An affine PI Hopf algebra not finite over a normal commutative Hopf subalgebra
Hopf bifurcation

Hopf bifurcationFrom Wikipedia, the free encyclopedia (Redirected from Andronov-Hopf bifurcation )Jump to: navigation , search In the mathematical theory of bifurcations , a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Eberhard Hopf , and Aleksandr Andronov , is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues of the linearization around the fixed point cross the imaginary axis of the complex plane . Under reasonably generic assumptions about the dynamical system, we can expect to see a small-amplitude limit cycle branching from the fixed point.For a more general survey on Hopf bifurcation and dynamical systems in general, see [1][2][3][4][5].Contents[hide ]● 1 Overview r 1.1 Supercritical / subcritical Hopf bifurcationsr 1.2 Remarks r1.3 Example ● 2 Definition of a Hopf bifurcation ● 3 Routh–Hurwitz criterionr 3.1 Sturm seriesr 3.2 Propositions ● 4 Example● 5 References●6 External links [edit ] Overview[edit ] Supercritical / subcritical Hopf bifurcationsThe limit cycle is orbitally stable if a certain quantity called the first Lyapunov coefficient is negative, and the bifurcation is supercritical. Otherwise it isunstable and the bifurcation is subcritical.The normal form of a Hopf bifurcation is:where z , b are both complex and λ is a parameter. WriteThe number α is called the first Lyapunov coefficient.●If α is negative then there is a stable limit cycle for λ > 0:whereThe bifurcation is then called supercritical.●If α is positive then there is an unstable limit cycle for λ < 0. The bifurcation is called subcritical.[edit ] Remarks The "smallest chemical reaction with Hopf bifurcation" was found in 1995 in Berlin, Germany [6]. The same biochemical system has been used in order to investigate how the existence of a Hopf bifurcation influences our ability to reverse-engineer dynamical systems [7].Under some general hypothesis, in the neighborhood of a Hopf bifurcation, a stable steady point of the system gives birth to a small stable limit cycle . Remark that looking for Hopf bifurcation is not equivalent to looking for stable limit cycles. First, some Hopf bifurcations (e.g. subcritical ones) do not imply the existence of stable limit cycles; second, there may exist limit cycles not related to Hopf bifurcations.[edit ] ExampleThe Hopf bifurcation in the Selkov system(see article). As the parameters change, a limitcycle (in blue) appears out of an unstableequilibrium.Hopf bifurcations occur in the Hodgkin–Huxley model for nerve membrane, the Selkov model of glycolysis , the Belousov–Zhabotinsky reaction , the Lorenz attractor and in the following simpler chemical system called the Brusselator as the parameter B changes:The Selkov model isThe phase portrait illustrating the Hopf bifurcation in the Selkov model is shown on the right. See Strogatz, Steven H. (1994). "Nonlinear Dynamics and Chaos" [1], page 205 for detailed derivation.[edit ] Definition of a Hopf bifurcationThe appearance or the disappearance of a periodic orbit through a local change in the stability properties of a steady point is known as the Hopf bifurcation. The following theorem works with steady points with one pair of conjugate nonzero purely imaginary eigenvalues . It tells the conditions under which this bifurcation phenomenon occurs.Theorem (see section 11.2 of [3]). Let J 0 be the Jacobian of a continuous parametric dynamical system evaluated at a steady point Z eof it. Suppose that all eigenvalues of J 0 have negative real parts except one conjugate nonzero purely imaginary pair. A Hopf bifurcation arises when these two eigenvalues cross the imaginary axis because of a variation of the system parameters.[edit ] Routh–Hurwitz criterionRouth–Hurwitz criterion (section I.13 of [5]) gives necessary conditions so that a Hopf bifurcation occurs. Let us see how one can use concretely this idea [8].[edit ] Sturm series Let be Sturm series associated to a characteristic polynomial P . They can be written in the form:The coefficients c i,0 for i in correspond to what is called Hurwitz determinants [8]. Their definition is related to the associated Hurwitz matrix .[edit ] PropositionsProposition 1. If all the Hurwitz determinants c i ,0 are positive, apart perhaps c k,0 then the associated Jacobian has no pure imaginary eigenvalues.Proposition 2. If all Hurwitz determinants c i ,0 (for all i in are positive, c k " 1,0 = 0 and c k" 2,1 < 0 then all the eigenvalues of the associated Jacobian have negative real parts except a purely imaginary conjugate pair.The conditions that we are looking for so that a Hopf bifurcation occurs (see theorem above) for a parametric continuous dynamical system are given by this last proposition.[edit ] Example Let us consider the classical Van der Pol oscillator written with ordinary differential equations:The Jacobian matrix associated to this system follows:The characteristic polynomial (in λ) of the linearization at (0,0) is equal to:P (λ) = λ2 " μλ + 1.The coefficients are: a 0 = 1,a 1 = " μ,a 2 = 1 The associated Sturm series is:The Sturm polynomials can be written as (here i = 0,1):The above proposition 2 tells that one must have:c 0,0 = 1 > 0,c 1,0 = " μ = 0,c 0,1 = " 1 < 0.Because 1 > 0 and 1 < 0 are obvious, one can conclude that a Hopf bifurcation may occur for Van der Pol oscillator if μ = 0.[edit ] References1. ^ a b Strogatz, Steven H. (1994). Nonlinear Dynamics and Chaos . Addison Wesley publishing company.2. ^ Kuznetsov, Yuri A. (2004). Elements of Applied Bifurcation Theory . New York: Springer-Verlag. ISBN 0-387-21906-4.3. ^ a b Hale, J.; Ko ak, H. (1991). Dynamics and Bifurcations . Texts in Applied Mathematics. 3. New York: Springer-Verlag.4. ^ Guckenheimer, J.; Myers, M.; Sturmfels, B. (1997). "Computing Hopf Bifurcations I". SIAM Journal on Numerical Analysis .5. ^ a b Hairer, E.; Norsett, S. P.; Wanner, G. (1993). Solving ordinary differential equations I: nonstiff problems (Second ed.). New York: Springer-Verlag.6. ^ Wilhelm, T.; Heinrich, R. (1995). "Smallest chemical reaction system with Hopf bifurcation". Journal of Mathematical Chemistry 17 (1): 1–14.doi :10.1007/BF01165134. http://www.fli-leibniz.de/~wilhelm/JMC1995.pdf .7. ^ Kirk, P. D. W.; Toni, T.; Stumpf, MP (2008). "Parameter inference for biochemical systems that undergo a Hopf bifurcation". Biophysical Journal 95 (2):540–549. doi :10.1529/biophysj.107.126086. PMC 2440454. PMID 18456830. /biophysj/pdf/PIIS0006349508702315.pdf .8. ^ a bKahoui, M. E.; Weber, A. (2000). "Deciding Hopf bifurcations by quantifier elimination in a software component architecture". Journal of SymbolicComputation 30 (2): 161–179. doi:10.1006/jsco.1999.0353. [edit] External links● Reaction-diffusion systems● The Hopf Bifurcation● Andronov–Hopf bifurcation page at ScholarpediaCategories: Bifurcation theoryPersonal tools● Log in / create accountNamespaces● Article● DiscussionVariantsViews● Read● Edit● View historyActionsSearchInteractionToolboxPrint/exportLanguages● This page was last modified on 25 May 2011 at 02:56.● Text is available under the Creative Commons Attribution-ShareAlike License; additional terms may apply. See Terms of use for details. Wikipedia is a registered trademark of the W ikimedia Foundation, Inc., a non-profit organization.● Contact us● Privacy policy● About Wikipedia● Disclaimers●●。
布基纳法索英文

布基纳法索英文Burkina Faso: A Gateway to West AfricaIntroductionBurkina Faso, a landlocked country in West Africa, is brimming with cultural diversity, natural wonders, and historical significance. Formerly known as Upper Volta, Burkina Faso gained independence from France in 1960 and has since become an emblem of resilience and progress. This article delves into the various aspects that make Burkina Faso an intriguing destination, including its history, geography, culture, and tourism opportunities.HistoryBurkina Faso boasts a rich historical heritage dating back thousands of years. The region was once part of the ancient Mossi Kingdoms, which played a pivotal role in shaping the local culture and traditions. In the late 19th century, European powers colonized the area, with France taking control until independence was achieved. Today, remnants of this colonial legacy can still be seen in the country's architecture and institutions.Geography and ClimatePositioned in the heart of West Africa, Burkina Faso is surrounded by six countries: Mali to the north, Niger to the east, Benin to the southeast, Togo and Ghana to the south, and Ivory Coast to the southwest. The country's landscape is predominantly characterized by the Sahel, a semi-arid region that transitions into the Sudanian savannah in the south. Despite its arid climate, Burkina Faso showcases stunning natural features such as the Waterfalls of Banfora and the stunning rock formations of Sindou.Culture and TraditionsBurkina Faso's diverse ethnic composition contributes to its vibrant culture. The Mossi, Fulani, Gourma, and Bobo people, among others, each bring their unique customs, languages, and music to the country's cultural tapestry. One of the most internationally renowned cultural events in Burkina Faso is the FESPACO (Pan-African Film and Television Festival of Ouagadougou), which attracts film enthusiasts and industry professionals from around the world.Tourism OpportunitiesWhile not as well-known as some of its neighboring countries, Burkina Faso offers a range of tourism opportunities that appeal to all types of travelers. Nature enthusiasts canembark on safaris in the national parks, bird-watching expeditions, or hiking adventures in the Sahel region. History buffs will find fascination in exploring the ancient ruins of Loropéni, a UNESCO World Heritage site, or immersing themselves in the history of the Mossi Kingdoms at the Moro-Naba Palace in Ouagadougou, the capital city.Furthermore, Burkina Faso hosts several cultural festivals throughout the year, providing visitors with a chance to witness vibrant dances, traditional music performances, and colorful local costumes. The Masked Carnival, celebrated annually in February, is particularly captivating as it showcases traditional African masks and costumes in a spirited parade.Challenges and OpportunitiesLike many developing nations, Burkina Faso faces various challenges that hinder its full potential for growth. Poverty, limited infrastructure, and political instability are some of the hurdles that the country must overcome. However, Burkina Faso also presents ample opportunities for investment in sectors such as agriculture, renewable energy, and tourism. With its strategic location and vast natural resources, the country has the potential to become an economic hub in West Africa.ConclusionBurkina Faso, with its captivating history, diverse culture, and untapped tourism potential, deserves greater recognition as a destination in West Africa. From its ancient ruins to its lively festivals, travelers can immerse themselves in the beauty and uniqueness of Burkina Faso. As the country continues to address its challenges and harness its opportunities, it is poised to thrive as a gateway to West Africa.。
Doubly Special Relativity

a rXiv:g r-qc/2749v 112J ul22gr-qc/0207049preprint version 1of Nature 418(2002)34-35Doubly Special Relativity Giovanni AMELINO-CAMELIA Dipartimento di Fisica,Universit`a “La Sapienza”,P.le Moro 2,I-00185Roma,Italy ABSTRACT I give a short non-technical review of the results obtained in recent work on “Doubly Special Relativity”,the relativistic theories in which the rota-tion/boost transformations between inertial observers are characterized by two observer-independent scales (the familiar velocity scale,c ,and a new observer-independent length/momentum scale,naturally identified with the Planck length/momentum).I emphasize the aspects relevant for the search of a solution to the cosmic-ray paradox.Galilei/Newton Relativity was abandoned because of the conflicting results of theMichelson-Morley experiments and because of its incompatibility with the mathemati-cal structure of the successful Maxwell theory of electromagnetism.After a century of successes,Einstein’s Special Relativity,the theory that replaced Galilei/Newton Rela-tivity,couldnow be questioned for similar reasons.A key Special-Relativity prediction appears to be violated by certain observations of ultra-high-energy cosmic rays [1],andsome Quantum-Gravityarguments appear to encourage a modification of Special Rel-ativity.I argued in Ref.[2]that this situation can provide motivation for consideringa change in the Relativity postulates somewhat analogous to the one needed for the transition from Galilei/Newton Relativity to Einstein’s Relativity:the introduction of a new absolute observer-independent scale.I analyzed in detail a first illustrative ex-ample of relativity postulates with an observer-independent length(momentum)scale,in addition to the familiar observer-independent velocity scale c ,and I showed that there is no in principle obstruction for the construction of such new relativistic theo-ries.That illustrative example of new relativistic theory also predicts some new effects of a type that could explaintheobservationsofultra-high-energy cosmic rays,but thepredicted magnitude of these effects turns out to be too weak for a description of thedata.For nearly a year,follow-up studies [3]focused on the example of new relativistictheory which I had used to illustrate the idea.In a very recent paper[4],Maguejio and Smolin constructed a second example of relativistic theory of the type proposed in Ref.[2],and this has generated increased interest[5,6,7,8,9,10,11]in research on relativity theories with two observer-independent scales.These theories are being called2“Doubly Special Relativity”(DSR)theories.Some of the key open issues that are being studies concern the search of other examples of DSR theories,the study of the multi-particle sector of given DSR theories,and attempts offinding a full solution of the cosmic-ray paradox within DSR.An aspect of cosmic-ray observations that is directly connected with relativity is the Greisen-Zatsepin-Kuzmin(GZK)limit.Ultra-high-energy cosmic rays are parti-cles,most likely protons,produced by distant active galaxies,which we detect through the particle-physics processes they ignite in the atmosphere.The GZK limit is related with the threshold energy,E GZK,required for such cosmic rays to interact with the “Cosmic Microwave Background Radiation”(CMBR):because of these interactions with the CMBR it should not be possible for cosmic rays with energies above E GZK to reach us.The value of the threshold energy E GZK is a purely kinematical prediction. In a given relativity theory it is obtained by combining the laws of energy-momentum conservation and the dispersion relation(the relation between the energy and the mo-mentum of a particle).Within Special Relativity onefinds E GZK≃5·1019eV,but several cosmic-ray events[1]are in disagreement with this prediction.As with all emerging experimental paradoxes it is of course possible that the cosmic-ray paradox is the result of an incorrect analysis of the experiment,for example it is legitimate to speculate that the identification of these ultra-high-energy cosmic rays as protons produced by distant active galaxies might eventually turn out to be incorrect.But,in spite of its preliminary status,this cosmic-ray paradox provides encouragement for the study of new relativity postulates.Besides this motivation coming for the experimental side,the idea of revising the relativity postulates alsofinds encouragement because of the role that the“Planck scale”E p≃1028eV plays in certain Quantum-Gravity scenarios.Various arguments lead to the expectation that for particles with energies close to E p it would be necessary to describe spacetime in terms of one form or another of new spacetime quanta,while for our readily available particles with energies much smaller than E p the familiarclassical-spacetime picture would remain valid.It would be appealing to introduce such a transition scale,a scale at which our description of physical phenomena changes significantly,as an observer-independent kinematical scale.Just like in going from Galilei/Newton Relativity to Einstein’s Special Relativity a key role is played by the law of composition of velocities,which for Einstein must reflect the special status of the speed-of-light constant c,in going then from Special Relativity to DSR a key role is played by the law of composition of energy-momentum,which, in the new framework,must attribute a special status to the Planck scale E p.This modification of the laws of energy-momentum conservation also affects the evaluation of the mentioned threshold energy E GZK that is relevant for the cosmic-ray paradox. Indeed the DSR theory which I considered as illustrative example in Ref.[2]predicts, besides the emergence of a maximum momentum of order E p for fundamental particles, a deformation of the laws of energy-momentum conservation.In turn the deformed laws of energy-momentum conservation of the DSR theory of Ref.[2]leads to a value of E GZK which is different from the one predicted by ordinary Special Relativity,but the difference is not as large as required for a full explanation of the cosmic-ray paradox. The DSR theory more recently proposed[4]by Maguejio and Smolin predicts that E p sets the maximum value of both energy and momentum for fundamental particles.The corresponding deformation[5]of the laws of energy-momentum conservation leads to yet another alternative prediction for E GZK,but that too is not sufficient to solve the cosmic-ray paradox.A lot has been understood of these DSR theories,but several issues must still be investigated.At present,since the status of the paradox is still preliminary,the search of a solution to the cosmic-ray paradox is not to be seen as a consistency condition for the DSR research programme,but the emergence of a compelling phenomenological result would legitimate interest in the rather speculative DSR idea.The recent study[4] by Magueijo and Smolin,by showing that there exist more than one example of DSR theories,provides indirect encouragement for the search of a DSR theory that would solve the cosmic-ray paradox.It appears[2,5,12]that a DSR theory capable of solving the cosmic-ray paradox should rely on the introduction of some structure not yet present in the DSR theories discussed in Refs.[2]and[4].This new structure should enter the law of composition of energy-momentum,which,through energy-momentum conservation,affects the evaluation of E GZK.Interestingly,the law of composition of energy-momentum also plays a role in an-other open problem for DSR theories:while Planck-scale deformed dispersion relations, generically predicted in DSR[2,4],are fully consistent with our observations of funda-mental/microscopic particles,they are clearly in conflict with observations of macro-scopic bodies.Therefore the rule that defines the total momentum of a macroscopic body in terms of the momenta of the composing microscopic particles must allow the emergence of different relativistic properties for macroscopic and microscopic entities3. Such a difference between macroscopic and microscopic entities could not be accom-modated in ordinary Special Relativity,but,remarkably,through the presence of an observer-independent energy/momentum scale,DSR naturally provides room[2,12] for a macro/micro separation.Unfortunately,it is still unclear in which specific way this macro/micro separation would be best implemented.In particular,it is unclear whether or not we should assume that the total energy-momentum of a multi-particle system is constructed in terms of the energy-momentum of each composing particle ac-cording to laws that are themself observer-independent laws.In addition to the already difficult task of describing a system of free particles both in terms of the momenta of each particle and in terms of the total momentum of the system,even more conceptually challenging for DSR theories is the description of the relativistic properties of bound states(macroscopic particles which are in a sense composed of several fundamental particles,but the composing particles are not free).Besides the indirect connection with the cosmic-ray paradox through the laws of composition of energy-momentum, this issue of the macro/micro separation could turn out to be even directly relevant for the analysis of the cosmic-ray paradox if it is established that(some of)the relevant particles(protons,pions,photons)must be described as composite objects in DSR.The role of certainκ-Poincar´e Hopf algebras[13]in DSR theories is also a lively subject of investigation[2,6,7,12].In the one-particle sector of the DSR theories so far considered the Lorentz sector of certainκ-Poincar´e Hopf algebras plays a role that is analogous4to the role of the Lorentz algebra in Einstein’s Special Relativity: the operators of the(Hopf)algebra are used to describe infinitesimal rotation/boost transformations between inertial observers.But for what concerns the delicate issues just mentioned above,the ones that involve the two-particle and multi-particle sec-tors,the role ofκ-Poincar´e Hopf algebras remains unclear[2,12].It would also be interesting to establish whether it is possible to construct DSR theories without any use ofκ-Poincar´e Hopf algebras,not even for the infinitesimal transformations of the one-particle sector.In fact,the DSR proposal[2]just requires that the laws of rota-tion/boost transformation between inertial observers have a lenght(momentum)and a velocity observer-independent scales,and it might be possible to realize this proposal in a variety of mathematical frameworks.The debate on these open issues is likely to keep busy the interested scientists for the next few years.Experimental help could come soon from improved data on the mentioned ultra-high-energy cosmic rays;moreover,in2006,when related stud-ies[14]will be performed on the GLAST space telescope,we should have conclusive information on another key prediction of some DSR theories:a possible wavelength dependence[2,12]of the speed of photons.References[1]D.J.Bird et al.,Astrophys.J.441(1995)144[arXiv:astro-ph/9410067].[2]G.Amelino-Camelia,Int.J.Mod.Phys.D11(2002)35[arXiv:gr-qc/0012051];Phys.Lett.B510(2001)255[arXiv:hep-th/0012238].[3]S.Alexander and J.Magueijo,hep-th/0104093;N.R.Bruno,G.Amelino-Cameliaand J.Kowalski-Glikman,Phys.Lett.B522(2001)133;J.Kowalski-Glikman Mod.Phys.Lett.A17(2002)1;S.Liberati,S.Sonego and M.Visser Annals Phys.298(2002)167.[4]J.Magueijo and L.Smolin,Phys.Rev.Lett.88(2002)190403.[5]G.Amelino-Camelia,D.Benedetti,F.D’Andrea,hep-th/0201245.[6]J.Kowalski-Glikman and S.Nowak,hep-th/0203040.[7]J.Lukierski and A.Nowicki,hep-th/0203065.[8]S.Judes,and M.Visser,gr-qc/0205067.[9]D.V.Ahluwalia and M.Kirchbach,gr-qc/0207004.[10]J.Rembielinski and K.A.Smolinski,hep-th/0207031.[11]A.Granik,hep-th/0207113.[12]G.Amelino-Camelia,gr-qc/0106004(in“Karpacz2001,New developments in fun-damental interaction theories”pag.137-150).[13]J.Lukierski,A.Nowicki,H.Ruegg,and V.N.Tolstoy,Phys.Lett.B264(1991)331;S.Majid and H.Ruegg,Phys.Lett.B334(1994)348;J.Lukierski,H.Ruegg and W.J.Zakrzewski Ann.Phys.243(1995)90.[14]G.Amelino-Camelia,J.Ellis,N.E.Mavromatos,D.V.Nanopoulos and S.Sarkar,Nature393(1998)763.5。
斐波那契 fft算法-概述说明以及解释

斐波那契fft算法-概述说明以及解释1.引言1.1 概述概述:斐波那契(Fibonacci)fft(Fast Fourier Transform)算法是一种高效的计算机算法,它结合了斐波那契数列以及快速傅里叶变换的特性。
该算法在信号处理、图像处理、音频处理等领域有着广泛的应用。
斐波那契数列是一种特殊的数列,每个数是前两个数之和。
这个数列在现实世界中有着很多的应用,如螺旋线、金融市场分析、自然界中的一些模式等。
斐波那契数列具有迅速增长的特点,其增长速度随着序号的增加而加快。
FFT算法(Fast Fourier Transform),即快速傅里叶变换算法,是一种在数字信号处理中广泛使用的算法。
它通过将信号在时域和频域之间进行转换,能够高效地计算信号的频谱分析。
FFT算法的核心思想是利用对称性质和递归分治策略,将原本复杂的傅里叶变换问题转化为一系列简单的子问题,从而提高计算效率。
本文将从斐波那契数列和FFT算法的基本原理入手,介绍它们的数学定义和应用场景。
随后,将详细解析斐波那契数列算法和FFT算法的实现过程,并对其优劣进行比较。
最后,总结整篇文章的主要内容,并展望斐波那契fft算法在未来的发展方向。
通过阅读本文,读者将对斐波那契算法和FFT算法有一个全面的了解,以及它们在不同领域的应用。
同时,读者还可以通过学习、实践这两种算法,提升自己在信号处理和数学计算方面的能力。
1.2 文章结构文章结构部分的内容可以参考以下写法:“文章结构”部分旨在介绍本文的整体结构和各个章节的内容安排,帮助读者快速了解文章的组织架构和主要内容。
本文分为引言、正文和结论三个部分。
在引言部分,我们会概述文章的主要内容,并阐明撰写本文的目的。
通过引言,读者可以初步了解本文的主题和动机,并对将要介绍的斐波那契算法和FFT算法有一个整体的认识。
在正文部分,我们将详细介绍斐波那契算法和FFT算法。
在斐波那契算法部分,我们会探讨斐波那契数列的计算方法和相关性质,包括它的递推公式、矩阵乘法形式等;在FFT算法部分,我们将介绍快速傅里叶变换的原理和应用,包括算法的基本思想、核心步骤和具体实现过程。
漫谈微分几何、多复变函数与代数几何(Differential geometry, functions

漫谈微分几何、多复变函数与代数几何(Differential geometry, functions of complex variable and algebraic geometry)Differential geometry and tensor analysis, developed with the development of differential geometry, are the basic tools for mastering general relativity. Because general relativity's success, to always obscure differential geometry has become one of the central discipline of mathematics.Since the invention of differential calculus, the birth of differential geometry was born. But the work of Euler, Clairaut and Monge really made differential geometry an independent discipline. In the work of geodesy, Euler has gradually obtained important research, and obtained the famous Euler formula for the calculation of normal curvature. The Clairaut curve of the curvature and torsion, Monge published "analysis is applied to the geometry of the loose leaf paper", the important properties of curves and surfaces are represented by differential equations, which makes the development of classical differential geometry to reach a peak. Gauss in the study of geodesic, through complicated calculation, in 1827 found two main curvature surfaces and its product in the periphery of the Euclidean shape of the space not only depends on its first fundamental form, the result is Gauss proudly called the wonderful theorem, created from the intrinsic geometry. The free surface of space from the periphery, the surface itself as a space to study. In 1854, Riemann made the hypothesis about geometric foundation, and extended the intrinsic geometry of Gauss in 2 dimensional curved surface, thus developing n-dimensional Riemann geometry, with the development of complex functions. A group of excellentmathematicians extended the research objects of differential geometry to complex manifolds and extended them to the complex analytic space theory including singularities. Each step of differential geometry faces not only the deepening of knowledge, but also the continuous expansion of the field of knowledge. Here, differential geometry and complex functions, Lie group theory, algebraic geometry, and PDE all interact profoundly with one another. Mathematics is constantly dividing and blending with each other.By shining the charming glory and the differential geometric function theory of several complex variables, unit circle and the upper half plane (the two conformal mapping establishment) defined on Poincare metric, complex function theory and the differential geometric relationships can be seen distinctly. Poincare metric is conformal invariant. The famous Schwarz theorem can be explained as follows: the Poincare metric on the unit circle does not increase under analytic mapping; if and only if the mapping is a fractional linear transformation, the Poincare metric does not change Poincare. Applying the hyperbolic geometry of Poincare metric, we can easily prove the famous Picard theorem. The proof of Picard theorem to modular function theory is hard to use, if using the differential geometric point of view, can also be in a very simple way to prove. Differential geometry permeates deep into the theory of complex functions. In the theory of multiple complex functions, the curvature of the real differential geometry and other series of calculations are followed by the analysis of the region definition metric of the complex affine space. In complex situations, all of the singular discrete distribution, and in more complex situations, because of the famous Hartogsdevelopment phenomenon, all isolated singularities are engulfed by a continuous region even in singularity formation is often destroyed, only the formation of real codimension 1 manifold can avoid the bad luck. But even this situation requires other restrictions to ensure safety". The singular properties of singularities in the theory of functions of complex functions make them destined to be manifolds. In 1922, Bergman introduced the famous Bergman kernel function, the more complex function or Weyl said its era, in addition to the famous Hartogs, Poincare, Levi of Cousin and several predecessors almost no substantive progress, injected a dynamic Bergman work will undoubtedly give this dead area. In many complex function domains in the Bergman metric metric in the one-dimensional case is the unit circle and Poincare on the upper half plane of the Poincare, which doomed the importance of the work of Bergman.The basic object of algebraic geometry is the properties of the common zeros (algebraic families) of any dimension, affine space, or algebraic equations of a projective space (defined equations),The definitions of algebraic clusters, the coefficients of equations, and the domains in which the points of an algebraic cluster are located are called base domains. An irreducible algebraic variety is a finite sub extension of its base domain. In our numerical domain, the linear space is the extension of the base field in the number field, and the dimension of the linear space is the number of the expansion. From this point of view, algebraic geometry can be viewed as a study of finite extension fields. The properties of algebraic clusters areclosely related to their base domains. The algebraic domain of complex affine space or complex projective space, the research process is not only a large number of concepts and differential geometry and complex function theory and applied to a large number of coincidence, the similar tools in the process of research. Every step of the complex manifold and the complex analytic space has the same influence on these subjects. Many masters in related fields, although they seem to study only one field, have consequences for other areas. For example: the Lerey study of algebraic topology that it has little effect on layer, in algebraic topology, but because of Serre, Weil and H? Cartan (E? Cartan, eldest son) introduction, has a profound impact on algebraic geometry and complex function theory. Chern studies the categories of Hermite spaces, but it also affects algebraic geometry, differential geometry and complex functions. Hironaka studies the singular point resolution in algebraic geometry, but the modification of complex manifold to complex analytic space and blow up affect the theory of complex analytic space. Yau proves that the Calabi conjecture not only affects algebraic geometry and differential geometry, but also affects classical general relativity. At the same time, we can see the important position of nonlinear ordinary differential equations and partial differential equations in differential geometry. Cartan study of symmetric Riemann space, the classification theorem is important, given 1, 2 and 3 dimensional space of a Homogeneous Bounded Domain complete classification, prove that they are all homogeneous symmetric domains at the same time, he guessed: This is also true in the n-dimensional equivalent relation. In 1959, Piatetski-Shapiro has two counterexample and find the domain theory of automorphic function study in symmetry, in the 4 and 5dimensional cases each find a homogeneous bounded domain, which is not a homogeneous symmetric domain, the domain he named Siegel domain, to commemorate the profound work on Siegel in 1943 of automorphic function. The results of Piatetski-Shapiro has profound impact on the theory of complex variable functions and automorphic function theory, and have a profound impact on the symmetry space theory and a series of topics. As we know, Cartan transforms the study of symmetric spaces into the study of Lie groups and Lie algebras, which is directly influenced by Klein and greatly develops the initial idea of Klein. Then it is Cartan developed the concept of Levi-Civita connection, the development of differential geometry in general contact theory, isomorphic mapping through tangent space at each point on the manifold, realize the dream of Klein and greatly promote the development of differential geometry. Cartan is the same, and concluded that the importance of the research in the holonomy manifold twists and turns, finally after his death in thirty years has proved to be correct. Here, we see the vast beauty of differential geometry.As we know, geodesic ties are associated with ODE (ordinary differential equations), minimal surfaces and high dimensional submanifolds are associated with PDE (partial differential equations). These equations are nonlinear equations, so they have high requirements for analysis. Complex PDE and complex analysis the relationship between Cauchy-Riemann equations coupling the famous function theory, in the complex case, the Cauchy- Riemann equations not only deepen the unprecedented contact and the qualitative super Cauchy-Riemann equations (the number of variables is greater than the number of equations) led to a strange phenomenon. This makes PDE and the theory ofmultiple complex functions closely integrated with differential geometry.Most of the scholars have been studying the differential geometry of the intrinsic geometry of the Gauss and Riemann extremely deep stun, by Cartan's method of moving frames is beautiful and concise dumping, by Chern's theory of characteristic classes of the broad and profound admiration, Yau deep exquisite geometric analysis skills to deter.When the young Chern faced the whole differentiation, he said he was like a mountain facing the shining golden light, but he couldn't reach the summit at one time. But then he was cast as a master in this field before Hopf and Weil.If the differential geometry Cartan development to gradually change the general relativistic geometric model, then the differential geometry of Chern et al not only affect the continuation of Cartan and to promote the development of fiber bundle in the form of gauge field theory. Differential geometry is still closely bound up with physics as in the age of Einstein and continues to acquire research topics from physicsWhy does the three-dimensional sphere not give flatness gauge, but can give conformal flatness gauge? Because 3D balls and other dimension as the ball to establish flat space isometric mapping, so it is impossible to establish a flatness gauge; and n-dimensional balls are usually single curvature space, thus can establish a conformal flat metric. In differential geometry, isometry means that the distance between the points on the manifold before and after the mapping remains the same. Whena manifold is equidistant from a flat space, the curvature of its Riemann cross section is always zero. Since the curvature of all spheres is positive constant, the n-dimensional sphere and other manifolds whose sectional curvature is nonzero can not be assigned to local flatness gauge.But there are locally conformally flat manifolds for this concept, two gauge G and G, if G=exp{is called G, P}? G between a and G transform is a conformal transformation. Weyl conformal curvature tensor remains unchanged under conformal transformation. It is a tensor field of (1,3) type on a manifold. When the Weyl conformal curvature tensor is zero, the curvature tensor of the manifold can be represented by the Ricci curvature tensor and the scalar curvature, so Penrose always emphasizes the curvature =Ricci+Weyl.The metric tensor g of an n-dimensional Riemann manifold is conformally equivalent to the flatness gauge locally, and is called conformally flat manifold. All Manifolds (constant curvature manifolds) whose curvature is constant are conformally flat, so they can be given conformal conformal metric. And all dimensions of the sphere (including thethree-dimensional sphere) are manifold of constant curvature, so they must be given conformal conformal metric. Conversely, conformally flat manifolds are not necessarily manifolds of constant curvature. But a wonderful result related to Einstein manifolds can make up for this regret: conformally conformally Einstein manifolds over 3 dimensions must be manifolds of constant curvature. That is to say, if we want conformally conformally flat manifolds to be manifolds of constant curvature, we must call Ric= lambda g, and this is thedefinition of Einstein manifolds. In the formula, Ric is the Ricci curvature tensor, G is the metric tensor, and lambda is constant. The scalar curvature S=m of Einstein manifolds is constant. Moreover, if S is nonzero, there is no nonzero parallel tangent vector field over it. Einstein introduction of the cosmological constant. So he missed the great achievements that the expansion of the universe, so Hubble is successful in the official career; but the vacuum gravitational field equation of cosmological term with had a Einstein manifold, which provides a new stage for mathematicians wit.For the 3 dimensional connected Einstein manifold, even if does not require the conformal flat, it is also the automatic constant curvature manifolds, other dimensions do not set up this wonderful nature, I only know that this is the tensor analysis summer learning, the feeling is a kind of enjoyment. The sectional curvature in the real manifold is different from the curvature of the Holomorphic cross section in the Kahler manifold, and thus produces different results. If the curvature of holomorphic section is constant, the Ricci curvature of the manifold must be constant, so it must be Einstein manifold, called Kahler- Einstein manifold, Kahler. Kahler manifolds are Kahler- Einstein manifolds, if and only if they are Riemann manifolds, Einstein manifolds. N dimensional complex vector space, complex projective space, complex torus and complex hyperbolic space are Kahler- and Einstein manifolds. The study of Kahler-Einstein manifolds becomes the intellectual enjoyment of geometer.Let's go back to an important result of isometric mapping.In this paper, we consider the isometric mapping between M and N and the mapping of the cut space between the two Riemann manifolds, take P at any point on M, and select two non tangent tangent vectors in its tangent space, and obtain its sectional curvature. In the mapping, the two tangent vectors on the P point and its tangent space are transformed into two other tangent vectors under the mapping, and the sectional curvature of the vector is also obtained. If the mapping is isometric mapping, then the curvature of the two cross sections is equal. Or, to be vague, isometric mapping does not change the curvature of the section.Conversely, if the arbitrary points are set, the curvature of the section does not change in nature, then the mapping is not isometric mapping The answer was No. Even in thethree-dimensional Euclidean space on the surface can not set up this property. In some cases, the limit of the geodesic line must be added, and the properties of the Jacobi field can be used to do so. This is the famous Cartan isometry theorem. This theorem is a wonderful application of the Jacobi field. Its wide range of promotion is made by Ambrose and Hicks, known as the Cartan-Ambrose-Hicks theorem.Differential geometry is full of infinite charm. We classify pseudo-Riemannian spaces by using Weyl conformal curvature tensor, which can be classified by Ricci curvature tensor, or classified into 9 types by Bianchi. And these things are all can be attributed to the study of differential geometry, this distant view Riemann and slightly closer to the Klein point of the perfect combination, it can be seen that the great wisdom Cartan, here you can see the profound influence of Einstein.From the Hermite symmetry space to the Kahler-Hodge manifold, differential geometry is not only closely linked with the Lie group, but also connected with algebra, geometry and topologyThink of the great 1895 Poicare wrote the great "position analysis" was founded combination topology unabashedly said differential geometry in high dimensional space is of little importance to this subject, he said: "the home has beautiful scenery, where Xuyuan for." (Chern) topology is the beauty of the home. Why do you have to work hard to compute the curvature of surfaces or even manifolds of high dimensions? But this versatile mathematician is wrong, but we can not say that the mathematical genius no major contribution to differential geometry? Can not. Let's see today's close relation between differential geometry and topology, we'll see. When is a closed form the proper form? The inverse of the Poicare lemma in the region of the homotopy point (the single connected region) tells us that it is automatically established. In the non simply connected region is de famous Rham theorem tells us how to set up, that is the integral differential form in all closed on zero.Even in the field of differential geometry ignored by Poicare, he is still in a casual way deeply affected by the subject, or rather is affecting the whole mathematics.The nature of any discipline that seeks to be generalized after its creation, as is differential geometry. From the curvature, Euclidean curvature of space straight to zero, geometry extended to normal curvature number (narrow Riemann space) andnegative constant space (Lobachevskii space), we know that the greatness of non Euclidean geometry is that it not only independent of the fifth postulate and other alternative to the new geometry. It can be the founder of triangle analysis on it. But the famous mathematician Milnor said that before differential geometry went into non Euclidean geometry, non Euclidean geometry was only the torso with no hands and no feet. The non Euclidean geometry is born only when the curvature is computed uniformly after the metric is defined. In his speech in 1854, Riemann wrote only one formula: that is, this formula unifies the positive curvature, negative curvature and zero curvature geometry. Most people think that the formula for "Riemann" is based on intuition. In fact, later people found the draft paper that he used to calculate the formula. Only then did he realize that talent should be diligent. Riemann has explored the curvature of manifolds of arbitrary curvature of any dimension, but the quantitative calculations go beyond the mathematical tools of that time, and he can only write the unified formula for manifolds of constant curvature. But we know,Even today, this result is still important, differential geometry "comparison theorem" a multitude of names are in constant curvature manifolds for comparison model.When Riemann had considered two differential forms the root of two, this is what we are familiar with the Riemann metric Riemannnian, derived from geometry, he specifically mentioned another case, is the root of four four differential forms (equivalent to four yuan product and four times square). This is the contact and the difference between the two. But he saidthat for this situation and the previous case, the study does not require substantially different methods. It also says that such studies are time consuming and that new insights cannot be added to space, and the results of calculations lack geometric meaning. So Riemann studied only what is now called Riemann metric. Why are future generations of Finsler interested in promoting the Riemann's not wanting to study? It may be that mathematicians are so good that they become a hobby. Cartan in Finsler geometry made efforts, but the effect was little, Chern on the geometric really high hopes also developed some achievements. But I still and general view on the international consensus, that is the Finsler geometry bleak. This is also the essential reason of Finsler geometry has been unable to enter the mainstream of differential geometry, it no beautiful properties really worth geometers to struggle, also do not have what big application value. Later K- exhibition space, Cartan space will not become mainstream, although they are the extension of Riemannnian geometry, but did not get what the big development.In fact, sometimes the promotion of things to get new content is not much, differential geometry is the same, not the object of study, the more ordinary the better, but should be appropriate to the special good. For example, in Riemann manifold, homogeneous Riemann manifold is more special, beautiful nature, homogeneous Riemann manifolds, symmetric Riemann manifold is more special, so nature more beautiful. This is from the analysis of manifold Lie group action angle.From the point of view of metric, the complex structure is given on the even dimensional Riemann manifold, and the complexmanifold is very elegant. Near complex manifolds are complex manifolds only when the near complex structure is integrable. The complex manifold must be orientable, because it is easy to find that its Jacobian must be nonnegative, whereas the real manifold does not have this property in general. To narrow the scope of the Kahler manifold has more good properties, all complex Submanifolds of Kahler manifolds are Kahler manifolds, and minimal submanifolds (Wirtinger theorem), the beautiful results captured the hearts of many differential geometry and algebraic geometry, because other more general manifolds do not set up this beautiful results. If the first Chern number of a three-dimensional Kahler manifold is zero, the Calabi-Yau manifold can be obtained, which is a very interesting manifold for theoretical physicists. The manifold of mirrors of Calabi-Yau manifolds is also a common subject of differential geometry in algebraic geometry. The popular Hodge structure is a subject of endless appeal.Differential geometry, an endless topic. Just as algebraic geometry requires double - rational equivalence as a luxury, differential geometry requires isometric transformations to be difficult. Taxonomy is an eternal subject of mathematics. In group theory, there are single group classification, multi complex function theory, regional classification, algebraic geometry in the classification of algebraic clusters, differential geometry is also classified.The hard question has led to a dash of young geometry and old scholars, and the prospect of differential geometry is very bright.。
千种植物拉丁学名

大花三色堇 大花溲疏 大花天竺葵 大花烟草 大丽花 大麻 大明竹 大吴风草 大岩桐 大叶桉 大叶冬青 大叶黄杨(冬青卫矛) 大叶莲 大叶落地生根 大叶紫薇 代代花 待宵草 倒挂金钟 德国鸢尾 地星 地中海绵枣儿 棣棠 吊金钱 吊兰 吊竹梅 东京樱花 冬青 兜兰 斗球花 豆蔻天竺葵 豆梨 杜鹃 杜梨 杜松 杜英 杜仲 短穗鱼尾葵 钝齿冬青 盾叶天竺葵 多花木蓝 多花紫藤 多枝柽柳 鹅掌柴 鹅掌楸(马褂木) 蛾蝶花 二乔木兰 二球悬铃木
六月雪(白马骨) 龙柏 龙柏 龙舌兰 龙吐珠 龙须海棠 龙牙花 龙爪槐 龙爪柳 芦荟(木立芦荟) 芦苇 芦竹 鹿角桧 栾树 罗汉松 罗汉竹 椤木石楠 络石 落羽杉 绿萝 麻栎 麻叶绣球 麻叶绣线菊 马棘 马甲子 马兰 马蹄金 马蹄金 马蹄莲 马尾松 马缨丹 麦冬 麦冬(沿阶草) 麦李 馒头柳 蔓生花烛 蔓性八仙花 蔓长春花 猫乳 毛白杨 毛白杨 毛刺槐 毛地黄 毛冬青 毛梾 毛泡桐 毛樱桃
狭叶十大功劳(十大功劳) 狭叶水塔花 夏腊梅 仙客来 线柏 腺柳 香椿 香榧 香果树 香荚 香荚蒾 香蕉 香桃木 香豌豆 香雪兰 香叶天竺葵 香橼 香樟 小蜡 小叶女贞 小叶朴 小叶野决明 孝顺竹 新疆杨 猩猩草 杏 杏梅 雄黄兰 熊耳草 宿根亚麻 须苞石竹 萱草 悬铃木 雪柳 雪片莲 雪松 鸭嘴花 雅容杜鹃 盐地柽柳 盐肤木 雁来红 燕子掌 羊蹄甲 杨梅 洋白蜡 洋常春藤 野决明
牛奶子 糯米条 女贞 欧洲白栎 欧洲夹竹桃 爬山虎 泡桐 炮仗花 蓬莱竹 枇杷 平枝栒子 苹果 铺地柏 葡萄 葡萄麝香兰 蒲葵 朴树 普通月见草 七姐妹 七叶树 桤木 杞柳 千里香 千里香 千里香 千日红 千头柏 千头赤松 牵牛 钱蒲 蔷薇 琴叶喜林芋 青枫(鸡爪槭) 青冈栎 青灰叶下珠 青木 青杄云杉(青扦) 青檀 青桐 青杨 清秀竹芋 秋英 楸树 球茎海棠 球兰 全缘栾树 雀梅藤
代数英语

(0,2) 插值||(0,2) interpolation0#||zero-sharp; 读作零井或零开。
0+||zero-dagger; 读作零正。
1-因子||1-factor3-流形||3-manifold; 又称“三维流形”。
AIC准则||AIC criterion, Akaike information criterionAp 权||Ap-weightA稳定性||A-stability, absolute stabilityA最优设计||A-optimal designBCH 码||BCH code, Bose-Chaudhuri-Hocquenghem codeBIC准则||BIC criterion, Bayesian modification of the AICBMOA函数||analytic function of bounded mean oscillation; 全称“有界平均振动解析函数”。
BMO鞅||BMO martingaleBSD猜想||Birch and Swinnerton-Dyer conjecture; 全称“伯奇与斯温纳顿-戴尔猜想”。
B样条||B-splineC*代数||C*-algebra; 读作“C星代数”。
C0 类函数||function of class C0; 又称“连续函数类”。
CA T准则||CAT criterion, criterion for autoregressiveCM域||CM fieldCN 群||CN-groupCW 复形的同调||homology of CW complexCW复形||CW complexCW复形的同伦群||homotopy group of CW complexesCW剖分||CW decompositionCn 类函数||function of class Cn; 又称“n次连续可微函数类”。
Cp统计量||Cp-statisticC。
沉浸在骑鹅旅行记英语作文

沉浸在骑鹅旅行记英语作文英文回答:Embarking on a Quixotic Odyssey: A Journey Astride Quills and Parchment.In the hallowed halls of literature, where flights of fancy take wing, there exists a tale that transcends the boundaries of time and imagination. It is the story of a knight-errant, Don Quixote, whose delusions of grandeur propelled him on a whimsical adventure astride his loyal steed, Rocinante. But what if, instead of a noble charger, Don Quixote had embarked on his quixotic quest perched upon a humble goose?This outlandish notion forms the comedic and poignant core of "The Goose Travels South," an unpublished masterpiece that weaves together the threads of adventure, absurdity, and a profound meditation on the nature of existence. The novel's protagonist, a modern-day DonQuixote named Ignatius McCracken, sets off on a journey across Europe, accompanied not by a burly squire, but by an unlikely companion: a garrulous and opinionated goose named Henrietta.Through their misadventures, Ignatius and Henrietta encounter a kaleidoscope of unforgettable characters and situations. There's a beautiful damsel in distress, a pompous literary critic, a wise-cracking witch, and a host of eccentric individuals who add depth and humor to their extraordinary voyage.As Ignatius and Henrietta negotiate the trials and tribulations of their goose-propelled odyssey, they embark on a parallel journey of self-discovery. Ignatius grapples with the complex nature of human existence, grappling with questions of identity, meaning, and the elusive nature of happiness. Henrietta, with her unconventional wisdom and unyielding loyalty, provides a unique and often irreverent perspective on life's absurdities and complexities.In an unexpected twist, Ignatius's feathered companionbecomes more than just a mere means of transportation. Henrietta transforms into a symbol of resilience, adaptability, and the boundless possibilities that lie hidden within the most unassuming of creatures. As the novel reaches its poignant climax, Ignatius and Henrietta find themselves at a crossroads, facing a choice that will forever alter the course of their lives."The Goose Travels South" is a literary tour de force that seamlessly blends comedy, adventure, and philosophical introspection. It is a story that asks us to embrace our own eccentricities, to cherish the bonds we forge, and to never cease seeking out the unexpected wonders that life has to offer.中文回答:沉浸在骑鹅旅行记中。
algebra thomas w.hungerford 简介 -回复

algebra thomas w.hungerford 简介-回复Thomas W. Hungerford is a highly renowned mathematician and author who has made significant contributions to the field of algebra. His works and publications have greatly influenced students and researchers around the world. In this essay, we will explore the life, achievements, and impact of Thomas W. Hungerford, focusing on his contributions to the field of algebra.Thomas W. Hungerford was born on October 15, 1936, in Chicago, Illinois, United States. He developed an early interest in mathematics and pursued it further during his academic career. Hungerford attended the University of Chicago, where he earned his undergraduate degree in 1958. He then went on to complete his Ph.D. in mathematics at Princeton University under the guidance of the eminent mathematician John Tukey in 1963.After completing his doctorate, Hungerford embarked on his career as a mathematician. His research primarily focused on algebra, with an emphasis on ring theory and homological algebra. Hungerford made significant contributions to these areas, particularly in commutative algebra and the theory of rings and modules.One of Hungerford's most notable achievements in algebra is the book "Abstract Algebra: An Introduction," which is widely recognized as one of the most comprehensive and influential textbooks in the field. First published in 1974, this book provides a rigorous introduction to the fundamental concepts of abstract algebra. It covers a wide range of topics, including group theory, ring theory, field theory, and Galois theory. The book has been widely used as a textbook in undergraduate and graduate courses in algebra, and it continues to be highly regarded for its clarity, rigor, and depth.In addition to "Abstract Algebra: An Introduction," Hungerford has authored several other books and research papers in algebra. Some of his other notable works include "Algebra," "Algebraic Geometry: A First Course," and "Introduction to Algebraic Structures." These works have further solidified Hungerford's reputation as an authority in the field and have continued to serve as valuable resources for students and researchers alike.Apart from his research and publications, Hungerford has also made significant contributions as an educator. He has taughtmathematics at various prestigious institutions, including the University of Rochester, Ohio State University, and Western Illinois University. Hungerford's teaching style is known for its clarity and precision, allowing students to grasp complex algebraic concepts with ease. Many of his former students have gone on to become successful mathematicians and researchers themselves, further highlighting the impact of his teaching and mentorship.Hungerford's contributions to the field of algebra extend beyond his own research and teaching. He has served as the editor or associate editor for several mathematical journals, including the "Journal of Algebra" and "Communications in Algebra." He has also been actively involved in various professional societies, such as the American Mathematical Society, serving on committees and contributing to the advancement of algebraic research.In recognition of his contributions to the field, Hungerford has received numerous awards and honors throughout his career. He was elected as a Fellow of the American Mathematical Society in 2012 for his contributions to teaching and research in algebra. His works continue to be referenced and studied by mathematicians worldwide, making him a highly respected figure in the field ofalgebra.In conclusion, Thomas W. Hungerford is an esteemed mathematician who has made significant contributions to the field of algebra. Through his research, publications, and teaching, he has greatly influenced the study and understanding of algebraic concepts. Hungerford's books, particularly "Abstract Algebra: An Introduction," continue to be widely used and revered in the mathematical community. His impact as an educator and mentor has also been significant, with many of his students going on to make their mark in the field. Overall, Thomas W. Hungerford's work and influence have solidified his place among the leading figures in the field of algebra.。
汉语动词的屈折机制与限定性问题

汉语动词的屈折机制与限定性问题*杨亦鸣蔡冰徐州师范大学语言研究所提要根据生成语法的动词混合形态理论,普遍语法中存在着两种不同类型的动词屈折机制。
本文依据这一理论,运用“否定结构测试”,确定了汉语动词的屈折类型,在此基础上修正了动词限定性的定义,提出限定性是动词屈折成分的一种本质属性,汉语动词存在抽象的限定性特征,并从理论依据、语言事实和实验证据等三个方面论证了这一观点。
关键词动词屈折特征动词混合形态理论抽象限定性一引言一般认为,与西语语法相比,汉语语法有两个最为重要的特点,一是汉语词类的多功能性,二是词组和句子构造上的一致性。
事实上,对这两个特点的认识都与对动词限定性的看法有着密切的关系(参见朱德熙1985)。
1.1关于动词的限定性按照通行的英语语法书的解释,限定性是指对动词的一种语法描述,根据动词在表达时制、体貌、情态和一致等语法范畴时形态标记的有无,可将动词区分为限定动词(finite verbs)和非限定动词(non-finite verbs)。
例如在英语中,限定动词在上述几个方面都体现出形式上的区分,而非限定动词则没有相应的形式区分:(1)a. I am/was walking. b. They are/were walking.c. I have/had walked. d. He has/had walked.在(1)中,动词be和have在表达时制和一致等语法范畴时,表现出形式上的区分,是限定动词,而分词walking和walked则不随时态和人称的变化而变化,是非限定动词。
此外,两者的句法表现也不同:限定动词只能充当谓语,非限定动词可以充当主语、宾语和定语等其他句子成分。
如:(2)a. He works in a factory. b. Working is a happy thing.c. He enjoys working.d. No talking during working time.在(2)中,works和enjoys充当句子的谓语,work和talk的非限定形式则出现在句子的主语、宾语和定语的位置上。
leptospira interrogans ss. icterohaemorrhagiae-感染的

LEPTOSPIRA INTERROGANS SSP.Aetiology Epidemiology Diagnosis Prevention and ControlPotential Impacts of Disease Agent Beyond Clinical Illness References AETIOLOGYClassification of the causative agentLeptospira interrogans, the causative agent of leptospirosis, consists of numerable serotypes capable of causing a variety of disease manifestations in a wide range of hosts. This motile and flagellated spirochete bacterium is recognizable via microscopy and earned its name from a characteristic hooked appearance that resembles a question mark. The taxonomic classifications within the Leptospira genus have been reorganized many times in accordance with new antigenic, genomic, and pathologic data. What was once over 250 serovars grouped into two Leptospira species is now 21 genomospecies of Leptospira with reclassified serovars. While the new taxonomic names are typically used in the scientific literature, historical names still circulate on product labels and in common use.Not all serovars of Leptospira are pathogenic, and many are associated with a reservoir species in which little disease is apparent. Many serovars are highly prevalent within maintenance host populations and persist in the kidneys or genital tract. Small antibody responses and low tissue burdens are typical in these animals. Incidental hosts, however, typically develop serious disease with high tissue burdens and robust antibody responses. These classifications are not always entirely distinct and some overlap between presentations can exist.Leptospirosis is a zoonotic disease but is typically associated with at-risk occupations (veterinarian, livestock owners, dairy workers, etc.) and exposure to contaminated water.Resistance to physical and chemical actionTemperature: Generally fails to persist at <10°C or >34°C;pasteurization and moist heat at 121°C/15 minutes are effective methodsof killing leptospirespH: Prefers neutral to slightly alkaline conditionsChemicals/Disinfectants: Inactivated by 1% sodium hypochlorite, 70%ethanol, formaldehyde, detergents, quaternary ammonium compounds,iodine based compounds, glutaraldehyde, and hydrogen peroxideSurvival: Warm, moist conditions greatly enhance survival; maypersist up to 6 weeks under favorable conditions; freezing, dehydration,and UV radiation inactivate leptospiresEPIDEMIOLOGYHosts●Virtually all mammals are vulnerable to pathogenic Leptospira serovars to varying degrees○Many serovars have specific maintenance hosts while others are more promiscuous●Leptospira serovars known to cause disease in mammals have been isolated from amphibians○Some serovars have also been isolated from invertebrates, reptiles, and birdsProminent host-serovar associations●Armadillos (Dasypus novemcinctus, Euphractus sexcinctus) - Autumnalis, Cynopteri, Hebdomadis,Pomona●Bandicoots (Isoodon macrourus, Perameles spp.) - numerous serovars have been associated withthese species●Brazilian tapir (Tapirus terrestris) - Pomona●Canids (Canis latrans, C. familiaris, C. lupus) - Bratislava, Canicola, Grippotyphosa, Hardjo,Icterohaemorrhagiae, Pomona●Cattle (Bos taurus, Syncerus caffer) - Hardjo and others●Cervids - Bratislava, Canicola, Grippotyphosa, Hardjo, Icterohaemorrhagiae, Pomona●European hedgehog (Erinaceus europaeus)●Felids (Felis silvestris silvestris, F. silvestris catus, Lynx spp.)●Flying foxes (Pteropus spp.) - a multitude of Leptospira serovars have been identified in variousspecies of bat●Foxes (Vulpes lagopus, V. vulpes, Urocyon cinereoargenteus, Lycalopex griseus) - Bratislava,Canicola, Grippotyphosa●Giant anteater (Myrmecophaga tridactyla) - Djasiman●Horses (Equus ferus) - Bratislava●Lagomorphs (Lepus europaeus, L. timidus, Oryctolagus cuniculus) - Grippotyphosa●Marine mammals (Eubalaena australis,Trichechus manatus ) - Australis, Manaua○Sea lions (Zalophus californianus, Z. wollebaeki) and seals (Callorhinus ursinus, Phoca vitulina, Mirounga angustirostris, Arctocephalus forsteri) - Canicola, Hardjo, Pomona ○There have been multiple mass-mortality events attributed to leptospirosis in California sea lions●Marsupials - Australis, Autumnalis, Ballum, Bataviae, Celledoni, Cynopteri, Djasiman,Grippotyphosa, Hardjo, Hebdomadis, Icterohaemorrhagiae, Javanica, Mini, Panama, Pomona, Pyrogenes, Sejroe, Tarassov, Topaz●Mongooses (Herpestes auropunctatus, Mungos mungo, Paracynictis selousi) - Bratislava, Hardjo●Mustelids (Meles meles, Martes fiona, M. martes, Mustela putorius, M. nivalis, M. ermine, Lutra lutra)●Platypus (Ornithorhynchus anatinus) - Autumnalis, Hardjo, Grippotyphosa●Raccoons (Procyon itor) and skunks (Mephitis mephitis) - Bratislava, Canicola, Grippotyphosa,Hardjo, Icterohaemorrhagiae, Pomona●Rodents and insectivores - Arborea, Australis, Ballum, Bindjei, Broomi, Canicola, Celledoni,Gryppotyphosa, Icterohaemorrhagiae, Javanica, Mini, Pomona, Pyrogenes, Sejroe, Tarrasovi, Zanoni○Rats are well-appreciated hosts for serotype Icterohaemorrhagiae●Swine (Sus scrofa and other spp.) - Bratislava, Hardjo, Pomona●Vervet monkey (Cercopithecus aethiops sabaeus) - Australis, Grippotyphosa, Javanica●Multiple snake, turtle, toad, and frog species have also been identified as PCR and/or serologicallypositiveTransmission●Ingestion●Contact with mucous membranes or wet, abraded skin●Some serovars can be transmitted venerally or transplacentallySources●Urine●Contaminated soil and water●Placental fluids●Genital secretions●Milk●BloodOccurrenceMany wildlife species are reservoirs for Leptospira and subsequently maintain host-bacterium interactions that do not negatively impact the animal. Over time, selection pressures on the leptospires many change and drive reservoir species relationships to shift accordingly. Therefore, it is important to assess the epidemiology of leptospirosis on a more local level to understand transmission risks and disease impacts.Leptospira is globally enzootic, but disease is more frequently seen in warm and moist environments. This may be seasonal (temperate zones) or more constant (tropical regions). Rainfall encourages persistence of the organism in the environment. Additionally, some serotypes are much more geographically dispersed and others are found in more limited regions.For more recent, detailed information on the occurrence of this disease worldwide, see the OIE World Animal Health Information System - Wild (WAHIS-Wild) Interface [http://www.oie.int/wahis_2/public/wahidwild.php/Index].DIAGNOSISAfter invasion of mucous membranes or damaged skin, there is a 4-20 day incubation period followed by a 7-10 day period of circulation in the bloodstream. Clinical signs of acute leptospirosis depend on the tissues colonized during this period of bacteraemia, the host species, and infecting serovar. A robust antibody response follows and is associated with a declining bacteraemia. Tissues may recover slowly or not at all depending on the degree of damage. Death is possible in severe cases.Incidental hosts maintain the bacterium in renal tubules for days to weeks and shed the organism in urine. Maintenance hosts, however, maintain the bacterium in the renal tubules, genital tract, and/or eyes and shed it in urine or genital secretions for months to years after infection.Clinical diagnosisLeptospirosis is a highly variable, systemic infection and the presentation depends on the infecting serovar, the host species, and the host’s general health and immune status. Maintenance hosts typically do not develop significant clinical disease. Incidental hosts typically experience severe, acute disease secondary to bacterial toxins and inflammatory responses generated by the immune system. Initially, animals may be febrile and anorectic. They may quickly develop signs of haemorrhage and haemolytic anaemia secondary to endothelial damage such as mucosal petechiation, icterus, haemoglobinuria/haematuria, dehydration, vomiting, and colic. Acute renal injury develops rapidly and is a significant contributor to mortality. Pneumonia, meningitis, uveitis, corneal opacification, photosensitization, myalgia, and pancreatitis are also possible.Reproductive disease is often characterised by abortion/stillbirth, mummified fetuses, infertility, blood in milk, or a cessation of milk production. If not aborted, neonates infected transplacentally are typically weak. Maintenance hosts do not develop reproductive disease acutely like incidental hosts, but instead remain subclinical for weeks to months.Lesions●Renal tubular necrosis and suppurative nephritis○Pale, oedematous parenchyma +/- pitting of the serosal surface and capsular adhesions○Subcapsular haemorrhage○Inflammation initially characterised by neutrophils but becomes lymphoplasmacytic○Mixed inflammatory processes are associated with higher mortality rates●Hepatomegaly +/- necrotizing hepatitis○The liver is often friable and discolored in a lobular pattern●Pulmonary haemorrhage●Petechiae and ecchymoses on mucous membranes and internal organs●Horses may develop uveitis with conjunctivitis, corneal oedema, synechia, or cataractsDifferential diagnoses●Ocular disease○Equine recurrent uveitis○Traumatic uveitis/reflex uveitis○Infectious conjunctivitis●Kidney disease○Toxin exposure (e.g., ethylene glycol)○Infectious nephritis, pyelonephritis, glomerulonephritis○Renal tubular acidosis○Nematodes (Stephanurus dentatus, Dioctophyma renale)●Reproductive failure or compromise○Brucellosis○Bovine viral diarrhea virus (BVDV)○Porcine reproductive and respiratory syndrome (PRRS)○Q-Fever (Coxiella burnetii)○Neospora spp.○Tritrichomonas foetus○Mastitis, metritis●Liver disease, icterus, and haemolytic anaemia○Viral hepatitis○Toxin exposure (e.g., heavy metals, anticoagulant rodenticides)○Rickettsial infection○Clostridium haemolyticum, C. perfringens A○Neonatal isoerythrolysis●Bacterial septicaemiaLaboratory diagnosisSamplesFor isolation of agent●Kidney●Blood●Urine●Other grossly affected tissue such as liverSerological tests●Serum●Whole bloodProceduresIdentification of the agent●Silver-stained histopathology slides allow for direct visualization of the organism in renal tubules●Immunohistochemistry (IHC)●Bacterial culture○Because the organism is low-growing, this may take 12-26 weeks○Best available method to determine infecting serovar●Polymerase chain reaction (PCR)○Widely variable protocols○Does not provide serovar-specific resultsSerological tests●Microscopic agglutination test (MAT)○Uses live, regionally common serovars of Leptospira○Requires diagnostic laboratory to maintain live cultures of serovars○Provides quantitative titre level●Antibody capture enzyme-linked immunosorbent assay (ELISA)○Currently used for domestic canines; detects antibodies to LipL32 protein○Results are qualitative (positive/negative) and may yield false positives in the event of prior vaccination●Immunofluorescence assay (IFA)●There is not yet a consensus on what a diagnostic titre for Leptospira should be, therefore pairedacute and convalescent sera are recommended for testing●Caution should be taken when interpreting serology data; antibody titre does not always correspondwith disease stateFor more detailed information regarding laboratory diagnostic methodologies, please refer to Chapter 3.1.12 Leptospirosis in the latest edition of the OIE Manual of Diagnostic Tests and Vaccines for Terrestrial Animals.PREVENTION AND CONTROLSanitary prophylaxis●Extra precautions should be taken when cleaning areas frequented by potential Leptospira hosts.Wear gowns, shoe covers, and gloves to prevent contamination of personal clothing. Face shields are recommended to protect mucous membranes from aerosols.Medical prophylaxis●There are a variety of Leptospira vaccines available for domestic animals, including livestock○Vaccine intent may vary from prevention of infection to reduction of renal colonization and urine shedding○Read vaccine labels to determine which serovars are targeted, as immunity is believed to be serovar-specificPOTENTIAL IMPACTS OF DISEASE AGENT BEYOND CLINICAL ILLNESS Risks to public health●Leptospirosis is a zoonotic disease. Because clinical signs can be vague and maintenance hostscan be asymptomatic carriers, basic protective measures are suggested for at-risk populations (veterinarians, livestock owners, dairy workers, etc.): protect eyes with safety glasses, wear gloves especially if there are openings in the skin, thoroughly wash hands after interacting with animals of unknown status and before consuming food or water, etc.○Pregnant individuals within at-risk populations are particularly advised to utilise protective measures.●Many domestic animal species, including dogs, horses, and livestock, are susceptible to leptospirosisand could potentially transmit it to humans. Individuals should speak with local veterinarians to determine risk and appropriate prevention strategies, including animal vaccines.Risks to agriculture●If livestock or working animals (horses, dogs) develop clinical disease due to Leptospira, decreasedthrift and reproductive compromise can significantly impact production. Working animals may not beable to do their jobs as efficiently, and livestock may demand increased resources for treatment while producing less.REFERENCES AND OTHER INFORMATION●Atherstone, C., Picozzi, K., & Kalema-Zikusoka, G. (2014). Seroprevalence of Leptospira hardjo incattle and African buffalos in southwestern Uganda. The American Journal of Tropical Medicine and Hygiene, 90(2), 288–290.●Ayral, F., Djelouadji, Z., Raton, V., Zilber, A. L., Gasqui, P., et al. (2016). Hedgehogs and mustelidspecies: major carriers of pathogenic Leptospira, a survey in 28 animal species in France (20122015). PloS One, 11(9), e0162549.●Biscola, N. P., Fornazari, F., Saad, E., Richini-Pereira, V. B., Campagner, M. V., et al. (2011).Serological investigation and PCR in detection of pathogenic leptospires in snakes. Pesquisa Veterinária Brasileira, 31(9), 806-811.●Buhnerkempe, M. G., Pragger, K. C., Strelloff, C. C., Greig, D. J., Laake, J. L., et al. (2017). Detectingsignals of chronic shedding to explain pathogen persistence: Leptospira interrogans in California sea lions. Journal of Animal Ecology, 86(3), 460-472.●Denkinger, J., Guevara, N., Ayala, S., Murillo, J. C., Hirschfeld, M., et al. (2017). Pup mortality andevidence for pathogen exposure in Galapagos sea lions (Zalophus wollebaeki) on San Cristobal Island, Galapagos, Ecuador. Journal of Wildlife Disease, 53(3), 491-498.●Gravekamp, C., Korver, H., Montgomery, J., Everard, C. O. R., Carrington, D., et al. (1991).Leptospires isolated from toads and frogs on the island of Barbados. Zentralblatt für Bakteriologie, 275(3), 403-411.●Jobbins, S. E., Sanderson, S. E., & Alexander, K. A. (2014). Leptospira interrogans at the human-wildlife interface in northern Botswana: a newly identified public health threat. Zoonoses and Public Health, 61, 113-123.●Karesh, W. B., Hart, J. A., Hart, T. B., House, C., Torres, A., et al. (1995). Health evaluation of fivesympatric duiker species (Cephalophus spp). Journal of Zoo and Wildlife Medicine, 26(4), 485-502.●Leighton, F. A. & Kuiken, T. (2001). Leptospirosis. In E. S. Williams and I. K. Barker (Eds.), InfectiousDiseases of Wild Mammals (3rd ed., pp. 498-502). Iowa State Press.●Loffler, G. S., Rago, V., Martinez, M., Uhart, M., Florin-Christensen, M., et al. (2015). Isolation of aseawater tolerant Leptospira spp. from a southern right whale (Eubalaena australis). PLoS One, 10(12), e0144974.●Lunn, K. F. (2018). Overview of leptospirosis. Merck Veterinary Manual.Accessed 2020:https:///generalized-conditions/leptospirosis/overview-of-leptospirosis?query=leptospira●Pedersen, K., Anderson, T. D., Maison, R. M., Wiscomb, G. W., Pipas, M. J., et al. (2018). Leptospiraantibodies detected in wildlife in the USA and the US Virgin Islands. Journal of Wildlife Diseases, 54(3), 450-459.●Spickler, A. R. & Leedom, L. K. R. (2013). Leptospirosis. Accessed 2020:/Factsheets/pdfs/leptospirosis.pdf●The World Organisation for Animal Health (2018). Leptospirosis. Accessed 2020:https://www.oie.int/fileadmin/Home/eng/Health_standards/tahm/3.01.12_LEPTO.pdf●Vieira, A. S., Pinto, P. S, & Lillenbaum, W. (2018). A systematic review of leptospirosis on wildanimals in Latin America. Tropical Animal Health and Production, 50(2), 229-238.●Wildlife Health Australia (2018). Leptospira infection in Australian mammals. Accessed 2020:https://.au/FactSheets.aspx●Wildlife Health Australia (2011). Leptospira infection in Australian seals. Accessed 2020:https://.au/FactSheets.aspx** *。
数学专业词汇及翻译

一、字母顺序表 (1)二、常用的数学英语表述 (7)三、代数英语(高端) (13)一、字母顺序表1、数学专业词汇Aabsolute value 绝对值 accept 接受 acceptable region 接受域additivity 可加性 adjusted 调整的 alternative hypothesis 对立假设analysis 分析 analysis of covariance 协方差分析 analysis of variance 方差分析 arithmetic mean 算术平均值 association 相关性 assumption 假设 assumption checking 假设检验availability 有效度average 均值Bbalanced 平衡的 band 带宽 bar chart 条形图beta-distribution 贝塔分布 between groups 组间的 bias 偏倚 binomial distribution 二项分布 binomial test 二项检验Ccalculate 计算 case 个案 category 类别 center of gravity 重心 central tendency 中心趋势 chi-square distribution 卡方分布 chi-square test 卡方检验 classify 分类cluster analysis 聚类分析 coefficient 系数 coefficient of correlation 相关系数collinearity 共线性 column 列 compare 比较 comparison 对照 components 构成,分量compound 复合的 confidence interval 置信区间 consistency 一致性 constant 常数continuous variable 连续变量 control charts 控制图 correlation 相关 covariance 协方差 covariance matrix 协方差矩阵 critical point 临界点critical value 临界值crosstab 列联表cubic 三次的,立方的 cubic term 三次项 cumulative distribution function 累加分布函数 curve estimation 曲线估计Ddata 数据default 默认的definition 定义deleted residual 剔除残差density function 密度函数dependent variable 因变量description 描述design of experiment 试验设计 deviations 差异 df.(degree of freedom) 自由度 diagnostic 诊断dimension 维discrete variable 离散变量discriminant function 判别函数discriminatory analysis 判别分析distance 距离distribution 分布D-optimal design D-优化设计Eeaqual 相等 effects of interaction 交互效应 efficiency 有效性eigenvalue 特征值equal size 等含量equation 方程error 误差estimate 估计estimation of parameters 参数估计estimations 估计量evaluate 衡量exact value 精确值expectation 期望expected value 期望值exponential 指数的exponential distributon 指数分布 extreme value 极值F factor 因素,因子 factor analysis 因子分析 factor score 因子得分 factorial designs 析因设计factorial experiment 析因试验fit 拟合fitted line 拟合线fitted value 拟合值 fixed model 固定模型 fixed variable 固定变量 fractional factorial design 部分析因设计 frequency 频数 F-test F检验 full factorial design 完全析因设计function 函数Ggamma distribution 伽玛分布 geometric mean 几何均值 group 组Hharmomic mean 调和均值 heterogeneity 不齐性histogram 直方图 homogeneity 齐性homogeneity of variance 方差齐性 hypothesis 假设 hypothesis test 假设检验Iindependence 独立 independent variable 自变量independent-samples 独立样本 index 指数 index of correlation 相关指数 interaction 交互作用 interclass correlation 组内相关 interval estimate 区间估计 intraclass correlation 组间相关 inverse 倒数的iterate 迭代Kkernal 核 Kolmogorov-Smirnov test柯尔莫哥洛夫-斯米诺夫检验 kurtosis 峰度Llarge sample problem 大样本问题 layer 层least-significant difference 最小显著差数 least-square estimation 最小二乘估计 least-square method 最小二乘法 level 水平 level of significance 显著性水平 leverage value 中心化杠杆值 life 寿命 life test 寿命试验 likelihood function 似然函数 likelihood ratio test 似然比检验linear 线性的 linear estimator 线性估计linear model 线性模型 linear regression 线性回归linear relation 线性关系linear term 线性项logarithmic 对数的logarithms 对数 logistic 逻辑的 lost function 损失函数Mmain effect 主效应 matrix 矩阵 maximum 最大值 maximum likelihood estimation 极大似然估计 mean squared deviation(MSD) 均方差 mean sum of square 均方和 measure 衡量 media 中位数 M-estimator M估计minimum 最小值 missing values 缺失值 mixed model 混合模型 mode 众数model 模型Monte Carle method 蒙特卡罗法 moving average 移动平均值multicollinearity 多元共线性multiple comparison 多重比较 multiple correlation 多重相关multiple correlation coefficient 复相关系数multiple correlation coefficient 多元相关系数 multiple regression analysis 多元回归分析multiple regression equation 多元回归方程 multiple response 多响应 multivariate analysis 多元分析Nnegative relationship 负相关 nonadditively 不可加性 nonlinear 非线性 nonlinear regression 非线性回归 noparametric tests 非参数检验 normal distribution 正态分布null hypothesis 零假设 number of cases 个案数Oone-sample 单样本 one-tailed test 单侧检验 one-way ANOVA 单向方差分析 one-way classification 单向分类 optimal 优化的optimum allocation 最优配制 order 排序order statistics 次序统计量 origin 原点orthogonal 正交的 outliers 异常值Ppaired observations 成对观测数据paired-sample 成对样本parameter 参数parameter estimation 参数估计 partial correlation 偏相关partial correlation coefficient 偏相关系数 partial regression coefficient 偏回归系数 percent 百分数percentiles 百分位数 pie chart 饼图 point estimate 点估计 poisson distribution 泊松分布polynomial curve 多项式曲线polynomial regression 多项式回归polynomials 多项式positive relationship 正相关 power 幂P-P plot P-P概率图predict 预测predicted value 预测值prediction intervals 预测区间principal component analysis 主成分分析 proability 概率 probability density function 概率密度函数 probit analysis 概率分析 proportion 比例Qqadratic 二次的 Q-Q plot Q-Q概率图 quadratic term 二次项 quality control 质量控制 quantitative 数量的,度量的 quartiles 四分位数Rrandom 随机的 random number 随机数 random number 随机数 random sampling 随机取样random seed 随机数种子 random variable 随机变量 randomization 随机化 range 极差rank 秩 rank correlation 秩相关 rank statistic 秩统计量 regression analysis 回归分析regression coefficient 回归系数regression line 回归线reject 拒绝rejection region 拒绝域 relationship 关系 reliability 可*性 repeated 重复的report 报告,报表 residual 残差 residual sum of squares 剩余平方和 response 响应risk function 风险函数 robustness 稳健性 root mean square 标准差 row 行 run 游程run test 游程检验Sample 样本 sample size 样本容量 sample space 样本空间 sampling 取样 sampling inspection 抽样检验 scatter chart 散点图 S-curve S形曲线 separately 单独地 sets 集合sign test 符号检验significance 显著性significance level 显著性水平significance testing 显著性检验 significant 显著的,有效的 significant digits 有效数字 skewed distribution 偏态分布 skewness 偏度 small sample problem 小样本问题 smooth 平滑 sort 排序 soruces of variation 方差来源 space 空间 spread 扩展square 平方 standard deviation 标准离差 standard error of mean 均值的标准误差standardization 标准化 standardize 标准化 statistic 统计量 statistical quality control 统计质量控制 std. residual 标准残差 stepwise regression analysis 逐步回归 stimulus 刺激 strong assumption 强假设 stud. deleted residual 学生化剔除残差stud. residual 学生化残差 subsamples 次级样本 sufficient statistic 充分统计量sum 和 sum of squares 平方和 summary 概括,综述Ttable 表t-distribution t分布test 检验test criterion 检验判据test for linearity 线性检验 test of goodness of fit 拟合优度检验 test of homogeneity 齐性检验 test of independence 独立性检验 test rules 检验法则 test statistics 检验统计量 testing function 检验函数 time series 时间序列 tolerance limits 容许限total 总共,和 transformation 转换 treatment 处理 trimmed mean 截尾均值 true value 真值 t-test t检验 two-tailed test 双侧检验Uunbalanced 不平衡的 unbiased estimation 无偏估计 unbiasedness 无偏性 uniform distribution 均匀分布Vvalue of estimator 估计值 variable 变量 variance 方差 variance components 方差分量 variance ratio 方差比 various 不同的 vector 向量Wweight 加权,权重 weighted average 加权平均值 within groups 组内的ZZ score Z分数2. 最优化方法词汇英汉对照表Aactive constraint 活动约束 active set method 活动集法 analytic gradient 解析梯度approximate 近似 arbitrary 强制性的 argument 变量 attainment factor 达到因子Bbandwidth 带宽 be equivalent to 等价于 best-fit 最佳拟合 bound 边界Ccoefficient 系数 complex-value 复数值 component 分量 constant 常数 constrained 有约束的constraint 约束constraint function 约束函数continuous 连续的converge 收敛 cubic polynomial interpolation method三次多项式插值法 curve-fitting 曲线拟合Ddata-fitting 数据拟合 default 默认的,默认的 define 定义 diagonal 对角的 direct search method 直接搜索法 direction of search 搜索方向 discontinuous 不连续Eeigenvalue 特征值 empty matrix 空矩阵 equality 等式 exceeded 溢出的Ffeasible 可行的 feasible solution 可行解 finite-difference 有限差分 first-order 一阶GGauss-Newton method 高斯-牛顿法 goal attainment problem 目标达到问题 gradient 梯度 gradient method 梯度法Hhandle 句柄 Hessian matrix 海色矩阵Independent variables 独立变量inequality 不等式infeasibility 不可行性infeasible 不可行的initial feasible solution 初始可行解initialize 初始化inverse 逆 invoke 激活 iteration 迭代 iteration 迭代JJacobian 雅可比矩阵LLagrange multiplier 拉格朗日乘子 large-scale 大型的 least square 最小二乘 least squares sense 最小二乘意义上的 Levenberg-Marquardt method 列文伯格-马夸尔特法line search 一维搜索 linear 线性的 linear equality constraints 线性等式约束linear programming problem 线性规划问题 local solution 局部解M medium-scale 中型的 minimize 最小化 mixed quadratic and cubic polynomialinterpolation and extrapolation method 混合二次、三次多项式内插、外插法multiobjective 多目标的Nnonlinear 非线性的 norm 范数Oobjective function 目标函数 observed data 测量数据 optimization routine 优化过程optimize 优化 optimizer 求解器 over-determined system 超定系统Pparameter 参数 partial derivatives 偏导数 polynomial interpolation method 多项式插值法Qquadratic 二次的 quadratic interpolation method 二次内插法 quadratic programming 二次规划Rreal-value 实数值 residuals 残差 robust 稳健的 robustness 稳健性,鲁棒性S scalar 标量 semi-infinitely problem 半无限问题 Sequential Quadratic Programming method 序列二次规划法 simplex search method 单纯形法 solution 解 sparse matrix 稀疏矩阵 sparsity pattern 稀疏模式 sparsity structure 稀疏结构 starting point 初始点 step length 步长 subspace trust region method 子空间置信域法 sum-of-squares 平方和 symmetric matrix 对称矩阵Ttermination message 终止信息 termination tolerance 终止容限 the exit condition 退出条件 the method of steepest descent 最速下降法 transpose 转置Uunconstrained 无约束的 under-determined system 负定系统Vvariable 变量 vector 矢量Wweighting matrix 加权矩阵3 样条词汇英汉对照表Aapproximation 逼近 array 数组 a spline in b-form/b-spline b样条 a spline of polynomial piece /ppform spline 分段多项式样条Bbivariate spline function 二元样条函数 break/breaks 断点Ccoefficient/coefficients 系数cubic interpolation 三次插值/三次内插cubic polynomial 三次多项式 cubic smoothing spline 三次平滑样条 cubic spline 三次样条cubic spline interpolation 三次样条插值/三次样条内插 curve 曲线Ddegree of freedom 自由度 dimension 维数Eend conditions 约束条件 input argument 输入参数 interpolation 插值/内插 interval取值区间Kknot/knots 节点Lleast-squares approximation 最小二乘拟合Mmultiplicity 重次 multivariate function 多元函数Ooptional argument 可选参数 order 阶次 output argument 输出参数P point/points 数据点Rrational spline 有理样条 rounding error 舍入误差(相对误差)Sscalar 标量 sequence 数列(数组) spline 样条 spline approximation 样条逼近/样条拟合spline function 样条函数 spline curve 样条曲线 spline interpolation 样条插值/样条内插 spline surface 样条曲面 smoothing spline 平滑样条Ttolerance 允许精度Uunivariate function 一元函数Vvector 向量Wweight/weights 权重4 偏微分方程数值解词汇英汉对照表Aabsolute error 绝对误差 absolute tolerance 绝对容限 adaptive mesh 适应性网格Bboundary condition 边界条件Ccontour plot 等值线图 converge 收敛 coordinate 坐标系Ddecomposed 分解的 decomposed geometry matrix 分解几何矩阵 diagonal matrix 对角矩阵 Dirichlet boundary conditions Dirichlet边界条件Eeigenvalue 特征值 elliptic 椭圆形的 error estimate 误差估计 exact solution 精确解Ggeneralized Neumann boundary condition 推广的Neumann边界条件 geometry 几何形状geometry description matrix 几何描述矩阵 geometry matrix 几何矩阵 graphical user interface(GUI)图形用户界面Hhyperbolic 双曲线的Iinitial mesh 初始网格Jjiggle 微调LLagrange multipliers 拉格朗日乘子Laplace equation 拉普拉斯方程linear interpolation 线性插值 loop 循环Mmachine precision 机器精度 mixed boundary condition 混合边界条件NNeuman boundary condition Neuman边界条件 node point 节点 nonlinear solver 非线性求解器 normal vector 法向量PParabolic 抛物线型的 partial differential equation 偏微分方程 plane strain 平面应变 plane stress 平面应力 Poisson's equation 泊松方程 polygon 多边形 positive definite 正定Qquality 质量Rrefined triangular mesh 加密的三角形网格 relative tolerance 相对容限 relative tolerance 相对容限 residual 残差 residual norm 残差范数Ssingular 奇异的二、常用的数学英语表述1.Logic∃there exist∀for allp⇒q p implies q / if p, then qp⇔q p if and only if q /p is equivalent to q / p and q are equivalent2.Setsx∈A x belongs to A / x is an element (or a member) of Ax∉A x does not belong to A / x is not an element (or a member) of AA⊂B A is contained in B / A is a subset of BA⊃B A contains B / B is a subset of AA∩B A cap B / A meet B / A intersection BA∪B A cup B / A join B / A union BA\B A minus B / the diference between A and BA×B A cross B / the cartesian product of A and B3. Real numbersx+1 x plus onex-1 x minus onex±1 x plus or minus onexy xy / x multiplied by y(x - y)(x + y) x minus y, x plus yx y x over y= the equals signx = 5 x equals 5 / x is equal to 5x≠5x (is) not equal to 5x≡y x is equivalent to (or identical with) yx ≡ y x is not equivalent to (or identical with) yx > y x is greater than yx≥y x is greater than or equal to yx < y x is less than yx≤y x is less than or equal to y0 < x < 1 zero is less than x is less than 10≤x≤1zero is less than or equal to x is less than or equal to 1| x | mod x / modulus xx 2 x squared / x (raised) to the power 2x 3 x cubedx 4 x to the fourth / x to the power fourx n x to the nth / x to the power nx −n x to the (power) minus nx (square) root x / the square root of xx 3 cube root (of) xx 4 fourth root (of) xx n nth root (of) x( x+y ) 2 x plus y all squared( x y ) 2 x over y all squaredn! n factorialx ^ x hatx ¯ x barx ˜x tildex i xi / x subscript i / x suffix i / x sub i∑ i=1 n a i the sum from i equals one to n a i / the sum as i runs from 1 to n of the a i4. Linear algebra‖ x ‖the norm (or modulus) of xOA →OA / vector OAOA ¯ OA / the length of the segment OAA T A transpose / the transpose of AA −1 A inverse / the inverse of A5. Functionsf( x ) fx / f of x / the function f of xf:S→T a function f from S to Tx→y x maps to y / x is sent (or mapped) to yf'( x ) f prime x / f dash x / the (first) derivative of f with respect to xf''( x ) f double-prime x / f double-dash x / the second derivative of f with r espect to xf'''( x ) triple-prime x / f triple-dash x / the third derivative of f with respect to xf (4) ( x ) f four x / the fourth derivative of f with respect to x∂f ∂ x 1the partial (derivative) of f with respect to x1∂ 2 f ∂ x 1 2the second partial (derivative) of f with respect to x1∫ 0 ∞the integral from zero to infinitylimx→0 the limit as x approaches zerolimx→0 + the limit as x approaches zero from abovelimx→0 −the limit as x approaches zero from belowlog e y log y to the base e / log to the base e of y / natural log (of) ylny log y to the base e / log to the base e of y / natural log (of) y一般词汇数学mathematics, maths(BrE), math(AmE)公理axiom定理theorem计算calculation运算operation证明prove假设hypothesis, hypotheses(pl.)命题proposition算术arithmetic加plus(prep.), add(v.), addition(n.)被加数augend, summand加数addend和sum减minus(prep.), subtract(v.), subtraction(n.)被减数minuend减数subtrahend差remainder乘times(prep.), multiply(v.), multiplication(n.)被乘数multiplicand, faciend乘数multiplicator积product除divided by(prep.), divide(v.), division(n.)被除数dividend除数divisor商quotient等于equals, is equal to, is equivalent to 大于is greater than小于is lesser than大于等于is equal or greater than小于等于is equal or lesser than运算符operator数字digit数number自然数natural number整数integer小数decimal小数点decimal point分数fraction分子numerator分母denominator比ratio正positive负negative零null, zero, nought, nil十进制decimal system二进制binary system十六进制hexadecimal system权weight, significance进位carry截尾truncation四舍五入round下舍入round down上舍入round up有效数字significant digit无效数字insignificant digit代数algebra公式formula, formulae(pl.)单项式monomial多项式polynomial, multinomial系数coefficient未知数unknown, x-factor, y-factor, z-factor 等式,方程式equation一次方程simple equation二次方程quadratic equation三次方程cubic equation四次方程quartic equation不等式inequation阶乘factorial对数logarithm指数,幂exponent乘方power二次方,平方square三次方,立方cube四次方the power of four, the fourth power n次方the power of n, the nth power开方evolution, extraction二次方根,平方根square root三次方根,立方根cube root四次方根the root of four, the fourth root n次方根the root of n, the nth root集合aggregate元素element空集void子集subset交集intersection并集union补集complement映射mapping函数function定义域domain, field of definition值域range常量constant变量variable单调性monotonicity奇偶性parity周期性periodicity图象image数列,级数series微积分calculus微分differential导数derivative极限limit无穷大infinite(a.) infinity(n.)无穷小infinitesimal积分integral定积分definite integral不定积分indefinite integral有理数rational number无理数irrational number实数real number虚数imaginary number复数complex number矩阵matrix行列式determinant几何geometry点point线line面plane体solid线段segment射线radial平行parallel相交intersect角angle角度degree弧度radian锐角acute angle直角right angle钝角obtuse angle平角straight angle周角perigon底base边side高height三角形triangle锐角三角形acute triangle直角三角形right triangle直角边leg斜边hypotenuse勾股定理Pythagorean theorem钝角三角形obtuse triangle不等边三角形scalene triangle等腰三角形isosceles triangle等边三角形equilateral triangle四边形quadrilateral平行四边形parallelogram矩形rectangle长length宽width附:在一个分数里,分子或分母或两者均含有分数。
HOPF ALGEBRAS

θ ⊗θ
/ B⊗B
θ
/B O
uB
k commute.
k
Definition. Let C and D be k -coalgebras. A linear map f : C → D is a k -coalgebra morphism if the diagrams C C ⊗C and C
HOPF ALGEBRAS
5
For example, if A is any associative k -algebra then A is a Lie algebra if we define [a, b] = ab − ba for all a, b ∈ A. In particular, when A = Mn (k ), we write this as gl(n, k ). The universal enveloping algebra of the Lie algebra g is the factor algebra of the tensor algebra T (g) by the ideal I (g) =< [x, y ] − xy + yx : x, y ∈ g > There is a bijective correspondence between left U (g)-modules and representations of the Lie algebra g, where the latter are - by definition - Lie algebra homomorphisms ρ : g → End(V ) for k -vector spaces V . Special case (A): Let n ≥ 1, g =
椭圆傅里叶描述符英文

椭圆傅里叶描述符英文The Elliptical Fourier DescriptorsThe Elliptical Fourier Descriptors (EFDs) are a powerful tool used in the field of image analysis and shape recognition. They provide a mathematical representation of the shape of an object or a closed contour, allowing for the quantification and comparison of shapes. The EFDs are particularly useful in applications where the shape of an object is an important feature, such as in biological studies, pattern recognition, and computer vision.The Fourier transform is a fundamental mathematical concept that allows for the decomposition of a periodic function into a sum of sine and cosine waves with different frequencies and amplitudes. The Elliptical Fourier Descriptors extend this idea to the description of closed contours in two-dimensional space. Instead of representing the contour as a function of a single variable (such as the angle around the contour), the EFDs represent the contour as a function of two variables, the x and y coordinates.The process of obtaining the Elliptical Fourier Descriptors for a given contour involves several steps. First, the contour is digitized,meaning that the coordinates of a finite number of points along the contour are recorded. These points are then used to calculate the Fourier coefficients that define the EFDs.The Fourier coefficients are calculated by considering the x and y coordinates of the contour as separate periodic functions. For each coordinate, the Fourier series expansion is computed, yielding a set of Fourier coefficients. These coefficients are then used to reconstruct the contour, with the lower-order coefficients capturing the overall shape of the contour and the higher-order coefficients capturing the finer details.One of the key advantages of the Elliptical Fourier Descriptors is their ability to provide a compact and efficient representation of the shape of an object. The shape can be described using a relatively small number of Fourier coefficients, making it possible to store and compare shapes efficiently. This is particularly useful in applications where large numbers of shapes need to be analyzed or compared, such as in biological studies or industrial quality control.Another advantage of the EFDs is their invariance to certain transformations of the shape, such as translation, rotation, and scaling. This means that the Fourier coefficients are not affected by these transformations, making it possible to compare shapes that have been subjected to different transformations.The Elliptical Fourier Descriptors have found numerous applications in various fields. In biology, they have been used to study the shapes of plant leaves, pollen grains, and other biological structures. In computer vision, they have been used for object recognition and shape-based image retrieval. In industrial applications, they have been used for quality control and defect detection.Despite their many advantages, the Elliptical Fourier Descriptors are not without their limitations. One of the main challenges is the selection of the appropriate number of Fourier coefficients to use in the representation of a shape. Too few coefficients may result in a poor approximation of the shape, while too many coefficients can lead to overfitting and increased computational complexity.Another challenge is the interpretation of the Fourier coefficients themselves. While the coefficients provide a compact and efficient representation of the shape, they do not necessarily have a clear physical interpretation. This can make it difficult to understand the underlying shape characteristics that are being captured by the EFDs.Despite these challenges, the Elliptical Fourier Descriptors remain an important and widely-used tool in the field of image analysis and shape recognition. As computational power and storage capabilities continue to increase, the use of EFDs is likely to become even morewidespread, with applications in an ever-widening range of fields.In conclusion, the Elliptical Fourier Descriptors are a powerful mathematical tool that provides a compact and efficient representation of the shape of an object or a closed contour. They have found numerous applications in fields such as biology, computer vision, and industrial quality control, and their use is likely to continue to grow in the years to come.。
pinesap音译

pinesap音译English Answer:A Quick Introduction to Pinesap.Pinesap is a genus of parasitic plants, and its members are commonly known as pinesaps. They are found in the understory of coniferous or hardwood forests and are often associated with beech trees. Pinesaps are parasitic on mycorrhizal fungi, primarily those associated with beech, oak, and pine trees. As such, they lack chlorophyll and obtain their nutrients from their host fungi. Their stems are typically pale and fleshy, with reddish or purplishtips that bear flowers. Pinesaps have small, scale-like leaves that are often reduced to bracts.Pinesap species are distributed globally, with the majority of species occurring in temperate regions of North America and Asia. There are approximately 15 recognized species of pinesap, with the most common species beingEastern pinesap (Pinesap squarrosa) and Western pinesap (Pinesap uniflora).Fascinating Facts about Pinesap.1. Parasitic Nature: Pinesaps are obligate parasites, meaning they cannot survive without their host fungi. They penetrate the fungal hyphae with specialized structures called haustoria, which allow them to absorb nutrients from the fungi.2. Lack of Chlorophyll: Pinesaps lack chlorophyll, the green pigment that enables photosynthesis in plants. Instead, they rely on their host fungi for nutrition.3. Pale and Fleshy Stems: Pinesaps have pale and fleshy stems that often appear translucent or whitish. The stems are often covered with reddish or purplish tips.4. Small, Scale-like Leaves: Pinesaps have small,scale-like leaves that are often reduced to bracts. These leaves are typically arranged in a spiral pattern along thestem.5. Inconspicuous Flowers: Pinesaps produce small, inconspicuous flowers that are often white or tinged with pink. The flowers are borne on the upper portion of the stem and are often hidden by the surrounding vegetation.Pinesap in the Environment.1. Habitat: Pinesaps are typically found in the understory of coniferous or hardwood forests. They are often associated with beech trees, as they primarily parasitize fungi associated with these trees.2. Ecological Role: Pinesaps play a minor ecological role in the forest ecosystem. They do not contribute significantly to the food web and are not known to have any major interactions with other organisms.Conclusion.Pinesap is a fascinating genus of parasitic plants thatrelies on mycorrhizal fungi for survival. Their lack of chlorophyll and reliance on host fungi for nutrients make them unique and intriguing members of the plant kingdom. While they play a minor ecological role, their presence in forest ecosystems adds to the overall biodiversity and complexity of these habitats.Chinese Answer:松叶兰简介。
花朵中的斐波那契数列(组图)

花朵中的斐波那契数列(组图)花朵中的斐波那契数列作者:西蒙妮.普罗伊斯拍摄人:Mack Hall1、图中的是紫色金光菊(又称紫锥花)自然界鬼斧神工:随意的几朵白云,溪水水中浑圆的鹅卵石,或海中白色的浪花等等。
多数情况下,看似毫无规律而言-好比野地里花花草草一样杂乱无章-但有些特却如花头按序排列的种子一样有序可循。
自然界和数学的完美结合,让我们惊叹之余不得不感慨自然界布局竟然完全符合数学领域严格的要求。
在此探讨的是自然界中的斐波纳契数列,借助一些花朵图片开始研究之旅。
这些看似平淡无奇的花朵如何一转眼成为令人叹为观止的艺术品。
拍摄人: Daaynos2、瓢虫毫不关心尖尖的紫锥花头。
而是被排列如此整齐的景象深深吸引。
中世纪数学家比萨的莱昂纳多(公元1170-1250年)发现了斐波纳契数列(拼写构成为fib-on-arch-ee)。
“斐波纳契”是拉丁语“弗立维.波纳切”的缩写,含义是“Bonaccio之子”,其父亲名为Guglielmo Bonaccio。
拍摄人:Daaynos3、令人想起斐波那契数列的花自于意大利比萨市的莱昂纳多,其父Guglielmo是一名海关官员,工作地点就是今天阿尔及利亚的贝贾亚省。
北非留学期间,常常与地中海附近的商旅打交道,莱昂纳多青年时就熟知算数及阿拉伯数字系统。
他发现阿拉伯数字0-9远比常用的罗马数字(I, V, X等等)更高级、更好用。
拍摄人:Rohit Sood4、业余植物学家眼中普普通通的绿芯雏菊斐波纳契如此喜爱数字系统,于是开始在整个欧洲推广数字系统,并著书立说,1202年,他的著作公开出版。
其著作《算盘书》(或者叫《计算之书》)被当时的欧洲同行和后辈数学家称作是推进”新的“十进制系统的开山之作。
拍摄人: Solidskorpion5、像牙齿一样洁白的白菊花花瓣这些历史和这些美轮美奂的花朵图片有什么联系呢?请耐心一点!马上,就给您揭晓答案。
《算盘书》第12章,斐波纳契记录了一组另后人十分着迷的数字序列。
高中英语课时作业(译林版选修第三册)单元测试卷(三)

单元测试卷(三)第一部分听力(共两节,满分30分)第一节(共5小题;每小题分,满分分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.Where does this conversation most probably take place?a bank. B.In a restaurant. C.In a hospital.2.What can we learn from this conversation?A.Mr. Davidson is busy right now.B.The man dialed the wrong number.C.The woman is quite familiar with the man.3.What are the speakers talking about?A.Colors. B.Mushrooms. C.Wallpaper.4.What do the speakers decide to do?A.Go out for dinner.B.Work overtime together.C.Bring some food back for dinner.5.Why doesn't the woman help the man?A.She is busy now. B.She is poor at physics.C.She has a headache.第二节(共15小题;每小题分,满分分)听下面5 段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各个小题将给出5秒钟的作答时间。
全球货币代码
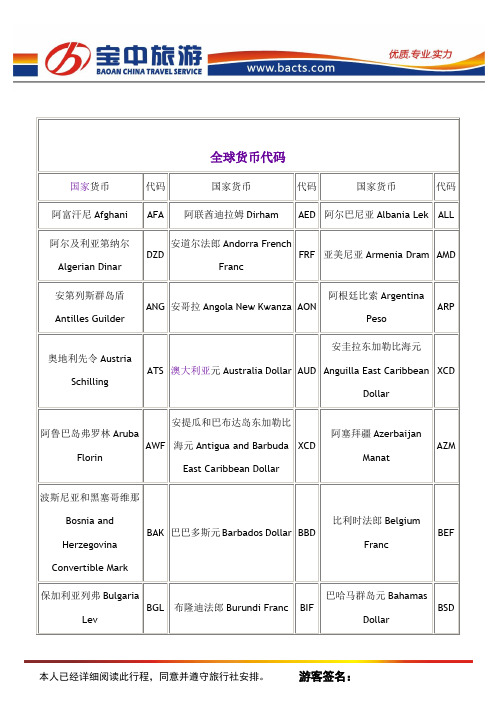
安哥拉Angola New Kwanza
AON
阿根廷比索Argentina Peso
ARP
奥地利先令Austria Schilling
ATS
澳大利亚元Australia Dollar
AUD
安圭拉东加勒比海元Anguilla East Caribbean Dollar
XCD
阿鲁巴岛弗罗林Aruba Florin
厄瓜多尔Ecuador Sucre
ECS
缅甸元Burma Kyat
MMK
爱沙尼亚Estonia Kroon
EEK
埃及镑Egypt Pound
EGP
厄立特里亚Eritrea Nakfa
ERN
西班牙彼萨塔Spain Peseta
ESP
柬埔寨Cambodia Riel
KHR
埃塞俄比亚Ethiopia Birr
ETB
喀麦隆Cameroon CFA Franc
XAF
欧元Euro
EUR
芬兰Finland Markka
FIM
斐济元Fiji Dollar
FJD
法国法郎France Franc
FRF
中非共和国Central African Republic CFA Franc
XAF
乍得Chad CFA Franc
XAF
JMD
约旦第纳尔Jordan Dinar
JOD
日圆Japan Yen
JPY
肯尼亚先令Kenya Shilling
KES
萨尔瓦多El Salvador Colon
SVC
朝鲜Korea (North) Won
KPW
赤道几内亚Equatorial Guinea CFA Franc
菲波那契螺旋

斐波那契螺旋斐波那契(Leonardo Fibonacci, 约1175-约1240)也许是在生活在丢番图(Diophantos)之后费尔马(Pierr e de Fermat)之前这2000年间欧洲最杰出的数论学家。
我们对他的生平知道得很少。
他出生在意大利那个后来因为伽里略做过落体实验而著名的斜塔所在的城市里,现在那里还有他的一座雕像。
他年轻是跟随经商的父亲在北非和欧洲旅行,大概就是由此而学习到了世界各地不同的算术体系。
在他最重要的著作《算盘书》(Liber Abaci,写于1202年)中,引进了印度-阿拉伯数码(包括0)及其演算法则。
数论方面他在丢番图方程和同余方程方面有重要贡献。
数学中有一个以他的名字命名的著名数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ……从第三项开始每一项都是数列中前两项之和。
这个数列是斐波那契在他的《算盘书》的“兔子问题”中提出的。
在问题中他假设如果一对兔子每月能生一对小兔(一雄一雌),而每对小兔在它出生后的第三个月,又能开始生小兔,如果没有死亡,由一对刚出生的小兔开始,一年后一共会有多少对兔子?将问题一般化后答案就是,第n个月时的兔子数就是斐波那契数列的第n项。
斐波那契数列和黄金分割数有很密切的联系。
斐波那契并没有把这个问题和这个数列看得特别重要,在《算盘书》中兔子问题只不过是书里许多问题中并不特别的其中一个罢了。
但是在此后的岁月中,这个数列似乎和题中的高产兔子一样,引发了为数众多的数学论文和介绍文章(本文似乎也在步此后尘)。
不过在这里我不想介绍浩如烟海的有关斐波那契数列的数学文章,只想欣赏大自然的造化。
在现实的自然世界中,《算盘书》里那样的神奇兔子自然是找不到的,但是这并不妨碍大自然使用斐波那契数列。
本期封面上是起绒草椭球状的花头,你可以看见那上面有许多螺旋。
很容易想像,如果从上面俯视下去的话,这些螺旋从中心向外盘旋,有些是顺时针方向的,还有些是逆时针方向的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(adl a)(b) = a1bS(a2), and (adr a)(b) = S(a1)ba2,
for a, b ∈ H, where ∆(a) = a1 ⊗ a2. Also recall that a Hopf subalgebra A of H is normal in H provided (adl H)(A) and (adr H)(A) are contained in A.
December 2001.
Abstract. In formulating a generalized framework to study certain noncommutative algebras naturally arising in representation theory, K. A. Brown asked if every finitely generated Hopf algebra satisfying a polynomial identity was finite over a normal commutative Hopf subalgebra. In this note we show that Radford’s biproduct, applied to the enveloping algebra of the Lie superalgebra pl(1, 1), provides a noetherian prime counterexample.
arXiv:math/0112038v1 [math.QA] 4 Dec 2001
AN AFFINE PI HOPF ALGEBRA NOT FINITE OVER
A NORMAL COMMUTATIVE HOPF SUBALGEBRA
Shlomo Gelaki and Edward S. Letzter
The first author’s research was supported by the Technion V.P.R. Fund - Loewengart research fund and by the Fund for the Promotion of Research at the Technion. The second author’s research was supported in part by NSF grant DMS-9970413. This research was begun during the second author’s visit to the Technion in August 2001, and he is grateful to the Technion for its hospitality.
The reader is referred to [9] for background on noncommutative rings, to [11] for background on Hopf algebras, and to [13] for background on Lie superalgebras.
the ordinary structure maps with morphisms in SuperVect. The resulting objects are referred to, respectively, as Lie superalgebras, superbialgebras, Hopf superalgebras, etc.
We will use SuperVect to denote the category of supervector spaces with homogeneous morphisms. For V, W ∈ SuperVect the commutativity constraint V ⊗ W → W ⊗ V is different from the classical one and is given by the formula
1. Introduction
Noncommutative affine PI Hopf algebras arise in fundamental representation-theoretic contexts: as enveloping algebras of finite dimensional restricted Lie algebras in positive characteristic, as group algebras of finitely generated abelian-by-finite groups, and as quantizations of algebraic groups – and their corresponding Lie algebras – at roots of unity. (By affine we mean “finitely generated over the ground field as an associative algebra,” and by PI we mean “satisfying a polynomial identity.”) In all of the preceding examples, the Hopf algebra of interest is finitely generated as a module over a normal affine commutative Hopf subalgebra. Therefore, in developing a general structure theory to handle these examples, K. A. Brown asked [3, Question B] whether every affine PI Hopf algebra was finitely generated as a left (or right) module over some normal commutative Hopf subalgebra (cf. [4]). In this note we present a counterexample; we describe a prime affine noetherian PI Hopf algebra not finitely generated as a left or right module over any of its normal commutative Hopf subalgebras. This counterexample also arises in a representation-theoretic context, resulting from an application of Radford’s biproduct [12] to the enveloping algebra of the Lie superalgebra pl(1, 1). (In the terminology of [10], the counterexample is the “bosonization” of the enveloping algebra of pl(1, 1).)
of algebras A and B in SuperVect is defined to be the vector space A ⊗ B equipped with
the multiplication
(a ⊗ b)(a′ ⊗ b′) := (−1)p(a′)p(b)aa′ ⊗ bb′,
for homogeneous a, a′ ∈ A and b, b′ ∈ B. (Hopf superalgebras are referred to as “graded Hopf algebr= (−1)p(a2)p(b1)a1b1 ⊗ a2b2
for all homogeneous a, b ∈ H (where ∆(a) = a1 ⊗ a2, ∆(b) = b1 ⊗ b2 and the
components are homogeneous). This formulation is required because the tensor product
For example, a Hopf superalgebra H is a Z2-graded associative algebra, possessing a coassociative multiplicative (in the super-sense) morphism ∆: H → H ⊗ H in SuperVect, and further equipped with a counit ǫ and antipode S satisfying the expected axioms. By “multiplicativity in the super-sense” we mean that ∆ satisfies the relation
Typeset by AMS-TEX 1
2
SHLOMO GELAKI AND EDWARD S. LETZTER
2. Preparatory Results
Let k be an algebraically closed field of characteristic zero. We assume throughout this note that k is the ground field for all of the vector spaces mentioned (explicitly or implicitly). In particular, all algebras (associative and otherwise) are over k. All of the associative algebras discussed below will be assumed to be unital.
