理论力学课后题参考答案
理论力学课后答案Word版
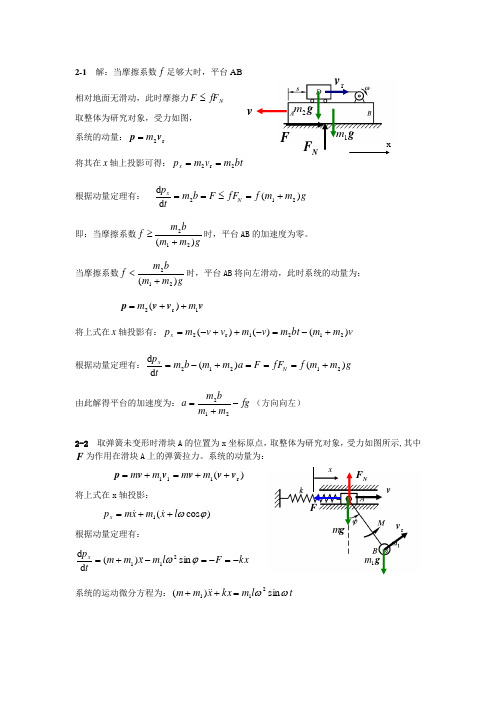
2-1 解:当摩擦系数f 足够大时,平台AB 相对地面无滑动,此时摩擦力N fF F ≤ 取整体为研究对象,受力如图, 系统的动量:r 2v p m =将其在x 轴上投影可得:bt m v m p x 2r 2==根据动量定理有:g m m f fF F b m tp N x)(d d 212+=≤== 即:当摩擦系数gm m bm f )(212+≥时,平台AB 的加速度为零。
当摩擦系数gm m bm f )(212+<时,平台AB 将向左滑动,此时系统的动量为:v v v p 1r 2)(m m ++=将上式在x 轴投影有:v m m bt m v m v v m p x )()()(2121r 2+-=-++-=根据动量定理有:g m m f fF F a m m b m tp N x)()(d d 21212+===+-= 由此解得平台的加速度为:fg m m bm a -+=212(方向向左)2-2 取弹簧未变形时滑块A 的位置为x 坐标原点,取整体为研究对象,受力如图所示,其中F 为作用在滑块A 上的弹簧拉力。
系统的动量为:)(r 111v v v v v p ++=+=m m m m将上式在x 轴投影:)cos (1ϕωl x m xm p x ++= 根据动量定理有:kx F l m xm m tp x-=-=-+=ϕωsin )(d d 211 系统的运动微分方程为:t l m kx x m m ωωsin )(211=++N Fg mg 1mFxvr vvr vN FFg 1mg 2mx2-4 取提起部分为研究对象,受力如图(a)所示,提起部分的质量为vt m ρ=,提起部分的速度为v ,根据点的复合运动可知质点并入的相对速度为r v ,方向向下,大小为v (如图a 所示)。
(a ) (b)根据变质量质点动力学方程有:v vt t t m m t t mρρr r )()(d d )(d d v g F v g F v ++=++= 将上式在y 轴上投影有:)()()()(d d 2r v vgt t F v v g vt t F tvm+-=--=ρρρ 由于0d d =tv,所以由上式可求得:)()(2v vgt t F +=ρ。
理论力学课后题参考答案

1.1 沿水平方向前进的枪弹,通过某一距离s 的时间为t 1,而通过下一等距离s 的时间为2t .试证明枪弹的减速度(假定是常数)为由题可知示意图如题1.1.1图: {{SSt t 题1.1.1图设开始计时的时刻速度为0v ,由题可知枪弹作匀减速运动设减速度大小为a .则有:()()⎪⎪⎩⎪⎪⎨⎧+-+=-=221210211021221t t a t t v s at t v s 由以上两式得 11021at t s v +=再由此式得 ()()2121122t t t t t t s a +-=1.26一弹性绳上端固定,下端悬有m 及m '两质点。
设a 为绳的固有长度,b 为加m 后的伸长,c 为加m '后的伸长。
今将m '任其脱离而下坠,试证质点m 在任一瞬时离上端O 的距离为解 以绳顶端为坐标原点.建立如题1.26.1图所示坐标系.题1.26.1图设绳的弹性系数为k ,则有 kb mg = ① 当 m '脱离下坠前,m 与m '系统平衡.当m '脱离下坠前,m 在拉力T 作用下上升,之后作简运.运动微分方程为 ()ym a y k mg &&=-- ② 联立①② 得 b b a g y b g y +=+&& ③ 0=+y bg y &&齐次方程通解 t b g A t b g A Y sin cos 211+= 非齐次方程③的特解 b a Y +=0 所以③的通解b a t bg A t b g A Y +++=sin cos 211代入初始条件:0=t 时,,c b a y ++=得0,21==A c A ;故有 b a t b g c y ++=cos 即为m 在任一时刻离上端O 的距离.'1.39 一质点受一与距离23次方成反比的引力作用在一直线上运动。
试证此质点自无穷远到达a 时的速率和自a 静止出发到达4a 时的速率相同。
理论力学课后习题与答案解析

第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
《理论力学》课后习题解答(赫桐生版)
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学课后习题及答案解析

理论力学课后习题及答案解析文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-MG129]第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A 点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力RB和一个力偶M B,且:如图所示;将RB向下平移一段距离d,使满足:最后简化为一个力R,大小等于RB。
其几何意义是:R 的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力RA和一个力偶M A,且:如图所示;将RA向右平移一段距离d,使满足:最后简化为一个力R,大小等于RA。
其几何意义是:R 的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
理论力学课后习题部分答案

B
A FAC FBA
P
(l)
(l1)
(l2)
(l3)
图 1-1
1-2 画出下列每个标注字符的物体的受力图。题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
(a)
B
FN1
C
FN 2
P2 P1
FAy
A
FAx
(a2)
(b)
FN1
A
P1
FN
(b2)
C
FN′
P2
(a1)
B
FN1
FN 2
FN
P1
F Ay
FCy
FAx (f2)
C FC′x
FC′y F2
FBy
FBx B (f3)
FAy A FAx
FB
C B
(g)
FAy
FAx A
D FT C FCx
(g2)
FB
B
F1
FB′ B
FAy
A
FAx
(h)
(h1)
P (g1)
FC′y
FT
C
FC′x
P (g3)
D
FCy
FB
F2
C FCx
B
(h2)
A FAx
FAy
FCy
D FAy
A
FAx
(k3)
6
FB
F1
FB′
B B
FD D
(l) FD′ D
A FA
(l1) F2
C
FC (l2)
F1
D
F2
B
A
E
FE
FA
(l3) 或
F1
FB′
理论力学第七版课后习题答案

理论力学第七版课后习题答案第一章: 引言习题1-11.问题描述:给定物体的质量m=2kg,加速度a=3m/s^2,求引力F。
2.解答:根据牛顿第二定律F=ma,其中m表示物体的质量,a表示物体的加速度。
代入已知值,可求得F=6N。
习题1-21.问题描述:给定物体的质量m=5kg,引力F=20N,求加速度a。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=4m/s^2。
第二章: 运动的描述习题2-11.问题描述:一个物体以恒定速度v=10m/s匀速直线运动,经过t=5s,求物体的位移。
2.解答:位移等于速度乘以时间,即s=vt。
代入已知值,可得s=50m。
习题2-21.问题描述:一个物体以初始速度v0=5m/s匀加速直线运动,加速度a=2m/s^2,经过t=3s,求物体的位移。
2.解答:由于物体是匀加速直线运动,位移可以通过公式s=v0t+0.5at^2计算。
代入已知值,可得s=(53)+(0.52*3^2)=45m。
第三章: 动力学基础习题3-11.问题描述:一个物体质量为m=4kg,受到的力F=10N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2.5m/s^2。
习题3-21.问题描述:一个物体质量为m=3kg,受到的力F=6N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2m/s^2。
第四章: 动力学基本定理习题4-11.问题描述:一个物体质量为m=8kg,受到的力F=16N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2m/s^2。
习题4-21.问题描述:一个物体质量为m=6kg,受到的力F=12N,求物体的加速度。
2.解答:根据牛顿第二定律F=ma,将已知值代入,可求得a=2m/s^2。
以上是理论力学第七版课后习题的答案。
希望能对你的学习有所帮助!。
理论力学课后习题及答案

应按下列要求进行设计(D )A.地震作用和抗震措施均按8度考虑B.地震作用和抗震措施均按7度考虑C.地震作用按8度确定,抗震措施按7度采用答题(共38分)1、什么是震级什么是地震烈度如何评定震级和烈度的大小(6分)震级是表示地震本身大小的等级,它以地震释放的能量为尺度,根据地震仪记录到的地震波来确定(2分)地震烈度是指某地区地面和各类建筑物遭受一次地震影响的强弱程度,它是按地震造成的后果分类的。
(2分)震级的大小一般用里氏震级表达(1分)地震烈度是根据地震烈度表,即地震时人的感觉、器物的反应、建筑物破坏和地表现象划分的。
(1分)D.地震作用按7度确定,抗震措施按8度采用4.关于地基土的液化,下列哪句话是错误的(A)A.饱和的砂土比饱和的粉土更不容易液化B.地震持续时间长,即使烈度低,也可能出现液化C.土的相对密度越大,越不容易液化D.地下水位越深,越不容易液化5.考虑内力塑性重分布,可对框架结构的梁端负弯矩进行调幅(B )A.梁端塑性调幅应对水平地震作用产生的负弯矩进行B.梁端塑性调幅应对竖向荷载作用产生的负弯矩进行C.梁端塑性调幅应对内力组合后的负弯矩进行D.梁端塑性调幅应只对竖向恒荷载作用产生的负弯矩进行6.钢筋混凝土丙类建筑房屋的抗震等级应根据那些因素查表确定( B )A.抗震设防烈度、结构类型和房屋层数B.抗震设防烈度、结构类型和房屋高度C.抗震设防烈度、场地类型和房屋层数D.抗震设防烈度、场地类型和房屋高度7.地震系数k与下列何种因素有关( A )A.地震基本烈度B.场地卓越周期一、 C.场地土类1.震源到震中的垂直距离称为震源距(×)2.建筑场地类别主要是根据场地土的等效剪切波速和覆盖厚度来确定的(√)3.地震基本烈度是指一般场地条件下可能遭遇的超越概率为10%的地震烈度值(×)4.结构的刚心就是地震惯性力合力作用点的位置(×)5.设防烈度为8度和9度的高层建筑应考虑竖向地震作用(×)6.受压构件的位移延性将随轴压比的增加而减小C.地震作用按8度确定,抗震措施按7度采用答题(共38分)1、什么是震级什么是地震烈度如何评定震级和烈度的大小(6分)震级是表示地震本身大小的等级,它以地震释放的能量为尺度,根据地震仪记录到的地震波来确定(2分)地震烈度是指某地区地面和各类建筑物遭受一次地震影响的强弱程度,它是按地震造成的后果分类的。
理论力学课后习题答案

第7章 点的合成运动一、是非题(正确的在括号内打“√”、错误的打“×”)1.点的速度和加速度合成定理建立了两个不同物体上两点之间的速度和加速度之间的 关系。
( √ ) 2.根据速度合成定理,动点的绝对速度一定大于其相对速度。
( × )3.应用速度合成定理,在选取动点和动系时,若动点是某刚体上的一点,则动系不可以固结在这个刚体上。
( √ )4.从地球上观察到的太阳轨迹与同时在月球上观察到的轨迹相同。
( × ) 5.在合成运动中,当牵连运动为转动时,科氏加速度一定不为零。
( × ) 6.科氏加速度是由于牵连运动改变了相对速度的方向而产生的加速度。
( √ ) 7.在图中,动点M 以常速度r v 相对圆盘在圆盘直径上运动,圆盘以匀角速度ω绕定轴O 转动,则无论动点运动到圆盘上的什么位置,其科氏加速度都相等。
( √ )二、填空题1.已知r 234=++v i j k ,e 63=-ωi k ,则k =a 18 i + -60 j + 36 k 。
2.在图中,两个机构的斜杆绕O 2的角速度均为2ω,O 1O 2的距离为l ,斜杆与竖直方向的夹角为θ,则图(a)中直杆的角速度=1ωθθωcos sin 2,图(b)中直杆的角速度=1ω2ω。
图 图3.科氏加速度为零的条件有:动参考系作平动、0=r v 和r e v ω//。
4.绝对运动和相对运动是指动点分别相对于定系和动系的运动,而牵连运动是指牵连点相对于定系的运动。
牵连点是指某瞬时动系上和动点相重合的点,相应的牵连速度和加速度是指牵连点相对于定系的速度和加速度。
5.如图所示的系统,以''Ax y 为动参考系,Ax'总在水平轴上运动,AB l =。
则点B 的相对轨迹是圆周,若kt ϕ= (k 为常量),点B 的相对速度为lk ,相对加速度为2lk 。
图6.当点的绝对运动轨迹和相对运动轨迹都是曲线时,牵连运动是直线平动时的加速度合成定理表达式是a e r =+a a a ;牵连运动是曲线平动时的加速度合成定理表达式是 a e r =+a a a ;牵连运动是转动时的加速度合成定理表达式是a e r k =++a a a a 。
《理论力学》课后习题解答(赫桐生_高教版)
第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
胡汉才编著《理论力学》课后习题答案 第1章静力学基本概念

第一章 静力学基本概念
1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量
B.自由矢量
C.定位矢量
1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相
反,则其合力可表为( C )。
A.1F –2F
B.2F - 1F
C.1F +2F
图1-18 图1-19 1-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小 x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6
B. 70.0
C. 136.6
D.25.9
1-4 力的可传性只适用于 A 。
A. 刚体
B. 变形体
1-5 加减平衡力系公理适用于 C 。
A. 刚体;
B. 变形体;
C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0
B. F/2
C. F/6
D.-F/3
1-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21。
理论力学课后习题答案

理论力学课后习题答案1. 第一题题目:一个质点从初始点A沿着一条直线运动到达点A,在此过程中质点受到一个恒定的力A的作用。
求解质点从A 到A的位移A和速度A与时间A的关系。
解答:根据牛顿第二定律A=AA,我们可以得到质点在恒定力作用下的运动方程为 $F = m \\frac{dv}{dt}$。
即:$$F = m \\frac{dx}{dt}$$将方程变形可得:$$dx = \\frac{F}{m} dt$$对上式两边同时积分可得:$$\\int_{x_A}^{x_B} dx = \\frac{1}{m} \\int_0^t F dt$$化简后可得:$$x_B - x_A = \\frac{1}{m} \\int_0^t F dt$$即质点从初始点A移动到达点A时的位移A与时间A的关系为:$$x = x_A + \\frac{1}{m} \\int_0^t F dt$$2. 第二题题目:一个滑块在一个光滑的水平轨道上,质量为A,受到一根拉力为A的绳子的作用。
求解滑块的加速度A。
解答:根据牛顿第二定律A=AA,可以得到滑块的加速度A与拉力A的关系为 $a = \\frac{F}{m}$。
3. 第三题题目:一个质点在一个弹簧的作用下振动,弹簧的劲度系数为A,质量为A。
求解质点的振动周期A。
解答:质点在弹簧的作用下振动,其运动方程为 $m\\frac{d^2x}{dt^2} = -kx$,其中A为质点的位移。
对上式进行变形可得:$$\\frac{d^2x}{dt^2} = -\\frac{k}{m}x$$该微分方程的通解为 $x = A \\sin(\\sqrt{\\frac{k}{m}} t + \\phi)$,其中A为振幅,$\\phi$ 为相位角。
振动周期A可以通过求解动能和势能的平衡关系来得到。
在振动过程中,动能 $K = \\frac{1}{2} m v^2$ 和势能 $U =\\frac{1}{2} k x^2$ 之和保持不变。
理论力学课后习题解答

《理论力学》课后习题解答(赫桐生,高教版)(总53页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
理论力学课后习题解答附答案

5.27证取广义坐标
因为
又因为
所以
5.28解 如题5.28.1图
(1)小环的位置可以由角 唯一确定,因此体系的自由度 ,取广义坐标 ,广义速度 。小球的动能:
以 为势能零点,则小环势能
所以拉氏函数
(2)由哈密顿原理
故
所以
又由于
所以
因为 是任意的,所以有被积式为0,即
化简得
5.29解 参考5.23题,设 ,体系的拉氏函数
⑶小球动能
又由
①式得
设小球势能为V,取固定圆球中心O为零势点,则
小球拉氏函数
= ①
根据定义
有
根据正则方程
④
⑤
对式两边求时间得:
故小球球心切向加速度
5.25解根据第二章§2.3的公式有:
①
根据泊松括号的定义:
②
所以
同理可知:
,
由②得:
同理可得:
,
5.26解 由题5.25可知 的表达式
因为
故
同理可求得:
势能:
根据定义式
故
因为
所以 为第一积分.又
故
得 为第二个第一积分.
同理
即
得 为第三个第一积分.
5.23解如题5.23.1图,
由5.6题解得小球的动能
①
根据定义
②
得
③
根据哈密顿函数的定义
代入③式后可求得:
④
由正则方程得:
⑤
⑥
代入⑤得
整理得
5.24如题5.24.1图,
⑴小球的位置可由 确定,故自由度
⑵选广义坐标 ,广义速度 .
①
根据哈密顿原理
故
②
理论力学课后习题及答案解析.pptx

理论力学教科书课后习题及解析
解:(1) 研究 BC 杆,受力分析,画受力图:
由图知:
习题 4-15.静定多跨梁的荷载及尺寸如图所示,长度单位为 m;求支座反力和 中间铰处压力。
列平衡方程:
8
解方程组: 研究 BC 杆,受力分析,画受力图: 列平衡方程:
理论力学教科书课后习题及解析 解方程组: (2) 研究 CD 杆,受力分析,画受力图:
解:(1) 研究 AB 杆,受力分析(注意 BC 是二力杆),画受力图: 列平衡方程:
由力三角形: 其中: (3) 研究 OE,受力分析,画受力图:
13
理论力学教科书课后习题及解析 解:(1) 研究 ABC 部分,受力分析(注意 AC 是二力杆),画受力图:
列平衡方程:
列平衡方程:
习题 4-20.图示液压升降装置,由平台和两个联动机构所组成,联动机构上的 液压缸承受相等的力(图中只画了一副联动机构和一个液压缸)。 连杆 EDB 和 CG 长均为 2a,杆端装有滚轮 B 和 C,杆 AD 铰结 于 EDB 的中点。举起重量 W 的一半由图示机构承受。设 W=9800N,a=0.7m,l=3.2m,求当 θ=60o 时保持平衡所需的液 压缸的推力,并说明所得的结果与距离 d 无关。
77kN,铅垂荷载 P=1350kN,风荷载 q=1.5kN/m, 水平力 F=50kN;求支座 A 的约束反力和撑杆 CD 所受的力。
列平衡方程:
解:(1) 研究整体,受力分析(CD 是二力杆),画受力图:
解方程组:
反力的实际方向如图示。 习题 4-14.圆柱 O 重 G=1000N 放在斜面上用撑架支承如图;不计架重,求铰链
列平衡方程: 解方程组: 4
反力的实际方向如图示。 校核:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、1 沿水平方向前进得枪弹,通过某一距离s 得时间为t,而通过下一等距离s 得时间为、试
证明枪弹得减速度(假定就是常数)为
由题可知示意图如题1、1、1图: 设开始计时得时刻速度为,由题可知枪弹作匀减速运动设减速度大小为、则有: 由以上两式得 再由此式得
1、26一弹性绳上端固定,下端悬有及两质点。
设为绳得固有长度,为加后得伸长,为加后得伸
长。
今将任其脱离而下坠,试证质点在任一瞬时离上端得距离为
解 以绳顶端为坐标原点、建立如题1、26、1图所示坐标系、
题1、26、1图
设绳得弹性系数为,则有 ① 当 脱离下坠前,与系统平衡、当脱离下坠前,在拉力作用下上升,之后作简运、运动微分方程为 ② 联立①② 得 ③
齐次方程通解 非齐次方程③得特解
所以③得通解
代入初始条件:时,得;故有 即为在任一时刻离上端得距离、 1、39 一质点受一与距离次方成反比得引力作用在一直线上运动。
试证
此质点自无穷远到达时得速率与自静止出发到达时得速率相同。
证
质点受一与距离
次方
成反比得力得作用。
设此力为① 又因为
即 ②
当质点从无穷远处到达时,对②式两边分别积分:
当质点从静止出发到达时,对②式两边分别积分:得 所以质点自无穷远到达时得速率与自静止出发到达时得速率相同。
1、43如质点受有心力作用而作双纽线、、、证 由毕耐公式
质点所受有心力做双纽线运动 故
故
()()⎥⎦⎤⎢⎣
⎡++-=--θθθθθ2cos 12cos 2sin 32cos 22cos 12522132a mh 1、44点所受得有心力如果为
式中及都就是常数,并且<,则其轨道方程可写成 试证明之。
式中(为积分常数)
证 由毕耐公式 将力带入此式 因为 所以
即令 上式化为
这就是一个二阶常系数废气次方程。
'
解之得 微积分常数,取,故 有
令 所以 3、10解 如题3、10、1图。
一均质圆盘,半径
为,放在粗糙水平桌上,绕通过其中心得竖直轴转动,开始时得角速度为。
已知圆盘与桌面得摩擦系数为,
问经过多少时间后盘将静止?
解:轴过点垂直纸面向外。
均质圆盘得密度为。
设盘沿顺时针转动,则沿得方向有 即 ① 为转盘绕轴得转动惯量:(为盘得质量),
② (为盘转动得角频率,负号因为规定顺时针转动) =③ 由①②③得 又因为 故 所以 得
3、11通风机得转动部分以初角速绕其轴转动。
空气阻力矩与角速成正比,比例常数为。
如
转动部分对其轴得转动惯量为,问经过多少时间后,其转动得角速减为初角速得一半?又在此时间内共转了多少转?
解: 如题3、11、1图所示,设轴通过点垂直纸面指向外。
则对轴有:设通风机转动得角速度大小为,由于通风机顺时针转动。
所以,将代入上式得: 。
又由于,解得:
故当时,㏑。
又由于 (为通风机转动得角度) 设, 故当㏑时,,时间
内通风机转动得转数
3、12解 如题3、12、1图,矩形均质薄片,边长为与,重为,
绕竖直轴以初角速转动。
此时薄片得每一部分均受到空气得阻
力,其方向垂直与薄片得平面,其量值与面积及速度平方成正比,比例系数为。
问经过多少时间后,薄片得角速减为初角速得一半?
解:坐标与薄片固连,则沿轴方向有: 且①
现取如图阴影部分得小区域,该区域受到得阻力
对轴得力矩 所以 ②
又薄片对轴得转动惯量 ③ 由①②③得: 当时,
3、15解 如题3、15、1图所示坐标系。
一轮得半径为,以匀速无滑动地沿一直线滚动。
求轮缘上任一点得速度及加速度。
又最高点及最低点得速度各等于多少?哪一点就是转动瞬心?
解:由于球作无滑滚动,球与地面得接触得速度与地面一致,等于零,所以点为转
题3.15.1图
动瞬心。
以为基点。
设球得角速度,则
设轮缘上任意一点,与轴交角为,则故
当时,得最高点得速度当与时分别得到最高点与最低点得加速度
3、19长为2得均质棒,以铰链悬挂于点上。
如起始时,棒自水平位置无初速地运动,并且当
棒通过竖直位置时,铰链突然松脱,棒成为自由体。
试证在以后得运动中,棒得质心得轨迹为一抛物线,并求当棒得质心下降距离后,棒一共转了几转?
解 :固定坐标系。
杆从水平位置摆到竖直位置过程中只有重力做功,故机械能守恒。
设此时得角速度为,则 右边第一项为质心运动动能,第二项为杆绕质心转动得动能。
解上式得
在杆脱离悬点后,根据动量定理与动量矩定理:①②③
③式中为杆绕质心得转动惯量,为沿过质心平行于轴得合力矩,易知,又,代入③式得 即杆将作匀速转动。
解①②得 所以质心得轨迹为一抛物线。
故当时,杆得质心下降,代入④式得 故时间内杆得转数 3、20质量为半径为得均质圆柱体放在粗糙水平面上。
柱得外面绕有
轻绳,绳子跨过一个很轻得滑轮,并悬挂一质量为得物体。
设圆柱体只滚
不滑,并且圆柱体与滑轮间得绳子就是水平得。
求圆柱体质心得加速度,物体得加速度及绳中张力。
解:设圆柱体得转动角速度为,设它受到地面得摩擦力为,由动量定理与动量矩
定理知:① ②对于滑块。
由动量定理知:③ ④ 以为基点: 假设绳不可拉伸。
则。
故⑤ 由①②③④⑤解得:
3、22一飞轮有一半径为得杆轴。
飞轮及杆轴对于转动轴得总转动惯量为。
在杆轴上绕有
细而轻得绳子,绳子得另一端挂一质量为得重物。
如飞轮受到阻尼力矩得作用,求飞轮得角加速度。
若飞轮转过角后,绳子与杆轴脱离,并再转过角后,飞轮停止转动,求飞轮所受到得阻尼力矩得量值。
解: 轴与速度方向一致,轴垂直纸面向外。
设球得半径为,则球绕任一直径得转动
惯量。
由动量定理与动量矩定理可知:①② ③ ④
由①②③④得:
设球与板得接触点为,则时刻点得速度为⑤ ⑥
球由滑
题3.20.1图
m
图
题1.22.3
动变为滚动得条件就是: ⑦ 由⑤⑥⑦解得:
3、23重为得木板受水平力得作用,在一不光滑得平面上运动,板与平面间得摩擦系数为。
在板上放一重为得实心圆柱,此圆柱在板上滚动而不滑动,
试求木板得加速度。
解:设圆柱得半径为,与木板
之间得摩擦力为,弹力为,木板受地面得摩擦力为,弹力为,对木板由动量定理得:
①② 对圆柱,由角动量定理与动量定理得:③ ④⑤ 其中为圆柱绕中心轴得转动惯量,所以⑥ ⑦ 无滑滚动得条件: ⑧ 由①~⑧式解得
5、13、1 半径为得光滑半球形碗,固定在水平面上。
一均
质棒斜靠在碗缘,一端在碗内,一端则在碗外,在碗内得长度为,试证棒得全长为 、
解 杆受理想约束,在满足题意得约束条件下杆得位置可由杆与水平方向夹角所唯一确定。
杆得自
由度为1,由平衡条件:
即 mgy =0①
变换方程y=2rcossin-= rsin2② 故③ 代回①式即
因在约束下就是任意得,要使上式成立必须
有:rcos2-=0 ④ 又由于 cos= 故 cos2= 代回④式得
5、2解 相同得两个均质光滑球悬在结于定点得两根绳子上,此两球同时又支持一个等重
得均质球,求角及角之间得关系。
解:三球受理想约束,球得位置可以由确定,自由度数为1,故。
得
由虚功原理 故
()()()0sin 2sin sin sin 0
332211=⋅++-+-+-=++δαδα
δβ
β
αδααδααδαδδδr r l r l r l y P y P y
P 1
f F
图
题1.23.3
题5.1.1
图
题5.2.1图
①
因在约束条件下就是任意得,要使上式成立,必须 故② 又由 得: ③ 由②③可得
4、10 质量为得小环,套在半径为得光滑圆圈上,并可沿着圆圈滑动。
如圆圈在水平面内以匀角速绕圈上某点转动,试求小环沿圆圈切线方向得运动微分方程。
解:平面运动,一个自由度、 选广义坐标为,广义速度
因未定体系受力类型,由一般形式得拉格朗日方程 ① 在 广义力 代入①得: ② 在极坐标系下:
()
⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢⎣
⎡⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝
⎛+⎪⎪⎪⎪⎭⎫
⎝⎛=+=
22222222cos 22cos 2212
1
dt t d a dt a d m r r m T ωθθθθ ③ 故 将以上各式代入②式得。
