八年级数学角平分线的性质及其逆定理同步练习

合集下载

人教版八年级数学上册《角平分线性质定理及逆定理》练习题

角均分线性质定理及逆定理练习一．选择题（共 11 小题）1．（ ?衢州）如图， OP 均分∠ MON ， PA ⊥ON 于点 A ，点 Q 是射线OM 上的一个动点，若 PA=2，则 PQ 的最小值为（A ．1B ． 2C ．3D ．4）2．（?恩施州）如图， AD 是 △ ABC 的角均分线， DF ⊥ AB ，垂足为 F ，DE=DG ，△ADG 和△AED 的面积分别为 50 和 39，则 △EDF 的面积为（）A11．． D 3.5B 5.5C 7．．3．（?柳州）如图，Rt △ABC 中，∠C=90°，∠ABC 的均分线 BD 交 AC 于 D ，若 CD=3cm ，则点 D 到 AB 的距离 DE 是（）A ．5cmB ．4cmC ．3cmD ．2cm4．（?鄂州）如图， AD 是△ABC 中∠ BAC 的均分线， DE ⊥ AB 于点 E ，DF ⊥AC 交 AC 于点 F ． S △ ABC =7， DE=2，AB=4 ，则 AC 长是（）A ．4B ．3C ．6D ．55．（?临沂）如图， OP 均分∠ AOB ， PA ⊥OA ， PB ⊥ OB ，垂足分别为 A ，B ．以下结论中不必定建立的是（）A ．PA=PBB ．PO 均分．．垂直均分 ∠ APBC OA=OBD ABOP6．（?中山）到三角形三条边的距离都相等的点是这个三角形的（）A ．三条中线的交点B ．三条高的交点C ．三条边的垂直均分线的交点D ．三条角均分线的交点7．（?贵港）已知：如图，AD 是△ ABC 的角均分线，且 AB ：AC=：，则 △ABD 与 △ACD 的面积之比为（）A ．3：2B ．：C ．2：3D ．：8．（?仙桃潜江江汉）如图，折叠直角三角形纸片的直角，使点 C 落在AB 上的点 E 处．已知 BC=12，∠ B=30°，则 DE 的长是（）A．6B．4C．3D．29．（?内江）如图，∠ AOB=30°， OP 均分∠ AOB， PC∥ OB， PD⊥ OB，假如 PC=6，那么 PD 等于（）A．4B．3C．2D．110．（?天津）如图，在△ABC 中，AQ=PQ，PR=PS，PR⊥AB 于 R，PS⊥AC 于 S，则三个结论① AS=AR ；②QP∥ AR ；③△ BPR≌△ QSP 中（）A ．所有正确B．仅①和②正确 C．仅①正确D．仅①和③正确11．（?安徽）如图，直线 l1、l2、l 3表示三条互订交错的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地点有（）A．1 处B．2 处C．3 处D．4 处二．填空题（共 4 小题）12．（ ?通辽）如图，△ABC 的三边 AB 、BC、CA 长分别为 40、50、60．其三条角均分线交于点 O，则 S△ABO：S△BCO：S△CAO=_________ ．13．（?岳阳）如图， AD ∥BC，∠ ABC 的角均分线 BP 与∠ BAD 的角均分线 AP 订交于点 P，作 PE⊥AB 于点 E．若 PE=2，则两平行线AD 与 BC 间的距离为 _________ ．14．（?随州）如图，△ ABC 的外角∠ ACD 的均分线 CP 与内角∠ABC 均分线 BP 交于点 P，若∠ BPC=40°，则∠ CAP= _________ ．15．（?河南）如图，在四边形ABCD 中，∠ A=90°， AD=4 ，连接 BD ，BD ⊥CD，∠ADB= ∠ C．若 P 是 BC 边上一动点，则 DP长的最小值为 _________ ．三．解答题（共 4 小题）16．（?牡丹江）在△ABC 中，∠ ACB=2 ∠B，如图①，当∠ C=90°，AD 为∠ BAC 的角均分线时，在 AB 上截取 AE=AC ，连结 DE，易证 AB=AC+CD ．（1）如图②，当∠ C≠90°， AD 为∠ BAC 的角均分线时，线段 AB 、 AC、 CD 又有如何的数目关系？不需要证明，请直接写出你的猜想：（2）如图③，当 AD 为△ ABC 的外角均分线时，线段 AB 、AC 、CD 又有如何的数目关系？请写出你的猜想，并对你的猜想赐予证明．17．（?西宁）（1）班同学上数学活动课，利用角尺均分一个角（以下图）．设计了以下方案：（Ⅰ）∠ AOB 是一个随意角，将角尺的直角极点 P 介于射线 OA 、OB 之间，挪动角尺使角尺两边同样的刻度与 M 、N 重合，即 PM=PN，过角尺极点 P 的射线 OP 就是∠ AOB 的均分线．（Ⅱ）∠ AOB 是一个随意角，在边 OA 、OB 上分别取 OM=ON ，将角尺的直角极点 P 介于射线OA 、OB 之间，挪动角尺使角尺两边同样的刻度与M 、N 重合，即PM=PN，过角尺极点P 的射线 OP 就是∠ AOB 的均分线．（1）方案（Ⅰ）、方案（Ⅱ）能否可行？若可行，请证明；若不行行，请说明原因；（2）在方案（Ⅰ） PM=PN 的状况下，持续挪动角尺，同时使PM⊥ OA ，PN⊥OB．此方案能否可行？请说明原因．18．（?福州）如图，直线 AC ∥BD ，连结 AB ，直线 AC ， BD 及线段 AB 把平面分红①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点 P 落在某个部分时，连结 PA，PB，构成∠ PAC，∠APB ，∠PBD 三个角．（提示：有公共端点的两条重合的射线所构成的角是 0°角）（1）当动点 P 落在第①部分时，求证：∠APB=∠ PAC+∠PBD；（2）当动点 P 落在第②部分时，∠ APB=∠ PAC+∠PBD 能否建立？（直接回答建立或不建立）（3）当动点 P 落在第③部分时，全面研究∠PAC，∠ APB ，∠PBD 之间的关系，并写出动点P的详细地点和相应的结论．选择此中一种结论加以证明．19．（?东城区）如图，CD⊥AB 于点 D，BE⊥AC 于点 E，BE，CD 交于点 O，且 AO 均分∠BAC ，求证： OB=OC．。

人教版八年级数学上册12.3角的平分线的性质同步练习解析版

人教版八年级数学上册12.3角的平分线的性质同步练习一．选择题（共11小题）1．下列作图属于尺规作图的是（）A．画线段MN＝3cmB．用量角器画出∠AOB的平分线C．用三角尺作过点A垂直于直线L的直线D．已知∠α，用没有刻度的直尺和圆规作∠AOB，使∠AOB＝2∠α2．如图△ABC中，∠ACB＝90゜，AD平分∠BAC交BC于D，DE垂直AB于E，若DE＝1.5cm，BD＝3cm，则BC＝（）A．3cm B．7.5cm C．6cm D．4.5cm3．如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC，交BC于D，CD＝4，则点D到AB的距离是（）A．4B．2C．3D．64．如图，AE为∠BAC的平分线，EB⊥AB，EF⊥AC，则下列结论不正确的是（）A．EF＝EB B．AF＝AB C．AE＝CE D．∠AEF＝∠AEB 5．如图，在△ABC中，∠B、∠C的角平分线交于点0，OD⊥AB于D，OE⊥AC于E，则OD与OE的大小关系是（）A．OD＞OE B．OD＜OE C．OD＝OE D．不能确定6．如图，PC⊥OC于C，PD⊥OD于D，若PC＝PD，则（）A．∠1＞∠2B．∠1＝∠2C．∠1＜∠2D．不能确定7．如图所示，点D在∠AOB的内部，DE⊥OA，DF⊥OB，垂足分别为E，F，DE＝DF，则∠AOD与∠BOD的大小关系是（）A．∠AOD＞∠BOD B．∠AOD＝∠BOD C．∠AOD＜∠BOD D．无法确定8．下列关于三角形角平分线的说法错误的是（）A．两角平分线交点在三角形内B．两角平分线交点在第三个角的平分线上C．两角平分线交点到三边距离相等D．两角平分线交点到三顶点距离相等9．给出下列结论，正确的有（）①到角两边距离相等的点，在这个角的平分线上；②角的平分线与三角形平分线都是射线；③任何一个命题都有逆命题；④假命题的逆命题一定是假命题．A．1个B．2个C．3个D．4个10．如图，已知点P、D、E分别在OC、OA、OB上，下列推理：①∵OC平分∠AOB，∴PD＝PE；②∵OC平分∠AOB，PD⊥OA，PE⊥OB，∴PD＝PE；③∵PD⊥OA，PE⊥OB，∴PD＝PE；其中正确的个数有（）A．0个B．1个C．2个D．3个11．如图所示，PD＝PE，PD⊥OA，PE⊥OB，垂足分别为D，E，则下列结论中错误的是（）A．∠DOP＝∠EOP B．OD＝OE C．∠DPO＝∠EPO D．PD＝OD二．填空题（共8小题）12．如图，∠B＝∠D＝90°，根据角平分线性质，填空：（1）若∠1＝∠2，则＝；（2）若∠3＝∠4，则＝．13．点M在∠AOB的平分线上，点M到OA的距离为6，则点M到OB的距离为．14．射线OC平分∠AOB，点P在OC上，且PM⊥OA于点M，PN⊥OB予点N，且PM＝2cm，则PN＝cm．15．如图所示，在△ABC中，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F．则下列结论：①DA平分∠EDF；②AE＝AF，DE＝DF；③AD上的点到B，C两点的距离相等；④图中共有3对全等三角形，正确的有．16．如图，△ABC中，∠C＝90°，AD为角平分线．若BC＝5，BD＝2，则点D到边AB 的距离为．17．如图，在△ABC中，∠C＝90°，AD是∠CAB的平分线，DE⊥AB于点E，且DE＝3cm，BD＝5cm，则BC＝cm．18．（1）如图，已知∠1＝∠2，DE⊥AB，DF⊥AC，垂足分别为E、F，则DE DF．（2）已知DE⊥AB，DF⊥AC，垂足分别为E、F，且DE＝DF，则∠1∠2．19．如图，△ABC中，∠C＝90°，AB＝13，AC＝5，BC＝12，点O为∠CAB和∠CBA的平分线的交点，则OP＝．三．解答题（共9小题）20．如图，在直线MN上找一点P，使点P到直线AB和直线CD的距离相等．21．如图，△ABC中，∠C＝90゜，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，且BE＝CF，求证：（1）DE＝DC；（2）BD＝DF．22．如图所示，D是△ABC外角∠ACG的平分线上的一点．DE⊥AC，DF⊥CG，垂足分别为E，F．求证：CE＝CF．23．如图，E是∠APB内的一点，CE⊥P A于点C，ED⊥PB于点D，CE＝ED，点F在P A 上，∠APB＝60°，∠PEF＝15°．求∠CFE的度数．24．∠B＝∠C＝90°，EB＝EC，DE平分∠ADC，求证：AE是∠DAB平分线．25．△ABC中，∠C＝90°，AD为角平分线，BC＝64，BD：DC＝9：7，求D到AB的距离．26．如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC＝90，AB＝18，BC＝12，求DE 的长．27．如图，若S△ABD：S△ACD＝AB：AC，求证：AD平分∠BAC．28．已知：如图所示，AQ，BM，CN是△ABC的三条角平分线．试说明AQ，BM，CN交于一点．参考答案一．选择题（共11小题）1．下列作图属于尺规作图的是（）A．画线段MN＝3cmB．用量角器画出∠AOB的平分线C．用三角尺作过点A垂直于直线L的直线D．已知∠α，用没有刻度的直尺和圆规作∠AOB，使∠AOB＝2∠α【解答】解：A、画线段MN＝3cm，需要知道长度，而尺规作图中的直尺是没有长度的，错误；B、用量角器画出∠AOB的平分线，量角器不在尺规作图的工具里，错误；C、用三角尺作过点A垂直于直线L的直线，三角尺也不在作图工具里，错误；D、正确．故选：D．2．如图△ABC中，∠ACB＝90゜，AD平分∠BAC交BC于D，DE垂直AB于E，若DE＝1.5cm，BD＝3cm，则BC＝（）A．3cm B．7.5cm C．6cm D．4.5cm【解答】解：∵∠ACB＝90°，∴AC⊥BC，∵DE⊥AB，AD平分∠BAC，∴DE＝DC＝1.5cm，∵BD＝3cm，∴BC＝BD+DC＝3cm+1.5cm＝4.5cm，故选：D．3．如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC，交BC于D，CD＝4，则点D到AB的距离是（）A．4B．2C．3D．6【解答】解：如图，过D点作DE⊥AB于点E，则DE即为所求，∵∠C＝90°，AD平分∠BAC交BC于点D，∴CD＝DE（角的平分线上的点到角的两边的距离相等），∵CD＝4，∴DE＝4．故选：A．4．如图，AE为∠BAC的平分线，EB⊥AB，EF⊥AC，则下列结论不正确的是（）A．EF＝EB B．AF＝AB C．AE＝CE D．∠AEF＝∠AEB 【解答】解：∵AE为∠BAC的平分线，EB⊥AB，EF⊥AC，∴EF＝EB，在Rt△ABE和Rt△AFE中，，∴Rt△ABE≌Rt△AFE（HL），∴AF＝AB，∠AEF＝∠AEB，∴结论不正确的是AE＝CE．故选：C．5．如图，在△ABC中，∠B、∠C的角平分线交于点0，OD⊥AB于D，OE⊥AC于E，则OD与OE的大小关系是（）A．OD＞OE B．OD＜OE C．OD＝OE D．不能确定【解答】解：如图，连接AO，∵∠B、∠C的角平分线交于点0，∴AO平分∠BAC，∵OD⊥AB，OE⊥AC，∴OD＝OE．故选：C．6．如图，PC⊥OC于C，PD⊥OD于D，若PC＝PD，则（）A．∠1＞∠2B．∠1＝∠2C．∠1＜∠2D．不能确定【解答】解：∵PC⊥OC，PD⊥OD，PC＝PD，∴P在∠COD的角平分线上，即∠1＝∠2，故选：B．7．如图所示，点D在∠AOB的内部，DE⊥OA，DF⊥OB，垂足分别为E，F，DE＝DF，则∠AOD与∠BOD的大小关系是（）A．∠AOD＞∠BOD B．∠AOD＝∠BOD C．∠AOD＜∠BOD D．无法确定【解答】解：∵DE⊥OA，DF⊥OB，DE＝DF，∴点D在∠AOB的平分线上，∴∠AOD＝∠BOD．故选：B．8．下列关于三角形角平分线的说法错误的是（）A．两角平分线交点在三角形内B．两角平分线交点在第三个角的平分线上C．两角平分线交点到三边距离相等D．两角平分线交点到三顶点距离相等【解答】解：A、两角平分线交点在三角形内，正确；B、两角平分线交点在第三个角的平分线上，正确；C、根据角平分线的性质，两角平分线交点到三边距离相等，正确；D、根据角平分线的性质，两角平分线交点到三边距离相等，不是到三顶点距离相等，故本选项错误．故选：D．9．给出下列结论，正确的有（）①到角两边距离相等的点，在这个角的平分线上；②角的平分线与三角形平分线都是射线；③任何一个命题都有逆命题；④假命题的逆命题一定是假命题．A．1个B．2个C．3个D．4个【解答】解：①根据角平分线性质的逆定理，在角的内部到角两边距离相等的点，在这个角的平分线上，故本选项错误；②角平分线是射线，三角形的角平分线是线段，故本选项错误；③任何一个命题都有逆命题，正确；④假命题的逆命题不一定是假命题，如：假命题“相等的两个角是对顶角”的逆命题“对顶角相等”是真命题，故本选项错误．故选：A．10．如图，已知点P、D、E分别在OC、OA、OB上，下列推理：①∵OC平分∠AOB，∴PD＝PE；②∵OC平分∠AOB，PD⊥OA，PE⊥OB，∴PD＝PE；③∵PD⊥OA，PE⊥OB，∴PD＝PE；其中正确的个数有（）A．0个B．1个C．2个D．3个【解答】解：∵OC平分∠AOB，PD⊥OA，PE⊥OB，∴PD＝PE．故选：B．11．如图所示，PD＝PE，PD⊥OA，PE⊥OB，垂足分别为D，E，则下列结论中错误的是（）A．∠DOP＝∠EOP B．OD＝OE C．∠DPO＝∠EPO D．PD＝OD【解答】解：A、根据HL可求得Rt△POE≌Rt△POD，∴∠DOP＝∠EOP，故正确；B、OD＝OE，正确；C、DPO＝∠EPO，正确；D、错误．故选：D．二．填空题（共8小题）12．如图，∠B＝∠D＝90°，根据角平分线性质，填空：（1）若∠1＝∠2，则BC＝DC；（2）若∠3＝∠4，则AB＝AD．【解答】解：（1）若∠1＝∠2，则BC＝DC；（2）若∠3＝∠4，则AB＝AD．故答案为：BC，DC；AB，AD．13．点M在∠AOB的平分线上，点M到OA的距离为6，则点M到OB的距离为6．【解答】解：∵点M在∠AOB的平分线上，点M到OA的距离为6，∴点M到OB的距离＝6．故答案为：6．14．射线OC平分∠AOB，点P在OC上，且PM⊥OA于点M，PN⊥OB予点N，且PM＝2cm，则PN＝2cm．【解答】解：∵OC平分∠AOB，点P在OC上，且PM⊥OA于M，PN⊥OB于N，PM ＝2cm，∴PN＝PM＝2cm．故答案为：2．15．如图所示，在△ABC中，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F．则下列结论：①DA平分∠EDF；②AE＝AF，DE＝DF；③AD上的点到B，C两点的距离相等；④图中共有3对全等三角形，正确的有①②．【解答】解：∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，∴DE＝DF，在Rt△ADE与Rt△ADF中，，∴Rt△ADE≌Rt△ADF，∴∠ADF＝∠ADE，AE＝AF，∴DA平分∠EDF；故①②正确，∵无法判定AD⊥BC且平分BC，∴AD上的点到B，C两点的距离相等错误，∵图中只有1对全等三角形，故③④错误．故答案为：①②．16．如图，△ABC中，∠C＝90°，AD为角平分线．若BC＝5，BD＝2，则点D到边AB 的距离为3．【解答】解：过D作DE⊥AB，∵BC＝5，BD＝2，∴CD＝5﹣2＝3，∵AD为角平分线，∴CD＝DE＝3，故答案为：3．17．如图，在△ABC中，∠C＝90°，AD是∠CAB的平分线，DE⊥AB于点E，且DE＝3cm，BD＝5cm，则BC＝8cm．【解答】解：∵∠C＝90°，AD是∠CAB的平分线，DE⊥AB，∴CD＝DE，∵DE＝3cm，BD＝5cm，∴BC＝CD+BD＝3+5＝8cm．故答案为：8．18．（1）如图，已知∠1＝∠2，DE⊥AB，DF⊥AC，垂足分别为E、F，则DE＝DF．（2）已知DE⊥AB，DF⊥AC，垂足分别为E、F，且DE＝DF，则∠1＝∠2．【解答】解：（1）∵已知∠1＝∠2∴AD为∠BAC的平分线又∵DE⊥AB，DF⊥AC，∴由角平分线性质得DE＝DF．（2）∵已知DE⊥AB，DF⊥AC，∴DE，DF为点D到角两边的距离．又∵DE＝DF，∴由角平分线性质知AD为角平分线．19．如图，△ABC中，∠C＝90°，AB＝13，AC＝5，BC＝12，点O为∠CAB和∠CBA的平分线的交点，则OP＝2．【解答】解：作OE⊥BC，OF⊥AC，∴∠C＝∠CFO＝∠OEC＝90°，∴四边形CFOE是矩形；∵∠CAB，∠CBA的平分线相交于点O，OE⊥BC，OF⊥AC，OP⊥AB，∴OE＝OP＝OF，∴四边形CFOE是正方形，设OE＝OP＝OF＝x，则AP＝AF＝5﹣x，BP＝BE＝12﹣x，∴5﹣x+12﹣x＝13，解得x＝2，∴OP＝OE＝2．故答案为2．三．解答题（共9小题）20．如图，在直线MN上找一点P，使点P到直线AB和直线CD的距离相等．【解答】解：点P如图所示．21．如图，△ABC中，∠C＝90゜，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，且BE＝CF，求证：（1）DE＝DC；（2）BD＝DF．【解答】证明：（1）∵∠C＝90°，AD是∠BAC的平分线，DE⊥AB，∴DE＝DC；（2）在△BDE和△FDC中，，∴△BDE≌△FDC（SAS），∴BD＝DF．22．如图所示，D是△ABC外角∠ACG的平分线上的一点．DE⊥AC，DF⊥CG，垂足分别为E，F．求证：CE＝CF．【解答】证明：∵CD是∠ACG的平分线，DE⊥AC，DF⊥CG，∴DE＝DF，在Rt△CDE和Rt△CDF中，，∴Rt△CDE≌Rt△CDF（HL），∴CE＝CF．23．如图，E是∠APB内的一点，CE⊥P A于点C，ED⊥PB于点D，CE＝ED，点F在P A 上，∠APB＝60°，∠PEF＝15°．求∠CFE的度数．【解答】解：∵CE⊥P A，ED⊥PB，CE＝ED，∴∠APE＝∠APB＝×60°＝30°，在△PEF中，∠CFE＝∠APE+∠PEF＝30°+15°＝45°．24．∠B＝∠C＝90°，EB＝EC，DE平分∠ADC，求证：AE是∠DAB平分线．【解答】证明：如图，过点E作EF⊥AD于F，∵DE平分∠ADC，∠C＝90°，∴EC＝EF，∵EB＝EC，∴EF＝BE，又∵∠B＝90°，∴AE是∠DAB平分线．25．△ABC中，∠C＝90°，AD为角平分线，BC＝64，BD：DC＝9：7，求D到AB的距离．【解答】解：∵BD：DC＝9：7，BC＝64，∴CD＝＝28，∵AD为角平分线，∠C＝90°，DE⊥AB，∴DE＝DC＝28．答：D到AB的距离为28．26．如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC＝90，AB＝18，BC＝12，求DE 的长．【解答】解：如图，过点D作DF⊥BC于F，∵BD是∠ABC的平分线，DE⊥AB，∴DE＝DF，∴S△ABC＝AB•DE+BC•DF＝90，即×18•DE+×12•DE＝90，解得DE＝6．27．如图，若S△ABD：S△ACD＝AB：AC，求证：AD平分∠BAC．【解答】证明：如图，过D作DM⊥AB于M，DN⊥AC于N，则S△ABD＝AB•DM，S△ACD＝AC•DN，∵S△ABD：S△ACD＝AB：AC，∴DM＝DN，∴AD平分∠BAC．28．已知：如图所示，AQ，BM，CN是△ABC的三条角平分线．试说明AQ，BM，CN交于一点．【解答】证明：设BM，CN交于点P，过点P作PD⊥AB，PE⊥BC，PF⊥AC，垂足分别为：D，E，F，∵BM平分∠ABC，CN平分∠ACB，∴PD＝PE，PE＝PF，∴PD＝PF，∴AP平分∠BAC，即AQ，BM，CN交于一点P．。

2018秋八年级数学上册第13章全等三角形13.5逆命题与逆定理13.5.3角平分线习题课件新版华东师大版

在这个角的平分线上．
推理格式：如图②，∵PD⊥OA 于点 D，PE⊥OB 于点 E，PD＝PE，∴点 P 在∠AOB 的平分线上．
图①
图②
2. 三角形的三条角平分线相交于一点到
三边的距离
一点
，并且这
相等．
知识点
角平分线的性质
1. 下列关于三角形的角平分线的说法错误的是 ( D ) A．两条角平分线的交点在三角形内 B．两条角平分线的交点在第三个角的平分线上 C．两条角平分线的交点到三边的距离相等 D．两条角平分线的交点到三顶点的距离相等
3. 如图，若点 P 到 BE、BD、AC 的距离恰好相等，则点 P 的位置：①在∠B 的平分线上；②在∠DAC 的平分线上；③在∠ECA 的平分线上；④恰是∠B、∠DAC、 ∠ECA 三条角平分线的交点．上述结论中，正确的有 ( D ) A．1 个 C．3 个 B．2 个 D ．4 个
第 3 题图
第 5 题图
6. 如图所示，DE⊥AB 于点 D，CE⊥BC 于点 C，且 DE＝CE，则下列结论不一定正确的是( A．BE 平分∠ABC B．EB 平分∠CED C．AE＋DE＝AC D．∠A＝∠ABE
D )
第 6 题图
1. 如图，OP 平分∠MON，PA⊥ON 于点 A，点 Q 是射线 OM 上的一动点，若 PA＝2，则 PQ 的最小值为 ( B ) A．1 C ．3 B．2 D．4
BD＝CD，中，∵ DE＝DF，
∴Rt△ BED≌Rt△ CFD(H. L. )，∴BE＝CF.
9. 如图，在 Rt△ ABC 中，AD 为斜边 BC 上的高， BE 平分∠ABC 交 AD 于点 F，交 AC 于点 E，EG⊥BC 于点 G. 求证：AF＝AE＝EG.

八年级数学角平分线的性质及其逆定理同步练习

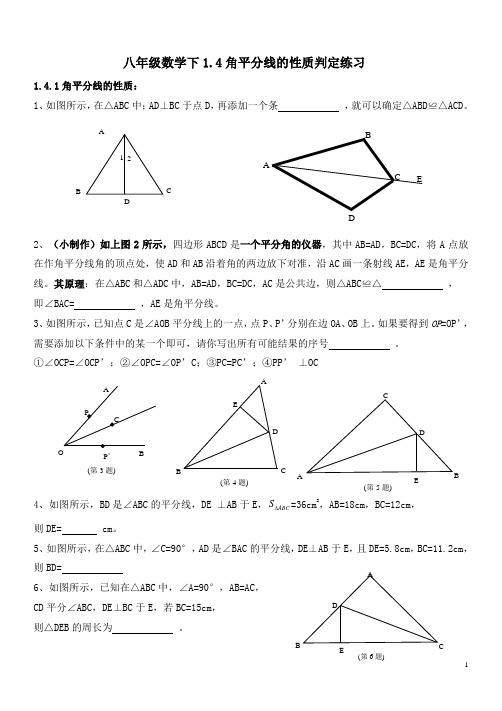
八年级数学下1.4角平分线的性质判定练习1.4.1角平分线的性质：1、如图所示，在△ABC 中；AD ⊥BC 于点D ，再添加一个条，就可以确定△ABD ≌△ACD 。

2、（小制作）如上图2所示，四边形ABCD 是一个平分角的仪器，其中AB=AD ，BC=DC ，将A 点放在作角平分线角的顶点处，使AD 和AB 沿着角的两边放下对准，沿AC 画一条射线AE ，AE 是角平分线。

其原理：在△ABC 和△ADC 中，AB=AD ，BC=DC ，AC 是公共边，则△ABC ≌△ ，即∠BAC= ，AE 是角平分线。

3、如图所示，已知点C 是∠AOB 平分线上的一点，点P 、P ’分别在边OA 、OB 上。

如果要得到OP =OP ’，需要添加以下条件中的某一个即可，请你写出所有可能结果的序号。

①∠OCP=∠OCP ’；②∠OPC=∠OP ’C ；③PC=PC ’；④PP ’ ⊥OC4、如图所示，BD 是∠ABC 的平分线，DE ⊥AB 于E ，ABC S =36cm 2，AB=18cm ，BC=12cm ，则DE= cm 。

5、如图所示，在△ABC 中，∠C=90°，AD 是∠BAC 的平分线，DE ⊥AB 于E ，且DE=5.8cm ，BC=11.2cm ，则BD=6、如图所示，已知在△ABC 中，∠A=90°，AB=AC ， CD 平分∠ABC ，DE ⊥BC 于E ，若BC=15cm ，则△DEB 的周长为。

BD CABCDEP ’B(第3题)ABCDE(第4题)ABE(第5题)ABCDE(第6题)7、如图所示，D 是△ABC 的∠BAC 的一个外角平分线上的一点，求证：AB+AC<DB+DC.8、如图所示，在△ABC 中，D 为BC 的中点，DE ⊥BC 交∠BAC 的平分线AE 于E ，EF ⊥AB 于F ， EG ⊥AC 交延长线于G ，求证：BF=CG 。

角平分线的性质专项练习(含解析)

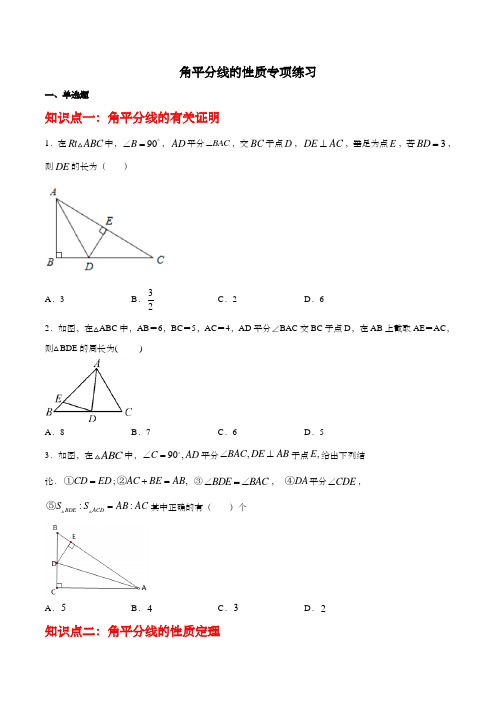
角平分线的性质专项练习一、单选题知识点一：角平分线的有关证明1．在Rt ABC 中，90B ︒∠=，AD 平分BAC ∠，交BC 于点D ，DE AC ⊥，垂足为点E ，若3BD =，则DE 的长为（）A ．3B ．32C ．2D ．62．如图，在△ABC 中，AB ＝6，BC ＝5，AC ＝4，AD 平分∠BAC 交BC 于点D ，在AB 上截取AE ＝AC ，则△BDE 的周长为( )A ．8B ．7C ．6D ．53．如图，在ABC 中，90,C AD ∠=平分,BAC DE AB ∠⊥于点,E 给出下列结论．CD ED =①;,AC BE AB +=② ③BDE BAC ∠=∠， DA ④平分CDE ∠，::BDE ACD S S AB AC =⑤其中正确的有（）个A ．5B ．4C ．3D ．2知识点二：角平分线的性质定理4．如图，在Rt ABC ∆中，90B =∠，以点A 为圆心，适当长为半径画弧，分别交AB AC 、于点,D E ，再分别以点D E 、为圆心，大于12DE 为半径画弧，两弧交于点F ，作射线AF 交边BC 于点1,4BG AC ==，则ACG ∆的面积是（）A ．1B ．32C ．2D ．525．如图，在△ABC 中，AB ＝AC ，AD 是中线，DE ⊥AB ，DF ⊥AC ，垂足分别为E ，F ，则下列四个结论中：①AB 上任一点与AC 上任一点到D 的距离相等；②AD 上任一点到AB ，AC 的距离相等；③∠BDE ＝∠CDF ；④∠1＝∠2；其中正确的有( )A ．1个B ．2个C ．3个D ．4个6．如图，AB ∥CD ，BP 和CP 分别平分∠ABC 和∠DCB ，AD 过点P ，且与AB 垂直．若AD ＝8，则点P 到BC 的距离是（）A ．8B ．6C ．4D ．27．如图，已知在四边形ABCD 中，90BCD ∠=︒，BD 平分ABC ∠，6AB =，9BC =，4CD =，则四边形ABCD 的面积是（）A．24 B．30 C．36 D．42知识点三：角平分线判定定理=，则（）8．如图，AC AD=，BC BDA．CD垂直平分AD B．AB垂直平分CDC．CD平分ACB∠D．以上结论均不对9．如图,已知AB∥CD，PE⊥AB，PF⊥BD，PG⊥CD，垂足分别E、F、G，且PF=PG=PE，则∠BPD=（）．A．60°B．70°C．80°D．90°10．如图所示，若DE⊥AB，DF⊥AC，则对于∠1和∠2的大小关系下列说法正确的是（）A．一定相等B．一定不相等C．当BD=CD时相等D．当DE=DF时相等11．如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是（）A ．线段CD 的中点B ．OA 与OB 的中垂线的交点C ．OA 与CD 的中垂线的交点 D ．CD 与∠AOB 的平分线的交点知识点四：角平分线性质的实际应用12．如图，在ABC ∆中，90︒∠=C ，8AC =，13DC AD =，BD 平分ABC ∠，则点D 到AB 的距离等于( )A ．4B ．3C ．2D ．113．如图，Rt △ABC 中，∠C=90°，AD 平分∠BAC ，交BC 于点D ，若AB=14，S △ABD=14，则CD=（）A ．4B ．3C ．2D ．114．如图，AD 是△ABC 的角平分线，DE ⊥AB ，垂足为E ，S △ABC ＝7，DE ＝2，AB ＝4，则AC 长是（）A ．6B ．5C ．4D ．3知识点五：尺规作图-角平分线15．尺规作图作AOB ∠的平分线方法如下：以O 为圆心，任意长为半径画弧交OA 、OB 于C 、D ，再分别以点C 、D 为圆心，以大于12CD 长为半径画弧，两弧交于点P ，作射线OP ，由作法得OCP ODP ≌的根据是（）A ．SASB ．ASAC ．AASD ．SSS16．如图，在ABC ∆中，,40AC BC A =∠=︒，观察图中尺规作图的痕迹，可知BCG ∠的度数为（）A ．40︒B ．45︒C ．50︒D ．60︒17．如图1，已知ABC ∠，用尺规作它的角平分线．如图2，步骤如下，第一步：以B 为圆心，以a 为半径画弧，分别交射线BA ，BC 于点D ，E ；第二步：分别以D ，E 为圆心，以b 为半径画弧，两弧在ABC ∠内部交于点P ；第三步：画射线BP ．射线BP 即为所求．下列正确的是（）A ．a ，b 均无限制B ．0a >，12b DE >的长C ．a 有最小限制，b 无限制D ．0a ≥，12b DE <的长18．如图,观察图中尺规作图痕迹,下列说法错误的是( )A ．OE 是AOB ∠的平分线B ．OC OD =C ．点C,D 到OE 的距离不相等D ．AOE BOE ∠=∠二、填空题知识点一：角平分线的有关证明19．如图，已知△ABC 的周长是21，OB ，OC 分别平分∠ABC 和∠ACB ，OD ⊥BC 于D ，且OD ＝4，△ABC 的面积是_____．20．如图,在平面直角坐标系xOy 中,点A 、B 分别在x 轴的正半轴、y 轴的正半轴上移动,点M 在第二象限，且MA 平分∠BAO ，做射线MB ，若∠1=∠2，则∠M 的度数是_______。

角平分线性质定理和逆定理备考练习

角平分线性质定理和逆定理备考练习
解答题（每题12分，共120分）
1、如图，在直线MN上求作一点P，使点P到射线OA和OB的距离相等。

2、如图，△ABC的∠ABC的外角的平分线BD与∠ACB的外角的平分线CE相交于点P，
求证：点P到三边AB，BC，CA所在的直线的距离相等。

3、如图，在△ABC中，AD是它的角平分线，且BD=CD，DE⊥AB，DF⊥AC，
垂足分别是E，F。

求证：EB=FC
4、如图，在△ABC中，AD是它的角平分线，P是AD上的一点，PE∥AB，交BC于点E，PF∥
AC，交BC于点F。

求证：点D到PE和PF的距离相等.
5、如图，P 点是△ABC 的两个外角平分线BM，CN 的交点，
求证：点P 在∠BAC 的平分线上．
6、如图，OC是∠AOB的平分线，P是OC上的一点，PD⊥OA，PE⊥OB，
垂足分别是D、E，F是OC上的另一点，连接DF，EF.
求证：DF=EF
7、如图，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别是E，F，
连接EF，EF与AD相交于点G，AD与EF垂直吗？证明你的结论：
8、如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC.
求证：AE是∠DAB的平分线.
9、如图，AD∥BC，DC⊥AD，AE平分∠BAD,且E是中点。

问：AD+BC与AB之间有何关系？
10、如图，已知△ABC中，∠BAC=2∠B，AB=2AC，AE平分∠BAC，
求证：∠C=90°。

角平分线的性质(4种题型)-2023年新八年级数学核心知识点与常见题型(人教版)(解析版)

角平分线的性质（4种题型）【知识梳理】一、角的平分线的性质角的平分线的性质：角的平分线上的点到角两边的距离相等.要点诠释：用符号语言表示角的平分线的性质定理：若CD平分∠ADB，点P是CD上一点，且PE⊥AD于点E，PF⊥BD于点F，则PE＝PF.二、角的平分线的逆定理角平分线的判定：角的内部到角两边距离相等的点在角的平分线上.要点诠释：用符号语言表示角的平分线的判定：三、角的平分线的尺规作图角平分线的尺规作图（1）以O为圆心，适当长为半径画弧，交OA于D，交OB于E.（2）分别以D 、E 为圆心，大于DE 的长为半径画弧，两弧在∠AOB 内部交于点C. （3）画射线OC.射线OC 即为所求. 【考点剖析】题型一：角平分线性质定理例1.（2023春·陕西榆林·八年级校考期末）如图，在四边形ABCD 中，90B C ∠=∠=︒，点E 为BC 的中点，且AE 平分BAD ∠．求证：DE 是ADC ∠的平分线．【详解】证明：如图，过点E 作EF AD ⊥于点F ，∴90B Ð=°，AE 平分BAD ∠，∴BE EF =．∴点E 是BC 的中点，∴BE CE =，∴CE EF =．又∵90C ∠=︒，EF AD ⊥，∴DE 是ADC ∠的平分线．【变式1】（2023春·山西太原·七年级校考阶段练习）如图，ABC 中，90C ∠=︒，AD 平分BAC ∠，5AB =，2CD =，求ABD △的面积．12【答案】5【详解】解：作DE AB ⊥如图，∵AD 平分BAC ∠，90C ∠=︒，2CD =，∴=2CD DE =，1152522ABD S AB DE ∴=⨯⨯=⨯⨯=△．【变式2】（2023春·湖南常德·八年级统考期末）如图，点P 是ABC 的三个内角平分线的交点，若ABC 的周长为24cm ，面积为236cm ，则点P 到边BC 的距离是（）A ．8cmB ．3cmC ．4cmD ．6cm【答案】B 【详解】解：过点P 作PD AB ⊥于，PE BC ⊥于E ，PF AC ⊥于F ，如图，∵点P 是ABC 的内角平分线的交点，∴PE PF PD ==，又ABC 的周长为24cm ，面积为236cm ，∴()11112222ABC S AB PD BC PE AC PF PE AB BC AC =⋅+⋅+⋅=++，∴124363PE ⨯⨯=∴3cm PE =【变式3】（湖南省郴州市2022-2023学年八年级下学期期末数学试题）如图，在ABC 中，90ACB ∠=︒，BD 平分ABC ∠，DE AB ⊥于点E ．如果8AC =，那么AD DE +=______．【答案】8【详解】解：∵在ABC 中，90ACB ∠=︒，BD 平分ABC ∠，DE AB ⊥，∴CD DE =，∵8AC =，∴8AD DE AD CD AC +=+==，【变式4】（2023春·广东深圳·七年级统考期末）把两个同样大小的含30︒角的三角尺像如图所示那样放置，其中M 是AD 与BC 的交点，若4CM =，则点M 到AB 的距离为______．【答案】4【详解】解：由题意，得：90,30D C ABC DAB ∠=∠=︒∠=∠=︒，∴,60MC AC CAB ⊥∠=︒，∴30MAC BAC MAB MAB ∠=∠−∠=︒=∠，∴AM 平分DAB ∠，过点M 作MN AB ⊥，交AB 于点N ，∴4MN MC ==．故答案为：4．【变式5】如图，P 为ABC 三条角平分线的交点，PH 、PN 、PM 分别垂直于BC 、AC 、AB ，垂足分别为H 、N 、M ．已知ABC 的周长为15cm ，3cm PH =，则ABC 的面积为______2cm ．【答案】22.5【详解】解：连接PM 、PN 、PH ，P 为ABC 三条角平分线的交点，PH 、PN 、PM 分别垂直于BC 、AC 、AB ，3cm PM PN PH ∴===，ABC ∴∆的面积ΔAPB =的面积ΔBPC +的面积ΔAPC +的面积111222AB PM BC PH AC PN =⨯⨯+⨯⨯+⨯⨯ 1()32AB BC AC =++⨯222.5(cm )=．七年级校考期末）如图，在ABC 中，【答案】(1)32︒ (2)6【详解】（1）解：∵40B ∠=︒，76C ∠=︒，∴180407664BAC ∠=︒−︒−︒=︒，∵AD 平分BAC ∠， ∴1322BAD BAC ∠=∠=︒；（2）如图，过点D 作DF AB ⊥于点F ，∵AD 平分BAC ∠，DE AC ⊥，∴DF DE =，∵2DE =，6AB =，∴2DF =， ∴ABD △的面积12662=⨯⨯=.题型二：角平分线性质定理及证明，且PMN 与OMN 的面积分别是【答案】(1)证明过程见详解(2)20OM ON +=【详解】（1）证明：如图所示，过P 作PC MN PD OA PE OB ⊥⊥⊥，，，∵MP 平分AMN ∠，NP 平分MNB ∠，∴PD PE =，PC PE =，∴PD PE =，∵PD AO PE BO ⊥⊥，，∴OP 平分AOB ∠．（2）解：如图所示，过P 作PC MN PD OA PE OB ⊥⊥⊥，，，连接OP ，∵18162PMN MN S MN PC ===△，，∴4PC =，由（1）可知4PD PE PC ===，∵1624PMN OMN S S ==△△，，∴40MONP S =四边形，即1122OPM ONP MONP S S S OM PD ON PE =+=+△△四边形，∴1140442222OM ON OM ON =⨯+⨯=+，∴20OM ON +=．【变式1】（2022秋·河南安阳·八年级校考阶段练习）如图，点E 是BC 的中点，AB BC DC BC ⊥⊥，，AE 平分BAD ∠．求证：(1)DE 平分ADC ∠；(2)AD AB CD +＝．【详解】（1）证明：如下图，过E 作EF AD ⊥于F ，∵AB BC ⊥，AE 平分BAD ∠，∴EB EF ＝，∵点E 是BC 的中点，∴EB EC ＝，∴EF EC ＝，∵DC BC EF AD ⊥⊥，，∴90EFD ECD ∠∠︒＝＝，在Rt EFD 和Rt ECD △中，EF EC ED ED =⎧⎨=⎩，∴Rt Rt HL EFD ECD ≌（），∴FDE CDE ∠∠＝，∴DE 平分ADC ∠；（2）解：由（1）知，Rt Rt EFD ECD ≌，∴FD CD ＝，在Rt AEF 和Rt AEB 中，EF EB AE AE =⎧⎨=⎩，∴Rt Rt HL AEF AEB ≌（），∴AF AB ＝，∵AD AF FD +＝，∴AD AB CD +＝．【变式2】（2022秋·北京朝阳·八年级校考期中）如图，在ABC ∆中，90C ∠=︒，DE AB ⊥，于点E ，AD 平分CAB ∠，点F 在AC 上，BD DF =．求证：BE FC =．【详解】证明：∵AD 平分CAB ∠，90C ∠=︒，DE AB ⊥，∴DE DC =，90C DEB ∠=∠=︒，∴在Rt DEB ∆和Rt DCF ∆中，∵DE DC BD DF =⎧⎨=⎩，∴()HL DEB DCF ∆≅∆，∴BE FC =．(1)求证：BE ＝CD ；(2)判断点O 是否在∠BAC 的平分线上，并说明理由．（1）证明：BE 、CD 是ABC ∆的高，且相交于点O ，90∴∠=∠=︒BEC CDB ，在BDO ∆和CEO ∆中，90CDB BEC BOD COEBD CE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，BOD COE ∴∆≅∆(AAS)，OD OE ∴=，OB OC =，OD OC OE OB ∴+=+，即CD BE =；（2）解：点O 在BAC ∠的平分线上，理由如下：连接AO ，如图所示：BE 、CD 是ABC ∆的高，且相交于点O ， 90ADC AEB ∴∠=∠=︒，由（1）得BE CD =，∴在ABE ∆和ACD ∆中，90ADC AEB CAD BAE CD BE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，ACD ABE ∴∆≅∆(AAS)， AD AE ∴=，由（1）得OD OE =，∴在AOD ∆和AOE ∆中，90AD AE ADC AEB OD OE =⎧⎪∠=∠=︒⎨⎪=⎩，AOD AOE ∴∆≅∆(SAS)，DAO EAO ∴∠=∠， ∴点O 在BAC ∠的平分线上．题型三：角平分线的判定定理例3.如图，90B C ∠=∠=︒，M 是BC 的中点，AM 平分DAB ∠，求证：DM 平分ADC ∠．【详解】证明：如图：过点M 作ME AD ⊥，垂足为E ，AM 平分DAB ∠，MB AB ⊥，ME AD ⊥，ME MB =∴（角平分线上的点到角两边的距离相等），又MC MB =，ME MC ∴=，MC CD ⊥，ME AD ⊥，DM ∴平分ADC ∠（到角的两边距离相等的点在这个角的平分线上）．【详解】（1）证明：如图，过点E 作EF DA ⊥于点F ，∵90C ∠=︒，DE 平分ADC ∠，∴CE EF =，∵E 是BC 的中点，∴BE CE =，∴BE EF =，又∵90B Ð=°，EF DA ⊥，∴AE 平分DAB ∠．（2）解：∵EF DA ⊥，90C ∠=︒，∴EFD △和ECD 都为Rt △，又∵DE 平分ADC ∠，∴EC EF =，在Rt EFD 和Rt ECD △中，ED ED EC EF =⎧⎨=⎩，∴()Rt Rt HL EFD ECD △≌△， ∴EFD ECD S S =△△，CED FED ∠=∠，∵EF DA ⊥，90B Ð=°，∴EFA △和EBA △都为Rt △，又∵AE 平分DAB ∠，∴EF EB =，在Rt EFA △和Rt EBA △中，EA EA EF EB =⎧⎨=⎩，∴()Rt Rt HL EFA EBA △≌△， ∴EFA EBA S S =△△，FEA BEA ∠=∠， ∴()111809022DEA DEF AEF CEF BEF ∠=∠+∠=∠+∠=⨯︒=︒， ∵4AE =，3DE =， ∴1143622AED S AE DE =⋅=⨯⨯=△， ∴EFD ECD EFA EBA ABCD S S S S S =+++△△△△四边形EFD EFD EFA EFA S S S S =+++△△△△()2EFD EFA S S =+△△2AED S =△ 26=⨯12=．∴四边形ABCD 的面积为12．【变式2】如图，在AOB 和COD △中，OA OB =，OC OD =（OA OC <），AOB COD α∠=∠=，直线AC ，BD 交于点M ，连接OM ．(1)求证：AC BD =；(2)用α表示AMB ∠的大小；(3)求证：OM 平分AMD ∠．【详解】（1）证明：AOB COD α∠=∠=，AOB BOC COD BOC ∴∠+∠=∠+∠，即AOC BOD ∠=∠，在AOC 和BOD 中，OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩，()SAS AOC BOD ∴≌， ∴AC BD =，（2）解：由三角形的外角性质得：AMB OBD OAC AOB ∠+∠=∠+∠，由（1）得()SAS AOC BOD ≌△△，∴OAC OBD ∠=∠，AMB AOB α∴∠=∠=，（3）证明：作OG AM ⊥于G ，OH DM ⊥于H ，如图所示，则90OGA OHB ∠=∠=︒，在OAG △和OBH △中，OGA OHB OAC OBDOA OB ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AAS OAG OBH ∴≌， OG OH ∴=，OG AM ⊥于G ，OH DM ⊥于H ，MO ∴平分AMD ∠，是ABC 的角平分线，且交于点(1)APB ∠=______．(2)求证：点P 在C ∠的平分线上．【详解】（1）解：证明：60C ∠=︒，AE ，BD 是ABC 的角平分线，12ABP ABC ∴∠=∠，12BAP BAC ∠=∠，11()(180)6022BAP ABP ABC BAC C ∴∠+∠=∠+∠=︒−∠=︒， 120APB ∴∠=︒；（2）如图，过P 作PF AB ⊥，PG AC ⊥，PH BC ⊥，AE ，BD 分别平分CAB ∠，CBA ∠，PF PG ∴=，PF PH =，PH PG ∴=，∴点P 在C ∠的平分线上；（3）如图，在AB 上取点M 使AM AD =，连接PM ，AE 是BAC ∠的平分线，PAM PAD ∴∠=∠，在AMP 与ADP △中，AP AP PAM PADAM AD =⎧⎪∠=∠⎨⎪=⎩，()SAS AMP ADP ∴≌， 18060APM APD APB ∴∠=∠=︒−∠=︒，180()60BPM APM APD ∴∠=︒−∠+∠=︒，60BPE APD ∠=∠=︒，BPM BPE ∴∠=∠，BD Q 是ABC ∠的角平分线，MBP EBP ∴∠=∠，在BPM △与BPE 中，MBP EBP BP BPBPE BPM ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ASA BPM BPD ∴≌，BM BE ∴=， AB AM BM AD BE ∴=+=+． (1)如图1，连接AC BD ，，交点为G ，连接OG ，求证：①AC BD =；②OG 平分DGC ∠；(2)如图2，若90AOD BOC ∠=∠=︒，E 是CD 的中点，过点在同一条直线上．∴AOD AOB BOC AOB ∠+∠=∠+∠，∴AOB AOC ∠=∠，又∵OA OD =，OB OC =，∴()SAS DOB AOC V V ≌，∴AC BD =；②如图所示，过点O 作OH DB ⊥于点H ，OF AC ⊥于点F ，∵DOB AOC ≌，OH DB ⊥，OF AC ⊥∴OH OF =，∴点O 在DGC ∠的角平分线上，∴OG 是DGC ∠的角平分线，∴OG 平分DGC ∠；（2）证明：连接OE ，并延长到N ，使NE OE =，连接CN ，∵E 是CD 的中点，∴CE DE =，又∵CEN DEO ∠=∠，NE OE =，∴()SAS CEN DEO ∠V V ≌，∴NCE ODE ∠=∠，CN OD =，∴CN OD ∥，∴180OCN COD CN OA ∠+∠=︒=，，90AOD BOC ∠=∠=︒，180AOB COD ∴∠+∠=︒，OCN AOB ∴∠=∠，在ONC 和BAO 中，OC OB OCN AOBCN OA =⎧⎪∠=∠⎨⎪=⎩，()SAS ONC BAO ∴≌， NOC ABO ∴∠=∠，OF AB ⊥，90ABO BOF ∴∠+∠=︒，90NOC BOF ∴∠+∠=︒，180NOC BOF BOC ∴∠+∠+∠=︒，∴点E O F ，，在同一条直线上．题型四：尺规作图—作角平分线例4．（2023春·陕西榆林·七年级校考期末）如图，已知ABC ，利用尺规，在AC 边上求作一点D ，使得ABD DBC ∠=∠.（保留作图痕迹，不写作法）【详解】解：如图点D 即为所求..【变式1】（2023春·福建福州·七年级福建省福州第十九中学校考期末）如图，Rt ABC △中，90BAC ∠=︒，AD 为BC 边上的高．(1)尺规作图，在AB 边上求作点P ，使得点P 到边BC 的距离等于AP （保留作图痕迹，不写做法）：(2)连接CP （P 为所求作的点）交AD 于点Q ，若30B ∠=︒，求AQC ∠的度数．【详解】（1）解：如图：点P 即为所求；作法：作ACB ∠的角平分线，与AB 的交点P 即为所求；理由：∵CP 是ACB ∠的角平分线，∴点P 到AC 的距离等于点P 到BC 的距离，∵90BAC ∠=︒，∴点P 到AC 的距离即为PA 的值，故点P 到边BC 的距离等于AP ．（2）解：如图：∵90BAC ∠=︒，30B ∠=︒，∴180903060ACB ∠=︒−−︒=︒，又∵AD 为BC 边上的高，∴90ADC ∠=︒，∴180906030DAC ∠=︒−−︒=︒，由（1）可知CP 是ACB ∠的角平分线， ∴1302ACQ QCD ACB ∠=∠=∠=︒，∴1803030128001ACQ DAC AQC ∠−∠=︒−︒−︒=︒∠=︒−．【变式2】（2023·甘肃兰州·统考中考真题）综合与实践问题探究：（1）如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9：“平分一个已知角．”即：作一个已知角的平分线，如图2是欧几里得在《几何原本》中给出的角平分线作图法：在OA 和OB 上分别取点C 和D ，使得OC OD =，连接CD ，以CD 为边作等边三角形CDE ，则OE 就是AOB ∠的平分线．请写出OE 平分AOB ∠的依据：____________；类比迁移：（2）小明根据以上信息研究发现：CDE 不一定必须是等边三角形，只需CE DE =即可．他查阅资料：我国古代已经用角尺平分任意角．做法如下：如图3，在AOB ∠的边OA ，OB 上分别取OM ON =，移动角尺，使角尺两边相同刻度分别与点M ，N 重合，则过角尺顶点C 的射线OC 是AOB ∠的平分线，请说明此做法的理由；拓展实践：（3）小明将研究应用于实践．如图4，校园的两条小路AB 和AC ，汇聚形成了一个岔路口A ，现在学校要在两条小路之间安装一盏路灯E ，使得路灯照亮两条小路（两条小路一样亮），并且路灯E 到岔路口A 的距离和休息椅D 到岔路口A 的距离相等．试问路灯应该安装在哪个位置？请用不带刻度的直尺和圆规．．．．．．．．．．在对应的示意图5中作出路灯E 的位置．（保留作图痕迹，不写作法）【详解】解：（1）∵OC OD =，CE DE =，DE DE =，∴()SSS OCE ODE ≌，∴AOE BOE ∠=∠，∴OE 是AOB ∠的角平分线；故答案为：SSS（2）∵OM ON =，CM CN =，OC OC =，∴()SSS OCM OCN ≌，∴AOC BOC ∠=∠，∴OC 是AOB ∠的角平分线；（3）如图，点E 即为所求作的点；．【变式3】（2023春·重庆九龙坡·七年级校考期末）如图，已知在ABC 中，90BAC ∠=︒，AD BC ⊥于点D ．（1）尺规作图：作ABC ∠的平分线交AC 于点E ，交AD 于点F ；（要求：保留作图痕迹，不写作法，不下结论）（2）在（1）的条件下，求证：AFE AEF ∠=∠．AD BC ⊥90ADB ∴∠=︒∴__________90BFD +∠=︒又BFD ∠=__________FBD ∴∠+__________90=︒90BAC ∠=︒ABF ∴∠+__________90=︒BF 平分ABC ∠ABF ∴∠=__________AFE AEF ∴∠=∠．【详解】（1）如图所示，（2）AD BC ⊥90ADB ∴∠=︒∴FBD ∠90BFD +∠=︒又BFD ∠=AEF ∠FBD ∴∠+AEF ∠90=︒90BAC ∠=︒ABF ∴∠+AFE ∠90=︒ BF 平分ABC ∠ABF ∴∠=FBD ∠AFE AEF ∴∠=∠．故答案为：FBD ∠；AEF ∠；AEF ∠；AFE ∠；FBD ∠．【过关检测】一、单选题 1．（2023春·四川泸州·八年级统考期末）如图，70AOB ∠=︒，点C 是AOB ∠内一点，CD OA ⊥于点D ，CE OB ⊥于点E ．且CD CE =，则DOC ∠的度数是（）A ．30︒B ．35︒C ．40︒D ．45︒【答案】B【分析】根据角平分线的判定定理可得OC 平分AOB ∠，再计算角度．【详解】解：∵CD OA ⊥，CE OB ⊥，CD CE =，∴OC 平分AOB ∠， ∴1352DOC AOB ∠=∠=︒，故选C ．【点睛】本题主要考查了角平分线的判定，注意：到角的两边距离相等的点在角平分线上． 2．（陕西省榆林市高新区2022-2023学年七年级下学期期末数学试题）如图，在Rt ABC △中，ABC ∠的平分线BD 交AC 于点D ，过点D 作DE AB ⊥交AB 于点E ．若9cm CD =，则点D 到AB 的距离是（）A ．9cmB ．6cmC ．4.5cmD ．3cm【答案】A 【分析】根据角平分线的性质，角平分线上的点到角两边的距离相等，即可求解．【详解】∵BD 平分ABC ∠，DE AB ⊥，AC BC ⊥，∴9DC DE ==，∴点D 到AB 的距离是9cm ．故选：A ．【点睛】本题考查角平分线的性质，解题的关键是掌握角平分线的性质．3．（2023春·河南焦作·七年级校考期末）如图，在四边形ABCD 中，90A ∠=︒，3AD =，连接BD ，BD CD ⊥，ADB C ∠=∠．若P 是BC 边上一动点，则DP 的长不可能是（）【答案】A【分析】根据余角的性质可得ABD CBD ∠=∠，即BD 平分ABC ∠，作DE BC ⊥于E ，则3AD DE ==，再根据垂线段最短即可得到答案．【详解】解：∵90A ∠=︒，BD CD ⊥，∴90,90ABD ADB CBD C ∠+∠=︒∠+∠=︒，∵ADB C ∠=∠，∴ABD CBD ∠=∠，即BD 平分ABC ∠，作DE BC ⊥于E ，则3AD DE ==，∵P 是BC 边上一动点，则DP DE ≥，即3DP ≥，∴DP 的长不可能是52；故选：A ．【点睛】本题考查了直角三角形的性质和角平分线的性质，得出BD 平分ABC ∠是解题的关键．A ．12∠=∠且CM DM =B ．13∠=∠且CM DM =C ．12∠=∠且OD DM =D ．23∠∠=且OD DM =【答案】A 【分析】由作图过程可得：,OD OC CM DM ==，再结合DM DM =可得()SSS COM DOM ≌，由全等三角形的性质可得12∠=∠即可解答．【详解】解：由作图过程可得：,OD OC CM DM ==，∵DM DM =，∴()SSS COM DOM ≌．∴12∠=∠．∴A 选项符合题意；不能确定OC CM =,则13∠=∠不一定成立，故B 选项不符合题意；不能确定OD DM =,故C 选项不符合题意，OD CM ∥不一定成立，则23∠∠=不一定成立，故D 选项不符合题意．故选A ．【点睛】本题主要考查了角平分线的尺规作图、全等三角形的判定与性质等知识点，理解尺规作图过程是解答本题的关键．，ABC 的面积为，则ABC 的周长为（ A ．4B ．6C ．24D ．12【答案】C 【分析】过点E 作EF AB ⊥，垂足为F ，过点E 作EG AC ⊥，垂足为G ，根据角平分线的性质可得1EG EF ED ===，然后根据三角形的面积公式进行计算即可解答．【详解】解：过点E 作EF AB ⊥，垂足为F ，过点E 作EG AC ⊥，垂足为G ，∵BE 平分ABC ∠，ED BC ⊥，EF AB ⊥，∴1EF ED ==，∵CE 平分ACB ∠，ED BC ⊥，EG AC ⊥，∴1ED EG ==，∴ABC 的面积ABE =的面积BEC +△的面积AEC +△的面积()11111122222AB EF BC ED AC EG AB BC AC =⋅+⋅+⋅=⨯⨯++=，∴24AB BC AC ++=，即ABC 的周长为24．故选：C ．【点睛】本题考查了角平分线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．A ．3PD =B ．3PD <C ．3PD ≤ D ．3PD ≥【答案】D 【分析】根据角平分线的性质得到3PF =，再根据垂线段最短即可解答．【详解】解：过点P 作PE AB ⊥于点E ，过点P 作PF BC ⊥于点F ，∵点P 在ABC ∠的平分线上，∴PE PF =， ∵3PE =，∴3PF =，∴根据垂线段最短可知：3PD ≥，故选D ．【点睛】本题考查了角平分线的性质，垂线段最短，掌握角平分线的性质是解题的关键．八年级统考期末）如图，在ABC 中， A ．83 B ．43 【答案】D【分析】由题意可求DC 的长，由角平分线的性质可求解．【详解】解：如图，过点D 作DH AB ⊥，垂足为H ，∵143AC DC AC ==，，∴1DC =，∵BD 平分ABC ∠，90C DH AB =︒∠，⊥，∴1CD DH ==，∴点D 到AB 的距离等于1，故选：D ．【点睛】本题考查了角平分线的性质，熟练运用角平分线的性质是本题的关键．8．（2023春·湖南娄底·八年级统考期末）如图，三条公路把A ，B ，C 三个村庄连成一个三角形区域，现决定在这个三角形区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，则这个集贸市场应建在（）A ．三角形三个内角的角平分线的交点B ．三角形三条边的垂直平分线的交点C ．三角形三条高的交点D ．三角形三条中线的交点【答案】A 【分析】根据角平分线上的点到角的两边的距离相等解答即可．【详解】解：根据角平分线的性质，集贸市场应建在三个角的角平分线的交点处．故选：A ．【点睛】本题主要考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．9．（2023春·陕西榆林·八年级统考期末）如图，OD 平分AOB ∠，DE AO ⊥于点E ，5DE =，F 是射线OB 上的任意一点，则DF 的长度不可能是（）【答案】A 【分析】过Ｄ点作DH OB ⊥于H ，根据角平分线的性质得5DH DE ==，再利用垂线段最短得到5DF ≥，然后对各个选项进行判断即可，【详解】过Ｄ点作DH OB ⊥于H ，OD 平分AOB ∠，DE OA ⊥，DH OB ⊥，5DH DE ∴==，DF DH ≥，5DF ∴≥，故选A【点睛】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等，也考查了垂线段最短，掌握角平分线的性质是解题的关键． 10．（2023春·河南开封·七年级统考期末）如图，在ABC 中，90C ∠=︒，AD 平分BAC ∠，DE AB ⊥于E ，则下列结论：①DE CD =；②AD 平分CDE ∠；③BAC BDE ∠=∠；④BE AC AB +=，其中正确的是（）A ．1个B ．2个C ．3个D ．4个【答案】D 【分析】①根据角平分线的性质得出结论：DE CD =；②证明ACD AED △≌△，得AD 平分CDE ∠；③由四边形的内角和为360︒得180CDE BAC ∠+∠=︒，再由平角的定义可得结论是正确的；④由ACD AED ∆≅∆得AC AE =，再由AB AE BE =+，得出结论是正确的．【详解】解：①90C ∠=︒，AD 平分BAC ∠，DE AB ⊥，DE CD ∴=；所以此选项结论正确；②DE CD =，AD AD =，90ACD AED ∠=∠=︒，ACD AED ∴≌，ADC ADE ∴∠=∠，AD ∴平分CDE ∠，所以此选项结论正确；③90ACD AED ∠=∠=︒，3609090180CDE BAC ∴∠+∠=︒−︒−︒=︒，180BDE CDE ∠+∠=︒，BAC BDE ∴∠=∠，所以此选项结论正确；④ACD AED ≌，AC AE ∴=，AB AE BE =+，BE AC AB ∴+=，所以此选项结论正确；本题正确的结论有4个，故选D ．【点睛】本题考查了全等三角形性质和判定，同时运用角平分线的性质得出两条垂线段相等；本题难度不大，关键是根据HL 证明两直角三角形全等，根据等量代换得出线段的和，并结合四边形的内角和与平角的定义得出角的关系．二、填空题七年级统考期末）如图，在ABC 中，ABC 的内部相交于点【答案】5【分析】先根据尺规作图描述得出AD 为BAC ∠的角平分线，再根据角平分线的性质得到点D 到AB 的距离5DE =，进而求出三角形的面积．【详解】由作法得AD 平分BAC ∠，如图所示，过点D 作DE AB ⊥于E ，∵90ACB ∠=︒，根据角平分线的性质，得43DC DE ==，ABD ∴的面积114102233AB DE AB =⋅⋅=⨯⨯=． ∴5AB =，故答案为：5．【点睛】本题考查角平分线的性质，解决本题的关键是熟知角平分线的性质并灵活应用．【答案】2【分析】根据尺规作图可得BF 平分ABC ∠，再利用角平分线的性质定理可得出2DF CF ==，最后根据垂线段最短即可得出FH 的最小值是2．【详解】解：如图，过点F 作FD AB ⊥于D ．由作图可知，BF 平分ABC ∠，∵FC BC ⊥，FD AB ⊥，∴2DF CF ==．根据垂线段最短可知，FH 的最小值为DF 的长，即为2．故答案为：2．【点睛】本题主要考查角平分线的性质，垂线段最短，解题的关键在于能够准确判断出BF 是ABC ∠的角平分线．13．（2023春·重庆沙坪坝·七年级重庆八中校考期末）如图，Rt ABC △中，90C ∠=︒，AD 平分BAC ∠交BC 于点D ，E 为线段AC 上一点，连接DE ，且B CED ∠=∠．若16AB =，6CE =，则AE 的长为________．【答案】4【分析】过点D 作DF AB ⊥于点F ，由角平分线的性质得出DC DF =，证明DCE DFB ≌，得出BF CE =，求出AF ，由HL 证明Rt Rt ADC ADF ≌，得出AC AF =，即可求出结果．【详解】解：过点D 作DF AB ⊥于点F ，如图所示：∵90C ∠=︒，AD 平分BAC ∠交BC 于点D ，，∴DC DF =，在DCE △和DFB △中，90=BFD DCE B CEDDC DF ∠=∠=︒⎧⎪∠=∠⎨⎪⎩，∴()AAS DCE DFB ≌，∴6BF CE ==，∴10AF AB BF =−=，在Rt ADC 与Rt ADF 中，==DC DF AD AD ⎧⎨⎩，∴Rt Rt ADC ADF ≌，∴10AC AF ==，∴1064AE AC CE =−=−=．故答案为：4．【点睛】此题考查全等三角形的判定和性质和角平分线的性质，解题的关键是作出辅助线，构造全等三角形，根据HL 证明直角三角形的全等解答．【答案】30【分析】由作图可知OC 是AOB ∠的角平分线，根据角平分线的定义即可得到答案．【详解】解：由题意可知，OC 是AOB ∠的角平分线，∴11603022AOC AOB ∠=∠=⨯︒=︒．故答案为：30【点睛】此题考查角平分线的作图、角平分线相关计算，熟练掌握角平分线的作图是解题的关键．，则POD 的面积是【答案】6【分析】过点P 作PF OB ⊥交OB 于点F ，由作图可知OP 是AOB ∠的平分线，根据角平分线的性质得3PF PC ==，即可求得POD 的面积．【详解】解：如图，过点P 作PF OB ⊥交OB 于点F ，由作图可知，OP 是AOB ∠的平分线，∵PC OA ⊥，PF OB ⊥，∴3PF PC ==，∴POD 的面积为：162OD PF ⋅=，故答案为：6．【点睛】本题考查了尺规作角平分线以及角平分线的性质定理：角平分线上的点到角两边的距离相等．16．（2023春·山东泰安·七年级统考期末）如图，在锐角ABC 中，60BAC ∠=︒，BE 、CD 为ABC 的角平分线．且BE 、CD 交于点F ，连接AF ．有下列四个结论：①120BFC ∠=︒；②BD CE =；③BC BD CE =+；④FBD FEC FBC S S S +=△△△．其中结论正确的序号是__________ ．【答案】①③④【分析】根据角平分线的定义和三角形内角和定理求出BFC ∠；在BC 上取BM BD =，证明()SAS DBF MBF ≌△△，再证明()ASA MCF ECF ≌△△；过点F 作FG AB ⊥于点G ，FH AC ⊥于点H ，FK BC ⊥于点K ，根据角平分线的性质和三角形面积公式分别对各个结论进行判断即可．【详解】解：∵ABC 的两条角平分线BE 和CD 交于点F ，60BAC ∠=︒，∴FBC FCB∠+∠()12ABC ACB =∠+∠()11802BAC ︒=−∠()1180602=⨯︒−︒60=︒， ∴()180********BFC FBC FCB ∠=︒−∠+∠=︒−︒=︒，故结论①正确； ∴18060BFD BFC CFE Ð=°-Ð=°=Ð，在BC 上取BM BD =，∵BE 平分ABC ∠，∴DBF MBF Ð=Ð，在DBF 和MBF V 中，BD BM DBF MBFBF BF =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS DBF MBF ≌△△， ∴60BFD BFM ∠=∠=︒，∴1206060CFM BFC BFM ∠=∠−∠=︒−︒=︒，∴60CFM CFE ∠=∠=︒，∵CD 平分ACB ∠，∴MCF ECF ∠=∠，在MCF △和ECF △中，CFM CFE CF CFMCF ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴()ASA MCF ECF ≌△△， ∴CM CE =，∴BC BM CM BD CE =+=+，故结论③正确；∵没有条件得出点M 是BC 的中点，∴不能得出BD 与CE 一定相等，故结论②错误；过点F 作FG AB ⊥于点G ，FH AC ⊥于点H ，FK BC ⊥于点K ，∵BE 、CD 为ABC 的角平分线，∴FG FK =，FK FH =，∴FG FK FE ==， ∵12FBD S BD FG =⋅△，12FEC S EC FH =⋅△，12FBC S BC FK =⋅△，∴FBD FEC S S +△△1122BD FG EC FH =⋅+⋅ 1122BM FK MC FK =⋅+⋅ ()12BM MC FK =+⋅ 12BC FK =⋅FBC S =△，∴FBD FEC FBC S S S +=△△△，故结论④正确，∴结论正确的序号是①③④．故答案为：①③④．【点睛】本题考查角平分线的性质，全等三角形的判定与性质，三角形内角和定理，三角形的面积，作出辅助线构造全等三角形是解题的关键．三、解答题 17．（2023春·重庆江北·七年级统考期末）完成下面的解答过程，并填上适当的理由．已知：如图，DE BC ∥，BD 平分ABC ∠，EF 平分AED ∠．解： ∵DE BC ∥（已知）∴ABC AED ∠=∠（ ① ）．∵BD 平分ABC ∠，EF 平分∠∴112ABC ∠=∠，122AED ∠=∠【答案】两直线平行，同位角相等 2∠ 等量代换同位角相等，两直线平行【分析】先分析角的位置关系，根据平行线的性质及判定定理，即可写出答案．【详解】证明：∵DE BC ∥（已知），∴ABC AED ∠=∠．∵BD 平分ABC ∠，EF 平分AED ∠，∴112ABC ∠=∠，122AED ∠=∠．∴12∠=∠（等量代换）．∴EF BD ∥（同位角相等，两直线平行）．故答案为：两直线平行，同位角相等； 2∠ ；等量代换同位角相等，两直线平行．【点睛】本题主要考查平行线的性质（两直线平行，同位角相等），及平行线的判定方法（同位角相等，两直线平行）．牢记平行线的性质和判定方法是解题的关键．18．（2023春·山东泰安·七年级统考期末）如图，在AOB 和COD △中，OA OB =，OC OD =，OA OC <，36AOB COD ∠=∠=︒，连接AC 、BD 交于点M ，连接OM ．求证：(1)36AMB ∠=︒；(2)MO 平分AMD ∠．【答案】(1)证明见解析 (2)证明见解析【分析】（1）证明()SAS AOC BOD ≌△△，由三角形全等的性质得出OAC OBD ∠=∠，由三角形的外角性质得：AMB OBD OAC AOB ∠+∠=∠+∠，可得出AMB ∠的度数；（2）作OG AC ⊥于G ，OH BD ⊥于H ，利用全等三角形对应边上的高相等，得出OG OH =，由角平分线的判定方法即可得证．【详解】（1）证明：∵36AOB COD ∠=∠=︒，∴AOB BOC COD BOC ∠+∠=∠+∠，即AOC BOD ∠=∠，在AOC 和BOD 中，OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS AOC BOD ≌△△， ∴OAC OBD ∠=∠，∵AEB ∠是AOE △和BME 的外角∴AEB AMB OBD AOB OAC ∠=∠+∠=∠+∠，∴36AMB AOB ∠=∠=︒；（2）如图所示，作OG AC ⊥于G ，OH BD ⊥于H ，∴OG 是AOC 中AC 边上的高，OH 是BOD 中BD 边上的高，由（1）知：AOC BOD ≌，∴OG OH =，∴点O 在AMD ∠的平分线上，即MO 平分AMD ∠．【点睛】本题考查全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识．证明三角形全等是解题的关键．七年级统考期末）如图，在ABC 中， (2)18【分析】（1）根据BD 平分ABC ∠，CD 平分ACB ∠得12DBC ABC ∠=∠，12DCB ACB ∠=∠，根据40ABC ∠=︒，70ACB ∠=︒得140202DBC ∠=⨯︒=︒，170352DCB ∠=⨯︒=︒，根据三角形内角和定理即可得；（2）过点D 作DF BC ⊥于点F ，根据BD 平分ABC ∠，DE AB ⊥，DF BC ⊥得DE DF =，根据4DE =得4DF =，即可得．【详解】（1）解：∵BD 平分ABC ∠，CD 平分ACB ∠，∴12DBC ABC ∠=∠，12DCB ACB ∠=∠，∵40ABC ∠=︒，70ACB ∠=︒，∴140202DBC ∠=⨯︒=︒，170352DCB ∠=⨯︒=︒，∴在BCD △中，1802035125BDC ∠=︒−︒−︒=︒；（2）解：过点D 作DF BC ⊥于点F ，∵BD 平分ABC ∠，DE AB ⊥，DF BC ⊥，∴DE DF =，∵4DE =，∴4DF =，∵9BC =， ∴11S 941822BCD BC DF =⨯⨯=⨯⨯=△．【点睛】本题考查了角平分线，三角形内角和定理，三角形的面积，解题的关键是理解题意，掌握这些知识点．八年级假期作业）如图，在ABC 中，【答案】6cm CD =，34B ∠=︒【分析】根据角平分线的性质可得CD DE =，28BAD CAD ∠=∠=︒，再根据直角三角形的两个锐角互余即可求出B ∠的度数．【详解】解：∵ABC 中，90C ∠=︒，AD 平分BAC ∠，DE AB ⊥，∴6cm CD DE ==，28BAD CAD ∠=∠=︒，∴256BAC CAD ∠=∠=︒，∴9034B CAD ∠=︒−∠=︒．【点睛】本题考查了角平分线的性质定理和直角三角形的两个锐角互余，属于基础题型，熟练掌握角平分线的点到一个角的两边距离相等是解题关键．21．（2023春·广西南宁·七年级南宁十四中校考期末）如图，已知ABC ．(1)尺规作图：作BAC ∠的角平分线交BC 于点G （不写作法，保留作图痕迹）；(2)如果6AB =，10AC =，ABG 的面积为18，求ACG 的面积．【答案】(1)见解析(2)30【分析】（1）根据角平分线的尺规作图方法作图即可；（2）如图所示，过点G 作GE AB GF AC ⊥⊥，垂足分别为E 、F ，证明AEF AFG △≌△，得到EG FG =，根据面积法求出6EG FG ==，再根据三角形面积公式求解即可．【详解】（1）解：如图所示：（2）解：如图所示，过点G 作GE AB GF AC ⊥⊥，垂足分别为E 、F ，∴90AEG AFG ∠=∠=︒，∵AG 是BAC ∠的角平分线，∴EAG FAG ∠=∠，又∵AG AG =，∴()AAS AEF AFG △≌△，∴EG FG =；∵6AB =，ABG 的面积为18，∴1182AB EG ⋅=，即16182EG ⨯=，∴6EG =，∴6EG FG ==，∴111063022ACG S AC FG =⋅=⨯⨯=△．【点睛】本题主要考查了全等三角形的性质与判定，三角形面积，角平分线的尺规作图，角平分线的定义等等，灵活运用所学知识是解题的关键． 22．（2023春·山西太原·七年级统考期末）如图，在ABC 中，AD 是它的角平分线，DE AB ⊥于点,E DF AC ⊥于点F ，且BE CF =．线段BD 与CD 相等吗？说明理由．【答案】BD CD =，见解析【分析】根据角平分线的性质得出DE DF =，根据垂直定义得出90DEB DFC ∠=∠=︒，根据SAS 证明DFC △D E B ≌△，得出BD CD =即可．【详解】解：BD CD =；理由如下：∵AD 是BAC ∠的角平分线，DE AB ⊥，DF AC ⊥，∴DE DF =，∵DE AB ⊥，DF AC ⊥，∴90DEB DFC ∠=∠=︒，又∵BE CF =，∴DFC △DE B ≌△， ∴BD CD =．【点睛】本题主要考查了角平分线的性质，垂线定义理解，三角形全等的判定和性质，解题的关键是熟练掌握三角形全等的判定方法，证明DFC △DE B ≌△． 23．（重庆市大渡口区2022-2023学年七年级下学期期末数学试题）如图，AD BC ∥，180B BCD ∠+∠=︒．(1)用直尺和圆规完成以下基本作图：过点A 作BAD ∠的角平分线，交CD 于点F ，与BC 的延长线交于点E ；（不写做法，保留作图痕迹）(2)求证：CFE FEC ∠=∠．证明：∵AD BC ∥（已知），∴DAF FEC ∠=∠（①__________）． ∵AE 平分BAD ∠，∴②__________（角平分线的定义）． ∴BAE FEC ∠=∠（③__________）． ∵180B BCD ∠+∠=︒（已知）， ∴④__________（⑤__________）． ∴BAE CFE ∠=∠（两直线平行，同位角相等）． ∴CFE FEC ∠=∠（等量代换）．【答案】(1)见解析(2)见解析【分析】（1）利用基本作图作BAD ∠的平分线即可；（2）先根据平行线的性质得到DAF FEC ∠=∠，再利用角平分线的定义得到BAE DAF ∠=∠，则BAE FEC ∠=∠，接着证明AB CD ∥得到BAE CFE ∠=∠，然后利用等量代换得到CFE FEC ∠=∠．【详解】（1）解：如图，BE 为所作；（2）证明：AD BC ∥（已知）， DAF FEC ∴∠=∠（两直线平行，内错角相等）．AE 平分BAD ∠，BAE DAF ∴∠=∠（角平分线的定义），BAE FEC ∴∠=∠（等量代换）．180B BCD ∠+∠=︒（已知），AB CD ∴∥（同旁内角互补，两直线平行）．BAE CFE ∴∠=∠（两直线平行，同位角相等）．CFE FEC ∴∠=∠（等量代换）．【点睛】本题考查了作图−基本作图：熟练掌握5种基本作图是解决问题的关键．也考查了角平分线的性质和平行线的判定与性质．七年级校考阶段练习）如图，ABC 中，若BCG 的面积为，则ABC 的面积为【答案】(1)120︒(2)3(3)6【分析】（1）根据作图方法可得BG 是ABC ∠的角平分线，则1302ABG ABC ==︒∠∠，再由三角形外角的性质可得120BGC A ABG =+=︒∠∠；（2）如图所示，过点G 作GD BC ⊥于D ，先求出3AG AC CG =−=，再证明ABG DBG △≌△，得到3DG AG ==，根据垂线段最短可知线段H G 的最小值为3；（3）证明BDG CDG △≌△，得到122BDG CDG BCG S S S ===△△△，进而求出2BDG ABG S S ==△△，则6ABC ABG CBG S S S =+=△△△．【详解】（1）解：由作图方法可知BG 是ABC ∠的角平分线， ∴1302ABG ABC ==︒∠∠，∵90A ∠=︒，∴120BGC A ABG =+=︒∠∠，故答案为：120︒；（2）解：如图所示，过点G 作GD BC ⊥于D ，∴90BAG BDG ==︒∠∠，∵96AC CG ==，，∴3AG AC CG =−=，∵BG 是ABC ∠的角平分线，∴ABG DBG ∠=∠，又∵BG BG =，∴()AAS ABG DBG △≌△，∴3DG AG ==，∵H 是边BC 上一动点，∴当点H 与点D 重合时，HG 最小，∴线段HG 的最小值为3，故答案为：3；（3）解：∵BG 是ABC ∠的角平分线，∴30ABG DBG ==︒∠∠，∵9030C ABC ∠=︒−∠=︒，∴GBD C ∠=∠，又∵90DG DG BDG CDG ===︒，∠∠，∴()AAS BDG CDG △≌△， ∴122BDG CDG BCG S S S ===△△△，∵ABG DBG △≌△，∴2BDG ABG S S ==△△，∴6ABC ABG CBG S S S =+=△△△，故答案为：6．【点睛】本题主要考查了全等三角形的性质与判定，三角形内角和定理，三角形外角的性质，角平分线的定义，角平分线的尺规作图等等，正确作出辅助线构造全等三角形是解题的关键．七年级统考期末）ABC 中， (2)如图2，若ABC 是锐角三角形．过点FED ∠，EDB ∠与ABC ∠ (3)若ABC 是钝角三角形，其中FED ∠，EDB ∠与ABC ∠之间的数量关系．【答案】(1)45 (2)12BDE FED ABC ∠=∠+∠，证明见解析 (3)12ABC BDE DEF ∠=∠+∠【分析】（1）首先证明AED ABC ∠=∠得到DE BC ∥，得到EDB DBC ∠=∠，再根据角平分线的定义得到1452DBC ABC ∠=∠=︒，即可证明；（2）延长ED 、BC 交于G ，利用平行线的性质得FED G ∠=∠，再利用三角形外角的性质可得结论；（3）由（2）同理解决问题．【详解】（1）解：DE AB ∵⊥，90AED ∴∠=︒．90ABC ∠=︒，AED ABC ∴∠=∠．DE BC ∴∥．EDB DBC ∴∠=∠．BD Q 平分ABC ∠，1452DBC ABC ∴∠=∠=︒．45EDB ∴∠=︒．（2）如图，12BDE FED ABC ∠=∠+∠，理由如下：延长ED 、BC 交于G ，EF BC ∥，FED G ∴∠=∠，BD Q 平分ABC ∠，。

人教版八年级上数学12.3 角的平分线的性质 _同步练习及答案(含答案)

第12章《全等三角形》同步练习班级学号姓名得分一、填空题（每题3分，共30分）1．到一个角的两边距离相等的点都在_________.2．∠AOB的平分线上一点M，M到OA的距离为1.5 cm，则M到OB的距离为_________. 3．如图，∠AOB=60°，CD⊥OA于D，CE⊥OB于E，且CD=CE，则∠DOC=_________.4．如图，在△ABC中，∠C=90°，AD是角平分线，DE⊥AB于E，且DE=3 cm，BD=5 cm，则BC=_________ cm．5．如图，已知AB、CD相交于点E，过E作∠AEC及∠AED的平分线PQ与MN，则直线MN与PQ的关系是_________．6．三角形内一点到三角形的三边的距离相等，则这个点是三角形_________的交点．7．△ABC中，∠C=90°，AD平分∠BAC交BC于D，且BD：CD=3：2，BC=15cm，则点D到AB的距离是__________．8．角平分线的性质定理：角平分线上的点_____________________________．9．（1）如图，已知∠1 =∠2，DE⊥AB，DF⊥AC，垂足分别为E、F，则DE____DF．（2）已知DE⊥AB，DF⊥AC，垂足分别为E、F，且DE = DF，则∠1_____∠2．10．直角三角形两锐角的平分线所夹的钝角为_______度．二、选择题（每题3分，共24分）11．如图，OP平分∠AOB，PC⊥OA，PD⊥OB，垂足分别是C、D．下列结论中错误的是（）A．PC = PD B．OC = ODC．∠CPO = ∠DPO D．OC = PC12．如图，△ABC中，∠C = 90°，AC = BC，AD是∠BAC的平分线，（第3题）（第4题）（第5题）21ABCDEF（第9题）ABCDOP（第11题）（第14题）DE ⊥AB 于E ，若AC = 10cm ，则△DBE 的周长等于( )A ．10cmB ．8cmC ．6cmD ．9cm13．到三角形三条边的距离都相等的点是这个三角形的（）A ．三条中线的交点B ．三条高的交点C ．三条边的垂直平分线的交点D ．三条角平分线的交点 14．如图所示，表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（）Ａ．1处Ｂ．2处Ｃ．3处Ｄ．4处 15．给出下列结论，正确的有（）①到角两边距离相等的点，在这个角的平分线上；②角的平分线与三角形平分线都是射线；③任何一个命题都有逆命题；④假命题的逆命题一定是假命题A ．1个B ．2个C ．3个D ．4个 16．已知，Rt △ABC 中，∠C=90°，AD 平分∠BAC 交BC 于D ，若BC =32，且BD ∶CD =9∶7，则D 到AB 的距离为（） A ．18 B ．16 C ．14 D ．12 17．两个三角形有两个角对应相等，正确说法是（）A ．两个三角形全等B ．两个三角形一定不全等C ．如果还有一角相等，两三角形就全等D ．如果一对等角的角平分线相等，两三角形全等18．如图，OB 、OC 是∠AOD 的任意两条射线，OM 平分∠AOB ，ON 平分∠COD ，若∠MON =α，∠BOC =β，则表示∠AOD 的代数式为（）A ．2α－βB ．α－βC ．α+βD ．2α三、解答题（共46分） 19．（7分）如图，已知OE 、OD 分别平分∠AOB 和∠BOC ，若∠AOB =90°，∠EOD =70°，求∠BOC 的度数．ED CB A （第12题）（第18题）20．（7分）已知：有一块三角形空地，若想在空地中找到一个点，使这个点到三边的距离相等，试找出该点．（保留画图痕迹）21．（8分）如图，点D 、B 分别在∠A 的两边上，C 是∠A 内一点，AB = AD ，BC = CD ，CE ⊥AD 于E ，CF ⊥AF 于F ．求证：CE = CF22．（8分）已知：如图，在△ABC 中，∠A =90°，AB = AC ，BD 平分∠ABC ．求证：BC = AB + ADF A B EC D D A23．（8分）如图，PB 和PC 是△ABC 的两条外角平分线． ①求证：∠BPC =90°-12∠BAC ． ②根据第①问的结论猜想：三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形？24．（8分）如图，BP 是△ABC 的外角平分线，点P 在∠BAC 的角平分线上．求证：CP 是△ABC 的外角平分线．PC B A DE参考答案一、填空题1．这个角的平分线上2．1.5cm 3．30°4．8 5．MN⊥PQ 6．三条角平分线7．6cm 8．到角的两边的距离相等9．（1）=（2）= 10．135二、选择题11．D 12．B 13．D 14．D 15．B 16．C 17．D 18．A三、解答题19．50°20．画两个角的角平分线的交点P 21．略22．提示：过点D做DM⊥BC 23．①略；②锐角三角形24．提示：过P作三边AB、AC、BC的垂线段PD、PE、PF。

《123角平分线的性质》同步测试题((有答案))-(新课标人教版数学八年级)AlHKMK

角平分线的性质测试题一、选择题（本大题共11小题，共33.0分）1.如图，AD是的角平分线，，垂足为E，交ED的延长线于点F，若BC恰好平分，给出下列四个结论：；；；，其中正确的结论共有A. 4个B. 3个C. 2个D. 1个2.如图，AD是的角平分线，，，垂足分别为点E、点F，连接EF与AD相交于点O，下列结论不一定成立的是A. B. C.D.3.如图，在中，，，点E在BC的延长线上，的平分线BD与的平分线CD相交于点D，连接AD，则下列结论中，正确的是A. B. C. D.4.如图，在中，，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若，，则的面积是A. 15B. 30C. 45D. 605.为促进旅游发展，某地要在三条公路围成的一块平地上修建一个度假村，如图所示，若要使度假村到三条公路的距离相等，则这个度假村应修建在A. 三角形ABC三条高线的交点处B. 三角形ABC三条角平分线的交点处C. 三角形ABC三条中线的交点处D. 三角形ABC三边垂直平分线的交点处6.如图，，，垂足分别为D、E，且，则与全等的理由是A. SASB. AAAC. SSSD. HL7.如图，OP平分，，垂足为A，，，Q是射线OM上的一个动点，则线段PQ的最小值是A. 10B. 8C. 4D. 68.三条公路将A、B、C三个村庄连成一个如图的三角形区域，如果在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，那么这个集贸市场应建的位置是A. 三条高线的交点B. 三条中线的交点C. 三条角平分线的交点D. 三边垂直平分线的交点9.如图：的两个外角平分线交于点P，则下列结论正确的是平分到AB，BC的距离相等平分．A. B. C. D.10.如图，BD是的平分线，于E，，，，则DE的长是A. 2cmB. 4cmC.D.11.如图，点P为定角的平分线上的一个定点，且与互补，若在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：恒成立；的值不变；四边形PMON的面积不变；的长不变，其中正确的个数为A. 4B. 3C. 2D. 1二、填空题（本大题共11小题，共33.0分）12.如图，，，，若，则______．13.如图，已知于点B，于点C，且，，，则______．14.如图，的三条角平分线交于点O，O到AB的距离为3，且的周长为18，则的面积为______．15.如图，在中，，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M、N，再分别以点M、N为圆心，大于的长为半径画弧，两弧交于点P，作射线AB交边BC于点D，若，，则的面积是______．16.已知：如图，中，，沿过点B的一条直线BE折叠，使点C恰好落在AB边的中点D处，则______ 度17.边长为7，24，25的内有一点P到三边距离相等，则这个距离为______ ．18.如图，OC平分，点P是OC上一点，于点M，点N是射线OA上的一个动点，若，则PN的最小值为______．19.如图，在中，，，AD平分，交BC边于点D，若，则的面积为______．20.如图，在中，，BD平分，若，则点D到AB的距离为______ cm．21.随着人们生活水平的不断提高，汽车逐步进入到千家万户，小红的爸爸想在本镇的三条相互交叉的公路如图所示，建一个加油站，要求它到三条公路的距离相等，这样可供选择的地址有______处22.已知OC平分，点P为OC上一点，于D，且，过点P作交OB于E，，求PE的长度______cm．三、计算题（本大题共3小题，共18.0分）23.如图，中，，，E，F分别是BC，AC的中点，若，求线段AB的长．24.如图，等腰梯形ABCD中，，，梯形周长为40，对角线BD平分，求梯形的腰长及两底边的长．25.某私营企业要修建一个加油站，如图，其设计要求是，加油站到两村A、B的距离必须相等，且到两条公路m、n的距离也必须相等，那么加油站应修在什么位置，在图上标出它的位置要有作图痕迹四、解答题（本大题共2小题，共16.0分）26.如图，BD是的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．请判断四边形EBGD的形状，并说明理由；若，，，点H是BD上的一个动点，求的最小值．两直角边分别与OA、OB相交于点C、D，问PC与PD相等吗？试说明理由．答案和解析【答案】1. A2. C3. B4. B5. B6. D7. D8. C9. C10. D11. B12. 413.14. 2715. 3016. 3017. 318. 519. 820. 321. 422. 623. 解：作BH平分交AC于H，连结HE，如图，平分，，，，为等腰三角形，点E为BC的中点，，，，，为的平分线，，，即，．24. 解：四边形ABCD是等腰梯形，，，，又BD平分，，，，又，，，，，，，即梯形腰长为8，两底边长为8和16，答：梯形的腰长是8，两底边的长分别是8，16．25. 解：作图如图，点P即为所求作的点．26. 解：四边形EBGD是菱形．理由：垂直平分BD，，，，，，，在和中，≌ ，，，四边形EBGD是菱形．作于M，于N，连接EC交BD于点H，此时最小，在中，，，，，，，，，，，在中，，，，，，在中，，，．，的最小值为10．27. 解：PC与PD相等理由如下：过点P作于点E，于点F．平分，点P在OM上，，，角平分线上的点到角两边的距离相等又，，四边形OEPF为矩形，，，又，，．在与中，，≌ ，．【解析】1. 解：，，平分，，，，是的角平分线，，，故正确，在与中，，≌ ，，，故正确；，，故正确．故选：A．根据等腰三角形的性质三线合一得到，，故正确；通过 ≌ ，得到，，故正确．本题考查了全等三角形的判定和性质，等腰三角形的性质，平行线的性质，掌握等腰三角形的性质三线合一是解题的关键．2. 解：是的角平分线，，，，，在和中，，≌ ，；是的角平分线，，在和中，，≌ ，；故选C．首先运用角平分线的性质得出，再由HL证明 ≌ ，即可得出；根据SAS 即可证明 ≌ ，即可得到．本题考查了角平分线的性质、全等三角形的判定与性质、等腰三角形的三线合一性质；熟练掌握全等三角形的判定方法是解决问题的关键．3. 解：，，，故A选项错误，平分，，在中，，，故B选项正确；平分，，平分，，，，故C选项错误；，，，故D选项错误．故选：B．根据三角形的内角和定理列式计算即可求出，再根据角平分线的定义求出，然后利用三角形的内角和定理求出，再根据对顶角相等可得，根据邻补角的定义和角平分线的定义求出，再利用三角形的内角和定理列式计算即可，判断出，根据，，即可判定．本题考查了角平分线的性质，三角形的内角和定理，角平分线的定义，熟记定理和概念是解题的关键．4. 解：由题意得AP是的平分线，过点D作于E，又，，的面积．故选：B．判断出AP是的平分线，过点D作于E，根据角平分线上的点到角的两边距离相等可得，然后根据三角形的面积公式列式计算即可得解．本题考查了角平分线上的点到角的两边距离相等的性质以及角平分线的画法，熟记性质是解题的关键．5. 解：度假村在三条公路围成的平地上且到三条公路的距离相等，度假村应该在三条角平分线的交点处．故选B．根据角平分线上的点到角的两边的距离相等的性质解答．本题考查了角平分线上的点到角的两边的距离相等的性质，是基础题，熟记性质是解题的关键．6. 解：，，，在和中，≌ ，故选：D．根据题中的条件可得和是直角三角形，再根据条件，可根据HL定理判定 ≌ ．本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、结合已知条件在图形上的位置选择判定方法．7. 解：当时，PQ的值最小，平分，，，，故选D．根据垂线段最短得出当时，PQ的值最小，根据角平分线性质得出，求出即可．本题考查了角平分线性质，垂线段最短的应用，能得出要使PQ最小时Q的位置是解此题的关键．8. 解：在这个区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，根据角平分线的性质，集贸市场应建在、、的角平分线的交点处．故选：C．根据角平分线上的点到角的两边的距离相等解答即可．本题主要考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．9. 解：过点P作与点D，于点E，于点F．平分，CP平分，．点P在的平分线上，P到AB，BC的距离相等．故正确．故选C．根据角平分线上的点到角的两边的距离相等，过点P作与点D，于点E，于点F，则点P在的平分线上．此题考查角平分线的性质：角平分线上的点到角的两边的距离相等；到角的两边距离相等的点在角的平分线上．10. 解：如图，过点D作于F，是的平分线，，，，，，解得．故选D．过点D作于F，根据角平分线上的点到角的两边距离相等可得，然后根据的面积列出方程求解即可．本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质是解题的关键．11. 解：如图作于E，于F．，，，，，平分，于E，于F，，在和中，，≌ ，，在和中，，≌ ，，，故正确，，定值，故正确，四边形四边形定值，故正确，MN的长度是变化的，故错误，故选：B．如图作于E，于只要证明 ≌ ， ≌ ，即可一一判断．本题考查全等三角形的性质、角平分线的性质定理、四边形的面积等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．12. 解：作于G，如图所示：，，，，，．故答案为：4．作于F，根据角平分线的性质得到EG的长度，再根据平行线的性质得到，然后利用三角形的外角和内角的关系求出，利用角所对的直角边是斜边的一半解题．本题考查了角平分线的性质、平行线的性质、含角的直角三角形的性质；熟练掌握角平分线的性质，证出是解决问题的关键．13. 解：于B，于C，且，是的平分线，，，．故答案为：先根据到角的两边距离相等的点在角的平分线上得到AD是的平分线，求出的度数，再根据三角形的一个外角等于与它不相邻的两个内角的和即可求解．本题考查了角平分线的判定与三角形的一个外角等于与它不相邻的两个内角的和的性质，仔细分析图形是解题的关键．14. 解：作于E，于F，于H，的三条角平分线交于点O，，，，，的面积，故答案为：27．作于E，于F，于H，根据角平分线的性质得到，根据三角形的面积公式计算即可．本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．15. 解：作于E，由基本尺规作图可知，AD是的角平分线，，，，的面积，故答案为：30．根据角平分线的性质得到，根据三角形的面积公式计算即可．本题考查的是角平分线的性质、基本作图，掌握角的平分线上的点到角的两边的距离相等是解题的关键．16. 解：在中，，与重合，，，又点D是AB的中点，，设，，．．只要证明，设列出方程即可解决问题．本题考查翻折变换、垂直平分线的性质等知识，解题的关键是灵活运用翻折不变性，学会设未知数列方程解决问题，属于中考常考题型．17. 解：，是直角三角形，根据题意画图，如图所示：连接AP，BP，CP．设，，，则，．故答案为：3．首先根据三边长确定三角形是直角三角形，再根据题意画出图形，连接AP，BP，CP，根据直角三角形的面积公式即可求得该距离的长．此题主要考查了勾股定理逆定理，以及三角形的面积注意构造辅助线，则直角三角形的面积有两种表示方法：一是整体计算，即两条直角边乘积的一半；二是等于三个小三角形的面积和，即，然后即可计算x的值．18. 解：当时，PN的值最小，平分，，，，的最小值为5．故答案为：5．根据垂线段最短可得时，PN最短，再根据角平分线上的点到角的两边的距离相等可得，从而得解．本题考查了角平分线上的点到角的两边的距离相等的性质，垂线段最短的性质，熟记性质是解题的关键．19. 解：作于E，平分，，，，的面积，故答案为：8．作于E，根据角平分线的性质求出DE的长，根据三角形的面积公式计算即可．本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．20. 解：如图，过点D作于E，，BD平分，，，，即点D到AB的距离为3cm．故答案为：3．过点D作于E，根据角平分线上的点到角的两边的距离相等可得，从而得解．本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．21. 解：如图所示，加油站站的地址有四处，故答案为：4．根据角平分线上的点到角的两边的距离相等作出图形即可得解．本题考查了角平分线的性质，掌握角平分线上的点到角的两边的距离相等的性质是解题的关键，作出图形更形象直观．22. 解：过P作于F，，OC平分，，，，，，平分，于D，于F，，，，故答案为：6．过P作于F，根据角平分线的定义可得，根据平行线的性质可得，从而可得，即可得出答案．此题主要考查：含度的直角三角形的性质：在直角三角形中，角所对的直角边等于斜边的一半，角平分线的性质：角的平分线上的点到角的两边的距离相等．23. 作BH平分交AC于H，连结HE，如图，由于，则，于是可判断为等腰三角形，根据等腰三角形的性质得，易得，根据平行线分线段成比例定理得，接着根据角平分线的性质定理得，则，然后把代入计算即可得到．本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例也考查了等腰三角形的判定与性质和角平分线性质．24. 根据等腰梯形性质得到，，根据角平分线性质推出，推出，根据已知梯形的周长求出即可．本题主要考查对等腰梯形的性质，平行线的性质，等腰三角形的性质，角平分线的性质等知识点的理解和掌握，能求出是解此题的关键．25. 连接A、B，作AB的垂直平分线，然后作两条公路m和n夹角的平分线，其交点即为加油站的位置．此题考查学生对角平分线的性质和线段垂直平分线的性质的理解和掌握特别要注意让学生牢记角平分线的性质定理．26. 结论四边形EBGD是菱形只要证明即可．作于M，于N，连接EC交BD于点H，此时最小，在中，求出EM、MC即可解决问题．本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识，解题的关键是利用对称找到点H的位置，属于中考常考题型．27. 先过点P作于点E，于点F，构造全等三角形：和，这两个三角形已具备两个条件：的角以及，只需再证，根据已知，两个角都等于减去，那么三角形全等就可证．本题考查了角平分线的性质，以及四边形的内角和是、还有三角形全等的判定和性质等知识正确作出辅助线是解答本题的关键．。

角平分线的性质定理及其逆定理习题精选及答案(一)

角平分线的性定理及其逆定理习题精选（一）1．（1）在角的平分线上的点到这个角的________相等。

（2）到一个角的_______相等的点，在这个角的平分线上。

2．如图，OP平分∠AOB，PC⊥OA于C，PD⊥OB于D，则下列结论中错误的是（）A．PC＝PDB．OC＝ODC．∠CPO＝∠DPOD．OC＝PC3．如图，△ABC中，AB＝AC，AD平分∠BAC，DE⊥AB，DF⊥AC，E、F为垂足，则下列四个结论：①AD上任意一点到点C，点D的距离相等；②AD上任意一点到AB，AC的距离相等；③AD⊥BC且BD＝CD；④∠BDE＝∠CDF，其中正确的个数是（）A．1个B．2个C．3个D．4个4．如图，OC是∠AOB的平分线，点P在OC上，PD⊥OA于D，PE⊥OB于E，求证：OD ＝OE，∠OPD＝∠OPE5．已知，如图，点A、B在OP上，AC⊥OM于点C，AD⊥ON于点D，BE⊥OM于点E，BF ⊥ON于点F，且AC＝AD，求证：BE＝BF。

6．如图，点D、点P在∠ABC的平分线上，PA⊥BA，PC⊥BC，A、C为垂足，求证：AD ＝CD，∠ADB＝∠CDB。

7．下列命题正确的是（）A．三角形一个外角等于两个内角的和B．有两边和一角对应相等的两个三角形一定全等C．有两边对应相等的两个直角三角形全等D．到角的两边距离相等的点在这个角的平分线上8．下列定理中有逆定理的是（）A．对顶角相等B．全等三角形的对应角相等C．同位角相等D．角平分线上的点到这个角的两边距离相等9．已知，如图，BD是∠ABC的平分线，AB＝BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M、N，求证：PM＝PN。

10．已知，△ABC中，P是角平分线AD、BE的交点，求证：点P在∠C的平分线上。

11．如图，在△ABC 中，请证明：（1）若AD 为角平分线，则ABD ACD S AB S AC∆∆=。

（2）设D 为BC 上一点，连结AD ，若ABD ACD S AB S AC ∆∆=，则AD 为角平分线。

八年级数学角平分线的性质及其逆定理同步练习

24.8 角平分线的性质及其逆定理第1题. 如图，△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB ，DF ⊥AC ，E 、F 为垂足，在以下结论中：①△ADE ≌△ADF ；②△BDE ≌△CDF ；③△ABD ≌△ACD ；④AE =AF ；⑤BE =CF ；⑥BD =CD ．其中正确结论的个数是（）A ．1B ．2C ．3D ．4 答案：B ．第2题. 如图，Rt △ABC 中，∠C =90º，BD 是角平分线，DE ⊥AB ，垂足为E ，BC =6，CD =3，AE =4，则DE =_______，AD =_______，△ABC 的周长是_______．答案：3，5，24第3题. 用三角尺画角平分线：如图，∠AOB 是一个任意角，在边O A ，OB 上分别取OM =ON ，再分别过M 、N 作OA ，OB 的垂线，交点为P ，画射线OP ，则这条射线即为角平分线．请解释这种做法的道理．你还能举出哪些作角平分线的方法，并说明这种做法的道理．答案：提示：OM =ON ，OP =OP ，∴Rt △OMP ≌Rt △ONP (HL)，∴∠MOP =∠NOP ，∴射线OP 是∠AOB 的平分线．第4题. 求证：三角形的三条角平分线相交于一点．AB CDEF ABCDE答案：提示：画出图形，写出已知、求证，证明两条角平分线的交点到第三个角的两边的距离相等．第5题. 如图，三条公路围成的一个三角形区域，要在这个区域中建一个加油站，使它到三条公路的距离都相等，加油站应建在什么位置？请用尺规作图，找出建造加油站的位置．答案：提示：作两个角的平分线，交点即为建加油站的位置．第6题. 如图，△ABC 中，∠C =90º，BD 平分∠ABC 交AC 于D ，DE 是AB的垂直平分线，DE =21BD ，且DE =1.5cm ，则AC 等于（）A ．3cmB ．7.5cmC ．6cmD ．4.5cm 答案：D ．第7题. 如图，△ABC 中，P 是角平分线A D ，BE 的交点．求证：点P 在∠C 的平分线上．答案：如图，过点P 作PM ⊥AB ，PN ⊥BC ，PQ ⊥AC ，垂足分别为M 、N 、B CDE AA BCDE PQ ．∵P 在∠BAC 的平分线AD 上，∴PM =PQ ．P 在∠ABC 的平分线BE 上，∴PM =PN 。

八年级数学上册《第十二章角平分线的性质》同步练习及答案(人教版)

八年级数学上册《第十二章角平分线的性质》同步练习及答案(人教版）学校:___________班级：___________姓名：___________考号：___________一、单选题1．两条平行线a、b被第三条直线c所截得的同旁内角的平分线的交点到直线c的距离是2cm，则a、b之间的距离是（）A．3cm B．4cm C．5cm D．6cm2．如图，△ABC的外角∠ACD的平分线CP与∠ABC平分线BP交于点P，若∠BPC=40°，则∠CAP的度数是（）A．30°；B．40°；C．50°；D．60°.3．如图所示，在△ABC中，AC⊥BC，AE为∠BAC的平分线，DE⊥AB，AB=7cm，AC=3cm，则BD等于（）A．1cm B．2cm C．3cm D．4cm4．如图，在Rt△ABC中∠C=90°，AC=8，BC=6，AB=10，∠CAB和∠ABC的平分线交于点O，OM⊥BC于点M，则OM的长为（）A．1 B．2 C．3 D．45．如图，已知AB//CD，∠ABE与∠CDE的角平分线相交于点F，若∠ABM=13∠ABF，∠CDM=13∠CDF，设∠BED=108°，则∠M的度数是（）A．24°B．36°C．42°D．54°6．△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线相交于O点，将△ABC分为三个三角形，则S△ABO︰S△BCO︰S△CAO等于（）A．1︰1︰1 B．1︰2︰3 C．2︰3︰4 D．3︰4︰57．如图，P是ΔABC的三条角平分线的交点，连接PA、PB、PC,若ΔPAB、ΔPBC、ΔPAC的面积分别为S1、S2、S2，则S1（）S2+S3．A．>B．=C．<D．无法确定8．如图，已知点P到BE，BD，AC的距离恰好相等，则点P的位置：①在∠B的平分线上；②在∠DAC的平分线上；③在∠ECA的平分线上；④恰是∠B，∠DAC，∠ECA三条角平分线的交点，上述结论中，正确结论的个数有（）A．1个B．2个C．3个D．4个二、填空题9．如图，已知在△ABC中，∠A=90°，AB=AC，CD平分∠ACB，DE⊥BC于E，若BC=15cm，则△DEB的周长为cm．10．如图，在ΔABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，BC=5，DE=2则ΔBCE的面积为；11．如图，AB∥CD,O是∠BAC和∠ACD的平分线的交点，OE⊥AC与E，OE=3，则AB与CD之间的距离为．12．如图，△ABC中，∠C=90°，AD是∠CAB的角平分线，DE⊥AB于点E，且BC=8cm，BD=5cm，则DE= cm．13．如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC面积是45cm2，AB=16cm，AC=14cm，则DE= ．三、解答题14．如图,已知直线AB//EF,AB//CD,∠ABE=50°,EC平分∠BEF,求∠DCE的度数.15．如图：已知BD=CD，BF⊥AC，CE⊥AB，求证：点D在∠BAC的平分线上．16．已知DE∥AC，∠3=∠4，CD平分∠BCA．试说明EF平分∠BED．17．在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，BD：DC＝2：1，BC＝7.8cm，求点D到AB的距离.18．如图，已知AB∥CD，AE平分∠BAD，DF平分∠ADC，EF交AD于点O，求证∠E＝∠F.19．已知：如图，D为△ABC外角∠ACP平分线上一点，且DA=DB，DM⊥BP于点M.（1）若AC=3，DM=1求△ACD的面积；（2）求证：AC=BM+CM .参考答案1．B2．C3．D4．B5．C6．C7．C8．D9．1510．511．612．313．3cm14．解：∵AB//EF ，∠ABE=50°（已知）∴∠ABE=∠BEF=50°（两直线平行，内错角相等） ∵EC 平分∠BEF （已知）∴∠CEF= 12 ∠BEF=25°（角平分线的意义） ∵AB//EF,AB//CD （已知）∴CD//EF （平行线的传递性）∴∠CEF+∠DCE=180°（两直线平行，同旁内角互补） ∴∠DCE=180-25=155°（等式性质）15．证明：∵BF ⊥AC ，CE ⊥AB∴∠BED=∠CFD=90°在△BED 和△CFD 中 {∠BED =∠CFD∠BDE =∠CDF BD =CD∴△BED ≌△CFD （AAS ）∴DE=DF又∵DE ⊥AB ，DF ⊥AC∴点D 在∠BAC 的平分线上．16．证明：∵DE∥AC（已知）∴∠BCA=∠BED（两直线平行，同位角相等）即∠1+∠2=∠4+∠5∵DE∥AC（已知）∴∠1=∠3（两直线平行，内错角相等）；∵∠3=∠4（已知）∴∠1=∠4（等量代换）∴∠2=∠5（等式性质）；∵CD平分∠BCA（已知）∴∠1=∠2（角平分线的定义）∴∠4=∠5（等量代换）∴EF平分∠BED（角平分线的定义）．17．解：过点D作DE⊥AB于E.∵AD平分∠BAC，DE⊥AB，DC⊥AC∴CD＝DE又BD：DC＝2：1，BC＝7.8cm∴DC＝7.8÷（2+1）＝7.8÷3＝2.6cm.∴DE＝DC＝2.6cm.∴点D到AB的距离为2.6cm.18．证明：∵AB//CD∴∠BAD=∠ADC∵AE平分∠BAD DF平分∠ADC∴∠EAD=12∠BAD∠FDA=12∠ADC∴∠EAD=∠FDA∴AE//FD∴∠E=∠F .19．（1）解：如图所示，过点D作DE⊥AC于E∵CD是∠ACM的角平分线，DE⊥AC，DM⊥BC ∴DE=DM=1∴S△ACD=12AC⋅DE=32；（2）证明：∵DE⊥AC，DM⊥BC∴∠DEA=∠DEC=∠DMB=90°∵AD=BD，DE=DM∴Rt△DEA≌Rt△DMB（HL）∴AE=BM∵∠DEC=∠DMC=90°，DE=DM，DC=DC ∴Rt△DEC≌Rt△DMC（HL）∴EC=CM∴AC=AE+EC=BM+CM。

2020-2021学年八年级数学北师大版下册角平分线的性质定理及其逆定理同步练习(附答案)

第1课时角平分线的性质定理及其逆定理1．下列各图中，OP 是∠MON 的平分线，点E ，F ，G 分别在射线OM ，ON ，OP 上，则可以解释定理“角平分线上的点到角的两边的距离相等”的图形是（）2．如图，点P 是∠AOB 的平分线上一点，PC ⊥OA 于点C ，PD ⊥OB 于点D ，连接CD 交OP 于点E ，下列结论不一定正确的是（）A ．PC ＝PDB ．OC ＝OD C ．OP 垂直平分CDD ．OE ＝CD第2题图第3题图3．如图，在△ABC 中，∠C ＝90°，AC ＝8，DC ＝13AD ，BD 平分∠ABC ，则点D 到AB 的距离等于（）A ．4B ．3C ．2D ．14．如图，点P 是∠AOC 的平分线上一点，PD ⊥OA ，垂足为D ，且PD ＝3，点M 是射线OC 上一动点，则PM 的最小值为．第4题图第5题图5．如图，BD 平分∠ABC ，DE ⊥BC 于点E ，AB ＝7，DE ＝4，则△ABD 的面积为． 6．已知：如图所示，点O 在∠BAC 的平分线上，OD ⊥AC ，OE ⊥AB ，垂足分别为D ，E，DO，EO的延长线分别交AE，AD的延长线于点B，C，求证：OB＝OC.7．如图，DA⊥AC，DE⊥BC.若AD＝5 cm，DE＝5 cm，∠ACD＝30°，则∠DCE＝（）A．30°B．40°C．50°D．60°8．如图，BE＝CF，DE⊥AB交AB的延长线于点E，DF⊥AC于点F，且DB＝DC，求证：AD是∠BAC的平分线．9．已知D，E分别是△ABC中AB边，AC边上的一点，在△ABC内有一点O，使OE ＝OD，则AO平分∠CAB吗？解：AO平分∠CAB，理由如下：因为点O到∠CAB两边的距离相等，所以点O在∠CAB的平分线上．所以AO平分∠CAB.以上解法是否正确？若不正确，请说明理由，并写出正确的结论．10．在正方形网格中，∠AOB的位置如图所示，到∠AOB两边距离相等的点应是（）A．M点B．N点C．P点D．Q点第10题图第11题图11．如图，在△ABC中，∠B＝30°，∠C＝45°，AD平分∠BAC交BC于点D，DE ⊥AB，垂足为E.若DE＝1，则BC的长为（）A．2＋ 2 B.2＋3C．2＋ 3 D．312．如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于点D，DE⊥BA于点E，AB＝6 cm，则△DEB的周长是cm.13．如图，在四边形ABCD中，∠B＝90°，AB∥CD，M为BC边上的一点，且AM 平分∠BAD，DM平分∠ADC.(1)求证：AM⊥DM；(2)若BC＝8，求点M到AD的距离．14．已知：如图，锐角△ABC的两条高BD，CE相交于点O，且OB＝OC.(1)求证：△ABC是等腰三角形；(2)判断点O是否在∠BAC的平分线上，并说明理由．15．如图，在△ABC中，∠BAC＝60°，AD是∠BAC的平分线，AC＝ 6.若点P是AD上一动点，且作PN⊥AC于点N，则PN＋PC2参考答案：第1课时角平分线的性质定理及其逆定理1．下列各图中，OP 是∠MON 的平分线，点E ，F ，G 分别在射线OM ，ON ，OP 上，则可以解释定理“角平分线上的点到角的两边的距离相等”的图形是(D)2．如图，点P 是∠AOB 的平分线上一点，PC ⊥OA 于点C ，PD ⊥OB 于点D ，连接CD 交OP 于点E ，下列结论不一定正确的是(D)A ．PC ＝PDB ．OC ＝OD C ．OP 垂直平分CDD ．OE ＝CD第2题图第3题图3．如图，在△ABC 中，∠C ＝90°，AC ＝8，DC ＝13AD ，BD 平分∠ABC ，则点D 到AB 的距离等于(C)A ．4B ．3C ．2D ．14．如图，点P 是∠AOC 的平分线上一点，PD ⊥OA ，垂足为D ，且PD ＝3，点M 是射线OC 上一动点，则PM 的最小值为3．第4题图第5题图5．如图，BD 平分∠ABC ，DE ⊥BC 于点E ，AB ＝7，DE ＝4，则△ABD 的面积为14．6．已知：如图所示，点O 在∠BAC 的平分线上，OD ⊥AC ，OE ⊥AB ，垂足分别为D ，E ，DO ，EO 的延长线分别交AE ，AD 的延长线于点B ，C ，求证：OB ＝OC.证明：∵点O 在∠BAC 的平分线上，OD ⊥AC ，OE ⊥AB ， ∴OE ＝OD ，∠BEO ＝∠CDO ＝90°. 在△BEO 和△CDO 中，⎩⎨⎧∠BEO ＝∠CDO ，OE ＝OD ，∠EOB ＝∠DOC ，∴△BEO ≌△CDO(ASA)． ∴OB ＝OC.7．如图，DA ⊥AC ，DE ⊥BC.若AD ＝5 cm ，DE ＝5 cm ，∠ACD ＝30°，则∠DCE ＝(A)A ．30°B ．40°C ．50°D ．60°8．如图，BE ＝CF ，DE ⊥AB 交AB 的延长线于点E ，DF ⊥AC 于点F ，且DB ＝DC ，求证：AD 是∠BAC 的平分线．证明：∵DE ⊥AB ，DF ⊥AC ， ∴∠BED ＝∠DFC ＝90°.在Rt △DEB 和Rt △DFC 中，⎩⎨⎧BE ＝CF ，DB ＝DC ，∴Rt △DEB ≌Rt △DFC(HL)． ∴DE ＝DF.∴AD 是∠BAC 的平分线．9．已知D ，E 分别是△ABC 中AB 边，AC 边上的一点，在△ABC 内有一点O ，使OE ＝OD ，则AO 平分∠CAB 吗？解：AO 平分∠CAB ，理由如下：因为点O 到∠CAB 两边的距离相等，所以点O 在∠CAB 的平分线上．所以AO 平分∠CAB.以上解法是否正确？若不正确，请说明理由，并写出正确的结论．解：不正确．以上解法忽视了OD ，OE 分别垂直于AB ，AC 的条件，故产生错误．正确的结论是“AO 不一定平分∠CAB ”．10．在正方形网格中，∠AOB 的位置如图所示，到∠AOB 两边距离相等的点应是(A) A ．M 点B ．N 点C ．P 点D ．Q 点第10题图第11题图11．如图，在△ABC 中，∠B ＝30°，∠C ＝45°，AD 平分∠BAC 交BC 于点D ，DE ⊥AB ，垂足为E.若DE ＝1，则BC 的长为(A)A ．2＋ 2 B.2＋3 C ．2＋ 3D ．312．如图，在△ABC 中，∠C ＝90°，AC ＝BC ，AD 平分∠CAB 交BC 于点D ，DE ⊥BA 于点E ，AB ＝6 cm ，则△DEB 的周长是6cm.13．如图，在四边形ABCD 中，∠B ＝90°，AB ∥CD ，M 为BC 边上的一点，且AM 平分∠BAD ，DM 平分∠ADC.(1)求证：AM ⊥DM ；(2)若BC ＝8，求点M 到AD 的距离．解：(1)证明：∵AM 平分∠BAD ，DM 平分∠ADC ， ∴∠MAD ＝12∠BAD ，∠ADM ＝12∠ADC.∵AB ∥CD ，∴∠BAD ＋∠ADC ＝180°.∴∠MAD ＋∠ADM ＝12(∠BAD ＋∠ADC)＝90°.又∵∠AMD ＋∠MAD ＋∠ADM ＝180°，∴∠AMD ＝90°. ∴AM ⊥DM.(2)过点M 作MN ⊥AD 于点N. ∵AB ∥CD ，∠B ＝90°，∴∠C ＝90°，即BM ⊥AB ，MC ⊥DC. 又∵AM ，DM 分别平分∠BAD ，∠ADC ， ∴BM ＝MN ，MN ＝MC. ∴MN ＝12BC ＝4.∴点M 到AD 的距离为4.14．已知：如图，锐角△ABC 的两条高BD ，CE 相交于点O ，且OB ＝OC. (1)求证：△ABC 是等腰三角形；(2)判断点O 是否在∠BAC 的平分线上，并说明理由．解：(1)证明：∵BD ，CE 是△ABC 的高， ∴∠BEC ＝∠CDB ＝90°. 又∵∠EOB ＝∠DOC ， ∴∠ABD ＝∠ACE. ∵OB ＝OC ， ∴∠OBC ＝∠OCB. ∴∠ABC ＝∠ACB.∴AB＝AC.∴△ABC是等腰三角形．(2)点O在∠BAC的平分线上．理由：∵∠BEO＝∠CDO＝90°，∠BOE＝∠COD，OB＝OC，∴△BOE≌△COD(AAS)．∴OE＝OD.又∵OD⊥AC，OE⊥AB，∴点O在∠BAC的平分线上．15．如图，在△ABC中，∠BAC＝60°，AD是∠BAC的平分线，AC＝ 6.若点P是AD上一动点，且作PN⊥AC于点N，则PN＋PC2。

湘教版八年级下册数学角平分线的性质定理的逆定理同步测试题

1.4 角平分线的性质第2课时角平分线的性质定理的逆定理要点感知角平分线的性质定理的逆定理：角的内部到角的两边距离相等的点在__________上.预习练习如图，P是∠MON内一点，PE⊥OM于点E，PF⊥ON 于点F，若PE=PF，则OP平分∠MON，其依据是____________________.知识点角平分线的判定1.如图，点D在BC上，DE⊥AB，DF⊥AC，且DE=DF，∠BAD=25°，则∠CAD=( )A.20°B.25°C.30°D.50°第1题图第2题图第3题图2.如图，在CD上求一点P，使它到OA，OB的距离相等，则P点是( )A.线段CD的中点B.OA与OB的中垂线的交点C.OA与CD的中垂线的交点D.CD与∠AOB的平分线的交点3.如图，已知点P在射线BD上，PA⊥AB，PC⊥BC，垂足分别为A，C，且PA=PC，下列结论错误的是( )A.AD=CPB.点D在∠ABC的平分线上C.△ABD≌△CBDD.∠ADB=∠CDB4.如图，是一个风筝骨架.为使风筝平衡，须使∠AOP=∠BOP.已知PC ⊥OA，PD⊥OB，那么PC和PD应满足__________，才能保证OP 为∠AOB的角平分线.第4题图第5题图5.如图，△ABC中，∠C=90°，∠A=36°，DE⊥AB于D，且EC=ED，则∠EBC的度数为__________.6.如图：在△ABC中，∠C=90°，DF⊥AB，垂足为F，DE=BD，CE=FB.求证：点D在∠CAB的角平分线上.7.如图，已知BE⊥AC，CF⊥AB，垂足分别为E，F，BE，CF相交于点D，若BD=CD.求证：AD平分∠BAC.8.下列说法：①角的内部任意一点到角的两边的距离相等；②到角的两边距离相等的点在这个角的平分线上；③角的平分线上任意一点到角的两边的距离相等；④△ABC中∠BAC的平分线上任意一点到三角形的三边的距离相等，其中正确的有( )A.1个B.2个C.3个D.4个9.如图，在△ABC中，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC 于S，则三个结论①AS=AR；②QP∥AR；③△BPR≌△QSP中( ) A.全部正确 B.仅①和②正确 C.仅①正确D.仅①和③正确第9题图第10题图10.如图，直线l1，l2，l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则供选择的地址有( ) A.1处 B.2处 C.3处D.4处11.点O是△ABC内一点，且点O到三边的距离相等，∠A=50°，则∠BOC=__________.12.如图，在△ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F，BE=CF.求证：AD是△ABC的角平分线.13.如图，某校八年级学生分别在M，N两处参加植树劳动，现要在道路AB，AC的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且使PM=PN，请你找出点P.14.已知：如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC.(1)若连接AM，则AM是否平分∠DAB？请你证明你的结论；(2)线段DM与AM有怎样的位置关系？请说明理由.参考答案要点感知角的平分线预习练习角平分线定理的逆定理1.B2.D3.A4.PC=PD5.27°6.证明：∵DF⊥AB，∠C=90°，∴∠DFB=∠C=90°.在Rt△CED和Rt△FBD中，DE=DB,CE=FB,∴△CED≌△FBD(HL).∴DC=DF.∵DF⊥AB，DC⊥AC，∴点D在∠CAB的角平分线上.7.证明：∵BE⊥AC，CF⊥AB，∴∠BFD=∠CED=90°.在△BDF与△CDE中，∠BFD=∠CED，∠BDF=∠CDE，BD=CD，∴△BDF≌△CDE(AAS).∴DF=DE.∴AD是∠BAC的平分线.8.B 9.B 10.D 11.115°12.证明：∵DE⊥AB，DF⊥AC，∴△BDE和△DCF是直角三角形.∵BD=CD，BE=CF，∴Rt△BDE≌Rt△CDF(HL).∴DE=DF.又∵DE⊥AB，DF⊥AC，∴AD是△ABC的角平分线.13.作法：(1)作出∠BAC的平分线AD；(2)连接MN，作MN的垂直平分线EF交AD于点P.∴点P就是所求的点.图略.14.(1)AM平分∠DAB.证明：过点M作ME⊥AD，垂足为E.∵DM平分∠ADC，∴∠1=∠2.∵MC⊥CD，ME⊥AD，∴ME=MC.又∵MC=MB，∴ME=MB.∵MB⊥AB，ME⊥AD，∴AM平分∠DAB.(2)AM⊥DM.理由：∵∠B=∠C=90°，∴DC⊥CB，AB⊥CB.∴CD∥AB.∴∠CDA+∠DAB=180°.又∵∠1=12∠CDA，∠3=12∠DAB，∴2∠1+2∠3=180°.∴∠1+∠3=90°.∴∠AMD=90°，即AM⊥DM.八年级下册数学期末测试卷一、选择题（本大题共8个小题，每小题3分，满分24分．请将正确答案的字母代号填在下表中．）1．（3分）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．2．（3分）以下列各组数为边长能构成直角三角形的是（）A．1，1，B．2，3，4 C．4，5，6 D．6，8，113．（3分）在下列所给出坐标的点中，在第三象限的是（）A．（2，3）B．（﹣2，﹣3） C．（﹣2，3）D．（2，﹣3）4．（3分）如图，在△ABC中，∠C=90°，∠A=30°，BC=4cm，点D 为AB的中点，则CD=（）A．3cm B．4cm C．5cm D．6cm5．（3分）已知▱ABCD的周长是26cm，其中△ABC的周长是18cm，则AC的长为（）A．12cm B．10cm C．8cm D．5cm6．（3分）菱形的两条对角线长为6cm 和8cm，那么这个菱形的周长为（）A．40 cm B．20 cm C．10 cm D．5 cm7．（3分）正方形具有而菱形不一定具有的性质是（）A．对角线平分一组对角B．对角线互相垂直平分C．对角线相等D．四条边相等8．（3分）汽车由重庆驶往相距400千米的成都，如果汽车的平均速度是100千米/时，那么汽车距成都的路程s（千米）与行驶时间t （小时）的函数关系用图象表示为（）A．B．C．D．二、填空题（本大题共8小题，每小题3分，满分24分）9．（3分）已知点P（3，2）在一次函数y=x+b的图象上，则b= ．10．（3分）一个多边形的内角和是外角和的2倍，则这个多边形的边数为．11．（3分）已知y与x成正比例，且当x=1时，y=2，则当x=4时，y= ．12．（3分）如图，AC⊥BC，AD⊥BD，垂足分别是C、D，若要用“HL”得到Rt△ABC≌Rt△BAD，则你添加的条件是．（写一种即可）13．（3分）将点P （﹣3，4）先向下平移3个单位，再向右平移2个单位后得到点Q，则点Q的坐标是．14．（3分）如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=2，则菱形ABCD的周长是．15．（3分）如图，矩形ABCD中，对角线AC、BD交于点O，过O 的直线分别交AD、BC于点E、F，已知AD=4cm，图中阴影部分的面积总和为6cm2，对角线AC长为cm．16．（3分）如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A4n+1（n为自然数）的坐标为（用n表示）．三、解答题（本大题共8个小题，共计72分）17．（6分）在边长为1的小正方形网格中，△AOB的顶点均在格点上，（1）B点关于y轴的对称点坐标为；（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；（3）在（2）的条件下，A1的坐标为．18．（8分）已知：如图，AC平分∠BAD，CE⊥AB于E CF⊥AD于F，且BC=DC．求证：BE=DF．19．（8分）已知一次函数y=（2m+1）x+m﹣3．（1）若这个函数的图象经过原点，求m的值；（2）若这个函数的图象经过一、三、四象限，求m的取值范围．20．（8分）已知：如图，四边形ABCD中，AB⊥BC，AB=1，BC=2，CD=2，AD=3，求四边形ABCD的面积．21．（10分）为了进一步了解某校八年级学生的身体素质情况，体育老师对该校八年级（1）班50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图，图表如下所示：组别次数x 频数（人数）第1组80≤x＜100 6第2组100≤x＜120 8第3组120≤x＜140 a第4组140≤x＜160 18第5组160≤x＜180 6请结合图表完成下列问题：（1）求表中a的值；（2）请把频数分布直方图补充完整；（3）若在一分钟内跳绳次数少于120次的为测试不合格，则该校八年级共1000人中，一分钟跳绳不合格的人数大约有多少？22．（10分）如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是32cm．求：（1）两条对角线的长度；（2）菱形的面积．23．（10分）甲、乙两地相距300km，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA表示货车离甲地距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地距离y（km）与时间x（h）之间的函数关系．请根据图象，解答下列问题：（1）线段CD表示轿车在途中停留了h；（2）货车的平均速度是km/h；（3）求线段DE对应的函数解析式．24．（12分）如图，在矩形ABCD中，AB=1cm，AD=3cm，点Q 从A点出发，以1cm/s的速度沿AD向终点D运动，点P从点C出发，以1cm/s的速度沿CB向终点B运动，当这两点中有一点到达自己的终点时，另一点也停止运动，两点同时出发，运动了t秒．（1）当0＜t＜3，判断四边形BQDP的形状，并说明理由；（2）求四边形BQDP的面积S与运动时间t的函数关系式；（3）求当t为何值时，四边形BQDP为菱形．2016-2017学年湖南省张家界市永定区八年级（下）期末数学试卷参考答案与试题解析一、选择题（本大题共8个小题，每小题3分，满分24分．请将正确答案的字母代号填在下表中．）1．（3分）（2017春•永定区期末）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【解答】解：不是轴对称图形，是中心对称图形，故本选项不符合题意；B、不是轴对称图形，是中心对称图形，故本选项不符合题意；C、既是轴对称图形，又是中心对称图形，故本选项符合题意；D、不是轴对称图形，是中心对称图形，故本选项不符合题意．故选C．【点评】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．2．（3分）（2017春•永定区期末）以下列各组数为边长能构成直角三角形的是（）A．1，1，B．2，3，4 C．4，5，6 D．6，8，11【分析】根据勾股定理的逆定理对各选项进行逐一判断即可．【解答】解：A、∵12+12=2=（）2，∴能构成直角三角形，故本选项正确；B、∵22+32=25≠42，∴不能构成直角三角形，故本选项错误；C、∵42+52=41≠62，∴不能构成直角三角形，故本选项错误；D、∵62+82=100≠112，∴不能构成直角三角形，故本选项错误．故选A．【点评】本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．3．（3分）（2017春•永定区期末）在下列所给出坐标的点中，在第三象限的是（）A．（2，3）B．（﹣2，﹣3） C．（﹣2，3）D．（2，﹣3）【分析】根据各象限内点的坐标特征解答即可．【解答】解：A、（2，3）第一象限，B、（﹣2，﹣3）第三象限，C、（﹣2，3）第二象限，D、（2，﹣3）第四象限，故选：B．【点评】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．4．（3分）（2017春•永定区期末）如图，在△ABC中，∠C=90°，∠A=30°，BC=4cm，点D为AB的中点，则CD=（）A．3cm B．4cm C．5cm D．6cm【分析】根据直角三角形的性质得到AB=2BC=8cm，根据直角三角形中，斜边上的中线等于斜边的一半计算即可．【解答】解：∵∠C=90°，∠A=30°，BC=4cm，∴AB=2BC=8cm，∵点D为AB的中点，∴CD=4cm，故选：B．【点评】本题考查的是直角三角形的性质，掌握直角三角形中，30°角所对的直角边等于斜边的一半、斜边上的中线等于斜边的一半是解题的关键．5．（3分）（2017春•永定区期末）已知▱ABCD的周长是26cm，其中△ABC的周长是18cm，则AC的长为（）A．12cm B．10cm C．8cm D．5cm【分析】根据题意得出平行四边形的邻边长的和为13cm，进而利用△ABC的周长是18cm求出AC即可．【解答】解：如图所示：∵▱ABCD的周长是26cm，∴AB+BC=13cm，∵△ABC的周长是18cm，∴AC=18﹣13=5（cm）．故选：D．【点评】此题主要考查了平行四边形的性质，得出AB+BC=13cm是解题关键．6．（3分）（2017春•永定区期末）菱形的两条对角线长为6cm 和8cm，那么这个菱形的周长为（）A．40 cm B．20 cm C．10 cm D．5 cm【分析】首先根据题意画出图形，由菱形ABCD中，AC=6，BD=8，即可得AC⊥BD，OA=AC=3，OB=BD=4，然后利用勾股定理求得这个菱形的边长．【解答】解：∵菱形ABCD中，AC=6，BD=8，∴AC⊥BD，OA=AC=3，OB=BD=4，∴AB==5．即这个菱形的周长为：20．故选B．【点评】此题考查了菱形的性质以及勾股定理．注意菱形的对角线互相平分且垂直．7．（3分）（2017春•博兴县期末）正方形具有而菱形不一定具有的性质是（）A．对角线平分一组对角B．对角线互相垂直平分C．对角线相等D．四条边相等【分析】根据正方形和菱形的性质容易得出结论．【解答】解：正方形的性质：正方形的四条边相等，四个角都是直角，对角线互相垂直平分且相等，并且每一条对角线平分一组对角；菱形的性质：菱形的四条边相等，对角线互相垂直平分，并且每一条对角线平分一组对角；因此正方形具有而菱形不一定具有的性质是：对角线相等；故选：C．【点评】本题考查了正方形和菱形的性质；熟练掌握正方形和菱形的性质是解题的关键；注意区别．8．（3分）（2004•四川）汽车由重庆驶往相距400千米的成都，如果汽车的平均速度是100千米/时，那么汽车距成都的路程s（千米）与行驶时间t（小时）的函数关系用图象表示为（）A．B．C．D．【分析】先根据题意列出s、t之间的函数关系式，再根据函数图象的性质和实际生活意义进行选择即可．【解答】解：根据题意可知s=400﹣100t（0≤t≤4），∴与坐标轴的交点坐标为（0，400），（4，0）．要注意x、y的取值范围（0≤t≤4，0≤y≤400）．故选C．【点评】主要考查了一次函数的图象性质，首先确定此函数为一次函数，然后根据实际意义，函数图象为一条线段，再确定选项即可．二、填空题（本大题共8小题，每小题3分，满分24分）9．（3分）（2017春•永定区期末）已知点P（3，2）在一次函数y=x+b 的图象上，则b= ﹣1 ．【分析】直接把点P（3，2）代入一次函数y=x+b即可．【解答】解：∵P（3，2）在一次函数y=x+b的图象上，∴3+b=2，解得b=﹣1．故答案为：﹣1．【点评】本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．10．（3分）（2016•乌鲁木齐）一个多边形的内角和是外角和的2倍，则这个多边形的边数为 6 ．【分析】利用多边形的外角和以及多边形的内角和定理即可解决问题．【解答】解：∵多边形的外角和是360度，多边形的内角和是外角和的2倍，则内角和是720度，720÷180+2=6，∴这个多边形是六边形．故答案为：6．【点评】本题主要考查了多边形的内角和定理与外角和定理，熟练掌握定理是解题的关键．11．（3分）（2017春•永定区期末）已知y与x成正比例，且当x=1时，y=2，则当x=4时，y= 8 ．【分析】首先根据y与x成正比例列出函数关系式，然后代入x、y的值即可求解．【解答】解：∵y与x成正比例，∴y=kx（k≠0）．∵当x=1时，y=2，∴k=2，∴y与x之间的函数解析式是y=2x，∴当x=4时，y=8．故答案为：8．【点评】本题考查的是利用待定系数法求一次函数的解析式，此类题目需灵活运用待定系数法建立函数解析式，然后将一对未知数的值代入解析式，利用方程解决问题．12．（3分）（2017春•永定区期末）如图，AC⊥BC，AD⊥BD，垂足分别是C、D，若要用“HL”得到Rt△ABC≌Rt△BAD，则你添加的条件是AC=BD ．（写一种即可）【分析】根据“HL”添加AC=BD或BC=AD均可．【解答】解：可添加AC=BD，∵AC⊥BC，AD⊥BD，∴∠C=∠D=90°，在Rt△ABC和Rt△BAD中，∵，∴Rt△ABC≌Rt△BAD（HL），故答案为：AC=BD．【点评】本题主要考查全等三角形的判定，熟练掌握直角三角形全等的判定是解题的关键．13．（3分）（2017春•永定区期末）将点P （﹣3，4）先向下平移3个单位，再向右平移2个单位后得到点Q，则点Q的坐标是（﹣1，1）．【分析】根据横坐标，右移加，左移减；纵坐标，上移加，下移减可得答案．【解答】解：根据题意，知点Q的坐标是（﹣3+2，4﹣3），即（﹣1，1），故答案为：（﹣1，1）．【点评】此题主要考查了坐标与图形的变化﹣﹣平移，关键是掌握点的坐标的变化规律．14．（3分）（2017春•永定区期末）如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=2，则菱形ABCD的周长是16 ．【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出BC，再根据菱形的周长公式列式计算即可得解．【解答】解：∵E、F分别是AB、AC的中点，∴EF是△ABC的中位线，∴BC=2EF=2×2=4，∴菱形ABCD的周长=4BC=4×4=16．故答案为16．【点评】本题主要考查了菱形的四条边都相等，三角形的中位线平行于第三边并且等于第三边的一半，求出菱形的边长是解题的关键．15．（3分）（2017春•永定区期末）如图，矩形ABCD中，对角线AC、BD交于点O，过O的直线分别交AD、BC于点E、F，已知AD=4cm，图中阴影部分的面积总和为6cm2，对角线AC长为 5 cm．【分析】根据矩形的性质，采用勾股定理求解即可．【解答】解：∵图中阴影部分的面积总和为6cm2，AD=4cm，则AD ×CD=×4×CD=6，CD=3，在直角三角形ACD中AD=4，CD=3，由勾股定理得AC=5，∴对角线AC长为5cm．故答案为5．【点评】本题主要考查矩形的性质、勾股定理，是基础知识比较简单．16．（3分）（2013•聊城）如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A4n+1（n为自然数）的坐标为（2n，1）（用n 表示）．【分析】根据图形分别求出n=1、2、3时对应的点A4n+1的坐标，然后根据变化规律写出即可．【解答】解：由图可知，n=1时，4×1+1=5，点A5（2，1），n=2时，4×2+1=9，点A9（4，1），n=3时，4×3+1=13，点A13（6，1），所以，点A4n+1（2n，1）．故答案为：（2n，1）．【点评】本题考查了点的坐标的变化规律，仔细观察图形，分别求出n=1、2、3时对应的点A4n+1的对应的坐标是解题的关键．三、解答题（本大题共8个小题，共计72分）17．（6分）（2014•湘潭）在边长为1的小正方形网格中，△AOB的顶点均在格点上，（1）B点关于y轴的对称点坐标为（﹣3，2）；（2）将△AOB向左平移3个单位长度得到△A1O1B1，请画出△A1O1B1；（3）在（2）的条件下，A1的坐标为（﹣2，3）．【分析】（1）根据关于y轴对称的点的横坐标互为相反数，纵坐标相等解答；（2）根据网格结构找出点A、O、B向左平移后的对应点A1、O1、B1的位置，然后顺次连接即可；（3）根据平面直角坐标系写出坐标即可．【解答】解：（1）B点关于y轴的对称点坐标为（﹣3，2）；（2）△A1O1B1如图所示；（3）A1的坐标为（﹣2，3）．故答案为：（1）（﹣3，2）；（3）（﹣2，3）．【点评】本题考查了利用平移变换作图，关于y轴对称点的坐标，熟练掌握网格结构准确找出对应点的位置是解题的关键．18．（8分）（2017春•永定区期末）已知：如图，AC平分∠BAD，CE⊥AB于E CF⊥AD于F，且BC=DC．求证：BE=DF．【分析】根据角平分线的性质就可以得出CE=CF，再由HL证明△CEB ≌△CFD就可以得出结论．【解答】证明：∵AC平分∠BAD，CE⊥AB于E CF⊥AD于F，∴∠F=∠CEB=90°，CE=CF．在Rt△CEB和Rt△CFD中，∴△CEB≌△CFD（HL），∴BE=DF．【点评】本题考查了角平分线的性质的运用，全等三角形的判定与性质的运用，解答时证明△CEB≌△CFD是关键．19．（8分）（2017春•永定区期末）已知一次函数y=（2m+1）x+m ﹣3．（1）若这个函数的图象经过原点，求m的值；（2）若这个函数的图象经过一、三、四象限，求m的取值范围．【分析】（1）由一次函数图象经过原点，可得出m﹣3=0，解之即可得出结论；（2）由一次函数图象经过一、三、四象限，即可得出关于m的一元一次不等式组，解之即可得出结论．【解答】解：（1）∵一次函数y=（2m+1）x+m﹣3的图象经过原点，∴m﹣3=0，解得：m=3．（2）∵一次函数y=（2m+1）x+m﹣3的图象经过一、三、四象限，∴，解得：﹣＜m＜3．【点评】本题考查了一次函数图象与系数的关系以及一次函数图象上点的坐标特征，解题的关键是：（1）根据一次函数图象上点的坐标特征，找出m﹣3=0；（2）根据一次函数图象与系数的关系，找出关于m的一元一次不等式组．20．（8分）（2017春•永定区期末）已知：如图，四边形ABCD中，AB⊥BC，AB=1，BC=2，CD=2，AD=3，求四边形ABCD的面积．【分析】先根据勾股定理求出AC的长度，再根据勾股定理的逆定理判断出△ACD的形状，再利用三角形的面积公式求解即可．【解答】解：连接AC．∵∠ABC=90°，AB=1，BC=2，∴AC==，在△ACD中，AC2+CD2=5+4=9=AD2，∴△ACD是直角三角形，∴S四边形ABCD=AB•BC+AC•CD，=×1×2+××2，=1+．故四边形ABCD的面积为1+．【点评】本题考查的是勾股定理的逆定理及三角形的面积，能根据勾股定理的逆定理判断出△ACD的形状是解答此题的关键．21．（10分）（2017春•永定区期末）为了进一步了解某校八年级学生的身体素质情况，体育老师对该校八年级（1）班50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图，图表如下所示：组别次数x 频数（人数）第1组80≤x＜100 6第2组100≤x＜120 8第3组120≤x＜140 a第4组140≤x＜160 18第5组160≤x＜180 6请结合图表完成下列问题：（1）求表中a的值；（2）请把频数分布直方图补充完整；（3）若在一分钟内跳绳次数少于120次的为测试不合格，则该校八年级共1000人中，一分钟跳绳不合格的人数大约有多少？【分析】（1）本题需先根据表中所给的数据以及频数与频率之间的关系即可求出答案；（2）本题需根据频数分布表中的数据即可将直方图补充完整；（3）从表格中可以知道在一分钟内跳绳次数少于120次的有两个小组，共6+8=14人，然后除以总人数即可求出该校九年级（1）班学生进行一分钟跳绳不合格的概率，然后即可得出人数；【解答】解：（1）a=50﹣（6+8+18+6）=12；（2）频数分布直方图如图所示：（3）抽样调查中不合格的频率为：=0.28，估计该年级学生不合格的人数大约有1000×0.28=280（个）答：估计该年级学生不合格的人数大约有280个人．【点评】此题主要考查读频数分布直方图的能力和利用统计图获取信息的能力．用到的知识点为：概率=所求情况数与总情况数之比．22．（10分）（2017春•永定区期末）如图，在菱形ABCD中，∠ABC 与∠BAD的度数比为1：2，周长是32cm．求：（1）两条对角线的长度；（2）菱形的面积．【分析】（1）首先证明△ABC是等边三角形，解直角三角形OAB即可解决问题；（2）菱形的面积等于对角线乘积的一半；【解答】解：（1）菱形ABCD的周长为32cm，∴菱形的边长为32÷4=8cm∵∠ABC：∠BAD=1：2，∠ABC+∠BAD=180°（菱形的邻角互补），∴∠ABC=60°，∠BCD=120°，∴△ABC是等边三角形，∴AC=AB=8cm，∵菱形ABCD对角线AC、BD相交于点O，∴AO=CO，BO=DO且AC⊥BD，∴BO=4cm，∴BD=8cm；（2）菱形的面积=AC•BD=×8×8=32（cm2）．【点评】本题考查菱形的性质、等边三角形的判定和性质、解直角三角形等知识，解题的关键是证明△ABC是等边三角形，属于中考常考题型．23．（10分）（2017春•永定区期末）甲、乙两地相距300km，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA表示货车离甲地距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地距离y（km）与时间x（h）之间的函数关系．请根据图象，解答下列问题：（1）线段CD表示轿车在途中停留了0.5 h；（2）货车的平均速度是60 km/h；（3）求线段DE对应的函数解析式．【分析】（1）根据点C、D的横坐标，即可求出轿车在途中停留的时间；（2）根据速度=路程÷时间，即可求出货车的平均速度；（3）观察函数图象，找出点的坐标，利用待定系数法即可求出线段DE对应的函数解析式．【解答】解：（1）2.5﹣2=0.5（h）．故答案为：0.5．（2）300÷5=60（km/h）．故答案为：60．（3）设线段DE对应的函数解析式为y=kx+b（2.5≤x≤4.5），将点D（2.5，80）、点E（4.5，300）代入y=kx+b，，解得：．∴线段DE对应的函数解析式为y=110x﹣195（2.5≤x≤4.5）．【点评】本题考查了一次函数的应用以及待定系数法求一次函数解析式，解题的关键是：（1）利用点D的横坐标﹣点C的横坐标，求出停留时间；（2）根据数量关系，列式计算；（3）根据点的坐标，利用待定系数法求出线段DE的函数解析式．24．（12分）（2017春•永定区期末）如图，在矩形ABCD中，AB=1cm，AD=3cm，点Q从A点出发，以1cm/s的速度沿AD向终点D运动，点P从点C出发，以1cm/s的速度沿CB向终点B运动，当这两点中有一点到达自己的终点时，另一点也停止运动，两点同时出发，运动了t秒．（1）当0＜t＜3，判断四边形BQDP的形状，并说明理由；（2）求四边形BQDP的面积S与运动时间t的函数关系式；（3）求当t为何值时，四边形BQDP为菱形．【分析】（1）先判断出AD∥BC，AD=BC=3，再由运动知，AQ=PC=t，即可得出结论；（2）利用平行四边形的面积公式即可得出结论；（3）利用勾股定理表示出BQ，再由BQ=BP建立方程求解即可得出结论．【解答】解：（1）∵四边形ABCD是矩形，∴AD∥BC，AD=BC=3，由运动知，AQ=t，PC=t，∴AQ=PC，∴AD﹣AQ=BC﹣PC，∴DQ=BP，∵AD∥BC，∴四边形BQDP为平行四边形，（2）由（1）知，四边形BQDP是平行四边形，∵PC=t，∴BP=BC﹣PC=3﹣t，∴S=BP×AB=（3﹣t）×1=﹣t+3（3）如图，在Rt△ABQ中，AQ=t，AB=1，根据勾股定理得，BQ==，由运动知，CP=t，∴BP=3﹣t，∵平行四边形BQDP是菱形，∴BQ=BP，∴=3﹣t，∴t=，当时，四边形BQDP为菱形．【点评】此题是四边形综合题，主要考查了矩形的性质，平行四边形的判定和性质，菱形的性质，解（1）的关键是得出AQ=PC，解（2）的关键是利用平行四边形的面积公式求解，解（3）的关键是表示出BQ，用BQ=BP建立方程求解，是一道中等难度的题目．厚薄读书法：复习课本要厚薄结合著名数学家华罗庚先生说:“书要能从薄读到厚,还要能从厚读到薄。

北师版八年级数学下册 1.4.1角平分线的性质定理及其逆定理培优训练(含答案)

北师版八年级数学下册1.4.1 角平分线的性质定理及其逆定理培优训练一、选择题（共10小题，3*10=30）1.如图，直线l 1，l 2，l 3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有( )A.1处B.2处C.3处D.4处2．如图，OP 为∠AOB 的平分线，PC ⊥OA ，PD ⊥OB ，垂足分别是C ，D ，则下列结论错误的是( )A ．PC ＝PDB ．∠CPO ＝∠DOPC ．∠CPO ＝∠DPOD ．OC ＝OD3．如图，点P 是∠BAC 内一点，且到AB ，AC 的距离(PE ，PF 的长)相等，则△PEA ≌△PFA 的依据是( )A ．HLB ．ASAC ．SSSD ．SAS4. 作∠AOB 的平分线时，以O 为圆心，某一长度为半径作弧，与OA ，OB 分别相交于C ，D ，然后分别以C ，D 为圆心，适当的长度为半径作弧，使两弧相交于一点，则这个适当的长度为( )A ．大于12CDB ．等于12CD C ．小于12CD D ．以上都不对 5. 如图，OP 平分∠AOB ，PA ⊥OA ，PB ⊥OB ，垂足分别为A ， B ．下列结论中不一定成立的是()A．PA＝PB B．PO平分∠APBC．OA＝OB D．AB垂直平分OP6. 如图在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于D，如果AC=3 cm，那么AE+DE 等于( )A.2cmB.3cmC.4cmD.5cm7. 如图，在Rt△ABC中，∠C=90°，BD是∠ABC的平分线，交AC于点D，若CD=n，AB=m，则△ABD的面积是( )A. 1mnB. 12mn C.2mn D.13mn8. 如图，AB=AD，CB=CD，AC、BD相交于点O，则下列结论正确的是( )A. OA=OCB. 点O到AB、CD的距离相等C. ∠BDA=∠BDCD. 点O到CB、CD的距离相等9. 如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD的面积是()A．24 B．30C．36 D．4210．如图，在△ABC中，AB＝AC，AD是中线，DE⊥AB，DF⊥AC，垂足分别为E，F.则下列4个结论：①AB上任一点与AC上任一点到点D的距离相等；②AD上任一点到AB，AC 的距离相等；③∠BDE＝∠CDF；④∠1＝∠2.正确的有()A．1个B．2个C．3个D．4个二．填空题（共8小题，3*8=24）11．在正方形网格中，∠AOB和点P，Q，M，N的位置如图所示，到∠AOB两边距离相等的点应是点________.12. 如图，∠AOB=60°，PD⊥OA于D，PE⊥OB于E，且PD=PE，则∠1=________13. 如图，△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，且AB＝6cm，则△DEB的周长为________.14．在Rt△ABC中，∠C＝90°，若BC＝10，AD平分∠BAC交BC于点D，且BD∶CD＝3∶2，则点D到线段AB的距离为___.15. 如图，AD是△ABC中∠BAC的平分线，DE⊥AB于点E，S△ABC＝7，DE＝2，AB＝4，则AC的长是_______.16．如图，在△ABC中，∠BAC＝60°，点D在BC上，DE⊥AB于点E，DF⊥AC于点F，且DE＝DF，若DE＝4，则AD＝______.17. 如图，在△ABC 中，∠C ＝90°，AC ＝8，DC ＝13AD ，BD 平分∠ABC ，则点D 到AB 的距离等于_______.18．如图，在△ABC 中，∠ABC ＝120°，∠C ＝26°，且DE ⊥AB ，DF ⊥AC ，DE ＝DF ，则∠ADC 的度数为_______.三．解答题（共7小题， 46分）19．(6分) 在△ABC 中，AB=BC ，∠ABC=84°，BD 是∠ABC 的平分线，DE ∥BC ；求∠EDB 的度数.20．(6分) 如图，AB ⊥AC ，BF 是∠ABC 的角平分线，若∠BFC=110°，求∠C 的度数？21．(6分)已知：如图△ABC中，AB=AC，CD、BE是△ABC的角平分线；求证：AD=AE．22．(6分) 如图，在△ABC中，∠B＝30°，∠C＝45°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E.若DE＝1，求BC的长.23．(6分) 如图，AB∥CD，BP和CP分别平分∠ABC和∠DCB，AD过点P，且与AB垂直．若AD＝8，求点P到BC的距离.24．(8分) 如图，四边形ABCD中，∠B＝90°，AB∥CD，M为BC边上的一点，且AM平分∠BAD，DM平分∠ADC.(1)求证：AM⊥DM；(2)若BC＝8，求点M到AD的距离．25．(8分)如图，在△ABC中，∠BAC＝90°，AD⊥BC，垂足为D，求作∠ABC的平分线，分别交AD，AC于P，Q两点；并证明AP＝AQ.(要求：尺规作图，保留作图痕迹，不写作法)参考答案1-5DBAAD 6-10 BBDBC11．M12. 30°13. 6cm14. 415．316. 817．218. 137°19. 解：因为AB=BC ，所以可知三角形ABC 是等腰三角形，即∠ABC=∠ACB=84°，因为BD 是∠ABC 的平分线，所以∠DBC=84°÷2=42°；因为DE ∥BC ，所以∠EDB=∠DBC=42°20. 解：∵∠BFC=110°，根据三角形的外角等于不相邻的两个内角之和，可以得到∠ABF+∠A=110° ∴∠ABF=110°—90°=20°，∵BF 是∠ABC 的角平分线，∴∠ABC=2∠ABF=40°，即在三角形ABC 中∠C=180°—90°—40°=50°21. 证明：∵AB=AC （已知），∴∠ABC=∠ACB ．∵CD 、BE 是△ABC 的角平分线（已知），∴∠1=12∠ABC ，∠2=12∠ACB ， ∴∠1=∠2．又∵∠A=∠A （已知），∴△ADC ≌△AEB ．∴AD=AE ．22. 解：如图，作DF ⊥AC 于点F.∵AD 为∠BAC 的平分线，且DE ⊥AB 于点E ，DF ⊥AC 于点F ， ∴DE ＝DF ＝1.在Rt △BED 中，∠B ＝30°，∴BD ＝2DE ＝2.在Rt △CDF 中，∠C ＝45°，∴∠CDF ＝45°＝∠C.∴CF ＝DF ＝1. ∴CD ＝ 2.∴BC ＝BD ＋CD ＝2＋ 2.23. 解：如图，过点P 作PE ⊥BC 于点E ，∵AB ∥CD ，PA ⊥AB ，∴PD ⊥CD.∵BP 和CP 分别平分∠ABC 和∠DCB ，∴PA ＝PE ，PD ＝PE.∴PE ＝PA ＝PD.∵PA ＋PD ＝AD ＝8，∴PA ＝PD ＝4.∴PE ＝4.24. (1)证明：∵AM 平分∠BAD ，DM 平分∠ADC ，∴∠MAD ＝12∠BAD ，∠ADM ＝12∠ADC. ∵AB ∥CD ，∴∠BAD ＋∠ADC ＝180°，∴∠MAD ＋∠ADM ＝12(∠BAD ＋∠ADC)＝90°. 又∵∠AMD ＋∠MAD ＋∠ADM ＝180°，∴∠AMD ＝90°，∴AM ⊥DM(2)过点M 作MN ⊥AD 于点N.∵AB ∥DC ，∠B ＝90°，∴∠C ＝90°，即BM ⊥AB ，MC ⊥DC.又∵AM ，DM 分别平分∠BAD ，∠ADC ，∴BM ＝MN ，MN ＝MC ，∴MN ＝12BC ＝4， ∴点M 到AD 的距离为425. 解：如图，BQ 就是∠ABC 的平分线．证明如下：作AM ⊥PQ 于点M ，则∠AMP ＝∠AMQ ＝90°.∵AD ⊥BC ，∴∠ADB ＝90°.∴∠BPD ＋∠PBD ＝90°. ∵∠BAC ＝90°，∴∠AQP ＋∠ABQ ＝90°. ∵∠ABQ ＝∠PBD ，∴∠BPD ＝∠AQP.∵∠BPD ＝∠APQ ，∴∠APQ ＝∠AQP.在△APM 和△AQM 中，⎩⎪⎨⎪⎧∠APQ ＝∠AQP ，∠AMP ＝∠AMQ ，AM ＝AM ，∴△APM ≌△AQM(AAS)．∴AP ＝AQ.。

八年级数学上册12.3角的平分线的性质同步练习含答案解析

编号：54158543442893744576892562学校：观音市阳沅镇普贤学校*教师：黑白双雄*班级：白云伍班*《12.3 角的平分线的性质》一、填空题1．如图，∠B=∠D=90゜，根据角平分线性质填空：（1）若∠1=∠2，则______=______．（2）若∠3=∠4，则______=______．2．如图，BD是∠ABC的平分线，DE⊥AB于E，DF⊥BC于F，AB=12，BC=15，S△ABD =36，则S△BCD=______．3．如图，△ABC的三边AB、BC、CA长分别是20、30、40，其三条角平分线将△ABC分成三个三角形，则S△ABO ：S△BCO：S△CAO等于______．4．如图，AD是△ABC的角平分线，若AB=2AC．则S△ABD ：S△ACD=______．二、选择题5．如图，已知点P、D、E分别在OC、OA、OB上，下列推理：①∵OC平分∠AOB，∴PD=PE；②∵OC平分∠AOB，PD⊥OA，PE⊥OB，∴PD=PE；③∵PD⊥OA，PE⊥OB，∴PD=PE；其中正确的个数有（）A．0个B．1个C．2个D．3个6．如图△ABC中，∠ACB=90゜，AD平分∠BAC交BC于D，DE垂直AB于E，若DE=1.5cm，BD=3cm，则BC=（）A．3cm B．7.5cm C．6cm D．4.5cm7．在△ABC中，∠C=90゜，AD平分∠BAC交BC于D，BD：DC=3：2，点D到AB的距离为6，则BC 长为（）A．10 B．20 C．15 D．258．如图，在△ABC中，∠B、∠C的角平分线交于点0，OD⊥AB于D，OE⊥AC于E，则OD与OE的大小关系是（）A．OD＞OE B．OD＜OE C．OD=OE D．不能确定三、解答题9．如图，△ABC中，∠C=90゜，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，且BE=CF，求证：（1）DE=DC；（2）BD=DF．10．如图，四边形ABCD中，AB=AD，CB=CD，点P是AC上一点，PE⊥BC于E，PF⊥CD于F，求证：PE=PF．11．已知，如图，BD是∠ABC的平分线，AB=BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M、N．试说明：PM=PN．=90，AB=18，BC=12，求DE的长．12．如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC13．如图．已知在△ABC中，∠A、∠B的角平分线交于点O，过O作OP⊥BC于P，OQ⊥AC于Q，OR ⊥AB于R，AB=7，BC=8，AC=9．（1）求BP、CQ、AR的长．（2）若BO的延长线交AC于E，CO的延长线交AB于F，若∠A=60゜，求证：OE=OF．《12.3 角的平分线的性质》参考答案与试题解析一、填空题1．如图，∠B=∠D=90゜，根据角平分线性质填空：（1）若∠1=∠2，则BC = DC ．（2）若∠3=∠4，则AB = AD ．【考点】角平分线的性质．【分析】（1）根据角平分线性质推出即可；（2）根据角平分线性质推出即可．【解答】解：（1）∵∠B=∠D=90°，∴AB⊥BC，AD⊥DC，∵∠1=∠2，∴BC=CD，故答案为：BC，DC．（2）∵AB⊥BC，AD⊥DC，∵∠3=∠4，∴AB=AD，故答案为：AB，AD．【点评】本题考查了角平分线性质的应用，注意：角平分线上的点到角两边距离相等．2．如图，BD是∠ABC的平分线，DE⊥AB于E，DF⊥BC于F，AB=12，BC=15，S△ABD =36，则S△BCD= 45 ．【考点】角平分线的性质．【分析】首先根据△ABD的面积计算出DE的长，再根据角平分线上的点到角两边的距离相等可得DE=DF，然后计算出DF的长，再利用三角形的面积公式计算出△BCD的面积即可．【解答】解：∵S△ABD=36，∴•AB •ED=36，×12×ED=36，解得：DE=6，∵BD 是∠ABC 的平分线，DE ⊥AB 于E ，DF ⊥BC 于F ，∴DE=DF ，∴DF=6，∵BC=15，∴S △BCD =•CB •DF=×15×6=45，故答案为：45．【点评】此题主要考查了角平分线的性质，关键是掌握角平分线上的点到角两边的距离相等．3．如图，△ABC 的三边AB 、BC 、CA 长分别是20、30、40，其三条角平分线将△ABC 分成三个三角形，则S △ABO ：S △BCO ：S △CAO 等于 2：3：4 ．【考点】角平分线的性质；三角形的面积．【专题】常规题型．【分析】由角平分线的性质可得，点O 到三角形三边的距离相等，即三个三角形的AB 、BC 、CA 的高相等，利用面积公式即可求解．【解答】解：过点O 作OD ⊥AC 于D ，OE ⊥AB 于E ，OF ⊥BC 于F ，∵O 是三角形三条角平分线的交点，∴OD=OE=OF ，∵AB=20，BC=30，AC=40，∴S △ABO ：S △BCO ：S △CAO =2：3：4．故答案为：2：3：4．【点评】此题主要考查角平分线的性质和三角形面积的求法，难度不大，作辅助线很关键．4．如图，AD 是△ABC 的角平分线，若AB=2AC ．则S △ABD ：S △ACD = 2 ．【分析】过D 作DM ⊥AC 于M ，DN ⊥AB 于N ，根据角平分线性质得出DM=DN ，根据三角形面积公式求出即可．【解答】解：过D 作DM ⊥AC 于M ，DN ⊥AB 于N ，∵AD 是△ABC 的角平分线，∴DM=DN ，∴S △ABD ：S △ACD =（AB ×DN ）：（AC ×DM ）=AB ：AC=2AC ：AC=2，故答案为：2．【点评】本题考查了角平分线性质的应用，注意：角平分线上的点到角两边的距离相等．二、选择题5．如图，已知点P 、D 、E 分别在OC 、OA 、OB 上，下列推理：①∵OC 平分∠AOB ，∴PD=PE ；②∵OC 平分∠AOB ，PD ⊥OA ，PE ⊥OB ，∴PD=PE ；③∵PD ⊥OA ，PE ⊥OB ，∴PD=PE ；其中正确的个数有（）A ．0个B ．1个C ．2个D ．3个【考点】角平分线的性质．【分析】直接根据角平分线的性质进行解答即可．【解答】解：∵OC 平分∠AOB ，PD ⊥OA ，PE ⊥OB ，∴PD=PE ．故选B ．【点评】本题考查的是角平分线的性质，即角平分线上的点到角两边的距离相等．6．如图△ABC 中，∠ACB=90゜，AD 平分∠BAC 交BC 于D ，DE 垂直AB 于E ，若DE=1.5cm ，BD=3cm ，则BC=（）A ．3cmB ．7.5cmC ．6cmD ．4.5cm【分析】根据角平分线的性质得出CD长，代入BC=BD+DC求出即可．【解答】解：∵∠ACB=90°，∴AC⊥BC，∵DE⊥AB，AD平分∠BAC，∴DE=DC=1.5cm，∵BD=3cm，∴BC=BD+DC=3cm+1.5cm=4.5cm，故选D．【点评】本题考查了角平分线性质的应用，注意：角平分线上的点到角两边的距离相等．7．在△ABC中，∠C=90゜，AD平分∠BAC交BC于D，BD：DC=3：2，点D到AB的距离为6，则BC 长为（）A．10 B．20 C．15 D．25【考点】角平分线的性质．【分析】过点D作DE⊥AB于E，根据角平分线上的点到角的两边的距离相等可得DC=DE，然后求出BD的长，再根据BC=BD+DE代入数据进行计算即可得解．【解答】解：如图，过点D作DE⊥AB于E，∵点D到AB的距离为6，∴DE=6，∵∠C=90°，AD平分∠BAC交BC于D，∴DC=DE=6，∵BD：DC=3：2，∴BD=×3=9，∴BC=BD+DE=9+6=15．故选C．【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键，作出图形更形象直观．8．如图，在△ABC中，∠B、∠C的角平分线交于点0，OD⊥AB于D，OE⊥AC于E，则OD与OE的大小关系是（）A．OD＞OE B．OD＜OE C．OD=OE D．不能确定【考点】角平分线的性质．【分析】根据三角形的角平分线相交于一点，连接AO，则AO平分∠BAC，然后根据角平分线上的点到角的两边的距离相等解答．【解答】解：如图，连接AO，∵∠B、∠C的角平分线交于点0，∴AO平分∠BAC，∵OD⊥AB，OE⊥AC，∴OD=OE．故选C．【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，根据三角形的角平分线相交于一点作辅助线并判断出AO平分∠BAC是解题的关键．三、解答题9．如图，△ABC中，∠C=90゜，AD是∠BAC的平分线，DE⊥AB于E，F在AC上，且BE=CF，求证：（1）DE=DC；（2）BD=DF．【考点】角平分线的性质；全等三角形的判定与性质．【专题】证明题．【分析】（1）根据角平分线上的点到角的两边的距离相等证明即可；（2）利用“边角边”证明△BDE和△FDC全等，再根据全等三角形对应边相等证明即可．【解答】证明：（1）∵∠C=90°，AD是∠BAC的平分线，DE⊥AB，∴DE=DC；（2）在△BDE和△FDC中，，∴△BDE≌△FDC（SAS），∴BD=DF．【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，全等三角形的判定与性质，是基础题，熟记性质是解题的关键．10．如图，四边形ABCD中，AB=AD，CB=CD，点P是AC上一点，PE⊥BC于E，PF⊥CD于F，求证：PE=PF．【考点】全等三角形的判定与性质；角平分线的性质．【专题】证明题．【分析】根据“SSS”可得到△ABC≌△ADC，则∠BCA=∠DCA，再利用角平分线的性质即可得到结论．【解答】证明：在△ABC和△ADC中，，∴△ABC≌△ADC（SSS），∴∠BCA=∠DCA，∵PE⊥BC于E，PF⊥CD于F，∴PE=PF．【点评】本题考查了全等三角形的判定与性质：三边都对应相等的两三角形全等；全等三角形的对应边相等，对应角相等．角平分线的性质：角的平分线上的点到角的两边的距离相等．11．已知，如图，BD是∠ABC的平分线，AB=BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M、N．试说明：PM=PN．【考点】角平分线的性质；全等三角形的判定与性质．【专题】证明题．【分析】根据角平分线的性质以及已知条件证得△ABD≌△CBD（SAS），然后由全等三角形的对应角相等推知∠ADB=∠CDB；再由垂直的性质和全等三角形的判定定理AAS判定△PMD≌△PND，最后根据全等三角形的对应边相等推知PM=PN．【解答】证明：在△ABD和△CBD中，AB=BC（已知），∠ABD=∠CBD（角平分线的性质），BD=BD（公共边），∴△ABD≌△CBD（SAS），∴∠ADB=∠CDB（全等三角形的对应角相等）；∵PM⊥AD，PN⊥CD，∴∠PMD=∠PND=90°；又∵PD=PD（公共边），∴△PMD≌△PND（AAS），∴PM=PN（全等三角形的对应边相等）．【点评】本题考查了角平分线的性质、全等三角形的判定与性质．由已知证明△ABD≌△CBD是解决的关键．=90，AB=18，BC=12，求DE的长．12．如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC【考点】角平分线的性质．【分析】过点D作DF⊥BC于F，根据角平分线上的点到角的两边的距离相等可得DE=DF，然后根据三角形的面积列出方程求解即可．【解答】解：如图，过点D作DF⊥BC于F，∵BD是∠ABC的平分线，DE⊥AB，∴DE=DF，∴S=AB•DE+BC•DF=90，△ABC即×18•DE+×12•DE=90，解得DE=6．【点评】本题考查了角平分线上的点到角的两边的距离相等的性质，三角形的面积，熟记性质并作出辅助线是解题的关键．13．如图．已知在△ABC中，∠A、∠B的角平分线交于点O，过O作OP⊥BC于P，OQ⊥AC于Q，OR ⊥AB于R，AB=7，BC=8，AC=9．（1）求BP、CQ、AR的长．（2）若BO的延长线交AC于E，CO的延长线交AB于F，若∠A=60゜，求证：OE=OF．【考点】角平分线的性质；全等三角形的判定与性质．【分析】（1）根据角平分线性质得出OR=OQ=OP，根据勾股定理起床AR=AQ，CQ=CP，BR=BP，得出方程组，求出即可；（2）过O作OM⊥AC于肘，ON⊥AB于N，求出OM=ON，证出△FON≌△EOM即可．【解答】解：连接AO，OB，OC，∵OP⊥BC，OQ⊥AC，OR⊥AB，∠A、∠B的角平分线交于点O，∴OR=OQ，OR=OP，∴由勾股定理得：AR2=OA2﹣OR2，AQ2=AO2﹣OQ2，∴AR=AQ，同理BR=BP，CQ=CP，即O在∠ACB角平分线上，设BP=BR=x，CP=CQ=y，AQ=AR=z，则x=3，y=5，z=4，∴BP=3，CQ=5，AR=4．（2）过O作OM⊥AC于M，ON⊥AB于N，∵O在∠A的平分线，∴OM=ON，∠ANO=∠AMO=90°，∵∠A=60°，∴∠NOM=120°，∵O在∠ACB、∠ABC的角平分线上，∴∠EBC+∠FCB=（∠ABC+∠ACB）=×（180°﹣∠A）=60°，∴∠FON=∠EOM，在△FON和△EOM中∴△FON≌△EOM，∴OE=OF．【点评】本题考查了角平分线性质和全等三角形的性质和判定的应用，注意：角平分线上的点到角两边的距离相等．。

八年级数学角平分线的性质及其逆定理同步练习

人教版八年级数学上册《角平分线性质定理及逆定理》练习题

人教版八年级数学上册12.3角的平分线的性质同步练习解析版

2018秋八年级数学上册第13章全等三角形13.5逆命题与逆定理13.5.3角平分线习题课件新版华东师大版

八年级数学角平分线的性质及其逆定理同步练习

角平分线的性质专项练习(含解析)

角平分线性质定理和逆定理备考练习

角平分线的性质(4种题型)-2023年新八年级数学核心知识点与常见题型(人教版)(解析版)

人教版八年级上数学12.3 角的平分线的性质 _同步练习及答案(含答案)

《123角平分线的性质》同步测试题((有答案))-(新课标人教版数学八年级)AlHKMK

角平分线的性质定理及其逆定理 习题精选及答案(一)

八年级数学角平分线的性质及其逆定理同步练习

八年级数学上册《第十二章 角平分线的性质》同步练习及答案(人教版)

2020-2021学年八年级数学北师大版下册角平分线的性质定理及其逆定理 同步练习(附答案)

湘教版八年级下册数学角平分线的性质定理的逆定理同步测试题

北师版八年级数学下册 1.4.1角平分线的性质定理及其逆定理 培优训练(含答案)

八年级数学上册12.3角的平分线的性质同步练习含答案解析

角平分线的性质定理及其逆定理习题精选及答案(一)

八年级数学上册《第十二章角平分线的性质》同步练习及答案(人教版)

2020-2021学年八年级数学北师大版下册角平分线的性质定理及其逆定理同步练习(附答案)

北师版八年级数学下册 1.4.1角平分线的性质定理及其逆定理培优训练(含答案)