数学期末复习试卷1

合集下载

五年级数学下册期末试卷复习练习(Word版含答案)(1)

五年级数学下册期末试卷复习练习(Word版含答案)(1)一、选择题1．将四个长10cm，宽5cm，高2cm的长方体盒子，用彩纸包在一起，最省包装纸的方法是（）。

A．B．C．D．2．一个长方体，它有一组相对的面是正方形，其余四个面的面积（）。

A．互不相等B．一定相等C．可能不等D．无法确定3．一个数的最大因数是36，这个数的最小倍数是（）。

A．1 B．36 C．18 D．94．暑假里，冬冬每6天去一次游泳，丁丁每4天去一次游冰。

8月1日他们同时去游泳，下一次他们同时去游泳将是8月（）日。

A．12 B．13 C．24 D．255．34与912这两个分数（）。

A．大小相等B．意义相同C．分数单位一样D．都是最简分数6．第一堆沙子x千克，比第二堆沙子重13，第二堆沙子重（）千克。

A．13x B．23x C．34x D．43x7．天柱山推出甲，乙两种购票优惠方案（如下）。

一家2个大人带3个小孩去游玩，选择（）方案更省钱。

甲方案：成人每位100元，小孩每位40元。

乙方案：团体5人及5人以上每位80元。

A．甲B．乙C．甲和乙8．古希腊人认为：如果一个数恰好等于它的所有因数（本身除外）相加之和，那么这个数就是“完美数”。

例如：6有四个因数1、2、3、6，除本身6以外，还有1、2、3三个因数，6＝1＋2＋3，恰好是本身除外的所有因数之和，所以6就是“完美数”。

下面的数中（）是“完美数”。

A．12 B．20 C．25 D．28二、填空题9．45000立方厘米＝（________）立方米 8.09立方米＝（________）立方分米6.7L＝（________）立方厘米 3670mL＝（________）立方分米10．分母是6的最大的真分数是（________），它的分数单位是（________），再加上（________）个这样的分数单位就是最小的质数。

11．一包糖果，无论是平均分给2个人，平均分给3个人，还是平均分给5个人，都正好分完。

七年级下册数学期末复习试卷(一附答案

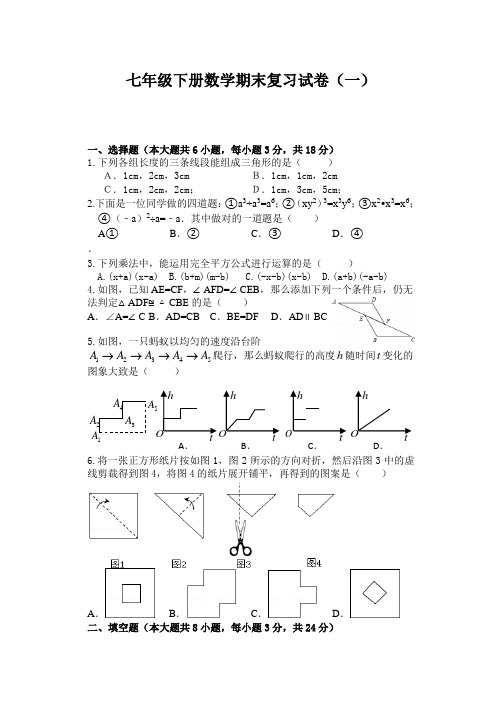
七年级下册数学期末复习试卷（一）一、选择题（本大题共6小题，每小题3分，共18分） 1.下列各组长度的三条线段能组成三角形的是（）Ａ．1cm ，2cm ，3cm Ｂ．1cm ，1cm ，2cm Ｃ．1cm ，2cm ，2cm ；Ｄ．1cm ，3cm ，5cm ；2.下面是一位同学做的四道题：①a 3+a 3=a 6；②（xy 2）3=x 3y 6；③x 2•x 3=x 6；2A.(x+a)(x-a)B.(b+m)(m-b)C.(-x-b)(x-b)D.(a+b)(-a-b) 4.如图，已知AE=CF ，∠AFD=∠CEB ，那么添加下列一个条件后，仍无法判定△ADF ≌△CBE 的是（）A ．∠A=∠CB ．AD=CBC ．BE=DFD ．AD ∥BC5.如图，一只蚂蚁以均匀的速度沿台阶12345A A AA A →→→→爬行，那么蚂蚁爬行的高度h 随时间t 变化的图象大致是（）6.将一张正方形纸片按如图1，图2所示的方向对折，然后沿图3中的虚线剪裁得到图4，将图4的纸片展开铺平，再得到的图案是（）A ．B ．C ．D ．二、填空题（本大题共8小题，每小题3分，共24分）1A 2A 3A 4A 5A A ．B ．C ．D ．7.计算21()2--= _______8.如图有4个冬季运动会的会标，其中不是轴对称图形的有______个9.已知等腰三角形的一边长为4，另一边长为8，则这个等腰三角形的周长为___________． 10.已知：2211,63a b a b -=-=，则22a b +=_______ 11.如图，是我们生活中经常接触的小刀，刀柄外形是一个直角梯形（挖去一小半圆），刀片上、下是平行的，转动刀片时会形成∠1、∠2，则∠1+∠2=_______． 12.如图所示，∠E=∠F=90°，∠B=∠C ，AE=AF ．给出下列结论：①∠1=∠2；②BE=CF ；③△ACN ≌△ABM ；④CD=DN ．其中正确的结论是．（将你认为正确的结论的序号都填上）第11题图第12题图第13题图13.如图是叠放在一起的两张长方形卡片，图中有∠1、∠2、∠3，则其中一定相等的是_____14.如果a 2+b 2+2c 2+2ac-2bc=0,那么2015a b+的值为三、（本大题共4小题，每小题6分，共24分） 15.已知：2x ﹣y=2，求：〔（x 2+y 2）﹣（x ﹣y ）2+2y （x ﹣y ）〕÷4y 的值．16.若2(1)()a a a b --- =4，求222a b ab +-的值17.已知：如图，AB ∥CD ，∠ABE=∠DCF ，说明∠E=∠F 的理由．18.如图,把宽为2cm的纸条ABCD沿EF，GH同时折叠，B、C两点恰好落在AD边的P点处，若△PFH的周长为10cm，求长方形ABCD的面积．四、（本大题共3小题，每小题8分，共24分）19.将一副直角三角尺BAC和BDE如图放置，其中∠BCA=30°，∠BED=45°，（1）若∠BFD=75°，判断AC与BE的位置关系，并说明理由；（2）连接EC，如果AC∥BE，AB∥EC，求∠CED的度数．20.投掷一枚普通的正方体骰子24次．（1）你认为下列四种说法中正确的为（填序号）；①出现1点的概率等于出现3点的概率；②投掷24次，2点一定会出现4次；③投掷前默念几次“出现4点”,投掷结果出现4点的可能性就会加大；④若只连续投掷6次，出现的点数之和不可能等于37．（2）求出现奇数的概率；（3）出现6点大约有多少次？21.如图所示，在△ABC中，DM、EN分别垂直平分AB和AC，交BC于D、E，(1)若∠DAE=50°，求∠BAC的度数；(2)若△ADE的周长为19cm，求BC的长．五、（本大题共2小题，每小题9分，共18分）22.小明的父亲在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便，他带了一些零钱备用．他先按市场价售出一些后，又降价出售．售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示，结合图像回答下列问题：(1)降价前他每千克西瓜出售的价格是多少?(2)随后他按每千克下降0.5元将剩余的西瓜售完，这时他手中的钱(含备用的钱)是450元，问他一共批发了多少千克的西瓜?(3)小明的父亲这次一共赚了多少钱?23.如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D 不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．（1）当∠BDA=115°时，∠BAD=°；点D从B向C运动时，∠BDA逐渐变（填“大”或“小”）；（2）当DC等于多少时，△ABD≌△DCE，请说明理由；（3）在点D的运动过程中，△ADE的形状也在改变，判断当∠BDA等于多少度时，△ADE是等腰三角形．六、（本大题共1小题，共12分）24.如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）①找出图1中的一对全等三角形并说明理由；②写出图1中线段DE、AD、BE满足的数量关系;（不必说明理由）（2）当直线MN绕点C旋转到图2的位置时, 探究线段DE、AD、BE之间的数量关系并说明理由；（3）当直线MN绕点C旋转到图3的位置时,问DE、AD、BE之间又具有怎样的数量关系？直接写出这个数量关系（不必说明理由）．七年级下册综合复习试卷（一）参考答案1~6. CBDBBB 7.4 8.3 9.20 10.1 11.90°12.①②③13.∠2=∠314.1 15. 1．16.8 17.略18.解：∵把宽为2cm的纸条ABCD沿EF，GH同时折叠，B、C两点恰好落在AD边的P点处，∴BF=PF，PH=CH，∵△PFH的周长为10cm，∴PF+FH+HC=BC=10cm，∴长方形ABCD的面积为：2×10=20（cm 2），19. （1）AC∥BE，理由略（2）45°．20. （1）①④（2）12（3）421. （1）∠BAC=115°；（2）BC=19cm．22（1）3.5元（2）120千克，（3）450﹣120×1.8﹣50=184元，②当DA=DE时，即∠DAE=∠DEA=（180°﹣40°）=70°，24. 解：（1）①△ADC≌△CEB．理由如下：：∵∠ACB=90°，∠ADC=90°，∠BEC=90°∴∠ACD+∠DAC=90°，∠ACD+∠BCE=90°，∴∠DAC=∠BCE，在△ADC与△BEC中，，∴△ADC≌△BEC（AAS）；②DE=CE+CD=AD+BE．理由如下：由①知，△ADC≌△BEC，∴AD=CE，BE=CD，∵DE=CE+CD，∴DE=AD+BE；（2）∵AD⊥MN于D，BE⊥MN于E．∴∠ADC=∠BEC=∠ACB=90°，∴∠CAD+∠ACD=90°，∠ACD+∠BCE=90°．∴∠CAD=∠BCE．在△ADC和△CEB中，∴△ADC≌△CEB．∴CE=AD，CD=BE．∴DE=CE﹣CD=AD﹣BE．（3）同（2），易证△ADC≌△CEB．∴AD=CE，BE=CD∵CE=CD﹣ED∴AD=BE﹣ED，即ED=BE﹣AD；当MN旋转到图3的位置时，AD、DE、BE所满足的等量关系是DE=BE﹣AD（或AD=BE﹣DE，BE=AD+DE等）．。

期末考试复习题及答案2021数学卷选做题 (1)

一、选择题1. [选做题]1-1.下列给出的赋值语句中正确的是B x=-161-2.做“紫菜鸡蛋汤”有一下几道工序......需要的最短时间是B 62[选做题]2-1.cos（a-B）cosB-sin（a-B）sinB＝A cos a2-2.若1/2a+√21-1-b I,则a,b的值分别为A 2，-√23[选做题]3-1.参数方程｛x=1+2t （t为参数）表示式的曲线是｛y＝-2+tB 直线3-2.如图，三角形所围成......最小值的点是B 点B（1,1）数学卷②一、选做题1.[选做题]1-1.在程序框图中下列图形符号叫判断框的是B 菱形1-2.某项工程的流程图如图所示（单位/min）.从开始节点①到终止节点⑦的路径有B 6条2.[选做题]2-1.在△ABC中,若sin A /a＝cos B/b,则B等于A π/22-2.复数＝1+√3i的模和幅角主值分别是A 2，60°3.[选做题]3-1.平移坐标轴，将坐标原点0,（-1，2 ），已知A……xOy中的坐标为C （2，4）3-2.下列不是线性规划问题的是C :＝6x+4y｛2x+3y≤10｛3x+2y≤12｛x≥0.y≥0一、选做题5-1.在△ABC中，若sin A/b＝cos B/b，则B等于（）C.π/45-2.在复数z＝1+√3i的模和辐角主值分别是（）A.2，60°6-1.平移坐标轴，将坐标原点移至0’（-1，2），已知点A在新坐标系X’O’y’中的坐标为（3，2），则A点在原坐标系，xOy中的坐标为（）C.（2，4）6-2.下列不是线性规划问题的是（）C.z＝6x+4y｛2x+3y≤10｛3x+2y≤12｛x≥0，y≥07-1.与A·B相等的是（）C. ——A+B7-2.某职业学校机电4班共36名学生，经统计，……扇形圆心角等于（）C.200°8-1.下列关于算法的说法，正确的有（）C.3个8-2.某项工程的网络图如图所示（单位:天），则完成该工程的最短工期为（）A.10. 59-1.函数y＝3sin（2x-π/6）的最小正周期为（）B.π9-2.复数2（3-4i）的实部和虚部分别是（）B.6，-810-1.若p、q是两个简单命题，且“p∧q”为真命题，则必有（）D.p真、q真10-2.小明的家庭全年各项支出的统计图如下图所示，以下判断中，不正确的是（）D.全年总支出为7000元11-1.如图所示程序框图的功能是（）C.求Ix-2I的值11-2.某项工程的横道图如下:若开工后第9天去检查工程，根据横道图显示，该工程应处于的工序是（）C. E、F12-1. 2sin（a+π/3）等于（）D. sin a+√3cos a12-2.复数z＝3-5i对应的点位于复平面的（）D.第四象限13-1.二进制数1011转化为十进制数是（）B. 1113-2.某校甲、乙、丙三位同学期中考试语文、数学、英语成绩如下表，则表示这三位同学数学的成绩数组是（）B.（85，89，83）14-1.下面描述的算法:第一部X=3:第二部Y＝X+4:第三部X＝X+Y:第四部输出X输出结果为（） D.1014-2.做“紫菜蛋汤”有一下几项工序:……以下说法错误的是（）D. B是E的紧前工作15-1.在△ABC中，已知AC＝2，∠ABC＝45°，∠ACB＝60°，则AB＝（）D.√615-2.下列各式复数三角形式的是（）D.2（cos65°+i sin65°）16-1.若p、q是两个简单命题，且“pVq”为假命题，则必有（）D.p假、q假16-2.下图是某品牌汽车2015年度销量直方图（单位:万辆），下列说法正确的是（）D.华南区全年销量总量最高17-1.一个完整的程序框图至少包括（）A.起、止框和输入、输出框17-2.某项工程的流程图如图所示（单位:min）.以下是关键路径的是（）A. A→E→H18-1.平移坐标轴，使点P（-4，3）在新坐标系中的坐标为P’（2，-1），则将坐标原点移至（）B. （-6，4）18-2.完成一项装修工程，请木工需付工资每人200元，……请工人的一个约束条件是（）B.（200x+180y≤5000）二、填空题4.[选做题]4-1.补充完成“按权展开式”:8844X10³+8X（10³）+4X10º10³4-2.某班从甲、乙、丙三名候选人中......，则学生乙的得票数是（27）273-1.将参数方程｛x=t （t是参数）化为普通方程是y＝4x²｛y=4t²3-2.右图中阴影部分平面区域的不等式是2x+3y≥64-1.平移坐标轴，将坐标原点移至O’（-5，6），则点A（8，-2）在新坐标系中的坐标为（13，-8）4-2.在已知P（0，0）、Q（1，0）、R（-2，4）、S（3，0）中，在不等式3x+y-6≥0所表示的平面区域的点是S5-1.将参数方程｛x＝cos6θ+1｛y=sinθ-2 （θ是参数）化为普通方程是（x-1）²+（y+2）²=15-2.设点A（0，0）、B（-1，3）、C（-1，3）、D（2，3），则与点P（1，2）位于直线x+y-1=0的同一侧的点是C（-1，3）6-1.函数y＝3/2sin（2x-π/6）的最大值为3/26-2.（3+2i）（4-i）＝14+5i。

人教版数学五年级下册期末测试卷(1-5)

五年级数学下册期末测试卷（一）（时间：７0分钟满分：100分）一、填一填。

1.12有（）个因数，17有（）个因数。

2.能同时被2、3、5整除的最大两位数是（）。

3.已知a =2×2×3×5，b =2×5×7，a 和b 的最小公倍数是（），它们的最大公约数是（）。

4.把两个棱长是10厘米的正方体粘合成一个长方体，这个长方体的表面积是（），体积是（）。

5.把3米长的绳子平均分成7段，每段长是全长的)()(，每段长（）米。

6.在a5里，当a 是（）时，这个分数是5，当a 是（）时，这个分数是1。

7.)()(15)(2416)(83==÷==（填小数）。

8.三个连续奇数的和是177，这三个数的平均数是（），其中最大的数是（）。

9.在下面每组的○里填上“＞”、“＜”或“＝”。

413829716 842831 10.3.85立方米＝（）立方分米 4升40毫升＝（）升二、我是小法官。

（对的打“√”，错的打“×”） 1.两个质数的积一定是合数。

（）2.一个假分数不能化成整数就一定能化成带分数。

（）3.长方体的6个面一定都是长方形。

（）4.五角星是轴对称图形，它只有1条对称轴。

（）5.做一个零件，甲用了21小时，乙用了31小时，甲的效率高。

（）6.把分数的分子和分母同时加上4，分数的大小不变。

（）7.大于51而小于53的分数有无数个。

（）8.一个正方体的棱长之和是12厘米，体积是1立方厘米。

（）三、选一选。

（在括号里填上正确答案的序号）1.下面几个分数中，不能化成有限小数的是（）。

A.53B.62C.81D.287 2.一个分数化成最简分数是134，原分数的分子扩大为原来的4倍后是96，那么原分数的分母是（）。

A.78 B.52 C.26 D.65 3.下列说法正确的是（）。

A.所有的质数都是奇数B.整数都比分数大C.两个奇数的差一定是奇数D.是4的倍数的数一定是偶数4.一个无盖的水桶，长a 厘米，宽b 厘米，高h 厘米，做这个水桶用料（）平方厘米。

冀教版八年级下册数学期末试卷 (1)

冀教版八年级下册数学期末试卷一、选择题（本大题共10个小题，每小题2分，满分20分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．（2分）在平面直角坐标系中，第二象限内的一点P到x轴的距离是3，到y轴的距离是2，则点P的坐标为（）A．（3，﹣2）B．（﹣3，2）C．（2，﹣3）D．（﹣2，3）2．（2分）下列调查方式，你认为最合适的是（）A．要检测一批节能灯的使用寿命，采用全面调查B．要了解滦河的水质，采用抽样调查C．某高铁站对乘车旅客实施安检，采用抽样调查D．要了解全市初中生的睡眠情况，采用全面调查3．（2分）在▱ABCD中，对角线AC、BD交于点O，若AD＝5，AC＝10，BD＝6，△BOC 的周长为（）A．13B．16C．18D．214．（2分）为了解全市6300名八年级学生的期中数学成绩，教研室随机从全部考生中抽取了500名学生的数学成绩进行分析，对于此次调查下列说法：①6300名学生是调查的总体；②500名学生的数学成绩是总体的一个样本；③每个学生的数学成绩是个体；④样本容量是500名学生．其中正确的有（）A．1个B．2个C．3个D．4个5．（2分）如图所示，在Rt△ABC中，∠A＝30°，BC＝3，D、E分别是直角边BC、AC 的中点，则DE的长为（）A．1.5B．2C．2.5D．36．（2分）据测试，拧不紧的水龙头每分钟滴出100滴水，每滴水约0.05毫升．小明洗手后没有把水龙头拧紧，水龙头以测试速度滴水，当小明离开x分钟后，水龙头滴水y毫升水，则y与x之间的函数关系式是（）A．y＝0.05x B．y＝5xC．y＝100x D．y＝0.05x+1007．（2分）如图，矩形ABCD中，对角线AC、BD交于点O，点P为AD边上一点，过点P 分别作AC、BD的垂线，垂足分别为E、F，若AB＝6，BC＝8，则PE+PF的值为（）A．4.8B．6C．8D．不能确定8．（2分）小明在计算某多边形的内角和时，由于马虎漏掉了一个角，结果得到970°，则原多边形是一个（）A．七边形B．八边形C．九边形D．十边形9．（2分）某仓库调拨一批物资，调进物资共用8小时，调进物资4小时后同时开始调出物资（调进与调出的速度保持不变）．该仓库库存物资m（吨）与时间t（小时）之间的函数关系如图所示．则这批物资从开始调进到全部调出所需要的时间是（）A．8.4小时B．8.6小时C．8.8小时D．9小时10．（2分）如图，△ABO缩小后变为△A'B'O，其中A、B的对应点分别为A'、B'，点A、B、A'、B'均在格点上，若线段AB上有点P（m，n），则点P在A'B'上的对应点P'的坐标为（）A．（，n）B．（m，n）C．（m，）D．（）二、填空题（本大题共10个小题，每小题3分，共30分，）11．（3分）把点A（3，1）向左平移2个单位，再向下平移3个单位后与点B重合，则点B 的坐标是．12．（3分）已知一组数据有40个，把它分成六组，第一组到第四组的频数分别是10，5，7，6，第五组的频率是0.2，则第六组的频率是．13．（3分）函数y＝的自变量x的取值范围是．14．（3分）如图所示，直线l1：y＝x+b与直线l2：y＝kx+4交于点A，则不等式x+b≥kx+4的解集是．15．（3分）如图，在菱形ABCD中，对角线AC、BD交于点O，过点A作AH⊥BC于点H，若AC＝6，BD＝8，则AH＝．16．（3分）已知点A（m﹣1，2m+3）在第二象限，则m的取值范围是．17．（3分）已知一次函数y＝kx+2k+3的图象交y轴于正半轴，且函数值y随x的增大而减小，则k所能取到的整数值为．18．（3分）已知，在▱ABCD中，∠A的平分线交BC边于点E，若BC边被点E分为4和5两部分，则▱ABCD的周长为．19．（3分）如图，菱形ABCD中，∠A＝120°，E是AD上的点，沿BE折叠△ABE，点A 恰好落在BD上的点F，那么∠BFC的度数是．20．（3分）如图所示，正方形ABCD和正方形CEFG的边长分别为2和3，则图中阴影部分的面积为．三、解答题：（本大题共6个小题，50分，解答过程应写出文字说明，证明过程或演算步骤）21．（6分）已知：▱ABCD中，对角线AC、BD交于点O，EF过点O交AD于点E，交BC 于点F．（1）求证：AE＝CF．（2）若▱ABCD的周长是18cm，且OE＝1.5cm，请直接写出四边形CDEF的周长是cm．22．（7分）某校开展“阳光体育活动”，开设了以下体育项目：篮球、羽毛球、乒乓球和跳绳要求每名学生必须且只能选择其中的一项，为了解选择各体育项目的学生人数，随机抽取了部分学生进行调查，并对调查获取的数据进行了整理，绘制出两幅不完整的统计图，请根据统计图回答下列问题：（1）在这次调查中，一共调查了名学生；（2）计算选择跳绳的人数并补全条形统计图；（3）在扇形统计图中，乒乓球项目所对应的扇形圆心角的度数是；（4）请根据此统计数据估算该校1800名学生中有多少人选择了球类项目．23．（8分）某水果店以6元/千克的价格购进油桃若干千克，销售了一部分后，余下的油桃每千克降价2元进行销售，直至全部售完．销售金额y（元）与销量x（千克）之间的函数关系如图所示．请根据图象提供的信息解决下列问题：（1）降价前油桃的销售单价是元/千克．（2）求降价后销售总金额y（元）与总销量x（千克）之间的函数关系式，并写出自变量的取值范围；（3）该水果店销售这些油桃总共盈利多少元？24．（9分）已知：如图，四边形ABCD中，M、N、P、Q分别是AD、BC、BD和AC的中点．（1）求证：四边形MPNQ是平行四边形．（2）若满足AB＝CD．试判断MN与PQ的位置关系（不用说明理由）．25．（10分）已知：如图所示，在平面直角坐标系中，过点A（﹣6，0）的直线l1与直线l2：y＝2x相交于点B（m，4），与y轴交于点M．（1）求直线l1的表达式．（2）求△BOM的面积．（3）点P（n，0）是x轴上一个动点，过点P垂直于x轴的直线分别与直线l1和l2交于C、D两点，当点C位于点D上方时，直接写出n的取值范围．26．（10分）已知：如图1所示，O是△ABC中AC边上一点，过点O的直线MN∥BA，D 是BA延长线上一点，∠BAC和∠DAC的角平分线分别交MN于点E、F．（1）请直接写出线段OA和EF的数量关系．（2）如图2所示，连接CE、CF，若点O是AC中点，试判断四边形AECF的形状并写出详细推理过程．（3）在（2）的条件下，在△ABC中添加什么条件能使四边形AECF是正方形．（直接写出结果即可）参考答案与试题解析一、选择题（本大题共10个小题，每小题2分，满分20分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．【分析】根据第二象限内点的坐标特征以及点到x轴的距离等于纵坐标的绝对值，到y轴的距离等于横坐标的绝对值解答．【解答】解：∵第二象限的点P到x轴的距离是3，到y轴的距离是2，∴点P的横坐标是﹣2，纵坐标是3，∴点P的坐标为（﹣2，3）．故选：D．2．【分析】根据调查对象的特点，结合普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果接近准确数值，从而可得答案．【解答】解：A．要检测一批节能灯的使用寿命，适合采用抽样调查，故本选项不合题意；B．要了解滦河的水质，适合采用抽样调查，故本选项符合题；C．某高铁站对乘车旅客实施安检，适合采用全面调查方式，故本选项不合题意；D．要了解全市初中生的睡眠情况，适合采用抽样调查，故本选项不合题意．故选：B．3．【分析】利用平行四边形的性质对角线互相平分，进而得出BO，CO的长，即可得出△BOC的周长．【解答】解：∵▱ABCD的两条对角线交于点0，AC＝10，BD＝6，AD＝5，∴BO＝DO＝3，AO＝CO＝5，BC＝AD＝5∴△BOC的周长为：BO+CO+BC＝3+5+3＝13．故选：A．4．【分析】总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．【解答】解：①6300名学生的数学成绩是调查的总体；故命题错误；②500名学生的数学成绩是总体的一个样本；故命题正确；③每个学生的数学成绩是个体；故命题正确；④样本容量是500．故命题错误；故选：B．5．【分析】根据直角三角形的性质求出AB，根据三角形中位线定理计算即可．【解答】解：在Rt△ABC中，∠A＝30°，∴AB＝2BC＝6，∵D，E分别是直角边BC，AC的中点，∴DE＝AB＝3，故选：D．6．【分析】每分钟滴出100滴水，每滴水约0.05毫升，则一分钟滴水100×0.05毫升，则x 分钟可滴100×0.05x毫升，据此即可求解．【解答】解：根据题意可得：y＝100×0.05x，即y＝5x．故选：B．7．【分析】首先连接OP．由矩形ABCD的两边AB＝6，BC＝8，可求得OA＝OD＝5，然后由S△AOD＝S△AOP+S△DOP求得答案．【解答】解：连接OP，∵矩形ABCD的两边AB＝6，BC＝8，∴S矩形ABCD＝AB•BC＝48，OA＝OC，OB＝OD，AC＝BD，AC＝＝10，∴S△AOD＝S矩形ABCD＝12，OA＝OD＝5，∴S△AOD＝S△AOP+S△DOP＝OA•PE+OD•PF＝OA（PE+PF）＝×5×（PE+PF）＝12，∴PE+PF＝＝4.8．故选：A．8．【分析】根据n边形的内角和公式，则内角和应是180°的倍数，且每一个内角应大于0°而小于180度，根据这些条件进行分析求解即可．【解答】解：∵970°÷180°＝5…70°，则边数是：5+1+2＝8，故选：B．9．【分析】通过分析题意和图象可求调进物资的速度，调出物资的速度；从而可计算最后调出物资20吨所花的时间．【解答】解：调进物资的速度是60÷4＝15吨/时，当在第4小时时，库存物资应该有60吨，在第8小时时库存20吨，从4小时到8小时，物资既调进也调出，共调进15×4＝60吨，实际这4个小时调出的物资是原来的60吨+调进的60吨减去仓库剩余的20吨，所以调出速度是＝25（吨/时），所以剩余的20吨完全调出需要20÷25＝0.8（小时）．故这批物资从开始调进到全部调出需要的时间是8+0.8＝8.8（小时）．故选：C．10．【分析】根据A，B两点坐标以及对应点A′，B′点的坐标得出坐标变化规律，进而得出P′的坐标．【解答】解：∵△ABO缩小后变为△A′B′O，其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上，即A点坐标为：（4，6），B点坐标为：（6，2），A′点坐标为：（2，3），B′点坐标为：（3，1），∴线段AB上有一点P（m，n），则点P在A′B′上的对应点P′的坐标为：（）．故选：D．二、填空题（本大题共10个小题，每小题3分，共30分，）11．【分析】根据横坐标，右移加，左移减；纵坐标，上移加，下移减可得答案．【解答】解：点P（3，1）向下平移3个单位，向左平移2个单位，得到点P'的坐标是（3﹣2，1﹣3），即（1，﹣2），故答案为：（1，﹣2）．12．【分析】根据频率＝频数÷总数，以及第五组的频率是0.2，可以求得第五组的频数；再根据各组的频数和等于1，求得第六组的频数，从而求得其频率．【解答】解：根据第五组的频率是0.2，其频数是40×0.2＝8；则第六组的频数是40﹣（10+5+7+6+8）＝4．故第六组的频率是，即0.1．13．【分析】根据二次根式的被开方数大于等于0，分母不等于0列式计算即可得解．【解答】解：根据题意得：x﹣2＞0，解得x＞2∴自变量x的取值范围是x＞2．故答案为：x＞2．14．【分析】写出直线l1在直线l2上方所对应的自变量的范围即可．【解答】解：∵直线l1：y＝x+b与直线l2：y＝kx+4交于点A（2，2），当x≥2时，直线l1在直线l2的上方，∴不等式x+b≥kx+4的解集是x≥2．故答案为x≥2．15．【分析】由菱形面积＝对角线积的一半可求面积，由勾股定理求出BC，然后由菱形的面积即可得出结果．【解答】解：∵四边形ABCD是菱形，∴AC⊥BD，OA＝OC，OB＝OD，∴BC＝，∵菱形ABCD的面积＝，∴AH＝，故答案为：．16．【分析】根据第二象限内点的坐标的符号特点列出关于m的不等式组，解之即可得出答案．【解答】解：∵点A（m﹣1，2m+3）在第二象限，∴，解不等式①，得：m＜1，解不等式②，得：m＞﹣1.5，则不等式组的解集为﹣1.5＜m＜1，故答案为：﹣1.5＜m＜1．17．【分析】由一次函数图象与系数的关系可得出关于k的一元一次不等式组，解不等式组即可得出结论．【解答】解：由题意得：，解得：﹣＜k＜0．∵k为整数，∴k＝﹣1，故答案为﹣1．18．【分析】根据AE平分∠BAD及AD∥BC可得出AB＝BE，BC＝BE+EC，从而根据AB、AD的长可求出平行四边形的周长．【解答】解：在平行四边形ABCD中，AD∥BC，则∠DAE＝∠AEB．∵AE平分∠BAD，∴∠BAE＝∠DAE，∴∠BAE＝∠BEA，∴AB＝BE，BC＝BE+EC，①当BE＝4，EC＝5时，平行四边形ABCD的周长为：2（AB+AD）＝2×（4+4+5）＝26．②当BE＝5，EC＝4时，平行四边形ABCD的周长为：2（AB+AD）＝2×（5+5+4）＝28．故答案为：26或28．19．【分析】根据菱形的性质可得AB＝BC，∠A+∠ABC＝180°，BD平分∠ABC，然后再计算出∠FBC＝30°，再证明FB＝BC，再利用等边对等角可得∠BFC＝∠BCF，利用三角形内角和可得答案．【解答】解：∵四边形ABCD是菱形，∴AB＝BC，∠A+∠ABC＝180°，BD平分∠ABC，∵∠A＝120°，∴∠ABC＝60°，∴∠FBC＝30°，根据折叠可得AB＝BF，∴FB＝BC，∴∠BFC＝∠BCF＝（180°﹣30°）÷2＝75°，故答案为：75°．20．【分析】用两个正方形面积减去三个空白三角形面积即可求得．【解答】解：由题意知，阴影面积S＝22+32﹣×（2+3）×3﹣×（3﹣2）×3﹣×22＝×22＝2，故答案为：2．三、解答题：（本大题共6个小题，50分，解答过程应写出文字说明，证明过程或演算步骤）21．【分析】（1）利用平行线的性质结合全等三角形的判定与性质得出即可．（2）根据全等三角形的性质和平行四边形的性质解答即可．【解答】证明：（1）∵四边形ABCD是平行四边形，∴AD∥BC，∴∠AEO＝∠CFO，在△AEO和△CFO中，∴△AEO≌△CFO（ASA），∴AE＝CF；（2）∵AE＝CF，∴CF+ED＝AE+ED＝AD，∵▱ABCD的周长是18cm，∴AD+DC＝9（cm），∴四边形CDEF的周长＝DE+CF+DC+EF＝AD+DC+EF＝9+1.5+1.5＝12（cm）．故答案为：12．22．【分析】（1）根据选择篮球的人数和所占的百分比，可以计算出本次调查的学生人数；（2）根据（1）中的结果和条形统计图中的数据，可以计算出选项跳绳的人数，然后即可将条形统计图补充完整；（3）根据（1）中的结果和条形统计图中的数据，可以计算出在扇形统计图中，乒乓球项目所对应的扇形圆心角的度数；（4）根据条形统计图中的数据，可以计算出该校1800名学生中有多少人选择了球类项目．【解答】解：（1）在这次调查中，一共调查了16÷32%＝50名学生，故答案为：50；（2）选择跳绳的学生有：50﹣16﹣12﹣10＝12（人），补全的条形统计图如右图所示；（3）在扇形统计图中，乒乓球项目所对应的扇形圆心角的度数是360°×＝72°，故答案为：72°；（4）1800×＝1368（人），答：估算该校1800名学生中有1368人选择了球类项目．23．【分析】（1）由函数图象可知：销售50千克所得销售收入为550元，由此可得降价前油桃的销售单价；（2）根据“余下的油桃每千克降价2元进行销售”求出降价后的销售单价，再利用减价后的收入为（730﹣550）元，可求减价后销售的油桃数，再利用待定系数法可求函数关系式；（3）根据盈利＝销售收入﹣成本可得．【解答】解：（1）由图象可知，降价前油桃的销售单价是550÷50＝11（元/千克），故答案为：11；（2）降价后销售的油桃数是：（730﹣550）÷（11﹣2）＝20（千克），∴销售的油桃总数为50+20＝70（千克），设降价后销售金额y（元）与销售量x（千克）之间的函数解析式是y＝kx+b（k≠0），把（50，550），（70，730）代入得：，解得，∴y＝9x+100（50＜x≤70）；（3）730﹣6×70＝310（元）．答：该水果店销售这些油桃总共盈利310元．24．【分析】（1）根据三角形中位线定理得到PM＝AB，PM∥AB，NQ＝AB，NQ∥AB，根据平行四边形的判定定理证明四边形PMQN是平行四边形，根据平行四边形的性质定理证明结论；（2）根据菱形的判定定理和性质定理解答即可．【解答】（1）证明：∵P、M分别是BD，AD的中点，∴PM＝AB，PM∥AB，同理NQ＝AB，NQ∥AB，∴PM∥NQ，PM＝NQ，∴四边形PMQN是平行四边形；（2）PQ⊥MN，理由如下：由（1）知，PM＝AB，PN＝CD，当AB＝CD时，PM＝PN，∴平行四边形PMQN是菱形，∴PQ⊥MN．25．【分析】（1）先求出点B坐标，再利用待定系数法即可解决问题．（2）把x＝0代入解析式，求出M坐标，利用三角形面积公式解答即可；（3）由图象可知直线l1在直线l2上方即可，由此即可写出n的范围．【解答】解：（1）∵点B（m，4）直线l2：y＝2x上，∴4＝2m，∴m＝2，∴点B（2，4），设直线l1的表达式为y＝kx+b，将A（﹣6，0），B（2，4）代入得：，解得，∴直线l1的表达式为y＝x+3；（2）将x＝0代入y＝x+3，得：y＝3，∴M（0，3），∴OM＝3，∴△BOM的面积＝OM•|x B|＝×3×2＝3；（3）当点C位于点D上方时，即是直线l1在直线l2上方，如图：由图象可知n＜2．26．【分析】（1）根据MN∥BA，得∠OEA＝∠BAE，由AE平分∠BAC，得∠BAE＝∠CAE，从而∠OEA＝∠CAE，则有OE＝OA，同理可证：OF＝OA，即可得出EF＝2OA；（2）先通过对角线互相平分得出：四边形AECF是平行四边形，再证AC＝EF即可；（3）添加∠BAC＝90°，可得∠EAC＝45°，从而CE＝AE，得出结论．【解答】解：（1）∵MN∥BA，∴∠OEA＝∠BAE，∵AE平分∠BAC，∴∠BAE＝∠CAE，∴∠OEA＝∠CAE，∴OE＝OA，同理可证：OF＝OA，∴EF＝2OA；故答案为：EF＝2OA；（2）四边形AECF是矩形，∵点O是AC中点，∴OC＝OA，AC＝2OA，由（1）知：OE＝OF，∴四边形AECF是平行四边形，∵EF＝2OA，∴EF＝AC，∴▱AECF是矩形；（3）添加∠BAC＝90°，能使四边形AECF是正方形，∵AE平分∠BAC，∠BAC＝90°，∴∠EAC＝45°，∴CE＝AE，∴矩形AECF是正方形，故添加：∠BAC＝90°．。

2022-2023扬州梅岭小学二年级数学上册期末复习试卷一(及答案)

二年级数学上册期末复习试卷一一、细心算一算。

（共 29分）1.直接写得数。

（20分，每题1分）4×8= 63÷7= 7×3= 6×7-7＝36÷6= 3×9= 42÷6= 3×2×3=9×8= 16÷4= 5×9= 8×3÷6=6×5= 56-7= 49÷7= 40÷8×2=48+8= 25÷5= （）×4=36 55厘米-（）厘米=25厘米2.列竖式计算。

（9分，每题3分）36+24+35= 75-27-18= 60-46+39=二、用心填一填。

（每空1分，共 33分）1. 把9+9+9=27改写成乘法算式是（），用到的乘法口诀是（），用这句口诀可以写成的除法算式是（）或（）。

2. ★★★★★★★★★★★★这些★可以平均分成（）份，每份（）个；还可以平均分成（）份，每份（）个。

3. 2个7相乘的积是（）；被除数和除数都是6，商是（）；比4个9多49的数是（）。

4. 在（）里填“米”或“厘米”。

教室门高约2（）；洗脸毛巾长约60（）；明明身高1（）28（）。

5.在○里填上“＞”“＜”或“＝”。

51-12 6×2 45÷5 3×3 4×4 4+4+4 80厘米 8米6.在（）里填上合适的数。

5×7＋7＝7×（） 12÷（）=（）×2 45厘米＋55厘米＝（）米7. 找规律填一填。

（1） 1,4,9,16，（），（）；（2） 42，3，35，6，28，9，（），（）；（3） 8.把一根绳子先对折一次，再对折一次，刚好长1米，这根绳子原来长（）米。

9. 画一条3厘米的线段，可以从直尺上的刻度“1”画到刻度“（）”；从刻度“3”画到从刻度“8”是（）厘米。

苏教版2022-2023扬州市育才小学五年级数学下册期末复习试卷(一)及答案

五年级数学下册期末复习试卷（一）一、选择题。

1. 一根绳被剪成两段，第一段长52米，第二段占全长的52。

比较两段的长度，发现（）。

A.第一段长 B.第二段长 C.一样长 D.无法判断2. 把 27 的分子加上10，要使分数的大小不变，分母应加上（）。

A.10B. 42C. 35 D ．283. 一个五位数万位上是最小的质数，十位上是最小的合数，其余各个数位上数字相同，这个五位数一定是（）。

A.2的倍数B.3的倍数C.5的倍数D.无法判断4. 小军、小明两人读同一篇文章，小军用51小时，小明用了61小时，（）读得快。

A.小军 B.小明 C.一样快 D.无法判断5. 分母是8的最简真分数有（）个。

A ．2B ．3C ．4D ．76．学校合唱社团，每组5人或每组8人都多1人，学校合唱社团最少有（）。

A ．81 人B ．41人C ．40 人D ．39人7. 右图中，正方形的面积是10平方厘米，圆的面积是（）。

A ．2.5π平方厘米B ．4π 平方厘米C ．5π平方厘米D ．6.25π平方厘米8. 古希腊人认为：如果一个数恰好等于它的所有因数（本身除外）相加之和，那么这个数就是“完美数”。

下面各数中，是“完美数”的是（）。

A.14B.28C.35D.519.要反映一个人一天的体温变化情况，应绘制（）。

A.复式统计表B.单式统计表C.条形统计图D.折线统计图10. 如右图，小红从甲地到乙地有两条路线可走，走哪一条路线近一些？（）。

A. 走①号路线近B. 走②号路线近C.一样近D.无法确定二、填空题。

1.（）÷20=)(15=53=15)(=（）（此空填小数）。

2. 一个数最大因数与最小倍数的和是36，把这个数分解质因数，是（）。

高等数学1期末试卷(5套)

试卷（一）一、1、下列等式中成立的是（ B ）.(A) e n nn =⎪⎭⎫⎝⎛+∞→21lim (B) e n n n =⎪⎭⎫ ⎝⎛++∞→211lim (C) e n nn =⎪⎭⎫ ⎝⎛+∞→211lim (D) e n nn =⎪⎭⎫⎝⎛+∞→211lim2、函数()x f 在点0x 处连续是在该点处可导的（）.(A) 必要但不充分条件 (B) 充分但不必要条件 (C)充分必要条件 (D) 既非充分也非必要条件 3、设函数()x f 可导，并且下列极限均存在，则下列等式不成立的是（）.(A) ()()()00limf x f x f x '=-→ (B) ()()()0000lim x f x x x f x f x '=∆∆--→∆(C) ()()()a f h a f h a f h '=-+→2lim(D) ()()()00002lim x f xx x f x x f x '=∆∆--∆+→∆ 4、若(),00='x f 则点0x x =是函数()x f 的（）.(A) 极大值点 (B) .最大值点 (C) 极小值点 (D) 驻点5、曲线12+=x x y 的铅直渐近线是（）.（A ）y =1 （B ）y =0 （C ）1-=x （D ）x =0 6、设xe-是)(x f 的一个原函数，则⎰=dx x xf )(（）.（A ）c x e x+--)1( （B ）c x e x++-)1( （C ）c x e x+--)1( （D ） c x e x++--)1( 二、1、当0x →时，(1cos )x -与2sin2xa 是等价无穷小，则常数a 应等于______ _. 2、若82lim =⎪⎭⎫⎝⎛-+∞→xx b x b x ，则=b .3、函数123++=x x y 的拐点是 .4、函数()x y y =是由方程y x y +=tan 给出，则='y ______________________.5、双曲线1xy =在点()1,1处的曲率为 .6、已知)(x f 在),(∞+-∞上连续，且2)0(=f ，且设2sin ()()x xF x f t dt =⎰，则(0)F '= .三、 1、求极限()xx x x x sin tan cos 1lim20-→ .2、设曲线的方程为33190x y (x )cos(y ),π++++=求此曲线在1x =-处的切线方程.3、求不定积分⎰++322x x xdx.4、求不定积分dx x x ⎰+31. 5、求定积分dx x x ⎰22cos π.6、求定积分⎰--+11242dx xx .四、1、求抛物线12+=x y 与直线1-=x y 所围成的图形. 2、设()f x ''连续，()1f π=，()()0sin 3f x f x xdx π''+=⎡⎤⎣⎦⎰，求()0f .试卷（二）一、1、=+→xx x 2)31(lim ．2、当=k 时，⎪⎩⎪⎨⎧>+≤=00e)(2x kx x x f x 在0=x 处连续．3、设x x y ln +=,则=dydx． 4、曲线x e y x -=在点)1,0(处的切线方程是．5、设两辆汽车从静止开始沿直线路径前进，下图中给出的两条曲线)(1t a a =和)(2t a a =分别是两车的速度曲线．那么位于这两条曲线和直线T t = )0(>T 之间的图形的面积A 所表示的物理意义是．二、1、若函数xx x f =)(，则=→)(lim 0x f x （）．A 、0B 、1-C 、1D 、不存在 2、下列变量中，是无穷小量的为（）.A 、 x 1ln（当+→0x ） B 、x ln （当1→x ） C 、x cos （当0→x ） D 、 422--x x （当2→x ） 3、满足关系式0)(='x f 的x 是函数)(x f y =的（）.A 、极大值点B 、极小值点C 、驻点D 、间断点 4、下列函数)(x f 在]1,1[-上适合罗尔中值定理条件的是（）.A 、32)(x x f =B 、x x x f 2)(=C 、32)(+=x x fD 、x x f sin )(= 5、下列无穷积分收敛的是（）.A 、⎰∞+ 0sin xdx B 、dx x ⎰∞+ 01C 、dx e x ⎰∞+- 0 2D 、dx x⎰∞+ 0 1三、1、求极限 xx x 2sin 24lim-+→ . 2、求极限 2cos 2cos 0lim x dte xx t x ⎰-→.3、设)1ln(25x x e y +++=，求y '.4、设)(x y f =由已知⎩⎨⎧=+=ty t x arctan )1ln(2，求22dx y d . 5、求不定积分dx xx x ⎰+)sin (ln 2.6、设⎪⎩⎪⎨⎧≥<+=-0011)(2x xe x x x f x ，求⎰-20d )1(x x f .四、1、设函数21)(xxx f +=，分别求其单调区间、极值、凹凸性与拐点. 2、设)(x f 在闭区间],[b a 上连续，在开区间),(b a 内可导)0(>a .试证在),(b a 内至少存在一点ξ满足：)(][)]()([2012201220122011ξξf a b a f b f '-=-.试卷（三）一、1．设)sin (cos )(x x x x f +=，则在0=x 处有（）.(A)2)0(='f (B) 1)0(='f (C) 0)0(='f (D) )(x f 不可导 2．设333)(,11)(x x xxx ⋅-=+-=βα，则当1→x 时（）. (A) )(x α与)(x β是同阶无穷小，但不是等价无穷小； (B) )(x α与)(x β是等价无穷小； (C) )(x α是比)(x β高阶的无穷小； (D) )(x β是比)(x α高阶的无穷小.3．函数2)4(121++=x xy 的图形（）. (A) 只有水平渐近线； (B) 有一条水平渐近线和一条铅直渐近线； (C) 只有铅直渐近线； (D) 无渐近线.4．设函数nn x xx f 211lim)(++=∞→，则下列结论正确的为（）.(A) 不存在间断点； (B) 存在间断点1=x ； (C) 存在间断点0=x ； (D) 存在间断点1-=x .5．设函数)(x f 是连续函数，且⎰+=1)(2)(dt t f x x f ，则)(x f = ( ).(A) 22x (B)222+x (C) 1-x (D) 2+x 6.广义积分)0( >⎰∞+a xdxap 当（）时收敛. (A) 1>p (B) 1<p (C) 1≥p (D) 1≤p二、1．=+→xx x sin 20)31(lim .2．曲线⎩⎨⎧=+=321ty t x 在t=2处的切线方程为 . 3．方程0162=-++x xy e y 确定隐函数)(x y y =，则)0(y '= .4．⎰--+2121 2211arcsin dx xx x = .5．已知x x cos 是)(x f 的一个原函数，则dx xxx f ⎰cos )(= . 6.=⎰→22 0sin lim2xtdt e xt x .三、1．（6分）已知tt t x x f ⎪⎪⎭⎫⎝⎛+=+∞→2sin 1lim )(，求)(x f '. 2．（6分）求不定积分dx xx⎰++cos 1sin 1. 3．（8分）设函数⎩⎨⎧≤<-≤=-1010)(2x x x xe x f x ，，，求dx x f ⎰-1 3 )(. 4．（8分）已知2)3(lim 2=++-∞→c bx ax x x ，求常数b a ,.5.（8分）求由曲线)1(2,4,22≥===x x y x y xy 所围图形的面积.6.（8分）由方程)ln(arctan22y x x y +=确定隐函数)(x f y =，求0=y dx dy . 7.（8分）设函数)(x f 在[0,1]上连续且单调递减，证明：对任意的],1,0[∈q ⎰⎰≥qdx x f q dx x f 01)()(.试卷（四）一、1.方程23cos2x y y y e x '''--=的特解形式为（）（A ）cos 2xaxe x ；（B ）cos 2sin 2xxaxe x bxe x +；（C ）cos 2sin 2xxae x be x +；（D ）22cos 2sin 2xxax e x bx e x +.2. 设a 不是π的整数倍，极限ax a x a x -→⎪⎭⎫⎝⎛1sin sin lim 的值是（）.（A ） 1 （B ）e （C ）a e cot （D ）ae tan3. 函数⎪⎩⎪⎨⎧=≠-+=0 ,0 ,1sin )(2x a x xe x xf ax 在0=x 处连续，则=a （）. （A ）1 （B ） 0 （C ）e （D ）1-4. 设2()()lim1()x af x f a x a →-=--，则在x a =处有（）（A ）()f x 的导数存在，且()0f a '≠；（B ）()f x 取得极大值；（C ）()f x 取得极小值；（D ）()f x 取得最大值.5. 设函数)(x f 在点0=x 的某个邻域内连续，且0)0(=f ，2cos 1)(lim0=-→xx f x ，则点0=x （）.（A ）是)(x f 的极大值点（B ）是)(x f 的极小值点(C)不是)(x f 的驻点（D ）是)(x f 的驻点但不是极值点二、1. 设tan 21, 0sin 2(), 0xx e x x f x ae x ⎧->⎪⎪=⎨⎪⎪≤⎩在0x =连续，则a =____________.2. 极限xaa x x ln )ln(lim0-+→（0>a ）的值是 .3. 设()(1)(2)(99)f x x x x x =---L ，则(0)f '=____________.4. 曲线21x xe y =的铅直渐近线是 . 5. 函数)4ln(x x y -=的单调递增区间为 .三、1. 计算极限412921612lim 2332-+-+-→x x x x x x . 2. 求不定积分10arctan d x x x ⎰. 3. 求定积分⎰+41)1(x x dx . 4. 求函数122+=x xy 的极值与拐点.5. 求微分方程52d 2(1)d 1y y x x x -=++的通解. 6. 设1>a ，函数a a x x a x a x y +++=，求dxdy . 四、证明题（本题8分）证明：当02x <<时，有24ln 240x x x x --+>.试卷（五）一、 1. 下列各式正确的是（）.(A)1)11(lim 0=++→x x x (B) e x x x =++→)11(lim 0(C) e x x x -=-∞→)11(lim (D)e xxx =+-∞→)11(lim 2. 设()f x 可导，()()(1sin )F x f x x =+，若欲使()0F x x =在可导，则必有（）.（A ）(0)0f '=（B ）(0)0f = （C ）(0)(0)0f f '+=（D ）(0)(0)0f f '-=3.为，则又设已知　)()20( d )()(21 110 )(12x F x t t f x F x x x x f x ⎰≤≤=⎩⎨⎧≤≤<≤=（）.⎪⎩⎪⎨⎧≤≤<≤21 10 31)(3x x x x A ⎪⎩⎪⎨⎧≤≤<≤-21 10 3131)(3x x x x B ⎪⎩⎪⎨⎧≤≤-<≤21 110 31)(3x x x x C ⎪⎩⎪⎨⎧≤≤-<≤-21 1103131)(3x x x x D 4.当0→x 时，与x ex cos 22-等价的无穷小是（）.（A ）2x . （B ）223x . （C ）22x . （D ）225x . 5.x e y y y x2cos 52=+'-''的一个特解应具有形式（）.（A ）x Ae x2cos （B ）)2sin 2cos (x B x A e x+（C ）)2sin 2cos (x B x A xe x+ （D ）)2sin 2cos (2x B x A e x x+ 二、1. 已知2sin ()d x f x x e C =+⎰,则()f x =____________.2.设函数22, 1()ln(1), 1a x x f x x x x ⎧+>-=⎨++≤-⎩在1x =-处连续，则a = . 3. 设),tan ln(sec x x y +=则='y .4. 设()f x 是连续函数，则dt t f a x x xaa x ⎰-→ )(lim= .5. 已知⎰+=C x dx x f arcsin )(，则=-⎰dx x f x )(12. 6. 由0 , 0)( , , =≥===y x f y b x a x 所围曲边梯形绕x 轴旋转而成的旋转体的体积公式为：V = . 则（应用你给的公式计算）由],[,)(22R R x x R x f y -∈-==与x 轴所围成的图形绕x 轴旋转而成的立体的体积=V . 三、1. (6分) 1.求函数22(,)(2)ln f x y x y y y =++的极值.2. (6分)设arctany x= 求dx dy .3.（6分）求微分方程满足初始条件的特解1,sin ==+=πx y xx x y dx dy . 4. (6分) 设由方程2cos()1x y e xy e +-=-确定y 是x 的函数，求d .0d yx x =5. (7分) 求函数22(,)(2)ln f x y x y y y =++的极值. 6 若函数)(x f 在]1,0[上连续，证明：=⎰π)(sin dx x xf ⎰)(sin 2ππdx x f ，并计算dx xxx ⎰+π2cos 1sin . 8. 过原点(0,0)O 作曲线ln y x =的切线，该切线与曲线ln y x =及x 轴围成一平面图形，求此平面图形的面积.《高等数学》试卷6（下）一.选择题（3分⨯10）1.点1M ()1,3,2到点()4,7,22M 的距离=21M M （）.A.3B.4C.5D.62.向量j i b k j i a+=++-=2,2，则有（）.A.a ∥bB.a ⊥bC.3,π=b aD.4,π=b a3. 设有直线1158:121x y z L --+==-和26:23x y L y z -=⎧⎨+=⎩，则1L 与2L 的夹角为（）（A ）6π；（B ）4π；（C ）3π；（D ）2π. 4.两个向量a 与b垂直的充要条件是（）.A.0=⋅b aB.0 =⨯b aC.0 =-b aD.0 =+b a5.函数xy y x z 333-+=的极小值是（）. A.2 B.2- C.1 D.1-6.设y x z sin =，则⎪⎭⎫ ⎝⎛∂∂4,1πyz ＝（）.A.22 B.22- C.2 D.2- 7. 级数1(1)(1cos ) (0)nn n αα∞=-->∑是（）（A ）发散；（B ）条件收敛；（C ）绝对收敛；（D ）敛散性与α有关.8.幂级数∑∞=1n n n x 的收敛域为（）.A.[]1,1- B ()1,1- C.[)1,1- D.(]1,1-9.幂级数nn x ∑∞=⎪⎭⎫⎝⎛02在收敛域内的和函数是（）.A.x -11 B.x -22 C.x -12 D.x -21 二.填空题（4分⨯5）1.一平面过点()3,0,0A 且垂直于直线AB ，其中点()1,1,2-B ，则此平面方程为______________________.2.函数()xy z sin =的全微分是______________________________.3.设13323+--=xy xy y x z ，则=∂∂∂yx z2_____________________________.4. 设L 为取正向的圆周：221x y +=，则曲线积分2(22)d (4)d Lxy y x xx y -+-=⎰Ñ____________.5. .级数1(2)nn x n ∞=-∑的收敛区间为____________.三.计算题（5分⨯6）1.设v e z usin =，而y x v xy u +==,，求.,yz x z ∂∂∂∂ 2.已知隐函数()y x z z ,=由方程05242222=-+-+-z x z y x 确定，求.,yz x z ∂∂∂∂ 3.计算σd y x D⎰⎰+22sin ，其中22224:ππ≤+≤y x D . 4.．计算1d d yxy x x⎰.试卷6参考答案一.选择题 CBCAD ACCBD 二.填空题1.0622=+--z y x .2.()()xdy ydx xy +cos .3.19622--y y x .4.()n n n n x ∑∞=+-0121. 5.()x e x C Cy 221-+= .三.计算题 1.()()[]y x y x y e x z xy +++=∂∂cos sin ，()()[]y x y x x e y z xy +++=∂∂cos sin . 2.12,12+=∂∂+-=∂∂z y y z z x x z . 3.⎰⎰=⋅πππρρρϕ202sin d d 26π-. 4.3316R . 5.x x e e y 23-=. 四.应用题1.长、宽、高均为m 32时，用料最省.2..312x y =《高数》试卷7（下）一.选择题（3分⨯10）1.点()1,3,41M ，()2,1,72M 的距离=21M M （）. A.12 B.13 C.14 D.152.设两平面方程分别为0122=++-z y x 和05=++-y x ，则两平面的夹角为（）. A.6π B.4π C.3π D.2π 3.点()1,2,1--P 到平面0522=--+z y x 的距离为（）. A.3 B.4 C.5 D.6 4.若几何级数∑∞=0n nar是收敛的，则（）.A.1≤rB. 1≥rC.1<rD.1≤r8.幂级数()nn xn ∑∞=+01的收敛域为（）.A.[]1,1-B.[)1,1-C.(]1,1-D. ()1,1- 9.级数∑∞=14sin n n na是（）. A.条件收敛 B.绝对收敛 C.发散 D.不能确定10. ．考虑二元函数(,)f x y 的下列四条性质：（1）(,)f x y 在点00(,)x y 连续；（2）(,),(,)x y f x y f x y 在点00(,)x y 连续（3）(,)f x y 在点00(,)x y 可微分；（4）0000(,),(,)x y f x y f x y 存在. 若用“P Q ⇒”表示有性质P 推出性质Q ，则有（）（A ）(2)(3)(1)⇒⇒；（B ）(3)(2)(1)⇒⇒ （C ）(3)(4)(1)⇒⇒；（D ）(3)(1)(4)⇒⇒ 二.填空题（4分⨯5）1. 级数1(3)nn x n ∞=-∑的收敛区间为____________.2.函数xye z =的全微分为___________________________.3.曲面2242y x z -=在点()4,1,2处的切平面方程为_____________________________________.4.211x +的麦克劳林级数是______________________. 三.计算题（5分⨯6）1.设k j b k j i a32,2+=-+=，求.b a ⨯2.设22uv v u z -=，而y x v y x u sin ,cos ==，求.,y z x z ∂∂∂∂ 3.已知隐函数()y x z z ,=由233=+xyz x 确定，求.,yz x z ∂∂∂∂ 4. 设∑是锥面1)z z =≤≤下侧，计算y z 2d d 3(1)d d xd d y z x z x y ∑++-⎰⎰四.应用题（10分⨯2）试用二重积分计算由x y x y 2,==和4=x 所围图形的面积.试卷7参考答案一.选择题 CBABA CCDBA. 二.填空题1.211212+=-=-z y x .2.()xdy ydx e xy +.3.488=--z y x .4.()∑∞=-021n n n x . 5.3x y =. 三.计算题1.k j i238+-.2.()()()y y x y y y y x yz y y y y x x z 3333223cos sin cos sin cos sin ,sin cos cos sin +++-=∂∂-=∂∂ .3.22,z xy xz y z z xy yz x z +-=∂∂+-=∂∂. 4. ⎪⎭⎫ ⎝⎛-3223323πa . 5.xx e C e C y --+=221. 四.应用题 1.316. 2. 00221x t v gt x ++-=.《高等数学》试卷3（下）一、选择题（本题共10小题，每题3分，共30分） 1、二阶行列式 2 -3 的值为（）4 5A 、10B 、20C 、24D 、222、设a=i+2j-k,b=2j+3k ，则a 与b 的向量积为（） A 、i-j+2k B 、8i-j+2k C 、8i-3j+2k D 、8i-3i+k3、点P （-1、-2、1）到平面x+2y-2z-5=0的距离为（） A 、2 B 、3 C 、4 D 、54、函数z=xsiny 在点（1，4π）处的两个偏导数分别为（） A 、,22 ,22 B 、,2222- C 、22- 22- D 、22- ,225、设x 2+y 2+z 2=2Rx ，则yzx z ∂∂∂∂,分别为（） A 、z y z R x --, B 、z y z R x ---, C 、zyz R x ,-- D 、zyz R x ,- 6、设圆心在原点，半径为R ，面密度为22y x +=μ的薄板的质量为（）（面积A=2R π） A 、R 2A B 、2R 2A C 、3R 2A D 、A R 221 7、级数∑∞=-1)1(n nnn x 的收敛半径为（）A 、2B 、21C 、1D 、3 8、cosx 的麦克劳林级数为（）A 、∑∞=-0)1(n n)!2(2n x n B 、∑∞=-1)1(n n )!2(2n x n C 、∑∞=-0)1(n n )!2(2n x n D 、∑∞=-0)1(n n)!12(12--n x n9、微分方程(y``)4+(y`)5+y`+2=0的阶数是（）A 、一阶B 、二阶C 、三阶D 、四阶 10、微分方程y``+3y`+2y=0的特征根为（） A 、-2，-1 B 、2，1 C 、-2，1 D 、1，-2 二、填空题（本题共5小题，每题4分，共20分） 1、直线L 1：x=y=z 与直线L 2：的夹角为z y x =-+=-1321___________。

五年级上册数学期末试卷(1)题目及解析版

2020-2021学年五年级上册数学期末试卷(一)一.选择题(共8小题)1. 晚上面对北极星，这时我们的左面是( ) 方 .A. 西B. 南C. 东2. 下面算式中，计算结果小于1的是( )A.0.92×4.3B. 0.61×0.71C. 8.2×0.473. 与5.45÷0.5的商相等的式子是( )A.54.5÷50B. 545÷5C.54.5÷54.35×102=35×100+35×2运用了( )A. 乘法交换律B. 乘法结合律C. 乘法分配律D. 减法简便计算5. 如果1平方米能站16人，那么1公顷大约能站( ) 人。

A. 160B. 1600C. 16000D. 1600006. 下面各式中， ( )是方程，A. 3x+4yB. 5x=0C. 1.8+1.2=37. 有三根同样长的铁丝，每根铁丝首尾相连，分别围成一个长方形、正方形和圆，它们的面积相比，( )的面积最小，A. 正方形B. 圆C. 长方形D. 无法确定8.8个同学在一起，其中小希的年龄不是最大的，那么小希的年龄是最小的概率是( )A. B. C. D.二.填空题(共10小题)9. (4.16×84-2.08×54-0.15×832)÷(0.3)2=10. 如果7x=1.4, 那么5- 1.8x 的值是11. 已知方程1.5+mx=28.5 的解是x=3, 那么m=12. 一个数的1.6倍是6.4,这个数是13.8.5×4.3的积有位小数，4.17×0.25的积有位小数.14. 如果我在野外迷了路，可用帮助我识别方向.15. 口袋中只有5个红球，任意摸1个，要使摸出的红球的可能性,还要往口袋中放个其他颜色的球.16.0 . 07升= 亭升2 5 平方米= 公顷 6 8 克= 千3 分米5 厘米= 米克17. 如图，两个边长为12厘米的正方形相互错开3厘米，那么图中阴影平行四边形的面积是平方厘米.18. 在一个布袋中有白、红、绿、黄四种颜色的乒乓球各5个，每次摸一个乒乓球，摸完后放回，共摸80次，可能摸到次红颜色乒乓球.三.判断题 ( 共5 小题)19. 一个正方体抛向空中，落地后，每个面朝上的可能性都, . ( 判断对错)20.0.25÷0.12的商一定小于0.25. . ( 判断对错)21. 4x=0,x+y=5,10+Y>20 都是方程. (判断对错)22. 用地毯铺满一间房的地面，地毯的大小就是这间房地面的面积. (判断对错)23.32×(7×3)=32×7+32×3.. ( 判断对错)四 .计算题(共4小题)24. 解方程.4x+8=1683x-3.6=5.16n÷4=3625. 用自己喜欢的方法计算.2.5×1.25×3.27.13×99+0.713×1026. 求图中阴影部分的面积. (单位：米)27. 列竖式计算下面各题。

2022-2023学年第一学期八年级数学期末复习冲刺卷(01)

2022-2023学年第一学期八年级数学期末复习冲刺卷（01）（考试时间：100分钟试卷满分：120分）考生注意：1．本试卷28道试题，满分120分，考试时间100分钟．2．本试卷分设试卷和答题纸．试卷包括试题与答题要求．作答必须涂（选择题）或写（非选择题）在答题纸上，在试卷上作答一律不得分．3．答卷前，务必用钢笔或圆珠笔在答题纸正面清楚地填写姓名、准考证号码等相关信息．一．选择题（共10小题每题3分，满分30分）1．第24届冬奥会将于2022年在北京和张家口举办．下列四个图分别是第24届冬奥会图标中的一部分，其中是轴对称图形的是（）A．B．C．D．2．如果某函数的图象如图所示，那么y随着x的增大而（）A．增大B．减小C．先减小后增大D．先增大后减小3．如果点P（m，1﹣2m）在第一象限，那么m的取值范围是（）A．0＜m＜B．﹣＜m＜0C．m＜0D．m＞4．点（3，﹣4）到x轴的距离是（）A．3B．4C．5D．75．函数y＝x的图象向左平移2个单位，相应的函数表达式为（）A．y＝x+1B．y＝x﹣1C．y＝x+2D．y＝x﹣26．若等腰三角形中有一个角为50度，则这个等腰三角形的顶角的度数为（）A．50°B．80°C．65°或50°D．50°或80°7．已知一次函数y＝（2m﹣1）x+2，y随x的增大而减小，则m的取值范围是（）A．m＜B．m＞C．m≥1D．m＜18．如图，函数y＝mx和y＝kx+b的图象相交于点P（1，m），则不等式﹣b≤kx﹣b≤mx的解集为（）A．0≤x≤1B．﹣1≤x≤0C．﹣1≤x≤1D．﹣m≤x≤m9．下列各组数据中，不能作为直角三角形三边长度的是（）A．9，12，15B．7，24，25C．，2，D．1，，10．如图，将风筝放至高30m，牵引线与水平面夹角约为45°的高空中，则牵引线AB的长度所在范围最有可能是（）A．36m至38m B．38m至40m C．40m至42m D．42m至44m二．填空题（共8小题，每题3分，满分24分）11．点P（﹣2，3）到x轴的距离是．12．在，2π，0，，0.454454445…，中，无理数有个．13．如图，△ABC≌△DEF，BE＝4，AE＝1，则DE的长是．14．已知一个直角三角形的两直角边长分别为3和4，则斜边长是．15．如图，在△ABC中，AC的垂直平分线交BC于点D，垂足为点E，△ABD的周长为12cm，AC＝5cm，则△ABC的周长是．16．如图，在平面直角坐标系中，函数y＝mx+n与y＝kx+b的图象交于点P（﹣2，1），则方程组的解为．17．将一次函数的图象平移，使得平移之后的图象经过点A（2，1），则平移之后的图象的解析式为．18．如图，点C的坐标是（2，2），A为坐标原点，CB⊥x轴于B，CD⊥y轴于D，点E是线段BC的中点，过点A的直线y＝kx交线段DC于点F，连接EF，若AF平分∠DFE，则k的值为．三．解答题（共10小题，满分66分）19．计算：（1）；（2）；（3）；（4）求（x﹣2）2﹣9＝0中x的值．20．化简：（1）；（2）．21．先化简再求值：，其中．22．如图，点D、E在△ABC的BC边上，AB＝AC，AD＝AE．求证：BD＝CE．23．如图，在四边形ABCD中，AD∥BC，AD＝2BC，点E是AC的中点，请仅用无刻度的直尺分别按下列要求画图．（不写画法，保留画图痕迹）（1）在图1中，画出△ACD的边AD上的中线CM；（2）在图2中，若AC＝AD，画出△ACD的边CD上的高AN．24．如图，在平面直角坐标系中，直线l1：y＝﹣x+5与x轴交于点B，直线l1与过点A（﹣4，0）的直线l2交于点P（﹣1，m）．（1）求直线l2的函数表达式；（2）点M在第一象限且在直线l2上，MN∥y轴，交直线l1于点N，若MN＝AB，求点M的坐标．25．如图，在等边三角形ABC中，AD是∠BAC的平分线，E为AD上一点，以BE为一边且在BE下方作等边三角形BEF，连接CF．（1）求证：△ABE≌△CBF；（2）求∠ACF的度数．26．抗击疫情，我们在行动．某药店销售A型和B型两种型号的口罩，销售一箱A型口罩可获利120元，销售一箱B型口罩可获利140元．该药店计划一次购进两种型号的口罩共100箱，其中B 型口罩的进货量不超过A型口罩的3倍．设购进A型口罩x箱，这100箱口罩的销售总利润为y 元．（1）求y与x的函数关系式；（2）该商店购进A型、B型口罩各多少箱，才能使销售利润最大？最大利润是多少？（3）若限定该药店最多购进A型口罩70箱，则这100箱口罩的销售总利润能否为12500元？请说明理由．27．【数学阅读】如图1，在△ABC中，AB＝AC，点P为边BC上的任意一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F，求证：PD+PE＝CF．小明的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE＝CF．【推广延伸】如图3，当点P在BC延长线上时，其余条件不变，请运用上述解答中所积累的经验和方法，猜想PD，PE与CF的数量关系，并证明．【解决问题】如图4，在平面直角坐标系中，点C在x轴正半轴上，点B在y轴正半轴上，且AB＝AC，点B到x 轴的距离为3．（1）点B的坐标为；（2）点P为射线CB上一点，过点P作PE⊥AC于E，点P到AB的距离为d，直接写出PE与d的数量关系为；（3）在（2）的条件下，当d＝1，A为（﹣4，0）时，求点P的坐标．28．如图，直线l：y＝2x﹣2与y轴交于点G，直线l上有一动点P，过点P作y轴的平行线PE，过点G作x轴的平行线GE，它们相交于点E．将△PGE沿直线l翻折得到△PGE′，点E的对应点为E′．（1）如图1，请利用无刻度的直尺和圆规在图1中作出点E的对应点E′；（2）如图2，当点E的对应点E′落在x轴上时，求点P的坐标；（3）如图3，直线l上有A，B两点，坐标分别为（﹣2，﹣6）（4，6），当点P从点A运动到点B的过程中，点E′也随之运动，请直接写出点E′的运动路径长为．答案与解析一．选择题（共10小题每题3分，满分30分）1．第24届冬奥会将于2022年在北京和张家口举办．下列四个图分别是第24届冬奥会图标中的一部分，其中是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，进行判断即可．【解答】解：A．不是轴对称图形，故此选项不合题意；B．不是轴对称图形，故此选项不合题意；C．是轴对称图形，故此选项符合题意；D．不是轴对称图形，故此选项不合题意；故选：C．【点评】本题考查的是轴对称图形的概念，正确掌握相关定义是解题关键．2．如果某函数的图象如图所示，那么y随着x的增大而（）A．增大B．减小C．先减小后增大D．先增大后减小【分析】根据函数图象可以得到y随x的增大如何变化，本题得以解决．【解答】解：由函数图象可得，y随x的增大而增大，故选：A．【点评】本题考查函数的图象，解答本题的关键是明确题意，利用数形结合的思想解答．3．如果点P（m，1﹣2m）在第一象限，那么m的取值范围是（）A．0＜m＜B．﹣＜m＜0C．m＜0D．m＞【分析】根据第一象限内点的横坐标与纵坐标都是正数，列出不等式组求解即可．【解答】解：∵点P（m，1﹣2m）在第一象限，∴，由②得，m＜，所以，m的取值范围是0＜m＜．故选：A．【点评】本题考查了各象限内点的坐标的符号特征以及解不等式组，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．4．点（3，﹣4）到x轴的距离是（）A．3B．4C．5D．7【分析】根据点到x轴的距离等于纵坐标的绝对值解答即可．【解答】解：点（3，﹣4）到x轴的距离是4．故选：B．【点评】本题考查了点的坐标，熟记点到x轴的距离等于纵坐标的绝对值是解题的关键．5．函数y＝x的图象向左平移2个单位，相应的函数表达式为（）A．y＝x+1B．y＝x﹣1C．y＝x+2D．y＝x﹣2【分析】根据“上加下减，左加右减”的原则进行解答即可．【解答】解：由“左加右减”的原则可知，将函数y＝x的图象向左平移2个单位，所得函数的解析式为y＝（x+2），即y＝x+1，故选：A．【点评】本题考查的是一次函数的图象与几何变换，熟知“上加下减，左加右减”的原则是解答此题的关键．6．若等腰三角形中有一个角为50度，则这个等腰三角形的顶角的度数为（）A．50°B．80°C．65°或50°D．50°或80°【分析】因为题中没有指明该角是顶角还是底角，所以要分两种情况进行分析．【解答】解：①50°是底角，则顶角为：180°﹣50°×2＝80°；②50°为顶角；所以顶角的度数为50°或80°．故选：D．【点评】根据等腰三角形的性质分两种情况进行讨论．7．已知一次函数y＝（2m﹣1）x+2，y随x的增大而减小，则m的取值范围是（）A．m＜B．m＞C．m≥1D．m＜1【分析】直接根据一次函数的性质得出关于m的不等式，求出m的取值范围即可．【解答】解：∵一次函数y＝（2m﹣1）x+2，y随x的增大而减小，∴2m﹣1＜0，解得m＜．故选：A．【点评】本题考查的是一次函数的图象与系数的关系，熟知一次函数的增减性是解答此题的关键．8．如图，函数y＝mx和y＝kx+b的图象相交于点P（1，m），则不等式﹣b≤kx﹣b≤mx的解集为（）A．0≤x≤1B．﹣1≤x≤0C．﹣1≤x≤1D．﹣m≤x≤m【分析】首先确定y＝mx和y＝kx﹣b的交点，作出y＝kx﹣b的大体图象，然后根据图象判断．【解答】解：∵y＝kx+b的图象经过点P（1，m），∴k+b＝m，当x＝﹣1时，kx﹣b＝﹣k﹣b＝﹣（k+b）＝﹣m，即（﹣1，﹣m）在函数y＝kx﹣b的图象上．又∵（﹣1，﹣m）在y＝mx的图象上．∴y＝kx﹣b与y＝mx相交于点（﹣1，﹣m）．则函数图象如图．则不等式﹣b≤kx﹣b≤mx的解集为﹣1≤x≤0．故选：B．【点评】本题考查了一次函数与不等式的关系，正确确定y＝kx﹣b和y＝mx的交点是关键．9．下列各组数据中，不能作为直角三角形三边长度的是（）A．9，12，15B．7，24，25C．，2，D．1，，【分析】先分别求出两小边的平方和和最长边的平方，再根据勾股定理的逆定理逐个判断即可．【解答】解：A．∵92+122＝81+144＝225，152＝225，∴92+122＝152，∴以9，12，15为边能组成直角三角形，故本选项不符合题意；B．∵72+242＝49+576＝625，252＝625，∴72+242＝252，∴以7，24，25为边能组成直角三角形，故本选项不符合题意；C．∵（）2+22＝3+4＝7，（）2＝5，∴（）2+22≠（）2，∴以，2，为边不能组成直角三角形，故本选项符合题意；D．∵12+（）2＝1+2＝3，（）2＝3，∴12+（）2＝（）2，∴以1，，为边能组成直角三角形，故本选项不符合题意；故选：C．【点评】本题考查了勾股定理的逆定理，能熟记勾股定理的逆定理是解此题的关键，注意：如果一个三角形的两边a、b的平方和等于第三边c的平方，那么这个三角形是直角三角形．10．如图，将风筝放至高30m，牵引线与水平面夹角约为45°的高空中，则牵引线AB的长度所在范围最有可能是（）A．36m至38m B．38m至40m C．40m至42m D．42m至44m【分析】过B作BC⊥水平面于C，证△ABC是等腰直角三角形，得AC＝BC＝30m，再由勾股定理求出AB的长，即可得出结论．【解答】解：如图，过B作BC⊥水平面于C，∵∠BAC＝45°，∴△ABC是等腰直角三角形，∴AC＝BC＝30m，∴AB＝＝＝30≈42.42（m），故选：D．【点评】本题考查了勾股定理的应用以及等腰直角三角形的判定与性质，熟练掌握勾股定理是解题的关键．二．填空题（共8小题，每题3分，满分24分）11．点P（﹣2，3）到x轴的距离是3．【分析】求得P的纵坐标的绝对值即可求得P点到x轴的距离．【解答】解：∵点P的纵坐标为3，∴P点到x轴的距离是|3|＝3．故答案为：3．【点评】本题考查了点的坐标，解答本题的关键在于熟练掌握点到x轴的距离为点的纵坐标的绝对值．12．在，2π，0，，0.454454445…，中，无理数有3个．【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．【解答】解：，是分数，属于有理数；0，是整数，属于有理数；无理数有2π，0.454454445…，，共3个．故答案为：3．【点评】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…（两个1之间依次多一个0），等有这样规律的数．13．如图，△ABC≌△DEF，BE＝4，AE＝1，则DE的长是5．【分析】先求出AB的长度，再根据全等三角形对应边相等解答即可．【解答】解：∵BE＝4，AE＝1，∴AB＝BE+AE＝4+1＝5，∵△ABC≌△DEF，∴DE＝AB＝5．故答案为：5．【点评】本题考查了全等三角形对应边相等的性质，先求出DE的对应边AB的长度是解题的关键．14．已知一个直角三角形的两直角边长分别为3和4，则斜边长是5．【分析】根据勾股定理计算即可．【解答】解：由勾股定理得，斜边长＝＝5，故答案为：5．【点评】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2＝c2．15．如图，在△ABC中，AC的垂直平分线交BC于点D，垂足为点E，△ABD的周长为12cm，AC＝5cm，则△ABC的周长是17cm．【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得AD＝CD，然后求出△ABD 的周长＝AB+BC，再根据三角形的周长公式列式计算即可得解．【解答】解：∵DE垂直平分AC，∴AD＝CD，∴△ABD的周长＝AB+BD+AD＝AB+BD+CD＝AB+BC，∴△ABC的周长＝AB+BC+AC＝12+5＝17cm．故答案为：17cm．【点评】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质，熟记性质并求出△ABD的周长＝AB+BC是解题的关键．16．如图，在平面直角坐标系中，函数y＝mx+n与y＝kx+b的图象交于点P（﹣2，1），则方程组的解为．【分析】利用方程组的解就是两个相应的一次函数图象的交点坐标进行判断．【解答】解：∵函数y＝mx+n的图象与y＝kx+b的图象交于点P（﹣2，1），∴方程组的解为，故答案为：．【点评】本题考查了一次函数与二元一次方程（组）：方程组的解就是使方程组中两个方程同时成立的一对未知数的值，而这一对未知数的值也同时满足两个相应的一次函数式，因此方程组的解就是两个相应的一次函数图象的交点坐标．17．将一次函数的图象平移，使得平移之后的图象经过点A（2，1），则平移之后的图象的解析式为．【分析】平移时k的值不变，只有b发生变化．【解答】解：新直线是由一次函数的图象平移得到的，∴新直线的k＝．可设新直线的解析式为：y＝x+b．∵经过点（2，1），则×2+b＝1．解得b＝0．∴平移后图象函数的解析式为y＝x．故答案是：y＝x．【点评】本题主要考查了一次函数图象与几何变换，本题要注意利用一次函数的特点，求出未知数的值从而求得其解析式，求直线平移后的解析式时要注意平移时k的值不变．18．如图，点C的坐标是（2，2），A为坐标原点，CB⊥x轴于B，CD⊥y轴于D，点E是线段BC的中点，过点A的直线y＝kx交线段DC于点F，连接EF，若AF平分∠DFE，则k的值为1或3．【分析】分两种情况：①当点F在DC之间时，作出辅助线，求出点F的坐标即可求出k的值；②当点F与点C重合时求出点F的坐标即可求出k的值．【解答】解：∵C的坐标是（2，2），A为坐标原点，CB⊥x轴于B，CD⊥y轴于D，∴四边形ABCD是正方形，①如图，作AG⊥EF交EF于点G，连接AE，∵AF平分∠DFE，∴DA＝AG＝2，在RT△ADF和RT△AGF中，，∴RT△ADF≌RT△AGF（HL），∴DF＝FG，∵点E是BC边的中点，∴BE＝CE＝1，∴AE＝＝，∴GE＝＝1，∴在RT△FCE中，EF2＝FC2+CE2，即（DF+1）2＝（2﹣DF）2+1，解得DF＝，∴点F（，2），把点F的坐标代入y＝kx得：2＝k，解得k＝3；②当点F与点C重合时，∵四边形ABCD是正方形，∴AF平分∠DFE，∴F（2，2），把点F的坐标代入y＝kx得：2＝2k，解得k＝1．故答案为：1或3．【点评】本题主要考查了一次函数综合题，涉及角平分线的性质，三角形全等的判定及性质，正方形的性质理，及勾股定解题的关键是分两种情况求出k．三．解答题（共10小题，满分66分）19．计算：（1）；（2）；（3）；（4）求（x﹣2）2﹣9＝0中x的值．【分析】（1）先计算开方、零次幂，后计算加减；（2）先变除法为乘法，再计算化简；（3）先计算二次根式、绝对值，后计算加减；（4）运用开平方法进行求解．【解答】解：（1）＝2﹣1+2＝1+2；（2）＝＝12；（3）＝3﹣+＝6﹣+＝5+；（4）移项，得（x﹣2）2＝9，开平方，得x﹣2＝3，或x﹣2＝﹣3，解得x＝5或x＝﹣1．【点评】此题考查了实数的混合运算和解一元二次方程的能力，关键是能确定正确的运算顺序和方法．20．化简：（1）；（2）．【分析】（1）把除化为乘，再约分即可；（2）分子、分母分解因式，约分后再算加减．【解答】解：（1）原式＝•＝；（2）原式＝﹣＝﹣＝．【点评】本题考查分式的混合运算，解题的关键是掌握分式通分、约分的方法，把分式化简．21．先化简再求值：，其中．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．【解答】解：原式＝÷＝•＝，当x＝时，原式＝＝．【点评】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．22．如图，点D、E在△ABC的BC边上，AB＝AC，AD＝AE．求证：BD＝CE．【分析】要证明线段相等，只要过点A作BC的垂线，利用三线合一得到P为DE及BC的中点，线段相减即可得证．【解答】证明：如图，过点A作AP⊥BC于P．∵AB＝AC，∴BP＝PC；∵AD＝AE，∴DP＝PE，∴BP﹣DP＝PC﹣PE，∴BD＝CE．【点评】本题考查了等腰三角形的性质，做题时，两次用到三线合一的性质，由等量减去等量得到差相等是解答本题的关键．23．如图，在四边形ABCD中，AD∥BC，AD＝2BC，点E是AC的中点，请仅用无刻度的直尺分别按下列要求画图．（不写画法，保留画图痕迹）（1）在图1中，画出△ACD的边AD上的中线CM；（2）在图2中，若AC＝AD，画出△ACD的边CD上的高AN．【分析】（1）延长BE交AD于M，证明△AEM≌△CEB得到AM＝BC＝AD，从而得到M点为AD的中点；（2）延长BE交AD于F，连接CF、DE，它们相交于点O，然后延长AO交CD于N，则AN满足条件．【解答】解：（1）如图1，CM为所作；（2）如图2，AN为所作．【点评】本题考查了作图﹣复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定与性质．24．如图，在平面直角坐标系中，直线l1：y＝﹣x+5与x轴交于点B，直线l1与过点A（﹣4，0）的直线l2交于点P（﹣1，m）．（1）求直线l2的函数表达式；（2）点M在第一象限且在直线l2上，MN∥y轴，交直线l1于点N，若MN＝AB，求点M的坐标．【分析】（1）将点P代入y＝﹣x+5，可求P点坐标，再由待定系数法求直线解析式即可；（2）求出AB的长，设M（t，2t+8），则N（t，﹣t+5），MN＝3t+3＝9，求出t的值即可求M 点坐标．【解答】解：（1）∵P（﹣1，m）在直线l1：y＝﹣x+5上，∴1+5＝m，∴m＝6，∴P（﹣1，6），设直线l2的解析式为y＝kx+b，∴，解得，∴y＝2x+8；（2）由y＝﹣x+5可得B（5，0），∵A（﹣4，0），∴AB＝9，设M（t，2t+8），则N（t，﹣t+5），∴MN＝3t+3，∵MN＝AB，∴3t+3＝9，∴t＝2，∴M（2，12）．【点评】本题考查一次函数的图象及性质，熟练掌握一次函数的图象及性质是解题的关键．25．如图，在等边三角形ABC中，AD是∠BAC的平分线，E为AD上一点，以BE为一边且在BE下方作等边三角形BEF，连接CF．（1）求证：△ABE≌△CBF；（2）求∠ACF的度数．【分析】（1）由△ABC是等边三角形的性质得出AB＝BC，∠ABE+∠EBC＝60°，EB＝BF，∠CBF+∠EBC＝60°，求出∠ABE＝∠CBF，根据SAS证出△ABE≌△CBF；（2）根据等边三角形的性质得出∠BAE＝30°，∠ACB＝60°，再根据△ABE≌△CBF，得出∠BCF＝∠BAE＝30°，从而求出∠ACF的度数．【解答】（1）证明：∵△ABC是等边三角形，∴AB＝BC，∠ABE+∠EBC＝60°，∵△BEF是等边三角形，∴BE＝BF，∠CBF+∠EBC＝60°，∴∠ABE＝∠CBF，在△ABE和△CBF，，∴△ABE≌△CBF（SAS）；（2）解：∵等边△ABC中，AD是∠BAC的角平分线，∴∠BAE＝30°，∠ACB＝60°，∵△ABE≌△CBF，∴∠BCF＝∠BAE＝30°，∴∠ACF＝∠BCF+∠ACB＝30°+60°＝90°．【点评】此题考查了等边三角形的性质和全等三角形的判定与性质等知识；熟练掌握等边三角形的性质，证明三角形全等是解题的关键．26．抗击疫情，我们在行动．某药店销售A型和B型两种型号的口罩，销售一箱A型口罩可获利120元，销售一箱B型口罩可获利140元．该药店计划一次购进两种型号的口罩共100箱，其中B 型口罩的进货量不超过A型口罩的3倍．设购进A型口罩x箱，这100箱口罩的销售总利润为y 元．（1）求y与x的函数关系式；（2）该商店购进A型、B型口罩各多少箱，才能使销售利润最大？最大利润是多少？（3）若限定该药店最多购进A型口罩70箱，则这100箱口罩的销售总利润能否为12500元？请说明理由．【分析】（1）根据题意即可得出y关于x的函数关系式；（2）根据题意列不等式得出x的取值范围，再根据一次函数的性质解答即可；（3）由题意得出x的取值范围为25≤x≤60，根据一次函数的性质可得x＝60时，总利润y最小，求出y的最小值，即可得出答案．【解答】解：（1）根据题意得，y＝120x+140（100﹣x）＝﹣20x+14000，答：y与x的函数关系式为：y＝﹣20x+14000；（2）根据题意得，100﹣x≤3x，解得x≥25，∵y＝﹣20x+14000，k＝﹣20＜0；∴y随x的增大而减小，∵x为正整数，∴当x＝25时，y有最大值，最大值为﹣20×25+14000＝13500，则100﹣x＝75，即商店购进A型口罩25箱、B型口罩75箱，才能使销售总利润最大，最大利润为13500元；（3）根据题意得25≤x≤70，∵y＝﹣20x+14000，k＝﹣20＜0；∴y随x的增大而减小，∵x为正整数，∴当x＝70时，y有最小值，最小值为﹣20×70+14000＝12600，∵12600＞12500，∴这100箱口罩的销售总利润不能为12500元．【点评】本题主要考查了一次函数的应用，一元一次不等式的应用，解题的关键是根据一次函数x值的增大而确定y值的增减情况．27．【数学阅读】如图1，在△ABC中，AB＝AC，点P为边BC上的任意一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F，求证：PD+PE＝CF．小明的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE＝CF．【推广延伸】如图3，当点P在BC延长线上时，其余条件不变，请运用上述解答中所积累的经验和方法，猜想PD，PE与CF的数量关系，并证明．【解决问题】如图4，在平面直角坐标系中，点C在x轴正半轴上，点B在y轴正半轴上，且AB＝AC，点B到x 轴的距离为3．（1）点B的坐标为（0，3）；（2）点P为射线CB上一点，过点P作PE⊥AC于E，点P到AB的距离为d，直接写出PE与d的数量关系为PE＝3+d或3﹣d；（3）在（2）的条件下，当d＝1，A为（﹣4，0）时，求点P的坐标．【分析】【数学阅读】由S△ABP+S△APC＝×AB×（DP+PE），S△ABC＝×AB×CF，再由面积相等即可证明；【推广延伸】由S△ABC+S△APC＝×AB×（CF+PE），S△ABP＝×AB×DP，再由面积相等即可求解；【解决问题】（1）由题意可直接求得；（2）由面积和差关系可求解；（3）由勾股定理可求AB的长，利用待定系数法可求直线BC解析式，分两种情况讨论，可求点P坐标．【解答】【数学阅读】证明：∵DP⊥AB，PE⊥AC，∴S△ABP＝×AB×DP，S△APC＝×AC×PE，∵AB＝AC，∴S△ABP+S△APC＝×AB×（DP+PE），∵CF⊥AB，∴S△ABC＝×AB×CF，∵S△ABP+S△APC＝S△ABC，∴PE+PD＝CF；【推广延伸】PE+CF＝DP，理由如下：连接AP，∵CF⊥AB，PE⊥AC，∴S△ABC＝×AB×CF，S△APC＝×AC×PE，∵AB＝AC，∴S△ABC+S△APC＝×AB×（CF+PE），∵DP⊥AB，∴S△ABP＝×AB×DP，∵S△ABC+S△APC＝S△ABP，∴PE+CF＝DP；【解决问题】（1）∵点B在y轴正半轴上，点B到x轴的距离为3，∴OB＝3，∴点B（0，3），故答案为：（0，3）；（2）如图4，当点P在线段BC上时，过点P作PH⊥AB于H，∵S△ABC＝S△ABP+S△ACP，∴AC×BO＝AC×PE+AB×PH，∵AB＝AC，点P到AB的距离为d，∴3＝PE+d，∴PE＝3﹣d；当点P在线段CB的延长线上时，过点P'作P'H⊥AB于H'，∵S△ABC＝S△ACP﹣S△ABP，∴AC×BO＝AC×PE﹣AB×PH，∵AB＝AC，点P到AB的距离为d，∴3＝PE﹣d，∴PE＝3+d，综上所述：PE＝3+d或3﹣d，故答案为：PE＝3+d或3﹣d；（3）∵点A为（﹣4，0），∴AO＝4，∴AB＝＝＝5，∴AB＝AC＝5，∴OC＝1，∴点C（1，0），设直线BC解析式为：y＝kx+3，∴0＝k+3，∴k＝﹣3，∴直线BC解析式为：y＝﹣3x+3，当点P在线段BC上时，PE＝3﹣d＝2，∴当y＝2时，x＝，∴点P（，2）；当点P在线段CB的延长线上时，PE＝3+d＝4，∴当y＝4时，x＝﹣，∴点P（﹣，4）；综上所述：点P坐标为：（，2）或（，2）．【点评】本题是三角形综合题，考查了等腰三角形的性质，勾股定理，三角形的面积公式，一次函数的应用，利用分类讨论思想解决问题是解题的关键．28．如图，直线l：y＝2x﹣2与y轴交于点G，直线l上有一动点P，过点P作y轴的平行线PE，过点G作x轴的平行线GE，它们相交于点E．将△PGE沿直线l翻折得到△PGE′，点E的对应点为E′．（1）如图1，请利用无刻度的直尺和圆规在图1中作出点E的对应点E′；（2）如图2，当点E的对应点E′落在x轴上时，求点P的坐标；（3）如图3，直线l上有A，B两点，坐标分别为（﹣2，﹣6）（4，6），当点P从点A运动到点B的过程中，点E′也随之运动，请直接写出点E′的运动路径长为6．【分析】（1）过点E画PG的垂线，再以G为圆心，GE为半径画圆与垂线交点即为点E'；（2）设直线l交x轴于点D，首先求出点C、D的坐标，利用平行线的性质和角平分线的定义得E'D＝E'G，设点P的坐标为（a，2a﹣2），则可得点E的坐标为（a，﹣2），在Rt△OGE'中，利用勾股定理得：22+（a﹣1）2＝a2，解方程即可；（3）分别过点A，B作y轴的平行线，与过点G垂直于y轴的直线分别交于点C，M，则点E在线段CM上运动，根据对称性知，点E'运动路径长度为CM的长，从而解决问题．【解答】解：（1）如图，点E'即为所求；（2）设直线l交x轴于点D，在y＝2x﹣2中，当y＝0时，x＝1，当x＝0时，y＝﹣2，∴D（1，0），G（0，﹣2），∴OD＝1，OG＝2，由对称得：E'G＝EG，∠EGD＝∠E'GD，∵GE∥x轴，∴∠EGD＝∠E'DG，∴∠E'GD＝∠E'DG，∴E'D＝E'G，∴E'D＝EG，设点P的坐标为（a，2a﹣2），则可得点E的坐标为（a，﹣2），∴EG＝E'D＝a，∴OE'＝E'D﹣OD＝a﹣1，在Rt△OGE'中，由勾股定理得：22+（a﹣1）2＝a2，解得a＝，当a＝时，2a﹣3＝2×﹣2＝3，∴P（）；（3）分别过点A，B作y轴的平行线，与过点G垂直于y轴的直线分别交于点C，M，则点E在线段CM上运动，根据对称性知，点E'运动路径长度为CM的长，∵A（﹣2，﹣6），B（4，6），∴CM＝4﹣（﹣2）＝6，∴点E'的运动路径长为6，故答案为：6．【点评】本题是一次函数综合题，主要考查了一次函数图象上点的坐标的特征，翻折的性质，勾股定理，尺规作图等知识，确定点E的运动路径长是解题的关键．。

人教版数学五年级上册期末真题试卷1(含答案)

人教版五上期末复习测试卷（一）2.（1）（2）根据，直接写出下面各式的得数．3.制作一套校服需要布料，现在制衣厂还有同样的布料，则可以制作套这样的校服．4.依据下图列出的方程是．5.图书角有本书，借出本，还剩下本，当时，还剩本书．6.街道上有大、小两种混凝土圆球（如下图），这些圆球是为了防止车辆停泊而设置的，每一个圆球都被牢固的固定在地面上的某一点，相邻两个圆球固定点之间相距米，在相邻两个大圆球之间放置了个小圆球，相邻两个大圆球固定点之间的距离是米．7.王叔叔骑车到离家千米的郊外游玩，他骑车的速度是千米/时，估一估，小时他到达目的地．（填“能”或“不能”）．8.下图是由两个等腰直角三角形和一个正方形拼成的一个大三角形，正方形的边长是，大三角形的面积是．1.（1）（2）在横线填上“”、””或“”．9.下面是某楼房一层到二层的楼梯示意图．每级台阶高米．总长度米总高度米10.约翰和父母来中国旅游，花了元人民币买了一个纪念品，折合成美元是美元．美元换人民币元美元换港币元港元换人民币元日元换人民币元11.1.2.3.4.5.判断对错．一个数除以，商一定大于这个数．（）两个面积相等的三角形一定可以拼成一个平行四边形．（）的倍比少，用方程表示是．（）将一个平行四边形框架拉成长方形，它的周长不变，面积变大．（）两个完全一样的三角形，不可能拼成一个正方形．（）12.A.个一B.个C.个D.个观察右边除法算式，方框内的数表示（）．13.A.B.C.D.将、、、按从大到小的顺序排列，排在第二位的是（）．14.平行四边形如图所示，计算其面积的正确算式是（）．A. B. C. D.15.A.黄球B.篮球C.红球D.白球在一个纸箱里装有个红球，个篮球，个黄球和个白球，它们的形状、大小、质量完全相同．欢欢从箱子中任意摸出一个球，拿到（）的可能性最大．16.A. B. C. D.如下图所示，不规则图形的面积大约是（）平方厘米．（每个小正方形的面积是平方厘米）．17.（1）（2）笔算．18.（1）（2）计算下面各题．．．19.（1）（2）（3）解方程．20.按要求画图并填空．（1）（2）在右图方格纸中（每小格代表平方厘米），先画一个面积是平方厘米的平行四边形，再用数对表示格顶点的位置分别是：（，）、（，）、（，）、（，）．请你再画出与平行四边形面积相等的三角形，这个三角形的底是厘米，高是厘米．21.计算下面图形中阴影部分的面积．厘米厘米厘米厘米22.研究表明，体育运动可以适当提高人体的肺活量，一名游泳运动员的肺活量可以达到普通小学生肺活量的倍．23.下面是张阿姨去便利超市的购物小票，不小心撕掉了一部分．24.假日里同学们一起去游乐园玩儿，儿童票每张元，元最多能买几张儿童票呢？25.少年宫合唱团共有学生人，其中男生人数是女生人数的倍，合唱团中男生、女生各有多少人？（用方程解答）26.A 套餐 78元/月包含：免费通话80分钟、免费使用8G 上网流量．B 套餐 128元/月包含：免费通话150分钟、免费使用20G 上网流量．两种套餐收费补充说明通话时间超出套餐部分按0.20元/分钟收费．上网流量超出套餐部分按5元/G 进行收费．免收短信费．（1）（2）电信公司推出两种手机套餐服务．李叔叔每月的通话时间大约是分钟，使用上网流量，他选择哪种套餐比较便宜？每月大约花费多少元？王阿姨购买了套餐，她月份共缴费元，其中使用上网流量，王阿姨这个月的通话时间是多少分钟？27.甲乙两车分别从、两地同时出发相向而行，乙车每小时行千米，乙车速度是甲车速度的倍，经过小时相遇．、两地相距多少千米？28.（1）（2）李大爷用米长的篱笆，在靠墙的地方围了一块梯形菜地（如图）．米梯形菜地的面积是多少平方米?如果用这些篱笆靠墙改围成一块长为米的长方形菜地，菜地的面积会增加多少平方米？人教版五上期末复习测试卷（一）(详解)2.（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】根据，直接写出下面各式的得数．因为相比于小数点向左移动了位，相比于小数点也向左移动了位，所以的小数点要向左移动两位，即﹒由，得，被除数小数点向左移动位，除数小数点向左移动位，则商的小数点向右移动位，最终结果为．3.【答案】制作一套校服需要布料，现在制衣厂还有同样的布料，则可以制作套这样的校服．1.（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】在横线填上“”、””或“”．一个数乘一个小于的数，积小于这个数本身，一个数除以一个小于的数，商大于这个数本身．【解析】【踩分点】制作一套校服需要米的布料，现在制衣厂有米同样的布料，那么可以制作套这样的校服．但是需要采用去尾法的方法舍掉整数后面的数字．因为剩余的布料无法再做出一套这样的校服，所以最多可以做套这样的校服．4.【答案】【解析】【踩分点】依据下图列出的方程是．从图中可知，左右两边的重量是相等的，所以左边三个物体的总重量为千克，故列方程为：，即，故答案为：．5.【答案】【解析】【踩分点】图书角有本书，借出本，还剩下本，当时，还剩本书．;剩下的本数（本），把代入算式为：（本）．6.【答案】【解析】街道上有大、小两种混凝土圆球（如下图），这些圆球是为了防止车辆停泊而设置的，每一个圆球都被牢固的固定在地面上的某一点，相邻两个圆球固定点之间相距米，在相邻两个大圆球之间放置了个小圆球，相邻两个大圆球固定点之间的距离是米．因为两个大圆球之间放了个小圆球，所以两个大圆球之间的距离就是个米，（米）．【踩分点】7.【答案】【解析】【踩分点】王叔叔骑车到离家千米的郊外游玩，他骑车的速度是千米/时，估一估，小时他到达目的地．（填“能”或“不能”）．不能（千米），．8.【答案】【解析】【踩分点】下图是由两个等腰直角三角形和一个正方形拼成的一个大三角形，正方形的边长是，大三角形的面积是．因为正方形的边长是，所以等腰直角三角形的两个直角边都是，所以大三角形的面积．9.【答案】【解析】【踩分点】下面是某楼房一层到二层的楼梯示意图．每级台阶高米．总长度米总高度米（米）．10.约翰和父母来中国旅游，花了元人民币买了一个纪念品，折合成美元是美元．【答案】【解析】【踩分点】美元换人民币元美元换港币元港元换人民币元日元换人民币元（美元）．11.1.2.3.4.5.【答案】1 ：2 ：3 ：4 ：5 ：【解析】判断对错．一个数除以，商一定大于这个数．（）两个面积相等的三角形一定可以拼成一个平行四边形．（）的倍比少，用方程表示是．（）将一个平行四边形框架拉成长方形，它的周长不变，面积变大．（）两个完全一样的三角形，不可能拼成一个正方形．（）×××✓×零除以任何非零的数都为零，所以一个数除以，商一定大于这个数的说法是错误的．故答案为：错误．例如：底边长为，高为和底边长为，高为的两个三角形，面积相等，但是不能拼成平行四边形．面积相等的两个三角形一定能拼成平行四边形，说法错误．故答案为：错误．的倍比少，即，说法错误．故答案为：错误．平行四边形活动框架拉成长方形之后，每条边的长度不变，所以周长不变；平行四边形活动框架拉成长方形之后，长方形的宽大于平行四边形的高，长方形的长等于原来平行四边形的底，所以长方形的面积比平行四边形的面积大，说法正确．故答案为：正确．要拼成一个长方形，需要两个完全一样的等腰直角三角形，以斜边为公共边来拼．如图：故：原题说法错误．12.A.个一B.个C.个D.个【答案】【解析】观察右边除法算式，方框内的数表示（）．C 方框中的表示，，所以方框中的表示个．故选．13.A.B.C.D.【答案】【解析】将、、、按从大到小的顺序排列，排在第二位的是（）．D 14.A.B. C. D.【答案】【解析】平行四边形如图所示，计算其面积的正确算式是（）．B 解：或，答：这个平行四边形的面积是．15.A.黄球B.篮球C.红球D.白球在一个纸箱里装有个红球，个篮球，个黄球和个白球，它们的形状、大小、质量完全相同．欢欢从箱子中任意摸出一个球，拿到（）的可能性最大．【答案】【解析】C红球的个数最多，可能性最大．16.A.B. C. D.【答案】【解析】如下图所示，不规则图形的面积大约是（）平方厘米．（每个小正方形的面积是平方厘米）．C数图中所占的格子数有个大格子和个半格子，所以面积为：（平方厘米）．故选．17.（1）（2）（1）（2）【答案】（1）（2）【解析】笔算．．3.5×2.7414024579.590．【踩分点】4.22·510·5.150518.（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】计算下面各题．．．．．．．19.（1）（2）（3）（1）（2）【答案】解方程．．．（3）（1）（2）（3）【解析】【踩分点】．，，．，，，．，，，，．20.（1）（2）（1）（2）【答案】按要求画图并填空．在右图方格纸中（每小格代表平方厘米），先画一个面积是平方厘米的平行四边形，再用数对表示格顶点的位置分别是：（，）、（，）、（，）、（，）．请你再画出与平行四边形面积相等的三角形，这个三角形的底是厘米，高是厘米．; ; ; ;; ; ;;（1）（2）【解析】【踩分点】方格纸的边长为厘米，；（答案正确即可，图正确即可），三角形的底为厘米，高是厘米；或底为厘米，高是厘米．（选其中一个填入即可，图正确即可）21.【答案】【解析】【踩分点】计算下面图形中阴影部分的面积．厘米厘米厘米厘米．小正方形里阴影部分三角形的面积是，大正方形里三角形的面积是，．22.研究表明，体育运动可以适当提高人体的肺活量，一名游泳运动员的肺活量可以达到普通小学生肺活量的倍．【答案】【解析】【踩分点】毫升．（毫升）．23.【答案】【解析】【踩分点】下面是张阿姨去便利超市的购物小票，不小心撕掉了一部分．元．（元），（元）．24.【答案】【解析】【踩分点】假日里同学们一起去游乐园玩儿，儿童票每张元，元最多能买几张儿童票呢？张．（张）（元）．答：元最多购买张儿童票．25.【答案】【解析】少年宫合唱团共有学生人，其中男生人数是女生人数的倍，合唱团中男生、女生各有多少人？（用方程解答）男生人，女生人．设：合唱团女生人数为，则男生人数为人，（人）．【踩分点】26.A 套餐 78元/月包含：免费通话80分钟、免费使用8G 上网流量．B 套餐 128元/月包含：免费通话150分钟、免费使用20G 上网流量．两种套餐收费补充说明通话时间超出套餐部分按0.20元/分钟收费．上网流量超出套餐部分按5元/G 进行收费．免收短信费．（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】电信公司推出两种手机套餐服务．李叔叔每月的通话时间大约是分钟，使用上网流量，他选择哪种套餐比较便宜？每月大约花费多少元？王阿姨购买了套餐，她月份共缴费元，其中使用上网流量，王阿姨这个月的通话时间是多少分钟？使用套餐便宜，元．分钟．如果使用套餐：，（G ），（元），（元），如果使用套餐，，需要花费元，，使用套餐便宜．，（元），（分），（分）．27.【答案】【解析】【踩分点】甲乙两车分别从、两地同时出发相向而行，乙车每小时行千米，乙车速度是甲车速度的倍，经过小时相遇．、两地相距多少千米？千米．（千米）．答：、两地相距千米．28.李大爷用米长的篱笆，在靠墙的地方围了一块梯形菜地（如图）．（1）（2）（1）（2）【答案】（1）（2）【解析】【踩分点】米梯形菜地的面积是多少平方米?如果用这些篱笆靠墙改围成一块长为米的长方形菜地，菜地的面积会增加多少平方米？梯形菜地的面积平方米．菜地的面积会增加平方米．根据题意，可用篱笆的长减去梯形的高米计算出梯形上底与下底的和，然后再利用梯形的面积（上底下底）高进行计算即可得到答案．（平方米），答：梯形菜地的面积平方米．已知篱笆的长，减去长方形菜地的长米，就是长方形的两个宽，再除以即可得到长方形菜地的宽，利用长方形的面积长宽即可解决．长方形菜地的宽为：（米），（平方米）；答：菜地的面积会增加平方米．。

四年级下册数学期末复习卷1

\四年级下册数学期末复习卷1一．选择题1．下面的小数从小到大排列正确的是（）A．10.90＜8.99＜10.09＜9.91B．8.99＜9.91＜10.90＜10.09C．10.90＜10.09＜9.91＜8.99D．8.99＜9.91＜10.09＜10.902．一个平底锅每次最多只能煎两个鸡蛋，两面都要煎，每面要煎2分钟，煎5个鸡蛋最少要用（）分钟。

A．5B．10C．15D．203．—只锅最多同时能煎2条鱼，鱼的两面都要煎。

煎一面要3分钟，煎完7条鱼，最少要用（）分钟。

A．24B．18C．21D．274．下列说法正确的是（）A．大于0.3元而小于0.5元的小数只有0.4元B．每年下半年的天数都一样多C．一袋鲜牛奶5.98元，这个小数中的“9”表示9分D．小丽身高是1米4厘米，用小数表示是1.40米5．小明主动做家务，需要做：用洗衣机洗衣服（20分钟）、扫地（10分钟）、整理书桌（10分钟）、晾衣服（5分钟）。

小明最少需要（）分钟。

A．20B．25C．456．如图，一个三角形被遮住了，这个三角形一定是（）A．锐角三角形B．钝角三角形C．直角三角形D．等腰直角三角形7．下面图中，三角形都被长方形纸板遮住了一部分。

一定是锐角三角形的是（）A．B．C．8．如图，用两个完全相同的小三角形拼出一个大三角形。

这个大三角形的内角和是（）A．180°B．360°C．540°9．一根电线长30米，第一次用去4.7米，第二次用去3.55米，这时这根电线还剩下（）米。

A．1.15B．4.7C．8.25D．21.7510．奇思有6.9元，买了一支4.4元的钢笔和一块1.3元的橡皮擦，还剩（）元。

A．2.5B．0.2C．1.2二．填空题11．m×7×n的简便写法是，5×a×a的简便写法是。

12．当2x＝10时，58﹣x＝，3x+16＝。

13．当d＝0.4时，2d＝，d+2＝。

冀教版小学二年级上册期末考试数学试卷(1)(解析版)

二年级上册数学期末综合测试题（一）一、选择题1.小方看到的茶壶的样子是哪一幅图?A. B. C.2.三角尺上的直角与黑板上的直角大小（）。

A. 不相等B. 相等C. 不能比较3.两个乘数都是9，积是（）。

A. 18B. 81C. 644.算式里没有括号，有乘法和加法，应该（）。

A. 从左往右的顺序进行计算B. 先算加法C. 先算乘法5.下面哪道算式可以用口诀“二六十二”算出得数?A. 6×2B. 6＋2C. 6÷26.小青连续走两步全长大约是1米，照这样，从教室的前面走到后面一共走了17步，大约一共走了多少米?A. 不到2米B. 不到9米C. 大约17米7.8乘4，正确列式是（）。

A. 8×4B. 8－4C. 8＋48.5×4改写成加法算式是（）。

A. 5＋4B. 4＋4＋4+4C. 5＋5＋5+59.图形里有几个角？（）A. 2个B. 3个C. 4个D. 没有10.□×5<29，□里可以填（）。

A. 4B. 6C. 811.下面三种分法，哪种不是平均分？（）A. ▲▲∣▲▲∣▲▲B. ▲▲▲∣▲▲▲C. ▲∣▲▲∣▲▲▲二、判断题12.每一个三角尺上都有两个直角。

（）13.同一个物体，不管从哪一个方向看都一样。

（）14.计算4×8=32，用口诀四八三十二。

（）15.3辆三轮车共有9个轮子。

（）16.18＋93-60先算加法，再算减法。

（）三、填空题17.横线上最大能填几？________×6＜27 ________＜3×74×________＜15 35＞7×________18.两个因数都是5，积是________；4个8相加的和是________；54与36的差是________。

19.有一堆糖，比30块多，比40块少，平均分给一些小朋友，每人分得的块数和小朋友的人数同样多。

这堆糖有________块。

人教版六年级数学上册期末试卷附答案 (1)

人教版六年级数学上册期末综合复习复习时间：80分钟满分：100分书写(2分)。

我能做到书写端正。

一、选择。

(将正确答案的序号填在括号里)(每题2分，共20分)1．已知a是一个不为0的自然数，下面算式中得数最小的是( )。

A.17÷a B．a÷17 C.17×a D．a＋172．下面说法正确的是( )。

A．在100 g水中放入10 g糖，糖的质量占糖水质量的10% B．一个假分数的倒数一定比这个假分数小C．生活中的百分数不可能超过100%D．圆的周长是它的直径的π倍3．冰化成水，体积减小110；水结成冰，体积会增大( )。

A.111 B.110 C.112 D.194．用12 m长的铁丝做直径是5 dm的圆形铁环，最多可以做( )个。

A．8 B．7 C．6 D．25．一项工程，甲队单独做要15天完成，乙队单独做要18天完成。

如果甲、乙两队合作，要( )天完成。

A.332B．10 C.9011D．336．一个圆环，内圆半径是4 cm，外圆直径是12 cm。

这个圆环的面积是( ) cm2。

A．20π B．128πC．80πD．48π7．甲、乙、丙三名同学用相同的正方形手工纸剪图形，甲剪了一个最大的扇形，乙剪了一个最大的圆，丙剪了四个最大的圆，如图。

他们对手工纸的利用率情况是( )。

A ．甲最高B ．乙最高C ．丙最高D ．三人都相同8．把一个比的前项扩大到原来的3倍，后项缩小到原来的13，这个比的比值( )。

A ．不变B ．扩大到原来的9倍C ．缩小到原来的19D ．以上都不对9．花生仁的出油率通常在40%～50%之间，500 kg 花生仁最少可以出油( )kg 。

A ．200B ．150C ．250D ．22510．一件上衣原价150元，先涨价10%，再降价10%，现价比原价( )。

A ．增加1元 B ．增加1% C ．减少1% D ．减少1元二、填空。

(每空1分，共23分)11. 1011÷( )＝58＝( )∶40＝( )%＝( )(填小数) 12．比240 kg 多18是( )kg ，( )元增加30%后是260元。

人教版二年级上册数学期末综合复习试卷(附答案)(1)

人教二年级数学上册期末试卷一、填空题1．在括号里填上“米”或“厘米”。

床长2( )；粉笔盒高8( )；旗杆高15( )。

2．一个乘数是8，另一个乘数是7，积是( )。

3．把口诀补充完整。

七八( )( )三十六四( )二十4．在括号里填上“＞”“＜”或“＝”。

-( )8644979+⨯( )44100厘米( )1米90厘米( )1米＋时，可以先算( )，再算( )，最后算( )。

5．口算45236．计算15＋（58－23）时，先算( )法，再计算( )法。

7．如图中有( )条线段，有( )个锐角。

8．按规律填一填。

（1）25，32，39，( )，53，( )，( )。

（2）85，80，75，( )，65，( )，( )。

9．猴妈妈摘了一些桃，比40个多，比50个少。

把它们平均分给8只小猴，正好分完。

猴妈妈摘了( )个桃。

10．用4、0、1这三张数字卡片可以摆出( )个不同的两位数；任意选取这些两位数中的两个数求和，得数有( )种可能。

11．下面用三角尺拼成的角中，（）是钝角。

A．B．C．12．下面的说法错误的是（）。

A．一个成年人的体重是70克B．一天是24小时C．5千克水和5000克棉花一样重13．晚上7：40时，动画片已经播出了45分，动画片是晚上（）开始播出的。

A．8：25 B．7：00 C．6：5514．用0、1和2组成两位数，每个两位数的个位与十位不能一样，能组成（）个两位数。

A．2 B．4 C．615．6×6＝□×9，□里应填（）。

A．6 B．9 C．416．小动物们跳一跳找“宝物”，“宝物”藏在“18”处。

它们都从0点开始跳，（）找不到“宝物”。

A．B．C．D．三、解答题17．直接写得数。

7×8＝36＋29＝56－7＝8×7－9＝61＋8＝6×4＝38－12＝6×9＋5＝9×8＝38＋16＝5×3＝65－30＋20＝18．竖式计算。

2019-2020学年人教版二年级(下)期末数学复习试卷(1)

2019-2020学年人教版二年级（下）期末数学复习试卷（1）学校:___________姓名：___________班级：___________考号：___________注意：本试卷包含Ⅰ、Ⅱ两卷。

第Ⅰ卷为选择题，所有答案必须用2B铅笔涂在答题卡中相应的位置。

第Ⅱ卷为非选择题，所有答案必须填在答题卷的相应位置。

答案写在试卷上均无效，不予记分。

一、填一填．1、24÷8＝__________ ，读作__________ 除以__________ 等于__________ ，其中__________ 叫做被除数，8叫做__________ ，商是__________ ．2、42÷6＝__________ ，42÷7＝__________ ，都是用口诀__________ 计算。

3、56里面有__________ 个7，30里面最多有__________ 个4．4、皮球原来13元一个，现在优惠促销，买4个32元。

促销的皮球每个__________ 元，每个比原来便宜__________ 元。

5、写4个商是6的除法算式：____________ 、____________ 、____________ 、_ ___________ ．二、选一选．（将正确答案的序号填在括号里）1、下面算式中，商最小的是（）A. 64÷8B. 18÷2C. 35÷72、被除数和除数相同（不为0），商是（）A. 1B. 无法确定C. 03、有40颗糖，最少拿出（）颗，剩下的刚好可以平均分给6个小朋友。

A. 6B. 4C. 2三、算一算1、在横线上填上合适的数。

36÷__________ ＝3×340÷5＝__________ ÷9__________ ÷6＝24÷38×__________ ＝4×428÷4＝__________ ÷79÷1＝9×__________2、里该填几？(1) __________ , __________ , __________(2) __________ . __________ , __________3、在横线上填上“+”“-”“×”或“÷”．72 __________ 8＝954 __________ 6＝604 __________ 8＝3281 __________ 9＝935 __________ 5＝408 __________ 8＝14、同学们去野营。

人教版六年级数学下册期末数与代数专项复习卷(1)附答案

人教版六年级数学下册数与代数专项复习卷(1)数的认识＋数的运算满分：100分试卷整洁分：2分(69分)一、用心思考，认真填写。

(每空1分，共19分)1．[数的写法、近似数]第六次全国人口普查显示，中国总人口数为十三亿七千零五十三万六千八百七十五人。

横线上的数写作（），省略“亿”后面的尾数约是（）。

2．[2，3，5的倍数]同时是2，3，5的倍数的最大两位数是（）。

3．[分数、小数和百分数的互化]0.75＝（）4＝（）%＝6÷（）＝（）折。

4．[倒数]29的倒数是（），0.35的倒数是（），（）没有倒数。

5．[小数、分数和百分数的大小比较]在0.66、66.7%、0.67··和23中，最大的数是（），最小的数是（）。

6．[负数]某天，北京凌晨的温度是－1 ℃，中午的温度上升了3 ℃，中午的温度是（）℃。

7．[百分数]一件衣服先降价10%，再涨价10%，现在售价是原价的（）%。

8．[分数单位、真分数、假分数]分数单位是19的最大真分数是（），再加上（）个这样的分数单位就是最小的假分数。

9．[小数点位置的移动引起小数大小的变化]一个数的小数点位置向左移动一位后，比原数小31.5，原数是（）。

10．[小数的近似数]一个三位小数用“四舍五入”法取近似数是12.30，这个数最大是（），最小是（）。

二、明辨是非。

(对的画“√”，错的画“×”)(6分)1．[倒数]假分数的倒数一定都是真分数。

（） 2．[分解质因数]12分解质因数是12＝1×2×2×3。

（） 3．[百分数]植树95棵，其中有5棵没成活，成活率是95%。

（） 4．[奇偶性]任意两个奇数的和一定是偶数。

（） 5．[小数的意义]0.7和0.70表示的意义相同。

（） 6．[运算性质]12÷⎝ ⎛⎭⎪⎫34＋45＝12÷34＋12÷45＝31。