三角高程测量原理

合集下载

三角高程测量

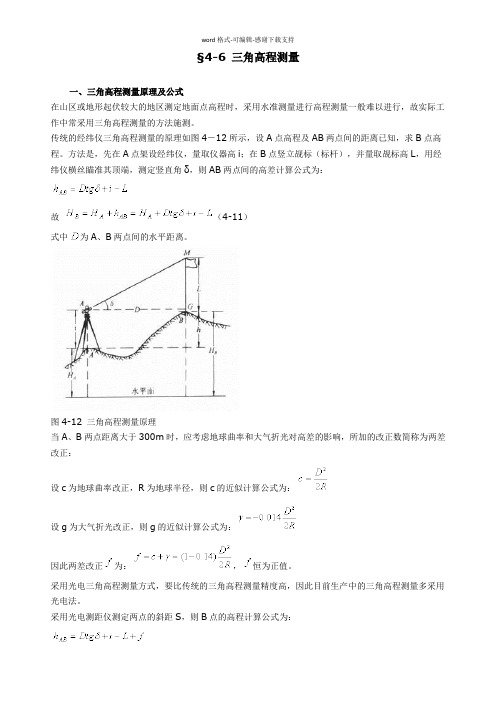
§4-6 三角高程测量一、三角高程测量原理及公式在山区或地形起伏较大的地区测定地面点高程时，采用水准测量进行高程测量一般难以进行，故实际工作中常采用三角高程测量的方法施测。

传统的经纬仪三角高程测量的原理如图4－12所示，设A点高程及AB两点间的距离已知，求B点高程。

方法是，先在A点架设经纬仪，量取仪器高i；在B点竖立觇标（标杆），并量取觇标高L，用经纬仪横丝瞄准其顶端，测定竖直角δ，则AB两点间的高差计算公式为：故（4-11）式中为A、B两点间的水平距离。

图4-12 三角高程测量原理当A、B两点距离大于300m时，应考虑地球曲率和大气折光对高差的影响，所加的改正数简称为两差改正：设c为地球曲率改正，R为地球半径，则c的近似计算公式为：设g为大气折光改正，则g的近似计算公式为：因此两差改正为：，恒为正值。

采用光电三角高程测量方式，要比传统的三角高程测量精度高，因此目前生产中的三角高程测量多采用光电法。

采用光电测距仪测定两点的斜距S，则B点的高程计算公式为：（4-12)为了消除一些外界误差对三角高程测量的影响，通常在两点间进行对向观测，即测定hAB和hBA，最后取其平均值，由于hAB和hBA反号，因此可以抵销。

实际工作中，光电三角高程测量视距长度不应超过1km，垂直角不得超过15°。

理论分析和实验结果都已证实，在地面坡度不超过8度，距离在1.5km以内，采取一定的措施，电磁波测距三角高程可以替代三、四等水准测量。

当已知地面两点间的水平距离或采用光电三角高程测量方法时，垂直角的观测精度是影响三角高程测量的精度主要因素。

二、光电三角高程测量方法光电三角高程测量需要依据规范要求进行，如《公路勘测规范》中光电三角高程测量具体要求见表4-6。

表4-6 光电三角高程测量技术要求往返各注：表4-6中为光电测距边长度。

对于单点的光电高程测量，为了提高观测精度和可靠性，一般在两个以上的已知高程点上设站对待测点进行观测，最后取高程的平均值作为所求点的高程。

三角高程测量的计算公式

三角高程测量的计算公式三角高程测量是地理测量中常用的一种方法，用于测量地面上的点的高程。

本文将介绍三角高程测量的计算公式，并解释其原理和应用。

三角高程测量是基于三角法原理的一种测量方法。

它利用三角形的一些特性和测量数据，通过计算可以得到被测点的高程。

三角高程测量适用于各种地形条件，无论是平原、山地还是高原，都可以通过三角高程测量来确定各个点的高程。

三角高程测量的计算公式如下：h = H + d * tan(a)其中，h表示被测点的高程，H表示参考点的高程，d表示两个测点之间的水平距离，a表示两个测点之间的夹角。

根据这个公式，我们可以通过测量参考点和被测点之间的距离和夹角，再加上参考点的高程，就可以计算出被测点的高程。

这个公式的原理是基于三角形的相似性原理，即两个三角形的对应边的比例相等。

在实际测量中，我们首先需要选择一个参考点，可以是已知高程的点或者固定测量设备的位置。

然后，利用测量仪器测量参考点和被测点之间的水平距离和夹角。

最后，根据测量数据和计算公式，我们可以计算出被测点的高程。

三角高程测量在地理测量中具有广泛的应用。

它可以用于绘制地形图、制作地图、建筑工程设计等。

通过三角高程测量，我们可以快速准确地确定地面上各个点的高程，为地理信息系统的建设和规划提供重要的数据支持。

在实际应用中，三角高程测量需要考虑一些误差因素。

例如，测量仪器的精度、天气条件、地形复杂度等都会对测量结果产生影响。

因此，在测量过程中要注意选择合适的测量仪器、控制测量误差，并进行合理的数据处理和分析。

三角高程测量是一种常用的地理测量方法，通过测量参考点和被测点之间的距离和夹角，再结合计算公式，可以准确地确定被测点的高程。

它在地理信息系统、地形图制作、建筑工程设计等领域具有重要的应用价值。

在实际应用中，我们需要注意测量误差的控制和数据处理，以提高测量结果的精度和可靠性。

通过三角高程测量，我们可以更好地了解地球表面的地形特征，为人类的生活和发展提供有益的信息。

第四章第三讲第5节三角高程和视距距测量2005年4月1日

式中：R=6371公里公式改写为：
在煤矿井下测量时，往往直接测量 A 、 B 两点间的斜距，则：
h＝Lsinδ + i — v
三角高程测量一般应进行往返观测，既由A向B观测(称为直觇)，又由B向A观测(称为反觇 )。这样的观测，称为对向观测。对向观测可以消除地球曲率和大气折光的影响。
第六节视距测量
仪器中心到测站点高度 i
利用视线水平时视距公式计算水平距离
注意事项：
1、安置仪器的方法与上次实验相同。 2、在水准尺上读三个数值（上、中、下丝） 3、测竖直角时不要忘记打开补偿装置。并观察和判断竖盘注计形式。 4、大坝的斜距可用钢尺直接量得。 5、测量仪器高，觇杆高，并做好记录。 6、认真思考测量的整个过程是否和理论公式相符合。
第四章第三讲三角高程测量和视距测量
华山莲花峰
金沙江
九寨沟
第五节三角高程测量
在以上图片中的山地或井下测定控制点的高程时，若用水准测量的方法速度慢困难大。故可采用三角高程测量的方法。但必须用水准测量的方法在测区内引测一定数量的水准点，作为高程起算的依据。以保证高程测量的精度。
Ｏ
但是，S′不是实际的尺间隔，实际测得的尺间隔是R及尺上的MN(即S)，因此需要找出S与S′间的关系。
于是
Ｏ
上式为视线倾斜时求水平视距的公式。
将式
则得用视距表示得三角高差计算公式：
上式为用上、下丝读数差和竖直角计算高差的公式。
二、视距测量方法
(1) 在A点安置经纬仪，进行对中、整平，并量取仪器高 i；（ 2 ）用望远镜瞄准 B 点上的视距尺，读取上丝、中丝 ( 即 7) 和下丝读数．然后用微动螺旋使指标水准管气泡居中，再读取竖盘读数。 (3) 计算尺间隔S及竖直角，按公式(4—19)和(4—20) 计算水平距离和高差 h。计算可用电子计算器进行。视距测量记录及计算格式如表4—3所示。

全站仪三角高程测量方法

全站仪三角高程测量方法全站仪是一种先进的测量仪器，具有测量水平角、垂直角和斜距的功能，因此在进行三角高程测量时，可以采用以下方法：1. 三角高程测量原理：三角高程测量是利用三角学原理进行测量的方法。

当我们在地面上选择三个测站，并测量出它们之间的水平角、垂直角和斜距时，根据三角关系可以计算出这些测站的高程。

2. 选择测站：在进行三角高程测量时，首先需要选择三个测站，并保证这三个测站之间形成一个合理的三角形。

测站的选择要考虑到其位置相对固定和稳定，同时要满足仪器观测范围的要求。

3. 测量水平角：使用全站仪测量水平角的方法有两种：反射测量和直接测量。

反射测量是将反光棱镜放置在测站上，然后使用全站仪对反射棱镜进行测量，得到水平角的数据。

直接测量是将全站仪直接对准目标，通过全站仪内置的水平角读数装置进行测量。

4. 测量垂直角：全站仪可以通过照准测量和激光测量两种方法来测量垂直角。

照准测量是将全站仪对准目标，然后通过全站仪内置的图像传感器来读取目标的中轴线，从而获得垂直角的数据。

激光测量是利用全站仪内置的激光器向目标发射激光束，然后通过在目标接收到光线的位置上读取垂直角的数据。

5. 测量斜距：通过使用全站仪的测距仪，可以实时测量出目标与测站之间的水平距离或斜距。

全站仪的测距仪可以通过使用红外线或激光技术来测量距离，并将测得的数据显示在仪器的屏幕上。

6. 计算高程：当我们完成三个测站的水平角、垂直角和斜距的测量后，可以利用三角关系计算出测站的高程。

常用的计算方法有正算法和反算法。

正算法是已知两个测站的高程和一个介于它们之间的斜距，通过三角关系计算出第三个测站的高程。

反算法是已知两个测站的高程和一个测站的高程，通过三角关系计算出这个测站到其他两个测站的斜距。

总结：全站仪的三角高程测量方法包括选择测站、测量水平角、测量垂直角、测量斜距和计算高程。

通过合理的测站选择和准确的观测操作，可以获得高精度的三角高程测量数据，从而为工程测量和地形测量提供可靠的高程数据支持。

三角高程测量的往返观测计算公式

三角高程测量是一种常用的测量方法，它可以用来测量地面上点的准确高程。

在这篇文章中，我们将着重介绍三角高程测量中的往返观测计算公式。

一、三角高程测量原理三角高程测量是利用三角形的相似性原理，通过已知两点的高程和这两点到待测点的水平距离，来计算待测点的高程。

三角高程测量的基本原理如下：1. 在地面上选择一个已知高程的点A，以及要测量高程的点P。

2. 通过测量仪器测量点A和点P之间的水平距离d和两点的高程差h。

3. 通过三角函数计算出点P的高程。

二、三角高程测量的往返观测在实际测量中，为了提高精度，常常采用往返观测的方法进行测量。

往返观测的原理是利用观测仪器来回测量两点之间的距离和高程差，然后取平均值作为最终结果，以减小由于观测仪器误差、大气温度、大气压力等因素造成的误差。

三、三角高程测量往返观测计算公式往返观测的三角高程测量计算公式如下：1. 求点P的高程差首先需要计算出点P的高程差，使用以下公式：\[ \Delta h = h_1 - h_2 \]其中，$h_1$ 为第一次测量的高程，$h_2$ 为第二次测量的高程。

2. 求两次测量的平均距离将两次测量的距离$d_1$和$d_2$求均值，得到平均距离：\[ \bar{d} = \frac{d_1 + d_2}{2} \]3. 计算点P的高程利用三角函数计算出点P的高程：\[ H = h_2 + \frac{\Delta h \times \bar{d}}{d_2} \]其中，$H$为最终计算出的点P的高程。

四、注意事项在进行三角高程测量的往返观测时，需要注意以下几点：1. 观测仪器的选择和校准非常重要，需要保证其精度和稳定性。

2. 大气温度和大气压力对测量结果有较大影响，需要进行相应的修正。

3. 观测时需要注意周围环境的影响，避免受到建筑物、树木、地形等因素干扰。

4. 测量终点的选取应当避免大坡度地形，以减小误差。

通过以上介绍，我们了解了三角高程测量中的往返观测计算公式及其应用注意事项。

三角高程

四、仪器高i和目标高v的测定误差 1．测定地形控制点的高程：对于测定地形控制点高程的三角高程测量，仪器高、觇标高的测定误差，仅要求精确到厘米级，这是很容易达到的，测量时认真丈量即可。 2．控制测量的高程：对于用光电测距三角高程代替四等水准测量时，仪器高和觇标高的测定要求达到毫米级，其丈量误差应注意控制，一般丈量两次取其平均值。
2 2 2 2 mh md m S S 2 S hBA AB BA AB
其容许值为：
2 2 S d容
二、三角高程测量的计算 1．三角高程路线的计算对于控制而言，三角高程导线都应进行往返观测，其起闭点都应是高级控制点。（1）高差计算外业成果检查、整理，不合格的应重测；画草图，计算相邻点间的高差、距离，当往返测高差互差符合规范要求后取其平均值。（2）三角高程路线成果整理计算高差闭合差： f h h ( H b H a ) 计算每公里高差改正数: 公里 f h / S公里计算每测段高差改正数： i S i 公里计算各待定点高程：
D
B p
v
r
EG=IE•tgα
hAB
r=0.08 • s2/R
p=s2/2R
C
HB
通常令 f=p-r,则 f=0.42 s2/R
S B0 R
HB= HA+Stgα+i-v+f
ε
O
HB= HA+Stgα+i-v+f
平距、斜距、视距
四、竖角的测定竖角的测定一般采用两种方法。 1．中丝法（1）在测站上安臵好仪器，对中、整平、量取仪器高i。（2）盘左位臵瞄准目标，使十字丝的中丝切目标于某一位臵，其高度即为v。（3）转动竖盘水准管微动螺旋，使竖盘水准管气泡居中。读取竖盘读数即为L。（4）同上法，以盘右位臵照准原目标，读取竖盘读数即为R。（注意气泡居中）

三角高程测量方法

三角高程测量方法一、三角高程网三角高程网是一种通过在地面上布设一系列三角形网状控制点的方法进行测量。

它的原理是，通过在地面上选取一些具有良好观测条件的点，然后利用这些点来构成一定数量的三角形，最后通过测量这些三角形的角和边长，就可以计算出地面的高程差。

三角高程网方法的步骤如下：1.选择控制点：根据实际情况选择一定数量的具有良好观测条件的点作为控制点。

2.观测角度：利用测量仪器观测每个控制点与相邻控制点之间的角度。

3.观测距离：利用测量仪器测量每个控制点与相邻控制点之间的水平距离。

4.计算高程差：根据观测角度和距离，利用三角形的计算公式计算出每个控制点之间的地面高程差。

三角高程网方法的优点是测量精度相对较高，适用于平面较大、高差较大的地区。

但是它的缺点是需要布设大量的控制点，工作量大且耗时，适用范围有限。

二、三角高程尺三角高程尺是一种通过仪器测量仰角和目标物与测站之间的水平距离来计算地面高程差的方法。

三角高程尺方法的步骤如下：1.设置测站：在需要测量地面高程的位置设置测站。

2.对准目标：将仪器对准目标物，记录仪器的仰角。

3.测量距离：利用测距仪等测量仪器测量目标物与测站之间的水平距离。

4.计算高程差：根据仰角和距离，利用三角形的计算公式计算出地面的高程差。

三角高程尺方法的优点是测量简单、迅速，适用于平面较小、高差较小的地区。

但是它的缺点是测量精度相对较低，主要适用于对地面高程差要求不严格的场合。

总结：三角高程测量方法是一种常用的测量地面高程差的方法，可以根据实际情况选择适合的方法进行测量。

三角高程网方法精度较高，适用于平面较大、高差较大的地区；三角高程尺方法测量简单、迅速，适用于平面较小、高差较小的地区。

在实际应用中，根据需要进行选择，并结合其他辅助工具和方法，可以提高测量的精度和有效性。

三角高程测量代替四等水准测量在实际工程中的应用

三角高程测量代替四等水准测量在实际工程中的应用【摘要】三角高程测量是在工程测量中常用的一种方法，它可以代替传统的四等水准测量，提高测量效率和精度。

本文首先介绍了三角高程测量和四等水准测量的原理，然后对两种方法进行了比较分析，指出了三角高程测量的优势。

接着针对三角高程测量在工程测量中的具体应用进行了探讨，并通过实际工程案例分析展示了其实用性。

最后总结了三角高程测量的优势以及对四等水准测量的替代性，同时展望了未来发展方向。

通过本文的研究，我们可以看到三角高程测量在实际工程中的重要性和应用前景，对工程测量技术的发展具有积极意义。

【关键词】三角高程测量、四等水准测量、工程测量、应用、原理、比较、案例分析、优势、替代性、发展方向1. 引言1.1 三角高程测量代替四等水准测量在实际工程中的应用三角高程测量是一种新型的测量方法，相较于传统的四等水准测量具有更高的效率和精度。

在实际工程中，三角高程测量的应用逐渐取代了四等水准测量，成为工程测量领域的重要技术手段。

传统的四等水准测量是通过在测量区域内设置一系列水准点，然后利用水准仪测量点之间的高差，确定各点的高程。

这一方法需要在地面上布设大量的水准点，测量效率低下，而且在复杂地形和环境条件下往往难以实施。

而三角高程测量则是通过测量三角形各角的方法，推算出各点之间的高程。

这种方法只需要设置少量的控制点，测量精度高，适用于各种地形和环境条件。

在实际工程中，三角高程测量被广泛应用于道路、桥梁、建筑等工程项目中。

通过对三角高程测量与四等水准测量的比较分析，可以得出三角高程测量在精度、效率和适用性等方面优于四等水准测量。

未来工程测量领域将更多地采用三角高程测量技术，以提高测量效率和精度，推动工程建设的发展。

2. 正文2.1 三角高程测量原理三角高程测量原理是一种利用三角学原理来测定地面上点的高程的方法。

其基本原理是利用三角形的内角和为180度的性质，结合测量角度和距离的数据来计算出目标点的高程。

三角高程测量的计算公式

三角高程测量的计算公式三角高程测量是一种常用的地理测量方法，随着测量技术的发展和应用领域的拓宽，其计算公式也越来越重要。

本文将从计算公式的基本原理、计算过程和误差控制三方面进行阐述，以期让读者更深入地了解三角高程测量的计算方法。

一、基本原理三角高程测量，顾名思义，是以三角形理论为基础进行测量的一种方法。

通常情况下，我们选取三个站点进行测量，这三个站点构成一个三角形，我们可以测量得到三个角的角度和三边的长度。

在此基础上，我们可以运用三角函数，求得这个三角形的高程。

具体来说，我们可以通过以下公式进行计算：H = L（a sin B + b sin A）/ sin C其中，H为目标点的高程，L为相邻两个点的距离，A 和B为相邻两点到目标点的水平角，C为相邻两点之间的斜线距离。

在实际操作中，我们一般采用三边测量和两边一角测量两种方法来进行三角高程测量。

无论采用哪种方法，都需要进行角度和距离的测量，然后通过计算公式求得目标点的高程。

二、计算过程在进行三角高程测量之前，我们需要对测量区域进行勘验，确定三个测量点的位置，并在每个站点上架设三角测量仪器。

在具体的测量过程中，我们首先测量站点之间的距离和角度。

这一步骤可以采用三边测量或两边一角测量方式。

如果采用三边测量方式，则需要同时测量两个角度。

如果采用两边一角测量方式，则需要测量三个角度。

在完成角度和距离的测量之后，我们可以将数据输入到计算公式中，求解目标点的高程。

需要注意的是，三角高程测量的计算精度受到多种因素的影响，例如测量仪器的精度、环境因素以及人为操作错误等。

因此，在进行计算之前，我们需要对数据进行校核，以确保计算结果的准确性。

三、误差控制三角高程测量存在着测量误差，这不可避免。

为了尽可能地减小误差对测量结果的干扰，我们可以采取一些措施。

具体来说，我们可以从以下几方面入手：（1）选择合适的测量仪器。

测量仪器的精度和稳定性对测量结果的影响很大。

因此，我们需要选用精度高、稳定性好的测量仪器来进行测量。

三角高程测量原理及应用

三角高程测量原理及应用 Revised by Hanlin on 10 January 2021三角高程测量及其误差分析与应用一、三角高程测量的基本原理三角高程测量是通过观测两点间的水平距离和天顶距（或高度角）求定两点间的高差的方法。

它观测方法简单，不受地形条件限制，是测定大地控制点高程的基本方法。

如图1,所示，在地面上A,B两点间测定高差hAB,A点设置仪器，在B点竖立标尺。

量取望远镜旋转轴中心I至地面点上A点的仪器高i1，用望远镜中的十字丝的横丝照准B点标尺上的一点M，它距B点的高度称为目标高i2，测出倾斜视线与水平线所夹的竖角为a，若A,B两点间的水平距离已知为S，则由图可得图1如图1,所示，在地面上A,B两点间测定高差hAB,A点设置仪器，在B点竖立标尺。

量取望远镜旋转轴中心至地面点上A点的仪器高i，用望远镜中的十字丝的横丝照准B点标尺，它距B点的高度称为目标高v，测出倾斜视线与水平线所夹的竖角为a，若A,B两点间的水平距离已知为s，则由图可得，AB两点间高差的公式为：若A点的高程已知为HA,则B点的高程为：但是，在实际的三角高程测量中，地球曲率、大气折光等因素对测量结果精度的影响非常大，必须纳入考虑分析的范围。

因而，出现了各种不同的三角高程测量方法，主要分为：单向观测法，对向观测法，以及中间观测法。

1.1单向观测法单向观测法是最基本最简单的三角高程测量方法，它直接在已知点对待测点进行观测，然后在①式的基础上加上大气折光和地球曲率的改正，就得到待测点的高程。

这种方法操作简单，但是大气折光和地球曲率的改正不便计算，因而精度相对较低。

1.2对向观测法对向观测法是目前使用比较多的一种方法。

对向观测法同样要在A点设站进行观测，不同的是在此同时，还在B点设站，在A架设棱镜进行对向观测。

从而就可以得到两个观测量：直觇：h AB =S往tanα往+i往-v往+c往+r往②反觇：h BA =S返tanα返+i返-v返+c返+r返③S——A、B间的水平距离；α——观测时的高度角；i——仪器高；v——棱镜高；c——地球曲率改正；r——大气折光改正。

三角高程测量的方法

三角高程测量的方法
三角高程测量是一种常用的测量方法，通常用于测量地表的高
程差异。

在三角高程测量中，有几种常用的方法：
1. 三角测量法，这是最常见的方法之一，利用三角形的相似性
原理，通过测量三角形的边长和角度来计算高程。

测量过程中需要
测量三角形的三条边和一个角度，然后利用三角函数计算出高程差。

2. 三角高程测量法，这是一种基于三角形相似原理的高程测量
方法。

在实际测量中，首先需要选择一个已知高程的点作为基准点，然后利用测距仪和测角仪测量目标点到基准点的水平距离和仰角，
再利用三角函数计算目标点的高程。

3. GPS测量法，全球定位系统（GPS）可以用于测量地表的高
程差异。

通过在不同位置接收卫星信号，可以计算出不同点的高程差。

这种方法通常精度较高，适用于大范围的高程测量。

4. 激光测距法，利用激光测距仪测量目标点到测量仪的距离，
再结合测量仪的仰角，可以计算出目标点的高程。

这种方法测量速
度快，精度高，适用于复杂地形的高程测量。

总的来说，三角高程测量方法有多种，每种方法都有其适用的场景和精度要求。

在实际应用中，需要根据具体情况选择合适的方法进行高程测量。

三角高程测量高差中误差计算公式

三角高程测量高差中误差计算公式1. 什么是三角高程测量三角高程测量是一种常用的测量方法，可以用于测量地面上两点间的高度差。

它的原理是通过三角形的性质来计算出两点间的高差，因此被称为三角高程测量。

2. 中误差的概念在三角高程测量过程中，由于测量数据的误差，会导致测量结果的精度受到影响。

为了评估测量结果的精度，需要计算中误差。

中误差是指样本中单个测量值与样本平均值之差的平均值。

通常用标准差来表示中误差，它是各单次测量值离样本平均值的差的平方和的平均数的算术平方根。

3. 三角高程测量中误差的计算公式在三角高程测量中，中误差可以通过测量数据的方差和协方差计算得出。

常用的计算公式如下：1) 方差公式：$$\sigma^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}$$其中，$x_i$表示第$i$次测量的结果，$\bar{x}$是所有结果的平均值，$n$是测量次数，$\sigma^2$表示样本方差。

2) 协方差公式：$$\text{cov}(x,y) = \frac{\sum_{i=1}^n (x_i -\bar{x})(y_i - \bar{y})}{n-1}$$其中，$x_i$和$y_i$分别表示第$i$次测量的两个测量值，$\bar{x}$和$\bar{y}$分别表示$x$和$y$的平均值，$\text{cov}(x,y)$表示$x$和$y$的协方差。

3) 中误差公式：$$\sigma_{\text{mid}} = \sqrt{\frac{\sigma^2_a +\sigma^2_b - 2\text{cov}(a,b)}{2}}$$其中，$\sigma_{\text{mid}}$表示中误差，$\sigma^2_a$和$\sigma^2_b$分别表示两个测量角度的方差，$\text{cov}(a,b)$表示两个测量角度的协方差。

4. 如何减小中误差为了减小三角高程测量中误差，可以采取以下措施：1) 提高仪器的精度，使用高精度的仪器进行测量。

测绘技术中的三角高程测量方法解析

测绘技术中的三角高程测量方法解析在测绘工作中，高程测量是非常重要的一项工作。

而在测量高程时，三角高程测量方法无疑是一种常用且有效的方法。

本文将对三角高程测量方法进行解析，探讨其原理和应用。

三角高程测量方法的原理基于三角形的几何性质。

在测量过程中，通过测量目标物体与测量仪器之间的角度和距离，利用三角关系计算出目标物体的高程。

这种方法的核心思想是将目标物体视为一个顶点，利用仪器与目标物体之间的两条边作为已知条件，计算出第三边（高程）的长度。

在实际应用中，三角高程测量方法有多种形式。

最常见的是直角三角高程测量法和斜角三角高程测量法。

直角三角高程测量法是指利用视线水平和垂直的两个角来计算高程，适用于附近地形较平缓的区域。

而斜角三角高程测量法则是利用斜角和水平角或垂直角来计算高程，适用于地形较为复杂的区域。

三角高程测量方法的应用范围广泛。

在土木工程领域中，三角高程测量方法可用于确定地面的高程，为建筑设计和施工提供基础数据。

在地理测绘领域中，三角高程测量方法可用于绘制地形图和等高线图，帮助研究地理地貌和地质构造。

在航空航天领域中，三角高程测量方法可用于飞机和导弹的导航和定位。

除了上述常见的测量方法外，还有一些辅助测量技术可以提高三角高程测量的精度和效率。

例如，使用全站仪等高精度测量设备可以提供更准确的角度和距离测量结果。

同时，使用GPS定位系统可以提供更准确的位置信息，进一步提高测量结果的可靠性。

然而，三角高程测量方法也存在一些局限性和挑战。

首先，该方法依赖于仪器的精度和操作人员的技术水平，对设备和人员要求较高。

其次，该方法只能测量目标物体与测量仪器之间的直线距离，无法直接测量地面上的高程。

因此，在地势复杂的区域中，需要采取多点测量和数据处理的方法来获得准确的高程信息。

尽管存在一些挑战，三角高程测量方法仍然是测绘工作中广泛应用的一种方法。

随着测量技术的不断进步和仪器设备的不断更新，三角高程测量方法也在不断优化和改进。

三角高程测量的原理

MPN MPC NPC
2 即圆弧PN的弦切角∠MPN等于圆心角 ε的一半。
三角高程测量
因ε很小， PN PN D，由图可
得 MPN MN MN
2 PN D
即
MN D
2
因
PN D
R' R'
所以
MN D2
若令
k
R
2R ' ,k称为大气折光系数
R' ，则 R ' R，代入上式得
hAB =D·tanα + i - v + f1 - f2
三角高程测量
在三角高程测量中，由于球差f1使高差减小，气差f2使高差增大，因此，在高差中应进行“ 加入球差减去气差”的改正，即球气差改正，亦称两差改正,通常用 f 表示。即
f = f1 - f2 将上式代入hAB =D·tanα + i v + f1 - f2 ，并整理得：
k f2
MN
D2 2R
k
三角高程测量
D2 f1 CE 2R
f2
MN
D2 2R
k
将上式代入 f = f1 - f2 得
f D2 D2 k (1 k) D2
2R 2R
2R
三角高程测量
4. 三角高程测量的观测方法
(1)直、反觇观测由已知高程点设站观测待定高程点的垂直角叫直
觇。由待定高程点设站观测已知高程点的垂直角叫反
由于R>>i+HA，故可以用R代替
i+HA+R，则
R2+D2=(CE+R)2
展开得 R2+D2=CE2+2R·CE+R2
则

中间法三角高程测量基本原理

中间法三角高程测量基本原理嘿，朋友们！今天咱来聊聊中间法三角高程测量的基本原理哈。

你看哈，这中间法三角高程测量就像是我们走路找方向一样。

我们要知道从哪儿出发，到哪儿去，中间经过哪些地方。

三角高程测量呢，就是要搞清楚地面上不同点之间的高差。

想象一下，我们在两个点之间拉一条线，就像搭了一座小桥。

然后呢，我们通过测量角度和距离，来算出这座“小桥”的坡度，这就是高差啦！这是不是很神奇呢？它呀，就像是一个聪明的小侦探，能通过各种线索找出地面的高低起伏。

我们用全站仪或者经纬仪这些厉害的工具，就像小侦探的放大镜和显微镜一样，去捕捉那些关键的信息。

比如说，我们在这边的点上观测那边的点，测量出角度，再量一下距离，然后通过一些巧妙的计算，就能得出高差啦！这可不像我们平时走路那么简单哦，这里面可有大学问呢！这中间法呀，就像是走在一条中间的道路上，不偏不倚，能更准确地测量出那些高差。

为啥要这么做呢？这就好比我们要去一个地方，走直路肯定比绕弯路来得快、来得准呀！你说这中间法三角高程测量是不是很有意思呢？它能帮我们搞清楚大地的起伏，就像给大地画了一幅立体的图画。

我们工程师们就靠着它来修路、建桥、盖房子呀！没有它，那可真是不行呢！而且哦，它还很实用呢！不管是在高山上，还是在平原上，都能发挥它的作用。

就好像一把万能钥匙，能打开各种地形的秘密之门。

你想想，如果没有它，我们怎么知道这里高那里低呀？那不就像闭着眼睛走路一样，容易摔跤嘛！所以说呀，这中间法三角高程测量可真是我们工程建设的好帮手呢！总之呢，中间法三角高程测量是个非常重要的测量方法，它就像我们生活中的指南针一样，指引着我们在工程建设的道路上稳步前行。

让我们好好利用它，为我们的生活创造更多美好的建筑和设施吧！。

三角高程测量原理

§ 三角高程测量三角高程测量的基本思想是根据由测站向照准点所观测的垂直角（或天顶距）和它们之间的水平距离，计算测站点与照准点之间的高差。

这种方法简便灵活，受地形条件的限制较少，故适用于测定三角点的高程。

三角点的高程主要是作为各种比例尺测图的高程控制的一部分。

一般都是在一定密度的水准网控制下，用三角高程测量的方法测定三角点的高程。

三角高程测量的基本公式1.基本公式关于三角高程测量的基本原理和计算高差的基本公式，在测量学中已有过讨论，但公式的推导是以水平面作为依据的。

在控制测量中，由于距离较长，所以必须以椭球面为依据来推导三角高程测量的基本公式。

如图5-35所示。

设0s 为B A 、两点间的实测水平距离。

仪器置于A 点，仪器高度为1i 。

B 为照准点，砚标高度为2v ，R 为参考椭球面上B A ''的曲率半径。

AF PE 、分别为过P 点和A 点的水准面。

PC 是PE 在P 点的切线，PN 为光程曲线。

当位于P 点的望远镜指向与PN 相切的PM 方向时，由于大气折光的影响，由N 点出射的光线正好落在望远镜的横丝上。

这就是说，仪器置于A 点测得M P 、间的垂直角为2,1a 。

由图5-35可明显地看出，B A 、两地面点间的高差为NB MN EF CE MC BF h --++==2,1 （5-54）式中，EF 为仪器高NB i ;1为照准点的觇标高度2v ；而CE 和MN 分别为地球曲率和折光影响。

由2021s R CE =2021s R MN '=式中R '为光程曲线PN 在N 点的曲率半径。

设,K R R='则 20202.21S RK S R R R MN ='=K 称为大气垂直折光系数。

图由于B A 、两点之间的水平距离0s 与曲率半径R 之比值很小（当km s 100=时,0s 所对的圆心角仅5'多一点），故可认为PC 近似垂直于OM ，即认为 90≈PCM ,这样PCM ∆可视为直角三角形。

三角高程测量原理

三角高程测量

三角高程测量的计算公式

第四章第三讲第5节三角高程和视距距测量2005年4月1日

全站仪三角高程测量方法

三角高程测量的往返观测计算公式

三角高程

三角高程测量方法

三角高程测量代替四等水准测量在实际工程中的应用

最新三角高程测量原理及应用

三角高程测量的计算公式

三角高程测量原理及应用

三角高程测量的方法

三角高程测量高差中误差计算公式

测绘技术中的三角高程测量方法解析

三角高程测量的原理

中间法三角高程测量基本原理

三角高程测量原理