2019年桂平市社坡高级中学高考数学选择题专项训练(一模)

合集下载

2019年桂平市麻垌中学高考数学选择题专项训练(一模)

2019年桂平市麻垌中学高考数学选择题专项训练（一模）抽选各地名校试卷，经典试题，有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。

第 1 题：来源： 2019高中数学第二章平面向量单元测试（一）新人教A版必修4若与满足，，则等于（）A． B． C．D．2【答案】B【解析】由题意得，故选B．第 2 题：来源：湖南省怀化市新晃侗族自治县2019届高三数学上学期期中试题理函数的图象是【答案】A第 3 题：来源：福建省霞浦县2018届高三数学上学期第二次月考试题理设为非零实数，则关于函数的以下性质中，错误的是A.函数一定是个偶函数B.函数一定没有最大值C.区间一定是的单调递增区间D.函数不可能有三个零点.【答案】 C第 4 题：来源：辽宁省沈阳市2018届高三数学10月月考试题理试卷及答案已知命题，；命题，，则下列命题中为真命题的是（）A. B. C. D.【答案】C第 5 题：来源：四川省成都市2018届高三数学上学期第三次月考（11月）试题理试卷及答案设数列的前项和，若，且，则等于（）A． B． C． D．【答案】C第 6 题：来源：内蒙古巴彦淖尔市临河三中2018_2019学年高一数学下学期第二次月考试题（宏志）已知，，，则的大小关系（）A. B. C. D.【答案】B第 7 题：来源：广东省中山市普通高中2017_2018学年高一数学11月月考试题试卷及答案06.若函数、分别是R上的奇函数、偶函数，且满足，则有（）A. B.C. D.【答案】D第 8 题：来源：广西钦州市钦州港区2016-2017学年高一数学12月月考试题试卷及答案设M是边BC上任意一点,N为AM的中点,若,则λ+μ的值为( )A．B．C．D．1【答案】 A第 9 题：来源：山东省济宁市2019届高三数学第一次模拟考试试题理已知当时，关于的方程有唯一实数解，则所在的区间是A．(3，4) B．(4，5) C．(5，6) D．(6．7)【答案】C第 10 题：来源：江西省南昌市2017_2018学年高一数学上学期第一次月考试题试卷及答案已知函数．若，则实数的取值范围是（）A． B．C． D．【答案】B 因为令，则就是．画出函数的图象可知，，或，即或．由得，或．由．由得，或．再根据图象得到，故选D.1第 11 题：来源：黑龙江省五常市2017_2018学年高三数学11月月考试题理试卷及答案.设函数f（x）满足2x2f（x）+x3f′（x）=ex，f（2）=，则x∈[2，+∞）时，f（x）（）A．有最大值 B．有最小值 C．有最大值 D．有最小值【答案】B第 12 题：来源：山东省临沂市2017届高三数学二模试卷理（含解析）“|x﹣1|+|x+2|≤5”是“﹣3≤x≤2”的（）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件【答案】C【考点】2L：必要条件、充分条件与充要条件的判断．【分析】由|x﹣1|+|x+2|≤5，对x分类讨论，解出即可判断出结论．【解答】解：由“|x﹣1|+|x+2|≤5”，x≥1时，化为：x﹣1+x+2≤5，解得1≤x≤2；﹣2≤x＜1时，化为：1﹣x+x+2≤5，化为0≤2恒成立，解得﹣2≤x＜1；x＜﹣2时，化为：1﹣x﹣x﹣2≤5，解得﹣3≤x＜﹣2．综上可得：“|x﹣1|+|x+2|≤5”的解集为：{x|﹣3≤x≤2}．∴“|x﹣1|+|x+2|≤5”是“﹣3≤x≤2”的充要条件．故选：C．第 13 题：来源：福建省晋江市季延中学2018_2019学年高一数学下学期期中试题已知△ABC中，∠A＝60°，a＝，b＝4，那么满足条件的△ABC的形状大小 ( )．A．有一种情形 B．有两种情形C．不可求出 D．有三种以上情形【答案】C第 14 题：来源：河北省大名县2017_2018学年高二数学上学期第二次月考试题 (1)已知△中，，，则等于（）A. B.1 C. D. 2【答案】A第 15 题：来源：高中数学第三章导数及其应用3.3导数的应用3.3.1利用导数判断函数的单调性课后导练新人教B版选修1_120171101245设f(x)在(a,b)内可导，则f′(x)<0是f(x)在(a,b)内单调递减的________条件( )A.充分不必要B.必要不充分C.充要D.既不充分也不必要【答案】A第 16 题：来源：河北省石家庄市第四中学2018_2019学年高二数学上学期期中试题命题“，”的否定是A. ，B. ，C. ，D. ，【答案】.B．第 17 题：来源：河北省博野县2016_2017学年高一数学3月月考试题试卷及答案设是等差数列的前项和,若,则（）A． B． C． D．【答案】A【解析】试题解析：,.故选A.考点：等差数列第 18 题：来源：河北省景县2017_2018学年高一数学上学期第一次调研考试试题试卷及答案将集合表示成列举法，正确的是A．{2,3} B．{（2,3）} C．{x＝2，y＝3} D．（2,3）【答案】B试题分析：集合为点集，点的坐标为方程组的解，通过解方程可知，所以集合为{（2,3）}第 19 题：来源：贵州省兴义市2017_2018学年高一数学上学期第二次月考（期中）试题试卷及答案某种生物的繁殖数量y(只)与时间x(年)之间的关系式为y＝alog2(x＋1)，设这种生物第一年有100只，则第7年它们发展到( )A．300只 B．400只 C．500只 D．600只【答案】A第 20 题：来源：福建省晋江市2017_2018学年高二数学上学期期中试题理试卷及答案已知椭圆的左，右焦点分别为，过的直线交椭圆于两点，若的最大值为5，则的值是( )A.1 B. C.D.【答案】D第 21 题：来源：广东省广州市2017_2018学年高一数学上学期10月段考试题试卷及答案下列各组函数中，表示同一函数的是（）A. B.C． D．【答案】D第 22 题：来源： 2016_2017学年高中数学每日一题（3月20日_3月26日）试卷及答案新人教A 版必修3抛掷一枚骰子，下列不是基本事件的是A．向上的点数是奇数 B．向上的点数是3C．向上的点数是4 D．向上的点数是6 【答案】A第 23 题：来源：聊城市2017年高考数学理科模拟试卷（一）含答案解析已知复数满足（是虚数单位），则的共轭复数为（）A． B． C． D．【答案】C第 24 题：来源：重庆市2017届高三数学下学期第一次段考试卷及答案理（含解析）已知椭圆+=1（a＞b＞0）的左、右焦点分别为F1，F2，焦距为2，若直线y=﹣（x+）与椭圆交于点M，满足∠MF1F2=∠MF2F1，则离心率是（）A． B．﹣1 C． D．【答案】B【考点】K4：椭圆的简单性质．【分析】由题意可知：∠MF1F2=，∠MF2F1=，∠F1MF2=90°．根据三角形的关系即可求得丨MF1丨+丨MF2丨=2a=（+1），根据椭圆的离心率公式即可求得椭圆的离心率．【解答】解：如图所示，由直线y=﹣（x+），由tanα=﹣，则α=．又椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1，则∠MF2F1=，则不满足三角形的内角和为π，∴∠MF1F2=，∠MF2F1=，∠F1MF2=90°．在Rt△F1MF2中，由丨F1F2丨=2c=2，丨MF1丨=丨F1F2丨=，丨MF2丨=丨F1F2丨=，由丨MF1丨+丨MF2丨=2a=（+1），∴该椭圆的离心率e===﹣1，椭圆的离心率e=﹣1，第 25 题：来源： 2016_2017学年安徽省蚌埠市高二数学上学期期中试题试卷及答案理已知函数在［10,+∞)上单调递增，则的取值范围是（）A． B.C. D．【答案】D第 26 题：来源：云南省腾冲市2017_2018学年高二数学上学期期中试题试卷及答案已知直线和平面，下列推理错误的是（）A．且B．∥且∥C．∥且 D．且∥或【答案】B第 27 题：来源：四川省新津县2018届高三数学10月月考试题理试卷及答案一个几何体的三视图如图所示，则该几何体的表面积为（）.A．B．C．D．【答案】B第 28 题：来源：黑龙江省伊春市2016_2017学年高一数学下学期期中试题试卷及答案已知，直线的倾斜角为，则直线的倾斜角为（）A. B. C. D.【答案】D【解析】∵直线l1的倾斜角为60∘，∴直线l1的斜率k1=tan60∘=，又l2⊥l1,设直线l2的斜率为k2，则k1⋅k2=−1，∴k2=−，故直线l2的倾斜角为150∘，本题选择D选项.第 29 题：来源：宁夏银川市2017_2018学年高一数学上学期期末考试试题试卷及答案已知过两点A(-3，m),B(m,5)的直线与直线3x+y-1=0平行，则m的值是（）A．3 B．7 C． -7 D．-9【答案】C第 30 题：来源：吉林省乾安县2017_2018学年高二数学上学期期中试题理试卷及答案已知，且，那么的大小关系是（）A. B.C. D.【答案】C第 31 题：来源：安徽省霍邱县第二中学2018_2019学年高二数学上学期期中试题理天气预报说，在今后的三天中，每一天下雨的概率均为40%．现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率：先利用计算器产生0到9之间取整数值的随机数，用1，2，3，4表示下雨，用5，6，7，8，9，0表示不下雨；再以每三个随机数作为一组，代表这三天的下雨情况．经随机模拟试验产生了如下20组随机数：907 966 191 925 271 932 812 458 569 68 3431 257 393 027 556 488 730 113 537 9 89据此估计，这三天中恰有两天下雨的概率近似为A．0.35 B．0.25 C．0.20 D．0.15 【答案】B第 32 题：来源： 2019年普通高等学校招生全国统一考试数学（浙江卷）（含答案）设0＜a＜1，则随机变量X的分布列是则当a在（0,1）内增大时，A．D（X）增大 B．D（X）减小C．D（X）先增大后减小 D．D（X）先减小后增大【答案】D第 33 题：来源：吉林省长春市2017年高考数学三模试卷（文科）含答案解析已知复数z=1+2i，则=（）A．5 B．5+4i C．﹣3 D．3﹣4i【答案】A【考点】复数代数形式的乘除运算．【分析】由已知直接利用求解．【解答】解：∵z=1+2i，∴=|z|2=．故选：A．第 34 题：来源： 2016_2017学年北京市昌平区高二数学6月月考试题试卷及答案文如图所示的程序框图，若输入m=8，n=3，则输出的S值为（）A．56 B．336 C．360 D．1440【答案】B第 35 题：来源：福建省龙海市2017_2018学年高二数学上学期第二次月考试题理试卷及答案已知抛物线的焦点与双曲线的右焦点重合，抛物线的准线与轴的交点，点在抛物线上，且，则点的横坐标为（）A． B．2 C. D．4【答案】B第 36 题：来源：湖北省黄冈中学2016-2017学年高二数学上学期期末模拟测试试题试卷及答案（1）理过点的直线与椭圆交于两点, 且点平分弦,则直线的方程为A． B．C． D．【答案】B第 37 题：来源：甘肃省白银市会宁县2016_2017学年高一数学下学期期中试题若圆上至少有三个不同的点到直线：的距离为，则取值范围为（）A．B．C．D．【答案】B第 38 题：来源：山西省平遥中学校2018_2019学年高二数学下学期期中试题理设复数，则（）A． B． C． D．【答案】C第 39 题：来源：广东省天河区普通高中2017_2018学年高二数学11月月考试题03 试卷及答案某观察站与两灯塔、的距离分别为300米和500米，测得灯塔在观察站北偏东30，灯塔在观察站南偏东30处，则两灯塔、间的距离为A、400米B、700米C、500米D、800米【答案】B第 40 题：来源：四川省内江市2019届高三数学上学期第一次模拟考试试题理（含解析）已知集合，，则（）A. B. C. D.【答案】A∵集合A＝{x|x≤1，x∈N}＝{0，1}，又，∴A∩B＝{0，1}．故选A.第 41 题：来源： 2016_2017学年江西省宜春市奉新县高二数学下学期期末考试试题试卷及答案理定义在R上的奇函数满足：当时，，则方程的实数根的个数是 ( )A. 1B. 2C. 3D. 5【答案】 C第 42 题：来源：江西省南昌市2017_2018学年高一数学上学期第一次月考试题试卷及答案幂函数上单调递增，则m的值为（）A. 2B. 3C. 4D. 2或4【答案】 C 由题意得：第 43 题：来源：湖南省双峰县2017_2018学年高二数学上学期第一次月考试题在已知中，内角所对边的长分别是，若，则的值为（）A、B、C、D、【答案】B第 44 题：来源：贵州省遵义市2016_2017学年高一数学下学期第一次月考试题试卷及答案已知函数()的图像与直线的两个相邻公共点之间的距离等于，则的单调递减区间是（）A. B.C. D.【答案】B第 45 题：来源： 2016-2017学年福建省漳州市芗城区高一数学上学期期中试题试卷及答案下列函数中，是偶函数且在上为减函数的是( )A. B. C. D.【答案】C第 46 题：来源：福建省龙海市程溪中学2016-2017学年高二数学上学期期末考试试题理如果执行右面的程序框图，那么输出的（）A、22B、46C、D、190【答案】C第 47 题：来源：广西陆川县2017_2018学年高二数学9月月考试题理试卷及答案等差数列{an}和{bn}的前n项和分别为Sn和Tn，且，则（）A． B． C． D．【答案】D第 48 题：来源：上海市2016届高三数学3月月考试题理试卷及答案．已知数列中，，若利用下面程序框图计算该数列的第2016项，则判断框内的条件是( )A． B．C．D．【答案】 C第 49 题：来源：江西省上饶市玉山县第一中学2018_2019学年高二数学下学期期中试题理（10_19班）极坐标方程为表示的曲线是（）A．双曲线B．圆C．两条相交直线D．两条射线【答案】C第 50 题：来源：黑龙江省伊春市2016_2017学年高二数学下学期期中试题理试卷及答案用数学归纳法证明时，在第二步证明从n＝k到n＝k＋1成立时，左边增加了的项数是（）A. B.C. D.【答案】A【解析】从到成立时，左边增加的项为，因此增加的项数是，选A.。

2019年桂平市石咀中学高考数学选择题专项训练(一模)

2019年桂平市石咀中学高考数学选择题专项训练（一模）抽选各地名校试卷，经典试题，有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。

第 1 题：来源：广东省湛江市普通高中2018届高考数学一轮复习模拟试题试卷及答案05三棱锥的外接球为球，球的直径是，且、都是边长为1的等边三角形，则三棱锥的体积是（）A．B．C． D．【答案】D第 2 题：来源： 2017年高中数学第一章坐标系第二章参数方程综合质量评估（含解析）新人教A 版选修4_4在极坐标系中,曲线ρ=4cosθ围成的图形面积为( )A.πB.4C.4πD.16【答案】C.由ρ=4cosθ得ρ2=4ρcosθ,直角坐标方程为x2+y2=4x,所以(x-2)2+y2=4,所以S=πr2=4π. 第 3 题：来源：宁夏石嘴山市2017_2018学年高二数学上学期期中试题理等差数列的值为（）A．66 B．99 C．144 D ．297【答案】B第 4 题：来源：河南省林州市2017_2018学年高二数学上学期开学检测试题试卷及答案.角θ的终边过点P(－1,2)，则sinθ等于( )A． B． C．－ D．－【答案】B【解析】由题意可得，x＝－1，y＝2，r＝|OP|＝，∴sinθ＝＝.第 5 题：来源：广东省天河区普通高中2017_2018学年高一数学10月月考试题试卷及答案08 下列函数中,在区间上是增函数的是A． B． C． D．【答案】A第 6 题：来源：安徽省赛口中学2018_2019学年高二数学下学期期中试题文已知双曲线的渐近线方程为，且其右焦点为（5,0），则双曲线的方程为A．B．C．D．【答案】B第 7 题：来源： 2017年成都市高考数学二诊试卷（理科）含答案解析若对∀m，n∈R，有g（m+n）=g（m）+g（n）﹣3，求的最大值与最小值之和是（）A．4 B．6 C．8 D．10【答案】B【考点】函数的最值及其几何意义．【分析】构造h（x）=g（x）﹣3，根据函数奇偶性的定义可判定函数h（x）为奇函数，利用奇函数图象的性质即可求出答案．【解答】解：∵∀m，n∈R，有g（m+n）=g（m）+g（n）﹣3，∴令m=n=0时，g（0）=g（0）+g（0）﹣3，∴g（0）=3，令m=﹣n时，g（0）=g（﹣n）+g（n）﹣3，∴g（x）+g（﹣x）=6，令h（x）=g（x）﹣3，则h（x）+h（﹣x）=0即h（x）为奇函数，奇函数的图象关于原点对称，它的最大值与最小值互为相反数，∴g（x）max+g（﹣x）min=6，设F（x）=，则F（﹣x）=﹣F（x），函数为奇函数，最大值与最小值之和为0，∴．的最大值与最小值之和是6．故选B．第 8 题：来源：广东省湛江市普通高中2018届高考数学一轮复习模拟试题试卷及答案09利用如图所示程序框图在直角坐标平面上打印一系列点，则打印的点落在坐标轴上的个数是（）A.0B.1C.2D.3【答案】B第 9 题：来源：高中数学第一章常用逻辑用语章末测试A新人教B版选修1_已知命题p：x∈R，x＋6＞0，则p是( )A．x∈R，x＋6≥0 B．x∈R，x＋6≤0C．x∈R，x＋6≥0 D．x∈R，x＋6≤0【答案】D第 10 题：来源：内蒙古集宁一中2016-2017学年高二数学上学期期末考试试题试卷及答案理过的直线与双曲线仅有一个公共点，则这样的直线有（）条A．1 B．2 C．3D．4【答案】B第 11 题：来源：江西省南昌市2018届高三数学上学期第三次月考试题理试卷及答案函数y=（a＞0，a≠1）的定义域和值域都是[0，1]，则loga+loga=A．1 B．2 C．3D．4【答案】C第 12 题：来源：甘肃省甘谷县第一中学2019届高三数学上学期第一次检测考试试题理（含解析）已知定义在上的函数满足条件：①对任意的，都有；②对任意的且，都有；③函数的图象关于轴对称，则下列结论正确的是（）A. B.C. D.【答案】C【解析】【分析】根据条件判断函数的周期性和对称性，利用函数对称性，周期性和单调性之间的关系将函数值进行转化比较即可得到结论．【详解】：∵对任意的，都有；∴函数是4为周期的周期函数，∵函数的图象关于轴对称∴函数函数）的关于对称，∵且，都．∴此时函数在上为增函数，则函数在上为减函数，则，，，则，即，故选C．【点睛】本题主要考查与函数有关的命题的真假判断，根据条件判断函数的周期性和对称性，和单调性之间的关系是解决本题的关键．第 13 题：来源：湖南省浏阳市2016_2017学年高二数学下学期第一次阶段性测试试题试卷及答案理已知p：x＞1，q：＜1，则p是q的( )(A) 充分不必要条件(B) 必要不充分条件 (C) 充要条件(D) 既不充分也不必要条件【答案】A第 14 题：来源：山东省淄博市2018届高三数学上学期开学考试试题试卷及答案理某程序框图如图所示，若该程序运行后输出的值是，则（）A．a=11 B．a=12 C．a=13 D．a=14【答案】B．第 15 题：来源： 2017届江西省南昌市十所省重点中学高三第二次模拟突破冲刺数学理科试题（五）含答案若不等式对恒成立，则实数a的最小值是（）A． B．0 C．2 D．4【答案】A第 16 题：来源：云南省玉溪市2017_2018学年高二数学上学期第二次月考试题理试卷及答案是抛物线上一点，是抛物线的焦点，以为始边、为终边的角，则（）【答案】B第 17 题：来源：北京市西城区2016_2017学年高一数学下学期期中试题试卷及答案如图所示，C、D、A三点在同一水平线上，AB是塔的中轴线，在C、D两处测得塔顶部B处的仰角分别是和，如果C、D间的距离是a，测角仪高为b，则塔高为（）A. B.C. D.【答案】A第 18 题：来源：山西省平遥中学校2018_2019学年高二数学下学期期中试题理设函数在区间[a－1，a＋1]上单调递减，则实数a的取值范围是( )A. [－∞，2)B. (1，2]C. (0，3]D. (4，＋∞]【答案】B第 19 题：来源： 2019高考数学一轮复习第7章不等式第1讲一元二次不等式的解法分层演练文不等式(x－2)(2x－3)<0的解集是( )A． B．RC． D．∅【答案】C.因为不等式(x－2)(2x－3)<0，解得<x<2，所以不等式的解集是.第 20 题：来源：安徽省滁州市定远县育才学校2018_2019学年高二数学下学期第一次月考试题（普通班）理已知函数f(x)＝则等于( )A．－B．＋C．＋D．－【答案】.B第 21 题：来源： 2017年普通高等学校招生全国统一考试数学试题文（全国卷2，参考解析）函数的最小正周期为A.4B.2C.D.【答案】C【解析】由题意，故选C.第 22 题：来源：甘肃省兰州市2016_2017学年高一数学下学期期末考试试题试卷及答案下列各式中，其值为的是（）A．B．C．D．【答案】B第 23 题：来源：江西省南昌市2018届高三数学上学期第三次月考试题理试卷及答案设函数是连续函数，且在x=1处存在导数，若函数及其导函数满足，则函数A. 既有极大值又有极小值B. 有极大值无极小值C. 有极小值无极大值D. 既无极大值有无极小值【答案】D第 24 题：来源：河南省郑州市2017_2018学年高一数学上学期第二次月考试题试卷及答案若幂函数是偶函数，且在上是减函数，则实数m的值可能为（）A. B. C. D.【答案】B第 25 题：来源： 2019_2020学年高中数学第二章等式与不等式2.2.3一元二次不等式的解法课后篇巩固提升（含解析）新人教B版必修1已知关于x的方程|x|-k(x+1)=0有正实数根,则实数k的取值范围是( )A.k≥1B.k≤-1C.k>1或k<-1D.0<k<1【答案】D由题意可知,(1-k)x=k,显然k≠1.由>0,得0<k<1.第 26 题：来源：江西省赣州市2016_2017学年高二数学下学期第二次（5月）月考试题理不等式|2x﹣1|+|x+1|＞2的解集为（）A．（﹣∞，0）∪（，+∞）B．（，+∞） C．（﹣∞，﹣1）∪（，+∞） D．（﹣∞，0）【答案】A第 27 题：来源： 2017_2018学年高中数学第三章直线与方程章末综合测评2试卷及答案新人教A 版必修经过点(2,1)的直线l到A(1,1)、B(3,5)两点的距离相等，则直线l的方程为( )A．2x－y－3＝0B．x＝2C．2x－y－3＝0或x＝2D．以上都不对【答案】C第 28 题：来源：宁夏青铜峡市高级中学2018_2019学年高一数学下学期开学考试试题已知函数，，则函数的图象可能是下面的哪个（）A． B． C． D．【答案】D第 29 题：来源： 2016_2017学年江苏省泰安市岱岳区高二数学下学期期中试题试卷及答案理一个三位自然数百位、十位、个位上的数字依次为，当且仅当时称为“凹数”（如213），若，且互不相同，则三位数中“凹数”有A．6个 B．7个 C．8个 D．9个【答案】C第 30 题：来源：河北省景县2017_2018学年高二数学开学摸底考试试题试卷及答案对于任意实数，不等式恒成立，则实数的取值范围（）A． B． C． D．【答案】C第 31 题：来源：甘肃省武威市第六中学2018_2019学年高二数学下学期第三次学段考试试题文已知椭圆以及椭圆内一点P(4，2)，则以P为中点的弦所在直线的斜率为( )A. －B.C. －2 D. 2【答案】A第 32 题：来源：辽宁省六校2017_2018学年高二数学上学期期初联考试题试卷及答案理从4件合格品和2件次品共6件产品中任意抽取2件检查，抽取的2件中至少有1件是次品的概率是A． B． C. D．【答案】C第 33 题：来源：宁夏银川市2018届高三数学上学期统练试题试卷及答案（二）理根据有关资料，围棋状态空间复杂度的上限M约为3361，而可观测宇宙中普通物质的原子总数N约为1080，则下列各数中与最接近的是（）（参考数据：lg3≈0.48）A.1033B.1053C.1073D.1093【答案】 D第 34 题：来源：吉林省延边州2019届高三数学2月复习质量检测试题文在一次庆教师节联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目,若选中男教师的概率为,则参加联欢会的教师共有A. B. C.D.【答案】A第 35 题：来源：安徽省定远重点中学2018_2019学年高二数学下学期开学考试试题理在△ABC中，若p：A＝60°，q：sinA＝，则p是q的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A第 36 题：来源：江西省南昌市2018届高三数学第二轮复习测试题（二）理（含解析）已知实数满足：.若目标函数（其中为常数）仅在处取得最大值，则的取值范围是A. B. C. D.【答案】A【解析】【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，利用为目标函数取得最大值时的唯一最优解，讨论目标函数的斜率满足的条件，从而求出a的取值范围．【详解】构造二次函数单调性可知，得到自变量离轴越远函数值越大，故，且得到可行域为如图所示，直线斜率为-a,由图像可得到满足-1<-a<1即-1<a<1.故答案选A.【点睛】利用线性规划求最值的步骤：(1)在平面直角坐标系内作出可行域．(2)考虑目标函数的几何意义，将目标函数进行变形．常见的类型有截距型（型）、斜率型（型）和距离型（型）．(3)确定最优解：根据目标函数的类型，并结合可行域确定最优解．(4)求最值：将最优解代入目标函数即可求出最大值或最小值。

2019年数学高考一模试卷附答案

2019年数学高考一模试卷附答案一、选择题1．已知回归直线方程中斜率的估计值为1.23，样本点的中心()4,5，则回归直线方程为（）A ． 1.2308ˆ.0yx =+ B ．0.0813ˆ.2yx =+ C ． 1.234ˆyx =+ D ． 1.235ˆyx =+ 2．定义运算()()a ab a b b a b ≤⎧⊕=⎨>⎩，则函数()12xf x =⊕的图象是（）．A ．B ．C ．D ．3．某学校开展研究性学习活动，某同学获得一组实验数据如下表： x 1.99 3 4 5.16.12 y1.54.04 7.51218.01对于表中数据，现给出以下拟合曲线，其中拟合程度最好的是( ) A ．22y x =-B ．1()2xy =C ．2y log x =D ．()2112y x =- 4．设集合(){}2log 10M x x =-<，集合{}2N x x =≥-，则M N ⋃=（） A ．{}22x x -≤<B ．{}2x x ≥-C ．{}2x x <D ．{}12x x ≤<5．一个正方体内接于一个球，过球心作一个截面，如图所示，则截面的可能图形是（）A ．①③④B ．②④C ．②③④D ．①②③6．如图，12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点，过2F 的直线与双曲线C 交于,A B 两点．若11::3:4:5AB BF AF =，则双曲线的渐近线方程为（）A ．23y x =±B ．22y x =±C ．3y x =±D ．2y x =±7．设双曲线2222:1x y C a b-=(00a b >>，)的左、右焦点分别为12F F ，，过1F 的直线分别交双曲线左右两支于点M N ，，连结22MF NF ，，若220MF NF ⋅=，22MF NF =，则双曲线C 的离心率为( ). A ．2B ．3C ．5D ．68．函数f (x )＝2sin(ωx ＋φ)(ω>0，－2π<φ<2π)的部分图象如图所示，则ω、φ的值分别是( )A ．2，－3πB ．2，－6π C ．4，－6πD ．4，3π 9．在ABC 中，若 13,3,120AB BC C ==∠=，则AC =（）A ．1B ．2C ．3D ．410．不等式2x 2-5x -3≥0成立的一个必要不充分条件是（） A ．1x <-或4x >B ．0x 或2x -C ．0x <或2x >D ．12x -或3x 11．已知锐角三角形的边长分别为2，3，x ，则x 的取值范围是（） A 513x << B 135x < C ．25x <<D 55x <<12．设双曲线22221x y a b-=（0a >，0b >）的渐近线与抛物线21y x =+相切，则该双曲线的离心率等于（） A ．3B ．2C ．6D ．5二、填空题13．在区间[﹣2，4]上随机地取一个数x ，若x 满足|x|≤m 的概率为，则m= _________ ． 14．设25a b m ==,且112a b+=,则m =______. 15．若x ，y 满足约束条件x y 102x y 10x 0--≤⎧⎪-+≥⎨⎪≥⎩，则xz y 2=-+的最小值为______．16．若函数3211()232f x x x ax =-++ 在2,3⎡⎫+∞⎪⎢⎣⎭上存在单调增区间，则实数a 的取值范围是_______.17．371()x x+的展开式中5x 的系数是 .（用数字填写答案）18．已知点()0,1A ，抛物线()2:0C y ax a =>的焦点为F ，连接FA ，与抛物线C 相交于点M ，延长FA ，与抛物线C 的准线相交于点N ，若:1:3FM MN =，则实数a 的值为__________．19．已知圆C 经过(5,1),(1,3)A B 两点，圆心在x 轴上，则C 的方程为__________． 20．设等比数列{}n a 满足a 1+a 3=10，a 2+a 4=5，则a 1a 2…a n 的最大值为．三、解答题21．选修4-5：不等式选讲设函数()|2||1|f x x x =-++.（1）求()f x 的最小值及取得最小值时x 的取值范围；（2）若集合{|()10}x f x ax +->=R ，求实数a 的取值范围.22．已知矩形ABCD 的两条对角线相交于点20M （，），AB 边所在直线的方程为360x y --=，点11T -（，）在AD 边所在直线上. （1）求AD 边所在直线的方程；（2）求矩形ABCD 外接圆的方程.23．四棱锥P ABCD -中，底面ABCD 是边长为2的菱形，3BAD π∠=，PAD ∆是等边三角形，F 为AD 的中点，PD BF ⊥.（1）求证：AD PB ⊥；（2）若E 在线段BC 上，且14EC BC =，能否在棱PC 上找到一点G ，使平面DEG ⊥平面ABCD ？若存在，求四面体D CEG -的体积. 24．选修4-5：不等式选讲：设函数()13f x x x a =++-. （1）当1a =时，解不等式()23f x x ≤+；（2）若关于x 的不等式()42f x x a <+-有解，求实数a 的取值范围.25．2016年某市政府出台了“2020年创建全国文明城市简称创文”的具体规划，今日，作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成，市有关部门准备对项目进行调查，并根据调查结果决定是否验收，调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分，并将结果绘制成如图所示的频率分布直方图，相关规则为：调查对象为本市市民，被调查者各自独立评分；采用百分制评分，内认定为满意，80分及以上认定为非常满意；市民对公交站点布局的满意率不低于即可进行验收；用样本的频率代替概率．求被调查者满意或非常满意该项目的频率；若从该市的全体市民中随机抽取3人，试估计恰有2人非常满意该项目的概率；已知在评分低于60分的被调查者中，老年人占，现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因，并从中选取2人担任群众督察员，记为群众督查员中老年人的人数，求随机变量的分布列及其数学期望．【参考答案】***试卷处理标记，请不要删除一、选择题1．A 解析：A 【解析】【分析】由题意得在线性回归方程ˆy bx a =+中 1.23b =，然后根据回归方程过样本点的中心得到a 的值，进而可得所求方程．【详解】设线性回归方程ˆy bx a =+中，由题意得 1.23b =， ∴ 1.23ˆy x a =+．又回归直线过样本点的中心()4,5， ∴5 1.234a =⨯+， ∴0.08a =，∴回归直线方程为 1.2308ˆ.0yx =+．故选A ．【点睛】本题考查线性回归方程的求法，其中回归直线经过样本点的中心时解题的关键，利用这一性质可求回归方程中的参数，也可求样本数据中的未知参数，属于基础题．2．A解析：A 【解析】【分析】【详解】由已知新运算a b ⊕的意义就是取得,a b 中的最小值，因此函数()1,0122,0xxx f x x >⎧=⊕=⎨≤⎩，只有选项A 中的图象符合要求，故选A.3．D解析：D 【解析】【分析】根据,x y 的数值变化规律推测二者之间的关系，最贴切的是二次关系. 【详解】根据实验数据可以得出，x 近似增加一个单位时，y 的增量近似为2.5，3.5，4.5，6，比较接近()2112y x =-，故选D.【点睛】本题主要考查利用实验数据确定拟合曲线，求解关键是观察变化规律，侧重考查数据分析的核心素养.4．B解析：B 【解析】【分析】求解出集合M ，根据并集的定义求得结果. 【详解】(){}{}{}2log 1001112M x x x x x x =-<=<-<=<< {}2M N x x ∴⋃=≥-本题正确选项：B 【点睛】本题考查集合运算中的并集运算，属于基础题.5．A解析：A 【解析】【分析】分别当截面平行于正方体的一个面时，当截面过正方体的两条相交的体对角线时，当截面既不过体对角线也不平行于任一侧面时，进行判定，即可求解. 【详解】由题意，当截面平行于正方体的一个面时得③；当截面过正方体的两条相交的体对角线时得④；当截面既不过正方体体对角线也不平行于任一侧面时可能得①；无论如何都不能得②.故选A. 【点睛】本题主要考查了正方体与球的组合体的截面问题，其中解答中熟记空间几何体的结构特征是解答此类问题的关键，着重考查了空间想象能力，以及推理能力，属于基础题.6．A解析：A 【解析】【分析】设1123,4,5,AB BF AF AF x ====，利用双曲线的定义求出3x =和a 的值，再利用勾股定理求c ，由by x a=±得到双曲线的渐近线方程. 【详解】设1123,4,5,AB BF AF AF x ====，由双曲线的定义得：345x x +-=-，解得：3x =，所以12||F F ==c ⇒=因为2521a x a =-=⇒=，所以b =所以双曲线的渐近线方程为by x a=±=±. 【点睛】本题考查双曲线的定义、渐近线方程，解题时要注意如果题干出现焦半径，一般会用到双曲线的定义，考查运算求解能力.7．B解析：B 【解析】【分析】本道题设2MF x =,利用双曲线性质,计算x ，结合余弦定理，计算离心率，即可．【详解】结合题意可知,设22,,,MF x NF x MN ===则则结合双曲线的性质可得,21122,2MF MF a MF MN NF a -=+-=代入,解得x =,所以122,NF a NF =+=,01245F NF ∠= 对三角形12F NF 运用余弦定理,得到()()()()()22202222cos45a c a ++-=+⋅,解得ce a== 故选B. 【点睛】本道题考查了双曲线的性质，考查了余弦定理，关键利用余弦定理，解三角形，进而计算x ，即可，难度偏难．8．A解析：A 【解析】【分析】由函数f （x ）＝2sin （ωx+φ）的部分图象，求得T 、ω和φ的值．【详解】由函数f （x ）＝2sin （ωx+φ）的部分图象知，3T 5π412=-（π3-）3π4=， ∴T 2πω==π，解得ω＝2；又由函数f （x ）的图象经过（5π12，2），∴2＝2sin （25π12⨯+φ）， ∴5π6+φ＝2kππ2+，k∈Z，即φ＝2kππ3-，又由π2-＜φπ2＜，则φπ3=-；综上所述，ω＝2、φπ3=-．故选A ．【点睛】本题考查了正弦型函数的图象与性质的应用问题，是基础题．9．A解析：A 【解析】余弦定理2222?cos AB BC AC BC AC C =+-将各值代入得2340AC AC +-=解得1AC =或4AC =-(舍去)选A.10．C解析：C 【解析】【分析】根据题意，解不等式2x 2-5x-3≥0可得x≤-12或x≥3，题目可以转化为找x≤-12或x≥3的必要不充分条件条件，依次分析选项即可得答案．【详解】根据题意，解不等式2x 2-5x-3≥0可得x≤-12或x≥3，则2x 2-5x-3≥0⇔x≤12-或3x ，所以可以转化为找x≤-12或x≥3的必要不充分条件；依次选项可得：x 1<-或x 4>是12x ≤-或x≥3成立的充分不必要条件； x 0≥或x 2≤-是12x ≤-或x≥3成立的既不充分也不必要条件x 0<或x 2>是12x ≤-或x≥3成立的必要不充分条件；x≤-12或x≥3是12x ≤-或x≥3成立的充要条件；【点睛】本题考查了充分必要条件，涉及一元二次不等式的解答，关键是正确解不等式2x 2-5x-3≥0．11．A解析：A 【解析】试题分析：因为三角形是锐角三角形，所以三角形的三个内角都是锐角，则设边3对的锐角为角α，根据余弦定理得22223cos 04x xα+-=>，解得x >x 边对的锐角为β，根据余弦定理得22223cos 012x β+-=>，解得0x <<x 的取值范x << A. 考点：余弦定理.12．D解析：D 【解析】由题意可知双曲线的渐近线一条方程为b y x a =，与抛物线方程组成方程组2,1b y xa y x ⎧=⎪⎨⎪=+⎩消y 得，2210,()40b b x x a a -+=∆=-=，即2()4b a =，所以e == D. 【点睛】双曲线22221x y a b-=（0a >，0b >）的渐近线方程为b y x a =±．直线与抛物线交点问题，直线与抛物线方程组方程组，当直线与抛物线对称轴平行时，直线与抛物线相交，只有一个交点．当直线与抛物线对称轴不平行时，当>0∆时，直线与抛物线相交，有两个交点．当0∆=时，直线与抛物线相切，只有一个交点．当∆<0时，直线与抛物线相离，没有交点．二、填空题13．3【解析】【分析】【详解】如图区间长度是6区间﹣24上随机地取一个数x 若x 满足|x|≤m 的概率为若m 对于3概率大于若m 小于3概率小于所以m=3故答案为3解析：3 【解析】【详解】如图区间长度是6，区间[﹣2，4]上随机地取一个数x ，若x 满足|x|≤m 的概率为，若m 对于3概率大于，若m 小于3，概率小于，所以m=3．故答案为3．14．【解析】【分析】变换得到代入化简得到得到答案【详解】则故故答案为：【点睛】本题考查了指数对数变换换底公式意在考查学生的计算能力 10【解析】【分析】变换得到2log a m =，5log b m =，代入化简得到11log 102m a b+==，得到答案. 【详解】25a b m ==，则2log a m =，5log b m =，故11log 2log 5log 102,10m m m m a b+=+==∴= 10 【点睛】本题考查了指数对数变换，换底公式，意在考查学生的计算能力.15．-1【解析】【分析】画出约束条件表示的平面区域由图形求出最优解再计算目标函数的最小值【详解】画出约束条件表示的平面区域如图所示由图形知当目标函数过点A 时取得最小值由解得代入计算所以的最小值为故答案为解析：-1 【解析】【分析】画出约束条件表示的平面区域，由图形求出最优解，再计算目标函数1z x y 2=-+的最小值．【详解】画出约束条件102100x y x y x --≤⎧⎪-+≥⎨⎪≥⎩表示的平面区域如图所示，由图形知，当目标函数1z x y 2=-+过点A 时取得最小值，由{x 0x y 10=--=，解得()A 0,1-，代入计算()z 011=+-=-，所以1z x y 2=-+的最小值为1-．故答案为1-．【点睛】本题考查了线性规划的应用问题，也考查了数形结合的解题方法，是基础题．16．【解析】【分析】【详解】试题分析：当时的最大值为令解得所以a 的取值范围是考点：利用导数判断函数的单调性解析：1(,)9-+∞ 【解析】【分析】【详解】试题分析：2211()2224f x x x a x a ⎛⎫=-++=--++ ⎪⎝⎭'．当23x ⎡⎫∈+∞⎪⎢⎣⎭，时，()f x '的最大值为22239f a ⎛⎫=+ ⎪⎝⎭'，令2209a +>，解得19a >-，所以a 的取值范围是1,9⎛⎫-+∞ ⎪⎝⎭．考点：利用导数判断函数的单调性．17．【解析】由题意二项式展开的通项令得则的系数是考点：1二项式定理的展开式应用解析：35【解析】由题意，二项式371()x x +展开的通项372141771()()r r r r r r T C x C x x--+==，令2145r -=，得4r =，则5x 的系数是4735C =. 考点：1.二项式定理的展开式应用.18．【解析】依题意可得焦点的坐标为设在抛物线的准线上的射影为连接由抛物线的定义可知又解得点睛：本题主要考查的知识点是抛物线的定义以及几何性质的应用考查了学生数形结合思想和转化与化归思想设出点在抛物线的准【解析】依题意可得焦点F 的坐标为04a ⎛⎫ ⎪⎝⎭，，设M 在抛物线的准线上的射影为K ，连接MK 由抛物线的定义可知MF MK =13FM MN =∶∶KN KM ∴=∶又01404FN K a a--==-，FN KN K KM ==-4a-∴=-a =点睛：本题主要考查的知识点是抛物线的定义以及几何性质的应用，考查了学生数形结合思想和转化与化归思想，设出点M 在抛物线的准线上的射影为K ，由抛物线的定义可知MF MK =，再根据题设得到KN KM =∶，然后利用斜率得到关于a 的方程，进而求解实数a 的值19．【解析】【分析】由圆的几何性质得圆心在的垂直平分线上结合题意知求出的垂直平分线方程令可得圆心坐标从而可得圆的半径进而可得圆的方程【详解】由圆的几何性质得圆心在的垂直平分线上结合题意知的垂直平分线为令解析：22(2)10x y -+=.【解析】【分析】由圆的几何性质得，圆心在AB 的垂直平分线上,结合题意知，求出AB 的垂直平分线方程，令0y =，可得圆心坐标，从而可得圆的半径，进而可得圆的方程.【详解】由圆的几何性质得，圆心在AB 的垂直平分线上,结合题意知，AB 的垂直平分线为24y x =-，令0y =，得2x =，故圆心坐标为(2,0)，所以圆的半径=22(2)10x y -+=.【点睛】本题主要考查圆的性质和圆的方程的求解,意在考查对基础知识的掌握与应用，属于基础题.20．【解析】试题分析：设等比数列的公比为由得解得所以于是当或时取得最大值考点：等比数列及其应用解析：64【解析】试题分析：设等比数列的公比为q ，由132410{5a a a a +=+=得，2121(1)10{(1)5a q a q q +=+=，解得18{12a q ==.所以2(1)1712(1)22212118()22n n n n n n n n a a a a q --++++-==⨯=，于是当3n =或4时，12na a a 取得最大值6264=.考点：等比数列及其应用三、解答题21．（1）min ()3f x =，此时x ∈[]1,2-（2）()1,2-【解析】【分析】（1）利用绝对值不等式公式进行求解；（2）集合(){}10x f x ax R +-=表示x R ∀∈，()1f x ax >-+，令()1g x ax =-+，根据几何意义可得()y f x =的图像恒在()y g x =图像上方，数形结合解决问题.【详解】解（1）因为()()21213x x x x -++≥--+=，当且仅当()()210x x -+≤，即12x -≤≤时，上式“=”成立，故函数()21f x x x =++-的最小值为3，且()f x 取最小值时x 的取值范围是[]1,2-.（2）因为(){}10x f x ax R +-=，所以x R ∀∈，()1f x ax >-+. 函数()21f x x x =-++化为()21,13,1221,2x x f x x x x -+<-⎧⎪=-≤≤⎨⎪->⎩.令()1g x ax =-+，其图像为过点()0,1P ，斜率为a -的一条直线.如图，()2,3A ，()1,3B -.则直线PA 的斜率131120k -==-，直线PB 的斜率231210k -==---. 因为()()f x g x >，所以21a -<-<，即12a -<<，所以a 的范围为()1,2-.【点睛】本题考查了绝对值不等式问题与不等式恒成立问题，不等式恒成立问题往往可以借助函数的图像来研究，数形结合可以将抽象的问题变得更为直观，解题时应灵活运用.22．（1）3x ＋y ＋2＝0；（2）(x －2)2＋y 2＝8.【解析】【分析】(1) 直线AB 斜率确定，由垂直关系可求得直线AD 斜率，又T 在AD 上，利用点斜式求直线AD 方程；（2）由AD 和AB 的直线方程求得A 点坐标，以M 为圆心，以AM 为半径的圆的方程即为所求.【详解】(1)∵AB 所在直线的方程为x －3y －6＝0，且AD 与AB 垂直，∴直线AD 的斜率为－3．又∵点T (－1,1)在直线AD 上，∴AD 边所在直线的方程为y －1＝－3(x ＋1)，即3x ＋y ＋2＝0．(2)由360320x y x y --=⎧⎨++=⎩,得02x y =⎧⎨=-⎩, ∴点A 的坐标为(0，－2)，∵矩形ABCD 两条对角线的交点为M (2,0)，∴M 为矩形ABCD 外接圆的圆心，又|AM |()()22200222-++= ∴矩形ABCD 外接圆的方程为(x －2)2＋y 2＝8．【点睛】本题考查两直线的交点，直线的点斜式方程和圆的方程,考查计算能力，属于基础题.23．（1）证明见解析；（2）112. 【解析】【分析】（1）连接PF ，BD 由三线合一可得AD ⊥BF ，AD ⊥PF ，故而AD ⊥平面PBF ，于是AD ⊥PB ；（2）先证明PF ⊥平面ABCD ，再作PF 的平行线，根据相似找到G ，再利用等积转化求体积．【详解】连接PF ，BD,∵PAD ∆是等边三角形，F 为AD 的中点，∴PF ⊥AD ，∵底面ABCD 是菱形，3BAD π∠=，∴△ABD 是等边三角形，∵F 为AD 的中点，∴BF ⊥AD ，又PF ，BF ⊂平面PBF ，PF ∩BF ＝F ，∴AD ⊥平面PBF ，∵PB ⊂平面PBF ，∴AD ⊥PB ．（2）由（1）得BF ⊥AD ，又∵PD ⊥BF ，AD ，PD ⊂平面PAD ，∴BF ⊥平面PAD ，又BF ⊂平面ABCD ，∴平面PAD ⊥平面ABCD ，由（1）得PF ⊥AD ，平面PAD ∩平面ABCD ＝AD ，∴PF ⊥平面ABCD ，连接FC 交DE 于H,则△HEC 与△HDF 相似，又1142EC BC FD ==，∴CH=13CF ， ∴在△PFC 中,过H 作GH //PF 交PC 于G ，则GH⊥平面ABCD ，又GH ⊂面GED ，则面GED⊥平面ABCD ，此时CG=13CP, ∴四面体D CEG -的体积111311223382312D CEG G CED CED V V S GH PF --==⋅=⨯⨯⨯⨯⨯=．所以存在G 满足CG=13CP, 使平面DEG ⊥平面ABCD ，且112D CEG V -=. 【点睛】本题考查了线面垂直的判定与性质定理，面面垂直的判定及性质的应用，考查了棱锥的体积计算，属于中档题．24．（1）15[,]42（2）(5,3)-【解析】【分析】（1）通过讨论x 的范围，求出不等式的解集即可；（2）问题等价于关于x 的不等式14x x a ++-<有解，()min 14x x a++-<，求出a的范围即可．【详解】解：（1）()1323f x x x a x =++-≤+可转化为 14223x x x ≥⎧⎨-≤+⎩或114223x x x -<<⎧⎨-≤+⎩或12423x x x ≤-⎧⎨-≤+⎩，解得512x ≤≤或114x ≤<或无解. 所以不等式的解集为15,42⎡⎤⎢⎥⎣⎦. （2）依题意，问题等价于关于x 的不等式14x x a ++-<有解，即()min 14x x a ++-<，又111x x a x x a a ++-≥+-+=+，当()()10x x a +-≤时取等号.所以14a +<，解得53a -<<，所以实数a 的取值范围是()5,3-.【点睛】含绝对值不等式的解法有两个基本方法，一是运用零点分区间讨论，二是利用绝对值的几何意义求解．法一是运用分类讨论思想，法二是运用数形结合思想，将绝对值不等式与函数以及不等式恒成立交汇、渗透，解题时强化函数、数形结合与转化化归思想方法的灵活应用。

2019年高考数学一模试题(及答案)

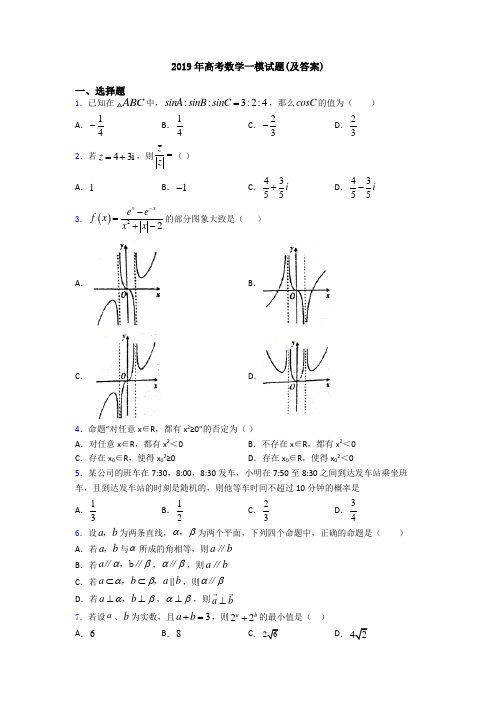
2019年高考数学一模试题(及答案)一、选择题1．已知在ABC 中，::3:2:4sinA sinB sinC =，那么cosC 的值为（）A ．14-B ．14C ．23-D ．232．若43i z =+，则zz=（） A ．1B ．1-C ．4355i + D ．4355i - 3．()22x xe ef x x x --=+-的部分图象大致是（）A ．B ．C ．D ．4．命题“对任意x ∈R ，都有x 2≥0”的否定为（） A ．对任意x ∈R ，都有x 2＜0 B ．不存在x ∈R ，都有x 2＜0 C ．存在x 0∈R ，使得x 02≥0D ．存在x 0∈R ，使得x 02＜05．某公司的班车在7:30，8:00，8:30发车，小明在7:50至8:30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是A ．13B ．12 C ．23 D ．346．设a b ，为两条直线，αβ，为两个平面，下列四个命题中，正确的命题是（） A ．若a b ，与α所成的角相等，则a b ∥B ．若a αβ∥，b ∥，αβ∥，则a b ∥C ．若a b a b αβ⊂⊂，，，则αβ∥D ．若a b αβ⊥⊥，，αβ⊥，则a b ⊥7．若设a 、b 为实数，且3a b +=，则22a b +的最小值是（） A ．6B ．8C ．26D ．428．已知集合1}{0|A x x -≥=，{0,1,2}B =，则A B =A ．{0}B ．{1}C ．{1,2}D ．{0,1,2}9．已知π,4αβ+=则(1tan )(1tan )αβ++的值是（） A ．-1B ．1C ．2D ．410．sin 47sin17cos30cos17-A ．32-B ．12-C ．12D ．3211．函数y ()y ()f x f x ==，的导函数的图像如图所示，则函数y ()f x =的图像可能是A ．B ．C ．D ．12．将函数()sin 2y x ϕ=+的图象沿轴向左平移8π个单位后，得到一个偶函数的图象，则ϕ的一个可能取值为( ) A ．B ．C ．0D ．4π-二、填空题13．函数()22,026,0x x f x x lnx x ⎧-≤=⎨-+>⎩的零点个数是________．14．若不等式|3|4x b -<的解集中的整数有且仅有1，2，3，则b 的取值范围是15．在ABC 中，60A =︒，1b =3sin sin sin a b cA B C ________．16．已知圆锥的侧面展开图是一个半径为2cm ，圆心角为23π的扇形，则此圆锥的高为________cm .17．在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若1sin 3α=，则cos()αβ-=___________. 18．已知函数()(ln )f x x x ax =-有两个极值点,则实数a 的取值范围是__________． 19．能说明“若f （x ）>f （0）对任意的x ∈（0，2］都成立，则f （x ）在［0，2］上是增函数”为假命题的一个函数是__________．20．从2位女生，4位男生中选3人参加科技比赛，且至少有1位女生入选，则不同的选法共有_____________种．（用数字填写答案）三、解答题21．某农场有一块农田，如图所示，它的边界由圆O 的一段圆弧MPN （P 为此圆弧的中点）和线段MN 构成．已知圆O 的半径为40米，点P 到MN 的距离为50米．现规划在此农田上修建两个温室大棚，大棚I 内的地块形状为矩形ABCD ，大棚II 内的地块形状为CDP ，要求,A B 均在线段MN 上，,C D 均在圆弧上．设OC 与MN 所成的角为θ．（1）用θ分别表示矩形ABCD 和CDP 的面积，并确定sin θ的取值范围；（2）若大棚I 内种植甲种蔬菜，大棚II 内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4:3．求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大．22．已知椭圆22221(0)x y a b a b +=>>的离心率为63，以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为22．（1）求椭圆的方程；（2）如图，斜率为k 的直线l 过椭圆的右焦点F ，且与椭圆交与,A B 两点，以线段AB 为直径的圆截直线1x =所得的弦的长度为5，求直线l 的方程．23．如图，在三棱柱111ABC A B C -中，H 是正方形11AA B B 的中心，122AA =1C H ⊥平面11AA B B ，且1 5.C H =（Ⅰ）求异面直线AC 与11A B 所成角的余弦值；（Ⅱ）求二面角111A AC B --的正弦值；（Ⅲ）设N 为棱11B C 的中点，点M 在平面11AA B B 内，且MN ⊥平面111A B C ，求线段BM 的长．24．已知矩形ABCD 的两条对角线相交于点20M （，），AB 边所在直线的方程为360x y --=，点11T -（，）在AD 边所在直线上. （1）求AD 边所在直线的方程；（2）求矩形ABCD 外接圆的方程.25．商场销售某种商品的经验表明，该商品每日的销售量(单位：千克)与销售价格(单位：元/千克)满足关系式，其中，为常数，已知销售价格为5元/千克时，每日可售出该商品11千克． (1) 求的值；(2) 若商品的成品为3元/千克, 试确定销售价格的值,使商场每日销售该商品所获得的利润最大【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【解析】【分析】【详解】::sin :sin :sin 3:2:4a b c A B C == ，不妨设3,2,4a k b k c k ===，,则()()()2223241cos 2324k k k C k k+-==-⨯⨯ ，选A.2．D解析：D 【解析】【详解】由题意可得：5z ==，且：43z i =-，据此有：4343555z i i z -==-. 本题选择D 选项.3．A解析：A 【解析】【分析】根据函数的奇偶性，排除D ；根据函数解析式可知定义域为{}1x x ≠±,所以y 轴右侧虚线部分为x=1，利用特殊值x=0.01和x=1.001代入即可排除错误选项．【详解】由函数解析式()22x x e e f x x x --=+-，易知()22x xe ef x x x ---=+-=() f x - 所以函数()22x xe ef x x x --=+-为奇函数，排除D 选项根据解析式分母不为0可知,定义域为{}1x x ≠±,所以y 轴右侧虚线部分为x=1，当x=0.01时，代入()f x 可得()0f x <，排除C 选项当x=1.001时，代入()f x 可得()0f x >，排除B 选项所以选A 【点睛】本题考查了根据函数解析式判断函数的图象，依据主要是奇偶性、单调性、特殊值等，注意图中坐标的位置及特殊直线，属于中档题．4．D解析：D 【解析】因为全称命题的否定是特称命题，所以命题“对任意x ∈R ，都有x 2≥0”的否定为．存在x 0∈R ，使得x 02＜0．故选D ．5．B解析：B 【解析】试题分析：由题意，这是几何概型问题，班车每30分钟发出一辆，到达发车站的时间总长度为40，等车不超过10分钟的时间长度为20，故所求概率为201402=，选B. 【考点】几何概型【名师点睛】这是全国卷首次考查几何概型,求解几何概型问题的关键是确定“测度”,常见的测度有长度、面积、体积等.6．D解析：D 【解析】【分析】【详解】试题分析：A 项中两直线a b ，还可能相交或异面,错误； B 项中两直线a b ，还可能相交或异面,错误； C 项两平面αβ，还可能是相交平面，错误；故选D.7．D解析：D 【解析】【分析】2a b+≤转化为指数运算即可求解。

2019年最新广西高考数学一模试卷(理)及答案解析

广西高考数学一模试卷（理科）一、选择题（共12小题，每小题5分，满分60分）1．已知集合A={x|﹣1≤x≤1}，B={x|x2﹣2x≤0}，则A∩B=（）A．[﹣1，0] B．[﹣1，2] C．[0，1] D．（﹣∞，1]∪[2，+∞）2．设复数z=1+i，i是虚数单位，则+（）2=（）A．1﹣3i B．1﹣i C．﹣1﹣i D．﹣1+i3．“log22x＞0”是“x＞1”成立的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件4．下列函数是偶函数，且最小正周期为π的是（）A．y=sin（π﹣2x）B．y=sin2xcos2x C．y=cos22x+1 D．y=cos（2x﹣π）5．阅读如图所示的程序框图，运行相应的程序，若判断框内是n≤6，则输出的S为（）A．B．C．D．6．已知双曲线，它的一个顶点到较近焦点的距离为1，焦点到渐近线的距离是，则双曲线C的方程为（）A．x2﹣=1 B．﹣y2=1 C．﹣y2=1 D．x2﹣=17．已知数列{a n}是等比数列，且a3=1，a5a6a7=8，则a9=（）A．2 B．4 C．6 D．88．一个几何体的三视图如图，则该几何体的表面积为（）A．8+6B．10+8 C．12+4 D．14+29．将函数y=sin2x的图象向左平移φ（φ＞0）个单位，得到g（x）的图象，若g（x）的图象关于直线x=对称，则φ的最小值为（）A．B．C．D．10．若x，y满足不等式组，z=x﹣y的最大值为4，则实数a=（）A．4 B．C．5 D．11．已知圆C：x2+y2﹣2x+4y=0关于直线3x﹣ay﹣11=0对称，则圆C中以（，﹣）为中点的弦长为（）A．1 B．2 C．3 D．412．已知曲线f（x）=e x﹣ax在点（0，f（0））处的切线方程为3x+y+b=0，则下列不等式恒成立的是（）A．f（x）≥2﹣4ln2 B．f（x）≤2﹣4ln2 C．f（x）≥4﹣8ln2 D．f（x）≤4﹣8ln2二、填空题（共4小题，每小题5分，满分20分）13．（2x﹣）6展开式中常数项为（用数字作答）．14．向量=（1，﹣2）与=（3，t）的夹角为θ，=（1，﹣3），⊥，则cosθ=．15．设函数f（x）=，若存在实数b，使函数y=f（x）﹣b有且只有2个零点，则实数b的取值范围是．16．已知等差数列{a n}的前n项和为S n，a1=﹣1，（a n+1﹣4）n=2S n，则S n= ．三、解答题（共5小题，满分60分）17．在三角形ABC中，角A，B，C的对边分别是a，b，c．若b=，c=3，B+C=3A．（1）求边a；（2）求sin（B+）的值．18．某地区交通执法部门从某日上午9时开始对经过当地的200名车辆驾驶人员驾驶的车辆进行超速测试并分组，并根据测速的数据制作了频率分布图：（Ⅱ）若在第2，3，4，5组用分层抽样的方法随机抽取12名驾驶人员做回访调查，并在这12名驾驶人员中任意选3人，这3人中超速在[20%，80%）内的人数记为ξ，求ξ的数学期望．19．如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AC⊥AD，AB⊥BC，PA=AB=BC=1，AC=AD，点E在棱PB上，且PE=2EB．（1）求证：PD∥平面EAC．（2）求平面ACE和平面ABCD所成锐二面角的余弦值．20．已知椭圆G：+=1（a＞b＞0）的离心率为，左顶点为A，上顶点为E，O是坐标原点，△OAE面积为．（1）求椭圆G的方程；（2）若过椭圆G的右焦点作垂直于x轴的直线m与G在第一象限内交于点M，平行于AM的直线l与椭圆G相交于B，C两点，判断直线MB，MC是否关于直线m对称，并说明理由．21．设函数f（x）=x3+ax2+bx（x＞0）的图象与x轴相切于M（3，0）．（1）求f（x）的解析式，并求y=+4lnx的单调减区间；（2）是否存在两个不等正数s，t（x＞t），当x∈[s，t]时，函数f（x）=x3+ax2+bx的值域也是[s，t]，若存在，求出所有这样的正数s，t，若不存在，请说明理由．请在第（22）、（23）、（24)三题中任选一题作答，如果多做，则按所做的第一题记分[选修4-1：几何证明选讲]22．如图，A，B，C，D四点在同一圆上，AB∥CD，AD的延长线与BC的延长线交于E点．（1）证明：EC=ED．（2）延长CD到F，延长DC到G，连接EF、EG，使得EF=EG，证明：A，B，G，F四点共圆．[选修4-4：坐标系与参数方程]23．已知曲线C1的参数方程为（θ为参数），曲线C2的极坐标方程为ρ=2cosθ+6sinθ．（1）将曲线C1的参数方程化为普通方程，将曲线C2的极坐标方程化为直角坐标方程；（2）曲线C1，C2是否相交，若相交请求出公共弦的长，若不相交，请说明理由．[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣1|+|x﹣a|（a∈R）．（1）若a=4，求不等式f（x）≥5的解集；（2）若存在x∈R，使f（x）≤4成立，求a的取值范围．参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．已知集合A={x|﹣1≤x≤1}，B={x|x2﹣2x≤0}，则A∩B=（）A．[﹣1，0] B．[﹣1，2] C．[0，1] D．（﹣∞，1]∪[2，+∞）【考点】交集及其运算．【分析】直接由一元二次不等式化简集合B，则A交B的答案可求．【解答】解：∵B={x|x2﹣2x≤0}={x|0≤x≤2}，∴A∩B={x|﹣1≤x≤1}∩{x|0≤x≤2}={x|0≤x≤1}．则A∩B的区间为：[0，1]．故选C．2．设复数z=1+i，i是虚数单位，则+（）2=（）A．1﹣3i B．1﹣i C．﹣1﹣i D．﹣1+i【考点】复数代数形式的混合运算．【分析】利用复数的运算法则和共轭复数的定义即可得出．【解答】解：复数z=1+i，i是虚数单位，则+（）2=+（1﹣i）2=1﹣i﹣2i=1﹣3i，故选：A3．“log22x＞0”是“x＞1”成立的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据充分条件和必要条件的定义进行判断即可．【解答】解：若log22x＞0，则2x＞1，得x＞0，则“log22x＞0”是“x＞1”成立的必要不充分条件，故选：B．4．下列函数是偶函数，且最小正周期为π的是（）A．y=sin（π﹣2x）B．y=sin2xcos2x C．y=cos22x+1 D．y=cos（2x﹣π）【考点】三角函数的周期性及其求法．【分析】根据正弦型函数及余弦型函数的性质，我们逐一分析四个答案中的四个函数的周期性及奇偶性，然后和题目中的条件进行比照，即可得到答案．【解答】D解：A中，函数y=sin（π﹣2x）=sin2x为奇函数，不满足条件；B中，函数y=sin2xcos2x=sin4x周期为，不满足条件；C中，函数y=cos22x+1=cos4x+周期为，不满足条件；D中，函数y=cos（2x﹣π）=﹣cos2x是最小正周期为π的偶函数，满足条件；故选：D．5．阅读如图所示的程序框图，运行相应的程序，若判断框内是n≤6，则输出的S为（）A．B．C．D．【考点】程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的S，n的值，当n=8时，此时应该不满足条件n≤6，退出循环，输出S的值为．【解答】解：模拟执行程序框图，可得：S=0，n=2满足条件n≤6，S=，n=4满足条件n≤6，S=，n=6满足条件n≤6，S=+=，n=8由题意，此时应该不满足条件n≤6，退出循环，输出S的值为，故选：C．6．已知双曲线，它的一个顶点到较近焦点的距离为1，焦点到渐近线的距离是，则双曲线C的方程为（）A．x2﹣=1 B．﹣y2=1 C．﹣y2=1 D．x2﹣=1【考点】双曲线的简单性质．【分析】由题意可得c﹣a=1，求出渐近线方程和焦点的坐标，运用点到直线的距离公式，可得b=，由a，b，c的关系，可得a，进而得到所求双曲线的方程．【解答】解：双曲线的一个顶点（a，0）到较近焦点（c，0）的距离为1，可得c﹣a=1，由双曲线的渐近线方程为y=x，则焦点（c，0）到渐近线的距离为d==b=，又c2﹣a2=b2=3，解得a=1，c=2，即有双曲线的方程为x2﹣=1．故选：A．7．已知数列{a n}是等比数列，且a3=1，a5a6a7=8，则a9=（）A．2 B．4 C．6 D．8【考点】等比数列的通项公式．【分析】设等比数列{a n}的公比为q，由a3=1，a5a6a7=8，可得=1，=8，解得q3，即可得出．【解答】解：设等比数列{a n}的公比为q，∵a3=1，a5a6a7=8，∴=1，=8，解得q3=2．则a9==4．8．一个几何体的三视图如图，则该几何体的表面积为（）A．8+6B．10+8 C．12+4 D．14+2【考点】由三视图求面积、体积．【分析】由三视图知该几何体是一个直四棱柱，由三视图求出几何元素的长度，由面积公式求出各个面的面积，加起来即可求出几何体的表面积．【解答】解：根据三视图可知几何体是一个直四棱柱，由俯视图知底面是等腰梯形：上底、下底分别是1、3，梯形的高是1，则腰长是，且直四棱柱的高是2，∴几何体的表面积S==12+4，故选：C．9．将函数y=sin2x的图象向左平移φ（φ＞0）个单位，得到g（x）的图象，若g（x）的图象关于直线x=对称，则φ的最小值为（）A． B．C．D．【考点】函数y=Asin（ωx+φ）的图象变换．【分析】由条件利用函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，求得φ的最小值．【解答】解：将函数y=sin2x的图象向左平移φ（φ＞0）个单位，得到g（x）=sin2（x+φ）=sin（2x+2φ）的图象，若g（x）的图象关于直线x=对称，则+2φ=kπ+，k∈Z，则φ的最小值为，故选：A．10．若x，y满足不等式组，z=x﹣y的最大值为4，则实数a=（）A．4 B．C．5 D．【考点】简单线性规划．【分析】作出可行域，变形目标函数，平移直线可得z的最值，可得a的方程，解方程可得．【解答】解：作出不等式组所对应可行域（如图△ABC），变形目标函数z=x﹣y可得y=x﹣z，平移直线y=x可知：当直线经过点A（a，3﹣a）时，直线截距最小值，z取最大值，代值可得a﹣（3﹣a）=4，解得a=，故选：B．11．已知圆C：x2+y2﹣2x+4y=0关于直线3x﹣ay﹣11=0对称，则圆C中以（，﹣）为中点的弦长为（）A．1 B．2 C．3 D．4【考点】直线与圆的位置关系．【分析】由已知直线3x﹣ay﹣11=0过圆心C（1，﹣2），从而得到a=4，点（1，﹣1）到圆心C（1，﹣2）的距离d=1，圆C：x2+y2﹣2x+4y=0的半径r=，由此能求出圆C中以（，﹣）为中点的弦长．【解答】解：∵圆C：x2+y2﹣2x+4y=0关于直线3x﹣ay﹣11=0对称，∴直线3x﹣ay﹣11=0过圆心C（1，﹣2），∴3+2a﹣11=0，解得a=4，∴（，﹣）=（1，﹣1），点（1，﹣1）到圆心C（1，﹣2）的距离d==1，圆C：x2+y2﹣2x+4y=0的半径r==，∴圆C中以（，﹣）为中点的弦长为：2=2=4．故选：D．12．已知曲线f（x）=e x﹣ax在点（0，f（0））处的切线方程为3x+y+b=0，则下列不等式恒成立的是（）A．f（x）≥2﹣4ln2 B．f（x）≤2﹣4ln2 C．f（x）≥4﹣8ln2 D．f（x）≤4﹣8ln2 【考点】利用导数研究曲线上某点切线方程．【分析】求出函数的导数，可得切线的斜率，由切线的方程可得斜率，解方程可得a，求出单调区间、极值和最值，即可得到结论．【解答】解：f（x）=e x﹣ax的导数为f′（x）=e x﹣a，可得在点（0，f（0））处的切线斜率为1﹣a，由切线方程为3x+y+b=0，可得1﹣a=﹣3，即有a=4，可得f′（x）=e x﹣4，当x＞ln4时，f′（x）＞0，f（x）递增；当x＜ln4时，f′（x）＜0，f（x）递减．可得f（x）在x=ln4处取得极小值，也为最小值4﹣8ln2．即为f（x）≥4﹣8ln2．故选：C．二、填空题（共4小题，每小题5分，满分20分）13．（2x﹣）6展开式中常数项为60 （用数字作答）．【考点】二项式定理．【分析】用二项展开式的通项公式得展开式的第r+1项，令x的指数为0得展开式的常数项．【解答】解：（2x﹣）6展开式的通项为=令得r=4故展开式中的常数项．故答案为6014．向量=（1，﹣2）与=（3，t）的夹角为θ，=（1，﹣3），⊥，则cosθ=．【考点】平面向量数量积的运算．【分析】根据向量的数量积的运算和向量的夹角公式计算即可．【解答】解：∵=（1，﹣2）与=（3，t）的夹角为θ，=（1，﹣3），⊥，∴3×1﹣3t=0，∴t=1，∴=（3，1），∴||=，||=，•=1×3﹣2×1=1，∴cosθ==故答案为：．15．设函数f（x）=，若存在实数b，使函数y=f（x）﹣b有且只有2个零点，则实数b的取值范围是（0，+∞）．【考点】函数零点的判定定理．【分析】由题意可得函数f（x）=的图象和直线y=b有2个交点，分类讨论，数形结合求得a的取值范围．【解答】解：由题意可得函数y=f（x）=的图象和直线y=b有且只有2个交点，当a=0 时，f（x）=，如图（1）所示，函数y=f（x）的图象和直线y=b之多有一个交点，不满足条件．当a＞0时，f（x）=的图象如图（2）所示，此时，应有b＞0．当a＜0时，f（x）=的图象如图（3）所示，此时，函数y=f（x）的图象和直线y=b之多有一个交点，不满足条件．综上可得，b＞0，故答案为：（0，+∞）．16．已知等差数列{a n}的前n项和为S n，a1=﹣1，（a n+1﹣4）n=2S n，则S n= ．【考点】等差数列的前n项和．【分析】设等差数列{a n}的公差为d，a1=﹣1，则a n+1=﹣1+nd，S n=﹣n+d，代入（a n+1﹣4）n=2S n，化简整理即可得出．【解答】解：设等差数列{a n}的公差为d，a1=﹣1，则a n+1=﹣1+nd，S n=﹣n+d，代入（a n+1﹣4）n=2S n，可得：（﹣5+nd）n=﹣2n+n（n﹣1）d，化为：d=3．则S n=﹣n+=．故答案为：．三、解答题（共5小题，满分60分）17．在三角形ABC中，角A，B，C的对边分别是a，b，c．若b=，c=3，B+C=3A．（1）求边a；（2）求sin（B+）的值．【考点】正弦定理的应用；两角和与差的正弦函数．【分析】（1）由条件利用余弦定理求得a的值．（2）由条件利用正弦定理求得sinB的值，可得cosB的值，再利用两角和差的正弦公式，求得sin（B+）的值．【解答】解：（1）三角形ABC中，∵b=，c=3，B+C=3A，∴A=，利用余弦定理可得a2=b2+c2﹣2bc•cosA=5，∴a=．（2）由正弦定理=，可得=，∴sinB=，再结合b＜c，可得B为锐角，∴cosB==，∴sin（B+）=sinBcos+cosBsin=+•=．18．某地区交通执法部门从某日上午9时开始对经过当地的200名车辆驾驶人员驾驶的车辆进行超速测试并分组，并根据测速的数据制作了频率分布图：（Ⅱ）若在第2，3，4，5组用分层抽样的方法随机抽取12名驾驶人员做回访调查，并在这12名驾驶人员中任意选3人，这3人中超速在[20%，80%）内的人数记为ξ，求ξ的数学期望．【考点】离散型随机变量的期望与方差；分层抽样方法．【分析】（Ⅰ）由频率=，能求出z，y，x的值．（Ⅱ）若在第2，3，4，5组用分层抽样的方法随机抽取12名驾驶人员，则第2，3，4，5组抽取的人数分别是4，3，2，1，设任意选取的3人超速在（20%，80%）的人数是ξ，则ξ=2或ξ=3，由此能求出ξ的数学期望．【解答】解：（Ⅰ）由题意得x=200×0.01=2，y=6÷200=0.03，z=0.88÷20=0.044．（Ⅱ）若在第2，3，4，5组用分层抽样的方法随机抽取12名驾驶人员，则第2，3，4，5组抽取的人数分别是4，3，2，1，设任意选取的3人超速在（20%，80%）的人数是ξ，则ξ=2或ξ=3，P（ξ=2）==，P（ξ=3）==，∴Eξ==．19．如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AC⊥AD，AB⊥BC，PA=AB=BC=1，AC=AD，点E在棱PB上，且PE=2EB．（1）求证：PD∥平面EAC．（2）求平面ACE和平面ABCD所成锐二面角的余弦值．【考点】二面角的平面角及求法；直线与平面平行的判定．【分析】（1）根据线面平行的判定定理即可证明PD∥平面EAC．（2）建立坐标系，求出平面的法向量，利用向量法即可求平面ACE和平面ABCD所成锐二面角的余弦值．【解答】证明：（1）∵AB⊥BC，AB=BC=1，∴AC=，∠BAC=，∵AC=AD，AC⊥AD，∴CD=2，∠ACD=，∴∠BAC=∠ACD，则AB∥CD，连接BD，交AC于M，连EM，则，又PE=2EB，在△BPD中，，∴PD∥EM，∵PD⊄平面EAC，EM⊂平面EAC，∴PD∥平面EAC（2）建立如图所示的空间坐标系如图：则A（0，0，0），P（0，0，1），B（0，1，0），C（1，1，0），E（0，，），设=（x，y，z）是平面AEC的一个法向量，则=（1，1，0），（0，，），则•=x+y=0，•=y+z=0，得，令y=1，则x=﹣1，z=﹣2，则=（﹣1，1，﹣2），同理平面ABCD的法向量为==（0，0，1），则cos＜，＞==，即平面ACE和平面ABCD所成锐二面角的余弦值是．20．已知椭圆G：+=1（a＞b＞0）的离心率为，左顶点为A，上顶点为E，O是坐标原点，△OAE面积为．（1）求椭圆G的方程；（2）若过椭圆G的右焦点作垂直于x轴的直线m与G在第一象限内交于点M，平行于AM的直线l与椭圆G相交于B，C两点，判断直线MB，MC是否关于直线m对称，并说明理由．【考点】椭圆的简单性质．【分析】（1）运用椭圆的离心率公式和实际行动面积公式，及a，b，c的关系，解得a，b，进而得到椭圆方程；（2）求得椭圆的右焦点坐标，M，A的坐标，求得斜率．可设BC的方程为y=x+t，代入椭圆方程3x2+4y2=12，可得x2+tx+t2﹣3=0，设B（x1，y1），C（x2，y2），运用韦达定理和直线的斜率公式，可得k MB+k MC=0，进而得到直线MB和直线MC关于直线m对称．【解答】解：（1）由题意可得e==，由A（﹣a，0），E（0，b），可得△OAE面积为，即有ab=，又a2﹣b2=c2，解得a=2，b=，c=1，即有椭圆的方程为+=1；（2）椭圆的右焦点为（1，0），可得M（1，），A（﹣2，0），k AM==，设BC的方程为y=x+t，代入椭圆方程3x2+4y2=12，可得x2+tx+t2﹣3=0，设B（x1，y1），C（x2，y2），即有x1+x2=﹣t，x1x2=t2﹣3，由k MB+k MC=+=+===0．即有直线MB和直线MC关于直线m对称．21．设函数f（x）=x3+ax2+bx（x＞0）的图象与x轴相切于M（3，0）．（1）求f（x）的解析式，并求y=+4lnx的单调减区间；（2）是否存在两个不等正数s，t（x＞t），当x∈[s，t]时，函数f（x）=x3+ax2+bx的值域也是[s，t]，若存在，求出所有这样的正数s，t，若不存在，请说明理由．【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．【分析】（1）由已知得f′（x）=3x2+2ax+b．依题意f（3）=0，f′（3）=0，解方程即可求出f（x）=x3﹣6x2+9x．（2）由函数的定义域是正数知，s＞0，故极值点x=3不在区间[s，t]上，由此利用分类讨论思想能求出不存在正数s，t满足要求．【解答】解：（1）∵f（x）=x3+ax2+bx，∴f′（x）=3x2+2ax+b．依题意则有f（3）=0，f′（3）=0，即27+9a+3b=0，①27+6a+b=0，②解得a=﹣6，b=9，∴f（x）=x3﹣6x2+9x．则y=+4lnx=x2﹣6x+9+4lnx，x＞0，y′=2x﹣6+==，由y′＜0得1＜x＜2，即y=+4lnx的单调减区间为（1，2）．（2）f′（x）=3x2﹣12x+9=3（x﹣1）（x﹣3），由f′（x）=0，得x=1或x=3．列表讨论，得：由函数的定义域是正数知，s＞0，故极值点x=3不在区间[s，t]上，①若极值点1∈[s，t]，此时0＜s≤1≤t＜3，在此区间上f（x）的最大值是4，不可能等于t，故在区间[s，t]上没有极值点；②若f（x）=x3﹣6x2+9x在[s，t]上单调增，即0＜s＜t≤1或3＜s＜t，则，即，解得不合要求．（3）若f（x）=x3﹣6x2+9x在[s，t]上单调减，即1≤s＜t＜3，则，两式相减并除s﹣t，得：（s+t）2﹣6（s+t）﹣st+10=0，①两式相除并开方，得[s（s﹣3）]2=[t（t﹣3）]2，即s（3﹣s）=t（3﹣t），整理，并除以s﹣t，得：s+t=3，②则①、②得，即s，t是方程x2﹣3x+1=0的两根，即s=，t=不合要求；综上，不存在正数s，t满足要求．…请在第（22）、（23）、（24)三题中任选一题作答，如果多做，则按所做的第一题记分[选修4-1：几何证明选讲]22．如图，A，B，C，D四点在同一圆上，AB∥CD，AD的延长线与BC的延长线交于E点．（1）证明：EC=ED．（2）延长CD到F，延长DC到G，连接EF、EG，使得EF=EG，证明：A，B，G，F四点共圆．【考点】与圆有关的比例线段．【分析】（1）根据四点共圆，得到四边形的一个外角等于不相邻的一个内角，根据两直线平行，同位角相等，等量代换得到两个角相等，从而两条边相等，得到结论；（2）根据第一问做出的边和角之间的关系，得到两个三角形全等，根据全等三角形的对应角相等，根据平行的性质定理，等量代换，得到四边形的一对对角相等，得到四点共圆．【解答】（1）证明：因为A，B，C，D四点在同一圆上，所以∠EDC=∠EBA因为CD∥AB，所以∠ECD=∠EBA，所以∠EDC=∠ECD，所以EC=ED．（2）解：由（1）知，AE=BE，因为EF=EG，故∠EFD=∠EGC从而∠FED=∠GEC连接AF，BG，△EFA≌△EGB，故∠FAE=∠GBE又CD∥AB，∠FAB=∠GBA，所以∠AFG+∠GBA=180°故A，B．G，F四点共圆．[选修4-4：坐标系与参数方程]23．已知曲线C1的参数方程为（θ为参数），曲线C2的极坐标方程为ρ=2cosθ+6sinθ．（1）将曲线C1的参数方程化为普通方程，将曲线C2的极坐标方程化为直角坐标方程；（2）曲线C1，C2是否相交，若相交请求出公共弦的长，若不相交，请说明理由．【考点】圆的参数方程；简单曲线的极坐标方程．【分析】（1）根据同角三角函数关系消去参数θ，即可求出曲线C1的普通方程，曲线C2的极坐标方程两边同乘ρ，根据极坐标公式进行化简就可求出直角坐标方程；（2）先求出两个圆心之间的距离与两半径和进行比较，设相交弦长为d，因为两圆半径相等，所以公共弦平分线段C1C2，建立等量关系，解之即可．【解答】解：（1）由得（x+2）2+y2=10∴曲线C1的普通方程为得（x+2）2+y2=10∵ρ=2cosθ+6sinθ∴ρ2=2ρcosθ+6ρsinθ∵ρ2=x2+y2，x=ρcosθ，y=ρsinθ∴x2+y2=2x+6y，即（x﹣1）2+（y﹣3）2=10∴曲线C2的直角坐标方程为（x﹣1）2+（y﹣3）2=10（2）∵圆C1的圆心为（﹣2，0），圆C2的圆心为（1，3）∴∴两圆相交设相交弦长为d，因为两圆半径相等，所以公共弦平分线段C1C2∴∴d=∴公共弦长为[选修4-5：不等式选讲]24．已知函数f（x）=|x﹣1|+|x﹣a|（a∈R）．（1）若a=4，求不等式f（x）≥5的解集；（2）若存在x∈R，使f（x）≤4成立，求a的取值范围．【考点】绝对值不等式的解法；绝对值三角不等式．【分析】（1）不等式即|x﹣1|+|x﹣4|≥5，通过去绝对值符号，列出不等式组，分别求出每个不等式组的解集，再取并集即得所求．（2）利用f（x）=|x﹣1|+|x﹣a|≥|a﹣1|，由题意可得|a﹣1|≤4，由此解得a的范围．【解答】解：（1）解：（Ⅰ）当a=4时，不等式f（x）≥5，即|x﹣1|+|x﹣4|≥5，等价于，或，或．解得：x≤0或x≥5．…故不等式f（x）≥6的解集为{x|x≤0，或x≥5}；（2）∵f（x）=|x﹣1|+|x﹣a|≥|（x﹣1）﹣（x﹣a）|=|a﹣1|．（当x=1时等号成立）所以：f（x）min=|a﹣1|．…由题意得：|a﹣1|≤4，解得：﹣3≤a≤5．…。

2019年高考数学一模试卷含答案

2019年高考数学一模试卷含答案一、选择题1．如图所示的圆锥的俯视图为（）A ．B ．C ．D ．2．123{3x x >>是12126{9x x x x +>>成立的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．即不充分也不必要条件3．已知集合{}{}x -1<x 1Q=x 0x 2P =<<<，，那么P Q=⋃ A ．（-1,2）B ．（0，1）C ．（-1,0）D ．（1,2）4．在△ABC 中，a ＝5，b ＝3，则sin A ：sin B 的值是（）A ．53 B ．35 C ．37 D ．575．若,,a b R i ∈为虚数单位，且()a i i b i +=+，则A ．1,1a b ==B ．1,1a b =-=C ．1,1a b ==-D ．1,1a b =-=-6．甲、乙、丙，丁四位同学一起去问老师询问成语竞赛的成绩。

老师说：你们四人中有两位优秀，两位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩，根据以上信息，则（） A ．乙、丁可以知道自己的成绩 B ．乙可以知道四人的成绩 C ．乙、丁可以知道对方的成绩D ．丁可以知道四人的成绩7．在△ABC 中，P 是BC 边中点，角、、A B C 的对边分别是，若0cAC aPA bPB ++=，则△ABC 的形状为（）A ．直角三角形B ．钝角三角形C ．等边三角形D ．等腰三角形但不是等边三角形. 8．当1a >时，在同一坐标系中，函数xy a-=与log a y x =-的图像是（）A ．B ．C ．D ．9．函数f (x )＝2sin(ωx ＋φ)(ω>0，－2π<φ<2π)的部分图象如图所示，则ω、φ的值分别是( )A ．2，－3πB ．2，－6π C ．4，－6πD ．4，3π 10．已知复数，则复数在复平面内对应的点位于（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限11．已知ABC 为等边三角形，2AB =，设P ，Q 满足AP AB λ=，()()1AQ AC λλ=-∈R ，若32BQ CP ⋅=-，则λ=（）A ．12B ．122± C ．1102± D ．322± 12．某公司的班车在7:30，8:00，8:30发车，小明在7:50至8:30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是A ．13B ．12C ．23D ．34二、填空题13．事件,,A B C 为独立事件，若()()()111,,688P A B P B C P A B C ⋅=⋅=⋅⋅=，则()P B =_____．14．已知函数21,1()()1a x x f x x a x ⎧-+≤=⎨->⎩，函数()2()g x f x =-，若函数()()y f x g x =-恰有4个不同的零点，则实数a 的取值范围为______．15．已知椭圆22195x y +=的左焦点为F ，点P 在椭圆上且在x 轴的上方，若线段PF 的中点在以原点O 为圆心，OF 为半径的圆上，则直线PF 的斜率是_______. 16．一个算法的伪代码如图所示，执行此算法，最后输出的S 的值为________．17．若,满足约束条件则的最大值．18．在平面上，若两个正三角形的边长的比为1：2，则它们的面积比为1：4，类似地，在空间内，若两个正四面体的棱长的比为1：2，则它们的体积比为 ▲ 19．设函数21()ln 2f x x ax bx =--，若1x =是()f x 的极大值点，则a 取值范围为_______________.20．已知集合P 中含有0,2,5三个元素,集合Q 中含有1,2,6三个元素,定义集合P+Q 中的元素为a+b ,其中a ∈P ,b ∈Q ,则集合P+Q 中元素的个数是_____.三、解答题21．已知向量()2sin ,1a x =+，()2,2b =-，()sin 3,1c x =-，()1,d k =(),x R k R ∈∈（1）若,22x ππ⎡⎤∈-⎢⎥⎣⎦，且()//a b c +，求x 的值.（2）若函数()f x a b =⋅，求()f x 的最小值.（3）是否存在实数k ，使得()()a dbc +⊥+？若存在，求出k 的取值范围；若不存在，请说明理由.22．我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行调查，通过抽样，获得某年100为居民每人的月均用水量（单位：吨），将数据按照分成9组，制成了如图所示的频率分布直方图.（1）求直方图的的值；（2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由；（3）估计居民月用水量的中位数.23．为评估设备生产某种零件的性能，从设备生产该零件的流水线上随机抽取100个零件为样本，测量其直径后，整理得到下表：经计算，样本的平均值，标准差，以频率值作为概率的估计值.（I ）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为，并根据以下不等式进行判定（表示相应事件的概率）： ①； ②； ③.判定规则为：若同时满足上述三个式子，则设备等级为甲；若仅满足其中两个，则等级为乙，若仅满足其中一个，则等级为丙；若全部都不满足，则等级为了.试判断设备的性能等级.（Ⅱ）将直径尺寸在之外的零件认定为是“次品”.①从设备的生产流水线上随机抽取2个零件，求其中次品个数的数学期望；②从样本中随意抽取2个零件，求其中次品个数的数学期望.24．在平面直角坐标系xOy 中,已知直线l 的参数方程为12312x t y t ⎧=⎪⎪⎨⎪=-⎪⎩（t 为参数）.在以坐标原点O 为极点,x 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线C的极坐标方程是4πρθ⎛⎫=+⎪⎝⎭. （1）求直线l 的普通方程与曲线C 的直角坐标方程；（2）设点()0,1P -.若直l 与曲线C 相交于两点,A B ,求PA PB +的值.25．已知A 为圆22:1C x y +=上一点，过点A 作y 轴的垂线交y 轴于点B ，点P 满足2.BP BA =（1）求动点P 的轨迹方程；（2）设Q 为直线:3l x =上一点，O 为坐标原点，且OP OQ ⊥，求POQ ∆面积的最小值.26．在直角坐标系xoy 中以O 为极点，x 轴正半轴为极轴建立坐标系.圆1C ，直线2C 的极坐标方程分别为4sin ,cos 4πρθρθ⎛⎫=-= ⎪⎝⎭. （I ）12C C 求与交点的极坐标；（II ）112.P C Q C C PQ 设为的圆心，为与交点连线的中点已知直线的参数方程为()33{,,.12x t a t R a b b y t =+∈=+为参数求的值【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】【分析】找到从上往下看所得到的图形即可．【详解】由圆锥的放置位置，知其俯视图为三角形．故选C. 【点睛】本题考查了三视图的知识，俯视图是从物体的上面看得到的视图，本题容易误选B ，属于基础题.2．A解析：A【解析】试题分析：因为123{3x x >>12126{9x x x x +>⇒>，所以充分性成立；1213{1x x ==满足12126{9x x x x +>>，但不满足123{3x x >>，必要性不成立，所以选A.考点：充要关系3．A解析：A 【解析】利用数轴，取,P Q 所有元素，得P Q =(1,2)-．【名师点睛】对于集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图处理．4．A解析：A 【解析】由正弦定理可得：sin 5sin 3A aB b == . 本题选择A 选项.5．C解析：C 【解析】【分析】利用复数乘法的运算法则化简原式，利用复数相等的性质可得结果. 【详解】因为()a i i b i +=+，即1ai b i -+=+，因为,,a b R i ∈为虚数单位，所以1,1a b ==-，故选C. 【点睛】本题主要考查复数的乘法运算以及复数相等的性质，属于基础题.6．A解析：A 【解析】【分析】根据甲的所说的话，可知乙、丙的成绩中一位优秀、一位良好，再结合简单的合情推理逐一分析可得出结果. 【详解】因为甲、乙、丙、丁四位同学中有两位优秀、两位良好，又甲看了乙、丙的成绩且还不知道自己的成立，即可推出乙、丙的成绩中一位优秀、一位良好，又乙看了丙的成绩，则乙由丙的成绩可以推出自己的成绩，又甲、丁的成绩中一位优秀、一位良好，则丁由甲的成绩可以推出自己的成绩. 因此，乙、丁知道自己的成绩，故选：A. 【点睛】本题考查简单的合情推理，解题时要根据已知的情况逐一分析，必要时可采用分类讨论的思想进行推理，考查逻辑推理能力，属于中等题.7．C解析：C 【解析】【分析】【详解】解答：由已知条件得；根据共面向量基本定理得：∴△ABC 为等边三角形。

2019年桂平市实验中学高考数学选择题专项训练(一模)

2019年桂平市实验中学高考数学选择题专项训练（一模）抽选各地名校试卷，经典试题，有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。

第 1 题：来源：黑龙江省哈尔滨市2016_2017学年高一数学6月月考试题试卷及答案设，若，则的最小值为（）8【答案】A第 2 题：来源：宁夏银川市孔德2016_2017学年高一数学下学期第一次（3月）月考试题某鱼贩一次贩运草鱼、青鱼、鲢鱼、鲤鱼及鲫鱼分别有80条、20条、40条、40条、20条，现从中抽取一个容量为20的样本进行质量检测，若采用分层抽样的方法抽取样本，则抽取的青鱼与鲤鱼共有( )A．6条 B．8条 C．10条 D．12条【答案】A【解析】设抽取的青鱼与鲤鱼共有x条，根据分层抽样的特点有＝，所以x＝6.考点：分层抽样．第 3 题：来源：黑龙江省哈尔滨市2016_2017学年高二数学6月月考试题试卷及答案理.离散型随机变量X的分布列为，则与依次为( )和和和和【答案】D第 4 题：来源： 2017-2018学年吉林省吉林市吉化高一（上）期末数学试卷（含答案解析）函数的定义域为（）A．（﹣∞，1） B．（0，1] C．（0，1） D．（0，+∞）【答案】C解：函数的定义域为：{x|}，解得{x|0＜x＜1}，第 5 题：来源：高中数学第二章推理与证明B章末测试试卷及答案新人教A版选修1-2用反证法证明命题“设a，b为实数，则方程x3＋ax＋b＝0至少有一个实根”时，要做的假设是( ) A．方程x3＋ax＋b＝0没有实根B．方程x3＋ax＋b＝0至多有一个实根C．方程x3＋ax＋b＝0至多有两个实根D．方程x3＋ax＋b＝0恰好有两个实根【答案】A第 6 题：来源：河南省六市2017届高三第二次联考数学试题（理）含答案.已知圆.设条件：，条件：圆上至多有2个点到直线的距离为1，则是的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C第 7 题：来源：重点班2017届高三数学一轮复习阶段检测试题三理试卷及答案如果a<b<0,那么下列不等式成立的是( )(A)-<- (B)ab<b2(C)-ab<-a2 (D)|a|<|b|【答案】A解析:因为a<b<0,所以-a>-b>0,ab>0,所以->-,即->-.选项A成立;由a<b<0得ab>b2,选项B不成立;由a<b<0,-a>0得-a2<-ab,选项C不成立;由a<b<0得|a|>|b|.选项D不成立.第 8 题：来源：安徽省巢湖市2017_2018学年高一数学上学期期中试题试卷及答案函数y=2|x|的图象是（）A. B. C. D.【答案】B第 9 题：来源：黑龙江省鹤岗市第一中学2018_2019学年高一数学下学期期末考试试题理已知都是正数,且，则的最小值等于A．B． C．D．【答案】C第 10 题：来源：甘肃省武威市2016_2017学年高一数学下学期期末考试试题试卷及答案已知角的终边经过点，且，则等于（）A．B． C．-4 D．4【答案】C第 11 题：来源：广东省中山市第一中学2017_2018学年高一数学上学期第一次段考试题（含解析）已知函数，则A. 是偶函数，且在上是增函数B. 是奇函数，且在上是增函数C. 是偶函数，且在上是减函数D. 是奇函数，且在上是减函数【答案】B【解析】试题分析：，所以该函数是奇函数，并且是增函数，是减函数，根据增函数−减函数=增函数，可知该函数是增函数，故选B.第 12 题：来源： 2017_2018学年高中数学第三章直线与方程章末综合测评2试卷及答案新人教A 版必修等腰直角三角形ABC的直角顶点为C(3,3)，若点A(0,4)，则点B的坐标可能是( )A．(2,0)或(4,6) B．(2,0)或(6,4)C．(4,6) D．(0,2)【答案】 A第 13 题：来源：黑龙江省大庆市2017_2018学年高二数学上学期开学考试试题试卷及答案下列说法正确的是（）A.若,则B.若为实数,且,则C.已知是空间两条不同的直线,是空间三个不同的平面，若,,则D.已知直线，若，则【答案】B第 14 题：来源： 2019高考数学一轮复习第2章函数的概念与基本初等函数第10讲变化率与导数导数的运算分层演练文某单位为鼓励职工节约用水，作出了以下规定：每位职工每月用水不超过10 m3的，按每立方米m元收费；用水超过10 m3的，超过部分加倍收费．某职工某月缴水费16m元，则该职工这个月实际用水为( )A．13 m3 B．14 m3 C．18 m3 D．26 m3 【答案】A.第 15 题：来源：河南省信阳市2017_2018学年高二数学上学期第一次月考试题理试卷及答案《九章算术》勾股章有一“引葭赴岸”问题：“今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐.问水深、葭长各几何.”其意思是：有一水池一丈见方，池中生有一颗类似芦苇的植物，露出水面一尺，若把它引向岸边，正好与岸边齐（如图所示），问水有多深，该植物有多长？其中一丈为十尺.若从该葭上随机取一点，则该点取自水下的概率为（）A. B.C. D.【答案】B第 16 题：来源：安徽省滁州市定远县育才学校2018_2019学年高二数学下学期期末考试试题（普通班）理已知集合，，全集，则等于（）A. B. C.D.【答案】D第 17 题：来源：内蒙古包头市第四中学2017_2018学年高一数学上学期期中试题已知三点A（-3，-1），B（0,2），C（m，4）在同一直线上，则实数m的值为（）A.1B.2C.3D.4【答案】B第 18 题：来源：宁夏2017_2018学年高二数学12月月考试题理“a≠1或b≠2”是“a＋b≠3”的（）A、充分不必要条B、必要不充分条件C、充要条件D、既不充分也不必要【答案】B第 19 题：来源：贵州省思南中学2018_2019学年2018_2019学年高一数学下学期期中试题设Sn为数列{an}的前n项和，an＝1＋2＋22＋…＋2n-1，则Sn的值为( )A． 2n－1 B． 2n-1－1 C． 2n－n－2 D． 2n+1－n－2【答案】D【解析】∵an＝1＋2＋22＋…＋2n－1＝2n－1，∴Sn＝2n＋1－n－2.第 20 题：来源：青海省西宁市2017_2018学年高一数学9月月考试题试卷及答案若，则 ( )（A）（B）（C）（D）【答案】D第 21 题：来源：云南省玉溪市2017_2018学年高二数学上学期期中试题理试卷及答案设集合，，那么“”是“”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【答案】B第 22 题：来源：福建省永春县2016_2017学年高二数学3月月考试题理曲线与直线围成的图形的面积为（）A．B．C．D．【答案】D第 23 题：来源：辽宁省沈阳市2018届高三数学11月阶段测试试题理试卷及答案在中,内角的对边分别为是外接圆的圆心,若,且,则的值是( ) SX050501A. B. C. D.【答案】 C第 24 题：来源： 2016-2017学年重庆市璧山中学高一数学上学期期中试题试卷及答案已知下列各组对象:①中国古代四大发明；②所有非常小的负数；③某班中个子高的男生；④底边长为3的等腰三角形的全体。

2019年桂平市历山中学高考数学选择题专项训练(一模)

2019年桂平市历山中学高考数学选择题专项训练（一模）抽选各地名校试卷，经典试题，有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。

第 1 题：来源：安徽省蚌埠市第二中学2018_2019学年高一数学下学期期中试题（含解析）函数在区间上的最小值是（）A. B. C. -1 D.【答案】D【详解】,,故故当时，函数取得最小值即当时，故选D【点睛】本题考查了同角三角函数关系，将其转化为关于的二次函数问题，注意的取值范围，较为基础第 2 题：来源：安徽省临泉县2017_2018学年高二数学12月阶段考（第三次月考）试题理试卷及答案实数满足且，由按一定顺序构成的数列（）A. 可能是等差数列，也可能是等比数列B. 可能是等差数列，但不可能是等比数列C. 不可能是等差数列，但可能是等比数列D. 不可能是等差数列，也不可能是等比数列【答案】B第 3 题：来源：湖北省孝感市七校教学联盟2017届高三数学上学期期末考试试题文在复平面内，复数对应的点P位于（）A.第一象限B. 第二象限C. 第三象限D. 第四象限【答案】C第 4 题：来源： 2019高中数学第三章数系的扩充与复数的引入测评（含解析）新人教A版选修1_2“m=1”是“复数z=(1+mi)(1+i)(m∈R,i为虚数单位)为纯虚数”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】C解析:z=(1+mi)(1+i)=1+i+mi-m=(1-m)+(1+m)i,若m=1,则z=2i为纯虚数;若z为纯虚数,则m=1.第 5 题：来源：山东省济南第一中学2017届高三数学10月阶段测试试题文（含解析）已知函数，则A. 在（0，2）单调递增B. 在（0，2）单调递减C. 的图像关于直线x=1对称D. 的图像关于点（1，0）对称【答案】C【解析】由题意知，，所以的图象关于直线对称，故C正确，D错误；又（），由复合函数的单调性可知在上单调递增，在上单调递减，所以A，B错误，故选C．【名师点睛】如果函数，，满足，恒有，那么函数的图象有对称轴；如果函数，，满足，恒有，那么函数的图象有对称中心．第 6 题：来源：甘肃省兰州市2017_2018学年高一数学上学期期中试题试卷及答案下列函数在上是增函数的是（）A．B．C．D．【答案】B第 7 题：来源： 2017年高中数学第一章坐标系单元质量评估（含解析）新人教A版选修4_4下列极坐标方程中,对应的曲线为如图的是( )A.ρ=6+5cosθB.ρ=6+5sinθC.ρ=6-5cosθD.ρ=6-5sinθ【答案】D.当θ=-时,ρ达到最大.第8 题：来源：广东省深圳市普通高中2017_2018学年高二数学下学期4月月考试题3201805241395在正三棱柱中，若AB=2，则点A到平面的距离为（）A． B． C．D．【答案】B第 9 题：来源：黑龙江省哈尔滨市2016_2017学年高二数学6月月考试题试卷及答案理二项式的展开式中所有二项式系数和为64，若展开式中的常数项为，则的值为( )【答案】D第 10 题：来源： 2019年普通高等学校招生全国统一考试理科数学（全国卷Ⅰ）（含答案）我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“——”，如图就是一重卦．在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是A． B． C．D．【答案】A第 11 题：来源：安徽省定远重点中学2017_2018学年高一数学上学期第三次月考试题函数f(x)＝ln(x2＋1)的图象大致是( )A．选项A B．选项BC．选项C D．选项D【答案】A【解析】本题考查的是对数函数的图象．由函数解析式可知f(x)＝f(－x)，即函数为偶函数，排除C；由函数过(0,0)点，排除B、D.第 12 题：来源：河南省安阳市2017_2018学年高一数学9月月考试题试卷及答案下列四个函数：①；②；③；④.其中值域为的函数有（）A．1个 B．2个 C．3个 D．4个【答案】B第 13 题：来源： 2016_2017学年河南省南阳市高一数学下学期第一次月考（3月）试题试卷及答案10名工人某天生产同一零件，生产的件数是15，17，14，10，15，17，17，16，14，12，设其平均数为a,中位数为b,众数为c，则有 ( )A．a>b>c B．b>c>a C ．c>a>b D ．c> b>a【答案】D第 14 题：来源：高中数学第三章导数及其应用3.3导数的应用3.3.3导数的实际应用自我小测新人教B版选修1_120171101256某工厂生产某种产品，已知该产品的月生产量x t与每吨产品的价格p(元/t)之间的关系式为p＝24 200－x2，且生产x t的成本为R＝50 000＋200x(元)，则该厂利润达到最大时的月产量为( ) A．100 B．20 C．400 D．200【答案】D第 15 题：来源：四川省广安市邻水县2017_2018学年高一数学上学期第一次月考试题试卷及答案函数的最值情况为( )(A)最小值0，最大值1 (B)最小值0，无最大值(C)最小值0，最大值5 (D)最小值1，最大值5【答案】B.x∈［-1,0］，f(x)的最大值为1，最小值为0；x∈(0,1］时，f(x)∈［1,+∞)无最大值，有最小值1，所以f(x)有最小值0，无最大值.第 16 题：来源：河北省承德市第一中学2018_2019学年高二数学下学期期中试题理函数的单调递减区间是( )A．(－∞,1) B．(－∞,0)和(0,1) C. (－∞,0) D．(0,1)【答案】B由题得，令，所以x<1,因为x≠0，所以x＜1，且x≠0，所以函数的单调减区间为和，故选B.第 17 题：来源：安徽省巢湖市2016_2017学年高二数学下学期第三次月考试题理函数f(x)＝(x－4)ex的单调递增区间是( )A．(－∞，3) B．(3，＋∞) C．(1,4) D．(0,3)【答案】B第 18 题：来源：安徽省东至二中2017_2018学年高二数学上学期12月份考试试题理（含解析）已知过双曲线右焦点，斜率为的直线与双曲线的第一象限交于点，点为左焦点，且，则此双曲线的离心率为( )A. B. C. D.【答案】C【解析】由题意，∵过双曲线右焦点的直线，∴，代入双曲线，可得，∴，∴，∴，∵，∴，故选C.第 19 题：来源：江西省樟树中学2017_2018学年高二数学下学期第三次月考试题文（含解析）已知集合，，则等于A. B. C. D.【答案】B【解析】【分析】根据集合交集的定义求解即可得到结果．【详解】∵，∴．第 20 题：来源：安徽省淮南市2017_2018学年高二数学上学期期中试题理试卷及答案椭圆的焦点坐标是（）A. B. C. D.【答案】C第 21 题：来源：河北省定州市2016_2017学年高一数学下学期期末考试试题试卷及答案已知直线与平行，则的值是（）A. 0或1B. 1或C. 0或D.【答案】C第 22 题：来源：黑龙江省虎林市2016_2017学年高二数学5月月考试题理试卷及答案某人进行射击训练,每次击中目标的概率为0.7,在10次射击中,未击中目标次数的期望为( ) A. 7 B. 3 C. 4 D. 5【答案】B第 23 题：来源：（通用版）2019版高考数学二轮复习4套“12＋4”限时提速练检测理（普通生，含解析）过抛物线y＝x2的焦点F的直线交抛物线于A，B两点，点C在直线y＝－1上，若△ABC为正三角形，则其边长为( )A．11 B．12C．13 D．14【答案】B 由题意可知，焦点F(0,1)，易知过焦点F的直线的斜率存在且不为零，则设该直线方程为y＝kx＋1(k≠0)，联立消去y，得x2－4kx－4＝0，设A(x1，y1)，B(x2，y2)，∴x1＋x2＝4k，x1x2＝－4，设线段AB的中点为M，则M(2k,2k2＋1)，设C(m，－1)，连接MC，∵△ABC为等边三角形，∴|AB|＝4(1＋k2)＝12.第 24 题：来源： 2017届北京市海淀区高三5月期末(二模)数学试题(理)含答案.已知两个半径不等的圆盘叠放在一起（有一轴穿过它们的圆心），两圆盘上分别有互相垂直的两条直径将其分为四个区域，小圆盘上所写的实数分别记为，大圆盘上所写的实数分别记为,如图所示.将小圆盘逆时针旋转次，每次转动，记为转动次后各区域内两数乘积之和，例如. 若，，则以下结论正确的是A.中至少有一个为正数B.中至少有一个为负数C.中至多有一个为正数D.中至多有一个为负数【答案】A第 25 题：来源：江西省吉安市新干县2018届高三数学上学期第一次月考试题理试卷及答案已知函数f（x）=e|x|+x2，（e为自然对数的底数），且f（3a﹣2）＞f（a﹣1），则实数a的取值范围是A．B．C．D．【答案】C第 26 题：来源：甘肃省镇原县二中2018_2019学年高二数学上学期期末考试试题理直线y＝x－3与抛物线y2＝4x交于A、B两点，过A、B两点向抛物线的准线作垂线，垂足为P、Q，则梯形APQB的面积为( )A．48 B．56 C．64 D．72【答案】A第 27 题：来源：甘肃省静宁县2018届高三数学上学期第一次月考试题理试卷及答案已知函数，则关于的不等式的解集为（）A. B. C. D.【答案】D第 28 题：来源： 2016_2017学年湖北省孝感市七校高二数学下学期期中试题试卷及答案理若椭圆经过原点，且焦点分别为则其离心率为【答案】C第 29 题：来源：山东省济南市2018届高三数学上学期12月考试试题试卷及答案理定义一种运算如下：，则复数（是虚数单位）的模长为（）A． B． C．D．【答案】C第 30 题：来源：重庆市2017届高三下第一次月段考试数学试题（理科）含答案在如图所示的程序框图中，若输出的值是3，则输入的取值范围是A. B. C. D.【答案】A第 31 题：来源： 2017届江西省南昌市十所省重点中学高三第二次模拟突破冲刺数学理科试题（五）含答案在四棱锥中，底面是正方形，底面，，，，分别是棱，，的中点，则过，，的平面截四棱锥所得截面面积为（）A． B． C. D．【答案】C第 32 题：来源：广西南宁市2017_2018学年高二数学上学期期中试题试卷及答案在中，内角A,B,C所对的边分别是a,b,c，若，则的值为（）A． B． C．1D．【答案】D【解析】由三角形的性质及正弦定理知，，又∵，∴，故选D.第 33 题：来源：西藏拉萨市2016_2017学年高二数学下学期第六次月考（期中）试卷理（含解析）观察下列各式：a+b=1，a2+b2=3，a3+b3=4，a4+b4=7，a5+b5=11，…，则a10+b10=（）A．28 B．76 C．123 D．199【答案】C【考点】F1：归纳推理．【分析】观察可得各式的值构成数列1，3，4，7，11，…，所求值为数列中的第十项．根据数列的递推规律求解．【解答】解：观察可得各式的值构成数列1，3，4，7，11，…，其规律为从第三项起，每项等于其前相邻两项的和，所求值为数列中的第十项．继续写出此数列为1，3，4，7，11，18，29，47，76，123，…，第十项为123，即a10+b10=123，．故选C．第 34 题：来源：湖南省益阳市2017_2018学年高一数学上学期10月月考试题试卷及答案已知是定义在上是减函数，则的取值范围是（）A． B． C. D．【答案】A第 35 题：来源：内蒙古乌兰察布市2015_2016学年高二数学下学期期末考试试题理函数是（）A．非奇非偶函数 B．既不是奇函数,又不是偶函数奇函数C．偶函数 D．奇函数【答案】 D第 36 题：来源： 2016-2017学年福建省漳州市芗城区高一数学上学期期中试题试卷及答案函数的定义域是( )A. B. C. D.【答案】B第 37 题：来源：广西钦州市钦州港区2016-2017学年高二数学12月月考试题试卷及答案理已知抛物线方程为，直线的方程为，在抛物线上有一动点P到y轴的距离为，P到直线的距离为，则的最小( )A．B．C．D．【答案】 D第 38 题：来源：广东省中山市普通高中2017_2018学年高一数学11月月考试题试卷及答案01 已知,点，，都在函数的图像上，则下列不等式中正确的是A. B.C. D.【答案】 A第 39 题：来源：江苏省扬州2017届高三下学期5月质量监测最后一模数学试卷含答案直角的三边满足，则面积的最大值是.【答案】;第 40 题：来源：贵州省铜仁市第一中学2019届高三数学上学期第二次月考试题理（含解析）我国古代数学著作《孙子算经》中有如下问题：“今有方物一束，外周一匝有三十二枚，问积几何？”设每层外周枚数为，如图是解决该问题的程序框图，则输出的结果为（）A. 121B. 81C. 74D. 49【答案】B【解析】满足，第一次循环：；满足，第二次循环：；满足，第三次循环：；满足，第四次循环：；满足，第五次循环：。

2019年高考数学一模试卷(附答案)

的渐近线的
距离为 3 c ，则双曲线的渐近线方程为（） 2
A． y 3x
B． y 2x
C． y x
12．在如图的平面图形中，已知
D． y 2x
OM 1,ON 2, MON 120 , BM 2MA,CN 2NA, 则 BC·OM 的值为
A． 15
C． 6 二、填空题
B． 9
D．0
D． b a c
3．如果，那么下列不等式成立的是（）
4
2
A． sin cos tan
B． tan sin cos
C． cos sin tan
D． cos tan sin
4．在“一带一路”知识测验后，甲、乙、丙三人对成绩进行预测．
甲：我的成绩比乙高．
乙：丙的成绩比我和甲的都高．
2019 年高考数学一模试卷(附答案)
一、选择题
1．若 tan 3 ，则 cos2 2sin 2 （
）
4
A． 64
B． 48
C．1
25
25
2．设 a sin 5 ， b cos 2 ， c tan 2 ，则（）
7
7
7
A． a b c
B． a c b
C． b c a
D． 16 25
【方法点拨】三角函数求值：①“给角求值”将非特殊角向特殊角转化，通过相消或相约消
去非特殊角，进而求出三角函数值；②“给值求值”关键是目标明确，建立已知和所求之间
分成 9 组，制成了如图所示的频率分布直方图. （1）求直方图的的值；（2）设该市有 30 万居民，估计全市居民中月均用水量不低于 3 吨的人数，说明理由；（3）估计居民月用水量的中位数.
23．如图，已知四棱锥 P ABCD 的底面为等腰梯形， AB//CD , AC BD ,垂足为 H ， PH 是四棱锥的高．

2019年数学高考一模试题(含答案)

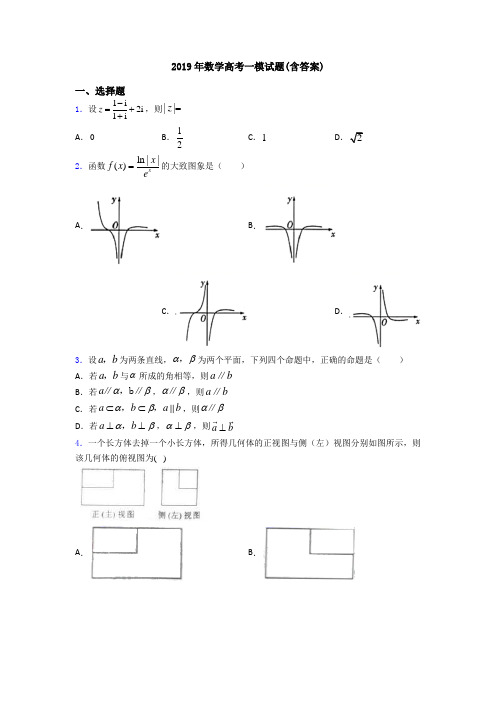
2019年数学高考一模试题(含答案)一、选择题1．设1i 2i 1i z -=++，则||z = A ．0B ．12C ．1D ．2 2．函数ln ||()xx f x e =的大致图象是（） A ． B ．C ．D ．3．设a b ，为两条直线，αβ，为两个平面，下列四个命题中，正确的命题是（） A ．若a b ，与α所成的角相等，则a b ∥B ．若a αβ∥，b ∥，αβ∥，则a b ∥C ．若a b a b αβ⊂⊂，，，则αβ∥D ．若a b αβ⊥⊥，，αβ⊥，则a b ⊥4．一个长方体去掉一个小长方体，所得几何体的正视图与侧（左）视图分别如图所示，则该几何体的俯视图为( )A ．B ．C ．D ．5．设ω>0,函数y=sin(ωx+3π)+2的图象向右平移43π个单位后与原图象重合，则ω的最小值是A ．23B ．43C ．32D ．36．抛掷一枚骰子，记事件A 为“落地时向上的点数是奇数”，事件B 为“落地时向上的点数是偶数”，事件C 为“落地时向上的点数是3的倍数”，事件D 为“落地时向上的点数是6或4”，则下列每对事件是互斥事件但不是对立事件的是（）A ．A 与B B ．B 与C C ．A 与D D ．C 与D7．已知命题p ：若x >y ，则－x <－y ；命题q ：若x >y ，则x 2>y 2.在命题①p ∧q ；②p ∨q ；③p ∧(⌝q )；④(⌝p )∨q 中，真命题是( )A ．①③B ．①④C ．②③D ．②④8．若角α的终边在第二象限，则下列三角函数值中大于零的是（）A ．sin(+)2πα B ．s(+)2co πα C ．sin()πα+ D ．s()co πα+9．圆C 1：x 2+y 2＝4与圆C 2：x 2+y 2﹣4x +4y ﹣12＝0的公共弦的长为（）A ．2B ．3C ．22D ．3210．南北朝时代的伟大数学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”.其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等，如图，夹在两个平行平面之间的两个几何体的体积分别为12,V V ，被平行于这两个平面的任意平面截得的两个截面的面积分别为12,S S ，则“12,S S 总相等”是“12,V V 相等”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件11．已知某几何体的三视图（单位：cm ）如图所示，则该几何体的体积是（）A ．108cm 3B ．100cm 3C ．92cm 3D ．84cm 312．在如图的平面图形中，已知1,2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 的值为A ．15-B ．9-C ．6-D ．0二、填空题13．如图所示，平面BCC 1B 1⊥平面ABC ，∠ABC ＝120︒，四边形BCC 1B 1为正方形，且AB ＝BC ＝2，则异面直线BC 1与AC 所成角的余弦值为_____．14．某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查．已知该校一年级、二年级、三年级、四年级的本科生人数之比为4：5：5：6，则应从一年级本科生中抽取_______名学生．15．函数2()log 1f x x =-________．16．记n S 为数列{}n a 的前n 项和，若21n n S a =+，则6S =_____________．17．能说明“若f （x ）>f （0）对任意的x ∈（0，2］都成立，则f （x ）在［0，2］上是增函数”为假命题的一个函数是__________．18．在ABC ∆中，若13AB =3BC =，120C ∠=︒，则AC =_____．19．设函数21()ln 2f x x ax bx =--，若1x =是()f x 的极大值点，则a 取值范围为_______________. 20．已知向量a 与b 的夹角为60°，|a |=2，|b |=1，则|a +2 b |= ______ .三、解答题21．已知直线352:{132x t l y t =+=+（t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为2cos ρθ=. （1）将曲线C 的极坐标方程化为直角坐标方程；（2）设点的直角坐标为(5,3)，直线l 与曲线C 的交点为A ，B ，求MA MB ⋅的值.22．若不等式2520ax x +->的解集是122xx ⎧⎫<<⎨⎬⎩⎭，求不等式22510ax x a -+->的解集．23．在直角坐标系xOy 中，直线l 1的参数方程为2+,,x t y kt =⎧⎨=⎩（t 为参数），直线l 2的参数方程为2,,x m m m y k =-+⎧⎪⎨=⎪⎩（为参数）.设l 1与l 2的交点为P ，当k 变化时，P 的轨迹为曲线C ．（1）写出C 的普通方程；（2）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设()3:cos sin 20l ρθθ+-=，M 为l 3与C 的交点，求M 的极径.24．如图，边长为2的正方形ABCD 中，E 、F 分别是AB 、BC 边的中点，将AED ，DCF 分别沿DE ，DF 折起，使得A ，C 两点重合于点M ．(1) 求证：MD EF ⊥；(2) 求三棱锥M EFD -的体积．25．在直角坐标平面内，以原点O 为极点，x 轴的非负半轴为极轴建立极坐标系．已知点A ，B 的极坐标分别为()π42，，5π224⎛⎫ ⎪⎝⎭，，曲线C 的方程为r ρ=（0r >）．（1）求直线AB 的直角坐标方程；（2）若直线AB 和曲线C 有且只有一个公共点，求r 的值．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【解析】分析：利用复数的除法运算法则：分子、分母同乘以分母的共轭复数，化简复数z ，然后求解复数的模. 详解：()()()()1i 1i 1i 2i 2i 1i 1i 1i z ---=+=++-+ i 2i i =-+=，则1z =，故选c.点睛：复数是高考中的必考知识，主要考查复数的概念及复数的运算．要注意对实部、虚部的理解，掌握纯虚数、共轭复数这些重要概念，复数的运算主要考查除法运算，通过分母实数化转化为复数的乘法，运算时特别要注意多项式相乘后的化简，防止简单问题出错，造成不必要的失分.2．A解析：A【解析】【分析】由函数解析式代值进行排除即可.【详解】解：由()x ln x f x =e ，得()f 1=0，()f 1=0- 又()1f e =0e e >，()1f e =0e e--> 结合选项中图像，可直接排除B ，C ，D故选A【点睛】本题考查了函数图像的识别，常采用代值排除法.3．D解析：D【解析】【分析】【详解】试题分析：A 项中两直线a b ，还可能相交或异面,错误；B 项中两直线a b ，还可能相交或异面,错误；C 项两平面αβ，还可能是相交平面，错误；故选D.4．C解析：C【解析】【分析】从正视图和侧视图上分析，去掉的长方体的位置应该在的方位，然后判断俯视图的正确图形．【详解】由正视图可知去掉的长方体在正视线的方向，从侧视图可以看出去掉的长方体在原长方体的右侧，由以上各视图的描述可知去掉的长方体在原长方体的右上方，其俯视图符合C 选项．故选C ．点评：本题考查几何体的三视图之间的关系，要注意记忆和理解“长对正、高平齐、宽相等”的含义．考点：三视图．5．C解析：C【解析】函数sin 23y x πω⎛⎫=++ ⎪⎝⎭的图象向右平移43π个单位后44sin 2sin 23333w y w x wx ππππ⎡⎤⎛⎫⎛⎫=-++=+-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 所以有43332013222w k k k w w k w ππ=∴=>∴≥∴=≥ 故选C 6．C解析：C【解析】分析：利用互斥事件、对立事件的概念直接求解判断即可.详解：在A 中，A 与B 是对立事件，故不正确；在B 中，B 与C 能同时发生，不是互斥事件，所以不正确；在C 中，A 与D 两个事件不能同时发生，但能同时不发生，所以是互斥事件，但不是对立事件，所以是正确的；在D 中，C 与D 能同时发生，不是互斥事件，所以是错误的.综上所述，故选C.点睛：本题主要考查了命题的真假判定，属于基础题，解答时要认真审题，注意互斥事件与对立事件的定义的合理运用，同时牢记互斥事件和对立事件的基本概念是解答的基础.7．C解析：C【解析】试题分析：根据不等式的基本性质知命题p 正确，对于命题q ，当,x y 为负数时22x y >不成立，即命题q 不正确，所以根据真值表可得,(p q p ∨∧q )为真命题，故选C.考点：1、不等式的基本性质；2、真值表的应用. 8．D解析：D【解析】【分析】利用诱导公式化简选项，再结合角α的终边所在象限即可作出判断.【详解】解：角α的终边在第二象限，sin +2πα⎛⎫ ⎪⎝⎭＝cos α＜0，A 不符； s +2co πα⎛⎫ ⎪⎝⎭＝sin α-＜0，B 不符； ()sin πα+＝sin α-＜0，C 不符；()s co πα+＝s co α-＞0，所以，D 正确故选D【点睛】本题主要考查三角函数值的符号判断，考查了诱导公式，三角函数的符号是解决本题的关键．9．C解析：C【解析】【分析】两圆方程相减，得到公共弦所在的直线方程，然后利用其中一个圆，结合弦长公式求解.【详解】因为圆C 1：x 2+y 2＝4与圆C 2：x 2+y 2﹣4x +4y ﹣12＝0，两式相减得20x y --=，即公共弦所在的直线方程.圆C 1：x 2+y 2＝4，圆心到公共弦的距离为2d =，所以公共弦长为：22222l r d =-=.故选：C【点睛】本题主要考查直线与圆，圆与圆的位置关系，还考查了运算求解的能力，属于基础题.10．A解析：A【解析】【分析】根据充分条件和必要条件的定义，结合祖暅原理进行判断即可.【详解】根据祖暅原理，当12,S S 总相等时，12,V V 相等，所以充分性成立；当两个完全相同的四棱台，一正一反的放在两个平面之间时，此时体积固然相等但截得的面积未必相等，所以必要性不成立.所以“12,S S 总相等”是“12,V V 相等”的充分不必要条件.故选：A【点睛】本题考查充分条件与必要条件的判断，属于基础题.11．B解析：B【解析】试题分析：由三视图可知：该几何体是一个棱长分别为6，6，3，砍去一个三条侧棱长分别为4，4，3的一个三棱锥（长方体的一个角）．据此即可得出体积．解：由三视图可知：该几何体是一个棱长分别为6，6，3，砍去一个三条侧棱长分别为4，4，3的一个三棱锥（长方体的一个角）．∴该几何体的体积V=6×6×3﹣=100．故选B ．考点：由三视图求面积、体积．12．C解析：C【解析】分析：连结MN ，结合几何性质和平面向量的运算法则整理计算即可求得最终结果. 详解：如图所示，连结MN ，由2,2BM MA CN NA == 可知点,M N 分别为线段,AB AC 上靠近点A 的三等分点，则()33BC MN ON OM ==-，由题意可知： 2211OM ==，12cos1201OM ON ⋅=⨯⨯=-，结合数量积的运算法则可得： ()2333336BC OM ON OM OM ON OM OM ⋅=-⋅=⋅-=--=-.本题选择C 选项.点睛：求两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．二、填空题13．【解析】【分析】将平移到和相交的位置解三角形求得线线角的余弦值【详解】过作过作画出图像如下图所示由于四边形是平行四边形故所以是所求线线角或其补角在三角形中故【点睛】本小题主要考查空间两条直线所成角的解析：64【解析】【分析】将AC 平移到和1BC 相交的位置，解三角形求得线线角的余弦值.【详解】过B 作//BD AC ，过C 作//CD AB ，画出图像如下图所示，由于四边形ABCD 是平行四边形，故//BD AC ，所以1C BD ∠是所求线线角或其补角.在三角形1BC D 中，1122,23BC C D BD ===16cos 22223C BD ∠==⨯⨯.【点睛】本小题主要考查空间两条直线所成角的余弦值的计算，考查数形结合的数学思想方法，属于中档题.14．60【解析】【分析】采用分层抽样的方法从该校四个年级的本科生中抽取一个容量为300的样本进行调查的【详解】∵该校一年级二年级三年级四年级的本科生人数之比为4:5:5:6∴应从一年级本科生中抽取学生人解析：60【解析】【分析】采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查的.【详解】∵该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6， ∴应从一年级本科生中抽取学生人数为：4300604556⨯=+++. 故答案为60. 15．2+∞）【解析】分析：根据偶次根式下被开方数非负列不等式解对数不等式得函数定义域详解：要使函数有意义则解得即函数的定义域为点睛：求给定函数的定义域往往需转化为解不等式（组）的问题解析：[2，+∞）【解析】分析：根据偶次根式下被开方数非负列不等式，解对数不等式得函数定义域.详解：要使函数()f x 有意义，则2log 10x -≥，解得2x ≥，即函数()f x 的定义域为[2,)+∞.点睛：求给定函数的定义域往往需转化为解不等式（组）的问题.16．【解析】【分析】首先根据题中所给的类比着写出两式相减整理得到从而确定出数列为等比数列再令结合的关系求得之后应用等比数列的求和公式求得的值【详解】根据可得两式相减得即当时解得所以数列是以-1为首项以2 解析：63-【解析】【分析】首先根据题中所给的21n n S a =+，类比着写出1121n n S a ++=+，两式相减，整理得到12n n a a +=，从而确定出数列{}n a 为等比数列，再令1n =，结合11,a S 的关系，求得11a =-，之后应用等比数列的求和公式求得6S 的值.【详解】根据21n n S a =+，可得1121n n S a ++=+，两式相减得1122n n n a a a ++=-，即12n n a a +=，当1n =时，11121S a a ==+，解得11a =-，所以数列{}n a 是以-1为首项，以2为公比的等比数列，所以66(12)6312S --==--，故答案是63-. 点睛：该题考查的是有关数列的求和问题，在求解的过程中，需要先利用题中的条件，类比着往后写一个式子，之后两式相减，得到相邻两项之间的关系，从而确定出该数列是等比数列，之后令1n =，求得数列的首项，最后应用等比数列的求和公式求解即可，只要明确对既有项又有和的式子的变形方向即可得结果.17．y=sinx （答案不唯一）【解析】分析：举的反例要否定增函数可以取一个分段函数使得f （x ）>f （0）且（02］上是减函数详解：令则f （x ）>f （0）对任意的x ∈（02］都成立但f （x ）在［02］上不解析：y =sin x （答案不唯一）【解析】分析：举的反例要否定增函数，可以取一个分段函数，使得f （x ）>f （0）且（0，2］上是减函数.详解：令0,0()4,(0,2]x f x x x =⎧=⎨-∈⎩，则f （x ）>f （0）对任意的x ∈（0，2］都成立，但f（x ）在［0，2］上不是增函数.又如，令f （x ）=sin x ，则f （0）=0，f （x ）>f （0）对任意的x ∈（0，2］都成立，但f （x ）在［0，2］上不是增函数.点睛：要判定一个全称命题是假命题，只要举出集合M 中的一个特殊值0x ，使0()p x 不成立即可.通常举分段函数.18．1【解析】【分析】由题意利用余弦定理得到关于AC 的方程解方程即可确定AC 的值【详解】由余弦定理得解得或（舍去）【点睛】本题主要考查余弦定理解三角形的方法方程的数学思想等知识意在考查学生的转化能力和计解析：1【解析】【分析】由题意利用余弦定理得到关于AC 的方程，解方程即可确定AC 的值.【详解】由余弦定理得21393AC AC =++，解得1AC =或4AC =-（舍去）.【点睛】本题主要考查余弦定理解三角形的方法，方程的数学思想等知识，意在考查学生的转化能力和计算求解能力.19．【解析】试题分析：的定义域为由得所以①若由得当时此时单调递增当时此时单调递减所以是的极大值点；②若由得或因为是的极大值点所以解得综合①②：的取值范围是故答案为考点：1利用导数研究函数的单调性；2利用解析：【解析】试题分析：()f x 的定义域为()()10,,'f x ax b x +∞=--，由()'00f =，得1b a =-，所以()()()11'ax x f x x+-=.①若0a ≥，由()'0f x =，得1x =，当01x <<时，()'0f x >，此时()f x单调递增，当1x >时，()'0f x <，此时()f x 单调递减，所以1x =是()f x 的极大值点；②若0a <，由()'0f x =，得1x =或1x a=-.因为1x =是()f x 的极大值点，所以11a->，解得10a -<<，综合①②：a 的取值范围是1a >-，故答案为()1,-+∞. 考点：1、利用导数研究函数的单调性；2、利用导数研究函数的极值. 20．【解析】【分析】【详解】∵平面向量与的夹角为∴∴故答案为点睛：(1)求向量的夹角主要是应用向量的数量积公式(2)常用来求向量的模解析：23【解析】【分析】【详解】∵平面向量a 与b 的夹角为060，21a b ==，∴021cos601a b ⋅=⨯⨯=.∴2222(2)4(2)44423a b a b a a b b +=+=+⋅+=++=故答案为23.点睛：(1)求向量的夹角主要是应用向量的数量积公式．(2) a a a =⋅ 常用来求向量的模．三、解答题21．（1）；（2）.【解析】【分析】【详解】试题分析：（1）在方程=2cos ρθ两边同乘以极径ρ可得2=2cos ρρθ，再根据222=,cos x y x ρρθ+=，代入整理即得曲线C 的直角坐标方程；（2）把直线的参数方程代入圆的直角坐标方程整理，根据韦达定理即可得到MA MB ⋅的值.试题解析：（1）=2cos ρθ等价于2=2cos ρρθ①将222=,cos x y x ρρθ+=代入①既得曲线C 的直角坐标方程为 2220x y x +-=，②（2）将5212x t y t ⎧=+⎪⎪⎨⎪=⎪⎩代入②得2180t ++=，设这个方程的两个实根分别为12,,t t则由参数t 的几何意义既知，1218MA MB t t ⋅==.考点：圆的极坐标方程与直角坐标方程的互化及直线参数方程的应用.22．132x x ⎧⎫-<<⎨⎬⎩⎭【解析】【分析】由不等式的解集和方程的关系，可知12，2是方程520ax x +-=的两根，利用韦达定理求出a ，再代入不等式22510ax x a -+->，解一元二次不等式即可.【详解】解：由已知条件可知0a <，且方程520ax x +-=的两根为12，2；由根与系数的关系得55221a a⎧-=⎪⎪⎨⎪-=⎪⎩解得2a =-．所以原不等式化为2530x x +-<解得132x -<<所以不等式解集为132x x ⎧⎫-<<⎨⎬⎩⎭【点睛】本题主要考查一元二次不等式的解法，还考查一元二次不等式解集与一元二次方程的关系以及利用韦达定理求值.23．（1）()2240x y y -=≠（2【解析】（1）消去参数t 得1l 的普通方程()1:2l y k x =-；消去参数m 得l 2的普通方程()21:2l y x k=+. 设(),P x y ,由题设得()()212y k x y x k ⎧=-⎪⎨=+⎪⎩，消去k 得()2240x y y -=≠. 所以C 的普通方程为()2240x y y -=≠. （2）C 的极坐标方程为()()222cos sin 402π,πρθθθθ-=<<≠. 联立()()222cos sin 4,cos sin 0ρθθρθθ⎧-=⎪⎨+=⎪⎩得()cos sin 2cos sin θθθθ-=+. 故1tan 3θ=-，从而2291cos ,sin 1010θθ==. 代入()222cos sin 4ρθθ-=得25ρ=，所以交点M【名师点睛】本题考查了极坐标方程的求法及应用，重点考查了转化与化归能力.遇到求曲线交点、距离、线段长等几何问题时，求解的一般方法是分别化为普通方程和直角坐标方程后求解，或者直接利用极坐标的几何意义求解.要结合题目本身特点，确定选择何种方程.24．（1）见解析；（2）13 【解析】【分析】（1）在正方形ABCD 中，有AB AD ⊥，CD BC ⊥，在三棱锥M DEF -中，可得MD MF ⊥，MD ME ⊥，由线面垂直的判定可得MD ⊥面MEF ，则MD EF ⊥；（2）由E 、F 分别是AB 、BC 边的中点，可得1BE BF ==，求出三角形MEF 的面积，结合()1及棱锥体积公式求解．【详解】（1）证明：在正方形ABCD 中，AB AD ⊥，CD BC ⊥，∴在三棱锥M DEF -中，有MD MF ⊥，MD ME ⊥，且ME MF M ⋂=， MD ∴⊥面MEF ，则MD EF ⊥；（2）解：E 、F 分别是边长为2的正方形ABCD 中AB 、BC 边的中点，1BE BF ∴==，111122MEF BEF S S ∴==⨯⨯=，由（1）知，111123323M DEF MEF V S MD -=⋅=⨯⨯=．【点睛】本题考查线面垂直的判定定理及性质定理的应用，考查棱锥体积的求法，是中档题．25．（1）340x y -+=；（2）2105【解析】【分析】（1）求得()04A ，，()22B --，，问题得解．（2）利用直线AB 和曲线C 相切的关系可得：圆心到直线A B 的距离等于圆的半径r ，列方程即可得解．【详解】（1）分别将()π42A ，，()5π224B ，转化为直角坐标为()04A ，，()22B --，，所以直线AB 的直角坐标方程为340x y -+=．（2）曲线C 的方程为r ρ=（0r >），其直角坐标方程为222x y r +=．又直线A B 和曲线C 有且只有一个公共点，即直线与圆相切，所以圆心到直线A B 的距离等于圆的半径r .又圆心到直线A B 22210431=+r 210．【点睛】本题主要考查了极坐标与直角坐标互化，还考查了直线与圆相切的几何关系，考查计算能力及点到直线距离公式，属于中档题．。

2019年高考数学一模试题(含答案)

(1)当 n=1 时, 12 1 <1+1,不等式成立.
(2)假设当 n=k(k∈N*)时,不等式成立,即 k2 k <k+1.
那么当 n=k+1
时, (k 1)2 k 1 k2 3k 2 k2 3k 2 k 2 (k 2)2 =(k+1)+1,
所以当 n=k+1 时,不等式也成立. 根据(1)和(2),可知对于任何 n∈N*,不等式均成立.
C． y log2 x
D． y 1 x2 1 2
2．通过随机询问 110 名不同的大学生是否爱好某项运动，得到如下的列联表：
男
女
总计
爱好
40
20
60
不爱好
20
30
50
总计
60
50
110
2
由K
n(ad bc)2
算得, K 2 110 (40 30 20 30)2 7.8
(a b)(c d )(a c)(b d )
2019 年高考数学一模试题(含答案)
一、选择题
1．某学校开展研究性学习活动，某同学获得一组实验数据如下表：
x 1.99 3
4
5.1 6.12
y 1.5 4.04 7.5 12 18.01
对于表中数据，现给出以下拟合曲线，其中拟合程度最好的是 ( )
A． y 2x 2
B． y ( 1 )x 2
是锐角，且 a 2
7
，
cosA
1 3
，则
△ABC
的面积为______．
19．设为第四象限角，且 sin3 ＝ 13 ，则 tan 2＝ ________. sin 5
20． sin 50 1 3 tan10 ________________.

2019年广西桂平市大洋中学高考数学选择题专项训练(一模)

2019年广西桂平市大洋中学高考数学选择题专项训练（一模）抽选各地名校试卷，经典试题，有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。

第 1 题：来源：广西桂林市七星区2017_2018年高二数学上学期期中检测试题试卷及答案等比数列的前项和为，已知，则（）.A. B. C.D.【答案】C第 2 题：来源：山东省枣庄市2016_2017学年高二数学3月月考试题试卷及答案已知集合，若，则的真子集个数为（）A． 5 B． 6 C. 7D． 8【答案】 C第 3 题：来源：内蒙古乌兰察布市2015_2016学年高一数学下学期期末考试试题若并且（）A． B. C.D.【答案】C第 4 题：来源：河南省郑州市、平顶山市、濮阳市2017届高考数学二模试卷（理科）含答案要计算1+++…+的结果，如图程序框图中的判断框内可以填（）A．n＜2017 B．n≤2017 C．n＞2017 D．n≥2017【答案】B【考点】程序框图．【分析】通过观察程序框图，分析为填判断框内判断条件，n的值在执行运算之后还需加1，故判断框内数字应减1，按照题意填入判断框即可．【解答】解：通过分析，本程序框图为“当型“循环结构，判断框内为满足循环的条件，第1次循环，S=1，n=1+1=2，第2次循环，S=1+，n=2+1=3，…当n=2018时，由题意，此时，应该不满足条件，退出循环，输出S的值．所以，判断框内的条件应为：n≤2017．故选：B．【点评】本题考查程序框图，通过对程序框图的分析对判断框进行判断，属于基础题．第 5 题：来源： 2017年普通高等学校招生全国统一考试数学试题理（全国卷2，参考解析）已知直三棱柱中，，，，则异面直线与所成角的余弦值为（）A．B． C．D．【答案】C【解析】，，分别为，，中点，则，夹角为和夹角或其补角（异面线所成角为）可知，，作中点，则可知为直角三角形．，中，，则，则中，则中，又异面线所成角为，则余弦值为．第 6 题：来源：福建省四地六校2016_2017学年高二数学下学期第二次联考（5月）试题理 (1) 已知随机变量服从正态分布，且，则（）A. 0.4B.0.1 C.0.6 D.0.9【答案】A第 7 题：来源：黑龙江省牡丹江市2017_2018学年高一数学上学期期中试题试卷及答案设，则（）A. B. C. D.【答案】D第 8 题：来源：新疆呼图壁县2017_2018学年高一数学上学期期中试题试卷及答案已知集合M＝{－1,0,1}，N＝{0,1,2}，则M∪N＝( )A．{－1,0,1} B．{－1,0,1,2}C．{－1,0,2} D．{0,1}【答案】B第 9 题：来源：河北省唐山市2017_2018学年高一数学上学期期中试题试卷及答案已知函数，且，则A． B． C． D．【答案】B第 10 题：来源：广东省佛山市高明区第一中学2017_2018学年高一数学上学期第9周考试试题（含解析）已知分别是定义在上的偶函数和奇函数，且，则（）A. 4B. 3C. 2D. 1【答案】D【解析】试题分析：由题意得，，,故选C．第 11 题：来源：高中数学第三章导数及其应用3.3导数的应用3.3.1利用导数判断函数的单调性自我小测新人教B版选修1_120171101248如果函数f(x)＝2x3＋ax2＋1在区间(－∞，0)和(2，＋∞)内单调递增，在区间(0,2)内单调递减，则a 的值为( )A．1 B．2 C．－6 D．－12 【答案】C第 12 题：来源：河北省永年县2017_2018学年高二数学上学期开学考试试卷及答案定义在R上的函数f(x)满足f(x)＝则f(3)的值为( )A．－1 B．－2 C．1 D．2【答案】B第 13 题：来源：江西省红色七校2019届高三数学第二次联考试题理已知若有最小值，则实数的取值范围是（）A B C D【答案】C第 14 题：来源：四川省成都市龙泉驿区第一中学校2019届高三数学12月月考试题理已知5台机器中有2台存在故障，现需要通过逐台检测直至区分出2台故障机器为止.若检测一台机器的费用为1000元，则所需检测费的均值为（）A．3200元 B．3400元 C．3500元 D．3600元【答案】C第 15 题：来源：宁夏银川市兴庆区2018届高三数学第四次月考试题理若函数f（x）=x2+x﹣lnx+1在其定义域的一个子区间（2k﹣1，k+2）内不是单调函数，则实数k的取值范围是（）A．（﹣，） B．[，3） C．[，） D．（﹣，3）【答案】C第 16 题：来源： 2017年普通高等学校招生全国统一考试数学试题文（天津卷，含解析）有5支彩笔（除颜色外无差别），颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔，则取出的2支彩笔中含有红色彩笔的概率为（A）（B）（C）（D）【答案】【考点】古典概型【名师点睛】本题主要考查的是古典概型及其概率计算公式.，属于基础题．解题时要准确理解题意，先要判断该概率模型是不是古典概型，利用排列组合有关知识，正确找出随机事件A包含的基本事件的个数和试验中基本事件的总数代入公式.第 17 题：来源：安徽省滁州市定远县育才学校2018_2019学年高二数学下学期期末考试试题（实验班）理在中，为边上一点，且，向量与向量共线，若，，，则（）A. 3B.C.2 D.【答案】B第 18 题：来源：安徽省滁州市定远县育才学校2018_2019学年高一数学下学期第一次月考试题（普通班）已知sinα＝，则cos等于( )A． B． C．－D．－【答案】C第 19 题：来源： 2016_2017学年天津市静海县高二数学3月学业能力调研试题试卷及答案理函数的定义域为，，对任意， f′(x)>2，则的解集为( )A． B． C． D．【答案】B第 20 题：来源：湖南省益阳市2016_2017学年高一数学下学期3月月考试题试卷及答案阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为( )A、7B、9C、10D、11【答案】B第 21 题：来源：江西省2018届高三数学上学期阶段性检测考试试题（二）理已知函数图象的一个对称中心为，且，要得到函数的图象可将函数的图象（）A．向左平移个单位长度 B．向左平移个单位长度C．向右平移个单位长度 D．向右平移个单位长度【答案】C第 22 题：来源：广西钦州市钦州港区2016-2017学年高一数学12月月考试题试卷及答案在平行四边形中，与交于点是线段的中点，的延长线与交于点．若，，则（）A．B．C．D．【答案】 C第 23 题：来源：安徽省滁州市定远县民族中学2018_2019学年高二数学12月月考试题理设F为抛物线y2=2px(p>0)的焦点,A,B,C为该抛物线上三点,当++=0,且++=3时,此抛物线的方程为( )A．y2=2x B．y2=4xC．y2=6x D．y2=8x【答案】A【解析】设A(x1,y1),B(x2,y2),C(x3,y3),∵++=0,∴(x1-)+(x2-)+(x3-)=0,即x1+x2+x3=p.又++=3,∴(x1+)+(x2+)+(x3+)=3,即3p=3,∴p=1,故抛物线方徎为y2=2x.第 24 题：来源：宁夏石嘴山市2018届高三数学上学期期中试题理若为不等式组表示的平面区域，当从连续变化到时，动直线扫过中的那部分区域的面积为（）A. B. C.D.【答案】A第 25 题：来源：江西省赣州市2017届高三第二次模拟考试数学试题(理)含答案已知复数满足，则在复平面内复数对应的点为（）A． B． C． D．【答案】A第 26 题：来源：云南省泸水市学2017_2018学年高一数学上学期期中试题试卷及答案若全集，则集合的真子集共有（）A．个 B．个 C．个 D．个【答案】C第 27 题：来源：广西南宁市2017_2018学年高一数学上学期期中试题试卷及答案如图，阴影部分表示的集合是（）A． B． C． D．【答案】A 解析：阴影部分是集合A之外部分与集合B的交集第 28 题：来源：河北省唐山市2017_2018学年高一数学上学期期中试题试卷及答案已知为偶函数，当时，，那么函数零点个数为A．2 B．4 C．6 D．8【答案】D第 29 题：来源：湖北省长阳县第一高级中学2018_2019学年高一数学下学期期中试题【答案】B第 30 题：来源：吉林省梅河口市2016_2017学年高一数学下学期期中试题试卷及答案理数列是递减的等差数列，的前项和是，且，有以下四个结论①；②若对任意都有成立，则的值等于7或8时；存在正整数，使；④存在正整数，使.其中所有正确结论的序号是（）A．①②B．①②③C．②③④D．①②③④【答案】 D第 31 题：来源：广东省汕头市潮南区2017年高考考前冲刺数学试题（理）含答案解析若复数,则的虚部为（）A．B．C．D．【答案】B第 32 题：来源：四川省眉山一中办学共同体2018_2019学年高二数学上学期期中试题理如图，在正方体ABCD－A1B1C1D1中，M，N分别是BC1，CD1的中点，则下列判断错误的是( )A．MN与CC1垂直B．MN与AC垂直C．MN与BD平行D．MN与A1B1平行【答案】D第 33 题：来源：吉林省实验中学2018_2019学年高二数学上学期期中试题文命题“”的否定是（）A．B．C．D．【答案】D第 34 题：来源：江西省南昌市第二中学2018_2019学年高二数学上学期第三次月考试题理函数f(x)＝x3－3ax－a在(0,1)内有最小值，则a的取值范围是( )A．0≤a<1 B．－1<a<1 C．0<a< D．0<a<1【答案】D第 35 题：来源：山东省新泰市2017_2018学年高一数学上学期第三次月考试题试卷及答案设f(x)＝则f(f(－2))的值为( )A. B．2 C. D．－2【答案】D第 36 题：来源：河北省鸡泽县2018届高三数学上学期第三次周测试题理试卷及答案焦点在轴上的双曲线的一条渐近线方程是，此双曲线的离心率为A. B. C. 2 D.【答案】C第 37 题：来源：内蒙古杭锦后旗2017_2018学年高一数学上学期期中试题（艺术班）试卷及答案函数的定义域为（）A． B． C． D.【答案】D第 38 题：来源：河北省定州市2016-2017学年高二数学下学期开学考试试题试卷及答案（承智班）若等比数列中，，若，，则等于（）A．16 B．27 C．36 D．82【答案】B第 39 题：来源：湖南省衡阳市2018届高三数学上学期第二次月考试题（实验班）理已知α为锐角，cos（α+）=，则sinα=（）A．B．C．D．【答案】D第 40 题：来源：广东省深圳市耀华实验学校2019届高三数学上学期第一次月考试题理已知向量，，若向量满足∥，，则（）A. B. C. D.【答案】D第 41 题：来源：安徽省黄山市2016_2017学年高二数学下学期期中试题理（含解析）某车队准备从甲、乙等7辆车中选派4辆参加救援物资的运输工作，并按出发顺序前后排成一队．要求甲、乙至少有一辆参加，且若甲、乙同时参加，则它们出发时不能相邻，那么不同的排法种数为 ( )．A. 360B. 520C. 600D. 720【答案】C【解析】若甲、乙只有一个参加，则有＝480(种)．若甲、乙同时参加，则有＝120(种)，所以共有600种排法．第 42 题：来源：甘肃省甘谷第一中学2018_2019学年高二数学下学期第一次月考试题理下列等式中，错误的是（）A．B．C．D．【答案】C第 43 题：来源： 2019高中数学第二章点、直线、平面之间的位置关系单元测试（一）新人教A 版必修2如图，α⊥β，α∩β＝l，，，A，B到l的距离分别是a和b，AB与α，β所成的角分别是θ和φ，AB在α，β内的射影长分别是m和n，若，则（）A． B．C． D．【答案】D【解析】由勾股定理得．又，∴．由已知得sinθ＝，sinφ＝，而，∴，又θ，φ，∴．故选D．第 44 题：来源：湖北省宜昌市部分重点中学2016-2017学年高一数学上学期期末考试试题函数，，在同一坐标系中的图象可能是（）【答案】C．（1）由指数函数和对数函数的单调性可知a＞1，此时直线y=x+a的截距不满足条件，其它类似。

2019年坡脚中学高考数学选择题专项训练(一模)

2019年坡脚中学高考数学选择题专项训练（一模）抽选各地名校试卷，经典试题，有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。

第 1 题：来源：辽宁省大连经济技术开发区得胜高级中学2019届高三数学上学期第二次月考试题理在△中，“”是“”的（）A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分又不必要条件【答案】C第 2 题：来源：四川省广元市2019届高三数学第一次适应性统考试题（含解析）定义域为的可导函数的导函数为，且满足，则下列关系正确的是（）A. B.C. D.【答案】A【解析】设，则在上递减，，即，化为，故选A.【方法点睛】本题主要利用导数研究函数的单调性、构造函数比较大小,属于难题. 联系已知条件和结论，构造辅助函数是高中数学中一种常用的方法，解题中若遇到有关不等式、方程及最值之类问题，设法建立起目标函数，并确定变量的限制条件，通过研究函数的单调性、最值等问题，常可使问题变得明了，准确构造出符合题意的函数是解题的关键；解这类不等式的关键点也是难点就是构造合适的函数，构造函数时往往从两方面着手：①根据导函数的“形状”变换不等式“形状”；②若是选择题，可根据选项的共性归纳构造恰当的函数.第 3 题：来源：内蒙古包头市第一中学2016-2017学年高一数学上学期期末考试试题试卷及答案下列图形中，不可能是函数y＝f(x)的图象的是( )【答案】B第 4 题：来源：广东省第二师范学院番禺附属中学2018_2019学年高二数学下学期期中试题理某工厂为提高生产效率，开展技术创新活动，提出了完成某项生产任务的两种新的生产方式．为比较两种生产方式的效率，选取40名工人，将他们随机分成两组，每组20人，第一组工人用第一种生产方式，第二组工人用第二种生产方式．根据工人完成生产任务的工作时间（单位：min）绘制了如右茎叶图：则下列结论中表述不正确的是A. 第一种生产方式的工人中，有75%的工人完成生产任务所需要的时间至少80分钟B. 第二种生产方式比第一种生产方式效率更高C. 这40名工人完成任务所需时间的中位数为80D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.【答案】D第 5 题：来源：内蒙古赤峰市2016_2017学年高二数学下学期第二次月考试题文（含解析）复数的虚部是（）A. -1B. 1C.D.【答案】B【解析】依题意，原式.第 6 题：来源：安徽省阜阳市第三中学2018_2019学年高二数学下学期开学考试试题（竞培中心）理已知的边上有一点满足，则可表示为A．B．C．D．【答案】D第 7 题：来源：河北省巨鹿县2018届高三数学上学期期中试题理几位大学生响应国家的创业号召，开发了一款应用软件。

2019年数学高考一模试卷及答案

2019年数学高考一模试卷及答案一、选择题1．已知回归直线方程中斜率的估计值为1.23，样本点的中心()4,5，则回归直线方程为（）A ． 1.2308ˆ.0yx =+ B ．0.0813ˆ.2yx =+ C ． 1.234ˆyx =+ D ． 1.235ˆyx =+ 2．()62111x x ⎛⎫++ ⎪⎝⎭展开式中2x 的系数为（） A ．15B ．20C ．30D ．353．已知命题p ：若x >y ，则－x <－y ；命题q ：若x >y ，则x 2>y 2.在命题①p ∧q ；②p ∨q ；③p ∧(⌝q )；④(⌝p )∨q 中，真命题是( ) A ．①③ B ．①④ C ．②③ D ．②④4．已知集合1}{0|A x x -≥=，{0,1,2}B =，则AB =A ．{0}B ．{1}C ．{1,2}D ．{0,1,2}5．函数2||()x x f x e -=的图象是（）A ．B ．C ．D ．6．下列四个命题中，正确命题的个数为( ) ①如果两个平面有三个公共点，那么这两个平面重合； ②两条直线一定可以确定一个平面； ③若M α∈，M β∈，l αβ= ，则M l ∈；④空间中，相交于同一点的三直线在同一平面内． A ．1B ．2C ．3D ．47．ABC ∆的内角A B C 、、的对边分别是a b c 、、，若2B A =，1a =，3b =c =( )A ．3B ．2C 2D ．18．在“近似替代”中，函数()f x 在区间1[,]i i x x +上的近似值（） A ．只能是左端点的函数值()i f xB ．只能是右端点的函数值1()i f x +C ．可以是该区间内的任一函数值()(i i f ξξ∈1[,]i i x x +）D ．以上答案均正确9．函数()sin(2)2f x x π=-的图象与函数()g x 的图象关于直线8x π=对称，则关于函数()y g x =以下说法正确的是（）A ．最大值为1，图象关于直线2x π=对称B ．在0,4π⎛⎫⎪⎝⎭上单调递减，为奇函数 C ．在3,88ππ⎛⎫-⎪⎝⎭上单调递增，为偶函数 D ．周期为π，图象关于点3,08π⎛⎫⎪⎝⎭对称 10．在ABC 中，若3,120AB BC C ==∠=，则AC =（） A ．1B ．2C ．3D ．411．已知,a b ∈R ，函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩，若函数()y f x ax b =--恰有三个零点，则（）A ．1,0a b <-<B ．1,0a b <->C ．1,0a b >-<D ．1,0a b >->12．设双曲线22221x y a b-=（0a >，0b >）的渐近线与抛物线21y x =+相切，则该双曲线的离心率等于（）AB ．2CD二、填空题13．设n S 是等差数列{}*()n a n N ∈的前n 项和，且141,7a a ==，则5______S =14．已知函数21,1()()1a x x f x x a x ⎧-+≤=⎨->⎩，函数()2()g x f x =-，若函数()()y f x g x =-恰有4个不同的零点，则实数a 的取值范围为______．15．某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查．已知该校一年级、二年级、三年级、四年级的本科生人数之比为4：5：5：6，则应从一年级本科生中抽取_______名学生．16．函数()f x =________．17．已知复数z=1+2i （i 是虚数单位），则|z|= _________ ． 18．计算：1726cos()sin 43ππ-+=_____． 19．若函数2()1ln f x x x a x =-++在(0,)+∞上单调递增，则实数a 的最小值是__________．20．已知双曲线1C：22221(0,0)x ya ba b-=>>的左、右焦点分别为1F、2F，第一象限内的点00(,)M x y在双曲线1C的渐近线上，且12MF MF⊥，若以2F为焦点的抛物线2C：22(0)y px p=>经过点M，则双曲线1C的离心率为_______．三、解答题21．已知a，b，c分别为ABC∆三个内角A,B,C的对边，3c asinC ccosA=-. (Ⅰ)求A；(Ⅱ)若a=2，ABC∆的面积为3，求b，c.22．如图，已知四棱锥P ABCD-的底面为等腰梯形，//AB CD,AC BD⊥,垂足为H，PH是四棱锥的高．（Ⅰ）证明：平面PAC⊥平面PBD;（Ⅱ）若AB6=,APB ADB∠=∠=60°,求四棱锥P ABCD-的体积．23．如图：在ABC∆中，10a=，4c=，5cos C=-.（1）求角A；（2）设D为AB的中点，求中线CD的长.24．在直角坐标系xOy中，直线l1的参数方程为2+,,x ty kt=⎧⎨=⎩（t为参数），直线l2的参数方程为2,,x mmmyk=-+⎧⎪⎨=⎪⎩（为参数）.设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．（1）写出C的普通方程；（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设()3:cos sin20lρθθ+=，M为l3与C的交点，求M的极径.25．已知(3cos ,cos )a x x =，(sin ,cos )b x x =，函数()f x a b =⋅.（1）求()f x 的最小正周期及对称轴方程；（2）当(,]x ππ∈-时，求()f x 单调递增区间.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【解析】【分析】由题意得在线性回归方程ˆy bx a =+中 1.23b =，然后根据回归方程过样本点的中心得到a 的值，进而可得所求方程．【详解】设线性回归方程ˆy bx a =+中，由题意得 1.23b =， ∴ 1.23ˆy x a =+．又回归直线过样本点的中心()4,5， ∴5 1.234a =⨯+， ∴0.08a =，∴回归直线方程为 1.2308ˆ.0yx =+．故选A ．【点睛】本题考查线性回归方程的求法，其中回归直线经过样本点的中心时解题的关键，利用这一性质可求回归方程中的参数，也可求样本数据中的未知参数，属于基础题．2．C解析：C 【解析】【分析】利用多项式乘法将式子展开,根据二项式定理展开式的通项即可求得2x 的系数. 【详解】根据二项式定理展开式通项为1C r n r r r n T a b -+=()()()66622111111x x x x x ⎛⎫++=++⋅+ ⎪⎝⎭则()61x +展开式的通项为16r rr T C x +=则()62111x x ⎛⎫++ ⎪⎝⎭ 展开式中2x 的项为22446621C x C x x ⎛⎫+⋅ ⎪⎝⎭ 则()62111x x ⎛⎫++ ⎪⎝⎭展开式中2x 的系数为2466151530C C +=+= 故选:C【点睛】本题考查了二项定理展开式的应用,指定项系数的求法,属于基础题.3．C解析：C 【解析】试题分析：根据不等式的基本性质知命题p 正确，对于命题q ，当,x y 为负数时22x y>不成立，即命题q 不正确，所以根据真值表可得,(p q p ∨∧q )为真命题，故选C.考点：1、不等式的基本性质；2、真值表的应用.4．C解析：C 【解析】【分析】由题意先解出集合A,进而得到结果．【详解】解：由集合A 得x 1≥, 所以{}A B 1,2⋂= 故答案选C. 【点睛】本题主要考查交集的运算，属于基础题．5．A解析：A 【解析】【分析】通过(0)1f =，和函数f(x)>0恒成立排除法易得答案A ．【详解】2||()x x f x e -=，可得f(0)=1,排除选项C,D;由指数函数图像的性质可得函数f(x)>0恒成立，排除选项B ，故选A 【点睛】图像判断题一般通过特殊点和无穷远处极限进行判断，属于较易题目．6．A解析：A 【解析】【分析】【详解】试题分析：如果两个平面有三个公共点，那么这两个平面重合或者是相交，故（1）不正确；两条异面直线不能确定一个平面，故（2）不正确；若M ∈α，M ∈β，α∩β=l ，则M ∈l ，故（3）正确；空间中，相交于同一点的三直线不一定在同一平面内（如棱锥的3条侧棱），故（4）不正确，综上所述只有一个说法是正确的，故选A ．7．B解析：B 【解析】1sin A ===cos A =,所以22212c c =+-2320,c c -+=求得1c =或 2.c若1c =，则三角形为等腰三角形，030,60A C B ===不满足内角和定理，排除. 【考点定位】本题考查正弦定理和余弦定理的应用，考查运算能力和分类讨论思想.当求出cos 2A =后，要及时判断出0030,60A B ==，便于三角形的初步定型，也为排除1c =提供了依据.如果选择支中同时给出了1或2，会增大出错率.8．C解析：C 【解析】【分析】【详解】根据近似替代的定义，近似值可以是该区间内的任一函数值()(i i f ξξ∈ []1,i i x x +），故选C ．9．B解析：B 【解析】【分析】先求出函数y=g(x)的解析式，再利用三角函数的图像和性质对每一个选项逐一分析判断. 【详解】设点P(x,y)是函数()y g x =图像上的任意一点，则点Q (x ,)4y π-+在函数y=f(x)的图像上，sin[2(-x+)]sin 2()42y x g x ππ=-=-=，对于选项A,函数y=g(x)的最大值为1，但是()012g π=≠±，所以图象不关于直线2x π=对称，所以该选项是错误的；对于选项B,()()g x g x -=-，所以函数g(x)是奇函数，解222+22k x k ππππ-≤≤得+44k x k ππππ-≤≤，)k Z ∈（,所以函数在0,4π⎛⎫⎪⎝⎭上单调递减，所以该选项是正确的；对于选项C,由前面分析得函数y=g(x)的增区间为3[+,]()44k k k Z ππππ+∈,且函数y=g(x)不是偶函数，故该选项是错误；对于选项D,函数的周期为π，解2,,2k x k x ππ=∴=所以函数图像的对称中心为,0)(k Z)2k π∈（,所以该选项是错误的. 故选：B 【点睛】本题主要三角函数的解析式的求法，考查三角函数的图像和性质，意在考查学生对这些知识的理解掌握水平和分析推理能力.10．A解析：A 【解析】余弦定理2222?cos AB BC AC BC AC C =+-将各值代入得2340AC AC +-=解得1AC =或4AC =-(舍去)选A.11．C解析：C 【解析】【分析】当0x <时，()(1)y f x ax b x ax b a x b =--=--=--最多一个零点；当0x 时，32321111()(1)(1)3232y f x ax b x a x ax ax b x a x b =--=-++--=-+-，利用导数研究函数的单调性，根据单调性画函数草图，根据草图可得．【详解】当0x <时，()(1)0y f x ax b x ax b a x b =--=--=--=，得1b x a=-；()y f x ax b =--最多一个零点；当0x 时，32321111()(1)(1)3232y f x ax b x a x ax ax b x a x b =--=-++--=-+-， 2(1)y x a x =+-'，当10a +，即1a -时，0y '，()y f x ax b =--在[0，)+∞上递增，()y f x ax b =--最多一个零点．不合题意；当10a +>，即1a >-时，令0y '>得[1x a ∈+，)+∞，函数递增，令0y '<得[0x ∈，1)a +，函数递减；函数最多有2个零点；根据题意函数()y f x ax b =--恰有3个零点⇔函数()y f x ax b =--在(,0)-∞上有一个零点，在[0，)+∞上有2个零点，如图：∴01b a <-且3211(1)(1)(1)032b a a a b ->⎧⎪⎨+-++-<⎪⎩，解得0b <，10a ->，310(116,)b a a >>-+∴>-．故选C ．【点睛】遇到此类问题，不少考生会一筹莫展.由于方程中涉及,a b 两个参数，故按“一元化”想法，逐步分类讨论，这一过程中有可能分类不全面、不彻底.12．D解析：D 【解析】由题意可知双曲线的渐近线一条方程为b y x a =，与抛物线方程组成方程组2,1b y xa y x ⎧=⎪⎨⎪=+⎩消y 得，2210,()40b b x x a a -+=∆=-=，即2()4b a =，所以e == D. 【点睛】双曲线22221x y a b-=（0a >，0b >）的渐近线方程为b y x a =±．直线与抛物线交点问题，直线与抛物线方程组方程组，当直线与抛物线对称轴平行时，直线与抛物线相交，只有一个交点．当直线与抛物线对称轴不平行时，当>0∆时，直线与抛物线相交，有两个交点．当0∆=时，直线与抛物线相切，只有一个交点．当∆<0时，直线与抛物线相离，没有交点．二、填空题13．25【解析】由可得所以解析：25 【解析】由141,7a a ==可得11,2,21n a d a n ===-，所以5(19)5252S +⨯==． 14．【解析】【分析】由函数把函数恰有个不同的零点转化为恰有4个实数根列出相应的条件即可求解【详解】由题意函数且函数恰有个不同的零点即恰有4个实数根当时由即解得或所以解得；当时由解得或所以解得综上可得：实解析：(]2,3【解析】【分析】由函数()2()g x f x =-，把函数()()y f x g x =-恰有4个不同的零点，转化为()1f x =恰有4个实数根，列出相应的条件，即可求解. 【详解】由题意，函数()2()g x f x =-，且函数()()y f x g x =-恰有4个不同的零点，即()1f x =恰有4个实数根，当1x ≤时，由11a x -+=，即110x a +=-≥，解得2=-x a 或x a =-，所以2112a a a a -≤⎧⎪-≤⎨⎪-≠-⎩，解得13a ；当1x >时，由2()1x a -=，解得1x a =-或1x a =+，所以1111a a ->⎧⎨+>⎩，解得2a >，综上可得：实数a 的取值范围为(]2,3.【点睛】本题主要考查了函数与方程的应用，其中解答中利用条件转化为()1f x =，绝对值的定义，以及二次函数的性质求解是解答的关键，着重考查了数形结合思想，以及推理与计算能力，属于中档试题.15．60【解析】【分析】采用分层抽样的方法从该校四个年级的本科生中抽取一个容量为300的样本进行调查的【详解】∵该校一年级二年级三年级四年级的本科生人数之比为4:5:5:6∴应从一年级本科生中抽取学生人解析：60 【解析】【分析】采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查的. 【详解】∵该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6， ∴应从一年级本科生中抽取学生人数为：4300604556⨯=+++.故答案为60.16．2+∞）【解析】分析：根据偶次根式下被开方数非负列不等式解对数不等式得函数定义域详解：要使函数有意义则解得即函数的定义域为点睛：求给定函数的定义域往往需转化为解不等式（组）的问题解析：[2，+∞）【解析】分析：根据偶次根式下被开方数非负列不等式，解对数不等式得函数定义域.详解：要使函数()f x 有意义，则2log 10x -≥，解得2x ≥，即函数()f x 的定义域为[2,)+∞.点睛：求给定函数的定义域往往需转化为解不等式（组）的问题.17．【解析】【分析】【详解】复数z=1+2i （i 是虚数单位）则|z|==故答案为解析：【解析】【分析】【详解】复数z=1+2i （i 是虚数单位），则|z|==．故答案为．18．【解析】【分析】利用诱导公式化简题目所给表达式根据特殊角的三角函数值求得运算的结果【详解】依题意原式【点睛】本小题主要考查利用诱导公式化简求值考查特殊角的三角函数值考查化归与转化的数学思想方法属于基 32+【解析】【分析】利用诱导公式化简题目所给表达式，根据特殊角的三角函数值求得运算的结果.【详解】依题意，原式17π26ππ2πcossin cos 4πsin 8π4343⎛⎫⎛⎫=+=+++ ⎪ ⎪⎝⎭⎝⎭π2πcos sin 43=+=. 【点睛】本小题主要考查利用诱导公式化简求值，考查特殊角的三角函数值，考查化归与转化的数学思想方法，属于基础题.利用诱导公式化简，首先将题目所给的角，利用诱导公式变为正角，然后转化为较小的角的形式，再利用诱导公式进行化简，化简过程中一定要注意角的三角函数值的符号.19．【解析】【分析】由函数单调递增可得导函数在区间内大于等于零恒成立根据分离变量的方式得到在上恒成立利用二次函数的性质求得的最大值进而得到结果【详解】函数在上单调递增在上恒成立在上恒成立令根据二次函数的解析：18【解析】【分析】由函数单调递增可得导函数在区间内大于等于零恒成立，根据分离变量的方式得到22a x x ≥-在()0,∞+上恒成立，利用二次函数的性质求得22x x -的最大值，进而得到结果.【详解】函数()21ln f x x x a x =-++在()0,∞+上单调递增 ()210a f x x x '∴=-+≥在()0,∞+上恒成立 22a x x ∴≥-在()0,∞+上恒成立令()22g x x x =-，0x > 根据二次函数的性质可知：当14x =时， ()max 18g x = 18a ∴≥，故实数a 的最小值是18本题正确结果：18 【点睛】本题考查根据函数在区间内的单调性求解参数范围的问题，关键是能将问题转化为导函数的符号的问题，通过分离变量的方式将问题转变为参数与函数最值之间的关系问题.20．【解析】【分析】由题意可得又由可得联立得又由为焦点的抛物线：经过点化简得根据离心率可得即可求解【详解】由题意双曲线的渐近线方程为焦点为可得①又可得即为②由联立①②可得由为焦点的抛物线：经过点可得且即解析：2+【解析】【分析】由题意可得00b y x a=，又由12MF MF ⊥，可得22200y x c +=，联立得0x a =，0y b =，又由F 为焦点的抛物线2C ：22(0)y px p =>经过点M ，化简得224ac 0c a --=，根据离心率c e a =，可得2410e e --=，即可求解．【详解】由题意，双曲线的渐近线方程为b y x a =±，焦点为()1,0F c -，()2,0F c ，可得00b y x a=，① 又12MF MF ⊥，可得00001y y x c x c ⋅=-+-，即为22200y x c +=，②由222a b c +=，联立①②可得0x a =，0y b =，由F 为焦点的抛物线2C ：22(0)y px p =>经过点M ，可得22b pa =，且2p c =，即有2224b ac c a ==-，即224ac 0c a --=由c e a=，可得2410e e --=，解得2e =+【点睛】本题考查了双曲线的几何性质——离心率的求解，其中根据条件转化为圆锥曲线的离心率的方程是解答的关键．求双曲线的离心率(或离心率的取值范围)，常见有两种方法：①求出a ，c 的值，代入公式c e a=；②只需要根据一个条件得到关于,,a b c 的齐次式，转化为,a c 的齐次式，然后转化为关于e 的方程(不等式)，解方程(不等式)，即可得e (e 的取值范围)．三、解答题21．(1)3A π=(2)b c ==2【解析】【分析】【详解】(Ⅰ)由sin cos c C c A =-及正弦定理得sin cos sin sin A C A C C -=由于sin 0C ≠，所以1sin 62A π⎛⎫-= ⎪⎝⎭，又0A π<<，故3A π=.(Ⅱ)ABC ∆的面积S =1sin 2bc A 故bc =4，而2222cos a b c bc A =+-故22c b +=8，解得b c ==222．（Ⅰ）证明见解析；（Ⅱ. 【解析】【分析】【详解】试题分析：（Ⅰ）因为PH 是四棱锥P-ABCD 的高．所以AC ⊥PH,又AC ⊥BD,PH,BD 都在平面PHD 内,且PH BD=H.所以AC ⊥平面PBD.故平面PAC ⊥平面PBD.（Ⅱ）因为ABCD 为等腰梯形，AB CD,AC ⊥.所以因为∠APB=∠ADR=600所以,HD=HC=1.可得等腰梯形ABCD 的面积为S=12所以四棱锥的体积为V=13x （33+ 考点：本题主要考查立体几何中的垂直关系，体积的计算．点评：中档题，立体几何题，是高考必考内容，往往涉及垂直关系、平行关系、角、距离、体积的计算．在计算问题中，有“几何法”和“向量法”．利用几何法，要遵循“一作、二证、三计算”的步骤，利用向量则能简化证明过程．本题（I ）较为简单，（II ）则体现了“一作、二证、三计算”的解题步骤．23．（1）4A π=；（2 【解析】【分析】（1）通过cos C 求出sin C 的值，利用正弦定理求出sin A 即可得角A ；（2）根据()sin sin B A C =+求出sin B 的值，由正弦定理求出边b ，最后在ACD ∆中由余弦定理即可得结果.【详解】（1）∵cos C =，∴sin C ===. 由正弦定理sin sin a c A C ==.得sin A =cos 0C =<，∴C 为钝角，A 为锐角，故4A π=.（2）∵()B A C π=-+，∴()sin sin sin cos cos sin B A C A C A C =+=+⎛=+= ⎝⎭. 由正弦定理得sin sin b a B A ==得b = 在ACD ∆中由余弦定理得：2222cos CD AD AC AD AC A =+-⋅⋅242222=+-⨯=，∴CD =. 【点睛】本题主要考查了正弦定理和余弦定理在解三角形中的应用，考查三角函数知识的运用，属于中档题.24．（1）()2240x y y -=≠（2【解析】（1）消去参数t 得1l 的普通方程()1:2l y k x =-；消去参数m 得l 2的普通方程()21:2l y x k=+. 设(),P x y ,由题设得()()212y k x y x k ⎧=-⎪⎨=+⎪⎩，消去k 得()2240x y y -=≠. 所以C 的普通方程为()2240x y y -=≠. （2）C 的极坐标方程为()()222cos sin 402π,πρθθθθ-=<<≠. 联立()()222cos sin 4,cos sin 0ρθθρθθ⎧-=⎪⎨+=⎪⎩得()cos sin 2cos sin θθθθ-=+.故1tan 3θ=-，从而2291cos ,sin 1010θθ==. 代入()222cos sin 4ρθθ-=得25ρ=，所以交点M【名师点睛】本题考查了极坐标方程的求法及应用，重点考查了转化与化归能力.遇到求曲线交点、距离、线段长等几何问题时，求解的一般方法是分别化为普通方程和直角坐标方程后求解，或者直接利用极坐标的几何意义求解.要结合题目本身特点，确定选择何种方程.25．(1) T π= ；26k x ππ=+（k Z ∈）. (2) 5(,]6ππ--，[,]36ππ-和2[,]3ππ 【解析】【分析】（1）化简得()1sin 262f x x π⎛⎫=++ ⎪⎝⎭，再求函数的周期和对称轴方程；（2）先求出函数在R 上的增区间为[,36k k ππππ-+] （k Z ∈），再给k 赋值与定义域求交集得解.【详解】解：（1）()23sin cos cos f x a b xx x =⋅=+ 111cos2sin 22262x x x π⎛⎫=++=++ ⎪⎝⎭ 所以()f x 的周期22T ππ==, 令262x k πππ+=+（k Z ∈），即26k x ππ=+（k Z ∈）所以()f x 的对称轴方程为26k x ππ=+（k Z ∈）. （2）令222262k x k πππππ-≤+≤+ （k Z ∈）解得36k x k ππππ-≤≤+ （k Z ∈），由于(],x ππ∈- 所以当1,0k =-或1时，得函数()f x 的单调递增区间为5,6ππ⎛⎤--⎥⎝⎦，,36ππ⎡⎤-⎢⎥⎣⎦和2,3ππ⎡⎤⎢⎥⎣⎦. 【点睛】本题主要考查三角恒等变换，考查三角函数的周期的求法和对称轴的求法，考查三角函数的单调区间的求法，意在考查学生对这些知识的理解掌握水平和分析推理能力.。

2019年桂平市第一中学高考数学选择题专项训练(一模)

2019年桂平市第一中学高考数学选择题专项训练（一模）抽选各地名校试卷，经典试题，有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。

第1 题：来源： 2019高考数学一轮复习第2章函数的概念与基本初等函数第4讲二次函数分层演练文若函数y＝x2－3x－4的定义域为[0，m]，值域为，则m的取值范围是( )A．[0，4] 【答案】D.二次函数图象的对称轴为x＝，且f＝－，f(3)＝f(0)＝－4，由图得m∈.第 2 题：来源：河北省衡水中学2018届高三数学上学期一轮复习周测试题理试卷及答案已知集合，则集合（）A． B． C. D．【答案】C第 3 题：来源：辽宁省六校2017_2018学年高一数学上学期期中试题试卷及答案下列函数是偶函数且在区间上为增函数的是（）【答案】D第 4 题：来源：黑龙江省鹤岗市第一中学2018_2019学年高二数学下学期第二次月考试题理（含解析）已知位学生得某次数学测试成绩得茎叶图如图，则下列说法正确的是( )A. 众数为7B. 极差为19C. 中位数为64.5D. 平均数为64 【答案】C【解析】【分析】根据茎叶图中的数据求得这组数据的众数、极差、中位数和平均数．【详解】根据茎叶图中的数据知，这组数据的众数为67，A错误；极差是75﹣57＝18，B错误；中位数是64.5，C正确；平均数为60（﹣3﹣1+1+2+7+7+12+15）＝65，D错误．故选：C．【点睛】本题考查了利用茎叶图求众数、极差、中位数和平均数的应用问题，是基础题．第 5 题：来源：山东省济南市2018届高三数学上学期12月考试试题理试卷及答案已知函数，则是（）A．奇函数，且在上单调递增 B．偶函数，且在上单调递增C．奇函数，且在上单调递减 D．偶函数，且在上单调递增【答案】D第 6 题：来源：湖北省荆州市沙市区2017_2018学年高二数学上学期第二次双周考试题理试卷及答案过点P(2，1）作直线交正半轴于两点，当取到最小值时，则直线的方程是（）A. B.C. D.【答案】A第 7 题：来源：山东省泰安第四中学2018_2019学年高一数学下学期2月月考试题直线2x-y=0与圆C:(x-2)2+(y+1)2=9相交于A、B两点,则△ABC(C为圆心)的面积等于( )(A)2 (B)2 (C)4(D)4【答案】A 解析:圆C的圆心C(2,-1),半径r=3,C到直线2x-y=0的距离d==, ∴|AB|=2=4, ∴S△ABC=×4×=2. 故选A.第 8 题：来源： 2017届陕西省西安市高三数学下学期第二次模拟考试试题试卷及答案理已知向量==,若,则的最小值为（）(B) (C) (D)(A)【答案】D第 9 题：来源：黑龙江省鹤岗市第一中学2018_2019学年高一数学下学期期末考试试题理下列命题正确的是（）A.有两个面平行，其余各面都是四边形的几何体叫棱柱。

2019年桂平兴桂中学高考数学选择题专项训练(一模)

2019年桂平兴桂中学高考数学选择题专项训练（一模）抽选各地名校试卷，经典试题，有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。

第 1 题：来源：江西省上高县2017届高三数学下学期开学考试（第七次）试题试卷及答案理若平面内共线的A、B、P三点满足条件，，其中{an}为等差数列，则a2008等于（）A． 1 B．﹣ 1 C．D．【答案】C第 2 题：来源：黑龙江省大庆实验中学2018_2019学年高二数学下学期第二次月考试题文（含解析）已知，则“”是“”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B【解析】试题分析：或,所以是的必要非充分条件.故选B.考点：充分必要条件第 3 题：来源：重庆市六校联考高一（上）期末数学试卷（含答案解析）已知函数f（x）=，若f（﹣1）=f（1），则实数a的值为（）A．1 B．2 C．0 D．﹣1【答案】B【解答】解：∵函数f（x）=，f（﹣1）=f（1），∴f（﹣1）=1﹣（﹣1）=2，f（1）=a，∵f（﹣1）=f（1），∴a=2．第 4 题：来源：江西省吉安市新干县2018届高三数学上学期第一次月考试题理试卷及答案若“”是“”的充分不必要条件，则的取值范围是A． B． C．D．【答案】A第 5 题：来源：广东省第二师范学院番禺附属中学2018_2019学年高一数学下学期期中试题一个几何体的三视图及其尺寸如图(单位:),则该几何体的表面积为( )A．B．C．D．【答案】A第 6 题：来源：黑龙江省双鸭山市第一中学2019届高三数学上学期第一次月考试题理（含解析）已知命题，命题,则（）A. 命题是假命题B. 命题是真命题C. 命题是真命题D. 命题是假命题【答案】C【详解】当x=10时，x-2=10-2=8，lg10=1，则不等式x-2＞lgx成立，即命题q是真命题，当x=0时，x2＞0不成立，即命题q是假命题，则命题p∧（￢q）是真命题，第 7 题：来源：江西省南昌市第二中学2018_2019学年高二数学上学期期中试题理分别是双曲线的左右焦点，过的直线与双曲线的左右两支分别交于两点．若为等边三角形，则的面积为（）A. 8B.C.D.16【答案】C第 8 题：来源：河北省曲周县一中2018_2019学年高二数学12月月考试题理在正方体中分别是和的中点，则异面直线与所成角的余弦值为（）A．0 B．C. D．【答案】D第 9 题：来源：四川省成都市龙泉驿区第一中学校2019届高三数学12月月考试题理已知集合，，则A∩B=（）A. B. C. （0，1] D. （0，3]【答案】D【解析】由解得，所以，由解得，所以，故，选D.第 10 题：来源：安徽省蚌埠市2017_2018学年高二数学上学期期中试题理试卷及答案在正方体中，分别为棱的中点，则在空间中与三条直线都相交的直线有A．无数条 B．３条Ｃ．１条Ｄ． 0条【答案】 A第 11 题：来源：云南省玉溪市2017_2018学年高二数学上学期第二次月考试题理试卷及答案经过椭圆的左焦点且斜率为的直线交椭圆于两点，则（）10 【答案】.D第 12 题：来源：陕西省黄陵县2017_2018学年高二数学上学期开学考试试题（重点班，含解析）设，则等于( )A. 4B.C. －D. －【答案】D【解析】∵f(tanx)＝tan2x ＝，∴f(2)＝＝－.本题选择D 选项.第 13 题：来源：四川省广元市2018_2019学年高一数学下学期期中试题等差数列，，，则当为何值时，达到最大值．A ．8B ．7C ． 6D ． 9 【答案】C第 14 题：来源：福建省福州市八县（市）一中2018_2019学年高一数学下学期期末联考试题将某选手的7个得分去掉1个最高分，去掉1个最低分，5个剩余分数的平均分为21，现场作的7个分数的茎叶图后来有1个数据模糊，无法辨认，在图中以x 表示：1 7 7 249x则5个剩余分数的方差为( )A. B. C ．36 D.【答案】B第 15 题：来源：浙江省温州市十校联合体高一（上）期末数学试卷（含答案解析）若集合P={y|y ≥0}，P ∩Q=Q ，则集合Q 不可能是（）A ．{y|y=x2，x ∈R}B ．{y|y=2x ，x ∈R}C ．{y|y=lgx ，x ＞0}D ．∅ 【答案】C 【解答】解：∵集合P={y|y ≥0}，P ∩Q=Q ， ∴Q ⊆P∵A={y|y=x2，x ∈R}={y|y ≥0}，满足要求 B={y|y=2x ，x ∈R}={y|y ＞0}，满足要求 C={y|y=lgx ，x ＞0}=R ，不满足要求 D=∅，满足要求第 16 题：来源：广东省湛江市2016-2017学年高一数学上学期期末调研考试试题试卷及答案已知函数，则A．1 B．2 C．3D．4【答案】B第 17 题：来源：江西省奉新县2018届高三数学上学期第四次月考试题理试卷及答案已知直线x+y﹣k=0（k＞0）与圆x2+y2=4交于不同的两点A、B，O是坐标原点，且有，那么k的取值范围是（）A． B． C． D．【答案】C第 18 题：来源：辽宁省实验中学分校2016-2017学年高二数学上学期期末考试试题理试卷及答案已知上是减函数，则的取值范围是（）A. B. C. D.【答案】C第 19 题：来源：山西省山西大学附中2018_2019学年高二数学下学期2月模块诊断试题理已知，则是的( )A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A第 20 题：来源：广东省惠州市惠城区2018届高三数学9月月考试题理试卷及答案若，则的大小关系A． B． C． D ．【答案】D第 21 题：来源： 2017年辽宁省大连市高考数学一模试卷（理科）含答案解析在平面内的动点（x，y）满足不等式，则z=2x+y的最大值是（）A．6 B．4 C．2 D．0【答案】A【考点】简单线性规划．【分析】根据约束条件画出可行域，再利用几何意义求最值，只需求出直线z=x+y的最优解，然后求解z 最大值即可．【解答】解：根据不等式，画出可行域，由，可得x=3，y=0平移直线2x+y=0，∴当直线z=2x+y过点A（3，0）时，z最大值为6．故选：A．第 22 题：来源：广东省深圳市普通高中2017_2018学年高二数学下学期4月月考试题6201805241398一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如下图所示,则该几何体的俯视图为（）【答案】C第 23 题：来源：福建省莆田市第二十四中学2016-2017学年高一数学上学期期末考试试题试卷及答案无论取何值，函数的图象必过（）点A． B． C． D．【答案】C第 24 题：来源：山东省泰安市三校2016_2017学年高一数学上学期期中联考试题试卷及答案函数y＝ax+2 (a＞0，且a≠1) 的图象经过的定点坐标是( )A．(0，1) B．(2，1) C．(－2，0) D．(－2，1)【答案】D第 25 题：来源：河北省唐山市2017_2018学年高一数学上学期期中试题要得到函数的图象，则只需将函数的图象A．向右平移1个单位 B．向左平移1个单位C．向右平移个单位 D．向左平移个单位【答案】C第 26 题：来源：辽宁省阜新二高2017_2018学年高二数学下学期期中试题理以点、、为顶点的三角形是以角C为直角的直角三角形，满足条件的三角形个数为（）A、 B、 C、 D、【答案】A第 27 题：来源：重庆市巴蜀中学2018_2019学年高二数学上学期期中复习试题已知，满足，的最小值、最大值分别为，，且对上恒成立，则的取值范围为（）A． B． C． D．【答案】B【解析】作出表示的平面区域（如图所示），显然的最小值为0，当点在线段上时，；当点在线段上时，；即，；当时，不等式恒成立，若对上恒成立，则在上恒成立，又在单调递减，在上单调递增，即，即．第 28 题：来源：山东省山东师范大学附属中学2019届高三数学上学期第五次模拟考试试题理已知复数满足，则A. B. C. D.【答案】C第 29 题：来源：福建省莆田市莆田第六中学2018届高三数学下学期第三次模拟考试试卷文（含解析）已知双曲线：与双曲线：，给出下列说法，其中错误的是（）A. 它们的焦距相等B. 它们的焦点在同一个圆上C. 它们的渐近线方程相同D. 它们的离心率相等【答案】D第 30 题：来源：福建省漳州市八校2017届高三数学下学期2月联考试题理已知平面向量、、为三个单位向量，且，满足，则的最大值为（）A．1 B． C． D．2【答案】B.第 31 题：来源：黑龙江省友谊县红兴隆管理局2016_2017学年高二数学下学期期中试题试卷及答案理已知某离散型随机变量X服从的分布列如图，则随机变量X的方差D(X)等于( )X 0 1P m 2mA．B．C．D．【答案】.B、第 32 题：来源：河南省兰考县2016_2017学年高二数学下学期期末考试试题试卷及答案理下列函数中，既是偶函数又在区间(0,+ ∞)上单调递减的是( )A. B. C. D.【答案】 C第 33 题：来源： 2017年江西省南昌市六校高二数学5月联考试题（理）及答案以图中的8个点为顶点的三角形的个数是（）A.56个B.48个C.45个D.42个【答案】D第 34 题：来源：浙江省台州市书生中学2018_2019学年高一数学下学期起始考试试题若实数满足，求的最小值为（）【答案】D第 35 题：来源：甘肃省武威市2016_2017学年高二数学下学期期末考试试题文试卷及答案圆ρ= (cosθ+sinθ)的圆心的坐标是( )A.(1, )B.( , )C.( , )D.(2, )【答案】A 解析 : 圆的方程可化为ρ=2cos(θ- ).这是ρ=2rcos(θ-θ 0 )的形式,它的圆心为O 1 (r,θ 0 ),本题也可化为直角坐标方程求解.答案 : A第 36 题：来源：云南省玉溪市峨山彝族自治县第一中学2016-2017学年高二数学上学期期末考试试题试卷及答案理某几何体的三视图如图所示，则它的体积是（）A. B.C. D.【答案】 A第 37 题：来源：云南省玉溪一中2018_2019学年高二数学下学期第一次月考试题理已知函数f（x）＝xlnx﹣aex（e为自然对数的底数）有两个极值点，则实数a的取值范围是（）A． B． C．D.【答案】A第 38 题：来源：湖北省襄阳市2017届高三第三次适应性考试数学试题（理）含答案在内随机取出两个数，则这两个数满足的概率为（）A． B．C． D．【答案】B第 39 题：来源：辽宁省抚顺市2016_2017学年高一数学上学期期中试题试卷及答案若函数y=x2﹣6x+8的定义域为x∈，值域为，则a的取值范围是（）A．（1，3） B．（1，5） C．（3，5） D．【答案】D第 40 题：来源：福建省漳州市八校2017届高三数学上学期期末联考试题理试卷及答案已知双曲线的右顶点为E，过双曲线的左焦点且垂直于x轴的直线与该双曲线相交于A、B两点，若∠AEB=90°，则该双曲线的离心率是（）A． B．2 C．或2 D．不存在【答案】．B第 41 题：来源：广东省中山市第一中学2017_2018学年高一数学上学期第一次段考试题（含解析）设集合，则图中阴影部分表示的集合是A. B. C. D.【答案】A【解析】略第 42 题：来源：青海省西宁市2016_2017学年高二数学下学期期中试题理某班新年联欢会原定的5个节目已排成节目单, 开演前又增加了两个新节目. 如果将这两个新节目插入原节目单中, 那么不同插法的种数为（）A．42 B．48 C． 96 D． 124 【答案】A第 43 题：来源： 2017年普通高等学校招生全国统一考试数学试题文（全国卷1，参考解析）已知F是双曲线C：x2-=1的右焦点，P是C上一点，且PF与x轴垂直，点A的坐标是(1,3).则△APF 的面积为A． B．C． D．【答案】D【解析】由得，所以，将代入，得，所以，又A的坐标是(1,3)，故APF的面积为，选D.第 44 题：来源：江西省吉安市新干县2018届高三数学上学期第一次月考试题理试卷及答案已知函数，则函数的大致图像为（）【答案】A第 45 题：来源：河北省沧州市2017_2018学年高一数学上学期第二次月考试题试卷及答案已知，函数与的图象可能是（）A. B. C.D.【答案】C第 46 题：来源：重点班2017届高三数学一轮复习阶段检测试题一理试卷及答案二f(x)=sin(ωx+) (ω>0,||<)的最小正周期是π,若其图象向左平移个单位后得到的函数为奇函数,则函数f(x)的图象( )(A)关于点(,0)对称(B)关于点(,0)对称(C)关于直线x=对称(D)关于直线x=对称【答案】C解析:因为f(x)最小正周期是π,所以ω==2,f(x)=sin(2x+),若其图象向左平移个单位,则得g(x)=sin(2x++),若g(x)=sin(2x++)为奇函数,则+=kπ,=kπ-,因为||<,所以=-,所以f(x)=sin(2x-),则关于直线x=对称.第 47 题：来源： 2017年高中数学模块综合测评1（含解析）新人教A版选修2_3若随机变量ξ服从正态分布N(0,1)，已知P(ξ＜－1.96)＝0.025，则P(|ξ|＜1.96)＝( )A．0.025 B．0.050 C．0.950 D．0.975【答案】C第 48 题：来源：湖南省湘潭市2019届高三数学上学期第一次模拟检测试题理（含解析）若满足约束条件，则的最大值是（）A. B. C. D. 3【答案】D【详解】画出可行域，如图所示，表示可行域内一点与点连线的斜率，由图可知，当，时，取得最大值3.【点睛】本题主要考查简单的线性规划问题，只需掌握目标函数的几何意义，即可求解，属于基础题型.第 49 题：来源： 2017年普通高等学校招生全国统一考试数学试题文（全国卷1，参考解析）△ABC的内角A、B、C的对边分别为a、b、c。

2019年广西贵港桂平市金田中学高考数学选择题专项训练(一模)

2019年广西贵港桂平市金田中学高考数学选择题专项训练（一模）抽选各地名校试卷，经典试题，有针对性的应对高考数学考点中的难点、重点和常规考点进行强化训练。

第 1 题：来源：安徽省合肥一六八中学2018_2019学年高二数学下学期期中试题理（含解析）三角形的面积为，（为三角形的边长，为三角形的内切圆的半径）利用类比推理，可以得出四面体的体积为 ( )A. （为底面边长）B. （分别为四面体四个面的面积，为四面体内切球的半径）C. （为底面面积，为四面体的高）D. （为底面边长，为四面体的高）【答案】B【解析】【分析】根据类比规则求解.【详解】平面类比到空间时，边长类比为面积，内切圆类比为内切球，调节系数也相应变化，因此四面体的体积为（分别为四面体四个面的面积，为四面体内切球的半径），选B.【点睛】本题考查类比推理，考查基本分析推理能力，属基本题.第 2 题：来源：湖北省武汉市2017届高三四月调研测试数学试题（理）含答案若等差数列的前项和满足，，则A. -1B. 0C. 1D. 3【答案】B第 3 题：来源：内蒙古包头市第四中学2016_2017学年高二数学上学期期中试题已知，为单位向量，当的夹角为时，在上的投影为（）A. B. C.D.【答案】Ｂ第 4 题：来源：山东省禹城市2017_2018学年高二数学上学期期中试题试卷及答案若圆与轴相切于点，与轴的正半轴交于两点，且，则圆的标准方程是（）A. B.C. D.【答案】 C第 5 题：来源：吉林省长春汽车经济技术开发区六中2017_2018学年高二数学上学期期末考试试题文已知椭圆则 ( )A．与顶点相同. B．与长轴长相同.C．与短轴长相同. D．与焦距相等.【答案】．D试题分析：中；中与焦距相等.第 6 题：来源：广东省深圳市红岭中学2019届高三数学第四次模拟考试试题理在平面直角坐标系xOy中，P是椭圆＋＝1上的一个动点，点A(1,1)，B(0，－1)，则|PA|＋|PB|的最大值为A．2 B．3 C．4 D．5 【答案】D第 7 题：来源： 2017年广东省汕头市高考数学一模试卷（文科）含答案命题“ax2﹣2ax+3＞0恒成立”是假命题，则实数a的取值范围是（）A．0＜a＜3 B．a＜0或a≥3 C．a＜0或a＞3 D．a≤0或a≥3【答案】B【考点】命题的真假判断与应用．【分析】命题“ax2﹣2ax+3＞0恒成立”是假命题，即存在x∈R，使“ax2﹣2ax+3≤0，分类讨论即可．【解答】解：命题“ax2﹣2ax+3＞0恒成立”是假命题，即存在x∈R，使“ax2﹣2ax+3≤0，当a=0时，不符合题意；当a＜0时，符合题意；当a＞0时，△=4a2﹣12a≥0⇒a≥3，综上：实数a的取值范围是：a＜0或a≥3．故选：B【点评】本题考查了命题的真假的应用，转化是关键，属于基础题．第 8 题：来源：湖南省岳阳县、汨罗市2017_2018学年高二数学10月月考试题理试卷及答案设命题：，则为（）（A）（B）（C）（D）【答案】 C第 9 题：来源：山西省2017届高三3月联考数学（理）试题 Word版含答案《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都是直角三角形的四面体称之为鳌膳.如图，网格纸上正方形小格的边长为1，图中粗线画出的是某几何体毛坯的三视图，第一次切削，将该毛坯得到一个表面积最大的长方体，第二次切削沿长方体的对角面刨开，得到两个三棱柱，第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳌膳和两个阳马，则阳马和鳌膳的体积之比为A. 3：1B. 2：1C. 1:1D.1:2【答案】B第 10 题：来源：河南省太康县2016-2017学年高一数学下学期开学考试试题试卷及答案该程序运行后，变量y的值是( )A．3 B．6C．9 D．27【答案】B第 11 题：来源：山东省济南市2017_2018学年高二数学上学期开学考试试题试卷及答案在△ABC中，若，则A等于（）A． B． C． D．【答案】D第 12 题：来源：内蒙古包头市2016_2017学年高一数学下学期期末考试试题理试卷及答案如图，四棱锥S—ABCD的底面为正方形，SD底面ABCD，则下列结论中错误的是A．AC⊥SBB．AB∥平面SCDC．SA与平面SBD所成的角等于SC与平面SBD所成的角D．AB与SC所成的角等于DC与SA所成的角【答案】D第 13 题：来源： 2019年普通高等学校招生全国统一考试文科数学（全国卷Ⅱ）（含答案）文档已知a∈（0，），2sin2α=cos2α+1，则sinα=A． B．C． D．【答案】B第 14 题：来源：湖北省部分重点中学2018届高三数学起点考试试题试卷及答案理某几何体的三视图如图所示(单位：)，则该几何体的体积等于( )A．B．C．D．【答案】D第 15 题：来源：吉林省通化市第十四中学2018_2019学年高一数学上学期期末考试试题与向量平行的单位向量为（）A． B．C． D．【答案】D【解析】，所求单位向量为．故选D．考点：单位向量，向量平行．第 16 题：来源：广西桂林市2016_2017学年高二数学下学期期中试题试卷及答案理设△ABC的内角A,B,C的对边分别为,若,,,且,则( )A. B.2 C.D.3【答案】B第 17 题：来源：河南省郑州市第一中学2017届高三数学上学期期中试题理.如果函数在区间I上是增函数，而函数在区间I上是减函数，那么称函数是区间I上“缓增函数”，区间I叫做“缓增区间”．若函数是区间I上“缓增函数”，则“缓增函数区间”I为（）A． B． C．D．【答案】D考点：1、函数的单调性；2、导数的应用.【方法点晴】本题考查函数的单调性、导数的应用，涉及函数与方程思想、数形结合思想和转化化归思想，考查逻辑思维能力、等价转化能力、运算求解能力，综合性较强，属于较难题型. 首先利用数形结合思想由在上是增函数，在上是减函数的缓增区间为．第 18 题：来源：江西省横峰县2017_2018学年高一数学上学期第一次月考试题试卷及答案下列各组函数的图象相同的是（）A． B．与g（x）=x+2C． D．【答案】D第 19 题：来源：江西省吉安市新干县2016_2017学年高二数学下学期第一次段考试题（1、2班）试卷及答案过两点A（1，），B（4，）的直线的倾斜角为（）A． B. C. D.【答案】A第 20 题：来源：辽宁省辽河油田第二高级中学2019届高三数学上学期期中试题理已知全集，，，则图中阴影部分表示的集合是（）A ．B ．C ．D ．【答案】C第 21 题：来源：内蒙古包头市2017_2018学年高二数学上学期期中试题理试卷及答案下列命题中正确的是( )A．若p∨q为真命题，则p∧q为真命题B．“x＝5”是“x2－4x－5＝0”的充分不必要条件C．命题“若x<－1，则x2－2x－3>0”的否定为：“若x≥－1，则x2－2x－3≤0”D．已知命题p：∃x∈R，x2＋x－1<0，则：∃x∈R，x2＋x－1≥0【答案】B第 22 题：来源：辽宁省六校2018届高三数学上学期期初联考试题试卷及答案理执行如图所示的程序框图，则输出的结果为（）【答案】B第 23 题：来源： 2017届山东省枣庄市高三数学4月阶段性自测试题试卷答案下列说法中正确的是（）A．“a＞b”是“log2a＞log2b”的充要条件B．若函数y=sin2x 的图象向左平移个单位得到的函数图象关于y轴对称C．命题“在△ABC 中，，则”的逆否命题为真命题D．若数列{an}的前n项和为Sn=2n，则数列{an}是等比数列【答案】B第 24 题：来源：安徽省滁州市定远县育才学校2018_2019学年高一数学下学期第一次月考试题（普通班）已知α是第二象限角，sinα＋cosα＝，则cos 2α等于( )A．－ B．－ C． D．【答案】A第 25 题：来源：甘肃省会宁县第一中学2019届高三数学上学期第三次月考试题理已知函数f（x）=x3﹣x2+cx+d无极值，则实数c的取值范围为（）A．B．C．D．【答案】C第 26 题：来源：重庆市巴蜀中学2018_2019学年高一数学上学期期中复习试题已知函数，若，则实数（）A． B．2 C．3D．或3【答案】D【解析】由题意得，∴．又，∴，即，解得或．故选D．第 27 题：来源：江西省南昌市2017_2018学年高二数学上学期第三次月考试题理试卷及答案点是曲线上的点，是直线上的点，则的最小值为（）A. B. C. D.【答案】B第 28 题：来源：广西南宁市2017_2018学年高一数学上学期期中试题试卷及答案如图，阴影部分表示的集合是（）A． B． C． D．【答案】A 解析：阴影部分是集合A之外部分与集合B的交集第 29 题：来源：黑龙江省大庆铁人中学2018_2019学年高二数学下学期期中试题理已知（为自然对数的底数），则下列说法错误的是A．函数的图象关于轴对称 B.函数的极小值为4C．函数在上为增函数 D.函数的值域为【答案】C第 30 题：来源：江西省南昌市2018届高三数学第二轮复习测试题（二）理（含解析）已知函数，若和图象有三条公切线，则的取值范围是（）A. B. C. D.【答案】A【解析】【分析】设公切线与分别相切于点,对，，根据题意可得，即，解得，代入化简得.【详解】设公切线与分别相切于点,,，解得，代入化简得，函数在区间递增，在区间递减，在区间递增，且，可知无上界，即时，方程有三解，故选A.【点睛】本题考查利用导数求公切线的斜率，属难题.第 31 题：来源：四川省德阳市三校2018届高三数学联合测试试题理试卷及答案执行如图所示的程序框图，若输入，输出的 1.75，则空白判断框内应填的条件为A．＜1B．＜0.5C．＜0.2D．＜0.1【答案】B第 32 题：来源：内蒙古巴彦淖尔市2018届高三数学12月月考试题理试卷及答案平面向量满足，在上的投影为，则的模为（）A. 2B. 4C. 8D.16【答案】B第 33 题：来源：安徽省2017_2018学年高二数学上学期期中试题理在平面直角坐标系中，定义d（P，Q）＝|x1－x2|＋|y1－y2|为点P（x1，y1）到点Q（x2，y2）的“折线距离”.在这个定义下，给出下列命题：①到原点的“折线距离”等于1的点的轨迹是一个正方形；②到原点的“折线距离”等于1的点的轨迹是一个圆；③到M（－1，0），N（1，0）两点的“折线距离”相等的点的轨迹方程是x＝0；④到M（－1，0），N（1，0）两点的“折线距离”之差的绝对值为1的点的轨迹是两条平行线.其中真命题有（）A．1个B．2个C．3个D．4个【答案】C第 34 题：来源： 2016-2017学年内蒙古集宁一中高二数学上学期期末考试试题试卷及答案理等比数列的前项和为，已知，，则（）A. B. C. D.【答案】C第 35 题：来源：河南省洛阳市2017届高考第二次统一考试（3月）数学（文）含答案已知均为非零向量，，则的夹角为A. B. C. D.【答案】A第 36 题：来源：江西省南昌市第二中学2018_2019学年高一数学上学期第一次月考试题已知集合，则满足条件的集合C的个数为A.1B.2C.3D.4【答案】D第 37 题：来源：陕西省黄陵县2018届高三数学上学期期中试题（高新部）理试卷及答案一束光线自点P(1,1,1)发出，被xOy平面反射，到达点Q(3,3,6)被吸收，那么光线自点P到点Q所走的距离是( )A． B．12 C． D．57【答案】C第 38 题：来源：甘肃省玉门一中2019届高三数学11月月考试题理如图所示，程序框图(算法流程图)的输出结果是( )A．3 B．4 C．5 D．8（第 5 题图）【答案】B第 39 题：来源：安徽省滁州市全椒县2016_2017学年高二数学上学期期末考试试题理已知复数满足,其中为虚数单位,则的共轭复数为( )A. B. C. D.【答案】D第 40 题：来源：黑龙江省牡丹江市2016_2017学年高一数学3月月考试题．若等差数列的公差为，且是与的等比中项，则该数列的前项和取最小值时，的值等于（） A.B. C. D.【答案】C第 41 题：来源：广东省深圳市普通高中2017_2018学年高二数学下学期4月月考试题5201805241397从{1,2,3,4,5}中随机选取一个数为a ，从{1,2,3}中随机选取一个数为b ，则的概率是（）A. B. C.D.【答案】D第 42 题：来源：辽宁省六校2017_2018学年高一数学上学期期中试题试卷及答案设集合，则下列对应中不能构成到的映射的是（）A. B.C. D.【答案】B第 43 题：来源：湖北省黄冈市某校2018_2019学年高二数学4月月考试题理设抛物线C ：y2＝2px(p ＞0)的焦点为F ，点M 在C 上，|MF|＝5.若以MF 为直径的圆过点(0,2)，则C 的方程为( )A ．y2＝4x 或y2＝8xB ．y2＝2x 或y2＝8xC ．y2＝4x 或y2＝16xD ．y2＝2x 或y2＝16x 【答案】C第 44 题：来源：内蒙古开来中学2018_2019学年高一数学5月月考（期中）试题理已知圆C的半径为2,圆心在x轴的正半轴上,直线3x+4y+4=0与圆C相切,则圆C的方程为( ).A. x2+y2-2x-3=0B. x2+y2+4x=0C. x2+y2+2x-3=0D. x2+y2-4x=0【答案】D【解析】本题考查圆的方程及直线与圆的位置关系,属于中档题.设圆C的圆心为(a,0),(a>0),因为直线3x+4y+4=0与圆C相切,而圆C的半径为2,所以=2,解得a=2,所以圆C的方程为(x-2)2+y2=4,即x2+y2-4x=0,故选D.第 45 题：来源：湖南省桃江县第一中学2018_2019学年高二数学下学期期中试题理.函数的部分图象大致为（）【答案】A第 46 题：来源： 2019高中数学第二章数列单元测试（一）新人教A版必修5已知等差数列的公差且，，成等比数列，则等于（）A． B． C．D．【答案】C【解析】因为，所以．所以．所以．故选C．第 47 题：来源：湖北省宜城市2016_2017学年高二数学3月月考试题理椭圆mx2+ny2+mn=0（m＜n＜0）的焦点坐标是（）A. B. C. D.【答案】C第 48 题：来源：福建省厦门外国语学校2019届高三数学11月月考试题理将函数y＝sin(x＋)的图象上各点的纵坐标不变，横坐标缩短到原来的倍，再向右平移个单位，所得到的图象解析式是（）A． B． C． D．【答案】A第 49 题：来源：浙江省东阳市2016_2017学年高一数学下学期期中试题试卷及答案已知函数，若存在，对于任意，不等式都成立，则实数a的取值范围是（）A． B．C．D．【答案】A第 50 题：来源：贵州省仁怀市2015-2016学年高一数学11月月考试题试卷及答案设偶函数在上是减函数，且，则不等式的解集是（A）（B）（C）（D）【答案】C。

广西壮族自治区贵港市桂平社坡高级中学高一数学理模拟试题含解析

广西壮族自治区贵港市桂平社坡高级中学高一数学理模拟试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知圆上任意一点M关于直线x+y=0的对称点N也在圆上，则m的值为（）A．-1 B．1C．-2 D．2参考答案：D2. （5分）某几何体的三视图如图，则该几何体的表面积为（）A．24 B．36 C．48 D．60参考答案：C考点：由三视图求面积、体积．专题：计算题；空间位置关系与距离．分析：三视图复原的几何体是底面为侧视图的三棱柱，高为4，根据三视图的数据，求出几何体的表面积．解答：三视图复原的几何体是底面为侧视图的三棱柱，高为4，所以三棱柱的表面积为：S底+S侧=2××4×3+2×（3+4+5）×3=48故选：C．点评：本题考查由三视图求几何体的面积、体积，考查对三视图的理解与应用，本题解题的关键是用三视图中的数据还原出实物图的数据，再根据相关的公式求表面积与体积，三视图的投影规则是：“主视、俯视长对正；主视、左视高平齐，左视、俯视宽相等”，本题是一个基础题．3. 已知幂函数的图像过点,则的值为( )A．B．C．D．参考答案：A略4. 与角终边相同的角的集合是A. B．C. D.参考答案：A5. 函数＝ln x＋2x－8的零点所在区间是( )A． (0,1) B． (1,2) C． (2,3) D．(3,4)参考答案：D6. 设M是△ABC边BC上任意一点，N为AM上一点且AN=2NM，若，则λ+μ=（）A．B．C．1 D．参考答案：B【考点】平面向量的基本定理及其意义．【专题】平面向量及应用．【分析】利用平面向量基本定理，用、表示出、，从而得出结论．【解答】解：如图所示，∵M是△ABC边BC上任意一点，设=m+n，∴则m+n=1，又∴AN=2NM，∴=，∴==m+n=λ+μ，∴λ+μ=（m+n）=．故选：B．【点评】本题考查了平面向量基本定理的应用问题，解题的关键是用、表示出向量，属于基础题．7. 设P=log23，Q=log32，R=log2(log32)，则 ( )A.Q＜R＜PB.P＜R＜QC. R＜Q＜PD.R＜P＜Q参考答案：C8. 已知集合A={﹣1，0，1，2，3}，B={x|（x+1）（x﹣2）＜0，x∈Z}，则A∩B=（）A．{1} B．{0，1} C．{﹣1，0，1，2} D．{﹣1，0，1，2，3}参考答案：B【考点】交集及其运算．【分析】直接解一元二次不等式化简集合B，再由交集运算性质得答案．【解答】解：∵A={﹣1，0，1，2，3}，B={x|（x+1）（x﹣2）＜0，x∈Z}={0，1}，∴A∩B={﹣1，0，1，2，3}∩{0，1}={0，1}．故选：B．9. 若圆台的上、下底面半径的比为3∶5，则它的中截面分圆台上、下两部分面积之比为（）A．3∶5 B．9∶25 C．5∶ D．7∶9参考答案：D略10. 若函数 f（x）=log a x（0＜a＜1）在区间上的最大值是最小值的2倍，则a的值为（）A．B．C．D．参考答案：B【考点】对数函数的值域与最值．【专题】函数的性质及应用．【分析】利用对数函数的单调性确定最大值和最小值，利用条件建立方程即可求a．【解答】解：∵0＜a＜1，∴对数函数 f（x）=log a x在上单调递减，∴最大值为f（a）=log a a=1，最小值为f（2a）=log a2a，∵f（x）在区间上的最大值是最小值的2倍，∴f（a）=2f（2a），即1=2log a2a，∴log a2a=，即，∴，解得a=，故选：B．【点评】本题主要考查对数函数的运算和求值，利用对数函数的单调性确定函数的最大值和最小值是解决本题的关键，比较基础．二、填空题:本大题共7小题,每小题4分,共28分11. 当时，函数取得最大值，则．参考答案：略12. 设都是锐角，且，则_________。