红绿灯的时间设置问题
红绿灯中的数学奥秘
红绿灯中的数学奥秘
“妈妈,怎么才挪动这么点路又红灯了?”我说,“这红绿灯是不是坏掉了!”
“玥玥,红绿灯肯定没坏掉,只是现在车子很多,我们还无法过十字路口。
”妈妈说,“其实交警叔叔按一定的数学知识来设计红绿灯时间长短,你可以去研究一下!”
我问:“怎么研究啊?”
“玥玥,你想红绿灯来指挥什么的?”妈妈回答到。
“妈妈,我知道是用来指挥车辆的!”我立马回答到。
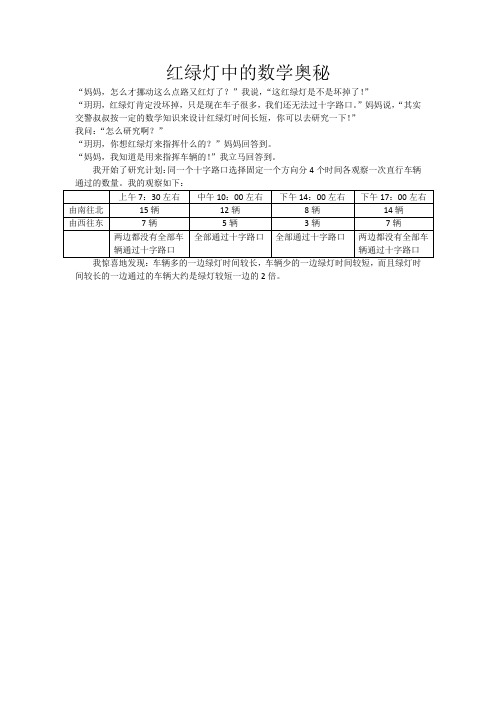
我开始了研究计划:同一个十字路口选择固定一个方向分4个时间各观察一次直行车辆
间较长的一边通过的车辆大约是绿灯较短一边的2倍。
苏教版六年级《数学与生活》一等奖获奖作品《红绿灯时间设置》
苏教版六年级《数学与生活》一等奖获奖作品
红绿灯时间设置调研
每天我们上学、上班的路上都会遇到很多的红绿灯,自觉遵守交通规则是我们长大后独自走路要学的第一节课——“红灯停、绿灯走”,我们的出行安全很大程度上都依靠红绿灯。
我们知道,每个红绿灯口的时间设置是不一样的。
有一次,妈妈带我去卡子门宜家,经过一个红绿灯口,我们以最快的速度过马路,因为马路太宽,而绿灯时间太短,我们竟然被拦在马路中间,马路上都是行驶的车辆,特别危险,于是我便提出了疑问——红绿灯的时间设置是否都是合理的呢?
带着这个疑问,爸爸妈妈陪着我对岔路口学校附近的两个红绿灯口进行了试验——一个是位于学校门口的红绿灯,因为东西方向没有马路,所以只有南北方向设置了红绿灯,东西向只有行人走路的指示灯;一个是位于金盛路与鞭鞍街交界处的红绿灯,南侧没有汽车道,只有东西方向和北侧有行车道。
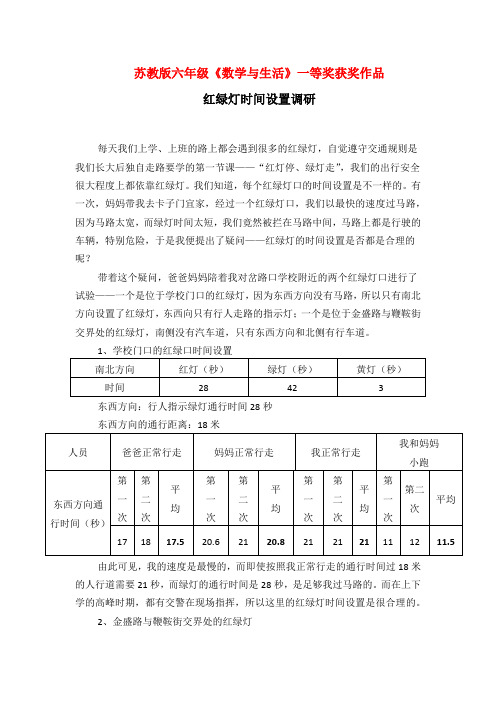
东西方向:行人指示绿灯通行时间28秒
东西方向的通行距离:18米
由此可见,我的速度是最慢的,而即使按照我正常行走的通行时间过18米的人行道需要21秒,而绿灯的通行时间是28秒,是足够我过马路的。
而在上下学的高峰时期,都有交警在现场指挥,所以这里的红绿灯时间设置是很合理的。
2、金盛路与鞭鞍街交界处的红绿灯
东西方向的通行距离:22米;
南北方向的通行距离:17米。
由此可见,东西方向按我的速度通行,需要27.6秒,而绿灯有55秒,是足够我过马路的,可见红绿灯的时间设置是很合理的;而南北方向即使按照爸爸的速度通行,需要16.5秒,而绿灯只有12秒,根本就不够时间通行的,而我和妈妈则很有可能被卡在马路中间,幸好此时东西方向仍是红灯,没有车辆通过,但是依然让人心惊肉跳,可见这里的红绿灯设置是很不合理的。
合理设置红绿灯时间的方法

合理设置红绿灯时间的方法红绿灯时间设置可太重要啦,就像给城市的交通脉搏在把节奏呢。
咱先说说路口的车流量情况。
要是一个路口啊,早高峰的时候,进城方向的车多得像蚂蚁搬家似的,出城方向车没多少,那这进城方向绿灯时间就得长点呀。
可以派人在路口统计统计,看看不同时段每个方向大概有多少辆车经过。
比如说早上七点到九点,观察个几天,算出平均数来。
如果某方向车流量特别大,绿灯时间就可以给到一分钟或者更久,车少的方向就给个二三十秒就成。
再讲讲路口的行人情况。
要是附近有学校或者大商场,那行人肯定多。
特别是上下学或者商场大促销的时候,那行人就像潮水一样。
这时候就得给行人过马路留够时间。
不能让人家小娃娃或者大爷大妈,刚走到路中间,红灯就亮了,那多危险呀。
一般来说呢,行人过马路的绿灯时间,得保证正常速度能从这头走到那头,还能有点富裕时间,以防有走得慢的。
要是路宽,那至少得给个三十秒往上。
还有哦,不同类型的路口也得区别对待。
像那种三岔路口,和十字路口的车流量走向就不一样。
三岔路口可能有一个方向的车流量特别小,那这个方向的绿灯时间就可以很短,主要照顾车流量大的那两个方向。
而十字路口呢,四个方向都得权衡好。
另外呀,要是这个路口经常有大货车经过,大货车启动慢呀,那绿灯亮起的时候,得给它们足够的启动时间,不然就容易造成后面堵车。
这就好比大货车是个慢性子的大块头,得给它点特殊照顾。
还有一种情况也不能忽略,就是这个路口如果连接着高速路的出入口,那在设置红绿灯时间的时候,得考虑到从高速下来的车的速度和流量。
从高速下来的车速度快,要是绿灯时间不合适,很容易造成交通事故或者拥堵呢。
总之呀,合理设置红绿灯时间就像给城市交通这个大机器上润滑油,要考虑到方方面面的情况,这样大家在路上才能顺顺利利的,少点堵心,多点舒心呢。
关于优化红绿灯设置的建议

关于优化红绿灯设置的建议可以从以下几个方面来考虑:
一、信号灯时长动态调整
根据道路的实际情况,如车流量、人流量等,动态调整红绿灯的时长。
在高峰时段,适当增加红灯时间,以减少路口的拥堵。
同时,在非高峰时段,可以适当减少绿灯时间,以更好地利用道路资源。
二、增加行人按钮
在有人行横道的路口,可以增加行人按钮。
当行人需要过马路时,可以按下按钮,信号灯将自动切换到行人绿灯,保证行人安全过马路。
三、设置左转待转区
在一些路口,可以设置左转待转区。
当左转车辆在绿灯时进入待转区,等待下一次信号灯变化时再行驶。
这样可以提高左转车辆的通过效率,减少路口的拥堵。
四、优化信号灯配时
对于一些路口,可以根据交通流量的变化,动态调整信号灯的配时。
例如,在上下班高峰期,可以增加红灯时间,减少绿灯时间;在非高峰期,则可以适当调整绿灯时间,提高车辆通过效率。
五、加强交通宣传教育
通过加强交通宣传教育,提高行人和驾驶员的交通安全意识,减少交通事故的发生。
同时,可以让行人和驾驶员更好地了解交通规则和信号灯的设置,从而更好地配合交通管理。
综上所述,优化红绿灯设置需要综合考虑多个方面,包括信号灯时长、行人按钮、左转待转区、信号灯配时和交通宣传教育等。
通过这些措
施,可以提高道路通行效率,减少交通事故的发生,为市民创造更加安全、便利的出行环境。
交通信号管理规范

交通信号管理规范行业背景:交通信号管理是指对交通信号设备及其周边环境进行规范化管理,以确保道路交通的顺畅与安全。
随着城市交通拥堵问题的日益严重,交通信号管理正变得越来越重要。
本文将从信号灯设置、信号灯配时、人行横道及停车场标线等几个方面,展开论述交通信号管理的规范要求。
一、信号灯设置规范信号灯的设置应遵循以下规范:1. 路口信号灯设置:信号灯的设置应根据道路交通流量、道路类型、交通环境等因素进行合理判断。
应根据交通流量大的主干道和次干道的交汇点来设立信号灯。
2. 信号灯类型选择:信号灯应根据道路类型和交通状况来选择合适的类型,包括红绿灯、箭头灯、倒计时灯等。
在特殊情况下,可以使用倒计时灯来提醒驾驶员剩余绿灯时间。
3. 信号灯高度设置:信号灯的高度应符合国家规定的标准,一般为2.5米至3.5米之间。
对于公交专用道、机动车道和非机动车道的信号灯高度应适当调整。
二、信号灯配时规范合理的信号灯配时可以提高交通效率,减少交通阻塞。
以下是信号灯配时的规范要求:1. 主干道通行时间:根据主干道交通流量及交通状况,合理设置绿灯通行时间。
对于主干道来说,绿灯时间要比辅助道路长,以保证主干道的通行流畅。
2. 调整绿灯时间:信号灯的绿灯时间可以根据交通流量的变化进行动态调整。
通过交通监测设备,实时获取道路交通状况,以保证信号灯配时的准确性。
3. 信号灯相位设置:信号灯的相位设置应根据道路的具体情况来决定,包括左转信号、直行信号、右转信号等。
相位设置应合理分配,以减少交叉流量的冲突。
三、人行横道规范人行横道是行人过马路的重要场所,以下是人行横道的规范要求:1. 人行横道标线:人行横道应使用标准的白色实线进行标示,并在夜间使用反光材料进行处理。
标线的宽度应根据道路宽度进行调整。
2. 人行横道信号灯:人行横道应设置交通信号灯,以保护行人的安全。
行人横道的红绿灯设置应与机动车信号灯配合,确保行人安全过马路。
3. 人行横道标志牌设置:人行横道两侧应设置明显的人行横道标志牌,提醒驾驶员减速并给予行人让行权。
红绿灯之间的规律

红绿灯之间的规律红绿灯,是道路交通中的重要设施,也是驾驶员遵守的信号指示之一。
它具有一定的规律,让车辆和行人能够有序通行,保障交通安全。
下面,我将从人类视角出发,用文字描述红绿灯之间的规律。
红绿灯的规律是有时间限制的。
当我们靠近红绿灯时,会发现它的上方有一个倒计时的数字。
这个数字代表了红绿灯的切换时间。
当数字递减到零时,红绿灯会从红灯切换到绿灯,表示车辆和行人可以通行了。
而当数字递减到一定范围内时,红绿灯的颜色会从绿灯变为黄灯,提示驾驶员要减速停车。
红绿灯的规律是有固定顺序的。
在交通路口,通常会设置有多个红绿灯,分别控制不同方向的车辆和行人。
这些红绿灯根据道路设计和交通流量的需要,按照一定的顺序进行切换。
比如,当东西向的红绿灯显示绿灯时,南北向的红绿灯就会显示红灯,以确保交叉方向的车辆和行人互不干扰。
这种有序的切换方式,有效地避免了交通事故的发生。
红绿灯的规律也与交通流量有关。
在高峰时段,道路上车流量比较大,红绿灯的切换时间会相应延长,以保证交通流畅。
而在低峰时段,道路上车流量相对较少,红绿灯的切换时间会相应缩短,以提高交通效率。
红绿灯的规律让道路交通变得有序,它不仅仅是一种交通设施,更是一种交通文明的象征。
当我们遵守红绿灯规则时,就是在保护自己和他人的安全。
红绿灯的存在,让我们能够更好地掌握交通情况,做出正确的决策,避免交通事故的发生。
在行人的角度看待红绿灯,它是我们安全过马路的保障。
当红灯亮起时,我们就要停下来等待,不得擅自闯红灯。
而当绿灯亮起时,我们才能放心地通过人行横道,确保自己的安全。
红绿灯的规律让我们能够有序地穿行于道路之间,避免了交通事故的发生,保护了行人的生命安全。
红绿灯之间的规律是为了保障道路交通的有序进行,它具有时间限制、固定顺序和与交通流量有关等特点。
我们应该遵守红绿灯的规则,做到文明驾驶、文明出行,共同营造一个安全、有序、畅通的交通环境。
信号灯时间标准

信号灯时间标准
信号灯时间标准因城市和具体路口的情况而异。
在中国的许多城市,常见的红绿灯时长间隔是30秒、40秒、45秒和60秒。
然而,也有部分城市的间隔时间是90秒。
每个城市和同一城市的不同路口的红绿灯时长都可能不同,这通常是根据该路口或相邻路段的交通流量进行综合考虑后设计的。
一些常见的指导原则包括:
1.当路口达到饱和状态时,红绿灯运行周期不宜超过180秒。
2.最小绿灯时间在主干道不宜少于15秒,次干道或采用感应式信号
控制方式的不宜少于8秒,行人过街不宜少于1至1.2米/秒。
3.机动车最大红灯时间非饱和交通状态下不宜大于120秒,饱和交
通状态下不宜大于150秒,行人与非机动车的最大红灯时间不宜大于90秒。
连续红灯不属于信号灯故障,而是属于人工干预,是调控绿灯时长的重要手段,根据各个流向的交通压力来决定。
以上信息仅供参考,具体时长可能会因各种因素而有所不同。
如果需要更详细的信息,建议咨询当地的交通管理部门。
红绿灯时间设置的原理是

红绿灯时间设置的原理是
红绿灯时间设置的原理基于交通流量和道路情况的实时监测与调整。
一般来说,红绿灯的时间设置包括以下几个方面的原理:
1. 交通流量监测:通过使用交通监测设备(例如车辆流量检测器、摄像头等),实时监测交通流量并记录数据。
这些数据包括车辆数量、速度、方向等信息。
2. 道路情况分析:将交通流量数据与道路情况进行分析,确定交通的瓶颈和拥堵区域。
例如,交叉口附近的道路可能容易造成交通堵塞,需要相应地调整红绿灯的时间。
3. 信号控制算法:基于交通流量和道路情况的分析结果,使用特定的信号控制算法来调整红绿灯的时间。
这些算法可以根据交通需求进行动态调整,以使交通流畅并减少拥堵。
4. 自适应调整:一些红绿灯系统还具备自适应能力,可以根据实时的交通情况来动态地调整红绿灯的时间。
例如,当监测到较大的车辆流量时,系统可以自动延长绿灯时间以减少拥堵。
综上所述,红绿灯时间设置的原理是基于实时监测和分析道路交通流量及道路情况,并通过信号控制算法动态调整红绿灯的时间,以达到交通流畅和减少拥堵的
目的。
交通中的趣味数学

交通中的趣味数学在我们日常生活中,交通是一个不可或缺的部分。
然而,你是否曾想过交通和数学之间存在着怎样的关系呢?其实,交通中隐藏着许多有趣的数学问题和原理。
本文将带你一起探索交通中的趣味数学。
一、红绿灯和时间红绿灯是我们交通中常见的信号灯,它的工作原理是通过时间控制交通流量。
红绿灯的时间设置往往是根据交通流量和道路情况来决定的。
那么,红绿灯的时间设置是否有数学依据呢?答案是肯定的。
在交通工程中,红绿灯的时间设置往往是通过数学模型来确定的。
交通流量的预测和分析需要考虑到车辆的到达率、通过率以及道路容量等因素。
通过数学建模和计算,交通工程师可以得出最优的红绿灯时间设置方案,以提高交通效率和减少拥堵。
二、交通信号的同步在城市中,我们经常看到一系列的交通信号灯,它们会按照一定的规律进行闪烁。
这一现象其实也涉及到了数学。
交通信号的同步是指多个路口的交通信号灯按照一定的规律进行变化,以实现交通的顺畅。
交通信号的同步需要考虑到车辆通过的时间和信号灯的变化周期。
通过数学计算和优化算法,可以确定最优的信号灯变化序列,以减少交通阻塞和提高车辆通过效率。
三、交通流量的模拟交通流量的模拟是交通工程中的一个重要研究领域。
通过数学模型和计算机仿真,可以模拟交通流量在不同道路和交叉口的运行情况。
这对于交通规划和道路设计非常重要。
交通流量的模拟需要考虑到车辆的速度、密度和流量等因素。
通过数学建模和仿真实验,可以得出不同交通流量条件下的道路通行能力和拥堵情况,从而指导交通规划和道路设计。
四、交通网络的优化交通网络的优化是指通过调整道路网和交通流量的分配,以提高整个交通系统的效率和可靠性。
这涉及到数学优化和图论等领域的知识。
交通网络的优化需要考虑到交通流量的分配、路段的容量和交通需求等因素。
通过数学建模和优化算法,可以得出最优的交通流量分配和路段的容量配置,以提高交通系统的性能和服务质量。
总结交通中的趣味数学不仅涉及到红绿灯的时间设置和交通信号的同步,还包括交通流量的模拟和交通网络的优化。
交通行业交通信号配时规范

交通行业交通信号配时规范导言在现代社会中,交通事故频发,交通拥堵问题日益严重,交通信号灯的配时规范对于维持道路秩序和保障交通安全起着至关重要的作用。
因此,制定并严格遵守交通行业的交通信号配时规范,是确保交通系统正常运行的关键之一。
一、交通信号灯的基本原则交通信号灯的配时规范应遵循以下基本原则:1. 合理性原则:根据道路的交通流量和车辆种类,合理分配不同方向的绿灯时间,并确保各路段的通行效率。
同时,还要考虑到周边道路的红绿灯配时情况,避免造成拥堵。
2. 安全性原则:在红灯亮起时,应保证道路上的车辆停车,而绿灯亮起时,应确保道路上车辆能够安全通行。
配时规范应确保行人过马路的时间充足,并与车辆的信号灯同步进行。
3. 灵活性原则:交通信号配时规范应考虑到不同时间段的交通流量变化,以及特殊情况下的应急处理。
在早晚高峰期间,信号配时应增加道路绿灯时间,以减少交通拥堵。
二、交通信号配时规范的具体要求1. 路口信号灯配时规范(1)绿灯时间计算:绿灯时间应根据道路的宽度、交通流量和车辆行驶速度进行合理计算。
一般来说,绿灯的时间应能够满足过路车辆的需要,但不宜过长,以免造成其他方向的等待时间过长。
(2)黄灯时间设置:为确保交通安全,黄灯时间应适当延长,以使通过红灯的车辆能够有足够的时间安全地停车。
黄灯时间的设置应根据道路条件和车辆行驶速度灵活调整。
(3)红灯时间设置:红灯时间的设置应根据交通流量、路口行人过街时间和清障时间来确定。
在人行横道线上,红灯时间应相对较长,以确保行人安全。
2. 路段信号灯配时规范(1)绿波带设置:对于一些在交通流量较大的主干道上设置的信号灯,应根据道路长度和流量情况设置绿波带。
绿波带的设置能够保持车辆的连续通行,减少交通拥堵。
(2)行人专用信号灯:在人行横道线和人行天桥出入口设置行人专用信号灯,以保障行人的交通安全。
行人专用信号灯的配时应与机动车的信号灯同步进行。
(3)左转信号灯:在一些需要调整转向的路段设置左转信号灯,以减少交通事故的发生。
过街红绿灯设置标准

过街红绿灯设置标准
过街红绿灯的设置标准通常由交通管理部门或交通工程规范规定,不同国家和地区可能存在一些差异。
以下是一些通常考虑的标准和指南:
1. 行人交叉流量:过街红绿灯的设置通常会考虑行人交叉的流量,以确定绿灯亮起的时间。
流量可能会根据不同时间段的变化而有所不同,例如交通高峰期和非高峰期。
2. 行人平均行进速度:行人的平均行进速度也是一个重要的考虑因素,以确保他们有足够的时间在绿灯时间内安全过马路。
3. 交叉口宽度:交叉口的宽度和形状可能影响信号的设置,尤其是对于大型交叉口。
4. 残疾人需求:根据残疾人需求,可能需要设置足够的过街时间,并在合适的位置安装无障碍设施,如视觉或听觉提示。
5. 交叉口流量:交叉口的车辆流量也是一个考虑因素,以确保行人有足够的时间安全穿越交叉口。
6. 交通信号控制类型:信号可能是定时控制,根据预设的时间间隔来切换,也可能是感应控制,根据实际交叉口的交通流量情况来调整。
7. 交叉口安全评估:在确定过街红绿灯设置时,通常会进行交叉口安全评估,以考虑交叉口的整体安全性。
8. 交叉口的类型:不同类型的交叉口,如T型交叉口、十字路口、环形交叉口等,可能需要不同的信号设置。
以上这些因素通常在制定交通规划、设计交叉口时得到综合考虑。
最终的标准和设置可能会因地区、国家和城市的法规和规范而异。
在具体情况下,最好咨询当地交通管理部门或专业交通工程师,以确保
过街红绿灯的设置符合当地的法规和标准。
关于调整优化红绿灯时间的建议

关于调整优化红绿灯时间的建议调整优化红绿灯时间是提高交通效率、减少拥堵的重要措施之一。
下面列举一些关于调整优化红绿灯时间的建议。
1. 根据交通流量进行调整根据不同时间段内的交通流量情况,合理调整红绿灯时间。
在高峰时段,可以延长绿灯时间,缩短红灯时间,以便更多的车辆通过。
而在低峰时段,可以适当缩短绿灯时间,增加红灯时间,减少车辆等待时间。
2. 考虑不同道路的通行能力不同道路的通行能力不同,因此,在调整红绿灯时间时,应该充分考虑道路的通行能力。
对于通行能力较大的主干道,可以适当延长绿灯时间,以提高交通效率;而对于通行能力较小的支路、小巷,可以适当缩短绿灯时间,避免造成拥堵。
3. 考虑不同车辆类型的需求不同车辆类型对红绿灯时间的需求也不同。
例如,公交车通常需要更多的绿灯时间,以确保能够按时到达站点;而对于行人来说,绿灯时间应该足够长,以确保他们能够安全过马路。
因此,在调整红绿灯时间时,应该综合考虑不同车辆类型的需求,以提高交通效率和交通安全。
4. 考虑道路交叉口的特点每个道路交叉口的特点不同,因此,在调整红绿灯时间时,应该充分考虑交叉口的特点。
例如,一些交叉口容易产生交通事故,可以适当延长红灯时间,增加安全因素;而一些交叉口容易产生拥堵,可以适当缩短红灯时间,提高交通效率。
5. 考虑行人通行的需要在城市交通规划中,行人通行也是非常重要的一环。
因此,在调整红绿灯时间时,应该充分考虑行人通行的需要。
例如,在繁华商业区的红绿灯中,可以适当延长绿灯时间,以便行人能够更方便地过马路;而在人流量较少的地方,可以适当缩短绿灯时间,提高车辆通行效率。
6. 考虑交通事故的影响交通事故往往会造成交通拥堵,影响交通效率。
因此,在调整红绿灯时间时,应该充分考虑交通事故的影响。
例如,在发生交通事故时,可以及时调整红绿灯时间,疏导交通,减少拥堵。
7. 利用智能交通系统进行调整利用智能交通系统,可以实时监测交通流量、车辆行驶速度等信息,根据实时数据进行红绿灯时间的调整。
红绿灯时间设置标准

红绿灯时间设置标准
红绿灯作为交通信号灯中的一种,是控制车辆和行人通行的重要设施。
它的时间设置标准直接关系到交通的顺畅和安全,因此,合理的红绿灯时间设置标准对于交通管理至关重要。
首先,红绿灯时间设置需要考虑的因素有很多,比如道路的宽度、车流量、行人通行情况、交通事故的发生情况等。
在实际操作中,需要根据不同的道路情况来进行具体的设置。
其次,对于不同类型的道路,红绿灯时间设置也有所不同。
比如在城市主干道上,车流量大,行人通行量也较大,因此红绿灯时间需要相对较长,以保证车辆和行人的通行顺利。
而在小区内或者乡村道路上,车流量相对较小,红绿灯时间可以相应缩短。
另外,红绿灯时间设置还需要考虑到不同时间段的交通情况。
比如在早晚高峰期,车流量大,红绿灯时间可以适当延长,以便疏通交通;而在夜间或者凌晨,车流量较小,红绿灯时间可以适当缩短,以节约能源和提高交通效率。
此外,红绿灯时间设置还需要考虑到行人通行的情况。
在人行横道处,需要设置行人过街时间,以保证行人安全通行。
行人过街时间需要根据人流量和行人通行速度来设置,以保证行人安全。
最后,红绿灯时间设置还需要考虑到特殊情况的处理。
比如在突发事件或者交通事故发生时,需要及时调整红绿灯时间,以保证交通秩序和安全。
总的来说,红绿灯时间设置标准需要综合考虑道路情况、车流量、行人通行情况等多种因素,以保证交通的顺畅和安全。
只有合理的红绿灯时间设置,才能有效地提高交通效率,减少交通事故的发生,保障行人和车辆的安全通行。
因此,交通管理部门在进行红绿灯时间设置时,需要严格按照标准进行操作,以保证交通的顺畅和安全。
对十字路口不规范红绿灯时间的整改措施

对十字路口不规范红绿灯时间的整改措施
如果发现十字路口的红绿灯时间规划存在不规范的情况,应该及时采取以下整改措施:
1. 进行现场检查和调研,了解具体情况。
确定交通流量、车速等数据,评估现状和可能存在的安全隐患,明确需要修改的地方。
2. 根据实际情况重新设定红绿灯时间。
遵循交通平稳、顺畅、安全的原则,充分考虑各方面的情况,制定出符合交通流量需要的时间。
3. 定期对红绿灯设置进行检查和维护,预防设备故障和人为损坏,确保设备正常运行,保证交通秩序和安全。
4. 加强宣传教育,提高公众的交通安全意识。
加强对行人、车辆等各方人员的教育和引导,让他们了解交通规则的重要性,共同维护交通秩序。
关于红绿灯时间设置的建议-概述说明以及解释

关于红绿灯时间设置的建议-概述说明以及解释1.引言1.1 概述红绿灯时间设置一直以来都是城市交通管理的重要内容之一。
它直接关系到交通流畅度、交通安全性以及对机动车和行人的交通管控能力。
正确设置红绿灯时间,可以合理分配交通各方的时间资源,提高道路通行效率,减少交通压力,降低交通事故的发生几率。
因此,研究和探讨如何优化红绿灯时间设置,具有重大的现实意义和深远的社会影响。
本文将从现行红绿灯时间设置存在的问题出发,提出两点建议。
首先,应根据交通流量合理设置红绿灯时间,以确保道路上的车辆和行人能够依据实际情况恰当通行。
其次,还应考虑道路的交通状况,根据道路情况的变化灵活调整红绿灯时间,使其更加适应实际交通需求。
通过对红绿灯时间设置的合理调整,我们可以提升交通运行效率,减少交通事故的发生,改善出行体验,提高城市交通管理水平。
因此,本文旨在为相关决策者提供建议与借鉴,促进红绿灯时间设置的优化和城市交通的可持续发展。
1.2 文章结构文章结构的设计是为了合理组织和展现文章的内容,使读者能够清晰地理解和接受作者所提出的观点和建议。
本文的结构主要包括引言、正文和结论三个部分。
引言部分旨在引起读者的兴趣、概述文章内容、明确文章的目的和重要性。
文章通过引言部分来为读者提供一个整体的背景,并激发读者对于红绿灯时间设置问题的思考与关注。
正文部分是文章的核心部分,它分为两个子部分,分别是红绿灯时间设置的重要性和现行红绿灯时间设置存在的问题。
在第一个子部分,文章将探讨红绿灯时间设置的重要性,包括它对于交通流量调控的意义、对交通安全和效率的影响等等。
在第二个子部分,文章将具体分析现行红绿灯时间设置存在的问题,如时间设置不合理造成的交通拥堵、行人过街不便等。
结论部分是对前文讨论的总结和归纳,并提出两点具体建议。
第一个建议是根据交通流量合理设置红绿灯时间,文章将解释其合理性以及对解决现行问题的具体作用。
第二个建议是考虑道路交通状况调整红绿灯时间,文章将说明该建议的可行性和实施方法。
红绿灯设置法规-概述说明以及解释

红绿灯设置法规-概述说明以及解释1.引言1.1 概述红绿灯是交通管理中一项重要的设施,用于指示车辆和行人在道路交通中的行进和停留。
随着城市的不断发展和交通流量的增加,红绿灯设置的合理性和科学性变得越来越重要。
红绿灯设置法规是针对红绿灯的设立和运行所制定的一系列规章制度,旨在确保道路交通安全和流畅。
这些规定涉及红绿灯的安装位置、信号灯颜色和频率、黄灯延迟时间等方面的内容。
在红绿灯设置的过程中,需要考虑到交通流量、交叉口形态、行人需求等多种因素。
科学合理的红绿灯设置可以提高交通效率和交通安全性,减少交通事故的发生。
同时,合理设置的红绿灯可以缓解交通压力,减少尾气排放和能源浪费。
然而,目前存在一些问题和挑战。
例如,部分地区红绿灯设置不够科学合理,导致交通拥堵和事故频发;某些红绿灯黄灯时间过短,容易导致交通违规行为;红绿灯信号同步不好,导致交叉口交通效率低下等。
为了解决这些问题,需要进一步加强红绿灯设置的规范性和科学性。
应该借鉴国内外的经验和技术,在红绿灯设置中充分考虑各种交通流量、行人需求、交叉口形态等因素,并采用智能化的控制系统进行管理和调控。
此外,还应该加强对红绿灯设置法规的宣传和培训,提高相关部门和驾驶员的意识和理解。
综上所述,红绿灯设置法规在维护道路交通安全和提高交通效率方面起着重要作用。
通过严格遵守法规和加强科学管理,我们可以建立更加安全、便捷和可持续的交通系统。
1.2 文章结构本文将分为三个主要部分,分别是引言、正文和结论。
每个部分将详细探讨与红绿灯设置法规相关的内容。
引言部分将首先概述本文的主题,即红绿灯设置法规。
随后,将介绍本文的结构,以便读者能够清晰地了解整个文章的框架和内容。
最后,还将说明本文的目的,即通过对红绿灯设置法规的探讨,提高交通管理的效率和安全性。
正文部分将从背景和意义入手,为读者介绍红绿灯设置的必要性和重要性。
接着,将介绍红绿灯设置的基本原则,包括公平、合理和科学等方面的要求。
红绿灯配时调整存在的问题及原因

红绿灯配时调整存在的问题及原因引言红绿灯配时调整是城市交通管理中的重要环节,合理的红绿灯配时可以提高交通效率、减少拥堵和事故发生的可能性。
然而,在实际的交通管理中,红绿灯配时常常存在一些问题,导致交通流量无法得到有效控制,进而影响交通的畅通。
本文将探讨红绿灯配时调整存在的问题及原因,并提出相应的解决方案。
问题一:红绿灯配时不合理原因分析1.缺乏科学依据:一些地区对红绿灯配时缺乏科学依据,仅凭经验和主观判断进行设置。
2.人为干预:有些地方存在人为干预红绿灯配时的情况,导致配时不合理。
解决方案1.制定科学准则:建立科学的红绿灯配时准则,包括车流量、路口类型、行人需求等因素,并根据实际情况进行优化调整。
2.自动化控制:引入智能交通系统,采用自动化控制的方式进行红绿灯配时,减少人为干预的可能性。
问题二:红绿灯配时不适应交通需求变化原因分析1.交通流量变化快:交通流量受到多种因素影响,如天气、节假日等,造成车流量的快速变化。
2.道路改建和拓宽:道路改建和拓宽会改变交通流量分布,导致原有的红绿灯配时不再适应新的交通需求。
解决方案1.实时监测和调整:利用传感器、摄像头等设备对交通流量进行实时监测,并根据监测结果及时调整红绿灯配时。
2.动态优化算法:采用动态优化算法对红绿灯配时进行调整,根据实际交通需求进行合理分配。
问题三:红绿灯配时不考虑行人需求原因分析1.行人流量被忽视:一些地区在红绿灯配时中只考虑车辆流量,而忽视了行人的需求。
2.行人过街时间不足:有些地方行人过街时间设置过短,导致行人不能及时通过。
解决方案1.考虑行人需求:在红绿灯配时中充分考虑行人的需求,设置合理的过街时间和绿灯时间。
2.增加人行道设施:增加人行道设施,提高行人通行的便利性和安全性。
问题四:红绿灯配时不协调原因分析1.路口之间配时不协调:一些地区红绿灯配时没有考虑到相邻路口之间的协调,导致交通流量无法顺畅过渡。
2.不同交通方式配时不协调:对于不同交通方式(如汽车、自行车、电动车等)的红绿灯配时没有进行统一规划和协调。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
红绿灯的时间设置问题
摘要
随着经济发展,人口和交通工具的增多,世界各国都面临着交通问题,如何科学地进行交通管理为人们所关注.现考察十字路口的交通管理办法.目前,各国对交叉路口实施交通管理的方法主要有两种,其中红绿灯管理是常见的一种方法.
假设平均流量已知,我们要通过建立数学模型,设定适当的红灯和绿灯时间,在道路保持通畅的基础上,使在一个红绿灯周期所有车辆在路口停滞的时间之和最短(一辆车在路口的滞留时间通常包括两部分,一部分是每辆车遇红灯后的停车等待时间,另一部分是停车后从启动到正常车速的时间)
在本次论文研究中,我们就此问题介绍如何运用Matlab软件进建立数学建模对实际问题进行最优化处理。
关键词:红绿灯管理 Matlab软件最优化处理
The timing of the traffic problem
summary
Along with the economic development, population and transport increases, the world are facing traffic problems, and how to scientifically, traffic management concern for people. Now examine intersection traffic management solution. Currently, countries in the intersection of traffic management method to basically have two kinds, including traffic management is a common method. The average flow hypothesis, we should known by establishing mathematics model, setting appropriate red and green time, on the basis of keeping unobstructed road, make in a traffic light cycle all vehicles at intersections stagnation total time shortest (a car in the intersection of retention time usually includes two parts, one is each car event of a red light after parking waiting time, another part is after parking from start-up to normal speed in this paper the time) study, we introduce how to use this software Matlab into establishing mathematical modeling of actual problem optimal processing.
Keywords: traffic management software Matlab optimum processing
目录
一、问题的提出
作为城市交通的指挥棒,红绿灯对交通的影响起着决定性作用。
如果红绿灯的设置不合理,不仅会影响到交通秩序;还有可能会影响到行人和自行车的安全。
目前杭城还有很多路口的红绿灯设置存在一些不合理的因素,我们以古墩路一个路口(界于天目山路和文苑路之间)的红绿灯设置为例,该路口是刚开通的,交管部门对路况和车流量的研究还不是很成熟,因此红绿灯的设置存在一些问题。
该路口的车流量相对比较小,有几个方向的车流量特别小,但绿灯时间设置太长,经常出现路口空荡荡但是车辆必须长时间等待的情况;同时在这样的路口,右转红灯显得有些多余。
另外,该路口不同时段的红绿灯设置没有什么区别,显然这是非常不合理的。
下面我们就针对该路口来研究一下红绿灯设置的合理方案。
我们主要研究两个方面:红绿灯周期的设置以及一个周期各个方面开绿灯的时间。
二、问题的假设
假设一个路口,只有东西方向和南北方向的两条干道。
且忽略黄灯,只考虑红灯和绿灯。
又设两个方向的车流量是稳定和均匀的,不考虑转弯的情形。
三、模型的建立 1、红绿灯周期
从《道路交通自动控制》中,我们可以找到有关红绿信号灯的最佳周期公式:
s
q L C ∑
-+=
15
其中 : C 为周期时间。
相位:同时启动和终止的若干股车流叫做一个相位。
L 为一个周期的总损失时间。
每一相位的损失时间I=启动延迟时间-结束滞后时间;而整个周期的总损失时间为各个相位总损失时间的和加上各个绿灯间隔时间R 。
(通俗地讲,启动延迟时间即司机看到绿灯到车子启动的反应时间,结束滞后时间即绿灯关闭到最后一辆车通过的时间。
)
即R I L +∑= q 为相应相位的车流量
s 为相应相位的饱和车流量。
(当车辆以大致稳定的流率通过路口时,该流率即该相位的饱和车流量。
)
2、南北方向和东西方向开绿灯时间的分配
将交通信号灯转换的一个周期取作单位时间,又设两个方向的车流量是稳定和均匀的,不考虑转弯的情形。
设E 是单位时间从东西方向到达路口的车辆数;S 是单位时间从南北方向到达路口的车辆数。
假设在一个周期,东西方向开红灯、南北方向开绿灯的时间为R ,那么在该周期,东西方向开绿灯、南北方向开红灯的时间为1-R 。
我们要确定交通灯的控制方案,即确定R 。
度量一个十字路口的串行效率的主要依据是单位时间所有车辆在路口滞留的时间总和。
因此要确定R ,只需保证在一个周期,所有车辆在路口滞留的时间总和最短即可。
一辆车在路口的滞留时间通常包括两部分,一部分是每辆车遇红灯后的停车等待时间,另一部分是停车后司机见到绿灯重新发动到开动的时间0t ,它是可以测定的。
首先,对任意给定的R (0<R<1),计算出所有车辆在路口滞留的总时间。
在一个周期中,从东西方向到达路口的车辆为E 辆,该周期中东西方向开红灯的比率为R ,需停车等待的车辆共为R E ⋅辆。
这些车辆等待信号灯改变的时间最短为0(刚停下就转绿灯),最长为R (到达路口时,刚转红灯),所以它们的平均等待时间为R/2。
由此可知,东西向行驶的所有车辆在一个周期中等待的时间总和为
2
22ER R R E =⨯⨯
同理可得,南北向行驶的所有车辆在一个周期中等待时间的总和为
2
)1(2R S - 凡遇红灯的车辆均需花费t 单位时间启动,这部分时间也必须计入总滞留时间。
一个周期中,各方向遇红灯停车的车辆总和为)1(R S R E -⋅+⋅,对应的这一部分滞留时间为
)]1([0R S R E t -⋅+⋅⋅
从而总滞留时间为
2
)1(2)]1([)(220R S ER R S R E t R T T -++-+⋅⋅==
2
])1[(20002S
S t R E t S t R S E ++-+-+=
])1([1
000Et t S S E R R -++==∴当
时,车辆总滞留时间最短。
令B=V+H ,表示一个周期中经过十字路口的车辆总数,上述表达式简化得最佳的0R 为
B
t E S S R 0
0)(⨯-+=
容易看到,最佳控制方案B
t E S S R 0
)(⨯-+=。
三、调查结果与数据处理 1、调查数据
2、数据处理
根据上述数据和前面建立的模型,我们可以计算出最佳周期和每个方向开绿灯的时间。
(见表中最后两列)
上面的表格已经给出了不同时段,该路口的红绿灯周期和各个方向的绿灯时间。
不过,事实上,红绿灯的设置是非常复杂的,它牵涉到各种因素,不可能用一个固定的模型解决一切问题,它必须根据实际情况不断调整。
我们上面给出的方案只是一种理想化的、近似的方案,不过相信它对交警部门会有一定的参考价值和实际意义。
