开侨中学第十三周周日测试题
九年级(上)第13周周考数学试题(含部分参考答案)

南川中学2018级17-18学年度上期A 班第十三周周考数学试题(考试时间120分钟 总分150分)一、选择题:(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上对应题目的正确答案标号涂黑. 1、下列汽车标志中既是轴对称图形又是中心对称图形的是( )A .B .C .D .2、如图,⊙O 的半径OD 垂直于弦AB ,垂足为点C ,连接AO 并延长交⊙O 于点E ,连接BE ,CE .若AB=8,CD=2,则△BCE 的面积为( )A .12B .15C .16D .183、某超市一月份的营业额为200万元,一月、二月、三月的营业额共1000万元,如果平均每月增长率为x ,根据题意列方程为( ) A .()1000%1200=+xB .()1000%12002=+xC .()()1000%1200%12002=+++x x D .()()1000%1200%12002002=++++x x4、要从小强、小华和小林三人中随机选两人作为旗手,则小强和小林同时入选的概率是( )A .32B .31C .21D .615、关于x 的一元二次方程()01212=+--x x a 有两个不相等的实根,则a 的取值范围是( ) A .2<a B .2>a C .2<a 且1≠a D .2-<a6、如图,矩形ABCD 的边AB=1,BE 平分∠ABC ,交AD 于点E ,若点E 是AD 的中点,以点B 为圆心,BE 为半径画弧,交BC 于点F ,则图中阴影部分的面积是( )A .42π-B .423π-C .82π-D .823π-7、如图,⊙O 的半径为6,△ABC 是⊙O 的内接三角形,连接OB 、OC ,若∠BAC 与∠BOC 互补,则线段BC 的长为( ) A .B .3C .D .68.若正比例函数y=mx (m ≠0),y 随x 的增大而减小,则它和二次函数y=mx 2+m 的图象大致是( )A .B .C .D .9、关于x 的一元二次方程(a ﹣1)x 2+2x+1=0有两个实数根,则a 的取值范围为( ) A .a ≤2 B .a <2 C .a ≤2且a ≠1 D .a <2且a ≠110、如图,半径为1的圆O与正五边形ABCDE相切于点A、C,劣弧AC的长度为()A.π B.π C.π D.π11、当﹣4≤x≤2时,函数y=﹣(x+3)2+2的取值范围为()A.﹣23≤y≤1 B.﹣23≤y≤2 C.﹣7≤y≤1 D.﹣34≤y≤212.若数a使关于x的分式方程+=4的解为正数,且使关于y的不等式组的解集为y<﹣2,则符合条件的所有整数a的和为()A.10 B.12 C.14 D.16(第2题图)(第6题图)(第7题图)(第10题图)二、填空题:(本大题共6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡...中对应的横线上.13、若关于x的方程(a+3)x|a|﹣1﹣3x+2=0是一元二次方程,则a的值为.14、若点M(3,a﹣4),N(b,a)关于原点对称,则a+b= .15、如图所示,点A是半圆上一个三等分点,点B是的中点,点P是直径 MN上一动点,若⊙O的直径为6,则AP+BP的最小值是.16、在如图所示的电路中,随机闭合开关S1,S2,S3中的两个,能让灯泡L1发光的概率是.17、二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有.18、如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.(第15题图)(第16题图)(第17题图)三.解答题:(本大题2个小题,每题8分,共16分)19.解方程:(1)x2-6x-16=0 (2) 2(2x-4)=5-6x20. 重庆某中学组织七、八、九年级学生参加“直辖20年,点赞新重庆”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.(1)扇形统计图中九年级参赛作文篇数对应的圆心角是度,并补全条形统计图;(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.四.解答题:(本大题5个小题,每题10分,共50分)21、如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,2),C(﹣2,2).(1)把△ABC绕B顺时针旋转90°得到对应的△A1B1C1,画出△A1B1C1,则BA扫过的面积为;(2)把△ABC绕O顺时针旋转90°得到对应的△A2B2C2,则点A经过的路径的长为;(3)画出与△ABC关于原点O对称的△A3B3C3,则C3的坐标为;22.如图,AC 为⊙O 的直径,B 为⊙O 上一点,∠ACB=30°,延长CB 至点D ,使得CB=BD ,过点D作DE ⊥AC ,垂足E 在CA 的延长线上,连接BE .(1)求证:BE 是⊙O 的切线;(2)当BE=3时,求图中阴影部分的面积.23.藏族小伙小游在九寨沟开店作牛肉生意,根据协议,每天他会用8880元购牦牛肉和黄牛肉共240千克,其中牦牛肉和黄牛肉的数量比为3:1,已知每千克牦牛肉的售价比千克黄牛肉的售价多15元,预计当天可以全部售出.(1)若小游预计每天盈利不低于2220千克,则牦牛肉每千克至少卖多少元?(2)若牦牛肉和黄牛肉在(1)的条件下以最低价格销售,但8月份因为九寨沟地震,游客大量减少,导致牛肉滞销,小游决定降价销售每天进够的牛肉,已知牦牛肉的单价下降a %,(其中a >0),但销量还是比进够数量下降了35a %,黄牛肉每千克下降3元,销量比进够数量下降了310a %,最终每天牦牛肉的销售额比黄牛肉的销售额的5倍还多350元,求a 的值.24. 在等腰直角三角形ABC 中,∠BAC=90°,AB=AC ,D 是斜边BC 的中点,连接AD .(1)如图1,E 是AC 的中点,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′,当AD=时,求AE 的值.(2)如图2,在AC 上取一点E ,使得CE=AC ,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′交BC 于点F ,求证:DF=CF .25.任意一个四位数n 可以看成由前两位数字和后两位数字组成,交换这两个两位数得到一个新四位数m ,计f (n )=99m n -,如n=1234,则m=3412,f (1234)=9934121234-=-22,(1)直接写出f (2222)= ,f (5025)= ; (2)求证:任意一个四位数n ,f (n )都是整数;(3)若s=1200+10a+b ,t=1000b+100a+14(1≤a ≤5, (1≤b ≤5,a 、b 均为整数),当f (s )+f (t )是一个完全平方数时,求满足条件S 的最大值.五.解答题:(本大题12分)26、如图,抛物线y=﹣x2﹣x+与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,已知点D(0,﹣).(1)求直线AC的解析式;(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD面积最大时,过P作PQ⊥x 轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM,NQ,求PM+MN+NQ的最小值;(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△BPQ′沿直线BD 平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E.则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长.南川中学2018级17-18学年度上期A班第十三周周考数学试题答案13. 3 14. ﹣1 15. 316. 17. ①④⑤ 18. 1212、若数a使关于x的分式方程+=4的解为正数,且使关于y的不等式组的解集为y<﹣2,则符合条件的所有整数a的和为()A.10 B.12 C.14 D.16解:分式方程+=4的解为x=且x≠1,∵关于x的分式方程+=4的解为正数,∴>0且≠1,∴a<6且a≠2.,解不等式①得:y<﹣2;解不等式②得:y≤a.∵关于y的不等式组的解集为y<﹣2,∴a≥﹣2.∴﹣2≤a<6且a≠2.∵a为整数,∴a=﹣2、﹣1、0、1、3、4、5,(﹣2)+(﹣1)+0+1+3+4+5=10.故选A.15、解:作点B关于MN的对称点B′,连接AB′交MN于点P,连接BP,此时AP+BP=AB′最小,连接OB′,如图所示.∵点B和点B′关于MN对称,∴PB=PB′.∵点A是半圆上一个三等分点,点B是的中点,∴∠AON=180°÷3=60°,∠B′ON=∠AON÷2=30°,∴∠AOB′=∠AON+∠B′ON=90°.∵OA=OB′=1,∴AB′=3.故答案为:3.17、二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有①④⑤.解:①∵开口向下∴a<0∵与y轴交于正半轴∴c>0∵对称轴在y轴右侧∴b>0∴abc<0,故①正确;∵二次函数的对称轴是直线x=1,即二次函数的顶点的横坐标为x=﹣=1,∴2a+b=0,故②错误;∵抛物线与x轴有两个交点,∴b2﹣4ac>0,故③错误;∵b=﹣2a,∴可将抛物线的解析式化为:y=ax2﹣2ax+c(a≠0);由函数的图象知:当x=﹣2时,y<0;即4a﹣(﹣4a)+c=8a+c<0,故④正确;∵二次函数的图象和x轴的一个交点是(﹣1,0),对称轴是直线x=1,∴另一个交点的坐标是(3,0),∴设y=ax2+bx+c=a(x﹣3)(x+1)=ax2﹣2ax﹣3a,即a=a,b=﹣2a,c=﹣3a,∴a:b:c=a:(﹣2a):(﹣3a)=﹣1:2:3,故⑤正确;故答案为:①④⑤.18、如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为__________.解:连接AP,A′P′,过点A作AD⊥PP′于点D,由题意可得出:AP∥A′P′,AP=A′P′,∴四边形APP′A′是平行四边形,∵抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3),平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),∴PO==2,∠AOP=45°,∴△ADO是等腰直角三角形,∴PP′=2×2=4,∴AD=DO=×3=,∴抛物线上PA段扫过的区域(阴影部分)的面积为:4×=12.24、解:(1)∵∠BAC=90°,AB=AC,D是斜边BC的中点,∴∠ADC=90°,∠ACD=45°,在Rt△ADC中,AC=AD×sin45°=2,∵E是AC的中点,∴CE=AC=,∵将△CDE沿CD翻折到△CDE',∴CE=CE'=,∠ACE'=90°,由勾股定理得:AE==;(2)证明:过B作AE’的垂线交AD于点G,交AC于点H,∵∠ABH+∠BAF=90°,∠CAF+∠BAF=90°,∴∠ABH=∠CAF,又∵AB=AC,∠BAH=∠ACE’=90°,∴△ABH≌△CAE',∴AH=CE’=CE,∵CE=AC,∴AH=HE=CE,∵D是BC中点,∴DE是△BCH的中位线,∴DE∥BH,∴G是AD中点,∵在△ABG和△CAF中,AB=AC,∠BAD=∠ACD=45°,∠ABH=∠CAF,∴△ABG≌△CAF,∴AG=CF,∵AG=AD,∴CF=AD=CD,∴DF=CF.22、解:(1)如图所示,连接BO,∵∠ACB=30°,∴∠OBC=∠OCB=30°,∵DE⊥AC,CB=BD,∴Rt△DCE中,BE=CD=BC,∴∠BEC=∠BCE=30°,∴△BCE中,∠EBC=180°﹣∠BEC﹣∠BCE=120°,∴∠EBO=∠EBC﹣∠OBC=120°﹣30°=90°,∴BE是⊙O的切线;(2)当BE=3时,BC=3,∵AC为⊙O的直径,∴∠ABC=90°,又∵∠ACB=30°,∴AB=tan30°×BC=,∴AC=2AB=2,AO=,∴阴影部分的面积=半圆的面积﹣Rt△ABC的面积=π×AO2﹣AB×BC=π×3﹣××3=﹣.解:(1)∵抛物线y=﹣x2﹣x+与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,∴A(﹣4,0),B(1,0),C(0,),设直线AC的解析式为y=kx+b,则有,∴k=,b=,∴直线AC的解析式为y=x+.(2)如图1中,分别过D、B作x轴,y轴的平行线交于点K,连接PK.设P(m,﹣m2﹣m+).S△PDB=S△PDK+S△PBK﹣S△DKB=•1•(﹣m2﹣m++)+••(1﹣m)﹣•1 =﹣(m+3)2+,∵﹣<0,∴m=﹣3时,△PBD的面积最大,此时P(﹣3,),Q(﹣3,0).如图2中,作Q关于y轴的对称点Q′,将Q′向左平移个单位得到Q″,连接PQ″交抛物线对称轴于M,此时PM+MN+NQ最短.易证四边形MNQ′Q″是平行四边形,∴NQ=NQ′=Q″M,∴PM+MN+NQ=PM+MQ″+MN=PQ″+MN,∵Q″(,0),∴PQ″==,∴PM+MN+NQ的最小值为+.(3)如图3中,由(2)可知直线PB的解析式为y=﹣x+,直线BD的解析式为y=x﹣,易证∠PBQ=30°,∠DBO=60°,PB⊥BD.①当点Q″与Q重合时,∵∠B′EQ=∠QB′E=30°,∴EQ=B′Q″=4,∴OE=QE+OQ=7.②如图4中,当B′E=B′Q″时作B′N⊥x轴于N.∵B′E=B′Q″=4,∠B′EN=30°,∴B′N=B′E=2,EN=2,∴B′(,﹣2),∴OE=2+=﹣1.③如图5中,当EQ″=EB′时,作B′N⊥x轴于N.易知EP′=EQ″=EB′=,B′N=,EN=2,∴B′(,﹣),∴EO=.④如图6中,当B′E=B′Q″时,易知B′E=B′Q″=4,在Rt△BEB′中,BE=EB′÷cos30°=,∴OE=OB+BE=+1,综上所述,满足条件的OE的值为7或﹣1或或+1.26、解:(1)∵抛物线y=﹣x2﹣x+与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,∴A(﹣4,0),B(1,0),C(0,),设直线AC的解析式为y=kx+b,则有,∴k=,b=,∴直线AC的解析式为y=x+.(2)如图1中,分别过D、B作x轴,y轴的平行线交于点K,连接PK.设P(m,﹣m2﹣m+).S△PDB =S△PDK+S△PBK﹣S△DKB=•1•(﹣m2﹣m++)+••(1﹣m)﹣•1 =﹣(m+3)2+,∵﹣<0,∴m=﹣3时,△PBD的面积最大,此时P(﹣3,),Q(﹣3,0).如图2中,作Q关于y轴的对称点Q′,将Q′向左平移个单位得到Q″,连接PQ″交抛物线对称轴于M,此时PM+MN+NQ最短.易证四边形MNQ′Q″是平行四边形,∴NQ=NQ′=Q″M,∴PM+MN+NQ=PM+MQ″+MN=PQ″+MN,∵Q″(,0),∴PQ″==,∴PM+MN+NQ的最小值为+.(3)如图3中,由(2)可知直线PB的解析式为y=﹣x+,直线BD的解析式为y=x﹣,易证∠PBQ=30°,∠DBO=60°,PB⊥BD.① 当点Q″与Q重合时,∵∠B′EQ=∠QB′E=30°,∴EQ=B′Q″=4,∴OE=QE+OQ=7.②如图4中,当B′E=B′Q″时作B′N⊥x轴于N.∵B′E=B′Q″=4,∠B′EN=30°,∴B′N=B′E=2,EN=2,∴B′(,﹣2),∴OE=2+=﹣1.③如图5中,当EQ″=EB′时,作B′N⊥x轴于N.易知EP′=EQ″=EB′=,B′N=,EN=2,∴B′(,﹣),∴EO=.④如图6中,当B′E=B′Q″时,易知B′E=B′Q″=4,在Rt△BEB′中,BE=EB′÷cos30°=,∴OE=OB+BE=+1,综上所述,满足条件的OE的值为7或﹣1或或+1.。
开侨中学第十二周周练习

开侨中学2017届理科数学第十三周综合测试命题人:周春峰一、选择题(共12小题,每小题5分,满分60分) 1.已知集合A={x |y=),B={x |x 2﹣1>0},则A ∩B=( )A .(﹣∞,﹣1)B .[0,1)C .(1,+∞)D .[0,+∞)2. 将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师和2名学生组成,不同的安排方案共有( ) A 、12种 B 、10种 C 、9种 D 、8种 3.复数的共扼复数是( ) A .﹣+i B .﹣﹣iC .﹣iD .+i4.已知双曲线C :(a >0,b >0)的离心率为,且过点(2,),则双曲线C 的标准方程为( ) A .B .C .D .x 2﹣y 2=15.已知等差数列{a n },满足a 1+a 5=6,a 2+a 14=26,则{a n }的前10项和S 10=( )A .40B .120C .100D .806.执行如图所示的程序框图,输出的结果是( )A .56B .36C .54D .647.一个几何体的三视图都是边长为1的正方形,如图,则该几何体的体积是( ) A .121 B .31 C .42 D.218.已知抛物线Γ:x 2=8y 的焦点为F ,直线l 与抛物线Γ在第一象限相切于点P ,并且与直线y=﹣2及x 轴分别交于A 、B 两点,直线PF 与抛物线Γ的另一交点为Q ,过点B 作BC∥AF 交PF 于点C ,若|PC |=|QF |,则|PF |=( ) A .﹣1 B .2C .3D .5 9.已知函数f (x )=|sinx |+|cosx |,则下列结论中错误的是( ) A .f (x )是周期函数 B .f (x )的对称轴方程为x=,k ∈Z C . f (x )在区间(,)上为增函数D . 方程f (x )=在区间[﹣π,0]上有6个根10.已知函数)(x f 是R 上的奇函数,且满足)()2(x f x f -=+,当]1,0[∈x 时,x x f =)(,则方程182)(+-=x x x f 在),0(+∞解的个数是( ) A .3 B .4 C .5 D.6 11.已知三棱锥ABC P -中,1===AC PB PA ,⊥PA 面ABC ,∠BAC =32π,则三棱锥ABC P -的外接球的表面积为( )A .π3B .π4C .π5 D.π8 12.若关于x 的不等式xln +x ﹣kx +3k >0对任意x >1恒成立,则整数k 的最大值为( )A .4B .3C .2D .5二、填空题(共4小题,每小题5分,满分20分) 13.已知||=2,||=,,的夹角为30°,( +2)∥(2+λ),则((+λ))•(﹣)= .14.若x ,y 满足不等式组,则z=|x ﹣3|+2y 的最小值为 .15.已知(1﹣x ﹣2y )2的展开式中不含x 项的系数和为m ,则x m dx= .16.已知数列{a n }的前n 项和为S n ,S 1=1,S 2=﹣,且S n ﹣S n ﹣2=3×(﹣)n ﹣1(n ≥3),则a n = .开侨中学2017届理科数学第十三周综合测试命题人:周春峰三、解答题(共5小题,满分60分)17.锐角△ABC 中,其内角A 、B 满足:B B ocsA cos 3sin 2-=.(1)求角C 的大小;(2)D 为AB 的中点,CD =1,求△ABC 面积的最大值.18.数列{}n a 中, 11=a ,11++=-n n n n a a a a ,*∈N n .(1)求数列{}n a 的通项公式;(2)n S 为{}n a 的前n 项和,n b =n n S S -2,求n b 的最小值.19.在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于60分的选手定为合格选手,直接参加第二轮比赛,不超过40分的选手将直接被淘汰,成绩在(40,60)内的选手可以参加复活赛,如果通过,也可以参加第二轮比赛.(1)已知成绩合格的200名参赛选手成绩的频率分布直方图如图,估计这200名参赛选手的成绩平分数和中位数;(40,50] (50,60)每名选手能够进入第二轮的概52,58,记这4名选手在复活赛中通过的人数为随机变量X,求X的分布列和数学期望.20.如图所示,在三棱锥ABC﹣A1B1C1中,底面△ABC为边长为6的等边三角形,点A1在平面ABC内的射影为△ABC的中心.(1)求证:BC⊥BB1;(2)若AA1与底面ABC所成角为60°,P为CC1的中点,求二面角B1﹣PA﹣C的余弦值.21.已知椭圆C:离心率为,右焦点F到直线x=的距离为1.(1)求椭圆C的方程;(2)过点F的直线l(与x轴不重合)与椭圆C交于A,B两点,线段AB中点为D,过点O,D的直线交椭圆于M、N两点(O为坐标原点),求四边形AMBN面积的最小值.22.已知f(x)=x,x∈(0,1).(1)若f(x)在(0,1)上是单调递增函数,求a的取值范围;(2)当a=﹣2时,f(x)≥f(x0)恒成立,且f(x1)=f(x2)(x1≠x2),求证:x1+x2>2x0.开侨中学2017届理科数学第十三周综合测试参考答案CADA DCBC CBCA13.1; 14. ; 15. ; 16.17. 解:(1)∵2cosA +cosB=sinB ,可得:cosA=sinB ﹣cosB=cos (﹣B ), (2)分又∵A ,B 为锐角, ∴0,<﹣B <,∴A=﹣B ,A +B=,可得:C=π﹣=.…5分(2)设∠ACD=α,延长CD 到E ,使CD=DE ,则AEBC 为平行四边形,在△ACE 中,AC=b ,AE=BC=α,CE=2,∠CAE=,∠AEC=﹣α,由正弦定理可得:==,所以,a=4sin α,b=4sin (﹣α),…7分S △ABC =absin ∠ABC=sin=4sin α•sin (﹣α)=2sin αcos α﹣2sin 2α =sin2α+cos2α﹣=2sin (2α+)﹣,…11分当α=时,△ABC 的面积取得最大值,最大值为2﹣.…12分18. 解:(1)∵a 1=1,a n ﹣a n +1=a n a n +1,n ∈N *.∴=1,∴数列是等差数列,公差为1,首项为1.∴=1+(n ﹣1)=n ,可得a n =.(2)由(1)可得:S n =1++…+.∴b n=S2n﹣S n=+…+.﹣b n=+…+++﹣(+…+)∴b n+1=+﹣=﹣>0,∴数列{b n}单调递增,∴b n的最小值为b1=.19.解:(1)由10(0.01+0.02+0.03+a)=1,解得:a=0.04,由平均数x¯=10×(65×0.01+75×0.04+85×0.02+95×0.03)=82,由图可知:前两个矩形面积之和为0.5,∴中位数为80;(2)由题意可知:成绩在(40,50],(50,60)内选手各由两名,则随机变量X的取值为0,1,2,3,4,P(X=0)=×××=,P(X=1)=××××+××××=,P(X=2)=×××+×××+×××××=,P(X=3)=××××+××××=,P(X=3)=×××=,0 1 2 3 4∴X数学期望E(X)=0×+1×+2×+3×+4×=.20.证明:(1)点A1在底面△ABC内的射影为O,连结A1O,取BC的中点E,连结AE,∵A1O⊥面ABC,BC⊂面ABC,∴A1O⊥BC,又∵AE⊥BC,AE∩A1O=O,∴BC⊥面A1AO,∵AA1⊂面A1AO,∴BC⊥AA1,∵AA1∥BB1,∴BC⊥BB1.解:(2)由(1)得A1O,AO,BC两两垂直,建立如图所示的空间直角坐标系,∵A1O⊥面ABC,∴∠A1AO为AA1与底面ABC所成角,∵AB=6,∴,,由,得A1O=6,∴A(2,0,0),B(﹣,3,0),C(),A1(0,0,6),由=,得C1(﹣3,﹣3,6),由=,得B1(),∴P(﹣2,﹣3,3),=(﹣4,﹣3,3),=(﹣),=(﹣3,﹣3,0),设平面PAB1的一个法向量=(x,y,z),则,取x=,得=(),设平面PAC的一个法向量=(a,b,c),则,取a=,得=(),设二面角B1﹣PA﹣C的平面角为θ,由图知θ为钝角,则cosθ=﹣=﹣.∴二面角B1﹣PA﹣C的余弦值为﹣.21. 解:(1)由题意可知:e==,﹣c=1,解得:a=,c=1,b2=a2﹣c2=1,∴椭圆方程为,(2)设A(x1,y1),B(x2,y2),D(x0,y0),设直线AB的方程为x=my+1,联立,整理得:(2+m2)y2+2my﹣1=0,由韦达定理可知:y1+y2=,y1•y2=,由弦长公式可知:丨AB丨=•丨y1﹣y2丨=,由中点坐标公式可知:y0==,x0=my0+1=+1=,∴D(,),直线OD的方程为y=﹣x,代入,整理得:x2=,M(,),N(,),M到直线AB的距离d1=,N到直线AB的距离d2=,∵M,N在直线AB的两侧,且MN关于原点对称,∴S AMBN=丨AB丨+(d1+d2)=••(+),=,∴S AMBN==2≥2,综上所述,四边形AMBN面积的最小值2.22. 解:(1)f(x)=x,x∈(0,1).则f′(x)=2x+a﹣,∵f(x)在(0,1)上是单调递增函数,∴f′(x)≥0恒成立,即2x+a﹣≥0可得:2x﹣≥﹣a恒成立,令g(x)=2x﹣,x∈(0,1).g′(x)=2﹣sin∵x∈(0,1)是g′(x)>0,且g′(0)>0,g′(1)<0;∴g′(x)在区间(0,1)上存在唯一零点x′;所以g(x)在区间(0,x′)上单调递增,在区间(x′,1)上单调递减,故有,解得:a.所以f(x)在(0,1)上是单调递增函数,a的取值范围是[,+∞)证明:(2)当a=﹣2时,f(x)=,x∈(0,1).则f′(x)=2x﹣2﹣,令h(x)=2x﹣2﹣,即f′(x)=h(x);则h′(x)=2﹣sin显然x∈(0,1)上,h′(x)是单调递减.又∵h′(0)=2>0,h′(1)=2<0,故存在唯一实数根ξ∈(0,1)使得h′(ξ)=0;所以h(x)在区间(0,ξ)上单调递增,在区间(ξ,1)上单调递减,即f′(x)在区间(0,ξ)上单调递增,在区间(ξ,1)上单调递减;又∵f′(0)=﹣2+<0,f′(1)=0;∴f′(ξ)>0;因为f(x)≥f(x0)恒成立,所以x0是f(x)的极小值点,由f′(x0)=0,可知0<x0<ξ<1.∴f(x)在区间(0,x0)上单调递减,在区间(x0,1)上单调递增.f′()=﹣1+,∴0<x0<;不妨设x1<x2,由题意:f(x1)=f(x2),则:0<x1<x0<x2<1.要证明:x1+x2>2x0,即证明:2x0﹣x1<x2,∵x0<2x0﹣x1<1,x0<x2<1,所以只要证:f(2x0﹣x1)<f(x2)<f(x1);即要证f(2x0﹣x1)<f(x1);设F(x)=f(2x0﹣x1)﹣f(x1);即证F(x)<0在x∈(0,1)上恒成立,F′(x)=﹣f′(2x0﹣x1)﹣f′(x1)=﹣h(2x0﹣x1)﹣h(x1)令M(x)=﹣h(2x0﹣x1)﹣h(x1)则M′(x)=h′(2x0﹣x1)﹣h′(x1)∵h′(x)在x∈(0,1)上单调递减.x0<2x0﹣x1<1,∴h′(2x0﹣x1)﹣h′(x1)<0即h(x)<0,x∈(0,1)上单调递减.h(x)>h(x0)=﹣2f′(x0)=0;可得F′(x)>0,在x∈(0,x0)上恒成立,则F(x)在x∈(0,x0)上单调递增,F(x)<F(x0)=0;所以:x1+x2>2x0.。
第十三中学初二上学期期中数学试卷(含答案) (2)

已知图中的两个三角形全等,则∠1 等于( A.50° C.60° B.58° D.72°
c
72°
b
5. 如图,△ABC≌Δ ADE,若∠B=80°,∠C=30°, ∠DAC=35°,则∠EAC 的度数为 ( ) A.40° B.35° C.30° D.25°
6.分式方程 A. x= -2
A. B. C. D. 2. 下列因式分解中,正确的个数为( ) 3 2 2 2 2 2 ①x +2xy+x=x(x +2y) ;②x +4x+4=(x+2) ;③﹣x +y =(x+y) (x﹣y) A. 3 个 B.2 个 C. 1 个 D. 0 个 3. 若分式 A. 0 4. 的值为零,则 x 的值为( ) B. 1 C. -1 D. ±1 )
初中毕业生重点卷
xxx 市第十三中学 2015-2016 学年度 初二数学期中测试
考 生 须 知 2.在试卷和答题卡上认真填写班级、姓名和准考证号。 3.试题答案一律填涂或书写在答题卡、答题纸上,在试卷上作答无效。 4.在答题纸上,选择题、作图题用 2B 铅笔作答,其他试题用黑色字迹签字笔作答。 5.考试结束,请将答题卡、答题纸和草稿纸一并交回。
A E F B
D
证 :
,错误!未找到引用源。错误!未找到引用源。.求 错误!未找到引用源。.
C
25.先化简,再求值: 1
1 a ,其中 a 3 1 . 2 a 1 a 2a 1
四、解答题(26 题 3 分,27-29 每题 6 分,本题共 21) 26.尺规作图: 已知: 如图, 试在 l 上找一点 P , 使点 P 到 A A 与直线 l . 的两边的距离相等.要求:保留痕迹,不写作法.
八年级英语上学期第13周本练习 试题

心尺引州丑巴孔市中潭学校武平县城郊二零二零—二零二壹八年级英语上学期第13周校本练习班级座号成绩Ⅰ、单项选择〔30分〕〔〕1.—Maria ,can you play basketball?— No, I can′t. But I can play piano.A. the; theB./; theC. the; /( ) 2. After knew the bad news, she felt very .A. happyB. sadC. well( )3. — are you going to stay here?—For three days.A. How longB. How oftenC. How soon( )4. —They are going to have a soccer game against Class Five next week.—Really? Let′s go toA. Cheer on themB. Cheer they onC. Cheer them on( )5. —There a wonderful movie tomorrow evening. would you like to watch it with me?—sure ,I′d love to.A. hasB. is going to haveC. is going to be( ) 6. We shouldn’t too much time computer games.A. spend ,inB. spend ,to playC. spend ,playing ( )7. — Would you mind not smoking here? — .A. Not at allB. Ok , I willC. sorry ,I won’t( )8.Michael enjoys basketball very much.A. plays B .playing C. to play( )9. —We should do our best when we are young.—I agree with youA. to learnB. learningC. learn( )10. We are all when we watch the football game.A. excited; excitedB. exciting; excitedC. excited; exciting( ) 11. The 30th Olympic Games was held in London in 2021. The 31st Olympic Games will be held .A. in 2021B. in 2016C. in 2021( )12. —Doctor, what’s wrong with my son? Is it serious?—No, . He didn’t have a good rest.A. anything seriousB. serious nothingC. nothing serious( ) 13. Running right after meals bad for our health.A. areB. isC. am( )14. — I borrow your bike , please? —sure , Here you are.A. MustB. MayC. Should( )15.It is important us to have healthy eating habitsA. toB. ofC. for( )16. — Is playing computer games too much good or bad? —A. Yes, it is.B. No, it isn’t.C. It’s bad.( )17. —Why are you so happy? —Because I won .A. the boy’s 400 meter raceB. the boys’ 400-meter raceC. the boys’ 400-meters race( )18. —Doing exercise every day our health.—Yes, that’s right.A. is good atB. is harmful to C .is good for( )19. — Must We finish the work just now?— .You can do it tomorrow.A. No, you mustn’tB. No, you needn’tC. No, you don’t( )20. He didn’t win the game ,but he never tryingA. gave upB. put upC. get upⅡ完形填空〔20分〕Oscar is a black bear. He likes going shopping.One day , Oscar 21 the shopping with his mother. When they 22 the supermarket , Oscar was very 23 .There were many things and many people 24 it. His mother told Oscar 25 her .They walked here and there and they 26 some things. When they came to a shelf (架子),Oscar 27 some boxes of chocolates. He wanted his mother to buy some 28 him. His mother gave 29 a box of black chocolates .Oscar shook(摇晃)his head and said,“I want a box of white chocolates.〞“Why?〞 asked his mother.“I may bite(咬)my fingers 30 I eat black chocolates at night,〞 answered Oscar quickly.21 ( ). A. did B. do C. does22. ( ) A. arrived in B. reached to C. got to23. ( ) A. sorry B .happy C. sad24. ( ) A. on B. in C. at25. ( ) A. followed B. follows C. to follow26. ( ) A. bought B. took C. carried27. ( ) A. looked B. saw C. read28. ( ) A .with B. for C. to29. ( ) A. him B. to him C. for him30. ( ) A. after B. before C. whenⅣ阅读理解〔20分〕(A)Tony was a 13-year-old boy. He was tall and strong . Everyone was proud of him because he ran fastest in his class. A month ago, a new student,Nick, came to his class. Nick was thin and short,but he ran very fast when he was playing basketball with his classmates. One of Tony’s good friends, Jimmy, told Tony about it. But Tony didn’t believe it at all. So he want to have a race with Nick on the school playground the next day.Early next morning, Tony and Nick both got ready for the race. All of their classmates came tothe school playground except Miss Wang, because they wanted to know if Nick could run faster than Tony. The race was over when Miss Wang came there. She asked Tony, “What’s the result,Tony?〞“I was the second, Miss Wang,〞 answered Tony.“Congratulations to you!〞 Miss Wang said happily.〞“And how was Nick?〞“He was the last but one(倒数第二).〞根据短文内容,选择正确答案。
广东省深圳市文汇中学14—15学年上学期八年级数学第13周周末作业(无答案)

广东省深圳市文汇中学14—15学年上学期八年级数学第13周周末作业1.16的平方根是 ( ) (A )4± (B )32± (C )2 (D ) 2±2.下列能构成直角三角形三边长的是 ( ) (A )1、2、3 (B )2、3、4 (C )3、4、5 (D )4、5、63.下列数中是无理数的是( ) (A )113355(B )16 (C )0.37373737 (D )2π4.下列计算错误的是( )(A )2)2(2=- (B )()2233-=-(C ) 3的平方根是3± (D )()232)3(-⨯-=-⨯-5.点P (﹣2,1)在平面直角坐标系中所在的象限是( ) (A )第一象限 (B ) 第二象限 (C )第三象限 (D )第四象限6若⎩⎨⎧-==12y x 是关于x 、y 的方程组⎩⎨⎧=+=-05by x y ax 的解,则a 、b 的值为( )A .⎩⎨⎧-==22b a B.⎩⎨⎧==22b a C. ⎩⎨⎧-=-=22b a D.以上都不正确7、下列图象中,能表示一次函数1+-=x y 的图象是( )8.如图所示圆柱形玻璃容器,高17cm ,底面周长为24㎝,在外侧下底面点S 处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处1㎝的点F 处有一苍蝇,急于捕获苍蝇充饥的蜘蛛,所走的最短路线的长度是( ) (A ) 20cm (B ) 138cm (C )433cm (D ) 24cm9、如图,函数y 1=ax+b 与y 2=bx+a 正确的图象为10、已知M (3,2),N (1,-1),点P 在y 轴上,且PM +PN 最短,则点P 的坐标是( ) (A )(0,21) (B )(0,0) (C )C 、(0,611) (D )(0,41-)二、填空题(前面4个小题每题3分,第15题4分,共16分)11.比较大小:-412.点P (3,-5)关于x 轴对称的点的坐标是 .13、函数25+-=x y 与x 轴的交点坐标是_________,与y 轴的交点坐标是_________。
初一新生入学分班考试卷(十三中)s

初一新生入学分班考试卷(一)语 文班级 姓名 得分一、基础部分。
(36分)1. 下列词语中加点字注音完全正确的一项是 ( )(3分)A.收敛.(liǎn) 屏.气(píng) 人行.道(xíng) B.沉郁.(yù) 提.防(tí) 河堤.(d ī) C.几.乎(j ī) 间.隔(jiān) 称.职(chèn) D.粗犷.(guǎng) 旷.野(kuàng) 胆怯.(qiè) 2.下列句中词语书写有两处错误的一项是 ( )(3分)A.读着女儿写给自己的信,妈妈第一次发现女儿的字写得那么漂亮,文章写得那么有 文彩。
B.影响中小学生学习成绩的主因是注意力不集中,如上课做不住、开小差、做作业摩蹭。
C.爸爸在儿子的衣袋里发现了来历不名的钱,他意识到问题的严重性。
D.“寻物启示”已经播出很多天了, 一点反映都没有,真另人着急啊。
3.下列语句中带点词语运用有错误的一项是 ( )(3分)A.元宵佳节,老街上的干果店独出心裁....,制成各样的冰灯,吸引顾客。
B.星期天,晶晶和爸爸一起去瞻仰一江山岛革命烈士纪念馆。
离开的时候,他们兴高采烈....。
C. 在本次篮球比赛中,六(1)班和六(2)班旗鼓相当....,最后以1:1握手言和....。
D.每个时代都有不同的英雄,战斗在一线救死扶伤....、迎难而上....的医务工作者就是伟大的英雄。
4. 下列句子中标点符号使用有错误的一项是 ( )(3分)有一次,我禁不住问他:“老班长,你怎么不吃鱼啊?”“我知道小狐仙在什么地方,”他低声说:“但是这并不等于说我愿意告诉你。
” “什么?爹!”我瞪着眼睛问父亲。
腊月二十三过小年,差不多就是过春节的“彩排”。
5. 选词填空。
( )(3分) ①这次挫折对他打击很大,这阵子他一直 ,振作不起来。
②一心去看球赛,排了两个钟头的队,结果竟然没买到票,他 地回到了家。
广东省江门市开侨中学2017-2018学年度第一学期高二文科数学第10周周练卷

广东省江门市开侨中学2017-2018学年度第一学期数学第10周周练卷一、选择题(本大题共12小题,每题5分,共60分) 1、下列命题中,正确的是( )A. 若d c b a ,,则 bd acB. 若bc ac ,则b aC. 若d c b a ,,则 d b c a --D. 若22bc ac ,则b a2、关于x 的不等式0 b ax -的解集是()∞+,1,则关于x 的不等式0)3)(( -+x b ax 的解集是( ) A. ()31,- B. ()31, C. ()),3(1+∞⋃∞-, D. ()),3(1+∞⋃-∞-,3、已知向量2,1==b a 且0=∙b a ,又d c b n a m d b a c//,,2-=+=,则=nm ( )A. 21- B. -1 C. 1 D. 24、已知{}n a 是首项为32的等比数列,n S 是前n 项和,且646536=S S ,则数列{}n a 2log 前10项和为( ) A. 58 B. 56 C. 50 D. 455、公比不为1的等比数列{}n a 的前n 项和为n S ,且321,,3a a a --成等差数列,若11=a ,则4S =( )A. -20B. 0C. 7D. 406、已知△ABC 中,∠A=30°,AB ,BC 分别是23,23-+的等差中项与等比中项,则△ABC 的面积等于( )A. 23B. 43C. 23 或3D. 23 或437、首项为正数的等差数列{}n a 的前n 项和为n S ,若1006a 和1007a 是方程020*******=--x x 的两根,则使0 n S 成立的正整数n 的最大值是( ) A. 1006 B. 1007 C. 2011 D. 20128、已知a ,b ,c 为△ABC 的三个内角A 、B 、C 的对边,向量)sin ,(cos )1,3(A A n m =-=,,若n m ⊥,且C c A b B a sin cos cos =+,则∠B=( ) πππ2π9、△ABC 的三内角A ,B ,C 的对边边长分别为a ,b ,c ,若B A b a 2,25==,则cosB=( ) A. 35 B. 45 C. 55 D. 6510、若a ,b ,c 为△ABC 的三边,直线0=++c by ax 与圆122=+y x 相离,则△ABC 一定是( )A. 直角三角形B. 等边三角形C. 锐角三角形D. 钝角三角形11、定义在R 上的偶函数f (x )满足:对[)()2121,0,x x x x ≠+∞∈∀,有()0)(1212 x x x f x f --,则( ) A. ()()()5.07.0666log 7.0f f f B. ()()()6log 67.07.05.06f f f C. ()()()65.07.07.066log f f f D. ()()()5.07.0666log 7.0f f f12、数列{}n a 满足12)1(1-=-++n a a n n n ,则{}n a 的前60项和为( )A. 3690B. 3660C. 1845D. 1830二、填空题(本大题共4小题,每小题5分,共20分)13、圆C 与直线x+y=0及x+y-4=0都相切,圆心在直线x-y=0上,则圆C 的方程为14、对任意实数x ,不等式()04)2(222 ----x a x a 恒成立,则实数a 的范围是15、数列{}n a 满足*221,5221...2121N n n a a a n n ∈+=+++,则n a =16、如右图,把正整数按上小下大,左小右大的原则排成如图三角形数表(每行比上一行多一个数):设()*,N j i a j i ∈,是位于这个三角形数表中从上往下数第i 行、从左往右第j 个数,如824=,a ,则2551,a 为 1 2 3 4 5 6 7 8 9 10三、解答题(本大题共6小题,共70分) 17、设()()112++-=x a ax x f (1)解关于x 的不等式f(x)>0(2)若对任意的[]1,1-∈a ,不等式f(x)>0恒成立,求x 的取值范围18、已知函数())(2cos 322cos R x x x x f ∈-⎪⎭⎫ ⎝⎛-=π(1)求函数()x f 的最小正周期和单调递增区间(2)△ABC 内角A 、B 、C 的对边分别为a 、b 、c ,若3,1,232==-=⎪⎭⎫⎝⎛c b B f ,且a >b ,求B 和C19、设数列{}n a 满足*11),1()1(,1N n n n a n na a n n ∈+++==+(1)证明:⎭⎬⎫⎩⎨⎧n a n 是等差数列(2)设n n n a b 3=,求数列{}n b 的前n 项和n S20、如图,在△ABC 中,3π=∠B ,AB=8,点D 在BC 上,且CD=2,71cos =∠ADC(1)求sin ∠BAD(2)求BD 、AC 的长21、如图,四棱锥P-ABCD 中,△PAB 是正三角形,四边形ABCD 是矩形,且平面PAB ⊥平面ABCD ,PA=2,PC=4,。
人教版八年级数学上册13周2.docx

初中数学试卷桑水出品八年数学周末卷(13--2)一、选择题1、在x 1、31、212+x 、πy +5、m a 1+中分式的个数有( )A 、2个B 、3个C 、4个D 、5个2 、使分式1122+-a a 有意义的a 的取值是( )A 、a ≠1B 、a ≠±1C 、a ≠-1D 、a 为任意实数3、把分式b a a+2中a 、b 都扩大2倍,则分式的值( )A 、扩大4倍B 、扩大2倍C 、缩小2倍D 、不变4、能使分式122--x xx 的值为零的所有x 的值是( )A 、 0=xB 、1=xC 、0=x 或1=xD 、0=x 或1±=x5、下列计算错误的是( )A 、253--=⋅a a aB 、326a a a =÷C 、33323a a a -=-D 、()1210=+-7、化简x y xx 1⋅÷的结果是( )A 、 1B 、 xyC 、 x yD 、 y x8、下列公式中是最简分式的是( )A 、21227ba B 、22()ab b a -- C 、22x y x y ++ D 、22x y x y --9、化简x y y x y x ---22的结果是( )A 、y x --B 、x y -C 、y x -D 、y x +10、一件工作,甲单独做a 小时完成,乙单独做b 小时完成,则甲、乙两人合作完成需要()小时。
A 、ba 11+ B 、ab 1 C 、b a +1 D 、b a ab + 二、填空题11、要使31-x 有意义,则x 的取值范围是 .12、当x 时,分式313+-x x 有意义;13、利用分式的基本性质填空:(1)())0(10 53≠=a axy xy a (2)()1422=-+a a ; 14、分式12x ,212y ,15xy-的最简公分母为 ; 三、解答题15、计算:(1)y x y y x x ---22 (2) 222246⎪⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛x y x y16、计算:(1)bc c b ab b a +-+ (2)÷+--4412a a a 214a a --17、先化简,再求值:22111x x x -⎛⎫+÷ ⎪⎝⎭,其中2=x 。
第十三周双休日作业

塘南中心小学第十三周双休日作业班级姓名家长签字一、判断正误。
1、一堆煤,用去了80%,还剩20%吨。
()2、李师傅加工了120个零件,个个合格,合格率就是120%。
()3、今年的产量比去年增加了20%,今年的产量就相当于去年的120%。
()4、56.5%读作百分之五六点五。
()5、一件衣服打九折,就是指衣服的现价是原价的90%。
()⒍比的前项不变,后项乘以2,比值扩大到原来的2倍。
()⒎甲数与乙数的比是5:4,乙数是甲数的45 。
()⒏一个真分数的倒数一定比这个真分数大。
()二、想一想,填一填。
1、18=()÷()=()∶()=()24=()%2、一个数是由5个一和3个百分之一组成的,这个数写成小数是(),写成百分数是(),这个百分数读作()。
3、甲乙两数的比是3∶4,甲数是乙数的()%。
4、比50米少40%的是()米,35米比()米多40%。
5、六(1)班有男生20人,女生30人,女生人数是男生人数的()%,男生人数约占全班人数的()%,女生比男生多()%。
6、果园今年种果树200棵,活了198棵,成活率是()。
7、商店五月份营业额50000元,如按营业额的4%缴纳营业税,五月份应纳税()元。
8、在3.145、3.14、π、3.14%中,最大的数是(),最小的数是()。
三、选一选。
1、下面的分数可以用百分数表示的是()。
A、小丽一步约走35米 B、大牛比小牛45多 C、一堆煤重910吨2、把25克盐溶化在100克水中,盐的重量占盐水的()。
A、20%B、25%C、125%3、六年级共有学生120人,今天有2人请病假。
六年级学生今天的出勤率是()。
A、98.3%B、98.4%C、118%4、小明家十月份用电80度,比上月节约了20度,比上月节约了( )。
A 、25%B 、20%C 、40%5、甲数是200,乙数比甲数大20%,乙数是( )。
A 、40B 、120C 、240⒍桃树的棵数比李树多15 ,桃树棵数和李树棵数的比是( )。
四会中学十三周数学周末测试及参考答案.doc
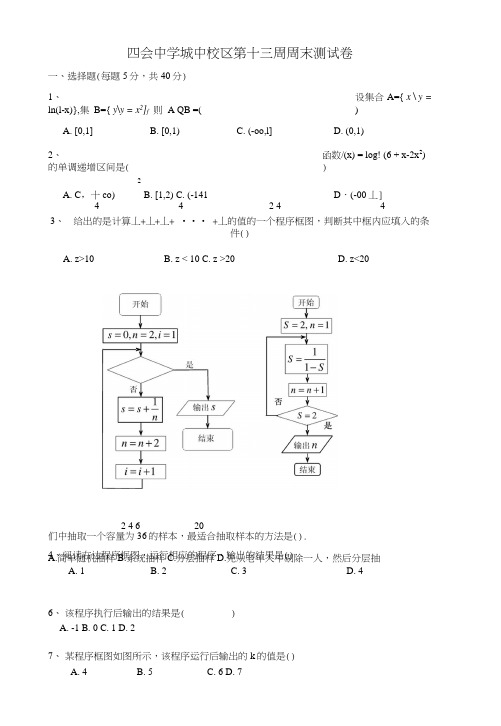
四会中学城中校区第十三周周末测试卷一、选择题(每题5分,共40分) 1、设集合 A={ x \ y = ln(l-x)},集 B={ y\y = x 2]f 则 A QB =()A. [0,1]B. [0,1)C. (-oo,l]D. (0,1)2、函数/(x) = log! (6 + x-2x 2)的单调递增区间是()2A. C ,十co)B. [1,2)C. (-141D ・(-00丄]4 42 443、 给出的是计算丄+丄+丄+ ••• +丄的值的一个程序框图,判断其中框内应填入的条件() 2 4 6 20们中抽取一个容量为36的样本,最适合抽取样本的方法是().A.简单随机抽样B.系统抽样C.分层抽样D.先从老年人中剔除一人,然后分层抽6、 该程序执行后输出的结果是( )A. -1B. 0C. 1D. 27、 某程序框图如图所示,该程序运行后输岀的k 的值是()A. 4B. 5C. 6D. 7A. z>10B. z < 10C. z >20D. z<204、阅读右边程序框图,运行相应的程序,输出的结果是() A. 1 B. 2 C. 3 D. 48>为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁一1 8岁的男生休重(kg),得到频率分布直方图如F:根据上图町得这100名学生中体重在[56.5,64.5)的学生人数是()A. 20B. 30C. 40D. 50n=5s=()WHILE s<15S=s + nn=n— 1WENDPRINT nEND(第6题)二、填空题(每题5分,共3()分)9、函数f(x) = / 1的定义域是V2 一4e x10、若指数函数在[0, 1]上的最大值与最小值的差为3,则a的值为____11、执行右边的程序框图,输出的______________12、某校有教师400人,男学牛3000人,女学生3200人现用分层抽样的方法,从所有师生中抽取一个容量为刃的样木,已知从男生中抽取的人数为100A,贝川= ___________ .体血(kg) 13、某初级中学领导采用系统抽样方法.,从该校预备年级全体800名学牛中抽50名学生做牙齿健康检杳。
八年级数学第十三周周练试题试题

创作;朱本晓 宁化城东中学2021-2021学年八年级第十三周周练数学试题〔无答案〕班级 座号 姓名 得分一、选择题〔30分〕1、以下不等式一定成立的是( ) A.5a >4aB.x +2<x +3C.-a >-2aD.aa 24> 2、以下各组线段中,不是成比例线段的是 ( )A. 4,2,6,3====d c b aB. 10,5,6,4====d c b aC.3,6,2,1====d c b aD.32,15,5,2====d c b a3、某今年一共有5万人参加研究生考试,为了理解5万名考生的成绩从中抽取1000名考生的英语成绩进展统计分析,以下说法正确的有( )个. ①5万名考生为总体 ②调查采用抽样调查方式③1000名考生是总体的一个样本 ④ 每名考生的英语成绩是个体 A. 4 B. 3 C. 2 D. 14、当分式2239)(--x x 的值是零时,x 的值是 ( ) A. 3 B. -3 C. 0 D. 3或者-3创作;朱本晓 E H FGA5.假设分式n m nm m、中的22+同时扩大2倍,那么分式的值〔 〕A 、扩大两倍B 、不变C 、缩小两倍D 、无法确定115122-=-++x mx x 会产生增根,那么m 等于 ( ) A. -10 B. -10或者-3 C. -3 D. -10或者-4323+-=x y 的图象如下图,当-3 < y < 3时, x 的取值范围是〔 〕 A .x >4 B .0<x <2 C .0<x <4 D .2<x <4第7题图 第8题图8、如图,△ABC 是等边三角形,被一平行于BC 的矩形所截,AB 被截成三等分,那么图中阴影局部的面积是△ABC 的面积的 〔 〕A.91 B.92 C.31 D.94 9、甲,乙两个小组各10名同学,在同一次英语口语测验中,两组成绩的平均数___x 相等,但方差不等,.36,26s 13.2,22==乙甲s 那么这次测验成绩比拟整齐的是〔 〕10.图中的圆点是有规律地从里到外逐层排列的.设y 为………创作;朱本晓第n 层〔n 为正整数〕圆点的个数,那么以下函数关系中正 确的是……………………………… 【 】A .44y n =-B .4y n =C .44y n =+D .2y n =二、填空题〔18分〕11、假设a+b=7,ab=10,那么22ab b a +的值应是12.如图,在□ABCD 中,E 为DC 边的中点,AE 交BD 于O,△DOE 的面积为9, 那么S AOB =___________12210,,,,-- 的方差是 ;14、假如线段AB=10㎝,点C 是AB 上靠近点B 的黄金分割点,那么AC 的值是 ㎝。
七年级上学期第13周周练试题(共6页)

2021—2021学年上期城东中学(zhōngxué)七年级语文第13周周练一、默写古诗〔8分〕1.无可奈何花落去,,。
2. ,天光云影一共彷徨。
3.商女不知亡国恨,。
4.乡书何处达?。
5.,小桥流水人家。
6.争渡,争渡,。
7. ,为有源头活水来。
二、以下语句没有语病的一项是哪一项:〔〕〔3分〕A.拥有坚强的意志,是能否改掉不良习惯的根本。
B.中国一共产HY走过的90多年的奋斗历程,为我们留下了勤劳英勇、自强不息的伟大民族精神。
C.他在做每道题时,都是经过认真考虑、深思熟虑之后才动笔。
D.“阳光体育〞活动有助于培养学生的身体素质,要大力提倡。
三、名著阅读〔6分〕1.在以下三个有关?西游记?的情节中,最能表达孙悟空对抗精神的是__________。
〔1分〕请你简要概述这一情节的主要内容。
(3分)A、大闹龙宫B、大闹天宫C、大闹地府情节内容:_______________________________________________________________________________ _______________________________________________________________________________ ______________________________________________________________________________________________________________________________________________________________ ________________四、文言文阅读〔22分〕虽有佳肴,弗食,不知其旨也。
虽有至道,弗学,不知其善也。
是故学然后知缺乏,教然后知困。
知缺乏然后能自反也;知困然后能自强也。
故曰:教学相长也。
?兑命?曰:“学学半。
〞其此之谓乎!1.划出以下句子的停顿〔每句停一处〕〔2分〕〔1〕是故学然后知不足〔2〕知困然后能自强也2.解释加点的字〔11分〕〔1〕虽.有至道,〔〕〔2〕弗.学〔〕〔3〕不知其旨.也〔〕〔4〕教学相长.也〔〕〔5〕学.学半〔〕〔6〕知困.然后能自强.也〔〕〔〕〔7〕不知其善.也〔〕〔8〕温故.而知新〔〕择其善.者而从之〔〕故.曰:教学相长也。
开侨中学理科数学十三周周末练习

开侨中学理科数学十三周周末练习1.已知集合M={x|(x+1)(x﹣3)<0,x∈R},N={﹣1,0,1,2,3},则M∩N等于()A.{0,1,2} B.{﹣1,0,1} C.{﹣1,0,2} D.{1,2,3}2.已知双曲线C:﹣=1(a>0,b>0)的离心率为,则C的渐近线方程为()A.y=±2x B.y=±x C.y=±x D.y=±x3.设向量,满足|+|=,||=1,||=2,则•等于()A.B.C.D.4.设复数满足,则()A.B.C.D.5.(1+ax)(1﹣x)2的展开式中x2的系数为5,则a等于()A.1 B.﹣1 C.2 D.﹣26.执行如图所示的程序框图,输出的k值为()A.3 B.4 C.5 D.67.若某物体的三视图如图所示,则该物体的体积是()A.10+6π B.10+20π C.14+5π D.14+20π8.已知不等式组,则目标函数z=2y﹣x的最大值是()A.1 B.﹣1 C.﹣5 D.49.设函数f(x)=sin2x+cos2x,若将函数f(x)的图象向右平移个单位,所得图象对应函数为g(x),则()A.f(x)的图象关于直线x=对称,g(x)图象关于原点对称B.f(x)的图象关于点(,0)对称,g(x)图象关于直线x=对称C.f(x)的图象关于直线x=对称,g(x)图象关于原点对称D.f(x)的图象关于点(,0)对称,g(x)图象关于直线x=对称10.已知函数f (x )=x 3+ax 2﹣9x+1,下列结论中错误的是( )A .∃x 0∈R ,f (x 0)=0B .“a=3”是“﹣3为f (x )的极大值点”的充分不必要条件C .若x 0是f (x )的极小值点,则f (x )在区间(x 0,+∞)单调递增D .若3是f (x )的极值点,则f (x )的单调递减区间是(﹣1,3)11.已知以F 为焦点的抛物线y 2=4x 上的两点A 、B 满足=3,则弦AB 的中点到准线的距离为( )A .B .C .2D .112.若存在x 使不等式xx me ->m 的取值范围为( ) A .B .C .(),0-∞D .()0,+∞13.若曲线y=aln (x+1)在点(0,0)处的切线方程为y=2x ,则a= _________ . 14.在△ABC 中,a=1,b=,cosC=﹣,则sinB=________15.若函数f (x )是定义在R 上的偶函数,且在区间[0,+∞)上是单调增函数.如果实数t 满足时,那么t 的取值范围是 _________ .16.将a ,b 都是整数的点(a ,b )称为整点,若在圆x 2+y 2﹣6x+5=0内的整点中任取一点M ,则点M 到直线2x+y ﹣12=0的距离大于的概率为 _________ .17.设数列{a n }是公比为正数的等比数列,a 1=2,a 3﹣a 2=12.(1)求数列{a n }的通项公式;(2)设数列{b n }是首项为1,公差为2的等差数列,求数列{a n +b n }的前n 项和S n .18.如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.(Ⅰ)求证:DE∥平面ABC;(Ⅱ)求二面角E﹣CD﹣B的余弦值.19.如图,已知椭圆的右顶点为A(2,0),点P(2e,)在椭圆上(e为椭圆的离心率).(1)求椭圆的方程;(2)若点B,C(C在第一象限)都在椭圆上,满足,且,求实数λ的值.20.已知函数f(x)=e x﹣m﹣ln(2x).(Ⅰ)设x=1是函数f(x)的极值点,求m的值并讨论f(x)的单调性;(Ⅱ)当m≤2时,证明:f(x)>﹣ln2.21.(选做题)在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的圆心的极坐标为(,),半径r=,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.(1)求圆C的直角坐标方程;(2)求|PA|•|PB|的值.24.函数f(x)=|x﹣4|﹣t,t∈R,且关于x的不等式f(x+2)≤2的解集为[﹣1,5].(1)求t值;(2)a,b,c均为正实数,且a+b+c=t,求证:++≥1.理数13周周末参考答案1.A 因为()(){}{}=130,13M x x x x R x x +-<∈=-<< {}{}{}131,0,1,2,30,1,2M N x x =-<<-=2.A 【解析】试题分析:由题设e =222222152c a b b ba a a a +⎛⎫==+=⇒= ⎪⎝⎭所以双曲线渐近线方程为: by x a=±即: 2y x =±3.D 【解析】试题分析:因为6a b +=,所以()222626a b a a b b +=⇒+⋅+=又因为1,2a b ==,所以1246a b +⋅+=,解得: 12a b ⋅=, 4.C 【解析】试题分析:因为 ,所以5.D 【解析】试题分析:因为的展开式中x 2的系数为,由题意: ,解得: ,故选 D .6.B 试题分析:运行第一次,01,311,100k s s ==⨯=≤成立; 运行第二次,12,1327,100k s s ==+⨯=≤成立;运行第三次,23,73334,100k s s ==+⨯=≤成立; 运行第四次,34,3434142,100k s s ==+⨯=≤不成立;退出循环,输出k 的值4;故选B . 7.C 试题分析:由三视图可知该几何体是一个长、宽、高分别为4、0.5、7的长方体与的个底面直径为1,高为5的圆柱组成的组合体,所以该几何体的体积2240.5751452V ππ⎛⎫=⨯⨯+⨯⨯=+ ⎪⎝⎭,故选 C .8.A 平面直角坐标系中,不等式组510x y x y y +≤⎧⎪-≥⎨⎪≥⎩所表示的平面区域如下图中的阴影部分所示,由2z y x =-,得:1122y x z =+,当z 变化时,它表示一组经过可行域且互相平行的直线,直线的斜率为12,在y 轴上的截距为2z ,截距越大z 越大,截距越小z 越小;由图可知当直线经过点A 时,在y 轴上的截距最大,解方程组15x y x y -=⎧⎨+=⎩得A 点的坐标为(3,2),所以当3,2x y ==时,max 2231z =⨯-=.9.C 试题分析:因为()12cos 2sin 2cos cos 2sin sin 22666f x x x x x x πππ⎛⎫=+=+=+ ⎪⎝⎭ 所以()sin 2sin 212126g x f x x x πππ⎛⎫⎛⎫⎛⎫=-=-+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为51sin 1,362f ππ⎛⎫==≠± ⎪⎝⎭所以选项A 不正确; 因为2sin 0,43f ππ⎛⎫==≠ ⎪⎝⎭所以选项B 不正确;因为sin 1,62f ππ⎛⎫== ⎪⎝⎭且()sin 2g x x =是奇函数,所以选项C 正确;因为5sin 0,sin 11263f g ππππ⎛⎫⎛⎫====≠± ⎪ ⎪⎝⎭⎝⎭所以选项D 不正确.本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
开侨中学高三理数周末练习(4)

开侨中学高三理数周末练习(4)一、单选题1.已知复数 满足 ,则 ( )A .B .C .D .2.已知 ,函数 的定义域为 , ,则下列结论正确的是( )A .B .C .D . 3.已知 、 都是实数,那么“ ”是“ ”的( )A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件 4.若变量 , 满足,则 的最大值为( )A .B .C .D .5.已知是函数 的一个极大值点,则 的一个单调递减区间是( )A .B .C .D .6.已知 、 分别是双曲线的左、右两个焦点,若在双曲线上存在点 ,使得 ,且满足 ,那么双曲线的离心率为( )A . B . C . D .7.某学校 位同学组成的志愿者组织分别由李老师和张老师负责,每次献爱心活动均需该组织 位同学参加.假设李老师和张老师分别将各自活动通知的信息独立,随机地发给 位同学,且所发信息都能收到.则甲同学收到李老师或张老师所发活动通知的信息的概率为( )A .B .C .D .8.已知,则( )A .B .C .D .9.执行如图所示的程序框图,输出的 值为( ) A . B . C . D .10.某一简单几何体的三视图如图所示,则该几何体的外接球的表面积是( ). A . B . C . D .11.给出下列函数:① ;② ;③ . ,使得的函数是( )A . ①②B . ①③C . ②③D . ①②③12.设直线 与曲线 的三个交点分别为 、 、 ,且 .现给出如下结论:① 的取A.B.C.D.二、填空题13.展开式的常数项是__________.14.已知向量,,,若为实数,,则的值为__________.15.宋元时期杰出的数学家朱世杰在其数学巨著《四元玉鉴》卷中“菱草形段”第一个问题“今有菱草六百八十束,欲令‘落一形’捶(同垛)之,问底子(每层三角形边菱草束数,等价于层数)几何?”中探讨了“垛积术”中的落一形垛(“落一形”即是指顶上束,下一层束,再下一层束,……,成三角锥的堆垛,故也称三角垛,如图,表示第二层开始的每层菱草束数),则本问题中三角垛底层菱草总束数为__________.16.在中,角、、的对边分别为、、,是的中点,,,则面积的最大值为__________.三、解答题17.已知数列的前项和为,且满足.(1)求数列的通项公式;(2)求数列的前项和.18.如图,三棱柱中,侧面侧面,,,,为棱的中点,在棱上,面.(1)求证:为的中点;(2)求二面角的余弦值.19.未来创造业对零件的精度要求越来越高.打印通常是采用数字技术材料打印机来实现的,常在模具制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有发展空间.某制造企业向高校打印实验团队租用一台打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取个零件,度量其内径的茎叶图如图(单位:).(1)计算平均值与标准差;(2)假设这台打印设备打印出品的零件内径服从正态分布,该团队到工厂安装调试后,试打了个零件,度量其内径分别为(单位:):、、、、,试问此打印设备是否需要进一步调试?为什么?参考数据:,,,,.20.已知椭圆:的一个顶点为,且焦距为,直线交椭圆于、两点(点、与点不重合),且满足.(1)求椭圆的标准方程;(2)为坐标原点,若点满足,求直线的斜率的取值范围.21.设常数,,.(1)当时,若的最小值为,求的值;(2)对于任意给定的正实数、,证明:存在实数,当时,.22.选修4-4:坐标系与参数方程已知直线的方程为,圆的参数方程为(为参数),以原点为极点,轴正半轴为极轴,建立极坐标系.(1)求直线与圆的交点的极坐标;(2)若为圆上的动点,求到直线的距离的最大值.开侨中学高三理数周末练习(4)参考答案1.C由题意,∴.2.A由题意,,∴.3.B【解析】,有可能为,故不能推出,反过来,则成立,故为必要不充分条件. 4.D作出可行域,如图五边形,作直线,平移直线,当过点时,为最大值.故选D.5.B函数的周期是,而,因此区间是其减区间.故选B.6.A【详解】∵,且满足,∴,又,∴,∴,,∴.7.C设甲同学收到李老师的信息为事件A,收到张老师的信息为事件B,A、B相互独立,,则甲同学收到李老师或张老师所发活动通知的信息的概率为.8.D试题分析:因,故,所以,故应选D.9.D程序运行时,变量值依次为;;;,,退出循环,.10.C【解析】几何体为一个正四棱柱,底面正方形边长为,侧棱长为3,外接球球心为上下底面中心连线的中点,球半径为 ,表面积是,选C.11.B是偶函数,,当时,,当时,,因此存在,使;当时,();是奇函数,=0(),因此①③是正确的.12.C ,,可知或时,,当时,,是极大值,是极小值,因此如图是函数的图象.在上的变化率逐渐减小,在上的变化率逐渐增大,因此的值先增大后减小,故存在最大值不存在最小值.故③错误,又由题意知是方程即的三个根,∴,,,∴,∴①②正确.故选C.13.由题意得,二项式展开式的通项为,当时,所以. 14.【详解】∵,∴=0,即,解得.故答案为.15.120解:由题意,第n层茭草束数为1 2 ... =,∴1 3 6 (680)即为[n(n+1)(2n+1)+n(n+1)]=n(n+1)(n+2)=680,即有n(n+1)(n+2)=15×16×17,∴n=15,∴=120.故答案为:12016.【详解】在中有,和中有,∴,即.∵,∴,∴,∴当时,取得最大值.故答案为.17.【详解】(1)当,,解得;当时,,,两式相减得,化简得,所以数列是首项为,公比为的等比数列.所以.(2)由(1)可得,所以,,,两式相减得,所以数列的前项和.因为,所以.18.【详解】(1)连接,因为为正三角形,为棱的中点,所以,从而,又面侧面,面侧面,面,所以面.以为原点,建立空间直角坐标系如图所示,不妨设,则,2,2,设,则2,2,因为平面,平面,所以,所以,解得,即1,所以为的中点.(2)1,1,,设平面的法向量为,则,即,解得,令,得33,显然平面的一个法向量为,所以,所以二面角的余弦值为.19.【详解】(1),,所以.(2)结论:需要进一步调试.理由如下:如果机器正常工作,则服从正态分布,,零件内径在123之外的概率只有,而123,根据原则,知机器异常,需要进一步调试.20.【详解】(1)依题意,,,则,解得,所以椭圆的标准方程为.(2)当直线垂直于轴时,由消去整理得,解得或,此时,直线的斜率为;当直线不垂直于轴时,设,,直线:,由,消去整理得,依题意,即,且,,又,所以,所以,即,解得满足,所以,故.故直线的斜率,当时,,此时;当时,,此时;综上,直线的斜率的取值范围为.21.【详解】(1),将代入得,由,得,且当时,,递减;时,,递增;故当时,取极小值,因此最小值为,令,解得.(2)因为,记,故只需证明:存在实数,当时,,,设,,则,易知当时,,故,又由,解得:,即,取,则当时,恒有,即当时,恒有成立.22.试题分析:(1)直线:,圆:,联立方程组,解得或, 利用极坐标转换公式即可求出结果;(2)设,则,当时,即可求出的最大值.试题解析:(1)直线:,圆:,联立方程组,解得或,对应的极坐标分别为,.(2)设,则,当时,取得最大值.考点:极坐标与参数方程.。
八年级上册数学第13周考试卷

八年级上册数学第13周考试卷满分:150分考试时间:120分钟班级:姓名:学号:A卷(共100分)第Ⅰ卷(选择题,共30分)一、选择题:(本大题共10个小题,每小题3分,共30分,答案写在答题卡上)1.下列各数中是无理数的是()A.3.1415926B.4C.D.392.在平面直角坐标系中,点(4,﹣2)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限3有意义的x的取值范围是()A.x<1B.x>1C.x≤1D.x≥14.下列各组数据中的三个数,可作为三边长构成直角三角形的是()A.1、2、3B.7、8、9C.5、12、13D.5、12、205.估计+1的值应在()A.3和4之间B.4和5之间C.5和6之间D.6和7之间6.将直线y=﹣2x向下平移两个单位,所得的直线是()A.y=﹣2x+2B.y=﹣2x﹣2 C.y=﹣2(x﹣2)D.y=﹣2(x+2)7.在平面直角坐标系中,点P(﹣2,﹣5)关于x轴对称的点的坐标为()A.(2,5)B.(﹣2,﹣5)C.(2,﹣5)D.(﹣2,5)8.下列命题为真命题的是()A.若a2=b2,则a=b B.等角的余角相等C.同旁内角相等,两直线平行D.=,S A2>S B2,则A组数据更稳定9.小明去超市买东西花20元,他身上只带了面值为2元和5元的纸币,营业员没有零钱找给他,那么小明付款有几种方式()A. 5种B. 4种C. 3种D. 2种10.下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是()A .B .C .D .第Ⅱ卷(非选择题,共70分)二、填空题:(本大题共4个小题,每小题4分,共16分,答案写在答题卡上) 11.32- 分母有理化后的值为 . 12.若y =(m +1)x 2﹣|m |+3是关于x 的一次函数,则m 的值为 .13.如图,正比例函数y =kx (k ≠0)和一次函数y =ax +4(a ≠0)的图象相交于点A (1,1),则不等式kx ≥ax +4的解集为 .14.如图,将长方形ABCD 沿对角线AC 折叠,得到如图所示的图形,点B 的对应点是点B ′,B ′C 与AD 交于点E .若AB =2,BC =4,则AE 的长是 . 三、解答题:(本大题共6个小题,共54分,答案写在答题卡上) 15. (本小题满分12分,每题6分) (1)计算: ()()021136333----+-π(2)解不等式组:并把它的解集在数轴上表示出来.16. (6分)已知关于x ,y 的二元一次方程组.(1)若方程组的解是正数,求m 的取值范围.(2)若方程组的解满足x ﹣y 不小于0,求m 的取值范围.17.(8分)为了解某校八年级体育科目训练情况,从八年级学生中随机抽取了部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:(1)图1中∠α的度数是,并把图2条形统计图补充完整.(2)抽取的这部分的学生的体育科目测试结果的中位数是在级;(3)依次将优秀、良好、及格、不及格记为90分、80分、70分、50分,请计算抽取的这部分学生体育的平均成绩.18.(8分)如图,在四边形ABCD中,∠ABC=∠ACD=90°,AB=BC.(1)当AD=7,CD=5时,求BC的长;(2)当AD=,BC=时,求BD的长.19. (本题10分) A、B两机场相距3000km,甲、乙两架飞机沿同一航线分别从A、B两机场出发相向而行,假设它们都保持匀速行驶,如图,线段AE、CD分别表示甲、乙两机离B机场的距离y(km)和所用去的时间x(h)之间的函数关系的图象,观察图象回答下列问题:(1)乙机在甲机出发几小时后才从B机场出发?甲、乙两机的飞行速度各为多少km/h?(2)求甲、乙两机各自的y与x的函数关系式;(3)甲、乙两机相遇时,乙机飞行了多长时间?距离A机场多少km?20. (本题10分)如图(a),已知点B(0,6),点C为x轴上一动点,连接BC,△ODC和△EBC都是等边三角形.(1)求证:BO=DE.(2)如图(b),当点D恰好落在BC上时,①求OC的长及点E的坐标;②在x轴上是否存在点P,使得△PEC为等腰三角形?若存在,写出点P的坐标;如不存在,说明理由.③如图(c),点M是线段BC上的动点(点B,C除外),过点M作MG⊥BE于点G,MH⊥CE于点H,当点M运动时,MH+MG的值是否发生变化?如不会变化,直接写出MH+MG的值;如会变化,简要说明理由.B卷(共50分)一、填空题:(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)21. 若点P(﹣3,a),Q(2,b)在一次函数y=﹣3x+c的图象上,则a与b的大小关系是.22. 若第二象限的点P(m+1,3m﹣5)到x轴的距离与到y轴的距离相等,则m的值为.23.如图,点P的坐标为(2,0),点B在直线y=x+2上运动,当线段PB最短时,PB的长度是.24.如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…,直线l n⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3,…,l n分别交于点A1,A2,A3,…,A n;函数y=2x的图象与直线l1,l2,l3,…,l n分别交于点B1,B2,B3,…,B n.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,…,四边形A n﹣1A n B n B n﹣1的面积记作S n,那么S2019=.25. 如图,正方形ABCD的边长是4,点E是BC的中点,连接DE,DF⊥DE交BA的延长线于点F.连接EF、AC,DE、EF分别与C交于点P、Q,则PQ=.二、解答题:(本大题共3个小题,共30分,解答过程写在答题卡上)26. (8分) 2010年6月5日是第38个世界环境日,世界环境日的主题为“多个物种、一颗星球、一个未来”.为了响应节能减排的号召,某品牌汽车4S店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共16辆,以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息:成本价(万元/辆)售价(万元/辆)A型3032B型4245(1)若经营者的购买资金不少于576万元且不多于600万元,则有哪几种进车方案?(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你做为一名购车者,将会选购哪一种型号的汽车?并说明理由.27.(10分)已知△ABC是等边三角形,点D是直线AB上一点,延长CB到点E,使BE=AD,连接DE,DC,(1)若点D在线段AB上,且AB=6,AD=2(如图①),求证:DE=DC;并求出此时CD的长;(2)若点D在线段AB的延长线上,(如图②),此时是否仍有DE=DC?请证明你的结论;(3)在(2)的条件下,连接AE,若,求CD:AE的值.28.(12分)已知:在直角坐标系中,A为x轴负半轴上的点,B为y轴负半轴上的点.(1)如图1,以A点为顶点、AB 为腰在第三象限作等腰Rt△ABC,若OA=2,OB=4,试求C点的坐标.(2)如图2,若点A的坐标为(﹣2,0),点B的坐标为(0,﹣m),点D的纵坐标为n,以B为顶点,BA为腰作等腰Rt△ABD.试问:当B点沿y轴负半轴向下运动且其他条件都不变时,整式2m+2n﹣5的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.(3)如图3,E为x轴负半轴上的一点,且OB=OE,OF⊥EB于点F,以OB为边作等边△OBM,连接EM交OF于点N,试探索:在线段EF、EN和MN中,哪条线段等于EM与ON的差的一半?请你写出这个等量关系,并加以证明.。
2022-2023学年广东省广东华侨中学八年级上学期数学期末考试试卷带讲解

广东侨中2022~2023学年八年级第一学期数学期末总结性练习一、选择题(共10小题,每题3分)1.下列几种著名的数学曲线中,不是轴对称图形的是()A. B.C. D.D【分析】根据轴对称的定义:如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴;据此解答即可.【详解】解:选项中A ,B ,C 均有对称轴为轴对称图形,D 不是轴对称图形,故选:D .【点睛】本题考查了轴对称的定义,熟记定义是解本题的关键.2.下列长度的三条线段中,能构成三角形的是()A.2cm ,4cm ,7cmB.4cm ,8cm ,12cmC.3cm ,7cm ,12cmD.4cm ,10cm ,12cmD【分析】根据“三角形任意两边之和大于第三边,任意两边之差小于第三边”对各选项进行进行逐一分析即可.【详解】解:A 、247+<,不能够组成三角形,故本选项不符合题意;B 、4812+=,不能组成三角形,故本选项不符合题意;C 、3712+<,不能够组成三角形,故本选项不符合题意;D 、41012+>,能够组成三角形,故本选项符合题意.故选:D .【点睛】此题主要考查了三角形三边关系,判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.3.2020年6月23日9时43分,我国成功发射了北斗系统第55颗导航卫星,其授时精度为世界之最,不超过0.0000000099秒.数据“0.0000000099”用科学记数法表示为()A.109910-⨯ B.109.910-⨯ C.99.910-⨯ D.89.910-⨯C【分析】根据科学记数法的表示方法解答即可.【详解】解:0.0000000099用科学记数法表示为99.910-⨯.故答案为:C .【点睛】此题考查了科学记数法的表示方法,科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.4.下列运算结果正确的是()A.235x x x += B.()235x x = C.()2239x x = D.55x x x ÷=C【分析】根据合并同类项,幂的乘方,积的乘方,同底数幂相除,逐项判断即可求解.【详解】解:A 、2x 和3x 不是同类项,无法合并,故本选项错误,不符合题意;B 、()236x x =,故本选项错误,不符合题意;C 、()2239x x =,故本选项正确,符合题意;D 、54x x x ÷=,故本选项错误,不符合题意;故选:C【点睛】本题主要考查了合并同类项,幂的乘方,积的乘方,同底数幂相除,熟练掌握相关运算法则是解题的关键.5.如图,用直尺和圆规作一个角等于已知角,能得出A O B AOB '''∠=∠的依据是()A.SASB.SSSC.AASD.ASAB【分析】首先连接CD 、C D '',从作图可知OD OD OC OC ''===,CD C D ''=,即可判定()SSS ODC O D C '''△≌△,然后根据全等三角形对应角相等的性质,即可得出A O B AOB '''∠=∠.【详解】解:A O B AOB '''∠=∠,理由是:连接CD 、C D '',从作图可知OD OD OC OC ''===,CD C D ''=,∵在ODC 和O D C '''△中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开侨中学2017届高三理科数学第十三周周日晚测试题
命题人:莫世理
1.在ABC △中,点M ,N 满足2AM MC = ,BN NC = .若MN xAB y AC =+
, 则x = ;y = .
2.已知函数12
22,1()log (1),1x x f x x x -⎧-≤=⎨-+>⎩ ,且()3f a =-,则(6)f a -=
3. 如图,斜线段AB 与平面α所成的角为60 ,B 为斜足,平面α上的动点P 满足30∠PAB = ,则点P 的轨迹是
4.设双曲线22
221x y a b
-=(a >0,b >0)的右焦点为F,右顶点为A,
过F 作AF 的垂线与双曲线交于B ,C 两点,过B ,C 分别作AC ,AB 的垂线交于点D .若D 到直线BC
的距离小于a +,
则该双曲线的渐近线斜率的取值范围是 5.在ABC ∆中,点M 是BC 上的一点,3BM =
,AC =45B ∠=
,cos 10
BAM ∠=
.(1)求线段AM 的长度; (2)求线段MC 的长度.
6. 已知二次函数f(x)=ax 2+bx 的图象过点(-4n,0),且f ′(0)=2n ,n ∈N *
.
(1)求f(x)的解析式;(2)若数列{a n }满足1a n +1=f ′(1
a n
),且a 1=4,求数列{a n }的通项公式;
(3)记b n =a n a n +1,数列{b n }的前n 项和T n ,求证:4
3
≤T n <2.
C
B
A
7.如图,平面ABCD ⊥平面ADEF ,四边形ABCD 为菱形,四边形ADEF 为矩形,M 、N 分别是EF 、BC 的中点,2AB AF =,60CBA ∠=
. (1)求证:DM ⊥平面MNA ;
(2)若三棱锥A DMN -
的体积为3
,求点A 到平面
DMN 的距离.
8.已知椭圆E :22
221(0)x y a b
+=>>的上顶点P 在圆22:(2)9C x y ++=上,且椭圆的
C 的圆心是直线与椭圆E 交于A 、B 两
B C
D
A
E
F
M N
理科数学第十三周周日晚测试题答案
117
1.,;
2.;
3.
4.(1,0)(0,1).264
--- 椭圆; 5.(1
)∵cos BAM ∠=(0,180)BAM ∠∈ ,
∴sin BAM ∠==.
∵sin 2
ABM ∠=,3BM =,
sin sin BM AM BAM B =∠∠
,∴3sin sin BM B AM BAM ⋅∠=
==∠ (2)cos cos()AMC BAM B ∠=∠+∠cos cos sin sin BAM B BAM B =∠∠-∠∠
cos cos sin sin BAM B BAM B =∠∠-∠
∠22=
=
,
∵AC =,222
2cos AC MC AM MC AM AMC =+-⋅⋅∠,
∴2
2
2
25
MC MC =+-⨯, ∴2
650MC MC -+=,∴1MC =,或5MC =.
6.(1)由题意及f ′(x)=2ax +b 得⎩
⎪⎨⎪⎧
b =2n ,
16n 2
a -4n
b =0,解之得⎩⎪⎨⎪⎧
a =12,
b =2n ,
即f(x)=12
x
2
+2nx(n ∈N *
).
(2)由条件得1a n +1=1a n +2n ,∴1a n +1-1a n =2n ,累加得1a n -14
=2+4+6+…+2(n -1)=n 2
-n ,
∴1a n =(n -12)2,所以a n =1 n -12
2=4 2n -1
2(n ∈N *). (3)b n =a n a n +1=2(12n -1-1
2n +1
), 则T n =b 1+b 2+…+b n
=a 1a 2+a 2a 3+…+a n a n +1=2[(1-13)+(13-15)+…+(12n -1-1
2n +1
)]=2(1-
12n +1)<2.∵2n +1≥3,故2(1-12n +1)≥43,∴43≤T n <2. 7.(1)证明:连接AC ,在菱形ABCD 中,
∵60CBA ∠=
且AB AC =,∴ABC ∆为等边三角形. ∵N 是BC 的中点, ∴AN BC ⊥,AN BC ⊥.
∵ABCD ⊥平面ADEF ,AN ⊂平面ADEF ,
ABCD 平面ADEF AD =,∴AN ⊥平面ABEF . ∵DM ⊂平面ADEF ,∴AN DM ⊥.
∵矩形ADEF 中,2AD AF =,M 是的中点, ∴AMF ∆为等腰直角三角形,∴45AMF ∠=
,
同理可证45DME ∠=
,∴90DAM ∠=
,∴DM AM ⊥.
∵AM AN N = ,AM ⊂平面MNA ,AN ⊂平面MNA ,∴DM ⊥平面MNA . (2)设AF x =,则22AB AF x ==, 在Rt ABN ∆中,2AB x =,BN x =,
H
N M
F E A
D C
B
60ABN ∠=
,∴AN =.
∴2
122
ADN S x ∆=⋅=.∵ABCD ⊥平面ADEF ,FA AD ⊥,
ABCD 平面ADEF AD =,∴FA ⊥平面ABCD . 设h 为点M 到平面ADN 的距离,则h FA x ==.
∴2
311333
M ADN CDF V V h x x -∆=⋅=⋅=,
∵3
M ADN D AMN V V --==,∴1x =.
作AH MN ⊥交MN 于点H . ∵DM ⊥平面MNA ,∴DM AH ⊥. ∴AH ⊥平面DMN ,
即AH 为求点A 到平面DMN 的距离,
∵在Rt MNA ∆
中,MA =
AN ,
∴5
AH =.
∴点A 到平面DMN
8.(1)依题意,令0x =,
得220(2)9y ++=,解得1y =或5y =, ∴点P 的坐标为(0,1),即1b =.
∵c e a ==,∴2a =,
∴椭圆E 1. (2)∵直线经过圆心,
①当直线的斜率不存在时,不合题意;
②当直线的斜率存在时,设直线的方程为2y kx =-,1122(,),(,)A x y B x y .
由22
214
y kx x y =-⎧⎪⎨+=⎪⎩,得22(1
4)16120k x kx +-+=, ∵2225648(14)0k k ∆=-+>,∴2
k > 121222
1612
,1414k x x x x k k
+==++, ∵11222,2y kx y kx =-=-,∴1212()4y y k x x +=+-,
2
(2)(2)2()4y y kx kx k x x k x x =--=-++,。
