庞皓版计量经济学课件 (5)
庞皓计量经济学简单线性回归模型教学ppt

中国旅游业成为国民经济战略性支柱产业
“国务院印发的《“十三五”旅游业发展规划》提出, 改革开放以来,中国实现了从旅游短缺型国家到旅游大 国的历史性跨越。中国已经成为世界第一大出境旅游客 源国和全国第四大入境旅游接待国。“十三五”旅游业 发展的主要目标是:到2020年,旅游市场总规模达到67 亿人次,旅游投资总额2万亿元,旅游业总收入达到7万 亿元。旅游业综合贡献度达12%”。
相关关系的类型
● 从所涉及的变量数量看
简单相关 —— 两个变量之间的相关关系 多重相关—— 多个变量之间的复相关关系
●从变量相关关系的表现形式看
线性相关——散布图接近一条直线 非线性相关——散布图接近一条曲线
●从变量相关关系变化的方向看
正相关——变量同方向变化,同增同减 负相关——变量反方向变化,一增一减
相关系数 rXY 为:
rXY
__
__
( Xi X )(Yi Y )
__
__
( Xi X )2 (Yi Y )2
其中:X i 和 Yi 分别是变量X和Y的样本观测值,
__ __
X 和 Y 分别是变量 X 和Y 样本值的平均值
注意 : 每一组样本观测值都可以计算一个 rXY , 所以 rXY 是随
只是相关分析还不能达到计量经济分析的目的
相关分析的局限:
相关系数只能反映变量间的线性相关程度,不能确 定变量间的因果关系。
相关系数只能说明两个变量线性相关的方向和程度, 不能说明相关关系具体接近哪条直线,也就不能说明一个 变量的变动会导致另一个变量变动的具体数量规律。
计量经济学关心的问题:
是经济变量间的因果关系以及隐藏在随机性后面的具体 统计规律性 在这方面回归分析方法可以发挥更为重要的作用。
计量经济学庞皓课件(第五章 异方差性)

绘制出
ei2
对
X
的散点图
i
◆如果 ui 不随 Xi 而变化,则表明不存在异方差;
◆如果 ui 随 Xi 而变化,则表明存在异方差。
19
二、Goldfeld-Quanadt检验
作用:检验递增性(或递减性)异方差。
基本思想:将样本分为两部分,然后分别对两个样 本进行回归,并计算两个子样的残差平方和所构成 的比,以此为统计量来判断是否存在异方差。
E(Yi ) 1 2 X 2i 3X3i ... k X ki (5.2)
的分散程度,因此同方差性指的是所有观测值的
分散程度相同。
6
异方差性的含义
设模型为
Yi 1 2 X2i 3 X3i ... k X ki ui i 1, 2,..., n
如果对于模型中随机误差项 ui 有:
即认为存在异方差性。
38
第四节 异方差性的补救措施
主要方法:
●模型变换法 ●加权最小二乘法 ●模型的对数变换
39
一、模型变换法
以一元线性回归模型为例:
Yi 1 2 X i ui
经检验 ui 存在异方差,且
var(ui )
2 i
2
f
(Xi)
其中 σ 2是常数,f (Xi ) 是 X i的某种函数。
40
变换模型时,用 f (Xi) 除以模型的两端得:
Yi = f(Xi )
β1 f(X i
)
+
β2
Xi + f(Xi )
ui f(Xi )
记 Yi* 则有:
Yi f (Xi)
;
X
* i
Xi f (Xi)
; 1*
Yi*
计量经济学第三版庞皓

第二章简单线性回归模型第一节回归分析与回归函数P15(一)相关分析与回归分析1、相关关系2、相关系数3、回归分析(二)总体回归函数(条件期望)(三)随机扰动项(四)样本回归函数第二节简单线性回归模型参数的估计P26(一)简单线性回归的基本假定(二)普通最小二乘法求样本回归函数(三)OLS回归线的性质(四)最小二乘估计量的统计性质1、参数估计量的评价标准(无偏性、有效性、一致性)2、OLS估计量的统计特性(线性特性、无偏性、有效性、高斯-马尔可夫定理)第三节拟合优度的度量(RSS、ESS、TSS)P35(一)总变差的分解(二)可决系数(三)可决系数与相关系数的关系第四节回归系数的区间估计与假设检验P38(一)OLS估计的分布性质(二)回归系数的区间估值(三)回归系数的假设检验1、Z检验2、t检验第五节回归模型预测P43第六节案例分析P48第三章多元线性回归模型第一节多元线性回归模型及古典假定P64一、多元线性回归模型二、多元线性回归模型的矩阵形式三、多元线性回归模型的古典假定第二节多元线性回归模型的估计P68一、多元线性回归性参数的最小二乘估计二、参数最小二乘估计的性质(线性特性、无偏性、有效性)三、OLS估计的分布性质四、随机扰动项方差的估计五、多元线性回归模型参数的区间估计第三节多元线性回归模型的检验P74一、拟合优度检验(多重可决系数、修正的可决系数)二、回归方程的显著性检验(F-检验)三、回归参数的显著性检验(t-检验)第四节多元线性回归模型的预测P79第五节案例分析P81第四章多重共线性第一节什么是多重共线性P94第二节多重共线性产生的后果第三节多重共线性的检验第四节多重共线性的补救措施第五节案例分析P109。
计量经济学(第五版)教学课件5

模型 统计量
1
2
样本容量 25 50 100 250 500 >500 25 50 100 250 500 >500 25 50 100 250 500 >500
0.01 -2.66 -2.62 -2.60 -2.58 -2.58 -2.58 -3.75 -3.58 -3.51 -3.46 -3.44 -3.43 3.41 3.28 3.22 3.19 3.18 3.18
– 则称该随机时间序列是平稳的(stationary),而该
随机过程是一平稳随机过程(stationary stochastic
process)。
宽平稳、广义平稳
• 白噪声(white noise)过程是平稳的: Xt=t , t~N(0,2)
• 随机游走(random walk)过程是非平稳的: Xt=Xt-1+t , t~N(0,2) Var(Xt)=t2
0.01 -4.38 -4.15 -4.04 -3.99 -3.98 -3.96 4.05 3.87 3.78 3.74 3.72 3.71 3.74 3.60 3.53 3.49 3.48 3.46
0.025 -3.95 -3.80 -3.73 -3.69 -3.68 -3.66 3.59 3.47 3.42 3.39 3.38 3.38 3.25 3.18 3.14 3.12 3.11 3.11
0.05 -3.60 -3.50 -3.45 -3.43 -3.42 -3.41 3.20 3.14 3.11 3.09 3.08 3.08 2.85 2.81 2.79 2.79 2.78 2.78
0.10 -3.24 -3.18 -3.15 -3.13 -3.13 -3.12 2.77 2.75 2.73 2.73 2.72 2.72 2.39 2.38 2.38 2.38 2.38 2.38
计量经济学课件(庞浩版)

劳动经济学中经常运用联立方程模型来研究劳动力市场中 的各种问题,如工资决定、就业与失业、劳动力流动等。 例如,可以构建一个包含工资方程和就业方程的联立方程 模型,以分析最低工资制度对就业和工资水平的影响。
06
CATALOGUE
面板数据计量经济学模型
面板数据基本概念与特点
面板数据定义
面板数据是指在时间序列上取多个截面,在这些截面上同时选取样本观测值所构成的样 本数据。
面板数据模型估计方法及应用举例
估计方法
面板数据模型的估计方法主要有最小二乘法 、广义最小二乘法和极大似然法等。
应用举例
面板数据模型在经济学、金融学、社会学等 领域有广泛的应用,如经济增长、劳动力市 场、金融市场、环境经济学等问题的研究。 例如,可以利用面板数据模型研究不同国家 经济增长的影响因素,或者分析某个政策对 不同地区或不同群体的影响效果。
模型设定
多元线性回归模型是描述多个自变量与一 个因变量之间线性关系的模型,形式为 Y=β0+β1X1+β2X2+...+βkXk+u。
假设ห้องสมุดไป่ตู้验
对各个自变量的回归系数进行假设检验, 判断其是否显著不为零。
参数估计
通过最小二乘法等方法对模型中的参数进 行估计,得到各个自变量的回归系数估计 值。
多重共线性问题
采用逐步回归法、岭回归法、主成分分析法等方法对多重 共线性进行修正,同时也可以通过增加样本容量或收集更 多信息来缓解多重共线性的影响。
04
CATALOGUE
时间序列计量经济学模型
时间序列基本概念与性质
时间序列定义
按时间顺序排列的一组数据,反映现象随时间 变化的发展过程。
计量经济学-(西南财大)庞皓-博导

●计量经济学对经济关系要作出定量的估计,
对经济理论提出经验的内容
18
2、计量经济学与经济统计学的关系
联系:
●经济统计侧重于对社会经济现象的描述性计量
●经济统计提供的数据是计量经济学据以估计参
数、验证经济理论的基本依据
●经济现象不能作实验,只能被动地观测客观经 济现象变动的既成事实,只能依赖于经济统计 数据
假定条件经常不能满足,需要建立一些专门的
经济计量方法
21
第二节 计量经济学的研究方法
需要做的工作
选择变量和数学关系式 —— 模型设定
确定变量间的数量关系 —— 估计参数
检验所得结论的可靠性 —— 模型检验
作经济分析和经济预测 —— 模型应用
22
一、模型设定
经济模型及设定
模型:对经济现象或过程的一种数学模拟 设定(Specification):
数据的要求:
真实性、完整性、可比性
37
四、计量经济模型的建立
经济模型是对实际经济现象或过程的一种数学模
拟,是对复杂经济现象的简化与抽象 特点:只能在一定假定前提下 忽略次要因素,突出主要因素
38
可利用来建立计量经济模型的关系:
行为关系(如生产、投资、消费)
生产技术关系 (如投入产出关系)
制度关系(如税率) 定义关系 计量经济模型的数学形式: 线性模型:如 非线性模型:如
8
特点
计量经济学的重要特点是它自身并没有固定的 经济理论,计量经济学中的各种计量方法和技 术,大多来自数学和统计学。
计量经济学产生的意义
从定性研究到定量分析的发展,是经济学更精 密、更科学的表现,是现代经济学的重要特征
计量经济学-ch_02_wooldridge_5e_ppt

Chapter 2 The Simple Regression Model
2.1 Definition of the Simple Regression Model (6/6)
f(y|x)
y = b0 + b1x + u
E u x = 0
E(y|x3) E(y|x2) E(y|x1)
y, E(y|x)
This means that the average value of the dependent variable can be expressed as a linear function of the explanatory variable Chapter End © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.
Chapter 2 The Simple Regression Model
2.2 Deriving the Ordinary Least Squares Estimates (2/10)
Fit as good as possible a regression line through the data points:
Chapter 2 The Simple Regression Model
2.2 Deriving the Ordinary Least Squares Estimates (1/10)
In order to estimate the regression model one needs data A random sample of observations
计量经济学第5章PPT学习教案

量保持不变的情况下,Xj每变化1个单位时,Y 的均值E(Y)的变化;
或者说j给出了Xj的单位变化对Y均值的“直
接”或“净”(不含其他变量)影响。
第1页/共49页
2
总体回归模型n个随机方程的矩阵表达式为 Y Xβ μ
其中
1 X 11
X
1
X 12
1 X 1n
所以,
ˆ ~ N(, 2(X X )1)
第24页/共49页
以cii表示矩阵(X’X)-1 主对角线上的第i个元素,于是参数估 计量的 方差为 : 其中,2为随机误差项的总体 方差, 由于总 体未知 ,故方 差也不 可知。 因此, 在实际 计算时 ,用它 的估计 量代替:
ˆi ~ N (i , 2cii )
2Q
ˆˆ
2X X是一个正定矩阵
ˆ (X X ) XY 1
是使方程最小化的解。
第13页/共49页
14
知识点:正定矩阵
对于任意的非零向量c,令
a cX Xc
则
a cXXc vv
vi2
除非v中的每一个元素为0, 否则a为正的。但是,若v为0, 则
v Xc 0
这与X中的向量线性无关的假设是矛盾的,故X满秩,则必
n
第7页/共49页
8
回忆:由线性代数可知
如果一个矩阵没有逆矩阵,则被称 为奇异矩阵,如果有则为非奇异矩 阵(non-singular)
对于n阶方阵A,A是非奇异矩阵的 证明: 充要条件是A的行列式不等于0
当r且an仅k(当X X矩)阵 满ran秩k时(X,) 其k行1列式不 X X为(k等+1于)(零k+1)阶方阵,所以,X X为非奇异矩阵,可逆.
计量经济学庞皓第五章练习题参考解答

第五章练习题参考解答练习题5.1 设消费函数为i i i i u X X Y +++=33221βββ式中,i Y 为消费支出;i X 2为个人可支配收入;i X 3为个人的流动资产;i u 为随机误差项,并且222)(,0)(i i i X u Var u E σ==(其中2σ为常数)。
试回答以下问题: (1)选用适当的变换修正异方差,要求写出变换过程;(2)写出修正异方差后的参数估计量的表达式。
5.2 根据本章第四节的对数变换,我们知道对变量取对数通常能降低异方差性,但须对这种模型的随机误差项的性质给予足够的关注。
例如,设模型为u X Y 21ββ=,对该模型中的变量取对数后得如下形式u X Y ln ln ln ln 21++=ββ(1)如果u ln 要有零期望值,u 的分布应该是什么? (2)如果1)(=u E ,会不会0)(ln =u E ?为什么? (3)如果)(ln u E 不为零,怎样才能使它等于零?5.3 由表中给出消费Y 与收入X 的数据,试根据所给数据资料完成以下问题: (1)估计回归模型u X Y ++=21ββ中的未知参数1β和2β,并写出样本回归模型的书写格式;(2)试用Goldfeld-Quandt 法和White 法检验模型的异方差性; (3)选用合适的方法修正异方差。
Y X Y X Y X 55 80 152 220 95 140 65 100 144 210 108 145 70 85 175 245 113 150 801101802601101607912013519012516584115140205115180981301782651301859514019127013519090125137230120200759018925014020574105558014021011016070851522201131507590140225125165651001372301081457410514524011518080110175245140225841151892501202007912018026014524090125178265130185981301912705.4由表中给出1985年我国北方几个省市农业总产值,农用化肥量、农用水利、农业劳动力、每日生产性固定生产原值以及农机动力数据,要求:(1)试建立我国北方地区农业产出线性模型;(2)选用适当的方法检验模型中是否存在异方差;(3)如果存在异方差,采用适当的方法加以修正。
庞皓版计量经济学课后习题答案
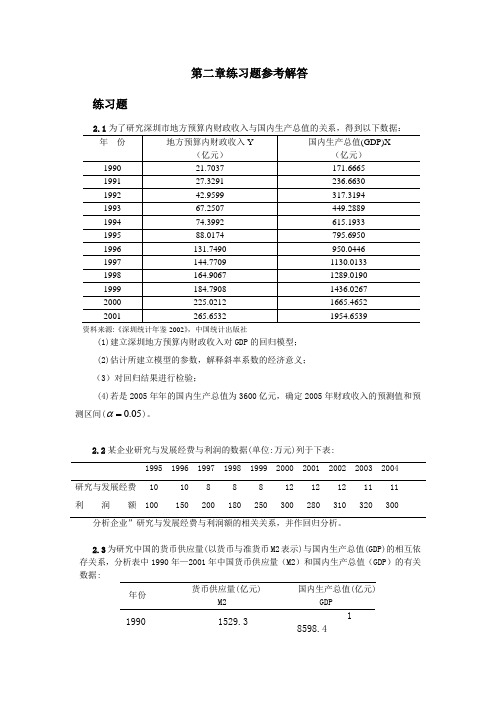
第二章练习题参考解答练习题资料来源:《深圳统计年鉴2002》,中国统计出版社(1)建立深圳地方预算内财政收入对GDP的回归模型;(2)估计所建立模型的参数,解释斜率系数的经济意义;(3)对回归结果进行检验;(4)若是2005年年的国内生产总值为3600亿元,确定2005年财政收入的预测值和预测区间(0.05α=)。
2.2某企业研究与发展经费与利润的数据(单位:万元)列于下表:1995 1996 1997 1998 1999 2000 2001 2002 2003 2004研究与发展经费 10 10 8 8 8 12 12 12 11 11利润额 100 150 200 180 250 300 280 310 320 300 分析企业”研究与发展经费与利润额的相关关系,并作回归分析。
2.3为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2001年中国货币供应量(M2)和国内生产总值(GDP)的有关数据:年份货币供应量(亿元)M2国内生产总值(亿元)GDP1990 1529.31 8598.41991 19349.92 1662.51992 25402.22 6651.91993 34879.83 4560.51994 46923.54 6670.01995 60750.55 7494.91996 76094.96 6850.51997 90995.37 3142.71998 104498.57 6967.21999 119897.98 0579.42000 134610.38 8228.12001 158301.99 4346.4资料来源:《中国统计年鉴2002》,第51页、第662页,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明分析结果的经济意义。
2.4表中是16支公益股票某年的每股帐面价值和当年红利:根据上表资料:(1)建立每股帐面价值和当年红利的回归方程;(2)解释回归系数的经济意义;(3)若序号为6的公司的股票每股帐面价值增加1元,估计当年红利可能为多少?2.5美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》(The Wall Street1。
经济学计量经济学第五章PPT课件

• 当a>0、0<b<1时,y 随着t 的增加而趋向于0
• 描述以几何极数递增或递减的现象
• 序列的观察值按指数规律变化
• 序列的逐期观察值按一定的增长率增长或衰减
• 参数估计方法 • 采用对数变换法将模型化为线性进行估计
29
第29页/共45页
修正指数型增长曲线模型
• 一般形式
y L ab •
•
~yi ˆ0 yi f xi , ˆ0 zi ˆ0 ˆ0
• 易平~y求方i 出和ˆ其式0参最数小zi 的ˆ0普 通ˆ最小二i 乘估计值
•
ˆ
,该估计值使得残差
2
ˆ1
n
S ˆ1
~yi ˆ0 zi ˆ0 ˆ1 2
i 1
17
第17页/共45页
Gauss-Newton迭代法(续2)
• 类别 • 多项式增长曲线模型 • 简单指数型增长曲线模型 • 修正指数型增长曲线模型 • Logistic增长曲线模型 • Gompertz增长曲线模型
27
第27页/共45页
多项式增长曲线模型
• 一般数学形式
•
y• t
yt:a第0t
期
的a1某t
个经a济2t指2
标
;t :时a间k t
k
• a0,a1,…,ak:模型参数
• 至此完成非线性模型的OLS估计
18
第18页/共45页
Gauss-Newton迭代法(续3)
• 步骤
• 给出参数估计值 近似值
的初值 ,将
ˆ
在 处展开泰勒级数,取一阶
ˆ0
f xi , ˆ
ˆ0
• 计算
和
的样本观z测i 值ˆ0
计量经济学ppt课件(完整版)

在进行模型选择与比较时,需要注意避免过拟合和欠拟合问题,以及确保模型的稳定性和可靠性。此外 ,还需要关注模型的异方差性、共线性等问题,以确保模型的准确性和有效性。
04
时间序列分析及应用
时间序列基本概念及性质
01
时间序列定义
按时间顺序排列的一组数据,反映 现象随时间变化的发展过程。
时间序列类型
03
广义线性模型与非线性模型
广义线性模型介绍
定义
广义线性模型是一类用于描述响 应变量与一组预测变量之间关系 的统计模型,其特点在于响应变 量的期望值通过一个连接函数与 预测变量的线性组合相关联。
连接函数
连接函数是广义线性模型中一个 关键组成部分,它将响应变量的 期望值与预测变量的线性组合连 接起来。常见的连接函数包括恒 等连接、对数连接、逆连接等。
模型的统计性质
深入探讨多元线性回归模型的统计性质,包括无偏性、有效性和一致性等,并解释这些 性质在多元回归分析中的重要性。
多重共线性问题
详细讲解多重共线性的概念、产生原因、后果以及诊断和处理方法,如逐步回归、岭回 归等。
回归模型检验与诊断
模型的拟合优度 介绍衡量模型拟合优度的指标, 如可决系数、调整可决系数等, 并解释这些指标在实际应用中的 意义。
微观计量经济学在因果推断和政策评 估方面发挥着重要作用。目前,研究 者们关注于如何运用实验设计、工具 变量、双重差分等方法识别和处理内 生性问题,以更准确地估计因果关系 和评估政策效果。
高维数据处理与机器 学习
随着大数据时代的到来,高维数据处 理成为微观计量经济学面临的新挑战 。目前,研究者们正在探索如何将机 器学习等先进的数据分析技术应用于 微观计量经济学中,以处理高维数据 和挖掘更多的有用信息。
计量经济学 庞皓

第八章 虚拟变量回归
8.1什么是虚拟变量?它在模型中有什么作用?
答:虚拟变量是人工构造的取值为0或1的作为属性变量代表的变量。虚拟变量的 作用主要有:(1)可以作为属性因素的代表,如性别、所有制等;(2)作为某 些非精确计量的数量因素的代表,如受教育程度、管理者素质等;(3)作为某 些偶然因素或政策因素的代表,如战争、灾害、改革前后等;(4)可以作为时 间序列分析中季节的代表;(5)可以实现分段回归,研究斜率、截距的变动, 或比较两个回归模型的结构差异。
第一章 绪论
1.1怎样理解产生于西方国家的计量经济学能够在中国的经济理论研究和现代化 建设中发挥重要作用?
答:计量经济学的产生源于对经济问题的定量研究,这是社会经济发展到一定 阶段的客观需要。计量经济学的发展是与现代科学技术成就结合在一起的,它 反映了社会化大生产对各种经济因素和经济活动进行数量分析的客观要求。经 济学从定性研究向定量分析的发展,是经济学逐步向更加精密、更加科学发展 的表现。我们只要坚持以科学的经济理论为指导,紧密结合中国经济的实际, 就能够使计量经济学的理论与方法在中国的经济理论研究和现代化建设中发挥 重要作用。
1.2理论计量经济学和应用计量经济学的区别和联系是什么?
答:计量经济学不仅要寻求经济计量分析的方法,而且要对实际经济问题加以 研究,分为理论计量经济学和应用计量经济学两个方面。
理论计量经济学是以计量经济学理论与方法技术为研究内容,目的在于为应用 计量经济学提供方法论。所谓计量经济学理论与方法技术的研究,实质上是指 研究如何运用、改造和发展数理统计方法,使之成为适合测定随机经济关系的 特殊方法。
第七章 分布滞后模型与自回归模型
7.1 什么是滞后现象?产生滞后现象的原因主要有哪些?
庞皓版计量经济学课后习题答案

第二章练习题参考解答练习题资料来源:《深圳统计年鉴2002》,中国统计出版社(1)建立深圳地方预算内财政收入对GDP的回归模型;(2)估计所建立模型的参数,解释斜率系数的经济意义;(3)对回归结果进行检验;(4)若是2005年年的国内生产总值为3600亿元,确定2005年财政收入的预测值和预测区间(0.05α=)。
2.2某企业研究与发展经费与利润的数据(单位:万元)列于下表:1995 1996 1997 1998 1999 2000 2001 2002 2003 2004研究与发展经费 10 10 8 8 8 12 12 12 11 11利润额 100 150 200 180 250 300 280 310 320 300 分析企业”研究与发展经费与利润额的相关关系,并作回归分析。
2.3为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系,分析表中1990年—2001年中国货币供应量(M2)和国内生产总值(GDP)的有关数据:年份货币供应量(亿元)M2国内生产总值(亿元)GDP1990 1529.31 8598.41991 19349.92 1662.51992 25402.22 6651.91993 34879.83 4560.51994 46923.54 6670.01995 60750.55 7494.91996 76094.96 6850.51997 90995.37 3142.71998 104498.57 6967.21999 119897.98 0579.42000 134610.38 8228.12001 158301.99 4346.4资料来源:《中国统计年鉴2002》,第51页、第662页,中国统计出版社对货币供应量与国内生产总值作相关分析,并说明分析结果的经济意义。
2.4表中是16支公益股票某年的每股帐面价值和当年红利:根据上表资料:(1)建立每股帐面价值和当年红利的回归方程;(2)解释回归系数的经济意义;(3)若序号为6的公司的股票每股帐面价值增加1元,估计当年红利可能为多少?2.5美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》(The Wall Street1。
庞皓计量经济学(第二版)第五、六章习题参考解答

第五章练习题及参考解答5.1 设消费函数为i i i i u X X Y +++=33221βββ式中,i Y 为消费支出;i X 2为个人可支配收入;i X 3为个人的流动资产;i u 为随机误差项,并且222)(,0)(i i i X u Var u E σ==(其中2σ为常数)。
试解答以下问题:(1)选用适当的变换修正异方差,要求写出变换过程;(2)写出修正异方差后的参数估计量的表达式。
练习题5.1参考解答:(1)因为22()i i f X X =,所以取221i iW X =,用2i W 乘给定模型两端,得 312322221i i iii i i Y X u X X X X βββ=+++ 上述模型的随机误差项的方差为一固定常数,即22221()()i i i iu Var Var u X X σ==(2)根据加权最小二乘法,可得修正异方差后的参数估计式为***12233ˆˆˆY X X βββ=--()()()()()()()***2****22232322322*2*2**2223223ˆii i i i i i i i i i i i i i i i i W y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑()()()()()()()***2****23222222332*2*2**2223223ˆii i i i i i i i i i i i i i i i i W y x W x W y x W x x W x W x W x x β-=-∑∑∑∑∑∑∑其中22232***23222,,i ii ii iiiiW X W X W Y XXYWWW===∑∑∑∑∑∑******222333i i i i i x X X x X X y Y Y =-=-=-5.2 下表是消费Y 与收入X 的数据,试根据所给数据资料完成以下问题: (1)估计回归模型u X Y ++=21ββ中的未知参数1β和2β,并写出样本回归模型的书写格式;(2)试用Goldfeld-Quandt 法和White 法检验模型的异方差性; (3)选用合适的方法修正异方差。
计量经济学(庞浩主编)第五章练习题参考解答

第五章练习题参考解答练习题5.1 设消费函数为ii i i u X X Y +++=33221βββ式中,为消费支出;为个人可支配收入;为个人的流动资产;为随机误差i Y i X 2i X 3i u 项,并且(其中为常数)。
试回答以下问题:222)(,0)(i i i X u Var u E σ==2σ (1)选用适当的变换修正异方差,要求写出变换过程;(2)写出修正异方差后的参数估计量的表达式。
5.2 根据本章第四节的对数变换,我们知道对变量取对数通常能降低异方差性,但须对这种模型的随机误差项的性质给予足够的关注。
例如,设模型为,对u X Y 21ββ=该模型中的变量取对数后得如下形式u X Y ln ln ln ln 21++=ββ(1)如果要有零期望值,的分布应该是什么?u ln u (2)如果,会不会?为什么?1)(=u E 0)(ln =u E (3)如果不为零,怎样才能使它等于零?)(ln u E 5.3 由表中给出消费Y 与收入X 的数据,试根据所给数据资料完成以下问题:(1)估计回归模型中的未知参数和,并写出样本回归模u X Y ++=21ββ1β2β型的书写格式;(2)试用Goldfeld-Quandt 法和White 法检验模型的异方差性;(3)选用合适的方法修正异方差。
YXYXYX558015222095140651001442101081457085175245113150801101802601101607912013519012516584115140205115180981301782651301859514019127013519090125137230120200759018925014020574105558014021011016070851522201131507590140225125165651001372301081457410514524011518080110175245140225841151892501202007912018026014524090125178265130185981301912705.4由表中给出1985年我国北方几个省市农业总产值,农用化肥量、农用水利、农业劳动力、每日生产性固定生产原值以及农机动力数据,要求:(1)试建立我国北方地区农业产出线性模型;(2)选用适当的方法检验模型中是否存在异方差;(3)如果存在异方差,采用适当的方法加以修正。
计量经济学演示课件 教学PPT 作者 庞皓 第二章 简单线性回归模型

E(Y Xi ) = f (Xi )
这个函数称为总体回归函数(PRF)
15
2.总体回归函数的表现形式
(1)条件均值表现形式 假如 Y的条件均值 E(Y是X解i ) 释变量 的X线性函数,可表示为:
尽可能“接近”总体回归函数中的参数1 和2 。
这样的“规则和方法”有多种,最常用的是最小二 乘法
27
第二节 简单线性回归模型的最小二乘估计
本节基本内容:
● 简单线性回归的基本假定 ● 普通最小二乘法 ● OLS回归线的性质 ● 参数估计式的统计性质
28
一、简单线性回归的基本假定
1. 为什么要作基本假定?
E(Yi Xi ) f (Xi ) 1 2 Xi
(2)个别值表现形式
Y
E(Y Xi ) Yi
对于一定的
X
,
i
的Y 各个别值
分Yi布
在 E(的Y 周Xi )围,若令各个 与条Y件i
均值 E(Y的X偏i )差为 , 显u然i 是随机变u i量,则有
ui Yi E(Yi Xi ) Yi 1 2 Xi
线性相关——散布图接近一条直线 非线性相关——散布图接近一条曲线
● 从变量相关关系变化的方向看
正相关——变量同方向变化,同增同减 负相关——变量反方向变化,一增一减 不相关
7
3.相关程度的度量—相关系数
总体线性相关系数:
Cov( X ,Y )
Var( X )Var(Y )
其中:Var(X ) ——X 的方差;Var(Y ) ——Y的方差
视为对 ui 的估计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
逐次代入可得:
∞
ut = vt + vt-1 + 2vt-2 + ... = r vt-r
r=0
这表明随机误差项 ut 可表示为独立同分布的随
机误差序列 vt , vt1 , vt2 , 的加权和,权
数分别为 1 , , 2 , 。当 0 1 时,
这些权数是随时间推移而呈几何衰减的;
而当 1 0 时,这些权数是随时间推移而
交错振荡衰减的。
6-23
可以推得:
∞
E(ut ) = r E(vt-r ) = 0
r=0
Var(vt ) =
∞ r=0
2 n V ar(vt -r
)
=
σv2
1-
2
=
2 u
表明,在 ut 为一阶自回归的相关形式时,随机 误差 ut 依然是零均值、同方差的误差项。
体回归模型(PRF)的随机项为 u1 , u2 , ..., un ,
如果自相关形式为
ut = ut-1 + vt
-1< <1
其中 为自相关系数, vt为经典误差项,即
E(vt ) 0 , Var(vt ) 2 , Cov(vt , vt+s ) 0 , s 0
则此式称为一阶自回归模式,记为 AR(1) 。因为
6-34
一个被低估了的标准误意味着一个较大的t统计
量。因此,当 0 时,通常t统计量都很大。
这种有偏的t统计量不能用来判断回归系数的显 著性。 综上所述,在自相关情形下,无论考虑自相关, 还是忽视自相关,通常的回归系统显著性的t检 验都将是无效的。 类似地,由于自相关的存在,参数的最小二乘估 计量是无效的,使得F检验和t检验不再可靠。
二、对参数估计的影响
在有自相关的条件下,仍然使用普通最小二乘 法将低估估计量 ˆ2 的方差 Var(ˆ2)
并且 ˆ 2 ei2 将低估真实的 2
n-k
6-27
对于一元线性回归模型,当 u为经典误差项时,
普通最小二乘估计量 ˆ2 的方差为: Var(ˆ2 Fra bibliotek =2
(X - X )2 =
=
Var(ˆ2) = E(ˆ2 -
2
+
Σxt ut Σxt2
2 )2
=
E
Σxtut Σxt2
2
n-1
n-2
=
2 u
n
(1+ 2
xt xt+1
t =1 n
+ 22
xt xt+2
t =1 n
+ ...+ 2 n-1
x1 xn
n
)
xt2
xt2
xt2
xt2
本章讨论四个问题:
●什么是自相关 ●自相关的后果 ●自相关的检验 ●自相关性的补救
6-4
第一节 什么是自相关
本节基本内容:
●什么是自相关 ●自相关产生的原因 ●自相关的表现形式
6-5
第一节 什么是自相关
一、自相关的概念
自相关(auto correlation),又称序列相关( serial correlation)是指总体回归模型的随机 误差项之间存在相关关系。即不同观测点上的 误差项彼此相关。
2 v
1- 2
Cov(ut , ut-2 )
E(utut-2 )
2
2 v
1- 2
6-25
以此类推,可得 :
Cov(ut , ut-k )
=
kVar(ut-k )
=
k
2 v
1- 2
这些协方差分别称为随机误差项 ut 的一阶自 协方差、二阶自协方差和k 阶自协方差
6-26
数,v t是经典误差项。此式称为二阶自回归模式,
记为 AR。(2)
6-19
一般地,如果 u1,u2 ,...,ut 之间的关系为
ut = 1ut-1 + 2ut-2 + ... + mut-m + vt
其中, v t 为经典误差项。则称此式为 m 阶自回 归模式,记为 AR(m) 。
在经济计量分析中,通常采用一阶自回归形式,
6-6
自相关系数 的定义与普通相关系的公式形式相同
n
utut-1
t=2
n
n
ut2
u2 t 1
t2
t2
的取值范围为 -1 1
(6.1)
式(6.1)中 ut-1 是 ut 滞后一期的随机误差项。 因此,将式(6.1)计算的自相关系数 称为一阶 自相关系数。
6-2
检验结果表明:回归系数的标准误差非常小,t 统
计量较大,说明居民收入X 对居民储蓄存款 Y 的
影响非常显著。同时可决系数也非常高,F统计量 为4122.531,也表明模型异常的显著。 但此估计结果可能是虚假的,t统计量和F统计量 都被虚假地夸大,因此所得结果是不可信的。为 什么?
6-3
第六章 自相关
即假定自回归形式为一阶自回归 AR(1)。
6-20
第二节 自相关的后果
本节基本内容:
●一阶自回归形式的性质 ●自相关对参数估计的影响 ●自相关对模型检验的影响 ●自相关对模型预测的影响
6-21
一、一阶自回归形式的性质
对于一元线性回归模型:
Y = 1 + 2 X + u
假定随机误差项 u 存在一阶自相关:
u t = u t -1 + vt
其中,ut 为现期随机误差,ut-1 为前期随机误差。
vt 是经典误差项,满足零均值 E(vt ) = 0 ,同方
差
Var(vt
)
=
2 v
,无自相关 E(vtvs ) 0
(t s)
的假定。
6-22
将随机误差项 ut 的各期滞后值: ut-1 = ut-2 + vt-1 , ut-2 = ut-3 + vt-2 , ...
6-7
二、自相关产生的原因
自
经济系统的惯性
相 关
经济活动的滞后效应
产 生
数据处理造成的相关
的
原
蛛网现象
因
模型设定偏误
6-8
原因1-经济系统的惯性
自相关现象大多出现在时间序列数据中, 而经济系统的经济行为都具有时间上的惯 性。
如GDP、价格、就业等经济指标都会随经 济系统的周期而波动。例如,在经济高涨 时期,较高的经济增长率会持续一段时间, 而在经济衰退期,较高的失业率也会持续 一段时间,这种现象就会表现为经济指标 的自相关现象。
自相关的性质可以用自相关系数的符号判断 即 0 为负相关, 0 为正相 关。 当 | | 接近1时,表示相关的程度很高。
自相关是 u1,u2,...,un 序列自身的相关,因随机误差
项的关联形式不同而具有不同的自相关形式。 自相关多出现在时间序列数据中。
6-17
自相关的形式
对于样本观测期为 n 的时间序列数据,可得到总
将低估估计量 的方差ˆ2
Va。r(ˆ2 )
ˆ 2 ei2 (n - k ) 将低估真实的 2。
6-30
三、对模型检验的影响
考虑自相关时的检 验
对模型检验的影响
忽视自相关时的 检验
6-31
由于 Var(ˆ2) 并不是所有线性无偏估计量中最小的, 使用t检验判断回归系数的显著性时就可能得到
6-15
例如,在消费行为中,一个家庭、一个地区的 消费行为可能会影响另外一些家庭和另外一些 地区,就是说不同观测点的随机误差项可能是 相关的。 多数经济时间序列在较长时间内都表现为上升 或下降的超势,因此大多表现为正自相关。但 就自相关本身而言是可以为正相关也可以为负 相关。
6-16
三、自相关的表现形式
6-14
模型形式设定偏误也会导致自相关现象。如将 形成本曲线设定为线性成本曲线,则必定会导致 自相关。由设定偏误产生的自相关是一种虚假自 相关,可通过改变模型设定予以消除。 自相关关系主要存在于时间序列数据中,但是在 横截面数据中,也可能会出现自相关,通常称其 为空间自相关(Spatial auto correlation)。
Yt = 1 + 2 X 2t + 3 X 3t + ut
而建立模型时,模型设定为: Yt = 1 + 2 X 2t + ut 则 X3t 对 Yt 的影响便归入随机误差项 ut 中,由
于 ut 在不同观测点上是相关的,这就造成了
在不同观测点是相关的,呈现出系统模式,此
时 ut 是自相关的。
σ2 x2
随机误差项 u 有自相关时,ˆ2 依然是无偏的,
即 E(ˆ2 ) = β2 ,这一点在普通最小二乘法无偏
性证明中可以看到。因为,无偏性证明并不需
要 u 满足无自相关的假定。那么,最小二乘估
计量 ˆ2 是否是有效呢?下面我们将说明。
6-28
例如,一元回归中
ˆ2
=
Σxt yt Σxt2
6-11
原因4-蛛网现象
许多农产品的供给呈现为
蛛网现象,供给对价格的
反应要滞后一段时间,因
为供给需要经过一定的时
间才能实现。如果时期 t 的价格 Pt 低于上一期的 价格 Pt-1 ,农民就会减少 时期 t 1 的生产量。如
此则形成蛛网现象,此时
的供给模型为:
蛛网现象是微观经济学中的 一个概念。它表示某种商品 的供给量受前一期价格影响 而表现出来的某种规律性, 即呈蛛网状收敛或发散于供 需的均衡点。
