天津市第一中学2018届高三上学期第三次月考数学(文)试题Word版含答案
天津市耀华中学2022-2023学年高三上学期第三次月考语文试题

天津市耀华中学2023届高三年级第三次月考语文试卷本试卷考试时间150分钟,总分150分。
第I卷一、(9分)阅读下面一段文字,完成下面1-3题。
苏州的美是含蓄的。
要是不下一番寻索的(),你就别想领略它。
_______走到山腰,站在“迎笑亭”前,回头一看,原来这么美!眼下是一片松树的海,没有风,但是闭上眼睛,就能听到一种()的声音,正如悠远的琴曲。
深吸一口气,就闻到松脂()的清香。
再远一点,有整齐的农田,有蜿蜒的小河,有模糊的远山。
传说这条小河是为西施到对面象山而开凿的。
你怎能相信这条满怀青春的小河倒有两千岁!正如我跟前这座“迎笑亭”,一个四角方方的房子,你怎能相信这就是传说中苏东坡到过的地方。
可是如果周围的美景把你迷得(),你是什么都会相信的,仿佛自己已经置身仙山。
1.依次填入括号内的词语,最恰当的一组是A.功夫飒飒沁人心脾神魂颠倒B.工夫铮铮神清气爽如痴如醉C.功夫飒飒神清气爽如痴如醉D.工夫铮铮沁人心脾神魂颠倒2.下列填入文中横线处的句子,衔接最恰当的一项是A.站在灵岩山跟前,觉得它不过是一个有树的山丘,所以没有什么出奇的。
B.站在灵岩山跟前,并不觉得它有什么出奇的,不过是一个有树的山丘罢了。
C.灵岩山不过是一个有树的山丘罢了,站在它跟前,不觉得它有什么出奇的。
D.灵岩山并不让人觉得它有什么出奇的,不过是一个有树的山丘罢了。
3.对选文中涉及的文化常识解说正确的一项是A.古代的琴曲有很多,比如著名的《高山流水》,据《列子》记载,俞伯牙弹琴,钟子期能听出他是“志在高山”还是“志在流水”,遂成知音。
B.西施是古代著名的美女,后世《红楼梦》中,曹雪芹却用“病如西子胜三分”来形容贾宝玉,别有一番趣味。
C.苏轼的文化思想非常丰富,儒、道、释三家对其均有影响,我们从其作品中就可以感受到。
比如“人生如梦”一句,可以品出《庄子》的意味,“逝者如斯”,源自《诗经》,而“造物者之无尽藏”,则是佛家用语。
D.中国古代传说海外有三座仙山,分别是蓬莱、方丈和瀛洲。
2016届高三上学期第一次月考数学(文)试题Word版含答案

2016届高三上学期第一次月考数学(文)试题Word版含答案2016届高三上学期第一次月考数学文试卷考试时间120分钟,满分150分一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合M ={x |x ≥0,x ∈R },N ={x |x 2<1,x ∈R },则M ∩N 等于( ) A .[0,1] B .[0,1) C .(0,1]D .(0,1)2.已知集合A ={1,2},B ={1,a ,b },则“a =2”是“A ?B ”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.已知命题p :所有有理数都是实数;命题q :正数的对数都是负数,则下列命题中为真命题的是( ) A .﹁p 或q B .p 且q C .﹁p 且﹁qD .﹁p 或﹁q4.设函数f (x )=x 2+1,x ≤1,2x ,x >1,则f (f (3))等于( )A.15B .3C.23D.1395.函数f (x )=log 12(x 2-4)的单调递增区间是( )A .(0,+∞)B .(-∞,0)C .(2,+∞)D .(-∞,-2)6.已知函数f (x )为奇函数,且当x >0时,f (x )=x 2+1x ,则f (-1)等于( )A .-2B .0C .1D .27. 如果函数f (x )=x 2-ax -3在区间(-∞,4]上单调递减,则实数a 满足的条件是( ) A .a ≥8 B .a ≤8 C .a ≥4D .a ≥-48. 函数f (x )=a x -2+1(a >0且a ≠1)的图像必经过点( ) A .(0,1) B .(1,1) C .(2,0)D .(2,2)9. 函数f (x )=lg(|x |-1)的大致图像是( )10. 函数f (x )=2x +3x 的零点所在的一个区间是( ) A .(-2,-1) B .(-1,0) C .(0,1)D .(1,2)11. 设f (x )=x ln x ,若f ′(x 0)=2,则x 0的值为( ) A .e 2B .eC.ln22D .ln212. 函数f (x )的定义域是R ,f (0)=2,对任意x ∈R ,f (x )+f ′(x )>1,则不等式e x ·f (x )>e x +1的解集为( ).A .{x |x >0}B .{x |x <0}C .{x |x <-1或x >1}D .{x |x <-1或0<1}<="" p="">二、填空题:本大题共4小题,每题5分.13. 已知函数y =f (x )及其导函数y =f ′(x )的图像如图所示,则曲线y =f (x )在点P 处的切线方程是__________.14. 若函数f (x )=x 2+ax +b 的两个零点是-2和3,则不等式af (-2x )>0的解集是________. 15. 函数y =12x 2-ln x 的单调递减区间为________.16. 若方程4-x 2=k (x -2)+3有两个不等的实根,则k 的取值范围是________.三、解答题:解答应写出文字说明、证明过程或演算步骤17.(10分) 化简:(1)3131421413223b a b a ab b a -(a >0,b >0);(2)(-278)23-+(0.002)12--10(5-2)-1+(2-3)0.18.(12分)已知函数f (x )=1a -1(a >0,x >0),(1)求证(用单调性的定义证明):f (x )在(0,+∞)上是增函数; (2)若f (x )在[12,2]上的值域是[12,2],求a 的值.19.(12分)已知定义在R 上的奇函数f (x )有最小正周期2,且当x ∈(0,1)时,f (x )=2x4x +1.(1)求f (1)和f (-1)的值; (2)求f (x )在[-1,1]上的解析式.20.(12分)已知函数f (x )=x 2+2ax +3,x ∈[-4,6]. (1)当a =-2时,求f (x )的最值;(2)求实数a 的取值范围,使y =f (x )在区间[-4,6]上是单调函数;(3)当a =1时,求f (|x |)的单调区间. 21.(12分)已知函数f (x )=x 3+x -16. (1)求曲线y =f (x )在点(2,-6)处的切线的方程;(2)直线l 为曲线y =f (x )的切线,且经过原点,求直线l 的方程及切点坐标; 22.(12分)已知函数f (x )=x 3-3ax -1,a ≠0. (1)求f (x )的单调区间;(2)若f (x )在x =-1处取得极值,直线y =m 与y =f (x )的图像有三个不同的交点,求m 的取值范围.2016届高三上学期第一次月考数学答题卡一、选择题(共12小题,每小题5分,共60分,每小题有一个正确答案)13、 14、15、 16、三、解答题17.(10分) 化简:(1)131421413223b a b a ab b a -(a >0,b >0);(2)(-278)23-+(0.002)12--10(5-2)-1+(2-3)0.18.(10分)已知函数f (x )=1a -1x(a >0,x >0),(1)求证(用单调性的定义证明):f (x )在(0,+∞)上是增函数; (2)若f (x )在[12,2]上的值域是[12,2],求a 的值.19.(12分)已知定义在R 上的奇函数f (x )有最小正周期2,且当x ∈(0,1)时,f (x )=2x4x +1.(1)求f (1)和f (-1)的值; (2)求f (x )在[-1,1]上的解析式.20.(12分)已知函数f(x)=x3+x-16.(1)求曲线y=f(x)在点(2,-6)处的切线的方程;(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;21.(13分)已知函数f(x)=x2+2ax+3,x∈[-4,6].(1)当a=-2时,求f(x)的最值;(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;(3)当a=1时,求f(|x|)的单调区间.22.(13分)已知函数f(x)=x3-3ax-1,a≠0.(1)求f(x)的单调区间;(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图像有三个不同的交点,求m的取值范围.2016届高三上学期第一次月考数学文试卷参考答案1.B2.A3.D4.D5.D6.A7.A8.D9.B10.B11.B12.A13. x -y -2=0 14. {x |-32<1}<="" p="">15. (0,1] 16. (512,34]17. 解 (1)原式=121311113233211212633311233().a b a b abab ab a b+-++----==(2)原式=(-278)23-+(1500)12--105-2+1=(-827)23+50012-10(5+2)+1=49+105-105-20+1=-1679. 18. (1)证明设x 2>x 1>0,则x 2-x 1>0,x 1x 2>0,∵f (x 2)-f (x 1)=(1a -1x 2)-(1a -1x 1)=1x 1-1x 2=x 2-x 1x 1x 2>0,∴f (x 2)>f (x 1),∴f (x )在(0,+∞)上是增函数. (2)解∵f (x )在[12,2]上的值域是[12,2],又f (x )在[12,2]上单调递增,∴f (12)=12,f (2)=2.易得a =25.19. 解(1)∵f (x )是周期为2的奇函数,∴f (1)=f (1-2)=f (-1)=-f (1),∴f (1)=0,f (-1)=0. (2)由题意知,f (0)=0. 当x ∈(-1,0)时,-x ∈(0,1).由f (x )是奇函数,∴f (x )=-f (-x )=-2-x4-x +1=-2x4x +1,综上,在[-1, 1]上,f (x )=2x4x +1,x ∈(0,1),-2x 4x+1,x ∈(-1,0),0,x ∈{-1,0,1}.20.解 (1)当a =-2时,f (x )=x 2-4x +3=(x -2)2-1,∵x ∈[-4,6],∴f (x )在[-4,2]上单调递减,在[2,6]上单调递增,∴f (x )的最小值是f (2)=-1,又f (-4)=35,f (6)=15,故f (x )的最大值是35. (2)∵函数f (x )的图像开口向上,对称轴是x =-a ,∴要使f (x )在[-4,6]上是单调函数,应有-a ≤-4或-a ≥6,即a ≤-6或a ≥4. (3)当a =1时,f (x )=x 2+2x +3,∴f (|x |)=x 2+2|x |+3,此时定义域为x ∈[-6,6],且f (x )=?x 2+2x +3,x ∈(0,6],x 2-2x +3,x ∈[-6,0],∴f (|x |)的单调递增区间是(0, 6],单调递减区间是[-6,0].21.解 (1)可判定点(2,-6)在曲线y =f (x )上.∵f ′(x )=(x 3+x -16)′=3x 2+1.∴f ′(x )在点(2,-6)处的切线的斜率为k =f ′(2)=13. ∴切线的方程为y =13(x -2)+(-6),即y =13x -32.(2)法一设切点为(x 0,y 0),则直线l 的斜率为f ′(x 0)=3x 20+1,∴直线l 的方程为y =(3x 20+1)(x -x 0)+x 30+x 0-16,又∵直线l 过点(0,0),∴0=(3x 20+1)(-x 0)+x 30+x 0-16,整理得,x 30=-8,∴x 0=-2,∴y 0=(-2)3+(-2)-16=-26,k =3×(-2)2+1=13. ∴直线l 的方程为y =13x ,切点坐标为(-2,-26.) 法二设直线l 的方程为y =kx ,切点为(x 0,y 0),则k=y0-0x0-0=x30+x0-16x0又∵k=f′(x0)=3x20+1,∴x30+x0-16x0=3x2+1,解之得x0=-2,∴y0=(-2) 3+(-2)-16=-26,k=3×(-2)2+1=13.∴直线l的方程为y=13x,切点坐标为(-2,-26).22.解(1)f′(x)=3x2-3a=3(x2-a),当a<0时,对x∈R,有f′(x)>0,∴当a<0时,f(x)的单调增区间为(-∞,+∞).当a>0时,由f′(x)>0,解得x<-a或x>a.由f′(x)<0,解得-a<x<a,< p="">∴当a>0时,f(x)的单调增区间为(-∞,-a),(a,+∞),单调减区间为(-a,a).(2)∵f(x)在x=-1处取得极值,∴f′(-1)=3×(-1)2-3a=0,∴a=1.∴f(x)=x3-3x-1,f′(x)=3x2-3,由f′(x)=0,解得x1=-1,x2=1.由(1)中f(x)的单调性可知,f(x)在x=-1处取得极大值f(-1)=1,在x=1处取得极小值f(1)=-3.∵直线y=m与函数y=f(x)的图像有三个不同的交点,结合如图所示f(x)的图像可知:实数m的取值范围是(-3,1).</x<a,<>。
天津市第一中学2022-2023学年高三上学期第三次月考数学试题(解析版)

天津一中2022-2023-1高三年级第三次月考数学试卷(答案)本试卷总分150分,考试用时120分钟。
考生务必将答案涂写在答题卡上,答在试卷上的无效。
一、选择题:本题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、已知集合3{Z |Z}1A x x=∈∈-,2{Z |60}B x x x =∈--≤,则A B ⋃=( ) A .{2} B .}{2,0,2- C .{}2,1,0,1,2,3,4-- D .}{3,2,0,2,4--【详解】{A x =∈2Z |x x --{2,1,0,1,2,3,4--.,b ,c 为非零实数,则“A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件【分析】根据不等式的基本性质可判定“a >b >c ”能推出“a +b >2c ”,然后利用列举法判定“a +b >2c ”不能推出“a >b >c ”,从而可得结论.【解答】解:∵a >b >c ,∴a >c ,b >c ,则a +b >2c , 即“a >b >c ”能推出“a +b >2c ”,但满足a +b >2c ,取a =4,b =﹣1,c =1,不满足a >b >c , 即“a +b >2c ”不能推出“a >b >c ”,所以“a >b >c ”是“a +b >2c ”的充分不必要条件, 故选:A .3、已知2log 0.8a =,0.12b =,sin 2.1c =,则( )A .a b c <<B .a c b <<C .c a b <<D .b<c<a 【答案】B【详解】因为22log 0.8log 10<=,0.10122>=,0sin 2.11<<, 所以a c b <<, 故选:B 4、函数2sin ()1x xf x x -=+的图象大致为 ( )A .B .C .D .【答案】A 【解析】【分析】根据函数的定义域、奇偶性以及2f π⎛⎫⎪⎝⎭的值来确定正确选项. 【详解】由题意,函数2sin ()1x xf x x -=+的定义域为R , 且22sin()sin ()()()11x x x xf x f x x x -----===--++,所以函数()f x 奇函数,其图象关于原点对称,所以排除C 、D 项,2120212f πππ-⎛⎫=> ⎪⎝⎭⎛⎫+ ⎪⎝⎭,所以排除B 项. 故选:A5、已知1F 、2F 分别为双曲线2222:1x y E a b-=的左、右焦点,点M 在E 上,1221::2:3:4F F F M F M =,则双曲线E 的渐近线方程为 ( ) A .2y x =± B .12y x =±C.y = D.y =【答案】C【解析】由题意,1F 、2F 分别为双曲线2222:1x y E a b-=的左、右焦点,点M 在E 上,且满足1221:||:2:3:4F F F M F M =,可得122F F c =,23F M c =,14F M c =, 由双曲线的定义可知21243a F M F M c c c =-=-=,即2c a =,又由b ==,所以双曲线的渐近线方程为y =.故选:C .6、设n S 是等比数列{}n a 的前n 项和,若34S =,4566a a a ++=,则96S S = ( )A .32B .1910 C .53D .196【答案】B【解析】设等比数列{}n a 的公比为q ,若1q =,则456133a a a a S ++==,矛盾. 所以,1q ≠,故()()33341345631111a q a q q a a a q S qq--++===--,则332q=, 所以,()()()63113631151112a q a q S q S qq--==+⋅=--, ()()()9311369311191114a q a q S q q S qq--==++=--, 因此,9363192194510S S S S =⋅=.故选:B . 7、直线1y kx =-被椭圆22:15x C y +=截得最长的弦为( ) A .3 B .52C .2D【答案】B【解析】联立直线1y kx =-和椭圆2215xy +=,可得22(15)100k x kx +-=,解得0x =或21015kx k =+,则弦长21015kl k =+,令215(1)k t t +=≥,则10l === 当83t =,即k =,l 取得最大值55242⨯=, 故选:B8、设函数()sin()(0)4f x x πωω=->,若12()()2f x f x -=时,12x x -的最小值为3π,则( )A .函数()f x 的周期为3πB .将函数()f x 的图像向左平移4π个单位,得到的函数为奇函数 C .当(,)63x ππ∈,()f x的值域为D .函数()f x 在区间[,]-ππ上的零点个数共有6个 【答案】D【解析】由题意,得23T π=,所以23T π=,则23T πω==,所以()sin(3)4f x x π=-选项A 不正确; 对于选项B :将函数()f x 的图像向左平移4π个单位,得到的函数是 ()sin[3()]cos344f x x x ππ=+-=为偶函数,所以选项B 错误;对于选项C :当时(,)63x ππ∈,则33444x πππ<-<,所以()f x的值域为,选项C 不正确;对于选项D :令()0,Z 123k f x x k ππ=⇒=+∈,所以当3,2,1,0,1,2k =---时,[,]x ππ∈-,所以函数()f x 在区间[,]-ππ上的零点个数共有6个,D 正确, 故选:D .9、设函数()(),01,,10,1xx mf x x x m x ⎧≤<⎪⎪=⎨-⎪-<<+⎪⎩,()()41g x f x x =--.若函数()g x 在区间()1,1-上有且仅有一个零点,则实数m 的取值范围是( )A .(]11,1,4⎡⎫--⋃+∞⎪⎢⎣⎭B .(]1,1,4⎡⎫-∞-+∞⎪⎢⎣⎭C .{}11,5⎡⎫-⋃+∞⎪⎢⎣⎭D .{}11,15⎛⎫-⋃ ⎪⎝⎭【答案】C 【详解】令()()410g x f x x =--=,则()41f x x =+,当01x ≤<时,41xx m=+,即4x mx m =+,即函数1y x =与24y mx m =+的交点问题,其中24y mx m =+恒过A 1,04⎛⎫- ⎪⎝⎭.当10x -<<时,()411x x m x -=++,即1114mx m x -+=++,即函数3111x y =-++与24y mx m =+的交点问题 分别画出函数1y ,2y ,3y 在各自区间上的图象: 当2y 与3y 相切时,有且仅有一个零点,此时()411xx m x -=++,化简得:()24510mx m x m +++=,由()2251160m m ∆=+-=得:11m =-,219m =-(舍去)当直线2y 的斜率,大于等于直线1y 的斜率时,有且仅有一个零点,把()1,1B 代入24y mx m =+中,解得:15m =,则15m ³综上,m 的取值范围是{}11,5⎡⎫-⋃+∞⎪⎢⎣⎭故选:C二、填空题:本大题共6小题,每小题5分,共30分.试题中包含两个空的,答对1个的给3分,全部答对的给5分.10、已知复数z 满足()2i i z -=,则5i z -=___________.【答案】3【解析】因为圆22:20(0)C x ax y a -+=>的标准方程为:()222x a y a -+=,所以圆必坐标为(,0)a ,半径为a ,由题意得:32a a += 解得:3a = ,故答案为:3.12、已知3π3sin 85α⎛⎫-= ⎪⎝⎭,则πcos 24α⎛⎫+= ⎪⎝⎭________. 【答案】725-【解析】2πcos 2cos 22cos 1488ππααα⎡⎤⎛⎫⎛⎫⎛⎫+=+=+- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦232cos 182ππα⎡⎤⎛⎫=-+- ⎪⎢⎥⎝⎭⎣⎦223372sin 1218525πα⎛⎫⎛⎫=--=⨯-=- ⎪ ⎪⎝⎭⎝⎭,故答案为:725- 13、直线l 与双曲线2222:1(0,0)x y E a b a b -=>>的一条渐近线平行,l 过抛物线2:4C y x =的焦点,交C 于A ,B 两点,若||5AB =,则E 的离心率为_______.【详解】依题意,点F 的坐标为(1,0),设直线l 的方程为1x my =+,联立方程组214x my y x=+⎧⎨=⎩,消去x 并整理得:2440y my --=,设1(A x ,1)y ,2(B x ,2)y ,则124y y m +=,124y y =-,则2212||()4(1)5AB y y m ++=,解得:12m =±,∴直线l 的方程为220x y +-=或220x y --=;直线的斜率为:2±.直线l 与双曲线2222:1(0,0)x y E a b a b -=>>的一条渐近线平行,可得2b a =,所以22224b a c a ==-,1e >,解得e =故14、已知1a >,1b >,且lg 12lg a b =-,则log 2log 4a b +的最小值为_______. 【答案】9lg2【解析】由已知,令lg 2log 2lg a m a ==,lg 4log 4lg b n b==, 所以lg 2lg a m =,lg 42lg 2lg b n n ==,代入lg 12lg a b =-得:lg 24lg 21m n+=, 因为1a >,1b >,所以lg 24lg 24log 2log 4()1()()5lg 2(lg 2lg 2)a b m nm n m n m n n m+=+⨯=++=++ 2lg 25lg 25lg 24lg 29lg 2n m≥+=+=.当且仅当4lg 2lg 2m n n m=时,即1310a b ==时等号成立. log 2log 4a b +的最小值为9lg2. 故答案为:9lg2.15、在Rt ABC 中,90C ∠=,若ABC 所在平面内的一点P 满足0PA PB PC λ++=,当1λ=时,222PA PB PC+的值为 ;当222PA PB PC+取得最小值时,λ的值为 .【答案】5;-1【解析】(1)如图5-26,以C 为坐标原点建立直角坐标系, 因为0PA PB PC λ++=,所以点P 为ABC 的重心,设BC a =,AC b =,所以(),0A b ,()0,B a ,易得,33a b P ⎛⎫⎪⎝⎭,所以222222222411499991199a b a b PA PBPC b a ++++=+5=. (2)设(,)P x y ,则(,),(,),(,)PA b x y PB x a y PC x y =--=--=--, 所以2,2,b x x a y y λλ-=⎧⎨-=⎩可得(2),(2),b x a y λλ=+⎧⎨=+⎩于是222222222||||()()||PA PB x b y x y a x y PC +-+++-=+()222222222x y bx ay a b x y +--++=+ 22222222(2)(2)2(2)2(2)2x y x y x y λλλλ+++-+-+=++()()222222222x y x y λλλλ+++=++ 2222(1)11λλλ=++=++…当1λ=-时取等号,所以222||||||PA PB PC +的最小值为1. 故答案为:5;-1.三、解答题:本大题共5小题,共75分.解答应写出文字说明,证明过程或演算步骤.16、如图,在平面四边形ABCD 中,对角线AC 平分BAD ∠,ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,cos cos cos 0B a C c A ++=. (1)求B ;(2)若2AB CD ==,ABC 的面积为2,求AD . 【答案】(1)34B π=;(2)4=AD .【分析】(1)利用正弦定理将边化角,再根据两角和的正弦公式及诱导公式即可得到cos B=出B;(2)由三角形面积公式求出a,再利用余弦定理求出AC,即可求出cos CAB∠,依题意cos cosCAB CAD∠=∠,最后利用余弦定理得到方程,解得即可;【详解】(1)cos cos cos0B aC c A++=,cos sin cos cos sin0B B AC A C++=,()cos sin0B B A C++=,cos sin0B B B+=,因为0Bπ<<,所以sin0B>,所以cos B=34Bπ=.(2)因为ABC的面积2S=,所以1sin22==ABCS ac B,2=,所以a=由余弦定理得AC==所以222cos2AB AC BCCABAB AC+-∠==⋅因为AC平分BAD∠,所以cos cosCAB CAD∠=∠,所以2222cosCD AC AD AC AD CAD=+-⋅⋅∠,所以24202AD AD=+-⨯28160AD AD-+=,所以4=AD.17、如图,在五面体ABCDEF中,四边形ABEF为正方形,DF⊥平面ABEF,//CD EF,2DF=,22EF CD==,2EN NC=,2BM MA=.(1)求证://MN平面ACF;(2)求直线AD与平面BCE所成角的正弦值;(3)求平面ACF与平面BCE夹角的正弦值.【答案】(1)见解析;(2;(3)45【详解】(1)证明:在EF上取点P,使2EP PF=,因为2EN NC=,所以//NP FC,于是//NP平面ACF,因为2BM MA=,四边形ABEF为正方形,所以//MP AF,所以//MP平面ACF,因为MP PN P =,所以平面//MNP 平面ACF ,因为MN ⊂平面MNP ,所以//MN 平面ACF ;(2)解:因为DF ⊥平面ABEF ,所以DF FA ⊥,DF EF ⊥, 又因为四边形ABEF 为正方形,所以AF EF ⊥,所以FA 、FE 、FD 两两垂直,建立如图所示的空间直角坐标系, (2AD =-,0,2),(2EB =,0,0),(0EC =,1-,2),设平面BCE 的法向量为(m x =,y ,)x , 2020EB m x EC m y z ⎧⋅==⎪⎨⋅=-+=⎪⎩,令1z =,(0m =,2,1), 所以直线AD 与平面BCE所成角的正弦值为||2||||22AD m AD m ⋅=⋅⋅ (3)解:(2FA =,0,0),(0FC =,1,2), 设平面ACF 的法向量为(n u =,v ,)w ,2020FA n u FC n v w ⎧⋅==⎪⎨⋅=+=⎪⎩,令1w =-,(0n =,2,1)-, 由(1)知平面BCE 的法向量为(0m =,2,1), 设平面ACF 与平面BCE 所成二面角的大小为θ,||33cos ||||55m n m n θ⋅===⋅⋅,4sin 5θ==.所以平面ACF 与平面BCE 所成二面角的正弦值为45. 18、已知椭圆2222:1(0)x y C a b a b +=>>的左、右焦点为12,F F ,P 为椭圆上一点,且212PF F F ⊥,12tan PF F ∠=. (1)求椭圆C 的离心率;(2)已知直线l 交椭圆C 于,A B 两点,且线段AB 的中点为11,2Q ⎛⎫- ⎪⎝⎭,若椭圆C 上存在点M ,满足234OA OB OM +=,试求椭圆C 的方程.【答案】(1)e =(2)22551164x y +=.【分析】(1)由212tan 2b a PF F c ∠==222a c b -=,建立关于e 的方程,即可得到结果; (2)设()()()112200,,,,,A x y B x yM x y ,由(1)可知224a b =,可设椭圆方程为22244x y b +=,根据234OA OB OM +=,可得120120234234x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩,设1:(1)2AB y k x =--将其与椭圆方程联立,由韦达定理和点M 满足椭圆方程,可求出2b ,进而求出结果.【详解】(1)解:因为2212tan 22b b a PF F c ac ∠==26b =,即()226a c -=, 则()261e -=,解得e =(2)设()()()112200,,,,,A x y B x y M x y ,由22234c e a ==,得2243a c =,所以222221134b a c c a =-==,所以224a b =设2222:14x y C b b+=,即22244x y b +=由于,A B 在椭圆上,则2221144x y b +=,2222244x y b +=,①由234OA OB OM +=,得120120234234x x x y y y +=⎧⎨+=⎩,即120120234234x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩ 由M 在椭圆上,则2220044x y b +=,即212222144232344x x y y b ⎛⎫+= ⎪++⎛⎫ ⎪⎝⎝⎭⎭, 即()()()222211121222441249464x y x x y y x y b +++++=,②将①代入②得:212124x x y y b +=,③线段AB 的中点为11,2Q ⎛⎫- ⎪⎝⎭,设1:(1)2AB y k x =--可知()22211244y k x x y b⎧=--⎪⎨⎪+=⎩ ()()22222148444410k x kk x k k b +-+++-+=212284121142k k x x k k ++==⨯⇒=+, 所以222220x x b -+-=,其中0∆>,解得212b >, 所以21222x x b ⋅=-,AB 方程为112y x =-又()2121212121111111122422b y y x x x x x x -⎛⎫⎛⎫=--=-++= ⎪⎪⎝⎭⎝⎭,④ 将④代入③得:22221422425b b b b --+⋅=⇒=, 经检验满足212b >, 所以椭圆C 的方程为22551164x y +=. 19、已知等差数列}{n a 的前n 项和为n S ,且455=S 455=S ,40342=+a a .数列}{n b 的前n 项和为n T ,满足n n b T 413=+)(*N n ∈.(1)求数列}{n a 、}{n b 的通项公式;(2)若1)23(+⋅-=n n n n n a a a b c ,求数列}{n c 的前n 项和n R ; (3)设n n n b S d =,求证:11248-=+-<∑n n k k n d . 【答案】(1)32+=n a n ,14-=n n b ;(2)51524-+=n R n n ;(2)证明见详解. 【详解】(2);(3)124n n n n n b c b b ++=, 112(3)44n n n n n n b n n c b b +-++∴==, 则12124)2(444--+=++<n n n n n n c ,122-+<n n . 设1122n n k k k S '-=+=∑, 11123422122nn k n k k n S '--=++∴==++⋯+∑ 213422222n n n S +'∴=++⋯+ 12111(1)121112422334122222221()2n n n n n n n n n S ---+++'∴=-+++⋯+=-+=--,1482n n n S -+'∴=- 综上,11248-=+-<∑n n k k n c . 20、已知函数()e cos x f x x =,()cos (0)g x a x x a =+<,曲线()y g x =在π6x =处的切线的斜率为32.(1)求实数a 的值;(2)对任意的π,02x ⎡⎤∈-⎢⎥⎣⎦,()'()0f x g x -≥恒成立,求实数t 的取值范围; (3)设方程()'()f x g x =在区间()ππ2π,2π32n n n +⎛⎫++∈ ⎪⎝⎭N 内的根从小到大依次为1x 、2x 、…、n x 、…,求证:12n n x x +->π.【答案】(1)1a =-;(2)1t ≥;(2)证明见详解.【分析】(1)由'π362g ⎛⎫= ⎪⎝⎭来求得a 的值. (2)由()'()0f x g x -≥,对x 进行分类讨论,分离常数t 以及构造函数法,结合导数求得t 的取值范围.(3)由()'()f x g x =构造函数()e cos sin 1x x x x ϕ=--,利用导数以及零点存在性定理,结合函数的单调性证得12n n x x +->π.【详解】(1)因为()cos (0)g x a x x a =+<,则()'1sin g x a x =-, 由已知可得'π131622g a ⎛⎫=-= ⎪⎝⎭,解得1a =-. (2)由(1)可知()'1sin g x x =+,对任意的π,02x ⎡⎤∈-⎢⎥⎣⎦,()'()0tf x g x -≥恒成立, 即e cos 1sin x t x x ≥+对任意的π,02x ⎡⎤∈-⎢⎥⎣⎦恒成立, 当2x π=-时,则有00≥对任意的R t ∈恒成立; 当π02x -<≤时,cos 0x >,则1sin e cos x x t x+≥, 令1sin ()e cos x x h x x +=,其中π02x -<≤, ()()2'2e cos e (cos sin )(1sin )e cos x x x x x x x h x x --+=2(1cos )(1sin )0e cos x x x x-+=≥且()'h x 不恒为零, 故函数()h x 在π,02⎛⎤- ⎥⎝⎦上单调递增,则max ()(0)1h x h ==,故1t ≥. 综上所述,1t ≥.(3)由()'()f x g x =可得e cos 1sin x x x =+,e cos 1sin 0x x x --=,令()e cos sin 1x x x x ϕ=--,则()'e (cos sin )cos x x x x x ϕ=--, 因为()ππ2π,2π32x n n n +⎛⎫∈++∈ ⎪⎝⎭N ,则sin cos 0x x >>,所以,()'0x ϕ<,所以,函数()ϕx 在()ππ2π,2π32n n n +⎛⎫++∈ ⎪⎝⎭N 上单调递减,因为π2π3ππ2πe cos 2π33n n n ϕ+⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭πsin 2π13n ⎛⎫-+- ⎪⎝⎭π2π31e 12n +=π2π3e 102+≥>,π2π202n ϕ⎛⎫+=-< ⎪⎝⎭, 所以,存在唯一的()ππ2π,2π32n x n n n +⎛⎫∈++∈ ⎪⎝⎭N ,使得()0n x ϕ=, 又1ππ2(1)π,2(1)π32n x n n +⎛⎫∈++++ ⎪⎝⎭()n +∈N ,则()1ππ2π2π,2π32n x n n n ++⎛⎫-∈++∈ ⎪⎝⎭N 且()10n x ϕ+=, 所以,()()12π112πe cos 2πn x n n x x ϕ+-++-=-()1sin 2π1n x +---12π11e cos sin 1n x n n x x +-++=--112π11e cos e cos n n x x n n x x ++-++=-()112π1e e cos 0n n x x n x ++-+=-<()n x ϕ=, 因为函数()ϕx 在()ππ2π,2π32n n n +⎛⎫++∈ ⎪⎝⎭N 上单调递减, 故12n n x x +-π>,即12n n x x +->π.。
天津市第一中学2023届高三上学期第一次月考物理试题 Word版含答案

C.P所受摩擦力方向先沿斜面向下后沿斜面向上D.斜面对P的作用力先变小后变大
三、实验题
11.某同学用橡皮条与弹簧测力计验证“力的平行四边形定则”,实验装置如图甲所示。其中A为固定橡皮条的图钉, 和 为细绳。
(1)本实验采用的科学方法是“等效替代法”,其含义是___________
4.电梯、汽车等交通工具在加速时会使乘客产生不适感,其中不适感的程度可用“急动度”来描述。急动度是描述加速度变化快慢的物理量,即 。汽车工程师用急动度作为评判乘客不舒适程度的指标,按照这一指标,具有零急动度的乘客,感觉较舒适。图为某汽车加速过程的急动度j随时间t的变化规律。下列说法正确的是( )
A.在0~5.0s时间内,汽车做匀加速直线运动
B.“福建舰”在码头补给充足后,它的惯性将变大
C.“福建舰”大角度转弯时,舰上各点的速度相同
D.研究战斗机在航母上的起落时,可以将“福建舰”看成质点
2.如图所示,音乐喷泉竖直向上喷出水流,喷出的水经3s到达最高点,把最大高度分成三等份,水通过起始的第一等份用时为 ,通过最后一等份用时为 。空气阻力不计,则 满足( )
A.
B.轻绳上的弹力与弹簧N上的弹力之比为
C.若剪断弹簧M,则在剪断的瞬间,b球处于失重状态
D.若剪断轻绳,则在剪断的瞬间,a球的加速度为
6.“血沉”是指红细胞在一定条件下沉降的速度,在医学中具有重要意义。测量“血沉”可将经过处理后的血液放进血沉管内,由于重力作用,血液中的红细胞将会下沉。设血沉管竖直放置且足够深,红细胞的形状为球体。已知红细胞下落受到血液的粘滞阻力表达式为 ,其中 为血液的粘滞系数,r为红细胞半径,v为红细胞运动的速率。若某血样中半径为r的红细胞,由静止下沉直到匀速运动的速度为 ,红细胞密度为 ,血液的密度为 。以下说法正确的是( )
天津市第一中学2021届高三上学期摸底考(零月考)化学试题 Word版含答案

天津一中 2020-2021-1 高三年级化学学科 0 月考试卷本试卷分为第 I 卷(选择题)、第II 卷(非选择题)两部分,共100 分,考试用时60 分钟。
第 I 卷 1 至 2 页,第 II 卷 3 至 4 页。
考生务必将答案涂写规定的位置上,答在试卷上的无效。
祝各位考生考试顺利!C:12 N:14 O:16 Na:23 Mg :24 Fe :56第Ⅰ卷选择题(单选)(共 12 道题,每题 3 分,共 36 分)1.化学与生活、生产密切相关。
下列说法正确的是 A.气象报告中的“PM2.5”是指一种胶体粒子 B.石英玻璃主要成分是硅酸盐,可制作化学精密仪器 C.“熬胆矾铁釜,久之亦化为铜”,该过程发生了置换反应 D.“天宫一号”使用的碳纤维,是一种新型有机高分子材料2. 下列说法错误的是A.淀粉和纤维素均可水解产生葡萄糖B.油脂的水解反应可用于生产甘油C.氨基酸是组成蛋白质的基本结构单元 D.淀粉、纤维素和油脂均是天然高分子3.设 N A 为阿伏加德罗常数的值。
下列叙述正确的是 A.标准状况下,22.4L CCl4 所含分子数为N A B.常温常压下,7.8g Na2O2 晶体中阳离子和阴离子总数为0.3N A C.7.8g 苯中含有的碳碳双键数为0.3N AD.室温下,1L pH=13 的 NaOH 溶液中,由水电离的OH- 数目为 0.1N A4.探究浓硫酸和铜的反应,下列装置或操作正确的是2 2 2 2 A .用装置甲进行铜和浓硫酸的反应B .用装置乙收集二氧化硫并吸收尾气C .用装置丙稀释反应后的混合液D .用装置丁测定余酸的浓度5. 吡啶()是类似于苯的芳香化合物,2-乙烯基吡啶(VPy )是合成治疗矽肺病药物的原料,可由如下路线合成。
下列叙述正确的是A .Mpy 只有两种芳香同分异构体B .Epy 中所有原子共平面C .Vpy 是乙烯的同系物D .反应②的反应类型是消去反应6. 反应 M n O + 4 H Cl(浓) Δ M n Cl + Cl ↑ +2 H O 量之比是 中,氧化产物与还原产物的物质的 A .1∶2B .1∶1C .2∶1D .4∶17.用如下图所示的装置进行实验(夹持仪器略去,必要时可加热),其中 a 、b 、c 中分别盛 有试剂 1、2、3,能达到相应实验目的的是8. 对于下列实验,能正确描述其反应的离子方程式是A.用 Na2SO3 溶液吸收少量Cl2:3SO2-+Cl2+H2O = 2HSO-+2Cl-+SO2-3 3 4B.向 CaCl2 溶液中通入 CO2:Ca2++H2O+CO2=CaCO3↓+2H+C.向 H2O2 溶液中滴加少量FeCl3:2Fe3+ +H2O2=O2↑+2H++2Fe2+D.同浓度同体积NH4HSO4 溶液与 NaOH 溶液混合:NH++OH -=NH3·H2O9. 下列离子在溶液中能共存,加OH- 有沉淀析出,加H+能放出气体的是- 2+ + - -A. Na+、Ca2+、Cl-、HCO3B. Ba 、K 、Cl 、NO3+ 2- -+ 2+ - 2-C. Ba2+、NH4 、CO3、NO3D. Na 、Cu 、Cl 、SO410. 由一种阳离子与两种酸根离子组成的盐称为混盐。
天津市第一中学2022届高三上学期第一次月考物理试题 Word版含答案

天津一中2021—2022学年度高三班级一月考物理学科试卷班级姓名成果本试卷分为第Ι卷(选择题)、第Ⅱ卷(非选择题)两部分,共100分,考试用时90分钟。
第Ι卷1至3页,第Ⅱ卷3至4页。
考生务必将答案涂写答题纸或答题卡的规定位置上,搭在试卷上的无效。
祝各位考生考试顺当!第Ι卷(选择题,共44分)一、单项选择题(本题共8小题,每题3分,共24分。
每小题只有一个正确选项。
)1.关于惯性,下列说法正确的是( )2.A.高速运动的物体不简洁让它停下来,所以物体运动速度越大,惯性越大3.B.用相同的水平力分别推放在地面上的两个材料不同的物体,则难以推动的物体惯性大4.C.两个物体只要质量相同,那么惯性就肯定相同5.D.在月球上举重比在地球上简洁,所以同一个物体在月球上比在地球上惯性小2.一个小滑块以肯定的初速度滑上倾角为37°的光滑斜面,在第ls内与前3s内通过的位移相等,取初速度方向为正方向,g=10m/s2,则下列推断正确的是( )A.滑块在前3s内的平均速度为9m/sB.滑块在前3s内的平均速率为3m/sC.滑块在第3s内的平均速度为3m/sD.滑块在第3s内的平均速率为3m/s3.如图所示,A和B两物块的接触面是水平的,A与B保持相对静止一起沿粗糙斜面加速下滑,在A和B下滑过程中,斜面保持静止不动,下列说法错误的是( )A.斜面对B的作用力方向为竖直向上B.斜面对B的摩擦力方向为沿斜面对上C.B对A的摩擦力方向为水平向左D.地面对斜面的摩擦力方向为水平向左4.如图所示,一小球左端固连一根轻杆(轻杆另一端插在墙内),右端连接一根弹簧,上面用轻绳连接,下面用平台托住(不连接)。
初始时,轻绳处于竖直方向,绳上张力小于小球的重力,弹簧处于水平方向拉伸状态。
除弹簧外,一切形变都可忽视不计。
则下列说法正确的是( )A.撤去绳的瞬间,平台对小球的支持力增大,小球有瞬时向上的加速度B.撤去杆的瞬间,弹簧对小球的作用力不变,小球有瞬时向右的加速度C.撤去弹簧的瞬间,杆对小球的作用力不变,小球有瞬时向左的加速度D.撤去平台的瞬间,绳对小球的拉力增大,小球有瞬时向下的加速度5.在升降电梯内的地板上放一体重计,电梯静止时,某同学站在体重计上,体重计示数为50kg,电梯运动过程中,某一段时间内该同学发觉体重计示数为40kg,已知重力加速度为g,则在这段时间内,下列说法中正确的是( )A.该同学处于失重状态,他所受的重力变小了B.该同学对体重计的压力与体重计对该同学的支持力是一对平衡力C.电梯的加速度大小为g/5,方向肯定竖直向下D.电梯肯定在竖直向下运动6.在粗糙水平地面上放着一个截面为四分之一圆弧的柱状物体A,A的左端紧靠竖直墙,A与竖直墙之间放一光滑圆球B,整个装置处于平衡状态,截面如图所示。
天津市第一中学2019届高三上学期第三次月考物理试题 PDF版含答案

天津一中 2018—2019—1 学年度高三年级三月考物理学科试卷 本试卷分为第 I 卷(选择题)、第 II 卷(非选择题)两部分,共120 分。
考生务必将 答案涂写答题纸或答题卡的规定位置上,答在试卷上的无效。
第Ⅰ卷(本卷共 8 道题,共 48 分)一、单选题:(每小题 6 分,共 30 分。
每小题中只有一个选项是正确的)1.在物理学的发展过程中,许多物理学家的科学发现推动了人类历史的进步,下列表述 符合物理学史实的是( )A.牛顿提出了万有引力定律并准确地测出了引力常量B.安培最早引入了电场概念,并提出用电场线表示电场C.奥斯特发现了电流的磁效应并总结出了判断电流与磁场方向关系的右手螺旋定则 D.法拉第发现了电磁感应现象,宣告了电磁学作为一门统一学科的诞生2.两个等量同种电荷固定于光滑水平面上,其连线的中垂线上有 A、B、C 三点,如图所 示。
一个比荷为 2C/kg 的小物块从该水平面内的 C 点静止释放,其运动的 v-t 图象如图 所示,其中 B 点处为整条图线切线斜率最大的位置(图中标出了该切线)。
则下列说法中 正确的是( )A.在 A、B、C 三点中,B 点电场强度最大,其电场强度 E=1V/mB.由 C 到A 的过程中,物块的电势能先增大后减小C.由 C 到 A 的过程中,电势逐渐升高D.A、B 两点电势差U AB=5 V3.地面附近空间中存在着纸面内水平方向的匀强电场(图中未画出)和垂直于纸面向里 的匀强磁场(如图所示)。
一个带电油滴沿着一条与竖直方向成α角的直线 MN运动。
以下说法中不正确的是( )A.油滴一定做匀速直线运动B.油滴一定从 M到 N运动C.油滴一定受水平向左的电场力D.油滴一定受垂直 MN 斜向右上的洛伦兹力4.如图为法拉第做过的电磁旋转实验,图中A 是可动磁铁,B 是固定导线,C 是可动导 线,D是固定磁铁。
图中灰色部分表示汞(磁铁和导线的下半部分都浸没在汞中),下部接在电源上。
天津市第一中学2022-2023学年高三上学期第一次月考数学试题(解析版)
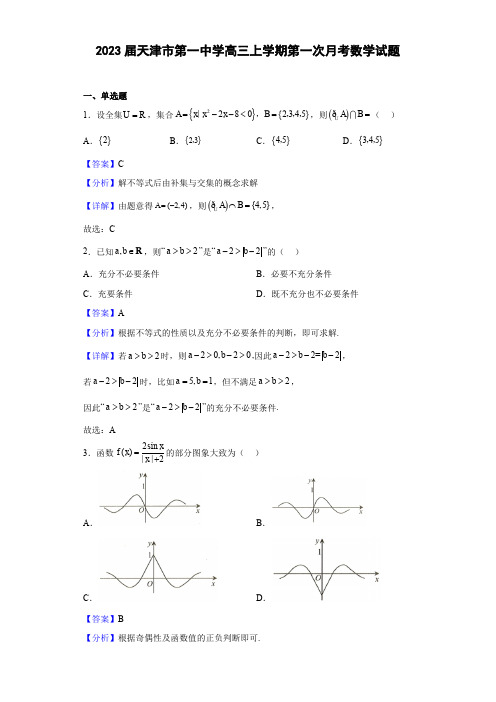
2023届天津市第一中学高三上学期第一次月考数学试题一、单选题1.设全集R U =,集合{}{}22802345A x x x B =--<=∣,,,,,则()U A B =ð( ) A .{}2 B .{}23,C .{}45,D .{}345,, 【答案】C【分析】解不等式后由补集与交集的概念求解 【详解】由题意得(2,4)A =-,则(){4,5}U A B ⋂=ð, 故选:C2.已知,a b ∈R ,则“2a b >>”是“22a b ->-”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】A【分析】根据不等式的性质以及充分不必要条件的判断,即可求解. 【详解】若2a b >>时,则20,20a b ->->,因此22=2a b b ->--, 若22a b ->-时,比如5,1a b ==,但不满足2a b >>, 因此“2a b >>”是“22a b ->-”的充分不必要条件. 故选:A 3.函数2sin ()||2xf x x =+的部分图象大致为( ) A . B .C .D .【答案】B【分析】根据奇偶性及函数值的正负判断即可.【详解】因为2sin ()2xf x x =+,定义域为R 所以2sin()2sin ()()22x xf x f x x x --==-=--++所以()f x 为奇函数,且(0)0f =,排除CD 当()0,x π∈时,sin 0x >,即()0f x >,排除A 故选:B.4.已知函数()11e xm f x x ⎛⎫=+ ⎪-⎝⎭是偶函数,则m 的值是( ) A .2- B .1-C .1D .2【答案】A【分析】先求出函数的定义域,然后根据偶函数的定义取特殊值求解 【详解】函数的定义域为{}0x x ≠,因为函数()11e xm f x x ⎛⎫=+ ⎪-⎝⎭是偶函数, 所以(1)(1)f f -=,所以11111e 1e m m -⎛⎫⎛⎫-+=⨯+ ⎪ ⎪--⎝⎭⎝⎭, e 11e 11em m--=+--,所以(e 1)21e m -=-, 得2m =-, 故选:A5.已知函数()f x 是(),-∞+∞上的偶函数,且()()11f x f x -=+,当[]0,1x ∈时,()21x f x =-,则()()20212022f f +的值为( )A .1B .2C .1-D .0【答案】A【分析】由偶函数可得()()f x f x -=,由()()11f x f x -=+可得对称性,再化简整理可得周期2T =,进而根据性质转换()()20212022f f +到[]0,1x ∈,再代入解析式求解即可.【详解】由题,因为偶函数,所以()()f x f x -=,又()()11f x f x -=+,所以()()()111f x f x f x -+=-=+,即()()2f x f x =+,所以()f x 是周期函数,2T =,故()()()()10202120221021211f f f f +=+=-+-= 故选:A6.已知函数()()||0.542π()2,log 3,log 5,cos 3x f x a f b f c f ⎛⎫==== ⎪⎝⎭,则( )A .a c b >>B .a b c >>C .b a c >>D .c a b >>【答案】B【分析】直接由指数、对数的运算以及特殊角的三角函数值求解即可. 【详解】0.52|log 3|log 3223a ===,4|log 5|log 22b ==2π1cos3222c ==a b c >>.故选:B . 7.已知35a b =且211a b+=,则a 的值为( ) A .3log 15 B .5log 15C .3log 45D .5log 45【答案】C【分析】令350a b k ==>,利用指对数互化,换底公式及对数的运算法则可得45k =,即得.【详解】令350a b k ==>, 则35log ,log a k b k ==,351111log 3,log 5log log k k a k b k ====,又211a b+=, ∴2log 3log 5log 451k k k +==,即45k =, ∴3log 45a =. 故选:C.8.设函数e e ()sin 2x x f x x --=+,不等式()e (ln 1)0xf a x f x x -+++≤对0x >恒成立,则实数a 的最大值为( ) A .e 1- B .1C .e 2-D .0【答案】D【分析】先由定义证()f x 为奇函数,结合均值不等式可证()1cos 0f x x '≥+≥,得()f x 在R 上单调递增,故结合奇偶性与单调性,恒成立转化为e ln 1x a x x x ≤---对0x >恒成立.令()e ln 1x g x x x x =---,用导数法求()g x 最小值,即有()min a g x ≤.【详解】因为e e ()sin 2x xf x x ---=-,所以()()f x f x -=-,所以()f x 为R 上的奇函数.因为e e ()cos cos 1cos 02x x f x x x x -+'=+≥=+≥,所以()f x 在R 上单调递增.不等式()e (ln 1)0x f a x f x x -+++≤可转化为()(ln 1)e xf x x f x a ++≤-,所以ln 1e x x x x a ++≤-,即e ln 1x a x x x ≤---对0x >恒成立. 令()e ln 1x g x x x x =---,则ln ln ()e e ln 1e (ln )1x x x x g x x x x x +=---=-+-, 令()e 1x h x x =--,则()e 1x h x '=-.当0x >时,()0h x '>,()h x 在(0,)+∞上单调递增;当0x <时,()0h x '<,()h x 在(,0)-∞上单调递减.所以0min ()(0)e 010h x h ==--=,即()0h x ≥,所以()0g x ≥,且当ln 0x x +=时,()g x 取最小值0, 故0a ≤,即实数a 的最大值为0. 故选:D.【点睛】1.通常函数不等式恒成立问题涉及奇偶性与单调性可先进行转化; 2.含参不等式恒成立问题,一般通过构造函数解决.一般将参数分离出来,构造函数用导数法讨论不含参数部分的最值;或者包含参数一起构造函数,用导数法对参数分类讨论.当参数不能分离出来时,也可尝试将不等式左右变形成一致形式,即可将该形式构造成函数,通过导数法分析单调性,将问题等价成对应自变量的不等式.9.已知函数()()212f x x mx x =++∈R ,且()y f x =在[]0,2x ∈上的最大值为12,若函数()()2g x f x ax =-有四个不同的零点,则实数a 的取值范围为( )A .1,02⎛⎫- ⎪⎝⎭B .()0,1C .1,14⎛⎫- ⎪⎝⎭D .51,4⎛⎫ ⎪⎝⎭【答案】B【分析】由()y f x =在[]0,2x ∈上的最大值为12,讨论可求出2m =-,从而()2122f x x x =-+,若()()2g x f x ax =-有4个零点,则函数()y f x =与2y ax =有4个交点,画出图象,结合图象求解即可【详解】若0m ≥,则函数()212f x x mx =++在[]0,2上单调递增, 所以()212f x x mx =++的最小值为12,不合题意,则0m <, 要使函数()212f x x mx =++在[]0,2x ∈上的最大值为12. 如果22m-≥,即4m ≤-,则()912222f m =+≤,解得522m -≤≤-,不合题意;若22m -<,即40m -<<,则2912,2211,242m m ⎧+≤⎪⎪⎨⎪-≤⎪⎩解得52,22,m m ⎧-≤≤-⎪⎨⎪≥-⎩即2m =-, 则()2122f x x x =-+. 如图所示,若()()2g x f x ax =-有4个零点,则函数()y f x =与2y ax =有4个交点,只有函数2y ax =的图象开口向上,即0a >.当2y ax =与(2y x =-122x -+)有一个交点时,方程221202ax x x +-+=有一个根,0∆=得1a =,此时函数()()2g x f x ax =-有二个不同的零点,要使函数()g x =()2f x ax -有四个不同的零点,2y ax =与2122y x x ⎛⎫=--+ ⎪⎝⎭有两个交点,则抛物线2y ax =的图象开口要比2y x =的图象开口大,可得1a <, 所以01a <<,即实数a 的取值范围为()0,1. 故选:B【点睛】关键点点睛:此题考查函数与方程的综合应用,考查二次函数的性质的应用,考查数形结合的思想,解题的关键是由已知条件求出m 的值,然后将问题转化为函数()y f x =与2y ax =有4个交点,画出函数图象,结合图象求解即可,属于较难题二、填空题 10.复数i2i=+_________. 【答案】12i 55+【分析】根据复数的除法运算直接求解.【详解】解:()()()i 2i i 12i 2i 2i 2i 55-==+++-. 故答案为:12i 55+.11.已知函数()f x 的导函数,满足()()321f x xf x '=+,则()1f 等于_______________.【答案】5-【分析】求导,令1x =,可解得()1f ',进而可得()1f .【详解】由()()321f x xf x '=+,得()()2213f x f x ''=+,令1x =,得()()1213f f ''=+,解得()13f '=-,所以()()()312112315f f '=+=⨯-+=-,故答案为:5-.12.为了保护水资源,提倡节约用水,某城市对居民生活用水,实行“阶梯水价”.计算方法如下表:若某户居民本月交纳的水费为90元,则此户居民本月用水量为___________. 【答案】320m 20立方米【分析】根据题设条件可得水费与水价的关系式,根据该关系式可求用水量. 【详解】设用水量为x 立方米,水价为y 元,则()3,01236612,1218729(18),18x x y x x x x ≤≤⎧⎪=+-<≤⎨⎪+->⎩,整理得到:3,012636,1218990,18x x y x x x x ≤≤⎧⎪=-<≤⎨⎪->⎩,当012x ≤≤时,036y ≤≤;1218x <≤时,3672y <≤;故某户居民本月交纳的水费为90元,则用水量大于18立方米, 令99090x -=,则20x =(立方米), 故答案为:320m .13.函数()f x 是定义在R 上的奇函数,满足(2)()f x f x +=-,当[0x ∈,1)时,2()f x x =,则23()2f =_______. 【答案】14-【分析】根据题意,分析可得(4)(2)()f x f x f x +=-+=,则函数()f x 是周期为4的周期函数,由此可得231()()22f f =-,结合函数的解析式计算可得答案. 【详解】根据题意,函数()f x 是定义在R 上的奇函数,满足(2)()f x f x +=-, 则(2)()()f x f x f x +=-=-,则有(4)(2)()f x f x f x +=-+=,则函数()f x 是周期为4的周期函数, 则23111()(12)()()2222f f f f =-+=-=-, 又由当[0x ∈,1)时,2()f x x =,则2111()()224f ==,则2311()()224f f =-=-,故答案为:14-.14.已知函数()212-,02=1+1,>02xx f x x x ≤⎧⎛⎫⎪ ⎪⎪⎝⎭⎨⎪⎪⎩,则不等式()313xf ->的解集为___________.【答案】()1,+∞【分析】分别在条件31>0x -,310x -≤下化简不等式,再求其解,由此可得不等式()31>3x f -的解集.【详解】当310x -≤时,即0x ≤时,()31131=22x x f ---⎛⎫ ⎪⎝⎭,所以不等式()31>3xf -可化为3112>32x --⎛⎫ ⎪⎝⎭,所以0x ≤且3111>2x --⎛⎫⎪⎝⎭,所以满足条件的x 不存在,即当0x ≤时,不等式无解,当31>0x -时,即>0x 时,()()2131=31+12xxf --,此时不等式()31>3x f -可化为()2131+1>32x-,得31>2x -或31<2x --,解得>1x , 所以不等式()31>3xf -的解集为()1,+∞,故答案为:()1,+∞.15.已知正数,a b 满足1,a b c +=∈R ,则222312a c bc b abc ab++++的最小值为__________.【答案】2【分析】把1a b +=平方得到2221,0,0a ab b a b ++=>>,代入结论构造基本不等式,再分析计算可求出最小值.【详解】解:由1a b +=,得2221,0,0a ab b a b ++=>>, 则222312a c bc b abc ab++++ 222213221a a ab b c c b ab ⎛⎫++=++ ⎪+⎝⎭2214221a b c c b a ⎛⎫=+++ ⎪+⎝⎭221221c c ⎛⎫+ ⎪ ⎪⎝⎭≥+()226212221c c =++-≥=+, 当且仅当4a bb a =,即2b a =,()226211c c =++,即()2213c +=时取“等号”,所以当212,,133a b c ==时,222312a c bc b abc ab++++的最小值为2.故答案为:2三、解答题16.在ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos (cos cos )C a B b A c +=.(1)若cos A =cos(2)A C +的值;(2)若c =ABC a ,b 的值.【答案】(1)(2)2a =,3b =或3a =,2b =【分析】(1)利用正弦定理将边化角,再由两角和的正弦公式求出C ,由同角三角函数的基本关系求出sin A ,即可求出sin 2A 、cos 2A ,最后利用两角和的余弦公式计算可得; (2)由面积公式及余弦定理得到方程组,解得即可.【详解】(1)解:因为2cos (cos cos )C a B b A c +=, 由正弦定理得2cos (sin cos sin cos )sin C A B B A C +=, 即2cos sin()2cos sin sin C A B C C C +==, 因为(0,)C π∈,sin 0C >,所以1cos 2C =, 由C 为三角形内角得3C π=;由cos A =,则sin A =所以sin 22sin cos 2A A A ===, 261cos 22cos 121164A A =-=⨯-=-,()cos 2cos 2cos sin 2sin A C A C A C +=-=1142-⨯=(2)解:因为ABC 的面积1sin 2S ab C ==6ab =①, 由余弦定理2222cos c a b ab C =+-得227a b ab =+-,则2213a b +=②, 由①②解得2a =,3b =或3a =,2b =17.如图,在四棱柱1111ABCD A B C D -中,1AA ⊥平面ABCD ,底面ABCD 满足AD BC ∥,且12AB AD AA ===,BD DC ==(1)求证:BD ∥平面11B CD .(2)求直线AB 与平面11B CD 所成角的正弦值. (3)求二面角111B CD C --的正弦值. 【答案】(1)证明见解析(3)正弦值为1【分析】(1)由四棱柱的性质证明11//BD B D ,根据线面平行判定定理证明BD 平面11B CD ;(2)建立空间直角坐标系,求直线AB 的方向向量和平面11B CD 的法向量利用空间向量求解线面角;(3)求平面11C CD 的法向量,利用向量夹角公式求二面角111B CD C --的夹角的余弦值,再由同角关系求其正弦值.【详解】(1)在四棱柱1111ABCD A B C D -中,11BB DD ,11BB DD =,故四边形11BB D D 是平行四边形,所以11//BD B D ,因为BD ⊄平面11B CD ,11B D ⊂平面11B CD , 所以BD ∥平面11B CD ;(2)因为1AA ⊥平面ABCD ,AB ,AD ⊂平面ABCD , 所以1AA AB ⊥,1AA AD ⊥,因为2AB AD ==,BD =所以222AB AD BD +=,=ABD ADB ∠∠,所以AB AD ⊥,=45ADB ∠,因为AD BC ∥,所以=45DBC ∠,又BD CD ==所以BDC △为等腰直角三角形,所以=4BC ,因为AB ,AD ,1AA 两两垂直,以A 为坐标原点,分别以AB ,AD ,1AA 为x 轴,y 轴,z 轴建立空间直角坐标系,则()0,0,0A ,()2,0,0B ,()2,4,0C ,()12,0,2B ,()10,2,2D 所以()2,0,0AB =,()1=0,4,2B C -,()11=2,2,0B D - 设平面11B CD 的法向量为(),,n x y z =∴111=0=0n B C n B D ⎧⋅⎪⎨⋅⎪⎩,即42=02+2=0y z x y --⎧⎨⎩,令=1x ,则=1y ,=2z ,∴()1,1,2n =设直线AB 与平面11B CD 所成角为θ,∴2sin =cos ,==2?6AB n AB nAB n⋅θ⋅所以直线AB 与平面11B CD .(3)平面11B CD 的法向量为()1,1,2n =,因为1AA ⊥平面ABCD ,11//AA DD ,所以1DD ⊥平面ABCD ,BD ⊂平面ABCD ,所以1DD BD ⊥,又B D D C ⊥,1=DD DC D ⋂,1,DD DC ⊂平面11CD C ,所以BD ⊥平面11CD C ,所以BD 为平面11CD C 的法向量,所以平面11CD C 的法向量为()=2,2,0m BD -= ∴cos ,==0m nm n m n⋅,∴sin ,1m n = 所以,二面角111B CD C --的正弦值为1.18.已知()f x 是定义在R 上的奇函数,当],(0x ∈-∞时,()93x xm f x -=-. (1)求()f x 在(0,)+∞上的解析式;(2)当[1,2]x ∈时,1()23x x f x a +⋅+…恒成立,求实数a 的取值范围;(3)关于x 的方程1()3160x f x n -++⋅+=在[2,1]--上有两个不相等的实根,求实数n 的取值范围.【答案】(1)()93x xf x =-+(2)15,2⎡⎫-+∞⎪⎢⎣⎭ (3)227,93⎡⎫--⎪⎢⎣⎭【分析】(1)根据函数的奇偶性求出m 的值,进而求出函数的解析式即可;(2)利用分离参数法将原不等式转化为932()22x xa g x ⎛⎫⎛⎫≥--⨯= ⎪ ⎪⎝⎭⎝⎭在[]1,2上恒成立,结合函数的单调性求出()max g x 即可;(3)令[]33,9xt -=∈,将原方程转化为直线13y n =-与函数()16h t t t=+的图象有两个交点.利用数形结合的思想即可求解.【详解】(1)依题意得()010f m =-=,解得1m =, 经检验1m =,符合题意.当()0,x ∈+∞时,(),0x -∈-∞,则()93x xf x -=-,因为()f x 是定义在R 上的奇函数,所以()()93x xf x f x =--=-+,即当()0,x ∈+∞时,()93x xf x =-+;(2)当[]1,2x ∈时,19323xxxx a +-+≤⋅+恒成立,即93222x xa ⎛⎫⎛⎫≥--⨯ ⎪ ⎪⎝⎭⎝⎭恒成立.设()93222x xg x ⎛⎫⎛⎫=--⨯ ⎪ ⎪⎝⎭⎝⎭,易知()g x 在[]1,2上是减函数,()()max 1512g x g ==-,所以152a ≥-,即实数a 的取值范围为15,2⎡⎫-+∞⎪⎢⎣⎭; (3)方程()13160x f x n -++⋅+=在[]2,1--上有两个不相等的实根, 即函数()()931316x xF x n --=+-⋅+在[]2,1--上有两个零点,令[]33,9xt -=∈,则关于t 的方程()231160t n t +-+=在[]3,9上有两个不相等的实根,由于2161613t n t t t+-==+,则直线13y n =-与()16h t t t=+的图象有两个交点.如图,因为()16h t t =+在[]3,4上单调递减,在[]4,9上单调递增, 且()48h =,()2533h =,()9799h =,所以258133n <-≤, 解得22793n -≤<-,即实数n 的取值范围为227,93⎡⎫--⎪⎢⎣⎭.19.设函数()222ln f x ax a x =--,()1eex g x x =-,其中a ∈R ,e 为自然对数的底数. (1)讨论()f x 的单调性; (2)证明:当1x >时,()0g x >;(3)若不等式()()f x g x >在()1,x ∈+∞时恒成立,求a 的取值范围. 【答案】(1)答案见解析(2)证明见解析 (3)1,4a ⎡⎫∈+∞⎪⎢⎣⎭【分析】(1)求导后分0a ≤与0a >两种情况讨论即可; (2)构造函数()1e-=-x s x x ,求导分析单调性与最值,证明当1x >时,1e x x ->即可;(3)结合(1)(2)讨论()(),f x g x 1的大小关系,构造函数()()()h x f x g x =-,求导放缩判断单调性,进而证明即可. 【详解】(1)()f x 定义域为()0,∞+,()241ax f x x-'=. 当0a ≤时,()0f x '<,()f x 在()0,∞+内单调递减;当0a >时,由()0f x '=,得x =x ⎛∈ ⎝⎭时,()0f x '<,()f x 单调递减;当x ⎫∈+∞⎪⎪⎝⎭时,()0f x '>,()f x 单调递增.综上所述,当0a ≤时,()f x 在()0,∞+内单调递减;当0a >时,()f x 在⎛ ⎝⎭上单调递减,在⎫+∞⎪⎪⎝⎭上单调递增. (2)令()1e-=-x s x x ,则()1e 1x s x -=-.当1x >时,()0s x '>,()s x 单调递增,()()10s x s >=, 所以1e x x ->,从而()1110e x g x x -=->. (3)由(2)得,当1x >时,()0g x >.当0a ≤时,1x >时,()()()221ln 0f x a x x g x =--<<,不符合题意.当104a <<1=>,由(1)得,当x ⎛∈ ⎝⎭时,()()()10f x f g x <=<,不符合题意. 当14a ≥时,令()()()h x f x g x =-,1x >. ()211e 4e x h x ax x x '=-+-2111x x x x >-+-()222111110x x x x x ->-+-=>()h x 在区间()1,+∞上单调递增.又因为()10h =,所以当1x >时,()()()0h x f x g x =->,即()()f x g x >恒成立. 综上,1,4a ⎡⎫∈+∞⎪⎢⎣⎭.【点睛】本题主要考查了求导分情况讨论函数单调性的问题,证明不等式与恒成立的问题,需要根据题意,结合极值点与区间端点的关系分情况讨论导函数的正负,求得函数的单调性,从而证明不等式的问题.属于难题.20.已知0a >,设函数()(2)ln ,()=-+'f x x a x x f x 是()f x 的导函数. (1)若2a =,求曲线()f x 在点(1,(1))f 处的切线方程;(2)若()f x 在区间(1,)+∞上存在两个不同的零点()1212,x x x x <, ①求实数a 范围; ②证明:()221(e)(2e)(3)12e---'<-x f x a a a x .注,其中e 2.71828=⋅⋅⋅⋅⋅⋅是自然对数的底数. 【答案】(1)y x =(2)①>a【分析】(1)把1x =代入原函数与导函数得到切点及斜率,利用点斜式即可得切线方程; (2)①可设()()2ln ln f x xg x x a x x==+-,因为1x >,所以()g x 与()f x 零点相同,可根据()g x 的单调性与极值情况来确定a 的范围;②根据题意,巧设函数,利用放缩构造等思路结合导数,可分别求出22()x f x '与111x -的范围,然后相乘即可,详细过程见解析.【详解】(1)当2a =时,2()2(1)ln ,()2ln 3=-+=-+'f x x x x f x x x,所以(1)1,(1)1f k f '===.根据点斜式可得曲线()f x 在(1,(1))f 处的切线方程为y x =.(2)①当1x >时,()0f x =等价于20ln +-=xx a x. 设()2ln =+-x g x x a x ,则22ln 1(ln 1)(2ln 1)()2ln ln '-+-=+=x x x g x x x.当1x <<()0,()g x g x '<单调递减;当x >()0,()'>g x g x 单调递增; 所以,当1x >时,min [()]==g x g a , 因为()f x 在区间(1,)+∞上存在两个不同的零点12,x x ,所以min [()]0<g x,解得>a当>a1=∈-a ax a ,则1ln 11<-=-a a x x a , 故()221201ln 111-=+->+-=>---a a a a a x a a a g x x a a x a a a ,又202ln 2⎛⎫=> ⎪⎝⎭a a g a , 所以()f x在区间和2⎫⎪⎭a 上各有一个零点.综上所述:>a②设()()[(3)2](2)ln (2)(2)=--+-=-+---F x f x a x a x a x a x a , 则2()2ln (2)2ln -=++=+'--x a aF x x a x a x x,它是[1,)+∞上的增函数. 又(1)0F '=,所以()0F x '≥,于是()F x 在[1,)+∞上递增.所以()(1)0F x F ≥=,即(2)ln (3)2-+≥-+-x a x x a x a ,当1x =时取等号. 因为11x >,所以()110(3)2=>-+-f x a x a ,解得11031<<--a x .(1) 因为()2ln 3=-'+af x x x,所以()222222ln 3-'=+x f x x x a x , 结合()()22222ln 0=-+=f x x a x x 知()()2222222222232222-=-+=---+-'-a x ax f x a x a x x a a x .处理1:设函数()ln xh x x =,则2ln 1()ln -='x h x x, 所以当0x e <<时,()0,()h x h x '<递减,当x e >时,()0,()h x h x '>递增,所以()()ln =≥=xh x h e e x,所以2222ln -=≥x a x e x .处理2:因为ln 1≤-x x ,所以ln 1⎛⎫≤- ⎪⎝⎭x xe e,即ln x x e ≤,当x e =时取等号,所以ln 022222-----⎛⎫=-+>-⋅+= ⎪⎝⎭a e a e a e a e a e f e e e . 由①可知,()f x 在[)2,x +∞上单调递增,且()20f x =,所以22-≤a ex ,即22-≥a x e . 因为22()2=--+a a g x t t 在[,)e ∞+上是减函数,且22-≥a x e ,且()()2222()(2)22()22--=-≤=--+='a a a e a e x f x g a x g e e e e.综上可知:()221()(2)(3) 12--'-<-x f x a e a e ax e.【点睛】导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.。
天津市第一中学、滨海一中2023届高三上学期第三次月考历史试题 附解析

一.选择题(每小题3分,共45分)
1.据历史学家研究,古代雅典官员在接受任职资格审查时,要回答:直系亲属姓名及男性亲属所在村社名称、崇拜的神祇及其圣所所在地、墓葬方位、是否善待双亲、是否纳税、是否服兵役等。以下哪些是古代雅典官员任职的前提条件()
2.英国学者马丁·贝尔纳在其著作《黑色雅典娜:古典文明的亚非之根》中,批判了关于希腊文明起源的传统观点,提出希腊文明的源头在西亚和北非。下列希腊文明成果,能印证这一观点的是( )
①字母文字 ②雕刻艺术 ③民主政治 ④冶铁技术
A.①②③B.①②④C.①③④D.②③④
【答案】B
【解析】
【详解】古希腊文字来源于腓尼基文字、古希腊的雕刻艺术受到古代埃及的影响、而西亚地区的赫梯人最早掌握冶铁技术,由此可知,①②④能够证明希腊文明起源于西亚和北非,B项正确;民主政治是雅典首先开创的,③错误,排除A、C、D项。故选B项。
A.①②B.③④C.①③D.①④
【答案】C
【解析】
【详解】“把屠宰和包装分成几道独立工序,利用传送带进行流水作业”体现了产业分工的不断细化,①正确;“并雇佣工程师设计冷冻车厢,以便长途运输鲜肉”说明当时铁路运输业得到发展,能够长距离的运输货物,③正确,根据以上分析可知,①③正确,C项正确;通过材料无法证实斯威夫特创办的肉类加工厂是西方近代工厂制度的开端,②错误,排除A项;而且肉类加工本身不属于机械生产,也不属于现代农业,④错误,排除B项;肉类加工不属于现代农业,排除D项。故选C项。
7.1870、80年代,美商斯威夫特创办了肉类加工厂,把屠宰和包装分成几道独立工序,利用传送带进行流水作业,并雇佣工程师设计冷冻车厢,以便长途运输鲜肉。他还陆续开办工厂,利用肉类加工厂的下脚料生产肥料、肥皂和甘油等。斯威夫特的经营模式()
天津市第一中学2023-2024学年高三第四次月考数学试卷(解析版)

天津一中2023—2024-2高三年级第四次月考数学试卷本试卷总分150分,考试用时120分钟.考生务必将答案涂写在答题卡上,答在试卷上的无效.一、选择题(本大题共9小题,每小题5分,共45分)1. 已知集合,则( )A. B. C. D. 【答案】C 【解析】【分析】根据题意,求得集合,结合集合交集的运算,即可求解.【详解】由不等式,解得,所以,又由,所以.故选:C.2. 将收集到的天津一中2021年高考数学成绩绘制出频率分布直方图,如图所示,则下列说法中不正确的是( )A. B. 高三年级取得130分以上的学生约占总数的65%C. 高三年级的平均分约为133.2D. 高三年级成绩的中位数约为125【答案】D 【解析】【分析】对于A ,由各个矩形面积之和为1即可列式求解;对于B ,求最右边两个矩形面积之和即可验算;对于C ,D 分别由平均数计算公式、中位数计算方法即可判断.{}{}2|3100,33A x x x B x x =--<=-≤≤A B = (2,3]-[)3,5-{1,0,1,2,3}-{3,2,1,0,1,2,3,4}---{}1,0,1,2,3,4A =-23100x x --<25x -<<{}1,0,1,2,3,4A =-{}33B x x =-≤≤{}1,0,1,2,3A B ⋂=-0.028a =【详解】对于A ,,故A 正确;对于B ,高三年级取得130分以上的学生约占总数的,故B 正确;对于C ,高三年级的平均分约为,故C 正确;对于D ,设高三年级成绩的中位数为,由于,所以,故D 不正确.故选;D.3. 已知,条件,条件,则是的( )A. 充分不必要条件 B. 必要不充分条件C 充要条件D. 既不充分也不必要条件【答案】A 【解析】【分析】结合绝对值的性质,根据不等式的性质及充分条件、必要条件的定义分析判断即可.【详解】因为,所以由得,故由能推出;反之,当时,满足,但是;所以是的充分不必要条件.故选:A .4. 函数的图象大致为( )A. B.C. D.【答案】B 【解析】.()1100.0010.0090.0250.037100.028a =-⨯+++÷=⎡⎤⎣⎦()0.0280.03710100%65%+⨯⨯=()1050.0011150.0091250.0251450.0281350.03710133.2⨯+⨯+⨯+⨯+⨯⨯=x 0.010.090.250.350.500.350.370.72++=<<+=130140x <<0a >:p a b >2:q a ab >p q 0a >a b >2a ab ab >≥:p a b >2:q a ab >10,2a b =>=-212a ab =>=-122a =<-=p q ()21cos 31x f x x ⎛⎫=-⋅ ⎪+⎝⎭【分析】根据函数奇偶性即可排除CD ,由特殊点的函数值即可排除A.【详解】,则的定义域为R ,又,所以为奇函数,图象关于原点对称,故排除CD ,当时,,故排除A .故选:B.5. 已知函数是上的偶函数,且在上单调递增,设,,,则a ,b ,c 的大小关系是( )A. B. C. D. 【答案】B 【解析】【分析】结合偶函数的性质,函数单调性,只需比较对数、分数指数幂的大小即可得解.【详解】因为函数是上的偶函数,且在上单调递增,所以,即.故选:B.6. 多项式展开式中的系数为( )A. 985B. 750C. 940D. 680【答案】A 【解析】分析】由二项式定理即可列式运算,进而即可得解.【详解】多项式展开式中的系数为.故选:A.7. 已知斜三棱柱中,为四边形对角线的交点,设三棱柱的体积【2()(1)cos 31xf x x =-⋅+()f x ()()()22321cos 1cos 1cos 313131x x x xf x x x x f x -⎛⎫⨯⎛⎫⎛⎫-=-⋅-=-⋅=-+⋅=- ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭()f x πx =()ππ22π1cos π103131f ⎛⎫-=< ⎪++⎝⎭=-+()f x R ()f x [0,)+∞12e a f ⎛⎫= ⎪⎝⎭12b f ⎛⎫= ⎪⎝⎭1ln 2c f ⎛⎫= ⎪⎝⎭a b c <<b<c<ac<a<bb a c<<()f x R ()f x [0,)+∞()()1211ln 2ln 1e 22b f f f c f ff a ⎛⎫⎛⎫⎛⎫=<==<<== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭b<c<a ()52(71)52x x++2x ()52(71)52x x++2x 32350555C 712C 7159805985⋅⋅⋅+⋅⋅⋅=+=111ABC A B C -O 11ACC A 111ABC A B C -为,四棱锥的体积为,则( )A. B. C. D. 【答案】A 【解析】【分析】如图,延长,连接,则、,进而得,即可求解.【详解】如图,延长,连接,则,所以,又O 为的中点,所以点到平面的距离是点到平面的距离的2倍,则,所以,即故选:A8. 已知函数(为常数,且)的一个最大值点为,则关于函数的性质,下列说法错误的有( )个.1V 11O BCC B -2V 21:V V =1:31:41:62:31OA 11,,OB OB A B 111123A BCC B V -=11122A BCC B V V -=12223V V =1OA 11,,OB OB A B 11111111,3A ABC A BCCB A ABC V V V V V ---=+=111123A BCCB V -=1AC 1A 11BCC B O 11BCC B 11111222A BCC B O BCC B V V V --==12223V V =2113V V =()sin cos f x a x b x =+,a b 0,0a b >>π3x =()sin 2cos 2g x a x b x =+①的最小正周期为;②的一个最大值点为;③在上单调递增;④的图像关于中心对称.A. 0个 B. 1个C. 2个D. 3个【答案】B 【解析】【分析】根据三角函数的性质,求的关系,再根据辅助角公式化简函数,再利用代入的方法,判断函数的性质.【详解】函数,,平方后整理为,所以,,函数的最小正周期为,故①正确;当时,,此时函数取得最大值,故②正确;当时,,位于单调递增区间,故③正确;,故④错误,所以错误的只有1个.故选:B9. 已知双曲线的左焦点为,过作渐近线的垂线,垂足为,且与抛物线交于点,若,则双曲线的离心率为( )A.B.C.D.【答案】B 【解析】()g x π()g x π6()g x 2π,π3⎛⎫⎪⎝⎭()gx 7π,012⎛⎫⎪⎝⎭,a b ()g x ()sin cos f x a x b x =+12b +=()20a =a π()sin 2cos 22sin 26g x x b x b x ⎛⎫=+=+ ⎪⎝⎭0b >()g x 2ππ2=π6x =πππ2662⨯+=()g x 2π,π3x ⎛⎫∈⎪⎝⎭π3π13π2,626x ⎛⎫+∈ ⎪⎝⎭77ππ4π2sin 22sin 0121263g b b π⎛⎫⎛⎫=⨯+=≠ ⎪ ⎪⎝⎭⎝⎭22221(0,0)x y a b a b-=>>1(,0)F c -1F P 212y cx =M 13PM F P =【分析】首先利用等面积法求出点坐标,再根据,求出坐标,再将坐标带入抛物线化简即可求解出双曲线离心率.【详解】据题意,不妨取双曲线的渐近线方程为,此时,,∴,且是直角三角形,设,则,,代入中,得,即;设,则,,由,则,,∴,则;又在抛物线上,,即,化简得,分子分母同时除以,,且,,.故选:B二、填空题(本大题共6小题,每小题5分,共30分)10. 已知,且满足(其中为虚数单位),则_________.【答案】2【解析】【分析】根据复数相等得到关于的方程组,解该方程组即可.【详解】由题意,可得,P 13PM F P =M M 212y cx =by x a=-1F P b =1OF c =OP a =1OPF (,)p p P x y 11122OPF p S ab cy== p aby c ∴=b y xa =-2p a x c =-2(,a ab P c c-(,)M xy 2,a ab PM x y c c ⎛⎫=+- ⎪⎝⎭ 221,,a ab b ab F P c cc c c ⎛⎫⎛⎫=-+= ⎪ ⎪⎝⎭⎝⎭ 13PM F P = 223a b x c c+=⋅3ab ab y c c -=⋅2234,b a ab x y c c -==2234(,)b a abM c c -M 212y cx =22243()12ab b a cc c-∴=()()()2222222222221612316123a b b aca c a c a a c ⎡⎤=-⇔-=--⎣⎦422491640c a c a -+=4a 4291640e e ∴-+=1e >2e ∴===e ∴=,R a b ∈(12i)(i)3i a b ++=-i 22a b +=,a b (12i)(i)3i a b ++=-(2)(2)i 3i a b a b -++=-所以,解得,所以.故答案为:211. 著名的“全错位排列”问题(也称“装错信封问题”是指“将n 个不同的元素重新排成一行,每个元素都不在自己原来的位置上,求不同的排法总数.”,若将个不同元素全错位排列的总数记为,则数列满足,.已知有7名同学坐成一排,现让他们重新坐,恰有两位同学坐到自己原来的位置,则不同的坐法有_________种【答案】【解析】【分析】根据数列递推公式求出项,再结合分步计数原理求解.【详解】第一步,先选出两位同学位置不变,则有种,第二步,剩下5名同学都不在原位,则有种,由数列满足,,则,,,则不同的做法有种.故答案为:.12. 已知在处的切线与圆相切,则_________.【答案】或【解析】【分析】根据导数的几何意义,求得切线方程,再由直线与圆相切,列出方程,即可求解.【详解】由函数,可得,则且,所以函数在处的切线方程为,即,又由圆,可得圆心,半径为,2321a b a b -=⎧⎨+=-⎩1575a b ⎧=⎪⎪⎨⎪=-⎪⎩222a b +=n n a {}n a 120,1a a ==()12(1)(3)n n n a n a a n --=-+≥9242776C 2121⨯==⨯5a {}n a 120,1a a ==()12(1)(3)n n n a n a a n --=-+≥()()321312a a a =-+=()()432419a a a =-+=()()5435144a a a =-+=2144924⨯=9242()ln f x x x =-1x =22:()4C x a y -+==a -0x y -=2()ln f x x x =-1()2f x x x=-'(1)1f '=(1)1f =()f x 1x =11y x -=-0x y -=22:()4C x a y -+=(,0)C a 2r =因为与圆,解得.故答案为:.13. 元旦前夕天津-中图书馆举办一年一度“猜灯谜”活动,灯谜题目中逻辑推理占,传统灯谜占,一中文化占,小伟同学答对逻辑推理,传统灯谜,一中文化的概率分别为,,,若小伟同学任意抽取一道题目作答,则答对题目的概率为______,若小伟同学运用“超能力”,抽到的5道题都是逻辑推理题,则这5道题目中答对题目个数的数学期望为______.【答案】 ①. ##②. 【解析】【分析】根据全概率公式求解概率,根据二项分布列的期望公式求解即可.【详解】设事件“小伟同学任意抽取一道题目作答,答对题目”,则.由题意小伟同学任意抽取一道逻辑推理题作答,则答对题目的概率为,根据二项式分布知,所以,即的数学期望为.故答案为:,14. 在中,设,,其夹角设为,平面上点满足,,交于点,则用表示为_________.若,则的最小值为_________.【答案】 ①. ②.【解析】【分析】由和三点共线,得到和,得出方程组,求得的值,得到,再由,化简得到,得出,结合基本不等式,即可求解.0x y -=C 2a =±±20%50%30%0.20.60.7X 0.5511201A =()0.20.20.50.60.30.70.55P A =⨯+⨯+⨯=0.2()5,0.2X B ~()50.21E X =⨯=X 10.551ABC ,AB a AC b ==u u u r r u u u r r θ,D E 2AD AB = 3AE AC =,BE DC O AO ,a b65AO DE DC BE ⋅=⋅ cos θ4355AO a b =+ ,,D O C ,,B O E 2(1)AO ta t b =+- ()33AO ua u b =+-2133t ut u =⎧⎨-=-⎩,t u 4355AO a b =+ 65AO DE DC BE ⋅=⋅ 2248209a b a b ⋅=+ 22209cos 48a b a bθ+=【详解】因为三点共线,则存在实数使得,又因为三点共线,则存在实数使得,可得,解得,所以,由,因为,可得,整理得,可得,所以又因为所以,当且仅当时,即时,等号成立,所以.故答案为:15. 设函数,若函数与直线有两个不同的公共点,则的取值范围是______.【答案】或或【解析】【分析】对于,当可直接去绝对值求解,当时,分和,,D O C t (1)2(1)AO t AD t AC ta t b =+-=+-,,B O E u ()()133AO u AB u AE ua u b =+-=+-2133t u t u =⎧⎨-=-⎩24,55t u ==4355AO a b =+ 32,2,3DE AE AD b a DC AC AD b a BE AE AB b a =-=-=-=-=-=- 65AO DE DC BE ⋅=⋅ 436()(32)(2)(3)555a b b a b a b a +⋅-=-⋅-2248209a b a b ⋅=+ 2248cos 209a b a b θ=+ 22209cos 48a b a bθ+=22209a b+≥ 22209cos 48a b a b θ+=≥ 22209a b = 3b cos θ4355AO a b =+ 22()21f x x ax ax =-++()y f x =y ax =a 2a <-21a -<<-2a >221y x ax =-+0∆≤0∆>a <-a >论,通过和图像交点情况来求解.详解】由已知,即,则必过点,必过,对于,当时,,此时恒成立,所以,令,即,要有两个不同的公共点,则,解得或或,当时,或当时,和图象如下:此时夹在其两零点之间的部分为,令,得无解,则有两个根有两个根,即有两个解,,符合要求;当和图象如下:【221y x ax =-+()1y ax x =-22()21f x x ax ax ax =-++=()2211x ax ax x -+=-()1y ax x =-()()0,0,1,0221y x ax =-+()0,1221y x ax =-+280a ∆=-≤a -≤≤2210x ax -+≥()222()2121f x x ax ax a x ax =-++=+-+()221a x ax ax +-+=()22210a x ax +-+=()21Δ442020a a a ⎧=-+>⎨+≠⎩2a -≤<-21a -<<-2a <≤280a ∆=->a <-a >a <-221y x ax =-+()1y ax x =-221y x ax =-+-2221x ax ax ax -+-=-+()221a x -=()2211x ax ax x -+=-()2211x ax ax x ⇔-+=-()22210a x ax +-+=()2Δ4420a a =-+>a <-a >221y x ax =-+()1y ax x =-或令,根据韦达定理可得其两根均为正数,对于①,则,解得,对于②,则,解得,综上所述,的取值范围是或或.【点睛】方法点睛:对于方程的根或者函数零点问题,可以转化为函数图象的交点个数问题,图象直观方便,对解题可以带来很大的方便.三、解答题(本大发共5小题,共75分)16. 已知中,角A ,B ,C 的对边分别为a ,b ,c ,且,.(1)求;(2)若,求的面积.【答案】(1(2【解析】【分析】(1)利用正弦定理求关系,再利用余弦定理求出,再利用两角和的正弦定理计算即可;(2)利用三角形的面积公式求解即可.【小问1详解】2210x ax -+=011⎧<<⎪⎪>3a >011⎧<<⎪⎪<3a <<a 2a <-21a -<<-2a >ABC sin cos sin 22C CB =2223a c b -=πsin 3B ⎛⎫+⎪⎝⎭1b =ABC ,,a b c cos B因为,所以,由正弦定理得,所以,即,所以,在中,,所以【小问2详解】由(1)得当时,,所以17. 已知四棱台,下底面为正方形,,,侧棱平面,且为CD 中点.(1)求证:平面;(2)求平面与平面所成角的余弦值;(3)求到平面的距离.【答案】(1)证明见详解 (2)sincos sin 22C CB =sin 2sinC B =2c b =2222223347b a b c b b +=+===a 222cos 2a cb B ac +-===ABC sin B ==π11sin sin 322B B B ⎛⎫+=== ⎪⎝⎭1b =2a c ==122ABC S =´´=1111ABCD A B C D -ABCD 2AB =111A B =1AA ⊥ABCD 12,AA E =1//A E 11BCC B 11ABC D 11BCC B E 11ABC D 15(3【解析】【分析】(1)直接使用线面平行的判定定理即可证明;(2)构造空间直角坐标系,然后分别求出两个平面的法向量,再计算两个法向量的夹角余弦值的绝对值即可;(3)使用等体积法,从两个不同的方面计算四面体的体积即可求出距离.【小问1详解】由于,,故,而,故四边形是平行四边形,所以,而在平面内,不在平面内,所以平面;【小问2详解】如上图所示,以为原点,为轴正方向,建立空间直角坐标系.则,,,,,,设平面与平面的法向量分别是和,则有和,1EAD B 11∥A B AB CE AB ∥11CEA B 1111122CE CD AB A B ====11CEA B 11A E B C ∥1B C 11BCC B 1A E 11BCC B 1//A E 11BCC B 1A 11111,,A A A D A B,,x y z ()2,0,0A ()10,1,0D ()2,0,2B ()10,0,1B ()10,1,1C ()()()()11110,0,2,2,1,0,2,0,1,0,1,0AB AD BB B C ==-=--=11ABC D 11BCC B ()1,,n p q r = ()2,,n u v w =11100n AB n AD ⎧⋅=⎪⎨⋅=⎪⎩ 212110n BB n B C ⎧⋅=⎪⎨⋅=⎪⎩即,,从而,,.故我们可取,,而,故平面与平面所成角的余弦值是.【小问3详解】设到平面的距离为,由于,而,所以.所以到平面18. 已知椭圆的左右顶点为A ,B ,上顶点与两焦点构成等边三角形,右焦点(1)求椭圆的标准方程;(2)过作斜率为的直线与椭圆交于点,过作l 的平行线与椭圆交于P ,Q 两点,与线段BM 交于点,若,求.【答案】(1)(2)【解析】【分析】(1)根据上顶点与两焦点构成等边三角形求出即可;(2)设出直线方程,利用弦长公式求出求出,,利用点到直线的距离求出点到直线的距离和点到直线的距离,再根据列式计算即可.【小问1详解】2020r p q =⎧⎨-+=⎩200u w v --=⎧⎨=⎩0r v ==2p q =20u w +=()11,2,0n = ()21,0,2n =-11cos ,5n 11ABC D 11BCC B 15E 11ABC D L 111111332E AD B AD B V LS L AD AB L -==⋅⋅⋅= 111142333E AD B B AD E AEB ABCD V V S S --==⋅⋅=⋅= 43=L =E 11ABC D 22221(0)x y a b a b +=>>(1,0)F A (0)k k >l M F N 2AMN BPQ S S =△△k 22143x y +=k =,a b AM PQ N AM B PQ 2AMN BPQ S S =△△由已知在等边三角形中可得,则椭圆的标准方程为为;【小问2详解】设直线的方程为:,联立消去得,则,得,,设直线的方程为:,设,联立,消去得,易知,则,所以,由得,所以直线的方程为,即,联立得,所以点到直线的22,a c b ====22143x y +=l ()2y k x =+()222143y k x x y ⎧=+⎪⎨+=⎪⎩y ()2222341616120k x k x k +++-=221612234M k x k --=+226834M k x k-=+226834Mk AM x k -=-=-=+PQ ()1y k x =-()()1122,,,P x y Q x y ()221143y k x x y ⎧=-⎪⎨+=⎪⎩y ()22223484120k x k x k +-+-=0∆>221212228412,3434k k x x x x k k-+==++PQ ==()2212134k k +=+226834M k x k -=+222681223434M k k y k k k ⎛⎫-=⋅+= ⎪++⎝⎭BM ()2221234268234kk y x k k +=---+()324y x k=--()()3241y x k y k x ⎧=--⎪⎨⎪=-⎩222463,4343k k N k k ⎛⎫+ ⎪++⎝⎭N AM点到直线,因为,所以,解得.【点睛】方法点睛:直线与椭圆联立问题第一步:设直线方程:有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,都可由点斜式设出直线方程.第二步:联立方程:把所设直线方程与椭圆方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式:计算一元二次方程根的判别式.第四步:写出根之间的关系,由根与系数的关系可写出.第五步:根据题设条件求解问题中的结论.19. 已知数列满足对任意的,均有,且,,数列为等差数列,且满足,.(1)求,的通项公式;(2)设集合,记为集合中的元素个数.①设,求的前项和;②求证:,.【答案】(1),B PQ 2AMN BPQ S S =△△()221211122234k k +=⨯+k =∆0∆>{}n a *N n ∈212n n n a a a ++=12a =24a ={}n b 11b =2105b b a +={}n a {}n b {}*1N n n k n A k a b a +=∈<≤n c n A ()2n n n p b c =+{}n p 2n 2n P *N n ∀∈122121111176n n c c c c -++++< 2n n a =32n b n =-(2)①;②证明过程见解析【解析】【分析】(1)根据等比中项的性质,结合等差数列的通项公式、等比数列的通项公式进行求解即可;(2)①根据不等式的解集特征,结合累和法、等比数列的前项和公式分类讨论求出的表达式,最后根据错位相减法进行求解即可;②运用放缩法,结合等比数列前项和公式进行运算证明即可.【小问1详解】因为数列满足对任意的,均有,所以数列是等比数列,又因为,,所以等比数列的公比为,因此;设等差数列的公差为,由;【小问2详解】因为,,所以由,因此有,即有,,当时,有于是有当为大于2的奇数时,()2122122n n P n n +=-⋅+-12322,n n k k +*<-≤∈N n n c n {}n a *N n ∈212n n n a a a ++={}n a 12a =24a ={}n a 212a a =1222n n n a -=⨯={}n b d ()210511932313132n b d d d b b n n a ⇒+++=⇒=⇒=+-=+-=2n n a =32n b n =-11,2322,nn n k n a b a k k k *+*+<≤∈⇒<-≤∈N N {}{}{}{}{}123452,3,4,5,6,7,8,9,10,11,12,13,,22A A A A A ===== {}623,24,,43,A =1234561,1,3,5,11,21,c c c c c c ======234512233445562,42,82,162,322,c c c c c c c c c c +=+==+==+==+== 12,n n n c c ++= 2,N n n *≥∈112,n n n c c --+=1112,n n n c c -+--=n ()()()243122431122221n n n n n n n c c c c c c c c -----=-+-+-+=+++++,显然也适合,当为大于2的偶数时,,显然也适合.①,,,设,则有,两式相减,得,,;②设,显然,,当时,有,因此,12214211143n n -⎛⎫- ⎪+⎝⎭=+=-11c =n ()()()244222442222221n n n n n n n c c c c c c c c -----=-+-++-+=+++++ 122214211143nn ⎛⎫- ⎪-⎝⎭=+=-21c =()()()21,21,N 221,2,Nn n n n n n n k k p b c n n k k **⎧+=-∈⎪=+=⎨-=∈⎪⎩()()212342121321242n n n n n P P P P P P P P P P P P P --=++++++=+++++++ ()()132124212132321221222424222n nn n n n -⎡⎤⎡⎤=⨯++⨯+++-⋅+-+⨯-+⨯-++⋅-⎣⎦⎣⎦()()()123212122232212221234212n n n n n n -⎡⎤=⨯+⨯+⨯++-⋅+⋅+-+-+--⎣⎦ ()()12321212223221222n n S n n -=⨯+⨯+⨯++-⋅+⋅ ()()234221212223221222nn S n n +=⨯+⨯+⨯++-⋅+⋅ 123212212222222n n n S n -+-=+++++-⋅ ()()2212121222212212n n n S n S n ++-⇒-=-⋅⇒=-⋅+-()2122122n n P n n +=-⋅+-()()11321k k k k c *+=∈+-N ()11332121k k k k c +=≤-+-()4213224k k k --⨯=-4,N k k *≥∈()()344213224042132212kk kkkk k--⨯=->⇒->⨯⇒<-()1133421221k k k k k c +=≤<-+-所以当时,,即,显然当时,有成立.【点睛】关键点点睛:本题的关键由可以确定从第几项开始放缩,根据数列的通项公式的形式,得到,这样可以进行放缩证明.20. 已知函数.(1)讨论的单调区间;(2)已知,设的两个极值点为,且存在,使得的图象与有三个公共点;①求证:;②求证:.【答案】(1)答案见解析 (2)证明见解析【解析】【分析】(1)首先求函数的导数,再讨论,结合函数的定义域,即可求函数的单调区间;(2)①要证,即证,只需证,构造函数,,借助导数即可得证;②同①中证法,先证,则可得,利用、是方程的两根所得韦达定理,结合即可得证.【小问1详解】,,N k *∈4512321111111111143222k k k c c c c c -⎛⎫+++++<++++++ ⎪⎝⎭ 43123211111111122114312k k k c c c c c --⎛⎫- ⎪⎝⎭⇒+++++<+++⨯- 312321111171171171322326k k k c c c c c --⎛⎫+++++<+-<+= ⎪⎝⎭ 2k n =122121111176n n c c c c -++++< 171111632=+++()1133421221k k k k k c +=≤<-+-2()24ln f x x ax x =-+()f x [4,6]a ∈()f x ()1212,λλλλ<b ∈R ()y f x =y b =()123123,,x x x x x x <<1212x x λ+>31x x -<∆1212x x λ+>2112x x λ>-()()1112f x f x λ<-()()()12x g x f x f λ=--()10,x λ∈2232x x λ+<()()2312123122x x x x x x λλ=++<---1λ2λ220x ax -+=[4,6]a ∈()()222422x ax f x x a x x-+'=-+=0x >其中,,当时,即,此时恒成立,函数在区间单调递增,当时,即或当时,在区间上恒成立,即函数在区间上单调递增,当,得或当时,,时,,所以函数的单调递增区间是和,单调递减区间是,综上可知,当的单调递增区间是;当的单调递增区间是和,单调递减区间是;【小问2详解】①由(1)知,当时,函数的单调递增区间是和,单调递减区间是,、是方程的两根,有,,又的图象与有三个公共点,故,则,()22tx x ax =-+28a ∆=-0∆≤a -≤≤()0f x '≥()f x ()0,∞+0∆>a <-a >a <-()0f x ¢>()0,∞+()f x ()0,∞+a >()0t x =1x =1x =0x <<x >()0f x ¢>x <<()0f x '<()f x ⎛ ⎝⎫+∞⎪⎪⎭a ≤()f x ()0,∞+a >()f x ⎛ ⎝⎫+∞⎪⎪⎭[4,6]a ∈()f x ()10,λ()2,λ+∞()12,λλ1λ2λ220x ax -+=122λλ=12a λλ+=()y f x =y b =()123123,,x x x x x x <<112230x x x λλ<<<<<1112x λλ->要证,即证,又,且函数在上单调递减,即可证,又,即可证,令,,由,则恒成立,故在上单调递增,即,即恒成立,即得证;②由,则,令,,则,故在上单调递增,即,1212x x λ+>2112x x λ>-1112x λλ->()f x ()12,λλ()()1122f x f x λ<-()()12f x f x b ==()()1112f x f x λ<-()()()12x g x f x f λ=--()10,x λ∈()()()()212222422x ax x x f x x a x x xλλ-+--'=-+==()()()()()112211122222x x xx x g x x λλλλλλλ------'=+-()()()()()1221112222x x x x x x x λλλλλλ+--+-=-⋅-()()222211*********x x x x x x xx x λλλλλλλλ-+++--+=-⋅-()()()()()12221111222420x x x x x x x λλλλλλλ--=-⋅=>--()g x '()10,λ()()()()111102g x g f f λλλλ<=--=()()1112f x f x λ<-112230x x x λλ<<<<<2322x λλ-<()()()22x h x f x f λ=--()2,x λ∈+∞()()()()()122221222222x x xx x h x x λλλλλλλ------'=+-()()()()()2112222222x x x x x x x λλλλλλ+--+-=-⋅-()()221122212222222x x x x x x xx x λλλλλλλλ-+++--+=-⋅-()()()()()22112222222420x x x x x x x λλλλλλλ--=-⋅=>--()h x '()2,λ+∞()()()()222202h x h ff λλλλ>=--=即当时,,由,故,又,故,由,,函数在上单调递减,故,即,又由①知,故,又,故.【点睛】关键点点睛:最后一问关键点在于先证,从而借助①中所得,得到.()2,x λ∈+∞()()22x f x f λ>-32x λ>()()3232f x f x λ>-()()32f x f x =()()3222f x f x λ>-2322x λλ-<122x λλ<<()f x ()12,λλ2322x x λ<-2232x x λ+<1212x x λ+>()()2312123122x x x x x x λλ=++<---2122λλ-==≤=31x x -<2232x x λ+<1212x x λ+>()()2312123122x x x x x x λλ=++<---。
天津市第一中学2023-2024学年高三下学期第四次月考试题语文含答案

天津一中2023-2024-2高三年级语文学科第四次月考本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试时间150分钟考生务必将答案涂写在答题卡的规定位置上,答在试卷上的无效。
祝各位考生考试顺利!I卷(共33分)一、阅读下面的文字,完成1-3题,共9分。
随着生成式人工智能的发展,数字人正在成为电商界的新宠。
数字人虚拟主播拥有栩栩如生的面容、()的表情、悦耳的声音,大有替代真人主播的架势。
成本更低成为虚拟主播受到热捧的驱动力。
数字人能24小时不间断直播,帮助商家()零散时段的流量,部分场景下的带货数据()。
但据此就得出“数字人吃上了主播饭”的结论还为时尚早。
数字人口型对不上、音画不同步、问答反馈慢……这些客观存在的痛点都指向一个问题,就是虚拟主播。
1.依次填入上文三个括号处的词语,最贴切的一项是()A.多变抓取精彩绝伦B.丰富捕获可圈可点C.丰富赚取精彩绝伦D.多变捕捉可圈可点2.上文画线句有语病,下列修改最恰当的一项是()A.成本更低以至虚拟主播受到热捧B.成本更低导致虚拟主播受到热捧C.成本更低赢得虚拟主播受到热捧D.成本更低是虚拟主播受到热捧的驱动力3.将下列短语依次填入上文横线处,衔接自然的一项是()A.交互性不足、缺乏真实感,影响了买家的消费体验B.真实感缺乏、交互性不足,影响了买家的消费体验C.真实感不足、缺乏交互性,影响了买家的消费体验D.影响了买家的消费体验—一缺乏真实感、交互性不足二、阅读下面的文字,完成4-6题,共9分。
材料一:(摘编自费孝通《乡土中国》第四章“差序格局”思维导图)材料二:《乡土中国》中“差序格局”一词高度概括了中国传统的社会结构、人际关系的逻辑和传统文化的特点,具有丰富的文化意蕴和鲜明的社会特征。
一是差序格局的等级性。
差序格局中的“序”,有等级之意。
在儒家文化中,我国社会结构尤为注重人伦。
“伦是有差等的次序。
”君臣、父子、夫妇、政事、长幼、上下等都有着严格的伦理界限,不可逾越。
天津市第一中学高三上学期第一次月考化学试题 解析版 Word版含解析

本试卷分为第I卷(选择题)、第II卷(非选择题)两部分,共100分,考试用时90分钟。
第I 卷1 至2页,第II卷2 至4 页。
考生务必将答案涂写答题纸或答题卡的规定位置上,答在试卷上的无效。
祝各位考生考试顺利!第Ⅰ卷(本卷共20 道题,每题2分,共40分)相对原子质量:H:1 C:12 N:14 O:16 S:32 Mg:24 Cu: 64 Fe: 56一.选择题(每题只有一个正确选项)1.化学与环境、材料、信息、能源关系密切,下列说法正确的是( )A.绿色化学的核心是应用化学原理对环境污染进行治理B.开发高效氢能、太阳能等新型电动汽车,以解决城市机动车尾气排放问题C.PM2.5是指大气中直径接近2.5×10-6m的颗粒物,分散在空气中形成胶体D.半导体行业中有一句话:“从沙滩到用户”,计算机芯片的材料是二氧化硅【答案】B【解析】【考点定位】考查常见的生活环境的污染及治理;硅和二氧化硅【名师点晴】本题考查化学与环境、材料、信息、能源关系密切相关的知识,为高频考点,侧重于基础知识的综合理解和运用的考查,注意能形成胶体的微粒直径在1-100nm之间,为易错点,注意绿色化学的核心高频考点。
若NA表示阿伏加德罗常数,下列说法中正确的是( )A.16 g CH4与18 g NH4+所含质子数相等B.常温下,5.6g 铁钉与足量浓硝酸反应,转移的电子数为0.3 NAC.1L 0.5 mol·L-1 Na2CO3溶液中,阴阳离子总数为1.5 NAD.常温常压下,11g CO2气体中所含的分子数为0.25NA【答案】D【解析】【考点定位】考查阿伏加德罗常数和阿伏加德罗定律【名师点晴】本题考查了阿伏伽德罗常的应用,主要考查质量换算物质的量计算微粒数,盐类水解的应用,关键常温下铁在浓硫酸、浓硝酸中发生钝化。
顺利解答该类题目的关键是:一方面要仔细审题,注意关键字词,熟悉常见的“陷阱”;另一方面是要把各种量转化为物质的量,以此为中心进行计算。
天津市第一中学2022-2023学年高三上学期第三次月考英语试题(含答案)

天津一中2022-2023-1高三年级英语学科第三次月考试卷第I卷(共95分)本试卷分为第I卷(选择题)、第II卷(非选择题)和第III卷(听力)三部分,共150 分, I卷、第II卷考试用时100分钟。
第I卷4页,第II卷1页,第III卷2页。
考生务必将答案涂写规定的位置上, 答在试卷上的无效。
祝各位考生考试顺利!第一部分英语知识运用(共两节,满分45分)第一节单项填空(共15小题;每小题1分,满分15分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
1. —Going to the pub Viking Burger to watch the final of the World Cup tonight?—______! Will you join us?A. You thereB. You betC. You got meD. You know better2. The Five Avenues Area is a very popular tourist ______ in Tianjin.A. digestB. drawC. distinctionD. division3. For a senior high student, ______ good use you have made of your time to study, there is still room for improvement.A. whateverB. howeverC. thoughD. whether4. With the ever-serious pollution, many species, including endangered ones, are known ______ by ocean plastics in the past decades.A. to have been affectedB. to have affectedC. having been affectedD. having affected5. Sometimes parents’ control of young kids will be thought to be such an invisible rope with which to tie them tightly that they ______ tried to cut it.A. extremelyB. thoroughlyC. desperatelyD. obviously6. There is a sign over there, saying no person ______ bring food and drinks into the reading room.A. shallB. shouldC. willD. must7. Such a simple experiment ca n effectively ______ people’s doubts about the new technology, so they are willing to embrace the innovation.A. bring forthB. go overC. put awayD. wipe out8. The Palace Museum is ______ the royal families used to live and it’s now a historical museum with collections of valuable antiques.A. whatB. whichC. whereD. how9. Prof. Wu says that the best way to help the tradition ______ is passing it down from generation to generation.A. surviveB. recoverC. preserveD. function10. Although members of one culture do not express their emotions as openly as _______ of another do, it does not mean that they do not experience emotions.A. itB. oneC. thatD. those11. Cambridge University says it ______ gaokao scores for years, requiring the admitted students to rank in the top 0.1 percent on the test in their province.A. has been consideringB. had consideredC. is consideringD. considers12. Hate speech on the internet causes violence, undermines diversity and social unity, thus ______ the common values and principles that bind us together.A. to threatenB. having threatenedC. threateningD. threatened13. Reciting does much good in language learning and it ______ helps to learn science subjects better.A. in returnB. by chanceC. in turnD. for once14. China will allow all couples to have three children, ______, in my opinion, is helpful to cope with the increasingly aging society.A. thatB. whichC. whatD. who15. —Because they were all team players, the task was fulfilled.—Well, ______.A. a bird in the hand is worth two in the bushB. a good beginning is half doneC. where there is a will, there is a wayD. many hands make light work第二节完形填空(共20小题;每小题1.5分,满分30分)阅读下面短文,从16-35各题所给的A、B、C、D四个选项中,选出最佳选项。
天津市第一中学2018届高三上学期第二次月考物理试题Word版含答案

本试卷分为第1卷(选择题)、第Ⅱ卷(非选择题)两部分,共100分,考试用时90分钟。
考生务必将答案涂写答题纸或答题卡的规定位置上,答在试卷上的无效。
祝各位考生考试顺利!第1卷(选择题,共44分)一、单项选择题(本题共8小题,每题3分,共24分。
每小题只有一个正确选项。
)1、2017年11月15日,我国自行研制的风云三号D星发射升空,这是一颗极轨气象卫星,运行周期约为100分钟。
而11月5日,北斗三号双星发射升空,标志着我国的北斗导航系统进入全球组网时代。
北斗系统中的同步定点卫星与风云卫星相比,下列说法正确的是( )A.两种卫星都可能经过天津上空B.北斗卫星的周期约为风云卫星的14.4倍C.北斗卫星的运行速度可能比风云卫星的大D.北斗卫星的向心力一定比风云卫星的大2、如图所示,A、B、C是水平面上同一直线上的三点,其中AB=BC,在A点正上方的O点以初速度v0水平抛出一小球,刚好落在B点,小球运动的轨迹与OC的连线交于D点,不计空气阻力,重力加速度为g,下列说法不正确的是( )A. 小球从O到D点的水平位移是从O到B点水平位移的1/2B.小球经过D点与落在B点时重力瞬时功率的比为1/2C.小球从O到D点与从D到B点两段过程中重力做功的比为1/3D.小球经过D点时速度与水平方向夹角的正切值是落到B点时速度与水平方向夹角的正切值的1/43、如图所示,有一个内壁光滑的圆锥形漏斗竖直放置,一个质量为m的小球在漏斗内壁某水平面内做匀速圆周运动。
若漏斗的侧壁与竖直方向夹角为θ,小球运动的圆平面到漏斗底端的距离为h,则下列说法正确的是( )A. 小球受到内壁的支持力与h 无关,随θ的增大而增大B .小球运动的向心加速度与θ无关,随h 的增大而增大C .小球运动的线速度与θ无关,随h 的增大而增大D .小球运动的角速度与h 无关,随θ的增大而增大4、如图所示,一小球以初速度v 做竖直上抛运动,到达的最大高度为H 。
2023届天津市滨海新区塘沽第一中学高三毕业班第三次月考语文试卷

塘沽一中2023届高三毕业班第三次月考语文本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷两部分,共150分,考试用时150分钟。
第Ⅰ卷1至9页,第Ⅱ卷10至16页。
答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共11小题,每小题3分,共33分。
在每小题给出的四个选项中,只有一项是最符合题目要求的。
一、(9分,每小题3分)阅读下面一段文字,完成1~3题。
吃喝当然是人生一大乐事,如果生活在太空,我们还能愉快地享用大餐吗?最早的太空餐是让人的“牙膏”:宇航员从管子里面挤出半流体的食物,不需要咀嚼便直接咽下去,没有咀嚼的快感,没有多样的选择,首代宇航员的饮食条件相当艰苦。
然而,吃货的生产力,很快,人们就发明了种种能在无重力环境中使用的餐具,甚至还有咖啡杯和煎锅。
如今,宇航员们已能在太空中自如地使用各种餐具,与地面用餐相当接近。
与此同时,太空食品的种类也丰富起来。
正因为目前国际空间站中有上百种餐品,使得宇航员可以自由选择自己的用餐计划——然而这一用餐计划是每八天循环一次的。
而且宇航员们还在不停地开发新的太空料理:小饼干、寿司、花生酱冰棍,甚至是“昨天的咖啡”——采访中一位航天飞机的指挥官曾自豪地展示过一批再生水,而原料是什么,自然。
然而,制订太空莱谱仍然受到很大的限制。
大部分蔬果在宇宙中最多只能保持两天鲜度,空间站中新鲜食品,绝大多数食品只能脱水或加工成罐头运上太空。
目前科学家们正想方设法解决这一难题。
1.依次填入文中横线上的词语,全都恰当的一项是()A.望而却步不胜枚举不言而喻寥寥无几B.踌躇不前不可低估心照不宣寥寥无几C.望而却步不可低估不言而喻极其稀缺D.踌躇不前不胜枚举心照不宣极其稀缺2.文中画横线的句子有语病,下列修改最恰当的一项是()A.目前国际空间站中有上百种餐品,宇航员可以自由选择自己的用餐计划——虽然这一用餐计划是每八天循环一次的。
天津市第一中学2022届高三上学期第三次月考语文试题 Word版含答案

Evaluation Only. Created with Aspose.Words. Copyright 2003-2016 Aspose Pty Ltd.天津一中、益中学校2020-2021-1高三班级语文学科三月考质量调查试卷本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试时间150分钟。
考生务必将答案涂写答题纸或答题卡的规定位置上,答在试卷上的无效。
祝各位考生考试顺当!第Ⅰ卷(36分)一、(12分,每小题3分)1.下列各句中,没有错别字且加点字的注音全都正确的一项是A.吐.(tǔ)槽社会不公,埋怨怀才不遇,因而踟.(c hí)蹰不前,这不过是找一个堂皇的借口而已。
当你拂去往日心灵的积弊与尘垢,用婴儿水晶般的瞳孔端详世界的时候,你会发觉即使是在严冬季节,周遭仍旧暗涌着奇迹抽芽带来的层层新绿。
B.中华文明硕果累累(lěi),仰韶的彩陶、良渚(z hǔ)的玉器、唐之金银、宋之陶瓷,元明清不胜枚举,这些手艺不经意间将生活艺术化,让后人仰而视之,诚惶诚恐。
C.雄心期决胜,壮志在必克。
我们要多些一往无前的进取意识、乘.(chénɡ)势而上的机遇意识、敢于担当的责任意识,汇聚全体国民的磅礴力气,再接再厉,砥砺攻艰,铿(kēng)锵前行,争取更大的成功。
D.站在兵马俑(yǒng)坑前,我们观察的秦朝文物几近全部。
细心倾听,甚至可以听见金戈铁马的嘶杀声。
这令人震惊的兵马俑,不过是秦文明中的沧海一粟(sù)。
2.依次填入下面横线上的词语最恰当的一项是(1)为了搞清事故的缘由,公安部门打算立案。
(2)我们必需学会如何在纷繁简单的干扰中剥离出“演绎”的成分,去伪存真,真相,呈现出万事万物的真实状态。
(3)为了弄清这句话的出处,推断对方说法的真伪,老先生跑了很多图书馆,了大量的文献资料。
A.侦查厘清披阅B.侦查理清批阅C.侦察理清披阅D.侦察厘清批阅3.下列各句中,没有语病的一句是A.蓟县滑雪场九成以上受伤者为初学滑雪者,大部分在未接受专业指导或训练的情况下直接进入中高级滑道,从而导致自己受伤或撞伤他人概率更大。
天津市滨海新区塘沽第一中学2023届高三三模数学试题

三、双空题 13.盒子里装有同样大小的 4 个白球和 3 个黑球,甲先从中取 2 球(不放回),之后 乙再从盒子中取 1 个球.(1)则甲所取的 2 个球为同色球的概率为____________;
(2)设事件 M 为“甲所取的 2 个球为同色球”, N 事件为“乙所取的球与甲所取的
球不同色”,则在事件 M 发生的条件下,求事件 N 发生的概率 P ( N M ) = __________
,
b
=
lnπ
,c
3
=
æ çè
4 5
ö ÷ø
4
,则(
)
A. a < c < b
B. c < a < b
C. b < a < c
D. c < b < a
6.点 F 是抛物线 x2 = 8 y 的焦点,A 为双曲线 C: x2 8
-
y2 b
= 1的左顶点,直线 AF 平
行于双曲线 C 的一条渐近线,则实数 b 的值为( )
AD × BC =
__________;若点 D 在边 BC 上(不包含端点),延长 AD 到 P,使得 AP = 9 ,且满足
uuur PA =
uuur mPBLeabharlann +æ çè
3 2
-
m
ö ÷ø
uuur PC
(m 为常数),则
uuur uuur DA + DB
= ____________.
试卷第41 页,共33 页
P,点
M,N
在
x
轴上,
PM∥QN,且直线 PM 与直线 QN 间的距离为 c,四边形 PQNM 的面积为 3c. (i)求直线 PF 的斜率; (ii)求椭圆的方程.
2022届天津市第一中学高三上学期12月月考数学试题(解析版)

2022届天津市第一中学高三上学期12月月考数学试题一、单选题1.已知集合()(){}210M x x x =+-<,{}10N x x =+<,则M N =( ) A .()1,1- B .()2,1- C .()2,1--D .()1,2【答案】C【分析】解出集合M 、N ,利用交集的定义可求得集合M N ⋂.【详解】()(){}()2102,1M x x x =+-<=-,{}()10,1N x x =+<=-∞-, 因此,()2,1M N =--.故选:C.2.若,a b ∈R ,且0ab ≠,则“a b >”是“11a b<”的 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件【答案】D【分析】根据充分必要条件的定义分别进行判断即可. 【详解】当0a b >>时,11a b <不成立;当110a b<<时,a b >不成立,所以“a b >”是“11a b<”的既不充分也不必要条件.故选D . 【点睛】本题考查了充分必要条件,考查了不等式的性质,是一道基础题. 3.函数2()22x x f x x -=--的图象大致为( )A .B .C .D .【答案】B【分析】根据函数的奇偶性可排除C ,再根据()()3,5f f 的符号即可排除AD ,即可得出答案.【详解】解:函数的定义域为R ,因为()2()22x xf x x f x --=--=,所以函数()f x 是偶函数,故排除C ;()17398088f =--=>,故排除A ;()1152532703232f =--=--<,故排除D. 故选:B.4.为了解学生课外使用手机的情况,某研究学习小组为研究学校学生一个月使用手机的总时间,收集了500名学生2019年12月课余使用手机的总时间(单位:小时)的数据.从中随机抽取了50名学生,将数据进行整理,得到如图所示的频率分布直方图.已知这50人中,恰有2名女生的课余使用手机总时间在[18,20]区间,现在从课余使用手总时间在[18,20]样本对应的学生中随机抽取2人,则至少抽到1名女生的概率为( )A .25B .710C .815D .715【答案】B【解析】由频率分布直方图求出在[18,20]区间的学生人数,然后求出抽取2人的总方法数和至少有1名女生的方法数,从而计算出概率.【详解】500.105⨯=,则[18,20]样本对应的学生为5人,即2名女生,3名男生,从中抽取2人有25C =10种方法,至少抽到一名女生有2253C C -=7种方法,概率为710. 【点睛】本题考查频率分布直方图,考查古典概型,正确理解频率分布直方图是解题基础,求出至少抽到1名女生所含有的基本事件的数量是解题关键.5.已知正方体ABCD -A 1B 1C 1D 1棱长为1,点P 在线段BD 1上,当∠APC 最大时,三棱锥P -ABC 的体积为A .124B .118 C .19D .112【答案】B【详解】连接AC 交BD 于O ,连接PO ,则∠APC=2∠APO ∵tan ∠APO=AOPO∴当PO 最小时,∠APO 最大, 即PO ⊥BD 1时,∠APO 最大, 如图,作PE ⊥BD 于E ,∵正方体ABCD-A 1B 1C 1D 1棱长为1, ∴2BD 13 ∵OP ⊥BD 1,PE ⊥BD , ∴△BDD 1∽△BPO ∽△PEO , ∴11OP OB DD BD =,1PE OPBD BD = ∴6,PE=13,∴三棱锥P-ABC 的体积V=ABC 11PE 318S⨯⨯=,, 故选项为:B点睛:立体几何的核心思想:空间问题平面化.本题把问题转化到平面BDD 1中,当PO 最小时,即∠APO 最大,借助平面几何知识易得:6PE=13,从而得到了三棱锥P-ABC 的体积.6.已知3log 1a a ⋅=,31b b ⋅=,21c c ⋅=,则a b c ,,的大小关系为( ) A .a b c << B .c a b << C .b c a << D .b a c <<【答案】C【分析】根据等式特征,构造函数,利用函数图象,结合数形结合思想进行判断即可.【详解】显然0,0,0a b c >>>, 331log 1log a a a a ⋅=⇒=,1313b b b b ⋅=⇒=,1212c cc c⋅=⇒=, 构造函数()()31log (0),20,30,(0),x xy x x y x y x y x x=>=≥=≥=>在同一直角坐标系画出它们的图象,如下图所示:有b c a <<成立, 故选:C7.函数()()2sin (0,0)f x x ωϕωϕπ=+><<的图象如图,把函数()f x 的图象上所有的点向右平移6π个单位长度,可得到函数()y g x =的图象,下列结论中: ①3πϕ=;②函数()g x 的最小正周期为π;③函数()g x 在区间,312ππ⎡⎤-⎢⎥⎣⎦上单调递增;④函数()g x 关于点,03π⎛-⎫⎪⎝⎭中心对称其中正确结论的个数是( ).A .4B .3C .2D .1【答案】C【分析】对①,先根据图象分析出ω的取值范围,然后根据()03f =ϕ的可取值,然后分类讨论ϕ的可取值是否成立,由此确定出,ωϕ的取值;对②,根据图象平移确定出()g x 的解析式,利用最小正周期的计算公式即可判断;对③,先求解出()g x 的单调递增区间,然后根据k 的取值确定出,312ππ⎡⎤-⎢⎥⎣⎦是否为单调递增区间;对④,根据3g π⎛⎫- ⎪⎝⎭的值是否为0,即可判断. 【详解】解:由图可知: 1112113124T T ππ⎧<⎪⎪⎨⎪>⎪⎩,11211129πππω∴<<, 即18241111ω<<, 又()02sin f ϕ==0ϕπ<<,由图可知:23ϕπ=, 又11112sin 21212f ππωϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭, 112,122k k Z ππωϕπ∴+=+∈, 且113,2122ππωπ⎛⎫∈ ⎪⎝⎭, 113,3122ππωϕπ⎛⎫⎛⎫∴+∈ ⎪ ⎪⎝⎭⎝⎭, 故1k =, 当23ϕπ=时,1111126πωπ=,解得:2ω=,满足条件,()22sin 23f x x π⎛⎫∴=+⎪⎝⎭, 故()22sin 22sin 2633g x x x πππ⎛⎫⎛⎫⎛⎫=-+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,对①,由上述可知①错误; 对②,()2sin 23g x x π⎛⎫=+ ⎪⎝⎭,()g x ∴的最小正周期为2=2ππ,故②正确; 对③,令222,232k x k k Z πππππ-≤+≤+∈,即5,1212k x k k Z ππππ-≤≤+∈, 令0k =,此时单调递增区间为5,1212ππ⎡⎤-⎢⎥⎣⎦,且5,,3121212ππππ⎡⎤⎡⎤-⊆-⎢⎥⎢⎥⎣⎦⎣⎦,故③正确;对④,2sin 230333g πππ⎛⎫⎛⎫⎛⎫-=⨯-+=-≠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ,03π⎛⎫∴- ⎪⎝⎭不是对称中心,故④错误; 故选:C.【点睛】方法点睛:已知函数()()sin g x A x ωϕ=+()0ω>, 若求函数()g x 的单调递增区间,则令ππ2π2π22k x k ωϕ-<+<+,Z k ∈; 若求函数()g x 的单调递减区间,则令π3π2π2π22k x k ωϕ+<+<+,Z k ∈; 若求函数()g x 图象的对称轴,则令ππ2x k ωϕ+=+,Z k ∈; 若求函数()g x 图象的对称中心或零点,则令πx k ωϕ+=,Z k ∈.8.如图,1F ,2F 是双曲线()222:103x y C a a -=>的左右焦点,过1F 的直线与双曲线C 的两条渐近线分别交于A ,B 两点,若点A 为1F B 的中点,且12F B F B ⊥,则12F F =( ).A .4B .43C .6D .9【答案】A【分析】结合已知条件得2//OA F B ,推出1260AOF AOB BOF ∠=∠=∠=︒,然后求出a ,即可求得12||F F .【详解】因为点A 为2F B 的中点,所以2//OA F B ,又12F B F B ⊥,所以1OA F B ⊥,12||||||OF OF OB ==,所以1260AOF AOB BOF ∠=∠=∠=︒,3tan 603=︒=1a =,所以132c =+=. 故12||24F F c ==. 故选:A.9.已知偶函数(),()y f x x R =∈,满足(2)()f x f x +=-且[1,0]x ∈-时()||f x x =,则6()log (1)0f x x -+=的解的个数是( )A .4B .5C .6D .7【答案】B【解析】已知函数()f x 是周期为2的周期函数,在同一个坐标系中,画出函数()y f x =和()6log 1y x =+的图像,可以得出两个图像的交点的个数是5个. 【详解】由()y f x =为偶函数, 得()(2)()f x f x f x +=-=, 所以()f x 的周期为2,由6()log (1)0f x x -+=可得6()log (1)f x x =+, 令()()6log 1g x x =+,即求6()log (1)0f x x -+=的解的个数转化为函数()y f x =与函数()y g x =的交点个数问题;在同一个坐标系中,画出函数()y f x =和()y g x =的图像,如图所示:观察图像可得两个函数共有5个交点. 故选:B.【点睛】本题主要考查了函数图像的交点个数,考查了数形结合思想.属于较易题. 二、填空题10.用()Re z 表示复数z 的实部,用()Im z 表示复数z 的虚部,若已知复数:满足()173z i i -=+,其中z 是复数z 的共轭复数,则()()Re Im z z +=______.【答案】3-【分析】根据复数除法运算求得z ,进而得到z ,实部加虚部即可得到结果.【详解】由题意得:()()()()73173410251112i i i iz i i i i ++++====+--+ 25z i ∴=- 则()()Re Im 253z z +=-=- 本题正确结果:3-【点睛】本题考查复数的除法运算、共轭复数的定义、复数的实部和虚部的定义,属于基础题.11.72x x ⎛⎫- ⎪⎝⎭的展开式中x 的系数为__________.【答案】280-【分析】写出72x x ⎛⎫- ⎪⎝⎭的展开式通项,令x 的指数为1,求出参数的值,再代入通项即可得解.【详解】72x x ⎛⎫- ⎪⎝⎭的展开式通项为()77217722rr r r rr r T C x C x x --+⎛⎫=⋅⋅-=⋅-⋅ ⎪⎝⎭,令721r -=,解得3r =.因此,72x x ⎛⎫- ⎪⎝⎭的展开式中x 的系数为()()3372358280C ⋅-=⨯-=-. 故答案为:280-.【点睛】本题考查利用二项式定理求展开式中指定项的系数,考查计算能力,属于基础题.12.据统计,连续熬夜48小时诱发心脏病的概率为0.055,连续熬夜72小时诱发心脏病的概率为0.19.现有一人已连续熬夜48小时未诱发心脏病,则他还能继续连续熬夜24小时不诱发心脏病的概率为______. 【答案】67【分析】由对立设事件的概率分别得到连续熬夜48小时和连续熬夜72小时未诱发心脏病的概率,再利用条件概率公式求解.【详解】设事件A 为48h 发病,事件B 为72h 发病, 由题意可知:()0.055P A =,()0.19P B =, 则()0.945P A =,()0.81P B =,由条件概率公式可得:()()()()()0.8160.9457P AB P B P B A P A P A ====.故答案为:67【点睛】本题主要考查对立事件和条件概率的求法,属于基础题.13.正数a ,b 满足1a +9b=1,若不等式a +b ≥-x 2+4x +18-m 对任意实数x 恒成立,则实数m 的取值范围是______. 【答案】[6,+∞)【分析】先利用基本不等式,求得a b +的最小值为16.再对题目所给的恒成立的不等式分离常数m ,求得含有x 的表达式的最小值,由此求得m 的取值范围.【详解】因为a >0,b >0,1a +9b =1,所以a +b =(a +b )·19a b ⎛⎫⎪⎝⎭+=10+b a +9a b ≥10+29=16,由题意,得16≥-x 2+4x +18-m ,即x 2-4x -2≥-m 对任意实数x 恒成立. 又x 2-4x -2=(x -2)2-6,所以x 2-4x -2的最小值为-6,所以-6≥-m ,即m ≥6. 【点睛】本小题主要考查利用基本不等式求和式的最小值,考查不等式恒成立问题的解决策略——分离常数法.属于中档题.14.法国数学家布丰提出一种计算圆周率π的方法——随机投针法,受其启发,我们设计如下实验来估计π的值:先请200名同学每人随机写下一个横、纵坐标都小于1的正实数对(),x y ;再统计两数的平方和小于1的数对(),x y 的个数m ;最后再根据统计数m 来估计π的值.已知某同学一次试验统计出156m =,则其试验估计π为______. 【答案】3.12【解析】横、纵坐标都小于1的正实数对(),x y 构成第一象限内的一个正方形, 两数的平方和小于1的数对(),x y 为单位圆在第一象限的部分.由几何概型概率的计算公式,及试验所得结果,即可估计π的值.【详解】横、纵坐标都小于1的正实数对(),x y 构成第一象限内的一个正方形, 两数的平方和小于1的数对(),x y 为单位圆在第一象限的部分.其关系如下图所示:则阴影部分与正方形面积的比值为1:14π由几何概型概率计算公式可知115642001π=解得15643.12200π⨯== 故答案为: 3.12【点睛】本题考查了几何概型概率的求法,根据题意得各部分的关系是解决问题的关键,属于基础题.15.已知向量a ,b 满足1a =,2b =,则a b a b ++-的最大值为______ 【答案】【分析】设a ,b 的夹角为θ,则a b a b ++-=y =平方后化简可求出其最大值,从而可求得a b a b ++-的最大值【详解】解:设a ,b 的夹角为θ([0,]θπ∈), 因为1a =,2b =, 所以()()22a b a b a b a b ++-=++-222222a a b b a a b b +⋅++-⋅+令y =210y =+因为[0,]θπ∈,所以2cos [0,1]θ∈,所以当2cos 0θ=时,2y 有最大值102520+⨯=,即y 有最大值所以a b a b ++-的最大值为 故答案为:三、解答题16.已知ABC 的内角,,A B C 的对边分别为,,a b c,且4B π=.(1)b =3a =,求sinA 的值;(2)若b =3ac +=,求ABC 的面积. 【答案】(1;(21.【分析】(1)直接利用正弦定理即可求出sin A 的值;(2)根据5b =,3a c +=,4B π=,利用余弦定理求出ac ,即可求出ABC 的面积. 【详解】解:(1)由正弦定理sin sin b a B A =得sin 310sin 10a B Ab ==. (2)由余弦定理2222cos b ac ac B =+-得2252a c ac =+-,所以25()(22)9(22)a c ac ac =+-+=-+,得422ac =-. 所以1sin 212ABC S ac B ==-. 17.如图,四棱锥P ABCD -的底面ABCD 中,ABD △为等边三角形,BCD △是等腰三角形,且顶角120BCD ∠=︒,PC BD ⊥,平面PBD ⊥平面ABCD ,M 为PA 中点.(1)求证://DM 平面PBC ;(2)若PD PB ⊥,求二面角C PA B --的余弦值大小.【答案】(1)见解析;(221 【解析】(1)设AB 中点为N ,连接MN 、DN ,首先通过条件得出CB AB ⊥,加DN AB ⊥,可得//DN BC ,进而可得//DN 平面PBC ,再加上//MN 平面PBC ,可得平面//DMN 平面PBC ,则//DM 平面PBC ;(2)设BD 中点为O ,连接AO 、CO ,可得PO ⊥平面ABCD ,加上BD ⊥平面PCO ,则可如图建立直角坐标系O xyz -,求出平面PAB 的法向量和平面PAC 的法向量,利用向量法可得二面角的余弦值.【详解】(1)证明:设AB 中点为N ,连接MN 、DN ,ABD 为等边三角形,DN AB ∴⊥,DC CB =,120DCB ∠=︒,30CBD ∴∠=︒,603090ABC ∴∠=︒+︒=︒,即CB AB ⊥,DN AB ⊥,//DN BC ∴,BC ⊂平面PBC ,DN ⊄平面PBC ,//DN ∴平面PBC ,MN 为PAB △的中位线,//MN PB ∴,PB ⊂平面PBC ,MN ⊄平面PBC ,//MN ∴平面PBC , MN 、DN 为平面DMN 内二相交直线,∴平面//DMN 平面PBC ,DM ⊂平面DMN ,//DM ∴平面PBC ;(2)设BD 中点为O ,连接AO 、COABD 为等边三角形,BCD △是等腰三角形,且顶角120BCD ∠=︒AO BD ∴⊥,CO BD ⊥,A ∴、C 、O 共线,PC BD ⊥,BD CO ⊥,PC CO C =,PC ,CO ⊂平面PCOBD ∴⊥平面PCO .PO ⊂平面PCOBD PO ∴⊥平面PBD ⊥平面ABCD ,交线为BD ,PO ⊂平面PBDPO ∴⊥平面ABCD .设2AB =,则3AO =在BCD △中,由余弦定理,得:2222cos BD BC CD BC CD BCD =+-⋅⋅∠又BC CD =,222222cos120BC BC ∴=-⋅︒, 233CB CD ∴==,33CO =, PD PB ⊥,O 为BD 中点,112PO BD ∴==, 建立直角坐标系O xyz -(如图),则C ⎛⎫ ⎪ ⎪⎝⎭,()0,0,1P ,)A,()0,1,0B . ()3,1,0BA ∴=-,()3,0,1PA =-, 设平面PAB 的法向量为(),,n x y z =,则,000y n BA n PA z ⎧-=⋅=⇒⎨⋅=-=⎩,取1x =,则y z == (1,3,n ∴=, 平面PAC 的法向量为()0,1,0OB =, 21cos ,7n OBn OB n OB ⋅==⋅ 二面角C PA B --为锐角,∴二面角C PA B --的余弦值大小为7. 【点睛】本题考查面面平行证明线面平行,考查向量法求二面角的大小,考查学生计算能力和空间想象能力,是中档题.18.设椭圆()2222:10x y C a b a b+=>>的右焦点为F ,以原点O 为圆心,短半轴长为半径的圆恰好经过椭圆C 的两焦点,且该圆截直线10x y +-=.(1)求椭圆C 的标准方程;(2)过定点()2,0P 的直线交椭圆C 于两点A 、B ,椭圆上的点M 满足OA OB OM +=,求直线AB 的方程.【答案】(1)2212x y +=;(2))2y x =-.【分析】(1)由题意可知,b c =,再由圆222x y b +=截直线10x y +-=得=,可求出b ,从而求出2a 的值,可得到椭圆的标准方程; (2)设过点P 的直线为2x my =+,与椭圆方程联立成方程组,消元后得()222420m y my +++=,先使判别式大于零,求出m 的取值范围,再利用根与系数的关系得到12242m y y m +=-+,然后结合OA OB OM +=将点M 的坐标表示出来代入椭圆方程中可出m 的值,从而可得直线AB 的方程.【详解】(1)以原点为圆心,短半轴长为半径的圆的方程为222x y b +=.∵ 圆222x y b +=过椭圆C 的两焦点, ∴b c =,∵ 圆222x y b +=截直线10x y +-=∴1b =, ∴ 222222a b c b =+==.∴ 椭圆C 的标准方程为2212x y +=. (2)设过点P 的直线方程为2x my =+.A ,B 两点的坐标分别为()11,x y ,()22,x y , 联立方程22122x y x my ⎧+=⎪⎨⎪=+⎩,得()222420m y my +++=,2281602m m ∆=->⇒>, ∴ 12242m y y m +=-+, ∵ OA OB OM +=,∴点()1212,M x x y y ++,∵ 点M 在椭圆C 上,∴有()()22121222x x y y +++=,即()()221212422m y y y y ++++=⎡⎤⎣⎦,∴ ()()()22121228140m y y m y y +++++=, 即()2222442814022m m m m m m ⎛⎫⎛⎫-++-+= ⎪ ⎪++⎝⎭⎝⎭,解得214m =,符合22m >, 直线AB方程为)214y x =±-. (2)方法二:由题意知直线AB 的斜率存在,设过定点()2,0P 的直线为()2y k x =-,()11,A x y ,()22,B x y ,则直线与y 轴交于点()0,2k -,因为OA OB OM +=,所以()1212,M x x y y ++,将直线()2y k x =-与椭圆2212x y +=联立并化简可得, ()2222218820k x k x k +-+-=,则()()()22228421820k k k ∆=--+->,解得k << 所以2122821k x x k +=+,21228221k x x k -=+, 所以()121224421k y y k x x k +=+-=-+, 因为点M 在椭圆上, 所以()1212,M x x y y ++满足椭圆方程2212x y +=, 将2122821k x x k +=+,122421k y y k +=-+代入得, ()()422222321612121k k k k +=++,化简得k ⎛= ⎝⎭, 直线AB方程为)2y x =-. 【点睛】此题考查了求椭圆的标准方程,直线与椭圆的位置关系,考查了运算能力,属于中档题.19.给定数列{c n },如果存在常数p 、q 使得c n+1=pc n +q 对任意n ∈N 都成立,则称{c n }为“M 类数列”.(1)若{a n }是公差为d 的等差数列,判断{a n }是否为“M 类数列”,并说明理由; (2)若{a n }是“M 类数列”且满足:a 1=2,a n +a n+1=3•2n .①求a 2、a 3的值及{a n }的通项公式;②设数列{b n }满足:对任意的正整数n ,都有a 1b n +a 2b n ﹣1+a 3b n ﹣2+…+a n b 1=3•2n+1﹣4n ﹣6,且集合M ={n|n nb a ≥λ,n ∈N}中有且仅有3个元素,试求实数λ的取值范围. 【答案】(1)见解析;(2)①234,8a a == ,2n n a =;②71,162λ⎛⎤∈ ⎥⎝⎦【分析】(1)通过a n+1=a n +d 与c n+1=pc n +q 比较可知p =1、q =d ,进而可得结论; (2)①通过a 1=2、a n +a n+1=3•2n 计算出a 2、a 3的值,进而利用数列{a n }是“M 类数列”代入计算可知数列{a n }是以首项、公比均为2的等比数列,计算可得结论;②通过①可知2b n +22b n ﹣1+23b n ﹣2+…+2n b 1=3•2n+1﹣4n ﹣6,利用2b n =(2b n +22b n ﹣1+23b n ﹣2+…+2n b 1)﹣(22b n ﹣1+23b n ﹣2+…+2n b 1)计算可知b n =2n ﹣1,从而M ={n|212nn -≥λ,n ∈N},分别计算出当n =1、2、3时λ的值,进而可得结论.【详解】(1)结论:公差为d 的等差数列是“M 类数列”.理由如下:∵数列{a n }是公差为d 的等差数列,∴a n+1=a n +d ,此时p =1、q =d ,即公差为d 的等差数列是“M 类数列”;(2)①∵a 1=2,a n +a n+1=3•2n ,∴a 2=3•2﹣a 1=4,232328a a =⋅-=,又∵数列{a n }是“M 类数列”,∴2132a pa q a pa q=+⎧⎨=+⎩,即4284p q p q =+⎧⎨=+⎩,解得:p =2,q =0, 即a n+1=2a n ,又∵a 1=2,∴数列{a n }是以首项、公比均为2的等比数列,∴数列{a n }的通项公式a n =2n ;②由①可知a 1b n +a 2b n ﹣1+a 3b n ﹣2+…+a n b 1=3•2n+1﹣4n ﹣6,即2b n +22b n ﹣1+23b n ﹣2+…+2n b 1=3•2n+1﹣4n ﹣6,∴2b n ﹣1+22b n ﹣2+23b n ﹣3+…+2n ﹣1b 1=3•2n ﹣4(n ﹣1)﹣6=3•2n ﹣4n ﹣2()2n ≥,∴22b n ﹣1+23b n ﹣2+…+2n b 1=3•2n+1﹣8n ﹣4,∴2b n =(2b n +22b n ﹣1+23b n ﹣2+…+2n b 1)﹣(22b n ﹣1+23b n ﹣2+…+2n b 1)=(3•2n+1﹣4n ﹣6)﹣(3•2n+1﹣8n ﹣4)=4n ﹣2,即b n =2n ﹣1()2n ≥,当1n =时,11b =也符合上式,所以b n =2n ﹣1.∴集合M ={n|n n b a ≥λ,n ∈N}={n|212n n -≥λ,n ∈N}, 当n =1时,λ≤21122-= ;当n =2时,λ≤2221324⨯-=; 当n =3时,λ≤3231528⨯-= ;当n≥4时,λ≤42417216⨯-=; 又∵集合M ={n|n n b a ≥λ,n ∈N}中有且仅有3个元素,∴71162λ<, 故实数λ的取值范围是71,162⎛⎤ ⎥⎝⎦. 【点睛】本题是一道关于数列与不等式的综合题,考查数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.20.已知函数()e 1e x xx f x a =--,其中0a >. (1)当2a =时,求曲线()y f x =在点(0,(0))f 处的切线方程;(2)若函数()f x 有唯一零点,求a 的值.【答案】(1)10x y -+=;(2)a 的值为1.【分析】(1)求出函数的导数,得出曲线在点(0,(0))f 处的切线的斜率,再求出切点坐标,得出切线方程.(2) 问题等价于关于x 的方程1(1)e e x x x a =+有唯一的解时,求a 的值,令1()(1)e e x x x g x =+,求出函数()g x 的导数,得出函数()g x 的单调性,从而得出答案.【详解】(1)当2a =时,()2e 1ex x x f x =--,所以1()2e e x x x f 'x -=-, 所以(0)211f '=-=;又(0)211f =-=,所以曲线()y f x =在点(0,(0))f 处的切线方程为1y x -=,即10x y -+=.(2)问题等价于关于x 的方程1(1)e e x x x a =+有唯一的解时,求a 的值. 令1()(1)e e x x x g x =+,则212e ()e xxx g'x --=. 令()12e x h x x =--,则()2e 0x h'x =--<,∴()h x 在(,)-∞+∞上单调递减.又(0)0h =,∴当(,0)x ∈-∞时,()0h x >,()0g x '>,∴()g x 在(,0)-∞上单调递增.当(0,)x ∈+∞时,()0h x <,)'(0g x <,∴()g x 在(0,)+∞上单调递减,∴()g x 的极大值即最大值为(0)1g =.∴当(,0]x ∈-∞时,()(,1]g x ∈-∞;当(0,)x ∈+∞时,()(0,1)g x ∈.又0a >,∴当方程1(1)e e x xx a =+有唯一的解时,1a =. 综上,当函数()f x 有唯一零点时,a 的值为1.【点睛】本题考查求曲线的切线方程,利用导数讨论函数的零点问题,属于中档题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R 天津一中 2017—2018 学年度高三年级三月考试卷数 学(文史类)
第Ⅰ卷 一.选择题:在每小题给出的
四个选项中,只有一项是符合题目要求的.每小题 5 分,共
40 分.
1.已知集合 A x Z || x 1 | 3 , B x | x 2 2x 3 0
,则 A (C
B)
()A. 2,1
2.若从集合 1,2,3,5 中随机地选出三个元素,则满足其中两个元素的和等于第三个元素的概率为()
A.1
4
2
4
2 D . 1
3
3.下列说法正确的是( )
A .若 a R ,则“ 1 1 ”是“ a 1 ”的必要不充分条件
a
B .“ p q 为真命题”是 “ p q 为真命题”的必要不充分条件
C .若命题 p :“ x R , s in os x
2
2 ”,则 p 是真命题
D .命题“ x 0 R , x 0
2x
3 0”的否定是“ x R,x
2x 3 0”
4.执行如右图所示的程序框图,则输出S 的值为()A. l g9
D.1
5.直线y kx 3被圆 x 2 2 y 3 2 4 2 3 ,则直线的倾斜角为()
5
A.或
6 6
B. 或
3 3
C. 或 D.
6 6 6
6.若f x 2cos 2x ( 0)的图像关于直线x
3
对称,且当 取最小值时,
x 0,
,使得 f x 0 a ,则 a 的取值范围是( ) 2
A . 1, 2
D. 2,1
7.已知f x 是定义在R 上的奇函数,对任意两个不相等的正数x1, x2 ,都有
f x1 x1f x2
x
2
f l o
g 4.1
0,记a , b , c
0.2 ,则
x 1 x 2 ( )
2.1
l og
4.1
0.2
A.a c b
B.a b c
x2 x 3,x 1,
8.已知函数 f ( x)
x
2
,x 1. x
设a R,若关于x 的不等式 f (x) | x a | 在R
2
上恒成
立,则a 的取值范围是()
A.[ 47 ,2]
16
B.[ 47 , 39]
16 16
C.[ 2 3,2]
D .
[ 2 3, 39 ]
16
第Ⅱ卷
二.填空题:本大题共 6 小题,每小题 5 分,共 30 分.
9.已知复数 z 满足 (1 2i )z i ,其中 i 为虚数单位,则复数
z 的虚部 为
10.已知函数 f (x ) 2 f '
(1) ln x x ,则 f (x ) 的极大值为
11.某几何体的三视图如右图所示,则该几何体的体积为
12.已知双曲线 C : x
2 y 2
1 (a 0,b 0)的右焦点为F ,抛物线E : x
2 4y 的焦点
a2 b2
B 是双曲线虚轴上的一个顶点,若线段BF 与双曲线
C 的右支交于点A ,且BA 3AF ,
则双曲线C 的离心率为
13.对任意的 (0, π) ,不等式
2
是
| 2x 1|恒成立,则实数x 的取值范围
14.在平行四边形ABCD 中,已知AB 6, BAD 600 ,点E 是BC 的中点,AE 与
BD 相交于点P ,若AP •PC 15,则BC
三.解答题:本大题共6 小题,共80 分.解答应写出文字说明,证明过程或演算步骤.15.(本小题满分13 分)
在△ABC 中,内角A,B,C 所对的边分别为a,b,c .已知a sin A 4b sin B ,
ac
5(a2 b2 c 2 )
(Ⅰ)求cos A 的值
(Ⅱ)求s i n(2B A) 的值
某营养学家建议:高中生每天的蛋白质摄入量控制在[60 ,90](单位:克),脂肪的摄入量控制在[18 ,27](单位:克)某学校食堂提供的伙食以食物A 和食物B 为主,1 千克食物A 含蛋白质60 克,含脂肪9 克,售价20 元;1 千克食物B 含蛋白质30 克,含脂肪27 克,售价15 元
(Ⅰ)如果某学生只吃食物A ,判断他的伙食是否符合营养学家的建议,并说明理由
(Ⅱ)为了花费最低且符合营养学家的建议,学生需要每天同时食用食物A 和食物B 各多少千克?并求出最低需要花费的钱数
如图,三棱柱ABC-A1B1C1 中,侧棱A1A⊥底面ABC,
且各棱长均相等,D,E,F 分别为棱AB,BC,A1C1 的中
点
(Ⅰ)证明EF∥平面A1CD
(Ⅱ)证明平面A1CD⊥平面A1ABB1
(Ⅲ)求直线B1C1与平面A1CD 所成角的正弦值
18.(本小题满分13 分)
已知数列 a n , b n ,S n 为数列 a n 的前n 项和,a2 4b1 ,S n 2a n 2,nb
n 1
n 1 b n
n n 2 n ( n N * )
(Ⅰ)求数列 a n 的通项公式
(Ⅱ)证明 b n
为等差数列
(Ⅲ)若数列 c n 的通项公式为 c n
{
T 2 n
a
n
b
n ,n为奇数2
a n b
n ,n为偶数
4
,令T n 为 c n 的前n 项的和,求
已知函数f ( x) x l n x ,g (x) (x 2 1) ( 为常数)(Ⅰ)若函数y
2 f ( x ) 与函数 y g ( x ) 在 x 1处有相同的切线,求实数 的值
(Ⅱ)若
1 ,且 x 1,证明: f ( x ) g ( x ) 2
(Ⅲ)若对任意 x [1, ) ,不等式恒 f ( x ) g ( x ) 成立,求实数 的取值范围
20.(本小题满分 14 分)
在平面直角坐标系中,焦点在 x 轴上的椭圆 C : x
8。
