2019年天津卷理数高考试题(含答案)
2019年天津市高考数学试卷(理科)-含答案
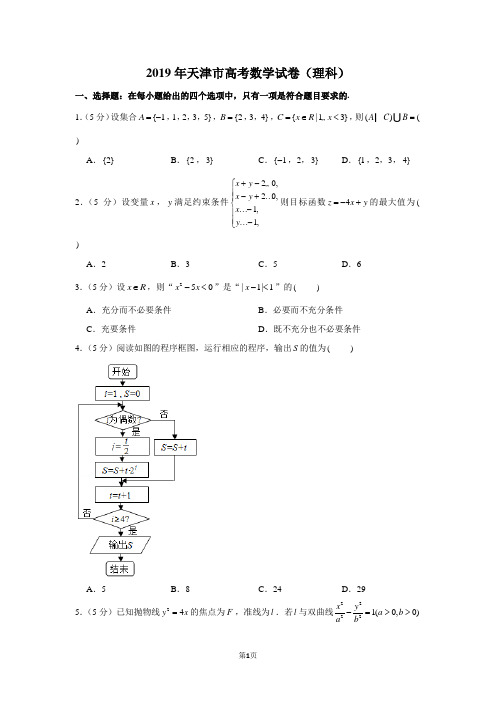
2019年天津市高考数学试卷(理科)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合{1A =-,1,2,3,5},{2B =,3,4},{|13}C x R x =∈<„,则()(A C B =I U)A .{2}B .{2,3}C .{1-,2,3}D .{1,2,3,4}2.(5分)设变量x ,y 满足约束条件20,20,1,1,x y x y x y +-⎧⎪-+⎪⎨-⎪⎪-⎩„………则目标函数4z x y =-+的最大值为() A .2B .3C .5D .63.(5分)设x R ∈,则“250x x -<”是“|1|1x -<”的( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件4.(5分)阅读如图的程序框图,运行相应的程序,输出S 的值为( )A .5B .8C .24D .295.(5分)已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||(AB OF O =为原点),则双曲线的离心率为()A B C .2D6.(5分)已知5log 2a =,0.5log 0.2b =,0.20.5c =,则a ,b ,c 的大小关系为( ) A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.(5分)已知函数()sin()(0f x A x A ωϕ=+>,0ω>,||)ϕπ<是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x的最小正周期为2π,且()4g π,则3()(8f π= )A .2-B .CD .28.(5分)已知a R ∈.设函数222,1,(),1x ax a x f x x alnx x ⎧-+=⎨->⎩g „若关于x 的不等式()0f x …在R 上恒成立,则a 的取值范围为( ) A .[0,1]B .[0,2]C .[0,]eD .[1,]e二、填空题:本大题共6小题,每小题5分,共30分. 9.(5分)i 是虚数单位,则5||1ii-+的值为 . 10.(5分)831(2)8x x -的展开式中的常数项为 .11.(5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为 .12.(5分)设a R ∈,直线20ax y -+=和圆22cos ,(12sin x y θθθ=+⎧⎨=+⎩为参数)相切,则a 的值为 .13.(5分)设0x >,0y >,25x y +=的最小值为 .14.(5分)在四边形ABCD 中,//AD BC ,AB =5AD =,30A ∠=︒,点E 在线段CB 的延长线上,且AE BE =,则BD AE =u u u r u u u rg .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(13分)在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c .已知2b c a +=,3sin 4sin c B a C =.(Ⅰ)求cos B 的值; (Ⅱ)求sin(2)6B π+的值.16.(13分)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.(Ⅰ)用X 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X 的分布列和数学期望;(Ⅱ)设M 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M 发生的概率.17.(13分)如图,AE ⊥平面ABCD ,//CF AE ,//AD BC ,AD AB ⊥,1AB AD ==,2AE BC ==.(Ⅰ)求证://BF 平面ADE ;(Ⅱ)求直线CE 与平面BDE 所成角的正弦值;(Ⅲ)若二面角E BD F --的余弦值为13,求线段CF 的长.18.(13分)设椭圆22221(0)x y a b a b+=>>的左焦点为F ,上顶点为B .已知椭圆的短轴长为45. (Ⅰ)求椭圆的方程;(Ⅱ)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若||||(ON OF O =为原点),且OP MN ⊥,求直线PB 的斜率.19.(14分)设{}n a 是等差数列,{}n b 是等比数列.已知14a =,16b =,2222b a =-,3324b a =+. (Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)设数列{}n c 满足11c =,11,22,,2,k k n kk n c b n +⎧<<⎪=⎨=⎪⎩其中*k N ∈. ()i 求数列22{(1)}n n a c -的通项公式; ()ii 求2*1()ni i i a c n N =∈∑.20.(14分)设函数()cos x f x e x =,()g x 为()f x 的导函数. (Ⅰ)求()f x 的单调区间; (Ⅱ)当[4x π∈,]2π时,证明()()()02f xg x x π+-…; (Ⅲ)设n x 为函数()()1u x f x =-在区间(24n ππ+,2)2n ππ+内的零点,其中n N ∈,证明20022sin cos n n e n x x x πππ-+-<-.2019年天津市高考数学试卷(理科)参考答案与试题解析一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合{1A =-,1,2,3,5},{2B =,3,4},{|13}C x R x =∈<„,则()(A C B =I U)A .{2}B .{2,3}C .{1-,2,3}D .{1,2,3,4}【分析】根据集合的基本运算即可求A C I ,再求()A C B I U ;【解答】解:设集合{1A =-,1,2,3,5},{|13}C x R x =∈<„,则{1A C =I ,2}, {2B =Q ,3,4},(){1A C B ∴=I U ,2}{2⋃,3,4}{1=,2,3,4};故选:D .【点评】本题主要考查集合的基本运算,比较基础.2.(5分)设变量x ,y 满足约束条件20,20,1,1,x y x y x y +-⎧⎪-+⎪⎨-⎪⎪-⎩„………则目标函数4z x y =-+的最大值为() A .2B .3C .5D .6【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.【解答】解:由约束条件20,20,1,1,x y x y x y +-⎧⎪-+⎪⎨-⎪⎪-⎩„………作出可行域如图:联立120x x y =-⎧⎨-+=⎩,解得(1,1)A -,化目标函数4z x y =-+为4y x z =+,由图可知,当直线4y x z =+过A 时,z 有最大值为5. 故选:C .【点评】本题考查简单的线性规划知识,考查数形结合的解题思想方法,是中档题. 3.(5分)设x R ∈,则“250x x -<”是“|1|1x -<”的( ) A .充分而不必要条件 B .必要而不充分条件C .充要条件D .既不充分也不必要条件【分析】充分、必要条件的定义结合不等式的解法可推结果 【解答】解:250x x -<Q ,05x ∴<<, |1|1x -<Q ,02x ∴<<, 05x <<Q 推不出02x <<, 0205x x <<⇒<<,05x ∴<<是02x <<的必要不充分条件,即250x x -<是|1|1x -<的必要不充分条件.故选:B .【点评】本题考查了充分必要条件,考查解不等式问题,是一道基础题. 4.(5分)阅读如图的程序框图,运行相应的程序,输出S 的值为( )A .5B .8C .24D .29【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案. 【解答】解:1i =,0s =;第一次执行第一个判断语句后,1S =,2i =,不满足条件; 第二次执行第一个判断语句后,1j =,5S =,3i =,不满足条件; 第三次执行第一个判断语句后,8S =,4i =,满足退出循环的条件; 故输出S 值为8, 故选:B .【点评】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题5.(5分)已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||(AB OF O =为原点),则双曲线的离心率为()A B C .2D【分析】推导出(1,0)F ,准线l 的方程为1x =-,2||bAB a=,||1OF =,从而2b a =,进而c =,由此能求出双曲线的离心率. 【解答】解:Q 抛物线24y x =的焦点为F ,准线为l . (1,0)F ∴,准线l 的方程为1x =-,l Q 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||(AB OF O =为原点), 2||b AB a ∴=,||1OF =,∴24b a=,2b a ∴=,c ∴==,∴双曲线的离心率为ce a=故选:D .【点评】本题考查双曲线的离心率的求法,考查抛物线、双曲线的性质等基础知识,考查运算求解能力,考查化归与转化思想,是中档题.6.(5分)已知5log 2a =,0.5log 0.2b =,0.20.5c =,则a ,b ,c 的大小关系为( ) A .a c b <<B .a b c <<C .b c a <<D .c a b <<【分析】本题先将a 、b 、c 的大小与1作个比较,发现1b >,a 、c 都小于1.再对a 、c 的表达式进行变形,判断a 、c 之间的大小. 【解答】解:由题意,可知: 5log 21a =<,110.5122221log 0.25log 5log 425b log log --====>=. 0.20.51c =<,b ∴最大,a 、c 都小于1.521log 25a log ==Q,10.2510.5()2c ===而22log 5log 42>=>∴215log <. a c ∴<,a cb ∴<<.故选:A .【点评】本题主要考查对数、指数的大小比较,这里尽量借助于整数1作为中间量来比较.本题属基础题.7.(5分)已知函数()sin()(0f x A x A ωϕ=+>,0ω>,||)ϕπ<是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且()4g π,则3()(8f π= )A .2-B.CD .2【分析】根据条件求出ϕ和ω的值,结合函数变换关系求出()g x 的解析式,结合条件求出A 的值,利用代入法进行求解即可. 【解答】解:()f x Q 是奇函数,0ϕ∴=, 则()sin()f x A x ω=将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x . 即1()sin()2g x A x ω=()g x Q 的最小正周期为2π,∴2212ππω=,得2ω=, 则()sin g x A x =,()sin 2f x A x =,若()4g π=,则()sin 44g A A ππ===2A =,则()2sin 2f x x =,则333()2sin(22sin 2884f πππ=⨯== 故选:C .【点评】本题主要考查三角函数的解析式的求解,结合条件求出A ,ω和ϕ的值是解决本题的关键.8.(5分)已知a R ∈.设函数222,1,(),1x ax a x f x x alnx x ⎧-+=⎨->⎩g „若关于x 的不等式()0f x …在R 上恒成立,则a 的取值范围为( ) A .[0,1]B .[0,2]C .[0,]eD .[1,]e【分析】分2段代解析式后,分离参数a ,再构造函数求最值可得. 【解答】解:当1x =时,f (1)12210a a =-+=>恒成立;当1x <时,22()22021x f x x ax a ax =-+⇔-厖恒成立,令2222(11)(1)2(1)11()(12)2)011111x x x x x g x x x x x x x -----+==-=-=-=--+--=-----„,2()0max a g x ∴=…,0a ∴>.当1x >时,()0xf x x alnx alnx=-⇔厔恒成立, 令()x h x lnx=,则2211()()()lnx x lnx x h x lnx lnx --'==g, 当x e >时,()0h x '>,()h x 递增, 当1x e <<时,()0h x ''<,()h x 递减,x e ∴=时,()h x 取得最小值h (e )e =, ()min a h x e ∴=…,综上a 的取值范围是[0,]e . 故选:C .【点评】本题考查了函数恒成立,属中档题. 二、填空题:本大题共6小题,每小题5分,共30分.9.(5分)i 是虚数单位,则5||1ii-+【分析】本题可根据复数定义及模的概念及基本运算进行计算. 【解答】解:由题意,可知:225(5)(1)56231(1)(1)1i i i i i i i i i i -+---+===-++--,5|||23|1ii i-∴=-+【点评】本题主要考查复数定义及模的概念及基本运算.本题属基础题. 10.(5分)831(2)8x x-的展开式中的常数项为 28 . 【分析】本题可根据二项式的展开式的通项进行计算,然后令x 的指数为0即可得到r 的值,代入r 的值即可算出常数项. 【解答】解:由题意,可知: 此二项式的展开式的通项为: 888188833111(2)()2()()(1)288r r r r rr r r r r r T C x C x C x x---+=-=-=-g g g g g 8484rr x --g .∴当840r -=,即2r =时,1r T +为常数项.此时22218(1)2T C +=-g 84228-⨯=.故答案为:28.【点评】本题主要考查二项式的展开式的通项,通过通项中未知数的指数为0可算出常数项.本题属基础题.11.(5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为4π.【分析】求出正四棱锥的底面对角线长度和正四棱锥的高度,根据题意得圆柱上底面的直径就在相对中点连线,有线段成比例求圆柱的直径和高,求出答案即可.【解答】解:由题作图可知,四棱锥底面正方形的对角线长为2,且垂直相交平分, 由勾股定理得:正四棱锥的高为2,由于圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,有圆柱的上底面直径为底面正方形对角线的一半等于1,即半径等于12; 由相似比可得圆柱的高为正四棱锥高的一半1, 则该圆柱的体积为:21()124v sh ππ==⨯=;故答案为:4π 【点评】本题考查正四棱锥与圆柱内接的情况,考查立体几何的体积公式,属基础题. 12.(5分)设a R ∈,直线20ax y -+=和圆22cos ,(12sin x y θθθ=+⎧⎨=+⎩为参数)相切,则a 的值为 34. 【分析】推导出圆心(2,1)到直线20ax y -+=的距离:2d r ===,由此能求出a 的值.【解答】解:a R ∈Q ,直线20ax y -+=和圆22cos ,(12sin x y θθθ=+⎧⎨=+⎩为参数)相切, ∴圆心(2,1)到直线20ax y -+=的距离:2d r ==,解得34a =. 故答案为:34. 【点评】本题考查实数值的求法,考查直线与圆相切的性质、圆的参数方程等基础知识,考查运算求解能力,是基础题.13.(5分)设0x >,0y >,25x y +=的最小值为【分析】利用基本不等式求最值. 【解答】解:0x >,0y >,25x y +=,===;由基本不等式有:=时,即:3xy=,25x y+=时,即:31xy=⎧⎨=⎩或232xy=⎧⎪⎨=⎪⎩时;等号成立,的最小值为故答案为:【点评】本题考查了基本不等式在求最值中的应用,属于中档题.14.(5分)在四边形ABCD中,//AD BC,AB=5AD=,30A∠=︒,点E在线段CB 的延长线上,且AE BE=,则BD AE=u u u r u u u rg1-.【分析】利用ADu u u r和ABu u u r作为基底表示向量BDu u u r和AEu u u r,然后计算数量积即可.【解答】解:AE BE=Q,//AD BC,30A∠=︒,∴在等腰三角形ABE中,120BEA∠=︒,又AB=2AE∴=,∴25BE AD=-u u u r u u u r,Q AE AB BE=+u u u r u u u r u u u r,∴25AE AB AD=-u u u r u u u r u u u r又BD BA AD AB AD=+=-+u u u r u u u r u u u r u u u r u u u r,∴2()()5BD AE AB AD AB AD=-+-u u u r u u u r u u u r u u u r u u u r u u u rg g227255AB AB AD AD=-+-u u u r u u u r u u u r u u u rg2272||||cos55AB AB AD A AD=-+-u u u r u u u u u r u u u u u r u u u rg721252555=-+⨯⨯-⨯1=-故答案为:1-.【点评】本题考查了平面向量基本定理和平面向量的数量积,关键是选好基底,属中档题.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(13分)在ABC∆中,内角A,B,C所对的边分别为a,b,c.已知2b c a+=,3sin 4sin c B a C =.(Ⅰ)求cos B 的值; (Ⅱ)求sin(2)6B π+的值.【分析】(Ⅰ)根据正余弦定理可得;(Ⅱ)根据二倍角的正余弦公式以及和角的正弦公式可得. 【解答】解(Ⅰ)在三角形ABC 中,由正弦定理sin sin b cB C=,得sin sin b C c B =,又由3sin 4sin c B a C =,得3sin 4sin b C a C =,即34b a =.又因为2b c a +=,得43a b =,23a c =,由余弦定理可得222222416199cos 22423a a a a cb B ac a a +-+-===-g g .(Ⅱ)由(Ⅰ)得sin B,从而sin 22sin cos B B B ==, 227cos2cos sin 8B B B =-=-,故71sin(2)sin 2cos cos2sin 66682B B B πππ+=+=-⨯=. 【点评】本小题主要考查同角三角函数的基本关系,两角和的正弦公式,二倍角的正余弦公式,以及正弦定理、余弦定理等基础知识.考查运算求解能力.属中档题. 16.(13分)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.(Ⅰ)用X 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X 的分布列和数学期望;(Ⅱ)设M 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M 发生的概率.【分析】()I 甲上学期间的三天中到校情况相互独立,且每天7:30之前到校的概率均为23,故2~()3X B ,可求分布列及期望;()II 设乙同学上学期间的三天中7:30到校的天数为Y ,则2~(3,)3Y B ,且{3M X ==,1}{2Y X ==⋃,0}Y =,由题意知{3X =,1}Y =与{2X =,0}Y =互斥,且{3}X =与{1}Y =,{2}X =与{0}Y =相互独立,利用相互对立事件的个概率公式可求【解答】解:()I 甲上学期间的三天中到校情况相互独立,且每天7:30之前到校的概率均为23,故2~(3,)3X B ,从而3321()()()33k k k P x k C -==,0k =,1,2,3.2()323E X =⨯=; ()II 设乙同学上学期间的三天中7:30到校的天数为Y ,则2~(3,)3Y B ,且{3M X ==,1}{2Y X ==⋃,0}Y =,由题意知{3X =,1}Y =与{2X =,0}Y =互斥,且{3}X =与{1}Y =,{2}X =与{0}Y =相互独立,由()I 知,()({3P M P X ==,1}{2Y X ==⋃,0}({3Y P X ===,1}{2Y P X =+=,0}Y = 824120(3)(1)(2)(0)279927243P X P Y P X P Y ===+===⨯+⨯=【点评】本题主要考查了离散型随机变量的分布列与期望,互斥事件与相互独立事件的概率计算公式,考查运算概率公式解决实际问题的能力.17.(13分)如图,AE ⊥平面ABCD ,//CF AE ,//AD BC ,AD AB ⊥,1AB AD ==,2AE BC ==.(Ⅰ)求证://BF 平面ADE ;(Ⅱ)求直线CE 与平面BDE 所成角的正弦值;(Ⅲ)若二面角E BD F --的余弦值为13,求线段CF 的长.【分析】(Ⅰ)以A 为坐标原点,分别以AB u u u r ,AD u u u r ,AE u u u r所在直线为x ,y ,z 轴建立空间直角坐标系,求得A ,B ,C ,D ,E 的坐标,设(0)CF h h =>,得(1F ,2,)h .可得(1,0,0)AB =u u u r是平面ADE 的法向量,再求出(0,2,)BF h =u u u r ,由0BF AB =u u u r u u u rg ,且直线BF ⊂/平面ADE ,得//BF 平面ADE ;(Ⅱ)求出(1,2,2)CE =--u u u r,再求出平面BDE 的法向量,利用数量积求夹角公式得直线CE与平面BDE 所成角的余弦值,进一步得到直线CE 与平面BDE 所成角的正弦值;(Ⅲ)求出平面BDF 的法向量,由两平面法向量所成角的余弦值为13列式求线段CF 的长.【解答】(Ⅰ)证明:以A为坐标原点,分别以AB u u u r ,AD u u u r ,AE u u u r所在直线为x ,y ,z 轴建立空间直角坐标系,可得(0A ,0,0),(1B ,0,0),(1C ,2,0),(0D ,1,0),(0E ,0,2). 设(0)CF h h =>,则(1F ,2,)h .则(1,0,0)AB =u u u r 是平面ADE 的法向量,又(0,2,)BF h =u u u r ,可得0BF AB =u u u r u u u rg .又Q 直线BF ⊂/平面ADE ,//BF ∴平面ADE ;(Ⅱ)解:依题意,(1,1,0)BD =-u u u r ,(1,0,2)BE =-u u u r ,(1,2,2)CE =--u u u r.设(,,)n x y z =r为平面BDE 的法向量,则020n BD x y n BE x z ⎧=-+=⎪⎨=-+=⎪⎩u u u r r g u u u rr g ,令1z =,得(2,2,1)n =r .4cos ,9||||CE n CE n CE n ∴<>==-u u u r r u u u r g r u u u r r g . ∴直线CE 与平面BDE 所成角的正弦值为49; (Ⅲ)解:设(,,)m x y z =r为平面BDF 的法向量, 则020m BD x y m BF y hz ⎧=-+=⎪⎨=+=⎪⎩u u u r r g u u u rr g ,取1y =,可得2(1,1,)m h =-r , 由题意,22|4|||1|cos ,|||||3432m n h m n m n h -<>===⨯+r rg r rr r g ,解得87h =.经检验,符合题意. ∴线段CF 的长为87.【点评】本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了利用空间向量求解线面角与二面角的大小,是中档题.18.(13分)设椭圆22221(0)x y a b a b+=>>的左焦点为F ,上顶点为B .已知椭圆的短轴长为4. (Ⅰ)求椭圆的方程;(Ⅱ)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若||||(ON OF O =为原点),且OP MN ⊥,求直线PB 的斜率. 【分析】(Ⅰ)由题意可得2b =,运用离心率公式和a ,b ,c 的关系,可得a ,c ,进而得到所求椭圆方程;(Ⅱ)(0,2)B ,设PB 的方程为2y kx =+,联立椭圆方程,求得P 的坐标,M 的坐标,由OP MN ⊥,运用斜率之积为1-,解方程即可得到所求值.【解答】解:(Ⅰ)由题意可得24b =,即2b =,c e a ==222a b c -=,解得a ,1c =,可得椭圆方程为22154x y +=;(Ⅱ)(0,2)B ,设PB 的方程为2y kx =+, 代入椭圆方程224520x y +=, 可得22(45)200k x kx ++=, 解得22045kx k =-+或0x =,即有220(45kP k -+,22810)45k k -+,2y kx =+,令0y =,可得2(M k-,0), 又(0,1)N -,OP MN ⊥,可得281011220k k k-=---g,解得k = 可得PB的斜率为 【点评】本题考查椭圆的方程和性质,考查直线和椭圆方程联立,求交点,考查化简运算能力,属于中档题.19.(14分)设{}n a 是等差数列,{}n b 是等比数列.已知14a =,16b =,2222b a =-,3324b a =+. (Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)设数列{}n c 满足11c =,11,22,,2,k k n kk n c b n +⎧<<⎪=⎨=⎪⎩其中*k N ∈. ()i 求数列22{(1)}n n a c -的通项公式; ()ii 求2*1()ni i i a c n N =∈∑.【分析】(Ⅰ)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,利用等差数列、等比数列的通项公式列出方程组,能求出{}n a 和{}n b 的通项公式.(Ⅱ)()i 由222(1)(1)n n n n a c a b -=-,能求出数列22{(1)}n n a c -的通项公式. (Tex translation failed),由此能求出结果.【解答】解:(Ⅰ)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q , 依题意有:26626124q d q d =+⎧⎨=+⎩,解得32d q =⎧⎨=⎩,4(1)331n a n n ∴=+-⨯=+,16232n n n b -=⨯=⨯.(Ⅱ)()i Q 数列{}n c 满足11c =,11,22,,2,k k n kk n c b n +⎧<<⎪=⎨=⎪⎩其中*k N ∈. 222(1)(1)(321)(321)941n n n n n n n a c a b ∴-=-=⨯+⨯-=⨯-,∴数列22{(1)}n n a c -的通项公式为:22(1)941n n n a c -=⨯-.(Tex translation failed)12(21)(243)(941)2n n nni i =-=⨯+⨯+⨯-∑2114(14)(3252)914n n n n ---=⨯+⨯+⨯--2112725212n n n +-=⨯+⨯--.*()n N ∈.【点评】本题考查等差数列、等比数列通项公式及前n 项和等基础知识,考查化归与转化思想和数列求和的基本方法以及运算求解能力.20.(14分)设函数()cos x f x e x =,()g x 为()f x 的导函数. (Ⅰ)求()f x 的单调区间; (Ⅱ)当[4x π∈,]2π时,证明()()()02f xg x x π+-…; (Ⅲ)设n x 为函数()()1u x f x =-在区间(24n ππ+,2)2n ππ+内的零点,其中n N ∈,证明20022sin cos n n e n x x x πππ-+-<-.【分析】(Ⅰ)求出原函数的导函数,可得当(24x k ππ∈+,52)()4k k Z ππ+∈时,()0f x '<,()f x 单调递减;当3(24x k ππ∈-,2)()4k k Z ππ+∈时,()0f x '>,()f x 单调递增; (Ⅱ)记()()()()2h x f x g x x π=+-,依题意及(Ⅰ),得到()(cos sin )x g x e x x =-,由()0h x '<,得()h x 在区间[4π,]2π上单调递减,有()()()022h x h f ππ==…,从而得到当[4x π∈,]2π时,()()()02f xg x x π+-…;(Ⅲ)依题意,()()10n n u x f x =-=,即cos 1n x n e x =,记2n n y x n π=-,则(,)42n y ππ∈,且2()()n n f y e x N π-=∈.由20()1()n n f y e f y π-==„及(Ⅰ),得0n y y …,由(Ⅱ)知,当(4x π∈,)2π时,()g x 在[4π,]2π上为减函数,有0()()()04n g y g y g π<=„,又由(Ⅱ)知,()()()02n n n f y g y y π+-…,得0222200000()2()()()sin cos (sin cos )n n n n n n y n n f y e e e e y g y g y g y x x e y y πππππ-----=-=<--剟, 从而证得20022sin cos n n e n x x x πππ-+-<-.【解答】(Ⅰ)解:由已知,()(cos sin )x f x e x x '=-,因此, 当(24x k ππ∈+,52)()4k k Z ππ+∈时,有sin cos x x >,得()0f x '<,()f x 单调递减; 当3(24x k ππ∈-,2)()4k k Z ππ+∈时,有sin cos x x <,得()0f x '>,()f x 单调递增. ()f x ∴的单调增区间为3[24k ππ-,2]()4k k Z ππ+∈,单调减区间为[,52]()4k k Z ππ+∈;(Ⅱ)证明:记()()()()2h x f x g x x π=+-,依题意及(Ⅰ),有()(cos sin )x g x e x x =-,从而()()()()()(1)()()022h x f x g x x g x g x x ππ'='+'-+-='-<g g .因此,()h x 在区间[4π,]2π上单调递减,有()()()022h x h f ππ==….∴当[4x π∈,]2π时,()()()02f xg x x π+-…; (Ⅲ)证明:依题意,()()10n n u x f x =-=,即cos 1n x n e x =.记2n n y x n π=-,则(,)42n y ππ∈,且22()cos cos(2)()n n y x n n n n n f y e y e x n e x N πππ--==-=∈.由20()1()n n f y e f y π-==„及(Ⅰ),得0n y y …,由(Ⅱ)知,当(4x π∈,)2π时,()0g x '<,()g x ∴在[4π,]2π上为减函数,因此,0()()()04n g y g y g π<=„, 又由(Ⅱ)知,()()()02n n n f y g y y π+-…,故0222200000()2()()()sin cos (sin cos )n n n n n n y n n f y e e e e y g y g y g y x x e y y πππππ-----=-=<--剟. 20022sin cos n n e n x x x πππ-∴+-<-.【点评】本题主要考查导数的运算,不等式的证明、运用导数研究函数的性质等基础知识和方法,考查函数思想和化归与转化思想,考查抽象概括能力、综合分析问题与解决问题的能力,属难题.。
2019年天津市高考数学试题(理科)(解析版)

2019年天津市高考数学试题(理科)一、单选题1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R …,则()A C B =( ) A .{}2 B .{}2,3C .{}1,2,3-D .{}1,2,3,4【答案】D【解析】先求A B ⋂,再求()A C B 。
【详解】 因为{1,2}A C =, 所以(){1,2,3,4}A C B =.故选D 。
【点睛】集合的运算问题,一般要先研究集合中元素的构成,能化简的要先化简,同时注意数形结合,即借助数轴、坐标系、韦恩图等进行运算.2.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为( )A .2B .3C .5D .6【答案】C【解析】画出可行域,用截距模型求最值。
【详解】已知不等式组表示的平面区域如图中的阴影部分。
目标函数的几何意义是直线4y x z =+在y 轴上的截距, 故目标函数在点A 处取得最大值。
由20,1x y x -+=⎧⎨=-⎩,得(1,1)A -,所以max 4(1)15z =-⨯-+=。
故选C 。
【点睛】线性规划问题,首先明确可行域对应的是封闭区域还是开放区域,分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值或范围.即:一画,二移,三求.3.设x R ∈,则“250x x -<”是“|1|1x -<”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件 【答案】B【解析】分别求出两不等式的解集,根据两解集的包含关系确定. 【详解】化简不等式,可知 05x <<推不出11x -<; 由11x -<能推出05x <<,故“250x x -<”是“|1|1x -<”的必要不充分条件, 故选B 。
2019年高考理科数学天津卷真题理数(附参考答案及详解)

文档说明绝密★启用前 6月7日15:00-17:002019年普通高等学校招生全国统一考试(天津卷)数学(理工农医类)总分:150分考试时间:120分钟★祝考试顺利★注意事项:1、本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证条形码粘贴在答题卡的指定位置。
2、选择题的作答:选出每小题答案后,用2B铅笔将答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸、答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内,写在试题卷、草稿纸、答题卡上的非答题区域均无效。
4、考试结束后,将本试卷和答题卡一并上交。
第I卷一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合{1,1,2,3,5}A=-,{2,3,4}B=,{|13}C x x=∈≤<R,则()A C B=I U()A.{2}B.{2,3}C.{1,2,3}- D.{1,2,3,4}2.设变量x y⋅满足约束条件20,20,1,1,x yx yxy+-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y=-+的最大值为()A.2B.3C.5D.63.设x ∈R ,则“250x x -<”是“|1|1x -<”的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.阅读如图的程序框图,运行相应的程序,输出S 的值为( )A.5B.8C.24D.29 5.已知抛物线24y x =的焦点为F ,准线为l .若l 与双曲线22221(0,0)x y a b a b -=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为( )C.26.已知52log a =,0.5log 0.2b =,0.20.5c =,则a ,b ,c 的大小关系为( ) A.a c b << B.a b c << C.b c a << D.c a b <<7.已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且π4g ⎛⎫= ⎪⎝⎭3π8f ⎛⎫= ⎪⎝⎭( )A.2-B. D.28.已知a ∈R ,设函数222,1()ln ,1x ax a x f x x a x x ⎧-+≤⎪=⎨->⎪⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为( )A.[0,1]B.[0,2]C.[0,e]D.[1,e]第Ⅱ卷二、填空题:本题共6小题,每小题5分。
2019年天津理科数学高考真题(含答案)

绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数 学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R ,则()A C B =I U A .{}2B .{}2,3C .{}1,2,3-D .{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y =-+的最大值为A .2B .3C .5D .63.设x ∈R ,则“250x x -<”是“|1|1x -<”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件4.阅读下边的程序框图,运行相应的程序,输出S 的值为 A .5 B .8C .24D .295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为A .2B .3C .2D .56.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭,则38f π⎛⎫= ⎪⎝⎭A .2-B .2-C .2D .28.已知a ∈R ,设函数222,1,()ln ,1.x ax a x f x x a x x ⎧-+≤=⎨->⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为 A .[]0,1 B .[]0,2C .[]0,eD .[]1,e绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数 学(理工类)第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷理数高考试题文档版有答案【备战高考】

绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R ,则()A C B =I U A .{}2B .{}2,3C .{}1,2,3-D .{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y =-+的最大值为A .2B .3C .5D .63.设x ∈R ,则“250x x -<”是“|1|1x -<”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4.阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 A 2B 3C .2D 56.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B .2-C 2D .28.已知a ∈R ,设函数222,1,()ln ,1.x ax a x f x x a x x ⎧-+≤=⎨->⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为 A .[]0,1B .[]0,2C .[]0,e D .[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
【2019高考真题天津卷】2019年天津卷理数高考试题(有答案)

绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P AB P A P B =+.·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R ,则()A CB =A .{}2B .{}2,3C .{}1,2,3-D .{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y =-+的最大值为A .2B .3C .5D .63.设x ∈R ,则“250x x -<”是“|1|1x -<”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4.阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为A BC .2D 6.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且4g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B .C D .28.已知a ∈R ,设函数222,1,()ln ,1.x ax a x f x x a x x ⎧-+≤=⎨->⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为 A .[]0,1B .[]0,2C .[]0,e D .[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年高考理数天津卷

数学试卷 第1页(共16页) 数学试卷 第2页(共16页)绝密★启用前2019年普通高等学校招生全国统一考试(天津市)数学(理工类)本试卷分为第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟.第Ⅰ卷本卷共8小题,每小题5分,共40分.参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U .·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R …,则()A C B =I U ( ) A .{}2B .{}23,C .{}123-,,D .{}1234,,, 2.设变量x ,y 满足约束条件20,20,1,1,x y x y x y +-⎧⎪-+⎪⎨-⎪⎪-⎩≤………则目标函数4z x y =-+的最大值为( )A .2B .3C .5D .63.设x ∈R ,则“05x <<”是“|1|1x -<”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4.阅读如图所示的程序框图,运行相应的程序,输出S 的值为( )A .5B .8C .24D .295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||A B O F =(O 为原点),则双曲线的离心率为( )ABC .2D6.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为( )A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若且()g x 的最小正周期为2π,且π4g ⎛⎫= ⎪⎝⎭,则3π8f ⎛⎫= ⎪⎝⎭( )A .2- B.CD .28.已知a ∈R ,设函数222,1,()ln ,1.x ax a x f x x a x x ⎧-+=⎨->⎩≤若关于x 的不等式()0f x …在R 上恒成立,则a 的取值范围为( )A .[]0,1B .[]0,2C .[]0,eD .[]1,e毕业学校_____________ 姓名________________ 考生号________________________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共16页) 数学试卷 第4页(共16页)第Ⅱ卷本卷共12小题,共110分.二.填空题:本大题共6小题,每小题5分,共30分.9.i 是虚数单位,则5i1i-+的值为 .10.83128x x ⎛⎫- ⎪⎝⎭的展开式中的常数项为 .11.的正方形,.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为 .12.设a ∈R ,直线20ax y -+=和圆22cos,12sinx y θθ=+⎧⎨=+⎩(θ为参数)相切,则a 的值为 . 13.设0,0,25x y x y +=>>的最小值为 .14.在四边形ABCD中,,5,30AD BC AB AD A ==∠=︒∥,点E 在线段CB 的延长线上,且AE BE =,则BD AE ⋅=uu u r uu u r.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)在ABC △中,内角,,A B C 所对的边分别为,,a b c .已知2b c a +=,3sin 4sin c B a C =. (Ⅰ)求cos B 的值;(Ⅱ)求sin 26πB ⎛⎫+ ⎪⎝⎭的值.16.(本小题满分13分)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.(Ⅰ)用X 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X 的分布列和数学期望;(Ⅱ)设M 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M 发生的概率.17.(本小题满分13分)如图,AE ⊥平面ABCD ,,CF AE AD BC ∥∥,AD AB ⊥,1AB AD ==,2AE BC ==.(Ⅰ)求证:BF ∥平面ADE ;(Ⅱ)求直线CE 与平面BDE 所成角的正弦值;(Ⅲ)若二面角E BD F --的余弦值为13,求线段CF 的长.数学试卷 第5页(共16页) 数学试卷 第6页(共16页)18.(本小题满分13分)设椭圆22221(0)x y a b a b +=>>的左焦点为F ,上顶点为B .已知椭圆的短轴长为4,离.(Ⅰ)求椭圆的方程;(Ⅱ)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若||||ON OF =(O 为原点),且OP MN ⊥,求直线PB 的斜率.19.(本小题满分14分)设{}n a 是等差数列,{}n b 是等比数列.已知1122334,622,24a b b a b a ===-=+,. (Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)设数列{}n c 满足111,22,,21,,k k n kk n c b n c +=⎧<<⎪=⎨=⎪⎩其中*k ∈N . (i )求数列(){}221n n a c -的通项公式; (ii )求()2*1ni ii a c n =∈∑N .20.(本小题满分14分) 设函数()e cos ,()x f x x g x =为()f x 的导函数.(Ⅰ)求()f x 的单调区间;(Ⅱ)当,42x ππ⎡⎤∈⎢⎥⎣⎦时,证明()()02f x g x x π⎛⎫+-≥ ⎪⎝⎭;(Ⅲ)设n x 为函数()()1u x f x =-在区间2,242n n ππ⎛⎫π+π+ ⎪⎝⎭内的零点,其中n ∈N ,证明20022sin c s e o n n n x x x -πππ+-<-.-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共16页) 数学试卷 第8页(共16页)2019年普通高等学校全国统一招生考试(天津市)数学(理工类)答案解析第Ⅰ卷一、选择题 1.【答案】D【解析】由条件可得{}1,2A C =I ,{}2,3,4B =,故{}()1,2,3,4A C B =I U . 【考点】集合的交运算与并运算 【考查能力】运算求解 2.【答案】C【解析】画出可行域如图中阴影部分所示.由4z x y =-+得4y x z =+,可知当直线过点A 时,z 取得最大值,由20,1,x y x -+=⎧⎨=-⎩,可得1,1,x y =-⎧⎨=⎩,所以A 的坐标为(1,1)-,.故max 4(1)15z =-⨯-+=.【考点】线性规划 【考查能力】数形结合 3.【答案】B【解析】由250x x -<可得05x <<,由11x -<,解得02x <<,由于区间(0,2)是(0,5)的真子集(0,2)(0,5)Ú,故“05x <<”是“11x -<”的必要而不充分条件.故选B .【考点】充分性与必要性的判断,简单的不等式求解【考查能力】运算求解 4.【答案】B【解析】由题意知,011S =+=,2i =;1j =,11225S ⨯=+=,3i =;538S =+=,4i =,满足4i ≥,输出的8S =.【考点】程序框图 【考查能力】运算求解 5.【答案】D【解析】由题意,可得(1,0)F ,直线l 的方程为1x =-,双曲线的渐近线方程为by x a=±.将1x =-代入by x a=±,得b y a =±,所以点A ,B 的纵坐标的绝对值均为b a ,由||4||ABOF =可得24ba =,即2b a =,224b a =,故双曲线的离心率c e a ===【考点】抛物线的标准方程与几何性质,双曲线的离心率 【考查能力】运算求解 6.【答案】A【解析】551log 2log 2a =<,而0.2110.50.52c ==>,故a c <;0.50.5log 0.2log 0.252b =>=,而0.200.50.51c ==<,故c b <,所以a c b <<【考点】利用指数函数与对数函数的性质比较大小 【考查能力】逻辑思维7.【答案】C【解析】由()f x 是奇函数,可得()k k ϕπ=∈Z ,又||ϕπ<,所以0ϕ=,所以1()s i n 2g x A x ω=,由()g x 的最小正周期为2π,可得2212ππω=,故=2ω,()sin 2f x A x =,()sin 4g x A =π,所以2A =,所以()2s i n 2f x x =,故332sin 84f ππ⎛⎫== ⎪⎝⎭.【考点】三角函数的图象与性质,三角函数的奇偶性、周期性数学试卷 第9页(共16页) 数学试卷 第10页(共16页)【考查能力】数形结合 8.【答案】C【解析】解法一 当0a =时,不等式()0f x …恒成立,排除D ;当a e =时,222,1,()eln ,1,x ex e x f x x x x ⎧-+=⎨->⎩…,当1x ≤时2()22f x x ex e =-+的最小值为(1)10f =>,满足()0f x …;当1x >时,由()eln f x x x =-可得()'1e x ef x x x-=-=,易得()f x f (x )在x e =处取得极小值(也是最小值)()0f e =,满足()0f x …恒成立,排除A ,B .故选C.解法二 若1x …,222()22()2f x x ax a x a a a =-+=--+,当1a ≤时,可得()f x 的最小值为2()2f a a a =-+,令()0f x …,解得02a ≤≤,故0a ≤≤1;当1a >时,可得()f x 的最小值为()110f =≥,满足条件。
【推荐】(精校版)2019年天津卷理数高考试题文档版(含答案)

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3-5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P AB P A P B =+.·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R …,则()A C B =A.{}2B.{}2,3C.{}1,2,3-D.{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为A.2B.3C.5D.6 3.设x R ∈,则“250x x -<”是“|1|1x -<”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4.阅读右边的程序框图,运行相应的程序,输出S 的值为 A.5 B.8 C.24D.295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为C.26.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为A.a c b <<B.a b c <<C.b c a <<D.c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数,将()y f x =的图像上所有点的横坐标伸长到原的2倍(纵坐标不变),所得图像对应的函数为()g x .若()g x 的最小正周期为2π,且4g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A.2-B.D.28.已知a R ∈,设函数222,1,()ln ,1,x ax a x f x x a x x ⎧-+=⎨->⎩…若关于x 的不等式()0f x …在R 上恒成立,则a 的取值范围为A.[]0,1B.[]0,2C.[]0,eD.[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷理数高考试题文档版含答案【精编】

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3-5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R „,则()A C B =I UA.{}2B.{}2,3C.{}1,2,3-D.{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为A.2B.3C.5D.6 3.设x R ∈,则“250x x -<”是“|1|1x -<”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件4.阅读右边的程序框图,运行相应的程序,输出S 的值为A.5B.8C.24D.295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 23256.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为A.a c b <<B.a b c <<C.b c a <<D.c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数,将()y f x =的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A.2-B.22 D.28.已知a R ∈,设函数222,1,()ln ,1,x ax a x f x x a x x ⎧-+=⎨->⎩„若关于x 的不等式()0f x …在R 上恒成立,则a 的取值范围为A.[]0,1B.[]0,2C.[]0,eD.[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷理数高考试题文档版含答案【高考真题】

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3-5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R „,则()A C B =I UA.{}2B.{}2,3C.{}1,2,3-D.{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为A.2B.3C.5D.6 3.设x R ∈,则“250x x -<”是“|1|1x -<”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件4.阅读右边的程序框图,运行相应的程序,输出S 的值为 A.5 B.8C.24D.295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 23256.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为A.a c b <<B.a b c <<C.b c a <<D.c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数,将()y f x =的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A.2-B.2-2 D.28.已知a R ∈,设函数222,1,()ln ,1,x ax a x f x x a x x ⎧-+=⎨->⎩„若关于x 的不等式()0f x …在R 上恒成立,则a 的取值范围为A.[]0,1B.[]0,2C.[]0,eD.[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷理数高考试题文档版有答案(真题)

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R ,则()A C B =I U A .{}2B .{}2,3C .{}1,2,3-D .{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y =-+的最大值为A .2B .3C .5D .63.设x ∈R ,则“250x x -<”是“|1|1x -<”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件4.阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 A 2B 3C .2D 56.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B .2-C 2D .28.已知a ∈R ,设函数222,1,()ln ,1.x ax a x f x x a x x ⎧-+≤=⎨->⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为 A .[]0,1B .[]0,2C .[]0,e D .[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
【精选】2019年天津卷理数高考试题文档版含答案

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3-5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P AB P A P B =+.·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R ,则()A CB =A.{}2B.{}2,3C.{}1,2,3-D.{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩则目标函数4z x y =-+的最大值为A.2B.3C.5D.6 3.设x R ∈,则“250x x -<”是“|1|1x -<”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件4.阅读右边的程序框图,运行相应的程序,输出S 的值为A.5B.8C.24D.295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 23256.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为A.a c b <<B.a b c <<C.b c a <<D.c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数,将()y f x =的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A.2-B.22 D.28.已知a R ∈,设函数222,1,()ln ,1,x ax a x f x x a x x ⎧-+=⎨->⎩若关于x 的不等式()0f x 在R 上恒成立,则a 的取值范围为A.[]0,1B.[]0,2C.[]0,eD.[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
【最新】2019年天津卷理数高考试题文档版含答案

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3-5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R „,则()A C B =I UA.{}2B.{}2,3C.{}1,2,3-D.{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为A.2B.3C.5D.6 3.设x R ∈,则“250x x -<”是“|1|1x -<”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件4.阅读右边的程序框图,运行相应的程序,输出S 的值为A.5B.8C.24D.295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 23256.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为A.a c b <<B.a b c <<C.b c a <<D.c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数,将()y f x =的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A.2-B.22 D.28.已知a R ∈,设函数222,1,()ln ,1,x ax a x f x x a x x ⎧-+=⎨->⎩„若关于x 的不等式()0f x …在R 上恒成立,则a 的取值范围为A.[]0,1B.[]0,2C.[]0,eD.[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷理数高考试题文档版含答案【优选真题】

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3-5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈<R „,则()A C B =I UA.{}2B.{}2,3C.{}1,2,3-D.{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨-⎪⎪-⎩……则目标函数4z x y =-+的最大值为A.2B.3C.5D.6 3.设x R ∈,则“250x x -<”是“|1|1x -<”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.既不充分也不必要条件4.阅读右边的程序框图,运行相应的程序,输出S 的值为A.5B.8C.24D.295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 23256.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为A.a c b <<B.a b c <<C.b c a <<D.c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数,将()y f x =的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A.2-B.22 D.28.已知a R ∈,设函数222,1,()ln ,1,x ax a x f x x a x x ⎧-+=⎨->⎩„若关于x 的不等式()0f x …在R 上恒成立,则a 的取值范围为A.[]0,1B.[]0,2C.[]0,eD.[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷理数高考试题文档版有答案【精】

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R ,则()A C B =I U A .{}2B .{}2,3C .{}1,2,3-D .{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y =-+的最大值为A .2B .3C .5D .63.设x ∈R ,则“250x x -<”是“|1|1x -<”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件4.阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 A 2B 3C .2D 56.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B .2-C 2D .28.已知a ∈R ,设函数222,1,()ln ,1.x ax a x f x x a x x ⎧-+≤=⎨->⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为 A .[]0,1B .[]0,2C .[]0,e D .[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷理数高考试题文档版有答案【优】

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R ,则()A C B =I U A .{}2B .{}2,3C .{}1,2,3-D .{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y =-+的最大值为A .2B .3C .5D .63.设x ∈R ,则“250x x -<”是“|1|1x -<”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件4.阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 A 2B 3C .2D 56.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B .2-C 2D .28.已知a ∈R ,设函数222,1,()ln ,1.x ax a x f x x a x x ⎧-+≤=⎨->⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为 A .[]0,1B .[]0,2C .[]0,e D .[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2019年天津卷理数高考试题文档(真题)

2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R ,则()A C B =I U A .{}2B .{}2,3C .{}1,2,3-D .{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y =-+的最大值为A .2B .3C .5D .63.设x ∈R ,则“250x x -<”是“|1|1x -<”的 A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件4.阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 A 2B 3C .2D 56.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B .2-C 2D .28.已知a ∈R ,设函数222,1,()ln ,1.x ax a x f x x a x x ⎧-+≤=⎨->⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为 A .[]0,1B .[]0,2C .[]0,e D .[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
(精校版)【高考真题】2019年天津卷理数高考试题文档

(Ⅱ)求 sin 2B
的值.
6
16.(本小题满分 13 分)
设甲、乙两位同学上学期间,每天 7: 30 之前到校的概率均为 情况互不影响,且任一同学每天到校情况相互独立.
绝密★启用前
2019 年普通高等学校招生全国统一考试(天津卷)
数学(理工类)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 第Ⅰ卷 1 至 2 页,第Ⅱ卷 3 至 5 页。
150 分,考试用时 120 分钟。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。 答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。考试结束后,将本试卷和答题卡一 并交回。
A 处取得最大值。
x y 2 0,
由
,得 A( 1,1) ,所以 zmax
x1
4 ( 1) 1 5。故选 C。
5
【点睛】 线性规划问题, 首先明确可行域对应的是封闭区域还是开放区域, 分界线是实线还是虚线,
其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线
的距离等等,最后结合图形确定目标函数最值或范围.即:一画,二移,三求.
设椭圆 x2 a2
y2 b2
1(a
b
0) 的左焦点为 F ,上顶点为 B .已知椭圆的短轴长为
4,离心率
为 5. 5
(Ⅰ)求椭圆的方程;
(Ⅱ)设点 P 在椭圆上,且异于椭圆的上、下顶点,点 M 为直线 PB 与 x 轴的交点,点 N 在 y 轴的负半轴上.若 | ON | | OF |( O 为原点),且 OP MN ,求直线 PB 的斜率.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题卡上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A 、B 互斥,那么()()()P A B P A P B =+U . ·如果事件A 、B 相互独立,那么()()()P AB P A P B =.·圆柱的体积公式V Sh =,其中S 表示圆柱的底面面积,h 表示圆柱的高. ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面面积,h 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,1,2,3,5},{2,3,4},{|13}A B C x x =-==∈≤<R ,则()A C B =I U A .{}2B .{}2,3C .{}1,2,3-D .{}1,2,3,42.设变量,x y 满足约束条件20,20,1,1,x y x y x y +-≤⎧⎪-+≥⎪⎨≥-⎪⎪≥-⎩则目标函数4z x y =-+的最大值为A .2B .3C .5D .63.设x ∈R ,则“250x x -<”是“|1|1x -<”的A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件4.阅读下边的程序框图,运行相应的程序,输出S 的值为A .5B .8C .24D .295.已知抛物线24y x =的焦点为F ,准线为l ,若l 与双曲线22221(0,0)x y a b a b-=>>的两条渐近线分别交于点A 和点B ,且||4||AB OF =(O 为原点),则双曲线的离心率为 A 2B 3C .2D 56.已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b <<B .a b c <<C .b c a <<D .c a b <<7.已知函数()sin()(0,0,||)f x A x A ωϕωϕ=+>><π是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且24g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A .2-B .2-C 2D .28.已知a ∈R ,设函数222,1,()ln ,1.x ax a x f x x a x x ⎧-+≤=⎨->⎩若关于x 的不等式()0f x ≥在R 上恒成立,则a 的取值范围为 A .[]0,1B .[]0,2C .[]0,e D .[]1,e第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2.本卷共12小题,共110分。
二.填空题:本大题共6小题,每小题5分,共30分. 9.i 是虚数单位,则5ii1-+的值为_____________. 10.83128x x ⎛⎫- ⎪⎝⎭的展开式中的常数项为_____________.11侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________. 12.设a ∈R ,直线20ax y -+=和圆22cos ,12sin x y θθ=+⎧⎨=+⎩(θ为参数)相切,则a 的值为_____________.13.设0,0,25x y x y >>+=_____________.14.在四边形ABCD 中,,5,30AD BC AB AD A ==∠=︒∥,点E 在线段CB 的延长线上,且AE BE =,则BD AE ⋅=u u u r u u u r_____________.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 15.(本小题满分13分)在ABC △中,内角,,A B C 所对的边分别为,,a b c .已知2b c a +=,3sin 4sin c B a C =. (Ⅰ)求cos B 的值; (Ⅱ)求sin 26B π⎛⎫+⎪⎝⎭的值. 16.(本小题满分13分)设甲、乙两位同学上学期间,每天7:30之前到校的概率均为23.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.(Ⅰ)用X 表示甲同学上学期间的三天中7:30之前到校的天数,求随机变量X 的分布列和数学期望; (Ⅱ)设M 为事件“上学期间的三天中,甲同学在7:30之前到校的天数比乙同学在7:30之前到校的天数恰好多2”,求事件M 发生的概率. 17.(本小题满分13分)如图,AE ⊥平面ABCD ,,CF AE AD BC ∥∥,,1,2AD AB AB AD AE BC ⊥====.(Ⅰ)求证:BF ∥平面ADE ;(Ⅱ)求直线CE 与平面BDE 所成角的正弦值; (Ⅲ)若二面角E BD F --的余弦值为13,求线段CF 的长.18.(本小题满分13分)设椭圆22221(0)x y a b a b+=>>的左焦点为F ,上顶点为B .已知椭圆的短轴长为4,离心率为55.(Ⅰ)求椭圆的方程;(Ⅱ)设点P 在椭圆上,且异于椭圆的上、下顶点,点M 为直线PB 与x 轴的交点,点N 在y 轴的负半轴上.若||||ON OF =(O 为原点),且OP MN ⊥,求直线PB 的斜率. 19.(本小题满分14分)设{}n a 是等差数列,{}n b 是等比数列.已知1122334,622,24a b b a b a ===-=+,. (Ⅰ)求{}n a 和{}n b 的通项公式;(Ⅱ)设数列{}n c 满足111,22,2,1,,k k n kk c n c b n +=⎧<<=⎨=⎩其中*k ∈N .(i )求数列(){}221n n a c -的通项公式; (ii )求()2*1ni ii a c n =∈∑N .20.(本小题满分14分)设函数()e cos ,()xf x xg x =为()f x 的导函数.(Ⅰ)求()f x 的单调区间;(Ⅱ)当,42x ππ⎡⎤∈⎢⎥⎣⎦时,证明()()02f x g x x π⎛⎫+-≥ ⎪⎝⎭;(Ⅲ)设n x 为函数()()1u x f x =-在区间2,242n n ππ⎛⎫π+π+ ⎪⎝⎭内的零点,其中n ∈N ,证明20022sin c s e o n n n x x x -πππ+-<-.绝密★启用前2019年普通高等学校招生全国统一考试(天津卷)数学(理工类)参考解答一、选择题1.【答案】D【分析】先求A B ⋂,再求()A C B I U 。
【详解】因为{1,2}A C =I ,所以(){1,2,3,4}A C B =I U .故选D 。
集合的运算问题,一般要先研究集合中元素的构成,能化简的要先化简,同时注意数形结合,即借助数轴、坐标系、韦恩图等进行运算. 2.【答案】D【分析】画出可行域,用截距模型求最值。
【详解】已知不等式组表示的平面区域如图中的阴影部分。
目标函数的几何意义是直线4y x z =+在y 轴上的截距,故目标函数在点A 处取得最大值。
由20,1x y x -+=⎧⎨=-⎩,得(1,1)A -,所以max 4(1)15z =-⨯-+=。
故选C 。
线性规划问题,首先明确可行域对应的是封闭区域还是开放区域,分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数最值或范围.即:一画,二移,三求. 3.【答案】B【分析】分别求出两不等式的解集,根据两解集的包含关系确定.【详解】化简不等式,可知 05x <<推不出11x -<;由11x -<能推出05x <<,故“250x x -<”是“|1|1x -<”的必要不充分条件,故选B 。
本题考查充分必要条件,解题关键是化简不等式,由集合的关系来判断条件。
4.【答案】B【分析】根据程序框图,逐步写出运算结果。
【详解】1,2S i ==→11,1225,3j S i ==+⋅==8,4S i ==,结束循环,故输出8。
故选B 。
解答本题要注意要明确循环体终止的条件是什么,会判断什么时候终止循环体. 5.【答案】D【分析】只需把4AB OF =用,,a b c 表示出来,即可根据双曲线离心率的定义求得离心率。
【详解】抛物线24y x =的准线l 的方程为1x =-,双曲线的渐近线方程为by x a=±, 则有(1,),(1,)b b A B a a ---,∴2b AB a =,24b a =,2b a =,∴c e a ===故选D 。
本题考查抛物线和双曲线的性质以及离心率的求解,解题关键是求出AB 的长度。
6.【答案】A【分析】利用10,,12等中间值区分各个数值的大小。
【详解】551log 2log 2a =<<,0.50.5log 0.2log 0.252b =>=,10.200.50.50.5<<,故112c <<,所以a c b <<。
故选A 。
本题考查大小比较问题,关键选择中间量和函数的单调性进行比较。
7.【答案】C【分析】只需根据函数性质逐步得出,,A ωϕ值即可。
【详解】因为()f x 为奇函数,∴(0)sin 0=,0,f A k k ϕϕπ==∴=,0ϕ=;又12()sin ,2,122g x A x T πωπω=∴==2ω=,2A =,又()4g π=∴()2sin 2f x x =,3()8f π=故选C 。
本题考查函数的性质和函数的求值问题,解题关键是求出函数()g x 。
8.【答案】C【分析】先判断0a ≥时,2220x ax a -+≥在(,1]-∞上恒成立;若ln 0x a x -≥在(1,)+∞上恒成立,转化为ln xa x≤在(1,)+∞上恒成立。
【详解】∵(0)0f ≥,即0a ≥,(1)当01a ≤≤时,2222()22()22(2)0f x x ax a x a a a a a a a =-+=-+-≥-=->, 当1a <时,(1)10f =>,故当0a ≥时,2220x ax a -+≥在(,1]-∞上恒成立; 若ln 0x a x -≥(1,)+∞上恒成立,即ln xa x≤在(1,)+∞上恒成立, 令()ln x g x x=,则2ln 1'()(ln )x g x x -=,当,x e >函数单增,当0,x e <<函数单减, 故max ()()g x g e e ==,所以a e ≤。
