过氧化环己酮[含量≤91%,含水≥9%]安全技术说明书MSDS
实验室试剂清单

序号1234567891011121314151617181920212223242526272829303132333436373839404142434445464748410实验室试剂清单49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 7374 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117118 119 120 121122123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148149 150 151 152 153 154 155 156 157 158 159 160 161 162 163164 165 166 167 168 169 170 171 172 173 174 175 176 177 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253254 255 256 257 258 259 260261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299300 302 303 304 305337339340341342343344345346347348349350351352353354355356357359360361362363364365366367368369370371372373374375376377378379380381382383384385386388389390391392393394395396397398399400401402403404405406407409440442443444445446447448449450451452453454455456457459460461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502503 504 505 506 507 508 509 510511 512 513 514 515 516 517 518 519520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553554 555 556 557 558 559 560 561 562563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606607 608 609 610 611 612 613615616617618619620621622623624625626627628629630631632633634635636637638639640641643644645646647648649650651652653654655656657658659660661662663664665667对甲砜基苯基丝氨酸乙酯668偏三甲基苯酸酐Trimellitic Anhydride669雷米普利母液Ramiprilat670双酚Z671抗氧剂(T501)672麝香草酚Thymol673NaSCN Sodium thiocyanate674胆酸钠Sodium tauroglycocholate675柱层析硅胶676邻硝基苯乙酮,对硝基苯677邻甲基苯胺o-Toluidine6782,4-二氯酚2,4-Dichlorophenol679喹啉黄Quinoline Yellow680对苯二甲酸Terephthalic acid681异长叶烷酮Isolongifolone6822,4-二硝基苯酚2,4-Dinitrophenol683十溴联苯醚Decabromodiphenyl oxide684BOPTA未精制浓缩物685苯酚CaO686DSD酸687二乙基羟羧胺688二甲基亚砜(DMSO)Dimethyl sulfoxide6902,6-二甲基吡啶2,6-Lutidine700甘油石酸酯701碘甲磺隆钠盐702甲基四氢苯酐703氯化亚砜Thionyl chloride704猪胆膏705白藜芦醇Resveratrol706100g明胶 浓HCl(37%)200707苯酚钠Sodium benzenolate708P2O5吸水成H3PO47092,6-萘二磺酸,2,7-萘二7102,6-二甲基吡啶2,6-Lutidine711松香Rosin712喹啉Quinoline713三氯化硼二水合物714紫胶红色素LACCAIC ACID715甲基硅油SILICONE OV-101716肉桂油Cinnamon oil717薄荷醇乳酸酯(-)-Menthyl lactate718乙酸柏木酯Cedryl acetate719双酚A Bisphenol A720莪术油ZEDOARY OIL721桉叶油Eucalyptus oil722一缩二乙二醇(三甘醇)Diethylene glycol7233,4-甲基吡啶母液724青蒿蜡725对甲硫基苯酚4-(Methylthio)phenol726松根油727吡啶Azabenzene728偏三甲基苯酸酐729乙醇胺和三乙烯二胺730 731 732 733 734 735 736 737 738 739740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781782 783 784 785 786 787 788 789 790 791 792 793 794795 796 797 798 799800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833834 835 836 837 838 839 840 841 842 843844清单A区上层AR A区上层AR A区上层AR A区上层A区上层A区上层AR A区上层AR500ml/瓶A区上层A区上层A区上层A区上层A区上层A区上层A区上层A区上层A区上层A区上层AR500ml A区上层500ml A区上层AR500ml A区上层A区上层A区上层CP500ml A区上层CP A区上层A区上层A区上层CP A区上层CP A区上层AR A区上层生化试剂A区上层A区上层AR A区上层CP A区上层AR A区上层AR100g A区上层AR100g A区上层CP250g A区上层生化试剂A区上层AR A区下层>98%A区下层A区下层A区下层A区下层A区下层A区下层AR A区下层AR A区下层AR A区下层 A区下层AR A区下层A区下层A区下层AR A区下层A区下层AR A区下层85-90%A区下层A区下层A区下层0.85A区下层A区下层AR A区下层AR A区下层AR A区下层A区下层A区下层AR A区下层A区下层A区下层A区下层CP A区下层0.99A区下层AR B区上层AR B区上层AR B区上层CP B区上层AR B区上层B区上层CP B区上层AR B区上层AR B区上层B区上层B区上层500g B区上层B区上层CP B区上层CP B区上层B区上层AR B区上层B区上层B区上层AR B区上层AR B区上层AR B区上层AR B区上层AR B区上层AR B区上层B区上层B区上层B区上层B区上层500g B区上层500g B区上层500g B区上层B区上层AR B区上层AR B区上层CP500g B区上层B区上层AR500g B区上层B区上层500g B区上层AR500g B区上层500g B区上层B区上层CP500g B区上层B区下层B区下层B区下层500g B区下层500g B区下层500g B区下层500g B区下层四厂昆山分厂500g B区下层500g B区下层500g B区下层500g B区下层工业级500g B区下层B区下层500g B区下层CP100g B区下层500g B区下层AR25g B区下层B区下层AR500g B区下层B区下层AR B区下层B区下层AR500g B区下层AR500g B区下层AR500g B区下层AR500g B区下层AR500g B区下层AR500g B区下层B区下层B区下层AR B区下层B区下层AR500g B区下层AR B区下层AR B区下层AR500g B区下层B区下层500g B区下层B区下层AR500g B区下层AR500g B区下层B区下层AR500g B区下层B区下层AR500g B区下层AR500g B区下层CP500ml C上层500ml C上层500ml C上层C上层500ml C上层AR500ml C上层CP500g C上层250g C上层AR500ml C上层C上层CP500ml C上层25g C上层C上层AR500ml C上层C上层AR500ml C上层AR500ml C上层AR500ml C上层AR500ml C上层C上层500ml C上层AR500ml C上层AR500mlX3C上层AR500ml C上层CP500ml C上层CP500ml C上层CP500ml C上层AR500mlX2C上层AR500ml C上层CP500ml C上层CP100g C上层CP100g X2C上层CP100g C上层CP250ml C上层CP250ml C上层CP250ml C上层CP250ml C上层AR250ml C上层AR250g C上层CP250ml C上层CP100g C上层CP1000g C上层CP100g C上层C上层AR250g C上层CP250ml C上层CP250ml C上层CP250ml C上层CP250ml C上层CP100g C上层AR25g C上层C上层C上层100g C上层100g C上层AR50ml C上层CP 98%C上层AR250ml C上层CP100g C上层AR500ml C上层C上层CP500ml C下层CP500mlX4C下层CP500ml C下层CP500ml C下层AR500ml C下层CP500ml C下层CP500ml C下层CP500ml C下层C下层C下层C下层AR500ml C下层C下层AR500ml C下层AR C下层C下层AR500ml C下层CP250ml C下层AR250ml C下层CP250ml C下层CP100g X 2C下层CP100ml C下层AR100g C下层AR100g C下层AR100g C下层CP100ml C下层CP100ml C下层CP500ml C下层C下层0.91C下层0.9850g C下层CP25g C下层CP250ml C下层CP100g C下层500g*2C下层AR500ml C下层AR500g D区上层500g D区上层AR500g D区上层D区上层AR500ml D区上层AR250ml D区上层D区上层AR500g D区上层D区上层AR500g D区上层AR500g D区上层CP100ml D区上层AR500g D区上层AR100g D区上层0.99100g D区上层500g D区上层500ml D区上层D区上层CP25g D区上层100g D区上层D区下AR500ml D区下CP500g D区下AR500ml D区下D区下D区下500g D区下D区下100g D区下 AR500g D区下AR500g D区下500g D区下 AR500g D区下500g D区下 AR500ml D区下AR500g D区下CP250ml D区下100ml D区下 CP100ml D区下 CP500ml E区下层CP500ml E区下层500g E区下层500ml E区下层500ml E区下层E区下层AR500mlX2E区下层E区下层AR500mlX2E区下层500g E区下层500ml E区下层500ml E区下层振兴化工一厂500ml E区下层100mlX2E区下层CP100g E区下层E区下层500g E区下层500mlX2E区下层CP500ml E区下层250g E区下层CP500g E区下层CP500ml E区下层CP E区下层100g E区下层CP E区下层E区下层CP500ml E区下层AR500ml E区下层CP500mlX2E区下层AR500mlX2E区下层AR500ml E区下层AR500ml E区下层AR500ml E区下层AR500ml E区下层AR500ml E区下层AR500ml E区下层E区下层E区上层99%500g E区上层AR E区上层CP100g E区上层CP500g E区上层AR500ml E区上层CP500ml E区上层500g E区上层CP500ml E区上层500ml E区上层CP500ml E区上层CP500ml E区上层AR500ml E区上层CP500g E区上层CP100g E区上层98%100g E区上层500g E区上层500mlX2E区上层CP500ml E区上层E区上层CP250ml E区上层CP E区上层化学试剂公司500mlX2E区上层AR E区上层CP500ml E区上层AR500ml E区上层AR500ml E区上层E区上层AR500ml E区上层CP500ml E区上层AR500ml E区上层CP500ml E区上层AR500ml E区上层CP500ml E区上层CP250ml E区上层CP500ml E区上层AR500ml E区上层AR500ml E区上层CP500g E区上层AR500ml E区上层AR500ml E区上层AR500ml E区上层AR500ml E区上层CP250ml E区上层CP500g E区上层98%100g E区上层CP500ml E区上层AR500ml E区上层E区上层CP500mlX2F区上层CP100ml F区上层CP100ml F区上层AR500g F区上层500ml F区上层AR500gX2F区上层AR500g F区上层AR250g F区上层AR500g F区上层CP500ml F区上层500g F区上层CP500g F区上层CP250g F区上层F区上层AR500g F区上层100ml F区上层F区上层F区上层F区上层F区上层F区上层AR500g F区下层F区下层F区下层F区下层AR500g F区下层F区下层CP250g F区下层AR500g F区下层AR500g F区下层CP500g F区下层AR500g F区下层AR500g F区下层CP500g F区下层AR500g F区下层AR500g F区下层CP500g F区下层CP500g F区下层AR500g F区下层AR500g F区下层AR500g F区下层AR500g F区下层AR500gX2F区下层CP500ml F区下层500ml F区下层CP500g F区下层CP500g F区下层AR500g F区下层AR500g F区下层AR500g F区下层AR500g F区下层AR250gX2F区下层CP100gX2F区下层CP500ml F区下层G区上层G区上层G区上层G区上层G区上层G区上层G区上层G区上层G区上层G区上层G区上层G区上层AR500g*2G区上层AR500ml G区上层500ml G区上层AR500ml G区上层500ml G区上层G区上层AR250g G区下层500g G区下层G区下层AR250g G区下层98%25g G区下层CP25g G区下层25%50ml G区下层10%50ml G区下层99%100ml G区下层99%100ml G区下层97%25ml G区下层98%25g G区下层20%100ml G区下层99%25ml G区下层G区下层CP500g G区下层200g G区下层AR500g G区下层G区下层G区下层G区下层1000g A区木板架99%500g A区木板架98%1000g A区木板架科技开发公司500ml A区木板架AR100ml A区木板架AR500mlX2A区木板架AR500mlX2A区木板架AR500g A区木板架化工有限公司A区木板架98%500g A区木板架AR250g A区木板架75%100g A区木板架A区木板架500ml A区木板架99.50%250g A区木板架AR500ml A区木板架AR500ml A区木板架AR500ml A区木板架AR500ml A区木板架AR500ml A区木板架AR500ml A区木板架AR500ml A区木板架65%-68% AR500ml A区木板架95% AR500ml A区木板架AR500ml B区木板架AR500ml B区木板架15%500mlX2B区木板架250ml B区木板架AR500ml B区木板架B区木板架AR500g B区木板架AR500gX3B区木板架AR500g B区木板架AR500g B区木板架AR500g B区木板架AR500g B区木板架AR500g B区木板架AR500g B区木板架B区木板架B区木板架500g B区木板架500ml B区木板架98%250g C区架子C区架子98.50%100g C区架子学试剂有限公司25g C区架子100g C区架子99%100g C区架子98%25g C区架子99%25g C区架子AR50g C区架子99%25g C区架子98%5g C区架子C区架子C区架子C区架子CP100ml C区架子98%25g C区架子99%100g C区架子99%100g C区架子99%25g C区架子98%5g C区架子25ml C区架子99%100ml C区架子99%100ml C区架子98%25g C区架子99%100g C区架子C区架子98%25g C区架子试剂有限公司25ml C区架子100g C区架子99%100g C区架子99%25ml C区架子100g C区架子BR100g C区架子98%25g C区架子D区木板架D区木板架D区木板架D区木板架D区木板架AR500ml D区木板架D区木板架D区木板架星化工有限公司1kg D区木板架D区木板架AR500mlX3D区木板架学试剂有限公司AR500ml D区木板架AR500ml D区木板架AR500ml D区木板架AR501ml D区木板架AR500ml D区木板架AR500ml D区木板架D区木板架D区木板架AR500ml D区木板架AR500ml D区木板架AR500ml D区木板架75%D区木板架500ml D区木板架95%25g D区木板架99%100g D区木板架AR500ml D区木板架AR500ml D区木板架E区木板架E区木板架97.02%200g E区木板架市新华化工厂E区木板架E区木板架E区木板架81.55%E区木板架E区木板架CR500g E区木板架50%*2E区木板架E区木板架E区木板架E区木板架*2E区木板架E区木板架E区木板架E区木板架≥89%E区木板架500g E区木板架E区木板架AR500g E区木板架E区木板架E区木板架85%E区木板架E区木板架E区木板架E区木板架E区木板架AR250g E区木板架E区木板架E区木板架20%E区木板架E区木板架93%E区木板架化学有限公司E区木板架E区木板架25g E区木板架80%100g E区木板架X2E区木板架93%E区木板架E区木板架250ml E区木板架E区木板架E区木板架10%E区木板架85%50g E区木板架85%500g E区木板架E区木板架E区木板架E区木板架75%E区木板架E区木板架E区木板架E区木板架E区木板架X2E区木板架E区木板架阳生化试剂厂E区木板架研究有限公司E区木板架50%X2E区木板架75-80%E区木板架E区木板架50%,80%FG大木架FG大木架FG大木架X2FG大木架FG大木架75%FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架试剂级FG大木架500g FG大木架400g FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架化工有限公司FG大木架FG大木架1000g FG大木架60%FG大木架100-200目FG大木架FG大木架50%FG大木架70%FG大木架70%FG大木架96%FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架60%FG大木架FG大木架FG大木架91%X2FG大木架1kg FG大木架FG大木架FG大木架20%FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架X2FG大木架FG大木架FG大木架FG大木架500CS FG大木架FG大木架99%FG大木架FG大木架FG大木架FG大木架80%FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架80%FG大木架FG大木架AR 99%FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架FG大木架试剂有限公司100g B抽屉AR500g B抽屉B抽屉B抽屉试剂有限公司100g B抽屉AR100g B抽屉AR500g B抽屉B抽屉CP B抽屉AR100g B抽屉AR100g B抽屉CP100g B抽屉CP B抽屉CP B抽屉CP25g B抽屉B抽屉CP100g B抽屉250g B抽屉CP25g B抽屉100g B抽屉试剂有限公司25g B抽屉25g B抽屉25g B抽屉25g B抽屉B抽屉B抽屉B抽屉5g B抽屉B抽屉6g B抽屉B抽屉B抽屉B抽屉实业有限公司B抽屉5g B抽屉B抽屉B抽屉10g B抽屉B抽屉B抽屉B抽屉AR25g B抽屉B抽屉10g B抽屉B抽屉B抽屉50g B抽屉B抽屉B抽屉B抽屉B抽屉B抽屉B抽屉B抽屉B抽屉99.80%100g F抽屉99.90%25g F抽屉99.90%100g F抽屉99.90%50g F抽屉AR F抽屉98%25g G抽屉1香料有限公司G抽屉125g G抽屉125g G抽屉1G抽屉1G抽屉1AR25g G抽屉1G抽屉1AR5g G抽屉1生物有限公司100g G抽屉197%G抽屉1AR5g G抽屉1G抽屉125g G抽屉125g G抽屉125g G抽屉1G抽屉1AR10g G抽屉1G抽屉125g G抽屉125g G抽屉1CP25ml G抽屉1G抽屉1G抽屉199%25ml G抽屉1G抽屉125g G抽屉125g G抽屉180%G抽屉125g G抽屉1试剂有限公司10g G抽屉1G抽屉110g G抽屉1AR25g G抽屉110g G抽屉1G抽屉1AR25g G抽屉1G抽屉125g G抽屉1G抽屉1G抽屉1G抽屉1科技开发中心G抽屉1G抽屉1G抽屉2G抽屉2G抽屉2G抽屉2G抽屉2G抽屉2G抽屉2G抽屉2G抽屉2G抽屉2G抽屉2G抽屉2。
N,N-二乙基间甲苯胺91-67-8

h) 蒸发速率
无数据资料
i) 可燃性(固体,气体) 无数据资料
j) 高的/低的燃烧性或爆炸性限度 无数据资料
k) 蒸气压
无数据资料
l) 相对蒸气密度
无数据资料
m) 相对密度
0.922 g/cm3 at 25 °C (77 °F)
n) 溶解性 / 水溶性 无数据资料
o) 辛醇/水分配系数的对数值 log Pow: 3.618
无数据资料
11 毒理学资料
11.1 毒理学影响的信息
急性毒性 半数致死浓度( LC50) 吸入 - 大鼠 - 4 h - 4,660 mg/m3 备注 : 感觉器官和特殊感觉(鼻、眼、耳和 味觉):嗅觉:其他改变。 行为的:震颤。 肺,胸,或者呼吸系统:其他变化 亚 急性毒性 无数据资料 刺激性(总述) 无数据资料 皮肤腐蚀/刺激 无数据资料 严重眼损伤 / 眼刺激 无数据资料
9 理化特性
9.1 基本的理化特性的信息
a) 外观与性状
形状 : 无数据资料
颜色 : 无数据资料
b) 气味
无数据资料
c) 气味临界值
无数据资料
d) pH值
无数据资料
e) 熔点/凝固点
无数据资料
f) 起始沸点和沸程
231 - 232 °C (448 - 450 °F) - lit.
g) 闪点
100 °C (212 °F) - closed cup
14 运输信息
14.1 UN编号
欧洲陆运危规 : 无数据资料
国际海运危规 : 无数据资料
国际空运危规 : 无数据资料
14.2 联合国(UN)规定的名称
欧洲陆运危规:TOLUIDINES,LIQUID 国际海运危规:TOLUIDINES,LIQUID 国际空运危规:Toluidines,liquid
ASCII码值对照表

最全ASCII码对照表ASCII码值对照表ASCII码值ASCII码中英文对照表0010 0000 32 20 空格0010 0001 33 21 !0010 0010 34 22 "0010 0011 35 23 #0010 0100 36 24 $0010 0101 37 25 %0010 0110 38 26 &0010 0111 39 27 '0010 1000 40 28 (0010 1001 41 29 )0010 1010 42 2A *0010 1011 43 2B +0010 1100 44 2C ,0010 1101 45 2D -0010 1110 46 2E .0010 1111 47 2F /0011 0000 48 30 00011 0001 49 31 10011 0010 50 32 20011 0011 51 33 30011 0100 52 34 40011 0101 53 35 50011 0110 54 36 60011 0111 55 37 70011 1000 56 38 80011 1001 57 39 90011 1010 58 3A :0011 1011 59 3B ;0011 1100 60 3C <0011 1101 61 3D =0011 1110 62 3E >0011 1111 63 3F ?0100 0000 64 40 @0100 0001 65 41 A0100 0010 66 42 B0100 0011 67 43 C0100 0100 68 44 D0100 0101 69 45 E0100 0110 70 46 F0100 0111 71 47 G0100 1000 72 48 H0100 1001 73 49 I0100 1010 74 4A J0100 1011 75 4B K0100 1100 76 4C L0100 1101 77 4D M0100 1110 78 4E N0100 1111 79 4F O0101 0000 80 50 P0101 0001 81 51 Q0101 0010 82 52 R0101 0011 83 53 S0101 0100 84 54 T0101 0101 85 55 U0101 0110 86 56 V0101 0111 87 57 W0101 1000 88 58 X0101 1001 89 59 Y0101 1010 90 5A Z 0101 1011 91 5B [ 0101 1100 92 5C \ 0101 1101 93 5D ] 0101 1110 94 5E ^ 0101 1111 95 5F _ 0110 0000 96 60 ` 0110 0001 97 61 a 0110 0010 98 62 b 0110 0011 99 63 c 0110 0100 100 64 d 0110 0101 101 65 e 0110 0110 102 66 f 0110 0111 103 67 g 0110 1000 104 68 h 0110 1001 105 69 i 0110 1010 106 6A j 0110 1011 107 6B k 0110 1100 108 6C l 0110 1101 109 6D m 0110 1110 110 6E n 0110 1111 111 6F o 0111 0000 112 70 p 0111 0001 113 71 q 0111 0010 114 72 r 0111 0011 115 73 s 0111 0100 116 74 t 0111 0101 117 75 u 0111 0110 118 76 v 0111 0111 119 77 w 0111 1000 120 78 x 0111 1001 121 79 y 0111 1010 122 7A z 0111 1011 123 7B { 0111 1100 124 7C | 0111 1101 125 7D } 0111 1110 126 7E ~ 0111 1111 127 7F DEL (delete)删除ESC键 VK_ESCA PE (27)回车键: VK_RETU RN (13) TAB键: VK_TAB(9)Caps Lock键: VK_CAPI TAL (20) Shift键: VK_SHIF T ()Ctrl键: VK_CONT ROL (17) Alt键:VK_MENU (18)空格键: VK_SPAC E (/32)退格键: VK_BACK (8)左徽标键: VK_LWIN (91)右徽标键: VK_LWIN (92)鼠标右键快捷键:VK_APPS (93) Insert键: VK_INSE RT (45) Home键: VK_HOME (36) Page Up: VK_PRIO R (33) PageDow n: VK_NEXT (34)End键: VK_END(35) Delete键: VK_DELE TE (46)方向键(←): VK_LEFT (37)方向键(↑):VK_UP (38)方向键(→): VK_RIGH T (39)方向键(↓): VK_DOWN (40)F1键:VK_F1 (112)F2键:VK_F2 (113)F3键:VK_F3 (114)F4键:VK_F4 (115)F5键:VK_F5 (116)F6键:VK_F6 (117)F7键:VK_F7 (118)F8键:VK_F8 (119)F9键:VK_F9 (120)F10键: VK_F10(121)F11键: VK_F11(122)F12键: VK_F12(123)Num Lock键:VK_NUML OCK (144)小键盘0: VK_NUMP AD0 (96)小键盘1: VK_NUMP AD0 (97)小键盘2: VK_NUMP AD0 (98)小键盘3: VK_NUMP AD0 (99)小键盘4: VK_NUMP AD0 (100)小键盘5: VK_NUMP AD0 (101)小键盘6: VK_NUMP AD0 (102)小键盘7: VK_NUMP AD0 (103)小键盘8: VK_NUMP AD0 (104)小键盘9: VK_NUMP AD0 (105)小键盘.: VK_DECI MAL (110)小键盘*: VK_MULT IPLY (106)小键盘+: VK_MULT IPLY (107)小键盘-: VK_SUBT RACT (109)小键盘/: VK_DIVI DE (111)Pause Break键: VK_PAUS E (19)ScrollLock键: VK_SCRO LL (145)注意:1.在ASCII码中,有4组字符:一组是控制字符,如LF,CR等,其对应ASCI I码值最小;第2组是数字0~9,第3组是大写字母A~Z,第4组是小写字母a~z。
数论之余数三大定理

第十四章数论之余数三大定理概念一般地,如果a是整数,b是整数(b旳)若有a H b=q……r,也就是a 二b旳+ r, 0孕v b ;我们称上面的除法算式为一个带余除法算式。
这里:⑴当r 0时:我们称a可以被b整除,q称为a除以b的商或完全商(2)当r 0时:我们称a不可以被b整除,q称为a除以b的商或不完全商三大余数定理1. 余数的加法定理a与b的和除以c的余数,等于a,b分别除以c的余数之和,或这个和除以c的余数。
2. 余数的乘法定理a与b的乘积除以c的余数,等于a,b分别除以c的余数的积,或者这个积除以c 所得的余数。
3. 同余定理若两个整数a、b被自然数m除有相同的余数,那么称a、b对于模m同余,用式子表示为:a M b ( mod m ),左边的式子叫做同余式。
同余式读作:a同余于b,模m。
由同余的性质,我们可以得到一个非常重要的推论:若两个数a,b除以同一个数m得到的余数相同,则a,b的差一定能被m 整除用式子表示为:如果有aM) ( mod m ),那么一定有a-b = mk,k是整数,即m|(a—b)例题1. 用某自然数a去除1992,得到商是46,余数是r,求a和r。
2. 甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数。
3. 一个两位数除310,余数是37,求这样的两位数。
4. 有两个自然数相除,商是17,余数是13,已知被除数、除数、商与余数之和为2113,则被除数是多少?5. 用一个自然数去除另一个自然数,商为40,余数是16.被除数、除数、商、余数的和是933,求这2个自然数各是多少?6. (真题)三个不同的自然数的和为2001,它们分别除以19,23,31所得的商相同,所得的余数也相同,这三个数是_______ ,______ , _____ 。
_7. 一个自然数,除以11时所得到的商和余数是相等的,除以9时所得到的商是余数的3倍,这个自然数是________ 。
2022-CSP-S(提高组)认证第一轮试题详细解析

2022CSP-S提高级第一轮认证C++语言试题考生注意事项:●试题纸共满分100分。
请在答题纸上作答,写在试题纸上的一律无效。
●不得使用任何电子设备(如计算器、手机、电子词典等)或查阅任何书籍资料。
一、单项选择题(共15题,每题2分,共计30分;每题有且仅有一个正确选项)1.在Linux系统终端中,用于切换工作日录的命令为()。
A.lsB.cdC.CPD.all答案:B ls命令用于显示指定工作目录下之内容(列出目前工作目录所含之文件及子目录)。
cd命令用于切换当前工作目录。
cp命令主要用于复制文件或目录。
all和Linux系统并无什么关联。
2.你同时用time命令和秒表为某个程序在单核CPU的运行计时。
假如time命令的输出如下:real0m30.721suser0m24.579ssys0m6.123s以下最接近秒表计时的时长为()。
A.30sB.24sC.18sD.6s答案:A Linux time命令用于统计给定命令所花费的总时间。
它报告了以下几个关键指标:实际时间(Real Time):从命令行开始执行到运行终止的实际消逝时间。
用户CPU时间(User CPU Time):命令行执行完成时用户模式下CPU消耗的总时间。
系统CPU时间(System CPU Time):命令行执行完成时内核模式下CPU消耗的总时间。
Real Time>User CPU Time+System CPU Time3.若元素a、b、c、d、e、f依次进栈,允许进栈、退栈操作交替进行,但不允许连续三次退栈操作,则不可能得到的出栈序列是()。
A.d ce b f aB.cb d a efC.b ca e f dD.af e d cb答案:D A选项abcd先依此进栈,d c再出栈,e进栈,e b出栈,f进栈后f a出栈。
BC符合题目进栈退栈操作,D连续退栈操作远超三次4.考虑对n个数进行排序,以下最坏时间复杂度低于O(n2)的排序方法是()。
新概念英语第二册Lesson91(共23页)

5.失去理智 out of one's wits
6.无意中遇到,碰上 bump into
7.海底下 深海底 under the sea
8.某物的供应 supply of sth.
9.缺少;不存在 absence of
10.结果是
as a result
invent 和discover的用法区别:
• invent 意为“发明”, 是发明或创造不曾存在 的东西。
2. Can you _m_a_k_e_o_ut_what they are talking about?
3. I can’t ___m_a_ke_o_u_t__the boss’s handwriting.
4.mJakaenheerisouatngry again. Sometimes I can’t _______at allm. Hakeeromutoods change quickly.
L91 Three men in a basket
齐绪友
1.他把身份证丢了,结果上不了火车
He lost his ID card, as a result, he can't board a train.
2.她被门外的枪声吓得惊慌失措。
She was frightened out of wits by the gunshot outside door.
离开加来后,那艘船便驶往多佛。
动词 make 的一些固定短语
(1)make out “辨出”、“听出”,“理解”、“弄清” : I can't make out what this picture is about. 我看不出这幅画的意思。
Can you make out what the child wants? 你能弄清那孩子想要什么吗?
加工中心G代码

CNC加工中心G代码:G00定位G01直线切削G02顺时针方向圆弧切削G03逆时针方向圆弧切削G04暂停指令G09正确停止检测G10补正设定G12顺时针方向圆周切削G13逆时针方向圆周切削G15极座标系统取消G16极座标系统设定G17XY平面设定G18XZ平面设定G19YZ平面设定G20英制单位设定G21公制单位设定G22软体极限设定G23软体极限设定取消G27机械原点复归检测G28自动经中间点复归机械原点G29自动从参考点复归G30自动复归到第二原点G40刀具半径补正取消G41刀具半径偏左补正G42刀具半径偏右补正G43刀具长度沿正向补正G44刀具长度沿负向补正G49刀具长度补正取消G45刀具位置补正增加G46刀具位置补正减少G47刀具位置补正两倍增加G48刀具位置补正两倍减少G50比例功能取消OFFG51比例功能设定ONG52回复到基本座标系统G53回复到机械座标系统G54第一工件座标系统G55第二工件座标系统G56第三工件座标系统G57第四工件座标系统G58第五工件座标系统G59第六工件座标系统G60 外部补正G70圆周等分段循环G71圆周分段循环G72直线分段循环G73高速喙钻循环G74左旋牙切削循环G76精搪孔循环G77反面搪孔循环G80固定循环取消G81钻孔循环G82沉头孔加工循环G83啄钻循环G84右旋牙切削循环G85搪孔循环G86搪孔循环G87搪孔循环G88搪孔循环G89搪孔循环G90绝对指令座标值设定G91增量指令座标值设定G92绝对程式零点设定G94每分钟进给量设定mm/minG95每转进给给设定mm/revG98固定循环,刀具复归到起始点G99固定循环,刀具复归到R点M04主轴逆时针旋转M05主轴停止M06刀具交换M07雾化冷却液开启M08冷却液开启M09冷却液关启M10工作台(B轴)锁住M11工作台(B轴)松开M13主轴顺时针转动及加切削液M14主轴逆时针转动及加切削液M15正方向运动M16负方向运动M19主轴定位M30程式结束记忆体回归M90程式中断取消M91程式中断设定M92多段暂存取消M93多段暂存设定M94镜像投影工能取消M95镜像投影工能设定M96刀具补正圆弧转角模式M97刀具补正交角转角模式M98副程式呼叫M99副程式结束代码名称-功能简述G00------快速定位G01------直线插补G02------顺时针方向圆弧插补G03------逆时针方向圆弧插补G04------定时暂停G05------通过中间点圆弧插补G07------Z 样条曲线插补G08------进给加速G09------进给减速G20------子程序调用22------半径尺寸编程方式G220-----系统操作界面上使用G23------直径尺寸编程方式G230-----系统操作界面上使用G24------子程序结束25------跳转加工G26------循环加工G30------倍率注销G31------倍率定义G32------等螺距螺纹切削,英制G33------等螺距螺纹切削,公制G53,G500-设定工件坐标系注销G54------设定工件坐标系一G55------设定工件坐标系二G56------设定工件坐标系三G57------设定工件坐标系四G58------设定工件坐标系五G59------设定工件坐标系六G60------准确路径方式G64------连续路径方式G70------英制尺寸寸G71------公制尺寸毫米G74------回参考点(机床零点)G75------返回编程坐标零点G76------返回编程坐标起始点G81------外圆固定循环G331-----螺纹固定循环G90------绝对尺寸G91------相对尺寸G92------预制坐标G94------进给率,每分钟进给G95------进给率,每转进给功能详解G00—快速定位格式:G00 X(U)__Z(W)__ 说明:(1)该指令使刀具按照点位控制方式快速移动到指定位置。
线切割G代码
Y
A1
A
O
X
Y
A
O
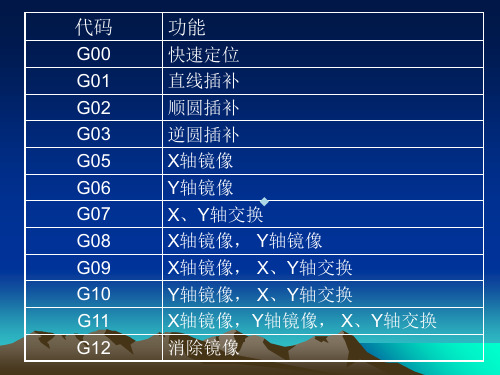
X 8——X轴镜像, Y轴镜像,函数关系式:X=X, Y=-Y;G08=G05+G06。
• G09——X轴镜像, X、Y轴交换;即 G09=G05+G07。
• G10——Y轴镜像, X、Y轴交换;即 G10=G06+G07。
• G11——X轴镜像, Y轴镜像, X、Y轴交换;即 G11=G05+G06+G7。
• 书写格式:G92 X__Y__
• 例4 ,分别采用增量坐标系和绝对坐标系编 写下图程序。
Y 30 20 10
0 10 20 30 40 X
• G90编程 N01 G92 X0 Y0; N02 G01 X1000 Y0; N03 G01 X1000 Y20000; N04 G02 X30000 Y20000 I10000 J0; N05 G01 X30000 Y0; N06 G01 X0 Y0;
• G00为快速定位指令:
在线切割机床不放电情况下,使指定的某轴以最 快的速度移动到指定位置。
1. 书写格式:G00 X__Y__
2. 注意:如果程序中指定了G01,G02等指令,
则G00无效,有些系统将这一常用命令作为外部
功能使用。
• G01 为直线插补指令
1. 书写格式:G01 X__Y__
• 锥度加工指令G50、 G51、 G52
– G51:左偏,沿着电极丝前进的方向看,电极 丝上段在底平面加工轨迹的左边,程序格式为: G51 A ____
– G52:右偏,沿着电极丝前进的方向看,电极 丝上段在底平面加工轨迹的右边,程序格式为: G52 A ____
– G50:取消锥度加工指令,程序格式为:
CNC代码

G08/G09—进给加速/减速 格式:G08 说明:它们在程序段中独自占一行,在程序中运行到这一段时,进给速度将增加10%, 如要增加20%则需要写成单独的两段。
G22(G220)—半径尺寸编程方式 格式:G22 说明:在程序中独自占一行,则系统以半径方式运行,程序中下面的数值也是 以半径为准的。 G23(G230)—直径尺寸编程方式 格式:G23 说明:在程序中独自占一行,则系统以直径方式运行,程序中下面的数值也是 以直径为准的。 G25—跳转加工 格式:G25 LXXX 说明: 当程序执行到这段程序时,就转移它指定的程序段。(XXX为程序段号)。 G26—循环加工 格式:G26 LXXX QXX 说明:当程序执行到这段程序时,它指定的程序段开始到本 段作为一个循环体, 循环次数由Q后面的数值决定。
G30—倍率注销 格式:G30 说明:在程序中独自占一行,与G31配合使用,注销G31的功能。
G31—倍率定义 格 式:G31 F_____
G32—等螺距螺纹加工(英制)
G33—等螺距螺纹加工(公制) 格式:G32/G33 X(u)____Z(w)____F____ 说明:(1)X、Z为终点坐标值,F为螺距 (2)G33/G32只能加工单刀、单头螺纹。 (3)X值的变化,能加工锥螺纹 (4)使用该指令时,主轴的转速不能太高,否则刀具磨损较大。
G91—增量方式编程 格式:G91 说明:G91编入程序时,之后所有坐标值均以前一个坐标位置作为起点来计算 运动的编程值。在下一段坐标系中,始终以前一点作为起始点来编程。 例: N0010 G91 G92 X20 Z85 N0020 G01 X20 Z-10 F100 N0030 Z-20 N0040 X20 Z-15 N0050 M02
辽宁省名校联盟2023届高考模拟调研卷数学(二)

2023年普通高等学校招生全国统一考试模拟试题数学(二)本试卷共4页,22小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹钢笔或签字笔将自己的姓名、准考证号、考场号和座位号填写在答题纸上.将条形码横贴在答题纸“贴条形码区”.2.作答选择题时,选出每小题答案后,用2B 铅笔把答题纸上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题纸各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题纸的整洁.考试结束后,将试卷和答题纸一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知()1i 75i z +=+,则z = A.6i − B.6i +C.32i −D.12i −2.已知集合{}2780U x xx =−−≤,{}0,1,2A =,{}2,1,0,1,2,3,4B =−−,则()U A B ∩=ð A.{}0,1,2B.{}3,4C.{}1,3,4−D.{}2,1,3,4−−3.下列函数不是偶函数的是A.()3sin 2f x x π=+B.()22x x f x −=+C.()21xxf x x =+−D.())lnf x x x =−4.使:0p x ∀>,4x a x+≥的否定为假命题的一个充分不必要条件是 A.4a ≥B.4a ≤C.2a ≥D.2a ≤5.某市要建立步行15分钟的核酸采样点,现有9名采样工作人员全部分配到3个采样点,每个采样点至少分配2人,则不同的分配方法种数为 A.1918B.11508C.12708D.186.石碾子是我国电气化以前的重要粮食加工工具.它是依靠人力或畜力把谷子、稻子等谷物脱壳或把米碾碎成碴子或面粉的石制工具.如图,石碾子主要由碾盘、碾滚和碾架等组成,一个直径为60cm 的圆柱形碾滚的最外侧与碾柱的距离为100cm ,碾滚最外侧正上方为点A ,若人推动拉杆绕碾盘转动一周,则点A 距碾盘的垂直距离约为A.15cmB.cmC.(30−cmD.45cm7.过圆锥内接正方体(正方体的4个顶点在圆锥的底面,其余顶点在圆锥的侧面)的上底面作一平面,把圆锥截成两部分,下部分为圆台,已知此圆台上底面与下底面的面积比为1:4,设圆台体积为1V ,正方体的外接球体积为2V ,则12V V =8.若200a =,()99lg 101b =,101lg 99c =,则a ,b ,c 的大小关系为 A.a c b >>B.c a b >>C.c b a >>D.a b c >>二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.设α为第一象限角,1cos 3α =,则 A.51sin 83πα−=−B.71cos 83πα+=−C.13sin 8πα−D.tan 8πα−−10.已知函数()()3220f x x bx cx b b =+++<在1x =−处有极值,且极值为8,则 A.()f x 有三个零点 B.b c =C.曲线()y f x =在点()()2,2f 处的切线方程为340x y ++= D.函数()2yf x −为奇函数11.已知抛物线2:4C x y =的焦点为F ,直线1l ,2l 过点F 与圆()22:21E x y −+=分别切于A ,B两点,交C 于点M ,N 和P ,Q ,则 A.C 与E 没有公共点B.经过F ,A ,B 三点的圆的方程为2220x y x y +−−=C.AB =D.1369MN PQ +=12.设正整数0110119999k k k k n a a a a −−=⋅+⋅++⋅+⋅ ,其中{}()0,1,2,3,4,5,6,7,80,1,2,,i a i k ∈= .记()01k n a a a ω=+++ ,当8n ≤时,()()()()129S n n ωωω=+++ ,则A.()()()19282S n S n n n −−=+≥B.()()9101n n ωω+=+C.数列()S n n为等差数列D.918n n ω −=三、填空题:本题共4小题,每小题5分,共20分.13.已知向量)1a =− ,(),1b m = ,若b a > ,2a b −=,则m =___________.14.已知随机变量21,2X N σ�,且10.252P X <−= ,()20.1P X >=,则112P X −−= ≤≤_____.15.如图①,在平行四边形ABCD 中,AB=ABD △沿BD 折起,使得点A 到达点P 处(如图②),PC =P BCD −的内切球半径为____________.16.已知椭圆()2222:10x y C a b a b+=>>的右焦点为F ,上顶点为B ,线段BF 的垂直平分线交C 于M ,N 两点,交y 轴于点P ,O 为坐标原点,2BP PO =,则C 的离心率为___________;若BMN △的周长为8,则b =______________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)记ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知2sin 3tan 2B CA +=. (1)求A ;(2)若ABC △,AB AC +=a .18.(12分)某校有A ,B 两个餐厅﹐为调查学生对餐厅的满意程度,在某次用餐时学校从A 餐厅随机抽取了67人,从B 餐厅随机抽取了69人,其中在A ,B 餐厅对服务不满意的分别有15人、6人,其他人均满意. (1)根据数据列出2×2列联表,并依据小概率值0.005α=的独立性检验,能否认为用餐学生与两家餐厅满意度有关联?(2)学校对大量用餐学生进行了统计﹐得出如下结论:任意一名学生第一次在校用餐时等可能地选择一家餐厅用餐,从第二次用餐起,如果前一次去了A 餐厅,那么本次到A ,B 餐厅的概率分别为14,34;如果前一次去了B 餐厅,那么本次到A ,B 餐厅的概率均为12.求任意一名学生第3次用餐到B 餐厅的概率. 附:()()()()()22n ad bc a b c d a c b d c −=++++,其中n a b c d =+++.α 0.100 0.050 0.025 0.010 0.005 0x2.7063.8415.0246.6357.87919.(12分)在数列{}n a 中,19a =,1312n n a a +=+. (1)证明:数列{}6n a −为等比数列; (2)求数列{}n na 的前n 项和n S .20.(12分)如图,在直四棱柱1111ABCD A B C D −中,底面ABCD 为矩形,点M 在棱AD 上,3AM MD =,12AB BB ==,1BD C M ⊥.(1)求AD ;(2)求二面角11A MC B −−的正弦值.21.(12分)已知一动圆与圆()22:318E x y ++=外切,与圆()22:32F x y −+=内切,该动圆的圆心的轨迹为曲线C .(1)求C 的标准方程;(2)直线l 与C 交于A ,B 两点,点P 在线段AB 上,点Q 在线段AB 的延长线上,从下面①②③中选取两个作为条件,证明另外一个成立:①()8,1P ;②AP BQ BP AQ ⋅=⋅;③Q 是直线l 与直线10x y −−=的交点. 注:如果选择不同的组合分别解答,按第一个解答计分. 22.(12分)已知函数()e x f x x =,()ln g x x x x =+. (1)证明:()()f x g x >;(2)若()()f x a ag x −>恒成立,求实数a 的取值范围.数学(二)一、选择题1.B 【解析】()()()()75i 1i 75i122i6i 1i1i 1i 2z +−+−====−++−,故6i z =+.故选B 项 2.C 【解析】由题意得{}18U x x =−≤≤,所以(){}U1,3,4A B ∩=−ð.故选C 项.3.C 【解析】对于A 项,()cos f x x =−,所以()()()cos cos f x x x f x −=−−=−=,所以()f x 为偶函数;对于B 项,()()22x x f x f x −−+,所以()f x 为偶函数;对于C 项,()f x 的定义域为()(),00,−∞∪+∞,()()21211221x x x xx xf x x x f x − −−=−=−+=≠ −−− ,所以()21x x f x x =+−不是偶函数;对于D项,()f x 的定义域为R,()))()lnln ln f x x x x x x f x −=−===,所以())lnf x x x =−是偶函数.故选C 项.4.D 【解析】由题得::0p x ∀>,4x a x+≥为真命题,又44x x +≥,当且仅当2x =时等号成立,反之也成立.所以4a ≤是p 为真命题的充要条件,4a ≥是p 为真命题的既不充分也不必要条件,2a ≥是p 为真命题的既不充分也不必要条件,2a ≤是p 为真命题的充分不必要条件.故选D 项.5.B 【解析】分组方法共有()2,2,5,()2,3,4,()3,3,3三种情况,所以分配方法共有225333323497596339742323C C C C C C A C C C 11508A A ++= .故选B 项. 6.A 【解析】由题意碾滚最外侧滚过的距离为2100cm 200cm ππ×=,碾滚的周长为230cm 60cm ππ×=,所以碾滚滚过20010603ππ=圈,即滚过了1036033601203×°=×°+°,所以点A 距碾盘的垂直距离为()3030cos 18012015cm −×°−°=.故选A 项.7.A 【解析】由圆台上底面与下底面的面积比为1:4,得圆台上底面与下底面的半径比为1212r r =,由题知正1,如图,在1Rt AA P △中,AP =,11A P r =,1A A =,即)22211r =+,解得1r =,则()1128228433V ππ=××++=,正方体的外接球半径为R =,2243V π==,所以12V V =.故选A 项.8.B 【解析】解法一:设()()()100lg 100f x x x =−+,[]1,1x ∈−,当[]1,1x ∈−时,()()100lg 100lg e100xf x x x−′=−+++,令()()100lg 100lg e100xg x x x−=−++⋅+,则()()21200lg e lg e 0100100g x x x ′=−−<++,所以函数()g x 在区间[]1,1−上单调递减,所以()101991011lg 99lg e lg e lg 9999g −=−+=−,又101299e e 99<<,所以()()10g x g <−<,所以函数()f x 在区间[]1,1−上单调递减,所以()()()()991101lg 990100lg100200199lg101lg 101f f f −=>==>==,故c a b >>.故选B 项.解法二:由题意得200100lg10lg100100lg100a==,99lg101b =.令函数()()200ln f x x x =−,()200200ln 1ln x f x x x x x −′=−=−−,当()90,x ∈+∞时,()2001ln 90090f x ′<−−<,所以()f x 在区间()90,+∞内单调递减,所以()()()99100101f f f >>,所以101ln 99100ln10099ln101>>,即1011009999100101>>,所以c a b >>.故选B 项. 二、选择题9.BD 【解析】由题意得8πα−也是第一象限角,所以sin 8πα−,51sin sin cos cos 828883πππππαααα−=+−=−=−=,A 项错误;71cos cos cos 8883πππααπα+=−+=−−=−,B 项正确;1331sin sin cos cos 828883πππππαααα−=+−=−−=−−=−,C 项错误;tan tan 88ππαα−=−−− D 项正确.故选BD 项. 10.AC 【解析】由题意得()232f x x bx c ′=++,又()1320f b c ′−=−+=,又()2118f b c b −=−+−+=,解得33b c = = (舍去)或27b c =− =−,故B 项错误;()32274f x x x x =−−+,()()()2347137f x x x x x ′=−−=+−,当(),1x ∈−∞−时,()0f x ′>,()f x 单调递增,当71,3x∈−时,()0f x ′<,()f x 单调递减,当7,3x∈+∞时,()0f x ′>,()f x 单调递增,又()30f −<,()10f −>,()10f <,()40f >,所以()f x 有三个零点,故A 项正确;又()23f ′=−,()210f =−,则曲线()y f x =在点()()2,2f 处的切线方程为()1032y x +=−−,即340x y ++=,故C 项正确;()()3222722f x x x x f x −−=−−++≠−+,故D 项错误.故选AC 项.11.BCD 【解析】联立()222421x yx y = −+=,得()422116x x −+=,因为2x =是方程的一个根,所以C 与E 有公共点,A 项错误;连接EA ,EB ,则EA FA ⊥,EB FB ⊥,所以F ,A ,B ,E 四点在以FE 为直径的圆上,圆的方程为()2215124x y−+−=,化简得2220x y x y +−−=,B 项正确;由题得2FA =,所以2AB EA FA EF ×==,所以AB =C 项正确;设过点F 且与圆()22:21E x y −+=相切的切线方程为1y kx =+1,解得0k =或43k =−.不妨设1:1l y =,24:13l y x =−+,则4MN =,联立24413x yy x = =−+得298290y y −+=,所以829P Qy y +=,所以10029P Q PQ y y ++,所以100136499MN PQ +=+=,D 项正确.故选BCD 项. 12.ACD 【解析】当2n ≥时,()()()()()()198979695S n S n n n n n ωωωω−−=−+−+−+−()()()()()949392919n n n n n ωωωωω+−+−+−+−+,又()01981919n n −=⋅+−⋅,所以()9811n n n ω−=+−=,同理()01972919n n −=⋅+−⋅,所以()97211n n n ω−=+−=+,…,()01918919n n −=⋅+−⋅,所以()91817n n n ω−=+−=+,09099n n =⋅+⋅,所以()9n n ω=,所以()()1928S n S n n −−=+,A 项正确;012101191009999991k k k k n a a a a +−+=⋅+⋅+⋅++⋅+⋅++ ,()()012910112k n a a a a n ωω+=++++++=+ ,B 项错误;当1n =时,()()()()1129128137S ωωω=+++=++++= ,当2n ≥时,()()()()()()()()()112211928912892S n S n S n S n S n S S S n n =−−+−−−++−+=++−+++× ()296596528912822n n n n ++++×+==,当1n =时也符合,所以()29652n nS n +=,所以()9652S n n n +=,所以()()196595691222S n S n n n n n −++−=−=−,所以数列()S n n为等差数列,C 项正确;()012311199199999819nn n −×−−==+++++− ,911118n n ω −=+++=,D 项正确.故选ACD 项.三、填空题13.【解析】由题意得2314a =+= ,221b m =+ ,1a b ⋅=− ,所以2222244164112a b a a b b m −−⋅+−+++ ,所以290m −+=,解得m =或m =当m =时,b a =,不符合题意;当m =时,b a > .所以m =14.0.15【解析】由题意知12µ=,所以()()120.1P X P X <−=>=,所以()11110.1522P X P X P X−−=<−−<−=≤≤.如图,过点D 作DE BC ∥,且DE BC =,连接PE ,CE ,由题意可知PD BD ⊥,BC BD ⊥,所以BD ⊥平面PDE ,所以BD PE ⊥,所以CE PE ⊥,所以2PE =.又BD ⊂平面BCED ,所以平面BCED ⊥平面PDE .取DE 的中点O ,连接OP ,则OP ⊥平面BCED ,且OP =所以三棱锥P BCD −的体积11122332P BCD BCD V S OP −=⋅=×××=△.又12222BCD S =××=△,122PBC PCDS S ==×=△△,122PBDS =×=△,所以三棱锥P BCD−的表面积(22BCD PBD PCD PBC S S S S S =+++=+△△△△,设三棱锥P BCD −的内切球半径为r ,则3V rS ==16.12【解析】由2BP PO = ,可得23BP b =,13OP b =,连接PF ,在Rt POF △中,由勾股定理得222OP OF PF +=,所以2221233b c b +=,整理得223b c =,所以2223a c c −=,即224a c =,所以C 的离心率12c e a ==.在Rt BOF △中,1cos 2OF c BFO BF a ∠===,所以60BFO ∠=°.设直线MN 交x 轴于点F ′,交BF 于点H ,在Rt HFF ′△中,由2cos HFFF a c BFO′===∠,所以F ′为C 的左焦点,又MB MF =,NB NF =,所以BMN △的周长等于FMN △的周长,又FMN △的周长为4a ,所以48a =,解得2a =,所以1c =,故b =四、解答题17.解:(1)由题得3sin 3cos 2222sin 3tan 2sin cos 222A AA A A A πππ− − ===−, 所以3cos24sin cos 22sin 2AA A A =,又0A π<<,所以022A π<<, 所以0cos12A <<,0sin 12A <<,所以23sin 24A ==,所以sin2A =,所以23A π=,故23A π=. (2)由题得11sin 22bc A bc ==4bc =,又AB AC +=,所以2222cos63b c bc π++=,故22610b c bc +=+=, 由余弦定理得22212cos 1024142a b c bc A=+−=−××−=,所以a =18.解:(1)零假设为0H :用餐学生与两家餐厅满意度无关联,依题意列出22×列联表如下:不满意 满意 合计 A 餐厅 15 52 67 B 餐厅6 63 69 合计21115136()220.0051361563526 4.8817.879676921115x c ××−×≈<=×××,根据小概率值0.005α=的独立性检验,没有充分证据推断0H 不成立,因此可以认为0H 成立,即认为用餐学生与两家餐厅满意度无关联.(2)设事件i A =“第i 次在A 餐厅用餐”,事件i B =“第i 次在B 餐厅用餐”,其中1,2,3i =, 由题意i A 与i B 互斥,且()()1112P A P B ==,()2114P A A =,()2134P B A =;()2112P A B =,()2112P B B =, 由全概率公式得()()()()()21211211111324228P A P A P A A P B P A B =+=×+×=, ()()22518P B P A =−=,又()3234P B A =,()3212P B B =,由全概率公式得()()()()()3232232335119848232P B P A P B A P B P B B =+=×+×=. 19.(1)证明:由1312n n a a +=+,得1123n n a a ++=,即()11261666333n n n n a a a a ++−−=−==−, 又163a −=,所以60n a −≠,所以数列{}6n a −是以3为首项,13为公比的等比数列. (2)解:由(1)可知,12116333n n n a −− −=×=,所以2163nn a −=+,故263nn n na n −=+,设数列{}6n 的前n 项和为n P ,数列23n n −的前n 项和为n T . 所以数列{}n na 的前n 项和n n n S T P =+, 所以()()216126332n n n P n n n +=+++=×=+ ,10211112333n n T n −− =×+×++×,①111111123333n n T n − =×+×++×,②由①-②得1121211111333333n n n T n −−−=++++−×,所以123911272312233443n n n n n T n −−+ =−−×=− × , 故数列{}n na 的前n 项和22272333443n n n n n S T P n n −+=+=++−×. 20.解:(1)连接CM ,由题意得1CC BD ⊥,又1BD C M ⊥,111CC C M C ∩=,所以BD ⊥平面1C CM , 又CM ⊂平面1C CM ,所以BD CM ⊥,在Rt BDC △和Rt CMD △中,因为BDC CMD ∠=∠,所以Rt Rt BDC CMD �△△, 所以MD DCDC BC=,又3AM MD =,所以4BC MD =, 即22244MD DC AB ===,所以1=,即44AD BC MD ===.(2)直四棱柱1111ABCD A B C D −中,底面ABCD 为矩形,所以以点D 为坐标原点,DA ,DC ,1DD 所在直线分别为x ,y ,z 轴,建立如图所示的空间直角坐标系,由(1)可得()0,0,0D ,()1,0,0M ,()14,0,2A ,()10,2,2C ,()4,2,0B ,则()11,2,2MC =− ,()13,0,2MA =,()3,2,0MB = ,设平面11A MC 的法向量为()111,,m x y z =, 由1111111220320m MC x y z m MA x z ⋅=−++= ⋅=+=取13z =−,得()2,4,3m =− ,设平面1BMC 的法向量为()222,,n x y z =,由122222220,320n MC x y z n MB x y ⋅=−++= ⋅=+=取23y =,可得()2,3,4n =−− ,20cos ,29m n m n m n⋅==⋅,所以21sin ,29m n = , 故二面角11A MC B −−的正弦值为2129. 21.(1)解:设动圆的圆心为(),M x y ,半径为r ,则ME r =+,MF r =,所以ME MF EF −=<,由双曲线定义可知,M 的轨迹是以E ,F为焦点,实轴长为所以2a =,26c =,即a =3c =,所以2221b c a =−=,所以C 的标准方程为2218x y −=,x ≥.(2)证明:若①②⇒③:由题可设直线():81l x m y −=−,()11,A x y ,()22,B x y ,()00,Q x y ,01y ≠, 由直线l 与C 交于A ,B两点,所以m −<<,联立()228118x m y x y −=−−=得()()()222828880m y m m y m −−−+−−=,所以()122288m m y y m −+=−,()2122888m y y m −−=−,由AP BQ BP AQ ⋅=⋅,得AP AQ BP BQ =,即01120211y y y y y y −−=−−,由题知1AQ BQ ≠,所以1APBP≠,即P 异于AB 的中点,所以122y y +≠,即1m ≠,得()()()2212121201212228162222681112822128m y y y y y y m y m m y y y y m m −−−−+−−==−+=−+=−−+−+−−−−, 又()0081x m y −=−,所以0081x m y −=−,故00061811y x y =−−−−,化简得0010x y −−=,所以点Q 在直线10x y −−=上,又Q 是l 上的点,所以③成立. 若①③⇒②:设()11,A x y ,()22,B x y ,()00,Q x y ,01y ≠,则0010x y −−=.由P ,A ,B ,Q 四点共线,设AP AQ λ= ,BP BQ µ=,其中0λ>且1λ≠,0µ<,则0181x x λλ−=−,0111y y λλ−=−,0281x x µµ−=−,0211y y µµ−=−, 又点A 在C 上,所以221118x y −=,所以2020811181x x λλλλ−−− −= −,整理得()()222000088161480x y x y λλ−−−−−+=, 又0010x y −−=,所以()2220088480x y λ−−+=,同理()2220088480x y µ−−+=,所以2222004888y x λµ==−+, 又0λ>,0µ<,所以λµ=−,故AP AQ µ=− ,BP BQ µ=,所以AP BP AQ BQµ== ,故AP BQ BP AQ ⋅=⋅ ,即AP BQ BP AQ ⋅=⋅成立,所以②成立. 若②③⇒①:由题设()11,A x y ,()22,B x y ,(),P x y ′′,()00,Q x y ,由AP BQ BP AQ ⋅=⋅,得APBPAQBQλ==, 又点P 为线段AB 上一点,点Q 为线段AB 延长线上一点,所以设AP AQ λ= ,BP BQ λ=−,其中0λ>且1λ≠,则011x x x λλ′−=−,011y y y λλ′−=−,021x x x λλ′+=+,021y y y λλ′+=+,又点A 在C 上,所以221118x y −=,所以20201181x x y y λλλλ′−′−− −= −, 整理得()()2222200008821616880x y x xy y x y λλ′′′′−−−−−+−−=,同理()()2222200008821616880x y x xy y x y λλ′′′′−−+−−+−−=,所以()00002161621616x x y y x x y y ′′′′−−=−−−,故00880x x y y ′′−−=,将001x y =+代入得()0880x y y x ′′′−+−=, 所以8080x y x ′′−=′−= 故81x y ′= ′=即①()8,1P 成立. 22.(1)证明:即证e 1ln xx >+恒成立, 设()e 1ln x h x x =−−,()1e xh x x′=−,显然()h x ′在区间()0,+∞内单调递增, 又121e 202h′=−<,()1e 10h ′=−>,所以存在唯一01,12x∈,使得()00h x ′=,即001e x x =,00ln x x =−.当()00,x x ∈时,()0h x ′<,()h x 单调递减;当()0,x x ∈+∞时,()0h x ′>,()h x 单调递增, 所以()()000001e 1ln 1xh x h x x x x =−−=+−≥, 又01,12x∈,所以0012x x +>,故()()0001110h x h x x x =+−>>≥, 所以e 1ln xx >+,即()()f x g x >.(2)解:由()()f x a ag x −>,得()e ln xx a a x x x −>+,0x >,当0a ≤时,e 0xx a −>,所以()e ln x x a a x x x −>+,即()e ln 1x x a x x x >++,设()ln 1t x x x x =++,则()2ln t x x ′=+,且()2e0t −′=,当()20,ex −∈时,()0t x ′<,()t x 单调递减; 当()2e ,x −∈+∞时,()0t x ′>,()t x 单调递增,所以()()22e1e 0t x t −−=−>≥,所以()ln 10a x x x ++≤,所以()e ln 1x x a x x x >++,即()()ln f x a a x x x −>+成立; 当0a >时,令()e x u x x a =−,0x >,则()()1e 0x u x x ′=+>, 所以()u x 在区间()0,+∞内单调递增, 又()00u a =−<,()()e 10au a a =−>,所以存在唯一()00,x a ′∈,使得()00u x ′=,即00e 0x x a ′′−=,当()00,x x ′∈时,()0u x <,由()e ln xx a a x x x −>+, 得()e ln x x a a x x x −+>+,即e ln 0xaa x a x−+−−>, 设()e ln xa p x a x a x =−+−−,则()2e 0x a ap x x x′=−−−<, 所以()p x 在区间()00,x ′内单调递减, 所以()()00000e ln ln 0x a p x p x a x a a x a x ′′′′>=−+−−=−−>′,解得01ex ′<. 当()0,x x ′∈+∞时,()0u x >,即e 0xx a −>, 由()e ln xx a a x x x −>+,得()e ln x x a a x x x −>+,即e ln 0xa a x a x −−−>,设()e ln x a q x a x a x =−−−,则()2e x a aq x x x′=+−, 由e 0xx a −>得e 0xa x −>,所以()2e 0x a aq x x x′=+−>,所以()q x 单调递增, 所以()()00000e ln ln 0x a q x q x a x a a x a x ′′′′>=−−−=−−>′,解得01ex ′<, 由00e x a x ′′=,得0111e e 01e e e ex a x −′′=<=,综上,实数a的取值范围为11e,e− −∞.。
等比数列前n项和公式的应用

【规律方法】 分组转化求和法的应用条件和解题步骤 (1)应用条件 一个数列的通项公式是由若干个等差数列或等比数列 或可求和的数列的通项公式相加组成. (2)解题步骤
[跟进训练] 1.求数列 214,418,6116,…,2n+2n1+1,…的前 n 项和 Sn. [解] Sn=214+418+6116+…+2n+2n1+1 =(2+4+6+…+2n)+14+18+…+2n1+1 =n2n2+2+1411--1212n=n(n+1)+12-2n1+1 =n2+n-2n1+1+12.
【规律方法】 与等差、等比数列有关的综合问题,其解题过程应注意 以下方法与技巧: 1转化思想:将非等差、等比数列转化构造成等差、等 比数列,以便于利用其公式和性质解题. 2等差比数列公式和性质的灵活应用. 3当题中有多个数列出现时,既要研究单一数列项与项 之间的关系,又要关注各数列之间的相互联系.
【规律方法】 1.在涉及奇数项和 S 奇与偶数项和 S 偶时,常考虑对其差或比进 行简化运算.若项数为 2n,则SS偶 奇=q(S 奇≠0);若项数为 2n+1, 则S奇S-偶a1=q(S 偶≠0). 2.等比数列前 n 项和为 Sn(且 Sn≠0),则 Sn,S2n-Sn,S3n-S2n 仍成等比数列,其公比为 qn(q≠-1).
(1)A (2)24 [(1)∵{an}为等比数列, ∴S2,S4-S2,S6-S4 也为等比数列, 即 7,S4-7,91-S4 成等比数列, ∴(S4-7)2=7(91-S4),解得 S4=28 或 S4=-21. ∵S4=a1+a2+a3+a4=a1+a2+a1q2+a2q2 =(a1+a2)(1+q2)=S2(1+q2)>S2,∴S4=28.
和.(重点、易错点)
学运算素养.
八年级数学上册经典几何题集

初中数学八年级上册经典几何题1、已知三角形的周长为9, 且三边长都是整数,则满足条件的三角形共有 个。
2、如图:在△ABC 中, D 为AC 的中点,E,F 为AB 上的两点,且AE=BF=41AB,求S △DEF :S △ABC 的值。
AEFB C3、在△ABC 中 ,AB=AC ,P 点是BC 上任意一点。
(1)如图,若P 是BC 边上任意一点,PF ⊥AB 于F 点,PE ⊥AC 于点E ,BD 为△ABC 的高线, 请探求PE,PF 与BD 之间的关系。
AF D E B P C (2)如图,若P 是BC 延长线上一点,PF ⊥AB 于F 点,PE ⊥AC 于点E ,CD 为△ABC 的高线, 请探求PE,PF 与CD 之间的关系。
AF DB C P E4、(1)如图,将△ABC 纸片沿DE 折叠成图①,此时点A 落在四边形BCDE 内部,则∠A 与∠1、∠2之间有一种数量关系保持不变,请找出这种数量关系并说明理由。
(2)若折成图②或图③,即点A 落在BE 或CD 上时,分别写出∠A 与∠2,∠A 与∠1之间的关系,并说明理由。
(3)若折成图④,写出∠A 与∠1、∠2之间的关系,并说明理由 (4)若折成图⑤,写出∠A 与∠1、∠2之间的关系,并说明理由。
B A E 图①C DBAE 图②C DB 图③EC A DB A 图④EC DB 图⑤EC A DD5、在5×5的方格中,已知格点A、B、C,请再取一个格点D,在这四个格点中任取三点组成格点三角形,按要求取格点D,(1)组成两对全等的格点三角形;(2)组成四对全等的格点三角形;(3)组成多于四对全等三角形的点D存在吗?6、如图,在△ABC中,AB=BC=AC,∠BAC=∠ABC=∠C,点D,E分别在BC,AC边上,且AE=CD,AD 与BE交于点F。
(1)线段AD与BE有什么关系?证明你的结论。
(2)求∠BFD的度数7、如图,在△ABC中,AD是BAC的外角的平分线,P是AD上异于点A的任意一点,试比较PB+PA 与AB+AC的大小,并说明理由。
最全的平面图形公式

1过两点有且只有一条直线2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行10 内错角相等,两直线平行11 同旁内角互补,两直线平行12两直线平行,同位角相等13 两直线平行,内错角相等14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理有两边和它们的夹角对应相等的两个三角形全等23 角边角公理有两角和它们的夹边对应相等的两个三角形全等24 推论有两角和其中一角的对边对应相等的两个三角形全等 25 边边边公理有三边对应相等的两个三角形全等26 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60° 34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a 2+b2=c247勾股定理的逆定理如果三角形的三边长a、b、c有关系a+b=c,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理 n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半L=(a+b)÷2 S=L×h83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84 (2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85 (3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三个点确定一条直线110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111推论1 ①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧112推论2 圆的两条平行弦所夹的弧相等113圆是以圆心为对称中心的中心对称图形114定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等115推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116定理一条弧所对的圆周角等于它所对的圆心角的一半117推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等118推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径119推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形120定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角121①直线L和⊙O相交 d﹤r②直线L和⊙O相切 d=r③直线L和⊙O相离 d﹥r122切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123切线的性质定理圆的切线垂直于经过切点的半径124推论1 经过圆心且垂直于切线的直线必经过切点125推论2 经过切点且垂直于切线的直线必经过圆心126切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角127圆的外切四边形的两组对边的和相等128弦切角定理弦切角等于它所夹的弧对的圆周角129推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等130相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等131推论如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项132切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项133推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等134如果两个圆相切,那么切点一定在连心线上135①两圆外离 d﹥R+r ②两圆外切 d=R+r③两圆相交 R-r﹤d﹤R+r(R﹥r)④两圆内切 d=R-r(R﹥r) ⑤两圆内含d﹤R-r(R﹥r)136定理相交两圆的连心线垂直平分两圆的公共弦137定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138定理任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆139正n边形的每个内角都等于(n-2)×180°/n140定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141正n边形的面积Sn=pnrn/2 p表示正n边形的周长142正三角形面积√3a/4 a表示边长143如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360°,因此k×(n-2)180°/n=360°化为(n-2)(k-2)=4144弧长计算公式:L=n∏R/180145扇形面积公式:S扇形=n∏R/360=LR/2146内公切线长= d-(R-r) 外公切线长= d-(R+r)。
各类化合物的质谱

2. 烯烃
1)由于双键的引入,分子离子峰增强。 2)相差14的一簇峰,(41+14 n)41、55、69、83…。 3)断裂方式有 β 断裂;γ-H、六元环、麦氏重排。 4)环烯烃及其衍生物发生 RDA 反应。
烯烃易发生烯丙基断裂:
CH3 CH2 CH CH2
CH3 CH2 CH CH3
CH3 + CH2 CH CH2
各类化合物的质谱
支链烷烃:1)分枝烷烃的分子离子峰强度较直链烷烃降低。 2)各峰簇顶点不再形成一平滑曲线,因在分枝处易 断裂,其离子强度增加。 3)在分枝处的断裂,伴随有失去单个氢原子的倾向, 产生较强的 CnH2n 离子。 4)有 M-15 的峰。
环烷烃:1)由于环的存在,分子离子峰的强度相对增加。 2)常在环的支链处断开,给出 CnH2n-1 峰, 也常伴随氢原子的失去,因此该 CnH2n-2 峰较强。 (41、55、56、69…) 3)环的碎化特征是失去 C2H4 (也可能失去 C2H5)。
C4H8 rH
C2H5CH OH m/z = 59
H2C OH m/z = 31
C2H5 rH
H H C OH
H2C C H H
醇的M 容易失水和失去(H2O + CnH2n)(当 n≥2)
C2H5
H
OH
C2H5
H
OH
rd
C2H5
C2H5
H
C2H5
OH
i
HOH
+ HOH
m/z = 18 3%
i
C2H5
1.校核质谱谱峰的m/z值 2.分子离子峰的确定 3.对质谱图作一总的浏览
分析同位素峰簇的相对强度比及峰形,判断是否有 Cl、Br S、Si、F、P、I 等元素。
词性转换总结与归纳

动词变名词1.V+ment结尾69.press—pressure压力70.mix—mixture混合,混合物10.n+or/er/ee/ist/ian/ant表人71.employ--employer雇主,老板--employee雇员72.work—worker工人82.s it--seat座位83.f ly—flight飞行Theflightwilltakefourhours.Therewasnoliftandwehadtoclimbsixflightsofstairs.84.d efend—defence/defense防守,防卫85.w eigh—weight重量,体重86.a dvi s e—advi c e建议87.p racti s e—practi c e练习88.b reathe—breath呼吸1.eventual—eventually最后地,终于地2.final—finally最后地,终于地3.brief—briefly简单地,简要地4.serious—seriously严肃地,认真地5.chemical—chemically化学地6.fluent—fluently流利地7.smooth—smoothly顺利地,平坦地8.hopeful—hopefully满怀希望地9.10.11.12.13.14.15.16.17.18.19.20.21.22.main------mainly主要地23.most多数-----mostly多半,大多24.normal---normally正常地25.quick—quickly迅速地26.quiet—quietly轻轻地,安静地27.real—really真正地28.recent----recently最近;近来29.sad—sadly悲伤地30.slow---slowly缓慢地31.special—specially专门,特殊地43.probable—probably很有可能地44.incredible—incredibly难以置信地45.true—truly真实地46.whole—wholly完全地47.full—fully完全地,全部地48.dull—dully迟钝地,呆滞地49.rare—rarely罕见地,稀有地50.mere--merely仅仅,只=only51.fortunate—fortunately幸运地52.53.54.55.56.57.58.59.60.61.62.63.4.辅音字母+y变ily64.easy—easily容易地65.heavy—heavily沉重地66.happy—happily开心地67.hungry—hungrily饥饿地68.healthy—healthily健康地69.lucky—luckily幸运地70.noisy—noisily嘈杂地5.辅音字母+y直接接ly(1)特殊:good—well好地well身体健康的,井(2)既是形容词又是副词:1有些以-ly结尾的词daily,weekly,monthly,yearly,fast,early,hard,late,far,alone,little,deep,high, straight,long△注意:1以下-ly结尾的词为adj.friendly、lovely、lively、elderly、brotherly、fatherly、motherly、lonely、deadly2high—deepwidehard—loud—closelate—late\lately3两个副词形式但意思不一样80.free--免费地freely--随便不拘束地81.hard--努力地、猛烈地hardly--几乎不82.just--恰好、仅仅、不久前justly--公正地te--迟lately--最新地、最近地84.most--最mostly--大部分地85.near--近nearly--几乎86.pretty--很(adv.)prettily--漂亮名词+y1.anger-----angry生气2.honest—honesty诚实的3.hunger---hungry饥饿的4.fog—foggy有雾的5.fur----furry毛皮的6.guilt---guilty内疚的7.health---healthy健康地8.luck---lucky幸运地9.cloud---cloudy多云地21.balance–balanced平衡的22.spot----spotted有斑点23.talent-----talented有天赋的名词+ful/less24.meaning—meaningful/meaningless有意义的/无意义的25.care—careful/careless小心的/粗心的26.help---helpful/helpless有帮助的/无助的27.home—homeless无家可归的28.colour---colourful多彩的38.courage—courageous勇敢的39.danger—dangerous危险的40.mystery----mysterious神秘的6.ce变t41.confidence----confident自信的42.difference---different不同的43.dependence—dependent依赖的44.independence--independent独立的7.n+al45.46.47.48.49.50.51.52.53.54.55.56.8.名词+ly57.friend—friendly58.live---lively活跃的,有生气的59.love—lovely可爱的60.month---monthly每月的9.+en结尾61.wood—wooden木制的62.wool—woolen羊毛的73.pride---proud骄傲的,自豪的74.scientist----scientific科学的形容词变名词75.efficient有效率的—efficiency效率76.patient—patience/impatience77.dependent—dependence依赖性78.independent—independence独立性79.true—truth80.high—height92.long—lengthen—length(n.)93.wide--widen94.less--lessen95.strong—strengthen—strength(n.)rge—enlarge名词变动词puter--computerize名词---形容词—副词98.beauty美,美人—beautiful—beautifully99.100.101.102.103.104.105.106.107.108.109.110.111.112.success—successful—successfully 113.truth—true—truly114.unluck—unlucky—unluckily115.wonder奇迹—wonderful—wonderfully方位的词名词—形容词116.east—eastern117.west—western118.south—southern119.north---northern。
第31讲 完全平方数和完全平方式

第三十一讲 完全平方数和完全平方式设n 是自然数,若存在自然数m ,使得n=m 2,则称n 是一个完全平方数(或平方数).常见的题型有:判断一个数是否是完全平方数;证明一个数不是完全平方数;关于存在性问题和其他有关问题等.最常用的性质有:(1)任何一个完全平方数的个位数字只能是0,1,4,5,6,9,个位数字是2,3,7,8的数一定不是平方数;(2)个位数字和十位数字都是奇数的两位以上的数一定不是完全平方数,个位数字为6,而十位数字为偶数的数,也一定不是完全平方数;(3)在相邻两个平方数之间的数一定不是平方数;(4)任何一个平方数必可表示成两个数之差的形式;(5)任何整数平方之后,只能是3n 或3n+1的形式,从而知,形如3n+2的数绝不是平方数;任何整数平方之后只能是5n ,5n+1,5n+4的形式,从而知5n+2或5n+3的数绝不是平方数;(6)相邻两个整数之积不是完全平方数;(7)如果自然数n 不是完全平方数,那么它的所有正因数的个数是偶数;如果自然数n 是完全平方数,那么它的所有正因数的个数是奇数;(8)偶数的平方一定能被4整除;奇数的平方被8除余1,且十位数字必是偶数. 例题求解【例1】 n 是正整数,3n+1是完全平方数,证明:n+l 是3个完全平方数之和. 思路点拨 设3n+1=m 2,显然3卜m ,因此,m=3k+1或m=3k+2(k 是正整数).若rn=3k+1,则k k m n 233122+=-=. ∴ n+1=3k 2+2k+1= k 2+ k 2+( k+1)2.若m=3k+2,则1433122++=-=k k m n ∴ n+1=3k 2+4k+2= k 2+(k+1)2+( k+1)2.故n+1是3个完全平方数之和.【例2】一个正整数,如果加上100是一个平方数,如果加上168,则是另一个平方数,求这个正整数.思路点拨 引入参数,利用奇偶分析求解.设所求正整数为x ,则x+100=m 2 ----①x+168==n 2 -----②其中m ,n 都是正整数, ②—①得n 2—m 2=68,即 (n —m )(n+m)=22×17.---- ③ 因n —m ,n+m 具有相同的奇偶性,由③知n —m ,n+m 都是偶数.注意到0<n —m<n+m ,由③可得 ⎩⎨⎧⨯=+=-1722m n m n . 解得n=18.代人②得x=156,即为所求.【例3】 一个正整数若能表示为两个正整数的平方差,则称这个正整数为“智慧数”,比如16=52—32,16就是一个“智慧数”.在正整数中从1开始数起,试问第1998个“智慧数”是哪个数?并请你说明理由.思路点拨 1不能表为两个正整数的平方差,所以1不是“智慧数”.对于大于1的奇正整数2k+1,有2k+1=(k+1)2-k 2(k=1,2,…).所以大于1的奇正整数都是“智慧数”. 对于被4整除的偶数4k ,有4k=(k+1)2—(k —1)2 (k=2,3,…).即大于4的被4整除的数都是“智慧数”,而4不能表示为两个正整数平方差,所以4不是“智慧数”.对于被4除余2的数4k+2 (k=0,1,2,3,…),设4k+2=x 2—y 2=(x+y)(x -y),其中x ,y 为正整数,当x ,y 奇偶性相同时,(x+y)(x -y)被4整除,而4k+2不被4整除;当x ,y 奇偶性相异时,(x+y)(x -y)为奇数,而4k+2为偶数,总得矛盾.所以不存在自然数x ,y 使得x 2—y 2=4k+2.即形如4k+2的数均不为“智慧数”.因此,在正整数列中前四个正整数只有3为“智慧数”,此后,每连续四个数中有三个“智慧数”.因为1998=(1+3×665)+2,4×(665+1)=2664,所以2664是第1996个“智慧数”,2665是第1997个“智慧数”,注意到2666不是“智慧数”,因此2667是第1998个“智慧数”,即第1998个“智慧数”是2667.【例4】(太原市竞赛题)已知:五位数abcde 满足下列条件:(1)它的各位数字均不为零;(2)它是一个完全平方数;(3)它的万位上的数字a 是一个完全平方数,干位和百位上的数字顺次构成的两位数bc 以及十位和个位上的数字顺次构成的两位数de 也都是完全平方数.试求出满足上述条件的所有五位数.思路点拨 设abcde M =2,且2m a =(一位数),2n bc = (两位数),2t de = (两位数),则 2224221010t n m M +⨯+⨯= ①由式①知 224222210210)10(t mt m t m M +⨯+⨯=+⨯= ②比较式①、式②得n 2=2mt .因为n 2是2的倍数,故n 也是2的倍数,所以,n 2是4的倍数,且是完全平方数. 故n 2=16或36或64.当n 2=16时,得8=mt ,则m=l ,2,4,8,t=8,4,2,1,后二解不合条件,舍去; 故116642=M 或41616.当n 2=36时,得18=mt .则m=2,3,1,t=9,6,18.最后一解不合条件,舍去. 故436812=M 或93636.当n 2= 64时,得32=mt .则m=1,2,4,8,t=32,16,8,4都不合条件,舍去. 因此,满足条件的五位数只有4个:11 664,41 616,43 681,93 636.【例5】 (2002年北京)能够找到这样的四个正整数,使得它们中任两个数的积与2002的和都是完全平方数吗?若能够,请举出一例;若不能够;请说明理由.思路点拨 不能找到这样的四个正整数,使得它们中任两个数的积与2002的和都是完全平方数.理由如下:偶数的平方能被4整除,奇数的平方被4除余1,也就是正整数的平方被4除余0或1.若存在正整数满足22002m n n j i =+;j i ,=1,2,3,4,rn 是正整数;因为2002被4除余2,所以j i n n 被4除应余2或3.(1)若正整数n 1,n 2,n 3,n 4中有两个是偶数,不妨设n 1,n 2是偶数,则200221+n n 被4除余2,与正整数的平方被4除余0或1不符,所以正整数n 1,n 2,n 3,n 4中至多有—个是偶数,至少有三个是奇数.(2)在这三个奇数中,被4除的余数可分为余1或3两类,根据抽屉原则,必有两个奇数属于同一类,则它们的乘积被4除余1,与j i n n 被4除余2或3的结论矛盾.综上所述,不能找到这样的四个正整数,使得褥它们中任两个数的积与2002的和都是完全平方数.【例6】 使得(n 2—19n+91)为完全平方数的自然数n 的个数是多少?思路点拨 若(n 2—19n+91)处在两个相邻整数的完全平方数之间,则它的取值便固定了. ∵ n 2一19n+91=(n-9)2 +(10一n)当n>10时,(n -10)2<n 2-19n+19<(n-9)2∴ 当n>10时(n 2—19n+19)不会成为完全平方数∴ 当n ≤10时,(n 2—19n+91)才是完全平方数经试算,n=9和n=10时,n 2—19n+91是完全平方数.所以满足题意的值有2个.【例7】 (“我爱数学”夏令营)已知200221a a a ,,, 的值都是1或—1,设m 是这2002个数的两两乘积之和.(1)求m 的最大值和最小值,并指出能达到最大值、最小值的条件;(2)求m 的最小正值,并指出能达到最小正值的条件.思路点拨 (1)m m a a a a a a 220022)(2200222212200221+=++++=+++ ,22002)(2200221-+++=a a a m . 当1200221====a a a 或1-时,m 取最大值2003001.当200221a a a ,,, 中恰有1001个1,1001个1-时,m 取最小值—1001.(2)因为大于2002的最小完全平方数为452=2025,且200221a a a +++ 必为偶数,所以,当46200221=+++a a a 或46-;即200221a a a ,,, 中恰有1024个1,978个1-或恰有1024个1-,978个1时,m 取最小值57)200246(212=-. 【例8】 (全国竞赛题)如果对一切x 的整数值,x 的二次三项式c bx ax ++2都是平方数(即整数的平方),证明:(1) 2a 、2b 都是整数;(2)a 、b 、c 都是整数,并且c 是平方数.反过来,如果(2)成立,是否对一切x 的整数值,c bx ax ++2的值都是平方数?思路点拨 (1) 令x=0,得c=平方数=2l ;令x=±1,得2m c b a =++,2n c b a =+-,其中m 、n 都是整数.所以,c n m a 2222-+=, 222n m b -=都是整数.(2) 如果2b 是奇数2k+l(k 是整数),令x=4得22416h l b a =++,其中h 是整数. 由于2a 是整数,所以16a 被4整除,有2416416++=+k a b a 除以4余2.而))((22l h l h l h -+=-,在h 、l 的奇偶性不同时,))((l h l h -+是奇数;在h 、l 的奇偶性相同时,))((l h l h -+能被4整除.因此,22416l h b a -≠+,从而2b 是偶数,b 是整数,b c m a --=2 ^也是整数. 在(2)成立时,c bx ax ++2不一定对x 的整数值都是平方数.例如,a=2,b=2,c=4,x=1时,c bx ax ++2=8不是平方数.另解(2):令x=±2,得4a+2b+c=h 2,4a —2b+c=k 2,其中h 、k 为整数.两式相减得4b=h 2—k 2=(h+k)(h —k).由于4b=2(2b)是偶数,所以h 、k 的奇偶性相同,(h+k)(h —k)能被4整除.因此,b 是整数,b c m a --=2也是整数.学力训练(A 级)1.(山东省竞赛题)如果a -是整数,那么a 满足( )A .a>0,且a 是完全平方数B .a<0,且-a 是完全平方数C .a ≥0,且a 是完全平方数D .a ≤0,且—a 是完全平方数2.设n 是自然数,如果n 2的十位数字是7,那么n 2的末位数字是( )A .1B .4C .5D .63.(五羊杯,初二)设自然数N 是完全平方数,N 至少是3位数,它的末2位数字不是00,且去掉此2位数字后,剩下的数还是完全平方数,则N 的最大值是 .4.使得n 2—19n+95为完全平方数的自然数n 的值是 .5.自然数n 减去52的差以及n 加上37的和都是整数的平方,则n= .6.两个两位数,它们的差是56,它们的平方数的末两位数字相同,则这两个数分别是.7.是否存在一个三位数abc (a ,b ,c 取从1到9的自然数),使得cab bca abc ++为完全平方数?8.求证:四个连续自然数的积加l ,其和必为完全平方数.(B 级)1.若x 是自然数,设1222234++++=x x x x y ,则 ( )A .y 一定是完全平方数B .存在有限个,使y 是完全平方数C .y 一定不是完全平方数D .存在无限多个,使y 是完全平方数2.已知a 和b 是两个完全平方数,b 的个位数字为l ,十位数字为x ;b 的个位数为6,十位数字为y ,则( )A .x ,y 都是奇数B .x ,y 都是偶数C .x 是奇数,y 是偶数D .x 为偶数,y 为奇数3.若四位数xxyy 是一个完全平方数,则这个四位数是 .4.设m 是一个完全平方数,则比m 大的最小完全平方数是 .5.(全国联赛题)设平方数y 2是11个连续整数的平方和,则y 的最小值是 .6.(北京市竞赛,初二)p 是负整数,且2001+p 是—个完全平方数,则p 的最大值为 .7.有若干名战士,恰好组成一个八列长方形队列.若在队列中再增加120人或从队列中减去120人后,都能组成一个正方形队列.问原长方形队列共有多少名战士?8.证明:10006999309个各n n 是一个完全平方数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一部分化学品及企业标识
化学品中文名:过氧化环己酮[含量≤91%,含水≥9%]
化学品英文名:cyclohexanone peroxide (not more than 91%, and water not less than 28%)
化学品别名:-
CAS No.:78-18-2
EC No.:201-091-1
分子式:C12H22O5
第二部分危险性概述
紧急情况概述
固体。
遇热有火灾危险。
有严重损害眼睛的危险。
对呼吸道有刺激作用。
GHS危险性类别
根据GB30000-2013化学品分类和标签规范系列标准(参阅第十六部分),该产品分类如下:有机过氧化物,C型;皮肤腐蚀/刺激,类别1;眼损伤/眼刺激,类别1;特定目标器官毒性-单次接触:呼吸道刺激,类别3。
标签要素象形图
警示词:危险
危险信息:加热可能起火,造成严重皮肤灼伤和眼损伤,造成严重眼损伤,可能造成呼吸道刺激。
预防措施:远离热源、热表面、火花、明火以及其它点火源。
禁止吸烟。
只能在原包装中存放。
保持低温。
容器和接收设备接地和等势联接。
不要吸入粉尘/烟/气体/烟雾/蒸气/喷雾。
作业后彻底清洗。
只能在室外或通风良好之处使用。
戴防护手套/穿防护服/戴防护眼罩/戴防护面具。
事故响应:如感觉不适,呼叫中毒急救中心/医生。
沾染的衣服清洗后方可重新使用。
如误吸入:将受人转移到空气新鲜处,保持呼吸舒适的体位。
如误吞咽:漱口。
不要诱导呕吐。
如皮肤(或头发)沾染:立即去除/脱掉所有沾染的衣服。
用水清洗皮肤或淋浴。
如进入眼睛:用水小心冲洗几分钟。
如戴隐形眼镜并可方便地取出,取出隐形眼镜。
继续冲洗。
安全储存:存放在通风良好的地方。
存放处须加锁。
防日晒。
分开存放。
存放在通风良好的地方。
保持容器密闭。
废弃处置:按照地方/区域/国家/国际规章处置内装物/容器。
物理化学危险:有爆炸性,遇热有火灾危险。
健康危害:吸入粉尘或烟雾(尤其是长期接触)可能引起呼吸道刺激,偶尔出现呼吸窘迫。
吸入该物质可能会引起对健康有害的影响或呼吸道不适。
意外食入本品可能对个体健康有害。
皮肤直接接触造成严重皮肤灼伤。
通过割伤、擦伤或病变处进入血液,可能产生全身损伤的有害作用。
眼睛直接接触本品能造成严重化学灼伤。
如果未得到及时、适当的治疗,可能造成永久性失明。
眼睛直接接触本品可导致暂时不适。
环境危害:请参阅SDS第十二部分。
第三部分成分/组成信息
第四部分急救措施
皮肤接触:立即脱去污染的衣物。
用大量肥皂水和清水冲洗皮肤。
如有不适,就医。
眼睛接触:用大量水彻底冲洗至少15分钟。
如有不适,就医。
吸入:立即将患者移到新鲜空气处,保持呼吸畅通。
如果呼吸困难,给于吸氧。
如患者食入或吸入本物质,不得进行口对口人工呼吸。
如果呼吸停止。
立即进行心肺复苏术。
立即就医。
食入:禁止催吐,切勿给失去知觉者从嘴里喂食任何东西。
立即呼叫医生或中毒控制中心。
第五部分消防措施
危险特性
加热时,容器可能爆炸。
暴露于火中的容器可能会通过压力安全阀泄漏出内容物。
受热或接触火焰可能会产生膨胀或爆炸性分解。
灭火方法与灭火剂
合适的灭火介质:
不合适的灭火介质:
灭火注意事项及措施
灭火时,应佩戴呼吸面具并穿上全身防护服。
在安全距离处、有充足防护的情况下灭火。
防止消防水污染地表和地下水系统。
第六部分泄漏应急处理
作业人员防护措施、防护装备和应急处置程序
保证充分的通风。
清除所有点火源。
迅速将人员撤离到安全区域,远离泄漏区域并处于上风方向。
使用个人防护装备。
避免吸入蒸气、烟雾、气体或风尘。
环境保护措施
在确保安全的情况下,采取措施防止进一步的泄漏或溢出。
避免排放到周围环境中。
泄漏化学品的收容、清除方法及处置材料
少量泄漏时,可采用干砂或惰性吸附材料吸收泄漏物,大量泄漏时需筑堤控制。
附着物或收集物应存放在合适的密闭容器中,并根据当地相关法律法规废弃处置。
清除所有点火源,并采用防火花工具和防暴设备。
第七部分操作处置与储存
操作注意事项
在通风良好处进行操作。
穿戴合适的个人防护用具。
避免接触皮肤和进入眼睛。
远离热源、火花、明火和热表面。
采取措施防止静电积累。
储存注意事项
保持容器密闭。
储存在干燥、阴凉和通风处。
远离热源、火花、明火和热表面。
存储于远离不相容材料和食品容器的地方。
第八部分接触控制/个体防护
职业接触限值:无资料。
生物限值:无资料。
监测方法:GBZ/T160.1~GBZ/T160.81-2004工作场所空气有毒物质测定(系列标准)。
工程控制:保持充分的通风,特别在封闭区内。
确保在工作场所附近有洗眼和淋浴设施。
使用防爆电器、通风、照明等设备。
设置应急撤离通道和必要的泄险区。
呼吸系统防护:如果蒸气浓度超过职业接触限值或发生刺激等症状时,请使用全面罩式多功能防毒面具。
眼睛防护:佩戴化学护目镜。
皮肤和身体防护:穿阻燃防静电防护服和抗静电的防护靴。
手防护:戴化学防护手套(例如丁基橡胶手套)。
其他防护工:作现场禁止吸烟、进食和饮水。
工作完毕,淋浴更衣。
保持良好的卫生习惯。
第九部分理化特性
第十部分稳定性和反应性
稳定性:在正确的使用和存储条件下是稳定的。
不相容的物质:无资料
应避免的条件:不相容物质,热、火焰和火花。
危险反应:无资料
分解产物:在正常的储存和使用条件下,不会产生危险的分解产物。
第十一部分毒理学信息
急性毒性:无资料。
眼睛刺激或腐蚀:造成严重眼损伤
皮肤致敏:无资料
呼吸致敏:无资料
生殖细胞突变性:无资料
生殖毒性:无资料
特异性靶器官系统毒性--一次接触可能:可能造成呼吸道刺激
特异性靶器官系统毒性--反复接触:无资料
吸入危害无资料
第十二部分生态学信息
急性水生毒性:无资料。
慢性水生毒性:无资料。
持久性和降解性:无资料
潜在的生物累积性:无资料
土壤中的迁移性:无资料
其他有害作用:无资料。
第十三部分废弃处置
废弃处置方法
产品:如需求医,随手携带产品容器或标签。
不洁的包装:包装物清空后仍可能存在残留物危害,应远离热和火源,如有可能返还给供应商循环使用。
废弃注意事项
请参阅“废弃物处理”部分。
第十四部分运输信息
联合国危险货物编号(UN):3104
联合国运输名称:固态C型有机过氧化物
联合国危险性分类:5.2
包装类别:满足Ⅱ类包装要求
包装标签
海洋污染物(是/否):否
包装方法
螺纹口玻璃瓶、铁盖压口玻璃瓶、塑料瓶或金属桶(罐)外普通木箱等。
按照生产商推荐的方法进行包装。
运输注意事项
严禁与酸类、易燃物、有机物、还原剂、自燃物品、遇湿易燃物品等混装混运。
运输时运输车辆应配备相应品种和数量的消防器材及泄漏应急处理设备。
运输前应先检查包装容器是否完整、密封。
运输工具上应根据相关运输要求张贴危险标志、公告。
第十五部分法规信息
【B】《重点环境管理危险化学品目录》,环保部办公厅2014年第33号文
【C】《中国严格限制进出口的有毒化学品目录》,环保部2013年第85号公告
【D】《麻醉药品和精神药品品种目录(2013年版)》,食药总局2013年第230号通知
【E】《重点监管的危险化学品名录(第1和第2批)》,安监总局2011年第95号和2013年第12号通知
【F】《中国进出口受控消耗臭氧层物质名录(第1到6批)》,环保部2000年至2012系列公告
【G】《易制爆危险化学品名录(2011年版)》,公安部2011年11月25日公告
【H】《高毒物品目录》,卫生部2003年第142号通知。
