19光的衍射习题思考题的解答
光的衍射习题思考题

习题1919-1.波长为nm 546的平行光垂直照射在缝宽为mm 437.0的单缝上,缝后有焦距为cm 40的凸透镜,求透镜焦平面上出现的衍射中央明纹的线宽度。
解:中央明纹的线宽即为两个暗纹之间的距离:93322546100.42 1.0100.43710f x m a λ---⨯⨯⨯∆===⨯⨯。
19-2.在单缝夫琅禾费衍射实验中,波长为λ的单色光的第三极亮纹与波长'630nm λ=的单色光的第二级亮纹恰好重合,求此单色光的波长λ。
解:单缝衍射的明纹公式为:sin (21)a k ϕ=+2λ, 当'630nm λ=时,'2k =,未知单色光的波长为λ、3=k ,重合时ϕ角相同,所以有:630sin (221)(231)22nm a λϕ=⨯+=⨯+,得:56304507nm nm λ=⨯=。
19-3.用波长1400nm λ=和2700nm λ=的混合光垂直照射单缝,在衍射图样中1λ的第1k 级明纹中心位置恰与2λ的第2k 级暗纹中心位置重合。
求满足条件最小的1k 和2k 。
解:由11sin (21)2a k λθ=+,22sin 22a k λθ=,有:122121724k k λλ+==, ∴12427k k +=,即:13k =,22k =。
19-4.在通常的环境中,人眼的瞳孔直径为mm 3。
设人眼最敏感的光波长为nm 550=λ,人眼最小分辨角为多大?如果窗纱上两根细丝之间的距离为mm 0.2,人在多远处恰能分辨。
解:最小分辨角为:rad D 439102.21031055022.122.1---⨯=⨯⨯⨯==λθ 如果窗纱上两根细丝之间的距离为2.0mm ,人在s 远处恰能分辨,则利用:42.210lrad sθ-==⨯,当2l mm =时,9.1s m =。
19-5.波长为nm 500和nm 520的两种单色光同时垂直入射在光栅常数为cm 002.0的光栅上,紧靠光栅后用焦距为m 2的透镜把光线聚焦在屏幕上。
光的衍射习题答案

思 考 题1 为什么隔着山可以听到中波段的电台广播,而电视广播却很容易被高大建筑物挡住 答:只有当障碍物的大小比波长大得不多时,衍射现象才显着。
对一座山来说,电视广播的波长很短,衍射很小;而中波段的电台广播波长较长,衍射现象比较显着。
2 用眼睛通过一单狭缝直接观察远处与缝平行的光源,看到的衍射图样是菲涅耳衍射图样还是夫琅和费衍射图样为什么答:远处光源发出的光可认为是平行光,视网膜在眼睛(相当于凸透镜)的焦平面上,所以观察到的是平行光的衍射。
由此可知,这时人眼看到的是夫琅和费衍射图样。
3 在单缝衍射图样中,离中央明纹越远的明纹亮度越小,试用半波带法说明。
答:在单缝衍射图样中,未相消的一个半波带决定着明纹的亮度。
离中央明纹越远处,衍射角越大,单缝处波阵面分的半波带越多,未相消的一个半波带的面积越小,故离中央明纹越远的明纹亮度越小。
4 根据惠更斯-菲涅耳原理,若已知光在某时刻的波阵面为S ,则S 的前方某点P 的光强度决定于波阵面S 上所有面积元发出的子波各自传到P 点的( )(A)振动振幅之和。
(B)光强之和。
(C)振动振幅之和的平方。
(D)振动的相干叠加。
答:衍射光强是所有子波相干叠加的结果。
选(D)。
5波长为?的单色平行光垂直入射到一狭缝上,若第一级暗纹的位置对应的衍射角为30o,则缝宽的大小( )(A) a =?。
(B) a =?。
(C)a =2?。
(D)a =3?。
答:[ C ]6波长为?的单色光垂直入射到单缝上,若第一级明纹对应的衍射角为30?,则缝宽a 等于( )(A) a =? 。
(B) a =2?。
(C) a =23?。
(D) a =3?。
答:[ D ]7在单缝夫琅和费衍射实验中波长为?的单色光垂直入射到单缝上,对应于衍射角为30?的方向上,若单缝处波面可分成3个半波带,则缝宽度a 等于( )(A) ? 。
(B) ?。
(C) 2?。
(D) 3?。
答:[ D ]8在单缝夫琅和费衍射实验中,波长为?的单色光垂直入射到宽度a=4?的单缝上,对应于衍射角为30?的方向,单缝处波面可分成的半波带数目为( ) (A)2个。
光的衍射习题答案

思 考 题1 为什么隔着山可以听到中波段的电台广播,而电视广播却很容易被高大建筑物挡住 答:只有当障碍物的大小比波长大得不多时,衍射现象才显着。
对一座山来说,电视广播的波长很短,衍射很小;而中波段的电台广播波长较长,衍射现象比较显着。
2 用眼睛通过一单狭缝直接观察远处与缝平行的光源,看到的衍射图样是菲涅耳衍射图样还是夫琅和费衍射图样为什么答:远处光源发出的光可认为是平行光,视网膜在眼睛(相当于凸透镜)的焦平面上,所以观察到的是平行光的衍射。
由此可知,这时人眼看到的是夫琅和费衍射图样。
3 在单缝衍射图样中,离中央明纹越远的明纹亮度越小,试用半波带法说明。
答:在单缝衍射图样中,未相消的一个半波带决定着明纹的亮度。
离中央明纹越远处,衍射角越大,单缝处波阵面分的半波带越多,未相消的一个半波带的面积越小,故离中央明纹越远的明纹亮度越小。
4 根据惠更斯-菲涅耳原理,若已知光在某时刻的波阵面为S ,则S 的前方某点P 的光强度决定于波阵面S 上所有面积元发出的子波各自传到P 点的( )(A)振动振幅之和。
(B)光强之和。
(C)振动振幅之和的平方。
(D)振动的相干叠加。
答:衍射光强是所有子波相干叠加的结果。
选(D)。
5波长为的单色平行光垂直入射到一狭缝上,若第一级暗纹的位置对应的衍射角为30o ,则缝宽的大小( )(A) a =。
(B) a =。
(C)a =2。
(D)a =3。
答:[ C ]6波长为的单色光垂直入射到单缝上,若第一级明纹对应的衍射角为30,则缝宽a 等于( )(A) a = 。
(B) a =2。
(C) a =23。
(D) a =3。
答:[ D ]7在单缝夫琅和费衍射实验中波长为的单色光垂直入射到单缝上,对应于衍射角为30的方向上,若单缝处波面可分成3个半波带,则缝宽度a 等于( )(A) 。
(B) 。
(C) 2。
(D) 3。
答:[ D ]8在单缝夫琅和费衍射实验中,波长为的单色光垂直入射到宽度a=4的单缝上,对应于衍射角为30的方向,单缝处波面可分成的半波带数目为( ) (A)2个。
光的衍射习题(附答案)

光的衍射(附答案)一.填空题1.波长λ = 500 nm(1 nm = 109 m)的单色光垂直照射到宽度a = mm的单缝上,单缝后面放置一凸透镜,在凸透镜的焦平面上放置一屏幕,用以观测衍射条纹.今测得屏幕上中央明条纹之间的距离为d = 12 mm,则凸透镜的焦距f 为3 m.2.在单缝夫琅禾费衍射实验中,设第一级暗纹的衍射角很小,若钠黄光(λ1 ≈589 nm)中央明纹宽度为mm,则λ2 ≈ 442 nm(1 nm = 109 m)的蓝紫色光的中央明纹宽度为mm.3.平行单色光垂直入射在缝宽为a = mm的单缝上,缝后有焦距为f = 400 mm的凸透镜,在其焦平面上放置观察屏幕.现测得屏幕上中央明纹两侧的两个第三级暗纹之间的距离为8 mm,则入射光的波长为500 nm(或5×104mm).4.当一衍射光栅的不透光部分的宽度b与透光缝宽度a满足关系b = 3a 时,衍射光谱中第±4, ±8, …级谱线缺级.5.一毫米内有500条刻痕的平面透射光栅,用平行钠光束与光栅平面法线成30°角入射,在屏幕上最多能看到第5级光谱.6.用波长为λ的单色平行红光垂直照射在光栅常数d = 2 μm(1 μm = 106 m)的光栅上,用焦距f= m的透镜将光聚在屏上,测得第一级谱线与透镜主焦点的距离l = m,则可知该入射的红光波长λ=或633nm.7.一会聚透镜,直径为3 cm,焦距为20 cm.照射光波长550nm.为了可以分辨,两个远处的点状物体对透镜中心的张角必须不小于×105rad.这时在透镜焦平面上两个衍射图样中心间的距离不小于μm.8.钠黄光双线的两个波长分别是nm和nm(1 nm = 109 m),若平面衍射光栅能够在第二级光谱中分辨这两条谱线,光栅的缝数至少是500.9.用平行的白光垂直入射在平面透射光栅上,波长为λ1 = 440 nm的第3级光谱线将与波长为λ2 =660 nm的第2级光谱线重叠(1 nm = 109 m).10.X射线入射到晶格常数为d的晶体中,可能发生布拉格衍射的最大波长为2d.二.计算题11.在某个单缝衍射实验中,光源发出的光含有两种波长λ1和λ2,垂直入射于单缝上.假如λ1的第一级衍射极小与λ2的第二级衍射极小相重合,试问:(1) 这两种波长之间有何关系(2) 在这两种波长的光所形成的衍射图样中,是否还有其它极小相重合解:(1) 由单缝衍射暗纹公式得a sinθ1= 1 λ1 a sinθ2= 2 λ2由题意可知θ1= θ2, sinθ1= sinθ2代入上式可得λ1 = 2 λ2(2) a sinθ1= k1λ1=2 k1λ2(k1=1, 2, …)sinθ1= 2 k1λ2/ aa sinθ2= k2λ2(k2=1, 2, …)sinθ2= 2 k2λ2/ a若k2= 2 k1,则θ1= θ2,即λ1的任一k1级极小都有λ2的2 k1级极小与之重合.12.在单缝的夫琅禾费衍射中,缝宽a = mm,平行光垂直如射在单缝上,波长λ= 500 nm,会聚透镜的焦距f= m.求中央亮纹旁的第一个亮纹的宽度Δx.解:单缝衍射第1个暗纹条件和位置坐标x1为a sinθ1= λx1 = f tanθ1≈ f sinθ1≈ f λ / a (∵θ1很小)单缝衍射第2个暗纹条件和位置坐标x2为a sinθ2 = 2 λx2 = f tanθ2≈ f sinθ2≈ 2 f λ / a (∵θ2很小)单缝衍射中央亮纹旁第一个亮纹的宽度Δx1 = x2x1≈ f (2 λ / a λ / a)= f λ / a=××107/×104) m=.13.在单缝夫琅禾费衍射中,垂直入射的光有两种波长,λ1 = 400 nm,λ2 = 760nm(1 nm = 109 m).已知单缝宽度a = ×102 cm,透镜焦距f = 50 cm.(1)求两种光第一级衍射明纹中心间的距离.(2)若用光栅常数a= ×10-3cm的光栅替换单缝,其它条件和上一问相同,求两种光第一级主极大之间的距离.解:(1) 由单缝衍射明纹公式可知a sinφ1= 12(2 k + 1)λ1 =12λ1(取k = 1)a sinφ2= 12(2 k + 1)λ2=32λ2tanφ1= x1/ f,tanφ2= x1/ f由于sinφ1≈ tanφ1,sinφ2≈ tanφ2所以x1= 32f λ1 /ax2= 32f λ2 /a则两个第一级明纹之间距为Δx1= x2x1= 32f Δλ/a = cm(2) 由光栅衍射主极大的公式d sinφ1= k λ1 = 1λ1d sinφ2= k λ2 = 1λ2且有sinφ = tanφ = x / f所以Δx1= x2x1 = fΔλ/a = cm14.一双缝缝距d = mm,两缝宽度都是a = mm,用波长为λ = 480 nm(1 nm =109 m)的平行光垂直照射双缝,在双缝后放一焦距f= m的透镜.求:(1) 在透镜焦平面的屏上,双缝干涉条纹的间距l;(2) 在单缝衍射中央亮纹范围内的双缝干涉数目N和相应的级数.解:双缝干涉条纹(1) 第k级亮纹条件:d sinθ = kλ第k级亮条纹位置:x1= f tanθ1≈ f sinθ1≈ k f λ / d相邻两亮纹的间距:Δx= x k +1x k = (k + 1) fλ / d k λ / d= f λ / d = ×103 m = mm(2) 单缝衍射第一暗纹:a sinθ1= λ单缝衍射中央亮纹半宽度:Δx= f tanθ1≈ f sinθ1≈ k f λ / d = 12 mm Δx0/ Δx = 5∴双缝干涉第±5级主极大缺级.∴在单缝衍射中央亮纹范围内,双缝干涉亮纹数目N = 9分别为k = 0, ±1, ±2, ±3, ±4级亮纹或根据d /a= 5指出双缝干涉缺第±5 级主极大,同样可得出结论。
高中物理(新人教版)选择性必修一课后习题:光的衍射、光的偏振 激光(课后习题)【含答案及解析】

光的衍射光的偏振激光课后篇巩固提升必备知识基础练1.(多选)对于光的衍射现象的定性分析,下列说法正确的是()A.只有障碍物或孔的尺寸可以跟光波波长相比甚至比光波长还要小的时候,才能产生明显的衍射现象B.光的衍射现象是光波相互叠加的结果C.光的衍射现象否定了光沿直线传播的结论D.光的衍射现象说明了光具有波动性,而小孔成像说明光沿直线传播,而要出现小孔成像,孔不能太小,光的直线传播规律只是近似的,只有在光的波长比障碍物小很多的情况下,光才可以看成直线传播的,所以光的衍射现象和直线传播是不矛盾的,它们是在不同条件下出现的两种现象,故上述选项中正确的是A、B、D。
2.(多选)关于衍射光栅,下列说法正确的是()A.衍射光栅是由许多等宽度的狭缝组成的B.衍射光栅分为透射光栅和反射光栅两类C.透射光栅中刻痕的部分相当于透光的狭缝D.透射光栅中未刻的部分相当于透光的狭缝,当光照到刻痕上时,由于光发生漫反射而不能透过,故选项C错误。
3.关于自然光和偏振光,下列观点正确的是()A.自然光能产生干涉和衍射现象,而偏振光却不能B.只有自然光透过偏振片才能获得偏振光C.自然光只能是白色光,而偏振光不能是白色光D.自然光和偏振光都能使感光底片感光,而振动沿着特定方向的光是偏振光,但自然光和偏振光都能发生干涉、衍射,所以选项A错误。
光的偏振现象并不罕见,除了从光源直接发出的光以外,我们通常看到的绝大部分光,都是偏振光,所以选项B错误。
光的颜色由光的频率决定,与光的振动方向无关,所以选项C错误。
自然光和偏振光都具有能量,都能使感光底片感光,选项D正确。
4.(多选)关于衍射,下列说法正确的是()A.衍射现象中条纹的出现是光叠加后产生的结果B.双缝干涉中也存在衍射现象C.一切波都很容易发生明显的衍射现象D.影子的存在是一个与衍射现象相矛盾的客观事实,双缝干涉中光通过两个狭缝时均发生衍射现象,一般现象中既有干涉又有衍射。
一切波都能发生衍射,但要发生明显的衍射,需要满足障碍物的尺寸小于或相当于波长的条件。
光的衍射习题、答案与解法(2010.11.1)

光衍射习题、答案与解法一、填空题1.根据惠更斯—菲涅耳原理,若已知光在某时间的波阵面为S ,则S 的前方某点P 的光强取决于波阵面S 上所有面积元发出的子波各自传到P 点( D )(A )振动振幅之和 (B )光强之和 (C )振动振幅之和的平方 (D )振动的相干叠加 2.在夫琅禾费单缝衍射实验中,对于给定的入射单色光,当缝宽度变大时,除中央明纹的中心位置不变外,各级衍射条纹 ( A ) (A )对应的衍射角变小 (B )对应的衍射角变大(C )对应的衍射角也不变 (D )光强也不变 参考答案:λϕk a =sin ⎪⎭⎫⎝⎛=-a k λϕ1sin 3.在单缝夫琅禾费单缝衍射实验中,波长λ为的单色光垂直入射到单缝上,对应于衍射角为030的方向上,若单缝处波面可分为6个半波带,则缝宽度a 等于( B )(A )λ (B )λ6 (C )λ2 (D )λ4 参考答案:2sin λϕka = λλλϕλ6212630sin 26sin 20=⨯=⨯==ka4.一束波长为λ的平行单色光垂直入射到一单色AB 上,装置如图1所示,在屏幕P 上形成衍射图样,如果Q 是中央PQCλfALB亮纹一侧第二个暗纹的中心所在位置,则BC 得长度为 ( D )(A )2/λ (B )λ (C )2/3λ (D )λ2 参考答案:λϕk a =sin λλϕ2sin ==k a5. 波长为nm 600=λ)m 10nm 1(9-=的单色光垂直照射到宽mm 3.0=a 的单缝上,单缝后面放置一凸透镜,在凸透镜的焦平面上放置一个屏幕,用以观测衍射条纹,今测得屏幕中央明条纹一侧第一个暗条纹和另一侧第一个暗条纹之间的距离为mm 4=∆x ,则凸透镜的焦距f 为 ( C )(A )m 2 (B ) m 1.0 (C )m 1 (D )m 5.0参考答案:⎪⎪⎩⎪⎪⎨⎧==-=∆=-12k x x x x k a f x k k k k λ ()m 1106002103.01042933=⨯⨯⨯⨯⨯=∆=---a x f λ6.一束平行单色光垂直入射在光栅上,当光栅常数()b a +,为下列哪种情况时(a 代表每条缝的宽度),k=3、6、9等级次的明纹均不出现 ( B )(A )a b a 2=+ (B )a b a 3=+(C )a b a 4=+(D )a b a 6=+参考答案:()⎪⎪⎪⎩⎪⎪⎪⎨⎧==='==+963sin sin k k k k a k b a λϕλϕ ===='=+392613k k a b a 7.一束白光垂直照射在一光栅上,在形成的同一级光栅谱中,离中央明纹最近的是 ( A )(A )紫光 (B )绿光 (C )黄光 (D )红光参考答案:()λϕk b a =+sin⎪⎭⎫ ⎝⎛+=-b a k λϕ1sin 红λλ〈3 8.若用衍射光栅准确测定一单色光可见光的波长,在下列各种光栅中选用那一种最为合适?( D )(A )mm 5.0(B ) mm 1(C )mm 01.0(D )mm 100.13-⨯参考答案:()⎪⎪⎩⎪⎪⎨⎧===+21sin πϕλϕk k b a()()mm 107nm 7001107001sin 49--⨯==⨯⨯==+ϕλk b a9.波长为λ的单色光垂直入射于光栅常数为d 、缝宽为a 、总缝数为N 的光栅上,取⋅⋅⋅⋅±±=2,1,0k ,则决定出现明纹的衍射角θ的公式可写成( C )(A )λθk Na =sin (B )λθk a =sin (C )λθk d =sin (D )λθk Nd =sin 参考答案:()λϕk b a =+sin λϕk d =sin10.提高光仪器分辨率本领的方法是:( B ) ( A )增大透光孔径,增大入射光的波长 ( B )增大透光孔径,减小入射光的波长 ( C ) 减小透光孔径,增大入射光的波长 ( D ) 减小透光孔径,减小入射光的波长 参考答案:λ22.1D R = Dλθ22.1= 二、填空题1.在单缝夫琅禾费衍射实验中,波长nm 400=λ的平行光垂直入射单缝,所用凸透镜焦距m 5.1=f ,第三级暗纹离中央明纹中心m 100.33-⨯,另一波长为0λ的光的第二级暗纹在屏的同一位置上,则单缝的缝宽m 103.5-4⨯=a ,波长nm 0060=λ。
光的衍射选择题解答与分析

7光的衍射7.1惠更斯—菲涅耳原理1. 根据惠更斯-菲涅耳原理,假设光在某时刻的波阵面为S ,那么S 的前方某点P 的光强度决定于波阵面S 上所有面积元发出的子波各自传到P 点的 (A) 振动振幅之和. (B) 光强之和. (C) 振动振幅之和的平方. (D) 振动的相干叠加. 答案:(D) 参考解答:惠更斯原理可以定性说明波遇到障碍物时为什么会拐弯,但是它不能解释拐弯之后波的强度的重新分布〔对光而言,表现为出现明暗相间的衍射条纹〕现象。
在杨氏双缝干预实验的启发下,注意到干预可导致波的能量出现重新分布,法国物理学家菲涅耳认为:同一波阵面上发出的子波是彼此相干的,它们在空间相遇以后发生相干迭加,使得波的强度出现重新分布,由此而形成屏上观察到的衍射图样。
这一经 “子波相干叠加〞思想补充开展后的惠更斯原理,称为惠更斯-菲涅耳原理。
对所有选择,均给出参考解答,进入下一步的讨论。
2. 衍射的本质是什么?干预和衍射有什么区别和联络?参考解答:根据惠更斯-菲涅耳原理,衍射就是衍射物所发光的波阵面上各子波在空间场点的相干叠加,所以衍射的本质就是干预,其结果是引起光场强度的重新分布,形成稳定的图样。
干预和衍射的区别主要表达在参与叠加的光束不同,干预是有限光束的相干叠加,衍射是无穷多子波的相干叠加。
7.2单缝衍射1. 在夫琅禾费单缝衍射实验中,对于给定的入射单色光,当缝宽度变小时,除中央亮纹的中心位置不变外,各级衍射条纹(A) 对应的衍射角变小. (B) 对应的衍射角变大. (C) 对应的衍射角也不变. (D) 光强也不变. 答案:(B) 参考解答:根据半波带法讨论的结果,单缝衍射明纹的角位置由下式确定,,2)12(sin λθ+±=k a 即...)3,2,1(2)12(sin =+±=k ak λθ.显然对于给定的入射单色光,当缝宽度a 变小时,各级衍射条纹对应的衍射角变大。
对所有选择,均给出参考解答,进入下一步的讨论。
光的衍射习题解答
•6
2-9 波长为546.1nm的平行光垂直地射在 1mm宽的缝上,若将焦 距为 100cm的透镜紧贴于缝的后面,并使光聚焦到屏上,试问 衍射图样的中央到(1)第一最小值;(2)第一最大值;(3) 第三最小值的距离分别为多少?
7•7
2-11 *以纵坐标表示强度,横坐标表示屏上的位置,粗略地画出 三缝的夫琅禾费衍射(包括缝与缝之间的干涉)图样。设缝宽
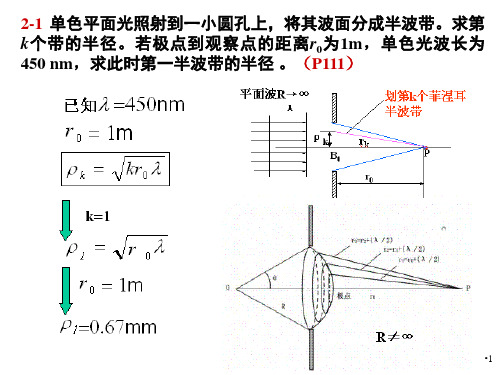
2-1 单色平面光照射到一小圆孔上,将其波面分成半波带。求第 k个带的半径。若极点到观察点的距离r0为1m,单色光波长为 450 nm,求此时第一半波带的半径 。(P111)
•1
2-3 波长为500nm的单色点光源离光阑 1m,光阑上有一内外半 径分别为 0.5mm 和1mm的透光圆环,接收点 P离光阑 1m,求 P点的光强 I与没有光阑时的光强度 I0之比。
为 b,相邻缝间的距离为 d, d = 3b。注意缺级问题。
8•8
2-13 用可见光(760~400 nm)照射全息光栅时,一级光谱和二级 光谱是否重叠?二级和三级怎样?若重叠,则重叠范围是多少?
•9
2-14 *用波长为589 nm的单色光照射一衍射光栅,其光谱的中央 最大值和第二十级主最大值之间的衍射角为15o10’,求该光栅 1 cm内的缝数是多少?
•10
2-15 用每毫米内有400 条刻痕的平面透射光栅观察波长为589 nm的纳光谱。试问: (1)光垂直入射时,最多能观察到几级光谱? (2)光以30o角入射时,最多能观察到几级光谱?
•11
2-16 白光垂直照射到一个每毫米250条刻痕的平面透射光栅上, 试问在衍射角为30o处会出现哪些波长的光?颜色如何?
•4
2-7 平面光的波长为480 nm,垂直照射到宽度为 0.4mm的狭缝 上,会聚透镜的焦距为 60 cm。分别计算当缝的两边到 P点的相 位差为 p/2和 p/6时, P点离焦点的距离。
光的衍射知识题目解析

思考题1 为什么隔着山可以听到中波段的电台广播,而电视广播却很容易被高大建筑物挡住?答:只有当障碍物的大小比波长大得不多时,衍射现象才显著。
对一座山来说,电视广播的波长很短,衍射很小;而中波段的电台广播波长较长,衍射现象比较显著。
2 用眼睛通过一单狭缝直接观察远处与缝平行的光源,看到的衍射图样是菲涅耳衍射图样还是夫琅和费衍射图样?为什么?答:远处光源发出的光可认为是平行光,视网膜在眼睛(相当于凸透镜)的焦平面上,所以观察到的是平行光的衍射。
由此可知,这时人眼看到的是夫琅和费衍射图样。
3 在单缝衍射图样中,离中央明纹越远的明纹亮度越小,试用半波带法说明。
答:在单缝衍射图样中,未相消的一个半波带决定着明纹的亮度。
离中央明纹越远处,衍射角越大,单缝处波阵面分的半波带越多,未相消的一个半波带的面积越小,故离中央明纹越远的明纹亮度越小。
4 根据惠更斯-菲涅耳原理,若已知光在某时刻的波阵面为S,则S的前方某点P的光强度决定于波阵面S上所有面积元发出的子波各自传到P点的( )(A)振动振幅之和。
(B)光强之和。
(C)振动振幅之和的平方。
(D)振动的相干叠加。
答:衍射光强是所有子波相干叠加的结果。
选(D)。
5波长为λ的单色平行光垂直入射到一狭缝上,若第一级暗纹的位置对应的衍射角为30º,则缝宽的大小()(A) a=0.5λ。
(B) a=λ。
(C)a=2λ。
(D)a=3λ。
答:[ C ]6波长为λ的单色光垂直入射到单缝上,若第一级明纹对应的衍射角为30︒,则缝宽a 等于( )(A) a =λ 。
(B) a =2λ。
(C) a =23λ。
(D) a =3λ。
答:[ D ]7在单缝夫琅和费衍射实验中波长为λ的单色光垂直入射到单缝上,对应于衍射角为30︒的方向上,若单缝处波面可分成3个半波带,则缝宽度a 等于( )(A) λ 。
(B) 1.5λ。
(C) 2λ。
(D) 3λ。
答:[ D ]8在单缝夫琅和费衍射实验中,波长为λ的单色光垂直入射到宽度a=4λ的单缝上,对应于衍射角为30︒的方向,单缝处波面可分成的半波带数目为( ) (A)2个。
光的色散与衍射练习题及

光的色散与衍射练习题及解答光的色散与衍射练习题及解答一、选择题1.当光通过一个介质界面从光密介质射入光疏介质时,发生的现象是()。
A.全反射B.衍射C.色散D.吸收答案:A.全反射解析:当光从光密介质射入光疏介质时,入射角大于临界角时会发生全反射。
2.在双缝干涉实验中,两个缝的间距减小,则干涉的条纹距离()。
A.增大B.减小C.不变D.无法确定答案:B.减小解析:根据双缝干涉的公式d·sinθ = m·λ,其中d为缝距,θ为条纹夹角,m为干涉级次,λ为波长。
当d减小时,根据公式可以得出条纹夹角θ减小,即干涉的条纹距离减小。
3.以下哪种现象与衍射无关?A.人耳对声音的听觉感受B.双缝干涉实验的条纹C.太阳光通过窄缝后形成的光条纹 D.水波通过狭缝后形成的波纹答案:A.人耳对声音的听觉感受解析:衍射是波动现象,与波的传播有关。
人耳对声音的听觉感受是由空气中的声音波传播到人耳中引起的,属于声波的传播过程,并不涉及衍射现象。
4.以下哪种现象与色散无关?A.水滴中的彩虹B.光通过三棱镜的偏折C.太阳光经大气层折射形成的赤橙黄绿蓝靛紫光带D.日落时太阳的颜色变化答案:D.日落时太阳的颜色变化解析:色散是指光在介质中传播时由于不同频率的光波速度不同而引起的偏离,而日落时太阳的颜色变化是由于大气中的散射现象引起的,并不涉及光的频率变化。
二、问答题1.请简述全反射的条件及应用。
全反射是指当光从光密介质射入光疏介质时,如果入射角大于临界角,则光将全部被反射回光密介质中,不会在光疏介质中传播。
全反射的条件是入射角大于临界角,临界角可以由光密介质与光疏介质的折射率决定。
全反射在光纤通信中有广泛应用,光纤的工作原理就是利用光从光纤的芯层表面发生全反射来传输信号。
2.请解释双缝干涉实验的原理,并简述其应用。
双缝干涉实验是一种观察光波干涉现象的实验。
实验中通过在一个遮光板上开两个狭缝,让光通过缝隙后形成干涉条纹。
光的衍射习题解答

习题19-1.波长为nm 546的平行光垂直照射在缝宽为mm 437.0的单缝上,缝后有焦距为cm 40的凸透镜,求透镜焦平面上出现的衍射中央明纹的线宽度。
解:中央明纹的线宽即为两个暗纹之间的距离 利用两者相等,所以:m a f x 339100.110437.04.010546222---⨯=⨯⨯⨯⨯==λ 19-2.波长为nm 500和nm 520的两种单色光同时垂直入射在光栅常数为cm 002.0的光栅上,紧靠光栅后用焦距为m 2的透镜把光线聚焦在屏幕上。
求这两束光的第三级谱线之间的距离。
解:两种波长的第三谱线的位置分别为x 1,x 2所以: 120.006m x x x ∆=-=19-3.在通常的环境中,人眼的瞳孔直径为mm 3。
设人眼最敏感的光波长为nm 550=λ,人眼最小分辨角为多大?如果窗纱上两根细丝之间的距离为mm 0.2,人在多远处恰能分辨。
解:最小分辨角为:rad D 439102.21031055022.122.1---⨯=⨯⨯⨯==λθ 如果窗纱上两根细丝之间的距离为mm 0.2,人在多远处恰能分辨。
19-4.已知氯化钠晶体的晶面距离nm 282.0=d ,现用波长nm 154.0=λ的X 射线射向晶体表面,观察到第一级反射主极大,求X 射线与晶体所成的掠射角.解: 212sin λϕ)(+±=k d 第一级即k=0。
19-5. 如能用一光栅在第一级光谱中分辨在波长间隔nm 18.0=∆λ,发射中心波长为nm 3.656=λ的红双线,则该光栅的总缝数至少为多少? 解:根据瑞利判据:)(λλλ∆+-=NkN k 1 )(18.06.65316.653+-=NN 所以N=3647。
19-6.一缝间距d=0.1mm ,缝宽a=0.02mm 的双缝,用波长 nm 600=λ的平行单色光垂直入射,双缝后放一焦距为f=2.0m 的透镜,求:(1)单缝衍射中央亮条纹的宽度内有几条干涉主极大条纹;(2)在这双缝的中间再开一条相同的单缝,中央亮条纹的宽度内又有几条干涉主极大?解: λϕk a ±=sin 所以中央亮条纹位置为:m a f x 12.01021060022259=⨯⨯⨯==--λ 中央明条纹位于:中心位置的上下方各0.06m 处。
光的衍射习题答案

第六章 光的衍射6-1 求矩形夫琅和费衍射图样中,沿图样对角线方向第一个次极大和第二个次极大相对于图样中心的强度。
解:对角线上第一个次极大对应于πβα43.1==,其相对强度为:0022.043.143.1sin sin sin 4220=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=ππββααI I 对角线上第二个次极大对应于πβα46.2==,其相对强度为:00029.046.246.2sin sin sin 4220=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛=ππββααI I6-2 由氩离子激光器发出波长488=λnm 的蓝色平面光,垂直照射在一不透明屏的水平矩形孔上,此矩形孔尺寸为0.75mm ×0.25mm 。
在位于矩形孔附近正透镜(5.2=f m )焦平面处的屏上观察衍射图样,试求中央亮斑的尺寸。
解:中央亮斑边缘的坐标为:63.175.010********±=⨯⨯±=±=-a f x λmm 26.32=x mm 88.425.010********±=⨯⨯±=±=-b f y λmm 76.92=y mm ∴中央亮斑是尺寸为3.26mm ×9.76mm 的竖直矩形6-3 一天文望远镜的物镜直径D =100mm ,人眼瞳孔的直径d =2mm ,求对于发射波长为5.0=λμm 光的物体的角分辨极限。
为充分利用物镜的分辨本领,该望远镜的放大率应选多大?解:当望远镜的角分辨率为: 636101.610100105.022.122.1---⨯=⨯⨯⨯==D λθrad 人眼的最小分辨角为: 4361005.3102105.022.122.1---⨯=⨯⨯⨯==d e λθrad ∴望远镜的放大率应为:50===dDM e θθ 6-4 一个使用汞绿光(546=λnm )的微缩制版照相物镜的相对孔径(f D /)为1:4,问用分辨率为每毫米380条线的底片来记录物镜的像是否合适? 解:照相物镜的最大分辨本领为: 375411054622.1122.116=⨯⨯⨯==-f D N λ/mm∵380>375∴可以选用每毫米380条线的底片。
光的衍射(有答案)

光的衍射一、光的衍射的基础知识1、发生明显衍射的条件只有当障碍物的尺寸跟光的波长相差不多,甚至比光的波长小的时候,衍射现象才会明显.2、衍射图样①单缝衍射a.单色光:明暗相间的不等距(等距、不等距)条纹,中央亮纹最宽最亮,两侧条纹具有对称性.b.白光:中间为宽且亮的白色条纹,两侧是窄且暗的彩色条纹,最靠近中央的是紫光,远离中央的是红光.②圆孔衍射:明暗相间的不等距(等距、不等距)圆环,圆环面积远远超过孔的直线照明的面积.③圆盘衍射:明暗相间的不等距(等距、不等距)圆环,中心有一亮斑称为泊松亮斑.二、衍射与干涉的比较三、习题1、对于光的衍射的定性分析,下列说法中不正确的是()A.只有障碍物或孔的尺寸可以跟光波波长相比甚至比光的波长还要小的时候,才能明显地产生光的衍射现象B.光的衍射现象是光波相互叠加的结果C.光的衍射现象否定了光的直线传播的结论D.光的衍射现象说明了光具有波动性答案 C解析光的干涉和衍射现象说明了光具有波动性,而小孔成像说明了光沿直线传播,而要出现小孔成像现象,孔不能太小,可见光的直线传播规律只是近似的,只有在光波波长比障碍物小得多的情况下,光才可以看做是直线传播的,所以光的衍射现象和直线传播并不矛盾,它们是在不同条件下出现的两种光现象,单缝衍射实验中单缝光源可以看成是无限多个光源排列而成,因此光的衍射现象也是光波相互叠加的结果.2、如图所示的4种明暗相间的条纹,分别是红光、蓝光通过同一个双缝干涉仪形成的干涉图样和黄光、紫光通过同一个单缝形成的衍射图样(黑色部分代表亮纹),那么1、2、3、4四个图中亮条纹的颜色依次是()123 4A.红黄蓝紫B.红紫蓝黄C.蓝紫红黄D.蓝黄红紫解析由于双缝干涉条纹是等间距的,而单缝衍射条纹除中央亮条纹最宽最亮之外,两侧条纹亮度、宽度都逐渐减小,因此1、3为双缝干涉条纹,2、4为单缝衍射条纹.又双缝干涉条纹的间距Δx=ldλ,在l、d都不变的情况下,干涉条纹间距Δx与波长λ成正比,红光波长比蓝光波长长,则红光干涉条纹间距比蓝光干涉条纹间距大,即1、3分别对应红光和蓝光.而在单缝衍射中,当单缝宽度一定时,波长越长,衍射越明显,即中央条纹越宽越亮,黄光波长比紫光波长长,则黄光的中央条纹较宽较亮,故2、4分别对应紫光和黄光.综上所述,1、2、3、4四个图中亮条纹的颜色依次是红、紫、蓝、黄,选项B正确.答案 B3、在单缝衍射实验中,下列说法正确的是()A.其他条件不变,将入射光由黄色换成绿色,衍射条纹间距变窄B.其他条件不变,使单缝宽度变小,衍射条纹间距变窄C.其他条件不变,换用波长较长的光照射,衍射条纹间距变宽D.其他条件不变,增大单缝到屏的距离,衍射条纹间距变宽答案ACD解析当单缝宽度一定时,波长越长,衍射现象越明显,条纹间距也越大,黄光波长大于绿光波长,所以条纹间距变窄,A、C正确;当光的波长一定时,单缝宽度越小,衍射现象越明显,衍射条纹间距越宽,B错误;当光的波长一定,单缝宽度也一定时,增大单缝到屏的距离,衍射条纹间距也会变宽,D正确.4、(2011·浙江·18)关于波动,下列说法正确的是()A.各种波均会发生偏振现象B.用白光做单缝衍射与双缝干涉实验,均可看到彩色条纹C.声波传播过程中,介质中质点的运动速度等于声波的传播速度D.已知地震波的纵波波速大于横波波速,此性质可用于横波的预警答案BD解析偏振现象是横波特有的现象,纵波不会发生偏振现象,故选项A错误.用白光做单缝衍射实验和双缝干涉实验看到的都是彩色条纹,故选项B正确.声波在传播过程中,质点在平衡位置附近振动,其振动速度周期性变化,而声波的传播速度是单位时间内声波传播的距离,故选项C错误.地震波的纵波传播速度比横波传播速度大,纵波可早到达地面,能起到预警作用,故选项D正确.5、在光的单缝衍射实验中可观察到清晰的明暗相间的图样,图4的四幅图片中属于光的单缝衍射图样的是()图4A.a、c B.b、c C.a、d D.b、d答案 D6、用单色光通过小圆盘和小圆孔分别做衍射实验,在光屏上得到衍射图形,则()A.用小圆盘时,图形中央是暗的,用小圆孔时,图形中央是亮的B.用小圆盘时,图形中央是亮的,用小圆孔时,图形中央是暗的C.两个图形中央均为亮点的同心圆形条纹D.两个图形中央均为暗点的同心圆形条纹答案 C7、(1)肥皂泡在太阳光照射下呈现的彩色是______现象;露珠在太阳光照射下呈现的彩色是________现象;通过狭缝看太阳光时呈现的彩色是________现象.(2)凡是波都具有衍射现象,而把光看作直线传播的条件是_____________.要使光产生明显的衍射,条件是______________________________________.(3)当狭缝的宽度很小并保持一定时,分别用红光和紫光照射狭缝,看到的衍射条纹的主要区别是____________________________________________________________.(4)如图6所示,让太阳光或白炽灯光通过偏振片P和Q,以光的传播方向为轴旋转偏振片P或Q,可以看到透射光的强度会发生变化,这是光的偏振现象,这个实验表明________________________________________________________________________________________________________________________________________________.图6答案见解析解析(1)肥皂泡呈现的彩色是光的干涉现象,露珠呈现的彩色是光的色散,通过狭缝看太阳光呈现的彩色是光的衍射现象.(2)障碍物或孔的尺寸比波长大得多时,可把光看作沿直线传播;障碍物或孔的尺寸跟波长相差不多或比波长更小时,可产生明显的衍射现象.(3)红光的中央亮纹宽,红光的中央两侧的亮纹离中央亮纹远.(4)这个实验说明了光是一种横波.。
第19章 光的衍射

第19章光的衍射第19章光的衍射第19章光的衍射思考题19-1在日常生活中,为什么声波的衍射比光波的衍射显著?答:因为耳朵能听到的声波波长在0.017-17米之间,这与通常的障碍物的尺寸基本相同,故声波的衍射很显著.而可见光的波长在400-700nm之间,远小于通常的障碍物的尺寸,故光的衍射在通常情况下不太容易观察到.19-2 夫琅禾费衍射实验中,透镜的作用是什么?图19-16 答:夫琅禾费衍射实验中,透镜的作用是把有限远的光源成像到无穷远,或把无穷远处的衍射图样成像到有限远处.19-3 夫琅禾费单缝衍射实验中,若入射的平行光束与狭缝平面不垂直(如图19-16),干涉条纹的分布将发生什么变化?答:夫琅禾费衍射实验中,若入射的平行光束与狭缝平面不垂直,干涉条纹在观察屏幕上的位置将发生偏移,即中央明纹将偏离观察屏的中心点O,但干涉花样的形状保持不变.19-4若放大镜的放大倍数足够高,是否能看清任何细小的物体?答:放大镜的放大倍数足够高,也不一定能看清任何细小的物体.因为,要看清细小物体不仅需要有一定的放大能力,还要有足够的分辨本领,才能把微小物体放大到清晰可见的程度.19-5 为什么天文望远镜的物镜直径都很大?答:由光学仪器的分辨率λθ22.11D R R ==,可知天文望远镜的分辨率与物镜直径D 成正比.物镜的直径越大,分辨率越高.为分辨无限远处的天体,天文望远镜的物镜直径都做得尽可能的大.19-6 如何理解光栅的衍射条纹是单缝衍射和多缝干涉的总效益?答:光栅是由许多等宽的狭缝等距离地排列起来构成的,光栅衍射实际上是每个狭缝的单缝衍射光再相互干涉的结果,所以多缝干涉的效果必然受到单缝衍射效果的影响,也即光栅的衍射条纹是单缝衍射和多缝干涉的总效益.19-7 光栅的光谱和棱镜的光谱有什么区别?答:光栅的光谱是由于光在光栅上的衍射引起的,而棱镜的光谱是光在棱镜两个表面的折射引起的.19-8 为什么用光栅的衍射比用杨氏双缝干涉实验能更准确的测量入射光的波长?答:因为杨氏双缝干涉的条纹间距太小,亮度很暗,不易观测,而光栅衍射的条纹间距较大、极细、亮度很高. 因此用光栅的衍射比用杨氏双缝干涉实验能更准确的测量入射光的波长.19-9 为什么不能用一般光栅观察X射线的衍射现象?答:X射线的波长很短(介于20~0.06nm),而普通光栅的缝宽在μm量级.由于X射线的波长远小于光栅的缝宽,因此无法观察到衍射现象. 习题19-1用波长为500nm的单色平行光,垂直入射到缝宽为1mm的单缝上,在缝后放一焦距f=50cm的凸透镜,并使光聚焦在观察屏上,求衍射图样的中央到一级暗纹中心、二级明纹中心的距离各是多少?解:(1)已知 =500nm,a=1mm,f=50cm.根据夫琅禾费单缝衍射公式,可知一级暗纹位置sin f x f a λθ==±可得衍射图样的中央到一级暗纹中心的距离为 7115050010cm 0.025cm 0.25mm 110f x a λ--⨯⨯≈===⨯ (2)二级明纹位置为5sin 2f x f a λθ==±可得衍射图样的中央到二级明纹中心的距离为 7221555050010sin cm 0.063cm 0.63mm 22110f x f a λθ--⨯⨯≈==⨯==⨯ 即衍射图样的中央到一级暗纹中心、二级明纹中心的距离分别为0.25mm 和0.63mm.19-2 在夫琅禾费单缝衍射实验中,以波长λ为589 nm 的平行光垂直入射到单缝上.若缝宽为0.10 mm ,试问一级暗纹中心出现在多大的角度上?若要使一级暗纹中心出现在0.50︒的方向上,则缝宽应多大?解:(1) 已知λ=589nm ,a =0.10mm.根据夫琅禾费单缝衍射公式,可得一级暗纹中心的角位置为661158910sin rad 5.8910rad 0.34a 0.1λθθ--⨯≈=±=±=±⨯=±故衍射图样的一级暗纹中心出现在0.34︒的方向上.(2) 若一级暗纹中心出现在0.50︒的方向上,即10.5θ=,则62158910a mm 6.7510mm 0.5/180 3.14λθ--⨯≈==⨯⨯ 即要使一级暗纹中心出现在0.50︒的方向上,则缝宽应为26.7510mm -⨯.19-3 波长λ=500nm 的平行单色光,垂直入射到缝宽为0.25mm 的单缝上,紧靠缝后放一凸透镜,在凸透镜的焦平面上测得第二条暗纹间距离为2x 2=2mm ,求凸透镜的焦距f 为多少?解:已知λ=500nm ,a =0.25mm ,x 2=1mm.根据夫琅禾费单缝衍射公式a f f x λθ2sin 2±==可得 260.251mm 250mm 25cm 2250010x a f λ-⨯====⨯⨯ 凸透镜的焦距f 为25cm.19-4 用水银灯发出的波长为546 nm 的绿色平行光垂直入射到一单缝上,紧靠缝后放一的焦距为40 cm 凸透镜,在位于凸透镜的焦平面处的观察屏上测得二级暗纹中心至衍射图样中心的线距离为0.30 cm. 若用一波长未知的光作实验时,测得三级暗纹中心到衍射图样中心的线距离为0.42 cm ,试求未知波长.解:已知1λ=546nm , f =40cm ,x 2=0.30cm ,x 3=0.42cm.根据夫琅禾费单缝衍射公式af k f x λθ±==sin 可得1122sin 2f x f a λθ==,2233sin 3f x f a λθ==解上述方程可得 232112220.42546nm 510nm 330.30x x λλ==⨯=即未知波的波长为510nm.19-5 在单缝夫琅禾费衍射装置中,用细丝代替单缝,就构成了衍射细丝测径仪.已知光波波长为632.8 nm, 透镜焦距为50 cm, 今测得零级衍射斑的宽度为1.0 cm, 试求该细丝的直径.解:已知λ=632.8 nm ,a =1 mm ,f =50 cm ,0x ∆=1.0 cm .根据夫琅禾费单缝衍射公式,得零级衍射斑的宽度02 1.0cm f x a λ∆==可得细丝的直径为295205010632.81022m 6.3310m 63.3μm 110f a x λ----⨯⨯⨯==⨯≈⨯≈∆⨯19-6 在迎面驶来的汽车上,两盏前灯相距1.0 m ,试问在汽车离人多远的地方,眼睛恰好能分辨这两盏灯?设夜间人眼瞳孔的直径为5.0 mm ,入射光波长为550 nm ,而且仅考虑人眼瞳孔的衍射效应.解:已知λ=550nm ,d =1.0m ,D =5.0mm.由最小的分辨角公式可得人眼的最小分辨角为943550101.22 1.22rad 1.3410rad 510λθ---⨯==⨯=⨯⨯R D设人和汽车的距离为x 时,眼睛恰好能分辨这两盏灯,则有θ≈R dx即341m 7.4610m=7.46km 1.3410θ-≈=≈⨯⨯R dx人和汽车的距离为7.46km 时,眼睛恰好能分辨这两盏灯.19-7 一架生物显微镜,物镜的标号为20×0.25, 即物镜的放大率为20倍,数值孔径sin n u 为0.25;若光波的波长以550 nm 计算,试问可分辨的最小距离是多大?目镜物方焦平面上恰可分辨的两物点的艾里斑中心间距是多大?解:已知λ=550nm ,sin n u =0.25,可得m μ3.1m 103.1m 25.01055061.0sin 61.069=⨯=⨯⨯==∆--u n y λ目镜物方焦平面上恰可分辨两物点的艾里斑中心间距等于物镜的放大率乘以y ∆, 即26μm .19-8 对于可见光,平均波长为λ = 550 nm ,试比较物镜直径为5.0 cm 的普通望远镜和直径为6.0 m 的反射式天文望远镜的分辨本领.解: 由光学仪器的分辨率公式,可知物镜直径为D 1 = 5.0 cm 和D 2 = 6.0 m 的望远镜的最小分辨角为:rad 103.1rad 100.51055022.122.152911---⨯=⨯⨯⨯==D λθ rad 101.1rad 0.61055022.122.17922--⨯=⨯⨯==D λθ它们的比值为12016100.522112=⨯==-D D θθ 即这台天文望远镜的分辨本领是普通望远镜的120倍19-9用λ=589.3nm 的钠黄光垂直入射到一个平面透射光栅上,测得第三级谱线的衍射角为10.18︒, 而用未知波长的单色光垂直入射时,测得第二级谱线的衍射角为 6.20︒, 试求此未知波长.解:已知1λ=589.3nm ,13θ=10.18︒,22θ=6.20︒.由光栅方程λθk d ±=sin 可得sin10.183589.3nm=⨯d ,2sin 6.203λ=⨯d解上述方程组,可得3589.3sin 6.20nm 540.15nm 2sin10.18λ⨯=⨯=19-10 用每毫米内有400条刻痕的平面透射光栅观察波长为589nm 的纳光谱.试问:光垂直入射时,最多能观察到几级光谱?解:已知1λ=589.3nm ,依题意可得光栅常数d =1mm/400=0.0025mm.由光栅方程λθk d ±=sin ,可知90θ=对应光栅光谱的最高衍射级次,即max 6sin 900.002514.2589.310λ-⨯==≈⨯d k即最多能观察到4级光谱2sin 6.203λ=⨯d解上述方程组,可得3589.3sin 6.20nm 540.15nm 2sin10.18λ⨯=⨯=19-11 以波长范围为400~700 nm 的白光,垂直入射到一块每厘米有6000条刻线的光栅上.试分别计算第一级和第二级光谱的角宽度,两者是否重叠?解:已知1λ=400nm ,2λ=700nm ,依题意可得光栅常数d =1/6000cm.由光栅方程λθk d ±=sin ,可得第一级和第二级光谱的角宽度11θ、21θ和12θ、22θ分别为711140010asin asin 0.24rad1/6000λθ-⨯==≈d722170010asin asin 0.43rad1/6000λθ-⨯==≈d71122240010asin asin 0.50rad1/6000λθ-⨯⨯==≈d72222270010asin asin 1.00rad1/6000λθ-⨯⨯==≈d即白光的一级衍射光谱的角范围为0.24~0.43rad ,二级衍射光谱的角范围为0.50~1.00rad. 一级衍射光谱的角宽度为0.19rad ,二级衍射光谱的角宽度为0.50rad. 显然,白光的第一级和第二级光谱的不会重叠. 19-12 用氦氖激光器发出的λ=632.8nm 的红光,垂直入射到一平面透射光栅上,测得第一级极大出现在38︒的方向上,试求这一平面透射光栅的光栅常量d ,这意味着该光栅在1 cm 内有多少条狭缝?第二级谱线的衍射角是多大? 解:(1) 已知λ=632.8nm ,1θ=38︒,k =1.由光栅方程λθk d ±=sin ,可得7411632.810cm 1.0010cmsin sin 38λθ--⨯⨯==≈⨯k d即光栅在1 cm 内有10000条狭缝. (2) 当k =2时,由光栅方程得22sin dλθ=,即72422632.810sin 1.211.0010d λθ--⨯⨯==≈>⨯表明该光栅的第二级谱线实际上是不存在的.19-13 已知氯化钠的晶体结构是简单的立方点阵,且相邻两离子之间的平均距离(即晶格常量)d =0.2819nm .若用波长λ = 0.154 nm 的X 射线照射在氯化钠晶体表面上,且只考虑与表面平行的晶面系,试问当X 射线与表面分别成多大掠射角时,可观察到第一级和第二级主极大谱线.解:(1) 已知λ=0.154nm ,a =0.2819nm ,k =1和k =2时,由布拉格方程得10.154arcsinarcsin15.85220.2819d λθ==≈⨯220.154arcsinarcsin 33.1120.2819d λθ==≈X射线与表面分别成15.85︒和33.11︒大掠射角时,可观察到第一级和第二级主极大谱线.。
(网工)《大学物理学》光的衍射练习题(解答) (1)

f
a
拓展题:在单缝衍射实验中,缝宽 a=0.2mm,透镜焦距 f=0.4m,入射光波长 =500nm,在距离中
央亮纹中心位置 2mm 处是亮纹还是暗纹?对应的波阵面分为几个半波带?
(D)
(A) 亮纹,3 个半波带; (B) 亮纹,4 个半波带;(C) 暗纹,3 个半波带; (D) 暗纹,4 个半波带。
(C) 不变;
(D) 改变无法确定。
【提示:衍射光栅公式变为 d sin a sin ' k ,最高级次 k 变大】
5.在光栅光谱中,假如所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上,因而实际上不出
现,那么此光栅每个透光缝宽度 a 和相邻两缝间不透光部分宽度 b 的关系为
(B)
/2
/2
拓展题:在单缝夫琅和费衍射中,若单缝两边缘点 A、B 发出的单色平行光到空间某点 P 的光程差
为 1.5 ,则 A、B 间可分为 个半波带,P 点处为 (填明或暗)条纹。若光程差为 2 ,则
A、B 间可分为 个半波带,P 点处为 (填明或暗)条纹。
a sin
【提示:根据公式
n 判断, n 3 ,奇数半波带对应明 条纹,2 是 4 个 / 2 ,偶数半波带对应
相等,则光谱上呈现的全部级数为
(B)
(A) 0 、 1、 2 、 3 、 4 ; (B) 0 、 1、 3 ;(C) 1、 3 ; (D) 0 、 2 、 4 。
【 提 示 : 根 据 衍 射 光 栅 公 式 d sin k , 取 =900 k 4.16 , 可 判 断 kmax 4 。 又 由 缺 级 公 式
ab
【提示:由缺级公式 k
k ' ,取 k 3k ' 】
第19章 光的衍射

第19章 光的衍射思考题19-1 在日常生活中,为什么声波的衍射比光波的衍射显著?答:因为耳朵能听到的声波波长在0.017-17米之间,这与通常的障碍物的尺寸基本相同,故声波的衍射很显著.而可见光的波长在400-700nm 之间,远小于通常的障碍物的尺寸,故光的衍射在通常情况下不太容易观察到.19-2 夫琅禾费衍射实验中,透镜的作用是什么? 图19-16 答:夫琅禾费衍射实验中,透镜的作用是把有限远的光源成像到无穷远,或把无穷远处的衍射图样成像到有限远处.19-3 夫琅禾费单缝衍射实验中,若入射的平行光束与狭缝平面不垂直(如图19-16),干涉条纹的分布将发生什么变化?答:夫琅禾费衍射实验中,若入射的平行光束与狭缝平面不垂直,干涉条纹在观察屏幕上的位置将发生偏移,即中央明纹将偏离观察屏的中心点O ,但干涉花样的形状保持不变.19-4若放大镜的放大倍数足够高,是否能看清任何细小的物体?答:放大镜的放大倍数足够高,也不一定能看清任何细小的物体.因为,要看清细小物体不仅需要有一定的放大能力,还要有足够的分辨本领,才能把微小物体放大到清晰可见的程度.19-5 为什么天文望远镜的物镜直径都很大? 答:由光学仪器的分辨率λθ22.11D R R ==,可知天文望远镜的分辨率与物镜直径D 成正比.物镜的直径越大,分辨率越高.为分辨无限远处的天体,天文望远镜的物镜直径都做得尽可能的大.19-6 如何理解光栅的衍射条纹是单缝衍射和多缝干涉的总效益?答:光栅是由许多等宽的狭缝等距离地排列起来构成的,光栅衍射实际上是每个狭缝的单缝衍射光再相互干涉的结果,所以多缝干涉的效果必然受到单缝衍射效果的影响,也即光栅的衍射条纹是单缝衍射和多缝干涉的总效益.19-7 光栅的光谱和棱镜的光谱有什么区别?答:光栅的光谱是由于光在光栅上的衍射引起的,而棱镜的光谱是光在棱镜两个表面的折射引起的.19-8 为什么用光栅的衍射比用杨氏双缝干涉实验能更准确的测量入射光的波长? 答:因为杨氏双缝干涉的条纹间距太小,亮度很暗,不易观测,而光栅衍射的条纹间距较大、极细、亮度很高. 因此用光栅的衍射比用杨氏双缝干涉实验能更准确的测量入射光的波长.19-9 为什么不能用一般光栅观察X 射线的衍射现象?答:X 射线的波长很短(介于20~0.06nm ),而普通光栅的缝宽在μm 量级.由于X 射线的波长远小于光栅的缝宽,因此无法观察到衍射现象.习题19-1 用波长为500nm 的单色平行光,垂直入射到缝宽为1mm 的单缝上,在缝后放一焦距f =50cm 的凸透镜,并使光聚焦在观察屏上,求衍射图样的中央到一级暗纹中心、二级明纹中心的距离各是多少?解:(1)已知λ=500nm ,a =1mm ,f =50cm.根据夫琅禾费单缝衍射公式, 可知一级暗纹位置sin f x f aλθ==±可得衍射图样的中央到一级暗纹中心的距离为 7115050010cm 0.025cm 0.25mm 110f x a λ--⨯⨯≈===⨯ (2)二级明纹位置为5sin 2f x f aλθ==±可得衍射图样的中央到二级明纹中心的距离为 7221555050010sin cm 0.063cm 0.63mm 22110f x f a λθ--⨯⨯≈==⨯==⨯ 即衍射图样的中央到一级暗纹中心、二级明纹中心的距离分别为0.25mm 和0.63mm.19-2 在夫琅禾费单缝衍射实验中,以波长λ为589 nm 的平行光垂直入射到单缝上.若缝宽为0.10 mm ,试问一级暗纹中心出现在多大的角度上?若要使一级暗纹中心出现在0.50︒的方向上,则缝宽应多大?解:(1) 已知λ=589nm ,a =0.10mm.根据夫琅禾费单缝衍射公式,可得一级暗纹中心的角位置为661158910sin rad 5.8910rad 0.34a 0.1λθθ--⨯≈=±=±=±⨯=± 故衍射图样的一级暗纹中心出现在0.34︒的方向上.(2) 若一级暗纹中心出现在0.50︒的方向上,即10.5θ=,则62158910a mm 6.7510mm 0.5/180 3.14λθ--⨯≈==⨯⨯ 即要使一级暗纹中心出现在0.50︒的方向上,则缝宽应为26.7510mm -⨯.19-3 波长λ=500nm 的平行单色光,垂直入射到缝宽为0.25mm 的单缝上,紧靠缝后放一凸透镜,在凸透镜的焦平面上测得第二条暗纹间距离为2x 2=2mm ,求凸透镜的焦距f 为多少?解:已知λ=500nm ,a =0.25mm ,x 2=1mm.根据夫琅禾费单缝衍射公式 af f x λθ2sin 2±== 可得 260.251mm 250mm 25cm 2250010x a f λ-⨯====⨯⨯ 凸透镜的焦距f 为25cm. 19-4 用水银灯发出的波长为546 nm 的绿色平行光垂直入射到一单缝上,紧靠缝后放一的焦距为40 cm 凸透镜,在位于凸透镜的焦平面处的观察屏上测得二级暗纹中心至衍射图样中心的线距离为0.30 cm. 若用一波长未知的光作实验时,测得三级暗纹中心到衍射图样中心的线距离为0.42 cm ,试求未知波长.解:已知1λ=546nm , f =40cm ,x 2=0.30cm ,x 3=0.42cm.根据夫琅禾费单缝衍射公式a f kf x λθ±==sin 可得 1122sin 2f x f a λθ==,2233sin 3f x f aλθ== 解上述方程可得 232112220.42546nm 510nm 330.30x x λλ==⨯= 即未知波的波长为510nm.19-5 在单缝夫琅禾费衍射装置中,用细丝代替单缝,就构成了衍射细丝测径仪.已知光波波长为632.8 nm, 透镜焦距为50 cm, 今测得零级衍射斑的宽度为1.0 cm, 试求该细丝的直径.解:已知λ=632.8 nm ,a =1 mm ,f =50 cm ,0x ∆=1.0 cm .根据夫琅禾费单缝衍射公式,得零级衍射斑的宽度021.0cm f x aλ∆== 可得细丝的直径为 295205010632.81022m 6.3310m 63.3μm 110f a x λ----⨯⨯⨯==⨯≈⨯≈∆⨯ 19-6 在迎面驶来的汽车上,两盏前灯相距1.0 m ,试问在汽车离人多远的地方,眼睛恰好能分辨这两盏灯?设夜间人眼瞳孔的直径为5.0 mm ,入射光波长为550 nm ,而且仅考虑人眼瞳孔的衍射效应.解:已知λ=550nm ,d =1.0m ,D =5.0mm.由最小的分辨角公式可得人眼的最小分辨角为943550101.22 1.22rad 1.3410rad 510λθ---⨯==⨯=⨯⨯R D 设人和汽车的距离为x 时,眼睛恰好能分辨这两盏灯,则有θ≈R d x 即 341m 7.4610m=7.46km 1.3410θ-≈=≈⨯⨯R dx 人和汽车的距离为7.46km 时,眼睛恰好能分辨这两盏灯.19-7 一架生物显微镜,物镜的标号为20×0.25, 即物镜的放大率为20倍,数值孔径sin n u 为0.25;若光波的波长以550 nm 计算,试问可分辨的最小距离是多大?目镜物方焦平面上恰可分辨的两物点的艾里斑中心间距是多大?解:已知λ=550nm ,sin n u =0.25,可得m μ3.1m 103.1m 25.01055061.0sin 61.069=⨯=⨯⨯==∆--u n y λ 目镜物方焦平面上恰可分辨两物点的艾里斑中心间距等于物镜的放大率乘以y ∆, 即26μm .19-8 对于可见光,平均波长为λ = 550 nm ,试比较物镜直径为5.0 cm 的普通望远镜和直径为6.0 m 的反射式天文望远镜的分辨本领.解: 由光学仪器的分辨率公式,可知物镜直径为D 1 = 5.0 cm 和D 2 = 6.0 m 的望远镜的最小分辨角为:rad 103.1rad 100.51055022.122.152911---⨯=⨯⨯⨯==D λθ rad 101.1rad 0.61055022.122.17922--⨯=⨯⨯==D λθ 它们的比值为12016100.522112=⨯==-D D θθ 即这台天文望远镜的分辨本领是普通望远镜的120倍19-9用λ=589.3nm 的钠黄光垂直入射到一个平面透射光栅上,测得第三级谱线的衍射角为10.18︒, 而用未知波长的单色光垂直入射时,测得第二级谱线的衍射角为6.20︒, 试求此未知波长.解:已知1λ=589.3nm ,13θ=10.18︒,22θ=6.20︒.由光栅方程λθk d ±=sin 可得 sin10.183589.3nm =⨯d ,2sin 6.203λ=⨯d解上述方程组,可得3589.3sin 6.20nm 540.15nm 2sin10.18λ⨯=⨯= 19-10 用每毫米内有400条刻痕的平面透射光栅观察波长为589nm 的纳光谱.试问:光垂直入射时,最多能观察到几级光谱?解:已知1λ=589.3nm ,依题意可得光栅常数d =1mm/400=0.0025mm.由光栅方程λθk d ±=sin ,可知90θ=对应光栅光谱的最高衍射级次,即max 6sin 900.00251 4.2589.310λ-⨯==≈⨯d k 即最多能观察到4级光谱 2sin 6.203λ=⨯d解上述方程组,可得3589.3sin 6.20nm 540.15nm 2sin10.18λ⨯=⨯= 19-11 以波长范围为400~700 nm 的白光,垂直入射到一块每厘米有6000条刻线的光栅上.试分别计算第一级和第二级光谱的角宽度,两者是否重叠?解:已知1λ=400nm ,2λ=700nm ,依题意可得光栅常数d =1/6000cm.由光栅方程λθk d ±=sin ,可得第一级和第二级光谱的角宽度11θ、21θ和12θ、22θ分别为711140010asin asin 0.24rad 1/6000λθ-⨯==≈d 722170010asin asin 0.43rad 1/6000λθ-⨯==≈d 71122240010asin asin 0.50rad 1/6000λθ-⨯⨯==≈d 72222270010asin asin 1.00rad 1/6000λθ-⨯⨯==≈d 即白光的一级衍射光谱的角范围为0.24~0.43rad ,二级衍射光谱的角范围为0.50~1.00rad. 一级衍射光谱的角宽度为0.19rad ,二级衍射光谱的角宽度为0.50rad. 显然,白光的第一级和第二级光谱的不会重叠.19-12 用氦氖激光器发出的λ=632.8nm 的红光,垂直入射到一平面透射光栅上,测得第一级极大出现在38︒的方向上,试求这一平面透射光栅的光栅常量d ,这意味着该光栅在1 cm 内有多少条狭缝?第二级谱线的衍射角是多大?解:(1) 已知λ=632.8nm ,1θ=38︒,k =1.由光栅方程λθk d ±=sin ,可得7411632.810cm 1.0010cm sin sin 38λθ--⨯⨯==≈⨯k d 即光栅在1 cm 内有10000条狭缝.(2) 当k =2时,由光栅方程得22sin dλθ=,即 72422632.810sin 1.211.0010d λθ--⨯⨯==≈>⨯ 表明该光栅的第二级谱线实际上是不存在的.19-13 已知氯化钠的晶体结构是简单的立方点阵,且相邻两离子之间的平均距离(即晶格常量)d =0.2819nm .若用波长λ = 0.154 nm 的X 射线照射在氯化钠晶体表面上,且只考虑与表面平行的晶面系,试问当X 射线与表面分别成多大掠射角时,可观察到第一级和第二级主极大谱线.解:(1) 已知λ=0.154nm ,a =0.2819nm ,k =1和k =2时,由布拉格方程得10.154arcsin arcsin 15.85220.2819d λθ==≈⨯ 220.154arcsin arcsin 33.1120.2819d λθ==≈ X 射线与表面分别成15.85︒和33.11︒大掠射角时,可观察到第一级和第二级主极大谱线.。
19光的衍射习题思考题[汇总]
![19光的衍射习题思考题[汇总]](https://img.taocdn.com/s3/m/93d820c17e192279168884868762caaedd33ba8d.png)
习题1919-1.波长为nm 546的平行光垂直照射在缝宽为mm 437.0的单缝上,缝后有焦距为cm 40的凸透镜,求透镜焦平面上出现的衍射中央明纹的线宽度。
解:中央明纹的线宽即为两个暗纹之间的距离:93322546100.42 1.0100.43710f x m a λ---⨯⨯⨯∆===⨯⨯。
19-2.在单缝夫琅禾费衍射实验中,波长为λ的单色光的第三极亮纹与波长'630nm λ=的单色光的第二级亮纹恰好重合,求此单色光的波长λ。
解:单缝衍射的明纹公式为:sin (21)a k ϕ=+2λ,当'630nm λ=时,'2k =,未知单色光的波长为λ、3=k ,重合时ϕ角相同,所以有:630sin (221)(231)22nm a λϕ=⨯+=⨯+,得:56304507nm nm λ=⨯=。
19-3.用波长1400nm λ=和2700nm λ=的混合光垂直照射单缝,在衍射图样中1λ的第1k 级明纹中心位置恰与2λ的第2k 级暗纹中心位置重合。
求满足条件最小的1k 和2k 。
解:由11sin (21)2a k λθ=+,22sin 22a k λθ=,有:122121724k k λλ+==,∴12427k k +=,即:13k =,22k =。
19-4.在通常的环境中,人眼的瞳孔直径为mm 3。
设人眼最敏感的光波长为nm 550=λ,人眼最小分辨角为多大?如果窗纱上两根细丝之间的距离为mm 0.2,人在多远处恰能分辨。
解:最小分辨角为:rad D 439102.21031055022.122.1---⨯=⨯⨯⨯==λθ如果窗纱上两根细丝之间的距离为2.0mm ,人在s 远处恰能分辨,则利用:42.210lrad sθ-==⨯,当2l mm =时,9.1s m =。
19-5.波长为nm 500和nm 520的两种单色光同时垂直入射在光栅常数为cm 002.0的光栅上,紧靠光栅后用焦距为m 2的透镜把光线聚焦在屏幕上。
高中物理-光的衍射

〖干涉和衍射归纳高中物理-光的衍射〗 等间距不等间距,∆x =λdl:d 越小,∆x 越大单缝越窄,条纹展开越宽∆x =λdl:λ越小,∆x 越小λ越小,中央亮纹越窄没有公式注:红光波长最大,紫光波长最小。
思考题:1.干涉、衍射都要产生明暗相间的条纹,它们究竟有什么区别?答:干涉图样是等间距条纹,衍射图样是中间宽、两边窄,对称分布的条纹。
干涉、行射都是波的叠加现象。
从本质上讲,两者并无区别。
区分干涉、衍射,是一种习惯说法,一般来说,双缝图样叫干涉,单缝或多缝图样叫衍射。
2.为什么在日常生活中,声波的衍射比光波更显著?答:可闻声波的波长范围是1.8cm ~ 18m ,和障碍物尺寸相近,容易发生衍射;可见光波长范围是400nm-760nm ,障碍物尺寸往往比光的波长大得多,所以不容易发生衍射。
只闻其声不见其人,物理本质就是声波容易衍射,光波不容易衍射。
〖思考与讨论~P59〗发生明显衍射的条件是:障碍物(或孔)测尺寸比波长小或跟波长差不多。
日常生活中的物体,跟可见光的波长(400nm-760nm )比,尺寸较大,所以衍射不明显,更多是呈现“沿直线传播”。
其实,也不是观察不到光的衍射,而是大部分人即使是观察到了也并没有在意。
〖做一做~P60、61〗用激光笔做单缝衍射实验如果家里有激光笔一定要做一做这个实验,能增加你对衍射的感性认识。
做的时候注意做好防护,尤其注意激光不要直接照射眼睛。
如果你做成了,拍下照片发到我们的教学班级群里。
用羽毛做光栅衍射实验能找到羽毛、翎毛是最好的(拆鸡毛掸子?)。
如果没有,还可以寻找替代品,比如纱巾,总之就是密集多缝或多孔的东西就行。
也有人眯缝眼睛,从上下眼睫毛交错构成的许多小缝隙中看灯光,也能看到彩色的衍射花样,没看到也不强求,但一定要注意保护好眼睛。
〖问题与练习~P4〗1.会观察到明暗相间的彩色条纹,因为当两支铅笔夹成的狭缝与光波波长接近时,会发生光的衍射现象。
说明1:也可以用两把直尺重叠并压紧后,对着日光灯观察光的衍射现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题
19-1.波长为nm 546的平行光垂直照射在缝宽为m m 437.0的单缝上,缝后有焦距为cm 40的凸透镜,求透镜焦平面上出现的衍射中央明纹的线宽度。
解:中央明纹的线宽即为两个暗纹之间的距离
a λϕϕϕ2210=
-=∆ f
x 20=∆ϕ 利用两者相等,所以:m a f x 339100.110
437.04.010546222---⨯=⨯⨯⨯⨯==λ 19-2.波长为nm 500和nm 520的两种单色光同时垂直入射在光栅常数为cm 002.0的光栅上,紧靠光栅后用焦距为m 2的透镜把光线聚焦在屏幕上。
求这两束光的第三级谱线之间的距离。
解:两种波长的第三谱线的位置分别为x 1,x 2
λϕk a ±=sin f
x ==ϕϕtan sin a f x 113λ= a
f x 223λ= 所以: 120.006m x x x ∆=-=
19-3.在通常的环境中,人眼的瞳孔直径为mm 3。
设人眼最敏感的光波长为
nm 550=λ,
人眼最小分辨角为多大?如果窗纱上两根细丝之间的距离为mm 0.2,人在多远处恰能分辨。
解:最小分辨角为:rad D 439
102.21031055022.122.1---⨯=⨯⨯⨯==λ
θ 如果窗纱上两根细丝之间的距离为mm 0.2,人在多远处恰能分辨。
m s mm l rad s
l 1.92102.24==⨯==
-,可得:,当θ 19-4.已知氯化钠晶体的晶面距离nm 282.0=d ,现用波长nm 154.0=λ的X 射线射向晶体表面,观察到第一级反射主极大,求X 射线与晶体所成的掠射角.
解: 2
12sin λ
ϕ)(+±=k d 第一级即k=0。
s i n 0.2762r a d
d λϕϕ=== 19-5. 如能用一光栅在第一级光谱中分辨在波长间隔nm 18.0=∆λ,发射中心波长为
nm 3.656=λ的红双线,则该光栅的总缝数至少为多少? 解:根据瑞利判据:)(λλλ∆+-=N
kN k 1 )(18.06.65316.653+-=N
N 所以N=3647。
19-6.一缝间距d=0.1mm ,缝宽a=0.02mm 的双缝,用波长 nm 600=λ的平行单色光垂直入射,双缝后放一焦距为f=2.0m 的透镜,求:(1)单缝衍射中央亮条纹的宽度内有几条干涉主极大条纹;(2)在这双缝的中间再开一条相同的单缝,中央亮条纹的宽度内又有几条干涉主极大?
解: λϕk a ±=sin 所以中央亮条纹位置为:m a f x 12.010
21060022259
=⨯⨯⨯==--λ 中央明条纹位于:中心位置的上下方各0.06m 处。
而干涉条纹的条纹间距为:m d f x 012.010
110600249=⨯⨯⨯==∆--λ 中央明条纹在中心位置的上下方各0.006m 的位置上,第K 级明条纹的位置为:
06.0012.0006.0 ⨯+=k x 所以对应的k=4,
即在单缝衍射中央亮条纹的宽度内有9条干涉主极大条纹(两边各四条+中央明纹)。
(2)在这双缝的中间再开一条相同的单缝, 干涉条纹的条纹间距将变为:m d f x 024.0105.01060022
149=⨯⨯⨯==∆--λ 中央明条纹在中心位置的上下方各0.012m 的位置上,第K 级明条纹的位置为:
06.0024.0012.0 ⨯+=k x 所以对应的k=2,
即在单缝衍射中央亮条纹的宽度内有5条干涉主极大条纹(两边各两条+中央明纹)。
19-7 一个平面透射光栅,当用光垂直入射时,能在30度角的衍射方向上得到600nm 的第二级主极大,并且第二级主极大能分辨nm 05.0=∆λ的两条光谱线,但不能得到400nm 的第三级主极大,求:(1)此光栅的透光部分的宽度a 和不透光部分的宽度b ;(2)此光栅的总缝数N 。
解:(1)利用: λϕk b a ±=+s i n )(
根据题意:30度角的衍射方向上得到600nm 的第二级主极大,所以:
nm b a 24002
1
6002sin 2=⨯==+ϕλ
不能得到400nm 的第三级主极大:说明第三级条纹缺级。
由缺级的定义可得到: 3=+a
b a 所以:a=800nm ,b=1600nm 。
(2)根据瑞利判据:)(λλλ∆+-=
N kN k 1
)(05.0600126002+-=
⨯N N 所以:N=6000。
19-8 波长400nm 到750nm 的白光垂直照射到某光栅上,在离光栅0.50m 处的光屏上测得第一级彩带离中央明条纹中心最近的距离为4.0cm ,求:(1)第一级彩带的宽度;(2)第三级的哪些波长的光与第二级光谱的光相重合。
解:(1)衍射光栅中a k x 212λ
)(+= 波长越小,则离中央明纹就越近,所以:a
210400304.07
-⨯⨯= 那么750nm 的波长的第一级条纹位置在:m a
x 075.021075037
=⨯⨯=- 第一级彩带的宽度:cm m x 5.3035.004.0075.0==-=∆
(2)第二级的750nm 的波长对应的光的位置:m a
x 125.021075057
2=⨯⨯=- 第三级中有一部分和它将重合:m a x 125.0103
72733≤⨯=⨯=λλ
对应的波长为400——500nm 的波
19-9 如要用衍射光谱区别氢原子巴尔末系第11条和第12条谱线,光栅的分辨本领应为多大?如光栅常数为每毫米200条的光栅,要想在第2级中能分辨这两条谱线,这光栅的宽度至少多宽?(提示:巴尔末系第11条和第12条谱线由量子数n 分别为13和14到n=2的跃迁所产生。
)
解:(1)根据瑞利判据:光栅的分辩本领为λλ∆=
R ,只要知道它们的波长就可以了。
n 从13→2:v ~ =R [1/22-1/132]=(3/4)R , λ2=676/(165R) n 从14→2:v
~ =R [1/22-1/142]=(5/36)R ,λ3=(49)/(12R) 所以:323
300R λλλλλ===∆- (2) 根据瑞利判据: )(λλλ∆+-=
N
kN k 1 k=2,所以:37341237222⨯-=⨯N
N 得出: N=151条, 如光栅常数为每毫米200条的光栅,那么只要光栅的宽度为:1510.75200mm =就可以满足要求了。
19-10 用每毫米500条栅纹的光栅,观察钠光光谱(
A 5900=λ)。
问:(1)光线垂直入射;(2)光线以入射角30。
入射时,最多能看到几级条纹?
解:(1)正入射时, m d 63
102500
10--⨯== λϕk d ±=sin 所以当1sin =ϕ,对应的级次(取整数)最大:3==
λd k
能看到的条纹为:3,2,1,0,-1,-2,-3。
(2)斜入射时,λθϕk d ±=±)(sin sin 所以当2330sin sin =
+ ϕ,对应的级次(取整数)最大:523==λ
d k 当2130sin sin -=+ ϕ,对应的级次(取整数)最小:12-=-=λd k
能看到的条纹为:5,4,3,2,1,0,-1。
思考题
19-1.要分辨出天空遥远的双星,为什么要用直径很大的天文望远镜? 答:最小分辨角为:D λ
θ22.1=,它的倒数为分辨本领,当D 越大,θ越小,那么分辨
本领就越大。
所以用的天文望远镜的直径很大,提高了分辨本领。
19-2.使用蓝色激光在光盘上进行数据读写较红色激光有何优越性? 答:最小分辨角为:D λ
θ22.1=,它的倒数为分辨本领,当λ越小,θ越小,那么分辨
本领就越大。
所以用的蓝色光比红色光好,提高了分辨本领。
19-3.光栅形成的光谱较玻璃棱镜形成的色散光谱有何不同?
答:两者都是分光元件。
不同点:
(1)光栅光谱有一系列的级次,每一级次都有正负两套光谱,零级光谱因波长重合而不能分光;而棱镜光谱只有一套零级光谱,相对强度大。
(2)低级次的光栅光谱波长与衍射角近似有正比关系,称为匀排光谱;而棱镜光谱的波长与角度为非线性关系,不是匀排光谱。
19-4.孔径相同的微波望远镜和光学望远镜相比较,哪个分辨本领大?为什么? 答:最小分辨角为:D λ
θ22.1=,它的倒数为分辨本领,当λ越小,θ越小,那么分辨
本领就越大。
由于微波的波长大于光波的波长,所以光波望远镜的分辨本领大。
19-5.登月宇航员声称在月球上唯独能够用肉眼分辨地球上的人工建筑是中国的长城。
你依据什么可以判断这句话是否真的?需要哪些数据?
答:可以根据瑞利判据。
