典型系统1的计算结果

合集下载

实验一电力系统潮流计算

实验一电力系统潮流计算
一、实验背景
潮流计算是电力系统的基础，也是电力系统优化设计的前提。

它是一种求解受非线性条件制约的线性方程组的数值方法，能够求解电力系统的稳态潮流，即电力系统在其中一种操作或运行状态下的电压、电流大小和方向。

潮流计算可以为电力系统的综合分析、可靠性分析、功率调度、故障分析、电压控制、电源接入分析、调节器诊断、可调装置分析等提供重要的输入参数。

二、实验步骤
（1）系统参数设置：确定潮流计算模型中的系统参数，包括拓扑结构、主变参数以及节点馈电和负荷数据。

（2）特性参数选择：确定潮流计算模型中特性参数，包括电抗器、变压器的损耗参数、电容器的补偿方式以及可调节装置参数等。

（3）潮流程序的编制：根据模型结构，以及确定的参数，编制潮流计算程序。

（4）潮流计算的运行：运行潮流计算程序，得到电力系统中的线路电流、电压、有功、无功等参数。

（5）潮流计算结果分析：分析潮流计算结果，验证潮流计算模型和输入参数的准确性，对电力系统的可靠性进行评价和优化设计。

三、实验过程
此次实验采用PSCAD/EMTDC软件。

电力拖动控制系统第三章习题答案

习题三3.1双闭环调速系统的ASR 和ACR 均为PI 调节器，设系统最大给定电压*nm U =15V ，Nn =1500r/min ，N I =20A ，电流过载倍数为2，电枢回路总电阻R =2Ω，s K =20，e C =0.127V ·min/r ，求：（1）当系统稳定运行在*n U =5V ，dL I =10A 时，系统的n 、n U 、*i U 、i U 和c U 各为多少？（2）当电动机负载过大而堵转时，*i U 和c U 各为多少？解：(1)*****0*/15/15000.01/55,5000.01/150.375/400.375*10 3.750.127*50010*24.17520500,5, 3.75,nm N nnim dm i d i d dL e N dL C s s s n i i c U n V rpm V rpmU VU V n rpmV rpmU V V AI AU I V U U E I R C n I R U V K K K n rpm U V U U V U ααββ==============+++=========当转速即4.175v=（2）堵转时，V I U dm i 15*==β，()040*2420e d d dm c s s s C n I R U I R U V K K K +=====3.2 在转速、电流双闭环调速系统中，两个调节器ASR ，ACR 均采用PI 调节器。

已知参数：电动机：N P =3.7kW ，N U =220V ，N I =20A ，N n =1000 r/min ,电枢回路总电阻R =1.5Ω,设cm im nm U U U ==** =8V ，电枢回路最大电流dm I =40A,电力电子变换器的放大系数s K =40。

试求：（1）电流反馈系数β和转速反馈系数α。

（2）当电动机在最高转速发生堵转时的,0d U c i i U U U ,,*值。

利用简单工具对一个典型办公大楼照明系统的设计进行关于日光照明和人工照明的能量分析

利用简单工具对一个典型办公大楼照明系统的设计进行关于日光照明和人工照明的能量分析内容摘要现今社会，能源欠缺和碳排放量是所有国家都正在面临的要紧挑战。

要解决那个问题有很多方式，能够通过在许多领域节约能源来实现。

照明被普遍应用在许多领域，其中之一确实是被用来提高能源利用效率从而减少能源消耗。

在这篇文章中，迪拜一座典型的办公大楼被用于分析考虑。

本文的第一部份对有效利用自然采光为一座办公大楼来提高能源效率进行了报告。

本研究利用威卢克斯日光可视化工具2进行仿真，对仿真结果具体讨论。

研究说明，在迪拜，一个理想办公空间有足够的潜能来获取自然光并减少人工照明的需要。

在第二部份中，人工照明被用来补充自然采光,以知足所需的照明标准。

德国专业照明设计软件版本照明向导软件用于设计和评估关于同一个办公空间，通过应用不同种类的灯具，人工照明打算和其相似的照明能力，评估结果被重点突出。

其造成的阻碍也被进行了研究。

对暖通系统利用自然采光和人工照明造成的阻碍也被用来调查和重点突出。

关键字人工照明，荧光灯，发光二极管（LED）1.介绍能源消耗是工程师、科学家和决策者们在全世界讨论中的一个要紧关注点。

照明是住宅和商业建筑能源消耗的要紧因素之一。

天天，每一个国家对能源消耗的需求都在不断增加，因此，有一个提高能源效率的研究需求。

在迪拜，和世界其他国家一样，在办公楼中，尽管自然采光存在着普遍的应用，用作功能性和装饰性目的的人工照明仍占总的电能消耗中相当大的一部份。

在少数建筑物中存在一个很严重的问题，那确实是过度照明和后续的本钱效益。

这些本钱能够通过利用一些照明策略而大大的降低，例如照明操纵系统来有效的获取日光来用作室内照明目的。

因此，照明现在代表了能源消耗中专门大的一部份，而且受到了大量的关注，尤其是在办公大楼的利用中。

本文的要紧目标是探讨在办公大楼中优化日光照明利用的可能性而且通过利用人工照明的同时限制其对冷负荷的阻碍从而减少能源消耗。

单元体吊装轨道系统计算(1)

采用sap2000 建模计算，钢梁及钢索自重由软件自动考虑。
计算模型及活荷载加载（KN）
计算模型及工字钢轨道自重荷载加载（KN）
挠度组合
强度组合（活荷载系数1.3*1.4=1.82 ）
6
轴力图（KN）
剪力图（KN）
弯矩图（KN*m）
挠度图（mm ）
7
钢梁最大内力荷载效应组合设计值轴力剪力 F a := 11.8kN F vy := 30.3 kN M x := 8.35 kN ⋅ m
< 80
fQ235B_t
235MPa
= "OK, Pass !"
无局部压应力，可不配置横向加劲肋
钢索验算
参考规范《高处作业吊篮》（GB19155-2003 ），有吊篮时，钢索安全系数不应小于 9 倍。钢索最大拉力设计值钢索最小破断力活荷载分项系数活荷载动力系数 F t1_cable := 55.48kN Tlim_ϕ23 = 281.5 KN γL := 1.4 η := 1.3 Tlim_ϕ23 ⋅ γL ⋅ η F t2_cable := 42.96kN
弯矩
4
强度校核 Fa A22a Mx Wx
截面正应力
σ a :=
+
= 82.49 ⋅ MPa
因此 σ a < fQ235B_t = "OK, Pass !"
(
)
(1.05 为塑性发展系数） F vy ⋅ S x Ix ⋅ 25mm
截面剪应力
τ v :=
= 8.76 ⋅ MPa
因此 τ v < fQ235B_v = "OK, Pass !"

热力系统计算模板

计算原始资料:1.汽轮机型式及参数（1）机组型式：亚临界、一次中间再热、四缸四排汽、单轴、凝汽式汽轮机；（2）额定功率：p e=600MW（3）主蒸汽参数（主汽阀前）：p0=，t0=537℃；（4）再热蒸汽参数（进汽阀前）：热段：p rh=，t rh=537℃冷段：pˊrh=，tˊrh=315℃（5）汽轮机排汽压力p c= MPa，排汽比焓：h c=Kg。

2.回热加热系统参数：（1）机组各级回热抽汽参数见表1-1；表1-1 回热加热系统原始汽水参数项目单位H1H2H3H4 H5 H6 H7 H8 Mpa抽汽压力pˊj抽汽比焓hKJ/Kg 3133 3016 3317 3108 2913 2750 2650 2491 j抽汽管道压% 3 3 3 3 3 3 3 3 损δpjMpa 20水侧压力pw加热器上端差δ℃0 0 0t℃316 429 323 137 抽汽温度twj加热器下端℃差δt1（2）最终给水温度：t fw=℃；（3）给水泵出口压力：p pu=，给水泵效率：ηpu=；（4）除氧器至给水泵高差:H pu== KJ/Kg（5）小汽机排汽压力：p e，xj= MPa；小汽机排汽焓：h c，xj3.锅炉型式及参数（1）锅炉型式：英国三井／541／541；（2）额定蒸发量:D b=2027t/h；（3）额定过热蒸汽压力p b=;额定再热蒸汽压力p r=；（4）额定过热气温t b=541℃额定再热气温t r=541℃；（5）汽包压力p du=；（6）锅炉热效率：ηb=%。

4.其他数据（1）汽轮机进汽节流损失δp1=4%，中压缸进汽节流损失δp2=2%=415KJ/Kg（2）轴封加热器压力p sg=98K Pa，疏水比焓：h d，sg（3）机组各门杆漏汽、轴封漏汽等小汽流量及参数见表1-2（4）锅炉暖风器耗汽、过热器减温水等全厂性汽水流量及参数见表1-3（5）汽轮机机械效率ηm=，ηg=（6）补充水温度t ma=20℃（7）厂用电率：ε=；（六）简化条件（1）忽略加热器和抽汽管道的散热损失；（2）忽略凝结水泵的介质比焓升。

《自动控制》一二阶典型环节阶跃响应实验分析报告

《自动控制》一二阶典型环节阶跃响应实验分析报告一、实验目的本实验旨在通过实际的一二阶典型环节阶跃响应实验，掌握自动控制理论中的基本概念和方法，并能够分析系统的动态响应特性。

二、实验原理1.一阶惯性环节：一阶惯性环节是工程实际中常见的系统模型，其传递函数为G(s)=K/(Ts+1)，其中K为传递函数的增益，T为时间常数。

2.二阶惯性环节：二阶惯性环节是另一类常见的系统模型，其传递函数为G(s)=K/((Ts+1)(αTs+1))，其中K为传递函数的增益，T为时间常数，α为阻尼系数。

3.阶跃响应：阶跃响应是指给定一个单位阶跃输入，观察系统的输出过程。

根据系统的阶数不同，其响应形式也不同。

实验仪器：电动力控制实验台，控制箱，计算机等。

三、实验步骤1.将实验台上的一阶惯性环节模型接入控制箱和计算机，并调整增益和时间常数的初始值。

2.发送一个单位阶跃信号给控制器，观察实验台上的输出响应，并记录时间和输出值。

3.根据记录的数据，绘制一阶惯性环节的阶跃响应图像。

4.类似地，将实验台上的二阶惯性环节模型接入控制箱和计算机，并调整增益、时间常数和阻尼系数的初始值。

5.发送一个单位阶跃信号给控制器，观察实验台上的输出响应，并记录时间和输出值。

6.根据记录的数据，绘制二阶惯性环节的阶跃响应图像。

四、实验结果与分析1.一阶惯性环节的阶跃响应图像如下：（在此插入阶跃响应图像）根据图像可以看出，随着时间的增加，输出逐渐趋于稳定。

根据实验数据，可以计算出一阶惯性环节的增益K和时间常数T的估计值。

2.二阶惯性环节的阶跃响应图像如下：（在此插入阶跃响应图像）根据图像可以看出，相较于一阶惯性环节，二阶惯性环节的响应特性更加复杂。

根据实验数据，可以计算出二阶惯性环节的增益K、时间常数T和阻尼系数α的估计值。

五、实验结论通过本实验，我们成功地进行了一二阶典型环节阶跃响应实验，并获得了实际的响应数据。

通过对实验数据的分析，我们得到了一阶惯性环节和二阶惯性环节的估计参数值。

【实验报告】一、二阶系统的电子模拟及时域响应测试

实验名称：一二阶系统的电子模拟及时域响应测试课程名称：自动控制原理实验目录（一）实验目的 (3)（二）实验内容 (3)（三）实验设备 (3)（四）实验原理 (3)（五）一阶系统实验结果 (3)（六）一阶系统实验数据记录及分析 (7)（七）二阶系统实验结果记录 (8)（八）二阶系统实验数据记录及分析 (11)（九）实验总结及感想............................................................................错误!未定义书签。

图片目录图片1 一阶模拟运算电路 (3)图片2 二阶模拟运算电路 (3)图片3 T=0.25仿真图形 (4)图片4 T=0.25测试图形 (4)图片5 T=0.5仿真图形 (5)图片6 T=0.5测试图形 (5)图片7 T=1仿真图形 (6)图片8 T=1测试图形 (6)图片9 ζ=0.25s仿真图形 (8)图片10 ζ=0.25s测试图形 (8)图片11 ζ=0.5s仿真图形 (9)图片12 ζ=0.5s测试图形 (9)图片13 ζ=0.8s仿真图形 (10)图片14 ζ=0.8s测试图形 (10)图片15 ζ=1s仿真图形 (11)图片16 ζ=1s测试图形 (11)表格目录表格1 一阶系统实验结果 (7)表格2 二阶系统实验结果 (11)一二阶系统的电子模拟及时域响应测试（一）实验目的1.了解一、二阶系统阶跃响应及其性能指标与系统参数之间的关系。

2.学习在电子模拟机上建立典型环节系统模型的方法。

3.学习阶跃响应的测试方法。

（二）实验内容1.建立一阶系统的电子模型,观测并记录在不同时间常数T时的跃响应曲线,并测定其过渡过程时间TS。

2.建立二阶系统的电子模型,观测并记录在不同阻尼比ζ时的跃响应曲线,并测定其超调量σ%及过渡过程时间TS。

（三）实验设备HHMN电子模拟机，实验用电脑，数字万用表（四）实验原理一阶系统：在实验中取不同的时间常数T，由模拟运算电路，可得到不同时间常数下阶跃响应曲线及不同的过渡时间。

实验一控制系统典型环节的模拟实验

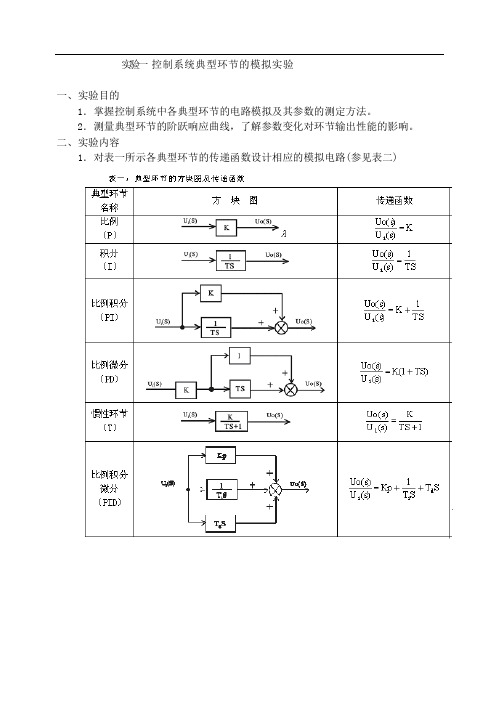
实验一控制系统典型环节的模拟实验一、实验目的1．掌握控制系统中各典型环节的电路模拟及其参数的测定方法。

2．测量典型环节的阶跃响应曲线，了解参数变化对环节输出性能的影响。

二、实验内容1．对表一所示各典型环节的传递函数设计相应的模拟电路(参见表二)2．测试各典型环节在单位阶跃信号作用下的输出响应。

3．改变各典型环节的相关参数，观测对输出响应的影响。

三、实验内容及步骤1．观测比例、积分、比例积分、比例微分和惯性环节的阶跃响应曲线。

①准备：使运放处于工作状态。

将信号发生器单元U1的ST端与+5V端用“短路块”短接，使模拟电路中的场效应管（K30A）夹断，这时运放处于工作状态。

②阶跃信号的产生：电路可采用图1-1所示电路，它由“阶跃信号单元”（U3）及“给定单元”（U4）组成。

具体线路形成：在U3单元中，将H1与+5V端用1号实验导线连接，H2端用1号实验导线接至U4单元的X端；在U4单元中，将Z端和GND端用1号实验导线连接，最后由插座的Y端输出信号。

以后实验若再用阶跃信号时，方法同上，不再赘述。

实验步骤：①按表二中的各典型环节的模拟电路图将线接好(先接比例)。

(PID先不接)②将模拟电路输入端(U i)与阶跃信号的输出端Y相连接；模拟电路的输出端(Uo)接至示波器。

③按下按钮(或松开按钮)SP时，用示波器观测输出端的实际响应曲线Uo(t)，且将结果记下。

改变比例参数，重新观测结果。

④同理得积分、比例积分、比例微分和惯性环节的实际响应曲线，它们的理想曲线和实际响应曲线参见表三。

2．观察PID环节的响应曲线。

实验步骤：①将U1单元的周期性方波信号(U1 单元的ST端改为与S端用短路块短接，S11波段开关置于“方波”档，“OUT”端的输出电压即为方波信号电压，信号周期由波段开关S11和电位器W11调节，信号幅值由电位器W12调节。

以信号幅值小、信号周期较长比较适宜)。

②参照表二中的PID模拟电路图，按相关参数要求将PID电路连接好。

自动控制原理1实验指导书

⾃动控制原理1实验指导书《⾃动控制原理Ⅰ》实验指导书2011年9⽉实验⼀典型环节及其阶跃响应⼀．实验⽬的1．学习构成典型环节的模拟电路。

2．熟悉各种典型环节的阶跃响应曲线，了解参数变化对典型环节动态特性的影响。

3．学会由阶跃响应曲线计算典型环节的传递函数。

4．掌握仿真分析软件multisim的使⽤。

⼆．物理模拟说明⽤电⼦线性运算放⼤器和各种反馈电路能够模拟线性系统典型环节。

同时，模拟典型环节是有条件的，即是将运算放⼤器视为满⾜以下条件的理想放⼤器：(1)输⼊阻抗为∞，进⼊运算放⼤器的电流为零，同时输出阻抗为零；(2)电压增益为∞；(3)通频带为∞；(4)输⼊与输出间呈线性特性．可是，实际运算放⼤器毕竟不是理想的；电⼦元件和电路仍然有惯性（尽管⾮常⼩）其通频带有限，并⾮达到∞，输⼊输出功率也是有限的；⼀般的运算放⼤器，在开环使⽤时，其通频带仅为10-100Hz，当将其接成K=1的⽐例器，其通频带也不过MHz左右。

所以，以线性运算放⼤器和各种反馈电路去模拟系统的各种线性和⾮线环节也不是⽆条件的，它仍然是在⼀定条件下，在⼀定程度上模拟出线性典型环节的特性，超出条件的范围和要求过份精确都是办不到的。

因此，需要说明以下⼏点事项：(1)⽤实际的运算放⼤器模拟线性系统各种典型环节都是有条件的近似关系，不可能得到理想化典型环节的特性。

其主要原因是：1实际运算放⼤器输出幅值受其电源所限，根本不可能达到∞，此即⾮线性影响；2实际运算放⼤器不是⽆惯性的。

尽管惯性很⼩，但通频带不会达到∞。

(2)实际运算放⼤器输出幅值受限的⾮线性因素对所有各种模拟环节都有影响，但情况迥异。

对⽐例环节、惯性环节、积分环节、⽐例积分环节和振荡环节，只要控制了输⼊量的⼤⼩或是输⼊量施加的时间长短(对于积分或⽐例积分环节），不使其输出在⼯作期间内达到最⾼饱和度，则⾮线性因素对上述环节特性的影响可以避免；但是⾮线性因素对模拟⽐例微分环节和微分环节的影响却⽆法避免。

天正防排烟计算1

天正防排烟计算1天正防排烟计算1一、相关常识介绍1.1防排烟系统的定义和作用防排烟系统是指在建筑物内的火灾或其他紧急情况下，通过合理的设计和安装排烟设备，将烟气排出建筑物外，使人员能够顺利疏散，降低烟气对人身安全和建筑物财产造成的威胁。

1.2防排烟系统的构成和设备一般防排烟系统主要包括烟气控制区域、烟气抽排区域、烟气排放口等组成部分。

常见的防排烟设备包括排烟风机、排烟阀门、排烟口、排烟道等。

二、天正防排烟计算的基本原理2.1烟气产生量的计算根据建筑物的设计容积和烟气产生速率，确定烟气产生量。

这需要考虑建筑物的使用功能、人员密度等因素。

2.2烟气排放速度的计算根据排烟通道的尺寸和形状，计算烟气排放速度。

一般来说，排烟速度应使烟气在通道内保持上升状态，以防止烟气进入室内。

2.3烟气温度和速度的分布通过计算分析，确定烟气在排烟通道内的温度和速度分布，以便确定合适的排烟口位置和数量。

三、天正防排烟计算的具体步骤及所需数据3.1建筑物参数的获取首先需要获取建筑物的尺寸、形状、楼层、使用功能等基本参数。

这些参数将作为计算的依据。

3.2确定防排烟系统的类型和布置方式根据建筑物的功能和建筑规范的要求，确定适合该建筑的防排烟系统类型和布置方式。

常见的防排烟系统包括自然排烟系统和强制排烟系统。

3.3计算烟气产生量根据建筑物内的使用功能和人员密度，计算火灾或紧急情况下烟气的产生量。

这需要考虑建筑物内部的燃烧物质种类和数量。

3.4计算烟气排放速度根据排烟道的尺寸、形状和烟气产生量，计算烟气排放速度。

一般来说，排烟速度应使烟气在排烟道内保持上升状态。

3.5确定排烟口位置和数量根据烟气排放速度的计算结果和建筑物内的布局，确定合适的排烟口位置和数量。

排烟口的位置应选择在烟气上升的区域，以便尽快将烟气排出建筑物。

3.6验证计算结果的合理性最后，需要验证计算结果的合理性，即通过模拟计算或实地测试，检查防排烟系统的性能是否符合设计要求，并对需要调整的参数进行优化。

计算说明书_悬架系统

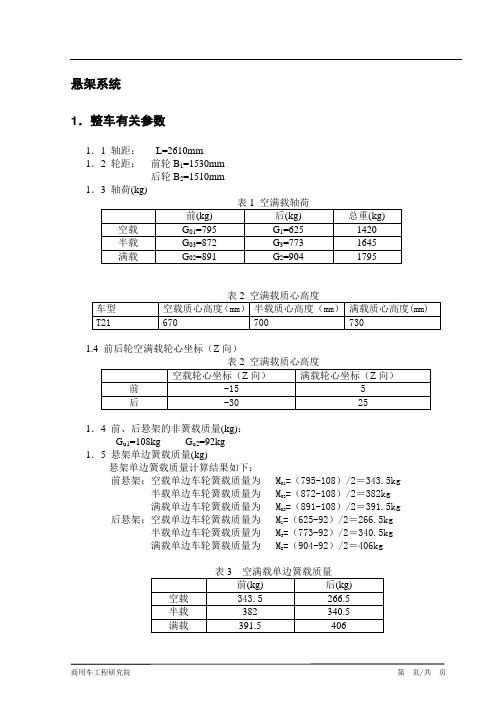
悬架系统1．整车有关参数1．1 轴距：L=2610mm1．2 轮距：前轮B1=1530mm后轮B2=1510mm1．3 轴荷(kg)1.4 前后轮空满载轮心坐标（Z向）1．4 前、后悬架的非簧载质量(kg)：G u1=108kg G u2=92kg1．5 悬架单边簧载质量(kg)悬架单边簧载质量计算结果如下：前悬架：空载单边车轮簧载质量为M01=（795-108）/2＝343.5kg 半载单边车轮簧载质量为 M03=（872-108）/2＝382kg满载单边车轮簧载质量为M02=（891-108）/2＝391.5kg 后悬架：空载单边车轮簧载质量为M1=（625-92）/2＝266.5kg半载单边车轮簧载质量为M3=（773-92）/2＝340.5kg满载单边车轮簧载质量为M2=（904-92）/2＝406kg2、前悬架布置前悬架布置图见图1图1 T21前悬架布置简图3、前悬架设计计算3．1 前悬架定位参数:3．2 前悬架采用麦弗逊式独立悬架，带稳定杆，单横臂，螺旋弹簧，双向双作用筒式减震器。

(1) 空满载时缓冲块的位置和受力情况空载时，缓冲块起作用，不受力满载时，缓冲块压缩量为13.8mm ，（由DMU 模拟得知，DMU 数据引自T21 M2数据）。

根据缓冲块的特性曲线，当缓冲块压缩13.8mm 时，所受的力为：125N (2) 悬架刚度计算螺旋弹簧行程杠杆比：1.06悬架刚度为K 1= （（391.5-343.5）*9.8-125/1.06）/（5-（-15））= 17.62N/mm（3）前螺旋弹簧①截锥螺旋弹簧②螺旋弹簧行程杠杆比：1.06③刚度C1=K1*（1.06）2*0.9=17.62*（1.06）2*0.9=17.81N/mm（4）静挠度和空满载偏频计算空载时挠度 f 1= N 1/K 1=( M 01*9.8)/K 1=(343.5*9.8)/17.81=18.9cm静挠度 f 01= f 1 +(5-(-15))/10=20.9 偏频n: 空载为 Hz f n 15.19.18/5/511=== 满载为 Hz f n 09.19.20/5/50101===结论：前悬架偏频在1.00～1.45Hz 之间，满足设计要求。

第7章简单系统的动态：一阶系统和二阶系统

R 速率（变化率）方程速率方程无一定格式；速率的值在DT时间内是不变的，其时间下标为KL。

A 辅助(Auxiliary)方程辅助方程定义为在反馈系统中描述信息的运算式； “辅助”的涵义就是帮助建立速率方程。

C T N
赋值予常数赋值予表函数中Y坐标为LEVEL方程赋予初始值
LEV与RT的指数增长
正反馈——指数增长的重要特点
以不同大小的时间坐标范围观察指数增长过程：
t≤15 Td 前，增长趋势不显著， t≥ 15 Td 后，状态变量猛然暴涨。
正反馈——超指数增长
如图，实线表示的非线性情况，其变化率的增长速度较虚线表示的线性增长情况快得多，这种增长过程称为超指数增长。系统时间常数变化的非线性系统比起线性系统具有更加突出的指数增长特性。
L
R
RT.KL=CONST*DISC.K
A DISC.K =GL－LEV.K 式中：
负反馈系统的典型流图
DT——计算时间间隔(时间)； CONST——常数（1/时间）； LEV——状态变量（单位）； RT——速率（单位/时间）； DISC ——偏差（单位）； GL ——目标值（单位）
负反馈系统——参数推导
带有不变外生输入速率的负反馈系统
推导：
RT1.KL=CONST*（GL－LEV.K） RT2.KL=CRT NTRT.KL＝CONST*（GL－ LEV.K）+CRT
系统新的动态平衡
速率—状态变量关系曲线当NTRT=0时， CRT=－CONST*(GL－LEV.K） =－CONST*GL+LEV*CONST LEV=NGL=（CRT/CONST）+GL 或以时间常数T(T=1/CONST)表示, NGL=T*CRT+GL 系统新的平衡值比原目标值GL增加了T*CRT

自动控制原理实验报告典型环节及其阶跃响应二阶系统阶跃响应连续系统串联校正

自动控制原理实验报告班级：自动化0906班学生: 伍振希（09213052）张小维（合作）任课教师：苗宇老师目录实验一典型环节及其阶跃响应 (1)一、实验目的 (1)二、实验仪器 (1)三、实验原理 (1)四、实验内容 (1)五、实验步骤 (2)六、实验结果 (3)实验二二阶系统阶跃响应 (6)一、实验目的 (6)二、实验仪器 (6)三、实验原理 (6)四、实验内容 (6)五、实验步骤 (7)六、实验结果 (7)实验三连续系统串联校正 (13)一、实验目的 (13)二、实验仪器 (13)三、实验内容 (13)四、实验步骤 (15)五、实验结果 (15)实验一典型环节及其阶跃响应一、实验目的1. 掌握控制模拟实验的基本原理和一般方法。

2. 掌握控制系统时域性能指标的测量方法。

二、实验仪器1．EL-AT-III型自动控制系统实验箱一台2．计算机一台三、实验原理1．模拟实验的基本原理：控制系统模拟实验采用复合网络法来模拟各种典型环节，即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节，然后按照给定系统的结构图将这些模拟环节连接起来，便得到了相应的模拟系统。

再将输入信号加到模拟系统的输入端，并利用计算机等测量仪器，测量系统的输出，便可得到系统的动态响应曲线及性能指标。

若改变系统的参数，还可进一步分析研究参数对系统性能的影响。

四、实验内容构成下述典型一阶系统的模拟电路，并测量其阶跃响应：1.比例环节的模拟电路及其传递函数如图1-1。

G（S）= R2/R12.惯性环节的模拟电路及其传递函数如图1-2。

G（S）= - K/TS+1K=R2/R1，T=R2C3.积分环节的模拟电路及传递函数如图1-3。

G（S）=1/TST=RC4.微分环节的模拟电路及传递函数如图1-4。

G（S）= - RCS5.比例微分环节的模拟电路及传递函数如图1-5（未标明的C=0.01uf）。

G（S）= -K（TS+1）K=R2/R1，T=R1C五、实验步骤1.启动计算机，在桌面双击图标 [自动控制实验系统] 运行软件。

一阶系统的频率响应 -回复

一阶系统的频率响应-回复一阶系统是控制系统中常见的一个基本模型，它具有简单的结构和一阶动态特性。

频率响应是研究系统在不同频率下的输出响应的方法之一。

本文将以一阶系统的频率响应为主题，逐步回答相关问题，帮助读者更好地理解和应用一阶系统的频率响应。

一、什么是一阶系统？一阶系统是指具有一个惯性成分和一个死时间成分的系统。

一阶系统的传递函数通常可以用以下形式表示：G(s) = K / (Ts + 1)，其中K为系统的增益，T为系统的时间常数，s为复平面上的复变量。

二、什么是频率响应？频率响应是描述系统对不同频率的输入信号的输出响应情况。

在控制系统中，一般通过系统的传递函数来计算系统的频率响应。

频率响应可以帮助我们了解系统对不同频率信号的衰减和相位延迟情况，从而更好地分析和设计控制系统。

三、如何计算一阶系统的频率响应？计算一阶系统的频率响应可以通过传递函数的频域分析方法来实现。

具体步骤如下：1. 将一阶系统的传递函数G(s)转化为频域表达式。

将s替换为jω，其中j为虚数单位，ω为频率。

2. 将传递函数的频域表达式分别表示为幅度和相位的形式。

幅度响应G(j ω)的计算公式为：G(jω) = K / (jωT + 1) ，相位响应Φ(jω)的计算公式为：Φ(jω) = arg(G(jω))。

3. 对于幅度响应，可以通过计算传递函数中分子和分母的模长来求解。

具体步骤如下：a. 将分子和分母的复数表示分别展开为实部和虚部的形式。

b. 将分子和分母的实部和虚部分别平方，并相加得到分子和分母的平方和。

c. 通过计算平方和的平方根，得到幅度响应的模长。

4. 对于相位响应，可以通过计算传递函数中分子和分母的虚部之差来求解。

具体步骤如下：a. 将分子和分母的复数表示分别展开为实部和虚部的形式。

b. 计算分子和分母的虚部之差，并计算arctan(虚部差/实部和)得到相位响应。

四、如何理解一阶系统的频率响应？一阶系统的频率响应可以帮助我们了解系统对不同频率信号的衰减和相位延迟情况。

利用热力学第一定律解决热力学问题

利用热力学第一定律解决热力学问题热力学是研究能量转化和宏观系统性质变化的学科，热力学第一定律是热力学的基本定律之一。

本文将重点讨论如何利用热力学第一定律解决热力学问题。

一、热力学第一定律的基本原理热力学第一定律是能量守恒定律的表达形式。

它指出，在封闭系统中，能量和物质可以相互转换，但总能量守恒。

即，能量不能从无到有，也不能从有到无，只能转换形式或从一处转移到另一处。

热力学第一定律的数学表达可以写作：ΔU = Q - W其中，ΔU表示系统内能的变化，Q表示系统吸收的热量，W表示系统对外做功。

二、应用热力学第一定律解决问题的步骤1. 确定问题的背景和条件在解决热力学问题之前，需要准确地了解问题的背景和所给出的条件。

只有了解清楚问题的具体情况，才能更好地应用热力学第一定律进行分析。

2. 选择合适的热力学过程根据问题的情况，选择适用的热力学过程。

常见的过程包括等温过程、等压过程、等容过程和绝热过程等。

选择合适的过程是分析问题的关键，需要根据问题中提供的信息进行判断。

3. 计算系统内能的变化根据热力学第一定律的表达式，计算系统内能的变化。

根据题目提供的信息，确定系统吸收的热量和对外做的功，然后代入公式求解即可。

4. 分析计算结果根据计算得到的结果，分析问题并得出结论。

根据热力学第一定律所描述的能量守恒原理，可以判断系统是否达到热平衡状态、能量转化是否合理等。

三、实例分析：汽车发动机工作过程以汽车发动机的工作过程为例，来说明如何利用热力学第一定律解决热力学问题。

汽车发动机是典型的热力学系统，其工作过程可以看作是一个循环过程。

在一个循环中，燃料燃烧释放热能，推动活塞工作，做功推动汽车运动，同时也有部分热能通过散热向外界传递。

在分析汽车发动机工作过程时，可以应用热力学第一定律进行计算和分析。

根据题目所给的条件，可以计算出活塞运动过程中系统吸收的热量和对外做的功，代入热力学第一定律的公式中，计算系统内能的变化。

通过分析计算得到的结果，可以判断发动机的效率、能量转化的合理性等。

第十二章差错控制编码习题解答

信息“101”的系统码为“110011”
方法2：信息与典型生成矩阵G计算得到系统码（不建议考试时使用，但是在实际中被使用）
1 0 0 1 0 1 [110] 0 1 0 1 1 0 0 0 1 0 1 1

1 1 00 11
方法3：典型生成矩阵G的某些行进行模2加运算（适合信息位中“1”的个数不多的场合） “110”
(3)写出信息码“110”所对应的系统码方法1：由监督方程
a4 a3 a2 a0 0 a4 a3 a1 0 a5 a3 a0 0 可得 a0 a5 a3 =1 0=1 a1 a4 a3 =1 0=1 a2 a4 a3 a0 =1 0 1=0
由 g ( x) x x x 1 可以直接画出编码器
门2 D0
4
2
⊕
D1
⊕
D2
D3
⊕
输出
门1
⊕
码组
输入信息码元
将非典型监督矩阵转换为典型监督矩阵
非典型
H
0 0 1
1 1 0
1 1 1
1 0 0
0 1 0
1 0 1
① ② ③
利用线性代数的初等变换， ① ⊕ ③
典型
①
1 0 0
H
1 0 1
1 1 0
0 1 1
0 1 0
0 0 1
Prk I r
典型
H
1 0 1
1 1 0
0 1 1
1 0 0
1 0 0 1 0 1 ① ② 典型生成矩阵G 0 1 0 1 1 0 ③ 0 0 1 0 1 0
①
⊕
③
1 1 00 11

实验一一,二阶系统阶跃响应

综合性实验：二阶系统的单位阶跃响应综合实验一、实验目的：1.在给定系统的内部结构、系统的阶跃响应性能指标，掌握系统的电路模拟方法。

2.掌握系统校正PID算法的实现和参数计算方法。

3.观察最优二阶系统的单位阶跃响应曲线，了解高阶系统的最优阶跃响应动、静态性能。

二、实验说明：1.本实验包括自控原理的线性定常系统分析的大部分内容，帮助学生复习、巩固书中的内容，提高学生的实验应用能力。

2.给定二阶系统的阶跃性能指标：o%=20% , t s=2s,设计一个电路模拟系统,计算电路的系统参数。

3.设计一个PID调节器，使系统具有二阶阶跃响应最优性能指标。

4.在实验平台上观察模拟系统的单位阶跃响应，观察系统校正前、后的输出响应。

说明最优二阶系统的动静态性能指标。

5.对模拟系统进行频域分析，计算其幅频和相频特性，在实验中观察系统的频率响应，对比计算和实验结果。

三、实验要求：按照实验过程作好实验前的准备工作＜包括安排布置软件、硬件设备，编写实验步骤，需要观察记录的数据准备）；记录好实验中的调试过程、数据变化，进行实验后的报告总结。

实验二二阶系统的阶跃响应实验二二阶系统的阶跃响应、实验目的1学习二阶系统阶跃响应曲线的实验测试方法2•研究二阶系统中无阻尼自然频率和阻尼比对阶跃瞬态响应指标的影响、实验设备1.XMN—2 型机；2.LZ3系列函数纪录仪或 CAE983.DT— 830数字万用表三、实验内容1对单一自然频率和阻尼比测量响应曲线2•保持阻尼比不变，改变自然频率记录响应曲线3•保持自然频率不变，改变阻尼比记录响应曲线四、实验步骤［步1］调整Rf和Ri使阻尼比为0.2，选择R，C使自然频率为1/0.47，假如幅度为1V的阶跃函数X(t＞，观察并记录响应曲线。

以下标称中电阻单位为千欧姆，电容为微法拉。

［步2］调整Rf和Ri使阻尼比为0.2，选择R，C使自然频率为1/1.47，假如幅度为1V的阶跃函数X(t＞，观察并记录响应曲线。