内蒙古科技大学马文蔚大学物理下册第六版答案

马文蔚《物理学》(第6版)(下册)章节题库-第十二章至第十三章【圣才出品】

则始、末两个状态气体内能之比为 E1/E2=
。
【答案】1.19
三、简答题 1．指出下列各式所表示的物理意义．
答：（1）表示理想气体分子每一自由度所具有的平均能量．表示单原子分子的平均动能或分子的平均平动动能．表示自由度为 i 的分子的平均能量．表示分子自由度为 i 的 1mol 理想气体的内能．表示质量为 m'的理想气体的内能．
3 / 124
圣才电子书十万种考研考证电子书、题库视频学习平台

图 12-2
【答案】（1）氧气；氢气；（2）2
【解析】由
可得。
2．1mol 氧气（视为刚性双原子分子的理想气体）贮于一氧气瓶中，温度为 27℃，这瓶氧气的内能为______J；分子的平均平动动能为______J；分子的平均总动能为______J。（摩尔气体常量 R＝8.31J·mol－1·K－1 玻耳兹曼常量 k＝1.38×10－23J·K－1）
【解析】由
可得。
2．理想气体处于平衡状态，设温度为 T，气体分子的自由度为 i，则每个气体分子所具
有的（）。
A．动能为 i/2kT
B．动能为 i/2RT
C．平均动能为 i/2kT
D．平均平动动能为 i/2RT
【答案】C
3．f（υ）为速率分布函数，则速率
的分子平均速率表达式为（）。
1 / 124
圣才电子书

【答案】B
十万种考研考证电子书、题库视频学习平台
【解析】由平均速率的定义，
区间内分子的平均速率应为：
分子、分母同除以 N，得
4．图 12-1 画了两条理想气体分子速率分布曲线（）。.
图 12-1
A．υp 是分子的最大速率

内蒙古科技大学马文蔚大学物理(下册)第六版答案解析

第九章振动习题：P37～39 1，2，3，4，5，6，7，8，16.9-4 一质点做简谐运动,周期为T,当它由平衡位置向X 轴正方向运动时,从1/2 最大位移处到最大位移处这段路程所需的时间( )A、T/12B、T/8C、T/6D、T/4分析(C)，通过相位差和时间差的关系计算。

可设位移函数y=A*sin(ωt),其中ω=2π/T；当y=A/2, ω t1= π /6 ；当y=A, ω t2= π /2 ；△ t=t2-t1=[ π /(2 ω )]-[ π /(6 ω )]= π/(3ω)=T/69-回图（a）中所阿的是两个简谐运动的曲线，若这两个简谐j⅛动可叠加* 则合成的余弦振动的初相位为（）3 1（A）-7W （B）—IT（C）F （D）O分析与解由振动曲线可以知道，这是两个同振动方向、同频率简谐运动, 它们的相位差是TT（即反相位）•运动方程分别为X I= Acos ωt利%2= -^-CoS（（（；« + 瓷）・它们的振幅不同.对于这样两个简谐运动M用旋转欠量送,如图（b）很方便A求得合运动方程为x=ycos ωt.因而正确答案为（D）.9-目有一个弹簧振子，振幅4 =2-0 X 10-2 m,周期T = 1.0 s,初相＜p = 3ιτ∕4.试写出它的运动方程,并作出X - 1图I e - i图和a - t图.解因3=X∕T,则运动方程/ 2πf≡½cos(ωt + φ) =ACUS根据题中给出的数据得X = 2. 0 Xio '2cos( 2irf + O- 75τr) ( m ) 振子的速度和加速度分别为t) = dx∕(It = -4π × 10^2Rin(2ττt + 0. 75ττ) (m * s^,)(Z = ∂2χ∕df2 = - 8TT2X 10 ^2cos( 2τrt + 0. 75τT) ( m ∙ s ^2) X-I^V-C及Oft图如图所示.9若简谐运动方程为x=0. 10 cθs(201r∕+0. 25ιτ)(m),求：(1)振幅，频率、角频率、周期和初相；(2) t=2s时的位移、速度和加速度.解(1)将x-0. IoeOS(20Trf + 0. 25Ir) ( m)与为=Λυos(<wi + ¢)比较后可得；振幅4=0. 10叫角频率e =20π√j,初相管=0. 25TF,则周期T = 2ττ∕ω = O. I s,频率P = 1∕71=10 Hz.(2) t=2s时的位移、速度、加速度分别为X =0. 10co√40π +0.25Tr) =7.07 ×W2 m1； = djj/dt = -2<ττsin(4θιτ +O.25ττ) = -4, 44 m ∙ E-Ia= d2x∕dt2= -40Ir i COS(40π +0.25TT) = -2. 79 X IO2m ∙ s^29-冋某振动质点的X"曲线如图(a)所示,试求：(1)运动方程；(2)点P对应的相位；(3)到达点尸相应位置所需的时间.第十章波动习题：P89～93 1，2，3，4，5，6，12，16，25，10-6 在驻波中,两个相邻波节间各质点的振动（）A.振幅相同,相位相同B.振幅不同,相位相同C.振幅相同,相位不同D.振幅不同,相位不同答案：波函数叠加检验.（C）振幅相同，相位相反优质. 参考. 资料IQ +冋已知一波动方程为y =0. 05sin( IO J ni -2χ)(m)I(1)求波长、频率、波速和周期；(2)说明-τ =0时方程的意义，并作图表示.解(1)将题给的波动方程改写为y =0. 05cos[ 10ιτ( i -x∕5ττ}~ ττ∕2]( m) 题1。

普通物理学第六版下册答案

普通物理学第六版下册答案【篇一：普通物理学第二版课后习题答案(全)】>1.1国际单位制中的基本单位是那些？解答，基本量：长度、质量、时间、电流、温度、物质的量、光强度。

基本单位：米（m）、千克（kg）、时间（s）、安培（a）、温度（k）、摩尔（mol）、坎德拉（cd）。

力学中的基本量：长度、质量、时间。

力学中的基本单位：米（m）、千克（kg）、时间（s）。

1.2中学所学习的匀变速直线运动公式为12s?v0t?at,2 各量单位为时间：s（秒），长度：m（米），若改为以h（小时）和km（公里）作为时间和长度的单位，上述公式如何？若仅时间单位改为h，如何？若仅v0单位改为km/h，又如何？解答，（1）由量纲dim v?3?lt?1，dim a?lt?2，改为以h（小时）和km（公里）作为时间和长度的单位时，1?3m/s?10km/h?10?3600km/h3600?3.6km/h12?3m/s?10km/(h)2?10?3?36002km/h23600?3.6?3600km/h212s?3.6v0t??3.6?3600at,2（速度、加速度仍为单位下的量值）验证一下:2siv0?2.0m/s, a?4.0m/s, t?3600s?1.0h12s?v0t?at,2利用计算得：12s?2?3600??4?36002?7200?25920000?25927200(m)12s?3.6v0t??3.6?3600at,2利用计算得 12s?3.6?2?1??3.6?3600?4?12?7.2?25920?25927.2(km)（2）. 仅时间单位改为h?1由量纲，dim adim v?lt?lt?2得若仅时间单位改为h，得：1m/s?m/h?3600m/h3600?3600m/h12m/s?m/(h)2?36002m/h2360022?3600m/h验证一下:122s?3600v0t??3600at,22v0?2.0m/s, a?4.0m/s, t?3600s?1.0h 12 s?v0t?at,2利用计算得：12s?2?3600??4?36002?7200?25920000?25927200(m)122s?3600v0t??3600at,2利用计算得： 122s?3600?2?1??3600?4?12?7200?25920000?25927200(m) （3）. 若仅v0单位改为km/h由量纲dim v?lt?3?1,得1m/s?10km/(h)?3.6km/h,36001km/h?m/s3.6仅v0单位改为km/h，因长度和时间的单位不变，将km/h换成m/s得验证一下:112s?v0t?at,3.62v0?2.0m/s, a?4.0m/s2, t?3600s?1.0h12s?v0t?at,2利用计算得：12s?2?3600??4?36002?7200?25920000?25927200(m)112s?v0t?at,3.62利用计算得： 12?10?312s???3600??4?36003.61/36002?7200?25920000?25927200(m)1.3设汽车行驶时所受阻力f与汽车的横截面积s成正比，且与速率 2vv之平方成正比。

内蒙古科技大学马文蔚大学物理下册第六版答案精编版

第九章振动习题：P37～39 1，2，3，4，5，6，7，8，16.9-4 一质点做简谐运动,周期为T,当它由平衡位置向X轴正方向运动时,从1/2最大位移处到最大位移处这段路程所需的时间( )A、T/12B、T/8C、T/6D、T/4分析（C），通过相位差和时间差的关系计算。

可设位移函数y=A*sin(ωt),其中ω=2π/T；当 y=A/2,ωt1=π/6；当 y=A,ωt2=π/2；△t=t2-t1=[π/(2ω)]-[π/(6ω)]=π/(3ω)=T/6第十章波动习题：P89～93 1，2，3，4，5，6，12，16，25，10-6在驻波中,两个相邻波节间各质点的振动（）：A.振幅相同,相位相同B.振幅不同,相位相同C.振幅相同,相位不同D.振幅不同,相位不同答案：波函数叠加检验.（C) 振幅相同，相位相反第十一章光学P177～182 1，2，3，4，5，6，7,8,11,23,26,31,37,38.11-4 、在迈克尔逊干涉仪的一条光路中,放入一片折射率为n=1.4的透明介质薄膜后，干涉条纹产生了7.0条条纹移动.如果入射光波长为589nm,则透明介质薄膜厚度为( )A 10307.5nmB 1472.5nmC 5153.8nmD 2945.0nm答案（C）由2(n-1)t=N得出11-26、某人用迈克尔逊干涉仪测量一光波的波长，当可动反射镜M 移动了0.310mm 的过程中，观察到干涉条纹移动了1100条，求该光波的波长解：d=N /2, =563.6nm第十二章气体动理论习题：P220～222 1，2，3，5，13,14,24.12-2 1 mol的氦气和1 mol的氧气（视为刚性双原子分子理想气体）。

当温度为T时，期内能分别为：A 3/2RT,5/2kTB 3/2kT,5/2kTC 3/2kT,3/2kTD 3/2RT,5/2RT答案：D （由1mol理想气体的内能定义式得出）12-13 当氢气和氦气的压强、体积和温度都相等时，它们的质量比和内能比各为多少？（氢气视为刚性双原子分子理想气体）解：质量比等于摩尔质量比，为1:2内能比等于自由度比，为5:3第十三章热力学基础习题：P270～275 1，2，3，4，5，6，7，9，11，12,15，25，27.13-4 气体经历如图所示的循环过程，在这个循环过程中，外界传给气体的净热量是答案：A 3.2*10^4JB 1.8*10^4JC 2.4*10^4JD 0J答案B，由循环所围成的面积计算得出。

马文蔚《物理学》（第6版）（下册）配套题库【名校考研真题＋课后习题＋章..

目　录第一部分　名校考研真题第9章　振　动第10章　波　动第11章　光　学第12章　气体动理论第13章　热力学基础第14章　相对论第15章　量子物理第二部分　课后习题第9章　振　动第10章　波　动第11章　光　学第12章　气体动理论第13章　热力学基础第14章　相对论第15章　量子物理第三部分　章节题库第9章　振　动第10章　波　动第11章　光　学第12章　气体动理论第13章　热力学基础第14章　相对论第15章　量子物理第四部分　模拟试题马文蔚等《物理学》配套模拟试题及详解第一部分　名校考研真题第9章　振　动一、选择题一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动．当重物通过平衡位置且向规定的正方向运动时开始计时，则其振动方程为（）．[电子科技大学2007研]A．B ．C ．D．E．二、填空题一物体作简谐振动，其振动方程为（国际单位制）．则此简谐振动的周期为______；当t ＝0.6s 时，物体的速度为______．[南京航空航天大学2008研]三、计算题1．考虑n ＝2摩尔的理想气体氦气，置于一垂直放置的圆柱体所缸中，如图9-1所示．水平放置的活塞可以在气缸中无摩擦上下运动．活塞质量为，气缸截面积为．活塞被一无质量的弹簧与气缸上端连接，活塞向下运动时将氦气向下压缩，活塞上方为真空．系统开始阶段活塞与氦气处于平衡状态时，弹簧处于未形变状态，氦气压强为B【答案】1.2s ；－20.9cm/s【答案】、温度为、体积为．假定弹簧弹性常数，气体常数，对于单原子氦气，热容比．活塞在平衡位置作小幅谐振动，计算其谐振频率f．[南京大学2006研]图9-1解：对弹簧，由牛顿第二定律可得：　①由于振动很快，系统来不及与外界发生热量交换，视为绝热过程，因此有：由于活塞在平衡位置作小幅谐振动，因此V0与V之间的变化很小，利用泰勒展开得： ②将②式代入①式有：　③初始时活塞处于平衡状态，有：　④将④代入③有：　整理得：　解得振动频率为： 2．质量分别为和的两个物体A、B，固定在倔强系数为的弹簧两端，竖直地放在水平桌面上，如图9-2所示．用一力垂直地压在A上，并使其静止不动．然后突然撤去，问欲使B离开桌面至少应多大？[中科院–中科大2007研]图9-2解：欲使B刚好弹起，则A到达最高点时弹簧的伸长量至少应为．假设力F作用下弹簧的压缩量为（初始位置），弹簧无变形时A的坐标为0（平衡位置）．运动方程为：当时，，则方程的解为：利用对称性，在最高点有．整理可得：又，于是：3．如图9-3所示，已知轻弹簧的劲度系数为k，定滑轮可看作质量为M，半径为R的均质圆盘，物体的质量为m，试求：（1）系统的振动周期；（2）当将m托至弹簧原长并释放时，求m的运动方程（以向下为正方向）．[南京理工大学2005研]图9-3　图9-4解：（1）受力分析如图9-4所示，设平衡位置为原点，向下为正，则将物体拉至处时：对m：对：　（为角加速度）解得：即：则系统振动圆频率：　振动周期：　（2）设振动方程，其中，．初始条件，当时：　解得：　求得m的运动方程为：第10章　波　动一、选择题一平面简谐波沿x 轴正方向传播，振幅为A ，频率为．设时刻的波形曲线如图10-1所示，则x=0处质点的振动方程为（）．[电子科技大学2006研]图10-1A．B ．C ．D．二、填空题1．一质点沿x 轴作简谐振动，它的振幅为A ，周期为T ．时，质点位于x 轴负向离平衡最大位移的一半处且向负方向运动，则质点的振动方程为x ＝______．在一周期内质点从初始位置运动到正方向离平衡位置为最大位移的一半处的时间为______．[南京航空航天大学2007研]2．一平面简谐机械波在弹性媒质中传播，一媒质质元在通过平衡位置时，其振动动能与弹性势能______（填相同或不同）．[湖南大学2007研]B 【答案】【答案】相同【答案】3．以波速u 向x 正方向传播的平面简谐波，振幅为A ，圆频率为，设位于坐标处的质点，t ＝0时，位移，且向y 负方向运动，则该质点的振动方程为______，该平面简谐波的波动方程（波函数）为______．[南京理工大学2005研]三、计算题1．火车以匀速行驶而过，铁路边探测器所测得的火车汽笛最高和最低频率分别为和，设声速为，求火车的行驶速度．[南京大学2006研]解：由多普勒效应可得： ① ②①、②两式相除，得：解得火车车速为：2．一列平面简谐纵波在均匀各向同性弹性介质中传播，求单位体积介质所具有的能量？（自设相关物理量）．[北京师范大学2008研]解：波动方程：振动速度：　设介质的密度为，用dV 表示体元体积，则该体积元动能：体积应变：则势能：　因为，所以：　则有：　所以，单位体积介质所具有的能量为：【答案】3．已知一平面简谐波的表达式为y＝0.25cos(125t－0.37x)（SI）．（1）分别求x1＝10m，x2＝25m两点处质点的振动方程．（2）求x1、x2两点间的振动相位差．（3）求x1点在t＝4s时的振动位移．[浙江大学2008研]解：（1），（2）由，可得：　所以：（3）时的振动位移为：4．甲火车以43.2千米/小时的速度行驶，其上一乘客听到对面驶来的乙火车鸣笛声的频率为v1＝512赫兹；当这一火车过后，听其鸣笛声的频率为v2＝428赫兹．求乙火车上的人听到乙火车鸣笛的频率v0和乙火车对于地面的速度u．设空气中声波的速度为340米/秒．[中科院—中科大2009研]解：由题可得：其中，v＝340m/s，v0＝43.2km/h＝12m/s．解得：v0＝468Hz，u＝18.4m/s＝66.3km/h5．如图10-2所示，一平面简谐波沿x轴正方向传播，已知振幅为A，频率为，波速为u．（1）若t＝0时，原点O处质元正好由平衡位置向位移正方向运动，写出此波的波函数．（2）若该波在离原点处被竖直的墙面反射，欲使坐标原点处为波节，求满足的条件（设反射时无能量损失）．[厦门大学2006研]图10-2解：（1）t＝0时，y0＝0，u0＞0，所以初始相位，故波动方程为：（2）欲使波在x0处反射后到达y0处与原行波叠加产生波节，则原点O处两振动必须反相．即：所以有：，k＝0，1，2，…6．已知一平面余弦波振幅A＝0.03m，波速u＝1ms-1，波长，若以坐标原点O处质点恰好在平衡位置且向负方向运动时作为计时起点，求：（1）O点振动方程．（2）波动方程．（3）与原点相距处，t＝1秒时，质点的位移、速度；（4）和两点间的相位差．[南京航空航天大学2006研]解：（1）设O点振动方程为：．其中，，由题意知：．于是：　（2）波动方程为：．得：（3）与原点相距处，波动方程：得质点速度：当t＝1秒时：　（4）相位差：　7．设入射波的表达式为，在处发生反射，反射点为一固定端，设反射时无能量损失，求：（1）反射波的表达式．（2）合成的驻波的表达式．（3）波腹和波节的位置．[湖南大学2007研]解：（1）反射波的表达式为：（2）驻波的表达式为：（3）由，可得波腹位置为：由，可得波节位置为：，8．图10-3所示为一沿x轴正方向传播的平面余弦行波在t＝2s时刻的波形曲线，波速u＝0.5m/s，求：（1）原点o的振动方程；（2）波动方程．[电子科技大学2007研]图10-3解：（1）由已知得：．可得振动方程：（2）波动方程为：　9．一横波沿绳子传播，其波的表达式为．（1）求此波的振幅、波速、频率和波长．（2）求绳子上各质点的最大振动速度和最大振动加速度．（3）求处和处二质点振动的相位差．[宁波大学2009研]解：（1）将波的表达式与标准形式比较，得：，（2）　（3），二振动反相．第11章　光　学一、选择题1．在迈克耳孙干涉仪的一条光路中，放入一折射率为n 厚度为d 的透明介质片后，两光路光程差的改变量为（）．[暨南大学2010研]A．B．C．D．【解析】迈克尔孙干涉仪的原理为光的干涉，两束光进过G1平面镜被分为两束光，这两束光发生干涉．当在其中一条光路中放入折射率为n 的厚透明介质时，被放入介质的那条光路光程将发生变化，由于需要两次穿过新加入的透明介质，故光程差的改变量为：．2．自然光从空气入射到某介质表面上，当折射角为30°时，反射光是完全偏振光，则此介质的折射率为（）．[暨南大学2010研]A．B．C．D．3．若把牛顿环装置（都是用折射率为1.52的玻璃制成的）由空气搬入折射率为1.33的水中，则干涉条纹（）．[暨南大学2010研]C【答案】B【答案】当折射光线与反射光线垂直时反射完全偏振光，由折射公式得．【解析】A ．中心暗斑变成亮斑B ．间距不变C ．变疏D ．变密【解析】设牛顿环中某处的空气薄层厚度为e ，互相干涉的两束反射光的光程差为，若n 增大，则每个位置处的光程差增大，形成更大级数的干涉条纹，所以条纹变密．4．根据惠更斯——菲涅耳原理，若已知光在某时刻的波阵面为S ，则S 的前方某点P 的光强度决定于波阵面S 上所有面积元发出的子波各自传到P 点的（）．[暨南大学2010研]A ．振动的相干叠加B ．振动振幅之和C ．光强之和D ．振动振幅平方之和5．在单缝夫琅和费衍射实验中，波长为l 的单色光垂直入射在宽度为a=4l 的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为（）．[暨南大学2010研]A ．2个B ．6个C ．4个D ．8个D【答案】A【答案】由惠更斯—菲涅耳原理，统一波阵面各点发出的子波，经传播而在空间某点相遇，发生的是相干叠加．【解析】C【答案】可近似将单缝所在平面看作波阵面，则每一半波带都沿单缝方向，设总半波带【解析】得N=4.6．一束白光垂直入射在光栅上，在形成的同一级光栅光谱中，偏离中央明纹最远的是（）．[暨南大学2010研]A ．紫光B ．黄光C ．红光D ．绿光【解析】根据光栅公式，同一级条纹满足，可见光中红光波长最长，故偏离中央明纹最远．7．光强为I 0的自然光依次垂直通过两个偏振片，且此两偏振片的偏振化方向夹角a=45°，若不考虑偏振片的反射和吸收，则透射偏振光的强度I 是（）．[暨南大学2010研]A．B．C．D．由此可得，8．一光波分别通过两种不同介质的光程相同，则（）．[暨南大学2011研]数为N ，则C【答案】A【答案】自然光经过任一偏振片后光强减半，再经过另一个偏振片，根据马吕斯定律【解析】A ．光波通过这两种介质的时间不相同B ．光波通过这两种介质的时间相同C ．光波通过这两种介质后的位相不相同D ．光波通过这两种介质后的位相相同9.在迈克耳孙干涉仪的一臂中放入一折射率为厚度为的透明介质片，同时在另一臂中放入一折射率为厚度为的透明介质片，设没有放两透明介质片时两臂的光程差为则放入两透明介质片后两臂的光程差为（）．[暨南大学2011研]A．；B ．C．D．10．关于光学仪器的分辨本领，下述表述错误的是（）．[暨南大学2011研]A ．分辨本领受到衍射极限的限制B ．分辨本领和光学仪器的通光口径有关C ．分辨本领和照明光的波长有关D ．分辨本领和照明光的强度有关B【答案】光程差公式为 L ＝nd ，在不同介质中光速不同，v ＝c/n,故传播时间为 t ＝d/v ＝L/c ，对不同的介质相同．出射光的位相与入射光有关，故不能确定．【解析】B【答案】放入介质片后，相应光路中的光两次经过此介质，光程变化为2nd ，所以放入两个介质片后，两臂的光程差变化为2（n2－n1）d【解析】D【答案】光学仪器的分辨率，与由衍射导致的像点的展宽有关，而衍射条纹与通光孔径【解析】11．自然光从空气入射到某透明介质表面上，则（）．[暨南大学2011研]A ．反射光一定是完全偏振光B ．反射光一定是部分偏振光C ．折射光一定是部分偏振光D ．折射光一定是完全偏振光12．眼镜片上的增透膜是根据光的以下什么现象做成的（）．[暨南大学2011研]A ．光的干涉B ．光的衍射C ．光的布儒斯特定律D ．光的马吕斯定律13．光强度（）．[暨南大学2011研]A ．和光波的振幅成正比B ．和光波的振幅的平方成正比C ．和光波的位相成正比D ．和光波的位相的平方成正比和波长有关，与光强无关．C【答案】根据菲涅耳反射折射公式，自然光入射产生的反射和折射光都将变成部分偏振光．但当入射角为布鲁斯特角时，反射光为完全偏振光．【解析】A【答案】增透膜的原理是通过在镜片表面镀膜，使得某波长的光在膜前后表面反射光之间光程差是半波长的奇数倍，从而使反射光相干抵消，增加透射．【解析】B【答案】光强度是单位面积单位时间内辐射光的平均能量，此平均能量与电场分量或磁场分量的振幅的平方成正比，而由于是时间平均效果，与位相无关．【解析】14．一束白光垂直入射在单缝上，在第一级夫琅和费衍射明纹中，靠近中央明纹的颜色是（）．[暨南大学2011研]A ．紫光B ．黄光C ．红光D ．绿光【解析】单缝衍射明纹满足，故条纹到中央明纹的距离与波长正相关，所以紫光一级明纹最靠近中间．15．光强为I0的自然光依次垂直通过三个偏振片，且第一和第三偏振片的偏振化方向夹角a=90°，第二和第三偏振片的偏振化方向夹角a=45°，若不考虑偏振片的反射和吸收，则从第三偏振片透射出的光强I 是（）．[暨南大学2011研]A．B．C．D．二、填空题1．一个平凸透镜的顶点和一平板玻璃接触，用单设光垂直照射，观察反射光形成的牛顿环，测得中央暗斑外第k 个暗环半径为r 1．现将透镜和玻璃板之间的空气换成某种液体（其折射率小于玻璃的折射率），第k 个暗环的半径变为变为r 2，由此可知该液体的折射率为______．[南京航空航天大学2008研]A【答案】C【答案】自然光经过第一个偏振片，光强减半．第一偏振片的偏振方向与第二个，第二个与第三个，夹角都是45°，根据马吕斯定律，【解析】2．自然光入射到空气和某玻璃的分界面上，当入射角为60°时，反射光为完全偏振光，则该玻璃的折射率为______；一束强度为的自然光垂直入射于两种平行放置且透光轴方向夹角为60°的偏振片上，则透射光强度为______．[南京理工大学2005研]三、计算题1．一平凸透镜置于一平板玻璃上，波长为6700Å的红光垂直从上方入射，由透镜凸表面和平板玻璃表面反射的光形成牛顿环干涉条纹．透镜和平玻璃的接触点处为暗纹，测得第12条暗纹的半径为11mm ，求透镜的曲率半径R ．[暨南大学2010研]解：牛顿环上r半径处空气层的厚度为第12条暗纹处与第一条暗纹处光程差相差11个波长，可得透镜的曲率半径为　2．（5分）将麦克耳孙干涉仪的一臂稍微调长（移动镜面），观察到有150条暗纹移过视场．若所用光的波长为480nm ，求镜面移动的距离．[暨南大学2010研]解：在迈克尔孙干涉仪中，沿两条光路的光发生干涉，它们之间光程差每变化一个波长，则有一条暗纹移过视场．设镜面移动距离为d，则得．3．在杨氏双缝实验中，两缝相距2mm ，用l ＝750nm 和l¢＝900nm 的混合光照明，若屏幕到缝的距离为2m ，问两种波长的光的干涉明纹重合的位置到中央明纹中线的最小距离为多少？[暨南大学2010研]解：双缝干涉第k级干涉明纹满足，【答案】【答案】要想使不同波长的两束光条纹重合，需要某级条纹距离相同，即可得，k最小值为6，故4．如何利用偏振片和波晶片（1/4波片、半波片等）将一束自然光转化为圆偏振光？又如何利用波晶片将一线偏振光的偏振方向旋转90度？[暨南大学2010研]解：（1）首先将自然光通过偏振片，变成线偏光．然后使线偏光通过1/4波片，保证线偏振方向与波片光轴方向呈45°角，从而出射的o光和e光方向相同，振幅相等，相位差，从而变成圆偏振光．（2）首先将线偏光通过一个1/4波片，变成圆偏光，再经过一个与原偏振方向垂直的偏振片，变成新方向的线偏光．5．白光垂直照射到一厚度为370nm的肥皂膜（膜的两侧都为空气）上，设肥皂的折射率为1.32，试问该膜的正面呈现什么颜色？[暨南大学2011研]解：肥皂膜前后表面反射光的光程差为青色光的波长范围是476－495 nm，所以L正好是青色光波长的二倍；红色光的波长范围是 620－750 nm，所以L正好是红色光波长的3/2倍．所以前后表面反射的红光相干相消，青光相干相长，所以呈青色．6．用波长500nm的单色光垂直照射到宽0.5mm的单缝上，在缝后置一焦距为0.5m的凸透镜，用一屏来观察夫琅和费衍射条纹，求在屏上中央明纹的宽度和第一级明纹的宽度？并定性解释级次越高，明纹的强度越低的原因．[暨南大学2011研]解：（1）单缝夫琅禾费衍射产生暗纹条件为中央和第一级明纹处衍射角很小，可以近似．所以各暗纹距离中央的位置为所以中央明纹和第一级明纹的宽度分别为（2）明纹级次越高，说明单缝两个位置单色光距明纹处的光程差越大，相位差越大．根据光振幅矢量性，相同幅值的相干光相位差越大，合成振幅越小，从而光强越低．7．请解释为什么劈尖干涉条纹是等间距的直条纹而牛顿环是非等间距的圆条纹？如果看到牛顿环的中央是暗纹，解释之？[暨南大学2011研]解：（1）根据干涉原理，不论是劈尖干涉条纹还是牛顿环条纹，相邻条纹处干涉光光程差的差为．因为劈尖上到顶点的距离和厚度成正比，而厚度和光程差成正比，所以会形成等间距的直条纹；而牛顿环空气层厚度与光程差成正比，但由于棱镜下表面是球形，使得厚度与到中心的水平距离不成正比，所以形成非等间距的圆条纹．（2）中央处空气层厚度为0，棱镜底面与平面玻璃表面发射光的光程差为0．但光由光疏介质（空气）进入光密介质（平面玻璃）进行反射时会产生半波损失，使得两束相干光完全相消，出现中央暗纹．8．杨氏双缝实验中，在两缝S1和S2前分别放置两偏振片P1和P2，在两缝S1和S2后放置一偏振片P3，如图11-1所示，照明光为一自然光．问 (1) 当P1和P2偏振化方向相同，P1和P3偏振片的偏振化方向夹角为45°，屏上是否会出现干涉条纹？为什么？（2）当P1和P2偏振化方向垂直，P1和P3偏振片的偏振化方向夹角为45°，屏上是否会出现干涉条纹？为什么？[暨南大学2011研]图11-1解：（1）会出现干涉条纹．因为经过两个偏振片的光具有相同的偏振方向，都沿P3的方向偏振，所以同频率的光会产生相干叠加，出现干涉条纹．（2）会出现干涉条纹．因为虽然经过第一个偏振片的两束光具有垂直的偏振方向，但由于两束光的偏振方向都与P3偏振化方向呈45°角，根据马吕斯定律，经过P3后的两束光偏振方向相同，且振幅相等．所以依然会产生干涉条纹．9．（1）迈克尔逊干涉仪的M2镜前，当插入一薄玻璃片时，可以观察到有150条干涉条纹向一方移过．若玻璃片的折射率为n=1.632，所用单色光的波长为500nm，试求玻璃片的厚度．（2）用钠光灯（，）照明迈克尔逊干涉仪，首先调整干涉仪得到最清晰的干涉条纹，然后移动M1，干涉图样逐渐变得模糊，到第一次干涉现象消失时，M1由原来位置移动了多少距离？[南京大学2006研]解：（1）插入玻璃片后，光程差改变量为，则：解得玻璃片厚度：　（2）干涉条纹消失，即、两个波长照射下的亮纹和暗纹重合，即：解得：　10．试按下列要求设计光栅：当白光垂直照射时，在30°衍射方向上观察到波长为600nm 的第二级主极大，且能分辨Δλ＝0.05nm的两条谱线，同时该处不出现其他谱线的主极大．[浙江大学2008研]解：由光栅方程：　．则：当时，可得：　当，．因为时，主极大，即缺级，因此有：所以有： 11．如图11-2所示，有一缝宽分别为a和2a、两缝中心相距为d的双缝衍射屏，今在缝宽为2a的左半缝前覆盖一个宽度为a的相移片．导出正入射时其夫琅禾费衍射强度分布公式．[山东大学1997研]图11-2解：x方向振幅：　y方向振幅：　光强：　12．如图11-3所示，在偏振化方向夹角为60°的两偏振片和之间插入一个四分之一波片C，其光轴与两偏振片偏振化方向的夹角均为30°．一强度为的自然光先后通过偏振片、四分之一波片C和偏振片，求出射的光强度．[厦门大学2006研]图11-3解：经过P1后：　，经过四分之一波片后：　，得出射光振幅：　出射光光强：　第12章　气体动理论一、选择题若为气体分子速率分布函数，则的物理意义是（）．[电子科技大学2005研]A ．速率区间内的分子数B ．分子的平均速率C ．速率区间内的分子数占总分子数的百分比D ．速率分布在附近的单位速率区间中的分子数二、填空题1．三个容器A 、B 、C 中装有同种理想气体，其分子数密度n 相同，而最概然速率之比为，则单位体积内的内能之比为______．[南京航空航天大学2007研]2．一定量的理想气体贮于某一容器中，温度为T ，气体分子的质量为m ．根据理想气体的分子模型和统计假设，分子速度在x 方向的分量平方的平均值为______．[北京工业大学2004研]3．由绝热材料包围的窗口被隔板隔为两半，左边是理想气体，右边真空，如果把隔板撤去，气体将进行自由膨胀过程，达到平衡后气体的温度______（填升高、降低或不变），气体的熵______（填增加、减小或不变）．[湖南大学2007研]4．27℃的1mol 氧气分子的最概然速率为______，其物理意义为______，分子的平均平动动能为______，1mol 理想氧气的内能为______．[南京理工大学2005研]三、计算题B【答案】1∶4∶9【答案】【答案】不变；增加【答案】【答案】1．设气体分子的速率分布满足麦克斯韦分布律．（1）求气体分子速率与最可几速率相差不超过0.5%的分子占全部分子的百分之几？（2）设氦气的温度为300K，求速率在3000～3010m/s之间的分子数与速率在1500～1510m/s之间的分子数之比．（3）某种气体的温度为100K和400K时的最可几速率分别为和．在100K时与相差不超过1m/s的分子数为总数的a%，求400K时与相差不超过1m/s的分子数占总数的百分比．[南京大学2006研]解：（1）设气体分子速率与最可几速率相差不超过0.5%的分子数为，全部分子数为，则：（2）设速率在3000～3010m/s之间的分子数为，速率在1500～1510m/s之间的分子数为，则：（3）2．1摩尔双原子理想气体的某一过程的摩尔热容量，其中为定容摩尔热容量，R 为气体的普适恒量．（1）导出此过程的过程方程；（2）设初态为（，），求沿此过程膨胀到时气体的内能变化，对外做功及吸热（或放热）．[北京师范大学2006研]解：（1）理想气体的状态方程为，其微分形式为：由热力学第一定律，则：由上述两式消去，得：则由的积分可得：上式即为双原子分子理想气体的过程方程．（2）初态，其中；末态．由过程方程，可知：所以，末态为．①气体内能的变化：②对外做功：　③吸收的热量：负号表示与题设相反，即此过程向外放热　．3．0.2g氢气盛于3.0 L的容器中，测得压强为8.31×104Pa，则分子的最概然速率、平均速率和方均根速率各为多大？[浙江大学2008研]解：气体状态方程：　最概然速率：平均速率：方均根速率：　4．设有N个气体分子组成的系统，每个分子质量为m，分子的速率分布函数为求：（1）常数a．（2）分子的平均速率．（3）若分子只有平动，且忽略分子间的相互作用力，求系统的内能E．[厦门大学2006研]解：（1）由归一化条件可得：解得：　（2）N个分子的平均速度：＝（3）由，得：5．许多星球的温度达到108K，在这温度下原子已经不存在了，而氢核（质子）是存在的，若把氢核视为理想气体，求：（1）氢核的方均根速率是多少？（2）氢核的平均平均平动动能是多少电子伏特？[宁波大学2009研]（普适气体常量，玻尔兹曼常量）解：（1）由于，而氢核，所以有：（2）第13章　热力学基础一、选择题在一定量的理想气体向真空作绝热自由膨胀，体积由增至，在此过程中气体的（）．[电子科技大学2007研]A．内能不变，熵增加B．内能不变，熵减少C．内能不变，熵不变D．内能增加，熵增加二、填空题热力学第二定律表明在自然界中与热现象有关的实际宏观过程都是不可逆的．开尔文表述指出了______的过程是不可逆的，而克劳修斯表述指出了______的过程是不可逆的．[北京工业大学2004研]三、计算题1．假设地球大气为干燥空气，导热性能不好．气流上升缓慢，可以视为准静态过程．试导出大气的垂直温度梯度dT/dz，并估算其量值的大小．[南京大学2005研]解：对于绝热过程有：　对上式两边同时求导，得：于是有：对于大气层，气压强变化满足，再结合理想气体状态方程，得：A【答案】功变热；热传导【答案】。

物理学马文蔚第1至8章课后习题答案详解

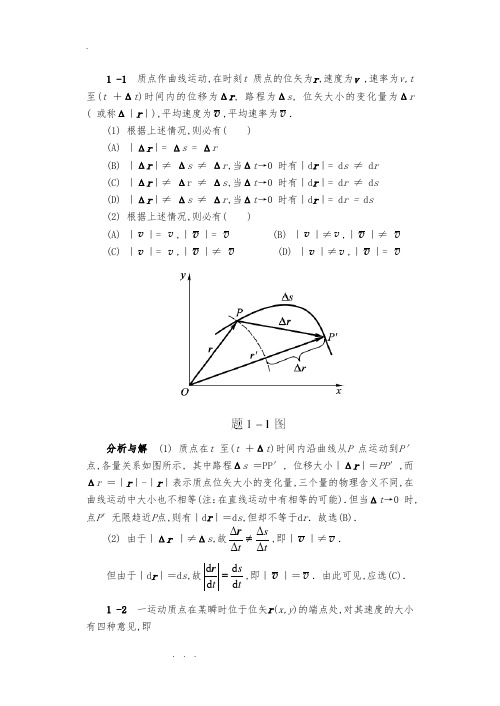
1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t ＋Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ｜r ｜),平均速度为v ,平均速率为v ．(1) 根据上述情况,则必有( )(A) ｜Δr ｜= Δs = Δr(B) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d s ≠ d r(C) ｜Δr ｜≠ Δr ≠ Δs ,当Δt →0 时有｜d r ｜= d r ≠ d s(D) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d r = d s(2) 根据上述情况,则必有( )(A) ｜v ｜= v ,｜v ｜= v (B) ｜v ｜≠v ,｜v ｜≠ v(C) ｜v ｜= v ,｜v ｜≠ v (D) ｜v ｜≠v ,｜v ｜= v分析与解 (1) 质点在t 至(t ＋Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs ＝PP′, 位移大小｜Δr ｜＝PP ′,而Δr ＝｜r ｜-｜r ｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt →0 时,点P ′无限趋近P 点,则有｜d r ｜＝d s ,但却不等于d r ．故选(B)．(2) 由于｜Δr ｜≠Δs ,故ts t ΔΔΔΔ≠r ,即｜v ｜≠v ．但由于｜d r ｜＝d s ,故ts t d d d d =r ,即｜v ｜＝v ．由此可见,应选(C)． 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即 (1)t r d d ； (2)t d d r ； (3)t s d d ； (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x ．下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解 tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量；td d r 表示速度矢量；在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解．故选(D)． 1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a ｔ表示切向加速度．对下列表达式,即(1)d v /d t ＝a ；(2)d r /d t ＝v ；(3)d s /d t ＝v ；(4)d v /d t ｜＝a ｔ．下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的(C) 只有(2)是对的 (D) 只有(3)是对的分析与解td d v 表示切向加速度a ｔ,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用；tr d d 在极坐标系中表示径向速率v r (如题1 -2 所述)；t s d d 在自然坐标系中表示质点的速率v ；而td d v 表示加速度的大小而不是切向加速度a ｔ．因此只有(3) 式表达是正确的．故选(D)．1 -4 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解加速度的切向分量a ｔ起改变速度大小的作用,而法向分量a n 起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于a ｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时, a ｔ恒为零；质点作匀变速率圆周运动时, a ｔ为一不为零的恒量,当a ｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．*1 -5 如图所示,湖中有一小船,有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动．设该人以匀速率v 0 收绳,绳不伸长且湖水静止,小船的速率为v ,则小船作( )(A) 匀加速运动,θcos 0v v = (B) 匀减速运动,θcos 0v v =(C) 变加速运动,θcos 0v v = (D) 变减速运动,θcos 0v v =(E) 匀速直线运动,0v v =分析与解本题关键是先求得小船速度表达式,进而判断运动性质．为此建立如图所示坐标系,设定滑轮距水面高度为h,t 时刻定滑轮距小船的绳长为l ,则小船的运动方程为22h l x -=,其中绳长l 随时间t 而变化．小船速度22d d d d h l t llt x -==v ,式中t l d d 表示绳长l 随时间的变化率,其大小即为v 0,代入整理后为θl h l cos /0220v v v =-=,方向沿x 轴负向．由速度表达式,可判断小船作变加速运动．故选(C)．讨论有人会将绳子速率v 0按x 、y 两个方向分解,则小船速度θcos 0v v =,这样做对吗？1 -6 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s ．求：(1) 质点在运动开始后 s 内的位移的大小；(2) 质点在该时间内所通过的路程；(3) t ＝4 s 时质点的速度和加速度．分析位移和路程是两个完全不同的概念．只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等．质点在t 时间内的位移Δx 的大小可直接由运动方程得到：0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了．为此,需根据0d d =tx 来确定其运动方向改变的时刻t p ,求出0～t p 和t p ～t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t ＝ s 时质点速度和加速度可用tx d d 和22d d t x 两式计算．解 (1) 质点在 s 内位移的大小m 32Δ04-=-=x x x(2) 由0d d =tx 得知质点的换向时刻为s 2=p t (t ＝0不合题意) 则m 0.8Δ021=-=x x x m 40Δ242-=-=x x x所以,质点在 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t ＝ s 时1 -7 一质点沿x 轴方向作直线运动,其速度与时间的关系如图(a)所示．设t ＝0 时,x ＝0．试根据已知的v -t 图,画出a -t 图以及x -t 图．分析根据加速度的定义可知,在直线运动中v -t 曲线的斜率为加速度的大小(图中AB 、CD 段斜率为定值,即匀变速直线运动；而线段BC 的斜率为0,加速度为零,即匀速直线运动)．加速度为恒量,在a -t 图上是平行于t 轴的直线,由v -t 图中求出各段的斜率,即可作出a -t 图线．又由速度的定义可知,x -t 曲线的斜率为速度的大小．因此,匀速直线运动所对应的x -t 图应是一直线,而匀变速直线运动所对应的x –t 图为t 的二次曲线．根据各段时间内的运动方程x ＝x (t ),求出不同时刻t 的位置x ,采用描数据点的方法,可作出x -t 图．解将曲线分为AB 、BC 、CD 三个过程,它们对应的加速度值分别为2s m 20-⋅=--=AB A B AB t t a v v (匀加速直线运动) 0=BC a (匀速直线运动)2s m 10-⋅-=--=CD C D CD t t a v v (匀减速直线运动) 根据上述结果即可作出质点的a -t 图［图(B)］．在匀变速直线运动中,有由此,可计算在0～2ｓ和4～6ｓ时间间隔内各时刻的位置分别为用描数据点的作图方法,由表中数据可作0～2ｓ和4～6ｓ时间内的x -t 图．在2～4ｓ时间内, 质点是作1s m 20-⋅=v 的匀速直线运动, 其x -t 图是斜率k ＝20的一段直线［图(c)］．1 -8 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为ｓ．求：(1) 质点的运动轨迹；(2) t ＝0 及t ＝2ｓ时,质点的位矢；(3) 由t ＝0 到t ＝2ｓ内质点的位移Δr 和径向增量Δr ；*(4) 2 ｓ内质点所走过的路程s ．分析质点的轨迹方程为y ＝f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到．对于r 、Δr 、Δr 、Δs 来说,物理含义不同,可根据其定义计算．其中对s 的求解用到积分方法,先在轨迹上任取一段微元d s ,则22)d ()d (d y x s +=,最后用⎰=s s d 积分求ｓ．解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为这是一个抛物线方程,轨迹如图(a)所示．(2) 将t ＝0ｓ和t ＝2ｓ分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t ＝0ｓ和t ＝2ｓ时质点所在位置．(3) 由位移表达式,得其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r 而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r *(4) 如图(B)所示,所求Δs 即为图中PQ 段长度,先在其间任意处取AB 微元d s ,则22)d ()d (d y x s +=,由轨道方程可得x x y d 21d -=,代入d s ,则2ｓ内路程为1 -9 质点的运动方程为式中x ,y 的单位为m,t 的单位为ｓ．试求：(1) 初速度的大小和方向；(2) 加速度的大小和方向．分析由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向．解 (1) 速度的分量式为当t ＝0 时, v o x ＝-10 m·ｓ-1 , v o y ＝15 m·ｓ-1 ,则初速度大小为设v o 与x 轴的夹角为α,则α＝123°41′(2) 加速度的分量式为2s m 60d d -⋅==ta x x v , 2s m 40d d -⋅-==t a y y v 则加速度的大小为设a 与x 轴的夹角为β,则β＝-33°41′(或326°19′)1 -10 一升降机以加速度 m·ｓ-2上升,当上升速度为 m·ｓ-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距 m ．计算：(1)螺丝从天花板落到底面所需要的时间；(2)螺丝相对升降机外固定柱子的下降距离．分析在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y 1 ＝y 1(t )和y 2 ＝y 2(t ),并考虑它们相遇,即位矢相同这一条件,问题即可解；另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度．升降机厢的高度就是螺丝(或升降机)运动的路程．解1 (1) 以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为当螺丝落至底面时,有y 1 ＝y 2 ,即(2) 螺丝相对升降机外固定柱子下降的距离为解2 (1)以升降机为参考系,此时,螺丝相对它的加速度大小a ′＝g ＋a ,螺丝落至底面时,有(2) 由于升降机在t 时间内上升的高度为则 m 716.0='-=h h d1 -11 一质点P 沿半径R ＝ m 的圆周作匀速率运动,运动一周所需时间为ｓ,设t ＝0 时,质点位于O 点．按(a )图中所示Oxy 坐标系,求(1) 质点P 在任意时刻的位矢；(2)5ｓ时的速度和加速度．分析该题属于运动学的第一类问题,即已知运动方程r ＝r (t )求质点运动的一切信息(如位置矢量、位移、速度、加速度)．在确定运动方程时,若取以点(0,3)为原点的O′x′y′坐标系,并采用参数方程x′＝x′(t )和y′＝y′(t )来表示圆周运动是比较方便的．然后,运用坐标变换x ＝x 0 ＋x ′和y ＝y 0 ＋y ′,将所得参数方程转换至Oxy 坐标系中,即得Oxy 坐标系中质点P 在任意时刻的位矢．采用对运动方程求导的方法可得速度和加速度．解 (1) 如图(B)所示,在O′x′y′坐标系中,因t T θπ2=,则质点P 的参数方程为 t T R x π2sin=', t TR y π2cos -=' 坐标变换后,在O x y 坐标系中有 t T R x x π2sin='=, R t TR y y y +-=+'=π2cos 0 则质点P 的位矢方程为 (2) 5ｓ时的速度和加速度分别为j j i r )s m π3.0(π2sin π2π2cos π2d d 1-⋅=+==t TT R t T T R t v i j i r a )s m π03.0(π2cos )π2(π2sin )π2(d d 222222-⋅-=+-==t TT R t T T R t 1 -12 地面上垂直竖立一高 m 的旗杆,已知正午时分太阳在旗杆的正上方,求在下午2∶00 时,杆顶在地面上的影子的速度的大小．在何时刻杆影伸展至 m ？分析为求杆顶在地面上影子速度的大小,必须建立影长与时间的函数关系,即影子端点的位矢方程．根据几何关系,影长可通过太阳光线对地转动的角速度求得．由于运动的相对性,太阳光线对地转动的角速度也就是地球自转的角速度．这样,影子端点的位矢方程和速度均可求得．解设太阳光线对地转动的角速度为ω,从正午时分开始计时,则杆的影长为s ＝h tg ωt ,下午2∶00 时,杆顶在地面上影子的速度大小为当杆长等于影长时,即s ＝h ,则即为下午3∶00 时．1 -13 质点沿直线运动,加速度a ＝4 -t2 ,式中a 的单位为m·ｓ-2 ,t 的单位为ｓ．如果当t ＝3ｓ时,x ＝9 m,v ＝2 m·ｓ-1 ,求质点的运动方程．分析本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决．由t a d d v =和tx d d =v 可得t a d d =v 和t x d d v =．如a ＝a (t )或v ＝v (t ),则可两边直接积分．如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分．解由分析知,应有得 03314v v +-=t t (1) 由 ⎰⎰=t x x t x 0d d 0v 得 00421212x t t t x ++-=v (2) 将t ＝3ｓ时,x ＝9 m,v ＝2 m·ｓ-1代入(1) (2)得v 0＝-1 m·ｓ-1,x 0＝ m ．于是可得质点运动方程为1 -14 一石子从空中由静止下落,由于空气阻力,石子并非作自由落体运动,现测得其加速度a ＝A -B v ,式中A 、B 为正恒量,求石子下落的速度和运动方程．分析本题亦属于运动学第二类问题,与上题不同之处在于加速度是速度v 的函数,因此,需将式d v ＝a (v )d t 分离变量为t a d )(d =v v 后再两边积分．解选取石子下落方向为y 轴正向,下落起点为坐标原点．(1) 由题意知 v v B A ta -==d d (1)用分离变量法把式(1)改写为t B A d d =-vv (2) 将式(2)两边积分并考虑初始条件,有得石子速度 )1(Bt e B A --=v 由此可知当,t →∞时,B A →v 为一常量,通常称为极限速度或收尾速度． (2) 再由)1(d d Bt e BA t y --==v 并考虑初始条件有得石子运动方程1 -15 一质点具有恒定加速度a ＝6i ＋4j ,式中a 的单位为m·ｓ-2 ．在t ＝0时,其速度为零,位置矢量r 0 ＝10 m i ．求：(1) 在任意时刻的速度和位置矢量；(2) 质点在Oxy 平面上的轨迹方程,并画出轨迹的示意图．分析与上两题不同处在于质点作平面曲线运动,根据叠加原理,求解时需根据加速度的两个分量a x 和a y 分别积分,从而得到运动方程r 的两个分量式x (t )和y (t )．由于本题中质点加速度为恒矢量,故两次积分后所得运动方程为固定形式,即20021t a t x x x x ++=v 和20021t a t y y y y ++=v ,两个分运动均为匀变速直线运动．读者不妨自己验证一下．解由加速度定义式,根据初始条件t 0 ＝0时v 0 ＝0,积分可得又由td d r =v 及初始条件t ＝0 时,r 0＝(10 m)i ,积分可得由上述结果可得质点运动方程的分量式,即x ＝10＋3t 2 y ＝2t 2 消去参数t ,可得运动的轨迹方程 3y ＝2x -20 m 这是一个直线方程．直线斜率32tan d d ===αx y k ,α＝33°41′．轨迹如图所示．1 -16 一质点在半径为R 的圆周上以恒定的速率运动,质点由位置A 运动到位置B,OA 和OB 所对的圆心角为Δθ．(1) 试证位置A 和B 之间的平均加速度为)Δ(/)Δcos 1(22θR θa v -=；(2) 当Δθ分别等于90°、30°、10°和1°时,平均加速度各为多少？并对结果加以讨论．分析瞬时加速度和平均加速度的物理含义不同,它们分别表示为t d d v =a 和tΔΔv =a ．在匀速率圆周运动中,它们的大小分别为Ra n 2v =,t a ΔΔv = ,式中｜Δv ｜可由图(B)中的几何关系得到,而Δt 可由转过的角度Δθ 求出．由计算结果能清楚地看到两者之间的关系,即瞬时加速度是平均加速度在Δt →0 时的极限值．解 (1) 由图(b)可看到Δv ＝v 2 -v 1 ,故而所以(2) 将Δθ＝90°,30°,10°,1°分别代入上式,得R a 219003.0v ≈,Ra 229886.0v ≈ R a 239987.0v ≈,Ra 24000.1v ≈ 以上结果表明,当Δθ→0 时,匀速率圆周运动的平均加速度趋近于一极限值,该值即为法向加速度R2v ． 1 -17 质点在Oxy 平面内运动,其运动方程为r ＝＋ )j ,式中r 的单位为m,t 的单位为s ．求：(1)质点的轨迹方程；(2) 在t 1＝到t 2 ＝时间内的平均速度；(3) t 1 ＝ｓ时的速度及切向和法向加速度；(4) t ＝时质点所在处轨道的曲率半径ρ．分析根据运动方程可直接写出其分量式x ＝x (t )和y ＝y (t ),从中消去参数t ,即得质点的轨迹方程．平均速度是反映质点在一段时间内位置的变化率,即tΔΔr =v ,它与时间间隔Δt 的大小有关,当Δt →0 时,平均速度的极限即瞬时速度td d r =v ．切向和法向加速度是指在自然坐标下的分矢量a ｔ和a n ,前者只反映质点在切线方向速度大小的变化率,即t t te a d d v =,后者只反映质点速度方向的变化,它可由总加速度a 和a ｔ得到．在求得t 1 时刻质点的速度和法向加速度的大小后,可由公式ρa n 2v =求ρ．解 (1) 由参数方程x ＝, y ＝消去t 得质点的轨迹方程：y ＝(2) 在t 1 ＝ｓ到t 2 ＝ｓ时间内的平均速度(3) 质点在任意时刻的速度和加速度分别为则t 1 ＝ｓ时的速度v (t )｜t ＝1ｓ＝切向和法向加速度分别为(4) t ＝ｓ质点的速度大小为则m 17.112==na ρv 1 -18 飞机以100 m·ｓ-1 的速度沿水平直线飞行,在离地面高为100 m 时,驾驶员要把物品空投到前方某一地面目标处,问：(1) 此时目标在飞机正下方位置的前面多远？ (2) 投放物品时,驾驶员看目标的视线和水平线成何角度？(3) 物品投出ｓ后,它的法向加速度和切向加速度各为多少？分析物品空投后作平抛运动．忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动．到达地面目标时,两方向上运动时间是相同的．因此,分别列出其运动方程,运用时间相等的条件,即可求解．此外,平抛物体在运动过程中只存在竖直向下的重力加速度．为求特定时刻t 时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β．由图可知,在特定时刻t ,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量v x 、v y 求出,这样,也就可将重力加速度g 的切向和法向分量求得．解 (1) 取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x ＝v t , y ＝1/2 gt 2飞机水平飞行速度v ＝100 m·s -1 ,飞机离地面的高度y ＝100 m,由上述两式可得目标在飞机正下方前的距离(2) 视线和水平线的夹角为(3) 在任意时刻物品的速度与水平轴的夹角为取自然坐标,物品在抛出2s 时,重力加速度的切向分量与法向分量分别为1 -19 如图(a)所示,一小型迫击炮架设在一斜坡的底端O 处,已知斜坡倾角为α,炮身与斜坡的夹角为β,炮弹的出口速度为v 0,忽略空气阻力．求：(1)炮弹落地点P 与点O 的距离OP ；(2) 欲使炮弹能垂直击中坡面．证明α和β必须满足αβtan 21tan =并与v 0 无关．分析这是一个斜上抛运动,看似简单,但针对题目所问,如不能灵活运用叠加原理,建立一个恰当的坐标系,将运动分解的话,求解起来并不容易．现建立如图(a)所示坐标系,则炮弹在x 和y 两个方向的分运动均为匀减速直线运动,其初速度分别为v 0cos β和v 0sin β,其加速度分别为g sin α和gcos α．在此坐标系中炮弹落地时,应有y ＝0,则x ＝OP ．如欲使炮弹垂直击中坡面,则应满足v x ＝0,直接列出有关运动方程和速度方程,即可求解．由于本题中加速度g 为恒矢量．故第一问也可由运动方程的矢量式计算,即20g 21t t +=v r ,做出炮弹落地时的矢量图［如图(B)所示］,由图中所示几何关系也可求得OP (即图中的r 矢量)．(1)解1 由分析知,炮弹在图(a)所示坐标系中两个分运动方程为αgt βt x sin 21cos 20-=v (1) αgt βt y cos 21sin 20-=v (2) 令y ＝0 求得时间t 后再代入式(1)得解2 做出炮弹的运动矢量图,如图(b)所示,并利用正弦定理,有从中消去t 后也可得到同样结果．(2) 由分析知,如炮弹垂直击中坡面应满足y ＝0 和v x ＝0,则0sin cos 0=-=αgt βx v v (3)由(2)(3)两式消去t 后得由此可知．只要角α和β满足上式,炮弹就能垂直击中坡面,而与v 0 的大小无关．讨论如将炮弹的运动按水平和竖直两个方向分解,求解本题将会比较困难,有兴趣读者不妨自己体验一下．1 -20 一直立的雨伞,张开后其边缘圆周的半径为R ,离地面的高度为h ,(1) 当伞绕伞柄以匀角速ω旋转时,求证水滴沿边缘飞出后落在地面上半径为g ωh R r /212+=的圆周上；(2) 读者能否由此定性构想一种草坪上或农田灌溉用的旋转式洒水器的方案？分析选定伞边缘O 处的雨滴为研究对象,当伞以角速度ω旋转时,雨滴将以速度v 沿切线方向飞出,并作平抛运动．建立如图(a)所示坐标系,列出雨滴的运动方程并考虑图中所示几何关系,即可求证．由此可以想像如果让水从一个旋转的有很多小孔的喷头中飞出,从不同小孔中飞出的水滴将会落在半径不同的圆周上,为保证均匀喷洒对喷头上小孔的分布还要给予精心的考虑．解 (1) 如图(a)所示坐标系中,雨滴落地的运动方程为t ωR t x ==v (1)h gt y ==221 (2) 由式(1)(2)可得 gh ωR x 2222= 由图(a)所示几何关系得雨滴落地处圆周的半径为(2) 常用草坪喷水器采用如图(b)所示的球面喷头(θ0 ＝45°)其上有大量小孔．喷头旋转时,水滴以初速度v 0 从各个小孔中喷出,并作斜上抛运动,通常喷头表面基本上与草坪处在同一水平面上．则以φ角喷射的水柱射程为为使喷头周围的草坪能被均匀喷洒,喷头上的小孔数不但很多,而且还不能均匀分布,这是喷头设计中的一个关键问题．1 -21 一足球运动员在正对球门前 m 处以 m·ｓ-1 的初速率罚任意球,已知球门高为 m ．若要在垂直于球门的竖直平面内将足球直接踢进球门,问他应在与地面成什么角度的范围内踢出足球？ (足球可视为质点)分析被踢出后的足球,在空中作斜抛运动,其轨迹方程可由质点在竖直平面内的运动方程得到．由于水平距离x 已知,球门高度又限定了在y 方向的范围,故只需将x 、y 值代入即可求出．解取图示坐标系Oxy ,由运动方程θt x cos v =, 221sin gt θt y -=v 消去t 得轨迹方程以x ＝ m,v ＝ m·ｓ-1 及 m≥y ≥0 代入后,可解得71．11°≥θ1 ≥69．92°27．92°≥θ2 ≥18．89°如何理解上述角度的范围？在初速一定的条件下,球击中球门底线或球门上缘都将对应有两个不同的投射倾角(如图所示)．如果以θ＞71．11°或θ ＜°踢出足球,都将因射程不足而不能直接射入球门；由于球门高度的限制,θ 角也并非能取°与°之间的任何值．当倾角取值为°＜θ ＜69．92°时,踢出的足球将越过门缘而离去,这时球也不能射入球门．因此可取的角度范围只能是解中的结果．1 -22 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量．(1) 求t 时刻质点的总加速度；(2) t 为何值时总加速度在数值上等于b ？(3) 当加速度达到b 时,质点已沿圆周运行了多少圈？分析在自然坐标中,s 表示圆周上从某一点开始的曲线坐标．由给定的运动方程s ＝s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a ｔ,而加速度的法向分量为a n ＝v 2 /R ．这样,总加速度为a ＝a ｔe ｔ＋a n e n ．至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs ＝s t -s 0．因圆周长为2πR,质点所转过的圈数自然可求得．解 (1) 质点作圆周运动的速率为其加速度的切向分量和法向分量分别为b t s a t -==22d d , Rbt R a n 202)(-==v v 故加速度的大小为其方向与切线之间的夹角为(2) 要使｜a ｜＝b ,由b bt b R R=-+4022)(1v 可得 (3) 从t ＝0 开始到t ＝v 0 /b 时,质点经过的路程为因此质点运行的圈数为1 -23 一半径为 m 的飞轮在启动时的短时间内,其角速度与时间的平方成正比．在t ＝ｓ时测得轮缘一点的速度值为 m·ｓ-1．求：(1) 该轮在t′＝ｓ的角速度,轮缘一点的切向加速度和总加速度；(2)该点在ｓ内所转过的角度．分析首先应该确定角速度的函数关系ω＝kt 2．依据角量与线量的关系由特定时刻的速度值可得相应的角速度,从而求出式中的比例系数k ,ω＝ω(t )确定后,注意到运动的角量描述与线量描述的相应关系,由运动学中两类问题求解的方法(微分法和积分法),即可得到特定时刻的角加速度、切向加速度和角位移．解因ωR ＝v ,由题意ω∝t 2 得比例系数所以 22)(t t ωω==则t ′＝ｓ时的角速度、角加速度和切向加速度分别为总加速度在ｓ内该点所转过的角度1 -24 一质点在半径为 m 的圆周上运动,其角位置为342t θ+=,式中θ 的单位为rad,t 的单位为ｓ．(1) 求在t ＝ｓ时质点的法向加速度和切向加速度．(2) 当切向加速度的大小恰等于总加速度大小的一半时,θ 值为多少？(3) t 为多少时,法向加速度和切向加速度的值相等？分析掌握角量与线量、角位移方程与位矢方程的对应关系,应用运动学求解的方法即可得到．解 (1) 由于342t θ+=,则角速度212d d t t θω==．在t ＝2 ｓ时,法向加速度和切向加速度的数值分别为(2) 当22212/t n t a a a a +==时,有223n t a a =,即得 3213=t此时刻的角位置为(3) 要使t n a a =,则有 t ＝ｓ1 -25 一无风的下雨天,一列火车以v 1＝ m·ｓ-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降．求雨滴下落的速度v2 ．(设下降的雨滴作匀速运动)分析这是一个相对运动的问题．设雨滴为研究对象,地面为静止参考系Ｓ,火车为动参考系Ｓ′．v 1 为Ｓ′相对Ｓ的速度,v 2 为雨滴相对Ｓ的速度,利用相对运动速度的关系即可解．解以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得1 -26 如图(a)所示,一汽车在雨中沿直线行驶,其速率为v 1 ,下落雨滴的速度方向偏于竖直方向之前θ 角,速率为v 2′,若车后有一长方形物体,问车速v 1为多大时,此物体正好不会被雨水淋湿？分析这也是一个相对运动的问题．可视雨点为研究对象,地面为静参考系Ｓ,汽车为动参考系Ｓ′．如图(a)所示,要使物体不被淋湿,在车上观察雨点下落的方向(即雨点相对于汽车的运动速度v 2′的方向)应满足hl αarctan ≥．再由相对速度的矢量关系122v v v -=',即可求出所需车速v 1．解由122v v v -='［图(b)］,有而要使h l αarctan ≥,则1 -27 一人能在静水中以 m·ｓ-1 的速度划船前进．今欲横渡一宽为 ×103 m 、水流速度为 m·ｓ-1 的大河．(1) 他若要从出发点横渡该河而到达正对岸的一点,那么应如何确定划行方向？到达正对岸需多少时间？ (2)如果希望用最短的时间过河,应如何确定划行方向？船到达对岸的位置在什么地方？分析船到达对岸所需时间是由船相对于岸的速度v 决定的．由于水流速度u 的存在, v 与船在静水中划行的速度v ′之间有v ＝u ＋v ′(如图所示)．若要使船到达正对岸,则必须使v 沿正对岸方向；在划速一定的条件下,若要用最短时间过河,则必须使v 有极大值．解 (1) 由v ＝u ＋v ′可知v'=u αarcsin ,则船到达正对岸所需时间为 (2) 由于αcos v v '=,在划速v ′一定的条件下,只有当α＝0 时, v 最大(即v ＝v ′),此时,船过河时间t ′＝d /v ′,船到达距正对岸为l 的下游处,且有1 -28 一质点相对观察者O 运动, 在任意时刻t , 其位置为x ＝v t , y ＝gt2 /2,质点运动的轨迹为抛物线．若另一观察者O′以速率v 沿x 轴正向相对于O 运动．试问质点相对O′的轨迹和加速度如何？分析该问题涉及到运动的相对性．如何将已知质点相对于观察者O 的运动转换到相对于观察者O′的运动中去,其实质就是进行坐标变换,将系O 中一动点(x ,y )变换至系O′中的点(x ′,y ′)．由于观察者O′相对于观察者O 作匀速运动,因此,该坐标变换是线性的．解取Oxy 和O′x′y′分别为观察者O 和观察者O′所在的坐标系,且使Ox 和O′x ′两轴平行．在t ＝0 时,两坐标原点重合．由坐标变换得。

科技大学大学物理下册第六版答案

第九章振动习题：P37〜39 1 , 2, 3, 4, 5, 6, 7, 8, 16.49-1 一个质点作简谐运动，振幅为忙在起始时刻质点的位移为-今，且向尤轴正方向运动，代表此简谐运动的旋转矢童为（）分析与解由振动曲线可知，初始时刻质点的位移为-冲/2.且向震轴负方向运动•图（町是其相应的錠转矢最图.山旋转矢童法可知初相位为2TT /3•振动曲线上给出质点从-A/2处运动到十M 处所需时间为I 矢由对应旋转矢量图可知相应的相位差A 甲=4ir/3，则角频率孙二、中£Z = （4ir/3） 6_ \故选（D ）»本题也可根分析与解（巧图中旋转矢量的矢端往耳轴上投影点的位移为-片/2,且投影点的运动方向指向0龙轴正向，即其速度的耳分量大于零*故满足题意因而正确答案为少-2已知某简谐运动的振动曲线如图心）所朋■则此简谐运动的运动方程为（（A ）（C ） X = 2 COS J -yTTi - -^-71 “2叫CTD )cm(R)工 h 2<X»s( ； TTi + -j-7T (D) x =+ y I ( cm )cm )据振动曲线所给信息，逐一代入方程来找出正确答案.9*3 两个同周期简i皆运动曲线如图（"所示*，的相位比勺的相位（）5）落后牙（R）超前壬（C）落后仃（D）超前7T分析与解由振动曲线图作出相应的旋转久量图（b）即可得到答案为（叭9-4 一质点做简谐运动，周期为T,当它由平衡位置向X轴正方向运动时,从1/2最大位移处到最大位移处这段路程所需的时间（）A、T/12B、T/8C、T/6D、T/4分析（C）,通过相位差和时间差的关系计算。

可设位移函数y=A*sin（w t）,其中w =2n /T ;当y=A/2, w t1= n /6 ;当y=A, w t2= n /2 ;△t=t2 -t1=［n /（2 w ）］-［n /（6 w ）］= n /（3 w ）=T/69 -目当质点以频率¥作简谐运动时，它的动能的变化频率为（）（A 】寺「B）P（（J）2胖（D） 4卩分析与解质点作简谐运动的动能表武为- （a +护），可见其周期为简谐运动周期的一半［则频率为简谐运动频率卩的两倍+因而止确答案为（C）.9- E ］图（町巾所啣的是两个简谐运动的曲线，若这两个简谐运动可叠加+ 则合成的余弦振动的初相位为（）31（A ）亍力（B ）（｛；） TT（D ） 0分析与解由振动曲线可以知道，这是两个同振动方向、同频率简谐运动, 它们的相位差是“（即反相位）+运动方程分别为口 = A cos a ）t 和x 2 = -^-cos （（ot+£灯）》它们的振幅不同•对于这样两个简谐运动，叮用旋转矢量法，如图（b ）很方便求得合运动方程为^=ycos 族.因而正确答案为（D ）.9-0有一个弹簧振子，振幅/ =2.0x107叫周期°趴初相炉二 3ir/4.试写出它的运动方程，并作出火"图卩“图和a"图.解因3=2IT /T\则运动方程根据题中给出的数据得x - 2. 0 x 10 _2€08（ 2衣 + 0. 75TT ）（in ）振子的速度和加速度分别为v = dx/dt 石x 10'2ftin(27TZ +0* 75ir) ( m • s'1)(i = d 2x/di 3 - - 8TT 2 x 10 2CDS (21TZ + 0* 75TF ) (m ・ s 1)尤- — f 及＜i 7图如图所示*X = /lcos( (dt + 少)=4cos/ 2打『9-0 若简谐运动方程为x=o. 10 ws(20m+0. 257T)(m)r求：(1)振幅、频率.角频率、周期和初相；(2) t=2合时的位移、速度和加速度.解(1 )将x =0, lOcos (20ir^ + 0. 25ir) ( ni)与女二A€os(t^(十炉)比较后可得;振幅4二①【0 m,角频率w = 20^-\初柑申 Z 25□则周期T = = 0. I筑频率卩=1/『二10 Hz.(2) t^2s时的位移、速度、加速度分别为x =0. 10CO9(40TT +O.25TT) =7J)7 xlO*2mv = dx/d/ =「27T5in(40ir +0. 25TT)=- 4.44 m - s« - d^/di1= -40ir2cos(407r +0. 25ir) = -2. 79 x 10L m ・少-凹某振动质点的工-丄曲线如图(町所示，试求：(1)运动方程；(2)点戶对应的相位；(3)到达点尸相应位置所需的时间.解（1）质点振动振幅=0. W m 而由振动曲线可画出q =0和=4 8 时旋转矢量，如图（b ）所示.由IS 可见初相気二亠忻/3（或純=5ir/3） t 而由-和)=ir/2 + TT /3得曲=5^/24 & ' +则运动方程为文=0.］仇0彳 - TT /3)( m)（2）图（町中点F 的位置是质点从A/2处运动到正向的端点处.对应的旋转矢量图如图（町所示.当初相取列=7用时’点P 的相位为和十。

内蒙古科技大学马文蔚大学物理(下册)第六版答案解析

内蒙古科技大学马文蔚大学物理(下册)第六版答案解析-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第九章振动习题：P37～39 1，2，3，4，5，6，7，8，16.9-4 一质点做简谐运动,周期为T,当它由平衡位置向X轴正方向运动时,从1/2最大位移处到最大位移处这段路程所需的时间( )A、T/12B、T/8C、T/6D、T/4分析（C），通过相位差和时间差的关系计算。

可设位移函数 y=A*sin(ωt),其中ω=2π/T；当 y=A/2,ωt1=π/6；当 y=A,ωt2=π/2；△t=t2-t1=[π/(2ω)]-[π/(6ω)]=π/(3ω)=T/6第十章波动习题：P89～93 1，2，3，4，5，6，12，16，25，10-6 在驻波中,两个相邻波节间各质点的振动（）：A.振幅相同,相位相同B.振幅不同,相位相同C.振幅相同,相位不同D.振幅不同,相位不同答案：波函数叠加检验.（C) 振幅相同，相位相反第十一章光学P177～182 1，2，3，4，5，6，7,8,11,23,26,31,37,38.11-4 、在迈克尔逊干涉仪的一条光路中,放入一片折射率为n=1.4的透明介质薄膜后，干涉条纹产生了7.0条条纹移动.如果入射光波长为589nm,则透明介质薄膜厚度为( )A 10307.5nmB 1472.5nmC 5153.8nmD 2945.0nm答案（C）由2(n-1)t=N得出11-26、某人用迈克尔逊干涉仪测量一光波的波长，当可动反射镜M移动了0.310mm的过程中，观察到干涉条纹移动了1100条，求该光波的波长解：d=N /2, =563.6nm习题：P220～222 1，2，3，5，13,14,24.12-2 1 mol的氦气和1 mol的氧气（视为刚性双原子分子理想气体）。

当温度为T时，期内能分别为：A 3/2RT,5/2kTB 3/2kT,5/2kTC 3/2kT,3/2kTD 3/2RT,5/2RT答案：D （由1mol理想气体的内能定义式得出）12-13 当氢气和氦气的压强、体积和温度都相等时，它们的质量比和内能比各为多少（氢气视为刚性双原子分子理想气体）解：质量比等于摩尔质量比，为1:2内能比等于自由度比，为5:3第十三章热力学基础习题：P270～275 1，2，3，4，5，6，7，9，11，12,15，25，27.13-4 气体经历如图所示的循环过程，在这个循环过程中，外界传给气体的净热量是答案：A 3.2*10^4JB 1.8*10^4JC 2.4*10^4JD 0J答案B，由循环所围成的面积计算得出。

物理学简明教程马文蔚第1至7章课后习题答案详解

1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v,t 至(t ＋Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ｜r ｜),平均速度为v ,平均速率为v ． (1) 根据上述情况,则必有( )(A) ｜Δr ｜= Δs = Δr(B) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d s ≠ d r(C) ｜Δr ｜≠ Δr ≠ Δs ,当Δt →0 时有｜d r ｜= d r ≠ d s(D) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d r = d s(2) 根据上述情况,则必有( )(A) ｜v ｜= v ,｜v ｜= v (B) ｜v ｜≠v ,｜v ｜≠ v(C) ｜v ｜= v ,｜v ｜≠ v (D) ｜v ｜≠v ,｜v ｜= v…分析与解 (1) 质点在t 至(t ＋Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs ＝PP′, 位移大小｜Δr ｜＝PP ′,而Δr ＝｜r ｜-｜r ｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt →0 时,点P ′无限趋近P 点,则有｜d r ｜＝d s ,但却不等于d r ．故选(B)．(2) 由于｜Δr ｜≠Δs ,故ts t ΔΔΔΔ≠r ,即｜v ｜≠v ．但由于｜d r ｜＝d s ,故ts t d d d d =r ,即｜v ｜＝v ．由此可见,应选(C)． 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即 (1)t r d d ； (2)t d d r ； (3)t s d d ； (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x ．下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解 tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量；td d r 表示速度矢量；在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解．故选(D)． 1 -3 一个质点在做圆周运动时,则有( );(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解加速度的切向分量a ｔ起改变速度大小的作用,而法向分量a n 起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于a ｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时, a ｔ恒为零；质点作匀变速率圆周运动时, a ｔ为一不为零的恒量,当a ｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．1 -4 质点的运动方程为23010t t x +-=和22015t t y -=，式中x ,y 的单位为m,t 的单位为ｓ。

大学物理学教程第二(马文蔚)练习册答案6第六章-机械波ppt

6-8 图示为平面简谐波在t=0时刻的波形图，此简谐波的频率为250Hz，且此图中P点的运动方向向上，求：（1）此波的波动方程；（2）距原点7.5m处质点的运动方程与t=0时该点的振动速度。 y/m
解：
距原点7.5m处质点的运动方程：
0.10
0.05
P
O
10.0m x /m
6-8 y 0.1cos[500 (t 7.5 ) ]
6-7
解：
u y
t0时2,y0 0,v0 0 2m1
Ac2os 2Tx
t
2
ux17216 cm
2
Acos
2
0.02
2 t
x
100
t
x
2
cm
6-8 图示为平面简谐波在t=0时刻的波形图，此简谐波的频率为250Hz，且此图中P点的运动方向向上，求：（1）此波的波动方程；（2）距原点7.5m处质点的运动方程与t=0时该点的振动速度。 y/m
1
2
波源振动方程：
y0
A cos
2
T
t
2
cm
6-7
波动方程：
y
Acos
2
T
t
x u
2
cm
A cos
100
t
x
2
cm
y15
A cos
100 t
15
2
cm
15 15.5
y5
Acos 100 t
5
2
cm
5 5.5
解： t 0时,y0 0, v0 0
1
2
6-7
波源振动方程：
y0
6-6 波源作简谐运动，其运动方程为

马文蔚《物理学》(第6版)(下册)课后习题-第九章至第十一章【圣才出品】

第二部分课后习题第9章振动一、问题9-1有人说谐振子是指作简谐运动的物体；也有人说谐振子是指一个振动系统。

你的看法如何？试表述之。

答：作简谐运动的振动系统，称为谐振子。

弹簧振子、单摆、复摆等都是谐振子。

谐振动是指振动物体在平衡位置附近往复运动，在这个振动形式下，物体受力的大小总是和它偏离平衡位置的距离（或角位移）成正比，并且受力方向始终指向平衡位置。

9-2符合什么规律的运动是简谐运动？说明下列运动是不是简谐运动：（1）完全弹性球在硬地面上的跳动；（2）活塞的往复运动；（3）如问题9-2图所示，一小球沿半径很大的光滑凹球面滚动（设小球所经过的弧线很短）；（4）竖直悬挂的弹簧上挂一重物，把重物从静止位置拉下一段距离（在弹性限度内），然后放手任其运动。

问题9-2图答：符合关系式F＝－kx或的运动都是简谐运动。

（1）不是简谐运动。

虽然完全弹性碰撞过程中能量守恒，但球在运动过程中受到的力不符合关系式F＝－kx。

（2）不是简谐运动。

有摩擦力做功，不符合关系式F＝－kx。

（3）是简谐运动。

运动过程类似单摆。

（4）是简谐运动。

重物所受的力符合关系式F＝－kx。

9-3弹簧的劲度系数k是材料常数吗？若把一个弹簧均分为二段，则每段弹簧的劲度系数还是k吗？将一质量为m的物体分别挂在分割前、后的弹簧下面，问分割前、后两个弹簧振子的振动频率是否一样，其关系如何？答：弹簧的劲度系数k不是材料常数。

若把一个弹簧均分为二段，则每段弹簧的劲度系数变为2k。

根据弹簧振子频率的公式，将一质量为m的物体分别挂在分割前、后两个弹簧的下面，分割前、后两个弹簧振子的振动频率之比为。

9-4一质量未知的物体挂在一劲度系数未知的弹簧上，只要测得此物体所引起的弹簧的静平衡伸长量，就可以知道此弹性系统的振动周期，为什么？答：当物体挂在一个劲度系数未知的弹簧上，平衡时，，其中是此物体所引起的弹簧的静平衡伸长量。

而弹性系统的振动周期，所以T＝，即只要测得此物体所引起的弹簧的静平衡伸长量，就可以知道此弹性系统的振动周期。

内蒙古科技大学马文蔚大学物理下册第六版答案

第九章振动习题：P37～39 1，2，3，4，5，6，7，8，16.9-4 一质点做简谐运动,周期为T,当它由平衡位置向X轴正方向运动时,从1/2最大位移处到最大位移处这段路程所需的时间( )A、T/12B、T/8C、T/6D、T/4分析（C），通过相位差和时间差的关系计算。

可设位移函数y=A*sin(ωt),其中ω=2π/T；当y=A/2,ωt1=π/6；当y=A,ωt2=π/2；△t=t2-t1=[π/(2ω)]-[π/(6ω)] =π/(3ω)=T/6第十章波动习题：P89～93 1，2，3，4，5，6，12，16，25，10-6在驻波中,两个相邻波节间各质点的振动（）：A.振幅相同,相位相同B.振幅不同,相位相同C.振幅相同,相位不同D.振幅不同,相位不同答案：波函数叠加检验.（C) 振幅相同，相位相反第十一章光学P177～182 1，2，3，4，5，6，7,8,11,23,26,31,37,38.11-4 、在迈克尔逊干涉仪的一条光路中,放入一片折射率为n=1.4的透明介质薄膜后，干涉条纹产生了7.0条条纹移动.如果入射光波长为589nm,则透明介质薄膜厚度为( )A 10307.5nmB 1472.5nmC 5153.8nmD 2945.0nm答案（C）由2(n-1)t=N得出11-26、某人用迈克尔逊干涉仪测量一光波的波长，当可动反射镜M 移动了0.310mm 的过程中，观察到干涉条纹移动了1100条，求该光波的波长解：d=N /2, =563.6nm第十二章气体动理论习题：P220～222 1，2，3，5，13,14,24.12-2 1 mol的氦气和1 mol的氧气（视为刚性双原子分子理想气体）。

当温度为T时，期内能分别为：A 3/2RT,5/2kTB 3/2kT,5/2kTC 3/2kT,3/2kTD 3/2RT,5/2RT答案：D （由1mol理想气体的内能定义式得出）12-13 当氢气和氦气的压强、体积和温度都相等时，它们的质量比和内能比各为多少？（氢气视为刚性双原子分子理想气体）解：质量比等于摩尔质量比，为1:2内能比等于自由度比，为5:3第十三章热力学基础习题：P270～275 1，2，3，4，5，6，7，9，11，12,15，25，27.13-4 气体经历如图所示的循环过程，在这个循环过程中，外界传给气体的净热量是答案：A 3.2*10^4JB 1.8*10^4JC 2.4*10^4JD 0J答案B，由循环所围成的面积计算得出。

物理学简明教程马文蔚第1至7章课后习题答案详解

1-1质点作曲线运动,在时刻t质点的位矢为r,速度为v,速率为v,t至(t＋Δt)时间内的位移为Δr,路程为Δs,位矢大小的变化量为Δr(或称Δ｜r｜),平均速度为v,平均速率为v．(1)根据上述情况,则必有()(A)｜Δr｜=Δs=Δr(B)｜Δr｜≠Δs≠Δr,当Δt→0时有｜d r｜=ds≠r d(C)｜Δr｜≠Δr≠Δs,当Δt→0时有｜d r｜=dr≠s d(D)｜Δr｜≠Δs≠Δr,当Δt→0时有｜d r｜=dr=ds(2)根据上述情况,则必有()(A)｜v｜=v,｜v｜=v(B)｜v｜≠v,｜v｜≠v(C)｜v｜=v,｜v｜≠v(D)｜v｜≠v,｜v｜=v分析与解(1)质点在t至(t＋Δt)时间内沿曲线从P点运动到P′点,各量关系如图所示,其中路程Δs＝PP′,位移大小｜Δr｜＝PP′而,Δr＝｜r｜-｜r｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt→0时,点P′无限趋近P点,则有｜d r｜＝ds,但却不等于dr．故选(B)．(2)由于｜Δr｜≠Δs,故ΔrΔsΔtΔt,即｜v｜≠v．但由于｜d r｜＝ds,故d rdsdtdt,即｜v｜＝v．由此可见,应选(C)．1-2一运动质点在某瞬时位于位矢r(x,y)的端点处,对其速度的大小有四种意见,即dr dt ；(2) d r dt ；(3) ds dt ；(4) dx dt 2 dydt 2 (1)．下述判断正确的是()(A)只有(1)(2)正确(B)只有(2)正确 (C)只有(2)(3)正确(D)只有(3)(4)正确分析与解d r dt表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量；d rdt表示速度矢量；在自然坐标系中速度大小可用公式dsv 计算,在dt直角坐标系中则可由公式22dxdyv 求解．故选(D)．dtdt1-3一个质点在做圆周运动时,则有() (A)切向加速度一定改变,法向加速度也改变 (B)切向加速度可能不变,法向加速度一定改变 (C)切向加速度可能不变,法向加速度不变 (D)切向加速度一定改变,法向加速度不变分析与解加速度的切向分量aｔ起改变速度大小的作用,而法向分量a n起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于aｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时,aｔ恒为零；质点作匀变速率圆周运动时,a ｔ为一不为零的恒量,当a ｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．1-4质点的运动方程为2x10t30t 和2y15t20t ，式中x,y 的单位为m,t 的单位为ｓ。

物理学简明教程马文蔚第1至7章课后习题答案详细讲解

1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v,t 至(t ＋Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ｜r ｜),平均速度为v ,平均速率为v ． (1) 根据上述情况,则必有( )(A) ｜Δr ｜= Δs = Δr(B) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d s ≠ d r(C) ｜Δr ｜≠ Δr ≠ Δs ,当Δt →0 时有｜d r ｜= d r ≠ d s(D) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d r = d s(2) 根据上述情况,则必有( )(A) ｜v ｜= v ,｜v ｜= v (B) ｜v ｜≠v ,｜v ｜≠ v(C) ｜v ｜= v ,｜v ｜≠ v (D) ｜v ｜≠v ,｜v ｜= v分析与解 (1) 质点在t 至(t ＋Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs ＝PP′, 位移大小｜Δr ｜＝PP ′,而Δr ＝｜r ｜-｜r ｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt →0 时,点P ′无限趋近P 点,则有｜d r ｜＝d s ,但却不等于d r ．故选(B)．(2) 由于｜Δr ｜≠Δs ,故ts t ΔΔΔΔ≠r ,即｜v ｜≠v ．但由于｜d r ｜＝d s ,故ts t d d d d =r ,即｜v ｜＝v ．由此可见,应选(C)． 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ； (2)t d d r ； (3)t s d d ； (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x ．下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解 tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量；td d r 表示速度矢量；在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解．故选(D)． 1 -3 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解加速度的切向分量a ｔ起改变速度大小的作用,而法向分量a n 起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于a ｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时, a ｔ恒为零；质点作匀变速率圆周运动时, a ｔ为一不为零的恒量,当a ｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．1 -4 质点的运动方程为23010t t x +-=和22015t t y -=，式中x ,y 的单位为m,t 的单位为ｓ。

大学物理活页作业答案（全套）马文蔚

⼤学物理活页作业答案（全套）马⽂蔚1.质点运动学单元练习（⼀）答案1．B 2．D 3．D 4．B5．3.0m ；5.0m （提⽰：⾸先分析质点的运动规律，在t <2.0s 时质点沿x 轴正⽅向运动；在t =2.0s 时质点的速率为零；，在t >2.0s 时质点沿x 轴反⽅向运动；由位移和路程的定义可以求得答案。

）6．135m （提⽰：质点作变加速运动，可由加速度对时间t 的两次积分求得质点运动⽅程。

）7．解：（1）)()2(22SI jt i t r -+=)(21m ji r+= )(242m ji r-=)(3212m ji r r r-=-=?)/(32s m ji t r v -=??=（2）)(22SI j t i dtrd v -== )(2SI jdt vd a -==)/(422s m j i v-=)/(222--=s m ja8．解：t A tdt A adt v totoωω-=ωω-==sin cos 2t A tdt A A vdt A x totoω=ωω-=+=??cos sin9．解：（1）设太阳光线对地转动的⾓速度为ωs rad /1027.73600*62/5-?=π=ωs m th dt ds v /1094.1cos 32-?=ωω==（2）当旗杆与投影等长时，4/π=ωth s t 0.31008.144=?=ωπ=10．解： ky yv v t y y v t dv a -====d d d d d d d -k =y v d v / d y+=-=-C v ky v v y ky 222121,d d 已知y =y o ，v =v o 则20202121ky v C --= )(2222y y k v v o o -+=2.质点运动学单元练习（⼆）答案1．D 2．A 3．B 4．C5．14-?==s m t dt ds v ；24-?==s m dtdva t ；2228-?==s m t Rv a n ；2284-?+=s m e t e a nt6．s rad o /0.2=ω；s rad /0.4=α；2/8.0s rad r a t =α=；22/20s m r a n =ω=7．解：（1）由速度和加速度的定义)(22SI ji t dt rd v +==；)(2SI idtvd a ==（2）由切向加速度和法向加速度的定义)(124422SI t t t dt d a t +=+=)(12222SI t a a a t n +=-=（3）())(122/322SI t a v n+==ρ8．解：⽕箭竖直向上的速度为gt v v o y -?=45sin ⽕箭达到最⾼点时垂直⽅向速度为零，解得s m gtv o /8345sin =?=3.⽜顿定律单元练习答案1．C 2．C 3．A 4．kg Mg T 5.36721==；2/98.02.0s m MT a == 5．x k v x 22=；x x xv k dtdxk dt dv v 222== 221mk dt dv mf x x == 6．解：（1）ma F F N T =θ-θsin cosmg F F N T =θ+θcos sinθ-θ=θ+θ=sin cos ;cos sin ma mg F ma mg F N T（2）F N =0时；a =g cot θ7．解：mg R m o ≥ωµ2Rg o µ≥ω 8．解：由⽜顿运动定律可得dtdv t 1040120=+ 分离变量积分()??+=tovdt t dv 4120.6 )/(6462s m t t v ++=()++=t oxdt t tdx 6462.5 )(562223m t t t x +++=9．解：由⽜顿运动定律可得dtdv mmg kv =+- 分离变量积分-=+t o vv o dt m k mg kv kdv ot m kmg kv mg o -=+ln+=???? ??+-=mg kv k m mg kv mg k m t o o 1ln ln10．解：设f 沿半径指向外为正，则对⼩珠可列⽅程 a v m f mg 2 cos =-θ，t vm mg d d sin =θ，以及 ta v d d θ=，θd d v a t =，积分并代⼊初条件得 )cos 1(22θ-=ag v ，)2cos 3(cos 2-=-=θθmg av m mg f ．4.动量守恒和能量守恒定律单元练习（⼀）答案1．A ； 2．A ； 3．B ； 4．C ； 5．相同 6．2111m m t F v +?=；2212m t F v v ?+=7．解：（1）t dt dxv x 10==；10==dtdv a x x N ma F 20==；m x x x 4013=-=?J x F W 800=?=（2）s N Fdt I ?==40318．解：()1'v m m mv +=()221221'2121o kx v m m mv ++= ()''m m k mm vx +=9．解：物体m 落下h 后的速度为 gh v 2=当绳⼦完全拉直时，有 ()'2v M m gh m +=gh mM m v 2'+=gh mM mMMv I I T 22'22+===10．解：设船移动距离x ，⼈、船系统总动量不变为零0=+mv Mu等式乘以d t 后积分，得0=+??totomvdt Mudt0)(=-+l x m Mx m mM mlx 47.0=+=5.动量守恒和能量守恒定律单元练习（⼆）答案1．C 2．D 3．D 4．C 5．18J ；6m/s 6．5/37．解：摩擦⼒mg f µ=由功能原理 2121210)(kx x x f -=+- 解得 )(22121x x mg kx +=µ.8．解：根据⽜顿运动定律 Rv m F mg N 2cos =-θ由能量守恒定律mgh mv =221质点脱离球⾯时 RhR F N -=θ=cos ;0 解得：3R h =9．解：(1)在碰撞过程中，两球速度相等时两⼩球间距离最⼩ v v v )(212211m m m m +=+ ①212211m m v m v m v ++=(2) 两球速度相等时两⼩球间距离最⼩，形变最⼤，最⼤形变势能等于总动能之差22122221)(212121v v v m m m m E p +-+=②联⽴①、②得 )/()(212122121m m m m E p +-=v v10．解：(1)由题给条件m 、M 系统⽔平⽅向动量守恒，m 、M 、地系统机械能守恒．0)(=--MV V u m ① mgR MV V u m =+-2221)(21 ②解得： )(2m M M gRmV +=；MgRm M u )(2+=(2) 当m 到达B 点时，M 以V 运动，且对地加速度为零，可看成惯性系，以M 为参考系 R mu mg N /2 =-M mg m M mg R mu mg N /)(2/2++=+= mg MmM M mg m M Mmg N 23)(2+=++=6.刚体转动单元练习（⼀）答案1．B 2．C 3．C 4．C5．v = 1.23 m/s ；a n = 9.6 m/s 2；α = –0.545 rad/ s 2；N = 9.73转。

物理学简明教程马文蔚第1至7章课后习题答案详解

1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t ＋Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ｜r ｜),平均速度为v ,平均速率为v ． (1) 根据上述情况,则必有( )(A) ｜Δr ｜= Δs = Δr(B) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d s ≠ d r(C) ｜Δr ｜≠ Δr ≠ Δs ,当Δt →0 时有｜d r ｜= d r ≠ d s(D) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d r = d s (2) 根据上述情况,则必有( )(A) ｜v ｜= v ,｜v ｜= v (B) ｜v ｜≠v ,｜v ｜≠ v(C) ｜v ｜= v ,｜v ｜≠ v (D) ｜v ｜≠v ,｜v ｜= v分析与解 (1) 质点在t 至(t ＋Δt )时间内沿曲线从P 点运动到P′点,各量关系如下图, 其中路程Δs ＝PP′, 位移大小｜Δr ｜＝PP ′,而Δr ＝｜r ｜-｜r ｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt →0 时,点P ′无限趋近P 点,则有｜d r ｜＝d s ,但却不等于d r ．故选(B)．(2) 由于｜Δr ｜≠Δs ,故ts t ΔΔΔΔ≠r ,即｜v ｜≠v ．但由于｜d r ｜＝d s ,故ts t d d d d =r ,即｜v ｜＝v ．由此可见,应选(C)． 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t r d d ； (2)t d d r ； (3)t s d d ； (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x ．下述判断正确的选项是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解 tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量；td d r 表示速度矢量；在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解．故选(D)． 1 -3 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解加速度的切向分量a ｔ起改变速度大小的作用,而法向分量a n 起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于a ｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时, a ｔ恒为零；质点作匀变速率圆周运动时, a ｔ为一不为零的恒量,当a ｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．1 -4 质点的运动方程为23010t t x +-=和22015t t y -=，式中x ,y 的单位为m,t 的单位为ｓ。

大学物理下光学部分答案(马文蔚版)

光的干涉一、选择题1、有下列说法：其中正确的是A 、从一个单色光源所发射的同一波面上任意选取的两点光源均为相干光源；B 、从同一单色光源所发射的任意两束光，可视为两相干光束；C 、只要是频率相同的两独立光源都可视为相干光源；D 、两相干光源发出的光波在空间任意位置相遇都以产生干涉现象。

[ A ]2、折射率为n 2、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为n 1和n 3，已知n 1＜n 2＜n 3，若用波长为λ的单色平行光垂直入射到该薄膜上，则从薄膜上、下两表面反射的光束（1）与（2）的光程差是 A 、2n 2e B 、2n 2e-λC 、2n 2e-λD 、2n 2e-λ/2n 2 [ A ]3、用两根直径分别为d 1和d 2的细金属丝将两块平板玻璃垫起来。

形成一个空气劈。

如果将两金属丝拉近，这时：A 、条纹宽度变宽，两金属丝间的条纹数变少；B 、条纹宽度不变，两金属丝间的条纹数变少；C 、条纹宽度变窄，两金属丝间的条纹数不变；D 、条纹宽度不变，两金属丝间的条纹数不变。

[ C ] 二、填空题4、如图所示，双缝干涉实验装置中两个缝用厚度均为e ，折射率分别为n 1和n 2的透明介质膜覆盖（ n 1 > n 2 ），波长为λ的平行单色光照射双缝，双缝间距为d ，在屏幕中央O 处（S 1O = S 2O ），两束相干光的位相差122()n n e πφλ∆=-5、用波长为λ的平行单色光垂直照射折射率为n 的劈尖薄膜，形成等厚干涉条纹，若测得相邻明条纹的间距为l ，则劈尖角θ=arcsin()2nlλ6、由两块玻璃片组成空气劈形膜，当波长为λ的单色平行光垂直入射时，测得相邻明条纹的距离为L 1。

在相同的条件下，当玻璃间注满某种透明液体时，测得两相邻明条纹的距离为L 2。

则此液体的折射率为12L L 。

7、已知在迈克尔逊干涉仪中使用波长为λ的单色光，在干涉仪的可动反射镜移动一距离d过程中，干涉条纹将移动2dλ条。

物理学简明教程马文蔚第1至7章课后习题答案详解

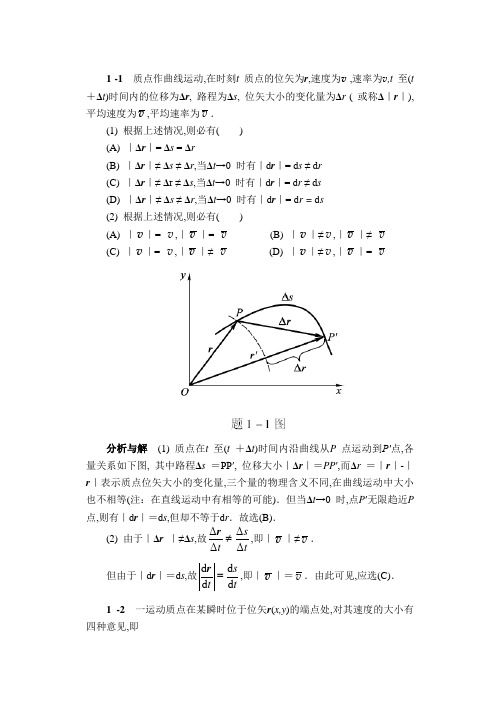
1-1 质点作曲线运动，在时刻t 质点的位矢为r,速度为v ,速率为v,t 至(t + A t)时间内的位移为A r,路程为A s,位矢大小的变化量为 & (或称r | ), 平均速度为V ,平均速率为V.⑴根据上述情况，则必有()(A) | A | =A s = A(B) | A r |M A s MA r,当 A t T 0 时有 dr | : =ds M d (C) | A r |M A M s,当A t T 0时有 dr | ==dr M s (D) | A | M A s MA r,当 A t T 0 时有dr | =dr = ds⑵ 根据上述情况，则必有()(A) | V | =V , | V | = V (B) | V | M V , | V | M V (C) | V | =V , | V | M V(D) | V | M V ,| V | = V分析与解⑴ 质点在t 至(t + A t)时间内沿曲线从P 点运动到P'点,各量关系如图所示,其中路程A s = PP ，位移大小| A r | = PP'而A r =| r | -| r |表示质点位矢大小的变化量小也不相等(注：在直线运动中有相等的可能).P 点，则有| dr | = ds 但却不等于dr .故选(B).,A rA s - (2)由于 | A | MA s,故，即 | VAA，三个量的物理含义不同，在曲线运动中大M V .d r 但由于| dr | = ds 故一 dt ds 亦ds ，即1V | = V .由此可见应选(C). 1 -2 一运动质点在某瞬时位于位矢四种意见，即r(x,y)的端点处，对其速度的大小有2dx dt10 60t系中叫径向速率•通常用符号V r 表示，这是速度矢量在位矢方向上的一个分1-3 —个质点在做圆周运动时，则有( )(C) 切向加速度可能不变，法向加速度不变起改变速度方向的作用.质点作圆周运动时，由于速度方向不断改变，相应法向加速度的方向也在不断改变，因而法向加速度是一定改变的.至于 a t 是否改变，则要视质点的速率情况而定•质点作匀速率圆周运动时，a t 恒为零；质点作匀变速率圆周运动时，a t 为一不为零的恒量，当a t 改变时，质点则作一般的变速率圆周运动•由此可见，应选(B).1-4 质点的运动方程为 x 10t 30t 2和y 15t 20t 2，式中x ，y 的单位为m ，t 的单位为s 。