聚类分析实验课件
合集下载
聚类分析实验课件

2020/8/10
4
目录 上页 下页 返回 结束
§3.7 计算步骤与上机实践
2020/8/10
5
目录 上页 下页 返回 结束
§3.7 计算步骤与上机实践
输出结果中,表3.9表示接近度矩阵,是反映样品之间相似性 或者相异性的矩阵。本例中由于计算距离使用的是平方欧氏距 离,所以样品间距离越大,样品越相异,如果我们计算距离选 择Pearson相关系数,则接近度矩阵是相似性矩阵。由表中矩 阵可以看出,Bangladesh(孟加拉国)与Cambodia(柬埔寨) 的距离是最小的,因此它们最先聚为一类。
我们可以看出全国城镇居民得消费结构大致可以分为三个方面,一类是各 种副食、日用品及交通通信、文化教育和住房等支出,这是在消费结构中 起主导作用的方面;其次是居民购买烟、酒、饮料及着装支出;粮食和水 电燃料是两项很重要的消费指标,但目前在城镇居民的消费中占的比例较 小,可将它们归并为同一类。
2020/8/10
计算步骤与上机实践
在这个数据文件中,我们选择的变量(Variables(s))有 Urban(城市人口比例),Lifeexpf(女性平均寿命)、 Lifeexpm(男性平均寿命)、Literacy(有读写能力的人 所占比例)、Gdp_cap(人均国内生产总值),以Country (国家或地区)来标识(Label Cases)本例中的17个亚洲国 家或地区,并以其他5个变量进行Q型聚类分析,即对国家 进行聚类。 这里我们将原始变量标准化(在Method选项下Transform Values的Standardize空白框内,选择Z Scores),在 Statistics选项中选择Agglomeration Schedule,聚类方 法选择组内联结法(Within-group linkage),计算距离选 择平方欧氏距离,输出冰柱图和树状聚类图。得到的结果 如下:
《聚类分析》PPT课件

应聘者 X Y Z
1 2 3 4 5 6 7 8 9 10 28 18 11 21 26 20 16 14 24 22 29 23 22 23 29 23 22 23 29 27 28 18 16 22 26 22 22 24 24 24
2021/8/17
5
2021/8/17
6
2021/8/17
Ch6 聚类分析
2021/8/17
1
聚类分析根据一批样品的许多观测指标,按 照一定的数学公式具体地计算一些样品或一些参 数(指标)的相似程度,把相似的样品或指标归为 一类,把不相似的归为一类。
例如对上市公司的经营业绩进行分类;据经 济信息和市场行情,客观地对不同商品、不同用 户及时地进行分类。又例如当我们对企业的经济 效益进行评价时,建立了一个由多个指标组成的 指标体系,由于信息的重叠,一些指标之间存在 很强的相关性,所以需要将相似的指标聚为一类, 从而达到简化指标体系的目的。
2021/8/17
29
(1) 所 选 择 的 亲 疏 测 度 指 标 在 实 际 应 用中应有明确的意义。如在经济变量分析 中,常用相关系数表示经济变量之间的亲 疏程度。
2021/8/17
30
(2)亲疏测度指标的选择要综合考虑已对样本观测 数据实施了的变换方法和将要采用的聚类分析方法。如在 标准化变换之下,夹角余弦实际上就是相关系数;又如若 在进行聚类分析之前已经对变量的相关性作了处理,则通 常就可采用欧氏距离,而不必选用斜交空间距离。此外, 所选择的亲疏测度指标,还须和所选用的聚类分析方法一 致。如聚类方法若选用离差平方和法,则距离只能选 用 欧氏距离。
剂的种类等。在名义尺度中只取两种特性状态的变量是很
重要的,如电路的开和关,天气的有雨和无雨,人口性别
聚类分析 PPT课件
(f) (f) p dij f 1 ij d (i, j) (f) p f 1 ij
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
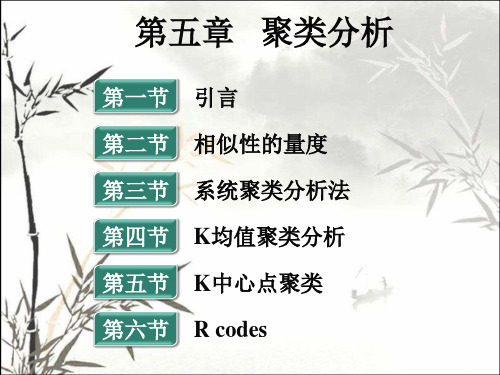
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
f is binary or nominal: dij(f) = 0 if xif = xjf , or dij(f) = 1 otherwise f is ordinal Compute ranks rif and Treat zif as interval-scaled
x1 x2 x3 x4
x1 0 3.61 5.1 4.24
x2 0 5.1 1
x3
x4
5
0 5.39
0
第二节 相似性的量度
一 样品相似性的度量
二 变量相似性的度量
含名义变量样本相似性度量
例: 学员资料包含六个属性:性别(男或女);外语语种
(英、日或俄);专业(统计、会计或金融);职业(教师 或非教师);居住处(校内或校外);学历(本科或本科以 下) 现有两名学员: X1=(男,英,统计,非教师,校外,本科)′ X2=(女,英,金融,教师,校外,本科以下)′ 对应变量取值相同称为配合的,否则称为不配合的 记配合的变量数为m1,不配合的变量数为m2,则样本之间 的距离可定义为
第五章 聚类分析
第一节 第二节 第三节 第四节 第五节 引言 相似性的量度 系统聚类分析法 K均值聚类分析 K中心点聚类
第六节
R codes
第一节 引言
“物以类聚,人以群分” 无监督分类聚类分析 分析如何对样品(或变量)进行量化分类的 问题 Q型聚类—对样品进行分类 R型聚类—对变量进行分类
用他们的序代替xif
zif
rif 1 M f 1
10
混合型属性
A database may contain all attribute types Nominal, symmetric binary, asymmetric binary, numeric, ordinal 可以用加权法计算合并的影响
聚类分析大数据课件

5
Techniques
第七章 聚类分析
• 什么是聚类分析? • 数据类型及其相似性与非相似性计算 • 算法复杂性及近似算法概念 • 划分方法
– k-center、k-cluster、k-means、谱聚类NCut • 层次方法
– 单链接与全链接
2024年8月6日星期二
Data Mining: Concepts and
Data Mining: Concepts and
26
Techniques
天河一号有关数据
• 天河一号由140个机柜组成,占地约70 0平方米,总重量约160吨。
• 6144个通用处理器, 5120个加速处理器,内 存总容量98TB,存储容量为2PB 。
• 峰值运算速度为每秒4700万亿次、持续运算 速度2507万亿次每秒浮点运算。
解决方案:启发式方法与近似算法!
2024年8月6日星期二
Data Mining: Concepts and
28
Techniques
一些定义
• P = {C1, C2, …, Ck}:n个对象的一个划分,满足条件
Ci (i = 1, 2, …, k), V = iCi, 及Ci Cj = (i j)。
• k-Center:最大半径最小化
min r(P)
PPnk
k 3: NP-Hard问题!
• k-Cluster:最大直径最小化:
min d (P)
PPnk
k 3: NP-Hard问题!
2024年8月6日星期二
Data Mining: Concepts and
30
Techniques
一些常见的优化准则
d(i, j) q (| xi1 x j1 |q | xi2 x j2 |q ...| xip x jp |q)
聚类分析法ppt课件全

8/21/2024
25
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(3)分类函数
按照修改原则不同,动态聚类方法有按批修改法、逐个修改法、混合法等。 这里主要介绍逐步聚类法中按批修改法。按批修改法分类的原则是,每一步修 改都将使对应的分类函数缩小,趋于合理,并且分类函数最终趋于定值,即计 算过程是收敛的。
8/21/2024
23
1.2.2 动态聚类分析法
1.2 聚类分析的种类
(2)初始分类 有了凝聚点以后接下来就要进行初始分类,同样获得初始分类也有不同的
方法。需要说明的是,初始分类不一定非通过凝聚点确定不可,也可以依据其 他原则分类。
以下是其他几种初始分类方法: ①人为分类,凭经验进行初始分类。 ②选择一批凝聚点后,每个样品按与其距离最近的凝聚点归类。 ③选择一批凝聚点后,每个凝聚点自成一类,将样品依次归入与其距离
8/21/2024
14
1.2 聚类分析的种类
(2)系统聚类分析的一般步骤 ①对数据进行变换处理; ②计算各样品之间的距离,并将距离最近的两个样品合并成一类; ③选择并计算类与类之间的距离,并将距离最ቤተ መጻሕፍቲ ባይዱ的两类合并,如果累的个
数大于1,则继续并类,直至所有样品归为一类为止; ④最后绘制系统聚类谱系图,按不同的分类标准,得出不同的分类结果。
8/21/2024
18
1.2 聚类分析的种类
(7)可变法
1 2 D kr
2 (8)离差平方和法
(D k 2 pD k 2 q)D p 2q
D k 2 rn n ir n n p i D i2 pn n ir n n q iD i2 qn rn in iD p 2 q
8/21/2024
聚类分析解析课件

类间距的度量
类:一个不严格的定义
定义9.1:距离小于给定阀值的点的集合 类的特征
◦ 重心:均值 ◦ 样本散布阵和协差阵 ◦ 直径
类间距的定义
最短距离法 最长距离法 重心法 类平均法 离差平方和法 等等
最小距离法(single linkage method)
极小异常值在实际中不多出现,避免极 大值的影响
类的重心之间的距离
对异常值不敏感,结果更稳定
离差平方和法(sum of squares
method或ward method)
W代表直径,D2=WM-WK-WL
即
DK2L
nL nk nM
XK XL XK XL
Cluster K
Cluster M
Cluster L
◦ 对异常值很敏感;对较大的类倾向产生较大的距 离,从而不易合并,较符合实际需要。
如表9.2所示,每个样品有p个指标,共 有n个样品
每个样品就构成p维空间中的一个点
:第i个样品的第k个指标对应的取值
◦ i=1……n; k=1……p
:第i个样品和第j个样品之间的距离
◦ i=1……n; j=1……n
点间距离测量问题
样品间距离与指标间距离 间隔尺度、有序尺度与名义尺度 数学距离与统计距离 相似性与距离:一个硬币的两面
类图上发现相同的类
饮料数据
16种饮料的热量、咖啡因、钠及价格四种变量
SPSS实现
选择Analyze-Classify-Hierarchical Cluster, 然 后 把 calorie ( 热 量 ) 、 caffeine ( 咖 啡
因)、sodium(钠)、price(价格)选入 Variables, 在Cluster选Cases(这是Q型聚类:对观测 值聚类),如果要对变量聚类(R型聚类) 则选Variables, 为 了 画 出 树 状 图 , 选 Plots , 再 点 Dendrogram等。 可以在Method中定义点间距离和类间距 离
聚类分析法ppt课件

7
(2)计算样品的距离。
d ij xi x j yi y j
8
G1
D(0)
G2 G3
G4
G5
G1 G2 G3 G4 G5
0 0.34 1.37 1.34 1.33
0 1.03 1 1.67
0 0.63 1.3
0 0.67
0
9
(3)找出D(0)非对角线上的最小元素, 将其对应的两个类合并为一个新类。
0 0.63 1.30 0 0.67
0
19
0
D(2)
1.37 0
1.67 1.30
0
20
0 1.67
D(3)
0
21
G1 G2 G3 G4 G5
0.4
0.8 1.2 1.6 2.0
聚类距离
பைடு நூலகம்22
G1 G2 G3 G4 G5
0.2 0.4 0.6 0.8 1.0
G1 G2 G3 G4 G5
0.4
0.8
1.2
1.6
2.0
聚类距离
聚类距离
23
某村对5个地块就其土壤质地和土壤有机 质含量进行了评估,结果如下。请分别 使用最长距离法和最短距离法对这5个地 块进行聚类分析,要求分为两类。
地块 A
B
C
D
E
质地 8
3
6
6
4
有机质 5
7
4
9
7
含量
24
聚类分析法
Cluster Analysis
1
聚类分析
将具有相似(similarity)性质(或距离)的 个体(样本)聚为一类,具有不同性质 的个体聚为不同的类。
聚类分析法 PPT课件

所以,根据一对零件亲疏的程度,Sij值在0到1之间变化。
(二)聚类方法和类相似系数
成组技术 GT
单一样品对之间可以根据原始数据构造一定的相似系数统 计量来描述它们之间的相似性。同样,当样品合并成类时, 也可以按一定的法则构造相似系数统计量,以描述样品与 类之间或类与类之间的相似程度。
这种构造样品与类与类之间的相似系数统计量的法则称为 聚类方法,该统计量称为类相似系数。
比如学生成绩数据就可以对学生按照理科或文科成绩(或 者综合考虑各科成绩)分类。
当然,并不一定事先假定有多少类,完全可以按照数据本 身的规律来分类。
如何度量远近?
成组技术 GT
如果想要对100个学生进行分类,如果仅仅知道他们的数 学成绩,则只好按照数学成绩来分类;这些成绩在直线上 形成100个点。这样就可以把接近的点放到一类。
如果还知道他们的物理成绩,这样数学和物理成绩就形成 二维平面上的100个点,也可以按照距离远近来分类。
三维或者更高维的情况也是类似;只不过三维以上的图形 无法直观地画出来而已。在饮料数据中,每种饮料都有四 个变量值。这就是四维空间点的问题了。
成组技术 GT
如果以n个数值型变量(n维空间)来描述某一类事物,则 一个事物就是n维空间中是一个点。
令加工零件Xi与Xj使用的机床总数目分别为CI与CJ,则 有:
Ci CI Cij C j CJ Cij 将以上两式代入式1得:
Sij
CI
Cij
(式2)
CJ —Cij
相似系数Sij可以用来判定一对零件的相似程度。若一对零 件加工机床的类型与数目完全相同,则Sij=1,若没有相同 的机床,则Sij=0 。
聚类分析作分类时各类群乃至类群数事先未知,而是根据数 据的特征确定的,又称为无师可循的分类。
(二)聚类方法和类相似系数
成组技术 GT
单一样品对之间可以根据原始数据构造一定的相似系数统 计量来描述它们之间的相似性。同样,当样品合并成类时, 也可以按一定的法则构造相似系数统计量,以描述样品与 类之间或类与类之间的相似程度。
这种构造样品与类与类之间的相似系数统计量的法则称为 聚类方法,该统计量称为类相似系数。
比如学生成绩数据就可以对学生按照理科或文科成绩(或 者综合考虑各科成绩)分类。
当然,并不一定事先假定有多少类,完全可以按照数据本 身的规律来分类。
如何度量远近?
成组技术 GT
如果想要对100个学生进行分类,如果仅仅知道他们的数 学成绩,则只好按照数学成绩来分类;这些成绩在直线上 形成100个点。这样就可以把接近的点放到一类。
如果还知道他们的物理成绩,这样数学和物理成绩就形成 二维平面上的100个点,也可以按照距离远近来分类。
三维或者更高维的情况也是类似;只不过三维以上的图形 无法直观地画出来而已。在饮料数据中,每种饮料都有四 个变量值。这就是四维空间点的问题了。
成组技术 GT
如果以n个数值型变量(n维空间)来描述某一类事物,则 一个事物就是n维空间中是一个点。
令加工零件Xi与Xj使用的机床总数目分别为CI与CJ,则 有:
Ci CI Cij C j CJ Cij 将以上两式代入式1得:
Sij
CI
Cij
(式2)
CJ —Cij
相似系数Sij可以用来判定一对零件的相似程度。若一对零 件加工机床的类型与数目完全相同,则Sij=1,若没有相同 的机床,则Sij=0 。
聚类分析作分类时各类群乃至类群数事先未知,而是根据数 据的特征确定的,又称为无师可循的分类。
聚类分析ppt课件

第七章 聚类分析
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
第一节 引言 第二节 相似性的量度 第三节 系统聚类分析法 第四节 K均值聚类分析 第五节 两步聚类分析
1
第一节 引言
什么是聚类分析? ❖ 聚类分析是根据“物以类聚”的道理,对样本或指
标进行分类的一种多元统计分析方法,它们讨论的 对象是大量的样本,要求能合理地按各自的特性进 行合理的分类,没有任何模式可供参考或依循,即 在没有先验知识的情况下进行的。
1.明考夫斯基距离
p
dij (q) (
X ik X jk )q 1/ q
k 1
明考夫斯基距离简称明氏距离。
(7.1)
13
按q的取值不同又可分成下面的几个式子
(1)绝对距离( q 1)
p
dij (1) X ik X jk k 1
பைடு நூலகம்
(7.2)
(2)欧氏距离( q 2)
p
dij (2) (
X ik X jk )2 1/ 2
22
第三节 系统聚类分析法
一 系统聚类的基本思想 二 类间距离与系统聚类法
23
一、系统聚类的基本思想
❖ 系统聚类的基本思想是:距离相近的样品(或变量)先聚成 类,距离相远的后聚成类,过程一直进行下去,每个样品( 或变量)总能聚到合适的类中。系统聚类过程是:假设总共 有n个样品(或变量),第一步将每个样品(或变量)独自 聚成一类,共有n类;第二步根据所确定的样品(或变量) “距离”公式,把距离较近的两个样品(或变量)聚合为一 类,其它的样品(或变量)仍各自聚为一类,共聚成n 1类 ;第三步将“距离”最近的两个类进一步聚成一类,共聚成 n 2类;……,以上步骤一直进行下去,最后将所有的样品 (或变量)全聚成一类。为了直观地反映以上的系统聚类过 程,可以把整个分类系统画成一张谱系图。所以有时系统聚 类也称为谱系分析。除系统聚类法外,还有有序聚类法、动 态聚类法、图论聚类法、模糊聚类法等。
聚类分析专题教育课件

❖ 由距离来构造相同系数总是可能旳,如令
cij
1 1 dij
这里dij为第i个样品与第j个样品旳距离,显然cij满足 定义相同系数旳三个条件,故可作为相同系数。
❖ 距离必须满足定义距离旳四个条件,所以不是总能 由相同系数构造。高尔(Gower)证明,当相同系 数矩阵(cij)为非负定时,如令
dij 2 1 cij
0
2
0
5
3
D(2) G7
0 3
G5 0 G5 0
表
D(3)
G6
G8
G6
0
G8
4
0
其中G6= G1∪G2
图6.3.2 最短距离法树形图
二、最长距离法
❖ 类与类之间旳距离定义为两类最远样品间旳 , jGL
dij
图6.3.3 最长距离法: DKL=d15
❖ 最长距离法与最短距离法旳并类环节完全相同,只 是类间距离旳递推公式有所不同。
注:
❖ 假如某一步D(m)中最小旳元素不止一种,相应这些 最小元素旳类能够同步合并。
❖ 因为最短距离法是用两类之间近来样本点旳距离来 聚旳,所以该措施不适合对分离得很差旳群体进行 聚类
❖ D(0)等均为对称阵 ❖ 一般距离采用绝对距离或欧氏距离
❖ 例6.3.1 设有五个样品,每个只测量了一种指标, 分别是1,2,6,8,11,试用最短距离法将它们分 类。
❖ 递推公式:
DMJ maxDKJ , DLJ
❖ 对例采用最长距离法,其树形图如图所示,它与图 有相同旳形状,但并类旳距离要比图大某些,仍提 成两类为宜。
图6.3.4 最长距离法树形图
三、中间距离法
❖ 类与类之间旳距离既不取两类近来样品间旳距离,也不取两 类最远样品间旳距离,而是取介于两者中间旳距离,称为中
聚类分析clusteranaly课件
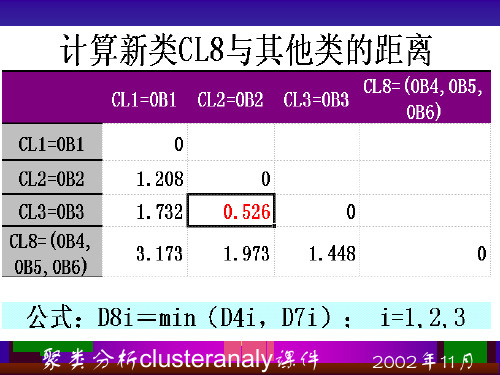
其中D.2. 为欧氏距离的平方
J
n.为各类中所含样品数
聚类分析clusteranaly课件 2002年11月
聚类分析clusteranaly课件 2002年11月
(六)可变类平均法
(flexible-beta method)
K
M
L
类平均法的变型
DM 2 J(1)nnM K DK 2JnnM L DL2JDK 2L J 1;SA软 S 件预置 0.25为
选项
人为固定分类数 ANOVA表,初
读写凝聚点 始凝聚点等
聚类分析clusteranaly课件 2002年11月
(二)SAS聚类分析
样品聚类:PROC CLUSTER pseudo
RSQUARE STD METHOD=(AVE, AVERAGE, CEN,
CENTROID, COM, COMPLETE, DEN, DENSITY, EML, FLE, FLEXIBLE, MCQ, MCQUITTY, MED, MEDIAN, SIN,
聚类分析clusteranaly课件
1,通常情况1下 ~0取 之- 间的数
聚类分析clusteranaly课件 2002年11月
(五)类平均法
(average linkage between group)
K
M
L SPSS作为默认方法 ,称为 between-
groups linkage
DM2 J
nK nM
DK2J
nL nM
DL2J
冰柱的方向
聚类分析clusteranaly课件 2002年11月
Method
聚类方法
亲疏关系指标
标准化变换
聚类分析clusteranaly课件
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图3.9是冰柱图,也是反映样品聚类情况的图,如果按照设定 的类数,在那类数的行上从左到右就可以找到各类所包含的样 品。比如我们希望分为三类,最左边的类数应选3,每个样品 右边都有一列X,如果某个样品右边的X个数少于3,那么它和 前面多于3个X的样品聚为一类,如此下去,直到找到全部三类 为止。例如,Hong Kong右边的列只有两个X,那么它就与Japan 和Singapore聚为一类了,而China右边的列只有一个X,那么 从Taiwan到China又被聚为一类,后面样品聚为另一类。
2015-1-25
目录 上页 下页 返回 结束
10
§3.8
社会经济案例研究
2015-1-25
目录 上页 下页 返回 结束
11
§3.8
社会经济案例研究
表3.16中最大的相关系数为r4,8=0.837,将G4和G8并成一新类G9,然后 计算G9与各类的相关系数,再找最大的相关系数,每次缩小一类得图3- 17。 我们可以看出全国城镇居民得消费结构大致可以分为三个方面,一类是各 种副食、日用品及交通通信、文化教育和住房等支出,这是在消费结构中 起主导作用的方面;其次是居民购买烟、酒、饮料及着装支出;粮食和水 电燃料是两项很重要的消费指标,但目前在城镇居民的消费中占的比例较 小,可将它们归并为同一类。
2015-1-25
目录 上页 下页 返回 结束
8
§3.7
计算步骤与上机实践
3.7.2 快速聚类法(K-means cluster)。 同样我们使用上面的数据文件World95.sav,从中筛 选出亚洲国家,试图将亚洲国家按经济和文教 水平分为3类。可以使用快速聚类法对样品进 行聚类。 我们使用的变量有Country(国家或地区)、Urban (城市人口比例),Lifeexpf(女性平均寿 命)、Lifeexpm(男性平均寿命)、Literacy (有读写能力的人所占比例)、Gdp_cap(人 均国内生产总值),以Country来标识本例中 的17个亚洲国家或地区,并以其他5个变量进 2015-1-25 行Q型聚类分析,即对国家进行聚类。 9
2015-1-25
目录 上页 下页 返回 结束
16
§3.8
社会经济案例研究
2015-1-25
目录 上页 下页 返回 结束
17
§3.8
社会经济案例研究
2015-1-25
目录 上页 下页 返回 结束
18
§3.8
社会经济案例研究
例3.6 我们仍以2005年31个省、市、自治区的城镇居民月平 均消费支出数据为例,在SPSS中利用K-均值法对31个省、市、 自治区的城镇居民消费水平进行聚类分析。 在SPSS中依次点击“Analyze”→“Classify” →“K-Means Cluster”,打开K-Means Cluster Analysis对话框,将8个变 量选入Variable框中,将表示地区的变量选入Label Cases By栏中,将分类数(Number of clusters)定为3。另外,点 击Iterate按钮可以在其中输入最大迭代次数(Maximum iterations)和收敛标准(Convergence criterion);在 Save按钮中可以选择保存样本的聚类结果(Cluster membership)和各样本距各自中心点的距离(Distance from cluster center);在Options按钮中可以选择输出初始类中 心点、方差分析表等结果,读者可以根据实际情况来选择。 点击“OK”得到聚类结果如下:
计算步骤与上机实践
在这个数据文件中,我们选择的变量(Variables(s))有 Urban(城市人口比例),Lifeexpf(女性平均寿命)、 Lifeexpm(男性平均寿命)、Literacy(有读写能力的人 所占比例)、Gdp_cap(人均国内生产总值),以Country (国家或地区)来标识(Label Cases)本例中的17个亚洲国 家或地区,并以其他5个变量进行Q型聚类分析,即对国家 进行聚类。 这里我们将原始变量标准化(在Method选项下Transform Values的Standardize空白框内,选择Z Scores),在 Statistics选项中选择Agglomeration Schedule,聚类方 法选择组内联结法(Within-group linkage),计算距离选 择平方欧氏距离,输出冰柱图和树状聚类图。得到的结果 如下:
2015-1-25
目录 上页 下页 返回 结束
1
聚类分析计算步骤与上机实践
2015-1-25
目录 上页 下页 返回 结束
2
§3.7
计步骤与上机实践
2015-1-25
目录 上页 下页 返回 结束
3
§3.7
计算步骤与上机实践
将表3-8的聚合系数利用Excel作出聚合系数随分类 数变化曲线,如图3-13.
2015-1-25
目录 上页 下页 返回 结束
19
§3.8
Initial Cluster Centers Cluster 2 21.50 122.39 29.08 51.64 55.04 11.30 54.88 288.13 x1 x2 x3 x4 x5 x6 x7 x8 1 21.30 124.89 35.43 73.98 93.01 20.58 43.97 433.73 3 16.16 139.92 12.98 23.58 24.87 10.76 32.35 144.21
2015-1-25
目录 上页 下页 返回 结束
7
§3.7
计算步骤与上机实践
图3.11是树状聚类图,从图中可以由分类个数得到 分类情况。如果我们选择分类数为3,就从距离为 10的地方往下切,得到分类结果如下。{1:孟加 拉国、柬埔寨、阿富汗、印度、巴基斯坦};{2: 香港、新加坡、日本};{3:泰国、越南、中国、 印度尼西亚、马来西亚、菲律宾、韩国、台湾和 朝鲜}。我们可以从经济发展水平和文化教育水平 来理解所作的分类。第2类应该是亚洲国家中经济 发达程度最高的国家或地区,第1类的经济水平和 文教水平都比较低,第3类国家的经济水平和文教 水平居中。
社会经济案例研究
a Iteration History
Iteration 1 2 3
Change in Cluster Centers 1 2 3 42.593 48.416 66.676 .000 12.213 3.742 .000 .000 .000
a. Convergence achieved due to no or small change in cluster centers. The maximum absolute coordinate change for any center is .000. The current iteration is 3. The minimum distance between initial centers is 152.938.
x1 x2 x3 x4 x5 x6 x7 x8
1 21.52 152.28 34.25 59.61 80.69 16.45 53.33 409.24
2015-1-25
目录 上页 下页 返回 结束
12
§3.8
社会经济案例研究
上面介绍的几种系统聚类方法,并类的原则和步 骤基本一致,所不同的是类与类的距离有不同的 定义。其实可以把这几种方法统一起来,有利于 在计算机上灵活地选择更有意义的谱系图。
2015-1-25
目录 上页 下页 返回 结束
13
§3.8
2015-1-25
目录 上页 下页 返回 结束
4
§3.7
计算步骤与上机实践
2015-1-25
目录 上页 下页 返回 结束
5
§3.7
计算步骤与上机实践
输出结果中,表3.9表示接近度矩阵,是反映样品之间相似性 或者相异性的矩阵。本例中由于计算距离使用的是平方欧氏距 离,所以样品间距离越大,样品越相异,如果我们计算距离选 择Pearson相关系数,则接近度矩阵是相似性矩阵。由表中矩 阵可以看出,Bangladesh(孟加拉国)与Cambodia(柬埔寨) 的距离是最小的,因此它们最先聚为一类。
6
目录 上页 下页 返回 结束
2015-1-25
§3.7
计算步骤与上机实践
表3.10是反映每一阶段聚类的结果,Coefficients表 示聚合系数,第2列和第3列表示聚合的类,比如第一 阶段时(Stage=1)第2个样品——Bangladesh(孟加 拉国)与第三个样品——Cambodia(柬埔寨)聚为一 类,注意这时有16类(17-1=16)。因此某阶段的分类 数等于总的样品数减去这个阶段的序号。 图3.10是聚合系数随分类数变化的曲线。由图可以看 出,当分类数为3或4时, 曲线变得比较平缓,这 个分类数也符合我们分类的目的。
2015-1-25
目录 上页 下页 返回 结束
15
§3.8
社会经济案例研究
那么究竟采用哪一种分类为好呢?一种方法是根据分类问题 本身的知识来决定取舍。另一种方法是将几种方法的共性取 出来,有争议的样品根据其实际情况再划分。综合考虑这两 点,笔者认为从全国各省、市、区的消费情况来看,分为三 类较为合适。 由分类结果可以看出,类平均法和最长距离法的分类结果基 本上一致,只是在西藏应该划入第二类还是第三类上存在差 异,从表3.15的实际情来看,西藏的经济发展和消费水平与 始终处在第二类的福建、天津、重庆和江苏有较大差距,因 此划入第三类较为合适,即这个聚类分析用类平均法较为合 适。
社会经济案例研究
对例3.5,我们采用欧氏距离分别用类平均 法、最短距离法、最长距离法把31个省市 分类。
类平均法聚类在SPSS中的操作为:点选 “Analyze”→“Classify” →“Hierarchical Cluster”,打开Hierarchical Cluster Analysis对话框,将八个聚类指标选入 Variables栏中,将表示地区的变量选入 Label Cases By栏中,按“Plots”按钮,在 弹出的窗口中选中Dendrogram(谱系图) 选项,按“Continue”返回主对话框,在按 “Method”按钮,在Cluster Method下拉菜 单中选择Between-groups linkage(组间 连接法,即类平均法)选项,返回主对话 框后按“OK”即可得到聚类结果。
2015-1-25
目录 上页 下页 返回 结束
10
§3.8
社会经济案例研究
2015-1-25
目录 上页 下页 返回 结束
11
§3.8
社会经济案例研究
表3.16中最大的相关系数为r4,8=0.837,将G4和G8并成一新类G9,然后 计算G9与各类的相关系数,再找最大的相关系数,每次缩小一类得图3- 17。 我们可以看出全国城镇居民得消费结构大致可以分为三个方面,一类是各 种副食、日用品及交通通信、文化教育和住房等支出,这是在消费结构中 起主导作用的方面;其次是居民购买烟、酒、饮料及着装支出;粮食和水 电燃料是两项很重要的消费指标,但目前在城镇居民的消费中占的比例较 小,可将它们归并为同一类。
2015-1-25
目录 上页 下页 返回 结束
8
§3.7
计算步骤与上机实践
3.7.2 快速聚类法(K-means cluster)。 同样我们使用上面的数据文件World95.sav,从中筛 选出亚洲国家,试图将亚洲国家按经济和文教 水平分为3类。可以使用快速聚类法对样品进 行聚类。 我们使用的变量有Country(国家或地区)、Urban (城市人口比例),Lifeexpf(女性平均寿 命)、Lifeexpm(男性平均寿命)、Literacy (有读写能力的人所占比例)、Gdp_cap(人 均国内生产总值),以Country来标识本例中 的17个亚洲国家或地区,并以其他5个变量进 2015-1-25 行Q型聚类分析,即对国家进行聚类。 9
2015-1-25
目录 上页 下页 返回 结束
16
§3.8
社会经济案例研究
2015-1-25
目录 上页 下页 返回 结束
17
§3.8
社会经济案例研究
2015-1-25
目录 上页 下页 返回 结束
18
§3.8
社会经济案例研究
例3.6 我们仍以2005年31个省、市、自治区的城镇居民月平 均消费支出数据为例,在SPSS中利用K-均值法对31个省、市、 自治区的城镇居民消费水平进行聚类分析。 在SPSS中依次点击“Analyze”→“Classify” →“K-Means Cluster”,打开K-Means Cluster Analysis对话框,将8个变 量选入Variable框中,将表示地区的变量选入Label Cases By栏中,将分类数(Number of clusters)定为3。另外,点 击Iterate按钮可以在其中输入最大迭代次数(Maximum iterations)和收敛标准(Convergence criterion);在 Save按钮中可以选择保存样本的聚类结果(Cluster membership)和各样本距各自中心点的距离(Distance from cluster center);在Options按钮中可以选择输出初始类中 心点、方差分析表等结果,读者可以根据实际情况来选择。 点击“OK”得到聚类结果如下:
计算步骤与上机实践
在这个数据文件中,我们选择的变量(Variables(s))有 Urban(城市人口比例),Lifeexpf(女性平均寿命)、 Lifeexpm(男性平均寿命)、Literacy(有读写能力的人 所占比例)、Gdp_cap(人均国内生产总值),以Country (国家或地区)来标识(Label Cases)本例中的17个亚洲国 家或地区,并以其他5个变量进行Q型聚类分析,即对国家 进行聚类。 这里我们将原始变量标准化(在Method选项下Transform Values的Standardize空白框内,选择Z Scores),在 Statistics选项中选择Agglomeration Schedule,聚类方 法选择组内联结法(Within-group linkage),计算距离选 择平方欧氏距离,输出冰柱图和树状聚类图。得到的结果 如下:
2015-1-25
目录 上页 下页 返回 结束
1
聚类分析计算步骤与上机实践
2015-1-25
目录 上页 下页 返回 结束
2
§3.7
计步骤与上机实践
2015-1-25
目录 上页 下页 返回 结束
3
§3.7
计算步骤与上机实践
将表3-8的聚合系数利用Excel作出聚合系数随分类 数变化曲线,如图3-13.
2015-1-25
目录 上页 下页 返回 结束
19
§3.8
Initial Cluster Centers Cluster 2 21.50 122.39 29.08 51.64 55.04 11.30 54.88 288.13 x1 x2 x3 x4 x5 x6 x7 x8 1 21.30 124.89 35.43 73.98 93.01 20.58 43.97 433.73 3 16.16 139.92 12.98 23.58 24.87 10.76 32.35 144.21
2015-1-25
目录 上页 下页 返回 结束
7
§3.7
计算步骤与上机实践
图3.11是树状聚类图,从图中可以由分类个数得到 分类情况。如果我们选择分类数为3,就从距离为 10的地方往下切,得到分类结果如下。{1:孟加 拉国、柬埔寨、阿富汗、印度、巴基斯坦};{2: 香港、新加坡、日本};{3:泰国、越南、中国、 印度尼西亚、马来西亚、菲律宾、韩国、台湾和 朝鲜}。我们可以从经济发展水平和文化教育水平 来理解所作的分类。第2类应该是亚洲国家中经济 发达程度最高的国家或地区,第1类的经济水平和 文教水平都比较低,第3类国家的经济水平和文教 水平居中。
社会经济案例研究
a Iteration History
Iteration 1 2 3
Change in Cluster Centers 1 2 3 42.593 48.416 66.676 .000 12.213 3.742 .000 .000 .000
a. Convergence achieved due to no or small change in cluster centers. The maximum absolute coordinate change for any center is .000. The current iteration is 3. The minimum distance between initial centers is 152.938.
x1 x2 x3 x4 x5 x6 x7 x8
1 21.52 152.28 34.25 59.61 80.69 16.45 53.33 409.24
2015-1-25
目录 上页 下页 返回 结束
12
§3.8
社会经济案例研究
上面介绍的几种系统聚类方法,并类的原则和步 骤基本一致,所不同的是类与类的距离有不同的 定义。其实可以把这几种方法统一起来,有利于 在计算机上灵活地选择更有意义的谱系图。
2015-1-25
目录 上页 下页 返回 结束
13
§3.8
2015-1-25
目录 上页 下页 返回 结束
4
§3.7
计算步骤与上机实践
2015-1-25
目录 上页 下页 返回 结束
5
§3.7
计算步骤与上机实践
输出结果中,表3.9表示接近度矩阵,是反映样品之间相似性 或者相异性的矩阵。本例中由于计算距离使用的是平方欧氏距 离,所以样品间距离越大,样品越相异,如果我们计算距离选 择Pearson相关系数,则接近度矩阵是相似性矩阵。由表中矩 阵可以看出,Bangladesh(孟加拉国)与Cambodia(柬埔寨) 的距离是最小的,因此它们最先聚为一类。
6
目录 上页 下页 返回 结束
2015-1-25
§3.7
计算步骤与上机实践
表3.10是反映每一阶段聚类的结果,Coefficients表 示聚合系数,第2列和第3列表示聚合的类,比如第一 阶段时(Stage=1)第2个样品——Bangladesh(孟加 拉国)与第三个样品——Cambodia(柬埔寨)聚为一 类,注意这时有16类(17-1=16)。因此某阶段的分类 数等于总的样品数减去这个阶段的序号。 图3.10是聚合系数随分类数变化的曲线。由图可以看 出,当分类数为3或4时, 曲线变得比较平缓,这 个分类数也符合我们分类的目的。
2015-1-25
目录 上页 下页 返回 结束
15
§3.8
社会经济案例研究
那么究竟采用哪一种分类为好呢?一种方法是根据分类问题 本身的知识来决定取舍。另一种方法是将几种方法的共性取 出来,有争议的样品根据其实际情况再划分。综合考虑这两 点,笔者认为从全国各省、市、区的消费情况来看,分为三 类较为合适。 由分类结果可以看出,类平均法和最长距离法的分类结果基 本上一致,只是在西藏应该划入第二类还是第三类上存在差 异,从表3.15的实际情来看,西藏的经济发展和消费水平与 始终处在第二类的福建、天津、重庆和江苏有较大差距,因 此划入第三类较为合适,即这个聚类分析用类平均法较为合 适。
社会经济案例研究
对例3.5,我们采用欧氏距离分别用类平均 法、最短距离法、最长距离法把31个省市 分类。
类平均法聚类在SPSS中的操作为:点选 “Analyze”→“Classify” →“Hierarchical Cluster”,打开Hierarchical Cluster Analysis对话框,将八个聚类指标选入 Variables栏中,将表示地区的变量选入 Label Cases By栏中,按“Plots”按钮,在 弹出的窗口中选中Dendrogram(谱系图) 选项,按“Continue”返回主对话框,在按 “Method”按钮,在Cluster Method下拉菜 单中选择Between-groups linkage(组间 连接法,即类平均法)选项,返回主对话 框后按“OK”即可得到聚类结果。
