2021年九年级中考数学考点:锐角三角函数
2021中考数学专题复习 解直角三角形2

αCBA2021中考数学专题复习:锐角三角函数一、知识网络⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⇒⇒⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=+=+⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧==+⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫∠∠=∠∠=∠∠=∠⇒测量应用定义)边角关系:(三角函数边边关系:角角关系:依据的过程。
已知元素求出未知元素定义:由直角三角形的解直角三角形系互余两锐角三角函数关同角三角函数关系的三角函数值、、的邻边的对边正切:斜边的邻边余弦:斜边的对边正弦:定义22202200090tan 1604530tan c b a B A Con Sin Con Sin A A A A A Cos A A Sin ααααα 二、根本知识点与典型题型 知识点1:锐角三角函数定义Rt △ABC 中,∠C=900,锐角A 的对边与斜边的比值叫∠A 的正弦,记作SinA=ca;锐角A 的邻边与斜边的比值叫∠A 的余弦,记作CosA=c b ; 锐角A 的对边与邻边的比值叫∠A 的正切,记作tanA=ba . 例1:〔1〕〔2021年贵州毕节〕在正方形网格中,ABC △的位置如下图,那么cos B ∠的值为〔 〕A .12B .22C .32D .33〔2〕〔2021 湖北孝感〕如图,△ABC 的三个顶点分别在正方形网格的格点上,那么A ∠tan 的值是 〔 〕A .56 B .65C .3102D .10103 〔3〕〔2021湖南常德〕在Rt△ABC 中,∠C=90°,假设AC=2BC,那么sin A 的值是( )A .12B .2C .55D .52〔4〕〔2021浙江金华〕“赵爽弦图〞是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.如果小正方形的面积为4,大正方形的面积为100,直角三角形中较小的锐角为α,那么tan α的值等于 ▲ .〔5〕如图,在Rt ABC △中,ACB ∠=Rt ∠,1BC =,2AB =,那么以下结论正确的选项是〔 〕 A .3sin 2A =B .1tan 2A = C .3cos 2B = D .tan 3B =(6)在Rt △ABC 中,∠C=90°,a = 1 , c = 4 , 那么sinA 的值是 ( )锐角三角三角函数αA 、1515 B 、41 C 、31D 、415 知识点2:同角三角函数关系:〔1〕122=+ααCon Sin;〔2〕αααtan =Con Sin例2.〔1〕在A ABC 中,∠C=90°,sinB=53,那么cosA 的值是 ( ) A .43 B .34 C .53 D .54 〔2〕〔2021 黄冈〕在△ABC 中,∠C =90°,sinA =45,那么tanB = 〔 〕 A .43 B .34 C .35 D .45〔3〕〔2021湖南怀化〕在Rt△ABC 中,∠C=90°,sinA=54,那么cosB 的值等于〔 〕 A .53 B. 54 C. 43D. 55〔4〕〔2021黔东南州〕x 为锐角,且31cos =α,求αααsin 1cos tan ++的值。
专题训练24:锐角三角函数-2021年中考数学一轮复习知识点课标要求

2021年中考数学一轮复习知识点课标要求专题训练24:锐角三角函数(含答案)一、知识要点:1、锐角三角函数 正弦:c a A A =∠=斜边的对边sin ; 余弦:cb A A =∠=斜边的邻边cos ; 正切:b a A A A =∠∠=的邻边的对边tan 。
常见三角函数值:锐角α三角函数 30° 45° 60°αsin 21 22 23 αcos 23 22 21 αtan33 1 32、解直角三角形 解直角三角形就是应用勾股定理、两锐角的关系、三角函数等进行求解。
除直角外,共5个元素(三边、两锐角),若知道其中2个元素(至少有一个是边),就可以求出其余3个未知元素。
二、课标要求:1、利用相似的直角三角形,探索并认识锐角三角函数(sin A ,cos A ,tan A ),知道30°,45°,60°角的三角函数值。
2、会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角。
3、能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题。
三、常见考点:1、30°,45°,60°角的三角函数值。
2、30°,45°,60°角的三角函数值与实数运算的结合。
3、解直角三角形。
4、用锐角三角函数的相关知识解决一些简单的实际问题。
四、专题训练:1.在Rt△ABC中,∠C=90°,AB=5,AC=3,则下列等式正确的是()A.sin A=B.cos A=C.tan A=D.cos A=2.如图,在塔AB前的平地上选择一点C,测出看塔顶的仰角为30°,从C点向塔底走100米到达D点,测出看塔顶的仰角为45°,则塔AB的高为()米.(≈1.7)A.145米B.135米C.125米D.120米3.在如图所示的网格中,小正方形网格的边长为1,△ABC的三个顶点均在格点上.则cos B 的值为()A.B.C.D.4.在Rt△ABC中,∠C=90°,cos B=,则Rt△ABC的三边a、b、c之比a:b:c为()A.2::3 B.1::C.1:2:3 D.2::5.在△ABC中,BC=2,AC=2,∠A=30°,则AB的长为()A.B.2 C.或4 D.2或46.用计算器求sin24°37'的值,以下按键顺序正确的是()A.B.C.D.7.如图,在△ABC中,AB=AC=4,∠C=72°,D是AB的中点,DE⊥AB交AC于点E,则cos A的值为()A.B.C.D.8.在△ABC中,∠C=90°,tan A=2,则sin A的值是()A.B.C.D.9.如图,在四边形ABCD中,∠ACB=∠CAD=90°,AC=CB,sin∠ACD=,则tan∠BDC 的值是()A.B.C.D.10.若α是锐角,sin(α+15°)=,那么锐角α等于()A.15°B.30°C.45°D.60°11.如图,CD是△ABC的高,若AB=10,CD=6,tan∠CAD=,则BD=.12.如图,△ABC的顶点都是正方形网格中的格点,则tan∠ACB等于.13.如图,在2×4的方格中,两条线段的夹角(锐角)为∠1,则sin∠1=.14.如图,在Rt△ABC中,∠A=90°,AB=AC,BD是AC边上的中线,则tan∠ADB的值是.15.如图,已知CD是△ABC的高,BD=4AD,CD=2AD,点E是BC上一点,EF⊥EA,AG=EG,tan∠EFA的值为.16.如图,测角仪CD竖直放在距建筑物AB底部8m的位置,在D处测得建筑物顶端A的仰角为50°.若测角仪CD的高度是1.5m,则建筑物AB的高度约为m.(结果精确到个位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)17.如图,已知P(4,3)为∠α边上一点,则cosα=.18.如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,通过测量可知河的宽度CD为50m.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,则AC=m(计算结果用含根号的式子表示).19.如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin∠ADE=,ED=5,如果△ECD的面积是6,那么BC的长是.20.如图,一山坡的坡度i=1:,小明从A处爬到B处所走的直线距离AB=10米,则他在垂直方向上升的高度CB为米.21.如图,在一次数学综合实践活动中,小亮要测量一教学楼的高度,先在坡面D处测得楼房项部A的仰角为30°,沿坡面向下走到坡脚C处,然后向教学楼方向继续行走10米到达E处,测得楼房顶部A的仰角为60°,已知坡面CD=16米,山坡的坡度i=1:,求楼房AB高度.(结果精确到0.1米)(参考数据:≈1.73,≈1.41)22.一种升降熨烫台如图所示,其原理是通过改变两根支撑杆夹角的度数来调整熨烫台的高度.AB和CD是两根相同长度的活动支撑杆,点O是它们的连接点,OA=OC,h(cm)表示熨烫台的高度.(1)如图1,若∠AOC=120°,h=60cm,求AB的长度;(2)小明发现,实际使用时将家里这种升降熨烫台的两根支撑杆的夹角∠AOC由120°变为60°(如图2),使用起来才顺手,请问在(1)的条件下,该熨烫台升高了多少?23.江阴芙蓉大道城市快速路在2020年5月份通车,在安装路灯过程中,工人师傅发现垂直于地面的灯柱OA与灯杆AB相交成一定的角度才能产生光照效果,路灯采用锥形灯罩,在地面上的照射区域OC长为8m,从O、C两处测得路灯B的仰角分别为∠BOC和∠BCO,且tan∠BOC=4,tan∠BCO=.(1)求路灯B到地面的距离;(2)若∠OAB=120°,求灯柱OA的高度(结果保留根号).24.如图所示,建筑物AB坐落在一斜坡的坡顶的平地上,当太阳光线与水平线夹角成60°时,测得建筑物AB在坡顶平地上的一部分影子BC=15米,在斜坡CE上的另一部分影子CD=5米,且斜坡CE的坡度为i(即tanα)=1:,求建筑物AB的高度.(结果保留根号)25.如图,楼和塔之间的距离AC为50m,小明在楼底A处测得塔顶的仰角为60°,爬到楼顶D测得塔顶的仰角为30°,求楼高AD.26.如图,某渔船在完成捕捞作业后准备返回港口C,途经某海域A处时,港口C的工作人员监测到点A在南偏东30°方向上,另一港口B的工作人员监测到点A在正西方向上.已知港口C在港口B的北偏西60°方向,且B、C两地相距120海里.(1)求出此时点A到港口C的距离(计算结果保留根号);(2)若该渔船从A处沿AC方向向港口C驶去,当到达点A'时,测得港口B在A'的南偏东75°的方向上,求此时渔船的航行距离(计算结果保留根号).参考答案1.解:如图所示:∵∠C=90°,AB=5,AC=3,∴BC=4,∴sin A=,故A错误;cos A=,故B正确;tan A=;故C错误;cos A=,故D错误;故选:B.2.解:在Rt△ABD中,∵∠ADB=45°,∴BD=AB.在Rt△ABC中,∵∠ACB=30°,∴=tan30°=,∴BC=AB.设AB=x(米),∵CD=100米,∴BC=(x+100)米.∴x+100=x,∴x=50(+1),即塔AB的高为50(+1)≈135米.故选:B.3.解:在Rt△BCD中,BD==2,所以cos B===.故选:B.4.解:∵∠C=90°,∴cos B==,设a=2x,c=3x,∴b==x,∴a:b:c=2x:x:3x=2::3.故选:A.5.解:作CD⊥AB交AB的延长线于点D,当B2C=2时,∵∠A=30°,∠ADC=90°,AC=2,∴CD=,∴AD==3,B2D==1,∴AB2=3﹣1=2,同理可得,AB1=3+1=4,即AB的长为2或4,故选:D.6.解:先按键“sin”,再输入角的度数24°37′,按键“=”即可得到结果.故选:A.7.解:∵在△ABC中,AB=AC=4,∠C=72°,∴∠ABC=∠C=72°,∠A=180°﹣∠C﹣∠ABC=36°.∵D是AB中点,DE⊥AB,∴AE=BE,AD=BD=AB=2,∴∠ABE=∠A=36°,∴∠BEC=∠A+∠ABE=72°=∠C,∴BE=BC=AE,设BC=AE=x,则CE=AC﹣AE=4﹣x.∵∠ABC=∠BEC,∠C=∠C,∴△ABC∽△BEC,∴=,即=,解得:x1=2﹣2,x2=﹣2﹣2(舍去),∴AE=2﹣2,∴cos A===,故选:C.8.解:∵∠C=90°,∴tan A==2,设AC=x,则BC=2x,∴AB==x,∴sin A===.故选:C.9.解:如图,过点D作DE⊥BC交BC的延长线于E,过点C作CH⊥BD于H.∵∠ACB=∠CAD=90°,DE⊥EC,∴∠ACE=∠E=90°,∴四边形ACED是矩形,∴AD=CE,AC=DE,∵sin∠ACD==,∴可以假设AD=3k,CD=5k,则AC=BC=DE=4k,∴BE=BC+CE=7k,∴BD===k,∵S△CBD=•BC•DE=•BD•CH,∴CH=k,∴DH===,∴tan∠BDC===.故选:C.10.解:∵sin45°=,∴α+15°=45°,∴α=30°,故选:B.11.解:∵CD是△ABC的高,∴∠ADC=90°,∵CD=6,tan∠CAD==,∴AD=CD=8,∵AB=10,∴BD=AB﹣AD=10﹣8=2,故答案为:2.12.解:过点B作BD⊥AC,垂足为D.∵AB=5,AC==,BC==5,∴CD=.∵S△ABC=15﹣﹣×4×3=,S△ABC=×AC×DB,∴××BD=,∴BD==.在Rt△BCD中,tan∠ACB==3.故答案为:3.13.解:如图,过点C作CE∥AB,连接DE,∵CE=,DE=,CD=,∴DE=CE,CE2+DE2=10=CD2,∴∠CED=90°,∴∠EDC=∠ECD=45°,∵CE∥AB,∴∠1=∠DCE=45°,∴sin∠1=,故答案为:.14.解:∵BD是AC边上的中线,∴AD=AC.∵AB=AC,∴AD=AB.在Rt△ABD中,tan∠ADB==2.故答案为:2.15.解:设AD=x,则CD=2x,BD=4x,∵CD为高,∴∠CDB=∠CDA=90°,∵==2,∴△ADC∽△CBD,∴∠CAD=∠BCD,∵∠CAD+∠ACD=90°,∴∠ACD+∠BCD=90°,即∠ACB=90°,∵AG=GE,∴CG=AG=GE,∵EF⊥EA,∴∠EFA+∠DAE=90°,∵∠DAE+∠AGD=90°,∴∠AGD=∠EFA,在Rt△AGD中,设DG=t,则AG=CG=2x﹣t,∵x2+t2=(2x﹣t)2,∴t=x,∴tan∠AGD===,∴tan∠EFA=.故答案为.16.解:作DE⊥AB于点E,由题意可得,DE=CD=8m,∵∠ADE=50°,∴AE=DE•tan50°≈8×1.19=9.52(m),∵BE=CD=1.5m,∴AB=AE+BE=9.52+1.52=11.2≈11(m),故答案为:11.17.解:过点P(4,3)作PQ⊥x轴,垂足为Q,则PQ=3,OQ=4,在Rt△POQ中,OP===5,所以cosα==,故答案为:.18.解:作AB⊥CD交CD的延长线于点B,在Rt△ABC中,∵∠ACB=∠CAE=30°,∠ADB=∠EAD=45°,∴AC=2AB,DB=AB.设AB=x,则BD=x,AC=2x,CB=50+x,∵tan∠ACB=tan30°,∴AB=CB•tan∠ACB=CB•tan30°.∴x=(50+x)•.解得:x=25(1+),∴AC=50(1+)(米).答:缆绳AC的长为50(1+)米.故答案为:50(1+)19.解:如图,过点E作EF⊥BC于F,过点A作AH⊥CB交CB的延长线于H.∵∠ABC=120°,∴∠ABH=180°﹣∠ABC=60°,∵AB=12,∠H=90°,∴BH=AB•cos60°=6,AH=AB•sin60°=6,∵EF⊥DF,DE=5,∴sin∠ADE==,∴EF=4,∴DF===3,∵S△CDE=6,∴•CD•EF=6,∴CD=3,∴CF=CD+DF=6,∵tan C==,∴=,∴CH=9,∴BC=CH﹣BH=9﹣6.故答案为:9﹣6.20.解:因为坡度i=1:,∴tan∠A==,∴∠A=30°,∴CB=AB=5(米).故答案为:5.21.解:过D作DG⊥BC于G,DH⊥AB于H,交AE于F,作FP⊥BC于P,如图所示:则DG=FP=BH,DF=GP,∵坡面CD=16米,山坡的坡度i=1:,∴∠DCG=30°,∴FP=DG=CD=8,∴CG=DG=8,∵∠FEP=60°,∴FP=EP=8,∴EP=,∴DF=GP=8+10+=+10,∵∠AEB=60°,∴∠EAB=30°,∵∠ADH=30°,∴∠DAH=60°,∴∠DAF=30°=∠ADF,∴AF=DF=+10,∴FH=AF=+5,∴AH=FH=16+5,∴AB=AH+BH=16+5+8=24+5≈24+5×1.73≈32.7(米),答:楼房AB高度约为32.7米.22.解:(1)如图1中,过点B作BH⊥AC于H.∵OA=OC,∠AOC=120°,∴∠OAC=∠OCA=(180°﹣120°)=30°,∵∠AHB=90°,BH=h=60cm,∴AB=2BH=120(cm).(2)如图2中,过点B作BT⊥AC于T.在Rt△ABT中,AB=120cm,∠A=60°,∠ATB=90°,∴BT=AB•sin60°=60(cm),∴熨烫台升高了(60﹣60)cm.23.解:(1)过点B作BF⊥OC于F,设BF=x.在Rt△BOF中,∵tan∠BOC==4,∴OF=x,在Rt△BCF中,∵tan∠BCO==,∴CF=x,∵OC=8,∴x+x=8,∴x=8,∴BF=8(m),即路灯B到地面的距离8m;(2)过点A作AG⊥BF于点G,∵∠OAB=120°,∴∠BAG=∠OAB﹣∠OAG=120°﹣90°=30°.∵OF=×8=2,∴AG=OF=2,在Rt△BCF中,∵tan∠BAG=,∴BG=tan30°×2=∴OA=GF=(8﹣)(m),即灯柱OA的高度为(8﹣)m.24.解:如图,延长BC交AD于F,过F作FG⊥CD于G,∵斜坡CE的坡度为i(即tanα)=1:,∴α=30°.∵BF∥EM,∴∠FCD=∠E=30°.∵∠AFB=60°.∴∠CDF=∠AFB﹣∠FCD=30°.∴∠ECD=∠FDC=30°.∴FC=FD.∴CG=CD=.∴CF===5(米).∴BF=BC+CF=15+5=20(米).∴AB=BF•tan60°=20(米).答:建筑物AB的高度是20米.25.解:由题意,可知∠BDE=30°,∠BAC=60°,四边形ACED是矩形,∴DE=AC=50m.在Rt△DBE中,∵tan∠BDE=,∴=,∴BE=(m).在Rt△ABC中,∵tan∠CAB=,∴=,∴BC=50(m),∴AD=CE=BC﹣BE=50﹣=(m).答:大楼AD的高为m.26.解:(1)如图所示:延长BA,过点C作CD⊥BA延长线与点D,由题意可得:∠CBD=30°,BC=120海里,则CD=BC=60海里,∵cos∠ACD==cos30°=,即=,∴AC=40(海里),答:此时点A到军港C的距离为40海里;(2)过点A′作A′N⊥BC于点N,如图:由(1)得:CD=60海里,AC=40海里,∵A'E∥CD,∴∠AA'E=∠ACD=30°,∴∠BA′A=45°,∵∠BA'E=75°,∴∠ABA'=15°,∴∠2=15°=∠ABA',即A′B平分∠CBA,∴A'E=A'N,设AA′=x,则AE=AA',A'N=A′E=AE=x,∵∠1=60°﹣30°=30°,A'N⊥BC,∴A'C=2A'N=x,∵A'C+AA'=AC,∴x+x=40,解得:x=60﹣20,∴AA'=(60﹣20)海里,答:此时渔船的航行距离为(60﹣20)海里.。
初中九年级数学中考锐角三角函数知识点总结

初中九年级数学中考锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 CA 90B 90∠-︒=∠︒=∠+∠得由B A6、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,8、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)9、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即hi l=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向) , 南偏东45°(东南方向), 南偏西60°(西南方向), 北偏西60°(西北方向)。
中考数学-锐角三角函数(解析版)

知识点一:锐角三角函数 1.三角函数定义 在 Rt△ABC 中,若∠C=90°
sin A A的对边 a
斜边
c
A的邻边
b
cos A
斜边
c
A的对边
a
tan A A的邻边 b
A的邻边
b
cot A A的对边 a
2.同角三角函数的关系
(1)平方关系: sin2 Acos2 A1
(1)三边之间的关系为 a2 b2 c2 (勾股定理)
(2)锐角之间的关系为∠A+∠B=90°
(3)30°角所对直角边等于斜边的一半。
(4)直角三角形斜边上的中线等于斜边的一半。
(5)边角之间的关系为:(三角函数定义)
2.其他有关公式
(1)
S
1 2
ab sin C
=
1 2
bc sin
A
=
1 2
ac sin
B
(2)Rt△面积公式:
S
1 2
ab
1 2
ch
(3)直角三角形外接圆的半径
R c 2
,内切圆半径
r abc 2
结论:直角三角形斜边上的高 h ab c
3.实际问题中术语的含义
(1)仰角与俯角
在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角。
(2)坡度:如图,我们通常把坡面的铅直高度和水平宽度的比叫做坡度(或坡比),用字母 i 表示,即 i h . l
见问题,这也是以后中考命题的趋势。 5.解决实际问题的关键在于建立数学模型,要善于把实际问题的数量关系转化为解直角三角形的问题.在 解直角三角形的过程中,常会遇到近似计算,应根据题目要求的精确度定答案.
锐角三角函数(公式、定理、结论图表) --中考数学知识必备
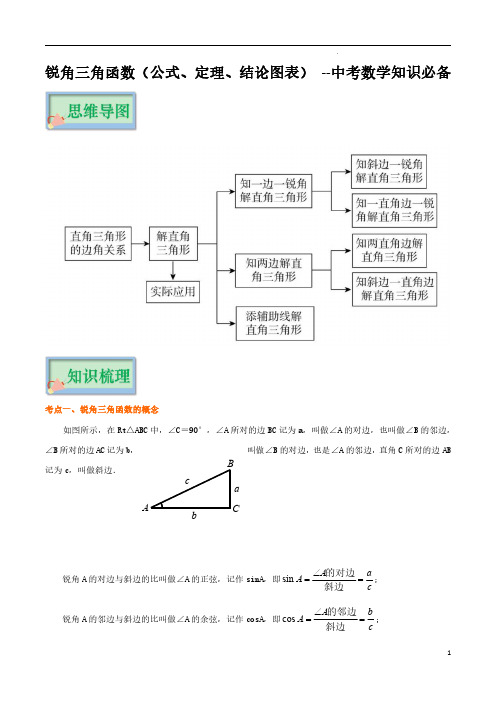
锐角三角函数(公式、定理、结论图表)--中考数学知识必备考点一、锐角三角函数的概念如图所示,在Rt△ABC 中,∠C=90°,∠A 所对的边BC 记为a,叫做∠A 的对边,也叫做∠B 的邻边,∠B 所对的边AC 记为b,叫做∠B 的对边,也是∠A 的邻边,直角C 所对的边AB记为c,叫做斜边.锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA,即sin A aA c ∠==的对边斜边;锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA,即cos A bA c∠==的邻边斜边;BCa c锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即tanA a AA b∠==∠的对边的邻边.同理sinB bBc∠==的对边斜边;cosB aBc∠==的邻边斜边;tanB bBB a∠==∠的对边的邻边.要点诠释:(1)正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化.(2)sinA,cosA,tanA分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成sin与∠A,cos与∠A,tan与∠A的乘积.书写时习惯上省略∠A的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan∠AEF”,不能写成“tanAEF”;另外,、、常写成、、.(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°之间变化时,,,tanA>0.典例1:(2022•扬州)在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,若b2=ac,则sin A的值为..【分析】根据勾股定理和锐角三角函数的定义解答即可.【解答】解:在△ABC中,∠C=90°,∴c2=a2+b2,∵b2=ac,∴c2=a2+ac,等式两边同时除以ac得:=+1,令=x,则有=x+1,∴x2+x﹣1=0,解得:x1=,x2=(舍去),当x=时,x≠0,∴x=是原分式方程的解,∴sin A==.故答案为:.【点评】本题主要考查了锐角三角函数,熟练掌握勾股定理和锐角三角函数的定义是解答本题的关键.考点二、特殊角的三角函数值利用三角函数的定义,可求出0°、30°、45°、60°、90°角的各三角函数值,归纳如下:要点诠释:(1)通过该表可以方便地知道0°、30°、45°、60°、90°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:sin0︒、、、、sin90︒的值依次为0、、、、1,而cos0︒、、、、cos90︒的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:当角度在0°<∠A<90°之间变化时,①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)②余弦值随锐角度数的增大(或减小)而减小(或增大).典例2:(2022•天津)tan45°的值等于()A.2B.1C.D.【分析】根据特殊角的三角函数值,进行计算即可解答.【解答】解:tan45°的值等于1,故选:B.【点评】本题考查了特殊角的三角函数值,熟练掌握特殊角的三角函数值是解题的关键.考点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;(2)平方关系:;(3)倒数关系:或;(4)商数关系:.要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.考点四、解直角三角形在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形.在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角.设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有:①三边之间的关系:a2+b2=c2(勾股定理).②锐角之间的关系:∠A+∠B=90°.③边角之间的关系:,,,,,.④,h为斜边上的高.要点诠释:(1)直角三角形中有一个元素为定值(直角为90°),是已知的值.(2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系).(3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤Rt△ABC两边两直角边(a,b)由求∠A,∠B=90°-∠A,斜边,一直角边(如c,a)由求∠A,∠B=90°-∠A,一边一角一直角边和一锐角锐角、邻边(如∠A,b)∠B=90°-∠A,,锐角、对边(如∠A,a)∠B=90°-∠A,,斜边、锐角(如c,∠A)∠B=90°-∠A,,要点诠释:1.在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算.2.若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边.典例3:(2022•丹东)如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.(1)请判断直线CD与⊙O的位置关系,并说明理由;(2)若sin∠ECD=,CE=5,求⊙O的半径.【分析】(1)结论:CD是⊙O的切线,证明OC⊥CD即可;(2)设OA=OC=r,设AE交OC于点J.证明四边形CDEJ是矩形,推出CD=EJ=4,CJ=DE=3,再利用勾股定理构建方程求解.【解答】解:(1)结论:CD是⊙O的切线.理由:连接OC.∵OC=OB,∴∠OCB=∠OBC,∵BC平分∠ABD,∴∠OBC=∠CBE,∴∠OCB=∠CBE,∴OC∥BD,∵CD⊥BD,∴CD⊥OC,∵OC是半径,∴CD是⊙O的切线;(2)设OA=OC=r,设AE交OC于点J.∵AB是直径,∴∠AEB=90°,∵OC⊥DC,CD⊥DB,∴∠D=∠DCJ=∠DEJ=90°,∴四边形CDEJ是矩形,∴∠CJE=90°,CD=EJ,CJ=DE,∴OC⊥AE,∴AJ=EJ,∵sin∠ECD==,CE=5,∴DE=3,CD=4,∴AJ=EJ=CD=4,CJ=DE=3,在Rt△AJO中,r2=(r﹣3)2+42,∴r=,∴⊙O的半径为.【点评】本题考查解直角三角形,切线的判定,垂径定理,矩形的判定和性质,勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型考点六、解直角三角形的应用解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是:(1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解.拓展:在用直角三角形知识解决实际问题时,经常会用到以下概念:(1)坡角:坡面与水平面的夹角叫做坡角,用字母表示.坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成=∶的形式.(2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图.(3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°.(4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.要点诠释:1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图.2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.例如:3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解.典例4:(2022•黑龙江)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,山高为()米A.600﹣250B.600﹣250C.350+350D.500【分析】设EF=5x米,根据坡度的概念用x表示出BF,根据勾股定理求出x,根据正切的定义列出方程,解方程得到答案.【解答】解:设EF=5x米,∵斜坡BE的坡度为5:12,∴BF=12x米,由勾股定理得:(5x)2+(12x)2=(1300)2,解得:x=100,则EF=500米,BF=1200米,由题意可知,四边形DCFE为矩形,∴DC=EF=500米,DE=CF,在Rt△ADE中,tan∠AED=,则DE==AD,在Rt△ACB中,tan∠ABC=,∴=,解得:AD=600﹣750,∴山高AC=AD+DC=600﹣750+500=(600﹣250)米,故选:B.【点评】本题考查的是解直角三角形的应用—坡度坡角问题,掌握坡度是坡面的铅直高典例5:(2022•湖北)如图,有甲乙两座建筑物,从甲建筑物A点处测得乙建筑物D点的俯角α为45°,C 点的俯角β为58°,BC为两座建筑物的水平距离.已知乙建筑物的高度CD为6m,则甲建筑物的高度AB为16m.(sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,结果保留整数).【分析】过点D作DE⊥AB于点E,则BE=CD=6m,∠ADE=45°,∠ACB=58°,在Rt△ADE中,∠ADE=45°,设AE=xm,则DE=xm,BC=xm,AB=AE+BE=(6+x)m,在Rt△ABC中,tan∠ACB =tan58°=≈1.60,解得x=10,进而可得出答案.【解答】解:过点D作DE⊥AB于点E,如图.则BE=CD=6m,∠ADE=45°,∠ACB=58°,在Rt△ADE中,∠ADE=45°,设AE=xm,则DE=xm,∴BC=xm,AB=AE+BE=(6+x)m,在Rt△ABC中,tan∠ACB=tan58°=≈1.60,解得x=10,∴AB=16m.故答案为:16.【点评】本题考查解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键典例6:(2022•资阳)小明学了《解直角三角形》内容后,对一条东西走向的隧道AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15°方向上,他沿西北方向前进100米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西60°方向上,(点A、B、C、D在同一平面内)(1)求点D与点A的距离;(2)求隧道AB的长度.(结果保留根号)【分析】(1)根据方位角图,易知∠ACD=60°,∠ADC=90°,解Rt△ADC即可求解;(2)过点D作DE⊥AB于点E.分别解Rt△ADE,Rt△BDE求出AE和BE,即可求出隧道AB的长.【解答】解;(1)由题意可知:∠ACD=15°+45°=60°,∠ADC=180°﹣45°﹣45°=90°,在Rt△ADC中,∴(米),答:点D与点A的距离为300米.(2)过点D作DE⊥AB于点E,∵AB是东西走向,∴∠ADE=45°,∠BDE=60°,在Rt△ADE中,∴(米),在Rt△BDE中,∴(米),∴(米),答:隧道AB的长为米.【点评】本题考查了解直角三角形的应用﹣方向角问题,掌握方向角的概念,掌握特殊角的三角函数值是解题的关键.考点七、解直角三角形相关的知识如图所示,在Rt△ABC 中,∠C=90°,(1)三边之间的关系:222a b c +=;(2)两锐角之间的关系:∠A+∠B=90°;(3)边与角之间的关系:sin cos a A B c ==,cos cos a A B c ==,cos sin b A B c ==,1tan tan a A b B==.(4)如图,若直角三角形ABC 中,CD⊥AB 于点D,设CD=h,AD=q,DB=p,则由△CBD∽△ABC,得a 2=pc;由△CAD∽△BAC,得b 2=qc;由△ACD∽△CBD,得h 2=pq;由△ACD∽△ABC 或由△ABC 面积,得ab=ch.(5)如图所示,若CD 是直角三角形ABC 中斜边上的中线,则①CD=AD=BD=12AB;②点D 是Rt△ABC 的外心,外接圆半径R=12AB.(6)如图所示,若r 是直角三角形ABC 的内切圆半径,则2a b c ab r a b c +-==++.直角三角形的面积:①如图所示,111sin 222ABC S ab ch ac B === △.(h 为斜边上的高)②如图所示,1()2ABCS r a b c=++△.典例7:(2022•黄石)我国魏晋时期的数学家刘徽首创“割圆术”:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长l6=6R,则π≈=3.再利用圆的内接正十二边形来计算圆周率,则圆周率π约为()A.12sin15°B.12cos15°C.12sin30°D.12cos30°【分析】利用圆内接正十二边形的性质求出A6A7=2A6M=2R×sin15°,再根据“圆周率等于圆周长与该圆直径的比”,即可解决问题.【解答】解:在正十二边形中,∠A6OM=360°÷24=15°,∴A6M=sin15°×OA6=R×sin15°,∵OA6=OA7,OM⊥A6A7,∴A6A7=2A6M=2R×sin15°,∴π≈=12sin15°,故选:A.【点评】本题主要考查了圆内接多边形的性质,解直角三角形等知识,读懂题意,计算出正十二边形的周长是解题的关键.。
2021年全国各省市中考真题分类汇编:锐角三角函数(含答案)

2021年全国各省市数学中考分类汇编锐角三角函数一、选择题1.(2021·山东省淄博市)如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为()A. 35B. √55C. 45D. 2√552.(2021·浙江省金华市)如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为()A. 4cosα米B. 4sinα米C. 4tanα米D. 4cosα米3.(2021·山东省泰安市)如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D 处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C 的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:√3≈1.732)()A. 136.6米B. 86.7米C. 186.7米D. 86.6米4.(2021·重庆市)如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B ,C ,D ,E 在同一平面内),在点D 处测得建筑物顶A 点的仰角为50°,则建筑物AB 的高度约为( )(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)A. 69.2米B. 73.1米C. 80.0米D. 85.7米5. (2021·广东省)如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P 、Q 两点分别测定对岸一棵树T 的位置,T 在P 的正北方向,且T 在Q 的北偏西70°方向,则河宽(PT 的长)可以表示为( )A. 200tan70°米B. 200tan70∘米C. 200sin 70°米D. 200sin70∘米 6. (2021·湖北省随州市)如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A 处,底端落在水平地面的点B 处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sinα=cosβ=35,则梯子顶端上升了( ) A. 1米 B. 1.5米 C. 2米 D. 2.5米7. (2021·广西壮族自治区桂林市)如图,在平面直角坐标系内有一点P (3,4),连接OP ,则OP 与x 轴正方向所夹锐角α的正弦值是( )A. 34B. 43 C. 35D. 458.(2021·广东省广州市)如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB′C′,使点C′落在AB边上,连结BB′,则sin∠BB′C′的值为()A. 35B. 45C. √55D. 2√559.(2021·贵州省毕节市)如图,拦水坝的横断面为梯形ABCD,其中AD∥BC,∠ABC=45°,∠DCB=30°,斜坡AB长8m,则斜坡CD的长为()A. 6√2mB. 8√2mC. 4√6mD. 8√3m10.(2021·福建省)如图,AB为⊙O的直径,点P在AB的延长线上,PC,PD与⊙O相切,切点分别为C,D.若AB=6,PC=4,则sin∠CAD等于()A. 35B. 23C. 34D. 45二、填空题11.(2021·湖北省黄石市)如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=5米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为45°,则电线杆AB的高度约为______ 米.(参考数据:√2≈1.414,√3≈1.732,结果按四舍五入保留一位小数)12.(2021·山东省烟台市)如图,在正方形网格中,每个小正方形的边长都是1,⊙O是△ABC的外接圆,点A,B,O在网格线的交点上,则sin∠ACB的值是______ .13.(2021·辽宁省本溪市)如图,由边长为1的小正方形组成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C和点D,则tan∠ADC= ______ .14.(2021·广东省梅州市)如图,在▱ABCD中,AD=5,AB=12,sin A=4.过点D作DE⊥AB,5垂足为E,则sin∠BCE= ______ .15.(2021·浙江省衢州市)图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE与地面平行,支撑杆AD,BC可绕连接点O转动,且OA=OB,椅面底部有一根可以绕点H转动的连杆HD,点H是CD的中点,FA,EB均与地面垂直,测得FA=54cm,EB=45cm,AB=48cm.(1)椅面CE的长度为______ cm.(2)如图3,椅子折叠时,连杆HD绕着支点H带动支撑杆AD,BC转动合拢,椅面和连杆夹角∠CHD的度数达到最小值30°时,A,B两点间的距离为______ cm (结果精确到0.1cm).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)16.(2021·湖北省荆州市)如图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,测量知BC=8cm,AB=16cm.当AB,BC转动到∠BAE=60°,∠ABC=50°时,点C到AE的距离为______ cm.(结果保留小数点后一位,参考数据:sin70°≈0.94,√3≈1.73)17.(2021·湖北省黄冈市)如图,建筑物BC上有一高为8m的旗杆AB,从D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则建筑物BC的高约为______ m(结果保留小数点后一位).(参考数据:sin53°≈0.80,cos53°≈0.60,tan53≈1.33)18.(2021·浙江省湖州市)如图,已知在Rt△ABC中,∠ACB=90°,AC=1,AB=2,则sin B的值是______ .19.(2021·广东省)如图,旗杆高AB=8m,某一时刻,旗杆影子长BC=16m,则tan C=______.20.(2021·江苏省常州市)如图,在△ABC中,AC=3,BC=4,D、E分别在CA、CB上,点F在△ABC内.若四边形CDFE是边长为1的正方形,则sin∠FBA= ______ .三、解答题3-π)0.21.(2021·湖南省岳阳市)计算:(-1)2021+|-2|+4sin30°-(√822.(2021·四川省达州市)计算:-12+(π-2021)0+2sin60°-|1-√3|.23.(2021·湖北省黄冈市)计算:|1−√3|−2sin60°+(π−1)0.)−2+4sin60°−(−1).24.(2021·湖南省怀化市)计算:(3−π)0−√12+(1325.(2021·浙江省金华市)已知:如图,矩形ABCD的对角线AC,BD相交于点O,∠BOC=120°,AB=2.(1)求矩形对角线的长.(2)过O作OE⊥AD于点E,连结BE.记∠ABE=α,求tanα的值.26.(2021·湖南省娄底市)我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角∠DPA为30°且A与P两点的距离为6千米,它沿铅垂线上升7.5秒后到达B处,此时在P 处测得B点的仰角∠DPB为45°,求天舟二号从A处到B处的平均速度.(结果精确到1m/s,取√3=1.732,√2=1.414)27.(2021·黑龙江省绥化市)一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为△ABC,点B、C、D在同一条直线上,测得∠ACB=90°,∠ABC=60°,AB=32cm,∠BDE=75°,其中一段支撑杆CD=84cm,另一段支撑杆DE=70cm.求支撑杆上的点E到水平地面的距离EF是多少?(用四舍五入法对结果取整数,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,√3≈1.732)28.(2021·湖北省荆门市)某海域有一小岛P,在以P为圆心,半径r为10(3+√3)海里的圆形海域内有暗礁.一海监船自西向东航行,它在A处测得小岛P位于北偏东60°的方向上,当海监船行驶20√2海里后到达B处,此时观测小岛P位于B处北偏东45°方向上.(1)求A,P之间的距离AP;(2)若海监船由B处继续向东航行是否有触礁危险?请说明理由.如果有触礁危险,那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域?29.(2021·湖南省益阳市)“2021湖南红色文化旅游节--重走青年毛泽东游学社会调查之路”启动仪式于4月29日在安化县梅城镇举行,该镇南面山坡上有一座宝塔,一群爱好数学的学生在研学之余对该宝塔的高度进行了测量.如图所示,在山坡上的A点测得塔底B的仰角∠BAC=13°,塔顶D的仰角∠DAC=38°,斜坡AB=50米,求宝塔BD的高(精确到1米).(参考数据:sin13°≈0.22,cos13°≈0.97,tan13°≈0.23,sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)30.(2021·湖南省湘西土家族苗族自治州)有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.芙蓉学校数学实践活动小组为测量“一心阁”CH的高度,在楼前的平地上A处,观测到楼顶C处的仰角为30°,在平地上B处观测到楼顶C处的仰角为45°,并测得A、B 两处相距20m,求“一心阁”CH的高度.(结果保留小数点后一位,参考数据:√2≈1.41,√3=1.73)参考答案1.A2.A3.A4.D5.B6.C7.D8.C9.B10.D11.10.512.2√5513.14.16.6.317.24.218.1219.1220.√101021.解:原式=-1+2+4×1-1=-1+2+2-1=2.222.解:原式=-1+1+2×√3-(√3-1)2=-1+1+√3-√3+1=1.23.解:原式=√3-1-2×√3+12=√3-1-√3+1=0.24.解:原式=1-2√3+9+4×√3+12=1-2√3+9+2√3+1=11.25.解:(1)∵∠BOC=120°,∴∠AOB=60°,∵四边形ABCD是矩形,∴∠BAD=90°,AC=BD,AO=OC,BO=DO,∴△AOB 是等边三角形,∴AB =AO =BO ,∵AB =2,∴BO =2,∴BD =2BO =4,∴矩形对角线的长为4;(2)由勾股定理得:AD =√BD 2−AB 2=√42−22=2√3,∵OA =OD ,OE ⊥AD 于点E ,∴AE =DE =12AD =√3,∴tanα=AE AB =√32.26.解:由题意可得:∠APD =30°,∠BPD =45°,AP =6km ,∠BDP =90°, 在Rt △BPD 中,∵∠APD =30°,AP =6km ,∠ADP =90°,cos ∠APD =cos30°=PDPA , ∴AD =12AP =3km ,PD =PA •cos30°=6×√32=3√3(km ), 在Rt △APD 中,∵∠BPD =45°,PD =3√3km ,∠BDP =90°,tan ∠BPD =tan45°=BDPD , ∴BD =PD tan45°=3√3(km ), 故AB =BD -AD =3√3-3≈5.196-3=2.196(km )=2196m ,则天舟二号从A 处到B 处的平均速度约为:2196÷7.5≈293(m /s ), 答:天舟二号从A 处到B 处的平均速度约为293m /s .27.解:方法一:如图1,过点D 作DM ⊥EF 于M ,过点D 作DN ⊥BA 交BA 延长线于N ,在Rt △ABC 中,∠ABC =60°,AB =32(cm ),∴BC =AB •cos60°=32×12=16(cm ), ∵DC =84(cm ),∴BD =DC +BC =84+16=100(cm ),∵∠F =90°,∠DMF =90°,∴DM ∥FN ,∴∠MDB=∠ABC=60°,,在Rt△BDN中,sin∠DBN=sin60°=DNBD∴DN=√3×100=50√3(cm),2∵∠F=90°,∠N=90°,∠DMF=90°,∴四边形MFND是矩形,∴DN=MF=50√3,∵∠BDE=75°,∠MDB=60°,∴∠EDM=∠BDE-∠MDB=75°-60°=15°,∵DE=70(cm),∴ME=DE•sin∠EDM=70×sin15°≈18.2(cm),∴EF=ME+MF=50√3+18.2≈104.8≈105(cm),答:支撑杆上的点E到水平地面的距离EF大约是105cm.方法二:如图2,过点D作DH⊥BA交BA延长线于H,过点E作EG⊥HD延长线于G,在Rt△ABC中,∠ABC=60°,AB=32(cm),∴BC=AB•cos60°=32×1=16(cm),2∵DC=84(cm),∴BD=DC+BC=84+16=100(cm),同方法一得,DH=BD•sin60°=50√3,∵在Rt△BDH中,∠DBH=60°,∴∠BDH=30°,∵∠BDE=75°,∴∠EDG=180°-∠BDH-∠BDE=180°-75°-30°=75°,∴∠DEG=90°-75°=15°,∴DG=DE•sin15°≈18.2(cm),∴GH=DG+DH=18.2+50√3≈104.8≈105(cm),∵∠F=90°,∠H=90°,∠G=90°,∴EF=EG≈105(cm),答:支撑杆上的点E到水平地面的距离EF大约是105cm.28.解:(1)过点P作PC⊥AB,交AB的延长线于点C,由题意得,∠PAC=30°,∠PBC=45°,AB=20√2,设PC=x,则BC=x,在Rt△PAC中,∵tan30°=PCAC =xx+20√2=√33,∴x=10√6+10√2,∴PA=2x=20√6+20√2,答:A,P之间的距离AP为(20√6+20√2)海里;(2)因为PC-10(3+√3)=10√6+10√2-30-10√3=10(√3+1)(√2-√3)<0,所以有触礁的危险;设海监船无触礁危险的新航线为射线BD,作PE⊥BD,垂足为E,当P到BD的距离PE=10(3+√3)海里时,有sin∠PBE=10(3+√3)√2⋅PC =10(3+√3)20(√3+1)=√32,∴∠PBD=60°,∴∠CBD=60°-45°=15°,90°-15°=75°即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域.29.解:在Rt△ABC中,sin∠BAC=BCAB ,cos∠BAC=ACAB,∴BC=AB•sin∠BAC=AB•sin13°≈50×0.22=11(米);AC=AB•cos∠BAC=AB•cos13°≈50×0.97=48.5(米);在Rt△ADC中,tan∠DAC=CDAC,∴CD=AC•tan∠DAC=AC•tan38°≈48.5×0.78-37.83(米);∴BD=CD-BC≈37.83-11=26.83≈27(米),答:宝塔BD的高约为27米.30.解:设CH为x m,由题意得:∠AHC=90°,∠CBH=45°,∠A=30°,∴BH=CH=xm,AH=√3CH=√3x m,∵AH-BH=AB,∴√3x-x=20,解得:x=10(√3+1)≈27.3(m),答:“一心阁”CH的高度约为27.3m.。
中考专项复习锐角三角函数

与几何图形有关的锐角三角函数问题
总结词
理解几何图形中的角度关系与边长关 系,掌握三角函数的定义及使用。
详细描述
在几何图形中,锐角三角函数通常被 用于求解角度、边长等问题。例如, 在直角三角形中,可以用正弦、余弦 、正切等函数来描述各边与斜边的关 系。
与实际生活有关的锐角三角函数问题
总结词
将实际问题转化为数学问题,通过锐 角三角函数求解。
余弦函数的图像与性质
图像描述
余弦函数图像也是周期性的,但其波形与正弦函数相反,波 峰和波谷随着x的增大而交替出现,且函数值先正后负,周期 为2π。
性质总结
余弦函数具有对称性和周期性,其对称轴为y轴,对称中心为 (kπ+π/2,0),其中k为整数。此外,余弦函数在区间[0,π/2] 上为增函数,在区间[π/2,π]上为减函数。
中考专项复习锐角三角函
数
汇报人:
2023-12-11
• 锐角三角函数概述 • 锐角三角函数的图像与性质 • 锐角三角函数的应用题解析 • 锐角三角函数的实际应用 • 中考中锐角三角函数的常见考点与题
型 • 中考真题解析与备考策略01锐角三角函数概述
锐角三角函数的定义
正弦函数(sine function): 锐角α的正弦值与直角三角形 斜边长度的比值,记作sin α。
总结
中考中锐角三角函数一般以填空题和选择题 的形式出现,主要考察的是锐角三角函数的 定义以及运用。题目会设定一个或者几个锐 角,然后利用锐角三角函数的定义,求出这 个锐角的三角函数值。
例子
例如,如果一个锐角A的对边长度为4,邻 边长度为3,那么我们可以使用锐角三角函 数的定义来求出这个锐角的正弦值和余弦值 。根据定义,正弦值=对边长度/斜边长度
中考数学考点:锐角三角函数公式

中考数学考点:锐角三角函数公式关于初中生来说中考就是一个重要的转机点,那么怎样才干在中考这场战役中取得成功呢?别担忧,看了中考数学考点:锐角三角函数公式以后你会有很大的收获:中考数学考点:锐角三角函数公式两角和与差的三角函数:sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinB ?cos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)三角和的三角函数:sin(++)=sincoscos+cossincos+coscossin-sinsinsincos(++)=coscoscos-cossinsin-sincossin-sinsincostan(++)=(tan+tan+tan-tantantan)/(1-tantan-tantan-ta ntan)辅佐角公式:Asin+Bcos=(A^2+B^2)^(1/2)sin(+t),其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsin+Bcos=(A^2+B^2)^(1/2)cos(-t),tant=A/B 倍角公式:sin(2)=2sincos=2/(tan+cot)cos(2)=cos^2()-sin^2()=2cos^2()-1=1-2sin^2() tan(2)=2tan/[1-tan^2()]三倍角公式:sin(3)=3sin-4sin^3()cos(3)=4cos^3()-3cos。
01选择题-2021中考数学真题知识点分类汇编-锐角三角形(含答案,30题)

01选择题-2021中考数学真题知识点分类汇编-锐角三角形(含答案,30题)一.锐角三角函数的定义(共1小题)1.(2021•云南)在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长是( )A.B.C.60D.80二.特殊角的三角函数值(共3小题)2.(2021•株洲)某限高曲臂道路闸口如图所示,AB垂直地面l1于点A,BE与水平线l2的夹角为α(0°≤α≤90°),EF∥l1∥l2,若AB=1.4米,BE=2米,车辆的高度为h (单位:米),不考虑闸口与车辆的宽度:①当α=90°时,h小于3.3米的车辆均可以通过该闸口;②当α=45°时,h等于2.9米的车辆不可以通过该闸口;③当α=60°时,h等于3.1米的车辆不可以通过该闸口.则上述说法正确的个数为( )A.0个B.1个C.2个D.3个3.(2021•天津)tan30°的值等于( )A.B.C.1D.24.(2021•泸州)在锐角△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,有以下结论:===2R(其中R为△ABC的外接圆半径)成立.在△ABC中,若∠A=75°,∠B=45°,c=4,则△ABC的外接圆面积为( )A.B.C.16πD.64π三.计算器—三角函数(共3小题)5.(2021•烟台)如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:按键的结果为m;按键的结果为n;按键的结果为k.下列判断正确的是( )A.m=n B.n=k C.m=k D.m=n=k 6.(2021•威海)若用我们数学课本上采用的科学计算器计算sin36°18′,按键顺序正确的是( )A.B.C.D.7.(2021•东营)如图,在△ABC中,∠C=90°,∠B=42°,BC=8,若用科学计算器求AC 的长,则下列按键顺序正确的是( )A.B.C.D.四.解直角三角形(共8小题)8.(2021•玉林)如图,△ABC 底边BC 上的高为h 1,△PQR 底边QR 上的高为h 2,则有( )A .h 1=h 2B .h 1<h 2C .h 1>h 2D .以上都有可能9.(2021•宜昌)如图,△ABC 的顶点是正方形网格的格点,则cos ∠ABC 的值为( )A .B .C .D .10.(2021•巴中)如图,点A 、B 、C 在边长为1的正方形网格格点上,下列结论错误的是( )A .sinB =B .sinC =C .tan B =D .sin 2B +sin 2C =111.(2021•淄博)如图,在Rt △ABC 中,∠ACB =90°,CE 是斜边AB 上的中线,过点E 作EF ⊥AB 交AC 于点F .若BC =4,△AEF 的面积为5,则sin ∠CEF 的值为( )A .B .C .D .12.(2021•黑龙江)如图,在△ABC 中,∠ACB =90°,点D 在AB 的延长线上,连接CD ,若AB =2BD ,tan ∠BCD =,则的值为( )A.1B.2C.D.13.(2021•宜宾)如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )A.B.2C.D.14.(2021•广东)如图,AB是⊙O的直径,点C为圆上一点,AC=3,∠ABC的平分线交AC 于点D,CD=1,则⊙O的直径为( )A.B.2C.1D.215.(2021•绍兴)如图,Rt△ABC中,∠BAC=90°,cos B=,点D是边BC的中点,以AD 为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连结CE,则的值为( )A.B.C.D.2五.解直角三角形的应用(共5小题)16.(2021•呼和浩特)如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径d,根据我国魏晋时期数学家刘徽的“割圆术”思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计π的值,下面d及π的值都正确的是( )A.d=,π≈8sin22.5°B.d=,π≈4sin22.5°C.d=,π≈8sin22.5°D.d=,π≈4sin22.5°17.(2021•长春)如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )A.30sinα米B.米C.30cosα米D.米18.(2021•十堰)如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )A.(15+)m B.5m C.15m D.(5+)m19.(2021•随州)如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sinα=cosβ=,则梯子顶端上升了( )A.1米B.1.5米C.2米D.2.5米20.(2021•温州)图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC=1,∠AOB=α,则OC2的值为( )A.+1B.sin2α+1C.+1D.cos2α+1六.解直角三角形的应用-坡度坡角问题(共4小题)21.(2021•德州)某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5米,调整后的楼梯会加长( )(参考数据:sin37°≈,cos37°≈,tan37°≈).A.6米B.3米C.2米D.1米22.(2021•潍坊)如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是( )A.15°B.30°C.45°D.60°23.(2021•衡阳)如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )A.7.5米B.8米C.9米D.10米24.(2021•金华)如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )A.4cosα米B.4sinα米C.4tanα米D.米七.解直角三角形的应用-仰角俯角问题(共6小题)25.(2021•济南)无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135m的A处测得试验田右侧边界N处俯角为43°,无人机垂直下降40m至B处,又测得试验田左侧边界M处俯角为35°,则M,N之间的距离为( )(参考数据:tan43°≈0.9,sin43°≈0.7,cos35°≈0.8,tan35°≈0.7,结果保留整数)A.188m B.269m C.286m D.312m 26.(2021•日照)如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB 的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m 到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1:,且点A,B,C,D,E在同一平面内,小明同学测得古塔AB的高度是( )A.(10+20)m B.(10+10)m C.20m D.40m 27.(2021•深圳)如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为( )A.15sin32°B.15tan64°C.15sin64°D.15tan32°28.(2021•泰安)如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)( )A.136.6米B.86.7米C.186.7米D.86.6米29.(2021•重庆)如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB 为30m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50m,测得山坡DF的坡度i=1:1.25.若ND=DE,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为(参考数据:≈1.41,≈1.73)( )A.9.0m B.12.8m C.13.1m D.22.7m 30.(2021•重庆)如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶点A的仰角为50°,则建筑物AB的高度约为( )(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)A.69.2米B.73.1米C.80.0米D.85.7米参考答案与试题解析一.锐角三角函数的定义(共1小题)1.(2021•云南)在△ABC中,∠ABC=90°.若AC=100,sin A=,则AB的长是( )A.B.C.60D.80【解析】解:∵AC=100,sin A=,∴BC=60,∴AB==80,【答案】D.二.特殊角的三角函数值(共3小题)2.(2021•株洲)某限高曲臂道路闸口如图所示,AB垂直地面l1于点A,BE与水平线l2的夹角为α(0°≤α≤90°),EF∥l1∥l2,若AB=1.4米,BE=2米,车辆的高度为h (单位:米),不考虑闸口与车辆的宽度:①当α=90°时,h小于3.3米的车辆均可以通过该闸口;②当α=45°时,h等于2.9米的车辆不可以通过该闸口;③当α=60°时,h等于3.1米的车辆不可以通过该闸口.则上述说法正确的个数为( )A.0个B.1个C.2个D.3个【解析】解:由题知,限高曲臂道路闸口高度为:1.4+2×sinα,①当α=90°时,h<(1.4+2)米,即h<3.4米即可通过该闸口,故①正确;②当α=45°时,h<(1.4+2×)米,即h<1.4+米即可通过该闸口,∵2.9>1.4+,∴h等于2.9米的车辆不可以通过该闸口,故②正确;③当α=60°时,h<(1.4+2×)米,即h<1.4米即可通过该闸口,∵3.1<1.4+,∴h等于3.1米的车辆可以通过该闸口,故③不正确;【答案】C.3.(2021•天津)tan30°的值等于( )A.B.C.1D.2【解析】解:tan30°=.【答案】A.4.(2021•泸州)在锐角△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,有以下结论:===2R(其中R为△ABC的外接圆半径)成立.在△ABC中,若∠A=75°,∠B=45°,c=4,则△ABC的外接圆面积为( )A.B.C.16πD.64π【解析】解:∵∠A+∠B+∠C=180°,∴∠C=180°﹣∠A﹣∠B=180°﹣75°﹣45°=60°,∵=2R,∴2R===,∴R=,∴S=πR2=π()2=π,【答案】A.三.计算器—三角函数(共3小题)5.(2021•烟台)如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序及结果如下:按键的结果为m;按键的结果为n;按键的结果为k.下列判断正确的是( )A.m=n B.n=k C.m=k D.m=n=k【解析】解:m=23﹣=8﹣4=4;n=﹣22=4﹣4=0;k=﹣cos60°=﹣=4;∴m=k,【答案】C.6.(2021•威海)若用我们数学课本上采用的科学计算器计算sin36°18′,按键顺序正确的是( )A.B.C.D.【解析】解:采用的科学计算器计算sin36°18′,按键顺序正确的是D选项中的顺序,【答案】D.7.(2021•东营)如图,在△ABC中,∠C=90°,∠B=42°,BC=8,若用科学计算器求AC 的长,则下列按键顺序正确的是( )A.B.C.D.【解析】解:在△ABC中,因为∠C=90°,所以tan B=,因为∠B=42°,BC=8,所以AC=BC•tan B=8×tan42°.【答案】D.四.解直角三角形(共8小题)8.(2021•玉林)如图,△ABC底边BC上的高为h1,△PQR底边QR上的高为h2,则有( )A.h1=h2B.h1<h2C.h1>h2D.以上都有可能【解析】解:如图,分别作出△ABC底边BC上的高为AD即h1,△PQR底边QR上的高为PE 即h2,在Rt△ADC中,h1=AD=5×sin55°,在Rt△PER中,h2=PE=5×sin55°,∴h1=h2,【答案】A.9.(2021•宜昌)如图,△ABC的顶点是正方形网格的格点,则cos∠ABC的值为( )A.B.C.D.【解析】解:法一、如图,在Rt△ABD中,∠ADB=90°,AD=BD=3,∴AB===3,∴cos∠ABC===.【答案】B.法二、在Rt△ABD中,∠ADB=90°,AD=BD=3,∴∠ABD=∠BAD=45°,∴cos∠ABC=cos45°=.【答案】B.10.(2021•巴中)如图,点A、B、C在边长为1的正方形网格格点上,下列结论错误的是( )A.sin B=B.sin C=C.tan B=D.sin2B+sin2C=1【解析】解:由勾股定理得:AB=,AC=,BC=,∴BC2=AB2+AC2,∴△ABC是直角三角形,∠BAC=90°,∴sin B=,sin C=,tan B=,sin2B+sin2C=,【答案】A.11.(2021•淄博)如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF ⊥AB交AC于点F.若BC=4,△AEF的面积为5,则sin∠CEF的值为( )A.B.C.D.【解析】解:连接BF,∵CE是斜边AB上的中线,EF⊥AB,∴EF是AB的垂直平分线,∴S△AFE=S△BFE=5,∠FBA=∠A,∴S△AFB=10=AF•BC,∵BC=4,∴AF=5=BF,在Rt△BCF中,BC=4,BF=5,∴CF==3,∵CE=AE=BE=AB,∴∠A=∠FBA=∠ACE,又∵∠BCA=90°=∠BEF,∴∠CBF=90°﹣∠BFC=90°﹣2∠A,∠CEF=90°﹣∠BEC=90°﹣2∠A,∴∠CEF=∠FBC,∴sin∠CEF=sin∠FBC==,【答案】A.12.(2021•黑龙江)如图,在△ABC中,∠ACB=90°,点D在AB的延长线上,连接CD,若AB=2BD,tan∠BCD=,则的值为( )A.1B.2C.D.【解析】解:过点D作DM⊥BC,交CB的延长线于点M,∵∠ACB=∠DMB=90°,∠ABC=∠DBM,∴△ABC∽△DBM,∴==,∵AB=2BD,∴===,在Rt△CDM中,由于tan∠MCD==,设DM=2k,则CM=3k,又∵==,∴BC=2k,AC=4k,∴==2,【答案】B.13.(2021•宜宾)如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )A.B.2C.D.【解析】解:如图:作OF⊥AB于F,∵AB=AC,AD平分∠BAC.∴∠ODB=90°.BD=CD=6.∴根据勾股定理得:AD==8.∵BE平分∠ABC.∴OF=OD,BF=BD=6,AF=10﹣6=4.设OD=OF=x,则AO=8﹣x,在Rt△AOF中,根据勾股定理得:(8﹣x)2=x2+42.∴x=3.∴OD=3.在Rt△OBD中,tan∠OBD===.法二:在求出AF=4后∵tan∠BAD==.∴=.∴OF=3.∴OD=OF=3.∴tan∠OBD==.【答案】A.14.(2021•广东)如图,AB是⊙O的直径,点C为圆上一点,AC=3,∠ABC的平分线交AC 于点D,CD=1,则⊙O的直径为( )A.B.2C.1D.2【解析】解:如图,过点D作DT⊥AB于T.∵AB是直径,∴∠ACB=90°,∴DC⊥BC,∵DB平分∠CBA,DC⊥BC,DT⊥BA,∴DC=DT=1,∵AC=3,∴AD=AC﹣CD=2,∴AD=2DT,∴∠A=30°,∴AB===2,解法二:AD=2DT由此处开始,可以在Rt△ADT中用勾股定理得AT=,再由垂径定理可得AB=2AT得解.【答案】B.15.(2021•绍兴)如图,Rt△ABC中,∠BAC=90°,cos B=,点D是边BC的中点,以AD 为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连结CE,则的值为( )A.B.C.D.2【解析】解:设DE交AC于T,过点E作EH⊥CD于H.∵∠BAC=90°,BD=DC,∴AD=DB=DC,∴∠B=∠DAB,∵∠B=∠ADE,∴∠DAB=∠ADE,∴AB∥DE,∴∠DTC=∠BAC=90°,∵DT∥AB,BD=DC,∴AT=TC,∴EA=EC=ED,∴∠EDC=∠ECD,∵EH⊥CD,∴CH=DH,∵DE∥AB,∴∠EDC=∠B,∴∠ECD=∠B,∴cos∠ECH=cos B=,∴=,∴==2,【答案】D.五.解直角三角形的应用(共5小题)16.(2021•呼和浩特)如图,正方形的边长为4,剪去四个角后成为一个正八边形,则可求出此正八边形的外接圆直径d,根据我国魏晋时期数学家刘徽的“割圆术”思想,如果用此正八边形的周长近似代替其外接圆周长,便可估计π的值,下面d及π的值都正确的是( )A.d=,π≈8sin22.5°B.d=,π≈4sin22.5°C.d=,π≈8sin22.5°D.d=,π≈4sin22.5°【解析】解:如图,连接AD,BC交于点O,过点O作OP⊥BC于点P,则CP=PD,且∠COP=22.5°,设正八边形的边长为a,则a+2×a=4,解得a=4(﹣1),在Rt△OCP中,OC==,∴d=2OC=,由πd≈8CD,则π≈32(﹣1),∴π≈8sin22.5°.【答案】C.17.(2021•长春)如图是净月潭国家森林公园一段索道的示意图.已知A、B两点间的距离为30米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )A.30sinα米B.米C.30cosα米D.米【解析】解:由图可知,在△ABC中,AC⊥BC,∴sinα==,∴BC=30sinα米.【答案】A.18.(2021•十堰)如图,小明利用一个锐角是30°的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为1.5m(即小明的眼睛与地面的距离),那么旗杆的高度是( )A.(15+)m B.5m C.15m D.(5+)m【解析】解:由题意可得,四边形ABCD是矩形,BC=15m,AB=1.5m,∴BC=AD=15m,AB=CD=1.5m,在Rt△ADE中,∠EAD=30°,AD=15m,∴DE=AD•tan∠EAD=15×=5(m),∴CE=CD+DE=(5+1.5)(m).【答案】D.19.(2021•随州)如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A处,底端落在水平地面的点B处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知sinα=cosβ=,则梯子顶端上升了( )A.1米B.1.5米C.2米D.2.5米【解析】解:如图所示,在Rt△ABC中,AC=sinα×AB==6(米);在Rt△DEC中,DC=cosβ×DE==6(米),EC===8(米);∴AE=EC﹣AC=8﹣6=2(米).【答案】C.20.(2021•温州)图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC=1,∠AOB=α,则OC2的值为( )A.+1B.sin2α+1C.+1D.cos2α+1【解析】解:∵AB=BC=1,在Rt△OAB中,sinα=,∴OB=,在Rt△OBC中,OB2+BC2=OC2,∴OC2=()2+12=.【答案】A.六.解直角三角形的应用-坡度坡角问题(共4小题)21.(2021•德州)某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,已知原楼梯长为5米,调整后的楼梯会加长( )(参考数据:sin37°≈,cos37°≈,tan37°≈).A.6米B.3米C.2米D.1米【解析】解:在Rt△BAD中,AB=5米,∠BAD=37°,则BD=AB•sin∠BAD≈5×=3(米),在Rt△BCD中,∠C=30°,∴BC=2BD=6(米),则调整后的楼梯会加长:6﹣5=1(米),【答案】D.22.(2021•潍坊)如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°,则平面镜的垂线与水平地面的夹角α的度数是( )A.15°B.30°C.45°D.60°【解析】解:如图,作CD⊥平面镜,垂足为G,交地面于D.∵EF⊥平面镜,∴CD∥EF,∴∠CDH=∠EFH=α,根据题意可知:AG∥DF,∴∠AGC=∠CDH=α,∴∠AGC=α,∵∠AGC=AGB=×60°=30°,∴α=30°.【答案】B.23.(2021•衡阳)如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB的倾斜角为37°,大厅两层之间的距离BC为6米,则自动扶梯AB的长约为(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)( )A.7.5米B.8米C.9米D.10米【解析】解:在Rt△ABC中,∠ACB=90°,BC=6米,∵sin∠BAC==sin37°≈0.6=,∴AB≈BC=×6=10(米),【答案】D.24.(2021•金华)如图是一架人字梯,已知AB=AC=2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )A.4cosα米B.4sinα米C.4tanα米D.米【解析】解:过点A作AD⊥BC于点D,∵AB=AC=2米,AD⊥BC,∴BD=DC,∴cosα==,∴DC=2cosα(米),∴BC=2DC=2×2cosα=4cosα(米).【答案】A.七.解直角三角形的应用-仰角俯角问题(共6小题)25.(2021•济南)无人机低空遥感技术已广泛应用于农作物监测.如图,某农业特色品牌示范基地用无人机对一块试验田进行监测作业时,在距地面高度为135m的A处测得试验田右侧边界N处俯角为43°,无人机垂直下降40m至B处,又测得试验田左侧边界M处俯角为35°,则M,N之间的距离为( )(参考数据:tan43°≈0.9,sin43°≈0.7,cos35°≈0.8,tan35°≈0.7,结果保留整数)A.188m B.269m C.286m D.312m【解析】解:由题意得:∠N=43°,∠M=35°,AO=135m,BO=AO﹣AB=95m,在Rt△AON中,tan N==tan43°,∴NO=≈150m,在Rt△BOM中,tan M==tan35°,∴MO=≈135.7m,∴MN=MO+NO=135.7+150≈286m.【答案】C.26.(2021•日照)如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔AB 的高度,他从古塔底部点B处前行30m到达斜坡CE的底部点C处,然后沿斜坡CE前行20m 到达最佳测量点D处,在点D处测得塔顶A的仰角为30°,已知斜坡的斜面坡度i=1:,且点A,B,C,D,E在同一平面内,小明同学测得古塔AB的高度是( )A.(10+20)m B.(10+10)m C.20m D.40m【解析】解:过D作DF⊥BC于F,DH⊥AB于H,∴DH=BF,BH=DF,∵斜坡的斜面坡度i=1:,∴=1:,设DF=xm,CF=xm,∴CD==2x=20m,∴x=10,∴BH=DF=10m,CF=10m,∴DH=BF=(10+30)m,∵∠ADH=30°,∴AH=DH=×(10+30)=(10+10)m,∴AB=AH+BH=(20+10)m,【答案】A.27.(2021•深圳)如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为( )A.15sin32°B.15tan64°C.15sin64°D.15tan32°【解析】解:∵∠CED=64°,∠F=32°,∠CED=∠F+∠EDF,∴∠EDF=∠CED﹣∠F=64°﹣32°=32°,∴∠EDF=∠F,∴DE=EF,∵EF=15米,∴DE=15米,在Rt△CDE中,∵sin∠CED=,∴CD=DE sin∠CED=15sin64°,【答案】C.28.(2021•泰安)如图,为了测量某建筑物BC的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡AD行走130米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为60°,建筑物底端B的俯角为45°,点A、B、C、D、E在同一平面内,斜坡AD的坡度i=1:2.4.根据小颖的测量数据,计算出建筑物BC的高度约为(参考数据:≈1.732)( )A.136.6米B.86.7米C.186.7米D.86.6米【解析】解:如图作DH⊥AB于H,延长DE交BC于F.在Rt△ADH中,AD=130米,DH:AH=1:2.4,∴DH=50(米),∵四边形DHBF是矩形,∴BF=DH=50(米),在Rt△EFB中,∠BEF=45°,∴EF=BF=50(米),在Rt△EFC中,FC=EF•tan60°,∴CF=50×≈86.6(米),∴BC=BF+CF=136.6(米).【答案】A.29.(2021•重庆)如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA和ND.甲在山脚点C处测得通信基站顶端M的仰角为60°,测得点C距离通信基站MA的水平距离CB 为30m;乙在另一座山脚点F处测得点F距离通信基站ND的水平距离FE为50m,测得山坡DF的坡度i=1:1.25.若ND=DE,点C,B,E,F在同一水平线上,则两个通信基站顶端M与顶端N的高度差为(参考数据:≈1.41,≈1.73)( )A.9.0m B.12.8m C.13.1m D.22.7m【解析】解:在Rt△MCB中,∠MCB=60°,CB=30m,tan∠MCB=,∴MB=CB•tan∠MCB=30×≈51.9(m),∵山坡DF的坡度i=1:1.25,EF=50m,∴DE=40(m),∵ND=DE,∴ND=25(m),∴两个通信基站顶端M与顶端N的高度差=40+25﹣51.9=13.1(m),【答案】C.30.(2021•重庆)如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度(或坡比)为i=1:2.4,坡顶D到BC的垂直距离DE=50米(点A,B,C,D,E在同一平面内),在点D处测得建筑物顶点A的仰角为50°,则建筑物AB的高度约为( )(参考数据:sin50°≈0.77;cos50°≈0.64;tan50°≈1.19)A.69.2米B.73.1米C.80.0米D.85.7米【解析】解:∵斜坡CD的坡度(或坡比)为i=1:2.4,∴DE:CE=5:12,∵DE=50米,∴CE=120米,∵BC=150米,∴BE=150﹣120=30(米),∴AB=tan50°×30+50≈85.7(米).【答案】D.。
【人教版】九年级下册数学《锐角三角函数》全章知识点复习及同步习题

c ,则有: s in A = a = cos B , cos A = = sin B , tan A = ,这就是锐角三角函数所以 cos B = sin(90 - B) = sin A = .在 Rt△BCD 中, cos B = ,所以 = ., cos A = , =(sin 2A 、cos 2A 分别表示 sin A 、cos A 2 2锐角三角函数我们知道,在 Rt△ABC 中,∠C =90°,∠A 、∠B 、∠C 的对边分别为 a 、b 、b ac c b的定义.根据锐角三角函数的定义,再结合直角三角形的性质,我们可以探索出锐角三角函数之间的三个特殊关系.一、余角关系由上面的定义我们已得到 sin A =cos B ,cos A =sin B ,而在直角三角形中,∠A+∠B =90°,即∠B =90°-∠A .因此有:sin A =cos (90°-A ),cos A =sin (90°-A ).应用这些关系式,可以很轻松地进行三角函数之间的转换.例1 如图,在 Rt△ABC 中,∠C =90°,CD ⊥AB 于 D ,已知 sin A ==2,求 BC 的长.解:由于∠A +∠B =90°,12BD 2 1BC BC 2所以 BC =4.二、平方关系a b 由定义知 sin A = c c1 2 ,BD所以 sin 2 A + cos 2 A = a 2 b 2 a 2 + b 2+ c c c 2的平方).又由勾股定理,知 a 2+b 2=c 2,所以 sin 2A +cos 2A = c 2 c 2=1.应用此关系式我们可以进行有关锐角三角函数平方的计算.例 2 计算:sin256°+sin245°+sin234°.=⎪⎪ + 1 = 由定义中 sin A = a, cos A = ,得 = c = ⨯ = = tan A .所以原式 = = =- .5 12 5 12所以 sin B = = .应选(B).5解:由余角关系知 sin56°=cos(90°-56°)=cos34°.所以原式=sin245°+(sin234°+cos234°)⎛ 2 ⎫2 ⎝ 2 ⎭3 2 .三、相除关系b c casin A a c a cos A b c b bc利用这个关系式可以使一些化简求值运算过程变得简单.例 3 已知 α 为锐角,tan α =2,求 3sin α + cos α 4cos α - 5sin α的值.解:因为 tan α = sin α cos α= 2 ,所以 sin α =2cos α ,6cos α + cos α 6 + 1 74cos α - 10cos α 4 - 10 6求三角函数值的方法较多,且方法灵活.是中考中常见的题型.我们可以根据已知条件结合图形选用灵活的求解方法.四、设参数法例 4 如图 △1,在 ABC 中,∠C =90°,如果 t a n A =(A)(B) (C) (D)13 13 12 55 12 ,那么 sin B 等于( )分析:本题主要考查锐角三角函数的定义及直角三角形的有关性质.因为 tan A = a 5 =b 12,所以可设 a =5k ,b =12k (k >0),根据勾股定理得 c =13k ,图 1b 12c 13五、等线段代换法例 5如图 2,小明将一张矩形的纸片 ABC D 沿 C E 折叠,B 点恰好落在 A D 边上,设此点为 F ,若 BA :BC =4:,则 c os∠DCF 的值是______.分析:根据折叠的性质可知 E △B C ≌ EF C ,所以 C F=CB ,又 C D=AB ,AB :BC =4:5, 所以 C D :C F=4:5,图 2=.113911,即=,所以C E=,在Rt△A E C中,tan∠CA E==3=.所以tanα=.C3445所以DB==,所以tanα=,选(A).在Rt D△C F中,c os∠D C F=DC4 CF5六、等角代换法例6如图3,C D是平面镜,光线从A点出发经C D上点E反射后照射到B点,若入射角为α(入射角等于反射角),AC⊥C D,B D⊥C D,垂足分别为C、D,且AC=3,B D=6,C D=11,则tanα的值为()B(A)(B)(C)(D)311119A分析:根据已知条件可得∠α=∠CA E,所以只需求出tan∠CA E.α根据条件可知△A C E∽B DE,所以AC CE3CE=BD ED611-CEC E图3D11311CE11AC39119七、等比代换法例7如图4,在Rt△ABC中,ACB=90,D⊥AB于点D,BC=3,AC=4,设BC D=α,tanα的值为()(A)(B)(C)(D)435分析:由三角形函数的定义知tanα=DB DC,由Rt△C D△B∽Rt ACB,BC33DC AC44图4( :锐角三角函数测试1.比较大小:sin41°________sin42°. 2.比较大小:cot30°_________cot22°. 3.比较大小:sin25°___________cos25°. 4.比较大小:tan52°___________cot52°. 5.比较大小:tan48°____________cot41°. 6.比较大小:sin36°____________cos55°.7、下列命题①sin α 表示角α 与符号 sin 的乘积;② 在△ABC 中,若∠C=90°,则 c=α sinA 成立;③任何锐角的正弦和余弦值都是介于 0 和 1 之间实数.其正确的为()A 、②③B.①②③C.②D. ③8、若 △R t ABC 的各边都扩大 4 倍得到 △R t A ′B ′C ′,那么锐角 A 和锐角 A ′正切值的关系为()A.tanA ′=4tanA B.4tanA ′=tanAC.tanA ′=tanAD.不确定.9(新疆中考题) 1)如图(1)、 2),锐角的正弦值和余弦值都随着锐角的确定而确定, 变化而变化.试探索随着锐角度数的增大.它的正弦值和余弦值变化的规律.(2)根据你探索到的规律,试比较 18°,34°,50°,62°,88°,这些锐角的正弦值的 大小和余弦值的大小。
中考数学:锐角三角函数试卷解析

中考数学:锐角三角函数试卷解析一、选择题1.(2021四川巴中,第8题3分)在Rt△ABC中,C=90,sinA=1/2,则t anB的值为()A.1B.3C.1/2D.2考点:锐角三角函数.分析:依照题意作出直角△ABC,然后依照sinA=,设一条直角边BC 为5x,斜边AB为13x,依照勾股定理求出另一条直角边AC的长度,然后依照三角函数的定义可求出tanB.解答:∵sinA=,设BC=5x,AB=13x,则AC==12x,故tanB==.故选D.点评:本题考查了互余两角三角函数的关系,属于基础题,解题的关键是把握三角函数的定义和勾股定理的运用.2.(2021山东威海,第8题3分)如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则AOB的正弦值是()A.1B.1/2C.3/5D.2/3考点:锐角三角函数的定义;三角形的面积;勾股定理分析:作ACOB于点C,利用勾股定理求得AC和AB的长,依照正弦的定义即可求解.解答:解:作ACOB于点C.则AC=AB===2,则sinAOB===.故选D.点评:本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.3.(2021四川凉山州,第10题,4分)在△ABC中,若|cosA﹣|+(1﹣tanB)2=0,则C的度数是()A.45B.60C.75D.105考点:专门角的三角函数值;非负数的性质:绝对值;非负数的性质:偶次方;三角形内角和定理分析:依照非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,依照三角形的内角和定理可得出C的度数.解答:解:由题意,得cosA=,tanB=1,A=60,B=45,C=180﹣A﹣B=180﹣60﹣45=75.故选:C.点评:此题考查了专门角的三角形函数值及绝对值、偶次方的非负性,属于基础题,关键是熟记一些专门角的三角形函数值,也要注意运用三角形的内角和定理.4.(2021甘肃兰州,第5题4分)如图,在Rt△ABC中,C=90,BC=3,A C=4,那么cosA的值等于()A.1/2B.3/5C.2D.1/5考点:锐角三角函数的定义;勾股定理.分析:第一运用勾股定理求出斜边的长度,再利用锐角三角函数的定义求解.解答:解:∵在Rt△ABC中,C=90,AC=4,BC=3,AB=.cosA=,故选:D.点评:本题要紧考查了锐角三角函数的定义:在直角三角形中,锐角的余弦为邻边比斜边.5.(2021广州,第3题3分)如图1,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,则().(A)(B)(C)(D)【考点】正切的定义.【分析】.【答案】D6.(2021浙江金华,第6题4分)如图,点A(t,3)在第一象限,OA与x 轴所夹的锐角为,则t的值是【】A.1B.1.5C.2D.3【答案】C.【解析】7.(2021滨州,第11题3分)在Rt△ACB中,C=90,AB=10,sinA=,c osA=,tanA=,则BC的长为()A.6B.7.5C.8D.12.5考点:解直角三角形分析:依照三角函数的定义来解决,由sinA==,得到BC==.解答:解:∵C=90AB=10,sinA=,BC=AB=10=6.故选A.点评:本题考查了解直角三角形和勾股定理的应用,注意:在Rt△AC B中,C=90,则sinA=,cosA=,tanA=.8.(2021扬州,第7题,3分)如图,已知AOB=60,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=()A.3B.4C.5D.6(第1题图)考点:含30度角的直角三角形;等腰三角形的性质分析:过P作PDOB,交OB于点D,在直角三角形POD中,利用锐角三角函数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN 中点,依照MN求出MD的长,由OD﹣MD即可求出OM的长.解答:解:过P作PDOB,交OB于点D,在Rt△OPD中,cos60==,OP=12,OD=6,∵PM=PN,PDMN,MN=2,MD=ND=MN=1,OM=OD﹣MD=6﹣1=5.故选C.点评:此题考查了含30度直角三角形的性质,等腰三角形的性质,熟练把握直角三角形的性质是解本题的关键.9.(2021四川自贡,第10题4分)如图,在半径为1的⊙O中,AOB=4 5,则sinC的值为()A.1B.1/2C.2D.3考点:圆周角定理;勾股定理;锐角三角函数的定义专题:压轴题.分析:第一过点A作ADOB于点D,由在Rt△AOD中,AOB=45,可求得AD与OD的长,继而可得BD的长,然后由勾股定理求得AB的长,继而可求得sinC的值.解答:解:过点A作ADOB于点D,∵在Rt△AOD中,AOB=45,OD=AD=OAcos45=1=,BD=OB﹣OD=1﹣,AB==,∵AC是⊙O的直径,ABC=90,AC=2,sinC=.故选B.点评:此题考查了圆周角定理、三角函数以及勾股定理.此题难度适中,注意把握辅助线的作法,注意数形结合思想的应用.10.(2021浙江湖州,第6题3分)如图,已知Rt△ABC中,C=90,AC =4,tanA=,则BC的长是()A.2B.8C.2D.4分析:依照锐角三角函数定义得出tanA=,代入求出即可.解:∵tanA==,AC=4,BC=2,故选A.点评:本题考查了锐角三角函数定义的应用,注意:在Rt△ACB中,C=90,sinA=,cosA=,tanA=.11.(2021广西来宾,第17题3分)如图,Rt△ABC中,C=90,B=30,BC=6,则AB的长为4考点:解直角三角形.分析:依照cosB=及专门角的三角函数值解题.解答:解:∵cosB=,即cos30=,AB===4.故答案为:4.点评:本题考查了三角函数的定义及专门角的三角函数值,是基础知识,需要熟练把握.12.(2021年贵州安顺,第9题3分)如图,在Rt△ABC中,C=90,A= 30,E为AB上一点且AE:EB=4:1,EFAC于F,连接FB,则tanCFB的值等于()A.30B.45C.60D.15考点:锐角三角函数的定义..分析:tanCFB的值确实是直角△BCF中,BC与CF的比值,设BC=x,则BC与CF就能够用x表示出来.就能够求解.解答:解:依照题意:在Rt△ABC中,C=90,A=30,∵EFAC,EF∥BC,∵AE:EB=4:1,=5,设AB=2x,则BC=x,AC=x.在Rt△CFB中有CF=x,BC=x.则tanCFB==.故选C.点评:本题考查锐角三角函数的概念:在直角三角形中,正弦等于对比斜;余弦等于邻边比斜边;正切等于对边比邻边.13.(2021年广东汕尾,第7题4分)在Rt△ABC中,C=90,若sinA=,则cosB的值是()A.1B.3C.2D.-1分析:依照互余两角的三角函数关系进行解答.解:∵C=90,B=90,cosB=sinA,∵sinA=,cosB=.故选B.点评:本题考查了互余两角的三角函数关系,熟记关系式是解题的关键.14.(2021毕节地区,第15题3分)如图是以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CDAB交AB于D.已知cosACD=,BC =4,则AC的长为()A.1B.4C.3D.2考点:圆周角定理;解直角三角形分析:由以△ABC的边AB为直径的半圆O,点C恰好在半圆上,过C作CDAB交AB于D.易得ACD=B,又由cosACD=,BC=4,即可求得答案.解答:解:∵AB为直径,ACB=90,ACD+BCD=90,∵CDAB,BCD+B=90,ACD,∵cosACD=,cosB=,tanB=,∵BC=4,tanB===,AC=.故选D.点评:此题考查了圆周角定理以及三角函数的性质.此题难度适中,注意把握数形结合思想的应用.15.(2021年天津市,第2题3分)cos60的值等于()A.1/2B.1C.3D.5点:专门角的三角函数值.分析:依照专门角的三角函数值解题即可.解答:解:cos60=.故选A.点评:本题考查专门角的三角函数值,准确把握专门角的函数值是解题关键.二、填空题1.(2021年贵州黔东南11.(4分))cos60=.考点:专门角的三角函数值.分析:依照专门角的三角函数值运算.解答:解:cos60=.点评:本题考查专门角三角函数值的运算,专门角三角函数值运算在中考中经常显现,要把握专门角度的三角函数值.2.(2021江苏苏州,第15题3分)如图,在△ABC中,AB=AC=5,BC=8.若BPC=BAC,则tanBPC=.考点:锐角三角函数的定义;等腰三角形的性质;勾股定理分析:先过点A作AEBC于点E,求得BAE=BAC,故BPC=BAE.再在Rt△BAE中,由勾股定理得AE的长,利用锐角三角函数的定义,求得tanBPC=tanBAE=.解答:解:过点A作AEBC于点E,∵AB=AC=5,BE=BC=8=4,BAE=BAC,∵BPC=BAC,BPC=BAE.在Rt△BAE中,由勾股定理得AE=,tanBPC=tanBAE=.故答案为:.点评:求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系式求三角函数值.3.(2021四川内江,第23题,6分)如图,AOB=30,OP平分AOB,P COB于点C.若OC=2,则PC的长是.考点:含30度角的直角三角形;勾股定理;矩形的判定与性质.专题:运算题.分析:延长CP,与OA交于点Q,过P作PDOA,利用角平分线定理得到PD=PC,在直角三角形OQC中,利用锐角三角函数定义求出QC的长,在直角三角形QDP中,利用锐角三角函数定义表示出PQ,由QP+PC=QC,求出PC的长即可.解答:解:延长CP,与OA交于点Q,过P作PDOA,∵OP平分AOB,PDOA,PCOB,PD=PC,在Rt△QOC中,AOB=30,OC=2,QC=OCtan30=2=,APD=30,在Rt△QPD中,cos30==,即PQ=DP=PC,QC=PQ+PC,即PC+PC=,解得:PC=.故答案为:点评:此题考查了含30度直角三角形的性质,锐角三角函数定义,熟练把握直角三角形的性质是解本题的关键.4.(2021四川宜宾,第16题,3分)规定:sin(﹣x)=﹣sinx,cos(﹣x)=co sx,sin(x+y)=sinxcosy+cosxsiny.据此判定下列等式成立的是②③④(写出所有正确的序号)①cos(﹣60②sin75③sin2x=2sinx④sin(x﹣y)=sinxcosy﹣cosxsiny.考点:锐角三角函数的定义;专门角的三角函数值.专题:新定义.分析:依照已知中的定义以及专门角的三角函数值即可判定.解答:解:①cos(﹣60)=cos60=,命题错误;②sin75=sin(30+45)=sin30cos45+cos30sin45=+=+=,命题正确;③sin2x=sinxcosx+cosxsinx═2sinxcosx,故命题正确;④sin(x﹣y)=sinxcos(﹣y)+cosxsin(﹣y)=sinxcosy﹣cosxsiny,命题正确.故答案是:②③④.点评:本题考查锐角三角函数以及专门角的三角函数值,正确明白得题目中的定义是关键.5.(2021甘肃白银、临夏,第15题4分)△ABC中,A、B差不多上锐角,若sinA=,cosB=,则C=.考点:专门角的三角函数值;三角形内角和定理.分析:先依照专门角的三角函数值求出A、B的度数,再依照三角形内角和定理求出C即可作出判定.解答:解:∵△ABC中,A、B差不多上锐角sinA=,cosB=,B=60.C=180﹣A﹣B=180﹣60﹣60=60.故答案为:60.点评:本题考查的是专门角的三角函数值及三角形内角和定理,比较简单.6.(2021广西贺州,第18题3分)网格中的每个小正方形的边长差不多上1,△ABC每个顶点都在网格的交点处,则sinA=.考点:锐角三角函数的定义;三角形的面积;勾股定理.分析:依照正弦是角的对边比斜边,可得答案.解答:解:如图,作ADBC于D,CEAB于E,由勾股定理得AB=AC=2,BC=2,AD=3,由BCAD=ABCE,观看内容的选择,我本着先静后动,由近及远的原则,有目的、有打算的先安排与幼儿生活接近的,能明白得的观看内容。
数学中考一轮复习:三角函数-锐角三角函数要点集锦
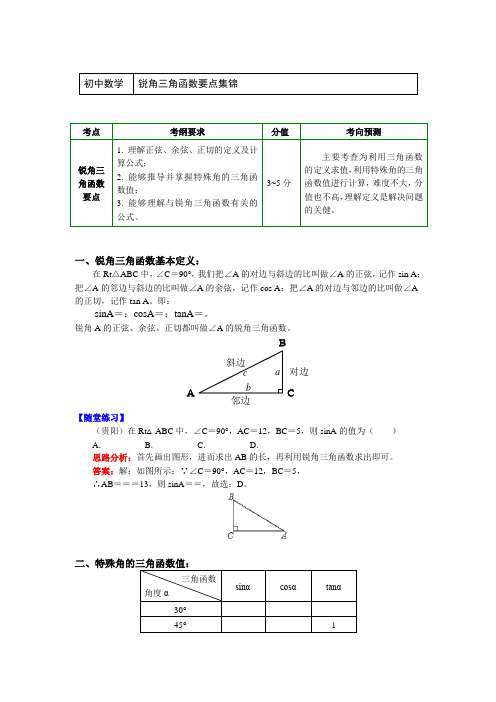
初中数学锐角三角函数要点集锦考点考纲要求分值考向预测锐角三角函数要点1. 理解正弦、余弦、正切的定义及计算公式;2. 能够推导并掌握特殊角的三角函数值;3. 能够理解与锐角三角函数有关的公式。
3~5分主要考查为利用三角函数的定义求值,利用特殊角的三角函数值进行计算,难度不大,分值也不高,理解定义是解决问题的关健。
一、锐角三角函数基本定义:在Rt△ABC中,∠C=90°,我们把∠A的对边与斜边的比叫做∠A的正弦,记作sin A;把∠A的邻边与斜边的比叫做∠A的余弦,记作cos A;把∠A的对边与邻边的比叫做∠A 的正切,记作tan A。
即:sinA=;cosA=;tanA=。
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。
ABCabc对边邻边斜边【随堂练习】(贵阳)在Rt△ABC中,∠C=90°,AC=12,BC=5,则sinA的值为()A. B. C. D.思路分析:首先画出图形,进而求出AB的长,再利用锐角三角函数求出即可。
答案:解:如图所示:∵∠C=90°,AC=12,BC=5,∴AB===13,则sinA==,故选:D。
三角函数角度αsinαcosαtanα30°45° 160°【重要提示】1. 各三角函数值可通过直角三角形性质及勾股定理求出边长从而求出比值;2. 锐角三角函数值的取值范围及增减情况:①∠A的正弦函数、余弦函数的取值范围是:0<sinA<1,0<cosA<1,即任意锐角的正弦、余弦值都大于0而小于1;而正切是两直角边的比,所以∠A的正切函数取值范围是:tanA>0,即任意锐角的正切值都大于0。
②当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小),余弦值随着角度的增大(或减小)而减小(或增大);正切值随着角度的增大(或减小)而增大(或减小)。
三、同角、互余两角的锐角三角函数值的关系:1. 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值;即:。
中考复习-锐角三角函数和解直角三角形

探究提高 在解斜三角形时,通常把斜三角形转化 为直角三角形,常见的方法是作高,作高 把斜三角形转化为直角三角形,再利用解 直角三角形的有关知识解决问题.
知能迁移3 一次数学活动课上,老师带领学生去 测一条南北流向的河宽,如图所示,某学生在 河东岸点A处观测到河对岸水边有一点C,测得 C在A北偏西31°的方向上,沿河岸向北前行 40m到达B处,测得C在B北偏西45°的方向上, 请你根据以上数据,求这条河的宽度.(参考 3 数值:tan 31°≈ ) 5
;
(2)角与角的关系:
(3)边与角的关系:
1 2 sinA=cosB=a ,cosA=sinB= b ; c c
;
tanA=b ,tanB= a
a
b
1.正确理解三角函数的概念 书写三角函数时,若锐角用一个大写字母 或者一个小写希腊字母表示的,表示它的正 弦时,习惯省略角的符号,如sin A;若锐角 是用三个大写字母或数字表示的,表示它的 正弦时,不能省略角的符号,如sin∠ABC, 余弦和正切的写法同理.由定义可以看出, 锐角A的正弦、余弦、正切都是它所在直角三 角形的两边的比,因此都是正数;因为锐角A 的取值范围是0<∠A<90°,则三角函数的取 值范围是0<sin A<1,0<cos A<1,tan A>0; 当∠A确定时,三个比值也分别有唯一确定的 值与之对应.
探究提高 此类问题常与仰角、俯角等知识相关,通 常由视线、水平线、铅垂线构成直角三角形, 再利用边与角之间存在的三角函数式,变形 求得物体高度.
知能迁移2 (2011· 潜江)五月石榴红,枝头 鸟儿歌.一只小鸟从石榴树上的A处沿直线 飞到对面一房屋的顶部C处.从A处看房屋 3 顶部C处的仰角为30°,看房屋底部D处的 俯角为45°,石榴树与该房屋之间的水平距 离为3 m,求出小鸟飞行的距离AC和房 屋的高度CD.
中考数学 锐角三角函数的实际应用

必考加练2 锐角三角函数的应用
5.(12 分)邓州市土城墙建于明代,它是穰邓生命的记录,历史的 见证,在这绵延起伏的土城墙里,蕴涵着深厚的古邓文化,目前花洲书 院东南角的一段土城墙保护的较为完整(如图1),邓州市某中学数学兴趣 小组在护城河东岸C处和D处分别测量了城墙顶端A的仰角及CD的长度 (如图2).
必考加练2 锐角三角函数的应用
∴BC=tanx37°≈0.7x54(m). ∵BC-BD=DC, ∴0.7x54-x=3,解得 x≈9.2. 答:土城墙 AB 的高度约为 9.2 m.
必考加练2 锐角三角函数的应用
6.(12 分)(2021 盐城)某种落地灯如图1所
示,AB为立杆,其高为84 cm;BC为支杆,它
必考加练2 锐角三角函数的应用
解:如答图 1,延长 BC 交 MN 于点 H,则 AD=BE=3.5 米.
设 MH=x 米.
∵∠MEC=45°,
∴EH=MH=x 米.
在 Rt△MHB 中,∠MBH=33°,
tan∠MBH=HEM+HEB=x+x3.5≈0.65.解得
答图 x=6.5.
1
∵HN=BA=1.6 米,∴MN=MH+HN=6.5+1.6=8.1≈8(米).
必考加练2 锐角三角函数的应用
在 Rt△BOC 中,∠BCO=45°, ∴OB=OC=OD-CD=(2 000 3-460)米. ∴AB=OB-OA=2 000 3-460-2 000≈1 004(米). ∴火箭的平均速度为 1 004÷3≈335(米/秒). 答:火箭从 A 到 B 处的平均速度约为 335 米/秒.
必考加练2 锐角三角函数的应用
3.(10分)(2021 泰州)如图,游客从旅游景区山脚下的地面A处出 发,沿坡角α=30°的斜坡AB步行50 m至山坡B处,乘直立电梯上升 30 m至C处,再乘缆车沿长为180 m的索道CD至山顶D处,此时观测C处 的俯角为19°30′,索道CD看作在一条直线上.求山顶D的高度.(精 确 到 1 m . 参 考 数 据 : sin 19°30′≈0.33 , cos 19°30′≈0.94 , tan 19°30′≈0.35)
九年级人教版数学第二学期第28章锐角三角函数整章知识详解

九年级数学第28章锐角三角函数
【例】求下列各式的值.
(1) cos260°+sin260°
(2) csoins4455
-tan45
【解析】(1)cos²60°+sin²60°
cos²60°表示 (cos60°)², 即cos60°的平方.
=( 12)²+(
3 2
)²
=1;
(2)cos 45 tan 45
九年级数学第28章锐角三角函数
2.(黄冈中考)在△ABC中,∠C=90°,sinA=
则tanB=( B )
A. 4
B. 3
C. 3
D. 4
3
4
5
5
3.(丹东中考)如图,小颖利用有一
个锐角是30°的三角板测量一棵树的高度, 30 已知她与树之间的水平距离BE为5m,AB为 °A
B 1.5m(即小颖的眼睛距地面的距离),那
九年级数学第28章锐角三角函数
【例】如图,在Rt△ABC中,∠C=90°,BC=6,sinA= 3 ,
求cosA,tanB的值.
5
B
【解析】 sinA BC ,
AB
6
AB BC 6 5 10,
sinA 3
又 AC AB2 BC2 102 62 8,
A
C
cosA AC 4 , tanB AC 4 .
100
D.不能确定
3.如图 A
B
1
3
,则 sinA=___2___ .
30°
C
7
九年级数学第28章锐角三角函数
1.(温州中考)如图,在△ABC中,∠C=90°, AB=13,
2021年九年级中考数学 一轮复习:锐角三角函数及其应用(含答案)

2021中考数学一轮复习:锐角三角函数及其应用一、选择题1. (2020·扬州)如图,由边长为1的小正方形构成的网格中,点A、B、C都在格点上,以AB为直径的圆经过点C、D.则sin∠ADC的值为()A.21313B.31313C.23D.322. 如图,点A,B,C在正方形网格的格点上,则sin∠BAC=()A.62 B.2626 C.1326 D.13133. (2019•江苏苏州)如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为183m的地面上,若测角仪的高度为1.5m,测得教学楼的顶部A处的仰角为30,则教学楼的高度是30°CDA.55.5m B.54m C.19.5m D.18m4. 如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中∠QMB的正切值是()A.12B. 1C. 3D. 25. (2019•湖南长沙•3分)如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60nmile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是A.303nmile B.60nmileC.120nmile D.(30+303)nmile6. (2019·浙江杭州)如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于A.asinx+bsinx B.acosx+bcosxC.asinx+bcosx D.acosx+bsinx7. (2020•湘西州)如图,在平面直角坐标系xOy中,矩形ABCD的顶点A在x轴的正半轴上,矩形的另一个顶点D在y轴的正半轴上,矩形的边AB=a,BC=b,∠DAO=x,则点C到x轴的距离等于()A.a cos x+b sin x B.a cos x+b cos x C.a sin x+b cos x D.a sin x+b sin x8. 如图,以O 为圆心,半径为1的弧交坐标轴于A ,B 两点,P 是AB ︵上一点(不与A ,B 重合),连接OP ,设∠POB =α,则点P 的坐标是( ) A . (sin α,sin α) B . (cos α,cos α) C . (cos α,sin α) D . (sin α,cos α)二、填空题9. 长为4 m 的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了________m .10. (2019•湖北荆门)计算23++|sin30°﹣π0|+3278-=__________.11. 齐河路路通电动车厂新开发的一种电动车如图,它的大灯A 射出的边缘光线AB ,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A 与地面的距离为1 m ,则该车大灯照亮的宽度BC 是________m .(不考虑其他因素,参考数据:sin 8°=425,tan 8°=17,sin 10°=910,tan 10°=528)12. (2019•湖北随州)计算:(π–2019)0–2cos60°=__________.13. 如图,一艘渔船位于灯塔P 的北偏东30°方向,距离灯塔18海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东55°方向上的B 处,此时渔船与灯塔P 的距离约为________海里.(结果取整数.参考数据:sin 55°≈0.8,cos 55°≈0.6,tan 55°≈1.4)14. 如图,在一次数学课外实践活动中,小聪在距离旗杆10 m 的A 处测得旗杆顶端B 的仰角为60°,测角仪高AD 为1 m ,则旗杆高BC 为__________m .(结果保留根号)15. 【题目】(2020·哈尔滨)在△ABC 中,∠ABC =60°,AD 为BC 边上的高,AD=36,CD =1,则BC 的长为 . 16. (2020·苏州)如图,已知MON ∠是一个锐角,以点O 为圆心,任意长为半径画弧,分别交OM 、ON 于点A 、B ,再分别以点A 、B 为圆心,大于12AB 长为半径画弧,两弧交于点C ,画射线OC .过点A 作AD ON ,交射线OC 于点D ,过点D 作DE OC ⊥,交ON 于点E .设10OA =,12DE =,则sin MON ∠=________.三、解答题17. 若河岸的两边平行,河宽为900米,一只船由河岸的A 处沿直线方向开往对岸的B 处,AB 与河岸的夹角是60°,船的速度为5米/秒,求船从A 处到B 处约需时间几分.(参考数据:3≈1.7)18. 如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC 于点E,GF⊥BC于点F,连接AG.(1)写出线段AG,GE,GF长度之间的等量关系,并说明理由;(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.19. 如图,在△ABC中,AB=AC,以AB为直径的☉O分别交AC,BC于点D,E,点F在AC的延长线上,且∠BAC=2∠CBF.(1)求证:BF是☉O的切线;(2)若☉O的直径为3,sin∠CBF=,求BC和BF的长.20. (2019·本溪)小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆DE,箱长BC,拉杆AB的长度都相等,B,F在AC上,C在DE 上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°,请根据以上信息,解决下列问题.(1)求AC的长度(结果保留根号);(2)求拉杆端点A到水平滑杆ED的距离(结果保留根号).21. 如图1,图2,在△ABC 中,AB =13,BC =14,5cos 13ABC ∠=.探究 如图1,AH ⊥BC 于点H ,则AH =_____,AC =______,△ABC 的面积S △ABC =________.拓展 如图2,点D 在AC 上(可与点A 、C 重合),分别过点A 、C 作直线BD 的垂线,垂足为E 、F .设BD =x ,AE =m ,CF =n .(当点D 与点A 重合时,我们认为S △ABD =0)(1)用含x ,m 或n 的代数式表示S △ABD 及S △CBD ;(2)求(m +n )与x 的函数关系式,并求(m +n )的最大值和最小值;(3)对给定的一个x 值,有时只能确定唯一的点D ,指出这样的x 的取值范围. 发现 请你确定一条直线,使得A 、B 、C 三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.图1 图22021中考数学 一轮复习:锐角三角函数及其应用-答案一、选择题1. 【答案】B【解析】本题考查了锐角三角函数的定义和圆周角的知识,解答本题的关键是利用圆周角定理把求∠ADC 的正弦值转化成求∠ABC 的正弦值.连接AC 、BC ,∵∠ADC 和∠ABC 所对的弧长都是AC ,∴根据圆周角定理知,∠ADC =∠ABC ,∴在Rt △ACB 中,根据锐角三角函数的定义知,sin ∠ABCACBC=,∵AC =2,CB=3,∴AB 13=,∴sin ∠ABC 33131313==,∴∠ADC 的正弦值等于31313,因此本题选B .2. 【答案】B【解析】过点B 作BD ⊥AC 于D 点D , 则∠ADB=90°,设小正方形方格的边长为1,根据勾股定理得AB=222313+=,BD=122,∴在Rt △ABD 中,sin ∠BAC=22622613BD AB ==,故选B .3. 【答案】C【解析】过D 作DE AB ⊥交AB 于E ,183DE BC ==在Rt ADE △中,tan30AEDE=, 318318(m)AE ∴==,18 1.519.5(m)AB ∴=+=,故选C .30°CDABE4. 【答案】D【解析】如解图,将AB平移到PE位置,连接QE, 则PQ=210,PE=22,QE=42,∵△PEQ中,PE2+QE2=PQ2,则∠PEQ=90°,∴tan∠QMB=tan∠P=QEPE=2.5. 【答案】D【解析】过C作CD⊥AB于D点,∴∠ACD=30°,∠BCD=45°,AC=60.在Rt△ACD中,cos∠ACD=CDAC,∴CD=AC•cos∠ACD=60×3=303.在Rt△DCB中,∵∠BCD=∠B=45°,∴CD=BD=303,∴AB=AD+BD=30+303.所以此时轮船所在的B处与灯塔P的距离是(30+303)nmile.故选D.6. 【答案】D【解析】如图,过点A作AE⊥OC于点E,作AF⊥OB于点F,∵四边形ABCD 是矩形,∴∠ABC=90°,∵∠ABC=∠AEC,∠BCO=x,∴∠EAB=x,∴∠FBA=x,∵AB=a,AD=b,∴FO=FB+BO=a•cosx+b•sinx,故选D.7. 【答案】A【解析】本题考查了矩形的性质、坐标与图形性质、三角函数定义等知识;熟练掌握矩形的性质和三角函数定义是解题的关键.作CE⊥y轴于E,如图:∵四边形ABCD是矩形,∴CD=AB=a,AD=BC=b,∠ADC=90°,∴∠CDE+∠ADO =90°,∵∠AOD=90°,∴∠DAO+∠ADO=90°,∴∠CDE=∠DAO=x,∵sin∠DAOODAD=,cos∠CDEDECD=,∴OD=AD×sin∠DAO=b sin x,DE=D×cos∠CDE=a cos x,∴OE=DE+OD=a cos x+b sin x,∴点C到x轴的距离等于a cos x+b sin x;因此本题选A.8. 【答案】C【解析】如解图,过点P作PC⊥OB于点C,则在Rt△OPC中,OC=OP·cos∠POB=1×cosα=cosα,PC=OP·sin∠POB=1×sinα=sinα,即点P的坐标为(cosα,sinα).二、填空题9. 【答案】2(3-2)【解析】开始时梯子顶端离地面距离为4×sin45°=4×2 2=22,移动后梯子顶端离地面距离为4×sin60°=4×32=23,故梯子顶端沿墙面升高了23-22=2(3-2)m .10. 【答案】1﹣3【解析】原式=2﹣3+1﹣12﹣32=1﹣3.故答案为:1﹣3.11. 【答案】1.4【解析】如解图,作AD ⊥MN 于点D ,由题意得,AD =1 m ,∠ABD =8°,∠ACD =10°,∠ADC =∠ADB =90°,∴BD =AD tan 8°=117=7 m ,CD =AD tan 10°=1528=285=5.6 m ,∴BC =BD -CD =7-5.6=1.4 m .12. 【答案】0【解析】原式=1–2×=1–1=0,故答案为:0.13. 【答案】11【解析】∵∠A =30°,∴PM =12PA =9海里.∵∠B =55°, sin B=PM PB ,∴0.8=9PB ,∴PB ≈11海里.14. 【答案】103+1 【解析】如解图,过点A 作AE ⊥BC ,垂足为点E ,则AE=CD =10 m ,在Rt △AEB 中,BE =AE·tan 60°=10×3=10 3 m ,∴BC =BE +EC =BE +AD =(103+1)m .15. 【答案】5或7【解析】本题考查了特殊三角函数,三角形的高,因为钝锐三角形的高的不同,此题有两种情况,①点D 在BC 延长线上,在△ABD 中 tan ∠ABD =BD AD ,∴3=BD36解得6=BD ,∴BC =BD - CD =6-1=5;②点D 在BC 上,在△ABD 中 tan ∠ABD =BD AD ,∴3=BD36解得6=BD ,∴BC =BD + CD =6+1=7,因此本题答案为5或7.D D A B B AC C16. 【答案】【答案】2425三、解答题17. 【答案】解:如解图,过点B 作BC 垂直于河岸,垂足为C ,则在R t △ACB 中,有AB =BC sin ∠BAC =900sin60°=600 3. 因而时间t =60035×60=23≈3.4(分) 即船从A 处到B 处约需3.4分.解图18. 【答案】【思维教练】求三条线段之间的关系,一般是线段的和差关系或线段平方的和差关系.由ABCD 是正方形,BD 是角平分线,可想到连接CG ,易得CG =AG ,再由四边形CEGF 是矩形可得AG 2=GE 2+GF 2;(2)给出∠AGF =105°,可得出∠AGB =60°,再由∠ABG =45°,可想到过点A 作BG 的垂线,交BG 于点M ,分别在两个直角三角形中得出BM 和MG 的长,相加即可得出BG 的长.解:(1)AG 2=GE 2+GF 2;(1分)理由:连结CG ,∵ABCD 是正方形,∴∠ADG=∠CDG=45°,AD=CD,DG=DG,∴△ADG≌△CDG,(2分)∴AG=CG,又∵GE⊥DC,GF⊥BC,∠GFC=90°,∴四边形CEGF是矩形,(3分)∴CF=GE,在直角△GFC中,由勾股定理得,CG2=GF2+CF2,∴AG2=GE2+GF2;(4分)(2)过点A作AM⊥BD于点M,∵GF⊥BC,∠ABG=∠GBC=45°,∴∠BAM=∠BGF=45°,∴△ABM,△BGF都是等腰直角三角形,(6分)∵AB=1,∴AM=BM=2 2,∵∠AGF=105°,∴∠AGM=60°,∴tan60°=AMGM,∴GM=66,(8分)∴BG=BM+GM=22+66=32+66.(10分)19. 【答案】解:(1)证明:连接AE,∵AB为直径,∴∠AEB=90°,∴AE⊥BC.∵AB=AC,∴BE=EC,∠BAE=∠CAE.∵∠BAC=2∠CBF,∴∠BAE=∠CBF.∵∠BAE+∠ABE=90°,∴∠CBF+∠ABE=90°,∴AB⊥BF,∴BF是☉O的切线.(2)由(1)得∠BAE=∠CBF,∴sin∠CBF=sin∠BAE=,∵∠AEB=90°,AB=3,∴BE=AB sin∠BAE=,∴BC=2BE=2.过点C作CH⊥BF于H点,在Rt△CBH中,CH=BC sin∠CBF=2,BH=2,∵CH⊥BF,AB⊥BF,∴AB∥CH,∴△FCH∽△F AB,∴=,∴=,∴BF=6.20. 【答案】(1)如图,过F作FH⊥DE于H,∴∠FHC=∠FHD=90°,∵∠FDC=30°,DF=30,∴FH=12DF=15,DH=323∵∠FCH=45°,∴CH=FH=15,∴3,∵CE:CD=1:3,∴DE=433∵AB=BC=DE,∴3;(2)过A作AG⊥ED交ED的延长线于G,∵∠ACG=45°,∴AG=2226,答:拉杆端点A 到水平滑杆ED 的距离为(20)cm .21. 【答案】探究 AH =12,AC =15,S △ABC =84.拓展 (1)S △ABD =12mx ,S △CBD =12nx . (2)由S △ABC =S △ABD +S △CBD ,得118422mx nx +=.所以168m n x +=. 由于AC 边上的高565BG =,所以x 的取值范围是565≤x ≤14. 所以(m +n )的最大值为15,最小值为12.(3)x 的取值范围是x =565或13<x ≤14. 发现 A 、B 、C 三点到直线AC 的距离之和最小,最小值为565.。
2021年中考数学真题 锐角三角函数(共65题)-(原卷版)

23锐角三角函数(共65题)一、单选题1.(2021·湖南中考真题)下列计算正确的是( )A .0(3)1π-= B .1tan 302=︒ C 2=± D .236a a a ⋅=2.(2021·福建中考真题)如图,某研究性学习小组为测量学校A 与河对岸工厂B 之间的距离,在学校附近选一点C ,利用测量仪器测得60,90,2km A C AC ∠=︒∠=︒=.据此,可求得学校与工厂之间的距离AB 等于( )A .2km B .3km C . D .4km3.(2021·浙江金华市·中考真题)如图是一架人字梯,已知2AB AC ==米,AC 与地面BC 的夹角为α,则两梯脚之间的距离BC 为( )A .4cos α米B .4sin α米C .4tan α米D .4cos α米 4.(2021·湖北随州市·中考真题)如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点A 处,底端落在水平地面的点B 处,现将梯子底端向墙面靠近,使梯子与地面所成角为β,已知3sin cos 5αβ==,则梯子顶端上升了( )A .1米B .1.5米C .2米D .2.5米5.(2021·湖南衡阳市·中考真题)如图是某商场营业大厅自动扶梯的示意图.自动扶梯AB 的倾斜角为37︒,大厅两层之间的距离BC 为6米,则自动扶梯AB 的长约为(sin370.6,cos370.8,tan370.75︒≈︒≈︒≈)( ).A .7.5米B .8米C .9米D .10米6.(2021·天津中考真题)tan 30︒的值等于( )A B C .1 D .27.(2021·湖南株洲市·中考真题)某限高曲臂道路闸口如图所示,AB 垂直地面1l 于点A ,BE 与水平线2l 的夹角为()090αα︒≤≤︒,12////EF l l ,若 1.4AB =米,2BE =米,车辆的高度为h (单位:米),不考虑闸口与车辆的宽度.①当90α=︒时,h 小于3.3米的车辆均可以通过该闸口;①当45α=︒时,h 等于2.9米的车辆不可以通过该闸口;①当60α=︒时,h 等于3.1米的车辆不可以通过该闸口.则上述说法正确的个数为( )A .0个B .1个C .2个D .3个8.(2021·重庆中考真题)如图,在建筑物AB 左侧距楼底B 点水平距离150米的C 处有一山坡,斜坡CD 的坡度(或坡比)为1:2.4i =,坡顶D 到BC 的垂直距离50DE =米(点A ,B ,C ,D ,E 在同一平面内),在点D 处测得建筑物顶A 点的仰角为50°,则建筑物AB 的高度约为(参考数据:sin 500.77︒≈;cos500.64︒≈;tan 50 1.19︒≈)A .69.2米B .73.1米C .80.0米D .85.7米9.(2021·浙江中考真题)如图,已知在矩形ABCD 中,1,AB BC ==,点P 是AD 边上的一个动点,连结BP ,点C 关于直线BP 的对称点为1C ,当点P 运动时,点1C 也随之运动.若点P 从点A 运动到点D ,则线段1CC 扫过的区域的面积是( )A .πB .4π+C .2D .2π10.(2021·浙江丽水市·中考真题)如图,AB 是O 的直径,弦CD OA ⊥于点E ,连结,OC OD .若O 的半径为,m AOD α∠=∠,则下列结论一定成立的是( )A .tan OE m α=⋅B .2sin CD m α=⋅C .cos AE m α=⋅D .2sin COD S m α=⋅11.(2021·浙江宁波市·中考真题)如图,在ABC 中,45,60,B C AD BC ∠=︒∠=︒⊥于点D ,BD =.若E ,F 分别为AB ,BC 的中点,则EF 的长为( )A B C .1 D 12.(2021·云南中考真题)在ABC 中,90ABC ∠=︒,若s n 3100,5i A A C ==,则AB 的长是( )A .5003B .5035C .60D .8013.(2021·山东泰安市·中考真题)如图,为了测量某建筑物BC 的高度,小颖采用了如下的方法:先从与建筑物底端B 在同一水平线上的A 点出发,沿斜坡AD 行走130米至坡顶D 处,再从D 处沿水平方向继续前行若干米后至点E 处,在E点测得该建筑物顶端C 的仰角为60°,建筑物底端B 的俯角为45°,点A 、B 、C 、D 、E 在同一平面内,斜坡AD 的坡度1:2.4i =.根据小颖的测量数据,计算出建筑物BC 的高度约为( ) 1.732≈)A .136.6米B .86.7米C .186.7米D .86.6米14.(2021·江苏连云港市·中考真题)如图,ABC 中,BD AB ⊥,BD 、AC 相交于点D ,47AD AC =,2AB =,150ABC ∠=︒,则DBC △的面积是( )A .14B .14C .7D .715.(2021·浙江绍兴市·中考真题)如图,Rt ABC 中,90BAC ∠=︒,1cos 4B =,点D 是边BC 的中点,以AD 为底边在其右侧作等腰三角形ADE ,使ADE B ∠=∠,连结CE ,则CE AD的值为( )A .32 B C D .216.(2021·重庆中考真题)如图,相邻两个山坡上,分别有垂直于水平面的通信基站MA 和N D .甲在山脚点C 处测得通信基站顶端M 的仰角为60°,测得点C 距离通信基站MA 的水平距离CB 为30m ;乙在另一座山脚点F 处测得点F 距离通信基站ND 的水平距离FE 为50m ,测得山坡DF 的坡度i =1:1.25.若58ND DE =,点C ,B ,E ,F 在同一水平线上,则两个通信基站顶端M 与顶端N 的高度差为( ) 1.41 1.73≈≈)A .9.0mB .12.8mC .13.1mD .22.7m17.(2021·四川南充市·中考真题)如图,在矩形ABCD 中,15AB =,20BC =,把边AB 沿对角线BD 平移,点'A ,'B 分别对应点A ,B .给出下列结论:①顺次连接点'A ,'B ,C ,D 的图形是平行四边形;①点C 到它关于直线'AA 的对称点的距离为48;①''A C B C -的最大值为15;①''A C B C +的最小值为确结论的个数是( )A .1个B .2个C .3个D .4个18.(2021·浙江温州市·中考真题)图1是第七届国际数学教育大会(ICME )的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若1AB BC ==.AOB α∠=,则2OC 的值为( )A .211sin α+B .2sin 1α+C .211cos α+D .2cos 1α+19.(2021·四川南充市·中考真题)如图,在菱形ABCD 中,60A ∠=︒,点E ,F分別在边AB ,BC 上,2AE BF ==,DEF 的周长为,则AD 的长为( )AB .C 1D .120.(2021·湖北荆州市·中考真题)如图,在菱形ABCD 中,60D ∠=︒,2AB =,以B 为圆心、BC 长为半径画AC ,点P 为菱形内一点,连接PA ,PB ,PC .当BPC △为等腰直角三角形时,图中阴影部分的面积为( )A .2132π- B .2132π- C .2π D .122π- 21.(2021·吉林长春市·中考真题)如图是净月潭国家森林公园一段索道的示意图.已知A 、B 两点间的距离为30米,A α∠=,则缆车从A 点到达B 点,上升的高度(BC 的长)为( )A .30sin α米B .30sin α米C .30cos α米D .30cos α米 22.(2021·湖北黄冈市·中考真题)如图,AC 为矩形ABCD 的对角线,已知3AD =,4CD =.点P 沿折线C A D --以每秒1个单位长度的速度运动(运动到D 点停止),过点P 作PE BC ⊥于点E ,则CPE △的面积y 与点P 运动的路程x 间的函数图象大致是( )A .B .C .D .23.(2021·四川达州市·中考真题)在平面直角坐标系中,等边AOB ∆如图放置,点A 的坐标为()1,0,每一次将AOB ∆绕着点О逆时针方向旋转60︒,同时每边扩大为原来的2倍,第一次旋转后得到11AOB ∆,第二次旋转后得到22AOB ∆,…,依次类推,则点2021A 的坐标为( )A .()202020202,2-B .()202120212,2C .()202020202,2D .()201120212,2-24.(2021·湖北十堰市·中考真题)如图,小明利用一个锐角是30的三角板测量操场旗杆的高度,已知他与旗杆之间的水平距离BC 为15m ,AB 为1.5m (即小明的眼睛与地面的距离),那么旗杆的高度是( )A .3m2⎛⎫+ ⎪⎝⎭ B . C . D .3m 2⎛⎫ ⎪⎝⎭ 25.(2021·浙江台州市·中考真题)如图,将长、宽分别为12cm ,3cm 的长方形纸片分别沿AB ,AC 折叠,点M ,N 恰好重合于点P .若①α=60°,则折叠后的图案(阴影部分)面积为( )A .(36-)cm 2 B .(36-cm 2 C .24 cm 2D .36 cm 2 26.(2021·湖南怀化市·中考真题)如图,菱形ABCD 的四个顶点均在坐标轴上,对角线AC 、BD 交于原点O ,AE BC ⊥于E 点,交BD 于M 点,反比例函数0)y x =>的图象经过线段DC 的中点N ,若4BD =,则ME 的长为( )A .53ME = B .43=ME C .1ME = D .23ME = 27.(2021·湖北十堰市·中考真题)如图,ABC 内接于,120,,O BAC AB AC BD ∠=︒=是O 的直径,若3AD =,则BC =( )A.B .C .3D .4二、填空题 28.(2021·江苏无锡市·中考真题)一条上山直道的坡度为1:7,沿这条直道上山,则前进100米所上升的高度为________米.29.(2021·广东中考真题)如图,在ABCD 中,45,12,sin 5AD AB A ===.过点D 作DE AB ⊥,垂足为E ,则sin BCE ∠=______.30.(2021·安徽中考真题)如图,圆O 的半径为1,ABC 内接于圆O .若60A ∠=︒,75B ∠=︒,则AB =______.31.(2021·海南中考真题)如图,ABC 的顶点B C 、的坐标分别是(1,0)、,且90,30ABC A ∠=︒∠=︒,则顶点A 的坐标是_____.32.(2021·甘肃武威市·中考真题)如图,在矩形ABCD 中,E 是BC 边上一点,90,30,AED EAD F ∠=︒∠=︒是AD 边的中点,4cm EF =,则BE =________cm .33.(2021·四川广元市·中考真题)如图,在44⨯的正方形网格图中,已知点A 、B 、C 、D 、O 均在格点上,其中A 、B 、D 又在O 上,点E 是线段CD 与O 的交点.则BAE ∠的正切值为________.34.(2021·湖南中考真题)如图,在ABC 中,5AB =,4AC =,4sin 5A =,BD AC⊥交AC 于点D .点P 为线段BD 上的动点,则35PC PB +的最小值为________.35.(2021·湖北武汉市·中考真题)如图,海中有一个小岛A ,一艘轮船由西向东航行,在B 点测得小岛A 在北偏东60︒方向上;航行12n mile 到达C 点,这时测得小岛A 在北偏东30方向上.小岛A 到航线BC 的距离是__________n mile 1.73≈,结果用四舍五入法精确到0.1).36.(2021·四川乐山市·中考真题)如图,为了测量“四川大渡河峡谷”石碑的高度,佳佳在点C 处测得石碑顶A 点的仰角为30,她朝石碑前行5米到达点D 处,又测得石顶A 点的仰角为60︒,那么石碑的高度AB 的长=________米.(结果保留根号)37.(2021·四川乐山市·中考真题)如图,已知点(4,3)A ,点B 为直线2y =-上的一动点,点()0,C n ,23n -<<,AC BC ⊥于点C ,连接AB .若直线AB 与x 正半轴所夹的锐角为α,那么当sin α的值最大时,n 的值为________.38.(2021·浙江衢州市·中考真题)图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面CE 与地面平行,支撑杆AD ,BC 可绕连接点O 转动,且OA OB =,椅面底部有一根可以绕点H 转动的连杆HD ,点H 是CD 的中点,F A ,EB 均与地面垂直,测得54cm FA =,45cm EB =,48cm AB =.(1)椅面CE 的长度为_________cm .(2)如图3,椅子折叠时,连杆HD 绕着支点H 带动支撑杆AD ,BC 转动合拢,椅面和连杆夹角CHD ∠的度数达到最小值30时,A ,B 两点间的距离为________cm (结果精确到0.1cm ).(参考数据:sin150.26︒≈,cos150.97︒≈,tan150.27︒≈)39.(2021·浙江中考真题)如图,已知在Rt ABC 中,90,1,2ACB AC AB ∠=︒==,则sin B 的值是______.40.(2021·浙江宁波市·中考真题)如图,在矩形ABCD 中,点E 在边AB 上,BEC△与FEC 关于直线EC 对称,点B 的对称点F 在边AD 上,G 为CD 中点,连结BG 分别与,CE CF 交于M ,N 两点,若BM BE =,1MG =,则BN 的长为________,sin AFE ∠的值为__________.41.(2021·四川乐山市·中考真题)在Rt ABC 中,90C ∠=︒.有一个锐角为60︒,4AB =.若点P 在直线AB 上(不与点A 、B 重合),且30PCB ∠=︒,则CP 的长为________.42.(2021·湖北荆州市·中考真题)如图1是一台手机支架,图2是其侧面示意图,AB ,BC 可分别绕点A ,B 转动,测量知8cm BC =,16cm AB =.当AB ,BC 转动到60=︒∠BAE ,50ABC ∠=︒时,点C 到AE 的距离为_____________cm .(结果保留小数点后一位,参考数据:sin 700.94︒≈ 1.73≈)43.(2021·山西中考真题)太原地铁2号线是山西省第一条开通运营的地铁线路,于2020年12月26日开通.如图是该地铁某站扶梯的示意图,扶梯AB 的坡度5:12i =(i 为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端A 以0.5米/秒的速度用时40秒到达扶梯顶端B,则王老师上升的铅直高度BC为__________米.44.(2021·湖北宜昌市·中考真题)“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为2厘米的等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”,该“莱洛三角形”的面积为____________平方厘米.(圆周率用π表示)45.(2021·湖北黄冈市·中考真题)如图,建筑物BC上有一高为8m的旗杆AB,从D处观测旗杆顶部A的仰角为53︒,观测旗杆底部B的仰角为45︒,则建筑物BC 的高约为_____m(结果保留小数点后一位).(参考数据sin530.80︒≈,︒≈,cos530.60 tan53 1.33︒≈)46.(2021·四川眉山市·中考真题)如图,在菱形ABCD 中,10AB AC ==,对角线AC 、BD 相交于点O ,点M 在线段AC 上,且3AM =,点P 为线段BD 上的一个动点,则12MP PB +的最小值是______.47.(2021·江苏苏州市·中考真题)如图,射线OM 、ON 互相垂直,8OA =,点B 位于射线OM 的上方,且在线段OA 的垂直平分线l 上,连接AB ,5AB =.将线段AB 绕点O 按逆时针方向旋转得到对应线段A B '',若点B '恰好落在射线ON 上,则点A '到射线ON 的距离d ≈______.48.(2021·新疆中考真题)如图,已知正方形ABCD 边长为1,E 为AB 边上一点,以点D 为中心,将DAE △按逆时针方向旋转得DCF ,连接EF ,分別交BD ,CD 于点M ,N .若25AE DN =,则sin EDM ∠=__________.49.(2021·四川达州市·中考真题)如图,在边长为6的等边ABC∆中,点E,F分别是边AC,BC上的动点,且AE CF=,连接BE,AF交于点P,连接CP,则CP的最小值为___________.三、解答题50.(2021·广东中考真题)如图,在Rt ABC中,90A∠=︒,作BC的垂直平分线交AC于点D,延长AC至点E,使CE AB=.(1)若1AE=,求ABD△的周长;(2)若13AD BD=,求tan ABC∠的值.51.(2021·内蒙古通辽市·中考真题)计算;101(3)2cos30|32π-⎛⎫+--︒+ ⎪⎝⎭ 52.(2021·湖南中考真题)“2021湖南红色文化旅游节——重走青年毛泽东游学社会调查之路”启动仪式于4月29日在安化县梅城镇举行.该镇南面山坡上有一座宝塔,一群爱好数学的学生在研学之余对该宝塔的高度进行了测量.如图所示,在山坡上的A 点测得塔底B 的仰角13BAC ∠=︒,塔顶D 的仰角38DAC ∠=︒,斜坡50AB =米,求宝塔BD 的高(精确到1米)(参考数据:sin130.22,cos130.97,tan130.23,sin380.62,cos380.79,tan380.78︒≈︒≈︒≈︒≈︒≈︒≈)53.(2021·湖南中考真题)已知锐角ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,边角总满足关系式:sin sin sin a b c A B C==.(1)如图1,若6,45,75a B C =∠=∠=︒︒,求b 的值;(2)某公园准备在园内一个锐角三角形水池ABC 中建一座小型景观桥CD (如图2所示),若,14CD AB AC ⊥=米,10AB =米,sin 14ACB ∠=,求景观桥CD 的长度. 54.(2021·湖南张家界市·中考真题)张家界大峡谷玻璃桥是我市又一闻名中外的五星景点.某校初三年级在一次研学活动中,数学研学小组设计以下方案测量桥的高度.如图,在桥面正下方的谷底选一观测点A ,观测到桥面B ,C 的仰角分别为30,60︒︒,测得BC 长为320米,求观测点A 到桥面BC 的距离.(结果保留整数,1.73≈)55.(2021·黑龙江绥化市·中考真题)一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为ABC ,点B C D 、、在同一条直线上,测得90,60,32cm ACB ABC AB ∠=︒∠=︒=,75BDE ∠=︒,其中一段支撑杆84cm CD =,另一段支撑杆70cm DE =,求支撑杆上的点E 到水平地面的距离EF 是多少?(用四舍五入法对结果取整数,参考数据sin150.26,cos150.97,tan15 1.732︒≈︒≈︒≈≈)56.(2021·浙江宁波市·中考真题)我国纸伞的制作工艺十分巧妙.如图1,伞不管是张开还是收拢,伞柄AP 始终平分同一平面内两条伞骨所成的角BAC ∠,且AB AC =,从而保证伞圈D 能沿着伞柄滑动.如图2是伞完全收拢时伞骨的示意图,此时伞圈D已滑动到点D的位置,且A,B,D三点共线,40cmAD'=,B 为AD'中点,当140∠=︒时,伞完全张开.BAC(1)求AB的长.(2)当伞从完全张开到完全收拢,求伞圈D沿着伞柄向下滑动的距离.(参考数︒≈︒≈︒≈)据:sin70094,cos700.34,tan70 2.7557.(2021·江西中考真题)图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA 与额头保持垂直量得胳膊28cmMB=,肘关节M与枪身端点A之间的MN=,42cm水平宽度为25.3cm(即MP的长度),枪身8.5cmBA=.图1(1)求ABC ∠的度数;(2)测温时规定枪身端点A 与额头距离范围为3~5cm .在图2中,若测得68.6BMN ∠=°,小红与测温员之间距离为50cm 问此时枪身端点A 与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)(参考数据:sin 66.40.92︒≈,cos 66.40.40=°,sin 23.60.40︒≈1.414≈) 58.(2021·甘肃武威市·中考真题)如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:方案设计:如图2,宝塔CD 垂直于地面,在地面上选取,A B 两处分别测得CAD ∠和CBD ∠的度数(,,A D B 在同一条直线上).数据收集:通过实地测量:地面上,A B 两点的距离为58m,42,58CAD CBD ∠=︒∠=︒.问题解决:求宝塔CD 的高度(结果保留一位小数).参考数据:sin 420.67,cos420.74,tan 420.90︒≈︒=︒≈,sin580.85,cos580.53,tan58 1.60︒=︒=︒=.根据上述方案及数据,请你完成求解过程.59.(2021·青海中考真题)如图1是某中学教学楼的推拉门,已知门的宽度2AD =米,且两扇门的大小相同(即AB CD =),将左边的门11ABB A 绕门轴1AA 向里面旋转35︒,将右边的门11CDD C 绕门轴1DD 向外面旋转45︒,其示意图如图2,求此时B 与C之间的距离(结果保留一位小数).(参考数据sin 350.6︒≈,cos350.8︒≈ 1.4≈).60.(2021·四川成都市·中考真题)越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A 处安置测倾器,测得点M 的仰角33MBC ∠=︒,在与点A 相距3.5米的测点D 处安置测倾器,测得点M 的仰角45MEC ∠=︒ (点A ,D 与N 在一条直线上),求电池板离地面的高度MN 的长.(结果精确到1米;参考数据:sin330.54,cos330.84,tan330.65︒≈︒≈︒≈)61.(2021·山东聊城市·中考真题)时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口A 处向正南方向走300米到达革命纪念碑B 处,再从B 处向正东方向走到党史纪念馆C 处,然后从C 处向北偏西37°方向走200米到达人民英雄雕塑D处,最后从D处回到A处.已知人民英雄雕塑在基地门口的南偏东65°方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)62.(2021·四川广元市·中考真题)如图,某无人机爱好者在一小区外放飞无人机,当无人机飞行到一定高度D点处时,无人机测得操控者A的俯角为75︒,测得小区楼房BC顶端点C处的俯角为45︒.已知操控者A和小区楼房BC之间的距离为45米,小区楼房BC的高度为(1)求此时无人机的高度;(2)在(1)条件下,若无人机保持现有高度沿平行于AB的方向,并以5米/秒的速度继续向前匀速飞行.问:经过多少秒时,无人机刚好离开了操控者的视线?(假定点A,B,C,D都在同一平面内.参考数据:︒=+tan152tan752︒=计算结果保留根号)63.(2021·四川资阳市·中考真题)资阳市为实现5G网络全覆盖,2020-2025年拟建设5G基站七千个.如图,在坡度为1:2.4i=的斜坡CB上有一建成的基站塔AB,小芮在坡脚C测得塔顶A的仰角为45︒,然后她沿坡面CB行走13米到达D处,在D处测得塔顶A的仰角为53︒(点A、B、C、D均在同一平面内)(参考数据:434︒≈︒≈︒≈)sin53,cos53,tan53553(1)求D处的竖直高度;(2)求基站塔AB的高.64.(2021·江苏连云港市·中考真题)我市的前三岛是众多海钓人的梦想之地.小明的爸爸周末去前三岛钓鱼,将鱼竿AB摆成如图1所示.已知 4.8mAB=,鱼竿尾端A离岸边0.4m,即0.4mAD=.海面与地面AD平行且相距1.2m,即 1.2mDH=.(1)如图1,在无鱼上钩时,海面上方的鱼线BC与海面HC的夹角37∠=︒,BCH海面下方的鱼线CO与海面HC垂直,鱼竿AB与地面AD的夹角22∠=︒.求点BADO到岸边DH的距离;(2)如图2,在有鱼上钩时,鱼竿与地面的夹角53BAD ∠=︒,此时鱼线被拉直,鱼线 5.46m BO =,点O 恰好位于海面.求点O 到岸边DH 的距离.(参考数据:3sin 37cos535︒=︒≈,4cos37sin 535=︒︒≈,3tan 374︒≈,3sin 228︒≈,15cos2216︒≈,2tan 225︒≈)65.(2021·四川凉山彝族自治州·中考真题)王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB 的高度,他在点C 处测得大树顶端A 的仰角为45︒,再从C 点出发沿斜坡走米到达斜坡上D 点,在点D 处测得树顶端A 的仰角为30︒,若斜坡CF 的坡比为1:3i =(点E C H ,,在同一水平线上).(1)求王刚同学从点C 到点D 的过程中上升的高度;(2)求大树AB 的高度(结果保留根号).。
【2021中考数学考前突破】锐角三角函数相关填空含答案

锐角三角函数相关填空压轴题1.如图,在△ABC中,AB=AC,点D为△ABC内部一点,且∠ADB+∠BAC=240°,∠ADC=2∠ABC,若3BD=2CD,则tan∠ADC的值为.2.如图2,有一块四边形的铁板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tan B=tan C=,若要从这块余料中裁出顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为cm2.3.如图,BE是△ABC的角平分线,F是AB上一点,∠ACF=∠EBC,BE、CF相交于点G.若sin∠AEB=,BG=4,EG=5,则S△ABE=.4.如图,在平面直角坐标系xOy中,已知Rt△ABC可运动(平移或旋转),且∠C=90°,BC=+4,tan A=,若以点M(3,6)为圆心,2为半径的⊙M始终在△ABC的内部,则△ABC的顶点C到原点O的距离的最小值为.5.如图,△ABC为等边三角形,点D在△ABC外,连接BD、CD.若∠ABD=2∠ACD,tan∠ACD=,BD=,则CD=.6.如图,Rt△ABC,∠C=90°,tan A=,D是AC中点,∠ABD=∠FBD,BC=6,CF ∥AB,则DF=.7.如图,C为射线AM上一点,以点C为直角顶点作∠BCD交射线AN于D,B两点,当tan A=时,的最大值为.8.如图,线段AC,BD交于点P,∠A=30°,∠ACD=120°,∠D=15°,AB=1,CD =,则BD的长为.9.如图,在等腰△ABC中,AB=AC,AD平分∠BAC,点E在BA的延长线上,ED=EC,DE交AC于点K,若EC=10,tan∠AED=,则AK=.10.在△ABC中,∠ABC=60°,BC=8,点D是BC边的中点,点E是边AC上一点,过点D作ED的垂线交边AC于点F,若AC=7CF,且DE恰好平分△ABC的周长,则△ABC的面积为.11.如图,已知四边形ABCD的一组对边AD、BC的延长线相交于点E.另一组对边AB、DC的延长线相交于点F,若cos∠ABC=cos∠ADC=,CD=5,CF=ED=n,则AD 的长为(用含n的式子表示).12.等腰三角形ABC,AB=BC,tan∠BAC=2,D为△ABC内一点,连接AD、BD、CD,AD=3,BD=2,CD=5,则AB=.13.如图,D是△ABC的边AC上一点,CD=2AD,AE⊥BC于点E,若BD=8,sin∠CBD =,则AE的长为.14.(按课改要求命制)如图,设P是等边三角形ABC内的一点,P A=1,PB=2,PC=,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是(不取近似值).15.如图,CD为Rt△ABC的斜边AB上的高,点E、F分别为CD、AD上的点,以EF为边在四边形ACEF的外部作等边△EFG,若∠A=60°,CE:AF=:2,tan∠GBA=,BG=2,则线段EF的长为.16.在△ABC中,tan∠ABC=,BD平分∠ABC交AC于点D,过A作AE⊥AB交BC 于点E,若AE=EC,BD=,则AB的长为.17.如图,在△ABC中,AB=6,E在AB边上,tan∠AEC=,D为BC中点,∠DEA=∠A,则△ABC的面积为.18.如图,在△ABC中,∠ABC=120°,AB=12,点D在边AC上,点E在边BC上,sin ∠ADE=,ED=5,如果△ECD的面积是6,那么BC的长是.19.已知在Rt△ABC中,∠C=90°,BC=1,AC=2,以点C为直角顶点的Rt△DCE的顶点D在BA的延长线上,DE交CA的延长线于点G,若tan∠CED=,CE=GE,那么BD的长等于.20.如图,AD是△ABC的中线,AD=5,tan∠BAD=,S△ADC=15,求线段AC的长.21.如图,在△ABC中,AH⊥BC于点H,在AH上取一点K,连接CK,使得∠HKC+∠HAC=90°,在CK上取一点N,使得CN=AC,连接BN,交AH于点M,若tan∠ABC =2,BN=15,则CH的长为.22.如图,在四边形ABCD中,AC与BD相交于点O,∠ABC=∠DAC=90°,tan∠ACB =,=,则=.23.如图,在边长为1的正方形网格中,端点在格点上的两条线段相交形成∠1,则tan∠1=.24.如图,在四边形ABCD中,tan∠ABC=,BD为对角线,∠ABD+∠BDC=90°,过点A作AE⊥BD于点E,连接CE,若AE=DE,EC=DC=5,则△ABC的面积为.参考答案1.解:在CD上取一点T,使得∠DAT=60°,过点T作TH⊥AD于H.∵∠ADB+∠BAC=240°,∴∠ADB+∠BAD+60°+∠CAT=240°,∴∠ADB+∠BAD+∠CAT=180°,∵∠ADB+∠BAD+∠ABD=180°,∴∠ABD=∠CAT,∵AB=AC,∴∠ABC=∠ACB,∵∠ADC=2∠ABC,∠ADT+∠DAT+∠ATD=180°,∠BAC+2∠ABC=180°,∴∠ABC=∠DAT+∠ATD=60°+∠ATD,∴∠ATC+∠ABC=∠ATC+∠ATD+∠DAT=240°,∴∠ADB=∠ATC,∴△ADB≌△CTA(AAS),∴BD=AT,AD=CT,∵3BD=2CD,∴可以假设BD=3k,CD=2k,则AH=AT•cos60°=k,HT=AT•sin60°=k,设AD=CT=x,则DH=x﹣k,在Rt△DHT中,DT2=DH2+HT2,∴(x﹣k)2+()2=(3k﹣x)2,∴x=k,∴DH=k,∴tan∠ADC===4,故答案为:4.2.解:如图,延长BA、CD交于点E,过点E作EH⊥BC于点H,交PQ于点G,如图,设矩形PQMN,∵tan B=tan C=,∴∠B=∠C,∴EB=EC,∵BC=108cm,且EH⊥BC,∴BH=CH=BC=54cm,∵tan B==,∴EH=BH=×54=72cm,∴EG=EH﹣GH=72﹣QM,∵PQ∥BC,∴△EQP∽△EBC,∴=,即=,∴PQ=(72﹣QM),设QM=x,则S矩形PQMN=PQ•QM=x(72﹣x)=﹣(x﹣36)2+1944,∴当x=36时,S矩形PQMN最大值为1944,所以当QM=36时,矩形PQMN的最大面积为1944cm2,答:该矩形的面积为1944cm2.故答案为:1944.3.解:如图,过点B作BT⊥AC于T,连接EF.∵BE平分∠ABC,∴∠ABE=∠CBE,∵∠ECG=∠ABE,∴∠ECG=∠CBE,∵∠CEG=∠CEB,∴△ECG∽△EBC,∴==,∴EC2=EG•EB=5×(5+4)=45,∵EC>0,∴EC=3,在Rt△BET中,∵sin∠AEB==,BE=9,∴BT=,∴ET===,∴CT=ET+CE=,∴BC===6,∴CG==10,∵∠ECG=∠FBG,∴E,F,B,C四点共圆,∴∠EFG=∠CBG,∵∠FGE=∠BGC,∴△EGF∽△CGB,∴=,∴=,∴EF=3,∵∠AFE=∠ACB,∠EAF=∠BAC,∴△EAF∽△BAC,∴===,设AE=x,则AB=2x,∵∠FBG=∠ECG,∠BGF=∠CGE,∴△BGF∽△CGE,∴=,∴=,∴BF=,∵AE•AC=AF•AB,∴x(x+3)=(2x﹣)•2x,解得x=,∴AE=ET=,∴点A与点T重合,∴AB=2AE=,∴S△ABE=×AB×AE=××=.故答案为.4.解:如图,设⊙M与AC相切于点J,与AB相切于点T,连接OC,MJ,MT,延长JM 交AB于F.∵AC,AB是⊙O的切线,∴MJ⊥AC,MT⊥AB,∴∠AJM=∠ATM=90°,∴∠A+∠JMT=180°,∵∠JMT+∠FMT=180°,∴∠A=∠FMT,∴tan A=tan∠FMT=,∵MT=2,∴TF=1,FM===,∴JF=MJ+MF=2+,∴AJ=2FJ=4+2,∵AC=2BC=8+2,∴CJ=4,∵∠CJM=90°,∴CM===2,∵M(3,6),∴OM==3,∵OC≥OM﹣CM,∴OC≥3﹣2,∴OC≥,∴OC的最小值为.故答案为.5.解:如图,连接AD,作BH⊥AD于H,作DE⊥CB交CB的延长线于E,作CM⊥DA 交DA的延长线于M.∵△ABC是等边三角形,∴∠ABC=∠ACB=60°,∵∠DBE=180°﹣∠ABD﹣∠ABC=120°﹣2∠ACD=120°﹣2(60°﹣∠BCD)=2∠BCD,又∵∠DBE=∠BDC+∠BCD,∴∠BCD=∠BDC,∴BD=BC,∴BD=BA=BC=AC=,∴△ADC的外接圆的圆心是点B,∴∠ADC=∠ABC=30°,∵BD=BA,BH⊥AD,∴∠ABH=∠DBH,∵∠ABD=2∠ACD,∴∠BDH=∠ACD,∴tan∠DBH=tan∠ACD==,设DH=2k,BH=5k,∴(2k)2+(5k)2=37,∴k=1或﹣1(舍弃),∴DH=AH=2,设CM=x,则DM=x,CD=2x,∴AM=x﹣4,在Rt△ACM中,∵AC2=AM2+CM2,∴37=(x﹣4)2+x2,解得x=(舍弃)或,∴CM=,∴CD=2x=11,故答案为11.6.解:如图:过点F作FG⊥AC于点G,∵∠ACB=90°,∴BC⊥AC,∴GF∥BC.∵tan∠A==,D是AC中点,∴BC=CD=AD,∴∠CBD=∠CDB=45°,∴∠ABD+∠A=45°,∠FBD+∠FBC=45°,∵∠ABD=∠FBD,∴∠FBC=∠A,∴tan∠EBC=tan∠A=,即在Rt△CBE中,tan∠EBC==,∴=,∴CE=3.根据勾股定理,得BE===3.∵CF∥AB,∴=,即=,∴EF=.∵GF∥BC.∴===,∴==,∴FG=2,EG=1.∴DG=DE﹣EG=3﹣1=2.∴Rt△FGE中,根据勾股定理,得DF===2.故答案为2.7.解:取BD的中点E,连接CE,过点E作EF⊥AM.设AD=x,BD=2y,在Rt△AEF中,tan∠A==,设EF=3k,AF=4k,则AE=5k,∵∠DCB=90°,DE=EB,∴EC=ED=EB=y,∵≥=,∴≥,∴≤,∴=≤,∴的最大值为.故最大值为.8.解:作BM⊥AC于M,CN⊥BD于N,在DB上取一点H,使得DH=CH,连接CH.∵∠D=15°,∠PCD=120°,∴∠CPD=∠APB=180°﹣120°﹣15°=45°,∵∠AMB=∠BMP=90°,∠A=30°,∴BM=PM=AB=,∴BP=BM=,设PN=x,则CN=PN=x,∵HC=HD,∴∠HCD=∠D=15°,∴∠CHN=30°,∴CH=DH=2x,NH=x,在Rt△CDN中,∵CN2+DN2=CD2,∴x2+(x+2x)2=()2,∴x=,∴PD=3x+x=(3+)x=,∴BD=BP+PD=2.解法二:如图,过点B作BM⊥AC于M,过点D作DN⊥AC交AC的延长线于N.由题意,△PBM,△PDN都是等腰直角三角形,∵BM=AB=,∴PB=,∴DN=CD•sin60°=,∴PD=DN=,∴BD=PB+PD=2.故答案为2.9.解:过点K作KM⊥EC,过D作DN∥AC,设KM=m,∠BED=∠α∵ED=EC=10,∴∠ECD=∠EDC=∠B+∠α,∵AB=AC,∴∠ACB=∠B,∴∠ECA=∠AED,∵tanα=,∴CM=2m,KC=m,∵DN∥AC,D是BC的中点,∴ND=AC,∠EAC=∠END,EC=ED,∴△EAC≌△DNE(AAS),∴AE=ND,∵AD⊥BC,AB=AC,∴ND=AB=AN=BN,∴4AK=AC,∵AC=AK+CK,∴AK=CK=,∴K是ED的中点,∴EK=5,在Rt△EKM中,EM=10﹣2m,KM=m,∴52=m2+(10﹣2m)2,∴m=3或m=5(舍)∴AK=;故答案为;10.解:如图,取AC的中点M,连接DM,作AH⊥BC于H.设DM=a,AE=b.∵BD=DC,AM=MC,∴AB=2DM=2a,∵AB+AE+BD=EC+DC,∴EC=2a+b,AC=2a+2b,∴AM=MC=a+b,∴EM=a,∴EM=DM,∴∠MED=∠MDE,∵∠MED+∠MFD=90°,∠MDE+∠MDF=90°,∴∠MFD=∠MDF,∴MD=MF=a,∴CF=AE=b,∵AC=7CF,∴2a+2b=7b,∴2a=5b,∵AB=5b,AC=7b,在Rt△ABH中,∵∠B=60°,∴BH=AB=b,AH=b,在Rt△ACH中,CH==b,∴BC=BH+HC=8b,∴8b=8,∴b=1,∴S△ABC=×8×=10,故答案为10.11.解:过C作CH⊥AD于H,∵cos∠ADC=,CD=5,∴DH=3,∴CH=4,∴tan∠E==,过A作AG⊥CD于G,设AD=5a,则DG=3a,AG=4a,∴FG=DF﹣DG=5+n﹣3a,∵CH⊥AD,AG⊥DF,∵∠CHE=∠AGF=90°,∵∠ADC=∠ABC,∴∠EDC=∠CBF,∵∠DCE=∠BCF,∴∠E=∠F,∴△AFG∽△CEH,∴,∴,∴a=,∴AD=5a=,故答案为:.12.解:作BE⊥AC于E,将△BCD绕点B逆时针旋转得到△ABF,连接DF交AB于O,作BH⊥DF于H.∵BC=BA,BD=BF,BE⊥AC,BH⊥DF,∴∠ABE=∠ABC,∠FBH=∠DBF,∵∠ABC=∠DBF,∴∠ABE=∠FBH,∵∠ABE+∠BAE=90°,∠FBH+∠BFH=90°,∴∠BAE=∠BFH,∴tan∠BAE=tan∠BFH=2,∴=2,∵BD=BF=2,∴FH=2,BH=4,∴DF=4,∵DF=4,AD=3,AF=CD=5,∴DF2+AD2=AF2,∴∠ADF=90°,∵∠ADO=∠BHO=90°,∴BH∥AD,∴=,∴=,∴OH=DH=,OD=DH=,∴BO===,OA===,∴AB=OB+OA=,故答案为.13.解:过点D作DH⊥BC,垂足为H.在Rt△BDH中,DH=BD•sin∠CBD=8×=6.∵DH⊥BC,AE⊥BC,∴DH∥AE,△CDH∽△CAE.∴===,∴AE=DH=×6=9.14.解:∵△ABC为等边三角形,∴∠BAC=60°.根据旋转的性质,有∠P AP′=60°,AP′=AP=1,CP′=BP=2.∴△APP′是等边三角形,PP′=1.在△PCP′中,PC=,PP′=1,CP′=2.∴PC2=P′P2+P′C2.∴△PCP′是直角三角形,且∠PP′C=90°.∴sin∠PCP′=.15.解:如图,作GK⊥AB于K,EN⊥AC于N,FM⊥AC于M,EH⊥FM于H.在Rt△BGK中,∵tan∠KBG==,BG=2,∴可以假设GK=k,BK=13k,则有(k)2+(13k)2=(2)2,解得k=1或﹣1(舍弃),∴GK=,BK=13,在Rt△AFM中,∵∠A=60°,∴∠AFM=30°,∴AF=2AM,∵△EFG是等边三角形,∴∠EFG=60°,EF=FG,∴∠AFM+∠EFG=90°,∴∠GFK+∠EFH=90°,∵∠GFK+∠FGK=90°,∴∠EFH=∠FGK,∵∠EHF=∠FKG=90°,EF=FG,∴△EHF≌△FKG(AAS),∴GK=FH=,∵FM=AF,EC=AF,∴FM=EC,在Rt△CEN中,∴∠ECN=30°,∴EN=EC=FM,∵四边形EHMN是矩形,∴EN=MH=FH=,∴FM=2,AM=2,AF=4,CN=3,设MN=EH=FK=x,∵AB=2AC,∴4+x+13=2(2+x+3),解得x=7,∴EF===2.故答案为2.16.解:如图,设BD交AE于J,作JH⊥BE于H,作DK⊥BC于K,作EF∥AC交AB于F.在Rt△ABE中,∵∠BAE=90°,∴tan∠ABE==,∴可以假设AE=5k,AB=12k,则BE=13k,∵EA=EC,∴EC=5k,BC=18k,∵BJ平分∠ABE,JA⊥AB,JH⊥BE,∴AJ=JH,设AJ=JH=x,易证AB=BH=12k,HE=k,在Rt△JEH中,∵JE2=JH2+HE2,∴(5k﹣x)2=x2+k2,∴x=k,∴tan∠ABJ=tan∠JBH===,∵BD=,∴DK=1,BK=5,∵EF∥AC,∴∠AEF=∠CAE,∠BEF=∠C,∵EA=EC,∴∠EAC=∠C,∴∠FEA=∠FEB=∠C,∵EF∥AC,∴==,∴AF=k,∴tan∠C=tan∠AEF===,∴KC=,∴BC=18k=5+,∴k=,∴AB=12k=.故答案为.17.解:延长ED到F,使得DF=DE,延长BA到G,使得AG=BE.作CH⊥AB于H,连接CF、CG.∵DE=DF,∠BDE=∠CDF,BD=CD,∴△BDE≌△CDF,∴BE=CF=AG,∠B=∠DCF,∴CF∥AB,∵∠CAE=∠AEF,∴四边形AEFC是等腰梯形,∴AC=EF,∠F=∠FCA=∠CAG,∴△CEF≌△GCA,∴CE=CG,∵CH⊥EG,∴EH=GH=EG=(AE+BE)=3,∵tan∠AEC==,∴CH=4,∴S△ABC=•AB•CH=12.18.解:如图,过点E作EF⊥BC于F,过点A作AH⊥CB交CB的延长线于H.∵∠ABC=120°,∴∠ABH=180°﹣∠ABC=60°,∵AB=12,∠H=90°,∴BH=AB•cos60°=6,AH=AB•sin60°=6,∵EF⊥DF,DE=5,∴sin∠ADE==,∴EF=4,∴DF===3,∵S△CDE=6,∴•CD•EF=6,∴CD=3,∴CF=CD+DF=6,∵tan C==,∴=,∴CH=9,∴BC=CH﹣BH=9﹣6.故答案为:9﹣6.19.解:如图,过点A作AH⊥CE于H.∵tan∠CED==tan∠BAC,∴∠E=∠BAC,∵CE=EG,∴∠CGE=∠ECG,∵∠BAC+∠GAK=180°,∴∠E+∠GAK=180°,∴∠AGE+∠AKE=180°,∵∠AKE+∠AKC=180°,∴∠AKC=∠CGE,∴∠AKC=∠ACK,∴AC=AK=2,∵AH⊥CK,∴KH=CH,∵∠AHE=∠DCK=90°,∴AH∥CD,∴KA=AD,∴DK=2AK=4,AD=AK=2,∵∠ACB=90°,BC=1,AC=2,∴AB===,∴BD=AB+AD=2+,故答案为:2+.20.解:过点D作DE⊥AB,垂足为D,过点A作AF⊥DC,垂足为F,在Rt△ADE中,∵AD=5,tan∠BAD=,∵AE=4,DE=3,∴AD==5,又∵AD是△ABC的中线,∴S△ADC=15=S△ADB=AB•DE,∴×3×AB=15,∴AB=10,BE=AB﹣AE=10﹣4=6,在Rt△BDE中,BD===3=CD,由S△ADC=15=CD•AF,可得AF=2,在Rt△ADF中,DF===,∴FC=CD﹣DF=3﹣=2,在Rt△AFC中,AF=FC=2,∴AC=DF=2,故答案为:2.21.解:如图,过点N作NJ⊥BC于J.设HJ=x.∵AH⊥BC,∴∠AHB=∠AHC=90°,∵tan∠ABH==2,∴可以假设BH=k,2k,∵∠HKC+∠HAC=90°,∠HKC+∠KCH=90°,∴∠HAC=∠KCH,∵NJ⊥BC,∴∠AHC=∠CJN=90°,∴△AHC∽△CJN,∴===2,∴CJ=k,∴CH=x+k,JN=(x+k),∴tan∠NBJ==,设NJ=y,BJ=2y,∵BN=15,∴5y2=152,∴y=3,∴NJ=3,∴CH=2NJ=6.22.解:如图,过点D作DM∥BC,交CA的延长线于点M,延长BA交DM于点N,∵DM∥BC,∴△ABC∽△ANM,△OBC∽△ODM,∴==tan∠ACB=,==,又∵∠ABC=∠DAC=90°,∴∠BAC+∠NAD=90°,∵∠BAC+∠BCA=90°,∴∠NAD=∠BCA,∴△ABC∽△DAN,∴==,设BC=4a,由==得,DM=3a,∴AB=2a,DN=a,AN=a,∴NB=AB+AN=2a+a=a,∴===.故答案为:.23.解:如图,设小正方形ABCD的边长为a,连接AC,BD交于点O,设EC交BD于J.∵BD=a,CD∥EB,∴==,∴JD=BD=a,∵OD=OB=OC=OA=a,∴OJ=OD﹣JD=a﹣a=a,∵AC⊥BD,∴∠COJ=90°,∴tan∠1===2,故答案为2.24.解:如图,延长CE交AB于点H,延长DC、AE相交于点K,∵AE⊥BD,∴∠AEB=∠AED=90°,∵∠ABD+∠BDC=90°,设∠ABD=α,则∠BDC=90°﹣α,∴∠BAE=90°﹣∠ABE=90°﹣α,∵EC=DC,∴∠CED=∠CDE=90°﹣α,∵∠AEH+∠DEC=180°﹣∠AED=90°,∴∠AEH=α,∴∠BHE=90°,∵∠K+∠KDE=90°,∠CDE+∠CEK=90°,∴∠K+∠CEK=α,∴sin K=sin∠ABD,即,∴,解得,∵,∴设CH=7a,BH=6a,∴HE=HC﹣CE=7a﹣5,AH=AB﹣BH=,∵∠AEH=∠EBH=tan∠ABE,∴tan∠AEH=tan∠ABE,即EH2=AH•BH,解得a=1(舍去),∴CH=7a=7,∴.故答案为:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021中考数学考点归类复习——专题五十六:锐角三角函数
一、选择题
1. (2020·天津)2sin45°的值等于( )
A. 1
B.
C. 3
D. 2
2.在ABC 中,90,13,12C AB BC ∠=︒==,则sin B 的值为( )
A .1213
B .512
C .513
D .135
3.在直角三角形中不能求解的是( )
A .已知一直角边和一锐角
B .已知斜边和一锐角
C .已知两边
D .已知两角 4.△ABC 中,tan A =1,cos B =
,则△ABC 为( ) A .锐角三角形 B .钝角三角形
C .直角三角形
D .不能确定 5. (2020·杭州)如图,在△ABC 中,∠C =90°,设∠A ,∠B ,∠C 所对的边分别为a ,b ,c ,则( )
A .c =b sin
B B .b =c sin B
C .a =b tan B
D .b =c tan B
6.如图,梯子地面的夹角为A ∠,关于A ∠的三角函数值与梯子的倾斜程度之间的关系,下列叙述正确的是( )
A .sin A 的值越小,梯子越陡
B .cos A 的值越小,梯子越陡
C .梯子的长度决定倾斜程度
D .梯子倾斜程度与A ∠的函数值无关
7. (2020·凉山州)如图所示,△ABC 的顶点在正方形网格的格点上,则tan A 的值为( )
C
B
A
A.1
2
B.2
2
C.2 D.22
8.如图所示,在矩形ABCD中,CE⊥BD于E,AB=5,BC=12,则sin∠DCE的值是()
A.
5
12
B.
12
13
C.
5
13
D.
12
5
9.如图,为测一河两岸相对两电线杆A、B间的距离,在距A点15米处的C点(AC⊥BA)测得∠C=50°,则A、B间的距离应为()
A.15sin50°米B.15cos50°米C.15tan50°米D.米
10. (2019•湖南长沙•3分)如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60nmile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A 的距离是
A.3nmile B.60nmile
C.120nmile D.3)nmile
11. (2019·浙江温州)某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB 的长为
A .
95sin α
米 B .95cos α米
C .59sin α米
D .59cos α米 二、填空题 1. (2020·湘潭)计算:sin 45︒=________.
2.cos60tan 45︒︒+=______.
3.等腰ABC 中,5,6AB AC BC ===,则sin B =__________
4.在△ABC 中,∠B =74°37′,∠A =60°23′,则∠C = ,sin A +cos B +tan C ≈ .
5.在Rt △ABC 中,∠C =90°,若cos B =,则tan A = ,若此时△ABC 的周长为48,那么△ABC 的面积 .
6. 如图①是小志同学书桌上的一个电子相框,将其侧面抽象为如图②所示的几何图形,已知BC =BD =15 cm ,∠CBD =40°,则点B 到CD 的距离为________cm (参考数据:sin 20°≈0.342,cos 20°≈0.940,sin 40°≈0.643,cos 40°≈0.766.结果精确到0.1 cm ,可用科学计算器).
7. (2019•江苏宿迁)如图,∠MAN=60°,若△ABC 的顶点B 在射线AM 上,且AB=2,点C 在射线AN 上运动,当△ABC 是锐角三角形时,BC 的取值范围是__________.
8.如图,菱形ABCD的周长为20cm,DE AB
⊥,
3
sin
5
A=,则这个菱形的面积为_________2
cm.
9.如图,小明想测量南塔的高度.她在A处仰望塔顶,测得仰角为30°,再往塔的方向前进20m至B处,测得仰角为60°,那么塔高约为m.(小明身高忽略不计,≈1.732)
10.如图,△ABC中,∠C=90°,BC=4,AB的垂直平分线MN交AC于D,且CD:DA=3:5,则sin A=.
三、解答题
1.已知∠A为锐角,且cos A=,求sin A、tan A.
2.在直角坐标系中,点P(x,6)在第一象限,且OP与x轴正半轴的夹角α的正切值是.求x的值,及角α的正弦和余弦值.
3. 如图,在△ABC中,∠C=150°,AC=4,tan B=1 8 .
(1)求BC的长;
(2)利用此图形求tan15°的值.(精确到0.1.参考数据:2=1.4,3=1.7,5=2.2)
4.如图,广场上空有一个气球A ,地面上点B ,C ,D 在一条直线上,BC =20m ,在点B ,C 分别测得气球A 的仰角∠ABD 为45°,∠ACD 为56°,求气球A 离地面的高度AD (精确到0.1m ).
5. 如图,大楼AB 右侧有一障碍物,在障碍物的旁边有一幢小楼DE ,在小楼的顶端D 处测得障碍物边缘点C 的俯角为30°,测得大楼顶端A 的仰角为45°(点B 、C 、E 在同一水平直线上),已知AB =80 m ,DE =10 m ,求障碍物B 、C 两点间的距离.(结果精确到0.1 m ,参考数据:2≈1.414,3≈1.732)
6.如图,为了测量河宽,在河的一边沿岸选取B 、C 两点,对岸岸边有一块石头A ,在ABC 中,测得
64B ∠=︒,45C ∠=︒,50BC =米,求河宽(即点A 到边BC 的距离)
(结果精确到0.1米). (参考数据:2 1.41≈,sin640.90︒=,cos640.44︒=,tan64 2.05︒=)
7. 某拉杆式旅行箱的侧面示意图如图10所示,已知箱体AB长50 cm,拉杆BC的伸长距离最大时可达35 cm,点A,B,C在同一条直线上,在箱体底端装有圆形滚轮⊙A,⊙A与水平地面MN相切于点D,在拉杆伸长到最大的情况下,点B距离水平地面34 cm,点C到水平地面的距离CE为55 cm,AF∥MN.
(1)求⊙A的半径;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为76 cm,∠CAF=64°,求此时拉杆BC的伸长距离(结果取整数.参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1).。
