2002年(首届)上海市TI杯高二年级数学竞赛
历届 最近十年 (新知杯)上海市初中数学竞赛试卷及答案(含模拟试题及解答)

新 知 杯 模 拟 试 题一、填空题(第1-5小题每题8分,第6-10题每题10分,共90分)1. 对于任意实数b a ,,定义b a *=b b a a ++)(,已知5.285.2=*a ,则实数a 的值是_________。
2. 在三角形ABC 中,,其中,,a CA a BC b AB 2122==-=b a ,是大于1的整数,则=-a b 。
3. 一个平行四边形可以被分成92个边长为1的正三角形,它的周长可能是 。
4. 已知关于x 的方程02)2()3(2234=++++++k x k x k x x 有实根,并且所有实根的乘积为-2,则所有实根的平方和为 。
5. 如图,直角三角形ABC 中1=AC ,2=BC ,P 为斜边AB 上一动点。
BC PE ⊥,CA PF ⊥,则线段EF 长的最小值为 。
6. 设b a ,是方程01682=++x x 的两个根,d c ,是方程01862=+-x x 的两个根,则()()()()d b d a c b c a --++的值为 。
7. 在平面直角坐标系中有两点()1,1-P ,()2,2Q ,函数1-=kx y 的图像与线段PQ 延长线相交(交点不包括Q ),则实数k 的取值范围是 。
8. 方程2009=xyz 的所有整数解有 组。
9. 如图,四边形ABCD 中CD BC AB ==,78=∠ABC ,162=∠BCD 。
设BC AD ,延长线交于E ,则=∠AEB _________________.EEC10. 如图,在直角梯形ABCD 中,90=∠=∠BCD ABC ,10==BC AB ,点M 在BC上,使得ADM ∆是正三角形,则ABM ∆与DCM ∆的面积和是________________。
二、(本题15分)如图,ABC ∆中,90=∠ACB ,点D 在CA 上,使得,,31==AD CD 并且,BAC BDC ∠=∠3求BC 的长。
2002年全国高中数学联赛获奖通知

2002年全国高中数学联赛获奖通知各县(市)教育局教研室:各有关学校:接省数学会通知,2002年全国高中数学联赛我省有13000余名学生参加。
经浙江省数学会、中国数学会2002年全国高中数学联合竞赛组织委员会评定,报浙江省学科竞赛委员会批准,评出全国一等奖45名、二等奖202名(由中国数学会颁发荣誉证书),浙江省一等奖176名、二等奖185名(由浙江省数学会颁发荣誉证书),浙江赛区团体优胜奖10个代表队(由浙江省数学会颁奖)。
嘉兴市有1579名学生参赛,获全国一等奖2名、二等奖19名,浙江省一等奖22名、二等奖9名。
嘉兴一中获浙江赛区团体优胜奖。
另由嘉兴市数学会评定嘉兴市一等奖31名、二等奖74名。
注:本次竞赛采用不重复设奖办法,即全国奖高于省级奖、省级奖高于市级奖。
嘉兴市全部获奖学生姓名、所在学校、指导老师姓名见附件。
嘉兴市教育局教研室嘉兴市数学会嘉兴市教育学会中学数学教学分会2003年1月附件:2002年全国高中数学联赛嘉兴市获奖名单团体优胜奖:嘉兴一中个人奖:共158名序号学生姓名奖次学校指导老师1林川全国一等奖嘉兴一中吕峰波2朱量全国一等奖嘉兴一中吕峰波1许枞全国二等奖嘉兴一中吕峰波2邵元龙全国二等奖桐乡高级中学姚福坤3严澄全国二等奖嘉兴一中吕峰波4徐震翔全国二等奖嘉善高级中学王书朝5王舟全国二等奖嘉兴一中吕峰波6徐竟杰全国二等奖元济高级中学胡水林7李瑞江全国二等奖嘉兴一中沈新权8陈飞全国二等奖嘉兴一中吕峰波9祁金佳全国二等奖桐乡高级中学姚福坤10沈峰全国二等奖嘉善高级中学王书朝11凌跃全国二等奖嘉兴一中许浩12许煜全国二等奖嘉兴一中邬佩弦13叶剑敏全国二等奖嘉兴一中吕峰波14吴一凡全国二等奖嘉善高级中学王书朝15徐磊全国二等奖嘉善高级中学王书朝16金益全国二等奖桐乡高级中学姚福坤17朱磊全国二等奖平湖中学周保国18顾国伟全国二等奖海宁高级中学吴娟红19苗洋全国二等奖嘉兴一中吕峰波1吕贤杰浙江省一等奖茅盾中学顾承坤2宋伟浙江省一等奖嘉兴一中沈新权3欧光亮浙江省一等奖元济高级中学胡水林4朱宇婧浙江省一等奖桐乡高级中学冯华5王晨杰浙江省一等奖海宁高级中学吴娟红6王槐欣浙江省一等奖嘉善高级中学王书朝7张李涛浙江省一等奖嘉善高级中学王书朝8徐涛浙江省一等奖元济高级中学胡水林9马杰浙江省一等奖海宁高级中学吴娟红10王海梁浙江省一等奖桐乡高级中学陈军1112王俊璞浙江省一等奖嘉兴一中吕峰波13倪成浩浙江省一等奖嘉善高级中学王书朝14华凌晖浙江省一等奖海宁高级中学顾贯石15范超杰浙江省一等奖嘉兴一中邬佩弦16杨颖浙江省一等奖嘉兴一中邬佩弦17丁一媛浙江省一等奖嘉兴一中邬佩弦18俞陈霄浙江省一等奖元济高级中学胡水林19吴春华浙江省一等奖桐乡高级中学姚福坤20朱赟超浙江省一等奖元济高级中学胡水林21黄周玮浙江省一等奖嘉兴一中曹必义22刘艺锋浙江省一等奖嘉兴一中沈新权1富彩萍浙江省二等奖元济高级中学祝锦如2黄荣益浙江省二等奖嘉善高级中学王书朝3顾也欣浙江省二等奖平湖中学高云4陆毅卿浙江省二等奖嘉兴高级中学邢川5俞春泉浙江省二等奖嘉善高级中学张幸6陆稼书浙江省二等奖海宁高级中学沈尔光7曹侃浙江省二等奖海宁高级中学顾贯石8顾惠勤浙江省二等奖嘉兴一中邬佩弦9陈亦龙浙江省二等奖嘉善高级中学王书朝1张瀛嘉兴市一等奖嘉兴一中许浩2赵连杰嘉兴市一等奖茅盾中学顾承坤3陆忠伟嘉兴市一等奖茅盾中学顾承坤4顾旻昊嘉兴市一等奖嘉兴一中吕峰波5王建锋嘉兴市一等奖平湖中学李美娟6曹信芳嘉兴市一等奖嘉兴一中吕峰波7陶文兵嘉兴市一等奖嘉兴一中吕峰波8李琦江嘉兴市一等奖嘉兴一中吕峰波9章福强嘉兴市一等奖嘉兴高级中学邢川10倪烨嘉兴市一等奖嘉善高级中学王书朝11柏琦峰嘉兴市一等奖嘉善高级中学王书朝12滕佳宇嘉兴市一等奖嘉善高级中学王书朝13龚晓春嘉兴市一等奖元济高级中学胡水林14马煜骞嘉兴市一等奖元济高级中学胡水林15苗智超嘉兴市一等奖桐乡高级中学姚福坤16李斌嘉兴市一等奖桐乡高级中学张国良17姜曦楠嘉兴市一等奖嘉兴一中吕峰波18张晨彬嘉兴市一等奖嘉善高级中学王书朝19朱鹏程嘉兴市一等奖元济高级中学胡水林2021许昊旻嘉兴市一等奖海宁高级中学顾贯石22高惠新嘉兴市一等奖桐乡高级中学姚福坤23陈坚嘉兴市一等奖平湖中学周保国24刘易嘉兴市一等奖嘉善高级中学刘朝阳25宋宁笛嘉兴市一等奖嘉兴一中吕峰波26刘珊珊嘉兴市一等奖元济高级中学胡水林27倪佳丽嘉兴市一等奖元济高级中学胡水林28高益范嘉兴市一等奖海宁高级中学顾贯石29唐杰晨嘉兴市一等奖桐乡高级中学程爱文30杨志宇嘉兴市一等奖桐乡高级中学陶庆芬31徐欢嘉兴市一等奖海宁高级中学吴飚1鲍翀嘉兴市二等奖嘉兴一中吕峰波2覃清硖嘉兴市二等奖嘉兴一中吕峰波3王燕嘉兴市二等奖嘉兴一中曹必义4祁晓凡嘉兴市二等奖嘉善高级中学王书朝5许正昱嘉兴市二等奖海宁高级中学顾贯石6吕忠嘉兴市二等奖海宁高级中学吴飚7余侃言嘉兴市二等奖桐乡一中沈松乾8金敏恒嘉兴市二等奖嘉善高级中学王书朝9王忠法嘉兴市二等奖元济高级中学胡水林10施朱明嘉兴市二等奖元济高级中学胡水林11汤浩彬嘉兴市二等奖海宁高级中学吴飚12施莉莉嘉兴市二等奖桐乡一中沈松乾13李昂嘉兴市二等奖平湖中学周保国14陈杰嘉兴市二等奖嘉善高级中学王书朝15徐松嘉兴市二等奖嘉善高级中学刘朝阳16沈承嘉兴市二等奖嘉善高级中学刘朝阳17沈弼凡嘉兴市二等奖嘉善高级中学陈轶才18蒋杰嘉兴市二等奖嘉善高级中学陈轶才19徐海超嘉兴市二等奖嘉善高级中学陈轶才20徐磊石嘉兴市二等奖桐乡一中沈松乾21水力嘉兴市二等奖平湖中学高云22许志锋嘉兴市二等奖嘉兴一中沈微微23王敏杰嘉兴市二等奖嘉善高级中学王书朝24张淳馨嘉兴市二等奖嘉善高级中学王书朝25郑灵杰嘉兴市二等奖平湖中学李美娟26郑典娜嘉兴市二等奖嘉兴一中许浩27高峰嘉兴市二等奖嘉兴高级中学邢川28陆蕙婷嘉兴市二等奖嘉善高级中学王书朝2930罗如迅嘉兴市二等奖嘉善高级中学陈轶才31施君源嘉兴市二等奖元济高级中学胡水林32王佳新嘉兴市二等奖海宁高级中学沈尔光33于浩崛嘉兴市二等奖平湖中学周保国34陈玥斐嘉兴市二等奖嘉兴一中吕峰波35徐跃嘉兴市二等奖平湖中学周保国36徐挺嘉兴市二等奖平湖中学周保国37赵汲嘉兴市二等奖海宁高级中学王增伟38徐梦茜嘉兴市二等奖元济高级中学祝锦如39冯峰嘉兴市二等奖嘉兴一中吕峰波40徐张廷嘉兴市二等奖嘉兴一中吕峰波41付石雨嘉兴市二等奖嘉兴一中曹必义42沈银海嘉兴市二等奖桐乡高级中学姚福坤43方蕴瑜嘉兴市二等奖嘉兴一中沈微微44陈晓权嘉兴市二等奖上外附属海宁宏达学校宋晓弟45王银燕嘉兴市二等奖上外附属海宁宏达学校宋晓弟46杨宇磊嘉兴市二等奖嘉善高级中学王书朝47郁杰嘉兴市二等奖元济高级中学胡水林48马茜岚嘉兴市二等奖桐乡高级中学姚福坤49陆灵锋嘉兴市二等奖茅盾中学顾承坤50陆飞嘉兴市二等奖桐乡高级中学冯华51陈咬其嘉兴市二等奖平湖当湖高级中学王晓卫52许磊叶嘉兴市二等奖平湖中学高云53俞洁琦嘉兴市二等奖海宁高级中学肖陆兴54陈晓强嘉兴市二等奖嘉善高级中学王书朝55周青松嘉兴市二等奖元济高级中学胡水林56曹圣杰嘉兴市二等奖桐乡高级中学陈军57沈翼嘉兴市二等奖桐乡高级中学姚福坤58张敏嘉兴市二等奖嘉善高级中学张幸59王仕超嘉兴市二等奖嘉善高级中学陈轶才60夏沈芳嘉兴市二等奖海盐高级中学宓全良61苏剑嘉兴市二等奖元济高级中学钟董甫62金雪萍嘉兴市二等奖元济高级中学金勤宏63吴雪峰嘉兴市二等奖嘉兴高级中学鲁建飞64李天明嘉兴市二等奖嘉兴高级中学邢川65富玲峰嘉兴市二等奖嘉兴高级中学邢川66王斌渊嘉兴市二等奖嘉兴高级中学胡贤辉67薛良宏嘉兴市二等奖嘉善第二高级中学车曦东68冷眩嘉兴市二等奖秀州中学周金娣6970鲁辰东嘉兴市二等奖嘉善一中张强71许振东嘉兴市二等奖洪波中学韩瑞玲72陈荣嘉兴市二等奖桐乡二中方新东73金新佳嘉兴市二等奖洪波中学韩瑞玲74徐伟嘉兴市二等奖王店中学郁培林。
2002年中国数学奥林匹克

则因点 D到A B和A C的距离
相等 , 以. 所 有
5- =S. ・ i } , z , -
从而, 有
召 - E= - I. 刀D D D C
图I
①
且 代 () :=只() 一二一) + xP () ( :) ( 1 , 一 , , '
n 23-. 二, - ,- ① 由余弦定理, 有 设 :为P z各项系数的绝对值之和, () 。 , 对于任 8 ' E 一 B " L E E =C' D + ' 2D - B = ' F D D E D B 二C 十D 2D D c 艺C F D P一 C " o D . Fe ② 意 数 。求非负整 , 正整 , 数k, 使得20。 奇数. -s为 + 因L E= D , B D L R 故由①和②可得 C ( 黄玉民 供题} B ' 班 二C2 P, D+ D +D ③ 三、 支足球队进行单循环赛, 1 8 即每轮将 I 支 8 球队分成 9 每组的两队赛一场, 组, 下一轮重新分组 R + D F D E二C + . D O ④ 由①和④可知下列两种情形之一成立: 进行比赛, 1轮, 共赛 7 使得每队都与另外 1支队各 7 ⑤ 赛一场. 按任盒可行的程序比赛了 二 轮之后, 总存在 4 支球队, 它们之间总共只赛了 1 求 二的最大可 场. ⑥ 能值 ( 李成幸 供题) 四、 对于平面上任意4 个不同的点 P, 2P iP I 因 占 c故式⑤不可能成立. < , 所以, 式⑥成立 凡, 求比值
从 每队都与另 2 队中 队 而, 外1支 的2 各赛1 所 场. 以, 有 8 至少 支队D, -, C, 均未赛 仇,-D 与 , - 。 几
即 2 > LB LA
IF LA 告 , D>D二二, C ;
2008年上海市TI杯高二年级数学竞赛
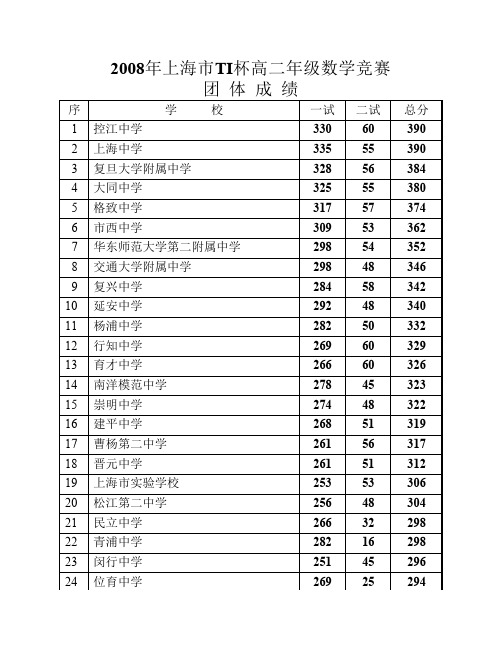
2008年上海市TI杯高二年级数学竞赛团体成绩序学校一试二试总分1控江中学33060390 2上海中学33555390 3复旦大学附属中学32856384 4大同中学32555380 5格致中学31757374 6市西中学30953362 7华东师范大学第二附属中学29854352 8交通大学附属中学29848346 9复兴中学28458342 10延安中学29248340 11杨浦中学28250332 12行知中学26960329 13育才中学26660326 14南洋模范中学27845323 15崇明中学27448322 16建平中学26851319 17曹杨第二中学26156317 18晋元中学26151312 19上海市实验学校25353306 20松江第二中学25648304 21民立中学26632298 22青浦中学28216298 23闵行中学25145296 24位育中学2692529425西南位育中学25635291 26南洋中学25530285 27七宝中学25330283 28南汇中学23348281 29向明中学21960279 30卢湾中学22748275 31大境中学244312752008年上海市TI杯高二年级数学竞赛个人获奖名单一等奖序姓名学校性别成绩1许弘毅上海中学男116 2鲁意上海中学男116 3张赜隐上海中学男116 4陈志浚控江中学男116 5薛钧元复旦大学附属中学男116 6武炳杰复旦大学附属中学男116 7陈玮骢复旦大学附属中学男116 8冯勇复旦大学附属中学男116 9阮凯茜大同中学女116 10应承隆大同中学男116 11顾丰交通大学附属中学男116 12蒋羽辰华东师范大学第二附属中学男116 13杨晟鑫复兴中学男116 14斯逸卿南洋模范中学男11615周鎏进才中学男116二等奖序姓名学校性别成绩1曹钦翔上海中学男1152毛杰申市西中学男1153陆奕骞控江中学男1124陈晟伟控江中学男1115刘赢延安中学男1096郭嘉骅复旦大学附属中学男1087王伟格致中学男1088叶云飞格致中学男1079沈之默控江中学男10710李观群控江中学男10711朱靓妤华东师范大学第二附属中学女10712蒋译瑶上海中学女10713姜雨晨南洋中学男10714陈睿源交通大学附属中学男10715罗珞交通大学附属中学男10616龚博易南洋模范中学男10617周昭奕延安中学男10418李汉平上海师范大学附属中学男10419沈楚雄位育中学男10420余玮骏行知中学男10321徐洋青浦中学男10322王殷超上海中学男10323徐梓榕格致中学女10324孟亦田格致中学男10325马吉锴格致中学男10226蔡迅捷格致中学男10227徐骥华东师范大学第二附属中学男10228谢飞延安中学男10229严一祥市西中学男10230陈皓复旦大学附属中学男10231唐鸿飞大同中学男10232高雄飞位育中学男10233曾加上海中学男102 34王久乐上海中学男102 35唐学卿控江中学男102 36魏传豪控江中学男101 37秦晨翔交通大学附属中学男101 38艾可华东师范大学第二附属中学男100 39宝鹏庆南洋模范中学男100 40纪宇诚松江第二中学男99 41蒋亚南交通大学附属中学男99 42陆竑斌向明中学男99 43熊一能复旦大学附属中学男98 44韩京俊复旦大学附属中学男98 45袁锴建平中学男98 46史奡建平中学男98 47张光耀七宝中学男98 48项刚七宝中学男98 49黄宇钦崇明中学男98 50胡一川曹杨第二中学男98 51朱呈岭嘉定第一中学男98 52陈嘉煜格致中学女98 53许婷婷行知中学女98 54林尧市西中学男98三等奖1徐捷复旦大学附属中学男97 2李宸上海中学男97 3袁君琦建平中学男97 4仲之越建平中学男97 5朱真维杨浦中学男97 6张定昊华东师范大学第一附属中学男97 7何俊杰闵行中学男97 8朱宇浩育才中学男97 9王浩民立中学男97 10杨方迪卢湾中学男97 11张子雨南洋模范中学男97 12夏茵南洋模范中学女9713傅超杰南洋模范中学男96 14宣炎复旦大学附属中学男96 15沈俊亮华东师范大学第二附属中学男96 16黄杰七宝中学男96 17张煜琪闵行中学男96 18王乃倩大同中学女96 19杨启帆大同中学男96 20孙雄毅上宝中学男96 21杨可人延安中学男96 22沈瑶青浦中学男96 23吴玮斌青浦中学男95 24张涛南洋模范中学男95 25倪翔南洋模范中学男95 26黄卯滢华东师范大学第二附属中学女93 27沈豪华东师范大学第二附属中学女93 28董俊翔复兴中学男93 29王玮毅控江中学男93 30林喆丰控江中学男93 31沈子骏大同中学男93 32周楚远曹杨第二中学男93 33严迟强民立中学男93 34应开元格致中学男93 35刘淳骅晋元中学男93 36沈睿上海市实验学校男93 37窦云雁建平中学男93 38顾易崇明中学男93 39沈宇豪崇明中学男93 40陈文哲交通大学附属中学男93 41孙轶凡杨浦中学男93 42陆桑田杨浦中学男92 43应碧丞大境中学男92 44秦奋育才中学男92 45朱灵市西中学男92 46马哲翱交通大学附属中学男92 47王佳军洋泾中学男92 48汪洋南洋模范中学男9149侯立豪华东师范大学第二附属中学男91 50刘达臻上海市实验学校男91 51沈昱西南位育中学男91 52周松年西南位育中学男91 53姜申俊风华中学男90 54丁佳靓晋元中学女90 55王凌志大同中学男89 56鲍志捷第八中学男89 57潘玫卢湾中学女89 58顾玥格致中学女89 59杨赟喆交通大学附属中学男89 60刘诗聪建平中学男89 61罗顺彦建平中学男88 62林望望建平中学男88 63丁栋复兴中学男88 64于人杰格致中学男88 65宋悦松江第二中学女88 66尹谷益崇明中学女88 67沈强南汇中学男88 68郑立元宜川中学男87 69哈元恺延安中学男87 70汪景云市西中学男87 71崔轶辰七宝中学女87 72郝隽一曹杨第二中学女87 73金嘉玮青浦中学男87 74章丽娜第二中学女87 75范佳斌位育中学男87 76郑超民立中学男87。
2002年全国高中数学联赛试题及解答

y
O
x
A.C100 B.C99 C.C100 D.C99 6.由曲线 x2=4y,x2=-4y,x=4,x=-4 围成的图形绕 y 轴旋转一周所得的旋转体的体积为 V1;满 足 x2+y2≤16,x2+(y-2)2≥4,x2+(y+2)2≥4 的点绕 y 轴旋转一周所得的旋转体的体积为 V2,则 1 A.V1= V2 2 2 B.V1= V2 3
y
D.4 个
O x
12|cosθ+sinθ-1| 设点 P(4cosθ,3sinθ). 点 P 与直线的距离 d= , 5 π 12 当 0≤θ≤ 时,d≤ ( 2-1),SABC≤6( 2-1)<3.即此时没有三角形面积=3; 2 5 π 12 当 <θ<2π 时,d≤ ( 2+1),SABC≤6( 2+1).即此时有 2 个三角形面积=3.选 B. 2 5 5.已知两个实数集合 A={a1,a2,a3,…,a100},与 B={b1,b2,…,b50},若从 A 到 B 的映射 f 使得 B 中每个元素都有原象,且 f(a1)≤f(a2)≤…≤f(a100),则这样的映射共有 A.C100 B.C99 C.C100 D.C99 解:不妨设b1≤b2≤…≤b50,在a1,a2,…,a100 的每两个数间有 1 个空档,共 99 个空档,其中任选 49 个空档插入 1 条竖杠, 把a1,a2,…,a100 分成 50 段,从前向后的第i段中的数映射到bi,即满足要求. 共有C99种插法,选D. 6.由曲线 x2=4y,x2=-4y,x=4,x=-4 围成的图形绕 y 轴旋转一周所得的旋转体的体积为 V1;满 2 足 x +y2≤16,x2+(y-2)2≥4,x2+(y+2)2≥4 的点绕 y 轴旋转一周所得的旋转体的体积为 V2,则 1 A.V1= V2 2 2 B.V1= V2 3 C.V1=V2 D.V1=2V2
2002年全国高中数学联合竞赛试题及解答.

2002年全国高中数学联合竞赛一试一、选择题:本大题共6个小题,每小题6分,共36分。
2002*1、函数)32(log )(221--=x x x f 的单调递增区间是A.()1,-∞- B.()1,∞- C.()+∞,1 D.()+∞,3◆答案:A★解析:由0322>--x x 解得1-<x 或3>x ,由复合函数的单调性可得选A 2002*2、若实数y x ,满足22214)12()5(=-++y x ,则22y x +的最小值为。
A.2B.1C.3D.2◆答案:B★解析:22214)12()5(=-++y x 可以看成以()12,5-为圆心,14为半径的圆,22y x +表示圆上的点到原点的距离的平方,因为圆心到原点的距离为13,所以11413222=-=+y x ,故选B2002*3、函数)(xx x f x --=A.是偶函数但不是奇函数B.是奇函数但不是偶函数C.既是偶函数又是奇函数D.既不是偶函数也不是奇函数◆答案:A★解析:计算出)(x f -的表达式整理到最简后对比即可发现,2002*4、直线134=+yx 与椭圆191622=+y x 相交于B A ,两点,该椭圆上点P ,使得PAB ∆面积等于3,这样的点P 共有A.1个 B.2个 C.3个 D.4个◆答案:B★解析:设()θθsin 3,cos 41P (20πθ<<),即点1P 在第一象限的椭圆上,如图,考虑四边形AOB P 1的面积S 。
可得⎪⎭⎫ ⎝⎛+=4sin 26πθS ,可知26max =S ,又6=∆OAB S 可知()3626max1<-=∆ABP S 所以点P 不可能在直线AB 的上方,显然在直线AB 的下方有两个点P ,故选B。
2002*5、已知两个实数集合{}10021,,,a a a A =与{}5021,,,b b b B =,若从A 到B 的映射f 使得B 中每个元素都有原象,且)()()(10021a f a f a f ≤≤≤ 则这样的映射共有A.50100C 个 B.4899C 个C.49100C 个D.4999C 个◆答案:D★解析:不妨设5021b b b <<< ,将A 中元素10021,,,a a a 按顺序分为非空的50组,定义映射B A f →:,使得第i 组的元素在f 之下的象都是i b (50,,2,1 =i ),易知这样的f 满足题设要求,每个这样的分组都一一对应满足条件的映射,于是满足题设要求的映射f 的个数与A 按足码顺序分为50组的分法数相等,而A 的分法数为4999C ,则这样的映射共有4999C ,故选D。
评2002年全国高中数学联赛

OH
在 △M O H 中 ,
MH = 3. OH
如果 N 在 CH 的延长线上 , 那么 M 将从上面所 说的位置 M 0 ( B M 0 = CH) 上移 , 这时有两种可能 : ( 1) M 在线段 M 0 H 内 . 由于 M 0 M = B M - B M 0 = CN - CH = HN , 所 以 M H + HN = M H + M 0 M = M 0 H , 根据上面所证 M0 H M H + HN + = 3.
= 27
2 ( v - v2 ) ( v - v2 ) ( 2× 1 6
3
1 - 2 v + 2 v2) 2
≤ 27
=
1 ( x1 + x2) . 2 3 2 a + 27 c - 9 ab 求 的最大值 . 3 λ 本题的解法很多 , 这里提供两种 . 解法 1 首先搞清 2 a3 + 27 c - 9 ab 的意义 . 如果 看不清楚 , 可先提出 27 , 将它写成 2 3 1 27 a ab + c 27 3 1 从ab 与 c 这两项可以猜出 . 3 1 2 3 1 f(a) = a ab + c , 3 27 3 而这立即可以验证是成立的 , 于是问题化为在条件 ( 1) , ( 2 ) 下 , 求 1 27 f ( a) 3 S = 3 λ 1 1 1 27 ( a - x1) ( a - x2) ( a - x3) 3 3 3 = 3 ( x2 - x1) 1 1 1 - 27 ( x 1 + a) ( x 2 + a) ( x 3 + a) 3 3 3 = 3 ( x2 - x1) 的最大值 .
3
2002年(首届)上海市TI杯高二年级数学竞赛
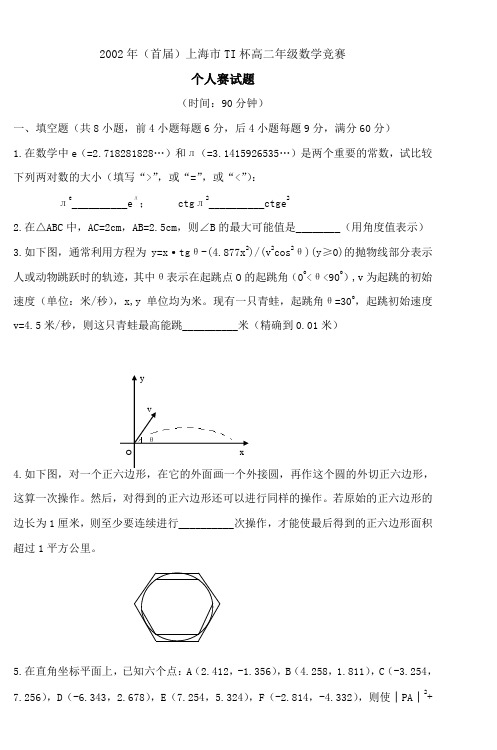
2002年(首届)上海市TI杯高二年级数学竞赛个人赛试题(时间:90分钟)一、填空题(共8小题,前4小题每题6分,后4小题每题9分,满分60分)1.在数学中e(=2.718281828…)和л(=3.1415926535…)是两个重要的常数,试比较下列两对数的大小(填写“>”,或“=”,或“<”):лe__________eл; ctgл2__________ctge22.在△ABC中,AC=2cm,AB=2.5cm,则∠B的最大可能值是________(用角度值表示)3.如下图,通常利用方程为y=x·tgθ-(4.877x2)/(v2cos2θ)(y≥0)的抛物线部分表示人或动物跳跃时的轨迹,其中θ表示在起跳点O的起跳角(0o<θ<90o),v为起跳的初始速度(单位:米/秒),x,y单位均为米。
现有一只青蛙,起跳角θ=30o,起跳初始速度v=4.5米/秒,则这只青蛙最高能跳__________米(精确到0.01米)θ4.这算一次操作。
然后,对得到的正六边形还可以进行同样的操作。
若原始的正六边形的边长为1厘米,则至少要连续进行__________次操作,才能使最后得到的正六边形面积超过1平方公里。
5.在直角坐标平面上,已知六个点:A(2.412,-1.356),B(4.258,1.811),C(-3.254,7.256),D(-6.343,2.678),E(7.254,5.324),F(-2.814,-4.332),则使│PA│2+│PB│2+│PC│2+│PD│2+│PE│2+│PF│2最小的点P的坐标是____________________ 6.海拔高度都是100米的三个雷达站A、B、C正好位于边长为1000米的正三角形的三个顶点上。
在某一时刻发现一个目标M,三个雷达站同时测得三个距离MA=2000米,MB=2000米,MC=1500米,此时这个目标位于海拔高度__________米的上空(精确到1米)7.已知AB是过双曲线x2/a2-y2/b2=1(a>0,b>0)右焦点F的弦,且AB⊥X轴,M是双曲线的右顶点,记∠BMA=θ,则用弧度值来表示θ的取值范围是___________________________(精确到10-4)8.通过函数y=sinx+1和y=x的图象交点可知方程x=sinx+1在(л/3,2л/3)内有一个解。
2002年全国高中数学联赛试题及答案

二○○二年全国高中数学联合竞赛试题参考答案及评分标准说明:1. 评阅试卷时,请依据本评分标准,选择题只设6分的0分两档,填空题只设9分和0分两档,其它各题的评阅,请严格按照本评分标准规定的评分档次给分,不要再啬其他中间档次。
2. 如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准适当档次评分,可以5分为一个档次,不要再增加其它中间档次。
一、 选择题(本题满分36分,每小题6分) 1、 函数f(x)=)32(log 221--x x 的单调递增区间是(A) (-∞,-1) (B) (-∞,1) (C) (1,+∞) (D) (3,+∞) 解:由x 2-2x-3>0⇒x<-1或x>3,令f(x)=u 21log , u= x 2-2x-3,故选A2、 若实数x, y 满足(x+5)2+(y12)2=142,则x 2+y 2的最小值为(A) 2 (B) 1 (C) 3 (D) 2 解:B 3、 函数f(x)=221xx x-- (A) 是偶函数但不是奇函数 (B) 是奇函数但不是偶函数(C) 既是奇函数又是偶函数 (D) 既不是奇函数又不是偶函数 解:A4、 直线134=+yx 椭圆191622=+y x 相交于A ,B 两点,该圆上点P ,使得⊿PAB 面积等于3,这样的点P 共有(A) 1个 (B) 2个 (C) 3个 (D) 4个 解:设P 1(4cos ,3sin ) (0<<2π),即点P 1在第一象限的椭圆上,如图,考虑四边形P 1AOB 的面积S 。
S=11OBP OAP S S ∆∆+=ααcos 4321sin 3421⨯⨯+⨯⨯=6(sin +cos )=)4sin(26πα+∴S max =62 ∵S ⊿OAB =6∴626)(max 1-=∆AB P S ∵626-<3∴点P 不可能在直线AB 的上方,显然在直线AB 的下方有两个点P ,故选B5、 已知两个实数集合A={a 1, a 2, … , a 100}与B={b 1, b 2, … , b 50},若从A 到B 的映射f 使得B 中的每一个元素都有原象,且f(a 1)≤f(a 2)≤…≤f(a 100),则这样的映射共有(A) 50100C (B) 5090C (C) 49100C (D) 4999C解:不妨设b 1<b 2<…<b 50,将A 中元素a 1, a 2, … , a 100按顺序分为非空的50组,定义映射f :A →B ,使得xyOA B P 1第i 组的元素在f 之下的象都是b i (i=1,2,…,50),易知这样的f 满足题设要求,每个这样的分组都一一对应满足条件的映射,于是满足题设要求的映射f 的个数与A 按足码顺序分为50组的分法数相等,而A 的分法数为4999C ,则这样的映射共有4999C ,故选D 。
2002年全国高中数学联赛试题及解答.doc

2002年全国高中数学联赛试题及解答一、选择题(本题满分36分,每小题6分)1.设全集是实数集,若A={x|≤0},B={x|=10x},则A∩是().A.{2}B.{-1}C.{x|x≤2}D.2.设sinα>0,cosα<0,且sin>cos,则的取值范围是().A.(2kπ+π/6,2kπ+π/3),k∈ZB.(2kπ/3+π/6,2kπ/3+π/3),k∈ZC.(2kπ+5π/6,2kπ+π),k∈ZD.(2kπ+π/4,2kπ+π/3)∪(2kπ+5π/6,2kπ+π),k∈Z3.已知点A为双曲线x2-y2=1的左顶点,点B和点C在双曲线的右分支上,△ABC是等边三角形,则△ABC的面积是().A./3 B.3/2 C.3 D.64.给定正数p,q,a,b,c,其中p≠q.若p,a,q是等比数列,p,b,c,q是等差数列,则一元二次方程bx2-2ax+c=0().A.无实根B.有两个相等实根C.有两个同号相异实根D.有两个异号实根5.平面上整点(纵、横坐标都是整数的点)到直线y=5/3x+4/5的距离中的最小值是().A./170 B./85 C.120 D.1306.设ω=cos+isin,则以ω,ω3,ω7,ω9为根的方程是().A.x4+x3+x2+x+1=0B.x4-x3+x2-x+1=0C.x4-x3-x2+x+1=0D.x4+x3+x2-x-1=0二、填空题〖HTK〗(本题满分54分,每小题9分)7.arcsin(sin2000°)=_______.8.设an是(3-)n的展开式中x项的系数(n=2,3,4,…),则=_______. 9.等比数列a+log23,a+log43,a+log83的公比是______. 10.在椭圆x2/a2+y2/b2=1(a>b>0)中,记左焦点为F,右顶点为A,短轴上方的端点为B.若该椭圆的离心率是,则∠ABF=______. 11.一个球与正四面体的六条棱都相切,若正四面体的棱长为a,则这个球的体积是______.12.如果:(1)a,b,c,d都属于{1,2,3,4};(2)a≠b,b≠c,c≠d,d≠a;(3)a是a,b,c,d中的最小值,那么,可以组成的不同的四位数的个数是______.三、解答题〖HTK〗(本题满分60分,每小题20分)13.设Sn=1+2+3+…+n,n∈N,求f(n)=的最大值.14.若函数f(x)=-1/2x2+13/2在区间[a,b]上的最小值为2a,最大值为2b,求[a,b].15.已知C0:x2+y2=1和C1:x2/a2+y2/b2=1(a>b>0),那么,当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为顶点、与C0外切、与C1内接的平行四边形?并证明你的结论.参考答案或提示一、1.D;2.D;3.C;4.A;5.B;6.B.提示:1.易得A={2},B={-1,2},则A∩=.2.由2kπ+π/2<α<2kπ+π,得2kπ/3+π/6<α<2kπ/3+π/3(k∈Z).又由sin>cos,得2kπ+π/4<<2kπ+5π/4(k∈Z).∴α∈(2kπ+π/4,2kπ+π/3)∪(2kπ+5π/6,kπ+π)(k∈Z).3.不妨设B点在x轴上方,则AB:y=/3x+/3,代入x2-y2=1,得B(2,).同理可得C(2,-).故S△ABC=3.4.由2b=p+c,2c=q+b,得b=2p+q3,c=p+2p3.于是从而Δ=4a2-4bc<0,方程无实根.5.整点(x0,y0)到直线5x-3y+12=0的距离为d=|25x0-15y0+12|/5.因25x0-15y0是5的倍数,所以|25x0-15y0+12|≥2,当x0=-1、y0=-1时等号成立.故/85即为所求.6.由ω=cos+isin知,ω,ω2,ω3,…,ω10(=1)是1的10个十次方根,则(x-ω)(x-ω2)(x-ω3)…(x-ω10)=x10-1.①又ω2,ω4,ω6,ω8,ω10是1的5个五次方根,则(x-ω2)(x-ω4)(x-ω6)(x-ω8)(x-ω10)=x5-1.②①÷②后,再两边同除以x-ω5(=x+1),得(x-ω)(x-ω3)(x-ω7)(x-ω9)=x4-x3+x2-x+1.二、7.-π/9;8.18;9.1/3;10.90°;11.a3;12.28.提示:7.原式=arcsin[sin(-π/9)]=-π/9.8.∵an=Cn2·3n-2,∴3n/an=…=18().∴原式=18= (18)9.公比,由等比定理,得10.由c/a=,得c2+ac-a2=0.又|AB|2=a2+b2,|BF|2=a2,故|AB|2+|BF|2=…=3a2-c2.而|AF|2=(a+c)2=…=3a2-c2=|AB|2+|BF|2,故∠ABF=90°.11.易知球心O为正四面体的中心,O点与棱的中点连线成为球的半径r,则r=,故球的体积为V=…=.12.按中所含不同数字的个数分三类:(1)恰有2个不同的数字时,组成=6个数;(2)恰有3个不同数字时,组成=16个数;(3)恰有4个不同数字时,组成=6个数.故符合要求的四位数共有6+16+6=24(个).三、13.,当且仅当n=64/n,即n=8时,上式等号成立,故f(n)max=1/50. 14.分三种情况讨论:(1)当0≤a<b时,f(a)=2b,f(b)=2a.解得[a,b]=[1,3].(2)当a<0<b时,f(0)=2b,f(a)=2a或f(b)=2a.解得[a,b]=[-2-,13/4].(3)当a<b≤0时,f(a)=2a,f(b)=2b.无解.综上,[a,b]=[1,3]或[-2-,13/4].15.所求条件为1/a2+1/b2=1.证明如下:必要性:易知,圆外切平行四边形一定是菱形,圆心即菱形中心.假设结论成立,则对点(a,0),有(a,0)为顶点的棱形与C1内接,与C0外切.(a,0)的相对顶点为(-a,0),由于菱形的对角线互相垂直平分,另外两个顶点必在y轴上,为(0,b)和(0,-b).菱形一条边的方程为x/a+y/b=1,即bx+ay=ab.由于菱形与C0外切,故必有,整理得1/a2+1/b2=1.必要性得证.充分性:设1/a2+1/b2=1,P是C1上任意一点,过P、O作C1的弦PR,再过O作与PR垂直的弦QS,则PQRS为与C1内接的菱形.设|OP|=r1,|OQ|=r2,则点P的坐标为(r1cosθ,r1sinθ),点Q的坐标为(r2cos(θ+),r2sin(θ+)),代入椭圆方程,得又在Rt△POQ中,设点O到PQ的距离为h,则同理,点O到QR,RS,SP的距离也为1,故菱形PQRS与C0外切.充分性得证.说明:今年高中数学联赛第4题由陕西省永寿县中学安振平老师提供,第6题和第10题由西安市西光中学刘康宁老师提供.。
2012年上海市TI杯高二年级数学竞赛

题号 5
6
7
1 44 4 8 , 8 9 4 ,4 96 8
8
2 4
答 案 1 5 15 ,2 51 6 , 2 、— 、, _ 一9 3 6 0 1 2 ,3 9 1 8 —9 , 9…
/ /
\ _ /
‘
二、解: 设A(ly)B(2y)则 x ,1, x ,2, lBI= (2 12 ( 一Y) A X 一X)+ Y 2 1。 = 2x 一x ). = (2 10 = 1 =、2X 一 【 ABI , 2 1. /l
解 答 以下 三 题 必须 写 出解 题 的必 要 步 骤 .
个 人赛试题 答案
一
二 、( 本题 满 分 2 分 )已知直线 X+Y= 0
4函 t ( ) (等) 与 数 =a z n ∈ u三 ] ,
的 图像 相交 于 A, B两 点, l BI 求 A 的值 ( 确 精
、
线.
相交 于 Q, 连结 R . R Q 则 Q就 是以点 A为投射 中心 , PG在 平 面 DMN 内的 中心 投 影 ;
A( ) 8
P E R
\ /
G
, ,
,
/
D( 0
\ /
图 1 0
A
Q
思路三: 图 1, 结 P 如 1连 F、 GF 设 PF与 1
D(’ C
图9
图1 1
思 路 二 : 如 图 1 ,分 别 延 长 AG、 DN、 0
AE、 设 A 与 DM 相 交于 R G与 DN D ,
以上思路所作 的投影就是在平面 DMN内 垂 直于平面A E的那条垂线 , 明留给读者. DF 证
2007年上海TI杯高二年级数学竞赛
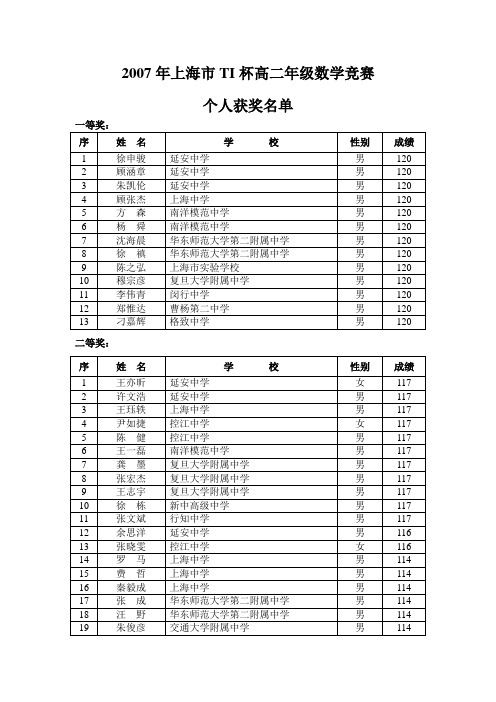
114
18
汪野
华东师范大学第二附属中学
男
114
19
朱俊彦
交通大学附属中学
男
114
20
李昕宇
交通大学附属中学
男
114
21
魏志一
交通大学附属中学
男
114
22
朱志尧
延安中学
男
114
23
王一珏
建平中学
男
114
24
朱劭宇
进才中学
男
113
25
罗涛
延安中学
男
111
26
张哲焘
控江中学
男
111
27
王钰
华东师范大学第二附属中学
9
陈之弘
上海市实验学校
男
120
10
穆宗彦
复旦大学附属中学
男
120
11
李伟青
闵行中学
男
120
12
郑惟达
曹杨第二中学
男
120
13
刁嘉辉
格致中学
男
120
二等奖:
序
姓名
学校
性别
成绩
1
王亦昕
延安中学
女
117
2
许文浩
延安中学
男
117
3
王珏轶
上海中学
男
117
4
尹如捷
控江中学
女
117
5
陈健
控江中学
男
117
6
王一磊
南洋模范中学
男
117
7
龚墨
复旦大学附属中学
男
2007年上海地区TI杯高二学年数学竞赛

108
14
王帅骏
民本中学
男
108
15
陈一镭
西南位育中学
男
108
16
张天伟
上南中学
男
108
17
顾宇丰
育才中学
男
108
18
李汝勇
行知中学
男
106
19
汤 艨
上海中学
男
105
20
陈文哲
交通大学附属中学
男
105
21
赵立毅
上海市实验学校
男
105
22
涂伟康
大同中学
男
105
23
徐 力
市西中学
男
105
24
武亦文
位育中学
35
朱 辉
闵行中学
男
102
36
朱晟祺
建平中学
男
102
37
蒋宇杰
位育中学
男
102
38
张尚骏
位育中学
女
102
39
陶 杰
进才中学
男
102
40
陈雨崴
敬业中学
男
102
41
宋家骥
杨浦高级中学
男
102
42
刘雄飞
育才中学
男
102
43
石宏霄
市西中学
男
101
44
刘基晟
上海中学
男
101
45
许 准
延安中学
男
101
46
吴 骥
格致中学
男
111
37
吕舒111
2007年上海市TI杯高二年级数学竞赛个人赛试

那0.0016、计算:tan1tan 2)tan 29)︒︒︒= . 7、底面直径为4,高为18的封闭圆柱,装半径为1的球,至多能装 个.
8、不等式组2
312,
23,34,1n
x x x n x n <<⎧⎪<<⎪⎪
<<⎨⎪⎪
⎪<<+⎩
的解集非空,则正整数n 的最大值为 .
解答以下三题必须写出解题的必要步骤. 二、(本题满分20分)
求正整数n ,使得[][][][][]33333log 1log 2log 3log 4log 2007n +++++= , 其中[]x 表示不超过x 的最大整数.
三、(本题满分20分)如图,正方形ABCD内接于椭圆,正方形EFGH和
正方形IJHK中的顶点E,F,I在椭圆上,顶点K,H,G在边AB上,顶点J在边HE 上.已知正方形ABCD与正方形EFGH的面积比为4∶1,求正方形IJHK与正方形EFGH 的面积比(精确到0.001).
四、(本题满分20分)我们知道,49
98
约分后是
1
2
,但按下面的方法,居然
也得1
2
:
4941
9882
==.试求出所有分子和分母都是十进制两位正整数,分子的个位数与
分母的十位数相同,且具有上述“奇怪”性质的真分数。
2002年少年数学初赛试卷

2002年少年数学初赛试卷一、解答题(共12小题,满分0分)1.“华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?2.长方形的各边长增加10%,那么它的周长和面积分别增加百分之几?3.如图所示的是一个正方体木块的表面展开图,若在正方体的各面填上数,使其对面两数之和为7,则A、B、C处填的数各是多少?4.在一列数:,,,,,,…中,从哪一个数开始,1与每个数之差都小于?5.“神舟五号”载人飞船载着航天英雄杨利伟于2003年10月16日清晨6时51分从太空返回地球,实现了中华民族的飞天梦.飞船绕地球共飞行14圈,其中后10圈沿离地面343千米的圆形轨道飞行.请计算飞船沿圆形轨道飞行了多少千米(地球半径为6371千米,圆周率π=3.14).6.如图,一块圆形的纸片分成4个相同的扇形,用红、黄两种颜色分别涂满各扇形,问共有几种不同的涂法?7.在9点至10点之间的某一时刻,5分钟前分针的位置与5分钟后时针的位置相同,此时刻是9点几分?8.一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数?9.任意写一个两位数,再将它依次重复3遍成一个8位数.将此8位数除以该两位数所得到的商再除以9,问:得到的余数是多少?10.一块长方形的木板,长为90厘米,宽为40厘米,将它锯成2块,然后拼成一个正方形,你能做到吗?11.如图,大小两个半圆,它们的直径在同一直线上,弦AB与小圆相切,且与直径平行,弦AB长12厘米.求图中阴影部分的面积(圆周率π=3.14).12.半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?2002年数学初赛试卷答案参考答案与解析一、解答题(共12小题,满分0分)1.“华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?考点:竖式数字谜.专题:填运算符号、字母等的竖式与横式问题.分析:根据整数加法的计算方法进行推算即可.解答:解:解法一:个位上:0+“杯”=4,可得“杯”=4;十位上:1+“华”的末尾是0,由1+9=10,可得“华”9,向百位上进1;百位上:9+1=10,向千位上进1;千位上:1+1=2;由以上可得:;因此,“华杯”代表的两位数是94.解法二:已知1910与“华杯”之和等于2004;那么“华杯”=2004﹣1910=94;因此,“华杯”代表的两位数是94.点评:本题非常巧妙地考察了对整数的加法运算法则及数位的进位等知识要点的熟悉掌握程度.2.长方形的各边长增加10%,那么它的周长和面积分别增加百分之几?考点:百分数的实际应用;长方形的周长;长方形、正方形的面积.专题:分数百分数应用题.分析:设长方形的长为a,宽为b,因此各边长增加10%时,则长为(1+10%)a=110%a,长为(1+10%)b=110%b,因此各边长增加10%时,周长增加2(1.1a+1.1b)﹣2(a+b)=2(a+b)×10%,即周长增加10%.面积增加1.1a×1.1b﹣ab=1.21ab﹣ab=ab×21%,即面积增加21%.解答:周长增加10%,面积增加21%解:设长方形的长为a,宽为b,边长增加10%时,则长为(1+10%)a=110%a,长为(1+10%)b=110%b,周长增加:2(110%a+110%b)﹣2(a+b)=220%a+220%b﹣2a﹣2b=2(a+b)×10%;面积增加:110%a×110%b﹣ab=121%ab﹣ab=ab×21%;答:周长增加了10%,面积增加了21%.点评:在求出长宽增加后的长度基础上,根据长方形的周长与面积公式计算是完成本题的关键.3.如图所示的是一个正方体木块的表面展开图,若在正方体的各面填上数,使其对面两数之和为7,则A、B、C处填的数各是多少?考点:正方体的展开图.专题:立体图形的认识与计算.分析:如图,是正方体展开图的“222”结构,把它折叠成正方体后,A面与1面相对,B面与2面相对,C面与4面相对,相使使其对面两数之和为7,A面填6,B面填5,C面填3.解答:解:如图,折成正方体后,A面与1面相对,B面与2面相对,C面与4面相对,要使其对面之各为7,则A面填6,B面填5,C面填3.点评:本题是考查正方体的展开图,关键是弄清把它折叠成正方体后,哪两个面相对.4.在一列数:,,,,,,…中,从哪一个数开始,1与每个数之差都小于?考点:数列中的规律.专题:探索数的规律.分析:这列数的特点是每个数的分母比分子大2,分子为奇数列,要使1﹣<,则n>999.5,即从n=1000开始,带入分数,即可得解.解答:解:这列数的特点是每个数的分母比分子大2,分子为奇数列,1﹣<,n>999.5,从n=1000开始,即从开始,满足条件.答:从开始,1与每个数之差都小于.点评:找出这列数的规律,根据已知列出等式求解.5.“神舟五号”载人飞船载着航天英雄杨利伟于2003年10月16日清晨6时51分从太空返回地球,实现了中华民族的飞天梦.飞船绕地球共飞行14圈,其中后10圈沿离地面343千米的圆形轨道飞行.请计算飞船沿圆形轨道飞行了多少千米(地球半径为6371千米,圆周率π=3.14).考点:有关圆的应用题.专题:平面图形的认识与计算.分析:先圆形轨道的半径,再根据圆的周长公式:C=2πr求出飞船沿圆形轨道飞行1圈的长度,再乘以10即可求出飞船沿圆形轨道飞行了多少千米.解答:解:2×3.14×(6371+343)×10=2×3.14×6714×10=3.14×134280=421639.2(千米);答:飞船沿圆形轨道飞行了421639.2千米.点评:考查了有关圆的应用题,关键是熟练掌握圆的周长公式.6.如图,一块圆形的纸片分成4个相同的扇形,用红、黄两种颜色分别涂满各扇形,问共有几种不同的涂法?考点:染色问题.专题:传统应用题专题.分析:根据四个扇形中有一个红色、两个、三个、四个分类列举即可.解答:解:按逆时针方向涂染各扇形:红红红红红红红黄红红黄黄红黄红黄红黄黄黄黄黄黄黄所以,共有6种.点评:本题考查了排列组合知识中的染色问题,还可以列式解答:4×(4﹣1)÷2=6(种).7.在9点至10点之间的某一时刻,5分钟前分针的位置与5分钟后时针的位置相同,此时刻是9点几分?考点:时间与钟面.专题:时钟问题.分析:可设当前是9点x分,则5分钟前分针指向x﹣5的位置,而分针转动的速度是时针的12倍,分针5分钟后指向x+5的位置,时针指向9刻度后刻度处,根据题意列出方程解答即可.解答:解:设当前时刻是9点x分.则5分钟后时针的位置为45+=x﹣5540+x+5=12x﹣6011x=605x=55;答:此时刻是9点55分.点评:本题主要考查钟表问题的实际应用,熟练掌握钟表的特征是解答本题的关键.8.一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数?考点:抽屉原理.专题:传统应用题专题.分析:建立抽屉:一副扑克牌有54张,大小鬼不相同,那么(54﹣2)÷4=13,所以一共有13+2=15个抽屉;分别是:1、2、3、…K、小鬼、大鬼,由此利用抽屉原理考虑最差情况,即可进行解答.解答:解:建立抽屉:54张牌,根据点数特点可以分别看做15个抽屉,考虑最差情况:每个抽屉都摸出了1张牌,共摸出15张牌,此时再任意摸出一张,无论放到哪个抽屉,都会出现有两张牌在同一个抽屉,即两张牌点数相同,15+1=16(张),答:至少抽取16张扑克牌,方能使其中至少有两张牌有相同的点数.点评:此类问题关键是根据点数特点,建立抽屉,这里要注意考虑最差情况.9.任意写一个两位数,再将它依次重复3遍成一个8位数.将此8位数除以该两位数所得到的商再除以9,问:得到的余数是多少?考点:带余除法.专题:余数问题.分析:先设这个两位数为10a+b,则可用含a、b的代数式表示将它依次重复写3遍成的一个8位数,再将此8位数除以该两位数得到商为1010101,然后将1010101除以9即可求解.解答:解:设这个两位数为10a+b,则将它依次重复3遍成的一个8位数为:1000000(10a+b)+10000(10a+b)+100(10a+b)+10a+b=1010101(10a+b),将此8位数除以该两位数得到的商为:1010101(10a+b)÷(10a+b)=1010101,则1010101÷9=112233…4.答:得到的余数是4.点评:本题考查了带余除法的定义及应用,难度中等,用含a、b的代数式正确表示将(10a+b)这个数依次重复写3遍成的一个8位数是解题的关键.10.一块长方形的木板,长为90厘米,宽为40厘米,将它锯成2块,然后拼成一个正方形,你能做到吗?考点:图形的拆拼(切拼).专题:平面图形的认识与计算.分析:因为这块长方形木板的面积为90×40=3600(平方厘米),又因为3600=60×60,即所求的正方形的边长为60厘米,如下图所示.解答:解:因为90×40=3600,3600=60×60,所求的正方形的边长为60厘米,可以如下图拼成:因此,能拼成一个正方形.点评:先求出总面积,看看是否能分成两个数的平方.11.如图,大小两个半圆,它们的直径在同一直线上,弦AB与小圆相切,且与直径平行,弦AB长12厘米.求图中阴影部分的面积(圆周率π=3.14).考点:组合图形的面积.专题:平面图形的认识与计算.分析:将小圆缩小至0,则AB就是大圆直径,阴影部分就是大圆的一半,利用圆的面积公式即可求解.解答:解:将小圆缩小至0,则AB就是大圆直径,阴影部分就是大圆的一半,所以阴影部分的面积是:×3.14×(12÷2)2=×3.14×36=56.52(平方厘米);答:图中阴影部分的面积是56.52平方厘米.点评:此题可以巧妙地利用“缩小法”,得出阴影部分的面积与直径为AB的圆的面积的关系,问题即可得解.12.半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?考点:有关圆的应用题.专题:平面图形的认识与计算.分析:由于小铁环的半径为25厘米,大铁环的半径为50厘米,可得小铁环的半径是大铁环半径的一半.根据周长与半径的关系可得大环周长是小环的2倍,即小环沿大环转2个周长时又回到原位,再减去公转的1圈,可得小环自身转动的圈数.解答:解:由于小铁环的半径是大铁环半径的一半,所以大环周长是小环的2倍,即小环沿大环转2个周长时又回到原位,其中有1个周长属于小环公转的,而另一个周长才是小环自身转动的,因此,小环自身转动1圈.点评:本题考查了圆与圆的位置关系,小铁环运动的圈数乘以它的周长就等于大铁环的周长.。
2004年上海市TI杯高二年级数学竞赛
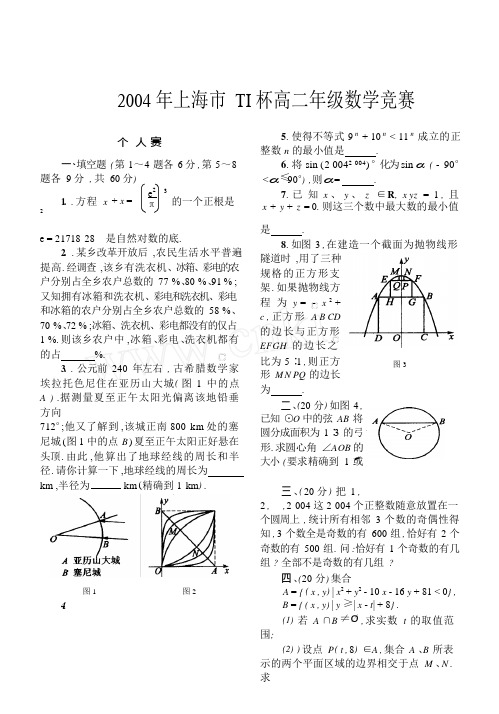
2004 年上海市TI 杯高二年级数学竞赛个人赛一、填空题( 第1~4 题各6 分, 第5~8题各9 分, 共60 分)5. 使得不等式9 n+ 10 n< 11 n成立的正整数n 的最小值是.6. 将sin ( 2 0042004) °化为sin α ( - 90°<α≤90°),则α= .1.. 方程x 2+ x =3的一个正根是7. 已知x 、y 、z ∈R, x yz = 1 , 且x + y + z = 0. 则这三个数中最大数的最小值e = 21718 28 是自然对数的底.2.. 某乡改革开放后,农民生活水平普遍提高. 经调查,该乡有洗衣机、冰箱、彩电的农户分别占全乡农户总数的77 %、80 %、91 % ; 又知拥有冰箱和洗衣机、彩电和洗衣机、彩电和冰箱的农户分别占全乡农户总数的58 %、70 %、72 % ;冰箱、洗衣机、彩电都没有的仅占1%. 则该乡农户中,冰箱、彩电、洗衣机都有的占%.3.. 公元前240 年左右, 古希腊数学家埃拉托色尼住在亚历山大城( 图1 中的点A ) .据测量夏至正午太阳光偏离该地铅垂方向712°;他又了解到,该城正南800 km 处的塞尼城(图1 中的点B ) 夏至正午太阳正好悬在头顶. 由此, 他算出了地球经线的周长和半径. 请你计算一下,地球经线的周长为km ,半径为km (精确到1 km) .图1 图24.是.8. 如图3 , 在建造一个截面为抛物线形隧道时,用了三种规格的正方形支架. 如果抛物线方程为y = - x 2+c , 正方形 A B CD的边长与正方形EFGH 的边长之比为5 ∶1 ,则正方图3形M N PQ 的边长为.二、(20 分) 如图4 ,已知⊙O 中的弦AB 将圆分成面积为1∶3 的弓形. 求圆心角∠A OB 的大小(要求精确到1′或三、( 20 分) 把1 ,2, , 2 004 这2 004 个正整数随意放置在一个圆周上, 统计所有相邻3 个数的奇偶性得知, 3 个数全是奇数的有600 组, 恰好有2 个奇数的有500 组. 问:恰好有1 个奇数的有几组? 全部不是奇数的有几组?四、(20 分) 集合A = { ( x , y) | x2+ y2- 10 x - 16 y + 81 < 0} ,B = { ( x , y) | y ≥| x - t| + 8} .(1)若A ∩B ≠Ø , 求实数t 的取值范围;(2)) 设点P ( t , 8) ∈A , 集合A 、B 所表示的两个平面区域的边界相交于点M 、N . 求e2 πPM ·PN PM ·PN ′22i 的最小值 2005 年第 3 期1 + 1 .| PM | | PN |团 体 赛33三、设恰好有 1 个奇数的有 x 组. 则全部不是奇数 的 有 2 004 - 600 - 500 - x = 904 - x .将圆周上的数从某个数开始 , 依次记为 x 1 , x 2 , , x 2 004 ,令一、(20 分) 已知 f ( x ) = ( x - 1) ( x - 2) · ·( x - 2 004) . - 1 , 当 x i 为奇数时 ,y i =1 , 当 x 为偶数时.问 :有多少个实数 x , 使得| f ( x ) | = 1 ?二、( 20 分) 集 合 M = { 12 , 22 , , 10002} . 问 :能否把集合 M 分拆成 2 个非空子 集 A 、B , 同时 , 满足(1) A ∪B = M , A ∩B = Ø ;(2) 集合 A 与集合 B 的元素和相等. 若可能 , 指出具体的分法 , 并给出证明; 若不能 , 说明理由.三、(20 分) 如图 5 , 有 2 个长方形的金属片零件 A B CD 和 EC FG 放在直角坐标平面 上 , 从原点 O 发出的激光将对零件作切割. 如果激光( l ) 一次从 2 个长方形上切割下的 2 个金属零件( 均在 l 上方) 的面积恰好相等 , 求 激 光 ( l ) 所 图 5 则 y 1 + y 2 + + y 2 004 = 0 , 且 A i = y i + y i + 1 + y i + 2 =- 3 , 当 x i 、x i + 1 、x i + 2全为奇数时 , - 1 , 当 x i 、x i + 1 、x i + 2恰好有 2 个奇数时 , 1 , 当 x i 、x i + 1 、x i + 2恰好有 1 个奇数时 , 3 , 当 x i 、x i + 1 、x i + 2全为偶数时.( x 2 004 + i = x i . )则 0 = 3 ( y 1 + y 2 ++ y 2 004 )= A 1 + A 2 + + A 2 004= - 3 ×600 - 500 + x + 3 (904 - x ) .解 得 x = 206 , 904 - x = 698.因此 ,恰好有 1 个奇数的有 206 组 , 全部不是奇数的有 698 组.四、(1) 集合 A = { ( x , y ) | ( x - 5) 2 + ( y - 8) 2 < (2 2) 2} .当射线 y = x - t + 8 ( x ≥t ) 与圆( x - 5) 2 + ( y - 8) 2 = (2 2) 2 相切时 ,有在的直线方程.参 考 答 案个 人 赛一、1. 31141 62. 513. 40 0006 3664.3= 2 2 .解得 t = 1 或 t = 9 (舍去) .当射线 y = t - x + 8 ( x ≤t ) 与圆( x - 5) 2 + ( y - 8) 2 = (2 2) 2相切时 ,有31079 15. 56. - 36°7.64 或 11587 4= 2 2 .解得 t = 1 (舍去) 或 t = 9.二、设 ⊙O 的半径为 r , M 为劣弧A B 上一点 ,A MB 的弧度为α. 则S 弓形AB M A = S 扇形OA MB - S OAB所以 , t 的取值范围是 1 < t < 9. (2) 如图 6 , 设集合 A 所表示的圆与 x 轴平行的直径为 CD , = 1 αr 2 - 1 r 2 sin α. M P 的延长线与圆的 2 2另一个交点为 N ′. 则则 1 αr 2 - 1 r 2 sin α= 1πr 2 ,即 1 1224| PM | +| PN |α- π = sin α.2 令β=α-π,则β= cos β.利用计算器算得β≈01739 1 弧度. 从而 ,α=β+ π≈2131 (弧度) .≥2 =2图 6| 5 - 8 - t + 8|2| 5 + 8 - t - 8|2PC ·PDk75k即 7k57k或 ′5 7 5·, =2≥ 2= 4 = 4 = 2 .PC + PD2CD 4 2 2 当 t = 5 时 ,上式等号成立. 故 1 + 1 的最小值为 2 . | PM | | PN | 2团 体 赛图 8一、如图 7 ,画出函数 f ( x ) 的草图.因为 S A ′C ′D = S G ′F ′G ,而Rt A ′C ′D Rt G ′F ′G , 故 Rt A ′C ′D Rt G ′F ′G.由 DC = GF ′,得 4 - 4 = 6k- 7. 所以 ,k =2 ∈3 , 6 .3 5 7(2) 当 k OE ≤k < k OF ,即4 ≤k <3时 ,设 l 与 2 个金属片零件的边界分别交于点 A ″、C ″、G ″、B ′( 如 图 7图 8 ) , 易 知 A ″( 4 , 4 k ) , C ″ 4 , 4 , G ″( 7 , 7 k ) , 由图像知 ,在 1~2 004 之间的每 2 个相邻整数之间 ,有 2 个实数使得| f ( x ) | = 1.在(0 , 1) 及(2 004 , + ∞) 中各有 1 个实数 x , 使得| f ( x ) | = 1.因此 ,共有 2 003 ×2 + 1 + 1 = 4 008 个实数 x , 使得| f ( x ) | = 1.二、结论是肯定的. 因为 12 + 22 + + 1 0002B ′(10 , 10 k ) . 由 S A ″C ″D = S 得 1 4- 4 (4 - 4 k ) = 1[ (6 - 7 k ) + (6 - 10 k ) ] 3 , 2 k 2 有 67 k 2- 68 k + 16 = 0.解 得 k 1 2 =2 (17 ± 21)≈01644 256 或 01370 669.4 3=1 ×1 000 ×1 001 ×2 001 = 333 833 500 , 易知 k 1 ,2 7 5 . 此时不可能.6所 以 ,333 833 500= 166 916 750.(3) 当 k OC < k < k OE , 2 5 < k < 4时 , 设 l 与 22而 12 + 22+ + 7932 < 166 916 750 < 12 + 22 + + 7942 = 167 170 745 , 则 167 170 745 - 166 916 750 = 253 995 = 5032 + 312 + 52 .个金属片零件的边界分别交于点 A ?、C ?、B ″( 如图 8) ,易知 A ?(4 , 4 k ) , C ″ 4, 4 , B ″(10 , 10 k ) . 由 S A ?C ?D = S 五边形EC ?B ″FG ,得S A ?C ?D = S 四边形ECFG - S B ″C ?C .取 A = { 12 , 22 , , 7942} \ { 52 , 312 , 5032} , B = { 7952 , 7962 , , 1 0002} ∪{ 52 , 312 , 5032} .1 4k 4 4 - 4 k则这样的 A 、B 满足题设条件.= 6 - 1 2 10 - 4 k (10 k - 4) .6 .7三 、易 知 k OC = 2 , k OE = 4, k OF设直线 l的方程为 y =k x .= 3, k OG = 有 29 k 2解得 k 1 ,2 =31 ± 33≈01633 5 或 01435. 只有 k = 31 - 33 ∈ 2 , 4 .585 7 (1) 当 k OF ≤k ≤k OG ,即3 ≤k ≤6 时 ,设 l 与 2综上所述 ,欲求的直线方程为个金属片零件的边界分别交于点 A ′、C ′、G ′、F ′( 如图 8 ) . 易知 A ′( 4 , 4 k ) , G ′ 4 , 4 , G ′( 7 , 7 k ) , y =2 3 x y = 31 - 33 (顾鸿达 提供)F 66 . k ∈ 则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2002年(首届)上海市TI杯高二年级数学竞赛
个人赛试题
(时间:90分钟)
一、填空题(共8小题,前4小题每题6分,后4小题每题9分,满分60分)
1.在数学中e(=
2.718281828…)和л(=
3.1415926535…)是两个重要的常数,试比较下列两对数的大小(填写“>”,或“=”,或“<”):
лe__________eл; ctgл2__________ctge2
2.在△ABC中,AC=2cm,AB=2.5cm,则∠B的最大可能值是________(用角度值表示)
3.如下图,通常利用方程为y=x·tgθ-(
4.877x2)/(v2cos2θ)(y≥0)的抛物线部分表示人或动物跳跃时的轨迹,其中θ表示在起跳点O的起跳角(0o<θ<90o),v 为起跳的初始速度(单位:米/秒),x,y单位均为米。
现有一只青蛙,起跳角θ=30o,起跳初始速度v=4.5米/秒,则这只青蛙最高能跳__________米(精确到0.01米)
θ
4.如下图,对一个正六边形,在它的外面画一个外接圆,再作这个圆的外切正六边形,这算一次操作。
然后,对得到的正六边形还可以进行同样的操作。
若原始的正六边形的边长为1厘米,则至少要连续进行__________次操作,才能使最后得到的正六边形面积超过1平方公里。
5.在直角坐标平面上,已知六个点:A(2.412,-1.356),B(4.258,1.811),C (-3.254,7.256),D(-
6.343,2.678),E(
7.254,5.324),F(-2.814,-4.332),则使│PA│2+│PB│2+│PC│2+│PD│2+│PE│2+│PF│2最小的点P的坐标是____________________
6.海拔高度都是100米的三个雷达站A、B、C正好位于边长为1000米的正三角形的三个顶点上。
在某一时刻发现一个目标M,三个雷达站同时测得三个距离MA=2000米,MB=2000米,MC=1500米,此时这个目标位于海拔高度__________米的上空(精确到1米)
7.已知AB是过双曲线x2/a2-y2/b2=1(a>0,b>0)右焦点F的弦,且AB⊥X轴,M 是双曲线的右顶点,记∠BMA=θ,则用弧度值来表示θ的取值范围是___________________________(精确到10-4)
8.通过函数y=sinx+1和y=x的图象交点可知方程x=sinx+1在(л/3,2л/3)内有一个解。
为了求出方程x=sinx+1精确到10-5的近似解可以采用下述的“迭代”方法进行:设x n=sinx n-1+1(n=1,2,3,…),取初始值x0=2,得x1=sin2+1=1909297427,x2=sin1.909297427+1=1.94325347,…直到│x n-x n-1│<10-6时,我们就把x=x n作为方程的近似解,则上述方程精确到10-5的近似解是__________
*解答以下三题必须写出解题的必要步骤
二、(本题满分20分)
已知函数f(x)=10+10sinxcosx-20cos2x,若方程f(x)=m(m为整数)在[0,л]内恰有两个不相等的实数根,求m的值。
三、(本题满分20分)
⑴写出一个以2002起首的十位完全平方数(应指出它是哪个自然数的平方)
⑵任给一个以2002起首的六位数,是否总能在其后面添加4个数字,使得到的十位数是一个完全平方数?证明你的结论
四、(本题满分20分)
椭圆x2/a2+y2/b2=1(a>0,b>0)的面积可用公式S=лab计算。
设F为椭圆x2/a2+y2/b2=1(a>0,b>0)的右焦点,且使以O为圆心,OF为半径的圆的面积恰好等于已知椭圆的面积,A为该圆与椭圆在第一象限内的交点,记∠XOA=θ(θ为锐角),求θ的大小(用角度值表示)。
