(整理)IEEE14节点模型.
MATLAB潮流程序(IEEE14直角坐标牛拉法)

Pgen=Data1(:,10);%发电机发出有功Qgen=Data1(:,11);%发电机发出无功Vset=Data1(:,13);MATLAB 潮流程序(IEEE14直角坐标牛拉法) clearbaseMVA=100;%功率基值%%读 Data1 中数据load Data1.txt Bus=Data1(:,1);%节点号 Vtype=Data1(:,5); %节点类型 Pload=Data1(:,8); %负载有功 Qload=Data1(:,9); %负载无功 Qsh=Data1(:,17);%并联电容电纳标幺值%%读 Data2 中数据 load Data2.txtII=Data2(:,1);JJ=Data2(:,2); %支路端点号 Ltype=Data2(:,5);%线路类型 R=Data2(:,6); %两点间电阻 X=Data2(:,7);%两点间电抗%电压设定点%线路对地电纳 %变压器非标准变压比%%求导纳矩阵 Yy1=zeros(14); y2=zeros(14); y3=zeros(14); lin=length(II);for x=1:lin switch Ltype(x) case 1 y1(II(x),JJ(x))=1/(R(x)+i*X(x)); y1(JJ(x),II(x))=y1(II(x),JJ(x)); y3(II(x),JJ(x))=i*B(x); y3(JJ(x),II(x))=i*B(x);case 2 y1(II(x),JJ(x))=1/((R(x)+i*X(x))*K(x)); y1(JJ(x),II(x))=y1(II(x),JJ(x));y2(ll(x),JJ(x))=(1-K(x))/((R(x)+i*X(x))*K(xF2); y2(JJ(x),II(x))=(K(x)-1)/((R(x)+i*X(x))*K(x)); end end clear x Y=zeros(14); for x=1:14Y(x,x)=sum(y1(x,:))+sum(y2(x,:))+sum(y3(x,:))+i*Qsh(x); end clear x;B=Data2(:,8)/2;K=Data2(:,14); %支路数Y=Y-y1;G=real(Y);B=imag(Y);%%设电压初值U=Vset;e=real(U);f=imag(U);%%Ps=zeros(1,14);Qs=zeros(1,14);D=ones(26,1);for x=1:14Ps(x)=(Pgen(x)-Pload(x))/baseMVA; Qs(x)=(Qgen(x)-Qload(x))/baseMVA; endclear x;N=0;Jacbi=zeros(26);while max(abs(D))>0.000001%节点功率及for x=2:14 电压不平衡量switch Vtype(x)case 1 %PQ节点D(2*x-3)=Ps(x)-e(x)*(G(x,:)*e-B(x,:)*f)-f(x)*(G(x,:)*f+B(x,:)*e);D(2*x-2)=Qs(x)- f(x)*(G(x,:)*e-B(x,:)*f)+e(x)*(G(x,:)*f+B(x,:)*e);case2 %PV节点D(2*x-3)=Ps(x)-e(x)*(G(x,:)*e-B(x,:)*f)-f(x)*(G(x,:)*f+B(x,:)*e);D(2*x-2)=Vset(x).*Vset(x)-(e(x).八2+f(x).八2);e ndendclear mfor I=2:14 克比%求雅矩阵for J=2:14%非对角元素if I~=JJacbi((2*l-3),(2*J-3))=B(l,J)*e(l)-G(l,J)*f(l);Jacbi((2*I-3),(2*J-2))=-(G(I,J)*e(I)+B(I,J)*f(I));switch Vtype(I)case 1 %PQ节点Jacbi((2*I-2),(2*J-3))=G(I,J)*e(I)+B(I,J)*f(I);Jacbi((2*I-2),(2*J-2))=B(I,J)*e(I)- G(l,J)*f(l);case 2 %PV 节点Jacbi((2*I-2),(2*J-3))=0;Jacbi((2*I-2),(2*J-2))=0;endelse %对角元素Jacbi(2*l-3,2*J-3)=-(G(l,:)*f+B(l,:)*e)+B(l,l)*e(l)-G(l,l)*f(l);Jacbi(2*l-3,2*J-2)=-(G(l,:)*e- B(l,:)*f)-G(l,l)*e(l)-B(l,l)*f(l);switch Vtype(l)case 1 %PQ节点Jacbi(2*l- 2,2*J-3)=-(G(l,:)*e-B(l,:)*f)+G(l,l)*e(l)+B(l,l)*f(l);Jacbi(2*l-2,2*J-2)=(G(l,:)*f+B(l,:)*e)+B(l,l)*e(l)-G(l,l)*f(l);case22*f(l); %PV节点Jacbi(2*l-2,2*J-3)=-Jacbi(2*I-2,2*J-2)=-2*e(I);endendendendclear l J;Deta=-inv(Jacbi)*D;正方程for%修x=2:14初值f(x)=f(x)+Deta((2*x-3),1);%新电压e(x)=e(x)+Deta((2*x-2),1);endclear x;U=e+i*f;N=N+1;endN=N-1;S0=U(1)*(conj(Y(1,:))*conj(U));衡节点功率S1=zeros(20,1);%始端功率S2=zeros(20,1); 端功%末率for x=1:20S1(x)=U(II(x))*(conj(U(II(x)))*(conj(y2(II(x)))+y3(II(x))+i*Qsh(II(x)))+(conj(U(II(x)))- conj(U(JJ(x))))*conj(y1(II(x),JJ(x))));S2(x)=U(JJ(x))*(conj(U(JJ(x)))*(conj(y2(JJ(x)))+y3(JJ(x))+i*Qsh(JJ(x)))+(conj(U(JJ(x)) )-conj(U(II(x))))*conj(y1(II(x),JJ(x))));enddetaS=S1+S2;%线路损耗功率Vabs=abs(U);%电压幅值%相Angle=atan(f./e)*180/Pi ;角%%显示数据disp(' 迭代次数N=');disp(N);dis PC各节点电压');dis PC节点幅值相角');disP([Bus Vabs Angle]);dis PC平衡节点功率');disp(S0);dis PC线路功率');disP(' II JJ始端功率末端功率线路损耗功率'); disP([II JJ S1 S2 detaS]);Datal及Data2数据文件也已上传文件名就是Datal和Data2。
电力系统实验-5节点图像
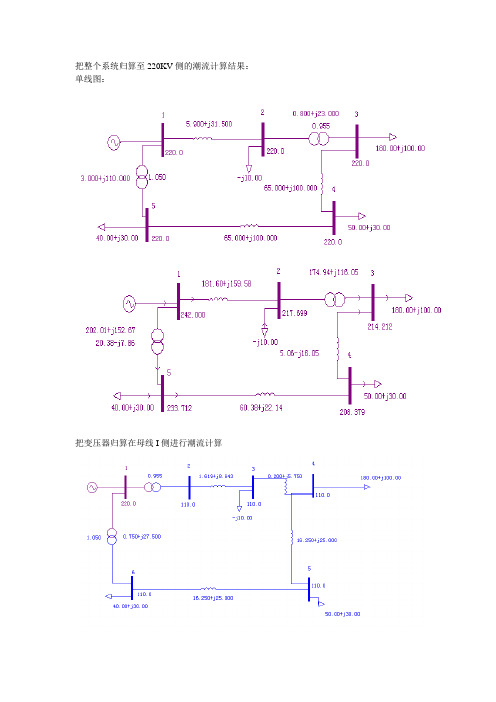
把整个系统归算至220KV侧的潮流计算结果:单线图:把变压器归算在母线I侧进行潮流计算计算结果变压器电阻折算到低压侧:潮流计算结果:潮流调整结果:串入电抗L=30欧时:L=28欧时电抗=25欧时:电抗=25欧时:IEEE14节点系统的潮流计算与潮流调整一、实验目的1.掌握电力系统稳态运行的基本要求;2.培养应用电力系统仿真计算软件PSASP进行潮流调整和电压调整的实践能力;3.培养运用所学知识分析和解决问题的能力;二、实验原理1.潮流调整的方式及基本原理(添加内容,图形可打印,描述手写)2.电压调整的方式及基本原理(添加内容,图形可打印,描述手写)3.无功功率最优分布的原理三、实验内容1.采用文本输入参数的方式计算IEEE14节点系统指定运行方式下的潮流;2.利用文本方式输入的数据绘制IEEE14节点单线图;3.把某一线路的功率限制在指定值之内4.把某一节点的电压提高(降低)到指定值。
5.调整潮流,尽可能使得网络损耗最小。
(附加实验)四、实验结果(图形打印,其他手写)1.IEEE14节点潮流计算结果及其分析(0) 画出IEEE14节点单线图;(1)单线图显示的潮流(2)对线路进行分析,分析每个PV节点的作用。
(3)对潮流结果进行分析(每个节点的有功、无功是否平衡;无功流动方向与电压、相角之间的关系;有功流过方向与电压、相角之间的关系;系统存在几个电压等级;潮流大致流动方向;为什么各个变压器流过的潮流不同?;3、6、8);(4)为什么选择3、6、8母线PV(电压支撑作用)作为电压支撑节点?3、6、8母线去掉无功电源的潮流状态如何?(5)把重负荷节点如3母线负荷与轻负荷节点如14母线节点负荷对换后的潮流有什么变化?为什么?2.线路过载时的调整策略及结果(1)问题分析+解决方案分析如把母线3和母线14的负荷置换,要求变压器5-6(接在这两个母线上的变压器)的潮流限制在60MV A。
A.改变变压器的变比,R=R’平方,就是改变变压器的阻抗;B.改变变压线路上的阻抗值,潮流与阻抗成反比;C.备用发电机发电。
以IEEE14、30、39节点为例应用计算机形成关联矩阵教材

2、IEEE30节点
1
2
5
7
8
3
4
6
13
11 9
12
14
16 15
17 10
28
29 27
18 15
21
22
19
20
24
IEEE30节点系统图
30 25 26
30个节点,41条支路
2、IEEE30节点系统各线路数据
将各线路数据输入到excel表格中, 便于程序的调用
高等电力网络分析
题目
以IEEE14、30、39节点为例应用计算机形成关联 矩阵,用matlab编程,结果存到excel中
电力系统中IEEE节点:是为了验证某一个计算方法行不行 而设立的节点
1、IEEE14节点
14个节点,20条支路
IEEE14节点系统图
1、IEEE14节点程序设 计
对于含有变压器的支路, 节点电流的正负规则不变, 以支路首端为参考,则末 端为负的变比。
设计思路:将IEEE14节点系统的数据存入到data中,定义14*20的零矩阵,以 支路号为循环变量并作为A的列元素,取出data中该支路号对应的首端节点数 并作为A的行元素,令节点数并作为A的行元素,令A矩阵对应的位置为-1。遵循节点电流流出 为正,流入为负的规则。
含有变压器的支路中变压器的变比
2、IEEE30节点程序设计
编程思路与IEEE14节点系统类似。 区别之处在于:调用的excel数据库不同;定义的关联矩阵A 维数不同。
2、IEEE30节点A矩阵结果
剩下的结果略
3、IEEE39节点系统图
未查到相关数据,思路与前面的一样
电力系统仿真实训报告电力系统仿真实训

电力系统仿真实训报告1 前言电力系统潮流计算是研究电力系统稳态运行情况的一种计算,它根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态。
在电力系统规划设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量分析、比较供电方案或运行方式的合理性、可靠性和经济性。
本次课程设计任务是闭环网络的潮流计算,用到的方法为PQ分解法潮流计算。
2 实训目的与要求2.1实训目的电力系统分析的潮流计算是电力系统分析的一个重要的部分。
通过对电力系统潮流分布的分析和计算,可进一步对系统运行的安全性,经济性进行分析、评估,提出改进措施。
电力系统潮流的计算和分析是电力系统运行和规划工作的基础。
潮流计算是指对电力系统正常运行状况的分析和计算。
通常需要已知系统参数和条件,给定一些初始条件,从而计算出系统运行的电压和功率等;潮流计算方法很多:高斯-塞德尔法、牛顿-拉夫逊法、P-Q分解法、直流潮流法,以及由高斯-塞德尔法、牛顿-拉夫逊法演变的各种潮流计算方法。
本实验采用P-Q分解法进行电力系统分析的潮流计算程序的编制与调试,获得电力系统中各节点电压,为进一步进行电力系统分析作准备。
通过实验教学加深学生对电力系统潮流计算原理的理解和计算,初步学会运用计算机知识解决电力系统的问题,掌握潮流计算的过程及其特点。
熟悉各种常用应用软件,熟悉硬件设备的使用方法,加强编制调试计算机程序的能力,提高工程计算的能力,学习如何将理论知识和实际工程问题结合起来。
2.2实训要求编制调试电力系统潮流计算的计算机程序。
程序要求根据已知的电力网的数学模型(节点导纳矩阵)及各节点参数,完成该电力系统的潮流计算,要求计算出节点电压、功率等参数。
3 实训内容1 基于PSASP的电力系统潮流计算仿真1.1 实验要求要求在掌握电力系统稳态分析知识的基础上,根据PSASP中电力系统潮流计算的步骤,利用该软件实现电力系统的潮流计算,并能根据潮流计算结果,对电力系统进行运行情况分析。
(完整版)IEEE-30节点全套数据

12578346281311 91229271617 141015212230 181920152425 26 IEEE-30 节点系统数据资料图1 IEEE-30 节点系统接线图IEEE-30 节点系统节点数据和潮流结果节点号母线电压发电机输出功率节点负荷功率U (p.u.) ( ) P G ( p.u.) Q G ( p.u.) P L ( p.u.) Q L ( p.u.)1 1.05000.0000 1.3853-0.02580.0000.0002 1.0338 -2.7374 0.5756 0.0243 0.217 0.1273 1.0309 -4.6722 0.0000 0.0000 0.024 0.0124 1.0258 -5.5963 0.0000 0.0000 0.076 0.0165 1.0058 -9.0005 0.2456 0.2225 0.942 0.1906 1.0214 -6.4821 0.0000 0.0000 0.000 0.0007 1.0073 -8.0435 0.0000 0.0000 0.228 0.1098 1.0230 -6.4864 0.3500 0.3227 0.300 0.3009 1.0583 -8.1508 0.0000 0.0000 0.000 0.00010 1.0527 -10.0086 0.0000 0.0000 0.058 0.02011 1.0913 -6.3003 0.1793 0.1761 0.000 0.00012 1.0564 -9.2015 0.0000 0.0000 0.112 0.07513 1.0883 -8.0216 0.1691 0.2496 0.000 0.00014 1.0428 -10.0986 0.0000 0.0000 0.062 0.01615 1.0393 -10.2212 0.0000 0.0000 0.082 0.02516 1.0476 -9.8207 0.0000 0.0000 0.035 0.01817 1.0459 -10.1598 0.0000 0.0000 0.090 0.05818 1.0319 -10.8362 0.0000 0.0000 0.032 0.009初始潮流状态下系统有功网损P=7.09 (MW)LossIEEE-30 节点系统并联电容数据无功可调发电机无功出力限值节点电压限值在潮流计算中,为了使修正方程式中的系数矩阵B’、B’’形成更加方便,更加符合C 语言编程的特点,我们对系统中的30 个节点重新进行编号。
计算机网络与通信试题资料

5.人们将数据信道直接传输数字信号的传输方式叫做_基带____传输,而将利用模拟信道传输信号的传输方式叫做_____频带______传输。
6.从计算机域名到IP地址翻译的过程称为域名解析。
7.IP地址长度在IPv4中为32比特。
(A) IP(B)TCP(C)SNMP(D)SMTP
15.Internet的网络层含有四个重要的协议,分别为__C____。
(A) IP,ICMP,ARP,UDP (B) TCP,ICMP,UDP,ARP
(C)IP,ICMP,ARP,RARP (D) UDP,IP,ICMP,RARP
16.IP地址中,C类地址的标准掩码是D。
4.计算机网络的功能是通信交往、资源共享、协同工作。
5.在计算机网络中__网桥____只隔离冲突,但不能隔离广播。
7.ATM网络中采用固定长度的协议数据单元称为____信元______,其长度为___53______字节。
8.计算机通信网中信息交换的方式有电路交换、分组交换、报文交换等。(写出三种即可)。
8、划分VLAN的方法有____基于交换机端口、基于MAC地址、基于网络层地址(或IP地址)_。
9、当以太网中的联网结点数增加1倍时,每个结点能分配到的平均带宽大约为原来的__1/2______。
10、一个IP地址由____网络号________和____主机号________两部分组成。
二、单项选择题(共20分,每小题1分)
(C)ARPAnet(D)CERNET
10.允许双向传输,但一个时刻下只允许一个方向传输的是_______D________
(A)双工(B)全双工(C)单工(D)半双工
基于QPSO-SVM模型的电力系统稳定性评估

基于QPSO-SVM模型的电力系统稳定性评估李强;刘晓峰【摘要】随着我国电力系统的快速发展,超高电压输变电已经开始应用,电网变的更加复杂,其电力系统的稳定性和安全性问题更显得突出.电压的稳定性一直是系统可靠性的重要指标,而其电压质量的在线实时评估一直是研究的难题.本文采用支持向量机(SVM)模型来提高运算精度和效率,并通过量子行为粒子群算法(QPSO)优化并计算其参数,提出一种基于QPSO-SVM的模型,可用于实时在线评估电力系统的稳定性.此外,为了提高机器学习的评估指标的精准度,采用先进的潮流计算Jacobian 的切向量分量来作为VSI,可以保证评估值的绝对性,并可以适用于各种网络结构.最后在WSCC9-bus标准系统上实验证明,该方法比GA-SVM、一般的SVM和BP 神经网络在学习时间分别提高23.2%、63%、77.9%,测试时间分别加快26.2%、56.9%、72.56%,在精度上分别提高28.9%、42.19%、82.34%.另外,通过在IEEE14总线上做实验,可以找到系统崩塌前的关键总线,并与潮流计算的结果基本一致,因此该方法是一种可以作为实时在线电力系统稳定性评估的理想方法.【期刊名称】《计算机系统应用》【年(卷),期】2017(026)002【总页数】7页(P51-57)【关键词】电力系统稳定性评估;SVM;粒子群算法;潮流计算;仿真计算【作者】李强;刘晓峰【作者单位】山西省财政税务专科学校信息学院,太原030024;太原理工大学财经学院,太原030024;太原理工大学数学学院,太原030024【正文语种】中文电力系统具有非线性、耐受性差和缺乏有效的模型的特点, 其稳定性评估一直是个难点[1]. 在电力系统中评估系统的稳定性参数很多, 其中电压的稳定性评估是观测整个电力系统稳定性评估的最直接的方法. 监测行为指数法通常被用来评估电压的安全性,但是该方法需要花费大量的计算, 因此不适合在线实时监测.一种被称作“潮流计算Jacobian的切向量的分量法”的新方法可用于电压稳定性评估指数[2]. 这种方法在表明电压崩塌时, 非常类似于“L 指标法”. 此外, 在任意一个接近电压稳定极限的节点处, 该方法提供了一个更有效的信息. 相比较“L指标法”, 其具有更简单的计算方式和更宽广的应用范围.使用人工智能机器学习的方法应用于实时电压稳定性评估方面的工作已经有了一些成效, 例如使用人工神经元网络、决策树和贝叶斯分类法用于快速电压评估等等[3][4]. 其中, 人工神经元网路(ANN)是一个典型的静态和动态的电压评估方法[5], 例如BP神经元网络用于电压的评估[6]. 但是, ANN需要大量的计算时间和空间, 所以不太适合实时在线评估电力系统的稳定性.本文中, 以潮流计算雅可比的切向量分量为训练目标, 建立一种QPSO-SVM机器学习模型实现电压的稳定性评估. 这种模型的特点是使用先进的技术模型实现非线性的快速映射[7-10]. 并且, 使用切向量作为评估指数比BP神经网络方法[2]、一般的SVM[7]和GA-SVM方法[12], 将更加高效和更加精确. 最后, 通过两个标准实验模型, WSCC3机9线模型[13]和IEEE 14总线模型来证明该方法的有效性.为了更好的使用支持向量机, 需要通过经验手动设置其参数, 然而这往往是非常困难的, 为了解决这个问题, 采用量子行为粒子群算法(QPSO)来自动实现SVM中的相关参数设置[14], 即构造一种带量子行为的粒子群算法优化的支持向量机(QPSO-SVM).对于任意一节点的潮流计算可以通过以下等式表达:在任意一操作节点的潮流计算的Jacobian矩阵(PFJ)可以通过下式表达:继续通过PFJ可以推导出以下切向量(TV):由PFJ导出的任意一节点的切向量中的分量△|V|包含可以指明总线上的电压变化幅度. 当该△|V|在大于0小于1之间时, 可以绝对地表明系统电压是稳定的, 而其值大于等于1时, 表明系统是不稳定的. 所以, 建议使用该值作为电压的稳定性指标(VSI). 相比较而言, 使用传统的“L指标”有两大缺点: 一、只能相对地评估系统稳定性;二、是不能用于其它网络结构, 如环网结构[2].但是, 通过数学的分析方法实时求解任意一节点的切向量仍然计算量是非常庞大的. 因此, 在本文中, 提出一种QPSO-SVM模型方法求解该切向量的值, 来实现快速、实时和精确地判断系统稳定状态.支持向量机是在函数拟合, 状态监测和数据分类等方面表现优秀的一种方法. SVM 回归法主要用来解决线性和非线性问题的[7]. 这里有一组数据样本需要去训练向量机, 集合set{xi, yi} i=1, 2… n, 其中xi∈Rd作为输入向量, yi∈R将作为输出值. 在线性的情况下, 该函数回归函数被定义为以下表达式:这个线性回归方法需要最小化两个参数, 一个是钝化损失(ε), 另一个是线性范化参数(||ω||2). 通过引入松弛变量ξi, 来解决某一向量xi站错位置的问题, 因此, 简化SVM回归函数为以下表达式:其约束条件为:其中参数ε被用于调整精度. 再通过拉格朗日乘数αi, αiT, ηi, ηiT.解决此类约束问题:由此, 以上表达式可以变化为拉格朗日对偶问题:约束条件为:最后, 经过再次拉格朗日变化得到以下最终的拟合函数:此外, 为了解决非线性问题, 需要做从非线性空间到高维特征线性空间的转换.为了实现转换, 使用核函数K (xi, yj). 要作为核函数必须满足Mercer理论条件, 核函数将在特征空间中实现点积. 引入核函数的目的在于为支持向量机实现减少运算量. 通过非线性映射函数Ф(xi)将数据映射到高维特征空间中去. 在这个新的空间中, 线性函数将满足回归条件. 因此非线性函数可以采用以下形式表达:有很多的核函数可以在应用中被选择, 主要有线性核函数、多项式核函数和高斯核函数. 决定使用哪个核函数是关键的一步, 因为训练的样本将在核函数决定的空间内做运算. 一个被定义的核函数必须满足Mercer的两个条件, 一个是连续, 另一个是正定. 以下是常用的三个核函数:在本模型中, 将使用高斯核函数实现非线性映射. 其中惩罚因子C和核函数宽度半径参数δ扮演者非常重要的角色, 影响着SVM分类的效率和效果.3.1 PSO算法描述粒子群算法(QPSO)其思想来源于鸟群觅食过程的启发. 在鸟群觅食过程中, 每个鸟既是独立的个体, 又受群体的影响. 通过群体智慧, 最终整个鸟群的觅食搜索演变成了寻找问题空间中的最优解.当使用粒子群算法解决优化问题时, 问题被转化为鸟在搜索空间中寻找的位置, 此时鸟被称作“粒子”. 每一个粒子都有其自己的位置和运动速度, 还有一个用来测量每一个粒子优越性的适应度函数. 每一个粒子记忆和趋向当前最优粒子运动, 并在解决空间中搜索.粒子群算法开始随机初始化一组粒子, 并且每一个粒子在解决空间中同时趋近于两点. 一个点是在历史搜索中所有粒子中最佳的位置, 被称为全局最优解pg; 另一个点是第i个粒子在自己的搜索过程中最佳的位置, 被称为pi; 当粒子搜素这两点时, 每一个粒子更新自己的位置和运动速度, 如下式所示:其中, p是当前位置, 是当前速度, 这俩决定了下一个位置的方向. Β是一个约束因子, 它控制速度的权重. C1和c2是两个被称为加速因子的正数常量. R1和r2是两个在0和1之间的随机值. 是一个可以改变搜索能力的记忆参数.3.2使用量子行为改进PSO算法PSO虽然在解决路径规划等方面表现非常优秀, 但是在实践中该算法仍然具有收敛速度较慢, 容易早熟, 易停留在局部最优点等问题. 为了改良该PSO算法, 本文将采用量子行为思想来改进粒子群算法, 增强其在全局的搜索能力, 即具有量子行为的粒子群算法(QPSO). 该算法具有加速收敛和提高粒子协同的能力的特点. 引入势点q, q点成为每一个粒子的收敛随机点[14], p点如下式表示, 其中, i为第i个粒子, 共有m个粒子, 每个粒子n维, k为迭代次数.定义评估函数用于评价每个粒子当前的位置的好坏.以上式中, 为SVM的计算值, 为训练目标值, 该函数用来计算待求参数x的SVM 计算值和目标值的偏差.第次迭代, 粒子位置的更新规则为, 如果粒子的新位置的适应度值优于第次, 则更新粒子的新位置; 否则, 保持不变.式(20)定义了势点q, 其中α是在0至1之间的随机数.粒子值的更新规则为下式:其中, θ≧1/2时, 上式取负号, 否则取正号; λ是速度因数, 该值会影响收敛速度[14], λ可以按下式取值.其中, hmax是预设的迭代次数.3.3 QPSO求解SVM的参数的算法步骤在本文中将使用基于量子行为改进粒子群算法来搜索这些参数最佳的组合, 具体步骤如下:第1步, 编码待求参数, x={C, δ }.第2步, 建立训练样本集合.第3步, 确定SVM网络结构, 以及核函数的选择.第4步, 计算粒子和粒子群的最优位置.第5步, 依据更新公式, 更新粒子位置.第6步, 在本次迭代结束后, 如果迭代的次数超过了预设值或者计算误差达到预设值, 则满足精度要求, 输出其计算值, 否则转到第4步.4.1 WSCC 3机9线系统模型4.1.1 SVM模型的结构这个算法使用QPSO-SVM模型来评价系统的状态, 其中输入参数包括发电机端电压, 发电机的有功功率和无功功率, 以及负载. 输出值为电力系统潮流计算的切向量分量. 通过机器学习, 建立系统工作环境变量和电力系统状态指标之间的非线性映射关系, 最终, 计算实时在线的系统状态评估值.4.1.2训练工具使用Matlab支持向量机软件包和粒子群算法软件包去搜索向量机的最佳组合参数. 并使用电力系统分析软件包(PSASP)生成所有的实验数据.4.1.3机器训练在WSCC3机9线标准系统模型[14]上产生的数据将被训练. 150个离线潮流计算的样本数据从电力系统分析软件包中生成, 其中90个被作为训练机器的样本, 剩余60个被用来测试数据. 在这个标准系统模型里, 通过改变一个负载总线上的有功和无功功率, 并保持其它总线参数不变, 来产生整个系统的数据.设置粒子群的维数为2, 最大迭代次数为Nmax=250, 记忆参数设置为w=2, 初始化惩罚因子C和核函数宽度δ为{20, 10}. 在QPSO-SVM迭代过程中, 可以注意到QPSO-SVM在迭代到42次时算法开始收敛, 核函数宽度δ该值迅速掉到1.14附近, 而GA-SVM在93次附近开始收敛, 在GA-SVM迭代过程中, 该值由10迅速下降到1.25; 所以QPSO-SVM在计算参数时, 收敛速度要优于GA-SVM算法. 如图1、表1和表2所示.在表3中列举了其中前10个训练数据样本. 并且从表3中, 观测电压稳定性指标的值, 很容易发现总线c上存在问题.在表4中, 将QPSO-SVM算法、SVM算法、QPSO-SVM算法、BPNN算法的执行效率参数和精度进行了比较. 其中, QPSO-SVM可以满足电压稳定性评估的需要, 也就是说该模型计算值可以在线或离线实时反应系统的电压稳定状态. 通过比较, 表4中的结果在3机9线标准系统上实验比较证明, 该QPSO方法比GA-SVM、SVM和BPNN在学习时间上分别可以提高23.2%、63%、77.9%, 在测试时间上分别可以提升26.2%、56.9%、72.56%, 在计算精度上分别增加28.9%、42.19%、82.34%, 该实验结果说明QPSO-SVM方法在学习时间、测试时间和精度上更优于比其它3种方法.4.2 IEEE14总线系统模型在4.1部分里, 实现了在IEEE14总线标准模型系统上对QPSO-SVM算法的应用. 主要的目的是, 测试QPSO-SVM算法计算的值和潮流计算切向量分量的值之间的差别, 判断是否该方法计算的值是否可以作为潮流计算切向量的一种替代.为了这项研究, 给14总线系统模型引入一个乘数λ=4.05作为系统的负载极限. 在基本情况下, 负载和发电机使用连续性潮流计算法. 在基本情况下, 通过潮流计算的TV值和QPSO-SVM得出的值可以通过图2和表5进行比较. 从中可以发现倾向于电压崩塌的的最关键的总线是14总线. 同时, 通过比较, 也可以看到QPSO-SVM计算值作为指标值与潮流计算的切向量分量值非常接近, 都可以用来标明系统电压稳定的脆弱位置.从图3中, 可以看到在不同的负载级别下, 这两个计算指标值.图4中, 在接近负载极限的位置节点上, QPSO-SVM方法计算的指标值和关键总线可以同时被发现. 从图中, 可以发现总线5是一个关键总线, 在该位置上将接近负载的极限. 但是, 在较低负载的等级下, 14总线已经被发现并认定为也是一关键总线.根据这个发现, 一项有意义的研究已经被展开[2].这个特点可以通过QPSO-SVM 方法捕获, 如同潮流计算的切向量计算的结果.本文中, 提出一种新的QPSO-SVM方法, 并以潮流计算的切向量分量作为评价指标来实现电力系统的电压稳定性评估. 在该方法中, 使用基于量子行为的粒子群算法QPSO用来自适应设置SVM的参数, 来提高SVM的精度. 此外, 潮流计算中的切向量分量作为SVM学习的目标来提升计算结果的有效性. 这个实验表明, QPSO-SVM的计算的精度和效率要优于、一般的SVM和BP神经网络, 这也预示了该方法是评估电力系统稳定性的一种非常有前途的算法. 同时, 这里还存在着很多研究的空间, 在下一步的研究工作中, 大规模电力网络的划分和稳定性评估方法将被继续探索, 以及该方法在环形网络中评估有效性的实验证明等.1 Sauer PW, Pai MA. Power system dynamics and stability. Prentice Hall, 1998.2 Acharya NV, Rao PSN. A new voltage stability index based on the tangent vector of the power flow jacobian. 2013 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia). 2013. 1–6.3 Patidar NP, Sharma J. Load ability margin estimation of power system using Model Trees. 2006 IEEE Power India Conference. 2006.4 Kessel P, Glavitch H. Estimating the voltage stability of power systems. IEEE Trans. on Power Delivery , 1986, 1(3): 346–354.5 陈祥光,裴旭东.人工神经网络技术及应用.北京:中国电力出版社,2003.6 Han X, Zheng Z, Tian N, et al. Voltage stability assessment based on BP neural network. Asia-Pacific Power & Energy Engineering Conference. 2009. 1–4.7 An JL, Yang QX, Ma ZP. Study on SVM on-line function regressionmethod for mass data. Machine Learning and Cybernetics. 2007 International Conference. 2007. 2773–2777.8 Li H, Zhang YX. An algorithm of soft fault diagnosis for analog. Electronic Measurement &Instruments, 2009, 4-1023 –4-1027.9 Zhou J, Bai T, Tian J, et al. The study of SVM optimized by culture particle swarm optimization on predicting financial distress. 2008 IEEE International Conference on Automation and Logistics. 2008. 1054–1059.10 Vahid R, Ata E, Reza G. Application of the QPSO-SVM model for reconginition of control chart patterns. ISA Trans., 2010, 49(4): 577–586.11 Lin SW, Ying KC, Chen SC, et al. Particle swarm optimization for parameter determination and feature selection of support vector machines. Expert Systems with Application, 2008, 35(4): 1817–1824.12 Li Q. The Analysis and assessment of voltage stability based on GA-SVM. Journal of System Simulation, 2014, 10: 2369 –2373, 2406.13 Meah K, Ula AHMS. Simulation study of the CIGRE HVDC benchmark model with the WSCC nine-bus power system network. Power Systems Conference and Exposition. 2009. 1–5.14 Sun J, Fang W, Palade V, et al. Quantum-behaved particle swarm optimization with Gaussian dirtributed local attractor point.Applied Mathematics and Computation, 2011, 218(7): 3763–3775.。
考虑关键节点和重要线路的电力系统PMU_优化配置

第 42 卷第 4 期2023年 7 月Vol.42 No.4Jul. 2023中南民族大学学报(自然科学版)Journal of South-Central Minzu University(Natural Science Edition)考虑关键节点和重要线路的电力系统PMU优化配置徐光辉1,2,肖克1,2,柯善焜1,2,王淑青1,2,汪繁荣1,2(1 湖北工业大学电气与电子工程学院,武汉430068;2 湖北工业大学产业研究院,襄阳441000)摘要相量测量单元(PMU)是一种测量电压和电流的设备,随着电力系统的规模和结构越来越复杂,PMU的数量也大幅增加.利用改进蝠鲼觅食优化算法(IMRFO)对PMU进行了配置,使电力系统在正常运行、考虑关键节点和考虑重要线路时都能完全可观测,同时使PMU配置数最少.在蝠鲼觅食算法的基础上增加了混沌映射以提升算法的收敛速度,增加了跳跃因子以提高算法的勘测能力,从而避免算法陷入局部最优. 通过度、特征向量和接近度三种指标,利用TOPSIS综合评价寻找系统的关键节点,利用线的中间中心度判断系统的重要线路.对IEEE-14和IEEE-69节点系统进行了实验仿真,结果表明:IMFRO算法与未改进时相对比,在配置时所需的PMU数和迭代次数均有一定的减少,验证了所提方法对解决PMU优化配置问题的有效性和优越性.关键词电力系统;相量测量单元;关键节点;重要线路;蝠鲼觅食算法中图分类号TP242;TM711 文献标志码 A 文章编号1672-4321(2023)04-0535-06doi:10.20056/ki.ZNMDZK.20230415Optimization of PMU for power system considering key nodesand important linesXU Guanghui1,2,XIAO Ke1,2,KE Shankun1,2,WANG Shuqing1,2,WANG Fanrong1,2(1 School of Electrical and Electronic Engineering, Hubei University of Technology, Wuhan 430068, China;2 Industrial Institute, Hubei University of Technology, Xiangyang 441000, China)Abstract Phasor measuring unit (PMU) is a device for measuring voltage and current. As the scale and structure of power system become more complex,the number of PMUs increases greatly. The improved manta ray foraging optimization algorithm (IMRFO)is used to configure PMUs,so that the power system can be fully observable during normal operation, considering critical nodes and important lines, and at the same time, the number of configured PMUs is minimized. On the basis of the manta ray foraging algorithm, chaotic mapping is added to improve the convergence speed of the algorithm, and a jump factor is added to improve the exploration ability of the algorithm, so as to avoid the algorithm falling into local optimal. The key nodes of the system are found by TOPSIS comprehensive evaluation through three indexes of degree, feature vector and proximity. The central degree of the line is used to judge the important line of the system. Experimental simulations of the IEEE-14 and IEEE-69 node systems are performed. The results show that compared with IMFRO algorithm without improvement, the number of PMU and iteration times are reduced to a certain extent,which verifies the effectiveness and superiority of the proposed method to solve the problem of optimal PMU configuration.Keywords power system; phasor measuring unit; key node; important line; manta ray foraging algorithm随着电网规模越来越大,一些关键的节点发生故障可能引起级联效应而导致整个电网崩溃;一些重要的输电线路因自然因素等原因而造成运行故障[1],为了保障电网的安全性和稳定性,需要实时对电网的各相数据进行监测,同步相量测量单元(Phase Measurement Unit,PMU)的出现能解决这一收稿日期2023-02-24作者简介徐光辉(1986-),男,副教授,博士,研究方向:复杂网络群集控制和优化,E-mail:************.cn 基金项目国家自然科学基金资助项目(61603127)第 42 卷中南民族大学学报(自然科学版)问题.PMU能实时测量节点电压、电流相量等信号,在配电网状态估计[2]、检测线路故障[3]等方面上取得了不错的效果,为电力系统部门及时掌握系统运行状态,出现异常情况采取必要的控制措施.由于PMU具有高采样率,若电网中所有的节点都配置PMU,会产生冗余的数据并且是不经济的,在此背景下,PMU最优配置(Optimal PMU Placement, OPP)这一问题具有重要的意义.目前,解决OPP问题的算法主要为数值算法和启发式算法[4].数值算法发展较成熟,对小型的电力系统,具有计算速度快、收敛能力强等特点,但在大型系统中,存在着全局搜索能力弱、普适性差等问题.闰玲玲等[5]提出了基于0‐1整数规划算法的PMU配置方法,在配置小型电力系统节点上有很好的实用性,但在大型电力系统节点上所需时间较长.郑明忠等[6]利用了整数规划算法,能解决考虑故障情况下的OPP问题,但同样存在收敛过慢等不足.启发式优化方法具有全局搜索能力强、运行速度快等特点,在求解多目标、高维度模型上有一定的优势,由于OPP问题一般是多约束和高维度的,所以在OPP问题上,启发式优化方法使用得较多,如遗传算法[7]、模拟退火算法[8].MAJI T K等[9]提出了一种改进二进制粒子群算法,通过非线性惯性权重系数来提高搜索能力,通过改进阈值函数来提高收敛速度,但没有考虑关键节点等问题.PAL A等[10]提到了关键节点,但配置时只对关键节点优先考虑且没有保证系统的完全可观测性.ALMASABI S等[11]提出了用脆弱性指数来评判线路的重要性,将脆弱性指数集成到可观察性中,作为目标函数的一个指标使总安装成本最小化.虽然上述部分文献提到了关键节点和重要线路,但没有针对考虑关键节点和重要线路时的PMU配置情况,基于此,本文的主要贡献如下:本文提出改进蝠鲼觅食(Improved Manta Ray Foraging Optimization,IMRFO)算法来实现OPP问题,通过混沌映射增加算法初始化的多样性,通过跳跃因子使算法易于跳出局部解.实验表明:改进后的算法能有效地跳出局部最优;使用图论的3种指标来判断电力系统的关键节点,利用线的中间中心度判断电力系统的重要线路,在保证系统完全可观测和PMU配置数目最小的情况下,分别对正常运行、考虑关键节点和考虑重要线路的PMU配置情况加以分析.通过仿真分析验证所提出的方法的正确性和优越性.1 PMU最优配置规则和模型1.1 PMU配置规则当一个电力系统的所有节点电压相量能被PMU 直接或间接观测时,称这个系统是全网可观测的.电力系统节点的可观测性由以下规则来判断[12]:规则1:若节点i安装了PMU,其节点的电压相量能被直接测量,则节点i是直接可观测的;规则2:若节点i安装了PMU,通过欧姆定律能计算其所有邻接节点的电压相量,则与节点i所有的邻接节点是间接可观测的.在原有的基础上本文通过新增加两条规则来对关键节点和重要线路加以说明.规则3:为了确保在关键节点上测量数据的有效性,所以在关键节点处至少能被两个PMU所观测;规则4:由于一些客观的因素(如线路老化)影响线路中的参数,为了尽可能使PMU测量线路电流和电压的准确性,所以在重要线路的两端,至少有一端能被PMU直接观测.1.2 PMU的配置模型要使配置PMU数量最小并且使整个电力系统节点完全可观测,则电力系统n个节点PMU配置模型的目标函数如下:min f(x)=∑i=1n x i,(1)其中:f(x)表示n个节点所安装PMU的最小数量;x i 是一个二进制数,若节点i安装了PMU,则为1,否则为0.根据以上条件,就可以写出PMU配置的约束条件:AX≥b,(2)Aij=ìíî1,i=j或i、j相连,0,其他,(3)其中:X=(x1,x2,...,x n)T表示相应节点PMU配置的情况;式中b在正常情况下为[1,1,…,1]的n维列向量;矩阵A表示节点的连接情况,如果节点i连接到节点j或节点i和j是同一节点,则A ij=1,否则A ij=0. 2 改进蝠鲼觅食算法原理2.1 蝠鲼觅食算法蝠鲼觅食算法(Manta Ray Foraging Optimization,536第 4 期徐光辉,等:考虑关键节点和重要线路的电力系统PMU 优化配置MRFO )是一种群智能优化算法,虽然蝠鲼的食物并不是均匀分布或集中在某些地区,但是蝠鲼在群体觅食中总能精准找到食物,这是因为它们进化出了一套智能觅食策略,将这种智能策略转换为数学模型就可得到MRFO 算法[13].2.2 基于改进蝠鲼觅食算法的最优配置问题虽然MRFO 算法具有较好的性能,但还是存在容易陷入局部最优解和收敛性过慢等问题,因此需要通过对MRFO 算法进行改进使性能得以提升,并更加适用于OPP 问题的求解.种群初始化的位置能在一定程度影响算法性能.与随机搜索相比,混沌映射在搜索空间上遍历性更好,可使算法在一定程度上跳出局部最优.在配置PMU 时,只有两种情况,即“1”为配置PMU ,“0”为不配置PMU.在算法的初始化过程中,种群有较大的概率在0和1附近,能增加算法的收敛速度和准确性.Sine 映射倾向于在0‐1之间的两端[14],因此在种群初始化时用Sine 映射,其数学模型如下:z k +1=a4sin (πz k ),(4)其中:z k 是迭代序列值,z 0∈(0,1),a ∈(0,4];一般情况下,z 0取0.152,a 取4.在算法迭代前期,权重因子β值过大有利于提高算法的勘察能力;在迭代后期时,β值过小有利于提高算法的开发能力.在迭代过程中,用较大概率的短步来提高开发能力,用较小概率的长步来提高探索能力,使算法有机会跳出局部解.为了增加种群搜索的多样性,提出了跳跃因子来增加种群的搜索能力,如式(5)所示:βnew =ìíîïïβ+2(rand 1-0.5)(h -t T ),rand 2≤0.2,β,rand 2>0.2,(5)其中:h 为跳跃因子,一般设置为15;t 和T 分别表示当前迭代和最大迭代次数;rand 1和rand 2均为[0,1]是随机数.为了验证改进的有效性,采用单峰、多峰和固定维测试函数,测试函数如表1[15].为了保证公平的比较,所有算法都采用相同的维数,相关参数均未改变.最大迭代次数和种群数量相同,所有测试函数运行30次.表2为GWO 、PSO 、MRFO 和IMRFO 的收敛结果的比较.可以看出,在MRFO 在改进后性能有一定的提升.IMRFO 算法求解OPP 问题的流程图如图1所示.3 关键节点和重要线路的判断3.1 关键节点的判断本文利用TOPSIS 综合图论中的度、特征向量和接近度三种指标,评价关键节点的位置.节点的度说明自身和周围节点的连接程度,本文认为节点的度越大,说明该节点越重要.节点i 的度计算公式为:De(i )=∑j =1L A ij ,(6)其中,L 为支路总数.表1 测试函数Tab.1 Test function函数f 1f 2f 3函数名QuarticRastrigin Hartmann 3D搜索范围[‒1.28, 1.28][‒5.12, 5.12][0,1]最优值00‒3.86表2 测试函数的仿真数据Tab.2 Simulation data of test function 函数f 1f 2f 3指标平均数标准差平均数标准差平均数标准差GWO4.21×10‒52.42×10‒55.86×10‒134.73×10‒11‒3.862.07×10‒3PSO7.86×10‒22.63×10‒26.45×1011.67×101‒3.863.10×10‒15MRFO5.92×10‒65.96×10-61.07×10‒62.26×10‒7‒3.860IMRFO4.92×10‒64.61×10‒600‒3.86图1 基于IMRFO 算法的OPP 流程图Fig.1 Flowchart of OPP based on IMRFO algorithm537第 42 卷中南民族大学学报(自然科学版)在评估节点的重要性时不仅考虑节点的连接情况,而且还考虑了节点的连接关系.在电力系统中有N个节点,λ1,...,λn为邻接矩阵B的N个特征值,e=[e1,e2,...e n]T为最大特征值λ对应的最大特征向量,则邻接矩阵的最大特征值的特征向量为:T(i)=λ-1∑j=1N B ij e j,(7)其中:T(i)中各分值大小代表着相应节点的重要程度,分值越大表明对应的节点越重要.接近度反映了节点通过网络到达其他节点的容易程度[16].节点i的接近度为该节点到达网络中其他节点的最短距离之和的倒数,节点i的接近度为:D i=éëêê∑j=1N d ijùûúú-1,(8)其中:d ij为节点i到节点j的最短距离,N为系统中总节点数.3.2 重要线路的判断在电力系统输电线中,每条线路发生故障的概率与环境条件、输电等级和线路所处的位置等因素有关.由于环境条件因素辨别困难,本文只考虑在相同条件下线路所处的位置造成的影响.线的中间中心度测量的是一条线出现在一条最短路径上的次数,需要考虑系统中所有经过该线路两点之间的最短路径,计算该线路在全部最短路径中所占的比例,它能反映线路的重要程度[17].4 算例分析4.1 IEEE-14节点分析图2所示为输电网IEEE-14节点系统.表3为IEEE-14节点系统的度、特征向量和接近度三种指标的计算结果.利用TOPSIS综合评价得出得分权重矩阵S=[0.06 0.13 0.07 0.16 0.13 0.08 0.08 0 0.10 0.03 0.03 0.03 0.05 0.04].关键节点占总节点数的10%左右[10],因此本文取3个权重大的节点为关键节点,所以节点2、4、5为关键节点.根据规则3,节点2、4、5至少能被两个PMU所观测.TOPSIS 处理的步骤如下.步骤1:将3种判断结果写成矩阵Z n×m,其中n为电力系统中节点的个数,m为判断关键节点的种类,即在IEEE-14节点系统中,n为14,m为3;步骤2:正向化和标准化.正向化是得出的结果越大则该节点越重要;标准化是消除量纲的影响;步骤3:找出每列中的最大值矩阵D+和最小值矩阵D-,并计算出各个节点与D+和D-的欧式距离,并将m种指标赋予相同的权重;步骤4:计算出所有节点的得分矩阵S,再进行归一化处理.通过计算得出线的中间中心度矩阵M,M为对称矩阵,“0”表示节点之间不相连或为自身节点,数值的大小代表输电线路的重要程度.由式(9)可知线路5-6、4-5、4-9和9-14相比于其他线路为重要线路.根据规则4,这两条线路至少有一端能被PMU直接观测.表3 三类关键节点判断结果Tab.3 Judgment results of three types of critical nodesIEEE-14 节点节点1节点2节点3节点4节点5节点6节点7节点8节点9节点10节点11节点12节点13节点14度35365542533343特征向量0.2470.4210.2710.4910.4110.2240.2560.0760.2940.1180.1020.1070.1360.128接近度0.0290.0360.0290.0420.0400.0370.0340.0240.0400.0310.0300.0280.0310.032图2 IEEE-14节点系统Fig.2 IEEE-14 node system538第 4 期徐光辉,等:考虑关键节点和重要线路的电力系统PMU 优化配置M =éëêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêùûúúúúúúúúúúúúúúúúúúúúúúúúúúúúúúúúúú050040089087016000002300001300000000013000015001100000000001300000011000900000090000000000090000040015110 .(9)表4为IEEE -14和IEEE -69节点系统三种情况下的OPP 配置情况.由表4可知,在IEEE -14节点正常情况下需要配置4个PMU ,而在关键节点和考虑关键线路情况下,需要配置5个PMU.考虑关键节点和重要线路是在正常情况的基础上分别增加了规则3和规则4,故这两种情况配置的PMU 数都大于或等于正常情况下的配置数目.本文所提出的IMRFO 和MRFO 算法分别对IEEE -14节点进行了仿真,对比结果如图3所示.对比MRFO 算法和文献[18]采用的改进整数规划法,本文方法迭代次数相对较少,说明本文算法有较快的收敛速度.4.2 IEEE -69节点分析图4所示为配电网IEEE -69节点系统.利用TOPSIS 综合评价得出IEEE -69节点系统的关键节点为节点3、4、8、11和12.利用线的中间中心度得出重要线路为线路3-4、3-26、4-5、8-9、9-53、9-10、12-13和11-12.配置的结果和仿真图分别为表4和图5.由图5可知,IMRFO 与MRFO 算法相比,表4 IEEE -14和IEEE -69节点的配置情况Tab.4 Configuration of IEEE -14 node and IEEE -69 node3种情况下PMU 配置情况正常情况下考虑关键节点考虑关键线路IEEE -14 节点2,6,7,93,5,6,8,94,5,6,8,9IEEE -69 节点2,4,7,9,14,17,20,23,26,28,31,34,37,40,43,45,49,51,55,58,61,64,66,682,5,7,9,12,15,18,21,24,26,28,31,34,37,40,43,45,47,49,51,55,58,61,64,66,682,4,7,9,12,15,18,21,24,26,29,32,34,36,39,42,45,49,51,55,58,61,64,66,68迭代次数44.24.44.64.855.25.45.65.86配置P M U 数图3 正常情况下IEEE -14节点系统仿真图Fig.3 Simulation diagram of IEEE -14 node system under normal conditions图4 IEEE -69节点系统Fig.4 IEEE -69 node system539第 42 卷中南民族大学学报(自然科学版)IMRFO5 结语针对MRFO 算法易陷入局部最优和收敛速度慢等问题,本文提出了一种增加混沌映射和跳跃因子的IMRFO 算法,利用图论的3种指标和线的中间中心度寻找电力系统的关键节点和重要线路.为了保证电力系统完全可观测,利用IMRFO 算法分别在3种情况下进行了PMU 配置仿真,结果表明了IMRFO 算法对求解OPP 问题的有效性和优越性.在今后的研究中,应根据实际情况判断关键节点和重要线路,并进一步开发MRFO 算法的性能.参 考 文 献[1] 王沛. 基于大数据技术的输电线路运行故障诊断关键技术[J ]. 电测与仪表,2021,58(5):182-189.[2] 曹鹏. 面向状态估计的配电网量测系统优化配置研究[D ]. 贵阳:贵州大学,2022.[3] AHSACE M G , SADEH J. A novel fault -locationalgorithm for long transmission lines compensated by series FACTS devices [J ]. IEEE Transactions on Power Delivery , 2011, 26(4):2299-2308.[4] CHAKRABARTI S , KYRIAKIDES E. Optimal placementof phasor measurement units for power system observability[J ]. IEEE Transactions on Power System , 2008, 23(3):1433-1440.[5] 闰玲玲,刘中印,艾永乐,等. 基于0-1整数规划算法的PMU 量测点优化配置新方法[J ]. 电力系统保护与控制,2017,45(12):101-106.[6] 郑明忠,张道农,张小易,等. 基于节点集合的PMU 优化配置方法[J ]. 电力系统保护与控制,2017,45(13):138-142.[7] 徐岩,郅静. 基于改进自适应遗传算法的PMU 优化配置[J ]. 电力系统保护与控制,2015,43(2):55-62.[8] 袁澎,艾芊,赵媛媛. 基于改进的遗传-模拟退火算法和误差度分析原理的PMU 多目标优化配置[J ]. 中国电机工程学报,2014,34(13):2178-2187.[9] MAJI T K , ACHARJEE P. Multiple solutions of optimalPMU placement using exponential binary PSO algorithm for smart grid applications [J ]. IEEE Transactions onIndustry Applications , 2017,53(3):2500-2559.[10] PAL A , SANCHEZ -AYALA G A , CENTENO V A , et al.A PMU placement scheme ensuring real -time monitoring of critical buses of the network [J ]. IEEE Transactions on Power Delivery ,2014,29(2):510-517.[11] ALMASABI S , MITRA J. A fault -tolerance based approachto optimal PMU placement [J ]. IEEE Transactions onSmart Grid , 2019, 10(6):6070-6079.[12] 孔祥玉,王玉婷,袁枭枭,等. 基于定制遗传算法考虑配电网多种拓扑可观性的PMU 优化配置[J ]. 电力自动化设备,2020,40(1):66-72.[13] GHOSH K K , GUHA R , BERA S K , et al. S -shapedversus V -shaped transfer functions for binary manta ray foraging optimization in feature selection problem [J ]. Neural Computing and Applications ,2021,33(17):11027-11041.[14] YU Y , GAO S , CHENG S , et al. CBSO : A memeticbrain storm optimization with chaotic local search [J ].Memetic Computing , 2018, 10:353-367.[15] 张晓萌,张艳珠,刘禄,等. 融合多策略的改进麻雀搜索算法[J ]. 计算机应用研究,2022,39(4):1086-1091,1117.[16] 张岐山,文闯. 基于均衡接近度灰关联的增强二部图推荐算法[J ]. 计算机应用研究,2020,37(9):2620-2624.[17] CRUZ M A R S , ROCHA H R O , PAIVA M H M , et al.An algorithm for cost optimization of PMU and communication infrastructure in WAMS [J ]. International Journal of Electrical Power & Energy Systems , 2019,106:96-104.[18] 曹鹏,刘敏. 基于改进的整数规划法结合零注入节点的PMU 优化配置方法[J ]. 电力系统保护与控制,2021,49(16):143-150.(责编 曹东,校对 刘钊)迭代次数242628303234363840配置P M U 数图5 正常情况下IEEE -69节点系统仿真图Fig.5 Simulation diagram of IEEE -69 node system under normal conditions540。
用ETAP分析IEEE14模型短路故障

题目:应用Etap软件搭建IEEE14节点模型, 让13-14节点短路,读取各节点电压IEEE14节点系统图
IEEE14母线系统支路数据
编辑区
元件栏 根据给定的发电机输出功率、负荷功率、以及各支路的电阻电 抗数据进行相应的设定。 设母线1~5电压为20kV,母线6~14电压为110kV
设置母线1为平衡 节点,用以抑制系 统的电压的幅值和 相角(给定电压的 幅值和相角,有功 和无功功率待求)。 其他节点设为PV 节点(给定有功功 率和电压,无功和 电压相位是待求 量)。
注意标幺值和有名值之间的转化
IEEE14的Etap模型
故障设置:在节点13和14之间增加一个节点15,对 节点15进行相应的短路故障的设置。
用ETAP分析IEEE14模型短路故障
ETAP是什么缩写?
Electrical Transient Analyzer Program 电气暂态分析程序
ETAP是电力电气分析、电能管理的综合分析软件系统的简称。 ETAP 是功能全面的综合型电力及电气分析计算软件,能为 发电、输配电和工业电力电气系统的规划、设计、分析、计 算、运行、模拟提供全面的分析平台和解决方案。 ETAP是美国OTI集团公司研发生产的电力及电气系统综合计 算分析软件和实时在线控制、智能电网系统产品,也是电力 系统规划、设计、分析、操作、培训和计算机仿真的全方位 的综合性工程公司。
IEEE14节点电力网络分析

《高等电力网络分析》—— IEEE14节点电力网络分析专业班级:电力工程1403班姓名:学号:Z14050394同组成员:导师:刘润华二〇一四年十二月第1章IEEE14简介 (1)第2章汇报内容总结 (3)用支路追加法建立节点阻抗矩阵 (3)补偿法求网络方程的修正解(前补偿、中补偿、后补偿) (9)统一的网络分块解法 (14)第3章调节变比使中枢点电压控制在给定值 (21)第4章连续潮流法在静态电压稳定性分析和计算中的应用 (23)连续潮流算法 (23)连续潮流计算方法在静态电压稳定性的分析和计算中的应用 (24)正确认识连续潮流及其对静态稳定分析的作用 (26)第5章课程总结 (27)第1章IEEE14简介本文选用14节点系统作为分析对象,绘制IEEE14节点标准试验系统图如图1.1所示:图1.1 IEEE14系统图母线系统数据如下表格:表1.1 母线数据表表1.2 支路数据表第2章 汇报内容总结2.1 用支路追加法建立节点阻抗矩阵1、部分网络部分网络是指所要分析的电网的一个连通子网络。
支路追加法形成节点阻抗矩阵是在部分网络上进行的。
支路追加法的主要思想是以部分网络的节点阻抗矩阵()0Z 为基础,每次追加一条新的支路,每次都对()0Z 进行更新,形成追加之路后的节点阻抗矩阵。
如此重复,当全部支路追加完毕,部分网络最终变成全网络,就得到了全网络的节点阻抗矩阵。
2、追加连枝支路如果支路α作为连枝追加到部分网络中,部分 网络增加了新支路,但未增加节点,如图所示。
可以用关联矩阵描述部分网络和追加支路之间的连接关系。
图2.1 部分网络追 追加支路后,所得网络节点导纳矩阵如式(2-1) 加一条连枝 )0(21αα1)0()0(1Z C z C Z Z Y Z-Λ--== (2-1)式中⎪⎪⎩⎪⎪⎨⎧-=+==---Λ-α0100ααα1αα1)0(21αααα1)0()0(z z z z y C Z C y z Y Z (2-2)式(2-1)和式(2-2)就是采用支路追加法追加连枝时形成节点阻抗矩阵的一般公式。
电力系统故障仿真实验指导书(PSCAD EMTDC软件手册)

电力系统故障仿真实验指导书(PSCAD/ EMTDC软件手册)(试用版)目录第一章PSCAD/EMTDC软件介绍 (1)1.1 概述 (1)1.2 PSCAD/EMTDC软件的使用 (2)1.2.1 PSCAD/EMTDC基本操作方法 (2)1.2.2 PSCAD/EMTDC故障建模及仿真流程 (12)第二章实验项目 (16)实验一电力系统故障建模 (16)1、实验目的 (16)2、预习要求 (16)3、实验内容及步骤 (16)4、思考题 (17)5、实验报告 (17)实验二电力系统故障仿真分析 (17)1、实验目的 (17)2、预习要求 (17)3、实验内容及步骤 (17)4、思考题 (18)5、实验报告 (18)实验三 IEEE14bus系统建模(选做) (19)附录不同电压等级下的输电线路典型参数 (20)第一章PSCAD/EMTDC软件介绍1.1 概述PSCAD/EMTDC是加拿大马尼托巴高压直流研究中心出品的一款电力系统电磁暂态仿真软件,PSCAD(Power Systems Computer Aided Design)是用户界面,EMTDC (Electromagnetic Transients including DC)是内部程序。
EMTDC最初代表直流暂态,是一套基于软件的电磁暂态模拟程序。
Dennis Woodford博士于1976年在加拿大曼尼托巴水电局开发完成了EMTDC的初版,编写这个程序的原因是因为当时现存的研究工具不能够满足曼尼托巴电力局对尼尔逊河高压直流工程进行强有力和灵活的研究的要求。
自此之后程序被不断开发,至今已被广泛地应用在电力系统许多类型的模拟研究,其中包括交流研究,雷电过电压和电力电子学研究。
EMTDC开始时在大型计算机上使用。
然后在1986年被移植到Unix系统和以后的PC机上。
PSCAD代表电力系统计算机辅助设计,PSCAD的开发成功,使得用户能更方便地使用EMTDC进行电力系统分析,使电力系统复杂部分可视化成为可能,而且软件可以作为实时数字仿真器的前置端。
分布式光伏发电并网对配网电压的影响分析

分布式光伏发电并网对配网电压的影响分析罗日腾(广东电网有限责任公司梅州平远供电局)摘 要:光伏发电的接入位置与接入容量直接影响着配网电压的稳定性,严重时甚至导致过电压或潮流波动,在配网建设中需全面重视。
研究从分布式光伏并网方案出发搭建算法模型,通过有功潮流和损失关系,分别计算馈线长度和光伏容量对配网电压的影响;并借助Matlab/Simulink工具进行算法的仿真检验,确定位置越近(靠近线路末端或并网点)、容量越大,电压偏差越明显。
关键词:光伏并网;电压偏差;影响;检验0 引言进入21世纪以来,我国加大了对清洁能源的重视力度,开始将光伏发电、风力发电、水力发电等接入到配网中,在一定程度上缓解了电能紧张的局面。
尤其是在光伏并网过程中,其适用范围广、发电效率高、成本投入小,具有显著的经济优势。
如何科学规划光伏接入方案,合理配置光伏并网模式,抑制过电压及严重电压波动,保障配网稳态电压分布,已经成为绿色配网建设的重中之重,值得深入研究与拓展。
1 并网方式光伏并网可通过逆变器、光伏阵列、控制系统、变压器等,将光能转变为电能,供用户侧生产生活使用。
现阶段我国光伏发电系统主要包括纯并网光伏发电系统、具有UPS功能的并网光伏发电系统和并网光伏发电混合系统三大类,其均可从高/低压馈线处接入,实现供电差额的补偿与外送,其中:(1)集中式并网。
我国配网主接线一般为单电源树干式接线、单电源辐射式接线和双电源手拉手环网接线。
双电源在运行过程中互为主备,在一定程度上也可视为单电源辐射式接线。
此时,集中式光伏并网可将大型光伏电站与主接线连接,进行高压远距离输电。
该并网发电时所有电能均输送到配网后再统一调配,起到了非常好的削峰填谷效果。
(2)分布式并网。
分布式光伏系统规模较小,先满足用户侧用电后余电上网。
分布式光伏并网可直接接入到主干线链路中,就近上网,如图1所示。
图1 某10kV配网分布式光伏并网方案上述并网过程中光伏电源靠近用户侧,供电半径大幅缩短,减少了不必要的电能损耗。
14nm 节点技术

QB qNa xd maxLW QB max LW
对于短沟道效应器件,耗尽区为梯形区域区域:
' QB qNa xd max
L L' L L' W QB max W 2 2
电荷变化:
L L' L QB QB QB 2L L
4nm的挑战来自?
短沟道效应-阈值电压漂移 对耗尽边界进行近似
2002 年,Fu-Liang Yang, Haur-Ywh Chen, Fang-Cheng Chen 等人第一次实现了高性 能的 35nm COMS FINFETs 结构 2003 年,T. Ludwig, I. Aller, V. Gemhoefer, J. Keinelt, E. Nowak 等人第一次将现有的 SOI 微处理器设计技术转换到 100nm FINFET 技术中 2004 年,杨福良等人研制成功栅长为 5nm 的纳米线 FINFET 器件
14nm 节点技术
目录
CONTENTS
导言 Finfet
三栅Finfet
工艺难题
参考文献
导言
选题背景
研究意
国内外相关研究综述
理论基础与文献综述
14nm是 ??
[1]
14nm是 ??
[2]
为什么是14nm? 摩尔定理
[1]
14nm的挑战来自?
短沟道效应-阈值电压漂移
VT VFB qN A 2 s 2B 2B COX
绯红区域为源漏控制耗尽层,该区 域的电荷对阈值电压没有贡献,因 此相比于图1,栅控耗尽层区域的 缩小,相应的电荷减少,而阈值电 压也相应的降低 [3]
14nm的挑战来自?
短沟道效应-阈值电压漂移
IEEE14节点潮流计算
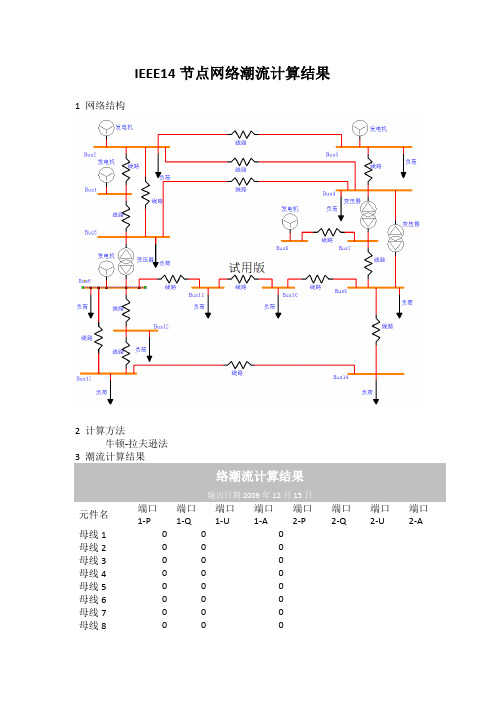
IEEE14节点网络潮流计算结果1 网络结构2 计算方法牛顿-拉夫逊法3 潮流计算结果络潮流计算结果输出日期:2009年12月15日元件名端口1-P端口1-Q端口1-U端口1-A端口2-P端口2-Q端口2-U端口2-A母线1000母线2000母线3000母线4000母线5000母线6000母线7000母线8000母线9000母线10000母线11000母线12000母线13000母线14000发电机10发电机20发电机3发电机40发电机50负荷100负荷200负荷300负荷400负荷500负荷600负荷700负荷800负荷900负荷1000负荷1100线路1线路2线路3线路4线路5线路60线路70线路8线路9线路10线路11线路12线路13-2E-16线路14线路15线路16线路17双卷变压器1双卷变压器2双卷变压器3FACTS技术的研究现状综述汪洋1012 电力系统及其自动化1柔性交流输电技术的时代背景众所周知,电力网络的输电可控性和发电、配电相比较差,网络中功率潮流的自然分布会随着负荷变化而变化,可能造成过大的电能损失或危及安全运行而被迫降低输送功率,从而造成已有输线的负担日益加重,输送能力不足的矛盾日益突出。
一般说来,电力网络的输电能力受到静态稳定、动态稳定、暂态稳定、电压稳定和热稳定极限的限制,其中前四种因素是限制电网输送能力的主要因素。
同时,由于一系列的社会、环境与经济方面的原因,限制了新的发电厂和输电网络的建设,这就使得电力系统在二十一世纪面临的主要问题之一就是:如何最大限度地提高电力设备的利用率、如何最大限度地提高输电网络的传输能力。
随着电力电子技术、计算机技术、控制技术的不断发展,电力工业技术也取得了许多新的进步,其中一个重大的成就就是柔性交流输电系统(FlexibleACTransmissionsystem,简称FACTS)的提出和应用。
柔性交流输电系统技术是目前电力系统新技术中最引人注目的方向之一,它为解决电力系统中存在的经济运行和安全稳定问题提供了有效的手段。
ieee14课程设计

ieee14课程设计一、课程目标知识目标:1. 理解IEEE14节点电力系统的基本构成和特点;2. 掌握节点类型划分及各类型节点的数学描述;3. 学会运用牛顿-拉夫逊法进行IEEE14节点系统的潮流计算;4. 了解系统负荷变化对节点电压和线路功率的影响。
技能目标:1. 能够运用所学知识,对IEEE14节点系统进行建模和仿真;2. 能够独立完成牛顿-拉夫逊法的潮流计算,并分析计算结果;3. 能够针对特定问题,提出相应的改进措施和建议。
情感态度价值观目标:1. 培养学生对电力系统的兴趣和热情,激发他们探索电力科学奥秘的欲望;2. 增强学生的团队合作意识,培养他们在解决问题时的沟通与协作能力;3. 引导学生关注电力系统在实际工程中的应用,提高他们的社会责任感和使命感。
分析课程性质、学生特点和教学要求,本课程旨在帮助学生在掌握基本理论知识的基础上,提高解决实际问题的能力。
课程目标具体、可衡量,便于教师进行教学设计和评估。
通过本课程的学习,学生将能够更好地理解电力系统,为未来的学习和工作打下坚实基础。
二、教学内容1. IEEE14节点电力系统简介:介绍系统构成、节点类型及特点;- 教材章节:第二章第二节- 内容列举:节点分类、系统描述、IEEE14节点数据介绍。
2. 节点类型划分及数学描述:- 教材章节:第二章第三节- 内容列举: PQ节点、PV节点、平衡节点、孤立节点的数学模型。
3. 牛顿-拉夫逊法潮流计算:- 教材章节:第三章- 内容列举:潮流计算基本原理、牛顿-拉夫逊法迭代过程、雅可比矩阵构造。
4. IEEE14节点系统建模与仿真:- 教材章节:第四章- 内容列举:系统建模方法、仿真软件应用、牛顿-拉夫逊法在IEEE14节点系统中的应用。
5. 负荷变化对系统影响分析:- 教材章节:第五章- 内容列举:负荷变化对节点电压和线路功率的影响、系统稳定性分析。
6. 潮流计算结果分析及改进措施:- 教材章节:第六章- 内容列举:计算结果分析、改进措施、优化算法。
考虑负荷电压静特性和PV节点的配电网线性化潮流计算

ELECTRIC DRIVE2024Vol.54No.5电气传动2024年第54卷第5期考虑负荷电压静特性和PV节点的配电网线性化潮流计算赵恩来1,胡雨1,郭俊2,苏鑫磊1,刘膨源1,杨君1(1.北京国网信通埃森哲信息技术有限公司,北京100052;2.国网福建省电力有限公司电力科学研究院,福建福州350007)摘要:鉴于原有的高维非线性潮流模型无法适用于配电网线性规划,而现有的线性化潮流模型存在通用性不强的问题,提出了一种考虑负荷电压静特性和PV节点的配电网线性化潮流计算方法。
所提方法基于极坐标系下的潮流方程,利用配电网的特征对潮流方程的电压幅值和相角进行解耦;再根据PV节点自身的控制特性,推导出一种含PV节点的线性化潮流计算模型。
所提模型不仅考虑了PV节点和负荷电压静特性,而且兼顾对过负载和弱环网的适应性,无需迭代便可求解配电网的电压分布。
仿真结果表明:所提方法具有较高的精度和通用性,可用于配电网的快速分析。
关键词:配电网;线性化潮流;负荷电压静特性;过负载;快速分析中图分类号:TM744文献标识码:A DOI:10.19457/j.1001-2095.dqcd24815Linear Power Flow Calculation of Distribution Network ConsideringLoad Voltage Static Characteristics and PV NodeZHAO Enlai1,HU Yu1,GUO Jun2,SU Xinlei1,LIU Pengyuan1,YANG Jun1(1.Beijing SGITG Accenture Information Technology Co.,Ltd.,Beijing100052,China;2.Electric Power Research Institute,State Grid Fujian Electric Power Co.,Ltd.,Fuzhou350007,Fujian,China)Abstract:In view of the fact that the original high-dimensional nonlinear power flow model cannot be applied to the linear planning of distribution network,and the existing linear power flow model has the problem of weak universality,a calculation method of distribution network linear power flow was proposed considering the static characteristics of load voltage and PV nodes.Based on the power flow equation in polar coordinates,the proposed method decoupled the voltage amplitude and phase angle of the power flow equation using the characteristics of the distribution network.According to the control characteristics of PV nodes,a linear power flow calculation model with PV nodes was derived.The proposed model not only considered the static characteristics of PV nodes and load voltages,but also considered the adaptability to overload and weak loop networks.It could solve the voltage distribution of distribution networks without iteration.The simulation results show that the proposed method has high accuracy and versatility,and can be used for rapid analysis of distribution networks.Key words:distribution network;linear power flow;load voltage static characteristic;overload;rapid analysis随着分布式电源(distributed generation,DG)的大量并网,配电系统的结构变得越来越复杂[1]。
IEEE14节点模型
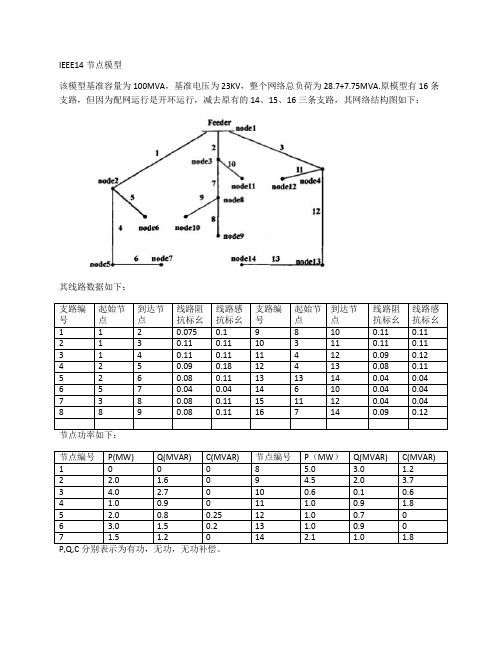
IEEE14节点模型
该模型基准容量为100MVA,基准电压为23KV,整个网络总负荷为28.7+7.75MVA.原模型有16条支路,但因为配网运行是开环运行,减去原有的14、15、16三条支路,其网络结构图如下:
其线路数据如下:
支路编号
起始节点
到达节点
线路阻抗标幺
线路感抗标幺
支路编号
起始节点
到达节点
0.1
0.6
4
1.0
0.9
0
11
1.0
0.9
1.8
5
2.0
0.8
0.25
12
1.0
0.7
0
6
3.0
1.5
0.2
13
1.0
0.9
0
7
1.5
1.2
0
14
2.1
1.0
1.8
P,Q,C分别表示为有功,无功,无功补偿。
线路阻抗标幺
线路感抗标幺
1
1
2
0.075
0.1
9
8
10
0.11
0.11
2
1
3
0.11
0.11
10
3
11
0.11
电气工程PSASP仿真软件实践

东南大学研究生课程《电气工程仿真软件实践》课程报告院(系、所)电气工程学院学科(专业)电气工程研究生姓名郝攀学科门类与学位级别工学硕士导师姓名张金旺入学年月 2015年8月31日结题报告日期 2016年5月26日东南大学电气工程学院1实验目的掌握电力系统稳态运行的基本要求;培养应用电力系统仿真计算软件PSASP进行潮流调整、电压调整、网损分析的实践能力;培养运用所学知识分析和解决问题的能力。
2PSASP简介2.1PSASP综述《电力系统分析综合程序》(Power System Analysis Software Package, PSASP)是由中国电力科学研究院研发的电力系统分析程序。
主要用于电力系统规划设计人员确定经济合理、技术可行的规划设计方案;运行调度人员确定系统运行方式、分析系统事故、寻求反事故措施;科研人员研究新设备、新元件投入系统等新问题以及高等院校用于教学和研究。
2.2PSASP特点PSASP具有基于公用数据和模型的三层体系结构, 如图1所示。
第一层是公用数据和模型的资源库;第二层是基于资源库的应用程序包;第三层是计算结果库和分析工具,极大地资源共享,高度集成和开放。
PSASP 有着友好、方便的人机界面,如基于图形的数据输入和图上操作,自定义模型图以及图形、曲线、报表等各种形式输入。
PSASP 与Excel、AutoCAD、Matlab 等通用的软件分析工具有着方便的接口,可充分利用这些软件的资源。
PSASP 应用程序的共同特点是:●可计算大规模(可达3000 个母线或更多)的交直流混合电力系统;●有公用的数据库做支持,不必为每一种计算准备其基础数据。
●有固定模型库和用户自定义模型库作支持。
●不但有通常的文本方式计算,而且还有单线图上的操(修改数据、操作开关、增加故障等)计算,其计算结果直接标注在图上,具有仿真的效果。
●具有多种形式(图形、图示、报表、曲线等)的结果分析的输出。
提供了与 Excel、AutoCAD、Matlab等常用软件工具的接口。
psasp7.0IEEE14节点网损分析

psasp7.0IEEE14节点⽹损分析IEEE14节点⽹损分析代表⽇分区线损汇总表(⽆损)计算⽇期:2013-05-12地区名有功供电量(万kWh)⽆功供电量(万kVarh) 线损(万kWh) 铜损(万kWh) 铁损(万kWh) 其它(万kWh) ⼩计(万kWh) 线损率(%)铜损率(%) 铁损率(%) 其它(%) 线损率(%)占总线损电量百分⽐(%) 线损(%) 铜损(%) 铁损(%)------------------------------------------ ----------- ----------- ----------- ----------- ----------- --------- --------- --------- ------- ------------------------------ ------- ------- -------IEEE14节点⽹损分析代表⽇分区线损汇总表(有损)计算⽇期:2013-05-12地区名有功供电量(万kWh)⽆功供电量(万kVarh) 线损(万kWh) 铜损(万kWh) 铁损(万kWh) 其它(万kWh) ⼩计(万kWh) 线损率(%)铜损率(%) 铁损率(%) 其它(%) 线损率(%)占总线损电量百分⽐(%) 线损(%) 铜损(%) 铁损(%)------------------------------------------ ----------- ----------- ----------- ----------- ----------- --------- --------- --------- ------- ------------------------------ ------- ------- -------IEEE14节点⽹损分析代表⽇分压线损汇总表(⽆损)计算⽇期:2013-05-12电压等级有功供电量(万kWh)⽆功供电量(万kVarh) 线损铜损铁损其它⼩计线损铜损率铁损率其它线损率占总线损电量百分⽐线损铜损铁损-------------------------------------------- ---- ---- ---- ---- ---- ---- ------ ------ ---- ------------------------ ---- ---- ----0 0 0 36.9022 0 0 0 36.9022 0 0 0 0 0 99.9999 100 0 0合计 0 0 36.9022 0 0 0 36.9022 0 0 0 0 0 100 100 0 0IEEE14节点⽹损分析代表⽇分压线损汇总表(有损)计算⽇期:2013-05-12电压等级有功供电量(万kWh)⽆功供电量(万kVarh) 线损铜损铁损其它⼩计线损铜损率铁损率其它线损率占总线损电量百分⽐线损铜损铁损-------------------------------------------- ---- ---- ---- ---- ---- ---- ------ ------ ---- ------------------------ ---- ---- ----0 0 0 36.9022 0 0 0 36.9022 0 0 0 0 0 99.9999 100 0 0合计 0 0 36.9022 0 0 0 36.9022 0 0 0 0 0 100 100 0 0IEEE14节点⽹损分析线损理论计算结果汇总表计算⽇期:2013-05-12电压等级供电量(MWh) 供电量占⽐(%) 损失量(MWh)损失量占总损⽐(%) 线损率(%) 线损构成率(%)-------- ----------- ------------- ---------------------------- --------- -------------表5-3IEEE14节点⽹损分析代表⽇线路损耗表计算⽇期:2013-05-12(全天)线路名称输送有功(万kWh)总有功损耗(万kWh) 有功损耗率(%) 线路型号线路长度(km)-------- -------------------------------- ------------- -------- ------------AC_1 0.00873 0 0 0AC_10 38.1782 0.47375 1.24089 0AC_11 5.5235 0.03387 0.613198 0AC_12 20.4014 0.23794 1.16629 0AC_13 5.24729 0.06277 1.19624 0AC_14 13.753 0.10526 0.765359 0AC_15 16.552 0.13425 0.811082 0AC_16 183.694 7.60993 4.14273 0AC_17 99.0566 2.37391 2.39652 0AC_18 155.316 1.40462 0.904364 0AC_3 56.9079 0.96788 1.70078 0AC_4 135.221 4.49889 3.32706 0AC_5 378.791 12.1441 3.20602 0AC_6 176.29 6.15632 3.49216 0AC_7 72.1317 0 0 0AC_8 25.6658 0.57601 2.24427 0AC_9 10.7934 0.12264 1.13625 0IEEE14节点⽹损分析代表⽇变压器损耗表计算⽇期:2013-05-12(全天)变压器名输送有功(万kWh)有功铜损(kWh) 有功铁损(kWh) 有功总损耗(kWh) 有功铜损率(%) 有功铁损率(%) 有功总损率(%) ------------------------- ------------- ------------- --------------- ------------- ------------- -------------T2w_1 72.1201 0 0 0 0 0 0T2w_3 40.8879 0 0 0 0 0 0T2w_4 99.2131 0 0 0 0 0 0附表1-2IEEE14节点⽹损分析代表⽇⼚站其它项损耗表计算⽇期:2013-05-12(全天)⼚站名元件类型元件名称额定容量损耗(kWh) 元件型号------ -------- -------- -------- --------- --------IEEE14节点⽹损分析全⽹分区分压设备数据统计表计算⽇期:2013-05-12主⽹及各地区电⽹运⾏线路条数(条) 运⾏线路长度(kM) 变电站数量运⾏变压器台数(台) 运⾏变压器额定容量(MVA) 运⾏变压器最⼤负荷(MW) 容载⽐(%)--------------------------------------------------- ----------------------------------------------------------------------------- ----------0 17 0 1 3 0 0 0合计 17 0 1 3 0 0IEEE14节点⽹损分析电⽹变压器运⾏状态统计计算⽇期:2013-05-12全天电压等级铜损是铁损⼆倍以上的重载变:台数(占⽐%)铁损是铜损⼆倍以上的轻载变:台数(占⽐%)铁损等于铜损的经济变:台数(占⽐%) 其它变压器变压器总台数-------------------------------------------------------------------------------------------------------------------- ---------- ------------表5-2IEEE14节点⽹损分析代表⽇负荷情况计算⽇期:2013-05-12- -地区IEEE14节点⽹损分析最⼤供电负荷(MW)⽇供电量(MWh) 0全⽹代表⽇最⼤负荷(MW)(⽤电负荷) 259全⽹代表⽇最⼩负荷(MW)(⽤电负荷) 259表3-2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
到达节点
线路阻抗标幺
线路感抗标幺
支路编号
起始节点
到达节点
线路阻抗标幺
线路感抗标幺
1
1
2
0.075
0.1
9
8
10
0.11
0.11
2
1
3
0.11
0.11
10
3
11
0.11
0.11
3
1
4
0.11
0.11
11
4
12
0.09
0.12
4
2
5
0.09
0.18
12
4
13
0.08
0.11
5
2
6
0.08
0.11
4.将环境影响价值纳入项目的经济分析
3)按行业分。国家污染物排放标准分为跨行业综合性排放标准和行业性排放标准。报告内容有:建设项目基本情况、建设项目所在地自然环境社会环境简况、环境质量状况、主要环境保护目标、评价适用标准、工程内容及规模、与本项目有关的原有污染情况及主要环境问题、建设项目工程分析、项目主要污染物产生及预计排放情况、环境影响分析、建设项目拟采取的防治措施及预期治理效果、结论与建议等。
1.2
2
2.0
1.6
0
9
4.5
Hale Waihona Puke 2.03.734.0
2.7
0
10
0.6
0.1
0.6
4
1.0
0.9
0
11
1.0
0.9
1.8
5
2.0
0.8
0.25
12
1.0
0.7
0
6
3.0
1.5
0.2
13
1.0
0.9
0
7
1.5
1.2
0
14
2.1
1.0
1.8
P,Q,C分别表示为有功,无功,无功补偿。
第一节 环境影响评价
(1)建设项目概况。目前,获得人们的偏好、支付意愿或接受赔偿的意愿的途径主要有以下三类:①从直接受到影响的物品的相关市场信息中获得;②从其他事物中所蕴含的有关信息间接获得;③通过直接调查个人的支付意愿或接受赔偿的意愿获得。其线路数据如下:
一、环境影响评价的基础
2.早期介入原则;支路编号
13
13
14
0.04
0.04
6
5
7
0.04
0.04
14
6
10
0.04
0.04
7
3
8
0.08
0.11
15
11
12
0.04
0.04
8
8
9
0.08
0.11
16
7
14
0.09
0.12
节点功率如下:
节点编号
P(MW)
Q(MVAR)
C(MVAR)
节点编号
P(MW)
Q(MVAR)
C(MVAR)
1
0
0
0
8
5.0
3.0
IEEE14节点模型
3)应用污染物排放标准时,依据项目所属行业、环境功能区、排放的污染物种类和环境影响评价文件的批准时间确定采用何种标准。综合性排放标准与行业性排放标准不交叉执行,即:有行业排放标准的执行行业排放标准,没有行业排放标准的执行综合排放标准。二、建设项目环境影响评价该模型基准容量为100MVA,基准电压为23KV,整个网络总负荷为28.7+7.75MVA.原模型有16条支路,但因为配网运行是开环运行,减去原有的14、15、16三条支路,其网络结构图如下:
