第三章(曲线拟合的最小二乘法-2)
第3章曲线拟合的最小二乘法计算方法

最小二乘拟合,特别是多项式拟合,是最流行的数据处理 方法之一.它常用于把实验数据(离散的数据)归纳总结为经 验公式(连续的函数),以利于进一步的推演分析或应用.
1
结束
§3.2 线性拟合和二次拟合函数
1. 线性拟合
计 已知数据点为 ( xi , yi ), i 1,2,..., n
算 用直线 p( x) a bx作为近似曲线,均方误差为
计
i xi yi xi yi xi2 xi2yi xi3
xi4
0 3 5 15 9 45 27
81
算
1 5 2 10 25 50 125 625
方
2 6 1 6 36 36 216 1296
法
3 8 2 16 64 128 512 4096
课
4 10 4 40 100 400 1000 10000
件
Y ln y, A ln a Y A bx
8
i
xi
0
1
yi
Yi
15.3
2.7279
xi2
xiYi
1
2.7279
1
2
20.5
3.0204
4
6.0408
计
2
3
27.4
3.3105
9
9.9315
算
3
4
36.6
3.6000
16
14.4000
方
4
5
49.1
3.8939
25
19.4695
法
5
6
65.6
4
例1 设5组数据如下表,用一多项式对其进行拟合。
x 3 5 6 8 10
计
计算方法 第三章曲线拟合的最小二乘法20191103

§2 多项式拟合函数
例3.1 根据如下离散数据拟合曲线并估计误差
x 1 23 4 6 7 8 y 2 36 7 5 3 2
解: step1: 描点
7
*
step2: 从图形可以看出拟
6 5
*
合曲线为一条抛物线:
4
y c0 c1 x c2 x2
3 2 1
* *
* * *
step3: 根据基函数给出法
法
18
定理 法方程的解是存在且唯一的。
证: 法方程组的系数矩阵为
(0 ,0 ) (1 ,0 )
G
(0
,1
)
(1 ,1 )
(0 ,n ) (1 ,n )
(n ,0 )
(
n
,
1
)
(n ,n )
因为0( x),1( x), ...,n( x)在[a, b]上线性无关,
所以 G 0,故法方程 GC F 的解存在且唯一。
第三章 曲线拟合的最小二乘法
2
最小二乘拟合曲线
第三章 曲线拟合的最小二乘
2021/6/21
法
3
三次样条函数插值曲线
第三章 曲线拟合的最小二乘
2021/6/21
法
4
Lagrange插值曲线
第三章 曲线拟合的最小二乘
2021/6/21
法
5
一、数据拟合的最小二乘法的思想
已知离散数据: ( xi , yi ), i=0,1,2,…,m ,假设我们用函
便得到最小二乘拟合曲线
n
* ( x) a*j j ( x) j0
为了便于求解,我们再对法方程组的导出作进一步分析。
第三章 曲线拟合的最小二乘
曲线拟合——最小二乘法算法

曲线拟合——最小二乘法算法一、目的和要求1)了解最小二乘法的基本原理,熟悉最小二乘算法;2)掌握最小二乘进行曲线拟合的编程,通过程序解决实际问题。
二、实习内容1)最小二乘进行多项式拟合的编程实现。
2)用完成的程序解决实际问题。
三、算法1)输入数据节点数n ,拟合的多项式次数m ,循环输入各节点的数据x j , y j (j=0,1,…,n-1)2)由x j 求S ;由x j ,y j 求T :S k =∑-=10n j k j x ( k=0,1,2, … 2*m ) T k = ∑-=10n j k j j x y ( k=0,1,2,… m )3)由S 形成系数矩阵数组c i,j :c[i][j]=S[i+j] (i=0,1,2,…m, j=0,1,2,…,m);由T 形成系数矩阵增广部分c i,m+1:c[i][m+1]=T[i] (i=0,1,2,…m)4)对线性方程组CA=T[或A C ],用列主元高斯消去法求解系数矩阵A=(a 0,a 1,…,a m )T四、实验步骤1)完成最小二乘法进行曲线拟合的程序设计及录入、编辑;2)完成程序的编译和链接,并进行修改;3)用书上P105例2的例子对程序进行验证,并进行修改;4)用完成的程序求解下面的实际问题。
5)完成实验报告。
五、实验结果1. 经编译、链接及例子验证结果正确的源程序:#include<stdio.h>#include<math.h>#define Q 100float CF(int,float);main(){int i,j,n1,n,p,k,q;float x[Q],y[Q],s[Q]={0},t[Q]={0},a[Q][Q]={0},l,sum=0;/*以下是最小二乘的程序*/printf("input 数据组数n");scanf("%d",&n);printf("input 拟合次数n1");scanf("%d",&n1);for(i=0;i<n;i++){printf("x[%d]=",i);scanf("%f",&x[i]);printf("y[%d]=",i);scanf("%f",&y[i]);}for(i=0;i<=2*n1;i++)for(j=0;j<n;j++){s[i]=s[i]+CF(i,x[j]);if(i<=n1)t[i]=t[i]+y[j]*CF(i,x[j]);}for(i=0;i<n1+1;i++)for(j=0;j<n1+2;j++){a[i][j]=s[i+j];if(j==n1+1)a[i][j]=t[i];}for(i=0;i<n1+1;i++)for(j=0;j<n1+2;j++)printf("a[%d][%d]=%f",i,j,a[i][j]); /*以下的是削去法的程序*/for(j=0;j<=n1-1;j++){p=j;for(i=j+1;i<=n1;i++){if(fabs(a[j][j])<fabs(a[i][j]))p=i;}if(p!=j)for(i=j;i<=n1+1;i++){l=a[p][i];a[p][i]=a[j][i];a[j][i]=l;}for(k=j+1;k<=n1;k++){l=a[k][j]/a[j][j];for(q=j;q<=n1+1;q++)a[k][q]=a[k][q]-l*a[j][q];}}for(i=0;i<n1+1;i++){for(j=0;j<n1+2;j++)printf("a[%d][%d]=%f\n",i,j,a[i][j]);printf("\n");}x[n1]=a[n1][n1+1]/a[n1][n1];for(i=n1-1;i>=0;i--){for(j=i+1;j<=n1;j++)sum=a[i][j]*x[j]+sum;x[i]=(a[i][n1+1]-sum)/a[i][i];sum=0;}for(i=0;i<=n1;i++)printf("x[%d]=%f\n",i,x[i]);}float CF(int i,float v){float a=1.0;while(i--)a*=v;return a;}2. 实例验证结果:1)输入初始参数:n=9,m=2X:1 3 4 5 6 7 8 9 10Y:10 5 4 2 1 1 2 3 42)结果输出:1.实际应用问题:作物体运动的观测实验,得出以下实验测量数据,用最小二乘拟合求物体的运动方程。
计算方法离散数据曲线拟合
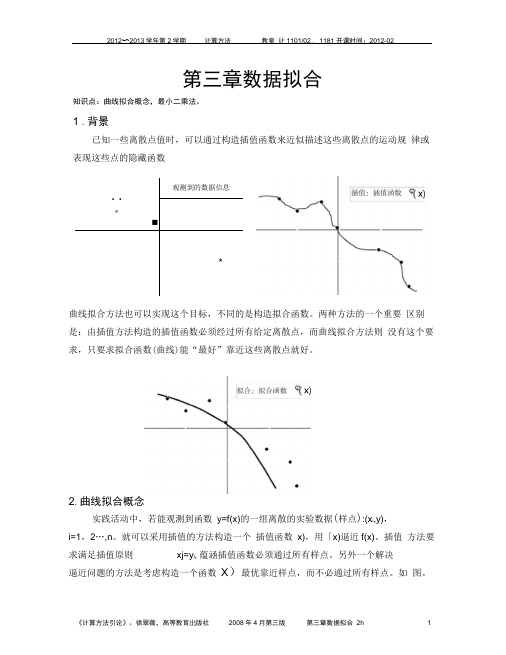
第三章数据拟合知识点:曲线拟合概念,最小二乘法。
1 .背景已知一些离散点值时,可以通过构造插值函数来近似描述这些离散点的运动规律或表现这些点的隐藏函数观测到的数据信息• •*■*曲线拟合方法也可以实现这个目标,不同的是构造拟合函数。
两种方法的一个重要区别是:由插值方法构造的插值函数必须经过所有给定离散点,而曲线拟合方法则没有这个要求,只要求拟合函数(曲线)能“最好”靠近这些离散点就好。
2.曲线拟合概念实践活动中,若能观测到函数y=f(x)的一组离散的实验数据(样点):(x i,y),i=1,2…,n。
就可以采用插值的方法构造一个插值函数x),用「x)逼近f(x)。
插值方法要求满足插值原则xj=y i,蕴涵插值函数必须通过所有样点。
另外一个解决逼近问题的方法是考虑构造一个函数X)最优靠近样点,而不必通过所有样点。
如图。
即向量T= (「X1),X2),•••「x n))与丫= (y1, y2, )的某种误差达到最小。
按T和丫之间误差最小的原则作为标准构造的逼近函数称拟合函数。
曲线拟合问题:如何为f(x)找到一个既简单又合理的逼近函数X)。
曲线拟合:构造近似函数x),在包含全部基节点x<i=1 , 2…,n)的区间上能“最好”逼近f(x)(不必满足插值原则)。
逼近/近似函数y=「x)称经验公式或拟合函数/曲线。
拟合法则:根据数据点或样点(xy), i=1 , 2…,n,构造出一条反映这些给定数据一般变化趋势的逼近函数y=「x),不要求曲线■- x)经过所有样点,但要求曲线x)尽可能靠近这些样点,即各点误差S i= x i)-y i按某种标准达到最小。
均方误差/误差平方和/误差的2-范数平方:n卜||2八1i 4常用误差的2-范数平方作为总体误差的度量,以误差平方和达到最小作为最优标准构造拟合曲线的方法称为曲线拟合的最小二乘法(最小二乘原理)。
3.多项式拟合2012〜2013学年第2学期计算方法 教案 计1101/02 , 1181 开课时间:2012-02年4月第三版 第三章数据拟合 2h 3(1) 线性拟合给定一组(x i ,y i ), i=1 , 2…,n 。
excel拟合曲线用的最小二乘法

Excel拟合曲线用的最小二乘法1. 介绍Excel作为一款常用的办公软件,被广泛应用于数据分析和处理,而拟合曲线是数据分析中常用的方法之一。
拟合曲线用的最小二乘法是一种常见的拟合方法,通过最小化数据点与拟合曲线之间的距离来找到最佳拟合曲线,从而对数据进行预测和分析。
在本文中,我将从深度和广度的角度来探讨Excel拟合曲线用的最小二乘法,带你深入探索这一主题。
2. 最小二乘法的原理在Excel中进行曲线拟合时,最小二乘法是一种常用的拟合方法。
其原理是通过最小化残差平方和来找到最佳拟合曲线。
残差是指每个数据点到拟合曲线的垂直距离,最小二乘法通过调整拟合曲线的参数,使得残差平方和最小化,从而得到最佳拟合曲线。
在Excel中,可以利用内置函数或插件来实现最小二乘法的曲线拟合,对于不同类型的曲线拟合,可以选择不同的拟合函数进行拟合。
3. Excel中的拟合曲线在Excel中进行拟合曲线时,首先需要将数据导入Excel,然后利用内置的数据分析工具或者插件来进行曲线拟合。
通过选择拟合函数、调整参数等操作,可以得到拟合曲线的相关信息,如拟合优度、参数估计值等。
可以根据拟合曲线的结果来对数据进行预测和分析,从而得到对应的结论和见解。
4. 个人观点与理解对于Excel拟合曲线用的最小二乘法,我认为这是一种简单而有效的数据分析方法。
它能够快速对数据进行拟合,并得到拟合曲线的相关信息,对于数据的预测和分析具有一定的帮助。
然而,也需要注意到拟合曲线并不一定能够准确描述数据的真实情况,需要结合实际背景和专业知识进行分析和判断。
在使用最小二乘法进行曲线拟合时,需要注意数据的可靠性和拟合结果的可信度,以避免出现不准确的结论和偏差的情况。
5. 总结通过本文的探讨,我们对Excel拟合曲线用的最小二乘法有了更深入的了解。
最小二乘法的原理、Excel中的实际操作以及个人观点与理解都得到了充分的展示和探讨。
在实际应用中,需要结合具体情况和专业知识来灵活运用最小二乘法进行曲线拟合,从而得到准确的分析和预测结果。
曲线拟合的最小二乘法

一、曲线拟合是什么?曲线拟合也就是求一条曲线,使数据点均在离此曲线的上方或下方不远处, 它既能反映数据的总体分布,又不至于出现局部较大的波动, 能反映被逼近函数的特性,使求得的逼近函数与已知函数从总体上来说其偏差按某种方法度量达到最小。
设函数y=f(x)在m个互异点的观测数据为求一个简单的近似函数φ(x),使之“最好”地逼近f(x),而不必满足插值原则。
这时没必要取φ(xi) = yi, 而要使i=φ(xi)yi 总体上尽可能地小。
这种构造近似函数的方法称为曲线拟合,称函数y=φ(x)为经验公式或拟合曲线。
如下为一个曲线拟合示意图。
清楚什么是曲线拟合之后,我们还需要了解一个概念——残差。
曲线拟合不要求近似曲线严格过所有的数据点,但使求得的逼近函数与已知函数从总体上来说其偏差按某种方法度量达到总体上尽可能地小。
若令(1-1)则为残向量(残差)。
“使(1-1)尽可能地小”有不同的准则(1)残差最大值最小(2)残差绝对值和最小(绝对值的计算比较麻烦)(3)残差平方和最小(即最小二乘原则。
计算比较方便,对异常值非常敏感,并且得到的估计量具有优良特性。
)二、最小二乘法是什么?个人粗俗理解:按照最小二乘原则选取拟合曲线的方法,称为最小二乘法。
百度百科:最小二乘法(又称最小平方法)是一种数学优化技术。
它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法还可用于曲线拟合。
其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
三、求解最小二乘法(包含数学推导过程)我们以最简单的线性模型来解释最小二乘法。
什么是线性模型呢?监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。
回归分析中,n个自变量,且因变量和自变量之间是线性关系,则称为一/多元线性回归分析。
python曲线拟合的最小二乘法

python曲线拟合的最小二乘法最小二乘法是一种常用的曲线拟合方法。
它的核心思想是寻找一条曲线,使得曲线上的点到实际数据点的距离之和最小。
在Python中,可以使用scipy库中的optimize.curve_fit函数来实现最小二乘法的曲线拟合。
该函数接受两个参数:要拟合的函数和实际数据点。
首先,需要定义一个函数,表示要拟合的曲线形式。
然后,通过curve_fit函数传入该函数和实际数据点,即可得到最小二乘法的曲线拟合结果。
以下是一个简单的示例代码:```pythonimport numpy as npfrom scipy import optimizeimport matplotlib.pyplot as plt# 定义要拟合的曲线形式def func(x, a, b, c):return a * np.exp(-b * x) + c# 实际数据点xdata = np.array([0, 1, 2, 3, 4, 5])ydata = np.array([1, 2, 3, 4, 5, 6])# 曲线拟合params, params_covariance = optimize.curve_fit(func, xdata, ydata)# 拟合结果a, b, c = paramsprint("拟合参数:a =", a, ", b =", b, ", c =", c)# 画出拟合曲线和实际数据点plt.plot(xdata, ydata, 'bo', label='实际数据点')plt.plot(xdata, func(xdata, a, b, c), 'r-', label='拟合曲线') plt.xlabel('x')plt.ylabel('y')plt.legend()plt.show()```在这个示例代码中,我们定义了一个指数形式的曲线函数func,并使用实际数据点进行拟合。
python曲线拟合的最小二乘法

Python曲线拟合的最小二乘法引言在实际应用中,我们经常需要通过已知数据去拟合一条曲线,以便更好地理解数据的趋势和规律。
曲线拟合是一种常用的数据分析方法,而最小二乘法则是其中最常见和重要的一种技术手段。
本文将介绍如何使用Python进行曲线拟合,并着重讨论最小二乘法的应用和原理。
1. 什么是最小二乘法?最小二乘法是一种数学优化方法,用于确定一组数据和一个数学关系式之间的最优拟合曲线。
具体来说,对于给定的一组数据点,最小二乘法的目标是找到一个数学模型,使得该模型计算出的值与实际观测值之间的残差平方和最小。
2. 最小二乘法的原理考虑一个简单的情况,假设我们有一组数据点(x1, y1), (x2, y2), … , (xn, yn),我们想要用一条直线y = ax + b来拟合这些数据。
最小二乘法的目标是找到最优的参数a和b,使得拟合后的直线与数据点之间的残差平方和最小。
为了求解最优参数,可以通过最小化残差平方和的方式来进行。
具体来说,可以定义一个损失函数,即残差平方和的平均值,如下所示:J(a, b) = (1/n) * Σ(yi - (axi + b))^2其中,n表示数据点的个数,xi和yi分别表示第i个数据点的横坐标和纵坐标。
通过最小化这个损失函数,可以得到最优的参数a和b。
对于更复杂的情况,比如需要拟合高阶曲线,最小二乘法的原理类似,只是拟合模型不同。
还可以通过增加更多的参数来适应更复杂的曲线形状。
3. 使用Python进行最小二乘法曲线拟合在Python中,使用最小二乘法进行曲线拟合非常方便,可以使用scipy库的optimize模块中的curve_fit函数来实现。
我们需要导入必要的库:import numpy as npfrom scipy.optimize import curve_fitimport matplotlib.pyplot as plt我们可以定义拟合的数学模型。
以拟合一条指数函数为例,定义一个指数函数的模型:def func(x, a, b, c):return a * np.exp(-b * x) + c接下来,我们可以生成一组测试数据:x = np.linspace(0, 4, 50)y = func(x, 2.5, 1.3, 0.5)使用curve_fit函数进行曲线拟合:params, params_covariance = curve_fit(func, x, y)我们可以绘制原始数据和拟合曲线的图像:plt.plot(x, y, 'bo', label='Original Data')plt.plot(x, func(x, params[0], params[1], params[2]), 'r-', label='Fitted Curv e')plt.legend()plt.show()4. 个人观点和总结最小二乘法在数据分析和曲线拟合中被广泛应用,其原理简单而有效。
2013218 第3章 曲线拟合的最小二乘法

换句话说 :求一条曲线,使数据点均在离此曲线的上方 为此 ,我们希望从给定的数据 (xi,yi)出发,构造一个 或下方不远处 , 所求的曲线称为拟合曲线 , 它既能反映 近似函数 , 不要求函数 完全通过所有的数 ( x) ( x) 数据的总体分布,又不至于出现局部较大的波动,更能 据点,只要求所得的近似曲线能反映数据的基本趋 反映被逼近函数的特性 势,如图 3.1所示。 ,使求得的逼近函数与已知函数 从总体上来说其偏差按某种方法度量达到最小,这就是 最小二乘法。
线。作拟合直线 y ( x ) a a x ,该直线不是通过所有的 0 1 数据点 x i, y i ,而是使偏差平方和
2 F ( a , a ) ( a a x y ) 0 1 0 1i i m
为最小,其中每组数据与拟合曲线的偏差为
i 1
y ( x ) y a a x y i 1 , 2 , , m i i 0 1 i i 根据最小二乘原理,应取 a 0 和 a 1 使 F(a0 , a1) 有极小 值,故 a 0 和 a 1应满足下列条件:
m F ( a 0,a 1) 2 ( a 0 a 1x i y i ) 0 a i 1 0 m F ( a 0,a 1) 2 ( a x 0 a 1x i y i) i 0 a i 1 1
即得如下正规方程组
m m a0 m a1 xi yi i 1 i 1 m m m 2 a x 1 i a0 xi xi yi i 1 i 1 i 1
两种逼近概念:
插值: 在节点处函数值相同.
拟合:
在数据点处误差平方和最小
函数插值是插值函数P(x)与被插函数f(x)在节点 处函数值相同,即 P 而曲线 i 0 , 1 , , n ) ( x f( x i) i) ( 拟合函数 ( x) 不要求严格地通过所有数据点 ( xi , y i ) ,也 就是说拟合函数 ( x) 在xi处的偏差(亦称残差)
最小二乘法曲线拟合原理

最小二乘法曲线拟合原理最小二乘法曲线拟合原理是指用曲线来拟合已知数据点的一种优化算法,也叫“误差最小化法”,更多的称之为“最小二乘法”,简称LSM。
最小二乘法曲线拟合的应用范围很广,拟合分析复杂数据的应用越来越多。
最小二乘法曲线拟合的原理最小二乘曲线拟合的基本原理是构造一个最适合拟合给定数据点的函数,使拟合后函数拟合数据点和真实数据点之间的均方误差(SSE)最小。
均方误差是指观测值和拟合函数值之间的差的平方(SSE = SΣ(Yi - Xk)^2)。
均方误差最小,表明拟合函数就是最适合拟合数据的函数,而最小二乘法的基本思想就是求均方误差最小,即求解最优解的函数,这个函数就是最合适拟合给定数据点的曲线函数,即最小二乘法曲线拟合函数。
最小二乘法曲线拟合的应用最小二乘法曲线拟合最常见的应用是拟合曲线,以解决未知函数形式的问题。
拟合曲线可以使用曲线来估计一组数据,曲线拟合可以使得模型更准确地拟合数据,并且可以获得该曲线的未知参数。
如果数据不符合一个函数,可以使用自定义函数进行拟合,比如指数函数、sin函数、双曲线等。
最小二乘法也可以用于拟合回归模型,这是一种统计学中常用的方法,它可以用来推断大量随机变量的变化趋势,或者用来分析一个可能受其他变量影响的变量之间的关系。
最小二乘法也可以用于数值估计,比如最小二乘法用于数值拟合,用于数值拟合可以求出未知函数的参数,用于回归分析中,可以估计因变量受自变量影响的参数。
最小二乘法曲线拟合的缺点最小二乘法曲线拟合的最大缺点是其依赖性强:由于拟合的曲线函数有固定形式,因此无法拟合数据点的异常值,也无法拟合数据不具有规律性的情况;另外,最小二乘法曲线拟合也可能因过拟合导致拟合出的函数复杂度较高,从而影响精度。
总结最小二乘法曲线拟合原理指用曲线来拟合已知数据点的一种优化算法,它的基本原理是构造一个最适合拟合给定数据点的函数,使拟合后函数拟合数据点和真实数据点之间的均方误差最小。
曲线拟合的最小二乘法原理及实现

曲线拟合的最小二乘法原理及实现任务名称简介在数据处理和统计分析中,曲线拟合是一种常见的技术,旨在通过数学函数找到最佳拟合曲线,以尽可能准确地描述给定数据集的变化趋势。
在曲线拟合的过程中,最小二乘法是一种常用的数学方法,用于选择最佳拟合曲线。
本文将详细介绍最小二乘法的原理和实现方法。
最小二乘法原理最小二乘法是一种通过最小化误差平方和来拟合数据的方法。
其基本原理是将数据集中的每个数据点与拟合曲线上对应点的差值进行平方,然后将所有差值的平方相加,得到误差平方和。
最小二乘法的目标是通过调整拟合曲线的参数,使得误差平方和达到最小值。
假设我们有一个包含n个数据点的数据集,每个数据点的横坐标为x,纵坐标为y。
我们希望找到一个拟合曲线,可以通过曲线上的点与数据点的差值来评估拟合效果。
拟合曲线的一般形式可以表示为:y = f(x, β)其中,β为拟合曲线的参数,f为拟合曲线的函数。
最小二乘法的基本思想是选择适当的参数β,使得误差平方和最小化。
误差平方和可以表示为:S(β) = Σ(y - f(x, β))^2其中,Σ表示求和操作,拟合曲线上的点的横坐标为x,纵坐标为f(x, β)。
为了找到误差平方和的最小值,我们需要对参数β进行求解。
最常用的方法是对参数β求导数,令导数为0,从而得到参数的估计值。
求解得到的参数估计值就是使得误差平方和最小化的参数。
最小二乘法实现步骤最小二乘法的实现可以分为以下几个步骤:1.确定拟合曲线的函数形式。
根据数据的特点和拟合的需求,选择合适的拟合曲线函数,例如线性函数、多项式函数等。
2.建立误差函数。
根据选择的拟合曲线函数,建立误差函数,即每个数据点与拟合曲线上对应点的差值的平方。
3.求解参数估计值。
对误差函数求导数,并令导数为0,求解得到参数的估计值。
4.进行拟合曲线的评估。
通过计算误差平方和等指标来评估拟合曲线的质量,可以使用残差平方和、R方值等指标。
5.优化拟合结果(可选)。
根据评估的结果,如有必要可以调整拟合曲线的参数或选择其他拟合曲线函数,以得到更好的拟合效果。
最小二乘法曲线拟合实验报告

竭诚为您提供优质文档/双击可除最小二乘法曲线拟合实验报告篇一:实验3曲线拟合的最小二乘法实验三曲线拟合的最小二乘法1、实验目的:在科学研究与工程技术中,常常需要从一组测量数据出发,寻找变量的函数关系的近似表达式,使得逼近函数从总体上与已知函数的偏差按某种方法度量能达到最小而又不一定过全部的点。
这是工程中引入最小二曲线拟合法的出发点。
充分掌握:1.最小二乘法的基本原理;2.用多项式作最小二乘曲线拟合原理的基础上,通过编程实现一组实验数据的最小二乘拟合曲线。
2、实验要求:1)认真分析题目的条件和要求,复习相关的理论知识,选择适当的解决方案和算法;2)编写上机实验程序,作好上机前的准备工作;3)上机调试程序,并试算各种方案,记录计算的结果(包括必要的中间结果);4)分析和解释计算结果;5)按照要求书写实验报告;3、实验内容:1)给定数据如下:x:0.15,0.4,0.6,1.01,1.5,2.2,2.4,2.7,2.9,3.5,3.8,4.4,4.6,5.1,6.6,7.6;y:4.4964,5.1284,5.6931,6.2884,7.0989,7.5507,7.5106,8.0756,7.8708,8.2403,8.5303,8.7394,8.9981,9.1450,9.5070,9.9115;试作出幂函数拟合数据。
2)已知一组数据:x:0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1y:-0.447,1.978,3.28,6.16,7.08,7.34,7.66,9.56,9.48,9.30,11.2;试用最小二乘法求多项式函数,使与此组数据相拟合。
4、题目:曲线拟合的最小二乘法5、原理:从整体上考虑近似函数同所给数据点(i=0,1,…,m)误差(i=0,1,…,m)的大小,常用的方法有以下三种:一是误差(i=0,1,…,m)绝对值的最大值,即误差向量的∞—范数;二是误差绝对值的和,即误差向量r的1—范数;三是误差平方和的算术平方根,即误差向量r的2—范数;前两种方法简单、自然,但不便于微分运算,后一种方法相当于考虑2—范数的平方,因此在曲线拟常采用误差平方和来度量误差(i=0,1,…,m)的整体大小.。
数值分析论文--曲线拟合的最小二乘法

---------------------------------------------------------------最新资料推荐------------------------------------------------------ 数值分析论文--曲线拟合的最小二乘法曲线拟合的最小二乘法姓名:徐志超学号:2019730059 专业:材料工程学院:材料科学与工程学院科目:数值分析曲线拟合的最小二乘法一、目的和意义在物理实验中经常要观测两个有函数关系的物理量。
根据两个量的许多组观测数据来确定它们的函数曲线,这就是实验数据处理中的曲线拟合问题。
这类问题通常有两种情况:一种是两个观测量 x 与 y 之间的函数形式已知,但一些参数未知,需要确定未知参数的最佳估计值;另一种是 x 与 y 之间的函数形式还不知道,需要找出它们之间的经验公式。
后一种情况常假设 x 与 y 之间的关系是一个待定的多项式,多项式系数就是待定的未知参数,从而可采用类似于前一种情况的处理方法。
在两个观测量中,往往总有一个量精度比另一个高得多,为简单起见把精度较高的观测量看作没有误差,并把这个观测量选作x,而把所有的误差只认为是y 的误差。
设 x 和 y 的函数关系由理论公式 y=f(x; c1, c2, cm)1 / 13(0-0-1)给出,其中 c1, c2, cm 是 m 个要通过实验确定的参数。
对于每组观测数据(xi, yi) i=1, 2,, N。
都对应于 xy 平面上一个点。
若不存在测量误差,则这些数据点都准确落在理论曲线上。
只要选取m 组测量值代入式(0-0-1),便得到方程组yi=f (x;c1,c2,cm)(0-0-2)式中 i=1,2,, m.求 m 个方程的联立解即得 m 个参数的数值。
显然Nm 时,参数不能确定。
在 Nm 的情况下,式(0-0-2)成为矛盾方程组,不能直接用解方程的方法求得 m 个参数值,只能用曲线拟合的方法来处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 曲线拟合的最小二乘法一、 曲线拟合的最小二乘法根据一组给定的实验数据点),(i i y x m i ,,1, =,求出)(x f y =的近似函数关系(1) 观测数据本身有误差(2) 反映实验数据规律的数学模型问题特点:所给数据本身不一定可靠,个别数据的误差甚至可能很大。
研究目标:设法构造一条曲线(所谓拟合曲线)反映所给数据点总的趋势,以消除其局部波动与插值问题不同,不要求通过点),(i i y x m i ,,1, =(否则将保留着一切观测误差),只要求在给定点i x 上的误差最小,即构造一条最佳拟合曲线......)(*x ϕ 节点i x 误差(偏差):),,1()(*m i y x i i i =-=ϕδ最佳标准:1)min max 1=≤≤i mi δ:误差绝对值最大达到最小(不易算)2)min1=∑=mi iδ:误差绝对值和最小(不易算)3)min12=∑=mi iδ:误差平方和达到最小(或平方误差,常用,最小二乘拟合)定义1:给定数据点m i y x i i ,,2,1),,( =,假设拟合曲线的函数形式为:)()()()()(11000x a x a x a x a x n n nk k k ϕϕϕϕϕ+++==∑=其中n k k x 0)}({=ϕ为已知的线性无关函数。
求系数**1*0,,,n a a a ,使得:min])([])([),,,(121210=-=-=∑∑∑===mi i nk i k k mi i i n y x a y x a a a S ϕϕ称∑==nk k k x a x 0**)()(ϕϕ为最小二乘拟合函数若n k x x kk ,,1,0,)( ==ϕ时称为最小二乘拟合多项式(S为误差平方和函数)注:若n k k x 0)}({=ϕ为定义在区间I 上的n+1个函数满足:I x x c x c x c n n ∈∀≡+++,0)()()(1100ϕϕϕ 010====⇔n c c c则称)(,),(),(10x x x n ϕϕϕ 是1+n 个线性无关函数如:n k x x kk ,,1,0,)( ==ϕ;线性无关如:x x 22sin ,cos ,1在整个数轴上是线性相关,因为1,1210-===c c c 时0sin cos 122≡--x x二、最小二乘拟合多项式的求法如:4=m ,2=n),,(),,(),,(),,(44332211y x y x y x y x 2210)(x a x a a x ++=ϕ为使min])[(),,(4122210210=-++=∑=i i ii y x a x a a a a a S由极值点必要条件有:⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧=⋅-++=∂∂=⋅-++=∂∂=-++=∂∂∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑===============412414142413120414141324121041414122411024122102412210141221000])[(20])[(20])[(2i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i i y x x a x a x a y x x a x a x a y x a x a a x y x a x a a a S x y x a x a a a S y x a x a a a S⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧=⋅-++=∂∂=⋅-++=∂∂=-++=∂∂∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑===============412414142413120414141324121041414122411024122102412210141221000])[(20])[(20])[(2i i i i i i i i i i ii i i i i i i i i i i i i i i i i i i i i i i i i i i i y x x a x a x a y x x a x a x a y x a x a a x y x a x a a a S x y x a x a a a S y x a x a a a S即:⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⋅⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑∑∑∑∑∑∑∑∑===========m i i i mi i i mi i i i i ii i i i i ii ii i i iy x y x y a a a x xx x x xx x121121041441341241341241412414 (法方程组)最小二乘拟合多项式求解一般情况)(m n < 假设给定数据m i y x i i ,,2,1),,( = 拟合多项式为:nn x a x a a x +++= 10)(ϕ为使:∑=-==mi i i n y x a a a S S 1210])([),,,(ϕ min])[(1210=-+++=∑=mi i n in i y x a x a a由n i a Si ,,2,1,0,0 ==∂∂可得:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⇔=+++=+++=+++∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑=====+==+=======+===+=====m i i ni m i i i m i i n m i n i mi n i m i n i m i n im i i m i i mi nimi im i m i ini n i n m i n i mi n i m i mi ii n i n m i i m i i m i mi i ni n m i i y x y x y a a a x x x x x x x xmy x x a x a x a y x x a x a x a y x a x a m a 11110121111112111112111101111211011110(法方程组,见书P74)//注:系数矩阵关于主对角线对称,次对角线元素相等定理1:以上法方程组在i x 互异时有解存在且唯一,而且其解即为min ])([),,,(1210=-=∑=mi i i n y x a a a S ϕ 的解(使误差取平方和最小的极小点)例1:已知一组实验数据如表所示.i 1 2 3 4 x i 2 4 6 8 y i 2 11 28 40试求最小二乘拟合曲线.0510152025303540450246810系列1解:作散点图,如图所示,说明它可用线性函数作曲 线拟合,即选择形如x a a x 10)(+=ϕ作为拟合曲线. 这里x a a x 10)(+=ϕ1,4,==n m ,故法方程⎩⎨⎧=+=+⇒⎪⎪⎩⎪⎪⎨⎧=+=+∑∑∑∑∑=====5361202081204)()()(41010411412041411410a a a a y x a x a x y a x a i ii i i i i i ii i 得55.6,5.1210=-=a a所求的最小二乘拟合曲线为:x x 55.65.12)(+-=ϕ例2:求下列数据)5,4,3,2,1,0)(,( i y x i i 对应的最小二乘拟合多项式i 1 2 3 4 5 6 x i 0 1 2 3 4 5 y i 5 3 1 1 2 3解:做散点图01234560123456系列1接近抛物线,因此2210)(x a x a a x ++=ϕ法方程组为:⎪⎪⎪⎩⎪⎪⎪⎨⎧⋅=++⋅=++=++∑∑∑∑∑∑∑∑∑∑∑∑============61261426131612061613261216106161226116101i i i i i i i i i i ii i i i i i i i ii i i i i y x x a x a x a y x x a x a x a y x a x a a⎪⎩⎪⎨⎧=++=++=++123979225553122555151555156210221210a a a a a a a a a解得:5.0,7857.2,7143.4210=-==a a a 从而:25.07857.27143.4)(x x x +-=ϕ三、非线性模型的线性化定义2:若拟合函数)(x ϕ与待定参数n a a a ,,,10 为线性关系,就称其为线性最小二乘拟合,如nn x a x a a x +++= 10)(ϕ 若拟合函数)(x ϕ与待定参数n a a a ,,,10 为非线性关系,就称其为非线性最小二乘拟合,如xa e a x y 10)(==ϕ 非线性模型有时可经过变换可化为线性模型,这些也应按线性模型处理。
注:对于线性最小二乘由∑=-==mi i i n y x a a a S S 1210])([),,,(ϕ 及n i a Si,,2,1,0,0 ==∂∂可得到关于n a a a ,,,10 的线性法方程组例3:给定数据)5,4,3,2,1,0)(,(=i y x i i 如下:i 1 2 3 4 5 x i 1.00 1.25 1.50 1.75 2.00 y i 5.10 5.79 6.53 7.45 8.46求bxae x y ==)(ϕ的最小二乘拟合曲线.(指数模型) 解:bxae x y ==)(ϕ不是多项式,但两端取对数得bx a y +=ln ln .若令a A y y ln ,ln ==,则有bx A y +=,它是线性最小二乘拟合问题,为求得A 和b ,先将),(i i y x 化为),(i i y x .转化后的数据表为故有法方程:⎩⎨⎧=+=+⇒⎪⎪⎩⎪⎪⎨⎧=+=+∑∑∑∑∑=====422.14875.115.7404.95.75)()()(551512515151b A b A y x b x A x y b x A i i i i i i i i ii i解得071.3,5056.0,122.1====Ae a b A ,于是得最小二乘拟合曲线xey 5056.0071.3=。
