longman math 4B08
long与double的转换规律

long与double的转换规律long和double是Java中的两种数据类型,用于表示不同范围的数值。
long用于表示整数类型的数据,而double用于表示浮点类型的数据。
在Java中,long和double之间可以进行转换,但需要注意转换规律和可能出现的精度损失。
我们来看一下long和double的定义和范围。
long是一个64位的有符号整数类型,可以表示的范围为-9223372036854775808到9223372036854775807。
而double是一个64位的浮点数类型,可以表示的范围为±4.9e-324到±1.8e+308。
在Java中,可以通过将long类型的变量直接赋值给double类型的变量来进行转换。
例如:```javalong num1 = 100L;double num2 = num1;```在这个例子中,我们将一个long类型的变量num1赋值给了一个double类型的变量num2。
由于long类型的范围比double类型更小,所以这种转换是安全的,不会导致精度损失。
而将double类型的变量赋值给long类型的变量时,就需要注意可能出现的精度损失和溢出的问题。
在Java中,可以使用强制类型转换来将double类型的数值转换为long类型。
例如:```javadouble num3 = 100.5;long num4 = (long) num3;```在这个例子中,我们将一个double类型的变量num3强制转换为long类型的变量num4。
由于double类型的范围比long类型更大,所以在进行强制转换时可能会导致精度损失。
在这个例子中,num4的值将变为100,小数部分被舍弃掉了。
需要注意的是,当将一个超出long类型范围的double数值转换为long类型时,会发生溢出。
例如:```javadouble num5 = 9223372036854775808.0;long num6 = (long) num5;```在这个例子中,double类型的数值9223372036854775808.0超出了long类型的范围,所以在进行强制转换时会发生溢出。
使用long来解决金额问题的具体方法

使用long来解决金额问题的具体方法在编程中,使用 long 类型来处理金额问题时,通常是因为需要处理大额的整数值。
这可能涉及到金融应用、计算、统计等领域。
在使用 long 处理金额时,需要考虑以下几个方面:单位选择:确定金额的基本单位,例如分。
将金额表示为整数的分数,而不是直接使用小数。
这有助于避免浮点数精度问题。
数据类型:选择合适的数据类型来表示金额,例如 long long。
在一些编程语言中,可能还有其他精度更高的整数类型,如 BigInteger。
格式化输出:在输出金额时,确保使用适当的格式化方法。
这可能包括将整数转换为字符串,并在适当的位置插入小数点。
下面是一个简单的示例,演示如何使用 long 处理金额问题的一些基本方法(这是一个假设单位为分的例子):# Python 示例# 定义金额(单位:分)amount_in_cents = 123456789012345# 将金额转换为字符串并插入小数点amount_str = str(amount_in_cents)formatted_amount = f"{amount_str[:-2]}.{amount_str[-2:]}"print(f"原始金额(分): {amount_in_cents}")print(f"格式化后金额: {formatted_amount}")在这个示例中,我们使用 long 表示金额(单位为分),然后将其转换为字符串,并在适当的位置插入小数点以进行格式化输出。
这样做可以避免浮点数精度问题,确保金额的准确表示。
请注意,具体的实现方式可能会因编程语言而异。
在使用long 或其他整数类型时,确保选择适当的类型和处理方法,以满足具体需求和语言特性。
在处理金融数据时,还应该注意遵循相关的法规和最佳实践,例如使用整数表示金额以避免浮点数舍入误差。
龙贝格算法——精选推荐

Romberg 算法一、 算法思路1)梯形法的递推化为了提高求积精度,实际计算时若精度不够可以将步长逐次分半,以此求积分 f (x )ba 的近似值。
首先将[a,b]分为n 等份,共有n+1个分点,注意到每个子区间[x k ,x k +1]经过二分只增加了一个分点:x k +12=12(x k ,+x k +1)。
然后利用复合梯形求积公式可以推导出二分前后的积分值递推关系(h 代表二分前的步长):T 2n =12T n +ℎ2f (x k +12)n −1k =0。
(1.1) 2)理查森外推加速从梯形公式出发,将区间[a,b]逐次二分可以提高求积公式精度,当[a,b]分为n 等份时,若记T n = T ℎ ,当区间[a,b]分为2n 等份时,则有T 2n =T ℎ2 。
再有泰勒公式展开为:T ℎ =I +α1ℎ2+α2ℎ4+⋯+αl ℎ2l+⋯,然后用h/2代替h 有T ℎ2=I +α1ℎ24+α2ℎ416+⋯+αl ℎ22l+⋯。
再记S ℎ =4T ℎ2−T ℎ3,这将复合梯形公式的的误差阶O(ℎ2)提高到了O(ℎ4),并且易知S ℎ =S n ,即将[a,b]分为n 等份得到的复合辛普森公式。
与上述做法类似,从S ℎ 出发,当n 在增加一倍,即h 减少一半时得到S ℎ2 ,然后记C ℎ =16S ℎ2−S ℎ3,易知C ℎ =C n ,即将[a,b]分为n 等份得到的复合柯特斯公式……如此继续下去就可以得到龙贝格公式。
我们重新引入记号T 0 ℎ = T ℎ ,T 1 ℎ = S ℎ 等,从而可以将上述公式写成统一的形式:T m ℎ =I +δ1ℎ2(m +1)+δ2ℎ2(m +2)+⋯.上述处理方法就称为理查森外推加速法。
3)龙贝格求积算法设以T 0(k )表示二分k 次后求得的梯形值,且以T m (k )表示序列 T 0(k )的m 次加速值,则依理查森外推加速公式,可以得到:T m(k )=4m 4m −1T m −1(k−1)−14m −1T m −1 k,k =1,2⋯.(1.2)这就是龙贝格求积算法。
2004amc8解析

2004amc8解析2004年的AMC 8数学竞赛是一场激烈而令人兴奋的比赛。
我记得当时我坐在教室里,心情紧张而充满期待。
这是我第一次参加这样的竞赛,我对自己的数学能力感到自豪。
当考试开始时,我专注地阅读题目,尽力想出解决方法。
第一道题目是一个关于几何的问题。
题目描述了一个矩形,要求我们计算矩形的对角线长度。
我回忆起几何课上学到的知识,知道矩形的对角线可以通过勾股定理来计算。
我用平方根计算出答案,然后继续解答下一道题目。
下一道题目是一个关于比例的问题。
题目描述了一个购买苹果的情境,要求我们计算每个苹果的价格。
我将问题转化为一个简单的比例方程,然后解出答案。
这道题目相对简单,我很快就得到了正确答案。
接下来的题目涉及到图形的旋转和对称性。
我回忆起几何课上学到的相关知识,然后运用这些知识来解决问题。
我注意到题目中给出了图形的一部分,然后要求我们计算另一部分的面积。
我使用了旋转和对称性的概念,将图形分成几个简单的部分,然后计算出整个图形的面积。
最后一道题目是一个关于概率的问题。
题目描述了一个抽奖的情境,要求我们计算中奖的概率。
我回忆起概率课上学到的知识,然后运用这些知识来解决问题。
我计算出中奖的可能性,然后将其转化为一个百分比。
整个竞赛过程充满了挑战和乐趣。
我在解题过程中遇到了一些困难,但通过坚持不懈和努力,我成功地解决了所有的问题。
我感到自豪和满足,因为我知道我在数学领域有了不小的进步。
参加这场竞赛让我意识到数学不仅仅是一门学科,更是一种思维方式。
通过解决问题和应用所学知识,我培养了逻辑思维和解决实际问题的能力。
这次竞赛经历让我更加热爱数学,并激发了我继续学习和探索数学的兴趣。
回顾这场竞赛,我意识到数学不仅仅是为了得到正确答案,更是为了培养我们的思维能力和解决问题的能力。
这场竞赛给我带来了很多启示和收获,我相信这对我未来的学习和职业发展都将有着积极的影响。
我期待着参加更多的数学竞赛,挑战自己,拓展自己的视野。
langchain大模型解数学题源码

langchain大模型解数学题源码《langchain大模型解数学题源码》
最近,一款名为langchain的大型模型在数学题解决方面取得了重要进展。
这一模型被设计成能够理解和解析各种未知数学问题,并给出相应的解答。
langchain的研发团队认为,他们的模型将对学生和教育工作者有着深远的影响。
下面是一段来自langchain研发团队的源码例子,它展示了这款大模型的工作原理:
```python
import langchain
# 定义数学问题
question = "解方程组:3x + 4y = 10; 2x - y = 5"
# 使用langchain模型解决问题
solution = langchain.solve_math_problem(question)
# 打印结果
print(solution)
```
在这个例子中,langchain大模型被调用来解决一个包含两个未知数的方程组。
该模型能够理解问题的语义,并给出正确的答案。
这种能力使得langchain成为学生们课堂上的得力助手,也是教育工作者备课和出题的得力工具。
除了解方程以外,langchain大模型还可以解决各种数学问题,包括简单的算术题、代数问题、几何问题等。
它的源码在许多教育机构和在线教育平台得到了广泛的应用,为学习者提供了更多的学习资源和帮助。
总的来说,langchain大模型的源码展示了它在解决数学问题方面的强大能力和应用潜力。
在未来,我们有望看到这样的大型模型成为学生学习和教育工作者教学的重要工具之一。
math.h常用函数

math.h常用函数什么是math.h?在C语言中,math.h是一个常用的库文件,它包含了很多数学函数的定义和声明。
通过引入math.h文件,我们可以使用这些函数来进行各种数学运算。
为什么要使用math.h?在编程过程中,我们经常需要进行各种数学运算,比如求平方根、取绝对值、进行三角函数运算等等。
这些运算不仅可以在通常的数学计算中使用,也可以用于解决实际问题和算法的设计。
而math.h库文件提供了这些数学函数的实现,使得我们能够更方便地进行数学运算。
常用的math.h函数有哪些?1. abs函数:用于求取一个整数的绝对值。
其定义如下:int abs(int x);其中x为待求取绝对值的整数。
返回值为x的绝对值。
2. sqrt函数:用于求取一个数的平方根。
其定义如下:double sqrt(double x);其中x为待求取平方根的数。
返回值为x的平方根。
3. pow函数:用于求取某个数的幂。
其定义如下:double pow(double x, double y);其中x为底数,y为指数。
返回值为x的y次幂。
4. sin函数:用于求取一个角的正弦值。
其定义如下:double sin(double x);其中x为角度值(以弧度为单位)。
返回值为x的正弦值。
5. cos函数:用于求取一个角的余弦值。
其定义如下:double cos(double x);其中x为角度值(以弧度为单位)。
返回值为x的余弦值。
6. tan函数:用于求取一个角的正切值。
其定义如下:double tan(double x);其中x为角度值(以弧度为单位)。
返回值为x的正切值。
这些只是math.h库文件中的部分函数,在实际使用时,根据需要可能会使用到更多的数学函数。
这些函数涵盖了基本的数学运算,可以帮助我们完成一些常见的数学计算任务。
现在,让我们逐步来解释每个函数的用途并举例说明。
首先是abs函数,它用于取一个整数的绝对值。
例如,如果我们要求取-5的绝对值,可以这样写:c#include <stdio.h>#include <math.h>int main() {int result = abs(-5);printf("绝对值为:d\n", result);return 0;}上述代码中,我们引入了stdio.h和math.h头文件,并使用了abs函数求取-5的绝对值。
八数码问题 算法流程

八数码问题算法流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!1. 问题定义:八数码问题是在一个 3x3 的棋盘上,有 8 个数字(1-8)和一个空格,通过移动空格,使得棋盘上的数字最终排列成目标状态。
c++算法 八数码问题

c++算法八数码问题八数码问题是一种经典的智力游戏,其规则是在有限的格子中,按照一定的顺序将数字旋转移动到目标位置。
为了解决这个问题,我们可以使用算法的思想来设计一种有效的解决方案。
一、问题描述八数码问题是一个有N×N的棋盘,其中每个格子代表一个数字。
玩家需要按照一定的顺序旋转数字,将它们移动到目标位置。
目标位置是预先设定好的,玩家需要按照规则移动数字,使得棋盘上的数字按照正确的顺序排列。
二、算法思想为了解决八数码问题,我们可以使用贪心算法的思想。
首先,我们需要找到一个初始状态,这个状态应该是最简单、最容易解决的问题。
然后,我们通过循环迭代的方式,不断尝试不同的旋转方式,直到找到一个能够满足目标位置的解决方案。
三、C语言实现下面是一个简单的C语言实现,用于解决八数码问题。
这个程序使用了递归和回溯的方法,通过穷举所有可能的旋转方式来找到解决方案。
```c#include <stdio.h>#include <stdlib.h>#include <stdbool.h>#define N 3// 定义棋盘状态结构体typedef struct {int nums[N][N];int num_count[N][N]; // 记录每个数字出现的次数} Board;// 判断两个数字是否相邻bool is_adjacent(int num1, int num2) {int dx[] = {-1, 0, 1};int dy[] = {0, -1, 1};for (int i = 0; i < 3; i++) {if (abs(nums[num1][i] - nums[num2][i]) <= 1) {return true;}}return false;}// 寻找最优解函数bool find_optimal_solution(Board& board, int target_row, int target_col) {// 初始化最优解为空状态bool optimal_solution = false;int optimal_score = INT_MAX; // 最优解的得分初始化为最大整数int best_score = INT_MAX; // 最优解的当前得分初始化为最大整数加一// 对当前棋盘进行遍历for (int row = 0; row < N; row++) {for (int col = 0; col < N; col++) {// 如果当前状态为空状态,则直接跳过if (board.nums[row][col] == 0) {continue;}// 记录当前状态的信息,包括得分和旋转次数等int score = calculate_score(board, row, col); // 计算得分函数在实现中定义了旋转方式的选择和得分计算规则等具体细节,这里省略了具体实现细节。
math.h常用函数 -回复

math.h常用函数-回复math.h是C语言标准库中一个重要的头文件,提供了许多与数学运算相关的常用函数。
本文将介绍math.h头文件中的常用函数,并解释它们的用途和功能。
以下是对math.h头文件中常用函数的详细说明。
1. abs函数:abs函数用于计算整数的绝对值,其语法如下:cint abs(int x);abs函数接受一个整数参数x,并返回其绝对值。
例如,abs(-5)将返回5。
2. fabs函数:fabs函数用于计算浮点数的绝对值,其语法如下:cdouble fabs(double x);fabs函数接受一个浮点数参数x,并返回其绝对值。
例如,fabs(-5.5)将返回5.5。
3. ceil函数:ceil函数用于向上取整,其语法如下:cdouble ceil(double x);ceil函数接受一个浮点数参数x,并返回大于或等于x的最小整数值。
例如,ceil(5.1)将返回6,ceil(5.9)也将返回6。
4. floor函数:floor函数用于向下取整,其语法如下:cdouble floor(double x);floor函数接受一个浮点数参数x,并返回小于或等于x的最大整数值。
例如,floor(5.1)将返回5,floor(5.9)也将返回5。
5. sqrt函数:sqrt函数用于计算平方根,其语法如下:cdouble sqrt(double x);sqrt函数接受一个浮点数参数x,并返回其平方根。
例如,sqrt(25.0)将返回5.0。
6. pow函数:pow函数用于计算幂值,其语法如下:cdouble pow(double x, double y);pow函数接受两个浮点数参数x和y,并返回x的y次幂。
例如,pow(2.0, 3.0)将返回8.0。
7. sin函数:sin函数用于计算正弦值,其语法如下:cdouble sin(double x);sin函数接受一个浮点数参数x(以弧度为单位)并返回其正弦值。
java8的lambda表达式

java8的lambda表达式
Java8的lambda表达式是一种新特性,它是一种匿名函数,可以作为参数传递给方法或者存储在变量中。
它的出现大大简化了Java 编程的复杂度,使得代码更加简洁易懂。
lambda表达式由三部分组成:参数列表、箭头符号和方法体。
使用lambda表达式可以替代传统的匿名内部类,从而减少代码量和提高代码可读性。
在使用lambda表达式时,需要注意以下几点:
1. lambda表达式需要一个函数式接口作为参数,函数式接口是只有一个抽象方法的接口。
2. lambda表达式没有访问权限修饰符、返回类型和方法名,它只有参数列表和方法体。
3. 参数列表可以省略类型声明,如果只有一个参数,括号也可以省略。
4. 如果方法体只有一条语句,可以省略大括号。
5. lambda表达式可以访问局部变量和类成员变量,但是局部变量必须是final或者事实上的final变量。
除了lambda表达式,Java8还引入了Stream API、默认方法和新的日期时间API等新特性,这些新特性都使得Java编程更加方便和高效。
- 1 -。
longdouble的取值范围

有关long double数据类型的取值范围,我们首先需要了解long double在不同编译器和计算机架构下的具体表现。
在C++语言中,long double是一种扩展精度浮点数类型,通常用来处理需要更高精度的计算,例如科学计算或者需要极高精度的金融运算。
下面我们将分别讨论long double在32位和64位系统下的取值范围。
1. 32位系统下的long double取值范围在32位系统下,long double通常是以80位格式存储的,它的取值范围与double类型相比更大。
其取值范围约为1.18 × 10^-4932 到3.4 × 10^4932,可以在大多数应用场景下满足高精度计算的需求。
然而,需要特别注意的是,在不同的编译器和系统环境下,long double类型的精度和取值范围可能会有所不同,因此在实际使用中应该遵循具体环境的规范。
2. 64位系统下的long double取值范围在64位系统下,long double通常是以128位格式存储的,这使得其精度和取值范围较之32位系统下更大。
在绝大多数情况下,long double的取值范围约为3.36 × 10^-4932 到1.18 × 10^4932,可以满足对极高精度计算的需求。
然而,仍然需要注意不同系统和编译器下的具体规范,以确保计算结果的准确性。
总结通过以上讨论,我们可以看出long double的取值范围在不同的系统环境下可能有所不同,但通常情况下都能满足对高精度计算的需求。
在实际编程中,应该遵循具体的系统规范和编译器要求,以确保long double类型能够发挥其最大作用。
在涉及对精度要求极高的计算时,应该对long double的取值范围有清晰的认识,并通过合理的算法设计和数据处理来保证计算结果的准确性。
在实际开发中,long double 类型常常用于处理需要非常高精度的计算,比如在科学计算、金融计算、工程领域和其他需要极高精度的计算场景中。
日娃编程笔记

日娃编程笔记
1)由数字、字母、下划线构成
2)变量名开头不能为数字
3)变量名的含义能够表达变量的用途
4)变量名不能与C语言中的关键字重名
5)区分大小写
1.基本数据类型(内存基于32位机器)字符型 char (1字节)
无符号字符型 unsigned char (1字节)短整型 short int (2字节)整形 int (4字节)长整形 long int (4字节)单精度浮点型f loat (4字节)双精度浮点型 double (8字节)
2.标准输入输出及运算符,在linux中用 man命令查找帮助手册 man scanf/man printf/ man stdio.h格式化输入输出:scanf printf占位符,单个字符,十进制有符号整形,十进制有符号长整形,有符号单精度浮点型,有符号双精度浮点型,十进制无符号整形,转化为16进制输出,转化为八进制树池,输出地址(初学代码常用的),字符串输出,自动控制小数位数。
java8 的lambda表达式

Java 8 引入了Lambda 表达式,它是一种简洁的表示匿名函数的方式。
Lambda 表达式可以让您更方便地编写简洁、功能强大的代码。
Lambda 表达式的语法如下:
(参数列表) -> { 函数体 }
其中,参数列表可以是零个或多个参数,用逗号分隔。
函数体是包含在花括号中的代码块,可以包含一个或多个语句。
下面是一个简单的 Lambda 表达式的示例:
// 定义一个Lambda表达式,将两个整数相加并返回结果
(int a, int b) -> a + b;
这个 Lambda 表达式接收两个整数作为参数,并将它们相加。
您可以像这样使用它:
// 调用Lambda表达式
int result = (int a, int b) -> a + b;
result = result(3, 4); // 输出 7
Lambda 表达式也可以用于简化和匿名接口的实现:
// 定义一个接口
interface MyInterface {
int myMethod(int a, int b);
}
// 使用Lambda表达式实现接口
MyInterface myObject = (int a, int b) -> a + b;
int result = myObject.myMethod(3, 4); // 输出 7
Lambda 表达式还可以用于方法引用和数组的过滤、映射和排序等操作。
double与long互转不丢失精度的方法

double与long互转不丢失精度的方法1. 引言1.1 背景介绍在计算机科学领域,double和long是两种常用的数据类型,分别用于存储浮点数和整数。
在实际编程中,我们有时需要在这两种类型之间进行转换,确保数据的精度不会丢失是非常重要的。
double是一种浮点数类型,通常用来表示带有小数部分的数字。
它可以存储非常大或非常小的数值,但由于浮点数的本质,存在精度丢失的风险。
与之相反,long是一种整数类型,适用于表示大范围的整数值。
由于整数不包含小数部分,long类型在精度上相对稳定。
在实际应用中,我们可能需要将一个double类型的数转换为long类型,或者将一个long类型的数转换为double类型。
在这个过程中,如何保证数据的精度不丢失是一个关键问题。
接下来,我们将介绍double与long的区别,以及转换方法,最后探讨如何确保在转换过程中不丢失精度的关键。
2. 正文2.1 double与long的区别在计算机科学中,double和long都是用来表示数字的数据类型,但它们有一些明显的区别。
double是一种浮点型数据类型,用于表示双精度浮点数。
它占用8个字节(64位)的内存空间,可以存储很大范围的数值,包括小数点后的精度。
而long是一种整型数据类型,用于表示长整型数值。
它占用4个字节(32位)的内存空间,只能存储整数值,不能表示小数。
在表示数值范围方面,double能够表示更大范围的数值,大约在-1.7E308到1.7E308之间。
而long的范围大约在-9223372036854775808到9223372036854775807之间。
当需要表示小数时,应该选择double类型;而如果只涉及整数运算,并且数值范围不会超出long类型的表示范围,那么可以选择long 类型。
需要注意的是,在进行double和long类型之间的转换时,可能会存在精度损失的问题,特别是当double类型的数值包含小数部分时。
encryptlong解密分段方法

encryptlong解密分段方法嘿,朋友们!今天咱来聊聊“encryptlong 解密分段方法”。
这可不是什么高深莫测的外星科技,其实就像我们生活中的小窍门一样。
你想想看,解密就像是打开一个神秘的宝盒。
而这个 encryptlong 解密分段方法呢,就是找到打开宝盒的那把钥匙的巧妙办法。
我们可以把这个过程比作是走一条曲曲折折的小路。
有时候,路会分成几段,每一段都有它独特的风景和挑战。
就像解密的时候,数据也被分成了不同的段,我们得一段一段地去攻克。
比如说,第一段可能就像是一个小谜题,需要我们细心去琢磨,找到其中的规律。
哎呀,这可不是随便猜猜就能搞定的哟!得动动脑筋,发挥我们的聪明才智。
然后呢,第二段可能就稍微复杂一些了,像是一个隐藏得更深的秘密。
这时候可不能着急,得慢慢来,一点点地去揭开它的面纱。
再往后,每一段都有不同的特点和难度。
但咱可不能被吓住啊,得像个勇敢的探险家一样,坚定地向前走。
那怎么去应对这些分段呢?首先,我们得有耐心,不能碰到一点困难就打退堂鼓。
解密可不是一蹴而就的事情,它需要我们一步一个脚印地去努力。
然后呢,我们得学会观察和分析。
就像侦探破案一样,从每一个细节中找到线索。
而且啊,我们还得不断尝试。
可能第一次不行,第二次也不行,但总有一次会成功的呀!难道不是吗?这就好像我们学骑自行车,一开始可能会摔倒很多次,但只要不放弃,最后总能骑得稳稳当当的。
总之呢,这个 encryptlong 解密分段方法虽然有点复杂,但只要我们掌握了正确的方法和技巧,加上足够的耐心和努力,就一定能够攻克它!相信自己,我们都可以成为解密的小高手哦!。
long类型的随机数

long类型的随机数【原创版】目录1.长整型随机数概述2.长整型随机数的生成方法3.长整型随机数的应用实例正文1.长整型随机数概述长整型随机数是指在计算机程序中生成的长整数值的随机数。
长整数通常是 64 位或更高位数的整数,它可以表示的数值范围很大。
在许多编程场景中,我们需要生成一个长整型的随机数来满足程序需求。
2.长整型随机数的生成方法生成长整型随机数的方法有很多,这里介绍两种常用的方法:(1)线性同余法线性同余法是一种基于模运算的随机数生成方法。
它的基本原理是:在一个模数很大的循环域内,通过线性方程来生成随机数。
具体步骤如下:1)选择一个很大的模数 M。
2)在 [0, M-1] 范围内选择一个随机数 a。
3)计算线性同余方程:x = a + M * (b % M),其中 b 为另一个随机数。
4)重复步骤 3,直到生成所需位数的长整数。
(2)梅森旋转算法梅森旋转算法是一种基于梅森数的随机数生成方法。
梅森数是指形如2^p - 1 的数,其中 p 为质数。
具体步骤如下:1)选择一个质数 p,并计算梅森数 M = 2^p - 1。
2)计算随机数 r,其中 0 <= r < M。
3)计算长整数:x = r * (M^i) mod M,其中 i 为正整数。
4)重复步骤 3,直到生成所需位数的长整数。
3.长整型随机数的应用实例长整型随机数在许多场景中都有应用,例如:(1)加密算法:在加密算法中,长整型随机数可以用作生成密钥或初始化向量,以提高加密安全性。
(2)随机数抽奖:在在线抽奖活动中,可以使用长整型随机数作为抽奖号码,确保抽奖结果的公平性。
long double的存储原理

long double的存储原理英文回答:The storage principle of long double is dependent on the underlying hardware and the compiler implementation. In general, long double is a floating-point data type that is designed to provide increased precision compared to regular double.On most modern systems, long double is typically implemented using the IEEE 754 standard for floating-point representation. This standard defines a format for representing and manipulating floating-point numbers, including long double.In the IEEE 754 standard, long double is usually represented using 80 bits or 128 bits, depending on the hardware and compiler. The extra bits allow for more precision in representing decimal numbers. The format includes a sign bit, an exponent, and a significand (alsoknown as the mantissa). The sign bit determines whether the number is positive or negative, the exponent represents the scale of the number, and the significand stores the actual digits of the number.The storage of long double can vary between different systems and compilers. For example, on some systems, long double may be stored using 10 bytes or 12 bytes, while on others it may be stored using 16 bytes. The actual size of long double can also depend on the compiler flags and settings used during compilation.Overall, the storage principle of long double is to provide increased precision for floating-point numbers by using more bits to represent the number. This allows for more accurate calculations and reduces the potential for rounding errors.中文回答:long double的存储原理取决于底层硬件和编译器的实现。
MathType怎么编辑倒L符号
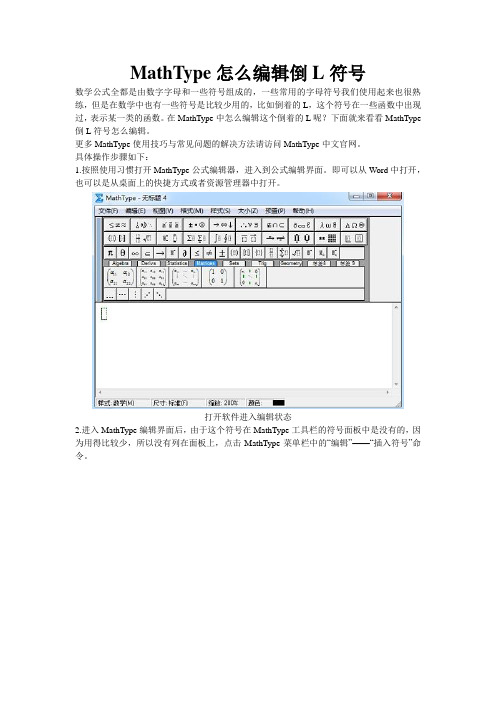
MathType怎么编辑倒L符号数学公式全都是由数字字母和一些符号组成的,一些常用的字母符号我们使用起来也很熟练,但是在数学中也有一些符号是比较少用的,比如倒着的L,这个符号在一些函数中出现过,表示某一类的函数。
在MathType中怎么编辑这个倒着的L呢?下面就来看看MathType 倒L符号怎么编辑。
更多MathType使用技巧与常见问题的解决方法请访问MathType中文官网。
具体操作步骤如下:1.按照使用习惯打开MathType公式编辑器,进入到公式编辑界面。
即可以从Word中打开,也可以是从桌面上的快捷方式或者资源管理器中打开。
打开软件进入编辑状态2.进入MathType编辑界面后,由于这个符号在MathType工具栏的符号面板中是没有的,因为用得比较少,所以没有列在面板上,点击MathType菜单栏中的“编辑”——“插入符号”命令。
点击“编辑”——“插入符号”3.在随后弹出的“插入符号”对话框中,将“查看”设置成“字体”——“Symbol”,其它设置保持默认不动,一般会默认“范围”是“全部已知字符”。
在符号面板中不用拉动滚动条就可以找到这个符号,然后点击符号后再点击一下插入,MathType编辑区域中就出现这个符号了。
从符号面板中对符号的描述可以看到这个符号的本质就是一个大写的希腊字母,只是我们不是很熟悉,用的也比较少,所以在编辑的时候用很生疏。
以上内容向大家介绍了MathType倒L符号的编辑方法,这个符号的编辑过程其实不难,用MathType插入特殊符号时常用的方法,连查看方式也是很平常的,基本不用设置,因为大多数人在使用MathType插入特殊符号时,都不会想到要去设置查看方式,而是直接使用默认状态,这也是很多人编辑不出符号时所犯的错误。
如果想要了解更多数学符号的编辑方法,比如MathType无穷符号,可以参考MathType中文官网教程:无穷符号怎么用MathType 编辑。
蓝桥杯研究兔子的土豪(疯狂雇主)矩阵快速幂

香港衣食住行香港人的日常穿着上海写字楼里的人们穿西装打领带的,但远没有香港这么严谨刻板。
不同的衣着装扮在这里被视为身份与地位的象征。
除非有特殊情况,在写字楼上班的男士一般都要求穿衬衫打领带,着西裤蹬皮鞋。
正式场合下,还必须穿与西裤相配的西装外套,否则就被视为不恭敬,缺乏教养。
在休闲风尚吹遍全球的今天,除了日韩,大概只有港督(憨大)统治过的香港,上班族才会对衣着依旧保持那种过气的不列颠传统。
两种情况下可以让自己随意些。
一是周六,这里大部分华资公司仍要上半天班,但可以在当天穿便服;还有就是不定期的香港公益金便服日,凡是资助过公益金(一种政府主持的慈善基金)的机构和公司,也都可以在规定的工作日里穿上便服。
事实上香港人心底里还是喜欢宽松的。
这里本来就有世界上最自由的经济和人文环境。
只要一到便服日,男男女女,老老少少都穿得五花八门、花枝招展的,而且越出挑、越标新立异越好。
因此如果那天有谁抱着芝麻街的大鸟公仔,或突然顶着一团火红的头发走进办公室的话,你大可不必为此感到诧异。
相反,在这样的日子里,如果马路上出现一帮西装笔挺、着装一丝不苟的人,则肯定会招来异样的眼光---这些人,要么是大陆旅行团的成员,要么就是世界其他什么偏僻地方跑出来的“巴子”。
有一点感触很深,就是如今对男人衣着的要求是越来越高,越来越严了,说不清社会在这方面是发展了,还是倒退了。
反正今天的正派男人,除了手臂、脖子、脑袋,其他任何地方是不能随便暴露在光天化日之下的,否则有伤风化。
我怀疑今天是不是又回到了维多利香港女人虽然从来没有在世界选美活动中占据过一席之地(就连本地男人也承认这里盛产“猪扒”,有的人不得已只好北上“炕热”),可这些都不会影响她们追求生活的兴致。
香港女人享有世界上最充分的“女权”,甚至在官场上也不例外(比如,董先生就最爱看《穆桂英挂帅》),因此就更别说穿着打扮了。
最有特征的是写字楼里女人的穿着。
时尚、飘逸、多姿多彩。
与男人正好相反,女人服饰发展的趋势是越来越单薄、越来越暴露,一句话,该露的地方都露了,不该露的地方也变着法儿露了。
