机构运动分析数据
机构运动简图测绘及分析

• 引言 • 机构运动简图测绘方法 • 机构运动简图分析 • 机构运动简图的实际应用案例 • 结论
01
引言
主题简介
机构运动简图测绘
机构运动简图是一种用于描述机构运动特性的图形表示方法,通过将实际机构 进行抽象化处理,将其简化为简单的几何图形,以便于分析和研究。
机构运动简图分析
测量尺寸
使用测量工具测量机构各部件 的实际尺寸,并标注在草图上。
确定测绘对象
明确需要测绘的机构运动简图 对象,了解其结构和工作原理。
绘制草图
根据观察结果,使用辅助工具 绘制出机构运动简图的草图。
整理成图
根据草图和实际尺寸,使用绘 图软件绘制出机构运动简图的 最终图纸。
测绘注意事项
准确性
确保测绘数据的准确性, 避免因测量误差导致简图 失真。
03
机构运动简图的应用价值
机构运动简图在机械设计、制造、维修等领域具有广泛的应用价值,本
研究为这些领域提供了有益的参考和借鉴。
对未研究的展望
1 2 3
机构运动简图的自动化测绘
未来研究可以进一步探索自动化测绘方法,提高 测绘效率和精度,降低人为误差和劳动强度。
机构运动简图的分析优化
基于精确的机构运动简图,未来研究可以进一步 开展运动学、动力学等方面的分析,为机构的优 化设计提供理论支持。
总结词
机器人是现代工业生产中常用的自动化设备,其运动简图测 绘及分析有助于提高机器人的工作效率和精度。
详细描述
通过对机器人的运动简图进行测绘和分析,可以了解机器人 的工作原理和运动轨迹,发现潜在的故障和问题,优化机器 人的运动性能,提高工作效率和精度。同时,也有助于机器 人自主导航和智能控制等方面的研究。
转动导杆机构的运动分析

% 转动导杆机构运动分析% 已知条件n=200;omega_1=pi*n/30; % 主动件导杆转速和角速度(rad/s)lambda=0.5; % 机构尺度系数alpha_p=45; % 机构许用压力角du=180/pi;hd=pi/180; % 角度与弧度转换系数disp ' ******** 已知条件********'fprintf (' 导杆转速n = %3.4f r/min \n',n)fprintf (' 导杆角速度omega_1 = %3.4f rad/s \n',omega_1)fprintf (' 机构尺度系数lambda = %3.4f \n',lambda)fprintf ('机构许用压力角alpha_p = %3.4f °\n',alpha_p)% 1-计算机构运动参数for phi_1=1:360phi_3(phi_1)=phi_1-asin(lambda*sin(phi_1*hd))*du; % 从动件曲柄角位移omega_3_z=lambda*cos(phi_1*hd);omega_3_m=sqrt(1-lambda^2*sin(phi_1*hd)^2);omega_3(phi_1)=omega_1*(1-omega_3_z/omega_3_m); % 从动件曲柄角速度i_31(phi_1)=omega_3(phi_1)/omega_1; % 机构传动比alpha(phi_1)=asin(lambda*sin(phi_1*hd))*du; % 机构压力角enddisp ' 'disp ' *** 转动导杆机构的运动参数***'disp ' 导杆转角曲柄角位移曲柄角速度'disp ' (°) (°) (rad/s) 'for phi_1=10:10:360ydcs=[phi_1 phi_3(phi_1) omega_3(phi_1)];disp(ydcs)end% 2-绘制机构的运动线图figure(1);subplot(2,1,1) % 曲柄角位移线图phi_1=1:360;plot(phi_1,phi_3);xlabel ('导杆转角\it \phi_1 / \rm( °)')ylabel ('\it \phi_3 / \rm(°)')title('从动件曲柄角位移线图');subplot(2,1,2) % 曲柄角速度线图phi_1=1:360;plot(phi_1,omega_3);xlabel ('导杆转角\it \phi_1 / \rm( °)')ylabel ('\it \omega_3 / \rm(rad/s)')title('从动件曲柄角速度线图');% 3-绘制机构的压力角线图figure(2);phi_1=1:360;plot(phi_1,alpha);xlabel ('导杆转角\it \phi_1 / \rm( °)');ylabel ('\it \alpha / \rm(°)');line([0,360],[alpha_p,alpha_p]);text(365,45,'\alpha_{max}=45°');line([0,360],[0,0]); % 横坐标line([0,360],[-alpha_p,-alpha_p]);text(365,-45,'\alpha_{min}=-45°');title('机构压力角线图');text(230,30,'可行域');% 4-绘制机构的传动比线图和传动比与尺度系数关系线图figure(3);subplot(1,2,1) % 机构传动比线图phi_1=1:360;plot(phi_1,i_31);xlabel ('导杆转角\it \phi_1 / \rm( °)')ylabel ('\it i_{31}')title('机构传动比线图(尺度系数是定值)');subplot(1,2,2) % 机构传动比与尺度系数关系线图line([0,sin(alpha_p*hd)],[1,1+sin(alpha_p*hd)]);line([0,sin(alpha_p*hd)],[1,1-sin(alpha_p*hd)]);line([sin(alpha_p*hd),sin(alpha_p*hd)],[1+sin(alpha_p*hd),1-sin(alpha_p*hd)]); xlabel ('尺度系数\it \lambda = e / l_3 ')ylabel ('\it i_{31}')title('传动比与尺度系数关系线图');text(0.25,1.4,'\it i_{31max}')text(0.32,1.0,'可行域')text(0.25,0.6,'\it i_{31min}')******** 已知条件********导杆转速n = 200.0000 r/min导杆角速度omega_1 = 20.9440 rad/s机构尺度系数lambda = 0.5000机构许用压力角alpha_p = 45.0000 °*** 转动导杆机构的运动参数***导杆转角曲柄角位移曲柄角速度(°) (°) (rad/s)10.0000 5.0191 10.592020.0000 10.1534 10.956430.0000 15.5225 11.577540.0000 21.2528 12.472550.0000 27.4790 13.657060.0000 34.3411 15.135170.0000 41.9757 16.886680.0000 50.5013 18.854790.0000 60.0000 20.9440100.0000 70.5013 23.0332 110.0000 81.9757 25.0013 120.0000 94.3411 26.7528 130.0000 107.4790 28.2309 140.0000 121.2528 29.4154 150.0000 135.5225 30.3104 160.0000 150.1534 30.9315 170.0000 165.0191 31.2959 180.0000 180.0000 31.4159 190.0000 194.9809 31.2959 200.0000 209.8466 30.9315 210.0000 224.4775 30.3104 220.0000 238.7472 29.4154 230.0000 252.5210 28.2309 240.0000 265.6589 26.7528 250.0000 278.0243 25.0013 260.0000 289.4987 23.0332 270.0000 300.0000 20.9440 280.0000 309.4987 18.8547 290.0000 318.0243 16.8866 300.0000 325.6589 15.1351 310.0000 332.5210 13.6570 320.0000 338.7472 12.4725 330.0000 344.4775 11.5775 340.0000 349.8466 10.9564 350.0000 354.9809 10.5920 360.0000 360.0000 10.4720。
平面机构的自由度与运动分析

平面机构的自由度与运动分析一、平面机构的自由度平面机构是指机构中的构件只能在一个平面内运动的机构,它由多个连接杆、转动副和滑动副组成。
平面机构的自由度是指机构中能够独立变换位置的最小的连接杆数目,也可以理解为机构中独立的变量的数量。
对于平面机构,其自由度可以通过以下公式计算:自由度=3n-2j-h其中,n表示连接杆的数量,j表示驱动链的数量,h表示外部约束的数量。
根据上述公式可以看出,自由度与平面机构中连接杆的数量和驱动链和外部约束的数量有关。
连接杆的数量越多,机构的自由度就越大,可以实现更复杂的运动。
驱动链的数量越多,机构中的动力驱动器越多,自由度就越小,机构的运动变得更加确定。
外部约束的数量越多,机构中的约束条件就越多,自由度就越小,机构的运动也会变得更加确定。
二、平面机构的运动分析1.闭合链和链架分析:首先需要确定机构中的闭合链和链架,闭合链是指机构中连接杆形成一个封闭的回路,闭合链中的连接杆数目应该为n 或n-1,n是机构中的连接杆数量。
链架是指机构中的连接杆形成一个开放的链路。
通过分析闭合链和链架中的链接关系和约束条件,可以确定机构中构件的位置和运动方式。
2.位置和速度分析:根据机构的连接杆的长度和角度,可以通过几何方法或代数方法确定机构中构件的位置和速度分量。
通过分析连接杆的长度和角度的变化规律,可以推导出机构中构件的位置和速度随时间的变化关系。
3.加速度和动力学分析:根据机构中各个构件的位置和速度,可以通过几何方法或动力学方法计算构件的加速度和动力学特性。
通过分析机构中构件的加速度和动力学特性,可以确定机构中构件的运动稳定性和质量分布。
4.动力分析:对于需要携带负载或进行力学传动的机构,需要进行动力学分析,确定机构中各个构件的受力和承载能力。
通过分析机构中构件的受力情况,可以确定机构的设计参数和强度要求。
总结起来,平面机构的自由度与运动分析是确定机构中构件位置和运动状态的重要方法,通过分析机构中的闭合链和链架、构件的位置和速度、加速度和动力学特性,可以确定机构的运动方式和特性,为机构的设计和优化提供依据。
机构运动简图及分析

一、实验目的
1、学习测绘实际机器和模型的机构运动简图。
2、学习巩固机构自由度计算。
3、分析一些四杆机构的化过程。验证其曲柄存在 的条件。
二、设备和工具
1、偏心泵模型 ;
2、冲床机构模型;
3、缝纫机的摆梭机构; 4、其他机构模型。 1
三、原理和绘制步骤
1、原理:由于机构的运动仅与机构中所有构件的
数目和构件所组成的运动副的数目、种类 、相对位 置有关。而与构件和运动副的具体结构、形状、剖 面尺寸以及组成构件的零件数等无关,因此,可以 忽略与机构的运动无关的因素,仅考虑与机构运动 有关的因素,用国标规定的简单符号和线条表示运 动副和构件,并以一定的比例尺绘制的简明图形称 为机构运动简图。
进料口
27
部分资料从网络收集整 理而来,供大家参考,
感谢您的关注!
3. 绘制机构运动简图的步骤
1)构件及其成副分析: 分析机构的构件个数;那些构件 之间成副关系,确定运动副的类型和数量。
2)机构运动尺寸的测绘:测量出运动副间相对位置尺寸
3)选择合适的比例尺μl 和恰当的视图 μl =实际尺寸 m /
图上长度mm 4)先确定基架位置,然后用规定的符号从原动件开始,
1000423323???????????????fpppnfhl精品资料进料口出料口精品资料进料口出料口精品资料进料口出料口精品资料进料口出料口精品资料进料口出料口精品资料进料口出料口精品资料进料口出料口精品资料进料口出料口精品资料进料口出料口精品资料进料口出料口精品资料机构运动简图及分析谢谢
机构运动简图测绘和分析
2
2、常用运动副及构件的表示方法
常见运动副符号的表示: 国标GB4460-84
3
运动副 名称
曲柄摇杆机构的运动分析

% 曲柄摇杆机构运动分析% (1)-计算连杆的输出角th3和摇杆的输出角th4% 设定各杆的长度(单位:毫米)rs(1)=304.8; % 设定机架1长度rs(2)=101.6; % 设定曲柄2长度rs(3)=254.0; % 设定连杆3长度rs(4)=177.8; % 设定摇杆4长度dr=pi/180.0;% 角度与弧度的转换系数% 设定初始推测的输入% 机构的初始位置th(1)=0.0; % 设定曲柄2初始位置角是0度(与机架1共线)th(2)=45*dr; % 连杆3的初始位置角是45度th(3)=135*dr; % 摇杆4的初始位置角是135度% 摇杆4的初始位置角可以用三角形的正弦定理确定th(3)=pi-asin(sin(th(2))*rs(3)/rs(4));dth=5*dr; % 循环增量% 曲柄输入角从0度变化到360度,步长为5度,计算th34for i=1:72[th3,th4]=ntrps(th,rs); % 调用牛顿—辛普森方程求解机构位置解非线性方程函数文件% Store results in a matrix-th34,in degrees% 在矩阵th34中储存结果,以度为单位;(i,:)表示第i行所有列的元素;(:,i)表示第i列所有行的元素th34(i,:)=[th(1)/dr th3/dr th4/dr]; % 矩阵[曲柄转角连杆转角摇杆转角]th(1)=th(1)+dth; % 曲柄转角递增th(2)=th3; % 连杆转角中间计算值th(3)=th4; % 摇杆转角中间计算值end% 求解曲柄摇杆机构中连杆的输出角th(3)和摇杆的输出角th(4)—函数文件function [th3,th4]=ntrps(th,rs)% 使用基于牛顿—辛普森方程解答四杆机构位置的非线性问题% 变量设置% th(1)=theta_2 % 输入变量% th(2)=theta_3_bar(starting guess) % 输出变量% th(3)=theta_4_bar(starting guess) % 输出变量% rs(1)=r_1,机架长度;rs(2)=r_2,曲柄长度;rs(3)=r_3,rs(4)=r_4,摇杆长度th2=th(1);th3bar=th(2);th4bar=th(3);% 设定收敛条件epsilon=1.0E-6;% 计算二维矢量的函数% 四杆机构闭环矢量方程的矩阵形式f=[rs(3)*cos(th3bar)-rs(4)*cos(th4bar)+rs(2)*cos(th2)-rs(1);rs(3)*sin(th3bar)-rs(4)*sin(th4bar)+rs(2)*sin(th2)];% 重复计算每个方程式的修正量因子while norm(f)>epsilonJ=[-rs(3)*sin(th3bar) rs(4)*sin(th4bar); rs(3)*cos(th3bar) -rs(4)*cos(th4bar)];dth=inv(J)*(-1.0*f);th3bar=th3bar+dth(1);th4bar=th4bar+dth(2);% 四杆机构闭环矢量方程的矩阵形式f=[rs(3)*cos(th3bar)-rs(4)*cos(th4bar)+rs(2)*cos(th2)-rs(1);rs(3)*sin(th3bar)-rs(4)*sin(th4bar)+rs(2)*sin(th2)];norm(f); % 计算矩阵或向量的范数(模)end;th3=th3bar; % 弧度值th4=th4bar; % 弧度值% 绘制输出角th(2)与th(3)—输入角th(1)的关系曲线subplot(2,2,1) % 选择第1个子窗口plot(th34(:,1),th34(:,2),th34(:,1),th34(:,3))axis([0 360 0 170])grid % 网格线ylabel('从动件角位移/deg')title('角位移线图')text(110,110,'摇杆4角位移')text(50,35,'连杆3角位移')% (2)-计算连杆的角速度om3和摇杆的角速度om4% Setting initial conditions% 设置初始条件om2=250; % 曲柄角速度(等速输入)T=2*pi/om2; % 机构周期-曲柄旋转1周的时间(秒)% 曲柄输入角从0度变化到360度,步长为5度,计算om34for i=1:72ct(2)=i*dth;A=[-rs(3)*sin(th34(i,2)*dr) rs(4)*sin(th34(i,3)*dr); rs(3)*cos(th34(i,2)*dr) -rs(4)*cos(th34(i,3)*dr)];B=[om2*rs(2)*sin(ct(2));-om2*rs(2)*cos(ct(2))];om=inv(A)*B; % 输出角速度矩阵om3=om(1);om4=om(2);om34(i,:)=[i om3 om4]; % 矩阵[序号连杆角速度摇杆角速度]t(i)=i*T/72;end% 绘制连杆的角速度om3和摇杆的角速度om4—时间Times的关系曲线subplot(2,2,2) % 选择第2个子窗口plot(t,om34(:,2),t,om34(:,3))axis([0 0.026 -190 210])grid % 网格线title('角速度线图')ylabel('从动件角速度/rad/s')text(0.001,170,'摇杆4角速度')text(0.013,130,'连杆3角速度')% (3)-计算连杆的角加速度a3和摇杆的角加速度a4a2=0; % 曲柄角速度是等速,角加速度a2=dom2/dt=0% 曲柄输入角从0度变化到360度,步长为5度,计算a34for i=1:72c(2)=i*dth;C=[-rs(3)*sin(th34(i,2)*dr) rs(4)*sin(th34(i,3)*dr); rs(3)*cos(th34(i,2)*dr) -rs(4)*cos(th34(i,3)*dr)];D(1)=a2*rs(2)*sin(c(2))+om2^2*rs(2)*cos(c(2))+om34(i,2)^2*rs(3)*cos(th34(i,2)*dr)-om34(i,3)^2*rs( 4)*cos(th34(i,3)*dr);D(2)=-a2*rs(2)*cos(c(2))+om2^2*rs(2)*sin(c(2))+om34(i,2)^2*rs(3)*sin(th34(i,2)*dr)-om34(i,3) ^2*rs(4)*sin(th34(i,3)*dr);a=inv(C)*D'; % 输出角加速度矩阵a3=a(1);a4=a(2);a34(i,:)=[i a3 a4]; % 矩阵[序号连杆角加速度摇杆加角速度]t(i)=i*T/72;end% 绘制连杆的角加速度a3和摇杆的角加速度a4—时间Times的关系曲线subplot(2,2,3) % 选择第3个子窗口plot(t,a34(:,2),t,a34(:,3))axis([0 0.026 -6*1e4 8*1e4])grid % 网格线title('角加速度线图')xlabel('时间/s')ylabel('从动件加速度/rad/s^{2}')text(0.003,6.2*1e4,'摇杆4角加速度')text(0.010,3.3*1e4,'连杆3角加速度')%% 输出1:四杆机构运动周期(0:5:360),时间,角位移,角速度,角加速度数据disp ' 曲柄转角连杆转角-摇杆转角-连杆角速度-摇杆角速度-连杆加速度-摇杆加速度' ydcs=[th34(:,1),th34(:,2),th34(:,3),om34(:,2),om34(:,3),a34(:,2),a34(:,3)];disp (ydcs)% 输出参数的数量级必须一致%% (4)-运动误差分析% 闭环矢量方程:r2+r3-r4-r1=0% 误差矢量E=r2+r3-r4-r1的模是表示仿真有效程度的标量(ex和ey是误差分量)ex=rs(2)*cos(th34(:,1)*dth)+rs(3)*cos(th34(:,2)*dth)-rs(4)*cos(th34(:,3)*dth)-rs(1); ey=rs(2)*sin(th34(:,2)*dth)+rs(3)*sin(th34(:,2)*dth)-rs(4)*sin(th34(:,3)*dth);ee=norm([ex ey]); % 计算误差矢量矩阵的范数(模) %% 输出2:四杆机构运动周期(0:5:360),时间,X向误差分量,Y向误差分量disp ' 曲柄转角时间(秒) X向误差Y向误差'wc=[th34(:,1),t(:),ex(:,1),ey(:,1)];disp (wc)fprintf (1,' 误差矢量矩阵的模ee = %3.4f \n',ee)%% 绘制均方根相容性误差曲线subplot(2,2,4) % 选择第4个子窗口plot(t,ex(:,1),t,ey(:,1))axis([0 0.026 -800 600])grid % 网格线title('均方根误差曲线')xlabel('时间/s')ylabel('均方根误差')text(0.012,350,'X向误差分量')text(0.003,-600,'Y向误差分量')。
四连杆机运动学分析报告

栏杆机四杆机构运动学分析1 四杆机构运动学分析1.1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
对四杆机构进行运动分析的意义是:在机构尺寸参数已知的情况下,假定主动件(曲柄)做匀速转动,撇开力的作用,仅从运动几何关系上分析从动件(连杆、摇杆)的角位移、角速度、角加速度等运动参数的变化情况。
还可以根据机构闭环矢量方程计算从动件的位移偏差。
上述这些内容,无论是设计新的机械,还是为了了解现有机械的运动性能,都是十分必要的,而且它还是研究机械运动性能和动力性能提供必要的依据。
机构运动分析的方法很多,主要有图解法和解析法。
当需要简捷直观地了解机构的某个或某几个位置的运动特性时,采用图解法比较方便,而且精度也能满足实际问题的要求。
而当需要精确地知道或要了解机构在整个运动循环过程中的运动特性时,采用解析法并借助计算机,不仅可获得很高的计算精度及一系列位置的分析结果,并能绘制机构相应的运动线图,同时还可以把机构分析和机构综合问题联系起来,以便于机构的优化设计。
1.2 机构的工作原理在平面四杆机构中,其具有曲柄的条件为:a.各杆的长度应满足杆长条件,即:最短杆长度+最长杆长度≤其余两杆长度之和。
b.组成该周转副的两杆中必有一杆为最短杆,且其最短杆为连架杆或机架(当最短杆为连架杆时,四杆机构为曲柄摇杆机构;当最短杆为机架时,则为双曲柄机构)。
三台设备测绘数据分别如下:第一组(2代一套)四杆机构L1=125.36mm,L2=73.4mm, L3=103.4mm,L4=103.52mm最短杆长度+最长杆长度(125.36+73.4) <其余两杆长度之和(103.4+103.52)最短杆为连架杆,四杆机构为曲柄摇杆机构图1-1 II-1型栏杆机机构测绘及其运动位置图第二组(2代二套)四杆机构L1=125.36mm,L2=50.1mm,L3=109.8mm,L4=72.85mm最短杆长度+最长杆长度(125.36+50.1) <其余两杆长度之和(109.8+72.85)最短杆为连架杆,四杆机构为曲柄摇杆机构图1-2 II-2型栏杆机机构测绘及其运动位置图第三组(3代)四杆机构L1=163.2mm,L2=64.25mm,L3=150mm,L4=90.1mm最短杆长度+最长杆长度(163.2+64.25) <其余两杆长度之和(150+90.1)最短杆为连架杆,四杆机构为曲柄摇杆机构图1-3 III型栏杆机机构测绘及其运动位置图在如下图1所示的曲柄摇杆机构中,构件AB为曲柄,则B点应能通过曲柄与连杆两次共线的位置。
机构运动参数测定实验报告

机构运动参数测定实验报告一、引言1.1 背景介绍1.2 目的和意义二、研究方法2.1 选取实验样本2.2 实验设备2.3 实验流程三、数据采集与分析3.1 数据采集方法3.2 数据处理与分析四、实验结果与讨论4.1 实验结果展示4.2 结果分析4.2.1 参数一的关系分析4.2.2 参数二的关系分析五、结论5.1 结果总结5.2 研究的局限性和不足之处六、进一步研究展望6.1 可改进的方法和方案6.2 后续研究工作的建议七、参考文献八、致谢一、引言1.1 背景介绍本实验旨在通过测定机构运动参数,深入研究运动特性及其相关因素。
机构运动参数是机构运动的重要指标,对于设计和控制机构具有重要意义。
准确测定机构运动参数是提高机构效能、优化机构设计的基础。
1.2 目的和意义本实验的目的是通过实际测定,获取机构运动参数,并对数据进行分析和处理,进一步了解机构运动的特性以及与参数之间的关系。
通过实验结果的分析,可以揭示不同因素对机构运动参数的影响,并为后续研究和应用提供理论基础。
二、研究方法2.1 选取实验样本根据研究目的,选取了具有代表性的机构样本作为实验对象,并根据一定的条件进行筛选和匹配。
2.2 实验设备实验所需设备包括测量仪器、数据采集系统和计算机等。
测量仪器要求具备高精度和稳定性,以确保数据的准确和可靠性。
数据采集系统需要能够实时采集和记录各项参数,并提供数据处理和分析的功能。
2.3 实验流程本实验的流程包括样本准备、测量数据采集、数据处理与分析等步骤。
在每个步骤中,需要按照规定的操作方法和流程进行实验,以保证实验结果的可靠性。
三、数据采集与分析3.1 数据采集方法通过实验设备和测量仪器对样本进行测量,并实时采集各项运动参数。
为了确保数据的准确性,需要重复多次实验,并在不同条件下进行测量。
3.2 数据处理与分析对采集到的数据进行处理和分析,包括数据清洗、统计分析、可视化展示等。
采用适当的数学模型和方法,对数据进行拟合和分析,揭示不同参数之间的关系及其影响因素。
导杆机构
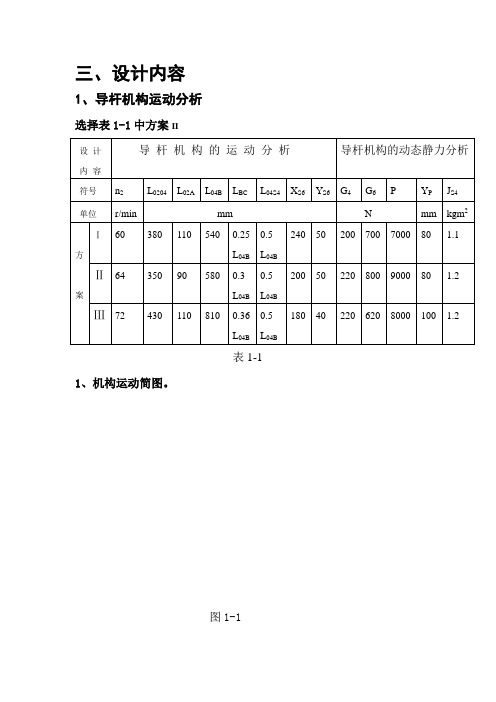
三、设计内容1、导杆机构运动分析选择表1-1中方案II设计内容导杆机构的运动分析导杆机构的动态静力分析符号n2 L0204 L02A L04B L BC L04S4 X S6 Y S6 G4 G6 P Y P J S4 单位r/min mm N mm kgm2方案Ⅰ60 380 110 540 0.25L04B0.5L04B240 50 200 700 7000 80 1.1 Ⅱ64 350 90 580 0.3L04B0.5L04B200 50 220 800 9000 80 1.2 Ⅲ72 430 110 810 0.36L04B0.5L04B180 40 220 620 8000 100 1.2表1-11、机构运动简图。
图1-12、曲柄位置“7”速度分析,加速度分析(列矢量方程,画速度图,加速度图)取曲柄位置“7”进行速度分析,其分析过程同曲柄位置“1”。
取构件3和4的重合点A进行速度分析。
列速度矢量方程,得υA4=υA3+υA4A3大小? √?方向⊥O4A⊥O2A∥O4B代表pa4 pa3 a3a4V A3=ω2l o2A=64/60×6.28×0.09=0.603m/s取速度极点P,速度比例尺µv=0.01(m/s)/mm,作速度多边形如图1-2则由图1-2知,υA4=pa4·μv=29×0.01=0.29m/sυA4A3=a3a4·μv=52×0.01m/s=0.52m/s图1-2υB5=υB4=υA4·O4B/ O4A=0.44m/s取5构件为研究对象,列速度矢量方程,得υC5=υB5+υC5B5大小? √?方向∥XX⊥O4B⊥BC代表pc5 pb4 b4b5其速度多边形如图1-2所示,有υC5=5Pc·μv=42×0.01=0.42m/s取曲柄位置“7”进行加速度分析,取曲柄构件3和4的重合点A进行加速度分析.列加速度矢量方程,得:a A4 =a A4n +a A4t= a A3n +a A4A3k+a A4A3r 大小? ω42l O4A ?√2ω4υA4A3 ? 方向? A→O4⊥O4B A→O2⊥O4B(向右)∥O4B代表pA4’pn4’n4’A4’p’A3’A3’k’k’A4’取加速度极点为P',加速度比例尺μa=0.02(m/s2)/mm作加速度多边形图1-3图1-3则由图1─3知:a A4t= n4’A4’·μa =137×0.02m/s2=2.74m/s2α4= a A4t/l O4A = 7.17 m/s2a A4 = pA4’·μa = 138×0.01m/s2 =2.76 m/s2用加速度影象法求得a B5 = a B4 = a A4 ×l O4B/l O4A=4.19m/s2取5构件的研究对象,列加速度矢量方程,得a C5=a B5+ a C5B5n+ a C5B5t大小?√√?方向∥xx √ C→B ⊥BC代表 P’c5’ P’B5’ n5’B5’ C5’n5’加速度比例尺μa=0.02(m/s2)/mm其加速度多边形如图1─4所示,有图1-4a C5B5t= n5’c5’·μa =31×0.02m/s2 =0.62m/s2a C5 = P’c5’·μa =179×0.02m/s2 =3.58m/s23、曲柄位置“10”速度分析,加速度分析(列矢量方程,画速度图,加速度图)取曲柄位置“10”进行速度分析。
第3章机构的运动分析-1

an EB
C 3 4
ω3
aE e'
b'
ω2
A
2
aB
1
w4
D
a
t EB
a
n EB
(P12 )
以曲柄滑块机构为例,进一步说明用矢量方程图 解法作机构的速度分析和加速度分析的具体步骤。
例 : 已知曲柄滑块机构原动件 AB 的运动规律和各构件尺寸。求: (1)图示位置连杆BC的角速度和 其上各点速度。 (2)连杆BC的角加速度和其上C点 加速度。 ω2 2
极点
C
vEC
vCB vEB
b
bc 代表 vCB 。
e
3)在速度多边形中,极点p 代表机构中速 度为零的点。 4)已知某构件上两点的速度 ,可用速度影 像法求该构件上第三点的速度。
速度多边形
E B
A
C
vC x
p
极点
C
vEC e
vCB
vB
vEB
b
△bce ~ △BCE
已知连杆上两点的速度vB 、vC 用速度影像法可以确定vE 。
④确定点的轨迹(连杆曲线)。
V型发动机运动简图
D
E
C B
A
3-1
机构运动分析的任务、目的及方法
1.机构运动分析的任务与目的
(2)速度分析
5 4
①掌握从动件的度变化规律 是否满足工作要求。如牛 头刨床; ②为加速度分析作准备。
2
1 3
6
3-1 机构运动分析的任务、目的及方法
1.机构运动分析的任务与目的
用三心定理可以确定ω3、ω4 的大小。
平面铰链四杆机构
例2:用三心定理分析凸轮机构速度 (v3)。 1
机械原理课程设计 六杆机构分析完整版

机械原理课程设计说明书设计题目:六杆机构运动分析学院:工程机械学院专业:机械设计制造及其自动化班级:25041004设计者:25041004指导老师:张老师日期:2013年01月07日目录1.课程设计题目以及要求————————————————————32.运用辅助软件对结构进行结构分析———————————————43.数据收集以及作图———————————————————————114.总结————————————————————————————17六杆机构运动分析1、分析题目对如图5所示的六杆机构进行运动与动力分析,各构件长度、滑块5的质量G 、构件1转速n1、不均匀系数δ的已知数据如表5所示。
2、分析内容(1)对机构进行结构分析:(2)绘制滑块D 的运动线图(即位移、速度和加速度线图):(3)绘制构件3和4的运动线图(即角位移、角速度和角加速度线图): (4)绘制S4点的运动轨迹。
图5表5方案号L CDmmL ECmmymm L AB mm L CS4 mm n 1r/mi n1 975 360 50 250 400 23.52 975 325 50 225 350 33.53 9003005020030035(一)对机构进行结构分析选取方案三方案号L CDmm L ECmmymmL ABmmL CS4mmn 1r/mi n3 900 300 50 200 300 35对六杆机构进行运动分析:(1)原始数据的输入:(2)基本单元的选取及分析:(3)各点运动参数:(4)长度变化参数(5)各构件角运动参数:(二)滑块D的运动线图(位移-速度-加速度线图):(三)构件3的运动线图(角位移-角速度-角加速度线图):(四)构件4的运动线图(角位移-角速度-角加速度线图):(五)S4点的运动轨迹:(六)数据收集以及作图(1)滑块D 点x 、y 方向的运动参数如表6.1所示表6..1由上表可以得到D 点运动线图如图6.1所示图6.1位置 0123456789101112位 移X 1188.097 1187.376 1058.394 848.5281 680.2758 607.9142 606.0113 651.5314 734.6896 848.5281 980.0058 1105.089 1188.097 Y 0 0 0 0 0 0 0 0 0 0 0 0 0 速 度X 332.4289 -434.0533 7293.698 -1466.08 -831.5157 -222.7902 169.5616 457.6898 699.4701 879.648 933.0263 776.3062 332.4289 Y 0 0 0 0 0 0 0 0 0 0 0 0 0 加 速度X -4255.382 -6281.231 -4679198 2533.081 4920.073 3387.318 2265.425 1834.254 1530.378 911.9092 -264.7796 -2020.469 -4255.382 y 0(2)构件3的运动参数如表6.2所示表6.2位置0 1 2 3 4 5 6 7 8 9 10 11 12角位移φ14.03624 -16.10211 -50.93532 -90 230.9353 196.1021 165.9638 139.1066 114.1333 90 65.86674 40.89339 14.03624角速度ω-3.4496 -3.947138 -4.561904 -4.886933 -4.561904 -3.947138 -3.4496 -3.1416 -2.981412 -2.93216 -2.981412 -3.1416 -3.4496角加速度ɛ-2.789002 -4.130385 -3.972855 -6.092957 3.972855 4.130385 2.789002 1.582846 0.7038764 2.368942 -0.703876 -1.582846 -2.789002由上表得构件3的运动线图如图6.2所示图6.2(3)构件4的运动参数如表6.3所示表6.3位置0 1 2 3 4 5 6 7 8 9 10 11 12 φ-4.63715 5.304571 14.99956 19.471122 14.99956 5.304571 -4.63715 -12.60438 -17.70998 -19.47122 -17.70998 -12.60438 -4.63715 角位移ω 1.119198 1.269533 0.992103 1.253846 -0.9921031 -1.269533 -1.119198 -0.8111576 -0.4265414 -1.775216 0.4265414 0.1811158 1.119198 角速度ɛ 1.768468 0.031558 -4.448388 -8.443604 -4.448388 0.031558 1.768468 2.468482 2.88811092 3.039697 2.881092 2.468482 1.768468 角加速度由表6.3参数可得构件4的运动线图如图6.3所示图6.3(4)S4点x、y方向的运动参数如表6.4所示表6.4位置0 1 2 3 4 5 6 7 8 9 10 11 12位移X 590.0608 586.9459 478.8375 282.8427 100.7192 10.48452 7.975251 65.99134 163.1245 282.8427 408.4406 519.5487 590.0608 Y 48.50713 -55.47002 755.287 -200 -155.287 -55.47002 48.50713 130.9307 182.5194 200 182.5194 130.9307 48.50713速度X 278.1398 -363.6323 -1139.637 -1466.08 -985.5764 -293.2113 223.8507 563.8953 777.3222 879.648 855.1742 670.1007 278.1398 Y -669.3207 -758.4576 -574.98 -8.42273 574.98 758.4576 669.3207 474.9653 243.7962 7.905602 -243.7962 -474.9653 -669.3207加速度X -3592.063 -5316.593 -4799.736 844.3604 4920.073 4351.956 2928.744 1896.326 1108.512 303.9697 -686.6455 -1958.397 -3592.063 y -1118.368 70.54837 2730.937 4776.623 2730.937 70.54837 -1118.368 -1531.544 -1679.939 -1719.512 -1679.939 -1531.544 -1118.368(七)总结:六杆机构的运动分析相比课本上的平面四杆机构来说难度大些,而且是用辅助软件进行运动分析,这看起来似乎难度更大。
机构运动简图实验报告

机构运动简图实验报告机构运动简图实验报告引言:机构运动是机械工程中的重要课题,它研究的是机械结构在特定条件下的运动规律。
本次实验旨在通过绘制机构运动简图,研究机构运动的特性和规律,以及对机构运动进行分析和优化。
实验目的:1. 了解机构运动的基本概念和术语;2. 学习使用绘图工具绘制机构运动简图;3. 分析机构运动的特性和规律;4. 探索机构运动的优化方法。
实验步骤:1. 确定实验所用机构:选择一种简单的机构,如四连杆机构;2. 绘制机构运动简图:使用绘图工具,按照机构的几何尺寸和运动规律,绘制机构运动简图;3. 分析机构运动的特性和规律:观察机构运动简图,记录机构各部分的运动轨迹和相对运动关系;4. 优化机构运动:根据机构运动的特性和规律,提出改进机构的方法,并进行实验验证。
实验结果:通过实验,我们得到了四连杆机构的运动简图。
在该机构中,我们观察到四个连杆的运动轨迹以及它们之间的相对运动关系。
通过分析机构运动的特性和规律,我们发现四连杆机构在运动过程中存在一些问题,如运动不平稳、能量损耗等。
为了优化机构运动,我们可以尝试调整连杆的长度、改变连杆的材料等方法,以提高机构的运动效率和稳定性。
讨论与分析:机构运动是机械工程中的重要研究课题,它与机械设计、控制系统等领域密切相关。
通过实验我们可以深入了解机构运动的特性和规律,为机械设计和控制系统的优化提供理论基础和实践经验。
在实验过程中,我们发现机构运动的特性受到多种因素的影响,如连杆长度、材料、运动速度等。
这些因素的改变会导致机构运动的变化,因此在机械设计中需要综合考虑这些因素,以达到最优的运动效果。
此外,机构运动的优化方法也是一个重要的研究方向。
通过改变机构的结构、优化连杆的长度和材料等方式,可以提高机构的运动效率和稳定性。
在实验中,我们可以尝试不同的优化方法,比较它们的效果,并根据实验结果进行改进。
结论:通过本次实验,我们了解了机构运动的基本概念和术语,并学会了使用绘图工具绘制机构运动简图。
机械设计-凸轮机构的运动规律分析

s
h
2h p
A
0
5v
1 6
2 7
3 8
a
φ
4φ
φ
φ
φ
φ
小结
1.运动过程分析
运动循环和运动参数
2.从动件的运动规 律
运动规律 等速运动规律 等加速等减速运动 余弦加速度运动规律 正弦加速度运动规律
运动特性
有刚性冲击
柔性冲击 柔性冲击 无冲击
适用场合
低速、轻载
中速、 轻载 中速、中载
✓ 等加速等减速运动规律(线运动规律(正弦加速度运动律)
1.等速运动规律
定义 从动件在推程或回程作等速运动。
启动瞬间: 速度由0→v0,a 由0→∞ 终止瞬间: 速度由v0→0,a 由0→-∞
冲击特性:始点、末点刚性冲击(F=ma) 适用场合:低速轻载
s h
O
v
O
a
∞
O
v0
φ φ
φ φ
φ φ
-∞
2.等加速等减速运动规律 定义 从动件在推程或回程的前半行程作等加速 运动,后半行程作等减速运动。
运动线图 从动件位移方程
抛物线
动力特性 加速度在运动的起始、中间和终止 位置有突变。
存在柔性冲击 (F=ma)
适用场合 中速轻载。
A
B
3.简谐(余弦加速度)运动规律
近休止:从动件在初始位置静止不动。 近休止角 :凸轮转过角度 Φs´ 凸轮与从动件的关系: 从动件的运动规律取决于凸轮的轮廓曲
二、从动件的运动规律
从动件的运动规律:从动件的位移(s)、速度(v)和加速 度(a)随时间(t)或凸轮转角(φ)的变 化规律。
牛头刨床导杆机构的运动分析、动态静力分析

摘要——牛头刨床运动和动力分析一、机构简介与设计数据1、机构简介牛头刨床是一种用于平面切削加工的机床,如图1-1a。
电动机经皮带和齿轮传动,带动曲柄2和固结在其上的凸轮8。
刨床工作时,由导杆机构2 –3 –4 –5 –6 带动刨头6和刨刀7作往复运动。
刨头右行时,刨刀进行切削,称工作行程,此时要求速度较低并且均匀,以减少电动机容量和提高切削质量;刨头左行时,刨刀不切削,称空回行程,此时要求速度较高,以提高生常率。
为此刨床采用有急回作用的导杆机构。
刨刀每切削完一次,利用空回行程的时间,凸轮8通过四杆机构1 – 9 – 10 – 11 与棘轮带动螺旋机构(图中未画),使工作台连同工件做一次进给运动,以便刨刀继续切削。
刨头在工作行程中,受到很大的切削阻力(在切削的前后各有一段约0.05H的空刀距离,图1-1b),而空回行程中则没有切削阻力。
因此刨头在整个运动循环中,受力变化是很大的,这就影响了主轴的匀速运转,故需安装飞轮来减小主轴的速度波动,以提高切削质量和减少电动机容量a b图目录摘要 (III)1设计任务 (1)2 导杆机构的运动分析 (2)导杆机构的动态静力分析 (4)3.1运动副反作用力分析 (4)3.2力矩分析 (6)4方案比较 (7)5总结 (10)6参考文献 (10)《机械原理课程设计》说明书1设计任务机械原理课程设计的任务是对机器的主题机构进行运动分析。
动态静力分析,确定曲柄平衡力矩,并对不同法案进行比较,以确定最优方案。
要求根据设计任务,绘制必要的图纸和编写说明书等。
2 导杆机构的运动分析2.1 速度分析取曲柄位置1’对其进行速度分析,因为2和3在以转动副相连,所以V A2=V A3,其大小等于ω2l02A,指向于ω2相同。
取构件3和4的重合点A进行速度分析。
列速度矢量方程,得υA4 = υA3 + υA4A3大小 ? √ ?方向⊥O4A ⊥O2A ∥O4B选比例尺μv=0.004(m/s)/mm,做出速度矢量图(见图a)νA4=0.088m/sνA3=0.816m/s取5构件作为研究对象,列速度矢量方程,得υC5 = υB5 + υC5B5大小 ? √ ?方向∥XX ⊥O4B ⊥BC取速度极点p,选比例尺μv=0.004(m/s)/mm,做出速度矢量图(见图a)νC5=0.16m/sνC5B5=0.044m/s2.2 加速度分析取曲柄位置“1”进行加速度分析。
四种门机构的运动分析

四种门机构的运动分析1.平面四杆机构:平面四杆机构是指由四个连杆构成的机构,它们在同一个平面内运动。
平面四杆机构可以实现转动和滑动运动。
其中,若有一个连杆固定,则该机构只能实现转动运动。
若没有连杆固定,则该机构可以实现平面内的任意运动。
根据连接方式和形状的不同,平面四杆机构有多种变体。
其中,常见的有四杆平行机构和四杆交叉机构。
四杆平行机构具有简单的结构和运动规律,适用于需要直线运动和平移运动的场景。
而四杆交叉机构则具有较复杂的结构和运动规律,适用于需要曲线运动和旋转运动的场景。
2.空间四杆机构:空间四杆机构是指由四个连杆构成的机构,它们在三维空间中运动。
与平面四杆机构不同,空间四杆机构的连杆不再在同一个平面内运动,而是可以在空间中的任意平面内运动。
空间四杆机构可以实现复杂的运动形式,如曲线运动、旋转运动和平移运动的组合。
空间四杆机构的应用十分广泛,例如工业机械中的抓取装置、自动化装配线中的定位装置、汽车工程中的转向机构等。
3.行程生成机构:行程生成机构是指一种能够产生规定轨迹的机构。
行程生成机构一般由连杆、滑块和曲柄等部件组成,通过这些部件的组合和运动,可以实现规定的曲线、平面或空间轨迹。
行程生成机构广泛用于工业制造、运动模拟和航空航天等领域。
例如,在汽车行业中,行程生成机构被用于模拟转向过程和悬挂系统的运动;在航空航天领域,行程生成机构被用于模拟飞机起降过程和空间站的姿态控制。
4.一维运动机构:一维运动机构是指一种只能在单一方向上进行运动的机构。
一维运动机构一般由连杆、齿轮和导向器等部件组成,通过这些部件的组合和运动,可以实现一维方向上的直线运动、旋转运动或平移运动。
一维运动机构的应用广泛,例如在自动化工程中的装配线上,一维运动机构被用于实现物品的进料、定位、装配和出料等操作;在机械制造中,一维运动机构被用于实现机械零件的加工和装配等工序。
综上所述,四种门机构分别具有不同的运动形式和应用场景。
机构运动简图的测绘与分析实验报告

指导教师签名:
项目
计 算 公 式
标准齿轮计算结果(mm)
变位齿轮计算结果(mm)
结果
备 注
分度圆直径d
齿顶圆直径da
齿根圆直径df齿厚s
分度圆齿槽宽e
最小变位系数xmin
齿形比较
注:“齿形比较”仅定性地说明两个齿轮的齿顶圆齿厚和齿根圆齿厚的差别,不用计算公式来计算;备注中填写变位齿轮相对标准齿轮的变化:增加用“+”号表示;减少用“-”号表示;不变用“0”表示。
实验日期: 年 月 日
一、机构名称:
机构编号: 比例尺μL= m/mm
机构运动尺寸:
机构自由度F=
二、机构名称:
机构编号: 比例尺μL= m/mm
机构运动尺寸:
机构自由度F=
三、机构名称:
机构编号:
机构自由度F=
四、机构名称:
机构编号:机构自由度F=
机构自由度F=
五、机构名称
机构编号:
机构自由度F=
附齿廓范成图
四、实验的心得体会和意见
指导教师签名:
基本机构的运动参数测定实验报告
院专业班级姓名学号
实验日期: 年 月 日
设备编号:
实验记录与理论计算曲线比较
机构示意图
运动尺寸
实测曲线
理论曲线
对比说明
滑
块
速
度
滑
块
加
速
度
曲柄
角
速
度
附图
指导教师签名:
院专业班级姓名学号
实验日期: 年 月 日
设备编号:
简要说明:
齿齿轮实验结果计算及比较项目计算公式标准齿轮计算结果mm变位齿轮计算结果mm结果备注分度圆直径齿顶圆直径da齿根圆直径df基圆直径dbpb分度圆齿厚分度圆齿槽宽e最小变位系数xmin齿形比较齿形比较仅定性地说明两个齿轮的齿顶圆齿厚和齿根圆齿厚的差别不用计算公式来计算
四连杆机运动学分析

栏杆机四杆机构运动学分析1 四杆机构运动学分析机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
对四杆机构进行运动分析的意义是:在机构尺寸参数已知的情况下,假定主动件(曲柄)做匀速转动,撇开力的作用,仅从运动几何关系上分析从动件(连杆、摇杆)的角位移、角速度、角加速度等运动参数的变化情况。
还可以根据机构闭环矢量方程计算从动件的位移偏差。
上述这些内容,无论是设计新的机械,还是为了了解现有机械的运动性能,都是十分必要的,而且它还是研究机械运动性能和动力性能提供必要的依据。
机构运动分析的方法很多,主要有图解法和解析法。
当需要简捷直观地了解机构的某个或某几个位置的运动特性时,采用图解法比较方便,而且精度也能满足实际问题的要求。
而当需要精确地知道或要了解机构在整个运动循环过程中的运动特性时,采用解析法并借助计算机,不仅可获得很高的计算精度及一系列位置的分析结果,并能绘制机构相应的运动线图,同时还可以把机构分析和机构综合问题联系起来,以便于机构的优化设计。
机构的工作原理在平面四杆机构中,其具有曲柄的条件为:a.各杆的长度应满足杆长条件,即:最短杆长度+最长杆长度≤其余两杆长度之和。
b.组成该周转副的两杆中必有一杆为最短杆,且其最短杆为连架杆或机架(当最短杆为连架杆时,四杆机构为曲柄摇杆机构;当最短杆为机架时,则为双曲柄机构)。
三台设备测绘数据分别如下:第一组(2代一套)四杆机构L1=,L2=, L3=,L4=最短杆长度+最长杆长度+ <其余两杆长度之和+最短杆为连架杆,四杆机构为曲柄摇杆机构图1-1 II-1型栏杆机机构测绘及其运动位置图第二组(2代二套)四杆机构L1=,L2=,L3=,L4=最短杆长度+最长杆长度+ <其余两杆长度之和+最短杆为连架杆,四杆机构为曲柄摇杆机构图1-2 II-2型栏杆机机构测绘及其运动位置图第三组(3代)四杆机构L1=,L2=,L3=150mm,L4=最短杆长度+最长杆长度+ <其余两杆长度之和(150+最短杆为连架杆,四杆机构为曲柄摇杆机构图1-3 III型栏杆机机构测绘及其运动位置图在如下图1所示的曲柄摇杆机构中,构件AB为曲柄,则B点应能通过曲柄与连杆两次共线的位置。
3-5用解析法做机构的运动分析

对时间求导得速度方程:
l2 sinθ2 ω2 - l3 sinθ3 ω3 =ω1 l1 sinθ1 l2 cosθ2 ω2 - l3 cosθ3 ω3 =-ω1 l1 cosθ1
写成矩阵形式:
- l2 sinθ2 l3 sinθ3 l2 cosθ2 - l3 cosθ3
ω2 ω3
=ω1
l1 sinθ1 -l1 cosθ1
α2 α3 =-
(8)
- l2 ω2 cosθ2 - l 2 ω2 sinθ2
l3 ω3 cosθ3 l3 ω3 sinθ3
ω2 ω3
+ω1
l1 ω1 sinθ1 l1 ω1 cosθ1
求解式(8)可得α2 ,α3。
速度方程的一般表达式: [A]{ω} =ω1{B}
其中[A]--机构从动件的位置参数矩阵;
θ3 Dx
改写成直角坐标的形式:
l2 cosθ2 - l3 cosθ3 = l4 -l1 cosθ1 l2 sinθ2 - l3 sinθ3 =- l1 sinθ1
解此方程即 可得θ2、θ3
2.速度分析 将上述位置方程:
l2 cosθ2 - l3 cosθ3 = l4 -l1 cosθ1 l2 sinθ2 - l3 sinθ3 =- l1 sinθ1
联立上两式可求得两个未知角速度ω2、 ω3 。
ω3 = ω1 l1 sin (θ1 -θ2 ) /[ l3 sin (θ3 -θ2 ) ] ω2 = - ω1 l1 sin (θ1 -θ3 ) /[ l2sin (θ2-θ3 ) ]
(三)、加速度分析
速度方程:
l11ei1 l22ei2 l33ei3 (5)
α3 =ω12 l1 cos (θ1 - θ2 ) + ω22 l2 -ω32 l3 cos (θ3 - θ2 ) /[ l3 sin (θ3 -θ2 ) ]
机构运动简图的测绘与分析

在机械设计中,机构运动简图还可以用于指导实际零件的设计和制造, 确保零件的尺寸和形状符合设计要求。
在机器人设计中的应用
机器人是一种复杂的机械系统,机构运动简图在机器人设计中扮演着重要 的角色。
通过机构运动简图,设计师可以快速地分析和理解机器人的运动特性,为 机器人的设计和优化提供依据。
处理。
05
机构运动简图的未来发展
运动简图与其他领域的结合
运动简图与机器人技术
通过将运动简图应用于机器人技术,可以实现更高效、灵活的机器人运动控制, 提高机器人执行任务的能力。
运动简图与生物医学工程
在生物医学工程领域,运动简图可用于分析和模拟人体骨骼、肌肉等系统的运 动,为医学诊断和治疗提供支持。
运动简图的分类
平面机构运动简图
适用于平面机构的分析, 包括平面连杆机构、凸轮 机构等。
空间机构运动简图
适用于空间机构的分析, 如螺旋机构、空间连杆机 构等。
机械系统运动简图
适用于复杂机械系统的分 析,如机床、自动化生产 线等。
运动简图的分析方法
运动分析
通过分析运动简图中各 构件的运动关系,确定
机构的运动特性。
受力分析
根据运动简图,分析机 构在运动过程中各构件
之间的相互作用力。
效率分析
通过分析运动简图,评 估机构的传动效率和功
率损失。
优化设计
基于运动简图的分析结 果,对机构进行优化设 计,提高性能和效率。
04
机构运动简图的应用
在机械设计中的应用
机构运动简图能够清晰地表示机械系统中各个构件之间的相对位置、运 动关系和相互作用,有助于设计师更好地理解机械系统的运动特性。
机构运动简图测绘及分析实验

实验一机构运动简图测绘与分析实验一、实验目的1.根据机构模型,掌握正确绘制平面机构运动简图的方法和技能。
2.验证和稳固机构自由度的计算,进一步理解机构自由度的概念。
3.应用机构自由度的计算方法,分析平面机构运动确实定性。
4.掌握平面机构的组成原理,能够对平面机构进展构造分析。
二、实验设备1、机构模型〔铆钉机构B1、简易冲床B2、装订机机构B3、鄂式破碎机B4、步进输送机B5、假肢膝关节机构B6、机械手腕部机构B7、抛光机B8、牛头刨床B9、制动机构B10等〕;2.所用工具:钢板尺、游标卡尺、三角板、铅笔、圆规、橡皮、纸〔除钢板尺和游标卡尺外,其余学生自备〕。
三、实验容1. 选择5种机构模型进展测量,绘制机构运动简图;2. 计算机构自由度,并注明其活动构件数、低副数、高副数,然后代入公式进展计算。
3.对所选择的机构进展构造分析,确定机构的级别。
四、实验原理、方法和手段在对现有机械设备进展分析或设计新的机械设备时,都需要运用其机构运动简图。
而机构各局部的运动是由其原动件的运动规律、该机构中各运动副的数目、类型,运动副相对位置和构件的数目来确定的,而与构件的外形、断面尺寸、组成构件的零件数目及运动副的具体构造等无关。
所以,只要根据机构的运动尺寸,按一定的比例尺定出各运动副的位置,就可以用运动副的代表符号和简单的线条把机构的运动简图画出来。
常用符号见下表:1、机构运动简图的概念抛开构件的复杂外形和运动副的具体构造,利用简单的线条和规定的符号来代表每一个构件和运动副,并按一定的比例将机构的运动特征表达出来的简单图形称为机构运动简图。
机构运动简图与原机构具有完全一样的运动特性,因而可以根据该图对机构进展运动分析和动力分析。
2、测绘方法〔1〕分析运动情况。
绘制机构运动简图时,首先要把该机器或模型的实际构造和运动情况搞清楚。
为此,先应确定出原动件和从动件,再使被测机器或模型缓慢运动,然后按照运动的传递路线,把原动件和从动件之间的各构件的运动情况观察清楚,尤其应注意有微小运动的构件,分清各构件间的接触情况及相对运动的性质,从而确定组成机构的运动构件数目、联接次序和运动副数目、种类等。
