2017年中考真题专题汇编——组合式归纳推论题
2017年中考历史试卷分类汇编:经济史专题(含答案)

经济史专题(经济、农业、农村、农民、工业化、民生)一、选择题◆(2017·河北)15.宣传画深深打上时代的印记。
下列宣传画共同反映了我国()AA.农业发展道路的探索 B.工业化的发展过程C.改革开放的历程 D.国有企业改革的经过◆(2017·湖北鄂州)7.小说《平凡的世界》中描述道:田福堂太痛苦了!当年搞合作化时,他曾怀着多么热烈的感情把左邻右舍拢合在一起,做梦也没想到二十多年后的今天,大家都散伙了。
小说中描述的“拢合在一起”和“都散伙了”分别是指()DA.农业合作化运动和人民公社化运动 B.土地改革和农业合作化运动C.土地改革和家庭联产承包责任制 D.农业合作化运动和家庭联产承包责任制◆(2017·江苏常州)1.生产工具是人类社会发展水平的重要标志。
下列生产工具中,代表人类社会发展水平最高的是A.钻孔石斧B.骨耜C.铁犁铧D.(青)铜铲◆(2017·黑龙江牡丹江)15.中国要强,农业必须强;中国要美,农村必须美;中国要富,农民必须富。
下列政策解放了农村生产力,调动了农民生产积极性的有()B①1950年土地改革②农业合作化③人民公社化运动④实行家庭联产承包责任制A.①②③ B.①②④C.①③④ D.②③④二、非选择题◆(2017·黑龙江龙东)25.中国要强农业必须强,中国要美农村必须美,中国要富农民必须富。
请跟随以下图片足迹,重温不同时期党和政府在农业建设方面的重大举措。
(6分)材料一图一图二河北邯郸市郊农民报名入社图三农民领取生产承包合同材料二这一时期大办公共食堂,吃饭不要钱,生产队及社员家庭的一些财产被无偿地收归公社所有,由公社统一调配。
这导致了“共产风”盛行,劳动纪律废弛,农业生产受到极大破坏。
——岳麓版八年级下册(1)图一反映的是哪一历史事件?(1分)(2)图二反映的是国家对农业的社会主义改造,改造中采取的主要方式是什么?(1分)(3)材料二反映了探索建设社会主义道路中出现的哪一失误?(1分)(4)图三契合了我国哪次重要会议的精神?随后,在中央的指导下,农村实行了什么制度?(2分)(5)哪个地方的农民率先进行农业生产责任制的尝试,实行包产到户?(1分)25.(6分)(1)土地改革;(1分)(2)农业生产合作社;(1分)(3)人民公社化运动;(1分)(4)十一届三中全会;家庭联产承包责任制;(2分)(5)安徽风阳小岗村。
2017年中考数学真题专题汇编----图形的展开与折叠

2017全国部分省市中考数学真题汇编----图形的展开与折叠一.选择题1.将一个无盖正方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )A.B.C.D.2.如图,四个图形是由立体图形展开得到的,相应的立体图形顺次是( )A.正方体、圆柱、三棱柱、圆锥B.正方体、圆锥、三棱柱、圆柱C.正方体、圆柱、三棱锥、圆锥D.正方体、圆柱、四棱柱、圆锥3.如图,点A,B,C是正方体三条相邻的棱的中点,沿着A,B,C三点所在的平面将该正方体的一个角切掉,然后将其展开,其展开图可能是( )A.B.C.D.4.如图所示的平面图形能折叠成的长方体是( )A.B.C.D.5.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A.B.C.D.6.如图,该几何体的展开图是( )A.B.C.D.7.如图是正方体的一个平面展开图,如果原正方体上前面的字为“友”,则后面的字为( )A.善B.国C.诚D.爱8.下列图形经过折叠不能围成棱柱的是( )A.B.C.D.二.填空题9.某个立体图形的侧面展开图形如图所示,它的底面是正三角形,这个立体图形一定是 .10.如图,是一个物体的展开图(单位:cm),那么这个物体的体积为 .11.如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A,B围成的正方体上的距离是 .12.如图1是边长为18cm的正方形纸板,截掉阴影部分后将其折叠成如图2所示的长方体盒子.已知该长方体的宽是高的2倍,则它的体积是 cm3.13.把如图所示的图形折成一个正方体的盒子,折好后与“顺”相对的字是 .14.图1是一个正方体的展开图,该正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格、第5格,此时这个正方体朝上一面的字是 .三.解答题15.如图,在无阴影的方格中选出两个画出阴影,使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图.(在图1和图2中任选一个进行解答,只填出一种答案即可)16.某长方体包装盒的表面积为146cm2,其展开图如图所示.求这个包装盒的体积.17.如图所示的是一个正方体,试在下列3×5方格中,画出它的平面展开图(要求:画出3种不同的情形)18.如图所示是长方体的平面展开图,设AB=x,若AD=4x,AN=3x.(1)求长方形DEFG的周长与长方形ABMN的周长(用字母x进行表示);(2)若长方形DEFG的周长比长方形ABMN的周长少8,求x的值;(3)在第(2)问的条件下,求原长方体的容积.19.如图是一个正方体的展开图,标有字母A的面是正方体的正面,如果正方体相对的两个面所标注的值均互为相反数,求字母A所标注的值.20.如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.(1)求该纸盒的体积;(2)求该纸盒的全面积(外表面积);(3)为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时x与y之间的倍数关系.(直接写出答案即可)21.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:(1)小明总共剪开了 条棱.(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.参考答案与解析一.选择题1.将一个无盖正方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )A.B.C.D.【分析】由平面图形的折叠及无盖正方体的展开图就可以求出结论.【解答】解:由四棱柱的四个侧面及底面可知,A、B、D都可以拼成无盖的正方体,但C拼成的有一个面重合,有两面没有的图形.所以将一个无盖正方体形状盒子的表面沿某些棱展开后不能得到的平面图形是C.故选C.【点评】本题考查了正方体的平面展开图,解答时熟悉四棱柱的特征及无盖正方体展开图的各种情形是关键.2.如图,四个图形是由立体图形展开得到的,相应的立体图形顺次是( )A.正方体、圆柱、三棱柱、圆锥B.正方体、圆锥、三棱柱、圆柱C.正方体、圆柱、三棱锥、圆锥D.正方体、圆柱、四棱柱、圆锥【分析】根据正方体、圆锥、三棱柱、圆柱及其表面展开图的特点解题.【解答】解:观察图形,由立体图形及其表面展开图的特点可知相应的立体图形顺次是正方体、圆柱、三棱柱、圆锥.故选A.【点评】可根据所给图形判断具体形状,也可根据所给几何体的面数进行判断.3.如图,点A,B,C是正方体三条相邻的棱的中点,沿着A,B,C三点所在的平面将该正方体的一个角切掉,然后将其展开,其展开图可能是( )A.B.C.D.【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.【解答】解:选项A、B、C折叠后都不符合题意,只有选项D折叠后两个剪去三角形与另一个剪去的三角形交于一个顶点,与正方体三个剪去三角形交于一个顶点符合.故选D.【点评】考查了截一个几何体和几何体的展开图.解决此类问题,要充分考虑带有各种符号的面的特点及位置.4.如图所示的平面图形能折叠成的长方体是( )A.B.C.D.【分析】根据两面相隔一个面是对面,相邻的面是邻面,可得答案.【解答】解:A、平面图形能折叠成的长方体正面的右邻面是阴影,故A错误;B、平面图形能折叠成的长方体上面的右邻面是阴影,故B错误;C、平面图形能折叠成的长方体正面是阴影,上面应是空白面,故C错误;D、平面图形能折叠成的长方体上面的右邻面是阴影,故D正确;故选:D.【点评】本题考查了展开图这个叠成几何体,确定折叠成长方体阴影面的邻面是解题关键.5.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A.B.C.D.【分析】根据立体图形平面展开图的特征进行判断即可.【解答】解:A.四棱锥的展开图有四个三角形,故A选项错误;B.根据长方体的展开图的特征,可得B选项正确;C.正方体的展开图中,不存在“田”字形,故C选项错误;D.圆锥的展开图中,有一个圆,故D选项错误.故选:B.【点评】本题主要考查了展开图折叠成几何体,解题时注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.6.如图,该几何体的展开图是( )A.B.C.D.【分析】由平面图形的折叠及正方体的展开图解题,注意带图案的两个面相邻.【解答】解:观察题干图形可知,带图案的两个面相邻.只有选项C中几何体的展开图带图案的两个面相邻.故选:C.【点评】本题主要考查了几何体的展开图.解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意做题时可亲自动手操作一下,增强空间想象能力.7.如图是正方体的一个平面展开图,如果原正方体上前面的字为“友”,则后面的字为( )A.善B.国C.诚D.爱【分析】根据展开图即可判断.【解答】解:“友”与“诚”属于同层,由同层隔一面可知:“友”相对的是“诚”故选(C)【点评】本题考查几何体的展开图,先找同层隔一面,再找异层隔两面,剩下两面必相对.8.下列图形经过折叠不能围成棱柱的是( )A.B.C.D.【分析】由平面图形的折叠及棱柱的展开图解题.【解答】解:A可以围成四棱柱,C可以围成五棱柱,D可以围成三棱柱,B选项侧面上多出一个长方形,故不能围成一个三棱柱.故选:B.【点评】熟记常见立体图形的表面展开图的特征是解决此类问题的关键.二.填空题(共11小题)9.某个立体图形的侧面展开图形如图所示,它的底面是正三角形,这个立体图形一定是 三棱柱 .【分析】根据侧面是三个矩形,底面是三角形,可得答案.【解答】解:由题意,得这个立体图形一定是三棱柱,故答案为:三棱柱.【点评】本题考查了几何体的展开图,利用侧面是三个矩形,底面是三角形是解题关键.10.如图,是一个物体的展开图(单位:cm),那么这个物体的体积为 250πcm3 .【分析】根据展开图可知此物体是圆柱,再利用圆柱的体积公式即可得出结。
2017年全国中考数学真题《函数与一次函数》分类汇编解析

2017年全国中考数学真题《函数与一次函数》分类汇编解析函数与一次函数考点一、平面直角坐标系 (3分) 1、平面直角坐标系在平面内画两条互相垂直且有公共原点的数轴,就组成了平面直角坐标系。
其中,水平的数轴叫做x 轴或横轴,取向右为正方向;铅直的数轴叫做y 轴或纵轴,取向上为正方向;两轴的交点O (即公共的原点)叫做直角坐标系的原点;建立了直角坐标系的平面,叫做坐标平面。
为了便于描述坐标平面内点的位置,把坐标平面被x 轴和y 轴分割而成的四个部分,分别叫做第一象限、第二象限、第三象限、第四象限。
注意:x 轴和y 轴上的点,不属于任何象限。
2、点的坐标的概念点的坐标用(a ,b )表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对,当b a ≠时,(a ,b )和(b ,a )是两个不同点的坐标。
考点二、不同位置的点的坐标的特征 (3分) 1、各象限内点的坐标的特征 点P(x ,y )在第一象限0,0>>⇔y x点P(x ,y )在第二象限0,0><⇔y x 点P(x ,y )在第三象限0,0<<⇔y x 点P(x ,y )在第四象限0,0<>⇔y x 2、坐标轴上的点的特征点P(x ,y )在x 轴上0=⇔y ,x 为任意实数 点P(x ,y )在y 轴上0=⇔x ,y 为任意实数点P(x ,y )既在x 轴上,又在y 轴上⇔x ,y 同时为零,即点P 坐标为(0,0) 3、两条坐标轴夹角平分线上点的坐标的特征点P(x ,y )在第一、三象限夹角平分线上⇔x 与y 相等 点P(x ,y )在第二、四象限夹角平分线上⇔x 与y 互为相反数 4、和坐标轴平行的直线上点的坐标的特征 位于平行于x 轴的直线上的各点的纵坐标相同。
位于平行于y 轴的直线上的各点的横坐标相同。
5、关于x 轴、y 轴或远点对称的点的坐标的特征点P 与点p’关于x 轴对称⇔横坐标相等,纵坐标互为相反数 点P 与点p’关于y 轴对称⇔纵坐标相等,横坐标互为相反数 点P 与点p’关于原点对称⇔横、纵坐标均互为相反数 6、点到坐标轴及原点的距离点P(x ,y )到坐标轴及原点的距离: (1)点P(x ,y )到x 轴的距离等于y(2)点P(x ,y )到y 轴的距离等于x(3)点P(x ,y )到原点的距离等于22y x +考点三、函数及其相关概念 (3~8分) 1、变量与常量在某一变化过程中,可以取不同数值的量叫做变量,数值保持不变的量叫做常量。
2017中考真题专题汇编——组合式归纳推论题.doc

2017中考真题专题汇编一一组合式归纳推论题题型分析:该考点的题型较为单一,主要是选择题的形式呈现,考查的内容以化学概念、化学原理为主,也包含元索化合物知识、化学用语、化学实验、环境保护、化学与生活等各个方面的相关内容,其最大的特点就是把多个有联系或共同点的知识点进行的整合,然后进行逻辑推理,并让学生判断•正误。
方法技巧:1.题目具有基础性。
知识点来源于教材,不拘于教材。
解题吋需从多角度、多层面思考问题、分析问题、解决问题,突出了化学学科的应用性。
解题时的难度在于能否用已学的知识和技能构建问题的模型。
2.题目具有丰富的信息资源。
考题一般跨度较大,需从阅读材料中筛选和破译出所需的信息资源,最后再根据题意要求,进行整合収舍。
3.该类题目将零散的化学知识整理归纳,具有开而不放的特点,解题吋可以使用排除法以加快解题速度、提高解题的儿率。
个别题目需通过某种现象,发掘其小隐含信息,联想到具体事例,才能轻松解决问题。
真题演练:1.(2017黄石)推理是一种重要的思维方法,以下推理合理的是(D )A.酸中--定含有孩元素,所以含有蛍元素的物质一定是酸B.置换反应有单质生成,所以有单质生成的反应一定是置换反应C.化学反应前后原子总数不变,所以化学反应前后分子总数也不变D.化学反应伴随能量变化,所以金屈腐蚀过程中一定伴随能量变化2.(2017随州)归纳推理是一种重要的化学思维方法。
下列归纳推理正确的是(B )A.碱溶液能使酚瞅溶液变红,那么能使酚瞅溶液变红的溶液一定是碱溶液B.镁、锌、铁能与盐酸反应生成氢气,那么它们与稀硫酸反应也能生成氢气C.屮和反应生成盐和水,那么生成盐和水的反应一定是屮和反应D.人体缺少必需微量元素会得病,那么应尽可能多吃含有这些元素的营养品3.(2017襄阳)推理是学习化学的一种重要方法,但推理必须科学、严谨。
下列推理正确的是(C)A.木炭在氧气中能燃烧,所以氧气具有可燃性B.不锈钢虽然是金属材料,但它属于混合物而不是金属单质C.原子核是由质子和中子构成的,故所有原子核中都一定含有质子和中子D.催化剂在反应前后质量不变,因此反应前后质量不变的物质一定是催化剂4.(2017孝感)推理是研究和学习化学的重要方法.以下推理正确的是(A)A.若某雨水的pH<7,则该雨水一定呈酸性B.过率可以除去水屮不溶性杂质,因此过滤后的水一定是软水C.一氧化碳和二氧化碳的组成元素相同,所以它们的化学性质相同D.可燃物燃烧时温度需要达到着火点,所以温度达到着火点时,可燃物就一定能燃烧5.(2017聊城)归纳总结和逻辑推理是化学学习中常用的思维方法。
2017中考政治真题分类汇编——考点25亲社会行为、热心公益

2017中考政治真题分类汇编——考点25亲社会行为、热心公益(2017河南)8.面对暗流汹涌的滔滔黄河,只要有救援需要,他们就毫不犹豫下水搜救;面对水波漂碧的深潭湖泊,只要有生命求救,他们就不假思索纵身跃入。
在郑州乃至全省,甚至全国范围内的水灾、溺水、户外被困、地震等事件现场,总能看到他们救援抢险的身影……他们,有一个共同的名字—义务救援队;他们,是河南人的道德标杆。
他们BCD A.自觉履行我国公民法定义务,积极促进社会和谐B.守护人民群众生命财产安全,生动诠释人间大爱C.传承了扶危济困的传统美德,弘扬志愿服务精神D.践行了社会主义核心价值观,彰显河南良好形象(2017浙江丽水)8.王某通过微信“轻松筹“平台,为因燃气爆炸而受重伤的某家庭捐款300元。
王某的捐款行为是( C )①乐善好施、无私奉献②法律要求的,必须做③为国分忧、勇担重任④法律鼓励的,积极做。
A.①② B.②③C.①④ D.③④(2017江苏苏州)11.从G20杭州峰会的“小青荷”到江苏发展大会的“小流苏”,青年志愿者们积极传递文明礼仪,制止不文明的行为。
该举动告诉我们要( A )A.学会亲近社会,自觉服务社会B.体验生活变化,领略现代文明C.提高文化素养,突出个人发展D.强调服务社会,不应获取回报(2017•吉林)5.(2分)(2017•吉林)某中学全体师生积极为身患重病的学生捐款、捐物,奉献爱心。
师生的行为是( C )①团结友爱的体现②在自觉履行公民的道德义务③宪法和法律规定公民必须履行的④在对自己的合法财产行使处分权。
A.①②③B.②③④C.①②④D.①③④(2017辽宁营口)4.被誉为篮球场上“中国长城”的姚明入选第三届“CCTV年度慈善人物”。
他一直以来致力于慈善和公益事业,由他发起的“姚基金”已援建和在建希望小学22所,“姚基金希望小学篮球季”更是为贫困地区32万青少年提供了学习篮球的机会。
为了更好地传递这种正能量我们应该( A )①热心公益,服务社会②积极承担责任,不言代价与回报③具有高度的社会责任感④从身边小事做起,只对自己负责。
专题10 四边形-2017年中考数学试题分项版解析汇编(解析版)

专题10:四边形一、选择题1.(2017北京第6题)若正多边形的一个内角是150°,则该正多边形的边数是( )A . 6B . 12C . 16D .18【答案】B .【解析】试题分析:设多边形的边数为n ,则有(n -2)×180°=n ×150°,解得:n =12.故选B .考点:多边形的内角与外角2. (2017河南第7题)如图,在ABCD 中,对角线AC ,BD 相交于点O ,添加下列条件不能..判定ABCD 是菱形的只有( )A .AC BD ⊥B .AB BC = C .AC BD = D .12∠=∠【答案】C .考点:菱形的判定.3. (2017湖南长沙第10题)如图,菱形ABCD 的对角线BD AC ,的长分别为cm cm 8,6,则这个菱形的周长为( )A .cm 5B .cm 10C .cm 14D .cm 20【答案】D【解析】试题分析:根据菱形的对角线互相垂直,可知OA =3,OB =4,根据勾股定理可知AB =5,所以菱形的周长为4×5=20.故选:D考点:菱形的性质4. (2017湖南长沙第12题)如图,将正方形ABCD 折叠,使顶点A 与CD 边上的一点H 重合(H 不与端点D C ,重合),折痕交AD 于点E ,交BC 于点F ,边AB 折叠后与边BC 交于点G ,设正方形ABCD 的周长为m ,CHG ∆的周长为n ,则mn 的值为( ) A .22 B .21 C .215- D .随H 点位置的变化而变化【答案】B【解析】试题分析:设正方形ABCD 的边长为2a ,正方形的周长为m =8a ,设CM =x ,DE =y ,则DM =2a -x ,EM =2a -y ,∵∠EMG =90°,∴∠DME +∠CMG =90°.∵∠DME +∠DEM =90°,∴∠DEM =∠CMG ,又∵∠D =∠C =90°△DEM ∽△CMG , ∴CG CM MG DM DE EM ==,即22CG x MG a x y a y==-- ∴CG =(2)(2)=,x a x x a y CG MG y y--= △CMG 的周长为CM +CG +MG =24ax x y-在Rt △DEM 中,DM 2+DE 2=EM 2即(2a -x )2+y 2=(2a -y )2整理得4ax -x 2=4ay∴CM +MG +CG =2444ax x ay a y y-===n . 所以12n m = 故选:B .考点:1、正方形,2、相似三角形的判定与性质,3、勾股定理5. (2017山东临沂第7题)一个多边形的内角和是外角和的2倍,这个多边形是( )A .四边形B .五边形C .六边形D .八边形【答案】C【解析】试题分析:根据多边形的外角和为360°,可知其内角和为720°,因此可根据多边形的内角和公式(n -2)·180°=720°,解得n =6,故是六边形.故选:C考点:多边形的内外角和6. (2017山东临沂第12题)在ABC V 中,点D 是边BC 上的点(与B 、C 两点不重合),过点D 作DE AC ∥,DF AB ∥,分别交AB ,AC 于E 、F 两点,下列说法正确的是( )A .若AD BC ⊥,则四边形AEDF 是矩形B .若AD 垂直平分BC ,则四边形AEDF 是矩形C .若BD CD =,则四边形AEDF 是菱形D .若AD 平分BAC ∠,则四边形AEDF 是菱形【答案】D【解析】试题分析:根据题意可知:DE AC ∥,DF AB ∥,可得四边形AEDF 是平行四边形.若AD ⊥BC ,则四边形AEDF 是平行四边形,不一定是矩形;选项A 错误;若AD 垂直平分BC ,则四边形AEDF 是菱形,不一定是矩形;选项B 错误;若BD =CD ,则四边形AEDF 是平行四边形,不一定是菱形;选项C 错误;若AD 平分∠BAC ,则四边形AEDF 是菱形;正确.故选:D考点:特殊平行四边形的判定7. (2017山东青岛第7题)如图,平行四边形ABCD 的对角线AC 与BD 相交于点O ,AE ⊥BC ,垂足为E ,3=AB ,AC =2,BD =4,则AE 的长为( )A .23B .23C .721D .7212 【答案】D考点:1、平行四边形的性质,2、勾股定理,3、面积法求线段长度8. (2017四川泸州第11题)如图,在矩形ABCD 中,点E 是边BC 的中点,AE BD ⊥,垂足为F ,则tan BDE ∠的值是 ( )A .24B .14C .13D .23【答案】A .【解析】试题分析:由AD ∥BC 可得△ADF ∽△EBF ,根据相似三角形的性质可得AD AF DF EB EF BF== ,因点E 是边BC 的中点且AD =BC ,所以AD AF DF EB EF BF ===2,设EF =x ,可得AF =2x ,在Rt △ABE 中,由射影定理可得BF =2x ,再由AD AF DF EB EF BF ===2可得DF =22x ,在Rt △DEF 中,tan BDE ∠=2422EF x DF x == ,故选A . 9. (2017江苏苏州第10题)如图,在菱形CD AB 中,60∠A =,D 8A =,F 是AB 的中点.过点F 作F D E ⊥A ,垂足为E .将F ∆AE 沿点A 到点B 的方向平移,得到F '''∆A E .设P 、'P 分别是F E 、F ''E 的中点,当点'A 与点B 重合时,四边形CD 'PP 的面积为A .283B .243C .323D .3238-【答案】A .【解析】试题分析:作,,DH AB PK AB FL AB ⊥⊥⊥在菱形CD AB 中,60∠A =,D 8A =,F 是AB 的中点 423,3AF EF EL ∴==∴=,P 是F E 的中点,32PK ∴= 43DH = 1373322PP CD ∴-= 高为4 7382832S ∴=⨯=L K H故答案选A .考点:平行四边形的面积,三角函数. 10.(2017江苏苏州第7题)如图,在正五边形CD AB E 中,连接BE ,则∠ABE 的度数为A .30B .36C .54D .72【答案】B .【解析】试题分析:∠ABE =3601=3652︒⨯︒ 故答案选B . 考点:多边形的外角,等腰三角形的两底角相等11.(2017浙江台州第10题) 如图,矩形EFGH 的四个顶点分别在菱形ABCD 的四条边上,BE BF =,将,AEH CFG ∆∆分别沿,EH FG 折叠,当重叠部分为菱形且面积是菱形ABCD 面积的116时,则AE EB 为 ( )A . 53B .2C . 52D .4 【答案】A考点:1、菱形的性质,2、翻折变换(折叠问题)二、填空题1.(2017天津第17题)如图,正方形ABCD 和正方形EFCG 的边长分别为3和1,点G F ,分别在边CD BC ,上,P 为AE 的中点,连接PG ,则PG 的长为 .【答案】5.【解析】试题分析:连结AC ,根据正方形的性质可得A 、E 、C 三点共线,连结FG 交AC 于点M ,因正方形ABCD 和正方形EFCG 的边长分别为3和1,根据勾股定理可求得EC =FG =2,AC =32,即可得AE =22,因P 为AE 的中点,可得PE =AP =2,再由正方形的性质可得GM =EM =22,FG 垂直于AC ,在Rt △PGM 中,PM =322,由勾股定理即可求得PG =5.2.(2017福建第15题)两个完全相同的正五边形都有一边在直线l 上,且有一个公共顶点O ,其摆放方式如图所示,则AOB ∠等于 度.【答案】108【解析】∵五边形是正五边形,∴每一个内角都是108°,∴∠OCD =∠ODC =180°-108°=72°,∴∠COD =36°,∴∠AOB =360°-108°-108°-36°=108°.D C3.(2017广东广州第16题)如图9,平面直角坐标系中O 是原点,OABC 的顶点,A C 的坐标分别是()()8,0,3,4,点,D E 把线段OB 三等分,延长,CD CE 分别交,OA AB 于点,F G ,连接FG ,则下列结论:①F 是OA 的中点;②OFD ∆与BEG ∆相似;③四边形DEGF 的面积是203;④453OD =;其中正确的结论是 .(填写所有正确结论的序号)【答案】①③【解析】试题分析:如图,分别过点A 、B 作AN OB ⊥ 于点N ,BM x ⊥ 轴于点M在OABC 中,(80)(34)(114)137A C B OB ∴= ,,,,,D E 、 是线段AB 的三等分点, 12OD BD ∴= ,CB OF ODF BDC ∴∆∆111222OF OD OF BC OA BC BD ∴==∴==, F ∴ 是OA 的中点,故①正确.(34)5C OC OA ∴=≠ ,,OABC ∴ 不是菱形.,DOF COD EBG ODF COD EBG ∴∠≠∠=∠∠≠∠=∠(40)17,F CF OC CFO COF ∴=<∴∠>∠ ,,DFO EBG ∴∠≠∠故OFD ∆ 和BEG ∆ 不相似.则②错误;由①得,点G 是AB 的中点,FG ∴ 是OAB ∆ 的中位线1137,22FG OB FG OB ∴== D E 、 是OB 的三等分点,1373DE ∴= 1118416222OAB S OB AN OA BM ∆=⋅=⋅=⨯⨯= 解得:1162AN OB= ,DF FG ∴ 四边形DEGH 是梯形()551202121223DEGF DE FG h S OB h OB AN -∴==⋅=⋅=四边形 则③正确 113733OD OB == ,故④错误. 综上:①③正确.考点: 平行四边形和相似三角形的综合运用4.(2017广东广州第11题)如图6,四边形ABCD 中,0//,110AD BC A ∠=,则B ∠=___________.【答案】70°【解析】试题分析:两直线平行,同旁内角互补,可得:B ∠=180°-110°=70°考点:平行线的性质5.(2017山东临沂第18题)在ABCD Y 中,对角线AC ,BD 相交于点O .若4AB =,10BD =,3sin 5BDC ∠=,则ABCD Y 的面积是 .【答案】24【解析】试题分析:作OE ⊥CD 于E ,由平行四边形的性质得出OA =OC ,OB =OD =12BD =5,CD =AB =4,由sin ∠BDC =35,证出AC ⊥CD ,OC =3,AC =2OC =6,得出▱ABCD 的面积=CD •AC =24. 故答案为:24.考点:1、平行四边形的性质,2、三角函数,3、勾股定理6.(2017山东青岛第13题)如图,在四边形 ABCD 中,∠ABC =∠ADC =90°,E 为对角线AC 的中点,连接BE 、ED 、BD ,若∠BAD =58°,则∠EBD 的度数为__________度.【答案】32 【解析】 试题分析:如下图由∠ABC =∠ADC =90°,E 为对角线AC 的中点,可知A ,B ,C ,D 四点共圆,圆心是E ,直径AC 然后根据圆周角定理由∠BAD =58°,得到∠BED =116°,然后根据等腰三角形的性质可求得∠EBD =32°. 故答案为:32.考点:1、圆周角性质定理,2、等腰三角形性质7.(2017山东滨州第16题)如图,将矩形ABCD 沿GH 对折,点C 落在Q 处,点D 落在AB 边上的E 处,EQ 与BC 相交于点F .若AD =8,AB =6,AE =4,则△EBF 周长的大小为___________.ABCDHQGFE【答案】8.【解析】由折叠的性质可得DH =EH ,设AH =x ,则DH =EH =8-x ,在Rt △AEH 中,根据勾股定理可得2224(8)x x +=- ,解得x =3,即可得AH =3,EH =5;根据已知条件易证△AEH ∽△BFE ,根据相似三角形的性质可得AH AE EH BE BF EF == ,即3452BF EF ==,解得BF =83 ,EF =103,所以△EBF 的周长为2+83+103=8. 8.(2017江苏宿迁第15题)如图,正方形CD AB 的边长为3,点E 在边AB 上,且1BE =.若点P 在对角线D B 上移动,则PA +PE 的最小值是 .【答案】10.9.(2017辽宁沈阳第16题)如图,在矩形ABCD 中,53AB BC ==,,将矩形ABCD 绕点B 按顺时针方向旋转得到矩形GBEF ,点A 落在矩形ABCD 的边CD 上,连接CE ,则CE 的长是 .【答案】3105. 【解析】试题分析:如图,过点C 作MN ⊥BG ,分别交BG 、EF 于点M 、N ,根据旋转的旋转可得AB =BG =EF =CD =5,AD =GF =3,在Rt △BCG 中,根据勾股定理求得CG =4,再由1122BCG S BC CG BG CM =⋅=⋅ ,即可求得CM =125 ,在Rt △BCM 中,根据勾股定理求得BM =22221293()55BC CM -=-=,根据已知条件和辅助线作法易知四边形BENMW 为矩形,根据矩形的旋转可得BE =MN =3,BM =EN =95,所以CN =MN -CM =3-125=35,在Rt △ECN 中,根据勾股定理求得EC =22223990310()()55255CN EN +=+==.考点:四边形与旋转的综合题.10.(2017江苏苏州第18题)如图,在矩形CD AB 中,将C ∠AB 绕点A 按逆时针方向旋转一定角度后,C B 的对应边C ''B 交CD 边于点G .连接'BB 、CC ',若D 7A =,CG 4=,G ''AB =B ,则CC '='BB (结果保留根号).【答案】745. 【解析】试题分析:连接AG ,设DG =x ,则 G=4+x ''AB =B在'Rt AB G ∆ 中,22492(4)1x x x +=+⇒= ,则5,7AB BC =='254974'55CC BB +∴==考点:旋转的性质 ,勾股定理 .11. (2017山东菏泽第11题)菱形ABCD 中, 60=∠A ,其周长为cm 24,则菱形的面积为____2cm . 【答案】183. 【解析】试题分析:如图,连接BD ,作DE ⊥AB ,已知菱形的周长为cm 24,根据菱形的性质可得AB =6;再由 60=∠A ,即可判定△ABD 是等边三角形;求得DE =33,所以菱形的面积为:6×33=183.12. (2017浙江湖州第13题)已知一个多边形的每一个外角都等于72,则这个多边形的边数是 . 【答案】5考点:多边形的外角和三、解答题1. (2017北京第20题) 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.,(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》) 请根据上图完成这个推论的证明过程.证明:()ADC ANF FGC NFGD S S S S ∆∆∆=-+矩形,ABC EBMF S S ∆=-矩形(____________+____________). 易知,ADC ABC S S ∆∆=,_____________=______________,______________=_____________. 可得NFGD EBMF S S =矩形矩形.【答案】,,,AEF CFM ANF AEF FGC CFM S S S S S ∆∆∆∆∆;;S . 【解析】试题分析:由矩形的对角线的性质,对角线把矩形分成两个面积相等的三角形计算即可. 本题解析:由矩形对角线把矩形分成两个面积相等的两部分可得:(),()ADC ANF FGC ABC AEF FMC NFGD EBMF S S S S S S S S ∆∆∆∆∆=-+=-+矩形矩形 ,∴,,ADC ABC ANF AEF FGC FMC S S S S S S ∆∆∆∆∆∆=== , ∴NFGD EBMF S S =矩形矩形 . 考点:矩形的性质,三角形面积计算.2. (2017北京第22题)如图,在四边形ABCD 中,BD 为一条对角线,0//,2,90AD BC AD BC ABD =∠=,E 为AD 的中点,连接BE .(1)求证:四边形BCDE 为菱形;(2)连接AC ,若AC 平分,1BAD BC ∠=,求AC 的长. 【答案】(1)证明见解析.(2)3. 【解析】试题分析:(1)先证四边形是平行四边形,再证其为菱形;(2)利用等腰三角形的性质,锐角三角函数,即可求解.本题解析:(1)证明:∵E 为AD 中点,A D =2BC ,∴BC =ED , ∵AD ∥BC , ∴四边形ABCD 是平行四边形,∵AD =2BE , ∠ABD =90°,AE =DE ∴BE =ED , ∴四边形ABCD 是菱形.(2)∵AD ∥BC ,AC 平分∠BAD ∴∠BAC =∠DAC =∠BCA ,∴BA =BC =1, ∵AD =2BC =2,∴sin ∠ADB =12,∠ADB =30°, ∴∠DAC =30°, ∠ADC =60°.在RT △ACD 中,AD =2,CD =1,AC = 3 .考点:平行线性质,菱形判定,直角三角形斜边中线定理.3. (2017天津第24题)将一个直角三角形纸片ABO 放置在平面直角坐标系中,点)0,3(A ,点)1,0(B ,点)0,0(O .P 是边AB 上的一点(点P 不与点B A ,重合),沿着OP 折叠该纸片,得点A 的对应点'A .(1)如图①,当点'A 在第一象限,且满足OB B A ⊥'时,求点'A 的坐标; (2)如图②,当P 为AB 中点时,求B A '的长;(3)当030'=∠BPA 时,求点P 的坐标(直接写出结果即可).【答案】(1)点A ’的坐标为(2,1);(2)1;(3)3333(,)22--或2333(,)22- . 【解析】试题分析:(1)因点)0,3(A ,点)1,0(B ,可得OA =3 ,OB =1,根据折叠的性质可得△A ’OP ≌△AOP ,由全等三角形的性质可得OA ’=OA =3,在Rt △A ’OB 中,根据勾股定理求得'A B 的长,即可求得点A的坐标;(2)在Rt △AOB 中,根据勾股定理求得AB =2,再证△BOP 是等边三角形,从而得∠OPA =120°.在判定四边形OPA ’B 是平行四边形,根据平行四边形的性质即可得B A '的长; 试题解析:(1)因点)0,3(A ,点)1,0(B , ∴OA =3 ,OB =1.根据题意,由折叠的性质可得△A ’OP ≌△AOP .∴OA ’=OA =3,由OB B A ⊥',得∠A ’BO =90°.在Rt △A ’OB 中,22''2A B OA OB =-=, ∴点A ’的坐标为(2,1). (2) 在Rt △AOB 中,OA =3 ,OB =1, ∴222AB OA OB =+= ∵当P 为AB 中点, ∴AP =BP =1,OP =12AB =1. ∴OP =OB =BP , ∴△BOP 是等边三角形 ∴∠BOP =∠BPO =60°, ∴∠OPA =180°-∠BPO =120°. 由(1)知,△A ’OP ≌△AOP ,∴∠OPA ’=∠OPA =120°,P ’A =PA =1,又OB =PA ’=1,∴四边形OPA ’B 是平行四边形. ∴A ’B =OP =1. (3)3333(,)22--或2333(,)22- .4. (2017福建第24题)如图,矩形ABCD 中,6,8AB AD ==,,P E 分别是线段AC 、BC 上的点,且四边形PEFD 为矩形.(Ⅰ)若PCD ∆是等腰三角形时,求AP 的长; (Ⅱ)若2AP =,求CF 的长.【答案】(Ⅰ)AP 的长为4或5或145;(Ⅱ)CF =324【解析】试题分析:(Ⅰ)分情况CP =CD 、PD =PC 、DP =DC 讨论即可得;(Ⅱ)连结PF 、DE ,记PF 与DE 的交点为O ,连结OC ,通过证明△ADP ∽△CDF ,从而得34CF CD AP AD == ,由AP =2 ,从而可得CF =324. 试题解析:(Ⅰ)在矩形ABCD 中,AB =6,AD =8,∠ADC =90°,∴DC =AB =6, AC =22AD DC + =10;要使△PCD 是等腰三角形,有如下三种情况: (1)当CP =CD 时,CP =6,∴AP =AC -CP =4 ;(2)当PD =PC 时,∠PDC =∠PCD ,∵∠PCD +∠PAD =∠PDC +∠PDA =90°,∴∠PAD =∠PDA ,∴PD =PA ,∴PA =PC ,∴AP =2AC,即AP =5;(3)当DP =DC 时,过D 作DQ ⊥AC 于Q ,则PQ =CQ ,∵S △ADC =12 AD ·DC =12AC ·DQ ,∴DQ =245AD DC AC = ,∴CQ =22185DC DQ -= ,∴PC =2CQ =365 ,∴AP =AC -PC =145. 综上所述,若△PCD 是等腰三角形,AP 的长为4或5或145;(Ⅱ)连结PF 、DE ,记PF 与DE 的交点为O ,连结OC ,∵四边形ABCD 和PEFD 都是矩形,∴∠ADC =∠PDF =90°,即∠ADP +∠PDC =∠PDC +∠CDF ,∴∠ADP =∠CDF ,∵∠BCD =90°,OE =OD ,∴OC =12 ED ,在矩形PEFD 中,PF =DE ,∴OC =12PF ,∵OP =OF =12PF ,∴OC =OP =OF ,∴∠OCF =∠OFC ,∠OCP =∠OPC ,又∵∠OPC +∠OFC +∠PCF =180°,∴2∠OCP +2∠OCF =180°,∴∠PCF =90°,即∠PCD +∠FCD =90°,在Rt △ADC 中,∠PCD +∠PAD =90°,∴∠PAD =∠FCD ,∴△ADP ∽△CDF ,∴34CF CD AP AD == ,∵AP =2 ,∴CF =324.5. (2017广东广州第24题)如图13,矩形ABCD 的对角线AC ,BD 相交于点O ,COD ∆关于CD 的对称图形为CED ∆.(1)求证:四边形OCED 是菱形;(2)连接AE ,若6cm AB =,5BC cm =. ①求sin EAD ∠的值;②若点P 为线段AE 上一动点(不与点A 重合),连接OP ,一动点Q 从点O 出发,以1/cm s 的速度沿线段OP 匀速运动到点P ,再以1.5cm /s 的速度沿线段PA 匀速运动到点A ,到达点A 后停止运动.当点Q 沿上述路线运动到点A 所需要的时间最短时,求AP 的长和点Q 走完全程所需的时间.【答案】(1)详见解析;(2)①2sin 3EAD ∠= ②32AP =和Q 走完全程所需时间为32s 【解析】(2)①连接OE ,直线OE 分别交AB 于点F ,交DC 于点GCOD ∆ 关于CD 的对称图形为CED ∆,OE DC DC AB ∴⊥ ,OF AB EF AD ∴⊥在矩形ABCD 中,G 为DC 的中点,且O 为AC 的中点OG ∴ 为CAD ∆ 的中位线 52OG GE ∴==同理可得:F 为AB 的中点,532OF AF ==, 22223593()22AE EF AF ∴=+=+= 32sin sin 932EAD AEFEAD AEF ∠=∠∴∠=∠==②过点P 作PM AB ⊥ 交AB 于点MQ ∴ 由O 运动到P 所需的时间为3s由①可得,23AM AP = ∴ 点O 以1.5/cm s 的速度从P 到A 所需的时间等于以 1/cm s 从M 运动到A 即:11OP PA OP MA t t t OP MA =+=+=+ Q ∴ 由O 运动到P 所需的时间就是OP +MA 和最小.如下图,当P 运动到1P ,即1PO AB 时,所用时间最短. 3t OP MA ∴=+=在11Rt APM ∆ 中,设112,3AM x APx == 2222211115(3)=(2)+()22AP AM PM x x =+∴ 解得:12x = 32AP ∴= 32AP ∴=和Q 走完全程所需时间为32s考点:菱形的判定方法;构造直角三角形求三角函数值;确定极值时动点的特殊位置6. (2017山东青岛第24题)(本小题满分12分)已知:Rt △EFP 和矩形ABCD 如图①摆放(点P 与点B 重合),点F ,B (P ),C 在同一条直线上,AB =EF =6cm ,BC =FP =8cm ,∠EFP =90°。
2017年全国各地中考化学真题分类汇编:最新科技之可燃冰(Word版,含答案)

2017中考真题专题汇编——最新科技之可燃冰1.(2017长沙)2017年5月18日,我国成为了世界上第一个连续海上开采可燃冰时间最长的国家,可燃冰的主要成分是CH4,其中碳元素的化合价是( )A.-4 B.-1 C.+1 D.+2【答案】A2.(2017株洲)下列过程中一定发生了化学变化的是A.蔗糖溶于水B.开采可燃冰C.生石灰变质D.金属拉成丝【答案】C3.(2017威海)2017年我国海域可燃冰开采取得重大突破。
下列有关可燃冰的叙述正确的是()A.可燃冰是一种纯净物B.可燃冰在常温常压下不易长久保存C.可燃冰的成功开发利用使“水变油”成为可能D.可燃冰作为一种清洁能源对环境没有任何危害【答案】B【解析】A.由两种或两种以上物质组成的物质叫混合物;由一种物质组成的物质叫纯净物;可燃冰的主要成分是甲烷,是由不同物质组成的混合物;B.可燃冰在甲烷和水在低温高压条件下形成的,所以常温常压下易分解,不易长久保存;C.化学变化中元素的种类不变,水不可能变成石油。
D.可燃冰作为一种相对清洁能源,燃烧时热值高,污染少,但不是对环境没有任何危害。
选B4.(2017枣庄)2017年5月18日,我国首次在南海神狐海域试采“可燃冰””(天然气水合物)成功,下列关于“可燃冰”说法正确的是()A.“可燃冰”外形像冰,是天然气冷却后得到的固体B.“可燃冰”燃烧后几乎不产生残渣和废气,被誉为“绿色能源”C.通常状况下,天然气和水就能结合成“可燃冰”D.“可燃冰”储量巨大,属于可再生能源【答案】B【解析】A.“可燃冰”外形像冰,主要含有甲烷水合物,还含有少量的二氧化碳气体,错误;B.“可燃冰”燃烧后几乎不产生残渣和废气,被誉为“绿色能源”,正确;C.“可燃冰”不是天然气和水结合成的,错误;D.“可燃冰”储量巨大,属于不可再生能源,错误。
故选B。
5.(2017娄底) 2017年5月18 日,我国首次在南海海域试采可燃冰成功,消息传出,举世关注.可燃冰外观似冰,主要含有的是甲烷水合物.请写出甲烷完全燃烧的化学方程式:.【答案】CH4+2O2点燃CO2+2H2O6.(2017泰州)2017年5月,我国载南海进行了天然气水合物(可燃冰)试开采,天然气的主要成分为____(填化学式),其完全燃烧的化学方程式为____________。
2017年中考真题专题汇编——工艺流程题

2017年中考真题专题汇编——工艺流程题1.(2107安徽)五氧化二钒(V2 O5)是一种工业催化剂,下图是制取V2 O5 的工艺流程。
(1)写出反应①的化学方程式。
(2)操作a 的名称是_________,实验室进行该操作所需的玻璃仪器有烧杯、玻璃棒和。
(3)反应②的反应类型是,物质X一定含有的元素是__________。
(4)写出副产物KCl 的一种用途___________。
【答案】(1) KVO3+NH4Cl=NH4VO3 (沉淀)+KCl;(2)过滤,漏斗(3)分解反应;(4)制备钾盐2. (2017广州)氯化亚铜(CuCl)广泛应用于冶金、电镀、医药等行业。
已知CuCl难溶于水和乙醇,在潮湿空气中易变质。
CuCl的制备流程如下:(1)“滤液1”中除了Na+、SO42-外,还存在较多的离子是、(写离子符号)(2)“反应”中发生的化学变化是2CuCl2+Na2SO3=2CuCl↓+2NaCl+SO3,产生的SO3迅速与水化合生成一种酸,该反应的化学方程式为。
(3)“操作a”的名称是。
本流程中可以循环利用的物质(水除外)是。
(写化学式)(4)可用“水洗”的原因是,“醇洗”的目的是。
(5)160g CuSO4与足量NaCl经上述制备流程,可生成的CuCl最多是g。
【答案】(1)Cl-、Cu2+;(2)SO3+H2O=H2SO4;(3)过滤;NaCl;(4)CuCl微溶于水;用水洗去可溶性杂质,保留CuCl;快速去除CuCl表面的水分,防止其氧化;(5)99.5。
3.(2017安顺)某种矿石由氧化镁、氧化铁、氧化铜和二氧化硅组成,用它制备氢氧化镁的流程示意图如图所示(已知:二氧化硅不溶于水也不与稀盐酸反应)。
请回答下列问题:(1)溶液A中共含有____种阳离子;写出矿石中的任意一种金属氧化物与稀盐酸反应的化学方程式:____________(只写一个)。
(2)在溶液A中加入熟石灰调节溶液的pH,可以使溶液中的金属阳离子逐步转化为沉淀。
2017年全国中考真题分类汇编 3.整式与因式分解(含答案)

整式与因式分解考点一、整式的有关概念 (3分)1、代数式用运算符号把数或表示数的字母连接而成的式子叫做代数式。
单独的一个数或一个字母也是代数式。
2、单项式只含有数字与字母的积的代数式叫做单项式。
注意:单项式是由系数、字母、字母的指数构成的,其中系数不能用带分数表示,如b a 2314-,这种表示就是错误的,应写成b a 2313-。
一个单项式中,所有字母的指数的和叫做这个单项式的次数。
如c b a 235-是6次单项式。
考点二、多项式 (11分)1、多项式几个单项式的和叫做多项式。
其中每个单项式叫做这个多项式的项。
多项式中不含字母的项叫做常数项。
多项式中次数最高的项的次数,叫做这个多项式的次数。
单项式和多项式统称整式。
用数值代替代数式中的字母,按照代数式指明的运算,计算出结果,叫做代数式的值。
注意:(1)求代数式的值,一般是先将代数式化简,然后再将字母的取值代入。
(2)求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入。
2、同类项所有字母相同,并且相同字母的指数也分别相同的项叫做同类项。
几个常数项也是同类项。
3、去括号法则(1)括号前是“+”,把括号和它前面的“+”号一起去掉,括号里各项都不变号。
(2)括号前是“﹣”,把括号和它前面的“﹣”号一起去掉,括号里各项都变号。
4、整式的运算法则 整式的加减法:(1)去括号;(2)合并同类项。
整式的乘法:),(都是正整数n m a a a nm nm+=∙),(都是正整数)(n m aa m nn m =)()(都是正整数n b a ab nnn = 22))((b a b a b a -=-+ 2222)(b ab a b a ++=+ 2222)(b ab a b a +-=- 整式的除法:)0,,(≠=÷-a n m aa a nm nm都是正整数注意:(1)单项式乘单项式的结果仍然是单项式。
(2)单项式与多项式相乘,结果是一个多项式,其项数与因式中多项式的项数相同。
2017年全国中考数学真题分类 课题研究2017(解答题)
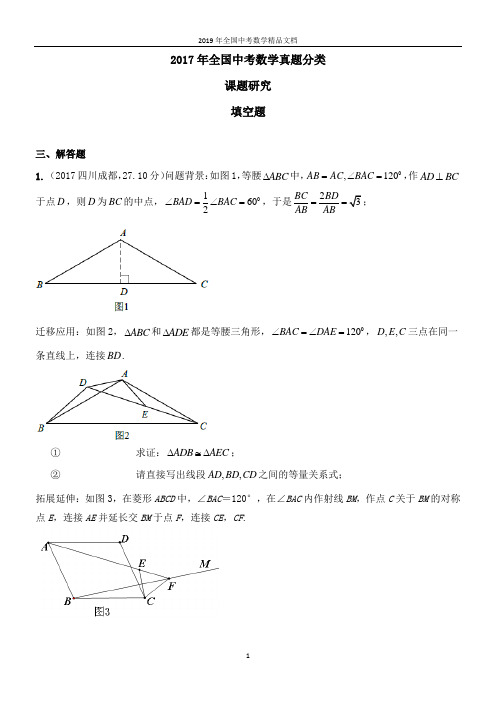
2017年全国中考数学真题分类课题研究 填空题三、解答题1. (2017四川成都,27.10分)问题背景:如图1,等腰ABC ∆中,0,120AB AC BAC =∠=,作AD BC⊥于点D ,则D 为BC 的中点,01602BAD BAC ∠=∠=,于是23BC BDAB AB==;迁移应用:如图2,ABC ∆和ADE ∆都是等腰三角形,0120BAC DAE ∠=∠=,,,D E C 三点在同一条直线上,连接BD .① 求证:ADB AEC ∆≅∆;②请直接写出线段,,AD BD CD 之间的等量关系式;拓展延伸:如图3,在菱形ABCD 中,∠BAC =120°,在∠BAC 内作射线BM ,作点C 关于BM 的对称点E ,连接AE 并延长交BM 于点F ,连接CE ,CF .① 证明:CEF ∆是等边三角形; ②若5,2AE CE ==,求BF 的长.解:迁移应用:①证明:∵ABC ∆和ADE ∆都是等腰三角形,0120BAC DAE ∠=∠=, ∴AD =AE ,AB =AC ,∵∠DAB =∠DAE -∠BAE ,∠CAE =∠BAC -∠BAE ,∴∠DAB =∠CAE ,∴△ADB ≌△AEC ; ②BD +3AD =CD .拓展延伸:①证明:如答图所示,连接BE ,作BG ⊥AE ,∵点C 关于BM 的对称点E ,∴BM 垂直平分CE , ∴FE =FC ,BE =BC ,∴△CEF 和△BEC 都是等腰三角形, ∴∠ABG =∠EBG ,∠EBF =∠CBF ,∴∠GBF =∠EBG +∠EBF =12∠ABC =60°, ∴∠GFB =30°,∴∠EFC =60°, ∴△CEF 是等边三角形;②∵AE =5,,在等腰三角形ABE 中,GF =GA =52. ∵EF =2,∴GF =GE +EF =9,2在直角三角形GBF 中,∵∠GFB =30°,∴FG =3BG =, ∴BF =2333⨯=.2. (2017安徽中考19.·10分)【阅读理解】我们知道,123+++…+n =(1)2n n +,那么, 12+22+32+…+n 2结果等于多少呢? 在图1所示三角形数阵中,第1行圆圈中的数为1,即12; 第2行两个圆圈中数的和为2+2,即22;……; 第n 行n 个圆圈中数的和为n +n +…+n ,即n 2.n 个n这样,该三角形数阵中共有(1)2n n +个圆圈,所有圆圈中数的和为12+22+32+…+n 2.【规律探究】将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n -1行的第一个圆圈中的数分别为n -1,2.n ),发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为:3(12+22+32+…+n 2)= .由此,12+22+32+…+n 2= .【解决问题】 根据以上发现,计算122232201721232017⨯⨯的结果为思路分析:【规律探究】①由特例可猜测任选这三个三角形数阵某行同一位置圆圈中的数(或代数式)求和得出每个位置上三个圆圈中数的和均为2n +1;②由【阅读理解】知三角形数阵中共有(1)2n n +个圆圈,每个圆圈上的数都是2n +1,所以这三个三角形数阵所有圆圈中数的总和为:3(12+22+32+…+n 2)=(1)(21)2n n n ++;③进而求得12+22+32+…+n 2的结果.【解决问题】把n =2017代入【规律探究】的结果,得122232201721232017⨯⨯=2017(20171)(220171)(220171)62017(20171)32⨯+⨯+⨯+=⨯+=1345. 解:【规律探究】2n +1;(1)(21)2n n n ++;(1)(21)6n n n ++.【解决问题】1345.3. (2017四川自贡,24,10分)(本小题满分10分))[探究函数4y x x=+的图象与性质] (1)函数4y x x=+的自变量x 的取值范围是 ;(2)下列四个函数图象中函数4y x x=+的图象大致是 ; (3)对于函数4y x x =+,求当x >0时,y 的取值范围.请将下列的求解过程补充完整. 解:∵x >0∴()2224y x x x xx x =+=+=+∵22x 0x ⎛⎫-≥ ⎪⎝⎭∴ y ≥ . [拓展运用]⑷若函数2x 5x 9y x-+=,则y 的取值范围 .思路分析:(1)根据分式的意义可知在4x中,x ≠0,故函数4y x x=+的自变量x 的取值范围yOA yOBxyOyO>,∴2224y x x⎛=+=+=+-⎝y ≥=2.(4)=2x 5x 99y x 5x x -+=+-,当x >0时,由(3)可知9x x +≥6,∴ y ∴y≥6-5,即y ≥1;当x <0时,9x x --=3)可知9x 6x --≥,∴+9x 6x≤-,∴y ≤-6-5,即y ≤-10.解:(1)x ≠0;(2)C ;(3)4 4;(4)y ≥1或y ≤-10. 4. (2017江苏盐城,26, 12分) 【探索发现】如图①,是一张直角三角形纸片,∠B =90°,小明想从中剪出一个以∠B 为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE 、EF 剪下时,所得的矩形的面积最大.随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 ▲ .【拓展应用】如图②,在△ABC 中,BC =a ,BC 边上的高AD =h ,矩形PQMN 的顶点P 、N 分别在边AB 、AC 上,顶点Q 、M 在边BC 上,则矩形PQMN 面积的最大值为 ▲ .(用含a 、h 的代数式表示) 【灵活应用】如图③,有一块“缺角矩形”ABCDE ,AB =32,BC =40,AE =20,CD =16,小明从中剪出了一个面积最大的矩形(∠B 为所剪出矩形的内角),求该矩形的面积. 【实际应用】如图④,现有一块四边形的木板余料ABCD ,经测量AB =50 cm ,BC =108 cm ,CD =60 cm ,且tan B =tan C =43,木匠徐师傅从这块余料中裁出了顶点M 、N 在边BC 上且面积最大的矩形PQMN ,求该矩形的面积.CQ D EAB NPM 第26题图②C D EFAB 第26题图① 第26题图③CEAB D思路分析:【探索发现】设BD =a ,BF =b ,分别表示出最大矩形BDEF 的面积及△ABC 的面积即可求解;【拓展应用】将图2看成是由两个图①组成,利用图①的结论求解;【灵活应用】将DE 向两侧分别延长与AB 、BC 的延长线相交,转化为图①求解;【实际应用】矩形PQMN 面积最大时顶点P 、Q 可能的位置有三种情形:①分别在点AB 、AD 上;②分别在边AB 、CD 上;③分别在边AD 、CD 上,其中第①种情形不存在,第②种情形利用图②的结论求解,第③种情形转化为第②种情形求解. 解:【探索发现】12. 【拓展应用】14ah .【灵活应用】如图①,设BFGK 是从“缺角矩形”中剪出的一个矩形,显然,当顶点G 在线段DE 上时,矩形的面积才可取最大值.作直线DE ,分别交线段BA 、BC 的延长线于点P 、Q ,过点E 作EH ⊥BC 于点H . ∵四边形ABCM 是矩形, ∴AM ∥BC . ∴△DEM ∽△DQC . ∴EM CQ =MDCD. ∵CD =16,CM =AB =32, ∴MD =CD =16. ∴EMCQ=1,即CQ =EM . ∵AE =20,AM =BC =40, ∴EM =AE =20.CDAB备用图CDAB 第26题图④∴AE =CQ .同理PA =MD =CD =16.∴当BK =12PB =24,即当顶点G 在DE 中点处时,矩形的面积最大,最大面积为14×60×48=720.【实际应用】分三种情形:(I )如图②,当矩形的另两个顶点P 、Q 分别在边AB 、CD 上时,延长BA 、CD 相交于点E . ∵∠EBC =∠DCG , ∴EB =EC .过点E 作EH ⊥BC 于点H . ∴BH =12BC =12×108=54.在Rt △EBH 中,EH =BH ·tan ∠B =54×43=72. ∴EB =90.由结论,当PB =12EB =45<AB 时,矩形面积有最大值为14×108×72=1944.(II )如图③,当矩形的另两个顶点P 、Q 分别在边AD 、CD 上时,延长BA 、CD 相交于点E ,延长QP 交AE 于点F ,过点F 作FG ⊥BC 于点G ,则矩形PQMN 的面积小于矩形FQMG 的面积. 由①知,矩形FQMG 的面积<1944.(III )当矩形另两个顶点P 、Q 分别在边AD 、CD 上时,此时不能裁出矩形.图②QP DEF G H A BN M CDEAB QHP图①MKF G综合知,矩形面积的最大值为1944.5.(2017山东临沂,25,11分)数学课上,张老师出示了问题:如图1,AC、BD是四边形ABCD 的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE ≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=G CDABEF图③QNPM∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.思路分析:(1)延长CB到E,使BE=CD,连接AE,构造△ADC≌△ABE,从而得到AE=AC,进而得出结论;(2)延长CB到E,使BE=CD,连接AE,构造△ADC≌△ABE,从而得到AE=AC,作AF⊥EC,,得∠E=α,则EB=AC,cosα从而得到结论.解:⑴结论:BC+CD=2AC证明如下:方法①,如图2,延长CB到E,使BE=CD,连接AE.∵∠ACB=∠ACD=∠ABD=∠ADB=45°∴∠BAD=90°,∠BCD=90°,AD=AB∴∠ABC+∠ADC=180°又∵∠ABE+∠ABC=180°∴∠ADC=∠ABE∴△ADC≌△ABE∴AC=AE,∠CAD=∠EAB∴∠EAC=∠BAD=90°∴CE=2AC∴BC+CD=2AC方法②,如图3,将△ABC绕着点A逆时针旋转90°至△ADF位置,使AB与AD重合,易得C、D、F三点共线,以下与方法①雷同,证略.⑵BC+CD=2ACcosα6. (2017江苏连云港,27,14分)问题呈现:如图1,点E 、F 、G 、H 分别在矩形ABCD 的边AB 、BC 、CD 、DA 上,AE DG . 求证:2ABCD EFGHS S 矩形四边形.(S 表示面积)实验探究:某数学实验小组发现:若图1中AH ≠BF ,点G 在CD 上移动时,上述结论会发生变化,分别过点E 、G 作BC 边的平行线,再分别过点F 、H 作AB 边的平行线,四条平行线分别相交于点1A 、1B 、1C 、1D ,得到矩形1111A B C D .如图2,当AH BF 时,若将点G 向点C 靠近(DG AE ),经过探索,发现:11112ABCDA B C D EFGHS S S 矩形矩形四边形.如图3,当AH BF 时,若将点G 向点D 靠近(DG AE ),请探索EFGH S 四边形、ABCD S 矩形与1111A B C D S 矩形之间的数量关系,并说明理由.迁移应用:请直接应用“实验探究”中发现的结论解答下列问题.(1)如图4,点E 、F 、G 、H 分别是面积为25的正方形ABCD 各边上的点,已知AH BF ,AE DG ,11EFGHS 四边形,29HF ,求EG 的长.(2)如图5,在矩形ABCD 中,3AB ,5AD ,点E 、H 分别在边AB 、AD 上,1BE ,2DH ,点F 、G 分别是边BC 、CD 上的动点,且10FG ,连接EF 、HG ,请直接写出四边形EFGH 面积的最大值.思路分析:问题呈现:根据矩形的性质,通过割补法利用三角形的面积和矩形的面积可得到结论;实验探究:由题意得当将点G 向点D 靠近(DG AE )时,通过割补法利用三角形的面积和矩形的面积可得到结论;迁移应用:(1)由上面的结论,结合图形,通过割补法利用三角形的面积和矩形的面积可得到结论;(2)直接根据规律写出结果即可. 解:问题呈现:因为四边形ABCD 是矩形,所以AB CD ∥,90A ∠°, 又因为AE DG ,所以四边形AEGD 是矩形, 所以AEGD HEG S AE EG s 矩形2121=⨯=∆,同理可得12FEG BCGE S S △矩形. 因为HEGFEG EFGH S S S △△四边形,所以2ABCD EFGHS S 矩形四边形.实验探究:由题意得,当将点G 向点D 靠近DG AE 时,如图所示,1112HECHAEC S S △矩形,1112EFB EBFB S S △矩形,1112FGA FCGA S S △矩形,1112GHD GDHD S S △矩形, 所以11111111HEC EFB FGA GHD A B C D EFGH S S S S S S △△△△矩形四边形, 所以1111111122HAEC EBFB FCGA CDHD A B C D EFGH S S S S S S 矩形矩形矩形矩形矩形四边形,即11112ABCDA B C D EFGH S S S 矩形矩形四边形.迁移应用:(1) 如图所示,由“实验探究”的结论可知11112ABCDA B C D EFGHS S S 矩形矩形四边形,所以S 矩形A1B1C1D1=S 矩形ABCD -2S 四边形EFGH =25-2×11=3=A 1B 1·A 1D 1, 因为正方形面积是25,所以边长为5, 又22211529254A D HF , 所以112A D ,1132A B , 所以22211910952544EG A B , 所以,109EG.(2) 四边形EFGH 面积的最大值为172.7. (2017四川达州1,11分)探究:小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意..两点()()111222Px y P x y ,,,,可通过构造直角三角形利用图1得到结论:()()22122121PP x x y y =-+-他还利用图2证明了线段12P P 的中点(),P x y P 的坐标公式:121222x x y y x y ++==,.图1 图2 图3(1)请你帮小明写出中点坐标公式的证明过程;运用:(2)①已知点()()2135M N--,,,,则线段MN长度为;②直接写出以点()()()222031A B C--,,,,,,D为顶点的平行四边形顶点D的坐标:;拓展:(3)如图3,点()2,P n在函数()43y x x=≥的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E F、,使PEF∆的周长最小,简要叙述作图方法,并求出周长的最小值.思路分析(1)利用三角形的中位线定理以及矩形的性质可证明出中点公式;(2)①直接利用两点间距离公式可求出MN的长度;②利用中点公式及分以那条边为对角线可得D的坐标;(3)先利用角平分线的性质和勾股定理求出n的值,再分别作出点P关于直线OL和x轴的对称点,连接两对称点与直线OL和x轴相交,即可得E,F两点,求出两对称点的坐标,然后利用两间距离公式,可得周长的最小值.解:(1)分别过点P1,P,P2作x轴的垂线,垂足分别为Q1,Q,Q2,过点P1作P1G⊥P2Q2,垂足为G.∴P1Q1∥PQ∥P2Q2∴11112112PP PH Q QPP PG Q Q==∵P1P2=2P1P∴P1G=2P1H,Q1Q2=2Q1Q即H,Q分别为P1G,Q1Q2的中点设P点的坐标为(m,n)∴m-x1=x2-m∴m=122x x+而P2G=P2Q2-GQ2= P2Q2-P1Q2=y2-y1=2PH=2(n-y1)∴n =122y y + ∴P 点的坐标为:(122x x +,122y y +)(2根据两点间距离公式,MN ②D 1(-3,3),D 2(7,1),D 3(-1,-3)如果以AB 为对角线,则AB 中点E 的坐标为(2-22,2+02),即为(0,1) 设D 1的坐标为(p ,q ),则根据中点公式,有3+0=2p ,-1+1=2q,解得P =-3,q =-3,∴D 1的坐标为:(-3,3).如果以BC ,AC 为对角线,同理可求得D 2(7,1),D 3(-1,-3).(3)如下图1,过点P 作ST ⊥x 轴,分别交OL 于S ,交x 轴于点T ,当x =2时,TS =83,由勾股定理可求得OS =103过点P 作PU ⊥OL 于点U ,垂足为U ,可得OU =OT =2,PU =PT =n ,∴SU =43,PS =83n -,∴22168()93n n +=-,解得n =1∴P点的坐标为(2,1)如图2,作点P 关于直线OL 的对称点P ′,P ′的坐标为(25,115), 作点P 关于x 轴的对称点P ′′, P ′′的坐标为(2,-1)根据两点间距离公式可得,P ′P ′′=图1 图28. (2017江苏淮安,27,12分)【操作发现】如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC 的三个顶点均在格点上.(1)请按要求画图:将△ABC 绕点A 按顺时针方向旋转90°,点B 的对应点为B ′,点C 的对应点为C ′,连接BB ′;(2)在(1)所画图形中,∠AB ′B =________. 【问题解决】如图②,在等边三角形ABC 中,AC =7,点P 在△ABC 内,且∠APC =90°,∠BPC =120°,求△APC 的面积.小明同学通过观察、分析、思考,对上述问题形成了如下想法:想法一:将△APC 绕点A 按顺时针方向旋转60°,得到△AP ′B ,连接PP ′,寻找PA 、PB 、PC三条线段之间的数量关系;想法二:将△APB 绕点A 按逆时针方向旋转60°,得到△AP ′C ′,连接PP ′,寻找PA 、PB 、PC 三条线段之间的数量关系.图①C ABAP图②……请参考小明同学的想法,完成该问题的解答过程.(―种方法即可) 【灵活运用】如图③,在四边形ABCD 中,AE ⊥BC ,垂足为E ,∠BAE =∠ADC ,BE =CE =2,CD =5,AD =k AB (k 为常数),求BD 的长(用含k 的式子表示).思路分析:【操作发现】(1)利用正方形网格的特征即可画出;(2)△AB ′B 是等腰直角三角形,且∠BAB ′=90°,所以∠AB ′B =45°;【问题解决】根据“想法一”或“想法二”并结合【操作发现】中的“经验”求解;【灵活运用】①连接AC ,证明AB =AC ;②将△ACD 绕点A 顺时针旋转∠CAB 的度数,得到△ABD ′;③证明∠BD ′D 为直角;④求DD ′长;⑤求BD 长. 解:【操作发现】 (1)如图所示.(2)45°. 【问题解决】如图,将△APC 绕点A 按顺时针方向旋转60°,得到△AP ′B ,连接PP ′,则AP ′=AP ,∠PAP ′=60°,∠AP ′B =∠APC . ∴△APP ′是等边三角形. ∴∠APP ′=∠AP ′P =60°. ∵AP ⊥PC , ∴∠APC =90°. 又∵∠BPC =120°,∴∠APB =360°-∠APC -∠BPC =360°-90°-120°=150°. ∴∠BPP ′=∠APB -∠APP ′=150°-60°=90°.∴∠BP ′P =∠AP ′B -∠AP ′P =∠APC -∠AP ′P =90°-60°=30°.C ABC 'B '图②CDE AB设BP=a.在Rt△BPP′中,∵∠BP′P=30°,∴P′B=2a,P′P.∴AP=,PC=2a.在Rt△APC中,由勾股定理得AP2+PC2=AC2.∴22)(2)a+=72.解得a∴AP=PC=∴S△APC=12AP·PC=12【灵活运用】连接AC.∵AE⊥BC,BE=CE,∴AB=AC.又∵AE⊥BC,∴∠BAE=∠CAE.设∠BAE=α,则∠CAE=α,∠ABE=90°-α,∠ADC=α.如图,将△ACD绕点A顺时针旋转2α,得到△ABD′,则BD′=CD=4,AD=AD′,∠DAD′=2α,∠BD′A=α.过点A作AF⊥DD′,垂足为点F,则∠D′AF=α,∠AD′F=90°-α,DD′=2D′F.∴∠BD′D=∠BD′A+∠AD′F=α+90°-α=90°.在Rt△AD′F中,D′F=AD′·cos∠AD′F=AD·cos(90°-α)=k AB·cos(90°-α)=k·BE =2k.∴DD′=4k.在Rt△BDD′中,由勾股定理得BDAP P'9. (2017湖南岳阳,本题满分10分)问题背景:已知∠EDF 的顶点D在△ABC 的边AB 上(不与A ,B 重合).DE 交AC 所在直线于点M ,DF 交BC 所在直线于点N .记△ADM 的面积为1S ,△BND 的面积为2S .(1) 初步尝试:如果①,当△ABC 是等边三角形,6AB =,EDF A ∠=∠,且DE BC ∥,2AD =时,则12_______S S ⋅=;(2) 类比探究:在(1)的条件下,先将点D 沿AB 平移,使4AD =,再将EDF ∠绕点D 旋转至如图②所示位置,求12S S ⋅的值;(3) 延伸拓展:当△ABC 为等腰三角形时,设B A EDF α∠=∠=∠=.(Ⅰ)如图③,当点D 在线段AB 上运动时,设AD a =,BD b =,求12S S ⋅的表达式(结果用a ,b 和α的三角函数表示).(Ⅱ)如图④,当点D 在BA 的延长线上运动时,设AD a =,BD b =,直接写出12S S ⋅的表达式,不必写出解答过程.③图②图①图ADD D解:(1)(2)过M ,N 分别作MG AB ⊥,NH AB ⊥垂足为G ,H∵180ADM MDN NDB ∠+∠+∠=︒180ADM MDN NDB ∠+∠+∠=︒EDF A ∠=∠∴NDB DMA ∠=∠C DE ABD 'F又∵A B ∠=∠ ∴△NDB ∽△DMA ∴AD AMBN BD=∵6AB =,4AD = ∴2BD =∴8BN AM AD BD ⋅=⋅=在Rt △AMG 中,MG =AM ·sinA AM∴112S AD MG =⨯⨯=同理:2S =∴123122S S AM BN ⋅=⋅=.(3)过M ,N 分别作MG AB ⊥,NH AB ⊥垂足为G ,H∵180ADM MDN NDB ∠+∠+∠=︒180ADM MDN NDB ∠+∠+∠=︒EDF A ∠=∠∴NDB DMA ∠=∠ 又∵A B ∠=∠ ∴△NDB ∽△DMA ∴AD AMBN BD=∵AD a =,BD b = ∴BN AM AD BD ab ⋅=⋅= 在Rt △AMG 中,MG =AM ·sin α ∴111sin 22S AD MG a AM α=⨯⨯=⋅⋅ 同理:21sin 2S b BN α=⋅⋅∴222121sin 4S S a b α⋅=.(4)222121sin 4S S a b α⋅=.10. (2017江苏泰州,25,12分)阅读理解:如图①,图形l 外一点P 与图形l 上各点连接的所有线段中,若线段i PA 最短,则线段i PA 的长度称为点P 到图形l 的距离.例如:图②中,线段i PA 的长度是点1P 到线段AB 的距离;线段2P H 的长度是点2P 到线段AB 的距离. 解决问题:如图③,平面直角坐标系xOy 中,点A 、B 的坐标分别为8,4,12,7,点P 从原点O 出发,以每秒1个单位长度的速度向x 轴正方向运动了t 秒. (1) 当4t 时,求点P 到线段AB 的距离; (2) t 为何值时,点P 到线段AB 的距离为5?(3) t 满足什么条件时,点P 到线段AB 的距离不超过6?(直接写出此小题的结果)思路分析: (1)要求线段PA 的长,构造以PA 为斜边的直角三角形,由题意求出两直角边的长,应用勾股定理求出斜边PA 的长即可.(2)根据题意,点P 到线段AB 的距离是5,即点P 到点A 的线段PA =5,也就是到点A 的距离为5的点P 的集合,是以A 为圆心,以5为半径的圆.此圆与x 轴相交于两点均符合条件. (3)根据题意,点P 到线段AB 的距离不超过6,就是到点A 的距离小于6或等于6;利用分类讨论方法,分点在点A 到横轴的垂足左边和右边两种情况讨论.解:(1)如图④,由题意知,点P的坐标为(4,0),连接AP,则线段AP的长就是此时点P到线段AB的距离.过点A作AH⊥x轴于点H.因为A(8,4),所以AH=4,OH=8,则PH=OH-OP=4.在Rt△APH中,由勾股定理得:AP=22224442PH AH+=+=;(2)如图④连接AP,作AH⊥x轴.设点P的坐标为(p,0),因为A(8,4),P(p,0),点P到线段AB的距离是5,即线段AP=5.所以根据题意,得(p-8)2+(0-4)2=52P2-16p+64=25,整理,得p2-16p+55=0解得:p1=5 ,p2=11.①当P点在H点左侧时,P点坐标是(5,0);②当P点在H点右侧时,P点坐标是(11,0);所以,当t=5或t=11时,点P到线段PA的距离是5。
2017年全国中考语文试题汇编(拼音)

2017年全国中考语文试题汇编拼音刘邦勇1.(2017•安徽省)阅读下面的文字,完成(1)题。
(3分)这里的石林斗姿百态,美不胜收。
怪石嶙峋,形态各异,或如走兽憨态可ju(),或如猛qin()展翅欲飞,或如仙女亭亭玉立,或如农夫默默耕耘。
在花海的印衬之下,婀娜多姿,楚楚动人。
(1)根据拼音写出相应的汉字,给加点的字注音。
憨态可ju( ) 猛qin()展翅婀( )娜多姿【答案】掬禽ě2.(2017•北京市)下列词语中加点字的读音完全正确的一项是()2分A.颁.发(bān)绮.丽(qí)不屈不挠.(náo)B.哺.育(bǔ)粗狂.(guǎng)刚正不阿.(ē)C.猝.然(cù)侥.幸(jiǎo)称.心如意(chèng)D.干涸.(kū)参.差(cēn)杳.无音信(yǎo)【答案】B3.(2017•福建省龙岩市)给加点字注音,根据拼音写汉字。
(2分)葱yù()晾.( )干【答案】郁liàng4.(2017•福建省福州市)下列加点字的注音,完全正确的一项是()A.妖娆(ráo) 重荷(hé) 苦心孤诣(yì)B.绯(fēi)红阔绰(chuò) 惟妙惟肖(xiāo)C.丰硕(shuò) 馈(kuì)赠根深蒂(dì)固D.芳馨(xīn) 鞭挞(dá) 叱咤(zhà)风云【答案】C5.(2017•福建省南平市)下列词语中加点字的读音全都正确的一项是:()A.宽恕(shù)归省(shěng)镂(lòu)空纤(xiān)细B.两栖(qī)静谧(mì)栅(zhà)栏诘(jié)问C.脸颊(xiá)鞭挞(tà)朔(shuò)方绯(fēi)红D.桑梓(zǐ)别墅(shù)蓦(mù)然雏(chú)形【答案】B6.(2017•福建省三明市)根据拼音写汉字,或给加点字选择正确的读音。
2017年中考数学试卷两套合集四附答案解析

2017年中考数学试卷两套合集四附答案解析中考数学试卷一.仔细选一选(本题有10小题,每题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确答案.1.是一个()A.整数 B.分数 C.有理数D.无理数2.下列计算正确的是()A.的平方根为±8 B.的算术平方根为8C.的立方根为2 D.的立方根为±23.小明想用图形1通过作图变换得到图形2,下列这些变化中不可行的是()A.轴对称变换B.平移变换 C.旋转变换 D.中心对称变换4.下列各式计算正确的有()A.(p5q4)÷(2p3q)=2p2q3B.(﹣a+5)(﹣a﹣5)=﹣a2﹣25C.D.5.如果圆内接四边形ABCD的对角线交点恰好是该圆的圆心,则四边形ABCD一定是()A.平行四边形B.矩形 C.菱形 D.正方形6.已知a﹣b=1,则a2﹣b2﹣2b的值为()A.1 B.2 C.3 D.47.某种数码产品原价每只400元,经过连续两次降价后,现在每只售价为256元,则平均每次降价的百分率为()A.20% B.80% C.180% D.20%或180%8.为了有效保护环境,某居委会倡议居民将生活垃圾进行可回收的、不可回收的和有害的分类投放,一天,小林把垃圾分装在三个袋中,则他任意投放垃圾,把三个袋子都放错位的概率是()A.B.C.D.9.一个多边形的内角中,锐角的个数最多有()A.3个B.4个C.5个D.6个10.已知抛物线y=a(x﹣m)2+n的顶点为A,与y轴的交点为B,若直线AB的解析式为y=﹣2x+b,点A,B关于原点的对称点分别为A′,B′,且四边形ABA′B′为矩形,则下列关于m,n,b的关系式正确的是()A.5m=4b B.4m=5b C.5n=3b D.3n=5b二、认真填一填(本题有6个小题,每小题4分,共24分)11.数据1,5,2,1,5,4的中位数是,方差为.12.把代数式4a2b﹣3b2(4a﹣3b)进行因式分解得:.13.函数y=x2﹣2x﹣3,当y<0时,x的取值范围为;当﹣1<x<2时,y的取值范围为.14.已知弦AB与CD交于点E,弧的度数比弧的度数大20°,若∠CEB=m°,则∠CAB= (用关于m的代数式表示).15.正方形ABCD的边长为acm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是 cm2.16.如图,△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从A出发,以2cm/s的速度沿△ABC 的边按A→B→C→A的顺序运动一周,则点P出发s时,△BCP为等腰三角形.三、全面答一答(本题有7小题,共66分,)解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.先化简,再求值:÷(x+2﹣),其中x满足x(x2﹣4)=0.18.为了深化我省义务教育课程改革,某校积极开展本校课程建设,计划成立“科普观察”、“架子鼓”、“足球”、“摄影”等多个社团,要求每个学生都自主选择其中一个社团.为此,随机调查了本校七、八、九年级部分学生选择社团的意向,并将调查结果绘制成如图统计表(不完整):某校被调查学生选择社团意向统计表架子鼓科普观察足球摄影其他选择意向所占30% a b 10% c百分比根据统计图表中的信息,解答下列问题:(1)求架子鼓和摄影社团的人数及a,b的值;(2)将条形统计图补充完整;(3)若该校共有1200名学生,试估计全校选择“科普观察”社团的学生人数.Array19.某政府大力扶持大学生创业,李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯,物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可看作一次函数:y=﹣10x+n.(1)当销售单价x定为25元时,李明每月获得利润w为1250元,求n的值;(2)当销售单价定为多少元时,每月可获得最大利润?并求最大利润是多少?20.如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过点A、C,并与y轴交于点E,反比例函数y=的图象经过点A.(1)点E的坐标是;(2)求反比例函数的解析式;(3)求当一次函数的值小于反比例函数的值时,x的取值范围.21.如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=.(1)求证:CD∥BF;(2)求⊙O的半径;(3)求弦CD的长.22.如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.(1)当AC的长度为多少时,△AMC和△BOD相似;(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;(3)连结BC.当S△AMC=S△BOC时,求AC的长.23.关于x的函数y=2mx2+(1﹣m)x﹣1﹣m(m是实数),探索发现了以下四条结论:①函数图象与坐标轴总有三个不同的交点;②当m=﹣3时,函数图象的顶点坐标是(,);③当m>0时,函数图象截x轴所得的线段长度大于;④当m≠0时,函数图象总经过两个定点.请你判断四条结论的真假,并说明理由.参考答案与试题解析一.仔细选一选(本题有10小题,每题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.注意可以用多种不同的方法来选取正确答案.1.是一个()A.整数 B.分数 C.有理数D.无理数【考点】无理数.【分析】根据无理数的定义即可作答.【解答】解:∵是一个无限不循环小数,∴是一个无理数.故选D.【点评】本题考查了无理数的定义:无限不循环小数为无理数.初中范围内学习的无理数有三类:①π类,如2π,等;②开方开不尽的数,如,等;③虽有规律但是无限不循环的数,如0.1010010001…,等.2.下列计算正确的是()A.的平方根为±8 B.的算术平方根为8C.的立方根为2 D.的立方根为±2【考点】立方根;平方根;算术平方根.【分析】依据平方根、算术平方根、立方根的性质求解即可.【解答】解:A、=8,8的平方根为±2,故A错误;B、=8,8的算术平方根为2,故B错误;C、=8,8的立方根为2,故C正确;D、=8,8的立方根为2,故D错误.故选:C.【点评】本题主要考查的是立方根、平方根、算术平方根的性质,熟练掌握相关知识是解题的关键.3.小明想用图形1通过作图变换得到图形2,下列这些变化中不可行的是()A.轴对称变换B.平移变换 C.旋转变换 D.中心对称变换【考点】几何变换的类型.【分析】根据轴对称变换、平移变换、旋转变换和中心对称变换的概念进行判断即可.【解答】解:连接AB,作线段AB的垂直平分线,垂足为O,∴图形1以直线l为对称轴通过轴对称变换得到图形2,A可行;图形1以O为旋转中心,旋转180°得到图形2,C、D可行;故选:B.【点评】本题考查的是几何变换的类型,掌握轴对称变换、平移变换、旋转变换和中心对称变换的概念是解题的关键.4.下列各式计算正确的有()A.(p5q4)÷(2p3q)=2p2q3B.(﹣a+5)(﹣a﹣5)=﹣a2﹣25C.D.【考点】分式的加减法;平方差公式;整式的除法.【分析】根据单项式的除法、平方差公式以及分式的加减法进行计算即可.【解答】解:A、(p5q4)÷(2p3q)=p2q3,故错误;B、(﹣a+5)(﹣a﹣5)=a2﹣25,故错误;C、+=,故错误;D、正确;故选D.【点评】本题考查了分式的加减、平方差公式以及分式的加减,掌握运算法则是解题的关键.5.如果圆内接四边形ABCD的对角线交点恰好是该圆的圆心,则四边形ABCD一定是()A.平行四边形B.矩形 C.菱形 D.正方形【考点】圆内接四边形的性质.【分析】由圆内接四边形ABCD的对角线交点恰好是该圆的圆心,根据直径所对的圆周角是直角,可求得四边形ABCD的四个内角都是直角,即可判定四边形ABCD一定是矩形.【解答】解:∵圆内接四边形ABCD的对角线交点恰好是该圆的圆心,∴∠A=∠B=∠C=∠D=90°,∴四边形ABCD一定是矩形.故选B.【点评】此题考查了矩形的判定以及圆的内接四边形的性质.注意直径所对的圆周角是直角定理的应用是解此题的关键.6.已知a﹣b=1,则a2﹣b2﹣2b的值为()A.1 B.2 C.3 D.4【考点】完全平方公式.【分析】由已知得a=b+1,代入所求代数式,利用完全平方公式计算.【解答】解:∵a﹣b=1,∴a=b+1,∴a2﹣b2﹣2b=(b+1)2﹣b2﹣2b=b2+2b+1﹣b2﹣2b=1.故选:A.【点评】本题考查了完全平方公式的运用.关键是利用换元法消去所求代数式中的a.7.某种数码产品原价每只400元,经过连续两次降价后,现在每只售价为256元,则平均每次降价的百分率为()A.20% B.80% C.180% D.20%或180%【考点】一元二次方程的应用.【分析】可先表示出第一次降价后的价格,那么第一次降价后的价格×(1﹣降低的百分率)=256,把相应数值代入即可求解.【解答】解:设平均每次降价的百分率为x,根据题意得:400(1﹣x)2=256解得:x=20%或x=1.8(舍去),故选A.【点评】考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.8.为了有效保护环境,某居委会倡议居民将生活垃圾进行可回收的、不可回收的和有害的分类投放,一天,小林把垃圾分装在三个袋中,则他任意投放垃圾,把三个袋子都放错位的概率是()A.B.C.D.【考点】列表法与树状图法.【专题】计算题.【分析】(装可回收的、不可回收的和有害的垃圾的三个袋分别用A、B、C表示,陈放可回收的、不可回收的和有害的垃圾的地方分别为a、b、c)画树状图展示所用6种等可能的结果数,再找出把三个袋子都放错位的结果数,然后根据概率公式求解.【解答】解:(装可回收的、不可回收的和有害的垃圾的三个袋分别用A、B、C表示,陈放可回收的、不可回收的和有害的垃圾的地方分别为a、b、c)画树状图:共有6种等可能的结果数,其中他任意投放垃圾,把三个袋子都放错位的结果数为2,所以他任意投放垃圾,把三个袋子都放错位的概率==.故选C.【点评】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.9.一个多边形的内角中,锐角的个数最多有()A.3个B.4个C.5个D.6个【考点】多边形内角与外角.【分析】利用多边形的外角和是360度即可求出答案.【解答】解:因为多边形的外角和是360度,在外角中最多有三个钝角,如果超过三个则和一定大于360度,多边形的内角与相邻的外角互为邻补角,则外角中最多有三个钝角时,内角中就最多有3个锐角.故选A.【点评】本题考查了多边形的内角问题.由于内角和不是定值,不容易考虑,而外角和是360度不变,因而内角的问题可以转化为外角的问题进行考虑.10.已知抛物线y=a(x﹣m)2+n的顶点为A,与y轴的交点为B,若直线AB的解析式为y=﹣2x+b,点A,B关于原点的对称点分别为A′,B′,且四边形ABA′B′为矩形,则下列关于m,n,b的关系式正确的是()A.5m=4b B.4m=5b C.5n=3b D.3n=5b【考点】二次函数的性质;一次函数图象上点的坐标特征.【分析】根据题意可知:A(m,n),B(0,b),所以B′的坐标为(0,﹣b),由题意可知:四边形ABA′B′为矩形,所以对角线AA′=BB′.【解答】解:由题意可知:A(m,n),B(0,b),∵点A,B关于原点的对称点分别为A′,B′,∴BB′=|2b|,∵四边形ABA′B′为矩形,∴AA′=BB′,∵OA2=m2+n2,∵AA′2=4OA2=4(m2+n2),∴4(m2+n2)=4b2,把(m,n)代入y=﹣2x+b,∴n=﹣2m+b,∴b2=m2+(﹣2m+b)2,化简可得:5m=4b,故选(A)【点评】本题考查了二次函数的性质,涉及矩形的性质,二次函数的性质,完全平方差公式,综合程度较高.二、认真填一填(本题有6个小题,每小题4分,共24分)11.数据1,5,2,1,5,4的中位数是 3 ,方差为 3 .【考点】方差;中位数.【专题】推理填空题.【分析】首先将这组数据按照从小到大的顺序排列,则中间两个数据的平均数就是这组数据的中位数;然后根据方差的含义和求法,求出数据1,5,2,1,5,4的方差是多少即可.【解答】解:∵数据1,5,2,1,5,4按照从小到大的顺序排列是:1,1,2,4,5,5,∴数据1,5,2,1,5,4的中位数是:(2+4)÷2=6÷2=3∵数据1,5,2,1,5,4的平均数是:(1+5+2+1+5+4)÷6=18÷6=3∴数据1,5,2,1,5,4的方差是:×[(1﹣3)2+(5﹣3)2+(2﹣3)2+(1﹣3)2+(5﹣3)2+(4﹣3)2]=×[4+4+1+4+4+1]=×18=3故答案为:3,3.【点评】此题主要考查了中位数、方差的含义和求法,要熟练掌握.12.把代数式4a2b﹣3b2(4a﹣3b)进行因式分解得:b(2a﹣3b)2.【考点】提公因式法与公式法的综合运用.【专题】计算题;因式分解.【分析】原式去括号整理后,提取b,再利用完全平方公式分解即可.【解答】解:原式=4a2b﹣12ab2+9b3=b(4a2﹣12ab+9b2)=b(2a﹣3b)2,故答案为:b(2a﹣3b)2【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.13.函数y=x2﹣2x﹣3,当y<0时,x的取值范围为﹣1<x<3 ;当﹣1<x<2时,y的取值范围为﹣4<y<0 .【考点】抛物线与x轴的交点.【分析】根据函数解析式可以确定图象与x轴的交点是(﹣1,0),(3,0),又当y<0时,图象在x轴的下方,由此可以确定x的取值范围,结合函数解析式求出y的取值范围.【解答】解:当y=0时,即x2﹣2x﹣3=0,∴x1=﹣1,x2=3,∴图象与x轴的交点是(﹣1,0),(3,0),当y<0时,图象在x轴的下方,此时﹣1<x<3.当﹣1<x<2时,y的取值范围为:﹣4<y<0,故答案为:﹣1<x<3,﹣4<y<0.【点评】本题主要考查了抛物线与x轴的交点问题,解答此题的关键是求出图象与x轴的交点,然后由图象找出当y<0时,自变量x的范围,锻炼了学生数形结合的思想方法.14.已知弦AB与CD交于点E,弧的度数比弧的度数大20°,若∠CEB=m°,则∠CAB=(用关于m的代数式表示).【考点】圆心角、弧、弦的关系.【分析】由弧BC与AD的度数之差为20°,根据圆周角定理,可得∠CAB﹣∠C=×20°=10°,又由∠CEB=60°,可得∠CAB+∠C=60°,继而求得答案.【解答】解:∵弧BC与AD的度数之差为20°,∴∠CAB﹣∠C=×20°=10°,∵∠CEB=∠CAB+∠C=m°,∴∠CAB=.故答案为:.【点评】此题考查了圆周角定理以及三角形外角的性质.此题难度不大,注意掌握方程思想与数形结合思想的应用.15.正方形ABCD的边长为acm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是 cm2.【考点】正方形的性质.【专题】几何图形问题.【分析】连接BD,可看出阴影部分的面积等于正方形的面积+一个三角形的面积,用相似求出三角形的面积,阴影部分的面积可证.【解答】解:连接BD,EF.∵阴影部分的面积=△ABD的面积+△BDG的面积(G为BF与DE的交点),∴△ABD的面积=正方形ABCD的面积=a2.∵△BCD中EF为中位线,∴EF∥BD,EF=BD,∴△GEF∽△GBD,∴DG=2GE,∴△BDE的面积=△BCD的面积.∴△BDG的面积=△BDE的面积=△BCD的面积=•a2=a2.∴阴影部分的面积=a2+a2=a2.故答案为: a2.【点评】本题考查正方形的性质,正方形的四个边长相等,关键是连接BD,把阴影部分分成两部分计算.16.如图,△ABC中,∠ACB=90°,BC=6cm,AC=8cm,动点P从A出发,以2cm/s的速度沿△ABC 的边按A→B→C→A的顺序运动一周,则点P出发2或2.5或11或1.4 s时,△BCP为等腰三角形.【考点】勾股定理;等腰三角形的判定.【专题】动点型.【分析】根据∠ACB=90°,BC=6cm,AC=8cm,利用勾股定理求出AB的长,①当点P在AB边上时;②当点P在BC边上时,不存在△BCP;③点P在AC边上时;利用P点的运动速度求出时间即可,注意分类讨论.【解答】解;∵△ABC中,∠ACB=90°,BC=6cm,AC=8cm,∴AB===10(cm),①当点P在AB边上时,当BP=BC=6cm时,∴AP=AB﹣BP=10﹣6=4,∵动点P从A出发,以2cm/s的速度沿AB移动,4÷2=2,∴点P出发2s时,△BCP为等腰三角形;当PC=PB时,P为斜边AB的中点,此时AP=BP=PC=5cm,5÷2=2.5,∴点P出发2.5s时,△BCP为等腰三角形;当BC=PC时,过点C作CD⊥AB于点D,如图1所示:则△BCD∽△BAC,∴=,即,解得:BD=3.6,∴BP=2BD=7.2,∴AP=10﹣7.2=2.8,2.8÷2=1.4,∴点P出发1.4s时,△BCP为等腰三角形;②当点P在BC边上时,不存在△BCP;③点P在AC边上时,CP=CB=6,AB+BC+CP=10+6+6=22,22×2=11,∴点P出发11s时,△BCP为等腰三角形.综上所述:点P出发2s或2.5s或11s或1.4s时,△BCP为等腰三角形;故答案为:2或2.5或11或1.4.【点评】此题主要考查勾股定理和等腰三角形的判定,解答此题的关键是首先根据勾股定理求出AB 的长,然后再利用等腰三角形的性质去判定.三、全面答一答(本题有7小题,共66分,)解答应写出文字说明、证明过程或推演步骤.如果觉得有的题目有点困难,那么把自己能写出的解答写出一部分也可以.17.先化简,再求值:÷(x+2﹣),其中x满足x(x2﹣4)=0.【考点】分式的化简求值.【专题】计算题.【分析】先把括号内通分和把除法运算化为乘法运算,再把分子分母因式分解,约分得到原式,接着解x(x2﹣4)=0,然后利用分式有意义的条件确定x的值,再把x的值代入计算即可.【解答】解:原式=÷=•==,解x(x2﹣4)=0得x=0或x=2或x=﹣2,因为x≠0且x≠2,所以x=﹣2,当x=﹣2时,原式==﹣.【点评】本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.18.为了深化我省义务教育课程改革,某校积极开展本校课程建设,计划成立“科普观察”、“架子鼓”、“足球”、“摄影”等多个社团,要求每个学生都自主选择其中一个社团.为此,随机调查了本校七、八、九年级部分学生选择社团的意向,并将调查结果绘制成如图统计表(不完整):某校被调查学生选择社团意向统计表架子鼓科普观察足球摄影其他选择意向所占30% a b 10% c百分比根据统计图表中的信息,解答下列问题:(1)求架子鼓和摄影社团的人数及a,b的值;(2)将条形统计图补充完整;(3)若该校共有1200名学生,试估计全校选择“科普观察”社团的学生人数.【考点】条形统计图;用样本估计总体;统计表.【分析】(1)根据统计图和表格中的数据可以求得本次抽查的人数,从而可以解答本题;(2)根据(1)中求得的架子鼓和摄影社团的人数,可以将条形统计图补充完整;(3)根据统计图和表格中的数据可以估计全校选择“科普观察”社团的学生人数.【解答】解:(1)由图可得,本次抽查的学生有:(70+40+10)÷(1﹣30%﹣10%)=120÷60%=200(人),∴架子鼓的人数为:200×30%=60,摄影社团的人数为:200×10%=20,a=,b=,即架子鼓的人数为60,摄影社团的人数为20,a的值是35%,b的值是20%;(2)由(1)知架子鼓的人数为60,摄影社团的人数为20,故补全的条形统计图如右图所示;(3)由题意可得,1200×35%=420(人),即全校选择“科普观察”社团的学生人数是420.【点评】本题考查条形统计图、统计表、用样本股及总体,解题的关键是明确题意,利用数形结合的思想解答.19.某政府大力扶持大学生创业,李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯,物价部门规定,这种护眼台灯的销售单价不得高于32元.销售过程中发现,月销售量y(件)与销售单价x(元)之间的关系可看作一次函数:y=﹣10x+n.(1)当销售单价x定为25元时,李明每月获得利润w为1250元,求n的值;(2)当销售单价定为多少元时,每月可获得最大利润?并求最大利润是多少?【考点】二次函数的应用;一元二次方程的应用.【分析】(1)根据题意可以列出相应的方程,得到n的值,本题得以解决;(2)根据题意可以得到w与x的函数关系式,然后化为顶点式即可解答本题.【解答】解:(1)由题意可得,(25﹣20)(﹣10×25+n)=1250,解得,n=500,即n的值是500;(2)w=(x﹣20)(﹣10x+500)=﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250,∴x=35时,w取得最大值,此时w=2250,即当销售单价定为35元时,每月可获得最大利润,最大利润是2250元.【点评】本题考查二次函数的应用、一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.20.如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过点A、C,并与y轴交于点E,反比例函数y=的图象经过点A.(1)点E的坐标是(0,﹣2);(2)求反比例函数的解析式;(3)求当一次函数的值小于反比例函数的值时,x的取值范围.【考点】反比例函数与一次函数的交点问题.【分析】(1)一次函数y=kx﹣2中代入x=0求得y的值,即可求得点E的坐标;(2)利用△ACD∽△CEO求得点A的坐标后代入反比例函数的解析式,即可求得反比例函数的解析式;(3)首先确定两个函数的交点坐标,然后结合图象确定x的取值范围即可.【解答】解:(1)一次函数y=kx﹣2中令x=0得y=﹣2,所以E(0,﹣2);(2)∵∠OCE=∠ACB,∴Rt△OCE∽Rt△BCA,∴=,即=,解得OC=4,∴C点坐标为(4,0);(2)把C(4,0)代入y=kx﹣2得4k﹣2=0,解得k=,∴一次函数解析式为y=x﹣2;∵OC=4,∴A点坐标为(6,1),把A(6,1)代入y=得m=6×1=6,∴反比例函数解析式为y=;(3)令解得,∴另一个交点(﹣2,﹣3),∴观察图象得:当x<﹣2或 0<x<6时次函数的值小于反比例函数的值.【点评】本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.21.如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=.(1)求证:CD∥BF;(2)求⊙O的半径;(3)求弦CD的长.【考点】切线的性质;勾股定理;垂径定理;圆周角定理;解直角三角形.【专题】证明题.【分析】(1)由BF是⊙O的切线得到AB⊥BF,而AB⊥CD,由此即可证明CD∥BF;(2)连接BD,由AB是直径得到∠ADB=90°,而∠BCD=∠BAD,cos∠BCD=,所以cos∠BAD=,然后利用三角函数即可求出⊙O的半径;(3)由于cos∠DAE=,而AD=3,由此求出AE,接着利用勾股定理可以求出ED,也就求出了CD.【解答】(1)证明:∵BF是⊙O的切线,∴AB⊥BF,∵AB⊥CD,∴CD∥BF;(2)解:连接BD,∵AB是直径,∴∠ADB=90°,∵∠BCD=∠BAD,cos∠BCD=,∴cos∠BAD=,又∵AD=3,∴AB=4,∴⊙O的半径为2;(3)解:∵∠BCD=∠DAE,∴cos∠BCD=cos∠DAE=,AD=3,∴AE=ADcos∠DAE=3×=,∴ED=,∴CD=2ED=.【点评】本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.22.如图,已知tan∠EOF=2,点C在射线OF上,OC=12.点M是∠EOF内一点,MC⊥OF于点C,MC=4.在射线CF上取一点A,连结AM并延长交射线OE于点B,作BD⊥OF于点D.(1)当AC的长度为多少时,△AMC和△BOD相似;(2)当点M恰好是线段AB中点时,试判断△AOB的形状,并说明理由;(3)连结BC.当S△AMC=S△BOC时,求AC的长.【考点】相似三角形的判定与性质.【分析】(1)由于∠MCA=∠BDO=Rt∠,所以△AMC和△BOD相似时分两种情况:①△AMC∽△BOD;②△AMC∽△OBD.则两种情况都可以根据相似三角形对应边的比相等及tan∠EOF=2列出关于AC的方程,解方程即可求出AC的长度;(2)先由MC∥BD,得出△AMC∽△ABD,根据相似三角形对应边的比相等及三角形中位线的性质求出BD=2MC=8,OD=4,CD=8,AC=CD=8,再利用SAS证明△AMC≌△BOD,得到∠CAM=∠DBO,根据平行线的性质及三角形内角和定理求出∠ABO=90°,进而得出△ABO为直角三角形;(3)设OD=a,根据tan∠EOF=2得出BD=2a,由三角形的面积公式求出S△AMC=2AC,S△BOC=12a,根据S=S△BOC,得到AC=6a.由△AMC∽△ABD,根据相似三角形对应边的比相等列出关于a的方程,解方△AMC程求出a的值,进而得出AC的长.【解答】解:(1)∵∠MCA=∠BDO=Rt∠,∴△AMC和△BOD中,C与D是对应点,∴△AMC和△BOD相似时分两种情况:①当△AMC∽△BOD时, =tan∠EOF=2,∵MC=4,∴=2,解得AC=8;②当△AMC∽△OBD时, =tan∠EOF=2,∵MC=4,∴=2,解得AC=2.故当AC的长度为2或8时,△AMC和△BOD相似;(2)△ABO为直角三角形.理由如下:∵MC∥BD,∴△AMC∽△ABD,∴,∠AMC=∠ABD,∵M为AB中点,∴C为AD中点,BD=2MC=8.∵tan∠EOF=2,∴OD=4,∴CD=OC﹣OD=8,∴AC=CD=8.在△AMC与△BOD中,,∴△AMC≌△BOD(SAS),∴∠CAM=∠DBO,∴∠ABO=∠ABD+∠DBO=∠AMC+∠CAM=90°,∴△ABO为直角三角形;(3)连结BC,设OD=a,则BD=2a.∵S△AMC=S△BOC,S△AMC=•AC•MC=2AC,S△BOC=•OC•BD=12a,∴2AC=12a,∴AC=6a.∵△AMC∽△ABD,∴,即,解得a1=3,a2=﹣(舍去),∴AC=6×3=18.【点评】本题主要考查了相似三角形的判定与性质,锐角三角函数的定义,三角形的面积,三角形中位线定理,综合性较强,有一定难度.进行分类讨论是解决第一问的关键.23.关于x的函数y=2mx2+(1﹣m)x﹣1﹣m(m是实数),探索发现了以下四条结论:①函数图象与坐标轴总有三个不同的交点;②当m=﹣3时,函数图象的顶点坐标是(,);③当m>0时,函数图象截x轴所得的线段长度大于;④当m≠0时,函数图象总经过两个定点.请你判断四条结论的真假,并说明理由.【考点】二次函数的性质;抛物线与x轴的交点.【分析】①通过反例即可判断;②把m=﹣3代入,然后化成顶点式即可判断;③求得与x轴的交点,进而求得|x1﹣x2|的值,即可判断;④由y=2mx2+(1﹣m)x﹣1﹣m=(2x2﹣x﹣1)m+x﹣1,可知当2x2﹣x﹣1=0时,y的值与m无关,此时x1=1,x2=﹣,当x1=1,y=0;当x2=﹣时,y2=﹣,从而判定函数图象总经过两个定点(1,0),(﹣,﹣).【解答】解:①假命题;当m=0时,y=x﹣1为一次函数与坐标轴只有两个交点,②真命题;当m=﹣3时,y=﹣6x2+4x+2=﹣6(x﹣)2+,∴顶点坐标是(,),③真命题;当m>0时,由y=0得:△=(1﹣m)2﹣4×2m(﹣1﹣m)=(3m+1)2,∴x=,∴x1=1,x2=﹣﹣,∴|x1﹣x2|=+>,∴函数图象截x轴所得的线段长度大于;④真命题;当m≠0时,y=2mx2+(1﹣m)x﹣1﹣m=(2x2﹣x﹣1)m+x﹣1,当2x2﹣x﹣1=0时,y的值与m无关此时x1=1,x2=﹣,当x1=1,y=0;当x2=﹣时,y2=﹣,∴函数图象总经过两个定点(1,0),(﹣,﹣).【点评】本题考查了二次函数的性质,抛物线与二次函数的交点,熟练掌握二次函数的性质是解题的关键.中考数学试卷一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中.只有一项符合题目要求.1.在数﹣3,2,0,3中,大小在﹣1和2之间的数是()A.﹣3 B.2 C.0 D.32.已知一个单项式的系数是2,次数是3,则这个单项式可以是()A.﹣2xy2B.3x2C.2xy3D.2x33.的算术平方根是()A.2 B.±2 C.D.±4.下面四个几何体中,俯视图为四边形的是()A.B.C.D.5.不等式组的解集在数轴上表示正确的是()A.B.C.D.6.为了考察一批电视机的使用寿命,从中任意抽取了10台进行实验,在这个问题中样本是()A.抽取的10台电视机B.这一批电视机的使用寿命C.10D.抽取的10台电视机的使用寿命7.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是()A.B.C.D.8.下列运算正确的是()A.()﹣1=﹣ B.6×107=6000000C.(2a)2=2a2D.a3•a2=a59.如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是()A.60° B.90° C.100°D.120°10.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是()A.B.C.D.二、填空题:本大题共5小题,每小题3分,共l5分.11.分解因式:2a2﹣4a+2= .12.设x1、x2是一元二次方程x2﹣5x﹣1=0的两实数根,则x12+x22的值为.13.在函数y=+中,自变量x的取值范围是.14.若m1,m2,…,m2016是从0,1,2这三个数中取值的一列数,若m1+m2+…+m2016=1526(m1﹣1)2+(m2﹣1)2+…+(m2016﹣1)2=1510,则在m1,m2,…,m2016中,取值为2的个数为.15.如图,一次函数的图象与x轴、y轴分别相交于点A、B,将△AOB沿直线AB翻折,得△ACB.若C(,),则该一次函数的解析式为.。
全国各地中考化学真题分类汇编综合计算题含答案

全国各地中考化学真题分类汇编综合计算题含答案Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#2017中考真题专题汇编——综合计算题1.(2017甘肃)某化学兴趣小组同学为回收一块质量为40 g 的铜锌合金中的铜,将该合金放人烧杯中,逐渐加入稀硫酸至不再产生气泡时,恰好用去稀硫酸100 g ,烧杯内剩余固体27 g 。
请完成下列计算:(1)40 g 铜锌合金中锌的质量是________g 。
(2)计算所用稀硫酸中溶质的质量分数。
【答案】(1)40 g 铜锌合金中锌的质量为40 g-27 g=13 g (2)解:设所用稀硫酸中溶质的质量为x 。
Zn+H 2SO 4═ZnSO 4+H 2↑ 65 98 13 g xx98g 1365= x = g所用稀硫酸中溶质的质量分数:%6.19%100g100g19.6=⨯。
答:所用稀硫酸中溶质的质量分数是%。
2.(2017安顺)某锥形瓶盛有盐酸和氯化铜的混合溶液100g,向其中逐滴加入溶质质量分数为10%的氢氧化钠溶液,锥形瓶内溶液质量与滴入的氢氧化钠溶液的质量的变化关系如图所示。
请计算:(l)反应至A点时加入氢氧化钠溶液的质量为__________;(2)计算反应至B点时锥形瓶内所得溶液的溶质质量分数为多少(计算结果保留至%)【答案】(1)40g(1分);(2)%3.(2017河南)将30.9 g 氯酸钾(KClO3)和二氧化锰的固体混合物装入试管中,加热制取氧气,同时生成氯化钾。
待反应完全后,将试管冷却,称量,可以得到21.3 g 固体物质。
请计算原固体混合物中氯酸钾的质量。
【答案】生成氧气的质量为30.9g-21.3g=9.6g,设原混合物中氯酸钾的质量为x2KClO3 2KCl+3O2↑245 96x 9.6g96245=gx 6.9 解得x = 24.5g 4.(2017黄石)向克稀盐酸中加入锌粉(仅含不溶于酸的杂质),所加锌粉的质量与产生气体的质量的关系如下图所示。
2017年全国中考数学真题分类之整式(选择题+填空题+解答题)解析版

2017全国中考数学真题分类知识点04整式(选择题+填空题+解答题)解析版一、选择题1. .(2017四川广安,2,3分)下列运算正确的是( )A .| 2 -1|= 2 -1B .x 3•x 2=x 6C .x 2+x 2=x 4D .(3x 2)2=6x 4答案:A ,解析:∵ 2 ≈1.414>1,∴ 2 -1>0,∴| 2 -1|=12-,故A 项正确;x 3•x 2=x 3+2=x 5,故B 项错误;x 2+x 2=(1+1)x 2=2x 2,故C 项错误;(3x 2)2=32×(x 2)2=9x 2×2=9x 4,故D 项错误.故选A . 2. (2017浙江丽水·2·3分)计算a 2·a 3的正确结果是( )A .a 5B .A 6C .A 8D .A 9答案:A .解析:根据同底数幂乘法法则,a 2·a 3=a 2+3=a 5,故选A .3. (2017四川泸州,3,3分)下列各式计算正确的是( )A .2x •3x =6xB .3x -2x =xC .(2x )2=4xD .6x ÷2x =3x答案:B ,解析:2x ·3x =6x 2,故A 错误;3x -2x =x ,故B 正确;(2x )2=4x 2,故C 错误;6x ÷2x =3,故D 错误. 4. (2017四川成都,3分)下列计算正确的是 A .5510a a a += B .76a a a ÷=C .326a a a ⋅=D .326()a a -=-答案:B ,解析:A .5552a a a +=,故A 错误;B .76a a a ÷=正确;C .325a a a ⋅=,故C 错误;D .326()a a -=,故D 错误.5. (2017浙江金华,5,3分)在下列的计算中,正确的是A .m 3+m 2=m 5B .m 5÷m 2=m 3C .(2m )3=6m 3D .(m +1)2=m 2+1答案:B ,解析:(1)根据“同类项定义”, m 3+m 2不能计算;(2)根据“同底数幂的除法”, m 5÷m 2=m 5-2=m 3;(3)根据“积的乘方”, (2m )3=23·m 3=8m 3;(4)根据“完全平方公式”, (m +1)2=m 2+2m +1. 6. (2017重庆,3,4分)计算x 6÷x 2正确的是( )A .3B .x 3C .x 4D .x 8答案:C 解析:先判断题目属于两个同底数幂相除,然后根据“同底数幂的除法:底数不变,指数相减”,得x 6÷x 2= x 6-2= x 4.7. (2017重庆,6,4分)若x =31-, y =4,则代数式3x +y -3的值为( )A . -6B .0C .2D .6答案:B 解析:把字母x , y 的值代入要求的代数式,然后按代数式指明的运算顺序进行计算.把x =31-, y =4代入3x +y -3,得3×(31-)+4-3=-1+4-3=0,故选择B . 8. (2017安徽中考·2.4分)计算32()a -的结果是( )A .6aB .6a -C .5a -D .5a答案:A .解析:根据幂的乘方的运算性质,(-a 3)2=a 3×2=a 6,故选A .9. (2017浙江衢州,3,3分)下列计算正确的是( )A .2a +b =2abB .(-a )2=a 2C .a 6÷a 2=a 3D .a 3·a 2=a 6答案:B ,解析:A 选项2a 与b 不是同类项,不能够合并;B 选项互为相反数的两数的平方相等;C 选项同底数幂相除,底数不变,指数相减,应为a 6÷a 2=a 4,D 选项同底数幂相乘,底数不变,指数相加,应为a 3·a 2=a 5.故A 、C 、D 错误,B 正确.10. (2017山东济宁,2,3分)单项式39m x y 与单项式24n x y 是同类项,则m n +的值是A .2B .3C .4D .5答案:D ,解析:根据“含有相同字母,相同字母的指数相同的单项式是同类项”,所以m =2,n =3,m +n =5. 11. (2017山东济宁,7,3分)计算()322323a a a a a -+-÷的结果为A .52a a -B .512a a- C .5a D .6a答案:D ,解析:根据“利用同底数幂的乘法,合并同类项,幂的乘方及负整数指数幂法则计算”,原式=6556a a a a +-=.12. (2017山东德州,5,3分)下列运算正确的是( ) A .(a 2)m =a 2mB .(2a )3=2a 3C .a 3·5-a =15-aD .a 3÷5-a =2-a答案:A 解析:(a 2)m =a 2m ,故A 正确;(2a )3=23a 3=8a 3,故B 错误;a 3·5-a =)15(3-+a =12-a,故C 错误;a 3÷5-a =)5(3--a=8a ,故D 错误.13. (2017山东威海,3,3分)下列运算正确的是( ) A .3x 2+4x 2=7x 4B .2x 3•3x 3=6x 3C .a -a -2=a 3D .(-12 a 2b 3)3=-16 a 6b 3答案:C ,解析:3x 2+4x 2=7x 2,故A 错误;2x 3·3x 3=6x 6,故B 错误;a ÷a -2=a 1―(-2)=a 3,C 正确;231()2a b -= 6318a b ,故D 错误.14. .(2017年四川南充,5,3分)下列计算正确的是( )A .a 8÷a 4=a 2B .(2a 2)3=6a 6C .3a 3-2a 2=aD .3a (1-a )=3a -3a 2 答案:D 解析:(1)a 8÷a 4=a 8-4=a 4.可见选项A 错误.(2)(2a 2)3=23(a 2)3=8a 6.可见选项B 错误. (3)多项式3a 3-2a 2不能化简,可见选项C 错误. (4)由单项式乘多项式的法则可知选项D 正确. 故选D .15. (2017重庆B ,3,4分)计算35a a ÷结果正确的是 A .aB .2aC .3aD .4a答案:B ,解析:根据“同底数幂相除,底数不变,指数相减”可得235a a a =÷,故答案为B .16.(2017重庆B ,6,4分)若x = -3,y =1,则代数式132+-y x 的值为A .-10B .-8C .4D .10答案:B ,解析:代入得:2×(-3)-3×1+1=-8.故答案为B 17. (2017四川攀枝花,2,3分)2.下列计算正确的是( )A .33=9B . (a -b )2=a 2-b 2C .(a 3)4 =a 12D .a 2⋅a 3=a 6答案:C解析:∵33=27,故A 项错误;(a -b )2=a 2-2ab +b 2,故B 项错误;(a 3)4=a 3×4=a 12,故C 项正确;a 2⋅a 3=a 2+3=a 5,故D 项错误.故选C .18. (2017江苏盐城,5,3分)下列运算中,正确的是A .7a a +=27aB .23a a ⋅=6aC .3a a ÷=2aD .2()ab =2ab答案:C ,解析:7a a +=(71)a +=8a ,选项A 不正确;23a a ⋅=32a +=5a ,选项B 不正确;3a a ÷=31a -=2a ,选项C 正确;2()ab =22a b ,选项D 不正确.19. (2017山东临沂,3,3分)下列计算正确的是( )A .-(a -b )=-a +bB .224a a a +=C .a 2·a 3=a 6D .()2224ab a b =答案:D解析:A 选项,-(a -b )=-a +b ,所以选项A 错误; B 选项,a ²+a ²是同类项,合并后为2a ²,所以选项B 错误; C 选项,a 2·a 3=a 32+=a 5,所以选项C 错误;D 选项,()2222224aba b a b ⨯==,所以选项D 正确.20. (2017山东泰安,2,3分)下列运算正确的是 A .2222a a a ⋅=B .224a a a +=C .22(12)124a a a +=++D .2(1)(1)1a a a -++=-答案:D ,解析:根据n m n m a a a +=•,所以选项A 中422a a a =•,错误;选项B 应为合并同类项,字母和字母的指数不变,系数相加,所以2222a a a =+,故选项B 错误;选项C 根据()2222b ab a b a +±=±可知,()2244121a a a ++=+,故选项C 错误;根据平方差公式()()22b a b a b a -=-+可知,()()2221111-a a a a -=-=++,故选项D 正确.21. (2017江苏连云港,2,3分)计算2a a 的结果是A .aB .2aC .22aD .3a答案:D ,解析:根据“同底数幂相乘,底数不变,指数相加”,可得2a a =3a .22. 3.(2017四川达州3,3分)下列计算正确的是( )A .235a b ab +=B 6±C .32122a b ab a ÷= D .()323526ab a b =答案:C ,解析:2a 与3b 不是同类项,不好合并,所以A 6,所以B 选项是错的;32122a b ab a ÷=,所以C 选项是对的;()323628ab a b =,所以D 选项是错的,故本题选C .23. 3.(2017四川德阳,3,3分)下列计算正确的是A . 632x x x =⋅B . 22532x x x -=+-C .2229)3(b a ab =-D .222)(b a b a +=+答案:C ,解析: A .选项考查的知识点是同底数幂的运算,底数不变,指数相加,A 错.B .选项考查合并同类项的知识点,显然错误.C .考查乘方的知识点,正确.D .完全平方公式的理解和应用,错误.24. 3.(2017江苏淮安,3,3分)计算23a a ⋅的结果是( )A .5aB .6aC .6aD .5a答案:D ,解析:根据“同底数幂相乘,底数不变,指数相加”,可知23a a ⋅=23a +=5a .25. (2017江苏淮安,10,3分)计算:()23x y y -+=________.答案:2x y +,解析:①去括号,得()23x y y -+=223x y y -+;②合并同类项,得()23x y y -+=2x y +.26. 3.(2017江苏无锡,3,3分)下列运算正确的是( )A . ()437a a = B .()22ab ab =C .824a a a ÷=D .246a a a ⋅=答案:D . 解析:∵()4312a a =,∴A 错;∵()222ab a b =,∴B 错;∵826a a a ÷=,∴C 错;∵246a a a ⋅=,∴D正确.27. 5.(2017江苏无锡,5,3分)若a -b =2,b -c =-3,则a -c 等于( )A .1B .1- C.5 D .5- 答案:B .解析:(a -b ) + (b -c )=a -c =2-3=-1.28. 1.(2017山东潍坊,1,3分)下列计算,正确的是( ) A .a 3×a 2=a 6 B .a 3÷a =a 3 C .a 2+a 2=a 4 D .(a 2)2=a 4答案:D ,解析:a 3×a 2= a 3+2=a 5,故A 错误;a 3÷a =a 3-1=a 2,故B 错误; a 2+a 2=2a 2,故C 错误; (a 2)2=a 2×2=a 4,故D 正确.29. (2017湖南岳阳,2,3分)下列运算正确的是 A .(x 3)2= x 5B .(x)5=- x 5C .x 3·x 2= x 6D .3 x 2+2 x 3= 5x 5答案:B ,解析:考察幂运算,单项式乘法,合并同类项,A 项的答案应为x 6,C 项的答案应为x 5,D 项不是同类项,不能合并.30. 2.(2017江苏扬州,,3分)下列算式的运算结果为6a 的是A .6a a ⋅ B .23()aC .33a a +D .6a a ÷【答案】B【解析】根据“同底数幂的乘法法则”67a a a =,根据“幂的乘方法则”236()a a =,根据“合并同类项法则”3332a a a +=,根据“同底数幂的除法法则”65a a a ÷=.31. 5.(2017甘肃酒泉,5,3分)下列计算正确的是( )A.224x x xB.824x x xC.236x x xD.220xx答案:D ,解析:根据合并同类项、同底数幂的乘法、除法等知识点进行判断, A 项错误,合并同类项应为22x ;B 项错误,根据同底数幂相除,底数不变,指数相减可知826x x x =;C 项错误,根据同底数幂相乘,底数不变,指数相加可知235x x x ;D 项正确,22220xx x x .故选D.32. 8.(2017甘肃酒泉,8,3分)已知,,a b c 是ABC △的三条边长,化简a b cc a b 的结果为( )A.222a b cB.22a bC.2cD.0答案:D ,解析:根据三角形三边满足的条件:两边和大于第三边,两边的差小于第三边,即可确定a b c >0,c a b <0,所以a b cc a b =a b c +c a b =0,故选D .33. (2017湖北黄冈,2,3分)下列计算正确的是 A .2x +3y =5xyB .(m +3) 2=m 2+9C .(xy 2) 3=xy 6D .a 10÷a 5=a 5答案:D ,解析:A .2x 与3y 不是同类项,不能合并;B .根据“完全平方公式()2222a b a ab b +=++”,可得:(m +3) 2=m 2+6m +9;C .根据“积的乘方法则:()mm m ab a b =”可得(xy 2) 3=x 3y 6 ;D .根据“同底数幂的除法法则:底数不变,指数相减”可得:a 10÷a 5=a 5.34. 4.(2017湖北荆门,4,3分)下列运算正确的是( )A .4x +5y =9xyB .(-m )3·m 7=m 10C .(x 2y )5=x 2y 5D .a 12÷a 8=a 4答案D ,解析:(1)选项A 的左边不能化简;(2)选项B 的正确结果是-m 10;(3)选项C 的正确结果是x 10y 5.(4)由同底数幂的除法法则可知选项D 是正确的,故选D .35. 2.(2017江苏泰州,2,3分)下列运算正确的是( )A.3362a a a ⋅=B.3362a a aC.236a a D.623a a a ÷=答案:C ,解析:根据同底数幂的乘法法则可知,336a a a ⋅=,故A 选项错误;根据合并同类项法则可知,336a a a +=,故B 选项错误;根据幂的乘方法则可知,236a a ,故C 选项正确;根据同底数幂的除法法则可知,624a a a ÷=,故D 选项错误;故选C .36. 9.(2017江苏泰州,9,3分)已知2m -3n =-4,则代数式m (n -4)-n (m -6)的值为 . 答案:8,解析:m (n -4)-n (m -6)=mn -4m -mn +6n =-4m +6n =-2(2m -3n )=-2×(-4)=8.37. 4.(2017江苏徐州,4,3分)下列运算正确的是( )A .()a b c a b c -+=-+B .235236a a a ⋅=C . 5302a a a += D .()2211x x +=+答案:B解析:A 中,a -(b +c )=a -b -c ,错误;B 中,2a 2·3a 3=6a 5,正确;C 中,a 5与a 3不是同类项,无法合并,错误;D 中,(x +1)2=x 2+2x +1,错误.38. (2017山西,5,3分)下列运算错误..的是( )A .()1130=-B .()414932=÷-C .5x 2-6x 2= -x 2D .()()422322m m m =÷答案:B ,解析:任何非零数的零次幂都是1,∴A 正确;(-3)2÷49=9×94=4,∴B 错误;5x 2-6x 2属于合并同类项,即5x 2-6x 2=(5-6)x 2=-x 2,∴C 正确;(2m 3)2÷(2m )2=【22×(m 3)2】÷【22×m 2】=4m 6÷4m 2=(4÷4)(m 6÷m 2)=m 4,∴D 正确.39.3.(2017湖北咸宁,3,3分)下列算式中,结果等于5a 的是( )A .32a a +B .32a a ⋅C .a a ÷5D .32)(a答案:B解析:∵32a a +中的23a a 、不是同类项,无法合并,∴A 错误; ∵23235=a a aa +⋅=,∴B 正确; ∵55145a a a a a -÷==≠,∴A 错误;∵232365()=a a a a ⨯=≠,∴D 错误.故选B.40. 5.(2017湖北咸宁,5,3分)由于受79H N 禽流感的影响,我市某城区今年2月份鸡的价格比1月份下降a%,3月份比2月份下降b%,已知1月份鸡的价格为24元/千克,设3月份鸡的价格为m 元/千克,则( ) A .%)%1(24b a m --= B .%%)1(24b a m -=C. %%24b a m --= D .%)1%)(1(24b a m --= 答案:D解析:∵1月份鸡的价格为24元/千克,2月份鸡的价格比1月份下降a%, ∴2月份鸡的价格为24(1%)a -. 又∵3月份比2月份下降b%,∴3月份鸡的价格%)1%)(1(24b a m --=.故选D.41. 7.(2017湖北宜昌,3分)下列计算正确的是( )A .a 2+a 3 =a 5B .a 3·a 2=a 5C .(a 2)3=a 5D .a 6÷a 2=a 3答案:B ,解析:根据幂的有关运算性质和整式的有关运算法则.分别从“同底数幂的乘法法则、幂的乘方法则、合并同类项的法则、同底数幂的除法法则”逐个验证各选项的正确性.选项A 中 a 2、a 3不是同类项,不能进行计算,选项B 中a 2·a 3=a 2+3=a 5;选项C 中(a 2) 3=a 2×3=a 6;选项D 中a 6÷a 2=a 6-2=a 4.故选择B .44. 8.(2017呼和浩特,3分)下列运算正确的是A .()()222222223a b a b a b +--+=+B .212111a aa a a +--=-- C .()()321mmm m a a a -÷=-D .()()26512131x x x x --=-- 答案:C ,解析:A 选项应为:()()222222222222223ab a b a b a b a +--+=++-=B 选项应为:()()22111121111a a a a a a a a a +----+--==---,D 选项应为:()()26512131x x x x -+=--43. 3.(2017湖北鄂州,3分)下列运算正确的是( )A .53x x -=2B .2(1)x -=21x -C .23(2)x -=66x -D .62x x ÷=4x答案:D ,解析:53x x -=(53)x -=2x ,选项A 不正确;2(1)x -=221x x -+,选项B 不正确;23(2)x -=323(2)()x -=68x -,选项C 不正确;62x x ÷=64x -=4x ,选项D 正确.44. (2017湖北随州,2,3分)下列运算正确的是( )A .336a a a +=B .222()a b a b -=-C .326()a a -=D .1226a a a ÷=答案:C ,解析:因为a 3+a 3=2a 3,(a -b )2=a 2-2ab +b 2,(-a 3)2=(-1)2⋅(a 3)2=a 6,a 12÷a 6=a 12-6=a 6,所以选项A 、B 、D 错误,选项C 正确.45. (2017江苏宿迁,3分)下列计算正确的是 A .222)(b a ab =B .1055a a a =+C .752)(a a =D .2816a a a =÷答案:A ,解析:根据nn nb a ab =)(知A 正确.46. (2017江苏南京,2,2分)计算106×(102)3÷104的结果是( )A .103B 107C .108D .109答案∶C ,解析∶根据乘方的意义及幂的乘方,可知106×(102)3÷104=106×106÷104=108.47. (2017甘肃庆阳,5,3分)下列计算正确的是( )A.224x x xB.824x x xC.236x x xD.220xx答案:D ,解析:根据合并同类项、同底数幂的乘法、除法等知识点进行判断, A 项错误,合并同类项应为22x ;B 项错误,根据同底数幂相除,底数不变,指数相减可知826x x x =;C 项错误,根据同底数幂相乘,底数不变,指数相加可知235x x x ;D 项正确,22220xx x x .故选D.48. (2017甘肃天水.3.4分)下列运算正确的是( )A .2x +y =2xyB .x ·2y 2=2xy 2C .2x ÷x 2=2xD .4x -5x =-1答案:B ,解析:A 选项2x 与y 不是同类项,不能够合并;B 选项单项式相乘,把它们的系数,相同字母分别相乘;C 选项同底数幂相除,底数不变,指数相减,应为2x ÷x 2=2x -1,D 选项合并同类项,同类项系数相加,相同字母及其指数不变,应为4x -5x =-x .故A 、C 、D 错误,B 正确.49. (2017湖南郴州,4,3分)下列运算正确的是A.()532a a = B.532a a a =⋅ C.a a ﹣﹣=1 D.(a +b )(a -b )=22b a + 答案:B ,解析:由()mn nm a a =知()632a a =,∴A 错误,由n m n m a a a +=⋅知532a a a =⋅,∴B 正确,由nn a a 1=-知aa 11=-,∴C 错误,由平方差公式知(a +b )(a -b )=22b a -,∴D 错误.50. (2017湖南衡阳,7,3分)下面各式中,计算正确的是( )A .235x y xy +=B .623x x x ÷= C.235x x x ⋅= D .()336xx -=答案:C ,解析:A 不是同类项不能合并,A 错误;B 是同底数幂相除,底数不变,指数相减,结果为x 4,所以B 错误;C 是同底数幂相乘,底数不变,指数相加,结果正确;故选C .51. (2017·湖南株洲,1,3分)计算a 4·a 2的结果是A . a 2B .a 4C .a 6D .a 8答案:C , 解析:根据同底数幂乘法法则,a 4·a 2=a 4+2=a 6,故选C .55. 2.(2017安徽中考·4分)计算32()a -的结果是( )A .6aB .6a -C .5a -D .5a答案:A .解析:根据幂的乘方的运算性质,(-a 3)2=a 3×2=a 6,故选A . 53.55.(2017新疆生产建设兵团,5,5分)下列运算正确的是( ) A.6a -5a=1 B.(a 2)3=a 5 C.3a 2+2a 3=5a 5 D.2a ×3a 2=6a 3答案:D 解析:根据合并同类项法则,6a -5a=(6-5)a=a ;根据幂的乘方法则,(a 2)3=a 2×3=a 6;3a 2与2a 3不是同类项,不能合并;根据单项式与单项式的乘法法则,2a ×3a 2=6a 3;故选D.55. 5.(2017湖北天门,5,3分)下列运算正确的是 A .(π-3)0=1B3=±C .2-1=﹣2D .(﹣a 2)3=a 6答案:A ,解析:任何 非零数的零次方都等于1,故(π-3)0=13,根据负指数运算法则1n na a -=,得2-1=12,根据积的乘方法则得到(﹣a 2)3=﹣a 6.56. 1. (2017宁夏,3分)下列各式计算正确的是A .4a -a =3B .a 4+a 2=a 3C .(-a 3)2=a 6D .a 3·a 2=6答案:C ,解析:根据合并同类项法则“同类项的系数相加,所得的结果作为系数,字母和字母指数保持不变”,可知4a -a =3a ,故选项A 错误;选项B 中“a 4 ”和“ a 2 ”不是同类项,故不能进行加减运算,所以选项B 错误;根据“(ab )n =a n b n ”和“(a m )n =a mn ”可知(-a 3)2=a 6成立,故选项C 正确;根据“a m ·a n =a m +n ”,可知a 3·a 2=a 5,故选项D 错误.57. 7. (2017宁夏,3分)如图,从边长为a 的大正方形中剪掉一个边长为b 的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形,根据图形的变化过程写出的一个正确的等式是A .(a -b )2=a 2-2ab +b 2B .a (a -b )=a 2-abC .(a -b )2=a 2-b 2D .a 2-b 2=(a +b )(a -b )答案:D ,解析:用两种不同的方式表示阴影部分的面积,从左图看,是边长为a 的大正方形减去边长为b 的小正方形,阴影面积是( a 2-b 2);从右图看,是一个长为(a +b ),宽为(a -b )的长方形,面积是(a +b )(a -b ),所以a 2-b 2=(a +b )(a -b ) .58. 12.(2017宁夏,3分)某种商品每件的进价为80元,标价为120元,后来由于该商品积压,将此商品打七折销售,则该商品每件销售利润为 元.答案:4,解析:由利润=售价-进价,可得120×0.7-80=4.59. (2017浙江宁波,2,4分)下列计算正确的是( )A .235a a aB .224a aC .a 2⋅a 3=a 5D .325a a【答案】C【解析】A 中,a 2与a 3不是同类项,不可以合并,错误;B 中,(2a)2=4a 2,错误;C 中,a 2﹒a 3=a 5,正确;D 中,(a 2)3=a 6,错误.故选C .60. .(2017黑龙江齐齐哈尔,4,3分)下列算式运算结果正确的是( )A. 5210(2)2x x =B. 21(3)9--= C.22(1)1a a +=+ D.a -(a -b)=-b 答案:B 解析:∵522521010(2)2()42x x x x ==≠,∴选项A 错误; ∵2211(3)=(3)9--=-,∴选项B 正确; ∵222(1)+211a a a a +=+=+,∴选项C 正确;∵a -(a -b)=a -a+b=b ,∴选项D 错误.故选B.61. (2017湖北襄阳,4,3分)下列运算正确的是( )A .3a -a =2B .(a 2)3=a 5C .a 2·a 3=a 5D .a 6÷a 3=a 2答案:C ,解析:3a -a=2a ;(a 2)3=a 2×3=a 6;a 2·a 3=a 2+3=a 5;a 6÷a 3=a 6-3=a 3.66. (2017山东聊城,3,3分)下列计算错误的是 ( )A .21()42-= B .21333-⨯= C .021224-÷= D .237(310) 2.710-⨯=-⨯答案:C ,解析:根据负指数幂的性质:1p p a a -=(p 为正整数),可得22111()4,112()24-===知A 正确;由同底数幂的乘法法则m n m n aa a +=(m 、n 为整数),可得()21213333+--⨯==,知B 正确;由同底数幂的除法法则m n m n a a a -÷=(m 、n 为整数),可得()0202222224---÷===,知C 错误;由积的乘方()m m n ab a b =(m 、n 为正整数),幂的乘方()m n mn aa =(m 、n 为正整数),可得()3232367(310)3(10)2710 2.710-⨯=-⨯=-⨯=-⨯,知D 正确.63. (2017新疆乌鲁木齐,3,4分)计算(ab 2)3结果是( )A. 3ab 2B. ab 6C.a 3b 5D. a 3b 6答案:D ,解析:根据积的乘方和幂的乘方的性质,(ab 2)3=a 3(b 2)3= a 3b 6,故选D.64. (2017广西百色,4,3分)下列计算正确的是( )A .33(3)27x x -=-B . 224()x x --=C .224x x x -÷=D .122x x x --=答案:A ,解析:224()x x -=,B 错误,C 不能合并成4x ,D 123x x x ---=.65. 3.(2017贵州安顺,3,3分)下列各式中运算正确的是( )A .2(a ﹣1)=2a ﹣1B .a 2b ﹣ab 2=0C .2a 3﹣3a 3=a 3D .a 2+a 2=2a 2 答案:D ,解析:A 、2(a ﹣1)=2a ﹣2,故此选项错误;B 、a 2b ﹣ab 2,无法合并,故此选项错误;C 、2a 3﹣3a 3=﹣a 3,故此选项错误;D 、a 2+a 2=2a 2,正确.66. 3.(2017年贵州省黔东南州,3,4分)下列运算结果正确的是A .3a -a = 2B .(a -b )2 = a 2-b 2C .6ab 2 ÷(-2ab ) = -3bD .a (a +b ) = a 2+b答案:C ,解析:3a -a = 2a ,A 错;(a -b )2 = a 2-2ab +b 2 ,B 错;a (a +b ) = a 2+ab , D 错;∴答案为C .67. 2.(2017江苏常州,2,3分)下列运算正确的是( )A .2m m m ⋅=B .33()mn mn =C . 236()m m =D .623m m m ÷= 【答案】C【解析】2m m m ⋅=故A 错误;333()mn m n =故B 错误;C 正确;624m m m ÷=故D 错误.68. 3. (2017江苏南通,3,3分)下列计算,正确的是A .a 2-a =aB .a 2·a 3=a 6C .a 9÷a 3=a 3D .(a 3)2=a 669. 4.(2017·辽宁大连,4,3分)计算(-2a 3)2的结果是A .-4a 6B .4a 5C .-4a 5D .4a 6 答案:D 解析:解析:根据幂的乘方的运算性质,(-2a 3)2=(-2)2a 3×2=4a 6,故选D .70. 4.(2017山东淄博,4,4分)下列运算正确的是 ( )A.a2·a3=a6B.(-a2)3=-a5 C.a10÷a9=a(a≠0) D.(-bc)4÷(-bc)2=-b2c2答案:C,解析:A项,a2·a3=a5,该项错误;B项,(-a2)3=-a6 ,该项错误;C项,a10÷a9=a10-9=a(a≠0),该项正确;D项,(-bc)4÷(-bc)2=b2c2,该项错误.71. 6.(2017山东淄博,6,4分)若a+b=3,a2+b2=7,则ab等于()A.2 B.1 C.-2 D.-1答案:B,解析:因为(a+b)2=a2+2ab+b2,所以ab=222()()2a b a b=2372=1.77. 3.(2017江苏省南通市,3,3分)下列计算,正确的是A.a2-a=a B.a2·a3=a6C.a9÷a3=a3D.(a3)2=a6答案:D 解析:A项不是同类项,不能合并;B项正确答案是a5,所以错误;C项应该底数不变,指数相减,正确答案是a6,所以错误;D项正确.73. 2.(2017青海西宁,2,3分)下列计算正确的是A.3m-m=2B.m4÷m3=mC.(-m2)3=m6D.-(m-n)=m + n答案:B,解析:有理数运算,同底数幂相除,底数不变,指数相减.74.(2017黑龙江绥化,3,3分)下列运算正确的是()A.3a+2a=5a2B.3a+3b=3ab C.2a2bc-a2bc=a2bc D.a5-a2=a3答案:C,解析:A、B、D不是同类项不能合并,所以错误;C是同类项,合并时,字母及字母的指数都不变,系数直接加减,C正确;故选C.75. 7.(2017辽宁沈阳,7,2分)下列运算正确的是A.x3+x5=x8B.x3+x5=x15C.(x+1)(x-1)=x2-1D.(2x)5=2x5答案:C,解析:根据“幂的运算法则:同底数幂相乘,底数不变,指数相加;合并同类项;平方差公式(a+b)(a-b)=a2-b2”,可得(a+b)(a-b)=a2-b2.76. 3.(2017年四川资阳,3,3分)下列运算正确的是( )A.(x+y)2=x2+y2B.(x2)3=x5C=|x|D.x6÷x2=x3答案:A解析:选项A的结果是x2+2xy+y2;选项B的结果是x6;选项D的结果是x4.只有选项C中的运算正确.故选C.77.(2017湖北恩施中考3·5分)下列计算正确的是( )A.a(a-1)=a 2-aB.(a 4)3=a 7C.a 4+a 3=a 7D.2a 5·a 3=a 23.A.解析:78. 3. (2017年武汉,3,3分)下列计算的结果是x 5的为( )A .x 10÷x 2B .x 6-xC .x 2·x 3D .(x 2)3答案:A ,解析:A 选项x 10÷x 2=x 10-2=x 8,B 选项x 6-x 没有同类项,不能合并,C 选项x 2·x 3= x 2+3= x 5,D选项(x 2)3= x 2×3= x 6.故选C .79. 5. (2017年武汉,5,3分)计算(x +1)(x +2)的结果为( )A .x 2+2B .x 2+3x +2C .x 2+3x +3D .x 2+2x +2答案:B ,解析:根据多项式乘法法则,(x +1)(x +2)= x 2+2x +x +2 = x 2+3x +2.故选B .80. 4.(2017内蒙古赤峰,4,3分)下列运算正确的是( )A .3x +2y =5(x +y )B .x +x 3=x 4C .x 2·x 3=x 6D .(x 2) 3=x 6答案:D ,解析:本题考查了整式的运算,正确掌握同类项概念、合并同类项的方法,同底数幂的乘法法则,幂的乘方法则是解题的关键.3x 与2y 不是同类项,不能合并,所以A 错;x 与x 3不是同类项,不能合并,所以B 错;由同底数幂相乘,底数不变,指数相加,得x 2·x 3=x 5,所以C 错;由幂的乘方,底数不变,指数相乘,得(x 2) 3=x 6,所以D 正确.81. 5. (2017广西贵港,5,3分)下列运算正确的是( )A .2333a a a +=B .()32522a a a -= C. 623422a a a += D .()22238a a a --= 答案D 解析:3a 2与a 不是同类项,不能合并,所以选项A 错误;2a 3•(﹣a 2)=[2×(﹣1)] •(a 3×a 2)=﹣2a 5,所以选项B 错误;4a 6与2a 2不是同类项,不能合并,所以选项C 错误;(﹣3a )2﹣a 2=9a 2﹣a 2=8a 2,所以选项D 正确,故选D .88. (2017贵州六盘水,3,4分)下列式子正确的是A .7m +8n =8m +7nB .7m +8n =15mnC .7m +8n =8n +7mD .7m +8n =56mn 答案:C ,解析:7m 和8n 不是同类项,无法合并计算,∴B 、D 选项错误;依据“加法的交换律”可知7m+8n =8n +7m 正确,∴C 选项正确.83. (2017贵州六盘水,14,5分)计算:2017×1983= .答案:3000711,解析:∵2017×1983=(2000+17) (2000-17),∴可以用平方差公式“(a +b )(a -b )=a 2-b 2”进行简便计算,2017×1983=(2000+17) (2000-17)=20002-172=3999711.84. 4.(2017湖北黄石,4,3分)下列运算正确的是( )A .00a =B .235a a a +=C .21a a a -⋅=D .111a b a b+=+ 答案:C ,解析:A 中不仅计算错误,说法也是又问题的,只能是这样: a 0=1(a ≠0);故A 错误;B,a 2与a 3不是同类项,不能合并,故B 错误;C,同底数幂相乘,法则是:底数不变,指数相加,即 a m ·a n =a m +n ,C 正确; 故选C.D,异分母的分式相加减,应该先通分,即ab b a ab a ab b b a +=+=+11,故D 错.85. (2017浙江台州,7,4分)下列计算正确的是( )A .()()2222a a a +-=-B .()()2122a a a a +-=+-C . ()222a b a b +=+D .()2222a b a ab b -=-+ 答案:D ,解析:∵()()2224a a a +-=-,∴选项A 错误;∵()()2122a a a a +-=--,∴选项B 错误;∵()2222a b a ab b +=++ ,∴选项C 错误;∵()2222a b a ab b -=-+,∴选项D 正确,因此选D . 88. (2017浙江台州,9,4分)滴滴快车是一种便捷的出行工具,计价规则如下表:小王与小张各自乘坐滴滴快车,行车里程分别为6公里和8.5公里,如果下车时间所付车费相同,那么这两辆滴滴快车的行车时间相差( )A . 10分钟B . 13分钟C . 15分钟D .19分钟答案:D ,解析:设小王坐车a 分钟,小张坐车b 分钟.则小王的车费为6×1.8+0.3a =10.8+0.3a ;小张的车费为8.5×1.8+0.3b +(8.5-7) ×0.8=16.5+0.3b ,∴10.8+0.3a =16.5+0.3b ,解得b -a =19,因此选D .87. (2017贵州遵义)下列运算正确的是( )A .2a 5-3a 5=a 5B .a 2·a 3=a 6 C.a 7÷a 5=a 2 D .(a 2b )3= a 5b 3答案:C ,解析:选项A ,根据整式的加减法则得2a 5-3a 5=-a 5,错误;选项B ,根据同底数幂的乘法法则得a 2·a 3=a 5,错误;选项C ,根据同底数幂的除法法则得a 7÷a 5=a 2,正确;选项D ,根据幂的乘方法则得(a 2b )3= a 6b 3,错误.88. 如图,将边长为3a 的正方形沿虚线剪成两块正方形和两块长方形,若拿掉边长为2b 的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为A .3a +2bB .3a +4bC .6a +2bD .6a +4b答案:A ,解析:根据剪拼的过程中面积不变,可得拼成的矩形面积是(3a )2-(2b )2,将其进行因式分解,即得(3a +2b )(3a -2b ),所以这块矩形的较长的边长是3a +2b .89. 3.(2017山东莱芜,3,3分)下列运算正确的是( )A .2x 2-x 2=1B .x 6÷x 3=x 2C .4x ·x 4=4x 5D .(3xy 2)2=6x 2y 4 答案:C ,解析:A 项, 2x 2-x 2=x 2,该项错误;B 项,x 6÷x 3=x 3,该项错误;C .4x ·x 4=4x 5,该项正确;D .(3xy 2)2=9x 2y 4,该项错误.90. (2017广西河池,5,3分)下列计算正确的是( )A .523a a a =+B .623a a a =⋅C . 632)(a a =D .236a a a =÷ 答案:C解析:325a a a +≠故A 错误,325a a a ⋅=故B 错误,632)(a a =故C 正确,633a a a ÷=故D 错误,故选C91. 4.下列运算正确的是( )A .﹣3(x ﹣4)=﹣3x+12B .(﹣3x )2•4x 2=﹣12x 4C .3x+2x 2=5x 3D .x 6÷x 2=x 3答案:A ,解析:∵﹣3(x ﹣4)=﹣3x+12,故选项A 正确,∵(﹣3x )2•4x 2=9x 2•4x 2=36x 4,故选项B 错误,∵3x+2x 2不能合并,故选项C 错误,∵x 6÷x 2=x 4,故选项D 错误99. (2017贵州毕节)下列计算正确的是( )A.a 3·a 3=a 9B.(a +b )2=a 2+b 2 C . a 2÷a 2=0 D. (a 2)3=a 6答案:D ,解析:(1)根据同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加,可得a 3·a 3=a 6,故A错误;(2)根据完全平方公式,可知(a +b )2=a 2+2ab +b 2,故B 错误;(3)根据同底数幂除法法则:同底数幂相除,底数不变,指数相减,可得:a 2÷a 2=a 0=1,故C 错误;(4)根据幂的乘方法则:底数不变,指数相乘,可知: (a 2)3=a 6,故 D 正确.因此本题正确选项为D.93. 2.(2017湖南怀化,4分)下列运算正确的是( )A .3m ﹣2m =1B .(m 3)2=m 6C .(﹣2m )3=﹣2m 3D .m 2+m 2=m 4答案:B .解析:A 、原式=(3﹣2)m =m ,故本选项错误;B 、原式=m 3×2=m 6,故本选项正确;C 、原式=(﹣2)3•m 3=﹣8m 3,故本选项错误;D 、原式=(1+1)m 2=2m 2,故本选项错误;94. 7. (2017四川巴中,3分)下列运算正确的是( )A .a 2 · a 3 = a 6B .C . (a + b )2 = a 2 + b 2D . (a 2)3 = a 6答案:D ,解析:a 2 · a 3 = a 5 (a +b )2 =a 2+2ab +b 2;(a 2)3=a 6,正确的为D ,故选D .二、填空题1. (2017浙江丽水·13·4分)已知a 2+a =1,则代数式3-a 2-a 的值为答案:2.解析:3-a 2-a =3-(a 2+a ),把a 2+a =1整体代入得原式=3-1=2.2. (2017四川内江,22,6分)若实数x 满足x 2-2x -1=0,则2x 3-7x 2+4x -2017= .答案:-2020,解析:由x 2-2x -1=0,得x 2=2x +1,把x 2=2x +1代入2x 3-7x 2+4x -2017,得2x 3-7x 2+4x -2017=2x (2x +1) -7(2x +1)+4x -2017=4x 2+2x -14x -7+4x -2017=4(2x +1)-8x -2024=-2020.3. .(2017江苏连云港,10,4分)计算22a a . 答案:,解析:根据整式的乘法公式(平方差公式)可得.4. 13.(2017四川德阳,13,3分)计算(x +3)(x -3)= .答案:92-x ,解析:平方差公式的应用.5. 11.(2017江苏苏州,11,3分)计算:()22a= .答案:4a ,解析:根据“幂的乘方运算法则”,幂的乘方,底数不变,指数相乘,()224a a =.6. (2017山西,12,3分)某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a 元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为 元.答案:1.08a ,解析:0.9(1+20%)a =1.08a .7. 13.(2017天津,3分)计算x 7÷x 4的结果等于________.答案:x 3,解析:根据同底数幂的除法法则“底数不变,指数相减”,可得x 7÷x 4=x 3.8. (2017湖北十堰,12,5分)若a -b =1,则代数式2a -2b -1的值为 .答案:1,解析:利用整体代入法求解,原式=2(a -b )-1=2×1-1=1.9. (2017江苏宿迁,3分)若a -b =2,则代数式5+2a -2b 的值是 .答案:9,解析:整体代入得原式=5+2(a -b )=5+4=9.24a()()22a b a b a b +-=-22a a 24a10. (2017江苏镇江,2,2分)计算:a 5÷a 3= .答案:a 2,解析:根据“同底数幂的除法法则:底数不变,指数相减”可得:a 5÷a 3=a 2.11. 11.(2017湖北天门,11,3分)已知2a -3b =7,则8+6b -4a = .答案:﹣6,解析:代数式求值,整体代入法,8+6b -4a =8﹣2(2a ﹣3b )=8﹣2×7=﹣6.12. 9.(2017宁夏,3分) 分解因式2a 2-8= .答案:2(a +2)(a -2),解析:先提取公因式2,再根据平方差公式得解.13. 15.(2017四川凉山,15,4分)若312m x y +-与3n y +是同类项,则2017()m n +=______. 【答案】-1【解析】∵y x m 321+-与342+n y x 是同类项,∴m+3=4,n+3=1,∴m =1,n =-2,∴1)21()(20172017-=-=+n m14. 15.(2017贵州安顺,15,4分)若代数式x 2+kx +25是一个完全平方式,则k=答案:±10,解析:∵代数式x 2+kx +25是一个完全平方式,∴k=±10.15. 17.(2017江苏省南通市,17,3分)已知x =m 时,多项式x 2+2x +n 2的值为-1,则x =-m 时,该多项式的值为________.答案:3 解析:当x =m 时,m 2+2m +n 2=-1,则(m +1)2+n 2=0,∴m +1=0,n =0.∴m =-1,n =0.∴x 2+2x +n 2=3.16.(2017青海西宁,11,2分)y x 231是 次单项式.答案:3,解析:单项式的相关知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年中考真题专题汇编——组合式归纳推论题题型分析:该考点的题型较为单一,主要是选择题的形式呈现,考查的内容以化学概念、化学原理为主,也包含元素化合物知识、化学用语、化学实验、环境保护、化学与生活等各个方面的相关内容,其最大的特点就是把多个有联系或共同点的知识点进行的整合,然后进行逻辑推理,并让学生判断正误。
方法技巧:1.题目具有基础性。
知识点来源于教材,不拘于教材。
解题时需从多角度、多层面思考问题、分析问题、解决问题,突出了化学学科的应用性。
解题时的难度在于能否用已学的知识和技能构建问题的模型。
2.题目具有丰富的信息资源。
考题一般跨度较大,需从阅读材料中筛选和破译出所需的信息资源,最后再根据题意要求,进行整合取舍。
3.该类题目将零散的化学知识整理归纳,具有开而不放的特点,解题时可以使用排除法以加快解题速度、提高解题的几率。
个别题目需通过某种现象,发掘其中隐含信息,联想到具体事例,才能轻松解决问题。
真题演练:1.(2017黄石)推理是一种重要的思维方法,以下推理合理的是( D )A.酸中一定含有氢元素,所以含有氢元素的物质一定是酸B.置换反应有单质生成,所以有单质生成的反应一定是置换反应C.化学反应前后原子总数不变,所以化学反应前后分子总数也不变D.化学反应伴随能量变化,所以金属腐蚀过程中一定伴随能量变化2.(2017随州)归纳推理是一种重要的化学思维方法。
下列归纳推理正确的是( B )A.碱溶液能使酚酞溶液变红,那么能使酚酞溶液变红的溶液一定是碱溶液B.镁、锌、铁能与盐酸反应生成氢气,那么它们与稀硫酸反应也能生成氢气C.中和反应生成盐和水,那么生成盐和水的反应一定是中和反应D.人体缺少必需微量元素会得病,那么应尽可能多吃含有这些元素的营养品3.(2017襄阳)推理是学习化学的一种重要方法,但推理必须科学、严谨。
下列推理正确的是(C)A.木炭在氧气中能燃烧,所以氧气具有可燃性B.不锈钢虽然是金属材料,但它属于混合物而不是金属单质C.原子核是由质子和中子构成的,故所有原子核中都一定含有质子和中子D.催化剂在反应前后质量不变,因此反应前后质量不变的物质一定是催化剂4.(2017孝感)推理是研究和学习化学的重要方法.以下推理正确的是(A)A.若某雨水的pH<7,则该雨水一定呈酸性B.过率可以除去水中不溶性杂质,因此过滤后的水一定是软水C.一氧化碳和二氧化碳的组成元素相同,所以它们的化学性质相同D.可燃物燃烧时温度需要达到着火点,所以温度达到着火点时,可燃物就一定能燃烧5.(2017聊城)归纳总结和逻辑推理是化学学习中常用的思维方法。
下列归纳推理正确的是(A)A.二氧化碳气体和氧气都能用浓H2SO4干燥B.Na2CO3溶滚和NaNO3溶液都能使无色酚酞试液变红C.稀有气体可做保护气,则可做保护气的一定是稀有气体D.中和反应生成盐和水,则生成盐和水的反应一定是中和反应6.(2017临沂)类推是化学学习中常川的思雄方法。
下列类推正确的是(D)A.活泼金属或酸反应有气体产生,则与酸反应产生气体的一定是活泼金属B.酸与碱发生中和反应生成盐和水,则生成盐和水的反应一定是中和反应C.单质一定是由同种元素组成的物质.则由同种元素组成的物质一定是单质D.碱性溶液能使酚酞溶液变红,则能使阶酞溶液变红的溶液一定是碱性溶液7.(2017泰安)类推是一种重要的学习方法,但如果不具体问题具体分析就会产生错误的结论。
下列类推结论错误的是(A)①CO能与Fe2O3反应生成Fe,CO也能与CuO反应生成Cu②NaOH溶液能使无色酚酞试液变红色,Cu(OH)2也能使无色酚酞试液变红色③有机化合物含碳元素,则含碳元索的化合物一定是有机化合物④中和反应生成盐和水,但生成盐和水的反应不一定是中和反应⑤碱的溶液呈碱性,则呈碱性的溶液一定是碱的溶液A. ②③⑤B. ①②⑤C. ①⑤D. ③④⑤8. (2017兰州)归纳是学习化学常用的方法。
下列归纳全部正确的是( C )9.(2017邵阳) 推理是一种重要的思维方法,以下推理合理的是( D )A.酸中一定含有氢元素,所以含有氢元素的物质一定是酸B.置换反应有单质生成,所以有单质生成的反应一定是置换反应C.化学反应前后原子总数不变,所以化学反应前后分子总数也不变D.化学反应伴随能量变化,所以金属腐蚀过程中一定伴随能量变化10. (2017龙东)推理是化学学习中常用的思维方法。
下列推理正确的是( B )A.中和反应生成盐和水,所以生成盐和水的反应一定是中和反应B.在一定温度下,硝酸钾饱和溶液不能再继续溶解硝酸钾,但可以继续溶解其它物质C.铝表面的氧化铝薄膜能起到保护作用,则铁表面的铁锈也能起到保护作用D.分子、原子可以构成物质,则物质都是由分子、原子构成的11.(2017绥化)分析和推理是学习和研究化学的重要方法。
下列说法正确的是( B )A.有机物一定含有碳元素,则含碳的化合物也一定是有机物B.同种元素的原子质子数相同,则质子数相同的原子一定是同种元素C.氧化物一定含有氧元素,则含有氧元素的化合物一定是氧化物D.中和反应能生成盐和水,则生成盐和水的反应一定是中和反应12.(2017青岛)(双选)分析推理是化学学习中常用的思维方法,下列说法正确的是( B C)A.活泼金属能与稀硫酸反应放出气体,能与稀硫酸反应放出气体的物质一定是活泼金属B.碱能跟酸反应生成盐和水,能跟酸反应生成盐和水的物质不一定是碱C.化合物是由不同种元素组成的纯净物,由不同种元素组成的纯净物一定是化合物D.有机物是含有碳元素的化合物,含有碳元素的化合物一定是有机物13.(2017南充)推理是一种重要的化学思维方法,以下推理正确的是( A )A.碳酸盐与酸反应会放出气体,能与酸反应放出气体的物质不一定是碳酸盐B.中和反应一定有盐和水生成,生成盐和水的反应一定是中和反应C.二氧化碳能使燃着的木条熄灭,能使燃着木条熄灭的气体一定是二氧化碳D.单质是由同种元素组成的,由同种元素组成的物质一定是单质14.(2017乌鲁木齐)推理是学习化学重要的方法之一。
下列叙述正确的是( B )A.通常情况下,物质燃烧需要氧气,所以有氧气参与的反应一定是燃烧B.氢气可用排水法收集,能用排水法收集的气体一定难溶于水、不与水反应C.性质活泼的全属在空气中容易被腐蚀,铝在空气中不易被腐蚀是因为其性质不活泼D.碱的溶液能使无色酚酞试液变红,能使无色酚酞试液变红的一定是碱的溶液15.(2017东营)推理和归纳是研究和学习化学的重要方法。
以下说法正确的是( A )A.氢气点燃前需验纯,则点燃任何可燃性气体前都需验纯B.含碳元素的物质充分燃烧会生成CO2,燃烧能生成CO2的物质不一定含碳元素C.单质由同种元素组成,由同种元素组成的物质一定是单质D. 室温下pH<7的溶液呈酸性,同理pH<7的雨水是酸雨16. (2017陕西)推理是常用的学习方法。
下列推理正确的是(D )A.化合物中含不同种元素,所以含不同种元素的物质都是化合物B.木炭、活性炭可用于净化空气,所以碳单质都能净化空气C.CO2、SO2均可与碱溶液反应,所以非金属氧化物一定能与碱溶液反应D.点燃可燃性气体前要验纯,所以点燃甲烷前一定要验纯17.(2017赤峰)推理是化学学习中常用的思维方法,下列推理正确的是(B)A.混合物中至少含有两种物质,则混合物中至少含有两种元素B.均一稳定的混合物是溶液,碘酒均一稳定,则碘酒属于溶液C.化学变化伴随有能量变化,则有能量变化的变化一定是化学变化D.利用红磷在空气中燃烧可以测定空气中氧气的含量,则利用木炭也可以18.(2017西宁)分析推理是化学学习中常用的思维方法。
下列分析推理正确的是A.碱溶液pH大于7,所以pH大于7的溶液一定是碱溶液(D )B.酸和碱作用生成盐和水的反应是中和反应,所以生成盐和水的反应一定是中和反应C.离子是带电荷的粒子,所以带电荷的粒子一定是离子D.单质是由同种元素组成的,所以由同种元素组成的纯净物一定是单质19.( 2017齐齐哈尔)推理是学习化学的一种方法,以下推理正确的是(A)A.氧气由氧元素组成,所以制取氧气的反应物一定含有氧元素B.质子数决定元素种类,所以质子数相同的粒子一定属于同种元素C.溶液是均一稳定的,所以均一稳定的物质一定是溶液D.催化剂可以加快化学反应速率,所以任何化学反应都需要催化剂20.(2017天水)类推是学习化学时常用的思维方式。
以下类推结果正确的是(C )A.有机物都含有碳元素,则含有碳元素的物质一定是有机物B.碱溶液能使酚酞溶液变红,则能使酚酞溶液变红的物质一定是碱C.化合物是由不同种元素组成的纯净物,则只含一种元素的物质一定不是化合物D.碳酸盐遇酸有气体产生,则与酸反应产生气体的一定是碳酸盐21. (2017广东)下表是部分知识的归纳,其中正确的一组是(B )22 .(2017贵港)下列对某一主题的知识归纳,有错误的一组是(B)23.(2017齐齐哈尔) 下列有关生产生活中的化学知识整理有错误的一组是( A )24. (2017随州)2017年6月1日,特朗普宣布美国退出《巴黎协定》,引起国际社会强烈反响,使能源和环境问题再次成为热点。
下列观点或做法完全正确的是( B )25.(2017娄底)小红同学对部分化学知识归纳如下,其中不完全正确的是( C ) A .A B .BC.CD .D26.(2017无锡)下列归纳和总结完全正确的一组是( A )27.(2017宿迁)下列归纳总结完全正确的一组是( A )29.(2017赤峰) 下表是某同学错题本中整理的部分内容,其中不需要修改的是( D )30.(2017西宁)善于梳理化学知识,是学好化学的有效方法。
以下归纳不完全正确的是( D )31.(2017菏泽) 化学与人类的生活密切相关。
下列对化学知识的应用归纳完全正确的一组是(A )32.(2017巴中)下列对有关主题知识的归纳错误的是(C )33.(2017遂宁市)化学知识涉及衣、食、住、行各个领域,下列有关说法全部正确的一组是( C )34.(2017烟台)下列主题知识的归纳中,完全正确的一组是(C)。
