数据结构图67311
数据结构ppt课件完整版

针对有序数据集合,每次通过中间元素将 待查找区间缩小为之前的一半,直到找到 元素或区间为空。
哈希查找
树形查找
通过哈希函数将数据映射到哈希表中,实 现快速查找。
如二叉搜索树、平衡树等,通过树形结构实 现高效查找。
排序算法分类及实现原理
插入排序
将待排序元素逐个插入到已排序序列中,直到所有元素均插入完毕。
由n(n>=0)个具有相同类型 的数据元素(结点)a1,a2,
...,an组成的有序序列。
同一性
每个元素必须是同一类型的数 据。
有序性
元素之间具有一对一的前驱和 后继关系,即除首尾元素外, 每个元素都有一个前驱和一个 后继。
可变性
线性表的长度可变,即可以插 入或删除元素。
顺序存储结构与链式存储结构比较
定义
用一段连续的存储单元依次存储线性 表的数据元素。
优点
可以随机存取表中任一元素,且存取 时间复杂度为O(1)。
顺序存储结构与链式存储结构比较
• 缺点:插入和删除操作需要移动大量元素,时间 复杂度高;需要预先分配存储空间,容易造成空 间浪费。
顺序存储结构与链式存储结构比较
定义
用一组任意的存储单元存储线性 表的数据元素(这组存储单元可 以是连续的,也可以是不连续的
查找操作
查找指定元素的位置。
遍历操作
访问线性表中的每个元素。
销毁操作
释放线性表占用的存储空间。
03
栈和队列
栈定义及特点
栈(Stack)是一种特殊的线性数据结构,其数据的存 取遵循后进先出(LIFO, Last In First Out)的原则。 栈的特点
具有记忆功能,能保存数据的状态。
栈的基本操作包括入栈(push)、出栈(pop)、查 看栈顶元素(top)等。 只能在栈顶进行数据的插入和删除操作。
《数据结构图》课件

层次分明
02
通过节点和边的关系,数据结构图能够清晰地表示数据的层次
结构,有助于理解数据的组织方式。
易于修改
03
相比文本或表格,数据结构图更易于修改和更新,能够快速适
应数据的变化。
数据结构图的缺点
制作难度大
制作一份高质量的数据结构图需要花费较多的时间和精力,特别 是在处理复杂的数据结构时。
表达能力有限
解数据结构。
辅助设计数据结构
在设计复杂的数据结构时,可以使 用数据结构图来辅助设计,使设计 过程更加清晰和有条理。
方便交流和讨论
数据结构图是一种可视化的表达方 式,可以方便地展示给其他人,有 助于团队成员之间的交流和讨论。
数据结构图的分类
01
02
03
树形结构图
树形结构图是一种层次结 构的数据结构图,它通过 节点和子节点的关系来表 示数据的层次关系。
随着用户需求的多样化,未来 的数据结构图将更加注重个性 化定制,满足不同用户对数据 可视化的需求和偏好。
为了提高数据可视化的可解释 性和透明度,未来的数据结构 图将更加注重对数据的处理和 分析过程的可视化呈现,使用 户能够更好地理解数据的来源 和含义。
2023 WORK SUMMARY
THANKS
未来的数据结构图将更加注重用户的交互 性,使用户能够更深入地探索数据,提高 数据理解的效率和准确性。
动态数据的实时呈现
多维度的数据呈现
随着大数据和实时数据处理技术的发展, 数据结构图将能够实时呈现动态数据的变 化,帮助用户更好地理解和分析数据。
未来的数据结构图将能够呈现多维度的数 据,包括时间序列数据、空间数据等,满 足用户对不同类型数据的可视化需求。
详细描述
数据结构ppt

数据结构ppt数据结构 PPT引言:数据结构是计算机科学中的重要基础,它探讨了数据的组织、存储和检索方法。
在计算机程序中,数据结构的选择对于程序的性能和效率起着至关重要的作用。
在本次演讲中,将介绍数据结构的基本概念、常见的数据结构类型以及它们的应用。
一、基本概念1.1 数据结构的定义数据结构是一种用于组织和存储数据的方式,它包括数据元素和它们之间的关系。
其中,数据元素是具有相同性质的数据的集合,关系是数据元素之间的逻辑关系。
1.2 数据结构的分类数据结构可以分为线性结构和非线性结构两大类。
1.2.1 线性结构线性结构中的数据元素之间存在一对一的关系,每个元素只有一个直接前驱和一个直接后继。
常见的线性结构有线性表、栈和队列。
1.2.2 非线性结构非线性结构中的数据元素之间存在一对多或多对多的关系,每个元素可以有多个直接前驱和直接后继。
常见的非线性结构有树和图。
二、常见的数据结构类型2.1 数组数组是一种线性结构,它由固定大小的相同类型的元素构成,可以通过索引直接访问元素。
数组的特点是随机访问速度快,但插入和删除操作较慢。
2.2 链表链表也是一种线性结构,它由一系列结点组成,每个结点包含数据和指向下一个结点的指针。
链表的特点是插入和删除操作快,但随机访问速度较慢。
2.3 栈栈是一种特殊的线性结构,它只能在表的一端进行插入和删除操作。
遵循先进后出(LIFO)的原则,所以栈也被称为后进先出(FILO)的数据结构。
2.4 队列队列也是一种特殊的线性结构,它只能在表的一端插入元素,在另一端删除元素。
遵循先进先出(FIFO)的原则。
2.5 树树是一种非线性结构,它由节点和节点之间的连接组成。
树的特点是每个节点可以有多个子节点,但只有一个根节点。
2.6 图图是一种非线性结构,它由节点和节点之间的连接组成。
图的特点是节点之间的关系可以是一对多或多对多的。
三、数据结构的应用3.1 数据库管理系统数据库管理系统是现代计算机应用中广泛使用的一种数据结构,它用于存储和管理大量的数据。
数据结构详解ppt课件

“数据结构知识导入全程目标•数据结构的基本概念–逻辑结构–物理结构–运算结构•数据结构的基本实现–堆栈–队列–链表–二叉树知识讲解数据结构的基本概念•数据结构是相互之间存在一种或多种特定关系的数据的集合•数据结构是计算机存储、组织数据的方式•数据结构的选择直接影响计算机程序的运行效率(时间复杂度)和存储效率(空间复杂度)•计算机程序设计=算法+数据结构•数据结构的三个层次–抽象层——逻辑结构–结构层——物理结构–实现层——运算结构识讲解•集合结构(集)–结构中的数据元素除了同属于一个集合外没有其它关系识讲解•线性结构(表)–结构中的数据元素具有一对一的前后关系识讲解•树型结构(树)–结构中的数据元素具有一对多的父子关系知识讲解实现双向线性链表•删除节点识讲解•树形结构的最简模型,每个节点最多有两个子节点•每个子节点有且仅有一个父节点,整棵树只有一个根节点•具有递归的结构特征,用递归的方法处理,可以简化算法•三种遍历序–前序遍历:D-L-R–中序遍历:L-D-R–后序遍历:L-R-D识讲解•二叉树的一般形式–根节点、枝节点和叶节点–父节点和子节点–左子节点和右子节点–左子树和右子树–大小和高度(深度)识讲解•满二叉树–每层节点数均达到最大值–所有枝节点均有左右子树知识讲解二叉树•完全二叉树–除最下层外,各层节点数均达到最大值–最下层的节点都连续集中在左边识讲解•顺序存储–从上到下、从左到右,依次存放–非完全二叉树需用虚节点补成完全二叉树识讲解•链式存储–二叉链表,每个节点包括三个域,一个数据域和两个分别指向其左右子节点的指针域识讲解•链式存储–三叉链表,每个节点包括四个域,一个数据域、两个分别指向其左右子节点的指针域和一个指向其父节点的指针域知识讲解实现有序二叉树•有序二叉树亦称二叉搜索树,若非空树则满足:–若左子树非空,则左子树上所有节点的值均小于等于根节点的值–若右子树非空,则右子树上所有节点的值均大于等于根节点的值–左右子树亦分别为有序二叉树•基于有序二叉树的排序和查找,可获得O(logN)级的平均时间复杂度知识讲解逻辑结构•网状结构(图)–结构中的数据元素具有多对多的交叉映射关系识讲解•顺序结构–结构中的数据元素存放在一段连续的地址空间中识讲解•顺序结构–随机访问方便,空间利用率低,插入删除不方便识讲解•链式结构–结构中的数据元素存放在彼此独立的地址空间中–每个独立的地址空间称为节点–节点除保存数据外,还需要保存相关节点的地址识讲解•链式结构–插入删除方便,空间利用率高,随机访问不方便知识讲解逻辑结构与物理结构的关系•每种逻辑结构采用何种物理结构实现,并没有一定之规,通常根据实现的难易程度,以及在时间和空间复杂度方面的要求,选择最适合的物理结构,亦不排除复合多种物理结构实现一种逻辑结构的可能知识讲解运算结构•创建与销毁–分配资源、建立结构、释放资源•插入与删除–增加、减少数据元素•获取与修改–遍历、迭代、随机访问•排序与查找–算法应用知识讲解数据结构的基本实现•堆栈–基于顺序表的实现–基于链式表的实现•队列–基于顺序表的实现–基于链式表的实现•链表–双向线性链表的实现•二叉树–有序二叉树(二叉搜索树)的实现知识讲解堆栈•后进(压入/push)先出(弹出/pop)识讲解•初始化空间、栈顶指针、判空判满识讲解•动态分配、栈顶指针、注意判空知识讲解队列•先进(压入/push)先出(弹出/pop)识讲解•初始化空间、前弹后压、循环使用、判空判满识讲解•动态分配、前后指针、注意判空知识讲解链表•地址不连续的节点序列,彼此通过指针相互连接•根据不同的结构特征,将链表分为:–单向线性链表–单向循环链表–双向线性链表–双线循环链表–数组链表–链表数组–二维链表识讲解•单向线性链表识讲解•单向循环链表识讲解•双向线性链表识讲解•双向循环链表识讲解•数组链表识讲解•链表数组识讲解•二维链表识讲解•结构模型识讲解•插入节点。
数据结构图结构(动态PPT)课件

结合实际问题
将数据结构图与实际问题相结合,通过分析问题的本质和 规律,选择合适的数据结构和算法进行求解。
创新应用方式
在传统的数据结构图应用基础上,探索新的应用方式和方 法,如基于数据结构图的机器学习模型、数据结构图在社 交网络分析中的应用等。
跨学科融合
将数据结构图与其他学科领域进行融合,如物理学、化学 、生物学等,通过借鉴其他学科的理论和方法,创新数据 结构图的应用场景和解决方案。
包括无向图、有向图、权 重图、邻接矩阵、邻接表 等。
图的遍历方法
深度优先搜索(DFS)和 广度优先搜索(BFS)的 原理和实现。
非线性数据结构图应用案例
树的应用案例
包括二叉搜索树、堆、哈夫曼树等在实际问题中的应用,如排序、优先队列、 编码等。
图的应用案例
包括最短路径问题(Dijkstra算法、Floyd算法)、最小生成树问题(Prim算法 、Kruskal算法)以及网络流问题等在实际问题中的应用,如交通网络规划、电 路设计等。
根据实际需求,选择适合的最小生 成树算法,如Prim算法、Kruskal算
法等。
B
C
D
可视化呈现结果
将算法的运行过程和结果以图形化的方式 呈现出来,方便用户直观地理解和掌握最 小生成树算法的原理和实现过程。
实现算法逻辑
编写代码实现最小生成树算法的逻辑,包 括节点的选择、边的添加和权重的计算等 。
拓展思考:如何创新应用数据结构图解决问题
作用
帮助理解复杂数据结构的组成和 关系,提高数据处理的效率。
常见类型及特点
01
02
03
04
线性数据结构图
元素之间一对一关系,如数组 、链表等。
树形数据结构图
数据结构 图

A
B
1
2
1
3
D
C
4
5
6
(a)强 连 通 图
(b)非 强 连 通 图
图 7-5 强 连 通 图 和 非 强 连 通 图
7.1 图及其抽象数据类型
图的基本概念
10. 连通分量(connected component)和强连通分量
无向图中,极大的连通子图为该图的连通分量。显然,任 何连通图的连通分量只有一个,即它本身,而非连通图有 多个连通分量。
7.1 图及其抽象数据类型
图的基本概念
1. 图(graph)的定义
u图G是由顶点(Vertex)集合V和顶点间的关系集合E (边Edge的集合)组成的一种数据结构,可以用二元 组定义为:G=(V,E)。
V={vi| vi ∈某个数据元素集合} E={(vi ,vj)|vi ,vi∈V} 或E = {〈vi ,vi〉|vi ,vi,∈V且Path}
对于上图中的非连通图,它的连通分量见下图。
1
2
5
4
3
图 7-6 图 7-4(b)的连通分量
7.1 图及其抽象数据类型
图的基本概念
10. 连通分量(connected component)和强连通分量
有向图中,极大的强连通子图为该图的强连通分量。显然, 任何强连通图的强连通分量只有一个,即它本身,而非强 连通图有多个强连通分量。
7.1 图及其抽象数据类型
图的基本概念
1. 图(graph)的定义
例如,对于下图所示的无向图G1和有向图G2,它们的数
据结构可以描述为:G1=(V1,E1), 其中 V1={a,b,c,d},E1={(a,b),(a,c),(a,d),(b,d),(c,d)},
《数据结构图》课件

欢迎来到《数据结构图》PPT课件!本课程将带您深入了解数据结构的定义、 常见类型以及应用领域。让我们一起开始探索这个精彩的主题吧!
概述
通过本节课,您将了解到数据结构的基本概念和作用。我们将探讨如何存储 和组织数据以及优化数据访问和操作的方法。
数据结构的定义
在这一节中,我们将介绍数据结构的定义,并探讨数据的抽象和表示方法。 了解数据结构的定义将有助于您理解数据在计算机中的常重要,因为不同的数据结构适用于不同的场景和数据操作需求。本节将深入 研究线性结构、树形结构和图形结构。
线性结构
线性结构是最简单且最常见的数据结构类型之一。我们将研究数组、链表和 栈等线性结构的特点、优点和缺点,并了解它们在实际应用中的使用情况。
树形结构
树形结构是一种层次化的数据结构,常用于表示层级关系。本节我们将探讨 二叉树、堆和AVL树等树形结构,并讨论它们在数据处理和搜索中的应用。
图形结构
图形结构是一种包含节点和边的数据结构,用于表示复杂的关联关系。本节我们将深入研究图的定义、遍历算 法和最短路径算法,并讨论图形结构在社交网络和地图导航中的应用。
数据结构的应用
数据结构是计算机科学领域中的核心概念,几乎应用于所有的软件开发领域。 本节我们将探讨数据结构在数据库、图形处理和算法设计中的实际应用。
数据结构图的设计原则
了解数据结构图的设计原则有助于我们创建清晰、易于理解的数据结构图。 本节我们将讨论数据结构图的设计原则,例如模块化、抽象和简洁性。
数据结构与算法思维导图-简单高清脑图_知犀
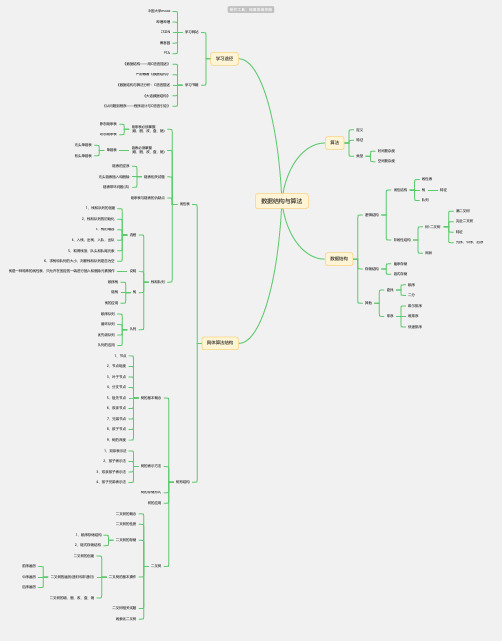
数据结构与算法算法定义特征类型时间复杂度空间复杂度数据结构逻辑结构线性结构线性表栈特征队列非线性结构树-二叉树满二叉树完全二叉树特征先序、中序、后序网状存储结构循序存储链式存储其他查找顺序二分排序希尔排序堆排序快速排序学习途径学习网站中国大学mooc哔哩哔哩CSDN 博客园PTA学习书籍《数据结构——用C语言描述》严蔚敏著《数据结构》《数据结构与算法分析:C语言描述《大话数据结构》《从问题到程序——程序设计与C语言引论》具体算法结构线性表顺序表必须掌握(增、删、改、查、销)静态顺序表动态顺序表链表必须掌握(增、删、改、查、销)单链表无头单链表有头单链表链表相关试题链表的逆序无头链表插入和删除链表带环问题(次)顺序表与链表的仇缺点栈和队列流程1、栈和队列的创建2、栈和队列的初始化3、栈的增容4、入栈,出栈,入队,出队5、取得栈顶,队头和队尾元索6、求栈和队列的大小、判断栈和队列是否为空说明栈是一种特殊的线性表,只允许在固定的一端进行插入和删除元素操作栈顺序栈链栈栈的应用队列顺序队列循环队列优先级队列队列的应用树形结构树的基本概念1、节点2、节点呃度3、叶子节点4、分支节点5、祖先节点6、双亲节点7、兄弟节点8、孩子节点9、树的深度树的表示方法1、双亲表示法2、孩子表示法3、双亲孩子表示法4、孩子兄弟表示法树的存储形式树的应用二叉树二叉树的概念二叉树的性质二叉树的存储1、顺序存储结构2、链式存储结构二叉树的基本搡作二叉树的创建二叉树的遍历(递归和非递归)前序遍历中序遍历后序遍历二叉树的增、删、改、查、销二叉树相关试题线索化二叉树。
2024版《数据结构图》ppt课件

良好的数据结构可以带来更高的运 行或存储效率,是算法设计的基础, 对程序设计的成败起到关键作用。
常见数据结构类型介绍
线性数据结构
如数组、链表、栈、队 列等,数据元素之间存
在一对一的关系。
树形数据结构
如二叉树、多叉树、森 林等,数据元素之间存
在一对多的关系。
图形数据结构
由顶点和边组成,数据 元素之间存在多对多的
队列定义、特点及应用场景
队列的特点 只能在队尾进行插入操作,队头进行删除操作。
队列是一种双端开口的线性结构。
队列定义、特点及应用场景
应用场景 操作系统的任务调度。 缓冲区的实现,如打印机缓冲区。
队列定义、特点及应用场景
广度优先搜索(BFS)。
消息队列和事件驱动模型。
串定义、基本操作及实现方法
最短路径问题 求解图中两个顶点之间的最短路径,即路径上边 的权值之和最小。
3
算法介绍 Prim算法、Kruskal算法、Dijkstra算法、Floyd 算法等。
拓扑排序和关键路径问题探讨
拓扑排序
对有向无环图(DAG)进行排序, 使得对每一条有向边(u,v),均有
u在v之前。
关键路径问题
求解有向无环图中从源点到汇点 的最长路径,即关键路径,它决
遍历二叉树和线索二叉树
遍历二叉树
先序遍历、中序遍历和后序遍历。遍历算 法可以采用递归或非递归方式实现。
VS
线索二叉树
利用二叉链表中的空指针来存放其前驱结 点和后继结点的信息,使得在遍历二叉树 时可以利用这些线索得到前驱和后继结点, 从而方便地遍历二叉树。
树、森林与二叉树转换技巧
树转换为二叉树
加线、去线、层次调整。将树中的每个结点的所有孩子结点用线连接起来,再去掉与原结点相连的线,最后 将整棵树的层次进行调整,使得每个结点的左子树为其第一个孩子,右子树为其兄弟结点。
数据结构课件图PPT培训课件

子 图:设有两个图 G=(V, E) 和 G’=(V’, E’)。若 V’ V 且
E’ E, 则称 图G’ 是 图G 的子图。
带权图:即边上带权的图。其中权是指每条边
可以标上具有某种含义的数值(即与 边相关的数)。
网 : →带权图
连通图:在无向图中, 若从顶点v1到顶点v2有
例3 : 有权图(即网络)的邻接矩阵如何表示?
定义: A.Edge[ i ][ j ]= 以有向网为例:
Wij <vi, vj> 或(vi, vj)∈VR ∞ 无边(弧)
N
v1
3 v6
1 v5
5 7 6
5
8
v2 4
顶点表: ( v1 v2 v3 v4 v5 v6 ) 邻接矩阵: ∞∞ 5∞5∞∞∞7∞7 ∞∞ ∞ v1
数据结构课件图
1. 哥尼斯堡七桥问题
德国古城—哥尼斯堡—普雷格尔河—七
2. 桥问题:从任一桥头出发,依次走过每
座
3. 桥,每座桥只走一次,最后回到出发点。
4.
——一笔画问
题
第7章 图
7.1 基本术语 7.2 存储结构 7.3 图的遍历 7.4 图的连通性 7.5 图的应用
7.1 图的基本术语
图:记为 G=( V, E )
V=vertex E=edge
其中:V 是G 的顶点集合,是有穷非空集;
E 是G 的边集合,是有穷集。
问:当E(G)为空时,图G存在否? 答:还存在!但此时图G只有顶点而没有边。
v1 v2
v3
v4
v5
v1 v2
有向图:图G中的每条边都是有方向的;
v3 v4
无向图:图G中的每条边都是无方向的;
