硬件加速的渐进式多边形模型布尔运算
赵汉理教授简介个人基本情况

赵汉理教授简介一、个人基本情况姓名:赵汉理学历/学位:博士研究生/博士职称职务:院长助理/瓯江特聘教授二、主要研究方向及研究团队专业领域:计算机图形图像处理主要研究兴趣:深度学习、医学图像分析与处理、图像识别、图像编辑、GPU并行计算、移动图形技术三、学习与工作经历2011年10月—现在温州大学硕士生导师2011年09月—现在温州大学副教授2009年12月—2011年09月温州大学讲师2008年11月—2009年05月香港中文大学研究助理2007年12月—2008年03月香港中文大学研究助理2004年09月—2009年12月浙江大学硕博连读2000年09月—2004年07月四川大学大学本科四、主要工作经历及业绩中国计算机学会(CCF)计算机辅助设计与图形学专业委员会委员。
曾两度在香港中文大学担任研究助理工作,曾赴土耳其、荷兰、加拿大等国家参加国际学术交流。
先后主持国家自然科学基金1项、浙江省自然科学基金2项、教育部产学合作协同育人项目1项、浙江大学CAD&CG国家重点实验室开放课题3项、市厅级项目4项、横向课题1项,曾获得国家发明专利授权15项、软件著作权登记12项,出版教材1部,在TVCG、Neurocomputing、CGA、C&G、TVC、计算机学报、计算机辅助设计与图形学学报、中国图象图形学报、浙江大学学报等高水平国际国内期刊以及CGI、CASA、CVM、CAD/Graphics、Chinagraph、ChinaCAD&CG等国内外主流学术会议上发表SCI论文23篇、国内一级期刊论文7篇。
担任CIDE-DEA2014、NICOGRAPH2016、ChinaVR2016、ChinaVR2017、ChinaVR2018、ChinaCAD&CG2018、ChinaCAD&CG2019等会议程序委员会委员,以及Neurocomputing、TVC、Information Sciences等SCI国际期刊论文评审专家。
学习Blender的几何建模工具 利用布尔运算与修剪建立复杂模型

学习Blender的几何建模工具:利用布尔运算与修剪建立复杂模型Blender是一个功能强大的三维建模软件,它提供了多种工具和技巧来创建复杂的模型。
其中,布尔运算和修剪是两个常用的几何建模工具,可以帮助我们建立多边形模型,实现复杂模型的快速建立。
1. 布尔运算布尔运算是一种基于多边形集合之间的逻辑操作,可以通过组合、相交和减去等操作来创建新的多边形形状。
在Blender中,布尔运算工具位于模型编辑模式下的“Mesh”菜单中。
首先,我们需要创建两个或多个多边形对象作为操作的输入。
选择第一个对象,然后按“Shift”键选择其他对象,最后按下Ctrl + J组合对象。
现在,我们可以选择布尔运算工具。
在布尔运算菜单中,选择合适的操作类型,如并集、相交或差异。
然后,选择要操作的对象,点击“应用”按钮。
Blender会根据选择的操作类型在3D视图中显示生成的新形状。
我们还可以通过调整对象的顺序和使用不同的操作类型来获得不同的结果。
2. 修剪工具修剪工具是一种常用的几何建模方法,可以通过删除或提取多边形的一部分来创建复杂的形状。
在Blender中,修剪工具位于模型编辑模式下的“Mesh”菜单中。
要使用修剪工具,我们首先要选择要进行操作的边或面。
通过按住Alt键并单击鼠标右键选择,我们可以选择一个或多个多边形的边或面。
选择完毕后,点击修剪工具按钮。
使用修剪工具可以实现两种不同的操作:通过删除选定部分来创建一个孔,或者通过提取选定部分来创建一个新的对象。
在修剪工具菜单中,选择适当的操作类型,并点击“应用”按钮。
修剪工具也可以与布尔运算相结合使用,以创建更复杂的模型。
通过使用布尔运算创建一个几何形状,然后使用修剪工具删除或提取部分内容,我们可以快速地建立出复杂的形状。
学习Blender的几何建模工具需要一定的实践和经验。
通过反复尝试和探索不同的操作类型和组合,我们可以逐渐掌握这些工具的使用技巧,并创建出更复杂、更精细的三维模型。
赵汉理教授简介个人基本情况

赵汉理教授简介一、个人基本情况姓名:赵汉理学历/学位:博士研究生/博士职称职务:院长助理/瓯江特聘教授二、主要研究方向及研究团队专业领域:计算机图形图像处理主要研究兴趣:深度学习、医学图像分析与处理、图像识别、图像编辑、GPU并行计算、移动图形技术三、学习与工作经历2011年10月—现在温州大学硕士生导师2011年09月—现在温州大学副教授2009年12月—2011年09月温州大学讲师2008年11月—2009年05月香港中文大学研究助理2007年12月—2008年03月香港中文大学研究助理2004年09月—2009年12月浙江大学硕博连读2000年09月—2004年07月四川大学大学本科四、主要工作经历及业绩中国计算机学会(CCF)计算机辅助设计与图形学专业委员会委员。
曾两度在香港中文大学担任研究助理工作,曾赴土耳其、荷兰、加拿大等国家参加国际学术交流。
先后主持国家自然科学基金1项、浙江省自然科学基金2项、教育部产学合作协同育人项目1项、浙江大学CAD&CG国家重点实验室开放课题3项、市厅级项目4项、横向课题1项,曾获得国家发明专利授权15项、软件著作权登记12项,出版教材1部,在TVCG、Neurocomputing、CGA、C&G、TVC、计算机学报、计算机辅助设计与图形学学报、中国图象图形学报、浙江大学学报等高水平国际国内期刊以及CGI、CASA、CVM、CAD/Graphics、Chinagraph、ChinaCAD&CG等国内外主流学术会议上发表SCI论文23篇、国内一级期刊论文7篇。
担任CIDE-DEA2014、NICOGRAPH2016、ChinaVR2016、ChinaVR2017、ChinaVR2018、ChinaCAD&CG2018、ChinaCAD&CG2019等会议程序委员会委员,以及Neurocomputing、TVC、Information Sciences等SCI国际期刊论文评审专家。
《3DMAX课程》五、复合建模和多边形建模

第五章 复合建模和多边形建模
2、 放样建模
5.2.3 “变形”卷展栏
“缩放”变形工具的应用。 简单的放样对象,通过缩放变形的控制改变截面在路径上大小,可以得到复杂的放样对象。左图 所示为圆环 形状的截面图形沿直线放样得到的圆管对象,如右图所示调整缩放变形曲线后,得到的花瓶模型。。
第五章 复合建模和多边形建模
第五章 复合建模和多边形建模
2、 放样建模
5.2.4 “变形”卷展栏
放样对象创建后,还可以对它的截面图形进行变形控制,产生更复杂的 造型。选择放样对象,切换到“修改”面板,在修改命令面板上出现了 “变形”卷展栏,如图所示。在该卷展栏中,主要有五种变形工具可以 应用于放样对象。 在每个工具按钮的右侧都有一个灯泡图标,单击可以切换该变形工具是 否启用。单击每个变形工具按钮,都会弹出相应的变形控制窗口,在变 形控制窗口调整变形曲线,放样对象就会产生相应的变形效果。
第五章 复合建模和多边形建模 1、布尔运算
5.1.2 布尔对象 在“布尔参数”卷展栏中,单击“添加运算对象”按钮可以实现添加操作对象;在“运算对象”列表中显 示布尔运算的所有操作对象,并可以选择要修改的操作对象;单击“移除运算对象”按钮可以将操作对象 从布尔运算中去除。可以选择多个操作对象并分别设置该对象与原始对象的布尔运算类型,如图所示为原 始长方体对象分别与球体进行并集运算、圆柱体进行差集运算的效果。
前几章介绍的多种建模方法可以用来制作简单或比较规则的模型,如果想要制作一些精细的、 表面造型复杂的模型就需要学习高级建模的方法来实现,多边形建模就是高级建模的方法之 一。所谓多边形建模是指,在较简单的模型上,通过对组成模型的点、边、面等等进行增减、 位置调整等编辑操作来产生所需模型。 多边形建模有两种方式:编辑多边形和编辑网格。多边形建模具有强大的建模功能,熟练掌 握这种建模方法,可以随心所欲地制作各种模型。 多边形建模方法比较容易理解,非常适合初学者学习,并且在建模的过程中可以按空间想象 进行编辑修改。几乎所有的几何体都可以使用多边形建模方法进行再次几何造型,封闭的样 条线也可以转换成曲面进行多边形建模。
OpenCASCADE布尔运算简介
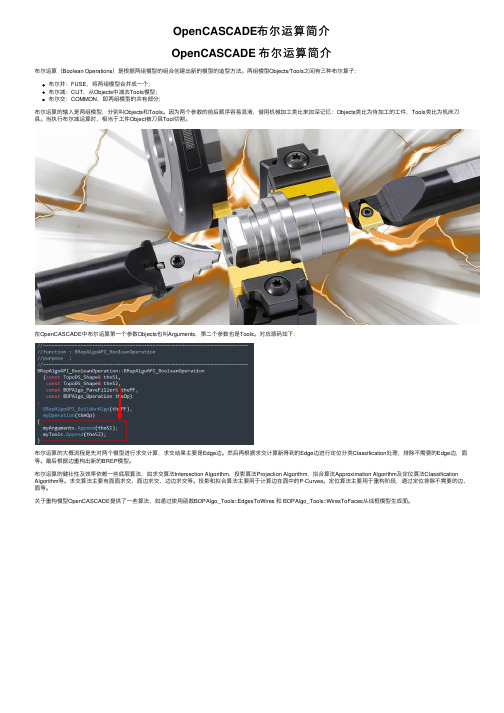
OpenCASCADE布尔运算简介OpenCASCADE 布尔运算简介布尔运算(Boolean Operations)是根据两组模型的组合创建出新的模型的造型⽅法。
两组模型Objects/Tools之间有三种布尔算⼦:布尔并:FUSE,将两组模型合并成⼀个;布尔减:CUT,从Objects中减去Tools模型;布尔交:COMMON,即两组模型的共有部分;布尔运算的输⼊是两组模型,分别叫Objects和Tools。
因为两个参数的前后顺序容易混淆,借⽤机械加⼯类⽐来加深记忆:Objects类⽐为待加⼯的⼯件,Tools类⽐为机床⼑具。
当执⾏布尔减运算时,相当于⼯件Object被⼑具Tool切割。
在OpenCASCADE中布尔运算第⼀个参数Objects也叫Arguments,第⼆个参数也是Tools。
对应源码如下:布尔运算的⼤概流程是先对两个模型进⾏求交计算,求交结果主要是Edge边。
然后再根据求交计算新得到的Edge边进⾏定位分类Classification处理,排除不需要的Edge边,⾯等。
最后根据边重构出新的BREP模型。
布尔运算的健壮性及效率依赖⼀些底层算法,如求交算法Intersection Algorithm,投影算法Projection Algorithm,拟合算法Approximation Algorithm及定位算法Classification Algorithm等。
求交算法主要有⾯⾯求交、⾯边求交、边边求交等。
投影和拟合算法主要⽤于计算边在⾯中的P-Curves。
定位算法主要⽤于重构阶段,通过定位排除不需要的边、⾯等。
关于重构模型OpenCASCADE提供了⼀些算法,如通过使⽤函数BOPAlgo_Tools::EdgesToWires 和 BOPAlgo_Tools::WiresToFaces从线框模型⽣成⾯。
关于定位算法,提供BOPTools_AlgoTools::ComputeState计算点、边、⾯相对于其他模型的位置状态。
Maya多边形模型建模的命令与工具Maya多边形模型建模的命令与工具

剪切面工具
剪切面工具是一个非常方便的剪切工具,它能够对不 规则的模型进行精确的剪切。但是我们一般更多是是用这个工具来进 行对不规则的模型和布线规律上去加线使用。 首先我们来示范一下剪切面命令来对模型加线如图:首先选中模 型然后点击剪切面命令鼠标左键点住不上移动鼠标来确定切线的方向, 确定好线的方向和位置之后鼠标左键松手就可以了,大家可以看到就 成功的加上了这样一条线条。
多边形填坑命令
填坑命令和补面命令很相似,但是填坑命令更加的快捷。 如果我的模型有空洞的地方存在那么我就可以执行填坑命令一次性进 行补面的操作。 如图左这个圆柱体是没有顶面的,我们选择模型之后执行填坑命 令。洞就被补上了(如图中),但是没有线条穿透。我们也可以通过 自由加线工具将其布线添补完整。如图右所示。
三、多边形模型的基础属性栏里面的可调整参数。创建并选中模型, 然后在基础通道栏里面。Translate(位移)、rotate(旋转) 、 scale(缩放)。
创建多边形以及多边形的基本属性
四、在INPUTS下面的polysphere1点击就可以展开模型的参数信息(模 型半径、长、宽、高、分段数等)。各种不同的几何体模型相应的参 数信息也有所不同。
就是普通复制模式(和ctrl+d效果一致)。 为关联 复制(被复制物体跟随原模型发生同样的变化),如图所示。
复制与特殊复制
复制的物体的位移值参数。如我想 让复制出来的模型美X轴5个单位复制出来一个的话就可以在第一个数 值输入5(默认排序X\Y\Z) 点击执行就 复制一个多次点击复制多个。
合并模型命令
所谓合并物体的意思就是把原本是两个物体的模型合并成同一个 物体。把这两个不同的模型进行合并为一个物体的话先选中两个模型 然后执行合并物体命令 后发现颜色都变成一致了并且是一个整体 了。那么我们就可以对它进行整理的调整和修改了。
3dmax的布尔运算

在创建几何体面板下面的创建合成物体面板,在这个区域包含了可以对三维模型进行更为复杂的解算命令,这些命令是以基本几何体或图形为构件进行不同形式的组合以达到相应的效果。
其中布尔运算命令在建筑模型制作中被广大设计师所利用。
如图001所示,布尔运算制作的穿透模型效果。
注:很多初学者常常把布尔运算理解为简单的“抠洞”,其实这种说法稍显片面。
当了解了布尔运算的操作原理后读者朋友就可以举一反三,并把这个有意思的工具加入到自己的工作流程中。
接下来我们先来看看布尔运算的定义,布尔是英国的数学家,在1847年发明了处理二值之间关系的逻辑数学计算法,包括联合、相交、相减。
在图形处理操作中引用了这种逻辑运算方法以使简单的基本图形组合产生新的形体。
并由二维布尔运算发展到三维图形的布尔运算。
、如图002是布尔运算制作的牌九。
从以上两个图示我们不难发现,布尔运算不仅可以穿透整个物体,也可以对物体的某一部分进行解算。
好了下面我们来详细的了解下关于布尔运算命令。
首先对于布尔运算要满足的条件是场景中至少包括两个或以上的模型物体用来解算,我们以下面两个物体为例,并把他们命名为物体“A”与物体“B”然后通过布尔运算命令会对“A”与”B”进行加法或者减法的相应操作。
如下图003注:假设盒子为A,球体为B.那么满足运算的前提条件是两个物体的位置一定要有交集,左图004的布置方式是错误的.步骤1首先选择盒子“A”,接下来点击创建面板下合成物体面板招到布尔运算命令,如图005,然后弹出的布尔运算命令面板。
步骤2点击“pick operand b”(拾取物体b)按钮。
然后回到视图,用鼠标左键拾取b物体也就是球体。
到此布尔运算的流程操作完毕,我们不难发现,在默认情况下,布尔运算是基于减法的计算,也就是说用盒子剪掉了盒子与球体相交后剩余的部分。
如下图007.我们说布尔运算的强大不仅仅是基于它的减法操作,适当的运用其他算法也可以优化我们的工作流程,当然这对于设计师的逻辑思维有一定的要求。
硬件加速算法的实现和优化

硬件加速算法的实现和优化随着计算机技术的发展和应用领域的不断扩展,对于算法的计算速度和计算复杂度的要求越来越高,尤其对于大数据处理、图像识别、物体跟踪等应用领域,传统的算法已经无法满足需求。
硬件加速算法的出现,使得算法可以在更短的时间内完成更加复杂的计算任务,对于提升算法的效率和精度起到了重要的作用。
本文将探讨硬件加速算法的实现和优化。
一、硬件加速算法的概念和实现1.1 硬件加速算法的概念硬件加速算法是指借助硬件加速器来完成高效计算和数据处理的算法。
与传统的基于CPU的软件算法相比,硬件加速算法利用了硬件加速器的并行处理能力、高速缓存和存储系统等特点,可以大幅提高算法的执行速度和效率。
1.2 硬件加速算法的实现硬件加速算法的实现需要硬件加速器的支持,通常有三种形式:FPGA、GPU和ASIC。
FPGA(可编程逻辑门阵列)是一种既可以进行硬件加速又可以进行重新编程的芯片。
它可以根据不同应用的需求重新调整部分硬件电路,使得计算密集型任务可以在更短的时间内完成,并且具有较低的功耗。
GPU(图形处理器)是一种专门用于图形处理的硬件加速器,其拥有数千个处理核心和高速存储单元等核心组件,可以高速并行地进行大规模数据处理,在深度学习、计算机视觉、图像处理等领域应用极广。
ASIC(专用集成电路)是一种专门设计用于特定应用领域的芯片。
它由一系列经过优化的电路组成,针对某一类任务进行专门设计,因此可以实现更高的性能和更低的功耗,但是需要更高的开发和生产成本。
二、硬件加速算法的优化2.1 优化空间复杂度硬件加速算法的优化需要从算法的空间复杂度和时间复杂度两个方面来考虑。
空间复杂度是指算法所需的内存空间大小。
为了减少硬件的资源占用,我们需要针对具体算法进行优化,节省内存使用。
例如,在卷积神经网络中,通常采用共享权重的方式来减少卷积核的数量,从而减少内存的使用。
同时,对于深度学习中的反向传播算法,可以采用梯度裁剪的方法来限制反向传播的梯度大小,进而降低内存的使用。
模型布尔运算

模型布尔运算布尔运算是数据处理中常用的基本运算之一,它主要用于逻辑判断和条件筛选等方面。
在模型计算中,布尔运算是不可或缺的一部分,它能够帮助我们更有效地处理数据,从而提高模型的精度和效率。
在模型布尔运算中,涉及到的主要操作符包括与(and)、或(or)、非(not)和异或(xor)等。
以下分别进行详细介绍。
1. 与(and)运算与运算是指当两个操作数都为真时,结果为真,否则结果为假。
在模型计算中,与运算常用于条件判断和筛选等方面,例如:if (a > 0 and b < 10):print("a大于0且b小于10")2. 或(or)运算或运算是指当两个操作数中至少有一个为真时,结果为真,否则结果为假。
在模型计算中,或运算常用于多重条件判断和筛选等方面,例如:if (a > 0 or b > 10):print("a大于0或b大于10")3. 非(not)运算非运算是指对一个操作数取反,即真变假,假变真。
在模型计算中,非运算常用于逆转条件判断等方面,例如:if not (a > 0 and b < 10):print("a不大于0且b不小于10")4. 异或(xor)运算异或运算是指当两个操作数中恰有一个为真时,结果为真,否则结果为假。
在模型计算中,异或运算常用于奇偶性判断或状态转换等方面,例如:if (a % 2 == 0) ^ (b % 2 == 0):print("a和b的奇偶性不同")在模型布尔运算中,除了上述基本操作符,还有一些衍生操作符,例如条件运算(a if b else c)、链式比较(a < b < c)和成员关系(a in b)等。
这些操作符能够帮助我们更快速、更灵活地处理数据,从而提高模型的实用性和适用范围。
总之,模型布尔运算是数据处理中不可或缺的一部分,它不仅能够帮助我们更精确、更高效地处理数据,还能够有效地优化模型的精度和效率。
掌握精准建模 Blender布尔运算和形状建模

掌握精准建模:Blender布尔运算和形状建模Blender是一款功能强大的开源3D建模软件,可以满足各种建模需求。
在Blender中,布尔运算和形状建模是非常重要的技巧之一,可以帮助我们快速精准地创建复杂的模型。
本文将介绍一些关于Blender布尔运算和形状建模的技巧,帮助读者更好地掌握这些技术。
首先,让我们先了解一下什么是布尔运算。
在Blender中,布尔运算是利用基本的几何体通过相交、相加或者相减等方式来创建复杂的模型的方法。
通过布尔运算,我们可以快速地在模型上添加、删除或者合并各种几何形状。
在Blender中,使用布尔运算的方式有很多种。
一种常用的方式是使用“布尔”修饰符。
在开始建模之前,我们需要先创建几个基本的几何体,可以是立方体、球体、圆柱体等。
然后,在编辑模式下选择一个目标对象,切换到“对象数据”选项卡中,选择“布尔修饰符”,并选择要进行布尔运算的几何体。
最后,选择相应的布尔运算方式,例如“相交”、“相减”或者“相加”。
点击“应用”按钮后,我们就可以看到运算后的结果了。
另一种常用的布尔运算方式是使用“差集”或者“交集”功能。
这些功能可以通过选择两个对象,然后使用Ctrl + - 或者Ctrl + J的快捷键来实现。
这些快捷键在编辑模式下非常方便,可以快速地完成布尔运算。
除了布尔运算,形状建模也是Blender中常用的技巧之一。
形状建模是在一个模型的基础上,通过修改顶点、边和面的位置,来创建新的形状。
形状建模可以用于创建各种有机体、建筑、车辆等复杂模型。
在使用形状建模时,我们需要了解一些基本的操作技巧。
首先是选择模型的不同部分。
在编辑模式下,我们可以使用点选择模式、边选择模式或者面选择模式来选择不同的顶点、边或者面。
使用快捷键1、2、3可以快速地切换选择模式。
接下来是移动、旋转和缩放模型的操作。
在编辑模式下,我们可以使用G键来移动选中的部分,使用R键来旋转选中的部分,使用S键来缩放选中的部分。
多边形建模技巧 Blender中处理复杂模型的方法

多边形建模技巧:Blender中处理复杂模型的方法Blender是一款功能强大的三维建模软件,它拥有许多强大的工具和功能,使其成为处理复杂模型的理想选择。
在本教程中,我们将分享一些在Blender中处理复杂模型的技巧和方法,帮助您更好地应对建模挑战。
1. 使用辅助网格:复杂模型往往具有许多细节和形状,使用辅助网格将有助于更好地控制模型的细节。
在Blender中,您可以通过添加额外的几何形状,如平面或立方体,来创建辅助网格。
然后,您可以将这些形状与主模型进行组合,以获得更好的曲线和细节。
2. 使用切割工具:当您需要将模型切割成不同的部分时,切割工具是非常有用的。
在Blender中,有多种切割工具可供选择,例如刀具和边界切割。
通过选中要切割的边缘或面,然后使用适当的切割工具,您可以轻松地将模型切割成多个部分,以便更好地编辑和修改。
3. 使用镜像模型:在处理复杂模型时,对称性往往是一个重要考虑因素。
使用Blender的镜像模型工具,您可以简化对称模型的制作过程。
只需选择适当的轴,将模型分割成两半,然后使用镜像模型工具进行对称复制。
这样一来,您只需要编辑和修改一半的模型,另一半将自动做出相应的调整。
4. 使用快照工具:为了处理复杂的模型,有时您可能需要在建模过程中参考其他对象或形状。
在Blender中,您可以使用快照工具来帮助您在场景中创建和管理快照。
通过将需要参考的形状保存为快照,您可以随时将其加载到场景中进行参考和编辑。
5. 使用边缘环工具:在处理复杂模型时,创造平滑的曲线和边缘往往是必需的。
使用Blender的边环工具,您可以轻松地创建平滑的边缘环,并对其进行调整和修改。
只需选中一条边或边环,然后使用适当的工具,您可以轻松地调整和修改其形状,以获得想要的效果。
6. 使用布尔运算:处理复杂模型时,将不同的形状合并成一个单一的对象往往是必须的。
在Blender中,您可以使用布尔运算工具来执行此操作。
通过选择两个或多个对象,并选择适当的布尔运算(如并集、差异或交集),您可以将这些对象合并成一个单一的对象,并在操作后进行进一步的修改和编辑。
使用Blender进行精确的多边形建模

使用Blender进行精确的多边形建模在进行3D建模时,精确的多边形建模是非常重要的。
在这个领域中,Blender是一个功能强大而受欢迎的工具。
本篇文章将介绍如何使用Blender进行精确的多边形建模,无废话,直奔主题。
1. 启动Blender并选择角度单位首先,启动Blender软件并进入建模界面。
在右上角的工具栏中,选择您习惯使用的角度单位,例如度数或弧度。
2.创建基础形状首先,我们需要创建一个基础形状来进行建模。
对于这个示例,我们将以立方体为例。
在3D视图中,按Shift+A或在左上角的"Add"菜单中选择立方体。
这将在场景中创建一个基础的立方体。
3. 进行精确的缩放和移动要对模型进行精确的缩放和移动操作,我们可以使用变换工具栏中的数值输入。
在顶部工具栏中,找到"Transform"选项,并确保开启数值输入。
然后,您可以在数值输入框中直接输入精确的数值来控制模型的缩放、移动和旋转。
4. 使用精确的测量工具在Blender中,我们可以使用精确的测量工具来确保模型的精确度。
在顶部工具栏中,找到"Measure"选项,并选择所需的工具,例如"Length"或"Angle"。
点击两个点或线来测量长度或角度,并在底部状态栏中看到结果。
这可以帮助您确保模型的尺寸和角度符合您的要求。
5. 使用网格工具进行细微调整当进行精确的多边形建模时,细微调整是不可避免的。
在Blender 中,我们可以使用网格工具来进行这些调整。
在左侧工具栏中,找到"Mesh Tools"选项,并选择所需的工具,例如"Vertex Slide"或"Edge Slide"。
这些工具可以帮助您将顶点或边缘移动到所需的位置,从而使模型更加精确。
6. 使用对齐工具来保持模型的对称性在建模过程中,保持模型的对称性非常重要。
多边形布尔运算-Read

U SING M AYA :P OLYGONAL M ODELING103多边形布尔运算用户可以使用多边形布尔运算来操作表面相交的物体。
根据选择的布尔运算类型——差、并或交,可以产生新的几何体。
注意要成功地进行布尔运算,表面不是必须相交,但如果表面不相交,那么操作的结果可能没有用处。
本章主要介绍如何使用布尔运算,包括下列内容: z 多边形布尔操作(103页) z 布尔运算的类型(104页)z 使用构造历史编辑布尔操作(108页) z 使用多边形布尔运算实现修剪功能(112页) z动画多边形布尔运算(113页)多边形布尔操作布尔操作是一个比较流行和直观的建模方法。
它使用一个形状来作用于另一个形状,直观的讲就是使用一个物体来雕刻另一个物体,如图所示。
选择的第一个物体的形状是产生结果形状的基础,选择的第二个物体是工具物体,它将作用于第一个物体。
作为一个操作的结果,布尔操作将产生一个新的形状节点。
并且如果构造历史被保留,当布尔操作完成后,用户可以使用通道盒、Hypergraph (超图)或Outliner6U SING M AYA P OLYGONAL M ODELING来选择原始的形状,并且可以使用原始的形状来编辑布尔操作的结果。
NURBS转换为多边形和布尔操作在进行布尔操作时,工具表面和基础表面相交的部分必须是完全闭合的,并且布尔操作对相交表面的质量是非常敏感的。
对于由NURBS表面转换而来的多边形表面(使用NURBSTo Polyous),有时可能需要进行一些编辑,才能用于布尔操作。
失败的布尔操作有时,因为拓扑运算方面的原因,布尔操作可能会失败,此时下面的错误信息就会显示出来:Cannot perform boolean operations for topological reasons。
当这种情况发生时,在操作之前选择的物体可能会变得不可见。
为恢复到原始的状态,使用命令Undo来恢复布尔操作。
occt 加速布尔切运算

Open CASCADE Technology (OCCT) 是一种开源的几何建模库,它提供了许多用于处理三维模型的功能,包括布尔运算。
布尔运算是一种将两个三维模型进行操作的方法,以产生一个新的模型。
这些操作包括交集(将两个模型的共有部分保留)、并集(将两个模型的所有部分都保留)、差集(从一个模型中减去另一个模型中的部分)和异或操作(只保留两个模型中不同的部分)。
在OCCT 中,布尔运算可以通过使用BRepTools::PerformBooleanOperation方法来进行。
以下是一个基本的示例:cpp复制代码// 创建两个 BRep 对象BRep_Builder builder1;builder1.MakeBox(gp_Pnt(0, 0, 0), gp_Pnt(10, 10, 10),Standard_Real(1), &shape1);BRep_Builder builder2;builder2.MakeBox(gp_Pnt(5, 5, 5), gp_Pnt(15, 15, 15),Standard_Real(1), &shape2);// 进行布尔交集运算BRepTools::PerformBooleanOperation(shape1, shape2,Standard_True, Standard_True, Standard_Real(0.001), &shape3); 在这个例子中,我们创建了两个盒子形状的BRep 对象,然后使用BRepTools::PerformBooleanOperation方法进行布尔交集运算。
参数Standard_True表示我们想要保留所有的交集,Standard_Real(0.001)是一个公差参数,用于确定交集的精度。
这只是一个基本的示例,实际使用中可能需要进行更复杂的操作,并处理更多的细节。
在OCCT 的文档和示例中可以找到更多关于如何使用这个库进行布尔运算的信息。
cura 布尔运算

cura 布尔运算布尔运算是计算机科学中一种基础的逻辑运算方法,其运算对象为两个逻辑值(真或假),运算结果也是一个逻辑值。
cura 布尔运算是基于 cura 算法的布尔运算,它是旨在对三维物体进行几何模型操作的一种方法。
本文将介绍 cura 布尔运算的原理、应用以及其在三维打印中的作用。
一、cura 布尔运算的原理cura 布尔运算是基于封闭多边形之间的交叉和重叠区域进行计算的。
具体而言,cura 布尔运算分为三种基本操作:并集、交集和补集。
并集操作将两个物体的空间合并为一个整体,交集操作提取两个物体共有的部分,而补集操作则取出一个物体相对于另一个物体的差异部分。
二、cura 布尔运算的应用cura 布尔运算在三维建模中有着广泛的应用。
首先,cura 布尔运算可以用于模型修复。
当我们通过扫描或其他方式获取到的三维模型存在空洞或错误时,可以通过cura 布尔运算来修复模型,使其符合要求。
其次,在模型设计中,cura 布尔运算可以将多个组件进行组合和重叠,生成新的复杂模型。
此外,cura 布尔运算还可以用于模型的切割和切割补偿,以满足不同的生产需求。
三、cura 布尔运算在三维打印中的作用在三维打印中,cura 布尔运算扮演着重要的角色。
首先,通过 cura布尔运算,可以对多个模型进行组合打印,提高打印效率。
例如,当需要打印一个由多个零件构成的物体时,可以通过 cura 布尔运算将各个零件合并为一个整体,减少打印时间和材料浪费。
其次,cura 布尔运算还可以解决打印过程中支撑结构的问题。
通过交集操作,可以生成支撑结构,并在打印完成后轻松去除。
此外,cura 布尔运算还可以用于模型修复,填补模型的空洞或错误,确保打印出的物体质量良好。
总结:cura 布尔运算作为一种基本的逻辑运算方法,在三维打印中发挥着重要的作用。
通过它,我们可以对物体进行模型修复、组合打印以及生成支撑结构等操作,提高打印效率和打印质量。
maya布尔运算怎么用?maya布尔运算的详细使用教程

maya布尔运算怎么⽤?maya布尔运算的详细使⽤教程布尔运算也是maya建模中⼀个经常不容易达到预期效果的领域,但是如果你能学会按照maya的运算规则来思考这些问题,并且及时找出症结的所在,那么⽤起布尔运算来会得⼼应⼿得多。
1、布尔运算的选择先后顺序有误。
这对并集和交集运算没有影响,但会导致在差集运算时达不到预期效果(如图⼀、图⼆)。
解决⽅法是按“Ctrl+Z”返回到上⼀步,重新调整模型的选择顺序,再次进⾏布尔差集运算即可。
2、布尔运算的其中⼀个模型与另⼀个模型法线整体相反(图三)。
此时进⾏布尔运算时模型会消失。
判断⽅法:单击菜单栏“显⽰”,将光标移动到⼀级下拉菜单⽬录“多边形”上,单击⼆级下拉菜单⽬录“⾯法线”,此时可以看到法线⽅向(图四)。
如果模型法线彼此整体相反,可选中需要恢复法线⽅向的模型,单击菜单栏“法线”,单击⼀级下拉菜单⽬录“反向”,将之前被反向的模型法线还原回来,然后即可成功进⾏布尔运算(图五)。
3、模型太过复杂多⾯。
此时进⾏布尔运算会占⽤⼤量内存,当电脑内存不⾜或maya版本较低时,运算将不能达到预期效果。
例如将⼀个按照图六属性创建的圆柱体与⼀个默认设置的圆环进⾏布尔差集运算,选择顺序是先选圆柱体后选圆环(图七),那么将产⽣图⼋的错误结果。
解决办法:建模初期尽可能减少⾯的数量,也不要执⾏任何光滑操作,如果要看效果,可以按“3”键观察⾼模。
4、进⾏布尔运算的多个模型相接触的地⽅没有任何线穿过。
例如图九中左边两个模型的接触⾯没有线穿过,右边有⼀条线穿过。
左右两种情况下布尔运算虽然都能达到预期效果,但左边模型在布尔运算结束后⽆法再进⾏交互式分割(图⼗、⼗⼀),因此为了防⽌后续操作⽆法进⾏,在布尔运算前⼀定要将模型的接触⾯添加⼀条线。
以本图中的模型为例,加分割线操作⽅法如下:选中圆柱体,单击菜单栏“编辑⽹格”,单击⼀级⽬录下拉菜单中的“交互式分割⼯具”(图⼗⼆),在圆柱体上单击确定第⼀个节点位置,再次单击确定下⼀个节点位置(图⼗三),直到分割线画好以后按“Enter”键即可。
rhino布尔运算

rhino布尔运算
Rhino布尔运算是指在Rhino软件中使用布尔运算进行3D建模操作。
布尔运算是指将两个或多个对象进行相交、差异或联合操作,以生成新的几何体。
在Rhino中,可以使用布尔运算来创建复杂的几何体,例如雕塑、建筑物或机械部件。
Rhino中支持的布尔运算包括求交(Intersection)、求差(Difference)和求并(Union)。
在执行布尔运算前,需要将要操作的对象转换为多边形网格(Mesh)或NURBS曲面(NURBS Surface)。
然后,通过选择要操作的对象和执行相应的布尔运算命令来创建新的几何体。
Rhino布尔运算具有以下优点:
1. 创建复杂几何体的速度比手动建模快。
2. 可以在不改变原始对象的情况下创建新的几何体。
3. 可以使用布尔运算来组合多个对象,从而创建更复杂的几何体。
使用Rhino布尔运算时,需要注意以下几点:
1. 对象的几何形状必须相互重叠,才能进行布尔运算。
2. 对象必须是有效的几何实体,即不能有开放的边缘或无效的曲面。
3. 对象的几何形状越复杂,执行布尔运算的速度越慢。
总之,Rhino布尔运算是一种强大的3D建模工具,可以帮助设计师快速创建复杂的几何体。
在使用时,需要注意对象几何形状的合
法性和复杂度,以保证操作的准确性和效率。
创建精确的多边形模型 Blender三角面和四边面技巧

创建精确的多边形模型:Blender三角面和四边面技巧Blender是一款功能强大的3D建模软件,它可以帮助我们创建各种复杂的模型。
在这篇文章中,我将与大家分享一些关于Blender中三角面和四边面技巧的内容。
首先,让我们来谈谈三角面和四边面之间的区别。
三角面是由三个顶点和三条边组成的面,而四边面则由四个顶点和四条边组成。
在建模过程中,我们通常会使用四边面来创建模型,因为它们更易于控制和编辑。
然而,在某些情况下,我们可能需要将四边面细分为三角面,以获得更好的拓扑结构和更流畅的曲线。
在Blender中,我们可以使用一些技巧来创建精确的多边形模型。
首先,确保在建模过程中使用最少的三角面。
这可以通过将四边面分割为更多的四边面来实现。
可以通过在四边面上选取两个相邻顶点,然后按下快捷键"J"来实现分割。
此操作将创建一条连接两个顶点的新边,并将四边面拆分为两个三角面。
除了分割四边面之外,我们还可以使用Blender中的额外工具来创建精确的多边形模型。
例如,我们可以使用Loop Cut工具在模型上创建额外的边缘环。
在编辑模式下选取一个面,然后按下快捷键"Ctrl + R",然后移动鼠标来调整边缘环的位置。
然后按下Enter键确认位置。
通过添加额外的边缘环,我们可以更方便地控制模型的细节。
另一个很有用的技巧是使用Blender中的布尔运算工具。
布尔运算工具可以将两个或多个物体组合在一起,创建出更复杂的形状。
例如,我们可以创造一个正方体和一个球体,在编辑模式下将它们选中,然后使用布尔运算工具将两个物体相交。
这样可以创建一个具有圆形拓扑结构的洞。
布尔运算工具可以帮助我们更高效地创建复杂的多边形模型。
此外,在使用Blender创建多边形模型时,还应注意保持模型的拓扑结构良好。
良好的拓扑结构有助于保持模型的形状和动画变形。
在建模过程中,我们应尽量避免创建尖锐的角或重叠的面。
当改变模型形状时,这些问题可能会导致不正常的变形。
ue布尔算法

ue布尔算法UE布尔算法是一种用于判断一个图形是否在另一个图形内部的算法。
UE布尔算法的全称是Unified Extensible Firmware Interface Boolean Algorithm,它是一种基于布尔运算的算法,可以快速而准确地判断一个图形的位置关系。
UE布尔算法的原理是将两个图形进行布尔运算,通过计算得到两个图形的交集、并集和补集,从而判断出一个图形是否包含另一个图形。
这个算法的优点是可以处理复杂的图形,而且计算速度非常快。
在UE布尔算法中,图形被表示为一组有序的点的集合。
通过对这些点进行布尔运算,可以得到图形的交集、并集和补集。
对于一个图形而言,如果它的交集为空集,那么说明它不在另一个图形内部;如果它的交集等于自身,那么说明它完全在另一个图形内部;如果它的交集不为空集,但也不等于自身,那么说明它部分在另一个图形内部。
UE布尔算法的应用非常广泛。
在计算机图形学中,它可以用来判断一个点是否在一个多边形内部,或者判断一个多边形是否在另一个多边形内部。
在地理信息系统中,它可以用来判断一个地理区域是否在另一个地理区域内部。
在计算机辅助设计中,它可以用来判断一个物体是否在另一个物体内部。
UE布尔算法的实现方式有很多种,可以通过编程语言来实现,也可以通过图形处理软件来实现。
在编程语言中,可以使用循环和条件语句来实现布尔运算,通过比较两个图形的点的位置关系来判断一个图形是否在另一个图形内部。
在图形处理软件中,可以使用图形界面来进行布尔运算,通过将两个图形进行组合和分割来得到交集、并集和补集。
虽然UE布尔算法非常强大和实用,但它也存在一些限制。
首先,它只能处理二维图形,不能处理三维图形。
其次,它对图形的表示方式有一定的要求,图形必须是由有序的点的集合组成,不能有重复的点。
此外,UE布尔算法对计算资源的要求比较高,需要有足够的内存和处理能力来进行运算。
UE布尔算法是一种用于判断一个图形是否在另一个图形内部的算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p r o x i ma t e t he e n c l os e d bo u n da r i e s o f po l y g o ns a n d t h e i n t e r s e c t i o n c a l c ul a t i o ns a r e p e r f o r me d a s t h e i n / o u t
l yg o na l r e c o n s t r uc t i o n ,wh e r e t h e p r e c i s i o n c o nt r o l a nd p r o c e s s i n g e ic f i e nc y a r e t wo ke y p r o b l e ms .To r e - d u c e t he Bo ol e a n o pe r a t i o n c o mp l e x i t y , t hi s pa pe r p r o pos e s a p r o g r e s s i v e a n d GP U a c c e l e r a t e d Bo o l e a n op ・
Zha o Ha nl i ¨
,
Me n g Qi n g r u ¨ , J i n Xi a o g a n g , H u a n g Hu i ¨ , a n d Wa n g Mi n g )
Ha n g z h o u 3 1 0 0 5 8 )
e r a t i o n a p pr oa c h t o ge ne r a t e l e ve l s — o f - d e t a i l po l yg o na l mo d e l s .La y e r e d d e p t h i ma ge s a r e e m pl o ye d t o a p -
第2 7卷 第 7 期
2 0 1 5年 7月
计 算 机 辅 助 设 计 与 图形 学 学 报
J o u r n a l o f Co mp u t e r - Ai d e d De s i g n& Co mp u t e r Gr a p h i c s
Vb1 . 27N O. 7 J u1 . 2 01 5
c l a s s i ic f a t i o n o f a xi s — a l i g n e d s a m pl i ng po i nt s .To a v oi d t he a d di t i o n a l s a mpl i n g p r o c e s s f o r l e ve l s - o f - d e t a i l mo de l s , t h e b ou n da r y po i n t s a r e pr o gr e s s i v e l y me r g e d i n t o l o w— r e s ol ut i o n c u be s . The f e a t ur e — pr e s e r vi ng d u a l
”( I n t e l l i g e n t I n f o r ma t i o n S y s t e m s I n s t i t u t e , We n z h o u U n i v e r s i t y , W e n z h o u 3 2 5 0 3实体的封闭边界,将多边形的求交计算简化为坐标轴平行的采样点的实体 内外
部 判 断 ;为 了 免 去 各 层 次 细 节 模 型 的重 复 采 样 过 程 ,渐 进 式 地 将 边 界采 样 点 归 并 到 低 分 辨 率 下 的立 方 体 中 ;运 用 特
征 保 持 的 多边 形 重 建 算 法 将 相 同 立方 体 内 的 边 界 采 样 点 转 换 成 多 边 形 顶 点 ,根据 邻 接 关 系 生 成 网 格 模 型 .上 述 算 法 使 用 支 持 图 形 硬 件加 速 的 C UD A 编 程并 行 实现 . 实 验 结 果 表 明 了算 法 的 可行 性 .
摘 要:多边形模 型的布尔运算 中包 含复杂的求交计算 以及多边形 重建 过程,精度 控制和处理效率是 其 中的关键 .
为 了 降 低 布 尔 运 算 复 杂 度 ,提 出一 种 适 合 硬 件加 速 的 基 于 渐 进 式 布 尔 运 算 的多 层 次 细 节 网格 模 型生 成 方 法 .该 方 法
关键 词 :布 尔 运 算 ;分 层 深 度 图像 ; GP U
中 图法 分 类 号 : T P 3 9 1 . 4 1
GPU- Ac c e l e r a t e d Pr o g r e s s i ve Bo o l e a n Ope r a t i o ns o n Po l y g o na l M o de l s
硬件 加速 的渐进式 多边形模 型布尔运算
赵汉理¨ , 孟庆如¨ , 金小冈 4 , 黄 辉n , 王 明 )
( 温州 大学智 能信 息系统研 究所 温州 3 2 5 0 3 5 )
( 浙 江大学 CAD&CG 国家重点 实验室 杭 州 3 1 0 0 5 8 ) ( h a n l i z h a o @g ma i l . c o m)
( S t a t e K e y L a b o r a t o r y o f C A D & C G Z h e j i a n g l v P
A bs t r a c t :Bo o l e a n o p e r a t i o ns o n po l y g o na l m od e l s i n v o l ve t he c o mp l e x i n t e r s e c t i o n c a l c ul a t i o ns a nd po -
