抚顺八中七年下应用题
抚顺市七年级数学下册第八单元《二元一次方程组》经典练习卷(含答案)(1)

一、选择题1.对于任意实数,规定新运算:x y ax by xy =+-※,其中a 、b 是常数,等式右边是通常的加减乘除运算.已知211=※,()322-=-※,则a b ※的值为( )A .3B .4C .6D .7 2.如图,天平上放有苹果、香蕉、砝码,且两个天平都平衡,则一个苹果的重量是一个香蕉的重量的( )A .23倍 B .32倍 C .2倍 D .3倍 3.甲、乙两人分别从相距40km 的两地同时出发,若同向而行,则5h 后,快者追上慢者;若相向而行,则2h 后,两人相遇,那么快者速度和慢者速度(单位:km/h)分别是( )A .14和6B .24和16C .28和12D .30和1 4.小明去买2元一支和3元一支的两种圆珠笔(一种圆珠笔至少买一支),恰好花掉30元,则购买方案有( )A .4种B .5种C .6种D .7种 5.将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有( )A .6种B .7种C .8种D .9种 6.方程组125x y x y +=⎧⎨+=⎩的解为( ) A .12x y =-⎧⎨=⎩B .21x y =⎧⎨=⎩C .43x y =⎧⎨=-⎩D .23x y =-⎧⎨=⎩ 7.若x m ﹣n ﹣2y m+n ﹣2=2007,是关于x ,y 的二元一次方程,则m ,n 的值分别是( ) A .m=1,n=0 B .m=0,n=1 C .m=2,n=1 D .m=2,n=3 8.若方程x-y=3与下面方程中的一个组成的方程组的解为41x y =⎧⎨=⎩,则这个方程可以( ) A .3x-4y=16B .1254x y +=C .1382x y -+=D .2(x-y)=6y 9.已知方程组2325x y x y +=⎧⎨-=⎩,则39x y +的值为( ) A .2- B .2 C .6- D .610.小明去商店购买A B 、两种玩具,共用了10元钱,A 种玩具每件1元,B 种玩具每件2元.若每种玩具至少买一件,且A 种玩具的数量多于B 种玩具的数量.则小明的购买方案有( )A .5种B .4种C .3种D .2种11.下列方程中,是二元一次方程的是( ).A .324x y z -=B .690+=xC .42x y =-D .123y x+= 12.下表为服饰店卖出的服装种类与原价对照表.某日服饰店举办大拍卖,外套按原价打六折出售,衬衫和裤子按原价打八折出售,各种服装共卖200件,营业额是24000元,则外套卖出了( )A .100件B .80件C .60件D .40件 13.若方程组21322x y k x y +=-⎧⎨+=⎩的解满足0x y +=,则k 的值为( ) A .1-B .1C .0D .不能确定 14.方程组320x y x y +=⎧⎨-=⎩的解是( ) A .11x y =⎧⎨=⎩ B .12x y =⎧⎨=⎩ C .21x y =⎧⎨=⎩ D .30x y =⎧⎨=⎩15.下列说法正确的是( )A .二元一次方程2317x y +=的正整数解有2组B .若52x y =⎧⎨=⎩是232x y k -=的一组解,则k 的值是12 C .方程组23321y x x y =-⎧⎨+=⎩的解是11x y =⎧⎨=-⎩ D .若3m n x +与22112m x y --是同类项,则2m =,1n = 二、填空题16.重庆某快递公司规定:寄件不超过1kg 的部分按起步价计费,超过1kg 不足2kg ,按照2kg 收费;超过2kg 不足3kg 按照3kg 收费,以此类推.某产家分别寄快递到重庆市内和北京,其中,寄往重庆市内的起步价为a 元,超过部分b 元/kg ;寄往北京的起步价为()7a +元,超过部分()4b +元/kg .已知一个寄往重庆市内的快件,质量为2kg ,收费13元;一个寄往北京的快件,质量为4.5kg ,收费42元.如果一个寄往北京的快件,质量为2.8kg ,应收费______元.17.若方程x |m|-2+(m+3)y 2m-n =6是关于x 、y 的二元一次方程,则m+n=_____ 18.已知关于x 、y 的方程组2326324x y k x y k +=+⎧⎨+=+⎩的解满足2x y +=,则k 的值为__. 19.已知2(2)0x y ++=,则y x 的值是_______. 20.设 a 、b是有理数,且满足等式2321a b ++=-则a+b=___________.21.关于,x y 的方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解是41x y =⎧⎨=⎩,则关于,x y 的方程组111222(1)()2(1)()2a x b y c a x b y c -+-=⎧⎨-+-=⎩的解是_____________. 22.甲、乙两人共同解方程组51542+=⎧⎨-=-⎩ax y x by ,由于甲看错了方程①中的a ,得到方程组的解为31x y =-⎧⎨=⎩,乙看错了方程②中的b ,得到方程组的解为54x y =⎧⎨=⎩,则a 2020+ (10b )2021=________. 23.如果()2 x 2y 1x y 50-+++-=,那么x =______,y =____ 24.已知关于,x y 的方程组231x ay bx y -=⎧⎨+=-⎩的解是13x y =⎧⎨=-⎩,则a b +=___________. 25.对于任意有理数a ,b ,c ,d ,我们规定a bad bc c d =-.已知x ,y 同时满足514x y=-,513y x =-,则xy =________.26.已知x ,y ,z 都不为0,且4330230x y z x y z --=⎧⎨-+=⎩,则式子346x y z x y z -+++的值为_____. 三、解答题27.解方程组:451122x y x y +=⎧⎨-=⎩. 28.解下列方程组(1)362x y y x +=⎧⎨=-⎩ (2)3510236x y x y -=⎧⎨+=-⎩(3)45321x yx y+=⎧⎨-=⎩(4)()31511212x yxy⎧-=+⎪⎨+=-⎪⎩29.若x,y2(2313)0x y+-=,求2x y-的值.30.近几年大部分家庭流行用不锈钢钢管做防盗窗,小芳家的防盗窗按设计要求,需要长为0.8米的钢管100根,及长为2.5米的钢管32根,两种长度的钢管粗细必须相同;并要求这些用料不能是焊接而成的,经市场调查,钢材市场中符合这种规格的钢管每根长均为6米.(1)将一根长为6米的钢管进行裁剪(余料作废),有下面几种方法,请完成填空:方法①:只裁长为0.8米的钢管时,最多可裁________根.方法②:先裁下1根2.5米长的钢管,余下部分最多能裁0.8米长的钢管____根.方法③:先裁下2根2.5米长的钢管,余下部分最多能裁0.8米长的钢管________根.(2)用(1)中的三种方法里面的两种进行结合来裁剪6米长的钢管,在尽量减少用料的情况下,如何裁剪才能得到所需要的相应数量的材料?。
抚顺市七年级数学下册第八单元《二元一次方程组》经典练习卷(含答案)(1)

一、选择题1.对于任意实数,规定新运算:x y ax by xy =+-※,其中a 、b 是常数,等式右边是通常的加减乘除运算.已知211=※,()322-=-※,则a b ※的值为( )A .3B .4C .6D .7D 解析:D【分析】根据新定义运算,得到关于a ,b 的方程组,求出a ,b 的值,再代入求解,即可.【详解】∵211=※,()322-=-※,∴221=1a b +-⨯,-32(3)22a b +--⨯=-,∴a=2,b=-1,∴a b ※=2(1)22(1)(1)2(1)7-=⨯+-⨯--⨯-=※,故选D .【点睛】本题主要考查解二元一次方程组,理解新定义的运算以及加减消元法解二元一次方程组,是解题的关键.2.若a 为方程250x x +-=的解,则22015a a ++的值为( )A .2010B .2020C .2025D .2019B 解析:B【分析】先根据a 为方程250x x +-=的解得到25a a +=,然后整体代入即可解答.【详解】解:∵a 为方程250x x +-=的解∴250a a +-=,即25a a +=∴22015a a ++=5+2015=2020.故答案为B .【点睛】本题考查了一元二次方程的解和整体法的应用,正确理解并灵活应用一元二次方程的解解答问题是解答本题的关键.3.下列方程中是二元一次方程的是( )A .(2)(3)0x y +-=B .-1x y =C .132x y=+ D .5xy = B 解析:B【分析】含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程.【详解】解:(2)(3)0x y +-=化简得3260xy x y -+-=,最高次是2次,故A 选项错误; -1x y =是二元一次方程,故B 选项正确;132x y=+不是整式方程,故C 选项错误; 5xy =最高次是2次,故D 选项错误.故选:B【点睛】本题主要考查的是二元一次方程的概念,正确的掌握二元一次方程的概念是解题的关键. 4.已知关于x ,y 的方程组232x y a x y a -=-⎧⎨+=⎩,其中﹣2≤a≤0.下列结论:①当a =0时,x ,y 的值互为相反数;②20x y =⎧⎨=⎩是方程组的解;③当a =﹣1时,方程组的解也是方程2x ﹣y =1﹣a 的解;其中正确的是( ) A .①②B .①③C .②③D .①②③B 解析:B【分析】把a =0代入方程组,可求得方程组的解,把20x y =⎧⎨=⎩代入方程组,可得a =1,可判断②;把a =﹣1代入方程可求得a 的值为2,可判断③;可得出答案.【详解】解:①当a =0时,原方程组为230x y x y -=⎧⎨+=⎩,解得11x y =-⎧⎨=⎩, ②把20x y =⎧⎨=⎩代入方程组得到a =1,不符合题意. ③当a =﹣1时,原方程组为242x y x y -=⎧⎨+=-⎩,解得02x y =⎧⎨=-⎩, 当02x y =⎧⎨=-⎩时,代入方程组可求得a =﹣1, 把02x y =⎧⎨=-⎩与a =﹣1代入方程2x ﹣y =1﹣a 得,方程的左右两边成立, 综上可知正确的为①③.故选:B .【点睛】本题主要考查二元一次方程组的解,熟练掌握二元一次方程组的解是解题的关键.5.已知关于,x y的方程组2106x ynx my+=⎧⎨+=⎩和10312mx y nx y-=⎧⎨-=⎩有公共解,则m n-的值为()A.1B.1-C.2D.2- A解析:A【分析】联立不含m与n的两个方程组成方程组,求出x与y的值,进而求出m与n的值,代入m-n,计算即可.【详解】解:联立得:210312x yx y+=⎧⎨-=⎩①②,①×3+②得:7x=42,解得:x=6,把x=6代入②得:y=-2,把62xy=⎧⎨=-⎩代入得:6266210n mm n-=⎧⎨+=⎩,解得:m=3,n=2,则m-n=3-2=1.故选A.【点睛】本题考查了二元一次方程组的解:一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.利用两个方程组有公共解得出x,y的值是解题关键.6.方程组2824x yx y⎧+=⎪⎨+=⎪⎩的解的个数为()A.1 B.2 C.3 D.4A解析:A【分析】分类讨论x与y的正负,利用绝对值的代数意义化简,求出方程组的解,即可做出判断.【详解】解:根据x、y的正负分4种情况讨论:①当x>0,y>0时,方程组变形得:2824x yx y+=⎧⎨+=⎩,无解;②当x>0,y<0时,方程组变形得:28 24 x yx y+=⎧⎨-=⎩,解得x=3,y=2>0,则方程组无解;③当x<0,y>0时,方程组变形得:28 24x yx y-+=⎧⎨+=⎩,此时方程组的解为16x y =-⎧⎨=⎩; ④当x <0,y <0时,方程组变形得:2824x y x y -+=⎧⎨-=⎩,无解, 综上所述,方程组的解个数是1.故选:A .【点睛】本题考查了解二元一次方程组,利用了分类讨论的思想,熟练掌握运算法则是解本题的关键.7.二元一次方程组22x y x y +=⎧⎨-=-⎩的解是( ) A .02x y =⎧⎨=-⎩B .02x y =⎧⎨=⎩C .20x y =⎧⎨=⎩D .20x y =-⎧⎨=⎩B 解析:B【解析】 分析:方程组利用加减消元法求出解即可.详解:22x y x y +⎧⎨--⎩=①=②, ①+②得:2x=0,解得:x=0,把x=0代入①得:y=2,则方程组的解为02x y ⎧⎨⎩==, 故选B .点睛:此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.8.已知x ,y 满足方程组4,5,x m y m +=⎧⎨-=⎩则无论m 取何值,x ,y 恒有的关系式是( ) A .1x y += B .1x y +=- C .9x y += D .9x y -=- C 解析:C【分析】由方程组消去m ,得到一个关于x ,y 的方程,化简这个方程即可.【详解】解:将5m y =-代入4x m +=,得54x y +-=,所以9x y +=.故选C.【点睛】解二元一次方程组的基本思想是“消元”,基本方法是代入法和加减法,此题实际是消元法的考核.9.解关于,x y 的方程组()()()1328511m x n y n x my ①②⎧+-+=⎪⎨-+=⎪⎩可以用①2+⨯②,消去未知数x ,也可以用①+②5⨯消去未知数y ,则mn 、的值分别为( ) A .23,39--B .23,40--C .25,39--D .25,40-- A 解析:A【分析】根据已知得出关于m 、n 的方程组,求出方程组的解即可.【详解】解:∵解关于x ,y 方程组()()()m 1x 3n 2y 85n x my 11⎧+-+=⎪⎨-+=⎪⎩①②可以用①×2+②,消去未知数x ;也可以用①+②×5消去未知数y ,2(1)(5)0(32)50m n n m ++-=⎧∴⎨-++=⎩∴27532m n m n -=-⎧⎨-=⎩解得:2339m n =-⎧⎨=-⎩, 故答案为:A .【点睛】本题考查了解二元一次方程组,能得出关于m 、n 的方程组是解此题的关键.10.二元一次方程组425x y x y +=⎧⎨-=⎩的解为( ) A .13x y =⎧⎨=⎩B .22x y =⎧⎨=⎩C .31x y =⎧⎨=⎩D .40x y =⎧⎨=⎩ C 解析:C【分析】先用加减消元法求出x 的值,再代回第一个方程求出y 的值即可. 【详解】解:425x y x y +⎧⎨-⎩=①=②, ①+②,得:3x=9,解得:x=3,将x=3代入①,得:3+y=4,解得:y=1,所以方程组的解为31 xy⎧⎨⎩==,故选:C.【点睛】本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.二、填空题11.金秋十月,丹桂飘香,重庆市綦江区某中学举行了创新科技大赛,该校初二年级某班共有18人报名参加航海组、航空组和无人机组三个项目组的比赛(每人限参加一项),其中航海组的同学比无人机组的同学的两倍少3人,航空组的同学不少于5人但不超过9人,班级决定为航海组的每位同学购买2个航海模型,为航空组的每位同学购买3个航空模型,为无人机组的每位同学购买若干个无人机模型,已知航海模型75元每个,航空模型98元每个,无人机模型165元每个,若购买这三种模型共需花费6939元,则其中购买无人机模型的费用是_______.4125元【分析】设无人机组有x个同学航空组有y个同学根据人数为18列出二元一次方程根据航空组的同学不少于5人但不超过9人得到xy的解再代入模型费用进行验证即可求解【详解】设无人机组有x个同学航空组解析:4125元.【分析】设无人机组有x个同学,航空组有y个同学,根据人数为18列出二元一次方程,根据航空组的同学不少于5人但不超过9人,得到x,y的解,再代入模型费用进行验证即可求解.【详解】设无人机组有x个同学,航空组有y个同学,则航海组有(2x-3)个同学,依题意得x+2x-3+y=18,解得x=21=733y y --,∵航空组的同学不少于5人但不超过9人,x,y为正整数,y为3的倍数,故方程的解为,56xy=⎧⎨=⎩,49xy=⎧⎨=⎩,设为无人机组的每位同学购买a个无人机模型,当56xy=⎧⎨=⎩时,依题意得5a×165+2×7×75+6×3×98=6939解得a=4125=5825,符合题意,故购买无人机模型的费用是4125元;当49xy=⎧⎨=⎩时,依题意得4a×165+2×5×75+9×3×98=6939解得a=3543660,不符合题意; 综上,答案为4125元.故答案为:4125元.【点睛】 此题主要考查二元一次方程的应用,解题的关键是根据题意列出方程,再分类讨论进行求解.12.已知x ,y 满足方程组612328x y x y +=⎧⎨-=⎩,则x +y 的值为__.5【分析】根据两个方程系数的关系将两个方程相加即可得到答案【详解】解:①+②得:4x+4y =20则x+y =5故答案为:5【点睛】此题考查解二元一次方程组—特殊法根据所求的式子中各系数与方程组的关系将解析:5【分析】根据两个方程系数的关系将两个方程相加即可得到答案.【详解】解:612328x y x y +=⎧⎨-=⎩①②, ①+②得:4x +4y =20,则x +y =5,故答案为:5.【点睛】此题考查解二元一次方程组—特殊法,根据所求的式子中各系数与方程组的关系,将原方程组对应相加或相减即可得到答案的方法更为简便.13.若2(321)4330x y x y -++--=,则x y -=_____.4【分析】根据非负数的性质两个非负数相加和为0这两个非负数的值都为0解出xy 的值再代入原式中即可【详解】解:∵∴①×3-②×2得把代入①得解得∴故答案为:4【点睛】本题考查了非负数的性质及二元一次方解析:4【分析】根据非负数的性质“两个非负数相加,和为0,这两个非负数的值都为0”解出x 、y 的值,再代入原式中即可.【详解】解:∵2(321)4330x y x y -++--=,∴32104330x y x y -+=⎧⎨--=⎩①②,①×3-②×2得,9x =-,把9x =-代入①得,27210y --+=,解得13y =-,∴9134x y -=-+=.故答案为:4.【点睛】本题考查了非负数的性质及二元一次方程组的解法.注意:几个非负数的和为零,则每一个数都为零.14.已知关于x 、y 的方程组2326324x y k x y k +=+⎧⎨+=+⎩的解满足2x y +=,则k 的值为__.0【分析】根据x+y=2求出5x+5y=10方程组的两方程的两边分别相加得出5x+5y=3k+10得出方程3k+10=10求出方程的解即可【详解】解:①②得:故答案为:0【点睛】本题考查了二元一次方解析:0【分析】根据x+y=2求出5x+5y=10,方程组的两方程的两边分别相加得出5x+5y=3k+10,得出方程3k+10=10,求出方程的解即可.【详解】解:2326324x y k x y k +=+⎧⎨+=+⎩①②, ①+②得:55310x y k +=+,2x y +=,5510x y ∴+=,31010k ∴+=,0k ∴=,故答案为:0.【点睛】本题考查了二元一次方程组的解,解一元一次方程和解二元一次方程组等知识点,能得出关于k 的一元一次方程是解此题的关键.15.鼠年新春佳节将至,小瑞准备去超市买些棒棒糖,送一份“甜蜜礼物”给他的好朋友.有甲、乙、丙三种类型的棒棒糖,若甲种买2包,乙种买1包,丙种买3包共23元;若甲种买1包,乙种买4包,丙种买5包共36元.则甲种买1包,乙种买2包,丙种买3包,共______元.22【分析】首先设买1包甲乙丙三种糖各abc 元根据买甲种糖2包和乙种1包丙种3包共23元列出方程2a +3c +b =23;根据买甲种1包乙4包丙种5包共36元列出方程a +4b +5c =36通过加减消元法求 解析:22【分析】首先设买1包甲,乙,丙三种糖各a ,b ,c 元.根据买甲种糖2包和乙种1包,丙种3包共23元,列出方程2a +3c +b =23;根据买甲种1包,乙4包,丙种5包,共36元,列出方程a +4b +5c =36.通过加减消元法求得b +c ,a +c 的值.题目所求买甲种1包,乙种2包,丙种3包,共需a +2b +3c =(a +c )+2(b +c ),因而将b +c 、a +c 的值直接代入即求得本题的解.【详解】解:设买1包甲,乙,丙三种糖各a ,b ,c 元.由题意得23234536a b c a b c ++=⎧⎨++=⎩①② 由②×2−①得:b +c =7③,由③代入①得:a +c =8④,由④+2×③得:a +2b +3c =(a +c )+2(b +c )=8+14=22.故答案为:22.【点睛】根据系数特点,通过加减消元法,得到b +c 、a +c 的值,再将其做为一个整体,代入求解.16.已知37m m n x y +-与653x y 是同类项,则m n -=_______.【分析】先根据同类项的定义可得mn 的值再代入计算即可得【详解】由题意得:解得则故答案为:【点睛】本题考查了同类项二元一次方程组的应用熟练掌握同类项的定义是解题关键解析:1-【分析】先根据同类项的定义可得m 、n 的值,再代入计算即可得.【详解】由题意得:365m m n =⎧⎨+=⎩, 解得23m n =⎧⎨=⎩, 则231m n -=-=-,故答案为:1-.【点睛】本题考查了同类项、二元一次方程组的应用,熟练掌握同类项的定义是解题关键. 17.已知关于x 、y 的方程组22332x y k x y k -=⎧⎨-=-⎩的解满足24x y -=,则k 的值为_______.6【分析】先利用方程组中的第二个方程减去第一个方程可得再根据方程的解满足可得一个关于k 的一元一次方程解方程即可得【详解】由②①得:由题意得:解得故答案为:6【点睛】本题考查了二元一次方程组的特殊解法解析:6【分析】先利用方程组中的第二个方程减去第一个方程可得22x y k -=-,再根据方程的解满足24x y -=可得一个关于k 的一元一次方程,解方程即可得.【详解】22332x y k x y k -=⎧⎨-=-⎩①②, 由②-①得:22x y k -=-,由题意得:24k -=,解得6k =,故答案为:6.【点睛】本题考查了二元一次方程组的特殊解法、解一元一次方程,熟练掌握方程组的解法是解题关键.18.若12,m m ,…,2019m 是从0,1,2这三个数中取值的一列数,若122019 2019m m m ++⋯+=,()()()22212201911 1 1510m m m -+-+⋯+-=,则在12,m m ,....,2019m 中,取值为0的个数为__________.755【分析】解决此题可以先设0有a 个1有b 个2有c 个根据据题意列出方程组求解即可【详解】设0有a 个1有b 个2有c 个由题意得列出方程组解得故取值为0的个数为755个故答案为:755【点睛】此题主要考解析:755【分析】解决此题可以先设0有a 个,1有b 个,2有c 个,根据据题意列出方程组求解即可【详解】设0有a 个,1有b 个,2有c 个,由题意得,列出方程组2019220191510a b c b c a c ++=⎧⎪+=⎨⎪+=⎩解得755509755a b c =⎧⎪=⎨⎪=⎩,故取值为0的个数为755个,故答案为:755.【点睛】此题主要考查列方程组解决问题,会根据题意设未知数列方程并正确求解是解题的关键.19.已知方程组32223x y mx y m+=+⎧⎨+=⎩的解适合8x y+=,则m=_______.19【分析】将m看做已知数表示出x与y代入x+y=8中计算即可求出m的值【详解】解:得5x=m+6即得:-5y=4-m即代入x+y=8中得:去分母得:2m+2=40解得:m=19故答案为:19【点睛解析:19【分析】将m看做已知数表示出x与y,代入x+y=8中计算即可求出m的值.【详解】解:322 23x y mx y m++⎧⎨+⎩=①=②32⨯-⨯①②得5x=m+6,即65mx+ =23⨯-⨯①②得:-5y=4-m,即45my-=代入x+y=8中,得:648 55m m+-+=去分母得:2m+2=40,解得:m=19.故答案为:19【点睛】此题考查了二元一次方程组的解,以及二元一次方程的解,熟练掌握运算法则是解本题的关键.20.若方程组18mx nynx my-=⎧⎨+=⎩的解是21xy=⎧⎨=⎩,则m=________,n=________.3【分析】把xy的值代入原方程组即可装化成关于mn的二元一次方程组进而求出mn的值【详解】解:把代入方程组得①×2+②得5m=10∴m=2将m=2代入②得n=3故答案为:2;3【点睛】本题考查二元一解析:3【分析】把x、y的值代入原方程组,即可装化成关于m、n的二元一次方程组,进而求出m、n的值.【详解】解:把21xy=⎧⎨=⎩代入方程组18mx nynx my-=⎧⎨+=⎩得2128m n n m -=⎧⎨+=⎩①② ①×2+②得5m=10∴m=2将m=2代入②得n=3故答案为:2;3.【点睛】本题考查二元一次方程组的定义及解法,其基本思路是消元,消元的方法有:加减消元法和代入消元法两种,当方程中相同的未知数的系数相等或者互为相反数时用加减消元法解方程组比较简单,灵活选择合适的方法是解题的关键.三、解答题21.数字“6”由于谐音“六六大顺”深受人们喜爱.若一个正整数各数位上的数字之和为6的倍数,则称这个正整数为“六六大顺”数.例如:正整数24,因为246+=且661÷=,所以24是“六六大顺”数;正整数125,因为1258++=且86÷商1余2,所以125不是“六六大顺”数.(1)判断96和615是否是“六六大顺”数?请说明理由;(2)求出所有大于600且小于700的“六六大顺”数的个数.解析:(1)96不是;615是;见解析;(2)15个【分析】(1)根据新定义.由9615+=,156÷商2余3即可判断96新特征“六六大顺”数.由61512++=,1262÷=,即可判断615新特征“六六大顺”数;(2)由N 为“六六大顺”数,满足定义6a b ++是6的倍数,由6,12,18a b +=,分类讨论不定方程①6a b +=时, ②12a b +=时, ③18a b +=时的非负整数解的个数即可.【详解】解:(1)96不是“六六大顺”数,615是“六六大顺”数,理由如下:∵9615+=,156÷商2余3,∴96不是“六六大顺”数;∵61512++=,1262÷=,∴615是“六六大顺”数;(2)∵ N 为“六六大顺”数,∴6a b ++是6的倍数,即+a b 是6的倍数.∴6,12,18a b +=①当6a b +=时,则有:0,1,2,3,4,5,6,6. 5. 4. 3. 2. 1.0.a a a a a a a b b b b b b b =======⎧⎧⎧⎧⎧⎧⎧⎨⎨⎨⎨⎨⎨⎨=======⎩⎩⎩⎩⎩⎩⎩此时,满足条件的“六六大顺”数共7个;②当12a b +=时,则有:3,4,5,6,7,8,9,9.8.7. 6. 5. 4. 3.a a a a a a a b b b b b b b =======⎧⎧⎧⎧⎧⎧⎧⎨⎨⎨⎨⎨⎨⎨=======⎩⎩⎩⎩⎩⎩⎩此时,满足条件的“六六大顺”数共7个;③当18a b +=时,则有:9,9.a b =⎧⎨=⎩此时,满足条件的“六六大顺”数共1个;∴77115++=(个).所以大于600且小于700的“六六大顺”数有15个.【点睛】本题考查新定义问题,认真阅读题目,掌握新定义的特征,会根据新定义的特征识别正整数的新特征,会根据新定义特征构造不定方程是解题关键.22.解方程组:()()41622358x y x y ⎧+=-⎪⎨-=-⎪⎩①② 解析:9412x y ⎧=-⎪⎪⎨⎪=-⎪⎩【分析】将原方程化简整理后再运用加减消元法求解即可.【详解】解:原方程组可化为233,252,x y x y -=-⎧⎨-=-⎩③④③-④,得21y =-, 12y , 将12y 代入③,得94x =-. 所以原方程组的解是9,41.2x y ⎧=-⎪⎪⎨⎪=-⎪⎩. 【点睛】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.23.解方程组:(1)35,24;x y x y +=⎧⎨-=⎩(2)3(1)1,5(1)2 1.x y y x --=⎧⎨-=+⎩解析:(1)21x y =⎧⎨=-⎩;(2)22x y =⎧⎨=⎩. 【分析】(1)利用加减消元法求解即可;(2)原方程整理后利用加减消元法求解即可.【详解】解:(1)3524x y x y +=⎧⎨-=⎩①② ①×2得:6210x y +=③,②+③得:714x =,解得2x =,代入①得:65y +=,解得1y =-,所以,该方程组的解为21x y =⎧⎨=-⎩; (2)原方程组整理得:34256x y x y -=⎧⎨-+=⎩①②, ①×5得:15520x y -=③,②+③得:1326x =,解得2x =,代入①得:64y -=,解得2y =,所以,该方程组的解为22x y =⎧⎨=⎩. 【点睛】本题考查解二元一次方程组.解二元一次方程组主要有两种方法,加减消元法和代入消元法,掌握“消元”思想是解题关键.24.为了防治“新型冠状病毒”,我市某小区准备用5400元购买医用口罩和洗手液发放给本小区住户,若医用口罩买800个,洗手液买120瓶,则钱还缺200元;若医用口罩买1200个,洗手液买80瓶,则钱恰好用完.(1)求医用口罩和洗手液的单价;(2)由于实际需要,除购买医用口罩和洗手液外,还需增加购买单价为6元的N 95口罩.若需购买医用口罩和N 95口罩共1200个,其中N 95口罩不超过200个,钱恰好全部用完,则有几种购买方案,.解析:(1)医用口罩的单价为2.5 元/个,洗手液的单价为30元/瓶;(2)有三种购买方案【分析】(1)设医用口罩的单价为x 元/个,洗手液的单价为y 元/瓶,根据题意得出方程组,解方程组即可;(2)设增加购买N95口罩a 个,洗手液b 瓶,则医用口罩(1200−a )个,根据题意得6a +2.5(1200−a )+30b =5400,解得b =80−760a ,可得a 为60的倍数,且a≤200,进而得出结论.【详解】(1)设医用口罩的单价为x 元/个,洗手液的单价为y 元/瓶,根据题意得:80012054002001200805400x y x y ++⎧⎨+⎩== 解得: 2.530x y ⎧⎨⎩==, 答:医用口罩的单价为2.5 元/个,洗手液的单价为30元/瓶;(2)设增加购买N95口罩a 个,洗手液b 瓶,则医用口罩(1200−a )个,根据题意得:6a +2.5(1200−a )+30b =5400,化简,得:7a +60b =4800,∴b =80−760a , ∵a ,b 都为正整数,∴a 为60的倍数,且a≤200,∴6073a b ⎧⎨⎩== ,12066a b ⎧⎨⎩== ,18059a b ⎧⎨⎩== , ∴有三种购买方案.【点睛】本题考查了二元一次方程组的应用以及二元一次方程的应用;由题意列出二元一次方程组或二元一次方程是解题的关键.25.解方程(组)(1)4,239,x y x y +=⎧⎨+=⎩(2)(x -1)2-25=0 解析:(1)31x y =⎧⎨=⎩;(2)x=6或x=-4. 【分析】(1)用加减消元法求二元一次方程组即可;(2)利用平方根的意义求解即可.【详解】(1)4(1)239(2)x y x y +=⎧⎨+=⎩, (2)−(1)×2,得y =1,将y =1代入(1),得x =3,∴原方程组的解为31x y =⎧⎨=⎩; (2)(x-1)2-25=0,∴(x-1)2=25,∴x-1=5或x-1=-5,∴x=6或x=-4.【点睛】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.也考查了利用平方根解方程.26.若方程12225m n m n x y --+-+=是二元一次方程,求m ,n 的值.解析:m=53,n=﹣13. 【分析】根据二元一次方程的定义,含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程,列出等式,即可求解.【详解】解:根据题意,得 11221m n m n --=⎧⎨+-=⎩, 解得53m =,13n =-. 【点睛】本题考查了二元一次方程组的概念以及解方程组,明确二元一次方程的定义是解题的关键.27.解下列方程组(1)3325y x x y =-⎧⎨-=⎩; (2)7239219x y x y -=⎧⎨+=-⎩; (3)322127x y x y +=⎧⎨-=⎩; (4)232491a b a b +=⎧⎨-=-⎩.解析:(1)14xy=-⎧⎨=-⎩;(2)15xy=-⎧⎨=-⎩;(3)53xy=⎧⎨=⎩;(4)1213ab⎧=⎪⎪⎨⎪=⎪⎩.【分析】(1)利用代入法解答;(2)利用加减法解答;(3)利用代入法解答;(4)利用加减法求解.【详解】(1)3325y xx y=-⎧⎨-=⎩①②,将①代入②,得3x-2(x-3)=5解得x=-1,将x=-1代入①,得y=-1-3=-4,∴方程组的解是14 xy=-⎧⎨=-⎩;(2)723 9219 x yx y-=⎧⎨+=-⎩①②由①+②,得16x=-16,解得x=-1,将x=-1代入①,得-7-2y=3,解得y=-5,∴这个方程组的解是15 xy=-⎧⎨=-⎩;(3)322127x yx y+=⎧⎨-=⎩①②,由②得:y=2x-7③,将③代入①得,3x+2(2x-7)=21,解得x=5,将x=5代入③得,y=3,∴这个方程组的解是53 xy=⎧⎨=⎩;(4)232491a ba b+=⎧⎨-=-⎩①②,由①3⨯得,6a+9b=6③,②+③得,10a=5,解得a=12,将a=12代入①,得1+3b=2,解得b=13,∴这个方程组的解是1213ab⎧=⎪⎪⎨⎪=⎪⎩.【点睛】此题考查解二元一次方程组,掌握解二元一次方程组的解法:代入法或加减法,根据每个方程组的特点选择恰当的解法是解题的关键.28.列方程解应用题:为让同学们幸福成长,年级准备组织师生秋游.关于租车问题:若只租45座的客车若干辆,则刚好坐满;若只租60座的客车,则可少租4辆,且余30个座位.(1)若只租45座的客车,求需要多少辆车?(2)已知一辆45座的客车租金每天2500元,一辆60座的客车租金每天3000元,若可以同时租用这两种类型的客车,则两种客车分别租多少辆最省钱?解析:(1) 18辆;(2) 租45座的客车2辆,租60座客车最省钱.【分析】(1)设单租45座客车x辆,则参加春游的师生总人数为45x人,根据人数与客车的数量关系建立方程求出其解即可;(2)等量关系为:45座客车能坐的人数+60座客车能坐的人数=秋游的师生总人数,选取正整数解,比较即可.【详解】解:(1)设单租45座客车x辆,则参加春游的师生总人数为45x人.根据题意,得45x=60(x−4)−30,解得:x=18.答:只租45座的客车,需要18辆车;(2)解:45×18=810(人)设租45座客车x辆,60座客车y辆.根据题意得:45x+60y=810.∵x,y均为正整数,∴x=2,y=12;或x=6,y=9;或x=10,y=6;或 x=14,y=3.2500×2+3000×12=41000(元)2500×6+3000×9=42000(元)2500×10+3000×6=43000(元)2500×14+3000×3=44000(元)∵41000﹤42000﹤43000﹤44000∴租45座的客车2辆,租60座客车12辆最省钱.【点睛】本题主要考查了用一元一次方程及二元一次方程解决实际问题,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系.。
抚顺市七年级下册末数学试卷及答案
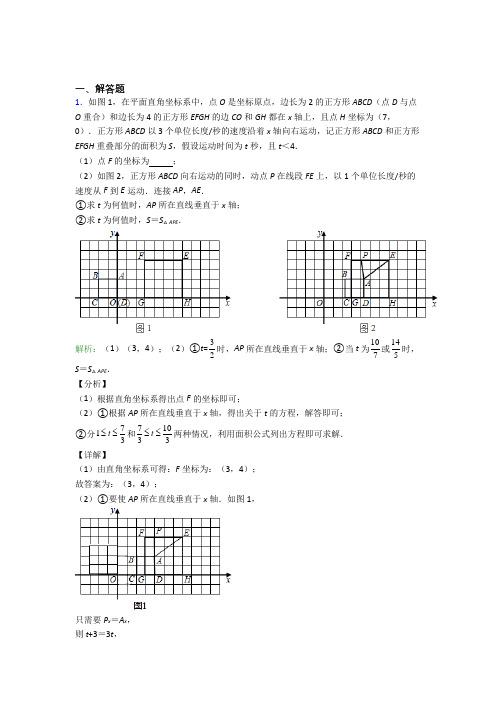
一、解答题1.如图1,在平面直角坐标系中,点O是坐标原点,边长为2的正方形ABCD(点D与点O重合)和边长为4的正方形EFGH的边CO和GH都在x轴上,且点H坐标为(7,0).正方形ABCD以3个单位长度/秒的速度沿着x轴向右运动,记正方形ABCD和正方形EFGH重叠部分的面积为S,假设运动时间为t秒,且t<4.(1)点F的坐标为;(2)如图2,正方形ABCD向右运动的同时,动点P在线段FE上,以1个单位长度/秒的速度从F到E运动.连接AP,AE.①求t为何值时,AP所在直线垂直于x轴;②求t为何值时,S=S△APE.解析:(1)(3,4);(2)①t=32时,AP所在直线垂直于x轴;②当t为107或145时,S=S△APE.【分析】(1)根据直角坐标系得出点F的坐标即可;(2)①根据AP所在直线垂直于x轴,得出关于t的方程,解答即可;②分713t≤≤和71033t≤≤两种情况,利用面积公式列出方程即可求解.【详解】(1)由直角坐标系可得:F坐标为:(3,4);故答案为:(3,4);(2)①要使AP所在直线垂直于x轴.如图1,只需要P x=A x,则t+3=3t,解得:32t =, 所以即32t =时,AP 所在直线垂直于x 轴;②由题意知,OH =7,所以当73t =时,点D 与点H 重合,所以要分以下两种情况讨论: 情况一:当713t ≤≤时, GD =3t ﹣3,PF =t ,PE =4﹣t ,∵S =S △APE ,∴BC ×GD =()12y y PE E A ⨯-, 即:2×(3t ﹣3)=()1422t -⨯, 解得:107t =; 情况二:当71033t ≤≤时,如图2,HD =3t ﹣7,PF =t ,PE =4﹣t ,∵S =S △APE ,∴BC ×CH =()12y y PE E A ⨯-, 即:2×[2﹣(3t ﹣7)]=()1422t -⨯, 解得:145t =, 综上所述,当t 为107或145时,S =S △APE . 【点睛】 本题考查了平面直角坐标系中点的移动,一元一次方程的应用等问题,理解题意,分类讨论是解题关键.2.如图,已知直线//AB 射线CD ,100CEB ∠=︒.P 是射线EB 上一动点,过点P 作PQ //EC 交射线CD 于点Q ,连接CP .作PCF PCQ ∠=∠,交直线AB 于点F ,CG 平分ECF ∠.(1)若点P,F,G都在点E的右侧,求PCG∠的度数;(2)若点P,F,G都在点E的右侧,30EGC ECG∠-∠=︒,求CPQ∠的度数;(3)在点P的运动过程中,是否存在这样的情形,使:4:3EGC EFC∠∠=?若存在,求出CPQ∠的度数;若不存在,请说明理由.解析:(1)40°;(2)65°;(3)存在,56°或20°【分析】(1)依据平行线的性质以及角平分线的定义,即可得到∠PCG的度数;(2)依据平行线的性质以及角平分线的定义,即可得到∠ECG=∠GCF=25°,再根据PQ∥CE,即可得出∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=4x-3x=x,分两种情况讨论:①当点G、F在点E 的右侧时,②当点G、F在点E的左侧时,依据等量关系列方程求解即可.【详解】解:(1)∵∠CEB=100°,AB∥CD,∴∠ECQ=80°,∵∠PCF=∠PCQ,CG平分∠ECF,∴∠PCG=∠PCF+∠FCG=12∠QCF+12∠FCE=12∠ECQ=40°;(2)∵AB∥CD∴∠QCG=∠EGC,∠QCG+∠ECG=∠ECQ=80°,∴∠EGC+∠ECG=80°,又∵∠EGC-∠ECG=30°,∴∠EGC=55°,∠ECG=25°,∴∠ECG=∠GCF=25°,∠PCF=∠PCQ=12(80°-50°)=15°,∵PQ∥CE,∴∠CPQ=∠ECP=65°;(3)设∠EGC=4x,∠EFC=3x,则∠GCF=∠FCD=4x-3x=x,①当点G、F在点E的右侧时,则∠ECG=x,∠PCF=∠PCD=32 x,∵∠ECD=80°,∴x+x+32x+32x=80°,解得x=16°,∴∠CPQ=∠ECP=x+x+32x=56°;②当点G、F在点E的左侧时,则∠ECG=∠GCF=x,∵∠CGF=180°-4x,∠GCQ=80°+x,∴180°-4x=80°+x,解得x=20°,∴∠FCQ=∠ECF+∠ECQ=40°+80°=120°,∴∠PCQ=12∠FCQ=60°,∴∠CPQ=∠ECP=80°-60°=20°.【点睛】本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补;两直线平行,内错角相等.3.已知,如图1,射线PE分别与直线AB,CD相交于E、F两点,∠PFD的平分线与直线AB相交于点M,射线PM交CD于点N,设∠PFM=α°,∠EMF=β°,且(40﹣2α)2+|β﹣20|=0(1)α=,β=;直线AB与CD的位置关系是;(2)如图2,若点G、H分别在射线MA和线段MF上,且∠MGH=∠PNF,试找出∠FMN 与∠GHF之间存在的数量关系,并证明你的结论;(3)若将图中的射线PM绕着端点P逆时针方向旋转(如图3),分别与AB、CD相交于点M1和点N1时,作∠PM1B的角平分线M1Q与射线FM相交于点Q,问在旋转的过程中1FPN Q∠∠的值是否改变?若不变,请求出其值;若变化,请说明理由. 解析:(1)20,20,//AB CD ;(2)180FMN GHF ∠+∠=︒;(3)1FPN Q∠∠的值不变,12FPN Q =∠∠ 【分析】(1)根据2(402)|20|0αβ-+-=,即可计算α和β的值,再根据内错角相等可证//AB CD ; (2)先根据内错角相等证//GH PN ,再根据同旁内角互补和等量代换得出180FMN GHF ∠+∠=︒;(3)作1PEM ∠的平分线交1M Q 的延长线于R ,先根据同位角相等证//ER FQ ,得1FQM R =∠∠,设PER REB x ==∠∠,11PM R RM B y ==∠∠,得出12EPM R ∠=∠,即可得12FPN Q=∠∠. 【详解】解:(1)2(402)|20|0αβ-+-=,4020α∴-=,200β-=,20αβ∴==,20PFM MFN ∴∠=∠=︒,20EMF ∠=︒,EMF MFN ∴∠=∠,//AB CD ∴;故答案为:20、20,//AB CD ;(2)180FMN GHF ∠+∠=︒;理由:由(1)得//AB CD ,MNF PME ∴∠=∠,MGH MNF ∠=∠,PME MGH ∴∠=∠,//GH PN ∴,GHM FMN ∴∠=∠,180GHF GHM ∠+∠=︒,180FMN GHF ∴∠+∠=︒;(3)1FPN Q ∠∠的值不变,12FPN Q=∠∠; 理由:如图3中,作1PEM ∠的平分线交1M Q 的延长线于R ,//AB CD ,1PEM PFN ∴∠=∠,112PER PEM ∠=∠,12PFQ PFN =∠∠, PER PFQ ∴∠=∠,//ER FQ ∴,1FQM R ∴∠=∠,设PER REB x ==∠∠,11PM R RM B y ==∠∠,则有:122y x R y x EPM =+∠⎧⎨=+∠⎩, 可得12EPM R ∠=∠,112EPM FQM ∴∠=∠, ∴112EPM FQM ∠=∠. 【点睛】本题主要考查平行线的判定与性质,熟练掌握内错角相等证平行,平行线同旁内角互补等知识是解题的关键.4.如图1,MN ∥PQ ,点C 、B 分别在直线MN 、PQ 上,点A 在直线MN 、PQ 之间. (1)求证:∠CAB =∠MCA +∠PBA ;(2)如图2,CD ∥AB ,点E 在PQ 上,∠ECN =∠CAB ,求证:∠MCA =∠DCE ;(3)如图3,BF 平分∠ABP ,CG 平分∠ACN ,AF ∥CG .若∠CAB =60°,求∠AFB 的度数.解析:(1)证明见解析;(2)证明见解析;(3)120°.【分析】(1)过点A 作AD ∥MN ,根据两直线平行,内错角相等得到∠MCA =∠DAC ,∠PBA =∠DAB ,根据角的和差等量代换即可得解;(2)由两直线平行,同旁内角互补得到∴、∠CAB +∠ACD =180°,由邻补角定义得到∠ECM +∠ECN =180°,再等量代换即可得解;(3)由平行线的性质得到,∠FAB =120°﹣∠GCA ,再由角平分线的定义及平行线的性质得到∠GCA ﹣∠ABF =60°,最后根据三角形的内角和是180°即可求解.【详解】解:(1)证明:如图1,过点A作AD∥MN,∵MN∥PQ,AD∥MN,∴AD∥MN∥PQ,∴∠MCA=∠DAC,∠PBA=∠DAB,∴∠CAB=∠DAC+∠DAB=∠MCA+∠PBA,即:∠CAB=∠MCA+∠PBA;(2)如图2,∵CD∥AB,∴∠CAB+∠ACD=180°,∵∠ECM+∠ECN=180°,∵∠ECN=∠CAB∴∠ECM=∠ACD,即∠MCA+∠ACE=∠DCE+∠ACE,∴∠MCA=∠DCE;(3)∵AF∥CG,∴∠GCA+∠FAC=180°,∵∠CAB=60°即∠GCA+∠CAB+∠FAB=180°,∴∠FAB=180°﹣60°﹣∠GCA=120°﹣∠GCA,由(1)可知,∠CAB=∠MCA+∠ABP,∵BF平分∠ABP,CG平分∠ACN,∴∠ACN=2∠GCA,∠ABP=2∠ABF,又∵∠MCA=180°﹣∠ACN,∴∠CAB=180°﹣2∠GCA+2∠ABF=60°,∴∠GCA﹣∠ABF=60°,∵∠AFB+∠ABF+∠FAB=180°,∴∠AFB=180°﹣∠FAB﹣∠FBA=180°﹣(120°﹣∠GCA)﹣∠ABF=180°﹣120°+∠GCA﹣∠ABF=120°.【点睛】本题主要考查了平行线的性质,线段、角、相交线与平行线,准确的推导是解决本题的关键.5.如图①,将一张长方形纸片沿EF对折,使AB落在''A B的位置;(1)若1∠的度数为a ,试求2∠的度数(用含a 的代数式表示);(2)如图②,再将纸片沿GH 对折,使得CD 落在''C D 的位置.①若//'EF C G ,1∠的度数为a ,试求3∠的度数(用含a 的代数式表示); ②若''B F C G ⊥,3∠的度数比1∠的度数大20︒,试计算1∠的度数.解析:(1)1902a ︒- ;(2)①1454a ︒+ ;②50︒ 【分析】(1)由平行线的性质得到4'B FC a ∠=∠=,由折叠的性质可知,∠2=∠BFE ,再根据平角的定义求解即可;(2) ①由(1)知,1902BFE a ∠=︒-,根据平行线的性质得到1BFE C'GB 902a ∠=∠=︒- ,再由折叠的性质及平角的定义求解即可;②由(1)知,∠BFE = 19012EFB '∠=︒-∠,由''B F C G ⊥可知:''90B FC FGC ∠+∠=︒,再根据条件和折叠的性质得到''11402190B FC FGC +=∠+∠=∠︒-∠︒,即可求解.【详解】解:(1)如图,由题意可知'//'A E B F ,∴14a ∠=∠=,∵//AD BC ,∴4'B FC a ∠=∠=,180BFB a '∴∠=︒-,∴由折叠可知1129022BFE BFB a '∠=∠=∠=︒-.(2)①由题(1)可知1902BFE a ∠=︒- , ∵//'EF C G ,1902BFE C'GB a ∴∠=∠=︒-, 再由折叠可知:113180*********HGC C GB a a ⎛⎫∠+∠=︒-∠=︒-︒-=︒+ ⎪⎝⎭', 13454HGC a ∴∠=∠=︒+;②由''B F C G ⊥可知:''90B FC FGC ∠+∠=︒,由(1)知19012BFE ∠=︒-∠, 11802180290112B FC BFE ⎛⎫'∴∠=︒-∠=︒-︒-∠=∠ ⎪⎝⎭, 又3∠的度数比1∠的度数大20︒,∴3=1+20∠∠︒,()18023180212014021FGC '∴∠=︒-∠=︒-∠+︒=︒-∠,''11402190B FC FGC +=∴∠+∠=∠︒-∠︒,1=50∴∠︒.【点睛】此题考查了平行线的性质,属于综合题,有一定难度,熟记“两直线平行,同位角相等”、“两直线平行,内错角相等”及折叠的性质是解题的关键.6.已知AB //CD .(1)如图1,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED .求证:∠BED =∠B +∠D ;(2)如图,连接AD ,BC ,BF 平分∠ABC ,DF 平分∠ADC ,且BF ,DF 所在的直线交于点F .①如图2,当点B 在点A 的左侧时,若∠ABC =50°,∠ADC =60°,求∠BFD 的度数. ②如图3,当点B 在点A 的右侧时,设∠ABC =α,∠ADC =β,请你求出∠BFD 的度数.(用含有α,β的式子表示)解析:(1)见解析;(2)55°;(3)1118022αβ︒-+ 【分析】(1)根据平行线的判定定理与性质定理解答即可; (2)①如图2,过点F 作//FE AB ,当点B 在点A 的左侧时,根据50ABC ∠=︒,60ADC ∠=︒,根据平行线的性质及角平分线的定义即可求BFD ∠的度数; ②如图3,过点F 作//EF AB ,当点B 在点A 的右侧时,ABC α∠=,ADC β∠=,根据平行线的性质及角平分线的定义即可求出BFD ∠的度数.【详解】解:(1)如图1,过点E 作//EF AB ,则有BEF B ∠=∠,//AB CD ,//EF CD ∴,FED D ∴∠=∠,BED BEF FED B D ∴∠=∠+∠=∠+∠;(2)①如图2,过点F 作//FE AB ,有BFE FBA ∠=∠.//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.BFE EFD FBA FDC ∴∠+∠=∠+∠.即BFD FBA FDC ∠=∠+∠,BF 平分ABC ∠,DF 平分ADC ∠,1252FBA ABC ∴∠=∠=︒,1302FDC ADC ∠=∠=︒, 55BFD FBA FDC ∴∠=∠+∠=︒.答:BFD ∠的度数为55︒;②如图3,过点F 作//FE AB ,有180BFE FBA ∠+∠=︒.180BFE FBA ∴∠=︒-∠,//AB CD ,//EF CD ∴.EFD FDC ∴∠=∠.180BFE EFD FBA FDC ∴∠+∠=︒-∠+∠.即180BFD FBA FDC ∠=︒-∠+∠,BF 平分ABC ∠,DF 平分ADC ∠,1122FBA ABC α∴∠=∠=,1122FDC ADC β∠=∠=, 1118018022BFD FBA FDC αβ∴∠=︒-∠+∠=︒-+. 答:BFD ∠的度数为1118022αβ︒-+. 【点睛】本题考查了平行线的判定与性质,解决本题的关键是熟练掌握平行线的判定与性质. 7.已知,//AE BD ,A D ∠=∠.(1)如图1,求证://AB CD ;(2)如图2,作BAE ∠的平分线交CD 于点F ,点G 为AB 上一点,连接FG ,若CFG ∠的平分线交线段AG 于点H ,连接AC ,若ACE BAC BGM ∠=∠+∠,过点H 作HM FH ⊥交FG 的延长线于点M ,且3518E AFH ∠-∠=︒,求EAF GMH ∠+∠的度数.解析:(1)见解析;(2)72︒【分析】(1)根据平行线的性质得出180A B ∠+∠=︒,再根据等量代换可得180B D ∠+∠=︒,最后根据平行线的判定即可得证;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB ,根据平行线的性质及等量代换可得出ECQ BGM DFG ∠=∠=∠,再根据平角的含义得出ECF CFG ∠=∠,然后根据平行线的性质及角平分线的定义可推出,BHF CFH CFA FAB ∠=∠∠=∠;设,FAB CFH αβ∠=∠=,根据角的和差可得出2AEC AFH ∠=∠,结合已知条件35180AEC AFH ∠-∠=︒可求得18AFH ∠=︒,最后根据垂线的含义及平行线的性质,即可得出答案.【详解】(1)证明://AE BD180A B ∴∠+∠=︒A D ∠=∠180B D ∴∠+∠=︒//AB CD ∴;(2)过点E 作//EP CD ,延长DC 至Q ,过点M 作//MN AB//AB CDQCA CAB ∴∠=∠,BGM DFG ∠=∠,CFH BHF ∠=∠,CFA FAG ∠=ACE BAC BGM ∠=∠+∠ECQ QCA BAC BGM ∴∠+∠=∠+∠ECQ BGM DFG ∴∠=∠=∠180,180ECQ ECD DFG CFG ∠+=︒∠+=︒ECF CFG ∴∠=∠//AB CD//AB EP ∴,PEA EAB PEC ECF ∴∠=∠∠=∠AEC PEC PEA ∠=∠-∠AEC ECF EAB ∴∠=∠-∠ECF AEC EAB ∴∠=∠+∠AF 平分BAE ∠ 12EAF FAB EAB ∴∠=∠=∠ FH 平分CFG ∠12CFH HFG CFG ∴∠=∠=∠ //CD AB,BHF CFH CFA FAB ∴∠=∠∠=∠设,FAB CFH αβ∠=∠=AFH CFH CFA CFH FAB ∠=∠-∠=∠-∠AFH βα∴∠=-,BHF CFH β∠=∠=222ECF AFH AEC EAB AFH AEC β∴∠+∠=∠+∠+∠=∠+22ECF AFH E BHF ∴∠+∠=∠+∠2AEC AFH ∴∠=∠35180AEC AFH ∠-∠=︒18AFH ∴∠=︒FH HM ⊥90FHM ∴∠=︒90GHM β∴∠=︒-180CFM NMF ∠+∠=︒90HMB HMN β∴∠=∠=︒-EAF FAB ∠=∠18EAF CFA CFH AFH β∴∠=∠=∠-∠=-︒189072EAF GMH ββ∴∠+∠=-︒+︒-=︒72EAF GMH ∴∠+∠=︒.【点睛】本题考查了平行线的判定及性质,角平分线的定义,能灵活根据平行线的性质和判定进行推理是解此题的关键.8.如图,直线HD //GE ,点A 在直线HD 上,点C 在直线GE 上,点B 在直线HD 、GE 之间,∠DAB =120°.(1)如图1,若∠BCG =40°,求∠ABC 的度数;(2)如图2,AF平分∠HAB,BC平分∠FCG,∠BCG=20°,比较∠B,∠F的大小;(3)如图3,点P是线段AB上一点,PN平分∠APC,CN平分∠PCE,探究∠HAP和∠N 的数量关系,并说明理由.∠HAP;理由见解解析:(1)∠ABC=100°;(2)∠ABC>∠AFC;(3)∠N=90°﹣12析.【分析】(1)过点B作BM//HD,则HD//GE//BM,根据平行线的性质求得∠ABM与∠CBM,便可求得最后结果;(2)过B作BP//HD//GE,过F作FQ//HD//GE,由平行线的性质得,∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,由角平分线的性质和已知角的度数分别求得∠HAF,∠FCG,最后便可求得结果;(3)过P作PK//HD//GE,先由平行线的性质证明∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,再根据角平分线求得∠NPC与∠PCN,由后由三角形内角和定理便可求得结果.【详解】解:(1)过点B作BM//HD,则HD//GE//BM,如图1,∴∠ABM=180°﹣∠DAB,∠CBM=∠BCG,∵∠DAB=120°,∠BCG=40°,∴∠ABM=60°,∠CBM=40°,∴∠ABC=∠ABM+∠CBM=100°;(2)过B作BP//HD//GE,过F作FQ//HD//GE,如图2,∴∠ABP=∠HAB,∠CBP=∠BCG,∠AFQ=∠HAF,∠CFQ=∠FCG,∴∠ABC=∠HAB+∠BCG,∠AFC=∠HAF+∠FCG,∵∠DAB=120°,∴∠HAB=180°﹣∠DAB=60°,∵AF平分∠HAB,BC平分∠FCG,∠BCG=20°,∴∠HAF=30°,∠FCG=40°,∴∠ABC=60°+20°=80°,∠AFC=30°+40°=70°,∴∠ABC>∠AFC;(3)过P作PK//HD//GE,如图3,∴∠APK=∠HAP,∠CPK=∠PCG,∴∠APC=∠HAP+∠PCG,∵PN平分∠APC,∴∠NPC=12∠HAP+12∠PCG,∵∠PCE=180°﹣∠PCG,CN平分∠PCE,∴∠PCN=90°﹣12∠PCG,∵∠N+∠NPC+∠PCN=180°,∴∠N=180°﹣12∠HAP﹣12∠PCG﹣90°+12∠PCG=90°﹣12∠HAP,即:∠N=90°﹣12∠HAP.【点睛】本题考查了角平分线的定义,平行线性质和判定:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用,理清各角度之间的关系是解题的关键,也是本题的难点.9.如图所示,A(1,0),点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,点C的坐标为(﹣3,2).(1)直接写出点E的坐标;(2)在四边形ABCD中,点P从点O出发,沿OB→BC→CD移动,若点P的速度为每秒1个单位长度,运动时间为t秒,请解决以下问题;①当t为多少秒时,点P的横坐标与纵坐标互为相反数;②当t为多少秒时,三角形PEA的面积为2,求此时P的坐标解析:(1)(-2,0);(2)①4秒;②(0,43)或(-3,43)【分析】(1)根据BC =AE =3,OA =1,推出OE =2,可得结论.(2)①判断出PB =CD ,即可得出结论;②根据△PEA 的面积以及AE 求出点P 到AE 的距离,结合点P 的路线可得坐标.【详解】解:(1)∵C (-3,2),A (1,0),∴BC =3,OA =1,∵BC =AE =3,∴OE =AE -AO =2,∴E (-2,0);(2)①∵点C 的坐标为(-3,2)∴BC =3,CD =2,∵点P 的横坐标与纵坐标互为相反数;∴点P 在线段BC 上,∴PB =CD =2,即t =(2+2)÷1=4;∴当t =4秒时,点P 的横坐标与纵坐标互为相反数;②∵△PEA 的面积为2,A (1,0),E (-2,0),∴AE =3,设点P 到AE 的距离为h ∴1322h ⨯⨯=, ∴h =43, 即点P 到AE 的距离为43, ∴点P 的坐标为(0,43)或(-3,43). 【点睛】本题考查坐标与图形变化-平移,三角形的面积等知识,解本题的关键是由线段和部分点的坐标,得出其它点的坐标.10.如图,在平面直角坐标系中,已知(),0A a ,(),0B b ,()0,4C ,a ,b 满足()220a +.平移线段AB 得到线段CD ,使点A 与点C 对应,点B 与点D 对应,连接AC ,BD .(1)求a ,b 的值,并直接写出点D 的坐标;(2)点P 在射线AB (不与点A ,B 重合)上,连接PC ,PD .①若三角形PCD 的面积是三角形PBD 的面积的2倍,求点P 的坐标;②设PCA α∠=,PDB β∠=,DPC θ∠=.求α,β,θ满足的关系式.解析:(1)(6,4)D ;(2)①(1,0)P 或(7,0);②点P 在B 点左侧时,αβθ+=;点P 在B 点右侧时,αβθ-=.【分析】(1)根据非负数的性质分别求出a 、b ,根据平移规律得到平移方式,再由平移的坐标变化规律求出点D 的坐标;(2)①设PB m =,根据三角形的面积公式列出方程,解方程求出m ,得到点P 的坐标; ②分点P 点P 在B 点左侧、点P 在B 点右侧时,过点P 作//PE AC ,根据平行线的性质解答.【详解】解:(1)()2240a b ++-, 20a ∴+=,40b -=,,解得,2a =-,4b =.(2,0)A ∴-,(4,0)B ,平移线段AB 得到线段CD ,使点(2,0)A -与点(0,4)C 对应,∴平移线段AB 向上平移4个单位,再向右平移2个单位得到线段CD ,∴(42,04)D ++,即(6,4)D ;(2)①设PB m =,∵线段AB 平移得到线段CD ,∴//AB CD ,∵6AB CD ==,4OC =∵2PCD PBD SS =, ∴11222CD OC PB OC =, ∵6AB CD ==,4OC =∴11642422m ⨯=⨯⨯ 解得3m =,当P 在B 点左侧时,坐标为(1,0),当P 在B 点右侧时,坐标为(7,0),(1,0)P ∴或(7,0);②I 、点P 在射线AB (不与点A ,B 重合)上,点P 在B 点左侧时,α,β,θ满足的关系式是αβθ+=.理由如下:如图1,过点P 作//PE AC ,,∴CPE PCA ∠=∠=α, CD 由AB 平移得到,点A 与点C 对应,点B 与点D 对应,//AC BD ∴,∴//PE BD∴DPE PDB ∠=∠=β,CPD CPE DPE αβ∴∠=∠+∠=+;即αβθ+=,II 、如图2,点P 在射线AB (不与点A ,B 重合)上,点P 在B 点右侧时,α,β,θ满足的关系式是αβθ-=.同①的方法得,CPE PCA ∠=∠=α,DPE PDB ∠=∠=β,CPD CPE DPE αβ∠=∠-∠=-;即:αβθ-=综上所述:点P 在B 点左侧时,αβθ+=.点P 在B 点右侧时,αβθ-=.【点睛】本题考查了坐标与图形平移的关系,坐标与平行四边形性质的关系,平行线的性质及三角形、平行四边形的面积公式.关键是理解平移规律,作平行线将相关角进行转化. 11.已知//AB CD ,点E 在AB 与CD 之间.(1)图1中,试说明:BED ABE CDE ∠=∠+∠;(2)图2中,ABE ∠的平分线与CDE ∠的平分线相交于点F ,请利用(1)的结论说明:2BED BFD ∠=∠.(3)图3中,ABE ∠的平分线与CDE ∠的平分线相交于点F ,请直接写出BED ∠与BFD ∠之间的数量关系.解析:(1)说明过程请看解答;(2)说明过程请看解答;(3)∠BED=360°-2∠BFD.【分析】(1)图1中,过点E作EG∥AB,则∠BEG=∠ABE,根据AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG=∠CDE,进而可得∠BED=∠ABE+∠CDE;(2)图2中,根据∠ABE的平分线与∠CDE的平分线相交于点F,结合(1)的结论即可说明:∠BED=2∠BFD;(3)图3中,根据∠ABE的平分线与∠CDE的平分线相交于点F,过点E作EG∥AB,则∠BEG+∠ABE=180°,因为AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG+∠CDE=180°,再结合(1)的结论即可说明∠BED与∠BFD之间的数量关系.【详解】解:(1)如图1中,过点E作EG∥AB,则∠BEG=∠ABE,因为AB∥CD,EG∥AB,所以CD∥EG,所以∠DEG=∠CDE,所以∠BEG+∠DEG=∠ABE+∠CDE,即∠BED=∠ABE+∠CDE;(2)图2中,因为BF平分∠ABE,所以∠ABE=2∠ABF,因为DF平分∠CDE,所以∠CDE=2∠CDF,所以∠ABE +∠CDE =2∠ABF +2∠CDF =2(∠ABF +∠CDF ), 由(1)得:因为AB ∥CD ,所以∠BED =∠ABE +∠CDE ,∠BFD =∠ABF +∠CDF ,所以∠BED =2∠BFD .(3)∠BED =360°-2∠BFD .图3中,过点E 作EG ∥AB ,则∠BEG +∠ABE =180°,因为AB ∥CD ,EG ∥AB ,所以CD ∥EG ,所以∠DEG +∠CDE =180°,所以∠BEG +∠DEG =360°-(∠ABE +∠CDE ),即∠BED =360°-(∠ABE +∠CDE ),因为BF 平分∠ABE ,所以∠ABE =2∠ABF ,因为DF 平分∠CDE ,所以∠CDE =2∠CDF ,∠BED =360°-2(∠ABF +∠CDF ),由(1)得:因为AB ∥CD ,所以∠BFD =∠ABF +∠CDF ,所以∠BED =360°-2∠BFD .【点睛】本题考查了平行线的性质,解决本题的关键是掌握平行线的性质. 12.如图,在平面直角坐标系xOy 中,已知(4,0)A ,将线段OA 平移至CB ,点D 在x 轴正半轴上,(,)C a b ,且2|3|0a b -+-=.连接OC ,AB ,CD ,BD .(1)写出点C 的坐标为 ;点B 的坐标为 ;(2)当ODC △的面积是ABD △的面积的3倍时,求点D 的坐标; (3)设OCD ∠=α,DBA ∠=β,BDC θ∠=,判断α、β、θ之间的数量关系,并说明理由.解析:(1)(2,3)C ,(6,3)B ;(2)点D 的坐标为(3,0)或(6,0);(3),,αβθ之间的数量关系θαβ=+,或θαβ=-,理由见解析.【分析】(1)由二次根式成立的条件可得a 和b 的值,由平移的性质确定BC ∥OA ,且BC=OA ,可得结论;(2)分点D 在线段OA 和在OA 延长线两种情况进行计算;(3)分点D 在线段OA 上时,α+β=θ和在OA 延长线α-β=θ两种情况进行计算;【详解】解:(1)∵2|3|0a b -+-=,∴a=2,b=3,∴点C 的坐标为(2,3),∵A (4,0), ∴OA=BC=4,由平移得:BC ∥x 轴,∴B (6,3),故答案为:(2,3)C ,(6,3)B ;(2)设点D 的坐标为,0)x ( ∵△ODC 的面积是△ABD 的面积的3倍∴3OCD ABD S S ∆∆=∴OD 3AD =①如图1,当点D 在线段OA 上时,由OD 3AD =,得03(4)x x -=-解得3x =∴点D 的坐标为(3,0)②如图2,当点D 在OA 得延长线上时,由OD 3AD =,得03(4)x x -=-解得6x =∴点D 的坐标为(6,0)综上,点D 的坐标为(3,0)或(6,0).(3)①如图1,当点D 在线段OA 上时,过点D 作DE ∥AB ,与CB 交于点E.由平移知OC ∥AB ,∴DE ∥OC∴,CDE BDE αβ=∠=∠又BDC CDE BDE θ=∠=∠+∠∴θαβ=+.②如图2,当点D 在OA 得延长线上时,过点D 作DE ∥AB ,与CB 得延长线交于点E由平移知OC ∥AB ,∴DE ∥OC∴,CDE BDE αβ=∠=∠又BDC CDE BDE θ=∠=∠-∠∴θαβ=-.综上,,,αβθ之间的数量关系θαβ=+,或θαβ=-.【点睛】此题考查四边形和三角形的综合题,点的坐标和三角形面积的计算方法,平移得性质,平行线的性质和判定,解题的关键是分点D 在线段OA 上,和OA 延长线上两种情况. 13.如果 x 是一个有理数,我们定义{x } 表示不小于 x 的最小整数. 如{3.2} = 4 , {-2.6} = -2 , {5} = 5 , {-6} = -6.由定义可知,任意一个有理数都能写成 x = {x } - b 的形式( 0≤b <1 ).(1)直接写出{x } 与 x , x + 1的大小关系;提示1:用“不完全归纳法”推导{x } 与 x , x + 1的大小关系;提示2:用“代数推理”的方法推导{x } 与 x , x + 1的大小关系.(2)根据(1)中的结论解决下列问题:① 直接写出满足{3m + 7} = 4 的 m 取值范围;② 直接写出方程{3.5n - 2} = 2n + 1 的解..解析:(1){}1x x x ≤<+;(2)①413m -<≤-;②32n =或2n =. 【分析】(1)提示1:先列出4个x 的值,分别得出{}x 与,1x x +的大小关系,再利用“不完全归纳法”即可得;提示2:先根据“{}x x b =-”得出{}b x x =-,再根据“01b ≤<”即可得;(2)①根据(1)的结论得出374371m m +≤<++,据此解不等式组即可得; ②先根据(1)的结论得出3.5221 3.521n n n -≤+<-+,再解不等式组求出n 的取值范围,从而可得21n 的取值范围,然后根据“21n 为整数”可得出方程,由此解方程即可得.【详解】(1)提示1:当 1.2x =时,{}{}1.22x ==,1 1.21 2.2x +=+=则{}1x x x <<+当 2.4x =-时,{}{}2.42x =-=-,1 2.41 1.4x +=-+=-则{}1x x x <<+当2x =时,{}{}22x ==,1213x +=+=则{}1x x x =<+当1x =-时,{}{}11x =-=-,x 1110+=-+=则{}1x x x =<+由“不完全归纳法”可得:{}1x x x ≤<+;提示2:{}x x b =-,且01b ≤<{}b x x ∴=-{}01x x ∴≤-<{}1x x x ∴≤<+;(2)①由(1)的结论得:{}3737371m m m +≤+<++{}374m +=374371m m ∴+≤<++ 解得413m -<≤-; ②由(1)的结论得:{}3.52 3.52 3.521n n n -≤-<-+{}3.5221n n -=+3.5221 3.521n n n ∴-≤+<-+ 解得423n <≤ 112153n ∴<+≤ {}3.5221n n -=+21n ∴+为整数则214n +=或215n += 解得32n =或2n =. 【点睛】本题考查了一元一次不等式组的应用、解一元一次方程等知识点,理解新定义,正确求解不等式组是解题关键.14.五一节前,某商店拟购进A 、B 两种品牌的电风扇进行销售,已知购进3台A 种品牌电风扇所需费用与购进2台B 种品牌电风扇所需费用相同,购进1台A 种品牌电风扇与2台B 种品牌电风扇共需费用400元.(1)求A、B两种品牌电风扇每台的进价分别是多少元?(2)销售时,该商店将A种品牌电风扇定价为180元/台,B种品牌电风扇定价为250元/台,商店拟用1000元购进这两种风扇(1000元刚好全部用完),为能在销售完这两种电风扇后获得最大的利润,该商店应采用哪种进货方案?解析:(1)A、B两种品牌电风扇每台的进价分别是100元、150元;(2)为能在销售完这两种电风扇后获得最大的利润,该商店应采用购进A种品牌的电风扇7台,购进B种品牌的电风扇2台.【分析】(1)设A种品牌电风扇每台进价x元,B种品牌电风扇每台进价y元,根据题意即可列出关于x、y的二元一次方程组,解出x、y即可.(2)设购进A品牌电风扇a台,B品牌电风扇b台,根据题意可列等式1001501000a b+=,由a和b都为整数即可求出a和b的值的几种可能,然后分别算出每一种情况的利润进行比较即可.【详解】(1)设A、B两种品牌电风扇每台的进价分别是x元、y元,由题意得:322400x yx y=⎧⎨+=⎩,解得:100150xy=⎧⎨=⎩,答:A、B两种品牌电风扇每台的进价分别是100元、150元;(2)设购进A种品牌的电风扇a台,购进B种品牌的电风扇b台,由题意得:100a+150b=1000,其正整数解为:16ab=⎧⎨=⎩或44ab=⎧⎨=⎩或72ab=⎧⎨=⎩,当a=1,b=6时,利润=80×1+100×6=680(元),当a=4,b=4时,利润=80×4+100×4=720(元),当a=7,b=2时,利润=80×7+100×2=760(元),∵680<720<760,∴当a=7,b=2时,利润最大,答:为能在销售完这两种电风扇后获得最大的利润,该商店应采用购进A种品牌的电风扇7台,购进B种品牌的电风扇2台.【点睛】本题主要考查了二元一次方程组的实际应用,根据题意找出等量关系列出等式是解答本题的关键.15.题目:满足方程组3512332x y kx y k+=+⎧⎨+=-⎩的x与y的值的和是2,求k的值.按照常规方法,顺着题目思路解关于x,y的二元一次方程组,分别求出xy的值(含有字母k),再由x+y=2,构造关于k的方程求解,从而得出k值.(1)某数学兴趣小组对本题的解法又进行了探究利用整体思想,对于方程组中每个方程变形得到“x+y”这个整体,或者对方程组的两个方程进行加减变形得到“x+y”整体值,从而求出k值请你运用这种整体思想的方法,完成题目的解答过程.(2)小勇同学的解答是:观察方程①,令3x=k,5y=1解得y=15,3x+y=2,∴x=95∴k=3×95=275把x=95,y=15代入方程②得k=﹣35所以k的值为275或﹣35.请诊断分析并评价“小勇同学的解答”.解析:(1)35;(2)“小勇同学的解答”错误,诊断分析和评价见解析【分析】(1)由两种方法分别得出2=5-5k,求解即可;(2)从二元一次方程的解和二元一次方程组的解的概念进行诊断分析,再从创新的角度进行评价即可.【详解】解:(1)方法一:②×2得:4x+6y=6-4k③,由③-①得:x+y=5-5k,∵x+y=2,∴2=5-5k,解得:k=35,方法二:由①-②得:x+2y=3k-2③,由②-③得:x+y=5-5k,∵x+y=2,∴2=5-5k,解得:k=35;(2)“小勇同学的解答”错误,理由如下:∵令3x=k,5y=1,求出的x、y的值只是方程①的一个解,而方程①有无数个解,根据方程组的解的概念,仅有方程①或方程②的某一个解中的x、y求出的k值不一定适合方程组中的另一个方程;只有当方程①、②取公共解时,k和x、y之间对应的数量关系才能成立,这时,求得的k=35才是正确答案;另一方面,小勇的解答虽然错误,但他的思维给我们有创新的感觉,也让我们巩固加深了对方程组解的概念的连接,同时启发我们平时在学习中,要善于多角度去探索问题,寻求新颖的解题方法.【点睛】本题考查了二元一次方程组的应用、二元一次方程的解、一元一次方程的解法以及整体思想的应用等知识;熟练掌握二元一次方程组的解法,由整体思想得出2=5-5k 是解题的关键.16.阅读下面资料:小明遇到这样一个问题:如图1,对面积为a 的△ABC 逐次进行以下操作:分别延长AB 、BC 、CA 至A 1、B 1、C1,使得A 1B =2AB ,B 1C =2BC ,C1A =2CA ,顺次连接A 1、B 1、C 1,得到△A 1B 1C 1,记其面积为S 1,求S 1的值.小明是这样思考和解决这个问题的:如图2,连接A 1C 、B 1A 、C 1B ,因为A 1B =2AB ,B 1C =2BC ,C 1A =2CA ,根据等高两三角形的面积比等于底之比,所以11∆∆=A BC B CA S S =11∆∆=A BC C AB S S =2S △ABC =2a ,由此继续推理,从而解决了这个问题. (1)直接写出S 1= (用含字母a 的式子表示).请参考小明同学思考问题的方法,解决下列问题:(2)如图3,P 为△ABC 内一点,连接AP 、BP 、CP 并延长分别交边BC 、AC 、AB 于点D 、E 、F ,则把△ABC 分成六个小三角形,其中四个小三角形面积已在图上标明,求△ABC 的面积.(3)如图4,若点P 为△ABC 的边AB 上的中线CF 的中点,求S △APE 与S △BPF 的比值.解析:(1)19a ;(2)315;(3)23. 【解析】【分析】(1)首先根据题意,求得S △A1BC =2S △ABC ,同理可求得S △A1B1C =2S △A1BC ,依此得到S △A1B1C1=19S △ABC ,则可求得面积S 1的值;(2)根据等高不等底的三角形的面积的比等于底边的比,求解,从而不难求得△ABC 的面积;(3)设S △BPF =m ,S △APE =n ,依题意,得S △APF =S △APC =m ,S △BPC =S △BPF =m .得出23APE BPF S S ∆∆=,从而求解.【详解】解:(1)连接A 1C ,∵B 1C=2BC ,A 1B=2AB ,∴122BCA ABC SS a ==,122BCA ABC S S a ==,1112A B C BCA S S =, ∴1144A B C ABC SS a ==, ∴1166A B B ABC S S a ==,同理可得出:11116A AC CB C S S a ==,∴S 1=6a+6a+6a+a=19a ;故答案为:19a ;(2)过点C 作CG BE ⊥于点G ,设BPF S x ∆=,APE S y ∆=,1·702BPC S BP CG ∆==;1·352PCE S PE CG ∆==, ∴1·7022135·2BPCPCE BP CG S S PE CG ∆∆===. ∴2BP EP=,即2BP EP =. 同理,APB APE S BP S PE ∆∆=. 2APB APE S S ∆∆∴=.842x y ∴+=.①8440APB BPD S AP x S PD ∆∆+==,3530APC PCD S AP y S PD ∆∆+==, ∴84354030x y ++=.②由①②,得5670x y =⎧⎨=⎩, 315ABC S ∆∴=.(3)设BPF S m ∆=,APE S n ∆=,如图所示.依题意,得APF APC S S m ∆∆==,BPC BPF S S m ∆∆==.PCE S m n ∆∴=-.BPC APB APE PCE S S BP S S PE∆∆∆∆==, ∴2m m n m n=-. 2()m m n mn ∴-=,0m ≠,22m n n ∴-=. ∴23n m =. ∴23APE BPF S S ∆∆=. 【点睛】此题考查了三角形面积之间的关系.(2)的关键是设出未知三角形的面积,然后根据等高不等底的三角形的面积的比等于底边的比列式求解.17.如图①,在平面直角坐标系中,点A 在x 轴上,直线OC 上所有的点坐标(,)x y ,都是二元一次方程40x y -=的解,直线AC 上所有的点坐标(,)x y ,都是二元一次方程26x y +=的解,过C 作x 轴的平行线,交y 轴与点B .(1)求点A 、B 、C 的坐标;(2)如图②,点M 、N 分别为线段BC ,OA 上的两个动点,点M 从点C 以每秒1个单位长度的速度向左运动,同时点N 从点O 以每秒1.5个单位长度的速度向右运动,设运动时间为t 秒,且0<t <4,试比较四边形MNAC 的面积与四边形MNOB 的面积的大小.解析:(1)(6,0)A ,(0,1)B ,(4,1)C ;(2)见解析.【分析】(1)令26x y +=中的0y = ,求出相应的x 的值,即可得到A 的坐标,将方程40x y -=和方程26x y +=联立成方程组,解方程组即可得到C 的坐标,进而可得到B 的坐标; (2)分别利用梯形的面积公式表示出四边形MNAC 的面积与四边形MNOB 的面积,然后根据t 的范围,分情况讨论即可.【详解】(1)令0y =,则206x +⨯=,解得6x =,(6,0)A ∴.4026x y x y -=⎧⎨+=⎩ 解得41x y =⎧⎨=⎩(4,1)C ∴.//BC x 轴,∴点B 的纵坐标与点C 的纵坐标相同,(0,1)B ∴ ;(2)(6,0)A ,(0,1)B ,(4,1)C ,6,4OA BC ∴==.∵点M 从点C 以每秒1个单位长度的速度向左运动,同时点N 从点O 以每秒1.5个单位长度的速度向右运动,, 1.5MC t ON t ∴==,4,6 1.5BM t NA t ∴=-=-,11()(4 1.5)12224MNOB t S BM ON OB t t ∴=+⋅=⨯-+⨯=+四边形, 11()(6 1.5)13224MNAC t S MC NA OB t t =+⋅=⨯+-⨯=-+四边形. 当2344t t +>-+时,即2t >时,MNOB MNAC S S >四边形四边形; 当2344t t +=-+时,即2t =时,MNOB MNAC S S =四边形四边形; 当2344t t +<-+时,即2t <时,MNOB MNAC S S <四边形四边形. 【点睛】本题主要考查二元一次方程及方程组的应用,数形结合并分情况讨论是解题的关键. 18.小语爸爸开了一家茶叶专卖店,包装设计专业毕业的小语为爸爸设计了一款纸质长方体茶叶包包装盒(纸片厚度不计).如图,阴影部分是裁剪掉的部分,沿图中实线折叠做成的长方体纸盒的上下底面是正方形,有三处长方形形状的“接口”用来折叠后粘贴或封盖.(1)若小语用长40cm ,宽34cm 的长方形纸片,恰好能做成一个符合要求的包装盒,盒高是盒底边长的2.5倍,三处“接口”的宽度相等.则该茶叶盒的容积是多少?(2)小语爸爸的茶叶专卖店以每盒200元购进一批茶叶,按进价增加18%作为售价,第一个月由于包装粗糙,只售出不到一半但超过三分之一的量;第二个月采用了小语的包装后,马上售完了余下的茶叶,但每盒成本增加了6元,售价仍不变,已知在整个买卖过程中共盈利1800元,求这批茶叶共进了多少盒?解析:(1)12803()cm ;(2)【分析】(1)根据题意设盒底边长,接口的宽度,分别为acm ,bcm ,根据题意列方程组,再根据长宽高求得体积;(2)分别设第一个月和第二个月的销售量为,x y 盒,根据题意列出方程和不等式组,根据不等式确定二元一次方程的解,两个月的销售总量为()x y +盒【详解】(1)设设盒底边长为acm ,接口的宽度为bcm ,则盒高是2.5acm ,根据题意得: 2.52240434a ab a b ++=⎧⎨+=⎩ 解得:82a b =⎧⎨=⎩茶叶盒的容积是:332.5 2.5 2.581280a a a a ⨯⨯=⨯=⨯=3()cm答:该茶叶盒的容积是12803()cm(2)设第一个月销售了x 盒,第二个月销售了y 盒,根据题意得:20018%(20018%6)1800x y ⨯⨯+⨯-⨯=化简得:65300x y +=①第一个月只售出不到一半但超过三分之一的量。
辽宁抚顺市七年级数学下册第九章【不等式与不等式组】提高练习(答案解析)

一、选择题1.已知关于x 的不等式组5210x x a -≥-⎧⎨->⎩无解,则a 的取值范围是( ) A .a <3B .a ≥3C .a >3D .a ≤3 2.不等式组20240x x +>⎧⎨-≤⎩的解集在数轴上表示正确的是( ) A . B .C .D .3.已知x=2是不等式()()5320x ax a --+≤的解,且x=1不是这个不等式的解,则实数a 的取值范围是( )A .a >1B .a≤2C .1<a≤2D .1≤a≤24.若|65|56x x -=-,则x 的取值范围是( )A .56x >B .56x <C .56x ≥D .56x ≤ 5.不等式组10840x x ->⎧⎨-≤⎩的解集在数轴上表示为( ) A . B . C . D . 6.下列说法中不正确的是( )A .若a b >,则a 1b 1->-B .若3a 3b >,则a b >C .若a b >,且c 0≠,则ac bc >D .若a b >,则7a 7b -<-7.若a >b ,则下列式子正确的是( )A .a +1<b +1B .a ﹣1<b ﹣1C .﹣2a >﹣2bD .﹣2a <﹣2b 8.如果点P(m ,1m -)在第四象限,则m 的取值范围是( )A .0m >B .01m <<C .1m <D .1m 9.若关于x 的一元一次方程x −m +2=0的解是负数,则m 的取值范围是A .m ≥2B .m >2C .m <2D .m ≤210.不等式组32153x x ->⎧⎨-<-⎩的解集在数轴上的表示是( ) A . B .C .D .11.某班共有48人,人人都会下棋,会下象棋的人数是会下围棋人数的2倍少3人,两种棋都会下的至多9人,但不少于5人,则会下围棋的有( )A .20人B .19人C .11人或13人D .19人或20人二、填空题12.不等式组3241112x x x x ≤-⎧⎪⎨--<+⎪⎩的整数解是_________. 13.不等式组2173112x x x -<⎧⎪⎨+-≥⎪⎩的解集是____. 14.a b ≥,1a -+_____1b -+15.若不等式组52355x x x a +≤-⎧⎨-+<⎩无解,则a 的取值范围是______. 16.不等式组210360x x ->⎧⎨-<⎩的解集为_______. 17.为改善教学条件,学校准备对现有多媒体设备进行升级改造,已知购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元.经过与经销商洽谈,键盘打八折,鼠标打八五折,若学校计划购买键盘和鼠标共50件,且总费用不超过1820元,则最多可购买键盘_____个.18.定义[]x 表示不大于x 的最大整数、{}[]x x x =-,例如[]22=,[]2.83-=-,[]2.82=,{}20=,{}2.80.8=,{}2.80.2-=,则满足{}[]2x x =的非零实数x 值为_______.19.在实数范围内规定一种新的运算“☆”,其规则是:a ☆b=3a+b ,已知关于x 的不等式:x ☆m>1的解集在数轴上表示出来如图所示.则m 的值是________ .20.如果不等式组2{223x a x b +≥-<的解集是01x ≤<,那么+a b 的值为 .21.若关于x 的不等式2x ﹣m≥1的解集如图所示,则m =_____.三、解答题22.已知点()39,210A m m --,分别根据下列条件解决问题:(1)点A 在x 轴上,求m 的值;(2)点A 在第四象限,且m 为整数,求点A 的坐标.23.解不等式组()41713843x x x x ⎧+≤+⎪⎨--<⎪⎩,并把它的解集在数轴上表示出来. 24.某商店需要购进A 型、B 型两种节能台灯共160盏,其进价和售价如下表所示. 类型价格A 型B 型 进价/(元/盏)15 35 销售价/(元/盏) 20 45(1)若商店计划销售完这批台灯后能获利1100元,问A 型、B 型两种节能台灯应分别购进多少盏(注:获利=售价-进价)?(2)若商店计划投入资金少于4300元,且销售完这批台灯后获利多于1260元,请问有哪几种进货方案?并直接写出其中获利最大的进货方案.25.学校需要购买一些篮球和足球,已知篮球的单价比足球的单价贵30元,买2个篮球和3个足球一共需要510元.(1)求篮球和足球的单价;(2)根据学生体育活动的需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的23,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?一、选择题1.程序员编辑了一个运行程序如图所示,规定:从“输入一个值x 到结果是否75>”为一次程序操作,如果要程序运行两次后才停止,那么x 的取值范围是( )A .18x >B .37x <C .1837x <<D .1837x <≤ 2.运行程序如图所示,规定:从“输入一个值x ”到“结果是否26>”为一次程序操作,如果程序操作进行了1次后就停止,则x 最小整数值取多少( )A .7B .8C .9D .103.某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )A .6折B .7折C .8折D .9折4.若|65|56x x -=-,则x 的取值范围是( )A .56x >B .56x <C .56x ≥D .56x ≤ 5.下列不等式组的解集,在数轴上表示为如图所示的是( )A .1x >-B .12x -<≤C .12x -≤<D .1x >-或2x ≤ 6.若关于x 的不等式组132(2)x a x x ≥-⎧⎨≤+⎩仅有四个整数解,则a 的取值范围是( ) A .12a ≤≤ B .12a ≤<C .12a <≤D .12a << 7.下列命题是假命题的是( ).A .两条直线被第三条直线所截,如果同位角相等,那么内错角的角平分线互相平行B .在实数7.5-15327-,π-,22中,有3个有理数,2个无理数 C .在平面直角坐标系中,点(21,7)P a a -+在x 轴上,则点P 的坐标为(7,0)-D .不等式组513(1)131722x x x x ->+⎧⎪⎨-≤-⎪⎩的所有整数解的和为7 8.不等式1322x x -+>的解在数轴上表示正确的是( ) A .B .C .D .9.下列不等式说法中,不正确的是( )A .若,2x y y >>,则2x >B .若x y >,则22x y -<-C .若x y >,则22x y >D .若x y >,则2222x y --<-- 10.某班共有48人,人人都会下棋,会下象棋的人数是会下围棋人数的2倍少3人,两种棋都会下的至多9人,但不少于5人,则会下围棋的有( )A .20人B .19人C .11人或13人D .19人或20人 11.已知实数x ,y ,且2<2x y ++,则下列不等式一定成立的是( )A .x y >B .44x y ->-C .33x y ->-D .22x y > 二、填空题12.已知关于x ,y 的方程组4375x y m x y m +=⎧⎨-=-⎩的解满足不等式2x+y>8,则m 的值是_____. 13.不等式21302x --的非负整数解共有__个. 14.已知关于x 的不等式组010x a x -≥⎧⎨->⎩的整数解共有3个,则a 的取值范围是________. 15.关于x 的不等式2x -a ≤-3的解集如图所示,则a 的值是______ .16.已知关于x 的不等式组0,10x a x +>⎧⎨->⎩的整数解共有3个,则a 的取值范围是___________. 17.点()1,2P x x -+不可能在第__________象限.18.若不等式a x c x c b +>⎧⎨≥-⎩的解为x≥-b+c ,则a ,b 的大小关系一定满足:a___b . 19.若a b >0,c b<0,则ac________0. 20.如果不等式组324x a x a +⎧⎨-⎩<<的解集是x <a ﹣4,则a 的取值范围是_______. 21.已知x ﹣y=3,且x >2,y <1,则x+y 的取值范围是_____.三、解答题22.台州某电视台组织知识竞赛,共设20道选择题,各题分值相同,答对一题得5分,可以选择不答,下表记录的是5名参赛者的得分情况.(1)由表格知,不答一题得________分,答错一题扣_________分.(2)某参赛者F 一共对了14题,不答题数与总得分有何关系?(3)某参赛者G 答错题数比不答题数的2倍多1题,最后得分为64分,他答对了几道题? (4)在前10道题中,参赛者N 答对8题,1题放弃不答,1题答错,则后面10题中,至少要答对几题才有可能使最后得分不低于79分?为什么?23.解下列方程(方程组)或不等式(组).(1)[]{}3213(21)35x x ---+=(2)2(53)3(12)x x x +≤--(3)解方程214163x x --=- (4)解方程组2538x y x y +=⎧⎨-=⎩(代入法解) (5)372(1)423133x x x x -<-⎧⎪⎨+≥-⎪⎩(6)0.35340.532m n m nm n m n+-⎧-=⎪⎪⎨+-⎪+=⎪⎩24.学校计划利用一片空地建造一个矩形的学生自行车棚(不考虑门),其中一面靠墙,这堵墙的长度为7.9米,计划建造车棚的面积为12平方米.现有可造车棚的建造材料总长为11米.(1)给出一种设计方案;(2)若矩形车棚的长、宽都要求为整数(单位:米),一共有几种方案?(3)若要使所有建造材料恰好用完,应怎么设计?25.学校需要购买一些篮球和足球,已知篮球的单价比足球的单价贵30元,买2个篮球和3个足球一共需要510元.(1)求篮球和足球的单价;(2)根据学生体育活动的需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的23,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?一、选择题1.已知关于x 的不等式组15x a x b -≥⎧⎨+≤⎩的解集是3≤x ≤5,则+a b 的值为( ) A .6 B .8 C .10 D .122.若点A (a ,b )在第二象限,则点B (﹣a ,b+1)在( )A .第一象限B .第二象限C .第三象限D .第四象限3.不等式组64325x x x -<⎧⎨≥+⎩的解集是( ) A .x ≥5 B .x ≤5 C .x >3 D .无解4.不等式组10,{360x x -≤-<的解集在数轴上表示正确的是( ) A . B . C .D .5.若a b >,则下列不等式中,不成立的是( )A .33a b ->-B .33a b ->-C .33a b > D .22a b -+<-+ 6.下列不等式中,是一元一次不等式的是( )A .2x 10->B .12-<C .3x 2y 1-≤-D .2y 35+> 7.若a b <,则下列各式中不一定成立的是( )A .11a b -<-B .33a b <C .a b ->-D .ac bc <8.关于x 的不等式620x x a -≤⎧⎨≤⎩有解,则a 的取值范围是( ) A .a <3 B .a≤3 C .a≥3 D .a >39.若01x <<,则下列选项正确的是( )A .21x x x <<B .21x x x <<C .21x x x <<D .21x x x<< 10.在数轴上,点A 2现将点A 沿数轴做如下移动,第一次点A 向左移动4个单位长度到达点1A ,第二次将点1A 向右移动8个单位到达点2A ,第三次将点2A 向左移动12个单位到达点3A ,第四次将点3A 向右移动16个单位长度到达点4A ,按照这种规律下去,第n 次移动到点n A ,如果点n A 与原点的距离不少于18,那么n 的最小值是( ) A .7 B .8 C .9 D .1011.若关于x?的不等式组2x 1x 3x a +<-⎧⎨>⎩无解,则实数 a?的取值范围是( ) A .a 4<- B .a 4=-C .a 4?≥-D . a 4>- 二、填空题12.随着中秋节的逐渐临近,红梅超市计划购进甜味型、咸味型、麻辣味型三种共50盒月饼,其中咸味型月饼数量不超过甜味型月饼数量,且咸味型月饼数量不少于麻辣味型月饼数量的一半.已知甜味型月饼每盒60元,咸味型月饼每盒80元,麻辣味型月饼每盒100元.在价格不变的条件下,小王实际购进甜味型月饼是计划的56倍,麻辣味型月饼购进了12盒,结果小王实际购进三种月饼共35盒,且比原计划少支付1240元,则小王原计划购进甜味型月饼_____盒.13.已知关于x 的不等式组221x a b x a b -≥⎧⎨-<+⎩的解集为55x -≤<,则a b 的值为___________. 14.已知关于x 的不等式24132m x mx +-≤的解集是34x ≥,那么m 的值是________. 15.已知:[]x 表示不超过x 的最大整数.例:[]4.84=,[]0.81-=-.现定义:{}[]x x x =-,例:{}[]1.5 1.5 1.50.5=-=,则{}{}{}3.9 1.81+--=________. 16.关于x ,y 的二元一次方程组23224x y m x y +=-+⎧⎨+=⎩的解满足x +y >﹣1,则m 的取值范围是_____. 17.若关于x 、y 的二元一次方程组23224x y m x y +=-+⎧⎨+=⎩的解满足32x y +>-,则满足条件的m 的取值范围是____________.18.若a b >0,c b<0,则ac________0. 19.不等式2x+9>3(x+4)的最大整数解是_____.20.为改善教学条件,学校准备对现有多媒体设备进行升级改造,已知购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元.经过与经销商洽谈,键盘打八折,鼠标打八五折,若学校计划购买键盘和鼠标共50件,且总费用不超过1820元,则最多可购买键盘_____个.21.已知关于x 的不等式组0{321x a x -≥->-的整数解共有5个,则a 的取值范围为_________.三、解答题22.某电器经销商计划同时购进一批甲、乙两种型号的微波炉,若购进1台甲型微波炉和2台乙型微波炉,共需要资金2600元;若购进2台甲型微波炉和3台乙型微波炉,共需要资金4400元.(1)求甲、乙型号的微波炉每台进价为多少元?(2)该店计划购进甲、乙两种型号的微波炉销售,预计用不多于1.8万元且不少于1.74万元的资金购进这两种型号的微波炉共20台,请问有几种进货方案?请写出进货方案; (3)甲型微波炉的售价为1400元,售出一台乙型微波炉的利润率为45%.为了促销,公司决定甲型微波炉九折出售,而每售出一台乙型微波炉,返还顾客现金m 元,要使(2)中所有方案获利相同,则m 的值应为多少?23.若关于x 的方程23244x m m x -=-+的解不小于7183m --,求m 的取值范围. 24.解不等式组:263235x x x x +>-⎧⎨->-⎩①②25.长沙市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品2件,乙种纪念品3件,需要400元;若购进甲种纪念品3件,乙种纪念品5件,需要650元.(1)求购进甲、乙两种纪念品每件各需多少元?(2)若该商店决定购进这两种纪念品共70件,其中乙种纪念品的数量不少于40件,考虑到资金周转,用于购买这70件纪念品的资金不能超过5750元,那么该商店共有几种进货方案?。
辽宁抚顺市七年级数学下册第八单元《二元一次方程组》经典练习(含答案)

一、选择题1.若12xy=⎧⎨=-⎩是方程3x+by=1的解,则b的值为()A.1 B.﹣1 C.﹣2 D.22.某工厂现有95个工人,一个工人每天可做8个螺杆或22个螺母,两个螺母和一个螺杆为一套,现在要求工人每天做的螺杆和螺母完整配套而没有剩余,若设安排x个工人做螺杆,y个工人做螺母,则列出正确的二元一次方程组为()A.958220x yx y+=⎧⎨-=⎩B.954220x yx y+=⎧⎨-=⎩C.9516220x yx y+=⎧⎨-=⎩D.9516110x yx y+=⎧⎨-=⎩3.若方程组a2b43a2b8+=⎧⎨+=⎩,则a+b等于()A.3 B.4 C.2 D.14.如果方程组54356x y kx y-=⎧⎨+=⎩的解中的x与y互为相反数,则k的值为()A.1 B.1或1-C.27-D.5-5.已知方程组512x yax by+=⎧⎨+=⎩和521613x ybx ay+=⎧⎨+=⎩的解相同,则a、b的值分别是()A.2,3 B.3,2 C.2,4 D.3,46.下列四组数值中,方程组2534a b ca b ca b c++=⎧⎪-+=-⎨⎪--=-⎩的解是( )A.11abc=⎧⎪=⎨⎪=-⎩B.121abc=-⎧⎪=⎨⎪=-⎩C.112abc=-⎧⎪=⎨⎪=-⎩D.123abc=⎧⎪=-⎨⎪=⎩7.已知关于,x y的方程组2106x ynx my+=⎧⎨+=⎩和10312mx y nx y-=⎧⎨-=⎩有公共解,则m n-的值为()A.1B.1-C.2D.2-8.若二元一次方程3x﹣y=﹣7,x+3y=1,y=kx+9有公共解,则k的取值为()A.3 B.﹣3 C.﹣4 D.49.已知:关于x、y的方程组2423x y ax y a+=-+⎧⎨+=-⎩,则x-y的值为( )A.-1 B.a-1 C.0 D.110.二元一次方程组22x y x y +=⎧⎨-=-⎩的解是( )A .02x y =⎧⎨=-⎩B .02x y =⎧⎨=⎩C .20x y =⎧⎨=⎩D .20x y =-⎧⎨=⎩11.若关于x y ,的二元一次方程组232320x y kx y k+=⎧⎨-=⎩的解也是二元一次方程236x y +=的解,则k 的值为( )A .34-B .34C .43D .43-12.小明去商店购买A B 、两种玩具,共用了10元钱,A 种玩具每件1元,B 种玩具每件2元.若每种玩具至少买一件,且A 种玩具的数量多于B 种玩具的数量.则小明的购买方案有( ) A .5种B .4种C .3种D .2种13.《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x ,y 的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是32=19423x y x y +⎧⎨+=⎩,在图2所示的算筹图所表示的方程组是( )A .2114327x y x y +=⎧⎨+=⎩B .21437x y x y +=⎧⎨+=⎩C .2274311x y x y +=⎧⎨+=⎩D .2114327y x y x +=⎧⎨+=⎩14.4辆板车和5辆卡车一次能运27吨货,10辆板车和3车卡车一次能运货20吨,设每辆板车每次可运x 吨货,每辆卡车每次能运y 吨货,则可列方程组( ) A .452710320x y x y +=⎧⎨-=⎩ B .452710320x y x y -=⎧⎨+=⎩ C .452710320x y x y +=⎧⎨+=⎩ D .427510203x yx y-=⎧⎨-=⎩15.二元一次方程组425x y x y +=⎧⎨-=⎩的解为( )A .13x y =⎧⎨=⎩B .22x y =⎧⎨=⎩C .31x y =⎧⎨=⎩ D .4x y =⎧⎨=⎩ 二、填空题16.金秋十月,丹桂飘香,重庆市綦江区某中学举行了创新科技大赛,该校初二年级某班共有18人报名参加航海组、航空组和无人机组三个项目组的比赛(每人限参加一项),其中航海组的同学比无人机组的同学的两倍少3人,航空组的同学不少于5人但不超过9人,班级决定为航海组的每位同学购买2个航海模型,为航空组的每位同学购买3个航空模型,为无人机组的每位同学购买若干个无人机模型,已知航海模型75元每个,航空模型98元每个,无人机模型165元每个,若购买这三种模型共需花费6939元,则其中购买无人机模型的费用是_______. 17.若关于x ,y 的方程组4,44ax by cx dy -=⎧⎨+=⎩的解是8,4,x y =⎧⎨=⎩则关于x ,y 的方程组()()()()214,2144a x b y c x d y ⎧+--=⎪⎨++-=⎪⎩的解是______. 18.甲、乙两筐苹果各有若干千克,从甲筐拿出20%到乙筐后,又从乙筐拿出25%到甲筐,这时甲、乙两筐苹果的质量相等,则原来乙筐的苹果质量是甲筐的__________ % . 19.若32x y =⎧⎨=⎩是方程24x ay -= 的一个解,则a =________. 20.如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知()8,5B -,则点A 的坐标为__________.21.某商店准备用每千克19元的A 糖果和每千克10元的B 糖果混合成什锦糖果出售,混合后糖果的价格是每千克16元.现在要配制这种什锦糖果150千克,需要两种糖果各多少千克?设A 糖果x 千克,B 糖果y 千克,根据题意可列二元一次方程组:_____. 22.对x ,y 定义一种新运算“※”,规定:x y mx ny =+※(其中m ,n 均为非零常数),若3213,218==※※.则12※的值是_______23.已知方程组2237x ay x y +=⎧⎨+=⎩的解是二元一次方程1x y -=的一个解,则a =________________.24.若方程组23103228a b a b -=⎧⎨+=⎩的解是82a b =⎧⎨=⎩,则方程组()()()()223110322128x y x y ⎧+--=⎪⎨++-=⎪⎩的解是____________. 25.若x a y b =⎧⎨=⎩是方程组2155x y x y -=⎧⎨-+=⎩的解,则a+4b =_____. 26.已知x y x x ++=,且490x y ,则5x y -的值为____________.三、解答题27.解方程或方程组: (1)7234(2)x x -=--;(2)2151136x x +--=;(按要求解方程并在括号里注明此步依据) 解:去分母,得____________________________.( ) 去括号,得_____________________________.( ) 移项,得______________________________.( ) 合并同类项,得_____________________________. 系数化为“1”,得_____________________________.(3)52253415x y x y +=⎧⎨+=⎩28.解方程组:3234x y x y +=⎧⎨-=-⎩29.如果(a ﹣2)x +(b +1)y =13是关于x ,y 的二元一次方程,则a ,b 满足什么条件? 30.若方程12225m n m n x y --+-+=是二元一次方程,求m ,n 的值.。
2023-2024学年辽宁省抚顺市新抚区七年级下学期期末数学试题

2023-2024学年辽宁省抚顺市新抚区七年级下学期期末数学试题1.在这个充满活力与希望的龙年,学校将举办一场别开生面的绘画大赛,通过画笔,大家可以描绘出心中龙的形象,展示龙年的独特魅力,在此次绘画比赛中有以下四个龙的图案,其中可以由如图平移得到的是()A.B.C.D.2.下列是二元一次方程的是()A.B.C.D.3.下列命题中,是真命题的是()A.相等的角是对顶角B.同旁内角互补C.若两个角的和为,则这两个角为邻补角D.同一平面内,垂直于同一条直线的两条直线互相平行4.下列实数,3.14159265,9,,0.4040040004…(相邻两个4之间0的个数逐次加1)中,无理数有()A.1个B.2个C.3个D.4个5.若,则下列变形错误的是()A.B.C.D.6.某学校为了了解学生对“禁止学生带手机进入校园”这一规定的意见,随机抽取100名学生进行调查,这一问题中的样本是()A.100B.被抽取的100名学生的意见C.被抽取的100名学生D.全校学生的意见7.《九章算术》有题如下:“仅有五雀、六燕,集称之衡,雀俱重,燕俱轻,一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?”意思是:五只雀、六只燕共重一斤,雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为斤,一只燕的重量为斤,则可列方程组为()A.B.C.D.8.将一副直角三角板按如图所示的方式叠放在一起,若.则的度数为()A.B.C.D.9.利用两块完全相同长方体测量一张桌子的高度,首先按图①方式放置,再交换木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是()A.B.C.D.10.如图,在平面直角坐标系中,各坐标分别为,,,,,,,,,,,……则依图中所示规律,的坐标为()A.B.C.D.11.比较大小:_____________5(填、或)12.的立方根是___________.13.将点A先向下平移3个单位,再向右平移2个单位后,则得到点B(2,5),则点A的坐标为_______________.14.如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知点B,则点A的坐标是________.15.如图,点,,,连接,,.若点D在y轴上,三角形与三角形的面积相等,则点D的坐标是______.16.计算:(1).(2)解方程组.(3)解不等式,并把解集在数轴上表示出来.17.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将沿方向平移,使点A的对应为点D,点E、F分别是B、C的对应点.(1)请画出平移后的;(2)若连接、,则这两条线段之间的关系是___________;(3)请在上找一点P,使得线段平分的面积,在图中作出线段;(4)线段扫过的图形面积为____________.18.为了创设全新的校园文化氛围,进一步组织学生开展课外阅读,让学生在丰富多彩的书海中,亲近母语,提高文学素养.某校准备开展“与经典为友、与名著为伴”的阅读活动(只写一项)的随机抽样调查,相关数据统计如图:请根据以上信息解答下列问题:(1)该校对多少名学生进行了抽样调查?(2)请将图和图补充完整;并求出扇形统计图中小说所对应的圆心角度数.(3)已知该校共有学生人,利用样本数据估计全校学生中最喜欢小说人数约为多少人?19.如图,点B、E分别在AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.证明:∵∠AGB=∠EHF()∠AGB=(对顶角相等)∴∠EHF=∠DGF,∴DB∥EC()∴∠=∠DBA(两直线平行,同位角相等)又∵∠C=∠D,∴∠DBA=∠D,∴DF∥(内错角相等,两直线平行)∴∠A=∠F().20.“换”出消费新活力,湖南家电启动以旧换新活动.在购买政策限定的新家电时对于以旧换新的消费者,国家给予新家电价格10%的补贴,其中,电脑最高补贴450元,空调最高补贴300元.某学校分两次更新部分电脑和空调,第一次购买1台电脑和2台空调,补贴前需花费10000元;第二次购买2台电脑和1台空调,补贴前需花费12200元.(1)补贴前.学校购买一台电脑和一台空调所需的资金分别是多少元?(2)若该校两次购买的所有电脑和空调均参加以旧换新活动,则一共能获得多少元的国家补贴?21.如图,于点D,于点F,,.(1)求的度数.(2)求证:.22.某体育用品商场销售两款足球,售价和进价如表:类型进价(元/个)售价(元/个)A款m120B款n90若该商场购进5个款足球和12个款足球共需1120元;若该商场购进10个款足球和15个款足球共需1700元.(1)求和的值;(2)已知商场购进10个款足球和20个款足球,售货员说:“每个款足球按售价进行打折销售,款足球不打折”.若两款足球全部售出后总盈利不少于640元,则每个款足球最多打几折?23.在平面直角坐标系中,,,满足,过点C作轴于点B.(1)如图1,连接,求三角形的面积.(2)如图2,连接,若过点B作交y轴于点D,且,分别平分,,求?(3)如图3,过C作垂直于点D,连接,点P从D点出发,沿“”移动,若点P的速度为每秒1个单位长度,运动时间t秒,当P运动到什么位置时,直线将四边形面积分为两部分?求出的坐标?。
抚顺市七年级数学下册第五单元《不等式与不等式组》检测(答案解析)

一、选择题1.下列各式中正确的是( ) A .若a b >,则11a b -<- B .若a b >,则22a b >C .若a b >,且0c ≠,则ac bc >D .若||||a b c c >,则a b > 2.不等式()31x -≤5x -的正整数解有( ) A .1个 B .2个 C .3个 D .4个 3.若a +b >0,且b <0,则a 、b 、-a 、-b 的大小关系为( )A .-a <-b <b <aB .-a <b <a <-bC .-a <b <-b <aD .b <-a <-b <a4.不等式组23x x ≥-⎧⎨<⎩的整数解的个数是( ) A .4个B .5个C .6个D .无数个5.若|65|56x x -=-,则x 的取值范围是( ) A .56x >B .56x <C .56x ≥D .56x ≤6.不等式组21x x ≥-⎧⎨<⎩的解集在数轴上表示正确的是( )A .B .C .D .7.若关于x 的不等式32x a +≤只有2个正整数解,则a 的取值范围为( ) A .74a -<<- B .74a -≤≤-C .74a -≤<-D .74a -<≤-8.不等式325132x x ++≤-的解集表示在数轴上是( ) A .B .C .D .9.关于x 的不等式620x x a -≤⎧⎨≤⎩有解,则a 的取值范围是( )A .a <3B .a≤3C .a≥3D .a >310.小圆想用7天的时间背诵若干首诗词,背诵计划如下: ①将诗词分为4组,第n 组有n x 首,1,2,3,4n =;②对于第n 组诗词,第n 天背诵第一遍,第(1)n +天背诵第二遍,第(3)n +天背诵第三遍,三遍后完成背诵,其它天无需背诵,1,2,3,4n =; ③每天最多背诵8首,最少背诵2首,第1天 第2天 第3天 第4天 第5天 第6天 第7天第1组 1x 1x1x第2组 2x2x2x第3组 3x3x3x第4组4x4x4xA .10首B .11首C .12首D .13首11.不等式1322x x -+>的解在数轴上表示正确的是( ) A . B .C .D .12.下列不等式说法中,不正确的是( ) A .若,2x y y >>,则2x > B .若x y >,则22x y -<- C .若x y >,则22x y >D .若x y >,则2222x y --<--二、填空题13.已知方程组3951x y a x y a +=+⎧⎨-=+⎩的解为正数,求a 的取值范围是_______.14.若关于x 、y 的二元一次方程组23242x y ax y a+=-⎧⎨+=+⎩的解满足1x y +<,则a 的取值范围为________.15.小张同学在解一元一次不等式时,发现一个不等式右边的数被墨迹污染看不清了,所看到的部分不等式是13x -<■,他查看练习本后的答案知道这个不等式的解是2x >,则被污染的数是__________.16.绝对值小于π的非负整数有____________.17.不等式组2021x x x -≥⎧⎨>-⎩的最小整数解是________.18.若关于x、y的二元一次方程组23224x y mx y+=-+⎧⎨+=⎩的解满足32x y+>-,则满足条件的m的取值范围是____________.19.不等式组213122xx->⎧⎪⎨-≤⎪⎩的解集是__________.20.若ab>0,cb<0,则ac________0.三、解答题21.解下列不等式(组):(1)2132x x-≤;(2)把它的解集表示在数轴上.3(2)41213x xxx--≤⎧⎪+⎨>-⎪⎩22.已知,点O是数轴的原点,点A、点B是数轴上不重合的两个点,且点A在点B的左边,点M是线段AB的中点.在上述条件下,解决问题:(1)如果点A表示的数是4,点B表示的数是6,那么点M表示的数是;(2)如果点A表示的数是-3,点M表示的数是2,那么点B表示的数是;(3)如果点A表示的数是a,点B表示的数是b,那么点M表示的数是;(用含a,b 的代数式表示) ,所以AM=BM.因此得到关于x的方程:x-a=b-x.你能解出这个方程吗?(4)如果点A表示的数是-2,点C表示的数是3,点B是线段OC上的一点,点M表示的数为m,则m的取值范围是;(5)如果点E表示的数是1,点F表示的数是x,点A从点E出发,以每分钟1个单位长度的速度向右运动,点B从点F出发,以每分钟3个单位长度的速度向右运动,设运动时间为t (t>0).①当x=5时,如果EM=6,那么t的值是;②当t≤3时,如果EM≤9,求x的取值范围.23.解方程组与不等式组.(1)解方程组24 4523 x yx y-=-⎧⎨-=-⎩.(2)解不等式组4(1)710853x xxx+≤+⎧⎪-⎨-<⎪⎩.24.为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A,B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.(1)求A,B两种型号家用净水器各购进多少台;(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,设每台A型号家用净水器的售价为x元,则每台A型号家用净水器的毛利润是元.每台B型号家用净水器的毛利润是元,并请列式求出每台A型号家用净水器的售价至少是多少元.(注:毛利率=售价-进价)25.学校计划利用一片空地建造一个矩形的学生自行车棚(不考虑门),其中一面靠墙,这堵墙的长度为7.9米,计划建造车棚的面积为12平方米.现有可造车棚的建造材料总长为11米.(1)给出一种设计方案;(2)若矩形车棚的长、宽都要求为整数(单位:米),一共有几种方案?(3)若要使所有建造材料恰好用完,应怎么设计?26.某企业在疫情复工准备工作中,为了贯彻落实“生命重于泰山,疫情就是命令,防控就是责任”的思想.计划购买300瓶消毒液,已知甲种消毒液每瓶30元,乙种消毒液每瓶18元.(1)若该企业购买两种消毒液共花费7500元,则购买甲、乙两种消毒液各多少瓶?(2)若计划购买两种消毒液的总费用不超过9600元,则最多购买甲种消毒液多少瓶?【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据不等式的性质,可得答案.【详解】A、不等式的两边都减1,不等号的方向不变,故A错误;B、当a<0时,不等式两边乘负数,不等号的方向改变,故B错误;C、当c<0时,ac<bc,故C错误;D、不等式两边乘(或除以)同一个正数,不等号的方向不变,故D正确;故选:D.【点睛】本题考查了不等式的基本性质.不等式的基本性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.2.B解析:B【分析】直接利用一元一次不等式的解法分析得出答案.【详解】解:3(x-1)≤5-x3x-3≤5-x,则4x≤8,解得:x≤2,故不等式3(x-1)≤5-x的正整数解有:1,2共2个.故选:B.【点睛】本题主要考查了一元一次不等式的整数解,正确解不等式是解题的关键.3.C解析:C【分析】根据不等式a+b>0得a>-b,-a<b,再根据b<0得b<-b,再比较大小关系即可.【详解】解:∵a+b>0,∴a>-b,-a<b.∵b<0,∴b<-b,∴-a<b<-b<a.故选C.【点睛】本题考查了不等式的性质与有理数的知识点,解题的关键是熟练的掌握有理数与不等式的性质.4.B解析:B【分析】本题首先求解该不等式组公共解集,继而在解集内确定整数解.【详解】由已知得:23x -≤<,该范围内包含5个整数解:2-,1-,0,1,2. 故选:B . 【点睛】本题考查求不等式的整数解,解题关键在于确定公共解集,其次确定答案时要确保不重不漏.5.D解析:D 【分析】先根据绝对值的性质判断出65x -的符号,再求出x 的取值范围即可. 【详解】∵6556x x -=-, ∴650x -≤,∴56x ≤. 故选:D . 【点睛】本题考查了绝对值的性质以及解一元一次不等式,解答此题的关键是熟知绝对值的性质:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,0的绝对值是0.6.A解析:A 【分析】先解出不等式组的解集,然后再根据选项解答即可. 【详解】解:由题意可得:不等式组的解集为:21x , 在数轴上表示为:故答案为A. 【点睛】本题主要考查了不等式组解集在数轴上的表示方法,在表示解集时“≥”或“≤”要用实心圆点表示,“<”,“>”要用空心圆点表示成为解答本题的关键.7.D解析:D 【分析】先解不等式得出23ax -≤,然后根据不等式只有2个正整数解可知正整数解为1和2,据此列出不等式组求解即可. 【详解】解:32x a +,32x a ∴-,则23ax-, ∵不等式只有2个正整数解, ∴不等式的正整数解为1、2,则2233a-≤<, 解得:74a -<-, 故答案为D . 【点睛】本题主要考查一元一次不等式的整数解,正确求解不等式并根据不等式的整数解的情况列出关于某一字母的不等式组是解答本题的关键.8.B解析:B 【分析】根据一元一次不等式的解法,去分母,去括号,移项,合并同类项,系数化为1即可得解. 【详解】 解:去分母,得, 2(3x +2)≤3(x +5)﹣6, 去括号,得 6x +4≤3x +15﹣6, 移项、合并同类项,得 3x ≤5,系数化为1,得, x ≤53, 在数轴上表示为:故选:B . 【点睛】本题考查了解一元一次不等式,以及在数轴上表示不等式的解集,>向右画,<向左画,≤与≥用实心圆点,<与>用空心圆圈.9.C解析:C 【分析】解不等式6-2x ≤0,再根据不等式组有解求出a 的取值范围即可. 【详解】解不等式6-2x ≤0,得:x ≥3,∵不等式组有解, ∴a ≥3. 故选:C . 【点睛】本题主要考查根据不等式组的解判断未知参数的范围,熟练掌握不等式组的解法是解题关键.10.D解析:D 【分析】根据表格及题意可得第2天、第3天、第4天、第5天的背诵最多的诗词,然后根据不等式的关系可进行求解. 【详解】解:由表格及题可得:∵每天最多背诵8首,最少背诵2首, ∴由第2天、第3天、第4天、第5天可得:128x x +≤①,238x x +≤②,1348x x x ++≤③,248x x +≤④,①+②+④-③得:2316x ≤, ∴2163x ≤, ∴123416181333x x x x +++≤+=, ∴7天后,小圆背诵的诗词最多为13首; 故选D . 【点睛】本题主要考查一元一次不等式的应用,熟练掌握不等式的性质与求法是解题的关键.11.B解析:B 【分析】根据解一元一次不等式基本步骤:移项、合并同类项、系数化为1可得. 【详解】解:∵1322x x -+>, ∴3122x x >+, ∴3322x <, ∴1x <,将不等式解集表示在数轴上如下:故选:B . 【点睛】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.12.B解析:B 【分析】根据不等式的基本性质,逐项判断即可. 【详解】 解:∵,2x y y >> ∴2x >,∴选项A 不符合题意; ∵x y >, ∴22x y ->-, ∴选项B 符合题意; ∵x y >, ∴22x y >, ∴选项C 不符合题意; ∵x y >, ∴22x y -<-, ∴2222x y --<-- ∴选项D 不符合题意. 故选:B . 【点睛】此题主要考查了不等式的基本性质:(1)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变;(2)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变;(3)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变.二、填空题13.-<<4【分析】先解方程组用含a 的式子表示方程组的解根据方程组的解是正数列出关于a 的不等式组再求解【详解】解:①+②得:①-②得:所以原方程组的解为:∵方程组的解为正∴>0且>0解得:-<<4故填:解析:-54<a <4 【分析】先解方程组用含a 的式子表示方程组的解,根据方程组的解是正数,列出关于a 的不等式组,再求解. 【详解】 解:3951x y a x y a +=+⎧⎨-=+⎩①②,①+②得:2810x a =+,45x a =+,①-②得:228y a =-+,4y a =-+,所以,原方程组的解为:454x a y a =+⎧⎨=-+⎩,∵ 方程组的解为正, ∴45a +>0且4a -+>0, 解得:-54<a <4, 故填:-54<a <4. 【点睛】本题考查了方程组的解法,以及一元一次不等式组的解法,解此类问题要先用字母a 表示方程组的解,再根据题意,列不等式组,最后求解.14.【分析】直接把两个方程相加得到然后结合即可求出a 的取值范围【详解】解:直接把两个方程相加得:∴∵∴∴故答案为:【点睛】本题考查了解二元一次方程组以及解一元一次不等式解题的关键是掌握运算法则正确得到解析:4a .【分析】直接把两个方程相加,得到337x y a +=+,然后结合1x y +<,即可求出a 的取值范围. 【详解】解:23242x y a x y a +=-⎧⎨+=+⎩,直接把两个方程相加,得:337x y a +=+,∴73ax y ++=, ∵1x y +<,∴713a+<, ∴4a .故答案为:4a.【点睛】本题考查了解二元一次方程组,以及解一元一次不等式,解题的关键是掌握运算法则,正确得到73ax y++=.15.−5【分析】设被污染的数为a表示出不等式的解集根据已知解集确定出a 的值即可【详解】解:设被污染的数为a不等式为1−3x<a解得:x>由已知解集为x>2得到=2解得:a=−5故答案为:−5【点睛】此题解析:−5【分析】设被污染的数为a,表示出不等式的解集,根据已知解集确定出a的值即可.【详解】解:设被污染的数为a,不等式为1−3x<a.解得:x>1-3a,由已知解集为x>2,得到1-3a=2,解得:a=−5,故答案为:−5【点睛】此题考查了不等式的解集,熟练掌握运算法则是解本题的关键.16.0123【分析】设所求的数为x再根据x的绝对值小于π得出关于x的不等式求出x的取值范围在此取值范围内找出符合条件的x的非负整数解的个数即可【详解】解:设该数为x∵x的绝对值小于π即|x|<π∴-π<解析:0,1,2,3【分析】设所求的数为x,再根据x的绝对值小于π得出关于x的不等式,求出x的取值范围,在此取值范围内找出符合条件的x的非负整数解的个数即可.【详解】解:设该数为x,∵x的绝对值小于π,即|x|<π,∴-π<x<π,∵π≈3.14,∴x的非负整数解为:0,1,2,3,故答案为:0,1,2,3.【点睛】本题考查了绝对值的性质及不等式组的整数解,解答此题的关键是根据题意得出关于x的不等式,再根据绝对值的性质求出x的取值范围.17.0【分析】求出不等式组的解集确定出最小整数解即可【详解】不等式组整理得:不等式组的解集为:-1<x≤2最小的整数解为0故答案为:0【点睛】本题主要考查一元一次不等式组的整数解掌握一元一次不等式组的求 解析:0【分析】求出不等式组的解集,确定出最小整数解即可.【详解】不等式组整理得:21x x ≤⎧⎨>-⎩, ∴不等式组的解集为:-1<x ≤2,∴最小的整数解为0.故答案为:0.【点睛】本题主要考查一元一次不等式组的整数解,掌握一元一次不等式组的求解是解题关键. 18.【分析】先将m 看做常数解方程组求出再代入可得关于m 的不等式解之可得答案【详解】①-②得:将代入②得:∵∴+∴故答案为:【点睛】本题主要考查了解二元一次方程组和解一元一次不等式熟练掌握运算法则是解本题 解析:72m <【分析】先将m 看做常数解方程组求出2x m =-、2y m =+,再代入32x y +>-可得关于m 的不等式,解之可得答案.【详解】 23224x y m x y +=-+⎧⎨+=⎩①② ①2⨯-②得:2x m =-,将2x m =-代入②得:2y m =+, ∵32x y +>-, ∴2m - +322m +>-, ∴72m <. 故答案为:72m <. 【点睛】本题主要考查了解二元一次方程组和解一元一次不等式,熟练掌握运算法则是解本题的关键.注意:不等式两边都乘以或除以同一个负数不等号方向要改变.19.【分析】先求出不等式组中每一个不等式的解集再求出它们的公共部分【详解】解:解①得:x>2解②得:x≥-4所以不等式组的解集是:x>2故答案为:x>2【点睛】本题考查的是一元一次不等式组的解解此类题目解析:2x>【分析】先求出不等式组中每一个不等式的解集,再求出它们的公共部分.【详解】解:21312?2xx->⎧⎪⎨-≤⎪⎩①②解①得:x>2,解②得:x≥-4.所以,不等式组的解集是:x>2.故答案为:x>2.【点睛】本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.20.<【分析】根据有理数的除法判断出ab同号再根据有理数的除法判断出bc 异号然后根据有理数的乘法运算法则判断即可【详解】解:∵>0∴ab同号∵<0∴bc异号∴ac异号∴ac<0故答案为<【点睛】本题考查解析:<【分析】根据有理数的除法判断出a、b同号,再根据有理数的除法判断出b、c异号,然后根据有理数的乘法运算法则判断即可.【详解】解:∵ab>0,∴a、b同号,∵cb<0,∴b、c异号,∴a、c异号,∴ac<0.故答案为<.【点睛】本题考查有理数的乘法,有理数的除法,熟记运算法则是解题关键.三、解答题21.(1)2x ≤;(2)1≤x <4,数轴见详解.【分析】(1)通过去分母,移项,合并同类项,未知数系数化为1,即可求解;(2)通过去分母,移项,合并同类项,未知数系数化为1,分别求出两个不等式的解,进而即可求解,然后再数轴上表示不等式组的解,即可.【详解】(1)2132x x -≤, 2(21)3x x -≤,423x x -≤, 432x x -≤,2x ≤;(2)3(2)41213x x x x --≤⎧⎪⎨+>-⎪⎩①② 由①得:x≥1,由②得:x <4,∴不等式组的解为:1≤x <4,在数轴上表示如下:【点睛】本题主要考查解一元一次不等式(组),熟练掌握解一元一次不等式的基本步骤,是解题的关键.22.(1)5;(2)7;(3)2a b +,2a b x +=;(4)﹣1≤m ≤12;(5)①2;②1<x ≤7 【分析】(1)设点M 表示的数是m ,分别表示出AM 和BM 的距离,再根据AM=BM 求解即可得出答案;(2)设点B 表示的数是b ,分别表示出AM 和BM 的距离,再根据AM=BM 求解即可得出答案;(3)设点M 表示的数是m ,分别表示出AM 和BM 的距离,再根据AM=BM 求解即可得出答案; x a b x -=-根据解一元一次方程的一般步骤即可得出答案;(4)设点B 表示的数是b ,根据点B 的位置在点O 和点C 之间建立不等式,再将点M 表示的数代入求解即可得出答案;(5)①分别表示出点M 表示的数、点A 表示的数及点B 表示的数,再根据2a b m +=代入求解即可得出答案; ②先表示出A 、B 、M 所表示的数,得出EM 的值,再根据给出的范围建立不等式求解即可得出答案.【详解】(1)设点M 表示的数是m ,则AM 之间的距离是4m -,BM 之间的距离是6m -,点M 是线段AB 的中点,∴AM=BM ,即46m m -=-,解得:5m =, 点M 表示的数是5;(2)设点B 表示的数是b点A 表示的数是-3,点M 表示的数是2,∴AM=5,BM=2b -点M 是线段AB 的中点,且点A 在点B 的左边,∴AM=BM ,5=2b ∴-解得:7b =∴点B 表示的数是7;(3)设点M 表示的数是m ,点A 表示的数是a ,点B 表示的数是b ,则AM 之间的距离是m a -,BM 之间的距离是b m -,点M 是线段AB 的中点,∴AM=BM ,即m a b m -=-,解得:2a b m +=, x a b x -=-移项,得x x b a +=+合并同类项,得2x a b将系数化为1,得2a b x +=(4)设点B 表示的数是b O 是原点,点A 表示的数是-2,点C 表示的数是3,点B 是线段OC 上的一点, 03b ∴≤≤22b m -+= 112m ∴-≤≤;(5)①点E 表示的数是1,EM=6,∴点M 表示的数是16=7+点F 表示的数是x ,且x=5 ∴点A 表示的数是1t +,点B 表示的数为53t +15372t t +++∴= 解得:2t =;②由题意得点A 表示的数是1t +,点B 表示的数为3x t +,∴点M 表示的数是132t x t +++ 点E 表示的数是1,∴1312t x t EM +++=-,1x > 即13192t x t +++-≤ 化简得194x t -≤3t ≤1934x -∴≥ 解得:7x ≤∴x 的取值范围为17x <≤.【点睛】本题考查了根据数轴表示两点间的距离、一元一次方程的应用、一元一次不等式的应用,解题的关键是结合数轴将点表示成具体的数.23.(1)125x y ⎧=⎪⎨⎪=⎩;(2)722x -≤< 【分析】(1)利用加减消元法求解可得;(2)分别求出各不等式的解集,再求出其公共解集.【详解】(1)244523x y x y -=-⎧⎨-=-⎩①②. ①5⨯得:10520x y -=-,③③-②得:63x =, ∴12x =, 将12x =代入①得:14y -=-, ∴5y =,∴方程组的解为125x y ⎧=⎪⎨⎪=⎩;(2)4(1)710853x x x x +≤+⎧⎪⎨--<⎪⎩①②, 由①得:44710x x +≤+,解得:2x ≥-,由②得:3(5)8x x -<-, 解得:72x <, ∴不等式组的解集为722x -≤<. 【点睛】 本题考查了解二元一次方程组与一元一次不等式组,熟知同大取大;同小取小;大小小大中间找;大大小小找不到的原则是解答此题的关键.24.(1)A 型号家用净水器购进了100台,B 型号家用净水器购进了60台. (2)(x-150);2(x-150);每台A 型号家用净水器的售价至少是200元.【分析】(1)设A 型号家用净水器购进了m 台,则B 型号家用净水器购进了(160-m )台,根据总价=单价×数量结合购进两种型号的家用净水器共用去36000元,即可得出关于m 的一元一次方程,解之即可得出结论;(2)设每台A 型号家用净水器的售价为x 元,则每台A型号家用净水器的毛利润为(x-150)元,每台B 型号家用净水器的毛利润为2(x-150)元,根据售完这160台家用净水器的毛利润不低于11000元,即可得出关于x 的一元一次不等式,解之取其最小值即可得出结论.【详解】(1)设A 型号家用净水器购进了m 台,则B 型号家用净水器购进了(160-m )台, 根据题意得:150m+350(160-m )=36000,解得:m=100,∴160-m=60.答:A 型号家用净水器购进了100台,B 型号家用净水器购进了60台.(2)设每台A 型号家用净水器的售价为x 元,则每台A 型号家用净水器的毛利润为(x-150)元,每台B 型号家用净水器的毛利润为2(x-150)元,根据题意得:100(x-150)+60×2(x-150)≥11000;解得:x≥200.答:每台A 型号家用净水器的售价至少是200元.【点睛】本题考查了一元一次不等式的应用以及一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)由总的毛利润不低于11000元,列出关于x 的一元一次不等式.25.(1)长为4米,宽为3米;(2)三种,宽为2m ,长为6m ;宽为3m ,长为4m ;宽为4m 时,长为3m ;(3)长为3米,宽为4米【分析】(1)根据矩形的面积公式计算即可,从中确定一种方案即可;(2)设矩形的长为y 米,宽为x 米,根据墙长7.9米,围成矩形的车棚面积为12平方米,列出方程和不等式,求出x ,y 的值,即可得出答案;(3)根据(2)得出的结果,选取宽为4米,长为3米时,正好使11米长的建造材料恰好用完.【详解】(1)∵长⨯宽=12平方米,∴当长为4米,宽为3米时,满足题意;(2)设矩形的长为y 米,宽为x 米,根据题意得:007.921112x y x y xy >⎧⎪<<⎪⎨+≤⎪⎪=⎩, ∵矩形的长、宽都是整数米,∴x=2,y=6或x=3,y=4或x=4,y=3,∴一共有3种方案:宽为2m 时,长为6m ,宽为3m 时,长为4m ,宽为4m时,长为3m;(3)∵要使11m长的建造材料恰好用完,则2x+y=11,由(2)得:x=4,y=3时,2x+y=11,∴要使11m长的建造材料恰好用完,应使宽为4m,长为3m.【点睛】本题主要考查了一元一次不等式组的综合应用,解题关键是要读懂题目,根据题目给出的条件,找出合适的等量关系,列出不等式组,注意园子的长、宽都为整数.26.(1)175,125;(2)350【分析】(1)设购买甲种消毒液x瓶,购买乙种消毒液y瓶,根据题意列出方程组求解;(2)设购买甲种消毒液a瓶,根据总费用不超过9600元,列不等式求解.【详解】解:(1)设购买甲种消毒液x瓶,购买乙种消毒液y瓶,依题意得:30030187500x yx y+=⎧⎨+=⎩,解得175125xy=⎧⎨=⎩,答:购买甲种消毒液175瓶,购买乙种消毒液125瓶;(2)设购买甲种消毒液a瓶,依题意得:30a+18(300-a)≤9600 ,解得a≤350 ,答:最多购买甲种消毒液350瓶.【点睛】本题考查二元一次方程组和不等式的应用,解题的关键是根据题意列出方程组和不等式进行求解.。
辽宁省抚顺市七年级第二学期数学精选常考选择题汇总含解析

辽宁省抚顺市七年级第二学期数学精选常考选择题汇总选择题有答案含解析1.下列调查:①了解某批种子的发芽率 ②了解某班学生对“社会主义核心价值观”的知晓率③了解某地区地下水水质 ④了解七年级(1)班学生参加“开放性科学实践活动”完成次数 适合采取全面调查的是( )A .①③B .②④C .①②D .③④2.下列语句中正确的是( )A .的平方根是B .的平方根是C .的算术平方根是D .的算术平方根是 3.如果∠α与∠β的两边分别平行,∠α比∠β的3倍少40°,则∠α的度数为( )A .20°B .125°C .20°或125°D .35°或110°4.人体中红细胞的直径约为0.000007m ,将0.000007m 用科学记数法表示数的结果是( ) A .50.710m -⨯B .60.710m -⨯C .5710m -⨯D .6710m -⨯ 5.如果,下列不等式中,不一定成立的是( ) A . B . C . D .6.疟原虫早期滋养体的直径约为0.00000122米,用科学记数法表示为( )米.A .61.2210-⨯B .60.12210-⨯C .612.210-⨯D .51.2210-⨯7.下列选项中,是二元一次方程的是( )A .xy +4x =7B .π+x =6C .x -y =1D .7x +3=5y +7x8.如图,在ABC ∆中,BC 边上的高是( )A .ECB .BHC .CD D .AF9.点P (5,-3)所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限10.如图,a ∥b ,点B 在直线a 上,且AB ⊥BC ,若∠1=56°,则∠2的度数是( )A .54°B .44°C .40°D .34°11. “已知:2m a =,3n a =,求m n a +的值”,解决这个问题需要逆用幂的运算性质中的哪一个?( ) A .同底数幂的乘法 B .积的乘方 C .幂的乘方 D .同底数幂的除法12.方程ax-4y=x-1是关于x,y 的二元一次方程,则a 的取值范围为( )A .a≠0B .a≠-1C .a≠1D .a≠213.下列四个统计图中,用来表示不同品种的奶牛的平均产奶量最为合适的是( )A .B .C .D .14.某车间工人刘伟接到一项任务,要求10天里加工完190个零件,最初2天,每天加工15个,要在规定时间内完成任务,以后每天至少加工零件个数为( )A .18B .19C .20D .2115.下列所示的四个图形中,∠1和∠2是同位角的是( )A .②③B .①②③C .①②④D .①④16.如图,在△ABC 中,AC 的垂直平分线交BC 于点D ,交AC 于点E ,BC =6,AB =5,则△ABD 的周长为( )A .13cmB .12cmC .11cmD .10cm17.将直尺和直角三角板按如图方式摆放,已知∠1=25°,则∠2的大小是( )A .45°B .55°C .65°D .75°18.一辆汽车在笔直的公路上行驶,在两次转弯后,前进的方向仍与原来相同,那么这两次转弯的角度可以是( )A .先右转80°,再左转100°B .先左转80°,再右转80°C .先左转80°,再左转100°D .先右转80°,再右转80°19.(6分)若x <y ,且(a+5)x >(a+5)y ,则a 的取值范围( )A .a 5>-B .a 5≥-C .a 5<-D .a 5<20.(6分)如图是运动员冰面上表演的图案,下列四个选项中,能由原图通过平移得到的是( )A .B .C .D .21.(6分)点P 在第二象限内,P 到x 轴的距离是4,到y 轴的距离是3,那么点P 的坐标为( )A .(43)-,B .(34)--,C .(34)-,D .(34)-,22.(8分)在平面直角坐标系中,点A'(2,﹣3)可以由点A (﹣2,3)通过两次平移得到,正确的是( )A .先向左平移4个单位长度,再向上平移6个单位长度B .先向右平移4个单位长度,再向上平移6个单位长度C .先向左平移4个单位长度,再向下平移6个单位长度D .先向右平移4个单位长度,再向下平移6个单位长度23.(8分)如果点在轴上,则点所在的象限是( )A .第四象限B .第三象限C .第二象限D .第一象限24.(10分)六边形的内角和为( )A .720°B .360°C .540°D .180°25.(10分)有下列长度的三条线段,其中能组成三角形的是A .3, 4, 8B .5, 6, 11C .3, 1, 1D .3, 4, 626.(12分)3的相反数是( )A .3B .3-C .3D .127.(12分)关于x 的不等式组0321x a x -≤⎧⎨+>-⎩的整数解共有4个,则a 的取值范围( ) A .3a = B .23a << C .23a ≤< D .23a <≤28.如图,一个运算程序,若需要经过两次运算才能输出结果,则x 的取值范围为( )A .1x >B .15x <≤C .15x ≤≤D .15x ≤<29.若m n >,则下列选项不正确的是( )A .22m n +>+B .33m n >C .m n -<-D .5252m n ->-30.将点()4,1A --向右平移2个单位长度,再向上平移3个单位长度得点'A ,则点'A 的坐标是( ) A .(2,2) B .(2,2)- C .(2,2)-- D .(2,2)-参考答案选择题有答案含解析1.B【解析】【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.【详解】①了解某批种子的发芽率适合采取抽样 调查;②了解某班学生对“社会主义核心价值观”的知晓率适合采取全面调查;③了解某地区地下水水质适合采取抽样调查;④了解七年级(1)班学生参加“开放性科学实践活动”完成次数适合采取全面调查;故选:B .【点睛】本题考查的是抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.2.D【解析】A 选项:-9没有平方根,故是错误的;B 选项:9的平方根有3和-3,故是错误的;C 选项:9的算术平方根是3,故是错误的;D 选项:9的算术平方根是3,故是正确的;故选D .3.C【解析】【分析】由两角的两边互相平行可得出两角相等或互补,再由题意,其中一个角比另一个角的3倍少40°,可得出答案.【详解】设∠β为x ,则∠α为3x ﹣40°,若两角互补,则x+3x ﹣40°=180°,解得x=55°,∠α=125°;若两角相等,则x=3x ﹣40°,解得x=20°,∠α=20°.故选C .【点睛】本题考查平行线的性质,关键在于根据两角的两边分别平行打开此题的突破口.4.D【解析】【分析】根据科学记数法的定义进行分析解答即可.【详解】60.000007710m m -=⨯.在把一个绝对值小于1的数用科学记数法表示为10n a ⨯的形式时,我们要注意两点:①a 必须满足:110a ≤<;②n 等于原来的数中从左至右第1个非0数字前面0的个数(包括小数点前面的0)的相反数.5.D【解析】【分析】根据不等式的性质,逐一分析,A 、B 一定成立,C 一定不成立,D 不一定成立.【详解】解:A 选项中不等式左右同时加上3,得出,成立; B 选项中不等式两边同时乘以,得出,成立;C 选项中不等式两边同时乘以2,得出,一定不成立;D 选项中当a 、b 为正数时成立,当a 、b 为负数时不成立,所以不一定成立;故选D.【点睛】此题主要考查不等式的性质,熟练掌握不等式的基本性质是解题关键.6.A【解析】【分析】科学记数法的表示形式为10n a ⨯ 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>10时,n 是正数;当原数的绝对值<1时,n 是负数.【详解】-60.00000122=1.2210⨯故选:A【点睛】此题考查的知识点是用科学记数法表示较小的数,关键用科学记数法表示较小的数,一般形式为10n a -⨯ ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.用科学记数法表示数,一定要注意a 的形式,以及指数n 的确定方法.7.C【详解】A选项:项xy的次数是2次,故是错误的;B选项:只有一个未知数x,是一元一次方程,故是错误的;C选项:x-y=1是二元一次方程,故是正确的;D选项:化简后为5y-3=0是一元一次方程,故是错误的;故选C.【点睛】二元一次方程定义关键是掌握二元一次方程需满足三个条件:①首先是整式方程.②方程中共含有两个未知数.③所有未知项的次数都是一次.不符合上述任何一个条件的都不叫二元一次方程.8.D【解析】【分析】根据三角形的高线的定义解答.【详解】根据高的定义,AF为△ABC中BC边上的高.故选D.【点睛】本题考查了三角形的高的定义,熟记概念是解题的关键.9.D【解析】【分析】根据各象限内点的坐标特征解答即可.【详解】点(5,−3)横坐标为正数,纵坐标为负数,故所在的象限是第四象限.故选:D.【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(−,+);第三象限(−,−);第四象限(+,−).10.D【解析】【分析】根据平行线的性质求得∠3的度数,即可求得∠2的度数.【详解】如图,∵a ∥b ,∴∠3=∠1=56°,∴∠2=180°﹣90°﹣56°=34°.故选D .【点睛】本题考查了平行线的性质,理解性质定理是关键.11.A【解析】【分析】根据同底数幂的乘法公式即可求解.【详解】∵m n a +=n m a a ⋅=2×3=6∴解决这个问题需要逆用同底数幂的乘法公式故选A .【点睛】此题主要考查幂的运算公式,解题的关键是熟知同底数幂的乘法公式的特点.12.C【解析】【分析】将方程整理得(a -1)x -4y =-1.因为此方程为关于x ,y 的二元一次方程,所以a -1≠0,所以a≠1.【详解】解:方程合并同类项后得 (a -1)x =4y -1根据题意 a -1≠0 ,即a≠1时这个方程才是关于x 、y 的二元一次方程,故选C.【点睛】本题考查二元一次方程的定义,掌握成立条件是解题关键.此题根据扇形统计图、折线统计图、条形统计图各自的特点来判断.扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.解:根据统计图的特点,知条形统计图能清楚地表示出每个项目的具体数目,也正符合这道题要把不同品种的奶牛的平均产奶量显示清楚的目的;而图B中的奶牛瓶这样一个立体物显示,容易使人们从体积的角度比较这几种不同品种奶牛的平均产奶量,从而扩大了它们的差距,是不合适的.故选D.14.C【解析】设平均每天至少加工x个零件,才能在规定的时间内完成任务,因为要求10天里加工完190个零件,最初2天,每天加工15个,还剩8天,依题意得2×15+8x≥190,解之得,x≥20,所以平均每天至少加工20个零件,才能在规定的时间内完成任务.故选C.【方法点睛】本题中存在的不等关系是,10天中能加工的零件数要大于或等于190个.根据这个不等关系就可以得到不等式.15.C【解析】【分析】此题在于考查同位角的概念,在截线的同侧,并且在被截线的同一方的两个角是同位角,所以①②④符合要求.【详解】图①、②、④中,∠1与∠2在截线的同侧,并且在被截线的同一方,是同位角;图③中,∠1与∠2的两条边都不在同一条直线上,不是同位角.故选C.【点睛】此题考查同位角,内错角,同旁内角的概念,关键是根据同位角,内错角,同旁内角的概念解答.判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.【分析】先根据DE是△ABC中AC边的垂直平分线,可得到AD=CD,即AD+BD=CD+BD=BC=6,即可解答【详解】∵DE是△ABC中AC边的垂直平分线,∴AD=CD,又∵BC=6,AB=5,∴AD+BD=CD+BD=BC=6,∴△ABD的周长=AB+(AD+BD)=AB+BC=6+5=1.故选C.【点睛】此题考查垂直平分线的性质,解题关键在于利用垂直平分线的性质得到AD+BD=CD+BD=BC=6 17.C【解析】【分析】先根据两角互余的性质求出∠3的度数,再由平行线的性质即可得出结论.【详解】如图,∵∠1+∠3=90°,∠1=25°,∴∠3=65°.∵直尺的两边互相平行,∴∠2=∠3=65°.故选C.【点睛】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.18.B【解析】根据两条直线平行的性质:两条直线平行,同位角相等.再根据题意得:两次拐的方向不相同,但角度相等画出图形,根据图形直接解答即可.【详解】解:如图所示:A、,故本选项错误;B、,故本选项正确;C、,故本选项错误;D、,故本选项错误.故选B.【点睛】本题考查平行线的性质,根据题意画出图形是解答此题的关键.19.C【解析】【分析】直接根据不等式的基本性质即可得出结论.【详解】<,且()()x y+>+,a5x a5y∴+<,即a5<-.a50故选C.【点睛】本题考查的是不等式的性质,熟知不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变是解答此题的关键.平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动.旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心.所以,它并不一定是绕某个轴的.然后根据平移与旋转定义判断即可.【详解】解:列四个图案中,可以通过右图平移得到的是:故选:C .【点睛】本题考查学生对平移和旋转的认识,知道平移和旋转只改变图形的位置,不改变图形的形状和大小. 21.C【解析】【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x 轴的距离等于纵坐标的长度,到y 轴的距离等于横坐标的长度解答.【详解】解:∵点P 在第二象限内,点P 到x 轴的距离是4,到y 轴的距离是3,∴点P 的横坐标是-3,纵坐标是4,∴点P 的坐标为(-3,4).故选C .【点睛】本题考查了点的坐标,熟记点到x 轴的距离等于纵坐标的长度,到y 轴的距离等于横坐标的长度是解题的关键.22.D【解析】【分析】利用点A 与点'A 的横纵坐标的关系确定平移的方向和平移的距离即可.【详解】把点()2,3A -先向右平移4个单位,再向下平移6个单位得到点()A'2,3-.本题考查了坐标与图形变化-平移:在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a ,相应的新图形就是把原图形向右(或向左)平移a 个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a ,相应的新图形就是把原图形向上(或向下)平移a 个单位长度.掌握平移规律是解题的关键.23.A【解析】【分析】 根据轴上的点横坐标为0,列方程求出m ,然后可得Q 点坐标,再判断即可.【详解】解:由题意得:m +1=0,解得:m =−1,m 2019=(−1)2019=−1∴Q (2,−1),∴Q 在第四象限.故选:D .【点睛】本题考查了平面直角坐标系,正确理解横坐标与纵坐标的意义是解题的关键.24.A【解析】【分析】根据多边形内角和公式2180()n -⨯︒ ,即可求出.【详解】根据多边形内角和公式2180()n -⨯︒,六边形内角和(62)180720=-⨯︒=︒故选A.【点睛】本题考查多边形内角和问题,熟练掌握公式是解题关键.25.D【解析】【分析】解:根据三角形任意两边的和大于第三边,A选项中,3+4=7<8,不能组成三角形;B选项中,5+6=11,不能组成三角形;C选项中,1+1=2<3,不能够组成三角形;D选项中,3+4>6,能组成三角形.故选:D.【点睛】本题考查能够组成三角形三边的条件:用两条较短的线段相加,如果大于最长的那条线段就能够组成三角形.26.B【解析】【分析】一个数的相反数就是在这个数前面添上“-”号,由此即可求解.【详解】故选B.【点睛】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“-”号:一个正数的相反数是负数,一个负数的相反数是正数,1的相反数是1.27.C【解析】【分析】分别求出每一个不等式的解集,根据不等式组的整数解的个数可得答案.【详解】解不等式x-a≤0得x≤a,解不等式3+2x>-1得x>-2,∵不等式组的整数解共有4个,∴这4个整数解为-1、0、1、2,则2≤a<3,故选:C.【点睛】【解析】【分析】根据运算流程结合需要经过两次运算可得出关于x 的一元一次不等式组,解不等式组即可得出结论.【详解】解:由题意得:()3x 21733x 2217+<⎧⎨++≥⎩, 解得:15x ≤<故选:D .【点睛】此题主要考查了一元一次不等式组的应用,关键是弄明白图示的意思,列出不等式组.29.D【解析】【分析】根据不等式的性质逐项分析即可.【详解】A. ∵m n >,∴ m 2n 2+>+,故正确;B. ∵m n >,∴ 3m 3n >,故正确;C. ∵m n >,∴ m n -<-,故正确;D. ∵m n >,∴2m 2n -<-,∴52m 52n -<-,故不正确;故选D.【点睛】本题考查了不等式的性质:①把不等式的两边都加(或减去)同一个整式,不等号的方向不变;②不等式两边都乘(或除以)同一个正数,不等号的方向不变;③不等式两边都乘(或除以)同一个负数,不等号的方向改变.30.B【解析】【分析】直接利用平移中点的变化规律求解即可.【详解】A(−4,−1)向右平移2个单位长度得到:(−4+2,−1),即(−2,−1),此题考查坐标与图形变化-平移,解题关键在于掌握平移的性质.。
辽宁省抚顺市七年级下学期数学期末考试试卷

辽宁省抚顺市七年级下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共20分)1. (2分)下面是某次数学测验同学们的计算摘录,其中正确的是()A . 2a+3b=5abB . (﹣2a2)3=6a6C . a3•a2=a6D . ﹣a5÷(﹣a)=a42. (2分)下列四个不等式:(1)ac>bc;(2)﹣ma<mb;(3)ac2>bc2;(4)>1,一定能推出a>b 的有()A . 1个B . 2个C . 3个D . 4个3. (2分)(2014·贺州) 不等式的解集在数轴上表示正确的是()A .B .C .D .4. (2分) (2020七下·慈溪期末) 下列各组数中,不是二元一次方程2x-5y=3的解是()A .B .C .D .5. (2分) (2016九上·海南期末) 如图,若∠A=27°,∠B=50°,∠C=38°,则∠BFE等于()A . 65°B . 115°C . 105°D . 75°6. (2分) (2018八上·上杭期中) 如图,用直尺和圆规作一个角等于已知角,能得出的依据是()A . (SAS)B . (SSS)C . (ASA)D . (AAS)7. (2分)(﹣)2015•()2016的计算结果是()A .B .C .D .8. (2分) (2020七下·河南月考) 若x2+8x+m是完全平方式,则m的值为()A . 4B . ﹣4C . 16D . ﹣169. (2分)在下列命题中,正确的是()A . 正多边形一个内角与一个外角相等,则它是正六边形B . 正多边形都是中心对称图形C . 边数大于3的正多边形的对角线长都相等D . 正多边形的一个外角为,则它是正十边形10. (2分) (2019八上·霍林郭勒月考) 如图,边长为的正方形纸片剪出一个边长为的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为,则另一边长为()A .B .C .D .二、填空题 (共8题;共8分)11. (1分)(2017·阿坝) 某种电子元件的面积大约为0.00000069平方毫米,将0.00000069这个数用科学记数法表示为________.12. (1分) (2019七下·新田期中) ________; =________.13. (1分) (2017七下·海安期中) 把方程3x-y-1=0改写成含x的式子表示y的形式得________.14. (1分) (2019八上·孝南月考) 若代数式2a2+3a+1的值是6,则代数式5-6a2-9a的值为________;15. (1分)(2018·玄武模拟) 如图,在□ABCD中,DB=DC,AE⊥BD,垂足为E,若∠EAB=46°,则∠C=________°.16. (1分)小亮解方程组的解为由于不小心滴上了两滴墨水,刚好遮住了两个数·和,请你帮他找回·和,·=________, =________.17. (1分) (2020·北京模拟) 在中,将、按如图所示方式折叠,点、均落于边上一点处,线段、为折痕.若,则 ________ .18. (1分) (2019九上·香坊月考) 如图,在△ABC中,AB=AC,点D在AB上,点E在AC延长线上,且BD =CE,连接DE交BC于点F,作DH⊥BC于点H,连接CD.若tan∠DFH=,S△BCD=18,则DE的长为________.三、解答题 (共9题;共76分)19. (10分) (2019八上·澄海期末) 计算:.20. (10分) (2018八上·翁牛特旗期末) 因式分解:(1)(2)21. (10分)(2019·广州模拟) 先化简,再求值:,其中a是满足不等式的最小整数解.22. (5分) (2019八上·安顺期末) 先化简,然后从的范围内选取一个合适的整数作为x的值代入求值。
辽宁省抚顺市七年级下学期数学期末考试试卷

辽宁省抚顺市七年级下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分)下列调查中,适合采用普查方式的是()A . 对河水水质情况的调查.B . 对端午节期间市场上粽子质量情况的调查.C . 对某班50名同学体重情况的调查.D . 对某类烟花爆竹燃放安全情况的调查.2. (2分)若(a-1)x<a-1的解集为x>1,那么a的取值范围是()A . a>0B . a<0C . a<1D . a>13. (2分)(2016·广元) 在平面直角坐标系中,点P(﹣2,x2+1)所在的象限是()A . 第一象限B . 第二象限C . 第三象限D . 第四象限4. (2分)(2019·温州模拟) 不等式x≤﹣1的解集在数轴上表示正确的是()A .B .C .D .5. (2分)(2017·文昌模拟) 如图,已知AB⊥GH,CD⊥GH,直线CD,EF,GH相交于一点O,若∠1=42°,则∠2等于()A . 130°B . 138°C . 140°D . 142°6. (2分) (2017八上·宝坻月考) 若a=0.32 , b=﹣3﹣2 , c= ,d= ,则它们的大小关系是()A . a<b<c<dB . b<a<d<cC . a<d<c<bD . c<a<d<b7. (2分) (2018八上·昌图期末) 下列句子中,不是命题的是()A . 动物都需要水B . 相等的角是对顶角C . 负数都小于零D . 过直线l外一点作l的平行线8. (2分)某款捷安特自行车进价是每辆1000元,标价是每辆1500元,店庆期间,商场为了答谢顾客,进行打折促销活动,若要保证利润不低于20%,则最多可打()折.A . 6B . 7C . 8D . 9二、填空题 (共6题;共6分)9. (1分)请你写出三个大于1的无理数:________.10. (1分) (2019八上·农安期末) 写出一个比-4大的负无理数________ .11. (1分) (2017七下·延庆期末) 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线AB,CD,并说出自己做法的依据.小琛、小萱、小冉三位同学的做法如下:小琛说:“我的做法的依据是内错角相等,两直线平行.”小萱做法的依据是________.小冉做法的依据是________.12. (1分) (2017七上·天门期中) 若|x-2|+(y- )2=0,则yx=________.13. (1分)经调查,某校学生上学所用的交通方式中.选择“自行车”、“公交车”、“其他”的比例为7:3:2,若该校学生有1200人,则选择“公交车”的学生人数是________ .14. (1分)(2019·滨城模拟) 如图,在一单位为1的方格纸上,△A1A2A3 ,△A3A4A5 ,△A5A6A7 ,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2019的坐标为________.三、解答题 (共9题;共66分)15. (5分)(2017·扬州) 计算或化简:(1)﹣22+(π﹣2017)0﹣2sin60°+|1﹣ |;(2)a(3﹣2a)+2(a+1)(a﹣1).16. (5分)已知,求代数式的值.17. (5分) (2019九下·常德期中) 解不等式组,并把它的解集在数轴上表示出来.18. (10分) (2019八上·长兴月考) 如图,每个小方格的边长为1,已知点A(2,2),把点A先向左平移4个单位,再向下平移2个单位到达点B;把点B先向右平移2个单位,再向下平移4个单位到达点C。
辽宁省抚顺市七年级第二学期数学精选常考解答题汇总含解析

辽宁省抚顺市七年级第二学期数学精选常考解答题汇总解答题有答案含解析1.如图,AB ∥CD ,点E 是CD 上一点,∠AEC =42°,EF 平分∠AED 交AB 于点F ,求∠AFE 的度数.2.如图,在平面直角坐标系xOy 中,四边形AOBC 为边长为6的正方形,点D 为OB 的中点,13BE BC =.动点(),P x y 在线段AD 和DE 上运动,另一动点(),Q x z 在线段AE 上运动. 用学过的知识解决下列问题:(1)①填空:点E 的坐标____________________; ②求三角形AOD 的面积;(2)求点P 在运动过程中,x 与y 的数量关系;(3)两个动点P Q 、在运动过程中,是否存在使线段PQ 的长等于2的时刻,如果存在,求出此时点P 坐标;如果不存在,请你说明理由.3.年是我市“创建国家卫生城市”第一年,为了了解本班50名学生对“创卫”的知晓率,某同学采取随机抽样的方法进行问卷调查,调查分为四个选项:A 非常了解,B 比较了解,C 基本了解,D 不甚了解.数据整理如下:DBCBC AACBA ABCBD ABBCB CABCB ABABB CBBCB CCBBC CABCD CDABD请画出条形图和扇形图来描述以上统计数据.4.如图,直线l 3,l 4与l 1,l 2分别相交于点A 、B 、C 、D ,且∠1+∠2=180°. (1)直线l 1与l 2平行吗?为什么?(2)点E 在线段AD 上,∠ABE =30°,∠BEC =62°,求∠DCE 的度数.5.细心解一解.(1)解方程组27 320 x yx y-=⎧⎨+=⎩(2)解不等式21321 34x x-+-6.(1)我国著名的数学家赵爽,早在公元3世纪,就把一个矩形分成四个全等的直角三角形,用四个全等的直角三角形拼成丁一个大的正方形(如图1),这个矩形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中两直角边a、b与斜边c满足关系式a2+b2=c2,称为勾股定理.证明:∵大正方形面积表示为S=c2,,又可表示为S=4×12ab+(b-a)2,∴4×12ab+(b-a)2=c2.∴______________即直角三角形两直角边的平方和等于斜边的平方.(2)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图2),也能验证这个结论,请你帮助小明完成验证的过程.(3)如图3所示,∠ABC=∠ACE=90°,请你添加适当的辅助线,证明结论a2+b2=c2.7.小明从家里到学校先是走一段平路然后走一段下坡路,假设他始终保持平路每分钟走80m,下坡路每分钟走90m,上坡路每分钟走60m,则他从家里到学校需20min,从学校到家里需25min.问:从小明家到学校有多远?8.化简22212(1)441x x xxx x x-+÷+⨯++-,并在-2≤x≤2中选择适当的值代入求值.9.如图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的坐标系.(1)写出汽车站和消防站的坐标;(2)某星期日早晨,小英同学从家里出发,沿,,,,,的路线转了一下,又回到家里,写出路上她经过的地方.10.某工程交由甲、乙两个工程队来完成,已知甲工程队单独完成需要60天,乙工程队单独完成需要40天(1)若甲工程队先做30天后,剩余由乙工程队来完成,还需要用时天(2)若甲工程队先做20天,乙工程队再参加,两个工程队一起来完成剩余的工程,求共需多少天完成该工程任务?11.在一个不透明的口袋中装有9个黄球,13个黑球,11个红球,它们除颜色外其余都相同.(1)求从袋中摸出一个球是红球的概率;(2)现从袋中取出若干个黄球,井放入相同数量的黑球,若要使搅拌均与后从袋中摸出一个球是黑球的概率不小于47,问至少要取出多少个黄球?12.“龟免赛跑”的故事同学们都非常热悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.(1)填空:折线OABC表示赛跑过程中_______(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是___________米.(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)乌龟用了多少分钟追上了正在睡觉的兔子?(4)兔子醒来假,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.13.如图,254267B D BCD ∠=︒∠=︒∠=︒,, ,试判断AB 和ED 的位置关系,并说明理由.14.用加减消元法解方程组:0.50.73520.820x y x y +=⎧⎨+=⎩15.探究与发现:探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?已知:如图1,∠FDC 与∠ECD 分别为△ADC 的两个外角,试探究∠A 与∠FDC +∠ECD 的数量关系. 探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?已知:如图2,在△ADC 中,DP 、CP 分别平分∠ADC 和∠ACD ,试探究∠P 与∠A 的数量关系. 探究三:若将△ADC 改为任意四边形ABCD 呢?已知:如图3,在四边形ABCD 中,DP 、CP 分别平分∠ADC 和∠BCD ,试利用上述结论探究∠P 与∠A +∠B 的数量关系.16.如图,(1,0)A -,(1,4)C ,点B 在x 轴上,且3AB =. (1)求点B 的坐标,并画出ABC ∆; (2)求ABC ∆的面积;(3)在y 轴上是否存在点P ,使以,,A B P 三点为顶点的三角形的面积为10?若存在,请直接写出点P 的坐标;若不存在,请说明理由.17.如图是由4个边长为1个单位长度的小正方形拼成,请你在图上添加一个小正方形,使添加后的图形是一个轴对称图形,要求画出三种.18.已知:如图,C ,D 是直线AB 上的两点,∠1+∠2=180°,DE 平分∠CDF,EF∥AB. (1)猜想:CE 和DF 是否平行?请说明理由; (2)若∠DCE=130°,求∠DEF 的度数.19.(6分)如图,Rt △ABC 中,∠ACB=90°,斜边AB 边上的高CD 与角平分线AE 交于点F ,经过垂足D 的直线分别交直线CA ,BC 于点M ,N . (1)若AC=3,BC=4,AB=5,求CD 的长;(2)当∠AMN=32°,∠B=38°时,求∠MDB 的度数;(3)当∠AMN=∠BDN 时,写出图中所有与∠CDN 相等的角,并选择其中一组进行证明.20.(6分)如图,ABC ∆的顶点都在每个边长为l 个单位长度的方格纸的格点上,将ABC ∆向右平移1格,再向上平移3格,得到A B C ∆''. (1)请在图中画出A B C ∆''; (1)ABC ∆的面积为________;(3)若AC 的长约为1.8,试求AC 边上的高为多少(结果保留分数)?21.(6分)七年级一班在召开期末总结表彰会前,班主任安排班长李小波去商店买奖品,下面是李小波与售货员的对话:李小波:阿姨,您好!售货员:同学,你好,想买点什么?李小波:我只有元,请帮我安排买支钢笔和本笔记本.售货员:好,每支钢笔比每本笔记本贵元,退你元,请清点好,再见.根据这段对话,你能算出钢笔和笔记本的单价各是多少吗?22.(8分)在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E 在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.23.(8分)进入六月以来,西瓜出现热卖.佳佳水果超市用760元购进甲、乙两个品种的西瓜,销售完共获利360元,其进价和售价如表:甲品种乙品种进价(元/千克) 1.6 1.4售价(元/千克) 2.4 2(1)求佳佳水果超市购进甲、乙两个品种的西瓜各多少千克?(2)由于销售较好,该超市决定,按进价再购进甲,乙两个品种西瓜,购进乙品种西瓜的重量不变,购进甲品种西瓜的重量是原来的2倍,甲品种西瓜按原价销售,乙品种西瓜让利销售.若两个品种的西瓜售完获利不少于560元,问乙品种西瓜最低售价为多少元?24.(10分)如图,∠1+∠2=180°,∠B=∠3.(1)判断DE与BC的位置关系,并说明理由:解:结论:______________.理由:∵∠1+∠2=180°,∴_________________∴∠ADE=∠3,∵∠B=∠3∴______________∴DE∥BC;(2)若∠C=65°,求∠DEC的度数.25.(10分)如图,∠BAD=∠CBE=∠ACF,∠FDE=64°,∠DEF=43°,求△ABC各内角的度数.26.(12分)解方程组:()()22171136x yx y⎧-++=⎪⎨+-=⎪⎩27.(12分)巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:(1)在上述变化过程中,自变量是______,因变量是______;(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?28.如图所示的一块草地,已知AD=4m,CD=3m,AB=12m,BC=13m,且∠CDA=90°,求这块草地的面积.29.如图,点C 是线段AB 上一点,AC <AB ,M ,N 分别是AB 和CB 的中点,AC=8,NB=5,求线段MN 的长.30.利用幂的运算性质 计算:363222⨯⨯.参考答案解答题有答案含解析 1.∠AFE =69°. 【解析】 【分析】由平角求出∠AED 的度数,由角平分线得出∠DEF 的度数,再由平行线的性质即可求出∠AFE 的度数. 【详解】解:∵∠AEC =42°,∴∠AED =180°-∠AEC =138°. ∵EF 平分∠AED , ∴∠DEF = ∠AED =69°.∵AB ∥CD ,∴∠AFE =∠DEF =69°.2.(1)①()6,2;②9;(2)62y x =-或263x y -=;(3)P 点坐标为3,32⎛⎫ ⎪⎝⎭或9,12⎛⎫⎪⎝⎭.【解析】 【分析】(1)由正方形边长和13BE BC =,求出BE 长即可得到点E 坐标. 由D 是OB 的中点可得OD=3,由三角形面积公式可求AOD S ∆.(2)分两种情况,①点P 在AD 上,②点P 在DE 上,设P 点坐标为(x ,y ),根据三角形面积求法用x 、y 表示已知三角形面积即可. (3)同(2)求出1823xz -=,结合(2)可知PQ=z-y.由(2)得两种情况即可求出对应的x 值,即可的出P 点坐标.【详解】解:(1)①∵四边形AOBC 为边长为6的正方形,∴B 点坐标为(6,0),C 点坐标为(6,6),A 点坐标为(0,6) ∵13BE BC ==163⨯=2,∴BE=2,∴E 点坐标为()6,2;②∵正方形AOBC 的边长为6,点D 为OB 的中点,, ∴3,2OD BE ==, ∴13692AOD S ∆=⨯⨯=; (2)①点P 在AD 上, ∴111369?222AOD S PM OA PN OD ∆=⨯⨯==+ ∴3618y x +=, ∴26,62y x y x +==-; ②点P 在DE 上,∴11· (22)DBE S PG DB PH EB ∆=+, ∴()11132632222y x ⨯⨯+⨯⨯-=⨯⨯ ∴236x y -=,263x y -=;(3)点Q 在AE 上,∴()()11111· (664622222)AEC S AC EC AC TQ CE QS z x ∆==+=⨯⨯-+⨯⨯- ∴1822318,3xx z z -+==,∴()PQ z y =-, ①点P 在AD 上,∴()1826223xx ---=, ∴32x =,P 点坐标为3,32⎛⎫ ⎪⎝⎭; ②点P 在DE 上, ∴18226233x x ---=, ∴92x =,P 点坐标为9,12⎛⎫ ⎪⎝⎭, 综上,P 点坐标为3,32⎛⎫ ⎪⎝⎭或9,12⎛⎫ ⎪⎝⎭.【点睛】本题考查三角形的面积、解一元一次方程组、坐标与图形的性质,解题的关键是灵活运用所学知识分类讨论、解决问题. 3.见解析 【解析】 【分析】先依次数出A,B,C,D 出现的次数,即可做出条形统计图,再求出A,B,C,D 四个选项各自的占比即可做出扇形统计图. 【详解】根据数据个数得到A 出现10次,B 出现20次,C 出现15次,D 出现5次, 故作出条形统计图如下:∵A 选项占比为10÷50=20%; B 选项占比为20÷50=40%; C 选项占比为15÷50=30%; D 选项占比为5÷50=10%; 故作扇形统计图如下:【点睛】此题主要考查统计图的作法,解题的关键是根据题意求出各选项的占比即可作图. 4.(1)见解析;(2)∠DCE=32°.【解析】【分析】(1)根据平行线的判定解答即可;(2)过点E作EF∥AB交BC于点F,利用平行线的判定和性质解答即可.【详解】(1)直线l1与l2平行,∵∠1+∠BAE=180°,∠1+∠2=180°,∴∠2=∠BAE,∴l1∥l2.(2)过点E作EF∥AB交BC于点F,可得:∠BEF=∠ABE=30°,∴∠FEC=62°﹣30°=32°,∵l1∥l2,∴EF∥CD,∴∠DCE=∠FEC=32°.【点睛】此题考查平行线的判定和性质,关键是根据平行线的判定和性质解答.5.(1)23xy=⎧⎨=-⎩;(1)x≥1【分析】(1)利用加减消元法即可求解;(1)将不等式去分母,去括号,移项合并,将x 系数化为1,即可求出解集.【详解】(1)27320x y x y -=⎧⎨+=⎩①②, ①2⨯+②得:x =1,把x =1代入①得:y =﹣3,所以方程组的解为:23x y =⎧⎨=-⎩; (1)去分母得:4(1x ﹣1)≤3(3x+1)﹣11,去括号得:8x ﹣4≤9x+6﹣11,解得:x ≥1.【点睛】本题考查了解二元一次方程组、解一元一次不等式,熟练掌握解一元一次不等式的步骤是解题关键. 6.(1)222+=a b c ;(2)答案见解析;(3)证明见解析.【解析】【分析】(1)通过化简即可证得;(2)根据四个全等的直角三角形的面积+阴影部分小正方形的面积=大正方形的面积,代入数值,即可证明;(3)作辅助线,构建矩形,根据矩形的面积可得结论.【详解】解答:证明:(1)∵大正方形面积表示为S =2c ,又可表示为S =4×()212ab b a +-, ∴4×()212ab b a +-=2c . ∴22222ab b ab a c +-+=,∴222+=a b c ,即直角三角形两直角边的平方和等于斜边的平方.故答案为:222+=a b c ;(2)证明:由图得,大正方形面积=12×ab ×4+2c =(a +b )×(a +b ), 整理得,22222ab c a b ab +=++,即222(3)如图,过A 作AF ⊥AB ,过E 作EF ⊥AF 于F ,交BC 的延长线于D ,则四边形ABDF 是矩形,∵△ACE 是等腰直角三角形,∴AC =CE =c ,∠ACE =90°=∠ACB +∠ECD ,∵∠ACB +∠BAC =90°,∴∠BAC =∠ECD ,∵∠B =∠D =90°,∴△ABC ≌△CDE (AAS ),∴CD =AB =b ,DE =BC =a ,S 矩形ABDF =b (a +b )=2×()()2111222ab c a b b a +++- , ∴222+=a b c .【点睛】本题考查了用数形结合来证明勾股定理,锻炼了同学们的数形结合的思想方法.7.1700m【解析】【分析】设出平路和坡路的路程,从家里到学校走平路和下坡路一共用10分钟,从学校到家里走上坡路和平路一共用15分钟,利用这两个关系式列出方程组解答即可.【详解】解:设平路有x 米,坡路有y 米,根据题意列方程得, 208090258060x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩ 解得:800900x y =⎧⎨=⎩ 总路程:8009001700m +=答:小明家到学校有1700m .【点睛】的变化,由此找出关系式,列方程组解决问题.8.2x x +;当x=1时,原式=1. 【解析】【分析】直接利用分式的混合运算法则化简得出答案.【详解】原式=()()()()21121112x x x x x x x +-+⨯⨯+-+ =2x x +, ∵-2≤x≤2,当x=-2,-1,1时都不合题意,∴当x=1时,原式=1.【点睛】此题主要考查了分式的化简求值,正确分解因式是解题关键.9.(1)汽车站(1,1),消防站(2,﹣2);(2)(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.【解析】【分析】(1)根据平面直角坐标系直接写出坐标即可;(2)根据平面直角坐标系找出各点对应的位置,然后写出经过的地方.【详解】(1)汽车站(1,1),消防站(2,﹣2);(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.10. (1) 1;(2)2天【解析】【分析】(1)总的工作量是“1”,甲的工作效率是160,乙的工作效率是140,根据题意,利用甲的工作量+乙的工作量=1列出方程并解答;(2)设共需x 天完成该工程任务,根据“甲的工作量+乙的工作量=1”列出方程并解答.【详解】(1)设剩余由乙工程队来完成,还需要用时x 天,依题意得: 3060+40x =1即剩余由乙工程队来完成,还需要用时1天.故答案为1;(2)设共需x 天完成该工程任务,根据题意得:60x +2040x -=1 解得:x=2.答:共需2天完成该工程任务.【点睛】本题考查了一元一次方程的应用.解题的关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.11. (1)摸出一个红球的概率是13; (2)至少去除6个黄球. 【解析】【分析】 (1)根据概率的定义公式,判断出m=11,n=33,即可得出摸出一个红球的概率是13; (2)首先设取出x 个黄球,则放入x 个黑球,根据题意得出摸出黑球的概率不小于47,列出不等式,解得417x ≥,所以至少去除6个黄球. 【详解】解:(1)摸出一个红球的概率是111913113=++ (2)设取出x 个黄球,则放入x 个黑球,根据题意得:134913117x x x +≥-+++ 解得:417x ≥ 所以至少去除6个黄球.【点睛】此题主要考查概率知识的实际应用问题,熟练掌握即可得解.12.(1)兔子 1500 (2)30米;(3)703;(4)46.5. 【解析】分析:(1)根据根据图象和点D 实际意义可得结论;(2)根据点A 实际意义知兔子起初速度,由点D 实际意义可知乌龟的速度;(3)利用兔子睡觉前行驶的路程是700米,结合乌龟的速度求出所用的时间;求解可得.详解:(1)由图可知,折线OABC 表示赛跑过程中兔子的路程与时间的关系,赛跑的全程是1500米.(2)结合图象得出:兔子在起初每分钟跑7002350÷=(米),乌龟每分钟爬15005030÷=(米).(3)70700303÷=(分钟), 所以乌龟用了703分钟追上了正在睡觉的兔子. (4)150********()-÷=(分钟),500.52246.5+--=(分钟), 所以兔子中间停下睡觉用了46.5分钟.点睛:本题考查了一次函数图象,理解两个函数图象的交点表示的意义,从函数图象准确获取信息是解题的关键.13.AB//ED ,理由见解析.【解析】【分析】先过C 点作CF ∥AB ,由平行线的性质得出∠B=∠BCF=25°,接下来计算出∠DCF 的度数,再根据∠DCF=∠D 得到结论成立.【详解】解:AB ∥ED .理由:如图,过C 作CF AB ∥,∵25B ∠=︒∴25BCF B ∠=∠=︒∴42DCF BCD BCF ∠=∠-∠=︒又∵42D ∠=︒∴DCF D ∠=∠.∴CF ED ∥.∴AB ∥ED .【点睛】本题考查了平行线的判定和性质,根据平行线的性质得到角的度数,解题的关键是熟练运用“内错角相等,两直线平行”的平行线的判定来证明,14.1460 xy=-⎧⎨=⎩【解析】【分析】首先将方程① ×4,再减去方程②,即可解得60y=,再将其代入②,即可得解. 【详解】解:0.50.735 20.820x yx y+=⎧⎨+=⎩①②4-⨯①②,得60y=代入②,得-14x=∴方程组的解为1460xy=-⎧⎨=⎩.【点睛】此题主要考查利用加减消元法进行二元一次方程组的求解.15.探究一:∠FDC+∠ECD=180°+∠A;探究二:∠P=90°+∠A;探究三:∠P =(∠A+∠B).【解析】【分析】探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;探究二:根据角平分线的定义可得∠PDC=∠ADC,∠PCD=∠ACD,然后根据三角形内角和定理列式整理即可得解;探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可.【详解】解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;探究二:∵DP、CP分别平分∠ADC和∠ACD,∴∠PDC =∠ADC,∠PCD =∠ACD,∴∠P=180°﹣∠PDC﹣∠PCD=180°﹣∠ADC﹣∠ACD=180°﹣(∠ADC+∠ACD )=180°﹣(180°﹣∠A )=90°+∠A ;探究三:∵DP 、CP 分别平分∠ADC 和∠BCD ,∴∠PDC =∠ADC ,∠PCD =∠BCD ,∴∠P =180°﹣∠PDC ﹣∠PCD=180°﹣∠ADC ﹣∠BCD=180°﹣(∠ADC+∠BCD )=180°﹣(360°﹣∠A ﹣∠B ) =(∠A+∠B ).故答案为探究一:∠FDC+∠ECD =180°+∠A ;探究二:∠P =90°+∠A ;探究三:∠P =(∠A+∠B ).【点睛】本题考查了三角形的外角性质,三角形的内角和定理,多边形的内角和公式,此类题目根据同一个解答思路求解是解题的关键.16. (1)B 点的坐标为(2,0),(4,0)-,画图见解析;(2) 6;(3)P 点的坐标为20(0,)3或20(0,)3- 【解析】【分析】(1)分点B 在点A 的左边和右边两种情况解答;(2)利用三角形的面积公式列式计算即可得解;(3)利用三角形的面积公式列式求出点P 到x 轴的距离,然后分两种情况写出点P 的坐标即可.【详解】(1)点B 在点A 的右边时,-1+3=2,点B 在点A 的左边时,-1-3=-4,所以,B 的坐标为(2,0)或(-4,0),(2)△ABC的面积=12×3×4=6;(3)设点P到x轴的距离为h,则12×3h=10,解得h=203,点P在y轴正半轴时,P(0,203),点P在y轴负半轴时,P(0,-203),综上所述,点P的坐标为(0,203)或(0,-203).【点睛】本题考查了坐标与图形性质,主要利用了三角形的面积,难点在于要分情况讨论.17.见解析【解析】【分析】根据轴对称图形的定义,即可得到答案.【详解】如图所示:【点睛】本题主要考查轴对称图形的定义,掌握轴对称图形的定义,是解题的关键.18.(1)CE∥DF.理由见解析;(2)25°【解析】(1)由∠1+∠DCE=180°,∠1+∠2=180°,可得∠2=∠DCE,即可得到CE∥DF;(2)由平行线的性质,可得∠CDF=50°,再由角平分线的性质得到∠CDE=25°,根据两直线平行,内错角相等即可得到结论.【详解】(1)CE∥DF.理由如下:∵∠1+∠2=180°,∠1+∠DCE=180°,∴∠2=∠DCE,∴CE∥DF;(2)∵CE∥DF,∠DCE=130°,∴∠CDF=180°﹣∠DCE=180°﹣130°=50°.∵DE平分∠CDF,∴∠CDE12=∠CDF=25°.∵EF∥AB,∴∠DEF=∠CDE=25°.【点睛】本题考查了平行线的判定与性质和角平分线的性质,注意平行线的性质和判定定理的综合运用.19.(1)CD125=;(2)∠MDB=110°;(3)与∠CDN相等的角有∠AFD,∠CFE,∠AEC,∠MNC;证明见解析.【解析】【分析】(1)根据三角形面积公式即可得到结论;(2)根据三角形的内角和定理求出∠MNC,进而得出∠MNB,再利用三角形外角的性质即可得到结论;(3)首先根据角平分线的定义和平行线的判定和性质证明AE∥MN,然后结合同角的余角相等可证明所有结论.【详解】解:(1)在Rt△ABC中,∠ACB=90°,∴S△ABC12=AC•BC12=⨯3×4=1.∵CD是斜边AB上是高,∴S△ABC12=AB•CD12=⨯5×CD=1,∴CD125 =;(2)∵∠ACB=90°,∠AMN=32°,∴∠MNC=180°﹣∠ACB﹣∠AMN=58°,∴∠MNB=180°﹣∠MNC=122°,∴∠MDB=∠MNB+∠B=122°+38°=110°;(3)与∠CDN相等的角有∠AFD,∠CFE,∠AEC,∠MNC;理由:∵∠AMN=∠BDN,∠BDN=∠ADM,∴∠CAB=∠AMN+∠ADM=2∠AMN,∵AE是∠CAB的角平分线,∴∠CAB=2∠CAE,∴∠AMN=∠CAE,∴AE∥MN,∴∠CDN=∠AFD=∠CFE,∵∠ACB=90°,∴∠AMN+∠MNC=90°,∵CD⊥AB,∴∠BDN+∠CDN=90°,∵∠AMN=∠BDN,∴∠CDN=∠MNC,∵AE∥MN,∴∠AEC=∠MNC,∴∠CDN=∠AEC.【点睛】本题考查了三角形的内角和定理,三角形外角的性质,角平分线的定义以及平行线的判定和性质等知识,正确的识别图形是解题的关键.20.(1)见解析;(1)3;(3)15 7.【解析】【分析】(1)根据平移的方向与距离进行作图;(1)根据△ABC中BC为3,BC边上的高为1,求得三角形的面积;(3)设AC边上的高为h,根据△ABC的面积为3,列出方程求解即可.【详解】(1)如图所示:(1)△ABC的面积为:12×3×1=3;(3)设AC边上的高为h,则12×AC×h=3,即12×1.8×h=3,解得h=15 7【点睛】本题主要考查了运用平移变换作图,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.21.钢笔每支为元,笔记本每本元,【解析】【分析】设钢笔每支为元,笔记本每本元,根据题意列出二元一次方程组求解即可.【详解】解:设钢笔每支为元,笔记本每本元,据题意得,解方程组得答:钢笔每支为元,笔记本每本元.【点睛】本题考查二元一次方程组的应用,根据题意找到等量关系是解题关键.22.64°32°【解析】【分析】(1)由∠BAC=100°,可求出∠ABC=∠ACB=40°,当∠DAC=36°时,根据∠BAD=∠BAC-∠DAC可求出∠BAD 的度数,根据等腰三角形的性质求出∠ADE=∠AED的度数,再根据三角形的外角的性质求解.(2)由思路(1)可知∠ABC=∠ACB=40°,以及∠ADE=∠AED=1802n-,∠CDE=∠ACB-∠AED,∠BAD=n-100°,即可求解.(3)根据(1)的思路,可知∠ABC=∠ACB=40°,∠ADE=∠AED=180n2︒-,∠CDE=∠ACD-∠AED,∠BAD=100°+n,即可求解.【详解】(1)∠BAD=∠BAC-∠DAC=100°-36°=64°.∵在△ABC中,∠BAC=100°,∠ABC=∠ACB,∴∠ABC=∠ACB=40°,∴∠ADC=∠ABC+∠BAD=40°+64°=104°.∵∠DAC=36°,∠ADE=∠AED,∴∠ADE=∠AED=72°,∴∠CDE=∠ADC-∠ADE=104°-72°=32°.故答案为64°,32°.(2)∠BAD=2∠CDE,理由如下:如图(2),在△ABC中,∠BAC=100°,∴∠ABC=∠ACB=40°.在△ADE中,∠DAC=n,∴∠ADE=∠AED=1802n︒-.∵∠ACB=∠CDE+∠AED,∴∠CDE=∠ACB-∠AED=40°-1802n︒-=1002n-︒.∵∠BAC=100°,∠DAC=n,∴∠BAD=n-100°,∴∠BAD=2∠CDE;(3)∠BAD=2∠CDE,理由如下:如图(3),在△ABC中,∠BAC=100°,∴∠ABC=∠ACB=40°,∴∠ACD=140°.在△ADE中,∠DAC=n,∴∠ADE=∠AED=180n2︒-.∵∠ACD=∠CDE+∠AED,∴∠CDE=∠ACD-∠AED=140°-180n2︒-=100n2︒+.∵∠BAC=100°,∠DAC=n,∴∠BAD=100°+n,∴∠BAD=2∠CDE.【点睛】此题主要考查了三角形的内角和及其外角的性质,熟练掌握三角形的内角和的性质和三角形的外角的性质是解题关键.23.(1)300千克,200千克;(2)1.1元/千克.【解析】【分析】(1)设佳佳水果超市购进甲品种西瓜x千克,购进乙品种西瓜y千克,根据总价=单价×数量结合总利润=每千克的利润×数量,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设乙品种西瓜的售价为m元/千克,根据总利润=每千克的利润×数量结合售完获利不少于560元,即可得出关于m的一元一次不等式,解之取其中的最小值即可得出结论.【详解】解:(1)设佳佳水果超市购进甲品种西瓜x千克,购进乙品种西瓜y千克,依题意,得:1.6 1.4760(2.4 1.6)(2 1.4)360x yx y+=⎧⎨-+-=⎩,解得:300200 xy=⎧⎨=⎩.答:佳佳水果超市购进甲品种西瓜300千克,购进乙品种西瓜200千克.(2)设乙品种西瓜的售价为m元/千克,依题意,得:300×2×(2.4﹣1.6)+200×(m﹣1.4)≥560,解得:m≥1.1.答:乙品种西瓜最低售价为1.1元/千克.【点睛】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.24.(1)DE∥BC,见解析;(2)115°【解析】【分析】(1)根据平行线的判定得出AB∥EF,根据平行线的性质得出∠ADE=∠3,求出∠ADE=∠B,根据平行线的判定得出即可;(2)根据平行线的性质得出∠C+∠DEC=180°,即可求出答案.【详解】(1). DE ∥BC ,理由: ∵∠1+∠2=180°,∴AB//EF∴∠ADE=∠3,∵∠B=∠3∴∠ADE=∠B∴DE ∥BC;(2)∵DE ∥BC ,∴∠C+∠DEC=180°,∵∠C=65°,∴∠DEC=115°.【点睛】考查了平行线的性质和判定,能熟练地运用定理进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然. 25.△ABC 各内角的度数分别为64°、43°、73°.【解析】【分析】根据三角形外角性质得到∠FDE=∠BAD +∠ABD ,而∠BAD=∠CBE ,则∠FDE=∠BAD +∠CBE=∠ABC=64°;同理可得∠DEF=∠ACB=43°,然后根据三角形内角和定理计算∠BAC=180°﹣∠ABC ﹣∠ACB 即可.【详解】∵∠FDE=∠BAD +∠ABD ,∠BAD=∠CBE ,∴∠FDE=∠BAD +∠CBE=∠ABC ,∴∠ABC=64°;同理:∠DEF=∠FCB +∠CBE=∠FCB +∠ACF=∠ACB ,∴∠ACB=43°;∴∠BAC=180°﹣∠ABC ﹣∠ACB=180°﹣64°﹣43°=73°,∴△ABC 各内角的度数分别为64°、43°、73°.【点睛】本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形外角的性质,熟记三角形的外角等于与它不相邻的两个内角之和是解题的关键.26.32x y ==,【解析】【分析】整理方程得27x y +=①和24x y -=②,再利用加减消元法求解即可.【详解】()()22171136x y x y ⎧-++=⎪⎨+-=⎪⎩()()2217x y -++=2227x y -++=27x y +=①1136x y +-= 226x y +-=24x y -=②①2+⨯②得515x =解得3x =将3x =代入27x y +=中327y +=24y =解得2y =故方程的解是32x y ==,.【点睛】本题考查了解二元一次方程组的问题,掌握加减消元法是解题的关键.27. (1)t ,s ;(2)2,6;(3)小明距起点的距离为300米.【解析】【分析】解析(1)观察函数图象即可找出谁是自变量谁是因变(2)根据速度=路程÷时间,即可分别算出朱老师以及小明的速度;(3)设t 秒时,小明第一次追上朱老师,列出关系式即可解答【详解】解:(1)在上述变化过程中,自变量是t ,因变量是s ;(2)朱老师的速度420200110-=2(米/秒),小明的速度为42070=6(米/秒); 故答案为t ,s ;2,6;(3)设t 秒时,小明第一次追上朱老师根据题意得6t =200+2t ,解得t =50(s),则50×6=300(米),所以当小明第一次追上朱老师时,小明距起点的距离为300米.【点睛】此题考查一次函数的应用,解题关键在于看懂图中数据28.14m 1.【解析】【分析】连接AC ,利用勾股定理可以得出三角形ACD 和ABC 是直角三角形,△ABC 的面积减去△ACD 的面积就是所求的面积.【详解】连接AC ,∵∠ADC=90°,AD=4m ,CD=3 m ,∴AC 1=AD 1+CD 1=41+31=15 ,又∵AC >0,∴AC=5 m ,又∵BC=13m ,AB=11m ,∴AC 1+AB 1=51+111=169,又∵BC 1=169,∴AC 1+AB 1=BC 1,∴∠ACB=90°,∴S △ABC =2115123022AC AB m ⨯⨯=⨯⨯= ∴S 四边形ABCD =S △ABC -S △ADC =30-6=14m 1.【点睛】此题考查了勾股定理,以及勾股定理的逆定理,熟练掌握定理及逆定理是解本题的关键.29.1.【解析】【分析】根据线段中点的性质,可得BC 的长,根据线段的和差,可得AB 的长,再根据线段中点的性质,可得BM的长,根据线段的和差,可得答案.【详解】解:由N 是CB 的中点,NB=5,得BC=2NB=2.由线段的和差,得AB=AC+BC=8+2=3.由M 是AB 的中点,得 MB=AB=×3=4.由线段的和差,得MN=MB ﹣NB=4﹣5=1.考点:两点间的距离.30.1.【解析】【分析】根据同底数幂的运算法则,即可求解.【详解】原式=1113623222⨯⨯⨯ =11123632++⨯=32⨯=6.【点睛】本题主要考查同底数幂的运算法则以及分数指数幂的性质,掌握“同底数幂相乘,底数不变,指数相加”是解题的关键.。
2022-2023学年抚顺市七年级数学下学期期中考试卷附答案解析

2022-2023学年抚顺市七年级数学下学期期中考试卷考试时间:100分钟试卷满分:120分一、选择题(每小题2分,共20分)1.4的平方根是()A .2B .-2C .2D .2±2.点P 的坐标是()23,1m +,则点P 在第()象限A .一B .二C .三D .四3.在实数227-,038,π-中,无理数的有()个A .0B .1C .2D .34.下列条件中不能够推理得到12//l l 的是()A .∠2=∠3B .∠1+∠4=180°C .∠2=∠5D .∠2+∠6+∠5=180°5.实数m ,n 在数轴上对应点的位置如图所示,则下列判断正确的是()A .1m <B .m -n <0C .mn >0D .m +1>06.方程132x y-=可以用含x 的式子表示y 的是()A .2133x y =-B .223x y -=C .223x y =-D .223xy =-7.一个长方形在平面直角坐标系中三个顶点坐标分别是()1,1--,()1,2-,()3,1-,则第四个顶点坐标是()A .()2,2--B .()3,2C .()3,3D .()2,38.关于x ,y 的二元一次方程组231ax by ax by +=⎧⎨-=⎩的解为11x y =⎧⎨=-⎩,则a -2b 的值是()A .-2B .2C .3D .-39.如图,三角形ABC 中任意一点()2,P m m +向左平移3个单位长度后,点P 的对应点恰好在y 轴上,将三角形ABC 作同样的平移得到三角形111A B C ,若点B 的坐标是()0,m ,则点1B 的坐标是()A .()0,1B .()3,1C .()3,1-D .()4,1-10.关于x ,y 的方程组343x y a x y a +=-⎧⎨-=⎩①②,给出下列结论:(1)51x y =⎧⎨=-⎩是方程组的一个解;(2)当a =-2时,方程①有一个正整数解;(3)若x 与y 互为相反数,则a 的值是-2;(4)无论a 为何实数时,x +2y 的值不变.结论正确的个数是______.A .1个B .2个C .3个D .4个二、填空题:(每题3分,共18分)11.点P 的坐标是()3,5-,则点P 到x 轴的距离是______.12.三角板ABC 如图所示摆放,其中∠CAB =30°,∠C =90°,若//AE BC ,//EF AB ,则∠E 的度数是______.13.一个正方体的体积是327cm ,则它的表面积是______2cm .14.小刚在做一道练习题时,书上写着方程组21x ay x y +=⎧⎨+=-⎩,该方程组的解是1x y =⎧⎨=⎩■,其中y 的值被墨迹掩盖住了,但仍能求出a 的值,则a 的值是______.15.天文学家以流星雨辐射所在的天空区域中的星座给流星命名,狮子座流星雨就是流星雨辐射点在狮子座中.如图,把狮子座的星座图放在网格中,若点A 的坐标是()2,6,点C 的坐标是()1,3-,则点B 的坐标是______.16.如图,在平面直角坐标系中,一动点按照图中箭头所示的方向运动,第1次从原点运动到点()1,1P -,第2次运动到点()12,0A ,第3次运动到点()23,2A ,第4次运动到点()34,0A ,第5次运动到点()45,1A -,…,按照这样的规律运动下去,则三角形2023OPA 的面积是______.三、解答题:(第17题6分,第18题8分,第19题8分,共22分)17.计算:(12233-(2)2380.043-18.解方程组:(1)32311y xx y =⎧⎨+=⎩(2)52327.5x y x y -=⎧⎨+=⎩19.如图,在平面直角坐标系中,三角形111A B C 是由三角形ABC 向左移动5个单位长度后得到的,且三个顶点的坐标分别为()13,0A -,()14,3B -,()10,1C .(1)请画出三角形ABC ;(2)求三角形ABC 的面积.四、解答题(第20题8分,第21题8分,共16分)20.如图,直线AB ,CD 相交于点O ,OE 平分∠AOD ,OF CD ⊥,若∠1=36°,求∠EOC 的度数.21.定义一种新运算“※”:规定m n am bn mn =+-※,其中a ,b 为常数,且615270=※,810360=※,求21-※的值.五、解答题(10分)22.如图,CA BE ⊥于点A ,DE BE ⊥于点E ,∠FAC +∠D =180°.求证:∠AFB =∠DCB .六、解答题(10分)23.每年5月的第二个星期日为母亲节,“谁言寸草心,报得三春晖”.某班学生在母亲节来临之际精心制作祝愿卡感恩母亲,祝福母亲.祝愿卡的制作需要彩带若干,2张A 类卡片和3张B 类卡片需要彩带26条,3张A 类卡片和1张B 类卡片需要彩带18条.1张A 类卡片和1张B 类卡片各需要彩带多少条.七、解答题(12分)24.如图,在平面直角坐标系中,()2,A a ,(),0B b ,其中a ,b 是方程组626a b b a +=⎧⎨-=⎩的解.(1)求点A 和点B 的坐标;(2)过点A 作//l x 轴交y 轴于点D ,E 是AD 上一点,F 是OD 上一点,连接FE ,FB ,且∠EFB =3∠FBO ,∠AEF =150°,求∠FBO 的度数.八、解答题(本题12分)25.如图1,()0,2A ,()4,0B ,我们能够容易地计算出AOB △的面积,根据所给的平面直角坐标系探究下列问题.(说明:三角形AOB 记作AOB △)【思维启迪】.(1)若点C 的坐标是()2,2,点D 的坐标是()5,2,则①COB △的面积是______,DOB △的面积是______;②AOB △的面积与COB △的面积之间的数量关系是______;③A ,C ,D 三点所在的直线与x 轴的位置关系是______.请利用你发现的结论,尝试解决以下问题.【学以致用】(2)E 是x 轴上方一点,点C 的坐标是()2,2,若COB △的面积与EOB △的面积相等,且3AC =4EC ,求点E 的坐标.【发散思维】(3)如图2,若点M 的坐标是()2,0,连接AM ,点P 在y 轴上,线段PB 与线段AM 相交于点H ,若PAH △的面积与BMH △的面积相等,请直接写出点P 的坐标.数学试题参考答案(※若有其他正确解法或证法参照此标准赋分)一、选择题(本题共10个小题,每小题3分,共30分)题号12345678910答案DABCBCBBCD二、填空题(本题共6小题,每小题3分,共18分)11.512.60°13.5414.12-15.()3,216.1012三、计算题(17题6分,第18题8分,第19题8分,共22分)17.(1)22(2)5.218.(1)13x y =⎧⎨=⎩(2)23.5x y =⎧⎨=⎩19.(1)如图所示,三角形ABC 即为所求;(2)过点B 作BE x ⊥轴,过点C 作CF x ⊥轴,∵ABC BEFC BEA CAF S S S S =--三角形梯形三角形三角形,∴()111134********ABC S =⨯+⨯-⨯⨯-⨯⨯=三角形.四、解答题(第20题8分,第21题8分,共16分)20.解:∵OF CD ⊥,∴∠COF =90°,∴∠3=180°-∠1-∠COF =180°-36°-90°=54°,∠BOC =∠COF +∠1=90°+36°=126°,∴∠AOD =∠BOC =126°.∵OE 平分∠AOD ,∴1121266322AOD ∠=∠=⨯︒=︒,∴∠EOC =∠2+∠3=63°+54°=117°.即:∠EOC 的度数是117°.21.解:根据题意可得:6159027081080360a b a b +-=⎧⎨+-=⎩,原方程组可化为2512045220a b a b +=⎧⎨+=⎩,解得:504a b =⎧⎨=⎩,∴2125041294-=-⨯+⨯+=-※.即:2194-=-※.五、解答题(本题10分)22.证明:∵CA BE ⊥,DE BE ⊥,∴∠BAC =∠BED =90°,∴//ED AC ,∴∠D +∠ACD =180°,∵∠FAC +∠D =180°,∴∠FAC =∠ACD ,∴//AF CD ,∴∠AFB =∠DCB .六、解答题(本题10分)23.解:设1张A 类卡片需要彩带x 条,1张B 类卡片需要彩带y 条.2326318x y x y +=⎧⎨+=⎩,解得:46x y =⎧⎨=⎩.答:1张A 类卡片需要彩带4条,1张B 类卡片需要彩带6条.七、解答题(本题12分)24.解:(1)626a b b a +=⎧⎨-=⎩①②,①+②得:3b =12,解得:b =4.将b =4代入①得:4+a =6,解得a =2,∴原方程组的解是24a b =⎧⎨=⎩,∴()2,2A ,()4,0B .(2)设∠FBO =x ,则∠EFB =3x .过点F 作//FM x 轴.∵//l x 轴,∴////FM l x 轴,∴∠MFB =∠FBO =x ,∠EFM =180°-∠AEF =180°-150°=30°,∵∠EFM +∠MFB =∠EFB ,∴30°+x =3x ,解得x =15°,即∠FBO =15°.八、解答题(本题12分)25.(1)①4,4②相等③平行(2)解:根据题意得://EC x 轴,AC =2,设点E 的坐标是(),2m ,当点E 在点C 右侧时,()4223m -=⨯,解得m =3.5,∴()3.5,2E .当点E 在点C 左侧时,()4223m -=⨯,解得m =0.5,∴()0.5,2E .综上所述:点E 的坐标是()3.5,2或()0.5,2.(3)()0,1P .。
2022-2023学年辽宁省抚顺市新抚区七年级(下)期中数学试卷(含解析)

2022-2023学年辽宁省抚顺市新抚区七年级(下)期中数学试卷一、选择题(本大题共10小题,共20.0分。
在每小题列出的选项中,选出符合题目的一项)1. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )A. B. C. D.2. 下列图中∠1与∠2是对顶角的是( )A. B.C.D. 3. 下列各式中,正确的是( )A. (−3)2=−3B. 32=3C. 32=±3D. 32=−34. 64的平方根为( )A. 8B. ±8C. −8D. ±45. 如果点P (2m +1,−1)在第四象限内,则m 的取值范围( )A. m >−12B. m <−12C. m ≥−12D. m ≤−126. 下列说法正确的是( )A. 827 的立方根是±23B. −125没有立方根C. 0的立方根是0D. 3−82=47. 在下列实数:π2、 3、 4、227、−1.010010001…中,无理数有( )A. 1个B. 2个C. 3个D. 4个8. 如图,三角板的直角顶点在直尺的一边上.若∠1=30°,∠2=70°,则∠3的度数是( )A. 30°B. 40°C. 50°D. 60°9.如图,A、B的坐标分别为(2,0)、(0,1).若将线段AB平移至A1B1,A1、B1的坐标分別(3,b)、(a,2),则a+b的值为( )A. 2B. 3C. 4D. 510. 某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知AB//CD,∠BAE=87°,∠DCE=121°,则∠E的度数是( )A. 28°B. 34°C. 46°D. 56°二、填空题(本大题共6小题,共18.0分)11. 已知点P(2a−6,a+1)在y轴上,则点P的坐标是______ .12. 比较大小:−4______ −15(填“>”“=”或“<”)13. 4的算术平方根是______ .14. 将点P(−3,y)向下平移3个单位,向左平移2个单位后得到点Q(x,−1),则x+y=______.15. 将一副三角板如图放置,使点A落在DE上,若BC//DE,则∠AFC的度数为______ .16. 如图,在平面直角坐标系中,从点P1(−1,0),P2(−1,−1),P3(1,−1),P4(1,1),P5(−2,1 ),P6(−2,−2),…,依次扩展下去,则P2023的坐标是______ .三、解答题(本大题共9小题,共82.0分。
抚顺市名校七年级第二学期数学解答题专项训练含解析

抚顺市名校七年级第二学期数学解答题专项训练解答题有答案含解析1.解不等式组(1)3(2)4 1213x xxx--≥-⎧⎪+⎨>-⎪⎩并把解集表示在数轴上.(2)已知关于,x y的二元一次方程组23224x y mx y+=-+⎧⎨+=⎩的解满足32x y+>-,求出满足条件的m的所有正整数值.2.某学校为了丰富学生的大课间活动,准备购进一批跳绳,已知2根短绳和1根长绳共需56元,1根短绳和2根长绳共需82元.(1)求每根短绳和每根长绳的售价各是多少元?(2)学校准备购进这两种跳绳共50根,并且短绳的数量不超过长绳数量的2倍,总费用不超过1020元,请设计出最省钱的购买方案,并说明理由.3.(1)如图(1),在△ABC中,∠A=62°,∠ABD=20°,∠ACD=35°,求∠BDC的度数.(2)图(1)所示的图形中,有点像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,观察“规形图”图(2),试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由.(3)请你直接利用以上结论,解决以下问题:①如图(3),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=42°,则∠ABX+∠ACX=°.②如图(4),DC平分∠ADB,EC平分∠AEB,若∠DAE=60°,∠DBE=140°,求∠DCE 的度数.③如图(5),∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=68°,求∠A的度数.4.为了了解学生毕业后就读普通高中或就读中等职业技术学校的意向,某校对八、九年级部分学生进行了一次调查,调查结果有三种情况:.A只愿意就读普通高中;.B只愿意就读中等职业技术学校;.C就读普通高中或中等职业技术学校都愿意.学校教务处将调查数据进行了整理,并绘制了尚不完整的统计图如下,请根据相关信息,解答下列问题:()1本次活动一共调查的学生数为______名;()2补全图一,并求出图二中A区域的圆心角的度数;()3若该校八、九年级学生共有2800名,请估计该校八、九年级学生只愿意就读中等职业技术学校的人数.5.如图,由4×4个小正方形组成的正方形网格图案,现已将其中的两个小正方形涂黑。
辽宁抚顺市七年级数学下册第六章【实数】提高练习(答案解析)

一、选择题1.观察下列运算:81=8,82=64,83=512,84=4 096,85=32 768,86=262 144,…,则81+82+83+84+…+82 017的和的个位数字是()A.2 B.4 C.6 D.82.下列实数中,是无理数的为()A.3.14 B.13C.5D.93.下列说法中,正确的是()A.64的平方根是8 B.16的平方根是4和-4C.()23-没有平方根D.4的平方根是2和-24.下列说法中,正确的是()A.正数的算术平方根一定是正数B.如果a表示一个实数,那么-a一定是负数C.和数轴上的点一一对应的数是有理数D.1的平方根是15.定义运算:132x y xy y=-※,若211a=-※,则a的值为()A.12-B.12C.2-D.26.如果32.37≈1.333,323.7≈2.872,那么32370约等于()A.287.2 B.28.72 C.13.33 D.133.37.数轴上表示下列各数的点,能落在A,B两个点之间的是()A.3B7C11D138.81的平方根是()A.9 B.-9 C.9和9-D.819.已知无理数m55π-的整数部分相同,则m为()A5B10C51D.5π-10.下列各组数中都是无理数的为( )A .0.07,23,π;B .0.7•,π;C ,π;D .0.1010101……101,π11.1的值在( )A .5~6之间B .6~7之间C .7~8之间D .8~9之间二、填空题12.已知一个正数的平方根是3a +和215a -.(1)求这个正数.(2的平方根和立方根.13.求下列各式中x 的值.(1)4(x ﹣3)2=9;(2)(x +10)3+125=0.14.先化简,再求值:()222233a ab a ab ⎛⎫---⎪⎝⎭,其中|2|a + 15.解方程:(1)2810x -=;(2)38(1)27x +=. 16.若一个正数的平方根是3m +和215m -,n 的立方根是2-,则2n m -+的算术平方根是______.17.27-的立方根是______________________;| 3.14|π-的绝对值是___________.18.小燕在测量铅球的半径时,先将铅球完全浸没在一个带刻度的圆柱形小水桶中,拿出铅球时,小燕发现小水桶中的水面下降了1cm ,小燕量得小水桶的直径为12cm ,于是她就算出了铅球的半径.你知道她是如何计算的吗?请求出铅球的半径.(球的体积公式343V r π=,r 为球的半径.) 19.计算:(1()23-.(2)()21183⎤⎛⎫-⨯-⎥ ⎪⎝⎭⎥⎦.20.若3109,b a =-且b 的算术平方根为4,则a =__________.21.设a ,b 是两个连续的整数,若a b <<,是,则a b =____.三、解答题22.计算:2(3)2--23.求下列各式中的x :(1)2940x -=;(2)3(1)8x -=24.小燕在测量铅球的半径时,先将铅球完全浸没在一个带刻度的圆柱形小水桶中,拿出铅球时,小燕发现小水桶中的水面下降了1cm ,小燕量得小水桶的直径为12cm ,于是她就算出了铅球的半径.你知道她是如何计算的吗?请求出铅球的半径.(球的体积公式343V r π=,r 为球的半径.)25. 1.414≈,于是我们说:的整数部分为1,小数部分则可记为1”.则:(11的整数部分是__________,小数部分可以表示为__________;(22的小数部分是a ,7-b ,那么a b +=__________;(3x 的小数部分为y ,求1(x y --的平方根.一、选择题1.给出下列各数①0.32,②227,③π,④5,⑤0.2060060006(每两个6之间依次多个0),⑥327,其中无理数是( )A .②④⑤B .①③⑥C .④⑤⑥D .③④⑤ 2.若227(7)0x y z -+++-=,则x y z -+的平方根为( )A .±2B .4C .2D .±43.下列各组数中,互为相反数的是( )A .2-与2B .2-与12-C .()23-与23-D .38-与38- 4.下列命题是真命题的是( )A .两个无理数的和仍是无理数B .有理数与数轴上的点一一对应C .垂线段最短D .如果两个实数的绝对值相等,那么这两个实数相等5.在实数﹣34,0,9,215中,是无理数的是( ) A .﹣34 B .0 C .9 D .2156.若“!”是一种运算符号,且1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,…,则计算2015!2014!正确的是( )A .2015B .2014C .20152014D .2015×2014 7.如果32.37≈1.333,323.7≈2.872,那么32370约等于( )A .287.2B .28.72C .13.33D .133.38.如图是一个按某种规律排列的数阵:根据数阵排列的规律,第n (n 是整数,且n ≥3)行从左向右数第(n ﹣2)个数是( )(用含n 的代数式表示)A 21n -B 22n -C 23n -D 24n -9.在223.14,, 5.12112111227π+--……中,无理数的个数为 ( ) A .5 B .2 C .3 D .410.下列有关叙述错误的是( )A B 是2的平方根 C .12<< D .2是分数11.已知下列结论:①;②无理数是无限小数;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.其中正确的结论是( ) A .① ③ B .②③ C .③④ D .②④二、填空题12.求x 的值:(1)2(3)40x +-=(2)33(21)240x ++=13.求下列各式中x 的值(1)21(1)64x +-=; (2)3(1)125x -=.14.解答下列各题.(1)已知2x +3与x -18是某数的平方根,求x 的值及这个数.(2)已知20c d -=,求d +c 的平方根.15.一个正方体的木块的体积是3343cm ,现将它锯成8块同样大小的小正方体木块,则每个小正方体木块的表面积是________.16.27-的立方根是______________________;| 3.14|π-的绝对值是___________.17.比较大小:|5|-________(填“>”“=”或“<”)18.在实数的原有运算法则中,我们补充新运算法则“*”如下:当a≥b 时,a*b=b 2,当a<b时,a*b=a ,则当时,()()1*-3*=x x x ______19.0.5325===的值是______________________.20.如图,一只蚂蚁从点A 沿数轴向右爬了2个单位长度到达点B ,点A 表示2-,设点B 所表示的数为m . (1)求11m m ++-的值;(2)在数轴上还有C 、D 两点分别表示实数c 和d ,且有2c d +与4d +互为相反数,求23c d -的平方根.21.若2(1)10a b -++=,则20132014a b +=___________.三、解答题22.计算:(1)﹣12+327-﹣(﹣2)×9(2)3(3+1)+|3﹣2| 23.如图所示的正方形纸板是由两张大小相同的长方形纸板拼接而成的,已知一个长方形纸板的面积为162平方厘米.(提示:182=324)(1)求正方形纸板的边长;(2)若将该正方形纸板进行裁剪,然后拼成一个体积为343立方厘米的正方体,求剩余的正方形纸板的面积.24.观察下列各式,并用所得出的规律解决问题:(12=1.414200=14.1420000=0.03=0.17323=1.732,300=17.32…由此可见,被开方数的小数点每向右移动 位,其算术平方根的小数点向 移动 位;(25=2.23650=7.0710.5= ,500= ;(331=131000=1031000000=100…小数点变化的规律是: .(4=2.154=4.642=,=.25.求下列x的值.(1)27x3=-8 (2)(3x-1)2=9一、选择题1.下列命题中,①81的平方根是9;②16的平方根是±2;③−0.003没有立方根;④−64的立方根为±4;⑤5,其中正确的个数有( )A .1B .2C .3D .42.下列实数:32233.14640.010*******-;;;; (相邻两个1之依次多一个0);52-,其中无理数有( )A .2个B .3个C .4个D .5个3.在0.010010001,3.14,π,10,1.51,27中无理数的个数是( ). A .5个 B .4个 C .3 D .2个4.如图,直径为1个单位长度的圆从A 点沿数轴向右滚动(无滑动)两周到达点B ,则点B 表示的数是( )A .1π-B .21π-C .2πD .21π+5.下列计算正确的是( )A 11-=-B 2(3)3-=-C 42=±D 31182-=- 6.下列选项中,属于无理数的是( )A .πB .227-C 4D .0 7.若53a =,则a 在( )A .3-和2-之间B .2-和1-之间C .1-和0之间D .0和1之间 864 )A .8B .8-C .22D .22±9.如图是一个按某种规律排列的数阵:根据数阵排列的规律,第n (n 是整数,且n ≥3)行从左向右数第(n ﹣2)个数是( )(用含n 的代数式表示)A 21n -B 22n -C 23n -D 24n - 10.下列各数中,属于无理数的是( )A .227B .3.1415926C .2.010010001D .π3- 11.下列说法中:①0是最小的整数;②有理数不是正数就是负数;③﹣2π不仅是有理数,而且是分数;④237是无限不循环小数,所以不是有理数;⑤无限小数不一定都是有理数;⑥正数中没有最小的数,负数中没有最大的数;⑦非负数就是正数;⑧正整数、负整数、正分数、负分数统称为有理数;其中错误的说法的个数为( )A .7个B .6个C .5个D .4个二、填空题12.求下列各式中x 的值(1)()328x -=(2)21(3)753x -=13.计算.(1)()113122⎛⎫⎛⎫---++ ⎪ ⎪⎝⎭⎝⎭; (2)()3328864---14.已知mn 、是两个连续的整数,且410m n <,则m n +=_______________________. 15.规定一种新的定义:a ★b b -a 2,若a =3,b =49,则(a ★b )★b =_________. 16.已知a 、b 2|3|0a b -++=,则(a +b )2021的值为________.17.实数2-2,227,π-327-中属于无理数的是________. 18.(1)求x 的值:2490x -=;(2()2325227-19.比较大小:312-___________12 20.如果3x -+(y +2)2=0,那么xy 的值为___________.21.已知实数,x y 满足()2380x y -++=,求xy -的平方根.三、解答题22.已知290x ,310y +=,求x y +的值.23.计算:31891224-++-+. 24.定义一种新运算;观察下列各式;131437=⨯+=()3134111-=⨯-=5454424=⨯+= ()4344313-=⨯-=(1)请你想一想:a b = ;(2)若a b ,那么a b b a (填“=”或“≠” );(3)先化简,再求值:()()2a b a b -+,其中1a =-,2b =.25.教材中的探究:如图,把两个边长为1的小正方形沿对角线剪开,用所得到的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法(数轴的单位长度为1).(1)阅读理解:图1中大正方形的边长为________,图2中点A 表示的数为________; (2)迁移应用:请你参照上面的方法,把5个小正方形按图3位置摆放,并将其进行裁剪,拼成一个大正方形.①请在图3中画出裁剪线,并在图3中画出所拼得的大正方形的示意图.②利用①中的成果,在图4的数轴上分别标出表示数-0.5以及 35-的点,并比较它们的大小.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用题
1、某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两1道侧门大小也相同.安全检查中,对4道门进行,、买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元,打折后,买50件A商品和50件B商品用了960元,比不打折少花多少钱?
2、甲、乙两人各有书若干本,如果甲从乙处拿来10本,那么甲拥有的书是乙所剩书的5倍;如果乙从甲处拿来10本,那么乙所有的书与甲所剩的书相等,问甲、乙两人原来各有几本书?
3.(本小题1分) 某种口服液礼品盒有大盒、小盒两种包装,现在知道3大盒、4小盒共装了108瓶;2大盒、3小盒共装了76瓶,现在有一个人一共买了6大盒、6小盒,问他一共买了多少瓶?
4. 张老师去文具店给美术小组的30名学生买铅笔和橡皮,到了商店后发现,若给全组每人都买2支铅笔和1块橡皮,则要按零售价计算,共需付款30元;若给全组每人都买3支铅笔和2块橡皮,则可按批发价,共需付款40.5元.已知铅笔每支批发价比零售价低0.05元,橡皮每块批发价比零售价低0.1元,求这家文具店每支铅笔和每块橡皮的批发价是多少?
5、汽车在相距70km的甲、乙两地之间往返行驶,因为行程中有一坡度均匀的小山,该汽车从甲地到乙地需要2小时30分钟,而从乙地回到甲地需要2小时48分钟,已知汽车在平地每小时行30km,上坡路每小时行20km,下坡路每小时行40km,求从甲地到乙地的行程中,平路、上坡路、下坡路各是多少?
6、某旅社在黄金旅游期间为一旅游团体安排住宿,若每间宿舍住5人,则有4人住不下;若每间住6人,则有一间只住了4人,且空两间宿舍,求该团体有多少人和宿舍间数.
7、有甲、乙两种债券,年利率分别是10%与12%,现有400元债券,一年后获利45元,问两种债券各有多少?
8、李明与王云分别从A、B两地相向而行,若两人同时出发,则经过80分钟两人相遇;若李明出发60分钟后王云再出发,则经过40分钟两人相遇,问李明与王云单独走完AB
全程各需多少小时?
9、在一次足球比赛中规定:胜一场得3分,平一场得1分,负一场得0分.某队在足球比赛的4场比赛中得6分,这个队胜了几场,平了几场,负了几场?
10、东风农场的两块试验田,去年共产花生470kg.改用良种后,今年共产花生523kg,已知第一块田的产量比去年增产16%,第二块田的产量比去年增产10%,这两块田改良种前每块田产量分别为多少千克?今年每块田各增产多少千克?。
