运筹学入门
运筹学

(一)基本知识一、图1、图的概念:图是反应对象之间关系的一种工具。
图由点和线构成,一般称为点线图,点代表所研究的对象,线代表对象之间的关联性质。
注:在一般情况下,图中的点对应的位置如何,点与点之间连线的长短曲直,对于反映对象之间的关系,并不重要。
2、图的分类:(1)无向图:图中线不带表示关联方向的箭头,称这样的线为边,这种图叫无向图。
(2)有向图:图中线带有表示关联方向的箭头,称这样的线为弧,这样的图叫有向图。
3、图的表示:G={V,E}其中V={V1,V2,……,Vn}为点集E={e1,e2,……,en}为边集(1)点的次数(度数):与点Vi关联的边数称为点Vi的次数,记为d(Vi)(2)一些特殊的点:悬挂点:次数为1的点。
孤立点:次数为0的点。
奇点:次数为奇数的点。
偶点:次数为偶数的点。
(3)一些特殊的边相邻边:与同一顶点关联的两条边。
多重边:与共同的两个相邻点关联的边。
悬挂边:与悬挂点关联的边。
环:与同一个点关联的边4、连通图:任意两点之间可用至少一条链连接起来相通的图叫连通图。
(1)所有点的次数之和为边数的二倍:因为计算个点的次数时,每条边均用了两次。
(2)奇点的个数必为偶数:所有点的次数之和为偶数,故所有奇点的次数之和也为偶数,即奇点成对出现。
5、设G1={V1,E1},G2={V2,E2}(1)子图:若V2包含于V1,E2包含于E1,则称G2是G1的子图。
(2)部分图:若V1=V2,E1包含于E2,则G2是G1的部分图,即包含原图全部顶点的子图。
(3)零图:由许多孤立点构成的图。
(4)空图:顶点个数为0的零图,。
二、树1、概念:无圈的连通图为树v2 v3 v2 v3v1 v6 v5 v4 v1 v6 v5 v42、组成:(1)树枝:树的边称为树枝。
(2)树叶:次数为1的点称为树叶,如V1,V4。
3、树的性质:任何树必有树叶树中任意两点之间有且仅有一条链连接相通,任意去掉一条树枝该树就被分割成两个互不连通的子图。
运筹学基础

1.运筹学的定义。
运筹学是一门研究如何有效地组织和管理人机系统的科学。
2.决策方法的分类:定性决策,定量决策,混合性决策。
1.1.1运筹学与管理决策运筹学(OR)是一门研究如何有效地组织和管理人机系统的科学。
对管理领域,运筹学也是管理决策工作进行决策的计量方法。
企业领导的主要职责是作出决策。
分析程序有两种基本形式:定性的和定量的。
运筹学的定义运筹学利用计划方法和有关多学科的要求,把复杂功能关系表示成数学模型,其目的是通过定量分析为决策和揭露新问题提供数量根据。
决策方法的分类:(1)定性决策。
基本上根据决策人员的主观经验或感受到的感觉或知识而制定的决策。
(2)定量决策。
借助于某些正规的计量方法而做出的决策。
(3)混合性决策。
必须运用定性和定量两种方法才能制定的决策。
1.2运筹学进行决策过程的几个步骤【选择】1观察待决策问题所处的环境。
问题域的环境有内部环境和外部环境,对企业来说,内部环境一般指问题内部人、财、物之间的交互活动,外部环境一般指问题域界面与外界的人、财、物之间的交互活动。
2分析和定义待决策的问题3拟定模型4选择输入资料5提出解并验证它的合理性6实施最优解第2章、2.1.1预测的概念和作用预测就是对未来的不确定的事件进行估计或判断。
预测方法的分类:(1)按其内容来分:①经济预测。
它分为宏观经济预测和微观经济预测。
宏观经济是对整个国民经济范围的经济预测,如对国民收入增长率、工农业总产值增长率的预测,为描述国民经济大系统以及相应经济变量的社会综合值的预测。
微观经济预测是指对单个经济实体(企业)的各项经济指标及其所涉及到国内外市场经济形势的预测,如市场需求、市场占有率、产品的销售量(额)等。
②科技预测。
它分为科学预测和技术预测。
科学预测包括:科学发展趋势和发明,科学发展、产品发展与社会生活的关系等。
技术预测包括:新技术发明可能应用的领域、范围和速度,新设备、新工艺、新材料的特点、性能及作用等。
运筹学(简化)
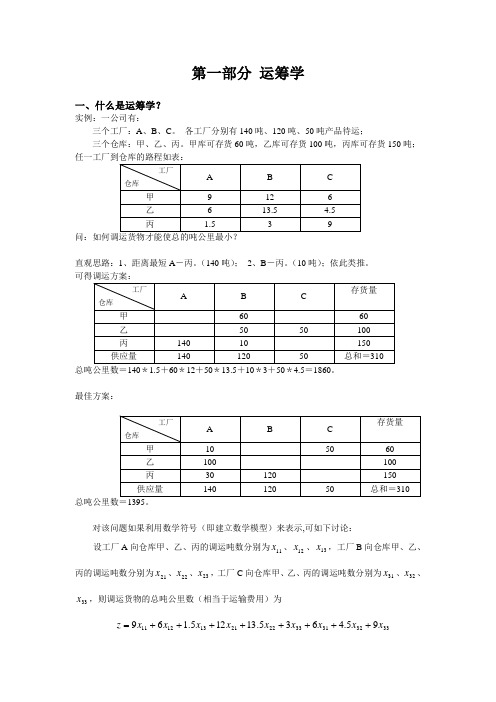
第一部分 运筹学一、什么是运筹学?实例:一公司有:三个工厂:A 、B 、C 。
各工厂分别有140吨、120吨、50吨产品待运;三个仓库:甲、乙、丙。
甲库可存货60吨,乙库可存货100吨,丙库可存货150吨;直观思路:1、距离最短A -丙。
(140吨); 2、B -丙。
(10吨);依此类推。
可得调运方案:总吨公里数=140*1.5+60*12+50*13.5+10*3+50*4.5=1860。
最佳方案:对该问题如果利用数学符号(即建立数学模型)来表示,可如下讨论:设工厂A 向仓库甲、乙、丙的调运吨数分别为11x 、12x 、13x ,工厂B 向仓库甲、乙、丙的调运吨数分别为21x 、22x 、23x ,工厂C 向仓库甲、乙、丙的调运吨数分别为31x 、32x 、33x ,则调运货物的总吨公里数(相当于运输费用)为33323133222113121195.4635.13125.169x x x x x x x x x z ++++++++=现在需要求该函数的最小值,而限制条件为:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥=++=++=++=++=++=++0,,,,,,,,1501006050120140333231232221131211332313322212312111333231232221131211x x x x x x x x x x x x x x x x x x x x x x x x x x x运筹学:以系统为研究对象,把系统的功能和特点用模型表示,通过对模型的定量分析,从总体上寻求最优策略,为决策和揭露新问题提供数量根据,并以研究结果的应用为目的,保证系统高效运行。
运筹学建立模型的最终目的是实现系统的最优化,帮助管理者作出正确的决策,使系统正常有效地运行。
这里的最优化是指在一定条件下求最优解(可以是求最大值,也可以是求最小值)。
运筹学研究系统的基本方法由以下5个阶段构成:第一阶段:观察所要研究的系统,确定存在的问题、影响问题的因素、约束、假设以及准备优化的目标。
运筹学 ( 第1次 )

运筹学 ( 第1次 )
1.运筹学是一门决策科学。
2.求解线性规划问题,就是求可行解中的最优解问题。
3.基可行解对应的基,称为可行基。
4.线性规划标准形式的约束式为小于等于。
5.原问题的决策变量个数等于对偶问题的等式约束个数。
6.隐枚举法是省去若干目标函数不占优势的基本可行解的一种检验过程。
7.运筹学有助于管理人员正确决策,因为它把研究对象当成有目标的系统。
8.资源价格大于影子价格时,应该卖出该资源。
9.敏感性分析假定可行基不变,分析参数的波动对最优解有什么影响。
10.从系统工程或管理信息预测决辅助系统的角度来看,管理科学与运筹学就其功能而言是等同或近似的。
11.闭回路的特点不包括每个顶点都是直角。
12.动态规划首先对一个多阶段的复杂动态问题进行分层处理。
13.运输问题分布m*n矩阵表的横向约束为供给约束或以上两者都有可能。
14.运筹学在系统观点下,强调可行性和总体最优化。
15.线性规划问题不包括混沌系统分析。
16.机会成本在一定时间地点只准用于有限种目的。
17.运输问题分布m*n矩阵表的纵向约束为需求约束或以上两者都有可能。
运筹学知识点

运筹学知识点:绪论1.运筹学的起源2.运筹学的特点第一章线性规划及单纯形法1.规划问题指生产和经营管理中如何合理安排,使人力、物力等各种资源得到充分利用,获得最大效益。
2.规划问题解决两类问题:一是给定一定数量的人力、物力等资源,研究如何充分利用,以发挥其最大效果;二是已给定计划任务,研究如何统筹安排,用最少的人力和物力去完成。
3.规划问题的数学模型包含三个组成要素:决策变量、目标函数(单一)、约束条件(多个)。
线性规划问题的数学模型要求:决策变量为可控的连续变量,目标函数和约束条件都是线性的。
4.线性规划问题的标准形式:目标函数为极大、约束条件为等式、决策变量为非负、变量为非负5.划标准型时添加的松驰变量、剩余变量和人工变量6.理解可行解、最优解、基、基解、基可行解等概念,且掌握各类解间的关系7.用图解法理解线性规划问题的四种解的情况:无穷多最优解、无界解、无可行解、唯一最优解8.用图解法只有解决两个变量的决策问题9.线性规划问题存在可行解,则可行域是凸集。
10.线性规划问题的基可行解对应线性规划问题可行域的顶点。
11.线性规划问题的解进行最优性检验:当所有的检验数小于等于零时为最优解;尤其当检验数小于零时(即不等于零)有唯一最优解;当某个非基变量检验数为时,有无穷多最优解;当存在某个检验数大于零且对应的系数又小于等于零时,有无界解。
12.单纯形法的计算过程,可能出计算题13.入单纯形表前首先要化成标准形式。
14.确定换出变量时根据θ值最小原则,且要求公式中对应的系数大于零。
15.当线性规划中约束条件为等式或大于等于时,划为标准型后,系数矩阵中又不包含单位矩阵时,需要添加人工变量构造一个单位矩阵作为基。
16.人工变量的系数为足够大的一个负值,用—M代表17.一般线性规划问题的数学建模题(生产计划问题、人才资源分配问题、混合配料问题等)第二章对偶问题1.原问题和对偶问题数学模型的对应关系,可能出填空题和数学模型题2.每一个线性规划必然有与之相伴而生的对偶问题3.对偶问题的性质:弱对偶性、无界性、强对偶性、最优性、互补松弛性,其中互补松弛性可能出计算题4.原问题与其对偶问题之间存在一对互补的基解,其中原问题的松弛变量对应对偶问题的变量,对偶问题的剩余变量对应原问题变量5.影子价格的定义,用互补松驰性理解影子价格的含义6.影子价格与企业的生产任务、产品结构、技术状况等相关,与市场需求无关7.理解影子价格是机会成本第三章运输问题1.运输问题的数学模型,出建模题2.掌握三个数字:m+n、m*n、m+n-13.解的退化及处理4.运输规划问题本质仍然是线性规划,系数矩阵的特殊性,利用表上作业法求解,核心依然是单纯形法5.表上作业法的计算过程,可能出大题6.什么是基格和空格及含义以及检验数的经济意义7.初始方案的方法,计算检验数的方法,调整方案的方法8.检验数的含义及检验规划与一般线性规划问题的差别9.产销不平衡问题的处理,包括产大于销和销大于产,假想地的单位运价设为零第四章整数规划1.整数规划的分类:纯整数、混合整数、0-1整数2.指派问题的数学模型,可能出建模题3.匈牙利法的计算过程4.解矩阵的特点:n个解1位于不同行不同列上5.分枝定界法分枝和定界的依据以及如何分枝和如何定界6.整数规划问题的求解方法及适用条件7.整数规划问题与其松弛问题解的关系第五章目标规划1.线性规划的局限:严格约束、单目标、约束同等重要2.目标规划问题的数学模型,可能会出建模题,强调目标函数由偏差变量、优先因素和权系数构成3.偏差变量的含义及特点,成对出现,非负且至少有一个为零4.目标约束是等式,等式左边添加一对偏差变量相减5.目标规划问题求解的单纯形表计算停止的规划:要么所有行的检验数均为非负,要么前i行检验数为非负,第i+1行存在负的检验数,但在负检验数上面存在正检验数6.目标规划的达成函数中的偏差变量的选择第六章图论与网络优化1.图论中的图研究对象间的关系,只关心图中有多少个点及点间有线相连2.树的定义及性质3.最小树的求解方法:避圈法和破圈法4.狄克斯屈拉算法的特点:不仅求出从始点到终点的最短路,还求出从始点其他任何各点的最短路5.有向图(点弧)非对称关系和无向图(点边)对称关系的应用6.可行流的定义:两大类的三个条件7.增广链的定义及特点8.最大流最小割定理9.用ford-fulkerson算法求网络中的最大流的计算过程10.算法的核心和实质是判断是否存在增广链,,即网络达到最大流的条件是网络中不存在增广链第七章网络计划技术1.关键路线的定点:持续时间最长、节点时差为零、不止一条2.工作持续时间的确定方法及使用条件3.节点最早时间、节点最迟时间的理解4.工作时间参数着重理解总时差和自由时差,即总时差是若干项工作共同拥有的机动时间,自由时差是某项工作单独拥有的机动时间5.绘制网络技术图的规则第八章动态规划1.动态规划是研究多阶段决策问题的理论和方法2.状态必须具备无后效性,及无后效性的定义3.动态规划和顺序解法和逆序解法的路径及应用条件。
运筹学--第一讲概论

田忌赛马
齐王要与大臣田忌赛马,双方各出上、 齐王要与大臣田忌赛马,双方各出上、中、下马 各一匹,对局三次,每次胜负1000 1000金 各一匹,对局三次,每次胜负1000金。田忌在 好友、著名的军事谋略家孙膑的指导下, 好友、著名的军事谋略家孙膑的指导下,做以下 安排: 安排: 齐王 上 中 下 田忌 下 上 中 最终净胜一局,赢得千金。 最终净胜一局,赢得千金。
运筹学形成于20 世纪 年代 运筹学形成于 20世纪 30年代( 第二次 世纪30 年代(
世界大战期间 ) 战斗机搜索潜艇(40年代) 年代) 战斗机搜索潜艇(40年代 军用物质运输(40年代 年代) 军用物质运输(40年代) 苏联著名数学家康托洛维奇:“生产组织与计划中的 苏联著名数学家康托洛维奇: 数学方” 数学方法”中提出合理调配和使用资源以便充分发挥 其效用的研究中所提出的新的数学方法和理论。 其效用的研究中所提出的新的数学方法和理论。
系统工程应用领域: 系统工程应用领域: 宏观经济: 宏观经济: 能源: 能源总体规划、 运输、 能源 : 能源总体规划 、 运输 、 产 供销: 石油如何分配、 水电、 供销 : 石油如何分配 、 水电 、 核 电发展规划。 电发展规划。 军事: 武器论证、 反坦克系统、 军事 : 武器论证 、 反坦克系统 、 高炮系统、 坦克系统、 作战模拟、 高炮系统 、 坦克系统 、 作战模拟 、 陆海空军作战。 陆海空军作战。 农业:农业规划、农业施肥。 农业:农业规划、农业施肥。
交通:全国交通网、城市交通网、 交通:全国交通网、城市交通网、 出租车、公交路线规划、港口选址、 出租车、公交路线规划、港口选址、 驳运、 河运( 航道堵塞) 驳运 、 河运 ( 航道堵塞 ) 、 空运 空中交通管制ATC) (空中交通管制ATC)、物流 工业企业:企业发展规划、 工业企业:企业发展规划、生产计 库存问题、新设备可行性、 划、库存问题、新设备可行性、下 料问题、全面质量管理、投入产出、 料问题、全面质量管理、投入产出、 生产调度问题、投资问题。 生产调度问题、投资问题。
运筹学基础

运筹学基础运筹学基础运筹学是一门研究问题的建模、分析和解决方法的学科,它涵盖了数学、统计学、计算机科学和工程等多个领域。
运筹学的目标是通过科学的方法,优化决策和资源利用,以达到最佳的效果。
运筹学的基础包括线性规划、整数规划、非线性规划、动态规划、排队论、网络流和图论等内容。
这些方法可以在许多领域中应用,包括物流、生产、供应链管理、交通运输、金融和资源分配等。
线性规划是运筹学中的一种基础方法。
它适用于求解具有线性目标函数和线性约束条件的问题。
线性规划常常涉及到资源的分配和决策的优化,例如在生产中如何最大化利润或者在供应链中如何最小化运输成本。
整数规划是在线性规划的基础上引入整数变量的一种问题求解方法。
这种方法可以用于求解一些离散决策问题,例如在物流中如何选择配送点和配送路线,以及如何安排生产任务等。
非线性规划是针对目标函数或约束条件中存在非线性项的问题的求解方法。
这种方法用于求解一些复杂的决策问题,例如在金融投资中如何优化投资组合,以及在环境保护中如何最小化排放量等。
动态规划是一种将多阶段决策问题转化为一系列单阶段决策问题的方法。
它适用于一些需考虑时序和状态转移的问题,例如旅行商问题和生产计划问题等。
排队论是研究顾客到达和服务系统间关系的数学方法。
它可以用于分析和优化服务系统的性能指标,例如等待时间和服务效率等。
排队论可以应用于各种排队系统,包括银行、餐厅和交通等。
网络流是研究网络中物质或信息流动的数学方法。
它可以用于解决一些网络中的最优路径或最小费用问题,例如在物流中如何选择最佳配送路径,以及在通信网络中如何优化数据传输等。
图论是研究图结构和图算法的学科。
它可以用于模型建立和问题求解,例如在地图上如何规划最短路径,以及在社交网络中如何分析人际关系等。
总之,运筹学提供了一系列数学方法和工具,用于解决决策和资源分配问题。
这些方法不仅可以优化决策效果,还可以提高经济效益和资源利用效率。
运筹学的应用范围广泛,对提高社会生产力和改善生活质量具有重要意义。
运筹学知识点总结

运筹学知识点总结一、线性规划线性规划是运筹学中最基础、最重要的一个分支。
它的基本形式可以表示为:Max cxs.t. Ax ≤ bx ≥ 0其中,c是一个n维的列向量,x是一个n维的列向量,A是一个m×n的矩阵,b是一个m维的列向量。
线性规划的目标是找到满足约束条件的x,使得目标函数cx取得最大值。
而当目标是最小化cx时,则是最小化问题。
线性规划问题有着很好的性质,它的最优解一定存在且一定在可行域边界上。
而且,很多非线性规划问题也可以通过线性化转化成线性规划问题,因此线性规划具有广泛的适用范围。
二、整数规划整数规划是线性规划的一个扩展,它在线性规划的基础上增加了对决策变量的整数取值限制。
这样的问题往往更加接近实际情况。
整数规划问题的一般形式可以表示为:Max cxs.t. Ax ≤ bx ∈ Zn整数规划问题的求解难度要比线性规划问题高很多。
因为整数规划问题是NP-hard问题,也就是说它没有多项式时间的算法可以解决。
但是对于特定结构的整数规划问题,可以设计专门的算法来求解。
比如分枝定界法、动态规划等。
整数规划问题在许多领域都有着广泛的应用,比如生产调度、设备配置、网络设计等。
三、动态规划动态规划是一种用来求解具有重叠子问题结构的最优化问题的方法。
它的核心思想是将原问题分解成一系列相互重叠的子问题,然后利用子问题的最优解来构造原问题的最优解。
动态规划问题的一般形式可以表示为:F(n) = max{F(n-1), F(n-2)+cn}其中,F(n)是问题的最优解,cn是问题的参数,n是问题的规模。
动态规划问题的求解是一个自底向上的过程,它依赖于子问题的最优解,然后通过递推关系来求解原问题的最优解。
动态规划在资源分配、路径优化、排程问题等方面有着广泛的应用。
四、决策分析决策分析是一种用来帮助人们做出最佳决策的方法。
它可以应用在各种风险决策、投资决策、生产决策等方面。
决策分析的一般形式可以表示为:Max E(u(x))其中,E(u(x))是对决策结果的期望效用,u(x)是决策结果的效用函数,x是决策变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江西省南昌市2015-2016学年度第一学期期末试卷(江西师大附中使用)高三理科数学分析一、整体解读试卷紧扣教材和考试说明,从考生熟悉的基础知识入手,多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力,立足基础,先易后难,难易适中,强调应用,不偏不怪,达到了“考基础、考能力、考素质”的目标。
试卷所涉及的知识内容都在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的大部分知识点均有涉及,其中应用题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学生感受到了数学的育才价值,所有这些题目的设计都回归教材和中学教学实际,操作性强。
2.适当设置题目难度与区分度选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较大,学生不仅要有较强的分析问题和解决问题的能力,以及扎实深厚的数学基本功,而且还要掌握必须的数学思想与方法,否则在有限的时间内,很难完成。
3.布局合理,考查全面,着重数学方法和数学思想的考察在选择题,填空题,解答题和三选一问题中,试卷均对高中数学中的重点内容进行了反复考查。
包括函数,三角函数,数列、立体几何、概率统计、解析几何、导数等几大版块问题。
这些问题都是以知识为载体,立意于能力,让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。
二、亮点试题分析1.【试卷原题】11.已知,,A B C 是单位圆上互不相同的三点,且满足AB AC →→=,则AB AC →→⋅的最小值为( )A .14-B .12-C .34-D .1-【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识,是向量与三角的典型综合题。
解法较多,属于较难题,得分率较低。
【易错点】1.不能正确用OA ,OB ,OC 表示其它向量。
2.找不出OB 与OA 的夹角和OB 与OC 的夹角的倍数关系。
【解题思路】1.把向量用OA ,OB ,OC 表示出来。
2.把求最值问题转化为三角函数的最值求解。
【解析】设单位圆的圆心为O ,由AB AC →→=得,22()()OB OA OC OA -=-,因为1OA OB OC ===,所以有,OB OA OC OA ⋅=⋅则()()AB AC OB OA OC OA ⋅=-⋅-2OB OC OB OA OA OC OA =⋅-⋅-⋅+ 21OB OC OB OA =⋅-⋅+设OB 与OA 的夹角为α,则OB 与OC 的夹角为2α所以,cos 22cos 1AB AC αα⋅=-+2112(cos )22α=--即,AB AC ⋅的最小值为12-,故选B 。
【举一反三】【相似较难试题】【2015高考天津,理14】在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ==则AE AF ⋅的最小值为 .【试题分析】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求,AE AF ,体现了数形结合的基本思想,再运用向量数量积的定义计算AE AF ⋅,体现了数学定义的运用,再利用基本不等式求最小值,体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现. 【答案】2918【解析】因为1,9DF DC λ=12DC AB =,119199918CF DF DC DC DC DC AB λλλλλ--=-=-==, AE AB BE AB BC λ=+=+,19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+,()221919191181818AE AF AB BC AB BC AB BC AB BCλλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥+= 当且仅当2192λλ=即23λ=时AE AF ⋅的最小值为2918. 2.【试卷原题】20. (本小题满分12分)已知抛物线C 的焦点()1,0F ,其准线与x 轴的交点为K ,过点K 的直线l 与C 交于,A B 两点,点A 关于x 轴的对称点为D . (Ⅰ)证明:点F 在直线BD 上; (Ⅱ)设89FA FB →→⋅=,求BDK ∆内切圆M 的方程. 【考查方向】本题主要考查抛物线的标准方程和性质,直线与抛物线的位置关系,圆的标准方程,韦达定理,点到直线距离公式等知识,考查了解析几何设而不求和化归与转化的数学思想方法,是直线与圆锥曲线的综合问题,属于较难题。
【易错点】1.设直线l 的方程为(1)y m x =+,致使解法不严密。
2.不能正确运用韦达定理,设而不求,使得运算繁琐,最后得不到正确答案。
【解题思路】1.设出点的坐标,列出方程。
2.利用韦达定理,设而不求,简化运算过程。
3.根据圆的性质,巧用点到直线的距离公式求解。
【解析】(Ⅰ)由题可知()1,0K -,抛物线的方程为24y x =则可设直线l 的方程为1x my =-,()()()112211,,,,,A x y B x y D x y -,故214x my y x =-⎧⎨=⎩整理得2440y my -+=,故121244y y m y y +=⎧⎨=⎩则直线BD 的方程为()212221y y y y x x x x +-=--即2222144y y y x y y ⎛⎫-=- ⎪-⎝⎭令0y =,得1214y yx ==,所以()1,0F 在直线BD 上.(Ⅱ)由(Ⅰ)可知121244y y m y y +=⎧⎨=⎩,所以()()212121142x x my my m +=-+-=-,()()1211111x x my my =--= 又()111,FA x y →=-,()221,FB x y →=-故()()()21212121211584FA FB x x y y x x x x m →→⋅=--+=-++=-,则28484,93m m -=∴=±,故直线l 的方程为3430x y ++=或3430x y -+=213y y -===±,故直线BD 的方程330x -=或330x -=,又KF 为BKD ∠的平分线,故可设圆心()(),011M t t -<<,(),0M t 到直线l 及BD 的距离分别为3131,54t t +--------------10分 由313154t t +-=得19t =或9t =(舍去).故圆M 的半径为31253t r +== 所以圆M 的方程为221499x y ⎛⎫-+= ⎪⎝⎭【举一反三】【相似较难试题】【2014高考全国,22】 已知抛物线C :y 2=2px(p>0)的焦点为F ,直线y =4与y 轴的交点为P ,与C 的交点为Q ,且|QF|=54|PQ|.(1)求C 的方程;(2)过F 的直线l 与C 相交于A ,B 两点,若AB 的垂直平分线l′与C 相交于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求l 的方程.【试题分析】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理,弦长公式的应用,解法及所涉及的知识和上题基本相同. 【答案】(1)y 2=4x. (2)x -y -1=0或x +y -1=0. 【解析】(1)设Q(x 0,4),代入y 2=2px ,得x 0=8p,所以|PQ|=8p ,|QF|=p 2+x 0=p 2+8p.由题设得p 2+8p =54×8p ,解得p =-2(舍去)或p =2,所以C 的方程为y 2=4x.(2)依题意知l 与坐标轴不垂直,故可设l 的方程为x =my +1(m≠0). 代入y 2=4x ,得y 2-4my -4=0. 设A(x 1,y 1),B(x 2,y 2), 则y 1+y 2=4m ,y 1y 2=-4.故线段的AB 的中点为D(2m 2+1,2m), |AB|=m 2+1|y 1-y 2|=4(m 2+1).又直线l ′的斜率为-m ,所以l ′的方程为x =-1m y +2m 2+3.将上式代入y 2=4x ,并整理得y 2+4m y -4(2m 2+3)=0.设M(x 3,y 3),N(x 4,y 4),则y 3+y 4=-4m,y 3y 4=-4(2m 2+3).故线段MN 的中点为E ⎝ ⎛⎭⎪⎫2m2+2m 2+3,-2m ,|MN|=1+1m 2|y 3-y 4|=4(m 2+1)2m 2+1m 2.由于线段MN 垂直平分线段AB ,故A ,M ,B ,N 四点在同一圆上等价于|AE|=|BE|=12|MN|,从而14|AB|2+|DE|2=14|MN|2,即 4(m 2+1)2+⎝ ⎛⎭⎪⎫2m +2m 2+⎝ ⎛⎭⎪⎫2m 2+22=4(m 2+1)2(2m 2+1)m 4,化简得m 2-1=0,解得m =1或m =-1, 故所求直线l 的方程为x -y -1=0或x +y -1=0.三、考卷比较本试卷新课标全国卷Ⅰ相比较,基本相似,具体表现在以下方面: 1. 对学生的考查要求上完全一致。
即在考查基础知识的同时,注重考查能力的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养,既考查了考生对中学数学的基础知识、基本技能的掌握程度,又考查了对数学思想方法和数学本质的理解水平,符合考试大纲所提倡的“高考应有较高的信度、效度、必要的区分度和适当的难度”的原则. 2. 试题结构形式大体相同,即选择题12个,每题5分,填空题4 个,每题5分,解答题8个(必做题5个),其中第22,23,24题是三选一题。
题型分值完全一样。
选择题、填空题考查了复数、三角函数、简易逻辑、概率、解析几何、向量、框图、二项式定理、线性规划等知识点,大部分属于常规题型,是学生在平时训练中常见的类型.解答题中仍涵盖了数列,三角函数,立体何,解析几何,导数等重点内容。
3. 在考查范围上略有不同,如本试卷第3题,是一个积分题,尽管简单,但全国卷已经不考查了。
四、本考试卷考点分析表(考点/知识点,难易程度、分值、解题方式、易错点、是否区分度题)。
