未分组数据茎叶图和箱线图
统计学-第三章-数据的图表展示

3.一般;4.满
意;5.非常满意。 合计
300 100.0 —
—
—
—
顺序数据的频数分布表(例题分析)
回答类别
乙城市家庭对住房状况评价的频数分布
乙城市
户数 百分比 (户) (%)
向上累积
户数 百分比 (户) (%)
向下累积
户数 百分比 (户) (%)
非常不满意 21
不满意
99
一般
78
满意
64
非常满意
7%
10% 8%
15% 21%
33% 36%
31% 26%
甲乙两城市家庭对住房状况的评价
非常不满意 不满意 一般 满意 非常满意
3.3数值型数据的整理与显示
1 数据分组
2
数值型数据的 图示
组距分组(要点)
☺~☺ ☺~☺ ☺~☺ ☺~☺ ☺~☺
1.将变量值的一个区间作为一组 2.适合于连续变量 3.适合于变量值较多的情况 4.需要遵循“不重不漏”的原则 5.可采用等距分组,也可采用不等距分组
等距分组表(上下组限重叠)
等距分组表(上下组限间断)
等距分组表(使用开口组)
1 数据分组
2
数值型数据的 图示
直方图和折线图
分组数据—直方图和折线图
Excel
分组数据—直方图(histogram)
用于展示分组数据分布的一种图形 用矩形的宽度和高度来表示频数分布 本质上是用矩形的面积来表示频数分布 在直角坐标中,用横轴表示数据分组,纵轴表 示频数或频率,各组与相应的频数就形成了一 个矩形,即直方图
分类数据整理—频数分布表(例题分析)
分类数据整理—频数分布表(例题分析)
分类数据整理—频数分布表(例题分析)
第二章 数据的描述性分析 图表展示

例:对学生成绩的分组可以分为0~20分、20~40分、
40~60分、60~80分、80~100组
• 不等距分组 适用于变动很不均匀,且变动幅度大 例:学生成绩分组也可分为0~60(D)、 60~80(C) 80~90(B)、90~100(A) 关键问题:分组数目的确定/组距的确定
3.2.1 数据分组
21
7.0 300 100.0
99
33.0
120
40.0 279
93.0
78
26.0
198
66.0 180
60.0
64
21.3
262
87.3 102
34.0
38
12.7
300
100.0
38
12.7
300 100.0
—
—
—
—
顺序数据的图示—累计频数分布图
400 累 积 300 户 数 200
(户1)00
根据上述资料编制频数分布表,向上向下累计频数,频率 分布表
居民户月消费品 支出额
751~800 801~850 851~900 901~950 951~1000 1001~1050 1051~1100 1101~1150
合计
频数
1 4 12 18 8 4 1 2 50
频率%
2 8 24 36 16 8 2 4 100
(1)表中数据属于顺序数据
(2)
学历 初中 高中或中专 本科 研究生及以上 合计
频数(人) 13 31 27 29 100
(3) 绘制条形图
学历分布
31
27
29
13
初中
高中或中专
本科
研究生及以上
统计学之统计数据的描述

则必然取2,而不能取其他
离散系数
离散系数
(coefficient of variation)
1. 标准差与其相应的均值之比 2.对数据相对离散程度的测度 3.消除了数据水平高低和计量单位的影
响
4v.用 较于对不同组别数v据s 离散程xs度的比
【 例 】某管理局抽查了所属的8家企业 ,其产品销售数据如表。试比较产品销售 额与销售利润的离散程度
累积的收入百分比
绝对公平线
A B
累积的人口百分比
基尼系数
1. 20世纪初意大利经济学家基尼(G. Gini)根据
洛伦茨曲线给出了衡收入分配平均程度的指
标 基尼系数=
A
A B
2. A表示实际收入曲线与绝对平均线之间的面积 3. B表示实际收入曲线与绝对不平均线之间的面
积
A B
• 如果A=0,则基尼系数=0,表示收入绝对 平均
一般用x表示变量;用f表示频数(次数) 。
2.1.3 次数分配图
分组数据—直方图和折线图
Excel
用直方形的宽度和高度来表示次数分 布的图形。
绘制直方图时,横轴表示各组组限, 纵轴表示次数(一般标在左方)和比 率(或频率,一般标在右方)。
分组数据的图示
我一眼就看 出来了,销 售量在170~ 180之间的天 数最多!
1. 一组数据中可以自由取值的数据的个数
2. 当样本数据的个数为 n 时,若样本均值x 确定后,只有n-1个数据可以自由取值,其
中必有一个数据则不能自由取值
3.
例如,样
x3=9,则
本有
x
3个数值,即
= 5。当 x
x=1=52,确x定2=4后,,x
1
(完整版)统计学思考题

1.1请举出统计应用的几个例子:1。
用统计识别作者:对于存在争议的论文,通过统计量推出作者 2.用统计量得到一个重要发现:在不同海域鳗鱼脊椎骨数量变化不大,推断所有各个不同海域内的鳗鱼是由海洋中某公共场所繁殖的3。
挑战者航天飞机失事预测1。
2请举出应用统计的几个领域:1.在企业发展战略中的应用2。
在产品质量管理中的应用3。
在市场研究中的应用 4.在财务分析中的应用 5.在经济预测中的应用1.3你怎么理解统计的研究内容:1。
统计学研究的基本内容包括统计对象、统计方法和统计规律. 2 .统计对象就是统计研究的课题,称谓统计总体。
3。
统计研究方法主要有大量观察法、数量分析法、抽样推断法、实验法等。
4.统计规律就是通过大量观察和综合分析所揭示的用数量指标反映的客观现象的本质特征和发展规律。
1.4举例说明分类变量、顺序变量和数值变量:1.分类变量:表现为不同类别的变量称为分类变量,如“性别”表现为“男”或“女”,“企业所属的行业”表现为“制造业”、“零售业"、“旅游业"等,“学生所在的学院”可能是“商学院"、“法学院"等2。
顺序变量:如果类别有一定的顺序,这样的分类变量称为顺序变量,如考试成绩按等级分为优、良、中、及格、不及格,一个人对事物的态度分为赞成、中立、反对。
这里的“考试成绩等级”、“态度"等就是顺序变量。
3。
数值变量:可以用数字记录其观察结果,这样的变量称为数值变量,如“企业销售额"、“生活费支出”、“掷一枚骰子出现的点数”。
1。
5获得数据的概率抽样方法有哪些?(1)简单随机抽样,简单随机抽样又称纯随机抽样,是指在特定总体的所有单位中直接抽取n个组成样本。
它最直观地体现了抽样的基本原理,是最基本的概率抽样。
(2)系统抽样,系统抽样也称等距抽样或机械抽样,是按一定的间隔距离抽取样本的方法.(3)分层抽样,分层抽样也叫分类抽样,就是先将总体的所有单位依照一种或几种特征分为若干个子总体,每一个子总体即为一类,然后从每一类中按简单随机抽样或系统随机抽样的办法抽取一个子样本,称为分类样本,它们的集合即为总体样本。
什么是箱线图

什么是箱线图什么是箱线图箱线图在文献中经常见到,是对数据分布的一种常用表示方法。
但是所见资料中往往说的不是特别清楚,因此需要了解一下箱线图的绘制过程,与部分的意义。
计算过程:1 计算上四分位数,中位数,下四分位数2 计算上四分位数和下四分位数之间的差值,即四分位数差(IQR,interquartile range)3 绘制箱线图的上下范围,上限为上四分位数,下限为下四分位数。
在箱子内部中位数的位置绘制横线。
4 大于上四分位数1.5倍四分位数差的值,或者小于下四分位数1.5倍四分位数差的值,划为异常值(outliers)。
5 异常值之外,最靠近上边缘和下边缘的两个值处,画横线,作为箱线图的触须。
6 极端异常值,即超出四分位数差3倍距离的异常值,用实心点表示;较为温和的异常值,即处于1.5倍-3倍四分位数差之间的异常值,用空心点表示。
7 为箱线图添加名称,数轴等。
在SPSS,SigmaPlot, R,SPlus,Origin等软件中,绘制箱线图非常方便。
下面是R中的一个箱线图举例箱线图举例:在R软件中输入如下命令:x<-c(25, 45, 50, 54, 55, 61, 64, 68, 72, 75, 75,78, 79, 81, 83, 84, 84, 84, 85, 86, 86, 86, 87, 89, 89, 89, 90, 91, 91, 92, 100)boxplot(x)对c向量绘制箱线图。
箱线图(Box plot)箱线图概述箱线图(Boxplot)也称箱须图(Box-whisker Plot),是利用数据中的五个统计量:最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法,它也可以粗略地看出数据是否具有有对称性,分布的分散程度等信息,特别可以用于对几个样本的比较。
[编辑]箱线图的绘制步骤[1](1)画数轴(2)画矩形盒两端边的位置分别对应数据的上下四分位数矩形盒:端边的位置分别对应数据的上下四分位数(Q1和Q3)。
(完整版)统计学思考题

1.1请举出统计应用的几个例子:1.用统计识别作者:对于存在争议的论文,通过统计量推出作者2.用统计量得到一个重要发现:在不同海域鳗鱼脊椎骨数量变化不大,推断所有各个不同海域内的鳗鱼是由海洋中某公共场所繁殖的3.挑战者航天飞机失事预测1.2请举出应用统计的几个领域:1.在企业发展战略中的应用2.在产品质量管理中的应用3.在市场研究中的应用4.在财务分析中的应用5.在经济预测中的应用1.3你怎么理解统计的研究内容:1.统计学研究的基本内容包括统计对象、统计方法和统计规律。
2 .统计对象就是统计研究的课题,称谓统计总体。
3.统计研究方法主要有大量观察法、数量分析法、抽样推断法、实验法等。
4.统计规律就是通过大量观察和综合分析所揭示的用数量指标反映的客观现象的本质特征和发展规律。
1.4举例说明分类变量、顺序变量和数值变量:1.分类变量:表现为不同类别的变量称为分类变量,如“性别”表现为“男”或“女”,“企业所属的行业”表现为“制造业”、“零售业”、“旅游业”等,“学生所在的学院”可能是“商学院”、“法学院”等2.顺序变量:如果类别有一定的顺序,这样的分类变量称为顺序变量,如考试成绩按等级分为优、良、中、及格、不及格,一个人对事物的态度分为赞成、中立、反对。
这里的“考试成绩等级”、“态度”等就是顺序变量。
3.数值变量:可以用数字记录其观察结果,这样的变量称为数值变量,如“企业销售额”、“生活费支出”、“掷一枚骰子出现的点数”。
1.5获得数据的概率抽样方法有哪些?(1)简单随机抽样 ,简单随机抽样又称纯随机抽样,是指在特定总体的所有单位中直接抽取n个组成样本。
它最直观地体现了抽样的基本原理,是最基本的概率抽样。
(2)系统抽样 ,系统抽样也称等距抽样或机械抽样,是按一定的间隔距离抽取样本的方法。
(3)分层抽样 ,分层抽样也叫分类抽样,就是先将总体的所有单位依照一种或几种特征分为若干个子总体,每一个子总体即为一类,然后从每一类中按简单随机抽样或系统随机抽样的办法抽取一个子样本,称为分类样本,它们的集合即为总体样本。
统计学期末试题_模拟试卷一及答案

模拟试卷一:统计学期末试题院系________姓名_________成绩________一. 单项选择题(每小题2分,共20分)1. 对于未分组的原始数据,描述其分布特征的图形主要有( )A. 直方图和折线图B. 直方图和茎叶图C. 茎叶图和箱线图 D 。
茎叶图和雷达图2. 在对几组数据的离散程度进行比较时使用的统计量通常是( )A. 异众比率 B 。
平均差 C. 标准差 D 。
离散系数3. 从均值为100、标准差为10的总体中,抽出一个50=n 的简单随机样本,样本均值的数学期望和方差分别为( )A. 100和2 B 。
100和0。
2 C 。
10和1.4 D 。
10和24. 在参数估计中,要求通过样本的统计量来估计总体参数,评价统计量标准之一是使它与总体参数的离差越小越好。
这种评价标准称为( )A 。
无偏性B 。
有效性C 。
一致性D 。
充分性 5. 根据一个具体的样本求出的总体均值95%的置信区间( )A. 以95%的概率包含总体均值B. 有5%的可能性包含总体均值C. 一定包含总体均值D. 可能包含也可能不包含总体均值6. 在方差分析中,检验统计量F 是( )A 。
组间平方和除以组内平方和B 。
组间均方和除以组内均方C 。
组间平方和除以总平方和D 。
组间均方和除以组内均方7. 在回归模型εββ++=x y 10中,反映的是( )A. 由于的变化引起的的线性变化部分B. 由于的变化引起的的线性变化部分C. 除和的线性关系之外的随机因素对的影响D. 由于和的线性关系对的影响8. 在多元回归分析中,多重共线性是指模型中( )A. 两个或两个以上的自变量彼此相关B. 两个或两个以上的自变量彼此无关C. 因变量与一个自变量相关D. 因变量与两个或两个以上的自变量相关9. 若某一现象在初期增长迅速,随后增长率逐渐降低,最终则以K 为增长极限。
描述该类现象所采用的趋势线应为( )A. 趋势直线 B 。
数值数据的整理与显示

• 16 • 17 • 18 • 19
. . . .
0358 01255667788 012356 0
4 11 6 1
未分组数据— 未分组数据—单批数据箱线图
(箱线图的构成) 箱线图的构成)
X 最小值 QL 中位数
QU
X 最大值
4
6
8
10
12
简单箱线图
未分组数据— 未分组数据—单批数据箱线图
(例题分析) 例题分析)
首先要依据数据的大小范围,确定“茎”的数字位和“叶”的 数字位。 确定“茎”的数字位时,要遵循“数据的‘茎’必须有变化 的原则”。 其次,将全部数据分成“茎”和“叶”两部分,“茎”在左, “叶”在右。“茎”“叶”之间用小数点隔开。 再次,把样本数据所有的茎,从小到大,从上到下纵向排列, 并在“茎”后标出小数点,小数点要纵向对齐。 • 树茎 树叶 数据个数
等距分组表
(上下组限重叠) 上下组限重叠)
等距分组表
(上下组限间断) 上下组限间断)
等距分组表
(使用开口组) 使用开口组)
数值型数据的图示
分组数据—直方图和折线图 分组数据—
分布图
直 方 图
折 线 图
曲 线 图
Exc el
分组数据— 分组数据—直方图
(histogram)
1. 用矩形的宽度和高度来表示频数分布的图 形,实际上是用矩形的面积来表示各组的 频数分布 2. 在直角坐标中,用横轴表示数据分组,纵 轴表示频数或频率,各组与相应的频数就 形成了一个矩形,即直方图 3. 直方图下的总面积等于1
最小值 141 下四分位数 中位数 170.25 182 上四分位数 197 最大值 237
140
150
统计学知识点(前四章)

统计学知识点(前四章)第1章导论1.统计学:收集、处理、分析、解释数据并从数据中得出结论的科学。
2.按数据分析方法分类:↗描述统计—数据收集、处理、汇总、图表描述↘推断统计—利用样本数据推断总体特征3.统计数据是对现象进行测量的结果。
4.按照计量尺度的不同,将统计数据分为分类数据、顺序数据和数值型数据。
1)分类数据:对事物分类的结果,用文字表述,数据表现为类别(男女);2)顺序数据:有序的类别,如,一等品二等品、小学初中高中、同意;3)数值型数据:按数字尺度测量的观察值,具体的数值。
5.数据的计量尺度:1)定/分类尺度:数据表现为类别,按照事物的属性平行的分类,计量层次最低,具有“=”或“≠”的数学特性;2)定/顺序尺度:数据表现为有序的类别,具有“>”或“<”的数学特性;3)定距/间隔尺度:数据表现为数字,没有绝对零点;4)定比/比率尺度:数据表现为数字,有绝对零点。
3、4统称数值型数据。
6.定性/品质数据:分类数据和顺序数据统称。
定量/数量数据:数值型数据。
7.按照数据的收集方法:观测数据和实验数据。
按时间状况:截面数据和时间序列数据。
(统计数据的分类)8.总体:是包含所研究的全部个体(数据)的集合。
组成总体的每个元素成为个体。
按包含数目是否可数,分为有限总体和无限总体。
9.样本:是从总体中抽取的一部分元素的集合。
构成样本的元素的数目成为样本量。
抽样的目的是为了根据样本提供的信息推断总体的特征。
10.参数:是用来描述总体特征的概括性数字度量。
是研究者想要了解的总体的某种特征值,如,总体平均数μ、总体标准差σ。
11.统计量:是用来描述样本特征的概括性数字度量。
是根据样本数据计算出来的量,如,样本平均数χ 、样本标准差s。
12.变量:是说明现象某种特征的概念。
如,商品销售额、受教育程度。
变量的具体值称为变量值,比如商品的销售额可以是20万、30万。
13.变量的分类——分类变量:性别、行业;顺序变量:产品等级、受教育程度;数值型变量:↗离散型变量:产品数量、企业数(取值以整数位断开)↘连续性变量:年龄、温度、零件尺寸(取值连续不断)随机变量和非随机变量,经验变量和理论变量第2章数据的搜集1.数据的来源:间接来源和直接来源2.间接来源的数据:对原信息重新加工、整理,数据可以取自系统外部或内部。
统计学原理-数据的整理

向下累积 户数 (户) 300 279 180 102 38 — 百分比 (%) 100.0 93.0 60.0 34.0 12.7 —
பைடு நூலகம்
提取甲 乙百分比 及回答 类别共 3列 列
非常不满 不满意 一般 满意 非常满意 合计
主要是分组整理 三,数值型数据的整理与显示(主要是分组整理 数值型数据的整理与显示 主要是分组整理)
– 完整性审核
检查应调查的单位或个体是否有遗漏 所有的调查项目或指标是否填写齐全
– 准确性审核
检查数据是否真实反映客观实际情况,内容是否符合实际 检查数据是否真实反映客观实际情况, 检查数据是否有错误,计算是否正确等 检查数据是否有错误, 审核数据准确性的方法
– 逻辑检查 从定性角度,审核数据是否符合逻辑,内容是否合理, 从定性角度,审核数据是否符合逻辑,内容是否合理, 各项目或数字之间有无相互矛盾的现象 主要用于对定类数据和定序数据的审核 – 计算检查 检查调查表中的各项数据在计算结果和计算方法上有无 错误 主要用于对定距和定比数据的审核
单变量值分组表
(实例)
表 某车间50名工人日加工零件数分组表
零件数 (个)
107 108 110 112 113 114 115 117 118
频数 (人)
1 2 1 2 1 1 1 3 3
零件数 (个)
119 120 121 122 123 124 125 126 127
频数 (人)
1 2 1 4 4 3 2 2 3
主要是分类整理 二,品质数据的整理与显示(主要是分类整理 品质数据的整理与显示 主要是分类整理)
一.分类数据的整理与显示 基本过程 分类数据的整理与显示(基本过程 分类数据的整理与显示 基本过程)
第五版统计学复习资料

第二章
1、概率抽样也称随机抽样,是遵循随机原则进行的抽样,不加主观因素,组成总体的每个单位都有被抽中 的概率(非零概率) ,可以避免样本出现偏差,样本对总体有很强的代表性。 特点: (1) (2) (3) 分类: (1) 简单随机抽样:从包括总体 N 个单位的抽样框中随机地、一个个地抽取 n 个单位作为样本,每个 单位的入样概率是相等的。也就是从总体中不加任何分组、划类、排队等,完全随机地抽取调查单 位。 特点是:每个样本单位被抽中的概率相等,样本的每个单位完全独立,彼此之间无一定的关联性 和排斥性。简单随机抽样是其他各种抽样形式的基础。通常只是在总体单位之间差异程度较小和 数目较少时,才采用这种方法。 (2) 分层抽样:将抽样单位按某种特征或某种规划划分为不同的层,然后从不同的层中独立、随机地 抽取样本。 特点是: 由于通过划类分层, 增大了各类型中单位间的共同性, 容易抽出具有代表性的调查样本。 抽样时是按一定的概率以随机原则抽取样本。 每个单位被抽中的概率是已知的,或是可以计算出来的。 当用样本对整体目标量进行估计时,要考虑到每个样本单位被抽中的概率。
称为向上累积,反之为向下累积。频率的最终累积值为 100%。 (三)数值型数据的图示 1、分组数据:直方图 用面积来表示频数分布矩形的高度表示每一组的频数或频率,宽度则表示各组的组距。 制作频数分布直方图的方法: ①集中和记录数据,求出其最大值和最小值。数据的数量应在 100 个以上,在数量不多的情况下,至 少也应在 50 个以上。我们把分成组的个数称为组数,每一个组的两个端点的差称为组距。 ②将数据分成若干组,并做好记号。分组的数量在 5-12 之间较为适宜。 ③计算组距的宽度。用最大值和最小值之差去除组数,求出组距的宽度。 ④计算各组的界限位。各组的界限位可以从第一组开始依次计算,第一组的下界为最小值减去最小测 定单位的一半,第一组的上界为其下界值加上组距。第二组的下界限位为第一组的上界限值,第二组的下 界限值加上组距,就是第二组的上界限位,依此类推。 ⑤统计各组数据出现频数,作频数分布表。 ⑥作直方图。以组距为底长,以频数为高,作各组的矩形图。
统计学贾俊平第3章数据的图表展示

组距(class width) :上限与下限之差
组中值(class midpoint) :下限与上限之间 的中点值
组中值 = 下限值+上限值 2
45
All rights reserved
【例】某电 脑公司连续 个月各天的 销售量数据( 单位:台)。 试对数据进 行分组
All rights reserved
29
All rights reserved 29
帕累托图
30
All rights reserved 30
例析
频数汇总
罪犯的例子
改造方式 监狱 文学课 总计
无新罪 22 32 54
新罪 18 6 24
总计 40 38 78
31
All rights reserved
Graphs are the most effective way to communicate using data
一图胜千言
John Tukey:“图形的最大价值就是使我 们注意到我们从来没有料到过的信息”
6
All rights reserved
图表的力量
历史上著名的统计图表
拿破仑的大军团进军俄国
向上累积
户数 百分比
(户)
(%)
向下累积
户数 百分比 (户) (%)
非常不满意 21
7.0
21
7.0 300 100.0
不满意
99 33.0 120
40.0 279
93.0
一般
78 26.0 198
66.0 180 60.0
满意
64 21.3 262
强烈推荐箱线图--举例.ppt
英语 经济数学
西方经济 学
市场营销
9
71
7 0
7 51
7 4
7 8
76 90 65 95
7 6
8 8
6 6
93 81
6 9
9
98 36
6 91 38 73 97 87
8 3
8 2
7 8
7 5
8 81 55 71 5
9 2
7 8
8 6
7 8
8 91 71 7
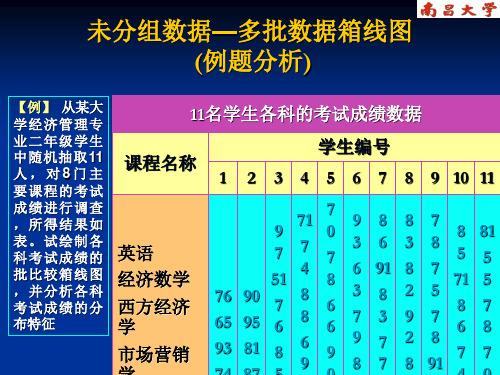
未分组数据—多批数据箱线图 (例题分析)
未分组数据—多批数据箱线图 (例题分析)
【例】 从某大
学经济管理专 业二年级学生 中 随 机 抽 取 11 人,对8门主 要课程的考试 成绩进行调查 ,所得结果如 表。试绘制各 科考试成绩的 批比较箱线图 ,并分析各科 考试成绩的分 布特征
11名学生各科的考试成绩数据
学生编号 课程名称
1 2 3 4 5 6 7 8 9 10 11
105 95 85 75 65 55 45
英语 经济数学 西方经济学 市场营销学 财务管理 基础会计学
统计学 计算机应用基础
8门课程考试成绩的箱线图
Min-Max 25%-75% Median value
2
未分组数据—多批数据箱线图 (例题分析)
105
95
85
75
65
55
45 学生1
学生3
学生5
学生7
学生9 学生11
学生2 学生4 学生6 学生8 学生10
min-max 25%-75% median value
11名学生8门课程考试成绩的箱线图
3
统计学第2章用图表展示数据

环形图
(doughnut chart )
北京、天津、上海和重庆地区按收入法计算的地区生产总值
第 2 章 用图表展示数据
2.2 用图表展示定量数据
2.2.1 生成频数分布表 2.2.2 定量数据的图示
2.2 用图表展示定量数据 2.2.1 生成频数分布表
【例2-3】某电 脑公司120天的 销售额数据(单 位:万元) 。生 成一张频数分
(定性数据)
【例2-1】为研究人们 对不同类型软饮料的偏 好情况,一家调查公司 在某超市随机调查了50 名消费者。右表是顾客 性别及其所偏好的饮料 类型记录。生成频数分 布表,观察不同性别的 消费者及其所偏好的饮 料类型的分布状况,并 进行描述性分析
制作频数分布表
生成频数分布表
(列联表—Excel)
用于研究结构 问题
简单饼图
(pie Chart)
主要用于展
示两个或多 个分类变量 的构成比较, 比如,在男 女分类的基 础上又增加 了饮料类型 的分类。
复式饼图
(pie Chart)
环形图
(doughnut chart)
1. 环形图中间有一个“空洞”,样本或 总体中的每一部分数据用环中的一段 表示
用哪些图形展示奖牌?
根据上面的数据,你认为可以选择哪些图形来展示 三个国家所获得的奖牌情况?学完本章的图表展示 技术,这样的问题就会迎刃而解
统计应用
把数据画图之后,要用用脑袋
➢ 沃德(Abraham Wald)和许多统计学 家一样,在第二次世界大战时也处理
了战争与相关的问题。他发明的一些
统计方法在战时被视为军事机密。以 下是他提出的概念中较简单的一种
3. 条形图主要用于展示定性数据,而直方 图则主要用于展示定量数据
统计(03)第3章__数据的图表展示

2. 数据筛选
3. 数据排序
4. 数据透视
统计学
STATISTICS (第四版)
数据审核
作者:贾俊平,中国人民大学统计学院
统计学
STATISTICS (第四版)
1.
–
–
数据审核—原始数据
(raw data)
完整性审核
应调查的单位或个体是否有遗漏 所有的调查项目或变量是否填写齐全
作者:贾俊平,中国人民大学统计学院
统计学
STATISTICS (第四版)
3.2 品质数据的整理与展示
3.2.1 分类数据的整理不图示 3.2.2 顺序数据的整理不图示
作者:贾俊平,中国人民大学统计学院
统计学
STATISTICS (第四版)
数据的整理不显示
(基本问题)
丌同类型的数据,采取丌同的处理方式和方法
统计学
STATISTICS (第四版)
数据排序
(方法)
1. 分类数据的排序 字母型数据,排序有升序降序之分,但习惯上
用升序 汉字型数据,可按汉字的首位拼音字母排列, 也可按笔画排序,其中也有笔画多少的升序降 序之分
2. 数值型数据的排序
–
–
逑增排序:设一组数据为x1,x2,…,xn,逑增 排序后可表示为:x(1)<x(2)<…<x(n) 逑减排序:可表示为:x(1)>x(2)>…>x(n)
甲城市家庭对住房状况评价的频数分布 甲城市 回答类别 户数 (户) 24 108 93 45 30 300 百分比 (%) 8 36 31 15 10 100.0 向上累积 户数 (户) 24 132 225 270 300 — 百分比 (%) 8.0 44.0 75.0 90.0 100.0 — 向下累积 户数 (户) 300 276 168 75 30 — 百分比 (%) 100.0 92 56 25 10 —
统计学知到章节答案智慧树2023年山东工商学院

统计学知到章节测试答案智慧树2023年最新山东工商学院第一章测试1.构成统计总体的前提是()。
参考答案:同质性2.指出下面哪一个属于分类变量()。
参考答案:购买商品时的支付方式3.指出下面哪一个属于数值型变量()。
参考答案:收入4.某研究部门准备在该市500万个家庭中随机抽取1000个家庭,据此推断该城市所有家庭的年人均收入。
这项研究的个体是()。
参考答案:500万个家庭中的每个家庭5.某研究部门准备在该市500万个家庭中随机抽取1000个家庭,据此推断该城市所有家庭的年人均收入。
这项研究的样本是()。
参考答案:1000个家庭6.一家研究机构从IT从业者中随机抽取500人作为样本进行调查,其中60%的人回答他们的月收入在5000元以上,50%的人回答他们的消费支付方式是使用信用卡。
这里的“月收入”是()。
参考答案:分类变量7.一名统计专业学生为了完成其统计作业,在《中国统计年鉴》中找到2019年全国各地区城镇居民人均可支配收入的数据,该数据属于()。
参考答案:截面数据8.一名统计专业学生为了完成其统计作业,在《中国统计年鉴》中找到2000-2014年全国城镇居民人均可支配收入的数据,该数据属于()。
参考答案:时间序列数据9.一名统计专业学生为了完成其统计作业,在《中国统计年鉴》中找到2000-2014年全国城镇居民人均可支配收入、农村居民纯收入等数据,该数据属于()。
参考答案:面板数据10.下列不属于描述统计的问题是()。
参考答案:根据样本信息对总体进行的推断11.在下列叙述中,采用推断统计的方法是()。
参考答案:根据36个橘子的平均重量估计果整个果园中橘子的平均重量12.一项民意调查的目的是确定年轻人愿意与父母讨论的话题。
调查结果表明:45%的年轻人愿意与其父母讨论家庭财务状况,38%的年轻人愿意与其父母讨论有关教育的问题,15%的年轻人愿意与其父母讨论爱情问题。
该调查所收集的数据是()。
参考答案:分类数据13.一项研究估计某城市拥有汽车的家庭比例是30%,这里的30%是()。
描述性统计

EX. 未分组数据—箱线图
(box plot)
1. 用于显示未分组的原始数据的分布 2. 由一组数据的5个特征值绘制而成,它由一个箱
子和两条线段组成
3. 绘制方法
首先找出一组数据的5个特征值,即最大值、最小 值 四分、位中数位Q数UM) e和两个四分位数(下四分位数QL和上
探索分析-I
探索分析-II
探索分析-III
探索分析-IV
探索分析-V
探索分析-VI
2.4.1列联表分析的功能与意义
SPSS的列联表分析过程(Crosstabs)是通过分 析多个变量在不同取值情况下的数据分布情 况,从而进一步分析多个变量之间相互关系 的一种描述性分析方法。
至少指定两个变量,分别为行变量和列变量, 如果要进行分层分析,则我们还要规定层变 量。
相关描述统计量主要有平均值、最大值 、最小值、方差、标准差、极差、平均 数标准误、偏度系数和峰度系数等。
2.2.2 描述性分析实例
【例2.2】下面的资料给出了山东省某 高校50名大一入学新生的体重。试对该 50名学生的体重进行描述性分析,了解 这50名学生体重的基本特征。
配书资料\源文件\2\正文\原始数据文 件\案例2.2.sav
意义。
描述性统计分析常用的有:频数分 析、描述性分析、探索分析、列联 表分析。下面我们一一介绍这几种 方法的功能和意义。
2.1.1 频数分析的功能与意义
频数分析过程(Frequencies)是描述性分析中 最基本也是最常用的方法之一。
可以得到详细的频数表以及平均值、最大值 、最小值、方差、标准差、极差、平均数标 准误、偏度系数和峰度系数等重要的描述统 计量,还可以通过分析得到合适的统计图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、未分组数据:茎叶图和箱线图(1)茎叶图:
(可根据实际所需,选择输出“两者都”)
(可根据实际所需,选择箱图)。
转至SPSS查看器可得:
(2)箱线图:
【例3.7】
(1)第一种方法:看每个学生考试成绩的分布情况,把学生考试成绩当变量来制作箱线图。
以下为初始数据,还有操作过程:
点击“箱图”,弹出如下框
选择“简单”还有“各个变量的摘要”,再点击“定义按钮”,有如下框:
将“学生1”等变量均选入“框的表征”,再点击,结果如下:
案例处理摘要
案例
有效缺失合计
N 百分比N 百分比N 百分比
学生1 8 100.0% 0 .0% 8 100.0% 学生2 8 100.0% 0 .0% 8 100.0% 学生3 8 100.0% 0 .0% 8 100.0% 学生4 8 100.0% 0 .0% 8 100.0% 学生5 8 100.0% 0 .0% 8 100.0% 学生6 8 100.0% 0 .0% 8 100.0% 学生7 8 100.0% 0 .0% 8 100.0% 学生8 8 100.0% 0 .0% 8 100.0% 学生9 8 100.0% 0 .0% 8 100.0% 学生10 8 100.0% 0 .0% 8 100.0% 学生11 8 100.0% 0 .0% 8 100.0% 得箱线图如下:
第二种方法:看各科考试成绩的分布情况,与第一种方法类似以下为转置后的数据:
操作过程为:
选择“简单”还有“各个变量的摘要”,再点击“定义”按钮,有如下框:
将各科选入“框的表征”,点击,输出如下结果:
案例处理摘要
案例
有效缺失合计
N 百分比N 百分比N 百分比
英语11 100.0% 0 .0% 11 100.0% 经济数学11 100.0% 0 .0% 11 100.0% 西方经济学11 100.0% 0 .0% 11 100.0% 市场营销学11 100.0% 0 .0% 11 100.0% 财务管理11 100.0% 0 .0% 11 100.0% 基础会计学11 100.0% 0 .0% 11 100.0% 统计学11 100.0% 0 .0% 11 100.0% 计算机应用基11 100.0% 0 .0% 11 100.0%
箱线图为:。
