塑性成形理论-Slip-line theory
塑性成形原理知识点总结

塑性成形原理知识点总结一、塑性成形的基本原理1. 塑性成形的基本原理是通过施加外部应力使材料受力,发生形变,从而改变其形状和尺寸。
外部应力可以是拉伸、压缩、弯曲等形式,材料受到应力后发生塑性变形,达到所需的形状和尺寸。
2. 塑性成形的基本原理还包括在一定的温度条件下进行成形。
材料在一定温度范围内会发生晶粒的滑移和再结晶等变化,使材料更容易流动和变形,这对于塑性成形的效果非常重要。
3. 塑性成形的基本原理还涉及到应变硬化和材料流动等方面的知识。
应变硬化是指材料在形变过程中发生的一种增加抗力的现象,材料流动则是指材料在应力作用下发生的形变过程,通过流动来实现所需的成形效果。
二、材料在塑性成形过程中的变形规律1. 材料在塑性成形过程中会发生各种形式的变形,包括平面应变变形、轴向应变变形、弯曲应变变形、扭曲应变变形等。
不同的成形方式会引起不同形式的变形,需要根据具体情况进行分析和处理。
2. 材料在塑性成形过程中的变形还受到横向压缩和减薄等因素的影响。
横向压缩会导致材料沿其厚度方向出现侧向膨胀的现象,减薄则是指材料在成形过程中产生的减小尺寸和厚度的现象。
3. 材料在塑性成形过程中还会出现显著的硬化现象。
随着形变量的增加,材料的硬度和抗力会逐渐增加,这对于成形过程的控制和调整非常重要。
三、材料在塑性成形过程中的流变规律1. 材料在塑性成形过程中会发生流变,即在应力的作用下发生形变的过程。
材料的流变规律是指在应力条件下材料的变形规律和流动规律,这对于塑性成形技术的研究和应用非常重要。
2. 材料在塑性成形过程中还会出现应力和应变的分布不均匀、表面变形、壁厚变化等现象。
这些现象会导致成形件质量的不稳定性和变形过程的复杂性,需要进行合理的控制和调整。
3. 材料在塑性成形过程中还会受到局部热和化学变化的影响。
局部热和化学变化会影响材料的微观结构和性能,对于成形过程的控制和调整也具有重要的参考意义。
四、塑性成形的热变形和冷变形1. 塑性成形通常分为热变形和冷变形两种方式。
百科知识精选滑移线

基本信息英文名:slip line中文名:滑移线隶属:塑性力学定义:试样表面出现的线纹时间:二十世纪20年代至40年代间简介材料在屈服时,试样表面出现的线纹称为滑移线。
滑移线理论是二十世纪20年代至40年代间,人们对金属塑性变形过程中,光滑试样表面出现"滑移带"现象经过力学分析,而逐步形成的一种图形绘制与数值计算相结合的求解平面塑性流动问题变形力学问题的理论方法.这里所谓"滑移线"是一个纯力学概念,它是塑性变形区内,最大剪切应力)等于材料屈服切应力(k)的轨迹线。
解释1、2节点相对位置判断构件接触碰撞点的轨迹称为滑移线.主节点所在的一侧称为主线主线上相邻节点之间的线段称为主段。
2、在塑性状态平面应变问题中,平面上每一点都存在两个相交的剪切破坏面,把各点的剪切破坏面连接起来,就可以得到两族相互正交曲线α和β,即称为滑移线。
3、0前言在塑性状态平面应变问题中,平面上每一点都存在两个相交的剪切破坏面,把各点的剪切破坏面连接起来,就可以得到两族相互正交曲线α和β,即称为滑移线.滑移线法按照其性质和边界条件,求出塑性区的应力和位移速度的分布,最后求出极限荷载。
4、滑移带晶体材料的滑移面与晶体表面的交线称为滑移线,滑移部分的晶体与晶体表面形成的台阶称为滑移台阶.由这些数目不等的滑移线或滑移台阶组成的条带称为滑移带。
5、塑料变形体内各点最大剪应力的轨迹称为滑移线.由于最大剪应力成对正交因此滑移线在变形体内成两族互相正交的线网组成所谓滑移线场。
6、这样的两组曲线在X、Y平面上形成一个曲线网称为滑移线.当物体处于屈服状态时,各点的最大剪应力达到K值,塑性变形就沿着这些曲线进行滑移。
塑性成形理论基础

主应力和应力不变量
J1、J2、J3分别为一阶、二阶、和三阶应力不变量, 方程 σ 3 − J 1σ 2 − J 2σ − J 3 = 0 有3个实根,即3个主应力,依其值从大到小依次记为 σ1、σ2、σ3。 3 以主应力表示时,3个应力不变量简化为:
J1 = σ1 +σ 2 +σ 3 J 2 = −(σ 1σ 2 + σ 2σ 3 + σ 3σ 1) J 3 = σ 1σ 2σ 3
塑性成形/ 塑性成形/加工
利用金属材料的塑性变形特性,用工 模具对金属材料施加机械(力)作用,使 其发生所希望的塑性变形,达到所要求 的形状、尺寸、精度和组织性能。 该过程中尺寸形状和组织性能同时改 变。
塑性成形一例
拉深成形
塑性加工
利用金属材料的塑性变形特性,用工模具加金属 材料施加机械作用,使其发生塑性变形,达到所 要求的形状、尺寸、精度和组织性能。 该过程中尺寸形状和组织性能都同时改变。 主要有: 成材的塑性加工:如轧制、挤压、拉拔等 成形的塑性加工:主要有锻造、拉深、冲压等 先进的塑性成形:主要有超塑性成形、液压胀 形、电磁成形等
应力状态
由单元体静力平衡可导出切应力互等,即: σxy = σyx; σxz = σzx; σyz = σzy 所以应力张量实际只有6个独立的分量。
σxx σxy σxz σij = ⋅ σyy σyz ⋅ ⋅ σzz
主应力和应力不变量
前面指出,只要将过一点Q处 三个相互垂直的面素上的应力矢量表示出来,就可以用三个面 素的应力矢量表示过该点的任一面素上的应力矢量。 现在知道了一点处三个相互垂直的面素上的应力矢量,即 应力张量σij,如何求任意一个截面上的应力呢?
材料加工/成形,有三个目的: 材料加工/成形,有三个目的: 获得所需要的形状、尺寸、精度, 获得所需要的形状、尺寸、精度, 材料的几何特征; 几何特征 材料的几何特征; 获得所需要的性能和内部组织, 获得所需要的性能和内部组织,材料 内在特征 特征; 的内在特征; 获得所需要的表面性能和表层组织, 获得所需要的表面性能和表层组织, 材料的表面特征。 材料的表面特征。 表面特征
第四章--塑性成形理论基础 物理基础

0916120232--王乐
滑移变形与位错运动
一个位错滑移过整个滑移面(距离L),产生的切应变
ε
为:
某位错 i 滑移任意距离xi产生的切应变(ε)i为:
0916120232--王乐
n个位错滑过n个任意距离xi产生的切应变为:
切应变速率为:
0916120232--王乐
两压一延,晶粒成纤维状,如挤压; 一压一延,晶粒成扁长形,如轧制; 一压两延,晶粒成饼状,如镦粗; 第二相也在延伸方向拉长拉碎呈链状排列,形成纤维状组织 沿纤维方向性能高,垂直于纤维方向性能低,产生各向异性。
0916120232--王乐
二、产生结构缺陷
塑性变形引入晶体的结构 缺陷有位错、空位、间隙 原子、堆垛层错、孪晶界、 亚晶界及至晶界。 冷变形后空位浓度:c =10-4e 塑性变形后位错密度可达: 1010 ~1011根/cm2。这高密度 的位错 可以形成位错胞等各种位错的低能组态。
0916120232--王乐
滑移与孪生
大多数bcc金属的孪生临 界切应力大于滑移临界 切应力,所以滑移先于 孪生进行;fcc金属的孪 生临界切应力远大于滑 移临界切应力
0916120232--王乐
孪生举例-AZ31中的孪晶
AZ31镁合金压缩变形(~2%)后的金相组织
0916120232--王乐
三、晶界滑移
0916120232--王乐
二、各向异性 由于冷变形时金属在主应变方向上形成 的纤维状组织,和金属晶粒转动产生的 晶体学择优取向(织构),使材料的宏观性 能产生了各向异性。 这种各向异性还会造成进一步深加工时 的缺陷——制耳。
0916120232--王乐
三、其他性能变化 冷加工还会造成:密度降低 导电性降低 导热性降低 耐蚀性变差 以及磁性变化等多种物理 化学性能的变化。
塑性理论第九章滑移线法

摩擦切应力为 K的接触面
σn= σm
摩擦切应力为 K的接触面
α
0 β α α σm σ3 σ3 K β β
0
σm K σ1 α
σ1 K β σm
K
σm 0 K
σm
代数值最大的 σm 主应力σ1的作用线
σ1
0
K σm
K
σ3
σm
K
σ1
σ3
摩擦切应力为K的接触表面的滑移线
(4)摩擦力为某一中间值的接触表面 1 1 xy cos 0 xy K 2 K
1 ( 1 3 ) k 2 1 ( 1 3 ) m 2
z σz= σm= σ2
σm +K
σy
σ1 τyx -K
σ1作用线
τxy
σm σx σ3
0 σx x
σy τxyτyx
y
P
τ
σy (σm,+K) y τyxቤተ መጻሕፍቲ ባይዱ
4
1 m k 2 m 3 m k
xy
0
y
r
y
y
m
K
xy
m
K
3
2
1
xy
0
x
xy
K K
xy
x
x
a
m
x
m
m
y
xy
a)
b)
摩擦切应力为某一中间值的接触面处的滑移线
2、常见的滑移线场类型
直线滑移线场,两族直线 简单滑移线场,一直一曲 有心和无心扇形场 直线与简单滑移线场组合 正交曲线滑移线场
塑性成形原理知识点

塑性成形原理知识点塑性成形是一种利用金属材料的塑性变形能力,在一定的条件下通过压力使金属材料发生塑性变形,从而获得所需形状的加工方法。
塑性成形技术是金属加工工艺中的重要分支,广泛应用于汽车、航空、航天、电子、家电、建筑等工业领域。
1.塑性变形:在塑性成形过程中,金属材料通过外力作用下的塑性变形使其形状发生改变。
塑性变形是金属材料中原子的相对位置发生改变而引起的宏观形变,其主要表现为材料的延伸、压缩、弯曲等。
塑性变形是金属材料的塑性性质所决定的,不同材料的塑性性能不同。
2.应力-应变关系:金属材料受到外力作用时,材料内部会产生应力,应力与应变之间存在一定的关系。
在塑性成形过程中,材料会发生塑性变形,使其产生应变。
应力-应变关系是描述材料塑性变形过程中应力和应变之间关系的数学模型,常用的模型有胡克定律模型和流变模型。
3.材料流动:塑性成形过程中,材料会发生流动从而获得所需的形状。
材料流动是指塑性材料在外力作用下,发生内部原子的相对位移和重新组合,从而使整个材料的结构发生变化。
材料流动是实现塑性成形的关键,其流动性能决定了成形工艺的可行性和成品质量。
4.成形工艺:塑性成形工艺是金属材料经过一系列工艺操作,通过压力使其发生塑性变形,最终获得所需形状的过程。
常见的塑性成形工艺包括冲压、拉伸、挤压、压铸、滚压等。
不同工艺适用于不同形状的零件,根据材料的性质和零件的要求选择合适的成形工艺。
5.工艺过程控制:塑性成形过程中,需要对各个环节进行控制以确保成品质量。
工艺过程控制包括工艺参数的选择、设备的调整、模具结构的设计等。
在塑性成形过程中,要控制好温度、应力、应变速率等因素,以避免过大的变形应力引起材料的断裂或变形过大导致零件尺寸偏差。
塑性成形技术不仅可以实现复杂形状的制造,而且可以提高材料的强度和刚度,降低材料的质量,节省原材料和能源。
因此,塑性成形技术在现代工业生产中具有重要的地位和应用价值。
机械制造基础塑性成形

回复温度较低,对于纯金属,可用下式计算:
T回 0.2 0.3T熔
式中 T回 ----金属的绝对回复温度;
T熔 ----金属的绝对熔化温度;
回复作用不改变晶粒的形状及晶粒变形时所构成的方 向性,也不能使晶粒内部的破坏现象及晶界间物质的破坏 现象得到恢复,只是逐渐消除晶格的扭曲程度。故回复作 用可以降低内应力,但力学性能变化不大,强度稍降低, 塑性稍提高。如图3-9b所示。
3)具有较高的劳动生产率。
4)适应性广。
缺点: 1)锻件的结构工艺性要求较高,内腔复杂零件难以锻造; 2)锻造毛坯的尺寸精度不高,一般需切削加工; 3)需重型机器设备和较复杂模具,设备费用与周期长; 4)生产现场劳动条件较差。
常用塑性成形加工方法有:1)自由锻造;2)模型锻 造;3)挤压;4)拉拔;5)轧锻;6)板料冲压。如图 3-1所示。
2)金属的组织状态:组织结构不同,锻造性能不同; 单一固溶体组成的合金,塑性好,锻造性能好;铸态柱 状组织和粗晶结构不如细小均匀的晶粒结构;金属内部 有缺陷也不一样。
2.金属的变形条件
1)变形温度:温度升高,塑性上升,降低变形抗力,易于 锻造;但温度过高也会产生相应的缺陷,如氧化,脱碳、 过热和过烧等。故要严格控制锻造温度范围。
多晶体的晶内变形方式和单晶体一样,也是滑移和双 晶,但各个晶粒所处的塑性变形条件不同,即晶粒内晶格 排列的方向性决定了其变形的难易,与外力成45度的滑移 面最易变形。因为其产生的切应力最大。如图3-7反映了 晶粒位向与受力变形的关系。
同时在多晶体的晶界处,由于相邻晶粒间的位向差别, 产生晶格的畸变,并有杂质的存在,以及晶粒间犬牙交错 状态,对多晶体的变形造成很大障碍。低温时,晶界强度 高于晶粒内部强度,变形抗力大不易变形;高温时,晶界 强度降低,晶粒易于相互移动。所以多晶体由于存在晶界 和各晶粒的位向差别,其变形抗力要远高于同种金属的单 晶体。
塑性成形7
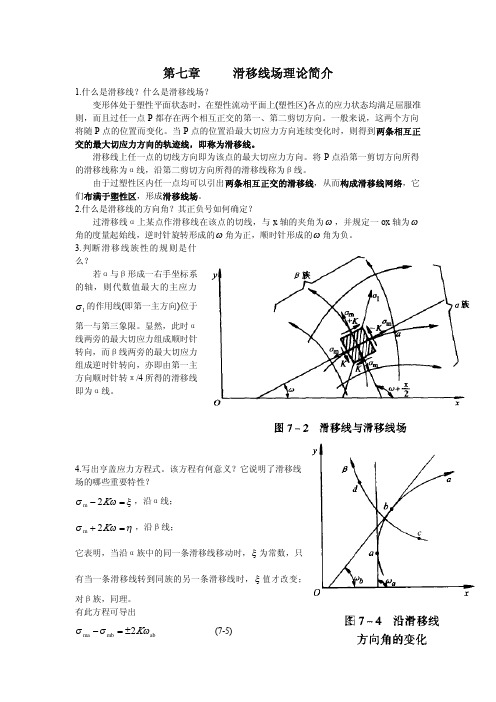
第七章滑移线场理论简介1.什么是滑移线?什么是滑移线场?变形体处于塑性平面状态时,在塑性流动平面上(塑性区)各点的应力状态均满足屈服准则,而且过任一点P 都存在两个相互正交的第一、第二剪切方向。
一般来说,这两个方向将随P 点的位置而变化。
当P 点的位置沿最大切应力方向连续变化时,则得到两条相互正交的最大切应力方向的轨迹线,即称为滑移线。
滑移线上任一点的切线方向即为该点的最大切应力方向。
将P 点沿第一剪切方向所得的滑移线称为α线,沿第二剪切方向所得的滑移线称为β线。
由于过塑性区内任一点均可以引出两条相互正交的滑移线,从而构成滑移线网络,它们布满于塑性区,形成滑移线场。
2.什么是滑移线的方向角?其正负号如何确定?过滑移线α上某点作滑移线在该点的切线,与x 轴的夹角为,并规定一ox 轴为ωω角的度量起始线,逆时针旋转形成的角为正,顺时针形成的角为负。
ωω3.判断滑移线族性的规则是什么?若α与β形成一右手坐标系的轴,则代数值最大的主应力的作用线(即第一主方向)位于1σ第一与第三象限。
显然,此时α线两旁的最大切应力组成顺时针转向,而β线两旁的最大切应力组成逆时针转向,亦即由第一主方向顺时针转π/4所得的滑移线即为α线。
4.写出亨盖应力方程式。
该方程有何意义?它说明了滑移线场的哪些重要特性?,沿α线;ξωσ=−K 2m ,沿β线;ηωσ=+K 2m 它表明,当沿α族中的同一条滑移线移动时,为常数,只ξ有当一条滑移线转到同族的另一条滑移线时,值才改变;ξ对β族,同理。
有此方程可导出(7-5)ab mb ma 2ωσσK ±=−式中,分别表示滑移线上a ,b 两点的平均应力;mb ma σσ、——a 、b 两点间的转角,亦即a 、b 两点的滑移线方向角的变化量;b a ab ωωω−=——分别为a 、b 两点的滑移线的方向角;b a ωω、——正号用于α线,负号用于β线。
±亨盖应力方程的重要意义在于,它揭示了滑移线上平均应力的变化规律。
塑性加工理论滑移线法

3
m k
O
1
k
m 3
m
图 9-19 无摩擦的接触表面
n=m 摩 擦 切 应 力
=k
为k 的接触面
O
xy k cos 2 0,
1 k m 3
n=m 摩 擦 切 应 力
=k
为k 的接触面
O
4
3 k m 1
k m
O
m
k
k
O
m
m
k
3
k m
1
(a)
1 m k 3 (b)
图 9-20 摩擦切应力达最大值 k 的接触表面
β β
β
O
α
O′
α
α
a) 中心扇形场 b) 无中心扇形场 图 9-23 简单滑移线场
(3)滑移线场由两族互相正交的光滑曲 线构成
属于这一类的滑移线场有以下几种
(a)当圆形界面为自由表面或作用有均 匀载荷时,其滑移线场为两族正交的对数 螺线所构成(如图9-24a所示);
β α
(a)对数螺旋线场
(b)在粗糙平行刚性模板间压缩 时, 相应于接触面上摩擦切应力达 到最大值的那一段滑移线场为正 交的圆摆线(如图9-24b所示)
1 arccos xy 1 arccos f
2
k2
k
y
=xy
0
y
m
xy k
m k
x
O xy
xy
x
k
k m
m
xy
y
(a)
y
r
y
3
1 O
xy
2 x
x
m
(b)
图 9-21 当 0 f k 时的接触表面
机械制造基础-塑性成形

机械制造基础-塑性成形引言塑性成形是机械制造中常用的一种方法,通过对金属材料施加压力,使其发生塑性变形,从而得到所需的形状和尺寸。
塑性成形广泛应用于汽车制造、航空航天、建筑等领域。
本文将介绍塑性成形的基本原理、常见的塑性成形工艺以及其在实际生产中的应用。
塑性成形的基本原理塑性成形是通过施加力量使金属材料发生塑性变形的一种加工方法。
金属材料在受到外力作用下会发生原子间的位移和形变,从而改变其晶体结构和形状。
塑性成形的基本原理可以归结为以下几个方面:1.塑性变形特性:金属材料具有较高的延展性和塑性,可以在外力作用下进行塑性变形,而不断变形后回弹至初始形状。
这种特性使得金属材料适合进行塑性成形加工。
2.金属的流动性:金属材料具有较好的流动性,即在塑性变形过程中,金属材料可以顺应应力分布的变化,在不同部位形成不同的变形形状。
这种流动性使得金属材料能够通过塑性成形加工来实现复杂的形状和结构。
3.应力与应变的关系:金属材料在受到外力作用下,会引起其内部产生应力,从而引起形变。
应力与应变之间的关系可以通过应力-应变曲线来表示,该曲线可以描述金属材料在不同应力下的塑性变形特性。
常见的塑性成形工艺塑性成形工艺根据其加工原理和特点的不同,可以分为压力成形和非压力成形两大类。
压力成形是通过施加压力使金属材料发生塑性变形的一种成形方式。
常见的压力成形工艺包括冲压、压铸、锻造等。
1.冲压:冲压是通过将金属材料放置在冲压模具中,并施加较大的冲击力使金属材料在模具中发生塑性变形。
冲压工艺可以实现高质量的金属零件加工,并能够高效率地进行批量生产。
2.压铸:压铸是通过将熔化的金属材料注入到压铸模具中,并施加高压将金属材料填充至模具中的空腔中,然后冷却固化,最终得到所需的零件形状。
压铸工艺适用于制造复杂形状的零件,可以获得高度精密的产品。
3.锻造:锻造是通过施加压力使金属材料发生塑性变形的一种成形方式。
锻造工艺分为冷锻和热锻两种。
塑性成形原理REV(last review)

chap3 —— strain
Engineering strain:
True strain is more convenient for large strains,
After integrating:
x
For small shear strains
x y
y
(3-5)
x
y
z
Review
chap1,2—— stress chap3 —— strain chap4,5,6 —— yield criterion chap7 —— slab chap8 —— Slip-line chap9 —— Extremum principles
chap1,2—— stress
应力:作用在单位截面上的内力。
I1 x y z
或者
等效应变表达式
2 i 3 2 i 3
1 2 2 2 3 2 3 1 2
x
y
2
y
z
2
z
2 2 2 x 3 ( xy yz zx ) 2 2
a 3 a 3 0
a 2a 0 ( 2a)( a) 0
3 2 2
1 2a, 2 0, 3 a 1 3 3a max 2 2
球应力张量、偏差应力张量概念 ,表达形式、分解意义?
1、球应力张量仅使物体体积发生弹性变形; 2、偏应力张量只引起塑性变形。 3、将应力分解为2个张量(球张量、偏张量),因为球应变 张量表示物体体积变形,仅与球应力张量有关;偏应变张量 表示物体的形状变形,仅与偏应力张量有关。 表达形式
塑性成形重要知识点总结

塑性变形:材料在一定外力作用下,利用其塑性而使其成型并获得一定力学性能的加工方法。
塑性:在外力作用下使金属材料发生塑性变形而不破坏其完整性的能力。
滑移:晶体在力的作用下,晶体的一部分沿一定的晶面和晶向相对于晶体的另一部分发生相对移动或切变。
滑移面:滑移中,晶体沿着相对滑动的晶面。
滑移方向:滑移中,晶体沿着相对滑动的晶向。
孪生:晶体在切应力作用下,晶体一部分沿着一定的晶面和一定的晶向发生均匀切变。
张量:由若干个当坐标改变时,满足转换关系的分量所组成的集合。
晶粒度:金属材料晶粒大小的程度。
变形织构:在塑性变形时,当变形量很大,多晶体中原为任意取向的各个晶粒,会逐渐调整其取向而彼此趋于一致。
这种由于塑性变形的结果而使晶粒具有择优取向的组织。
动态再结晶:在热塑性变形过程中发生的再结晶。
主应力:切应力为0的微分面上的正应力。
主方向:主应力方向,主平面法线方向。
主应力空间:由三个主方向组成的空间主切应力:切应力达到极值的平面上作用得切应力。
主切应力平面:切应力达到极值的平面。
主平面:应力空间中,可以找到三个互相垂直的面,其上均只有正应力,无切应力,此面就称为主平面。
平面应力状态:变形体内与某方向轴垂直的平面上无应力存在,并所有应力分量与该方向轴无关的应力状态。
平面应变状态:物体内所有质点都只在同一个坐平面内发生变形,而该平面的法线方向没有变形的变形状态。
理想刚塑性材料:研究塑性变形时,既不考虑弹性变形,又不考虑变形过程中的加工硬化的材料。
理想弹塑性材料:塑性变形时,需考虑塑性变形之前的弹性变形,而不考虑硬化的材料。
弹塑性硬化材料:塑性变形时,既要考虑塑性变形前的弹性变形,又要考虑加工硬化的材料。
刚塑性硬化材料:研究塑性变形时,不考虑塑性变形之前的弹性变形,需考虑变形过程中的加工硬化的材料。
屈服轨迹:两相应力状态下屈服准则的表达式在主应力坐标平面上的几何图形,一条封闭的曲线。
屈服表面:屈服准则的数学表达式在主应力空间中的几何图形是一个封闭的空间曲面称为屈服表面。
塑性成形重要知识点总结

塑性成形重要知识点总结塑性成形是一种通过应变作用将金属材料变形为所需形状的加工方法,也是金属加工领域中的一种重要工艺。
以下是塑性成形的重要知识点总结。
1.塑性成形的原理塑性成形是通过施加外力使金属材料发生塑性变形,使其形状和尺寸发生改变。
塑性成形的原理包括应力与应变关系、材料的流动规律和力学模型等。
2.塑性成形的分类塑性成形可以根据加工过程的不同进行分类,主要包括拉伸、压缩、挤压、弯曲、冲压等。
不同的成形方法适用于不同的材料和形状要求。
3.塑性成形的设备塑性成形通常需要使用专门的设备进行加工,包括拉伸机、压力机、挤压机、弯曲机、冲床等。
这些设备提供必要的力量和变形条件,使金属材料发生塑性变形。
4.金属材料的选择不同的金属材料具有不同的塑性特性,因此在塑性成形中需要根据不同的应用需求选择合适的材料。
常用的金属材料包括钢、铝、铜、镁等。
5.塑性成形的加工方法塑性成形的加工方法非常多样,包括冲压、拉伸、挤压、压铸、锻造等。
不同的加工方法适用于不同的材料和形状要求,可以实现复杂的金属成形。
6.塑性成形的工艺参数塑性成形的工艺参数对成形质量和效率具有重要影响。
常见的工艺参数包括温度、应变速率、应力等。
合理的工艺参数可以提高成形质量和生产效率。
7.塑性成形的变形行为塑性成形过程中金属材料的变形行为是研究的重点之一、金属材料的变形行为包括弹性变形、塑性变形和弹变回复等,通常通过应力-应变曲线来描述。
8.塑性成形的缺陷与控制塑性成形过程中可能发生一些缺陷,如裂纹、皱纹、细化等。
为了控制这些缺陷,需要采取合适的工艺和工艺措施,如加热、模具设计优化等。
9.塑性成形的优点与局限塑性成形具有成本低、加工效率高、灵活性好等优点,可以制造出复杂的金属零件。
然而,塑性成形也存在一些局限性,如对材料性能有一定要求、成形限制等。
10.塑性成形的应用领域塑性成形广泛应用于各个领域,如汽车制造、航空航天、电子、家电等。
不仅可以生产大批量的零部件,还可以满足不同产品的形状和性能要求。
金属塑性成形11)slip line

specify a stress state of a point under plastic plane strain condition?
τ
The shape? The size?
τmax
Plane strain
τmax
1 (σ1 −σ2 )2 + (σ2 −σ3 )2 + (σ3 −σ1)2 = σs 2
Chapter 12 Slip Line Method §12.3 The HENCKY Equation
The Hencky Equation is useful in slip line field analysis. To deduce the Hencky Equation we need to use the following Figures.
σm11 = (cα1 + cβ1 );
Chapter 12 Slip Line Method
1 (cα1 − cα 2 ) 4k 1 ∆ω2 = ω22 −ω12 = (cα1 − cα 2 ) 4k ∆ω1 = ∆ω2 ∆ω1 = ω21 −ω11 =
(塑性成形力学)4滑移线场理论及应用

存在速度不连续线的速端图:
两条速度不连续线相交于一点附近的速度不连续量的矢量和为零。
4.6滑移线场的绘制
建立变形区内滑移线场通常是一个相当复杂的问题。
在给定的应力边界条件下,作滑移线场的方法: 1. 积分滑移线的微分方程; 2. 图解法; 3. 数值积分法。
相关规定:
1. 使单元体产生顺时针转效果的剪应力方向为α线,反之为β线;(例题)
2. 分别以α线和β线构成一右手坐标系时的横轴和纵轴,则代数值最大的主应力
σ1的作用线在穿过原点条件下是在第Ⅰ和第Ⅲ象限内;(例题)
3. α线各点的切线与所取的x轴的夹角为φ,逆时针转为正,顺时针转为负。
y
右手坐标系: 姆指指向α线正方向 食指指向β线正方向 中指指向自己
不少的塑性加工过程,由于变形区域 沿某一方向(z轴方向)的尺寸较大, 沿该方向的相对变形量很小,可近似 认为是平面变形问题。 如:薄板轧制 矩形件压缩
莫尔圆 (应力圆)
单辉祖,“材料力学教程”, 国防工业出版社,1982
-p
k
4.1.2 基本假设
各向同性的理想刚-塑性材料 变形抗力为常数 忽略热应力和惯性力等
(①+②)/2 (①-②)/4
① ②
式(4.25) 式(4.26)
式(4.27) 式(4.28)
4.5 滑移线场求解的应力边界条件和步骤
4.5.1 应力边界条件 4.5.2 滑移线求解的一般步骤
4.5.1 应力边界条件
常见边界: 工件与工具接触表面:σ、τ 自由表面
单辉祖,“材料力学教程”,国防工 业出版社,1982,P208
图1.28 理想刚-塑性材料
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1 Basic concepts and assumptions 6.2 Slip line field definition 6.3 Hencky stress equations 6.4 Geometrical properties of slip lines 6.5 Geiringer velocity equations 6.6 Hodograph and velocity discontinuities 6.7 Stress boundary conditions 6.8 Construction of slip line field 6.9 Applications of slip line field theory
A→D along βline, pD 2kD pA 2kA
D→C along αline,
pD 2kD pC 2kC
pC pA 2k(A C 2D ) (6(-21)6)
Slip line field
6.4 Geometrical properties of slip lines
Useful deductions:
(1) If a slip line is straight, the other slip-lines of the family is also straight.
(2) The slip-lines in one family have the same curvature.
x
y y
0
②
( x
y )2
4
2 xy
4k2
K2
③
Volume constant: Plastic flow criteria:
vx vy 0
④
x y
x y x y
xy
xy
Slip line field
Fundamental equations for plane strain
The above equation can written as
Assumations: (1) rigid-perfectly plastic materials (2) Plain strain (3) Effects of temperature, strain rate and time are not considered (4) Constant shear stress at the interfacial boundary
vx x
vy y
x y
⑤
vx vy
2 xy
y x
Form the above five equations the variables x, y, z, xy ,vx,vy can be soluted.
6.2 Slip line field definition
Slip line field
x p k cos 2 2 p 2k cos 2
x x
x x
x
(6-7)
y p k cos 2 2 p 2k cos 2
y y
y y
y
(6-8)
6.3 Hencky stress equations
xy k sin 2 2 2k sin 2
x
x
x
derived in two possible ways using the Henkey stress equations as
follows:
A→B along αline,
pA 2kA pB 2kB
B→C along βline,
pB 2kB pC 2kC
pC pA 2k(A C 2B ) ((61-)15)
dx
2
6.3 Hencky stress equations
Slip line field
The state of stress at a point can be expressed by equations (6) in
terms of the independent quantities p, k and . The force
following ,
p S
2k
S
0
p
2k
0
S
S
along an line along a line
(6-12)
Integrating along the slip line produces
the following relationships,
p 2k C ( ) p 2k C ( )
Plane strain: x, y, z, xy
z
1 2
( x
y)
(6-1)
3
m
1 3
(
x
y
z)
1 2
( x y )
Ⅰ: max
k
(6-2)
xy y
x
y
y
x
1
yx
yx
x
2
1
m ( x y ) / 2 p
Ⅱ: max k
3
6.2 Slip line field definition
Combining equations (15) and (16) then gives
B C A D
(6-17)
There is a constant angle between the tangents to two slip
lines of one family () at their intersection with a slip line of the other family (). ——Hencky’s first theorem.
chosen x direction is then considered to be positive.
6.2 Slip line field definition
Slip line field
Along line, Along line,
dy tan
dx
dy tan( ) cot
y
0
p
2k
sin
2
2k
cos 2
0
y
x
y
(6-11)
6.3 Hencky stress equations
Slip line field
However, the choice of the x and y axes is arbitrary. If the x (S)
and y (S) axes coincide with the and directions at the point P under consideration and = 0. Equations (11) reduce to the
xy k sin 2 2 2k sin 2
y
y
y
Slip line field
(6-9) (6-10)
Substitute (6-7,8,9,10) into the equilibrium equations,
x
x
xy
y
0
xy
x
y
y
0
p x
2k
cos 2
x
2k sin 2
Slip line field
When the and lines form a right-handed coordinate system of axes then the line of action of 1 is contained in the first and third quadrants. The anticlockwise rotation, , of the line from the
(6-6)
6.2 Slip line field definition
Slip line field
From equations (6-6), the stress state at every point throughout the plastically deforming region is characterized by the superposition of a hydrostatic stress, p, on a pure shear stress, k.
one slip line to another.
Along an αline,
pA 2kA pB 2kB C pA pB 2k(B A )
(6-14)
H. Hencky
Slip line field
6.4 Geometrical properties of slip lines
The difference in the hydrostatic pressure between C and A can be
6.2 Slip line field definition
Slip line field
Slip lines or shear lines
The directions of these surfaces on which the shear stress
attains a maximum value k are usually designated the alpha () and beta () directions.
Slip line field
6.1 Basic concepts and assumptions
Plane strain problem
Provide information about deformation from point to point in plastically deformation region.
