高中数学必修2-知识点总结
数学必修二知识点归纳

数学必修二知识点归纳一、函数的概念与性质1. 函数的定义:函数是从一个集合(称为定义域)到另一个集合(称为值域)的映射,每个定义域中的元素都有一个唯一的值与之对应。
2. 函数的表示方法:常用f(x) = y,其中x是自变量,y是因变量。
3. 函数的性质:包括单调性、奇偶性、周期性和有界性等。
- 单调性:函数在某个区间内单调递增或递减。
- 奇偶性:函数可能是奇函数(f(-x) = -f(x))或偶函数(f(-x) = f(x))。
- 周期性:函数如果存在一个非零常数T,使得对于所有x都有f(x + T) = f(x),则称函数具有周期T。
- 有界性:函数的值在某个范围内,即存在上界和下界。
二、基本初等函数1. 幂函数:形如y = x^n的函数,其中n是实数。
2. 指数函数:形如y = a^x的函数,其中a > 0且a ≠ 1。
3. 对数函数:形如y = log_a(x)的函数,其中a > 0且a ≠ 1。
4. 三角函数:包括正弦函数、余弦函数、正切函数等。
- 正弦函数:y = sin(x)- 余弦函数:y = cos(x)- 正切函数:y = tan(x)三、函数的图像与变换1. 函数图像的绘制:通过坐标系中的点来表示函数的图像。
2. 函数的平移:包括水平平移(左加右减)和垂直平移(上加下减)。
3. 函数的伸缩:包括水平伸缩(y = af(x))和垂直伸缩(y =f(bx))。
4. 函数的对称性:函数图像关于x轴、y轴或原点的对称性。
四、函数的应用1. 实际问题的建模:将实际问题转化为函数关系式进行求解。
2. 最值问题:求解函数的最大值和最小值。
3. 函数的复合:两个或多个函数的组合,如(f ∘ g)(x) = f(g(x))。
五、极限与连续性1. 极限的概念:描述函数在某一点附近的行为。
2. 极限的性质:包括唯一性、局部有界性、保号性等。
3. 连续函数:在定义域内任意一点都连续的函数。
高中数学必修2知识点总结:第一章-空间几何体

高中数学必修2知识点总结第一章 空间几何体1.1柱、锥、台、球的结构特征 1.2空间几何体的三视图和直观图1 三视图:正视图:从前往后 侧视图:从左往右 俯视图:从上往下 2 画三视图的原则:长对齐、高对齐、宽相等 3直观图:斜二测画法 4斜二测画法的步骤:(1).平行于坐标轴的线依然平行于坐标轴;(2).平行于y 轴的线长度变半,平行于x ,z 轴的线长度不变; (3).画法要写好。
5 用斜二测画法画出长方体的步骤:(1)画轴(2)画底面(3)画侧棱(4)成图1.3 空间几何体的表面积与体积 (一 )空间几何体的表面积1棱柱、棱锥的表面积: 各个面面积之和2 圆柱的表面积3 圆锥的表面积2r rl S ππ+= 4 圆台的表面积22R Rl r rl S ππππ+++= 5 球的表面积24R S π=(二)空间几何体的体积1柱体的体积 h S V ⨯=底 2锥体的体积 h S V ⨯=底313台体的体积 h S S S S V ⨯++=)31下下上上( 4球体的体积 334R V π=222r rl S ππ+=第一章空间几何体1.1 空间几何体的结构一、选择题1、下列各组几何体中是多面体的一组是()A 三棱柱四棱台球圆锥B 三棱柱四棱台正方体圆台C 三棱柱四棱台正方体六棱锥D 圆锥圆台球半球2、下列说法正确的是()A 有一个面是多边形,其余各面是三角形的多面体是棱锥B 有两个面互相平行,其余各面均为梯形的多面体是棱台C 有两个面互相平行,其余各面均为平行四边形的多面体是棱柱D 棱柱的两个底面互相平行,侧面均为平行四边形3、下面多面体是五面体的是()A 三棱锥B 三棱柱C 四棱柱D 五棱锥4、下列说法错误的是()A 一个三棱锥可以由一个三棱锥和一个四棱锥拼合而成B 一个圆台可以由两个圆台拼合而成C 一个圆锥可以由两个圆锥拼合而成D 一个四棱台可以由两个四棱台拼合而成5、下面多面体中有12条棱的是()A 四棱柱B 四棱锥C 五棱锥D 五棱柱6、在三棱锥的四个面中,直角三角形最多可有几个()A 1 个B 2 个C 3个D 4个二、填空题7、一个棱柱至少有————————个面,面数最少的棱柱有————————个顶点,有—————————个棱。
高中数学必修2知识点总结

高中数学必修2知识点总结高中数学必修二知识点总结1. 一元二次方程一元二次方程的标准形式为ax^2+bx+c=0,并且a≠0。
求解一元二次方程的方法是配方法、公式法和因式分解法。
2. 三角函数常用的三角函数有正弦函数、余弦函数、正切函数和余切函数。
三角函数的定义域和值域以及其性质和图像都是必须掌握的。
3. 三角恒等式包括正弦、余弦和正切等三角函数的恒等式,例如正弦函数的和差公式、倍角公式、半角公式等。
三角恒等式是解决三角函数问题的重要工具。
4. 二次函数的图像和性质二次函数的标准形式为y=ax^2+bx+c,其中a≠0。
二次函数的图像是一个开口朝上或开口朝下的抛物线,其对称轴为x=-b/2a。
必须掌握二次函数的顶点、零点、对称轴等性质,这些性质是判断图像和求解问题的重要方法。
5. 平面向量平面向量包括向量的定义、向量之间的运算、向量的坐标表示等。
向量的运算包括向量的加法、减法、数量积和向量积。
向量的坐标表示是将向量投影在坐标轴上来表示的。
6. 点、直线、平面和空间几何点、直线、平面和空间几何的基本概念和性质是必须掌握的,例如点的坐标、直线的一般式方程、平面的法向量等。
此外,必须掌握两条直线和两个平面之间的位置关系、垂直平分线以及中垂线等概念。
7. 三视图和轴测图三视图是立体图形的三个视图,包括正视图、左视图和俯视图。
轴测图是用于三维图形表示的一种图形表示方法,包括斜二测和等轴测。
8. 四边形和圆的性质四边形和圆的主要性质包括四边形内角和定理、对角线定理、圆的周长和面积计算公式、圆内部和圆外部点与圆的位置关系等。
9. 三角形和圆的性质三角形和圆的主要性质包括三角形内角和、三角形的面积计算公式、圆心角和圆弧、圆的切线和切点等。
10. 函数及其应用函数的概念和图像、定义域和值域、单调性等性质必须掌握。
函数的应用包括函数的极值、最大值和最小值等问题。
以上是高中数学必修二知识点的总结,这些知识点是高中数学教育的重点和难点,学好这些知识点对于提高数学成绩和发展数学思维能力都具有重要的意义。
高中数学必修2知识点总结归纳全

高中数学於修2知5点一、丸戏与方程HJ直戌的慎斜角定义:x朝正勺与直爱,上方•句之间所成的角制宜发的倾斜角.特别地,当宜爱与x轴平行式重合时,我们规定它的倾斜角为0度.因此,倾斜角的取值闽是0° <a <180°〔2〕直钱的科率①定义:倾斜角不是90°的直爱,它的倾斜角的正切叫做这条立线的斜率.直爱的斜率常用k就示.即々 =tana.斜率反映直线与轴的倾斜程度.当ae[〔r,90°〕时,AN0;当a e〔90° ,180°〕时,k<0;当a = 90°时,k不存在.②过两点的左线的斜率公式:k = > —〞〔2W x、〕为一匹'注意下面四点:⑴当西=々时,公式右边无意义,直发的斜率不存在,领斜角为90.;Q〕k与汽、E的顺序无关;〔3〕以后求斜率可不通过倾斜角而由直发上两点的生标宜林求得;⑷求在线的倾斜角可由直线上两皮的生标先求斜率得列.〔3〕女院方程①点号K: y-y =k〔x-X1〕直发斜率片且过点〔X],yj注意:当直戈的斜率为0°时,k=0,直发的方程是片必.当直发的斜率为90°时,直发的斜率不存在,它的方程不能用点斜式表示,但因/上每一点的横生标都等于不,所以它的方程是4小.②寻&犬;y = kx+〃,直线斜率为片直发在y轴上的熊痘卫b③两点K: -—— = -—― 〔 x l^x2,y i *>', J直发两点〔演,四〕,〔方,以〕%一凹占一芯④就矩式:- + y = l a h其中成发/与X轴交于点〔a,o〕,与y轴交于点〔0⑼.即/与X轴.y轴的就足分别为a,b o⑤一般式:Ax+3y+C = 0 〔A, B不全为0〕注意:①各式的适.用国©特殊的方程如:平行于x轴的立线:y = h fb为常泰J;平行于V轴的立线:x = a fa为常数〕;⑸卢晓东方程:即具有某一具同性质的友然f-J平行直娱氽平行于立线A/ + 8°y + Co=.但凡不全为.的常数〕的女线条:-X + B o y + C = 0 〔 C 为常教Jr二〕过定点的直珑东〔〕斜率%々的直发余:>一〕’0=女〔无一玉〕〕,成线过定点〔八,九〕;()过两条立线J] :4x + 8]〉+ G =0,,2 :+ + =0的交点的直战条方程为(A l x+B l y + C l)+A(A2x + B2y + C2) = 0(2为参数人其中直线不在立战东中. (6)两直线平行与妻直当/1 : y = k i x + b l, 4 : 4 = k?x + b?时,L 〃/2 <=>〃]= k?,b、W 与,i,,2 = k1k? = —1 当4 : 4工+8]),+ £ =.,l2: A X+^2>? + C2 = 0 时/|/〃2 =察=导工9 |/J/2OAA + 8H =._______ A2 .2|注意:利用仰牟其新女戏的平行与垂支时,要注专舒卒的存在与否. (7)两条直送的支支4 :A{x+B1y + C[ =0 l2 :A2x + B2y + C2 = 0 和交 ,交点生标即方程组、4"+4y + G =°的一组斛.A2x + B2y + C2 = 0方程组无筹O/J〃2 ;方程组有无数解O,|与乙重合f8J两8间距喜公式:设AJ,y),以电,必)是平面直角生标条中的两个点,那么IA81= 丁5一3尸+⑵一凹尸J9)点灯友我J&害公式:一点凡飞,打)到直发/1 :Ax + By + C = O的痘毒<, _ I"'.+ B、.+q\A2 +B'no;两平行直战距*公式在任一直线上任取一A,再转化为A到直发的跑雷进行求二、团的才•程1、圆的定义:平面到一定点的距禽等于定长的点的集合例回,定点为回心,定长为回的半饯.2,回的方程HJ标准方程(X —4)2+()」〃『=〃,回心(4力),半及%r;(2)一般方程V+V+DX + EF + /7 = 0当O? +石?一4尸> 0时,方程表示回,此时回心为j ,半校为,=L X!D2+E2-4F2当.2+E? - 4尸=0时,表示一个皮;当£>2+石2—4尸 <.时,方程不就示任何图形.(3)求固4r做的方法:一般却采用柠走余数法:先设后求.确定一个回需要三个独立条件,假设利用回的标准方程,需求出a, b, r;假设利用一般方程,需要求出D, E, F;另外要过专多利用圆的几何枝质:七弦的中垂戡於^过原点,以凡泉碉定国心的枚五.3、女钱与圆的住置关东:直我与回的位置关未有和禽,粕切,粕交三种情况,根本上由以下两种方法判断:(1)设立线/: Ax+3y+C = 0,圆+(y-bp =户,囿7、C(a,b)到 / 的距南为,_\^Bb +C\ , 5,,j 有">/• =/与C相离;d = ro,与C 相切;"<,• = /与.相交(2)设立爱/: Ax+&y + C = O,回C:(x-a)2+(y-〃)2 =/,先将方程麟立曲元, 得到一个一元二次方程之后,令其中的判别式为△,那么有△ v 0 <=> /与C相离;△ = 0 o /与C相切;△ > 0 <=> /与C相交注:如果回心的核置在原点,可使用公式刀〞+ »o =都去解直发与回和切的问题,其中(小,为)表示切点生标,r表示半役.(3)过圆上一点的切然疗技:,①回/+)/=/,回上一点为(Xo,y0)>那么过此点的切发方程为xx()+ »o =,(课本命题).②回仅^^+付上了二*,回上一点为自,yo).那么过此点的切线方程为(x(ra)(x-a)-l-(y(rb)(y-b)= t2 (课本命题的推广).4,圆与圆的位JL关东:通过两回半发的和(爰人与囿心距(d)之间的大小比较来确定.1殳回C[ : (x-%+(V —仇F = / , C, : (x - u2 y + (y - b2 )2 = R2两圆的位置关系后通过两圆半法的和(爰人与囿心距(d)之间的大小比拟来确定.当d>R + r时两回外南,此时有公切珑四条;当4 = 7? +r时两回外切,连心爱过切点,有外公切珑两条,公切岗一条;当R-r<d<H + r时两回粕交,连心线垂直平分公共弦,有两条外公切珑;当"=7?一r时,两回切,连心战经过切点,只有一条公切珑;当c/vR-r时,两回含;当4=0时,为同心回.三、立体几何初步1,粒.底面flj极桂:定义:有两个面互相平行,其余各面都是刃边形,且每相邻两个囚边形的公共边都互相平行,由这些面所闺成的几何体.分类:以底面多边形的边数作为分类的标准分为三核粒.四梗粒.五枚粒等.表示:用各顶点字母,如五极柱A8C.石一48 co E或用对角戏的满点字母, 如五根板A.几何将征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧极平行且相等;平行于底面的脱面是与底面令等的多边形.(2) «定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所闽成的几何体分类:以底面多边形的边数作务分类的标准分为三极雄、四极/、五极椎苦袅示:用各顶点字母,如五根椎P — A B C D E几何特征:倒面、对狗面都是三角形;平行于底面的机面与底面相似,其粕仞比等于顶点到机面距禽与高的比的平方.(3J机台:定义:用一个平行于被碓底面的平面去截极般,截面和底面之间的局部分美:以底面多边形的边教作为分类的标准分为三极台.四极台.五极台等表示:用各顶点字母,如五极台P — ABC DE几何就征:①上下底面是相似的平行多边形②侧面是梯形⑶侧长交于原校钺的顶A(4)圆桩:定义:以矩形的一边所在的直爱为轴旗转,其余三边施转所成的曲面所囱成的几何体几何特征:①底面是全等的回;②母线与轴平行;G)轴与底面回的半役垂直;© 侧面展开图是一个矩形. (5)圆靠:丈义:以直角三角形的一条直角边为旗转朝.夜特一周所成的曲面所囱成的几何体几何将征:①底面是一个回;②母线交于回推的顶点;⑶侧面展开图是一个扇形. (6)回台:定义:用一个平行于回碓底面的平面去也回钺,机面和底面之间的局部几何聘征:①上下底面是两个回;②例面母线交于原回雄的顶点;⑶侧面展开图是一个弓形.(7)冰体:定义:以半回的直彼所在直发为旅转轴,半回面旋转一周形成的几何体几何特征:①球的机面是圆;②球面上任意一点到球7、的能害等于半投.2、空问几何体的三视图定义三视图:正视图(光线从几何体的的面曲后面正投影人侧视图(从左右右人俯视图(从上向下)注:正视图反映了物体上下.左右的位置关余,即反映了物体的高度和长度;俯视图反映了物体左右.看后的位置关东,即反映了物体的长度和宽度; 侧视图反映了物体上下、前后的住匿关系,即反映了物体的高度和宽度.3、空间几何体妁直现圄——当二测量柒仰二洲面濡将点:①原来与x轴平行的线段仍然与x平行旦长度不变;②原来与y轴平行的线段仍然与y平行,长度为原来的一半. 4,粒体、碓体、台体的森面积与体软H)几何体的薮面收为几何体各个面的面稹的新.(2)特珠几何体袅面余公式化处底面周长,h为高,力为号高,I 为母钱)〔3〕壮体.碓体.台体的体积公式<4J 球体的外表积新体新公式:V 球二〔汗R 、; S 球而二4乃太 4、空间点、直战、平面的秩JL 关东0〕平面① 平面的机念:A.描述性说明;B.平面是无限伸展的;②平面的袅示:通常用希腊字母a, 0, 丫就示,如平面a 〔通行写在一个锐 角〕;也可以用两个相对顶点的字母来就示,如平面BC .③ 点与平面的关东:点/在平面a ,记作A e 2 ;点A 不在平面a ,记作Aea 点与近端的关东:点4的直发/上,记作:/4 € /; 皮工在立线/外,记作4m我戡与平面的关东:成爱/在平面a,记作ya ;直发/不在平面a ,记作 /2 oc o〔2〕小以1:如枭一条直线的两点在一个平面,那么这条直戈是所有的点都在 这个平面.〔即直为在平面,或者平面经过直线J应用:检除案面是否平;判新直我是否在平面 用符号语言袅示公a1: Ae/,3w/,Aea,3ea = /ua〔3〕心理2:经过不在同一条直线上的三点,有且只有一个平面.推论:一直我和直战外一点确定一平面;两相交直均确定一平面;两平行 我或确定一平面.公痉2及其推先作用:①它是空间确定平面的依据 ②它是证实平面重合的依 据〔4〕公痉3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直爱符号:平面a 科6粕交,交线是a,记作ar)6二a . 符号语言:PeaCl) = an4=,,Pe/ 公双3的作用:①它是判定两个平面相交的方生.S 宜极柱侧面积-ch Sgi 柱例=29力S 正梭惟侧面积=2.〞S|用锥侧面积=加S 正技台M 向枳=]〔G +c 2〕h'S 圜台〔M 面枳=〔r + R 〕就“锥表=•〔,. +,〕5阳台?■> =而'+ H + RI + R‘V 柱=Sh嗫柱=Sh = "h K. 3h雄3网惟3E. =1(S +V?S+S)/?匕帕=_L(S + 4^S + S)h = -7r(r 2+ rR + R 2)h33上联缩小上恢犷d 枝缩生J②它说明两个平面的交线与两个平面公共点之间的关余:文战必过公共方、.③它可以判新点在直线上,即证假设干个疝共线的重要依据.(5)公延4:平行于同一条直发的两条直发互相平行⑸空间直战与友然之河的信五关东①异面立端定义:不同在任何一个平面的两条我为②畀面近端性质:既不平行,又不相交.③畀面女族打走:过平面外一点与平面一皮的jt线与平面不过,该点的直爱是异面直发④畀时立端所成角:直爱狼b是界面直发,经过空问任意一点O,分别引直线,//a, b II b,叫把.玄线3'科〞所成的锐角(或直角)叫做界面直发d和b 所成的角.两条界面直战所成角的闺是(0° ,90° ],假设两条界面宜爱所成的角是直角,我们就说这两条弁面玄端互相妻女.说明:(1)判定•空间直珑是界面直发方法:①根据界而立线的定义;②弁面直发的判定定理(2)在界面成线所成角定义中,无间一点.是任取的,而和点.的位置无关. ②束弁面直我所成角步骤:A.利用定义构爱角,可固定一条,平移另一条,或两条同时平移列架个特殊的位置,顶点选在特殊的住置上.B.证实作出的角即为所求角C,利用三角形来求角(7)等角定理:的系一小角的西也/另一小角的西也分别平行,坪以这两食和等贰M补.⑻空间直战与平面之河的柱,关东直为在平面——有无数个公共点.直线不在平面内理交一一只有一个公共点.(或直线在平面外)(平行一一没有公共点.三种枚五关东的符号袅示:oua;aQa = A ; alia(9)平面与平面之间的桂丑关东:平行——没有公共点;allp相交----- 有一条公共立为.aC\P = b5、文词中的平行问题HJ直或与平面平行的州定及其性质端面平行的村定走M:平面外一条直戏与此平面一条直或平行,那么核克瑞与此平面平行.线线平行=> 版而平行然面平行的性质定理:如枭一条直发"一个平面平行,经过这条直爱的平面和这个平面相交,那么这条直线的父战平行.爱而平行=>为疑平行(2)平面与平面平行的打走及其性质两个平面平行的利走走双(V如果一个平面的两条和交直线都平行于另一个平面,那么这两个平面平行 (爱而平行一面面平行人(2)如果在两个平面,各有两组相交成线对应平行,邛么这两个平面平行.(发线平行一面面平行人(3)垂克于同一条我爱的两个平面平行,两个平面平行的性质定双(1)如果两个平面平行,那么某一个平面的直珑与另一个平面平行.(面面平行一线面平行)(2)如果两个平行平面都的第三个平面相交,那么它们的交战平行.(面面平行一线线平行)7、空间中的塞女问题fU族然、面面、然面妻友的定义①两条界面直线的垂直:如果两条界面立线所成的角是直角,就说这两条界面直线互粕垂直.②为面生直:如果一条直或和一个平面的任何一条在爱垂直,就说这条直戏打这个平面垂直.③平面和平面垂皮:如果两个平面相交,所成的二面角(从一条左发出发的两个率平面所组成的图形)是左二面角(平面角是衣角人就说这两个平面垂去.⑵垂女关东的划定利性质定理①婉面妻女利定定理R性质定理判定定理:如果一条直线和一个平面的两条相交由线都垂直,那么这条直战垂直这个平面.性质定理:如果两条直发同垂直于一个平面,那么这两条直发平行.②面面妻女的利定定理R性质定理判定定理:如果一个平面经过另一个平面的一条垂珑,那么这两个平面互相垂直. 性质定理:如果两个平面互相垂直,那么在一个平面垂直于他们的交爱的直爱垂直于另一个平面.9,空间角问题HJ直婉与女戡所成的角①两平行直发所成的角:规定为0,②两条相交直发所成的角:两条直线相交其中不大于五角的角,叫这两条直戏所成的角.③两条异面直发所成的角:过空间任意一点.,分别作与两条弁面在爱a, 5平行的直珑〃,〃',形成两条粕交直珑,这两条相交直爱所成的不大于五角的希叫做两条弁面直线所成的角.(2)女姚/平面所出的角①平面的平行或与平面所成的角:规定为0°. ②平面的垂发与平面所成的角:规定为90」③平面的斜线与平面所成的角:平面的一条仰端和它在平面的射影所成的优角, 叫做这条直戈和这个平面所成的角.求仰武与聿面所成富的思路类效于求界面立线所成角:“一作.二证,三计算〞. 在“作角〞时依定义关缄作射影,由豺影定义知关使在于向爱上一点到面的垂战, 在斛题时,注意挖掘题设中两个主要信息:(1)斜珑上一点到面的垂发;(2)过斜戈上的一点或过斜戈的平面与面垂直,由面面垂直性质易径垂发.(3)二面角/二面角的平面角①二面角的定义:从一条在戏出发的两个半平面所组成的图形叫做二面角,这条直均叫做二面角的枝,这两个半平面叫做二面角的面.②二面角的平面角:以二面角的极上任意一点为顶点,在两个面分别作垂直于极• • • •的两条射发,这两条封发所成的角叫二面角的平面角.③直二面角:平面角是直角的二面角叫直二面角.两粕交平面如果所组晟的二面角是直二面角,那么这两个平面垂加反过来,如果两个平面垂直,那么所成的二面角为直二面角④求二面角的方决定义法:在枝上选择有关点,过这个点分别在两个面作垂直于极的射线得到平面角垂面头:二面角一点到两个面的垂线时,过两垂战作平面与两个面的交战所成的角为二面角的平面角_____ Q 7、空间直角生标东B1 Zj 71D,flj定义:如图,OBCD — DABC关隼伉正方体.以A为原点, 分别以ODQ A ,OB的方力为正方白,建立三条数轴x轴.y轴.z轴o. A……沙T 这时建立了一个空间直角生标条Oxyz. ^ 1J.叫做坐标点点2) x轴,y轴,z轴叫做生标轴.3)过每两个尘标轴的平面叫做生标面.(2)右手袅示法:令右孑大拇指、食指和中指粕互垂直时,可能形成的伉置. 大拇指指指为x轴正方白,食指指指为y轴正白,中指指右那么为2轴正白,这样也可以决定三轴间的粕位匿.C3)任意点生标嘉示:空间一点M的生标可以用有序实数组a,),,,z)来表示,有序实救组(x,y,z)叫做点M在此空间直角生标系中的生标,记作M(x,y,z) (x 叫做点M的横生标,y叫做点M的纵支标,z叫做点M 的竖坐标)(4)会间两点距禽生标公K:d = yl(X2 -Xj)2 +(% - Jl)2 +(句一句)2资资。
高中数学必修2知识点归纳

高中数学必修2知识点归纳高中数学必修2知识点归纳高中数学必修2是数学学科的一门重要课程,主要内容包括函数、二次函数与一元二次方程、直线和三角形的研究等。
下面是对这些知识点的归纳总结。
一、函数1. 函数的概念:函数是具有输入输出关系的一种映射关系。
通常用f(x)表示函数关系,其中x是自变量,f(x)是因变量。
2. 函数的性质:可递性、奇偶性、周期性、单调性等。
3. 特殊函数:常数函数、一次函数、幂函数、指数函数、对数函数、三角函数等。
4. 函数的运算:函数的四则运算、复合函数、反函数等。
5. 函数的图像:函数的图像可以通过函数的定义域和值域来确定,常见的有常数函数图像、线性函数图像、幂函数图像、指数函数图像、对数函数图像、三角函数图像等。
二、二次函数与一元二次方程1. 二次函数的概念:二次函数是一个带有二次项的函数,一般定义为f(x) = ax² + bx + c,其中a、b、c为常数,a ≠ 0。
2. 二次函数的性质:最值、对称轴、开口方向、零点等。
3. 一元二次方程:一元二次方程是一个以变量x为未知数的二次方程,一般表示为ax² + bx + c = 0,其中a、b、c为常数,且a ≠ 0。
4. 一元二次方程的解:一元二次方程有两个解,可以通过求根公式或配方法求得。
5. 一元二次方程与二次函数的关系:一元二次方程的解即为对应二次函数的零点,可以通过一元二次方程的解来求二次函数的零点。
三、直线1. 直线的表示:直线可以通过斜率截距式、一般式、点斜式等表示。
2. 直线的性质:平行直线、垂直直线、两直线交点的坐标、直线的倾斜角等。
3. 直线方程的求解:通过已知条件,可以利用直线的性质来求解直线的方程。
四、三角形1. 三角形的分类:根据边的长、内角的大小,三角形可以分为等边三角形、等腰三角形、直角三角形、锐角三角形、钝角三角形等。
2. 三角函数:正弦函数、余弦函数、正切函数等。
3. 三角函数关系:倍角公式、半角公式、和差化积公式等。
高中数学必修2知识点总结

高中数学必修2知识点总结一、函数基础1. 函数的概念- 定义:一个从非空数集A到非空数集B的映射,记为y=f(x)。
- 函数的表示:解析式、图象、表格。
- 函数的符号:f(x),x∈A。
2. 函数的性质- 单调性:函数在某个区间内,随着x的增加,y值单调递增或递减。
- 奇偶性:f(-x)=f(x)为偶函数,f(-x)=-f(x)为奇函数。
- 周期性:存在正数T,使得f(x+T)=f(x)。
3. 函数的运算- 四则运算:两个函数的和、差、积、商。
- 复合函数:f(g(x))。
- 反函数:满足f(f^(-1)(x))=x的函数。
4. 基本初等函数- 幂函数:y=x^a,a∈R。
- 指数函数:y=a^x,a>0,a≠1。
- 对数函数:y=log_a(x),a>0,a≠1。
- 三角函数:正弦、余弦、正切等。
二、三角函数1. 三角函数的定义- 正弦、余弦、正切函数的定义。
- 弧度制与角度制的转换。
2. 三角函数的图象与性质- 周期性、单调性。
- 最大值、最小值。
- 特殊角的三角函数值。
3. 三角函数的运算- 三角函数的和差公式。
- 二倍角公式、半角公式。
- 积化和差与和差化积公式。
4. 解三角形- 正弦定理、余弦定理。
- 三角形面积公式。
三、数列1. 数列的概念- 定义:按照一定顺序排列的一列数。
- 有穷数列与无穷数列。
2. 等差数列与等比数列- 定义与通项公式。
- 求和公式。
- 性质与判定。
3. 数列的极限- 极限的概念。
- 极限的性质。
- 极限的运算法则。
四、解析几何1. 平面直角坐标系- 点的坐标。
- 距离公式、中点坐标公式。
2. 直线的方程- 点斜式、斜截式、一般式。
- 两直线的交点、平行与垂直。
3. 圆的方程- 标准方程。
- 一般方程。
4. 圆锥曲线- 椭圆、双曲线、抛物线的方程与性质。
五、概率与统计1. 随机事件与概率- 事件的概率定义。
- 条件概率、独立事件。
2. 随机变量及其分布- 离散型随机变量与连续型随机变量。
高中数学必修2--空间向量与立体几何知识点归纳总结

空间向量与立体几何知识点归纳总结一.知识要点。
1. 空间向量的概念:在空间,我们把具有大小和方向的量叫做向量。
注:(1)向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量。
(2)向量具有平移不变性2. 空间向量的运算。
定义:与平面向量运算一样,空间向量的加法、减法与数乘运算如下(如图)。
OB OA AB a b =+=+;BA OA OB a b =-=-;()OP a R λλ=∈运算律:⑴加法交换律:a b b a+=+⑵加法结合律:)()(c b a c b a++=++⑶数乘分配律:b a b aλλλ+=+)(运算法则:三角形法则、平行四边形法则、平行六面体法则 3. 共线向量。
(1)如果表示空间向量的有向线段所在的直线平行或重合,那么这些向量也叫做共线向量或平行向量,a平行于b ,记作b a//。
(2)共线向量定理:空间任意两个向量a 、b(b ≠0 ),a //b 存在实数λ,使a=λb 。
(3)三点共线:A 、B 、C 三点共线<=>AC AB λ=<=>)1(=++=y x OB y OA x OC 其中 (4)与a共线的单位向量为a ±4. 共面向量(1)定义:一般地,能平移到同一平面内的向量叫做共面向量。
说明:空间任意的两向量都是共面的。
(2)共面向量定理:如果两个向量,a b 不共线,p 与向量,a b 共面的条件是存在实数,x y 使p xa yb =+。
(3)四点共面:若A 、B 、C 、P 四点共面<=>AC y AB x AP += <=>)1(=++++=z y x OC z OB y OA x OP 其中 5. 空间向量基本定理:如果三个向量,,a b c 不共面,那么对空间任一向量p ,存在一个唯一的有序实数组,,x y z ,使p xa yb zc =++。
若三向量,,a b c 不共面,我们把{,,}a b c 叫做空间的一个基底,,,a b c 叫做基向量,空间任意三个不共面的向量都可以构成空间的一个基底。
高中数学必修2知识点总结归纳

高中数学必修2知识点总结归纳
1、二次函数及其图像的性质:二次函数的定义,形式,及其未知量的解析解,二次
函数图像的性质,凹凸性和极值点位置,及其判定方法。
2、三角函数及其图形:正弦函数、余弦函数、正切函数的定义,平面直角坐标系下
的正弦余弦正切函数图像的性质及其判定方法,正弦定理,余弦定理,根据图形求三角函
数值,及其应用。
3、小数和分数的运算:常用的小数转分数的方法,小数和分数的加减乘除运算,及
其规律性的分析。
4、指数及对数:指数的定义,特殊指数的运算及其规律性,指数函数的图像及性质,对数的定义及其特殊性质,对数函数及其图形性质,及其一元二次多项式的变换。
5、多项式及其因子分解:多项式的基本定义,及其分母和分子的几何概念,多项式
的因子分解,及其唯一性的判断。
6、不定积分及其应用:不定积分的定义及其特殊性,常用的不定积分计算方法,及
其实际应用,求积分近似值的方法,以及实际的应用案例。
7、应用题中的数字变换:应用题中常见的实数变化,及其最高次数的判定,同时变
化的最小公倍数及其关系,求解应用题中特殊方程组的方法,及其实际案例。
8、圆的参数方程及极坐标方程:圆的定义,参数方程与极坐标方程的转换,园的性质,及其圆上点的定位方法,过定点且与圆的关系及应用。
9、高等函数及应用:高次函数的定义,及其图像的特点,高次函数的求解及其实际
应用,对数及指数函数的求解及应用,以及多项式、二次曲线等拟合应用。
10、三角型函数与几何图形的关系:三角型函数的定义及其特殊性质,三角型函数的
变换及其图形改变,及其三角函数与几何图形联系的应用。
高中数学必修2知识点归纳
--必修2知识点归纳第一章 空间几何体1、空间几何体的结构:空间几何体分为多面体和旋转体和简单组合体 ⑴常见的多面体有:棱柱、棱锥、棱台;常见的旋转体有:圆柱、圆锥、圆台、球。
简单组合体的构成形式:一种是由简单几何体拼接而成,例如课本图1.1-11中(1)(2)物体表示的几何体;一种是由简单几何体截去或挖去一部分而成,例如课本图1.1-11中(3⑵棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
⑶棱台:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台。
1、空间几何体的三视图和直观图把光由一点向外散射形成的投影叫中心投影,中心投影的投影线交于一点;把在一束平行光线照射下的投影叫平行投影,平行投影的投影线是平行的。
(1)定义:正视图:光线从几何体的前面向后面正投影得到的投影图;侧视图:光线从几何体的左面向右面正投影得到的投影图; 俯视图:光线从几何体的上面向下面正投影得到的投影图。
几何体的正视图、侧视图和俯视图统称为几何体的三视图。
(2)三视图中反应的长、宽、高的特点:“长对正”,“高平齐”,“宽相等”2、空间几何体的直观图(表示空间图形的平面图). 观察者站在某一点观察几何体,画出的图形.3、斜二测画法的基本步骤:①建立适当直角坐标系xOy (尽可能使更多的点在坐标轴上) ②建立斜坐标系'''x O y ∠,使'''x O y ∠=450(或1350),注意它们确定的平面表示水平平面;③画对应图形,在已知图形平行于X轴的线段,在直观图中画成平行于X ‘轴,且长度保持不变;在已知图形平行于Y轴的线段,在直观图中画成平行于Y ‘轴,且长度变为原来的一半; 一般地,原图的面积是其直观图面积的S 原图直观=4、空间几何体的表面积与体积 ⑴圆柱侧面积;l r S ⋅⋅=π2侧面⑵圆锥侧面积:l r S ⋅⋅=π侧面⑶圆台侧面积:l r S ⋅⋅=π侧面⑷体积公式:h S V ⋅=柱体;h S V ⋅=31锥体;()13V h S S =+下台体上 ⑸球的表面积和体积:32344R V R S ππ==球球,.一般地,面积比等于相似比的平方,体积比等于相似比的立方。
高中数学必修2知识点归纳

高中数学必修2知识点归纳1、函数:函数就是定义在一个一个自变量之间的确定的关系,可以用一条曲线或者说一个方程表示的。
函数的概念是数学的基础,除了最简单的对称函数外,函数还可以是多项式函数、参数方程以及三角函数等多种类型。
2、直线:直线就是两个点连接而成的一维几何图形,它可以唯一确定一条直线。
在高中数学中,通过两点式我们可以表示方程,通过斜截式我们可以求出斜率。
四边形或者多边形的边就是一条直线。
3、圆:圆是椭圆的特例,半径r表示圆心到圆上任一点的距离,周长l表示圆的外接正多边形的边的长度,面积s表示圆的外接正多边形的面积。
以圆心为终点,以半径为边长的等腰三角形称为直径等腰三角形。
4、椭圆:椭圆是一种几何图形,它是一条穿过两个特殊点的椭圆形曲线,内切圆的弦长为短轴,外接圆的弦长为长轴。
椭圆的面积公式是s=(ab)π,其中a表示长轴,b表示短轴,π大约等于3.14。
5、抛物线:抛物线是二次函数的一类,它是一条开启或关闭的凹凸曲线,形状像箭头或者翅膀,舍入时具有“s”形。
它的一般方程为y=ax2+bx+c,交点为顶点,抛物线的突出可以用幂函数或者等比数列来表示。
6、向量:向量是固定长度和方向的线段,把向量看做一个矢量,可以用矢量和能够推导出向量或者向量的方程来构造。
向量可以表示一个物体在某个特定时刻的状态,也可以用于计算数量积或者力学加速度等。
7、平面向量:平面向量是一类几何性质,它指向一个平面上的点,标识某种分数形式。
平面向量可以用来表示平面之间的距离、某种物理量或者在空间中的位置。
向量的线积表示的是平面的投影距离,而其向量积表示的是两个向量之间的夹角。
8、误差:误差是指测量结果与标准值之间的差距,有时也称为模糊度、精度的偏差等。
它的分类有绝对误差和相对误差两类。
绝对误差是指实际测得的数与真值之间的差距,而相对误差则可以通过变化百分比来表示实际测得与真值之间的相对关系。
高中数学必修2知识点总结(史上最全).doc
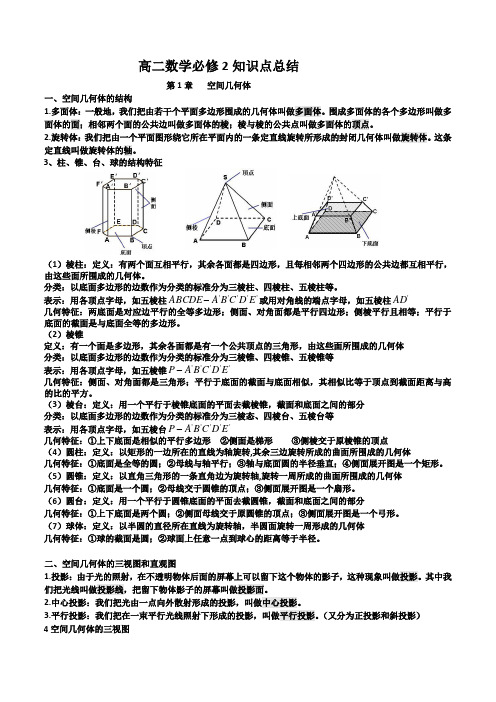
高二数学必修2知识点总结第1章空间几何体一、空间几何体的结构1.多面体:一般地,我们把由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
2.旋转体:我们把由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体。
这条定直线叫做旋转体的轴。
3、柱、锥、台、球的结构特征(1)棱柱:定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱'''''EDCBAABCDE-或用对角线的端点字母,如五棱柱'AD几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
(2)棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥'''''EDCBAP-几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
(3)棱台:定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如五棱台'''''EDCBAP-几何特征:①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。
必修二数学知识点归纳

必修二数学知识点归纳高中数学必修二的内容主要包括立体几何初步、平面解析几何初步。
以下是对这些知识点的详细归纳:一、立体几何初步1、空间几何体多面体:由若干个平面多边形围成的几何体叫做多面体。
旋转体:一条平面曲线绕着它所在的平面内的一条定直线旋转所形成的曲面叫作旋转面,封闭的旋转面围成的几何体叫作旋转体。
2、棱柱、棱锥、棱台棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
棱台:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台。
3、圆柱、圆锥、圆台、球圆柱:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体叫做圆柱。
圆锥:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体叫做圆锥。
圆台:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台。
球:以半圆的直径所在直线为轴,半圆面旋转一周形成的旋转体叫做球体,简称球。
4、中心投影与平行投影中心投影:光由一点向外散射形成的投影,叫做中心投影。
平行投影:在一束平行光线照射下形成的投影,叫做平行投影。
5、直观图斜二测画法:建立直角坐标系,在已知水平放置的平面图形中取互相垂直的 x 轴和 y 轴,两轴相交于点 O。
画直观图时,把它们画成对应的 x'轴和 y'轴,两轴交于点 O',且使∠x'O'y' = 45°(或 135°),它们确定的平面表示水平平面。
已知图形中平行于 x 轴或 y 轴的线段,在直观图中分别画成平行于 x'轴或 y'轴的线段。
已知图形中平行于 x 轴的线段,在直观图中长度不变;平行于 y 轴的线段,长度变为原来的一半。
6、三视图正视图:光线从几何体的前面向后面正投影得到的投影图。
高中数学必修2 全册知识点
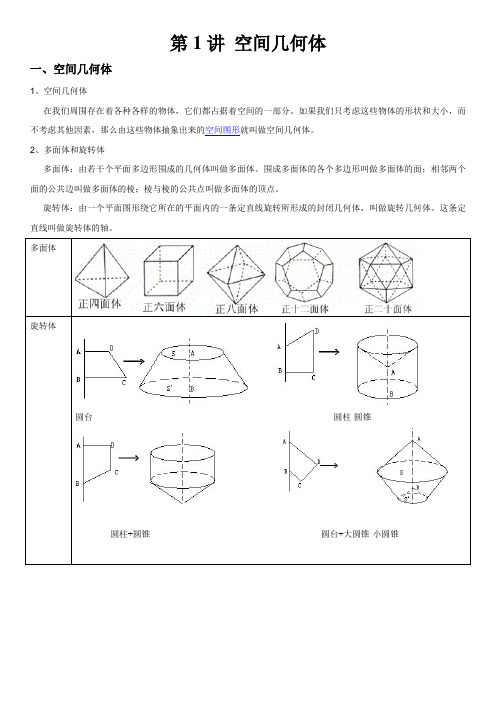
第1讲空间几何体一、空间几何体1、空间几何体在我们周围存在着各种各样的物体,它们都占据着空间的一部分。
如果我们只考虑这些物体的形状和大小,而2、多面体和旋转体多面体:由若干个平面多边形围成的几何体叫做多面体。
围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点。
旋转体:由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体,叫做旋转几何体。
这条定直线叫做旋转体的轴。
二、柱、锥、台、球的结构特征1.棱柱2.棱锥三棱台4.圆锥7.球的结构特征1、球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球。
(1)半圆的半径叫做球的半径。
(2)半圆的圆心叫做球心。
(3)半圆的直径叫做球的直径。
2、球的表示:用表示球心的字母表示,如球O3、球的性质(1)用一个平面去截球,截面是圆面;用一个平面去截球面,截线是圆。
大圆---截面过圆心,半径等于球半径;小圆---截面不过圆心。
(2)球心和截面的圆心的连线垂直于截面。
(3)球心到截面的距离d 与球的半径R 及截面的半径r ,有下面的关系:r =解题方法:将立体中相关问题转化为平面几何问题棱锥内由某些线段组成的直角三角形,在计算有关问题时很重要,它是将立体中相关问题转化为平面几何问题的根据,如图2-7中的△AOE,△AOC,△ACE及△OCE.这四个直角三角形中,若知道AE、AC、AO、OE、OC及CE 这六条线段中的若干条时,则可以通过这些直角三角形间的关系求出其他线段.总结三、空间几何体的三视图和直观图1、中心投影与平行投影2、三视图正视图——从正面看到的图侧视图——从左面看到的图俯视图——从上面看到的图画物体的三视图时,要符合如下原则:位置:正视图侧视图俯视图大小:长对正,高平齐,宽相等.3、直观图-----斜二测画法重点:用斜二测画法画水平放置的平面图形的直观图,步骤如下:⑴在已知图形中取互相垂直的x轴和y轴,两轴相交于点O. 画直观图时,把它们画对应的x'轴与y'轴,两轴交于点O' ,且使∠x'O'y' =45º(或135º),它们确定的平面表示水平面.⑵已知图形中平行于x轴或y轴的线段,在直观图中分别画成平行于x'轴或y'轴的线段;⑶已知图形中平行于x轴的线段,在直观图中保持原长度不变;平行于y轴的线段,长度为原来的一半.例1 用斜二测画法画水平放置的正六边形的直观图.说明:1. 保持平行关系不变.2.水平长度保持不变;纵向长度取其一半.例3 用斜二测画法画长、宽、高分别是4cm、3cm、2cm的长方体ABCD-A'B'C'D'的直观图.四、 空间几何体的表面积与体积(一 )空间几何体的表面积1棱柱、棱锥的表面积: 各个面面积之和2 圆柱的表面积3 圆锥的表面积2Srl r ππ=+4 圆台的表面积22S rl r Rl R ππππ=+++5 球的表面积24SR π=6扇形的面积公式213602n R S lr π==扇形(其中l 表示弧长,r 表示半径)(二)空间几何体的体积 1柱体的体积 VS h =⨯底2锥体的体积 13V S h =⨯底 3台体的体积1)3V S S h =++⨯下上(4球体的体积343V R π= 222rrl S ππ+=第2讲 空间点、直线、平面之间的位置关系一、平面1、平面及其表示2、平面的基本性质 ①公理1:②公理2:不共线的三点确定一个平面③公理3:A lB l l A B ααα∈⎫⎪∈⎪⇒⊂⎬∈⎪⎪∈⎭P l P l P ααββ∈⎫⇒⋂=∈⎬∈⎭则二、点与面、直线位置关系1、点与平面有2种位置关系2、点与直线有2种位置关系三、空间中直线与直线之间的位置关系1、异面直线2、直线与直线的位置关系⎧⎧⎨⎪⎨⎩⎪⎩相交共面平行异面3、公理4和定理 公理4:定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
数学必修二知识点归纳_图文

2、判定定理:一条直线与一个平面内的两条相交直线都 垂直,则该直线与此平面垂直。 注意点: a)定理中的“两条相交直线”这一条件不可忽 视; b)定理体现了“直线与平面垂直”与“直线与直线垂直” 互相转化的数学思想。
2.3.2平面与平面垂直的判定
1、二面角的概念:表示从空间一直线出发的两个
行,那么这两个角相等或互补 4 、注意点:
① a‘与b’所成的角的大小只由a、b的相互位置来确定,与O的选择 无关,为了简便,点O一般取在两直线中的一条上;
② 两条异面直线所成的角θ∈(0, ); ③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线
互相垂直,记作a⊥b; ④ 两条直线互相垂直,有共面垂直与异面垂直两种情形; ⑤ 计算中,通常把两条异面直线所成的角转化为两条相交直线所
成的角。
2.1.3 — 2.1.4 空间中直线与平面、 平面与平面之间的位置关系
1、直线与平面有三种位置关系:
(1)直线在平面内 —— 有无数个公共点
(2)直线与平面相交 —— 有且只有一个 公共点
(3)直线在平面平行 —— 没有公共点
指出:直线与平面相交或平行的情况统称 为直线在平面外,可用a α来表示
·αLβ
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点 的公共直线。
符号表示为:P∈α∩β =>α∩β=L,且P∈L
β
公理3作用:判定两个平面是否相交的依据
α
·
PL
2.1.2 空间中直线与直线之间的位置关系
1 空间的两条直线有如下三种关系:
相交直线:同一平面内,有且只
两个平面平行的判定定理:一个平面内的 两条交直线与另一个平面平行,则这两个 平面平行。
数学必修二所有知识点总结

数学必修二所有知识点总结数学必修二是高中数学课程的一部分,主要涵盖了解析几何、三角函数、数列和递推、概率统计等知识点。
这些知识点既有理论基础又有实际应用,对学生的数学思维能力和解决问题的能力有较高要求。
下面将对数学必修二中的各知识点进行总结和归纳。
一、函数与方程1.函数的概念函数是一种对应关系,将自变量的值映射到因变量的值。
函数通常用f(x)表示,其中x为自变量,f(x)为因变量。
函数的定义域、值域、性质等都是研究函数的重要内容。
2.特殊函数常见的特殊函数有一次函数、二次函数、幂函数、指数函数、对数函数和三角函数等。
这些函数在数学中有着广泛的应用,学生需要了解它们的图像、性质和变化规律。
3.方程与不等式一元一次方程、一元二次方程、一元一次不等式、一元二次不等式等都是学生需要掌握的内容。
解方程和不等式是数学中的基本技能,对于建模和解决实际问题有着重要的意义。
二、直线和圆1.直线的性质直线是解析几何中的基本对象,学生需要了解直线的斜率、方程、位置关系等内容。
直线的方程可以用点斜式、截距式、一般式等形式表示,学生需要熟练掌握这些表示方法并能灵活运用。
2.圆的性质圆是解析几何中的常见图形,学生需要了解圆的半径、直径、周长、面积等基本概念,同时还要掌握圆的方程和位置关系,以及与直线的关系等内容。
三、三角函数1.三角函数的概念三角函数是数学中的重要分支,是三角学的基础。
学生需要了解正弦函数、余弦函数、正切函数、余切函数等三角函数的定义和性质,包括周期性、奇偶性、单调性、图像等方面。
2.三角函数的变换学生需要了解三角函数的基本变换,包括平移、伸缩、反转等操作,以及将三角函数图像与三角函数方程相联系的应用问题。
四、数列和递推1.数列的概念数列是由一系列按照一定规律排列的数构成的序列。
学生需要了解等差数列、等比数列、等差数列和等比数列的和等基本概念,以及它们的性质和应用。
2.递推公式递推公式是数列中常见的一种表示方法,通过递推公式可以方便地表示数列的通项公式和前n项和。
高中数学必修二知识点

高中数学必修二知识点
一、函数基本概念
函数是一种中介关系,即一个输入和另一个输出之间的数学关系,是由一个变量与另一个变量之间的对应关系组成,也可用“自变量与因变量之间的函数关系”来表示。
自变量表示“输入”,因变量表示“输出”,函数则表示输入与输出之间的关系
二、函数的基本性质
1、唯一性。
假定函数f(x)是定义在D上的连续函数,若对x∈D有f(x)=f(y)(x≠y),那么令x=y,从而可得矛盾结论,即函数的值有唯一性。
2、有界性。
函数值的范围是定义域D或定义域D的子集,取值有边界,且返回的值不会超出这个范围。
3、连续性。
函数取值连续,不可突变,这是状态变化的基础。
三、函数的表达式
1、定义式。
定义式表示指定某函数时用来决定函数关系的公式。
常用的函数定义式包括一次函数式,二次函数式,指数函数式,对数函数式等。
2、函数图像。
函数图像就是将函数定义式替换成对应的点对连线图形,可以帮助我们更好地理解函数表达式与函数关系。
四、函数的分类
1、多项式函数。
多项式函数是按照指数大小进行组合,其图像是一段一段连续的连线图形。
2、三角函数。
三角函数是通过极坐标和直角坐标间的关系来研究函数关系的函数,其图像是一段一段的波浪曲线。
3、指数函数。
指数函数是按照指数的大小组成的函数,其图像是一条以负斜率上升的连线图形。
4、对数函数。
对数函数就是以底数为参数,参数为10时为常用对数,其图像是一条以正斜率上升的连线图形。
高中数学必修2全册知识点总结(理科)

高中数学必修2知识点第一章空间几何体1.1柱、锥、台、球的结构特征(1)棱柱:定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱'''''E D C B A ABCDE -或用对角线的端点字母,如五棱柱'AD几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
(2)棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥'''''E D C B A P -几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
(3)棱台:定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如五棱台'''''ED C B A P -几何特征:①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。
(5)圆锥:定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
(6)圆台:定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修2知识点总结第一章 立体几何初步1、特殊几何体表面积公式(c 为底面周长,h 为高,'h 为斜高,l 为母线)ch S =直棱柱侧面积'21ch S =正棱锥侧面积 ')(2121h c c S +=正棱台侧面积 rhS π2=圆柱侧()l r r S +=π2圆柱表rl S π=圆锥侧面积()l r r S +=π圆锥表lR r S π)(+=圆台侧面积()22R Rl rl r S +++=π圆台表2、柱体、锥体、台体的体积公式 V Sh =柱13V Sh=锥'1()3V S S h =台2V Sh r h π==圆柱h r V 231π=圆锥'2211()()33V S S h r rR R h π=+=++圆台3球体的表面积和体积公式: V 球=343R π ; S 球面=24R π第二章 直线与平面的位置关系空间点、直线、平面之间的位置关系1 2 三个公理:(1符号表示为A ∈lB ∈l=> l α⊂ A ∈α B ∈α公理1作用:判断直线是否在平面内.(2符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A ∈α、B ∈α、C ∈α。
公理2作用:确定一个平面的依据。
作用:判定两个平面是否相交的依据.2.1.2 空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点。
符号表示为:设a 、b 、c 是三条直线a ∥bLA· αCB ·A· α共面直线=>a ∥cc∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.4 注意点:① a'与b'所成的角的大小只由a、b的相互位置来确定,与O的选择无关,为了简便,点O一般取在两直线中的一条上;②两条异面直线所成的角θ∈(0, );③当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a⊥b;④两条直线互相垂直,有共面垂直与异面垂直两种情形;⑤计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
2.1.3 —空间中直线与平面、平面与平面之间的位置关系1、直线与平面有三种位置关系:(1)直线在平面内——有无数个公共点(2)直线与平面相交——有且只有一个公共点(3)直线在平面平行——没有公共点指出:直线与平面相交或平行的情况统称为直线在平面外,可用a α来表示a α a∩α=A a∥α.直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定1、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,2则该直线与此平面平行。
简记为:线线平行,则线面平行。
符号表示:a αb β => a∥αa∥b2.2.2 平面与平面平行的判定1、两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。
符号表示:aβbβa∩b =pβ∥αa∥αb∥α2、判断两平面平行的方法有三种:(1)用定义;(2)判定定理;(3)垂直于同一条直线的两个平面平行。
2.2.3 —直线与平面、平面与平面平行的性质1、直线与平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
简记为:线面平行则线线平行。
符号表示:a ∥αa β a∥bα∩β= b作用:利用该定理可解决直线间的平行问题。
2、两个平面平行的性质定理:如果两个平行的平面同时与第三个平面相交,那么它们的交线平行。
符号表示:α∥βα∩γ=a a∥bβ∩γ=b作用:可以由平面与平面平行得出直线与直线平行直线、平面垂直的判定及其性质2.3.1直线与平面垂直的判定1、定义:如果直线L与平面α内的任意一条直线都垂直,我们就说直线L与平面α互相垂直,记作L⊥α,直线L叫做平面α的垂线,平面α叫做直线L的垂面。
如图,直线与平面垂直时,它们唯一公共点P叫做垂足。
PaL2、直线与平面垂直的判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
注意点: a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想。
2.3.2平面与平面垂直的判定1、二面角的概念:表示从空间一直线出发的两个半平面所组成的图形A梭 l βBα2、二面角的记法:二面角α-l-β或α-AB-β— 直线与平面、平面与平面垂直的性质12第三章 直线与方程(1)直线的倾斜角定义:x 轴正向与直线向上方向之间所成的角叫直线的倾斜角。
特别地,当直线与x 轴平行或重合时,我们规定它的倾斜角为0度。
因此,倾斜角的取值范围是(2)直线的斜率①定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。
直线的斜率常用k 当直线l 与x 轴平行或重合时, α=0°, k = tan0°=0; 当直线l 与x 轴垂直时, α= 90°, k 不存在.当[) 90,0∈α时,0≥k ; 当() 180,90∈α时,0<k ; 当 90=α时,k 不存在。
②过两点的直线的斜率公式:)(211212x x x x y y k ≠--= ( P1(x1,y1),P2(x2,y2),x1≠x2)注意下面四点:(1)当21x x =时,公式右边无意义,直线的斜率不存在,倾斜角为90°;(2)k 与P 1、P 2的顺序无关;(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得;(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。
(3)直线方程注意:当直线的斜率为0°时,k=0,直线的方程是y =y 1。
当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示.但因l 上每一点的横坐标都等于x 1,所以它的方程是x =x 1。
注意:○1各式的适用范围 ○2特殊的方程如:(4)两直线平行与垂直注意:利用斜率判断直线的平行与垂直时,要注意斜率的存在与否。
(5)两条直线的交点0:1111=++C y B x A l 0:2222=++C y B x A l 相交交点坐标即方程组⎩⎨⎧=++=++0222111C y B x A C y B x A 的一组解。
方程组无解21//l l ⇔ ; 方程组有无数解⇔1l 与2l 重合(6设1122(,),A x y B x y ,()是平面直角坐标系中的两个点,(7一点()00,y x P 到直线0:1=++C By Ax l 的距离(8已知两条平行线直线1l 和2l 的一般式方程为1l :01=++C By Ax ,2l :02=++C By Ax ,则1l 与2l第四章 圆与方程1、圆的定义:平面内到一定点的距离等于定长的点的集合叫圆,定点为圆心,定长为圆的半径。
2、圆的方程(1点00(,)M x y 与圆222()()x a y b r -+-=的位置关系: 当2200()()x a y b -+->2r ,点在圆外 当2200()()x a y b -+-=2r ,点在圆上 当2200()()x a y b -+-<2r ,点在圆内(2当0422>-+F E D 时,方程表示圆,此时圆心为⎪⎭⎫ ⎝⎛--2,2E D ,半径为F E D r 42122-+=当0422=-+F E D 时,表示一个点;当0422<-+F E D 时,方程不表示任何图形。
(3)求圆方程的方法:一般都采用待定系数法:先设后求。
确定一个圆需要三个独立条件,若利用圆的标准方程,需求出a ,b ,r ;若利用一般方程,需要求出D ,E ,F ;另外要注意多利用圆的几何性质:如弦的中垂线必经过原点,以此来确定圆心的位置。
3、直线与圆的位置关系:直线与圆的位置关系有相离,相切,相交三种情况:(1)设直线0:=++C By Ax l ,圆()()222:r b y a x C =-+-,圆心()b a C ,到l 的距离为则有相离与C l r d ⇔>;相切与C l r d ⇔=;相交与C l r d ⇔<(2)过圆外一点的切线:①k 不存在,验证是否成立②k 存在,设点斜式方程,k ,得到方程【一定两解】(3)过圆上一点的切线方程:圆(x-a)2+(y-b)2=r 2,圆上一点为(x 0,y 0),则过4、圆与圆的位置关系:通过两圆半径的和(差),与圆心距(d )之间的大小比较来确定。
设圆()()221211:r b y a x C =-+-,()()222222:R b y a x C =-+-两圆的位置关系常通过两圆半径的和(差),与圆心距(d )之间的大小比较来确定。
①当r R d +>时两圆外离,此时有公切线四条;②当r R d +=时两圆外切,连心线过切点,有外公切线两条,内公切线一条; ③当r R d r R +<<-时两圆相交,连心线垂直平分公共弦,有两条外公切线;④当R d -=圆的辅助线一般为连圆心与切线或者连圆心与弦中点。
