2020年4月温州二模通用技术试题
2020年高中通用技术学业水平合格性考试模拟及答案

2020年高中学业水平合格性考试通用技术模拟试题1.下列不属于技术活动的是A.数学猜想的证明过程B.氢氧燃料电池的发明C.电梯的承载能力试验D.环保材料的设计运用2.市场上某款镍锌充电电池,其放电电流大,但使用寿命短。
下列关于该镍锌充电电池说法错误的是A.该电池运用了材料学、化学等多学科知识,体现了技术的综合性B.该电池放电电流大,但使用寿命短,体现了技术的两面性C.该电池与干电池相比,可反复充电使用,体现了技术的创新性D.该镍锌电池尽管有大量缺点,但还是可以申请专利3.小华同学想设计一个简易的床头灯,在设计分析时他不需要考虑的是A.支撑架的强度B.底座的大小C.灯罩的材料D.灯泡的生产过程4.某公司设计了一款平板电脑,机身80%都是由植物性材质组成,被弃置后机身可以分解为水和二氧化碳。
该机身技术设计主要体现的设计原则是A.法律、道德规范原则B.经济性原则C.美观性原则D.可持续发展原则5.小明发现工人依靠吊绳进行玻璃幕墙清洗非常危险,于是他想设计一款可用于玻璃幕墙清洗的爬壁机器人。
关于该设计步骤排序合理的是①制定设计方案,画出技术加工图②收集整理相关信息,确定设计目标③制作模型并进行相关测试④撰写使用说明书A.②①④③B.②①③④C.③①②④D.③②①④6.农场拖拉机表面多处出现严重锈蚀,为延长拖拉机的使用寿命,同时提高其美观程度,下列处理工艺最合理的是A.在生锈的地方直接刷上油漆B.在生锈的地方先进行表面打磨去掉铁锈,然后再喷涂油漆C.在生锈的地方用砂纸磨光D.在生锈的地方进行电镀处理7.火车卫生间一般设置有状态指示灯,红色表示“有人”,绿色表示“无人”,该设计主要考虑到A.更好地实现经济的目标B.更符合人体的动态尺寸要求C.更好地实现健康的目标D.更方便地传递信息8.一般用来展示产品设计效果的图样是A.效果图B.草图C.机械加工图D.电子电路图9.物体主视图和俯视图中,尺寸相等的是A.长度B.宽度C.高度D.厚度10.物体的三视图在位置上的安排是A.以主视图为主,俯视图在它的正下方,左视图在它的正右方B.以主视图为主,俯视图在它的正前方,左视图在它的正右方C.以主视图为主,俯视图在它的正下方,左视图在它的正左方D.以主视图为主,俯视图在它的正上方,左视图在它的正右方11.以下是某小组对其设计制作的便携折叠椅的评价总结:“①我们小组在加工椅面、椅子腿和转轴时采用分工合作的策略。
2020年通用技术学业水平测试模拟试题3

2020年通⽤技术学业⽔平测试模拟试题32020年通⽤技术模拟题3⼀、单项选择题(每题3分,25⼩题,共75分。
在每⼩题给出的四个选项中,只有⼀个选项是最符合题⽬要求的)1. 智能⼿机应⽤了多项新技术,从技术的性质⾓度分析,以下说法不正确的是()A.应⽤⼈脸识别技术开锁提⾼安全性,体现了技术的创新性B.具有通讯.播放.拍照.上⽹等功能,体现了技术的⽬的性C.应⽤程序的设计者可以要求使⽤者⽀付费⽤,体现了技术的专利性D.⼿机的价格⾮常的贵,体现了技术的两⾯性2. 这是⼀款可折叠⾃⾏车头盔。
传统头盔厚且笨重,不适合随⾝携带,因此⼤多数⼈骑车都不喜欢带头盔。
这种由交织塑料制成的⾃⾏车头盔,它与传统同类产品⼀样坚固(符合美国和欧洲的⼀般安全要求),⾜够灵活,⼏乎可以完全折叠。
设计者希望这款可折叠头盔能够帮助⾃⾏车爱好者养成戴头盔的好习惯。
这个案例说明技术具有()A.优化⼈的作⽤B.发展⼈的作⽤C.保护⼈的作⽤D.解放⼈的作⽤3. ⽯墨烯具有优异的光学.电学.⼒学特性,是⼀种未来⾰命性的材料。
随着⽯墨烯制备技术及批量化⽣产以及⼤尺⼨等难题的逐步突破,⽯墨烯的产业化应⽤步伐正在加快,基于已有的研究成果,研究⼈员已经⽤⽯墨烯制造出了⼀块柔性触摸屏,并表⽰,从理论上来讲,⼈们可以卷起智能⼿机,然后像铅笔⼀样将其别在⽿后。
该案例体现了()A.技术的发展为设计提供了⼴阔的空间B.新的设计会促进技术的⾰新,以满⾜新的设计需求C.只要有设计,相应的技术就⾃然出现D.设计是推动技术发展的驱动⼒,可以发挥技术的价值4. 如图所⽰是⼀款测游标卡尺,测量时可显⽰所量取要素的长度值。
从⼈机关系⾓度分析,该设计主要考虑了( )A.⼈体的静态尺⼨与动态尺⼨B.信息的交互C.普通⼈群和特殊⼈群D.⼈的⽣理需求与⼼理需求5.下图是⼀款蓝⽛⽿机,下列关于该蓝⽛⽿机的设计分析和评价中,正确的是( )A.该⽿机⼩巧轻便,⽅便随⾝携带, 主要是从“物”的⾓度考虑的B.采⽤了硅胶材质的弧形⽀撑架设计,主要是从“⼈”的⾓度考虑的C.具有IPX4防⽔等级,能够配合⾬天骑⾏使⽤,主要是从“环境”的⾓度考虑的D.配备了⼀枚便携式充电盒,⽿机本体续航3⼩时,配合充电盒可以额外再提供6⼩时,续航可约达9⼩时,体现了设计的可持续发展原则。
2020年通用技术学业水平测试模拟试题2

2020年通用技术合格考模拟试题2一、单项选择题:本题25小题,每小题3分,共75分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.1929年,在电灯发明50周年的时候,包括美国总统在内的500多名社会名流在华盛顿隆重集会庆祝。
爱迪生在经久不息的掌声中出场,他激动地说:“倘若我做的工作给这个社会哪怕只带来一丝幸福,那我也就因此而满足了”。
这个案例说明了技术可以()A.解放人B.发展人C.保护人D.赚钱2.“20世纪中叶,美国施乐公司发明的复印机(申请并获得了专利)掀起了一场划时代的办公室革命,购买复印机的公司趋之若鹜。
昂贵的售价为施乐公司带来了巨额的利润”。
这一案例说明了专利保护制度()A.体现了人们对知识产权的尊重和保护B.对发展中国家的利益是一种损害。
C.会阻碍技术创新活动的良性循环D.使得技术产品价格高昂,损害了普通大众的利益3.在市场上我们发现,有的铁锹头被设计成尖头的,有的铁锹头被设计成平口的,如下图所示,依据你对这种不同设计目的的理解,以下评论正确的是()A.尖头的铁锹比平口的好看,是为了满足设计的美观性原则B.平头的铁锹和尖头的形状不同,是为了满足设计的创新性原则C.制造尖头的铁锹比平头的用的材料少,是为了满足设计的经济性原则D.由于它们的力学特征不同,所以用途也不同,是为了满足设计的实用性原则4.早在100多年前,恩格斯就曾警告人类,“不要过分陶醉于人类对自然的胜利”,“人类每一次对自然界的胜利都必然受到大自然的报复”。
你认为以下理解正确的是()A.人类不需要技术,发明技术本身就是错误的,B.人们不能相信技术、依赖技术C.技术的进一步发展可以消除它所带来的一切危害D.我们应该理性地看待技术,以更为负责、更有远见、更具道德的方式使用和发展技术5.陈晓丽同学准备购买一个电热毯来取暖,在去商场前列出了几个对各种品牌电热毯的评价指标。
下列指标中,不属于性能评价的是()A.是否有温度调节及防漏电保护装置B.是否具有通断电指示装置C.设计是否新颖,花色是否美观D.通电多长时间可以达到预定温度6.如图所示是为空调室外机工作人员设计的一把专业扳手,工作人员只需站在室内,把螺母和螺栓吸在套筒内,把螺母和螺栓吸在套筒内,借助该工具就可以将空调用螺栓螺母固定在支架上。
2020年4月17日浙江省学考选考高2020届高2017级高三温州二模技术试题参考答案

2020年4月份温州市普通高中选考适应性测试技术试题参考答案及评分标准信息技术部分一、选择题(本大题共12小题,每小题2分,共24分。
在每小题给出的四个选项中,只有一个符合题目要求)题号123456789101112答案C B B A A C D A C D B C二、非选择题(本大题共4小题,其中第13小题4分,第14小题8分,第15小题7分,第16小题7分,共26分)DSSDA?DSA13.(1)=(D3+F3+H3)/J3*100(1分)或者=SUM(D3,F3,H3)/J3*100(2)品牌,2019年累计销量或列C,列J(1分)(3)ABD(2分)(全选对得2分,漏选得1分,不选、错选不得分)14.(1)ABD(2分)(2)动画补间(1分)(3)选中“标题”图层最后1帧(或第50帧)执行“清除关键帧”操作。
或选中“标题”图层第1(2-49帧的任意一帧都行)帧执行“复制帧”操作,在最后1帧执行“粘贴帧”操作。
或者选中“标题”图层第2(3-49帧的任意一帧都行)帧,移动到第50帧(2分)(4)A(1分)(5)蜻蜓或标题(根据第(3)题答题情况给分)stop();(2分)15.(1)3(1分)(2)①Int(Rnd*9)*10+19(1分)或者Int(Rnd*9+1)*10+9②d(i)=d(j)(2分)③Mid(s,1,Len(s)-1)或Mid(s,1,Len(s)-2)(1分)(3)d(k)<d(j)Or d(k)>=d(i-1)(2分)16.(1)1(1分)(2)①sum+b(i)或sum+2^(4–i)(2分)②ans(sum-b(i)-b(j))=1(2分)③x+Val(Mid(s,i,1))*2^(Len(s)-i)或者x+Val(Mid(s,i,1))*2^(5-i)或者x+Val(Mid(s,Len(s)-i+1,1))*2^(i-1)或者x+Val(Mid(s,6-i,1))*2^(i-1)或者x*2+Val(Mid(s,i,1))(2分)2020年4月份温州市普通高中选考模拟考试技术(测试卷)参考答案第二部分通用技术(共50分)一、选择题(本大题共13小题,每小题2分,共26分。
2020年浙江省温州市高考数学二模试卷(理科)含答案解析

浙江省温州市2020年高考数学二模试卷(理科)(解析版)一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U={1,2,3,4,5},集合A={1,2,3},B={3,4,5},则A∩∁U B=()A.{3}B.{1,2,4,5} C.{1,2}D.{1,3,5}2.已知实数x,y满足,则z=x﹣y()A.最小值为﹣1,不存在最大值B.最小值为2,不存在最大值C.最大值为﹣1,不存在最小值D.最大值为2,不存在最小值3.直线l1:mx+y﹣1=0与直线l2:(m﹣2)x+my﹣1=0,则“m=1”是“l1⊥l2”的()A.充分不必要条件B.充要条件C.必要不充分条件D.既不充分也不必要条件4.已知某个几何体的三视图如下,根据图中标出的尺寸,可得这个几何体的体积是()A.4 B.C.8 D.5.设集合S={A0,A1,A2,A3},在S上定义运算⊕为:A i⊕A j=A k,其中k为i+j被4除的余数,i,j=0,1,2,3.若(A2⊕A3)⊕A m=A0,则m的值为()A.0 B.1 C.2 D.36.点P到图形C上所有点的距离的最小值称为点P到图形C的距离,那么平面内到定圆C 的距离与到圆C外的定点A的距离相等的点的轨迹是()A.射线 B.椭圆 C.双曲线的一支 D.抛物线7.数列{a n}是递增数列,且满足a n+1=f(a n),a1∈(0,1),则f(x)不可能是()A .f (x )=B .f (x )=2x ﹣1C .f (x )=D .f (x )=log 2(x +1)8.棱长为2的正方形ABCD ﹣A 1B 1C 1D 1中,E 为棱CC 1的中点,点P ,Q 分别为面A 1B 1C 1D 1和线段B 1C 上的动点,则△PEQ 周长的最小值为( )A .2B .C .D .2二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分) 9.以椭圆=1的焦点为顶点,长轴顶点为焦点的双曲线的渐近线方程是 ,离心率为 . 10.函数的图象如图所示,则ω= ,φ= .11.已知等差数列{a n }的公差为﹣3,且a 3是a 1和a 4的等比中项,则通项a n = ,数列{a n }的前n 项和S n 的最大值为 . 12.设奇函数f (x )=,则a +c 的值为 ,不等式f (x )>f (﹣x )在x ∈[﹣π,π]上的解集为 . 13.若正数a ,b 满足log 2a=log 5b=lg (a +b ),则的值为 .14.若存在x 0∈[﹣1,1]使得不等式10002124+≤+•-x x x a 成立,则实数a 的取值范围是 .15.如图,矩形ABCD中,AB=3,AD=4,M,N分别为线段BC,CD上的点,且满足,若,则x+y的最小值为.三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.在△ABC中,角A,B,C所对的边分别为a,b,c,已知=,sinA=.(Ⅰ)求sinC的值;(II)设D为AC的中点,若△ABC的面积为8,求BD的长.17.如图,矩形ABCD中,=λ(λ>1),将其沿AC翻折,使点D到达点E的位置,且二面角C﹣AB﹣E为直二面角.(1)求证:平面ACE⊥平面BCE;(2)设F是BE的中点,二面角E﹣AC﹣F的平面角的大小为θ,当λ∈[2,3]时,求cosθ的取值范围.18.已知二次函数f(x)=ax2+bx+c(a>0)的图象过点(1,0).(1)记函数f(x)在[0,2]上的最大值为M,若M≤1,求a的最大值;(2)若对任意的x1∈[0,2],存在x2∈[0,2],使得f(x1)+f(x2)>a,求的取值范围.19.已知椭圆=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.(1)求该椭圆方程;(2)过x轴上的一点M(m,0)作一条斜率为k的直线l,与椭圆交于点A,B两点,问是否存在常数k,使得|MA|2+|MB|2的值与m无关?若存在,求出这个k的值;若不存在,请说明理由.=n2﹣m2 20.设正项数列{a n}满足:a1=1,且对任意的n,m∈N+,n>m,均有a2n+m a2n﹣m成立.(1)求a2,a3的值,并求{a n}的通项公式;+a2n+1与2a2n的大小;(2)(ⅰ)比较a2n﹣1(ⅱ)证明:a2+a4+…+a2n>.2020年浙江省温州市高考数学二模试卷(理科)参考答案与试题解析一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集U={1,2,3,4,5},集合A={1,2,3},B={3,4,5},则A∩∁U B=()A.{3}B.{1,2,4,5} C.{1,2}D.{1,3,5}【分析】由全集U及B,求出B的补集,找出A与B补集的交集即可.【解答】解:∵全集U={1,2,3,4,5},集合A={1,2,3},B={3,4,5},∴∁U B={1,2},则A∩∁U B={1,2},故选:C.【点评】此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.2.已知实数x,y满足,则z=x﹣y()A.最小值为﹣1,不存在最大值B.最小值为2,不存在最大值C.最大值为﹣1,不存在最小值D.最大值为2,不存在最小值【分析】作出不等式组对应的平面区域,利用z的几何意义进行求解即可.【解答】解:作出不等式组对应的平面区域如图:由z=x﹣y,得y=x﹣z表示,斜率为1纵截距为﹣z的一组平行直线,平移直线y=x﹣z,当直线y=x﹣z经过点A时,即和直线AD:x﹣y=﹣1平行时,直线y=x ﹣z的截距最大,此时z最小,最小为﹣1,无最大值,故选:A.【点评】本题主要考查线性规划的基本应用,利用z的几何意义是解决线性规划问题的关键,注意利用数形结合来解决.3.直线l1:mx+y﹣1=0与直线l2:(m﹣2)x+my﹣1=0,则“m=1”是“l1⊥l2”的()A.充分不必要条件B.充要条件C.必要不充分条件D.既不充分也不必要条件【分析】对m分类讨论,利用两条直线相互垂直的充要条件即可得出.【解答】解:当m=0时,两条直线分别化为:y﹣1=0,2x+1=0,此时两条直线相互垂直,∴m=0.当m≠0时,若l1⊥l2,则﹣m(﹣)=﹣1,解得m=1.综上可得:m=0,或m=1,故“m=1”是“l1⊥l2”的充分不必要条件,故选:A.【点评】本题考查了简易逻辑的判定方法、两条直线相互垂直的充要条件,考查了推理能力与计算能力,属于基础题.4.已知某个几何体的三视图如下,根据图中标出的尺寸,可得这个几何体的体积是()A.4 B.C.8 D.【分析】由三视图知该几何体是一个四棱锥,由三视图求出几何元素的长度,由锥体的体积公式求出几何体的体积.【解答】解:根据三视图可知几何体是一个四棱锥,底面是一个矩形:两条边分别是4、2,且四棱锥的高是2,∴几何体的体积V==,故选:B.【点评】本题考查三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.5.设集合S={A0,A1,A2,A3},在S上定义运算⊕为:A i⊕A j=A k,其中k为i+j被4除的余数,i,j=0,1,2,3.若(A2⊕A3)⊕A m=A0,则m的值为()A.0 B.1 C.2 D.3【分析】根据新定义进行推理计算即可.【解答】解:∵2+3=5,5除4的余数为1,∴A2⊕A3=A1,则A1⊕A m=A0,则1+m是4的倍数,则m=3,故选:D.【点评】本题主要考查推理的应用,根据新定义是解决本题的关键.比较基础.6.点P到图形C上所有点的距离的最小值称为点P到图形C的距离,那么平面内到定圆C 的距离与到圆C外的定点A的距离相等的点的轨迹是()A.射线 B.椭圆 C.双曲线的一支 D.抛物线【分析】根据题意可知|PC|﹣r=|PA|,即P到C与A的距离之差为常数,故而P在双曲线上运动.【解答】解:设圆C的半径为r,由题意可知P到圆C的距离为|PC|﹣r,∴|PC|﹣r=|PA|,即|PC|﹣|PA|=r.∴P点轨迹为以A,C为焦点的双曲线靠近A点的一只.故选:C.【点评】本题考查了圆锥曲线的定义,属于基础题,7.数列{a n}是递增数列,且满足a n+1=f(a n),a1∈(0,1),则f(x)不可能是()A.f(x)=B.f(x)=2x﹣1 C.f(x)=D.f(x)=log2(x+1)【分析】A.由a1∈(0,1),可得>a n,即可判断出数列{a n}的单调性;B.由a1∈(0,1),不妨取a1=,则a2=﹣1=﹣1,即可判断出数列{a n}的单调性;C:f(x)=,令2x﹣x2≥0,可得得0≤x≤2.由f(x)==,利用二次函数的单调性及其a1∈(0,1),即可判断出数列{a n}的单调性;D.利用几何画板画出图象y=log2(x+1),y=x,可知:在x∈(0,1)时,log2(x+1)>x,即可判断出数列{a n}的单调性.【解答】解:对于A.∵a1∈(0,1),∴>a n,可得数列{a n}是递增数列;对于B.∵a1∈(0,1),不妨取a1=,则a2=﹣1=﹣1,因此数列{a n}不是递增数列;对于C:f(x)=,令2x﹣x2≥0,解得0≤x≤2.由f(x)==,可知:当0≤x≤1时,函数f(x)单调递增;当1≤x≤2时,函数f(x)单调递减.∵a1∈(0,1),∴数列{a n}是递增数列;对于D.利用几何画板画出图象y=log2(x+1),y=x,可知:在x∈(0,1)时,log2(x+1)>x,∴a n+1=log2(a n+1)>a n,因此数列{a n}是递增数列.故选:B.【点评】本题考查了数列的单调性,考查了数形结合方法、推理能力与计算能力,属于中档题.8.棱长为2的正方形ABCD﹣A1B1C1D1中,E为棱CC1的中点,点P,Q分别为面A1B1C1D1和线段B1C上的动点,则△PEQ周长的最小值为()A.2 B. C. D.2【分析】由题意,△PEQ周长取得最小值时,P在B1C1上,在平面B1C1CB上,设E关于B1C的对称点为M,关于B1C1的对称点为N,求出MN,即可得出结论.【解答】解:由题意,△PEQ周长取得最小值时,P在B1C1上,在平面B1C1CB上,设E关于B1C的对称点为M,关于B1C1的对称点为N,则EM=2.EN=,∠MEN=135°,∴MN==.故选:B.【点评】本题考查棱柱的结构特征,考查对称点的运用,考查余弦定理,考查学生的计算能力,属于中档题.二、填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分)9.以椭圆=1的焦点为顶点,长轴顶点为焦点的双曲线的渐近线方程是y=±x,离心率为.【分析】由椭圆=1的焦点坐标为(,0),长轴顶点为(±2,0),求出双曲线的标准方程,由此能求出结果.【解答】解:∵椭圆=1的焦点坐标为(,0),长轴顶点为(±2,0),∴以椭圆=1的焦点为顶点,长轴顶点为焦点的双曲线的标准方程为:=1,∴双曲线的渐近线方程是y=±x,离心率e==.故答案为:,.【点评】本题考查双曲线的渐近线方程和离心率的求法,是基础题,解题时要认真审题,注意椭圆、双曲线的性质的合理运用.10.函数的图象如图所示,则ω=2,φ=.【分析】通过函数的图象,求出T然后求出ω,利用图象经过(π,0)求出φ的值.【解答】2,解:由图象可知T=π,,则ω=2,∵函数经过点(π,1),∴1=2sin(2×π+φ),sinφ=,|φ|<,故φ=;故答案为2,.【点评】本题是基础题,考查三角函数的图象的应用,学生的视图能力,注意角的范围的应用.11.已知等差数列{a n}的公差为﹣3,且a3是a1和a4的等比中项,则通项a n=﹣3n+15,数列{a n}的前n项和S n的最大值为30.【分析】由题意可得(a1﹣6)2=a1(a1﹣6),解之可得a1,代入通项公式得到a n=﹣3n+15,再判断数列{a n}的前n项和S n的最大值的n的情况,即可求出,【解答】解:由题意可得(a1﹣6)2=a1(a1﹣9),解得a1=12,∴a n=12+(n﹣1)×(﹣3)=﹣3n+15,∴a n=﹣3n+15≥0,解得n≤5,∴S5=5×12+=30,故答案为:﹣3n+15,30.【点评】本题考查等差数列的前n项和公式和等比中项的定义,属基础题.12.设奇函数f(x)=,则a+c的值为0,不等式f(x)>f(﹣x)在x∈[﹣π,π]上的解集为.【分析】根据函数奇偶性的定义和性质求出a,b,c的值,利用分类讨论的思想进行求解即可得到结论.【解答】解:∵f(x)是奇函数,∴f(0)=0,即f(0)=acos0﹣sin0+c=a+c=0,即a+c=0,则f(x)=,若x<0,则﹣x>0,则f(﹣x)=acosx+sinx﹣a=﹣cosx﹣bsinx﹣a,则a=﹣1,b=﹣,c=1,即f(x)=,若0≤x≤π,则由f(x)>f(﹣x)得﹣cosx﹣sinx+1>cosx+sinx﹣1,即cosx+sinx<1,即cos(x﹣)<,∵0≤x≤π,∴﹣≤x﹣≤,则<x﹣≤,即<x≤π,若﹣π≤x<0,则由f (x )>f (﹣x )得cosx ﹣sinx ﹣1>﹣cosx +sinx +1,即cosx ﹣sinx >1,即cos (x +)>, ∵﹣π≤x <0,∴﹣≤x +<,则﹣<x +<,即﹣<x <0,综上不等式的解集为,故答案为:.【点评】本题主要考查不等式的求解,根据函数奇偶性的性质求出a ,b ,c 的值,利用分类讨论的思想结合三角函数的图象和性质是解决本题的关键.13.若正数a ,b 满足log 2a=log 5b=lg (a +b ),则的值为 1 .【分析】设log 2a=log 5b=lg (a +b )=k ,可得a=2k ,b=5k ,a +b=10k ,可得a +b=ab .即可得出. 【解答】解:设log 2a=log 5b=lg (a +b )=k , ∴a=2k ,b=5k ,a +b=10k , ∴ab=10k , ∴a +b=ab , 则=1.故答案为:1.【点评】本题考查了对数与指数的运算性质,考查了推理能力与计算能力,属于中档题.14.若存在x 0∈[﹣1,1]使得不等式10002124+≤+•-x x x a 成立,则实数a 的取值范围是[0,] .【分析】将不等式进行等价转化,利用换元法,结合基本不等式的性质进行转化求解,建立不等式关系进行求解即可得到结论. 【解答】解:不等式|4﹣a2+1|≤2等价为≤2,即|2+﹣a |≤2,即﹣2≤2+﹣a≤2,即a﹣2≤2+≤2+a,设t=2,当x0∈[﹣1,1]是t∈[,2],设y=t+,则函数在[,1]上是减函数,在[1,2]上是增函数,则当t=1时,函数取得最小值y=1+1=2,当t=2或t=,函数取得最大值y=+2=,则2≤y≤,∵即a﹣2≤y≤2+a,∴若[a﹣2,a+2]与[2,]没有公共点,则a+2<2或a﹣2>,即a<0或a>,则若[a﹣2,a+2]与[2,]有公共点,则0≤a≤,故答案为:[0,]【点评】本题主要考查不等式恒成立问题,将不等式进行转化,利用不等式求出不等式的范围,建立不等式关系是解决本题的关键.15.如图,矩形ABCD中,AB=3,AD=4,M,N分别为线段BC,CD上的点,且满足,若,则x+y的最小值为.【分析】由题意建立平面直角坐标系,设点M(3,a),N(b,4),0<a<4,0<b<3;求得b=,a=,从而可得+=(x+y﹣1)2,再设x+y=m,则x=m﹣y;利用判别式即可求出m的最小值.【解答】解:由题意建立如图所示坐标系,如图所示;设点M(3,a),N(b,4),且0<a<4,0<b<3;∵=(3,4),=(3,a),=(b,4);又∵=x+y,∴(3,4)=x(3,a)+y(b,4),即,∴b=,a=,∴+=+=+=1,即+=(x+y﹣1)2,设x+y=m,则x=m﹣y;则+=(m﹣1)2,即25y2﹣18my+9m2﹣144(m﹣1)2=0,故△=(18m)2﹣4×25×(9m2﹣144(m﹣1)2)≥0,即24m2﹣50m+25≥0,解得,m≥或m≤(舍去);∴x+y的最小值.故答案为:.【点评】本题考查了平面向量的应用问题,也考查了数形结合的思想与转化思想的应用问题,是较难的题目.三、解答题(本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.在△ABC中,角A,B,C所对的边分别为a,b,c,已知=,sinA=.(Ⅰ)求sinC的值;(II)设D为AC的中点,若△ABC的面积为8,求BD的长.【分析】(1)利用向量的数量积和正玄定理得出sinBcosA=sinAcosB,根据三角公式得出A=B,根据诱导公式求解即可.(2)利用面积公式,以及余弦定理求解即可.【解答】解:在△ABC中,∵=,∴cbcosA=cacosB,即bcosA=acosB,sinBcosA=sinAcosB,sin(A﹣B)=0,∴A=B,∵sinA=.∴sinC=sin(π﹣2A)=sin(2A)=2sinAcosA=2××=.(2)设AC=BC=m,∵△ABC的面积为8,∴×=,m=3,cosC=,根据余弦定理得出:BD2=m2×=m2=BD=.【点评】本题考查了向量数量积以及正弦定理和余弦定理的运用,在判断三角形形状时,要注意对角的范围进行分析,即求角的大小需要两个条件:该角的一个三角函数值和该角的范围,缺一不可,正、余弦定理是解三解形必用的数学工具17.如图,矩形ABCD中,=λ(λ>1),将其沿AC翻折,使点D到达点E的位置,且二面角C﹣AB﹣E为直二面角.(1)求证:平面ACE⊥平面BCE;(2)设F是BE的中点,二面角E﹣AC﹣F的平面角的大小为θ,当λ∈[2,3]时,求cosθ的取值范围.【分析】(Ⅰ)推导出AB⊥BC,BC⊥AE,从而AE⊥平面BCE,由此能证明平面ACE⊥平面BCE.(Ⅱ)以E为坐标原点,以AD长为一个单位长度,建立空间直角坐标系,利用向量法能求出cosθ的取值范围.【解答】(本题15分)证明:(Ⅰ)∵二面角C﹣AB﹣E为直二面角,AB⊥BC,∴BC⊥AE平面,∴BC⊥AE…(2分)∵AE⊥CE,BC∩CE=C,∴AE⊥平面BCE…(4分)∵AE⊂平面ACE,∴平面ACE⊥平面BCE…(6分)解:(Ⅱ)如图,以E为坐标原点,以AD长为一个单位长度,建立如图空间直角坐标系,则AB=λ…(8分)则设平面EAC的法向量为则,取x=1,则…(10分)同理设平面FAC的法向量为…(12分)∴…(14分)∵…(15分)【点评】本题考查面面垂直的证明,考查二面角的余弦值的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.18.已知二次函数f(x)=ax2+bx+c(a>0)的图象过点(1,0).(1)记函数f(x)在[0,2]上的最大值为M,若M≤1,求a的最大值;(2)若对任意的x1∈[0,2],存在x2∈[0,2],使得f(x1)+f(x2)>a,求的取值范围.【分析】(1)方法一:由f(x)是开口向上的抛物线,可得:M=max{f(0),f(2)},即,两式相加可得a的最大值;方法二:=,结合M≤1,可得a的最大值(2)存在,使,结合二次函数的图象和性质,分类讨论,最后综合讨论结果,可得答案.【解答】解:(1)∵f(x)过点(1,0),∴f(1)=a+b+c=0,…(1分)∴c=﹣a﹣b,f(x)=ax2+bx﹣a﹣b∵f(x)是开口向上的抛物线,∴M=max{f(0),f(2)}…(3分)∴…(5分)两式相加得a≤1,即a的最大值为1…(6分)解法二:由解得:=≤=1 …(6分)(2)由题意,存在,使,∴…(8分)∵a+b+c=0∴f(x)=ax2+bx﹣a﹣b其对称轴为①当,即时,f(x)在[0,2]上单调递增,∴∴>0均符合题意…(10分)②当,即时,f(x)在[0,]上递减,在[,2]上递增且f(0)<f(2),∴∴由得:,符合题意…(12分)③当,即时,f(x)在[0,]上递减,在[,2]上递增且f(0)≥f(2),∴由得:∴符合题意…(13分)④当即时,f(x)在[0,2]上单调递减,∴,∴均符合题意…(14分)综上所述:∴或…(15分)【点评】本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.19.已知椭圆=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形.(1)求该椭圆方程;(2)过x轴上的一点M(m,0)作一条斜率为k的直线l,与椭圆交于点A,B两点,问是否存在常数k,使得|MA|2+|MB|2的值与m无关?若存在,求出这个k的值;若不存在,请说明理由.【分析】(Ⅰ)根据题意,有,由此能求出椭圆方程.(Ⅱ)联立方程组,得:(3+4k2)x2﹣8k2mx+4m2﹣12=0,由此利用根的判别式、韦达定理、弦长公式,结合已知条件推导出|MA|2+|MB|2=7与m无关符合题意.【解答】(本题15分)解:(Ⅰ)∵椭圆=1(a>b>0)的两个焦点为F1,F2,焦距为2,设点P(a,b)满足△PF1F2是等腰三角形,∴根据题意,有…(4分)解得:,故所求椭圆方程为.…(6分)(Ⅱ)联立方程:,整理得:(3+4k2)x2﹣8k2mx+4m2﹣12=0在△>0的情况下有:…(9分)令﹣24k2+18=0,得,即…(13分)此时|MA|2+|MB|2=7与m无关符合题意,…(15分)【点评】本题考查椭圆方程的求法,考查满足条件的实数是否存在的判断与证明,是中档题,解题时要认真审题,注意根的判别式、韦达定理、弦长公式的合理运用.20.设正项数列{a n}满足:a1=1,且对任意的n,m∈N+,n>m,均有a2n+m a2n=n2﹣m2﹣m成立.(1)求a2,a3的值,并求{a n}的通项公式;+a2n+1与2a2n的大小;(2)(ⅰ)比较a2n﹣1(ⅱ)证明:a2+a4+…+a2n>.【分析】(1)先令m=1,求得a3,n=m+2,求得a2,分类讨论n为奇数或偶数,分别求得通项公式,+a2n+1与2a2n的通项公式,化简、比较大小,采用分析法,写出所以偶数项和奇(2)a2n﹣1数项整理即可.【解答】解:(1)令m=1,得,从而,所以,令n=m+2,得从而,,又=,∴,,从而,∴当n为偶数时,;令n=m+1,,可知当n为奇数时,综上可得(n∈N+).+a2n+1﹣2a2n(2)(i)a2n﹣1==<0,+a2n+1<2a2n所以a2n﹣1(ii)即证明由(i)得,,…,将上述的n个式子相加,得所以,所以,只需证,事实上,当k=0,1,2,…,n时,+﹣1﹣=﹣≥0,(∵,1),∴从而。
2024年浙江省温州市高考数学二模试卷(含解析)

2024年浙江省温州市高考数学二模试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知z ∈C ,则“z 2∈R ”是“z ∈R ”的( )A. 充分条件但不是必要条件 B. 必要条件但不是充分条件C. 充要条件D. 既不是充分条件也不是必要条件2.已知集合M ={x |y =x +1},N ={y |y = x +1},则M ∩N =( )A. ⌀B. RC. MD. N3.在正三棱台ABC−A 1B 1C 1中,下列结论正确的是( )A. V ABC−A 1B 1C 1=3V A 1−BB 1C 1 B. AA 1⊥平面AB 1C 1C. A 1B ⊥B 1CD. AA 1⊥BC4.已知a =sin 0.5,b =30.5,c =log 0.30.5,则a ,b ,c 的大小关系是( )A. a <b <cB. a <c <bC. c <a <bD. c <b <a5.在(3−x )(1−x )5展开式中,x 的奇数次幂的项的系数和为( )A. −64B. 64C. −32D. 326.已知等差数列{a n }的前n 项和为S n ,公差为d ,且{S n }单调递增.若a 5=5,则d ∈( )A. [0,53)B. [0,107)C. (0,53)D. (0,107)7.若关于x 的方程|x 2+mx +1|+|x 2−mx +1|=2|mx |的整数根有且仅有两个,则实数m 的取值范围是( )A. [2,52)B. (2,52)C. (−52,−2]∪[2,52)D. (−52,−2)∪(2,52)8.已知定义在(0,1)上的函数f (x )={1n ,x 是有理数m n (m ,n 是互质的正整数)1,x 是无理数,则下列结论正确的是( )A. f (x )的图象关于x =12对称 B. f (x )的图象关于(12,12)对称C. f (x )在(0,1)单调递增D. f (x )有最小值二、多选题:本题共3小题,共18分。
2020年高考模拟试卷通用技术卷(含答案)

目录1 2020年高考模拟试卷通用技术卷命题双向细目表 (1)2 2020年高考模拟试卷通用技术试卷 (3)3 2020年高考模拟试卷通用技术答题卷 (13)4 2020年高考模拟试卷通用技术卷参考答案与评分标准 (15)2020年高考模拟试卷通用技术卷命题双向细目表2020年高考模拟试卷 通用技术卷总分:50分 考试时间:45分钟一、选择题(本大题共13小题.每小题2分.共26分。
每小题列出的四个备选项中只有一个是符合题目要求的.不选、多选、错选均不得分)1.【原创】如图所示是一款某品牌水质TDS 检测笔.TDS 值代表水中可溶性总固体含量.可在一定程度反映水质.通常TDS 值越低.表明水中重金属离子等可溶性盐类越少.水质越纯。
把该水质检测笔放入待检测的水中.按一下开关.显示屏就会立刻显示水中的TDS 值.让你了解水的纯度。
关于该产品以下说法错误的是( ) A.结合了电子、信息、生物等技术.体现了技术的综合性 B.具有专利号.体现了技术的专利性C.能马上显示出水中的TDS 值.体现了技术的目的性D.价格较高.体现了技术的两面性 参考答案:D解析:本题考核技术的基本特征——两面性。
两面性特别强调技术在使用过程中给人们以及社会带来的危害。
2.【原创】如图所示为一款热熔胶枪.可以用于材料涂胶.使用时只用按压扳机.就可从喷嘴挤出溶胶;暂不使用时.还可以打开支架将胶枪斜放。
下列关于该热熔胶枪的分析中.不是从人机关系角度考虑的是( ) A .轻松按压扳机.方便挤出溶胶 B .外壳采用隔热、绝缘材料C .打开支架可防止喷嘴直接与桌子接触D .可通过调节按钮.调节不同的功率 参考答案:C解析:本题主要考查人机关系相关知识。
当人们使用物品时.物品就与人产生了一种相互的关系.这种相互的关系成为人机关系。
3.【原创】如图所示是一款“指套型”光电鼠标及其评价坐标图.以下对坐标图分析中不恰当的是( )第1题图第2题图喷嘴支架扳机A .套在食指上只用拇指操作即可.操作性好B .指套结构.形态较新颖C .可在衣服、桌面等多种可反光介面上操作.实用性好D .鼠标移动速度快.性能价格比高 参考答案:D解析:本题考查坐标图的分析。
温州市平阳县2020届高三普通高中选考适应性测试通用技术试题清晰版.docx
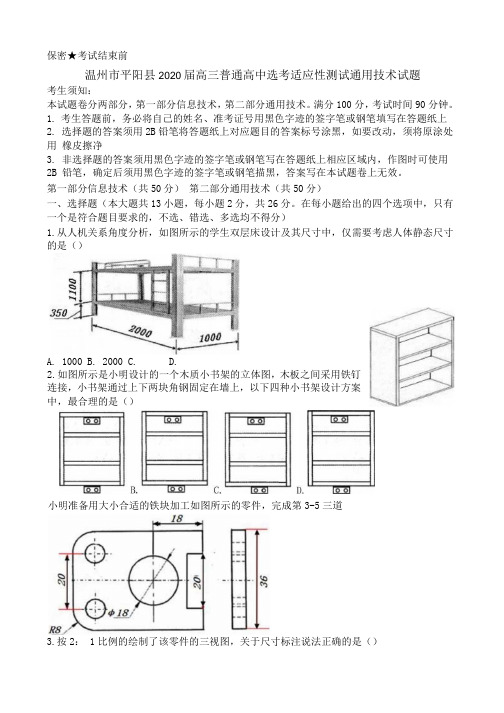
保密★考试结束前温州市平阳县2020届高三普通高中选考适应性测试通用技术试题考生须知:本试题卷分两部分,第一部分信息技术,第二部分通用技术。
满分100分,考试时间90分钟。
1.考生答题前,务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上2.选择题的答案须用2B铅笔将答题纸上对应题目的答案标号涂黑,如要改动,须将原涂处用橡皮擦净3.非选择题的答案须用黑色字迹的签字笔或钢笔写在答题纸上相应区域内,作图时可使用2B 铅笔,确定后须用黑色字迹的签字笔或钢笔描黑,答案写在本试题卷上无效。
第一部分信息技术(共50分)第二部分通用技术(共50分)一、选择题(本大题共13小题,每小题2分,共26分。
在每小题给出的四个选项中,只有一个是符合题目要求的,不选、错选、多选均不得分)1.从人机关系角度分析,如图所示的学生双层床设计及其尺寸中,仅需要考虑人体静态尺寸的是()A. 1000B. 2000C.D.2.如图所示是小明设计的一个木质小书架的立体图,木板之间采用铁钉连接,小书架通过上下两块角钢固定在墙上,以下四种小书架设计方案中,最合理的是()小明准备用大小合适的铁块加工如图所示的零件,完成第3-5三道3.按2: 1比例的绘制了该零件的三视图,关于尺寸标注说法正确的是()A. 该零件加工好后实际高度为72mmB. 现有标注中有1处错误C. 漏标5处尺寸D. 现有标注中重复尺寸有1处5. 加工该零件时,以下操作中不正确的是()A. 划线工具只需用到划针、划规、钢直尺或钢角尺B. 钻孔时要戴防护眼镜,但是不能戴手套C. 如果锯割较坚硬的金属材料,应选用细齿锯条D. 起锯时,用用大拇指抵住工件,挡住锯条的一面,防止锯割线偏移6. 用薄钢板加工如图所示的结构,两孔心的位置有精度要求(即两 孔的轴心线尽量在同一直线上,两孔对齐),则最合理的加工流程为 ()A. 划线一锯割一理削一钻孔一折弯一划线一钻孔B. 划线一锯割一铿削一折弯一划线一钻孔C. 划线一锯割一折弯一锂削一划线一钻孔D. 划线一钻孔一锯割一锂削一划线一折弯7. 如图所示的某双向夹具,可以在右边的小夹缝夹装 工件,也可以在左边的大夹缝中夹持工件。
2020年4月17日浙江省学考选考高2020届高2017级高三温州二模物理试题参考答案

一、选择题Ⅰ(本题共 13 小题,每小题 3 分,共 39 分。每小题列出的四个备选项中只有一个
是符合题目要求的,不选、多选、错选均不得分) 题号 1 2 3 4 5 6 7 8 答案 B D C D B D D C
9 10 11 12 13 CB ADD
)
(1分)(其它形式正确的也得1分)
(或 Q
4Rm2g 2 B 2 L2
t
48m3g 2R2 B 4 L4
)
(3)由 3mg
mg
B 2 L2v 2R
得: a
4mgR B 2 L2
(1分)
物理(选考试题)参考答案及评分标准 第 2 页(共 4 页)
由 3mg
mg
2BL
2BLv / 2R
得: b
mgR B 2 L2
物理(选考试题)参考答案及评分标准 第 1 页(共 4 页)
(2)甲物块由 C 至 D
vC2 vD2 2g (2R) (或动能定理写出)(1 分)
甲乙两物块碰撞: mvD (m 3m)v
(1 分)
碰后一起运动至静止: v2 2( g)x
(或动能定理写出) (1 分)
最终静止的位置离 D 点的距离 x 1 R 4
(2 分)
得 Ff =2.0×105 N (1 分)
③C(ห้องสมุดไป่ตู้ 分)
(3)A 到 C 位移 x (L1 L2 )2 h2 2002 62m 200m (1 分)
时间 t v v0 0.5 4s (1 分) a
平均速度 v x 50m / s (1 分) t
(三个式子只要写出二个得 2 分,结果 1 分。如果未得出 50m/s,其他都对,得 2 分。算
浙江省2020届高三4月联考试题 技术 试题(含答案)

浙江省4月联考技术注意事项:1.本试题卷分两部分,第一部分为信息技术,第二部分为通用技术,共16页,满分100分,考试时间90分钟。
2.答题前,考生务必将自己的姓名、准考证号等填写在答题卡的相应位置。
3.全部答案在答题卡上完成,答在本试题卷上无效。
4.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
5.考试结束后,将本试题卷和答题卡一并交回。
第一部分信息技术(共50分)一、选择题(本大题共12小题,每小题2分,共24分。
在每小题给出的四个选项中,只有一个符合题目要求,不选、多选、错选均不得分)1.下列有关信息和信息安全的说法,错误的是A.日常生活中随便填写传单资料存在信息被泄露的风险B.网络上的信息不能随意转发C.高考试卷设置为绝密等级的目的是防止信息在共享过程中产生损耗D.信息不可以脱离载体而单独存在2.下列应用中,体现人工智能技术的有①使用某软件识别拍摄植物照片并返回该植物相关信息②使用Word软件的查找替换功能把某文档中所有的“博客”替换为“Blog”③使用某软件过程中用语音方式设置闹钟④使用微信的视频聊天功能和朋友进行交流⑤人与人在围棋APP平台上对弈A.①②③B.①③⑤C.①③D.①⑤3.使用Access软件打开数据表,部分界面如图所示。
下列说法正确的是A.“卡号”字段属于“文本”类型,故“卡号”的字段值可以相同B.“卡状态”字段的有效输入值可以为“已挂失”C.数据表中每一行称为一条记录,该数据表有6条记录D.当前状态下不可以对“校园卡信息”数据表重命名4.使用UltraEdit软件观察字符内码,部分界面如图所示。
下列说法正确的是A.字符“!”的内码占两个字节B.字符“你”的交换码是“C4 E3”C.字符“2”在计算机内部是以十六进制“32”存储的D.图中共有6个ASCII码字符5.小明进行音频文件创作时遇到以下问题:①选中区域的音量和其它部分不一致,如图a;②选中区域的部分为不需要的信号,需要去除,如图b。
2020年浙江省温州市鹿城区中考数学二模试卷(解析版)
2020年浙江省温州市鹿城区中考数学二模试卷一、选择题(共10小题,每小题4分,共40分):1.计算:(﹣2)+3的结果是()A.﹣5B.﹣1C.1D.52.我国第六次全国人口普查总数约为1340000000人,用科学记数法表示为()A.13.4×108B.1.34×109C.1.34×108D.1.34×107 3.如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是()A.B.C.D.4.下列计算正确的是()A.a3+a2=2a5B.a3•a2=a6C.a3÷a2=a D.(a3)2=a9 5.不等式组的解集是()A.x>﹣1B.x>3C.﹣1<x<3D.x<3 6.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.7.某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如表:人数(人)1341分数(分)80859095那么这9名学生所得分数的众数和中位数分别是()A.90,90B.90,85C.90,87.5D.85,85 8.若分式=0,则x的值是()A.±2B.2C.﹣2D.09.在我国古代数学著作《九章算术》“勾股”章中有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何?”大意是说:如图,推开双门(AD和BC),门边缘D,C两点到门槛AB的距离为1尺(1尺=10寸),双门间的缝隙CD为2寸,那么门的宽度(两扇门的和)AB为()A.103寸B.102寸C.101寸D.100寸10.如图,一个坡角为15°的看台横截面上看旗杆CD,在这横截面上进行测量得到以下数据:在点A和点B处测得旗杆顶端的仰角分别为60°和30°,点A离地面高度为1米,且测得点A到点B的距离为8米,则旗杆的高度为()A.25米B.24米C.23米D.26米二、填空题(共6小题,每小题5分,共30分):11.(5分)因式分解:x2﹣4x=.12.(5分)一次函数y=﹣x+2的图象与y轴的交点坐标为.13.(5分)若一个反比例函数的图象位于二、四象限,则它的解析式可能是(写出一个即可).14.(5分)如图,将四边形ABCD绕顶点A顺时针旋转45°至四边形AB′C′D′的位置,若AB=16cm,则图中阴影部分的面积为cm2.15.(5分)如图,四边形OABC是一张矩形纸片,将边BC折叠,使点B落在边OA的点D处.已知折痕CE=5,且tan∠BCD=,则CO=.16.(5分)图1是一个高脚杯截面图,杯体CBD呈抛物线状(杯体厚度不计),点B是抛物线的顶点,AB=9,EF=2,点A是EF的中点,当高脚杯中装满液体时,液面CD =4,此时最大深度(液面到最低点的距离)为12,将高脚杯绕点F缓缓倾斜倒出部分液体,当∠EFH=30°时停止,此时液面为GD,则液面GD到平面l的距离是;此时杯体内液体的最大深度为.三、解答题(共8小题,共80分):17.(10分)(1)计算:;(2)先化简,再求值:(3﹣m)(3+m)+m(m﹣4)﹣7,其中.18.(10分)为关注学生出行安全,调查了某班学生出行方式,调查结果分为四类:A﹣骑自行车,B﹣步行,C﹣坐社区巴士,D﹣其它,并将调查结果绘制成以下两幅不完整的统计图.请你根据统计图,解答下列问题:(1)本次一共调查了多少名学生?(2)C类女生有名,D类男生有名,并将条形统计图补充完整.(3)若从被调查的A类和D类学生中分别随机选取一位同学进行进一步调查,请用列表法或画树状图的方法求出所选同学中恰好是一位男同学和一位女同学的概率.19.(8分)如图,在四边形ABCD中,E是AB的中点,AD∥EC,∠AED=∠B.(1)求证:△AED≌△EBC.(2)当AB=6时,求CD的长.20.(8分)如图1、图2是两张形状、大小完全相同的5×5方格纸,方格纸中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.(1)在图1中画出一个以点A、B为顶点的面积为3的平行四边形(要求所作的平行四边形且各顶点都在格点上).(2)在图2中画出一个以点A、B为顶点的面积为8的的平行四边形(要求所作的平行四边形各顶点都在格点上).21.(10分)如图,在平面直角坐标系中,抛物线y=﹣x2+x+6与x轴交于点A,B两点,B点在点A的右边,与y轴交于点C,点P是x轴上方抛物线上的一点,点D坐标为(0,2).(1)求线段AB的长度;(2)如图,以BD,BP为边作▱DBPE,当抛物线的对称轴恰好经过▱DBPE对称中心时,求点P的坐标,并说明此时点E是否在抛物线上.22.(10分)如图,Rt△ABC中,∠C=90°,点O在边AB上,以O点为圆心、OB为半径作圆,分别与BC、AB相交于点D、E,连接AD,AD是⊙O的切线.(1)求证:∠CAD=∠B;(2)若BC=4,tan B=,求⊙O半径.23.(10分)某校计划采购凳子,商场有A、B两种型号的凳子出售,并规定:对于A型凳子,采购数量若超过250张,则超出部分可在原价基础上每张优惠a元;B型凳子的售价为40元/张.学校经测算,若购买300张A型凳子需要花费14250元;若购买500张A 型凳子需要花费21250元.(1)求a的值;(2)学校要采购A、B两种型号凳子共900张,且购买A型凳子不少于150张且不超过B型凳子数量的2倍,请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少?最少是多少元?24.(14分)如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2,0),点D是对角线AC上一动点(不与A,C重合),连接BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.(1)填空:B的坐标为;(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式,并求出y的最小值.(4)如图2,若点E边OC上,EF与BC相交于点G,连接BE及DG,BE和DG相交于点H,若BH=3HE,记△GEC的面积为S1,△BGF的面积为S2,请直接写出的值.2020年浙江省温州市鹿城区中考数学二模试卷参考答案与试题解析一、选择题(共10小题,每小题4分,共40分):1.计算:(﹣2)+3的结果是()A.﹣5B.﹣1C.1D.5【分析】根据有理数的加法法则:绝对值不等的异号两数相加,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0.【解答】解:(﹣2)+3=3﹣2=1故选:C.2.我国第六次全国人口普查总数约为1340000000人,用科学记数法表示为()A.13.4×108B.1.34×109C.1.34×108D.1.34×107【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:1340000000=1.34×109,故选:B.3.如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是()A.B.C.D.【分析】根据主视图是从正面看得到的视图,可得答案.【解答】解:从正面看下面是一个比较长的矩形,上面是一个比较窄的矩形.故选:B.4.下列计算正确的是()A.a3+a2=2a5B.a3•a2=a6C.a3÷a2=a D.(a3)2=a9【分析】根据合并同类项法则、同底数幂的乘法法则、同底数幂的除法法则、积的乘方法则计算,判定即可.【解答】解:a3与a2不是同类项,不能合并,A错误;a3•a2=a5,B错误;a3÷a2=a,C正确;(a3)2=a6,D错误,故选:C.5.不等式组的解集是()A.x>﹣1B.x>3C.﹣1<x<3D.x<3【分析】利用不等式的性质,先求出两个不等式的解集,再求其公共解.【解答】解:,由①式得x>﹣1;由②式得x>3,所以不等式组的解集为x>3.故选:B.6.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形的定义判断,得到答案.【解答】解:A、不是轴对称图形,是中心对称图形;B、是轴对称图形,是中心对称图形;C、是轴对称图形,不是中心对称图形;D、是轴对称图形,不是中心对称图形;故选:B.7.某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如表:人数(人)1341分数(分)80859095那么这9名学生所得分数的众数和中位数分别是()A.90,90B.90,85C.90,87.5D.85,85【分析】众数是一组数据中出现次数最多的数据;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;可得答案.【解答】解:在这一组数据中90是出现次数最多的,故众数是90;排序后处于中间位置的那个数是90,那么由中位数的定义可知,这组数据的中位数是90.故选:A.8.若分式=0,则x的值是()A.±2B.2C.﹣2D.0【分析】分式的值为0时,分子等于0且分母不等于0.【解答】解:依题意得:x2﹣4=0且x﹣2≠0,解得x=﹣2.故选:C.9.在我国古代数学著作《九章算术》“勾股”章中有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何?”大意是说:如图,推开双门(AD和BC),门边缘D,C两点到门槛AB的距离为1尺(1尺=10寸),双门间的缝隙CD为2寸,那么门的宽度(两扇门的和)AB为()A.103寸B.102寸C.101寸D.100寸【分析】画出直角三角形,根据勾股定理即可得到结论.【解答】解:设OA=OB=AD=BC=r,过D作DE⊥AB于E,则DE=10,OE=CD=1,AE=r﹣1.在Rt△ADE中,AE2+DE2=AD2,即(r﹣1)2+102=r2,解得2r=101.故门的宽度(两扇门的和)AB为101寸.故选:C.10.如图,一个坡角为15°的看台横截面上看旗杆CD,在这横截面上进行测量得到以下数据:在点A和点B处测得旗杆顶端的仰角分别为60°和30°,点A离地面高度为1米,且测得点A到点B的距离为8米,则旗杆的高度为()A.25米B.24米C.23米D.26米【分析】过A作AE⊥CD于E,AF⊥BC于点F,解直角三角形即可得到结论.【解答】解:过A作AE⊥CD于E,AF⊥BC于点F,∵∠BAC=180°﹣15°﹣60°=105°,∠ABC=45°∴∠ACB=30°,∵AB=8,∴AF=BF=AB=8,∴AC=2AF=16,∵∠AEC=90°,∠ACE=30°,∴CE=AC=24,∵DE=1,∴CD=24+1=25(米),答:旗杆的高度为25米,故选:A.二、填空题(共6小题,每小题5分,共30分):11.(5分)因式分解:x2﹣4x=x(x﹣4).【分析】直接提取公因式x,进而分解因式得出即可.【解答】解:x2﹣4x=x(x﹣4).故答案为:x(x﹣4).12.(5分)一次函数y=﹣x+2的图象与y轴的交点坐标为(0,2).【分析】根据y轴上点的坐标特征把x=0代入一次函数解析式,求出对应的函数值即可得到与y轴的交点坐标.【解答】解:把x=0代入y=﹣x+2得y=2,所以一次函数y=﹣x+2的图象与y轴的交点坐标为(0,2).故答案为(0,2).13.(5分)若一个反比例函数的图象位于二、四象限,则它的解析式可能是y=﹣(写出一个即可).【分析】根据反比例函数的性质可列式子.答案不唯一,要注意符合题意,只写一个即可.【解答】解:反比例函数的图象位于二、四象限,k<0,则它的解析式可能是y=﹣.14.(5分)如图,将四边形ABCD绕顶点A顺时针旋转45°至四边形AB′C′D′的位置,若AB=16cm,则图中阴影部分的面积为32πcm2.【分析】由旋转的性质得:∠BAB'=45°,四边形AB'C'D'≌四边形ABCD,图中阴影部分的面积=四边形ABCD的面积+扇形ABB'的面积﹣四边形AB'C'D'的面积=扇形ABB'的面积,代入扇形面积公式计算即可.【解答】解:由旋转的性质得:∠BAB'=45°,四边形AB'C'D'≌四边形ABCD,则图中阴影部分的面积=四边形ABCD的面积+扇形ABB'的面积﹣四边形AB'C'D'的面积=扇形ABB'的面积==32π;故答案为:32π.15.(5分)如图,四边形OABC是一张矩形纸片,将边BC折叠,使点B落在边OA的点D 处.已知折痕CE=5,且tan∠BCD=,则CO=8.【分析】首先证明tan∠EDA=,设AE=3t,则AD=4t,再根据勾股定理表示出DE=5t,即BE=5t,所以OC=AB=8t,再证明两个相似三角形,得到CD=10t,从而在直角三角形CDE中,根据勾股定理列方程计算.【解答】解:∵四边形ABCD是矩形,∴∠B=∠O=∠A=90°,OC=AB,由翻折的性质可知,∠B=∠CDE=90°,BE=DE,∴∠BCD+∠DEB=180°,∵∠DEA+∠DEB=180°,∴∠BCD=∠DEA,∴tan∠DEA=tan∠BCD==,∴设AE=3t,则AD=4t,由勾股定理得DE=5t,∴OC=AB=AE+EB=AE+DE=8t,∵∠CDO+∠EDA=90°,∠EDA+∠AED=90°,∴∠CDO=∠AED,∴△OCD∽△ADE,∴=,∴=,∴CD=10t,在△DCE中,∵CD2+DE2=CE2,∴(10t)2+(5t)2=(5)2,解得t=1,∴OC=8,故答案为8.16.(5分)图1是一个高脚杯截面图,杯体CBD呈抛物线状(杯体厚度不计),点B是抛物线的顶点,AB=9,EF=2,点A是EF的中点,当高脚杯中装满液体时,液面CD =4,此时最大深度(液面到最低点的距离)为12,将高脚杯绕点F缓缓倾斜倒出部分液体,当∠EFH=30°时停止,此时液面为GD,则液面GD到平面l的距离是10;此时杯体内液体的最大深度为.【分析】以A为原点,直线EF为x轴,直线AB为y轴,建立平面直角坐标系,由待定系数法求得抛物线的解析式;将高脚杯绕点F倾斜后,仍以A为原点,直线EF为x轴,直线AB为y轴,建立平面直角坐标系,分别用待定系数法求得直线l的解析式和直线GD的解析式,过点M作MP⊥l于点P,用三角函数求得液面GD到平面l的距离;过抛物线最低点Q作QL∥l,再将QL的解析式与抛物线的解析式联立,得出关于x的一元二次方程,由判别式求得q,最后用三角函数求得答案.【解答】解:以A为原点,直线EF为x轴,直线AB为y轴,建立平面直角坐标系,如图:由题意得:A(0,0),B(0,9),C(﹣2,21),D(2,21),设抛物线的解析式为:y=ax2+9,将D(2,21)代入得:21=a×+9,解得:a=1,∴y=x2+9.将高脚杯绕点F倾斜后,仍以A为原点,直线EF为x轴,直线AB为y轴,建立平面直角坐标系,如图:由题意得:A(0,0),F(,0),E(﹣,0),B(0,9),C(﹣2,21),D(2,21),由题可知,直线l与x轴的夹角为30°,GD∥l,∵l经过点F(,0),且∠EFH=30°,∴设直线l的解析式为:y=x+b,将F(,0)代入,解得b=﹣1,∴y=x﹣1,又∵GD∥l,∴k GD=k l=,∴设直线GD的解析式为y=x+p,将D(2,21)代入,解得p=19,∴y=x+19,∴M(0,19),N(0,﹣1),过点M作MP⊥l于点P,∵∠EFH=30°,∠F AN=90°,∴∠ANF=60°,∴MP=MN•sin60°=[19﹣(﹣1)]×=10.过抛物线最低点Q作QL∥l,L为QL于MP的交点,设直线QL的解析式为y=x+q,由得:x2﹣x+9﹣q=0,∵只有一个交点Q,∴△=0,∴﹣4(9﹣q)=0,∴q=,∴ML=(19﹣)×sin60°=.故答案为:10,.三、解答题(共8小题,共80分):17.(10分)(1)计算:;(2)先化简,再求值:(3﹣m)(3+m)+m(m﹣4)﹣7,其中.【分析】(1)直接利用二次根式的性质、特殊角的三角函数值和幂的性质分别化简得出答案;(2)原式首先利用平方差公式以及单项式乘以多项式法则计算,然后合并同类项,把m 的值代入计算即可求出值.【解答】解:(1)原式=5+﹣(﹣1)=5+1+1=7.(2)原式=9﹣m2+m2﹣4m﹣7=﹣4m+2.当时,原式==﹣1+2=1.18.(10分)为关注学生出行安全,调查了某班学生出行方式,调查结果分为四类:A﹣骑自行车,B﹣步行,C﹣坐社区巴士,D﹣其它,并将调查结果绘制成以下两幅不完整的统计图.请你根据统计图,解答下列问题:(1)本次一共调查了多少名学生?(2)C类女生有3名,D类男生有1名,并将条形统计图补充完整.(3)若从被调查的A类和D类学生中分别随机选取一位同学进行进一步调查,请用列表法或画树状图的方法求出所选同学中恰好是一位男同学和一位女同学的概率.【分析】(1)用步行的人数除以所占的百分比即可得出调出的总人数;(2)用调查的总人数乘以所占的百分比,即可求出C类和D类的人数,从而补全统计图;(3)根据题意先画出树状图得出所以等情况数和恰好是一位男同学和一位女同学的情况数,然后根据概率公式即可得出答案.【解答】解:(1)本次调查的学生数=10÷50%=20(名);(2)C类女生数有20×25%﹣2=3名;D类男生数有20×(1﹣50%﹣25%﹣15%)﹣1=1名,条形统计图为:故答案为:3,1;(3)画树状图为:共有6种等可能的结果数,其中恰好是一位男同学和一位女同学的结果数为3种,所以所选A,D两类同学中恰好是一位男同学和一位女同学的概率是=.19.(8分)如图,在四边形ABCD中,E是AB的中点,AD∥EC,∠AED=∠B.(1)求证:△AED≌△EBC.(2)当AB=6时,求CD的长.【分析】(1)利用ASA即可证明;(2)首先证明四边形AECD是平行四边形,推出CD=AE=AB即可解决问题;【解答】(1)证明:∵AD∥EC,∴∠A=∠BEC,∵E是AB中点,∴AE=EB,∵∠AED=∠B,∴△AED≌△EBC.(2)解:∵△AED≌△EBC,∴AD=EC,∵AD∥EC,∴四边形AECD是平行四边形,∴CD=AE,∵AB=6,∴CD=AB=3.20.(8分)如图1、图2是两张形状、大小完全相同的5×5方格纸,方格纸中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.(1)在图1中画出一个以点A、B为顶点的面积为3的平行四边形(要求所作的平行四边形且各顶点都在格点上).(2)在图2中画出一个以点A、B为顶点的面积为8的的平行四边形(要求所作的平行四边形各顶点都在格点上).【分析】(1)构造底为1,高为3的平行四边形即可.(2)构造对角线分别为2,4的菱形即可.【解答】解:(1)如图1中,平行四边形ABCD即为所求.(2)如图2中,平行四边形ABCD即为所求.21.(10分)如图,在平面直角坐标系中,抛物线y=﹣x2+x+6与x轴交于点A,B两点,B点在点A的右边,与y轴交于点C,点P是x轴上方抛物线上的一点,点D坐标为(0,2).(1)求线段AB的长度;(2)如图,以BD,BP为边作▱DBPE,当抛物线的对称轴恰好经过▱DBPE对称中心时,求点P的坐标,并说明此时点E是否在抛物线上.【分析】(1)根据题意求出A、B两点坐标即可求出线段AB的长度;(2)根据抛物线的对称轴恰好经过▱DBPE对称中心即可求出点P的坐标,再根据平行四边形的性质即可求出点E的坐标,将E点横坐标代入y=﹣x2+x+6即可判断此时点E是否在抛物线上.【解答】解:(1)令y=0可得++6=0,解得x1=﹣3,x2=4,∴A(﹣3,0),B(4,0),∴AB=4﹣(﹣3)=7;(2)由题可得y=﹣x2+x+6抛物线的对称轴为x=,∴设▱DBPE的对称中心为(,a),∴P(1,6),由平移的性质可得E的坐标为(﹣3,8),∵当x=﹣3时,y=0,∴此时点E不在抛物线上.22.(10分)如图,Rt△ABC中,∠C=90°,点O在边AB上,以O点为圆心、OB为半径作圆,分别与BC、AB相交于点D、E,连接AD,AD是⊙O的切线.(1)求证:∠CAD=∠B;(2)若BC=4,tan B=,求⊙O半径.【分析】(1)连接OD,由切线的性质以及圆的半径构成的等腰三角形即可证明∠CAD =∠B;(2)设圆的半径为r,利用锐角三角函数定义求出AB的长,再利用勾股定理列出关于r 的方程,求出方程的解即可得到结果.【解答】解:(1)证明:∵AD是⊙O的切线,∴OD⊥AD,∴∠ADO=90°,∴∠ODB+∠ADC=90°,∵∠C=90°,∴∠ADC+∠DAC=90°,∴∠DAC=∠ODB,∵OD=OB,∴∠B=∠ODB,∴∠CAD=∠B;(2)设圆O的半径为r,在Rt△ABC中,AC=BC tan B=2,根据勾股定理得:AB==2,∴OA=2﹣r,在Rt△ACD中,tan∠CAD=tan B=,∴CD=AC tan∠CAD=1,根据勾股定理得:AD2=AC2+CD2=4+1=5,在Rt△ADO中,OA2=OD2+AD2,即(2﹣r)2=r2+5,解得:r=,∴⊙O半径为.23.(10分)某校计划采购凳子,商场有A、B两种型号的凳子出售,并规定:对于A型凳子,采购数量若超过250张,则超出部分可在原价基础上每张优惠a元;B型凳子的售价为40元/张.学校经测算,若购买300张A型凳子需要花费14250元;若购买500张A 型凳子需要花费21250元.(1)求a的值;(2)学校要采购A、B两种型号凳子共900张,且购买A型凳子不少于150张且不超过B型凳子数量的2倍,请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少?最少是多少元?【分析】(1)设A型凳子的售价为x张,根据题意列方程组解答即可;(2)设购买A型凳子m张,则购买B型凳子(900﹣m)张,根据题意求出m的取值范围;设总采购费用为w元,根据题意得出w与m的函数关系式,再根据一次函数的性质解答即可.【解答】解:(1)设A型凳子的售价为x元/张,根据题意得,解得,答:a的值为15.(2)设购买A型凳子m张,则购买B型凳子(900﹣m)张,根据题意得,解得150≤m≤600,设总采购费用为w元,根据题意得当150≤m≤250时,w=50m+40(900﹣m)=10m+36000;当250<m≤600时,w=50×250+(50﹣15)×(m﹣250)+40(900﹣m)=﹣5m+39750,∴,当150≤m≤250时,10>0,w随m的增大而增大,m=150时,w的最小值为37500;当250<m≤600时,﹣5<0,w随m的增大而减小,m=600时,w的最小值为36750.∵37500>36750,∴购买A型凳子600张,购买B型凳子300张时总采购费用最少,最少是36750元.24.(14分)如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2,0),点D是对角线AC上一动点(不与A,C重合),连接BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.(1)填空:B的坐标为(2,2);(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;(3)设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式,并求出y的最小值.(4)如图2,若点E边OC上,EF与BC相交于点G,连接BE及DG,BE和DG相交于点H,若BH=3HE,记△GEC的面积为S1,△BGF的面积为S2,请直接写出的值.【分析】(1)求出AB、BC的长即可得出结果;(2)先推出∠ACO=30°,∠ACD=60°由△DEC是等腰三角形,分两种情况:①当E 在线段CO上时,观察图象可知,只有ED=EC,∠DCE=∠EDC=30°,推出∠DBC =∠BCD=60°,可得△DBC是等边三角形,推出DC=BC=2,即可得出结果;②当E在OC的延长线上时,只有CD=CE,∠DBC=∠DEC=∠CDE=15°,得出∠ABD=∠ADB=75°即可得出结果;(3)①先表示出DN,BM,证出△BMD∽△DNE,即可得出结论;②作DH⊥AB于H,用x表示BD、DE的长,构建二次函数即可解决问题.【解答】解:(1)∵四边形AOCB是矩形,∴BC=OA=2,OC=AB=2,∠BCO=∠BAO=90°,∴B(2,2).故答案为(2,2).(2)存在;理由如下:∵OA=2,OC=2,∵tan∠ACO===,∴∠ACO=30°,∠ACB=60°,分两种情况:①当E在线段CO上时,△DEC是等腰三角形,观察图象可知,只有ED=EC,如图1所示:∴∠DCE=∠EDC=30°,∴∠DBC=∠BCD=60°,∴△DBC是等边三角形,∴DC=BC=2,在Rt△AOC中,∠ACO=30°,OA=2,∴AC=2AO=4,∴AD=AC﹣CD=4﹣2=2,∴当AD=2时,△DEC是等腰三角形;②当E在OC的延长线上时,△DCE是等腰三角形,只有CD=CE,∠DBC=∠DEC=∠CDE=15°,如图2所示:∴∠ABD=∠ADB=75°,∴AB=AD=2,综上所述,满足条件的AD的值为2或2.(3)过点D作MN⊥AB交AB于M,交OC于N,如图3所示:∵A(0,2)和C(2,0),∴直线AC的解析式为y=﹣x+2,设D(a,﹣a+2),∴DN=﹣a+2,BM=2﹣a,∵∠BDE=90°,∴∠BDM+∠NDE=90°,∠BDM+∠DBM=90°,∴∠DBM=∠EDN,∵∠BMD=∠DNE=90°,∴△BMD∽△DNE,∴===,在Rt△ADM中,∵AD=x,∠DAM=∠ACO=30°,∴DM=AD=x,AM===x,∴BM=2﹣x,在Rt△BDM中,BD===﹣6x+12,∴DE=BD=•,∴矩形BDEF的面积为y=•()2=x2﹣2x+4,∴y=(x﹣3)2+,∵>0,∴x=3时,y有最小值,即当点D运动到距A点的距离为3时,y有最小值.(4)如图4中,设,DE=BF=m,则BD=EF=m,∵EG∥BD,∴==3,∴EG=m,∴FG=m,∴BG===m,∵∠CGE=∠BGF,∠ECG=∠F=90°,∴△ECG∽△BFG,∴=()2=()2=.。
2020.4温州二模信息技术参考答案

2020年4月份温州市普通高中选考适应性测试技术试题参考答案及评分标准信息技术部分一、选择题(本大题共12小题,每小题2分,共24分。
在每小题给出的四个选项中,只有一个符合题目要求)二、非选择题(本大题共4小题,其中第13小题4分,第14小题8分,第15小题7分,第16小题7分,共26分)DSSDA?DSA13. (1)=(D3+F3+H3)/J3*100 (1分)或者=SUM(D3,F3,H3)/J3*100(2)品牌, 2019年累计销量或列C,列J (1分)(3)ABD (2分)(全选对得2分,漏选得1分,不选、错选不得分)14. (1)ABD (2分)(2)动画补间(1分)(3)选中“标题”图层最后1帧(或第50帧)执行“清除关键帧”操作。
或选中“标题”图层第1(2-49帧的任意一帧都行)帧执行“复制帧”操作,在最后1帧执行“粘贴帧”操作。
或者选中“标题”图层第2(3-49帧的任意一帧都行)帧,移动到第50帧(2分)(4)A (1分)(5)蜻蜓或标题(根据第(3)题答题情况给分) stop(); (2分)15. (1)3 (1分)(2)① Int(Rnd * 9) * 10 + 19 (1分)或者Int(Rnd * 9 + 1) * 10 + 9② d(i) = d(j) (2分)③ Mid(s, 1, Len(s) - 1) 或Mid(s, 1, Len(s) - 2) (1分)(3)d(k) < d(j) Or d(k) >= d(i - 1) (2分)16. (1) 1 (1分)(2)① sum + b(i) 或sum + 2 ^ (4 – i) (2分)② ans(sum - b(i) - b(j)) = 1 (2分)③ x + Val(Mid(s, i, 1)) * 2 ^ (Len(s) - i)或者x + Val(Mid(s, i, 1)) * 2 ^ (5 - i)或者 x + Val(Mid(s, Len(s) - i + 1, 1)) * 2 ^ (i - 1)或者 x + Val(Mid(s, 6 - i, 1)) * 2 ^ (i - 1)或者 x * 2 + Val(Mid(s, i, 1)) (2分)技术(选考试题)参考答案及评分标准第1页(共 1 页)。
温州市2022年4月二模考试技术试卷

温州市2022年4月二模考试技术试卷1、1学习老舍写的《我的母亲》一文,我们会由衷敬佩母亲坚忍、善良、宽容、勤俭和好客的品性,也会为儿子子欲养而亲不待的痛悔之情感动不已。
[判断题] *对(正确答案)错2、“参”字是个多音字,在“参军”“人参”“参差”三个词语中的读音各不相同。
[判断题] *对(正确答案)错3、13. 下列各句中,没有语病的一句是()[单选题] *A.我们欣赏古代诗词,应该全面了解作者的生平以及他所处的时代环境。
(正确答案) B.为了提高同学们的语文素养,我校团委今年积极开展了“读经典作品、建书香校园”。
C.通过全市上下的共同努力,让江油市交出了一份提升城乡人居环境满意的成绩单。
D.为了防止“新冠”疫情不再大规模扩散,我国各级政府都及时采取了防范措施。
4、1写说明文要根据说明对象的特点及写作目的,选用最佳的说明方法。
常见的说明方法有举例子、分类别、列数据、作比较、画图表、下定义等。
[判断题] *对(正确答案)5、1老刘庆祝生日,对好友说:“明天是我的生日,特邀请你来贵府一叙,你不会拒绝吧?”他这样表述是得体的。
[判断题] *对(正确答案)错6、1《诗经》分为风、雅、颂三类,普遍运用赋、比、兴的手法,语言以四言为主,其中不少篇章采用重章叠句的艺术形式。
[判断题] *对(正确答案)错7、下列词语中,加着重号字的注音正确的一项是()[单选题] *A、虹霓(ní)哂笑(xī)B、抽噎(yē)铿锵(kēng)(正确答案)C、茶峒(dòng)跬步(guǐ)D、残羹冷炙(zì)刮痧(shā)8、1“爱而不见”的下一句是“俟我于城隅。
”[判断题] *对(正确答案)错9、1巴金的爱情三部曲是《雾》《雨》《电》。
[判断题] *对(正确答案)错10、下列词语中,加着重号字的注音正确的一项是()[单选题] *A、将进酒(qiāng)岑夫子(chén)欢谑(xuè)馔玉(zhuàn)B、虾蟆陵(há)贾人(jiǎ)钿头(diàn)荻花(dí)C、樯橹(qiáng)酹(lèi) 凝噎(yè)兰舟催发(fà)D、郯子(tán)六艺经传(zhuàn)或不焉(fǒu)句读(dòu)(正确答案)11、“间隔”“亲密无间”的“间”读音都是“jiàn”。
温州通用技术会考模拟试题二及答案

方面着手?()①是否符合基本的科学原理 ③是否是多个问题中的主要问题A.①②④ B .①②③ ②能否确认该问题尚未得到充分解决 ④现有的技术条件能否解决这个问题C .②③④D .①②③④ 20XX 年温州市通用技术会考模拟试题 (二)(考试时间90分钟,满分100分)一、选择题(每小题只有一个正确选项,共 20题,每小题2分,共40分)1 .下列活动是科学活动而不是技术活动的是( )。
A.蒸汽机的制造 B .电视的转播 C .万有引力的发现D.桥梁的设计2、 客车的座椅旁都设有一个把手或按钮,可借此调节靠背的倾斜度,此设计主要体现了人 机关系的()。
A.健康原则 B.高效原则C.舒适原则D.安全原则3、 我们在设计制作的过程中,为了降低制作成本和制作难度,常希望使用一些“标准件” 你对“标准件”的理解是()。
A .国家给予统一标准代号的零部件 B.经国家检验合格或免检的零部件 C .全国统一价格的零部件D .已经获得专利并得到保护的零部件4、 明确问题内容之后,还需确定问题是否有价值。
判断一个问题的价值可以从以下哪几个5、 在学生台灯的设计过程中,需要对台灯的各个部件进行设计分析,你认为以下分析不合 理的是()。
A. 灯泡的主要功能在于照明,一般要选择没有频闪或频闪度较低的灯泡B. 灯罩主要起美观作用,设计时主要考虑其造型C. 支撑架主要起支撑作用,并决定台灯的高度,从而影响学生的坐姿D. 台灯开关多种功能,选择那种开关要考虑学生的需要6、 浙江图书馆计划展出某书画家的作品,为了保证书画展的社会效果和经济效益,组委会 提前制作了许多资料。
这些资料中,不属于技术图样的是( )。
A .去图书馆的交通线路图B .展览的宣传广告图 8、为使金属工件符合设计所要求的形状和粗糙度,往往需要进行挫削和检查工作面的垂直C.展馆的布置平面图D.书画家的原稿草图7、在下面给出的模具中,相应主视图的正确左视图是()。
温州市高三三项考试第二次适应性测试通用技术试卷清晰版有完整答案

温州市⾼三三项考试第⼆次适应性测试通⽤技术试卷清晰版有完整答案温州市2011届⾼三三项考试第⼆次适应性测试通⽤技术试卷本试卷分第Ⅰ卷和第Ⅱ卷两部分。
満分100分,考试时间90分钟。
请考⽣按规定⽤笔将所有试卷的答案涂、写在答题纸上。
⼀、选择题(本⼤题20⼩题,每⼩题2分,共40分。
在每⼩题给出的四个选项中,只有⼀个是符合题⽬要求的)1.图为通⽤汽车公司为未来的⼈们设计制造的⼀款双⼈座EN—V电动联⽹概念车,具有⾃动驾驶模式,在遇到障碍物或者⾏驶条件发⽣变化时能够做出迅速的调整。
微⼩的车⾝以及能旋转360度的功能,为⽤户解决交通拥堵和缺少停车空间带来的烦恼。
下列选项中不属于未来汽车发展趋势的是(C)A.动⼒来源更多地来⾃电能B.汽车更加智能化C.各类汽车体积更加微⼩D.汽车安全性能不断提⾼2.下列有关汽车及其配件的设计中,不能实现快速传递信息的是(A)A.货车后部低位防撞杆B.汽车仪表盘C.轮胎⽓压监测系统D.车⾝尾部及侧部粘帖反光条3.室外⽔龙头容易造成⾃来⽔被盗⽤、⽔龙头被⼈恶意拧开等现象。
于是有⼚商发现这⼀商机⽽设计了如图的带锁⽔龙头。
以下说法错误的是(B)A.防⽌长流⽔现象的出现体现可持续发展原则B.锁跟与钥匙相配套,体现技术规范性原则C.有效防⽌⾃来⽔被盗⽤的现象,体现实⽤原则D.为⽔龙头了增加新的功能,体现创新原则4.两个并排的插座很容易因为插头过⼤⽽⽆法同时使⽤,针对这个问题的创新设计如图所⽰。
在这个产品的设计过程中不需要收集的A.插头的形状和尺⼨B.插座的种类C.国家有关插座的设计规范D.插头的制作⼯艺5.图甲所⽰,是⼀款多功能的硬质⽊材制作的梯凳,将它的A处向上折叠180度后,并上下翻转就成了椅⼦,如图⼄所⽰。
下列对这款梯凳的评价中,不合理的是(B)A.该款梯凳通过结构上的改变,增加了使⽤功能,实现了技术创新B.该梯凳通过胶接实现功能的转变C.材料采⽤硬质⽊材,保证了⾜够的强度。
D.作为梯凳使⽤时,有较⼤的⽀撑⾯,提⾼了稳定性6.某学⽣打算利⽤铝块加⼯如右图所⽰的⼯件,要求⼯件的表⾯光滑,在划线、锉削、钻孔及锯割⼯序中,选⽤⼯具不合理的是(B)A. B. C. D.7.陈晨同学⽤⼩块铝⽚(图甲)加⼯成图⼄所⽰的零件,下列操作⽅法中不正确的是(D)甲⼄A.冲眼时,样冲顶端要对准划线的交点B.划线时,划针要紧贴导向⼯具,尽量⼀次划成C.弯折时,将该铝⽚装夹在台虎钳上操作D.钻孔时,⽤⼿紧拿铝⽚,进⾏操作8.伦敦设计师朱利安?海克斯在沙滩上散步时,看到⾃⼰脚底的受⼒点主要前脚掌和脚后跟,于是他设计了⼀双没有底板的鞋⼦(如右图所⽰)。
2020年浙江省普通高职单独考试温州市二模

2020年浙江省普通高职单独考试温州市二模《数学》试卷本试卷共三大题,全卷共4页. 满分150分,考试时间120分钟.注意事项:1. 所有试题均需在答题卷上作答,未在规定区域内答题,每错一个区域扣卷面总分1分,在试卷和草稿纸上作答无效.2. 答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题卷上.3. 选择题每小题选出答案后,用2B 铅笔把答题卷上对应题目的答案标号涂黑. 如需改动,用橡皮擦干净后,再选涂其他答案标号. 非选择题用黑色字迹的签字笔或钢笔将答案写在答题卷上.4. 在答题卷上作图,可先使用2B 铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑.一、单项选择题(本大题共20小题,1—10小题每题2分,11—20小题每题3分,共50分)(每小题列出的四个备选答案中,只有一个是符合题目要求的,错涂、多涂或未涂均不得分) 1. 设集合{13}A ,,{1357}B ,,,,则集合A M B 的集合M 有( ) A. 2个 B. 3个 C. 4个D. 8个2. 下列不等式(组)解集为{|0}x x 的是( ) A.3323x x B.20231x xC. 220x xD. |1|2x3. 在数列{}n a 中,“*13()nna a n N ”是“数列{}n a 为等差数列”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 4. 在等比数列{}n a 中,若93a ,149a ,则4a ( ) A.1 B. 1C. 1D.135. 已知平面向量(1,2)a ,(2,)b m ,且//a b ,则||a b ( )A. (1,2)B. 3C.D. 6. 下列不等式成立的是( ) A. sin 20200 B. cos20200 C. tan 20 D. cos(1)07. 如果4sin5,且α为钝角,则cos 的值为( ) A. 35 B. 35 C. 34 D. 348. 已知直线l 1:230mx my 与l 2:350x my 互相垂直,则m ( )A. 0B.32C. 6D. 0或329. 曲线C 的方程为2222(4)(4)10x y x y ,则曲线C 的离心率为( )A.43B.53C.35D.4510.已知直线a ,b 是平面α外的两条直线,若a ,且//b ,则一定有( ) A. //a bB. abC. a 与b 相交D. a 与b 异面11. 若0x ,则9x x( ) A. 有最大值6B. 有最小值6C. 有最大值6D. 有最小值612.已知函数()3x f x ,任意12x x R ,,且12x x ,则下列说法正确的是( )A. 1212[()()]()0f x f x x xB.2121()()0()f x f x x xC. 若21x x ,则21()()f x f xD. 若120x x ,则12()0f x x13.某校高一段共8个班级,现举行篮球单循环赛(即每个班级都要和其它班级各打一场),则共举行 比赛的场数为( ) A. 28AB. 18AC. 28CD. 2814.已知角α的终边过点(1,3)P ,则sin ( )A. 2B.32C.4D.1215.已知cos78a ,那么sin 66( )A. 21aB. 221aC. 212aD. 212a 16.已知直线过点(1,1)A ,(2,)B t ,(4,1)C ,则t ( ) A. 2 B. 3 C. 4 D. 517.已知圆C 过点(0,2)M ,(4,0)N ,则下列说法错误的是( ) A. 圆C 的圆心一定不在第二象限B. 圆C 可能与y 轴相切C. 圆C 可能经过原点D. 圆C 的面积可能为4π18.已知双曲线2242x y m 的实轴长为4,则m ( ) A. 1 B. 2 C. 4或2D. 1或219.曲线24yx 与直线3y kx 有公共点,则k 的取值范围为( )A. 33[,]22B. 55[,]22 C. 33(][,)22, D. 55(][,)22,20.某快递公司的省内运费计算规则如下:(1)一般按实际重量计费,当重量不超过1kg 时,计费8元,超过1kg 时,超过部分按2元/kg 计费(不足1kg 以1kg 计算);(2)当需寄快件的“体积重量”大于实际重量时按体积重量计收运费,计算方法为:运费=体积重量(kg)×4+6. 注:“体积重量”的计算公式为:物品的体积重量(kg )=最长(cm )×最宽(cm )×最高(cm )÷6000(cm 3/kg ). 现有一件货物,外包装尺寸为20cm ×30cm ×40cm ,重量为3.5kg ,由该快递公司寄到省内某城市,需付运费为( ) A. 13元 B. 14元 C. 22元 D. 24元 二、填空题(本大题共7小题,每小题4分,共28分) 21.函数1()31f x x x 的定义域为__________.22.一个袋子里有2个红球,2个绿球,2个白球,1个黑球,这7个球大小相同. 从中任取两个球, 颜色相同的概率为__________.23.等差数列{}n a 中,32a ,986a ,则其前100项的和为__________.24.已知椭圆的焦点恰为双曲线221169x y 的焦点,且椭圆的长轴长是短轴长的2倍,则椭圆的标准方程为__________.25.计算:1032020642lg 10C __________.26.函数()3sin 2f x x 的图象向右平移6个单位得到函数()g x 的图象,则函数()g x 的解析式为__________.27.已知一个正方体木箱的容积为64cm 3,则能放入该木箱的最大球的体积为__________cm 3. 三、解答题(本大题共8小题,共72分,解答应写出必要的文字说明、演算步骤) 28.(本题满分7分)(2)n x 的二项展开式中第二项的系数为16,求展开式中含3x 项的系数.29.(本题满分8分)如图所示,在△ABC 中,D 为BC 边上一点,4BD ,6AD ,210AB,60C ,求:(1)ADB 的余弦值;(4分) (2)边AC 的长.(4分)30.(本题满分9分)已知函数()cos (sin 3cos )f x x x x .(1)求(0)f ,()12f 的值;(3分)(2)求函数()f x 的最小正周期;(3分)(3)点A ,B 为该函数图象上相邻的两个最高点,点O 为坐标原点,求△ABO 的面积.(3分)31.(本题满分9分)已知圆C 的方程为2264120x y x y ,(1)求圆C 的圆心坐标和半径;(4分) (2)求过点(4,4)P 的圆的切线方程.(5分)32.(本题满分9分)如图所示,已知圆柱OO 1的底面半径为2,高为4,矩形ABCD 为圆柱轴截面,点E 为弧BC 的中点.(1)求圆柱OO 1的侧面积;(3分)(2)求二面角--E AD C 的正切值.(6分)33.(本题满分10分)已知抛物线的顶点在原点,以y 轴为对称轴,开口向下,焦点到准线的距离为4. (1)求抛物线的方程;(3分)(2)若点M ,N 在抛物线上,且点M ,N 到直线30x y 的距离均为MN 的长.(7分)34.(本题满分10分)酱油肉是温州人非常喜欢的食品,某酱油肉加工企业对历年市场行情进行了调查. 调查发现酱油肉每斤售价1y (元)与月份x (月)满足150(112,y x x 且)x N ,每斤生产成本2y (元)与月份x (月)满足221(112,8y x bx c x 且)x N ,其函数图象如图所示. (1)求b ,c 的值;(3分)(2)假定酱油肉当月生产当月销售,求每斤酱油肉的销售利润y (元)与月份x (月)之间的函数关系式;(3分)(3)在几月份生产并销售酱油肉时,每斤获得的利润最大?并求最大利润.(4分)35.(本题满分10分)已知函数()2([0,1])x f x x ,如图a 所示,点11(,0)4A ,21(,0)2A ,33(,0)4A将区间[0,1]四等分,过点1A ,2A ,3A 及4(1,0)A 作x 轴的垂线,交函数()2([0,1])x f x x 的图象分别于点1B ,2B ,3B ,4B ,以11A B ,22A B ,33A B ,44A B 为一边作四个矩形,且使每个矩形 的宽度为14,这四个矩形的面积依次记为1S ,2S ,3S ,4S . (1)求点1B ,2B ,3B 的坐标;(3分) (2)求1234S S S S 的值;(3分) (3)类似地,如图b 所示,点11(,0)A n ,22(,0)A n ,33(,0)A n,…11(,0)n n A n 将区间[0,1]进行 n 等分,过点1A ,2A ,3A ,…1n A 及(1,0)n A 作x 轴的垂线,交函数()2([0,1])x f x x 的图象分别于点1B ,2B ,3B ,…n B ,以11A B ,22A B ,33A B ,…n n A B 为一边作n 个矩形,且 使每个矩形的宽度均为1n,这n 个矩形的面积依次记为1S ,2S ,3S ,…,n S . 求 123n S S S S …的值.(4分)。
2020年4月温州市普通高中选考模拟测试通用技术试卷(温州二模含答案)
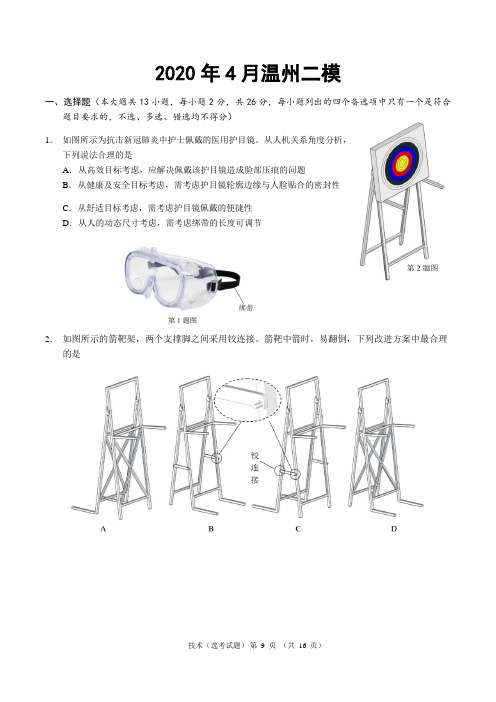
2020年4月温州二模一、选择题(本大题共13小题,每小题2分,共26分,每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.如图所示为抗击新冠肺炎中护士佩戴的医用护目镜。
从人机关系角度分析,下列说法合理的是A.从高效目标考虑,应解决佩戴该护目镜造成脸部压痕的问题B.从健康及安全目标考虑,需考虑护目镜轮廓边缘与人脸贴合的密封性C.从舒适目标考虑,需考虑护目镜佩戴的便捷性D.从人的动态尺寸考虑,需考虑绑带的长度可调节2.如图所示的箭靶架,两个支撑脚之间采用铰连接。
箭靶中箭时,易翻倒,下列改进方案中最合理的是3.如图所示是小明制作的桥梁摆件,侧板采用10mm厚的铝板,其中曲线轮廓为半径5cm的圆弧。
小明加工侧板时,从结构合理性的角度考虑,下列加工工艺及对应的工具选择不合理...的是通用技术实践课上,某小组准备制作一个垂直式夹具,用于锯割、锉削等操作。
将把手推至图1所示的状态,橡胶压头与工件直接形成挤压,起到夹紧的作用。
请完成4~5题。
4.图2是在制作底座前,绘制的平面图,圆弧与直线都相切,多标的尺寸共有A.1处B.2处C.3处D.4处5.用大小合适的材料加工该夹具时,下列有关说法合理的是A.材料可选用2.5mm厚的铝板B.将两个把手叠在一起进行锯割、钻孔、锉削和弯折,可提高加工的效率和准确度C.底座的加工可以为:划线→冲眼→钻孔→锯割→弯折→钻孔D.压头螺丝高度调好后,需拧紧上、下螺母且转动的方向相反6.如图所示的锁紧结构,水平转动手柄将工作台上的工件夹紧时,各构件主要受力形式分析合理的是A.杆1受拉、杆3受压B.杆2受弯曲、杆3受压C.杆2受弯曲、丝杠受压D.杆1受压、丝杠受拉7.如图所示是某市学校新冠肺炎疫情突发事件应急处置流程图。
下列有关说法不合理...的是A.“测量体温”与“120送医”两个环节不可同时进行B.学生家长被确诊感染新冠肺炎病毒,校园可能不需要消毒C.“联系家长”与“消息报送”属于并行环节D.该流程不包含对疑似感染的密切接触者的进一步处置措施如图所示是香梨分级自动控制系统。
