人教版八年级下册数学复习题
人教版 初中数学八年级下册 第十八章 平行四边形 复习习题 (含答案解析)
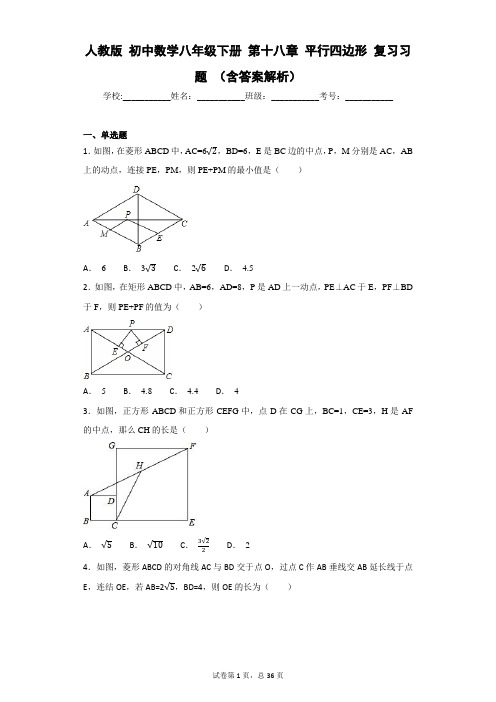
人教版初中数学八年级下册第十八章平行四边形复习习题(含答案解析)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,在菱形ABCD中,AC=6,BD=6,E是BC边的中点,P,M分别是AC,AB 上的动点,连接PE,PM,则PE+PM的最小值是()A.6B.3C.2D.4.52.如图,在矩形ABCD中,AB=6,AD=8,P是AD上一动点,PE⊥AC于E,PF⊥BD 于F,则PE+PF的值为()A.5B.4.8C.4.4D.43.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF 的中点,那么CH的长是()A.B.C.D.24.如图,菱形ABCD的对角线AC与BD交于点O,过点C作AB垂线交AB延长线于点E,连结OE,若AB=2,BD=4,则OE的长为()A.6 B.5 C.2D.45.如图,将正方形纸片ABCD折叠,使边AB,BC均落在对角线BD上,得到折痕BE,BF,则∠EBF的大小为( )A.15°B.30°C.45°D.60°6.下列命题正确的是()A.对角线相等的四边形是平行四边形B.对角线相等的四边形是矩形C.对角线互相垂直的平行四边形是菱形D.对角线互相垂直且相等的四边形是正方形7.如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD 是平行四边形的条件是()A.OA=OC,AD∥BC B.∠ABC=∠ADC,AD∥BCC.AB=DC,AD=BC D.∠ABD=∠ADB,∠BAO=∠DCO8.如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于()A.B.C.D.9.(题文)(2018•徐州一模)如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是()A.AE=CF B.BE=DF C.∠EBF=∠FDE D.∠BED=∠BFD10.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF 一定为平行四边形的是()A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF11.如图,在▱ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF与AD 的延长线相交于点G,下面给出四个结论:①BD=BE;②∠A=∠BHE;③AB=BH;④△BCF≌△DCE.其中正确的结论是( )A.①②③B.①②④C.②③④D.①②③④12.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为()A.1B.C.4-2D.3-413.如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=BC=1,则下列结论:①∠CAD=30°②BD=③S平行四边形ABCD=AB•AC④OE=AD⑤S△APO=,正确的个数是()A.2B.3C.4D.514.如图,在中,是的中点,将沿翻折得到,连接,则线段的长等于( )A.2 B.C.D.15.如图,已知在正方形中,点、分别在、上,△是等边三角形,连接交于,给出下列结论:①;②;③垂直平分; ④.其中结论正确的共有( ).A.1个B.2个C.3个D.4个16.如图,在梯形中,,中位线与对角线交于两点,若cm, cm,则的长等于( )A.10 cm B.13 cm C.20 cm D.26 cm17.如图,在△ABC中,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当点A 在x轴上运动时,点C随之在y轴上运动.在运动过程中,点B到原点的最大距离是( )A.6B.2C.2D.2+218.如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )A.5 B.C.D.19.如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A2017的坐标是()A.(0,21008)B.(21008,21008)C.(21009,0)D.(21009,-21009)20.如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使D1AC,连接AC1,再以AC1为边作第三个菱形AC C D,使D AC;…,按此规律所作的第六个菱形的边长为()A.9B.C.27D.21.如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N,设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( ).A.6B.8C.10D.1222.已知菱形ABCD在平面直角坐标系的位置如图所示,A(1,1),B(6,1),AC点P是对角线AC上的一个动点,E(0,2),当EPD周长最小时,点P的坐标为().A.(2,2)B.(2,C.D.二、填空题23.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为_____.24.如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处, 折痕为AF,若CD=6,则AF等于__________.25.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.∠BAD=60°,AC平分∠BAD,AC=2,BN的长为_____.26.如图,在菱形OABC中,点B在x轴上,点A的标为(2,3),则点C的坐标为__.27.如图,正方形CEGF的顶点E、F在正方形ABCD的边BC、CD上,且AB=5,CE=3,连接BG、DG,则图中阴影部分的面积是_____28.如图,Rt△ABC中,∠ACB=90°,AB=6,D是AB的中点,则CD=_____.29.如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH.若OB=4,S菱形ABCD=24,则OH的长为______________.30.如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD 的中点,则PQ的的长度为________.31.如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE这些结论中正确的是_____.32.如图,正方形ABCD的边长为4,E为BC上的点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为_____.33.如图,在正方形ABCD的外侧,作等边三角形ADE. AC,BE相交于点F,则∠BFC为_______°34.如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点B落在点B′处.已知折痕EF=13,则AE的长等于_________.35.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为__.36.如图,在Rt△ABC中,∠C=90°,将△ABC绕点C顺时针旋转90°得到△A′B′C,M 、M′分别是AB、A′B′的中点,若AC=4,BC=2,则线段MM′的长为____.37.平面直角坐标系中,已知平行四边形ABCD的四个顶点坐标分别是A(a,b),B(n,2n-1),C(-a,-b),D (),则m的值是_________38.如图,在矩形ABCD中,点G在AD上,且GD=AB=1,AG=2,点E是线段BC上的一个动点(点E不与点B,C重合),连接GB,GE,将△GBE关于直线GE对称的三角形记作△GFE,当点E运动到使点F落在矩形任意一边所在的直线上时,则所有满足条件的线段BE的长是__________.39.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.40.如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为6,则GE+FH的最大值为_____.41.如图,在△ABC中,BC=AC=4,∠ACB =90°,点M是边AC的中点,点P是边AB上的动点,则PM+PC的最小值为_______.42.如图,点E、F是正方形ABCD内两点,且BE=AB,BF=DF,∠EBF=∠CBF,则∠BEF 的度数_____________.43.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D 的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是______.44.已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相交于点O.以点O 为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系.以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,A n,则点A n的坐标为____________.45.已知直角三角形ABC,∠ABC=90°,AB=3,BC=5,以AC为边向外作正方形ACEF,则这个正方形的中心O到点B的距离为______.46.如图,□ABCD中,∠A=60°,点E、F分别在边AD、DC上,DE=DF,且∠EBF=60°,若AE=2,FC=3,则EF的长度为_________________.47.如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.48.如图,在矩形ABCD中,O为AC中点,EF过点O且EF⊥AC分别交DC于点F,交AB于点E,点G是AE中点且∠AOG=30°,给出以下结论:①∠AFC=120°;②△AEF是等边三角形;③AC=3OG;④S△AOG=S△ABC其中正确的是______.(把所有正确结论的序号都选上)三、解答题49.如图,在▱ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.(1)求证:▱ABCD是菱形;(2)若AB=5,AC=6,求▱ABCD的面积.50.如图,已知□ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.(1)求证:四边形BECD是矩形;(2)连接AC,若AD=4,CD= 2,求AC的长.51.如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC 于E,F,连接BE,DF.求证:四边形BFDE是菱形.52.如图,在矩形ABCD中,E是BC上的点,AE=BC,DF⊥AE,垂足为F,连接DE.(1)求证:△ABE≌△DFA;(2)如果AD=10,AB=6,求DE的长.53.如图,在□ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.(1)求证:四边形ABEF是菱形;(2)连接CF,若∠ABC=60°,AB= 4,AF =2DF,求CF的长.54.54.如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.(1)求证:△AGE≌△BGF;(2)试判断四边形AFBE的形状,并说明理由.55.如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.56.如图,已知E、F分别是▱ABCD的边BC、AD上的点,且.求证:四边形AECF是平行四边形;若四边形AECF是菱形,且,,求BE的长.57.已知,□ABCD中∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE.求证:四边形AFCE为平行四边形.(2)如图1,求AF的长.(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P 的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为t秒,若当A、P、C、Q 四点为顶点的四边形是平行四边形时,求t的值.58.如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD 相交于点O,与BC相交于点N,连接BM、DN.求证:四边形BMDN是菱形;若,,求菱形BMDN的面积和对角线MN的长.59.如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.(1)求证:EF=DF﹣BE;(2)若△ADF的周长为,求EF的长.60.如图,在边长为4的正方形ABCD中,E是CD的中点,F是BC上的一点,且∠AEF=90°,延长AE交BC的延长线于点G.(1)求GE的长;(2)求证:AE平分∠DAF;(3)求CF的长.61.如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:的值为:(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC= .62.在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G.(1)如图,点D在线段CB上,四边形ACDE是正方形.①若点G为DE中点,求FG的长.②若DG=GF,求BC的长.(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.63.(1)问题发现如图1,△ABC和△DCE都是等边三角形,点B、D、E在同一直线上,连接AE.填空:①∠AEC的度数为;②线段AE、BD之间的数量关系为.(2)拓展探究如图2,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,点B、D、E在同一直线上,CM为△DCE中DE边上的高,连接AE.试求∠AEB的度数及判断线段CM、AE、BM之间的数量关系,并说明理由.(3)解决问题如图3,在正方形ABCD中,CD=2,点P在以AC为直径的半圆上,AP=1,①∠DPC=°;②请直接写出点D到PC的距离为.64.如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.(1)求证:D是BC的中点;(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.65.如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于点F,连接AD、CF.(1)求证:四边形ADCF是平行四边形;(2)当△ABC满足什么条件时,四边形ADCF是菱形?为什么?66.如图,中,是上一点,于点,是的中点,于点,与交于点,若,平分,连接,.(1)求证:;(2)小亮同学经过探究发现:.请你帮助小亮同学证明这一结论.(3)若,判定四边形是否为菱形,并说明理由.67.67.如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.(1)请直接写出线段AF,AE的数量关系;(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论.68.如图,在平面直角坐标系中,直线分别与轴、轴交于点、,且与直线交于点.(1)若是线段上的点,且△的面积为,求直线的函数表达式.()在()的条件下,设是射线上的点,在平面内是否存在点,使以、、、为顶点的四边形是菱形?若存在,直接写出点的坐标,若不存在,请说明理由.69.如图,AB为⊙O的直径,点E在⊙O上,过点E的切线与AB的延长线交于点D,连接BE,过点O作BE的平行线,交⊙O于点F,交切线于点C,连接AC(1)求证:AC是⊙O的切线;(2)连接EF,当∠D=°时,四边形FOBE是菱形.70.如图,正方形ABCD的边长为,点P为对角线BD上一动点,点E在射线BC上,(1)填空:BD=______;(2)若BE=t,连结PE、PC,求PE+PC的最小值(用含t的代数式表示);(3)若点E是直线AP与射线BC的交点,当△PCE为等腰三角形时,求∠PEC的度数.71.如图①,在正方形ABCD中,P是对角线BD上的一点,点E在CD的延长线上,且 C E,PE交AD于点F.求证: A C;求 A E的度数;如图②,把正方形ABCD改为菱形ABCD,其它条件不变,当 ABC,连接AE,试探究线段AE与线段PC的数量关系,并给予证明.72.如图:在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连结CD,BE,(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由(2)在(1)的条件下,当∠A=时四边形BECD是正方形.73.如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.(1)求证:AE=DF;(2)当四边形BFDE是矩形时,求t的值;(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.×74.已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD 于点E、F,连接BD、EF.(1)求证:BD、EF互相平分;(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.75.如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,M,N分别是BC,DE的中点.求证:MN⊥DE(提示:连接ME,MD).76.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图1,求证:矩形DEFG是正方形;(2)若AB=2,CE=,求CG的长度;(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.77.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD 边于点E,F.(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.78.定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180°时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.特例感知:(1)在图2,图3中,△ABC与△DAE互为“顶补三角形”,AM,AN是“顶心距”.①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;②如图3,当∠BAC=120°,BC=6时,AN的长为.猜想论证:(2)在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明.拓展应用(3)如图4,在四边形ABCD,AD=AB,CD=BC,∠B=90°,∠A=60°,CD=2,在四边形ABCD的内部是否存在点P,使得△PAD与△PBC互为“顶补等腰三角形”?若存在,请给予证明,并求△PBC的“顶心距”的长;若不存在,请说明理由.79.问题提出(1)如图1,将直角三角板的直角顶点P放在正方形ABCD的对角线AC上,一条直角边经过点B,另一条直角边交边DC于点E,线段PB和线段PE相等吗?请证明;问题探究(2)如图2,移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由;问题解决(3)继续移动三角板,使三角板的直角顶点P在对角线AC上,一条直角边经过点B,另一条直角边交DC的延长线于点E,(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.80.在直角梯形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm。
人教版 八年级数学下册 18.1 ---18.2复习题(含答案)
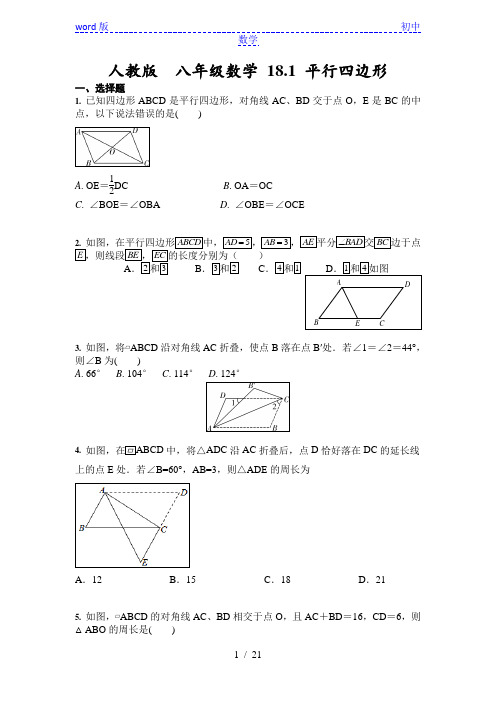
人教版八年级数学18.1 平行四边形一、选择题1. 已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是()A. OE=12DC B. OA=OCC. ∠BOE=∠OBAD. ∠OBE=∠OCE2. 如图,在平行四边形ABCD中,5AD=,3AB=,AE平分BAD∠交BC边于点E,则线段BE,EC的长度分别为()A.2和3B.3和2C.4和1D.1和4如图DCEBA3. 如图,将▱ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为()A. 66°B. 104°C. 114°4. 如图,在ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为A.12 B.15 C.18 D.215. 如图,▱ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是()A . 10B . 14C . 20D . 226. 点A 、B 、C 、D 在同一平面内,从①AB CD ∥,②AB CD =,③BC AD ∥,④BC AD =.这四个条件中任选两个,能使四边形ABCD 是平行四边形的选法有( )种A .3B .4C .5D .67. 在平行四边形ABCD 中,点1A 、2A 、3A 、4A 和1C 、2C 、3C 、4C 分别为AB 和CD 的五等分点,点1B 、2B 和1D 、2D 分别是BC 和DA 的三等分点,已知四边形4242A B C D 的面积为1,则平行四边形ABCD 面积为( )A .2B .35C .53D .158. 如图,D 是△ABC内一点,BD ⊥CD ,AD=7,BD=4,CD=3,E 、F 、G 、H分别是AB 、BD 、CD 、AC 的中点,则四边形EFGH 的周长为A .12B .14C .24D .219.已知四边形的四条边长分别a b c d ,,,其a b ,对边,并且满足222222a b c d ab cd +++=+)A .任意四边形B .平行四边形C .对角线相等的四边形D .对角线垂直的四边形10.(2020·P 是面积为S 的ABCD 内任意一点,PAD ∆的面积为1S,PBC∆的面积为2S,则()A.122SS S+> B.122SS S+<C.212SS S+= D.21S S+的大小与P点位置有关二、填空题11. 如图,在平行四边ABCD中,120A∠=︒,则D∠=︒.EAB C图图1DCBA如图,在平行四边形ABCD中,DB DC=,65A∠=︒,CE BD⊥于E,则BCE∠=︒.EEAB C图AB CD图2D13. 如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件________(写一个即可),使四边形ABCD是平行四边形.14. (2020·凉山州)如图,平行四边形ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E.若OA=1,△AOE的周长等于5,则平行四边形ABCD的周长等于.OE DCBA15. 如图,已知等边三角形的边长为10,P是ABC∆内一点,PD AC∥,PE AB PF BC∥,∥,点D E F,,分别在AB BC AC,,上,则PD PE PF++=P FEDCBA16. 如图,在▱ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=52°,∠DAE=20°,则∠FED′的大小为________.三、解答题17. 如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.(1)求证:四边形ACDF是平行四边形;(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.18. (2020·淮安)如图,在□ABCD中,点E、F分别在BC、AD上,AC与EF 相交于点O,且AO=CO.(1)求证∶△AOF≌△COE;(2)连接AE、CF,则四边形AECF_______________(填"是"或"不是")平行四边形.19. 如图,在等腰ABC∆中,延长边AB 到点D ,延长边CA 到点E ,连接DE ,恰有AD BC CE DE ===.求证:100BAC ∠=︒.EDCB A20. 如图,在ABC ∆中,AB AC AD BC =⊥,于D ,点P 在BC 上, PE BC ⊥交BA 的延长线于E ,交AC KHF FABCD EPPE D C BA21. 如图所示,在平行四边形ABCD 中,求证222222AC BD AB BC CD DA +=+++.DCBA人教版 八年级数学 18.1 平行四边形 培优训练-答案一、选择题1. 【答案】D 【解析】A 、B 、C 均正确,因为OB 不一定等于OC ,所以∠OBE 不一定等于∠OCE .2. 【答案】B3. 【答案】C 【解析】设∠ACD =x ,∠B =y ,则根据题意可列方程组⎩⎨⎧x +y +44°=180°180°-y -(44°-x )=44°,解得y =114°.4. 【答案】C【解析】由折叠可得,∠ACD=∠ACE=90°,∴∠BAC=90°, 又∵∠B=60°,∴∠ACB=30°,∴BC=2AB=6,∴AD=6, 由折叠可得,∠E=∠D=∠B=60°, ∴∠DAE=60°,∴△ADE 是等边三角形, ∴△ADE 的周长为6×3=18, 故选C .5. 【答案】B【解析】∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD .由AC +BD =16可得OA +OB =8,又∵AB =CD =6,∴△ABO 的周长为OA +OB +AB =8+6=14.6. 【答案】B7. 【答案】C8. 【答案】A【解析】∵BD ⊥CD ,BD=4,CD=3, ∴BC=2222=43BD CD ++=5,∵E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点, ∴EH=FG=12BC ,EF=GH=12AD , ∴四边形EFGH 的周长=EH+GH+FG+EF=AD+BC , 又∵AD=7,∴四边形EFGH 的周长=7+5=12.故选A .9. 【答案】B10. 【答案】C然后使分割后的图形与PAD∆的面积1S ,PBC ∆的面积2S 发生关联,然后求出其数量关系,如下图,过点P 作AD 的平行线,分别交ABCD 的边于点M 、N :2111(21222)AMND MbCN AMND MbCN SS S S S S S =+++==.11. 【答案】60︒12. 【答案】25︒【解析】∵四边形ABCD 是平行四边形 ∴65A DCB ∠=∠=︒ 又∵DB DC =∴65DBC DCB ∠=∠=︒,∴50CDB ∠=︒ 又∵CE BD ⊥,∴40ECD ∠=︒ ∴654025BCE ∠=︒-︒=︒.13. 【答案】AD ∥BC (答案不唯一) 【解析】根据平行四边形的判定,在已有AB ∥DC 的条件下,可再加另一组对边平行即可证得它是平行四边形,即加“AD ∥BC”.14. 【答案】16【解析】∵四边形ABCD 是平行四边形,∴OA =OC ,AB =CD ,AD =BC .∵OE ∥AB ,∴OE 是△ACD 的中位线.∴AE,OE.∵OA =1,△AOE 的周长等于5,∴AE +OE =4.∴AD +8ABCD 的周长=16.故答案为16.15.16. 【答案】36° 【解析】∵在▱ABCD 中,∠D =∠B =52°,∴∠AEF =∠DAE +∠D =20°+52°=72°,∴∠AED =180°-∠AEF =108°,由折叠的性质得,∠AED ′=∠AED =108°,∴∠FED ′=∠AED′-∠AEF =108°-72°=36°.三、解答题17. 【答案】解:(1)证明:∵四边形ABCD 是矩形, ∴AB ∥CD ,∴∠F AE=∠CDE , ∵E 是AD 的中点,∴AE=DE ,又∵∠FEA=∠CED ,∴△F AE ≌△CDE ,∴CD=F A , 又∵CD ∥AF ,∴四边形ACDF 是平行四边形. (2)BC=2CD.理由:∵CF 平分∠BCD ,∴∠DCE=45°, ∵∠CDE=90°,∴△CDE 是等腰直角三角形, ∴CD=DE ,∵E 是AD 的中点,∴AD=2CD , ∵AD=BC ,∴BC=2CD.18. 【答案】(1)∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠FAO=∠ECO , 中∴△AOF和△COE(ASA).(2)由(1)△AOF和△COE,∴OF=OE,又∵OA=OC,∴四边形AEOF为平行四边形.19.20. 【答案】分析:加倍中线构造平行四边形,然后再通过等量线段证明原式成立。
人教版数学八年级下册19.1---19.3考点复习题(含答案)

人教版数学八年级下册19.1《函数》一、选择题1.如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )A.凌晨4时气温最低为-3 ℃B.14时气温最高为8 ℃C.从0时至14时,气温随时间增长而上升D.从14时至24时,气温随时间增长而下降2.小丽的父亲饭后去散步,从家中走20分钟到离家1000米的报亭看了10分钟的报纸后,用15分钟返回家里,下列各图中表示小丽父亲离家的时间与距离之间的关系是()3.某人骑自行车沿直线旅行,先前进了akm,休息了一段时间后又按原路返回bkm(b<a),再前进ckm,则此人离出发点的距离s与时间t的关系示意图是()4.小明家所在学校离家距离为2千米,某天他放学后骑自行车回家,行使了5分钟后,因故停留10分钟,继续骑了5分钟到家、下面哪一个图象能大致描述他回家过程中离学校的距离S(千米)与所用时间t(分)之间的关系()5.随着移动互联网的快速发展,OFO、摩拜等互联网共享单车应运而生并快速发展.小冬骑的摩拜单车,爸爸骑的摩托车,沿相同路线由A地到B地,行驶过程中路程y和时间x的函数关系的图象如图,根据图象分析,何时俩人相遇,谁先到( )A.4分钟时相遇,爸爸先到B.20分钟时相遇,爸爸先到C.4分时相遇,小冬先到D.20分钟时相遇,小冬先到.6.向最大容量为60升的热水器内注水,每分钟注水10升,注水2分钟后停止注水1分钟,然后继续注水,直至注满.则能反映注水量与注水时间函数关系的图象是( )7.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是()A.小明中途休息用了20分钟B.小明休息前爬山的速度为每分钟60米C.小明在上述过程中所走路程为7200米D.小明休息前后爬山的平均速度相等8.小亮同学骑车上学,路上要经过平路、下坡、上坡和平路(如图),若小亮上坡、平路、下坡的速度分别为v1,v2,v3,v1<v2<v3,则小亮同学骑车上学时,离家的路程s与所用时间t 的函数关系图象可能是()9.如图,李老师早晨出门锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是()10.一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程随时间变化的图象如图所示,下列结论错误的是( )A.轮船的速度为20千米/小时B.快艇的速度为错误!未找到引用源。
数学 八年级下册 人教版 二次根式 单元复习(+答案)

第十六章单元复习二次根式一、选择题1.(青海海东模拟)下列的式子一定是二次根式的是( ) A.-x-2B.x C.x2+2D.x2-22.(新疆和田质检)要使x+12有意义,则x的取值范围为( )A.x>0 B.x≥-1 C.x<0 D.x>-13.(内蒙古包头模拟)下列二次根式中,为最简二次根式的是( )A.45B.a2+b2C.12D. 3.64.(重庆中考)计算14×7-2的结果是( )A.7 B.62C.72D.275.(恩施中考)从2,-3,-2这三个实数中任选两数相乘,所有积中小于2的有________个.( )A.0 B.1 C.2 D.36.(河北中考)与32-22-12结果相同的是( )A.3-2+1 B.3+2-1 C.3+2+1 D.3-2-17.(甘肃定西模拟)实数a在数轴上的位置如图所示,则(a-5)2+(a-13)2化简后为( )A.8 B.-8 C.2a-18 D.无法确定8.设a=7+2,则( )A.2<a<3 B.3<a<4C.4<a<5 D.5<a<69.(宁夏石嘴山模拟)若x为实数,在“(3+1)□x”的“□”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则x不可能是( )A.3+1 B.3-1 C.23D.1-310.(兰州模拟)甲、乙两人计算a+1-2a+a2的值,当a=5的时候得到不同的答案,甲的解答是a+1-2a+a2=a+(1-a)2=a+1-a=1;乙的解答是a+1-2a+a2=a+(a-1)2=a+a-1=2a-1=9.下列判断正确的是( )A.甲、乙都对B.甲、乙都错C.甲对,乙错D.甲错,乙对二、填空题11.(衡阳中考)若二次根式x-3有意义,则x的取值范围是____.12.(内蒙古乌兰察布模拟)2-5 的倒数是__ __.13.若两个连续整数x ,y 满足x <5 +1<y ,则x +y 的值是 __ __.14.(荆州中考)已知:a =(12 )-1+(-3 )0,b =(3 +2 )(3 -2 ),则a +b =____.15.(青海玉树模拟)计算:(12 -43 )×3 =__ __.16.当x =__ __时,2x -5 有最小值.17.(安徽中考)埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰三角形.底面正方形的边长与侧面等腰三角形底边上的高的比值是5 -1,它介于整数n 和n +1之间,则n 的值是__ __. 18.(新疆阿勒泰模拟)若|1 001-a |+a -1 002 =a ,则a -1 0012=__ __ __.三、解答题19.(1)(上海中考)计算:912 +|1-2 |-2-1×8 .(2) (仙桃中考)计算:(3-2 )0×4-(23 -6)+3-8 +12 .20.(宁夏中考)先化简,再求值:(a +1a +2 +1a -2 )÷2a 2-4,其中a =2 .21. (甘肃嘉峪关模拟)已知长方形的长为a ,宽为b ,且a =32 12 ,b =1248 .(1)求长方形的周长;(2)当S 长方形=S 正方形时,求正方形的周长.22.已知a ,b ,c 满足|a -8 |+b -5 +(c -3 2 )2=0.(1)求a ,b ,c 的值.(2)试问以a ,b ,c 为边能否构成三角形?如果能构成,请求出三角形的周长,如果不能,请说明理由.23.(乌鲁木齐模拟)观察、思考、解答:( 2 -1)2=( 2 )2-2×1×2 +12=2-2 2 +1=3-2 2 , 反之3-2 2 =2-2 2 +1=( 2 -1)2. ∴3-2 2 =( 2 -1)2,∴3-2 2 = 2 -1.(1) 仿上例,化简:6-2 5 .(2)若a +2b =m +n ,则m ,n 与a ,b 的关系是什么?并说明理由.(3)已知x =4-12 ,求⎝ ⎛⎭⎪⎫1x -2+1x +2 ·x 2-42(x -1)的值(结果保留根号).第十六章单元复习二次根式一、选择题1.(青海海东模拟)下列的式子一定是二次根式的是(C) A.-x-2B.x C.x2+2D.x2-22.(新疆和田质检)要使x+12有意义,则x的取值范围为(B)A.x>0 B.x≥-1 C.x<0 D.x>-13.(内蒙古包头模拟)下列二次根式中,为最简二次根式的是(B)A.45B.a2+b2C.12D. 3.64.(重庆中考)计算14×7-2的结果是(B)A.7 B.62C.72D.275.(恩施中考)从2,-3,-2这三个实数中任选两数相乘,所有积中小于2的有________个.(C)A.0 B.1 C.2 D.36.(河北中考)与32-22-12结果相同的是(A)A.3-2+1 B.3+2-1 C.3+2+1 D.3-2-17.(甘肃定西模拟)实数a在数轴上的位置如图所示,则(a-5)2+(a-13)2化简后为(A)A.8 B.-8 C.2a-18 D.无法确定8.设a=7+2,则(C)A.2<a<3 B.3<a<4C.4<a<5 D.5<a<69.(宁夏石嘴山模拟)若x为实数,在“(3+1)□x”的“□”中添上一种运算符号(在“+,-,×,÷”中选择)后,其运算的结果为有理数,则x不可能是(C)A.3+1 B.3-1 C.23D.1-310.(兰州模拟)甲、乙两人计算a+1-2a+a2的值,当a=5的时候得到不同的答案,甲的解答是a+1-2a+a2=a+(1-a)2=a+1-a=1;乙的解答是a+1-2a+a2=a+(a-1)2=a+a-1=2a-1=9.下列判断正确的是(D)A.甲、乙都对B.甲、乙都错C.甲对,乙错D.甲错,乙对二、填空题11.(衡阳中考)若二次根式x -3 有意义,则x 的取值范围是__x ≥3__.12.(内蒙古乌兰察布模拟)2-5 的倒数是.13.若两个连续整数x ,y 满足x <5 +1<y ,则x +y 的值是 __7__.14.(荆州中考)已知:a =(12 )-1+(-3 )0,b =(3 +2 )(3 -2 ),则a +b =__2__.15.(青海玉树模拟)计算:(12 -43 )×3 =__4__.16.当x =__52 __时,2x -5 有最小值.17.(安徽中考)埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰三角形.底面正方形的边长与侧面等腰三角形底边上的高的比值是5 -1,它介于整数n 和n +1之间,则n 的值是__1__. 18.(新疆阿勒泰模拟)若|1 001-a |+a -1 002 =a ,则a -1 0012=__1__002__.三、解答题19.(1)(上海中考)计算:912 +|1-2 |-2-1×8 .(2)(仙桃中考)计算:(3-2 )0×4-(23 -6)+3-8 +12 .【解析】(1)原式=912 +2 -1-12 ×22 =912 +2 -1-2 =812 .(2)原式=1×4-23 +6-2+23 =4-23 +6-2+23 =8. 20.(宁夏中考)先化简,再求值:(a +1a +2 +1a -2 )÷2a 2-4 ,其中a =2 .【解析】原式=(a +1)(a -2)+a +2a 2-4 ·a 2-42 =a 2-a -2+a +22 =a 22 , 当a =2 时,原式=(2)22=1.21. (甘肃嘉峪关模拟)已知长方形的长为a ,宽为b ,且a =32 12 ,b =12 48 .(1)求长方形的周长;(2)当S 长方形=S 正方形时,求正方形的周长.【解析】(1)∵a =32 12 =3 3 ,b =12 48 =23 ,∴长方形的周长是:2(a +b )=2(3 3 +2 3 )=10 3 . (2)设正方形的边长为x ,则有x 2=ab , ∴x =ab =33×2 3 =18 =3 2 ,∴正方形的周长是4x =12 2 . 22.已知a ,b ,c 满足|a -8 |+b -5 +(c -3 2 )2=0.(1)求a ,b ,c 的值.(2)试问以a ,b ,c 为边能否构成三角形?如果能构成,请求出三角形的周长,如果不能,请说明理由.【解析】(1)根据题意得,a -8 =0,b -5=0,c -3 2 =0, 解得a =2 2 ,b =5,c =3 2 .(2)∵2 2 +3 2 >5,即a +c >b ,∴能构成三角形, ∴C △ABC =2 2 +3 2 +5=5 2 +5. 23.(乌鲁木齐模拟)观察、思考、解答:( 2 -1)2=( 2 )2-2×1×2 +12=2-2 2 +1=3-2 2 , 反之3-2 2 =2-2 2 +1=( 2 -1)2. ∴3-2 2 =( 2 -1)2,∴3-2 2 = 2 -1.(1)仿上例,化简:6-2 5 .(2)若a +2b =m +n ,则m ,n 与a ,b 的关系是什么?并说明理由.(3)已知x =4-12 ,求⎝ ⎛⎭⎪⎫1x -2+1x +2 ·x 2-42(x -1) 的值(结果保留根号).【解析】(1)6-2 5 =5-25+1 =(5-1)2 = 5 -1.(2)a =m +n ,b =mn ,理由:∵a +2 b =m +n , ∴a +2 b =m +2mn +n ,∴a =m +n ,b =mn ;(3)∵x =4-12 =3-23+1 =(3-1)2 = 3 -1,∴⎝ ⎛⎭⎪⎫1x -2+1x +2 ·x 2-42(x -1) =x +2+x -2(x -2)(x +2) ·(x -2)(x +2)2(x -1) =2x (x -2)(x +2) ·(x -2)(x +2)2(x -1) =x x -1. 当x = 3 -1时,原式=3-13-1-1 =3-13-2 =(3-1)(3+2)(3-2)(3+2)=-1- 3 .。
人教版初中八年级数学下册第十六章《二次根式》复习题(含答案解析)(2)

一、选择题1.下列是最简二次根式的是( )A B CD2.已知x+y =﹣5,xy =4,则 ) A .4 B .﹣4 C .2 D .﹣23. ) A .1 B .2 C .3 D .4 4.下列二次根式中是最简二次根式的是( )A BC D 5.下列计算正确的是( ). A .()()22a b a b b a +-=- B .224x y xy +=C .()235a a -=-D .=6.下列计算正确的是( )A 2=±B .22423x x x +=C .()326328a b a b -=-D .()235x x x -=÷ 7.下列算式中,正确的是( )A .3=B =C =D 4= 8.下列各式中,错误的是( )A .2(3=B .3=-C .23=D 3=- 9.下列四个数中,是负数的是( )A .2-B .2(2)-C . D10.已知y 3,则x y 的值为( ). A .43 B .43- C .34D .34- 11.下列各式不是最简二次根式的是( )A B C D12.估计- )A .0到1之间B .1到2之间C .2到3之间D .3到4之间 13.下列二次根式:4、12、50、12中与2是同类二次根式的个数为( ) A .1个 B .2个 C .3个 D .4个14.下列运算正确的是( ) A .628+= B .66-= C .623÷= D .()266-=15.计算-23的结果是( )A .-3B .3C .-9D .9二、填空题16.计算1248⨯的结果是________________.17.若53x =-,则()234x +-的值为__________.18.实数a ,b 在数轴上的位置如图所示,化简:|a +1|﹣22(1)()b a b -+-=_____.19.若224y x x =--,则y x 的平方根是__________.20.)3750a b b >=________.21.2210(15)=_____818+=______.22.已知a 、b 为有理数,m 、n 分别表示5721amn bn +=,则3a b +=_________.23.若最简二次根式132-+b a 与a b -4是同类二次根式,则a+b =___. 24.已知223y x x =--,则()x x y +的值为_________.25.使式子32xx -+有意义的x 的取值范围是______.26.220x y -=,则x y +=________.三、解答题27.先阅读,后回答问题:x ()x x 3-解:要使该二次根式有意义,需x(x-3)≥0,由乘法法则得030? x x ≥⎧⎨-≥⎩或0 30x x ≤⎧⎨-≤⎩,解得x 3≥或x 0≤,即当x 3≥或x 0≤体会解题思想后,解答:x 28.计算: (1)1301(2)(2)53π-⎛⎫+-⨯-+ ⎪⎝⎭;(2)21)-++-.29.计算:20201|1-30.计算(1)2)。
【3套】人教版八年级下册数学第十八章平行四边形复习题(含答案)

人教版八年级下册数学第十八章平行四边形复习题(含答案)一、选择题1.如图,在□ ABCD中,已知∠ ODA= 90°, AC= 10cm, BD= 6cm,则 BC的长为()A. 4cmB. 5cmC. 6cmD. 8cm2.如图,在平行四边形ABCD中,连结对角线AC、BD,图中的全等三角形的对数()A. 1 对B. 对2C. 对3D. 对43.正方形的一条对角线长为 2 厘米,则正方形的面积(A. 2B. 3C. 4D.4.如图,矩形ABCD 的对角线AC、 BD 订交于点O, CE∥ BD, DE∥ AC,若 AC=4,则四边形CODE的周长()A. 4B. 6C. 8D. 105.如图,将△ABC沿 BC 方向平移获得△DCE,连结AD,以下条件中能够判断四边形ACED为菱形的是 ( )A. AB= BC B∠. ACB= 60°C∠. B= 60° D. AC= BC6.如图,在菱形 ABCD中,∠ ABC=60°,AB=1,E为 BC的中点,则对角线BD 上的动点P 到 E、C 两点的距离之和的最小值为()A. B. C. D.7.八个边长为 1 的正方形如图摆放在平面直角坐标系中,经过P 点的一条直线l 将这八个正方形分红面积相等的两部分,则该直线l 的分析式为()A. B. y=x+C. D.8.如图,在正方形 ABCD中, E,F 分别为 AD,CD 的中点, BF 与 CE订交于点 H,直线 EN 交CB 的延伸线于点 N,作 CM⊥ EN 于点 M ,交 BF 于点 G,且 CM=CD,有以下结论:① BF ⊥CE;② ED=EM ;③ tan ∠ ENC=;④S 四边形DEHF=4S△CHF,此中正确结论的个数为()A. 1 个B. 个2C. 个3D. 个49.如图,在正方形ABCD中,△BPC是等边三角形,BP、 CP的延伸线分别交AD 于点 E、 F,连结 BD、DP,BD 与 CF 订交于点H,给出以下结论:①BE=2AE;②△DFP∽△ BPH;③△PFD ∽△ PDB;④DP 2=PH?PC此中正确的选项是()A. ①②③④B. ②③C. ①②④D.①③④10.如图, ?ABCD中, AB=4,BC=6,AC 的垂直均分线交 AD 于点 E,则△CDE的周长是()A. 6B. 8C. 10D. 1211.如图,△ABC 周长为 1,连结△ABC 三边中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,以此类推,第2016 个三角形的周长为()A. 22016B. 22017C.D.12.如图,将边长为2cm 的菱形ABCD 沿边AB 所在的直线l 翻折获得四边形ABEF,若∠DAB=30°,则四边形CDFE的面积为()A. 2cm 2222B. 3cmC. 4cmD. 6cm13.如图,已知正方形ABCD边长为 1,连结 AC、BD,CE均分∠ ACD交 BD 于点 E,则 DE长为()A. 2-2B.-1C.-1D. 2-14.如图,P 为正方形 ABCD的对角线 BD 上任一点,过点 P 作 PE⊥ BC于点 E,PF⊥ CD 于点 F,连结 EF.给出以下 4 个结论:① △FPD是等腰直角三角形;②AP=EF;③AD=PD ;④∠ PFE=∠BAP.此中,全部正确的结论是()A. ①②B. ①④C. ①②④D. ①③④二、填空题15.在平行四边形ABCD中,∠ B=100°,则∠ A=________,∠ D= ________16.如图,已知△ABC 的三个极点的坐标分别为A(﹣ 2, 0),B(﹣ 1, 2), C( 2, 0).请直接写出以A, B, C 为极点的平行四边形的第四个极点 D 的坐标 ________17.如图,在 ?ABCD中, DE 均分∠ ADC, AD=6, BE=2,则 ?ABCD的周长是 ________.18.如图,平行四边形ABCD 中, AF、 CE分别是∠ BAD 和∠ BCD 的角均分线,依据现有的图形,请增添一个条件,使四边形AECF为菱形,则增添的一个条件能够是________ .(只要写出一个即可,图中不可以再增添其余“点”和“线”)19.如图,平行四边形的四个内角均分线订交,如能构成四边形,则这个四边形是________20.如图,正方形 ABCD被分红两个小正方形和两个长方形,假如两个小正方形的面积分别是18cm2和 10cm2,那么两个长方形的面积和为________cm 2.21.如图,在矩形ABCD中, AB=2,AD=4,点E是BC边上一个动点,连结AE,作 DF⊥AE 于点 F,当 BE的长为 ________时,△CDF是等腰三角形.三、解答题22.如图,四边形ABCD是平行四边形,E、 F 是对角线AC 上的两点,∠ 1=∠ 2.(1)求证: AE=CF;(2)求证:四边形 EBFD是平行四边形.F, G 是 EF 的中点,连结CG.求证:① △ABM≌△ CBM;②CG⊥CM.24.如图,在矩形ABCD中, M 、N 分别是 AD、BC 的中点, P、 Q 分别是 BM、 DN 的中点.(1)求证:△MBA≌△ NDC;(2)求证:四边形 MPNQ 是菱形.25.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D, AN 是△ABC 外角∠ CAM 的平分线, CE⊥ AN,垂足为点E,(1)求证:四边形 ADCE为矩形;(2)当△ABC知足什么条件时,四边形ADCE是一个正方形?并给出证明.26.如图,矩形 OABC的边 OA 在 x 轴正半轴上,边 OC在 y 轴正半轴上, B 点的坐标为(1,3).矩形 O′ A′是BC矩′形 OABC绕 B 点逆时针旋转获得的.O′点恰幸亏x 轴的正半轴上,O′ C′交 AB 于点 D.(1)求点 O′的坐标,并判断△O′DB的形状(要说明原因)(2)求边 C′O所′在直线的分析式.(3)延伸 BA 到 M 使 AM=1,在( 2)中求得的直线上能否存在点P,使得△POM 是以线段OM 为直角边的直角三角形?若存在,请直接写出P 点的坐标;若不存在,请说明原因.参照答案一、选择题1. A2.D3. A4.C5. D6. C7.B8.D9. C10. C11. D12. C13. C14. C二、填空题15.80 ;°100 °16.( 3,2 ),(﹣ 5,2),( 1,﹣ 2)17.2018.AC⊥ EF19.矩形20.21.2 或 2或 4﹣ 2三、解答题22.( 1)证明:如图:∵四边形ABCD是平行四边形,∴AD=BC, AD∥ BC,∠ 3=∠4,∵∠ 1=∠ 3+∠5,∠ 2=∠4+∠ 6,∠ 1=∠ 2∴∠ 5=∠ 6∵在△ADE 与△CBF中,∴△ ADE≌△ CBF( ASA),∴A E=CF(2)证明:∵∠ 1=∠ 2,∴DE∥BF.又∵由( 1)知△ADE≌△ CBF,∴DE=BF,∴四边形 EBFD是平行四边形.23.证明:① ∵四边形ABCD是正方形,∴A B=CB,∠ ABM=∠ CBM,在△ABM 和△CBM 中,,∴△ ABM≌△ CBM( SAS),② ∵△ ABM≌△ CBM,∴∠ BAM=∠ BCM,∵∠ ECF=90°, G 是 EF的中点,∴GC=GF,∴∠ GCF=∠F,又∵ AB∥ DF,∴∠ BAM=∠ F,∴∠ BCM=∠ GCF,∴∠ BCM+∠ GCE=∠ GCF+∠ GCE=90°,∴GC⊥ CM.24.( 1)证明:∵四边形 ABCD是矩形,∴AB=CD, AD=BC,∠ A=∠ C=90°,∵在矩形 ABCD中, M、 N 分别是 AD、 BC的中点,∴AM=AD, CN=BC,∴AM=CN,在△MAB 和△NDC中,∵,∴△ MBA≌△ NDC( SAS)(2)证明:四边形 MPNQ 是菱形.原因以下:连结 AP, MN ,则四边形 ABNM 是矩形,∵AN 和 BM 相互均分,则A,P,N 在同一条直线上,易证:△ABN≌△ BAM,∴AN=BM ,∵△ MAB≌△ NDC,∴BM=DN,∵P、 Q 分别是 BM、 DN 的中点,∴PM=NQ,∵,∴△ MQD≌△ NPB( SAS).∴四边形MPNQ 是平行四边形,∵M 是 AD 中点, Q 是 DN 中点,∴MQ=AN,∴MQ=BM,∵MP=BM,∴MP=MQ ,∴平行四边形MQNP 是菱形.25.(1)证明:在△ABC中, AB=AC, AD⊥ BC,∴∠ BAD=∠ DAC,∵AN 是△ABC外角∠ CAM 的均分线,∴∠ MAE=∠ CAE,∴∠ DAE=∠ DAC+∠CAE=180°=90°,又∵ AD⊥ BC,CE⊥AN,∴∠ ADC=∠ CEA=90°,∴四边形ADCE为矩形(2)当△ABC知足∠ BAC=90°时,四边形ADCE是一个正方形.原因:∵ AB=AC,∴∠ ACB=∠ B=45°,∵AD⊥ BC,∴∠ CAD=∠ ACD=45°,∴DC=AD,∵四边形ADCE为矩形,∴矩形 ADCE是正方形.∴当∠ BAC=90°时,四边形ADCE是一个正方形26.(1)解:如图,连结OB, O′B,则 OB=O′B,∵四边形OABC是矩形,∴AO=AO′,∵B 点的坐标为( 1, 3),∴O A=1,∴A O′=1,∴点 O′的坐标是( 2,0 ),△O′ DB为等腰三角形,原因以下:在△BC′D与△O′AD中,,∴△ BC′D≌△ O′AD(AAS),∴BD=O′D,∴△ O′DB是等腰三角形(2)解:设点 D 的坐标为( 1, a),则 AD=a,∵点 B 的坐标是( 1, 3),∴O′D=3﹣ a,222在 Rt△ADO′中, AD +AO′=O′D,∴a2+12=( 3﹣ a)2,解得 a=,∴点 D 的坐标为( 1,),设直线 C′O的′分析式为y=kx+b,则,解得,∴边 C′O所′在直线的分析式:y=﹣x+(3)解:∵ AM=1, AO=1,且 AM⊥AO,∴△ AOM 是等腰直角三角形,① PM 是另向来角边时,∠ PMA=45°,∴P A=AM=1,点P 与点O′重合,∴点 P 的坐标是( 2, 0),② PO 是另向来角边,∠ POA=45°,则 PO 所在的直线为 y=x,∴,解得,∴点 P 的坐标为P( 2, 0)或(,).人教版八年级数学下单元测试题:第十八章平行四边形一、填空题 (每题 3 分,共 24 分 )1.如图, ?ABCD 中, AC,BD 订交于点O,若 AD = 6,AC+BD = 16,则△BOC 的周长为________.2.如图,四边形ABCD 是对角线相互垂直的四边形,且OB= OD ,请你增添一个适合的条件____________,使四边形 ABCD 成为菱形 (只要增添一个即可 ).3.若以A(- 0.5, 0), B(2, 0), C(0, 1)三点为极点画平行四边形,则第四个极点不行能在第________象限.4.如图,在平面直角坐标系中,菱形OABC 的极点 B 的坐标为 (8, 4),则 C 点的坐标为________.5.如图, BD 为正方形ABCD 的对角线, BE 均分∠ DBC,交 DC 于点 E,延伸 BC 到 F ,使CF= CE,连结 DF .若 CE= 1 cm,则 BF= __________ .6.矩形 ABCD 中, AB= 3, AD= 4, P 是 AD 上一动点, PE⊥ AC 于 E, PF⊥ BD 于 F,则PE+ PF 的值为 ________.7.以正方形ABCD 的 AD 作等三角形ADE,∠ BEC 的度数是 __________.8.如,在 1 的菱形 ABCD 中,∠ DAB = 60°.接角AC,以 AC 作第二个菱形 ACEF ,使∠ FAC= 60°.接 AE,再以 AE 作第三个菱形AEGH ,使∠ HAE =60°⋯⋯按此律所作的第n 个菱形的是________.二、 (每 3 分,共 30 分 )9.如,在 ?ABCD 中,已知 AC= 4 cm,若△ACD 的周13 cm, ?ABCD 的周 ()A . 26 cm B. 24 cm C. 20 cm D. 18 cm10.如, ?ABCD 中,角AC ,BD 交于点 O,点 E 是 BC 的中点.若O E =3 cm,AB 的 ()A . 12 cm B. 9 cm C. 6 cm D. 3 cm11.以下四条件中,不可以判断四形ABCD 是平行四形的是()A . AB= DC , AD= BC B. AB∥ DC , AD∥ BCC.AB ∥DC , AD= BC D.AB ∥DC , AB= DC12.如,在平行四形ABCD 中,已知∠ ODA = 90°,AC =10 cm , BD = 6 cm, AD 的()13.如图,在菱形ABCD 中,∠ B= 60°,AB= 4,则以 AC 为一边的正方形ACEF 的周长为()A . 14B. 15C. 16D. 1714.以下说法中,正确的个数有()①对顶角相等;②两直线平行,同旁内角相等;③对角线相互垂直的四边形为菱形;④对角线相互垂直均分且相等的四边形为正方形.A . 1 个B. 2 个C. 3 个D. 4 个15.如图,已知在菱形ABCD 中,对角线AC 与 BD 交于点 O,∠ BAD = 120 °,AC =4,则该菱形的面积是()A . 16 3B . 16C. 8 3D. 816.用尺规在一个平行四边形内作菱形ABCD ,以下作法中错误的选项是()17.如图,在矩形ABCD 中, AD =3AB,点 G, H 分别在 AD,BC 上,连结BG,DH ,且AG=()时,四边形 BHDG 为菱形.BG∥ DH ,当AD4B.343A. 55 C.9 D.818.如图,在 ?ABCD 中, CD = 2AD, BE⊥ AD 于点 E,F 为 DC 的中点,连结EF ,BF ,以下结论:①∠ ABC= 2∠ ABF;② EF = BF;③ S 四边形DEBC= 2S△EFB;④∠ CFE = 3∠ DEF ,此中正确的结论有 ()A . 1 个B . 2 个C.3 个 D . 4 个三、解答题 (19 题 8 分, 20~ 22 题每题 10 分,其余每题14 分,共 66 分 )19.如图,在 ?ABCD 中,点 E, F 分别在边CB, AD 的延伸线上,且BE= DF , EF 分别与AB, CD 交于点 G,H .求证 AG =CH.20.如图,正方形 ABCD 中,E 是 BC 上的一点,连结 AE,过 B 点作 BH ⊥ AE,垂足为点 H ,延伸 BH 交 CD 于点 F,连结 AF .(1)求证 AE= BF;(2)若正方形的边长是5, BE= 2,求 AF 的长.21.如图,矩形A BCD 中, E 是 AD 的中点,连结CE 并延伸与BA 的延伸线交于点F,连接AC、 DF .(1)求证:四边形ACDF 是平行四边形;(2)当 CF 均分∠ BCD 时,写出BC 与 CD 的数目关系,并说明原因.22.在△ABC 中, AD 是 BC 边上的中线, E 是 AD 的中点,过点 A 作 BC 的平行线交BE 的延伸线于点F,连结 CF .(1)求证 AF= DC ;(2)若 AB⊥ AC,试判断四边形ADCF 的形状,并证明你的结论.23.如图,△ABC 中,∠ ACB= 90°, D 为 AB 的中点,四边形BCED 为平行四边形,DE ,AC 订交于 F .连结 DC, AE.(1)试确立四边形ADCE 的形状,并说明原因.(2)若 AB= 16, AC= 12,求四边形ADCE 的面积.(3)当△ABC 知足什么条件时,四边形ADCE 为正方形?请赐予证明.24.我们给出以下定义:按序连结随意一个四边形各边中点所得的四边形叫做中点四边形.(1)如图①,在四边形ABCD 中,点 E,F , G,H 分别为边 AB, BC,CD , DA 的中点,求证:中点四边形 EFGH 是平行四边形;(2)如图②,点 P 是四边形 ABCD 内一点,且知足点E,F , G, H 分别为边 AB, BC, CD ,DA PA= PB,PC= PD,∠ APB =∠ CPD ,的中点,判断中点四边形 EFGH 的形状,并说明原因;(3)若改变 (2) 中的条件,使∠APB=∠ CPD= 90°,其余条件不变,直接写出中点四边形EFGH 的形状 (不用证明 ).答案一、 1.142.OA=OC(答案不独一)3.三4.(3,4)5.(2+2) cm126.57.30°或150°8.(3)n-1二、 9-18: DCCAC BCCCD三、 19.证明:∵四边形ABCD是平行四边形,∴AD= BC,AD∥ BC,∠ A=∠ C.∴∠ F=∠ E.∵BE= DF,∴AD+ DF= CB+BE,即 AF=CE.在△AGF和△CHE中,∠ A=∠ C,AF= CE,∠ F=∠ E,∴△ AGF≌△ CHE(ASA).∴AG= CH.20.(1)证明:∵四边形ABCD是正方形,∴AB= BC,∠ ABE=∠ BCF= 90°.∴∠ BAE+∠ AEB= 90°.∵BH⊥ AE,∴∠ BHE=90°.∴∠ AEB+∠ EBH= 90°.∴∠ BAE=∠ EBH.在△ABE 和△BCF中,∠BAE=∠ CBF,AB= BC,∠ABE=∠ BCF,∴△ABE≌△BCF(ASA).∴AE= BF.∴BE= CF.∵正方形的边长是5, BE= 2,∴DF= CD- CF= CD- BE= 5- 2=3.在Rt△ADF 中,由勾股定理得: AF= AD2+ DF2= 52+ 32= 34. 21.(1)证明:∵四边形ABCD是矩形,∴AB∥ CD.∴∠ FAE=∠ CDE.∵E 是 AD 的中点,∴ AE= DE.又∵∠ FEA=∠ CED,∴△ FAE≌△ CDE(ASA).∴CD= FA.又∵ CD∥ FA,∴四边形 ACDF是平行四边形.(2)解: BC= 2CD.原因以下:∵CF均分∠BCD,∴∠ DCE= 45°.∵∠ CDE= 90°,∴△ CDE是等腰直角三角形.∴CD=DE.∵E是AD 的中点,∴ AD= 2DE.∴AD= 2CD.∵AD= BC,∴ BC= 2CD.22.(1)证明:∵AF∥BC,∴∠ AFE=∠ DBE.∵E 是 AD 的中点,∴ AE= DE.在△AFE 和△DBE 中,∠AFE=∠ DBE,∠FEA=∠ BED,AE= DE,∴△ AFE≌△ DBE(AAS).∴A F=BD.∵AD 是 BC边上的中线,∴DC= BD.∴A F= DC.(2)解:四边形ADCF是菱形.证明:由 (1)得 AF=DC,又 AF∥ BC,∴四边形ADCF是平行四边形.∵ AC⊥ AB, AD 是斜边 BC 上的中线,1∴AD=2BC= DC.∴?ADCF是菱形.23.解:(1)四边形ADCE是菱形.原因:∵四边形BCED为平行四边形,∴CE∥ BD, CE= BD, BC∥ DE.∵D 为 AB 的中点,∴ AD= BD.∴CE∥ AD, CE= AD.∴四边形ADCE为平行四边形.又∵ BC∥ DF,∴∠ AFD=∠ ACB=90°,即 AC⊥ DE.∴四边形ADCE为菱形.(2)在 Rt△ABC中,∵ AB= 16, AC=12 ,∴ BC= 4 7.而 BC= DE,∴ DE=4 7.1∴四边形ADCE的面积=2AC·DE= 24 7.(3)当 AC= BC 时,四边形ADCE为正方形.证明:∵ AC= BC,D 为 AB 的中点,∴ CD⊥ AB,即∠ ADC=90°.∴菱形 ADCE为正方形.24.(1)证明:如图①,连结BD.∵点 E, H 分别为边AB, DA 的中点,1∴EH∥ BD, EH=2BD.∵点 F, G 分别为边BC,CD 的中点,1∴FG∥BD,FG=2BD.∴EH∥ FG,EH= FG.∴中点四边形EFGH是平行四边形.(2)解:中点四边形EFGH是菱形.原因:如图②,连结AC,BD.∵∠ APB=∠ CPD,∴∠ APB+∠ APD=∠ CPD+∠ APD,即∠ BPD=∠ APC.在△APC和△BPD 中,PA= PB,∠APC=∠ BPD,PC= PD,∴△ APC≌△ BPD(SAS).∴AC= BD.∵点 E, F, G 分别为边AB, BC, CD 的中点,11∴EF=2AC, FG=2BD.∴EF= FG.又由 (1)中结论知中点四边形EFGH是平行四边形,∴中点四边形EFGH是菱形.(3)解:中点四边形EFGH是正方形.人教版数学八年级下册第十八章《平行四边形》检测卷一、选择题 (每题 3 分,共 30 分 )1. 平行四边形的周长为24 cm,相邻两边的差为 2 cm,则平行四边形的各边长为()A . 4 cm, 8 cm, 4 cm, 8 cm B. 5 cm, 7 cm,5 cm, 7 cmC.5.5 cm , 6.5 cm, 5.5 cm, 6.5 cm D. 3 cm, 9 cm,3 cm, 9 cm2. 如图,在? ABCD中,AB>AD,按以下步骤作图:以点 A 为圆心,小于AD 的长为半径画弧,分别交AB,AD 于点 E,F ;再分别以点E, F 为圆心,大于12EF 的长为半径画弧,两弧交于点G;作射线AG 交 CD 于点 H ,则以下结论中不可以由条件推理得出的是()A . AG 均分∠ DAB B. AD= DHC.DH = BC D. CH = DH第 2 题第3题3.如图,在 ? ABCD 中, AB= 4,BC =6,AC 的垂直均分线交 AD 于点 E,则△ CDE 的周长是 ()A . 7B .10C. 11 D . 124. 正方形的一条对角线长为4,则这个正方形面积是()A . 8B .42C. 82D. 165.如图,? ABCD 的对角线 AC 的长为 10 cm,∠ CAB= 30°,AB 的长为 6 cm,则? ABCD 的面积为 ()A . 60 cm2B. 30 cm2C. 20 cm2D. 16 cm2第 5 题第6题6.如图, ? ABCD 的对角线 AC 与 BD 订交于点 O,AE⊥ BC,垂足为 E, AB= 3, AC=2, BD = 4,则 AE 的长为 ()3321221A.2B. 2C.7D.77. 如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB边上一动点,以PA, PC 为边作 ? PAQC,则对角线PQ 长度的最小值为 ()A . 6B. 8C. 2 2 D .4 2第 7 题第8题8.如图,在矩形 ABCD 中, E, F 分别是 AD, BC 中点,连结 AF, BE, CE, DF 分别交于点 M, N,四边形EMFN 是 ()A .正方形B.菱形C.矩形D.没法确立9. 将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD ,转动这个四边形,使它形状改变,当∠ B= 90°时,如图 1,测得 AC= 2,当∠ B= 60°时,如图 2,AC 的长是 ()A.2 B . 2 C. 6D. 22第 9 题第 10 题10.如图, ? ABCD 中, AB= 8 cm, AD= 12 cm,点 P 在 AD 边上以每秒 1 cm 的速度从点A 向点 D 运动,点 Q 在 BC 边上以每秒 4 cm 的速度从点 C 出发,在 CB 间来回运动,两个点同时出发,当点P 抵达点 D 时停止 (同时点 Q 也停止 ),在运动此后,以P, D, Q,B 四点构成平行四边形的次数有()A . 4 次B. 3 次C. 2 次D. 1 次二、填空题 (每题 3 分,共 24 分 )11. 若平行四边形中两个内角度数比为1∶ 2,则此中较大的内角是度.12. 如图,在菱形ABCD中,AC,BD订交于点O,若∠BCO=55°,则∠ADO=.第 12 题第13题13.如图, ? ABCD 与? DCFE 的周长相等,且∠ BAD = 60°,∠ F= 110 °,则∠ DAE 的度数为.14.已知直角坐标系内有四个点O(0, 0),A(3,0),B(1,1),C(x,1),若以 O, A,B,C 为极点的四边形是平行四边形,则x=.15.如图,在四边形 ABCD 中, P 是对角线 BD 的中点, E, F 分别是 AB, CD 的中点,AD =BC,∠ PEF = 18°,则∠ PFE 的度数是.第 15 题第16题16.如图,在 ? ABCD 中,对角线 AC 与 BD 交于点 E,∠ AEB= 45°,BD= 2,将△ ABC 沿 AC 所在直线翻折,若点 B 的落点记为B′,则 DB′的长为.17.如图,正方形 ABCO 的极点 C,A 分别在 x 轴、y 轴上, BC 是菱形 BDCE 的对角线,若∠ D= 60°, BC= 2,则点 D 的坐标是.第 17 题第18题18.如图,边长为 4 的正方形 ABCD,点 P 是对角线 BD 上一动点,点 E 在边 CD 上,EC= 1,则 PC+ PE 的最小值是.三、解答题 (共 66 分 )19.(8 分)如图,已知四边形 ABCD 是平行四边形,点 E, B,D , F 在同向来线上,且BE= DF .求证: AE= CF .20.(8 分 )如图,在 Rt△ABC 中,∠ C=90°,∠ B= 60°,AB = 8 cm,E,F 分别为边 AC,AB 的中点.(1)求∠ A 的度数;(2)求 EF 的长.21.(9 分)如图, ? ABCD 的对角线 AC, BD 交于点 O, EF 过点 O 且与 BC, AD 分别交于点E,F.试猜想线段 AE, CF 的关系,并说明原因.22. (9分)如图,E是? ABCD的边CD的中点,延伸AE 交 BC 的延伸线于点 F.(1)求证:△ ADE≌△ FCE;(2)若∠ BAF = 90°, BC =5, EF= 3,求 CD 的长.23. (10分)如图,在正方形ABCD 中, E 是 AB 上一点, F 是 AD 延伸线上一点,且DF =BE .(1)求证: CE= CF;(2)若点 G 在 AD 上,且∠ GCE =45°,则 GE= BE+GD 建立吗?为何?24.(10 分 )如图, ? ABCD 的对角线 AC,BD 订交于点 O,EF 过点 O 且与 AB, CD 分别订交于点 E, F ,连结 EC.(1)求证: OE=OF ;(2)若 EF ⊥ AC,△ BEC 的周长是10,求 ? ABCD 的周长.25.(12 分 )以下图,在四边形 ABCD 中, AD ∥BC ,AD= 24 cm, BC= 30 cm,点 P 从点A 向点 D 以 1 cm/ s 的速度运动,到点 D 即停止.点 Q 从点 C 向点 B 以 2 cm/ s 的速度运动,到点 B 即停止.直线PQ 将四边形ABCD 截成两个四边形,分别为四边形ABQP 和四边形 PQCD ,则当 P,Q 两点同时出发,几秒后所截得两个四边形中,此中一个四边形为平行四边形?参照答案1. B2. D3. B4. A5. B6. D7. D8. B9. A10. B11.12012.35°13.25°14.4 或- 215.18°16.217.(2+ 3, 1)18.519.证明:∵四边形 ABCD 是平行四边形,∴ AB∥ CD,AB= CD . ∴∠ ABD =∠ CDB . ∴∠ ABE =∠ CDF .AB=CD ,在△ ABE 和△CDF 中,∠ABE=∠CDF,∴△ABE≌△CDF (SAS).∴AE=CF .BE=DF ,20.解: (1)∵∠ C= 90°,∴∠ A+∠ B= 90°.∴∠ A=90°-∠ B=90°- 60°= 30°.1(2) 在 Rt△ABC 中,∠ A=30°, AB= 8 cm,∴ BC=2AB= 4 cm. ∵ E, F 分别是 AC, AB 的中1点,∴ EF 是△ ABC 的中位线.∴EF=2BC= 2 cm.21.解: AE= CF 且 AE∥ CF. 原因:∵四边形 ABCD 为平行四边形,∴ OA= OC,AD ∥ BC.∠AFO =∠CEO ,∴∠ AFO =∠ CEO.在△ AOF和△ COE中,∠AOF =∠COE ,OA=OC,∴△ AOF ≌△ COE(AAS) .∴ OF= OE. 又∵ OA= OC,∴四边形 AECF 是平行四边形.∴ AE =C F 且 AE∥ CF .22. 解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC.∴∠DAE=∠F,∠D=∠ECF .∠DAE =∠ F,∵E是CD的中点,∴ DE=CE.在△ ADE和△ FCE中,∠D=∠ECF,DE =CE,∴△ ADE ≌△ FCE (AAS) .(2) ∵△ ADE≌△ FCE ,∴ AE= EF = 3.∵AB ∥CD,∴∠ AED=∠ BAF= 90°. 在 ? ABCD 中,AD =BC= 5,∴ DE = AD 2- AE 2=52- 32= 4. ∴CD= 2DE = 8.23.解: (1) 证明:∵四边形 ABCD 是正方形,∴ BC= CD ,∠ B=∠ CDF . 又∵ BE = DF ,∴△ CBE≌△ CDF (SAS) .∴ CE= CF .(2) GE= BE + GD 建立.原因:由 (1) ,得△ CBE≌△ CDF ,∴∠ BCE =∠ DCF . ∴∠ BCE +∠ECD =∠ DCF +∠ ECD,即∠ BCD =∠ ECF = 90°. 又∵∠ GCE = 45°,∴∠ GCF=∠ GCE =45°. ∵ CE= CF ,∠ GCE=∠ GCF ,GC= GC,∴△ ECG≌△ FCG(SAS) .∴GE= GF. ∴ GE =D F + GD = BE+ GD.24.解:(1) 证明:∵四边形 ABCD 是平行四边形,∴ OD = OB,DC ∥ AB. ∴∠ FDO =∠ EBO.∠FDO =∠ EBO,在△ DFO 和△ BEO 中,OD =OB,∴△ DFO≌△ BEO(ASA).∴ OE=OF .∠FOD =∠ EOB,(2) ∵四边形ABCD 是平行四边形,∴AB=CD ,AD = BC,OA= OC. ∵ EF ⊥ AC,∴ AE= CE.∵△ BEC 的周长是 10,∴ BC+BE + CE=BC +BE+ AE=BC+ AB=10. ∴ C? ABCD= 2(BC+ AB)=20.25.略。
2022-2023学年人教版八年级下册数学期末复习综合测试题

2022-2023学年人教版八年级下学期数学期末复习综合测试题一、选择题(每小题3分,共30分)1.若二次根式√x−1有意义,则x的取值范围是()A.x≥1B.x≤1C.x>1D.x≠12.以下列长度的线段为边,能组成直角三角形的是()A.1,2,3B.32,42,52C.√3,√4,√5D.5,12,13 3.下列说法中正确的个数为()①对角线互相平分且垂直的四边形是菱形;②对角线相等且垂直的四边形是正方形;③对角线相等的菱形是正方形;④经过平行四边形对角线交点的直线平分该平行四边形的面积.A.0个B.1个C.2个D.3个4.某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是()A.150B.200m2C.250m2D.300m25.在某时段有50辆车通过一个雷达测速点,工作人员将测得的车速绘制成如图所示的条形统计图,则这50辆车的车速的众数(单位:km/h)为()A .60B .50C .40D .156.下列计算正确的是( )A .√2+√3=√5B .√9=±3C .2√2−√2=√2D .√18=2√37.若一次函数y =kx +b 的图象经过第一、二、三象限,则k 、b 的取值范围是( )A .k >0,b >0B .k >0,b <0C .k <0,b <0D .k <0,b >08.两张全等的矩形纸片ABCD 、AECF 按如图方式交叉叠放在一起.若AB =AF =2,AE =BC =6,则图中重叠(阴影)部分的面积为( )A .163B .203C .4√3D .89.如图,在四边形ABCD 中,E ,F 分别是AD ,BC 的中点,G ,H 分别是BD ,AC 的中点,AB =CD ,∠ABD =20°,∠BDC =70°,则∠GEF 的大小是( )A .25°B .30°C .45°D .35°10.如图,在平面直角坐标系中,点A 1,A 2,A 3,…和B 1,B 2,B 3,…分别在直线y =12x +b和x 轴上,四边形OB 1A 1C 1、B 1B 2A 2C 2、B 2B 3A 3C 3、…都是正方形.如果点A 1(1,1),那么点A 2022的纵坐标是( )A.无法确定B.22021C.22022D.22023二、填空题(每小题3分,共18分)11.化简(√3)2=;√(−5)2=;√27=.12.本学期小伟同学报名参加了学校书法社团用活动班,他的7次考评成绩分别为90,85,85,95,85,100,90,那么小伟同学考评成绩的众数为.13.已知一次函数的图象经过(1,0)且与直线y=﹣4x+3平行,则该一次函数解析式是.14.(3分)如图,在菱形ABCD中,AC、BD交于点O,AC=4,E为AD边中点,菱形ABCD 的面积为4√5,则OE的长为.15.如图,已知直线y=mx+n交x轴于点A(4,0),直线y=ax+b交x轴于点B(﹣3,0),且两直线交于点C(﹣2,3),则不等式0<mx+n<ax+b的解集为.16.如图,在矩形ABCD中点E为AD上一点,将△CDE沿CE翻折至△CFE,EF交AB 于G点,且GA=GF,若CD=10,BC=6,则AE的值是.三、解答题(共8小题,共72分)17.(8分)(1)计算:√18+√12−2√6×√34÷5√2;(2)已知一次函数的图象经过点(2,6)和(﹣4,﹣9),求这个函数的解析式.18.(8分)如图,四边形ABCD中,AB=CD,AD=BC,对角线AC,BD相交于点O,且OA=OD.求证:四边形ABCD是矩形.19.(8分)如图,已知四边形ABCD的对角线AC、BD交于点O,AO=OC,OB=OD且∠1=∠2.(1)求证:四边形ABCD是菱形;(2)E为AO上一点,连接BE,若AE=4,AB=6,EB=2√3,求AO的长.20.(8分)为落实“双减”政策,加强“五项管理”,某校建立了作业时长调控制度,以及时采取措施调控作业量,保证初中生每天作业时长控制在90分钟之内.该校就“每天完成作业时长”的情况随机调查了本校部分初中学生,并根据调查结果制成了如下不完整的统计图,其中分组情况是:A组:t≤0.5h,B组:0.5h<t≤1h,C组:1h<t≤1.5h,D 组:t>1.5h.请根据以上信息解答下列问题:(1)这次共抽取了名学生进行调查统计;(2)请补全条形统计图;(3)扇形统计图中C组所在扇形的圆心角的大小是;(4)若该约有2000名初中学生,请估计每天完成作业时长在90分钟之内的初中生人数.21.(10分)如图,是由边长为1的小正方形构成6×6的网格,每个小正方形的顶点叫格点,A、B、D是格点,E是AD与网格线的交点,仅用无刻度直尺在给定的网格中画图,画图过程用虚线,画图结果用实线表示.(1)直接写出图中AE的长=;(2)在图①中画出等腰Rt△EBG,使∠EBG=90°;(3)在图②中先平移线段AB至DC(A对应D,B对应C),再在线段DC上画一点H;使得EH=AE+CH.22.(10分)如图,直线y=x+9与直线y=﹣2x﹣3交于点C,它们与y轴分别交于A、B 两点.(1)求A、B、C三点的坐标;(2)点F在x轴上,使S△BFC=10,求点F的坐标;(3)点P在x轴上,使∠PBO+∠P AO=90°,直接写出点P的坐标.23.(10分)某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)求每台A型电脑和B型电脑的销售利润;(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.①求y关于x的函数关系式;②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.24.(10分)正方形ABCD的边长为4.(1)如图1,点E在AB上,连接DE,作AF⊥DE于点F,CG⊥DE于点G.①求证:DF=CG;②如图2,对角线AC,BD交于点O,连接OF,若AE=3,求OF的长;(2)如图3,点K在CB的延长线上,BK=2,点N在BC的延长线上,CN=4,点P在BC上,连接AP,在AP的右侧作PQ⊥AP,PQ=AP,连接KQ.点P从点B沿BN方向运动,当点P运动到BC中点时,设KQ的中点为M1,当点P运动到N点时,设KQ的中点为M2,直接写出M1M2的长为.。
新人教版八年级数学(下册)期末复习题及答案

新人教版八年级数学(下册)期末复习题及答案 班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.将直线23y x =-向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )A .24y x =-B .24y x =+C .22y x =+D .22y x =-2.下列各数中,313.14159 8 0.131131113 25 7π-⋅⋅⋅--,,,,,,无理数的个数有( )A .1个B .2个C .3个D .4个3.对于函数y =2x ﹣1,下列说法正确的是( )A .它的图象过点(1,0)B .y 值随着x 值增大而减小C .它的图象经过第二象限D .当x >1时,y >04.如图,在四边形ABCD 中,∠A=140°,∠D=90°,OB 平分∠ABC ,OC 平分∠BCD ,则∠BOC=( )A .105°B .115°C .125°D .135°5.某旅店一共70个房间,大房间每间住8个人,小房间每间住6个人,一共480个学生刚好住满,设大房间有x 个,小房间有y 个.下列方程正确的是( )A .7086480x y x y +=⎧⎨+=⎩B .7068480x y x y +=⎧⎨+=⎩C .4806870x y x y +=⎧⎨+=⎩D .4808670x y x y +=⎧⎨+=⎩6.如果2a a 2a 1-+,那么a 的取值范围是( )A .a 0=B .a 1=C .a 1≤D .a=0a=1或715 )A.点P B.点Q C.点M D.点N8.如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为()A.90°B.60°C.45°D.30°9.如图所示,下列推理及括号中所注明的推理依据错误的是()A.∵∠1=∠3,∴AB∥CD(内错角相等,两直线平行)B.∵AB∥CD,∴∠1=∠3(两直线平行,内错角相等)C.∵AD∥BC,∴∠BAD+∠ABC=180°(两直线平行,同旁内角互补)D.∵∠DAM=∠CBM,∴AB∥CD(两直线平行,同位角相等)10.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD二、填空题(本大题共6小题,每小题3分,共18分)1.分解因式:29a-=__________.21a+8a=__________.3x2-x的取值范围是________.4.如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式组22{20x m xx+----<<的解集为________.5.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= _________度。
人教版初中八年级数学下册第十六章《二次根式》经典复习题(含答案解析)

一、选择题1.下列是最简二次根式的是( )A B CD2.下列说法:①带根号的数是无理数;③实数与数轴上的点是一一对应的关系;④两个无理数的和一定是无理数;⑤已知a =2b =2a 、b 是互为倒数.其中错误的个数有( )A .1个B .2个C .3个D .4个3.下列计算正确的是( )A =±B .=C =D 2=4.x 的取值范围为( )A .x 2≥B .x 2≠C .x 2>D .x 2<5.的结果估计在( ) A .10到11之间 B .9到10之间C .8到9之间D .7到8之间 6.当x在实数范围内有意义( ) A .1x > B .1≥x C .1x < D .1x ≤7.x 的取值范围是( )A .x <1B .x >1C .x≥1D .x≤18.( )A .B .C .D .无法确定 9.下列式子中无意义的是( )A .B .C .D . 10.下列算式中,正确的是( )A .3=B =C =D 4=11.下列计算正确的是( )A . 3B .1122+=C.3=D312.)A.1个B.2个C.3个D.4个13.下列各式中,一定是二次根式的个数为()10),232a a a⎫+<⎪⎭A.3个B.4个C.5个D.6个14.n为().A.2 B.3 C.4 D.515.)0a<得()A B.C D.二、填空题16.3+=__________.17.化简题中,有四个同学的解法如下:========他们的解法,正确的是___________.(填序号)18.________________.19.已知b>0=_____.20.23()a-=______(a≠0),2-=______,1-=______.21.如图,在长方形内有两个相邻的正方形A,B,正方形A的面积为2,正方形B的面积为6,则图中阴影部分的面积是__________.22.已知5ab =,则b a a b=__. 23.比较大小:310524.已知223y x x =--,则()x x y +的值为_________. 25.已知8817y x x =--,则x y +的平方根为_________.26.(1031352931643-⎛⎫++= ⎪⎝⎭__________. 三、解答题27.计算:(183(26)27+(211513(1)(0.5)2674÷; (3)52311x y x y +=⎧⎨+=⎩; (4)4(2)153123x y y x +=-⎧⎪+⎨=-⎪⎩. 28.(1232;(2)计算:122729.计算(1)3222(2333 30.计算:(11850(2)73)(73)。
人教版数学八年级下册期末综合培优复习题(四)(含答案)

期末综合培优复习题(四)一.选择题(每题3分,满分36分)1.下列一定是二次根式的是()A.B.C.D.2.直线y=3x+1向下平移2个单位,所得直线的解析式是()A.y=3x+3 B.y=3x﹣2 C.y=3x+2 D.y=3x﹣13.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度()A.保持不变B.逐渐变小C.先变大,再变小D.逐渐变大4.已知n是一个正整数,是整数,则n的最小值是()A.3 B.5 C.15 D.455.有下列说法:①有一个角为60°的等腰三角形是等边三角形;②三边分别是1,,3的三角形是直角三角形;③直角三角形斜边上的中线等于斜边的一半;④三个角之比为3:4:5的三角形是直角三角形,其中正确的有()A.1个B.2个C.3个D.4个6.若a=1﹣,b=1+,则代数式的值为()A.2B.﹣2C.2 D.﹣27.有20个班级参加了校园文化艺术节感恩歌咏大赛,他们的成绩各不相同,其中李明同学在知道自己成绩的情况下,要判断自己能否进入前十名,还需要知道这十个班级成绩的()A.平均数B.加权平均数C.众数D.中位数8.已知直线y=x+b和y=ax﹣3交于点P(2,1),则关于x,y的方程组的解是()A.B.C.D.9.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是()A.1 B.2018 C.2019 D.202010.在菱形ABCD中,∠ADC=120°,点E关于∠A的平分线的对称点为F,点F关于∠B的平分线的对称点为G,连结EG.若AE=1,AB=4,则EG=()A.2B.2C.3D.11.如图所示的图象(折线ABCDE)描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)与行驶时间t(时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了140千米;②汽车在行驶途中停留了1小时;③汽车在整个行驶过程中的平均速度为30千米/时;④汽车出发后6小时至9小时之间行驶的速度在逐渐减小.其中正确的说法共有()A.1个B.2个C.3个D.4个二.填空题(每题3分,满分18分)13.若点A (2,y 1),B (﹣1,y 2)都在直线y =﹣2x +1上,则y 1与y 2的大小关系是 . 14.使二次根式有意义的x 的取值范围是 .15.某公司招聘员工一名,某应聘者进行了三项素质测试,其中创新能力为70分,综合知识为80分,语言表达为90分,如果将这三项成绩按5:3:2计入总成绩,则他的总成绩为 分.16.已知一次函数y =kx ﹣3的图象与x 轴的交点坐标为(x 0,0),且2≤x 0≤3,则k 的取值范围是 .17.在平行四边形ABCD 中,连接AC ,∠CAD =40°,△ABC 为钝角等腰三角形,则∠ADC 的度数为 度.18.如图,过点N (0,﹣1)的直线y =kx +b 与图中的四边形ABCD 有不少于两个交点,其中A (2,3)、B (1,1)、C (4,1)、D (4,3),则k 的取值范围 .三.解答题 19.(6分)计算 (1)(3﹣2+)÷2 (2)×﹣(+)(﹣)20.已知一次函数y =(2m +1)x +3﹣m(1)若y 随x 的增大而减小,求m 的取值范围; (2)若图象经过第一、二、三象限,求m 的取值范围.21.(8分)为弘扬泰山文化,我市某校举办了“泰山诗文大赛”活动,小学、初中部根据初赛成绩,各选出5名选手组成小学代表队和初中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如下图所示.(1)根据图示填写图表;平均数(分)中位数(分)众数(分)小学部85初中部85 100 (2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.22.(6分)如图,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13.求BC的长.23.(8分)如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB =2∠OAD.(1)求证:四边形ABCD是矩形;(2)若∠AOB:∠ODC=4:3,求∠ADO的度数.24.(6分)已知y+m与x﹣n成正比例,(1)试说明:y是x的一次函数;(2)若x=2时,y=3;x=1时,y=﹣5,求函数关系式;(3)将(2)中所得的函数图象平移,使它过点(2,﹣1),求平移后的直线的解析式.25.(9分)为迎接“五一”国际劳动节,某商场计划购进甲、乙两种品牌的T恤衫共100件,已知乙品牌每件的进价比甲品牌每件的进价贵30元,且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.(1)求甲、乙两种品牌每件的进价分别是多少元?(2)商场决定甲品牌以每件50元出售,乙品牌以每件100元出售.为满足市场需求,购进甲种品牌的数量不少于乙种品牌数量的4倍,请你确定获利最大的进货方案,并求出最大利润.参考答案一.选择题1. A .2. D .3. A .4. B .5. C .6. A .7. D .8. B .9. D 10. B .11. A . 二.填空题 13. y 1<y 2. 14. x ≤2. 15. 77. 16. 1≤k ≤. 17. 100或40. 18. <k ≤2. 三.解答题19.解:(1)原式=(9﹣+4)÷2=12÷2=6; (2)原式=﹣(5﹣3)=3﹣2 =1.20.解:(1)由2m +1<0,可得m <﹣, ∴当m <﹣时,y 随着x 的增大而减小; (2)由,可得﹣<m <3, ∴当﹣<m <3时,函数图象经过第一、二、三象限.21.解:(1)填表:小学部平均数 85( 分),众数85(分);初中部中位数 80( 分). 故答案为85,85,80.(2)小学部成绩好些.因为两个队的平均数都相同,小学部的中位数高,所以在平均数相同的情况下中位数高的小学部成绩好些.(3)∵=[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,,∴,因此,小学代表队选手成绩较为稳定.22.解:∵AD⊥BC,∴∠ADB=∠ADC=90°,∵AB=15,AD=12,AC=13,∴BD===9,CD===5,∴BC=BD+CD=9+5=14.23.(1)证明:∵AO=OC,BO=OD,∴四边形ABCD是平行四边形,∵∠AOB=∠DAO+∠ADO=2∠OAD,∴∠DAO=∠ADO,∴AO=DO,∴AC=BD,∴四边形ABCD是矩形;(2)解:∵四边形ABCD是矩形,∴AB∥CD,∴∠ABO=∠CDO,∵∠AOB:∠ODC=4:3,∴∠AOB:∠ABO=4:3,∴∠BAO:∠AOB:∠ABO=3:4:3,∴∠ABO=54°,∵∠BAD=90°,∴∠ADO=90°﹣54°=36°.24.解:(1)已知y+m与x﹣n成正比例,设y+m=k(x﹣n),(k≠0),y=kx﹣kn﹣m,因为k≠0,所以y是x的一次函数;(2)设函数关系式为y=kx+b,因为x=2时,y=3;x=1时,y=﹣5,所以2k+b=3,k+b=﹣5,解得k=8,b=﹣13,所以函数关系式为y=8x﹣13;(3)设平移后的直线的解析式为y=ax+c,由题意可知a=8,且经过点(2,﹣1),可有2×8+c=﹣1,c=﹣17,平移后的直线的解析式为y=8x﹣17.25.解:(1)设甲品牌每件的进价为x元,则乙品牌每件的进价为(x+30)元,,解得,x=30经检验,x=30是原分式方程的解,∴x+30=60,答:甲品牌每件的进价为30元,则乙品牌每件的进价为60元;(2)设该商场购进甲品牌T恤衫a件,则购进乙品牌T恤衫(100﹣a)件,利润为w元,∵购进甲种品牌的数量不少于乙种品牌数量的4倍,∴a≥4(100﹣a)解得,a≥80w=(50﹣30)a+(100﹣60)(100﹣a)=﹣20a+4000,∵a≥80,∴当y=80时,w取得最大值,此时w=2400元,100﹣a=20,答:获利最大的进货方案是:购进甲品牌T恤衫80件,购进乙品牌T恤衫20件,最大利润是2400元.。
人教版八年级下册数学 第17章:勾股定理 复习训练题 含答案

17.1勾股定理一.选择题1.一个直角三角形两条直角边的长分别为5,12,则其斜边上的高为()A.B.13C.6D.252.如图,以数轴的单位长线段为边做一个正方形,数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是()A.1B.1.4C.D.3.在锐角△ABC中,AB=13,AC=20,BC边上的高为12,则△ABC的面积是()A.66B.126C.120D.684.如图1,分别以直角三角形三边为边向外作正方形,面积分别为S1,S2,S3;如图2,分别以直角三角形三边长为直径向外作半圆,面积分别为S4,S5,S6.其中S1=1,S2=3,S5=2,S6=4,则S3+S4=()A.10B.9C.8D.75.如图,“赵爽弦图”由4个全等的直角三角形所围成,在Rt△ABC中,AC=b,BC=a,∠ACB=90°,若图中大正方形的面积为48,小正方形的面积为6,则(a+b)2的值为()A.60B.79C.84D.906.如图,△ABC是等边三角形,AB=4,D是AB的中点,DF⊥AC于点F,FE⊥BC于点E,则EF的长是()A.B.C.D.37.如图,这是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长是3、5、2、3,则最大正方形E的边长是()A.13B.C.47D.8.如图,Rt△ABC中,∠C=90°,AC=6,BC=8.以点A为圆心,BC的长为半径作弧交AB于点D,再分别以点A,D为圆心,以AB,AC的长为半径作弧交于点E,连接AE,DE,若点F为AE的中点,则DF的长为()A.4B.5C.6D.89.如图,在△ABC中,∠A=90°,AB=6,AC=8,∠ABC与∠ACB的平分线交于点O,过点O作OD⊥AB于点D,则AD的长为()A.B.2C.D.410.勾股定理是人类最伟大的科学发明之一.如图1,以直角三角形ABC的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大的正方形内,三个阴影部分面积分别记为S1,S2,S3,若已知S1=1,S2=2,S3=3,则两个较小正方形纸片的重叠部分(四边形DEFG)的面积为()A.5B.5.5C.5.8D.6二.填空题11.在直角三角形中,两直角边分别为6和8,则第三边上中线长是.12.如图,在△ABC中,已知AB=2,AC=4,BC=6.则△ABC的面积为.13.如图,在Rt△ABC中,∠ACB=90°,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若AB=,则图中阴影部分的面积为.14.已知,在△ABC中,∠ACB=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F是垂足,且AB=17,BC=15,则OF、OE、OD的长度分别是.15.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC、BD交于点O.若AD=2,BC=4,则AB2+CD2=.三.解答题16.如图,在△ABC中,AD⊥BC,垂足为点D,AB=13,BD=5,AC=15.(1)求AD的长;(2)求BC的长.17.两块三角板如图放置,已知∠BAC=∠ADC=90°,∠ABC=45°,∠ACD=30°,BC =6cm.(1)分别求线段AD,CD的长度;(2)求BD2的值.18.教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c),也可以表示为4×ab+(a﹣b)2,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.(2)如图③,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2,画在如图4的网格中,并标出字母a,b所表示的线段.参考答案一.选择题1.解:∵直角三角形的两条直角边的长分别为5,12,∴斜边为=13,∵S△ABC=×5×12=×13h(h为斜边上的高),∴h=.故选:A.2.解:由勾股定理得,OB==,则OA=OB=,∴点A表示的数是,故选:C.3.解:在锐角△ABC中,∵∠B为锐角时,如图所示,在Rt△ABD中,BD===5,在Rt△ADC中,CD===16,∴BC=BD+CD=21,∴△ABC的面积为×21×12=126;故选:B.4.解:如右图所示,∵S1=a2,S2=b2,S3=c2,a2+b2=c2,∴S1+S2=S3,同理可得,S5+S6=S4,∵S1=1,S2=3,S5=2,S6=4,∴S3+S4=(1+3)+(2+4)=4+6=10,故选:A.5.解:由图可知,(b﹣a)2=6,4×ab=48﹣6=42,∴2ab=42,∴(a+b)2=(b﹣a)2+4ab=6+2×42=90.故选:D.6.解:∵△ABC为等边三角形,∴AC=BC=AB=4,∠A=∠B=∠C=60°,∵D是AB的中点,∴AD=AB=2,在Rt△ADF中,∠A=60°,∴∠ADF=30°,∴AF=AD=1,∴FC=AC﹣AF=3,在Rt△CFE中,∠C=60°,∴∠CFE=30°,∴EC=FC=,∴EF==,故选:A.7.解:设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,由勾股定理得:x2=32+52=34;y2=22+32=13;z2=x2+y2=47;即最大正方形E的面积为:z2=47,边长为z=.故选:B.8.解:根据作图知,AD=BC,AE=AB,DE=AC,∴△ADE≌△BCA(SSS),∴∠ADE=∠BCA=90°,AE=AC,∵Rt△ABC中,∠C=90°,AC=6,BC=8,∴AB===10,∴AE=AB=10,∵点F为AE的中点,∴DF=AE=5,故选:B.9.解:过O作OE⊥CB,OF⊥AC,又∵∠BAC=90°,∴四边形ADOF是矩形,∵∠ABC与∠ACB的平分线交于点O,∴DO=EO=FO,∴四边形ADOF是正方形,∴AD=DO,∵∠BAC=90°,AB=6,AC=8,∴BC=10,∴S△ABC==24,连接AO,设DO=x,则FO=EO=x,∴×6x+×8x+×10x=24,解得:x=2,∴DO=2,∴AD=2.故选:B.10.解:设直角三角形的斜边长为a,较长直角边为c,较短直角边为b,由勾股定理得,a2=c2+b2,∴a2﹣c2﹣b2=0,∴S阴影=a2﹣c2﹣(b2﹣S四边形DEFG)=a2﹣c2﹣b2+S四边形DEFG=S四边形DEFG ∴S四边形DEFG=S1+S2+S3=1+2+3=6,故选:D.二.填空题11.解:已知直角三角形的两直角边为6、8,则斜边长为=10,故斜边的中线长为×10=5,故答案是:5.12.解:如图,过A作AD⊥BC于D,设BD=x,则CD=6﹣x,依题意有(2)2﹣x2=(4)2﹣(6﹣x)2,解得x=2,在Rt△ADB中,AD===4,则△ABC的面积为×6×4=12.故答案为:12.13.解:在Rt△ABC中,AB2=AC2+BC2,AB=,所以,S阴影=S△AHC+S△BFC+S△AEB=×()2+×()2+×()2,=(AC2+BC2+AB2),=×()2,=.故答案为:.14.解:如图,连接OB,∵在Rt△ABC中,∠ACB=90°,AB=17,BC=15,∴AC===8,∵点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F 分别是垂足,∴OE=OF=OD,又∵OB是公共边,∴Rt△BOF≌Rt△BOD(HL),∴BD=BF,同理AE=AF,CE=CD,∵∠C=90°,OD⊥BC,OE⊥AC,OF⊥AB,OD=OE,∴四边形OECD是正方形,设OE=OF=OD=x,则CE=CD=x,BD=BF=15﹣x,AF=AE=8﹣x,∴15﹣x+8﹣x=17,解得x=3.∴OE=OF=OD=3.故答案为:3.15.解:∵AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,由勾股定理得,AB2+CD2=AO2+BO2+CO2+DO2,AD2+BC2=AO2+DO2+BO2+CO2,∴AB2+CD2=AD2+BC2,∵AD=2,BC=4,∴AB2+CD2=22+42=20.故答案为:20.三.解答题16.解:(1)∵AD⊥BC,∴∠ADB=∠CDA=90°.在Rt△ADB中,∵∠ADB=90°,∴AD2+BD2 =AB2,∴AD2=AB2﹣BD2=144.∵AD>0,∴AD=12.(2)在Rt△ADC中,∵∠CDA=90°,∴AD2+CD2 =AC2 ,∴CD2=AC2﹣AD2=81.∵CD>0,∴CD=9.∴BC=BD+CD=5+9=14.17.解:(1)在Rt△ABC中,∠ABC=45°,∴AB=AC=BC=6,在Rt△ADC中,∠ACD=30°,∴AD=AC=3,由勾股定理得,CD==3;(2)过点B作BE⊥AD交DA的延长线于E,由题意得,∠BAE=180°﹣90°﹣60°=30°,∴BE=AB=3,由勾股定理得,AE==3,∴DE=AE+AD=3+3,∴BD2=BE2+DE2=32+(3+3)2=45+18.18.解:(1)梯形ABCD的面积为,也可以表示为,∴,即a2+b2=c2;(2)在Rt△ABD中,AD2=AB2﹣BD2=42﹣x2=16﹣x2;在Rt△ADC中,AD2=AC2﹣DC2=52﹣(6﹣x)2=﹣11+12x﹣x2;所以16﹣x2=﹣11+12x﹣x2,解得;(3)如图,由此可得(a+b)(a+2b)=a2+3ab+2b2.17.2 勾股定理的逆定理一、选择题(共10小题;共60分)1. 下列各组数中,能构成直角三角形的是A. ,,B. ,,C. ,,D. ,,2. 以下各组数据能作为直角三角形的三条边的边长的是A. ,,B. ,,C. ,,D. ,,3. 下列命题的逆命题是假命题的是A. 等腰三角形的两底角相等B.C. 全等三角形的对应角相等D. 若,则4. 下列各组线段中,能够组成直角三角形的一组是A. ,,B. ,,C. ,,D. ,,5. 下列命题与它的逆命题都为真命题的是A. 已知非零实数,如果为分式,那么它的倒数也是分式B. 如果的相反数为,那么为C. 如果一个数能被整除,那么这个数也能被整除D. 如果两个数的和是偶数,那么它们都是偶数6. 以下组数据,能组成三角形的是A. ,,B. ,,C. ,,D. ,,7. 下列命题与它的逆命题都为真命题的是A. 已知非零实数,如果为分式,那么它的倒数也是分式B. 如果的相反数为,那么为C. 如果一个数能被整除,那么这个数也能被整除D. 如果两个数的和是偶数,那么它们都是偶数8. 下列长度的三条线段能组成直角三角形的是A. B. C. D.9. 下列各命题的逆命题成立的是A. 全等三角形的对应角相等B. 如果两个数相等,那么它们的绝对值相等C. 两直线平行,同位角相等D. 如果两个角都是10. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为里,问这块沙田面积有多大?题中的“里”里米,则该沙田的面积为A. 平方千米B. 平方千米C. 平方千米D.平方千米二、填空题(共5小题;共25分)11. 命题“同位角相等,两直线平行”的逆命题是:.12.三边都是整数的直角三角形叫做勾股三角形.有一条边长为的勾股三角形有个.13. 命题“等腰三角形两腰上的高相等”的逆命题是.14. 判定以如下的为边长的三角形是否是直角角形,是的打,不是的打.15. 写出下列命题的逆命题,并判断逆命题是否成立.()如果两个角是直角,那么它们相等;()对顶角相等.三、解答题(共5小题;共65分)16. 写出下列命题的逆命题,并在后面的括号里判断逆命题是否正确.(1)同旁内角互补,两直线平行;()(2)全等三角形的对应角相等.()17. 如图,在中,,,在中,为边上的高,,的面积为,是否为直角三角形?18. 下列各命题都成立,写出它们的逆命题,并判断逆命题的真假.(1)内错角相等,两直线平行;(2)对顶角相等;(3)全等三角形的对应角相等;(4)如果两个实数相等,那么它们的绝对值相等.19. 若的三边,,满足,试判断的形状.20. 利用线段垂直平分线性质定理及其逆定理证明以下命题.已知:如图,,,点在上.求证:.答案第一部分1. B 【解析】A不能构成直角三角形,故A错误,B能构成直角三角形,故B正确,C不能构成直角三角形,故C错误,D不能构成直角三角形,故D错误.2. D3. C4. D A不能构成三角形;B不能构成直角三角形;C不能构成直角三角形;D能构成直角三角形.5. B【解析】A.已知非零实数为分式,那么它的倒数也是分式是假命题;B.如果的相反数为为是真命题,它的逆命题是如果为么的相反数为C.如果一个数能被整除,那么这个数也能被整除是真命题,它的逆命题是如果一个数能被整除,那么这个数也能被整除,是假命题;D.如果两个数的和是偶数,那么它们都是偶数,是假命题.故选:B.6. B 【解析】A、B、C、D、故选:B.7. B 【解析】A、已知非零实数为分式,那么它的倒数也是分式是假命题;B、如果的相反数为为是真命题,它的逆命题是如果为么的相反数为C、如果一个数能被整除,那么这个数也能被整除是真命题,它的逆命题是如果一个数能被整除,那么这个数也能被整除,是假命题;D、如果两个数的和是偶数,那么它们都是偶数,是假命题.故选:B.8. C三条线段不能组成直角三角形;三条线段不能组成直角三角形;三条线段能组成直角三角形;三条线段不能组成直角三角形.9. C【解析】A 逆命题是三个角对应相等的两个三角形全等,错误;B 绝对值相等的两个数相等,错误;C 同位角相等,两条直线平行,正确;D 相等的两个角都是10. A第二部分11. “两直线平行,同位角相等”.【解析】命题:“同位角相等,两直线平行.”的题设是“同位角相等”,结论是“两直线平行”.所以它的逆命题是“两直线平行,同位角相等.”故答案为:“两直线平行,同位角相等”.12.13. 两边上的高相等的三角形是等腰三角形14.15. 如果两个角相等那么它们是直角,不成立,如果两个角相等,那么它们是对顶角,不成立第三部分16. (1)两直线平行,同旁内角互补;正确(2)对应角相等的三角形全等;不正确17. 在中,在是直角三角形.18. (1)两直线平行,内错角相等,为真命题.(2)相等的角是对顶角,为假命题.(3)对应角相等的三角形是全等三角形,为假命题.(4)如果两个实数的绝对值相等,那么这两个实数相等,为假命题.19. 设又是等腰直角三角形.20. 连接,点在线段的垂直平分线上.,点在线段的垂直平分线上,是线段的垂直平分线(两点确定一条直线).点在上,。
八年级数学下册复习题(人教版)

第十六章 分式一、分式的概念:1、下列式子是分式的有(1)21+x 、(2)12-x x 、(3)112+-x x 、(4)2-πx、(5)23+x、(6)21-x 、 (7)x 322、下列式子是分式的有(1)21--x x 、(2)、x 21(3)32-x 、(4)121-x 、(6)、242--x x (7)12-x二、分式有无意义的条件:1、当x 时,分式12-+x x 有意义;当x 时,分式12-+x x 无意义。
2、当a 为任何实数时,下列分式中一定有意义的是( )A 、21aa +B 、11+aC 、112-+a aD 、112++a a3、如果代数式1-x x有意义,那么x 的取值范围是( ) A 、x ≥0 B 、x ≠0 C 、x>0 D 、x ≥0且x ≠14、当x 时,分式12+-x x 有意义;当x 时,分式12-+x x 无意义。
5、当a 为任何实数时,下列分式中一定有意义的是( )A 、1122--a aB 、22aa -C 、112++a aD 、212++a a6、如果代数式22-+x x 有意义,那么x 的取值范围是( ) A 、x ≥-2 B 、x ≠2 C 、x ≥-2且x ≠2 D 、x>-2 7、如果代数式22+-x x 有意义,那么x 的取值范围是( )A 、x ≥-2B 、x ≠2C 、x ≥-2且x ≠2D 、x>-2三、分式的值为0的条件: 1、分式22--x x 的值为0,则x 的值为( )A 、 0B 、2C 、-2D 、2或-22、若分式32122---x x x 的值为0,则x 的值为 。
3、分式33+-x x 的值为0,则x 的值为( )A 、 0B 、-3C 、3D 、3或-34、若分式43422---x x x 的值为0,则x 的值为 。
四、分式的值为正、为负的条件:1、若分式21+a 的值为正,则a ;若分式21+a 的值为负,则a 。
人教版八年级数学下册-第十六章复习2

《二次根式》复习一、选择题1. 下列式子一定是二次根式的是( )A .2--xB .xC .22+xD .22-x 2.若b b -=-3)3(2,则( )A .b>3B .b<3C .b ≥3D .b ≤3 3.若13-m 有意义,则m 能取的最小整数值是( ) A .m=0 B .m=1 C .m=2 D .m=3 4.下列二次根式中属于最简二次根式的是( ) A .14 B .48 C .ba D .44+a5.如果)6(6-=-•x x x x ,那么( )A .x ≥0B .x ≥6C .0≤x ≤6D .x 为一切实数 6.小明的作业本上有以下四题: ①24416a a =;②a a a 25105=⨯;③a aa a a =•=112; ④a a a =-23。
做错的题是( ) A .① B .② C .③ D .④7.若最简二次根式a a 241-+与的被开方数相同,则a 的值为( ) A .43-=a B .34=a C .a=1 D .a= —1 8.化简)22(28+-得( )A .—2B .22-C .2D . 224-二、填空题9.①=-2)3.0( ;②=-2)52( 。
10.若m<0,则332||m m m ++= 。
11.1112-=-•+x x x 成立的条件是 。
12.比较大小:13.=•y xy 82 ,=•2712 。
14.若35-=x ,则562++x x 的值为 。
三、解答题15.求使下列各式有意义的字母的取值范围: (1)43-x (2)a 831- (3)42+m (4)x 1-16.化简:(1))169()144(-⨯- (2)22531-(3)5102421⨯- (4)n m 21817.计算:(1)21437⎪⎪⎭⎫ ⎝⎛- (2)225241⎪⎪⎭⎫⎝⎛-- (3))459(43332-⨯ (4)⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-126312817(5)2484554+-+ (6)2332326--四、综合题 18.若代数式||112x x -+有意义,则x 的取值范围是什么?19.若x ,y 是实数,且2111+-+-<x x y ,求1|1|--y y 的值。
人教版八年级下册数学习题课件-复习题18

∴BG=AG=EC=BE,∠BGE=∠BEG=45°.
∵CF是正方形ABCD外角的平分线,A
D
1
∴∠DCF=45°.
G
F
∵∠AGE=180°-∠BGE=135°, ∠ECF=∠DCE+∠DCF=135°,
B
3
2
E
C
∴∠AGE=∠ECF .
在△AGE中,∠1+∠3=180°-∠AGE=45°,
∠2+∠3=180°-∠AEF-∠BEG A
人教版
八(下)数学教材习题
复习题18
1.选择题.
(1) 若平行四边形中两个内角的度数比为1︰2,则其中较
小的内角是( B ).
A.90°
B.60° C.120° D.45°
(2) 若菱形的周长为8,高为1,则菱形两邻角的度数比为
( C ).
A.3︰1
B.4︰1 C.5︰1 D.6︰1
(3) 如图,在正方形ABCD的外侧,作等边三角形ADE, 则∠AEB为( B ). A.10° B.15° C.20° D.125°
2.如图,将□ABCD的对角线BD向两个方向延长,分别
至点E和点F,且使BE=DF. 求证:四边形AECF是平
行四边形.
证明:如图,连接AC交BD于点O.
O
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
又∵BE=DF,∴BE+BO=FD+DO,即EO=FO.
∴四边形AEFC是平行四边形.
PF=DE.因为PQ=CD,所以△PQF≌△DCE.所以FQ=
A
P
D
B
F
Q
EC
EC=26-24=2(cm).当点Q在点F右侧时,BF+FQ+QC=26,
人教版八年级下册数学专题复习及练习(含解析):等腰三角形

专题13.3 等腰三角形知识点1:等腰三角形1.等腰三角形的定义:有两条边相等的三角形叫做等腰三角形.相等的两边叫做腰,另一边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫底角.2.等腰三角形的性质:(1)等腰三角形的两个底角相等(简写成“等边对等角”).(2)等腰三角形的顶角平分线,底边上的中线、 底边上的高互相重合(通常称作“三线合一”).3.等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).知识点2:等边三角形1.定义:三条边相等的三角形叫做等边三角形.2.等边三角形的性质和判定:(1)等边三角形的三个内角都相等,并且每一个角都等于60°。
(2)三个角都相等的三角形是等边三角形。
(3)有一个角是60°的等腰三角形是等边三角形。
知识点3:直角三角形的一个定理在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.【例题1】如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求:△ABC各角的度数.【例题2】证明:在直角三角形中,如果一个锐角等于30°, 那么它所对的直角边等于斜边的一半. 已知:如图,在Rt △ABC 中,∠C=90°,∠BAC=30°.求证:BC=AB .【例题7】已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )A .B .C .D .不能确定【例题3】如图,已知AC ⊥BC ,BD ⊥AD ,AC 与BD 交于点O ,AC=BD.求证:(1)BC=AD ;(2)△OAB 是等腰三角形.一、选择题1.已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( )12C AA.B.C.D.不能确定2.如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是()A.AC>BC B.AC=BC C.∠A>∠ABC D.∠A=∠ABC3.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN 为等边三角形,则满足上述条件的△PMN有()A.1个B.2个C.3个D.3个以上4.如图所示,底边BC为2,顶角A为120°的等腰△ABC中,DE垂直平分AB于D,则△ACE的周长为()A.2+2B.2+C.4 D.3二、解答题5.已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.求证:△ABC是等边三角形.6.如图,在△ABC中,过C作∠BAC的平分线AD的垂线,垂足为D,DE∥AB交AC于E.求证:AE=CE.7.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.已知:∠CAE 是△ABC 的外角,∠1=∠2,AD ∥BC (如图).求证:AB=AC .8.已知:如图,AD ∥BC ,BD 平分∠ABC .求证:AB=AD .9.证明:等腰三角形两底角的平分线相等.已知:如图,在△ABC 中,AB=AC ,BD 、CE 是△ABC 的平分线.求证:BD=CE .10.证明:等腰三角形两腰上的高相等.已知:如图,在△ABC 中,AB=AC ,BE 、CF 分别是△ABC 的高.E DCAB11.证明:等腰三角形两腰上的中线相等.已知:如图,在△ABC 中,AB=AC ,BD 、CE 分别是两腰上的中线.求证:BD=CE .12.已知:如图,在△ABC 中,AB=AC=2a ,∠ABC=∠ACB=15°,CD 是腰AB 上的高.求:CD 的长.13.已知:如图,△ABC 中,∠ACB=90°,CD 是高,∠A=30°.求证:BD=AB .14.已知直角三角形的一个锐角等于另一个锐角的2倍,这个角的平分线把对边分成两条线段.求证:其中一条是另一条的2倍.已知:在Rt △ABC 中,∠A=90°,∠ABC=2∠C ,BD 是∠ABC 的平分线.1415.已知:如图,在Rt △ABC 中,∠C=90°,BC=AB .求证:∠BAC=30°.16.已知,如图,点C 为线段AB 上一点,△ACM 、△CBN 是等边三角形.求证:AN=BM .17.一个直角三角形房梁如图所示,其中BC ⊥AC ,∠BAC=30°,AB=10cm , CB 1⊥AB ,B 1C ⊥AC 1,垂足分别是B 1、C 1,那么BC 的长是多少?18.如图,△ABC 中,AB=AC ,∠A=36°,AC 的垂直平分线交AB 于E ,D 为垂足,连接EC .(1)求∠ECD 的度数;(2)若CE=5,求BC 长.12专题13.3 等腰三角形知识点1:等腰三角形1.等腰三角形的定义:有两条边相等的三角形叫做等腰三角形.相等的两边叫做腰,另一边叫做底边,两腰所夹的角叫做顶角,底边与腰的夹角叫底角.2.等腰三角形的性质:(1)等腰三角形的两个底角相等(简写成“等边对等角”).(2)等腰三角形的顶角平分线,底边上的中线、 底边上的高互相重合(通常称作“三线合一”).3.等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).知识点2:等边三角形1.定义:三条边相等的三角形叫做等边三角形.2.等边三角形的性质和判定:(1)等边三角形的三个内角都相等,并且每一个角都等于60°。
人教版 八年级数学下册 期末综合复习(含答案)

人教版 八年级数学下册 期末综合复习一、选择题(本大题共12道小题) 1. 计算(2x +1)(2x -1)的结果为 ( ) A .4x 2-1B .2x 2-1C .4x -1D .4x 2+12. 把分式方程2x +4=1x 转化为一元一次方程时,方程两边需同乘( ) A .xB .2xC .x +4D .x (x +4)3. 若a 2+ab +b 2=(a -b )2+X ,则整式X 为()A .abB .0C .2abD .3ab4. 如图,△ABE ≌△ACD ,∠A =60°,∠B =25°,则∠DOE 的度数为()A .85°B .95°C .110°D .120°5.(2020·临沂)如图,在ABC ∆中,AB AC =,40A ∠=︒,//CD AB ,则BCD ∠=( )A.40°B.50°C.60°.D.70°6. 下列哪一个度数可以作为某一个多边形的内角和 () A .240° B .600°C .540°D .2180°7. (2020·天津)计算221(1)(1)x x x +++的结果是( )A.11x+B.21(1)x+C. 1D. 1x+8. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于12BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是A.2 B.3C3D59. 下列长度的三条线段能组成钝角三角形的是( )A. 3,4,4B. 3,4,5C. 3,4,6D. 3,4,710.如图,平行河岸两侧各有一城镇P,Q,根据发展规划,要修建一条公路连接P ,Q两镇.已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )11. 如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3等于( )A.90°B.120 C.135°D.150°12.如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD ,则∠A的度数是( )A.45°B.50°C.55°D.80°二、填空题(本大题共12道小题)13.图中的虚线,哪些是图形的对称轴,哪些不是?是对称轴的是______;不是对称轴的是______.(填写序号)14. (2020·武威)分解因式:a2+a=.15.如图,已知在△ABC和△DEF中,∠B=∠E,BF=CE,点B,F,C,E在同一条直线上,若使△ABC≌△DEF,则还需添加的一个条件是________(只填一个即可).16.如图,两车从南北方向的路段AB的A端出发,分别向东、向西行进相同的距离,到达C,D两地,此时可以判断C,D到B的距离相等,用到的数学道理是____ ____.17.将两块完全相同的三角尺在∠AOB的内部如图摆放,两块三角尺较短的直角边分别与∠AOB的两边重合,且含30°角的顶点恰好也重合于点C,则射线OC即为∠AOB的平分线,理由是______________________.18.如图,∠AOB=40°,C为OB上的定点,M,N分别为OA,OB上的动点,当CM +MN的值最小时,∠OCM的度数为________.19. 将分式1a2-9和a3a-9进行通分时,分母a2-9可因式分解为____________,分母3a-9可因式分解为__________,因此最简公分母是____________.20. 若a-b=3x-y=2则a2-2ab+b2-x+y=________.21.如图,BO平分∠CBA,CO平分∠ACB,MN过点O且MN∥BC,设AB=12,AC =18,则△AMN的周长为________.22. 计算:1x2-6x+9÷x+3x-3·(9-x2).解:原式=1(x-3)2÷x+3x-3·(3+x)(3-x)……第一步=1(x-3)2·x-3x+3·(3+x)(3-x)……第二步=1.……第三步回答:(1)上述过程中,第一步使用的公式用字母表示为__________________________;(2)由第二步得到第三步所使用的运算方法是____________;(3)以上三步中,从第________步开始出现错误,本题的正确答案是__________.23. 一个等腰三角形的一边长是2,一个外角是120°,则它的周长是________.24. 画图:试画出下列正多边形的所有对称轴,并完成表格.根据上表,猜想正n边形有条对称轴.三、作图题(本大题共2道小题)25.利用刻度尺和三角尺作图:如图所示,已知四边形ABCD和直线m.请你作出四边形A1B1C1D1,使得四边形A1B1C1D1和四边形ABCD关于直线m成轴对称.26. 如图,在河岸l的同侧有两个居民小区A,B,现欲在河岸边建一个长为a的绿化带CD(宽度不计),使C到小区A的距离与D到小区B的距离之和最小.在图中画出绿化带的位置,并写出画图过程.四、解答题(本大题共6道小题)27. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D 和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG 的周长为16,GE=3,求AC的长.28. 我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质.小学时,把分子比分母小的分数叫做真分数.类似地,我们把分子的次数小于分母的次数的分式称为真分式,反之,称为假分式.对于任何一个假分式都可以化成整式与真分式的和的形式,如==+=1+. (1)下列分式中,属于真分式的是()A.B.C.-D.(2)将假分式化成整式与真分式的和的形式.29. 整体代入阅读下面文字,并解决问题.已知x2y=3,求2xy(x5y2-3x3y-4x)的值.分析:考虑到满足x2y=3的x,y的可能值较多,不可能逐一代入求解,故考虑整体思想,将x2y=3整体代入.解:2xy(x5y2-3x3y-4x)=2x6y3-6x4y2-8x2y=2(x2y)3-6(x2y)2-8x2y=2×33-6×32-8×3=2×27-6×9-8×3=-24.请你用上述方法解决问题:已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值.30.如图,已知AP∥BC,∠P AB的平分线与∠CBA的平分线相交于点E,过点E的直线分别交AP,BC于点D,C.求证:AD+BC=AB.31. 在△ABC中,∠A=90°,∠B=30°,AC=6 cm,点D从点A出发以1 cm/s的速度向点C运动,同时点E从点C出发以2cm/s的速度向点B运动,设运动时间为t s,解决以下问题:(1)当t为何值时,△DEC为等边三角形?(2)当t为何值时,△DEC为直角三角形?32. 已知有理数x ,y ,z 满足2|2|(367)|334|0x z x y y z --+--++-=,求3314n n n x y z x--的值.人教版 八年级数学下册 期末综合复习-答案一、选择题(本大题共12道小题) 1. 【答案】A2. 【答案】D3. 【答案】D4.【答案】C [解析]∵△ABE ≌△ACD ,∴∠B =∠C =25°.∵∠A =60°,∠C =25°,∴∠BDO =∠A +∠C =85°.∴∠DOE =∠B +∠BDO =85°+25°=110°.5. 【答案】D【解析】 根据三角形内角和定理和等腰三角形的等边对等角且AB AC =,40A ∠=,可得:70ABC ACB ∠=∠=;然后根据两直线平行内错角相等且//CD AB 可得:70BCD ABC ∠=∠=,所以选D .6. 【答案】C[解析] ∵多边形内角和公式为(n -2)×180°,∴多边形内角和一定是180°的倍数. ∵540°=3×180°,∴540°可以作为某一个多边形的内角和.7. 【答案】A【解析】本题考查分式的加减运算,主要运算技巧包括通分,约分,同时常用平方差、完全平方公式作为解题工具.本题可先通分,继而进行因式约分求解本题.221(1)(1)x x x +++21(1)x x +=+,因为10x +≠,故211=(1)1x x x +++.故选:A .8. 【答案】D【解析】由作法得CE ⊥AB ,则∠AEC=90°, AC=AB=BE+AE=2+1=3,在Rt △ACE 中,=.故选D .9.【答案】C【解析】①∵32+42=52,∴三条线段3、4、5组成直角三角形,∴B 选项不正确;②当把斜边5变成7时,3+4=7,不满足三角形两边之和大于第三边,不能构成三角形,∴D 选项不正确;③当把斜边5稍微变小一点为4时,三条线段为3、4、4组成锐角三角形,∴A 选项不正确;④当把斜边5稍微变大一点为6时,三条线段为3、4、6组成钝角三角形,∴C 选项正确.10.【答案】C [解析]如图,作PP′垂直于河岸L ,使PP′等于河宽,连接QP′,与河岸L 相交于点N ,将P′N 沿竖直方向向上平移河宽个单位长度,得到PM ,PM -MN -NQ 即所求.根据“两点之间,线段最短”,QP′最短,即PM +NQ 最短.观察选项,选项C 符合题意.11.【答案】C [解析]在图中容易发现全等三角形,将∠3转化为与其相等的对应角后可以看出∠3与∠1互余.故∠1+∠3=90°.易得∠2=45°,故∠1+∠2+∠3=135°.12. 【答案】B[解析] 如图,连接AC 并延长交EF 于点M.∵AB ∥CF ,∴∠3=∠1. ∵AD ∥CE ,∴∠2=∠4.∴∠BAD =∠3+∠4=∠1+∠2=∠FCE.∵∠FCE =180°-∠E -∠F =180°-80°-50°=50°,∴∠BAD =∠FCE =50°.二、填空题(本大题共12道小题)13. 【答案】②④⑥①③⑤14. 【答案】a 2+a =a (a +1).故答案为:a (a +1).15. 【答案】答案不唯一,如AB =DE[解析] ∵BF =CE ,∴BC =EF. 在△ABC 和△DEF 中,⎩⎪⎨⎪⎧AB =DE ,∠B =∠E ,BC =EF ,∴△ABC ≌△DEF(SAS).16. 【答案】线段垂直平分线上的点与这条线段两个端点的距离相等17. 【答案】角的内部到角的两边距离相等的点在角的平分线上18.【答案】10° [解析]作点C 关于OA 的对称点D ,过点D 作DN ⊥OB 于点N ,交OA 于点M ,则此时CM +MN 的值最小.∵∠OEC =∠DNC =90°,∠DME =∠OMN , ∴∠D =∠AOB =40°.∵MD=MC,∴∠DCM=∠D=40°,∠DCN=90°-∠D=50°.∴∠OCM=10°.19. 【答案】(a+3)(a-3)3(a-3)3(a+3)(a-3)20. 【答案】7[解析] a2-2ab+b2-x+y=(a-b)2-(x-y).把a-b=3x-y=2代入得原式=32-2=7.21. 【答案】30 [解析] ∵MN∥BC,∴∠MOB=∠OBC.∵∠OBM=∠OBC,∴∠MOB=∠OBM.∴MO=MB.同理NO=NC.∴△AMN的周长=AM+MO+AN+NO=AM+MB+AN+NC=AB+AC=30.22. 【答案】(1)a2-2ab+b2=(a-b)2,a2-b2=(a+b)(a-b)(2)约分(3)三-123. 【答案】 6 [解析] 已知三角形的一外角为120°,则相邻内角度数为60°,那么含有60°角的等腰三角形是等边三角形.已知等边三角形的一边长为2,则其周长为6.24. 【答案】解:如图.故填3,4,5,6,n.三、作图题(本大题共2道小题)25. 【答案】解:如图,四边形A1B1C1D1即为所求.26. 【答案】解:如图,作线段AP∥l,使AP=a,且点P在点A的右侧;作点P关于直线l的对称点P',连接BP'交l于点D;在l上点D的左侧截取DC=a,则CD就是所求绿化带的位置.四、解答题(本大题共6道小题)27. 【答案】解:∵DE垂直平分线段AB,GF垂直平分线段BC,∴EB=EA,GB=GC.∵△BEG的周长为16,∴EB+GB+GE=16.∴EA+GC+GE=16.∴GA+GE+GE+GE+EC=16.∴AC+2GE=16.∵GE=3,∴AC=10.28. 【答案】解:(1)C(2)==+=m-1+.29. 【答案】解:(2a3b2-3a2b+4a)·(-2b)=-4a3b3+6a2b2-8ab=-4(ab)3+6(ab)2-8ab=-4×33+6×32-8×3=-108+54-24=-78.30. 【答案】证明:如图,在AB 上截取AF =AD ,连接EF.∵AE 平分∠PAB ,∴∠DAE =∠FAE.在△DAE 和△FAE 中,⎩⎪⎨⎪⎧AD =AF ,∠DAE =∠FAE ,AE =AE ,∴△DAE ≌△FAE(SAS).∴∠AFE =∠ADE.∵AD ∥BC ,∴∠ADE +∠C =180°.又∵∠AFE +∠EFB =180°,∴∠EFB =∠C.∵BE 平分∠ABC ,∴∠EBF =∠EBC.在△BEF 和△BEC 中,⎩⎪⎨⎪⎧∠EFB =∠C ,∠EBF =∠EBC ,BE =BE ,∴△BEF ≌△BEC(AAS).∴BF =BC.∴AD +BC =AF +BF =AB.31. 【答案】(1)根据题意可得AD =t ,CD =6-t ,CE =2t. ∵△DEC 为等边三角形,∴CD =CE ,即6-t =2t ,解得t =2.∴当t 的值为2时,△DEC 为等边三角形.(2)∵∠A =90°,∠B =30°,∴∠C =60°. ①当∠DEC 为直角时,∠EDC =30°,∴CE =12CD ,即2t =12(6-t),解得t =65;②当∠EDC 为直角时,∠DEC =30°,∴CD =12CE ,即6-t =12·2t ,解得t =3.综上,当t 的值为65或3时,△DEC 为直角三角形.32. 【答案】【解析】由题意得2036703340x z x y y z --=⎧⎪--=⎨⎪+-=⎩,解方程组得3131x y z =⎧⎪⎪=⎨⎪⎪=⎩,代入所求代数式得313133143411313331333033n n n n n n n x y z x ---⎛⎫⎛⎫-=⋅⋅-=⋅⨯⋅-=-= ⎪ ⎪⎝⎭⎝⎭.。
人教版八年级数学下册第十八章:平行四边综合复习训练
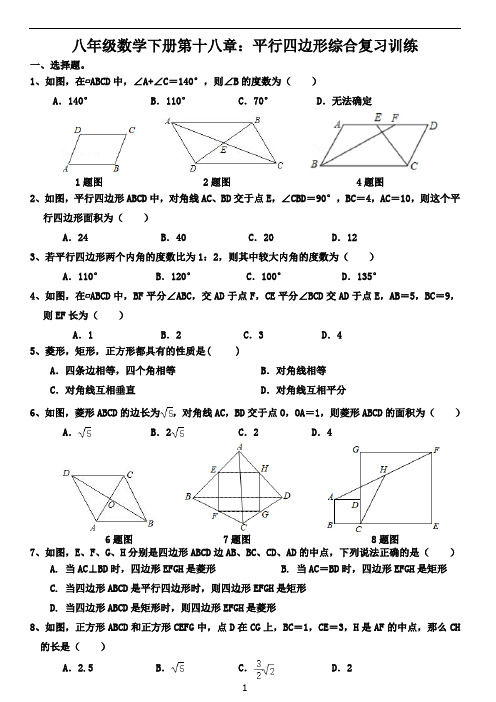
八年级数学下册第十八章:平行四边形综合复习训练一、选择题。
1、如图,在▱ABCD中,∠A+∠C=140°,则∠B的度数为()A.140° B.110° C.70° D.无法确定1题图 2题图 4题图2、如图,平行四边形ABCD中,对角线AC、BD交于点E,∠CBD=90°,BC=4,AC=10,则这个平行四边形面积为()A.24 B.40 C.20 D.123、若平行四边形两个内角的度数比为1:2,则其中较大内角的度数为()A.110° B.120° C.100° D.135°4、如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD交AD于点E,AB=5,BC=9,则EF长为()A.1 B.2 C.3 D.45、菱形,矩形,正方形都具有的性质是( )A.四条边相等,四个角相等 B.对角线相等C.对角线互相垂直 D.对角线互相平分6、如图,菱形ABCD的边长为,对角线AC,BD交于点O,OA=1,则菱形ABCD的面积为()A. B.2 C.2 D.46题图 7题图 8题图7、如图,E、F、G、H分别是四边形ABCD边AB、BC、CD、AD的中点,下列说法正确的是()A. 当AC⊥BD时,四边形EFGH是菱形B. 当AC=BD时,四边形EFGH是矩形C. 当四边形ABCD是平行四边形时,则四边形EFGH是矩形D. 当四边形ABCD是矩形时,则四边形EFGH是菱形8、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH9题图 10题图9、如图,已知正方形ABCD的边长为12,BE=EC,将正方形的边CD沿DE折叠到DF,延长EF交AB于G,连接DG.现有如下3个结论:①AG+EC=GE;②∠GDE=45°;③五边形DAGEC的周长是44,其中正确的个数为()A.0 B.1 C.2 D.310、如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④4FH=BD;其中正确结论的是()A.①②③ B.①②④ C.①③④D.②③④二、填空题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.选择。
1.下列多项式能因式分解的是 ( )A .2a b -B .21a +C .22a b b ++。
D .244a a -+2.人数相等的八(1)和八(2)两个班学生进行了一次数学测试,班级平均分和方差如下:22121286,86,259,186X X s s --====.则成绩较为稳定的班级是 ( ) A .八(1)班 B .八(2)班 C .两个班成绩一样稳定 D .无法确定. 3.下列语句是命题的是 ( ) A .同旁内角互补 B .两直线平行,同位角吗? C .画线段AB=CD D .量线段AB 的长度4.如图,1l 反映的是某公司产品的销售收入与销售量的关系,2l 反映的该公司产品的销售成本与销售量的关系,根据图象判断该公司盈利时销售 ( )A .小于4件;B .等于4件;C .大于14件;D .大于或等于4件。
5.下列不等式一定成立的是 ( )A .43a a >B .2a a ->-C .34x x -<-D .32a a> 6.在比例尺为1:100 000的地图上,海军参谋量得从海岸到A 岛的距离为2厘米,并且知道船在此海上行使的最快速度为4 0千米/时,那么海军要到达A 岛至少需要 ( ) A .6分钟 B .5分钟 C .4分钟 D .3分钟 7.下列说法中:①两个图形位似也一定相似;②相似三角形对应中线的比等于对应周长的比;③一组数据的极差、方差或标准差越小,该组数据就越稳定; ④三角形的外角一定大于它的内角.其中不正确的个数有 ( ) A . 1个 B .2个 C .3个 D .4个 8.在学校对学生进行的晨检体温测试中,学生甲连续10天的体温与36~C 的上下波动数据为0.2、0.3、0.1、0,1、0、0.2、0.1、0、0.1,则在这10天中该学生的体温波动数据中不正确的是A .平均数是0.12B , 方差是0.02C .中位数是0.1D .众数是0.19.若22(3)16x m x +-+是完全平方式,则m 的值是 ( )A .1-B .7C .1-或7D .5或110.赵强同学借了一本书,共260页,要在两周借期内读完。
当他读了一半时,发现平均每天要多读23页才能在借读完。
他读前一半时,平均每天读多少页?如果设读前一半时平均每天读X 页,则下面所列方程中,正确的是 ( )A .1301301423x x +=- B .1301301423x x +=+ C .2602601423x x +=- D .2602601423x x +=+11.己知xy mn =则把它改写成比例式后,错误的是 ( ) A .x y m n = B .y nm x= C .x m n y = D .x n m y =12.如图(1),在△脚中,若∠AED=∠B ,DE=6,AB=10,AE=8,则BC 的长为( )A .154 B .7 C .245 D .15213.如上图右:AB//CD ,直线HE MN ⊥交MN 于E ,∠1=130︒,则∠2等于 A .50︒ B .40︒ C .30︒ D .60︒14.如图,E 是正方形ABCD 的边BC 上一点,下列条件中: ①∠BAE=∠CEF ;③∠AEB=∠EFG ;③AE ⊥EF ; ④AB BE EC CF =;⑤AE ABEF EC=.其中能使△ABE ∽△ECF 的有A .2个B .3个C .4个D .5个15.如图,如果AB//CD ,则角a 、b 、y 之间的关系式为 A .360a b y ++=︒ B .180a b y -+=︒ C .180a b y ++=︒ D .180a b y +-=︒16.下列四个等式:①4)4(2=-;②(-4)2=16;③(4)2=4;④4)4(2-=-. 正确的是( )A .①②B .③④C .②④D .①③ 17.方程x2-25=0的解是( )A. x1=x2=5B. x1=x2=25C. x1=5,x2=-5D. x1=25,x2=-25 18.如果(m -1)x2+2x -3=0是一元二次方程,则( )A. m ≠0B. m ≠1C. m=0D. m ≠-1219.一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可以分( )A .10组B .9组C .8组D .7组20.某市对2400名年满15岁的男生的身高进行了测量,结果身高(单位:m)在1.68~1.70这一小组的频率为0.25,则该组的人数为( )A . 600人B . 150 人C .60人D . 15人 21.如图,,直线PQ 分别交AB ,CD 于点E ,F ,FG 是EFD ∠的平分线,交AB 于点G .若40PFD ∠=°,那么FGB ∠等于( ) A .80° B .100° C .110° D .120° 22.下列各组所述几何图形中,一定全等的是( )A.一个角是45°的两个等腰三角形B.腰长相等的两个等腰直角三角形C.两个等边三角形D.各有一个角是40°,腰长都为5㎝的两个等腰三角形23.如果一个正多边形绕它的中心旋转60°才和原来的图形重合,那么这个正多边形是( )A. 正三角形B. 正方形C. 正五角形D. 正六角形24.在下列四种边长均为a 的正多边形中,能与边长为a 的正三角形作平面镶嵌的正多边形有( )①正方形;②正五边形;③正六边形;④正八边形. A.4种 B.3种 C.2种 D.1种25.已知等腰梯形的大底等于对角线的长,小底等于高,则该梯形的小底与大底的长度之比是( )A . 3∶5B .3∶4C .2∶3D .1∶226.下列各式中,31-x 、12+a b 、πy x +2、21--m 、a +21、22)()(y x y x +-、x 12-、115-分式的个数有( ).A. 2个B. 3个C. 4个D. 5个 27.反比例函数y = 1x的图象在( )A .第一、二象限B .第一、三象限C .第二、四象限D .第三、四象限 28.分别以下列四组数为一个三角形的边长:(1)6、8、10;(2)5、12、13;(3)8、15、17; (4)4、5、6,其中能构成直角三角形的有( )A.四组B.三组C.二组D.一组 29.把分式(0)xyx y x y+≠+中的x 、y 都扩大3倍,那么分式的值( ). A. 扩大3倍 B. 缩小3倍 C. 扩大9倍 D. 不变 30.顺次连结四边形各边中点所得的四边形是( ).A. 平行四边形B. 矩形C. 菱形D. 以上都不对31.为筹备班级的中秋联欢会,班长对全班学生爱吃哪几种水果作了民意调查.那么最终买什么水果,下面的调查数据中最值得关注的是( )A .中位数B .平均数C .众数D .加权平均数32.如图,等腰梯形ABCD 中,AD ∥BC ,AE ∥DC ,∠B=60º,BC=3,△ABE 的周长为6,则等腰梯形的周长是( ).A BCD PF EG QA .8 B.10 C.12 D. 1633.解分式方程032222=+---x x x x 时,利用换元法设y x x=-22,把原方程变形成整式方程为( )(A )0132=++y y (B )0132=+-y y (C )0132=--y y (D )0132=-+y y 34.如图所示,正方形ABCD 的面积为12,ABE △是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD PE +的和最小,则这个最小值为( ) A .23 B .26 C .3 D .6 35.22,2,,3,1y x x ab b a c b a --π中,分式的个数为( )A .2个B .3个C .4个D .5个36.下列运算正确的是( )A .y x y y x y --=--B .3232=++y x y xC .y x y x y x +=++22D .y x yx x y -=-+122 37.若A (a ,b )、B (a -1,c )是函数x y 1-=的图象上的两点,且a <0,则b 与c 的大小关系为( )A .b <cB .b >cC .b=cD .无法判断38.如图,已知点A 是函数y=x 与y=x 4的图象在第一象限内的交点,点B 在x 轴负半轴上,且OA=OB ,则△AOB 的面积为( )A .2B .2C .22D .4第4题图 第5题图 第8题图 第10题图39.如图,在三角形纸片ABC 中,AC=6,∠A=30º,∠C=90º,将∠A 沿DE 折叠,使点A 与点B 重合,则折痕DE 的长为( )A .1B .2C .3D .2AB O y x A BCDE A B E D C40.△ABC 的三边长分别为a 、b 、c ,下列条件:①∠A=∠B -∠C ;②∠A :∠B :∠C=3:4:5;③))((2c b c b a -+=;④13:12:5::=c b a ,其中能判断△ABC 是直角三角形的个数有( )A .1个B .2个C .3个D .4个41.一个四边形,对于下列条件:①一组对边平行,一组对角相等;②一组对边平行,一条对角线被另一条对角线平分;③一组对边相等,一条对角线被另一条对角线平分;④两组对角的平分线分别平行,不能判定为平行四边形的是( )A .①B .②C .③D .④ 42.如图,已知E 是菱形ABCD 的边BC 上一点,且∠DAE=∠B=80º,那么∠CDE 的度数为( ) A .20º B .25º C .30º D .35º43.某班抽取6名同学进行体育达标测试,成绩如下:80,90,75,80,75,80. 下列关于对这组数据的描述错误的是( )A .众数是80B .平均数是80C .中位数是75D .极差是15 44.某居民小区本月1日至6日每天的用水量如图所示,那么这6天的平均用水量是( ) A .33吨 B .32吨 C .31吨 D .30吨45.如图,直线y=kx (k >0)与双曲线y=x 1交于A 、B 两点,BC ⊥x 轴于C ,连接AC 交y 轴于D ,下列结论:①A 、B 关于原点对称;②△ABC 的面积为定值;③D 是AC 的中点;④S △AOD=21. 其中正确结论的个数为( )A .1个B .2个C .3个D .4个第11题图 第12题图 第16题图 第18题图46.如图,在梯形ABCD 中,∠ABC=90º,AE ∥CD 交BC 于E ,O 是AC 的中点,AB=3,AD=2,BC=3,下列结论:①∠CAE=30º;②AC=2AB ;③S △ADC=2S △ABE ;④BO ⊥CD ,其中正确的是( )A .①②③B .②③④C .①③④D .①②③④ 47.下列各式中计算正确的是( ) A 、416±=B 、12223=-C 、565253=⨯D 、()13132=-48.将5张分别画有等边三角形、直角三角形、平行四边形、等腰梯形、正六边形的卡片任意放入袋中,从中抽取一张,抽得中心对称图形的概率是( )A B C DO x yAB C E D O A B O x y XY A D B C P OA 、51B 、52C 、53D 、5449.将一张矩形纸片ABCD 按如图方法折叠,定点C 落在C '处,已知AB=2∠DEC=30°,则折痕的长为( )C'DABA 、2B 、32C 、4D 、150.如果x-3是m x x 2+-的一个因式,那么m 的值为( ) A 、6B 、-6C 、3D 、-3填空。
