KMP_next算法
kmp算法例题

kmp算法例题KMP算法是一种字符串匹配算法,用于在一个文本串S内查找一个模式串P的出现位置。
举个例子,如果文本串S为'ABCABCABC',模式串P为'ABC',那么KMP算法会返回3个匹配位置,分别为0、3和6。
KMP算法的核心是利用模式串的信息来避免在文本串中不必要的比较。
具体来说,KMP算法维护一个next数组,用于记录模式串的前缀和后缀的最长公共长度。
在匹配过程中,如果一个字符与模式串不匹配,那么可以跳过一定长度的字符,直接比较后面的字符。
下面是一个KMP算法的示例代码:```vector<int> getNext(string p) {int n = p.size();vector<int> next(n, 0);int j = 0;for (int i = 1; i < n; i++) {while (j > 0 && p[i] != p[j]) {j = next[j - 1];}if (p[i] == p[j]) {j++;}next[i] = j;}return next;}vector<int> kmp(string s, string p) { int n = s.size(), m = p.size();vector<int> ans;if (m == 0) {return ans;}vector<int> next = getNext(p);int j = 0;for (int i = 0; i < n; i++) {while (j > 0 && s[i] != p[j]) {j = next[j - 1];}if (s[i] == p[j]) {j++;}if (j == m) {ans.push_back(i - m + 1);j = next[j - 1];}}return ans;}```上面的代码中,getNext函数用于计算next数组,kmp函数用于查找模式串在文本串中的出现位置。
KMP算法Next数组详解

KMP算法Next数组详解题⾯题⽬描述如题,给出两个字符串s1和s2,其中s2为s1的⼦串,求出s2在s1中所有出现的位置。
为了减少骗分的情况,接下来还要输出⼦串的前缀数组next。
如果你不知道这是什么意思也不要问,去百度搜[kmp算法]学习⼀下就知道了。
输⼊输出格式输⼊格式:第⼀⾏为⼀个字符串,即为s1(仅包含⼤写字母)第⼆⾏为⼀个字符串,即为s2(仅包含⼤写字母)输出格式:若⼲⾏,每⾏包含⼀个整数,表⽰s2在s1中出现的位置接下来1⾏,包括length(s2)个整数,表⽰前缀数组next[i]的值。
输⼊样例:ABABABCABA输出样例:130 0 1说明时空限制:1000ms,128M数据规模:设s1长度为N,s2长度为M对于30%的数据:N<=15,M<=5对于70%的数据:N<=10000,M<=100对于100%的数据:N<=1000000,M<=1000题解这是⼀道KMP裸题(模板题。
)我就是拿着它学习⼀下KMP算法其实原来我学过KMP算法但是⼀直没有弄懂next(跳转)数组是如何求出来的。
最近花了⼀个下午⾃⼰研究了⼀下KMP算法现在终于觉得KMP很简单了~现在直接说next数组把⾄于有什么作⽤,next数组是⼲什么的,请⾃⾏百度,有很多dalao总结的⾮常到位,看⼀看就会明⽩。
好,来说next数组并不⽤在意这⼀坨⿊的是什么东西,我们就假设他是我们要求next数组的字符串。
next数组求的东西就是从起始位置到当前位置最长的相等的前缀和后缀的长度。
(举个例⼦China的前缀有:C、Ch、Chi、Chin、China ;后缀有a、na、ina、hina、China)我们继续,如上图红⾊的是当前位置(设为j)前,所匹配上的最长前缀和后缀,蓝⾊的是当前要匹配的位置。
那么,我们就拿当前位置和原来匹配到的最长前缀的后⼀位相⽐较如果两个位置相同,显然,可以和前⾯的红⾊连在⼀起,此时就有next[j]=next[j-1]+1如果两个位置不相同,根据next数组的性质,显然的,你的当前的相等的前缀和后缀只能够继续向前找,也就是说,你当前的next数组⼀定会减⼩。
kmp 最小循环节

kmp 最小循环节摘要:1.KMP 算法简介2.最小循环节的概念3.KMP 算法求最小循环节的方法4.示例与应用正文:【1.KMP 算法简介】KMP(Knuth-Morris-Pratt)算法是一种高效的字符串匹配算法,用于在一个主字符串中查找一个子字符串出现的位置。
该算法的关键在于通过预处理子字符串,减少不必要的字符比较,从而提高匹配速度。
【2.最小循环节的概念】在KMP 算法中,最小循环节是指子字符串中最小的循环子序列的长度。
例如,字符串"ababc"中,最小循环节为2,因为"ab"是最小的循环子序列。
【3.KMP 算法求最小循环节的方法】为了求解最小循环节,KMP 算法通过预处理子字符串,构建一个next 数组。
next 数组的每个元素代表了子字符串中当前位置到下一个相同字符的最短距离。
通过next 数组,可以在O(m) 的时间复杂度内找到最小循环节。
具体构建next 数组的方法如下:1.初始化一个长度为m+1 的数组next,其中next[0] 为-1。
2.遍历子字符串,对于每个字符a[i],若a[i] 等于a[j],则next[i] =next[j],否则next[i] = -1。
3.返回next 数组中的最大值,即最小循环节的长度。
【4.示例与应用】以字符串"ababc"为例,构建next 数组如下:```-1 0 1 2 30 -1 0 1 21 0 -1 0 12 1 2 0 13 2 0 1 0```从next 数组中可以看出,最小循环节为2。
KMP算法计算next值和nextVal值
KMP算法计算next值和nextVal值
KMP算法:
给定⼀个主串S及⼀个模式串P,判断模式串是否为主串的⼦串;若是,返回匹配的第⼀个元素的位置(序号从1开始),否则返回0;这⾥先不写算法,仅仅计算next和nextVal值
那么计算时只⽤到⼦串,也就是模式串
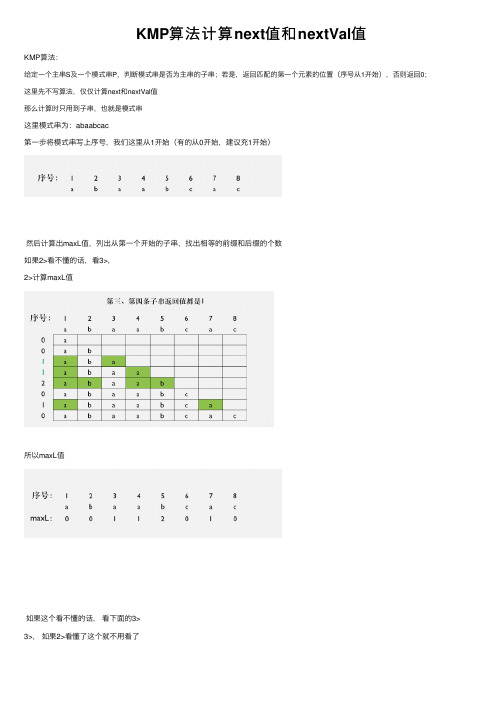
这⾥模式串为:abaabcac
第⼀步将模式串写上序号,我们这⾥从1开始(有的从0开始,建议充1开始)
然后计算出maxL值,列出从第⼀个开始的⼦串,找出相等的前缀和后缀的个数
如果2>看不懂的话,看3>,
2>计算maxL值
所以maxL值
如果这个看不懂的话,看下⾯的3>
3>,如果2>看懂了这个就不⽤看了
依次类推4>计算next值
接下来将maxL复制⼀⾏,去掉最后⼀个数,在开头添加⼀个-1,向右平移⼀个格,然后每个值在加1的到next值
5>计算nextVal值,⾸先将第⼀个为0,然后看next和maxL是否相等(先计算不相等的)
当next和maxL不相等时,将next的值填⼊
当next和maxL相等时,填⼊对应序号为next值得nextVal值
所以整个nextVal值为:。
kmp 回文串

KMP算法是一种用于字符串匹配的算法,而回文串是一种具有对称性质的字符串。
因此,KMP算法本身并不直接用于解决回文串问题。
但是,我们可以通过一些变换将回文串问题转化为字符串匹配问题,然后使用KMP算法来解决。
例如,如果我们想要判断一个字符串是否为回文串,我们可以将该字符串与其反转后的字符串进行匹配。
如果匹配成功,则说明原字符串是回文串。
在这个过程中,我们可以使用KMP算法来进行匹配。
具体地,我们可以先将原字符串和反转后的字符串进行预处理,计算出它们的部分匹配表(也称为失效函数表或next数组)。
然后,我们使用KMP算法进行匹配,如果在匹配过程中发现原字符串的某个后缀与反转后的字符串的某个前缀匹配成功,则说明原字符串是回文串。
需要注意的是,这种方法只能用于判断一个字符串是否为回文串,而不能用于查找一个字符串中的所有回文子串。
如果需要查找所有回文子串,可以使用其他算法,例如Manacher算法。
KMP算法以及优化(代码分析以及求解next数组和nextval数组)

KMP算法以及优化(代码分析以及求解next数组和nextval数组)KMP算法以及优化(代码分析以及求解next数组和nextval数组)来了,数据结构及算法的内容来了,这才是我们的专攻,前⾯写的都是开胃⼩菜,本篇⽂章,侧重考研408⽅向,所以保证了你只要看懂了,题⼀定会做,难道这样思想还会不会么?如果只想看next数组以及nextval数组的求解可以直接跳到相应部分,思想总结的很⼲~~⽹上的next数组版本解惑先总结⼀下,⼀般KMP算法的next数组结果有两个版本,我们需要知道为什么会存在这种问题,其实就是前缀和后缀没有匹配的时候next数组为0还是为1,两个版本当然都是对的了,如果next数组为0是的版本,那么对于前缀和后缀的最⼤匹配长度只需要值+1就跟next数组是1的版本⼀样了,其实是因为他们的源代码不⼀样,或者对于模式串的第⼀个下标理解为0或者1,总之这个问题不⽤纠结,懂原理就⾏~~那么此处,我们假定前缀和后缀的最⼤匹配长度为0时,next数组值为1的版本,考研⼀般都是⽤这个版本(如果为0版本,所有的内容-1即可,如你算出next[5]=6,那么-1版本的next[5]就为5,反之亦然)~~其实上⾯的话总结就是⼀句话next[1]=0,j(模式串)数组的第⼀位下标为1,同时,前缀和后缀的最⼤匹配长度+1即为next数组的值,j所代表的的是序号的意思408反⼈类,⼀般数组第⼀位下标为1,关于书本上前⾯链表的学习⼤家就应该有⽬共睹了,书本上好多数组的第⼀位下标为了⽅便我们理解下标为1,想法这样我们更不好理解了,很反⼈类,所以这⾥给出next[1]=0,前缀和后缀的最⼤匹配长度+1的版本讲解前⾔以及问题引出我们先要知道,KMP算法是⽤于字符串匹配的~~例如:⼀个主串"abababcdef"我们想要知道在其中是否包括⼀个模式串"ababc"初代的解决⽅法是,朴素模式匹配算法,也就是我们主串和模式串对⽐,不同主串就往前移⼀位,从下⼀位开始再和模式串对⽐,每次只移动⼀位,这样会很慢,所以就有三位⼤神⼀起搞了个算法,也就是我们现在所称的KMP算法~~代码以及理解源码这⾥给出~~int Index_KMP(SString S,SString T,intt next[]){int i = 1,j = 1;//数组第⼀位下标为1while (i <= S.length && j <= T.length){if (j == 0 || S.ch[i] == T.ch[j]){//数组第⼀位下标为1,0的意思为数组第⼀位的前⾯,此时++1,则指向数组的第⼀位元素++i;++j; //继续⽐较后继字符}elsej = next[j]; //模式串向右移动到第⼏个下标,序号(第⼀位从1开始)}if (j > T.length)return i - T.length; //匹配成功elsereturn 0;}接下来就可以跟我来理解这个代码~~还不会做动图,这⾥就⼿画了~~以上是⼀般情况,那么如何理解j=next[1]=0的时候呢?是的,这就是代码的思路,那么这时我们就知道,核⼼就是要求next数组各个的值,对吧,⼀般也就是考我们next数组的值为多少~~next数组的求解这⾥先需要给出概念,串的前缀以及串的后缀~~串的前缀:包含第⼀个字符,且不包含最后⼀个字符的⼦串串的后缀:包含最后⼀个字符,且不包含第⼀个字符的⼦串当第j个字符匹配失败,由前1~j-1个字符组成的串记为S,则:next[j]=S的最长相等前后缀长度+1与此同时,next[1]=0如,模式串"ababaa"序号J123456模式串a b a b a anext[j]0当第六个字符串匹配失败,那么我们需要在前5个字符组成的串S"ababa"中找最长相等的前后缀长度为多少再+1~~如串S的前缀可以为:"a","ab","aba","abab",前缀只不包括最后⼀位都可串S的后缀可以为:"a","ba","aba","baba",后缀只不包括第⼀位都可所以这⾥最⼤匹配串就是"aba"长度为3,那么我们+1,取4序号J123456模式串a b a b a anext[j]04再⽐如,当第⼆个字符串匹配失败,由前1个字符组成的串S"a"中,我们知道前缀应当没有,后缀应当没有,所以最⼤匹配串应该为0,那么+1就是取1~~其实这⾥我们就能知道⼀个规律了,next[1]⼀定为0(源码所造成),next[2]⼀定为1(必定没有最⼤匹配串造成)~~序号J123456模式串a b a b a anext[j]014再再⽐如,第三个字符串匹配失败,由前两个字符组成的串S"ab"中找最长相等的前后缀长度,之后再+1~~前缀:"a"后缀:"b"所以所以这⾥最⼤匹配串也是没有的长度为0,那么我们+1,取1序号J123456模式串a b a b a anext[j]0114接下来你可以⾃⼰练练4和5的情况~~next[j]011234是不是很简单呢?⾄此,next数组的求法以及kmp代码的理解就ok了~~那么接下来,在了解以上之后,我们想⼀想KMP算法存在的问题~~KMP算法存在的问题如下主串:"abcababaa"模式串:"ababaa"例如这个问题我们很容易能求出next数组序号J123456模式串a b a b a anext[j]011234此时我们是第三个字符串匹配失败,所以我们的next[3]=1,也就是下次就是第⼀个字符"a"和主串中第三个字符"c"对⽐,可是我们刚开始的时候就已经知道模式串的第三个字符"a"和"c"不匹配,那么这⾥不就多了⼀步⽆意义的匹配了么?所以我们就会有kmp算法的⼀个优化了~~KMP算法的优化我们知道,模式串第三个字符"a"不和主串第三个字符"c"不匹配,next数组需要我们的next[3]=1,也就是下次就是第⼀个字符"a"和主串中第三个字符"c"对⽐,之后就是模式串第⼀个字符"a"不和"c"匹配,就是需要变为next[1]=0,那么我们要省去步骤,不就可以直接让next[3]=0么?序号J12345模式串a b a b anext[j]01123nextval[j]00那么怎么省去多余的步骤呢?这就是nextval数组的求法~~nextval的求法以及代码理解先贴出代码for (int j = 2;j <= T.length;j++){if (T.ch[next[j]] == T.ch[j])nextval[j] = nextval[next[j]];elsenextval[j] = next[j];}如序号J123456模式串a b a b a anext[j]011234nextval[j]0⾸先,第⼀次for循环,j=2,当前序号b的next[2]为1,即第⼀个序号所指向的字符a,a!=当前序号b,所以nextval[2]保持不变等于next[2]=1序号J123456模式串a b a b a anext[j]011234nextval[j]01第⼆次for循环,j=3,当前序号a的next[3]为1,即第⼀个序号所指向的字符a,a=当前序号a,所以nextval[3]等于nextval[1]=0序号J123456模式串a b a b a anext[j]011234nextval[j]010第三次for循环,j=4,当前序号b的next[4]为2,即第⼆个序号所指向的字符b,b=当前序号b,所以nextval[4]等于nextval[2]=1序号J123456模式串a b a b a anext[j]011234nextval[j]0101就是这样,你可以练练5和6,这⾥直接给出~~序号J123456模式串a b a b a anext[j]011234nextval[j]010104⾄此nextval数组的求法你也应该会了,那么考研要是考了,那么是不是就等于送分给你呢?⼩练习那么你试着来求⼀下这个模式串的next和nextval数组吧~~next[j]nextval[j]⼩练习的答案序号j12345模式串a a a a b next[j]01234 nextval[j]00004。
kmp算法next函数详解

kmp算法next函数详解KMP算法在介绍KMP算法之前,先介绍⼀下BF算法。
⼀.BF算法BF算法是普通的模式匹配算法,BF算法的思想就是将⽬标串S的第⼀个字符与模式串P的第⼀个字符进⾏匹配,若相等,则继续⽐较S的第⼆个字符和P的第⼆个字符;若不相等,则⽐较S的第⼆个字符和P的第⼀个字符,依次⽐较下去,直到得出最后的匹配结果。
举例说明:S: ababcababaP: ababaBF算法匹配的步骤如下i=0 i=1 i=2 i=3 i=4第⼀趟:a babcababa 第⼆趟:a b abcababa 第三趟:ab a bcababa 第四趟:aba b cababa 第五趟:abab c ababaa baba ab aba ab a ba aba b a abab aj=0 j=1 j=2 j=3 j=4(i和j回溯)i=1 i=2 i=3 i=4 i=3第六趟:a b abcababa 第七趟:ab a bcababa 第⼋趟:aba b cababa 第九趟:abab c ababa 第⼗趟:aba b cababaa baba a baba ab aba ab a ba a babaj=0 j=0 j=1 j=2(i和j回溯) j=0i=4 i=5 i=6 i=7 i=8第⼗⼀趟:abab c ababa 第⼗⼆趟:ababc a baba 第⼗三趟:ababca b aba 第⼗四趟:ababcab a ba 第⼗五趟:ababcaba b aa baba a baba ab aba ab a ba aba b aj=0 j=0 j=1 j=2 j=3i=9第⼗六趟:ababcabab aabab aj=4(匹配成功)代码实现:int BFMatch(char*s,char*p){int i,j;i=0;while(i<strlen(s)){j=0;while(s[i]==p[j]&&j<strlen(p)){i++;j++;}if(j==strlen(p))return i-strlen(p);i=i-j+1; //指针i回溯}return-1;}其实在上⾯的匹配过程中,有很多⽐较是多余的。
深度剖析KMP

深度剖析KMP,让你认识真正的NextKMP算法,想必大家都不陌生,它是求串匹配问题的一个经典算法(当然如果你要理解成放电影的KMP,请退出本页面直接登录各大电影网站,谢谢),我想很多人对它的理解仅限于此,知道KMP能经过预处理然后实现O(N*M)的效率,比brute force(暴力算法)更优秀等等,其实KMP算法中的Next函数,功能十分强大,其能力绝对不仅仅限于模式串匹配,它并不是KMP的附属品,其实它还有更多不为人知的神秘功能^_^先来看一个Next函数的典型应用,也就是模式串匹配,这个相信大家都很熟悉了:POJ 3461 Oulipo——很典型的模式串匹配问题,求模式串在目标串中出现的次数。
#include<cstdio>#include<iostream>#include<cmath>#include<cstring>#include<algorithm>using namespace std;#define MAX 1000001char t[MAX];char s[MAX];int next[MAX];inline void calnext(char s[],int next[]){int i;int j;int len=strlen(s);next[0]=-1;j=-1;for(i=1;i<len;i++){while(j>=0&&s[i]!=s[j+1])j=next[j];if(s[j+1]==s[i])//上一个循环可能因为j=-1而不做,此时不能知道s[i]与s[j+1]的关系。
故此需要此条件。
j++;next[i]=j;}}int KMP(char t[],char s[]){int ans=0;int lent=strlen(t);int lens=strlen(s);if(lent<lens)return 0;int i,j;j=-1;for(i=0;i<lent;i++){while(j>=0&&s[j+1]!=t[i])j=next[j];if(s[j+1]==t[i])j++;if(j==lens-1){ans++;j=next[j];}}return ans;}int main(){int testcase;scanf("%d",&testcase);int i;for(i=1;i<=testcase;i++){scanf("%s%s",s,t);calnext(s,next);printf("%d\n",KMP(t,s));}return 0;}—————————————————————————————————————————————POJ 2406 Power Strings这道题就比较有意思了,乍看之下,怎么看貌似都与KMP无关,呵呵,这就是因为你没有深入理解Next 的含义;我首先来解释下这道题的题意,给你一个长度为n的字符串,首先我们找到这样一个字符串,这个字符串满足长度为n的字符串是由这个字符串重复叠加得到并且这个字符串的长度要最小.,然后输出重复的次数。
next数组的一般公式

next数组的一般公式Next数组是一种常用的数据结构,它在字符串匹配、模式识别以及图像处理等领域中具有重要的应用。
本文将介绍Next数组的一般公式及其应用。
一、Next数组的定义和作用Next数组是一个用于字符串匹配的辅助数组,它记录了每个字符在匹配失败时应该跳转到的位置。
具体而言,对于一个长度为n的字符串S,Next[i]表示S中以第i个字符结尾的子串的最长公共前后缀的长度。
利用Next数组,我们可以在O(n)的时间复杂度内完成字符串匹配操作。
二、Next数组的计算方法Next数组的计算可以通过动态规划的方法来实现。
具体而言,我们可以通过以下递推关系式计算Next数组:1. 初始化Next[0] = -1,Next[1] = 0;2. 设j为当前位置,如果S[i-1] == S[j-1],则Next[i] = Next[j] + 1;3. 如果S[i-1] != S[j-1],则令j = Next[j],继续比较S[i-1]与S[j-1],直到找到满足S[i-1] == S[j-1]或者j = 0为止;4. 重复步骤2和3,直到计算完整个Next数组。
三、Next数组的应用1. 字符串匹配:通过Next数组,我们可以在主串中找到模式串的出现位置。
具体而言,我们可以在O(n)的时间复杂度内完成字符串匹配操作,这在大规模文本的搜索中非常高效。
2. 模式识别:在模式识别中,我们经常需要寻找图像或者信号中的特定模式。
利用Next数组,我们可以快速计算出模式的相似度或者匹配程度,从而实现模式识别的任务。
3. 图像处理:在图像处理中,我们经常需要进行特征提取或者图像比对。
Next数组可以帮助我们快速计算出图像中的特征序列,并进行相似度的比对,从而实现图像处理的任务。
四、Next数组的优化算法在实际应用中,为了进一步提高字符串匹配的效率,可以对Next数组的计算方法进行优化。
其中最著名的算法是KMP算法,它通过预处理得到一个优化后的Next数组,从而在匹配过程中减少了不必要的比较操作,提高了匹配效率。
详解KMP算法中Next数组的求法

详解KMP算法中Next数组的求法例如:1 2 3 4 5 6 7 8模式串 a b a a b c a cnext值0 1 1 2 2 3 1 2next数组的求解方法是:第一位的next值为0,第二位的next 值为1,后面求解每一位的next值时,根据前一位进行比较。
首先将前一位与其next值对应的内容进行比较,如果相等,则该位的next 值就是前一位的next值加上1;如果不等,向前继续寻找next值对应的内容来与前一位进行比较,直到找到某个位上内容的next值对应的内容与前一位相等为止,则这个位对应的值加上1即为需求的next值;如果找到第一位都没有找到与前一位相等的内容,那么需求的位上的next值即为1。
看起来很令人费解,利用上面的例子具体运算一遍。
1.前两位必定为0和1。
2.计算第三位的时候,看第二位b的next值,为1,则把b和1对应的a进行比较,不同,则第三位a的next的值为1,因为一直比到最前一位,都没有发生比较相同的现象。
3.计算第四位的时候,看第三位a的next值,为1,则把a和1对应的a进行比较,相同,则第四位a的next的值为第三位a的next 值加上1。
为2。
因为是在第三位实现了其next值对应的值与第三位的值相同。
4.计算第五位的时候,看第四位a的next值,为2,则把a和2对应的b进行比较,不同,则再将b对应的next值1对应的a与第四位的a进行比较,相同,则第五位的next值为第二位b的next值加上1,为2。
因为是在第二位实现了其next值对应的值与第四位的值相同。
5.计算第六位的时候,看第五位b的next值,为2,则把b和2对应的b进行比较,相同,则第六位c的next值为第五位b的next 值加上1,为3,因为是在第五位实现了其next值对应的值与第五位相同。
6.计算第七位的时候,看第六位c的next值,为3,则把c和3对应的a进行比较,不同,则再把第3位a的next值1对应的a与第六位c比较,仍然不同,则第七位的next值为1。
KMP算法中next数组的理解与算法的实现(java语言)

KMP算法中next数组的理解与算法的实现(java语⾔)KMP 算法我们有写好的函数帮我们计算 Next 数组的值和 Nextval 数组的值,但是如果是考试,那就只能⾃⼰来⼿算这两个数组了,这⾥分享⼀下我的计算⽅法吧。
计算前缀 Next[i] 的值:我们令 next[0] = -1 。
从 next[1] 开始,每求⼀个字符的 next 值,就看它前⾯是否有⼀个最长的"字符串"和从第⼀个字符开始的"字符串"相等(需要注意的是,这2个"字符串"不能是同⼀个"字符串")。
如果⼀个都没有,这个字符的 next 值就是0;如果有,就看它有多长,这个字符的next 值就是它的长度。
计算修正后的 Nextval[i] 值:我们令 nextval[0] = -1。
从 nextval[1] 开始,如果某位(字符)与它 next 值指向的位(字符)相同,则该位的 nextval 值就是指向位的 nextval 值(nextval[i] = nextval[ next[i] ]);如果不同,则该位的 nextval 值就是它⾃⼰的 next 值(nextvalue[i] = next[i])。
举个例⼦:计算前缀 Next[i] 的值:next[0] = -1;定值。
next[1] = 0;s[1]前⾯没有重复⼦串。
next[2] = 0;s[2]前⾯没有重复⼦串。
next[3] = 0;s[3]前⾯没有重复⼦串。
next[4] = 1;s[4]前⾯有重复⼦串s[0] = 'a'和s[3] = 'a'。
next[5] = 2;s[5]前⾯有重复⼦串s[01] = 'ab'和s[34] = 'ab'。
next[6] = 3;s[6]前⾯有重复⼦串s[012] = 'abc'和s[345] = 'abc'。
kmp next算法

kmp next算法KMP算法(Knuth-Morris-Pratt Algorithm)是一种字符串匹配算法,它的核心思想是利用已经得到的匹配结果,尽量减少字符的比较次数,提高匹配效率。
本文将详细介绍KMP算法的原理、实现方法以及应用场景。
一、KMP算法的原理KMP算法的核心是构建next数组,用于指导匹配过程中的回溯操作。
next数组的定义是:对于模式串中的每个字符,记录它前面的子串中相同前缀和后缀的最大长度。
next数组的长度等于模式串的长度。
具体来说,KMP算法的匹配过程如下:1. 初始化主串指针i和模式串指针j为0。
2. 逐个比较主串和模式串对应位置的字符:- 若主串和模式串的字符相等,i和j同时后移一位。
- 若主串和模式串的字符不相等,根据next数组的值,将模式串指针j回溯到合适的位置,继续匹配。
二、KMP算法的实现KMP算法的实现可以分为两个步骤:构建next数组和利用next数组进行匹配。
1. 构建next数组:- 首先,next[0]赋值为-1,next[1]赋值为0。
- 然后,从第2个位置开始依次计算next[i],根据前一个位置的next值和模式串的字符进行判断:- 若前一个位置的next值为-1或模式串的字符与前一个位置的字符相等,则next[i] = next[i-1] + 1。
- 若前一个位置的next值不为-1且模式串的字符与前一个位置的字符不相等,则通过next数组的回溯操作,将模式串指针j回溯到合适的位置,继续判断。
2. 利用next数组进行匹配:- 在匹配过程中,主串指针i和模式串指针j会同时后移:- 若主串和模式串的字符相等,i和j同时后移一位。
- 若主串和模式串的字符不相等,则根据next数组的值,将模式串指针j回溯到合适的位置,继续匹配。
三、KMP算法的应用场景KMP算法在字符串匹配中有广泛的应用,特别是在大规模文本中的模式匹配问题上具有明显的优势。
以下是KMP算法的几个应用场景:1. 子串匹配:判断一个字符串是否是另一个字符串的子串。
kmp算法next数组构造过程

kmp算法next数组构造过程
KMP算法的核心部分就是构造next数组,它的作用是在模式
串与目标串不匹配时,快速确定模式串需要移动的位置,从而避免不必要的比较操作。
下面是KMP算法中next数组的构造过程:
1. 首先,创建一个长度与模式串相同的数组next[],用于存储
每个位置的next值。
2. 将next[0]初始化为-1,next[1]初始化为0,这是因为当模式
串只有一个字符时,无法进行移动,所以next[1]为0。
3. 从位置2开始,使用一个指针i遍历整个模式串。
在遍历的
过程中,不断更新next[i]的值。
4. 对于每个位置的next[i],需要判断模式串中位置i之前的子
串的前缀与后缀是否存在重复。
具体操作如下:
- 首先,将next[i-1]的值赋给一个临时变量j,并递归比较j
与i-1位置的字符是否相等。
如果相等,则next[i]的值为j+1;如果不相等,则将next[j]的值再赋给j,重新进行比较。
- 重复上述过程,直到找到一个相等的前缀和后缀,或者不
能再递归比较为止。
5. 当指针i遍历完整个模式串后,next数组的构造过程完成。
这个构造过程的时间复杂度为O(m),其中m是模式串的长度。
通过构造好的next数组,可以快速确定模式串的移动位置,
从而提高匹配效率。
KMP算法的next函数求解和分析过程

KMP算法的next函数求解和分析过程转⾃:/wang0606120221/article/details/7402688假设KMP算法中的模式串为P,主串为S,那么该算法中的核⼼是计算出模式串的P的next函数。
KMP算法是在已知的模式串的next函数值的基础上进⾏匹配的。
由于本次只讨论next的求值过程,因此KMP算法的数学推理过程这⾥不再讲解。
从KMP算法的数学推理可知,此next函数只取决与模式匹配串⾃⾝的特点和主串没有任何关系,此函数默认认为next[1]=0,由于next[j]=k表⽰的意义是当模式串和主串的第j个字符不匹配时,那么接下来和主串的第j个字符匹配的字符是模式串的第k个字符。
因此,next[1]=0表⽰当主串的当前字符和模式串的第1个字符不匹配,接下来需要⽤模式串的第0个字符和主串的当前字符匹配,由于模式串下标是从1开始的,所以不可能存在第0个字符,即接下的匹配动作是主串和模式串同时向右移动⼀位,继续模式匹配。
例如:主串:a c a b a a b a a b n a c模式串:a b a a b主串:a c a b a a b a a b n a c模式串: a b a a b主串:a c a b a a b a a b n a c模式串: a b a a b此时,主串和模式串不匹配,⽽next[1]=0,因此,模式串的第0个字符和主串的第2个字符⽐较,⽽模式串没有第0个字符,此时可以把第0个字符理解为空字符,即模式串向右移动⼀位,主串再继续喝模式串匹配,⽽此时的主串的当前字符是第3个字符,整体来看是当主串和模式串的第1个字符不匹配时,主串和模式串同时右移⼀位,然后继续匹配。
接下来讲解⼀般情况下的next函数值求解过程。
设next[j]=k,根据KMP算法的模式串的特点可知,‘p1p2......pk-1’=‘pj-k+1......pj-1’,其中k必须满⾜1<k<j,并且不可能存在k‘>k满⾜上⾯等式。
邝斌的ACM模板

字符串处理............................................................................................................................... 2 1、KMP 算法 .................................................................................................................... 2 2、扩展 KMP .................................................................................................................... 5 3、Manacher 最长回文子串 ........................................................................................... 6 4、AC 自动机 ................................................................................................................... 7 5、后缀数组..................................................................................................................... 9 6、后缀自动机....................
计算模式串t的next数组和nextval数组的值。

计算模式串t的next数组和nextval数组的值。
模式串的ne某t数组和ne某tval数组是用来加快KMP算法中匹配过程的重要辅助数组。
首先,我们来定义ne某t数组和ne某tval数组。
1. ne某t数组:ne某t[i]表示模式串前i个字符组成的字符串的最长相同前缀后缀的长度。
即,在模式串中以i为末尾字符的子串的最长相同前缀后缀的长度。
2. ne某tval数组:ne某tval[i]表示当模式串中以i为末尾字符的子串的ne某t值为0时,下一个字符与其前缀的最长相同前缀后缀的长度。
即,当ne某t[i]=0时,ne某tval[i]表示模式串前缀0~i-1的最长相同前缀后缀的长度。
接下来,我们来计算ne某t数组和ne某tval数组。
计算ne某t数组:1. 首先,ne某t[0]=-1,ne某t[1]=0,表示只包含一个字符的模式串不存在相同的前缀后缀,即长度为0。
2. 然后,我们从第2个字符开始,依次计算ne某t[i]的值。
- 如果模式串的前i-1个字符组成的字符串的最长相同前缀后缀的长度不为0,并且下一个字符与最后一个字符相等,则ne某t[i]=ne某t[i-1]+1。
- 否则,我们需要递归地查找前i-1个字符组成的字符串的次长相同前缀后缀。
假设最长相同前缀后缀的长度为k,则我们将次长相同前缀后缀的长度ne某t[k]赋值给ne某t[i]。
计算ne某tval数组:1. 首先,我们将ne某tval[0]=0,表示模式串的第一个字符不存在次长相同前缀后缀。
2. 然后,我们从第1个字符开始,依次计算ne某tval[i]的值。
- 如果ne某t[i]=0,即模式串的前缀0~i-1的最长相同前缀后缀的长度为0,那么我们需要找到前缀0~i-1的次长相同前缀后缀。
- 我们可以通过递归查找前i-1个字符组成的字符串的次长相同前缀后缀的长度k,然后将ne某tval[k]赋值给ne某tval[i]。
通过以上的计算步骤,我们可以得到模式串的ne某t数组和ne某tval数组。
kmp算法中的next数组实例解释

kmp算法中的next数组实例解释假设求串′ababaaababaa′的next数组模式串a b a b a a a b a b a a下标1234567891011121、前两位:next数组前两位⼀定是0,1 即前两位ab对应的next数组为01,则:模式串a b a b a a a b a b a a下标123456789101112next数组012、接下来看第三位,按照next数组求解⽅法。
第三位a的前⼀位为第⼆位的b,b的next值为1对应内容为a,b与a不同,向前继续寻找next值对应的内容来与前⼀位进⾏⽐较。
因为找到第⼀位都没有找到与前⼀位相等的内容,所以第三位a的next值为1,则:模式串a b a b a a a b a b a a下标123456789101112next数组0113、接下来看第四位b,b的前⼀位a的next值1对应内容为a,相同,所以该位b的next值就是前⼀位a的next值加上1,即为2模式串a b a b a a a b a b a a下标123456789101112next数组01124、接下来看第五位a,a的前⼀位b的next值2对应内容为b,相等,所以该位a的next值就是前⼀位b的next值加上1,即为3模式串a b a b a a a b a b a a下标123456789101112next数组011235、接下来看第六位a,a的前⼀位a的next值3对应内容为a,相等,所以该位a的next值就是前⼀位a的next值加上1,即为4模式串a b a b a a a b a b a a下标123456789101112next数组0112346、接下来看第七位a,a的前⼀位a的next值4对应内容为b,不相等,向前继续寻找next值对应的内容来与前⼀位进⾏⽐较,b的next值2对应的内容为b,依旧不相等,继续向前寻找,第⼆位b的next值1对应内容为a,相等。
JavaKMP算法代码

JavaKMP算法代码1. KMP 算法(字符串匹配算法)较 BF(朴素的字符串匹配)算法有哪些改进1)在主串和⼦串匹配的过程中,主串不再回退,只改变⼦串的⽐较位置。
2)为⼦串⽣成对应的next数组,每次匹配失败,通过访问next数组获知⼦串再⼀次开始匹配的位置。
2. 在KMP算法中,为了确定在匹配不成功时,下次匹配时j的位置,引⼊了next[]数组,next[j]的值表⽰P[0...j-1]中最长后缀的长度等于相同字符序列的前缀。
因此KMP算法的思想就是:在匹配过程称,若发⽣不匹配的情况,如果next[j]>=0,则⽬标串的指针i不变,将模式串的指针j移动到next[j]的位置继续进⾏匹配;若next[j]=-1,则将i右移1位,并将j置0,继续进⾏⽐较。
public class KMP {public static void main(String[] args) {String a="aawsadabbb";String b="abb";System.out.println(KMP(a,b));}public static int KMP(String s,String t ){int i=0;int j=0;int []next=getNext(t);while (i<s.length()&&j<t.length()){if(j==-1||s.charAt(i)==t.charAt(j)){i++;j++;}else {j=next[j];}}if(j==t.length()){return i-j;}else {return -1;}}// 求取next数组private static int[] getNext(String t) {int k=-1;int j=0;int []next=new int[t.length()];next[0]=-1;while (j<t.length()-1){if(k==-1||t.charAt(k)==t.charAt(j)) {k++;j++;next[j]=k;}else {k=next[k];}}return next;}}。
KMP算法(推导方法及模板)

KMP算法(推导⽅法及模板)介绍克努斯-莫⾥斯-普拉特算法Knuth-Morris-Pratt(简称为KMP算法)可在⼀个主⽂本S内查找⼀个词W的出现位置。
此算法通过运⽤对这个词在不匹配时本⾝就包含⾜够的信息来确定下⼀个匹配将在哪⾥开始的发现,从⽽避免重新检查先前匹配的。
此算法可以在O(n+m)时间数量级上完成串的模式匹配操作,其改进在于:每当⼀趟匹配过程中出现字符⽐较不等时,不需回溯i的指针,⽽是利⽤已经得到的“部分匹配”的结果将模式向右“滑动”尽可能远的距离后,继续进⾏⽐较。
kmp的核⼼之处在于next数组,⽽为了⽅便理解,我先介绍KMP的思想KMP匹配当开始匹配时,如果匹配过程中产⽣“失配”时,指针i(原串的下标)不变,指针j(模式串的下标)退回到next[j] 所指⽰的位置上重新进⾏⽐较,并且当指针j退回⾄零时,指针i和指针j需同时加⼀。
即主串的第i个字符和模式的第⼀个字符不等时,应从主串的第i+1个字符起重新进⾏匹配。
简单来说,就是两个串匹配,如果当前字符相等就⽐较两个字符串的下⼀个字符,如果当前匹配不相等时,就让j(待匹配串的下标)回到next[j] 的位置,因为我们已经知道next数组的作⽤是利⽤已经得到的“部分匹配”的结果将模式向右“滑动”尽可能远的距离,如ababac与abac⽐较时i=4,j=4时不匹配,则利⽤next数组让j=2继续匹配⽽不⽤重新开始。
(⽬前先不⽤管next数组的值时如何得到的,只要明⽩它的作⽤即可,下⾯回介绍)所以我们可以写出kmp的代码int KMP(char str[],char pat[]){int lenstr=strlen(str);int lenpat=strlen(pat);int i=1,j=1;while(i<=lenstr){if(j==0 || str[i]==pat[j]) //匹配成功继续往后匹配++i,++j;elsej=next[j]; //否则根据next数组继续匹配if(j==lenpat) //说明匹配完成return 1;}return 0;}接下来就是关键的求next数组了next数组⾸先,next数组取决于模式串本⾝⽽与相匹配的主串⽆关,我们可以对其递推得到。
KMP算法

KMP算法在传统的字符串匹配算法中,最常用的算法是朴素的模式匹配算法。
该算法的基本思想是:从主串的第一个字符开始,逐个字符地与模式串进行比较,如果发现不匹配的字符,则回溯到主串的下一个字符重新开始匹配。
这种算法的时间复杂度是O(m*n),其中m为主串的长度,n为模式串的长度。
在主串与模式串长度相等时,该算法的时间复杂度甚至会达到O(n^2)。
KMP算法的核心思想是利用模式串的信息,避免不必要的比较。
它通过预处理模式串,构建一个部分匹配表(prefix table),来提供匹配失败时的回溯位置。
这样,在匹配的过程中,只需要根据部分匹配表的内容来调整主串和模式串的位置即可。
这种优化使得KMP算法的时间复杂度降低到O(m+n)。
具体来说,KMP算法在预处理模式串时,对于模式串的每个前缀子串,求出其最长的相等的前缀和后缀的长度。
这个长度被称为部分匹配值。
例如,对于模式串"ababc",它的前缀子串有"","a","ab","aba",而其相等的后缀子串有"","c","bc","abc"。
其中,最长的相等的前缀和后缀的长度是2,因此,部分匹配值为2、在KMP算法中,这个信息会被存储在部分匹配表中,即prefix table。
当进行匹配时,如果发现匹配失败,那么根据部分匹配表中的值来进行回溯。
具体来说,如果当前字符匹配失败,那么将模式串向右移动的距离为:当前字符之前的最长相等前缀的长度-1、这样,就可以将模式串与主串对齐继续匹配。
1. 预处理模式串,求出部分匹配表(prefix table)。
2.根据部分匹配表,进行匹配操作。
3.如果匹配成功,返回匹配的位置;否则,返回匹配失败。
总之,KMP算法是一种高效的字符串匹配算法,通过预处理模式串,提供了匹配失败时的快速回溯位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
首先看看next数组值的求解方法。
例如:模式串abaabcac next值01122312 nextval值next数组的求解方法是:第一位的next值为0,第二位的next值为1,后面求解每一位的next值时,根据前一位进行比较。
首先将前一位与其next值对应的内容进行比较,如果相等,则该位的next值就是前一位的next值加上1;如果不等,向前继续寻找next值对应的内容来与前一位进行比较,直到找到某个位上内容的next值对应的内容与前一位相等为止,则这个位对应的值加上1即为需求的next 值;如果找到第一位都没有找到与前一位相等的内容,那么需求的位上的next 值即为1。
看起来很令人费解,利用上面的例子具体运算一遍。
1.前两位必定为0和1。
2.计算第三位的时候,看第二位b的next值,为1,则把b和1对应的a 进行比较,不同,则第三位a的next的值为1,因为一直比到最前一位,都没有发生比较相同的现象。
3.计算第四位的时候,看第三位a的next值,为1,则把a和1对应的a进行比较,相同,则第四位a的next的值为第三位a的next值加上1。
为2。
因为是在第三位实现了其next值对应的值与第三位的值相同。
4.计算第五位的时候,看第四位a的next值,为2,则把a和2对应的b进行比较,不同,则再将b对应的next值1对应的a与第四位的a进行比较,相同,则第五位的next值为第二位b的next值加上1,为2。
因为是在第二位实现了其next值对应的值与第四位的值相同。
5.计算第六位的时候,看第五位b的next值,为2,则把b和2对应的b 进行比较,相同,则第六位c的next值为第五位b的next值加上1,为3,因为是在第五位实现了其next值对应的值与第五位相同。
6.计算第七位的时候,看第六位c的next值,为3,则把c和3对应的a进行比较,不同,则再把第3位a的next值1对应的a与第六位c比较,仍然不同,则第七位的next值为1。
7.计算第八位的时候,看第七位a的next值,为1,则把a和1对应的a进行比较,相同,则第八位c的next值为第七位a的next值加上1,为2,因为是在第七位和实现了其next值对应的值与第七位相同。
在计算nextval之前要先弄明白,nextval是为了弥补next函数在某些情况下的缺陷而产生的,例如主串为“aaabaaaab”、模式串为“aaaab”那么,比较的时候就会发生一些浪费的情况:比较到主串以及模式串的第四位时,发现其值并不相等,据我们观察,我们可以直接从主串的第五位开始与模式串进行比较,而事实上,却进行了几次多余的比较。
使用nextval可以去除那些不必要的比较次数。
求nextval数组值有两种方法,一种是不依赖next数组值直接用观察法求得,一种方法是根据next数组值进行推理,两种方法均可使用,视更喜欢哪种方法而定。
我们使用例子“aaaab”来考查第一种方法。
1.试想,在进行模式匹配的过程中,将模式串“aaaab”与主串进行匹配的时候,如果第一位就没有吻合,即第一位就不是a,那么不用比较了,赶快挪到主串的下一位继续与模式串的第一位进行比较吧,这时,模式串并没有发生偏移,那么,模式串第一位a的nextval值为0。
2.如果在匹配过程中,到第二位才发生不匹配现象,那么主串的第一位必定是a,而第二位必定不为a,既然知道第二位一定不为a,那么主串的第一、二两位就没有再进行比较的必要,直接跳到第三位来与模式串的第一位进行比较吧,同样,模式串也没有发生偏移,第二位的nextval值仍然为0。
3.第三位、第四位类似2的过程,均为0。
4.如果在匹配过程中,直到第五位才发生不匹配现象,那么主串的第一位到第四位必定为a,并且第五位必定不为b,可是第五位仍然有可能等于a。
如果万一第五位为a,那么既然前面四位均为a,所以,只要第六位为b,第一个字符串就匹配成功了。
所以,现在的情况下,就是看第五位究竟是不是a了。
所以发生了下面的比较:123456aaaa**aaaabaaaab
前面的三个a都不需要进行比较,只要确定主串中不等于b的那个位是否为a,即可以进行如下的比较:如果为a,则继续比较主串后面一位是否为b;如果不为a,则此次比较结束,继续将模式串的第一位去与主串的下一位进行比较。
由此看来,在模式串的第五位上,进行的比较偏移了4位(不进行偏移,直接比较下一位为0),故第五位b的nextval值为4。
我们可以利用第一个例子“abaabcac”对这种方法进行验证。
a的nextval值为0,因为如果主串的第一位不是a,那么没有再比较下去的必要,直接比较主串的第二位是否为a。
如果比较到主串的第二位才发生错误,则主串第一位肯定为a,第二位肯定不为b,此时不能直接跳到第三位进行比较,因为第二位还可能是a,所以对主串的第二位再进行一次比较,偏移了1位,故模式串第二位的nextval值为1。
以此类推,nextval值分别为:01021302。
其中第六位的nextval之所以为3,是因为,如果主串比较到第六位才发生不匹配现象,那么主串的前五位必定为“abaab”且第六位必定不是“c”,但第六位如果为“a”的话,那么我们就可以从模式串的第四位继续比较下去。
所以,这次比较为:1234 5678910 11 12abaab*******abaabcac
而不是:1234 5678910 11 12abaab*******abaabca
因为前两位a和b已经确定了,所以不需要再进行比较了。
所以模式串第六位的nextval值为这次比较的偏移量3。
再来看求nextval数组值的第二种方法。
模式串abaabcac next值01122312nextval值01021302
1.第一位的nextval值必定为0,第二位如果于第一位相同则为0,如果不同则为1。
2.第三位的next值为1,那么将第三位和第一位进行比较,均为a,相同,则,第三位的nextval值为0。
3.第四位的next值为2,那么将第四位和第二位进行比较,不同,则第四位的nextval值为其next值,为2。
4.第五位的next值为2,那么将第五位和第二位进行比较,相同,第二位的next值为1,则继续将第二位与第一位进行比较,不同,则第五位的nextval值为第二位的next值,为1。
5.第六位的next值为3,那么将第六位和第三位进行比较,不同,则第六位的nextval值为其next值,为3。
6.第七位的next值为1,那么将第七位和第一位进行比较,相同,则第七位的nextval值为0。
7.第八位的next值为2,那么将第八位和第二位进行比较,不同,则第八位
的nextval值为其next值,为2。
在“aaaab”内进行验证。
模式串aaaabnext值01234nextval值00004。
