习题课-光的干涉
光的干涉 习题课 - 2015.10.20

B
S S`
S1 O
S2
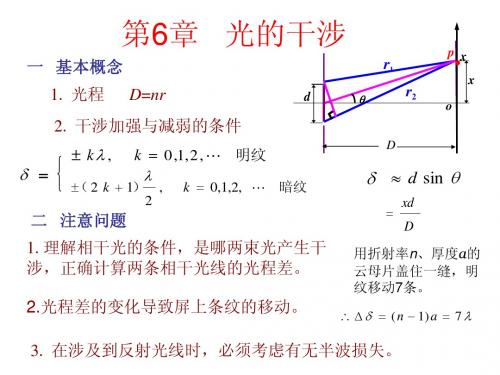
在双缝干涉实验中,波长=550 nm的单色平行 光垂直入射到缝间距d=2×10-4 m的双缝上,屏到 双缝的距离D=2 m.求:(1) 中央明纹两侧的两条 第10级明纹中心的间距; (2) 用一厚度为e= 6.6×10-5 m、折射率为n=1.58的玻璃片覆盖一缝 后,零级明纹将移到原来的第几级明纹处?(1 nm = 10-9 m) x 解: (1) d K 10 2 x 0.11m D (2) 覆盖云玻璃后,附加光程差 (n-1)e = k k=(n-1) e / =6.96≈7 零级明纹移到原第7级明纹处
M1
如图所示,波长为的平行单色光垂直照射到两 个劈形膜上,两劈尖角分别为1和 2,折射率分 别为n1和n2,若二者分别形成的 干涉条纹的明条纹间距相等,则1 , n n n11 = n22 . 2,n1和n2之间的关系是___________
1 1 2
2
波长为的单色光垂直照射到折射率为n2的形膜 上,如图所示,图中n1<n2<n3,观察反射光形成 的干涉条纹. (1) 从劈形膜顶部O开始向右数起, 第五条暗纹中心所对应的薄膜厚度是多少? (2) 相邻的二明纹所对应的薄膜厚度之差是多少? n 解(1) 2n2 e = (2k +1)/ 2 k =0,1,2, … n e 4 9 / 4 n2 令k =4 O n (2)相邻二明纹所对应的膜厚度之差 e = / (2n2)
d si n d si n , (2)当θ很小时, si n d 上式给出 k si n S2 d (k 1) sin ] [ k sin ] k 1 k [ d d (它与 φ 无关) d
第一章光的干涉习题和答案解析

λdr y 0=∆第一章 光的干涉●1.波长为nm 500的绿光投射在间距d 为cm 022.0的双缝上,在距离cm 180处的光屏上形成干涉条纹,求两个亮条纹之间的距离.若改用波长为nm 700的红光投射到此双缝上,两个亮条纹之间的距离又为多少?算出这两种光第2级亮纹位置的距离.解:由条纹间距公式λd r y y y j j 01=-=∆+ 得:cm 328.0818.0146.1cm146.1573.02cm818.0409.02cm573.010700022.0180cm 409.010500022.018021222202221022172027101=-=-=∆=⨯===⨯===⨯⨯==∆=⨯⨯==∆--y y y drj y d rj y d r y d r y j λλλλ●2.在杨氏实验装置中,光源波长为nm 640,两狭缝间距为mm 4.0,光屏离狭缝的距离为cm 50.试求:(1)光屏上第1亮条纹和中央亮条纹之间的距离;(2)若p 点离中央亮条纹为mm 1.0,问两束光在p 点的相位差是多少?(3)求p 点的光强度和中央点的强度之比.式: 解:(1)由公得λd r y 0=∆ =cm 100.8104.64.05025--⨯=⨯⨯(2)由课本第20页图1-2的几何关系可知52100.01sin tan 0.040.810cm 50y r r d d dr θθ--≈≈===⨯521522()0.8106.4104r r πππϕλ--∆=-=⨯⨯=⨯(3) 由公式2222121212cos 4cos 2I A A A A A ϕϕ∆=++∆= 得8536.042224cos 18cos 0cos 421cos 2cos42cos 422202212212020=+=+==︒⋅=∆∆==πππϕϕA A A A I I pp●3. 把折射率为1.5的玻璃片插入杨氏实验的一束光路中,光屏上原来第5级亮条纹所在的位置为中央亮条纹,试求插入的玻璃片的厚度.已知光波长为6×10-7m.解:未加玻璃片时,1S 、2S 到P 点的光程差,由公式2rϕπλ∆∆=可知为 Δr =215252r r λπλπ-=⨯⨯=现在1S 发出的光束途中插入玻璃片时,P 点的光程差为()210022r r h nh λλϕππ'--+=∆=⨯=⎡⎤⎣⎦所以玻璃片的厚度为421510610cm 10.5r r h n λλ--====⨯-4. 波长为500nm 的单色平行光射在间距为0.2mm 的双狭缝上.通过其中一个缝的能量为另一个的2倍,在离狭缝50cm 的光屏上形成干涉图样.求干涉条纹间距和条纹的可见度.解:6050050010 1.250.2r y d λ-∆==⨯⨯=mm122I I = 22122A A =12A A =()()122122/0.94270.941/A A V A A ∴===≈+5. 波长为700nm 的光源与菲涅耳双镜的相交棱之间距离为20cm ,棱到光屏间的距离L 为180cm,若所得干涉条纹中相邻亮条纹的间隔为1mm ,求双镜平面之间的夹角θ。
华理大学物理第13章习题课

1 e2 e1 4.5(2 1 )=225 2
【填空题6】检验滚珠大小的干涉装置示意如图 (a)。S为单色光源,波长为λ,L为会聚透镜,M为 半透半反镜。在平晶T1、T2之间放置A、B、C三 个滚珠,其中A为标准件,直径为d0。在M上方观
察时,观察到等厚条纹如图(b)所示.若轻压C端 d0 ,条纹间距变小,则可算出B珠的直径d1=______
其右边条纹的执行部分的切线相切。则工件的上
表面缺陷是【】 (A)不平处为凸起纹,最大高度为500nm; (B)不平处为凸直纹,最大高度为250nm ; (C)不平处为凹槽,最大深度为500nm ; (D)不平处为凹槽,最大深度为250nm 。 a
b
【选择题4】在双缝干涉实验中,入射光的波长为 λ,用玻璃纸遮住双缝中的一个缝,若玻璃纸中光
相干光的光程差应为 ;从劈尖棱边算起,第
三条明纹中心离棱边的水平距离为
。
n1=1 n2=1.25 n3=1.15
2n2 e
2n2e
2
2.5e k
2
2
2.5e 3
2
2.5 e
l sin l sin
(1)形状——直线
e
级次——外小中间大,
中间疏,两侧密
2e k 2 2d 0 kmax (d0 2) 2 kmax 4.5
r k 1, 2,3, 4 (2 ) e d 0 2R r2 2e 2(d0 ) k 2 2R 2
【选择题6】在折射率n3=1.60的玻璃片表面镀一层 折射率n2=1.38的MgF2薄膜作为增透膜。为了使波 长为λ=500nm的光,从折射率n1=1.00的空气垂直 入射到玻璃片上的反射尽可能地减少, MgF2 薄
光的干涉习题课共55页

31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
光的干习题课
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
光的干涉、衍射(习题课)

x
(二)、起偏和检偏
起偏:使自然光(或非偏振光)变成线偏振光的过程。 检偏:检查入射光的偏振性。
(三)、 马吕斯定律 如果入射线偏振光的光强为I1,透过检偏器后, 透射光的光强 I 为 I I cos 2
2 1
消光——透射光强 I 为零的情况
(四)、布儒斯特定律
入射角等于某一特定值i0且满足:
解(1)
xk D k级 明 纹 位 置 : xk k , 又 tan d D D 相邻两 条 纹 的间距: Δx λ d
相 邻 两 条 纹 的 角 间 距 : 同理:
x
D
d
x
D
d
而: (1 0.1)
( 1 0.1 ) 648.2 ( nm )
D
在恰能分辨时,两个点光源在透镜 前所张的角度,称为最小分辨角。
最小分辨角的倒数
(四)、光栅衍射
1
R
称为光学仪器的分辨率
1、光栅衍射是单缝衍射与多缝干涉的综合效应,即:它
是一种被单缝衍射调制的多缝干涉条纹。
2、屏幕上主极大位置由光栅公式决定
(a+b)sin =k
k=0,±1, ±2, ±3 · · ·
(2) 放入水中后, 钠黄光的波长变为
此 时 相 邻 两 条 纹 的 角 距 间变为: 1 0.20 o 0.15 nd d n n 1.33
n
1
o
2、 在空气中垂直入射的白光从肥皂膜 上反射(假定膜的厚度是均匀的) ,在可见光谱 中630nm处有一干涉极大,而在525nm处 有一干涉极小,在这极大与极小之间没有另 外的极大和极小。求这膜的厚度。 (肥皂水的折射率看作与水相同,为1.33。)
高中物理(新人教版)选择性必修一课后习题:光的干涉(课后习题)【含答案及解析】

光的干涉课后篇巩固提升必备知识基础练1.(多选)下列关于双缝干涉实验的说法正确的是()A.单缝的作用是获得频率保持不变的相干光源B.双缝的作用是获得两个振动情况相同的相干光源C.频率相同、相位差恒定、振动方向相同的两列单色光能够发生干涉现象D.照射单缝的单色光的波长越小,光屏上出现的条纹宽度越宽,单缝的作用是获得一个线光源,双缝的作用是获得两个振动情况完全相同的光源,故选项A错误,B正确;频率相同、相位差恒定的两列光可以发生干涉现象,选项C正确;由Δx=ldλ可知,波长越短,条纹间距越窄,选项D错误。
2.(2021河北博野中学高二开学考试)某一质检部门为检测一批矿泉水的质量,利用干涉原理测定矿泉水的折射率。
方法是将待测矿泉水填充到特制容器中,放置在双缝与光屏之间(可视为双缝与光屏之间全部为矿泉水),如图所示,特制容器未画出,通过比对填充后的干涉条纹间距x2和填充前的干涉条纹间距x1就可以计算出该矿泉水的折射率。
则下列说法正确的是(设空气的折射率为1)()A.x2=x1B.x2>x1C.该矿泉水的折射率为x1x2D.该矿泉水的折射率为x2x1n=cv和v=fλ可知光在水中的波长小于在空气中的波长,根据双缝干涉条纹的间距公式Δx=ldλ可知填充矿泉水后的干涉条纹间距x2小于填充前的干涉条纹间距x1,所以A、B错误;根据n=cv 和v=fλ可得n=λ1λ2,又由x1=ldλ1和x2=ldλ2得n=x1x2,故C正确,D错误。
3.如图所示,用频率为f 的单色光垂直照射双缝,在光屏上的P 点出现第3条暗条纹,已知光速为c ,则P 点到双缝距离之差S 2P-S 1P 应为( )A.c 2fB.3c 2fC.3c fD.5c 2fλ=c f ,又P 点出现第3级暗条纹,即S 2P-S 1P=5×λ2=5c 2f ,选项D 正确。
4.某同学自己动手利用如图所示的器材,观察光的干涉现象,其中,A 为单缝屏,B 为双缝屏,C 为像屏。
33光的干涉习题课

白光入射 肥皂膜的等厚干涉条纹 单色光入射
这也可以通过肥皂液薄膜来观察。取一洁净的线 框,浸入肥皂溶液中,取出时,使框面竖直。肥 皂膜由于重力作用,而逐渐变薄。
起初看见彩色条纹之间的距离逐渐增加,最后彩 色条纹消失。在反射光中,已看不见薄膜,在透 射光中由于没有额外光程差,所以看起来薄膜透 明无色。
9
牛顿环: 同心圆形干涉条纹, 级次“内低外高” 间距 “内疏外密”
2n2 d
2
k
(2k
明环
1)
2
明环半径
rk
R (2k 1)
n2
2
暗环
暗环半径
rk
R (k 1)
n2
10
6.干涉条纹的变化和移动
(1) 干涉场中某一固定点P的光程差,每增加或减少一个波 长,就有一个条纹移过该点,故有:
2
b
n1 n
L
n n / 2 D
n1
b
劈尖干涉
讨论
1)劈尖 d 0
Δ 为暗纹.
2
(k 1) (明纹)
d 2 2n k 2n (暗纹)
2)相邻明纹(暗纹)间的厚度差
di1
di
2n
n
2
D L n 2
b
3)条纹间距(明纹或暗纹)
b D n L L
2)属于等厚干涉,条纹间距不等,为什么?
3)将牛顿环置于 n 1 的液体中,条纹如何变?
4)应用例子:可以用来测 量光波波长,用于检测透镜质 量,曲率半径等.
工件 标准件
测量透镜的曲率半径
光的干涉习题(附答案)

π
S1
S2
3λ 4
4. 用波长为 λ 的单色光垂直照射牛顿环装置,观察牛顿环,如图所示。若使凸 透镜慢慢向上垂直移动距离 d, 移过视场中某固定观察点的条纹数等于 2d/λ 。
5. 空气中两块玻璃形成的空气劈形膜, 一端厚度为零, 另一端厚度为 0.005 cm, 玻璃折射率为 1.5,空气折射率近似为 1。如图所示,现用波长为 600 nm 的 单色平行光, 沿入射角为 30°角的方向射到玻璃板的上表面, 则在劈形膜上形 成的干涉条纹数目为 144 。
6. 维纳光驻波实验装置示意如图。MM 为金属反射镜,NN 为涂有极薄感光层 的玻璃板。MM 与 NN 之间夹角 φ=3.0×10-4 rad,波长为 λ 的平面单色光通过 NN 板垂直入射到 MM 金属反射镜上,则反射光与入射光在相遇区域形成光 驻波, NN 板的感光层上形成对应于波腹波节的条纹。 实验测得两个相邻的驻 波波腹感光垫 A、B 的间距 1.0 mm,则入射光的波长为 6.0×10-4 mm 。
8. 如图所示,折射率为 n2,厚度为 e 的透明介质薄膜的上、下方透明介质的折 射率分别为 n1 和 n3,且 n1<n2<n3,若用波长为 λ 的单色平行光垂直入射到该 薄膜上,则从薄膜上下两表面反射的光束之间的光程差为 2长为 λ 的单色平行光垂直照射两个劈尖上,两劈尖角分别为 θ1 和 θ2,折射 率分别为 n1 和 n2, 若两者分别形成的干涉条纹的明条纹间距相等, 则 θ1, θ2, n1,n2 之间的关系为 n1θ1= n2θ2 。
2h c arcsin 0.1 5.7 o arcsin 2hf
11. 油船失事,把大量石油(n=1.2)泄漏在海面上,形成一个很大的油膜。试求: (1)如果你从飞机上竖直地向下看油膜厚度为 460nm 的区域,哪些波长的 可见光反射最强? (2 ) 如果你戴了水下呼吸器从水下竖直的向上看这油膜同 一区域,哪些波长的可见光透射最强?(水的折射率为 1.33) 答:因为在油膜上下表面反射光都有半波损失, (1)反射光干涉加强:2nd=k
光的干涉习题课

2 如果第一条暗纹对应k=0, 则中心暗斑是 k=20。
对暗纹, 2ne = (2k + 1)
λ
n=1.4
, k = 0, 1, 2L
n=1.5
2ne = (20 + 1 )λ , e = 4100nm 2
如果第一条暗纹对应k=1, 则中心暗斑是 k=21。
2ne = (2k − 1)
λ
2
, k = 1, 2 L
k = 0, 1, 2 L
在油膜边缘处, 是明纹。 在油膜边缘处 e=0 (k=0), 是明纹。 所以第五条明纹对应 k=4。
kλ −6 ∴e = = 1.0 ×10 m 2n2
习题9-14 习题
δ = 2ne = (2k + 1) , k = 0
4n 习题9-15 习题 emin =
λ
λ
2
= 99.6nm
习题9-1 d=0.60mm, D=2.5m, 习题
d∆x (1)∆x = 2.3mm, λ = = 550nm D D D ′ = 3λ2 (2)λ1 = 480nm, x3 = 3λ1 ; λ2 = 600nm, x3 d d D ∆x = 3(λ2 − λ1 ) = 1.5mm d
习题9-2 习题
3、条纹 k 值的确定 、
δ = 2n2e + δ = 2n2e −
λ λ
2
= kλ = kλ
k = 1,2,3 k = 0,1,2,3
2
k的取值可以从零开始,也可以从1开始,取决于光程差的表达 的取值可以从零开始,也可以从 开始 开始, 的取值可以从零开始 一般从光程差最小的第一条纹开始计数, 式。一般从光程差最小的第一条纹开始计数,来判断某一条纹 值为多少。 的k值为多少。 值为多少 四、条纹移动和光程差的关系。 产生干涉条纹移动的原因是 条纹移动和光程差的关系。 光程差发生变化。条纹移动一条,光程差改变一个波长。 光程差发生变化。条纹移动一条,光程差改变一个波长。
光的干涉习题课

20 10
2
k 0,1,2 相干加强 k 0,1,2 相干减弱
k ( 2k 1) 2
光程差 dsin D k d x ( 2k 1) D 2d 条纹宽度(条纹间距)
2、杨氏双缝干涉的基本公式
3、相干光的获得 把由光源上同一点发出的光设法分成两部分, 再叠加起来。
分波阵面法
分振幅法
4、光程与光程差
L nr n2 r2 n1r1
5、半波损失
பைடு நூலகம்
2 2 ( n2 r2 n1r1 )
6、波的干涉
处理光的干涉的方法
1、干涉加强与减弱的条件
2 E1 A1 cos t ( n1r1 ) 10 2 E 2 A2 cos t ( n2 r2 ) 20 2 20 10 ( n2 r2 n1r1 ) k 0,1,2 相干加强 2k k 0,1,2 相干减弱 ( 2k 1)
1.已知:S2 缝上覆盖 的介质厚度为 h ,折射 率为 n ,设入射光的 波长为.
S1
S2
r1
r2
h 问:原来的零级条纹移至何处?若移至原来的第
k 级明条纹处,其厚度 h 为多少?
解:从S1和S2发出的相干光所对应的光程差
(r2 h nh) r1
当光程差为零时,对应 零条纹的位置应满足:
ZnS的最小厚度
k 1,2,3
( 2k 1) d1 |k 1 67.3nm 4n1
2d 2 n2 / 2 k
MgF2的最小厚度
k 1,2,3
( 2k 1) d2 |k 1 114.6nm 4n2
光学练习题光的干涉与衍射实验

光学练习题光的干涉与衍射实验光学练习题:光的干涉与衍射实验实验目的:本实验旨在通过实际操作探究光的干涉与衍射现象,并深入理解光的波动性质。
实验器材:1. 光源(例如激光、白光等)2. 狭缝3. 透镜4. 平面反射镜5. 光屏6. 测量尺7. 实验台8. 其他所需器材实验原理:干涉是指两个或多个波相互叠加时发生的现象。
在光学中,干涉分为两类,即构筑干涉和在自由空间中的干涉。
而衍射则是光通过一个或多个狭缝、小孔等时,发生的波的传播现象。
实验步骤:1. 实验器材的准备:将光源设置在实验台上,安装狭缝和透镜,并调整光源位置以确保它的稳定性。
2. 平面反射镜的调节:将平面反射镜固定在实验台上,调整其位置和角度,使得反射光线能够准确投射到光屏上。
3. 衍射实验:在光路中设置一个狭缝,使光通过狭缝后形成衍射图样,同时利用光屏捕捉并观察到衍射光的形状,记录相关数据。
4. 干涉实验:在光路中设置两个狭缝或小孔,通过调整狭缝或小孔之间的距离,观察到干涉现象,并使用光屏记录干涉光的分布情况。
实验结果和讨论:通过实验观察和记录,我们可以得出以下结论:1. 当光通过一个狭缝或小孔时,会产生衍射现象,具有明暗相间的衍射图样。
2. 当光通过两个狭缝或小孔时,会产生干涉现象,形成明暗相间的干涉图样。
3. 干涉和衍射的图样的分布与光的波长和狭缝(或小孔)的尺寸有关。
4. 实验结果与理论推导相符,从而验证了光的波动性质。
5. 通过调整狭缝或小孔的距离,可以改变干涉图样的间距和形状。
结论:通过本次实验,我们成功地观察到了光的干涉和衍射现象,深入了解了光的波动性质。
通过实验结果和讨论,我们验证了理论推导,并掌握了一些调节干涉和衍射图样的方法。
这对于了解光的行为和性质有着重要的意义,并在光学研究中具有广泛的应用前景。
参考文献:[待添加]。
光学光干涉习题

习题课-光的干涉
例1 在杨氏双缝实验中,双缝间距d=0.20mm,缝屏间距D=1.0m,
试求:(1) 若第二级明条纹离屏中心的距离为6.0mm,计算此单
色光的波长; (2)相邻两明条纹间的距离.
解: 其任意点P的光程差为:
y
r2 r1 k
由几何关系:r2
r1
d
y D
由明纹干涉条件可得:
2ne
2
k
(2k
1)
明纹
暗纹
2
其中:e r 2 / 2R
对明纹来说:
当n=1时,
38R (1.40102 )2
r2 (2k 1)R / 2n
当n=?时,
38R / n (1.27102 )2
即第10级亮环直径为
d120 38R / n
n 1.402 /1.272 1.22
习题课-光的干涉
s1
d
s2
r1
P
r2
O
D
(1)明条纹离屏中心的距离y k D
d
(2)相邻明条纹间距离 y D
d
yd kD
600.0nm
y 3.0mm
习题课-光的干涉
例2 在双缝装置中,用一很薄的云母片(n=1.58)覆盖其中的一条 缝,结果使屏幕上的第七级明条纹恰好移到屏幕中央原零级明 纹的位置.若入射光的波长为550.0nm,求此云母片的厚度.
则用1时第3条暗环的半径为:
r kR1 1.85mm
e r2 / 2R
R
re
2e
2
k
(2k
1)
明纹
暗纹
2
习题课-光的干涉
例7 当牛顿环状之中的透镜与玻璃之间的空间充以液体时,第 10级亮环的直径由d1=1.40×10-2m变为d2=1.27×10-2m ,求液体 的折射率。
光的干涉习题与答案解析

组合产生的第 10 个暗环半径分别为 rBC 4.5mm 和 rAC 5mm ,试计算 RA 、 RB 和 RC 。
h r2
解:
2R
OA
hAB
hA
hB
rAB 2 2RA
rAB 2 2RB
rAB 2 2
1 ( RA
1 )
RB
同理, hBC
rBC 2
1 ( RB
1 RC
)
RA
hAC
rAC 2
P2
2mm
P1
P0
0.4m
1.5m
题图
y r0 1500 500106 0.1875mm
解:(1)干涉条纹间距
d
4
(2)产生干涉区域 P1P2 由图中几何关系得:设 p2 点为 y2 位置、 P1 点位置为 y1
则干涉区域
y y2 y1
y2
1 2
r0
r tan2
1 2
r0
r
1 2
1 2
r0
y r0 500 500106 1.25
解: d 0.2
mm
I1 2I2
A12 2 A22
A1 2 A2
V
1
2
A1 A1
/ /
A2 A2
2
22 1 2
0.9427
0.94
5. 波长为 700nm 的光源与菲涅耳双镜的相交棱之间距离为 20cm,棱到光屏间的距离 L 为 180cm,若所得干涉条纹中相邻亮条纹的间隔为 1mm,求双镜平面之间的夹角θ。
1 ( RA
1 RC
解:对于亮环,有
rj
(2 j 1) R 2
( j 0,1,2,3,)
光的干涉习题答案

光学干涉测量技术
利用光的干涉现象测量长度、角 度、表面粗糙度等物理量,具有 高精度和高灵敏度。
光学干涉滤镜
利用光的干涉现象制作出的滤镜, 可以实现对特定波长的光进行过 滤或增强。
光学干涉仪
利用光的干涉现象测量光学元件 的表面形貌、折射率等参数,广 泛应用于光学研究和制造领域。
02 光的干涉原理
光的波动理论
光的干涉习题答案
目录
• 光的干涉现象 • 光的干涉原理 • 光的干涉实验 • 光的干涉习题解析 • 光的干涉理论的发展
01 光的干涉现象
光的干涉现象定义
1 2
光的干涉现象
当两束或多束相干光波在空间某一点叠加时,由 于光波的相互加强或减弱,形成明暗相间的干涉 条纹的现象。
相干光波
频率相同、振动方向相同、相位差恒定的光波。
题目:一束单色光垂直入射到一对相互平行的狭缝上, 光通过狭缝后形成的光斑可看作是什么图形?
解析:根据光的干涉原理,当单色光垂直入射到一对相 互平行的狭缝上,光通过狭缝后形成的光斑是圆形干涉 图样。
进阶习题解析
题目
如何通过双缝干涉实验验证光的波动性?
答案
通过观察干涉条纹的形状和分布,可以证明光具有波动性 。
光的波动理论。
20世纪初,爱因斯坦提出光的 量子理论,解释了光的干涉现象
的微观机制。
光的干涉理论在现代物理学中的应用
光的干涉理论在光学、 量子力学和凝聚态物 理学等领域有广泛应 用。
在量子力学中,光的 干涉被用于研究量子 纠缠和量子计算等前 沿领域。
在光学中,光的干涉 被用于制造高精度光 学仪器和检测技术。
光的干涉理论的前沿研究
01
目前,光的干涉理论的前沿研究主要集中在量子光 学和量子信息领域。
光学习题课

光学习题课
光学小结
一、光的干涉
Ⅰ 基本概念
1 光的相干条件:
振动频率相同 振动方向相同
位相相同或位相差恒定
只能利用同一原子的同一波列
2、相干光的获得:
把由光源上同一点发出的光设法分成两部分,再迭
加起来。
分波阵面法
分振幅法
2020/3/2
2
长江大学物理教程
3、光程与光程差
相邻明纹的间距:
x xk1 xk D / d
2020/3/2
19
长江大学物理教程
3.已知:S2 缝上覆盖的介质
厚度为 h ,折射率为 n ,设 入射光的波长为.
S1
r1
问:原来的零级条纹移至何处?S2
r2
若移至原来的第 k 级明条纹处, h
其厚度 h 为多少?
原来 k 级明条纹位置满足:
s
(o') (R2' r2' ) (R1' r1' ) 0
R1' s1
R1 R2
R2'
s2
r1 r2
X
o
r1'
r2'
o'
R2' R1'
r2' r1'
(o) (R1' r1) (R2' nt t r2 )
零级明纹下移,则整个条纹下移. (R1' R2' ) (r1 r2 ) (n 1)t 0
解:从S1和S2发出的相干 光所对应的光程差
r2 r1 k
设有介质时零级明条纹移到原
(r2 h nh) r1 来第 k 级处,它必须同时满足:
大学物理光的干涉习题课
2 n 2 e cos k
k max 2n2e 2 1 . 50 1 . 00 10 6 . 328 10
7 5
S
n1
R n2 e f
中心亮斑的干涉级最高,为kmax,其 = 0,有:
47 . 4
d
应取较小的整数,kmax = 47(能看到的最高干涉级为第47级亮斑). 最外面的亮纹干涉级最低,为kmin,相应的入射角为 im = 45(因R=d), 相应的折射角为m,据折射定律有
2.如图所示,在双缝干涉实验中 SS1= SS2,用波长 为 的光照射双缝 S1和 S2 ,通过空气后在屏幕E 上形成干涉条纹,已知 P 点处为第三级明条纹, 3 则 S1 和 S2 到 P 点的光程差为,若将整个 装置放在某种透明液体中,P 点为第四级明条纹, 则该液体的折射率 n =______。 1.33
ek 1 ek
A B 图 a
2
[ B ] 4. 用波长为1的单色光照射空气劈形膜,从反射光干涉条纹中观察到劈 形膜装置的A点处是暗条纹.若连续改变入射光波长,直到波长变为2 (2>1)时,A点再次变为暗条纹.求A点的空气薄膜厚度. 解:设A点处空气薄膜的厚度为e,则有
2e 1 2
S1 S S2
r1 r2
P
r2 r1 k , ( k 3 )
n ( r2 r1 ) 4 , 3n 4 n 4 / 3 1 . 33
3. 如图a所示,一光学平板玻璃A与待测工件B之间形成空气劈尖,用波 长=500 nm (1 nm=10-9 m)的单色光垂直照射.看到的反射光的干涉条 纹如图b所示.有些条纹弯曲部分的顶点恰好与其右边条纹的直线部分 的连线相切.则工件的上表面缺陷是 (A) 不平处为凸起纹,最大高度为500 nm. (B) 不平处为凸起纹,最大高度为250 nm. (C) 不平处为凹槽,最大深度为500 nm. (D) 不平处为凹槽,最大深度为250 nm.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2e
2
2k
2
明纹数 2kmax 8
k max 4 . 5 4
由暗纹条件 2e
2
(2k 1)
2
k max 4
(3)由中心向两侧移动
完
D
d D D d
x
1 10 %
(1 10%) 589 . 3 1 . 1 648.2(nm)
(2)
1 n
1 n
0 . 20 1 . 33
0.15
完
3. 一射电望远镜的天线设在湖岸上,距湖面的高度 为h,对岸地平线上方有一恒星刚在升起,恒星发出 波长为 的电磁波。试求,当天线测得第一级干涉极 大时恒星所在的角位置 (提示:作为洛埃镜干涉分 析)。
x=0处为第k=7级明纹时 ( n 1) l k
l k
n 1
7
550 10
9
1 . 58 1
6.64 10 (m)
完
6
2. 在双缝干涉实验装置中,屏幕到双缝的距离D远 大于双缝之间的距离d,对于钠黄光(=589.3nm), 产生的干涉条纹,相邻两明条纹的角距离(即相邻两 明条纹对双缝处的张角)为0.20。 (1)对于什么波长的光,这个双缝装置所得相邻两条 纹的角距离比用钠黄光测得的角距离大10%? (2)若将此装置浸入水中(水的折射率n=1.33),用钠 黄光垂直照射时,相邻两明条纹的角距离有多大? 解:(1)
1. 用很薄的云母片(n=1.58)覆盖在双缝实验中的 一条缝上,这时屏幕上的零级明条纹移到原来的第七 级明条纹的位置上。如果入射光波长为550nm,试问 此云母片的厚度为多少? 解:设云母的厚度为l。有云母时,光程差 xd ( n 1) l D x=0处的光程差 ( n 1) l
l sin
2n
sin
2nl
589 . 3 10
9 3
2 1 . 52 5 . 0 10
3 . 88 10
5
8
完
5. 柱面平凹透镜A,曲率半径为R,放在平玻璃片B 上,如图所示。现用波长为 的平行单色光自上方垂 直往下照射,观察A和B间空气薄膜的反射光的干涉条 纹。设空气膜的最大厚度d=2。 (1)求明条纹极大位置与 凹透镜中心线的距离r ; d (2)共能看到多少条明条 纹; (3)若将玻璃片B向下平 移,条纹如何移动?
h
解:
B
2
A
AC h / sin BC AC cos 2
光程差满足
C h
ቤተ መጻሕፍቲ ባይዱ
( AC BC )
h sin (1 cos 2 )
2
2
sin
1
4h
完
4. 利用劈尖的等厚干涉条纹可以测得很小的角度。 今在很薄的劈尖玻璃板上,垂直地射入波长为 589.3nm的钠光,相邻暗条纹间距离为5.0mm,玻璃 的折射率为1.52,求此劈尖的夹角。 解:
r
A
B R
解:
d e
2e 2e
r
2
2
2R
2k
2
k=1,2,3…明纹极大
(2k 1)
2
k=0,1,2,3…暗纹极小
2
(1)
r r
2 R (d 2 R (d
2k 1 4 k 2
) k=1,2,3…明纹极大
k=0,1,2,3…暗纹极小
)
(2) e max d 2 由明纹条件
