人教版高中数学选修2-3课件:2.1离散型随机变量的分布列 第二课
合集下载
人教课标版高中数学选修2-3《离散型随机变量的分布列》参考课件

2.1.2 离散型随机变量的分布列
1. 随机变量 如果随机试验的结果可以用一个变量来表示,(或
随着试验结果变化而变化的变量),那么这样的变量 叫做随机变量.
随机变量常用希腊字母X、Y、ξ、η等表示。
2. 离散型随机变量 所有取值可以一一列出的随机变量,称为离散型随
机变量。
如果随机变量可能取的值是某个区间的一切值,这 样的随机变量叫做连续型随机变量.
分布列的是( B )
A
0
1
P
0.6 0.3
B
0
1
2
P 0.9025 0.095 0.0025
C 0 1 2 …n D 0 1 2 … n
P 1 1 1 …1
2 48
2n1
P
1 3
12 33
1 3
2 3
2
…
1 3
2 3
n
2、设随机变量
的分布列为
P(
ቤተ መጻሕፍቲ ባይዱ
i)
a
1
i
,
i
1,2,3
则 a的值
27
ξ 2 3 4 5 6 7 8 9 10 11 12
p
1 36
2 36
34 36 36
5 36
6 36
5 36
4 36
32 36 36
1 36
例1:某一射手射击所得环数ξ 的分布列如下:
ξ 4 5 6 7 8 9 10 P 0.02 0.04 0.06 0.09 0.28 0.29 0.22
求此射手”射击一次命中环数≥7”的概率. 分析: ”射击一次命中环数≥7”是指互斥事
3
为
. 13
课堂练习:
3、设随机变量的分布列如下:
1. 随机变量 如果随机试验的结果可以用一个变量来表示,(或
随着试验结果变化而变化的变量),那么这样的变量 叫做随机变量.
随机变量常用希腊字母X、Y、ξ、η等表示。
2. 离散型随机变量 所有取值可以一一列出的随机变量,称为离散型随
机变量。
如果随机变量可能取的值是某个区间的一切值,这 样的随机变量叫做连续型随机变量.
分布列的是( B )
A
0
1
P
0.6 0.3
B
0
1
2
P 0.9025 0.095 0.0025
C 0 1 2 …n D 0 1 2 … n
P 1 1 1 …1
2 48
2n1
P
1 3
12 33
1 3
2 3
2
…
1 3
2 3
n
2、设随机变量
的分布列为
P(
ቤተ መጻሕፍቲ ባይዱ
i)
a
1
i
,
i
1,2,3
则 a的值
27
ξ 2 3 4 5 6 7 8 9 10 11 12
p
1 36
2 36
34 36 36
5 36
6 36
5 36
4 36
32 36 36
1 36
例1:某一射手射击所得环数ξ 的分布列如下:
ξ 4 5 6 7 8 9 10 P 0.02 0.04 0.06 0.09 0.28 0.29 0.22
求此射手”射击一次命中环数≥7”的概率. 分析: ”射击一次命中环数≥7”是指互斥事
3
为
. 13
课堂练习:
3、设随机变量的分布列如下:
高中数学选修2-3优质课件:2.1.2 离散型随机变量的分布列(二)

知识点二 超几何分布
思考
在含有5名男生的100名学生中,任选3人,求恰有2名男生的概 率表达式. 答案 CC25C3100195.
答案
梳理
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则 CkMCnN--kM
P(X=k)=____C__nN____,k=0,1,2,…,m,其中m=min{M,n},且n≤N,
人数不超过1人的概率为___5_____.
解析 设所选女生数为随机变量X,则X服从超几何分布,
所以 P(X≤1)=P(X=0)+P(X=1)=CC02C36 34+CC12C36 24=,可以参加一次摸奖,一袋中有同样大小的球10个,其中8个 标有1元钱,2个标有5元钱,摸奖者只能从中任取2个球,他所得奖励是 所抽2球的钱数之和,求抽奖人所得钱数的分布列.
C47×C68 C1105
的是
A.P(X=2)
B.P(X≤2)
√C.P(X=4)
D.P(X≤4)
解析 X 服从超几何分布,基本事件总数为 C1105,
所求事件数为 CX7C810-X,
∴P(X=4)=C47C×1105C68.
1234
解析 答案
3.从4名男生和2名女生中任选3人参加数学竞赛,则所选3人中,女生的 4
1 20
9 20
9 20
1 20
解答
引申探究 在本例条件下,若记取到白球的个数为随机变量η,求随机变量η的分布列.
解 由题意可知η=0,1,服从两点分布. 又 P(η=1)=CC2536=12, 所以η的分布列为
η 01
P
1 2
1 2
解答
反思与感悟
超几何分布的求解步骤 (1)辨模型:结合实际情景分析所求概率分布问题是否具有明显的两部分 组成,如“男生、女生”,“正品、次品”“优劣”等,或可转化为明 显的两部分.具有该特征的概率模型为超几何分布模型. (2)算概率:可以直接借助公式 P(X=k)=CkMCCnNNn--kM求解,也可以利用排列组 合及概率的知识求解,需注意借助公式求解时应理解参数 M,N,n,k 的 含义.
数学:2.1.2《离散型随机变量的分布列》课件(新人教A版选修2-3)

P
的变 0.2 离散型随机变量分布列 .如在 化情况可以用图象表示 ,掷出的点数 0.1 X 掷骰子试验中 的分布列在直角坐标系 中的 O 2 . 图象如图 .1− 2所示
1
2 3
4 5
6
X
在图 2.1 − 2 中, 横坐标是随 机变量的取值, 纵坐标为概 率 .从中可以看出, X 的取值 范围是 { ,2,3,4,5, 6},它取每 1 1 个值的概率都是 . 6
表2 −1
X P
1 1 6
2 1 6
3 1 6
4 1 6
5 1 6
6 1 6
利用表2 − 1可以求出能由X表示的事件的概率.例如, 在这个随机试验中事件{X < 3} = {X = 1} ∪ {X = 2}, 由概率的可加性得 1 1 1 P(X < 3 ) = P(X = 1) + P(X = 2) = + = . 6 6 3
3 3 4 4 5 5 C10C5−−10 C10C5−−10 C10C5−−10 30 30 30 = + + ≈ 0.191. 5 5 5 C30 C30 C30 55 左右 , 思考 如果要将这个游戏的中 奖控制在 % 那么应该如何设计中奖 ? 规则
Байду номын сангаас 作业:P49A组(4—6)和B组 P49A 4—6 B
X
P
0
0 n CMCN−0 −M n CN
1
n C1 CN−1 M −M n CN
⋅⋅⋅ ⋅⋅⋅
3
m n CMCN−m −M n CN
.如果随机变量 的分布列为 X 为 超几何分布列 , 超几何分布列 则称随机变量X服从超几何分 布(hypergeome tric distributi on).
人教a版数学【选修2-3】2.1.2《离散型随机变量的分布列习题课》课件

∴X 的分布列为 X P 0 1 210 1 4 35 2 3 7 3 8 21 4 1 14
第二章
2.1
2.1.2
第1课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
典例探究学案
第二章
2.1
2.1.2
第1课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
27 B.38 27 D.19
[答案] B
[解析]
2 2 2 27 2 3 ∵m3+3 +3 =1,∴m=38. Biblioteka 第二章2.12.1.2
第1课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
3.袋中有6个红球、4个白球,从袋中任取4个球,则至少
有2个白球的概率是________.
[答案]
23 42
[解析] 设取出的白球个数为离散型随机变量 X,则 X 的 所有可能取值为 0、1、2、3、4,则 P(X≥2)=P(X=2)+P(X=
2 3 1 4 0 90+24+1 115 23 C2 C C C C 4 6 4 6 4C6 3) + P(X = 4) = C4 + C4 + C4 = = 210 = 42 . 故至 210 10 10 10
2.1.2 离散型随机变量的分布列
第2课时 离散型随机变量的分布列习题课
第二章
随机变量及其分布
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
1
自主预习学案
2
典例探究学案
3
巩固提高学案
第二章
2.1
2.1.2
2019人教A版高中数学选修2-3 2.1.2离散型随机变量的分布列教学课件 (共21张PPT)教育精品.ppt

CNn
CNn
C C m nm M NM CNn
为 超 几 何 分 布 列.如果随机变量X的分布列为
超几何分布列 , 则称随机变量 X服 从 超 几 何 分
布
注:⑴超几何分布模型是不放回抽样 ⑵超几何分布中的参数 是M,N,n,变量是X
变式:从装有 3 个红球,2 个白球的袋中随机取出 3 个 球,设其中有X个红球,求X的分布列.
2.1.2离散型随机变量 的分布列
莱西市实验学校 吕淑丽
离散型随机变量的分布列是 高中阶段的重点内容,它作为概 率与统计的桥梁与纽带,是本章 的关键知识之一,也是第三节离 散型随机变量的均值和方差的基 础。从近几年的高考观察,这部 分内容有加强命题的趋势。2016、 2017年全国高考都考了分布列解 答题。
解:X的取值有1、2、3、4、5、6 则P(X=1)=1/6, P(X=2)=1/6,
P(X=3)=1/6, P(X=4)=1/6, P(X=5)=1/6, P(X=6)=1/6 列成表格形式为 表2 1
X
1
2
3
4
5
6
1
1
1
1
1
1
P
6
6
6
6
6
6
4、求离散型随机变量的分布列的步骤:
(1)找出随机变量ξ的所有可能的取值(明确随机变量的具体取
1、设某项试验的成功率是失败率的2倍,用随机变量 X描述一次该项试验的成功次数,则P(X=0)=( 1/3 )
2、由经验得知:在人民商场付款处排队等候付款的人数X及 其概率分布表如下:
X0
1
P 0.10 a
2
3
4
5
0.30 0.30 0.10 0.04
人教高中数学选修2-3第二章 2.1.2离散型随机变量的分布列 课件

我们可以先固定N=30,M=10,n=5.,通过调整k 到达目的.
∵从中摸5个球,至少摸到2个红球的概率为
P(X≥2)=P(X=2)+P(X≥55.1% . C3 50
∵游戏规那么定为至少摸到2个红球就中奖,中奖的 概率大约为55.1%.
练习:课本P56页练习T3.
复习回忆
1. 随机变量:
随着随机试验的结果变化而变化的量叫做随 机变量.
2.离散型随机变量:
对于随机变量可能取的值,我们可以 按一定次序一一列出,这样的随机变量叫做 离散型随机变量.
新课讲授
引例: 抛掷一枚骰子,所得的点数X有哪些值?X取每
个值的概率是多少?能否用表格的形式来表示呢?
解:随机变量X的取值有1、2、3、4、5、6
课堂小结:
1.离散型随机变量的分布列及其性质;
2.两点分布(或0-1分布或伯努利分布);
2.超几何分布.
在含有 M 件次品的 N 件产品中, 任取 n 件, 求取到
的次品数X的分布列.
(N≥M)
其中恰有X件次品数,那么事件{X=k}发生的概率为
P(Xk)C M kC C N n N n k M(k0,1,2, ,m )
其中 m minM, n,且 n≤ N ,M ≤ N ,n ,M ,N N *
注:这个两个性质是判断分布列是否正确的重 要依据
运用〔一〕分布列性质的运用
1、设随机变量X的分布列如下:
1
1
1
p
6
3
6
1
那么p的值为 3
.
2、设随机变量 的分布列为P( i) a1i, i 1,2,3
27
3
那么a的值为 13
.
3、随机变量X的分布列为
∵从中摸5个球,至少摸到2个红球的概率为
P(X≥2)=P(X=2)+P(X≥55.1% . C3 50
∵游戏规那么定为至少摸到2个红球就中奖,中奖的 概率大约为55.1%.
练习:课本P56页练习T3.
复习回忆
1. 随机变量:
随着随机试验的结果变化而变化的量叫做随 机变量.
2.离散型随机变量:
对于随机变量可能取的值,我们可以 按一定次序一一列出,这样的随机变量叫做 离散型随机变量.
新课讲授
引例: 抛掷一枚骰子,所得的点数X有哪些值?X取每
个值的概率是多少?能否用表格的形式来表示呢?
解:随机变量X的取值有1、2、3、4、5、6
课堂小结:
1.离散型随机变量的分布列及其性质;
2.两点分布(或0-1分布或伯努利分布);
2.超几何分布.
在含有 M 件次品的 N 件产品中, 任取 n 件, 求取到
的次品数X的分布列.
(N≥M)
其中恰有X件次品数,那么事件{X=k}发生的概率为
P(Xk)C M kC C N n N n k M(k0,1,2, ,m )
其中 m minM, n,且 n≤ N ,M ≤ N ,n ,M ,N N *
注:这个两个性质是判断分布列是否正确的重 要依据
运用〔一〕分布列性质的运用
1、设随机变量X的分布列如下:
1
1
1
p
6
3
6
1
那么p的值为 3
.
2、设随机变量 的分布列为P( i) a1i, i 1,2,3
27
3
那么a的值为 13
.
3、随机变量X的分布列为
人教课标版高中数学选修2-3《离散型随机变量及其分布列(第2课时)》名师课件

离散型随机变量及其分布列 (第2课时)
知识回顾 问题探究 课堂小结 随堂检测
检测下预习效果:
点击“随堂训练” 选择“《离散型随机变量及其分布列(第2课时)》预习自测”
知识回顾 问题探究 课堂小结 随堂检测
探究一:两点分布的概念、分布列及其特征★ ●活动一 透过掷骰子看分布列 例:投掷一枚硬币,正面成功的概率为 ,反面成功的概率为 .写出其 概率分布列. 详解:选取正反面作为随机变量.根据制作分布列步骤给出分布列表. 典型的分布列 (1)概念:两点分布又称0-1分布,是一种有两种可能结果的分布, 是二项分布的特殊情况. (2)两点分布的概率函数
此次抽样合格率为: 由此可知该批产品合格度不高,而且检测合格产品的标准低,对此可以 给出修改标准的意见. 点拨:考察了互斥事件的概率问题;组合思想在概率中的应用.
知识回顾 问题探究 课堂小结 随堂检测
针对此类问题我们可对其进行数学建模,具体思想如下: 1. 概念及其分布列表示 一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品, 则该事件(X=x)发的概率分布为超几何分布.
.则称满足上述分布列
知识回顾 问题探究 课堂小结 随堂检测
补充:若随机变量X服从超几何分布,则记作X~H(n,M,N).简写为H(k,n,M,N).
分析:由超几何分布的概率公式不难看出,在分析X件次品的可能情况中, 我们采用了分步乘法计数原理和组合的应用方法.然后严格根据概率的定义 得出所求取的结果. 注意:
知识回顾 问题探究 课堂小结 随堂检测
重难点突破
1.超几何分布随机变量的确定. 2.超几何分布概率的算法(结合排列组合思想解题;互斥事件的概率 加法原则).
解决此类问题的关键是根据题设条件找到X的可能取值,再利用概 率的有关知识求出相应的概率,最后根据分布列的定义写出分布列并 利用性质检验分布列的正确性.
知识回顾 问题探究 课堂小结 随堂检测
检测下预习效果:
点击“随堂训练” 选择“《离散型随机变量及其分布列(第2课时)》预习自测”
知识回顾 问题探究 课堂小结 随堂检测
探究一:两点分布的概念、分布列及其特征★ ●活动一 透过掷骰子看分布列 例:投掷一枚硬币,正面成功的概率为 ,反面成功的概率为 .写出其 概率分布列. 详解:选取正反面作为随机变量.根据制作分布列步骤给出分布列表. 典型的分布列 (1)概念:两点分布又称0-1分布,是一种有两种可能结果的分布, 是二项分布的特殊情况. (2)两点分布的概率函数
此次抽样合格率为: 由此可知该批产品合格度不高,而且检测合格产品的标准低,对此可以 给出修改标准的意见. 点拨:考察了互斥事件的概率问题;组合思想在概率中的应用.
知识回顾 问题探究 课堂小结 随堂检测
针对此类问题我们可对其进行数学建模,具体思想如下: 1. 概念及其分布列表示 一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品, 则该事件(X=x)发的概率分布为超几何分布.
.则称满足上述分布列
知识回顾 问题探究 课堂小结 随堂检测
补充:若随机变量X服从超几何分布,则记作X~H(n,M,N).简写为H(k,n,M,N).
分析:由超几何分布的概率公式不难看出,在分析X件次品的可能情况中, 我们采用了分步乘法计数原理和组合的应用方法.然后严格根据概率的定义 得出所求取的结果. 注意:
知识回顾 问题探究 课堂小结 随堂检测
重难点突破
1.超几何分布随机变量的确定. 2.超几何分布概率的算法(结合排列组合思想解题;互斥事件的概率 加法原则).
解决此类问题的关键是根据题设条件找到X的可能取值,再利用概 率的有关知识求出相应的概率,最后根据分布列的定义写出分布列并 利用性质检验分布列的正确性.
人教a版数学【选修2-3】2.1.2《离散型随机变量的分布列》ppt课件

离散型随机变量的分布列 温故知新 回顾复习古典概型的特点及概率计算、离散型随机变量的 特点.
第二章
2.1
2.1.2
第1课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
思维导航 1 .想一想,投掷一颗骰子,所得点数记为 ξ ,则 ξ 可取哪 些数字?ξ取各个数字的概率分别是多少?可否用列表法表示ξ 的取值与其概率的对应关系?投掷两颗骰子,将其点数之和记
X P0Βιβλιοθήκη 1-p1 p这样的分布列叫做两点分布列.如果随机变量 X的分布列 两点分布 .而称 p = P(X = 1) 为 为两点分布列,就称 X 服从 __________ 成功概率 . __________
第二章
2.1
2.1.2
第1课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
若其中所含教师人数记为ξ,则ξ可能的取值有哪些?怎样求其
概率?你能将这一问题一般化表达,并再找出类似的例子吗? 其一般概率公式如何推导?
第二章
2.1
2.1.2
第1课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
新知导学 2.两个特殊分布列
(1)两点分布列
如果随机变量X的分布列是
为ξ,则ξ可能的取值有哪些,你能列表表示ξ取各值的概率与ξ
取值的对应关系吗?
第二章
2.1
2.1.2
第1课时
成才之路 · 高中新课程 · 学习指导 · 人教A版 · 数学 · 选修2-3
新知导学
1.离散型随机变量的分布列 (1)定义:一般地,若离散型随机变量X可能取的不同值为 x1、x2、„、xi、„、xn,X取每一个值xi(i=1,2,„,n)的概率 P(X=xi)=pi,以表格的形式表示如下: X P x1 p1 x2 p2 „ „ xi pi „ „ xn pn
数学:2.1《离散型随机变量及其分布列-离散型随机变量分布列》课件(新人教A版-选修2-3)

P 1 p, P 0 q, 0 p, q 1,
p q 1.
想一想
X 2 5 是两点分布吗? P 0.3 0.7 提示:不是.两点分布的X的取值只能是0,1. 分布列
什么是超几何分布? 先思考一个例子: 思考 1.在含有 5 件次品的 100 件产品中,任取 3 件,求:(1)取到的次品数 X 的分布列.
例1
甲、乙两人参加一次数学知识竞赛 , 已知在备
选的 10 道试题中 , 甲能答对其中的 6 道试题 , 乙能答
对其中的8道试题.规定每次考试都从备选试题中
随机抽出3题进行测试,答对一题得5分,答错一题得 0分.求: (1)甲答对试题数X的分布列; (2)乙所得分数Y的分布列.
【解】
(1)X 的可能取值为 0,1,2,3. C3 4 1 4 P(X=0)= 3 = = ,2 分 C10 120 30 1 C2 36 3 4C6 P(X=1)= 3 = = 3分 C10 120 10 2 C1 60 1 4C6 P(X=2)= 3 = = ,4 分 C10 120 2 C3 20 1 6 P(X=3)= 3 = = .5 分 C10 120 6 所以甲答对试题数 X 的分布列为 X 0 1 1 3 P 30 10 6分
设摸出的红球的个数为 X k n k CM CN M 则 P( X k ) (k 0,1, 2 , m), m min M , n n CN
C
1分
2 1 2
3 1 6
(2)乙答对试题数可能为 1,2,3,所以乙所得分数 Y=5,10,15. 1 C2 C 8 1 2 8 P(Y=5)= 3 = = ,9 分 C10 120 15 2 C1 C 56 7 2 8 P(Y=10)= 3 = = ,10 分 C10 120 15 C3 56 7 8 P(Y=15)= 3 = = .11 分 C10 120 15 所以乙所得分数 Y 的分布列为 Y 5 10 15 1 7 7 P 15 15 15 12 分
p q 1.
想一想
X 2 5 是两点分布吗? P 0.3 0.7 提示:不是.两点分布的X的取值只能是0,1. 分布列
什么是超几何分布? 先思考一个例子: 思考 1.在含有 5 件次品的 100 件产品中,任取 3 件,求:(1)取到的次品数 X 的分布列.
例1
甲、乙两人参加一次数学知识竞赛 , 已知在备
选的 10 道试题中 , 甲能答对其中的 6 道试题 , 乙能答
对其中的8道试题.规定每次考试都从备选试题中
随机抽出3题进行测试,答对一题得5分,答错一题得 0分.求: (1)甲答对试题数X的分布列; (2)乙所得分数Y的分布列.
【解】
(1)X 的可能取值为 0,1,2,3. C3 4 1 4 P(X=0)= 3 = = ,2 分 C10 120 30 1 C2 36 3 4C6 P(X=1)= 3 = = 3分 C10 120 10 2 C1 60 1 4C6 P(X=2)= 3 = = ,4 分 C10 120 2 C3 20 1 6 P(X=3)= 3 = = .5 分 C10 120 6 所以甲答对试题数 X 的分布列为 X 0 1 1 3 P 30 10 6分
设摸出的红球的个数为 X k n k CM CN M 则 P( X k ) (k 0,1, 2 , m), m min M , n n CN
C
1分
2 1 2
3 1 6
(2)乙答对试题数可能为 1,2,3,所以乙所得分数 Y=5,10,15. 1 C2 C 8 1 2 8 P(Y=5)= 3 = = ,9 分 C10 120 15 2 C1 C 56 7 2 8 P(Y=10)= 3 = = ,10 分 C10 120 15 C3 56 7 8 P(Y=15)= 3 = = .11 分 C10 120 15 所以乙所得分数 Y 的分布列为 Y 5 10 15 1 7 7 P 15 15 15 12 分
人教版高中数学选修2-3课件:2.1 离散型随机变量及其分布列(共52张PPT)

预习探究
[探究] 以下随机变量是离散型随机变
量的是
.
①某部手机一小时内收到短信的次数
ξ;
②电灯泡的寿命ξ; ③某超市一天中的顾客量ξ; ④将一颗骰子掷两次出现的点数之和
ξ.
⑤连续不断地射击,首次命中目标所需
要的射击次数ξ.
④将一颗骰子掷两次出现点数之和ξ的取
值为2,3,…,12,是离散型随机变量;
三维目标
3.情感、态度与价值观 使学生感悟数学与生活的和谐之美,学会合作探讨,体验成功,提 高学习数学的兴趣.
重点难点
[重点] (1)随机变量、离散型随机变量的意义; (2)离散型随机变量的分布列的概念.
[难点] (1)随机变量、离散型随机变量的意义; (2)求简单的离散型随机变量的分布列.
教学建议
例1 指出下列变量中,哪些是随机变量, 哪些不是随机变量,并说明理由. (1)任意掷一枚质地均匀的硬币5次,出 现正面向上的次数; (2)投一颗质地均匀的骰子出现的点数 (最上面的数字); (3)某个人的属相随年龄的变化; (4)在标准状况下,水在0℃时结冰.
(3)属相是出生时便确定的,不随年龄的变化 而变化,不是随机变量. (4)标准状况下,水在0℃时结冰是必然事件, 不是随机变量.
P
分别求出随机变量η1=2ξ1,η2=ξ2的分布列.
当ξ取-1与1时,η2=ξ2取相同的值,故η2的分布 列为 η2 0 1 4 9
考点类析
例2 指出下列随机变量是不是离散型 随机变量,并说明理由. (1)从10张已编好号码的卡片(从1号到 10号)中任取1张,被取出的卡片的号数; (2)一个袋中装有5个白球和5个黑球,从 中任取3个,其中所含白球的个数; (3)某林场树木最高达30 m,则此林场中 树木的高度; (4)某加工厂加工的某种铜管的外径与 规定的外径尺寸之差.
《离散型随机变量的分布列》人教版高中数学选修2-3PPT课件(第2.1.2课时) (1)

A表示事件“第一名同学没有抽到中奖奖券”.
课前导入
思考 已知第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢? 在这个问题中,知道第一名同学没有抽到中奖奖券,等价于知道事件 A 一定会发生,导致可能出 现的基本事件必然在事件 A 中,从而影响事件 B 发生的概率,使得 P(B|A)≠P ( B ) .
人教版高中数学选修2-3
第2章 随机变量及其分布
2.2.1 条件概率
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-3
讲解人:XXX 时间:2020.6.1
课前导入
思考 三张奖券中只有一张能中奖,现分别由三名同学无放回地抽取,问最后一名同学抽到中奖奖券的概 率是否比前两名同学小. 若抽到中奖奖券用“Y”表示,没有抽到用“Y ”,表示,那么三名同学的抽奖结果共有三种可能: Y YY,YYY 和YYY.用 B 表示事件“最后一名同学抽到中奖奖券” , 则 B 仅包含一个基本事件 YYY.由古典概型计算公式可知,最后一名同学抽到中奖奖券的概率为:
(1)当收报台收到信号“·”时,发报台确实发出信号“·”的概率; (2)当收报台收到信号“-”时,发报台确实发出信号“-”的概率.
新知探究
分析: 完成该事件分两步:第一步发出信号“.” “-”,分别设为A1,A2,第二步收到信号“.” “-”,分别 设为B,C,则本题要求:P(A1|B),P(A2|C). 设A1表示发报台发出信号“.”,设A2表示发报台发出信号“-”. B表示收报台收到信号“.”,C表示收报台收到信号“-”.
解: 设事件A, B分别表示设备A, B有效.
已知 PA 0.92 PB 0.93
课前导入
思考 已知第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢? 在这个问题中,知道第一名同学没有抽到中奖奖券,等价于知道事件 A 一定会发生,导致可能出 现的基本事件必然在事件 A 中,从而影响事件 B 发生的概率,使得 P(B|A)≠P ( B ) .
人教版高中数学选修2-3
第2章 随机变量及其分布
2.2.1 条件概率
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-3
讲解人:XXX 时间:2020.6.1
课前导入
思考 三张奖券中只有一张能中奖,现分别由三名同学无放回地抽取,问最后一名同学抽到中奖奖券的概 率是否比前两名同学小. 若抽到中奖奖券用“Y”表示,没有抽到用“Y ”,表示,那么三名同学的抽奖结果共有三种可能: Y YY,YYY 和YYY.用 B 表示事件“最后一名同学抽到中奖奖券” , 则 B 仅包含一个基本事件 YYY.由古典概型计算公式可知,最后一名同学抽到中奖奖券的概率为:
(1)当收报台收到信号“·”时,发报台确实发出信号“·”的概率; (2)当收报台收到信号“-”时,发报台确实发出信号“-”的概率.
新知探究
分析: 完成该事件分两步:第一步发出信号“.” “-”,分别设为A1,A2,第二步收到信号“.” “-”,分别 设为B,C,则本题要求:P(A1|B),P(A2|C). 设A1表示发报台发出信号“.”,设A2表示发报台发出信号“-”. B表示收报台收到信号“.”,C表示收报台收到信号“-”.
解: 设事件A, B分别表示设备A, B有效.
已知 PA 0.92 PB 0.93
高二数学选修2-3离散型随机变量及其分布列(2)_ppt
6
6
12 34
1
1
1
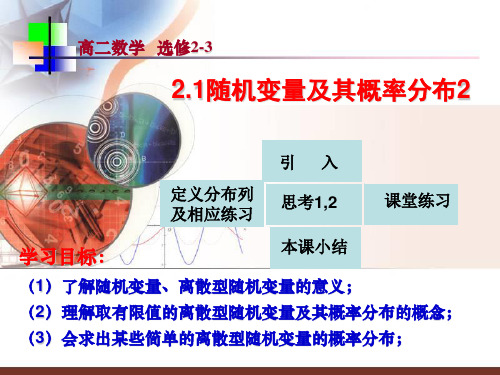
1
P(6)1 ξ的分布列
6
56
1
1
形式 P 6
6
6
6
6
6
该表不仅列出了随机变量 的所有取值. ξ的分布表
而且列出了 的每一个取值的概率.
建构定义
1.定义:概率分布( ξ分布列与分布表)
设离散型随机变量ξ可能取的值为 x1,x2,x3, ,xi
ξ取每一个值 xi(i1,2, )的概率 P(xi)pi
(3)会求出某些简单的离散型随机变量的概率分布;
新课导入
对于一个随机试验,仅仅知道试验的可能结果是不
够的,还要能把握每一个结果发生的概率.
引例:抛掷一枚骰子,所得的点数 有哪些值? 取
每个值的概率是多少?
解: 的取值有1、2、3、4、5、6
则 P(1)1
6
P(2)1
6
P(3)1
6
列成 表的
P(4)1 P(5)1
1
2
3
4
1
P
6
1
1
p
3
6
则 p 的值为 1 .
4.设随机变量
则 a 的值为
3
的分布列为
27
P(
i)a13i
,
i
1,2,3
13
.
1
0
1
5.设随机变量
则 q (
A、1
的分布为
D
B、1
)
2 2
C、
1
P
2 2
1 2
D、
1 2q 1 2
2
q2
6.设随机变量 只能取5、6、7、···、16这12个值,
高中数学人教A版选修2-3第二章:2.1离散型随机变量及其分布列课件

2.1.1离散型随机变量
复习回顾:
1、什么是随机事件?什么是基本事件?
在一定条件下可能发生也可能不发生的事件,叫做 随机事件。试验的每一个可能的结果称为基本事件。
2、什么是随机试验?
凡是对现象或为此而进行的实验,都称之为试验。
如果试验具有下述特点: (1)试验可以在相同条件下重复进行; (2)每次试验的所有可能结果都是明确可知的,并且 不止一个; (3)每次试验总是恰好出现这些结果中的一个,但在 一次试验之前却不能肯定这次试验会出现哪一个结果。
X 4 5 6 7 8 9 10 P 0.02 0.04 0.06 0.09 0.28 0.29 0.22
则此射手“射击一次命中环数≥7”的概率是_0_._8__8__
例 2.在含有 5 件次品的 100 件产品中,任取 3 件, 求:(1)取到的次品数 X 的分布列; (2)至少取到 1 件次品的概率。
例、袋子中有3个红球,2个白球,1个黑球,这些球 除颜色外完全相同,现要从中摸一个球出来,若摸到
黑球得1分,摸到白球得0分,摸到红球倒扣1分,试写 出从该盒内随机取出一球所得分数X的分布列.
解:因为只取1球,所以X的取值只能是1,0,-1
P( X 1) 1 , P( X 0) 2 1 ,
0分,1分,2分用数字来表
示呢? (3)抛掷一枚硬币,可能出现的结果有几种情况?
正面向上,反面向上
思考:在上述试验开始之前,你能确定结果是哪一 种情况吗?
分析:不行,虽然我们能够事先知道随机试验可能出 现的所有结果,但在一般情况下,试验的结果是随机出 现的。
一、随机变量的概念:
在前面的例子中,我们把随机试验的每一个结果 都用一个确定的数字来表示,这样试验结果的变化就 可看成是这些数字的变化。
复习回顾:
1、什么是随机事件?什么是基本事件?
在一定条件下可能发生也可能不发生的事件,叫做 随机事件。试验的每一个可能的结果称为基本事件。
2、什么是随机试验?
凡是对现象或为此而进行的实验,都称之为试验。
如果试验具有下述特点: (1)试验可以在相同条件下重复进行; (2)每次试验的所有可能结果都是明确可知的,并且 不止一个; (3)每次试验总是恰好出现这些结果中的一个,但在 一次试验之前却不能肯定这次试验会出现哪一个结果。
X 4 5 6 7 8 9 10 P 0.02 0.04 0.06 0.09 0.28 0.29 0.22
则此射手“射击一次命中环数≥7”的概率是_0_._8__8__
例 2.在含有 5 件次品的 100 件产品中,任取 3 件, 求:(1)取到的次品数 X 的分布列; (2)至少取到 1 件次品的概率。
例、袋子中有3个红球,2个白球,1个黑球,这些球 除颜色外完全相同,现要从中摸一个球出来,若摸到
黑球得1分,摸到白球得0分,摸到红球倒扣1分,试写 出从该盒内随机取出一球所得分数X的分布列.
解:因为只取1球,所以X的取值只能是1,0,-1
P( X 1) 1 , P( X 0) 2 1 ,
0分,1分,2分用数字来表
示呢? (3)抛掷一枚硬币,可能出现的结果有几种情况?
正面向上,反面向上
思考:在上述试验开始之前,你能确定结果是哪一 种情况吗?
分析:不行,虽然我们能够事先知道随机试验可能出 现的所有结果,但在一般情况下,试验的结果是随机出 现的。
一、随机变量的概念:
在前面的例子中,我们把随机试验的每一个结果 都用一个确定的数字来表示,这样试验结果的变化就 可看成是这些数字的变化。
高中数学人教A版选修2-3课件2-1-2离散型随机变量的分布列

付款,其利润为250元;分4期或5期付款,其利润为300元.若η表示经
销一件该商品的利润,求η的分布列.
探究一
探究二
探究三
探究四
思维辨析
当堂检测
解:由题易得,η的可能取值为200元,250元,300元,
则P(η=200)=P(ξ=1)=0.12,
P(η=250)=P(ξ=2)+P(ξ=3)=0.24+0.18=0.42,
=1
【做一做1】 离散型随机变量X的分布列为
X
1
1
4
)
P
则m的值为(
A.
C.
1
2
1
4
B.
2
3
m
4
1
3
1
3
1
D.
6
1
1
1
1
4
3
6
4
解析:由概率分布列的性质知, +m+ + =1,得 m= .
答案:C
1
6
2.两点分布
随机变量X的分布列为
X
P
0
1-p
1
p
若随机变量X的分布列具有上表的形式,则称X服从两点分布,并
C 345
C 350
C 350
.
,
探究一
探究二
探究三
探究四
思维辨析
当堂检测
离散型随机变量的分布列
例1 从装有除颜色外完全相同的6个白球,4个黑球和2个黄球的箱
中随机地取出两个球,规定每取出1个黑球赢2元,而每取出1个白球
输1元,取出黄球无输赢.
(1)以X表示赢得的钱数,随机变量X可以取哪些值?求X的分布列;
销一件该商品的利润,求η的分布列.
探究一
探究二
探究三
探究四
思维辨析
当堂检测
解:由题易得,η的可能取值为200元,250元,300元,
则P(η=200)=P(ξ=1)=0.12,
P(η=250)=P(ξ=2)+P(ξ=3)=0.24+0.18=0.42,
=1
【做一做1】 离散型随机变量X的分布列为
X
1
1
4
)
P
则m的值为(
A.
C.
1
2
1
4
B.
2
3
m
4
1
3
1
3
1
D.
6
1
1
1
1
4
3
6
4
解析:由概率分布列的性质知, +m+ + =1,得 m= .
答案:C
1
6
2.两点分布
随机变量X的分布列为
X
P
0
1-p
1
p
若随机变量X的分布列具有上表的形式,则称X服从两点分布,并
C 345
C 350
C 350
.
,
探究一
探究二
探究三
探究四
思维辨析
当堂检测
离散型随机变量的分布列
例1 从装有除颜色外完全相同的6个白球,4个黑球和2个黄球的箱
中随机地取出两个球,规定每取出1个黑球赢2元,而每取出1个白球
输1元,取出黄球无输赢.
(1)以X表示赢得的钱数,随机变量X可以取哪些值?求X的分布列;
《离散型随机变量的分布列》人教版高中数学选修2-3PPT课件(第2.1.2课时)

ξ0
1
2
3
4
5
P 0.95 0.5×0.94 0.1×0.93 0.01×0.92 4.5×0.14 0.15
课堂练习
(2) 下列给出的是不是某个随机变量的分布列?
①
1 0.5
3 0.3
05.2
②
1 0.7
2 0.1
03.1
0 1
2 n
③
1 2
1 1 2 3
1 1 2
2 3
1 1 n
讲解人:XXX 时间:20XX.6.1
人教版高中数学选修2-3
第2章 随机变量及其分布
2.3.1离散型随机变量的均值
PEOPLE'S EDUCATION PRESS HIGH SCHOOL MATHEMATICS ELECTIVE 2-3
讲解人: 时间:2020.6.1
课前导入
(1)离散型随机变量的分布列:
它是三种糖果价格的一种加权平均,这里的权数分别是1/2,1/3和1/6. 权是秤锤,权数是起权衡轻重作用的数值.加权平均是指在计算若干个数量的平均数时,考虑到 每个数量在总量中所具有的重要性不同,分别给予不同的权数. 如果混合糖果中每一颗糖果的质量都相等,你能解释权数的实际含义吗?
新知探究
根据古典概型计算概率的公式可知,在混合糖果中,任取一颗糖果,这颗糖果为第一、二、三种 糖果的概率分别为1/2,1/3,1/6,即取出的这颗糖果的价格为18元/kg,24元/kg或36元/kg的概 率分别是1/2,1/3,1/6.用X表示这颗糖果的价格,则它是一个离散型随机变量,其分布列为
所求的概率为 P(ξ≥7)=0.09+0.28+0.29+0.22=0.88 .
高中数学选修2-3精品课件:2.1.2 离散型随机变量的分布列(二)

2.超几何分布 一般地,在含有 M 件次品的 N 件产品中,任取 n 件,其中 恰有 X 件次品,则事件{X=k}发生的概率为 P(X=k)= CkMCCnnNN--kM,k=0,1,2,…,m,其中 m=min{M,n},且 n≤N, M≤N,n,M,N∈N*,
则称分布列
X
0
1
…
P
C0MCnN--0M C1MCnN--1M
2.只取两个不同值的随机变量一定服从两点分布吗?举例 说明. 答 只取两个不同值的随机变量并不一定服从两点分布.例 如:随机变量X的分布列如下:
X2 5
P 0.3 0.7
则X不服从两点分布,因为X的取值不是0或1.
[预习导引] 1.两点分布 若随机变量X的分布列为
X
0
1
P 1-p p
则称该分布列为两点分布列.若随机变量X的分布列为两点 分布列,则称X服从两点 分布,称p=P(X=1)为成功概率.
CnN
CnN
…
m
CmMCnN--mM CnN
为 超几何分布列 .如果随机变量X的分布列为超几何分布列, 则称随机变量X服从 超几何分布 .
要点一 两点分布 例1 袋中有红球10个,白球5个,从中摸出2个球,如果只 关心摸出两个红球的情形,问如何定义随机变量X,才能使 X满足两点分布,并求分布列. 解 从含有10个红球,5个白球的袋中摸出2个球,其结果 是随机的, 可能是一红一白、两红、两白三种情况,为此我们定义随 机变量如下:
P(ξ=2)=CC21280=2485,P(ξ=6)=CC81C21012=1465, P(ξ=10)=CC21220=415. 故ξ的分布列为 ξ 2 6 10
P
28 45
16 45
人教A版高中数学选修2-3课件《2.1.2离散型随机变量的分布列(2)》

X
0
3 C50C95 3 C100
1 5
1
CC 3 • C100
2 95
2 5
2
CC 3 C100
1 95
3
3 0 C5 C95 3 C100
P
2、超几何分布
一般地,在含有M件次品的N件产品中,任取n件, 其中恰有X件产品数,则事件{X=k}发生的概率为
k nk CM CN M P( X k ) , k 0,1, 2, n CN
变式引申:
1、某射手射击目标的概率为0.9,求从开始射击到击中目标 所需的射击次数的概率分布。
2、数字1,2,3,4任意排成一列,如果数字k恰好在第k个 位置上,则称有一个巧合,求巧合数的分布列。
•
一盒中放有大小相同的红色、绿色、黄色三种小球,已 知红球的个数是绿球个数的两倍,黄球个数是绿球个数 的一半,现从该盒中随机取出一球,若取出红球得1分, 取出绿球得0分,取出黄球得-1分,试写出从该盒内随机 取出一球所得分数ξ的分布列. 解:设黄球的个数为 n,由题意知
,m
其中m min{ M , n}, 且n N , M N , n, M , N N *
称分布列为 超几何分布
X P 0 1
…
…
m
m nm CM CN M n CN
1 n 1 0 n 0 C C CM CN M N M M n n C CN N
记为:x 则称随机变量 X 服从超几何分布. •
H(n,M,N),
例4:在某年级的联欢会上设计了一个摸奖游戏,在
一个口袋中装有10个红球和个20白球,这些球除颜 色外完全相同。一次从中摸出5个球,至少摸到3个 红球就中奖。求中奖的概率。
人教A版数学选修2—3 2.1.2 离散型随机变量的分布列(共20张PPT)

离散型随机变量及其分布列(二)
问题提出
1.离散型随机变量X的分布列的概念?
若离散型随机变量X的所有可能取值 为x1,x2,…,xi,…, xn,X取每一个 值xi(i=1,2,…,n)的概率P(X=xi)=
pi,则下列表格称为X的分布列.
X x1 x2 … xi … xn P p1 p2 … pi … pn
解:设黄球的个数为 n,由题意知
绿球个数为 2n,红球个数为 4n,盒中的总数为 7n.
∴ P(
1)
4n 7n
4 7
,P(
0)
n 7n
1 7
,P(
1)
2n 7n
2 7
.
所以从该盒中随机取出一球所得分数 ξ 的分布列为
1
0
-1
P
4
1
2
7
7
7
多做练习:
2.设袋中有 N 个球,其中有 M 个红球, N M 个黑球, 从中任取 n 个球,问恰有 k 个红球的概率是多少?
X01
P 1-p p
思考3:将上述两个分布列取名为两点分 布列,那么在什么情况下,随机变量X的 分布列可成为为两点分布列?
随机试验只有两个可能结果.
思考4:如果随机变量X的分布列为两点
分布列,则称X服从两点分布,在两点分
布中随机变量的值域是什么?分布列
P(X=2)=0.4,P(X=5)=0.6是否为两
P{X≥3}=P{X=3}+P{X=4}+P{X=5} ≈0.191
思考:若将这个游戏的中奖概率控制在 55%左右,应如何设计中奖规则?
游戏规则可定为至少摸到2个红球就中奖.
练习
从1~10这10个数字中随机取出5个数字,令X
问题提出
1.离散型随机变量X的分布列的概念?
若离散型随机变量X的所有可能取值 为x1,x2,…,xi,…, xn,X取每一个 值xi(i=1,2,…,n)的概率P(X=xi)=
pi,则下列表格称为X的分布列.
X x1 x2 … xi … xn P p1 p2 … pi … pn
解:设黄球的个数为 n,由题意知
绿球个数为 2n,红球个数为 4n,盒中的总数为 7n.
∴ P(
1)
4n 7n
4 7
,P(
0)
n 7n
1 7
,P(
1)
2n 7n
2 7
.
所以从该盒中随机取出一球所得分数 ξ 的分布列为
1
0
-1
P
4
1
2
7
7
7
多做练习:
2.设袋中有 N 个球,其中有 M 个红球, N M 个黑球, 从中任取 n 个球,问恰有 k 个红球的概率是多少?
X01
P 1-p p
思考3:将上述两个分布列取名为两点分 布列,那么在什么情况下,随机变量X的 分布列可成为为两点分布列?
随机试验只有两个可能结果.
思考4:如果随机变量X的分布列为两点
分布列,则称X服从两点分布,在两点分
布中随机变量的值域是什么?分布列
P(X=2)=0.4,P(X=5)=0.6是否为两
P{X≥3}=P{X=3}+P{X=4}+P{X=5} ≈0.191
思考:若将这个游戏的中奖概率控制在 55%左右,应如何设计中奖规则?
游戏规则可定为至少摸到2个红球就中奖.
练习
从1~10这10个数字中随机取出5个数字,令X
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n 1 P(ξ=-1)= 7 n= 7 .
所以从该盒中随机取出一球
ξ P
1
0
-1
所得分数ξ的分布列为:
4 7
2 7
1 7
3.已知随机变量 的分布列如下:
-2
1 12
-1
1 4
0
1 3
1
1 12
2
1 6
2
3
1 12
P
分别求出随机变量⑴ 1 ;⑵ 2
1 2
的分布列.
象上面这样的分布列称为两点分布列。如 果随机变量X的分布列为两点分布列,就称X服 从两点分布,而称p=P(X=1)为成功概率。
练习1:200件产品中,有190件合格品,10件不合
格品,现从中随机抽取一件, 若规定
1, 取得不合格品, 0,取得合格品.
则随机变量
pk
0
190 200
1
P(ξ=8)=0.28,
=0.09+0.28+0.29+0.22=0.88
注:离散型随机变量在某一范围内取值的概率等 于它取这个范围内各个值的概率之和 .
例 3、在掷一枚图钉的随机试验中,令
1, 针尖向上 X 0, 针尖向下
如果会尖向上的概率为p,试写出随机变量X的分布列
解:随机变量X的分布列是: X P 0 1—p 1 p
2 1 B、 2
P
1 2
1
0
1 2q
1 2 2
1
q2
2 C、 1 2
D、
求离散型随机变量的概率分布的方法步骤:
1、找出随机变量ξ的所有可能的取值 xi (i 1, 2, ); 2、求出各取值的概率 3、列成表格。
P( xi ) pi ;
练习1.随机变量ξ的分布列为 ξ 0 1 -1
2.概率分布还经常用图象来表示.
p
0.2
0.1 O 1 2 3 4 5 6 7 8
可以看出 的取值 范围是{1,2,3,4,5,6}, 它取每一个值的概 率都是 1/6 。
1、离散型随机变量的分布列完全描述了由这个随机 变量所刻画的随机现象。 2、函数可以用解析式、表格或图象表示,离散型随
机变量可以用分布列、等式或图象来表示。
x1
p1
x2
p2
· · · · · ·
xi
pi
· · ·
· · · P 为随机变量 的概率分布,简称 的分布列. 注: 1、分布列的构成 ⑴列出了随机变量 的所有取值. ⑵求出了 的每一个取值的概率.
2、分布列的性质
(1)pi 0, i 1, 2, ,n (2)p1 p2 P n 1
10 200
服从(0 —1)分布.
两点分布是最简单的一种分布,任何一个只有 两种可能结果的随机现象, 比如新生婴儿是男还 是女、明天是否下雨、种籽是否发芽等, 都属于
两点分布.
1.设随机变量 的分布列如下:
P
1
1 6
2
1 3
3
1 6
4
p
.
i
则
p的值为
1 i 1, 2, 3 2.设随机变量 的分布列为 P ( i ) a ,
例1:抛掷两枚骰子,点数之和为ξ,则ξ可能取 第二次抛掷 3 4 5 6 的值有: 2,3,4,……,12. 1 2
ξ的概率分布为:
第 一 次 抛 掷
1 2
3
2
3 4
3
4
4
5
6 7
6
7 8
7
8 9
5
6
5
6
7 8
4 5 6
5
6 7
7
8 9
8
9 10
9
10 11
10
11 12
ξ
2
3
4
3 36
5
4 36
2
3
p
0.16
a/10
a2
a/5
0.3
(1)求常数a;(2)求P(1<ξ<4)
解:(1)由离散型随机变量的分布列的性质有
a a 2 0.16 a 0.3 1 10 5
9 3 a (舍)或 a 解得: 10 5
(2)P(1<ξ<4)=P(ξ=2)+P(ξ=3)=0.12+0.3=0.42
2. 一盒中放有大小相同的红色、绿色、黄色三种小球, 已知红球的个数是绿球个数的两倍,黄球个数是绿球个 数的一半,现从该盒中随机取出一球,若取出红球得 1分, 取出绿 球得0分,取出黄球得-1分,试写出从该盒内随 机取出一球所得分数ξ的分布列. 解:设黄球的个数为n,则绿球的个数为2n,红球的个 数为4n,盒中球的个数为7n,所以 2 2n 4n 4 P(ξ=1)= 7 n = 7 ,P(ξ=0)= = , 7 7n
6
7
8
5 36
9
10 11 12
p
1 2 36 36
5 6 36 36
4 3 36 36
2 1 36 36
此表从概率的角度指出了随机变量在随机试验中取值 的分布情况,称为随机变量ξ的概率分布.
• 例 2 某一射手射击所得环数 的分布列如下:
4567 Nhomakorabea8
9
10
P
0.02 0.04 0.06 0.09 0.28 0.29 0.22
随机变量ξ的线性组合η=aξ+b(其中a、b是常 数)也是随机变量.
随机变量ξ是关于试验结果的函数,即每一个 试验结果对应着一个实数.
二、离散型随机变量的分布列
设随机变量 的所有可能的取值为 x1 , x2 , x3 , , xn ,
x (i 1,2, ) 的每一个取值 的概率为 P( xi ) pi 则称表格 , i
1 3
则 a 的值为
3.设随机变量 的分布列为 则 q ( D )
A、 1
27 13
.
3
4.设随机变量 只能取5、6、7、· · · 、16这12个值,且 1 2 P ( ) 8 取每一个值的概率均相等,则 ,若P ( x ) 3 12 则实数 x 的取值范围是 5,6 .
求此射手 “射击一次命中环数 7 ” 的概率 .
P(ξ=7)=0.09,
件P(ξ=9)=0.29, P(ξ=10)=0.22, “ = 7 ” “ = 8 ” “ = 9 ” “ = 10 ” 的和 . 所求的概率为P(ξ ≥7) 利用互斥事件的概率加法公式即可求得结果 .
分析:“ 射击一次命中环数 7 ” 是指互斥事
全国名校高中数学人教版优质课件汇编
一、复习引入:
概念 随机变量 离散型 随机变量 具体内容 如果随机试验的结果可以用一个变量来 表示,那么这样的变量叫做随机变量。 随机变量可能取的值可以按一定次序 一一列出,这样的随机变量叫做离散 型随机变量。
连续型 随机变量可以取某一曲间内的一切值, 随机变量 这样的随机变量叫作连续型随机变量。
