模式识别大作业
模式识别大作业

Iris 数据聚类分析-----c 均值和模糊c 均值一.问题描述Iris 数据集包含150个数据,共有3类,每一类有50个数据,其每个数据有四个维度,每个维度代表鸢尾花特征(萼片,花瓣的长度)中的一个,其三类数据名称分别setosa,versicolor,virginica ,这些就是 Iris 数据集的基本特征。
现在使用c 均值和模糊c 均值的方法解决其聚类分析,并且计算比较两种方法得到的分类结果的正确率。
二.算法介绍1.c-均值算法C 均值算法属于聚类技术中一种基本的划分方法,具有简单、快速的优点。
其基本思想是选取c 个数据对象作为初始聚类中心,通过迭代把数据对象划分到不同的簇中,使簇内部对象之间的相似度很大,而簇之间对象的相似度很小。
其主要思想:(1) 计算数据对象两两之间的距离;(2) 找出距离最近的两个数据对象,形成一个数据对象集合A1 ,并将它们从总的数据集合U 中删除;(3) 计算A1 中每一个数据对象与数据对象集合U 中每一个样本的距离,找出在U 中与A1 中最近的数据对象,将它并入集合A1 并从U 中删除, 直到A1 中的数据对象个数到达一定阈值;(4) 再从U 中找到样本两两间距离最近的两个数据对象构成A2 ,重复上面的过程,直到形成k 个对象集合;(5) 最后对k 个对象集合分别进行算术平均,形成k 个初始聚类中心。
算法步骤:1.初始化:随机选择k 个样本点,并将其视为各聚类的初始中心12,,,k m m m ;2.按照最小距离法则逐个将样本x 划分到以聚类中心12,,,k m m m 为代表的k 个类1,k C C 中;3.计算聚类准则函数J,重新计算k 个类的聚类中心12,,,k m m m ; 4.重复step2和3知道聚类中心12,,,k m m m 无改变或目标函数J 不减小。
2.模糊c-均值模糊C 均值算法就是,在C 均值算法中,把硬分类变为模糊分类。
设()j i μx 是第i 个样本i x 属于第j 类j G 的隶属度,利用隶属度定义的准则函数为211[()]C N b f j i i jj i J μ===-∑∑x x m其中,b>1是一个可以控制聚类结果的模糊程度的常数。
模式识别作业三道习题

K7 ( X ) K6 ( X ) 1 第八步:取 X 4 w2 , K 7 ( X 4 ) 32 0 ,故 0 K8 ( X ) K 7 ( X ) 0 第九步:取 X 1 w1 , K8 ( X 1 ) 32 0 ,故 1 K 9 ( X ) K8 ( X ) 0 第十步:取 X 2 w1 , K9 ( X 2 ) 32 0 ,故 1 K10 ( X ) K9 ( X )
2
K ( X , X k ) exp{ || X X k || 2} exp{[( x 1 xk 1) 2 ( x 2 xk 2 ) 2]} x1 X = x2 ,训练样本为 X k 。 其中
模式识别大作业

模式识别大作业模糊聚类算法模糊聚类算法概述模糊聚类算法是一种基于函数最优方法的聚类算法,使用微积分计算技术求最优代价函数。
在基于概率算法的聚类方法中将使用概率密度函数,为此要假定合适的模型,模糊聚类算法的向量可以同时属于多个聚类,从而摆脱上述问题。
在模糊聚类算法中,定义了向量与聚类之间的近邻函数,并且聚类中向量的隶属度由隶属函数集合提供。
对模糊方法而言,在不同聚类中的向量隶属函数值是相互关联的。
硬聚类可以看成是模糊聚类方法的一个特例。
模糊聚类算法的分类模糊聚类分析算法大致可分为三类[4]:1)分类数不定,根据不同要求对事物进行动态聚类,此类方法是基于模糊等价矩阵聚类的,称为模糊等价矩阵动态聚类分析法。
2)分类数给定,寻找出对事物的最佳分析方案,此类方法是基于目标函数聚类的,称为模c均值聚类。
3)在摄动有意义的情况下,根据模糊相似矩阵聚类,此类方法称为基于摄动的模糊聚类分析法。
模糊c均值(FCM)聚类算法算法描述模糊c均值聚类算法的步骤还是比较简单的,模糊c均值聚类(FCM),即众所周知的模糊ISODATA,是用隶属度确定每个数据点属于某个聚类的程度的一种聚类算法。
1973年,Bezdek提出了该算法,作为早期硬c均值聚类(HCM)方法的一种改进。
FCM把n个向量x i(i=1,2,…,n)分为c个模糊组,并求每组的聚类中心,使得非相似性指标的价值函数达到最小。
FCM与HCM的主要区别在于FCM用模糊划分,使得每个给定数据点用值在0,1间的隶属度来确定其属于各个组的程度。
与引入模糊划分相适应,隶属矩阵U允许有取值在0,1间的元素。
不过,加上归一化规定,一个数据集的隶属度的和总等于1:∑==∀=ciijnju1,...,1,1(3.1)那么,FCM的价值函数(或目标函数)就是:∑∑∑====c i njijm ij c i i c d u J c c U J 1211),...,,(, (3.2)这里u ij 介于0,1间;c i 为模糊组I 的聚类中心,d ij =||c i -x j ||为第I 个聚类中心与第j 个数据点间的欧几里德距离;且[)∞∈,1m 是一个加权指数。
中科院模式识别大作业——人脸识别

中科院模式识别大作业——人脸识别人脸识别是一种广泛应用于安全领域的技术,它通过对图像或视频中的人脸进行特征提取和比对,实现对个体身份的自动识别。
中科院模式识别大作业中的人脸识别任务主要包括了人脸检测、人脸对齐、特征提取和人脸比对等步骤。
下面将详细介绍这些步骤。
首先,人脸检测是人脸识别的第一步。
它的目的是在图像或视频中准确地定位人脸区域,去除背景和其他干扰信息。
传统的人脸检测算法主要基于特征匹配、分类器或神经网络等方法,而近年来深度学习技术的兴起也为人脸检测带来了重大突破。
深度学习方法通过构建卷积神经网络,在大规模数据上进行训练,可以准确地检测出各种姿态、光照和遮挡条件下的人脸区域。
接下来是人脸对齐,它的目的是将检测到的人脸区域进行准确的对齐,使得不同人脸之间的几何特征保持一致。
人脸对齐算法通常包括了关键点检测和对齐变换操作。
关键点检测通过在人脸中标注一些特定点(如眼睛、鼻子和嘴巴)来标定人脸的几何结构。
对齐变换操作则根据标定的关键点信息,对人脸进行旋转、尺度调整和平移等变换操作,使得不同人脸之间具有一致的几何结构。
人脸对齐可以提高后续特征提取的准确性,从而提高整个人脸识别系统的性能。
特征提取是人脸识别的核心步骤之一,它将对齐后的人脸图像转化为能够表示个体身份信息的特征向量。
传统的特征提取方法主要基于手工设计的特征描述子,如LBP、HOG等。
这些方法需要针对不同任务进行特征设计,且往往存在一定的局限性。
相比之下,深度学习方法可以通过网络自动地学习出适用于不同任务的特征表示。
常用的深度学习模型有卷积神经网络和人工神经网络等,它们通过在大规模数据上进行监督学习,可以提取出能够表达人脸细节和结构的高层次特征。
最后是人脸比对,它根据提取的特征向量进行个体身份的匹配。
人脸比对算法通常需要计算两个特征向量之间的相似度,常用的计算方法有欧氏距离、余弦相似度等。
在实际应用中,为了提高匹配的准确性,通常会结合分数归一化、阈值设定等技术来进行优化。
模式识别大作业1

模式识别大作业--fisher线性判别和近邻法学号:021151**姓名:**任课教师:张**I. Fisher线性判别A. fisher线性判别简述在应用统计方法解决模式识别的问题时,一再碰到的问题之一是维数问题.在低维空间里解析上或计算上行得通的方法,在高维里往往行不通.因此,降低维数就成为处理实际问题的关键.我们考虑把维空间的样本投影到一条直线上,形成一维空间,即把维数压缩到一维.这样,必须找一个最好的,易于区分的投影线.这个投影变换就是我们求解的解向量.B.fisher线性判别的降维和判别1.线性投影与Fisher准则函数各类在维特征空间里的样本均值向量:,(1)通过变换映射到一维特征空间后,各类的平均值为:,(2)映射后,各类样本“类内离散度”定义为:,(3)显然,我们希望在映射之后,两类的平均值之间的距离越大越好,而各类的样本类内离散度越小越好。
因此,定义Fisher准则函数:(4)使最大的解就是最佳解向量,也就是Fisher的线性判别式。
2.求解从的表达式可知,它并非的显函数,必须进一步变换。
已知:,, 依次代入上两式,有:,(5)所以:(6)其中:(7)是原维特征空间里的样本类内离散度矩阵,表示两类均值向量之间的离散度大小,因此,越大越容易区分。
将(4.5-6)和(4.5-2)代入(4.5-4)式中:(8)其中:,(9)因此:(10)显然:(11)称为原维特征空间里,样本“类内离散度”矩阵。
是样本“类内总离散度”矩阵。
为了便于分类,显然越小越好,也就是越小越好。
将上述的所有推导结果代入表达式:可以得到:其中,是一个比例因子,不影响的方向,可以删除,从而得到最后解:(12)就使取得最大值,可使样本由维空间向一维空间映射,其投影方向最好。
是一个Fisher线性判断式.这个向量指出了相对于Fisher准则函数最好的投影线方向。
C.算法流程图左图为算法的流程设计图。
II.近邻法A. 近邻法线简述K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
模式识别大作业
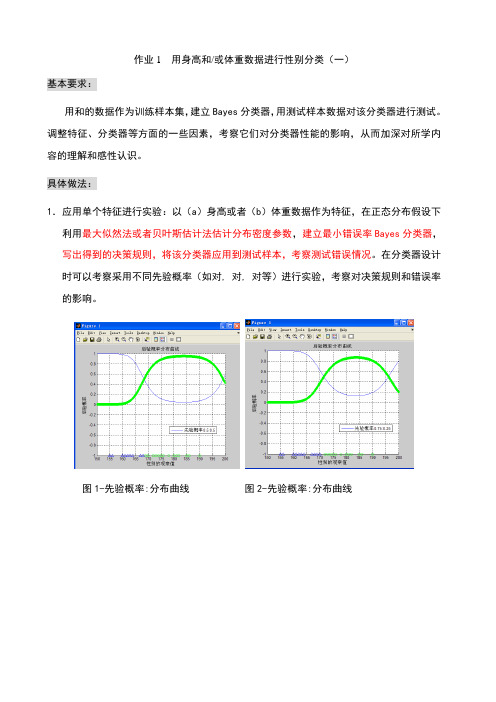
作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes 分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如 vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率 vs. 图2先验概率 vs.图3先验概率 vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
设以ceshi1单个特征身高进行试验:决策表W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2); error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
模式识别大作业-许萌-1306020
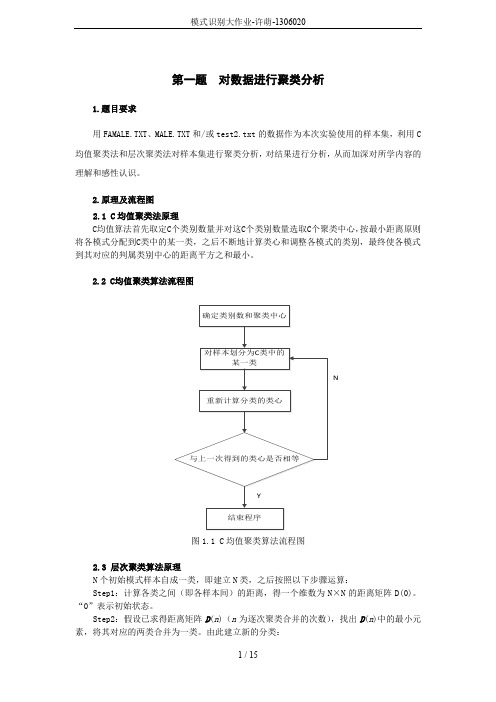
第一题对数据进行聚类分析1.题目要求用FAMALE.TXT、MALE.TXT和/或test2.txt的数据作为本次实验使用的样本集,利用C 均值聚类法和层次聚类法对样本集进行聚类分析,对结果进行分析,从而加深对所学内容的理解和感性认识。
2.原理及流程图2.1 C均值聚类法原理C均值算法首先取定C个类别数量并对这C个类别数量选取C个聚类中心,按最小距离原则将各模式分配到C类中的某一类,之后不断地计算类心和调整各模式的类别,最终使各模式到其对应的判属类别中心的距离平方之和最小。
2.2 C均值聚类算法流程图N图1.1 C均值聚类算法流程图2.3 层次聚类算法原理N个初始模式样本自成一类,即建立N类,之后按照以下步骤运算:Step1:计算各类之间(即各样本间)的距离,得一个维数为N×N的距离矩阵D(0)。
“0”表示初始状态。
Step2:假设已求得距离矩阵D(n)(n为逐次聚类合并的次数),找出D(n)中的最小元素,将其对应的两类合并为一类。
由此建立新的分类:Step3:计算合并后所得到的新类别之间的距离,得D (n +1)。
Step4:跳至第2步,重复计算及合并。
直到满足下列条件时即可停止计算:①取距离阈值T ,当D (n )的最小分量超过给定值 T 时,算法停止。
所得即为聚类结果。
②或不设阈值T ,一直到将全部样本聚成一类为止,输出聚类的分级树。
2.4层次聚类算法流程图N图1.2层次聚类算法流程图3 验结果分析对数据文件FAMALE.TXT 、MALE.TXT 进行C 均值聚类的聚类结果如下图所示:图1.3 C 均值聚类结果的二维平面显示将两种样本即进行聚类后的样本中心进行比较,如下表:从下表可以纵向比较可以看出,C 越大,即聚类数目越多,聚类之间差别越小,他们的聚类中心也越接近。
横向比较用FEMALE,MALE 中数据作为样本和用FEMALE,MALE ,test2中),1(),1(21++n G n G数据作为样本时,由于引入了新的样本,可以发现后者的聚类中心比前者都稍大。
模式识别大作业
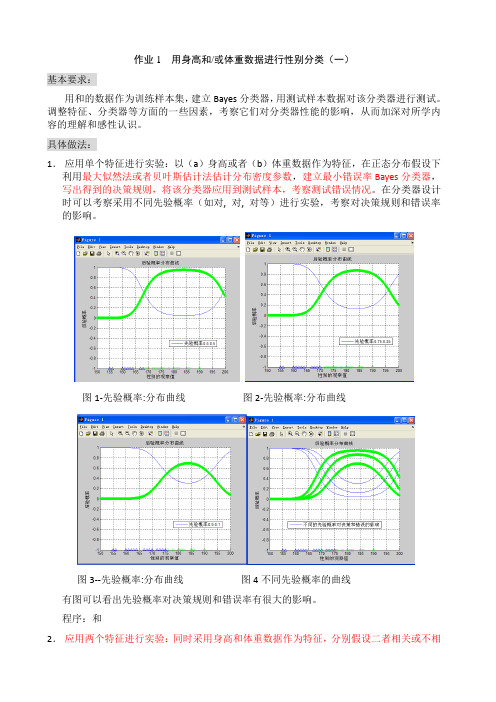
作业1 用身高和/或体重数据进行性别分类(一)基本要求:用和的数据作为训练样本集,建立Bayes分类器,用测试样本数据对该分类器进行测试。
调整特征、分类器等方面的一些因素,考察它们对分类器性能的影响,从而加深对所学内容的理解和感性认识。
具体做法:1.应用单个特征进行实验:以(a)身高或者(b)体重数据作为特征,在正态分布假设下利用最大似然法或者贝叶斯估计法估计分布密度参数,建立最小错误率Bayes分类器,写出得到的决策规则,将该分类器应用到测试样本,考察测试错误情况。
在分类器设计时可以考察采用不同先验概率(如对, 对, 对等)进行实验,考察对决策规则和错误率的影响。
图1-先验概率:分布曲线图2-先验概率:分布曲线图3--先验概率:分布曲线图4不同先验概率的曲线有图可以看出先验概率对决策规则和错误率有很大的影响。
程序:和2.应用两个特征进行实验:同时采用身高和体重数据作为特征,分别假设二者相关或不相关(在正态分布下一定独立),在正态分布假设下估计概率密度,建立最小错误率Bayes 分类器,写出得到的决策规则,将该分类器应用到训练/测试样本,考察训练/测试错误情况。
比较相关假设和不相关假设下结果的差异。
在分类器设计时可以考察采用不同先验概率(如vs. , vs. , vs. 等)进行实验,考察对决策和错误率的影响。
训练样本female来测试图1先验概率vs. 图2先验概率vs.图3先验概率vs. 图4不同先验概率对测试样本1进行试验得图对测试样本2进行试验有图可以看出先验概率对决策规则和错误率有很大的影响。
程序和3.自行给出一个决策表,采用最小风险的Bayes决策重复上面的某个或全部实验。
W1W2W10W20close all;clear all;X=120::200; %设置采样范围及精度pw1=;pw2=; %设置先验概率sample1=textread('') %读入样本samplew1=zeros(1,length(sample1(:,1)));u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布figure(1);subplot(2,1,1);plot(X,y1);title('F身高类条件概率分布曲线');sample2=textread('') %读入样本samplew2=zeros(1,length(sample2(:,1)));u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布subplot(2,1,2);plot(X,y2);title('M身高类条件概率分布曲线');P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);figure(2);subplot(2,1,1);plot(X,P1);title('F身高后验概率分布曲线');subplot(2,1,2);plot(X,P2);title('M身高后验概率分布曲线');P11=pw1*y1;P22=pw2*y2;figure(3);subplot(3,1,1);plot(X,P11);subplot(3,1,2);plot(X,P22);subplot(3,1,3);plot(X,P11,X,P22);sample=textread('all ') %读入样本[result]=bayes(sample1(:,1),sample2(:,1),pw1,pw2);%bayes分类器function [result] =bayes(sample1(:,1),sample2(:,1),pw1,pw2);error1=0;error2=0;u1=mean(sample1(:,1));m1=std(sample1(:,1));y1=normpdf(X,u1,m1); %类条件概率分布u2=mean(sample2(:,1));m2=std(sample2(:,1));y2=normpdf(X,u2,m2); %类条件概率分布P1=pw1*y1./(pw1*y1+pw2*y2);P2=pw2*y2./(pw1*y1+pw2*y2);for i = 1:50if P1(i)>P2(i)result(i)=0;pe(i)=P2(i);elseresult(i)=1;pe(i)=P1(i);endendfor i=1:50if result(k)==0error1=error1+1;else result(k)=1error2=error2+1;endendratio = error1+error2/length(sample); %识别率,百分比形式sprintf('正确识别率为%.2f%%.',ratio)作业2 用身高/体重数据进行性别分类(二)基本要求:试验直接设计线性分类器的方法,与基于概率密度估计的贝叶斯分离器进行比较。
模式识别大作业

模式识别大作业对sonar数据进行分类,用Fisher线性判别法和最近邻算法对其进行分类,并用MATLAB写程序对其进行模拟。
Fisher线性判别法的源程序如下clear,close all%¶ÁÈ¡È«²¿Êý¾ÝRock=xlsread('C:\Users\Administrator\Documents\data\rock');Mine=xlsread('C:\Users\Administrator\Documents\data\mine');%²úÉúËæ»úÊýr1=randperm(97,48);r2=randperm(111,56);%È¡³öѵÁ·Ñù±¾for i=1:48vtrainrock(i,:)=Rock(r1(1,i),:);endtrainrock=vtrainrock';for i=1:56vtrainmine(i,:)=Mine(r2(1,i),:);endtrainmine=vtrainmine';%È¡³ö²âÊÔÑù±¾Rock(r1',:)=[];testrock=Rock';Mine(r2',:)=[];testmine=Mine';%¼ÆËã¾ùÖµÏòÁ¿mrock=mean(trainrock,2);mmine=mean(trainmine,2);%¼ÆËãÀàÄÚÀëÉ¢¶È¾ØÕófor j=1:48s1=(trainrock(:,j)-mrock);sr=s1*s1';srock=zeros(60);srock=sr+srock;endfor j=1:56s2=(trainmine(:,j)-mmine);sm=s2*s2';smine=zeros(60);smine=sm+smine;endSw=srock+smine;%¼ÆËãÀà¼äÀëÉ¢¶È¾ØÕóSb=(mrock-mmine)*(mrock-mmine)';%¼ÆËã×î¼ÑͶӰ·½ÏòW=inv(Sw)*(mrock-mmine);%¶ÔѵÁ·Ñù±¾½øÐÐͶӰintestrock=W'*testrock;intestmine=W'*testmine;%¼ÆËãÅбðãÐÖµµãintrainrock=W'*trainrock;intrainmine=W'*trainmine;w0=(mean(intrainrock,2)*48+mean(intrainmine,2)*56)/104;%·ÖÀಢ¼ÆËã׼ȷÂÊ%¶Ô´ý²âÑù±¾½øÐзÖÀàj1=1;k1=1;RocksortRock1=zeros(size(intestrock));%¼ì²âÑù±¾Rock±»ÕýÈ·µØ·ÖΪRockµÄÊýRocksortMine1=zeros(size(intestmine));%¼ì²âÑù±¾Rock±»´íÎóµØ·ÖΪMineµÄÊýRocksortRocknumber1=zeros(size(intestrock));%¼ì²âÑù±¾Rock±»ÕýÈ·µØ·ÖΪRockµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅRocksortMinenumber1=zeros(size(intestmine));%¼ì²âÑù±¾Rock±»´íÎóµØ·ÖΪMineµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅfor i=1:49if(intestrock(1,i)>w0)RocksortRock1(1,j1)=intestrock(1,i);RocksortRocknumber1(1,j1)=i;j1=j1+1;elseRocksortMine1(1,k1)=intestrock(1,i);RocksortMinenumber1(1,k1)=i;k1=k1+1;endendj2=1;k2=1;MinesortMine2=zeros(size(intestmine));%¼ì²âÑù±¾Mine±»ÕýÈ·µØ·ÖΪMineµÄÊýMinesortRock2=zeros(size(intestrock));%¼ì²âÑù±¾Mine±»´íÎóµØ·ÖΪRockµÄÊýMinesortMinenumber2=zeros(size(intestmine));%¼ì²âÑù±¾Mine±»ÕýÈ·µØ·ÖΪMineµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅMinesortRocknumber2=zeros(size(intestrock));%¼ì²âÑù±¾Mine±»´íÎóµØ·ÖΪRockµÄÊýÔÚ¼ì²âÑù±¾ÀïµÄÐòºÅfor i=1:55if(intestmine(1,i)<=w0)MinesortMine2(1,j2)=intestmine(1,i);MinesortMinenumber2(1,j2)=i;j2=j2+1;elseMinesortRock2(1,k2)=intestmine(1,i);MinesortRocknumber2(1,k2)=i;k2=k2+1;endend%¼ÆËã·ÖÀà½á¹ûµÄÕýÈ·ÂÊright=(j1+j2-2)/(j1+j2+k1+k2-4);disp(right);最近邻算法的源程序如下clear,close all%¶ÁÈ¡È«²¿Êý¾ÝRock=xlsread('C:\Users\Administrator\Documents\data\rock'); Mine=xlsread('C:\Users\Administrator\Documents\data\mine'); %²úÉúËæ»úÊýr1=randperm(97,48);r2=randperm(111,56);%È¡³öѵÁ·Ñù±¾for i=1:48vtrainrock(i,:)=Rock(r1(1,i),:);endtrainrock=vtrainrock';for i=1:56vtrainmine(i,:)=Mine(r2(1,i),:);endtrainmine=vtrainmine';%È¡³ö²âÊÔÑù±¾Rock(r1',:)=[];testrock=Rock';Mine(r2',:)=[];testmine=Mine';%×î½üÁÚ·ÖÀàrocklast=zeros(size(Rock'));minelast=zeros(size(Mine'));rgr=0;rwm=0;mgm=0;mwr=0;for i=1:49for j=1:48Ar(j,1)=(testrock(:,i)-trainrock(:,j))'*(testrock(:,i)-trainrock(:,j)) ;endfor k=1:56Br(k,1)=(testrock(:,i)-trainmine(:,k))'*(testrock(:,i)-trainmine(:,k)) ;end%¶Ô´ý²âÑù±¾½øÐзÖÀàif(min(Ar)<=min(Br))rocklast(:,i)=testrock(:,i);rgr=rgr+1;Ar=zeros(48,1);Br=zeros(56,1);elseminelast(:,i)=testrock(:,i);rwm=rwm+1;Ar=zeros(48,1);Br=zeros(56,1);endendfor i=1:55for j=1:48Am(j,1)=(testmine(:,i)-trainrock(:,j))'*(testmine(:,i)-trainrock(:,j)) ;endfor k=1:56Bm(k,1)=(testmine(:,i)-trainmine(:,k))'*(testmine(:,i)-trainmine(:,k)) ;end%¶Ô´ý²âÑù±¾½øÐзÖÀàif(min(Am)<min(Bm))rocklast(:,i)=testmine(:,i);mwr=mwr+1;Am=zeros(48,1);Bm=zeros(56,1);elseminelast(:,i)=testmine(:,i);mgm=mgm+1;Am=zeros(48,1);Bm=zeros(56,1);endendright=(rgr+mgm)/(rgr+mgm+rwm+mwr);disp(right);以上为两种算法在MATLAB里的源代码。
模式识别_作业3

作业一:设以下模式类别具有正态概率密度函数: ω1:{(0 0)T , (2 0)T , (2 2)T , (0 2)T }ω2:{(4 4)T , (6 4)T , (6 6)T , (4 6)T }(1)设P(ω1)= P(ω2)=1/2,求这两类模式之间的贝叶斯判别界面的方程式。
(2)绘出判别界面。
答案:(1)模式的均值向量m i 和协方差矩阵C i 可用下式估计:2,111==∑=i x N m i N j ij i i2,1))((11=--=∑=i m x m x N C i N j Ti ij i ij i i 其中N i 为类别ωi 中模式的数目,x ij 代表在第i 个类别中的第j 个模式。
由上式可求出:T m )11(1= T m )55(2= ⎪⎪⎭⎫ ⎝⎛===1 00 121C C C ,⎪⎪⎭⎫⎝⎛=-1 00 11C 设P(ω1)=P(ω2)=1/2,因C 1=C 2,则判别界面为:24442121)()()(2121211112121=+--=+--=----x x m C m m C m x C m m x d x d T T T(2)作业二:编写两类正态分布模式的贝叶斯分类程序。
程序代码:#include<iostream>usingnamespace std;void inverse_matrix(int T,double b[5][5]){double a[5][5];for(int i=0;i<T;i++)for(int j=0;j<(2*T);j++){ if (j<T)a[i][j]=b[i][j];elseif (j==T+i)a[i][j]=1.0;elsea[i][j]=0.0;}for(int i=0;i<T;i++){for(int k=0;k<T;k++){if(k!=i){double t=a[k][i]/a[i][i];for(int j=0;j<(2*T);j++){double x=a[i][j]*t;a[k][j]=a[k][j]-x;}}}}for(int i=0;i<T;i++){double t=a[i][i];for(int j=0;j<(2*T);j++)a[i][j]=a[i][j]/t;}for(int i=0;i<T;i++)for(int j=0;j<T;j++)b[i][j]=a[i][j+T];}void get_matrix(int T,double result[5][5],double a[5]) {for(int i=0;i<T;i++){for(int j=0;j<T;j++){result[i][j]=a[i]*a[j];}}}void matrix_min(int T,double a[5][5],int bb){for(int i=0;i<T;i++){for(int j=0;j<T;j++)a[i][j]=a[i][j]/bb;}}void getX(int T,double res[5],double a[5],double C[5][5]) {for(int i=0;i<T;i++)double sum=0.0;for(int j=0;j<T;j++)sum+=a[j]*C[j][i];res[i]=sum;}}int main(){int T;int w1_num,w2_num;double w1[10][5],w2[10][5],m1[5]={0},m2[5]={0},C1[5][5]={0},C2[5][5]={0};cin>>T>>w1_num>>w2_num;for(int i=0;i<w1_num;i++){for(int j=0;j<T;j++){cin>>w1[i][j];m1[j]+=w1[i][j];}}for(int i=0;i<w2_num;i++){for(int j=0;j<T;j++){cin>>w2[i][j];m2[j]+=w2[i][j];}}for(int i=0;i<w1_num;i++)m1[i]=m1[i]/w1_num;for(int i=0;i<w2_num;i++)m2[i]=m2[i]/w2_num;for(int i=0;i<w1_num;i++){double res[5][5],a[5];for(int j=0;j<T;j++)a[j]=w1[i][j]-m1[j];get_matrix(T,res,a);for(int j=0;j<T;j++){for(int k=0;k<T;k++)C1[j][k]+=res[j][k];}matrix_min(T,C1,w1_num);for(int i=0;i<w2_num;i++){double res[5][5],a[5];for(int j=0;j<T;j++)a[j]=w2[i][j]-m2[j];get_matrix(T,res,a);for(int j=0;j<T;j++){for(int k=0;k<T;k++)C2[j][k]+=res[j][k];}}matrix_min(T,C2,w2_num);inverse_matrix(T,C1);inverse_matrix(T,C2);double XX[5]={0},C_C1[5]={0},C_C2[5]={0};double m1_m2[5];for(int i=0;i<T;i++){m1_m2[i]=m1[i]-m2[i];}getX(T,XX,m1_m2,C1);getX(T,C_C1,m1,C1);getX(T,C_C2,m2,C1);double resultC=0.0;for(int i=0;i<T;i++)resultC-=C_C1[i]*C_C1[i];for(int i=0;i<T;i++)resultC+=C_C2[i]*C_C2[i];resultC=resultC/2;cout<<"判别函数为:"<<endl;cout<<"d1(x)-d2(x)=";for(int i=0;i<T;i++)cout<<XX[i]<<"x"<<i+1;if(resultC>0)cout<<"+"<<resultC<<endl;elseif(resultC<0)cout<<resultC<<endl;return 0;}运行截图:。
模式识别作业(全)

模式识别大作业一.K均值聚类(必做,40分)1.K均值聚类的基本思想以及K均值聚类过程的流程图;2.利用K均值聚类对Iris数据进行分类,已知类别总数为3。
给出具体的C语言代码,并加注释。
例如,对于每一个子函数,标注其主要作用,及其所用参数的意义,对程序中定义的一些主要变量,标注其意义;3.给出函数调用关系图,并分析算法的时间复杂度;4.给出程序运行结果,包括分类结果(只要给出相对应的数据的编号即可)以及循环迭代的次数;5.分析K均值聚类的优缺点。
二.贝叶斯分类(必做,40分)1.什么是贝叶斯分类器,其分类的基本思想是什么;2.两类情况下,贝叶斯分类器的判别函数是什么,如何计算得到其判别函数;3.在Matlab下,利用mvnrnd()函数随机生成60个二维样本,分别属于两个类别(一类30个样本点),将这些样本描绘在二维坐标系下,注意特征值取值控制在(-5,5)范围以内;4.用样本的第一个特征作为分类依据将这60个样本进行分类,统计正确分类的百分比,并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志(正确分类的样本点用“O”,错误分类的样本点用“X”)画出来;5.用样本的第二个特征作为分类依据将这60个样本再进行分类,统计正确分类的百分比,并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志画出来;6.用样本的两个特征作为分类依据将这60个样本进行分类,统计正确分类的百分比,并在二维坐标系下将正确分类的样本点与错误分类的样本点用不同标志画出来;7.分析上述实验的结果。
8.60个随即样本是如何产生的的;给出上述三种情况下的两类均值、方差、协方差矩阵以及判别函数;三.特征选择(选作,15分)1.经过K均值聚类后,Iris数据被分作3类。
从这三类中各选择10个样本点;2.通过特征选择将选出的30个样本点从4维降低为3维,并将它们在三维的坐标系中画出(用Excell);3.在三维的特征空间下,利用这30个样本点设计贝叶斯分类器,然后对这30个样本点利用贝叶斯分类器进行判别分类,给出分类的正确率,分析实验结果,并说明特征选择的依据;。
模式识别大作业要求从专业杂志或国际会议上选择一篇或多篇模式

模式识别大作业要求:
从专业杂志或国际会议上选择一篇或多篇模式识别相关领域的论文进行研读,并撰写读书报告。
所选论文需满足以下要求:
1.与模式识别相关的最新研究成果。
例如:基于深度学习的人脸识别,基于模式识别
技术的股票预测,等等。
2.反映模式识别某个研究方向研究现状的综述。
例如,深度学习综述,等等。
需提交的材料:
1.论文原文的电子文档。
2.论文读书报告。
侧重于表达阅读过程中涉及的理解、分析、归纳及提炼等思维活动。
读书报告须以Word文档形式提交。
提交时间:2017年5月26日(课程考试日)之前。
需提交的电子文档:1.论文(pdf文档),2.读书报告(Word文档)。
读书报告宣讲:
1.抽签决定宣讲人选(共选6人)。
2.宣讲时间:5月19日下午15:55~18:20。
每人25分钟,课间不休息。
3.宣讲形式:以播放幻灯片的方式口头宣讲。
由抽签决定的宣讲人选如下:
BC16010025,张英迪;
SA16010030,施炀明;
SA16010039,温忻;
SA16023041,陈昱衡;
SC16009020,徐宝泉;
SC16011003,李靓。
请以上同学做好准备。
请至少提交宣讲ppt。
希望同时提交读书报告(Word文档)。
模式识别大作业许萌1306020

第一题 对数据进行聚类分析用、和/或test2.txt 的数据作为本次实验利用的样本集,利用C 均值聚类法和层次聚类法对样本集进行聚类分析,对结果进行分析,从而加深对所学内容的明白得和感性熟悉。
2.1 C 均值聚类法原理C 均值算法第一取定C 个类别数量并对这C 个类别数量选取C 个聚类中心,按最小距离原那么将各模式分派到C 类中的某一类,以后不断地计算类心和调整各模式的类别,最终使各模式到其对应的判属类别中心的距离平方之和最小。
2.2 C 均值聚类算法流程图N图1.1 C 均值聚类算法流程图2.3 层次聚类算法原理N 个初始模式样本自成一类,即成立N 类,以后依照以下步骤运算:Step1:计算各类之间(即各样本间)的距离,得一个维数为N ×N 的距离矩阵D(0)。
“0”表示初始状态。
Step2:假设已求得距离矩阵D (n )(n 为逐次聚类归并的次数),找出D (n )中的最小元素,将其对应的两类归并为一类。
由此成立新的分类:),1(),1(21++n G n GStep3:计算归并后所取得的新类别之间的距离,得D(n+1)。
Step4:跳至第2步,重复计算及归并。
直到知足以下条件时即可停止计算:①取距离阈值T,当D(n)的最小分量超过给定值T 时,算法停止。
所得即为聚类结果。
②或不设阈值T,一直到将全数样本聚成一类为止,输出聚类的分级树。
初始化分类找出D(n)中的最小元素将其对应的两类合并为一类N计算合并后新类别之间的距离是否满足停止条件Y结束程序图1.2层次聚类算法流程图3 验结果分析对数据文件、进行C均值聚类的聚类结果如以下图所示:图1.3 C均值聚类结果的二维平面显示将两种样本即进行聚类后的样本中心进行比较,如下表:从下表能够纵向比较能够看出,C越大,即聚类数量越多,聚类之间不同越小,他们的聚类中心也越接近。
横向比较用FEMALE,MALE中数据作为样本和用FEMALE,MALE,test2中数据作为样本时,由于引入了新的样本,能够发觉后者的聚类中心比前者都稍大。
模式识别大作业

模式识别大作业1.最近邻/k近邻法一.基本概念:最近邻法:对于未知样本x,比较x与N个已知类别的样本之间的欧式距离,并决策x与距离它最近的样本同类。
K近邻法:取未知样本x的k个近邻,看这k个近邻中多数属于哪一类,就把x归为哪一类。
K取奇数,为了是避免k1=k2的情况。
二.问题分析:要判别x属于哪一类,关键要求得与x最近的k个样本(当k=1时,即是最近邻法),然后判别这k个样本的多数属于哪一类。
可采用欧式距离公式求得两个样本间的距离s=sqrt((x1-x2)^2+(y1-y2)^2)三.算法分析:该算法中任取每类样本的一半作为训练样本,其余作为测试样本。
例如iris中取每类样本的25组作为训练样本,剩余25组作为测试样本,依次求得与一测试样本x距离最近的k 个样本,并判断k个样本多数属于哪一类,则x就属于哪类。
测试10次,取10次分类正确率的平均值来检验算法的性能。
四.MATLAB代码:最近邻算实现对Iris分类clc;totalsum=0;for ii=1:10data=load('iris.txt');data1=data(1:50,1:4);%任取Iris-setosa数据的25组rbow1=randperm(50);trainsample1=data1(rbow1(:,1:25),1:4);rbow1(:,26:50)=sort(rbow1(:,26:50));%剩余的25组按行下标大小顺序排列testsample1=data1(rbow1(:,26:50),1:4);data2=data(51:100,1:4);%任取Iris-versicolor数据的25组rbow2=randperm(50);trainsample2=data2(rbow2(:,1:25),1:4);rbow2(:,26:50)=sort(rbow2(:,26:50));testsample2=data2(rbow2(:,26:50),1:4);data3=data(101:150,1:4);%任取Iris-virginica数据的25组rbow3=randperm(50);trainsample3=data3(rbow3(:,1:25),1:4);rbow3(:,26:50)=sort(rbow3(:,26:50));testsample3=data3(rbow3(:,26:50),1:4);trainsample=cat(1,trainsample1,trainsample2,trainsample3);%包含75组数据的样本集testsample=cat(1,testsample1,testsample2,testsample3);newchar=zeros(1,75);sum=0;[i,j]=size(trainsample);%i=60,j=4[u,v]=size(testsample);%u=90,v=4for x=1:ufor y=1:iresult=sqrt((testsample(x,1)-trainsample(y,1))^2+(testsample(x,2) -trainsample(y,2))^2+(testsample(x,3)-trainsample(y,3))^2+(testsa mple(x,4)-trainsample(y,4))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar);class1=0;class2=0;class3=0;if Ind(1,1)<=25class1=class1+1;elseif Ind(1,1)>25&&Ind(1,1)<=50class2=class2+1;elseclass3=class3+1;endif class1>class2&&class1>class3m=1;ty='Iris-setosa';elseif class2>class1&&class2>class3m=2;ty='Iris-versicolor';elseif class3>class1&&class3>class2m=3;ty='Iris-virginica';elsem=0;ty='none';endif x<=25&&m>0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),ty));elseif x<=25&&m==0disp(sprintf('第%d组数据分类后为%s类',rbow1(:,x+25),'none'));endif x>25&&x<=50&&m>0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),ty));elseif x>25&&x<=50&&m==0disp(sprintf('第%d组数据分类后为%s类',50+rbow2(:,x),'none'));endif x>50&&x<=75&&m>0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),ty));elseif x>50&&x<=75&&m==0disp(sprintf('第%d组数据分类后为%s类',100+rbow3(:,x-25),'none'));endif (x<=25&&m==1)||(x>25&&x<=50&&m==2)||(x>50&&x<=75&&m==3)sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/75));totalsum=totalsum+(sum/75);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));测试结果:第3组数据分类后为Iris-setosa类第5组数据分类后为Iris-setosa类第6组数据分类后为Iris-setosa类第7组数据分类后为Iris-setosa类第10组数据分类后为Iris-setosa类第11组数据分类后为Iris-setosa类第12组数据分类后为Iris-setosa类第14组数据分类后为Iris-setosa类第16组数据分类后为Iris-setosa类第18组数据分类后为Iris-setosa类第19组数据分类后为Iris-setosa类第20组数据分类后为Iris-setosa类第23组数据分类后为Iris-setosa类第24组数据分类后为Iris-setosa类第26组数据分类后为Iris-setosa类第28组数据分类后为Iris-setosa类第30组数据分类后为Iris-setosa类第31组数据分类后为Iris-setosa类第34组数据分类后为Iris-setosa类第37组数据分类后为Iris-setosa类第39组数据分类后为Iris-setosa类第41组数据分类后为Iris-setosa类第44组数据分类后为Iris-setosa类第45组数据分类后为Iris-setosa类第49组数据分类后为Iris-setosa类第53组数据分类后为Iris-versicolor类第54组数据分类后为Iris-versicolor类第55组数据分类后为Iris-versicolor类第57组数据分类后为Iris-versicolor类第58组数据分类后为Iris-versicolor类第59组数据分类后为Iris-versicolor类第60组数据分类后为Iris-versicolor类第61组数据分类后为Iris-versicolor类第62组数据分类后为Iris-versicolor类第68组数据分类后为Iris-versicolor类第70组数据分类后为Iris-versicolor类第71组数据分类后为Iris-virginica类第74组数据分类后为Iris-versicolor类第75组数据分类后为Iris-versicolor类第77组数据分类后为Iris-versicolor类第79组数据分类后为Iris-versicolor类第80组数据分类后为Iris-versicolor类第84组数据分类后为Iris-virginica类第85组数据分类后为Iris-versicolor类第92组数据分类后为Iris-versicolor类第95组数据分类后为Iris-versicolor类第97组数据分类后为Iris-versicolor类第98组数据分类后为Iris-versicolor类第99组数据分类后为Iris-versicolor类第102组数据分类后为Iris-virginica类第103组数据分类后为Iris-virginica类第105组数据分类后为Iris-virginica类第106组数据分类后为Iris-virginica类第107组数据分类后为Iris-versicolor类第108组数据分类后为Iris-virginica类第114组数据分类后为Iris-virginica类第118组数据分类后为Iris-virginica类第119组数据分类后为Iris-virginica类第124组数据分类后为Iris-virginica类第125组数据分类后为Iris-virginica类第126组数据分类后为Iris-virginica类第127组数据分类后为Iris-virginica类第128组数据分类后为Iris-virginica类第129组数据分类后为Iris-virginica类第130组数据分类后为Iris-virginica类第133组数据分类后为Iris-virginica类第135组数据分类后为Iris-virginica类第137组数据分类后为Iris-virginica类第142组数据分类后为Iris-virginica类第144组数据分类后为Iris-virginica类第148组数据分类后为Iris-virginica类第149组数据分类后为Iris-virginica类第150组数据分类后为Iris-virginica类k近邻法对wine分类:clc;otalsum=0;for ii=1:10 %循环测试10次data=load('wine.txt');%导入wine数据data1=data(1:59,1:13);%任取第一类数据的30组rbow1=randperm(59);trainsample1=data1(sort(rbow1(:,1:30)),1:13);rbow1(:,31:59)=sort(rbow1(:,31:59)); %剩余的29组按行下标大小顺序排列testsample1=data1(rbow1(:,31:59),1:13);data2=data(60:130,1:13);%任取第二类数据的35组rbow2=randperm(71);trainsample2=data2(sort(rbow2(:,1:35)),1:13);rbow2(:,36:71)=sort(rbow2(:,36:71));testsample2=data2(rbow2(:,36:71),1:13);data3=data(131:178,1:13);%任取第三类数据的24组rbow3=randperm(48);trainsample3=data3(sort(rbow3(:,1:24)),1:13);rbow3(:,25:48)=sort(rbow3(:,25:48));testsample3=data3(rbow3(:,25:48),1:13);train_sample=cat(1,trainsample1,trainsample2,trainsample3);%包含89组数据的样本集test_sample=cat(1,testsample1,testsample2,testsample3);k=19;%19近邻法newchar=zeros(1,89);sum=0;[i,j]=size(train_sample);%i=89,j=13[u,v]=size(test_sample);%u=89,v=13for x=1:ufor y=1:iresult=sqrt((test_sample(x,1)-train_sample(y,1))^2+(test_sample(x ,2)-train_sample(y,2))^2+(test_sample(x,3)-train_sample(y,3))^2+( test_sample(x,4)-train_sample(y,4))^2+(test_sample(x,5)-train_sam ple(y,5))^2+(test_sample(x,6)-train_sample(y,6))^2+(test_sample(x ,7)-train_sample(y,7))^2+(test_sample(x,8)-train_sample(y,8))^2+( test_sample(x,9)-train_sample(y,9))^2+(test_sample(x,10)-train_sa mple(y,10))^2+(test_sample(x,11)-train_sample(y,11))^2+(test_samp le(x,12)-train_sample(y,12))^2+(test_sample(x,13)-train_sample(y, 13))^2); %欧式距离newchar(1,y)=result;end;[new,Ind]=sort(newchar);class1=0;class 2=0;class 3=0;for n=1:kif Ind(1,n)<=30class 1= class 1+1;elseif Ind(1,n)>30&&Ind(1,n)<=65class 2= class 2+1;elseclass 3= class3+1;endendif class 1>= class 2&& class1>= class3m=1;elseif class2>= class1&& class2>= class3m=2;elseif class3>= class1&& class3>= class2m=3;endif x<=29disp(sprintf('第%d组数据分类后为第%d类',rbow1(:,30+x),m));elseif x>29&&x<=65disp(sprintf('第%d组数据分类后为第%d类',59+rbow2(:,x+6),m));elseif x>65&&x<=89disp(sprintf('第%d组数据分类后为第%d类',130+rbow3(:,x-41),m));endif (x<=29&&m==1)||(x>29&&x<=65&&m==2)||(x>65&&x<=89&&m==3) sum=sum+1;endenddisp(sprintf('第%d次分类识别率为%4.2f',ii,sum/89));totalsum=totalsum+(sum/89);enddisp(sprintf('10次分类平均识别率为%4.2f',totalsum/10));第2组数据分类后为第1类第4组数据分类后为第1类第5组数据分类后为第3类第6组数据分类后为第1类第8组数据分类后为第1类第10组数据分类后为第1类第11组数据分类后为第1类第14组数据分类后为第1类第16组数据分类后为第1类第19组数据分类后为第1类第20组数据分类后为第3类第21组数据分类后为第3类第22组数据分类后为第3类第26组数据分类后为第3类第27组数据分类后为第1类第28组数据分类后为第1类第30组数据分类后为第1类第33组数据分类后为第1类第36组数据分类后为第1类第37组数据分类后为第1类第43组数据分类后为第1类第44组数据分类后为第3类第45组数据分类后为第1类第46组数据分类后为第1类第49组数据分类后为第1类第54组数据分类后为第1类第56组数据分类后为第1类第57组数据分类后为第1类第60组数据分类后为第2类第61组数据分类后为第3类第63组数据分类后为第3类第65组数据分类后为第2类第66组数据分类后为第3类第67组数据分类后为第2类第71组数据分类后为第1类第72组数据分类后为第2类第74组数据分类后为第1类第76组数据分类后为第2类第77组数据分类后为第2类第79组数据分类后为第3类第81组数据分类后为第2类第82组数据分类后为第3类第83组数据分类后为第3类第84组数据分类后为第2类第86组数据分类后为第2类第87组数据分类后为第2类第88组数据分类后为第2类第93组数据分类后为第2类第96组数据分类后为第1类第98组数据分类后为第2类第99组数据分类后为第3类第102组数据分类后为第2类第104组数据分类后为第2类第105组数据分类后为第3类第106组数据分类后为第2类第110组数据分类后为第3类第113组数据分类后为第3类第114组数据分类后为第2类第115组数据分类后为第2类第116组数据分类后为第2类第118组数据分类后为第2类第122组数据分类后为第2类第123组数据分类后为第2类第124组数据分类后为第2类第133组数据分类后为第3类第134组数据分类后为第3类第135组数据分类后为第2类第136组数据分类后为第3类第140组数据分类后为第3类第142组数据分类后为第3类第144组数据分类后为第2类第145组数据分类后为第1类第146组数据分类后为第3类第148组数据分类后为第3类第149组数据分类后为第2类第152组数据分类后为第2类第157组数据分类后为第2类第159组数据分类后为第3类第161组数据分类后为第2类第162组数据分类后为第3类第163组数据分类后为第3类第164组数据分类后为第3类第165组数据分类后为第3类第167组数据分类后为第3类第168组数据分类后为第3类第173组数据分类后为第3类第174组数据分类后为第3类2.Fisher线性判别法Fisher 线性判别是统计模式识别的基本方法之一。
模式识别大作业

模式识别专业:电子信息工程班级:电信****班学号:********** 姓名:艾依河里的鱼一、贝叶斯决策(一)贝叶斯决策理论 1.最小错误率贝叶斯决策器在模式识别领域,贝叶斯决策通常利用一些决策规则来判定样本的类别。
最常见的决策规则有最大后验概率决策和最小风险决策等。
设共有K 个类别,各类别用符号k c ()K k ,,2,1 =代表。
假设k c 类出现的先验概率()k P c以及类条件概率密度()|k P c x 是已知的,那么应该把x 划分到哪一类才合适呢?若采用最大后验概率决策规则,首先计算x 属于k c 类的后验概率()()()()()()()()1||||k k k k k Kk k k P c P c P c P c P c P P c P c ===∑x x x x x然后将x 判决为属于kc ~类,其中()1arg max |kk Kk P c ≤≤=x若采用最小风险决策,则首先计算将x 判决为k c 类所带来的风险(),k R c x ,再将x 判决为属于kc ~类,其中()min ,kkk R c =x可以证明在采用0-1损失函数的前提下,两种决策规则是等价的。
贝叶斯决策器在先验概率()k P c 以及类条件概率密度()|k P c x 已知的前提下,利用上述贝叶斯决策规则确定分类面。
贝叶斯决策器得到的分类面是最优的,它是最优分类器。
但贝叶斯决策器在确定分类面前需要预知()k P c 与()|k P c x ,这在实际运用中往往不可能,因为()|k P c x 一般是未知的。
因此贝叶斯决策器只是一个理论上的分类器,常用作衡量其它分类器性能的标尺。
最小风险贝叶斯决策可按下列步骤进行: (1)在已知)(i P ω,)(i X P ω,i=1,…,c 及给出待识别的X 的情况下,根据贝叶斯公式计算出后验概率:∑==cj iii i i P X P P X P X P 1)()()()()(ωωωωω j=1,…,x(2)利用计算出的后验概率及决策表,按下面的公式计算出采取i a ,i=1,…,a 的条件风险∑==cj j j i i X P a X a R 1)(),()(ωωλ,i=1,2,…,a(3)对(2)中得到的a 个条件风险值)(X a R i ,i=1,…,a 进行比较,找出使其条件风险最小的决策k a ,即()()1,min k i i aR a x R a x ==则k a 就是最小风险贝叶斯决策。
华南理工大学《模式识别》大作业报告

华南理工大学《模式识别》大作业报告题目:模式识别导论实验学院计算机科学与工程专业计算机科学与技术(全英创新班)学生姓名黄炜杰学生学号 201230590051指导教师吴斯课程编号145143课程学分2 分起始日期 2015年5月18日实验内容【实验方案设计】Main steps for the project is:1.To make it more challenging, I select the larger dataset, Pedestrian, rather than thesmaller one. But it may be not wise to learning on such a large dataset, so Inormalize the dataset from 0 to 1 first and perform a k-means sampling to select the most representative samples. After that feature selection is done so as to decrease the amount of features. At last, a PCA dimension reduction is used to decrease the size of the dataset.2.Six learning algorithms including K-Nearest Neighbor, perception, decision tree,support vector machine, multi-layer perception and Naïve Bayesian are used to learn the pattern of the dataset.3.Six learning algorithm are combing into six multi-classifiers system individually,using bagging algorithm.实验过程:NormalizationThe input dataset is normalized to the range of [0, 1] so that make it suitable for performing k-means clustering on it, and also increase the speed of learning algorithms.SamplingThere are too much sample in the dataset, only a smallpart of them are enough to learn a good classifier. To select the most representative samples, k-means clustering is used to cluster the sample into c group and select r% of them.There are 14596 samples initially, but 1460 may be enough, so r=10. The selection of c should follow three criterions:a) Less drop of accuracyb) Little change about ratio of two classesc) Smaller c, lower time complexitySo I design two experiments to find the best parameter c:Experiment 1:Find out the training accuracy of different amountof cluster. The result is shown in the figure on the left. X-axis is amount of cluster and Y-axis is accuracy. Red line denotes accuracy before sampling and blue line denotes accuracy after sampling. As it’s shown in the figure, c=2, 5, 7, 9, 13 may be good choice since they have relative higher accuracy.Experiment 2:Find out the ratio of sample amount of two class. The result is shown in the figure on the right. X-axis is amount of cluster and Y-axis is the ratio. Red line denotes ratio before sampling and blue line denotes ratio after sampling. As it’s shown in the figure, c=2, 5, 9 may be good choice since the ratio do not change so much.As a result, c=5 is selected tosatisfy the three criterions.Feature selection3780 features is much more than needed to train a classifier, so I select a small part of them before learning. The target is to select most discriminative features, that is to say, select features that have largest accuracy in each step. But there are six learning algorithm in our project, it’s hard to decide which learning algorithm this feature selection process should depend on and it may also has high time complexity. So relevance, which is the correlation between feature and class is used as a discrimination measurement to select the best feature sets. But only select the most relevant features may introduce rich redundancy. So a tradeoff between relevance and redundancy should be made. An experiment about how to make the best tradeoff is done:the best amount of features isFind out the training accuracy of different amountof features. The result is shown below. X-axis is amount of features and Y-axis is accuracy. Red line denotes accuracyPCATo make the dataset smaller, features with contribution rate of PCA ≥ 85% is selected. So we finally obtain a dataset with 1460 samples and 32 features. The size of the dataset drops for 92.16% but accuracy only has 0.61% decease. So these preprocessing steps are successful to decrease the size of the dataset.Learning6 models are used in the learning steps: K-Nearest Neighbor, perception, decision tree, support vector machine, multi-layer perception and Naïve Bayesian. I designed a RBF classifier and MLP classifier at first but they are too slow for the reason that matrix manipulation hasn’t been designed carefully, so I use the function in the library instead. Parameter determination for these classifiers are:①K-NNWhen k≥5,the accuracy trends to be stable, so k=5②Decision treeMaxcrit is used as binary splitting criterion.③MLP5 units for hidden is enough。
模式识别方法大作业实验报告

《模式识别导论》期末大作业2010-2011-2学期第 3 组《模式识别》大作业人脸识别方法一---- 基于PCA 和欧几里得距离判据的模板匹配分类器一、 理论知识1、主成分分析主成分分析是把多个特征映射为少数几个综合特征的一种统计分析方法。
在多特征的研究中,往往由于特征个数太多,且彼此之间存在着一定的相关性,因而使得所观测的数据在一定程度上有信息的重叠。
当特征较多时,在高维空间中研究样本的分布规律就更麻烦。
主成分分析采取一种降维的方法,找出几个综合因子来代表原来众多的特征,使这些综合因子尽可能地反映原来变量的信息,而且彼此之间互不相关,从而达到简化的目的。
主成分的表示相当于把原来的特征进行坐标变换(乘以一个变换矩阵),得到相关性较小(严格来说是零)的综合因子。
1.1 问题的提出一般来说,如果N 个样品中的每个样品有n 个特征12,,n x x x ,经过主成分分析,将它们综合成n 综合变量,即11111221221122221122n n n n n n n nn ny c x c x c x y c x c x c x y c x c x c x =+++⎧⎪=+++⎪⎨⎪⎪=+++⎩ij c 由下列原则决定:1、i y 和j y (i j ≠,i,j = 1,2,...n )相互独立;2、y 的排序原则是方差从大到小。
这样的综合指标因子分别是原变量的第1、第2、……、第n 个主分量,它们的方差依次递减。
1.2 主成分的导出我们观察上述方程组,用我们熟知的矩阵表示,设12n x x X x ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦是一个n 维随机向量,12n y y Y y ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦是满足上式的新变量所构成的向量。
于是我们可以写成Y=CX,C 是一个正交矩阵,满足CC ’=I 。
坐标旋转是指新坐标轴相互正交,仍构成一个直角坐标系。
变换后的N 个点在1y 轴上有最大方差,而在n y 轴上有最小方差。
上海交大模式识别大作业

x
i 1
m
i
gi
T
(2) D( x, G) x G (3)相似度
1
( x G)
2
xi g i ( x G) i 1 R ( x, G ) 1/ 2 x G m 2 m 2 x i g i i 1 i 1
阅读材料: (参考资料的阅读以下面的题目为导向,不需要细致的研读代码。 ) 边肇祺、张学工编著《模式识别》第二版,第十五章 求是科技 张宏林编著《Visual C++数字图像模式识别技术及工程实践》 ,第五、六、七、八 章 题目: (请对问题一一作答。 解答要尽量表达明白、 条理清楚。 不要求给出具体的代码实现。 ) 1)汉字识别是与生活紧密相关的一种二维信号识别问题。通过对上述材料的研读,同学们 应该对模式识别方法如何应用于实际中、 以及在实际应用中需要考虑哪些问题有了一些深入 的认识。问题: A.一般解决模式识别问题有哪几个关键步骤?给出处理一般模式识别问题步骤的流程图。 B.以汉字识别为例,预处理步骤是哪些(举出 3 种)?汉字的哪些特性可以被提取作为模 式特征(举出 5 种)?利用特征进行汉字识别分类时,要注意什么问题?有什么样的解决方 法?一般可采取哪些判别准则进行分类? 2)工厂对打上来的鱼进行分类,不同种类的鱼处理方式不 同。可是鱼的数量过大,人工分类不现实。如何利用模式识 别的方法让计算机帮我们分类? A.可能需要进行哪些预处理?你能想到哪些鱼类特性作为 分类特征?可以采取哪些对应的分类决策方法? B.在分类过程中,可能会遇到分类算法错误率高、性能不 够鲁棒,你能想出什么方法有效解决? C.文字说明一种你设计的、认为可以准确处理大多数鱼类 分类问题的分类算法,并写出算法流程图。 左图是利用传感器(如摄像机)对鱼类采样,以进行自动分 类的工厂流水线示意图。 3)人类具有很强的模式识别能力。通过视觉信息识别文字、图片和周围的环境,通过听觉 信息识别与理解语言。模式识别能力是人类智能的重要组成部分。今天,虽然人们可以利用 计算机部分实现人的视觉,听觉等模式识别能力,但是相对于浩瀚的人类智能,今天的模式 识别无论是在理论研究还是在应用水平上都仅仅只处于初级阶段。请以“模式识别,让明天 更美好”为题,设想 2000 年后,模式识别在理论上将会有那些突破,在应用中将会怎样深 刻的影响人类的工作和生活。要求: a、 体裁不限,字数不限,可以写成故事,小说或科技论文等等。 b、 文章应建立在对现存模式识别的理论分析基础之上, 通过分析统计模式识别的优点和不 足,设想 2000 年后模式识别将会得到怎样的发展。 c、 设想 2000 年模式识别应用的时候,应尽可能全面地描述模式识别在人类生活和生产中 的应用,如在工业,生活,娱乐,医疗,通信,战争等等。想象的翅膀能飞多远,就让 它飞多远。 d、 如果可以包含心理学,生理学,神经学,或数学,信息学等方面的描述更好。
模式识别大作业(二)

模式识别大作业(二)k-means 算法的应用一、 问题描述用c-means 算法对所给数据进行聚类,并已知类別数为2,随机初始样本聚类中心,进行10次求解,并计算聚类平均正确率。
二、 算法简介(1)J.B.MacQueen 在 1967 年提出的K-means 算法[22]到目前为止用于科学和工业应用的诸多聚类算法中一种极有影响的技术。
它是聚类方法中一个基本的划分方法,常常采用误差平方和准则函数作为聚类准则函数。
若i N 是第i 聚类i Γ中的样本数目,i m 是这些样本的均值,即1ii y m y N∈Γ=∑把i Γ中的各样本y 与均值i m 间的误差平方和对所有的类相加后为21ice i i y J y m =∈Γ=-∑∑e J 是误差平方和聚类准则,它是样本集y 和类别集Ω的函数。
e J 度量了用c 个聚类中心12,,...,c m m m 代表c 个样本子集12,,...,c ΓΓΓ时所产生的总的误差平方。
(2)K-means 算法的工作原理:算法首先随机从数据集中选取 K 个点作为初始聚类中心,然后计算各个样本到聚类中的距离,把样本归到离它最近的那个聚类中心所在的类。
计算新形成的每一个聚类的数据对象的平均值来得到新的聚类中心,如果相邻两次的聚类中心没有任何变化,说明样本调整结束,聚类准则函数 已经收敛。
本算法的一个特点是在每次迭代中都要考察每个样本的分类是否正确。
若不正确,就要调整,在全部样本调整完后,再修改聚类中心,进入下一次迭代。
如果在一次迭代算法中,所有的样本被正确分类,则不会有调整,聚类中心也不会有任何变化,这标志着 已经收敛,因此算法结束。
三、具体步骤1、 数据初始化:类别数c=2,样本类标trueflag(n,1) (其中n 为样本个数);2、 初始聚类中心:用随机函数随机产生1~n 中的2个数,选取随机数所对应的样本为初始聚类中心(mmnow);3、更新样本分类:计算每个样本到两类样本中心的距离,根据最小距离法则,样本将总是分到距离较近的类别;4、更替聚类中心:根据上一步的分类,重新计算两个聚类中心(mmnext);5、判断终止条件:当样本聚类中心不再发生变化即mmnow==mmnext时,转5);否则,更新mmnow,将mmnext附给mmnow,即mmnow=mmnext,转2);6、计算正确率:将dtat(i,1)与trueflag(i,1)(i=1~n)进行比较,统计正确分类的样本数,并计算正确率c_meanstrue(1,ii)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、问题描述
现有sonar 和wdbc 这两个样本数据集,取一半数据作为训练样本集,其余数据作为测试样本集,通过编程实现分别用C 均值算法对测试样本集中的数据进行分类,进行10次分类求正确率的平均值。
二、算法描述
1.初始化:选择c 个代表点,...,,321c p p p p
2.建立c 个空间聚类表:C K K K ...,21
3.按照最小距离法则逐个对样本X 进行分类:
),(),,(min arg J i i
K x add p x j ∂=
4.计算J 及用各聚类列表计算聚类均值,并用来作为各聚类新的代表点(更新代表点)
5.若J 不变或代表点未发生变化,则停止。
否则转2.
),(1∑∑=∈=c
i K x i i p x J δ
6.计算正确率:将dtat(i,1)与trueflag(i,1)(i=1~n )进行比较,统计正确分类的样本数,并计算正确率将上述过程循环10次,得到10次的正确率,并计算平均正确率ave
算法流程图
三、实验数据
表1 实验数据
四、实验结果
表2 实验结果准确率(%)
注:表中准确率是十次实验结果的平均值
五、程序源码
用C均值算法对sonar分类(对wdbc分类的代码与之类似)clc;clear;
accuracy = 0;
for i = 1:10
data = xlsread('sonar.xls');
data = data';
%初始划分2个聚类
rand(:,1:size(data,2)) = data(:,randperm(size(data,2))'); %使矩阵元素按列重排
A(:,1) = rand(:,1);
B(:,1) = rand(:,2); %选取代表点
m = 1;
n = 1;
for i = 3:size(rand,2)
temp1 = rand(:,i) - A(:,1);
temp2 = rand(:,i) - B(:,1);
temp1(61,:) = [];
temp2(61,:) = []; %去掉标号后再计算距离
if norm(temp1) < norm(temp2)
m = m + 1; %A类中样本个数
A(:,m) = rand(:,i);
else
n = n + 1; %B类中样本个数
B(:,n) = rand(:,i);
end
end
%划分完成
m1 = mean(A,2);
m2 = mean(B,2);
%计算Je
J = 0;
for i = 1:m
temp = A(:,i) - m1;
temp(61,:) = []; %去掉标号的均值
J = J + norm(temp)^2;
end
for i = 1:n
temp = B(:,i) - m2;
temp(61,:) = [];
J = J + norm(temp)^2;
end
test = [A,B];
N = 0; %Je不变的次数
while N < m + n
rarr = randperm(m + n); %产生1-208即所有样本序号的随机不重复序列向量
y = test(:,rarr(1,1));
if rarr(1,1) <= m %y属于A类时
if m == 1
continue
else
temp1 = y - m1;
temp1(61,:) = [];
temp2 = y - m2;
temp2(61,:) = [];
p1 = m / (m - 1) * norm(temp1);
p2 = n / (n + 1) * norm(temp2);
if p2 < p1
test = [test,y];
test(:,rarr(1,1)) = [];
m = m - 1;
n = n + 1;
end
end
else %y属于B类时
if n == 1
continue
else
temp1 = y - m1;
temp1(61,:) = [];
temp2 = y - m2;
temp2(61,:) = [];
p1 = m / (m + 1) * norm(temp1);
p2 = n / (n - 1) * norm(temp2);
if p1 < p2
test = [y,test];
test(:,rarr(1,1)) = [];
m = m + 1;
n = n - 1;
end
end
end
A(:,1:m) = test(:,1:m);
B(:,1:n) = test(:,m + 1:m + n);
m1 = mean(A,2);
m2 = mean(B,2);
%计算Je
tempJ = 0;
for i = 1:m
temp = A(:,i) - m1;
temp(61,:) = []; %去掉标号的均值
tempJ = tempJ + norm(temp)^2;
end
for i = 1:n
temp = B(:,i) - m2;
temp(61,:) = [];
tempJ = tempJ + norm(temp)^2;
end
if tempJ == J
N = N + 1;
else
J = tempJ;
end
end %while循环结束
%判断正确率
correct = 0;
false = 0;
A(:,1:m) = test(:,1:m);
B(:,1:n) = test(:,m + 1:m + n);
c = mean(A,2);
if abs(c(61,1) - 1) < abs(c(61,1) - 2) %聚类A中大多为1类元素
for i = 1:m
if A(61,i) == 1
correct = correct + 1;
else
false = false + 1;
end
end
for i = 1:n
if B(61,i) == 2
correct = correct + 1;
else
false = false + 1;
end
end
else %聚类A中大多为2类元素
for i = 1:m
if A(61,i) == 2
correct = correct + 1;
else
false = false + 1;
end
end
for i = 1:n
if B(61,i) == 1
correct = correct + 1;
else
false = false + 1;
end
end
end
accuracy = accuracy + correct / (correct + false);
end
aver_accuracy = accuracy / 10
fprintf('用C均值算法对sonar进行十次分类的结果的平均正确率为%.2d %%.\n',aver_accuracy*100)
六.实验心得
本算法确定的K 个划分到达平方误差最小。
当聚类是密集的,且类与类之间区别明显时,效果较好。
对于处理大数据集,这个算法是相对可伸缩和高效的,计算的复杂度为O(NKt),其中N是数据对象的数目,t是迭代的次数。
但
它需要根据初始聚类中心来确定一个初始划分,然后对初始划分进行优化。
这个初始聚类中心的选择对聚类结果有较大的影响,一旦初始值选择的不好,可能无法得到有效的聚类结果。
