用excel的线性规划计算 9、16、25宫格

合集下载

EXCEL规划求解功能操作说明

Excel规划求解功能操作说明以Microsoft Excel2003为例，说明使用Excel的求解线性规划问题功能的使用方法。

一、加载规划求解功能1.点击【工具】按钮，在下拉菜单中选择【加载宏】功能。

2.在弹出的【可加载宏】选项卡中勾选【规划求解】，点击确定按钮。

此时，【工具】下拉菜单中增加规划求解功能，表示加载成功。

二、构造表格Excel表格并填入各项数据以教材18页【例题2-8】为例，构造表格如下：1.录入约束条件系数约束条件（1）为5x1+x2-x3+x4=3，则在约束系数的第一行的x1,x2,x3,x4,x5，限制条件，常数b列下分别录入5,1，-1,1,0，=，3如下图所示。

约束系数区的第二行录入约束条件（2）的系数、限制符号及常数b，即-10,6,2,0,1，=，2；约束系数区的第三行录入约束条件（3）（x1≥0）的系数、限制符号及常数b，即1,0,0,0,0，≥，0；约束系数区的第四行录入约束条件（4）（x2≥0）的系数、限制符号及常数b，即0,1,0,0,0，≥，0；约束系数区的第五行录入约束条件（5）（x3≥0）的系数、限制符号及常数b，即0,0,1,0,0，≥，0；约束系数区的第六行录入约束条件（6）（x4≥0）的系数、限制符号及常数b，即0,0,0,1,0，≥，0；约束系数区的第七行录入约束条件（7）（x5≥0）的系数、限制符号及常数b，即0,0,0,0,1，≥，0。

如下图所示。

2.录入目标函数系数目标函数为maxZ=4x1-2x2-x3，则在目标函数的x1,x2,x3,x4,x5列下分别录入4，-2，-1,0,0，如下图所示。

3. 录入约束条件的计算公式双击约束条件（1）行的“总和”单元格，录入以下内容：“=B3*B12+C3*C12+D3*D12+E3*E12+F3*F12”说明：录入的内容即是约束条件（1）的计算公式，其中“B3*B12”代表5x 1; “C3*C12”代表1x 2；“D3*D12”代表-1x 3；“E3*E12”代表1x 4；“F3*F12”代表0x 5。

用EXCEL求解线性规划

用EXCEL求解线性规划
要用EXCEL求解线性规划问题，需要遵循以下步骤：
1. 给定问题中的约束条件和目标函数。

2. 打开EXCEL，建立一个新的工作表。

3. 在工作表中输入问题的约束条件和目标函数。

在输入目标函数时，需要将所有项移动到等号左侧，使它成为一个线性方程。

需要注意将不等式约束条件转化为等式约束条件，可以通过添加松弛变量来实现。

4. 使用EXCEL的“规划”工具，在工具栏中点击“数据”-“分
析”-“规划器”，打开“规划器”。

5. 在“规划器”中，选择需要优化的目标单元格，在“约束条件”
中输入所有约束条件所在的单元格，设置变量单元格的范围。

6. 可以在“选项”中添加其他约束条件。

例如，可以设定变量的整数或二元特性等。

7. 单击“求解”按钮，EXCEL将自动求解最优解，并输出最优
值和变量值。

需要注意的是，线性规划问题求解的结果是一个数值，而不是图形。

因此，需要谨慎分析问题以确保从数值结果中得到了正确的结论。

EXCEL规划求解功能操作说明

EXCEL规划求解功能操作说明Excel规划求解功能是Excel内置的解决最优化问题的工具，可用于线性规划、整数规划、非线性规划等诸多领域。

该功能十分便捷灵活，可以帮助用户快速找到问题的最优解。

一、添加求解功能1.打开Excel表格，点击“文件”>“选项”>“加载项”。

2.在弹出的窗口中选择“Excel加载项”>“转到”>“excel加载项”>“管理”。

在“可用的加载项”中勾选“求解器”并关闭窗口。

3.返回Excel表格，在数据选项卡中选择“分析”>“求解”，弹出求解对话框。

二、建立规划模型1.确定目标：需要确定最终要达到的目标或绩效指标，例如最大化利润、最小化成本等。

2.确定决策变量：需要确定影响目标的变量，例如销售量、成本等。

3.建立约束：需要确定影响决策变量的条件，例如材料成本、生产时间等。

注意约束需要用等式、不等式等数学形式表示。

例如，在一个玩具生产厂家的例子中，有以下规划问题：在有限的资源下，最大化玩具的利润。

目标：最大化利润。

决策变量：生产每种玩具的数量。

三、设置求解参数1.目标单元格：选择Excel表格中目标单元格，该单元格包含要优化的方程式。

4.变量单元格必须满足约束：勾选此项，保证变量单元格满足约束条件。

5.求解方法：选择要使用的求解算法，包括线性规划、非线性规划和整数规划等。

1.点击“求解”按钮，系统会自动寻找目标单元格、变量单元格和约束单元格区域。

2.系统执行计算，找到最优解并将其展示在新的单元格区域中。

3.若求解成功，单击“继续”将结果保存在Excel表中。

总之，利用Excel规划求解功能，用户可以通过建立规划模型，设置求解参数和运行求解功能轻轻松松地优化各种最优化问题。

怎么利用EXCEL求解线性规划

利用线性回归方法求解生产计划方法一：1、建立数学模型:①设变量：设生产拉盖式书桌x台，普通式书桌y台，可得最大利润②确定目标函数及约束条件目标函数：y=max+115P90x约束条件：200x .....................⑴+y10≤20x .....................⑵4≤+y16128x .....................⑶+y1015≤220yx ..........................⑷,≥2、在Excel中求解线性规划①首先，如图1所示，在Excel工作表格输入目标函数的系数、约束方程的系数和右端常数项：图1②将目标方程和约束条件的对应公式输入各单元格中F2=MMULT（B6:C6,F6:F7)；F3=MMULT（B3:C3,F6:F7)；F2=MMULT（B4:C4,F6:F7)；F2=MMULT（B5:C5,F6:F7)；出现图2样式：图2线性规划问题的电子表格模型建好后，即可利用“线性规划”功能进行求解。

选择“工具”→“规划求解”出现“规划求解参数”窗口，如图3所示:图3在该对话框中，目标单元格选择F2，问题类型选择“最大值”，可变单元格选择F6：F7，点击“添加”按钮，弹出“添加约束条件”窗口，如图4所示:图4根据所建模型，共有4个约束条件，针对约束（1）：2002010≤+y x ，左端“单元格所引用位置”选择F3，右端“约束值”选择D3，符号类型选择“<=”，同理继续添加约束（2）（3）（4），完成后选择“确定”，回到“规划求解参数”对话框，如5图所示：图5④点击“选项”按钮，弹出“规划求解选项”对话框，选择“采用线性模型”和“假定非负”两项，如图6所示：图6⑤点击“确定”→“求解”，选择“运算结果报告”“敏感性报告”“极限值报告”三项，最后点击“确定”，输出结果：运算结果报告：敏感性报告：极限报告：方法二：1、建立数学模型设生产拉盖式书桌x 台，普通式书桌y 台，总利润为Z 元确定目标函数及约束条件目标函数：y x Z 90115max += 约束条件：⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0,22010151281642002010..y x y x y x y x t s 2、在Excel 中规划求解在Excel 中建立线性规划模型，如图1所示：图11)在E2中输入“=B2*B6+C2*C6”如图2所示，同理 E3=B3*B6+C3*C6E4=B4*B6+C4*C6B7=B5*B6+C5*C6图22)单击“工具”菜单下的“规划求解”，在弹出的“规划求解参数”对话框输入各项参数：✓目标单元格选择B7✓问题类型选择“最大值”✓可变单元选择B6:C6✓约束条件选择B6:C6≥0；E2:E4≤D2:D4参数设置完毕，如图3：图33）点击“选项”，弹出“规划求解选项”对话框，选择“采用线性模型”、“假定非负”和“显示迭代结果”，说明要求求解的问题是线性模型且所求的变量必须为非负，如图4所示：图44）点击“确定”→“求解”，选择“运算结果报告”“敏感性报告”“极限值报告”三项，最后点击“确定”，输出结果：运算结果报告：敏感性报告：极限值报告：。

应用Excel软件求解线性规划问题

使用变量xij代表第i种原料用于生产第j种产品的数量（桶）
1
i=1, 2, 3分别代表催化裂化汽油、异戊烷和直馏汽油
2
j=1, 2, 3分别代表80#、100#汽油和燃料油
3
物料平衡约束
4
物料平衡约束
蒸汽压限制
01
辛烷值限制
02
变量非负约束
03
各类约束
Excel求解步骤
打开Excel，建立新工作表，输入公式
应用软件求解线性规划问题
添加副标题
202X
1.1 Excel的规划求解工具
Excel软件提供了求解一般规模数学规划问题的“规划求解”工具该工具具有界面友好、操作简单、与Excel无缝集成等优点可用于化学化工常见中、小规模线性规划、非线性规划、整数规划问题的求解
Excel提供的规划求解工具对模型规模有一定限制：求解模型的决策变量数不超过200个。当“规划求解选项”对话框中的“采用线性模型”复选框处于选中状态时，对约束条件的数量没有限制；而对于非线性问题，每个可变单元格除了变量的范围和整数限制外，还可以有最多达100个约束条件
Excel结果分析-3
整数规划的运行结果
由于工程实际问题中存在各种不确定性，因此线性规划模型中的系数C、aji、bj等均可能偏离原来的计算值，因此决策者必须掌握这些系数改变时对原最优解的影响，也就是必须进行线性规划的灵敏度分析。
可以应用Excel方便地实现
线性规划的灵敏度分析
The End
Excel求解步骤-1
打开规划求解窗口
Excel求解步骤-2
设置目标单元格设置可变单元格约束的输入
Excel求解步骤-3
设置规划求解选项

Excel求解线性规划问题实验教程要点

数学与信息科学学院Excel求解线性规划问题实验教程二零一三零八月目录1.关于“规划求解” (1)2.如何加载“规划求解” (2)3.“规划求解”各参数解释和设置 (3)4.“规划求解”的步骤 (6)5.Excel求解线性规划问题 (8)6.Excel求解运输问题 (14)7.Excel求解目标规划问题 (18)8.Excel求解整数规划问题 (22)1.关于“规划求解”“规划求解”是Excel中的一个加载宏，借助“规划求解”，可求得工作表上某个单元格（被称为目标单元格）中公式（公式:单元格中的一系列值、单元格引用、名称或运算符的组合，可生成新的值。

公式总是以等号（=）开始）的最优值。

“规划求解”将对直接或间接目标单元格中公式相关联的一组单元格中的数值进行调整，最终在目标单元格公式中求得期望的结果。

“规划求解”通过调整所指定的可更改的单元格（可变单元格）中的值，从目标单元格公式中求得所需的结果。

在创建模型过程中，可以对“规划求解”中的可变单元格数值应用约束条件（约束条件：“规划求解”中设置的限制条件。

可以将约束条件应用于可变单元格、目标单元格或其它与目标单元格直接或间接相关的单元格。

而且约束条件可以引用其它影响目标单元格公式的单元格。

使用“规划求解”可通过更改其它单元格来确定某个单元格的最大值或最小值。

）Microsoft Excel的“规划求解”工具取自德克萨斯大学奥斯汀分校的Leon Lasdon 和克里夫兰州立大学的Allan Waren共同开发的Generalized Reduced Gradient(GRG2)非线性最优化代码。

线性和整数规划问题取自Frontline Systems公司的John Watson 和Dan Fylstra提供的有界变量单纯形法和分支边界法。

2.如何加载“规划求解”安装office的时候，系统默认的安装方式不会安装宏程序，需要用户根据自己的需求选择安装。

下面是加载“规划求解”宏的步骤：（1）在“工具”菜单上，单击“加载宏”。

使用Excel求解线性规划问题

使用Excel 求解线性规划问题利用单纯形法手工计算线性规划问题是很麻烦的。

office 软件是一目前常用的软件，我们可以利用office 软件中的Excel 工作表来求解本书中的所有线性规划问题。

对于大型线性规划问题，需要应用专业软件，如Matlab ，Lindo ，lingo 等，这些软件的使用这里我们不作介绍，有需要的，自己阅读有关文献资料。

用Excel 工作表求解线性规划问题，我们需要先设计一个工作表，将线性规划问题中的有关数据填入该工作表中。

所需的工作表可按下列步骤操作：步骤 1 确定目标函数系数存放单元格，并在这些单元格中输入目标函数系数。

步骤 2 确定决策变量存放单元格，并任意输入一组数据。

步骤 3 确定约束条件中左端项系数存放单元格，并输入约束条件左端项系数。

步骤 4 在约束条件左端项系数存放单元格右边的单元格中输入约束条件左端项的计算公式，计算出约束条件左端项对应于目前决策变量的函数值。

步骤 5 在步骤4的数据右边输入约束条件中右端项（即常数项）。

步骤 6 确定目标函数值存放单元格，并在该单元格中输入目标函数值的计算公式。

例建立如下线性规划问题的Excell 工作表：解：下表是按照上述步骤建立的线性规划问题的Excell 工作表。

其中：D4=B2*B4+C2*C4, D5=B2*B5+C2*C5 , D6=B2*B6+C2*C6, C7= B2*B1+C2*C1 。

建立了Excel 工作表后，就可以利用其中的规划求解功能求相应的线性规划问题的解。

求解步骤如下：步骤1 单击[工具]菜单中的[规划求解]命令。

步骤2 弹出[规划求解参数]对话框，在其中输入参数。

置目标单元格文本框中输入目标单元格；[等于]框架中选中[最大值＼最小值］单选按钮。

步骤3 设置可变单元格区域，按Ctrl 键，用鼠标进行选取，或在每选一个连续区域后，在其后输入逗号“，”。

步骤4 单击[约束］框架中的[添加]按钮。

利用Excel解线性规划问题

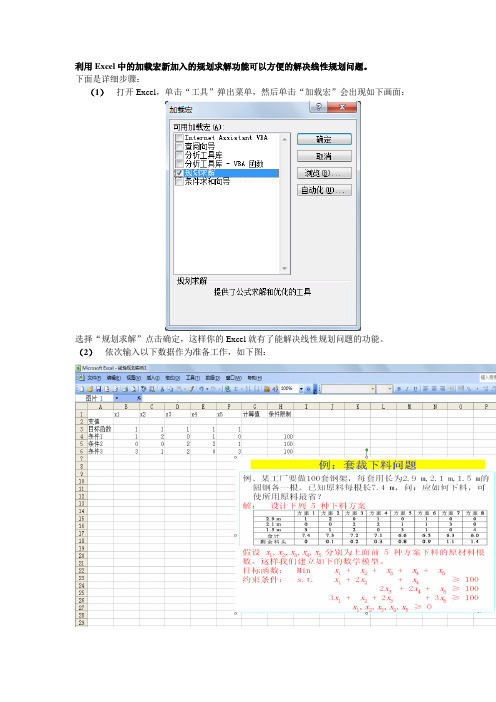
利用Excel中的加载宏新加入的规划求解功能可以方便的解决线性规划问题。

下面是详细步骤：
（1）打开Excel，单击“工具”弹出菜单，然后单击“加载宏”会出现如下画面：
选择“规划求解”点击确定，这样你的Excel就有了能解决线性规划问题的功能。

（2）依次输入以下数据作为准备工作，如下图：
（3）然后在表中选中“G3”位置如下图
输入以下公式“=$B$2*B3+$C$2*C3+$D$2*D3+$E$2*E3+$F$2*F3”（输入公式时必须在英文输入状态），然后回车即可。

（4）选中“G3”位置可以看到公式了，则用填充柄拖动让G4,G5,G6都相应填上公式
（5）再次选中“G3”点击“工具”----“规划求解”，出现下图：
根据题意选择目标单元格为“$G$3”，等于最小值，可变单元格为“$B$2:$C$2:$D$2:$E$2:$F$2”。

然后点击“添加”添加约束条件。

一共有八个约束条件要加入。

下图为其中之一：
（6）添加完约束条件后的图片是：
（7）如上图点击“求解”即可得到结果，如下图：。

用excel的线性规划计算 9、16、25宫格

0 0 0 0 0 x5 x6 0 0 0 0 0 x7 x8 x9 0 0 x7 0 0
x5
0 0 x8 0 0 x6 0 0 x9 x5 0 0 0 x9 x5 0 x7 0 0
这个目标函数按道理来说就是刚才所说的从19个自然数中挑选数字填到矩阵的各个元素位置上但是我们做不到将这个汉语直接翻译成代数式刚才我们也用了4个约束条件只满足了这个语文句子的前半句
用 excel 的线性规划计算 9、16、25 宫格 Statist3927 暨南大学经济学硕士前阵子外甥女突然问我，“姨酱，你会填 9 宫格吗？就是 9 个格子分别填入 1-9 这 9 个数字，使得每一行，每一竖排，对角线加起来都等于 15？” 这个问题真难倒我了，因为我想起了高中那会儿给化学方程式配平，总是按下葫芦浮起瓢，填好这个系数那个系数又不平衡了。不过后来我还是用线性代数+R 语言后搞定了这一心中遗憾。于是我脑海里灵光一闪：会不会用线性代数的方法也可以解出这个问题呢？我觉得这个思路还是靠谱的。为什么这么说呢？我们看，九宫格其实就相当于一个 3×3 的矩阵，要求每个矩阵的元素按照特定的方向求和后，代数和为相等的一个值，也就是 15。
的范式，直接代入到 excel 你是无法计算的。究竟怎么转变呢？其实不难首先要有个目标函数。这个目标函数按道理来说就是刚才所说的“从 1-9 这 9 个自然数中挑选数字填到矩阵的各个元素位置上” ，但是我们做不到将这个汉语直接翻译成代数式，刚才我们也用了 4 个约束条件，只满足了这个语文句子的前半句。因此，我们必须转变一下思路：将目标函数设定的简单一些，然后把约束条件加多一些，这样就可以间接实现了。请看如下操作目标函数：

利用excel求解线性规划问题

利用excel求解线性规划问题线性规划（Linear Programming，LP）是一种用于求解最优化问题的数学方法。

它在经济学，管理学，工程学等领域得到了广泛应用。

Excel是一种功能强大的电子表格软件，提供了一些内置的工具和函数，可以帮助我们求解线性规划问题。

在Excel中求解线性规划问题，通常需要使用“规划求解”工具，该工具位于“数据”选项卡的“分析”分组中。

下面将逐步介绍如何使用Excel求解线性规划问题。

步骤1：建立模型首先，我们需要建立线性规划模型。

模型通常包括目标函数和约束条件。

目标函数：我们需要定义一个目标函数，它表示我们希望最大化或最小化的目标。

在Excel中，可以使用单元格引用和各种数学运算符来定义目标函数。

约束条件：我们需要定义一系列约束条件，这些约束条件是对决策变量的限制。

在Excel中，可以使用不等式和等式来表示约束条件。

每个约束条件都可以转化为一个单元格引用和数学运算符的组合。

步骤2：输入数据在建立模型之后，我们需要输入相关数据。

这包括目标函数中的系数和约束条件中的系数和约束值。

在Excel中，我们可以使用单元格来输入这些数据。

步骤3：设置规划求解选择“数据”选项卡，在“分析”分组中找到“规划求解”工具。

如果没有找到该工具，可能需要先启用“加载项”中的“分析工具包”。

点击“规划求解”，将会打开一个对话框。

在这个对话框中，我们需要输入一些参数来设置求解过程。

目标单元格：这是包含目标函数结果的单元格。

调整变量单元格：这是包含决策变量的单元格范围。

约束条件：这是包含约束条件的单元格范围。

约束条件中的系数：这是一个选择项，用于指定约束条件中的系数是包含在单元格范围中还是直接输入。

约束条件的约束值：这是一个选择项，用于指定约束条件中的约束值是包含在单元格范围中还是直接输入。

约束条件的约束类型：这是一个选择项，用于指定约束条件的类型（大于等于，小于等于等）。

非负约束：这是一个复选框，用于指定决策变量是否具有非负约束。

用EXCLE求解线性规划问题

4.在约束条件左端项系数存放单元格右边的单元格中输入约束条件左端项的计算公式，计算出约束条件左端项对应于目前决策变量的函数值。 5.在步骤4的的数据右边输入约束条件中右端项（即常数项）
6.确定目标函数值存放单元格，并在该单元格中输入目标函数值电容计算公式。
例.求下列线性规划问题
SUMPRODUCT(B3:C3,B10:C10)
例.求解如下的线性规划问题某企业的产品生产数据如下
分共厂门生产时间窗 0 2小时 2小时 500 4小时 12小时 18小时每周可利用时间
s.t
第一步：选择决策变量单元格决策变量的一般初始值赋0。
第二步：目标单元格，用函数公式表示。
用EXCLE求解线性规划问题
1.“线性规划求解”的安装(文件
选项)
加载项规划求解加载项选择在数据加载项
转到
加载数据规划求解选项以后,在“数据”菜单中就会出现“规划求解”
线性规划求解的步骤：
1.确定目标函数系数存放单元格，并在这些单元格中输入目标函数系数。 2.确定决策变量存放单元格，并任意输入一组数据； 3.确定约束条件中左端项系数存放单元格，并输入约束条件左端项系数；
G 11 Total Proft 12 =sumproduct（C4:D4，C12:D12）
第三步：约束条件左边项用函数表示
5 6 7 8 9
E Hours Used SUMPRODUCT(C7:D7,$C$12:$D$12) SUMPRODUCT(C8:D8,$C$12:$D$12) SUMPRODUCT(C9:D9,$C$12:$D$12)
第四步：激活规划求解，确定可变单元格和目标单元格
第五步：增加约束条件

excel 线性规划

excel 线性规划Excel是一种非常强大的电子表格软件，可以用来进行各种类型的数学和统计分析，包括线性规划。

线性规划是一种最常见的优化方法，广泛应用于工程、经济和管理等领域。

它通过线性数学模型来找到最佳解决方案，以满足一组约束条件。

在Excel中进行线性规划，我们可以使用Excel的Solver插件。

Solver插件可以帮助我们找到目标函数的最大值或最小值，同时满足约束条件。

下面是一个示例，通过Excel进行线性规划的步骤：1.首先，我们需要创建一个Excel表格，其中包括如下内容：目标函数、约束条件、可调整的单元格等。

2.输入目标函数。

在一个单元格中输入目标函数，例如“=A1*10+B2*15+C3*20”，其中A1、B2、C3是可调整的单元格的引用，而10、15和20是目标函数中每个单元格对应的系数。

3.输入约束条件。

在另一行中，输入约束条件。

例如，“A1>=10”、“B2<=20”等等。

4.确保所需的单元格被定义为可调整单元格，并设置目标单元格为需要最小或最大化的目标函数单元格。

5.打开Solver插件。

在“数据”选项卡中，点击“Solver”。

6.在Solver对话框中，选择“最小化”或“最大化”的目标设置，输入目标函数单元格的引用，并设置约束条件。

7.点击“确定”按钮，Solver会自动计算并找到最佳解决方案。

需要注意的是，Excel的Solver插件对于较大的线性规划问题可能需要更复杂的方法。

解决大规模问题时，可能需要使用更专业的线性规划软件。

总之，Excel是一个非常方便和灵活的工具，可以用来进行线性规划分析。

通过使用Excel的Solver插件，我们可以快速而准确地找到最佳解决方案，并满足所有的约束条件。

无论是对于学生、专业人士还是研究人员，使用Excel进行线性规划都是一种方便和高效的方法。

运用EXCEL求解线性规划模型-文档资料

（1）两种新产品的每周产量：C12、D12，试验解为0。
（2）实际使用工时计算（三种方法） 1）分别在E7、E8、E9中输入相应的计算公
式： E7：C7*C12+D7*D12 E8：C8*C12+D8*D12 E9：C9*C12+D9*D12
9
EXCEL求解线性规划模型
2）复制、粘贴方法：在E7中输入：C7*$C$12+D7*$D$12
百分之一百法则：对于所有变化的目标函数决策变量系数（或约束条件右边常数），当其所有允许增加百分比和允许减少百分比之和不超过百分之一百时，最优解不变。
46
EXCEL求解线性规划模型
允许增加量百分比= 实际增加量（上限-现在值）/允许增加量
允许减少量百分比= 实际减少量（现在值-下限）/允许减少量
28
EXCEL求解线性规划模型
规划求解过程
29
EXCEL求解线性规划模型
课堂练习3：P25 1
使用单元格命名法有何好处？
使用名称比使用字母更容易理解公式的含义
在“规划求解参数”对话框中使用名称更容易理解线性规划模型的含义。
增强了公式和模型的可读性
30
建模求解要点回顾
输入数据标识数据每个数据对应唯一单元格在电子表格中显示完整模型数据、公式分离保持简单化使用区域名称使用相对和绝对地址简化公式并复制使用边框、底色区分单元格类型
• 百分之一百法则是判断最优解变与不变的充分条件，
复制E7单元格到E8、E9 3）公式法：
在E7中输入： =SUMPRODUCT（C7：D7，$C$12：$D$12）
复制E7单元格到E8、E9
10
EXCEL求解线性规划模型

excel做线性规划

2007进行该功能加载的方法
规划求解加载宏是一个Microsoft Office Excel 加载项（加载项：为Microsoft Office 提供自定义命令或自定义功能的补充程序。

）程序，安装Microsoft Office 或Excel 后即可使用该程序。

但是，要在Excel 中使用它，您需要先进行加载。

1.单击“Office 按钮”按钮图像，然后单击“Excel 选项”。

2.单击“加载项”，然后在“管理”框中，选择“Excel 加载宏”。

3.单击“转到”。

4.在“可用加载宏”框中，选中“规划求解加载项”复选框，然后单击“确定”。

5.提示如果“规划求解加载项”未在“可用加载宏”中列出，请单击“浏览”找到该加载宏。

6.如果出现一条消息，指出您的计算机上当前未安装规划求解加载宏，请单击“是”进行安
装。

7.加载规划求解加载宏后，“规划求解”命令将出现在“数据”选项卡的“分析”组中。

利用excel软件求解线性规划问题

数学规划模型实验指导手册Excel的规划求解加载宏求解数学规划问题一、什么是规划求解加载宏？规划求解加载宏（简称规划求解）是Excel的一个加载项1，可以用来解决线性规划与非线性规划优化问题。

规划求解可以用来解决最多有200个变量，100个外在约束和400个简单约束（决策变量整数约束的上下边界）的问题。

可以设置决策变量为整型变量。

规划求解加载宏的开发商是Fronline System公司。

用户通过自定义安装MS-Office所使用的是标准版本规划求解加载宏，Fronline System公司同时提供增强的Premium Solver工具。

规划求解工具在Office典型安装状态下不会安装，可以通过自定义安装选择该项或通过添加/删除程序增加规划求解加载宏。

二、怎样加载规划求解加载宏？加载规划求解加载宏的方法如下：（1）打开“工具”下拉列菜单，然后单击“加载宏”，打开“加载宏”对话框。

（2）在“可用加载宏”框中，选中“规划求解”旁边的复选框2，然后单击“确定”按钮。

1加载项的功能是为Microsoft Office 提供自定义命令或自定义功能的补充程序2如果“规划求解”未列出，请单击“浏览”进行查找。

（3）如果出现一条消息，指出您的计算机上当前没有安装规划求解，请单击“是”用原Office安装盘进行安装。

（4）单击菜单栏上的“工具”。

加载规划求解后，“规划求解”命令会添加到“工具”菜单中。

三、怎样使用规划求解加载宏求解数学规划？规划求解加载宏是一组命令构成的一个子程序，这些命令有时也称作假设分析3工具，其功能是可以求出线性和非线性数学规划问题的最优解和最优值。

使用规划求解加载宏求解数学规划的步骤首先，在Excel工作表中输入目标函数的系数向量、约束条件的系数矩阵和右端常数项（每一个单元格输入一个数据）；其次，选定一个单元格存储目标函数（称为目标单元格），用定义公式的方式在这个目标单元格内定义目标函数；再次，选定与决策变量个数相同的单元格（称为可变单元格），用以存储决策变量；再选择与约束条件个数相同的单元格，用定义公式的方式在每一个单元格内定义一个约束函数（称为约束函数单元格）；最后，点击下拉列菜单中的规划求解按钮，打开规划求解参数设定对话框（如图4所示），完成规划模型的设定模型设定方法如下：（1）设定目标函数和优化方向：光标指向规划求解参数设定对话框中的“设置目标单元格”提示后的域，点击鼠标左键，然后选中Excel工作表中的目标单元格。