三种排序

合集下载

Excel电子表格排序的三种实用方法

Excel电子表格排序的三种实用方法排序是数据处理中的经常性工作，Excel排序有序数计算（类似成绩统计中的名次）和数据重排两类。

本文以几个车间的产值和名称为例，介绍Excel2000/XP的数据排序方法。

一、数值排序1、RANK函数RANK函数是Excel计算序数的主要工具，它的语法为：RANK（number，ref，order），其中number 为参与计算的数字或含有数字的单元格，ref是对参与计算的数字单元格区域的绝对引用，order是用来说明排序方式的数字（如果order为零或省略，则以降序方式给出结果，反之按升序方式）。

例如要计算E2、E3、E4单元格存放一季度的总产值，计算各车间产值排名的方法是：在F2单元格内输入公式“=RANK（E2，$E$2E$4）”，敲回车即可计算出铸造车间的产值排名是2。

再将F2中的公式复制到剪贴板，选中F3、F4单元格按Ctrl+V，就能计算出其余两个车间的产值排名为3和1。

美文坊提醒大家如果B1单元格中输入的公式为“=R ANK（E2，$E$2E$4，1）”，则计算出的序数按升序方式排列，即2、1和3。

需要注意的是：相同数值用RAN K函数计算得到的序数（名次）相同，但会导致后续数字的序数空缺。

假如上例中F2单元格存放的数值与F3相同，则按本法计算出的排名分别是3、3和1（降序时）。

2、COUNTIF函数COUNTIF函数可以统计某一区域中符合条件的单元格数目，它的语法为COUNTIF（range，criteria）。

其中range为参与统计的单元格区域，criteria是以数字、表达式或文本形式定义的条件。

其中数字可以直接写入，表达式和文本必须加引号。

仍以上面的为例，F2单元格内输入的公式为“=COUNTIF（$E$2E$4，”>“&E2）+1”。

计算各车间产值排名的方法同上，结果也完全相同，2、1和3。

此公式的计算过程是这样的：首先根据E2单元格内的数值，在连接符&的作用下产生一个逻辑表达式，即“>176。

常见三种排序方法PPT参考课件

(2) 除第1个数外，其余n-1个数再按(1)的方法选出次小的数，与第2个数交换位置;
(3) 重复(1)n-1遍，最后构成递增序列。
实现方法：采用双重循环（循环的嵌套）
外循环为i：控制排序趟数内循环为j：第i趟排序过程中的下标变量
C Programming Language
6
实现方法：采用双重循环（循环的嵌套）
C Programming Language
9
交换排序：俩俩比较待排序记录的键值，若逆序，则交换，直到全部满足为止
25 25 25 25 11 11 11
56 49 49 11 25 25 25
（2）冒泡排序 49 56 11 49 41 36 36
78 11 56 41 36 41
for(j = i + 1;j < N;j++) if(a[k] > a[j]) k = j; if(k != i) { t = a[k]; a[k] = a[i]; a[i] = t; } } for(i = 0;i<N;i++) printf("%5d",a[i]); printf("\n");
}
C Programming Language
8
第二种：“冒泡法”（由小到大排序）
基本思想：
(1)从第一个元素开始，对数组中两两相邻的元素比较，将值较小的元素放在前面，值较大的元素放在后面，一轮比较完毕，最大的数存放在a[N-1] 中；
(2)然后对a[0]到a[N-2]的N-1个数进行同（1）的操作，次最大数放入a[N-2]元素内，完成第二趟排序；依次类推，进行N-1趟排序后，所有数均有序。

C语言中三种常见排序算法分析

C语言中三种常见排序算法分析C语言中三种常见排序算法分析C语言的设计目标是提供一种能以简易的方式编译、处理低级存储器、产生少量的机器码以及不需要任何运行环境支持便能运行的编程语言。

那么C语言中三种常见排序算法的分析情况是怎样的呢。

以下仅供参考！一、冒泡法（起泡法）算法要求：用起泡法对10个整数按升序排序。

算法分析：如果有n个数，则要进行n-1趟比较。

在第1趟比较中要进行n-1次相邻元素的两两比较，在第j趟比较中要进行n-j次两两比较。

比较的顺序从前往后，经过一趟比较后，将最值沉底（换到最后一个元素位置），最大值沉底为升序，最小值沉底为降序。

算法源代码：# includemain(){int a[10],i,j,t;printf("Please input 10 numbers: ");/*输入源数据*/for(i=0;i<10;i++)scanf("%d",&a[i]);/*排序*/for(j=0;j<9;j++) /*外循环控制排序趟数，n个数排n-1趟*/for(i=0;i<9-j;i++) /*内循环每趟比较的次数，第j趟比较n-j次*/ if(a[i]>a[i+1]) /*相邻元素比较，逆序则交换*/{ t=a[i];a[i]=a[i+1];a[i+1]=t;}/*输出排序结果*/printf("The sorted numbers: ");for(i=0;i<10;i++)printf("%d ",a[i]);printf(" ");}算法特点：相邻元素两两比较，每趟将最值沉底即可确定一个数在结果的位置，确定元素位置的顺序是从后往前，其余元素可能作相对位置的调整。

可以进行升序或降序排序。

算法分析：定义n-1次循环，每个数字比较n-j次，比较前一个数和后一个数的大小。

排序—时间复杂度为O（n2）的三种排序算法

排序—时间复杂度为O（n2）的三种排序算法1 如何评价、分析⼀个排序算法？很多语⾔、数据库都已经封装了关于排序算法的实现代码。

所以我们学习排序算法⽬的更多的不是为了去实现这些代码，⽽是灵活的应⽤这些算法和解决更为复杂的问题，所以更重要的是学会如何评价、分析⼀个排序算法并在合适的场景下正确使⽤。

分析⼀个排序算法，主要从以下3个⽅⾯⼊⼿：1.1 排序算法的执⾏效率1）最好情况、最坏情况和平均情况时间复杂度待排序数据的有序度对排序算法的执⾏效率有很⼤影响，所以分析时要区分这三种时间复杂度。

除了时间复杂度分析，还要知道最好、最坏情况复杂度对应的要排序的原始数据是什么样的。

2）时间复杂度的系数、常数和低阶时间复杂度反映的是算法执⾏时间随数据规模变⼤的⼀个增长趋势，平时分析时往往忽略系数、常数和低阶。

但如果我们排序的数据规模很⼩，在对同⼀阶时间复杂度的排序算法⽐较时，就要把它们考虑进来。

3）⽐较次数和交换（移动）次数内排序算法中，主要进⾏⽐较和交换（移动）两项操作，所以⾼效的内排序算法应该具有尽可能少的⽐较次数和交换次数。

1.2 排序算法的内存消耗也就是分析算法的空间复杂度。

这⾥还有⼀个概念—原地排序，指的是空间复杂度为O(1)的排序算法。

1.3 稳定性如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变，那么这种排序算法叫做稳定的排序算法；如果前后顺序发⽣变化，那么对应的排序算法就是不稳定的排序算法。

在实际的排序应⽤中，往往不是对单⼀关键值进⾏排序，⽽是要求排序结果对所有的关键值都有序。

所以，稳定的排序算法往往适⽤场景更⼴。

2 三种时间复杂度为O(n2)的排序算法2.1 冒泡排序2.1.1 原理两两⽐较相邻元素是否有序，如果逆序则交换两个元素，直到没有逆序的数据元素为⽌。

每次冒泡都会⾄少让⼀个元素移动到它应该在的位置。

2.1.2 实现void BubbleSort(int *pData, int n) //冒泡排序{int temp = 0;bool orderlyFlag = false; //序列是否有序标志for (int i = 0; i < n && !orderlyFlag; ++i) //执⾏n次冒泡{orderlyFlag = true;for (int j = 0; j < n - 1 - i; ++j) //注意循环终⽌条件{if (pData[j] > pData[j + 1]) //逆序{orderlyFlag = false;temp = pData[j];pData[j] = pData[j + 1];pData[j + 1] = temp;}}}}测试结果2.1.3 算法分析1）时间复杂度最好情况时间复杂度：当待排序列已有序时，只需⼀次冒泡即可。

Excel排序的三种方法

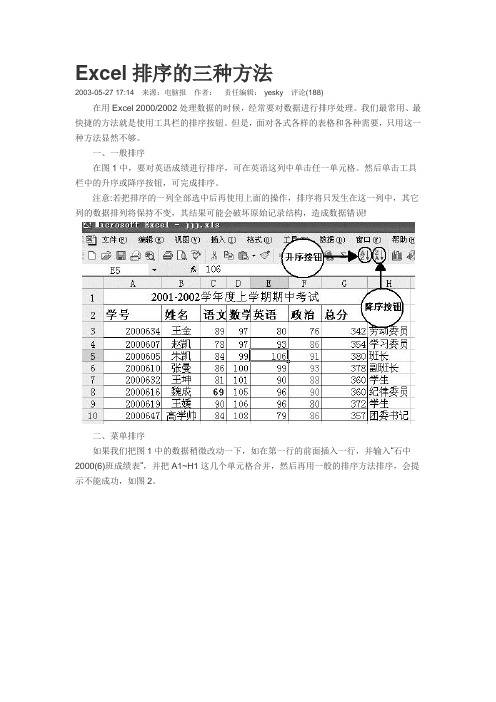
Excel排序的三种方法2003-05-27 17:14来源：电脑报作者：责任编辑：·yesky评论(188)在用Excel 2000/2002处理数据的时候，经常要对数据进行排序处理。

我们最常用、最快捷的方法就是使用工具栏的排序按钮。

但是，面对各式各样的表格和各种需要，只用这一种方法显然不够。

一、一般排序在图1中，要对英语成绩进行排序，可在英语这列中单击任一单元格。

然后单击工具栏中的升序或降序按钮，可完成排序。

注意:若把排序的一列全部选中后再使用上面的操作，排序将只发生在这一列中，其它列的数据排列将保持不变，其结果可能会破坏原始记录结构，造成数据错误!二、菜单排序如果我们把图1中的数据稍微改动一下，如在第一行的前面插入一行，并输入“石中2000(6)班成绩表”，并把A1~H1这几个单元格合并，然后再用一般的排序方法排序，会提示不能成功，如图2。

如果对这样的表格排序，可选中要排序的所有数据，包括标题行(学号、姓名等所在的行)，然后单击“数据/排序”菜单，弹出如图3所示窗口。

在主关键字的下拉列表中，选择要排序的列，如英语，在右侧选择“升序排列”或“降序排列”。

至于次要关键字和第三关键字可添可不添，但是它起到什么样的作用呢?在这儿举个例子，如果按英语排序，有两个学生都得了96分，但又必须分出高低，这样我们可选择数学成绩作为排名次的次要标准，谁得分高谁排在前面，那么这儿的次要关键字就是数学。

一切做完后，单击“确定”就可以看到结果了。

三、自定义排序在这个成绩表中，如果我们想按职务这列排序，如先后顺序是:团委书记、班长、副班长、学习委员、学生。

但是不管用上面的哪种方法都不会得到我们需要的结果。

在这儿利用Excel 2000/2002提供的自定义排序，就可以解决这个问题。

1.在“工具”菜单上，单击“选项”，再单击“自定义序列”选项。

2.在右侧的输入序列框中依次输入团委书记、班长、副班长、学习委员、学生，然后单击“确定”。

中班数学《按规律排序》

中班数学《按规律排序》数学是一门有趣又实用的学科，而在中班的数学学习中，我们将学习如何按规律排序。

通过这个主题，我们可以培养孩子们的观察力、逻辑思维和数学能力。

下面，我们将以一些简单的例子来介绍按规律排序的方法。

1. 第一种排序方法 - 数字排序首先，我们可以教孩子们按照数字的大小来排序。

举个例子，我们可以给孩子们一组数字：5、9、2、1、6，并要求他们按照从小到大的顺序排列这些数字。

孩子们可以将数字从左到右排列：1、2、5、6、9。

通过这种方法，他们可以发现数字的顺序与大小的关系，并培养出对数字排序的能力。

2. 第二种排序方法 - 图形排序除了数字排序，我们还可以用图形来进行排序。

例如，我们可以用不同的图形来让孩子们按照规定的顺序排列。

比如，给孩子们几个形状：圆形、三角形、正方形、长方形，并要求他们按照从简单到复杂的顺序排列这些形状。

孩子们可以先将圆形放在第一位，然后是三角形、正方形和长方形。

通过这种方法，他们可以锻炼观察和比较的能力。

3. 第三种排序方法 - 图案排序除了按照数字和图形排序，我们还可以让孩子们按照图案的规律来排序。

例如，给孩子们一系列的图案：星星、花朵、波浪线、方格，并要求他们按照由简到复杂的顺序进行排序。

孩子们可能会选择先排列星星，然后是花朵、波浪线和方格。

通过这种方法，他们可以学会观察和辨认不同图案的能力。

通过以上介绍的三种排序方法，我们可以培养孩子们的观察力、逻辑思维和数学能力。

在教学中，我们可以通过游戏和练习的方式来帮助孩子们掌握按规律排序的技巧。

例如，我们可以利用卡片游戏，让孩子们自己动手将卡片按照规定的排序进行排列。

这样，孩子们既能够学到知识，又能够保持兴趣，加深对数学的喜爱。

总之，在中班的数学学习中，按规律排序是一个重要的主题。

通过教孩子们不同的排序方法，我们可以培养他们的观察力、逻辑思维和数学能力。

通过游戏和练习的方式，让孩子们在愉快的学习氛围中提高自己的排序能力。

Excel2007中数据排序的三种方法

Excel2007中数据排序的三种方法排序是数据处理中的经常性工作，Excel排序有序数计算(类似成绩统计中的名次)和数据重排两类。

以几个车间的产值和名称为例，今天，店铺就教大家在Excel2007中数据排序的三种方法。

Excel2007中数据排序的三种步骤如下：一、数值排序1、RANK函数RANK函数是Excel计算序数的主要工具，它的语法为：RANK(number，ref，order)，其中number为参与计算的数字或含有数字的单元格，ref是对参与计算的数字单元格区域的绝对引用，order是用来说明排序方式的数字(如果order为零或省略，则以降序方式给出结果，反之按升序方式)。

例如要计算E2、E3、E4单元格存放一季度的总产值，计算各车间产值排名的方法是：在F2单元格内输入公式“=RANK(E2，$E$2:$E$4)”，敲回车即可计算出铸造车间的产值排名是2。

再将F2中的公式复制到剪贴板，选中F3、F4单元格按Ctrl+V，就能计算出其余两个车间的产值排名为3和1。

美文坊提醒大家如果B1单元格中输入的公式为“=RANK(E2，$E$2:$E$4，1)”，则计算出的序数按升序方式排列，即2、1和3。

需要注意的是：相同数值用RANK函数计算得到的序数(名次)相同，但会导致后续数字的序数空缺。

假如上例中F2单元格存放的数值与F3相同，则按本法计算出的排名分别是 3、3和1(降序时)。

2、COUNTIF函数COUNTIF函数可以统计某一区域中符合条件的单元格数目，它的语法为COUNTIF(range，criteria)。

其中range为参与统计的单元格区域，criteria是以数字、表达式或文本形式定义的条件。

其中数字可以直接写入，表达式和文本必须加引号。

仍以上面的为例，F2单元格内输入的公式为“=COUNTIF($E$2:$E$4，”>“&E2)+1”。

计算各车间产值排名的方法同上，结果也完全相同，2、1和3。

【转】三种快速排序算法以及快速排序的优化

【转】三种快速排序算法以及快速排序的优化⼀. 快速排序的基本思想快速排序使⽤分治的思想，通过⼀趟排序将待排序列分割成两部分，其中⼀部分记录的关键字均⽐另⼀部分记录的关键字⼩。

之后分别对这两部分记录继续进⾏排序，以达到整个序列有序的⽬的。

⼆. 快速排序的三个步骤1) 选择基准：在待排序列中，按照某种⽅式挑出⼀个元素，作为 “基准”（pivot）；2) 分割操作：以该基准在序列中的实际位置，把序列分成两个⼦序列。

此时，在基准左边的元素都⽐该基准⼩，在基准右边的元素都⽐基准⼤；3) 递归地对两个序列进⾏快速排序，直到序列为空或者只有⼀个元素；三. 选择基准元的⽅式对于分治算法，当每次划分时，算法若都能分成两个等长的⼦序列时，那么分治算法效率会达到最⼤。

也就是说，基准的选择是很重要的。

选择基准的⽅式决定了两个分割后两个⼦序列的长度，进⽽对整个算法的效率产⽣决定性影响。

最理想的⽅法是，选择的基准恰好能把待排序序列分成两个等长的⼦序列。

⽅法⼀：固定基准元（基本的快速排序）思想：取序列的第⼀个或最后⼀个元素作为基准元。

/// <summary>/// 1.0 固定基准元（基本的快速排序）/// </summary>public static void QsortCommon(int[] arr, int low, int high){if (low >= high) return; //递归出⼝int partition = Partition(arr, low, high); //将 >= x 的元素交换到右边区域，将 <= x 的元素交换到左边区域QsortCommon(arr, low, partition - 1);QsortCommon(arr, partition + 1, high);}/// <summary>/// 固定基准元，默认数组第⼀个数为基准元，左右分组，返回基准元的下标/// </summary>public static int Partition(int[] arr, int low, int high){int first = low;int last = high;int key = arr[low]; //取第⼀个元素作为基准元while (first < last){while (first < last && arr[last] >= key)last--;arr[first] = arr[last];while (first < last && arr[first] <= key)first++;arr[last] = arr[first];}arr[first] = key; //基准元居中return first;}注意：基本的快速排序选取第⼀个或最后⼀个元素作为基准。

大班数学优秀教案《排序》

大班数学优秀教案《排序》一、教学内容•目标：通过本课的学习，让学生能够掌握一定的排序算法，并对排序有初步理解。

•内容：–排序的定义–常见排序算法：冒泡排序、选择排序、插入排序二、教学重点难点1. 教学重点•定义排序，介绍排序算法思想。

•学习三种常规的排序算法，理解三种算法的优劣。

2. 教学难点•排序算法思想的理解。

•学生对于常见排序算法的初步掌握。

三、教学过程1. 教学准备•制作PPT及相关教学课件，准备讲义、白板、笔等教学工具。

2. 学生自学时间1.学生先通过网上资源或其他资料，学习排序算法的相关概念。

3. 教师讲授1.热身：老师可以先引入“让同桌按身高排一排”的小游戏，让学生将自己按照身高顺序排列。

2.内容讲解：–首先介绍排序的概念，即将一组无序的数据，按照一定规则排列为有序的数据。

–然后分别详细介绍三种排序算法：冒泡排序、选择排序、插入排序。

分析三种排序算法的优劣。

3.示例演示：–以冒泡排序为例，具体演示每个过程。

4.练习：老师出题，让学生自己练习并运用三种排序方法进行排序。

5.总结：–总结排序的概念和重要性。

–总结并回顾三种常规算法的特点和优劣。

4. 作业布置通过编写程序，至少实现其中一种排序算法。

5. 教学总结•强调排序的重要性，学生应该在日常生活中会使用到排序算法。

•回顾三种常规算法，引导学生反思，并对未来升级和优化打下基础。

四、教学效果评价•通过课堂练习和课后作业的相结合，可以评估学生的掌握程度。

同时，可以对教学效果进行评价。

•通过学习情况和学生成绩评估，可以有效地评估学生成果和教孔水平。

五、注意事项•此课程适用于大班数学学习，建议紧扣常规算法，通过例子讲解和演示等方式提高学生的学习兴趣。

•老师应该注重学生自主学习和实际操作，学生应该将学到的知识应用于实际问题，形成技能习惯。

EXCEL表格排序的三种实用方法

步骤/方法一、数值排序1、RANK函数RANK函数是Excel计算序数的主要工具，它的语法为：RANK(number，ref，order)，其中number为参与计算的数字或含有数字的单元格，ref是对参与计算的数字单元格区域的绝对引用，order是用来说明排序方式的数字(如果order为零或省略，则以降序方式给出结果，反之按升序方式)。

例如要计算E2、E3、E4单元格存放一季度的总产值，计算各车间产值排名的方法是：在F2单元格内输入公式 =RANK(E2，$E$2:$E$4)，敲回车即可计算出铸造车间的产值排名是2。

再将F2中的公式复制到剪贴板，选中F3、F4单元格按 Ctrl+V，就能计算出其余两个车间的产值排名为3和1。

美文坊提醒大家如果B1单元格中输入的公式为 =RANK(E2，$E$2:$E$4，1)，则计算出的序数按升序方式排列，即2、1和3。

需要注意的是：相同数值用RANK函数计算得到的序数(名次)相同，但会导致后续数字的序数空缺。

假如上例中F2单元格存放的数值与F3相同，则按本法计算出的排名分别是 3、3和1(降序时)。

2、COUNTIF函数COUNTIF函数可以统计某一区域中符合条件的单元格数目，它的语法为COUNTIF(range，criteria)。

其中range为参与统计的单元格区域，criteria是以数字、表达式或文本形式定义的条件。

其中数字可以直接写入，表达式和文本必须加引号。

仍以上面的为例，F2单元格内输入的公式为=COUNTIF($E$2:$E$4，;&E2)+1。

计算各车间产值排名的方法同上，结果也完全相同，2、1和3。

此公式的计算过程是这样的：首先根据E2单元格内的数值，在连接符&的作用下产生一个逻辑表达式，即;176。

7、 ;167。

3等。

COUNTIF函数计算出引用区域内符合条件的单元格数量，该结果加一即可得到该数值的名次。

详解排序算法（一）之3种插入排序（直接插入、折半插入、希尔）

详解排序算法（⼀）之3种插⼊排序（直接插⼊、折半插⼊、希尔）直接插⼊排序打过牌的⼈都知道，当我们拿到⼀张新牌时，因为之前的牌已经经过排序，因此，我们只需将当前这张牌插⼊到合适的位置即可。

⽽直接插⼊排序，正是秉承这⼀思想，将待插⼊元素与之前元素⼀⼀⽐较，从⽽找到合适的插⼊位置。

那么使⽤直接插⼊排序，具体是怎样操作的呢？我们取 3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48 来进⾏⽰范。

（1）第1轮排序，3之前⽆可⽐较值，因此我们从44开始操作，取44和3⽐较，⼤于3，顺序保持不变。

得数据3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48（2）第2轮排序，取38和44⽐较，38 < 44，再将38与3⽐较，38 > 3，故将38放于第2位，得数据3, 38, 44, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48（3）第3轮排序，取5与44⽐较，5 < 44，再将5与38⽐较，5 < 38，再将5与3⽐较，5 > 3, 置于第2位，得数据3, 5, 38, 44, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48（4）如此经过14轮排序后，得到最终结果2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50动态图javascript实现function directInsertSort (arr) {let compare, // 对⽐元素下标current // 待插⼊元素值for (let i = 1; i < arr.length; i++) {current = arr[i]compare = i - 1while (current < arr[compare] && compare >= 0) {arr[compare + 1] = arr[compare]compare--}arr[compare + 1] = current}return arr}折半插⼊排序细⼼的同学可能已经注意到，当我们要将⼀个元素插⼊合适的位置时，其之前的元素是有序的，因此，我们可以⽤折半查找的⽅式来⽐对并插⼊元素，也就是所谓的折半插⼊排序。

幼儿园数学教案：认识排序的方法

幼儿园数学教案：认识排序的方法
教学主题：认识排序的方法
教学目标：
1. 学习认识排序的方法；
2. 控制不同物品的大小；
3. 通过游戏加深对排序方法的理解。

教材准备：
1. 图片卡片（包括大小不同的物品）；
2. 排序游戏。

教学流程：
一、课前导入（5分钟）
老师与幼儿们一起唱歌、做体操等活动以集中幼儿们的注意力，让幼儿们准备好进入数学课堂。

二、新知讲解（20分钟）
（1）认识排序
老师拿出不同大小的物品图片，让幼儿们看一会儿，让大家分享，哪个物品最大，哪个最小？老师引导幼儿们认识：不同物品之间的大小关系，可以按照“大、中、小”或“高、中、低”等不同的标准来进行排序。

（2）排序方法
老师介绍了三种基本的排序方法：
①按大小排序：将小的放在前面，大的放在后面；
②按颜色排序：将相同颜色的放在一起；
③按形状排序：将相同形状的放在一起。

三、游戏操作（25分钟）
老师出示一些图片，幼儿们要将这些图片按照不同的排序方法排列出来。

游戏过程中，老师可以引导幼儿们，出示一些比较复杂的图片，让幼儿们思考如何进行排序。

四、知识总结（10分钟）
老师引导幼儿们回顾今天所学的知识，特别是三种排序方法，强化幼儿们对于排序知识的理解。

五、课后拓展（5分钟）
老师出示一些图片，让幼儿们回家完成排序游戏，巩固所学知识。

课后反思：
今天的课程中，幼儿们学会了排序的方法，锻炼了他们的排序能力，同时游戏化的教学方法让幼儿们更快乐的接受知识。

下一步，我将再结合一些活动与课程，让幼儿们对于数学知识有更加深入和全面的了解和掌握。

幼儿园大班数学优秀教案《按规律排序》

活动目标一、引导幼儿通过观看发觉事物间的简单规律(自然现象及特定的规律)。

二、培育幼儿细致观看、勤于动手的好适应;体验思维训练的乐趣。

3、增进幼儿的创新思维与动作和谐进展。

4、乐于探讨、交流与分享。

活动预备一、教具预备：三种排列规律的范例条各一(○□○□○□;○□□○□□○□□;○□△○□△○□△);“奇异的书”(封面是彩虹，从第一页到第七页依次是一颗红色的草莓、两只橙色的橘子、三根黄色的香蕉、四只绿色的西瓜、五只青色的苹果、六颗蓝色的梅子、七串紫色的葡萄;几组图片(从儿童到青年到成人再到老年人;从树芽到小树再到大树;从鸡蛋到小鸡再到母鸡，等等)。

二、学具预备：操作纸、记号笔、三角形、圆形、正方形各假设干。

活动进程一、开始部份导人：小朋友有无发觉，今天咱们座位排列的顺序有什么专门的地址?(一个男孩、一个女孩)有一组图形宝宝排列的顺序和咱们很相似，咱们一路来看看它们是谁。

二、大体部份一、依次出示三种排列规律的范例，请幼儿读一读每张范例条上的图形是什么，发觉了什么规律。

1)出示范例条○□○□○□，提问：有哪些图形在排队?它们的队伍是怎么排列的?后面还能够怎么排?它们排列得很整齐，咱们用字母来表示能够看得更清楚，用A表示圆形，用B表示正方形(引导幼儿用ABABAB分组，教师在范例条的下方记录，帮忙幼儿小结规律。

)2)出示范例条○□□○□□○□□，提问：它们是谁?都是怎么排的?后面应该怎么排列呢?(引导幼儿ABBABBABB分组，教师在范例条下方记录，帮忙幼儿小结规律。

)3)一样，出示范例条○□△○□△○□△，引导幼儿小结ABCABCABC排列的规律。

二、引导幼儿观看“奇异的书”，找出书中的规律。

1)引导幼儿观看“奇异的书”从封面到第三页。

封面是彩虹，颜色依次为红、橙、黄、绿、青、蓝、紫;第一页上是一颗红草莓;第二页上是两只橙色的橘子;第三页上是三根黄香蕉。

;.来源快思教师教。

案网;请幼儿依次猜猜后面几页上有什么，是怎么猜的。

PowerBI技巧之Power BI之power query多条件排序

Power BI之power query多条件排序业务场景三种排序要求：①按照销售额，员工销售额排序；——优先级：销售额②根据销售额，员工在部门中的排序；——优先级：部门、销售额③根据销售额，员工在部门、级别中的排序；——优先级：部门、级别、销售额实际操作：①销售额排序先对销售额降序排列—添加索引。

= Table.Sort(删除的列,{{"销售额", Order.Descending}})= Table.AddIndexColumn(排序的行, "销售额排名", 1, 1, Int64.Type)②部门-销售额排序：分组降序排：选中部门，对所有行分组，同时按照销售额降序排。

= Table.Group(已添加索引, {"部门"}, {{"组合", each Table.Sort(_,{{"销售额", Order.Descending}}), type table [员工=n ullable text, 部门=nullable text, 级别=nullable text, 销售额=nullable number, 销售额排名=number]}})添加自定义列-部门销售额排名，并添加索引。

= Table.AddColumn(分组的行, "部门销售额排名", each Table.AddIndexColumn([组合], "部门销售额排名", 1, 1))删除其他列，只保留“部门销售额排名”，展开表= Table.SelectColumns(已添加自定义,{"部门销售额排名"})= Table.ExpandTableColumn(删除的其他列, "部门销售额排名", {"员工", "部门", "级别", "销售额", "销售额排名", "部门销售额排名"}, {"员工", "部门", "级别", "销售额", "销售额排名", "部门销售额排名"})展开后如下图：③部门-级别-销售额排序：同上面的操作，分组是对部门、级别组合分组降序排：选中部门，级别，对所有行分组，同时按照销售额降序排。

三种基本排序算法

三种基本排序算法在计算机科学所使⽤的排序算法通常被分类为：计算的时间复杂度（最差、平均、和最好性能），依据列表（list）的⼤⼩(n)。

⼀般⽽⾔，好的性能是O(n log n)，且坏的性能是O(n^2)。

对于⼀个排序理想的性能是O(n)。

仅使⽤⼀个抽象关键⽐较运算的排序算法总平均上总是⾄少需要O(n log n)。

存储器使⽤量（以及其他电脑资源的使⽤）稳定性：稳定排序算法会让原本有相等键值的纪录维持相对次序。

也就是如果⼀个排序算法是稳定的，当有两个相等键值的纪录R和S，且在原本的列表中R出现在S之前，在排序过的列表中R也将会是在S之前。

依据排序的⽅法：插⼊、交换、选择、合并等等。

依据排序的⽅法分类的三种排序算法:冒泡排序冒泡排序对⼀个需要进⾏排序的数组进⾏以下操作:1. ⽐较第⼀项和第⼆项;2. 如果第⼀项应该排在第⼆项之后, 那么两者交换顺序;3. ⽐较第⼆项和第三项;4. 如果第⼆项应该排在第三项之后, 那么两者交换顺序;5. 以此类推直到完成排序;实例说明:将数组[3, 2, 4, 5, 1]以从⼩到⼤的顺序进⾏排序:1. 3应该在2之后, 因此交换, 得到[2, 3, 4, 5, 1];2. 3, 4顺序不变, 4, 5也不变, 交换5, 1得到[2, 3, 4, 1, 5];3. 第⼀次遍历结束, 数组中最后⼀项处于正确位置不会再有变化, 因此下⼀次遍历可以排除最后⼀项;4. 开始第⼆次遍历, 最后结果为[2, 3, 1, 4, 5], 排除后两项进⾏下⼀次遍历;5. 第三次遍历结果为[2, 1, 3, 4, 5];6. 最后得到[1, 2, 3, 4, 5], 排序结束;代码实现:function swap(items, firstIndex, secondIndex){var temp = items[firstIndex];items[firstIndex] = items[secondIndex];items[secondIndex] = temp;};function bubbleSort(items){var len = items.length, i, j, stop;for (i = 0; i < len; i++){for (j = 0, stop = len-i; j < stop; j++){if (items[j] > items[j+1]){swap(items, j, j+1);}}}return items;}外层的循环决定需要进⾏多少次遍历, 内层的循环负责数组内各项的⽐较, 还通过外层循环的次数和数组长度决定何时停⽌⽐较.冒泡排序极其低效, 因为处理数据的步骤太多, 对于数组中的每n项, 都需要n^2次操作来实现该算法(实际⽐n^2略⼩, 但可以忽略, 具体原因见 ),即时间复杂度为O(n^2).对于含有n个元素的数组, 需要进⾏(n-1)+(n-2)+...+1次操作, ⽽(n-1)+(n-2)+...+1 = n(n-1)/2 = n^2/2 - n/2, 如果n趋于⽆限⼤, 那么n/2的⼤⼩对于整个算式的结果影响可以忽略, 因此最终的时间复杂度⽤O(n^2)表⽰选择排序选择排序对⼀个需要进⾏排序的数组进⾏以下操作:1. 假定数组中的第⼀项为最⼩值(min);2. ⽐较第⼀项和第⼆项的值;3. 若第⼆项⽐第⼀项⼩, 则假定第⼆项为最⼩值;4. 以此类推直到排序完成.实例说明:将数组["b", "a", "d", "c", "e"]以字母a-z的顺序进⾏排序:1. 假定数组中第⼀项"b"(index0)为min;2. ⽐较第⼆项"a"与第⼀项"b", 因"a"应在"b"之前的顺序, 故"a"(index1)为min;3. 然后将min与后⾯⼏项⽐较, 由于"a"就是最⼩值, 因此min确定在index1的位置;4. 第⼀次遍历结束后, 将假定的min(index0), 与真实的min(index1)进⾏⽐较, 真实的min应该在index0的位置, 因此将两者交换, 第⼀次遍历交换之后的结果为["a", "b", "d", "c", "e"];5. 然后开始第⼆次遍历, 遍历从第⼆项(index1的位置)开始, 这次假定第⼆项为最⼩值, 将第⼆项与之后⼏项逐个⽐较, 因为"b"就在应该存在的位置, 所以不需要进⾏交换, 这次遍历之后的结果为"a", "b", "d", "c", "e"];6. 之后开始第三次遍历, "c"应为这次遍历的最⼩值, 交换index2("d"), index3("c")位置, 最后结果为["a", "b", "c", "d", "e"];7. 最后⼀次遍历, 所有元素在应有位置, 不需要进⾏交换.代码实现:function swap(items, firstIndex, secondIndex){var temp = items[firstIndex];items[firstIndex] = items[secondIndex];items[secondIndex] = temp;};function selectionSort(){let items = [...document.querySelectorAll('.num-queue span')].map(num => +num.textContent);let len = items.length, min;for (i = 0; i < len; i++){min = i;for(j = i + 1; j < len; j++){if(items[j] < items[min]){min = j;}}if(i != min){swap(items, i, min);}}return items;};外层循环决定每次遍历的初始位置, 从数组的第⼀项开始直到最后⼀项. 内层循环决定哪⼀项元素被⽐较.选择排序的时间复杂度为O(n^2).插⼊排序与上述两种排序算法不同, 插⼊排序是稳定排序算法(stable sort algorithm), 稳定排序算法指不改变列表中相同元素的位置, 冒泡排序和选择排序不是稳定排序算法, 因为排序过程中有可能会改变相同元素位置. 对简单的值(数字或字符串)排序时, 相同元素位置改变与否影响不是很⼤.⽽当列表中的元素是对象, 根据对象的某个属性对列表进⾏排序时, 使⽤稳定排序算法就很有必要了.⼀旦算法包含交换(swap)这个步骤, 就不可能是稳定的排序算法. 列表内元素不断交换, ⽆法保证先前的元素排列为⽌⼀直保持原样. ⽽插⼊排序的实现过程不包含交换, ⽽是提取某个元素将其插⼊数组中正确位置.插⼊排序的实现是将⼀个数组分为两个部分, ⼀部分排序完成, ⼀部分未进⾏排序. 初始状态下整个数组属于未排序部分, 排序完成部分为空.然后进⾏排序, 数组内的第⼀项被加⼊排序完成部分, 由于只有⼀项, ⾃然属于排序完成状态. 然后对未完成排序的余下部分的元素进⾏如下操作:1. 如果这⼀项的值应该在排序完成部分最后⼀项元素之后, 保留这⼀项在原有位置开始下⼀步;2. 如果这⼀项的值应该排在排序完成部分最后⼀项元素之前, 将这⼀项从未完成部分暂时移开, 将已完成部分的最后⼀项元素移后⼀个位置;3. 被暂时移开的元素与已完成部分倒数第⼆项元素进⾏⽐较;4. 如果被移除元素的值在最后⼀项与倒数第⼆项的值之间, 那么将其插⼊两者之间的位置, 否则继续与前⾯的元素⽐较, 将暂移出的元素放置已完成部分合适位置. 以此类推直到所有元素都被移⾄排序完成部分.实例说明:现在需要将数组var items = [5, 2, 6, 1, 3, 9];进⾏插⼊排序:1. 5属于已完成部分, 余下元素为未完成部分. 接下来提取出2, 因为5⽐2⼤, 于是5被移⾄靠右⼀个位置, 覆盖2, 占⽤2原本存在的位置. 这样本来存放5的位置(已完成部分的⾸个位置)就被空出, ⽽2在⽐5⼩, 因此将2置于这个位置, 此时结果为[2, 5, 6, 1, 3, 9];2. 接下来提取出6, 因为6⽐5⼤, 所以不操作提取出1, 1与已完成部分各个元素(2, 5, 6)进⾏⽐较, 应该在2之前, 因此2, 5, 6各向右移⼀位, 1置于已完成部分⾸位, 此时结果为[1, 2, 5, 6, 3, 9];3. 对余下未完成元素进⾏类似操作, 最后得出结果[1, 2, 3, 5, 6, 9];代码实现:function insertionSort(items) {let len = items.length, value, i, j;for (i = 0; i < len; i++) {value = items[i];for (j = i-1; j > -1 && items[j] > value; j--) {items[j+1] = items[j];}items[j+1] = value;}return items;};外层循环的遍历顺序是从数组的第⼀位到最后⼀位, 内层循环的遍历则是从后往前, 内层循环同时负责元素的移位.插⼊排序的时间复杂度为O(n^2)以上三种排序算法都⼗分低效, 因此实际应⽤中不要使⽤这三种算法, 遇到需要排序的问题, 应该⾸先使⽤JavaScript内置的⽅法Array.prototype.sort();参考:1.2.。

快速排序常见三种写法

快速排序常见三种写法排序的基本知识排序是很重要的，⼀般排序都是针对数组的排序，可以简单想象⼀排贴好了标号的箱⼦放在⼀起，顺序是打乱的因此需要排序。

排序的有快慢之分，常见的基于⽐较的⽅式进⾏排序的算法⼀般有六种。

冒泡排序（bubble sort）选择排序（selection sort）插⼊排序（insertion sort）归并排序（merge sort）堆排序（heap sort）快速排序（quick sort）前三种属于⽐较慢的排序的⽅法，时间复杂度在O(n2)级别。

后三种会快⼀些。

但是也各有优缺点，⽐如归并排序需要额外开辟⼀段空间⽤来存放数组元素，也就是O(n)的空间复杂度。

快速排序的三种实现这⾥主要说说快速排序，通常有三种实现⽅法：顺序法填充法交换法下⾯的代码⽤java语⾔实现可以⽤下⾯的测试代码，也可以参考⽂章底部的整体的代码。

public class Test {public static void main(String[] args) {int[] nums = {7,8,4,9,3,2,6,5,0,1,9};QuickSort quickSort = new QuickSort();quickSort.quick_sort(nums, 0, nums.length-1);System.out.println(Arrays.toString(nums));}}递归基本框架所有的快速排序⼏乎都有着相同的递归框架，先看下代码public void quick_sort(int[] array, int start, int end) {if(start < end){int mid = partition(array, start, end);quick_sort(array, start, mid-1);quick_sort(array, mid+1, end);}}代码有如下特点因为快速排序是原地排序（in-place sort），所以不需要返回值，函数结束后输⼊数组就排序完成传⼊quick_sort函数的参数有数组array，起始下标start和终⽌下标end。

关于“主键-次键”排序的三种方法比较。

关于“主键-次键”排序的三种⽅法⽐较。

⾃⼰给⾃⼰放了七天假，回家休息⼀下。

在家懒，七天就写了300多⾏代码，还质量不⾼...在《计算机编程艺术——vlo3》中（以下简称Art3），在排序内容前⾔的习题中谈到关于带主键和次键的排序问题，其实就类似与字符串的排序⽅式，即⽐完主键看次键1，再次键2...。

三种⽅法： A：先按主键排序，再在排完序的序列⾥将主键相同的划分为⼀个个区域，再⽐较次键1，递归的进⾏下去，直到次键全部⽐较完或区域中只剩下⼀个元素。

B：先以最⼩的次键n排序，再以次键n-1排序，...⼀直到主键。

C：排序时⽐较是以字典排序法⽐较，⼀次搞定。

以下是我的实现和测试代码：代码1/*对于具有主键（唯⼀）和次键（>=0）的排序，有三种⽅式：2 1.先对主键进⾏排序进⾏分组，在每个分组内再依次对各个次键进⾏排序分组3 2.先对优先级最低的键进⾏排序，然后再逐步上升4 3.对于排序的元素⽐较⽅式是字典排序法56注意：要使三种排序的结果⼀致，前提条件是排序是稳定的。

78实验表明三种⽅案中，C（字典排序法）是最稳定的，效率最⾼的。

9 */10//for timeval and gettimeofday11#include<sys/time.h>1213 #include<stdio.h>14 #include<stdlib.h>1516#define A 117#define B 218#define C 31920 typedef21struct22 {23int keys[100];24 }elem;2526//记录三种策略的总时间（单位usec）27 unsigned int total_A_u=0;28 unsigned int total_B_u=0;29 unsigned int total_C_u=0;3031323334 typedef int (*msort_func)(void* a,void* b,int at);3536//merge sort 保证排序的稳定性37//参数：38// array为代排序的序列39// n序列元素的个数40// size序列元素的⼤⼩41// f为⽐较函数42//43void msort(elem** array,size_t n,int key_num,msort_func f);4445//模拟情形1：已经排好序的序列，但序列中的元素数值是随机的46void sorted_random(elem** pe,unsigned int n,int key_num);47//模拟情景2：完全反序48void res_sorted_random(elem** pe,unsigned int n,int key_num);49//模拟情景3：完全随机50void unsorted(elem** pe,unsigned int n,int key_num);5152//分析函数：统计分析每⼀种情形下的三种排序⽅法的复杂度：53// 1.⽐较次数54// 2.总时间55void analysis(elem** pe,unsigned int n,int key_num,int type);565758void print_keys(elem** pe,int n,int key_num)59 {60int i,j;61for(i=0;i<n;i++)62 {63 printf("The %dth element is:",i+1);64for(j=0;j<key_num;j++)65 {66 printf("%d ",pe[i]->keys[j]);67 }68 printf("\n");69 }70 }7172int sort_func(void* a ,void * b,int at)73 {74 elem *x = (elem*)a;75 elem *y = (elem*)b;76return (x->keys[at]-y->keys[at]);77 }7879int main()80 {81 unsigned int elem_num;82 scanf("%u",&elem_num);83 elem **pelems = (elem**)malloc(sizeof(elem*)*elem_num);84int i;85for(i=0;i<elem_num;i++)86 pelems[i]=(elem*)malloc(sizeof(elem));87int key_num;88for(key_num=10;key_num<=30;key_num++)89 {90 sorted_random(pelems,elem_num,key_num);91 printf("SORTED:\n");92 print_keys(pelems,elem_num,key_num);93 analysis(pelems,elem_num,key_num,A);94 analysis(pelems,elem_num,key_num,B);95 analysis(pelems,elem_num,key_num,C);9697 res_sorted_random(pelems,elem_num,key_num);98 printf("RES SORTED\n");99 print_keys(pelems,elem_num,key_num);100 analysis(pelems,elem_num,key_num,A);101 analysis(pelems,elem_num,key_num,B);102 analysis(pelems,elem_num,key_num,C);103104 unsorted(pelems,elem_num,key_num);105 printf("RANDOM\n");106 print_keys(pelems,elem_num,key_num);107 analysis(pelems,elem_num,key_num,A);108 analysis(pelems,elem_num,key_num,B);109 analysis(pelems,elem_num,key_num,C);110111 printf("Total time of A:%ld B:%ld C:%ld\n",total_A_u,total_B_u,total_C_u); 112 }113for(i=0;i<elem_num;i++)114 free(pelems[i]);115 free(pelems);116return0;117 }118119void msort(elem** array,size_t n,int key_num,msort_func f)120 {121if(n<=1)122return;123int mid = n/2;124 msort(array,mid,key_num,f);125 msort(array+mid,n-mid,key_num,f);126127 elem** tmp = (elem**)malloc(n*sizeof(elem*));128int i,j,k;129 k=i=0;j=mid;130while(i<mid && j<n)131 {132//[i] > [j]133if(f(array[i],array[j],key_num)>0)134 {135 tmp[k]=array[j];136 j++;137 }138//[i] <= [j]139else140 {141 tmp[k]=array[i];142 i++;143 }144 k++;146if(k!=n)147 {148if(i<mid)149 {150while(i<mid)151 tmp[k++]=array[i++];152 }153else154 {155while(j<n)156 tmp[k++]=array[j++];157 }158 }159for(i=0;i<n;i++)160 array[i]=tmp[i];161 }162163 inline unsigned int gen_rand(unsigned int last)164 {165static unsigned int add=0;166 add+=last;167 srand(time(NULL)+(add));168return rand();169 }170171void sorted_random(elem** pe,unsigned int n,int key_num) 172 {173int at =0;174for(;at<key_num;at++)175 {176int highest = 10000;177 unsigned int remain = n;178int now =0;179 unsigned int last =0;180while(remain)181 {182 last=gen_rand(last);183if((last%highest)<remain)184 {185 pe[n-remain]->keys[at]=now;186 remain--;187 }188else189 {190 now++;191 highest--;192 }193 }194 }195 }196197198199200void res_sorted_random(elem** pe,unsigned int n,int key_num) 201 {202int at =0;203for(;at<key_num;at++)204 {205int highest = 10000;206 unsigned int remain = n;207int now =0;208 unsigned int last=0;209while(remain)210 {211 last=gen_rand(last);212if((last%highest)<remain)213 {214 pe[remain-1]->keys[at]=now;215 remain--;216 }217else218 {219 now++;220 highest--;221 }222 }223 }224 }225void unsorted(elem** pe,unsigned int n,int key_num)226 {227int at =0;228for(;at<key_num;at++)230int highest = 10000;231int i;232 unsigned int last=0;233for(i=0;i<n;i++)234 {235 last=gen_rand(last);236 pe[i]->keys[at]=(last%highest);237 }238 }239 }240241void plan_A(elem** pelems,unsigned int n,int key_num,int now) 242 {243if(now==key_num || n==1)244return;245 msort(pelems,n,now,sort_func);246int group_val = (*pelems)->keys[now];247int i=1;248 elem** group=pelems;249 elem** end = pelems+n;250while(group+i!=end)251 {252if(pelems[i]->keys[now]==group_val)253 {254 i++;255 }256else257 {258 plan_A(group,i,key_num,now+1);259 group+=i;260 i=1;261if(group!=end)262 group_val = (*group)->keys[now];263 }264 }265 }266void plan_B(elem** pelems,unsigned int n,int key_num)267 {268 elem ** tpelems = (elem**)malloc(sizeof(elem*)*n);269int i;270for(i=0;i<n;i++)271 tpelems[i]=pelems[i];272int now = key_num-1;273while(now>=0)274 {275 msort(tpelems,n,now,sort_func);276 now--;277 }278279 print_keys(tpelems,n,key_num);280 free(tpelems);281 }282int sort_func_C(void* a,void* b,int key_num)283 {284 elem* x = (elem*)a;285 elem* y = (elem*)b;286int i;287for(i=0;i<key_num;i++)288 {289if(x->keys[i]!=y->keys[i])290return (x->keys[i]-y->keys[i]);291 }292return0;293 }294void plan_C(elem** pelems,unsigned int n,int key_num)295 {296 elem ** tpelems = (elem**)malloc(sizeof(elem*)*n);297int i;298for(i=0;i<n;i++)299 tpelems[i]=pelems[i];300301 msort(tpelems,n,key_num,sort_func_C);302 print_keys(tpelems,n,key_num);303 free(tpelems);304 }305306307308309void analysis(elem** pelems,unsigned int n,int key_num,int type) 310 {311struct timeval tv1;312struct timeval tv2;313 unsigned long micro_time_passed;314switch(type)315 {316case A:317 {318 gettimeofday(&tv1,NULL);319320 elem ** tpelems = (elem**)malloc(sizeof(elem*)*n);321int i;322for(i=0;i<n;i++)323 tpelems[i]=pelems[i];324325 plan_A(tpelems,n,key_num,0);326327 print_keys(tpelems,n,key_num);328 free(tpelems);329330 gettimeofday(&tv2,NULL);331332 micro_time_passed=(__sec)*1000+(__usec)/1000;333 total_A_u+=(__usec + (__sec)*1000000);334 printf("plan A cost %ld micro seconds sec:%ld usec %ld\n",micro_time_passed,(__sec),(__usec));335break;336337 }338case B:339 {340 gettimeofday(&tv1,NULL);341342 plan_B(pelems,n,key_num);343344 gettimeofday(&tv2,NULL);345346 micro_time_passed=(__sec)*1000+(__usec)/1000;347348 total_B_u+=(__usec + (__sec)*1000000);349 printf("plan B cost %ld micro seconds sec:%ld usec %ld\n",micro_time_passed,(__sec),(__usec));350break;351 }352case C:353 {354 gettimeofday(&tv1,NULL);355356 plan_C(pelems,n,key_num);357358 gettimeofday(&tv2,NULL);359360 micro_time_passed=(__sec)*1000+(__usec)/1000;361362 total_C_u+=(__usec + (__sec)*1000000);363 printf("plan C cost %ld micro seconds sec:%ld usec %ld\n",micro_time_passed,(__sec),(__usec));364break;365 }366 }367 }368369 从测试结果来看，毫⽆疑问：肯定是第三种⽅法平均效率最⾼，但我⼀直以为⽅法B凭借着⽅法的简单性，要⽐⽅法A要快，可是实际上必不是如此...究其原因应该是B⽅法太呆板，⽆论源数据是什么情况全都是⼀股脑的从n键排到主键。