高三综合题强化训练1

合集下载

重庆市2024届高三下学期强化训练(一)物理含答案

重庆市2024届高考强化一考卷物理（答案在最后）一、单项选择题：本题共7小题，每小题4分，共28分。

在每小题给出的四个选项中，只有一项符合题目要求。

1.如图所示，风对帆面的作用力F 垂直于帆面，它能分解成两个分力12F F 、，其中2F 垂直于航向，会被很大的横向阻力平衡，1F 沿着航向，提供动力。

若帆面与航向之间的夹角为θ，下列说法正确的是（）A.21tan F F θ=B.sin F F θ=₂C.船受到的横向阻力为cos FθD.船前进的动力为2tan F θ2.地球本身是一个大磁体，其磁场分布如图所示。

目前学术界对于地磁场的形成机制尚无共识。

一种理论认为地磁场主要源于地表电荷随地球自转产生的环形电流。

基于此理论，下列判断正确的是（）A.地表电荷为正电荷B.若地球自转角速度减小，则地表上任一位置的磁感应强度均减小C.地球赤道上方各点处地磁场的磁感应强度相同D.赤道上穿过地表单位面积的磁通量比两极处大3.如图所示，从左往右看，各线圈在匀强磁场中绕轴匀速顺时针转动，从图示位置开始计时，设电流从2流出线圈为正方向，能产生图甲所示交变电流的是（）A.线圈平面与磁场垂直B.线圈平面与磁场平行C.线圈平而与磁场垂直D.线圈平面与磁场平行4.“场离子显微镜”的金属钨针尖处于球形真空玻璃泡的球心O ，玻璃泡内壁有一层均匀导电膜：在钨针和导电膜间加上高电压后，玻璃泡上半部分的电场线如图所示。

a 、b 、c 、d 、O 为同一平面上的5个点，abc 是一段以O 为圆心半径为r 的圆弧，d 为Ob 的中点。

O 、a 、b 、c 、d 五点场强分别为E O 、E a 、E b 、E c 、E d ，电势分别为φO 、φa 、φb 、φc 、φd ，则下面说法正确的是（）A.a 、b 、c 三点场强相同B.d a c b ϕϕϕϕ<==C.()2()O a O d ϕϕϕϕ-<- D.()2d b d R E ϕϕ-=⋅5.如图所示，某种材料制成太阳能电池的主体部分由P 型半导体和N 型半导体结合而成。

2020-2021年高考化学一轮易错点强化训练：化学反应原理综合题01【含答案】

2020-2021年高考化学一轮易错点强化训练：化学反应原理综合题011．（2020·贵州铜仁高三三模）CO和H2的混合气体俗称合成气，是一种重要的工业原料气。

工业上利用天然气(主要成分为CH4)与水进行高温重整制备合成气。

（1）已知：CH4、H2和CO 的燃烧热(ΔH)分别为−890.3 kJ/mol、−285.8 kJ/mol和−283.0kJ/mol，且1 mol 液态水汽化时的能量变化为44.0 kJ。

则甲烷与水蒸气在高温下反应制取合成气的热化学方程式为_______。

（2）在一定温度下，向体积为2L的密闭容器中充入0.40 mol CH4(g)和0.60 mol H2O (g)，测得CH4(g)和H2(g)的物质的量浓度随时间变化如表所示：①计算该反应第一次达平衡时的平衡常数K=_____。

②3 min时改变的反应条件可能是_____。

（3）已知温度、压强、投料比X[n(CH4)/n(H2O)]对该反应的影响如图所示。

①图1中的两条曲线所示的投料比的关系：X1____X2(填“=”“＞”或“＜”，下同)。

②图2中两条曲线所示的压强的关系：p1_______ p2。

（4）以合成气为原料可以制备二甲醚，将n(H2):n(CO)=3:1 投入体积固定密闭容器中发生反应：3CO(g)+3H2(g)⇌CH3OCH3(g)+CO2(g) ΔH＜0，2 分钟达平衡。

升温，反应重新达平衡。

下列关于两次平衡的比较中正确的是_______。

A．H2体积分数不变B．CO 体积分数增大C．混合气体平均摩尔质量不变D．反应速率和平衡常数均增大（5）以二甲醚(设杂质不参与反应)、KOH溶液为原料可设计成燃料电池：①放电时，负极的电极反应式为________。

②设装置中盛有100.0 mL 3.0 mol/L KOH 溶液，放电时参与反应的氧气在标准状况下的体积为6.72 L，放电过程中没有气体逸出，则放电完毕后，所得溶液中各离子浓度由大到小的关系为_______。

2021届河北省唐山市玉田县第一中学高三下学期5月三轮强化练物理试题(解析版)

河北省唐山市玉田县第一中学2021届高三下学期5月三轮强化训练（一）注意事项：一、单项选择题：本题共7小题，每小题4分，共28分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 如图为玻尔解释氢原子光谱画出的氢原子能级图，一群处于n=4激发态的氢原子，当它们自发地跃迁到较低能级时，以下说法符合玻尔理论的是A.这群氢原子跃迁时最多可产生3种不同频率的光子B.核外电子的轨道半径减小、动能增大,电势能变小,总能量不变C.由n=4能级跃迁到n=1能级时发出光子的波长最短D.已知金属钾的逸出功为2.25eV，从n=3能级跃迁到n=2能级释放的光子可使金属钾发生光电效应2.跳伞运动被视为“勇敢者的运动”，惊险又刺激。

在一次跳伞训练中，一名跳伞运动员打开降落伞后，先减速下降一段时间，此后匀速向下直线运动下列说法正确的是A.在减速下降阶段，下降同样的高度，运动员的动能变化量可能不相等B.在减速下降阶段，下降同样的高度，运动员的重力势能变化量不相等C.在匀速下降阶段，运动员所受合外力为零机械能守恒D.在匀速下降阶段，运动员的重力势能不变3. 一辆汽车从静止开始以恒定功率启动，汽车受到的阻力恒定，则在汽车加速运动过程中（）A 、汽车克服阻力做功的功率恒定B 、汽车克服阻力做功的功率越来越小C 、汽车合力做功的功率恒定D 、汽车合力做功的功率越来越小4.如图所示，一个质量为m ，带电量为+q 的粒子在匀强电场中运动，依次通过等腰直角三角形的三个顶点A 、C 、B ，粒子在A 、B 两点的速率均为v 0，在C 点的速率为055v ，已知AC=d ，匀强电场在ABC 平面内，粒子仅受电场力作用。

则A. 场强方向垂直于AB 背离 C 场强大小为2038mv qdB. 场强方向垂直于AB 指向C 场强大小为2225mv qdC. 场强方向垂直于AB 指向C 场强大小为2038mv qdD. 场强方向垂直于AB 背离 C 场强大小为222mv5.如图所示，一倾角为30°的斜面固定在水平地面上，一质量为M 的物块A 放在斜面上恰好不下滑。

高考生物二轮专题强化训练1 细胞的基本组成

高考生物二轮专题强化训练训练1 细胞的基本组成一、选择题1．关于如下四图的叙述中，不正确的是()A．图甲和图丙分别是生命活动主要承担者和遗传信息携带者的基本单位B．图乙小麦种子在晒干过程中所失去的水是结合水C．若图丙中a为脱氧核糖，则m有A、T、C、G四种D．在小鼠的体细胞内检测到的化合物丁很可能是乳糖2．分子伴侣是一类能循环发挥作用，协助多肽折叠、组装、转运、降解等生理活动的蛋白质。

Hsp70蛋白是分子伴侣系统的核心成员之一，包括核苷酸结合结构域和底物结合结构域，通过核苷酸结合结构域水解ATP引发自身构象改变，实现底物结合结构域与蛋白质结合进行生理活动。

下列说法错误的是()A．Hsp70蛋白的核苷酸结合结构域可特异性识别腺苷三磷酸B．与无机催化剂相比，Hsp70蛋白降低活化能的作用更显著C．Hsp70蛋白的空间结构一旦发生改变，会永久失活D．变性后的Hsp70蛋白与双缩脲试剂反应呈紫色3．载脂蛋白apoA－1是一种血浆蛋白，主要在肝脏合成，基本功能是运载脂类物质，其含量下降会导致胆固醇在血管中堆积，形成动脉粥样硬化。

下列叙述错误的是()A．胆固醇与磷脂一样都参与动物细胞膜的构成B．核糖体合成的多肽链在高尔基体中形成一定的空间结构C．载脂蛋白apoA－1是内环境成分之一，其含量变化会影响内环境的稳态D．apoA－1的空间结构改变可能导致动脉粥样硬化4．科研人员从某生物体内提取出一个核酸分子，经过检测，该分子中鸟嘌呤(G)的数量与胞嘧啶(C)的数量不相等。

据此分析，下列叙述正确的是()A．该生物体不具有细胞结构B．该核酸彻底水解产物中有两种不含氮C．该分子中G与C之间无法形成氢键D．该生物体内氢键的数量等于碱基的数量5．研究人员发现了一种感染兔子的新型病毒，现利用放射性同位素标记的方法，以体外培养的兔子细胞为材料，设计可相互印证的A、B两组实验，以确定该病毒的核酸类型。

下列有关实验设计思路的叙述，错误的是()A．先将A、B两组兔子细胞分别培养在含同位素标记的尿嘧啶或胸腺嘧啶的培养基中B．应选用35S、32P分别标记该病毒的蛋白质和核酸C．再将病毒分别接种到含有A、B两组兔子细胞的培养液中D．一定时间后离心并收集、检测病毒的放射性，以确定病毒的类型6．糖组是一个生物体或细胞中全部糖类的总和，包括简单的糖类和缀合的糖类。

高考数学强化复习训练精选题及答案

高三数学强化训练（1）1. 若集合M=｛y | y =x -3｝，P=｛y | y =33-x ｝，则M∩P=A ｛y | y >1｝B ｛y | y ≥1｝C ｛y | y >0｝D ｛y | y ≥0｝2210,(0)ax x a ++=≠有一个正根和一个负根的充分不必要条件是：A ．0a <B ．0a >C ．1a <-D ．1a > 3. 设命题甲:0122>++ax ax 的解集是实数集R;命题乙:10<<a ,则命题甲是命题乙成立的A . 充分非必要条件 B.必要非充分条件C. 充要条件D. 既非充分又非必要条件4. 函数f(x)=⎩⎨⎧∈-∈,,,,M x x P x x 其中P ，M 为实数集R 的两个非空子集，又规定f(P)={y|y=f(x),x ∈P}，f(M)={y|y=f(x),x ∈M}.给出下列四个判断：①若P∩M=∅，则f(P)∩f(M)=∅； ②若P∩M≠∅，则f(P)∩f(M) ≠∅；③若P ∪M=R ，则f(P)∪f(M)=R ； ④若P ∪M≠R ，则f(P) ∪f(M)≠R.其中正确判断有A 0个B 1个C 2个D 4个5. 已知全集U {}5,4,3,2,1=，A {}3,1=，B {}4,3,2=，那么=⋃)(B C A U ___. 6. 设二次函数)0()(2≠++=a c bx ax x f ，若)()(21x f x f =（其中21x x ≠），则)2(21x x f +等于 _____. 022>++bx ax 的解集为)31,21(-，求b a +的值8. 已知集合A {}0652=+-=x x x ，B {}01=+mx x ，且A B A =⋃，求实数m 的值组成的集合。

参考答案(一)CBBB. {}5,3,1, ab ac 442- 7. 由题意知方程022=++bx ax 的两根为31,2121=-=x x ，又⎪⎪⎩⎪⎪⎨⎧=-=+a x x a b x x 22121，即⎪⎪⎩⎪⎪⎨⎧=⨯--=+-aa b 231213121，解得⎩⎨⎧-=-=212b a ， 14-=+∴b a 8.{}{}A B A B A x x x A ⊆∴=⋃==+-=,,3,20652 ① A B B m ⊆Φ==,,0时；② 0≠m 时，由mx mx 1,01-==+得。

2014届高三理综化学“7 5”专题强化训练(1)

理综化学7+5（一）7．14C常用于测定生物遗骸的年份。

下列说法中正确的是（）A．14C相对原子质量等于14 B．14C与12C互为同分异构体C．14C与C60互为同素异形体D．14C与14N中子数一定不同8．世界上60％的镁是从海水中提取的，其主要步骤如下：①把贝壳制成生石灰；②在海水中加入生石灰，过滤，洗涤沉淀物；③将沉淀物与盐酸反应，结晶、过滤；④在氯化氢热气流中加热晶体；⑤电解上述所得盐（熔融条件下）。

下列说法正确的是（）A．向洗涤液中滴加碳酸钠溶液可检验沉淀是否洗涤干净B．上述变化过程中包括了分解、化合、复分解、置换等四种反应类型C．在氯化氢热气流中干燥晶体的目的是为了加快干燥速度D．步骤⑤也可以采用电解该盐水溶液的方法9．下列说法正确的是（）A．58.5g氯化钠中约含有6.02×1023个氯化钠分子B．1.4gC2H4中含有共用电子对的数目为0.3×6.02×1023C．在含4molSi—O键的石英晶体中，氧原子的数目为4×6.02×1023D．25℃时pH=1的醋酸溶液中含有H+的数目为0.1×6.02×102310、下列离子方程式表达正确的是（）A、将SO2通入次氯酸钠溶液中：SO2 + ClO－+H2O= SO32－+Cl-+2H+B、向三氯化铝溶液中滴入过量的浓氨水：Al3+ + 4NH3·H2O = AlO2－+ 4NH4+ +2H2OC、用KI、稀硫酸及淀粉检验碘盐中IO3－：IO3－+5I－+6H+ = 3I2+3H2OD、用两根铜棒电解稀盐酸：2H+ + 2Cl－H2↑ + Cl2↑11、相对分子质量为100的烃完全燃烧后，生成CO2和H2O的物质的量之比以及分子结构中有四个甲基的同分异构体的数目分别是（）A．6：7和2 B．6：7和3 C．7：8和3 D．7：8和4 12．—定质量的Al、Mg合金与适量的稀硫酸恰好完全反应，将反应后的溶液蒸干，所得固体(不含结晶水)质量比原固体增加了7.2g，则该合金的物质的量可能为（）A．0. 06mol B．0. 05mol C．0.08mol D．0.09mol13．下列说法正确的是（）A．分别在0.1mol/L的盐酸和0.1mol/L的NaOH溶液中加入足量铝粉，后者产生的H2多B．通常情况下，溴是液态，碘是固态，所以I—I键比Br-Br强C．向K2SO4溶液中滴加盐酸，得到PH=3的溶液，则溶液中c（K+）=2c（SO2-4）D．PCl5分子中各原子最外层都满足8电子稳定结构26．（14分）R、W、X、Y、Z是五种短周期元素，原子序数逐渐增大，R与W可组成某有机物，W与Y、X与Y组成的化合物是机动车排出的大气污染物，Y和Z能形成原子个数比为1：1和l：2的两种离子化合物。

2021年高三上学期第二次强化训练理科综合能力测试化学试题含答案

2021年高三上学期第二次强化训练理科综合能力测试化学试题含答案第丨卷（选择题共42分）一•选择题（本大题共7小題，每小题6分，共42分。

在每小题给出的四个选项中，只有一项是符合题目要求的）仁含NaOH 20. 0g的稀溶液与足量的稀盐酸反应，放出28. ZkJ 的热量，表示该反应中和热的热化学方程式正确的是（A.NaOH+HCI—NaCI+H2O(1)；AH=+2& 7kJ/mo 1B.NaOH+HCI—NaCI+H2O(1):AH= - 28. 7kJ/mo 1C.NaOH+HCI—NaCI+H20(1);AH 二+57. 4kJ/mo1D.NaOH+HCI—NaCI+H2OAH二一57. 4kJ/mol下列说法正确的是（A.7.1g氯气与足量的氢氧化钠溶液反应转移的电子束为0-2X6. 02X1023B.VLamol • U1的氯化铁溶液中'若的数目为6. 02X1023,则CI・的数目大于3X6. 02X1023C.标准状况下，22. 4LN0和11 • 21A混合后气体的分子总数为1.0X6. 02X1033D.工业用电解法进行粗铜精炼时，每转移lmol电子，阳极上溶解的铜原子数为0.5X6. 02X10353> lmol乙烯与Cl.完全加成后再与C1：发生最大程度的取代，两个过程共需C1, ）A. 3 mol B • 4 mol C. 5 mol D. 6 mol4、下列离子方程式正确的是（）A.O.Olmol/LNHiAl （S04） 2 溶液与0. 02mol/L Ba （OH） 2 溶液等体积混合:NHZ+A1X+2SO：•+2Ba*+4OH —2BaSO< I +A1 （OH） 31+NH3 • ILO—lOOO'C1200^0时间一1200*010009B. FeCl ：酸性溶液放在空气中变质：2Fe 3l +4H ++03—2Fe s++2HaOC. 用 CH»COOH 溶解 CaCO 9： CaC0#+2H +—Ca 3*+HaO+CO31D. 电解MgCla 水溶液的离子方程式：2Cr+2H 30H 3t+Clat+20H*5、已知X 、Y 、Z 、W 是原子序数依次增大的前四周期元素.X 最外层电子数是次外层电子数的3倍，Y 和W 同主族，且Y 是电负性最大的元索.Z 基态原子的M 层全充满，“层有1个电子•下列说法正确的是() A. X 、Y 均没有最高正价B. W 最高价氧化物的水化物是最强的含氧酸c. z 的焰色反应显紫色D.在XY ：中’X 显・2价6、下列实验设计能完成或实验结论合理的是()A. 证明一瓶红棕色气体是漠蒸气还是二氧化氮，可用湿润的碘化钾■淀粉试纸检验，观察试纸颜色的变化B •铝热剂溶于足量稀盐酸再滴加KSCN 溶液，未出现血红色，铝热剂中一定不含铁的氧化物C. 测氯水的pH,可用玻璃棒龍取氯水点在pH 试纸上，待其变色后和标准比色卡比较D. 用浓硫酸吸收二氧化硫中混有少量SO,气体7、已知：4NH3 (g) +502 (g) =4NO (g) +6H2O (g), A H=・ 1025kJ/mol,该反应是一个可逆反1000 V 有催化时间时间第I【卷三、非选择题：包括必考题和选考题两部分。

2013届高三文科数学专题强化训练附解析(一)

专题强化测评（一）A 组一、选择题1.(2011·江西高考)若全集U={1,2,3,4,5,6},M={2,3},N={1,4},则集合{5,6}等于( )(A)M ∪N (B)M ∩N (C)()()U U M N U 痧 (D)()()U U M N I 痧2.(2011·陕西高考)设a,b r r 是向量，命题“若a b,=-r r 则|a ||b |=r r ”的逆命题是( )(A)若a b ≠-r r ,则|a ||b |≠r r (B)若a b =-r r ,则|a ||b |≠r r(C)若|a ||b |≠r r ,则a b ≠-r r (D)若|a ||b |=r r ,则a b =-r r3.(2011·济南模拟)下列命题正确的是( )(A)“a=2”是“直线ax+2y=0平行于直线x+y=1”的充分不必要条件(B)“x=-1”是“x 2-5x-6=0”的必要不充分条件(C)命题“若x=y,则sinx=siny ”的逆否命题为真命题(D)命题“∃x ∈R 使得x 2+x+1＜0”的否定是：“∀x ∈R ，均有x 2+x+1＜0”4.(2011·杭州模拟)已知直线l 过定点(-1,1)，则“直线l 的斜率为0”是“直线l 与圆x 2+y 2=1相切”的( )(A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件5.(2011·蚌埠模拟)集合A={(x,y)|y=a,x ∈R}，集合B={(x,y)|y=b x +1,b ＞0,b ≠1},若集合A ∩B=Ø,则实数a 的取值范围是( )(A)(-∞,1］ (B)(-∞,1) (C)(1,+∞) (D)R6.命题“函数y=f(x)(x ∈M)是偶函数”的否定是( )(A)∃x ∈M,f(-x)≠f(x)(B)∀x ∈M,f(-x)≠f(x) (C)∀x ∈M,f(-x)=f(x) (D)∃x ∈M,f(-x)=f(x)7.已知命题p 1:函数y=2x -2-x 在R 上为增函数，p 2：函数y=2x +2-x 在R 上为减函数.则在命题q 1：p 1∨p 2,q 2：p 1∧p 2,q 3：(⌝p 1)∨p 2和q 4：p 1∧(⌝p 2)中，真命题是( )(A)q 1,q 3 (B)q 2,q 3 (C)q 1,q 4 (D)q 2,q 48.已知A ，B 均为集合U={1,3,5,7,9}的子集，且A ∩B={3},(U B ð)∩A={9},则A=( )(A){1,3} (B){3,7,9} (C){3,5,9} (D){3,9}9.已知p:2x1x1<-,q:(x-a)(x-3)>0,若⌝p是⌝q的必要不充分条件，则实数a的取值范围是( )(A)(-∞,1) (B)［1,3］(C)［1,+∞) (D)［3,+∞)10.定义差集A-B={x|x∈A,且x∉B}，现有三个集合A、B、C分别用圆表示，则集合C-(A-B)可表示下列图中阴影部分的为( )二、填空题11.(2011·陕西高考)设n∈N+，一元二次方程x2-4x+n=0有整数根的充要条件是n=____________.12.已知集合A={3,m2},B={-1,3,2m-1}.若A⊆B则实数m的值为________.13.(2011·淄博模拟)命题p:∃x∈R，x2+2x+a≤0.若命题p是假命题，则a的取值范围是______.(用区间表示)14.A、B是非空集合，定义A×B={x|x∈(A∪B)且x∉(A∩B)},若A={x|y=x},则A×B=__________.B组一、选择题1.(2011·山东高考)设集合M={x|x2+x-6<0},N={x|1≤x≤3}，则M∩N=( )(A)［1,2) (B)［1,2］(C)(2,3］(D)［2,3］2.(2011·安徽高考)命题“所有能被2整除的整数都是偶数”的否定是( )(A)所有不能被2整除的整数都是偶数(B)所有能被2整除的整数都不是偶数(C)存在一个不能被2整除的整数是偶数(D)存在一个能被2整除的整数不是偶数3.已知m、a都是实数，且a≠0,则“m∈{-a,a}”是“|m|=a”成立的( )(A)充分不必要条件(B)必要不充分条件(C)充分必要条件 (D)既不充分也不必要条件4.已知命题p:关于x 的函数y=x 2-3ax+4在［1,+∞)上是增函数，命题q:函数y=(2a-1)x 为减函数，若“p 且q ”为真命题，则实数a 的取值范围是( )(A)a ≤23 (B)0<a<12 (C)12<a ≤23 (D)12<a<1 5.已知命题p ：抛物线y=2x 2的准线方程为y=-12;命题q ：若函数f(x)为偶函数，则f(x-1)关于x=1对称，则下列命题是真命题的是( )(A)p ∧q (B)p ∨(⌝q) (C)( ⌝p)∧(⌝q) (D)p ∨q6.(2011·深圳模拟)已知a,b r r 是非零向量，则a r 与b r 不共线是|a b ||a ||b |+<+r r r r 的( )(A)充分非必要条件 (B)必要非充分条件(C)充分必要条件 (D)既非充分也非必要条件7.若集合M={1,m 2}，集合N={2，4}，M ∪N={1，2，4}，则实数m 的值的个数是( )(A)1 (B)2 (C)3 (D)4 8.已知A={x|-3≤x ≤2}，B={x|2m-1≤x ≤2m+1},且A ⊇B ，则实数m 的取值范围是 (A)(-1,12］ (B)［-1,12］ (C)［-1,12) (D)(-1,12) 9.对于复数a,b,c,d ，若集合S={a,b,c,d}具有性质“对∀x,y ∈S ，必有xy ∈S ”，则当22a 1b 1c b =⎧⎪=⎨⎪=⎩时,b+c+d 等于( )(A)1 (B)-1 (C)0 (D)i10.(2011·福建高考)在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为［k ］,即［k ］={5n+k|n ∈Z},k=0,1,2,3,4.给出如下四个结论：①2011∈［1］；②-3∈［3］;③Z=［0］∪［1］∪［2］∪［3］∪［4］; ④“整数a,b 属于同一类”的充要条件是“a-b ∈［0］”.其中，正确结论的个数是( )(A)1 (B)2 (C)3 (D)4二、填空题11.(2011·山东高考改编)已知a,b,c ∈R,命题“若a+b+c=3,则a 2+b 2+c 2≥3”的否命题是______.12.某班有学生60人，其中体育爱好者有32人，电脑爱好者有40人，还有7人既不爱好体育也不爱好电脑，则班上既爱好体育又爱好电脑的学生有_____人.13. (2011·济南模拟)在命题p的四种形式(原命题、逆命题、否命题、逆否命题)中，正确命题的个数记为f(p),已知命题p：“若两条直线l1：a1x+b1y+c1=0,l2：a 2x+b2y+c2=0平行，则a1b2-a2b1=0”，那么f(p)= __________.14. (2011·宿州模拟)给出下列命题：①已知a,b都是正数，且a1ab1b++＞，则a＜b;②当x∈(1,+∞)时，函数y=x3,y=12x的图像都在直线y=x的上方；③命题“∃x∈R，使得x2-2x+1＜0”的否定是真命题；④“x≤1，且y≤1”是“x+y≤2”的充要条件.其中正确命题的序号是______.(把你认为是正确命题的序号都填上)专题强化测评（一）A 组1.【解析】选D.由M={2,3},N={1,4}得,M ∪N={1,2,3,4},即U ð(M ∪N)={5,6},所以{5,6}=U ð(M ∪N)=(U M ð)∩(U N ð).故选D.2.【解析】选D.原命题的条件是a b =-r r ，作为逆命题的结论；原命题的结论是|a ||b |=r r ,作为逆命题的条件，即得逆命题“若|a ||b |=r r ,则a b =-r r ”，故选D.3.【解析】选C.选项A 中，“a=2”是“直线ax+2y=0平行于直线x+y=1”的充要条件，故A 不正确；选项B 中，“x=-1”是“x 2-5x-6=0”的充分不必要条件，故B 不正确；选项C 中，原命题为真命题，故逆否命题为真命题，故C 正确；选项D 中，原命题的否定是“∀x ∈R ，均有x 2+x+1≥0”，故D 不正确.4.【解析】选A.当直线l 的斜率为0时，直线l 与圆x 2+y 2=1相切，反之当直线l 与圆x 2+y 2=1相切时，直线l 的斜率可能为0，也可能不存在，故选A.5.【解析】选A.∵y=b x +1＞1,数形结合知当a ≤1时，A ∩B=Ø即a ∈(-∞，1］.6.【解析】选A.命题“函数y=f(x)(x ∈M)是偶函数”等价于“∀x ∈M,f(-x)=f(x)”是全称命题，故其否定为“∃x ∈M,f(-x)≠f(x)”.7.【解析】选C.p 1是真命题，则⌝p 1为假命题；p 2是假命题，则⌝p 2是真命题.∴命题q 1：p 1∨p 2是真命题，命题q 2：p 1∧p 2是假命题，命题q 3：(⌝p 1)∨p 2是假命题，命题q4：p 1∧(⌝p 2)是真命题.故真命题是q 1,q 4.8.【解析】选D.作出表示集合U ，A ，B 的Venn 图，可知：A=(A ∩B)∪(U B A I ð)={3}∪{9}={3,9}.故选D.9.【解析】选C.2x x 1100x 1x 1+-<⇒<-- ⇒(x-1)(x+1)<0⇒p:-1<x<1;当a ≥3时，q:x<3或x>a ；当a<3时，q:x<a 或x>3.⌝p 是⌝q 的必要不充分条件，即p 是q 的充分不必要条件，即p ⇒q 且q ¿p ，可推出a 的取值范围是a ≥1.10.【解析】选A.如图所示，A-B 表示图中阴影部分.故C-(A-B)所含元素属于C ，但不属于图中阴影部分，故选A.11.【解析】x 2==因为x 是整数，即2±为整数，所为整数，且n ≤4，又因为n ∈N +，取n=1，2，3，4，验证可知n=3，4符合题意；反之n=3，4时可推出一元二次方程x 2-4x+n=0有整数根.答案：3或412.∵A ⊆B,∴m 2=2m-1,或m 2=-1(舍).由m 2=2m-1得m=1.经检验m=1时符合题意.答案：113.因为p 是假命题，所以“∀x ∈R ，x 2+2x+a ＞0”为真命题，因此Δ=4-4a<0，解得a ＞1.14.【解析】{A x |y {x |x 0x 3}===≤≥或，B={y|y=3x }={y|y>0}， ∴A ∪B=R,A ∩B={x|x ≥3}，∴A ×B={x|x<3}.答案：{x|x<3}B 组1.【解析】选A.∵M={x|-3<x<2},∴M ∩N={x|1≤x ＜2}.2.【解】选D.全称命题的否定为相应的特称命题，即将所有变为存在，并且将结论进行否定.3.【解析】选B.若m ∈{-a,a},则a>0时|m|=a,a<0时，|m|=-a,若|m|=a,则m ∈{-a,a}一定成立.故“m ∈{-a,a}”是“|m|=a ”成立的必要不充分条件.4.【解析】选C.命题p 等价于3a 12≤,即2a .3≤命题q 等价于0<2a-1<1，即12<a<1.因为“p 且q ”为真命题，所以p 和q 均为真命题，故12a .23<≤ 5.【解析】选D.抛物线y=2x 2的准线方程为1y ,8=-故命题p 是假命题，函数y=f(x-1)图象是函数y=f(x)的图象向右平移1个单位得到的，故命题q 是真命题，∴命题p ∨q 是真命题.6.【解析】选A.若a r 与b r 不共线，则|a b ||a ||b |+<+r r r r 成立，反之，若|a b ||a ||b |+<+r r r r ，则a r 与b r 可能不共线也可能反向共线，故选A.7.【解析】选D.∵M ∪N={1，2，4}，∴m 2=2或m 2=4，∴m =m=±2,故选D.8.【解析】选B.∵A ⊇B,∴2m 132m 12-≥-⎧⎨+≤⎩，∴11m .2-≤≤ 9.【解析】选B.∵22a 1b 1c b =⎧⎪=⎨⎪=⎩,集合中的元素具有互异性，∴2a 1b 1,c 1⎧=⎪=-⎨⎪=-⎩∴(1)当a 1b 1c i =⎧⎪=-⎨⎪=⎩时，S={1,-1,i,d},又∵∀x,y ∈S ，必有xy ∈S,∴d=-i,∴b+c+d=-1;∴(2)当a1b1c i=⎧⎪=-⎨⎪=-⎩时,S={1,-1,-i,d},又∵∀x,y∈S,必有xy∈S,∴d=i,∴b+c+d=-1;综上所述：b+c+d=-1.10.【解析】选C.对于①:2011=5×402+1,∴2011∈［1］,对于②:-3=5×(-1)+2,∴-3∈［２］,故②不正确；对于③：∵整数集Z被5除，所得余数共分为五类. ∴Z=［0］∪［1］∪［2］∪［3］∪［4］,故③正确；对于④：若整数a,b属于同一类，则a=5n1+k,b=5n2+k,∴a-b=5n1+k-(5n2+k)=5(n1-n2)=5n,∴a-b∈［0］,若a-b∈［0］,则a-b=5n,即a=b+5n,故a与b被5除的余数为同一个数，∴a与b属于同一类，∴“整数a,b属于同一类”的充要条件是“a-b∈［0］”,故④正确，∴正确结论的个数是3.11.【解析】直接否定条件和结论可得，否命题为“若a+b+c≠3,则a2+b2+c2<3”.12.【解析】设既爱好体育又爱好电脑的学生有x人，画出Venn图，易得(32-x)+x+(40-x)+7=60.解之得x=19.13.【解析】由l1∥l2⇒a1b2-a2b1=0,但a1b2-a2b1=0¿l1∥l2，故命题p的原命题，逆否命题正确，但逆命题和否命题错误.∴f(p)=2.答案：214.【解析】①中，由a1a,b1b++＞a,b都是正数，得ab+b＞ab+a,即a＜b,故①正确；②中，当x∈(1,+∞)时，函数12y x=的图像在直线y=x的下方，故②不正确；③中原命题是假命题，故其否定是真命题，故③正确；④中“x≤1且y≤1”是“x+y ≤2”的充分不必要条件，故④不正确.答案：①③。

黑龙江省五常市2018届高三第一次强化训练语文试卷(附答案)

黑龙江省五常市2018届高三第一次强化训练语文一、现代文阅读（一）论述类文本阅读阅读下面的文字，完成下列小题。

我觉得，中国文化似乎有一个特征，是主体和客体往往会合而为一，按照今天的话来说，很像“行为艺术”。

它体现在操守、品行、生活方式、礼仪活动上，当我们看见天坛、地坛，还有那些巨大的青铜器时，也许我们就不难想象，古代那些祭祀的仪式该是多么的宏伟壮观。

孔子周游列国，在一个交通特别不发达、人对于距离相当敬畏的年代，一个人坐着马车上路，一个国家接一个国家地宣传他的理论，这不也正像行为艺术吗？《史记·刺客列传》中有这样一个故事：豫让曾臣事智伯，智伯死后他决意为其报仇，第一次刺杀赵襄子未果，被赵放了，豫让将自己毁容弄哑，企图再次刺杀。

朋友问：你要报仇，何苦用这种方法，尽可以假装臣服于赵乘机行刺。

豫让答：我不能为人臣怀二心。

第二次要刺杀赵时被抓住,赵问:你曾是范氏、中行氏的人,他们都被智伯杀死,你为什么只是忠于智伯?豫让答:他们是以奴仆待我,而智伯却是以国士待我,是有知遇之恩,我亦要以国士的品级回报。

豫让“请赵之衣而击之”后伏剑自杀。

豫让的忠诚有着人性、尊严、情感的美学内容,他的复仇也像是一个艺术仪式,只是这种艺术行为会在时间的流逝中消失,不可能客观地保存下来。

许多民间的习俗也是艺术化的。

我曾目睹过一场葬礼。

村子中最壮的十六个男子，先是喝酒，然后大喝一声“起杠”，拾起厚重无比的棺材出发了。

在后面跟随的，第一批是家中的男眷，他们用三寸的棍子拄地，弓着腰，发出低沉的呜咽的声音；接下来一批是家中的女眷，她们身披重孝以高音的啼泣诉说着。

艺术就是这样存在于我们的日常生活中的。

多年以来，这个场景在我的记忆中不断地翻新，让我联想起礼乐中的“乐”。

在莫言的《红高粱》中我也见到了相似的葬礼。

这种存在于中国人的日常生活中的艺术，同样依附于时间之上，随波逐流。

中国的诗词仿佛对水有一种特别的情感。

也许人们用“水”这个字眼的时候，正是在想象那些附在“水”上一去不返的东西，中国人似乎从来不在乎把一一些东西留下来，在他们的眼中，一切都是载在时间上，总在流逝，一旦欣赏之后享受之后，就只能撒手放开，随它去了。

2023届高三地理一轮复习同步选择题强化训练(1)---地球与地图基础知识

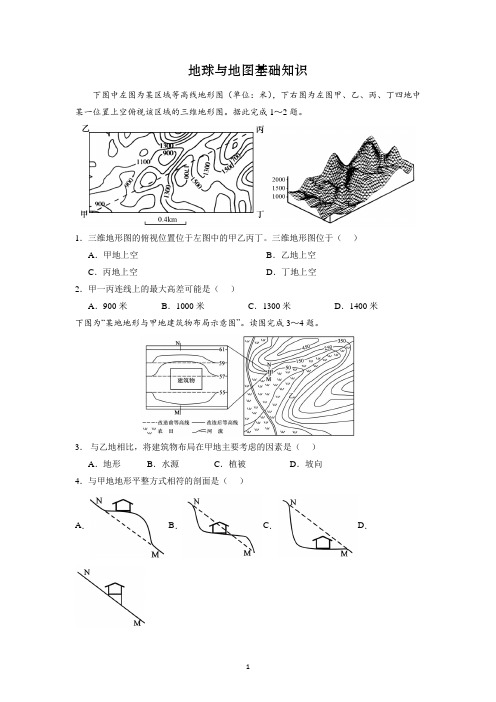
地球与地图基础知识下图中左图为某区域等高线地形图（单位：米），下右图为左图甲、乙、丙、丁四地中某一位置上空俯视该区域的三维地形图。

据此完成1～2题。

1．三维地形图的俯视位置位于左图中的甲乙丙丁。

三维地形图位于（）A．甲地上空B．乙地上空C．丙地上空D．丁地上空2．甲一丙连线上的最大高差可能是（）A．900米B．1000米C．1300米D．1400米下图为“某地地形与甲地建筑物布局示意图”。

读图完成3～4题。

3．与乙地相比，将建筑物布局在甲地主要考虑的因素是（）A．地形B．水源C．植被D．坡向4．与甲地地形平整方式相符的剖面是（）A．B．C．D．下图为我国江南某地等高线图，该地山清水秀，水流常年奔腾不息。

读图完成5～6题。

5．B处陡崖的顶部与④处的相对高度可能是（）A．60米B．90米C．100米D．150米6．当地山清水秀，夏季云雾缭绕。

村民在甲、乙两个地方发展了农家乐，但每到冬季乙农家乐生意冷淡，其中可能的原因是乙地（）A．降雨较多，湿冷B．坡度较陡，视线不佳C．光照不足，阴冷D．地势险要，泥石流多发雅万高铁连接印尼首都雅加达和重要城市万隆，位于印尼人口最多的爪哇岛上。

下图为雅万高铁沿线地区示意图。

据此完成7～8题。

7．图示岛屿的山脉主体走向大致为（）A．南北B．东西C．东北—西南D．西北—东南8．雅万高铁全长约为（）A．100km B．150km C．250km D．300km下图为浙江省中部某地新城规划区三维地形模拟图，某山脉主峰是图中区域最高点，海拔206.5米，区内最低点为83.9米，在最低点观测正午太阳时，太阳位于山脉主峰的正上方。

据此完成9～10题。

9．最适合眺望城市的景观点为（）A．7 B．3 C．5 D．110．从景观点8到景观点6，其山脊的走向大致是（）A．自西向东B．自东向西C．自西南向东北D．自东南向西北扎当冰川（30°28.57'N，90°38.71'E）位于念青唐古拉山北坡，面积约1.98km²，冰川厚度差别较大。

2021届高三化学一轮复习自我强化练化学反应原理综合训练

2021届高三化学一轮复习自我强化练化学反应原理综合训练 1 •现有两个图像：下列反应中符合图像的是（）B. 4NH 5(g)+5O,(g)^=±4NO(g)+6H,O(g)<0C. 2SO 3(g) ^=^2SO 2(g)+O 2(g) AH>0D. H 2(g)+co(g) ^=±C ⑸+H2(g) A^>0 2 •某同学设计如图所示实验，探究反应中的能量变化。

A. 由实验可知,（a ）、（b ）、（c ）所涉及的反应都是放热反应B. 将实验（a ）中的等质量的铝片换成铝粉后，释放出的热量有所增加C. 实验（c ）中将环形玻璃搅拌棒改为铁质搅拌棒对实验结果没有影响D. 若用NaOH 固体测定中和热，则测定结果偏高3•下列关于热化学反应的描述正确的是（）ifi 度计环形玻琥搅拥*泡沫那料板碎泡沫樂料（C ）A. M(g)+3比(g)—』2NHs(g) 、H <0稀盐酸下列判断正确的是（）A.稀盐酸和稀NaOH溶液反应的中和热A27=-57.3kJ mol-1则含lmol H2SO4 的稀硫酸与足量氢氧化顿溶液反应放出的热量为114.6kJB.H2(g)的燃烧热为285.8kJ.mol1,则反应2H2O(l)=2H2(g)+O2(g)的A^+571.6kJmor,C.放热反应比吸热反应容易发生D.lmol丙烷燃烧生成水和二氧化碳所放出的热量是丙烷的燃烧热4.下列事实能用勒夏特列原理来解释的是()A.SO?被氧化为SO),往往需要使用催化剂：2SO,(g)+O,(g) 12SOj(g)B.500 °C温度比室温更有利于合成氨反应：N2(g)+3Hjg) =2N比(g) \H <0C.H r I r HI平衡混合气体加压后颜色加深：H2(g)+I：(g) =2HI(g)D.实验室采用排饱和食盐水的方法收集氯气：CI2+H2O =H++CI-+HCIO5.下表是几种弱酸在常温下的电离平衡常数：则下列说法不正确的是()A.碳酸的酸性强于氢硫酸B.多元弱酸的酸性主要由第一步电离决定C.反应HS- +COf =S2- + HCO；可以发生稀盐酸，电离D.向弱酸溶液中加少量常数不变6.常温下，下列各组离子在指定溶液中一定能大量共存的是（）A.在水电离岀的c（H+） = 10-"mol/L： Na\ K\ S2\ SO；-B.在c（Fe3+） =lmol/L 的溶液中：K\ NH：、SCN\ IC.在0.1 mol/L 的NH4HCO3溶液中：Na\ Al"、Cl、NO；D.使甲基橙溶液变红的溶液中：Al*、Cu2\ SO/、NO；7.常温下某一元碱BOH溶液与0.01mol/L的一元强酸HA溶液等体积混合后所得溶液的pH为7.下列说法中正确的是（）□反应前，O.Olmol/L的一元强酸HA溶液中水电离出的IT的浓度为IX1012mol/L□反应前，一元碱BOH其溶液中溶质物质的量浓度一定大于0.01mol/L□反应后，溶液中离子浓度大小排列顺序一定是c（B+） = c（A ）＞c（Hj =c（OH ）□反应后，混合溶液中HA与M的浓度总和等于0.01mol/L・A.①②B.①③C.②④D.①②④&下列事实：①NaHSQ溶液呈酸性；②长期施用化肥（NH4）2SO4会使土壤酸性增强，发生板结；③配制eg,溶液时，用稀盐酸溶解CuCl,固体；®NaHS 溶液中C（H2S）＞C（S2"）；⑤氯化镀溶液可去除金属制品表而的锈斑;⑥蒸干FC—溶液，往往得不到Fed,固体。

2022-2023学年高三二模强化训练卷(新高考I)语文试题(含答案)

2022-2023学年高三二模强化训练卷(新高考I)语文考试时间：150分钟试卷分数：150分注意事项：1．答题前填写好自己的姓名、班级、考号等信息。

2．请将答案正确填写在答题卡上。

一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，19分）阅读下面的文字，完成1～5题。

材料一：中国人的最高信仰，乃是天、地、人三者之合一。

借用耶教术语来说，便是天、地、人之“三位一体”。

在中国，天地可合称为天，人与天地合一，便是所谓“天人合一”。

中国的社会风俗里面也有“三位一体”的信仰之存在。

如言时令，有二十四个节气，但同时有人造的节日。

中国人把此二项混合看待，不加区别，如清明、冬至是自然节，端午、中秋、重阳是人造节。

中国人在节日中，又多增添一些神话故事，使得人文自然益加亲密配合，社会礼俗随着天时节气而多彩多姿。

这亦是一种天人相应，把我们的日常生活推衍到大自然变化中而与之呼应。

这就是那人文参加进自然里面而演化成为一体了。

此中有信仰、有希望、有娱乐，极富礼乐意义，极富艺术性，亦极富传统性，极富有关于民族文化信仰之启示性与教育性。

但到最近，大家对自己文化无了解、无信心，因此对此种节日亦觉无趣味、无意义。

中国社会上之新年节日不废而渐废，耶诞节日代之而兴。

中国社会并非一耶教社会，中国文化亦非一耶教文化，而中国人则追步西方，来过耶诞节日。

这里面自不免夹杂着许多无情无理之盲目效颦。

再讲中国的艺术，一幅山水画，就是天、地、人三位一体的一种结构。

一幅画上定有空白，有春、夏、秋、冬四季分别，那都是天。

一座山、一溪水、一栋房子、一座亭榭，那都是地。

中间画着一渔翁，或是赶着骡子做生意的，或是读书弹琴的，或是倚着一杖在那里看天看地的，这都是人。

这是画中之主。

天有气象，地有境界，人有风格。

在此气象境界之中有此风格，配合起来，这是一个艺术的世界。

中国画便要此“气象”“境界”与“风格”之三者合一。

中国画也不愿酷肖自然，而要把人文意境融入，另成一天地。

2020届高三化学知识点强化训练—共价键对分子构型、性质的影响

2020届高三化学知识点强化训练一共价键对分子构型、性质的影响1.2mol金属钠和1mol氯气反应的能量关系如图所示，下列说法不正确的是()2Na(s)-Cl^g)切J&CKs)AH：AH42Xa(g)+2Cl(g)AHj AH52Na*(g)，2CT(g)-^*2NaCl(g)A.相同条件下，K(s)的(A H2,+AH3,)<Na的(△H?+△H3)B.的值数值上和Cl-Cl共价键的键能相等C.AH5<0,在相同条件下，2Br(g)的△H5‘>AH5D.AH7<0,且该过程形成了分子间作用力2,设N a为阿伏加德罗常数的值，下列说法正确的是()A.Imol羟基含有的电子数目为ION aB.Imol乙醇分子的C-H键数目为6N aC.标况下，22.4L己烷充分燃烧后产生的气态产物分子数为5N aD.两种气体炷组成的混合气体O.lmol,完全燃烧得0.16molC02,说明该混合气体中一定有甲烷3,物质结构包括原子结构、分子结构、晶体结构。

下列关于物质结构与性质的说法正确的是()A.Si。

?晶体为原子晶体，CO?晶体为分子晶体B.。

键都是由两个p轨道“头碰头”重叠形成的C.VSEPR模型就是分子的空间构型D.HF、HC1、HBr、HI的热稳定性和还原性从左到右依次减弱4,根据表中的信息判断下列说法正确的是()物质金刚石石墨外观无色，透明固体灰黑，不透明固体熔点?燃烧热/KJ-mor1395.4393.5A.表示石墨燃烧热的热化学方程式为C(石墨，s)+|02(g)=CO(g)△H=-393.5kJ•mol-1B.由表中信息知C（石墨，s）=C（金刚石，s）△H=+1.9kJ•mo]TC.由表中信息可得如图所示的图象D.由表中信息可推知相同条件下金刚石的熔点高于石墨的5.设N a为阿伏加德罗常数的值.下列说法正确的是()A.12g金刚石晶体中含有的C-C的数目为2N aB.1L1mol•LTAICI3溶液中含有的AH+数目为N aC.在标况下，11.2L氯气通入足量的NaOH溶液中转移电子数为N aD.常温常压下，22g C02气体中含有的。

圆锥曲线的综合问题强化训练-2023届高三数学二轮专题复习(含解析)

冲刺2023年高考二轮圆锥曲线的综合问题强化训练（原卷+答案）考点一证明问题——等价转化，直击目标圆锥曲线中证明问题的两种常见类型圆锥曲线中的证明问题，主要有两类：一是证明点、直线、曲线等几何元素中的位置关系，如：某点在某直线上，某直线经过某个点、某两条直线平行或垂直等；二是证明直线与圆锥曲线中的一些数量关系(相等或不等)．例 1已知椭圆E 的中心为坐标原点，对称轴为x 轴、y 轴，且过A (0，－2)，B (32，－1)两点．(1)求E 的方程；(2)设过点P (1，－2)的直线交E 于M ，N 两点，过M 且平行于x 轴的直线与线段AB 交于点T ，点H 满足MT⃗⃗⃗⃗⃗⃗ ＝TH ⃗⃗⃗⃗⃗ .证明：直线HN 过定点．对点训练已知直线y ＝3与曲线C ：x 2＋2py ＝0的两个公共点之间的距离为4√6. (1)求C 的方程；(2)设P 为C 的准线上一点，过P 作C 的两条切线，切点为A ，B ，直线P A ，PB 的斜率分别为k 1，k 2，且直线P A ，PB 与y 轴分别交于M ，N 两点，直线AB 的斜率为k 0.证明：k 1·k 2为定值，且k 1，k 0，k 2成等差数列．考点二定点问题——目标等式寻定点解析几何中的定点问题一般是指与解析几何有关的直线或圆(其他曲线过定点太复杂，高中阶段一般不涉及)过定点的问题，其实质是：当动直线或动圆变化时，这些直线或圆相交于一点，即这些直线或圆绕着定点在转动，这类问题的求解一般分为以下三步：一选：选择变量，定点问题中的定点，随某一个量的变化而固定，可选择这个量为变量(有时可选择两个变量，如点的坐标、斜率、截距等，然后利用其他辅助条件消去其中之一)．二求：求出定点坐标所满足的方程，即把需要证明为定点的问题表示成关于上述变量的方程．三定点：对上述方程进行必要的化简，即可得到定点坐标．例 2 已知椭圆M ：x 2a 2+y 2b 2＝1(a >b >0)的离心率为√22，AB 为过椭圆右焦点的一条弦，且AB 长度的最小值为2.(1)求椭圆M 的方程；(2)若直线l 与椭圆M 交于C ，D 两点，点P (2，0)，记直线PC 的斜率为k 1，直线PD 的斜率为k 2，当1k 1+1k 2＝1时，是否存在直线l 恒过一定点？若存在，请求出这个定点；若不存在，请说明理由．对点训练已知抛物线C ：y 2＝2px (p >0)的焦点为F ，S (t ，4)为C 上一点，直线l 交C 于M ，N 两点(与点S 不重合)．(1)若l 过点F 且倾斜角为60°，|FM |＝4(M 在第一象限)，求C 的方程；(2)若p ＝2，直线SM ，SN 分别与y 轴交于A ，B 两点，且OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ ＝8，判断直线l是否恒过定点？若是，求出该定点；若否，请说明理由．考点三定值问题——巧妙消元寻定值定值问题一般是指在求解解析几何问题的过程中，探究某些几何量(斜率、距离、面积、比值等)与变量(斜率、点的坐标等)无关的问题，其求解步骤一般为：一选：选择变量，一般为点的坐标、直线的斜率等．二化：把要求解的定值表示成含上述变量的式子，并利用其他辅助条件来减少变量的个数，使其只含有一个变量(或者有多个变量，若是能整体约分也可以)．三定值：化简式子得到定值．由题目的结论可知要证明为定值的量必与变量的值无关，故求出的式子必能化为一个常数，所以只需对上述式子进行必要的化简即可得到定值．例 3 已知双曲线C ：x 2a2−y 2b 2＝1(a >0，b >0)的左、右焦点分别为F 1、F 2，双曲线C 的右顶点A 在圆O ：x 2＋y 2＝3上，且AF 1⃗⃗⃗⃗⃗⃗⃗ ·AF 2⃗⃗⃗⃗⃗⃗⃗ ＝－1.(1)求双曲线C 的方程；(2)动直线l 与双曲线C 恰有1个公共点，且与双曲线C 的两条渐近线分别交于点M 、N ，设O 为坐标原点．求证：△OMN 的面积为定值．对点训练已知F 1(－√3，0)，F 2(√3，0)分别是双曲线C ：x 2a 2−y 2b 2＝1(a >b >0)的左、右焦点，A 为双曲线在第一象限的点，△AF 1F 2的内切圆与x 轴交于点P (1，0)．(1)求双曲线C 的方程；(2)设圆O ：x 2＋y 2＝2上任意一点Q 处的切线l ，若l 与双曲线C 左、右两支分别交于点M 、N ，问：QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ 是否为定值？若是，求出此定值；若不是，说明理由．考点四圆锥曲线中的最值、范围问题——巧设变量，引参搭桥圆锥曲线中的最值 (1)椭圆中的最值 F 1，F 2为椭圆x 2a2+y 2b 2＝1(a ＞b ＞0)的左、右焦点，P 为椭圆上的任意一点，B 为短轴的一个端点，O 为坐标原点，则有：①|OP |∈________；②|PF 1|∈________；③|PF 1|·|PF 2|∈________；④∠F 1PF 2≤∠F 1BF 2.(2)双曲线中的最值F 1，F 2为双曲线x 2a 2−y 2b 2＝1(a ＞0，b ＞0)的左、右焦点，P 为双曲线上的任一点，O为坐标原点，则有：①|OP |≥________；②|PF 1|≥________． (3)抛物线中的最值点P 为抛物线y 2＝2px (p ＞0)上的任一点，F 为焦点，则有：①|PF |≥________；②A (m ，n )为一定点，则|P A |＋|PF |有最小值；③点N (a ，0)是抛物线的对称轴上一点，则|PN |min ＝{|a |(a ≤p )，√2pa −p 2(a ＞p)．例 4如图，已知椭圆x 212＋y 2＝1.设A ，B 是椭圆上异于P (0，1)的两点，且点Q (0，12)在线段AB 上，直线P A ，PB 分别交直线y ＝－12x ＋3于C ，D 两点．(1)求点P 到椭圆上点的距离的最大值； (2)求|CD |的最小值．对点训练已知抛物线C ：x 2＝2py (p ＞0)的焦点为F ，且F 与圆M ：x 2＋(y ＋4)2＝1上点的距离的最小值为4.(1)求p ；(2)若点P 在M 上，P A ，PB 是C 的两条切线，A ，B 是切点，求△P AB 面积的最大值．[典例] 已知圆(x ＋√3)2＋y 2＝16的圆心为M ，点P 是圆M 上的动点，点N (√3，0)，点G 在线段MP 上，且满足(GN⃗⃗⃗⃗⃗ +GP ⃗⃗⃗⃗⃗ )⊥(GN ⃗⃗⃗⃗⃗ −GP ⃗⃗⃗⃗⃗ )． (1)求点G 的轨迹C 的方程；(2)过点T (4，0)作斜率不为0的直线l 与轨迹C 交于A ，B 两点，点A 关于x 轴的对称点为D ，连接BD 交x 轴于点Q ，求△ABQ 面积的最大值．(1)因为(GN ⃗⃗⃗⃗⃗⃗ +GP ⃗⃗⃗⃗⃗ )⊥(GN ⃗⃗⃗⃗⃗⃗ −GP ⃗⃗⃗⃗⃗ )，所以(GN ⃗⃗⃗⃗⃗⃗ +GP ⃗⃗⃗⃗⃗ )·(GN ⃗⃗⃗⃗⃗⃗ −GP ⃗⃗⃗⃗⃗ )＝0，即GN ⃗⃗⃗⃗⃗⃗ 2－GP ⃗⃗⃗⃗⃗ 2＝0，所以|GP |＝|GN |，所以|GM |＋|GN |＝|GM |＋|GP |＝|MP |＝4>2√3＝|MN |，所以点G 在以M ，N 为焦点，长轴长为4的椭圆上，设椭圆的方程为x 2a 2+y 2b 2＝1(a >b >0)，则2a ＝4，2c ＝2√3，即a ＝2，c ＝√3，所以b 2＝a 2－c 2＝1，所以点G 的轨迹C 的方程为x 24＋y 2＝1. (2)依题意可设直线l ：x ＝my ＋4. 由{x =my +4，x 24+y 2=1消去x ，得(m 2＋4)y 2＋8my ＋12＝0.设A (x 1，y 1)，B (x 2，y 2)，由Δ＝64m 2－4×12×(m 2＋4)＝16(m 2－12)>0，得m 2>12. ①且y 1＋y 2＝－8mm 2+4，y 1y 2＝12m 2+4.②因为点A 关于x 轴的对称点为D ，所以D (x 1，－y 1)，可设Q (x 0，0)，所以k BD ＝y 2+y 1x 2−x 1＝y 2+y 1m (y 2−y 1)，所以BD 所在直线的方程为y －y 2＝y 2+y 1m (y2−y 1)(x －my 2－4)．令y ＝0，得x 0＝2my 1y 2+4(y 1+y 2)y 1+y 2. ③将②代入③，得x 0＝24m−32m−8m＝1，所以点Q 的坐标为(1，0)．因为S △ABQ ＝|S △TBQ －S △TAQ |＝12|QT ||y 2－y 1|＝32√(y 1+y 2)2−4y 1y 2＝6√m 2−12m 2+4，令t ＝m 2＋4，结合①得t >16，所以S △ABQ ＝6√t−16t＝ 6√−16t 2+1t ＝6√−16(1t −132)2+164.当且仅当t ＝32，即m ＝±2√7时，(S △ABQ )max ＝34. 所以△ABQ 面积的最大值为34.参考答案考点一[例1] 解析：(1)设椭圆E 的方程为mx 2＋ny 2＝1(m >0，n >0，m ≠n )．将点A (0，－2)，B (32，－1)的坐标代入，得{4n =1，94m +n =1，解得{m =13，n =14. 所以椭圆E的方程为x 23+y 24＝1. (2)证明：方法一设M (x 1，y 1)，N (x 2，y 2)．由题意，知直线MN 与y 轴不垂直，设其方程为x －1＝t (y ＋2)．联立得方程组{x −1=t (y +2)，x 23+y 24=1. 消去x 并整理，得(4t 2＋3)y 2＋(16t 2＋8t )y ＋16t 2＋16t －8＝0，所以y 1＋y 2＝－16t 2+8t 4t 2+3，y 1y 2＝16t 2+16t−84t 2+3.设T (x 0，y 1)．由A ，B ，T 三点共线，得y 1+2x 0＝y 1+1x 0−32，得x 0＝32y 1＋3.设H (x ′，y ′)．由MT ⃗⃗⃗⃗⃗⃗ ＝TH ⃗⃗⃗⃗⃗ ，得(32y 1＋3－x 1，0)＝(x ′－32y 1－3，y ′－y 1)，所以x ′＝3y 1＋6－x 1，y ′＝y 1，所以直线HN 的斜率k ＝y 2−y ′x 2−x ′＝y 2−y 1x 2+x 1−(3y 1+6)＝y 2−y 1t (y 1+y 2)−3y 1+4t−4，所以直线HN 的方程为y －y 2＝y 2−y 1t (y 1+y 2)−3y 1+4t−4·(x －x 2)．令x ＝0，得y ＝y 2−y 1t (y 1+y 2)−3y 1+4t−4·(－x 2)＋y 2＝(y 1−y 2)(ty 2+2t+1)t (y 1+y 2)−3y 1+4t−4＋y 2＝(2t−3)y 1y 2+(2t−5)(y 1+y 2)+6y 1t (y 1+y 2)−3y 1+4t−4＝(2t−3)·16t 2+16t−84t 2+3+(5−2t )·16t 2+8t4t 2+3+6y 1−t(16t 2+8t)4t 2+3−3y 1+4t−4＝－2.所以直线NH 过定点(0，－2)．方法二由A (0，－2)，B (32，－1)可得直线AB 的方程为y ＝23x －2. a ．若过点P (1，－2)的直线的斜率不存在，则其直线方程为x ＝1.将直线方程x ＝1代入x 23+y 24＝1，可得N (1，2√63)，M (1，－2√63)．将y ＝－2√63代入y ＝23x －2，可得T (3－√6，－2√63)．由MT⃗⃗⃗⃗⃗⃗ ＝TH ⃗⃗⃗⃗⃗ ，得H (5－2√6，－2√63)．此时直线HN 的方程为y ＝(2＋2√63)(x －1)＋2√63，则直线HN 过定点(0，－2)． b ．若过点P (1，－2)的直线的斜率存在，设此直线方程为kx －y －(k ＋2)＝0，M (x 1，y 1)，N (x 2，y 2)．联立得方程组{kx −y −(k +2)=0，x 23+y 24=1. 消去y 并整理，得(3k 2＋4)x 2－6k (2＋k )x ＋3k (k ＋4)＝0. 所以{x 1+x 2=6k (2+k )3k 2+4，x 1x 2=3k (4+k )3k 2+4，则{y 1+y 2=−8(2+k )3k 2+4，y 1y 2=4(4+4k−2k 2)3k 2+4，且x 1y 2＋x 2y 1＝−24k3k 2+4.①联立得方程组{y =y 1，y =23x −2，可得T (3y 12＋3，y 1)．由MT⃗⃗⃗⃗⃗⃗ ＝TH ⃗⃗⃗⃗⃗ ，得H (3y 1＋6－x 1，y 1)．则直线HN 的方程为y －y 2＝y 1−y 23y 1+6−x 1−x2(x －x 2)．将点(0，－2)的坐标代入并整理，得2(x 1＋x 2)－6(y 1＋y 2)＋x 1y 2＋x 2y 1－3y 1y 2－12＝0.②将①代入②，得24k ＋12k 2＋96＋48k －24k －48－48k ＋24k 2－36k 2－48＝0，显然成立．综上可得，直线HN 过定点(0，－2)．对点训练解析：(1)将y ＝3代入x 2＋2py ＝0，得x 2＝－6p . 当p ≥0时，不合题意；当p <0时，x ＝±√−6p ，则2√−6p ＝4√6，解得p ＝－4，故C 的方程为x 2＝8y .(2)证明：由(1)可知C 的准线方程为y ＝－2，不妨设P (m ，－2)，A (x 1，y 1)，B (x 2，y 2)，设过点P 且与C 相切的直线l 的斜率为k ，则l ：y ＝k (x －m )－2，且k ≠0，联立{y =k (x −m )−2，x 2=8y ，得x 2－8kx ＋8(km ＋2)＝0，则Δ＝64k 2－32(km ＋2)＝0，即k 2－12mk －1＝0，由题意知，直线P A ，PB 的斜率k 1，k 2为方程k 2－12mk －1＝0的两根，则k 1＋k 2＝m2，k 1k 2＝－1，故k 1·k 2为定值．又x 2－8kx ＋8(km ＋2)＝(x －4k )2＝0，则x 1＝4k 1，同理可得x 2＝4k 2，则k 0＝y 1−y 2x 1−x 2＝18x −1218x 22x 1−x 2＝x 1+x 28，因此k 0＝4(k 1+k 2)8＝k 1+k 22，故k 1，k 0，k 2成等差数列．考点二[例2]解析：(1)因为x 2a 2+y 2b 2＝1(a >b >0)的离心率为√22，过椭圆右焦点的弦长的最小值为2b 2a＝2，所以a ＝2，c ＝√2，b ＝√2，所以椭圆M 的方程为x 24+y 22＝1. (2)设直线l 的方程为m (x －2)＋ny ＝1，C (x 1，y 1)，D (x 2，y 2)，由椭圆的方程x 2＋2y 2＝4，得(x －2)2＋2y 2＝－4(x －2)．联立直线l 的方程与椭圆方程，得(x －2)2＋2y 2＝－4(x －2)[m (x －2)＋ny ]，即(1＋4m )(x －2)2＋4n (x －2)y ＋2y 2＝0，(1＋4m )(x−2y )2＋4n x−2y＋2＝0，所以1k 1+1k 2＝x 1−2y 1+x 2−2y 2＝－4n 1+4m＝1，化简得m ＋n ＝－14，代入直线l 的方程得m (x －2)＋(−14−m)y ＝1，即m (x －y －2)－14y ＝1，解得x ＝－2，y ＝－4，即直线l恒过定点(－2，－4)．对点训练解析：(1)抛物线C ：y 2＝2px (p >0)的焦点为F (p2，0)，因为l 过点F 且倾斜角为60°，所以l ：y ＝√3(x －p2)，联立y 2＝2px (p >0)，可得12x 2－20px ＋3p 2＝0，解得x ＝32p 或x ＝p6，又M 在第一象限，所以x M ＝32p ，因为|FM |＝4，所以32p ＋p2＝4，解得p ＝2，所以抛物线C 的方程为y 2＝4x ；(2)由已知可得抛物线C 的方程为y 2＝4x ，点S (4，4)，设直线l 的方程为x ＝my ＋n ，点M (y 12 4，y1)，N (y 22 4，y2)，将直线l 的方程与抛物线C ：y 2＝4x 联立得y 2－4my －4n ＝0，所以Δ＝16m 2＋16n >0，y 1＋y 2＝4m ，y 1y 2＝－4n (*)，直线SM 的方程为y －4＝y 1−4y 12 4－4(x －4)，令x ＝0求得点A 的纵坐标为4y 1y 1+4，同理求得点B 的纵坐标为4y 2y2+4，由OA ⃗⃗⃗⃗⃗ ·OB ⃗⃗⃗⃗⃗ ＝16y 1y 2y 1y 2+4(y 1+y 2)+16＝8，化简得y 1y 2＝4(y 1＋y 2)＋16，将上面(*)式代入得－4n ＝16m ＋16，即n ＝－4m －4，所以直线l 的方程为x ＝my －4m －4，即x ＋4＝m (y －4)，所以直线l 过定点(－4，4)．考点三[例3] 解析：(1)不妨设F 1(－c ，0)，F 2(c ，0), 因为A (a ，0)，从而AF 1⃗⃗⃗⃗⃗⃗⃗ ＝(−c −a ，0)，AF 2⃗⃗⃗⃗⃗⃗⃗ ＝(c －a ，0) ，故有 AF 1⃗⃗⃗⃗⃗⃗⃗ ·AF 2⃗⃗⃗⃗⃗⃗⃗ ＝a 2－c 2＝－1, 又因为a 2＋b 2＝c 2, 所以 b ＝1，又因为A (a ，0) 在圆 O ：x 2＋y 2＝3 上，所以 a ＝√3，所以双曲线C的标准方程为x 23－y 2＝1.(2)证明：设直线l 与x 轴交于D 点，双曲线的渐近线方程为y ＝±√33x ，由于动直线l 与双曲线C 恰有1个公共点，且与双曲线C 的两条渐近线分别交于点M 、N ，当动直线l 的斜率不存在时， l ：x ＝±√3，|OD |＝√3，|MN |＝2，S △OMN ＝12×√3×2＝√3，当动直线l 的斜率存在时，且斜率k ≠±√33，不妨设直线 l ：y ＝kx ＋m,故由{y =kx +m x 23−y 2=1⇒(1－3k 2)x 2－6mkx －3m 2－3＝0，依题意，1－3k 2≠0且m ≠0，Δ＝(－6mk )2－4(1－3k 2)(－3m 2－3)＝0, 化简得 3k 2＝m 2＋1，故由{y =kx +my =√33x ⇒x M ＝√33−k ，同理可求，x N ＝－√33+k，所以|MN |＝√1+k 2|xM−x N |＝2√3|m|√k 2+1|1−3k 2|，又因为原点O 到直线l ：kx －y ＋m ＝0的距离d ＝√k 2+1，所以S △OMN ＝12|MN |d ＝√3m 2|1−3k 2|，又由3k 2＝m 2＋1，所以S △OMN ＝√3|m|√k 2+1|1−3k 2|＝√3，故△OMN 的面积为定值，定值为√3.对点训练解析：(1)如图，设AF 1，AF 2与△AF 1F 2的内切圆分别交于G ，H 两点，则2a ＝|AF 1|−|AF 2|＝|F 1P |−|PF 2| ＝(1＋√3)－(√3－1)＝2，所以a ＝1，则b 2＝c 2－a 2＝2，则双曲线C 的方程为x 2－y 22＝1.(2)由题意得，切线l 的斜率存在．设切线l 的方程为y ＝kx ＋m ，M (x 1，y 1)，N (x 2，y 2)．因为l 与圆O ：x 2＋y 2＝2相切，所以√1+k 2＝√2，即m 2＝2k 2＋2.联立{y =kx +m ，x 2−y 22=1，消去y 并整理得(2－k 2)x 2－2kmx －m 2－2＝0，所以x 1＋x 2＝2km2−k 2，x 1x 2＝−m 2−22−k 2.又QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ ＝(QO ⃗⃗⃗⃗⃗ +OM ⃗⃗⃗⃗⃗⃗ )·(QO ⃗⃗⃗⃗⃗ +ON ⃗⃗⃗⃗⃗ ) ＝|QO ⃗⃗⃗⃗⃗ |2－OQ ⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗ −OQ ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ +ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ ＝|QO ⃗⃗⃗⃗⃗ |2－|OQ ⃗⃗⃗⃗⃗ |·|ON ⃗⃗⃗⃗⃗ |cos ∠QON －|OQ ⃗⃗⃗⃗⃗ |·|OM ⃗⃗⃗⃗⃗⃗ |cos ∠QOM ＋ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ ＝|QO ⃗⃗⃗⃗⃗ |2－|OQ ⃗⃗⃗⃗⃗ |·|OQ ⃗⃗⃗⃗⃗ |−|OQ ⃗⃗⃗⃗⃗ |·|OQ ⃗⃗⃗⃗⃗ |+ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ ＝|QO ⃗⃗⃗⃗⃗ |2－|QO ⃗⃗⃗⃗⃗ |2－|QO ⃗⃗⃗⃗⃗ |2＋ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ ＝ON ⃗⃗⃗⃗⃗ ·OM ⃗⃗⃗⃗⃗⃗ −|OQ ⃗⃗⃗⃗⃗ |2. 又OM ⃗⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗ ＝x 1x 2＋y 1y 2 ＝x 1x 2＋(kx 1＋m )(kx 2＋m )＝(k 2＋1)x 1x 2＋km (x 1＋x 2)＋m 2 ＝(k 2+1)(−m 2−2)2−k 2+2k 2m 22−k2＋m 2＝m 2−2k 2−22−k 2，将m 2＝2k 2＋2代入上式得OM ⃗⃗⃗⃗⃗⃗ ·ON ⃗⃗⃗⃗⃗ ＝0.所以QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ ＝0－|OQ ⃗⃗⃗⃗⃗ |2＝－2. 综上所述，QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ 为定值，且QM ⃗⃗⃗⃗⃗⃗ ·QN ⃗⃗⃗⃗⃗ ＝－2.考点四(1)[b ，a ] [a －c ，a ＋c ] [b 2，a 2] (2)a c －a (3)p2[例4] 解析：(1)设M (2√3cos θ，sin θ)是椭圆上一点，P (0，1)，则|PM |2＝12cos 2θ＋(1－sin θ)2＝13－11sin 2θ－2sin θ＝14411－11(sin θ＋111)2≤14411.故|PM |的最大值为12√1111.(2)由题意，知直线AB 的斜率存在，故设直线AB 的方程为y ＝kx ＋12.将直线方程与椭圆方程联立，得{y =kx +12，x 212+y 2=1.消去y 并整理，得(k 2＋112)x 2＋kx －34＝0. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－kk 2+112，x 1x 2＝－34(k 2+112).直线P A ：y ＝y 1−1x 1x ＋1与直线y ＝－12x ＋3交于点C ，则x C ＝4x 1x1+2y 1−2＝4x 1(2k+1)x 1−1. 同理可得，x D ＝4x 2x 2+2y 2−2＝4x 2(2k+1)x 2−1，则|CD |＝ √1+14|x C －x D | ＝√52|4x1(2k+1)x1−1−4x2(2k+1)x2−1|＝2√5|x 1−x 2[(2k+1)x1−1][(2k+1)x 2−1]|＝2√5|x 1−x 2(2k+1)2x 1x 2−(2k+1)(x 1+x 2)+1|＝3√52·√16k 2+1|3k+1|＝6√55·√16k 2+1· √916+1|3k+1| ≥6√55，当且仅当k ＝316时等号成立．故|CD |的最小值为6√55.对点训练解析：(1)由题意知M (0，－4)，F (0，p2)，圆M 的半径r ＝1，所以|MF |－r ＝4，即p2＋4－1＝4，解得p ＝2.(2)由(1)知，抛物线方程为x 2＝4y ，由题意可知直线AB 的斜率存在，设A (x 1，x 12 4)，B (x2，x 22 4)，直线AB 的方程为y ＝kx ＋b ，联立得{y =kx +bx 2=4y，消去y 得x 2－4kx －4b ＝0，则Δ＝16k 2＋16b >0(※)，x 1＋x 2＝4k ，x 1x 2＝－4b ，所以|AB |＝√1+k 2|x 1－x 2|＝√1+k 2·√(x 1+x 2)2−4x 1x 2＝4√1+k 2·√k 2+b . 因为x 2＝4y ，即y ＝x 24，所以y ′＝x 2，则抛物线在点A 处的切线斜率为x12，在点A 处的切线方程为y −x 12 4＝x 12(x －x 1)，即y ＝x 12x −x 12 4，同理得抛物线在点B 处的切线方程为y ＝x 22x −x 22 4，联立得{y =x 12x −x 124y ＝x22x －x 22 4，则{x =x 1+x 22=2ky =x 1x 24=−b ，即P (2k ，－b )．因为点P 在圆M 上，所以4k 2＋(4－b )2＝1 ①，且－1≤2k ≤1，－5≤－b ≤－3，即－12≤k ≤12，3≤b ≤5，满足(※)．设点P 到直线AB 的距离为d ，则d ＝2√1+k 2，所以S △P AB ＝12|AB |·d ＝4√(k 2+b )3.由①得，k 2＝1−(4−b )24＝−b 2+8b−154，令t ＝k 2＋b ，则t ＝−b 2+12b−154，且3≤b ≤5. 因为t ＝−b 2+12b−154在[3，5]上单调递增，所以当b ＝5时，t 取得最大值，t max ＝5，此时k ＝0，所以△P AB 面积的最大值为20√5.。

河北省普通示范高中2014届高三考前强化模拟训练数学文1

河北省普通示范高中2014届高三考前强化模拟训练数学文1一.选择题:(共60分,每小题5分,每小题给出的四个选项中,只有一项符合题目要求） 1．已知R 是实数集，2{|1},{|M x N y y x===＜，则R N C M ⋂=( ) A.（1，2）B. [0，2]C.∅D. [1，2]2．已知a ＋2ii ＝b －i, (a ，b∈R)，其中i 为虚数单位，则a ＋b ＝（）A.－1 B ．1 C ．2 D ．33.设,l m 是两条不同的直线，α是一个平面，则下列命题正确的是（） A ．若,l m m α⊥⊂，则l α⊥ B ．若,//l l m α⊥，则m α⊥C ．若//,l m αα⊂，则//l mD ．若//,//l m αα，则//l m4．如下图，已知()32()0,f x ax bx cx d a =+++≠记()243,b ac ∆=-则当5．数列{}n a 是公差不为0的等差数列，且137,,a a a 为等比数列{}n b 的连续三项，则数列{}n b 的公比为（）A B ．4 C ．2 D ．126．已知向量a =(x －1，2)，b =(y ，－4)，若a ∥b ，则向量,12y x ⎛⎫=+ ⎪⎝⎭c 与向量()0,1=-d 的夹角为（）A ．45°B ．60°C ．135°°D ． 120 7．已知某个几何体的三视图如下，那么可得这个几何体的体积是（）A.31 B ．32 C ．34 D ．388．若右边的程序框图输出的S 是126，则条件①可为（）A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤9.A ，B 是抛物线y 2＝2px （p ＞0）上两点，F 为该抛物线的焦点，若FA →＋4FB →＝0，则直线AB 的倾斜角的余弦值为A.± 12B.± 35C.± 23D.± 5710.已知函数))2,0((cos )(π∈=x x x f 有两个不同的零点21,x x ，且方程m x f =)(有两个不同的实根43,x x ，若把这四个数按从小到大排列构成等差数列，则实数m 的值为（）A21 B 21- C 23 D 23-11.已知),(y x P 是直线)0(04>=++k y kx 上一动点，PB PA ,是圆C ：0222=-+y y x 的两条切线，B A ,是切点，若四边形PACB 的最小面积是2，则k 的值为（） A. 3 B.212 C.22 D. 212.函数21(0)()(1)(0)x x f x f x x -⎧-≤=⎨->⎩若方程()f x x a =+有且只有两个不等的实数根,则实数a 的取值范围为A.(-∞,0)B.[0,1)C.(-∞,1)D.[0,+∞)二.填空题:( 每小题5分共20分) 13若a 是12b +与12b -的等比中项，则22aba b+的最大值为14．椭圆13422=+y x 上有一个动点P ，圆E ：2220x y x +-=，过圆心E 任意作一条直线与圆E 交于A ，B 两点。

2022届高三化学一轮复习专题强化加强训练：物质的结构与性质(一)

2022届高三化学一轮复习专题强化加强训练：物质的结构与性质（一）-原卷一、单选题1.在抗击“2019新型冠状病毒”的过程中，大量防护和消毒用品投入使用。

下列有关说法正确的是（）A．新型冠状病毒由C、H、O三种元素组成B．聚丙烯和聚四氟乙烯为生产防护服的主要材料，二者均属于有机高分子材料C．二氧化氯泡腾片和酒精均可杀灭新型冠状病毒，二者的消毒原理相同D．84消毒液是以NaClO为主要有效成分的消毒液，与医用酒精混合可以提升消毒效果2.用示意图或图示的方法能够直观形象地理解化学知识，下列示意图或图示正确的是()A．砷原子的结构示意图B．-BF的结构式4C．HF分子间的氢键D．丙氨酸的手性异构3.下列关于晶体说法正确的是()A．金属晶体的熔沸点均高于分子晶体B．含有阳离子的晶体一定是离子晶体C．SiO2一定具有多面体外形D．金属导电和熔融电解质（或电解质溶液）导电的原理不一样4.下列说法正确的是()A．分子的稳定性与分子间作用力无关B．键长等于成键两原子的半径之和C．分子中中心原子若采用sp3杂化轨道成键，则该分子一定为正四面体结构D．可燃冰（CH4·nH2O）中甲烷分子与水分子之间形成了氢键5.下列说法不正确的是()A．Xe元素的所在族的原子的价电子排布式均为26ns np，属于非金属元素B．在元素周期表中，s区，d区和ds区的元素都是金属(氢元素除外)C．某基态原子的核外电子排布图为, 它违背了泡利原理D．某价电子排布为123d4s的基态原子，该元素位于周期表中第四周期第ⅢB族6.设N为阿伏加德罗常数的值，下列说法正确的是()AA．36g冰晶体中氢键的数目为4NAB．干冰晶胞熔化时，1mol干冰要断裂2mol碳氧双键C．1mol氯化钠中含有N个离子键AD．在含2mol Si-O键的SiO2晶体中，氧原子有2N个A7.下列说法正确的是()A．稳定性：HF<HCl<HBr<HIB．沸点：H O>HF>NH23C．熔点：晶体Si>金刚石>SiCl4D．阴离子的配位数：CsCl< NaCl <CaF28.下列提供了有关物质的熔点，根据表中的数据，下列判断错误的是（）33B．AlF3晶体的晶格能小于NaCl晶体的晶格能C ．同族元素的氧化物可以形成不同类型的晶体D ．不同族元素的氯化物可以形成相同类型的晶体 9.下列现象与氢键有关的是() ①冰的密度比液态水的密度小；②3NH 的稳定性比第VA 族其他元素的氢化物的高； ③尿素的熔沸点比醋酸的高； ④水分子在高温下也很稳定；⑤小分子的羧酸、醇可以和水以任意比例互溶； ⑥邻羟基苯甲酸的熔沸点比对羟基苯甲酸的低 A ．①②③④B ．①③④⑤C ．①③⑤⑥D ．②③⑤⑥10.下列关于酸性强弱比较正确的是() A ．HClO<HBrOB ．2HClO <HClOC ．2434H SO <H POD ．2324H SO <H SO11.已知信息：()344Cu NH SO ⎡⎤⎣⎦的电离方程式为()()2+2-4343444SO Cu NH SO = Cu NH + SO ⎡⎤⎡⎤⎣⎦⎣⎦。