Aspects of nonlocality in atom-photon interactions in a cavity
基于金刚石氮–空位色心的微波磁场成像技术的可靠性研究

Vol. 40, No. 6航 天 器 环 境 工 程第 40 卷第 6 期682SPACECRAFT ENVIRONMENT ENGINEERING2023 年 12 月https:// E-mail: ***************Tel: (010)68116407, 68116408, 68116544基于金刚石氮–空位色心的微波磁场成像技术的可靠性研究唐雨桐1,叶 安1,付鼎元1,李晓林1,张 超2*(1. 华东理工大学 物理学院,上海 200237; 2. 北京卫星环境工程研究所,北京 100094)摘要:相对于单片微波集成电路(MMIC)芯片的设计与制造工艺发展,芯片的测试与失效分析研究进展缓慢。
文章首先调研了基于金刚石氮–空位(NV)色心的高空间分辨率微波磁成像应用及通过磁成像技术反演电流分布的技术进展;继而进行了基于NV色心系综微波磁场成像技术的MMIC热态可靠性研究。
结果表明:利用基于金刚石NV色心的微波磁场成像技术,对毫米波微波芯片表面的二维矢量场进行高空间分辨率、高灵敏度的快速成像与重构,可以采集芯片在正常和非正常工作状态下的磁场成像信息;进一步对微波芯片内部的信息进行反演重建,可以实现芯片内部故障点的精确定位诊断和潜在故障点排除。
所做研究有望为芯片设计、生产、测试提供可靠性诊断。
关键词:单片微波集成电路;失效模式分析;磁成像;氮−空位色心;芯片热态可靠性中图分类号:TN707; V443文献标志码:A文章编号:1673-1379(2023)06-0682-10 DOI: 10.12126/see.2023043Study on the reliability of microwave magnetic field imaging technique based ondiamond nitrogen-vacancy color centersTANG Yutong1, YE An1, FU Dingyuan1, LI Xiaolin1, ZHANG Chao2*(1. School of Physics, East China University of Science and Technology, Shanghai 200237, China;2. Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)Abstract: Compared with the development of chip design and manufacturing of monolithic microwave integrated circuits (MMIC), the research on testing and failure analysis of chips has been progressing slowly. In this paper, the application of high-spatial resolution microwave magnetic imaging based on diamond nitrogen-vacancy (NV) color center and the technical progress of inversion current distribution by magnetic imaging were firstly reviewed. On this basis, the thermal reliability of MMIC based on NV color center ensemble microwave magnetic field imaging technology was studied. The results show that, by using the microwave magnetic field imaging technology based on the diamond NV color center, through the rapid imaging and reconstruction of the two-dimensional vector field on the surface of the millimeter wave microwave chip with high spatial resolution and high sensitivity, the magnetic field imaging information of both normal and abnormal working states of chips can be collected. The precise positioning and diagnosis of the fault points inside the chip and the elimination of potential fault points can be realized by further inversion and reconstruction of the internal information of the microwave chip. The proposed research is expected to provide reliability diagnosis for chip design, production and testing.Keywords: monolithic microwave integrated circuit; failure mode analysis; magnetic imaging; nitrogen-vacancy color center; chip thermal reliability收稿日期:2023-04-06;修回日期:2023-12-01基金项目:民用航天预研项目D040301引用格式:唐雨桐, 叶安, 付鼎元, 等. 基于金刚石氮–空位色心的微波磁场成像技术的可靠性研究[J]. 航天器环境工程, 2023, 40(6): 682-691TANG Y T, YE A, FU D Y, et al. Study on the reliability of microwave magnetic field imaging technique based on diamond nitrogen-vacancy color centers[J]. Spacecraft Environment Engineering, 2023, 40(6): 682-6910 引言自20世纪60年代以来,以微带线[1]为代表的微波与毫米波混合集成电路(microwave integrated circuits, MIC)以其结构紧凑、体积小、重量轻、造价低以及便于同有源器件相连等优点而得到迅速发展;继而随着新型集成介质传输线、介质波导以及谐振器/谐振腔在MIC的使用[2]以及MIC加工工艺的进一步成熟,出现了将大量有源器件和无源器件/组件或模块集成于一块集成电路(integrated circuit, IC)[3]的单片微波集成电路(monolithic microwave integrated circuit, MMIC)[4]。
最新物理实验报告(英文)

最新物理实验报告(英文)Abstract:This report presents the findings of a recent physics experiment conducted to investigate the effects of quantum entanglement on particle behavior at the subatomic level. Utilizing a sophisticated setup involving photon detectors and a vacuum chamber, the experiment aimed to quantify the degree of correlation between entangled particles and to test the limits of nonlocal communication.Introduction:Quantum entanglement is a phenomenon that lies at the heart of quantum physics, where the quantum states of two or more particles become interlinked such that the state of one particle instantaneously influences the state of the other, regardless of the distance separating them. This experiment was designed to further our understanding of this phenomenon and its implications for the fundamental principles of physics.Methods:The experiment was carried out in a controlled environment to minimize external interference. A pair of photons was generated and entangled using a nonlinear crystal. The photons were then separated and sent to two distinct detection stations. The detection process was synchronized, and the data collected included the time, position, and polarization state of each photon.Results:The results indicated a high degree of correlation between the entangled photons. Despite being separated by a significant distance, the photons exhibited a consistent pattern in their polarization states, suggesting a strong entanglement effect. The data also showed that the collapse of the quantum state upon measurement occurred simultaneously for both particles, supporting the theory of nonlocality.Discussion:The findings of this experiment contribute to the ongoing debate about the nature of quantum entanglement and its potential applications. The consistent correlations observed between the entangled particles provide strong evidence for the nonlocal properties of quantum mechanics. This has implications for the development of quantum computing and secure communication technologies.Conclusion:The experiment has successfully demonstrated the robustness of quantum entanglement and its potential for practical applications. Further research is needed to explore the broader implications of these findings and to refine the experimental techniques for probing the quantum realm.References:[1] Einstein, A., Podolsky, B., & Rosen, N. (1935). Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review, 47(8), 777-780.[2] Bell, J. S. (1964). On the Einstein Podolsky RosenParadox. Physics, 1(3), 195-200.[3] Aspect, A., Grangier, P., & Roger, G. (1982). Experimental Tests of Realistic Local Theories via Bell's Theorem. Physical Review Letters, 49(2), 91-94.。
Ultra- and extremely high energy neutrino astronomy

Underwater/ice neutrino telescopes (UNTs) represent a 3-D arrays of photomultipliers deployed deep in the lake, ocean or in the polar ice at the depth of 1 to 4 kilometers to provide with a shield against the sun and moon light background and background of atmospheric muons. Detection principle is based on registration of the Cherenkov photons emitted by charged leptons (including those emitted by secondaries produced along their way in the water or ice and by their decay products) which are generated in CC neutrino interactions νl N −C→C l X (see Fig. 1). Also hadronic showers produced in NC neutrino interactions νl N −N→C νl X inside UNT sensitive volume can be
MeV-range neutrino astronomy have been existing for forty years with two neutrino sources identified so far,
基于金纳米粒子局域表面等离子体共振吸收检测卡托普利
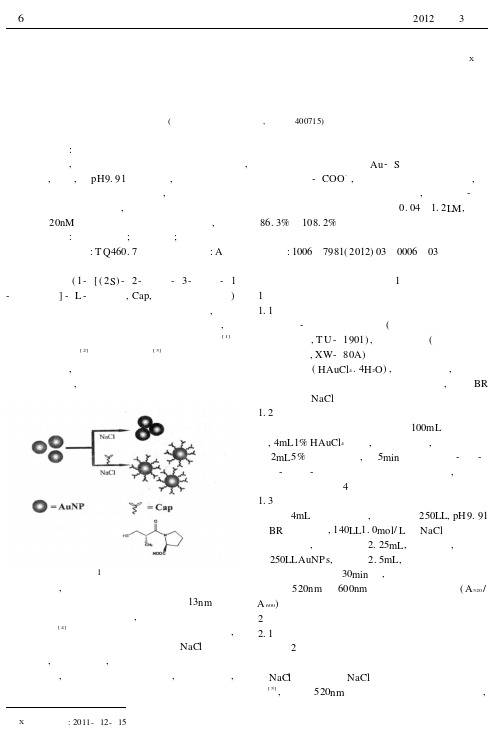
基于金纳米粒子局域表面等离子体共振吸收检测卡托普利X许 丹(西南大学化学化工学院,重庆 400715) 摘 要:柠檬酸根稳定的金胶在一定盐浓度下由于盐的电荷屏蔽效应而发生聚集。
加入一定浓度的卡托普利后,由于卡托普利分子中含有巯基和羧基,其分子中的巯基可以通过Au -S 键连在金纳米粒子表面,同时,在pH9.91的条件下,其分子中的羧基去质子化形成-COO -,导致金胶表面负电荷增多,纳米粒子之间的静电排斥力增大,金胶的聚集得到了抑制。
基于金胶由聚集到分散的现象,利用紫外-可见吸收光谱进行表征,建立了定量检测卡托普利含量的方法。
该方法的线性范围为0.04~1.2L M ,检出限为20nM 。
将此方法用于合成样的检测,回收率在86.3%~108.2%之间。
关键词:金纳米粒子;卡托普利;表面等离子体共振吸收 中图分类号:T Q460.7 文献标识码:A 文章编号:1006—7981(2012)03—0006—03 卡托普利(1-[(2S )-2-甲基-3-巯基-1-氧化丙基]-L -脯氨酸,Cap,结构如下图所示)是一种人工合成的血管紧张素转换酶抑制剂,目前广泛应用于治疗高血压及心力衰竭等疾病。
目前,定量测定卡托普利的分析方法有高效液相色谱法[1]、氧化还原滴定法[2]及化学发光法[3]等。
这些方法虽然灵敏度较高,但存在一些缺点如仪器设备昂贵、操作繁琐等。
因此,建立简便、快速、灵敏度高的检测卡托普利的方法仍然具有十分重要的意义。
图1 实验原理图近年来,金纳米粒子由于其独特的表面等离子体共振吸收性质被广泛用于色度传感。
13nm 柠檬酸根包被的金胶呈现酒红色,一旦发生聚集则呈现紫色或蓝色[4]。
这种颜色的改变很容易用肉眼捕获,不需要复杂的仪器。
金胶在一定浓度的NaCl 溶液中发生聚集,在本研究中,我们发现当体系中同时存在卡托普利后,金胶的聚集能得到抑制,基于此现象,建立了一种金胶由聚集到分散的状态来高灵敏检测卡托普利的新方法。
具有强抗噪声能力的图像分割方法

第31卷第3期 红外与激光工程 2002年6月Vol.31No.3 Infrared and Laser Engineering J un.2002具有强抗噪声能力的图像分割方法曹永锋,郑建生,万显容(武汉大学电子信息学院通信系,湖北武汉 430079) 摘要:尽可能多地综合利用图像整体和细部信息,是精确分割图像、提取特征的关键。
流域思想利用了整体信息,应用于梯度图像上,兼顾了细部信息。
引入待分割物体全局连通性,将这种方法用于物体与背景的分割,得到了极好的分割效果,对噪声有极强的抑制能力,同时具有原理简单、分割结果为连续单像素边缘、边缘定位准确、可以同时标记多个区域等优点。
给出了形态学流域算法的基本原理及数学实现,同时也总结了方法的缺点和解决途径。
关 键 词: 数学形态学; 流域算法; 抗噪声; 图像分割; 轮廓提取中图分类号:TP391 文献标识码:A 文章编号:100722276(2002)0320208204Method of im age segmentation with high anti2noise perform anceCAO Y ong2feng,ZHEN G Jian2sheng,WAN Xian2rong(Department of Communication,College of Electronic Information,Wuhan University,Wuhan430079,China)Abstract:The key problem of accurate image segmentation and character extraction is to utilize information of both whole image and local sections as much as possible.Idea of drainage area based onwhole image information takes account of local information when it is applied on gradient image.Ex2cellent segmentation result and the ability of restraining image noise are obtained when this approach isused in the segmentation of object and background and the overall connectivity of object to be segment2ed is lead in.Advantages,such as simple principle,connected single pixel edge output,accurate edgeorientation and simultaneous output of different signaled areas,are proven.The principle and mathe2matical description of the watershed algorithm are shown,and the disadvantages and resolving strategyare summarized.K ey w ords: Mathematical morphology; Watershed algorithm; Anti2noise;Image segmen2tation; Contour extraction 收稿日期:2001212204作者简介:曹永锋(19762),男,河北省冀州市人,助教,在职研究生,主要从事图像处理、机器视觉和SAR图像处理分析等方面的研究。
图像去雾增强算法的研究-文献综述

福州大学专业英语文献综述题目:图像去雾增强算法的研究姓名:学号:专业:一、引言由于近年来空气污染加重,我国雾霾天气越来越频繁地出现,例如:2012底到2013年初,几次连续七日以上的雾霾天气笼罩了大半个中国,给海陆空交通,人民生活及生命安全造成了巨大的影响。
因此,除降低空气污染之外,提高雾霾图像、视频的清晰度是亟待解决的重要问题。
图像去雾实质上就是图像增强的一种现实的应用。
一般情况下,在各类图像系统的传送和转换(如显示、复制、成像、扫描以及传输等)总会在某种程度上造成图像质量的下降。
例如摄像时,由于雾天的原因使图像模糊;再如传输过程中,噪声污染图像,使人观察起来不满意;或者是计算机从中提取的信息减少造成错误,因此,必须对降质图像进行改善处理,主要目的是使图像更适合于人的视觉特性或计算机识别系统。
从图像质量评价观点来看,图像增强技术主要目的是提高图像可辨识度。
通过设法有选择地突出便于人或机器分析的某些感兴趣的信息,抑制一些无用信息,以提高图像的使用价值,即图像增强处理只是增强了对某些信息的辨别能力[1].二、背景及意义近几年空气质量退化严重,雾霾等恶劣天气出现频繁,PM2。
5[2]值越来越引起人们的广泛关注。
在有雾天气下拍摄的图像,由于大气中混浊的媒介对光的吸收和散射影响严重,使“透过光"强度衰减,从而使得光学传感器接收到的光强发生了改变,直接导致图像对比度降低,动态范围缩小,模糊不清,清晰度不够,图像细节信息不明显,许多特征被覆盖或模糊,信息的可辨识度大大降低。
同时,色彩保真度下降,出现严重的颜色偏移和失真,达不到满意的视觉效果[3—6]。
上述视觉效果不佳的图像部分信息缺失,给判定目标带来了一定的困难,直接限制和影响了室外目标识别和跟踪、智能导航、公路视觉监视、卫星遥感监测、军事航空侦察等系统效用的发挥,给生产与生活等各方面都造成了极大的影响[7—9].以公路监控为例,由于大雾弥漫,道路的能见度大大降低,司机通过视觉获得的路况信息往往不准确,进一步影响对环境的判读,很容易发生交通事故,此时高速封闭或者公路限行,给人们的出行带来了极大的不便[10]。
表面等离子体亚波长光学原理和新颖效应_顾本源

传说中的 / 照妖镜 0大概也是金属所为. 其实不 然, 光子与金属之间的相互作用, 会引发出许多迷人的 现象 . 导体中表面等离子体激元 ( surface plasm on po laritons, SPP s)的激发 , 使人们得以利用金属等导体 材料来控制光的传播. SPPs 是光波与可迁移的表面 电荷 ( 例如金属中自由电子 ) 之间相互作用产生的
2 2 2
向 ) , 无论是 穿透进真 空和金属 , 都是 以指数衰 减 的, 而沿着表面是传播波 , 这正是人们所企求得到的 SPP s电磁模特性. E m 与频率 X 有关, 故 ( 4) 式给出 SPP s电磁模的频率与波矢 k spp之间的依赖关系 , 称 为色散关系. 它描述了 SPP s重要内在禀性 . 由于 k spp > k0, SPPs的动量 与入射光子的动 量不匹配 , 所以 在通常情况下 , SPP s 不能被激发. 只有 采用特殊的 手段 , 例如 , 外加耦合作用, 才能激发 SPP s . 另外, 由 于 SPP s电磁场的法向分量不连续性 , 导致表面电荷 密度的出现. 在真空中 ( z > 0 ), E 1z ( 0 ) = - ( 在金属中 ( z < 0 ) ,
2
2
SPPs 产生来由和色散关系
考虑一平坦的半无限金属表面 , 当一束可见光
或红外光照射到这一表面上时, 金属中可迁移的自 由电子的电 荷密度波将与入射电磁波 产生耦合作 用 , 导致电荷密度涨落 , 引发集体振荡, 感生的 SPPs 沿着金属表面传播. 下面简单地讨论一下如何激发 SPPs, 激发条件又是什么 ? 这主要取决于 SPPs 色散 关系. 既然 SPPs是外来电磁场激发引起的金属中电 荷密度涨落 , 产生集体振荡, 辐射出电磁模 , 当然它 要满足电磁场的基本方程 ) ) ) 麦克斯韦方程组. 众 所周知 , 麦克斯韦方程容纳各种各样的解 , 像个聚宝 盆 . 要根据人们的需求 , 加以挖掘出来 . 例如, 麦克斯 韦方程的解有平面波、 柱面波、 球面波、 贝塞尔函数、 高斯光束等等. 现在让我们来开发 SPP s电磁模 . 它 的特征是被限制于金属表面传播, 在垂直表面的两 个方向上, 电磁场急剧地衰减. 那么, 要问麦克斯韦 方程是否存在这种解 ? 解的具体形式又是什么样? 为确定起见 , 我们假定金属 /介 电界面是躺在 xy 面 上 , 其法向为 z 轴, 入射光的磁场方向指向 y 轴 ( TE 波 ) , 金属表面位于 z = 0 , 金属填充半无限空间 z < 0 区 ( 介电常数为 E m ) , 而 z > 0 区为真空或者介电材 料所占有 (介电常数 E 1 或 E 1 = E d ) , SPP s 沿 x 方向 传播, ( 如图 1 所示 ) . 根据 SPP s 的 特性 , 设 定 电磁 场的 形式
表面等离子体激元纳米激光器技术及应用研究进展

表面等离子体激元纳米激光器技术及应用研究进展陈泳屹;佟存柱;秦莉;王立军;张金龙【摘要】Conventional semiconductor lasers suffer from the scale of the diffraction limit due to the light to be confined by the optical feedback systems. Therefore, the scales of the lasers cannot be miniaturized because their cavities cannot be less than the half of the lasing wavelength. However, lasers based on the Surface Plas- mon Polaritons(SPPs) can operate at a deep sub-wavelength, even nanometer scale. Moreover, the develop- ment of modern nanofabrication techniques provides the fabrication conditions for micro - or even nanometer scale lasers. This paper reviews the progress in nano-lasers based on SPPs that have been demonstrated re-cently. It describes the basic principles of the SPPs and gives structures and characteristics for several kinds of nanometer scale lasers. Then, it points out that the major defects of the nanometer scale lasers currently are focused on higher polariton losses and the difficultiesin fabrication and electronic pumping technologies men- tioned above. Finally, the paper considers the research and application prospects of the nanometer scale lasers based on the SPPs.%传统半导体激光器由于采用光学系统反馈而存在衍射极限,其腔长至少是其发射波长的一半,因此难以实现微小化。
遥感与地理信息系统方面的好的期刊

遥感与地理信息系统方面的好杂志国内的期刊:1)遥感学报(98年前《环境遥感》杂志,国内比较好的遥感专业杂志,主编是原遥感所所长、现国家科技部部长徐冠华院士,遥感文章比较多,象国内比较牛的遥感理论研究的大牛复旦大学的金亚秋教授和北京师范大学的新当选的院士李小文教授经常有文章发表;基于遥感和GIS资源环境等应用的文章也比较好,主要是中科院地理所和遥感所的;还有就是图像处理的算法研究或新型的遥感方法如雷达干涉测量、高光谱方面的研究,主要由武汉大学测绘遥感信息工程国家重点实验室(L)和中科院遥感所的文章。
(2)测绘学报(侧重测量基础理论的研究,但经常有非常好的综述型的文章,上面的测绘学博士论文摘要是非常好,还有主编陈俊勇院士治学非常严谨,一般的假冒伪劣文章很难找到市场,该刊宁缺勿滥,2001年仍然是季刊,文章少,但很精。
不过该刊刊登的文章比较偏重大地测量(GPS),GIS的文章相比比较少)。
(3)武测学报(2001年改名《武汉大学学报》信息科学版)本杂志是原武汉测绘科技大学学报,主编是中国科学院和中国工程院双院士李德仁教授,很多具有创新性和理论性的测绘研究成果都在该刊发表,展示中国测绘学术研究的最高水平,引导测绘理论研究的方向。
我认为上面的博士论文摘要比较好,真正体现了我国3S技术的研究动向和学术水准。
本刊出版内容包括综述与瞻望、学术论文和研究报告、本领域重大科技新闻等,涉及测绘学研究的主要方面,尤其是摄影测量与遥感、大地测量与地球重力场、工程测量、地图制图、地球动力学、全球定位系统(GPS)、地理信息系统(GIS)、图形图像处理等。
该刊现同时有英文版,名为GEO-SPATIAL INFORMATION SCIENCE,是中文版的精华版,万方科技期刊网上可以下载全文。
(4)中国图象图形学报1996年创刊,由中国图象图形学会、中科院遥感所、中科院计算所共同主办,主编是科技部部长徐冠华院士。
2001年起《中国图象图形学报》分A、B版。
粒子群优化算法PSO介绍中英文翻译word版

粒子群优化算法(PSO)介绍在频谱资源日趋紧张的今天,想要通过增加频谱宽度来提高系统容量的方式已经很难实现;同时,想在时域、频域或码域进一步提高系统容量已经十分困难。
在这种情形下,人们把目光投向了空域,期望能够从中寻觅新的源泉。
随着人们对于无线移动通信的要求愈来愈高,专门是对高速多媒体传输的迫切需求,与之相关能够提高系统容量的技术也开始受到人们的特别重视。
20世纪90年代以来,对于群体智能的研究逐渐兴起。
Eberhart和Kennedy于1995年提出的粒子群优化算法(PSO),作为一种简单有效的优化算法迅速在各个领域取得了普遍的应用。
PSO算法的思想来源是鸟群在觅食进程中表现的群体智慧。
通常单个自然生物并非是智能的,可是整个生物群体却表现出处置复杂问题的能力,这就是群体智能。
各类生物聚集成生物种群,都有其内在行为规律,而人类作为高级生物,研究并掌握了这种规律,模拟设计出各类优化算法并运用于各类问题。
类似的还有按照生物繁衍特性产生的遗传算法,对蚂蚁群落食物收集进程的模拟产生的蚁群算法。
PSO算法目前已经普遍用于函数优化、神经网络训练、模糊系统控制和其他遗传算法涉及到的应用领域。
PSO算法较之其他的优化算法实现简单,也没有许多参数需要调整。
可是它也有着收敛过快、易收敛于局部极值的现象,专门是面对高维复杂的问题时如阵列天线方向图综合问题。
人们提出了很多的改良算法,来提高PSO算法的性能。
惯性权重和紧缩因子是目前应用比较普遍的对大体粒子群算法的改良,能够改善优化性能可是收敛较慢。
文献中将粒子群算法和遗传算法在方向图综合上的应用做了比较,能够看出粒子群算法较之遗传算法有计算量小易于实现等特点,但也能够看到大体的PSO算法和遗传算法的收敛速度都不快或往往在某个局部极值停滞太久很难跳出。
粒子群优化算法(PSO粒子群优化(PSO:Particle Swarm Optimization))是一种进化计算技术(evolutionary computation)是一种有效的全局优化技术,有Eberhart 博士和kennedy博士发明。
非线性光学 (Nonlinear Optics)

Robert W. Boyd
• Yujie Ding: B.S., Electronic Sciences, Jilin University; M.S., Electrical Engineering, Purdue Univ.; Ph.D.,Electrical Engineering, Johns Hopkins Univ.; now professor at Lehigh Univ..
• 其中虚线代表的是偏振
和电场 之间的线性关系,而实线代表非线性关系。
(a)在小电场情况下,偏振与电场的时间变化接近。 (b)电场强度加大后,偏振响应产生了非对称性,在负电场情况下具有较大的偏离。 • 以上这种失真的输出在电路理论中可以解释为高阶简谐成份的出现。
二、光学非线性的物理起源
Non-resonant nonlinearities 非共振非线性 •由 ,令 ,有 。 • 即在 不为零时,频率为ω的入射光场在介质中产生了频率为2ω的出射光场。
• 将一个电子束缚到一个原子中的电场幅度在1010-1011 V m-1左右,在光电场幅 度与该数值接近时非线性效应开始凸显。
•由
,此时光强需要达到1019 W m-2,可以由高功率激光来实现。
• 实际上并不需要上述的高光强,因为大量原子的微弱非线性效应可以叠加在 一起产生可观的宏观非线性效应 – 需要相位同步即“phase matching”条件。
原子跃迁的光谱线型函数
二、光学非线性的物理起源
Resonant nonlinearities 共振非线性 • 同样可以得到介质的单位时间内添加到光束中的受激发射光子数目:
• 此时单位时间内减少的光子数目为
,即净吸收速率。
• 随着光束在介质中的传播,其强度逐渐减小:定义z处的光强为I(z),dz内光强的变化 为dI ,此时有 。 • 由于光束强度定义为单位时间在单位面积上通过的能量(W m-2),有 ,即 。
冷原子光谱法 英语

冷原子光谱法英语Okay, here's a piece of writing on cold atom spectroscopy in an informal, conversational, and varied English style:Hey, you know what's fascinating? Cold atom spectroscopy! It's this crazy technique where you chill atoms down to near absolute zero and study their light emissions. It's like you're looking at the universe in a whole new way.Just imagine, you've got these tiny particles, frozen in place almost, and they're still putting out this beautiful light. It's kind of like looking at a fireworks display in a snow globe. The colors and patterns are incredible.The thing about cold atoms is that they're so slow-moving, it's easier to measure their properties. You can get really precise data on things like energy levels andtransitions. It's like having a super-high-resolution microscope for the quantum world.So, why do we bother with all this? Well, it turns out that cold atom spectroscopy has tons of applications. From building better sensors to understanding the fundamental laws of nature, it's a powerful tool. It's like having a key that unlocks secrets of the universe.And the coolest part? It's just so darn cool! I mean, chilling atoms to near absolute zero? That's crazy science fiction stuff, right?。
表面等离子体激元的原理与应用

材料研究与应用 2024,18(1):81‐94Materials Research and ApplicationEmail :clyjyyy@http ://mra.ijournals.cn 表面等离子体激元的原理与应用王强1,陈泳竹2*(1.广东技术师范大学光电工程学院,广东 广州 510665; 2.广东技术师范大学研究生院,广东 广州 510665)摘要: 光与物质之间的相互作用,被视为光学应用的最基础物理问题。
由光与凝聚态物质之间的相互作用形成的表面等离子体激元(Surface Plasmon Polaritons, SPPs ),是一种新型的元激发准粒子,因其具有独特的色散和局域场增强特性引起广泛关注。
SPPs 器件打破了传统光学衍射限制,在纳米光子器件中有独特优势,应用于微纳光子学的前沿研究。
阐述了SPPs 的色散关系、激发方式、传播形式和物理性质,重点探讨了SPPs 在波导、近场光学、传感器、生物医疗、光子芯片、表面增强拉曼散射和太阳能电池等方面的应用,并提出了研究前景。
关键词: 表面等离子体激元;衍射极限;局域场增强;表面等离子体共振;亚波长光学应用;波导;光子芯片;原理中图分类号:O436 文献标志码: A 文章编号:1673-9981(2024)01-0081-14引文格式:王强,陈泳竹.表面等离子体激元的原理与应用[J ].材料研究与应用,2024,18(1):81-94.WANG Qiang ,CHEN Yongzhu.Principles and Applications of Surface Plasmon Polaritons [J ].Materials Research and Applica‐tion ,2024,18(1):81-94.0 引言新世纪以来,计算机技术的迅猛发展和理论知识的不断创新,给人类生活带来极大便利的同时也加快了科学发展的脚步。
电子线路固有的发热现象和数据传输能力不足,极大地限制了计算机运行速度的大幅度提高。
量子保密通信器件发展概述

展 。 目前 实用 的量子保 密通信 技术依 赖于光 纤光缆 和精 密光学器 件 、本 文概述 了量子保 密通信 技术 用光纤 光缆 、光 器件的 发展热 点 ,包括 超低损 大有效 面积光纤 、高速 的窄脉;中半导体激 光器 、基于 lnGaAs/InP近 红外单 光子探测 器 、基 于单光子 时 间分辨 的量 子 随 机 数 发 生 器 等 。 The unconditional security of quantum key distribution is ensured by the No—cloning theorem,Uncertainty principle and Quantnm nonlocality W ith the completion ofthe”Beijing—Shanghai trunk line”and the completion ofthe three major research tasks ofthe”Mo—tse”quantum satellite.
表面等离子体纳米结构若干光学性质的研究毕业论文

摘要表面等离子体的发现及应用,为实现纳米尺度的光学控制提供了有力的工具。
金属纳米粒子对表面等离子体的研究至关重要,选择合适形状、尺寸以及排列结构的纳米粒子结构,可以提高表面等离子体的光场强度,更好地实现基于纳米粒子阵列的表面等离子体的聚焦和导波。
本文主要研究了金膜上纳米粒子抛物链在外电场激励下的表面等离子体的聚焦和导波:(1)针对格林函数分量计算中涉及到的Sommerfeld积分,研究了快速算法实现高效的积分运算,给出了沿最陡下降路径积分的计算实例,并与国外的结果进行分析对比,证明了运用的计算方法结果正确,算法快。
基于Sommerfeld积分的快速算法,分析和计算了半空间中任意方向的电偶极子的辐射和散射。
(2)从电磁基本理论出发,深入研究了金膜上基于纳米粒子抛物链的表面等离子体的相互作用,由并矢格林函数求解波动方程,建立分层参考系统的电磁场模型。
将纳米粒子抛物链划分为一系列立方单元,并利用耦合偶极子法将该积分方程转化为矩阵方程,从而计算出空间任意点的电场。
(3)应用格林函数体积积分法,研究了金膜上球形纳米粒子链在高斯光束照射下的SPPs激发、聚焦和导波。
研究了入射光斑大小、入射光沿链的位置、粒子间距和粒子链的曲率半径对SPPs激发、聚焦和导波影响。
结果表明,粒子间距、入射光斑大小对SPPs聚焦及其分布有很大影响。
入射光斑尺寸减小,激发的SPPs光束的衍射发散的增加,SPPs聚焦效果减弱。
SPPs场在很大程度上也取决于粒子间距,在粒子间距小于SPPs波长时,可以实现较好的SPPs聚焦和导波效果。
关键词表面等离子体;纳米粒子;格林函数法;耦合偶极子法;数值模拟AbstractSurface plasmon polaritons (SPPs) have been proved to better powerful tool for the optical manipulation on nanoscale. The nanoparticle on the metal thin film plays an important role of surface plasmon polaritons. If the metallic nanoparticles are designed with suitable shape, size and arrangement, electric field magnitude can be highly improved. Further, excitation, focusing and directing of surface plasmon polaritons with nanoparticles located on a finite metal layer could be accomplished theoretically.No matter which method is used for the calculation of scattered fields, there will be a common difficulty: the evaluation of Sommerfeld integrals, which is extremely time consuming. The integration along steepest descent paths is introduced to evaluate these Sommerfeld integrals. Numerical results show that the fast method can greatly accelerate the computation for scattering problems.Based on the fast evaluation of Sommerfeld integrals, the radiation of an arbitrarily oriented electric dipole in a half space is first analyzed and computed.Excitation, focusing and directing of surface plasmon polaritons with curved chains of nanoparticles located on a finite gold layer are investigated theoretically. The theory of Green’s dyadic functions on a layered reference system is outlined and electromagnetic properties of surface plasmons are discussed. A curved chain of nanoparticles in upper half-space is divided into a number of cubic cells and the integral equation is reduced to a matrix equation using coupled dipole formalism. Then we calculate the electric fields at any point on gold surface.Numerical simulations of the configuration investigated experimentally are carried out based on the Green’s tensor formalism and dipole approximation. We demonstrate that, by using a relatively narrow Gaussian beam (at normal incidence) interacting only with a portion of a curved chain of nanoparticles, one can excite an SPP beam whose divergence and propagation direction are dictated by the incident light spot size and its position along the chain. It is also found that the SPPs focusing regime is strongly influenced by the chain inter-particle distance. Comparison of numerical results with experimental data shows good agreement with respect to the observed features in SPPs focusing and directing, providing the guidelines for a proper choice of the system parameters.Keywords surface plasmon polaritons (SPPs); nanoparticles; Green’s dyadic function; coupled dipole formalism; numerical modelingII目录毕业设计(论文)原创性声明和使用授权说明原创性声明本人郑重承诺:所呈交的毕业设计(论文),是我个人在指导教师的指导下进行的研究工作及取得的成果。
FemtosecondZ-scanMeasurement:飞秒激光Z扫描测量

Off-Resonant Third-Order Optical Nonlinearity of Au Nanoparticle Array byFemtosecond Z-scan Measurement*WANG Kai(王凯)1,LONG Hua(龙华)1,FU Ming(付明)1,YANG Guang(杨光)1**,LU Pei-Xiang(陆培祥)1,2** 1Wuhan National Laboratory for Optoelectronics,Huazhong University of Science and Technology,Wuhan430074 2School of Science,Wuhan Institute of Technology,Wuhan430073(Received21January2010)A periodic triangular-shaped Au nanoparticle array is fabricated on a quartz substrate using nanosphere lithogra-phy and pulsed laser deposition,and the linear and nonlinear optical properties of metal particles are studied.The morphology of the polystyrene nanosphere mask(D=820nm)and the Au nanoparticle array are investigated by scanning electron microscopy.The surface plasmon resonance absorption peak is observed at606nm,which is in good agreement with the calculated result using the discrete dipole approximation method.By performing the Z-scan method with femtosecond laser(800nm,50fs),the optical nonlinearities of Au nanoparticle array are determined.The results show that the Au particles exhibit negative nonlinear absorption and positive nonlinearrefractive index with the effective third-order optical nonlinear susceptibilityχ(3)eff can be up to(8.8±1.0)×10−10esu under non-resonant femtosecond laser excitation.PACS:42.70.Mp,81.16.Nd DOI:10.1088/0256-307X/27/12/124204Noble metal nanoparticles such as Au,Ag and Cu have been of particular interest for a long time because of their unique optical properties called sur-face plasmon resonance(SPR),which is caused by the collective resonance of the conductive electrons in re-sponse to incident light and is widely used in applica-tions such as catalysis,biological sensors and molecu-lar rulers.[1−3]Recently,many studies have focused on the nonlinear properties of noble metal nanoparticles due to their large nonlinear optical effects and fast re-sponse time,which have great potential applications for all-optical switching and computing.[4−7] It is well known that the optical nonlinearities of noble metal nanoparticles can be greatly enhanced at the SPR position and strongly dependent on the nanoparticles’size,shape and distribution.However, among most of the previous works,the metal particles are comprised of spheres of various sizes or random distributed,which leads to broad SPR spectra and weak optical enhancement.The nanosphere lithogra-phy(NSL)has been proved to be a powerful tool de-veloped from natural lithography by Van Duyne[8,9]in 1995,to fabricate periodic particle array(PPA)with tunable shape,size and height,which make it possi-ble to quantitatively study the optical properties of nanoparticles.Recently,several studies on the nonlinear opti-cal properties of metal nanoparticle array have been reported.Both theoretical[10,11]and experimental studies[12,13]indicate that anisotropy of the shape and geometric distribution of the metal nanoparticles could enhance greatly the optical nonlinearityχ(3). However,up to now,the measurement of the nonlin-ear optical properties of the Au periodic nanoparticle array excited by ultrafast laser(50fs)at a wavelength of800nm has seldom been reported.In this Letter,we study the optical nonlinearities of an Au nanoparticle array determined by femtosecond laser.The morphology of the Au nanoparticle array is observed by scanning electron microscopy(SEM). The third-order nonlinear property is measured by Z-scan method,which is a useful tool to measure the nonlinear optical properties such as nonlinear absorp-tion and refraction.[14]The real and imaginary parts of the third-order nonlinear susceptibility,Reχ(3)and Imχ(3),are determined by performing open-aperture (OA)and closed-aperture(CA)Z-scan measurements, respectively.In the NSL processing step,the monodisperse polystyrene(PS)nanosphere suspensions were pur-chased from Duke Scientific Corp.,and the diame-ter of the spheres used in the experiment was820±5nm.The details of the NSL have been described elsewhere.[15]For the PLD processing step,a KrF (Lambda Physik,248nm)laser beam was used as the laser source with the laser energy density of about 2J/cm2focused on the target and the laser repetition frequency was6Hz.The deposition time was set to be 30min.The surface morphology of the NSL mask and the Au PPAs was observed by SEM(FEI QUANTA 200).The SPR spectra were measured by UV-visible absorption spectroscopy(U-3310UV Solutions)in a wavelength range from340nm to900nm.The inci-dent light was perpendicular to the samples through a small aperture with diameter of2mm to measure the absorption properties of small area.In order to*Supported by the National Natural Science Foundation of China under Grant No10974062,the National Science Fund for Distinguished Young Scholars under Grant No60925021,and the National Basic Research Program of China under Grant No 2010CB923203.**Email:***************;********************c○2010Chinese Physical Society and IOP Publishing Ltdcompare with the experimental result,the theoretical calculations based on the discrete dipole approxima-tion (DDA)method were also performed.The third-order nonlinear optical properties of the sample were determined by the Z-scan method.In our experiments,a femtosecond laser system,which consisted of a mode-locked Ti:sapphire oscil-lator and a regenerative amplifier (Spitfire,Spectra-Physics,800nm,50fs,1kHz),was used as the light source.The sample was scanned along the optical axis (z -direction)and focused by a lens with a focal length of 200mm.When there is no aperture in front of the detector,OA Z-scan curves are obtained and the nonlinear absorption coefficient βcan be deter-mined,while the nonlinear refractive index γis deter-mined by CA Z-scan curves using a small aperture.The radius of the beam waist ω0was 33µm,which iscalculated from the equation ω(z )2=ω02(1+z 2/z 20),where z 0=πω20/λis the Rayleigh length.The value of z 0was calculated to be 4.2mm,much larger than the thickness of either the 0.2-mm substrate or the sam-ple.The transmitted beam energy through OA or CA is received by silicon diodes (PC20-6,Silicon Sensor GmbH)and double-phase lock-in amplifier (SR830,Stanford ResearchSystem).nmFig.1.SEM image of large area (20×15µm 2)of a well-packed nanosphere mask with diameter D =820nm.The inset shows the SEM image of the details of the nanosphere mask.a =190 nm5 m m Fig.2.The SEM image of large area (25×20µm 2)of anAu nanoparticle array.The inset shows the cell of trian-gular Au nanoparticle array.Figure 1shows the SEM image (20×15µm 2)of the polystyrene nanosphere mask.It can be seen that most of the area is occupied by well-packednanospheres.The inset in Fig.1shows the details of the mask that the triangular-shaped gaps between nanospheres can only allow the deposited source to go through.Figure 2shows the SEM image of the Au nanoparticles at a scale of 25×20µm 2and the Au PPAs can be observed clearly.The inset in Fig.2shows clearly the shape and the size of the Au triangu-lar prism.The size of the nanoparticle can be defined with two parameters:the in-plane perpendicular bi-sector a and the out-of-plane particle height b .By a geometrical calculation,D =0.233a ,the value of a is calculated to be 190nm,which is in good agreement with the experimental results shown in the inset in Fig.2.Fig.3.Absorption spectrum of Au nanoparticle array with SPR peak at 606nm.The dotted line shows the DDA calculation result of absorption properties for a sin-gle Au particle with the same cross section,and a particle height of 16nm.The dashed line shows the average DDA results of three Au particles with the same cross section and different height:14nm,16nm and 18nm.The linear absorption of the Au PPAs was mea-sured in the wavelength range from 340nm to 900nm and the black line shows the absorption spectrum in Fig.3.It can be seen that the absorption peak due to SPR of Au particles is found to be located at 606nm.With the Mie theory,when εr (λ)+2εd =0and εi (λ)is small,the SPR condition occurs.Here εd is the dielectric constant of the medium surround-ing the metal nanoparticle,εr (λ)and εi (λ)are the real and the imaginary parts of dielectric function of the metal particles.The optical enhancement un-der laser excitation near the SPR position is much stronger than that in the off-resonant position such as λ=800nm.In comparison,the optical proper-ties of Au particles with the same cross section and particle height of 14nm,16nm and 18nm were calcu-lated using the DDA method.[16,17]The dotted line shows the absorption spectrum for a single 16-nm-height particle.It can be seen that the position of the SPR peak is located at 606nm,which is the same as the experimental results.The dashed line shows the average DDA results of three Au particles with differ-ent heights 14nm,16nm and 18nm.The deviationof the Au particles shape and height from theoretical values leads to the SPR peaks shifting and a broader SPR spectrum.Thus it is reasonable that the particle height is estimated to be16±2nm.Fig.4.Z-scan measurements at I0=59.5GW/cm2.(a) Open-aperture Z-scan results of Au nanoparticle array,the solid line indicates the theoretical fit.(b)Closed-aperture Z-scan result of Au nanoparticle array,the solid line indi-cates the theoretical fit.Figure4shows the typical OA and CA Z-scan results for the Au PPAs.The black dots indicate the experimental data and the solid curve represents the theoretical fit.The laser pulse energy at the fo-cal spot,E0,was100nJ and the laser intensity at the focal point,I0=E0/πω2τ,was calculated to be 59.5GW/cm2.Under the repetition rate of1kHz,the accumulative thermal effects can be neglected.The transmitted energy at each position was measured16 times to obtain a reliable average value.One can see that the curve in Fig.4(a)comprises a normalized peak,indicating the presence of saturation of absorp-tion(SA)in the Au PPAs.Under these conditions, as the shape of the Z-scan results for the substrate is flat,the substrates have a very small nonlinear opti-cal effect that can be neglected and the large nonlinear absorption observed here results from the Au PPAs.Figure4(b)shows the CA Z-scan data for Au PPAs.In order to obtain nonlinear refraction infor-mation,an approximate method was used where the closed-aperture transmittance was divided by the cor-responding open-aperture data.It can be seen that the shape of the curve exhibits a positive value for the nonlinear refractive index.From Fig.4(b),one can find that the distance between the peak and the val-ley(∆Z p−v)is about7.6mm as compared to1.71z0, which indicates that the observed nonlinear effect is the third-order response.The difference between nor-malized transmittances at peak and valley∆T p−v is 0.04,and S=0.18is the transmittance of the small aperture.The nonlinear absorption coefficientβ(m/W)and the nonlinear optical refractive index(m2/W)can be calculated using the method described in detail elsewhere.[14]The values ofβandγof Au PPAs were calculated to be(−1.3±0.1)×10−8m/W and (1.3±0.2)×10−15m2/W,respectively.The real and imaginary parts ofχ(3)of the Au PPAs can be ob-tained by the equations Reχ(3)(esu)=cn20γ/120π2 and Imχ(3)(esu)=cn20β/240π2k,where k=2π/λis the wave vector.The values of Reχ(3)and Imχ(3)were calculated to be(7.4±1.0)×10−10esu and(−4.7±0.4)×10−10esu,respectively.The absolute value of χ(3)was obtained to be about(8.8±1.0)×10−10esu, indicating the large third-order nonlinear optical prop-erties in Au PPAs using the femtosecond laser excita-tion.Fig.5.(a)Open-aperture Z-scan results of Au nanoparti-cle array in different exciting energy.(b)Intensity depen-dence of the nonlinear absorption coefficientβ(m/W).Figure5(a)shows the OA Z-scan results for Au PPAs at different excitation energies.With the increasing laser intensity at the focal point I0=29.5GW/cm2,46.4GW/cm2,59.5GW/cm2, 89.3GW/cm2and178GW/cm2,the normalized transmittance peak becomes progressively larger and exhibits SA process.The excited intensity induces ground-state plasmon to be bleached,which leads to the increasing OA transmittance with the increasing excited intensity.Figure5(b)shows the laser inten-sity dependence of values ofβthat are independent of the laser intensity when the intensity is relatively low (<60GW/cm2)and starts to decrease when the laser energy is higher.The high(>60GW/cm2)inten-sity results in the free carrier absorption dominating the region and the transmittance decreases with the increasing intensity and the reverse saturation of ab-sorption(RSA)process becomes considerable.In the ultrashort pulse temporal regime(smaller than a few picoseconds),the contribution of the hot electron phenomenon toχ(3)m is expected to be significant.[15]Hereχ(3)m and the corresponding sus-ceptibility response to the local field E loc,χ(3)eff,are related by[18]χ(3)eff=pf2|f|2χ(3)m,(1) where p is the metal volume fraction and f the ratio between the local field E loc and the applied field E0.E loc=3εdεm+2εdE0.(2) In the large particle limit,it is appropriate to calcu-late theεm value from the data for bulk Au.[19]Here εd=1is the dielectric constant of the host material for air matrices.The value of local-field factor|f|is estimated to be0.15at the wavelength of800nm for spherical particles using Eq.(2).However,in the case of triangular-shaped nanoparticle arrays,the local-field factor f cannot be calculated using Eq.(2).Using the following equation,the value of local-field factor can be estimated,[20]α=pωn0c|f|2ε′′m,(3)whereα0=8.5×103cm−1is the linear absorption coefficient at the wavelength of800nm,ωis the an-gular frequency of the incident light,c is the velocity of light.For the nanoparticle array in this experi-ment,p=0.08,which is a very low value of volume fraction of metal nanoparticles.The value of local-field factor|f|is estimated to be1.6,which is about 11times larger than that for the spherical particles. Thus the enhancement observed in Au PPA is prob-ably due to the stronger local field in the triangular-shaped nanoparticles.For comparison,the nonlinear coefficients of sev-eral thin films in the near infrared region under the ex-citation of femtosecond laser pulses are listed in Table 1.It is suggested that the Au nanoparticle array ex-hibits large optical nonlinear coefficients and has great potential applications in nonlinear photonics devices.Table1.Femtosecond optical nonlinearities of several films/particles in the near infrared region.Films/Particlesλ(nm)I0(GW/cm2)Pulse width(fs)β(m/W)γ(m2/W) Au PPAs80059.550−1.3×10−81.3×10−15DWNT a[21]800 1.5501.4×10−10−2.6×10−15BiFeO3[22]7801563501.6×10−101.5×10−17LGF b[23]8000.51503×10−82×10−17VO2[24]80016.91202.7×10−9−7.1×10−16a Double walled carbon nanotubes(DWNT).b lead-germanium based films(LGF).In summary,a triangular-shaped Au nanoparticle array has been fabricated by NSL and the PLD tech-nique.The nonlinear optical properties of the sample are investigated by the Z-scan method at a wavelength of800nm with pulse duration of50fs.The third-order nonlinear optical susceptibility is determined to be(8.8±1.0)×10−10esu.The large third-order non-linearity shows that Au nanoparticle arrays have great potential applications in ultrafast nonlinear photonic devices such as all-optical switching and computing. References[1]Haes J,Hall W P,Chang L,Klein W L and Van Duyne RP2004Nano Lett.41029[2]Park S J,Taton T A and Mirkin C A2002Science2951503[3]Narayanan R and El-Sayed M A2004Nano Lett.41343[4]Okada N,Hamanaka Y,Nakamura A,Pastoriza-Santos Iand Liz-Marzán L M2004J.Phys.Chem.B1088751 [5]Hamanaka Y,Nakamura A,Hayashi N and Omi S2003J.Opt.Soc.Am.B201227[6]Jayabalan J,Singh A,Chari R and Oak S M2007Nan-otechnology18315704[7]Tran P1997J.Opt.Soc.Am.B142589[8]Hulteen J C and Van Duyne R P1995J.Vac.Sci.Technol.A131553[9]Haynes C L and Van Duyne R P2001J.Phys.Chem.B1055599[10]Yuen K P,Law M F and Sheng P1997Phys.Rev.E56R1322[11]Huang J P and Yu K W2005J.Opt.Soc.Am.B221640[12]Shen H,Cheng B,Lu G W,Ning T Y,Guan D Y,Zhou YL and Chen Z G2006Nanotechnology174274[13]Nahata A,Linke R A and Ohashi K2003Opt.Lett.28423[14]Sheik-Bahae M,Said A A,Wei T H,Hagan D J and VanStryland E W1990IEEE J.Quantum Electron.26760 [15]Huang W Y,Qian W and El-Sayed M A2005J.Phys.Chem.B10918881[16]Draine B T and Flatau P J1994J.Opt.Soc.Am.A1114919[17]Draine B T and Flatau P J2008User Guide to theDiscrete Dipole Approximation Code DDSCAT7.0 arXiv:0809.0337v5[18]Ricard D,Roussignol P and Flytzanis C1985Opt.Lett.10511[19]Lide D R2001Handbook of Chemistry and Physics(Florida:CRC)[20]Uchida O K,Kaneko S,Omi S,Hata C,Tanji H,AsaharaY,Ikushima A J,Tokizaki T and Nakamura A1994J.Opt.Soc.Am.B111236[21]Kamaraju N,Kumar S,.Karthikeyan B,Moravsky A,Loutfy R O and Sood A K2008Appl.Phys.Lett.93 091903[22]Gu B,Wang Y,Wang J and Ji W2009Opt.Express1710970[23]Rativa D,Araujo R E,Araújo C B,Gomes A S L andKassab L R P2007Appl.Phys.Lett.90231906[24]Lopez R,Haglund R F,Feldman L C,Boatner L A andHaynes T E2004Appl.Phys.Lett.855191。
金属纳米材料表面等离子共振吸收的表征及其应用

aspect ratio 1.94 2.35 2.48 3.08
金球
金纳米棒
顶部: 计算的紫外可见吸收光谱 底部: 实验的光谱
Au vol% 10 30 50 60 70
金薄膜separationFra biblioteknm∞
15 7.5 1.5 1 0
多层金薄膜
Luis M., Langmuir, 2006, 22, 32
电磁波辐射与金属纳米材料作用的示意图 (a) 球型粒子 (b) 纳米棒
Luis M., Langmuir, 2006, 22, 32
diameter/nm 10 20 50 100
金球
diameter/nm 9 22 48 99
aspect ratio 2.0 2.2 2.4 2.6 2.8 3.0
21903
17469
6530
(a, b and c) 10-8M的罗丹明B在不同形状的Ag纳米材料上的SERS谱图 (d) 10-8M的罗丹明B水溶液的拉曼光谱
Jiatao Zhang, J. Phys. Chem. B 2005, 109, 12544
2180
2129 1596
1208 1167 2180 2129
纳米尺寸的金属粒子内部自由电子按其固有频率作协同 振荡,电子的运动可与一定波长的光作用发生共振,从而 产生金属粒子的表面等离子体共振 (surface plasmon resonance, SPR),其共振频率与电子密度、粒子大小和形 状等密切相关。UV-Vis 吸收光谱是表征等离子体共振的有 效工具之一。
Correa-Duarte, M. A., Angew. Chem. Int. Ed. 2005, 44, 4375
氮化硅薄膜中纳米非晶硅颗粒的键合结构及光致发光

表 1 不同配比样品的各键密度Π1022 cm - 3
R
013
018
112
于 威 李亚超 丁文革 张江勇 杨彦斌 傅广生
(河北大学物理科学与技术学院 ,保定 071002) (2007 年 9 月 4 日收到 ;2007 年 10 月 24 日收到修改稿)
采用螺旋波等离子体化学气相沉积技术以 N2ΠSiH4ΠH2 为反应气体制备了镶嵌有纳米非晶硅颗粒的氢化氮化 硅薄膜 ,通过改变 N2 流量实现了薄膜从红到蓝绿的可调谐光致发光. 傅里叶红外透射和紫外2可见光吸收特性分 析表明 ,所生长薄膜具有较高的氢含量 ,N2 流量增加使氢的键合结构发生变化 ,非晶硅颗粒尺寸减小 ,所对应的薄 膜的光学带隙逐渐增加和微观结构有序度减小. 可调光致发光 ( PL) 主要来源于纳米硅颗粒的量子限制效应发光 , 随 N2 流量增加 ,PL 的谱线展宽并逐渐增强.
Si —N
1170
2104
215
N —H
0122
0193
1140
Si —H
1173
1140
1114
© 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved.
SiH4 流量条件下 ,增加 N2 流量所引起的硅团簇成核
位置数密度增大及整体氮化硅成分的增加必将导致
硅纳米硅粒子尺寸的下降[13] .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a rXiv:q uant-ph/05123v215M ar21Aspects of nonlocality in atom-photon interactions in a cavity A.S.Majumdar ∗1and N.Nayak †21S.N.Bose National Centre for Basic Sciences,Block JD,Sector III,Salt Lake,Calcutta 700098,India 2Department of Physics,Texas A&M University,College Station,Texas 77843-4242,USA We investigate a Bell-type inequality for probabilities of detected atoms formulated using atom-photon interactions in a cavity.We consider decoherence brought about by both atomic decay,as well as cavity photon loss,and study its quantitative action in diminishing the atom-field and the resultant atom-atom secondary correlations.We show that the effects of decoherence on nonlocality can be observed in a controlled manner in actual experiments involving the micromaser and also the microlaser.PACS number(s):03.65.Bz,42.50.Dv I.INTRODUCTION Nonlocality at the quantum level manifests itself in various kinds of phenomena.The study of this so far,has been predominantly confined to the study of interactions amongst similar kinds of particles,for example,photon-photon interactions or the interaction of subatomic particles among themselves.With the advance of technology over the last several years,it has now become conceivable to investigate a new kind of nonlocality in a controllable fashion,viz.,the nonlocality generated through the interaction of distinct entities,like atoms and photons inside a high quality cavity.The mathematical framework for demonstrating the violation of local realism in quantum mechanics was first provided by Bell [1]through his famous inequalities.This work was subsequently generalized and also extended to consider the interaction of more than two particles [2,3].A different kind of proof of nonlocality without the use of inequalities,also exists [4].Furthermore,it has been shown that quantum nonlocality continues to persist even for the case of a large number of particles,or large quantum numbers [5].This has raised certain questions regarding the issue of the macroscopic or classical limit of quantum mechanics in examples where both the number of particles,and their quantum number is made arbitrarily large [6].The phenomenon of environment induced decoherence is of direct relevance here.It would be interesting if decoherence could be experimentally controlled and its effect on nonlocality be quantitatively monitored in particular examples of study.Experimental proposals of demonstrating nonlocality have mostly been concerned with spin-1/2particles [7],pho-tons [8,9],or mesons [10].In recent times,several schemes involving two-level Rydberg atoms have been proposed [11,12].In such schemes two-level rydberg atoms are considered in analogy to the spin system in Bell’s original rea-soning.The role of the polarization axis of the Stern-Gerlach apparatus used for spin-1/2systems is played here by the phase of an auxiliary electromagnetic field.The primary advantages of the experiments using atoms,compared to those with photons or spin half particles are two-fold.First,the realization of spacelike separation for Rydberg atoms is easier because of their smaller velocities than photons or electrons.Secondly,the efficiencies of detectors used for the former is much larger in general in comparison with the detectors used for elementary particles.In addition,the interaction of large-sized atoms with the environment can be significant enough to be monitored in certain cases.In fact,in the experimental schemes which involve the interaction of Rydberg atoms with photons in a microwave cavity,dissipation through the loss of cavity photons always occurs.The effect of this is manifested in the form of loss of coherence in the atom-photon interactions.Thus,this is a natural arena to study the effects of decoherence on quantum nonlocality in a quantitative manner.In this paper we propose a realistic experiment to test Bell’s inequality for real micromasers/microlasers by taking experimentally attainable data in the presence of both atomic decay and cavity dissipation under the influence of their respective reservoirs.The approach followed by us enables us to analyze both micromaser as well as microlaser dynamics within the framework of a single formalism in presence of decoherence.Our aim is to study the effects of decoherence on the magnitude of violation of Bell’s inequality in an experimentally controllable fashion.As an interesting sidelight,we are also able to demonstrate the effect of decoherence on multiparticle correlations thatarea natural outcrop of experimental schemes using microwave cavity that we use for our analysis.In the next section we describe the experimental arrangement and the relevant Bell-type inequality(BI).We wish to emphasize thatalthough the BI used by us is the same as in[12],the cavity dynamics considered by us(the steady-state dynamics is discussed in Section III)differs crucially form the one used in[12].We are hence able to take into account micromaserdissipation in a more realistic manner,and also analyse the microlaser by incorporating atomic decay.In Section IV we present and discuss our results.Section V is reserved for some concluding remarks.II.VIOLATIONS OF BELL’S INEQUALITY IN A MICROCA VITYWe consider the following experimental scenario.A two-level atom initially in its upper excited state|e>traverses a high-Q single mode cavity.The cavity is in a steady state and tuned to a single mode resonant with the transition|e>→|g>.The emerging single-atom wavefunction is a superposition of the upper|e>and lower|g>state,and it leaves an imprint on the photonic wavefunction in the cavity.After leaving the cavity,the atom passes through anelectromagneticfield which gives it aπ/2pulse the phase of which can be varied for different atoms.The atom then reaches the detector,placed at a sufficient distance,capable of detecting the atom only in the upper or lower state. Thus,the role of theπ/2pulse may be considered as a component of the detection mechanism in the experiment [13].During the whole process,dissipation takes place,and is taken into account.Next,this process is repeated for a similar second atom.The important difference is that the second atom interacts with a photonic wavefunction which has been modified due to the passage of thefirst atom.There is no direct interaction between the two atoms, although secondary correlations develop between them.In other words,though there is no spatial overlap between the two atoms,the entanglement of their wavefunctions with the cavity photons can be used to formulate local-realist bounds on the detection probabilities for the two atoms[11,12].The interplay of the atomic statistics with the photonic statistics plays a crucial role in the investigation of non-locality here.The initial state of the cavity is built up by the passage of a large number of atoms,but only one at a time,through it.The pump parameter and the atom-photon interaction time are key inputs for the profile of the resultant photonic wavefunction which in turn governs the nature of entanglement between two successive experimental atoms detected in their upper or lower states by the detector.As stated earlier,dissipation due to the interaction of the pumping atoms with their reservoir,as well as the loss of cavity photons can be controlled,and their effects on the statistics of detected atoms can be studied.The formalism used by us has another generic feature. The effects of decoherence on nonlocality can be studied in context of the micromaser,as well as the microlaser,its optical counterpart.It is easy to obtain a Bell-type inequality suitable for the scenario considered by us in analogy to Bell’s originalreasoning.Two level Rydberg atoms are analogous to spin-1/2systems,and the phase of the electromagneticfield plays the role of the polarization axis of the Stern-Gerlach apparatus used for spin-1/2systems.In fact,several local realist bounds have earlier been derived to tailor such a situation[11,12].Let us very briefly describe one such derivation[12]which we shall use in the present analysis.Assigning the value+1for the atom detected in the upper state|e>,and−1for the lower state|g>,one can in any local realist theory define functions f(φ1)=±1;g(φ2)=±1 describing the outcome of measurement on the atom1and2when the phase of the electromagneticfield givingπ/2 pulse to the atoms is set to beφ1andφ2for the respective atoms.The ensemble average for double click events is therefore defined asEλ(φ1,φ2)= dλf(φ1)g(φ2)(1)whereλis a suitable probability measure on the space of all possible states.The quantum mechanical expectation value for double click events is calculated from the probabilities of all possible double-click sequences.This is given byE(φ1,φ2)=P ee(φ1,φ2)+P gg(φ1,φ2)−P eg(φ1,φ2)−P ge(φ1,φ2)(2) where P eg(φ1,φ2)stands for the probability that thefirst atom is found to be in state|e>after traversing theπ/2 pulse with phaseφ1,and the second atom is found to be in state|g>with the phase of theπ/2pulse beingφ2for its case.Defining E0=Eλ(φ1=φ2)and M0=P ee(φ1=φ2)+P gg(φ1=φ2),and assuming perfect detections,it follows that E0=2M0−1.Further,it is easy to see that f(φ)=+g(φ)with probability M0,and f(φ)=−g(φ)with probability(1−M0).Hence,Eλ(φ1,φ2)can be written asEλ(φ1,φ2)=E0 dλf(φ1)f(φ2)(3)2Now,one can define a Bell sumB ≡|E λ(φ1,φ2)−E λ(φ1,φ3)|+sign (E 0)[E λ(φ2,φ3)−E 0](4)It follows immediately from (2-4)that B ≤0.In the next section we shall calculate this Bell sum B and see how it evolves for various values of the cavity parameters.It is convenient to set the values of the phases φ1=0,φ2=π/3,and φ3=2π/3,as for these values the Bell-type inequality is always violated,i.e.,B >0for the case of an idealised micromaser [12].III.STEADY-STATE MICROMASER/MICROLASER PHOTON STATISTICSIn realistic situations,one must consider the interacting systems (atoms as well as cavity field)coupled to their respective reservoirs.The couplings are governed by their equations of motion [14],˙ρ|atom −reservoir =−γ(1+¯n th )(s +s −ρ−2s −ρs ++ρs +s −)−γ¯n th (s −s +ρ−2s +ρs −+ρs −s +)(5)for the atom and˙ρ|field −reservoir =−κ(1+¯n th )(a †aρ−2aρa †+ρa †a )−κ¯n th (aa †ρ−2a †ρa +ρaa †)(6)for the field.ρis the reduced density operator obtained after tracing over the reservoir.γand κare the decay constants for the atom and the field respectively.¯n th is the average photon number representing the reservoir.s +and s −are the usual Pauli operators for the pseudo-spin representation of the two-level model of the atom.a (a †)is the photon annihilation (creation)operator.The dynamics we are interested in,involves two-level atoms steamed into a single mode cavity in such a way that there is at most one atom in the cavity at any time.Thus we have sequences of events (atom-field interactions)taking place randomly,but with each event of a fixed duration τ.This interaction is governed by˙ρ|atom −field =−i [H,ρ](7)where H =g (s +a +s −a †)is the well known Jaynes-Cummings [15]Hamiltonian with g being the coupling constant.Thus,we have to solve the equation of motion˙ρ=˙ρ|atom −reservoir +˙ρ|field −reservoir +˙ρ|atom −field (8)where the terms on the r.h.s.are the r.h.s’of (5),(6)and (7)respectively.For the duration between two events,we have to solve the equation of motion (6)only.The steady-state photon statistics of the cavity field undergoing such dynamics has been derived in [16].In thecavity photon number representation,the probabilities P n =<n |ρ(ss )f |n >are given byP n =P 0n m =1v m (9)P 0is obtained from the normalisation ∞n =0P n =1.The v n are given by the continued fractionsv n =f (n )3/(f (n )2+f (n )1v n +1)(10)with f (n )1=(Z n +C n )/κ,f (n )2=−2N +(Y n +B n )/κand f (n )3=−(X n +A n )/κ.κis the cavity bandwidth and N =R/2κis the number of atoms passing through the cavity in a photon lifetime.A n =2nκ¯n th ,B n =−2κ(n +¯n th +2n ¯n th )and C n =2(n +1)(¯n th +1)κ.X n ,Y n and Z n are given byX n =R sin 2(g √Y n =1n +1τ]−12(γ/κ+2n +1)−F 2(n −1)]exp {−[γ+(2n −1)κ]τ} ,and Z n =12(γ/κ+2n +3)+F 2(n )]exp {−[γ+(2n +1)κ]τ}−[1(√n +1)2 γn +2−√mτ)−γmτ)−[2n +3+2n +2−√mτ) +κ/4g n +2+√κ(√n +1)sin (2g √g cos (2g √(n +1)(n +2)](√n +1)sin (2g √2[A ρ(ss )f A †+D ρ(ss )f D †−{e −iφ1A ρ(ss )f D †+e iφ1D ρ(ss )f A †}]P g =1a †a +1)D =−ia †sin(gt √√(since Tr.f P e=1/2).The phase of theπ/2pulse is set toφ2for the second atom.P e for the second atom is given by P(2)e=1N) for the case of the micromaser in Figure1.500.10.20.30.40.50.60.70510********BD FIG.1.Violation of Bell’s inequality in a micromaser [20].Atoms in the upper of the two Rydberg levels are streamed into a cavity,one at a time,in such a way that the flight time of an atom τis much shorter than the lifetime of the long-lived Rydberg levels.Hence,we set the atomic decay constant γ=0.The average thermal photons ¯n th =0.15in the cavity represent its temperature at 0.5K .The leakage of the cavity photons is represented by κ/g =0.1×10−6.The pump rate N ,the number of individual atoms that pass through the cavity in a photon lifetime,=20(full),50(broken),and 100(dotted).D =φ√00.10.20.30.40.50.60.700.51 1.522.533.544.55BD FIG.2.Enhancement of nonlocality for increased N in the micromaser.The maximum value of B is 0.5812for N =20(full line),0.6079for N =50(broken),and 0.6241for N =100(dotted).Let us now consider the violation of BI in the microlaser.It is well known that atomic decay is an important factor in the microlaser where atomic levels at optical frequencies are involved.Although decay is unimportant for the dynamics of a single atom interacting with the field up to a certain interaction time,its accumulated effect for a large number of atoms is crucial for the evolution of the microlaser field to a steady state.Furthermore,the interaction time of the atom with the π/2pulse (in this case it is gt =π/2)is far less compared to even individual atom-field interaction times of interest in microlaser dynamics.For this reason the effect of atomic decay can be neglected during interaction of the atom with the π/2pulse.Our results for the microlaser are shown in Figure 3.00.10.20.30.40.50.60510********BD FIG.3.Demonstration of nonlocality in a microlaser,the optical counterpart of the micromaser.The results of our numerical simulations can be tested in a microlaser of the type in [21].Atomic levels having transition frequency in the optical regime have shorter lifetimes compared to Rydberg levels,and hence,we set γ/g =0.1.At optical frequencies,thermal photons are very close to zero,and thus we take ¯n th =0.N =100.The cavity leakage rate is κ/g =0.01(full),0.001(broken)and 0.0001(dotted).The effect of decoherence (cavity leakage rate κ/g )on the violation of BI is clearly seen in the microlaser.One can7check,similar to the case of the micromaser that the value of Bell sum B decreases with the increase of pump rate N for a large range of interaction timesτ.But in case of the microlaser,atomic dampingγis a dominating factor, in contrast to the cavity photon loss in the micromaser.This makes the Bell sum fall offrapidly for large values of τ.The second peak in B however,is a consequence of the Jaynes-Cummings dynamics and survives such dissipation [19].V.CONCLUSIONSTo summarize,we have shown that a demonstration of nonlocality,encompassing several of its varied aspects in atom-photon interactions in cavities and the effects of decoherence on it,can be possible in experimental set-ups already in operating conditions for the micromaser[20],as well as for the microlaser[21].The formalism chosen enables us to consider the steady-state dynamics of both the micromaser as well as the microlaser in the presence of atomic decay and cavity dissipation within a unified framework.Their distinguishing features are brought about by the different values of the parameters chosen to analyze the violation of BI in them separately.Certain notable features,such as enhancement of nonlocality for increased number of atoms,when decoherence effects are small,can be observed.We have seen how such features can be quantitatively monitored by control of decoherence.In an actual experiment,certain points have to be borne in mind.A few atoms may go undetected between two detector clicks.However,the steady state nature of the cavityfield contributes to making the effect of this on the Bell sum insignificant compared to the effect of decoherence which we have probed in detail.Finally,the observed magnitude of violation of BI would be brought down byfinite detector efficiency.Nevertheless,our selection of the particular type of BI[12],and the phases ofφ,ensure that this BI is always violated for the range of parameters chosen irrespective of the efficiency factor of the detector,which can in any case be accounted for easily by the introduction of appropriate scaling factors in the expressions of the various probabilities appearing in the Bell sum.[21]K.An,J.J.Childs,R.R.Dasari,and M.S.Feld,Phys.Rev.Lett.73,3375(1994).Uniform atom-field coupling constantin the cavity,an essential feature of the dynamics[19]considered here,has been obtained by them in,K.An,R.R.Dasari and M.S.Feld,Opt.Lett.22,1500(1997).Our present investigation shows that nonlocality can be demonstrated in such a device with strictly single-atom events.The MIT group is near attaining such events,R.R.Dasari(Private communication).9。
