16周量子力学基础
理论物理

19世纪末,物理学理论在当时看来已经发展到 相当完善的阶段。主要表现在以下两个方面:
(1) 应用牛顿方程成功的讨论了从天体到地上各种尺 度的力学客体的运动,将其用于分子运动上,气体分 子运动论,取得有益的结果。 1897年汤姆森发现了电 子,这个发现表明电子的行为类似于一个牛顿粒子。 (2) 光的波动性在 1803 年由杨的衍射实验有力揭示出 来,麦克斯韦在 1864年发现的光和电磁现象之间的联 系把光的波动性置于更加坚实的基础之上。
1898年Curie夫妇发现了放射性元素钚与镭 电子与放射性的发现揭示出:原子不再是物质组成的永 恒不变的最小单位,它们具有复杂的结构,并可相互转化。 原子既然可以放出带负电的β粒子来,那么原子是怎样由带 负电的部分(电子)与带正电的部分结合起来的?这样, 原子的内部结构及其运动规律的问题就提到日程上来了。
§2 量子论的诞生
(一)Planck 黑体辐射定律 (二)光量子的概念和光电效应理论 (三)Compton 散射 ——光的粒子性的进一步证实 (四)波尔(Bohr)的量子论
(一)Planck 黑体辐射定律
究竟是什么机制使空腔的原子产生出所观察 到的黑体辐射能量分布,对此问题的研究导 致了量子物理学的诞生。
这些问题,经典物理学不能给于解释。首先,经典物理 学不能建立一个稳定的原子模型。根据经典电动力学, 电子环绕原子核运动是加速运动,因而不断以辐射方式 发射出能量,电子的能量变得越来越小,因此绕原子核 运动的电子,终究会因大量损失能量而“掉到”原子核 中去,原子就“崩溃”了,但是,现实世界表明,原子 稳定的存在着。除此之外,还有一些其它实验现象在经 典理论看来是难以解释的,这里不再累述。 总之,新的实验现象的发现,暴露了经典理论的局限性, 迫使人们去寻找新的物理概念,建立新的理论,于是量 子力学就在这场物理学的危机中诞生。
北大物理学院课程

22 PHY-1-5 核物理与粒子物理导论 11 PHY-1-5 12 PHY-1-5 辐射物理 13 PHY-1-5 现代电子测量与实验 21 PHY-1-5 快电子学及实验 22 PHY-1-5 核天体物理 23 PHY-1-6 加速器物理基础 11 PHY-1-6 等离子体和离子束物理 12 PHY-1-6 医学物理导论 21 PHY-2-2 01 PHY-2-2 群论 I 02 PHY-2-2 量子统计物理 03 PHY-2-2 量子场论 04 PHY-2-2 群论 II(李群李代数) 05 PHY-2-2 量子规范场论 06 4 4 春季 3 3 春季 4 4 秋季 4 4 秋季 3 3 秋季 量子力学 III(高等量子力 4 学) 4 秋季 3 3 秋季 3 3 春季 3 3 春季 3 3 秋季 3 3 秋季 4 3 春季 3 3 秋季 核物理与粒子物理专题实 4 验 2 春季 3 3 春季
至 PHY-0-811系列的低年级选修棵。第二层次包括 PHY-1-01x 系列的数学物理方法、 PHY-1-04x 和 PHY-1-05x 系列两种类型的物理专业基础课、PHY-1-06x 系列的近代物理实验 以及 PHY-1-1xy 系列的高年级基础性选修课。第三层次包括 PHY-1-2xy 至 PHY-1-6xy 系列 的物理专业性选修课、PHY-2-20x 和 PHY-2-30x 系列的研究生课以及 PHY-1-9xy 系列(正在 建设中)的交叉学科类选修课。 对于不同类型的培养目标,除总学分要求都是140外,物理学院采用不同的培养方案和 不同的学分要求。在所有类型中,(1)必修课高等数学 I、II、线性代数可由数学学院内容 相近的 A 类课程代替, (2)全院必修课中超出规定学分部分可作为选修课, (3)在专业选修课 中,物理基础类和物理专业类课程中超出规定学分部分可作为跨学科类课程。 (一) 、宽基础型 总学分:140学分,其中:
学年第学期学院专业级-暨南大学理工学院

7、8节
15:00-16:50
一
高等数学Ⅱ
A605(10物理/光电系内招合班101人)
李全国
必修5学分
人生修养
A604(10理工全体/信息/生科部分学院外招合班76人)
金焱
必修2学分
电磁学
A312
刘彭义
必修3学分
思想道德修养与法律基础(3节)
A103(10级物理/光电系内招合班101人)
A314
古宇
必修3学分
半导体物理与器件(3节)
A314(08/09应物合班)
谢伟广
选修3学分
注:课室号“A”字头是教学楼,“B”字头是成人教育楼。
2010~2011学年第2学期理工学院应用物理学专业2009级
本科生课程表(校本部)
学生人数:内招23人,外招5人
1、2节
8:00-9:50
3、4节
10:20-12:10
四
大学英语二级
商务英语二级
多媒体
必修4学分
热学(1-15周)
A314
刘绘
必修3学分
五
电工技术
A314
张杰
必修3学分
大学英语二级
商务英语二级
多媒体
必修4学分
高等数学Ⅱ(3节)
A510(10物理/光电/电子系外招合班)
李全国
必修5学分
注:课室号“A”字头是教学楼,“B”字头是成人教育楼。
选修3学分
计算机网络(1-12周/单周)
A1208(09光电系2专业/08应物共95人合班)
姚立军
选修3学分
量子力学(双周)
A314
古宇
必修3学分
量子力学基本原理与基本概念小结-第16讲

薛定谔方程的评论
2、薛定谔方程是时间一次、坐标二次偏微分方程, 不具有相对论协变性(时空对称性),因而不是 微观粒子的相对论性量子力学运动方程。薛定谔 方程是建立在非相对论时空和非相对论运动学基 础之上的非相对论量子力学。
3、非相对论性量子多体理论,虽然引进了粒子产生、 消灭算符和二次量子化表象,但它们描述的是粒子 从一个量子态向另一个量子态的跃迁与转变,并没 有真正涉及粒子的产生和消灭。
薛定谔方程中的波函数的物理本质是什么呢?
波恩的观点:
薛定谔方程中的波函数代表的是一种概率,而 绝对不是薛定谔本人所理解的是电荷(电子) 在空间中的实际分布。波函数,准确地说 r 2 代表了电子在某个地点出现的概率,电子本身 不会像波那样扩展开去,但它的出现概率则像 一个波。
“微观粒子的运动状态用波函数描述,描写粒 子的波是概率波”,这是量子力学的一个基本 假设(基本原理)
WII
WII
N
III
(c e c e ) III iknIII ( xb) n
III iknIII ( xb) n
n1
2 ny
sin( ).
WIII
WIII
超晶格结构中电子的薛定谔方程与波函数如何写?
理想超晶格
d
含缺陷结构超晶格
复杂体系中电子运动
多粒子系统的Schrődinger方程
原则上只要对上式进行求解即可得出所有物理性质,然而由于电子之间的相互作用的复杂性, 要严格求出多电子体系的Schrődinger方程解是不可能的,必须在物理模型上进一步作一系列 的近似。
(一)薛定谔方程
Schrodinger 的方程一般表达式
i
(r,t)
Hˆ (r, t )
《量子力学基础和原子、分子及晶体结构》习题和思考题

《结构化学》课程作业题第一部分:《量子力学基础和原子结构》思考题与习题1. 经典物理学在研究微观物体的运动时遇到过哪些困难?举例说明之。
如何正确对待归量子论?2. 电子兼具有波动性的实验基础是什么?宏观物体有没有波动性?“任何微观粒子的运动都是量子化的,都不能在一定程度上满足经典力学的要求”,这样说确切吗?3. 怎样描述微观质点的运动状态?为什么?波函数具有哪些重要性质?为什么?4. 简述薛定谔方程得来的线索。
求解该方程时应注意什么?5. 通过一维和三维势箱的解,可以得出哪些重要結論和物理概念?6. 写出薛定谔方程的算符表达式。
你是怎样理解这个表达式的? *7. 量子力学中的算符和力學量的关系怎样?8. 求解氢原子和类氢离子基态和激发态波函数的思想方法是怎样的? 9. 通过氢原子薛定谔方程一般解的讨论明确四个量子数的物理意义。
10. 怎样根据波函数的形式讨论“轨道”和电子云图象?为什么不能说p +1和p -1就是分别代表p x 和p y ? 11. 样来研究多电子原子的结构?作过哪些近似?用过哪些模型?试简单说明之。
12. 电子的自旋是怎样提出的?有何实验依据?在研究原子内电子运动时,我们是怎样考虑电子自旋的?*13. 哈特里-福克SCF 模型考虑了一些什么问题?交换能有何意义?14. 怎样表示原子的整体状态?光谱项、光谱支项各代表什么含义?洪特规则、选择定则又是讲的什么内容?15. 原子核外电子排布的规律是什么?现在哪些问题你比过去理解得更加深入了?通过本部分的学习,你对微观体系的运动规律和特点掌握了多少?在思想方法上有何收获?16. 巴尔末起初分析氢原子光谱是用波长)(422-=n n c λ,其中c 为常数,n 为大于2的正整数,试用里德伯常数H R ~求出c 值。
17. 试计算氢原子中电子处于波尔轨道n = 1和n = 4时的动能(单位:J )和速度(单位:m·s -1)。
18. 已知电磁波中电场强度ε服从波动方程222221t c x ∂∂⋅=∂∂εε,试说明如下函数⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=t x t x y νλπεε2c o s 0),(是这个方程的解。
量子力学公式

(2)
(3)
都是常数,总动量平方 总能量是:
=
=
但 正整数.
#
[3]平面转子的转动惯量为 ,求能量允许值.
(解)解释题意:平面转子是个转动体,它的位置由一坐标(例如转角 )决定,它的运动是一种
刚体的平面平行运动.例如双原子分子的旋转.按刚体力学,转子的角动量 ,但 是角速度,能量是
利用量子化条件,将 理解成为角动量, 理解成转角 ,一个周期内的运动理解成旋转一周,则有
(1)
又利用量子化条件,令 电荷角动量 转角
(2)
即 (3)
由(1)(2)求得电荷动能=
再求运动电荷在磁场中的磁势能,按电磁学通电导体在磁场中的势能= , 是电荷的旋转频率, ,代入前式得
运动电荷的磁势能= (符号是正的)
点电荷的总能量=动能+磁势能=E= ( )
#Hale Waihona Puke [5]对高速运动的粒子(静质量 )的能量和动量由下式给出:
(1)
(2)
试根据哈密顿量 (3)
及正则方程式来检验以上二式.由此得出粒子速度和德布罗意的群速度相等的关系.计算速度并证明它大于光速.
(解)根据(3)式来组成哈氏正则方程式组: ,本题中 , ,因而
(4)
从前式解出 (用 表示)即得到(2).又若将(2)代入(3),就可得到(1)式.
其次求粒子速度 和它的物质波的群速度 间的关系.运用德氏的假设: 于(3)式右方,又用 于(3)式左方,遍除 :
(2)光的波动论的拥护者曾向光的微粒论者提出下述非难:
如认为光是粒子,则其运动遵守最小作用量原理 认为 则 这将导得下述折射定律
这明显违反实验事实,即使考虑相对论效应,则对自由粒子: 仍就成立,E是粒子能量,从一种媒质到另一种媒质E仍不变,仍有 ,你怎样解决矛盾?
2013-2014(1)课程表汇总0904(本科生部分)
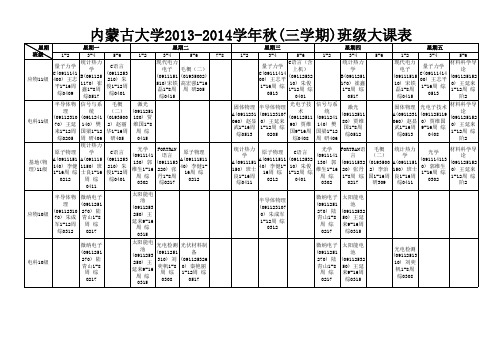
星期 班级 1-2 量子力学 C(0911141 应物11级 400) 王志 平1-16周 综0409 半导体物 理 (09112310 电科11级 70) 王延 来1-12周 综0205 原子物理 A(0911151 140) 李健 1-16周 综 0212 星期一 3-4 统计热力 学 B(091125 1170) 崔 鑫1-8周 综0517 信号与系 统 (0911241 140) 樊 国梁1-12 周 研406 统计热力 学 A(091115 1150) 班 士良1-16 周 综 0411 微纳电子 (0911251 270) 陆 青山1-8 周 综 0217 微纳电子 (0911251 270) 陆 青山1-8 周 综 0217 星期二 5-6 C语言 (0911253 210) 朱 俊1-12周 综0401 毛概 激光 (二) (0911251 (0193500 180) 贾 2) 赵丽 维国1-8 华1-16周 周 综 研405 0415 光学 FORTRAN C语言 原子物理 (0911141 语言 (0911253 A(09111511 130) 郭 (0911153 210) 朱 40) 李健1维生1-16 220) 张 俊1-12周 16周 综 周 综 丹1-8周 综0401 0212 0302 综0217 太阳能电 池 (0911253 250) 王 延来9-16 周 综 0315 太阳能电 池 (0911253 250) 王 延来9-16 周 综 0315 1-2 3-4 现代电力 电子 (0911151 510)宋铁 磊1-8周 综0415 5-6 毛概(二) (01935002) 高宏强1-16 周 研205 固体物理 A(0911231 060) 赵显 武1-16周 综0513 7-8 1-2 星期三 3-4 量子力学 C(09111414 00) 王志平 1-16周 综 0513 半导体物理 (091123107 0) 王延来 1-12周 综 0205 5-6 C语言(含 上机) (09112532 10) 朱俊 1-12周 综 0401 光电子技 术 (09112511 90) 贾维 国9-16周 综0408 1-2 星期四 3-4 统计热力 学 B(0911251 170) 崔鑫 1-8周 综 0517 5-6 1-2 现代电力 电子 (09111515 10) 宋铁 磊1-8周 综0415 固体物理 A(0911231 060) 赵显 武1-16周 综0513 星期五 3-4 量子力学 C(09111414 00) 王志平 1-16周 综 0513 光电子技术 (091125119 0) 贾维国 9-16周 综 0408 5-6 材料科学导 论 (091125152 0) 王延来 1-12周 综 阶2 材料科学导 论 (091125152 0) 王延来 1-12周 综 阶2
量子力学知识点总结

量子力学期末复习完美总结一、 填空题1.玻尔-索末菲的量子化条件为:pdq nh =⎰,(n=1,2,3,....),2.德布罗意关系为:hE h p k γωλ====; 。
3.用来解释光电效应的爱因斯坦公式为:212mV h A υ=-, 4.波函数的统计解释:()2r t ψ,代表t 时刻,粒子在空间r 处单位体积中出现的概率,又称为概率密度。
这是量子力学的基本原理之一。
波函数在某一时刻在空间的强度,即其振幅绝对值的平方与在这一点找到粒子的几率成正比,和粒子联系的波是概率波。
5.波函数的标准条件为:连续性,有限性,单值性 。
6.,为单位矩阵,则算符的本征值为:1± 。
7.力学量算符应满足的两个性质是 实数性和正交完备性 。
8.厄密算符的本征函数具有: 正交性,它们可以组成正交归一性。
即()m n mn d d λλφφτδφφτδλλ**''==-⎰⎰或。
9.设 为归一化的动量表象下的波函数,则 的物理意义为:表示在()r t ψ,所描写的态中测量粒子动量所得结果在p p dp →+范围内的几率。
10.i ;ˆxi L ;0。
11.如两力学量算符有共同本征函数完全系,则_0__。
12.坐标和动量的测不准关系是: ()()2224x x p ∆∆≥。
自由粒子体系,_动量_守恒;中心力场中运动的粒子__角动量__守恒13.量子力学中的守恒量A 是指:ˆA不显含时间而且与ˆH 对易,守恒量在一切状态中的平均值和概率分布都不随时间改变。
14.隧道效应是指:量子力学中粒子在能量E 小于势垒高度时仍能贯穿势垒的现象称为隧道效应。
15. 为氢原子的波函数,的取值范围分别为:n=1,2,3,… ;l=0,1,…,n -1;m=-l,-l+1,…,0,1,…l 。
16.对氢原子,不考虑电子的自旋,能级的简并为: 2n ,考虑自旋但不考虑自旋与轨道角动量的耦合时,能级的简并度为 22n ,如再考虑自旋与轨道角动量的耦合,能级的简并度为 12+j 。
上海理工大学大物A2-11第十九章 量子力学基础2作业及期末复习题

(D) -r2Bcos.
5、2107 一电子以 v = 105 m·s-1 的速率,在垂直于均匀磁场的平面内作半径 R = 1.2 cm 的圆周运动,
求此圆周所包围的磁通量. (忽略电子运动产生的磁场,已知基本电荷 e = 1.6×10-19 C,电子质量
B
n
me = 9.11×10-31 kg)
为它所占据的空间内场是均匀的.当此线圈的 pm 与 z 轴平行时,所受磁力矩大小为 M =5×10-9 N·m,方向沿 x 轴负方向;
当此线圈的 pm 与 y 轴平行时,所受磁力矩为零.则空间 A 点处的磁感强度 B 的大小为____________,方向为______________.
12、2133 载有恒定电流 I 的长直导线旁有一半圆环导线 cd,半圆环半径 为 b,环面与直导线垂直,且半圆环两端点连线的延长线与直导线相交, I
14、2769 由质量为 m、电阻为 R 的均匀导线做成的矩形线框,宽为 b,在 t =0 时由静止下
落,这时线框的下底边在 y =0 平面上方高度为 h 处(如图所示). y =0 平面以上没有磁场;
b
y =0 平面以下则有匀强磁场 B ,其方向在图中垂直纸面向里.现已知在时刻 t = t1 和 t = t2, t = 0
,它在基态的电子组态为
.
【答】
5. (自测提高 18)如果电子被限制在边界 x 与 x +x 之间,x =0.5 Å,则电子动量 x 分量的不确定量近似地为 kg·m/s. (不确定关系式x·p≥h)
【答】
三. 计算题
1. (基础训练 23)已知粒子在无限深势阱中运动,其波函数为 子的概率为最大的位置. 解:
课程大纲-西安建筑科技大学研究生院

课程大纲课程编号(理学院)课程名称随机规划学时40基本预备知识 1. 概率统计2. 最优化理论与算法3. 随机过程授课方式讲授、研讨基本要求掌握随机规划模型的类型。
(3TKH 主要类型),了解分布问题中参数LP 及其最优值得表达式,了解Z(3 )的可测性及其概率分布,掌握简单分布问题的计算方法,了解逼近方法和最优值的数学期望的估计,掌握有补偿的二阶段问题和二阶段问题的数值解法,了解概率约束规划和随机拟次梯度法,了解上图收敛性。
教材及参考书《随机规划》,王全德编著,南京大学出版社,1990 年。
《随机线性规划》,Kall 著,王金德译,南京大学出版社。
讲授的主要内容:(每章后附学时数)1.随机规划的模型(6 学时)1.1分布问题,二阶段有补偿问题,概率约束问题;1.2多阶段有补偿问题和多阶段概率约束计划;1.3各类问题的统一形式与相互关系。
2.分布问题:(6 学时)2.1参数LP;2.2Z(3)的可测性;2.3最优化Z(3 )的概率分布;2.4简单分布问题的计算方法;2.5逼近方法与最优值的数学期望的估计。
3.有补偿二阶段问题(8 学时)3.1一般有补偿二阶段的问题;3.2具有固定补偿矩阵的情形;3.3具有完备和简单补偿矩阵的二阶段问题。
4.二阶段问题的数值解法(8 学时)4.1具有离散随机变量的二阶段问题的解法;4.2简单补偿问题的解法。
5.概率约束规划(6 学时)可行解集合的特性,约束函数的分析性质,数值解法,逼近方法。
6.随机拟次梯度法(* )(2 学时)7. 应用举例(2 学时)8. 上图收敛性(2 学时)注:(*)只做了解课程名称学时基本预备知识值代数601. 数学分析2. 线性代数3. 矩阵论4. 计算方法授课方式讲授基本要求1. 知道矩阵计算的基本工具,熟悉Vandermonde、Toeplitz 等方程组的解法及某些迭代法的收敛性,了解多项式加速技巧。
2.掌握不完全分解预先共轭梯度法,广义共轭剩余法,Lanczos 方法,求解特征值问题的同伦方法和分而治之法以及求解Jacobi 矩阵特征值反问题的正交约化法。
量子力学练习题答案

一、 简答题 1. 简述光电效应中经典物理学无法解释的实验现象。 答:光电效应中经典物理学无法解释的实验现象有: (1)对入射光存在截止频率ν0 ,小于该频率的入射光没有光电子逸出;(2) 逸出的光电子的能量只与入射光的频率ν 有关,入射光的强度无关;(3) 截止频率只与材料有关而与光强无关;(4)入射光的强度只影响逸出的光 电子的数量;(5)无论多弱的光,只要其频率大于截止频率,一照射到金 属表面,就有光电子逸出。 2. 简述 Planck 的光量子假设。 答:Planck 的光量子假设为,对于一定的频率为ν 的辐射,物体吸收或发 射的能量只能以 hν 为单位来进行。 3. 写出 Einstein 光电方程,并阐述 Einstein 对光电效应的量子解释。 答:Einstein 光电方程为 hν = 1 mv2 + W 。
⎤ ⎥ ⎦
16. 简述粒子动量与位置的不确定关系。
答:若要想精确地知道粒子的动量值,就无法得知粒子的具体位置;要想
精确地知道粒子的位置,就无法得知粒子的具体动量值,位置分布的均方
差和动量分布的均方差受到下面关系的制约
Δx ⋅ Δp ≥ = 2
17. 简述量子力学的态叠加原理。
答:量子力学的态叠加原理是指如果ψ1 、ψ 2 、ψ 3 ……均是体系的可能状态,
ψ ( x, t) = eip0x / = ⋅ e−iEt / = = e−i(Et− p0x)/ =
14. 写出动量算符、动能算符以及在直角坐标系中角动量各分量的算符的
表达式。 答:动量算符 lpK = −i=∇
动能算符 Tl = 1 (−i=∇)2
2m
角动量各分量的算符
L x
=
−i=
⎛ ⎜
量子力学常用数学公式

n = 1,2,3 正整数
#
[2]用量子化条件,求限制在箱内运动的粒子的能量,箱的长宽高分别为 a, b, c.
(解)三维问题,有三个独立量子化条件, 可设想粒子有三个分运动,每一分运动是自由运动.设粒子与器壁作弹性碰撞,则每碰一次时,
p p 与此壁正交方向的分动量变号(如 → − ),其余分动量不变,设想粒子从某一分运动完
=
υλ
=
ω k
(υ 是频率)
利用(5)式得知
v= p
m2c4 ℏ2k 2
+ c2
>c
(6)
故相速度(物质波的)应当超过光速。
v v 最后找出 和 的关系,将(1)(2)相除,再运用德氏波假设:
G
p
E ℏω c 2 c 2
=
v p
ℏk
=
v
=
,
v v G
c2 =
p G
(7)
# [6](1)试用 Fermat 最小光程原理导出光的折射定律
8m a
b
c
但 nx , ny , nz = 1,2,3 正整数.
#
[3] 平面转子的转动惯量为 Ι ,求能量允许值. (解)解释题意:平面转子是个转动体,它的位置由一坐标(例如转角ϕ )决定,它的运动是一种
刚体的平面平行运动.例如双原子分子的旋转.按刚体力学,转子的
角动量 Ι
ω
,但 ω
⋅
=ϕ
是角速度,能量是
Ev 这明显违反实验事实,即使考虑相对论效应,则对自由粒子: p = 仍就成立,E 是
c2
∫ 粒子能量,从一种媒质到另一种媒质 E 仍不变,仍有 δ pdl = 0 ,你怎样解决矛盾?
16-1-2 波函数及其统计诠释

5. 波函数满足态叠加原理。 ——量子力学理论的一个基本假设
如果波函数 1 (r , t ) , 2 (r , t ), …都是描述系统的可能 的量子态,那么它们的线性叠加
(r ,t ) c1 1 (r ,t ) c2 2 (r ,t ) ci i (r ,t )
二、在量子力学中波函数的统计意义 1、经典物理学中的波函数 力学: 电磁学:
y( x, t ) A cos(t kx)
E (r , t ) E0 cos(k r t ) B(r , t ) B0 cos(k r t )
在经典物理学中,从波动现象中得到波函数, 波函数表达出某一个具体的物理量随时间的变化 规律,以及该物理量随空间位置的变化规律。 波函数是具有物理意义的。
t 时刻粒子出现在空间某点 r 附近体积元 dV
中的概率,与波函数平方及 dV 成正比。 出现在 dV 内概率:
dW Ψ (r , t ) dV
2
dV=dx dy dz
( x, y, z, t ) dxdydz 或 ( x, y, z, t ) ( x, y, z, t )dxdydz
2
则在t 时刻、在空间(x,y,z)附近的单位体积内粒子 出现的概率,即概率密度,为
( x , y , z , t ) ( x, y , z , t )
2
( x, y, z, t ) ( x, y, z, t )
1882~1970
他的相关作品: 《晶体点阵动力学》(1915年) 《爱因斯坦相对论》(1920年) 《固态原子理论》(1923年) 《原子动力学问题》(1926年) 《原子物理学》(1935年) 《晶格动力学》(1954年) 《物理学实验与理论》(1943年) 《我们一代的物理学》(1956年) 《物理学与政治学》(1962年)
北华大学2013-2014学年秋(两学期)班级大课表1
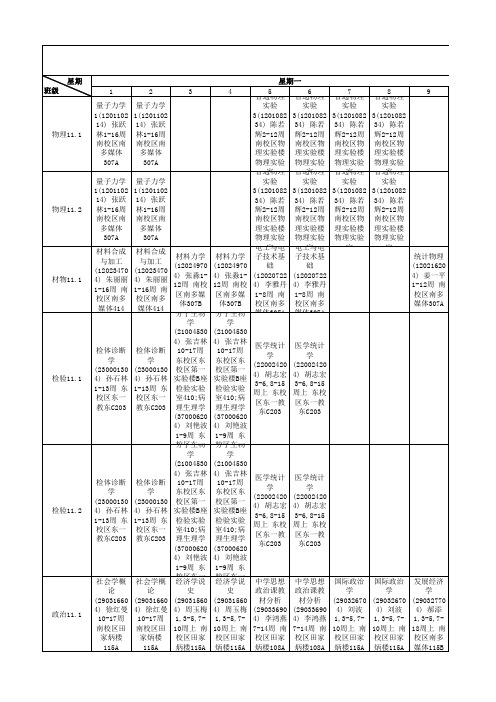
经济学说 史 (29031560 4) 周玉梅 1,3-5,710周上 南 校区田家 炳楼115A 教学系统 设计 (05021660 4) 张春苏 1-16周 东 校区东多 媒体电109
中学思想 政治课教 材分析 (29033690 4) 李鸿燕 7-14周 南 校区田家 炳楼108A 数据库应 用技术 (05020370 4) 宫慧颖 1-16周 东 校区东多 媒体E306
临药11.1
内科学 (23000420 4) 化工117周 东校 区东一教 东C102
内科学 (23000420 4) 化工117周 东校 区东一教 东C102
生物技术 制药 (32011870 4) 安丽萍 7-15周 东 校区东多 媒体E201
生物技术 制药 (32011870 4) 安丽萍 7-15周 东 校区东多 媒体E201
免疫学 (370083 东一教东 C206
免疫学 (37008320 4) 母润红 \李坚1-13 周 东校区 东一教东 C206
天然药物 化学 (32010160 4) 孙晶波 \崔龙1-10 周 东校区 东多媒体 E201
天然药物 化学 (32010160 4) 孙晶波 \崔龙1-10 周 东校区 东多媒体 E201
政治11.2
社会学概 论 (29031660 4) 徐红曼 10-17周 南校区田 家炳楼 115A
社会学概 论 (29031660 4) 徐红曼 10-17周 南校区田 家炳楼 115A
经济学说 史 (29031560 4) 周玉梅 1,3-5,710周上 南 校区田家 炳楼115A 教学系统 设计 (05021660 4) 张春苏 1-16周 东 校区东多 媒体电109
物理11.1
物理11.2
量子力学基础简答题(经典)

量子力学基础简答题1、简述波函数的统计解释;2、对“轨道”和“电子云”的概念,量子力学的解释是什么3、力学量Gˆ在自身表象中的矩阵表示有何特点 4、简述能量的测不准关系;5、电子在位置和自旋z S ˆ表象下,波函数⎪⎪⎭⎫ ⎝⎛=ψ),,(),,(21z y x z y x ψψ如何归一化解释各项的几率意义。
6、何为束缚态7、当体系处于归一化波函数ψ(,) r t 所描述的状态时,简述在ψ(,)r t 状态中测量力学量F 的可能值及其几率的方法。
8、设粒子在位置表象中处于态),(t rψ,采用Dirac 符号时,若将ψ(,)r t 改写为ψ(,)r t 有何不妥采用Dirac 符号时,位置表象中的波函数应如何表示9、简述定态微扰理论。
10、Stern —Gerlach 实验证实了什么 11、一个物理体系存在束缚态的条件是什么 12、两个对易的力学量是否一定同时确定为什么 13、测不准关系是否与表象有关14、在简并定态微扰论中,如 ()H 0的某一能级)0(n E ,对应f 个正交归一本征函数i φ(i =1,2,…,f ),为什么一般地i φ不能直接作为()H H H'+=ˆˆˆ0的零级近似波函数15、在自旋态χ12()s z 中, S x 和 S y的测不准关系( )( )∆∆S S x y 22•是多少 16、在定态问题中,不同能量所对应的态的迭加是否为定态Schrodinger 方程的解同一能量对应的各简并态的迭加是否仍为定态Schrodinger 方程的解17、两个不对易的算符所表示的力学量是否一定不能同时确定举例说明。
18说明厄米矩阵的对角元素是实的,关于对角线对称的元素互相共轭。
19何谓选择定则。
20、能否由Schrodinger 方程直接导出自旋21、叙述量子力学的态迭加原理。
22、厄米算符是如何定义的23、据[aˆ,+a ˆ]=1,a a N ˆˆˆ+=,n n n N =ˆ,证明:1ˆ-=n n n a 。
量子力学作业习题

第一章 量子力学的诞生[1] 在宏观世界里,量子现象常常可以忽略.对下列诸情况,在数值上加以证明: ( l )长l=lm ,质量M=1kg 的单摆的零点振荡的振幅;( 2 )质量M=5g ,以速度10cm/s 向一刚性障碍物(高5cm ,宽1cm )运动的子弹的透射率;( 3 )质量M= 0.1kg ,以速度0.5m/s 运动的钢球被尺寸为1×1.5m 2时的窗子所衍射.[2] 用h,e,c,m (电子质量), M (质子质量)表示下列每个量,给出粗略的数值估计: ( 1 )玻尔半径(cm ) ; ( 2 )氢原子结合能(eV ) ; ( 3 )玻尔磁子;( 4 )电子的康普顿波长(cm ) ; ( 5 )经典电子半径(cm ) ; ( 6 )电子静止能量(MeV ) ; ( 7 )质子静止能量( MeV ) ; ( 8 )精细结构常数;( 9 )典型的氢原子精细结构分裂[3]导出、估计、猜测或背出下列数值,精确到一个数量级范围内,( 1 )电子的汤姆逊截面;( 2 )氢原子的电离能;( 3 )氢原子中基态能级的超精细分裂能量;( 4 )37Li ( z=3 )核的磁偶极矩;( 5 )质子和中子质量差;( 6 )4He 核的束缚能;( 7 )最大稳定核的半径;( 8 )Π0介子的寿命;( 9 )Π-介子的寿命;( 10 )自由中子的寿命.[4]指出下列实验中,哪些实验表明了辐射场的粒子性?哪些实验主要证明能量交换的量子性?哪些实验主要表明物质粒子的波动性?简述理由.( 1 )光电效应;( 2 )黑体辐射谱;( 3 ) Franck – Hertz 实验;( 4 ) Davisson -Ger - mer 实验;( 5 ) Compton 散射.[5]考虑如下实验:一束电子射向刻有A 、B 两缝的平板,板外是一装有检测器阵列的屏幕,利用检测器能定出电子撞击屏幕的位置.在下列各种情形下,画出入射电子强度随屏幕位置变化的草图,给出简单解释. ( 1 ) A 缝开启,B 缝关闭; ( 2 ) B 缝开启,A 缝关闭; ( 3 )两缝均开启. [6]验算三个系数数值:(1)h 2e m ;(2)h 2nm ;(3)hc第二章 波函数与Schr ödinger 方程[1] 试用量子化条件,求谐振子的能量[谐振子势能2221)(x m x V ω=] [2] 一维运动的粒子处在⎩⎨⎧<≥=-0,00,)(x x Axe x x 当当λψ的状态,其中0>λ,求:(1)粒子动量的几率分布函数;(2)粒子动量的平均值。
量子力学复习资料

量⼦⼒学复习资料第⼀章知识点:1. ⿊体:能吸收射到其上的全部辐射的物体,这种物体就称为绝对⿊体,简称⿊体.2. 处于某⼀温度 T 下的腔壁,单位⾯积所发射出的辐射能量和它所吸收的辐射能量相等时,辐射达到热平衡状态。
3. 实验发现:热平衡时,空腔辐射的能量密度,与辐射的波长的分布曲线,其形状和位置只与⿊体的绝对温度 T 有关⽽与⿊体的形状和材料⽆关。
4. 光电效应---光照射到⾦属上,有电⼦从⾦属上逸出的现5. 光电效应特点:1.临界频率ν0 只有当光的频率⼤于某⼀定值ν0时,才有光电⼦发射出来.若光频率⼩于该值时,则不论光强度多⼤,照射时间多长,都没有电⼦产⽣.光的这⼀频率ν0称为临界频率。
2.光电⼦的能量只是与照射光的频率有关,与光强⽆关,光强只决定电⼦数⽬的多少(爱因斯坦对光电效应的解释)3. 当⼊射光的频率⼤于ν0时,不管光有多么的微弱,只要光⼀照上,⽴即观察到光电⼦(10-9s )6. 光的波粒⼆象性:普朗克假定a.原⼦的性能和谐振⼦⼀样,以给定的频率ν振荡;b.⿊体只能以 E = h ν为能量单位不连续的发射和吸收能量,⽽不是象经典理论所要求的那样可以连续的发射和吸收能量.7. 总结光⼦能量、动量关系式如下:把光⼦的波动性和粒⼦性联系了起来8.波长增量 Δλ=λ′–λ随散射⾓增⼤⽽增⼤.这⼀现象称为康普顿效应.散射波的波长λ′总是⽐⼊射波波长长(λ′ >λ)且随散射⾓θ增⼤⽽增⼤。
9.波尔假定:1.原⼦具有能量不连续的定态的概念. 2.量⼦跃迁的概念. 10.德布罗意:假定:与⼀定能量 E 和动量 p 的实物粒⼦相联系的波(他称之为“物质波”)的频率和波长分别为:E = h ν ? ν= E/h ? P = h/λ ? λ= h/p ? 该关系称为de. Broglie 关系.德布罗意波:ψde Broglie 关系:ν= E/h ?ω = 2πν= 2πE/h = E/ λ= h/p ?k = 1/ = 2π /λ = p/n k h k n n h n C h n C E p h E ==========πλπλνων22其中波长。
量子力学基础简答题(经典)教学文案

量⼦⼒学基础简答题(经典)教学⽂案量⼦⼒学基础简答题(经典)量⼦⼒学基础简答题1、简述波函数的统计解释;2、对“轨道”和“电⼦云”的概念,量⼦⼒学的解释是什么?3、⼒学量G在⾃⾝表象中的矩阵表⽰有何特点? 4、简述能量的测不准关系;5、电⼦在位置和⾃旋z S ?表象下,波函数=ψ),,(),,(21z y x z y x ψψ如何归⼀化?解释各项的⼏率意义。
6、何为束缚态?7、当体系处于归⼀化波函数ψ(,)?r t 所描述的状态时,简述在ψ(,)?r t 状态中测量⼒学量F 的可能值及其⼏率的⽅法。
8、设粒⼦在位置表象中处于态),(t r ?ψ,采⽤Dirac 符号时,若将ψ(,)?r t 改写为ψ(,)?r t 有何不妥?采⽤Dirac 符号时,位置表象中的波函数应如何表⽰?9、简述定态微扰理论。
10、Stern —Gerlach 实验证实了什么? 11、⼀个物理体系存在束缚态的条件是什么? 12、两个对易的⼒学量是否⼀定同时确定?为什么? 13、测不准关系是否与表象有关?14、在简并定态微扰论中,如?()H0的某⼀能级)0(n E ,对应f 个正交归⼀本征函数i φ(i =1,2,…,f ),为什么⼀般地i φ不能直接作为()H H H'+=0的零级近似波函数?15、在⾃旋态χ12()s z 中,?S x 和?S y的测不准关系(?)(?)??S S x y 22?是多少? 16、在定态问题中,不同能量所对应的态的迭加是否为定态Schrodinger &&⽅程的解?同⼀能量对应的各简并态的迭加是否仍为定态Schrodinger &&⽅程的解? 17、两个不对易的算符所表⽰的⼒学量是否⼀定不能同时确定?举例说明。
18说明厄⽶矩阵的对⾓元素是实的,关于对⾓线对称的元素互相共轭。
19何谓选择定则。
20、能否由Schrodinger &&⽅程直接导出⾃旋?21、叙述量⼦⼒学的态迭加原理。
量子力学基础习题课send

(3) ( x y )( 1 2 ) x( 1 2 )+y ( 1 2 )
x 1 x 2 y 1 y 2 ( x y ) 1 ( x y ) 2
* * * ( x y ) d ( x y ) d [( x y ) ] 2 2 1 d 1 2 * 1 为实数 坐标算符
2 n x n ( x) sin( ), a a
对比可知
n2 h2 En 8ma 2
n 1, 2, 3,
( x) 2 1 ( x) 3 2 ( x)
根据态叠加原理知,线性组合态也是粒子的可能状态。 要弄清楚能量是否有确定值,就是要求解函数 ( x) 是否 为哈密顿算符的本征函数,即
dx ==== 0
为奇函数
被积函数
因此
x p
x x
2
1 4
2
p
2
p
满足不确定度关系
1 xp 4
2
判断下列算符是否是线性厄米算符:
d (1) dx
(2)
2
(3) x y
(4)e
x2
解: 线性厄米算符要满足如下两个表达式:
线性算符 厄米算符
ˆ ) A ˆ A ˆ A( 1 2 1 2
结构化学习题课
量子力学基础
2015. 4. 16
REVIEW
------- 能量量子化 ------- 光电效应 “紫外灾难” ------- 波粒二象性 ------- 不确定度关系 量子力学基本假设 波函数 算符 本征方程 态叠加 Pauli原理 箱中粒子的Schrö dinger方程
大学物理课程思政教学大纲(最新)

大学物理课程思政教学大纲(最新)大学物理课程思政教学大纲课程名称:大学物理课程代码:000000000000000001课程时长:16周授课教师:__X适用专业:物理学课程目标:本课程的目标是使学生掌握物理学的基本概念、基本理论和基本方法,同时融入思想政治教育,培养学生科学思维、科学精神、科学方法和科学品质,提高综合素质和创新能力。
教学要求:1.掌握物理学的基本概念、基本理论和基本方法,能够正确运用物理原理和方法分析问题和解决问题。
2.培养学生的科学思维、科学精神、科学方法和科学品质,提高学生的综合素质和创新能力。
3.培养学生的爱国情怀、民族自豪感和社会责任感,增强学生的国际视野和跨文化交流能力。
4.注重物理实验技能的培养,提高学生的实验技能和实践能力。
5.培养学生的科学文化素养,提高学生的科学文化素质和社会文化素质。
教学内容:一、质点运动学1.运动的描述2.匀变速直线运动3.非匀变速直线运动4.曲线运动与运动的合成与分解二、牛顿力学1.牛顿三定律2.动力学基本定理和定律3.万有引力定律三、热学基础1.分子动理论2.热力学第一定律和第二定律3.热平衡原理和热力学第一、第二定律的数学表达式四、电磁学基础1.电荷守恒定律和库仑定律2.电场和电场强度3.电势能和电势差4.高斯定理和电场强度通量5.磁感应强度和磁场6.安培环路定理和磁场强度通量7.法拉第电磁感应定律和自感系数与互感系数物理大学教学大纲教学大纲是指有关教学方面的书面的、官方的东西。
教学大纲的着眼点在掌握有关学科领域的基本知识上面,如基础知识、基本技能、基本态度和基本方法,而教学设计主要研究教与学,试图解决的是如何使学生掌握知识,形成各种技能技巧,发展能力,磨练意志,指导行为的问题。
《普通高中物理课程标准(实验)》规定的高中物理课程总目标是:学习终身发展必备的物理基础知识和技能;了解物理学科的特征,知道物理知识****于生产生活实践,服务于社会发展和人类文明进步;了解科学研究的过程,掌握科学研究的方法,提高科学探究能力;形成科学的世界观,勇于探索,勇于创新;逐步形成适应21世纪社会发展需要的必备素质,为学生的终身发展奠定基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
赖曼系 1 氢原子能级图 −hcR=13.6eV
的激发态时, 例2、当大量氢原子处于n=4的激发态时,原子跃迁将 、当大量氢原子处于 的激发态时 发出? 发出?种波长的光
6种 种
若是从n=3跃迁呢? 跃迁呢? 若是从 跃迁呢
3种 种
例3 计算莱曼系的最短波长和最长波长及其光子的能量 解:
1 1 莱曼系 σ = = R ( 2 − 2 ) , n = 2,3,⋯ λ 1 n
电子在原子中,可以在一些特定 特定的轨道上 假设一 电子在原子中,可以在一些特定的轨道上 稳定状态 运动而不辐射电磁波,这时原子处于稳定状态(定态), 运动而不辐射电磁波,这时原子处于稳定状态(定态), 并具有一定的能量. 并具有一定的能量. 假设二 电子以速度 v在半径为 的圆周上绕核运 动时,只有电子的角动量 整数倍的那些 动时,只有电子的角动量 L 等于 h 2π 的整数倍的那些 稳定的 轨道是稳定 轨道是稳定的 .
1
1
当n=2时,此时辐射出光子的波长最长: 时 此时辐射出光子的波长最长: 所以: 所以:
λmax
1 1 3 7 = R ( 2 − 2 ) = 1.097 × 10 × = 0.823 × 10 7 1 2 4 −7 λmax = 1.22 × 10 = 122nm
c
ε min = hvmin = h
n 巴耳末公式 λ = 365.46 2 nm , n = 3,4,5, ⋯ 2 n −2
1890 年瑞典物理学家里德伯给出氢原子光谱公式 波数
2
ɶ = 1 = R( 1 − 1 ) υ λ 22 n2
n = 3, 4, 5........
里德伯常量
R = 1.0973731534 × 10 m
7
n =1−13.6 Nhomakorabea(4) 玻尔理论对氢原子光谱的解释 )
me 1 ⋅ 2 En = − 2 2 8ε 0 h n
4
4
En − Ek me 1 1 v = = ( 2 − 2) 2 3 h 8ε 0 h k n
目的状态
4
电子由n激发态跃迁到 激发态 电子由 激发态跃迁到k激发态 激发态跃迁到 辐射光子能量: 辐射光子能量:h ν = E − E
解:由巴末尔系公式: 由巴末尔系公式:
1 1 σ = = R ( 2 − 2 ) , n = 3, 4,⋯ λ 2 n 1 1 1 5 得: 7 7 σ = = R ( 2 − 2 ) = 1.097 × 10 × = 0.15 × 10 λ 2 3 36
所以: 所以:
1
λ = 6.67 × 10 −7 m = 667 nm
−1
氢原子光谱规律启发人们对原子内部结构的畅想和探索. 氢原子光谱规律启发人们对原子内部结构的畅想和探索
1 1 紫外 莱曼系 σ = = R ( 2 − 2 ) , n = 2,3, ⋯ λ 1 n 1 1 1 可见光 巴尔末系 σ = = R ( 2 − 2 ) , n = 3, 4, ⋯ λ 2 n 1 1 1 帕邢系 σ = = R ( 2 − 2 ) , n = 4,5, ⋯ λ 3 n
1
1 1 布拉开系 σ = = R ( 2 − 2 ) , λ 4 n
1
1
n = 5,6, ⋯
1 1 普丰德系 σ = = R ( 2 − 2 ) , n = 6,7 , ⋯ λ 5 n 1 1 1 汉弗莱系 σ = = R ( 2 − 2 ) , n = 7 ,8, ⋯ λ 6 n
例题1 例题 氢原子从n=3的能级状态跃迁到 的能级状态跃迁到k=2的能级时,求所辐射 的能级时, 氢原子从 的能级状态跃迁到 的能级时 的光子的波长?能量是多少? 的光子的波长?能量是多少?
c
3 × 10 8 ε = hv = h = 6.63 × 10 −34 × = 2.98 × 10 −19 J 6.67 × 10 −7 λ
2.98 ε = hv = eV = 1.86 eV 1.602
~ = 1 = R( 1 − 1 ) υ λ k 2 n2
n=4 n=3 n=2 n=1 r =a1
r
−e
+e F +
v
−e
+e +
(2)玻尔的三个假设 玻尔( 玻尔(Niels Henrik David Bohr, , 1885—1962)丹麦理论物理学家,现 )丹麦理论物理学家, 代物理学的创始人之一, 代物理学的创始人之一,1913年发表 年发表 论原子构造与分子构造》 了《论原子构造与分子构造》等三篇 文章, 文章,正式提出了关于原子稳定性和 量子跃迁理论的假设, 量子跃迁理论的假设,完满地解释了 氢原子光谱的规律. 氢原子光谱的规律 更重要的是讨论 了多电子原子, 了多电子原子,提出所有原子中有定 态结构,推动量子物理学的形成. 态结构,推动量子物理学的形成 玻尔的创新点 ) 玻尔的创新点: 1) 第一个将量子化概念用到原子 创新 结构上. ) 结构上 2) 第一个将原子光谱与原子中电子跃迁联系 起来. 将卢瑟福的原子模型, 起来 将卢瑟福的原子模型, 量子化概念和光谱统一 了起来. 这简直是思维上最和谐的乐章 这简直是思维上最和谐的乐章” 爱因斯坦 了起来 “这简直是思维上最和谐的乐章” —爱因斯坦
e2
电离能= 电离能 U ∞ − U1 = 13.6eV
(n = 1) me 4 E1 = − 8 ε 02 h 2 = − 13 .6 eV
能 能
自 由 态 激 发 态
氢原子能级图
E / eV n =∞
n=4 n =3 n=2
0 −0.85 −1.51 −3.4
(n > 1)
2
E n = E1 n
ɶ = 1 = R( 1 − 1 ) υ λ 22 n2 n = 3, 4, 5........
巴耳末系
486.1nm 410.2nm 434.0nm 656.3nm
③每一谱线的波数都可表达为两个光谱项之差。 每一谱线的波数都可表达为两个光谱项之差。
ɶ υ = T (k ) − T (n)
二 卢瑟福的原子有核模型 第一个钻到原子中心的人——卢瑟福 卢瑟福 第一个钻到原子中心的人 P R F S T
1 1 紫外 莱曼系 σ = = R ( 2 − 2 ) , n = 2,3, ⋯ λ 1 n 1 1 1 可见光 巴尔末系 σ = = R ( 2 − 2 ) , n = 3, 4, ⋯ λ 2 n 1 1 1 帕邢系 σ = = R ( 2 − 2 ) , n = 4,5, ⋯ λ 3 n
红外
第十二章
量子力学基础
第一节 玻尔的氢原子结构理论 氢原子光谱的规律 卢瑟福原子核模型 玻尔氢原子理论
原子发光 一 氢原子光谱的规律性 1885年瑞士数学家 1885年瑞士数学家 巴耳末发现氢原子光谱 可见光部分的规律
原子内部结构 红
蓝
n2 λ = 365.46 2 2 nm n −2
其中
紫
n = 3,4,5, ⋯
红外
1
1 1 布拉开系 σ = = R ( 2 − 2 ) , λ 4 n
1
1
n = 5,6, ⋯
1 1 普丰德系 σ = = R ( 2 − 2 ) , n = 6,7 , ⋯ λ 5 n 1 1 1 汉弗莱系 σ = = R ( 2 − 2 ) , n = 7 ,8, ⋯ λ 6 n
实验表明: 实验表明: ①原子具有线光谱; 原子具有线光谱; ②各谱线间具有一定的关系
2 vn = m rn
h 由假设 2 量子化条件 m v n rn = n 2π
rn =
ε 0h
2 2
π me
n
2
( n = 1, 2 ,3, ⋯ )
ε 0h
2 2
n = 1 , 玻尔半径 r1 = a0 =
2
π me
= 5.29 × 10
−11
m
rn = n r1 ( n = 1, 2 ,3, ⋯ )
λmax
3 × 108 = 6.63 × 10 −34 = 16.3 × 10 −19 = 10.2 eV 1.22 × 10 −7
当n
→∞
1
λmin
1 = R ( 2 − 0) = 1.097 × 10 7 1
λmin = 1.097 × 10 7 = 0.912 × 10 −7 m = 91.2 nm
四 氢原子玻尔理论的意义和困难 (1)正确地指出原子能级的存在(原子能量量子化); 正确地指出原子能级的存在(原子能量量子化); 原子能级的存在 (2)正确地指出定态和角动量量子化的概念; 正确地指出定态和角动量量子化的概念; 定态 的概念 (3)正确的解释了氢原子及类氢离子光谱; 正确的解释了氢原子及类氢离子光谱; (4)无法解释比氢原子更复杂的原子; 无法解释比氢原子更复杂的原子; 比氢原子更复杂的原子 (5)把微观粒子的运动视为有确定的轨道是不正确的; 把微观粒子的运动视为有确定的轨道是不正确的; 轨道是不正确的 (6)是半经典半量子理论,存在逻辑上的缺点,即把 经典半量子理论,存在逻辑上的缺点, 理论 微观粒子看成是遵守经典力学的质点,同时, 微观粒子看成是遵守经典力学的质点,同时,又 赋予它们量子化的特征 .
子 散 射 实 验 原子核
电子
α , , 15 来
子 . 果
卢瑟福提出有核模型: 卢瑟福提出有核模型: 有核模型 1. 全部正电荷 集中在原子球体中心,大约占原子 全部正电荷Ze集中在原子球体中心 集中在原子球体中心, 体积几万分之一大小的范围内,构成原子核 体积几万分之一大小的范围内,构成原子核. 2. 原子质量几乎全(99.9%以上)集中于此 原子质量几乎全( 以上) 以上 集中于此. 3. Z个电子在核外凭借其与正电荷的库仑力做绕核 个电子在核外凭借其与正电荷的库仑力做绕核 运动,也就类似于行星那样的运动 运动,也就类似于行星那样的运动.
