测控仪器设计第2章第3节PPT课件
合集下载
测控仪器设计节PPT课件

对光速的测定。
当时的人们认为光在太空中传播需要
介质“以太”,正如声音的传递需要
介质(空气等)。
7
美国物理学家。1852 年12月19日出生于普鲁士斯特 雷诺(现属波兰),后随父母移居美国,毕业于美国海军学 院,曾任芝加哥大学教授,美国科学促进协会主席,美国科 学院院长;还被选为法国科学院院士和伦敦皇家学会会员, 1931年5月9日在帕萨迪纳逝世。
(1)首先要能够正确得到仪器作用方程; (2)对于不能列入仪器作用方程的源误差,不能用
微分法求其对仪器精度产生的影响,例如仪器中经常遇到的 测杆间隙、度盘的安装偏心等,因为此类源误差通常产生于 装配调整环节,与仪器作用方程无关。
6
补充:迈克尔逊干涉仪(Michelson interferometer)
c
d
v
t1 t2
10
结果: 观察者先看到投出后的球,
后看到投出前的球。
球 投
c
出
d
前
球 投
v c v
出
后
t1
d c
t2
c
d
v
t1 t2
11
机械波的传播需要媒质,当时物理学家们认为光波在 宇宙中传播也需要一种媒质----以太。
12
十九世纪中叶,麦克斯韦建立了电磁场理论,并预 言了以光速C传播的电磁波的存在。到十九世纪末,实验 完全证实了麦克斯韦理论。电磁波是什么?它的传播速度 C是对谁而言的呢?当时流行的看法是整个宇宙空间充满 一种特殊物质叫做“以太”,电磁波是以太振动的传播。 但人们发现,这是一个充满矛盾的理论。如果认为地球是 在一个静止的以太中运动,那么根据速度叠加原理,在地 球上沿不同方向传播的光的速度必定不一样,但是实验否 定了这个结论。如果认为以太被地球带着走,又明显与天 文学上的一些观测结果不符。
测控仪器设计第二章习题ppt课件
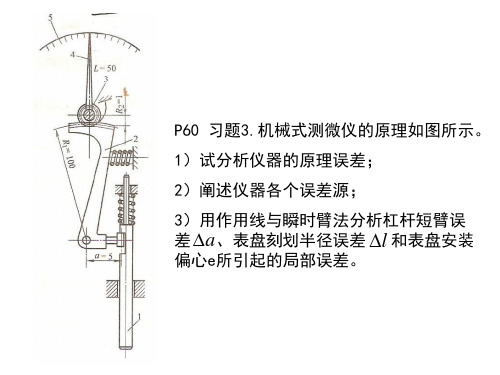
P60 习题3.机械式测微仪的原理如图所示。
1)试分析仪器的原理误差;
2)阐述仪器各个误差源;
3)用作用线与瞬时臂法分析杠杆短臂误
差 a、表盘刻划半径误差 l 和表盘安装
偏心e所引起的局部误差。
D
L50 R2 1
解: (1)原理误差推导。 测杆1感受尺寸变化,其位移S经过一级杠 杆传动(正弦机构)和一级齿轮传动使长
D L R R 1 2 S a S a1 6 S a 3 1 6L R R 1 2 S a 3 (4 )
此为指示端的原理误差。 在输入端的原理误差为:
S
D L R1
a
S
3
6 a
(5)
a R2
(2)误差源:
原理误差:
其中:
D1LR1S3 6 R2 a
L 指针长度
14
y = 0.2083x + 5.9773 R2 = 0.9647
14
13
13
12
12
11
11
10
10
9
9
8
8
7
7
6
6
5
10
15
20
25
30
5
14 y = 0.0004x3 - 0.0183x2 + 0.4007x + 5.6133
14
13
R2 = 0.9957
13
12
12
11
11
10
10
9
9
8
8
0.0-1(-30.003 .0)16m
测杆的最大倾斜角:
D1
tan 0.01 5 6 .3 3 1 4 0 ra
1)试分析仪器的原理误差;
2)阐述仪器各个误差源;
3)用作用线与瞬时臂法分析杠杆短臂误
差 a、表盘刻划半径误差 l 和表盘安装
偏心e所引起的局部误差。
D
L50 R2 1
解: (1)原理误差推导。 测杆1感受尺寸变化,其位移S经过一级杠 杆传动(正弦机构)和一级齿轮传动使长
D L R R 1 2 S a S a1 6 S a 3 1 6L R R 1 2 S a 3 (4 )
此为指示端的原理误差。 在输入端的原理误差为:
S
D L R1
a
S
3
6 a
(5)
a R2
(2)误差源:
原理误差:
其中:
D1LR1S3 6 R2 a
L 指针长度
14
y = 0.2083x + 5.9773 R2 = 0.9647
14
13
13
12
12
11
11
10
10
9
9
8
8
7
7
6
6
5
10
15
20
25
30
5
14 y = 0.0004x3 - 0.0183x2 + 0.4007x + 5.6133
14
13
R2 = 0.9957
13
12
12
11
11
10
10
9
9
8
8
0.0-1(-30.003 .0)16m
测杆的最大倾斜角:
D1
tan 0.01 5 6 .3 3 1 4 0 ra
测控仪器设计课件(第四次课)

l
分度圆
o2
图2—19 齿轮传动
例2-6 测杆与导套之间的配合间隙所引起的作用误差 测杆与导套为摩擦传动作用副,专用线为导套中心先,
由于两着之间存在间隙使测杆倾斜 h ,引起的作
用误差可按几何关系折算为
F s(1 cos ) s
2
2
总结
大体上可以按照上面所述三种情况来计算一对 运动副作用误差。通常,能转换成瞬时臂误差的源
1.源误差可以转换成瞬时臂误差时的作用误差计算
设一对运动副的理论瞬时 臂是 r0 ( ) ,若运动副中存在一源误差直接表现为瞬时臂误差 r0 ( ) ,那么位移沿作用 线传递的基本公式为
dl [r0 ( ) r0 ( )]d
由瞬时臂误差
r0 ( ) 而引起的作用线上的附加位移(作用误差)为
(一)机构传递位移的基本公式
• 推力传动 传递位移时一对运动副之间的相互作用力为推力
•
摩擦力传动 传递位移时一对运动副之间的相互作用力为摩擦力
作用线 为一对运动副之间瞬时作用力的方向线
• 推力传动,其作用线是两构件接触区的公法线
•
摩擦力传动,其作用线是两构件接触区的公切线
如图2-17
位移沿作用线传递的基本公式为
arctan( r0 / R)
图2—21 小模数渐开线齿形检查仪
1—被测齿轮 2—基圆盘 3—主拖板 4—传动丝杠 5—斜尺 6—主导轨
7—手柄 8—测量拖板 9—测杆 10—测微仪 11—测量导轨 12—推力弹簧
测量拖板的位移距离为
s Ltan L r0 R r0
上式表明:测量拖板水平位移与基圆盘的转角位移之间的位移关系形成的是 一种以r0为基圆半径的标准渐开线。当被测齿形的展开长度有误差时,测微仪输
测控仪器设计

• 第四代智能仪器。随着微电子技术的发展 和微处理器的普及,20世纪80年代出现了 在数字化的基础上,以微处理器为核心的 第四代测控仪器。 • 1)高精度、高可靠性 • 2)通用化、标准化与高效率 • 3)应用新原理、新技术 • 4)多维化、多功能化 • 5)高智能化
• • • •
6)网络化 1.3.2 虚拟仪器 1)概念 随着微电子技术、计算机软、硬件技术和 网络技术的迅速发展及其在现代仪器中的 广泛应用,新的测试领域和需求不断产生, 新的测试理论、测试方法、测试技术以及 仪器结构也不断涌现,这在许多方面已经 并将继续改变传统仪器的概念。
第1章 概论
• 1.1 概述 • 1.1.1 测控仪器的概念 • 仪器是人们认识世界、改造世界的手段和 工具,是用来对客观物质实体及其本质属 性进行观察、监视、测量、记录、传输、 转换、显示、分析、处理以及控制的各种 器具、设备与系统的总称,是信息技术的 源头。
• 测量是为确定被测对象的量值而进行的实 验过程,也是通过实验(试验)对客观事 物取得定量意义(或叫信息)的过程。 • 测量仪器:将被测量取出并与测量标准进 行比较,准确地表示被测量的真实数值, 其主要测量对象是各种物理量。 • 测量仪器可分为: • (1)几何量测量仪器 • (2)热工量测量仪器
• 第一代模拟指针式仪器是以电磁感应定律为 基础的,起源于20世纪40年代,主要是针对 某种测试目的而专门设计制造的专用仪器。 • 第二代分立元件仪器。当20世纪50年代出现 电子管,60年代出现晶体管时便产生了以电 子管或晶体管为基础的第二代测控仪器。
• 第三代数字化仪器。20世纪70年代集成电路 出现,随之诞生了以集成电路芯片为基础的 第三代测控仪器——数字化仪器。
示器等各种输出设备、数模转换器和信号 驱动器等构成,其作用是将输出数据以数 据、曲线、图形甚至多维测试结果模型来 显示、打印、存储或再转换成模拟信号输 出。 • 联网是虚拟仪器通信接口中重要的选件, 经过它可以使本仪器与其他计算机系统或 仪器相联,进行广泛的信息交换。 • 2)特点
测控仪器设计第2章——第3节

迈克尔逊等倾干涉条纹
等倾干涉
24
迈克尔逊干涉仪产生的等倾干涉条纹及M1和M2的相应位置
迈克尔逊等倾干涉条纹
25
迈克耳逊-莫雷实 验测到以太漂移速度 为零,对以太理论是 一个沉重的打击,被 人们称为是笼罩在19 世纪物理学上空的一 朵乌云。
26
对此实验结果,洛仑兹提出了一个假设, 认为一切在以太中运动的物体都要沿运动方向 收缩。由此他证明了,即使地球相对以太有运 动,迈克尔逊也不可能发现它。而爱因斯坦从
优点:简单、快速。
局限性:
(1)首先要能够正确得到仪器作用方程; (2)对于不能列入仪器作用方程的源误差,不能用微 分法求其对仪器精度产生的影响,例如仪器中经常遇到的测
杆间隙、度盘的安装偏心等,因为此类源误差通常产生于装 配调整环节,与仪器作用方程无关。
7
补充:迈克尔逊干涉仪(Michelson interferometer)
① 以太不存在,光的传播不需任何媒质,可在 真空中传播,以太不能作绝对参照系。 ② 地球上各方向光速相同,与地球运动状态无 关。 迈克尔逊干涉仪由于可进行精密测量, 1907年迈克尔逊获诺贝尔物理学奖。
21
迈克尔逊干涉仪结构
反射镜 M1
M1 M 2
反 射 镜
M1 移动导轨
单 色 光 源 分光板 G1 补偿板 G 2
13
十九世纪中叶,麦克斯韦建立了电磁场理论,并预言 了以光速C传播的电磁波的存在。到十九世纪末,实验完 全证实了麦克斯韦理论。电磁波是什么?它的传播速度C 是对谁而言的呢?当时流行的看法是整个宇宙空间充满一 种特殊物质叫做“以太”,电磁波是以太振动的传播。但 人们发现,这是一个充满矛盾的理论。如果认为地球是在 一个静止的以太中运动,那么根据速度叠加原理,在地球 上沿不同方向传播的光的速度必定不一样,但是实验否定 了这个结论。如果认为以太被地球带着走,又明显与天文 学上的一些观测结果不符。 1887年迈克尔逊和莫雷利用光的干涉现象进行了非常 精确的测量,仍没有发现地球有相对于以太的任何运动。
测控仪器设计(全)PPT课件

量程是7 ℃。
✓ 测量范围
• 测量仪器误差允 许范围内的被测 量值。
如光学计的示值范围 为±0.1mm,但其悬臂可 沿立柱调节180mm,在该 范围内仍可保证仪器的测 量精度,则其测量范围为 180±0.1mm。
光学计
✓ 灵敏度
• 测量仪器输出的变化与对应的输入变化的 比值。 s=△y/△x
• 表征仪器对被测量变化的反应能力。 • 当输出值与输入值为同一量纲时,灵敏度
又称为放大比。
第四节 对测控仪器设计的要求和设计程序
一、设计要求
(1)精度要求 精度是测控仪器的生命,精度是第一位的。
精度本身只是一种定性的概念。为表征一台仪器的性能和 达到的水平,应有一些精度指标要求,如静态测量的示值 误差、重复性误差、复现性、稳定性、回程误差、灵敏度、 鉴别力、线性度等,动态测量的稳态响应误差、瞬态响应
2009年9月,Intel总裁兼 CEO Paul Otellini展示世界 上第一块基于22nm工艺的 晶圆。该晶圆上的每个指甲 盖大小的单独硅片内都集成 了多达29亿个晶体管。
↓
努力于2016年实现10nm工 艺。
16
一、精度及其重要性
精度:是误差的反义词,精度的高低是用误差的大小来衡量的。 误差大,精度低;反之,误差小,精度高。
17
二、 精度分析的目的
❖ 仪器误差的客观存在性:决定了仪器的精度无论多高,总存 在误差。
大等
光准直式、显微镜式、投影放大、摄 光学式放大部件 影放大式、莫尔条纹、光干涉等
前置放大、功率放大等 电子放大部件
光电放大部件 光电管放大、倍增管放大等
名称 机械系统
光学系统 电子信息处 理系统 光电系统
6
4.瞄准部件
✓ 测量范围
• 测量仪器误差允 许范围内的被测 量值。
如光学计的示值范围 为±0.1mm,但其悬臂可 沿立柱调节180mm,在该 范围内仍可保证仪器的测 量精度,则其测量范围为 180±0.1mm。
光学计
✓ 灵敏度
• 测量仪器输出的变化与对应的输入变化的 比值。 s=△y/△x
• 表征仪器对被测量变化的反应能力。 • 当输出值与输入值为同一量纲时,灵敏度
又称为放大比。
第四节 对测控仪器设计的要求和设计程序
一、设计要求
(1)精度要求 精度是测控仪器的生命,精度是第一位的。
精度本身只是一种定性的概念。为表征一台仪器的性能和 达到的水平,应有一些精度指标要求,如静态测量的示值 误差、重复性误差、复现性、稳定性、回程误差、灵敏度、 鉴别力、线性度等,动态测量的稳态响应误差、瞬态响应
2009年9月,Intel总裁兼 CEO Paul Otellini展示世界 上第一块基于22nm工艺的 晶圆。该晶圆上的每个指甲 盖大小的单独硅片内都集成 了多达29亿个晶体管。
↓
努力于2016年实现10nm工 艺。
16
一、精度及其重要性
精度:是误差的反义词,精度的高低是用误差的大小来衡量的。 误差大,精度低;反之,误差小,精度高。
17
二、 精度分析的目的
❖ 仪器误差的客观存在性:决定了仪器的精度无论多高,总存 在误差。
大等
光准直式、显微镜式、投影放大、摄 光学式放大部件 影放大式、莫尔条纹、光干涉等
前置放大、功率放大等 电子放大部件
光电放大部件 光电管放大、倍增管放大等
名称 机械系统
光学系统 电子信息处 理系统 光电系统
6
4.瞄准部件
测控仪器设计第2章——第3节

是否满足设计要求。 是否满足设计要求。 设计成功; 设计失败,需要进行调整。 满足 设计成功;不满足 设计失败,需要进行调整。
4
P33
一、误差分析的理论基础:误差独立作用原理 误差分析的理论基础:
P33
除仪器输入以外, 除仪器输入以外,另有影响仪器输出的因素 qi (i = 1,2,L n ) 。假设某一 因素的变动(源误差) 使仪器产生一个附加输出,称为局部误差。 因素的变动(源误差)∆qi 使仪器产生一个附加输出,称为局部误差。
运行误差总结: 运行误差总结:
仪器在使用过程中产生的误差,属于随机误差。始终存在,无法消除。 仪器在使用过程中产生的误差,属于随机误差。始终存在,无法消除。
3
第三节 仪器误差的分析
精度:是误差的反义词。 精度:是误差的反义词。误差大 精度低; 精度低;误差小 精度高 所以,仪器误差分析又称为仪器精度分析
∆Qi = Pi ∆qi
局部误差 影响系数 源误差
∆y = ∑ Pi ∆qi = ∑ ∆Qi
i =1 i =1
n
n
仪器总误差
误差独立作用原理的内容: 误差独立作用原理的内容: ①一个源误差仅使仪器产生一个局部误差。局部误差是源误差的线性函 一个源误差仅使仪器产生一个局部误差。 与其他源误差无关。 数,与其他源误差无关。 ②仪器总误差是局部误差的综合。 仪器总误差是局部误差的综合。 意义: 意义:
具体步骤: 具体步骤: 1. 列出仪器的作用方程; 列出仪器的作用方程;
∆y =
∑
i =1
n
∂y ∆ qi = ∂ qi
∑ P ∆q
i i =1
n
i
=
∑ ∆Q
i =1
n
4
P33
一、误差分析的理论基础:误差独立作用原理 误差分析的理论基础:
P33
除仪器输入以外, 除仪器输入以外,另有影响仪器输出的因素 qi (i = 1,2,L n ) 。假设某一 因素的变动(源误差) 使仪器产生一个附加输出,称为局部误差。 因素的变动(源误差)∆qi 使仪器产生一个附加输出,称为局部误差。
运行误差总结: 运行误差总结:
仪器在使用过程中产生的误差,属于随机误差。始终存在,无法消除。 仪器在使用过程中产生的误差,属于随机误差。始终存在,无法消除。
3
第三节 仪器误差的分析
精度:是误差的反义词。 精度:是误差的反义词。误差大 精度低; 精度低;误差小 精度高 所以,仪器误差分析又称为仪器精度分析
∆Qi = Pi ∆qi
局部误差 影响系数 源误差
∆y = ∑ Pi ∆qi = ∑ ∆Qi
i =1 i =1
n
n
仪器总误差
误差独立作用原理的内容: 误差独立作用原理的内容: ①一个源误差仅使仪器产生一个局部误差。局部误差是源误差的线性函 一个源误差仅使仪器产生一个局部误差。 与其他源误差无关。 数,与其他源误差无关。 ②仪器总误差是局部误差的综合。 仪器总误差是局部误差的综合。 意义: 意义:
具体步骤: 具体步骤: 1. 列出仪器的作用方程; 列出仪器的作用方程;
∆y =
∑
i =1
n
∂y ∆ qi = ∂ qi
∑ P ∆q
i i =1
n
i
=
∑ ∆Q
i =1
n
测控技术第二章优秀课件

T0 / 2 T0 / 2
x
(t
)
co
s
n
0td
t
4 T0
T0 / 2 ( A
0
2A T0
t) cos
n 0tdt
4A n 2 2
n 1, 3, 5
4A n 2 2
sin 2
n 2
0
n 2,4,6
奇函数关于原点对称
奇函数
b n
2 T0
T0 / 2 T0 / 2
x(t) sin
n 0tdt
0
T0 /2
a n
2 T0
T0 /2 T0 /2
x
(t)
co
s
n
0td
t;
b n
2 T0
T0 /2 T0 /2
x (t) sin
n
0td t;
T0 周 期
0圆 频 率 ,
0
2 T0
常值分量 余弦分量幅值 正弦分量幅值
变形为:x (t )
a0 2
n 1
An
co s( n 0t
n)
An
a
2 n
第三节 周期信号和离散频谱
一、周期信号的分解
1、傅立叶级数的三角函数展开式:
Dirichlet条件
要将一周期信号分解为三角级数应当满足下列条件:
在一周期内,函数是绝对可积的,即 应为有限值;
| t1 T t1
f t| dt
在一周期内,函数的极值数目为有限;
在一周期内,函数f(t)或者为连续的,或者具有有限
个这样的间断点,即当t从较大的时间值和较小的时间
值分别趋向间断点时,函数具有两个不同的有限的函
测控仪器设计第2章

一、误差独立作用原理 y0 f ( x, q01 , q02 ......,q0n )
若仪器特性参数有误差
q1 q01 q1
q2 q02 q2
qn q0n qn
实际仪器输出方程:
y f ( x, q1 , q2 ......,qn )
仪器误差:
y y y0
仪器的工作原理:氦氖激光器l射出的激光经反射镜3、透镜4(用来减小光 束的发散)、反射镜2和用同步电动机带动的多面棱镜5,再经过透镜6对被 测工件7进行扫描.然后经过透镜8由光电二极管9接收实现光信号—电信号 的转换。由于多面棱镜以角速度ω 旋转使棱镜转过 θ 角,则反射光转过 2θ 角,实现对工件的扫描。在激光光束被工件遮挡的时间内,计数器所 计的脉冲数与被测工件的直径有一定的对应关系。为了保证扫描信号与计 算电路中计数脉冲同步,用同一晶体振荡器控制。
瞬时臂的由来:
例2-4 齿轮齿条传动机构 位移沿 l l 传递 dl r0 ( )d r cosd
L r cosd r cos
0
dl ds cos
dl r cos ds d rd cos cos
齿条位移方程:
S ds rd r
第二节 仪器误差的来源与性质
仪器误差:仪器本身所固有的误差。在仪器制成后,在规 定的使用条件下仪器误差就基本固定了。
仪器测量误差: 既包括仪器误差,由包括仪器使用和运行 时,因为一些使用的环境条件、测量方法以及测量人员主 观因素的等各项原因造成的综合误差,它以测量结果与被 测量值的偏差值来表示。
求仪器精度 ----各项误差来源分析-----找出主要因素-----控 制减小其影响 仪器误差产生的原因: 在仪器的设计、制造和使用的各个阶段可能产生误差,分 别称为原理误差制造误差和运行误差。从数学特性亡看。 原理误差多为系统误差、而制造误差和运行误差多为随机 误差。
测控仪器设计第章ppt课件

(3)滚柱和滚珠导轨的组合
灵活运用了滚珠导轨运动的灵活性和滚柱导轨承 载大的优点。
(4)滚柱与长圆柱轴导轨组合
轻载部件中使用
滚动导轨计算
1、运动导轨的长度
L
LB
l 2
2、滚动体的尺寸和数量
Z柱
W 4l
3、强度与刚度计算
Z珠
W 9.5
d
六、静压导轨及设计要点
静压导轨是在动导轨与静导轨之间,因液体压力油 或气体静压力而使动导轨及工作台浮起,两导轨之 间工作面不接触,而形成完全的液体或气体摩擦
(1)导轨的几何精度
二、导轨部件设计的基本要求 (一)导向精度
导向精度是指动导轨运动轨迹的准确度。
对一副导轨来说其直线度是非常重要的精 度指标,它取决于导轨面的几何精度、接 触精度、导轨和基座的刚度、导轨油膜刚 度及导轨与基座的热变形等。
(1)导轨的几何精度
(2)接触精度
减少接触面的表面粗糙度:滑动导轨—动导轨Ra 0.8-0.2µm ,静导轨0.4-0.1µm 。滚动导轨面Ra 小于0.2µm
运动灵敏度较高,能承受不大的倾复力矩
(2)双圆弧滚珠导轨
计量光学仪器中(如小型工具显微镜、投影仪等)使用
接触面积较大,接触点应力较小,变形也较小,承载能力强、 寿命长。
(3)四圆柱棒滚道的滚珠导轨
优点:运动精度和灵活性较高,维修方便
缺点是承载能力不大,故多适用于较轻巧的仪器 上(如掩膜检查显微镜工作台)
a)两滚道型导轨结构简图 b) 四滚道型导轨结构简图
第四节 主轴系统及设计
一、主轴系统设计的基本要求
主轴系统设计的主要要求:
是主轴在一定载荷下具有一定的回转精度,同时还要 求有一定的刚度和热稳定性
灵活运用了滚珠导轨运动的灵活性和滚柱导轨承 载大的优点。
(4)滚柱与长圆柱轴导轨组合
轻载部件中使用
滚动导轨计算
1、运动导轨的长度
L
LB
l 2
2、滚动体的尺寸和数量
Z柱
W 4l
3、强度与刚度计算
Z珠
W 9.5
d
六、静压导轨及设计要点
静压导轨是在动导轨与静导轨之间,因液体压力油 或气体静压力而使动导轨及工作台浮起,两导轨之 间工作面不接触,而形成完全的液体或气体摩擦
(1)导轨的几何精度
二、导轨部件设计的基本要求 (一)导向精度
导向精度是指动导轨运动轨迹的准确度。
对一副导轨来说其直线度是非常重要的精 度指标,它取决于导轨面的几何精度、接 触精度、导轨和基座的刚度、导轨油膜刚 度及导轨与基座的热变形等。
(1)导轨的几何精度
(2)接触精度
减少接触面的表面粗糙度:滑动导轨—动导轨Ra 0.8-0.2µm ,静导轨0.4-0.1µm 。滚动导轨面Ra 小于0.2µm
运动灵敏度较高,能承受不大的倾复力矩
(2)双圆弧滚珠导轨
计量光学仪器中(如小型工具显微镜、投影仪等)使用
接触面积较大,接触点应力较小,变形也较小,承载能力强、 寿命长。
(3)四圆柱棒滚道的滚珠导轨
优点:运动精度和灵活性较高,维修方便
缺点是承载能力不大,故多适用于较轻巧的仪器 上(如掩膜检查显微镜工作台)
a)两滚道型导轨结构简图 b) 四滚道型导轨结构简图
第四节 主轴系统及设计
一、主轴系统设计的基本要求
主轴系统设计的主要要求:
是主轴在一定载荷下具有一定的回转精度,同时还要 求有一定的刚度和热稳定性
仪器设计的基本原则ppt课件

② 在设计的整个过程中采用集多人智慧,互相启发来寻求解决问题的途径; 也可通过有针对性、有系统地提问来激发智慧,寻找解决办法
③ 通过对现有产品的观察,优缺点分析,或采用数学建模,或采用系统分析 及形态学矩阵的理论分析方法寻求各种解决办法。
举例子说明:采用系统分析方法解决防止螺纹松动的结构措施。
螺钉锁紧力矩公式为
结论:许多线值
测量系统的仪器,很 难做到使各个坐标方 向或一个坐标方向上 的各个平面内均能遵 守阿贝原则。
15
图3-3 a)
图3-3 b)
16
基于上述实际情况,引出了扩展阿贝原则的思路和方法。 美国学者布莱恩(J.B.Bryan)建议将扩展了的阿贝原则表达如下: “位移测量系统工作点的路程应和被测位移作用点的路程位于一条直线上。
其中图3-3 b)为YZ平面,测头1在该平面内的行程所构成的尺寸线与Z方向读数 线共线,但与Y方向读数线相距为L,在该平面内不符合阿贝原则。
13
图3-2 工件的直径测量
b)用阿贝比较仪测量
1—被测工件 2—工作台 3—底座 4—基准刻线尺 5—支架
14
图3-3 三坐标测量机 1-测头的触球 2-被测工件
如图3-3所示的三坐标测量机,其测量点的轨迹是测头1的行程所构成的尺寸 线,而仪器读数线分别在图示的X、Y与Z直线位置处,显然,在图示情况下测量 时,X与Y坐标方向均不遵守阿贝原则。
其中图3-3 a)为XZ平面,测头1在该平面内的行程所构成的尺寸线与Z方向读数 线共线,但与X方向读数线相距为L,在该平面内不符合阿贝原则。
消除了操作者的人为误差,实现了自动化、 数字化、微米级的测量精度。
结论
这种由光学投影式瞄准原理发展为利用计算机视觉系统进行瞄准的创新,开创了 新一代刀具预调仪的发展,也为生产厂家带来了较大的经济利润和社会效益。
③ 通过对现有产品的观察,优缺点分析,或采用数学建模,或采用系统分析 及形态学矩阵的理论分析方法寻求各种解决办法。
举例子说明:采用系统分析方法解决防止螺纹松动的结构措施。
螺钉锁紧力矩公式为
结论:许多线值
测量系统的仪器,很 难做到使各个坐标方 向或一个坐标方向上 的各个平面内均能遵 守阿贝原则。
15
图3-3 a)
图3-3 b)
16
基于上述实际情况,引出了扩展阿贝原则的思路和方法。 美国学者布莱恩(J.B.Bryan)建议将扩展了的阿贝原则表达如下: “位移测量系统工作点的路程应和被测位移作用点的路程位于一条直线上。
其中图3-3 b)为YZ平面,测头1在该平面内的行程所构成的尺寸线与Z方向读数 线共线,但与Y方向读数线相距为L,在该平面内不符合阿贝原则。
13
图3-2 工件的直径测量
b)用阿贝比较仪测量
1—被测工件 2—工作台 3—底座 4—基准刻线尺 5—支架
14
图3-3 三坐标测量机 1-测头的触球 2-被测工件
如图3-3所示的三坐标测量机,其测量点的轨迹是测头1的行程所构成的尺寸 线,而仪器读数线分别在图示的X、Y与Z直线位置处,显然,在图示情况下测量 时,X与Y坐标方向均不遵守阿贝原则。
其中图3-3 a)为XZ平面,测头1在该平面内的行程所构成的尺寸线与Z方向读数 线共线,但与X方向读数线相距为L,在该平面内不符合阿贝原则。
消除了操作者的人为误差,实现了自动化、 数字化、微米级的测量精度。
结论
这种由光学投影式瞄准原理发展为利用计算机视觉系统进行瞄准的创新,开创了 新一代刀具预调仪的发展,也为生产厂家带来了较大的经济利润和社会效益。
最新测控仪器第2章ppt教学课件

三、运行误差
仪器在使用过程中所产生的误差。如力变形误差、磨损和间隙造成的 误差,温度变形引起的误差,材料的内摩擦所引起的弹性滞后和弹性后效, 以及振动和干扰等 。
(一)力变形误差
由于仪器的测量装置(测量头架等) 在测量过程中的移动,使仪器结构件 (基座和支架等)的受力大小和受力点的 位置发生变化,从而引起仪器结构件 的变形。
非独立误差:相关系数非 “零”
(三)误差的表示方法
1.绝对误差 :被测量测得值 x与其真值(或相对真值) x 0 之差
xx0
特点:有量纲、能反映出误差的大小和方向。
2.相对误差 :绝对误差与被测量真值的比值
特点:无量纲
x0
表示方法 •引用误差 绝对误差的最大值与仪器示值范围的比值。 •额定相对误差 示值绝对误差与示值的比值。
(五)总结
(1)采用近似的理论和原理进行设计是为了简化设计、简化制造工 艺、简化算法和降低成本 。
(2)原理误差属于系统误差,使仪器的准确度下降,应该设法减小 或消除。
(3)方法: • 采用更为精确的、符合实际的理论和公式进行设计和参数计算 。 • 研究原理误差的规律,采取技术措施避免原理误差。 • 采用误差补偿措施 。
•摇臂式坐标测量
设横臂a×b=50×200mm为的等截面梁, 选用铝合金材料,长度l=3000mm, l1 =400mm,测头部件的自重W=200N。
图2—10 悬臂式坐标测量机原理图
1—立柱 2—平衡块 3—读数基尺 4—横臂 5—测头部件 6—z向测量轴
产生误差的原因 当测头部件位于横臂最外端A处和最里端B处时,由于测头部件的 集中负荷在横臂上的作用点发生变化引起立柱和横臂的受力状态发生变化,引起横 臂上A、B两点处的挠曲变形和截面转角变化,从而引起测量误差。
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
①光从G1
M1
①光从M1
G1
来回时间
t1
l l cv cv
c 1
2l
v2 c2
光速 c –v 顶风,
光速 c +v 顺风,
具体步骤: 1. 列出仪器的作用方程; 2. 对作用方程求全微分(包含各个源误差)。
-
3
Lm:测量光路长度
例2-1 激光干涉测长仪的误差分析与计算
Lc:参考光路长度
P34
当干涉仪处于起始位置,其初始光程差为 2n(LmLc) ,对应的干涉条纹数为
K1
2n(Lm Lc)
0
n:空气折射率 λ0:真空中激光波长
迈克尔逊主要从事光学和光谱学方面的研究,他以毕生
精力从事光速的精密测量,在他的有生之年,一直是光速测
定的国际中心人物。他发明了一种用以测定微小长度、折射
率和光波波长的干涉仪(迈克尔逊干涉仪),在研究光谱线
方面起着重要的作用。1887年他与美国物理学家E.W.莫雷
合作,进行了著名的迈克尔逊-莫雷实验,这是一个最重大的
-
6
补充:迈克尔逊干涉仪(Michelson interferometer)
阿尔伯特·亚伯拉罕·迈克尔逊
(Albert Abrahan Michelson) (1852~1931)
因发明精密光学仪器和借助这些仪器在光谱学和度量学的研 究工作中所做出的贡献,被授予1907年度诺贝尔物理学奖。
也是美国第一位诺贝尔物理奖得主。
②测量过程中由于测量镜的移动使仪器基座受力状态发生变化,使测量光路与参
考光路长度差发生改变 (LmLc) ;
③计数器的计数误差 K。
根据微分法,源误差引起的仪器误差 L 2 n 0 K 2 K n 0 K 2 n 2 0 n (L m L c )
若测量开始时计数器“置零”,在理想情况下, L K0
当反射镜M2移动到M2位置时,设
被测长度为L,那么,此时的干涉
条纹数为
KK 2K 12 n 0 L 2n(L m 0L c)
由上式可以得到:
LK0
2n
(LmLc)
上式称为激光干涉仪的测量方程
图2-14 激光干涉光路图
-
4
针对激光干涉仪的测量方程:
LK0
2n
(LmLc)
可能存在的误差:
①测量环境的变化如温度、湿度、气压等,使空气折射率发生变化n 、激光波 长发生变化 0 ;
P33
一、误差分析的理论基础:误差独立作用原理
除仪器输入以外,另有影响仪器输出的因素 qi(i1,2, n) 。假设某一
因素的变动(源误差)qi 使仪器产生一个附加输出,称为局部误差。
n
n
y Qi Piqi
i1
i1
仪器总误差
局部误差
误差独立作用原理的内容:
影响系数
源误差
①一个源误差仅使仪器产生一个局部误差。局部误差是源误差的线性函
-
2
(一)微分法
设仪器的作用方程为 yf(x,q 1,q2, ,qn),其中 qi(i1,2, n)为仪器各特性参
数,x为仪器被测量。对作用方程求全微分来求各源误差 qi(i1,2, n) 对 仪器精度的影响(局部误差)即 yi n1 q yi qi i n1P i qi i n1 Q i
否定性实验,它动摇了经典物理学的基础。
-
8
①真空中的光速(30万Km/s)相对于何物而言? ②真空中的光速是否适用牛顿的绝对时空观?
c c v ?
y
s s'
y ' cv
o o'
x'
x
z z'
-
9
例 试计算球被投出前后的瞬间,所 发出的光波达到观察者所需时间。
球 投 出 前
球 投 出
c
d
v cv
t1
d c
t2
c
d
v
后
t1 t2
-
10
结果: 观察者先看到投出后的球,
后看到投出前的球。
球 投 出 前
球 投 出
c
d
v cv
t1
d c
t2
c
d
v
后
t1 t2
-
11
机械波的传播需要媒质,当时物理学家们认为光波在 宇宙中传播也需要一种媒质----以太。
-
12
十九世纪中叶,麦克斯韦建立了电磁场理论,并预言 了以光速C传播的电磁波的存在。到十九世纪末,实验完 全证实了麦克斯韦理论。电磁波是什么?它的传播速度C 是对谁而言的呢?当时流行的看法是整个宇宙空间充满一 种特殊物质叫做“以太”,电磁波是以太振动的传播。但 人们发现,这是一个充满矛盾的理论。如果认为地球是在 一个静止的以太中运动,那么根据速度叠加原理,在地球 上沿不同方向传播的光的速度必定不一样,但是实验否定 了这个结论。如果认为以太被地球带着走,又明显与天文 学上的一些观测结果不符。
数,与其他源误差无关。Leabharlann ②仪器总误差是局部误差的综合。
③意义:
④根据误差独立作用原理,在进行仪器误差分析时,可以:
⑤1)首先计算每个源误差所造成的局部误差;
⑥2)然后将每个局部误差综合成仪器总误差。
-
1
⑦注意:误差独立作用原理是近似原理,但在大多数情况下都能适用。
二、误差分析的具体方法:
①微分法 ②几何法 ③作用线与瞬时臂法(难点) ④数学逼近法 ⑤控制系统的误差分析法 ⑥其他方法
突出贡献:
迈克尔逊干涉仪
迈克尔逊-莫雷实验 (这也是迈克尔逊一生中最重要的贡献 ) 通过光学实验否定了“以太”的存在。
对光速的测定。
当时的人们认为光在太空中传播需要
介质“以太”,正如声音的传递需要介
质(空- 气等)。
7
美国物理学家。1852 年12月19日出生于普鲁士斯特雷 诺(现属波兰),后随父母移居美国,毕业于美国海军学院, 曾任芝加哥大学教授,美国科学促进协会主席,美国科学院 院长;还被选为法国科学院院士和伦敦皇家学会会员, 1931年5月9日在帕萨迪纳逝世。
1887年迈克尔逊和莫雷利用光的干涉现象进行了非常
精确的测量,仍没有发现地球有相对于以太的任何运动。
-
13
迈克尔逊—莫雷实验
迈克尔逊为了
验证以太的存在, 设计了测量地球在 以太中运动速度的 实验。
M2 M1
G1 G2
地球相对以太 以 v 运动,以太风 从右至左吹来。
v
-
以太风
14
1.在实验室S’系观察
有
2n
激光测长仪仪器误差 L L ( K K 0 n n ) (L m L c)
即令 LmLc
-
5
微分法总结:
优点:简单、快速。 局限性:
(1)首先要能够正确得到仪器作用方程; (2)对于不能列入仪器作用方程的源误差,不能用微
分法求其对仪器精度产生的影响,例如仪器中经常遇到的测 杆间隙、度盘的安装偏心等,因为此类源误差通常产生于装 配调整环节,与仪器作用方程无关。
