北师大版八年级数学上册3.2 平面直角坐标系第3课时建立适当的坐标系描述图形的位置

合集下载

北师大版八年级数学上册《3.2平面直角坐标系(共3课时)》课件

第一象限
-3
-2
-1 O -1
1
2
3
X
第三象限
-2 -3
第四象限
平面直角坐标系
坐标轴上的点不在任何一个象限内！
平面直角坐标系内点的位置的表示
对于平面内任x轴、y轴上对应的数a、 b分别叫做点P 的横坐标、纵坐标，有序数对（a， b）叫做点 P 的坐标。
到了坐标为（３，２）和（３，－２）的两个标志点，并且知道藏宝地点的坐标为（４，４），除此外不知道其他信息，如何确定直角坐标系找到“宝藏”？与同伴进行交流．
x C
B
⑵ 图中A与D，B与C的纵坐标相同吗？为什么？A与B，C与D的横坐标相同吗？为什么？
随堂练习
在图中，以中心广场为坐标原点，取正东方向为x轴的正方向,取正北方向为y轴的正方向，一个方格的边长作为一个长度单位，建立直角坐标系分别写出图中各个景点的坐标。
y
雁塔钟楼中心广场碑林北
情景引入
图示是某市旅游景点的示意图。
⑴ 你是怎样确定各个景点位置的？
北
⑵“大成殿”在“中心广场”西、南各多少格？“碑林”在“中心广场”东、北各多少格？
雁塔
钟楼
中心广场大成殿
碑林
⑶ 如果以“中心广场”为原点作两条互相垂直的数轴，分别取向右和向上的方向为正方向，一个格的边长看做一个单位长度，那么你能表示碑林的位置吗？“大成殿”的位置呢？
课堂小结
⑴ 已知一点的坐标，如何在直角坐标系内描出
这个点？
⑵ 如何建立适当的直角坐标系来确定已知点的坐标？
1.平面直角坐标系是如何建立的？
在平面内，有公共原点的互相垂直的两条数轴，就构成了平面直角坐标系，其中水平数轴称为x轴或横轴，铅直数轴称为ｙ轴或纵轴．

八年级数学上册平面直角坐标系(第三课时) 教案北师大版

一、教学设计思想本节课是在前两节课的基础上，由“在坐标系中由点找坐标”发展为“根据已知条件，建立适当的直角坐标系”。

建立直角坐标系由多种方法，老师不直接把这些方法告诉学生，而是让学生主动探索，分析选择不同坐标系对计算简繁程度的影响。

二、教学目标知识与技能1．进一步巩固画平面直角坐标系，在给定的直角坐标系中，会根据坐标描出点的位置，由点的位置写出它的坐标．2．能在方格纸上建立适当的直角坐标系，描述物体的位置．3．能结合具体情境灵活运用多种方式确定物体的位置．过程与方法根据已知条件有不同的解决问题的方式，灵活地选取既简便又易懂的方法求解是本节的重点，通过多角度的探索既可以拓宽学生的思维，又可以从中找到解决问题的捷径，使大家的解决问题的能力得以提高．情感态度与价值观1．通过学习建立直角坐标系有多种方法，体验数学活动充满着探索与创造．2．通过确定旅游景点的位置，认识数学与人类生活的密切联系，提高学习数学的兴趣．三、教学重点根据实际问题建立适当的坐标系，并能写出各点的坐标．四、教学难点根据已知条件，建立适当的坐标系．五、教学方法探讨法．六、教具准备方格纸若干张．投影片三张：第一张：练习（记作§5．2．3 A）；第二张：补充练习（记作§5．2．3 B）；第三张：补充练习（记作§5．2．3 C）．七、教学过程Ⅰ．创设问题情境，引入新课在前两节课中我们学习了在直角坐标系下由点找坐标，和根据坐标找点，并把点用线段连接起来组成不同的图形，还自己设计出了不少漂亮的图案．这些都是在已知的直角坐标系下进行的，如果给出一个图形，要你写出图中一些点的坐标，那么你必须建立直角坐标系，直角坐标系应如何建立？是惟一的情形还是多种情况，这就是本节课的内容．Ⅱ．讲授新课［例］如下图，矩形ABCD的长与宽分别是6，4，建立适当的直角坐标系，并写出各个顶点的坐标．［师］在没有直角坐标系的情况下是不能写出各个顶点的坐标的，所以应先建立直角坐标系，那么应如何选取直角坐标系呢？请大家思考．［生甲］如下图所示，以点C为坐标原点，分别以CD、CB所在直线为x轴、y轴，建立直角坐标系．由CD长为6，CB长为4，可得A、B、C、D的坐标分别为A（6，4），B（0，4），C（0，0），D（6，0）．［生乙］如下图所示．以点D为坐标原点，分别以CD、AD所在直线为x轴、y轴，建立直角坐标系．由CD长为6，BC长为4，可得A、B、C、D的坐标分别为A（0，4），B（－6，4），C（－6，0），D（0，0）．［师］这两位同学选取坐标系的方式都是以矩形的某一顶点为坐标原点，矩形的相邻两边所在直线分别作为x轴、y轴，建立直角坐标系的．这样建立直角坐标系的方式还有两种，即以A、B为原点，矩形两邻边分别为x轴、y轴建立直角坐标系．除此之外，还有其他方式吗？［生］有，如下图所示．以矩形的中心（即对角线的交点）为坐标原点，平行于矩形相邻两边的直角为x轴、y轴，建立直角坐标系．则A、B、C、D的坐标分别为A（3，2），B（－3，2），C（－3，－2），D（3，－2）．［师］这位同学做的很棒．较前两种有难度，那还有没有其他建立直角坐标系的方式呢？［生］有，如下图所示．建立直角坐标系，则A、B、C、D的坐标系分别为A（4，3），B（－2，3），C（－2，－1），D（4，－1）．［师］还有其他情况吗？［生］有，把上图中的横坐标逐渐向上移动，纵坐标左、右移动，则可得到不同的坐标系，从而得到A、B、C、D四点的不同坐标．［师］从刚才我们讨论的情况看，大家能发现什么？［生］建立直角坐标系有多种方法．［师］非常正确．［例题］对于边长为4的正三角形ABC，建立适当的直角坐标系，写出各个顶点的坐标．解：如下图，以边BC所在直线为x轴，以边BC的中垂线为y轴建立直角坐标系．由正三角形的性质，可知AO=23，正△ABC各个顶点A、B、C的坐标分别为A（0，23），B（－2，0），C（2，0）．［师］正三角形的边长已经确定是4，则它一边上的高是不是会因所处位置的不同而发生变化呢？［生］不会，只是位置变化，而长度不会变．［师］除了上面的直角坐标系的选取外，是否还有其他的选取方法．［生］有，如下图所示．以点B为坐标原点，BC所在的直线为x轴，建立直角坐标系．因为BC=4，AD=23，所以A、B、C三点的坐标为A（2，23），B（0，0），C（4，0）．［师］很好，其他同学还有不同意见吗？［生］有．分别以A、C为坐标原点，以平行于线段BC或线段BC所在的直线为x轴，建立直角坐标系，则A、B、C的坐标相应地发生变化．［师］很棒，其他情况我们就不一一列举了，请大家在课后继续．议一议在一次“寻宝”游戏中，寻宝人员已经找到了坐标为（3，2）和（3，－2）的两个标志点，并且知道藏宝地点的坐标为（4，4），除此外不知道其他信息．如何确定直角坐标系找到“宝藏”？与同伴进行交流．［生］因为（3，2）和（3，－2）到x轴的距离都为2，所以x轴肯定通过连接两个点的线段的中点．［生］因为这两点的横坐标都是3，所以y轴应在这两点的左侧，且连接（3，－2），（3，2）的线段向左移动3个单位长度就与y轴相重合．［师］说的对，下面我完整地给大家叙说一次．如下图，设A（3，2），B（3，－2），C （4，4）．因为点A、B到x轴的距离相等，所以线段AB垂直于x轴，则连接线段AB，作线段AB的垂直平分线即为x轴，并把线段AB四等份，其中的一份为一个单位长度，以线段AB的中点D为起点，向左移动3个单位长度的点为原点O，过点O作x轴的垂线即为y轴，建立直角坐标系，再在新建的直角坐标系内找到（4，4）点，即是藏宝地点．Ⅲ．课堂练习（一）随堂练习投影片（§5．2．3 A）如下图，五个儿童正在做游戏，建立适当的直角坐标系，写出这五个儿童所在位置的坐标．［师］请大家每5个人组成一个小组，每个同学建立直角坐标系的方式不同．请在自己准备的方格纸上建立直角坐标系，并写出在此坐标系下的坐标．［生甲］我是以中间的儿童（即A）为坐标原点，以方格的横线、纵线所在直线为横轴、纵轴，建立直角坐标系，这样，五个儿童所在位置的坐标分别为A（0，0），B（－5，0），C （0，－4），D（4，0），E（0，3），如上图所示．［生乙］我是以图中的B为坐标原点，以方格的横线、纵线所在直线为横轴、纵轴建立直角坐标系，五个儿童所在位置的坐标分别为A（5，0），B（0，0），C（5，－4），D（9，0），E（5，3）．如下图所示．［师］另外以C、D、E为坐标原点，以方格的横线、纵线所在直线为横轴、轴纵建立直角坐标系的方法我们就不一一说明了，我相信大家做的一定很棒．除这五种方法外，是否就没有其他方法了呢？请大家思考．［生］还有，以方格纸的横线、纵线所在直线为横轴、纵轴，横线、纵线的任一交点为原点，都可建立直角坐标系，相应的可求出五个位置的坐标．（二）补充练习投影片（§5．2．3 B）某地为了发展城市群，在现有的四个中小城市A、B、C、D附近新建机场E，试建立适当的直角坐标系，并写出各点的坐标．解：若以A点为坐标原点，过A点的方格的横线、纵线所在直线为横轴、纵轴，建立直角坐标系．这时，A、B、C、D、E五个点的坐标分别为A（0，0），B（8，2），C（8，7），D（5，6），E（1，8）．投影片（§5．2．3 C）如下图，四边形ACEG和四边形BDFH都是正方形，BF的长为8，建立适当的直角坐标系，写出点A、B、C、D、E、F、G、H的坐标．［师］要写出这八个点的坐标，首先要做什么？［生］要求出各线段的长．［师］很好．由已知的BF的长能求出哪些线段的长呢？［生］AC=CE=EG=AG=BF=8AB=BC=CD=DE=EF=FG=GH=HA=4［师］下面请大家建立适当的直角坐标系．［生］如下图所示．以BF所在直线为x轴，DH所在直线为y轴，建立直角坐标系，BF、DH的交点O为坐标原点．这时八个点的坐标为A（－4，4），B（－4，0），C（－4，－4），D （0，－4），E（4，－4），F（4，0），G（4，4），H（0，4）．［师］这是惟一方法吗？［生］不是，还有许多方法．如上图所示，以点C为坐标原点，CA所在的直线为y轴，CE所在的直线为x轴，建立直角坐标系．这时两个正方形的八个顶点的坐标分别为A（0，8），B（0，4），C（0，0），D （4，0），E（8，0），F（8，4），G（8，8），H（4，8）．Ⅳ．课时小节本节课的目的是能在方格纸上建立适当的直角坐标系，描述物体的位置．Ⅴ．课后作业习题5．5Ⅵ．活动与探究如下图，建立两个不同的直角坐标系，在各个直角坐标系下，分别写出八角星8个角的顶点的坐标，并比较同一顶点在两个坐标系中的坐标．解：如上图所示建立直角坐标系，则八个顶点的坐标分别为A（－5，10），B（－7，5），C（－5，0），D（0，－2），E（5，0），F（7，5），G（5，10），H（0，12）．第二种：如下图所示建立直角坐标系．这时八个顶点的坐标分别为A（－5，7），B（－7，2），C（－5，－3），D（0，－5），E （5，－3），F（7，2），G（5，7），H（0，9）．比较同一顶点在两种坐标系下的坐标：A（－5，10），A（－5，7），可知横坐标不变，纵坐标减小了；B（－7，5）、B（－7，2），横坐标不变，纵坐标减小了……比较所有顶点的坐标可知，在这两种直角坐标系下，同一顶点的坐标的横坐标不变，纵坐标减小了．八、板书设计。

平面直角坐标系(共16张PPT)

二、新课讲解
例1 如图, 长方形ABCD的长与宽分别是6 , 4 , 建立适当的直角坐标系,并写出各个顶点的坐标.
二、新课讲解
解：以点C为坐标原点, 分别以CD , CB所在直线为x轴、y 轴，建立直角坐标系，如图. 此时点C的坐标是（0 ，0） .
由CD=6, CB=4, 可得D , B , A的坐标分别为D（6，
二、新课讲解
解： x BC 在坐标系中，A点坐标为（4，4），B点坐标为（0，4），C点坐标为（0，0），D点坐标为（4，0）；
八年级数学北师大如版·上图册，以边BC所在直线为轴，以边的中垂线为y轴建立
直角坐标系. 例1 如图, 长方形ABCD的长与宽分别是6 , 4 , 建立适当的直角坐标系,并写出各个顶点的坐标.
0），B（0，4），A（6，4）.
二、新课讲解
在例1中，你还可以怎样建立直角坐标系？与同伴进行交流.
还可以分别以A、B、D为坐标原点建立适当的直角坐标系.如：以A为坐标原点，则B，C，D的坐标分别为（-6，0），（-6，4），（0，-4）.
二、新课讲解
例2 对于边长为4的等边三角形ABC（如图），建立适当的直角坐标系，写出各个顶点的坐标.
二、新课讲解
在一次“寻宝”游戏中，寻宝人已经找到了A（3，2）和B（3，-2）两个标志点（如图），并且知道藏宝地点的坐标为（4，4），除此之外不知道其他信息.如何确定直角坐标系找到“宝藏”？与同伴进行交
流.
二、新课讲解
先根据点A（3，2）、B（3，-2）建立相应的平面直角坐标系，再由藏宝地点的坐标，即（4，4）确定“宝藏”的位置.
八年级数学北师大版·上册
第三章位置与坐标
3.2 平面直角坐标系（第3课时）

北师大版-数学-八年级上册-3.2《平面直角坐标系(3)》教学设计

3.2《平面直角坐标系（3）》教学设计教学目标：1.能结合所给图形的特点，建立适当的坐标系，写出点的坐标；2.能根据一些特殊点的坐标复原坐标系；3.经历建立坐标系描述图形的过程，进一步发展数形结合意识。

教学重点：建立适当的坐标系，确定点的坐标教学难点：建立适当的坐标系，确定点的坐标教学过程：一、导入新课活动过程：确定适当的直角坐标系，确定各个关键点的坐标。

活动成果：根据坐标系确定点的坐标。

【设计意图】：借助于大家熟悉的长方形着手，建立适当的直角坐标系，确定各个顶点的坐标，引入课题。

二、探究新知活动一：活动过程：通过建立不同的直角坐标系，感受点与坐标之间的对应关系。

活动成果：巩固坐标与点的对应关系。

【设计意图】：通过活动感受点与坐标之间的对应关系，并通过观察、猜想并验证坐标之间的特征，提升能力。

三、例题讲解：讲解过程：先确定如图所示的坐标系，然后再确定各个顶点的坐标。

解题思路：在具体情景中根据建立坐标系确定点的坐标。

解题方法：观察分析法答案：略四、课堂练习1.课本随堂练习五、课堂总结本节课我们通过活动更好的感受点与坐标之间的对应关系，建立适当的直角坐标系，确定各个点的坐标。

通过本节课的学习，你还有什么新的收获？请与大家分享。

六、课后作业课内作业：课本课后习题习题3.4 1、2、3七、板书设计课题：3.2 平面直角坐标系（3）1.建立适当的坐标系：2.例题八、教学反思本节课的内容主要通过建立适当的坐标系，确定图形各个顶点的坐标，增强学生解决问题的能力。

在坐标轴上的点学生易弄错坐标。

北师大版八年级数学上册：3.2《平面直角坐标系》教学设计2

北师大版八年级数学上册：3.2《平面直角坐标系》教学设计2一. 教材分析《北师大版八年级数学上册：3.2《平面直角坐标系》》是学生在学习了坐标轴的基础上，进一步探究平面直角坐标系的相关知识。

本节内容主要包括坐标系的定义、坐标系的性质以及坐标系中的应用。

通过本节的学习，使学生能更好地理解和运用坐标系，为后续函数、几何等知识的学习打下基础。

二. 学情分析学生在七年级已经学习了坐标轴的知识，对坐标轴有一定的认识和了解。

但坐标系的概念、性质以及应用可能还存在一些困惑。

因此，在教学过程中，要注重引导学生从实际问题中认识坐标系，通过观察、操作、思考、探究等活动，加深对坐标系的理解。

三. 教学目标1.了解平面直角坐标系的定义、性质，能正确地在平面直角坐标系中描述点的位置。

2.能运用坐标系解决实际问题，提高解决问题的能力。

3.培养学生的观察能力、操作能力、思考能力和团队协作能力。

四. 教学重难点1.重点：平面直角坐标系的定义、性质以及应用。

2.难点：坐标系在实际问题中的应用。

五. 教学方法采用问题驱动法、案例教学法、合作学习法等多种教学方法，引导学生从实际问题中认识坐标系，通过观察、操作、思考、探究等活动，深入理解坐标系的性质和应用。

六. 教学准备1.准备相关的教学案例和实际问题。

2.准备平面直角坐标系的图片和模型。

3.准备黑板、粉笔等教学工具。

七. 教学过程1.导入（5分钟）通过展示实际问题，引导学生思考如何用数学工具描述和解决这些问题。

例如，某城市有两个公园，分别位于东西方向和南北方向，如何用坐标系表示这两个公园的位置？2.呈现（10分钟）呈现平面直角坐标系的定义、性质和表示方法。

用图片和模型展示坐标系的特点，让学生直观地理解坐标系的概念。

3.操练（10分钟）让学生通过观察、操作、思考、探究等活动，掌握坐标系的性质。

例如，让学生在坐标系中找出给定的点，或判断两个点的位置关系。

4.巩固（10分钟）通过解决实际问题，巩固坐标系的应用。

北师大版八年级数学上册《平面直角坐标系》第3课时示范课教学设计

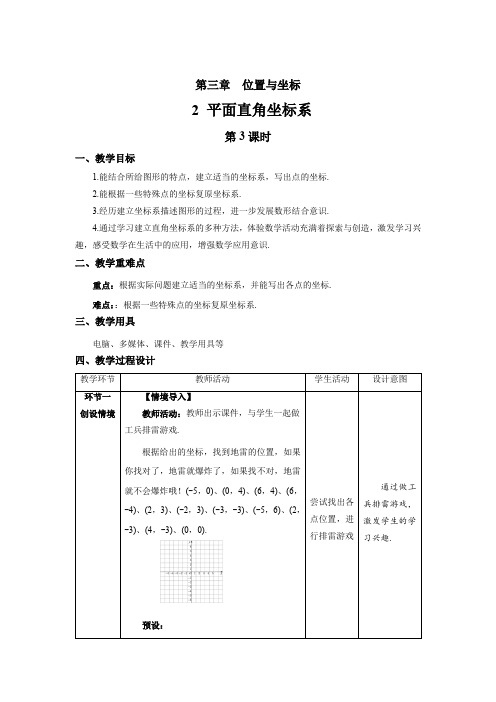
第三章位置与坐标2 平面直角坐标系第3课时一、教学目标1.能结合所给图形的特点，建立适当的坐标系，写出点的坐标.2.能根据一些特殊点的坐标复原坐标系.3.经历建立坐标系描述图形的过程，进一步发展数形结合意识.4.通过学习建立直角坐标系的多种方法，体验数学活动充满着探索与创造，激发学习兴趣，感受数学在生活中的应用，增强数学应用意识.二、教学重难点重点：根据实际问题建立适当的坐标系，并能写出各点的坐标.难点：：根据一些特殊点的坐标复原坐标系.三、教学用具电脑、多媒体、课件、教学用具等四、教学过程设计【情境导入】教师活动：教师出示课件，与学生一起做工兵排雷游戏.根据给出的坐标，找到地雷的位置，如果你找对了，地雷就爆炸了，如果找不对，地雷就不会爆炸哦！(-5，0)、(0，4)、(6，4)、(6，-4)、(2，3)、(-2，3)、(-3，-3)、(-5，6)、(2，-3)、(4，-3)、(0，0).预设：思考：你能写出图中几个点的坐标吗？预设：不能，因为没有建立直角坐标系.给出一个平面图形，要想写出图形中一些点的坐标，必须建立直角坐标系，而直角坐标系如何建立?建立方法是否唯一呢?我们一起来探索下！【探究】教师活动：通过探究活动，引导学生探究如何建立适当的平面直角坐标系.如图，长方形ABCD的长与宽分别是6和4，建立适当的直角坐标系，并写出各个顶点的坐标.思考：你是如何建立的直角坐标系?各顶点坐标如何求得?预设：(1)确定坐标原点；(2)确定x轴和y轴，建立直角坐标系；(3)根据条件中线段长度表示各顶点的坐标.解：如图，以点C为坐标原点，分别以CD，CB所在的直线为x轴，y轴建立直角坐标系. 此时C点坐标为( 0，0 ).由CD长为6，CB长为4，可得D，B，A的坐标分别为：D( 6 ，0 )，B( 0，4 )，A( 6，4).【议一议】还可以建立其他平面直角坐标系，表示长方形的四个顶点A，B，C，D的坐标吗？预设：成果展示教师引导学生多尝试，方法多样，合理即可.【想一想】由上得知，建立的平面直角坐标系不同，则【典型例题】教师活动：教师提出问题，学生先独立思考，解答.然后再小组交流探讨，如遇到有困难的学生适当点拨，最终教师展示答题过程.例如图，对于边长为4的等边三角形ABC，建立适当的直角坐标系，并写出各个顶点的坐标.解：如图，以边BC所在直线为x轴，以边BC的中垂线为y轴建立直角坐标系.由等边三角形的性质可知AO=23，顶点A，B，C的坐标分别为A (0，23)；B (-2，0)；C (2，0).提问：想一想，还有其他方法吗？预设：其他方法展示【议一议】在一次“寻宝”游戏中，寻宝人已经找到了坐标为(3，2)和(3，-2)的两个标志物A，B，并且知道藏宝地点的坐标为(4，4)，除此外不知道其他信息.如何确定直角坐标系找到“宝藏”？预设：连接AB，作线段AB的中垂线，并以这条直线为横轴；将线段AB分成四等份，以其中的一份为单位长度，以线段AB的中点为起点，向【随堂练习】教师活动：教师给出练习，随时观察学生完成情况并相应指导，最后给出答案，根据学生完成情况适当分析讲解.1.如图，建立适当的直角坐标系，并写出这个四角星的八个顶点的坐标.2.如图，围棋棋盘放在某平面直角坐标系内，已知黑棋(甲)的坐标为(-2，2)，黑棋(乙)的坐标为(-1，-2)，则白棋(甲)的坐标为__________.3.对于边长为4的正方形，建立适当的直角坐标系，并写出各个顶点的坐标.4.如图所示，在某次行动中，当我方两架飞机处于A(-1，2）与B(3，2)位置时，雷达探测到有一架可疑飞机C 在(1，-2)位置. 请你建立适当的直角坐标系，找出可疑飞机C的位置.答案：1.解：各顶点坐标如下图：2.解：白棋(甲)的坐标为（2，1）.3.解：如图，以顶点A为原点，AB所在直线为x轴，AD所在直线为y轴建立平面直角坐标系．正方形四个顶点A，B，C，D的坐标分别为：A(0，0)，B(4，0)，C(4，4)，D(0，4).方法不唯一.4.解：点C的位置如图所示：思维导图的形式呈现本节课的主要内容：。

北师大版数学八年级上册3.2平面直角坐标系建立适当的平面坐标系(教案)

针对本次教学，以下是我认为需要改进的地方：
1.在实践活动和小组讨论中，增加与生活实际相关的案例，让学生更好地感受到平面直角坐标系的应用。
2.在教学过程中，加强对学生的观察和引导，关注他们的思考过程，及时发现问题并给予指导。
3.注重个体差异，针对不同学生的需求进行分层教学，提高教学效果。
4.加强课堂互动，鼓励学生提问和发表观点，营造积极向上的学习氛围。
二、核心素养目标
1.培养学生的空间观念和几何直观：通过平面直角坐标系的建立，使学生能够在坐标系中表示点、线、图形，提高对空间位置关系的理解和判断能力。
2.提升数据分析与解决问题的能力：指导学生运用坐标分析图形的性质，解决实际问题，培养数据分析、逻辑推理和问题解决的核心素养。
3.增强数学建模意识：通过实际案例，让学生学会如何建立适当的坐标系，将现实问题转化为数学问题，提高数学建模能力。
3.坐标系的建立：通过实际例子，指导学生如何在实际问题中建立适当的平面直角坐标系，理解建立坐标系的意义和作用。
4.坐标与图形的关系：探讨如何利用坐标来描述图形的位置和性质，以及如何根据坐标关系解决实际问题。
5.练习题：针对本节课所学内容，设计具有代表性的练习题，巩固学生对平面直角坐标系的理解和应用。
4.发展数学抽象和逻辑推理能力：在教学过程中，引导学生从具体的坐标点抽象出一般规律，培养学生的数学抽象和逻辑推理能力。
5.培养合作交流意识：鼓励学生在小组讨论中分享观点，倾听他人意见，提高合作交流能力，为未来学习奠定基础。
三、教学难点与重点
1.教学重点
-理解平面直角坐标系的概念：包括坐标系由两条互相垂直的数轴组成，横坐标和纵坐标的定义。
此外，在学生小组讨论中，虽然大部分学生能够积极参与，提出自己的观点，但在引导与启发方面，我觉得还可以做得更好。今后，我将更加关注学生的思考过程，及时给予他们反馈和指导，以提高讨论效果。

数学北师大版八年级上册建立适当的平面直角坐标系(第三课时)

教学设计首页平面直角坐标系------ 如何建立适当的平面直角坐标系静态自习课自习安排：1、自习课本65页例3、例4、议一议，并完成课本内容2、完成学导练69页自学检测部分3、思考：1）给定一个图形，有几种建系方法，不同坐标系下坐标相同吗？ 2）给定一个图形，如何建立平面直角坐标系较为简便 3）给定点的坐标，应如何建立平面直角坐标系动态展示课（一）基础检测（共4分）1、右图是某市几个主要景点示意图，根据图中信息可确定九疑山的中心位置C 点的坐标为＿＿(3,1)＿＿．（1分）2、下图均为边长为4的正方形，写出各图中点C 的坐标（1）图一：C （4，4）（1分）（2）图二：C （0，4）（1分）（3）图三：C （2，4）（1分）阅卷组起立，评分（二）知识构建 1、（师）：昨日自习课中，你学到了什么？（生）：同一图形，可以建立不同的平面直角坐标系，坐标系不同，点的坐标也不同 2、展示小组对学导练69页自学检测部分进行展示汇报一组展示题：例1.（1）如图，矩形ABCD 的长与宽分别是6，4，建立适当的直角坐标系，并写出各个顶点的坐标。

（2）在上面的问题中，你还可以怎样建立直角坐标系？与同伴交流。

（3）对比不同的建立坐标系的方法，你更喜欢哪一种？谈谈你的看法二组展示题：（生）：在讲解自己解题过程中结合学生的互动，并讲解清楚了不同坐标的具体求法，注意顶点落到不同象限对应的正负（师）：总结刚刚两个小组的展示，我们再次看到同一图形可以建立不同的平面直角坐标系，坐标系不同，对应点的坐标也不相同。

那如何进行选择，需要我们进一步讨论（师）：汇报自习检测情况，小组报分，错误多的小组说明错误原因（三）解惑提升学生困惑：1、给定一个图形，怎样建立平面直角坐标系最简便 2、平面直角坐标系的坐标原点一定要在顶点上吗？ 3、答题格式是什么？学生补充困惑：老师质疑：如图，矩形ABCD 中，AB=8，CB=4，AF//CE,且AE=5,建立恰当的平面直角坐标系，并表示各顶点的坐标小组讨论困惑，给出你的回答（生）：1、答：建系原则：1）让尽可能多的点落在坐标轴上；2）坐标运算要简便3）先定原点，X 轴Y 轴，再标坐标，根据长度及所在位置确定点的坐标 2、答：平面直角坐标系的坐标原点不一定要在顶点上，是以方便建系，方便标坐标为原则建系的。

北师大版八年级数学上册第3章位置与坐标建立平面直角坐标系确定点的坐标

上其它点的坐标呢？的位置关系？
归纳总结
点的位置
横坐标的符号
纵坐标的符号
在 x 轴的正半轴上
+
0
在 x 轴的负半轴上
-
0
在 y 轴的正半轴上
0
+
在 y 轴的
负半轴上
0
-
y
5
4 3B 2
C
1
A
-4 -3 -2 -1-O1 1 2 3 4 x -2
-3
-4 E
与坐标轴平行的直线上的点的坐标特征：
解：如图，作辅助线.
∵A(2，－1)，B(4，3)，C(1，2)，
∴BD＝3，CD＝1，CE＝3，AE＝1，
AF＝2，BF＝4，
∴S△ABC＝S长方形BDEF－S△BDC－S△CEA－S△BFA
＝BD·DE－ 1 DC·DB－ 1 CE·AE－ 1 AF·BF
2
2
2
＝12－1.5－1.5－4
＝5.
别以 O、P 为圆心 OP 为半径画弧，与 y 轴
有三个交点 Q2，Q4，Q3，当以 OP 为底时， OP 的垂直平分线与 y 轴有一个交点 Q1.
4.写出平行四边形 ABCD 各个顶点的坐标.
y
(-3，3) 4
A
3
2
(6，3) D
1 O
-6 -5 -4-3-2 -1 1 2 3 4 5 6 -1
Ay
面积为 6，点 A 的横坐标为 -1，
那么点 A 的坐标为 (-1，2)或(-1，-2) ．
(-4，B 0)
(2，0) OC x
3. 在平面直角坐标系 xOy 中，已知点 P（2，2），点 Q 在 y 轴上，△PQO 是等腰三角形，则满足条件的点 Q 共有( B ) A．5 个 B．4个 C．3 个 D．2 个【解析】如图所示，当以 OP 为腰时，分

北师大版八年级数学上册：3.2《平面直角坐标系》教学设计

北师大版八年级数学上册：3.2《平面直角坐标系》教学设计一. 教材分析《北师大版八年级数学上册：3.2平面直角坐标系》这一节主要让学生掌握平面直角坐标系的定义、特点以及坐标轴上的点的坐标特征。

通过本节课的学习，使学生能够理解并运用平面直角坐标系解决实际问题。

二. 学情分析学生在学习本节课之前，已经掌握了实数、坐标等基础知识，但对平面直角坐标系的概念和应用可能还不够熟悉。

因此，在教学过程中，需要注重引导学生通过观察、操作、思考、交流等途径，逐步掌握平面直角坐标系的相关知识。

三. 教学目标1.让学生了解平面直角坐标系的定义、特点及其作用。

2.使学生能够正确地确定平面直角坐标系中点的坐标。

3.培养学生运用平面直角坐标系解决实际问题的能力。

四. 教学重难点1.重点：平面直角坐标系的定义、特点及其作用。

2.难点：平面直角坐标系中点的坐标的确定。

五. 教学方法采用问题驱动法、案例教学法、合作学习法等，引导学生通过观察、操作、思考、交流等途径，掌握平面直角坐标系的相关知识。

六. 教学准备1.准备平面直角坐标系的图片、PPT等教学资源。

2.准备一些实际问题，用于引导学生运用平面直角坐标系解决。

七. 教学过程1.导入（5分钟）利用PPT展示一些生活中的实例，如商场、学校、电影院等，引导学生思考如何用数学方法表示这些实例的位置。

从而引出平面直角坐标系的概念。

2.呈现（10分钟）讲解平面直角坐标系的定义、特点及其作用。

通过PPT展示平面直角坐标系的图片，让学生直观地了解坐标系的特点。

同时，解释坐标轴上的点的坐标特征，如正负号、绝对值等。

3.操练（10分钟）让学生分组进行操作，利用平面直角坐标系确定一些给定点的坐标。

教师巡回指导，解答学生遇到的问题。

4.巩固（10分钟）出示一些实际问题，如两个人在商场购物，要求学生运用平面直角坐标系解决这些问题。

教师选取部分学生的问题进行讲解和评价。

5.拓展（10分钟）讲解一些与平面直角坐标系相关的拓展知识，如斜率、直线方程等。

北师大版数学八年级上册建立平面直角坐标系确定点的坐标

坐标系找到“宝藏”？解：如图所示
（-2，2）3
·2 1
· -3 -2 -1-O1 1
-2
·（3，2）
234 x
·（3，-2）
1.已知 A(1，4)，B(-4，0)，C(2，
y A (1，4)
0). △ABC的面积是＿1＿2 ＿．
O
B(-4，0)
C (2，0)x
2.若 BC 的坐标不变，△ABC 的
y
●
●●●●
●
●●
●●
●●
●●
●
●●
●
●
●
●●
O
x
1.图形中哪些点在坐
y
标轴上，它们的坐
●
标有什么特点？
●●●●Βιβλιοθήκη D●●●●●
2.线段 EC 与 x 轴有
E● ● F
●●
●
●●
●
BC
什么位置关系？点 E 和点 C 的坐标有什么特点？线段 EC
●
●
●●
G
AO
x
3.点 F 和点 G 的横坐标有什么共同特点？线段 FG 与 y 轴有怎样
建立适当的直角坐
1
B
标系，写出各个顶 –4 –3 –2 –1 O
C 1234
x
点的坐标.
–1
解:A(0，2 3)， B(-2，0) ， –2
–3
C(2，0).
–4
练一练在一次“寻宝”游戏中，寻宝人已经找到了坐标
为（3，2）和（3，-2）的两个标志点，并且知道藏宝地
点的坐标为（-2，2），如何确定直角 y
求△ABC 的面积．
解析：本题宜用补形法．
分别过点 A 作 x 轴的平行线，过点 C 作 y 轴的平行线，两条平行线交于点 E，过点 B 分别作 x 轴、y 轴的平行线，分别交 EC 的延长线于点 D，交 EA 的延长线于点 F，然后根据 S△ABC＝S长方形BDEF －S△BDC－S△CEA－S△BFA 即可求出△ABC 的面积．

3.2第3课时建立直角坐标系求坐标(新教案)-2023-2024学年八年级上册数学(北师大版)

3.2第3课时建立直角坐标系求坐标（新教案）-2023-2024学年八年级上册数学（北师大版）
一、教学内容
《3.2第3课时建立直角坐标系求坐标》选自2023-2024学年八年级上册数学（北师大版）第三章第二节的第三课时内容。本节课将围绕以下教学内容展开：
1.理解平面直角坐标系的概念及作用；
2.学会建立平面直角坐标系，并能正确画出坐标系；
举例：通过典型例题，让学生掌握点的平移、对称等坐标运算的规律，并能应用于实际问题。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《建立直角坐标系求坐标》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要确定位置的情况？”（如电影院选座、地图定位等）。这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索直角坐标系求坐标的奥秘。
（2）对坐标概念的理解，特别是对坐标值的正负判断；
难点解析：学生对坐标值的正负容易混淆，需要通过实例进行讲解和强调。
举例：利用具体图形，让学生观察不同象限内点的坐标值特点，强化对坐标正负的理解。
（3）在直角坐标系中进行坐标运算的规律和方法；
难点解析：坐标运算涉及到点的平移、对称等操作，学生需要掌握相应的运算规律和方法。
3.掌握在直角坐标系中，点的坐标的表示方法；
4.能够根据给定的点，快速准确地求出其坐标；
5.通过实例，让学生学会在直角坐标系中进行简单的坐标运算。
教学内容与教材紧密关联，旨在帮助学生掌握直角坐标系的基本知识，为后续学习平面几何和函数等知识打下基础。
二、核心素养目标
《3.2第3课时建立直角坐标系求坐标》一课的核心素养目标如下：
5.激发学生的创新意识，鼓励他们在坐标系中进行探索和发现，培养其勇于尝试和创新的科学精神。

北师大版八年级数学上册3.2平面直角坐标系_教案

四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《平面直角坐标系》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要确定位置的情况？”（例如，在地图上找到学校的位置）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索坐标系在定位中的奥秘。
3.重点难点解析：在讲授过程中，我会特别强调第一象限和第四象限的点的坐标特征，以及坐标轴上点的特殊情况。对于难点部分，我会通过图示和实际例子来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与坐标系相关的问题，如如何在坐标系中表示一些日常生活中的位置信息。
（二）新课讲授（用时10分钟）
1.理论介绍：首先，我们要了解平面直角坐标系的基本概念。平面直角坐标系是由横轴和纵轴组成的，它能够帮助我们精确地确定平面内的点的位置。这是解决几何问题的重要工具，广泛应用于科学、工程和日常生活中。
2.案例分析：接下来，我们来看一个具体的案例。这个案例展示了如何使用坐标系来确定平面内的点的位置，以及如何通过坐标解决几何问题。
5.引导学生自主探究、发现规律，培养他们的数学抽象和数学建模的核心素养。
三、教学难点与重点
1.教学重点
-理解平面直角坐标系的概念，明确坐标轴、坐标点等基本元素；
-掌握坐标平面内各个象限的点的坐标特征，横坐标与纵坐标的正负关系；
-学会使用坐标描述点的位置，理解点、线、图形在坐标平面上的表示方法；
-能够应用平面直角坐标系解决简单的实际问题。
5.应用平面直角坐标系解决简单的实际问题。
二、核心素养目标
1.让学生通过探究平面直角坐标系的概念和性质，培养直观想象和逻辑推理的核心素养；

北师大版数学8年级上册学案第3课时建立适当的坐标系描述图形的位置

第3课时建议适当的坐标系描述图形的位置1.能结合所给图形的特点，建立适当的坐标系，写出点的坐标；2.能根据一些特殊点的坐标复原坐标系；3.经历建立坐标系描述图形的过程，进一步发展数形结合意识.知识探究自学指导：阅读课本P65，完成下列问题.建立直角坐标系的一般步骤：1.建立坐标系，选择一个适当的参考点为原点，确定坐标轴正方向；2.根据具体问题，确定恰当的比例尺，在坐标轴上标出单位长度.自学反馈1.如图，方格纸上有M，N两点，若以N为原点建立平面直角坐标系，则点M的坐标为（3，4）；若以M点为原点建立平面直角坐标系，则点N的坐标为（）A.（-3，-4）B.（4，0）C.（0，-2）D.（2，0）2.某市区的几个旅游景点在平面直角坐标系中的位置如图所示，已知图中每个小正方形的边长均为1个单位长度，且山峡会馆的坐标是（4，-1），则其他各景点的坐标分别为：光岳楼；金凤广场；动物园；湖心岛．活动1 小组讨论例1如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的坐标系,并写出各个顶点的坐标.解: 如图,以点C为坐标原点, 分别以CD , CB所在的直线为x 轴,y 轴建立直角坐标系. 此时C点坐标为( 0 , 0 ).由CD长为6, CB长为4, 可得D , B , A的坐标分别为D( 6 , 0 ), B( 0 , 4 ),A( 6 , 4 ) .在上面的问题中，你还可以怎样建立直角坐标系？与同伴交流.例2 如图，正三角形ABC 的边长为 4 , 建立适当的直角坐标系 ,并写出各个顶点的坐标 .解:如图,以边BC 所在的直线为x 轴,以边BC 的中垂线y 轴建立直角坐标系.由正三角形的性质可知AO=32 ,正三角形ABC 各个顶点A , B , C 的坐标分别为A (0 , 32 )，B ( -2 , 0 )，C ( 2 , 0).活动2 跟踪训练1.如图所示，四边形ABCD 是边长为6的正方形，请你建立一个适当的平面直角坐标系，并分别写出A ，B ，C ，D 的坐标．2.如图是某市旅游景点的示意图.试建立适当的平面直角坐标系，并用坐标表示出各景点的位置.3.如图，在一次部队军事对抗演习中甲方已经找到了乙方坐标为A （2，1）和B （-2，1）的两个警卫营的位置，并且知道乙方的指挥所的位置为（3，3），除此之外不知道其他信息，如何确定乙方的指挥所所处的位置？课堂小结关于建立平面直角坐标系，你有哪些经验？教学至此，敬请使用《名校课堂》相关课时部分.【预习导学】自学反馈1.A2.（0，0）（-2，-1.5）（6，5）（-1.5，1）【合作探究】活动2 跟踪训练1.（答案不唯一）以AB所在的直线为x轴，AD所在的直线为y轴，并以点A为坐标原点，则点A，B，C，D的坐标分别是（0，0），（6，0），（6，6），（0，6）．2.答案不唯一，如建立如图所示的平面直角坐标系，则各景点位置的坐标分别为：科技大学（0，0），大成殿（2，3），钟楼（1，6），雁塔（3，8），中心广场（5，4），映月湖（9，1），碑林（9，8）.3.连接AB，作线段AB的中垂线记为y轴，以AB的中点为起点，以AB的四分之一为一个单位长度向下作一个单位为坐标原点，过原点作AB的平行线记为x轴，建立平面直角坐标系，找到（3，3）即可．。

北师大版八年级数学上册：3.2.3《建立直角坐标系》

基础自主导学
考点梳理
自主测试
考点四
分式的运算
��
��± �� . �� 异分母的分式相加减,先通分,变为同分母的分式,再相加减,即 ± �� ± �� = . ��
1.分式的加减法
同分母的分式相加减,分母不变,把分子相加减,即 ±
=
2.分式的乘除法分式乘分式,用分子的积作为积的分子,分母的积作为积的分母, �� 即�� ·�� = ��.分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘,即�� ÷ �� = �� ·�� = �� . 3.分式的乘方分式乘方要把分子、分母分别乘方,即
轻松尝试应用 1 2 3 4
1.已知在等腰直角三角形ABC中,斜边AB的长为2.以AB所在直线为x轴,AB的垂直平分线为y轴建立直角坐标系,则点C的坐标是( )
A.(0,1)
B.(0,-1)
D.(1,0)或(-1,0)
C.(0,1)或(0,-1)
关闭
本题运用了分类讨论思想,根据题意可求得 OC=1,所以①当点 C 在 y 轴的正半轴时,点 C 的坐标是(0,1);②当点 C 在 y 轴的负半轴时,点 C 的坐标是(0,-1).
关闭
C 综上可知 ,点 C 的坐标是(0,1)或(0,-1),故选 C.
解析解析答案答案
轻松尝试应用 1 2 3 4