扭转轴在冲击载荷作用下冲击应力和动载系数的计算
起重机钢结构总体设计时常用地载荷系数

在进行起重机总体设计时,特别是钢结构设计时,考虑的载荷和工民建钢结构厂房设计考虑的载荷有很大不同,其特点就是起重机是动态使用的,在考虑载荷时,都要乘一个系数,现在我把整体设计时最常用的载荷系数简单得说一下,使对起重机钢结构设计不了解的人有一个初步的认识,同时,也请这方面的专家指出不足之处。
《规范》中可没有这么详细啊!一、自重冲击系数当货物突然起升离地、货物下降制动、起重机运行通过轨道接缝或运动机构起动、制动时,起重机的的自身重量将产生冲击和振动。
由于这种冲击和振动,起重机各部分质量会产生附加的加速度,虽然可用计算机计算这种加速度,但计算工作量较大,所以,实际计算时是将自重乘以一个冲击系数,以考虑这种附加动载的影响。
按照《起重机设计规范》(GB3811-83),的规定,自重冲击系数分两种情况,一是货物离地或货物下降制动对自重的冲击,将起重机自重乘以起升冲击系数φ1,二是吊着货物的起重机运行通过轨道接缝,将起重机自重和起升载荷均乘以相同的运行冲击系数φ4,他们都是经验值。
1、起升冲击系数φ1《规范》规定:0.9≤φ1≤1.1这个系数的应用分两种情况:当自重对要计算的元件起增大作用时,取φ1=1.0~1.1,否则取φ1=0.9~1.0。
2、运行冲击系数φ4《规范》规定,φ4用下式计算:φ4=1.10+0.058v√h (注:√h为h开更号)式中v-----起重机(或小车)的运行速度(m/s)h----轨道接缝处二轨道面的高度差(mm)理论表明,当速度较大时(v≤2m/s),冲击系数并不随速度增大,只要控制h≤2mm,系数不会大于1.1。
二、起升载荷动载系数φ2这是一个最重要的系数。
φ2一般取1≤φ2≤2当起升质量突然离地上升或下降制动时起升质量将产生附加的加速度,由这个附加加速度引起的惯性力,将对机构和结构产生附加的动应力,我国《规范》规定,将起升载荷乘以系数φ2予以增大,φ2即为起升载荷动载系数。
1、φ2的估算值φ2=1+cv√[1/δg(λ0+yo)]各符号的意义见《起重机设计规范》(GB3811-83)附录B为了检验上式的正确性,曾对通用桥式起重机、塔式起重机、门座起重机等做过测定,φ2值与实测值很接近。
材料力学典型例题及解析 12.冲击问题典型习题解析

击构件瞬间的速度为 υ
,只须将前面(a)式右端改为
1 2
⋅
Pυ2 g
= Vε
,即可导出 kd
=
υ2 。 g∆st
(4)、前面推导过程中,冲击物的势能取为 Ep = P(h + ∆d ) ,一般情况下 ∆d << h ,可将其忽
略,取 Ep = Ph ,读者可仿照上面推导一下,并讨论忽略后对 kd 有什么影响。
所以本问题的动载荷因数为: kd
=
∆d ∆st
=1+
1+ 2h = 1+ ∆st
1+
2
× 440 ×10 −3 2 ×10 −3 m
m
= 22
讨论:(1)、在线弹性范围内,载荷、变形、应变、应力之间都是线性关系,也就是说,当
外载荷被放大 kd 倍,则变形、应力、应变也同样被放大 kd 倍。所以有σ d = kdσ st 。有了 kd 很
动能完全转化为橡皮筋的应变能。即 Ek = Vε 。
解:设小球离开木拍瞬间速度为υ ,则其动能 Ek
=
1 2பைடு நூலகம்
W g
υ 2 ;而橡皮筋被拉至最长时应变能
Vε
=
1 2
F ⋅ ∆L ,其中
F
为小球速度为零时橡皮筋所受拉力。由于假设橡皮筋为线弹性变形,
3
所以 F
=σ
A
=
Eε
A=
∆L L0
EA ,于是Vε
=
∆d
=
∆d ∆st
P 。定义
∆d ∆st
= kd 为动载荷因数,则有
Fd P
=
∆d ∆st
= σd σ st
机械设计复习题

一、螺纹联接与螺旋传动概念、填空、选择题1、按牙型螺纹可分( )、( )、( )、( ).2、按螺旋的作用分( )、( )。
2、螺纹联接的防松方式有( )、( )、( )。
4、螺纹联接的基本类型有( )、( )、( )、( ).5、承受横向工作载荷的普通螺栓联接,螺栓受( )应力和( )应力作用,可能发生的失效形式是( );承受横向工作载荷的铰制孔用螺栓联接,靠螺栓受( )和( )来传递载荷,可能发生的失效形式是( )和( )。
6、螺栓组的受力分析类型,如何解决。
7、某螺纹联接在工作时承受较大的横向力作用,为使螺纹直径不至于过大,采用( )联接为宜。
A 普通螺栓B 铰制孔螺栓C 双头螺柱D 螺钉8、经过优选、简化、统一,并给以标准代号的零部件称为( ).A 通用件B 系列件C 标准件D 专用件9、在螺纹联接中,可以实现自锁性能的是( ),可以实现传动性能最好的是( ).A 三角形螺纹B 矩形螺纹C 锯齿形螺纹D 梯形螺纹10、用于薄壁形零件连接时,应采用( )A 多线三角粗牙螺纹B 三角细牙螺纹C 锯齿形螺纹D 梯形螺纹11、拧紧可以使一定公称直径的普通螺栓取得一定的预紧力,如果要以比较小的拧紧力矩T 来得到要求的预紧力,可采用( )。
A 细牙螺纹B 双线螺纹C 适当润滑D 增加螺母与被联接件支撑面间的面积12、在螺纹联接中,按防松原理,采用双螺母属于( )A 摩擦防松B 机械防松C 破坏螺纹副的关系防松D 增加预紧力防松13、当两被联接件之一太厚,不宜制成通孔,不需要经常拆卸时,往往采用( )A 螺栓联接B 螺钉联接C 双头螺柱连接D 紧定螺钉联接14、某单个螺栓联接,要求被联接件结合面不分离,假定螺栓的刚度b C 与被联接件的刚度m C 相等,联接的预紧力为0F .现在对联接施加轴向载荷,当外载荷F 达到与预紧力0F 的大小相等时( ) A 被联接件发生分离,联接失效B 被联接件即将发生分离,联接不可靠C 联接可靠,但不能继续加载D 联接可靠,只要螺栓强度足够,载荷F 还可以继续增加到接近预紧力0F 的两倍15、受轴向变载荷的螺栓联接中,已知预紧力0F =8000N,工作载荷N F F 4000,0max min ==,螺栓和被联接件刚度相等,则在最大工作载荷下,残余预紧力为( )A2000N B4000N C6000N D8000N16、当螺栓组承受横向载荷或旋转力矩时,该螺栓组中的螺栓( )A 必受剪切力作用B 必受拉力作用C 同时受到剪切和拉伸D 既可能受剪切,也可能受拉伸17、对于受轴向载荷的紧螺栓联接,在限定螺栓总拉力的条件下,提高螺栓疲劳强度的措施( )A 增加螺栓刚度,减小被联接件的刚度B 减小螺栓刚度,增加被联接件的刚度C 同时增加螺栓和被联接件的刚度D 同时减小螺栓和被联接件的刚度18、随着被联接件刚度的增大,螺栓的疲劳强度( )A 提高B 降低C 不变D 可能提高也可能降低19、受轴向变载荷作用的紧螺栓联接,当增大螺栓直径时,螺栓的疲劳强度( )A 提高B 降低C 不变D 可能提高,也可能降低20、一普通螺栓的螺栓头标记着6。
材料力学常用基本公式

面积A,拉应力为正)d,拉伸后试样直径 d1)纵向线应变和横向线应变外力偶P 功率, n 转速)弯矩、剪力和荷载集度之间的关系式轴向拉压杆横截面上正应力的计算公式杆件横截面轴力F N,横截面1.2.3.4.5.6.7.8.9.10.11.12.泊松比胡克定律受多个力作用的杆件纵向变形计算公式轴向拉压杆斜截面上的正应力与切应力计算公式夹角a 从x 轴正方向逆时针转至外法线的方位角为正)纵向变形和横向变形(拉伸前试样标距l ,拉伸后试样标距 l1 ;拉伸前试样直径承受轴向分布力或变截面的杆件,纵向变形计算公式轴向拉压杆的强度计算公式许用应力,脆性材料延伸率截面收缩率剪切胡克定律拉压弹性模量,塑性材料切变模量G,切应变gE、泊松比和切变模量圆截面对圆心的极惯性矩( a)实心圆b)空心圆)G之间关系式圆轴扭转时横截面上任一点切应力计算公式圆截面周边各点处最大切应力计算公式扭转截面系数,( a)实心圆扭矩T,所求点到圆心距离r )13.14.15.16.17.18.19.20.21.22.23.24.薄壁圆管(壁厚 δ≤ R 0 /10 ,R 0 为圆管的平均半径)扭转切应力计算公式圆轴扭转角 与扭矩 T 、杆长 l 、 扭转刚度 GH p 的关系式 同一材料制成的圆轴各段内的扭矩不同或各段的直径不同(如阶梯轴)时等直圆轴强度条件受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式平面应力状态下斜截面应力的一般公式b )空心圆25.26. 27. 28. 29. 30.31.32.33.或 塑性材料或 扭转圆轴的刚度条件 ? ;脆性材料平面应力状态的三个主应力 主平面方位的计算公式 ,面内最大切应力 三向应力状态最大切应力 广义胡克定律 四种强度理论的相当应力34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之 和的关系式平行移轴公式(形心轴 z c 与平行轴 z 1的距离为 a ,图形面积为 A )纯弯曲梁的正应力计算公式45. 46.47.48.49. 50.51.52.53.54., 组合图形的形心坐标计算公式 截面图形对轴 z 和轴y 的惯性半径 ?矩形、圆形、空心圆形的弯曲截面系数几种常见截面的最大弯曲切应力计算公式( 轴 z 的静矩, b 为横截面在中性轴处的宽度)为中性轴一侧的横截面对中性横力弯曲最大正应力计算公式工字形截面梁腹板上的弯曲切应力近似公式轧制工字钢梁最大弯曲切应力计算公式 圆形截面梁最大弯曲切应力发生在中性轴处弯曲正应力强度条件弯曲梁危险点上既有正应力 σ 又有切应力 τ 作用时的强度条件 或,梁的挠曲线近似微分方程 轴向荷载与横向均布荷载联合作用时杆件截面底部边缘和顶部边缘处的正应力计弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式55.56.57.58.59. 60.61.62.63.64.65. 66.算公式偏心拉伸(压缩) 圆环形薄壁截面梁最大弯曲切应力发生在中性轴处 几种常见截面梁的弯曲切应力强度条件梁的转角方程梁的挠曲线方程圆截面杆横截面上有两个弯矩 和 同时作用时,合成弯矩为圆截面杆横截面上有两个弯矩和同时作用时强度计算公式弯拉扭或弯压扭组合作用时强度计算公式剪切实用计算的强度条件挤压实用计算的强度条件 等截面细长压杆在四种杆端约束情况下的临界力计算公式 压杆的约束条件:( a )两端铰支 μ =l( b )一端固定、一端自由 μ =2( c )一端固定、一端铰支d )两端固定 μ =0.567.68.69.70.71.72.73. 74. 75. 76. 77.μ=0.778.压杆的长细比或柔度计算公式79.细长压杆临界应力的欧拉公式80.欧拉公式的适用范围81.压杆稳定性计算的安全系数法82.压杆稳定性计算的折减系数法83. 关系需查表求得3截面的几何参数4应力和应变5应力状态分析6内力和内力图7强度计算刚度校核9 压杆稳定性校核10 动荷载11 能量法和简单超静定问题材料力学公式汇总、应力与强度条件1、拉压maxmax2、剪切max3、4、挤压挤压圆轴扭转P挤压A挤压TWtmax平面弯曲①maxM maxy t maxI z*③ Q max S z max②t max5、斜弯曲max M z M yW z W yW z maxtmaxt maxmax注意:“5”与“ 6”两式仅供参考 ②第四强度理论r4w 2 3 n 2M w 20.75M n 2r4 w 3 n WWz二、变形及刚度条件1拉压LNLNLN i L iN ( x) dxEA EA LEA2扭转TLT i L i T x dx T 180 0( /GI pGI pGI pL GI p3弯曲(1) 积分法 : EIy ''( x) M(x) E Iy '(x) EI (x) M(x)dx CEIy ( x) [ M (x)dx]dx Cx D(2)叠加法 : f P 1,P 2 ⋯= f P 1 f P 2 +⋯, P 1, P 2 = P 1 P 2 ⋯M 2L =M i 2L i =M 2xdx2EI 2EI i 2EI(5)卡氏第二定理 ( 注:只给出线性弹性弯曲梁的公式 ) 三、应力状态与强度理论 1、 二向应力状态斜截面应力2、 二向应力状态极值正应力及所在截面方位角 3、 二向应力状态的极值剪应力注:极值正应力所在截面与极值剪应力所在截面夹角为 4504、 三向应力状态的主应力: 1 2 36、拉(压)弯组合 maxNM7、圆轴弯扭组合:①第三强度理论M w 2 M n2Wz(3)基本变形表 ( 注意:以下各公式均指绝对值,使用时要根据具体情 况赋予正负号 )ML3EI, A MLA6EIBA PL 216EI qL3 24EI (4)弹性变形能 ( 注:以下只给出弯曲构件的变形能 响, 其他变形与此相似 ,不予写出 ) 并忽略剪力影 B最大剪应力 : max1 325、二向应力状态的广义胡克定律(1)、表达形式之一(用应力表示应变) (2)、表达形式之二(用应变表示应力) 6、三向应力状态的广义胡克定律 强度理论 1) r1 1 1 bnb2)r 3 1 3五、动载荷(只给出冲击问题的有关公式)能量方程TVU7、 sn s8、平面应力状态下的应变分析sin 2x y x y1)2 2xys i n222tg2 0 xyxy四、压杆稳定1、临界压力与临界应力公式(若把直杆分为三类) ① 细长受压杆 p ② 中长受压杆 p ③ 短粗受压杆s2EI minPcr 2PcrL2cr a b“ cr ”2Ecr22、关于柔度的几个公式 或 b2Epasb3、惯性半径公式 i I Az短边长度 ))圆截面 i d4,矩形截面 i min b12(b 为2cos 2xyc o 2s2冲击系数 K d 1 1 2hst (自由落体冲击)K dgv0st(水平冲击)六、截面几何性质1、 惯性矩(以下只给出公式,不注明截面的形状) 442 d D 4 d132 DI P 2dA =2、惯性矩平移轴公式32。
轴的设计计算校核

轴的设计、计算、校核以转轴为例,轴的强度计算的步骤为:一、轴的强度计算1、按扭转强度条件初步估算轴的直径机器的运动简图确定后,各轴传递的P和n为已知,在轴的结构具体化之前,只能计算出轴所传递的扭矩,而所受的弯矩是未知的;这时只能按扭矩初步估算轴的直径,作为轴受转矩作用段最细处的直径dmin,一般是轴端直径;根据扭转强度条件确定的最小直径为:mm式中:P为轴所传递的功率KWn为轴的转速r/minAo为计算系数,若计算的轴段有键槽,则会削弱轴的强度,此时应将计算所得的直径适当增大,若有一个键槽,将d min增大5%,若同一剖面有两个键槽,则增大10%;以dmin为基础,考虑轴上零件的装拆、定位、轴的加工、整体布局、作出轴的结构设计;在轴的结构具体化之后进行以下计算;2、按弯扭合成强度计算轴的直径l绘出轴的结构图2绘出轴的空间受力图3绘出轴的水平面的弯矩图4绘出轴的垂直面的弯矩图5绘出轴的合成弯矩图6绘出轴的扭矩图7绘出轴的计算弯矩图8按第三强度理论计算当量弯矩:式中:α为将扭矩折合为当量弯矩的折合系数,按扭切应力的循环特性取值:a扭切应力理论上为静应力时,取α=;b考虑到运转不均匀、振动、启动、停车等影响因素,假定为脉动循环应力,取α=;c对于经常正、反转的轴,把扭剪应力视为对称循环应力,取α=1因为在弯矩作用下,转轴产生的弯曲应力属于对称循环应力;9校核危险断面的当量弯曲应力计算应力:式中:W为抗扭截面摸量mm3,;为对称循环变应力时轴的许用弯曲应力,;如计算应力超出许用值,应增大轴危险断面的直径;如计算应力比许用值小很多,一般不改小轴的直径;因为轴的直径还受结构因素的影响;一般的转轴,强度计算到此为止;对于重要的转轴还应按疲劳强度进行精确校核;此外,对于瞬时过载很大或应力循环不对称性较为严重的轴,还应按峰尖载荷校核其静强度,以免产生过量的塑性变形;二、按疲劳强度精确校核按当量弯矩计算轴的强度中没有考虑轴的应力集中、轴径尺寸和表面品质等因素对轴的疲劳强度的影响,因此,对于重要的轴,还需要进行轴危险截面处的疲劳安全系数的精确计算,评定轴的安全裕度;即建立轴在危险截面的安全系数的校核条件;安全系数条件为:式中:为计算安全系数;、分别为受弯矩和扭矩作用时的安全系数;、为对称循环应力时材料试件的弯曲和扭转疲劳极限;、为弯曲和扭转时的有效应力集中系数,为弯曲和扭转时的表面质量系数;、为弯曲和扭转时的绝对尺寸系数;、为弯曲和扭转时平均应力折合应力幅的等效系数;、为弯曲和扭转的应力幅;、为弯曲和扭转平均应力;S为最小许用安全系数:~用于材料均匀,载荷与应力计算精确时;~用于材料不够均匀,载荷与应力计算精确度较低时;~用于材料均匀性及载荷与应力计算精确度很低时或轴径>200mm时;三、按静强度条件进行校核静强度校核的目的在于评定轴对塑性变形的抵抗能力;这对那些瞬时过载很大,或应力循环的不对称性较为严重的的轴是很有必要的;轴的静强度是根据轴上作用的最大瞬时载荷来校核的;静强度校核时的强度条件是:式中:——危险截面静强度的计算安全系数;——按屈服强度的设计安全系数;=~,用于高塑性材料≤制成的钢轴;=~,用于中等塑性材料=~制成的钢轴;=~2,用于低塑性材料制成的钢轴;=2~3,用于铸造轴;——只考虑安全弯曲时的安全系数;——只考虑安全扭转时的安全系数;式中:、——材料的抗弯和抗扭屈服极限,MPa ;其中=~;Mmax、Tmax——轴的危险截面上所受的最大弯矩和最大扭矩,;Famax——轴的危险截面上所受的最大轴向力,N;A——轴的危险截面的面积,m;W、W T——分别为危险截面的抗弯和抗扭截面系数,m;四、轴的设计用表表1 轴的常用材料及其主要力学性能材料牌号热处理毛坯直径mm硬度HBS抗拉强度极限σb屈服强度极限σs弯曲疲劳极限σ-1剪切疲劳极限τ-1许用弯曲应力σ-1备注Q235A 热轧或锻后空冷≤100400~42022517010540用于不重要及受载荷不大的轴>100~250375~39021545正火回火≤10170~21759029522514055应用最广泛>100~300162~217570285245135调质≤200217~2556403552751556040Cr 调质≤100>100~300241~28673568554049035535520018570用于载荷较大,而无很大冲击的重要轴40CrNi 调质≤100>100~300270~300240~27090078573557043037026021075用于很重要的轴38SiMnMo 调质≤100>100~300229~286217~26973568559054036534521019570用于重要的轴,性能近于40CrNi38CrMoAlA 调质≤60>60~100>100~160293~321277~302241~27793083578578568559044041037528027022075用于要求高耐磨性,高强度且热处理氮化变形很小的轴20Cr 渗碳淬火回火≤60渗碳56~62HRC64039030516060用于要求强度及韧性均较高的轴3Cr13调质≤100≥24183563539523075用于腐蚀条件下的轴1Cr18Ni9Ti 淬火≤100≤19253019519011545用于高低温及腐蚀条件下的轴180110100~200490QT600-3190~270600370215185用于制造复杂外形的轴QT800-2245~335800480290250表2 零件倒角C与圆角半径R的推荐值直径d>6~10>10~18>18~30>30~50>50~80>80~120>120~180 C或R表3 轴常用几种材料的和A0值轴的材料Q2351Cr18Ni9Ti354540Cr,35SiMn,2Cr13,20CrMnTi 12~2012~2520~3030~4040~52A0160~135148~125135~118118~107107~98表4 抗弯抗扭截面模量计算公式。
轴的失效形式和原因分析

轴的失效形式和原因分析轴的失效形式与特征轴是各种机械中最为普通⽽不可缺少的重要零件,根据使⽤条件的差异,轴有很⼤不同的类型,按其功能和所受载荷的不同,⼀般可分为⼼轴、转轴和传动轴三类。
⼼轴主要承受弯矩⽽不承受扭矩,它只能旋转零件起⽀撑作⽤,并不传递动⼒。
传动轴主要承受扭矩,其基本功能只传输动⼒,⽽转轴既承受弯矩⼜承受扭矩,它兼有⽀撑与传输动⼒的双倍功能。
由于各类轴⾃⾝的材质、结构和承载条件不同、运⾏环境和使⽤操作的差异可能发⽣各种不同类型的失效时有发⽣,失效的形式和特征也各异。
⼀.疲劳断裂疲劳断裂是指轴在交变应⼒的作⽤下,经过多次反复后发⽣的突然断裂。
是轴类零件在其服役过程中主要的失效形式。
轴在疲劳断裂前没有明显的塑性变形,反映在宏观形态上属于脆性断裂。
断⼝形貌有其本⾝的特征,在宏观形貌上可分为三个区域:图1 疲劳断裂⽰意图1)疲劳源区:通常是指断⼝上的放射源的中⼼点,源区表⾯细密光滑,多发⽣于轴的表⾯。
由于表⾯常存在缺⼝、⼑痕、沟槽等缺陷,导致应⼒集中,从⽽诱发疲劳裂纹。
疲劳断⼝上可能只有⼀个疲劳裂纹源,也可能出现⼏个裂源。
疲劳源区有时存在疲劳台阶,这是由于不同⾼度的多源疲劳裂纹在其扩展过程中连接形成的。
2)疲劳扩展区:是断⼝上最重要的特征区域,海滩花样(贝壳花样、疲劳弧线、疲劳条带)的存在是鉴别疲劳断裂的宏观依据。
有时必须借住⾼倍的电⼦显微镜才能观察到疲劳条带。
根据弧线数量和间距可以略微地判断零件所承受交变应⼒幅值,弧线规律分布表⽰交变载荷是平稳的。
承受应⼒状态、⼯作环境以及材料性质的不同,疲劳裂纹扩展的形貌所异。
每条疲劳条带表⽰载荷的⼀次循环,条带间距离与外加载荷的应⼒幅值有关。
当交变载荷变化不⼤、零件内的残余应⼒很⼩时,往往不出现弧线或不明显,所以不是所以疲劳断⼝有存在疲劳条带,低周疲劳断⼝有时可呈现韧窝状,有时也可出现轮胎花样(图2),所以疲劳条带并不是疲劳断裂的唯⼀显微特征。
⾼频疲劳断⼝或腐蚀疲劳断⼝上的疲劳条带⽐较模糊,较难判断。
大学材料力学习题及答案(题库)

一.是非题:(正确的在括号中打“√”、错误的打“×”)(60小题)1.材料力学研究的主要问题是微小弹性变形问题,因此在研究构件的平衡与运动时,可不计构件的变形。
( √ )2.构件的强度、刚度、稳定性与其所用材料的力学性质有关,而材料的力学性质又是通过试验测定的。
( √ )3.在载荷作用下,构件截面上某点处分布内力的集度,称为该点的应力。
(√ )4.在载荷作用下,构件所发生的形状和尺寸改变,均称为变形。
( √ )5.截面上某点处的总应力p可分解为垂直于该截面的正应力σ和与该截面相切的剪应力τ,它们的单位相同。
( √ )6.线应变ε和剪应变γ都是度量构件内一点处变形程度的两个基本量,它们都是无量纲的量。
( √ )7.材料力学性质是指材料在外力作用下在强度方面表现出来的性能。
( )8.在强度计算中,塑性材料的极限应力是指比例极限σ,而脆性材p料的极限应力是指强度极限σ。
( )b9.低碳钢在常温静载下拉伸,若应力不超过屈服极限σ,则正应力sσ与线应变ε成正比,称这一关系为拉伸(或压缩)的虎克定律。
( ) 10.当应力不超过比例极限时,直杆的轴向变形与其轴力、杆的原长成正比,而与横截面面积成反比。
( √ )11.铸铁试件压缩时破坏断面与轴线大致成450,这是由压应力引起的缘故。
( )12.低碳钢拉伸时,当进入屈服阶段时,试件表面上出现与轴线成45o的滑移线,这是由最大剪应力τ引起的,但拉断时截面仍为横截max面,这是由最大拉应力σ引起的。
( √ )max13.杆件在拉伸或压缩时,任意截面上的剪应力均为零。
( )14.EA 称为材料的截面抗拉(或抗压)刚度。
( √ )15.解决超静定问题的关键是建立补充方程,而要建立的补充方程就必须研究构件的变形几何关系,称这种关系为变形协调关系。
( √ )16.因截面的骤然改变而使最小横截面上的应力有局部陡增的现象,称为应力集中。
(√ )17.对于剪切变形,在工程计算中通常只计算剪应力,并假设剪应力在剪切面内是均匀分布的。
(9) 减速器轴的设计计算.doc

轴的设计1、轴的机构设计 (1) 轴的设计计算① 轴的直径的确定(Ⅰ轴) 按扭转强度条件计算: 3npA do ≥ 其中:首选45号钢进行设计,查表A O =120,P=10.56 ,n=486.7r/min 于是d 1≥33.47取d 1=34m②作用在齿轮上的力F t =112d T =31033.7723.2072⨯⨯=5.34⨯103N (其中:T 1为Ⅰ轴受到的转矩,d 1为齿轮1的直径)F r =F t βcos tan n a ⨯=2⨯103N (其中:αn 为齿轮的压力角,β为螺旋角)F a =F t ·tan β=1342N同理可求得Ⅱ轴、Ⅲ轴的直径和轴上齿轮的受力: Ⅱ轴 d 2≥42.4 mm 取d 2=45 mm 轴上齿轮的受力:F t =2700 N 、F r = 1023 N 、 F a =780 NⅢ轴 d 3≥63.7 mm 取d 3=65 mm 轴上齿轮的受力:F t =8340 N 、F r =3100 N 、 F a =1800 N (2) 校核轴上轴承的受力和轴承的寿命 Ⅰ轴1、求轴承受到的径向载荷F r1和F r2将轴系部件受到的空间力系分解为铅垂面和水平面的两个力系,如下图所示根据图示力的分析可知道:由图(b )得F r1v =5.1905.6625.661+⨯-⨯d Fa Fr =5.1905.6625.678145.661007.13+⨯-⨯⨯=170N F r2v =F r -F r1v =1070-170=900NF r1H =5.1905.665.66+F t =7.29⨯102F r2H =F r -F r1H =2820-729=2091F r1=2211Hr F F v r +=22900170+=748.6 NF r2=2222H r v r F F +=222091729+=2276.5 N 2 求两轴承的计算轴向力F a1和F a2对于70000AC 型轴承,按表13-7轴承的派生轴向力为F d =0.68⨯F r (5-8)F d1=0.68×F r1=0.68×748.6=509.6 N F d2=0.68×F r2=0.68×2276.5=1547.99 N 根据轴向力和轴承的安装方向分析可知,轴承2压紧:∴ F a1=F d1=509.6 NF a2=F a +F d1=1323 N3 求轴承的当量动载荷 11r a F F =6.7486.509=0.68=e(5-9)22r a F F =5.22761323=0.58<e 由表13-5分别进行查表或插值计算得径向载荷系数和轴向载荷系数为: 对与轴承1: X 1=1 ; Y 1=0 对轴承2: X 2=1 ; Y 2=0 因轴承运转中有轻微的冲击载荷,按照表13-6,f p =1.0~1.2则 P 1=f p(X 1F r1+Y 1F a1)=1.1×(1×748.6+0×2362)=823.46(5-10)P 2=f p (X 2F r2+Y 2F a22)=1.1×(1×2276.5+0)=2504.15 (5-11) 4 计算轴承的寿命L h =ε⎪⎪⎭⎫⎝⎛266010P C n =72060106⨯⨯315.250423500⎪⎭⎫ ⎝⎛=19131 h<28800 h(5-12)寿命不能满足工作要求,所以应选择中载系列,选用型号为7307AC,在次进行验证:L h ’=72060106⨯⨯398.259732800⎪⎭⎫ ⎝⎛=420839 h>28800 h(5-13)满足工作寿命的要求,所以轴承选用7307AC 系列。
机械设计习题1

一、填空题(11分,每空1分)1、由机械零件强度疲劳试验可知:________________、________________和________________只对应力幅有影响。
2、在套筒滚子链设计中,在满足承载能力要求的前题下,节距选得______,齿数选得___________,传动越平稳。
(越大;越小)3、带传动工作时的应力有__________________、__________________和________________。
4、在闭式齿轮传动中,软齿面齿轮常发生 ____________ 破坏,硬齿面齿轮常发生 ____________破坏,开式齿轮传动中,常发生____________ 破坏。
二、选择题(20分,每空2分)1、滚动轴承的基本额定寿命是指同一批轴承中______的轴承所能达到的寿命。
(A、99%;B、90%;C、98%;D、50%)2、在作轴的疲劳强度校核计算时,对于一般单向转动的转轴,其弯曲应力应按______ 计算。
(A、脉动循环变应力; B、静应力;C、非对称循环变应力;D、对称循环变应力)3、对蜗杆传动进行热平衡计算,其主要目的是为了防止温升过高导致______。
(A、材料的机械性能下降;B、润滑油变质;C、蜗杆热变形过大;D、润滑条件恶化而产生胶合失效)4、一对正确啮合的标准渐开线齿轮减速传动,z1=18,z2=72,两轮材料、热处理相同,工作时轮齿根部危险截面上的弯曲应力_______。
(A、 s F1 > s F2;B、 s F1< s F2; C、s F1 =s F2)5、两轮轴线不在同一水平面的链传动,链条的紧边应布置在上面,松边应布置在下面,这样可以使______。
(A、链条平稳工作,降低运行噪声B、松边下垂量增大后不致与链轮卡死;C、链条的磨损减小;D、链传动达到自动张紧的目的)6、各种型号的三角带,其截面的槽角均为40°.为使三角带的工作面能与轮槽保持良好接触,必须使带轮槽角 ______。
起重机钢结构总体设计时常用的载荷系数

起重机钢结构总体设计时常用的载荷系数————————————————————————————————作者:————————————————————————————————日期:ﻩ在进行起重机总体设计时,特别是钢结构设计时,考虑的载荷和工民建钢结构厂房设计考虑的载荷有很大不同,其特点就是起重机是动态使用的,在考虑载荷时,都要乘一个系数,现在我把整体设计时最常用的载荷系数简单得说一下,使对起重机钢结构设计不了解的人有一个初步的认识,同时,也请这方面的专家指出不足之处。
《规范》中可没有这么详细啊!ﻫ一、自重冲击系数ﻫ当货物突然起升离地、货物下降制动、起重机运行通过轨道接缝或运动机构起动、制动时,起重机的的自身重量将产生冲击和振动。
由于这种冲击和振动,起重机各部分质量会产生附加的加速度,虽然可用计算机计算这种加速度,但计算工作量较大,所以,实际计算时是将自重乘以一个冲击系数,以考虑这种附加动载的影响。
ﻫ按照《起重机设计规范》(GB3811-83),的规定,自重冲击系数分两种情况,一是货物离地或货物下降制动对自重的冲击,将起重机自重乘以起升冲击系数φ1,二是吊着货物的起重机运行通过轨道接缝,将起重机自重和起升载荷均乘以相同的运行冲击系数φ4,他们都是经验值。
ﻫ1、起升冲击系数φ1《规范》规定:0.9≤φ1≤1.1这个系数的应用分两种情况:当自重对要计算的元件起增大作用时,取φ1=1.0~1.1,否则取φ1=0.9~1.0。
ﻫﻫ2、运行冲击系数φ4《规范》规定,φ4用下式计算:ﻫφ4=1.10+0.058v√h(注:√h为h开更号)式中v-----起重机(或小车)的运行速度(m/s)h----轨道接缝处二轨道面的高度差(mm)ﻫ理论表明,当速度较大时(v≤2m/s),冲击系数并不随速度增大,只要控制h≤2mm,系数不会大于1.1。
二、起升载荷动载系数φ2ﻫ这是一个最重要的系数。
φ2一般取1≤φ2≤2ﻫ当起升质量突然离地上升或下降制动时起升质量将产生附加的加速度,由这个附加加速度引起的惯性力,将对机构和结构产生附加的动应力,我国《规范》规定,将起升载荷乘以系数φ2予以增大,φ2即为起升载荷动载系数。
(整理)机械设计思考题答案

2012机械设计思考题参考答案(此为自行整理的答案,仅供参考)第一篇1.机器的基本组成要素是什么?p1(课本,下同)答:机器的基本组成要素是机械零件。
2.机械零件分哪两大类?答:通用零件,专用零件。
3.什么叫部件?(摘自百度文库)为完成共同任务而结合起来的一组零件成为部件,是装配的单元,eg.滚动轴承、联轴器4.机器的基本组成部分是什么?p3答:原动机部分,传动部分,执行部分。
5.机械零件的主要失效形式有那些?p10-11答:整体断裂,过大的残余变形,零件的表面破坏,破坏正常工作条件引起的失效。
6.机械零件的设计准则是什麽?其中最基本的准则是什麽?p11-14答:机械零件的设计准则是设计时对零件进行计算所依据的准则;其中最基本的准则有强度准则,刚度准则,寿命准则,振动稳定性准则,可靠性准则。
(是强度准则,刚度准则,寿命准则,振动稳定性准则,可靠性准则;最基本的准则是强度准则)7.什麽叫静应力、变应力和稳定循环变应力?稳定循环变应力有那三种形式?静应力:应力幅等于零的应力(p24);大小和方向不随时间转移而产生变化或变化较缓慢的应力。
其作用下零件可能产生静断裂或过大的塑性变形,即应按静强度进行计算。
(百度文库)变应力:大小和方向均随时间转移而产生变化的应力。
它可以是由变载荷引起的,也可能因静载荷产生的(如电动机重量给梁带来的弯曲应力)。
变应力作用的零件主要发生疲劳失效。
(百度文库)稳定循环变应力:变应力的最大、最小应力始终不变。
(百度文库)(不稳定循环变应力:变应力的最大、最小应力呈周期性变化。
)稳定循环变应力:单向稳定变应力,单向不稳定变应力,双向稳定变应力三种形式。
8.什麽是疲劳极限?何为有限寿命疲劳极限阶段和无限寿命疲劳阶段?疲劳极限:在疲劳试验中,应力交变循环大至无限次而试样仍不破损时的最大应力。
(百度百科)有限寿命疲劳极限阶段:在σ-N曲线上,试件经过一定次数的交变应力作用后总会发生疲劳破坏的范围,即CD段;无限寿命疲劳阶段:在σ-N曲线上,作用的变应力的最大应力小于持久疲劳极限(即D点的应力),无论应力变化多少次,材料都不会破坏的范围,即D点以后的线段。
材料力学11动载荷_2冲击载荷

st
P
[例5] 如图,在转轴 AB 的B 端有一个质量很大的飞轮,在 A 端有 制动装置。若在飞轮转速 n = 100 r/min 时突然在 A 端急刹车,瞬 间停止转动,试求轴内的最大切应力。 已知轴的长度 l = 1 m,直 径 d = 100 mm ,切变模量 G = 80 GPa,飞轮对轴的转动惯量 J = 500 kg·m2 ,轴的质量可以忽略不计。
1.8 MPa
梁内的动荷最大弯曲正应力
d max Kd st max 71.7 1.8 MPa = 129.1 MPa
[例4] 如图,钢丝绳的下端悬挂一重为 P 的重物,以速度 v 匀速下 降,当钢丝绳长度为 l 时,滑轮突然被卡住,试求钢丝绳内的动荷 应力。已知钢丝绳的横截面面积为 A,弹性模量为 E,滑轮与钢丝 绳的质量均忽略不计 。
2)重物落在弹簧上 此时的静荷位移
st
Pl EA
ห้องสมุดไป่ตู้
P k
7.074 106
m + 500106
m
=
507.074 106
m
2)重物落在弹簧上
静荷位移
st 507.074106 m
动荷因数
2h
Kd 1
1 15.08
st
杆内的动荷应力
d Kdst 15.08 0.7074 MPa = 10.7 MPa
4
P
hP
l
d
4)计算动荷应力
d Kdst 126.2 0.0424 MPa = 5.35 MPa
◆ 此时的动荷应力是静荷应力的126.2倍,可见,冲击载荷是 非常大的。
[例2] 钢制圆截面杆如图,其上端固定,下端固连一无重刚性托盘 以承接落下的环形重物。已知杆的长度 l = 2 m ,直径 d = 30 mm , 弹性模量 E = 200 GPa。若环形重物的重力 P = 500 N,自相对高度 h = 50 mm 处自由落下,使杆受到冲击。试求在下列两种情况下, 杆内的动荷应力:(1)重物直接落在刚性托盘上;(2)托盘上放 一刚度系数量 k = 1 MN/m的弹簧,环形重物落在弹簧上。
【精选】滚动轴承的受力分析、载荷计算、失效和计算准则

1.滚动轴承的受力分析滚动轴承在工作中,在通过轴心线的轴向载荷(中心轴向载荷)Fa作用下,可认为各滚动体平均分担载荷,即各滚动体受力相等。
当轴承在纯径向载荷Fr作用下(图6),内圈沿Fr方向移动一距离δ0,上半圈滚动体不承载,下半圈各滚动体由于个接触点上的弹性变形量不同承受不同的载荷,处于Fr作用线最下位置的滚动体承载最大,其值近似为5Fr/Z(点接触轴承)或4.6Fr/Z(线接触轴承),Z为轴承滚动体总数,远离作用线的各滚动体承载逐渐减小。
对于内外圈相对转动的滚动轴承,滚动体的位置是不断变化的,因此,每个滚动体所受的径向载荷是变载荷。
2.滚动轴承的载荷计算(1)滚动轴承的径向载荷计算一般轴承径向载荷Fr作用中心O的位置为轴承宽度中点。
角接触轴承径向载荷作用中心O的位置应为各滚动体的载荷矢量与轴中心线的交点,如图7所示。
角接触球轴承、圆锥滚子轴承载荷中心与轴承外侧端面的距离a可由直接从手册查得。
接触角α及直径D,越大,载荷作用中心距轴承宽度中点越远。
为了简化计算,常假设载荷中心就在轴承宽度中点,但这对于跨距较小的轴,误差较大,不宜随便简化。
图8角接触轴承受径向载荷产生附加轴向力1)滚动轴承的轴向载荷计算当作用于轴系上的轴向工作合力为FA,则轴系中受FA作用的轴承的轴向载荷Fa=FA,不受FA作用的轴承的轴向载荷Fa=0。
但角接触轴承的轴向载荷不能这样计算。
角接触轴承受径向载荷Fr时,会产生附加轴向力FS。
图8所示轴承下半圈第i个球受径向力Fri。
由于轴承外圈接触点法线与轴承中心平面有接触角α,通过接触点法线对轴承内圈和轴的法向反力Fi将产生径向分力Fri;和轴向分力FSi。
各球的轴向分力之和即为轴承的附加轴向力FS。
按一半滚动体受力进行分析,有FS ≈ 1.25 Frtan α(1)计算各种角接触轴承附加轴向力的公式可查表5。
表中Fr为轴承的径向载荷;e为判断系数,查表6;Y 为圆锥滚子轴承的轴向动载荷系数,查表7。
2019力学竞赛材料力学辅导(冲击)

全国周培源大学生力学竞赛辅导材料力学
——冲击应力分析
•冲击应力分析
第三届力学竞赛题6
第四届力学竞赛题3
第五届力学竞赛题6
第七力学竞赛题4
注意在冲击过程中的能量转化
冲击物的能量(动能或势能)转化为被冲击物的变形能
第七届竞赛题4例题5-冲击
冲击称载荷作用下外伸梁
F
l a st h K d Δ++=211冲击动载荷系数:
m EI
l Fa EI Fa st 03146.03323=+=Δ静位移利用叠加法(逐段刚
化法)求:
2565.7211=Δ++=st h K d MPa W
a F K W M d d d 02.78**===σ将运动员视为弹性体,最大
动应力减少。
力学模型:
m
图示两根完全相同的悬臂梁,弯曲刚度为,在自由端两者有一间隙,今有一重物P 从高度落下,试求重物对梁的最大冲击力?假设:两梁变形均在弹性范围内,冲击物为刚体,被冲击梁质量不计,在冲击过程中,两梁共同运动。
EI Δ
h 练习题。
(完整)滚动轴承的寿命计算
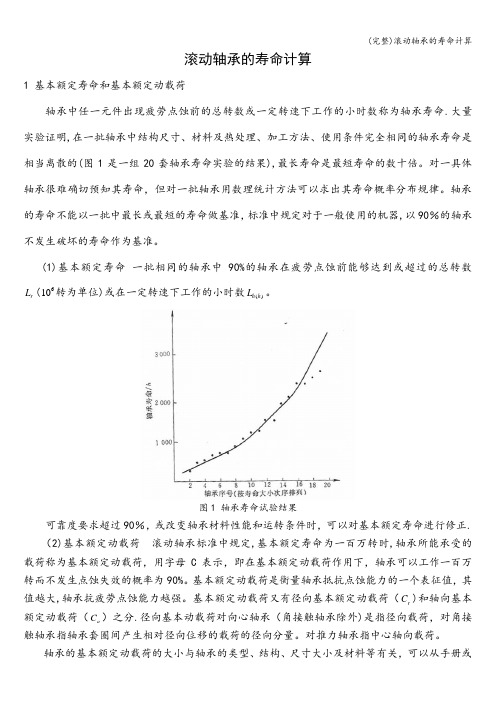
滚动轴承的寿命计算1 基本额定寿命和基本额定动载荷轴承中任一元件出现疲劳点蚀前的总转数或一定转速下工作的小时数称为轴承寿命.大量实验证明,在一批轴承中结构尺寸、材料及热处理、加工方法、使用条件完全相同的轴承寿命是相当离散的(图1是一组20套轴承寿命实验的结果),最长寿命是最短寿命的数十倍。
对一具体轴承很难确切预知其寿命,但对一批轴承用数理统计方法可以求出其寿命概率分布规律。
轴承的寿命不能以一批中最长或最短的寿命做基准,标准中规定对于一般使用的机器,以90%的轴承不发生破坏的寿命作为基准。
(1)基本额定寿命 一批相同的轴承中90%的轴承在疲劳点蚀前能够达到或超过的总转数r L (610转为单位)或在一定转速下工作的小时数()h h L 。
图1 轴承寿命试验结果可靠度要求超过90%,或改变轴承材料性能和运转条件时,可以对基本额定寿命进行修正.(2)基本额定动载荷 滚动轴承标准中规定,基本额定寿命为一百万转时,轴承所能承受的载荷称为基本额定动载荷,用字母C 表示,即在基本额定动载荷作用下,轴承可以工作一百万转而不发生点蚀失效的概率为90%。
基本额定动载荷是衡量轴承抵抗点蚀能力的一个表征值,其值越大,轴承抗疲劳点蚀能力越强。
基本额定动载荷又有径向基本额定动载荷(r C )和轴向基本额定动载荷(a C )之分.径向基本动载荷对向心轴承(角接触轴承除外)是指径向载荷,对角接触轴承指轴承套圈间产生相对径向位移的载荷的径向分量。
对推力轴承指中心轴向载荷。
轴承的基本额定动载荷的大小与轴承的类型、结构、尺寸大小及材料等有关,可以从手册或轴承产品样本中直接查出数值。
2 当量动载荷轴承的基本额定动载荷C (r C 和a C )是在一定条件下确定的。
对同时承受径向载荷和轴向载荷作用的轴承进行寿命计算时,需要把实际载荷折算为与基本额定动载荷条件相一致的一种假想载荷,此假想载荷称为当量动载荷,用字母P 表示。
当量动载荷P 的计算方法如下:同时承受径向载荷r F 和轴向载荷a F 的轴承()P r a P f XF YF =+(1)受纯径向载荷r F 的轴承(如N 、NA 类轴承)P r P f F =(2)受纯轴向载荷a F 的轴承(如5类、8类轴承)P a P f F =(3)式中:X ——径向动载荷系数,查表1; Y ——轴向动载荷系数,查表1; P f 冲击载荷系数,见表2。
南京工业大学材料力学材料力学冲击问题

2. 计算轴AB横截面上的最大切应力
任一横截面上的扭矩为:
TTd
MMdd
00..55ππ((kkNNmm)) 33
轴横截面上的最大扭转切应力为:
dmmaaxxWWTPdt
00..55ππ 110033NNmm 33
ππ 110000110033mm 33
22..6699110066PPaa 22..6699MMPPaa
总伸长。
解:⒈ 求杆内最大动应力
向心加速度为 an 2 x
到轴线距离为x处杆单位长度上的动载荷为
qd
(x)
A
g
2
x
因此,距轴线距离为x的截面上的轴力为
FNd
l
x qd (x)dx
l A 2 xdx A 2 (l 2 x2 )
xg
2g
FNd
A 2
2g
(l 2
x2)
相应的动应力为
d (x)
P
速度开始下降至0,同时弹簧变形达到最
h
P
大值 d 。
P
d
此时,全部(动)势能转化为应变能, 杆内动应力达最大值(以后要回跳)。就
以此时来计算:
•释放出的动能(以势能的降低来表示)
弹簧
T P(h d )
•增加的应变能,在弹性极限内
Ve
1 2
Pdd
根据力和变形之间的关系:Fd kd
F
Fd
Fd :冲击物速度为0时,作用于杆之力。
d Kd st
通常情况下,Kd 1 。
•关于动荷系数 K d 的讨论:
1.若冲击物是以一垂直速度v 作用于构件上,则由 v2 2gh
可得:
v2
Kd 1
工程力学动载荷

y
x
A
B
工程力学动载荷
例:重为P的重物从h处自由落下,冲击梁上的D点. 梁的EI及W均为已知.求:梁内max及梁中点处的挠度
h
A
CD B
P
A
CD B
yD=Pbx(l2-x2-b2)/6lEI
A
CD B
工程力学动载荷
h
A
CD B
P
A
CD B
1
A
B
工程力学动载荷
例 已知:重为G的重物以水平速度v冲击到圆形截面AB 梁的C点,EI已知. 求:σd max
解:水平冲击问题 ※确定动荷系数
静载时σmax出现于固定端A处
工程力学动载荷
图示钢杆的下端有一固定圆盘,盘上放置弹簧.弹簧在1kN 的静载荷作用下缩短0.0625cm.钢杆的直径d=4cm,l=4m许 用应力 =120Mpa,E=200GPa.若重为15kN的重物自由落下, 求其许可高度H.又若没有弹簧,许可高度H将等于多大?
注意:上面的论述是对等截面杆而言的,不能用于变截面杆的 情况。
工程力学动载荷
三、变截面杆同等截面杆的比较:
如图所示:一变截面杆,一等截面杆,同样受到重量 为Q,速度为v的重物的冲击,试比较它们的动应力。
根据机械能守恒定律,可求得两杆的冲击载荷分别为:
工程力学动载荷
于是两杆的冲击应力分别为: (a)
上升。若只考虑工字钢的重量而不计吊索自重,试求吊索的
动应力,以及工字钢在危险点的动应力d,max 欲使工字钢中的 d,max 减至最小,吊索位置应如何安置?
2m 4m 4m 2m
ACB a
(a)
z y
冲击应力和变形的计算

解:飞轮的惯性力矩为
M d I 0
d
A
n
(1)
在掣动时,若为匀减速旋转,则,
2n n t 60t 30t 代入式(1),得
(a)Байду номын сангаас
n a
πn M d I0 ( ) (2) 30t 沿与 相反的转向,将 Md
作用于轴上 (图b),得到一个 假想的平衡力偶系。可得轴横截 面上的扭矩 Td 为
材料力学
§12-2 构件作匀加速直线运动或 匀速转动时的应力计算
一、起重机匀加速吊杆问题(或:杆件匀加速运动问题)
a L m X n
材料力学
原始数据:杆件的长度:L 横截面面积:A 材料的比重: 加 速 度 :a
解:采用动静法(理论力学中的达朗伯原理) 1.受力分析:如图所示,在距下端为x的 横截面mn处将杆件分成两部分,并研究截 面以下的部分。 作用其上的重力集度为:
材料力学
二、圆环在匀角速旋转时的动应力计算问题(动静法)
w
t
D
qd
d
Nd
Nd
原始数据:环的平均直径D ;环的匀角速度w ;环的比重 环的厚度t ;环的横截面积A
材料力学
1.受力分析:沿圆环直径将它分成两部分,研究其上 半部分;由已知条件可知, 环内各点的向心加速度 :
2 D an r 2 2
材料力学
略去负值,得:
2h d j 1 1 j
(g)
令:
d 2h Kd 1 1 j j
——冲击动荷系数
d Kd j
代入(f)、(g)式得
讨论:
Pd K d Q
动载荷计算

动载荷计算第14章动载荷14.1 动载荷的概念及分类在以前各章中,我们主要研究了杆件在静载荷作用下的强度、刚度和稳定性的计算问题。
所谓静载荷就是指加载过程缓慢,认为载荷从零开始平缓地增加,以致在加载过程中,杆件各点的加速度很小,可以忽略不计,并且载荷加到最终值后不再随时间而改变。
在工程实际中,有些高速旋转的部件或加速提升的构件等,其质点的加速度是明显的。
如涡轮机的长叶片,由于旋转时的惯性力所引起的拉应力可以达到相当大的数值;高速旋转的砂轮,由于离心惯性力的作用而有可能炸裂;又如锻压汽锤的锤杆、紧急制动的转轴等构件,在非常短暂的时间内速度发生急剧的变化等等。
这些部属于动载荷研究的实际工作问题。
实验结果表明,只要应力不超过比例极限,虎克定律仍适用于动载荷下应力、应变的计算,弹性模量也与静载下的数值相同。
动载荷可依其作用方式的不同,分为以下三类:1(构件作加速运动。
这时构件的各个质点将受到与其加速度有关的惯性力作用,故此类问题习惯上又称为惯性力问题。
2(载荷以一定的速度施加于构件上,或者构件的运动突然受阻,这类问题称为冲击问题。
3(构件受到的载荷或由载荷引起的应力的大小或方向,是随着时间而呈周期性变化的,这类问题称为交变应力问题。
实践表明:构件受到前两类动载荷作用时,材料的抗力与静载时的表现并无明显的差异,只是动载荷的作用效果一般都比静载荷大。
因而,只要能够找出这两种作用效果之间的关系,即可将动载荷问题转化为静载荷问问题处理。
而当构件受到第三类动载荷作用时,材料的表现则与静载荷下截然不同,故将在第15章中进行专门研究。
下面,就依次讨论构件受前两类动载荷作用时的强度计算问题。
14.2 构件作加速运动时的应力计算本节只讨论构件内各质点的加速度为常数的情形,即匀加速运动构件的应力计算。
14.2.1 构件作匀加速直线运动设吊车以匀加速度a吊起一根匀质等直杆,如图14-1(a)所示。
杆件长度为l,横截面面积为A,杆件单位体积的重量为,,现在来分析杆内的应力。
起重机械的计算载荷与计算方法

数和许用应力及机构传动零件的强度安全系数见下页表中。
感谢下 载
⑤下弦杆为方形钢管、腹杆为圆管的三角形截面空间桁架, 在侧向风力作用下,其风力系数可取1.3。
⑥当风与结构长轴(或表面)成某一角度吹来时,结构所 受的风力可按其夹角分解成两个方向的分力来计算。 ★ 迎风面积A
指受风部位在垂直风向平面上的投影面积。
结构受风面积还应考虑充实率 , 见表中所示。
5、其它载荷 (1)冰雪、地震载荷一般不考虑。若有特殊要求,则进行 专门计算。 (2)安装及运输载荷在设计计算时视实际情况考虑。 (3)坡度载荷:流动起重机需要时,按具体情况考虑;轨 道起重机若轨道是永久性的,且坡度不超过0.5%,可不考虑, 否则按实际坡度计算;临时性轨道,按其安装误差计算。 (4)碰撞载荷:
q ——计算风压
A ——起重机或悬吊物品垂直于风向的迎风面积 ★ 计算风压 q
风压按空旷地区离地10 m 高度处的计算风速确定: q 0.613v2
v ——风速(m / s ),工作状态按瞬时风速考虑;非
工作状态按两分钟时距平均风速考虑。
计算风压分三种,qI ——起重机正常工作状态下计算风
压,用于选择电动机功率及发热验算;qII ——工作状态最大
1、起升载荷 PQ
是由起升机构吊起的货物和取物装置及其它随同升降的 装置重量吊钩起重机, =PQ(Q+ Q)0 ·g, —Q—0 吊钩重量
2、自重载荷 PG
包括机械部分、金属结构及电气设备和其它装置的总重 量。自重在设计前是未知的。
自重载荷的作用形式: 机械及电气设备的自重,一般看作是集中载荷; 桁架结构的自重,视作分布在相应节点上; 箱形板梁结构,视为连续分布。 3、动载荷 是由运动速度改变引起的质量力,即惯性力,包括惯性 载荷、振动载荷和冲击载荷。
