支撑刚度
钢管支撑刚度及稳定性计算

件段范围的最大弯矩M x 的计算 备注
考虑5kN施工荷载
M1
1.35*
gAl 2 8
1 4
*5l
取 1 偏心弯矩与0.02m的较大值
1000
M 2 Ne0 M x M1 M2
备注
Wx
2I D
N Ex
2 EA 1 .1 x 2
式中 An A, Wnx Wn
N Mx f
A 4
I ix A
x
l ix
n
x
fy E
Hale Waihona Puke 按b类截面计算:当λn ≤0.215时:
x 1 0.65n 2
当λn >0.215时:
x
1 2n 2
(0.965
0.3n
n 2
)
(0.965 0.3n n2 )2
4n 2
0.810
计算参数
所计算构件段范围的最大弯矩M x 的计算 计算数值
自重及施工荷载产生的最大弯
176.31
矩M 1(kN.m)
附加偏心距e 0(m)
附加弯矩M 2(kN.m) 所计算构件段范围的最大弯矩 M x (kN.m) 等效弯矩系数βmx
0.0200
119.44 295.75
1.00
M 2 Ne0 M x M1 M2
)
205
稳定性验算
通过
钢管计算长度 l (m) 16.47
钢管密度 ρ(kg/m3)
7850
钢管弹性模量 钢管抗拉强度设计值
E(N/mm2)
f (N/mm2)
钢管支撑刚度及稳定性计算

稳定性验算
通过
钢管计算长度 l (m) ϕ 16.47
钢管密度 ρ(kg/m ) 7850
3
钢管弹性模量 钢管抗拉强度设计值 E(N/mm2) 206000 f (N/mm2) 215
内的轴心受压构件稳定系数
x 的计算
I
A
D2 (D 2t)2
4
I A
D 4 ( D 2t ) 4 ) 64
计算数值
在弯矩作用平面内对较大受压 纤维的毛截面模量W x (m3) 截面塑性发展系数23044.6
M x N An x W nx
强度验算
165 通过
N
xA
mx M
x
x W 1 x (1 0 . 8
N ) ` N Ex
205
件段范围的最大弯矩M x 的计算 备注 考虑5kN施工荷载
M1 1.35*
gA
1 l 2 * 5l 8 4
取 1 偏心弯矩与0.02m的较大值
1000
M 2 Ne0 M x M1 M 2
备注
Wx
2I D
N Ex
2 EA 2 1 . 1 x
式中 An A, Wnx Wn
备注
ix
x
l ix
n
x
fy E
按b类截面计算: 当λn ≤0.215时:
x 1 0.65n 2
当λn >0.215时:
2 1 (0.965 0.3n n ) x 2 2n (0.965 0.3n n 2 ) 2 4n 2
基本参数 钢管直径 D(m) 0.8 钢管壁厚 t(m) 0.018 ϕ
支撑刚度及承载能力计算

mm
g=
7.85E+03
kg/m^3
E=
2.06E+05
N/mm^2
DN=
577
mm
A= [(D/2)^2-(D/2-t)^2]*3.142
=
29811.296
mm^2
I= (D^4-DN^4)*3.142/64
=
1.31E+09
mm^4
W= 0.0982*[(D^4-(DN)^4]/D
=
4.31E+06
N
=
7.30E+06
考虑受弯作 用稳定性
σ2=
βmx×Mx/〔γx×W1x(1-0.8× N/NEX)〕
=
48.3
Mpa
(考虑钢 稳定计算 支撑自重
影响)
σ=
σ1+σ2
f=
215
NEX
钢支撑承载力计算
压弯构件的整体稳定性 数据代名
钢支撑直径 钢支撑壁厚 钢构件自重 钢弹性模量 钢支撑内空
直径 支撑面积
转动惯量I
截面抵抗矩
塑性发展系 数 等效弯矩系 数 钢支撑单位
长度重量
钢管的截面类型
钢支撑长度 钢支撑轴力 钢管自重及 初偏心引起 跨中最大弯 矩
求λ
查表C-1
D=
609
mm
t=
16
=
210
mm
λ= =
sqrt(215/235)*L0*1000/i 87
φ=
0.641
DD TT GG EE DN AA II
WW GAMA BETA
GA GAA
LL NN
MZ
IK LAM FAI
支撑刚度计算
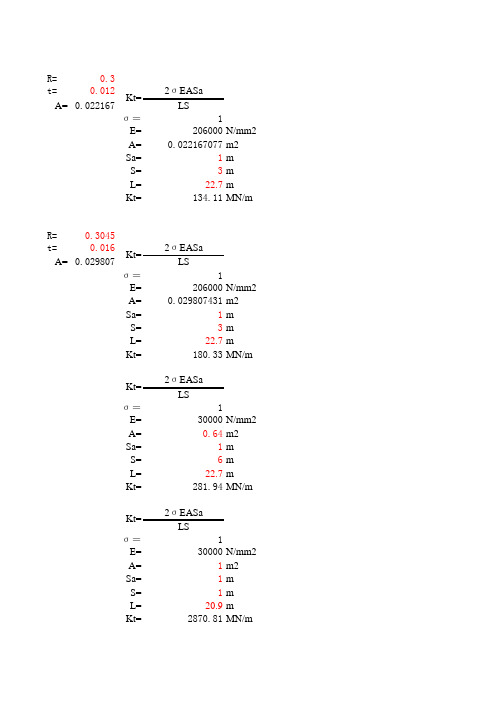
R=0.3t=0.0122σEASa A=0.022167LS σ=1E=206000N/mm2A=0.022167077m2Sa=1m S=3m L=22.7m Kt=134.11MN/mR=0.3045t=0.0162σEASa A=0.029807LS σ=1E=206000N/mm2A=0.029807431m2Sa=1m S=3m L=22.7m Kt=180.33MN/m2σEASa LS σ=1E=30000N/mm2A=0.64m2Sa=1m S=6m L=22.7m Kt=281.94MN/m 2σEASa LS σ=1E=30000N/mm2A=1m2Sa=1m S=1m L=20.9m Kt=2870.81MN/m Kt=Kt=Kt=Kt=钢支撑与支撑松弛有关的系数,取0.8~1.0支撑构件材料的弹性模量(N/mm2)支撑构件断面面积(m2)计算宽度(排桩水平荷载计算宽度取桩的中心距;地下连续墙取单位宽度。
)支撑的水平间距(m)支撑构件的受压计算长度支撑结构水平刚度系数钢支撑与支撑松弛有关的系数,取0.8~1.0支撑构件材料的弹性模量(N/mm2)支撑构件断面面积(m2)计算宽度(排桩水平荷载计算宽度取桩的中心距;地下连续墙取单位宽度。
)支撑的水平间距(m)支撑构件的受压计算长度支撑结构水平刚度系数混凝土支撑与支撑松弛有关的系数,取0.8~1.0支撑构件材料的弹性模量(N/mm2)支撑构件断面面积(m2)计算宽度(排桩水平荷载计算宽度取桩的中心距;地下连续墙取单位宽度。
)支撑的水平间距(m)支撑构件的受压计算长度支撑结构水平刚度系数混凝土支撑与支撑松弛有关的系数,取0.8~1.0支撑构件材料的弹性模量(N/mm2)支撑构件断面面积(m2)计算宽度(排桩水平荷载计算宽度取桩的中心距;地下连续墙取单位宽度。
)支撑的水平间距(m)支撑构件的受压计算长度支撑结构水平刚度系数理正软件、同济启明星、勘察软件联系QQ603481026。
钢支撑刚度

钢支撑承载力计算
D=
609
mm
t=
16
mm
g=
7.85E+03
kg/m^3
钢弹性模量
E=
2.06E+05
N/mm^2
钢支撑内空 直径
DN=
577
mm
支撑面积 转动惯量I
A= [(D/2)^2-(D/2-t)^2]*3.142
=
29811.296
mm^2
I= (D^4-DN^4)*3.142/64
=
29811.296
mm^2
KT
2a Ez LS
Az
(
1
1 a Ez Az x4
) sin
12 L S E j I j
式中,a 与支撑松弛有关的系数,取0.5~1.0;
1
Ez 支撑构 件的弹性模 量;
C30-30000/stell-206000
Az 支撑构件断面积; L 支撑的长度; S 支撑的水平间距;
BETA
GA GAA
LL NN
MZ
IK LAM
FAI
f=
215
NEX
f=
215
钢支撑直径 钢支撑壁厚 钢构件容重
D=
609
mm
t=
16
mm
g=
7.85E+03
kg/m^3
钢弹性模量
E=
2.06E+05
N/mm^2
钢支撑内空 直径
DN=
577
mm
支撑面积 支撑刚度计算
A= [(D/2)^2-(D/2-t)^2]*3.142
2.10E+05 N/mm^2
支撑体系支锚刚度及材料抗力计算

钢管支撑支锚刚度计算
钢管内撑材料抗力计算
矩形混凝土支撑支锚刚度计算
矩形混凝土内撑材料抗力计算
钢管截
矩形混凝土
钢管截面特性
混凝土截面特性
Kt=[(2×α×E×A)/L]×(Sa/S)
Kt:支撑结构水平刚度系数
α:与支撑松弛有关的系数,取0.8~1.0
E:支撑构件材料的弹性模量
A:支撑构件断面面积
L:支撑构件的受压计算长度
S:支撑水平间距
Sa:规程第4.2.1条确定的计算宽度(排桩水平荷载可取其中心距)
在不考虑塑性设计前提下,柱的λ限值为150,如考虑塑性设计,柱的λ限值为130*sqrt(235/fy)
T=φ×ζ×A×fy
T:支撑结构材料抗力
φ:轴心受压构件稳定系数
ξ:与工程有关的调整系数,取1.0
fy:钢材抗压强度设计值
λ=L/√(I/A)=l/i
hd+2r(b-d)+0.8584(r2-r12)L*7.85*1/1000
t1(H-2t2)+2Bt2+0.858r
圆形断面:A=Πd2/4(1-α)2
b2(3h-b)/6
Ix=ab3/12方管钢材Ix=(BH3-bh3)/12
圆管钢材Ix=[π(D4-d4)]/64
qrt(235/fy)。
刚度的计算公式

刚度的计算公式
在机械设计过程中,刚度的计算公式是一个重要的工具。
它可以帮助工程师正确计算材料刚度和构件位移、变形等参数。
在此,本文将阐述刚度计算的常见方法和公式。
一、刚度的概念
刚度是指一个物体受力时结构的阻力,它是一个测量材料强度和形状的比值(一般单位是MPa/mm),这个比值越大,材料耐受力越大,可以承受更大的应力,形状也更加稳定。
二、刚度计算公式
(1)有偏力的情况下:
刚度=支撑力/位移
其中,位移是指支撑力的作用下物体的距离变化量,支撑力是指根据正常荷载或指定力介质施加的所有外力。
(2)无偏力的情况下:
刚度=应力/应变
其中,应力是指物体在正常荷载或指定力介质作用下受到的外力,应变是指按照特定外力情况下物体形变量。
三、刚度计算实例
假设一个圆形截面受到一个偏载,半径为20mm,偏载作用时,
物体位移为8mm,刚度计算公式为:
刚度=支撑力/位移=0.25MPa/mm
四、刚度计算的实际应用
刚度的计算是机械设计过程中一个重要的环节。
它可以帮助设计人员准确地估算机构的可靠性、精度及构件的位移变形,以及它们抗载荷的能力。
此外,它还可以帮助设计人员准确地估算材料的强度和形状,以便采用最合适的材料来构建机构。
另外,刚度计算也可用于估算滑动系统动态性能,以及振动、噪音等。
以上就是有关刚度计算公式的详细介绍。
总之,在机械设计中,刚度计算公式是一种重要的手段,可以用于确定材料和机构的力学性能,以及估算滑动系统的动态性能和振动噪音。
支撑刚度计算(理正)
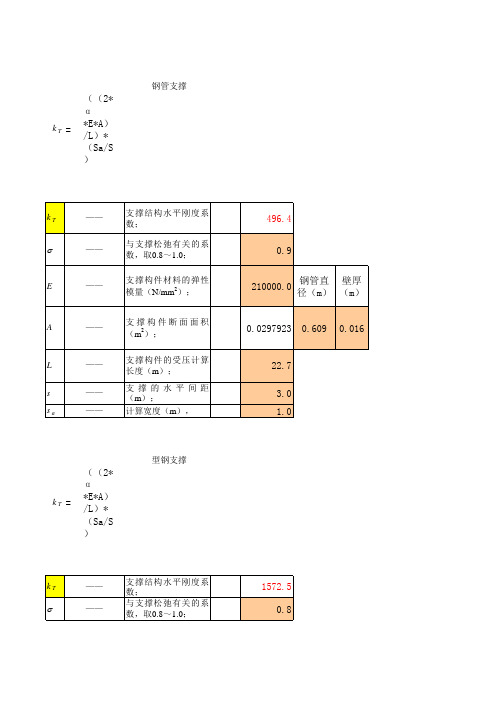
((2*α *E*A)/L)*(Sa/S)
kT
——
支撑结构水平刚度系 数; 与支撑松弛有关的系 数,取0.8~1.0; 支撑构件材料的弹性 2 模量(N/mm ); 支撑构件断面面积 (m2); 支撑构件的受压计算 长度(m); 支 撑 的 水 平 间 距 (m); 计算宽度(m),
支撑结构水平刚度系 数; 与支撑松弛有关的系 数,取0.8~1.0; 支撑构件材料的弹性 2 模量(N/mm ); 支撑构件断面面积 2 (m ); 支撑构件的受压计算 长度(m); 支 撑 的 水 平 间 距 (m); 计算宽度(m),
1572.5 0.8 210000.0 0.0234 5.0 4.0 1.0 5.704
kT =
混凝土支撑 ((2*α *E*A)/L)*(Sa/S)
kT
——
支撑结构水平刚度系 数; 与支撑松弛有关的系 数,取0.8~1.0; 支撑构件材料的弹性 2 模量(N/mm ); 支撑构件断面面积 (m2); 支撑构件的受压计算 长度(m); 支 撑 的 水 平 间 距 (m); 计算宽度(m),
1570.9 0.9 支撑宽 (m)
s
——
E
——
30000.0
A
——
0.64
0.8
L s sa
—— —— ——
22.0 6.0 6.0
支撑高 (m)
0.8
496.4 0.9 钢管直 壁厚 径(m) (m)
s
——
E
——
210000.0
A
——
0.0297923
0.609
0.016
L .0
型钢支撑 kT =
((2*α *E*A)/L)*(Sa/S)
厂房纵向支撑体系的设计强度和刚度要求

bL )
b L
.
( 10)
图 3 有初始缺陷体系 F ig . 3 M odel w ith initial imper fectio ns
第 i 根系杆的压力记为 Fi ( i = 1, 2, …, n- 1) , 初始倾斜值 0= L / 500 n [ 3] . 因为柱子数量越 多, 不同柱子初始缺陷方向可能不同, 产生的不利影
厂房纵向承载力通常由纵向支撑体系提供, 厂 房柱平面外稳定性也是由侧向支撑来保证. 对支撑 体系本身的设计, 通常由纵向受力决定, 很少从保证 稳定性的角度对支撑强度和刚度提出设计要求. 本 文考虑实际工程中的初始缺陷, 研究为保证框架柱 列纵向稳定性而对支撑体系提出的设计强度和刚度 要求.
1 单根柱子的情况
5
12. 344
6
17. 207
7
22. 881
8
29. 365
9
36. 660
10
44. 766
从式( 9) 推得 k 1. 0 2. 8 5. 4 8. 8 13. 0 18. 0 23. 8 30. 4 37. 8 46. 0
将式( 9) 代入式( 10) 得到用强度要求形式表达的对
系杆的刚度要求:
不同柱子初始缺陷方向可能不同产生的不利影618的关系必须利用并从下式得到响可能相互抵销所以引入统计折减系数根柱的平衡方程为d7对系杆的承载力要求其中已经包含刚度要求15表示了系杆内力和系杆两端相互缩短的关系曲线这条曲线的斜14c考虑系杆初弯可以看出支撑的轴压线刚度与理想压杆相比有所b500代入得到折减系数为15可以得到系杆的承载力相对于柱子轴压力的比因为图中每一根刚性系杆的内力不同所以每根系杆的线刚度折减系数也不同式16a16b表示一个平衡状态这个平衡状态是否稳定可以通过施加一个微量干扰来判定于干扰而引起的量用3标记式14ab500可以得到500000500000利用式14a同理由式14b变化得到16b从以上两式利用曲线曲线有一个极值点如果在式16a16b中取柱子和系杆的初始缺陷为零得到一个特征值问题结果为式14a14c表示的临界荷载与支撑刚度的关系如果柱子有初始倾16a16b得到的是系杆内力与柱荷载的关系当受力最大系杆的内力达到其本身的欧拉荷载时结构达到极限承载力状态如果柱子和系杆都有初始缺陷给定由于增量微小内力增量与变形增量为切线刚度关式15变为21利用式192021可以得到如下结构体系处于临界状态的条件方程
支撑刚度及强度计算
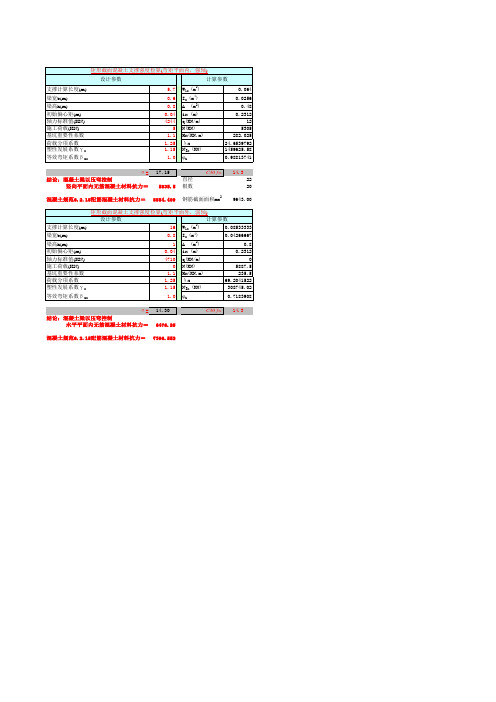
Ix (m4) A (m2) ix (m) q(KN/m) N(KN) Mx(KN.m) λ x N'Ex (KN) φx C30 f=
0.04266667 0.8 0.2312 0 5887.5 235.5 69.2041522 308745.02 0.7183908 14.3
σ = 14.30 结论:混凝土梁以压弯控制 水平平面内无筋混凝土材料抗力= 6476.25 混凝土规范6.2.15配筋混凝土材料抗力= 7396.552
2
0.064 0.0256 0.48 0.2312 12 5305 282.025 24.6539792 1459625.58 0.98813741 14.3 22 20 9643.00
σ = 17.15 结论:混凝土梁以压弯控制 竖向平面内无筋混凝土材料抗力= 5835.5 混凝土规范6.2.15配筋混凝土材料抗力= 8554.409
矩形截面混凝土支撑强度检算(弯矩平面内,强轴) 设计参数 支撑计算长度(m) 梁宽b(m) 梁高h(m) 初始偏心矩(m) 轴力标准值(KN) 施工荷载(KN) 基坑重要性系数 荷载分项系数 塑性发展系数γ x 等效弯矩系数β
mx
计算参数 5.7 0.6 0.8 0.04 4244 5 1.1 1m ) ix (m) q(KN/m) N(KN) Mx(KN.m) λ x N'Ex (KN) φx C30 f= 直径 根数 钢筋截面面积mm2
矩形截面混凝土支撑强度检算(弯矩平面外,弱轴) 设计参数 计算参数 3 支撑计算长度(m) 16 W1x (m ) 0.08533333 梁宽b(m) 梁高h(m) 初始偏心矩(m) 轴力标准值(KN) 施工荷载(KN) 基坑重要性系数 荷载分项系数 塑性发展系数γ x 等效弯矩系数β
支撑刚度对模态的影响

支撑刚度对模态的影响
支撑刚度是指杆件、构件等结构物件与支座之间的连接部位强度和刚度,它是影响结构体系抗震性能的重要因素之一。
支撑刚度对结构模态的影响主要表现在以下几个方面:
1. 支撑刚度的增加会增加结构的初始刚度,使得结构的固有频率升高。
这对于一些需要避免共振的结构体系尤为重要,比如高层建筑、桥梁等。
2. 在地震作用下,支撑刚度的增加会使结构的刚性增加,从而减小结构的变形,从而降低结构的振动幅值和加速度响应。
3. 支撑刚度的变化还会影响结构的阻尼比,从而影响结构的耗能性能。
在地震作用下,结构的耗能能力可以减轻地震的破坏。
综上所述,支撑刚度对结构模态有着重要的影响,因此在结构设计和抗震评估中,需要对支撑刚度进行合理的考虑和设置。
- 1 -。
圆形支撑刚度计算方法

圆形支撑刚度计算方法
圆形支撑的刚度可以通过多种方法进行计算。
其中一种常用的
方法是使用弹性力学的理论来计算圆形支撑的刚度。
在这种方法中,可以使用以下公式来计算圆形支撑的刚度:
K = (E A) / L.
其中,K代表支撑的刚度,E代表弹性模量,A代表支撑的横截
面积,L代表支撑的长度。
这个公式适用于简单的圆形支撑,比如
弹簧或者柱状支撑。
另一种常用的方法是有限元分析。
有限元分析是一种工程计算
方法,通过将结构分割成许多小的有限元素,然后对每个元素进行
力学分析,最后将它们组合起来得到整个结构的行为。
通过有限元
分析可以更精确地计算圆形支撑的刚度,考虑到了材料的非线性和
几何形状的复杂性。
除了这两种方法,还有其他一些方法可以用来计算圆形支撑的
刚度,比如试验测定法、理论推导法等。
不同的方法适用于不同的
情况,选择合适的方法需要考虑到支撑的具体形状、材料特性、工
程要求等因素。
总的来说,计算圆形支撑的刚度需要考虑到多个因素,包括支撑的形状、材料特性、工程要求等,可以根据具体情况选择合适的计算方法来进行计算。
上弦横向水平支撑布置原则

上弦横向水平支撑布置原则横向水平支撑是结构工程中常见的一种构造方法,用于增加结构的稳定性和刚度。
上弦横向水平支撑是一种特殊的支撑方式,它被广泛应用于大跨度建筑的结构设计中。
本文将详细介绍上弦横向水平支撑布置的原则和注意事项。
上弦横向水平支撑是指将水平支撑安装在主梁的上弦部分。
它主要通过与主梁上弦部分的紧密连接,增加主梁的抗弯刚度,改善结构的整体性能。
下面是上弦横向水平支撑布置的原则:1. 布置密度合理:上弦横向水平支撑的布置密度应根据主梁的跨度、结构的承载能力和设计要求来确定。
一般来说,支撑的间距不宜过大,以保证结构的稳定性和刚度。
同时,也不宜过密,以充分利用支撑的作用,避免资源的浪费。
2. 支撑位置合适:上弦横向水平支撑的位置应在主梁上弦部分的节点处或中跨段。
节点处是主梁的关键位置,是结构力学性能最好的部位,因此在节点处设置支撑可以有效提高结构的刚度和稳定性。
中跨段也是主梁的薄弱位置,需要增加支撑来改善结构的整体性能。
3. 连接可靠性:上弦横向水平支撑与主梁的连接应牢固可靠,确保支撑能够有效地传递荷载和力矩。
连接方式可以采用焊接、螺栓连接或预埋连接等,具体要根据结构的特点和设计要求来确定。
无论采用何种连接方式,都需要进行充分的强度计算和结构分析,确保连接的可靠性和安全性。
4. 支撑刚度匹配:上弦横向水平支撑的刚度应与主梁的刚度匹配。
支撑的刚度过大或过小都会对结构的性能产生不利影响。
刚度过大会导致主梁的变形受限,增加结构的应力和变形,从而影响结构的承载能力和稳定性。
刚度过小则无法起到支撑的作用,无法有效改善结构的刚度和稳定性。
因此,在设计上要进行充分的刚度计算和分析,确保支撑的刚度与主梁的刚度相匹配。
5. 维护便捷性:上弦横向水平支撑的设计应考虑到后期的维护和检修工作。
支撑的位置和布置要便于检查和维护,避免不必要的麻烦和成本。
同时,在支撑的设计上也要考虑到材料的耐久性和防腐蚀性能,确保支撑的使用寿命和稳定性。
支撑刚度及强度计算

支撑刚度及强度计算一、理论基础1.支撑刚度:支撑刚度指结构在受力作用下,支撑的刚度程度。
通过支撑刚度的计算,可以确定结构在外力作用下的变形程度,以及刚度不足等问题。
2.支撑强度:支撑强度指支撑所能承受的最大荷载。
支撑强度的计算可以帮助设计师确定结构的荷载能力,以及保证结构安全稳定的能力。
二、计算方法1.支撑刚度计算方法:(1)静力方法:静力方法根据固定边界条件和材料力学性质,通过平衡方程计算支撑的变形和刚度。
(2)刚度矩阵法:刚度矩阵法是一种应力-应变关系的分析方法,通过将结构离散成小单元,计算各个单元的刚度矩阵,最后组装成整个结构的刚度矩阵,并求解结构的位移和刚度。
(3)有限元方法:有限元方法是一种近似求解结构问题的数值计算方法,通过将结构分割成若干有限元,建立有限元模型,通过迭代计算得到结构的位移和应变,从而求解支撑的刚度。
2.支撑强度计算方法:(1)静力法:静力法是最常用的计算支撑强度的方法。
通过计算结构各部分的静力平衡和变形情况,确定支撑的强度。
(2)极限平衡法:极限平衡法是一种基于结构的理论极限承载力的计算方法。
通过分析结构的受力分布,确定结构的极限承载力,从而计算支撑的强度。
三、实际应用1.结构设计:支撑刚度和强度的计算可以帮助设计师确定结构的大小、形状和材料,从而满足结构受力和稳定性的要求。
2.施工监测:支撑刚度和强度的计算还可以用于施工中的结构安全监测和评估,及时发现结构的变形和损坏,采取相应的维修措施。
3.工程验收:支撑刚度和强度的计算也是工程验收的重要内容之一、通过计算支撑的刚度和强度是否满足设计要求,从而确认结构的安全性和稳定性。
总结:。
基坑内支撑刚度

基坑内支撑刚度
基坑内支撑刚度是指在基坑开挖过程中,为了保证基坑的稳定性和安全性,所采用的支撑结构的刚度。
基坑支撑结构的刚度是指支撑结构在受到外力作用时,抵抗变形的能力。
基坑支撑结构的刚度越大,其抵抗变形的能力就越强,从而保证基坑的稳定性和安全性。
基坑支撑结构的刚度主要受到以下几个因素的影响:
1.支撑结构的材料和形式:不同材料和形式的支撑结构具有不同的刚度。
例如,钢支撑结构的刚度比木质支撑结构的刚度大。
2.支撑结构的尺寸和间距:支撑结构的尺寸和间距越小,其刚度就越大。
3.支撑结构的连接方式:支撑结构的连接方式也会影响其刚度。
例如,焊接连接的支撑结构的刚度比螺栓连接的支撑结构的刚度大。
4.基坑周围土体的性质:基坑周围土体的性质也会影响支撑结构的刚度。
例如,土体的密实程度和土壤类型等因素都会影响支撑结构的刚度。
在基坑开挖过程中,为了保证基坑的稳定性和安全性,需要根据实际情况选择合适的支撑结构,并控制其刚度。
如果支撑结构的刚度过小,就会导致支撑结构变形过大,从而影响基坑的稳定性和安全性;如果支撑结构的刚度过大,就会导致支撑结构的成本过高,从
而增加工程造价。
因此,在基坑开挖过程中,需要根据实际情况选择合适的支撑结构,并控制其刚度,以保证基坑的稳定性和安全性,同时控制工程造价。
支撑刚度计算范文

支撑刚度计算范文支撑刚度是指物体在受到外部力或应力作用时,能够保持其形状和结构稳定的能力。
它是一个描述物体抵抗弯曲、扭转或变形的特性,是衡量物体受力能力的重要指标之一、支撑刚度计算是工程设计中的重要一环,它对结构的稳定性和安全性起着至关重要的作用。
为了进行支撑刚度计算,首先需要了解物体所受到的外部力或应力。
外部力可以是重力、风力、地震等,应力则是指物体内部受到的压力或拉力。
这些力或应力会导致物体产生弯曲、扭转或变形,而支撑刚度的作用就是限制这些变形,保持结构的稳定性。
在计算支撑刚度时,一般采用线性弹性理论。
线性弹性理论假设物体的应力与应变之间存在线性关系,并且物体的弯曲、扭转或变形都处于弹性范围内。
根据胡克定律,弹性应变与应力之间的关系可以表示为:σ=Eε其中,σ为应力,E为弹性模量,ε为弹性应变。
根据这个关系,我们可以得到物体的受力分析方程。
受力分析方程可以通过进行材料力学和结构分析计算得到。
在进行支撑刚度计算时,还需要考虑物体的几何特性。
物体的形状和尺寸对其支撑刚度有着重要影响。
例如,梁的支撑刚度与其截面的大小、形状和材料的强度有关。
梁的支撑刚度可以通过弯曲刚度和剪切刚度来表示。
弯曲刚度与梁的截面形状和尺寸相关,可以通过弯曲方程进行计算。
剪切刚度与梁的材料的剪切模量和截面的形状相关,可以通过剪切方程进行计算。
通过这些计算,可以得到完整的支撑刚度。
最后,在进行支撑刚度计算时,还需要考虑物体的边界条件。
边界条件是指物体在受到外力或应力作用时,与周围环境的接触情况。
常见的边界条件包括固定边界、自由边界和约束边界。
在计算支撑刚度时,需要考虑边界条件对物体的支撑刚度的影响,从而得到准确的计算结果。
总结来说,支撑刚度计算是工程设计中的重要一环。
它通过分析物体受力和形变特性,计算物体的支撑刚度。
在计算过程中,需要考虑物体的外部力或应力、线性弹性理论、物体的几何特性和边界条件等因素。
通过支撑刚度计算,可以为工程设计提供准确的数据,保证结构的稳定性和安全性。
钢管支撑刚度及稳定性计算

钢管支撑刚度及稳定性计算钢管支撑设计中的刚度和稳定性是非常重要的考虑因素。
在设计过程中,需要通过计算和评估来确定合适的钢管尺寸、材料和支撑间距,以满足支撑的刚度和稳定性要求。
本文将从钢管支撑的刚度计算和稳定性计算两个方面进行介绍。
一、钢管支撑的刚度计算钢管支撑的刚度计算是指钢管在受到加载时的刚度特性。
钢管支撑的刚度主要取决于材料的特性、钢管截面形状和尺寸以及支撑间距。
其中,材料的特性可以通过弹性模量来表示,钢管截面形状和尺寸可以通过惯性矩来表征,支撑间距则是指支撑点之间的距离。
钢管支撑的刚度可以通过弹性变形来衡量。
根据梁弯曲理论,弯曲刚度与弹性模量、惯性矩和长度有关。
在计算钢管支撑的弯曲刚度时,可以采用梁的弯曲刚度公式:EI=1/2*p*t^3其中,E为钢管的弹性模量,I为钢管的惯性矩,p为弯矩,t为钢管的厚度。
一个简单的钢管支撑的弯曲刚度计算可以通过以下步骤进行:1.确定钢管的截面形状和尺寸。
2.根据钢管的材料特性,确定钢管的弹性模量。
3.根据钢管截面形状和尺寸,计算钢管的惯性矩。
4.根据设计要求,确定钢管支撑的弯矩。
5.根据钢管的厚度,计算钢管支撑的弯曲刚度。
根据计算结果,可以评估钢管支撑的刚度是否满足设计要求。
如果刚度不足,可以通过增加钢管的尺寸或者减小支撑间距来提高刚度。
钢管支撑的稳定性计算是指在受到加载时,钢管是否能够保持稳定的能力。
稳定性计算主要考虑的是钢管支撑在受到压力作用时的稳定性,即屈曲稳定性。
在钢管支撑的稳定性计算中,需要考虑钢管支撑的临界压力,即支撑失稳时的应力状态。
根据欧拉公式和Euler-Bernoulli梁理论,可以得到支撑的临界压力表达式:Pcr = (π^2 * E * I) / (L^2)其中,Pcr为临界压力,E为钢管的弹性模量,I为钢管的惯性矩,L 为支撑长度。
钢管支撑的稳定性评估可以通过以下步骤进行:1.确定钢管的截面形状和尺寸。
2.根据钢管的材料特性,确定钢管的弹性模量。
