vc++第十一章
第十一章营养强化剂

一、营养强化剂的定义和分类
-VH (生物素、维生素B7):生物素 -胆碱:酒石酸氢胆碱、氯化胆碱 √ Vc : L-抗坏血酸,抗坏血酸棕榈酸酯、抗坏血酸磷酸酯镁、抗坏
血酸钠; √肌醇(类维生素) :肌醇 √肉碱(类维生素):左旋肉碱(L-肉碱),左旋肉碱酒石酸盐
* 无机盐类:10类共54种
-强化的无机盐有:铁、钙、锌、碘、硒、镁、铜、猛、钾、氟10类;
8
我国人民的营养素摄入状况
由卫生部、农业部、公安部及国家统计局共同组 织的1992年第三次全国营养调查数据表明,我国人民 有如下营养素的摄入量没有达到要求: 视黄醇当量(维生素A),B2,Ca,Fe,Zn, Se。
强化状况
9
我国营养强化食品的市场情况
1986年11月14日,我国卫生部首次公布了《食品营养强化剂使 用卫生标准(试行)》和《食品营养强化剂卫生管理办法》,可 作强化营养素仅11种。 1993年卫生部对原有的《营养强化剂使用卫生标准(试行)》 进行修改,1994年6月8日发布实施《食品营养强化剂使用卫生标 准》(GB14880—94) 在1996年又进行了补充(GB2760—1996)。 至此,明确规定了可作为强化营养有31个(87种化合物),其 中氨基酸及含氮化合物有3个,维生素17个(24种化合物),微 量元素10个(59种化合物)以及γ-亚麻油酸,并进一步规定了使 用范围、添加量及卫生标准的实施细则。
29
OSeO2
CH2OH
O
硒化卡拉胶
O O
OH
型
O O
OH
亚硒酸钠(NaSeO3)
Se是人体必需微量元素,与机体 抗氧化作用有关,保护细胞膜的 完整性
OSeO2 CH2OH
O
食品分析第十一章 维生素的测定

Heat at 100 deg C for 30 mins in a watert to pH4.5 with 2.5 M NaOAc
Extraction of Vitamin A
1. Weigh 5-10 g of the previously crushed food substance into a 1 L round flask. 2. Add 20 ml of a 50% NaOH solution and warm the mixture in a water bath. 3. Then, add 100 ml of diethyl alcohol and 2 ml of a hydroquinone solution that
脂溶性维生素提取的一般步骤及注意事项
步骤: 1、取样(如鱼肝) 2、加乙醇研磨或匀浆机均质化(常加入抗氧化剂(如焦性没食子酸,抗 坏血酸等)) 3、加碱加热皂化(Vk除外)(使脂肪水解成脂肪酸进而形成水溶性的脂 肪酸盐) 4、水洗去除脂肪酸盐 5、从水洗后的残渣中用有机溶剂提取脂溶性维生素 6、必要时进行减压回旋蒸发浓缩 7、HPLC分析 (UV DETECTOR + REVERSE PHASE COLUMN)
维生素B6(吡哆素)
Vitamin B6, pyridoxine
维生素B7(生物素)
Vitamin B7, vitaminH,biotin
维生素B11(叶酸)
Vitamin B11, folic acid, folacin
维生素B12(钴维生素)
Petroyl glutamic acid?
维生素C
Vitamin B12, cobalamins
water. 6. Add 50 ml of ethylic ether and shake. 7. Add 50 ml of petroleum ether. Shake and allow it to decant. 8. Extract once or twice with 50 ml of petrol ether. 9. Wash the ether phase three times with 100 ml of water. 10. Filter, evaporate, and concentrate until 1 ml is obtained.
第11章 气源装置及辅助元件

压缩空气站的净化流程装置(图10-1 )
二、空气压缩机 气动系统的动力源,把电机输出的机械能转换成气压能输送
给气动系统。 种类:(按工作原理分)容积式、速度式(叶片式)两种。 (1)容积式压缩机——压缩机内部的工作容积被缩小来提高气 体压力,使单位体积内气体的分子密度增加而形成的。
具体有:活塞式、膜片式和螺杆式。 (2)速度式压缩机——气体分子在高速流动时突然受阻而停滞 下来提高气体压力,使动能转化为压力能而达到的。
油雾器在使用中一定要垂直安装,可以单独使用。也可以 空气过滤器、减压阀和油雾器三件联合使用,组成气源调节装置 (通常称气动三大件),使之具有过滤、减压和油雾的功能。 联合使用时,顺序为空气过滤器—减压阀—油雾器(不能颠 倒) 。 安装注意:气源调节装置 应尽量靠近气动设备附近, 距离不应大于5cm。
五、储气罐 作用:消除压力波动,保证输出气流的连续性;储存一定数量 的压缩空气,调节用气量或以备发生故障和临时需要应急使用, 进一步分离压缩空气中的水分和油分。 结构:圆筒状焊接结构,有立式和卧式两种,以立式居多。 储气罐的容积Vc选择:以空气压缩机每分钟 的排气量q为依据进行选择,即: (1)当q<6.0m3/min时,取Vc=1.2m3; (2)当q=6.0~30m3/min时,取Vc=1.2~4.5m3; (3)当q>30m3/min时,取Vc=4.5m3。
具体有:离心式和轴流式等。 使用最广泛的是活塞式压缩机。
§11.2气源净化装置
一、空气过滤器 在空气进入压缩机之前,必须经过空气过滤器。
过滤原理——根据固体物质和空气分子的大小和质量不同,利用惯性、阻 隔和吸附的方法将灰尘和杂质与空气分离。 空气过滤器组成:壳体和滤芯 工作原理:压缩空气从输入口进入,被引入 旋风叶子1,并产生强烈旋转。空气中较大的 水、油滴和灰尘依靠自身的惯性与存水杯3的 内壁碰撞,并分离沉到杯底。微粒灰尘和雾 状水汽则由滤芯2滤除。为防止气体旋转将存 水杯中积存的污水卷起,在滤芯下部设有挡水 板4。
第十一章 透射显微术电子像衬度原理

=
1 = 0.245 2d 200
Å-1,由图查出
f(e)=5.41Å,则Fg=4f(e)=21.64Å。
(4)求
ξ g : 当V=100kV时,λ=0.037 Å
πVC 3.14 × 68.36 = = 268 Å λFg 0.037 × 21.64
ξ g = ξ 200 =
以上算出的消光距离 ξ g 仅适用于s=0的情况,原 则上 ξ g 是动力学理论中的一个物理量,对有限 的s,需要用有效消光距离 ξ geff (小于 替 ξg。
1.等厚消光条纹(衍射强度随样品厚度的变化)
晶体保持确定取向,s保持不变
sin 2 ( πst ) Ig = ( sξ g ) 2
a 当t=1/s;2/s;3/s……n/s Ig=0 b 当t=1/2s;3/2s;5/2s……2n+1/2s
1
Ig
Ig=1/(sζg
)2
( sξ g ) 2
楔形试样边缘
振幅衬度
钢的衍射衬度像
相位衬度: 当试样很薄(10纳米以下),试样相邻晶柱出射的透射振 幅的差异不足以区分相邻的两个像点的程度。这时得不到振幅衬度。 但我们可以利用电子束在试样出口表面上相位不一致,使相位差转换 成强度差而形成的衬度,这种程度称为相位衬度
A:高分辨像,B:原子序数衬度(Z contrast)像
11.2 衍射衬度
由于晶体试样满足布拉格反射条件程度不同及结构振幅 不同而形成衍射强度差异而导致的衬度。 设两取相不同晶粒 A 和 B , A 不满足布拉格衍射条件,强 度为I0的入射束穿过试样,A不产生衍射,透射束与衍射束 强度相同,即IA=I0 B 满足布拉格衍射条件,产生衍射,衍射束强度为 Ihkl , 透射束强度IB=I0-Ihkl, 让透射束通过物镜光阑,将衍射束挡掉,则在荧光屏上 ,A晶粒比B晶粒亮,明场(Bright Field)像。 用物镜光阑孔套某hkl衍射斑,让对应与衍射点hkl的电子 束Ihkl 通过,挡掉透射束,B比A亮,暗场(Dark Field)像。 明场像的衬度特征是跟暗场像互补的,即某个部分在明 场像中是亮的,则它在暗场像中是暗的, 反之亦然。
C++PrimerPlus第六版第十一章课后习题

1.头文件#ifndef STONEWT_H_#define STONEWT_H_namespace VECTOR{class Vector{public:enum Mode { RECT, POL};private:double x;double y;double mag;doubleang;Mode mode;voidset_x();voidset_y();voidset_mag();voidset_ang();public:Vector();Vector(double n1, double n2, Mode form = RECT);void Reset(double n1, double n2, Mode form = RECT);~Vector();doublexval () const { return x;}doubleyval () const { return y;}doublemagval () const { return mag;}doubleangval () const { return ang;}voidpolar_mode();voidrect_mode();Vector operator + (const Vector & v) const;Vector operator - (const Vector & v) const;Vector operator - () const;Vector operator * (double m) const;friend Vector operator * ( double m, const Vector & v);friendstd::ostream& operator << (std::ostream&os, const Vector & v);};}#endif;函数定义#include <iostream>#include "stonewt.h"#include <cmath>usingstd::sqrt;usingstd::sin;usingstd::cos;usingstd::atan;usingstd::atan2;usingstd::cout;namespace VECTOR {const double Rad_to_deg = 45.0/atan(1.0); void Vector::set_x(){x = mag * cos (ang);}void Vector::set_y(){y = mag * sin (ang);}void Vector::set_mag(){mag = sqrt (x * x + y * y);}void Vector::set_ang(){if (x ==0 && y == 0)ang = 0.0;elseang = atan2 (y, x);}Vector::Vector(){x = y = mag = ang = 0;mode = RECT;}Vector::Vector(double n1, double n2, Mode form ) {mode = form;if ( mode == RECT ){x = n1;y = n2;set_mag();set_ang();}else if ( mode == POL ){mag = n1;ang = n2;set_x();set_y();}else{cout<< "Vector set to 0.\n";x = y = mag = ang = 0;mode = RECT;}}void Vector::Reset(double n1, double n2, Mode form ) {mode = form;if ( mode == RECT ){x = n1;y = n2;set_mag();set_ang();}else if ( mode == POL ){mag = n1;ang = n2;set_x();set_y();}else{cout<< "Vector set to 0.\n";x = y = mag = ang = 0;mode = RECT;}}Vector::~Vector(){}void Vector::polar_mode(){mode = POL;}void Vector::rect_mode(){mode = RECT;}Vector Vector::operator + (const Vector & v) const{return Vector(x + v.x, y + v.y);}Vector Vector::operator - (const Vector & v) const{return Vector(x - v.x, y - v.y);}Vector Vector::operator - () const{return Vector(-x, -y);}Vector Vector::operator * (double m) const{return Vector(m * x, m * y);}Vector operator * ( double m, const Vector & v){return ( v * m );}std::ostream& operator << (std::ostream&os, const Vector & v) {if ( v.mode == Vector::RECT ){os<< "(x,y) = (" <<v.x<< " , " <<v.y<< " )\n";}else if ( v.mode == Vector::POL ){os<< "(mag, ang) = (" <<v.mag<< " , " <<v.ang<< " )\n";}elseos<< "Vector object mode is invaild.\n";returnos;}}主函数#include<iostream>#include<cstdlib>#include<ctime>#include<fstream>#include"stonewt.h"int main(){using namespace std;using VECTOR::Vector;srand(time(0));double director;Vector step;Vector result(0.0,0.0);unsigned long steps = 0;double target;doubledstep;fstreamfout;fout.open( "step.text" );cout<< "Enter target distance ( q to quit); ";while (cin>> target ){cout<< "Enter step length : ";if (!(cin>>dstep))break;while (result.magval() < target ){director = rand() % 360;step.Reset(dstep, director, Vector::RECT);result = result + step;steps ++;}cout<< "After " << steps << " steps, the subject has the following location :\n";cout<< result <<endl;result.polar_mode ();cout<< " or \n" << result <<endl;cout<< "Average outward distance per step = " <<result.magval()/steps <<endl;steps = 0;result.Reset(0.0,0.0);cout<< "Enter target distance ( q to quit); ";}cout<< "Bye!" <<endl;cin.clear();while (cin.get() != '\n')continue;system("Pause");return 0;}2.头文件#ifndef STONEWT_H_#define STONEWT_H_namespace VECTOR{class Vector{public:enum Mode { RECT, POL};private:double x;double y;Mode mode;void set_x(double mag, double ang);void set_y(double mag, double ang);double set_mag();double set_ang();public:Vector();Vector(double n1, double n2, Mode form = RECT);void Reset(double n1, double n2, Mode form = RECT);~Vector();double xval () const { return x;}double yval () const { return y;}double magval () { return set_mag();}double angval () { return set_ang();}void polar_mode();void rect_mode();Vector operator + (const Vector & v) const;Vector operator - (const Vector & v) const;Vector operator - () const;Vector operator * (double m) const;friend Vector operator * ( double m, const Vector & v);friend std::ostream& operator << (std::ostream&os, Vector & v);};}#endif;函数定义#include <iostream>#include "stonewt.h"#include <cmath>using std::sqrt;using std::sin;using std::cos;using std::atan;using std::atan2;using std::cout;namespace VECTOR {const double Rad_to_deg = 45.0/atan(1.0); void Vector::set_x(double mag, double ang){x = mag * cos(ang);}void Vector::set_y(double mag, double ang){y = mag * sin(ang);}double Vector::set_mag(){return sqrt (x * x + y * y);}double Vector::set_ang(){if (x ==0 && y == 0)return (0.0);elsereturn atan2 (y, x);}Vector::Vector(){x = y = 0;mode = RECT;}Vector::Vector(double n1, double n2, Mode form ) {mode = form;if ( mode == RECT ){x = n1;y = n2;set_mag();set_ang();}else if ( mode == POL ){set_x(n1, n2/Rad_to_deg);set_y(n1, n2/Rad_to_deg);}else{cout<< "Vector set to 0.\n";x = y = 0;mode = RECT;}}void Vector::Reset(double n1, double n2, Mode form ) {mode = form;if ( mode == RECT ){x = n1;y = n2;set_mag();set_ang();}else if ( mode == POL ){set_x(n1, n2/Rad_to_deg);set_y(n1, n2/Rad_to_deg);}else{cout<< "Vector set to 0.\n";x = y = 0;mode = RECT;}}Vector::~Vector(){}void Vector::polar_mode(){mode = POL;}void Vector::rect_mode(){mode = RECT;Vector Vector::operator + (const Vector & v) const{return Vector(x + v.x, y + v.y);}Vector Vector::operator - (const Vector & v) const{return Vector(x - v.x, y - v.y);}Vector Vector::operator - () const{return Vector(-x, -y);}Vector Vector::operator * (double m) const{return Vector(m * x, m * y);}Vector operator * ( double m, const Vector & v){return ( v * m );}std::ostream& operator << (std::ostream&os, Vector & v){if ( v.mode == Vector::RECT ){os<< "(x,y) = (" <<v.x<< " , " <<v.y<< " )\n";}else if ( v.mode == Vector::POL ){os<< "(mag, ang) = (" <<v.set_mag() << " , " <<v.set_ang() * Rad_to_deg<< " )\n";}elseos<< "Vector object mode is invaild.\n";return os;}}主函数#include<iostream>#include<cstdlib>#include<ctime>#include"stonewt.h"int main()using namespace std;using VECTOR::Vector;srand(time(0));double director;Vector step;Vector result(0.0,0.0);unsigned long steps = 0;double target;double dstep;cout<< "Enter target distance ( q to quit); ";while (cin>> target ){cout<< "Enter step length : ";if (!(cin>>dstep))break;while (result.magval() < target ){director = rand() % 360;step.Reset(dstep, director, Vector::RECT);result = result + step;steps ++;}cout<< "After " << steps << " steps, the subject has the following location :\n";cout<< result <<endl;result.polar_mode ();cout<< " or \n" << result <<endl;cout<< "Average outward distance per step = "<<result.magval()/steps << endl;steps = 0;result.Reset(0.0,0.0);cout<< "Enter target distance ( q to quit); ";}cout<< "Bye!" <<endl;cin.clear();while (cin.get() != '\n')continue;system("Pause");return 0;}3.头文件#ifndef STONEWT_H_#define STONEWT_H_namespace VECTOR{class Vector{public:enum Mode { RECT, POL};private:double x;double y;double mag;double ang;Mode mode;void set_x();void set_y();void set_mag();void set_ang();public:Vector();Vector(double n1, double n2, Mode form = RECT);void Reset(double n1, double n2, Mode form = RECT);~Vector();double xval () const { return x;}double yval () const { return y;}double magval () const { return mag;}double angval () const { return ang;}void polar_mode();void rect_mode();Vector operator + (const Vector & v) const;Vector operator - (const Vector & v) const;Vector operator - () const;Vector operator * (double m) const;friend Vector operator * ( double m, const Vector & v);friend std::ostream& operator << (std::ostream&os, Vector & v);};}#endif;函数定义#include <iostream>#include "stonewt.h"#include <cmath>using std::sqrt;using std::sin;using std::cos;using std::atan;using std::atan2;using std::cout;namespace VECTOR {const double Rad_to_deg = 45.0/atan(1.0); void Vector::set_x(){x = mag * cos(ang);}void Vector::set_y(){y = mag * sin(ang);}void Vector::set_mag(){mag = x * x + y * y;}void Vector::set_ang(){if (x ==0 && y == 0)ang = 0.0;elseang = atan2 (y, x);}Vector::Vector(){x = y = mag = ang = 0 ;mode = RECT;}Vector::Vector(double n1, double n2, Mode form ) {mode = form;if ( mode == RECT ){x = n1;y = n2;set_mag();set_ang();}else if ( mode == POL ){mag = n1;ang = n2;set_x();set_y();}else{cout<< "Vector set to 0.\n";x = y = 0;mode = RECT;}}void Vector::Reset(double n1, double n2, Mode form ) {mode = form;if ( mode == RECT ){x = n1;y = n2;set_mag();set_ang();}else if ( mode == POL ){mag = n1;ang = n2;set_x();set_y();}else{cout<< "Vector set to 0.\n";x = y = mag = ang = 0;mode = RECT;}}Vector::~Vector(){}void Vector::polar_mode(){mode = POL;}void Vector::rect_mode(){mode = RECT;}Vector Vector::operator + (const Vector & v) const{return Vector(x + v.x, y + v.y);}Vector Vector::operator - (const Vector & v) const{return Vector(x - v.x, y - v.y);}Vector Vector::operator - () const{return Vector(-x, -y);}Vector Vector::operator * (double m) const{return Vector(m * x, m * y);}Vector operator * ( double m, const Vector & v){return ( v * m );}std::ostream& operator << (std::ostream&os, Vector & v){if ( v.mode == Vector::RECT ){os<< "(x,y) = (" <<v.x<< " , " <<v.y<< " )\n";}else if ( v.mode == Vector::POL ){os<< "(mag, ang) = (" <<v.mag<< " , " <<v.ang<< " )\n";}elseos<< "Vector object mode is invaild.\n";return os;}}主函数#include<iostream>#include<cstdlib>#include<ctime>#include"stonewt.h"int main(){using namespace std;using VECTOR::Vector;srand(time(0));double director;Vector step;Vector result(0.0,0.0);unsigned long steps = 0;double target;double dstep;int N;intnum;double average, max, min, sum;cout<< "Enter a number :" ;cin>>num;cout<< "Enter target distance ( q to quit); ";cin>> target;cout<< "Enter step length : ";cin>>dstep;N = num;average = max = min = sum = 0;while ( num ){while (result.magval() < target ){director = rand() % 360;step.Reset(dstep, director, Vector::POL);result = result + step;steps ++;}cout<< "After " << steps << " steps once walk.\n";if ( max == 0 || min == 0)max = min = steps;if ( max < steps )max = steps;if ( min > steps )min = steps;sum += steps;num --;steps = 0;result.Reset(0.0,0.0);}average = sum/N;cout<< "Average = " << average <<endl;cout<< "max = " << max <<endl;cout<< "min = " << min <<endl;cout<< "Bye!" <<endl;cin.clear();while (cin.get() != '\n')continue;system("Pause");return 0;}4.头文件#ifndef STONEWT_H_#define STONEWT_H_#include <iostream>class Time{private:int minutes;int hours;public:Time();Time(int h, int m = 0);void Addmin(int m);void Addhr(int h);void reset(int h = 0, int m = 0);friend Time operator + (const Time & t1, const Time & t2 ) ;friend Time operator - (const Time & t1, const Time & t2 ) ;friend Time operator * (double m, const Time & t) ;friend std::ostream& operator << (std::ostream&os, const Time & t) ; };#endif;函数定义#include"stonewt.h"Time::Time(){hours = minutes = 0;}Time::Time(int h, int m){hours = h;minutes = m;}void Time::Addmin(int m){minutes = minutes + m;hours = hours + minutes / 60;minutes = minutes % 60;}void Time::Addhr(int h){hours = hours + h;}void Time::reset(int h , int m ){hours = h;minutes = m;}Time operator + (const Time & t1, const Time & t2 ){Time temp;temp.minutes = t1.minutes + t2.minutes;temp.hours = temp.minutes / 60 + t1.hours + t2.hours;temp.minutes = temp.minutes % 60;return temp;}Time operator - (const Time & t1, const Time & t2 ){Time differ;int tol1, tol2;tol1 = t1.minutes + t1.hours * 60;tol2 = t2.minutes + t2.hours * 60;differ.minutes = tol1 - tol2;differ.hours = differ.minutes / 60;differ.minutes = differ.minutes % 60;return differ;}Time operator * (double m, const Time & t){Time temp;temp.minutes = t.hours * 60 * m + t.minutes * m;temp.hours = temp.minutes / 60;temp.minutes = temp.minutes % 60;return temp;}std::ostream& operator << (std::ostream&os, const Time & t) {os<<t.hours<< " hour, " <<t.minutes<< " minutes.\n";return os;}主函数#include"stonewt.h"int main(){using namespace std;Time aida(3, 35);Time tosca(6, 48);cout<< "Aida and Tosca :" <<aida<< " , " <<tosca<<endl;Time temp;temp = aida + tosca;cout<< "Aida + Tosca: " << temp <<endl;temp = tosca - aida;cout<< "Aida - Tosca: " << temp <<endl;temp = 10.0 * tosca;cout<< "10.0 * Tosca: " << temp <<endl;system("Pause");return 0;}5.头文件#ifndef STONEWT_H_#define STONEWT_H_usingnamespace std;class Stonewt{public:enum Mode{STN,INP, DP};private:enum { Lbs_per_stn = 14 };int stone;double pds_left;int pounds_int;double pounds;Mode mode;void set_stone();void set_pds();void set_pds_int();public:Stonewt(double lbs, Mode form);Stonewt(int stn, double lbs, Mode form);Stonewt();~Stonewt();void stn_mode();void intpounds_mode();void boupounds_mode();operatorint() const;operatordouble () const;Stonewt operator + (const Stonewt&st) const;Stonewt operator - (const Stonewt&st) const;Stonewt operator * (double m)const;friend Stonewt operator * (double n, const Stonewt&st);friend ostream&operator<< (ostream&os, const Stonewt&st); };#endif;函数定义#include<iostream>#include"stonewt.h"void Stonewt::set_stone(){stone = int(pounds)/Lbs_per_stn;pds_left = int(pounds)%Lbs_per_stn + pounds - int(pounds); }void Stonewt::set_pds(){pounds = stone * Lbs_per_stn + pds_left;}void Stonewt::set_pds_int(){pounds = int (pounds);}Stonewt::Stonewt(double lbs, Mode form){mode = form;if( mode == STN){stone = (int)lbs / Lbs_per_stn;pds_left = (int)lbs % Lbs_per_stn + lbs - (int)lbs;set_pds();set_pds();}elseif(mode ==INP){pounds_int = int(lbs);pounds = lbs;set_stone();}elseif ( mode == DP){pounds = lbs;set_stone();set_pds_int();}else{std::cout<<"Stonewt set to 0."<<std::endl;stone = pounds = pds_left = 0;mode = STN;}}Stonewt::Stonewt(int stn, double lbs, Mode form) {mode = form;if( mode == STN){stone = stn;pds_left = lbs;set_pds();set_pds_int();}elseif ( mode == INP ){pounds_int = int ( stn * Lbs_per_stn + lbs);pounds = stn * Lbs_per_stn + lbs ;set_stone();}elseif ( mode == DP ){pounds = stn * Lbs_per_stn + lbs ;set_stone();set_pds_int();}else{std::cout<<"Stonewt set to 0."<<std::endl;stone = pounds = pds_left = 0;mode = STN;}}Stonewt::Stonewt(){stone = pds_left = pounds = 0;mode = STN;}Stonewt::~Stonewt(){}void Stonewt::stn_mode(){mode = STN;}void Stonewt::intpounds_mode(){mode = INP;}void Stonewt::boupounds_mode(){mode = DP;}Stonewt::operatorint() const{returnint(pounds + 0.5);}Stonewt::operatordouble () const{return pounds;}StonewtStonewt::operator + (const Stonewt&st) const {return Stonewt(pounds + st.pounds, st.mode);}StonewtStonewt::operator - (const Stonewt&st) const {return Stonewt(pounds - st.pounds, st.mode);}StonewtStonewt::operator * (double m)const{return Stonewt( pounds * m, mode);}Stonewt operator * (double n, const Stonewt&st) {return Stonewt(n * st.pounds, st.mode);}ostream&operator<< (ostream&os, const Stonewt&st){if( st.mode == Stonewt::STN)os<<st.stone<<" stone, "<<st.pds_left<<" pounds.\n";if ( st.mode == Stonewt::INP)os<<st.pounds_int<<" int pounds.\n";if ( st.mode == Stonewt::DP )os<<st.pounds<<" double pounds.\n";return os;}主函数#include<iostream>#include"stonewt.h"int main(){Stonewt tiger (275, Stonewt::DP);Stonewt wolf(285.7, Stonewt::STN);Stonewt dog (21, 8, Stonewt::INP);Stonewt temp;cout<<"The tiger weight is "<< tiger <<endl;cout<<"The wolf weight is "<< wolf <<endl;cout<<"The dog weight is "<< dog <<endl;temp = tiger - wolf;cout<<"Tiger - wolf "<< temp <<endl;temp = tiger + wolf;cout<<"Tiger + wolf "<< temp <<endl;temp = 10.0 * dog;cout<<"10.0 * dog = "<< temp <<endl;temp = dog * 10.0;cout<<"dog * 10.0 = "<< temp <<endl;system("Pause");return 0;}6.头文件#ifndef STONEWT_H_#define STONEWT_H_#include <iostream>class Stonewt{private:enum { Lbs_per_stn = 14 };int stone;double pds_left;double pounds;public:Stonewt(double lbs);Stonewt(int stone, double lbs);Stonewt();~Stonewt();bool operator < (constStonewt&st) const;bool operator <= (constStonewt&st) const;bool operator > (constStonewt&st) const;bool operator >= (constStonewt&st) const;bool operator == (constStonewt&st) const;bool operator != (constStonewt&st) const;friend std::ostream& operator << (std::ostream&os, constStonewt&st); };#endif;函数定义#include"stonewt.h"Stonewt::Stonewt(double lbs){stone = int(lbs) / Lbs_per_stn;pds_left = int(lbs) % Lbs_per_stn + lbs - int (lbs);pounds = lbs;}Stonewt::Stonewt(intsto, double lbs){stone = sto;pds_left = lbs;pounds = stone * Lbs_per_stn + lbs;}Stonewt::Stonewt(){stone = pds_left = pounds = 0;}Stonewt::~Stonewt(){}boolStonewt::operator < (constStonewt&st) const {if (pounds <st.pounds)return true;elsereturn false;}boolStonewt::operator <= (constStonewt&st) const {if (pounds <= st.pounds)return true;elsereturn false;}boolStonewt::operator > (constStonewt&st) const {if (pounds >st.pounds)return true;elsereturn false;}boolStonewt::operator >= (constStonewt&st) const {if (pounds >= st.pounds)return true;elsereturn false;}boolStonewt::operator == (constStonewt&st) const {if (pounds == st.pounds)return true;elsereturn false;}boolStonewt::operator != (constStonewt&st) const {if (pounds != st.pounds)return true;elsereturn false;}std::ostream& operator << (std::ostream&os, constStonewt&st) {os<<st.pounds<< " pounds.\n";return os;}主函数#include"stonewt.h"int main(){using namespace std;Stonewtsto[6] = { 10.0, 20.0, 30.0};Stonewt temp (11.0);for (int i = 3; i < 6; i++){double number;cout<< "Enter a number: " ;cin>> number;sto[i] = number;}int count = 0;Stonewt max = sto[0];Stonewt min = sto[0];for (int i = 0; i < 6; i++){if (max <sto[i])max = sto[i];else if (min >sto[i])min = sto[i];if (sto[i] >= temp)count ++;}cout<< "Max : " << max <<endl;cout<< "Min : " << min <<endl;cout<< "The number of >= 11.0 pounds : " << count <<endl;system("Pause");return 0;}7.头文件#ifndef COMPLEX0_H_#define COMPLEX0_H_#include <iostream>using namespace std;class Complex{private:double real;double imaginary ;public:Complex();Complex(double m, double n);~Complex();//重载运算符Complex operator + (const Complex & c)const; //加法Complex operator - (const Complex & c)const;//减法Complex operator * (const Complex & c)const;//乘法Complex operator * (double a)const;//数乘Complex operator ~ ()const;//共轭friend Complex operator * (double m, const Complex & c);friendostream& operator << (ostream&os, const Complex & c);friendistream& operator >> (istream& is, Complex & c); };#endif;函数定义#include "complex0.h"Complex::Complex(){real = imaginary = 0;}Complex::Complex(double m, double n){real = m;imaginary = n;}Complex::~Complex(){}//重载运算符Complex Complex::operator + (const Complex & c)const //加法{return Complex(real + c.real, imaginary + c.imaginary) ;}Complex Complex::operator - (const Complex & c)const//减法{return Complex(real - c.real, imaginary - c.imaginary) ;}Complex Complex::operator * (const Complex & c)const//乘法{return Complex(real * c.real - imaginary * c.imaginary, real * c.imaginary + imaginary * c.real);}Complex Complex::operator * (double a)const//数乘{return Complex(real* a, imaginary * a);}Complex Complex::operator ~ ()const//共轭{return Complex(real, -imaginary);}Complex operator * (double m, const Complex & c){return Complex(m * c.real, m * c.imaginary);}ostream& operator << (ostream&os, const Complex & c){os<< "(integer, imaginary) = ( " <<c.real<< " , " <<c.imaginary<< "i )\n";returnos;}istream& operator >> (istream& is, Complex & c){cout<< "Real:";if (is >>c.real){cout<< "Imaginary;";is>>c.imaginary;}return is;}主函数#include"complex0.h"int main(){Complex a (3.0, 4.0);Complex c;cout<< "Enter a complex number (q to quit): \n";while (cin>> c){cout<< "c is " << c << "\n";cout<< "complex conjugate is " << ~c << "\n";cout<< "a is " << a << "\n";cout<< "a + c is " << a + c << "\n";cout<< "a - c is " << a - c << "\n";cout<< "a * c is " << a * c << "\n";cout<< "2 * c is " << 2 * c << "\n";cout<< "Enter a complex number (q to quit): \n";}cout<< "Done!\n";system("Pause");return 0;}。
第十一章 非线性药物动力学

第一节 概述 第二节 非线性药物动力学方程 第三节 函数方程及Vm和Km的计算 第四节 动力学参数的计算
1
第一节 概述
一、非线性药物动力学定义:
药物的体内过程不服从一级速度过程,为遵循米 氏方程的动力学过程,称为非线性动力学,也称 剂量依赖药物动力学、饱和动力学或容量限制动 力学
4)从药-时曲线中求算动力学参数,从药动学参数的
改变中评价非线性
9
第二节 非线性药物动力学方程
Michealis-Menten方程及意义
dc vm c dt km c
dc :药物在t 时间的下降速率 dt
vm :酶促过程理论最大速率
k m :米氏常数,即达最大速率一半时的血药浓度
10
vm 越大,酶活性越强,难以达到饱和
cdt km c dc vm
取从0─∞积分:
cdt
0 ( vm c )dt
0
c0
vm
则有:
AUC
c02 2vm
c0 vm
km
即AUC与剂量的平方成正比,剂量增大使AUC超比例增大。
27
本章要求
1、掌握非线性药物动力学的定义,特点与识别方法 2、熟悉非线性动力学的参数Vm与Km的估算方法 3、熟悉非线性药物动力学与线性药物动力学的清除
km 越小,剂量对酶饱和影响越大,剂量对非线
性形成有显著作用
vm km
也称药物固有的清除率(Cl int )
11
当C很小时,km c
则有:
dc vm c k c dt km
(线性过程)
当C很大时, c km
则有:
dc dt
vm c c
vm
数电第十一章习题答案

• 13.图题(a)为心律失常报警电路,经放大后的 .图题( )为心律失常报警电路, V 如图( )所示, 的幅值Vm=4V。试 心电信号VI 如图(b)所示,I 的幅值 。 回答以下问题: 回答以下问题: 1)对应分别画出图中的A,B,C三点电压波形 三点电压波形; (1)对应分别画出图中的A,B,C三点电压波形; (2)所明电路的组成及工作原理。 )所明电路的组成及工作原理。
VTRI
VTHRቤተ መጻሕፍቲ ባይዱ
VTRI
为低电平(< 1 VCC
3
时,VC 为高电平,VTHR > 时, VC 为低电 平
2 V CC 3
• 第一级555定时器构成施密特触发器,将心律信 号整形为脉冲信号;第二级的是由单稳态触发器 加上BJT构成可重复触发的单稳态触发器。当心 律正常时,VA的频率较高,周期较短,使得VB不 能充电至
第十一章习题
• 11.下图所示电路是由555定时器构成的锯齿波发 .下图所示电路是由 定时器构成的锯齿波发 生器, 构成恒流源电路, 生器,BJT和电阻 R 1 R R3构成恒流源电路,给定时 和电阻 电容C充电 充电。 输入负脉冲后, 电容 充电。当触发输入端 v1 输入负脉冲后,画出 电容电压 vc及555输出端v0 的波形,并计算电容C 输出端 的波形,并计算电容 充电时间。 充电时间。
C
duc =I dt
,
• 12.由555定时器组成的脉冲宽度鉴别电路及输 . 定时器组成的脉冲宽度鉴别电路及输 VT 波形如图题所示。 入 VI波形如图题所示。集成施密特电路VT + =3V, − , =1.6V,单稳的输出脉宽 TW有 t1 <TW < t2的关系。 的关系。 单稳的输出脉宽 画出电路中B, , , 各点波形 各点波形, 对应 VI 画出电路中 ,C,D,E各点波形,并说 端输出负脉冲的作用。 明D,E端输出负脉冲的作用。 , 端输出负脉冲的作用
第十一章动能定理

)2
vC ? d?
Ek
?
1 2
mvc2
?
1 2
J c?
2
例11-1 四连杆机构如图所示,OA=DB=AB=l。质量均为m。 若OA绕O轴以匀角速度? 转动,求系统的动能。
vA A vC vB B 解: 杆OA和DB定轴转动,杆AB平动
C
vC = vA= vB= l ?
?
?
O
D
Ek = EkOA + EkDB+ EkAB
第十一章 动能定理
第一节 动能的概念和计算 第二节 功的概念和计算 第三节 动能定理 第四节 功率·功率方程 第五节 机械能守恒定理 第六节 动力学普遍定理的综合应用
本章重点
1.动能、功的计算 2.动能定理 3.动力学普遍定理的综合应用
第一节 动能的概念和计算
一、质点的动能
动能:物体机械运动强弱的一种度量。动能恒为正值。
? ? W ?
C2 C1
FR
?d rC
?
?2 ?1
MC
d?
F1
7、内力的功
r12
r1
r2
O
F2
δW = F1·dr1 + F2·dr2 = F1·(dr1-dr2) = F1·dr12
讨论:1)对于刚体F1·dr12?0 ; δW=0。内力不作功.
2)对于一般质点系,dr12?0。 内力作功.
为 r,质量为 m。求系统的动能。
解: 杆OA定轴转动,轮A平面运动, I为瞬心。
?
O
A? A
I
vA
vA= (R+r) ? = r ? A
?
A
?
?R ?
十一章动能定理

解:
取平衡位置为零势位,重力和弹簧旳静伸长抵消:
T1
1 2
P g
v2
T2 0
W k2
2
max st
T2 T1 W
1 P v2 k 2
2g
2
Pv
kg
Fmax P k P
Pk v g
自然位置
St 平衡位置
P
max
讨论:当:k =3.35kN/mm, v=0.5m/s, P=2.5 kN,
1 2g
vC2
(
2
Q1
3 2
vC R2
Q2
Q2 g
)
R22
M
l R1
Q2l
Q2
sin
F
FN
Fx
Q1
解得
vC 2
( M Q2 R1 sin )gl
R1( 2Q1 3Q2 )
例11-8:均质杆OA=l,重P,圆盘重Q,半径r,可绕A轴自 由旋转,初始时,杆垂直,系统静止,设OA杆无初速度释放。 求:杆转至水平位置时,杆旳角速度、角加速度。
T2 T1 W
v 2gL( 1 cos )
n
P
F
l
质点方程: Pv2 P cos F
gl
F P 2gL( 1 cos ) P cos P(2 3cos)
g 当:=时, F=5P
例11-5:电梯旳鼓轮重W,半径r,轿厢重P。 求:轿厢下落到任意高度时,钢索旳张力。
解: 动能定理
2
R2
r2 4R2
)
W
x
A
M R
mg(
1 2
3 2
fs
5r 12 R
)
理论力学第十一章动能定理
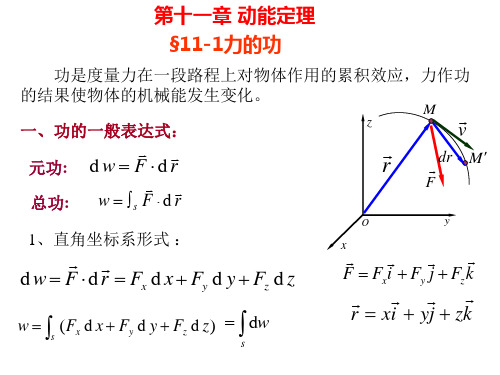
由于刚体上任意两点之间的距离始终保持不变。因此
d rB
cos
d rA
cos
d w 0
5、约束力的功 (1)光滑固定面力的功 d w FN d r 0 (2)摩擦力的功
FN dr
FN
静滑动摩擦力不做功
纯滚动摩擦力: dW F dr F vI dt 0
IF
动滑动摩擦力的功:dW F ds fd FN ds
1 2
mivr2i
柯尼希定理: 质点系的动能等于随同其质心平动的动 能与相对其质心运动的动能之和。
三、刚体的动能
1、平移刚体的动能:
T
1 2
mi
vi2
1 2
mi
v
2
1 mv2 2
2、定轴转动刚体的动能:
T
1 2
mi
vi2
1 2
(mi
i
2
)
2
1 2
J z 2
3、刚体作平面运动
设刚体上任一质点到瞬心的垂直距离为 i,则该
/
h2
a |90 3.14m/s 2 ( 90 )
例5:已知:mA=m,mB=m/2,mC=m/3,鼓轮的回转半径为,质 量为m,鼓轮小半径为r,大半径为R,外力偶M,C轮的半径为r, 物体A接触的摩擦系数为fd,系统初始静止,求物体A的速度(表 示成物体A位移xA的函数)。
解: “系统” T1 0
解 :BC杆及重物D(以 杆BC的水平位置为零势能位 )
V1
P1
l 2
cos
P2l
cos
( P1 2
P2 )l
cos
弹簧(选弹簧的原长处为势能的零位置)
B
V2
C++第11章习题解答

第十一章标准模板库(STL)习题一. 基本概念与基础知识自测题11.1填空题11.1.1 STL大量使用继承和虚函数是(1)(填对或错)。
因为(2)。
答案:(1)错(2)它使用的是模板技术,追求的是运行的效率,避免了虚函数的开销11.1.2 有两种STL容器:(1)和(2)。
STL不用new和delete,而用(3)实现各种控制内存分配和释放的方法。
答案:(1)第一类容器(2)近容器(3)分配子(allocator)11.1.3 五种主要迭代子类型为(1)、(2)、(3)、(4)和(5)。
STL算法用(6)间接操作容器元素。
sort算法要求用(7)迭代子。
答案:(1)输入(InputIterator)(2)输出(OutputIterator)(3)正向(ForwardIterator)(4)双向(BidirectionalIterator)(5)随机访问(RandomAccessIterator)(6)迭代子(7)随机访问(RandomAccessIterator)11.1.4 三种STL容器适配器是(1)、(2)和(3)。
答案:(1)stack(栈)(2)queue(队列)(3)priority_queue(优先级队列)11.1.5 成员函数end()得到容器(1)的位置,而rend得到容器(2)的位置。
算法通常返回(3)。
答案:(1)最后一个元素的后继位置(2)引用容器第一个元素的前导位置。
实际上这是该容器前后反转之后的end()(3)迭代子11.1.6 适配器是(1),它依附于一个(2)容器上,它没有自己的(3)函数和(4)函数,而借用其实现类的对应函数。
答案:(1)不独立的(2)顺序(3)构造函数(4)析构函数11.1.7 返回布尔值的函数对象称为(1),默认的是(2)操作符。
答案:(1)谓词(predicate)(2)小于比较操作符“<”11.1.8C++标准库中给出的泛型算法包括(1)种算法。
第十一章 国家垄断资本主义及其对经济的干预

第十一章国家垄断资本主义及其对经济的干预投资经营分散、非长期化异类性二、金融资本及其垄断统治银行垄断形成银行资本集中垄断银行的新作用万能的垄断者金融资本:银行垄断资本与工业垄断资本融和生长而形成的一种新型资本金融资本形成途径:1.资本相互参与2. 人事结合金融寡头:是指掌握庞大金融资本的最大的金融资本家或金融资本家财团。
金融寡头统治:经济上—参与制政治上—个人联合三、国家垄断资本主义的形成和发展1.含义国家垄断资本主义是国家资本同私人垄断资本相结合的一种垄断资本主义。
2.形成3.迅速发展的原因⑴它是解决科技进步和生产社会化带来的一系列新矛盾新问题的需要;⑵它是经济恢复的需要;⑶它是克服经济危机,实现经济稳定发展的需要;⑷它是适应日趋激烈的国际市场竞争的需要。
四、国家垄断资本主义的形式和实质㈠国家垄断资本主义的基本形式1.国有企业—最典型、最高层次⑴途径:国家财政拨款直接投资开办企业;实行私人垄断企业国有化。
⑵分类①满足国家机构自身需要的国有企业②从事公用事业的国有企业③高科技、高风险新兴工业部门中的国有企业④一般工业部门中的国有企业2.国私共有企业—战后的主要形式•国有企业将一部分股份出售给私人•国家和私人共同投资开办合资企业•由国有企业与私人垄断资本企业合并而成•国有企业对私人企业参股•国有企业转由私人承包或租赁经营3.国家通过多种方式参与私人垄断资本的再生产过程⑴国家向私人垄断企业大量订货⑵国家通过各种形式的津贴和补助⑶国家用大量资金发展教育和社会福利事业⑷国家科研投资委托私人企业进行科研㈡国家垄断资本主义的实质资产阶级国家与私人垄断资本在社会再生产过程的各个主要方面紧密地结合起来,以保证垄断资产阶级获取更高的垄断利润;资产阶级国家代表垄断资产阶级的整体利益并凌驾于个别垄断资本之上,调节社会经济和各种阶级矛盾,以推动资本主义经济的运转和维护资本主义经济制度的生存。
第十三章资本主义的历史地位和发展趋势一、资本积累及其后果㈠资本积累1.概念在扩大再生产需要增加投资的情况下,把剩余价值转化为资本,叫做资本积累。
ly_新标准C++程序设计教材11-20章课后题答案

新标准C++程序设计教材11-20章课后题答案第11章:1.简述结构化程序设计有什么不足,面向对象的程序如何改进这些不足。
答案:结构化程序设计的缺点:(1)用户要求难以在系统分析阶段准确定义,致使系统在交付使用时产生许多问题。
(2)用系统开发每个阶段的成果来进行控制,不适应事物变化的要求。
(3)系统的开发周期长。
面向对象的程序设计如何改进这些不足:面向对象程序设计技术汲取了结构忧程序设计中好的思想,并将这些思想与一些新的、强大的理念相结台,从而蛤程序设计工作提供了一种全新的方法。
通常,在面向对象的程序设计风格中,会将一个问题分解为一些相互关联的子集,每个子集内部都包含了相关的数据和函数。
同时会以某种方式将这些子集分为不同等级,而一个对象就是已定义的某个类型的变量。
2.以下说怯正确的是( )。
A.每个对象内部都有成员函数的实现代码B.一个类的私有成员函数内部不能访问本类的私有成员变量C.类的成员函数之间可以互相调用D.编写一个类时,至少要编写一个成员函数答案:C3.以下对类A的定义正确的是( )。
A.class A{ B.class A{private: int v; int v; A * next;public: void Func() {} void Func() {}} };C.class A{ D. class A{int v; int v;public: public:void Func(); A next;}; void Func() {}A::void Func() { } };答案:B4.假设有以下类A:class A{public:int func(int a) { return a * a; }};以下程序段不正确的是( )。
A.A a; (5);B.A * p = new A; p->func(5);C.A a;A&r =a ; (5);D.A a,b; if(a!=b) (5);答案:D5.以下程序段不正确的是(A)。
第十一章钢筋混凝土设计原理课后习题答案

第十一章1什么是单双向板?怎样加以区别?其传力路线有和特征?单向板:荷载作用下,只在一个方向或主要在一个方向弯曲的板。
双向板:荷载作用下,在两个方向弯曲,且不能忽略任一方向弯曲的板.(1)对两对边支承的板,应按单向板计算。
(2)对于四边支承的板l b≤时应按双向板计算;/2l b<<时宜按双向板计算;按沿短边方向受力的单向板计算2/3时,应沿长边方向布置足够数量的构造钢筋;/2l b≤时可按沿短边方向受力的单向板计算。
单向板沿短边方向受力,特征个方向弯曲双向板双向受力特征两个方向弯曲2什么叫截面的弯曲刚度?什么叫截面竖向弯曲刚度?截面的弯曲刚度:使构件截面产生单位曲率需施加的弯矩值截面竖向弯曲刚度:使构件截面产生单位挠度需施加的竖向均布荷载3现浇单向板的设计步骤是什么?(1) 结构平面布置,并拟定板厚和主、次梁的截面尺寸(2) 确定梁、板得计算简图(3)梁、板的内力分析(4)截面配筋及构造设施(5)绘制施工图4单向板肋梁楼盖其板、次梁、主梁的跨度如何确定?工程常用的数值分别是多少?板的跨度:次梁的间距单向板:1.7-2.5 m荷载大时取较小值,一般≤3m次梁的跨度:主梁的间距次梁: 4--6 m主梁的跨度:柱或墙的间距主梁: 5——8 m5单向板肋梁楼盖的布置方式都有哪几种?1)主梁横向布置,次梁纵向布置优点:主梁与柱可形成横向框架,横向抗侧移刚度大各榀横向框架间由纵向的次梁相连,房间整体性较好由于外墙处仅设次梁,故窗户高度可开大些,对采光有利(2)主梁纵向布置,次梁横向布置(3)优点:减小了主梁的截面高度,增加了室内净高适用于:横向柱距比纵向柱距大的多的情况3)只布置次梁适用于:有中间走道的砌体墙承重的混合结构房屋6什么是结构物的计算简图?包括那几方面的内容?结构物的计算简图包括计算模型,计算荷载两个方面1)简化假定和计算模型:简化假定1)支座可以自由转动,无竖向位移2)不考虑薄膜效应对板内力的影响3)忽略板、次梁连续性,按简支构件计算支座反力4)实际跨数≥5跨时等跨或跨度差≤10%且各跨受荷相同的连续梁按5跨计算 计算模型: 连续板或连续梁(2)计算单元及从属面积板计算单元:1m 宽板带次梁荷载范围 :次梁左右各半跨板主梁荷载范围 :主梁左右各半个主梁间距,次梁左右各半个次梁间距(3)弹性理论计算跨度中间跨 0c l l =边跨 板0min 1.025222n n b h b l l l =+++(,) 梁0min 1.025222n n b a b l l l =+++(,) (4)荷载取值板和次梁的折算荷载为了考虑次梁或主梁的抗扭刚度对内力的影响,采用增大恒载,减小活载的办法板 12g g q '=+ 12q q '= 次梁 14g g q '=+ 34q q '= 7、单向板肋梁楼盖的计算假定有哪些?答:⑴、支座可以自由转动,但没有竖向位移;⑵、不考虑薄膜效应对板内力的影响;⑶、在确定板传给次梁的荷载以及次梁传给主梁的荷载时,分别忽略板、次梁的连续性,按简支构件计算支座竖向反力;⑷、跨数超过5跨的连续梁、板,当各跨荷载相同,且跨数相差不超过10%时,可按5跨的等跨连续梁、板计算。
第十一章 特殊磁共振成像原理

(一)名词解释1.STIR序列2.脂肪探测器3.层流4.双极性流动相位编码梯度5.黑血技术6.弥散加权成像7.弥散8.弥散系数9.表观弥散系数10.弥散张量成像11.磁共振灌注成像12.脑血容量13.脑血流量14.平均通过时间15.达峰时间16.动脉自旋标记磁共振灌注法17.ppm18.半高宽19.组块设计20.事件相关设计21.血氧合水平依赖功能磁共振22.磁敏感加权成像23.磁化传递技术(二)填空题1.脂肪抑制成像常用的方法有:STIR, 、、和综合法;其中除了STIR之外,其余四种方法都是利用了水和脂肪中的质子存在差异。
在3T场强下,要实现水和脂肪信号的同相,TE应该满足。
2.水抑制成像一般采用序列。
如果水的T1弛豫为3600ms,要实现较好效果的水抑制,TI时间应该设定为 ms。
3.血管内血液的流动主要包括层流、、。
其中层流主要出现在(静脉/动脉)中。
层流的特点是。
流动效应主要包括和相位弥散效应。
前一类效应包括流空效应和。
该类效应出现的本质是。
一般(快速/慢速)血流容易出现流空效应。
流速高于截止流速Vc时,血管信号为。
Vc的计算公式为。
相位效应可以分为两种,一种是奇数回波弥散效应和。
4.血管成像的本质是将血流信号与信号体现出强烈对比信号。
根据不同的流动效应,血管成像的方法包括、PC法.CE-MRA。
第一种方法中,流速越高,血管信号越。
PC法中,采用进行流动相位效应编码。
CE-MRA图像中,与静息组织相比,血管信号为、信号。
2D血管成像技术中,对于每个层面的血管信号通过算法进行堆砌重建得到血管的影像。
黑血技术成像中,采用、建得到黑色血管图像,其固有缺陷在于。
5.弥散加权成像是一种主要体现组织内情况的技术。
作为目前在人体上进行测量与成像的唯一方法,它为磁共振成像提供了一种崭新的影像对比。
6.弥散是分子在媒介中的一种、的热运动,也就是,它与温度、分子浓度等有关,其量化单位为。
7.弥散系数是指水分子弥散运动的速度,即水分子内随机弥散运动的 ,单位为: 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.3 冲突、支配规则和赋值兼容性 11.3.1 冲突 如果一个派生类的不同的基类之间有同名的成员, 则在派生类中便出现了成员同名的情况,从而造成成员 访问的不唯一性,这种情况称为冲突。为了解决此类问 题,可以在访问同名的成员时用作用域运算符“:: ::”指定 :: 其所属的类。
11.3.2 支配规则 当派生类中新增的成员与基类中的成员同名时, 则在没有使用作用域运算符时缺省指代的是派生类中 新增的同名成员。这种优先关系称为支配规则。
11.1.3 私有派生和保护派生 在私有派生中,基类的所有成员在派生类中均变为私 有的。 在保护派生中,基类的公有成员和保护成员在派生 类中均变为保护的,而基类中的私有成员继承到派生类 中,其特性仍为私有的.
11.2 初始化基类成员和对象成员 如果一个类由另外的类派生而来,或类中含有对象成 员,则对基类成员或对象成员的初始化要通过该类的构 造函数来调用基类的构造函数和成员对象的构造函数来 完成,该类的构造函数定义形式如下: 类名(形参):基类(实参),对象(实参),… 其中,各基类、对象的构造函数的排列次序不是固定的。
基类 A
基类 A
基类 B
基类 C
派生类 D
11.3.3 基类和对象成员 基类在派生类中只能继承一次,否则,由于重复继承 所带来的冲突即使使用作用域运算符也没法解决。如果程 序中确实需要某个类的成员在另一类中重复几次,则可以 通过对象成员来解决。
11.3.4 赋值兼容性 对于一个公有派生,可以将一个派生类的对象赋 给基类的对象,这个赋值是将派生类中从基类中继承 来的成员赋给基类对象相应的成员。与此相对应,还 可以将一个派生类对象的指针赋给基类对象的指针, 也可以用派生类对象来初始化基类对象的引用,但是, 在这两种情况下,只能访问从相应基类中继承来的成 员,而不能访问其它的成员。这种赋值规则称为赋值 的兼容性。
11.4 虚基类 如果类B和类C均由类A派生 而成,而类D又是由类B和类C 共同派生而成,则在派生类D 中就出现了基类A的两个拷贝, 从而产生了冲突。为了解决此 问题,VC++中引入了虚基类的 概念,即在由类A派生类B和类 C时,如果将基类A说明为虚基 类,则类A在此后的派生类中 只生成一个拷贝。
派生类的定义格式如下: class <派生类> :[继承方式]<基类1>, [继承方式]<基类2>, … { <派生类新定义成员> };
派生类继承基类成员的方式有三种: 公有继承(public) 私有继承(private) 保护继承(protected) 如果继承方式缺省,则为私有派生。
11.1.2 公有派生 在公有派生中,基类成员继承到派生类中时其访问特性 不变,即: 基类中的公有成员在派生类中仍为公有成员,在派生类 的内部或外部均可直接使用这些成员; 基类中的保护成员在派生类中仍为保护成员,在派生类 内部可以直接使用这些成员,但在派生类外部则不可以 直接使用这些成员; 基类中的私有成员继承到派生类中,其访问特性仍是私 有的,并且在派生类内部和外部均不能直接使用这些成 员,只能通过基类中相应的成员函数使用这些成员。
第11章 继承和派生类 类的数据封装特性提高了VC++程序设计的数据安全性, 而类的继承和派生则赋予了VC++程序设计的灵活性。通过类 的继承机制,可以简化程序设计的方法,提高程序代码的重 复利用率和软件的可维护性 11.1 继承 11.1.1 基本概念 在原有的类的基础上生成新的类原有的类则称 为基类或父类。
