实验二---一般信道容量迭代算法教案资料
实验二 计算信道容量

PXi[i] = ((PXi[i] * a[i]) / sum);
}
n ++;
}
}while(cap_max-cap_result>= e);
printf("\n\n迭代次数为:%d\n" ,n);
for(i=0;i<X_num;i++)
{
printf("最佳信源概率:%f\n" ,PXi[i]);
}
/**************************************************************************
函数名:double Calculate_cap_result(double PXi[],double a[])
功能:计算并输出迭代法所需的参数cap_result
double Calculate_cap_max(double a[])
{
int i;
double max_a = a[0];
for(i=0;i<X_num;i++)
{
if(a[i] > max_a)
{
max_a = a[i];
}
}
printf("较大值=%f",log(max_a));
return log(max_a);
for(i=0;i<X_num;i++)
{
for(j=0;j<Y_num;j++)
{
printf("P[%d][%d]=",i,j);
scanf("%lf",&P[i][j]);
实验二:信道容量的迭代算法

实验二信道容量迭代算法一、实验目的:了解信道容量的计算方法二、实验内容与原理:内容:1.令pe1=pe2=0.1和pe1=pe2=0.01,分别计算该对称信道的信道容量和最佳分布;2.令pe1=0.15,pe2=0.1和pe1=0.075pe2=0.01,分别计算该信道的信道容量和最佳分布;信道容量是信息传输率的极限,当信息传输率小于信道容量时,通过信道编码,能够实现几乎无失真的数据传输;当数据分布满足最佳分布时,实现信源与信道的匹配,使得信息传输率能够达到信道容量。
本实验利用信道容量的迭代算法,使用计算机完成信道容量的计算。
三、程序代码#include<stdio.h>#include<math.h>int main(){double Pe1,Pe2,Pa1_=0,Pa2_=0; double b1a1,b2a1,b1a2,b2a2;double Pa1=0,Pa2=0;double I=0,max=0;//平均互信息量,最大平均互信息量int count=0;printf("输入信道容量参数Pe1:");scanf("%lf",&Pe1);printf("输入信道容量参数Pe2:");scanf("%lf",&Pe2);printf("信道容量参数:Pe1=%lf Pe2=%f\n",Pe1,Pe2);b1a1=1-Pe1;b2a1=Pe1;b1a2=Pe2;b2a2=1-Pe2;for(Pa1=0.01;Pa1<=1;Pa1=Pa1+0.01){ Pa2=1-Pa1;count=count+1;I=Pa1*b1a1*( log( b1a1/(Pa1*b1a1+Pa2*b1a2) )/log(2) )+Pa1*b2a1*( log(b2a1/(Pa1*b2a1+Pa2*b2a2) )/log(2) )+Pa2*b1a2*( log(b1a2/(Pa1*b1a1+Pa2*b1a2) )/log(2) )+Pa2*b2a2*( log(b2a2/(Pa1*b2a1+Pa2*b2a2) )/log(2) );printf("%10lf",I);if (I>max){max=I;Pa1_=Pa1,Pa2_=Pa2;}elsecontinue;}printf("\n");printf(" 一共计算机了:%d\n",count);printf(" 最大互信息量为:%lf\n",max);printf(" 最大互信息量的P(a1)=%lf;P(a2)=%lf\n",Pa1_,Pa2_); }四、运行结果。
《信息论与编码技术》实验教案

技术选型
根据实际需求选择合适的差错控制编码技术, 包括线性分组码、卷积码等。
实现与测试
通过编程实现所选差错控制编码技术的编码和解码过程,并进行测试和性能分 析。
04
现代编码技术实验
Turbo码编译码原理及性能评估
Turbo码基本原理
介绍Turbo码的结构、编码原理、迭代译码原理等基本概念。
编译码算法实现
《信息论与编码技术》实验教案
目录
• 课程介绍与实验目标 • 信息论基础实验 • 编码技术基础实验 • 现代编码技术实验 • 信息论与编码技术应用案例分析 • 课程总结与展望
01
课程介绍与实验目标
信息论与编码技术课程概述
课程背景
信息论与编码技术是通信工程、 电子工程等专业的核心课程,主 要研究信息的传输、存储和处理 过程中的基本理论和方法。
2. 根据概率分布生成模拟信源序列;
03
离散信源及其数学模型
3. 计算信源熵、平均符号长度等参数;
4. 分析实验结果,理解信源熵的物理 意义。
信道容量与编码定理验证
实验目的
理解信道容量的概念、计算方法和物理意义,验证香农编码定理的正确性。
实验内容
设计并实现一个信道模拟器,通过输入不同的信道参数和编码方案,计算并输出信道容量、误码率等关键参数。
数据存储系统中纠删码技术应用
纠删码基本原理
阐述纠删码的基本概念、原理及其在数据存储系统中的应用价值。
常用纠删码技术
介绍常用的纠删码技术,如Reed-Solomon码、LDPC码等,并分 析其性能特点。
纠删码技术应用实践
通过实验,将纠删码技术应用于数据存储系统中,评估其对系统可 靠性、数据恢复能力等方面的提升效果。
迭代求解信道容量

谢谢~~
Page
15
j
H (Y / X ) p (ai ) p (b j / ai ) log p (b j / ai ) p (b j / ai ) log p (b j / ai ) H (Y / xi )
j i j
•输出对称
1 p (b j ) p (ai ) p (b j / ai ) p (b j / ai ) n i i
迭代算法计算信道容量
信道的基本概念
信道分类:
研究信道主要考虑信道中受干扰的影响,由于信道存在的干扰使输入信号和输出 信号之间没有固定的函数关系,只有统计依赖关系,因此可以通过分析输入和输出信 号之间的统计特性来研究信道。 实际通信系统中,信道的种类很多,包含的设备也不相同,因此可以按照不同的 角度对信道进行分类。 根据用用户数量:信道可以分为单用户信道和多用户信道。 单用户信道只有一个输入端和一个输出端,信息只朝一个方向单向传输; 多用户信道的信号输入和输出端至少有一端有两个以上用户,信息在两个方向都能传 输。 根据输入端和输出端关系:无反馈信道、有反馈信道 根据信道参数与时间的关系:固定参数信道(光纤、电缆)、时变参数信道(无线信 道)。 根据噪声种类: 随机差错信道(高斯白噪声为主题的信道)、突发差错信道(噪声干 扰的影响前后相关,如:衰落信道、码间干扰信道)。 根据输入输出信号的特点:离散信道、连续信道、半离散半连续信道以及波形信道。
0.3 0.1 0.6; 0.2 0.5 0.3;
C1=logm(PX*B') C2=logm(max(B)) while (1) if abs(C1-C2)<e break; end for i=1:1:S(1) PX(i)=PX(i)*B(i)/(PX*B'); end for k=1:1:S(1) I=0; PY=zeros(1,S(2)); for j=1:1:S(2) for i=1:1:S(1) PY(j)=PY(j)+PX(i)*PY_X(i,j); end I=I+PY_X(k,j)*log2(PY_X(k,j)/PY(j)); end B(k)=expm(I); end C1=logm(PX*B'); C2=logm(max(B)); end C=C1
实验二 计算信道容量

实验二 一般信道容量迭代算法

是任意给定的一组初始输入分布,其所有分量 P0 (ai ) 均不为零。按下式不断对输入分布进行迭代、更新
P
n 1
(ak ) p (ak )
n
k ( PXn )
p
i 1
r
n
(ai ) i ( PXn )
其中
k ( P ) exp[ I ( x ak ; Y )] |P
n X
X
n PX
exp{ P(b j | ak ) log
j 1
s
P(b j | ak )
P
i 1
r
}
n
(ai ) P(b j | ai )
信道容量的迭代算法流程图
在迭代算法流程图中
当c(n)与c’(n)的差值小于某个给定值时,迭代结束。
三、实验内容
用matlab软件编程实现一般信道容量迭代算法 设定不同的迭代精度 设定不同的信道
关于输入概率分布Px的最大值问题。
一般DMC信道容量
一般DMC信道容量的计算非常困难,信道容量计算的
迭代算法能在给定的精度下用有限步数计算出一般
DMC的信道容量。
信道容量的迭代算法
设DMC的转移概率矢量为 Py| x {P(b j | ai )}i , j ,记
PX0 {P 0 (ai )}i
信道容量的定义
C max R max I ( X ; Y )bit / 符号
Px Px
1 C max Rt max I ( X ; Y ) bit / s Px Px t
信道
核心问题是信道容量和最佳输入分布。 根据定义,求信道容量问题就是求平均互信息量I(X;Y)
信道容量迭代算法

附录:实验代码(C++)
#include<iostream> using namespace std; #include<math.h> #define MAX 50 double Calculate_C1(double p[],double a[]); double Calculate_C2(double a[]); int r,s; double P[MAX][MAX]; int main() { int i,j; double C1,C2,E; double a[MAX],p[MAX]; E=0.000001; cout<<"请输入信源符号个数 r:\n"; cin>>r; cout<<"请输入信宿符号个数 s:\n"; cin>>s; cout<<"请输入信道转移概率矩阵 P[bj][ai]:\n"; for(i=0;i<r;i++) for(j=0;j<s;j++) cin>>P[i][j]; for(i=0;i<r;i++) p[i]=1.0/r; do { for(i=0;i<r;i++) { int w,j; double temp,sum2=0; for(j=0;j<s;j++) { double qj=0; for(w=0;w<r;w++) { qj+=p[w]*P[w][j]; } temp=P[i][j]/qj;
算法原理
1. 2.
1 (0) 初始化信源分布:pi= ,循环变量 k=1,门限△,C =- r
信道容量的迭代算法

输入
s P(y j | x i ) ai(n) exp y j | x i ) ln q(y j ) j 1 (i=1,2...)
u (n) p(x i )ai (n)
i
I L log 2 (u (n) ), IU log 2 (max(a i(n) ))
I (X; Y) p(x i ) p(y j | x i ) ln
i j
p(x ) p(y
i i
p(y j | x i )
j
| xi )
(1)
要求信道容量 C 就是要在 p(x i ) 的约束下,求 I (X; Y) 的极大值。 首先引入后验概率,即:
q(x i | y j )
p(x ) p(y
表 1.1 ε的选取与信道容量关系 因此,使用该算法计算 C 的时候要选取适当的ε值,才能保证 值的准确性。
四 程序说明 1、程序采用的是C++语言,编译环境为visual studio 2010 2、信道矩阵放在“Channel_matrix.txt”中,其中初始信源为等概 1/R(R表示信源个数),并放在vector<float> pxi中。 3、本程序使用#define wucha ε 定义误差,因此通过改变 wucha 的值就可以控制迭代的次数 4、程序为:channel_code.cpp 信道矩阵为:Channel_matrix.txt
信道容量的迭代算—彭海军
研究信道的目的是要讨论信道中平均每个符号所能传送的信息 量,而将最大的信息传输率称为信道容量。由于对于普通的线性信 道(信道矩阵 r=s),直接可以采用 C ln e 求解信道容量。但当
求解一般信道容量的方法分析

( Y) 到极大值( 于信 X; 达 等 } 满足
p ̄ 0 i
在通 讯系统 中经常要计 算信道 的容量 ,传 统的计算 方 法是人 工进 行的 , 其中要涉 及到大量 的数据 , 工计算不仅 人
() (iY) 对所有 x, p= 2 I ; s C, x i其 i0 这时 C就是所求的信道容量 。 2 .信 道容 量的求解方法
a( P
信道 每秒 钟平均传输的信息量 为
R= (; ) t }I Y =IHX 一, (l ( 特/ x ()  ̄HX ) 比 秒) l V
一
∑P0 1 (= a
值, 然后再求解 出信道容量 C。因为
I Y ( xI )
。
(2 2) .
般称此为信息传输率 。
可 以先求 出达 到极值 的概率分 布和拉格 朗 日乘 子 入的
个方程式两 边分别乘 以达 到极值 的输 入概率 P, i 并求 和得
p (j 。 i b g P l
i
+。 1ge
(_ 25 )
上 式 左 边 即 是信 道 容 量 , 以得 C h lge 所 = +o 。
根 据 式 23和 25可 得 . .
图 1 信道 容量迭代算法流 程图
一 =
Pa l (0 0 N g e
0
作 者简 介 : 陈长 生 , , 南驻 马 店人 , 男 河 本科 , 助教 , 究 方向 :信 息技 术 , R 嵌入 式 技 术 ,DA技 术 。 研 AM E
~
6 — 8
对 i 12 3 … … 、 都 成 立 。 = … r
又因 为∑P D (l =( 和∑ P j = (1 、 ( b k P ) a P i) a (l 1 i 、 b) = 2  ̄
迭代求信道容量

迭代法求(非对称)信道容量前言:对于给定的信道,除了对称信道之外,信道容量的计算是比较复杂的,但可以用迭代算法实现近似的信道容量。
具体细节:1..设输入变量为A (ai ),输出为B(bi),对于给定的信道,信道转移矩阵一般都为定值,设为已知,用矩阵Pa2b 表示。
2.为了提高计算效率,将累加求和等运算尽量用矩阵运算而不是循环运算。
实验数据分析:实验发现,当输入的信道转移矩阵为对称信道时,输入分布很快收敛于等概分布,然后很快的退出迭代运算而输出结果,当然这时候的结果是经检验不正确的。
具体分析原因如下:当迭代至输入分布赋值为等概(或接近等概)时,事实上我们一开始就初始化输入分布P (ai )为等概分布,由])|()()|(ln)|(exp[∑∑=j i i j ii j i j i a b P a P a b P a b P α其中)(j b P =)|()(i j i ia b P a P ∑,当)(i a P 等概分布且信道为准对称时易得)(j b P 等概记为P(b0)。
所以])()|(log )|(exp[0b P a b P a b P i j i j j i ∑=α,由对称矩阵性质易得每行求和后数值相等。
故得到i α是相等的(记为0α)。
所以:C(n ,n)=)ln())(ln())(ln())(ln(000αααα===∑∑∑ii i i i i i a P a P a P 而另一变量: C '(n+1,n)=)ln()max ln(0αα=i i可见C=C ',则C-C '<ε恒成立,故退出整个迭代过程,而得不到正确的结果。
具体实现代码(matlab )如下:%通过迭代算法求某信道的信道容量%%设输入变量为A (ai ),输出为B(bi),对于给定的信道,信道转移矩阵一般都为定值,设为已知,用矩阵Pa2b 表示%%为了提高计算效率,讲累加求和等运算尽量用矩阵运算而不是循环运算%%最后为了方便调用,将其封装成一个函数。
实验二---一般信道容量迭代算法.doc

实验二---一般信道容量迭代算法.doc实验二一般信道容量迭代算法1.实验目的掌握一般离散信道的迭代运算方法。
2.实验要求1)理解和掌握信道容量的概念和物理意义2)理解一般离散信道容量的迭代算法3)采用Matlab 编程实现迭代算法4)认真填写试验报告3.算法步骤①初始化信源分布),,,,,(21)0(p p p p P ri =(一般初始化为均匀分布) ,置迭代计数器k=0 ,设信道容量相对误差门限为δ ,δ>0 ,可设-∞=C )0(;②∑=i k i ij k i ij k ji p p p p )()()(? s j r i ,??=??=,1;,,1 ③∑∑∑??=+i k ji j ij k ji j ij k i p p p ??)()()1(ln exp ln exp r i ,,1??= ④??=∑∑+ik ji j ij k p C ?)()1(ln exp ln ⑤如果δ≤-++C C Ck k k )1()()1( ,转向⑦;⑥置迭代序号k k →+1,转向②;⑦输出p k i )1(+和C k )(1+的结果;⑧停止。
4.代码P=input('转移概率矩阵P=')e=input('迭代精度e=')[r,s]=size(P);n=0;C=0;C_k=0;C_k1=0;X=ones(1,r)/r;A=zeros(1,r);B=zeros(r,s);%初始化各变量while(1)n=n+1;for i=1:rfor j=1:sB(i,j)=log(P(i,j)/(X*P(:,j))+eps); if P(i,j)==0B(i,j)=0;elseendendA(1,i)=exp(P(i,:)*B(i,:)');endC_k=log2(X*A');C_k1=log2(max(A));if (abs(C_0-C_1)。
信道容量迭代计算实验报告

信道容量迭代计算实验报告王升信科1002信道容量迭代计算实验报告一、实验目的:了解信道容量的定义和计算方法,能编写出正确的程序进行迭代计算得出信道容量。
二、实验要求:1)输入:输入信源个数、信宿个数和信道容量的精度,程序能任意生成随机的信道转移概率矩阵。
2)输出:输出最佳信源分布和信道容量。
三、实验环境:Matlab四、实验原理:五、源程序代码:clear;r=input('输入信源个数:');s=input('输入信宿个数:');deta=input('输入信道容量的精度: ');Q=rand(r,s); %创建m*n随机分布矩阵A=sum(Q,2);B=repmat(A,1,s);disp('信源转移概率矩阵:'),p=Q./B %信源转移概率矩阵i=1:1:r;q(i)=1/r;disp('原始信源分布:'),qc=-10e-8;C=repmat(q',1,s);for k=1:1:100000m=p.*C; %后验概率的分子部分a=sum(m); %后验概率的分母部分su1=repmat(a,r,1);t=m./su1; %后验概率矩阵D=exp(sum(p.*log(t),2)); %信源分布的分子部分su2=sum(D); %信源分布的分母部分q=D/su2; %信源分布C=repmat(q,1,s);c(k+1)=log(sum(exp(sum(p.*log(t),2))))/log(2); kk=abs(c(k+1)-c(k))/c(k+1);if(kk<=break;endenddisp('最大信道容量时的信源分布:q='),disp(q') disp('最大信道容量:c='),disp(c(k+1))六、实验结果:。
实验一:信道容量的迭代算法
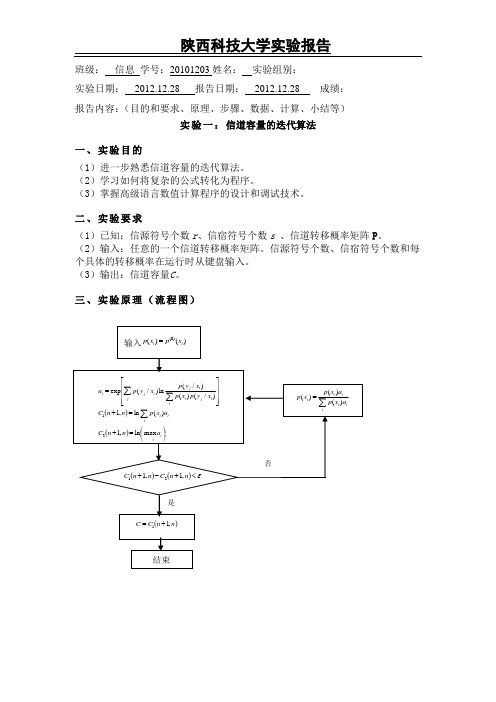
陕西科技大学实验报告 班级: 信息 学号:20101203姓名: 实验组别:实验日期: 2012.12.28 报告日期: 2012.12.28 成绩: 报告内容:(目的和要求、原理、步骤、数据、计算、小结等)实验一:信道容量的迭代算法一、实验目的(1)进一步熟悉信道容量的迭代算法。
(2)学习如何将复杂的公式转化为程序。
(3)掌握高级语言数值计算程序的设计和调试技术。
二、实验要求(1)已知:信源符号个数r 、信宿符号个数s 、信道转移概率矩阵P 。
(2)输入:任意的一个信道转移概率矩阵。
信源符号个数、信宿符号个数和每个具体的转移概率在运行时从键盘输入。
(3)输出:信道容量C 。
三、实验原理(流程图)是 否 ()()⎪⎭⎫ ⎝⎛=+=+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=∑∑∑i i i i i j i i j i i j i j i a n n C a x p n n C x y p x p x y p x y p a max ln ,1)(ln ,1)/()()/(ln )/(exp 21 输入)()()0(i i x p x p = ()()ε<+-+n n C n n C ,1,121 ()n n C C ,11+= ∑=i i i i i i a x p a x p x p )()()( 结束四、实验数据(源代码)#include <stdio.h>#include <math.h>//以2为底的对数为logx#include <stdlib.h>void main(){register int i,j;register int k;int N,M;//行,列float *p=0;float *q=0;float *d=0;float *a=0;float *sum=0; //sum数组为各行概率累加求和float **p_yx=0; //二维数组p_yx存放信道矩阵float C,b,u,max,IL,IU; //C为信道容量,b为迭代精度printf("请输入信源符号个数: "); //输入行列scanf("%d",&N);printf("请输出信宿符号个数: ");scanf("%d",&M);p=(float *)calloc(N,sizeof(float)); //初始化需要用到的数组q=(float *)calloc(M,sizeof(float));d=(float *)calloc(N,sizeof(float));a=(float *)calloc(N,sizeof(float));sum=(float *)calloc(N,sizeof(float));p_yx=(float **)calloc(N,sizeof(float));for(i=0;i<N;i++){p_yx[i]=(float *)calloc(M,sizeof(float));}printf("请输入信道转移概率矩阵:\n"); //输入信道矩阵for(i=0;i<N;i++){for(j=0;j<M;j++){printf("p_yx[%d][%d]=",i,j);scanf("%f",&p_yx[i][j]);}printf("\n");}for(i=0;i<N;i++) //判断输入的信道矩阵是否符合概率分布{sum[i]=0.0;for(j=0;j<M;j++)sum[i]=sum[i]+p_yx[i][j];}for(i=0;i<N;i++){if(sum[i]<=0.999999||sum[i]>=1.000001)printf("不符合概率分布");elseif(sum[N-1]>=0.999999&&sum[N-1]<1.000001) {printf("请输入迭代精度:");scanf("%f",&b);}break;}for(i=0;i<N;i++) //取初始概率为均匀分布p[i]=1.0/N;for(j=0;j<M;j++) //计算q[j]{q[j]=0;for (i=0;i<N;i++)q[j]=q[j]+p[i]*p_yx[i][j];}for(i=0;i<N;i++) //计算a[i]{d[i]=0;for(j=0;j<M;j++){if(p_yx[i][j]==0)d[i]=d[i]+0;elsed[i]=d[i]+p_yx[i][j]*log(p_yx[i][j]/q[j]); }a[i]=exp(d[i]);}u=0.0;for(i=0;i<N;i++) //计算uu=u+p[i]*a[i];IL=log(u)/log(2.0); //计算ILmax=a[0];for(i=0;i<N;i++){if(a[i]>=max)max=a[i];}IU=log(max)/log(2.0); //计算IUk=1;C=IL;while((IU-IL)>=b)//迭代计算{for(i=0;i<N;i++)p[i]=p[i]*a[i]/u;for(j=0;j<M;j++) //计算q[j]{q[j]=0;for (i=0;i<N;i++)q[j]=q[j]+p[i]*p_yx[i][j];}for(i=0;i<N;i++) //计算a[i]{d[i]=0;for(j=0;j<M;j++){if(p_yx[i][j]==0)d[i]=d[i]+0;elsed[i]=d[i]+p_yx[i][j]*log(p_yx[i][j]/q[j]); }a[i]=exp(d[i]);}u=0.0;for(i=0;i<N;i++) //计算uu=u+p[i]*a[i];IL=log(u)/log(2.0); //计算ILmax=a[0];for(i=0;i<N;i++){if(a[i]>=max)max=a[i];}IU=log(max)/log(2.0); //计算IUk=k+1;}C=IL;printf("信道矩阵为:\n"); //输出for(i=0;i<N;i++){for(j=0;j<M;j++){printf("%.2f ",p_yx[i][j]);}printf("\n");}printf("此次信道的迭代次数:k=%d\n",k);printf("信道容量C=%f比特/符号\n",C);}五、程序运行结果:六、实验小结:本次试验是建立在迭代的基础上,首先要深刻理解信道容量的迭代算法,其次是如何将复杂的公式转化为程序通过此次实验,我了解了信道容量的迭代算法的基本知识,学会了如何将复杂的公式如何用程序语言描述出来,掌握了高级语言数值计算过程程序的设计和调试的相关知识,对于将实际问题公式转化为程序的能力有提高。
大学信息论_信道容量的迭代算法

陕西科技大学实验报告 班级: XXXX 学号:XXXXXXXXX 姓名:XXX 实验组别: 实验日期: 报告日期: 成绩: 报告内容:(目的和要求、原理、步骤、数据、计算、小结等)实验名称:信道容量的迭代算法一、实验目的(1) 进一步熟悉信道容量的迭代算法。
(2) 学习如何将复杂的公式转化为程序。
(3) 掌握高级语言数值计算程序的设计和调试技术。
二、实验要求(1)已知:信源符号个数r 、信宿符号个数s 、信道转移概率矩阵P 。
(2)输入:任意的一个信道转移概率矩阵。
信源符号个数、信宿符号个数和每个具体的转移概率在运行时从键盘输入。
(3)输出:信道容量C 。
三、实验原理(流程图):1: procedure ChannelCapacity(r, s, (ji p ))2: initialize: 信源分布1i p r =,相对误差门限δ,C =-∞ 3: repeat4: 1i jiij r ijii p p p p φ=←∑ 5: 111exp log exp log s ji ij j i r s ji ij i j p p p φφ===⎛⎫ ⎪⎝⎭←⎛⎫ ⎪⎝⎭∑∑∑ 6: 11log exp log r s ji ij i j C p φ==⎡⎤⎛⎫←⎢⎥ ⎪⎢⎥⎝⎭⎣⎦∑∑ 7: until C Cδ∆≤ 8: output C9: end procedure四、实验数据(源代码):#include<stdio.h>#include<math.h>#define MAX 100double Calculate_a(int k,double pa[]); double Calculate_C1(double pa[],double a[]); double Calculate_C2(double a[]);int r,s;double pba[3][3];void main(){int i,j;double C1,C2,E;double a[MAX],pa[3];E=0.000001;r=3;s=3;pa[0]=0.2;pa[1]=0.3;pa[2]=0.5;pba[3][3]={0.5,0.33333333,0.16666666,0.16666666,0.5,0.333333333,0.333 33333,0.16666666,0.5};do{for(i=0;i<r;i++)a[i]=Calculate_a(i,pa);C1=Calculate_C1(pa,a);C2=Calculate_C2(a);if(C2-C1>=E){double sum=0;for(i=0;i<r;i++)sum+=pa[i]*a[i];for(i=0;i<r;i++)pa[i]=pa[i]*a[i]/sum;}else{printf("最佳信源概率:\n");for(i=0;i<r;i++)printf(" %lf \n",pa[i]);}}while(C2-C1>=E);printf("信道容量为:%lf\n",C1/log(2));}double Calculate_a(int k,double pa[]){int i,j;double temp,sum2=0;for(j=0;j<s;j++){double sum1=0;for(i=0;i<r;i++){sum1+=pa[i]*pba[i][j];}temp=pba[k][j]/sum1;temp=log(temp);sum2+=pba[k][j]*temp;}return exp(sum2);}double Calculate_C1(double pa[],double a[]){int i;double sum=0;for(i=0;i<r;i++)sum+=pa[i]*a[i];return log(sum);}double Calculate_C2(double a[]){int i;double max=a[0];for(i=0;i<r;i++)if(max<a[i]) max=a[i];return log(max);}五、程序运行结果:最佳信源概率:0.3333300.3333340.333337信道容量为:0.125815Press any key to continue六、实验小结:通过本次实验,我了解了信道容量的迭代算法,在理论的掌握基础上,更进一步的实现了程序的运行算法,同时又加深了编程语言上的一些不足和毛病.。
一般信道的信道容量求解

一般信道的信道容量求解组员:文枝传李红井任富绳马增敏指导教师:张坤老师一:实验目的使学生学会利用Matlab求解信道容量及最佳概率分布,帮助学生巩固所学知识,同时拓展学生的知识。
二:实验内容已知信道的转移矩阵P_YX为3.03.01.03.01.01.01.07.03.0 2.04.0 1.009.02.065.006 .03.03.02.02.027.04.023.01.0求该信道的信道容量和最佳概率输入分布。
三:实验步骤及编码方法(1) 建立一个名为contmax的文件,输入以下内容:%任意信道的信道容量C及最佳输入分布P_X源程序function [P_X,C,N]=contmax(P_YX,e)% 计算任意信道的信道容量C及最佳输入分布P_X% P_X -------最佳概率输入分布% C----------信道容量N----------迭代次数% P_YX-----DMC信道的转移矩阵e-----------精度if length(find(P_YX<0)~=0)error('Not a probable vector.Negtive component');endif abs(sum(P_YX')-1)>10e-10error('Not a probable vector,Component do not add up to "1" '); end% 变量初始化C1=1;C=0;N=0;r=size(P_YX);P_X=ones(1,r(1))/r(1);% 调整P_YX的零元素值Pyx=(P_YX==0).*eps;P_YX=P_YX+Pyx;% 迭代求解while (abs(C1-C))>eP_Y=P_X*P_YX;I1=sum((P_YX.*log2(P_YX))');I2=log2(P_Y)*(P_YX'); BETA=exp(I1-I2);B=P_X*(BETA');C1=log(B);C=log(max(BETA));P_X=P_X.*BETA/B;N=N+1;(2) 在命令窗口输入信道的转移矩阵P_YX>> P_YX=[0.1 0.23 0.4 0.27;0.2 0.2 0.3 0.3;0.06 0.65 0.2 0.09;0.1 0.4 0.2 0.3;0.7 0.1 0.1 0.1;0.3 0.1 0.3 0.3]P_YX =0.1000 0.2300 0.4000 0.27000.2000 0.2000 0.3000 0.30000.0600 0.6500 0.2000 0.09000.1000 0.4000 0.2000 0.30000.7000 0.1000 0.1000 0.10000.3000 0.1000 0.3000 0.3000四:实验结果[P_X,C,N]=contmax(P_YX,0.01)P_X =0.1495 0.0005 0.4101 0.0021 0.4299 0.0080C =0.4290N =37>> [P_X,C,N]=contmax(P_YX,0.001)P_X =0.1647 0.0000 0.4037 0.0001 0.4304 0.0011C =0.4215N =64五:实验分析由上比较分析得,当精度e=0.01时,P_X为最佳概率输入分布,即P_X =0.1495 0.0005 0.4101 0.0021 0.4299 0.0080此时,信道容量C = 0.4290(bit/符号)。
信息论实验报告(实验二、离散信道容量的计算)

学生实验报告院别电子信息学院课程名称信息论语编码实验班级实验名称实验二、离散信道容量的计算姓名实验时间学号指导教师成绩报告内容一、实验目的和任务1、理解和掌握信道容量的概念和物理意义;2、了解信道容量的计算方法3、采用计算机编程实现(MATLAB)二、实验原理介绍三、实验设备介绍1、计算机2、编程软件MATLAB6.5以上四、实验内容和步骤分别求出如下信道的信道容量1、信道转移概率矩阵为1/31/31/61/61/61/61/31/3P ⎡⎤=⎢⎥⎣⎦2、信道转移概率矩阵为:1/31/31/61/61/61/31/61/3P ⎡⎤=⎢⎥⎣⎦1、面出程序设计的流程图。
2、写出在调试过程中出现的问题。
3、 对实验的结果进行分析。
五、实验数据记录六、实验结论与心得通过本次实验,加强了对matlab 程序的学习,进一步提高了我的编程能力。
尊敬的赞助商:**于200X年X月X日举办一个全校性的综合型运动会,历时一周。
期间包括三个部分:开幕式文艺演出、运动会和闭幕式颁发奖项(两天)。
我们校学生会外联部是此类校园活动指定宣传策划单位,对商家赞助大学生活动的可行性,特别是赞助我校运动会活动的可行性有较深入的了解。
现在就让我们为贵公司作此赞助可行性报告。
一、行性分析1、本次运动会得到了学院团委和学校相关部门的大力支持,规模大、参与者多,能吸引更多师生及其家属来观看,深受同学欢迎,并推动学校体育事业的发展,必引起全校性的轰动。
2、在校大学生达XXXX余人,人流量大达到运动会每天入场观看人次为XXXX左右。
人口密集,而且本校的消费能力较高,为贵公司宣传的成效更明显。
3、本次活动得到师生关注,贵公司的产品也将得到大力的宣传。
二、宣传方式1、横幅:为期一周的大横幅宣传,在学校内悬挂横幅,(横幅内容为运动会的内容和公司的相关宣传--赞助商名称)活动前三天粘贴在运动场等人流量最多的位置。
悬挂时间是一天24小时不间断性。
2、我们将在运动会的宣传海报中点明贵公司为赞助单位。
信道容量的计算

§4.2信道容量的计算这里,我们介绍一般离散信道的信道容量计算方法,根据信道容量的定义,就是在固定信道的条件下,对所有可能的输入概率分布)(x P 求平均互信息的极大值。
前面已知()Y X I ;是输入概率分布的上凸函数,所以极大值一定存在。
而);(Y X I 是r 个变量)}(),(),({21r x p x p x p 的多元函数。
并且满足1)(1=∑=ri i x p 。
所以可用拉格朗日乘子法来计算这个条件极值。
引入一个函数:∑-=iix p Y X I )();(λφ解方程组0)(])();([)(=∑∂-∂∂∂i ii i x p x p Y X I x p λφ1)(=∑iix p (4.2.1)可以先解出达到极值的概率分布和拉格朗日乘子λ的值,然后在解出信道容量C 。
因为)()(log)()();(11i i i i i ri sj i y p x y Q x y Q x p Y X I ∑∑===而)()()(1i iri ii x yQ x p y p ∑==,所以e e y p y p i i i i i x y Q i x p i x p log log ))(ln ()(log )()()(==∂∂∂∂。
解(4.2.1)式有0log )()()()()()(log )(111=--∑∑∑===λe y p x y Q x y Q x p y p x y Q x y Q ii i i i r i s j i i i i sj i i (对r i ,,2,1 =都成立) 又因为)()()(1j k krk ky p x yQ x p =∑=ri x y Q sj i j,,2,1,1)(1==∑=所以(4.2.1)式方程组可以转化为),,2,1(log )()(log)(1r i e y p x y Q x y Q j i j sj i j =+=∑=λ1)(1=∑=ri ix p假设使得平均互信息);(Y X I 达到极值的输入概率分布},,{21r p p p 这样有e y p x y Q x y Q x p j i j i j r i sj i log )()(log)()(11+=∑∑==λ从而上式左边即为信道容量,得 e C log +=λ 现在令)()(log)();(1j i j sj i j i y p x y Q x y Q Y x I ∑==式中,);(Y x I i 是输出端接收到Y 后获得关于i x X =的信息量,即是信源符号i x X =对输出端Y 平均提供的互信息。
信道编码第二次试验实验报告

信道编码第二次试验实验报告一、实验目的1、实现F2(x)多项式的加法、乘法以及除法运算;求多项式的周期;2、编写同余类域的生成、加法计算、乘法运算、除法运算、幂运算、元素求阶以及求解极小多项式的程序;二、实验原理1、多项式运算:加、乘多项式相加:同次项系数按照二元域中的加法相加;多项式相乘:按普通多项式的乘法相乘,计算系数按二元域上的加法和乘法运算。
2、多项式的除法:给定任意两个多项式f(x)、g(x),一定存在唯一的多项式q(x)和r(x),使:f(x)=q(x)g(x)+r(x) ə(r(x))≤ə(g(x))r(x)称为f(x)模g(x)的余式3、多项式的周期:定义:设f(x)为二元域上次数不为0的多项式,且f(0)≠0,则f(x)|(xn+1)的最小正整数n称为多项式f(x)的周期,(n>=ə(f(x)))实现方法:方法一:长除法求多项式周期用多项式f(x)按升幂排列去除1,当所得余式是单项xn时,f(x)的周期即为n。
方法二:利用欧拉-费尔马定理4、GF(2)的扩域GF(2^n)扩域GF(2^n):设p(x)为GF(2)上的n次既约多项式,模p(x)的所有2^n个余式在模p(x)加法和乘法下构成2^n元域,称为GF(2)的扩域(也称为模p(x)的剩余类域),记为GF(2^n)。
5、幂运算:元素累乘6、元素求阶:具有性质a^n=e的最小正整数n称为a的阶7、求解元素的极小多项式:最小多项式:以扩域GF(2m)上的非零元素β为根的最低次多项式称为β的最小多项式,记为M (x)求解方法:待定系数法三、实验结果我在我的函数中规定:代表多项式的向量,从左到右为多项式高次到低次1、多项式的加、乘运算:在进行多项式的加法、乘法运算的编程时,思路来自于老蒋蒋凌云。
加法:二元域上的多项式加法遵从模2加的运算规则。
在编程时,输入的两个向量必须维度一致,MATLAB才能对其进行处理和运算。
因此,先将输入的两个多项式向量维度设定一致,再运用mod函数求出最终结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二---一般信道容量迭代算法
实验二 一般信道容量迭代算法
1.实验目的
掌握一般离散信道的迭代运算方法。
2.实验要求
1)理解和掌握信道容量的概念和物理意义
2)理解一般离散信道容量的迭代算法
3)采用Matlab 编程实现迭代算法
4)认真填写试验报告
3.算法步骤
①初始化信源分布),,,,,(21)0(p p p p P r
i ⋯⋯⋯⋯=(一般初始化为均匀分布),置迭代计数器k=0,设信道容量相对误差门限为δ,δ>0,可设-∞=C )0(; ②∑=i k i ij k i ij k ji p p p p )()
()
(ϕ s j r i ,⋯⋯=⋯⋯=,1;,,1 ③∑∑∑⎪⎭
⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=+i k ji j ij k ji j ij k i p p p ϕϕ)()()1(ln exp ln exp r i ,,1⋯⋯= ④⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=∑∑+i
k ji j ij k p C ϕ)()1(ln exp ln ⑤如果δ≤-++C C C k k k )1()()1(,转向⑦;
⑥置迭代序号k k →+1,转向②;
⑦输出p k i )
1(+和C k )(1+的结果;
⑧停止。
4.代码P=input('转移概率矩阵P=')
e=input('迭代精度e=')
[r,s]=size(P);
n=0;
C=0;
C_k=0;
C_k1=0;
X=ones(1,r)/r;
A=zeros(1,r);
B=zeros(r,s);%初始化各变量
while(1)
n=n+1;
for i=1:r
for j=1:s
B(i,j)=log(P(i,j)/(X*P(:,j))+eps);
if P(i,j)==0
B(i,j)=0;
else
end
end
A(1,i)=exp(P(i,:)*B(i,:)');
end
C_k=log2(X*A');
C_k1=log2(max(A));
if (abs(C_0-C_1)<e) C=C_0; %检验是否满足迭代精度 fprintf('迭代次数n=\n',n)%满足则输出相关的被求量
fprintf('信道容量:C=\n',C)
disp('最佳分布P(x)=');disp(X);
break; else %不满足则继续迭代
X=(X.*A)/(X*A');
continue;
end
end
5.计算下列信道的信道容量
例一:
0.980.02 0.050.95⎡⎤⎢⎥⎣⎦
P =
0.9800 0.0200
0.0500 0.950
e =
1.0000e-005
迭代次数: n=5
信道容量: C=0.785847比特/符号最佳分布P(x)=
0.5129 0.4871
例二:
0.60.4 0.010.99⎡⎤⎢⎥⎣⎦
P =
0.6000 0.4000
0.0100 0.9900
e =
1.0000e-005
迭代次数: n=17
信道容量: C=0.368768比特/符号最佳分布P(x)=
0.4238 0.5762
例三:
0.790.160.05 0.050.150.8⎡⎤⎢⎥⎣⎦
P =
0.7900 0.1600 0.0500
0.0500 0.1500 0.8000
e =1.0000e-005
迭代次数: n=6
信道容量: C=0.571215比特/符号
最佳分布P(x)=
0.5009 0.4991
.思考题:
迭代精度指的是什么?它对计算结果的影响?
迭代精度小数点的位数与迭代次数相同,迭代精度越小,信道容量越大。
