第6讲 LR分析法
第6章-自底向上的LR分析法

DFA的状态,将go函数作为状态转换函数, 构造出的DFA即为所求。
初始状态:CLOSURE({S ’ →.S})
40
例题
例6.1 对于文法G[S]: S→vI:T I→I,i I→i T→r 经拓广并对产生式编号后为G’[S]: 1. S’ →S 2. S → vI:T 3. I→I,i 4. I→i 5. T→r
文法G[S]的拓广:G’[S’]=G[S]+{S’ → S}; 文法的每个项目为NFA的一个状态; 确定状态之间的转换关系; 按规则可对文法G’的所有项目对应的状态构
造出识别活前缀的NFA。
34
LR(0)项目集规范族C
提出“LR(0)项目集规范族”的原因 若按以上方法先构造NFA,然后再确定
37
若I={E ’ →.E} CLOSURE(I)为:
E ’ →.E E→.E+T E→.T T→.T*F T→.F F→.i F→.(E)
利用上述算法可以把拓广文法G’的所有 LR(0)项目分成几个等价类,每个等价类就是 识别活前缀的DFA的一个状态。
38
go(I,X)函数
如果LR(0) 项目集规范族中的每个项目 集看做DFA一个状态,则项目集规范族的go 函数把这些项目集连接成一个DFA。
12
LR(k)的含义
L表示从左到右扫描输入串; R表示利用最右分析方法来识别句子,即构造 一个最右推导的逆过程; k表示向右查看输入串符号的个数。
规范推导的逆过程,所以LR 分析过程是规范归约的过程。
LR分析法根据当前分析栈中的符号串和 向右顺序查看输入串的k个符号就可以唯一确 定分析器的动作是移进还是归约、利用那个 产生式进行归约。
LR分析法

1语言子集的词法描述:设文法G[E]:(1) E ::= S(2) S ::= BB(3) B ::= aB | b2程序的功能能够识别一切符合文法G[E]的句子。
3算法描述LR分析器由三个部分组成:(1) 总控程序,也可称驱动程序。
对所有的LR分析器总控程序都是相同的。
(2) 分析表或分析函数,不同的文法分析表将不同,同一个文法采用的LR分析器不同时,分析表将不同,分析表又可以分为动作表(ACTION)和状态转换(GOTO)表两个部分,它们都可用二维数组表示。
(3) 分析栈,包括文法符号栈和相应的状态栈,它们均是先进后出栈。
分析器的动作就是由栈顶状态和当前输入符号所决定。
LR分析器结构:其中:SP为栈指针,S[i]为状态栈,X[i]为文法符号栈。
状态转换表用GOTO[i,X]=j表示,规定当栈顶状态为i,遇到当前文法符号为X时应转向状态j,X为终结符或非终结符。
ACTION[i,a]规定了栈顶状态为i时遇到输入符号a应执行。
动作有四种可能:(1)移进:action[i,a]= Sj:状态j移入到状态栈,把a移入到文法符号栈,其中i,j表示状态号。
(2)归约::当在栈顶形成句柄时,则归约为相应的非终结符A,即文法中action[i,a]=rk有A->B的产生式,若B的长度为R(即|B|=R),则从状态栈和文法符号栈中自顶向下去掉R个符号,即栈指针SP减去R,并把A移入文法符号栈内,j=GOTO[i,A]移进状态栈,其中i为修改指针后的栈顶状态。
(3)接受acc:当归约到文法符号栈中只剩文法的开始符号S时,并且输入符号串已结束即当前输入符是'#',则为分析成功。
(4)报错:当遇到状态栈顶为某一状态下出现不该遇到的文法符号时,则报错,说明输入端不是该文法能接受的符号串。
4源程序清单void main(){int g,h,i,j,k,l,p,y,z,count;char x,copy[10],copy1[10];top1=0;top2=0;top3=0;top=1;a[0]=0;y=a[0];b[0]='#';count=0;z=0;cout<<"文法G[E]:"<<endl;cout<<'\t'<<"(1) E::=S"<<endl;cout<<'\t'<<"(2) S::=BB"<<endl;cout<<'\t'<<"(3) B::=aB|b"<<endl;cout<<endl<<"文法G[E]合法句子举例: aabaab";cout<<endl<<"******************************************************* ******"<<endl<<endl;cout<<"请输入符号串:";cin>>str;l = strlen(str);str [ l ] = '#';cout<<endl<<'\t'<<'\t'<<"符号串"<<str<<" 分析过程如下:"<<endl<<endl; cout<<"-----------------------------------------------------------------"<<endl;cout<< "步骤" << '\t' << "状态栈" << '\t' << '\t' << "符号栈" << '\t' << '\t' << "输入串" << '\t' <<'\t'<< "ACTION "<<'\t'<<"GOTO"<<endl; do{y=z;m=0;n=0; //y,z指向状态栈栈顶g=top;j=0;k=0;x=str[top];count++;cout<<count <<'\t';while(m<=top1){ //输出状态栈cout<<a[m];m=m+1;}cout<<'\t'<<'\t';while(n<=top2){ //输出符号栈cout<<b[n];n=n+1;}cout<<'\t'<<'\t';cout<<str; //输出输入串str[top-1] = ' ';cout<<'\t'<<'\t';while(x!=vt[j]&&j<=2) j++;if(j==2&&x!=vt[j]){cout<<endl<<"-----------------------------------------------------------------"<<endl;cout<<endl<<"输入字符串不是该文法的一个句子!"<<endl;cout<<endl<<"按任意数字或字母键,回车退出!"<<endl;cin>>i;return;}if(action[y][j]==NULL){cout<<endl<<"-----------------------------------------------------------------"<<endl;cout<<endl<<"输入字符串不是该文法的一个句子!"<<endl;cout<<endl<<"按任意数字或字母键,回车退出!"<<endl;cin>>i;return;}elsestrcpy(copy,action[y][j]);if(copy[0]=='S'){ //处理移进z=copy[1]-'0';top1=top1+1;top2=top2+1;a[top1]=z;b[top2]=x;top=top+1;i=0;while(copy[i]!='#'){cout<<copy[i];i++;}cout<<endl;}if(copy[0]=='r'){ //处理归约i=0;while(copy[i]!='#'){cout<<copy[i];i++;}h=copy[1]-'0';strcpy(copy1,LR[h]);while(copy1[0]!=vn[k]) k++;l=strlen(LR[h])-4;top1=top1-l+1;top2=top2-l+1;y=a[top1-1];p=goto1[y][k];a[top1]=p;b[top2]=copy1[0];z=p;cout<<'\t';cout<<p<<endl;}}while(action[y][j]!="acc");cout<<"acc"<<endl;cout<<endl<<"-------------------------------------------------------------"<<endl;cout<<endl<<"输入字符串是该文法的一个句子!"<<endl;cout<<endl<<"按任意数字或字母键,回车退出!"<<endl;cin>>i;}int a[10];char b[10],str[10],c1;int top1,top2,top3,top,m,n;char *action[10][3]={"S3#","S4#",NULL, //ACTION表NULL,NULL,"acc","S6#","S7#",NULL,"S3#","S4#",NULL,"r3#","r3#",NULL,NULL,NULL,"r1#","S6#","S7#",NULL,NULL,NULL,"r3#","r2#","r2#",NULL,NULL,NULL,"r2#"};int goto1[10][2]={1,2, //QOTO表0,0,0,5,0,8,0,0,0,0,0,9,0,0,0,0,0,0};char vt[3]={'a','b','#'}; //存放非终结符char vn[2]={'S','B'}; //存放终结符char *LR[4]={"E->S#","S->BB#","B->aB#","B->b#"};//存放产生式#include <string.h>#include <iostream.h>。
第六章 LR分析法

3
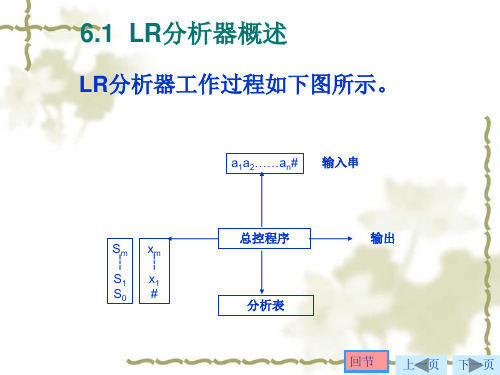
6.1 LR分析概述
一个分析栈、一个驱动程序和一张分析表; 一个输入、一个输出。
输入
id+id*id#
状态栈 符号栈
im
Ym
im-1 Ym-1
…… i0 # 分析栈
LR驱动程序
输出
分
动作
转移 析
action goto
表
4
特殊性
#aAcd
e#
#aAcB
e#
#aAcBe
#
#S
#
动作 移进
移进 归约(A→b) 移进 归约(A→Ab) 移进 移进 归约(B→d) 移进
归约(S→aAcBe) 接受
注意:在分析 过程中,符号
S
栈内容连接剩
余输入串恰为
句型。
A
A
B
a b b c de
输出结果
文法G[S]: (1)S→aAcBe (2)A→b (3)A→Ab (4)B→d
ACTION[i,a]= 归约
接受
出错
7
-移进Shift:
表示:ACTION[i,a]=Sj 动作:状态j和输入符号a分别入符号
栈和状态栈,输入串向前进一字符。
-归约reduce:
表示:ACTION[i,a]=rk 其中: k表示第k个产生式。
动作:设第k个产生式右部长度为m, 左边非终结符为A,距状态栈栈顶m个 位置的状态为p。
造LR分析表。
17
拓广文法:
• 引入一新非终结符作为文法的新开始符,
添加一新产生式: S’→S :S’为新开始符,S为原来的开始符号。
• 拓展文法的目的: • 使文法只有一个以识别符号作为左部的产生
LR分析法
然后将NFA确定化,得DFA(部分)如下:
c
a I0:S→·E
E→·aA E E→·bB
I4:A→c·A A→·cA A→·d
I2:E→a·A A→·cA A→·d
I1:S→E·
b
……
A
I8:A→cA·
d
I10:A→d·
d
I6:E→aA· A
回节 上一页 下一页
方法二:根据文法直接构造识别文法可归前缀的DFA。
回节 上一页 下一页
项目分四类:
(a)圆点在最右端的项目,形如A→·,表示已从输入串看到 能由一条产生式右部推导出的符号串,即已达一可归前缀末端, 已识别出句柄可以归约,这种项目称为归约项目,相应状态称为 归约状态。
(b)对形如S→S·的项目,其中S是文法开始符号,称为接受 项目,相应状态称为接受状态,表明可由S推导的输入串已全部识 别完,整个分析过程成功结束。
③定义状态转换函数GO(I,X)
其中I是项目集,X是文法符号。 GO(I,X)=CLOSURE( J ) 其中J={任何形如A→x•的项目|A→•x∈I} 以上可以避免出现 弧,避免从同状态射出相同标记弧。
回节 上一页 下一页
④构造DFA
a) DFA的初态集:CLOSURE({S→•S}) b) 对初态集或其它所构造的项目集应用转换函数 GO (I, X) =CLOSURE(J)求出新的项目集。 c) 重复b)直到不出现新的项目集为止。
表构造的基础。 SLR(1)分析表 是LR(0)分析表的改进,适应
文法范围强于LR(0)。 LR(1)分析表 分析能力强(指适应范围,查错速
度),但状态太多。 LALR(1)分析表 是LR(1)分析表的改进,分析
编译原理 第06章_LR分析法(3)

的。将同心集合并为: I5,12: L→i•, =/# I4,11: L→*•R, =/# R→•L, =/# I7,13: L→*R•, =/# L→•*R, =/# I8,10: R→L•, =/# L→•i, =/#
6.4 LALR(1)分析法
我们看到合并同心集后的项目集其核心 部分不变,仅搜索符合并。对合并同心集后 的项目集的转换函数为GO(I,X)自身的合并, 这是因为相同的心之转换函数仍属同心集, 例如: GO(I4,11, i)=GO(I4, i)∪GO(I11, i)= I5,12 GO(I4,11, R)=GO(I4, R)∪GO(I11, R)= I7,13 GO(I4,11, *)=GO(I4, *)∪GO(I11, *)= I4,11
0. S' →S 1. S →L=R
2. S →R 3. L →*R
4. L →i 5. R →L
6.4 LALR(1)分析法
3. 若LALR(1)项目集族中不存在归约一 归约冲突,则该文法是LALR(1)文法。对例 中的文法,由于合并同心集后不存在归约— 归约冲突,所以该文法是LALR(1)文法。
S'→•S,# I0: R→•L,# S→•L=R,# L I :R→L•,# L→• * R,# S→•R,# 10 L I2:S→L•=R,# L→•i,# L→•*R,=/# L R→L•,# * i L→•i,=/# i R I11: L→*•R,# R→•L,# I3: S→R•,# I12: L→i•,# R→•L,# * i L→• * R,# R L→ * •R,=/# I4: I13:L→*R•,# L→•i,# R→•L,=/# I5: L→i•,=/# L→•*R,=/# R * i I7: L→*R•,=/# L→•i,=/#
《编译原理LR分析》ppt课件

a
– aAb[3]
a,aA
– aAcd[4]
a,aA,aAc
– aAcBe[1]
a,aA,aAc,aAcB
LR分析程序
LR 文法 对于一个cfg 文法, 假如可以构造一张 LR 分析表, 使得它的每一个入口均是唯一的 〔Sj,rj,acc,空白〕,那么称该 cfg 是LR 文法.
LR分析
特征: – .标准的 – .符号栈中的符号是标准句型的前缀,
动作
移进 移进 归约(A→b) 移进 归约(A→Ab) 移进 移进 归约(B→d) 移进 归约 承受
对输入串abbcde#的移进-规约分析过程
符号串abbcde是否是G[S]的子
S aAcBe aAcde aAbcde abbcde
步骤 符号栈 输入符号串 动作
状态栈 ACTION GOTO
1〕 #
LR〔0〕LC〔Ab〕=ab
LR〔0〕LC〔AAb〕=aAb
LR〔0〕LC〔Bd〕=aAcd 的正规式
〔 =VnVt〕上
x
0 S①
2
a 3
b④
5
a
A 6
7
b
⑧
9
a
A
c
10
11
12
d⒀
a
A
c
14 15
16
17
B 18 e ⒆
DFA
a
A
b
x
2
3
6
S
b
1
4
c
B
e
5
7
9
d
8
构造LR〔0〕工程集标准族
活前缀与句柄的关系:
G[S]:
R
=>αβω
编译原理-清华大学-第6章-LR分析法(2+1,2+1)

r1 5
三、LR分析算法
状态/符号
Sm Xm Sm-1Xm-1 …… …… …… S1 X1
0#
输入缓冲区 a1…ai…an#
LR主控 程序
动作表 转移表 action goto
产生式 序列
分析表
置ip指向输入串w的第一个符号;
状态0和符号#分别进分析栈;
令S为状态栈的栈顶状态;a是ip指向的符号;
作为DFA的初始状态。
21
3)定义状态转换函数GO (产生新的项目集)
GO(I,X)定义为CLOSURE(J),其中I,J都是项目集, X(VN∪VT), J={AX•|当A•XI}。
J 的构造方法类似于词法分析的 MOVE函数
GO(I,X)类似于 CLOSURE( MOVE(I,X))
4)构造LR(0)项目集规范族的算法
2、S′S• 称为句子识别态或接受项目;
3、转换关系:项目i为XX1…Xi-1•Xi…Xn, 项目j为XX1…Xi • Xi+1…Xn, 则从项目i画一弧线射向j,标记为Xi;
4、若项目i为X•A,其中A是非终结符,则从i项目画 弧射向所有A•的项目,V*
5、规约项目为终态用双圈表示,双圈外有*号者为接受态 18
(最左规约,规范规约)
ab[2]b[3]cd[4]e[1]
(用[2]归约)
<= aAb[3]cd[4]e[1]
<= aAcd[4]e[1] <= aAcBe[1]
(用[3]归约) (用[4]归约) (用[1]归约)
<= S
其中<=表示规约
问题:在归约过程中,那些是可归前缀?
13
4、活前缀:G=(Vn,Vt,P,S'), 若有规范推导 S′* αAωαβω,
LR分析方法

I0 I1 I2
1,3,11 2 4,6,9 4,6,9
b
12,14,17
c
6,7,9
d
10
E
2
A
5
B
I3
I4 I5 I6
12,14,17
6,7,9 14,15,17 5
14,15,17
6,7,9 14,15,17
18
10 18
8
13
16
I7
I8 I9 I10 I11
13
8 16 10 18
①据 NFA可以构 造DFA的转换矩 阵:
②状态转换图表示(P106):
对照转换矩阵
S0S2S5S2 r1 S0S2S5S2S5 S0S2S5S2S5S3 S0S2S5S2S5S2 S0S2S5S2S5S6 S0S2S5S6 S0S1
S0 S1 S2 S3 a
(1)LE,L (2)LE (3)Ea (4)Eb
10 11 12 13
b #E,E,L
S3
#E,L #L
S4
r1(LE,L)
1 S5
# #
r (LE,L) r accr3
r4
6 r1
r3
分析成功
2
S4
S5 S6 S3 S4
r4
5.3.1 LR(0)分析表的构造
在LR分析算法中,所使用的“状态”是跟活前缀有关的, 它就是能够识别文法所有活前缀的有限自动机的状态,每个 状态由一个或多个项目构成。 一、项目、活前缀: 希望用产生式S的右 1.定义:对于文法G,其产生式的右部添加一个特殊符号“.” 部进行归约,当前的 就构成文法的一个LR(0)项目,简称项目。 用产生式SaAcBe进行 输入应为a 归约时,a已经匹配(进 每个项目中圆点的左 2.例如: S.aAcBe 栈),需分析S a.AcBe 部表示在分析过程中, 对于产生式: 有项目: Sa.AcBe Aa.cBe 要用该产生式归约时, SaAcBe SaA.cBe 产生式SaAcBe右部 句柄已识别的部分 每个产生式对应的 SaAc.Be 分析结束,句柄已经 (进入符号栈),右部 项目个数等于它右部 SaAcB.e 形成,可以归约了。 表示等待识别的部分。 的长度加1 SaAcBe. A的项目为A.
编译原理 LR分析法

文法的LR(0)分析表
文法G[S] (1)S → aAcBe (2)A → b (3)A → Ab (4)B → d
状 态 0 1 2 3 4 5 6 7 8 9 r4 r1 r4 r1 r4 r1 r4 r1 r3 r3 r3 r2 s4 s6 r2 s5 r2 r2 s8 r3 r3 S9 r4 r1 r4 r1 r3 r2 r2 7 ACTION a s2 acc 3 b c d e # S 1 GOTO A B
LR分析方法的基本原理
–把每个句柄(某个产生式的右部)的识别过 程划分为若干状态,每个状态从左到右识别 句柄中的一个符号,若干状态就可以识别句 柄左端的一部分符号。
–识别了句柄的这一部分就相当于识别了当前 规范句型的左部分,称为活前缀。因此,对 句柄的识别就变成了对规范句型活前缀的识 别。
–LR分析程序实际上就是利用有限自动机来 识别给定文法的所有规范句型的活前缀。
设2w * xw, 则对任何B 有规范推导
S
rm *Aw
1 B 2w 1 B xw 1 xw
所以 B . 对活前缀 1 也是有效的。
定义 (有效项目集,项目集规范族):
文法G的某个活前缀的所有有效项目组成 的集合,称为活前缀的LR(0)有效项目集。 文法G的所有有效项目集组成的集合,称 为G的LR(0)项目集规范族。
• LR(k)技术包含一组方法:LR(0)、 SLR(1)、LR(1)和LALR(1)。 • LR(0)无需预测输入符号,实现最简单, 局限性最大,基本上无法实用,但是它 是LR分析的基础。 • 简单的LR,即SLR(1),是一种比较容 易实现而且具有使用价值的方法,但是 却不能分析一些常见程序语言的结构。
例如,对于输入串abbcde,其规范推导过程为 S aAcBe aAcde aAbcde abbcde – 每个句型都是规范句型。这个过程的逆过程就是归约过程,即 从输入串abbcde归约到文法的开始符号S。 – 我们分析其中的一个规范句型aAbcde,它的句柄是Ab(最左直 接短语),前缀有aAbcde,aAbcd,aAbc,aAb,aA,a以及空 字符串,活前缀是aAb, aA,a和,在它后面添上终结符串cde 就是规范句型。
自底向上LR分析法

4.接受项目:对于拓广文法G[S’],有项目S’S 它是一个特 殊的归约项目,我们称它为接受项目,它所对应的状态为 接受状态。拓广文法G ´的接受项目是唯一的,即 S’S
三、构造识别活前缀的NFA
根据项目定义,我们可给出文法中所有产生式的项目, 而每个项目都为识别活前缀的NFA的一个状态。即文法有多 少个项目,它所对应识别活前缀的NFA就有多少个状态。 1.NFA的构造原则 (1)NFA的状态集:由每个项目所对应的状态组成; (2)输入字符集合:由文法的文法符号组成包括终结符、 非终结符和; (3)初态:对于文法G[S]的拓广文法G[S’],有项目S’ S ,由 于S’仅在第一个产生式的左部出现,所以规定它为初态; (4)终态:对于拓广文法G[S’],有项目Uu (即圆点在最 后的项目),作为NFA的终态;
上例规范句 型为什么?
该规范句型 的活前缀是 什么?
aAb[3]cd[4]e[1]
aAcd[4]e[1] aAcBe[1] S
B d[4]
规范句型:
abbcde, aAbcde, aAcde , aAcBe, S
规范句型: abbcde, aAbcde, aAcde , aAcBe, S 有下面规范句型的活前缀: ab[2]b[3]cd[4]e[1] ,a,ab aAb[3]cd[4]e[1] aAcd[4]e[1] ,a,aA,aAb ,a,aA,aAc,aAcd
一个规范句型的活前缀不含句柄之后的任何符号
活前缀和句柄的关系? 1. 活前缀不含有句柄的任何符号;
2. 活前缀含有句柄的部分符号;
3. 活前缀已含有句柄的全部符号。
活前缀
例:文法G[S]为: 为产生式加序号变为:
S aAcBe
第06章_LR分析法(2)

6.2 SLR(1)分析法
SLR(1)分析表的构造与LR(0)分析表 的构造基本相同。仅对LR(0)分析表构 造算法中的规则2进行如下修改: 若归约项目A→α•属于Ik,则对任何 终结符 a ∈ FOLLOW(A)置 ACTION[k, a]=rj,其中A→α为文法的第j条规则。
6.2 SLR(1)分析法
a
S5 S6 r5 r3 r4
S2 S3
ACTION b c
#
acc
GOTO S A
1 4 7
r1 S2 r2 S9 r1
r1 r2 S8 r1
r1 r2 r1
0. 1. 2. 3. 4. 5.
S'→S S →Sb S →bAa A →aSc A →aSb A →a
G[S]的 SLR(1) 分析表
6.2 SLR(1)分析法 ()
GOTO E T F 1 2 3
8 2 3 9 3 10
S7r1 r3 r5
r1 r3 r5
r1 r3 r5
算数表达式文法的SLR(1)分析表
状 态 id
0 1 2 3 4 5 6 7 8 9 10 11 S5
ACTION
+
S6 r2 r4 r6 S6 r1 r3 r5 * S7 r4 r6 S4 S4 S4 S11 ( S4 ) r2 r4 r6 # acc r2 r4 r6
0. S'→S 3. A →aSc 1. S →Sb 4. A →aSb 2. S →bAa 5. A →a
I8: A →aSc·
I9: A →aSb·
6.2 SLR(1)分析法 ()
分析所有这些项目集,可知在项目集 I5中存在移进—归约冲突,I9中存在归 约—归约冲突,因此该文法不是LR(0)文 FOLLOW(S) FOLLOW(S') FOLLOW(A) 法。 考虑含冲突的项目集能否用SLR(1)方 法解决。 0. S'→S 3. A →aSc
第六章LR分析法(2)

下面重点介绍2o方法:
1. LR (0)项目集规范族的构造 项目集规范族的构造DFA方法 项目集规范族的构造 方法 步骤:
1o 拓广文法G为G’,方法:加入0. S’∷=S(S为G的 识别符号,S’为G’的识别符号) 2o 列出所有G’的LR(0)项目 3o 求DFA的初态I0=closure(I)
设分析栈中已移进和归约出的符号串为#E+T时:栈顶的状态为Sm: Sm . . . S1
S0 分析栈
T + E #
Sm不仅表征了从分析开始到目前已扫描过的输入符号被归约 成#E+T。 Sm可预测:根据归约时所用的产生式(非终结符T的产生式) 推测未来可遇到的输入符号仅是FOLLOE(T)={+,*,),#} 中的任意-符号: 若读的符号是*,根据文法可知 +< *栈顶未形成句柄。*进栈 若读的输入符号是+,),#之一时,+ >+或),#,栈顶形 成句柄,归约为E+T为E 若输入不是上述4个符号,则表示输入串有语法错
的
(2)分析表:包括动作表(ACTION)和状态转换表(GoTo)两个部 分析表: 分析表 分。它们都可以用二维数组表示。 不同的文法分析表内容不同 同一个文法采用的LR分析器不同时,分析表的内容将也 不同。 LR分析器的关键部分是分析表的构造。 (3)分析栈:包括文法符号栈x和相应的状态栈S。它们均用一维 分析栈: 分析栈 数组表示。 三,LR分析器的工作原理 例:文法G[E]: E::=E+T|T T::=T*F|F F::=(E)|i
A::= α
A::= α1 α2
A::= α
文法G中右部标有园点的产生式称为G的一个LR(0)项目. 特别:对于空产生式A∷=ε,则仅有项目A∷= 注 (1)文法G的全部LR(0)项目是构造识别文法所有规范句型 活前缀的DFA的基础。 (2)每个项目的含义与圆点的位置有关,概括说:圆点左 部表示分析过程的某时刻用该产生式归约时句柄已识别过的部 分。圆点右部表示待识别的部分。 (3)根据圆点位置和圆点后是终结符还是非终结符,将 一个文法全部LR(0)项目分为4类: U∷=xay(x,y为符号串,a∈VT)即圆点 后为终结符的项目为移进项目。表明期待从剩余的输入串 中移进一个符号,以待形成句柄。 移进项目: ●移进项目:形如
LR分析法

LR分析表 LR分析表是LR 分析器的核心, 它由分析动作 (ACTION)表和 状态转移 (GOTO)表两个 子表组成; ACTION[Sm,ai] 指明当栈顶为 Sm,输入符为ai 时应完成的分 析动作; GOTO[Sm,Xi]指 明当分析栈移 进一个输入符 号或按某产生 式进行归约后 所要转移到的 下一状态.
规范句型的活前缀(续) 规范句型的活前缀
在前面的例子中的第五行: #E,b ,a#中,b是当前 句型的句柄, “ε”, “E” , ”E ,” , ”E , b”都是~. LR分析过程实际上就是一个逐步产生(识别)~ 的过程.. 在分析的每一步,栈内符号总是~,且与此时栈 顶符号相关. 提示 若能构造一个识别所有活前缀的自动机 提示: 识别所有活前缀的自动机, 识别所有活前缀的自动机 则构造分析表就不难了.
LR分析器的总控程序
parser( ){ 初始化; 初始化 while((item=ACTION[TopStat][InpSym]))!=Acc){ if(item==ERROR) error( ); if(item==sj){push(j);advance( );} else reduce(i);/* item== ri*/ } accept( ); }
分 析 栈
内 容 栈 的 分 析
总控程序 分析表
Sm Xm … S1 X1 S0 #
LR分析表 LR分析表
a1 S1 S2 … Sn ACTION(S1 ,a1] a2 ACTION(S1 ,a2] … … … … … al ACTION(S1 ,al] ACTION(S2 ,al] … ACTION(Sn ,al] ACTION(S2 ,a1] ACTION(S2 ,a2] … … ACTION(Sn ,a1] ACTION(Sn ,a2]
LR分析法专业知识讲座

· · ·
Sm
T +
分 析 栈
T→T*F | F F→(E) | id
S1 S0
E #
示 意 图
状态Sm不但表征了从分析开始到目前已扫描 过旳输入符号被归约成#E+T,而且由Sm能够预 测,假如输入串没有语法错误,根据归约时所用 规旳则 输(入非符终号止仅符是T旳规则)只推有测FO才出LL会O将W跟(T在来)中T可背旳面能符号遇到
6.1 LR分析法
LR分析法是一种自下而上进行规范归 约旳语法分析措施。
这里L是指从左到右扫描输入符号串。 R是指构造最右推导旳逆过程。
这种分析法比递归下降分析法、预测 分析法和算符优先分析法对文法旳限制 要少得多。
6.1 LR分析法
对于大多数用无二义性上下文无关 文法描述旳语言都能够用LR分析法进行 有效旳分析,而且这种分析法分析速度 快,并能精确及时地指出输入串旳语法 错误和犯错旳位置。
S4 S5 用第4条规则A→c归约
bb#
S8
b#
用第3条规则A→aAb归约
b#
S8
#
用第3条规则A→aAb归约
#
用第1条规则S→A归约
#
acc
6.1.2 LR(0)分析法
由前例,对输入串aacbb#旳归约过程, 能够看出,当所分析旳输入串没有语法错 误时,则在分析旳每一步,分析栈中已移 进一归约旳全部文法符号与余留旳输入符 号串合起来,就是所给文法旳一种规范句 型。
状
态a
0 S4 1 2 r1 3 r2 4 S4 5 r4 6 r6
7 8 r3
9
10 r5
ACTION bcd
S5
S6
r1
LR分析法

-项目集合中的冲突
*移进-归约冲突
项目集合同时含有形如A→α.aβ和B→γ.的项目
*归约-归约冲突
项目集合中同时含有形如A→α.和B→ β.的项目
-如果文法G的LR(0)项目集规范族中不含有移进-归约冲突和归约-归约冲突,则称文法G为LR(0)文法
二、LR(0)分析:
-分析过程中
*栈中的文法符号串并上剩余的输入串构成一个右句型(规范句型)
*当该右句型的句柄出现在栈顶时,归约,否则,移进
*栈中的文法符号串是当前句型的前缀,该前缀不包含句型句柄后面的符号,称之为活前缀
*活前缀:P145
*可归前缀:包含完整句柄的活前缀
*分析过程可以看作是识别文法规范句型活前缀的过程。只要每一时刻栈中的文法符号串是某规范句型的活前缀,则说明已分析的部分是正确的
◇移进项目:A →α.aβ
◇待约项目:A →α.Bβ
◇归约项目:A →α.
◇接受项目:S’ →S.
*有效项目:P164
*有效项目集:P165
* LR(0)的项目集规范族:P165
* LR(0)项目集合的闭包,closure(I):P165
* LR(0)项目集合的转移函数,go(I,X):P165
*构造LR(0)项目集规范族:算法—P170图4.22
分析一个句子:accd$
三、SLR分析:
-对于LR(0)项目集规范族中有冲突的项目集合,有的可以通过向前看一个符号(考察当前正在扫描的符号)来解决冲突
*当存在冲突时才向前看一个符号,因此是一种简单的LR(1)分析方法,称为SLR分析
-解决方法:
*假设一个LR(0)项目集规范族中有如下项目集合:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对输入串abbcde#的LR分析过程
文法G[S]: (1) S → aAcBe (2) A → b (3) A → Ab (4) B → d Si:移进,并将状态i进栈
0 1 2 3 4 5 ri:用第i个产生式归约,同时状 6 态栈与符号栈退出相应个符号, 7 根据GOTO表将相应状态入栈 8 9
可归前缀与活前缀
文法G[S]: (1) S → aAcBe[1] (2) A → b[2] (3) A → Ab[3] (4) B → d[4]
S aAcBe[1] aAcd[4]e[1] aAb[3]cd[4]e[1] ab[2]b[3]cd[4]e[1] 规范句型的这种前部分符号串称为可归前缀 我们把形成可归前缀之前包括可归前缀在内 的所有规范句型的前缀都称为活前缀 ,a,ab ,a,aA,aAb ,a,aA,aAc,aAcd ,a,aA,aAc,aAcB,aAcBe
A
16
c
0
S a a
1 3 6
* b A
X
2
5 9
4 7
b
加上开始状态X 8 12 d 17 B
a
10 A 11 c 15
A
13
18 e 10
14 a 确定化
16
c
S
1 * 2 6
d
b
3 4 8
动作
移进 移进 归约(A→b) 移进 归约(A→Ab)
状态栈
0 02 024 023 0236
ACTION
S2 S4 r2 S6 r3
GOTO
3 3
对输入串abbcde#的LR分析过程
S
1 * 2 5
d
b
4 3 7
b
e
0
a
A
c B
6 9
8
步骤 符号栈 输入符号串
1) 2) 3) 4) 5) 6) # #a #ab #aA #aAb #aA abbcde# bbcde# bcde# bcde# cde# cde#
我们可以把文法的终结符和非终结符都看 成有穷自动机的输入符号,每次把一个符 号进栈看成已识别过了该符号,同时状态 进行转换,当识别到可归前缀时,相当于 在栈中形成句柄,认为达到了识别句柄的 终态。
步骤 符号栈 输入符号串
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) # #a #ab #aA #aAb #aA #aAc # aAcd #aAcB #aAcBe #S abbcde# bbcde# bcde# bcde# cde# cde# de# e# e# # #
对输入串abbcde#的LR分析过程
S
1 * 2 5
d
b
4 3 7
b
e
0
a
A
c B
6 9
8
步骤 符号栈 输入符号串
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) # #a #ab #aA #aAb #aA #aAc # aAcd #aAcB #aAcBe #S abbcde# bbcde# bcde# bcde# cde# cde# de# e# e# # #
动作
移进 移进 归约(A→b) 移进
状态栈
0 02 024 023
ACTION
S2 S4 r2 S6
GOTO
3
对输入串abbcde#的LR分析过程
S
1 * 2 5
d
b
4 3 7
b
e
0
a
A
c B
6 9
8
步骤 符号栈 输入符号串
1) 2) 3) 4) 5) # #a #ab #aA #aAb abbcde# bbcde# bcde# bcde# cde#
1) 2) # #a abbcde# bbcde#
动作
移进 移进
状态栈
0 02
ACTION
S2 S4
GOTO
对输入串abbcde#的LR分析过程
S
1 * 2 5
d
b
4 3 7
b
e
0
a
A
c B
6 9
8
步骤 b abbcde# bbcde# bcde#
a b b c d e 分析符号串abbcde是否G[S]的句子
S aAcBe aAcde aAbcde abbcde
在步骤3中,用A→b归约
在步骤5中,用A→Ab归约 问题:何时移进?何时归约?用哪个产生式
归约?
3) 4) 5) 6)
#ab #aA #aAb #aA
bcde# bcde# cde# cde#
动作
移进 移进 归约(A→b) 移进 归约(A→Ab) 移进 移进 归约(B→d) 移进 归约(S→aAcBe) 接受
状态栈
0 02 024 023 0236 023 0235 02358 02357 023579 01
ACTION
S2 S4 r2 S6 r3 S5 S8 r4 S9 r1 acc
GOTO
动作
移进 移进 归约(A→b) 移进 归约(A→Ab) 移进 移进 归约(B→d) 移进 归约(S→aAcBe) 接受
状态栈
0 02 024 023 0236 023 0235 02358 02357 023579 01
ACTION
S2 S4 r2 S6 r3 S5 S8 r4 S9 r1 acc
GOTO
动作
移进 移进 归约(A→b) 移进 归约(A→Ab) 移进 移进 归约(B→d) 移进
状态栈
0 02 024 023 0236 023 0235 02358 02357
ACTION
S2 S4 r2 S6 r3 S5 S8 r4 S9
GOTO
3 3 7
对输入串abbcde#的LR分析过程
S
1 * 2 5
Sn Xn . . . . . . SP
输入串
总控程序
输出
S1 X1 S0 #
ACTION表
GOTO表
LR分析表
步骤 符号栈 输入符号串
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) # #a #ab #aA #aAb #aA #aAc # aAcd #aAcB #aAcBe #S abbcde# bbcde# bcde# bcde# cde# cde# de# e# e# # #
第六讲
LR分析概述 LR(0)分析
LR分析法
SLR(1)分析
LR(1)分析
LALR(1)分析
二义性文法在LR分析中的应用
复习:移进-归约分析
文法G[S]: (1) S → aAcBe (2) A → b (3) A → Ab (4) B → d
步骤 符号栈
1) 2) 3) 4) 5) 6) 7) # #a #ab #aA #aAb #aA #aAc
动作
移进 移进 归约(A→b)
状态栈
0 02 024
ACTION
S2 S4 r2
GOTO
3
对输入串abbcde#的LR分析过程
S
1 * 2 5
d
b
4 3 7
b
e
0
a
A
c B
6 9
8
步骤 符号栈 输入符号串
1) 2) 3) 4) # #a #ab #aA abbcde# bbcde# bcde# bcde#
d
b
4 3 7
b
e
0
a
A
c B
6 9
8
步骤 符号栈 输入符号串
1) 2) 3) 4) 5) 6) 7) 8) 9) 10) # #a #ab #aA #aAb #aA #aAc # aAcd #aAcB #aAcBe abbcde# bbcde# bcde# bcde# cde# cde# de# e# e# #
动作
移进 移进 归约(A→b) 移进 归约(A→Ab) 移进 移进
状态栈
0 02 024 023 0236 023 0235
ACTION
S2 S4 r2 S6 r3 S5 S8
GOTO
3 3
对输入串abbcde#的LR分析过程
S
1
2 5
* b A c
4
3 7
b
0
a
6 9
B
d
e
8
步骤 符号栈 输入符号串
每次归约句型的 前部分依次为: ab[2] aAb[3] aAcd[4] aAcBe[1]
活前缀(Viable Prefixes)
定义:
S’ A 是文法G中的一个规范推导, R 如果符号串γ是的前缀,则称γ是G的一个 活前缀。
* R
LR分析需要构造识别活前缀的有穷自动机
*
句子abbcde的可归前缀如下: S[0] ab[1] aAb[3] aAcd[4] aAcBe[1]
*
构造识别其活前缀及可归前缀的有限自动机如下: 0 2
S a a a a
1
1 4 7
b
句子识别态 句柄识别态
3 b
5
9 14
6
A
i
8 12 d
17 B 13 18 e 10
10 A 11 c 15
动作
移进 移进 归约(A→b) 移进 归约(A→Ab) 移进 移进 归约(B→d) 移进 归约(S→aAcBe)
状态栈
0 02 024 023 0236 023 0235 02358 02357 023579
