信号与系统期末考试试题
信号与系统期末考试试题(第二套)

信号与系统期末考试试题(第二套)符号说明:为符号函数,为单位冲击信号,为单位脉冲序列,为单位阶跃信号,为单位阶跃序列。
一、填空(共30分,每小题3分)1. 已知,求。
2. 已知,求。
3. 信号通过系统不失真的条件为系统函数。
4. 若最高角频率为,则对取样的最大间隔是。
5. 信号的平均功率为。
6. 已知一系统的输入输出关系为,试判断该系统是否为线性时不变系统 。
7. 已知信号的拉式变换为,求该信号的傅立叶变换=。
8. 已知一离散时间系统的系统函数,判断该系统是否稳定。
9. 。
10. 已知一信号频谱可写为是一实偶函数,试问有何种对称性。
二、计算题(共50分,每小题10分)1.已知一LTI 系统当输入为时,输出为,试写出系统在输入为时的响应的时间表达式,并画出波形(上述各信号波形如图A-1所示)。
图A-12.已知信号的波形如图A-2所示,且。
)sgn(t )(t δ)(k δ)(t ε)(k ε)()4()(2t t t f ε+=_______)("=t f }4,2,4,3{)(},1,2,2,1{)(=-=k h k f ______)()(=*k h k f _______)(=ωj H )(t f m ω)4(t f ______t t t f ππ30cos 220cos 4)(+=______)3()(t f t y =______)1)(1(1)(2-+=s s s F )(ωj F ______2121)(---+=z z z H ______=+-+⎰∞∞-dt t t t )1()2(2δ______)(,)()(3ωωωωA e A j F j -=)(t f ______()t x 1()t y 1()t x 2()t y2()t x ()()ωj X t x ↔图A-2(1)试求的相位;(2)试求?(3)试求?3.已知线性时不变因果连续系统的频率响应函数(1)求系统的冲激响应;(2)若系统输入,求系统的零状态响应。
信号与系统试题五(1)

期末考试试题五一、选择题(共10题,每题3分 ,共30分,每题给出四个答案,其中只有一个正确的) 1、 卷积f 1(k+5)*f 2(k-3) 等于 。
(A )f 1(k)*f 2(k) (B )f 1(k)*f 2(k-8)(C )f 1(k)*f 2(k+8)(D )f 1(k+3)*f 2(k-3) 2、 积分dt t t ⎰∞∞--+)21()2(δ等于 。
(A )1.25(B )2.5(C )3(D )5 3、 序列f(k)=-u(-k)的z 变换等于 。
(A )1-z z (B )-1-z z(C )11-z (D )11--z4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。
(A ))2(41t y (B ))2(21t y (C ))4(41t y (D ))4(21t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时,系统的零状态响应y f (t)等于(A )(-9e -t +12e -2t )u(t) (B )(3-9e -t +12e -2t )u(t)(C ))(t δ+(-6e -t +8e -2t )u(t) (D )3)(t δ +(-9e -t +12e -2t )u(t)6、 连续周期信号的频谱具有(A ) 连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于(A ) 1(B )2(C )3(D )4 8、序列和()∑∞-∞=-k k 1δ等于(A )1 (B) ∞ (C) ()1-k u (D) ()1-k ku 9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u tet f t的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s()()()2323++-s se C s ()()332++-s s e D s二、填空题(共9小题,每空3分,共30分)1、卷积和[(0.5)k+1u(k+1)]*)1(k -δ=________________________2、单边z 变换F(z)=12-z z的原序列f(k)=______________________ 3、已知函数f(t)的单边拉普拉斯变换F(s)=1+s s,则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换ss s s s F +++=2213)(的原函数f(t)=__________________________ 6、已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ,则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=20)()(t dx x f t y 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ,=kt 22三、(8分)已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dt t df t s =求⎪⎭⎫⎝⎛2ωs 的傅里叶逆变换。
信号及系统期末考试试题及答案

信号及系统期末考试试题及答案一、选择题(每题2分,共20分)1. 信号x(t)=3cos(2π(5t+π/4))是一个:A. 周期信号B. 非周期信号C. 随机信号D. 确定性信号2. 系统分析中,若系统对单位阶跃函数的响应为u(t)+2,则该系统为:A. 线性时不变系统B. 线性时变系统C. 非线性时不变系统D. 非线性时变系统3. 下列哪个是连续时间信号的傅里叶变换:A. X(k)B. X(n)C. X(f)D. X(z)4. 信号通过线性时不变系统后,其频谱:A. 仅发生相位变化B. 仅发生幅度变化C. 发生幅度和相位变化D. 不发生变化5. 单位脉冲函数δ(t)的拉普拉斯变换是:A. 1B. tC. e^(-st)D. 1/s二、简答题(每题5分,共10分)1. 解释什么是卷积,并给出卷积的数学表达式。
2. 说明傅里叶变换与拉普拉斯变换的区别。
三、计算题(每题15分,共30分)1. 给定连续时间信号x(t)=e^(-t)u(t),求其傅里叶变换X(f)。
2. 给定离散时间信号x[n]=u[n]-u[n-3],求其z变换X(z)。
四、分析题(每题15分,共30分)1. 分析信号x(t)=cos(ωt)+2cos(2ωt)通过理想低通滤波器后输出信号的表达式,其中滤波器的截止频率为ω/2。
2. 讨论线性时不变系统的稳定性,并给出判断系统稳定性的条件。
五、论述题(每题10分,共10分)1. 论述信号的采样定理及其在数字信号处理中的应用。
参考答案一、选择题1. A2. A3. C4. C5. A二、简答题1. 卷积是信号处理中的一种运算,它描述了信号x(t)通过系统h(t)时,输出信号y(t)的计算过程。
数学表达式为:y(t) = (x * h)(t) = ∫x(τ)h(t-τ)dτ。
2. 傅里叶变换用于连续时间信号的频域分析,而拉普拉斯变换则适用于连续时间信号,并且可以处理有初始条件的系统。
三、计算题1. X(f) = 3[δ(f-5) + δ(f+5)]。
信号与系统 期末复习试卷1

, 22t k
第2页共4页
三、(10 分)如图所示信号 f t,其傅里叶变换
F jw F
f t,求(1)
F
0
(2)
F
jwdw
四 、( 10
分)某
LTI
系统的系统函数
H s
s2
s2 2s 1
,已知初始状态
y0 0, y 0 2, 激励 f t ut, 求该系统的完全响应。
参考答案 一、选择题(共 10 题,每题 3 分 ,共 30 分,每题给出四个答案,其中只有一 个正确的)1、D 2、A 3、C 4、B 5、D 6、D 7、D 8、A 9、B 10、A
二、填空题(共 9 小题,每空 3 分,共 30 分)
1、 0.5k uk 2、 (0.5)k1u(k)
3、
s s
2 5
5、 (t) u(t) etu(t)
8、 et cos2tut
三、(10 分)
6、 1 0.5k1 uk
9、 66 , 22k!/Sk+1 s
解:1)
F ( ) f (t)e jt dt
Atut Btut 2 Ct 2ut Dt 2ut 2
10、信号 f t te3tut 2的单边拉氏变换 Fs等于
A
2s
s
7 e 2s3 32
C
se
s
2 s 3
32
B
e 2s
s 32
D
e 2s3
ss 3
二、填空题(共 9 小题,每空 3 分,共 30 分)
1、卷积和[(0.5)k+1u(k+1)]* (1 k) =________________________
信号与系统试题及答案(大学期末考试题)

信号与系统试题及答案(大学期末考试题)一、选择题(每题2分,共40分)1. 下列哪个信号是周期信号?A. 方波B. 单位冲激信号C. 随机信号D. 正弦信号答案:A2. 信号x(t)的拉普拉斯变换为X(s)。
若x(t)的区间平均功率为P,则X(s)的区间平均功率是多少?A. PB. 2πPC. P/2D. πP答案:D3. 系统的冲激响应为h(t)=e^(-2t)sin(3t)u(t)。
则该系统为什么类型的系统?A. 线性非时变系统B. 线性时不变系统C. 非线性非时变系统D. 非线性时不变系统答案:B4. 信号x(t)通过系统h(t)并得到输出信号y(t)。
若x(t)为周期为T的信号,则y(t)也是周期为T的信号。
A. 正确B. 错误答案:A5. 下列哪个信号不是能量有限信号?A. 常值信号B. 正弦信号C. 方波D. 三角波答案:B...二、填空题(每题4分,共40分)1. 离散傅里叶变换的计算复杂度为$O(NlogN)$。
答案:NlogN2. 系统函数$H(z) = \frac{1}{1-0.5z^{-1}}$的极点为0.5。
答案:0.5...三、简答题(每题10分,共20分)1. 请简要说明信号与系统的基本概念和关系。
答案:信号是波动的物理量的数学描述,而系统是对信号进行处理的方式。
信号与系统的关系在于信号作为系统的输入,经过系统处理后得到输出信号。
信号与系统的研究可以帮助我们理解和分析各种现实世界中的波动现象。
2. 请简要说明周期信号和非周期信号的区别。
答案:周期信号是在一定时间间隔内重复出现的信号,具有周期性。
非周期信号则不能被表示为简单的周期函数,不存在固定的重复模式。
...以上是关于信号与系统试题及答案的文档。
希望能对您的大学期末考试复习有所帮助。
祝您考试顺利!。
信号系统期末考试

常熟理工学院20 ~20 学年第 学期信号与系统考试试卷试卷库01试题总分: 100 分 考试时限:120 分钟一、选择题15分,每题3分1、信号)(t f 波形如右图所示,则其表达式为 B ;A )]1()1([+--t u t u tB )]1()1([--+t u t u tC )]1()1([++-t u t u tD )]1()1([/1+--t u t u t2、下列说法错误的是 B ;A 系统的零状态响应包括自由响应和强迫响应两部分;B 若系统初始状态为零,则系统的零状态响应就是系统的强迫响应;C 零状态响应与系统起始状态无关,而由系统的激励信号产生;D 零输入响应与系统激励无关,而由系统的起始状态产生;3、已知()f t 的频谱函数为()F j ω,则()cos c f t t ω的频谱函数 为 A ;A[])()(21c c j j F j j F ωωωω-++ B [])()(21c c j j F j j F ωωωω--+ C [])()(21c c j j F j j F ωωωω+-- D [])()(41c c j j F j j F ωωωω--+4、已知)(t f 的拉普拉斯变换为)(s F ,则dtt df )(的单边..拉普拉斯变换为 B ; A. )(s sF B.)0()(--f s sF C. )0()(-+f s sF D. ⎰-∞-+0)(1)(ττd f ss sF5、已知1()f k 的Z 变换为1()F z ,2()f k 的Z 变换为2()F z ,则12()*()f k f k 的Z 变换结果为 C ;A 12()*()F z F zB 121()*()2F z F z π C 12()()F z F z D 121()()2F z F z π二、填空题15分,每题3分1、所谓线性系统是指其具有_________齐次性_______和___________ 叠加性____;2、积分(3)t t e dt δ∞--∞+⎰=______3e ____________;3、频谱函数)2()2()(++-=ωδωδωj F 的傅立叶逆变换)(t f 为t 2cos 1π;4、已知信号的最高频率为f ,要抽样后的信号能完全恢复原信号,则最大抽样间隔为 1/2f ;5、函数)(2cos t tu 的拉普拉斯变换为_____24ss +;三、计算卷积14分,每题7分1)()(2t u e t u e t t --*⎰⎰------==*tttt ttt u d eet u d eet u et u e 020)(22)()()()(τττττ4分)()()()1(22t u e e t u e e t t t t ----=-=3分2已知两个有限序列}3,2,1{)(-=k x ,}1,1,1,1{)(-=k h ,求)()(k h k x *;利用就地相乘法方法4分,结果2分1 1 1 1 × 123 = 3 3 3 3 2 2 2 2 1 1 1 1=1 3 6 6 5 3其中,k =0时的值为11分四、试判断系统)()(2t e t r =是否为线性的,时不变的,因果的 并证明之;9分 解:令)()]([)(2t e t e T t r ==,其中][⋅T 代表系统函数;)]([)(11t e T t r =,)]([)(22t e T t r =那么2221122112222112211)]()([)]()([)()()()(t e C t e C t e C t e C T t e C t e C t r C t r C +=+≠+=+ ∴系统是非线性的; 3分)]([)()-(0020t t e T t t e t t r -=-= ,∴系统是时不变的;3分由于)()(2t e t r =可知,系统输出只与当前的输入值有关,因而系统是因果的;五、已知)(t f 的双边拉普拉斯变换为)(s F ,试证明⎰∞-td f ττ)(的双边拉氏变换为s s F /)(;6分 证明:[])(t f L 代表)(t f 的拉普拉斯变换;⎥⎦⎤⎢⎣⎡⎰∞-ττd f L t )(=)](*)([t u t f L 3分 ⎥⎦⎤⎢⎣⎡⎰∞-ττd f L t)(=[]s s F s s F t u L t f L /)(/1)()]([)(=•=• 3分六、已知矩形脉冲信号)(t f 如右图所示, (1) 写出)(t f 的时域表达式; (2) 求)(t f 的频谱函数; (3) 画出)(t f 频谱图;12分 解:1)21()21()(--+=t u t u t f 3分2)(t f 中1=A ,1=τ1分⎪⎭⎫⎝⎛↔=2)()(ωτττSa A t g t f 4分-1/21/20t所以,)2()(ωωSa j F =1分34分其中,E =1,1=τ七、描述某系统的微分方程为)()(2)(t f t y t y =+',求输入)()(t u e t f t -=时系统的响应;14分解:取傅氏变换,有)()(2)(ωωωωj F j Y j Y j =+2分21)()()(+==ωωωωj j F j Y j H 2分输入信号11)()()(+=↔=-ωωεj j F t e t f t 3分 故:1111)1)(2(1)()()(+-+=++==ωωωωωωωj j j j j F j H j Y 4分 取反变换)()()(2t e e t y t t ε---=3分八、已知线性时不变系统的差分方程为()()()n u n y n y 512=-+ ,()11=-y ,求系统的全响应;15分 解:202-==+r r齐次解()()nh C n y 21-=3分特解()()(常数)时全为 5 05≥=n n u n x ()C n y p =∴)0(52≥=+n C C35=∴C 3分 全解()()()()3521+-=+=np h C n y n y n y 2分()迭代出由11=-y 3)1(25)0( 0=--==y y n 3分()(),得代入 解3521+-=nC n y()35301+==C y341=∴C 2分 ()()035234≥+-=∴n n y n 2分常熟理工学院20 ~20 学年第 学期信号与系统考试试卷试卷库02试题总分: 100 分 考试时限:120 分钟一、选择题15分,每题3分1、函数)(t f 的波形如下图所示,则)(t f 的一次积分的波形为A ;A B C D2、连续周期信号的频谱具有 D ;A 连续性、周期性B 连续性、收敛性C 离散性、周期性D 离散性、收敛性3、已知)()(ωF t f ↔,则)24(t f -的频谱函数为 A ; A ωω2)2(21j e F -- B ωωj e F --)2(21 C ωω2)2(21j e F - D ωω2)2(21j e F ---4、拉普拉斯变换性质中,卷积定理的形式正确的是 A ;A )()()()(2121s F s F t f t f ↔*B )()(2)()(2121s F s jF t f t f *↔*πC )()(21)()(2121s F s F jt f t f π↔* D )()(2)()(2121s F s jF t f t f *↔π5、序列)(])1(1[21k u k -+的Z 变换为 B ;A 221z z +B 221z z -C 21z z +D 21z z -二、填空题15分,每题3分1、系统的全响应可分解为 零状态响应 和零输入响应两部分响应之和,又可以分解为 自由响应和强迫响应两部分响应之和; 2、积分⎰+∞∞-⋅dt t tt)(22sin δ等于 4 ;3、频谱结构中,当脉宽减小时,信号的频宽____增大 _;4、信号)()1()(t u e t f t α--=的象函数为_________()as s a +;5、12()2F z z z --=+对应的原始时间序列为 (1)2(2)k k δδ-+- 三、已知信号ft=)]23cos(31)22cos(21)2[cos(2111πωπωπωπ-+-+-t t ,画出ft 的单边、双边幅度频谱图和相位频谱图;12分解:单边谱:每图3分 双边谱:每图3分111四、设)()(ωj F t f ↔,求下列各式的频谱函数;15分,每题5分 1)3()3(t f t -- 解:由展缩特性)31(31)3(ωj F t f -↔-2分由频域微分特性)31(31)]31(31[)3(ωωωωj F d d j j F d d jt tf -=-↔-2分 因此)31()31(31)3(3)3()3()3(ωωωj F j F d d j t f t tf t f t ---↔---=--1分2dtt df )42(+-解:由展缩和时移特性,得ωωj e j F t f 2)21(21)42(--↔+-3分 再根据时域微分特性ωωωj e j F j t f dt d 2)21(21)42(--↔+-2分 3t j e t f 2)23(-- 解:由展缩和时移特性,得ωωj e j F t f 32)31(31)23(-↔-3分再根据频移特性)2(322)]2(31[31)23(+--+↔-ωωj tj e j F et f 2分 下方程和非零起始条件表示的连续时间因果LTI 系统,⎪⎩⎪⎨⎧==+=++--5)0(',2)0()(52)(4522y y t f dtdft y dt dy dt y d 五.已知输入)()(2t u e t f t-=时,试用拉普拉斯变换的方法求系统的零状态响应)(t y zs 和零输入响应)(t y zi ,0≥t 以及系统的全响应),(t y 0≥t ;15分 解:方程两边取拉氏变换:)(455245)0(5)0(')0()()()(22s F s s s s s y y sy s Y s Y s Y zi zs ⋅++++++++=+=---3分 455221459222+++⋅+++++=s s s s s s s 43/713/134592)(2+-+=+++=s s s s s s Y zi 2分 )()37313()(4t u e e t y t t zi ---=3分42/122/111459221)(2+-+-+=+++⋅+=s s s s s s s s Y zs 3分 )()2121()(42t u e e e t y tt t zi -----=2分 )()61721316()()()(42t u e e e t y t y t y t t t zi zs -----=+=2分六、有一因果离散时间LTI 系统,激励为)()21()(1n u n f n =时,全响应为)()21()(2)(1t u n u n y n n -=;起始状态不变,激励为)()21(2)(2n u n f n =时,其全响应为)()21(2)(23)(2n u n u n y n n -⋅⋅=,求:1系统的零输入响应,2激励为)()21(5.0)(3n u n f n ⋅=时的完全响应起始状态保持不变;14分 解:设相同初始条件下,零输入响应分量)(n y zi ,则 )()()(11n y n y n y zi f +=2分 由线性关系)()(2)()()(122n y n y n y n y n y zi f zi f +=+=3分解得:)()21()(22)(1n u n u n y n n f -⋅=2分因此)(2)()()(11n u n y n y n y n f zi -=-=2分所以)()(5.0)()()(133n y n y n y n y n y zi f zi f +=+=3分)()21(21)(3n u n y n⋅-=2分 七、已知系统框图如下,求该系统的单位样值响应;14分解:可得()()()()()261523---+--=n y n y n x n x n y即()()()()()232615--=-+--n x n x n y n y n y 4分 求得齐次解n n C C 2321+2分假定差分方程式右端只有xn 项起作用,不考虑3xn-2项作用,此时系统单位样值响应为)(1n h ; 由1)0(1=h ,0)1(1=-h 可得⎪⎩⎪⎨⎧+=+=2121213101C C C C解得31=C ,22-=C())(23)(111n u n h n n ++-=4分当-3xn-2项起作用时,由线性时不变特性 ())2(233)(112---=--n u n h n n 2分)2()23(3)()23()()()(111121----=+=--++n u n u n h n h n h n n n n 2分也可通过Z 变换得到常熟理工学院20 ~20 学年第 学期信号与系统考试试卷试卷库03试题总分: 100 分 考试时限:120 分钟一、填空题本大题共10小题,每小题2分,共20分;不写解答过程,将正确的答案写在每小题的空格内;错填或不填均无分;1、对于连续的线性系统,若输入为)(1t f 时的响应为)(1t y ,输入为)(2t f 时的响应为)(2t y ,则对于任意常数1a 和2a , 输入为)()(2211t f a t f a +时的响应为______)()(2211t y a t y a +2、某连续系统的输入信号为f t,冲激响应为h t,则其零状态响应为____)(*)(t h t f3、一线性时不变连续时间系统是稳定系统的充分且必要条件是系统函数的极点位于S 平面的 左半平面 ;4、=--)(*)(2τδt t u e t )()(2ττ---t u e t5、()dt t e t 12-⎰+∞∞--δ= e -2 ; 6、已知 ft 的傅里叶变换为Fj ω, 则f2t-3的傅里叶变换为 )2(2123ωωj F e j - ; 7、已知 651)(2+++=s s s s F ,则=+)0(f 1 ; =∞)(f 0 ;8、、若描述某线性时不变连续系统的微分方程为)(3)()(2)(2)(t f t f t y t y t y +'=+'+'',则该系统的系统函数Hs=__223)(2+++=s s s s H ___________; 9、信号)(n u a n 的z 变换为_____az z- ________;10、已知信号的最高频率为m f ,要使抽样后的信号能完全恢复原信号,则最大的抽样间隔为mf 21 二、选择题本大题共10小题,每小题2分,共20分;在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题后的括号内;1、假如周期矩形脉冲信号的周期为T ,脉冲宽度为τ,高度为A ,下列关于对周期矩形脉冲信号的频谱叙述不正确的是 B ;A. 当T 不变,将τ减小时,频谱的幅度将减小B. 当T 不变,将τ减小时,相邻谱线的间隔将变密C. 当T 不变,将τ减小时,频谱包络线过零点的频率将增高D. 当τ不变,将T 增大到∞时,频谱将由离散谱变为连续谱 2、题2图中信号)(t f 的表达式是 A ;A. )1()]1()([-+--t u t u t u tB. )]1()([--t u t u tC. )]1()()[1(---t u t u tD. )]2()([--t u t u t3、已知)(t f 的波形如题3a 图所示,则)22(--t f 为图3b 图中的的波形为 A ;4、积分⎰∞∞--+dt t t )2()1(2δ的值为 D ;A.1B.3C.4D.55、已知)(t f 的拉普拉斯变换为)(s F ,则dtt df )(的拉普拉斯变换为 B ; A. )(s sF B.)0()(--f s sFC. )0()(-+f s sFD. ⎰-∞-+0)(1)(ττd f s s sF6、周期信号)(t f 如题6图所示,其三角形式傅里叶级数的特点是 B ;A. 含余弦项的偶次谐波且含直流分量B. 含余弦项的奇次谐波且无直流分量C. 含正弦项的奇次谐波且无直流分量D. 含正弦项的偶次谐波且含直流分量7、已知dtt d t f )()(δ=,则其频谱)(ωj F 等于 C ; A.ωj 1 B.)(1ωπδω+jC. ωjD.)(21ωπδω+j 8、题8图a 中ab 段电路是某复杂电路的一部分,其中电感L 和电容C 都含有初始状态其初始状态分别为)0(-L i 和)0(-C u ,请在题8图b 中选出该电路的s 域模型为 B ;_题8图(a))(t u c b-L 1题8图(b)sc -A.-L 1sc -B.-L 1sc -C.-L 1sc -D.9、已知某离散序列,其它, , ⎩⎨⎧=≤=n N n n f 0||1)(该序列还可以表述为 C ; A. )()()(N n u N n u n f --+= B. )()()(N n u N n u n f ---+-= C. )1()()(---+=N n u N n u n f D. )1()()(----+-=N n u N n u n f 10、离散信号fn 是指 BA .n 的取值是连续的,而fn 的取值是任意的信号B .n 的取值是离散的,而fn 的取值是任意的信号C .n 的取值是连续的,而fn 的取值是连续的信号D .n 的取值是连续的,而fn 的取值是离散的信 三、计算题本题共16分1已知 6116332)(232+++++=s s s s s s F ,试求其拉氏逆变换ft ;8分解:1找极点())3)(2)(1(3322+++++=s s s s s s F 2分2展成部分分式 ()321321+++++=s k s ks k s F 2分 362511)( +++-++=s s s s F 所以 2分()[]1e αs t u L t +=-α根据 ()0e 6e 5e )(:32≥+-=---t t f tt t 得 2分2()。
武汉理工大学08级信号与系统期末试卷——武汉理工03级09级期末试卷(均有答案)资料文档

(1 分) (1 分) (1 分)
yzs
t
1 3
e2t
2 3
e3t
t
(2 分)
(4) 原点处有一单阶级点,所以系统临界稳定。
(5 分)
十一、解:(1)系统差分方程的表示式 yk 0.5yk 1 xk
(2)对差分方程两边取 z 变换并利用位移性质,得
Y z X z 0.5z1Y z
第 2 页,共 7 页
武汉理工大学教务处
试题标准答案及评分标准用纸
课程名称 信号与系统
信息工程学院 08 级
一、
f t F j
(A 卷)
f
t 4
4F
j
4
(1 分)
f
t 4
2
4F
j4 e
j 8
(1 分)
tf
1 4
t
2
d j4
F
j4 e j8
d
(2 分)
二、解:利用傅里叶变换的对称性
(1)系统函数 H (s) ;
(2)画出系统的模拟框图;
(3)当 e(t) 2et t 时,求系统的零状态响应 rzs (t) ;
(4)判断系统稳定性。
十一、(20 分)离散系统如下图所示,
xk
yk
z 1 0.5
(1)列写系统差分方程; (2)求系统函数 H(z),并求系统的单位样值响应; (3)画 H(z)的零、极点分布图并指出收敛域; (4)求该系统的频率响应,并绘制系统幅频响应曲线。
所以系统稳定
十、
(1)
H
s
s3
s 1 5s2
6s
(2)
(2 分) (5 分) (5 分)
信号与系统+复试、期末试题+哈工大

−
π
jω
) |2 d ω = 3 。
求该序列 x (n ) 的可能表达式。
2 四、(12 分)某二阶线性时不变系统 d r (t ) + a 0 d r (t ) + a1 r (t ) = b0 d e(t ) + b1e(t ) 在激
dt
dt
dt
励 e −2t u(t ) 作用下的全响应为 [−e − t + 4e −2t − e −3t ]u(t ) ,而在激励 δ (t ) − 2e −2t u(t ) 作 用下的全响应为 [3e − t + e −2t − 5e −3t ]u(t ) (设起始状态固定)。求: 1.待定系数 a0 , a1 ;(3 分) 2.系统的零输入响应 rzi (t ) ;(3 分) 3.系统的单位冲激响应 h(t);(3 分) 4.待定系数 b0 , b1 。(3 分)
第 2 页 共 4 页
10.已知 f (t ) = e −3t u(t ) ,则 f s (t ) = f (t )δ T (t ) , T = 2 的拉氏变换为
⒀
。
11.若 f (t ) 是一个奈奎斯特角频率为 ω 0 的信号,则 f (t ) + f (t − t 0 ) 的奈奎斯特 角频率为 ⒁ , f (t ) cos(ω 0 t ) 的奈奎斯特角频率为 ⒂ 。
12.已知 f (t ) = [cos 2t ]u (t ) 的拉氏变换为 FL (s ) ,傅立叶变换为 FF ( jω ) , 则 FF ( jω ) − FL ( jω ) = ⒃ 。 (暂态响应还是稳态响应)。
s + 2 s + 3s
13.稳定系统的自由响应属于 ⒄
长安大学信号与系统期末试卷

长安大学试题
课程 系别 专业班号 姓名
信号与系统
考试日期 2006 年 6 月 25 日 学号
一 、(10 分)已知某连续时间信号如图所示。
1.绘出信号
x1 (t
)
=
x(4
−
t) 2
的波形;
2.若 x(t ) 的频谱是 X (ω) ,试用 X (ω) 表
示信号 x1(t)(n) = ∑δ (n − 8k) ;
k =−∞
3. y(n) 是如图所示的方波序列
七 、(10 分)已知 x(t) 是一个最高频率为 3kHz 的带限连续时间信号,y(t) 是最高频率为 2kHz
的带限连续时间信号。试确定对下列信号理想抽样时,允许的最低抽样频率。
1. f (t) = x(t) ; 2. f (t) = x(t)∗ y(t) ; 3. f (t) = x(t) y(t) ; 4. f (t) = x(t) + y(t) ; 5. f (t) = y(2t) 。
, X (Ω) 是信号 x(n) 的傅立叶变换。
1.求 X (0) 的值;
π
∫ 2.求 X (Ω)dΩ 的值; −π
∫ 3.求 π X (Ω) 2dΩ 的值. −π
七、(13 分)已知某离散时间序列 x(n) ,其傅立叶变换 X (Ω) 如图所示。
⎧x(n) , n = 2k
x1(n) = x(2n) , x2 (n) = ⎨ ⎩
二、(10 分)已知某离散时间 LTI 系统的单位脉冲响应为 h(n) = u(n) ,该系统对输入信号
x(n)
的输出响应为
y(n)
=
⎜⎛
1
n
⎟⎞ u(n)
[北京科技大学]《信号与系统》期末考试试题
![[北京科技大学]《信号与系统》期末考试试题](https://img.taocdn.com/s3/m/1290bb23a417866fb94a8e11.png)
北京科技大学远程与成人教育学院2020学年第1次远程课程《信号与系统》测验学习中心批次/专业/层次学号姓名________一、选择题(20分,每题2分)从各选项中选择唯一符合题干要求的选项。
1、信号()()()sin5+2cos2f t t t=的周期为()。
(A)5π (B)2π/5 (C)π (D)2π2、以下为计算机产生的信号的是()(A)(B)(C)(D)3、系统1()()y t f tt=为()系统。
(A)线性时不变(B)线性时变(C)非线性时不变(D)非线性时变4、πcos()()d2t t tδ+∞-∞⋅-⎰的结果为()。
(A)0 (B)π()2tδ-(C)1 (D)25、[]2,10kf k r r=-<<可以表示为图()。
(A)(B)(C)(D)题号一二三四五总分得分6、已知周期为T 0的周期信号f (t )的傅里叶系数为C n ,则02j ()()e tx t f t ω-=的傅里叶系数为( )。
(A )C n +1 (B )C n +2 (C )C n -1 (D )C n -27、当系统初始状态为零时,由系统的外部激励f (t )产生的响应称为系统的为系统的( )。
(A )零状态响应 (B )零输入响应 (C )齐次响应 (D )强迫响应8、由系统的外部激励f (t )产生的响应称为系统的零状态响应,可以用f (t )和冲激响应h (t )的卷积积分得到,其定义为: (A )()()()()d f t h t f h t τττ+∞-∞*=⋅-⎰ (B )()()()()d f t h t f t h t ττ+∞-∞*=⋅-⎰(C )()()()()d f t h t f h t τττ+∞-∞*=⋅-⎰(D )()()()(+)d f t h t f h t τττ+∞-∞*=⋅⎰9、非周期信号的频谱为( )频谱,周期信号的频谱为( )频谱。
(A )离散,离散 (B )离散,连续 (C )连续,离散(D )连续,连续 10、某离散系统的系统函数为()H z ,若系统同时存在()H j ω,则此系统为 ( )。
11-5-技术专-信号与系统期末考试试题答案

学号___________ 姓名_________ 贵州函授站得分______中国传媒大学远程与继续教育学院2010级广播电视技术专科第五学期《信号与系统》期末试卷一.单项选择题(本大题共10小题,每小题2分,共20分)。
1. 如右下图所示信号,其数学表示式为 (B)A. f (t ) = tu(t) − tu(t− 1)B. f (t ) = tu(t) − (t− 1)u (t− 1)C. f (t) = (1 − t )u (t) − (t− 1)u (t− 1)D. f (t ) = (1 + t )u (t) − (t + 1)u (t + 1)∞2. 序列和∑δ ( n ) 等于( A )n = − ∞C.u ( n)D. (n + 1)u ( n)A. 1B. ∞3. 已知:f (t ) = sgn(t ) 傅里叶变换为F ( jw) =2,则:F(jw)=jπsgn(w)的傅里叶jw1反变换f1(t)为(C)A. f1 (t ) =1B. f1 (t) = −2C. f1(t) = −1D. f1 (t ) =2t t t t24. 积分∫−2e tδ ( t− 3 ) dt等于(A)A. 0B. 1C. e3D. e−35. 周期性非正弦连续时间信号的频谱,其特点为 (C)A. 频谱是连续的,收敛的B. 频谱是离散的,谐波的,周期的C. 频谱是离散的,谐波的,收敛的D. 频谱是连续的,周期的6. 设: f (t ) ↔ F ( jw ) ,则: f 1 (t ) = f ( at − b ) ↔ F 1 ( jw ) 为( C ) A. F ( jw ) = aF ( j w ) ⋅ e − jbw B. F ( jw ) = 1 F ( j w ) ⋅ e − jbw1 a 1a aC. F ( jw ) = 1 F ( j w ) ⋅ e − j b wa 1 a a7. 已知某一线性时不变系统对信号H ( s ) = ( B )w − j b w D. F ( jw ) = aF ( j ) ⋅ e a1 a X (t ) 的零状态响应为 4 dX (t − 2) ,则该系统函数 dtA. 4 F ( s )B. 4 s⋅ e - 2SC. 4 e−2S / sD. 4 X ( s ) ⋅ e - 2S8. 单边拉普拉斯变换F ( s ) = 1 + s的原函数f (t ) = (D)A. e−t u (t )B. (1 + e−t )u (t )C. (t + 1)u (t )D. δ (t ) + δ' (t )9.如某一因果线性时不变系统的系统函数H(s)的所有极点的实部都小于零,则( C )A. 系统为非稳定系统B. | h(t) |<∞∞C. 系统为稳定系统D.∫0h (t )dt = 010. 离散线性时不变系统的单位序列响应h( n ) 为(A)A.输入为δ ( n ) 的零状态响应B.输入为u ( n ) 的响应C.系统的自由响应D.系统的强迫响应二.填空题(本大题共10小题,每小题2分,共20分)1. δ( −t ) =___ δ (t ) __ (用单位冲激函数表示 )。
信与系统期末考试试题

期末试题一、选择题每小题可能有一个或几个正确答案,将正确的题号填入 内 1.f 5-2t 是如下运算的结果———————— A f -2t 右移5 B f -2t 左移5 C f -2t 右移25 D f -2t 左移252.已知)()(),()(21t u e t f t u t f at -==,可以求得=)(*)(21t f t f ————— A1-at e - B at e -C )1(1at e a --D at e a-13.线性系统响应满足以下规律————————————A 若起始状态为零,则零输入响应为零;B 若起始状态为零,则零状态响应为零;C 若系统的零状态响应为零,则强迫响应也为零;D 若激励信号为零,零输入响应就是自由响应;4.若对ft 进行理想取样,其奈奎斯特取样频率为f s ,则对)231(-t f 进行取样,其奈奎斯特取样频率为————————A3f s Bs f 31 C3f s -2 D )2(31-s f 5.理想不失真传输系统的传输函数Hjω是 ————————A 0j tKe ω- B 0t j Keω- C 0t j Keω-[]()()c c u u ωωωω+--D 00j t Keω- 00,,,c t k ωω为常数6.已知Z 变换Z 1311)]([--=zn x ,收敛域3z >,则逆变换xn 为—— A )(3n u n C 3(1)nu n -B )(3n u n -- D )1(3----n u n二.15分已知ft 和ht 波形如下图所示,请计算卷积ftht,并画出ftht 波形;三、15分四.20分已知连续时间系统函数Hs,请画出三种系统模拟框图直接型/级联型/并联型;.五.20分某因果离散时间系统由两个子系统级联而成,如题图所示,若描述两个子系统的差分方程分别为:)()1(31)()1(6.0)(4.0)(11n y n y n y n x n x n y =---+=x (n )y 1(n )(n )H 1(z )H 2(z )1.求每个子系统的系统函数H 1z 和H 2z ; 2.求整个系统的单位样值响应hn ;3.粗略画出子系统H 2z 的幅频特性曲线;ss s s s H 10755)(23+++=信号与系统试题一标准答案说明:考虑的学生现场答题情况,由于时间问题,时间考试分数进行如下变化:1第六题改为选做题,不计成绩,答对可适当加分;2第五题改为20分;一、1.C 2. C 3. AD 4. B二、三、四.20分已知连续时间系统函数Hs,请画出三种系统模拟框图直接型/级联型/并联型;.ss s s s H 10755)(23+++=五、答案:1. 1123()52()0.40.60z H z z z z-+=+=>2111()113133zH z z z z -==>-- 2. 121312111()()(1)()(1)53531553nn nh n u n u n n u n δ-⎛⎫⎛⎫⎛⎫=+-=+- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭3.Re zj Im z0 ⨯132()j H e Ω32 34π2πΩ期末试题2 一、选择题2分/题,共20分1) 信号xn , n=0,1,2,3,…是能量有限的意思是a xn 有限;b |xn |有界;c()2n x n ∞=<∞∑; d()01Nn x n N=<∞∑; c2) 一个实信号xt 的偶部是a xt+x-t ;b xt+x-t ;c |xt |-|x-t |;d xt-x-t; b 3) LTI 连续时间系统输入为(),0ate u t a ->,冲击响应为ht=ut , 则输出为a()11at e a --; b ()()11at e t a δ--; c ()()11ate u t a --; d ()()11at e t aδ---; c 4) 设两个LTI 系统的冲击响应为ht 和h 1t ,则这两个系统互为逆系统的条件是 a ()()()1h t h t t δ*=; b ()()()1h t h t u t *=; a c ()()()1h t h t u t *=-; d ()()10h t h t *=;5) 一个LTI 系统稳定指的是a) 对于周期信号输入,输出也是周期信号;b 对于有界的输入信号,输出信号趋向于零;c 对于有界输入信号,输出信号为常数信号;d 对于有界输入信号,输出信号也有界 d6) 离散信号的频谱一定是a 有界的;b 连续时间的;c 非负的;d 连续时间且周期的; d 7) 对于系统()()()dy t y t x t dtτ+=,其阶跃响应为 a ()/1t eu t τ-⎡⎤-⎣⎦; b ()/1t e t τδ-⎡⎤-⎣⎦; c ()/1t e u t τ-⎡⎤+⎣⎦; d ()/1t e t τδ-⎡⎤+⎣⎦. a8) 离散时间LTI 因果系统的系统函数的ROC 一定是a 在一个圆的外部且包括无穷远点;b 一个圆环区域;c 一个包含原点的圆盘;d 一个去掉原点的圆盘; a 9) 因果系统的系统函数为11,01a az ->-,则a 当a>2时,系统是稳定的;b 当a<1 时,系统是稳定的;c 当a=3时,系统是稳定的;d 当a 不等于无穷大时,系统是稳定的; b10) 信号的傅立叶变换可以看成是拉普拉斯变换的特例,如果 a 拉普拉斯变换的收敛域不包含虚轴;b 拉普拉斯变换的收敛域包含单位圆;c 拉普拉斯变换的收敛域包含虚轴;d 拉普拉斯变换的收敛域不包含单位圆; c二、填空题 3分/题,共24分1. 信号()()()2cos 101sin 41x t t t =+--的基波周期是 π2.信号()1, 380, n x n ≤≤⎧=⎨⎩其它和()1, 4150, n h n ≤≤⎧=⎨⎩其它的卷积为 ()6, 7116, 121824, 19230,n n n y n n n -≤≤⎧⎪≤≤⎪=⎨-≤≤⎪⎪⎩其它3.信号()252cos 4sin 33x t t t ππ⎛⎫⎛⎫=++⎪ ⎪⎝⎭⎝⎭的傅立叶系数为*0225512,,22a a a a a j --=====-4.因果LTI 系统差分方程()()()1y n ay n x n --=,1a <,则该系统的单位冲击响应为 hn=a nun5.信号()1112n u n -⎛⎫- ⎪⎝⎭的傅立叶变换为 12j j e e ωω---6.连续时间LTI 系统的系统函数是()0j t H j e ωω-=,则系统的增益和相位是 1和0t ω-7.理想低通滤波器()01,0,H j ωωωωω⎧≤⎪=⎨>⎪⎩的冲击响应是 ()sin c t h t t ωπ=8.系统函数()32221148z z zH z z z -+=++表示的系统的因果特性为回答因果或非因果 非因果三、简答题 6分/题,共24分1. 试给出拉普拉斯变换、Z 变换与傅立叶变换的定义并简述它们间的关系; 拉普拉斯变换()()st X s x t e dt +∞--∞=⎰Z 变换()()nn X z x n z+∞-=-∞=∑傅立叶变换()X如果拉普拉斯变换的收敛域包含j ω轴,当s j ω=时,拉普拉斯变换就是连续时间傅立叶变换;如果Z 变换的收敛域包含复平面单位圆,当Z=expj ω时,Z 变换就是离散时间傅立叶变换; 当上述条件不成立时傅立叶变换不存在,但是拉普拉斯变换或Z 变换可能存在,这说明这两种变换确实是傅立叶变换的推广;2. 试回答什么是奈奎斯特率,求信号()()2sin 4000t x t t ππ⎛⎫= ⎪⎝⎭的奈奎斯特率;带限信号xt 当Max ωω>时,对应的傅立叶变换()0X j ω=,则有当采样频率22sampling Max Tπωω=>时,信号xt 可以由样本(),0,1,2,...x nT n =±±唯一确定,而2Max ω即为奈奎斯特率;16000pi3. 试叙述离散时间信号卷积的性质,求出信号()()()122nn x n u n u n ⎛⎫=+- ⎪⎝⎭和()()h n u n =卷积;离散或连续卷积运算具有以下性质:交换率,分配律,结合率()()()()()()122nn x n h n u n u n u n u n ⎛⎫*=*+-* ⎪⎝⎭=()11112, 0212, 012n n n u n n ++⎛⎫⎛⎫- ⎪ ⎪≥⎧⎝⎭ ⎪+⎨ ⎪<⎩- ⎪⎝⎭4. 试回答什么是线性时不变系统,判定系统()()21y t t x t =-是否为线性的,是否为时不变的;系统满足线性性,即()()12ay t by t +是()()12ax t bx t +的响应同时满足是不变性,即()x t 的输出为()y t 则()0x t t -的输出为()0y t t - 该系统是线性的,但不是时不变的四、计算题 8分/题,32分1. 连续时间LTI 系统的系统函数为()2KH s s =+,采用几何分析法画出其幅频相应图,说明该系统对应的滤波器是何种频率选择性滤波器;解:2)(+=s Ks H ,2->σ 当jwes =,即取纵坐标轴上的值,)()(ωj es e H s H jw==AK e H j =|)(|ω讨论A 随着Ω的变化而发生的变化:0=Ω,A=2, 2|)(|Ke H j =ω,2=Ω,A=22, 22|)(|K e H j =ω,∞→Ω,A ∞→, 0|)(|→ωj e H 则频率响应的模特性大概如图:2.利用傅立叶级数的解析公式计算连续时间周期信号基波频率为0ωπ=() 1.5,011.5,12t x t t ≤<⎧=⎨-≤<⎩的系数;该傅立叶级数系数为/20,03sin 2,0k jk k k a e k k πππ-=⎧⎪⎪⎛⎫=⎨⎪⎝⎭⎪≠⎪⎩3. 对于()2132X s s s =++求出当Re{s}<-2和-2<Re{s}<-1时对应的时域信号()x t ; 分别是()()[]2,Re 2t tx t e e u t s --⎡⎤=-+-<-⎣⎦和()()()2t t x t e u t e u t --=---,[]2Re 1s -<<4.求系统函数()12111148H z z z --=+-对应的时域中的差分方程系统,并画出其并联型系统方框图; 差分方程为()()()()111248y n y n y n x n +---=信号与系统期末考试试题3课程名称: 信号与系统一、选择题共10题,每题3分 ,共30分,每题给出四个答案,其中只有一个正确的1、 卷积f 1k+5f 2k-3 等于 ;Af 1kf 2k Bf 1kf 2k-8Cf 1kf 2k+8Df 1k+3f 2k-32、 积分dt t t ⎰∞∞--+)21()2(δ等于 ;ABC3D53、 序列fk=-u-k 的z 变换等于 ;A1-z z B-1-z zC 11-zD 11--z4、 若yt=ftht,则f2th2t 等于 ;A)2(41t y B )2(21t y C )4(41t y D )4(21t y 5、 已知一个线性时不变系统的阶跃相应gt=2e -2tut+)(t δ,当输入ft=3e —tut 时,系统的零状态响应y f t 等于A-9e -t +12e -2t ut B3-9e -t +12e -2t utC )(t δ+-6e -t +8e -2t ut D3)(t δ +-9e -t +12e -2t ut6、 连续周期信号的频谱具有(A ) 连续性、周期性 B 连续性、收敛性 C 离散性、周期性 D 离散性、收敛性x nyn7、 周期序列2)455.1(0+k COS π的 周期N 等于(A )1B2C3D4 8、序列和()∑∞-∞=-k k 1δ等于A1 B ∞ C ()1-k u D ()1-k ku9、单边拉普拉斯变换()se ss s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u tet f t的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s ()()()2323++-s se C s ()()332++-s s e D s二、填空题共9小题,每空3分,共30分1、卷积和k+1uk+1)1(k -δ=________________________2、单边z 变换Fz=12-z z的原序列fk=______________________ 3、已知函数ft 的单边拉普拉斯变换Fs=1+s s,则函数yt=3e -2t ·f3t 的单边拉普拉斯变换Ys=_________________________4、频谱函数Fj ω=2u1-ω的傅里叶逆变换ft=__________________5、单边拉普拉斯变换ss s s s F +++=2213)(的原函数ft=__________________________ 6、已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ,则系统的单位序列响应hk=_______________________7、已知信号ft 的单边拉氏变换是Fs,则信号⎰-=20)()(t dx x f t y 的单边拉氏变换Ys=______________________________8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应ht=9、写出拉氏变换的结果()=t u 66 ,=k t 22三、8分已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数 ()(),dt t df t s =求⎪⎭⎫⎝⎛2ωs 的傅里叶逆变换;四、10分如图所示信号()t f ,其傅里叶变换()()[]t f jw F F =,求1 ()0F 2()⎰∞∞-dw jw F五、12分别求出像函数()25232+-=z z zz F 在下列三种收敛域下所对应的序列12〉z 2 5.0〈z 325.0〈〈z六、10分某LTI 系统的系统函数()1222++=s s s s H ,已知初始状态()(),20,00=='=--y y 激励()(),t u t f =求该系统的完全响应;信号与系统期末考试参考答案一、选择题共10题,每题3分 ,共30分,每题给出四个答案,其中只有一个正确的1、D2、A3、C4、B5、D6、D7、D8、A9、B 10、A二、填空题共9小题,每空3分,共30分1、()()k u k5.0 2、)()5.0(1k u k + 3、52++s s 4、()tj e t jt πδ+5、)()()(t u e t u t t -++δ6、()[]()k u k 15.01+-+ 7、 ()s F s e s2-8、()()t u t e t 2cos - 9、s66, 22k/S k+1 三、8分解: 由于()()()()()ωωωF j dtt df t s F t f ↔=↔ 利用对称性得()()ωπ-↔S jt F jt 2 利用尺度变换a=-1得()()ωπS jt F jt 2↔-- 由()jt F 为偶函数得 ()()ωπS jt F jt↔-2 利用尺度变换a=2得 ()⎪⎭⎫⎝⎛↔-221222ωπS t j F t j()⎪⎪⎩⎪⎪⎨⎧>〈=↔⎪⎭⎫⎝⎛∴21,12,021,12,2222t t t t j tt j F j t S 即即ππω四、10分 解:12)()0()()(==∴=⎰⎰∞∞--∞∞-dt t f F dte tf F t j ωω2ωωπωd e F t f t j ⎰∞∞-=)(21)(ππωω4)0(2)(==∴⎰∞∞-f d F五、12分 解:()()21221223125232---=⎪⎭⎫ ⎝⎛--•=⎪⎭⎫ ⎝⎛+-=z zz z z z z z z z z F1) 右边 ()()()k u k u k f kk⎪⎭⎫⎝⎛-=2122) 左边 ()()1221--⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛=k u k f kk3) 双边 ()()()1221---⎪⎭⎫⎝⎛-=k u k u k f k k六、10分 解:由)(S H 得微分方程为)()()(2)(t f t y t y t y ''=+'+'')()()0(2)(2)0()0()(22S F S S Y y S SY y Sy S Y S =+-+'-----12)0()0()2()(12)(222++'+++++=∴--S S y y S S F S S S S Y将SS F y y 1)(),0(),0(='--代入上式得 222)1(1)1(1)1(2)(+-++++=S S S S S Y11)1(12+++=S S )()()(t u e t u te t y t t --+=∴。
信号与系统期末考试试题

信号与系统期末考试试题题目一1.请简要介绍信号与系统的定义和基本概念。
2.什么是连续时间信号和离散时间信号?请分别给出它们的数学定义。
3.请解释线性系统和时不变系统的概念,并给出它们的数学表示。
4.什么是因果系统和稳定系统?请给出它们的定义和判别条件。
题目二1.请说明卷积操作在时域和频域的意义,并给出它们的数学表达式。
2.如何计算信号的自相关函数和互相关函数?请给出计算公式。
3.请解释频谱和功率谱密度的概念,并说明它们的物理意义。
4.如何通过傅里叶变换求解系统的频率响应?请给出计算步骤和公式。
题目三1.请解释采样定理的概念和应用,并给出采样定理的数学表达式。
2.如何通过离散时间傅里叶变换(DTFT)和离散傅里叶变换(DFT)分析离散时间信号的频谱特性?请给出计算公式。
3.请说明数字滤波器的分类和设计方法,并给出常见的滤波器类型。
4.请解释理想低通滤波器和巴特沃斯低通滤波器的设计原理和特点。
题目四1.请简要介绍拉普拉斯变换的定义和性质,并给出常见信号的拉普拉斯变换表达式。
2.如何通过拉普拉斯变换求解连续时间系统的频率响应?请给出计算步骤和公式。
3.请解释卷积定理的概念和应用,并给出卷积定理的数学表达式。
4.请解释单位冲激响应和单位阶跃响应的概念,并给出它们的计算方法和物理意义。
题目五1.请说明离散时间系统的稳定性判别方法,并给出判别条件。
2.如何通过离散时间系统的单位冲激响应和输入信号求解系统的输出响应?请给出计算方法。
3.请解释差分方程和差分方程的解的概念,并给出一阶差分方程的解析表达式。
4.请解释状态空间表示法的概念和优点,并给出状态空间模型的数学表达式。
结束语以上是信号与系统期末考试试题的内容。
希望通过这些题目,能够对信号与系统的基本理论和方法有一个全面的了解。
如果能够正确回答这些问题,那么对信号与系统的掌握程度就会更进一步。
祝愿大家在期末考试中取得好成绩!。
北交期末信号与系统期末(总复习)
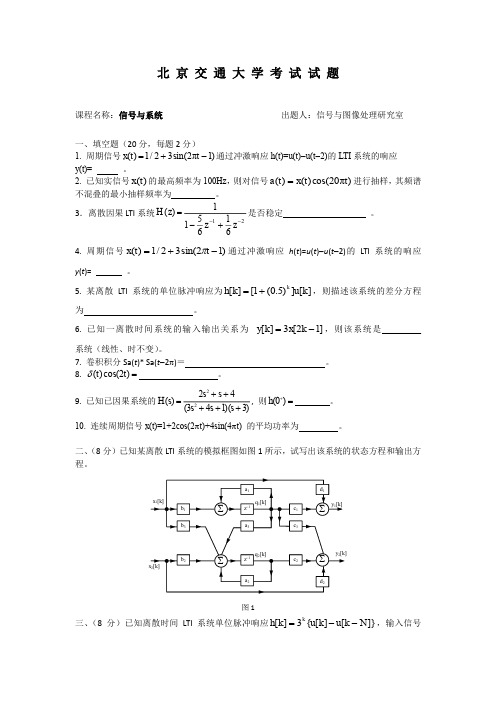
Im(z)
Re(z)
3 2 1 0
图2
三、(9 分)已知某离散时间系统如错误!未找到引用源。所示,试求系统的单位脉冲响应 h[k]。 其中 h1[k] u[k 1], h2[k] 0.5k u[k] 。
h1[k] x[k]
h2[k]
y[k]
图3
四、(9 分)已知某连续时间系统的模拟框图如图 4 所示,试写出该系统的状态方程和输出 方程.
并画出 x (1 0.2t )的波形。
x (t)
1
(1)
1 0 1
t 12 3
图2
3
五、(8 分)已知一系统的输入输出关系为 y[k] x[k n] , n2
(1)证明该系统是线性非时变系统; (2)求该系统的单位脉冲响应 h[k];
六、(8 分)在下图 3 所示系统中,H ( j) 是一个截止频率为c 的理想高通滤波器,求出该 理想低通滤波器的截止频率lc ,并求冲激响应 h(t) 。
6
图A
九、(15 分)
(1) yzi[k
k
k] u[k],
Yzs [k ]
[1 6
1 (1)k 2
4 (2)k 3
]u[k ]
y[k]
yzi[k]
yzs[k]
[7 (1)k 2
8 (2)k 3
1 ]u[k ] 6
(2)
H (z)
Yzs (z) X (z)
1 1 3z 1
2z 2
, h[k] [(1)k
q1(t) q2(t)
=
0 1
1 3
q1(t) q2(t)
+
0 1
x(t)
y(t) = 0
50
《信号与系统》考卷
2011/2012 学年 第 一 学期末考试试题(B 卷) 课程名称 信号与系统使用班级:09050341,09050342 ,09050343,09051041一、计算与画图(20分) [每题5分]1、 计算 dt t t t t x )6()2sin ()(0πδπ-+=⎰的值。
2、 已知信号1()x t 和2()x t 如图一所示图一试计算)(*)()(21t x t x t s =。
3、 计算信号)2()2()(--+=t u t u t x 傅立叶变换)(w X 。
4、 计算信号)2sin()(t e t x t -=的拉普拉斯变换)(s X 。
二、简答题(20分) [每题5分]1、 无失真传输系统在时域和频域应具备什么样的条件,才能实现无失真传输?2、 利用什么样的信号作系统的测试信号可测得系统的带宽C ω?3、 对于非带限信号)(t x ,如何实现抽样获得其样值序列{()}x kT ?4、 时域分析、频域分析、复频域分析对信号和系统分析而言,各自有什么特点?三、证明题(10分) [每题10分]非周期信号的时频功率守恒定理:ωωπd F dt t x 22)(21)(⎰⎰∞∞-∞∞-=四、分析与计算(30分) [第一题10分、第二题20分]1、 一线性系统在相同的初始状态下,当输入为)(1t x 时的全响应为)()2cos 2()(1t u t e t y t +=-,当输入为)(2)(12t x t x =时的全响应为)()2cos 2()(2t u t e t y t +=-。
试确定当输入为)(4)(31t x t x =时的全响应。
2、 已知信号()x t 如图二所示,且设其傅立叶变换式为()X ω,试分析以下特征:(1)其相位谱()φω。
(2)(0)X 。
(3)()X d ωω∞-∞⎰。
(4)1{Re[]}f X ω-()五、计算题(20分) [每题10分]1、 已知线性时不变系统传输函数()H s 的零极点分布如图四所示,单位冲激响应()h t 的初值(0)2h +=,求:(1)求系统函数()H s ;(2)求频率转移函数()H j ω;(3)求系统的单位冲激响应()h t ;(4)求激励()100cos(445)()x t t u t =+。
信号与系统期末考试试题(有答案的)

信号与系统期末考试试题6课程名称: 信号与系统一、选择题(共10题,每题3分 ,共30分,每题给出四个答案,其中只有一个正确的)1、 卷积f 1(k+5)*f 2(k-3) 等于 。
(A )f 1(k)*f 2(k) (B )f 1(k)*f 2(k-8)(C )f 1(k)*f 2(k+8)(D )f 1(k+3)*f 2(k-3)2、 积分dt t t ⎰∞∞--+)21()2(δ等于 。
(A )1.25(B )2.5(C )3(D )5 3、 序列f(k)=-u(-k)的z 变换等于 。
(A )1-z z (B )-1-z z(C )11-z (D )11--z4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。
(A ))2(41t y (B ))2(21t y (C ))4(41t y (D ))4(21t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时,系统的零状态响应y f (t)等于(A )(-9e -t +12e -2t )u(t) (B )(3-9e -t +12e -2t )u(t)(C ))(t δ+(-6e -t +8e -2t )u(t) (D )3)(t δ +(-9e -t +12e -2t )u(t)6、 连续周期信号的频谱具有(A ) 连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于(A ) 1(B )2(C )3(D )4 8、序列和()∑∞-∞=-k k 1δ等于(A )1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u tet f t的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s()()()2323++-s se C s ()()332++-s s e D s二、填空题(共9小题,每空3分,共30分)1、卷积和[(0.5)k+1u(k+1)]*)1(k -δ=________________________2、单边z 变换F(z)=12-z z的原序列f(k)=______________________ 3、已知函数f(t)的单边拉普拉斯变换F(s)=1+s s,则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换ss s s s F +++=2213)(的原函数f(t)=__________________________ 6、已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ,则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dx x f t y 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ,=k t 22三、(8分)已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dt t df t s =求⎪⎭⎫⎝⎛2ωs 的傅里叶逆变换。
2020年西南交通大学期末真题及答案信号与系统

《信号与系统》2005 年期末试题A 卷班级姓名学号成绩一一 30 分二二 30 分三三 26 分分四四 14 分分1 2 3 4 5 1 2 3 1 2 3一、共 5 5 小题,总分为 0 30 分1 、试判断下列式子代表的系统是否为线性系统,并说明理由(其中 y t为系统响应, 0 y 为初始条件, f t为系统输入)(8 分)201 0 2ty t y f d2 0 cos5 0 y t y t y f t2 33 3 0 y t y t f t3 2 2245 2d y t d y t d f ty t f tdt dt dt2、、试确定信号 1 cos 1000 sin 2000 x t t t 的奈奎斯特频率。
(3 分)3 、已知描述系统的方程为4 4 2y t y t y t f t ,初始条件为 0 0 2 y y 。
求(1 )系统传递算子 H p;;(2 )系统零输入响应 xy t。
(7 分)4 、已知系统的单位冲击响应 2h t t ,当系统输入为142f t t t t 时,用时域分析法求系统零状态响应 fy t。
(6 分)5 、已知 f t的波形如下图,求 F j 。
(6 分)二、共 3 3 小题,总分为 0 30 分1 、系统的微分方程为 5 62 8y t y t y t f t f t ,,激励 tf t e t ,利用复频域分析法求系统的零状态响应。
(7 分)2 、系统传递函数为 N sH sD s ,试分析下列系统是否渐近稳定。
(9 分)21 1 2D s s s s 5 3 22 4 3 2 9 D s s s s s 5 4 3 23 2 3 4 11 8 D s s s s s s 3 、作出下列系统直接实现形式的模拟框图和信号流图。
(注假定系统为零状态)(14 分)113sH ss 2423 2sH ss s 三、共 3 3 小题,总分为 6 26 分1 、系统信号流图如下图所示,求系统的传递函数 H s。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆大学信号与线性系统期末考试试题
一、填空题:(30分,每小题3分)
1.
=-⎰∞
∞-dt t t )()5cos 2(δ 。
2. ()dt t e t 12-⎰+∞
∞--δ= 。
3. 已知 f (t )的傅里叶变换为F (j ω), 则f (2t -3)的傅里叶变换为 。
4. 已知 6
51)(2+++=s s s s F ,则=+)0(f ; =∞)(f 。
5. 已知 ωωπδεj t FT 1)()]([+
=,则=)]([t t FT ε 。
6. 已知周期信号)4sin()2cos()(t t t f +=,其基波频率为 rad/s ;
周期为 s 。
7. 已知)5(2)2(3)(-+-=n n k f δδ,其Z 变换
=)(Z F ;收敛域为 。
8. 已知连续系统函数1
3423)(23+--+=
s s s s s H ,试判断系统的稳定性: 。
9.已知离散系统函数1.07.02)(2+-+=z z z z H ,试判断系统的稳定性: 。
10.如图所示是离散系统的Z 域框图,该系统的系统函数H(z)= 。
二.(15分)如下方程和非零起始条件表示的连续时间因果LTI 系统,
⎪⎩⎪⎨⎧==+=++--
5)0(',2)0()(52)(4522y y t f dt df t y dt dy dt y d 已知输入)()(2t e t f t ε-=时,试用拉普拉斯变换的方法求系统的零状态响应
)(t y zs 和零输入响应)(t y zi ,0≥t 以及系统的全响应),(t y 0≥t 。
三.(14分)
① 已知2
3662)(22++++=s s s s s F ,2]Re[->s ,试求其拉氏逆变换f (t ); ② 已知)2(235)(2>+-=
z z z z z X ,试求其逆Z 变换)(n x 。
四 (10分)计算下列卷积:
1. }1,0,6,4,3{}4,1,2,1{)()(21--*=*k f k f ;
2.)(3)(23t e t e t t εε--* 。
五.(16分)已知系统的差分方程和初始条件为:
)()2(2)1(3)(n n y n y n y ε=-+-+,5.0)2(,0)1(=-=-y y
1. 求系统的全响应y (n );
2. 求系统函数H (z ),并画出其模拟框图;
六.(15分)如图所示图(a )的系统,带通滤波器的频率响应如图(b)所示,其
相位特性0)(=ωϕ,若输入信号为:
)1000cos()(,2)2sin()(t t s t t t f ==π
试求其输出信号y(t),并画出y(t)的频谱图。
答案
一填空题(30分,每小题3分)
2. 1 ; 2. e -2 ;
3. )2(2123
ωωj F e j - ; 4. 1 ,0 ;
5. 21
)('ωωπδ-j ; 6. 2 л ;
7. 5223)(--+=z z z F ,|z|>0; 8. 不稳定; 9. 稳定 10.
214
14111)(--+-=z z z H 二.(15分)⎪⎩⎪⎨⎧==+=++--
5)0(',2)0()(52)(4522y y t f dt df t y dt dy dt y d 方程两边取拉氏变换:
)()6
1721316()()()(;)()2
121()(4
2/122/111459221)()()37313()(;)4
3/713/134592)(4
552214592)(4
55245)0(5)0(')0()()()(42422422222t e e e t y t y t y t e e e t y s s s s s s s s Y t e e t y s s s s s s Y s s s s s s s s F s s s s s y y sy s Y s Y s Y t t t zi zs t t t zi zs t t zi zi zi zs εεε-------------=+=--=+-+-+=+++⋅+=-=+-+=+++=+++⋅+++++=⋅++++++++=+=
三.1.(7分)
)
0(22)(2)(221222
32223662)(2222≥-+=+-+++=+++=++++=--t e e t t f s s s s s s s s s F t t δ
2.(7分)
)()12(5)(,2;2515)2)(1(5)
(;235)(2k k f z z z z z z z F z z z
z F n ε-=>-+--=--=+-=为右边序列
四. 1. (5分) {}4,1,22,21,4,11,2,3)(----=k f
2.(5分)
)()(3|)(36)()(6)(3)(230220)(33t e e e e d e
e d t e e t e t e t t t t t t
t t t εττ
τετεεεττττ---------∞
∞
----=-⋅==-⋅=*⎰⎰
五. 解:(16分)
(1)对原方程两边同时Z 变换有:
1
)]1()2()([2)]1()([3)(121-=-+-++-++---z z y z y z Y z y z Y z z Y 2
32121161)2)(1)(1()(2+-++-=++-=∴z z z z z z z z z z z Y )(])2(3
2)1(2161[)(n n y n n ε---+= (2)212311
)(--++=z z z H
六(15分)
)1000cos()(,2)2sin()(t t s t t t f ==π
)(5.0)(412)(2)2sin(4412)2sin()(44ωωππωππg g j F t t t t t f =⨯⨯=⨯⨯== )1000cos(22sin )()()
()()()(,
01001||999,1)()()]}1000()1000([*)(4
1{)
()()()
(*)()()]1000()1000([*)(4)(*)(21)()1000cos(22sin )()()(4t t
t t x t y j X j H j X j Y 其它j H j H g j H j X j Y t h t x t y g j S j F j X t t t t s t f t x ⋅====∴⎩⎨⎧≤≤=-++===-++==
⋅=
=πωωωωωωωωδωδωωωωωδωδωπ
πωωπωπτ。
