十一学校奥数升学考试真题7
北京市十一学校小升初考试数学真题

北京市十一学校小升初考试数学真题这篇北京市十一学校小升初考试数学真题是查字典数学网特地为大家整理的,希望对大家有所帮助!一、填空题(20分)1.二亿六千零四万八千写作( ),改写成用“万”作单位的数是()万。
2、,0.76和68%这三个数中最大的数是( ),最小的数是()。
3.能同时被2、3、5整除的最大的三位数是( )。
4.某班男生和女生人数的比是4:5,则男生占全班人数的( ),女生占全班人数的( )。
5.爸爸说:“我的年龄比小明的4倍多3。
” 小明说:“我今年a岁。
”用含有字母的式子表示爸爸的年龄,写作( );如果小明今年8岁,那么爸爸今年( )岁。
6.一个数除以6或8都余2,这个数最小是( );一个数去除160余4,去除240余6,这个数最大是()。
7. ÷( )=( )÷60=2:5=( )%=( )成。
8.在3.014,3 ,314%,3.1 和3. 中,最大的数是(),最小的数是( )。
9.一个圆的周长是12.56厘米,它的面积是( )平方厘米。
10.如果a= (c≠0),那么( )一定时,()和( )成反比例;( )一定时,( )和( )成正比例。
二、选择题(将正确答案的序号填入括号内)(5分)1.一个周长是l的半圆,它的半径是( )A.l÷2B. l÷C.l÷( +2)D.l÷( +1)2. 的值是一个( )。
A.有限小数B.循环小数C.无限不循环小数3.一台电冰箱的原价是2400元,现在按七折出售,求现价多少元?列式是( )。
A.2400÷70% B.2400×70%C.2400×(1-70%)4.在下列年份中,( )是闰年。
A.1990年 B.1994年 C.2019年5.下列各式中,a和b成反比例的是( )。
A.a× =1B.a×8=C.9a=6aD.三.判断题(对的在括号内打“√”,错的打“×”)(5分)1. 6千克:7千克的比值是千克。
2024年陕西省西安十一中小升初数学试卷

2024年陕西省西安十一中小升初数学试卷一、填空题。
(每小题3分,共30分)1.(3分)在5、5.5和55.5%这三个数中,最小的数是,最大的数是.2.(3分)一个三角形的三个角的度数比是1:4:5,这个三角形是三角形.3.(3分)甲、乙、丙三人,平均体重60千克,甲与乙的平均体重比丙的体重多3千克,甲比丙重3千克,则乙的体重为千克。
4.(3分)一个两位数,其十位与个位上的数字交换以后,所得的两位数比原来小27,则满足条件的两位数共有个.5.(3分)已知一个圆柱的侧面展开图恰好是一个边长为6.28厘米的正方形,这个圆柱的体积是立方厘米。
(保留一位小数)6.(3分)A,B,C,D,E是五个人的年龄数,已知A是B的2倍,C的3倍,D的4倍,E的6倍,则A+B+C+D+E最小为。
7.(3分)如图,阴影部分的面积是。
(用a,b表示,π=3)8.(3分)如图是一个正方体的表面展开图,若在正方体的表面填上数,使得对面两数之和为8,则A,B,C处填的数分别是、、。
9.(3分)有一堆糖果,其中奶糖占45%,再放入14颗水果糖后,奶糖就只占,那么这堆糖中有奶糖颗。
10.(3分)在如图的长方形内,有四对正方形(标号相同的两个正方形为一对),每一对是相同的正方形,那么中间这个小正方形的周长为。
二、计算题。
(每小题5分,共20分)11.(5分)计算:÷[32×(1﹣)+]+1。
12.(5分)计算题。
13.(5分)计算题。
14.(5分)计算题。
三、解答题。
(共50分)15.(6分)某学校在开学前两周开展“暑假作业完成量”调查活动,随机调查了部分学生的假期作业剩余情况,并将调查结果统计后绘制成如图所示的不完整统计图。
(1)被调查学生人数为人.(2)把条形统计图补充完整.(3)若该学校有学生10000人,请估计该学校今年暑假的假期作业完成情况为“剩少量”的学生有多少人?16.(5分)某商品按原价的八折出售,仍能获利20%,由于该商品成本降低,按原价的七五折出售,能获利25%,该商品成本降低了多少?17.(5分)正方形边长为8,求阴影部分面积.18.(5分)甲、乙两人爬山,下山速度是上山速度的2倍,当甲到达山顶时,乙距山顶还有400米,当甲下到山脚时,乙才下到半山腰,从山脚到山顶有多远?19.(10分)下面是某电影大世界的影片广告:片名《哈利•波特》票价45元优惠办法上午场六折下午场八折夜场不优惠张老师一家3口去看某一场次的电影,票价共节省了27元,那么张老师一家看的是那个场次的电影?优惠票价是多少元?20.(10分)如图是一个长4厘米、宽3厘米的长方形.(1)在长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形.(2)求出这个梯形的面积.(3)以等腰直角三角形的一条直角边为轴,旋转一周,会形成.算出旋转形成的这个立体图形的体积.21.(9分)将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起。
十一学校历年分班试题

十一学校历年分班试题
一、填空题: 1.在 1991,1992,1993,1994,1995,1996,1997 这七个数中,不能写成两个自然数的平方 差的数是____ 解: 由平方差公式 a 2 b 2 a b a b 知任意一个奇数 2n+1 有 2n+1=1× (2n+1) = (n+1-n) ×(n+1+n)=(n+1)2-n2,故任意一个奇数都能写成两个自然数的平方差,所以我们只需要 看偶数。因为 1992=2×996=(499-497)×(499+497)=4992-4972,1996=2×998=(500-498) ×(500+498)=5002-4982,所以只有 1994 不能写成两个自然数的平方差。 2.如图,阴影部分 S1 的面积比阴影部分 S2 的面积大 12 平方厘米,且 BD=4 厘米,DC=1 厘 米,则线段 AB=______厘米.
使每一横行,每一竖行,两对角线斜行中三个数的和都相等.
8.有本数学书共有 600 页,则数码 0 在页码中出现的次数是______. 9.张明骑自行车,速度为每小时 14 千米,王华骑摩托车,速度为每小时 35 千米,他们分别 从 A、B 两点出发,并在 A、B 两地不断往返行驶,且两人第四次相遇(两人同时到达同一地 点叫做相遇)与第五次相遇的地点恰好相距 120 千米,那么,A、B 两地之间的距离是______ 千米. 10.某次数学竞赛原定一等奖 8 人,二等奖 16 人,现在将一等奖中最后 4 人调整为二等奖, 这样得二等奖的学生的平均分提高了 1.2 分,得一等奖的学生的平均分提高了 4 分,那么原 来一等奖平均分比二等奖平均分多______分. 二、解答题: 11.学校要建一段围墙,由甲、乙、丙三个班完成,已知甲班单独干需要 20 小时完成,乙班 单独干需要 24 小时完成,丙班单独干需要 28 小时完成,如果先由甲班工作 1 小时,然后由乙 班接替甲班干 1 小时,再由丙班接替乙班干 1 小时,再由甲班接替丙班干 1 小时,„„三个班 如此交替着干,那么完成此任务共用了多少时间?
北京市十一学校2018-2019学年七年级分班测试数学试卷(含答案)

【答案】100!=100⨯99=9900(1)96×19+4×19(2)36⨯(1北京市十一学校初一分班测试题一、基础考察:(每题4分,共24分)1.如果甲比乙多五分之一,乙比丙多五分之一,则甲比丙多%.【答案】442.要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要分钟完成。
【答案】183.一个完全平方数有5个约数,那么这个数的立方有个约数。
【答案】134.715的分母减少3后,要使分数的大小不变,分子应减少.【答案】1.45.观察按下顺序排列的等式:9⨯0+1=01,9⨯1+2=11,9⨯2+3=21,9⨯3+4=31,9⨯4+5=41,按以上各式成立的规律,写出第12个等式是:【答案】9⨯11+12=1116.观察下列等式,(式子中的“!”是一种数学运算符号)1!=1,2!=2⨯1,3!=3⨯2⨯1,4!=4⨯3⨯2⨯1……;则计算100!= 98!98!二、能力提高:(每题4分,共52分)7.简便运算能力11-+)234【答案】(1)1900(2)158.小青坐在教室的第3排第4列,用(4,3)表示,那么小明座在教室的第5排第2列应当表示为【答案】(2,5)9.一次数学测验以后,张老师根据某班成绩绘制了如图所示的扇形统计图(80~89分的百分比因故模糊不清),若80分以上(含80分)为优秀等级,则本次测验这个班的优秀率为.(70分以下)12%(70~79分)20%36%(90~100分)(80~89)分)【答案】68%11.已知组成网格的小正方形的面积是1,则正方形ACDE的面积S=1正方形BCFG的面积S=2由此发现S、S、S三者关系是123,正方形ABHI的面积S=3A BFDEC【答案】9,16,25,S+S=S12312.如上面右图,长方形AFEB和长方形FDCE拼成了长方形ABCD,长方形ABCD的长是20,宽是12,则它内部阴影部分的面积是【答案】12013.如图,路线1是以AB为直径的半圆,路线2是四个半圆组成的曲线,一只蚂蚁要从A 爬到B,则沿路线1和沿路线2所走的路程()(A)路线1少(B)路线2少(C)路线1和路线2一样(D)无法确定路线12米路线2A B3米【答案】C15.已知某个台阶的宽度和高度如上面右图所示,现在要在台阶上铺满地毯,则需要地毯的长度是米。
十一学校小升初考试真题汇总

参考答案1、给下列加红字注音。
(10分)档dàng次给jǐ予模mú样惩chéng罚潜qián能歼jiān灭造诣yì膝xī盖尽jǐn管拖累lěi2、(10分)巧妙绝(伦) 抑扬顿(挫) 言简意(赅) 无动于(衷) 眼花(缭)乱脉搏渊博臂膊鄙薄锡箔3.C(2分) 4、D(2分) 5、D(2分) 6、D(2分) 7、D(2分)8、补全下列句子。
(10分)良药苦口利于病,忠言逆耳利于行。
书读百遍,其义自见。
世事洞明皆学问,人情练达即文章。
落红不是无情物,化作春泥更护花。
但使龙城飞将在,不教胡马度阴山。
天行健,君子以自强不息。
无边落木萧萧下,不尽长江滚滚来。
小荷才露尖尖角,早有蜻蜓立上头。
王师北定中原日,家祭无忘告乃翁。
借问酒家何处有,牧童遥指杏花村。
9、断句每错一处扣0.5分。
(5分)赵高欲为乱/恐群臣不听/乃先设验/持鹿献于二世/曰/马也/二世笑曰/丞相误邪/谓鹿为马/问左右/左右或言马/以阿顺赵高/或言鹿者/高因阴中诸言鹿者以法/后群臣皆畏高。
(1)(4分)欲:想要乃:于是误:错或:有的人(2)与选文相关的成语是:指鹿为马 (2分)(3)赵高(2分)(4)高因阴中诸言鹿者以法(2分)10.(2分)参考:假币风波11.(6分)甩掉:这里指“我们”想把这张50元的假币用掉。
翻船:这里指爸爸在大商场里使用假币时被验钞机验了出来,这张假币没能用掉。
自告奋勇:这里指“我”自己主动要求担当用掉这张假币的任务。
12.(4分)三心二意、五颜六色、千军万马、千呼万唤、十拿九稳等。
13.(2分)老板娘拿到钱后,先是对着亮处看了看,然后又用手揉一揉,最后还甩了两下,确定是真的后才找钱给那两个人。
14.(4分)略 15.(4分)略 16.(4分)略十一学校小升初面试真题(往年)试题题目:选择一首古典七律或绝句想象一个小故事。
分析:这道题考点有三个,一是对古诗的记忆和理解能力,二是语言的综合运用能力,三是创新能力。
十一学校2020-2021学年第二学期期末考试初一数学试题及答案

十一学校2020-2021学年第二学期期末考试初一数学一、选择题(每题3分,共24分)1.下面的图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.2.下列说法中,正确的是()A.±3是(﹣3)2的算术平方根B.﹣3是(﹣3)2的算术平方根C.的平方根是﹣3D.﹣3是的一个平方根3.如图,△ABC中,AC=BC,∠ACB=120°,AB=4,M为AB的中点,MN⊥BC,则△MNB的面积为()A.B.C.D.4.如图,在4×4的网格中,每个小正方形的过长均为1,点A、B、C都在格点上,则下列结论错误的是()A.AB=2B.∠BAC=90°C.△ABC的面积为10 D.点A到直线BC的距离是25.如图,平行四边形ABCD的对角线交于点O,且AD>CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么平行四边形ABCD的周长是()A.8 B.16 C.18 D.206.已知x,y为实数,xy=5,那么x+y的值为()A.B.2C.±2D.57.如图,在梯形ABCD中,AB∥DC,AB⊥BC,E是AD的中点,连接BE,若∠EBA=30°,BE=6,则梯形ABCD 的面积等于()A.6B.9C.15D.188.如图,△ABC中,AB>AC,AE平分∠BAC,BD⊥AE于D,CE⊥AE于E,F为BC的中点,给出结论:①FD ∥AC;②FE=FD;③AB﹣AC=DE;④∠BAC+∠DFE=180°.其中正确的是()A.①②B.①②③C.①②④D.①②③④二、填空题(每题3分,共30分)9.有一个数值转换器,原理如图,那么输入的x为729时,输出的y是.10.如图,数轴上A点表示的数为﹣2,B点表示的数是1.过点B作BC⊥AB,且BC=2,以点A为圆心,AC的长为半径作弧,若弧与数轴交点D表示的数为a,则a的平方为.11.如图,在△ABC中,AB=2,AC=,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为.12.三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB ∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是.13.如图,在平行四边形ABCD中,AB=5,AD=10,BF=3,BC的中点为E,连接EF,EF⊥AB.连接DF,DE,则△DEF的面积为.14.如图,在平行四边形ABCD中,E是BC的中点,AE=9,AD=10,若点B和点D之间的距离为12,则平行四边形ABCD的面积是.15.如图,在Rt△ABC中,∠ACB=90°,AC=6,CD为中线,延长CB至点E,使BE=BC,连接DE,F为DE 的中点,连接BF,若BF=3,则BC的长为.16.如图,在Rt△ABC中,∠BAC=90°,点D是BC的中点,连接AD.分别以点A,C为圆心,AD的长为半径在△ABC外画弧,两弧交于点E,连接AE,CE,过点D作DF⊥CE于点F.若AB=12,AC=16,则DF的长为.17如图,四边形ABCD为菱形,对角线AC,BD相交于点O,点E为OC上的一点,且AD=AE,若OE=1,OD =5,则菱形ABCD的面积为.18如图,矩形ABCD中,AB=6,BC=8,E为BC上一点,且BE=2,F为AB边上的一个动点,连接EF,将EF 绕着点E顺时针旋转45°到EG的位置,连接FG和CG,则CG的最小值为.三、解答题(共46分)19计算:(1)(﹣2)0﹣+(﹣1)2+|1﹣|;(2)×()+.20如图,在菱形ABCD中,BE⊥CD于点E,DF⊥BC于点F.(1)求证:BF=DE;(2)分别延长BE和AD,交于点G,若∠A=45°,BE=4,求DG的值.21已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且.(1)求证:BF=EF﹣ED;(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.22如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.(1)求证:DF∥AC;(2)连接DE、CF,若2AB=BF,若G恰好是CD的中点,求证:四边形CFDE是矩形;(3)在(2)的条件下,若四边形CFDE是正方形,且BC=80,求AB的长.23如图1,四边形ABCD是正方形,将线段CD绕点C逆时针旋转α(0°<α<90°),得到线段CE,连接DE,过点B作BF⊥DE交DE的延长线于F,连接BE.依题意补全图1,并解答下列问题:(1)当BE=CE时,直接写出旋转角α的度数;(2)当旋转角α的大小发生变化时,∠BEF的度数是否发生变化?如果变化,请用含α的代数式表示;如果不变,请写出∠BEF的度数,并证明;(3)连接AF,用等式表示线段AF与DE的数量关系,并证明.参考答案一.选择题(共8小题)1.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;B、不是轴对称图形,是中心对称图形,故此选项不合题意;C、既是轴对称图形又是中心对称图形,故此选项符合题意;D、是轴对称图形,不是中心对称图形,故此选项不合题意;故选:C.2.【分析】根据平方根、算术平方根的定义解答即可.【解答】解:A、3是(﹣3)2的算术平方根,故此选项不符合题意;B、3是(﹣3)2的算术平方根,故此选项不符合题意;C、,的平方根是±3,故此选项不符合题意;D、﹣3是的一个平方根,正确,故此选项符合题意;故选:D.3.【分析】由题意可知△ABC为等腰三角形,∠A=∠B=30°,由M为AB中点,则MB==2,在Rt△MNB中,MN=,BN=cos30°•MB=3,则根据S△MNB=可求答案.【解答】解:∵AC=BC,∠ACB=120°,∴△ABC为等腰三角形,∠A=∠B=30°.∵M为AB中点,AB=4,∴MB==2,又MN⊥BC,则在Rt△MNB中,MN==,BN=cos30°•MB==3,故S△MNB===.故选:A.4.【分析】根据勾股定理、勾股定理的逆定理以及三角形面积的计算分别对各个选项进行判断即可.【解答】解:A、∵AB==2,∴选项A不符合题意;B、∵AC2=12+22=5,AB2=22+42=20,BC2=32+42=25,∴AC2+AB2=BC2,∴△ABC是直角三角形,∠BAC=90°,∴选项B不符合题意;C、∵S△ABC=4×4﹣×3×4﹣×1×2﹣×2×4=5,∴选项C符合题意;D、设点A到直线BC的距离为h,∵BC2=32+42=25,∴BC=5,∵S△ABC=×5×h=5,∴h=2,即点A到直线BC的距离是2,∴选项D不符合题意;故选:C.5.【分析】由线段垂直平分线的性质可得AM=MC,即可求解.【解答】解:∵四边形ABCD是平行四边形,∴AO=CO,∵OM⊥AC,∴AM=MC,∵△CDM的周长为8,∴CM+DM+CD=8=AM+DM+CD=8,∴AD+CD=8,∴平行四边形ABCD的周长=2×8=16,故选:B.6.【分析】先化简所求式子,然后利用分类讨论的方法,可以求得所求式子的值.【解答】解:x+y=,∵x,y为实数,xy=5,∴x、y同号,当x<0,y<0时,原式=+=﹣﹣=﹣﹣=﹣2,当x>0,y>0时,原式=+==+=2,由上可得,x+y的值是,故选:C.7.【分析】过E作EF∥AB交BC于点F,再求出BF==3,EF=,BC=6,由EF为梯形中位线,则EF=(AB+DC)=,最后由梯形面积公式得到答案.【解答】解:过E作EF∥AB交BC于点F,则EF为梯形的中位线,EF=(AB+DC),又∠EBA=30°,∴∠FEB=30°,∴BF==3,EF=,∴BC=6,∴梯形ABCD的面积为==.故选:D.8.【分析】延长CE交AB于G,延长BD交AC延长线于H,根据三角形中位线定理和矩形的判定和性质解答即可.【解答】解:延长CE交AB于G,延长BD交AC延长线于H,∵AE平分∠GAC,AE⊥GC,∴AG=AC,GE=CE,同理可得,AB=AH,BD=HD,∵BF=CF,BD=HD,∴DF∥CH,即DF∥AC,故①正确,∴DF=CH,∵GE=CE,BF=CF,∴EF=BG,∵GB=AB﹣AG=AH﹣AC=CH,即GB=CH,∴GB=CH,即EF=DF,故②正确,∴AB﹣AC=AB﹣AG=BG,过G作GI⊥BH于I,∵∠GED=∠EDI=∠GID=90°,∴四边形GIDE是矩形,∴GI=ED,∴BG>GI=ED,∴AB﹣AC>DE,故③错误;∵EF∥BG,DF∥HC,∴∠FED=∠BAD,∠FDE=∠HAD,∴∠FED+∠FDE=∠BAD+∠HAD=∠BAC,∵∠FED+∠FDE+∠EFD=180°,∴∠BAC+∠EFD=180°,故④正确;故选:C.二.填空题(共8小题)9.【分析】先求729的立方根是9,再求9的算术平方根是3,由于3是有理数,再次求3的算术平方根是,由于是无理数,则可直接输出.【解答】解:输入x=729时,∴729的立方根是9,∵9的算术平方根是3,是有理数,∴3的算术平方根是,是无理数,∴输出为,故答案为.10.【分析】求出AB的长度为3,根据勾股定理求出AC的长为,所以AD=AC=,所以a=﹣2+,根据完全平方公式求a2即可.【解答】解:∵A点表示的数为﹣2,B点表示的数是1,∴AB=1﹣(﹣2)=3,∵BC⊥AB,且BC=2,∴AC===,∴AD=AC=,∴a=﹣2+,∴a2=(﹣2)2=13﹣4+4=17﹣4,故答案为:17﹣4.11.【分析】由旋转可知∠BAC1=90°,再用勾股定理求BC1的长即可得答案.【解答】解:由旋转性质可知,AC1=AC=,∠BAC1=∠BAC+∠CAC1=30°+60°=90°,则在Rt△BAC1中,BC1===.故答案为:.12.【分析】过点B作BM⊥FD于点M,根据题意可求出BC的长度,然后在△EFD中可求出∠EDF=45°,进而可得出答案.【解答】解:过点B作BM⊥FD于点M,在△ACB中,∠ACB=90°,∠A=60°,AC=10,∴∠ABC=30°,BC=10×tan60°=10 ,∵AB∥CF,∴BM=BC×sin30°==5,CM=BC×cos30°=15,在△EFD中,∠F=90°,∠E=45°,∴∠EDF=45°,∴MD=BM=5 ,∴CD=CM﹣MD=15﹣5 .故答案是:15﹣5.13.【分析】延长FE交DC的延长线于点G,由中点性质可得BE=5,利用ASA证明△BEF≌△CEG,从而CG =BF=3,∠G=∠BFE=90°,由勾股定理定理可得EF=4,最后可根据S△DEF=来计算面积得到答案.【解答】解:如图,延长FE交DC的延长线于点G,由四边形ABCD为平行四边形,∴AB∥CD,∴∠B=∠BCG,又BC中点为E,∴BE=CE==5,在△BEF和△CEG中,,∴△BEF≌△CEG(ASA),∴CG=BF=3,∠G=∠BFE=90°,∴EF==4,∴S△DEF===16.故答案为:1614.【分析】连接BD,如图所示,过点B作BF∥AE交DA延长线于点F,可得四边形AEBF为平行四边形,BF =AE=9,AF=BE=5,DF=15.再运用勾股定理逆定理证明△DBF为直角三角形,可求出DF边上高h为,最后根据S ABCD=AD•h求面积即可得到答案.【解答】解:连接BD,如图所示,过点B作BF∥AE交DA延长线于点F,∴四边形AEBF为平行四边形.∴BF=AE=9,AF=BE===5,∴DF=AD+AF=10+5=15,又BD=12,92+122=225=152,即BD2+BF2=DF2,∴△DBF为直角三角形.则设DF上的高为h,根据面积公式有DF•h=BF•BD,即15h=9×12,解得h=.∴S ABCD=AD•h=10×=72.故答案为:72.15.【分析】利用三角形中位线定理求出CD,再利用直角三角形斜边中线的性质求出AB,利用勾股定理求出BC 即可.∴CD=2BF=6,∵AD==DB,∠ACB=90°,∴AB=2CD=12,∴BC===6,故答案为:6.16.【分析】证明四边形ADCE是菱形,根据菱形的面积即可以求出DF的长.【解答】解:在Rt△ABC中,∠BAC=90°,点D是BC的中点,∴AD=CD,AE=EC=AD,AE=EC=AD=CD,∴四边形ADCE是菱形,如图,过点A作AH⊥BC于点H,∵AB=12,AC=16,∴BC==20,∴AH===,∵四边形ADCE是菱形,∴CD=CE,∴S菱形ADCE=EC•DF=CD•AH,∴DF=AH=.故答案为.17【考点】菱形的性质.【专题】矩形菱形正方形;运算能力;推理能力.【答案】120.【分析】根据菱形的性质得到AC⊥BD,AC=2AO,BD=2DO=10,求得AD=AE=AO+OE=1+OA,由勾股定理可求AO=12,由菱形的面积公式可求解.∴AC⊥BD,AC=2AO,BD=2DO=10,∵AD=AE,∴AD=AE=AO+OE=1+OA,∵AD2=OD2+AO2,∴(1+OA)2=25+AO2,∴AO=12,∴AC=24,∴菱形ABCD的面积===120,故答案为:120.18【考点】全等三角形的判定与性质;矩形的性质;旋转的性质.【专题】图形的全等;矩形菱形正方形;平移、旋转与对称;运算能力;推理能力.【答案】2+3.【分析】如图,将线段BE绕点E顺时针旋转45°得到线段ET,连接DE交CG于J.首先证明∠ETG=90°,推出点G的在射线TG上运动,推出当CG⊥TG时,CG的值最小.【解答】解:如图,将线段BE绕点E顺时针旋转45°得到线段ET,连接GT,连接DE交CG于J.∵四边形ABCD是矩形,∴AB=CD=6,∠B=∠BCD=90°,∵∠BET=∠FEG=45°,∴∠BEF=∠TEG,在△EBF和△ETG中,,∴△EBF≌△ETG(SAS),∴∠B=∠ETG=90°,∴点G的在射线TG上运动,∴当CG⊥TG时,CG的值最小,∵BC=8,BE=2,CD=6,∴CE=CD=6,∴∠CED=∠BET=45°,∴∠TEJ=90°=∠ETG=∠JGT=90°,∴四边形ETGJ是矩形,∴DE∥GT,GJ=TE=BE=2,∴CJ⊥DE,∴JE=JD,∴CJ=DE=3,∴CG=CJ+GJ=2+3,∴CG的最小值为2+3,故答案为2+3.19【考点】零指数幂;分母有理化;二次根式的混合运算.【专题】二次根式;运算能力.【答案】(1)4﹣.(2).【分析】(1)由二次根式的混合运算的运算顺序,先算乘方并化简,将化简为1﹣++,进而解决此题.(2)根据二次根式的混合运算的运算顺序,先算乘除后算加减.【解答】解:(1)=1﹣++=1﹣=4﹣.(2)===.=.20【考点】全等三角形的判定与性质;菱形的性质.【专题】图形的全等;矩形菱形正方形;运算能力;推理能力.【答案】(1)见解析;(2)8﹣4.【分析】(1)根据菱形的性质得到CB=CD,根据全等三角形的性质即可得到结论;(2)根据菱形的性质得到∠C=∠A=45°,AG∥BC,推出△DEG与△BEC是等腰直角三角形,根据等腰直角三角形的性质即可得到结论.【解答】(1)证明:∵四边形ABCD是菱形,∴CB=CD,∵BE⊥CD于点E,DF⊥BC于点F,∴∠BEC=∠DFC=90°,在△BEC与△DFC中,,∴△BEC≌△DFC(AAS),∴EC=FC,∴BF=DE;(2)解:∵∠A=45°,四边形ABCD是菱形,∴∠C=∠A=45°,AG∥BC,∴∠CBG=∠G=45°,∴△DEG与△BEC是等腰直角三角形,∵BE=CE=4,∴BC=AD=4,∵∠A=∠G=45°,∴AB=BC,∠ABG=90°,∴AG=8,∴DG=AG﹣AD=8﹣4.21【考点】全等三角形的判定与性质;等边三角形的判定与性质;等腰梯形的性质;旋转的性质.【专题】计算题;证明题;压轴题.【答案】见试题解答内容【分析】(1)旋转△BCF使BC与CD重合,从而根据SAS证得△FCE≌△F′CE,从而可证得结论.(2)根据等腰三角形的性质可得出∠BAC=∠BCA=50°,∠DEC=∠FEC=∠ECB=70°,从而可得出∠DCE 的度数,也就得出了∠BCF的度数,再结合∠BCA=50°即可得出答案.【解答】(1)证明:旋转△BCF使BC与CD重合,∵AD∥BC,AB=DC,即梯形ABCD为等腰梯形,∴∠A=∠ADC,∠A+∠ABC=180°,∴∠ADC+∠ABC=180°,由旋转可知:∠ABC=∠CDF′,∴∠ADC+∠CDF′=180°,即∠ADF′为平角,∴A,D,F′共线,∵FC=F′C,EC=EC,∠ECF'=∠BCF+∠DCE=∠ECF,∴△FCE≌△F′CE,∴EF′=EF=DF′+ED,∴BF=EF﹣ED;(2)解:∵AB=BC,∠B=80°,∴∠ACB=50°,由(1)得∠FEC=∠DEC=70°,∴∠ECB=70°,而∠B=∠BCD=80°,∴∠DCE=10°,∴∠BCF=30°,∴∠ACF=∠BCA﹣∠BCF=20°.22【考点】平行四边形的性质;矩形的判定与性质.【专题】图形的全等;等腰三角形与直角三角形;多边形与平行四边形;矩形菱形正方形;运算能力;推理能力.【答案】(1)证明见解析;(2)证明见解析;(3)16.【分析】(1)连接BD,交AC于点O,证出OE是△BDF的中位线,得OE∥DF即可;(2)先证△DFG≌△CEG(AAS),得FG=EG,则四边形CFDE是平行四边形,再证CD=EF,即可得出结论;(3)设AB=2a,则BF=4a,BE=EF=CD=2a,证△DEG是等腰直角三角形,得DE=DG=a,再证△ABE是等腰直角三角形,得AE=AB=2a,然后在Rt△ADE中,由勾股定理得出方程,解得a=8,即可求解.【解答】(1)证明:连接BD,交AC于点O,如图所示:∵四边形ABCD是平行四边形,∴BO=DO,∵BE=EF,∴OE是△BDF的中位线,∴OE∥DF,即DF∥AC;(2)证明:如图所示:由(1)得:DF∥AC,∴∠DFG=∠CEG,∠GDF=∠GCE,∵G是CD的中点,∴DG=CG,在△DFG和△CEG中,,∴△DFG≌△CEG(AAS),∴FG=EG,∴四边形CFDE是平行四边形,∵四边形ABCD是平行四边形,∴AB=CD,∵2AB=BF,∴2CD=BF,又∵EF=BE,∴CD=EF,∴平行四边形CFDE是矩形;(3)解:设AB=2a,则BF=4a,BE=EF=CD=2a,∵四边形ABCD是平行四边形,∴AD=BC=80,AB∥CD,∵四边形CFDE是正方形,∴∠DEC=90°,CD⊥EF,DG=EG=CD=a,∴∠AED=90°,△DEG是等腰直角三角形,∴DE=DG=a,∵AB∥CD,CD⊥EF,∴AB⊥BF,∴△ABE是等腰直角三角形,∴AE=AB=2a,在Rt△ADE中,由勾股定理得:AD2=DE2+AE2,即802=(a)2+(2)2,解得:a=8,∴AB=2a=16.23【考点】几何变换综合题.【专题】矩形菱形正方形;平移、旋转与对称;几何直观;应用意识.【答案】(1)30°;(2)不变,45°;(3)DE=AF.【分析】(1)证△BEC是等边三角形,得出α=∠BCD﹣∠BCE=90°﹣60°=30°;(2)由等腰三角形的性质可得∠CED=∠CDE==90°﹣,∠CEB=∠CBE==45°+,故∠BEF=180°﹣∠CED﹣∠CEB=45°,即,∠BEF的度数不变始终是45°;(3)设AB与DF交于点P,过点A作AG∥DF与BF的延长线交于点G,过点A作AH∥GF与DF交于H,过点C作CI⊥DF于I,证四边形AGFH是正方形,得出AH=AF,根据AAS证△AHD≌△DIC,得AH=DI,再根据CD=CE,得出DE=2DI=2AH=AF.【解答】解:补图如图1所示,(1)在正方形ABCD中,BC=CD,由旋转可知,CE=CD,∵BE=CE,∴BE=CE=BC,∴△BEC是等边三角形,∴∠BCE=60°,∵∠BCD=90°,∴α=∠DCE=90°﹣60°=30°;(2)不变,∠BEF=45°,证明如下:在△CED中,CE=CD,∴∠CED=∠CDE==90°﹣,在△CEB中,CE=CB,∠BCE=90°﹣α,∴∠CEB=∠CBE==45°+,∴∠BEF=180°﹣∠CED﹣∠CEB=45°;(3)DE=AF,证明如下:如图2,设AB与DF交于点P,过点A作AG∥DF与BF的延长线交于点G,过点A作AH∥GF与DF交于H,过点C作CI⊥DF于I,则四边形AGFH是平行四边形,∵BF⊥DF,∴平行四边形AGFH是矩形,∵∠BAD=∠BFP=90°,∠BPF=∠APD,∴∠ABG=∠ADH,∵∠AGB=∠AHD=90°,AB=AD,∴△ABG≌△ADH(AAS),∴AG=AH,∴矩形AGFH是正方形,∴∠AFH=∠FAH=45°,∴AH=AF,∵∠DAH+∠ADH=∠CDI+∠ADH=90°,∴∠DAH=∠CDI,∵∠AHD=∠DIC=90°,AD=DC,∴△AHD≌△DIC(AAS),∴AH=DI,∵CD=CE,CI⊥DE,∴DE=2DI,∴DE=2AH=AF.。
北京市海淀区十一学校小升初数学考试题(及答案)

4. 四个同样大小的圆柱拼成一个高为 40 厘米的大圆柱时,表面积减少了 72 平方厘米,原 来小圆柱的体积是__________立方厘米.
【考点】圆柱与圆锥 【难度】☆☆ 【答案】120 【分析】只能是四个小圆柱垒在一起,故一个小圆柱的高为 40 4 10(cm) ,表面积减少了
你 祝
前似锦
程
9. 一个圆柱体和一个圆锥体,底面半径之比 1:2,高之比为 2:3,它们的体积比为__________.
【考点】圆柱与圆锥
【难度】☆☆ 【答案】1: 2 【分析】设圆柱体与圆锥体的底面半径分别是 r 和 2r ,高分别是 2h 和 3h ,故它们的体积之
比为:
r2 2h
:
1 3
原数是__________. 2. 一个三位数,十位数上的数字是“1”,这个数既能被 2、5 整除,又是 3 的倍数,这个数
最小是__________. 3. 一辆汽车从甲地开往乙地用了 4 个小时,返回时速度提高了 25%,这样少用了__________
小时. 4. 四个同样大小的圆柱拼成一个高为 40 厘米的大圆柱时,表面积减少了 72 平方厘米,原
9. 一个圆柱体和一个圆锥体,底面半径之比 1:2,高之比为 2:3,它们的体积比为__________. 10. 一个三角形三个内角的比是 3:3:6,且最短边长为 10 厘米,则它的面积是__________. 二、填空题 B 组(每空 3 分,共 30 分) 1. 一个数的小数点,先向右移动一位,再向左移动三位,所得到的新数比原数少 35.64,
2. 一个三位数,十位数上的数字是“1”,这个数既能被 2、5 整除,又是 3 的倍数,这个数 最小是__________.
【考点】整除 【难度】☆☆ 【答案】210 【分析】设这个三位数是 a1b ,既能被 2 整除,又能被 5 整除,可得 b 0 ,又是 3 的倍数,
十一学校奥数升学考试真题6

一、填空题1.4、6、8的最小公倍数是2.甲数的65等于乙数的54,甲数与乙数的比是3.一块长方形水田,在比例尺为1:1000的地图上,它长3厘米,宽2厘米;水田的实际面积是平方米。
4.已知摄氏温度(单位:°C)和华氏温度(单位:°F)的换算方法是:摄氏温度=(华氏温度-3259⨯÷,则15°C用华氏温度表示是°F5.把下面小数四舍五入(精确到千分位)3.1215≈6.8乘2.5的积,加上12除以2.4的商得7.比较235347、、这三个数的大小,用小于号连接起来是8.当分数38的分子加上6时,为了使分数的大小不变,分母要加上9.某工厂第二车间的人数比第一车间的人数少10人,如果从第二车间调10人到第一车间,那么第一车间的人数就是第二车间的4倍。
第一车间原有人,第二车间原有人。
10.小虎是个粗心大意的孩子,在做一道除法算式时,把除数58看成了56来计算,算出的结果是90,这道算式的正确答案是11.四个数的平均数是12,如果每个数减少a,那么所得的四个新平均数是12.某商店同时出售两件商品,售价都是1200元,一件是正品,可赚20%;另一件是处理品,要赔20%,以这两件商品而言,该商店(填“赚”或“赔”)了元13.给出下列算式:21-1=10⨯22-2=21⨯23-3=32⨯观察上面一列算式,则第n个算式为14.如上图,在一块长为a米,宽为b米的长方形草地上,有一条弯曲的柏油小路(图中的阴影部分表示小路,小路任何地方的水平宽度都是1米),则空白部分表示的草地面积是 米215. 如上图,多边形ABCDEFGH 相邻的边互相垂直,要求出它的周长,最少需要知道 条边的边长。
二、 填空题16. 有这样的两位数,交换个位和十位上的数字所得的两位数与原数的和是一个完全平方数。
则这样的两位数共有 个17. 一列数,我们可以分别用123x x x 、、来表示;已知111=22123n nx x n x +=-=,(,,)则2009x =18. 用12厘米的铁丝围成一个直角三角形,这个三角形三边的长度比是3:4:5,这个直角三角形斜边上的高是 厘米19. 有一张长方体铁皮(如图),剪下图中两个圆及一块长方形,正好可以做成一个圆柱体,这个圆柱体的底面半径为10厘米,那么圆柱的体积是 立方厘米(结果保留π)20. 将一些宽6厘米、长12厘米的长方形按如图规律摆放,共摆10层,则一共有 个长方形,整个图形的周长为 厘米。
2022-2023学年十一学校直升初一第1学段数学试卷(解析版)

北京市十一学校2022-2023学年度第1学段直升初一数学能力诊断(2022.10)总分:150分时间:120分钟命题人:许文昌王继沈天成一.填空题(每题3分,共72分)1.微电子技术使半导体材料的精细加工尺寸大幅度缩小,某种电子元件的而积大约为0.00000069平方亳米,用科学记数法表示为平方亳米.答案:6.9×10-72.己知冇理数a的相反数是它自身,冇理数b的倒数是它自身,则a+b=.答案:1或-1解析:相反数是它自身为0,倒数是它自身为1或-1,则a+b=0+1=1或0+(-1)=-13.计算:12+(-12)3×2÷12-|12-1|=.答案:-解析:+(-)3×2÷-|-1|=+(-)×2×2-=+(-)-=-4.己知有理数a,b,c在数轴上的位置如图所示.化简代数式:3|c-a|+2|b+c|-3|a+b|=.答案:c+b解析:通过数轴可知,c-a>0,b+c<0,a+b<0,则3|c-a|+2|b+c|-3|a+b|=3(c-a)-2(b+c)+3(a +b)=3c-3a-2b-2c+3a+3b=c+b5.==.答案:解析:原式=202320222=202320222(20232022-1)2+(20232022+1)2202320222-2×20232022+1+202320222+2×20232022+1-2 =202320222=2×2023202226.x3+y3=1000,且x2y-xy2=-500,则(x3-y3)+(4xy2-2x2y)-2(xy2-y3)=.答案:0解析:原式=x3-y3+4xy2-2x2y-2xy2+2y3=x3+y3+2xy2-2x2y=x3+y3+2(xy2-x2y)=1000+2×(-500)=07.已知多项式x5+3x4-2x3+5x+k有因式x+3,则k=.答案:-39解析:利用短除法,将x5+3x4-2x3+5x+k除以x+3,得另一个因式为x4-2x2+6x-13,则k=3×(-13)=-39 8.多项式(3x+my-2)(4x+8y+5)展开后不含xy项,则m=.答案:-6解析:(3x+my-2)(4x+8y+5)=12x2+24xy+15x+4mxy+8my2+5my-8x-16y-10所以24+4m=0,m=-69.已知m满足32m+1×4m+1-18m×2m+1=360,则m=.答案:1解析:32m+1×4m+1-18m×2m+1=32m×3×4m×4-(2×9)m×2m×2=9m×3×4m×4-2m×9m×2m×2=9m×3×4m×4-2m×2m×9m×2=9m×3×4m×4-(2×2)m×9m×2=9m×3×4m×4-4m×9m×2=9m×4m×(3×4-2)=9m×4m×10=360所以9m×4m=36,即(9×4)m=36m=36,所以m=110.如图所示的运算程序中,若开始输入的x值为24,我们发现第1次输出的结果为12,第2次输出的结果为6,......,则第2022次输岀的结果为.答案:6解析:由运算程序可得,若开始输入的x值为24,第一次输结果为12,第2次输出的结果为6,第3次输出的结果为3,第4次输出的结果为6,第5次输出的结果为3,......,我们发现,从第2次输出结果开始,以6、3、6、3、6、3,......,每两次一循环,因为(2022-1)÷2=2021÷2=1010...1,所以2022次输岀的结果为611.写出一个只含字母x的多项式,且同时满足以下三个条件:(1)二次三项式;(2)各项系数绝对值为1;(3)对于任何有理数x,多项式的取值恒为正数..答案:x2+x+1(答案不唯一)12.计算:1×(-1)1+2×(-1)2+3×(-1)3+4×(-1)4+...+2022×(-1)2022=.答案:1011解析:原式=-1+2-3+4-5+6...+2022,结果为1至2022的奇数之和的相反数与1至2022的偶数之和.1至2022的奇数之和为1+3+5+...+2021=(1+2021)×1011÷2=1011×1011,相反数为-1011×1011;1至2022的偶数之和为2+4+6+...+2022=(2+2022)×1011÷2=1012×1011;则结果为-1011×1011+1012×1011=1011×(-1011+1012)=1011×1=101113.化简(p+q)3-3(p+q)2(p-q)+3(p+q)(p-q)2-(p-q)3=.答案:8q3解析:假设p+q=x,p-q=y因为(x-y)3=(x-y)(x-y)2=(x-y)(x2-2xy+y2)=x3-2x2y+xy2-x2y+2xy2-y3=x3-3x2y+3xy2-y3,对比原式可知,原式=[(p+q)-(p-q)]3=(2q)3=23q3=8q314.已知(x-2)5=ax5+bx4+cx3+dx2+ex+f,则16a+4c+e=.答案:44解析:本题采用赋值法求解;当x=2时,(2-2)5=25a+24b+23c+22d+2e+f=32a+16b+8c+4d+2e+f=0①当x=-2时,(-2-2)5=(-2)5a+(-2)4b+(-2)3c+(-2)2d+(-2)e+f=-32a+16b+(-8c)+4d+(-2e)+f=-45②①-②得:64a+16c+4e=45,等式两边同时除以4,所以16a+4c+e=44.15.若n2+n-l=0,则2n3+9n2+5n+2022=.答案:2029解析:原式=2n3+2n2+7n2+7n-2n+2022=2n(n2+n)+7(n2+n)-2n+2022;因为n2+n-l=0,所以n2+n=1,则原式=2n×1+7×1-2n+2022=2n-2n+7+2022=202916.己知实数a、b满足|a+2|+|1-a|=9-|b-5|-|1+b|,设a+b的最大值为m,最小值为n,则mn的值为.答案:-18解析:观察a、b满足的等式,可知无论a、b为何值,等式恒成立,则等式化简后应不含a、b,即2+1=9-5-1,所以等式化简为(a+2)+(1-a)=9-(5-b)-(1+b),即a+2≥0,1-a≥0,b-5≤0,1+b≥0,可得a≥-2,a≤1,b≤5,b≥-1,可得-2≤a≤1,-1≤b≤5.所以a+b最大值为1+5=6,即m=6;a+b最小值为-2+(-1)=-3,即n=-3,则mn的值为6×(-3)=-18.17.己知a=22021+122022+1,b=22020+122021+1,则a b.(用“<,>,=,”之一填写)答案:<解析:利用a÷b与1比较大小,判断a与b的大小关系;a÷b=2B+2B+÷22+2B+=2B+2B+×2B+22+=(2B+p(2B+p(2B+p(22+p=2B+H2B×r 2B+2B+22+=2B+2B+2B+2B+22+明显,分母与分子均为正数,且分母比分子大,所以a÷b<1,即a<b18.已知关于x、y的二次式x2+7x y+a y2-5x+10y-24可分解为两个一次因式的乘积,则a=.答案:6解析:本题利用待定系数法求解;假设原式可分解为(x+ay+m)(x+y+n)=x2+x y+n x+axy+a y2+nay+mx+my+mn=x2+(a+1)x y+a y2+(n+m)x+(na+m)y+mn对比原式可知,a+1=7,n+m=-5,na+m=10,mn=-24,可得m=-8,n=3,a=6时,等式成立,则a=619.若x+y=1,x 3+y 3=14,则x 5+y 5=.答案:1解析:若x+y=1,x 3+y 3=,则(x+y)3=x 3+3x 2y+3xy 2+y 3=x 3+y 3+3xy (x+y),可得xy =;又因为x+y=1,即y=1-x,可得xy =x(1-x)=,所以x=,y=,所以x 5+y 5=()5+()5=B +B=120.已知2a=24,3b=24,则(a-3)(b-1)=.答案:3解析:因为2a =24,所以2a-3=2a÷23=24÷8=3;因为3b=24,所以3b -1=3b÷31=24÷3=8,所以3b -1=(2a-3)b -1=2(a-3)(b -1)=8=23,所以(a-3)(b-1)=3.21.若a 1,a 2,a 3,a 4为互不相等的整数,满足(2022-a 1)(2022-a 2)(2022-a 3)(2022-a 4)=9,则|x -a 1|+|x -a 2|+|x -a 3|+|x -a 4|的最小值为.答案:8解析:若a 1,a 2,a 3,a 4为互不相等的整数,则2022-a 1、2022-a 2、2022-a 3、2022-a 4也为互不相等的整数,又因为1×3×(-1)×(-3)=9,所以a 1=2021,a 2=2019,a 3=2023,a 4=2025;|x -a 1|+|x -a 2|+|x -a 3|+|x -a 4|表示数轴上的一点x 到a 1,a 2,a 3,a 4四个点的距离之和,所以当2021≤x≤2023时,|x -2021|+|x -2019|+|x -2023|+|x -2025|的最小值为2023-2021+2025-2019=2+6=8.22.已知多项式a x 3+b x 2+cx +d 除以x-1时,所得的余数是1,除以x-2时,所得的余数是3,那么多项式a x 3+b x 2+cx +d 除以(x-1)(x-2)时,所得的余式是.答案:2x-1解析:a x 3+b x 2+cx +d 除以x-1时,所得的余数是1,假设a x 3+b x 2+cx +d=m(x-1)+1,当x=1时,a x 3+b x 2+cx +d=1;a x 3+b x 2+cx +d 除以x-2时,所得的余数是3,假设a x 3+b x 2+cx +d=n(x-2)+3,当x=2时,a x 3+b x 2+cx +d=3;因为(x-1)(x-2)展开为二次多项式,所以多项式a x 3+b x 2+cx +d 除以(x-1)(x-2)时,所得的余式是一次多项式,可以假设余式为px+q,商为z,则a x 3+b x 2+cx +d=z(x-1)(x-2)+px+q;当x=1时,a x 3+b x 2+cx +d=1,即p+q=1;当x=2时,a x 3+b x 2+cx +d=3,即2p+q=3,解得p=2,q=-1,所以所得的余式是2x-1.23.已知:x-y=5-2a,4x y +12a 2=4a-33,则a =.答案:-1解析:因为x-y=5-2a,所以(x-y)2=(5-2a)2,即x2-2xy+y2=25-20a+4a2①又因为4x y+12a2=4a-33②,所以①+②得x2+2xy+y2+12a2=-16a-8+4a2,所以x2+2xy+y2+8a2+16a+8=0,即(x+y)2+8(a2+2a+1)=(x+y)2+8(a+1)2=0,因为(x+y)2≥0,(a+1)2≥0,所以x+y=0,a+1=0,即a=-1.24.(a+b)3-a3-b3=9,(a+b)5-a5-b5=120,(a+b)7-a7-b7=.二.解答题(25题32分,26题10分,27题10分,28题26分)25.分解因式:⑴(b2+a2-c2)2-4a2b2;原式=(b2+a2-c2)2-(2ab)2=(b2+a2-c2+2ab)(b2+a2-c2-2ab)=(b2+2ab+a2-c2)(b2-2ab+a2-c2)=[(b+a)2-c2][(b-a)2-c2]=(b+a+c)(b+a-c)(b-a+c)(b-a-c)平方差公式法(2)x3+2x2+4xy+y3+2y2;原式=x3+y3+2x2+4xy+2y2=(x+y)(x2-xy+y2)+2(x2+2xy+y2)=(x+y)(x2-xy+y2)+2(x+y)2=(x+y)[x2-xy+y2+2(x+y)]=(x+y)(x2-xy+y2+2x+2y)分组分解法(3)x2+xy-6y2+3x+19y-10;原式=(x+3y)(x-2y)+3x+19y-10=(x+3y)(x-2y)+3x+19y-2×5=(x+3y-2)(x-2y+5)双十字相乘法(4)(x+l)(x+3)(x+4)(x+12)+5x2;原式=(x+l)(x+12)(x+3)(x+4)+5x2=(x2+13x+l2)(x2+7x+l2)+5x2令x2+l2=a,原式=(a+13x)(a+7x)+5x2=a2+20ax+91x2+5x2=a2+20ax+91x2=(a+12x)(a+8x)整体设元及十字相乘(5)x4-x3-4x2-x+1;已知当x=-1时,x4-x3-4x2-x+1=0,则x4-x3-4x2-x+1有一个因式是(x+1),用短除法可得另一个因式为x3-2x2-2x+1;又已知当x=-1时,x3-2x2-2x+1=0,则x3-2x2-2x+1有一个因式是(x+1)用短除法可得另一个因式为x2-3x+1,所以x4-x3-4x2-x+1=(x+1)2(x2-3x+1)赋值法(6)x4+2022x2+2021x+2022;(7)(x+y)4-8xy(x2+y2);(8)(x+y-2xy)(x+y-2)+(xy-1)2.26.己知多项式(2x2+ax+y2-1)-(2bx2-3x+1Oy-m)的值与字母x的取值无关.(1)求a,b的值;(2)不论y取何值,多项式的值恒大于0,求m的取值范围.解:(1)(2x2+ax+y2-1)-(2bx2-3x+1Oy-m)=2x2+ax+y2-1-2bx2+3x-1Oy+m=(2-2b)x2+(a+3)x+y2-1Oy+m因为多项式的值与字母x的取值无关,所以2-2b=0,a+3=0,所以b=1,a=-3(2)因为b=1,a=-3,所以多项式为y2-1Oy+m;y2-1Oy+m=y2-1Oy+25-25+m=(y-5)2-25+m,若不论y取何值,多项式的值恒大于0,即(y-5)2-25+m>0,因为(y-5)2≥0,所以-25+m>0,即m>25.27.小明最近在数学学习过程中遇到题目:己知n为正整数,计算:1×2+2×3+3×4+・・・+n(n+1).可他觉得无从下手,这时小红说可以考虑裂项,注意到:n(n+1)=13[(n+2)-(n-1)]n(n+l)=13[n(n+1)(n+2)-(n-1)n(n+1)].(1)请你借用小红的思路,计算:1×2+2×3+3×4+...+n(n+1);(2)己知n 为正整数,记S n =1×2×3+2×3×4+3×4×5+...+n(n +1)(n +2),证明:4S n +1为完全平方数.解:(1)由题意思路可知:1×2+2×3+3×4+...+n(n+1)=13(1×2×3-0×1×2)+13(2×3×4-1×2×3)+13(3×4×5-2×3×4)+...+13[n(n +1)(n +2)-(n -1)n(n +1)]=13×1×2×3-13×0×1×2+13×2×3×4-13×1×2×3+13×3×4×5-13×2×3×4+13n(n +1)(n +2)-13(n -1)n(n +1)=13n(n +1)(n +2)(2)由题意思路可知:S n =1×2×3+2×3×4+3×4×5+...+n(n +1)(n +2)=14(1×2×3×4-0×1×2×3)+14(2×3×4×5-1×2×3×4)+14(3×4×5×6-2×3×4×5)+...+14[n(n +1)(n +2)(n +3)-(n -1)n(n +1)(n +2)]=14×1×2×3×4-14×0×1×2×3+14×2×3×4×5-14×1×2×3×4+14×3×4×5×6-14×2×3×4×5+...+14n(n +1)(n +2)(n +3)-14(n -1)n(n +1)(n +2)=14n(n +1)(n +2)(n +3)则4S n +1=4×14n(n +1)(n +2)(n +3)+1=n(n +1)(n +2)(n +3)+1=n(n +3)(n +1)(n +2)+1=(n 2+3n)(n 2+3n +2)+1令n 2+3n=A,则4S n +1=A(A +2)+1=A 2+2A+1=(A +1)2,还原得4S n +1=(n 2+3n+1)2,因为n 为正整数,所以4S n +1为完全平方数.28.对于正整数n,若存在正整数x,y使得x2-3y2=n,则称n是一个佩尔数,并称(x,y,n)为佩尔数组,例如4=42-3×22,6=32-3×12,所以4,6均为佩尔数,(4,2,4)、(3,1,6)均为佩尔数组.(1)证明1为佩尔数;(2)已知m为正整数,证明m2为佩尔数;(3)已知m为正整数,且(x,3,m2)为佩尔数组,求x的值;(4)证明若n被4除余3,则n一定不是佩尔数;(5)2是佩尔数吗?若是请给出相应的x、y,若不是,请说明理由;(6)若n1,n2均为佩尔数,证明n1n2为佩尔数;(7)证明存在无穷组正整数x、y,使得(x,y,1)为佩尔数组.解:(1)因为1=22-3×12,所以1为佩尔数;(2)(3)若(x,3,m2)为佩尔数组,则x2-3×32=m2,即x2-m2=27,可得(x+m)(x-m)=27,因为x,m为正整数,所以(6+3)(6-3)=27,所以x的值为6.。
十一学校分班考试真题

十一学校分班考试真题一、填空题:1.在1991,1992,1993,1994,1995,1996,1997这七个数中,不能写成两个自然数的平方差的数是____2.如图,阴影部分S1的面积比阴影部分S2的面积大12平方厘米,且BD=4厘米,DC=1厘米,则线段AB=______厘米.3.一个人在河中游泳,逆流而上,在A处将帽子丧失,他向前游了15分后,才发现帽子丢了,立即返回去找,在离A处15千米的地方追到了帽子,则他返回来追帽子用了______分.4.乒乓球单打决赛在甲、乙、丙、丁四位选手中进行,赛前,有些人预测比赛结果,A说:甲第4;B说:乙不是第2,也不是第4;C说:丙的名次在乙的前面;D说:丁将得第1.比赛结果说明,四个人中只有一人预测错了.那么,甲、乙、丙、丁四位选手的名次分别为:_______.5.如图,正立方体边长为2,沿每边的中点将每个角都切下去,则所得到的几何体有______条棱.6.一本书,如果每天读50页,那么5天读不完,6天又有余;如果每天读70页,那么3天读不完,4天又有余;如果每天读n页,恰可用n天读完〔n是自然数〕.这本书的页数是______.7、使每一横行,每一竖行,两对角线斜行中三个数的和都相等.8.有本数学书共有600页,则数码0在页码中出现的次数是______.9.张明骑自行车,速度为每小时14千米,王华骑摩托车,速度为每小时35千米,他们分别从A、B两点出发,并在A、B两地不断往返行驶,且两人第四次相遇〔两人同时到达同一地点叫做相遇〕与第五次相遇的地点恰好相距120千米,那么,A、B两地之间的距离是______千米.10.某次数学竞赛原定一等奖8人,二等奖16人,现在将一等奖中最后4人调整为二等奖,这样得二等奖的学生的平均分提高了1.2分,得一等奖的学生的平均分提高了4分,那么原来一等奖平均分比二等奖平均分多______分.二、解答题:11.学校要建一段围墙,由甲、乙、丙三个班完成,已知甲班单独干需要20小时完成,乙班单独干需要24小时完成,丙班单独干需要28小时完成,如果先由甲班工作1小时,然后由乙班接替甲班干1小时,再由丙班接替乙班干1小时,再由甲班接替丙班干1小时,……三个班如此交替着干,那么完成此任务共用了多少时间?12.如图甲、乙、丙三个皮带轮的半径比分别为:5∶3∶7,求它们的转数比.当甲轮转动7圈时,乙、丙两轮各转多少圈?13.甲、乙、丙三个小孩分别带了假设干块糖,甲带的最多,乙带的较少,丙带的最少.后来进行了重新分配,第一次分配,甲分给乙、丙,各给乙、丙所有数少4块,结果乙有糖块最多;第二次分配,乙给甲、丙,各给甲、丙所有数少4块,结果丙有糖块最多;第三次分配,丙给甲、乙,各给甲、乙所有数少4块,经三次重新分配后,甲、乙、丙三个小孩各有糖块44块,问:最初甲、乙、丙三个小孩各带糖多少块?14.甲容器中有纯桔汁16升,乙容器中有水24升,问怎样能使甲容器中纯桔汁含量为60%,乙容器中纯桔汁含量为20%,甲、乙容器各有多少升?15.有12头羊14天可以吃完12亩草,13头羊44天可以吃完22亩草,问多少头羊60天可以吃完50亩草?16.如图,一个棱长为5的正方体,在它的上下、左右、前后各面中心挖去一个底面是1的正方形,高为2的长方体洞,求挖后此形体的外表积是多少?17.其余88人是群众,则此工厂共有多少人.18.某钟表,在6月29日零点比标准时间慢5分,它一直走到7月6日上午6时,比标准时间快5分,那么这只表所指时间是正确的时刻应该是在哪月哪日哪时?〔“零点”和“7时”都指的是标准时间〕19.某出版社出版某种书,今年每册书的成本比去年增加10%,但售价不变,因此每本利润下降了40%,那么今年这种书的成本在售价中所占的百分数是多少?20.两个整数A、B的最大公约数是C,最小公倍数是D,并且已知C不等于1,也不等于A或B,C+D=187,那么A+B等于多少?21. 老师在黑板上写了从11开始的假设干个连续自然数〔如11,12,13…〕,后来擦掉了其中一个数,剩下的数的平均数是 。
十道奥数题及答案

十道奥数题及答案1. 题目:一个数字问题,如果将数字1234567890的每一位数字都乘以2,得到的新数字是多少?答案:将每一位数字乘以2,得到的新数字是 2468135180。
2. 题目:一个数列问题,数列的前五项是1, 1, 2, 3, 5,求第六项。
答案:这是一个斐波那契数列,每一项都是前两项的和。
所以第六项是5+3=8。
3. 题目:一个几何问题,一个圆的半径是10厘米,求圆的面积。
答案:圆的面积公式是A = πr²,代入 r = 10 得到A = π *10² = 100π 平方厘米。
4. 题目:一个组合问题,有5个不同的球和3个不同的盒子,求将所有球放入盒子中的方法总数。
答案:每个球都有3种选择,所以总的方法数是 3^5 = 243种。
5. 题目:一个概率问题,抛掷一枚均匀的硬币两次,求至少出现一次正面的概率。
答案:至少一次正面的概率等于1减去两次都是反面的概率,即 1 - (1/2) * (1/2) = 3/4。
6. 题目:一个逻辑问题,有5个盒子,每个盒子里都有一个数字,分别是1, 2, 3, 4, 5。
如果将数字1放入数字2的盒子,数字2放入数字3的盒子,以此类推,问最后数字5会在哪里?答案:数字5会被放入数字4的盒子。
7. 题目:一个算术问题,求1到100所有整数的和。
答案:这是一个等差数列求和问题,公式为 (首项 + 末项) * 项数 / 2,即 (1 + 100) * 100 / 2 = 5050。
8. 题目:一个时间问题,如果现在是3点15分,那么45分钟后是几点?答案:45分钟后是3点60分,即4点。
9. 题目:一个速度问题,一辆车以每小时60公里的速度行驶,求它在2小时内行驶的距离。
答案:距离等于速度乘以时间,即 60 公里/小时 * 2 小时 = 120 公里。
10. 题目:一个体积问题,一个长方体的长、宽、高分别是10厘米、8厘米和6厘米,求它的体积。
北京市海淀区十一学校2022年七年级数学第一学期期末复习检测试题含解析

2022-2023学年七上数学期末模拟试卷请考生注意:1.请用2B 铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,C ,D ,E 是线段AB 上的三个点,下面关于线段CE 的表示:①CE=CD+DE ;②CE=CB ﹣EB ;③CE=CD+DB ﹣AC ;④CE=AE+CB ﹣AB .其中,正确的是( )A .①②B .①②③C .①②④D .①②③④2.下列说法正确的是( )A .射线PA 和射线AP 是同一条射线B .两点之间,直线最短C .延长射线APD .过两点有且只有一条直线 3.已知:2|2|(1)0m n -+-=,则方程2m x n +=的解为( )A .-3B .0C .6D .94.下列说法中正确的是( )A .2是单项式B .3πr 2的系数是3C .12abc -的次数是1 D .a 比-a 大 5.甲仓库与乙仓库共存粮450 吨、现从甲仓库运出存粮的60%.从乙仓库运出存粮的40%.结果乙仓库所余的粮食比甲仓库所余的粮食多30 吨.若设甲仓库原来存粮x 吨,则有( )A .(1-60%)x -(1-40%)(450-x )=30B .60%x -40%•(450-x )=30C .(1-40%)(450-x )-(1-60%)x =30D .40%•(450-x )-60%•x =306.为了解某市参加中考的25000名学生的身高情况,抽查了其中1200名学生的身高进行统计分析.下列叙述正确的是( )A .25000名学生是总体B .1200名学生的身高是总体的一个样本C .每名学生是总体的一个个体D .以上调查是全面调查781 )A .9B .9或-9C .3D .3或-38.已知关于x 的方程35a x -=的解是1x =-,则a 的值为( )A .43B .2C .-8D .8 9.在平面内的线段AB 上任取两点,可以得到的线段的条数为( )A .2条B .3条C .4条D .6条10.按一定规律排列的一列数依次是23、1、87、119、1411、1713…按此规律,这列数中第100个数是( ) A .299199 B .299201C .301201D .303203 11.a 、b 两数在数轴上位置如图所示,将a 、b 、a -、b -用“<” 连接,其中正确的是( )A .a <a -<b <b -B .b -<a <a -<bC .a -<b <b -<aD .b -<a <b <a - 12.已知622x y 和313m n x y -是同类项,则29517m mn --的值是( ) A .1- B .2- C .3- D .4-二、填空题(每题4分,满分20分,将答案填在答题纸上)13.按照下列程序计算输出值为2018时,输入的x 值为_____.14.如图,点B 是线段AC 上一点,点O 是线段AC 的中点,且AB =20,BC =1.则线段OB 的长为_____.15.如图是小琴同学的一张测试卷,他的得分应是______.16.实验室里,水平圆桌面上有甲乙丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,用两根相同的管子在容器的5cm 高度处连接(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm ,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位高度为56cm ,则开始注入________分钟的水量后,甲与乙的水位高度之差是16cm.17.如图,射线OC ,OD 在AOB ∠内,AOB ∠和BOC ∠互为补角13BOD AOB =∠∠,若COD ∠比BOD ∠大m ︒(30m <),则AOC ∠=___________︒(用含m 的式子表示)三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18.(5分)甲乙两地相距160千米,一辆汽车和一辆拖拉机同时由甲、乙两地相向而行,1小时20分相遇.相遇后,拖拉机继续前进,汽车在相遇处停留1个小时后调头按原速返回,汽车在返回后半个小时追上了拖拉机.(1)在这个问题中,1小时20分= 小时; (2)相向而行时,汽车行驶 小时的路程+拖拉机行驶 小时的路程=160千米;同向而行时,汽车行驶 小时的路程=拖拉机行驶 小时的路程;(3)全程汽车、拖拉机各自行驶了多少千米?19.(5分)人在运动时的心跳速率通常和人的年龄有关,如果用a 表示一个人的年龄,用b 表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么b =0.8(220﹣a ).(1)正常情况下,在运动时一个15岁的少年所能承受的每分钟心跳最高次数是多少?(2)一个45岁的人运动时每10秒心跳的次数是22次,请问他有危险吗?为什么?20.(8分)如图:在数轴上A 点表示数,a B 点示数,b C 点表示数,c b 是最大的负整数,A 在B 左边两个单位长度处,C 在B 右边5个单位处()1a = ;b = _;c = _;()2若将数轴折叠,使得A 点与C 点重合,则点B 与数_ __表示的点重合;()3点、、A B C 开始在数轴上运动,若点A 以每秒2个单位长度的速度向左运动,同时,点B 和点C 分别以每秒3个单位长度和5个单位长度的速度向右运动,假设t 秒钟过后,若点A 与点B 之间的距离表示为,AB 点A 与点C 之间的距离表示为,AC 点B 与点C 之间的距离表示为BC ,则AB =_ _,AC =_ _,BC =__ _;(用含t 的代数式表示)()4请问:52BC AB -的值是否随着时间t 的变化而改变﹖若变化,请说明理由;若不变,请求其值.21.(10分)一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请你画出从正面、左面看到的这个几何体的形状图.22.(10分)现在,家电商场进行促销活动,有两种促销方式,方式一:出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物:方式二:若不买卡,则打9.5折销售(1)买一台标价为3500的冰箱,方式一应付_____元,方式二应付_____元.(2)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?如何购物合算?(只需给出结论,不用写计算过程)(3)小张按合算的方案把这台冰箱买下,如果家电商场还能盈利25%,这台冰箱的进价是多少元?23.(12分)已知:直线AB与直线CD交于点O,过点O作OE⊥AB.(1)如图1,∠BOC=1∠AOC,求∠COE的度数;(1)如图1.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与1∠EOF度数相等的角.参考答案一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1、C【分析】根据图示可以找到线段间的和差关系.【详解】解:如图,①CE =CD +DE ,故①正确;②CE =BC −EB ,故②正确;③CE =CD +BD −BE ,故③错误;④∵AE +BC =AB +CE ,∴CE =AE +BC −AB =AB +CE −AB =CE ,故④正确;故选C.【点睛】考查两点间的距离,连接两点间的线段的长度叫做两点间的距离.注意数学结合思想在解题中的应用.2、D【分析】根据射线的表示法以及两点之间的距离的定义即可作出判断.【详解】解:A 、射线PA 的端点是P ,射线AP 的端点是A ,故不是同一条射线,故选项错误;B 、两点之间,线段最短,选项错误;C 、射线是无限的,不用延长,故选项错误;D 、过两点有且只有一条直线,正确.故选:D .【点睛】本题考查了射线的表示法以及两点之间的距离的定义,理解定理是关键.3、A【分析】根据绝对值和偶次方不可能为负数,可得|2|0-=m ,2(1)0-=n ,解得m 、n 的值,然后代入方程即可求解.【详解】解:因为2|2|(1)0m n -+-=,且|2|0-≥m ,2(1)0-≥n ,所以|2|0-=m ,2(1)0-=n ,解得:m =2,n =1,将m =2,n =1代入方程2m +x =n ,得4+x =1移项,得:x =−1.故选:A .此题主要考查学生对解一元一次方程和非负数的性质的理解和掌握,解答此题的关键是根据绝对值和偶次方不可能为负数,解得m、n的值.4、A【分析】根据单项式的次数、系数以及正数和负数的相关知识解答即可.【详解】解:A. 2是单项式,正确;B. 3πr2的系数是3π,故B选项错误;C.12abc的次数是3,故C选项错误;D.当a为负数时,a比-a小,故D选项错误.故答案为A.【点睛】本题主要考查了单项式的定义、次数、系数以及正数和负数的相关知识,灵活应用相关知识成为解答本题的关键.5、C【解析】试题分析:要求甲,乙仓库原来存粮分别为多少,就要先设出未知数,找出题中的等量关系列方程求解.题中的等量关系为:从甲仓库运出存粮的60%,从乙仓库运出存粮的40%.结果乙仓库所余的粮食比甲仓库所余的粮食30吨.解:设甲仓库原来存粮x吨,根据题意得出:(1﹣40%)(450﹣x)﹣(1﹣60%)x=30;故选C.考点:由实际问题抽象出一元一次方程.6、B【解析】试题解析:A、总体是25000名学生的身高情况,故A错误;B、1200名学生的身高是总体的一个样本,故B正确;C、每名学生的身高是总体的一个个体,故C错误;D、该调查是抽样调查,故D错误.故选B.7、D【分析】根据算术平方根的定义和平方根的定义计算即可.3或-3故选D.此题考查的是算术平方根和平方根的计算,掌握算术平方根的定义和平方根的定义是解决此题的关键.8、A【分析】将1x =-代入方程中可得到一个关于a 的方程,解方程即可得出答案.【详解】将1x =-代入方程35a x -=中,得3(1)5a --= 解得43a = 故选:A .【点睛】本题主要考查根据方程的解求其中的字母,掌握方程的解是解题的关键.9、D【分析】根据题意画出图形,再根据线段的定义即可确定线段的条数.【详解】解:如下图所示,再线段AB 上取C 、D 两点,可以得到线段:AC 、CD 、DB 、AD 、AB 、CB ,∴可以得到的线段的条数为6条,故答案为:D .【点睛】本题考查了线段的定义,解题的关键是熟知线段的定义.10、B【解析】观察发现,是不变的,变的是数字,不难发现数字的规律,代入具体的数就可求解.【详解】解:由23、1、87、119、1411、1713……可得第n 个数为3121n n -+. ∵n=100,∴第100个数为:299201故选:B .【点睛】本题考查学生的观察和推理能力,通过观察发现数字之间的联系,找出一般的规律,解决具体的问题;关键是找出一般的规律.11、B【分析】根据a 、b 在数轴上的位置和相反数的意义在数轴上标出表示-a ,-b 的点,利用数轴进行比较.【详解】解:如图,根据数轴上右边的数总比左边大,则可得:-b <a <-a <b .故选:B .【点睛】本题考查了有理数的大小比较及相反数、数轴等知识,根据数据上右边的数总比左边大来进行数的比较是解决本题的关键.12、A【分析】先根据同类项的定义求出m 、n 的值,再将其代入所求式子即可得.【详解】由同类项的定义得:362m n =⎧⎨=⎩,解得:22m n =⎧⎨=⎩ 将其代入得:2295179252217m mn --=⨯-⨯⨯-362017=--1=-故选:A .【点睛】本题考查了同类项的定义、有理数含乘方的混合运算,依据同类项的定义求出m 、n 的值是解题关键.二、填空题(每题4分,满分20分,将答案填在答题纸上)13、1【分析】根据程序图中运算顺序逆推即可.【详解】解:∵程序计算输出值为2018∴输入的x 值为[2018÷2-(-1)]÷5=(1009+1)÷5=1故答案为:1.【点睛】此题考查的是有理数的混合运算,掌握有理数的各个运算法则是解决此题的关键.14、2【分析】由线段的中点,线段的和差计算出线段OB 的长为2.【详解】解:如图所示:∴AC =AB +BC ,AB =20,BC =1,∴AC =20+1=21,又∵点O 是线段AC 的中点,∴AO =CO =112822AC =⨯=14, 又∵OB =OC ﹣BC ,∴OB =14﹣1=2,故答案为2.【点睛】本题综合考查了线段的中点,线段的和差等相关知识点,重点掌握两点间距离计算方法.15、75【分析】根据相反数的定义、倒数、绝对值的意义及立方的定义,逐一判断即可得.【详解】解:①2的相反数是2-,此题正确;②倒数等于它本身的数是1和1-,此题正确;③1-的绝对值是1,此题正确;④3-的立方是27-,此题错误;∴小琴的得分是75分;故答案为:75.【点睛】本题主要考查立方、绝对值、相反数及倒数,解题的关键是掌握相反数的定义、倒数、绝对值性质及立方的定义.16、1,75,17340. 【分析】先根据题意算出乙和丙每分钟注水量,随着时间变化可以分三种情况讨论,①当甲比乙高,②乙比加高,③乙溢出到甲后,乙比甲高.【详解】试题分析:∵甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,∴甲、乙、丙三个圆柱形容器的底面积之比为1:4:1,∵每分钟同时向乙和丙注入相同量的水,注水1分钟,乙的水位上升56cm , ∴注水1分钟,丙的水位上升510463⨯=cm , ①当甲比乙高16cm 时,此时乙中水位高56cm ,用时1分;②当乙比甲水位高16cm 时,乙应为76cm, 757=665÷分, 当丙的高度到5cm 时,此时用时为5÷103=32分, 因为73<52,所以75分乙比甲高16cm. ③当丙高5cm 时,此时乙中水高535624⨯=cm ,在这之后丙中的水流入乙中,乙每分钟水位上升55263⨯=cm ,当乙的水位达到5cm 时开始流向甲,此时用时为355+5243⎛⎫-÷ ⎪⎝⎭=154分,甲水位每分上升1020233⨯=cm ,当甲的水位高为546cm 时,乙比甲高16cm ,此时用时155201734146340⎛⎫+-÷= ⎪⎝⎭分; 综上,开始注入1,75,17340分钟的水量后,甲与乙的水位高度之差是16cm. 【点睛】本题考查圆柱体与水流变化的结合,关键在于找到三个分类节点.17、6365m ︒- 【分析】先根据题意用含m 的代数式表示出AOB ∠和BOC ∠,然后利用AOC AOB BOC ∠=∠-∠即可求出答案.【详解】∵AOB ∠和BOC ∠互为补角∴180AOB BOC ∠+∠=︒又∵COD BOD m ∠-∠=︒ ∴2BOC m BOD ∠-︒∠= ∵13BOD AOB =∠∠ ∴1(180)23BOC m BOC ∠-︒=︒-∠ 3725BOC m ∴∠=︒+ 31085AOB m ∴∠=︒- AOC AOB BOC ∠=∠-∠6365AOC m ∴∠=︒- 故答案为:6365m ︒-. 【点睛】本题主要考查角的和与差以及代数式,能够用含m 的代数式表示出AOB ∠和BOC ∠是解题的关键.三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)18、(1)113;(2)113,113,12,112;(3)汽车行驶的路程为165千米,拖拉机行驶的路程为85千米. 【分析】(1)根据1小时=60分进行单位换算即可;(2)相向而行,相遇时两者行驶时间相同,行驶距离之和为160千米,同向而行,汽车追上拖拉机时,汽车行驶时间为12小时,拖拉机行驶112小时,据此填写即可; (3)设汽车、拖拉机的速度分别是,x y 千米/小时,根据(2)中的等量关系建立方程求出汽车和拖拉机的速度,再用速度乘以行驶的总时间求出行驶路程.【详解】(1)20分=201=603小时, ∴1小时20分=111=133+小时 故答案为:113. (2)相向而行,相遇时,两者行驶时间均为113小时,同向而行,汽车追上拖拉机时,汽车行驶时间为12小时,拖拉机行驶111=122⎛⎫+ ⎪⎝⎭小时 故答案为:113,113,12,112. (3) 解:设汽车、拖拉机的速度分别是,x y 千米/小时,依题意有:11111603311(1)22x y x y ⎧+=⎪⎪⎨⎪=+⎪⎩,解之得:9030x y =⎧⎨=⎩ 全程汽车行驶的路程为1141(1)()90120451653232x +=+⨯=+=(千米) 全程拖拉机行驶的路程为1141(11)(1)30403015853232++=++⨯=++=y (千米) 答:全程汽车行驶的路程为165千米,拖拉机行驶的路程为85千米.【点睛】本题考查了二元一次方程组的应用,熟练掌握相向而行与同向而行中的等量关系是解题的关键.19、(1)164;(2)没有危险,理由见解析【分析】(1)直接把a=15代入b=0.8(220-a )计算即可;(2)先把a=45代入b=0.8(220-a )计算得到这个人在运动所能承受的每分钟心跳的最高次数为140次;而每10秒心跳的次数是22次,即每分种心跳的次数是132次,即可判断他没有危险.【详解】解:(1)∵a =15,∴b =0.8×(220﹣15)=0.8×205 =164;∴正常情况下,在运动时一个15岁的少年所能承受的每分钟心跳最高次数是164次;(2)没有危险.∵a =45,b =0.8(220﹣45)=140,即这个人在运动所能承受的每分钟心跳的最高次数为140次.又∵每10秒心跳的次数是22次,∴他每分种心跳的次数是132次,小于140次,∴他没有危险.【点睛】本题考查了代数式求值:把符合条件的字母的值代入代数式进行计算,然后根据计算的结果解决实际问题.20、(1)﹣3,﹣1,4;(2)2;(3)2+5t ,7+7t ,2t+5;(4)5BC ﹣2AB 的值不会随着时间t 的变化而改变,该值是1.【分析】(1)根据b 为最大的负整数可得出b 的值,再根据A 在B 左边两个单位长度处,C 在B 右边5个单位处即可得出a 、c 的值;(2)根据折叠的性质结合a 、b 、c 的值,即可找出与点B 重合的数;(3)根据运动的方向和速度结合a 、b 、c 的值,即可找出t 秒后点A 、B 、C 分别表示的数,利用数轴上两点间的距离即可求出AB 、AC 、BC 的值;(4))将(3)的结论代入52BC AB -中,可得出52BC AB -的值不会随着时间的变化而变化,即为定值,此题得解.【详解】(1)b 是最大的负整数,∴1b =-A 在B 左边两个单位长度处,C 在B 右边5个单位处∴3a =-,c 4=(2)将数轴折叠,使得A 点与C 点重合∴()3412a c b +-=-+--=(3)点A 以每秒2个单位长度的速度向左运动,同时,点B 和点C 分别以每秒3个单位长度和5个单位长度的速度向右运动∴t 秒钟过后,根据s vt =得:s 2A t =,s 3B t =,s 5C t = 又3a =-,1b =-,c 4=∴点A 表示的数为23t --,点B 表示的数为31t -,点C 表示的数为54t +,∴25AB t =+,77AC t =+,2+5BC t =;(4)由(3)可知:25AB t =+,2+5BC t =∴()()52=525225102541021BC AB t t t t -⨯+-+=+--=∴52BC AB -的值为定值1.故答案为:(1)﹣3,﹣1,4;(2)2;(3)2+5t ,7+7t ,2t+5;(4)5BC ﹣2AB 的值不会随着时间t 的变化而改变,该值是1.【点睛】本题考查了数轴及两点间的距离,根据点运动的方向和速度找出点A 、B 、C 运动后代表的数是解题的关键.21、画图见解析;【分析】由已知条件可知,主视图有3列,每列小正方形数目分别为3,1,2,左视图有3列,每列小正方数形数目分别为3,2,1.据此可画出图形.【详解】解:如图:【点睛】本题主要考查了作图-三视图,由三视图判断几何体,掌握作图-三视图,由三视图判断几何体是解题的关键.22、(1)3100,3325 (2)2000,顾客购买小于2000元金额的商品时,不买卡花钱划算;顾客购买2000元金额的商品时,买卡与不买卡花钱相等;顾客购买大于2000元金额的商品时,买卡花钱划算. (3)2480【分析】(1)根据题意计算两种方式的花费即可.(2)顾客购买x 元金额的商品时,买卡与不买卡花钱相等,根据题意列出方程求解,再分情况判断如何购物合算. (3)结合(1)可得小张买冰箱的花费,除以()1+25%,即可求出这台冰箱的进价.【详解】(1)方式一:30035000.83100+⨯=(元)方式二:35000.953325⨯=(元)故买一台标价为3500的冰箱,方式一应付3100元,方式二应付3325元.(2)顾客购买x 元金额的商品时,买卡与不买卡花钱相等3000.80.95x x +=x=解得2000故顾客购买2000元金额的商品时,买卡与不买卡花钱相等由此可得,顾客购买大于2000元金额的商品时,买卡花钱的折扣力度更大故顾客购买小于2000元金额的商品时,不买卡花钱划算;顾客购买2000元金额的商品时,买卡与不买卡花钱相等;顾客购买大于2000元金额的商品时,买卡花钱划算.(3)由(1)得,购买此冰箱方式一更划算÷=(元)3100 1.252480故这台冰箱的进价是2480元.【点睛】本题考查了一元一次方程的简单应用,掌握解一元一次方程的方法是解题的关键.23、(1)∠COE=30°;(1)与1∠EOF度数相等的角是:∠AOD,∠BOC,∠FON,∠EOM.【分析】(1)先根据平角的定义可得∠AOC=60︒,再利用垂直的定义可得∠AOE=90︒,从而得结论;(1)根据(1)中∠AOC=60︒,分别计算各角的度数,得其中∠EOF=60︒,根据各角的度数可得结论.【详解】(1)如图1,∵∠AOC+∠BOC=180︒,且∠BOC=1∠AOC,∴∠AOC=60︒,∵OE⊥AB,∴∠AOE=90︒,∴∠COE=90︒﹣60︒=30︒;(1)如图1,由(1)知:∠AOC=60︒,∵射线OM平分∠BOD,∴∠BOM=∠DOM=∠AON=∠CON=30︒,∵OE⊥AB,OC⊥OF,∴∠AOE=∠COF=90︒,∴∠AOC=∠EOF=60︒,∴∠AOD=∠BOC=∠FON=∠EOM=180︒﹣60︒=110︒=1∠EOF,∴与1∠EOF度数相等的角是:∠AOD,∠BOC,∠FON,∠EOM.【点睛】本题考查的是垂直的性质,角平分线的定义,以及对顶角和邻补角,熟练掌握这些性质和定义是关键,并会识图,明确角的和与差.。
十一学校新初一分班数学考试试卷及答案

北京市十一学校初一分班测试题一、基础考察:(每题4分,共24分)1. 如果甲比乙多五分之一,乙比丙多五分之一,则甲比丙多%.2. 要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要分钟完成。
3. 一个完全平方数有5个约数,那么这个数的立方有个约数。
4.715的分母减少3 后,要使分数的大小不变,分子应减少____.5. 观察按下顺序排列的等式:90101,⨯+=91211,⨯+=92321,⨯+=93431,⨯+=94541,⨯+=按以上各式成立的规律,写出第12个等式是:6.观察下列等式,(式子中的“!”是一种数学运算符号)。
1!1=,2!21=⨯,3!321=⨯⨯,4!4321=⨯⨯⨯……;则计算100!98!=______。
二、能力提高:(每题4分,共52分)7.简便运算能力(1)96×19+4×19 (2)111 36()234⨯-+8.小青坐在教室的第3排第4列,用(4,3)表示,那么小明座在教室的第5排第2列应当表示为9.一次数学测验以后,张老师根据某班成绩绘制了如图所示的扇形统计图(80~89分的百分比因故模糊不清),若80分以上(含80分)为优秀等级,则本次测验这个班的优秀率为___________.11.已知组成网格的小正方形的面积是1,则正方形ACDE 的面积1S = 正方形BCFG 的面积2S = ,正方形ABHI 的面积3S = 由此发现1S 、2S 、3S 三者关系是F E DCBA(80~89)分)(70~79分) 12%36%20%(90~100分)(70分以下)12.如上面右图,长方形AFEB 和长方形FDCE 拼成了长方形ABCD,长方形ABCD 的长是20,宽是12,则它内部阴影部分的面积是13.如图,路线1是以AB 为直径的半圆,路线2是四个半圆组成的曲线,一只蚂蚁要从A 爬到B ,则沿路线1和沿路线2所走的路程( )(A )路线1少 (B )路线2少 (C )路线1和路线2一样 (D )无法确定BA路线2路线13米2米15.已知某个台阶的宽度和高度如上面右图所示,现在要在台阶上铺满地毯,则需要地毯的长度是 米。
十一学校点招试题——小升初真题汇总

填空題二(毎踴2分.共20分)L、观票冃烤武,(式子中的“严罡一种敲学运茸符号>」=1* =仪2』=1*2心丿=1次2乂3"…2i四个数ftl平均数罡⑸如果昂个数增加爲那么所得的四个新数的平均数为____________3、问:4,9,12的最“险倍数是:_____________4、如右圈己知$小正方形%则次正方形的面积,$正方形二5>如图、用八块相同的长方形地碑拼成一个矩形,则毎个乐方形地眸的寃是:_____J某中学的课外关副起对較园阳近愉段公跖上机讷丰的丰邊俊了一;刑腔b如下图反映他nX夭在某一段时何内,检査餉若干帘车的车谏〈车遶取整数,单位:千米册D情况•⑴妇果车遼大于40“/h且不韜过60h/h为正當行赂统代资料表明正堆行驶车请的百分比为B5环那么这天在这段时间中地们抽2f的车辆言 ______ 辅.⑵俎臬全天超還(大于処小>的车帶有240话,则当夭的车炭量大纣为________ ?7、如右图,把这个農开酣斤成一个长方(♦, (1)如果人面在底話那么_____面在上面“ (2)九臬F面在前面P从左面看是B面,那______ 在上面。
B C D&“△”表示一种运算符马苴竜义罡:aAb二Mb,如果次△(2山)二3,则尸 __________________二.填空题:(每空2分.共32分)9、老师为了需察甲、乙两个同学的卑明現度,就对这两名咼学说:“找这里有三顶惘子’ 一顶经红色,两顶直色的,老刪巴侏们的眼盼養上并给身人廉一顶懈孔去掉養布以后,你们只繼通过看对方的帽子m 帥邑来獪目己所融帽子的數鱼/说芫,老师軌按上述过程標作,当两人都去掉裁布已甲发现乙迟迟不说自己帽子的做色,便说出了自己所瞬子挪I色是邑<如“红”或者嗨臥10.扑克购游戏,小明诗对引浹,让4浜按下列四个步玻操怕第一步:分发左、中.右三堆他每唯媲不少于两张,且各堆牌的张數相同。
第二步;从左边一堆空出两张,敞入中间一區第三步;从右边一堆宝出一张'放入中间一堆s第四步:左边一堆育几张斷从中间一肚几张理放入左边一坡。
2022年重庆十一中小升初数学试卷word版附详细答案
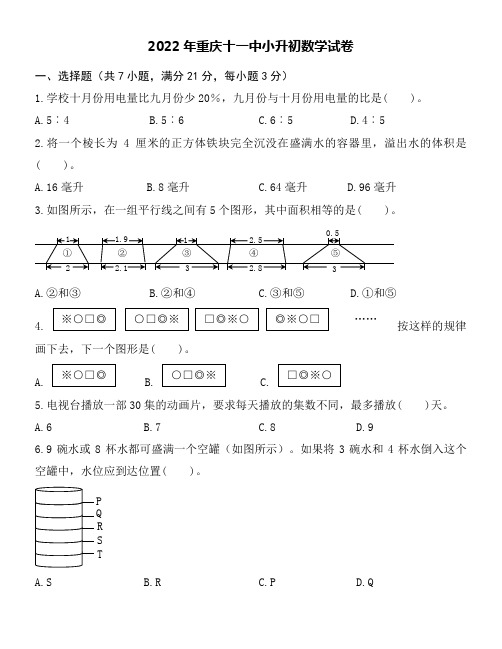
2022年重庆十一中小升初数学试卷一、选择题(共7小题,满分21分,每小题3分)1.学校十月份用电量比九月份少20%,九月份与十月份用电量的比是( )。
A.5︰4B.5︰6C.6︰5D.4︰52.将一个棱长为4厘米的正方体铁块完全沉没在盛满水的容器里,溢出水的体积是( )。
A.16毫升B.8毫升C.64毫升D.96毫升3.如图所示,在一组平行线之间有5个图形,其中面积相等的是( )。
A.②和③B.②和④C.③和⑤D.①和⑤按这样的规律画下去,下一个图形是( )。
5.电视台播放一部30集的动画片,要求每天播放的集数不同,最多播放( )天。
A.6B.7C.8D.96.9碗水或8杯水都可盛满一个空罐(如图所示)。
如果将3碗水和4杯水倒入这个空罐中,水位应到达位置( )。
A.SB.RC.PD.QSTR……7.一个圆柱和一个圆锥的高相等,体积也相等,圆柱的底面积与圆锥底面积的比是( )。
A.3︰1B.1︰3C.2︰1D.1︰2 二、计算题(共2小题,满分10分,每小题5分) 8.(5分)求阴影部分图形的面积。
(单位:厘米)9.(5分)求下面阴影部分的面积。
(单位:厘米)三、计算题(共2小题,满分28分) 10.解下列方程。
(每小题4分,共8分) 5x +114=5.25; 78x −35×57=10.11.计算下面各题,能简算的要简算。
(每小题5分,共20分)79÷[(415−15)×25] 49÷85+38÷941001×13125−13125617÷58×1718815 (1)(2)四、应用题(共4小题,12~13题每题6分,14题9分,15题10分,满分31分)12.华颖小学高年级共有学生360人,占全校学生总人数的27,全校学生总人数的720是中年级学生。
中年级学生有多少人?13.修一条公路,甲工程队单独修要8天完成,乙工程队单独修要10天完成。
北京市海淀区十一学校小升初入学数学试卷

数学测试卷(时间120分钟,满分120分)I 卷(满分100分)一、填空题(每题21.24、36、722.如果4203b a -=34.712的分母减少3减5.四个数的平均数是是6如果x △(2△3)=37.一个数的小数点,数少27,原数是8.如图,已知大正方形的面积是a ,则小正方形的面积是第8题第9题第10题9.如图,有一张长方体铁皮,剪下图中两个圆及一块长方形,正好可以做成一个圆柱体,这个圆柱体的底面半径为10厘米,那么圆柱的体积是B 、C 、D 、E 、F 将圆周六等分,分)12.扑克牌游戏:小明背对小亮,让小亮按下列四个步骤操作:堆牌的张数相同;边一堆.这时,间一堆的张数是.13.6的成本是每千克元14.若361x个15从A、B宽为2m第15题图第16题图第17FDCE拼成了长方形ABCD, 24,则它内部阴影部分的面____种放法.D为边BC的中点,点E为线段ED,则△ABC面积是△BDE的面题图的等圆两两相切,则图中阴影(边长取整厘米数).其18分)23.一个长方形的周长为54cm ,这个长方形的长减少2cm ,宽增加1cm ,就可成为一个正方形,22425.如图,将一些宽9规律摆放,共摆10个长方形,这10第24题图第2526.如图,由棱长为127.体,最少需要个这样的小正方体.28.长度相等,粗细不同的两枝蜡烛,其中的一枝可燃3小时,另一枝可燃4小时.将这两枝316分) 2)75136(1294⨯+- 50.347⨯(4)5分,共10分) 15分钟,3,相遇时甲比乙少走6千米,求甲乙两车的速度和两地的36只,已知每只茶 六、解决实际问题(本题6分)32.现在有两种照明灯:一种是10瓦(即0.01千瓦)的节能灯,售价60元;另一种是60瓦(即0.06千瓦)白炽灯,售价3元.两种灯的照明效果相同,使用寿命也相同.电费0.5元/(1(2)七、数学阅读(本题633.读一读:式子“1+2+“1+2+3+…+100这“∑(即从1开始的100连续偶数的和)可表示为“1031n n =∑”,同学们通过对以上材料的阅读,请回答以下问题: (1)1+3+5+…+101可以用求和符号表示为(2)计算421n n =∑=II 卷(满分20分)40题,每题3分,共2012×231=132×21;将等号左边的乘积和右边的乘积都64×21已知声音的速度是每秒340米,听到回响时汽车离山谷的距离是米.36.某商场经销一种商品,由于进货时价格比原进价降低了6.4%,使得利润率增加了8个百分371加密后再传输.的每个1都变成10成01.我们用AA串1A,对1A2A,依此类推,….若数字串A共有4相等的数对至少..有对38.有一个边长为4m第39题图第40题图39.如图是由若干个正方体形状的木块堆成的,平放于桌面上,其中,上面正方体的下底面四个顶点恰是下面相邻8,那么正方体2中共用7个3中共有19个可以看得见小4图中共有个看得为正整数)中共有个看得见的。
最近第十一中数学七年级上册升学试卷及答案分析

最近第十一中数学七年级上册升学试卷及答案分析第Ⅰ卷选择题(共30分)一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)1.实效m,n在数轴上的对应点如图所示,则下列各式子正确的是()A.B.C.D.2.满足下列条件的△ABC,不是直角三角形的是( )A、b2=c2-a2B、a∶b∶c=3∶4∶5C、∠C=∠A-∠BD、∠A∶∠B∶∠C=12∶13∶153、若a是最小的自然数,b是最大的负整数,c是绝对值最小的有理数。
则 a + b + c=( )A. —1B. 0C. 1D. 不存在4.青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米,将2500000用科学记数法表示应为( )A.25×105B.2.5×106C.0.25×107D.2.5×1075.下列选项中正确表示数轴的是( )A.B.C.D.6.把弯曲的道路改直,能够缩短行程,其道理用数学知识解释应是……………( ) A.垂线段最短B.两点确定一条直线C.线段可以大小比较D.两点之间,线段最短7.若|a|=7,|b|=5,a+b>0,那么a-b的值是( ) A.2或12 B.2或-12 C.-2或-12 D.-2或128.一根绳子弯曲成如图1的形状,用剪刀像图2那样沿虚线a把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线b(b∥a)把绳子再剪一次时,绳子就被剪为9段.若用剪刀在虚线a,b之间把绳子再剪(n-2)次(剪开的方向与a平行),这样一共剪n次时绳子的段数是( )A.4n+1 B.4n+2 C.4n+3 D.4n+59.四个互不相等整数的积为9,则和为()A.9 B.6C.0D.﹣3.10、火车票上的车次号有两个意义:一是数字越小表示车速越快,1~98次为特快列车,101~198次为直快列车,301~398次为普快列车,401~598次为普客列车;二是单数与双数表示不同的行驶方向,其中单数表示从北京开出,双数表示开往北京。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四套试题一、填空
1. 1.4⨯4
7
-1
1
5
÷(1.8-
1
5
)= .
2.把2
3
、0.6、66.7、0.67按照从小到大的顺序排序
3.盒里各色圆珠笔,其中红色占1
4
,后来又往盒里放了8支红色圆珠笔,这时红色圆珠笔占
总数的
5
12
,则原有红色圆珠笔支。
4.某项工作,甲单独干15天可完成,现甲做了9天另有任务,剩下的工作由乙完成,用了8
天,若这项工作全部由乙单独完成需天。
5.甲、乙两人分别从A、B两地同时出发,相向而行,甲的速度是乙的速度的2倍,两人相
遇后继续往前走,各自到达B、A后立即返回。
已知两人第二次相遇的地点距第一次相遇地点是12千米,那么A、B两地相距千米。
6.正方形的一组对边增加6厘米,另一组对边减少4厘米,结果得到的长方形与原正方形面
积相等,则原正方形的面积是平方厘米。
7.如图1,已知每个小正方形格的面积是1平方厘米,则不规则图形的面积是平方厘
米
8.有一个数,除以3的余数是2,除以4的余数是1,则这个数除以12的余数是
9.规定一种新运算:a℘b=a b-(a÷b)+2a,如3℘4=3⨯4-(3+4)+2⨯3.
则:5℘4 4℘6 (填“>”、“=”或“<”)
10.如图所示,在正方形ABCD中,红色、绿色正方形的面积分别是27和12,且红、绿两个
正方形有一个顶点重合,黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,则黄色正方形的面积为.
11.如果用(4,3)表示小青坐在教室的第3排第4列,那么小明坐在教室的第5排第2列应
当表示为
12.如图2.图中空白部分占正方形面积的比例是.
13.如右图,四边形ABCD的面积是42平方米,其中两个小三角形的面积分别是3平方米和4
平方米,那么最大的一个三角形面积是平方米。
14. 如图3,数一数图中共有三角形 个
15. 如图4所示的运算程序中,若开始输入的x 值为48,我们发现第1次输出的结果为24,第
2次输出的结果为12, 第2009次输出的结果为 。
16. 观察下列几何体,从正面看,左面看以及从上面看都是长方形的是( )
17. 有9张相同的卡片,上面写有汉字:我、参、与、我、奉、献、我、快、乐。
9张卡片任
意搅乱后,一个人随机抽取一张,卡片上写有汉字“我”的可能性是( )
A .
19 B. 29 C. 13 D. 23
18. 为了求1+2+22+23+ 22008的值,可令S=1+2+22+23+ 22008, 则2S=2+22+23+24 22009,因此2S-S=22009-1, 所以1+2+22+23+ 22008=22009-1,
仿照以上推理计算出1+5+52+53+ +52009的值是( )
A .5
2009
-1 B.5
2010
-1 C. 20095-14 D. 20105-1
4
19. 利用一副三角板上已知度数的角,不能画出的角是( ) A. 15︒ B. 100︒ C. 100︒ D. 165︒
20. 观察下列图形,则第n 个图形中三角形的个数是( )
A .4n B. 4n-4 C. 4n+4 D. 2n+2 三、计算题
21. 19.98⨯37-199.8⨯1.9+1998⨯0.82
22. 12.5⨯1.86+42÷12
5
+25.4⨯1
1
4
23.
1
24
⨯
+
1
46
⨯
+
1
68
⨯
+ +
1
98100
⨯
24. 1
21
+
202
2121
+
50505
212121
+
13131313
21212121
四、解答题
25. 小明一家四口人的年龄之和是147岁,爷爷比爸爸大38岁,妈妈比小明大27岁,爷爷的年龄是小明与妈妈年龄之和的2倍,问小明一家四口人的年龄各是多少岁?
26.看图,回答问题。
五、解决问题
27. 将11至17这七个数字,填入右图中的圈内,使每条线上的三个数的和相等。
28.李明对某校九年级(2)班进行了一次社会实践活动调查,从调查的内容中抽出两项, 调查一:对小聪,小亮两位同学的毕业成绩进行调查,其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算,计算的方法按4:4:2进行,毕业成绩达80分以上(含80分)为“优秀毕业生”,小聪、小亮的三项成绩如右表:(单位:分)
调查二:对九年级(2)班50名同学某项跑步成绩进行调查,并绘制了一个不完整的扇形统计图,如图1,请你根据以上提供的信息,解答下列问题:
(1) 不小聪和小亮谁能达到“优秀毕业生”水平?哪位同学的毕业成绩更好些?
(2)扇形统计图中“优秀率”是多少?
(3)“不及格”在扇形统计图中所占的圆心角是多少度?
29. 你能比较两个数20002001和20002000的大小吗?
为了解决这个问题,我们先把它抽象成数学问题,写出它的一般形式,即比较n n+1和(n+1)n 的大小(n是非零自然数),然后,我们从分析n=1,n=2,n=3, 这些简单的情形入手,从中发现规律,经过归纳,再猜想出结论
(1)通过计算,比较下列各组中两个数的大小(在空格内填写“>”、“=”或“<”)
1)1221 2) 2332
3)3443 4) 4554
(2)从第(1)题结果经过归纳,猜想n n+1与(n+1)n的大小关系是:
(3)根据上面的归纳猜想,试比较下面两个数的大小:2000200120012000
六、拓展提高题
请阅读下面两份材料,并解答后面的问题
阅读材料一:
在小学,我们学习了数的加、减、乘、除和乘方运算,但在现实生活中,有些问题仅用这五种运算是无法解决的,例如,已知一个正方形的面积是2平方厘米,那么它的边长是多少厘米?解决这个问题就要运用一种新的运算方法,这种运算叫做开方,开方运算与乘方运算一张张为逆运算
定义:设x2=2,则2的算术平方根,即2=2,因此,上面问题中正方形的
x2=4,则4的算术平方根,即2=4,而我们知道,
22=4=2,即2是4的算术平方根,类似的,我们还可以得到:
阅读材料二:
用完全相同的四个直角三角形,我们可以拼成如图所示的图形.
此时S 大正方形=S 小正方形+4S 三角形 即:C 2=(a-b )2+4 12
ab 化简整理得到a 2+b 2=c 2(a 、b 是直角边,c 是斜边) 解决以下问题:
30. 计算下列各式的值:
= , = , = ,
=
31. 如图,每个小正方形的边长为1,把阴影部分剪下来,用剪下来的阴影部分拼成一个正方
形,那么新正方形的边长是( )
A B.
C. D. 2
32.如图,细心观察图形,认真分析各式,然后解答问题。
)2+1=2 S 1=
2
2+1=3 S 2=
2
2+1=4 S 3(1) 观察上述变化规律,写出第四组对应的等式: (2) 推算出OA 10的长:
(3) 求出21S +22S + +2
10S 的值。
解:
33. 2002年8月在北京召开的国际数学在大会会标取村于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的不小小正方形拼成的一个大正方形(如图),如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,那么a2+2ab+b2的值为()
A.13 B. 19 C. 25 D. 169
34.现有5个边长为1的正方形,排列形式如图1,请把它们分割后拼接成一个新的正方形。
要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形,小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的
面积相等,有x2=5,解得
由此可知新正方形的边长等于两个小正方形组成得长方形对角线的长,于是,画出如图2所示的分割线,拼出如图3所示的新正方形。
请你参考小东同学的做法,解决如下问题:现有10个边长为1的正方形,排列形式如图4,请把它们分割后拼接成一个新的正方形,要求:在图4中画出分割线,并在图5的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。
